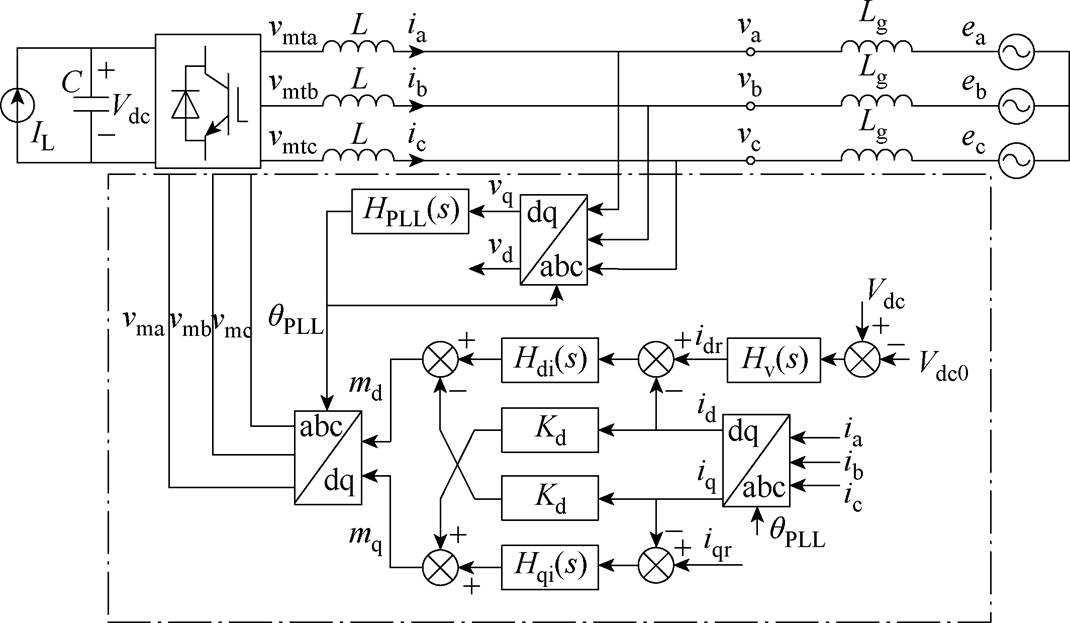
图1 逆变器并网系统结构
Fig.1 Grid-connected inverter control structure diagram
摘要 电力电子设备的广泛应用使得宽频振荡事件频发，尤其是次/超同步振荡问题突出，严重影响电力系统的稳定运行。由于宽频量测装置尚未广泛应用，现有基于宽频量测信息的振荡源定位方法难以适用。因此，该文研究基于工频测量阻抗的次/超同步振荡源定位方法，首先推导了次/超同步分量存在时工频电压电流的动态响应过程，揭示了次/超同步振荡发生时工频量的变化规律；然后针对振荡阈值难以准确获取的问题，构造多场景下的振荡训练样本集，基于支持向量机算法获取了振荡阈值的函数表达式，形成基于工频测量阻抗的次/超同步振荡源定位判据；最后依据新能源并网系统的典型拓扑结构搭建时域仿真模型，构建测试数据集并对所提方法进行验证。结果表明，所提方法对不同运行工况有较好的适应性，在新能源并网系统中能够实现次/超同步振荡源的准确定位。
关键词：次/超同步振荡 振荡源定位 支持向量机 工频测量阻抗
随着以风电、光伏为代表的新能源迅猛发展，电力电子设备在电力系统中的渗透率不断提高，由此引发了多起电力电子集群间以及电力电子集群与电网间相互作用导致的振荡事件，对新能源并网系统的安全稳定运行构成严重威胁。例如，在2009年，美国德州南部电力可靠性委员会（ERCOT）系统中发生了由双馈与串补相互作用而引发的振荡事件[1-2]，造成大量风机跳闸和撬棒电路的损坏；2015年，中国新疆哈密地区发生了直驱风机与弱电网相互作用而引发的次/超同步振荡事件，振荡信号传播到300 km外的汽轮机组，使其轴系发生扭振并跳闸[3]；2019年，渝鄂柔直鄂侧发生了1 810 Hz的高频谐振，渝侧发生了700 Hz和665 Hz的高频谐振，造成一个换流单元停运[4]。振荡所带来的谐波和间谐波会恶化电能质量和设备性能[5]，例如，会导致变压器功率降低或感应电机绕组温度升高[6-7]。由此可见，如果系统持续处于振荡状态，则极有可能造成系统中其他设备的事故甚至导致系统停运。然而如果能在振荡初期能够及时准确地检测到振荡来源并采取相应的抑制措施[7]，将能够极大地避免振荡带来的危害。
电力系统中的振荡问题可分为强迫振荡和自由振荡两类，强迫振荡通常由持续周期性的小扰动（原动机输入功率脉动、周期性负荷）诱发，具有起振快、扰动消失后衰减迅速的特点[8-9]。自由振荡通常由电路理论中的负阻尼效应引发，在新能源并网系统中电力电子设备与电网相互作用导致的自由振荡更为突出。本文主要关注新能源并网引发的振荡问题，因此下面提到的振荡均指自由振荡。
近年来，国内外对于振荡源检测与定位问题已开展了相关研究。目前，振荡源定位方法可分为基于机理模型的方法和基于量测数据的方法。基于机理模型的方法可分为基于状态空间的时域分析[3, 10]和基于阻抗的频域分析[10-15]。文献[10]建立了双馈风机经串补电容并网系统的状态空间模型，通过计算风电场的参与因子从而确定振荡源机组；文献[11]提出了风电场次同步频域聚合等值方法，文献[12-13]首先建立系统中各模块的阻抗模型，然后根据网络拓扑结构得到阻抗网络矩阵，通过频域模态分析得到不同机组的频域参与因子进而确定振荡源。文献[15]通过在线量测风电场阻抗，将阻抗结果汇总并处理，计算振荡主导模态下的聚合阻抗，通过聚合阻抗中的负电阻发散特性实现振荡源的定位与切除。然而基于机理模型的振荡源定位方法通常需要风机的控制参数以及网络拓扑结构，由于风机制造商不愿提供控制器信息以及网络拓扑的时变性，使得此类方法难以开展应用。
广域测量系统（Wide Area Measurement System,WAMS）在国内外的广泛应用[14]为基于量测数据的方法奠定了基础。相量测量装置主要分为同步相量测量装置和宽频测量装置两种。同步相量测量装置主要测量50 Hz处的相量，其对电压电流波形的采样频率应不低于4 kHz，子站向主站的上传速率可达50～100 Hz[16]；而宽频测量装置可以测量0～2 500 Hz的谐波、间谐波，其采样频率应不低于12.8 kHz，子站向主站的上传速率一般为1 Hz[17-18]。基于量测数据的定位方法有基于耗散能量的方法、基于次同步功率的方法以及基于次同步阻抗的方法。文献[19]通过自适应投影多元经验模态分解的方法提取强迫振荡的固有模态函数，进而计算各节点的耗散能量流，根据耗散能量流实现振荡源定位。文献[20-21]引入次同步功率的概念，分析表明次同步功率驱动了次同步振荡现象，进而通过次同步功率的流向识别振荡源。文献[22]采用Prony分析和矩阵束算法提取次同步分量并计算次同步阻抗，通过次同步阻抗实部的正负判断振荡源。基于量测数据的方法多针对次同步频段的振荡，对于次/超同步振荡的适用性未做深入研究。
人工智能技术的迅速发展消除了对参数化模型的依赖，人们提出了基于深度学习方法来探索振荡数据与振荡源之间的关系[23-26]。文献[23]利用有向加权图构建宽频振荡因果网络，在此基础上确定振荡源位置，并通过保留因果强度系数最大的支路，确定振荡的主要传播路径。文献[24]提出了一种基于深度迁移学习的次同步振荡定位方法，在仿真系统中获取数据样本运用卷积神经网络进行特征提取最后通过迁移学习迁移到实际系统中以实现振荡源定位。文献[25]为克服实际电力系统标记数据不足的问题，提出了一种深度迁移学习架构用来检测多种机制引发的振荡。然而基于深度学习的方法面临着可解释性差、泛化能力不足的问题，尚未进行实际应用。
综上所述，由于高维非线性机理模型难以建立以及深度学习方法可解释性差的问题，使得基于机理和人工智能的方法难以实际应用。同时由于宽频量测装置的应用尚不广泛，基于量测数据的方法也难以使用[27]。因此本文主要针对以逆变器为能量传输接口的新能源并网系统，从振荡发生时工频量的变化规律出发，提出了一种基于工频测量阻抗的次/超同步振荡源定位方法。首先推导了次/超同步分量存在时工频电压电流的动态响应过程，进而揭示了系统中各节点工频测量阻抗的变化规律；然后针对振荡阈值难以通过机理分析准确获取的问题，构造了多场景下的振荡样本数据集，进而基于支持向量机（Support Vector Machine, SVM）算法获取了振荡阈值，形成了次/超同步振荡源定位判据；最后通过测试数据集验证了所提次/超同步振荡源定位方法的有效性和准确性。
1.1.1 系统描述
新能源通常以逆变器作为接口传输能量，逆变器并网系统的典型结构如图1所示，主要由功率传输电路和控制电路组成。
图1 逆变器并网系统结构
Fig.1 Grid-connected inverter control structure diagram
逆变器直流侧由一个电流源等效，ea、eb、ec为电网电压，va、vb、vc为并网点电压，vmta、vmtb、vmtc为逆变器端口电压，ia、ib、ic为逆变器电感电流，Vdc为直流电压，C为直流侧电容，L为滤波电感。控制系统采用dq坐标下的电压外环、电流内环双闭环控制，Hv(s)、Hi(s)、Hpll(s)分别为电压环控制器传递函数、电流环控制器传递函数和锁相环控制器传递函数，qpll为锁相角，Kd为解耦增益系数。
1.1.2 直流电容的能量平衡方程
逆变器的直流电容通常用以缓冲直流侧和交流侧的能量交换，维持直流侧电压稳定，同时抑制直流侧谐波电压，稳定运行时其能量平衡方程为
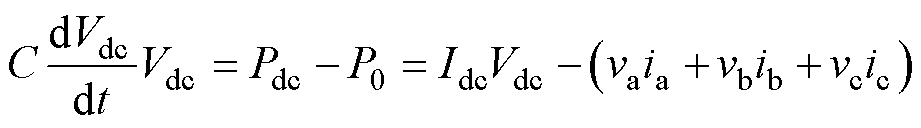（1）
式中，Pdc为直流侧功率；P0为交流侧功率。当交直流侧功率相等时，电容电压也保持恒定。
当系统存在次/超同步分量时会使交流侧功率出现小信号分量DP0，而直流侧功率Pdc保持不变[28]，此时会使得直流电压也出现小信号分量DVdc，次/超同步分量作用下直流电容动态方程为
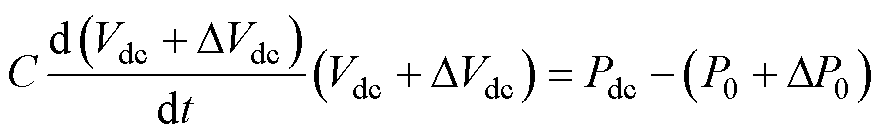（2）
将其展开后仅保留小信号分量可以得到
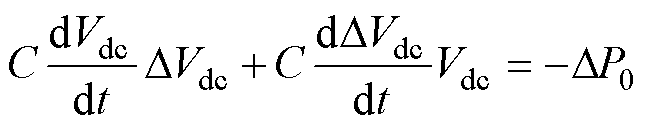（3）
在系统中存在次/超同步分量时，DVdc和DP0中不仅包含周期性分量，同时还包含非周期性分量。直流电容的动态响应与有功功率的小信号分量 相关。
1.1.3 瞬时有功的小信号分量
在以逆变器作为能量传输接口的新能源并网系统中，由于频率耦合作用，发生振荡时系统中会存在一对关于50 Hz对称频率为fp和fn的振荡分量。 a相电压、电流的时域表达式为
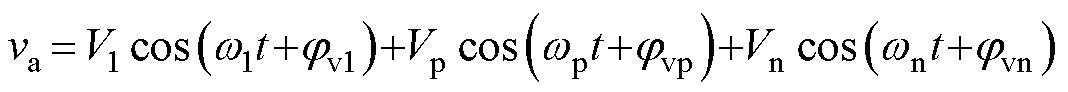（4）
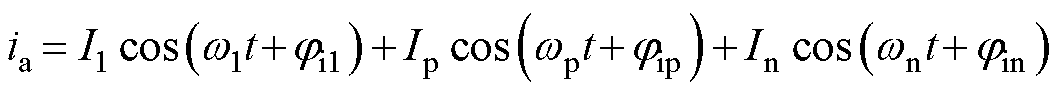（5）
其中
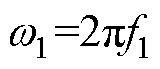
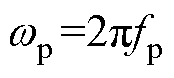
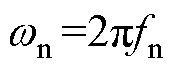
式中，f1为基波频率；fp为次同步分量频率；fn为超同步分量频率；V1、I1分别为基波电压、电流幅值；jv1、ji1分别为基波电压、电流相角；Vp、Ip分别为次同步电压、电流幅值；jvp、jip分别为次同步电压、电流相角；Vn、In分别为超同步电压、电流幅值；jvn、jin分别为超同步电压、电流相角。
当电压电流中同时存在工频量和振荡分量时，需要采用瞬时功率理论分析系统受扰后的能量平衡过程[28]。系统的瞬时有功功率表达式为
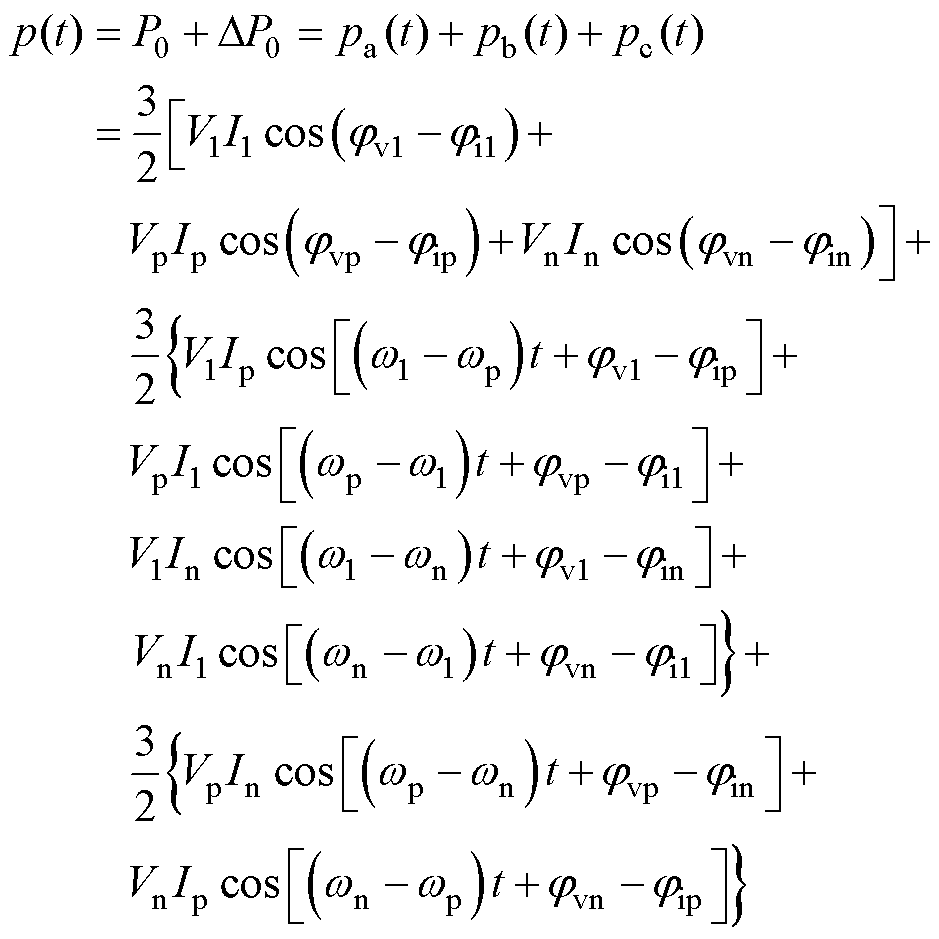（6）
由式（6）可知，三相瞬时有功功率由稳态量和小信号分量构成，DP0为次/超同步分量作用下瞬时有功功率的小信号分量，DP0又可以分为周期小信号分量和非周期小信号分量，其中DP0dc为瞬时有功功率的非周期小信号分量，即
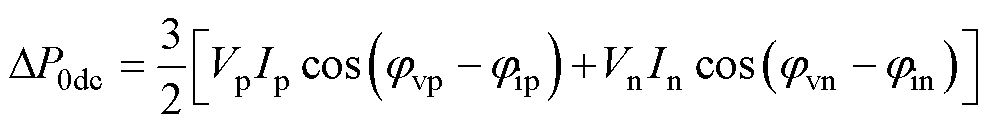（7）
DP0dc为系统中振荡电压电流间相互作用所产生，它会导致直流电容电压出现非周期性变化。
1.1.4 控制系统中非周期小信号分量的响应过程
将式（7）代入式（3）可以得到非周期小信号分量作用下直流电容的动态过程，即
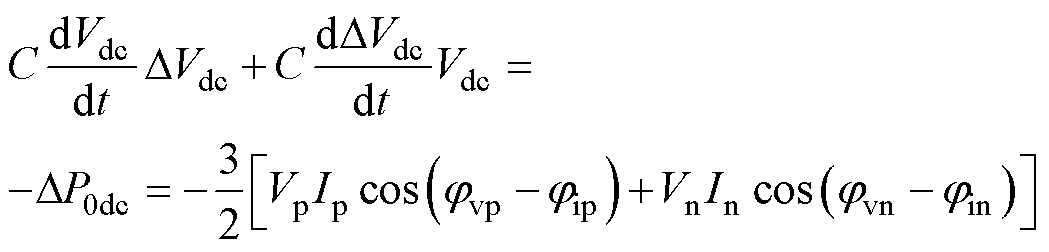（8）
由式（8）可知，系统中瞬时有功功率非周期小信号分量会使得直流电容电压中也响应出非周期的小信号分量DVdc，从而与直流电压参考值Vdc0出现偏差。在控制系统电压环的调节作用下，直流电容重新恢复平衡，直流电压的非周期分量DVdc也将重新变为0，然而在控制系统调节的过程中将导致输出的参考电流和参考电压发生变化。
设直流电容从受扰后直流电压发生变化到控制调节重新恢复平衡经历的时间为t，则在直流电压调节过程中造成的d轴参考电流变化量为
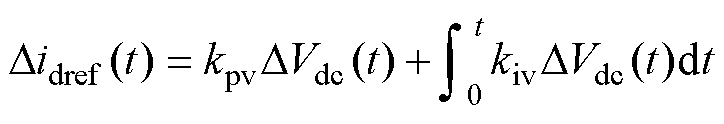（9）
同样d轴参考电流发生变化后，电流环开始调节，由于电流环的控制带宽较宽，所以d轴电流的跟踪速度更快。d轴电流参考值与d轴电流测量值的差Didr为
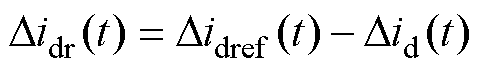（10）
电流环的调节过程也会使得d轴电压参考值产生一个非周期小信号分量Dvmd，即
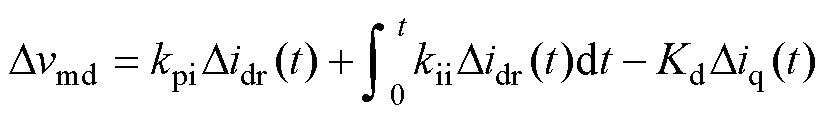（11）
由于dq轴控制间解耦环节的影响，q轴电压参考值也会产生一个非周期小信号分量Dvmq，即
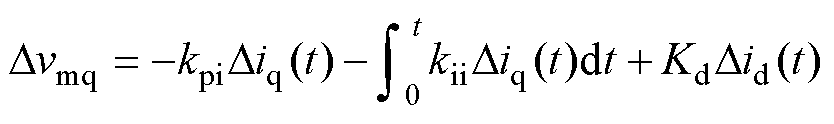（12）
q轴电压发生变化后进一步影响锁相环，导致锁相角也产生非周期小信号分量Dqpll，即
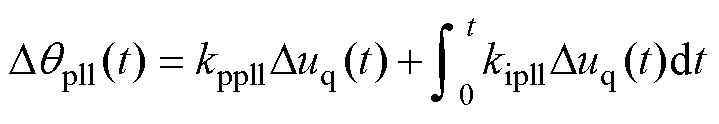（13）
在进行Park变换时，锁相角的非周期小信号分量会进一步导致电压电流发生变化。
1.1.5 次/超同步分量与工频量交互响应过程
受扰后控制系统输出的参考电压变化量Dvmdt、Dvmqt由两部分组成，一部分为受控制系统调节影响产生的变化量Dvmd、Dvmq，另一部分为受锁相角变化量影响在dq变换过程中产生的变化量Dqpllvmq、Dqpllvmd。
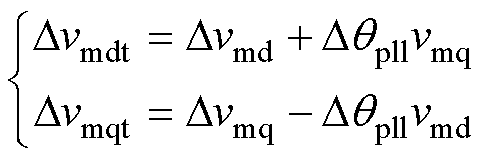（14）
a相端电压非周期小信号分量为
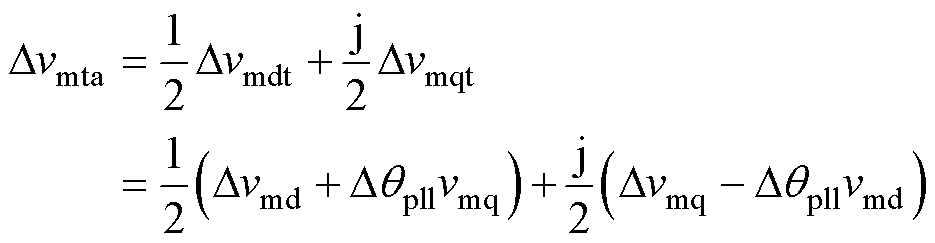（15）
a相电流非周期小信号分量为
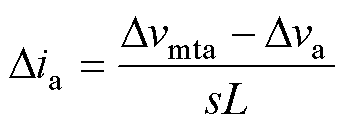（16）
系统中存在次/超同步分量时直流电容和控制系统的响应过程可由图2表示。
当系统中存在次/超同步分量时会产生瞬时有功非周期小信号分量DP0dc，从而打破交直流侧的能量平衡，在式（8）的作用下电容电压产生非周期小信号分量DVdc，进而在式（9）电压环反馈调节作用下，其输出的d轴电流参考值中也会产生一个非周期小信号分量Didref，然后在式（11）和式（12）电流环调节作用下，其输出的电压参考值中也产生一个非周期小信号分量Dvmd、Dvmq，进而考虑锁相环的作用可以得到Dvmdt、Dvmqt。经dq变换后逆变器端口电压中便会存在一个非周期小信号分量Dvmt，进而在电网的作用下电流中也存在非周期小信号分量Di，以上即为次/超同步分量影响工频电压电流的响应过程。
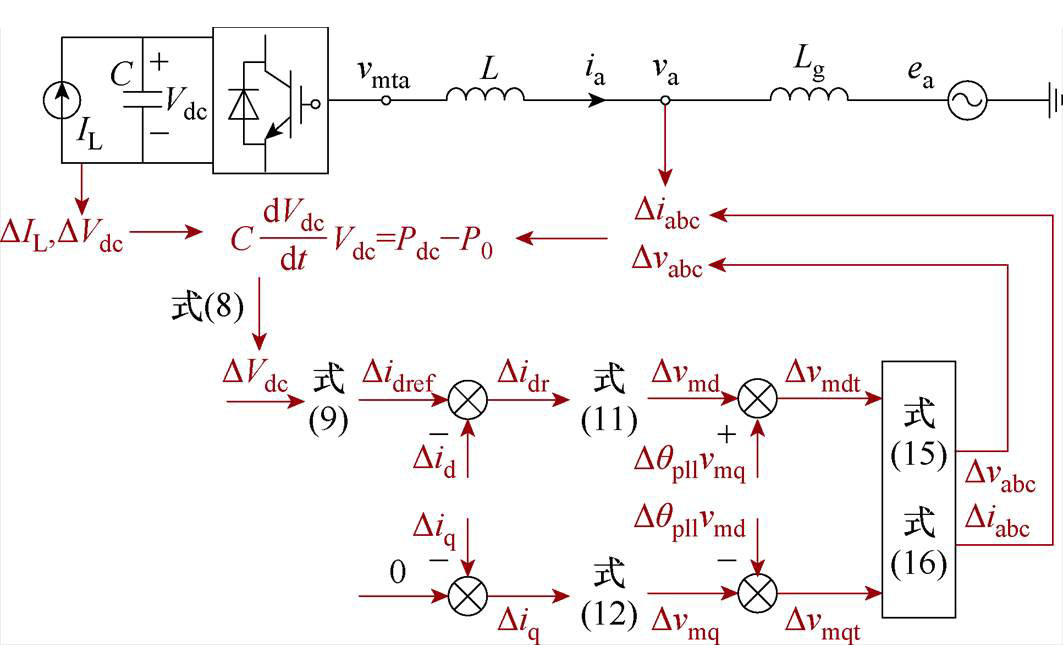
图2 次/超同步分量作用下系统响应过程
Fig.2 Response process of system with disturbance
1.2.1 工频测量阻抗
由1.1节分析可知，次/超同步分量的存在会对工频电压电流产生影响，本节将从时域的角度继续推导工频电压、电流和次/超同步分量之间的关系，推导时忽略Dqpllvmq、Dqpllvmd的影响。
式（8）是关于DVdc的一阶线性非齐次微分方程，整理可得
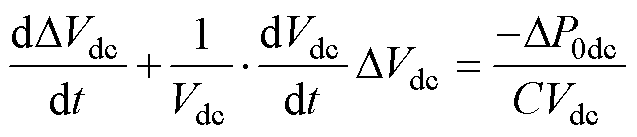（17）
式（17）的解为
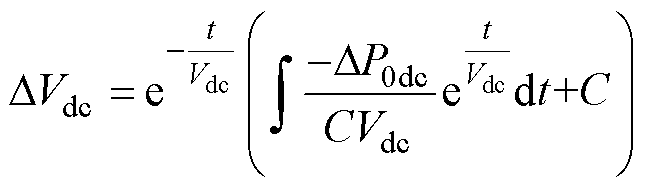（18）
式中，C为由初始状态决定的积分常数。
将式（8）～式（12）代入式（15）可得
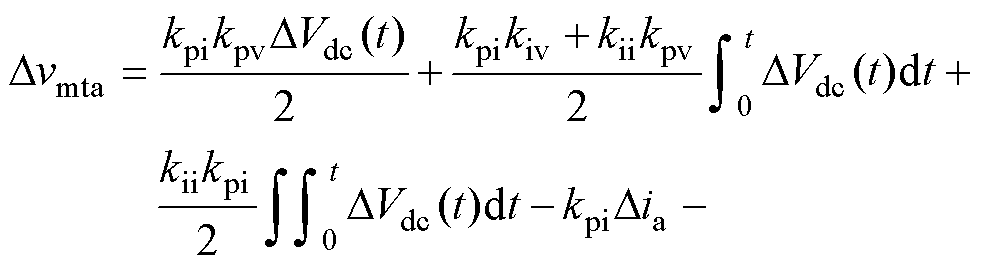
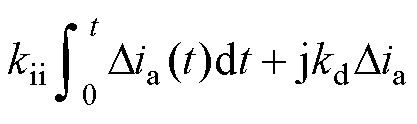（19）
将式（18）代入式（19）并除以Dia可得
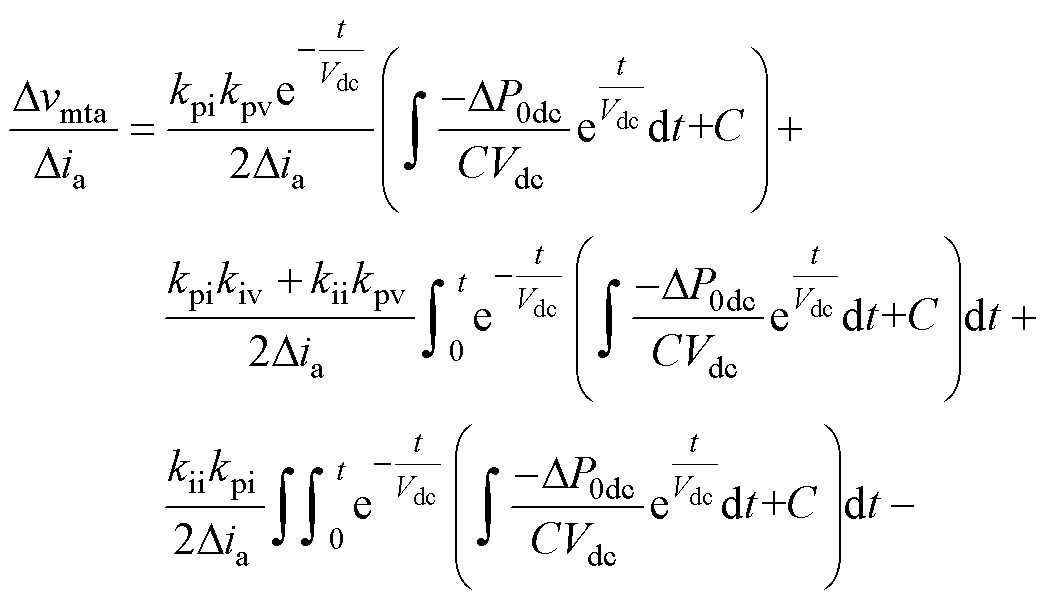
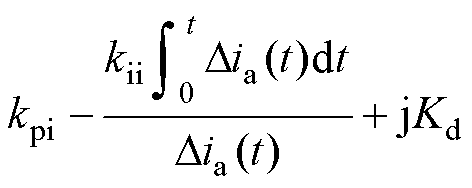（20）
式（20）的前三项主要与由次/超同步分量产生的DP0dc有关，后三项主要与控制参数有关。由此可以看出，当系统中存在DP0dc时，会导致Dvmt/Di发生变化。因此将工频电压电流相量的比值定义为工频测量阻抗Zm，来表征工频量受振荡分量影响的 程度。
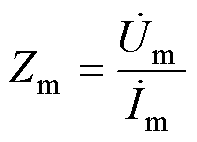（21）
式中，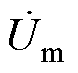
为电压相量；
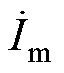为电流相量。
1.2.2 不同运行状态时的工频测量阻抗变化规律
新能源并网系统的振荡模态与电流环的控制参数密切相关[29]，因此主要分析逆变器在不同出力水平时，阻抗变化量标幺值DZ随注入扰动分量大小和逆变器电流环控制带宽变化的情况，如图3所示。
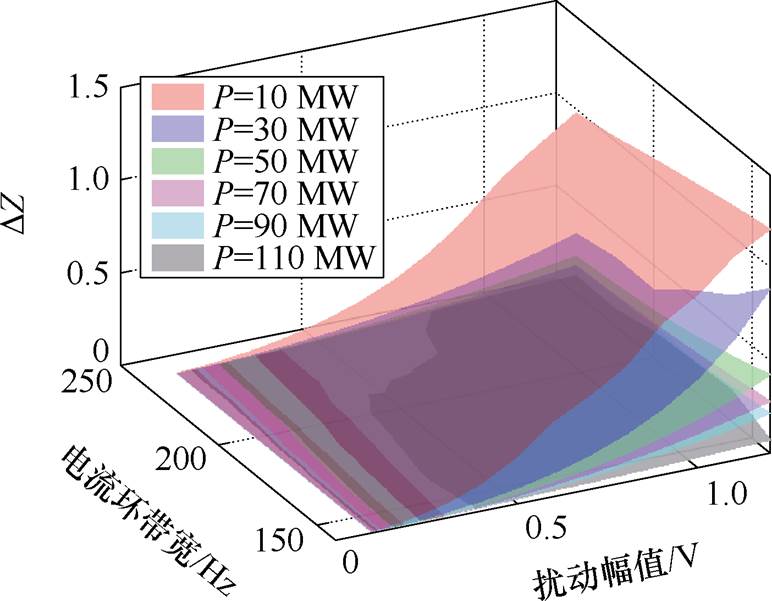
图3 扰动分量和逆变器电流环控制带宽变化时DZ变化
Fig.3 The variation of DZ with the disturbance component and the control bandwidth of the inverter current loop
由图3可知，DZ随着扰动幅值的增大而增大，由式（20）可知，当注入的扰动幅值越大时，产生的DP0dc也越大，其所导致的DZ变化也更加明显。当扰动幅值大小一定时，DZ随着电流环控制带宽的减小而增大。当扰动幅值和电流环带宽都不变时，逆变器输出功率P越小时DZ变化越大。
1.2.3 工频测量阻抗空间变化规律
新能源并网系统拓扑结构如图4所示。图4并网系统中标出了关键节点，其中s1、s2、s3表示电源节点，m1、m2、m3表示网络节点。
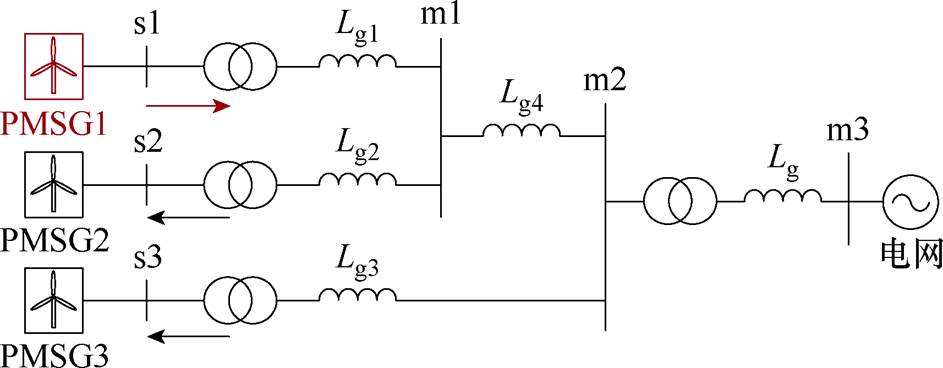
图4 新能源并网系统拓扑结构
Fig.4 Renewable energy grid-connected system topology
当PMSG1与弱电网发生相互作用导致次/超同步振荡时，振荡分量由节点s1经支路Lg1向系统中其他节点扩散。振荡源节点工频电压电流变化量表示为Dv、Di，系统中其他节点的工频电压电流变化量表示为ev、ei。由于振荡传播的衰减，振荡源节点的Dv、Di要远大于其他节点ev、ei。
电源节点振荡前后阻抗变化量DZs1为
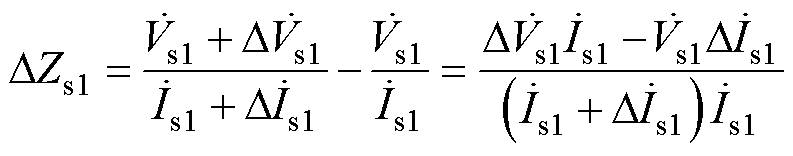（22）
通常情况下逆变器并网点电压相同，由式（22）可知，DZs1与工频电压、电流的变化量以及工频电流的大小密切相关。
网络节点振荡前后阻抗变化量eZm1为
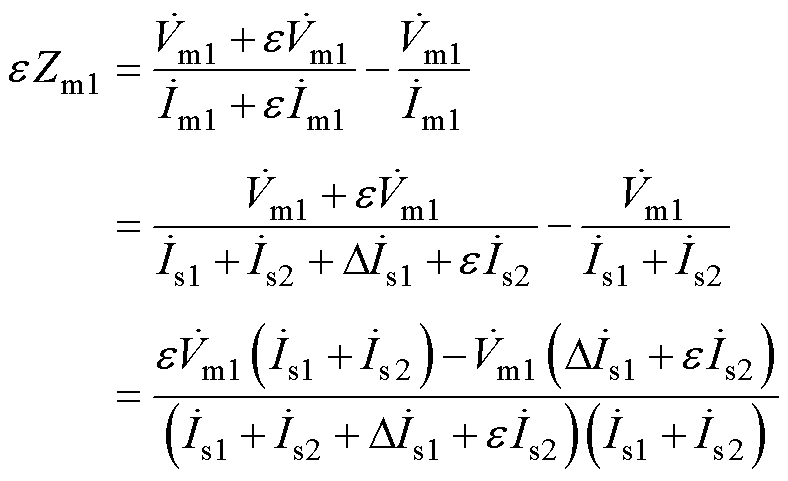（23）
由式（23）可知，eZm1与节点s1和s2工频电压、电流的变化量以及工频电流的大小密切相关。由于网络节点存在非振荡源机组电流的汇入，从而使得eZm1＜DZs1。如图4所示，由于节点m1有来自节点s1和s2的电流汇入，所以网络节点m1的测量阻抗小于电源节点s1和s2处的测量阻抗。节点m2、m3工频测量阻抗变化规律与节点m1类似。
工频测量阻抗在空间中各节点的变化规律如图5所示。图5中红色直线表示各节点DZ变化与自身的百分比，工频测量阻抗的变化在振荡流通路径上逐渐减小，振荡源和非振荡源的DZ大小差异显著。同时结合式（20）可知，系统中不同节点的DZ与DP0dc成正比，DP0dc从振荡源向系统中的无源元件传播衰减，DP0dc的传播受线路阻抗特性影响[28]。振荡源与非振荡源DZ的大小与线路阻抗密切相关并且总是会有一个明确的界限，因此通过设定一个振荡阈值m 可以区分振荡节点。
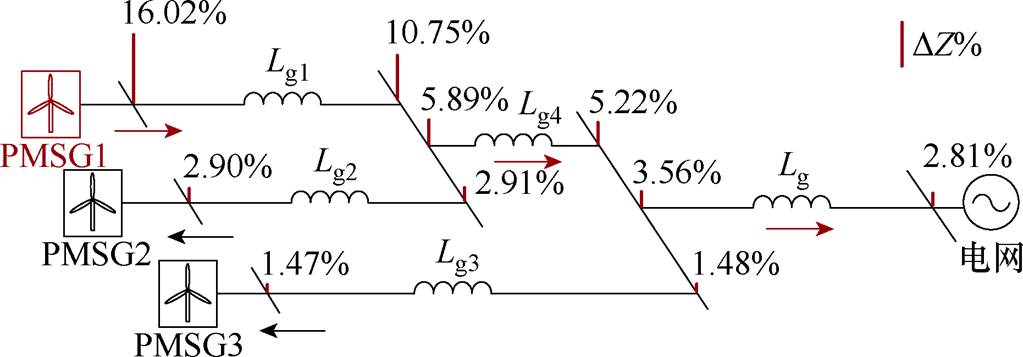
图5 DZ空间变化规律
Fig.5 DZ spatial variationcharacteristics
综上所述，系统中存在次/超同步分量时在控制环节的调节作用下最终会影响输出的工频电压、电流，可通过工频测量阻抗表征工频量受次/超同步分量的影响程度。系统中振荡源和非振荡源节点工频测量阻抗变化差异明显，可将工频测量阻抗作为定位次/超同步振荡源的依据。本节的分析为后续振荡阈值的获取和振荡判据的形成奠定了基础。
振荡阈值m 是区分振荡源与非振荡源的关键。然而在实际运行过程中，难以通过机理分析获得一个固定的振荡阈值，因此可以通过数据驱动的方法得到不同运行工况下的阈值。
振荡阈值的获取是一个典型的二分类问题，支持向量机在分类和回归问题中有广泛的应用，其主要优点包括：具有较强的泛化能力；适用于小样本数据；具有较好的鲁棒性和可解释性等。
2.1.1 支持向量机原理
支持向量机（SVM）是一种强鲁棒性的二分类模型。支持向量机的基本思想是建立一个最优决策超平面，使得该平面两侧距平面最近的两类样本之间的距离最大化，从而对分类问题提供良好的泛化能力。
支持向量机示意图如图6所示，距离超平面最近的几个样本点被称为“支持向量”，两个异类支持向量到超平面的距离之和被称为“间隔”，即
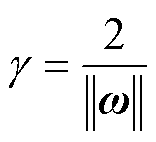（24）
支持向量机模型就是找到能够正确划分样本数据集并且使间隔最大的超平面。线性可分数据集的最大间隔分离超平面通常是存在且唯一的。
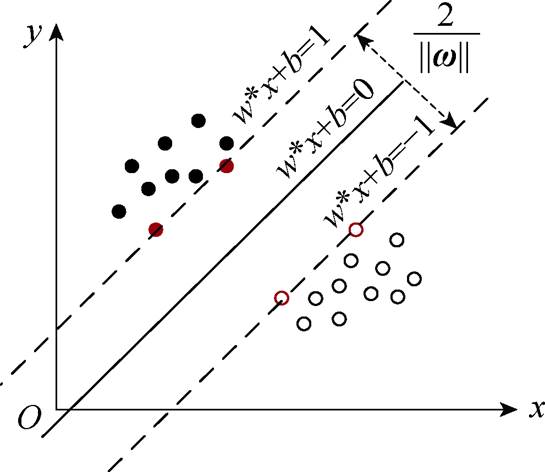
图6 支持向量机示意图
Fig.6 Support vector machine
2.1.2 构建训练样本数据集
支持向量机是监督学习的一种算法，因此支持向量机的训练需要构造已赋予不同标签的数据样本。振荡源和非振荡源的样本数据集的构造流程如下：
（1）收集各电源节点相量测量单元（Phasor Measurement Unit, PMU）测量得到的电压、电流相量和输出功率。
（2）计算振荡前后工频测量阻抗变化量并进行归一化，对输出功率进行傅里叶变换计算振荡频率。
（3）将振荡源节点的数据标签赋为1，非振荡源节点的数据标签赋为-1。
最终得到的样本数据集共包含四种类型的数据，即输出功率、振荡频率、工频测量阻抗变化量和数据标签。得到的样本集在三维坐标中如图7 所示。
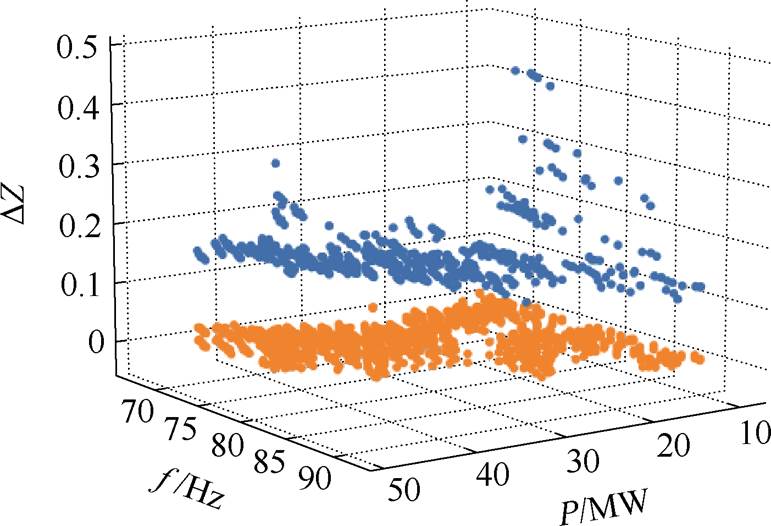
图7 样本集
Fig.7 Sample dataset
图7中横、纵坐标分别为振荡频率和输出功率，竖坐标为工频测量阻抗的变化量，蓝色的点为振荡源数据，橙色的点为非振荡源数据。
2.1.3 基于支持向量机的振荡阈值
在构造工频测量阻抗的样本集后便可基于支持向量机算法训练得到区分振荡源和非振荡源的 阈值。
首先需要构造求解最大间隔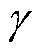
的约束最优化问题，由式（24）可知最大化
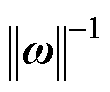等价于最小化
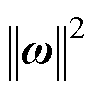，表达式为
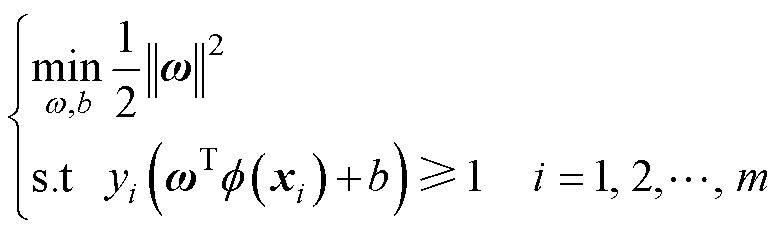（25）
式（25）本身是一个凸二次规划问题，通过序列最小最优化算法等方法可求解支持向量机问题，进而确定决策边界，即振荡源与非振荡源间的阈 值m。
支持向量机算法可以选择线性核函数、多项式核函数和高斯核函数获得使间隔最大的决策平面。然而复杂的核函数只能对特定的分类问题有效，且泛化能力弱，容易出现过拟合问题。简单的决策边界往往具有更强的泛化能力，因此这里选择线性核函数获得区分振荡源和非振荡源的超平面。
通过支持向量机算法选择线性核函数得到的决策平面如图8所示。
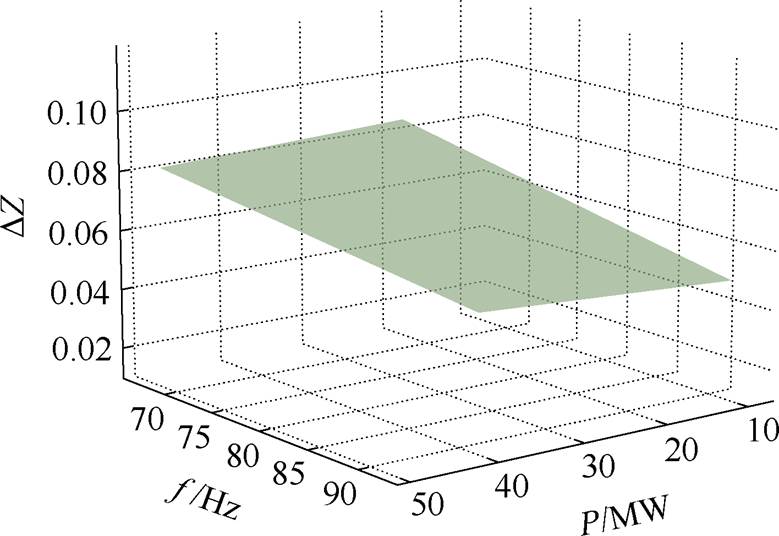
图8 决策平面
Fig.8 Decision plane
图8所示的决策平面即为不同振荡频率和不同功率时的振荡阈值m，阈值m 是关于频率和功率的线性函数。
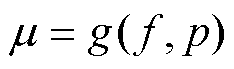（26）
对于新的各节点振荡数据，根据式（26）便可判断该节点是否超过振荡阈值。
T表示系统中收集到的所有电源节点DZ集合，即
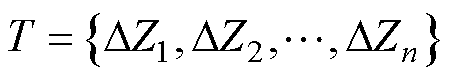（27）
在发生振荡时，系统中振荡源节点的DZ最大，此时的振荡源定位判据表达式为
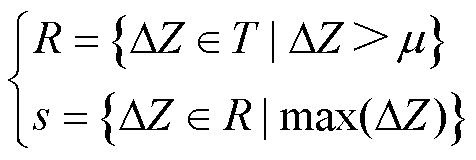（28）
式中，R为大于阈值的节点集合；s为仅包含振荡源节点的集合。振荡源定位判据由两部份组成，首先通过阈值筛选出振荡风险较大的节点；如果有多个节点超过阈值时需进一步选取DZ最大的节点作为振荡源节点。
本节针对工频测量阻抗振荡阈值难以获取的问题，构造了多场景下的振荡样本数据集，基于支持向量机算法获取振荡阈值的线性函数表达式，进而形成了次/超同步振荡源定位判据。
基于深度学习的振荡源定位方法是首先使用可采集的电气量构造已分类数据集，然后对数据集进行特征提取，将数据放到深度学习模型中进行训练，得到一个可判断振荡源和非振荡源的分类器。此类方法训练得到的分类器是一个黑箱模型，缺乏机理性解释，泛化能力不足。本文所提方法首先找到了可以用来区分振荡源和非振荡的特征，即工频测量阻抗。然而难以确定的是在各种运行工况下不同节点的振荡阈值，因此本文构造关于工频测量阻抗的数据集，进而通过SVM算法得到关于振荡源和非振荡源的阈值。最终得到的振荡阈值是一个关于频率和功率的函数，因此对于样本中未包含的工况有较好的泛化能力。
新能源电力系统中可能存在多个振荡源产生的不同频率振荡以及不同振荡源间单一频率的交互振荡。对于不同振荡源间单一频率的交互振荡，发生交互作用的两个电源节点DZ远大于系统中其他节点，而这两个节点的DZ由于变流器控制参数的不同而稍有差别。因此两台变流器节点均可作为振荡源节点，切除任意一台变流器均可破环振荡条件，可优先选择DZ变化最大的节点作为振荡源节点。对于多振荡源的多模态振荡，不同模态的振荡相互独立、互不影响，然而同一节点不同频率振荡分量的幅值不同，这里将某节点电压振荡幅值最大的振荡模态称为该节点的主导振荡模态。本文得到的振荡阈值是关于振荡频率和输出功率的函数，当有多个振荡源发生不同模态的振荡时，应首先得到该节点的主导振荡模态，然后判断该节点的DZ是否会超出阈值。不同振荡源节点的工频测量阻抗变化量均会超出阈值，本文所提方法仍可准确定位振荡源。
本文所提基于工频测量阻抗和支持向量机的振荡源定位具体流程如图9所示。
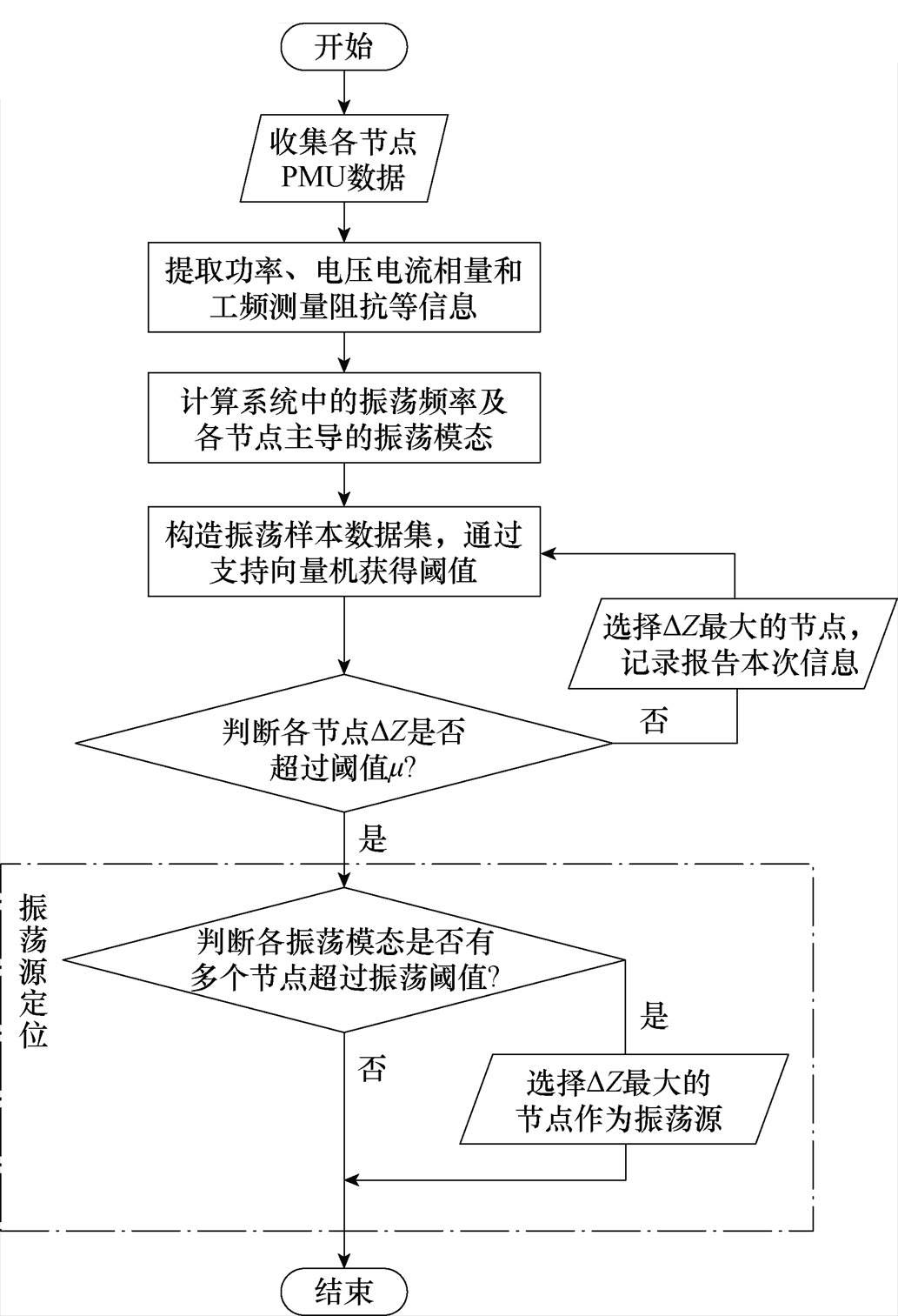
图9 振荡源定位流程
Fig.9 Oscillation source location process
振荡源定位流程简要描述如下：
（1）收集系统中各节点PMU量测得到的电压电流相量及输出功率。
（2）通过电压电流相量计算振荡前后的工频测量阻抗变化量，通过输出功率计算系统中的振荡频率及各节点主导的振荡模态。
（3）收集仿真和历史振荡数据，构造样本集，通过支持向量机获取振荡阈值。
（4）判断收集到的各节点DZ是否超过主导振荡模态的阈值，若超过阈值则进行下一步，若不超阈值则选择DZ最大的节点输出为振荡风险节点并记录本次信息作为训练的样本集。
（5）当某个振荡模态有多个节点DZ超过阈值时，选择DZ最大的节点作为振荡源；若只有一个节点DZ超过阈值则输出该节点为振荡源。
下面本文将从单模态振荡、单模态交互振荡以及多模态振荡三个方面验证所提方法的有效性。
中国新疆哈密风电系统为典型的新能源送端并网系统，其拓扑连接结构[21]如图10所示。
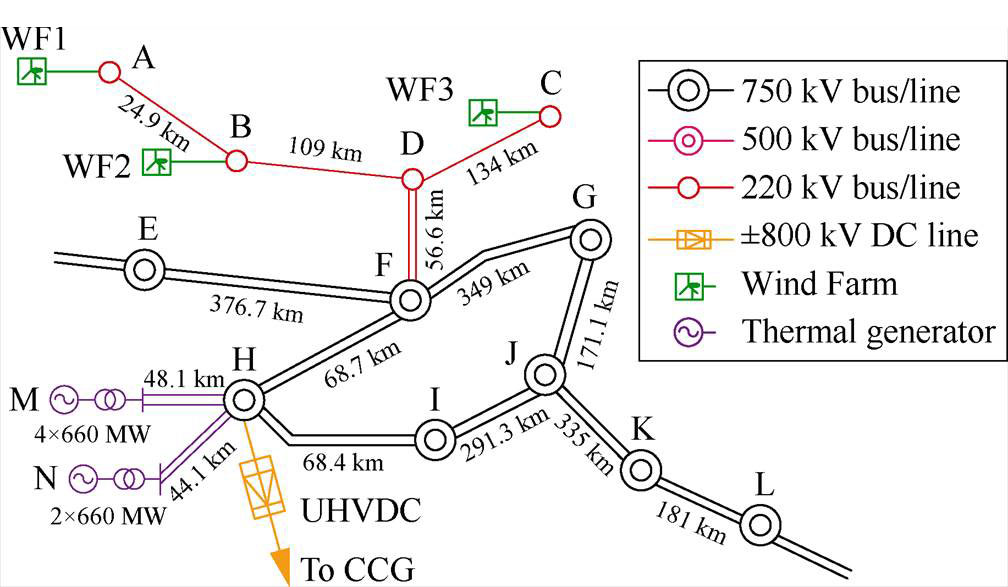
图10 哈密风电系统拓扑
Fig.10 Hami wind power system topology diagram
图4便是根据图10中节点A、B、C、D、F间的拓扑连接关系得到新能源并网系统典型结构。在PSCAD/EMTDC中搭建拓扑结构如图4所示的并网系统电磁暂态仿真模型，通过时域仿真获取不同运行工况下的数据。系统参数在附录中给出，PMSG的控制结构如图1所示。
3.2.1 训练样本集构造
在图4所示的系统中，调节PMSG的输出功率以及电流环的控制带宽，在不同运行工况下改变电网强度激发振荡，共获得不同出力水平下不同振荡频率的训练样本数据500组，如图11所示。
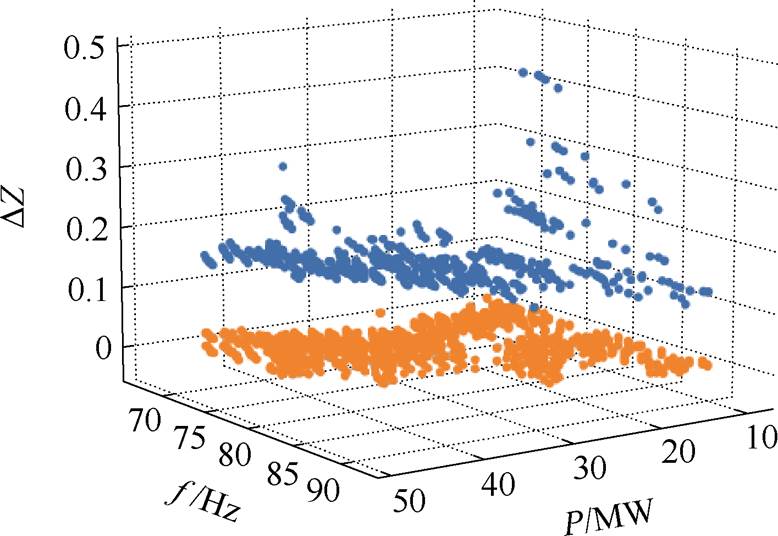
图11 DZ样本集
Fig.11 Sample dataset of DZ
如图11所示，蓝色的点为振荡源数据分布，橙色的点为非振荡源数据分布。由图11可知，风机出力较高时通常振荡频率较低，而风机出力较低时振荡频率的范围比较广泛，且振荡源和非振荡源的DZ之间存在明显的间隔区。
3.2.2 振荡阈值获取
训练样本数据集基于支持向量机算法使用线性核函数得到的决策平面如图12中绿色平面所示。
图12中的决策平面便是振荡阈值m1，阈值m1是关于频率和功率的线性函数。
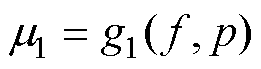（29）
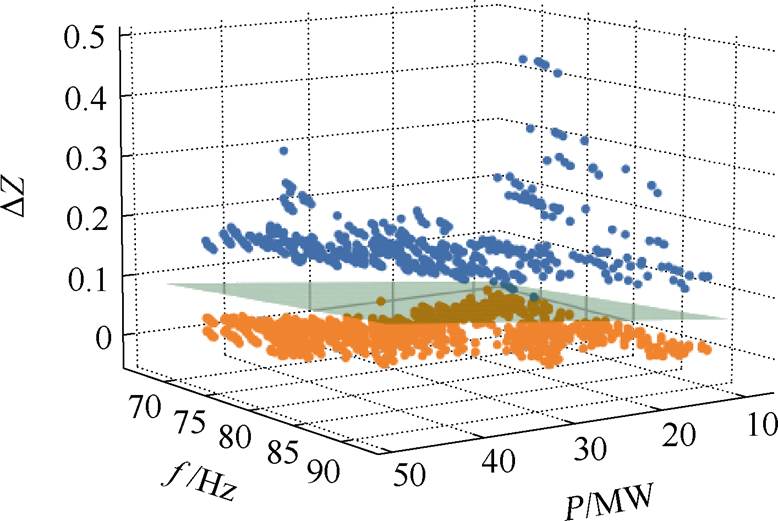
图12 DZ样本集决策平面
Fig.12 Data decision plane of DZ
对于新的测试数据集，通过训练得到的分类器判断是否超过振荡阈值便可筛选出振荡风险节点，进而再选择振荡源节点。
调节PMSG的输出功率以及控制结构中电流环的控制带宽，在不同运行工况下改变电网强度激发振荡，获得不同出力水平下不同振荡频率的测试数据集100组，如图13所示。
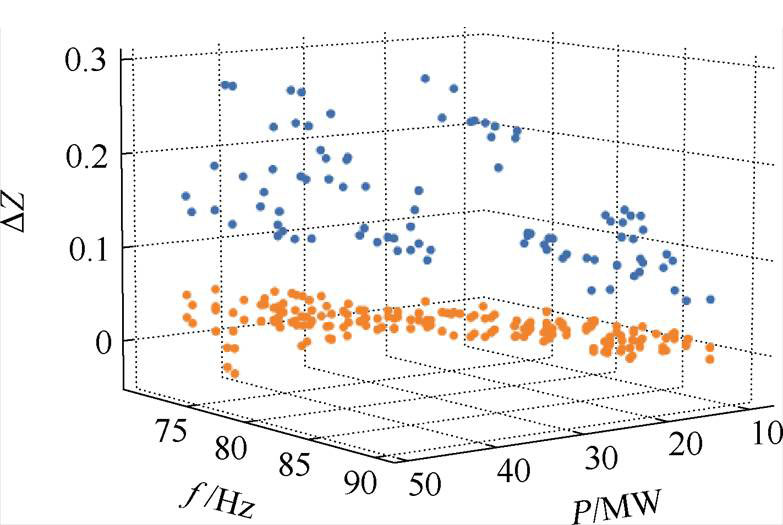
图13 单模态振荡测试集
Fig.13 Test dataset of single-mode oscillation
多层感知机（Multilayer Perceptron, MLP）和随机森林（Random Forest, RF）均为常用的机器学习分类算法。在此使用MLP和RF获取振荡阈值进行定位作为SVM的对比，所用机器学习算法的关键参数在附录中给出。SVM、MLP和RF的测试数据分类结果分别如图14～图16所示。
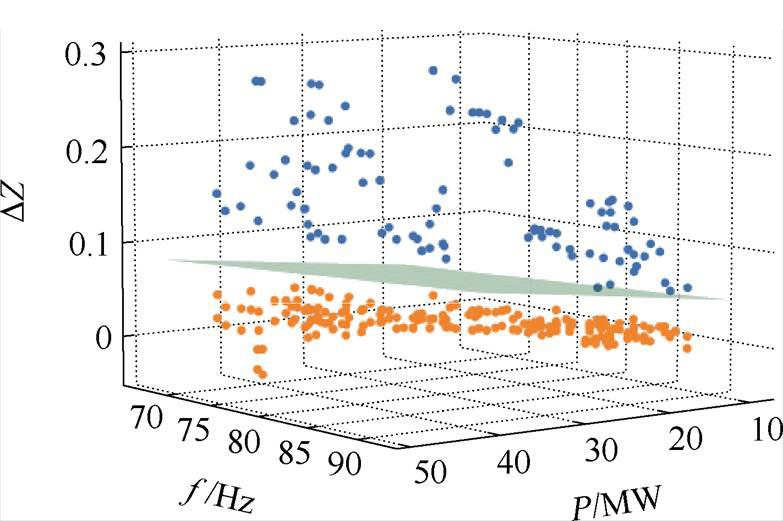
图14 单模态振荡SVM测试集分类结果
Fig.14 Test dataset classification results with SVM of single-mode oscillation
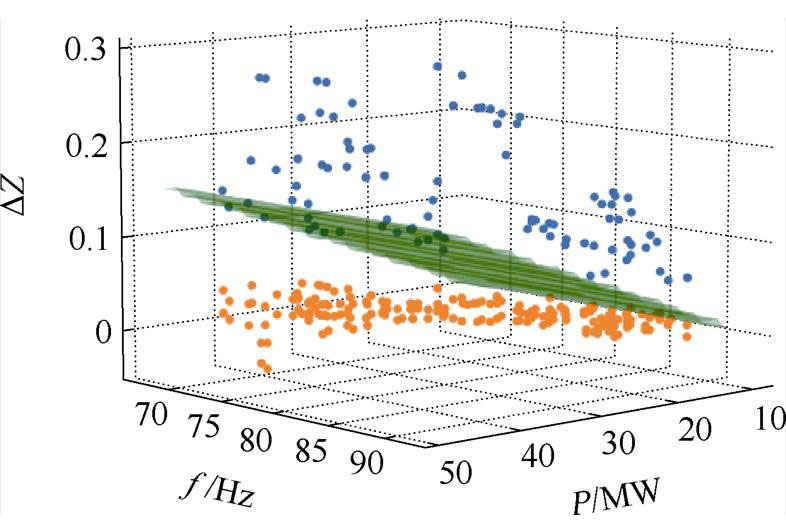
图15 单模态振荡MLP测试集分类结果
Fig.15 Test dataset classification results with MLP of single-mode oscillation
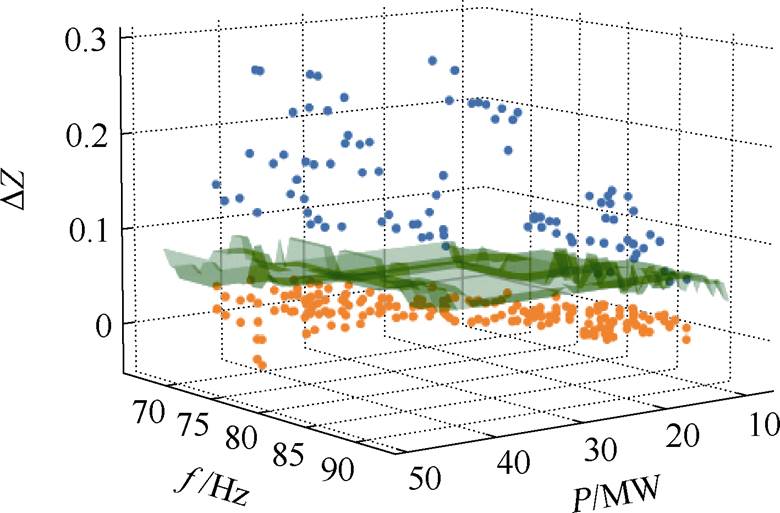
图16 单模态振荡RF测试集分类结果
Fig.16 Test dataset classification results with RF of single-mode oscillation
SVM、MLP和RF的测试数据定位准确率对比见表1。
表1 振荡源定位准确率对比
Tab.1 Location accuracy comparison
模 型综合准确率(%) MLP97.40 RF98.88 SVM100
由图14可知，即使在考虑多种不同运行状态的情况，测试集中的数据通过SVM得到的振荡阈值均能够正确分类。然而在图15和图16中，由MLP和RF得到的振荡阈值将某些振荡源判断为非振荡源，此时可选择DZ变化最大的节点作为振荡风险节点，并记录本次数据，更新训练结果。如果有多个节点超过振荡阈值时，则需要根据振荡源定位流程，进一步选择振荡源节点。
调节PMSG的输出功率以及控制结构中电流环的控制参数，在不同运行工况下改变电网强度激发不同电源节点间的交互振荡，获得测试数据集50组，采用3.3节中SVM算法获得的振荡阈值，测试数据集的分类结果如图17所示。
发生单模态交互振荡时不同节点的振荡频率相同，由图17可知，图中蓝色和绿色的点为发生交互振荡的电源节点的DZ变化，橙色的点为非振荡源节点。在测试集的50组数据中，有49组数据交互振荡的两个节点的DZ均大于振荡阈值，可进一步选择DZ最大的节点作为振荡源。有1组数据交互振荡的节点中仅有一个节点的DZ大于振荡阈值，也可准确定位振荡源。
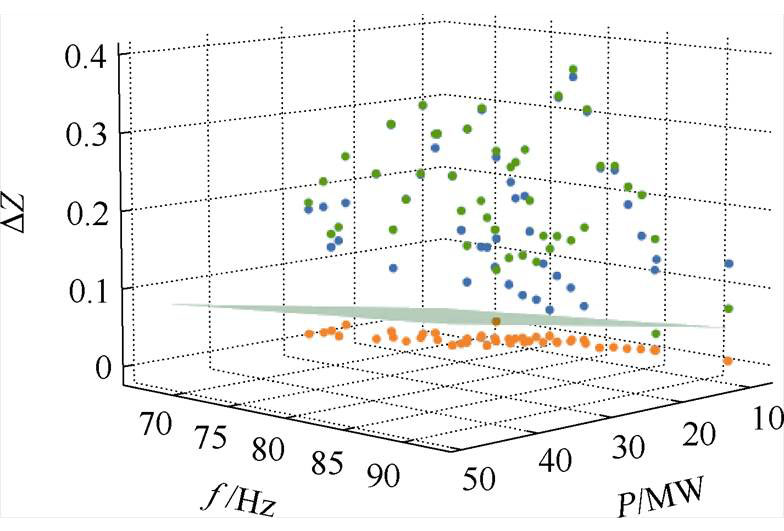
图17 单模态交互振荡SVM测试集分类结果
Fig.17 Test dataset classification results with SVM of single-mode interactive oscillation
调节PMSG的输出功率以及控制结构中电流环的控制参数，在不同运行工况下改变两个电源节点的电网强度激发多模态振荡，获得测试数据集50组，采用3.3节中SVM算法获得的振荡阈值，测试数据集的分类结果如图18所示。
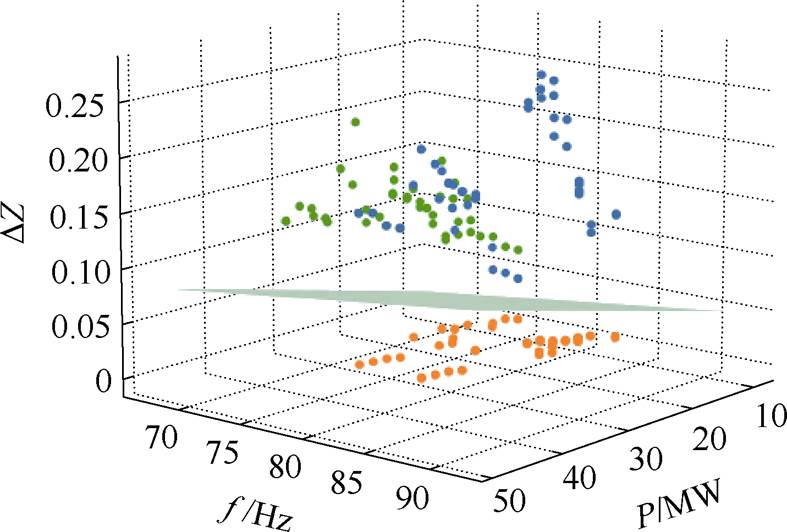
图18 多模态振荡SVM测试集分类结果
Fig.18 Test dataset classification results with SVM of multi-mode oscillation
发生多模态振荡时不同节点的振荡频率不同，由图18可知，图中蓝色和绿色的点为发生交互振荡的电源节点的DZ变化，橙色的点为非振荡源节点。在测试集的50组数据中，不同运行工况下多模态振荡的所有振荡源节点DZ均大于振荡阈值，因此所提方法在多模态振荡的情况下可准确定位振荡源。
本文提出了一种基于工频测量阻抗的振荡源定位方法，所提方法以工频电压电流作为数据来源，避免了宽频量测装置应用尚不广泛的问题。针对振荡阈值难以获取的问题，通过时域仿真构造振荡样本集，基于支持向量机算法获取了振荡阈值，形成了次/超同步振荡源定位判据。最后通过测试集验证了所提方法的准确性，主要结论总结如下：
1）本文分析了系统中存在次/超同步分量时通过控制环节影响工频电压电流的动态过程，揭示了次/超同步振荡发生时系统中各节点工频测量阻抗的变化规律，进而论证了工频测量阻抗作为振荡源定位依据的合理性和可行性。
2）本文针对振荡阈值难以准确获取的问题，采取数据驱动的方法构造了多运行场景下的振荡样本集，然后基于支持向量机算法获取了振荡阈值的线性函数表达式，进而形成了次/超同步振荡源定位判据。本文所提方法不依赖宽频量测装置，所需的仿真模型易于实现，有着较强的实用性。
3）本文依据新能源并网系统的典型拓扑结构，搭建了时域仿真模型进行算例研究，从单模态振荡、单模态交互振荡和多模态振荡三个方面验证了所提方法的准确性，结果表明，本文所提方法对于不同类型的振荡源定位有较好的泛化能力。
附 录
1. 仿真系统参数
附表1 仿真系统参数
App.Tab.1 System simulation parameters
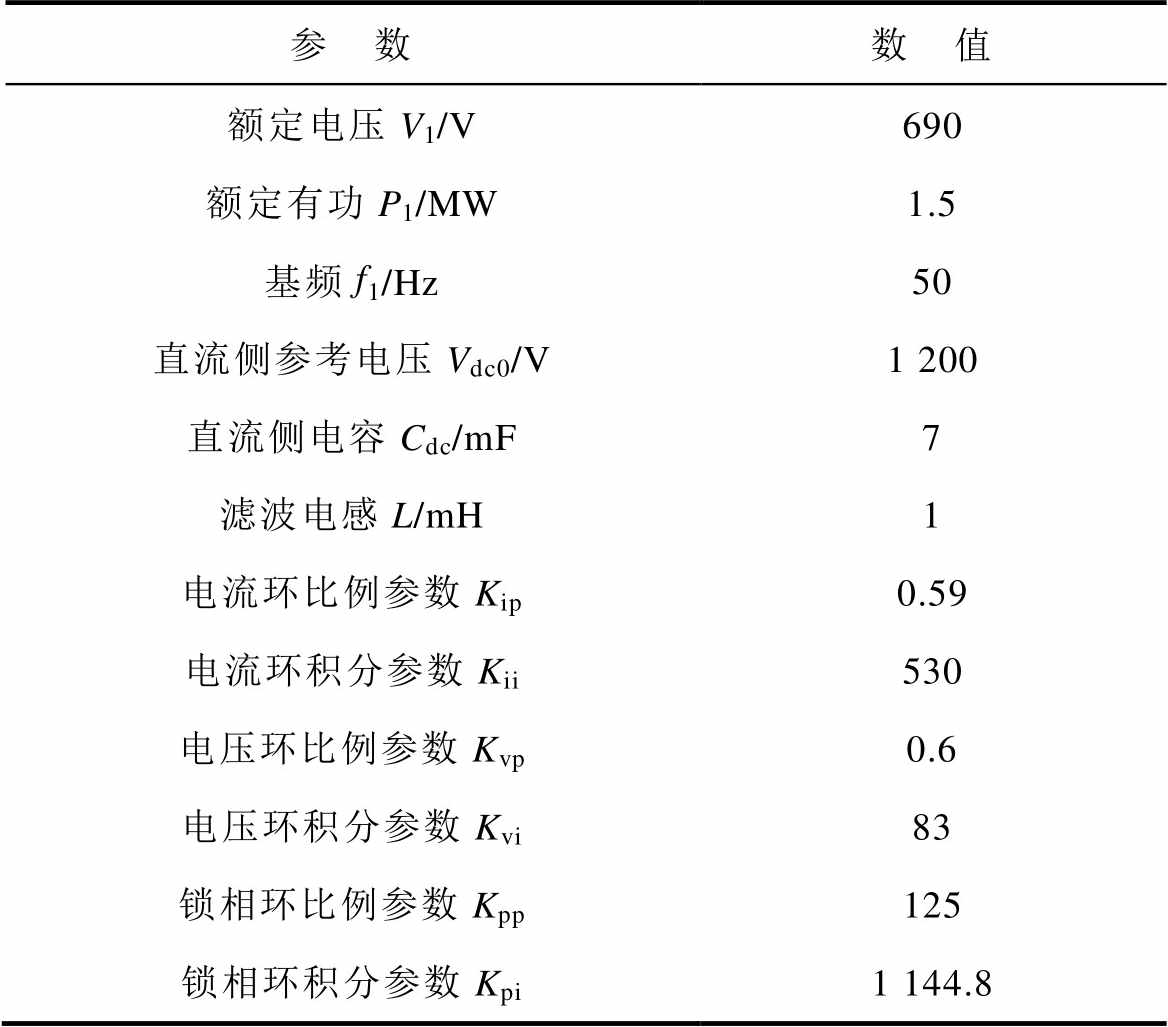
参 数数 值 额定电压V1/V690 额定有功P1/MW1.5 基频f1/Hz50 直流侧参考电压Vdc0/V1 200 直流侧电容Cdc/mF7 滤波电感L/mH1 电流环比例参数Kip0.59 电流环积分参数Kii530 电压环比例参数Kvp0.6 电压环积分参数Kvi83 锁相环比例参数Kpp125 锁相环积分参数Kpi1 144.8
2. 机器学习算法参数
文中所用的SVM、MLP、RF机器学习算法均来自于python中scikit-learn库。
SVM中核函数kernel='linear'，惩罚系数C=100；
MLP中求解器solver='lbfgs'，隐藏层神经元数量hidden_layer_sizes=(10,4);
RF中决策树数量n_estimators=10，随机种子random_ state=10。
参考文献
[1] Adams J, Pappu V A, Dixit A. Ercot experience screening for sub-synchronous control interaction in the vicinity of series capacitor banks[C]//2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 2012: 1-5.
[2] Leon A E, Solsona J A. Sub-synchronous interaction damping control for DFIG wind turbines[J]. IEEE Transactions on Power Systems, 2015, 30(1): 419- 428.
[3] 谢小荣, 刘华坤, 贺静波, 等. 直驱风机风电场与交流电网相互作用引发次同步振荡的机理与特性分析[J]. 中国电机工程学报, 2016, 36(9): 2366- 2372.
Xie Xiaorong, Liu Huakun, He Jingbo, et al. mechanism and characteristics of subsynchronous oscillation caused by the interaction between full- converter wind turbines and AC systems[J]. Pro- ceedings of the CSEE, 2016, 36(9): 2366-2372.
[4] 杨万开, 王兴国, 王书扬. 渝鄂柔性直流输电接入电网高频谐振与抑制分析[J]. 发电技术, 2022, 43(3): 492-500.
Yang Wankai, Wang Xingguo, Wang Shuyang. Analysis of high frequency resonance and suppression in Yu to E VSC-HVDC project connected to power grid[J]. Power Generation Technology, 2022, 43(3): 492-500.
[5] Testa A, Akram M F, Burch R, et al. Interharmonics: theory and modeling[J]. IEEE Transactions on Power Delivery, 2007, 22(4): 2335-2348.
[6] Testa A, Langella R. Power system subharmonics[C]// IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 2005: 2237-2242.
[7] 柳劲松, 马宁宁, 刘舒. 高比例风电系统宽频振荡紧急控制策略研究[J]. 全球能源互联网, 2024, 7(5): 558-566.
Liu Jinsong, Ma Ningning, Liu Shu. Study on emergency control strategy of wideband oscillation in power systems with high-percentage wind power[J]. Journal of Global Energy Interconnection, 2024, 7(5): 558-566.
[8] Xu Yanhui, Gu Zheng, Sun Kai, et al. Understanding a type of forced oscillation caused by steam-turbine governors[J]. IEEE Transactions on Energy Con- version, 2020, 35(3): 1719-1722.
[9] Ye Hua, Liu Yutian, Zhang Peng, et al. Analysis and detection of forced oscillation in power system[J]. IEEE Transactions on Power Systems, 2017, 32(2): 1149-1160.
[10] Ali Mohammadpour H, Santi E. Modeling and control of gate-controlled series capacitor interfaced with a DFIG-based wind farm[J]. IEEE Transactions on Industrial Electronics, 2015, 62(2): 1022-1033.
[11] Xu Yanhui, Gao Tianchu. Sub-synchronous frequency domain-equivalent modeling for wind farms based on rotor equivalent resistance characteristics[J]. Global Energy Interconnection, 2022, 5(3): 293-300.
[12] 占颖, 吴琛, 谢小荣, 等. 风电并网系统次同步振荡的频域模式分析[J]. 电力系统自动化, 2020, 44(18): 90-97.
Zhan Ying, Wu Chen, Xie Xiaorong, et al. Frequency domain modal analysis of subsynchronous oscillation in grid-connected wind power system[J]. Automation of Electric Power Systems, 2020, 44(18): 90-97.
[13] Zhan Ying, Xie Xiaorong, Wang Yang. Impedance network model based modal observability and controllability analysis for renewable integrated power systems[J]. IEEE Transactions on Power Delivery, 2021, 36(4): 2025-2034.
[14] Fan Xugen, Xiong Fei, Jiang Leihai. PMU-WAMS research and application in Brazil[J]. Global Energy Interconnection, 2019, 2(1): 85-93.
[15] Xie Xiaorong, Liu Wei, Liu Hui, et al. A system-wide protection against unstable SSCI in series- compensated wind power systems[J]. IEEE Transa- ctions on Power Delivery, 2018, 33(6): 3095-3104.
[16] 国家能源局. 电力系统同步相量测量装置通用技术条件: DL/T 280-2012[S]. 北京: 中国电力出版社, 2012.
[17] 樊陈, 姚建国, 常乃超, 等. 电力系统宽频测量装置技术规范解读及应用展望[J]. 电力系统自动化, 2023, 47(5): 190-199.
Fan Chen, Yao Jianguo, Chang Naichao,et al. Inter- pretation of technical specification for wide frequency measurement device of power system and prospect of its application[J]. Automation of Electric Power System, 2023, 47(5): 190-199.
[18] 国家电网有限公司. 电力系统宽频测量装置技术规范: Q/GDW12214-2022[S]. 北京: 中国电力出版社, 2022.
[19] 姜涛, 刘博涵, 李雪, 等. 基于自适应投影多元经验模态分解的电力系统强迫振荡源定位[J]. 电工技术学报, 2023, 38(13): 3527-3538.
Jiang Tao, Liu Bohan, Li Xue, et al. Forced oscillation location in power systems using adaptive projection intrinsically transformed multiple empi- rical mode decomposition[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3527-3538.
[20] Gao Bo, Wang Yang, Xu W, et al. Identifying and ranking sources of SSR based on the concept of subsynchronous power[J]. IEEE Transactions on Power Delivery, 2020, 35(1): 258-268.
[21] Xie Xiaorong, Zhan Ying, Shair J, et al. Identifying the source of subsynchronous control interaction via wide-area monitoring of sub/super-synchronous powerflows[J]. IEEE Transactions on Power Delivery, 2020, 35(5): 2177-2185.
[22] Wang Yang, Jiang Xiaolong, Xie Xiaorong, et al. Identifying sources of subsynchronous resonance using wide-area phasor measurements[J]. IEEE Transactions on Power Delivery, 2021, 36(5): 3242- 3254.
[23] 冯双, 杨浩, 崔昊, 等. 基于Copula传递熵的设备级和网络级宽频振荡传播路径分析及振荡源定位方法[J]. 电工技术学报, 2024, 39(16): 4996-5010.
Feng Shuang, Yang Hao, Cui Hao, et al. Device and network level wideband oscillations propagation path analysis and source localization method based on copula transfer entropy[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 4996-5010.
[24] 陈剑, 杜文娟, 王海风. 基于对抗式迁移学习的含柔性高压直流输电的风电系统次同步振荡源定位[J]. 电工技术学报, 2021, 36(22): 4703-4715.
Chen Jian, Du Wenjuan, Wang Haifeng. Location method of subsynchronous oscillation source in wind power system with VSC-HVDC based on adversarial transfer learning[J]. Transactions of China Electro- technical Society, 2021, 36(22): 4703-4715.
[25] Dong Xin, Du Wenjuan, Wang Haifeng. Measurement- driven diagnostics of mechanism and source of subsynchronous oscillations in power systems with
renewable power generation[J]. IEEE Transactions on Power Systems, 2024, 39(3): 5366-5381.
[26] Liu Hui, Cheng Yundan, Xu Yanhui, et al. Locali- zation method of subsynchronous oscillation source based on high-resolution time-frequency distribution image and CNN[J]. Global Energy Interconnection, 2024, 7(1): 1-13.
[27] Chisti Y. IEEE approved draft guide for syn- chronization, calibration, testing, and installation of phasor measurement units (PMU) for power system protection and control[J]. Education. physical Training. sport, 2013, 167(1):1-125.
[28] Yang Na, Ma Wenda, Wang Xitian, et al. Defining SSO power and characterizing SSO propagation in power system with wind farms integration[J]. IEEE Transactions on Power Systems, 2021, 36(4): 3531- 3540.
[29] 李光辉, 王伟胜, 刘纯, 等. 直驱风电场接入弱电网宽频带振荡机理与抑制方法(一): 宽频带阻抗特性与振荡机理分析[J]. 中国电机工程学报, 2019, 39(22): 6547-6562.
Li Guanghui, Wang Weisheng, Liu Chun, et al. mechanism analysis and suppression method of wideband oscillation of PMSG wind farms connected to weak grid (part I): analysis of wideband impedance characteristics and oscillation mechanism[J]. Pro- ceedings of the CSEE,2019, 39(22): 6547-6562.
Abstract With the rapid development of renewable energy represented by wind power and photovoltaics, the penetration rate of power electronic equipment in the power system has continued to increase. It has triggered several oscillation incidents caused by the interaction between power electronic equipment and the power grid, posing a serious threat to the safe and stable operation of the new energy grid-connected system. If the oscillation source can be detected promptly and accurately at the early stage and corresponding suppression measures can be taken, the harm caused by oscillation can be avoided. The oscillation source positioning can be divided into mechanism-model-based and measurement-data-based methods. Due to the difficulty in establishing high- dimensional nonlinear mechanism models and the poor interpretability of deep learning methods, mechanism- based and artificial intelligence-based methods are difficult to apply in practice. Meanwhile, broadband measurement devices are not yet widely used, and the existing methods for locating oscillation sources based on broadband measurement information are challenging.
Firstly, the dynamic response process of fundamental frequency voltage and current in the presence of sub/super-synchronous components is deduced, revealing the change rule of fundamental frequency quantity when sub/super-synchronous oscillation occurs. Then, for the problem that the oscillation threshold is difficult to obtain accurately, the oscillation training sample set under multiple scenarios is constructed, and the functional expression of the oscillation threshold is obtained based on the support vector machine algorithm. The sub/super-synchronous oscillation source localization criterion is formed based on the fundamental frequency measured impedance. Finally, a time domain simulation model is constructed based on the typical topology of new energy grid-connected systems, and the proposed method is validated by constructing a test data set. The results show that the proposed method is adaptableto different operating conditions and can realize the accurate localization of sub/super-synchronous oscillation sources in renewable energy grid-connected systems.
The main conclusion of this paper can be summarized as follows:
(1) When there are sub/super-synchronous components in the system, the voltage and current of power frequency are affected by the regulation of the control link. The fundamental frequency measurement impedance (FFMI) can be used to characterize the degree to which the fundamental frequency quantity is affected by the sub/super-synchronous components.
(2) The changes of FFMI in oscillation source and non-oscillation source nodes are significantly different, and the FFMI can be used to locate the sub/super-synchronous oscillation source. The support vector machine (SVM) is a robust binary classification model. An oscillation threshold of a binary function of frequency and power is finally obtained by constructing an oscillation training sample set under multiple scenarios.
(3) The FFMI-based oscillation source location method can accurately locate the oscillation source from three aspects: single-mode oscillation, single-mode interactive oscillation, and multi-mode oscillation. The proposed method has good generalization ability.
keywords：Sub/supersynchronous oscillation, oscillation source location, support vector machine, fundamental frequency measurement impedance
DOI: 10.19595/j.cnki.1000-6753.tces.241053
中图分类号：TM712
国家电网有限公司总部管理科技项目资助（5100-202499006A- 1-1-ZN）。
收稿日期 2024-06-17
改稿日期 2024-08-11
徐衍会 男，1978年生，教授，博士生导师，研究方向为动态电力系统分析和负荷建模。E-mail: xuyanhui23@sohu.com（通信作者）
李佳晏 男，1997年生，博士研究生，研究方向为新能源经柔直并网的稳定性分析。E-mail: lijiayan@ncepu.edu.cn
（编辑 郭丽军）