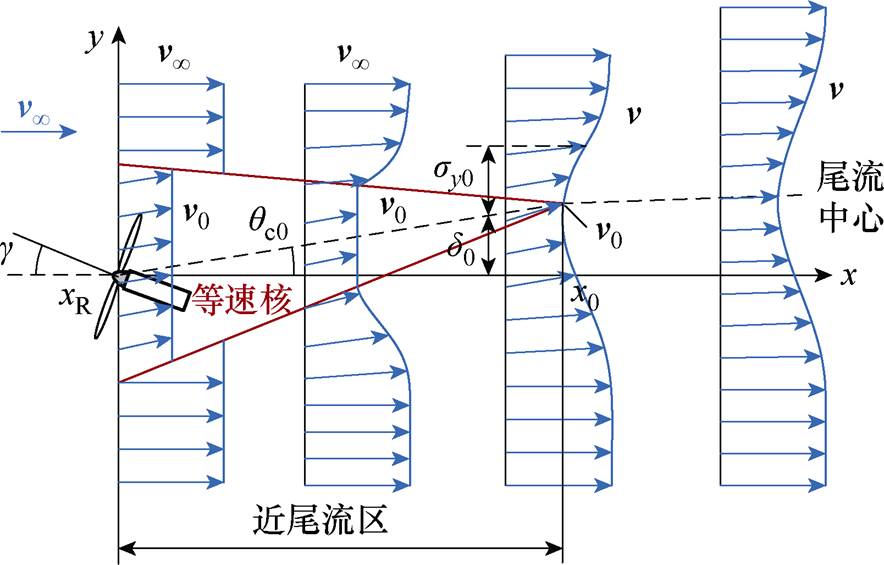
图1 Gauss尾流模型示意图
Fig.1 Schematic diagram of Gauss wake model
摘要 分布式海上风电制氢并集中送出的模式是高效利用深远海风资源并实现低碳清洁制氢的重要途径。尾流效应会导致海上风电的制氢量下降,仅考虑尾流效应以提升风电场制氢量为优化目标会导致场内风机疲劳分布不均,增加风电场维护成本。同时,风速预测精度与海上风电制氢优化问题紧密相关,预测精度不足会增大风速的不确定性,进而影响优化效果。为此,该文首先基于Gauss尾流模型、风机疲劳系数及分布式海上风电制氢模型提出一种同时考虑尾流效应与疲劳分布的分布式海上风电制氢多目标滚动优化运行方法。其次,为提高多目标优化问题的寻优效率,提出一种基于PID的多目标搜索算法(MO-PSA)。最后,在包含25台风机的5×5正方形布局海上风电场进行仿真验证。结果表明,所提滚动优化方法能在提高分布式海上风电制氢量的同时平衡各机组疲劳分布。与现有的多种优化算法相比,在计算时长相近的情况下,MO-PSA算法在所提多目标优化问题上可以提升0.915%~4.973%的制氢量,降低1.943%~47.153%风机累积疲劳系数标准差。
关键词:海上风电制氢 尾流效应 风机疲劳平衡 多目标优化 滚动优化
“双碳”目标背景下,我国海上风电进入大规模发展阶段,并逐步向深远海迈进[1-2]。但随着海上风电场离岸距离增加,输电的成本、损耗也显著增加[3-4],弃风问题日益严重成为深远海海上风电发展面临的重要难题。此外,氢能作为一种清洁高效的二次能源,正逐步成为未来能源脱碳转型的关键驱动力[5-6]。目前氢气主要来自化石能源制氢和工业副产制氢,绿氢占比偏低[7],低碳制氢仍是氢能产业面临的重要挑战。由于输氢成本低、效率高,100%分布式海上风电制氢并集中送出的模式在高效利用深远海风资源的同时,成为解决绿氢生产的重要途 径[8-10]。2019年全球首个海上制氢项目PosHYdon正式启动,在未来,瑞典Vattenfall的HT1(Hydrogen Turbine 1)、英国资助的Dolpyn等GW级分布式海上制氢项目也将陆续投建。然而,分布式海上风电制氢面临尾流效应与机组疲劳分布不均等问题,如何在提升整场制氢量的同时平衡风机疲劳亟待研究。
据统计,尾流效应导致风电场整场发电量的损失可高达2%~30%,将不同风向的尾流效应平均后,海上风电场尾流损失可能比陆上高40%~50%[11],这将显著降低风电场制氢量。通过调整风机的轴向诱导因子[12]与偏航角[13-14]可以协调风机出力、使尾流中心产生偏转,从而缓解尾流效应造成的不利影响,以期提高风电场的总功率输出[15]及制氢量。然而由于海上环境恶劣,可达性差,单次检修所需费用较高[16],上述文献未考虑风机疲劳分布不均匀的问题将导致多次派遣人员与船只进行检查维护,无法实现风电场统一检修、集中维护,大大增加了风电场的维护成本。因此,文献[17]采用粒子群优化算法同时对风场发电量与疲劳进行优化,但其未考虑风机偏航控制,且采用的Jensen尾流模型在垂直于每个圆锥轴的截面上采用了相等的风速,模型适用性较差。文献[18]对风电场进行非耦合分区,在每个分区内采用第二代非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm-Ⅱ, NSGA-Ⅱ)优化风机偏航角,实现风电场输出功率增加的同时减少风机疲劳。由于风机疲劳为各时段的累积量,上述文献仅对单一时段进行优化不具有前瞻性,无法保证日内疲劳均匀分布,需要对机组疲劳进行全时段统一优化。传统日前全时段优化方法采用日前预测风速值,由于日前预测风速误差较大,具有很大的不确定性,影响优化效果,难以为日内实际运行提供有效参考。
针对考虑风速不确定性的风电场运行研究,现有文献主要采用随机规划[19]、机会约束[20]、鲁棒优化[21]等方法,但对于非凸非线性的尾流模型,较难直接采用上述方法进行优化,文献[19]对尾流模型进行了线性化处理,文献[20-21]将风电场内因尾流造成的风速亏损视为定值来计算各风机处风速。然而采用上述方法刻画风电场内尾流效应会损失部分计算精度。同时,由于预测时间越接近预测域、预测时间范围越短,风速预测精度越高,基于滚动预测数据的滚动优化方法为减小风速不确定性带来的不利影响提供了一种新的思路[22-23]。滚动优化不仅可以使用精度更高的方法预测风速,降低风速不确定性对优化带来的影响,还可以前瞻未来一段时间内风况,均衡风机疲劳。
在复杂非线性的风电场优化模型求解方面,现有考虑尾流效应与疲劳分布的风电场优化研究以多目标粒子群(Multi-Objective Particle Swarm Optimi- zation, MO-PSO)、NSGA-Ⅱ等算法为主。然而,由于风电制氢模型的加入,优化问题变得更加复杂,需要寻优效果更好的算法来求解该问题。文献[24]所提出的基于PID的搜索算法(PID-based Search Algorithm, PSA)通过模拟增量式PID调控过程以校正每个个体与历史最优个体的偏差,使整个种群达到更优的状态,该算法已被证明在多数测试函数上具有较好的寻优效果。但PSA为单目标优化算法,无法直接应用于多目标优化问题。本文在PSA的基础上,提出适用于求解多目标优化问题的MO- PSA,以求解考虑尾流效应与疲劳分布的分布式海上风电制氢优化问题。
综上所述,本文首先基于Gauss尾流模型刻画海上风电场的风速分布以计算风机出力,通过疲劳系数衡量风机的疲劳程度,并建立分布式海上风电制氢模型计算风电场的制氢量;其次,提出一种考虑尾流效应与疲劳分布的分布式海上风电制氢滚动优化运行方法,在应对风速不确定性的同时实现海上风电场制氢量提升与疲劳均匀分布,可以为分布式海上风电制氢运行提供参考;最后,提出一种MO-PSA多目标优化算法,与现有的多种优化算法相比,在计算时长相近的情况下,该算法在本文多目标优化问题上可以得到更高的制氢量和更低的风机累积疲劳系数标准差。
海上风电场内由于尾流效应导致不同位置风机处的风速存在差异,进而影响风机的输出功率和制氢能力。Jensen尾流模型认为垂直于每个圆锥轴截面的风速相等,适用性较差,而Gauss尾流模型[25]采用Gauss函数来描述远场尾流的速度剖面,具有更高的精度。为了更加准确地刻画海上风电场内的风速分布情况,本文采用Gauss尾流模型对风速亏损、尾流偏转进行计算。Gauss尾流模型的示意图如图1所示。

图1 Gauss尾流模型示意图
Fig.1 Schematic diagram of Gauss wake model
1.1.1 风速亏损计算
因尾流效应的存在,无穷远处风速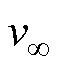 与风机下游
与风机下游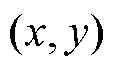 处的风速存在差值,该差值
处的风速存在差值,该差值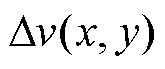 称为风速亏损,其计算方式为
称为风速亏损,其计算方式为
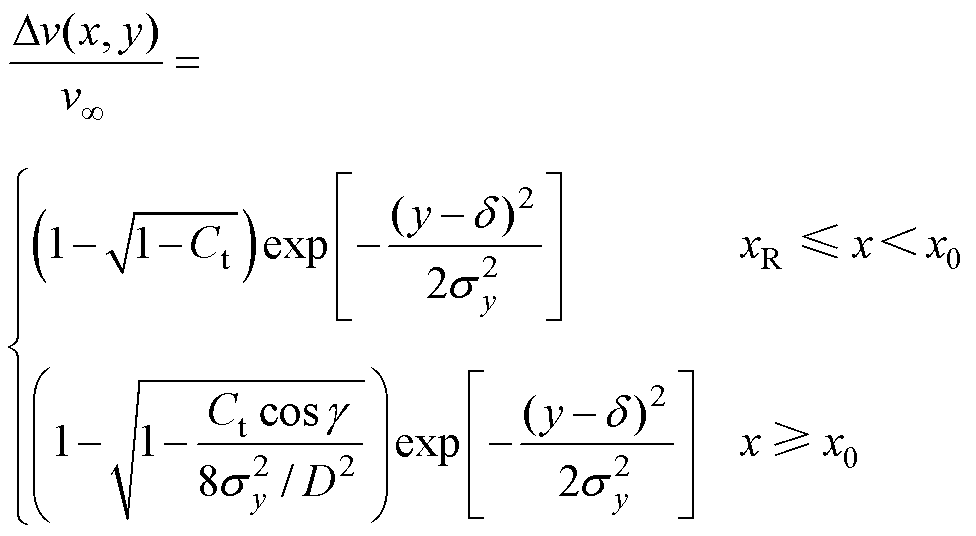 (1)
(1)
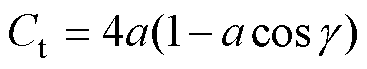 (2)
(2)
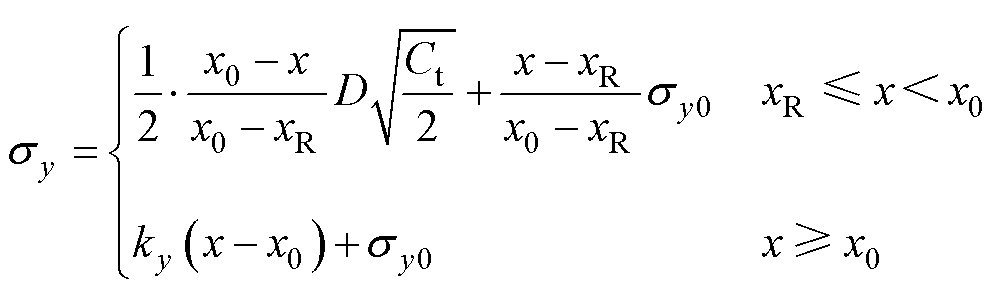 (3)
(3)
式中,g 为风机的偏航角;D为风机转子直径;d 为尾流中心的偏转量;Ct为风机的推力系数;a为风机的轴向诱导因子;sy为y方向尾流宽度;sy0为x=x0处y方向的尾流宽度;xR为风机转子所在位置横坐标;x0为近尾流区终止点的横坐标,xR≤ x<x0表示近尾流区,x≥x0表示远尾流区;ky为y方向的尾流增长率。
式(3)的其他参数计算式为
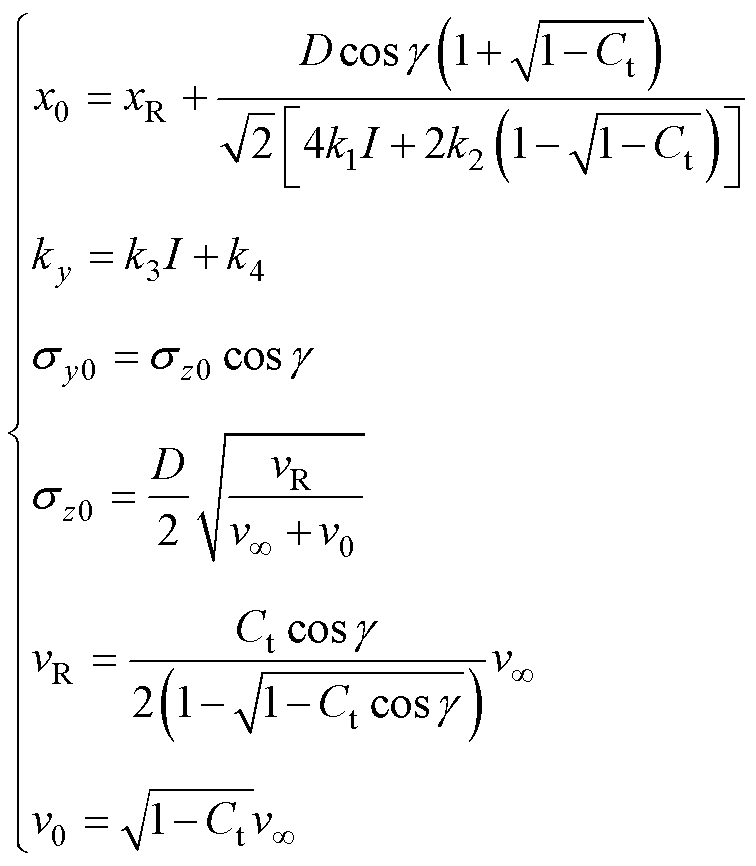 (4)
(4)
式中,I为湍流强度;k1、k2、k3、k4为拟合系数;sz0为x=x0处、z方向尾流宽度;vR为风机转子处的风速;v0为等速核内的风速。
1.1.2 尾流偏转计算
尾流中心会在风机偏航角的调整下产生偏转,其偏转量可表示为
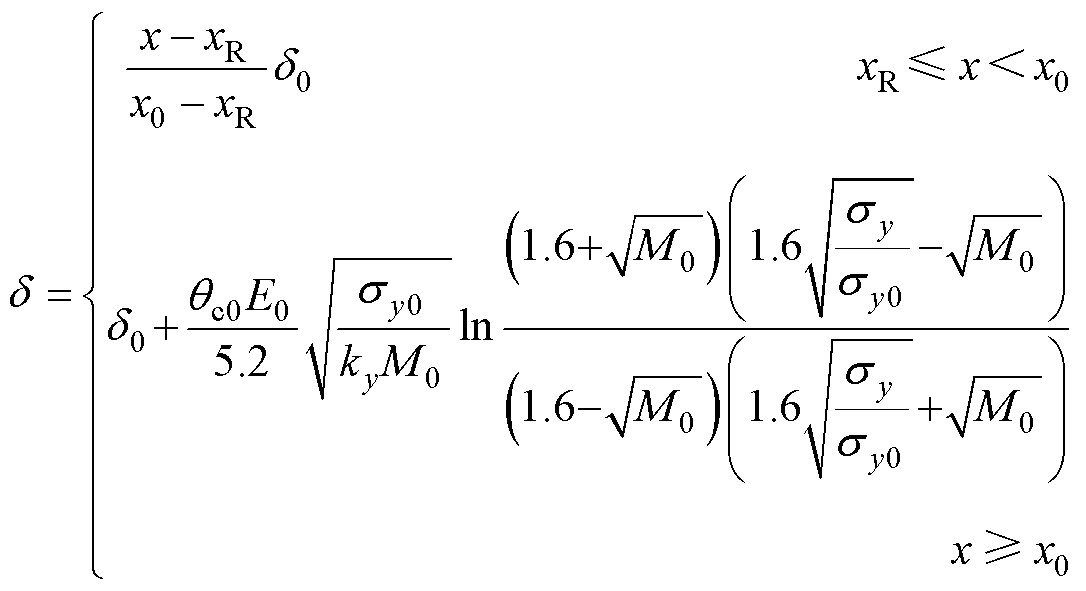 (5)
(5)
式(5)的其他参数计算方法如下。
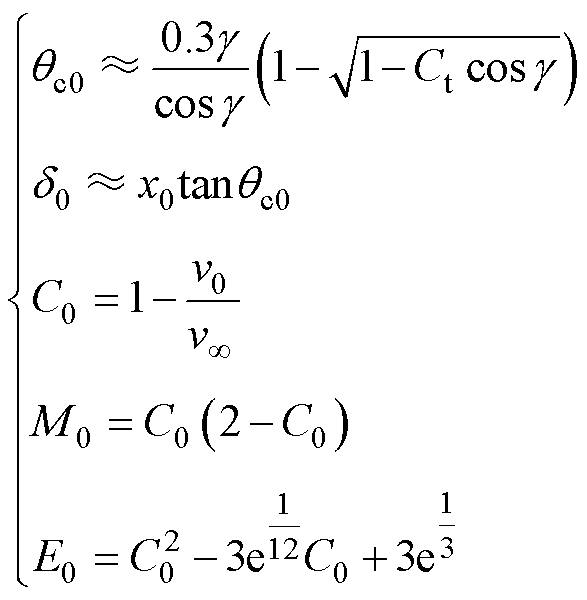 (6)
(6)
式中,qc0为尾流中心的偏转角;d0为x=x0处尾流中心的偏转量;C0、M0、E0为中间参数。
由于海上风电场内下游风机可能处在上游多个风机尾流影响下,为了计算这些风机处的风速,本文采用自由流平方和叠加(Sum of Square Freestream Superposition, SOSFS)模型对上游多个单台风机的尾流进行叠加。设K是位于风向上游且其尾流对下游风机i产生影响的风机集合,则风机i处的风速计算式为
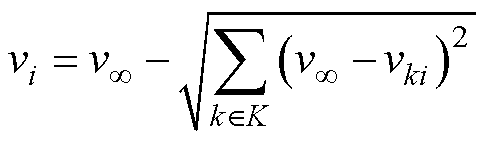 (7)
(7)
式中,vki为位于风向上游的风机k(k∈K)所产生尾流的影响下的风机i处的风速。
第i台风机的输出功率为
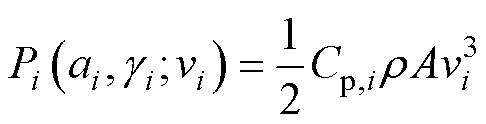 (8)
(8)
式中,ai、gi分别为第i台风机的轴向诱导因子和偏轨角;r 为空气密度;A为风轮扫过的面积,A= pD2/4;Cp,i为第i台风机的风能利用系数,即
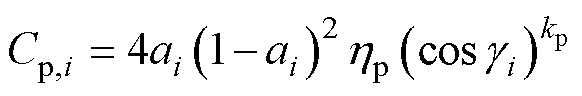 (9)
(9)
式中,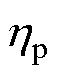 为能量转换效率;kp为拟合系数。
为能量转换效率;kp为拟合系数。
由于仅针对制氢量进行优化无法保证各风机疲劳的均匀分布,容易导致风电场频繁维护,文献[26]定义的疲劳系数不仅反映了风机因发电产生的工作疲劳fwork,还将真实气流中存在的湍流影响产生的扰动疲劳fdis考虑在内,较为全面,故本文采用该疲劳系数来衡量风机运行过程中产生的疲劳。
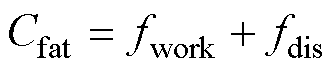 (10)
(10)
如果定义x 为湍流造成的疲劳与风机发电造成的疲劳之比,则可以计算自安装时刻(0时刻)起到t时刻风机产生的累积疲劳系数为
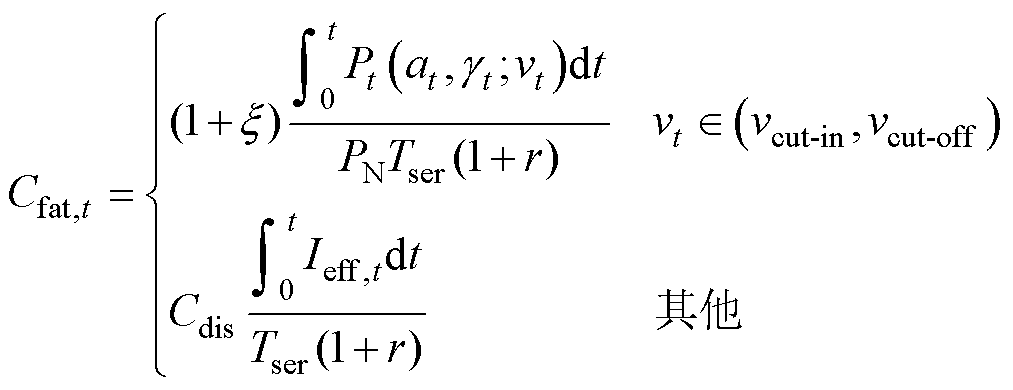 (11)
(11)
式中,vt为t时刻风机处的实际风速;PN为风机的额定功率;Tser为风机的设计服役年限;r为常规维修系数,若取r=0则认为风机均为新投入使用的;Cdis为扰动系数;vcut-in和vcut-off分别为风机的切入、切出风速;Ieff,t为t时刻的有效湍流强度,可通过式(12)计算。
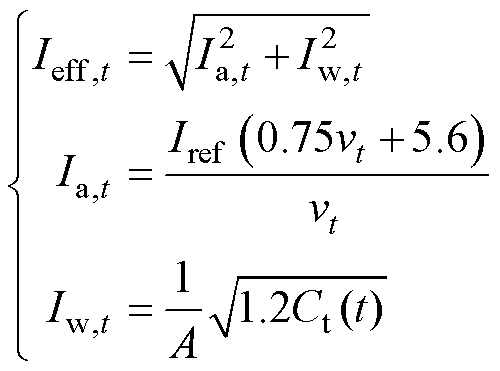 (12)
(12)
式中,Iref为参考湍流强度。
海上风电场与制氢设施有三种布置方式,分别为集中式陆上制氢、集中式海上制氢和分布式海上制氢。分布式海上风电制氢指将电解槽和风机集成在浮式平台上,每个风机与电解槽都构成一个独立的制氢系统,将电力转化的氢气通过管道或船舶集中送至陆上[27]。相较于集中式陆上制氢与集中式海上制氢,由于不需要大规模电制氢平台、电缆以及海上变电站,分布式海上制氢成本更低,可行性更高,而且当某个电解槽或风机发生故障时不会影响其他机组与电解槽的正常工作,此种布置方式更加可靠,正成为海上风电制氢的主流方式[28]。除此之外,由于质子交换膜(Proton Exchange Membrane, PEM)电解槽因其不需电解液,只需要纯水,具有效率高、响应速度快、较碱性电解槽安全可靠的特 点[29-30],适合与海上风电联合运行。故本节将电解槽设备选为PEM,建立分布式海上风电制氢模型。
单台风电制氢机组由风机与电制氢系统构成,变流器、电解槽、海水淡化装置是电制氢系统电气部分的主要组成部分[31]。电制氢系统中的功率关系为
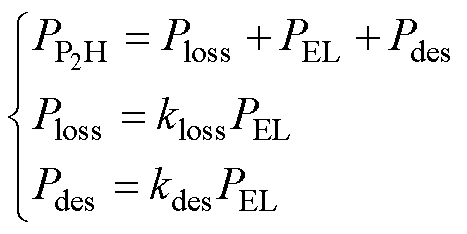 (13)
(13)
式中,Ploss为变流器损耗;Pdes为海水淡化装置功耗;PEL为电解槽输入功率,计算方式见第2.2节;kloss为变流器损耗与电解槽输入功率之比;kdes为反渗透海水淡化系统的电力消耗与电解水所需电量之比。
电解槽输入功率PEL的计算公式为
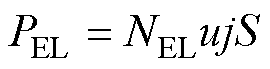 (14)
(14)
式中,NEL为串联的电解槽数量;u、j分别为单个电解槽的运行电压、运行电流密度;S为单个电解槽交换膜的面积。
单个电解槽的电压组成[32]为
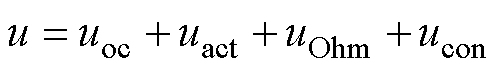 (15)
(15)
式中,uoc为开路电压;uact为激活电压;uOhm为欧姆电压;ucon为浓差电压。分别为
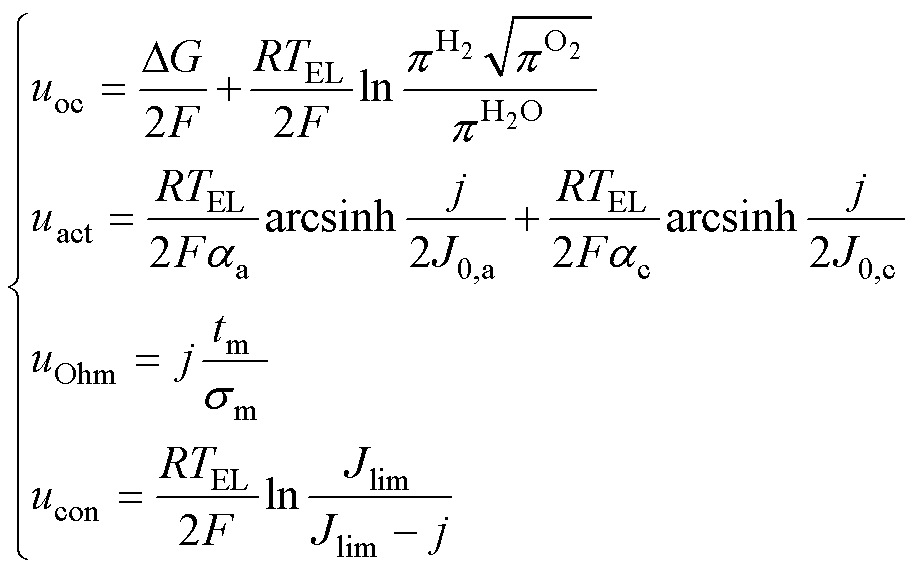 (16)
(16)
式中,DG为Gibbs自由能的变化;F为Faraday常数;R为理想气体常数;TEL为电解槽运行温度;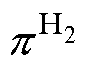 、
、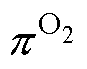 、
、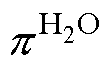 分别为电解槽中氢气、氧气、水的压力;
分别为电解槽中氢气、氧气、水的压力;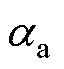 、
、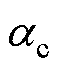 分别为阳极、阴极电荷转移系数;J0,a、J0,c分别为阳极、阴极转移电流密度;
分别为阳极、阴极电荷转移系数;J0,a、J0,c分别为阳极、阴极转移电流密度;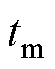 、
、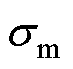 分别为单个电解槽交换膜的厚度、电导率;Jlim为极限电流密度。
分别为单个电解槽交换膜的厚度、电导率;Jlim为极限电流密度。
电解槽单位小时内的制氢量,即制氢速率为
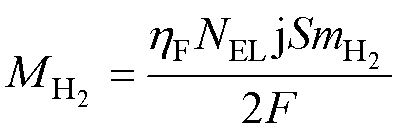 (17)
(17)
式中,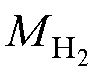 为氢气的摩尔质量;
为氢气的摩尔质量;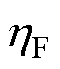 为Faraday效率,即
为Faraday效率,即
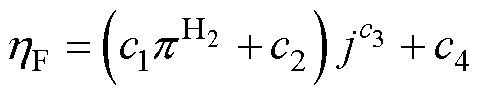 (18)
(18)
式中,c1、c2、c3、c4均为拟合系数。
电解槽的制氢效率为
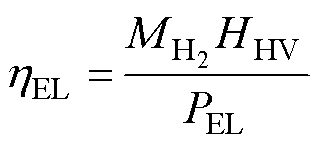 (19)
(19)
式中,HHV为氢气的高热值。
在运行温度TEL=323 K的条件下,利用式(14)~式(19)以及附表1中的相关参数取值,可以计算得到PEM电解槽输入功率与制氢速率和效率的关系如附图1所示。由附图1可以看出,当PEM电解槽的输入功率较小时,制氢效率随输入功率的增加而迅速提升;但当输入功率增加到一定程度后,由于电解槽无法将输入的电能完全转化为化学能,使得制氢效率增加的趋势逐渐趋于平缓,甚至开始下降。由此,PEM电解槽的制氢效率随着输入功率的增加并非是单调、线性增长的,不能简单地将电解槽输入功率等价为制氢速率。在后文中,将基于PEM电解槽的特性建立分布式海上风电制氢优化模型。
由于尾流效应的存在,不同风电机组之间的运行状态存在一定的耦合关系。为了在应对风速不确定性的同时提高海上风电场一天内的制氢量,并兼顾平衡一天内各风机之间的累积疲劳,本节以每台风机的轴向诱导因子a、偏航角g 作为优化变量建立多目标滚动优化模型。与日前预测次日24 h风速所进行的优化调度相比,滚动优化所用风速的预测时间尺度不同。滚动优化可以不断通过当前时刻监测得到的实际风速数据以及历史数据更新预测域的风速值,所用风速精度更高,可以有效地减小风速不确定性对优化产生的影响[22]。
设一天内共有T个优化时间段,预测域长度为m,控制域长度为n(n≤m),滚动优化步长为1,滚动优化原理如图2所示。图2中,以t∈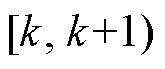 时段进行的滚动优化为例说明本节采用的滚动优化运行方法。
时段进行的滚动优化为例说明本节采用的滚动优化运行方法。
由于在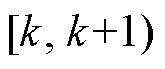 时段内,已经制定好了t<k+1时段内风机的调度计划,且t<k时段的调度计划已实际执行,故本次滚动优化的目的是制定风机在
时段内,已经制定好了t<k+1时段内风机的调度计划,且t<k时段的调度计划已实际执行,故本次滚动优化的目的是制定风机在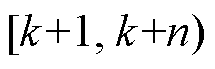 时段内的调度计划。本次滚动优化根据历史风速数据以及t≤k时段内的实际风速数据对预测域
时段内的调度计划。本次滚动优化根据历史风速数据以及t≤k时段内的实际风速数据对预测域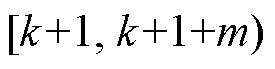 内m个时刻的风速
内m个时刻的风速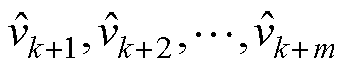 进行预测,然后根据预测风速在预测域
进行预测,然后根据预测风速在预测域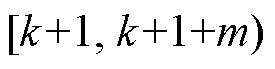 时段内求解第3.2节描述的多目标优化问题,最后取控制域
时段内求解第3.2节描述的多目标优化问题,最后取控制域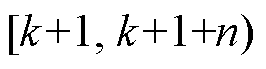 时段内的优化结果作为分布式海上风电制氢运行参考。
时段内的优化结果作为分布式海上风电制氢运行参考。
当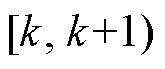 时段的调度计划执行完成后,进入下一次滚动,每次滚动优化的原理同前文,直至完成所有时间段的滚动优化。
时段的调度计划执行完成后,进入下一次滚动,每次滚动优化的原理同前文,直至完成所有时间段的滚动优化。
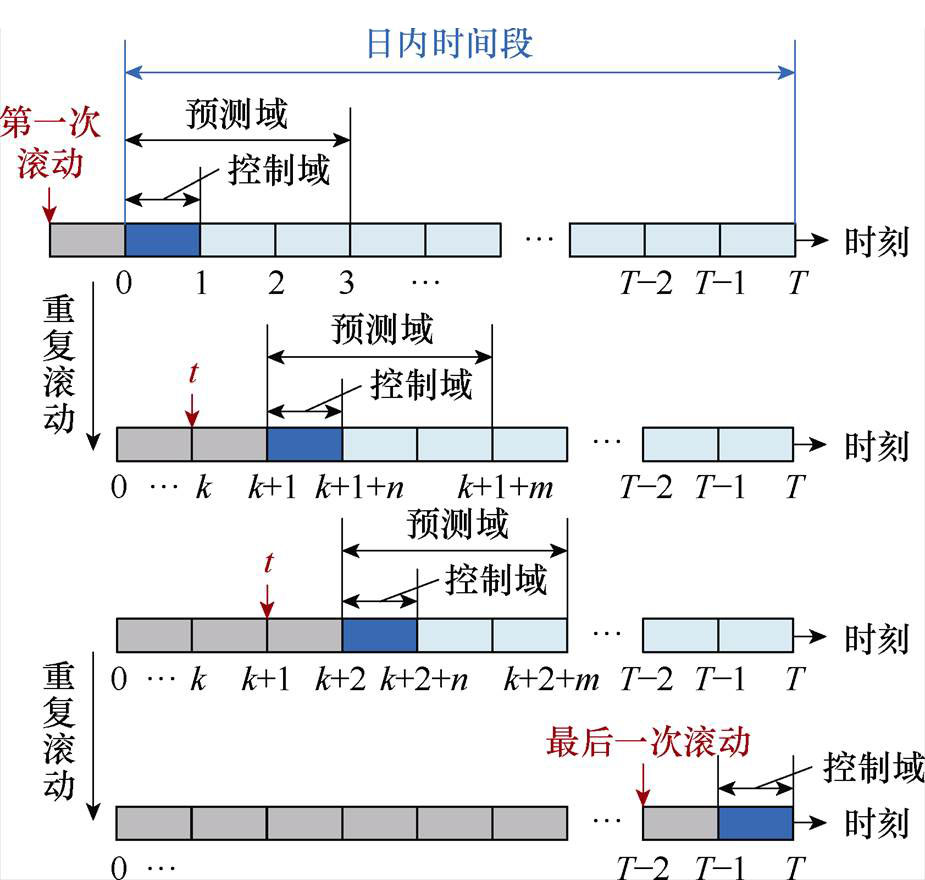
图2 滚动优化原理
Fig.2 Principle of rolling optimization
考虑到分布式海上风电制氢优化中各时段制氢量相互独立,而风电场内风机疲劳为累积量,为了在提高海上风电场制氢量的同时平衡场内各风机累积疲劳,设置如下优化目标。
优化目标1: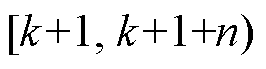 时段内海上风电场总制氢量最大。
时段内海上风电场总制氢量最大。
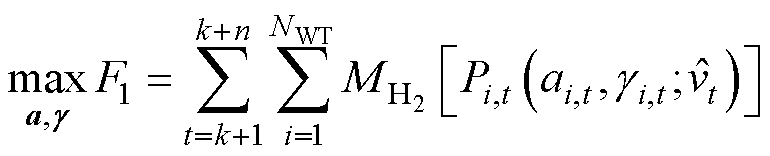 (20)
(20)
式中,a、g 分别为所有风机在预测域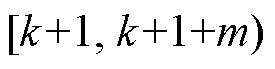 时段内的轴向诱导因子、偏航角;NWT为风电场内的风机数量;
时段内的轴向诱导因子、偏航角;NWT为风电场内的风机数量;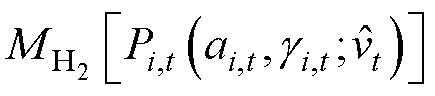 为第i台风机处于预测风速
为第i台风机处于预测风速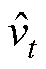 下、输出功率为Pi,t时的制氢量,功率的计算方式见式(8)和式(9),制氢量的计算方式由2.2节描述。
下、输出功率为Pi,t时的制氢量,功率的计算方式见式(8)和式(9),制氢量的计算方式由2.2节描述。
优化目标2:t<k+1+m时段内各风机累积疲劳系数的标准差最小。
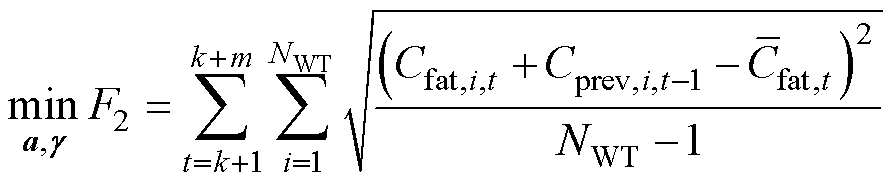 (21)
(21)
式中,Cfat,i,t为第i台风机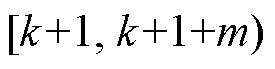 时段内产生的疲劳系数;
时段内产生的疲劳系数;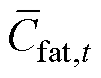 为
为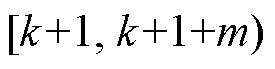 时段末所有风机疲劳系数的平均值,即
时段末所有风机疲劳系数的平均值,即
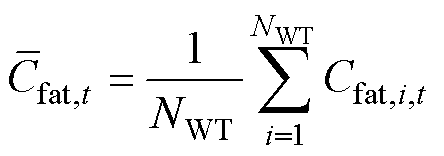 (22)
(22)
Cprev,i,t-1为第i台风机在t≤k时段的历史累积疲劳系数,表示为
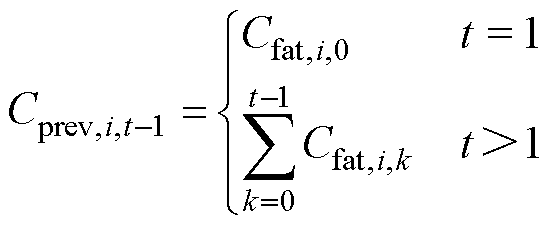 (23)
(23)
式中,Cfat,i,0为第i台风机疲劳系数初值。
需要指出的是,在使用式(11)和式(12)计算Cprev,i,t-1时使用的风速都是日内实际值,而在每次滚动优化的过程中Cfat,i,t和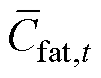 均使用预测风速计算。
均使用预测风速计算。
约束条件为
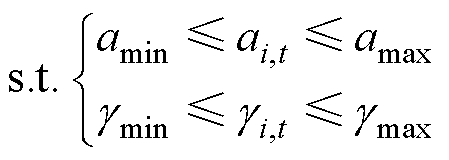 (24)
(24)
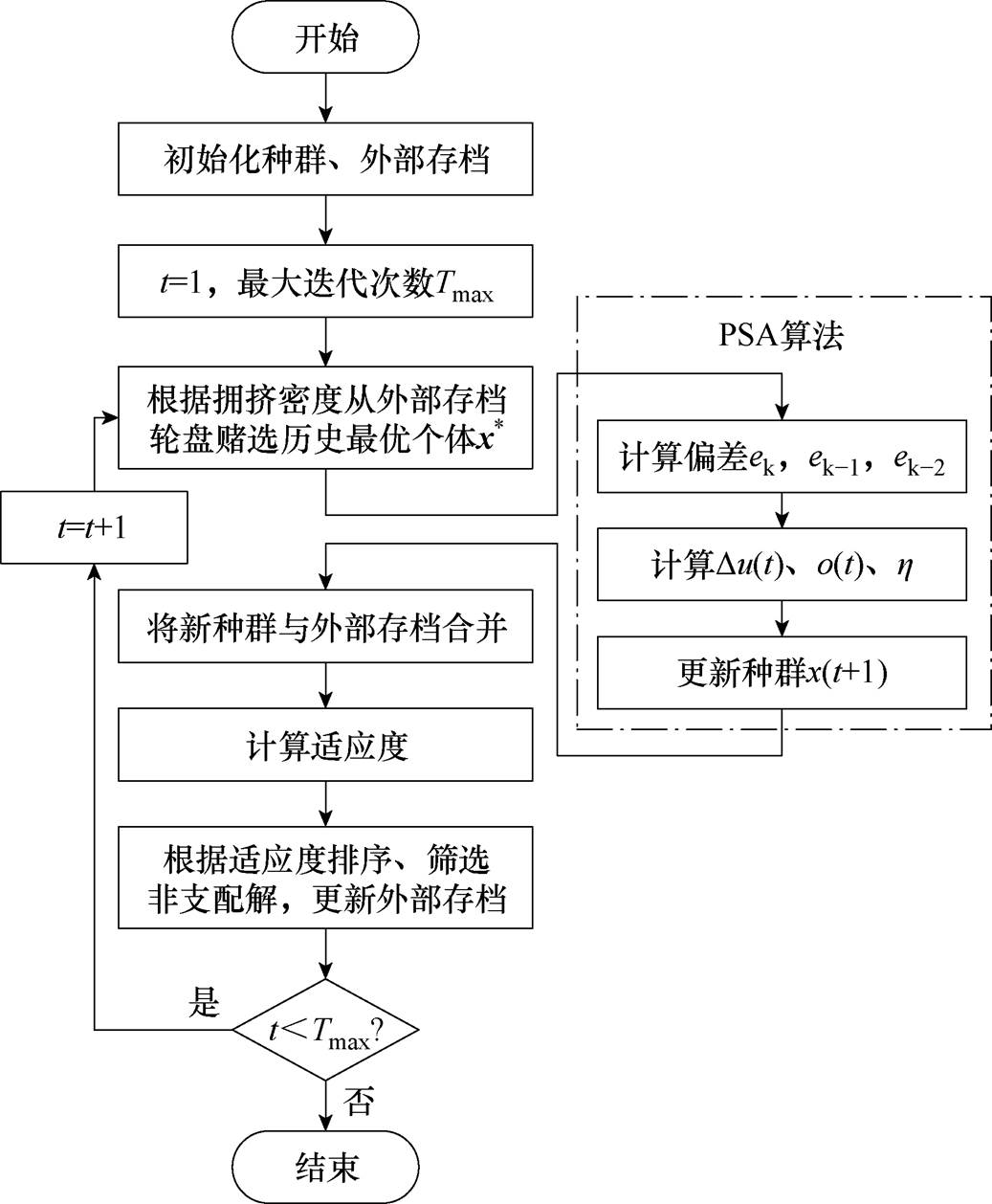
为了求解第3.2节建立的分布式海上风电制氢非线性多目标优化问题,本文基于PSA算法迭代更新种群的原理,对该算法历史最优个体的获取原理作了改进,以此建立MO-PSA多目标优化算法。MO-PSA算法的详细流程如附图2所示,主要步骤如下。
3.3.1 MO-PSA算法原理
1)种群初始化
设种群数量为N,维度为d,初始化操作为
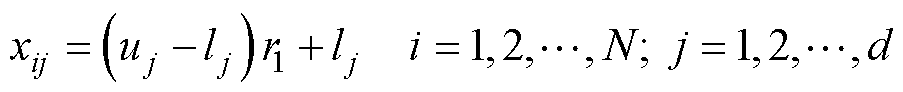 (25)
(25)
式中,uj和lj分别为第j维变量的上、下界;r1为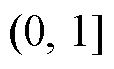 随机数。
随机数。
2)适应度计算和外部存档初始化
设极小化问题的目标函数为F,种群内第i个个体的适应度值为
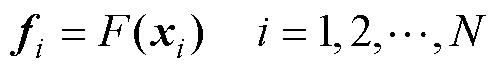 (26)
(26)
根据适应度对个体进行支配关系比较,将所有的非支配个体存入外部存档中,完成外部存档的初始化。
3)历史最优个体的选取
采用自适应网格法对外部存档中个体进行划分,并计算个体拥挤密度,采用轮盘赌的方式随机选择一个个体作为历史最优个体,其中拥挤密度越小的个体被选中的概率越高。第i个个体的拥挤密度的计算公式为
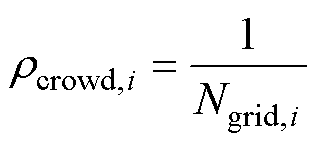 (27)
(27)
式中,Ngrid,i为个体i所在网格的所有个体总数。
4)偏差计算
定义在第t次迭代时种群的偏差ek(t)为
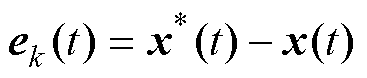 (28)
(28)
式中,x*(t)为第t次迭代时的历史最优个体。
定义种群第t次迭代与第t-1次迭代的偏差ek-1(t)为
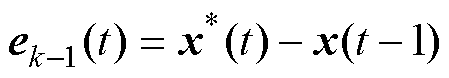 (29)
(29)
为了减少算法的空间复杂度,文献[24]将式(28)代入式(29)得到实用的ek-1(t)计算方式为
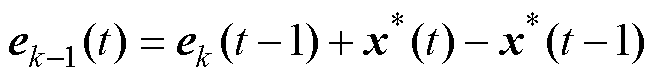 (30)
(30)
定义种群第t-1次迭代与第t-2次迭代的偏差ek-2(t)为
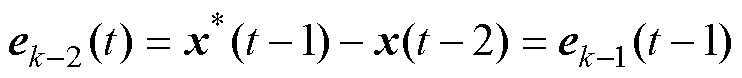 (31)
(31)
特别地,当t=1时,ek-2(t)=ek-1(t)=ek(t)。
5)种群更新
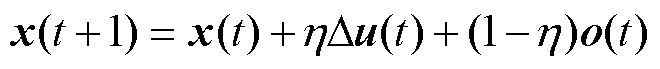 (32)
(32)
式中,Du(t)为新控制量,类比于增量式PID控制;o(t)为零输出。
Du(t)的计算公式为
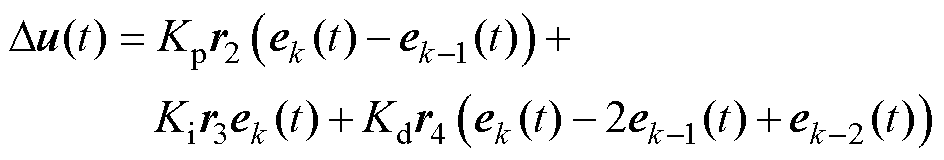 (33)
(33)
式中,r2、r3、r4为N×1维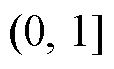 随机数矩阵;Kp、Ki、Kd分别为比例、积分、微分系数。
随机数矩阵;Kp、Ki、Kd分别为比例、积分、微分系数。
零输出o(t)用于防止算法过早地陷入局部最优,即
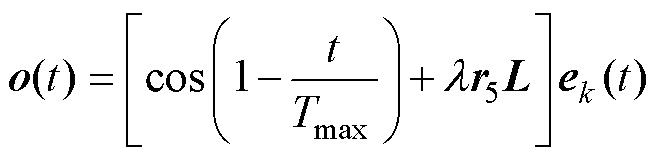 (34)
(34)
式中,Tmax为最大迭代次数;r5为N×d维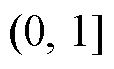 随机数矩阵。
随机数矩阵。
式(32)、式(34)中的其余参数计算式为
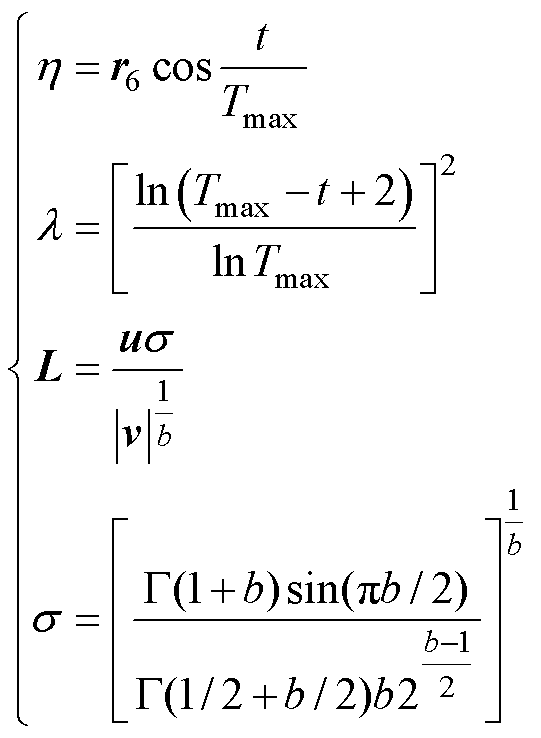 (35)
(35)
式中,r6为N×1维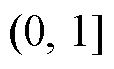 随机数矩阵;L为Lévy飞行函数;u、v为N×d维服从标准正态分布的随机数
随机数矩阵;L为Lévy飞行函数;u、v为N×d维服从标准正态分布的随机数
矩阵;b为固定参数;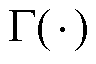 为Gamma函数。
为Gamma函数。
6)外部存档的更新
比较更新后的个体与外部存档中个体的支配关系,对外部存档进行更新。当外部存档中个体数量超过存档容量时,计算个体拥挤密度,随机删除拥挤密度最大的网格中的一个个体,重复该操作直到外部存档中个体数量与规定容量相同。
3.3.2 最优折中解的选取
本文在第3.2节建立的多目标优化问题经MO- PSA求解后将得出多组由a、g 确定的非支配解,这些非支配解对应的目标函数值组成Pareto前沿。考虑到制氢量和累积疲劳系数标准差的数量级差异,本文采用文献[22]的梯形型隶属度函数选择一个最优折中解(Optimal Compromise Solution, OCS)作为分布式海上风电制氢运行参考。
第j个非支配解xj对于第i个目标函数Fi的模糊隶属度为
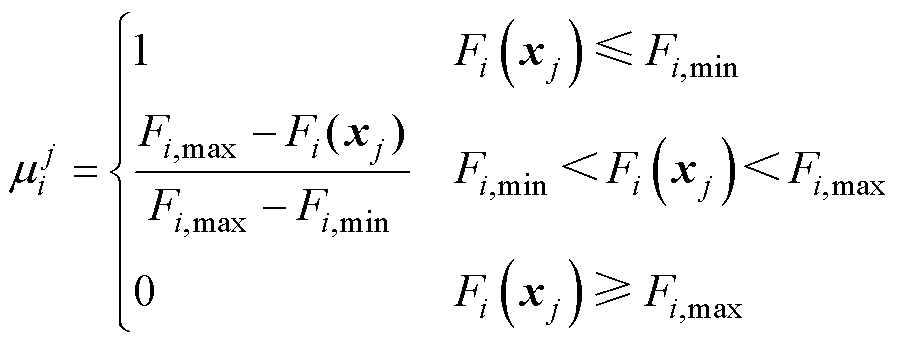 (36)
(36)
式中,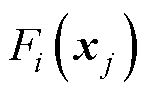 为当解为xj时目标函数Fi的值;Fi,max、Fi,min分别为Pareto前沿中目标函数最大、最小值。
为当解为xj时目标函数Fi的值;Fi,max、Fi,min分别为Pareto前沿中目标函数最大、最小值。
对式(36)进行标准化处理为
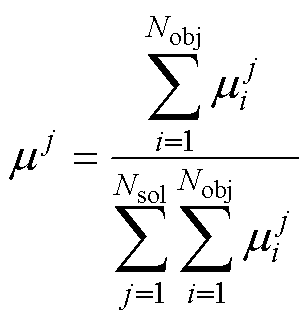 (37)
(37)
式中,Nobj为目标函数个数,对本文而言Nobj=2;Nsol为非支配解个数。选取式(37)最大者作为OCS。
分布式海上风电制氢滚动优化运行方法总体框架如图3所示。
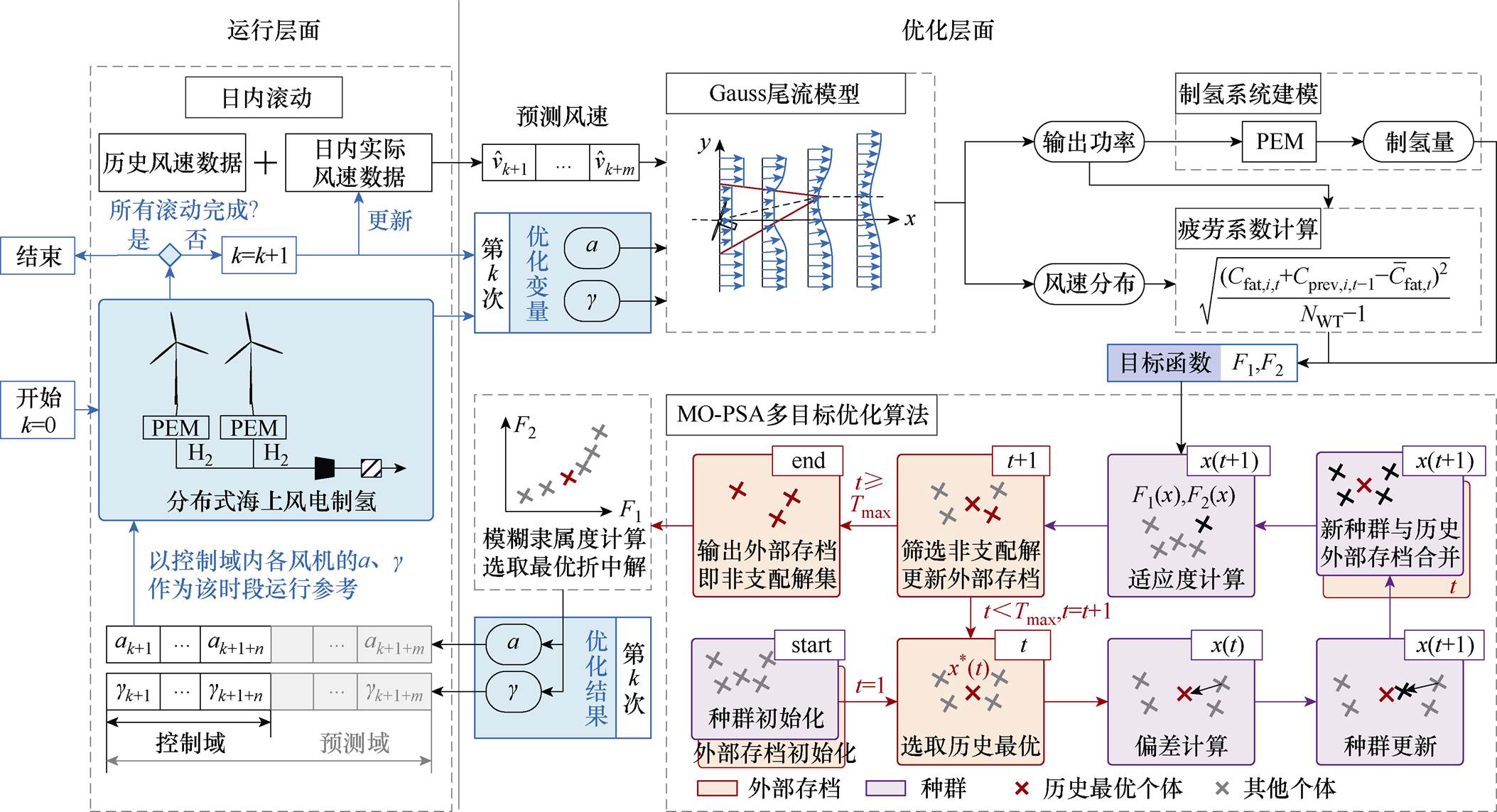
图3 分布式海上风电制氢滚动优化运行方法总体框架
Fig.3 The overall rolling optimal operation method framework of distributed hydrogen production by offshore wind power
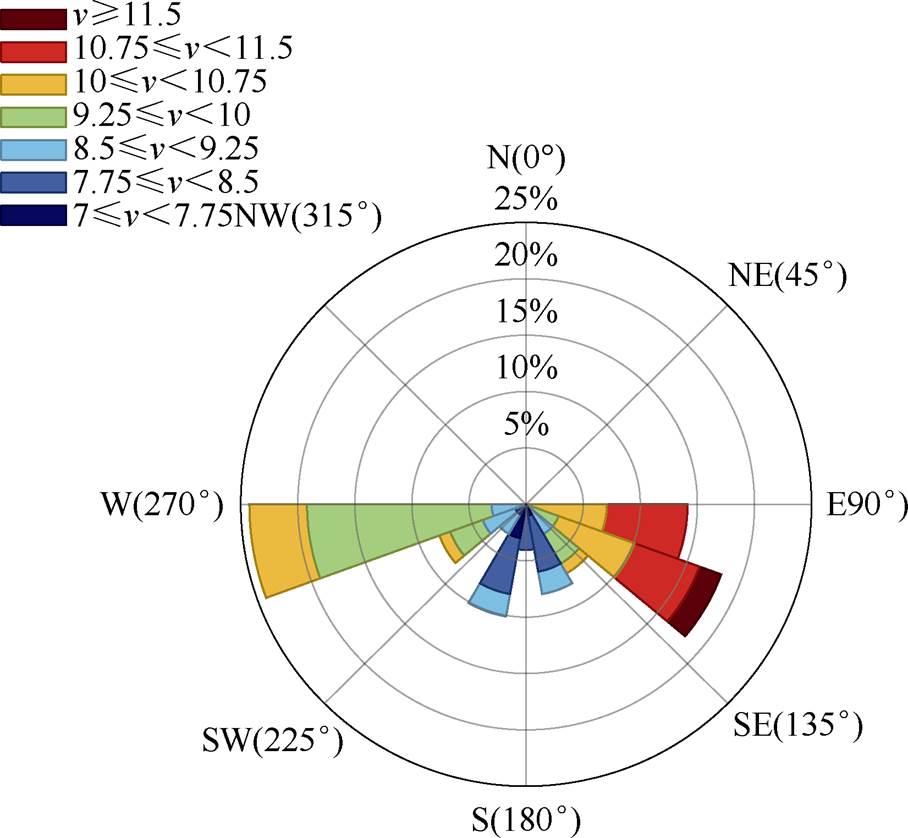
本文借鉴丹麦的HornsRev、江苏大丰H-4等风电场以近似规则的布局安装风机,将算例海上风电场设置为包含25台风机的5×5正方形布局,如附图3所示,风机与风机之间的横、纵向距离均为7D。风机类型为美国可再生能源国家实验室(National Renewable Energy Laboratory, NREL)提供的5MW风机,参数见附表2。日内实际风速、风向数据取自NREL所提供的2019年4月北太平洋某地区风速、风向数据,日前预测风速采用各时间节点与实际风速的预测偏差绝对值在15%内的随机分布得到,日内滚动更新的风速预测值由ARMA模型计算得到,如附图4、附图5所示。Gauss尾流模型参数见附表3,风机疲劳系数计算参数见附表4。仿真硬件:Intel(R)Core(TM)i9-14900HX CPU@2.20 GHz,内存DDR5 32 GB,软件运行环境:Matlab R2024a、Python 3.11.9。
以15 min为时间间隔,对24 h风机的运行情况进行滚动优化,即取优化时间段数T=96,预测域长度m=4(60 min),控制域长度n=1(15 min),算例参数见表1。
表1 算例参数
Tab.1 Parameters of calculation examples
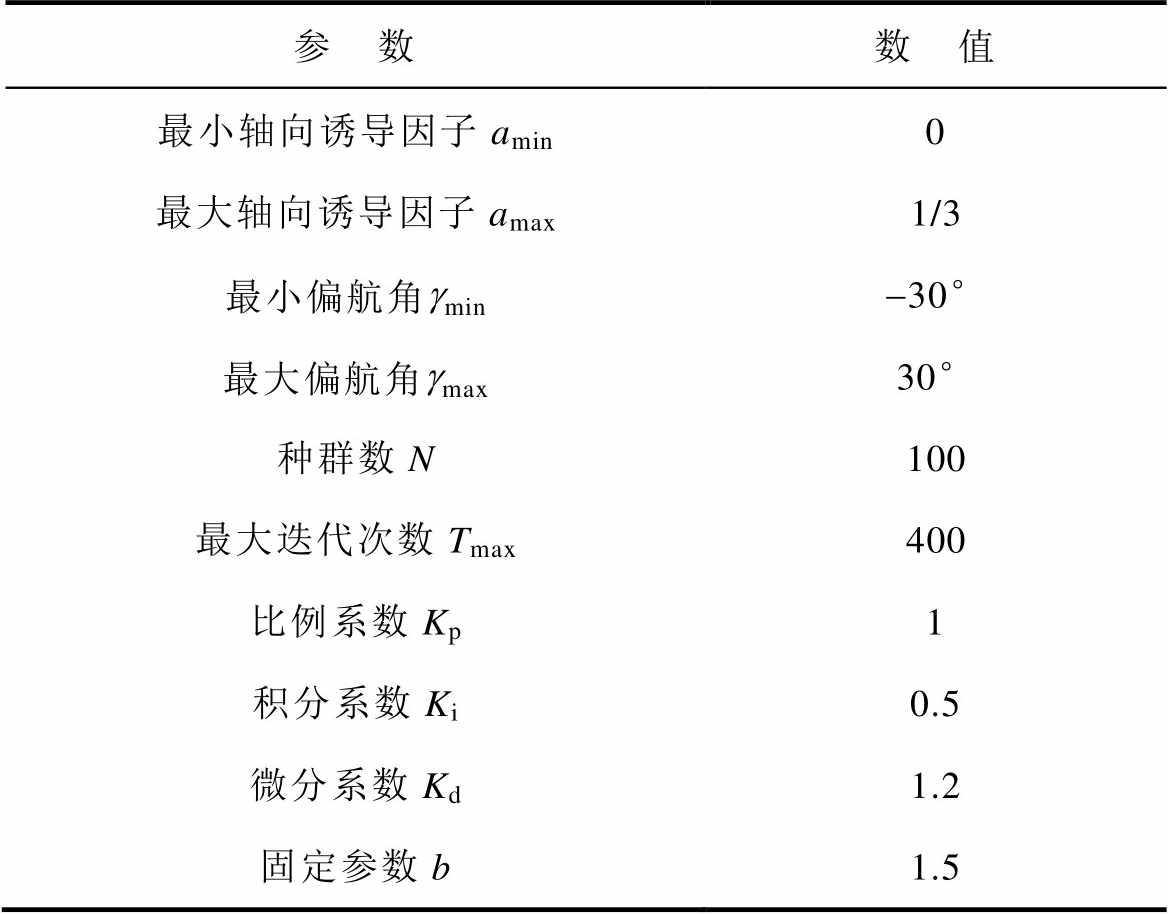
参 数数 值 最小轴向诱导因子amin0 最大轴向诱导因子amax1/3 最小偏航角gmin-30° 最大偏航角gmax30° 种群数N100 最大迭代次数Tmax400 比例系数Kp1 积分系数Ki0.5 微分系数Kd1.2 固定参数b1.5
为验证考虑尾流与疲劳的分布式海上制氢滚动优化运行方法的有效性,设置如下算例进行对比:
算例1:不进行优化,海上风电场内的所有风机均按照ai=1/3,gi=0(i∈NWT)的贪婪策略运行于日内实际风速。
算例2:单独优化每个时段的制氢量和疲劳系数,风速采取日内滚动更新的预测值。
算例3:全时段统一优化制氢量和疲劳系数,风速采取日前预测值。
算例4:滚动优化制氢量和疲劳系数,风速采取日内滚动更新的预测值。
计算海上风电场分别采取以上4个算例所述方法在日内24 h实际风速运行下的制氢量与累积疲劳系数标准差进行对比。
不同算例下,海上风电场优化运行结果见表2。算例4进行1次滚动优化用时3.912 min<15 min,能够在控制域内完成优化。
表2 不同算例下海上风电优化运行结果对比
Tab.2 Comparison of optimized operation results of offshore wind power under different calculation examples
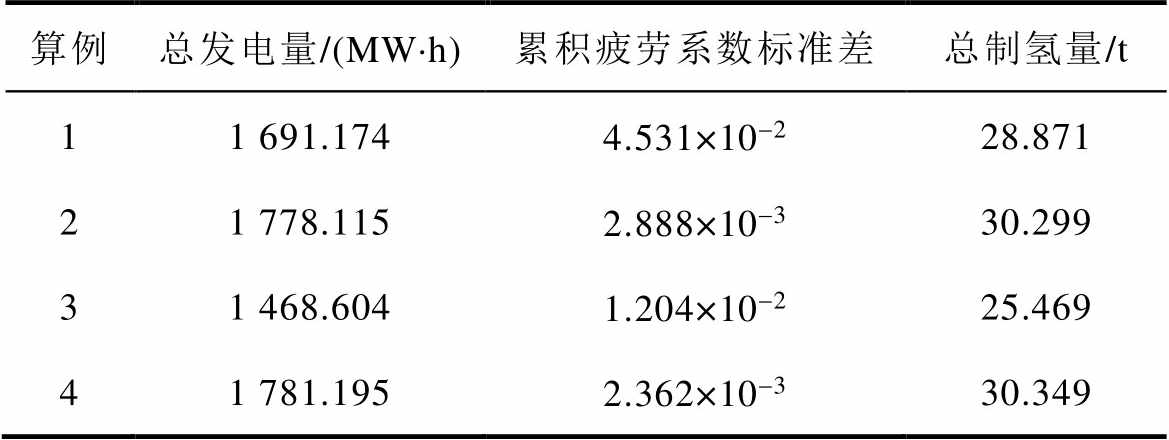
算例总发电量/(MW×h)累积疲劳系数标准差总制氢量/t 11 691.1744.531×10-228.871 21 778.1152.888×10-330.299 31 468.6041.204×10-225.469 41 781.1952.362×10-330.349
由表2可知,算例2因考虑了尾流效应与疲劳分布,较算例1提升4.95%的总制氢量并降低了疲劳标准差;算例3进行的全时段统一优化由于只能使用日前预测误差较大的风速,使得优化结果相对保守,虽然累积疲劳系数标准差较算例1下降73.43%,但总制氢量亦降低了11.78%;算例4采用滚动优化,通过滚动更新预测风速,减少风速不确定性带来的影响,总制氢量的优化结果较算例1和算例3分别提升5.12%和19.16%。算例4的总制氢量较算例2略有提升,且累积疲劳系数标准差较算例2降低了18.21%。
4.2.1 制氢量优化效果分析
图4分别给出了算例1与4、算例3与4海上风电各小时的制氢量对比。
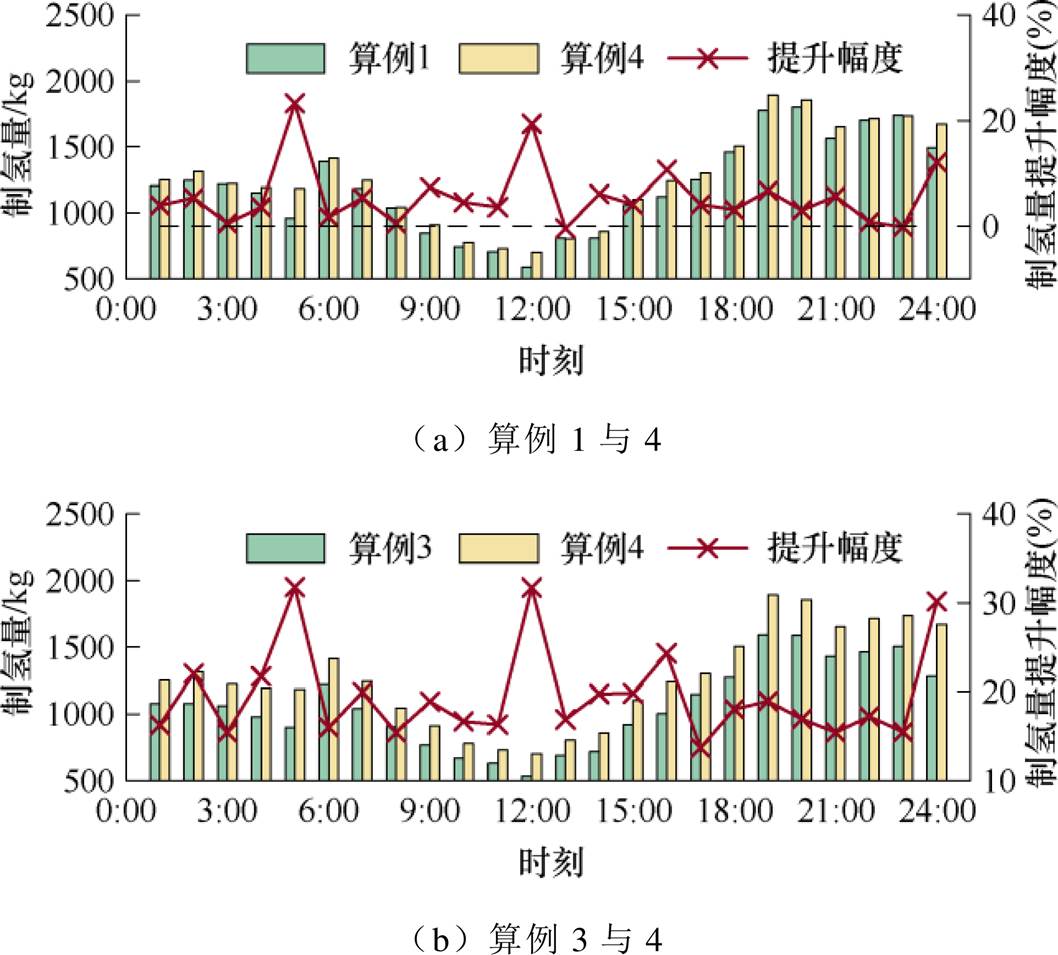
图4 算例1与4、算例3与4各小时制氢量对比
Fig.4 Comparison of hydrogen production amount within each hour between calculation examples 1 and 4, 3 and 4
据图4a可见,算例4在4 00—5
00—5 00、11
00、11 00—12
00—12 00、23
00、23 00—24
00—24 00时段内制氢量提升幅度较大,以4
00时段内制氢量提升幅度较大,以4 00—5
00—5 00时段内第1个15 min为例作一说明,该时段风速为9.35 m/s、风向为268.14°。在此风况下,得到尾流效应对分布式海上风电制氢的影响如图5所示。可以看到,算例1风机由于采取固定的运行方式,无法根据实际风向做出相应的调整,使得下游风机暴露在上游T1~T5风机的尾流中,风速损失较大,对制氢量产生不利影响。而算例4在优化目标中考虑了尾流效应对制氢量产生的影响,在该时段内通过调整各个风机的轴向诱导因子与偏航角,协调风机出力,使尾流中心产生偏转,较好地缓解了上游风机尾流对下游风机的不利影响,该15 min内海上风电场制氢总量为253.563 kg,较算例1的132.094 kg有显著提升。
00时段内第1个15 min为例作一说明,该时段风速为9.35 m/s、风向为268.14°。在此风况下,得到尾流效应对分布式海上风电制氢的影响如图5所示。可以看到,算例1风机由于采取固定的运行方式,无法根据实际风向做出相应的调整,使得下游风机暴露在上游T1~T5风机的尾流中,风速损失较大,对制氢量产生不利影响。而算例4在优化目标中考虑了尾流效应对制氢量产生的影响,在该时段内通过调整各个风机的轴向诱导因子与偏航角,协调风机出力,使尾流中心产生偏转,较好地缓解了上游风机尾流对下游风机的不利影响,该15 min内海上风电场制氢总量为253.563 kg,较算例1的132.094 kg有显著提升。
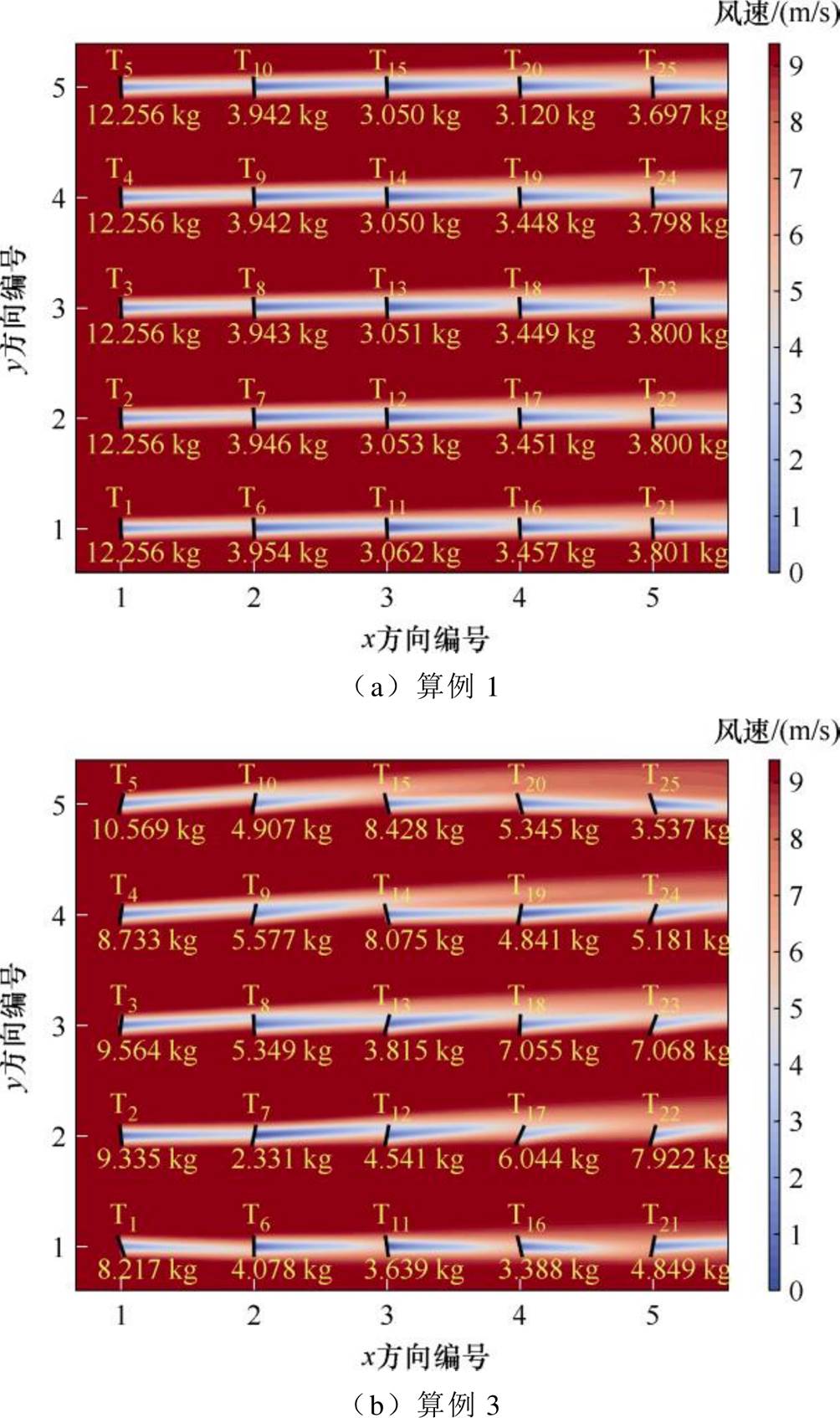
图5 尾流效应对分布式海上风电制氢的影响
Fig.5 Wake effect on distributed hydrogen production by offshore wind power
此外,据图4a可见,在12 00—13
00—13 00、22
00、22 00—23
00—23 00的部分时段内,算例4优化得到的制氢量略低于算例1。以12
00的部分时段内,算例4优化得到的制氢量略低于算例1。以12 00—13
00—13 00时段内第1个15 min为例作说明,该时段内风速为7.70 m/s、风向为169.78°。在此风况下,算例1的尾流分布情况如图6所示。从图6可以看出,即使采用算例1不调整轴向诱导因子与偏航角的运行方式,风电场内上游风机T1/T6/T11/T16/T21的尾流对下游风机的影响亦并不显著。而算例4采取的滚动优化由于兼顾了平衡各风机累积疲劳这一目标,使得该时段的制氢量略有下降。
00时段内第1个15 min为例作说明,该时段内风速为7.70 m/s、风向为169.78°。在此风况下,算例1的尾流分布情况如图6所示。从图6可以看出,即使采用算例1不调整轴向诱导因子与偏航角的运行方式,风电场内上游风机T1/T6/T11/T16/T21的尾流对下游风机的影响亦并不显著。而算例4采取的滚动优化由于兼顾了平衡各风机累积疲劳这一目标,使得该时段的制氢量略有下降。
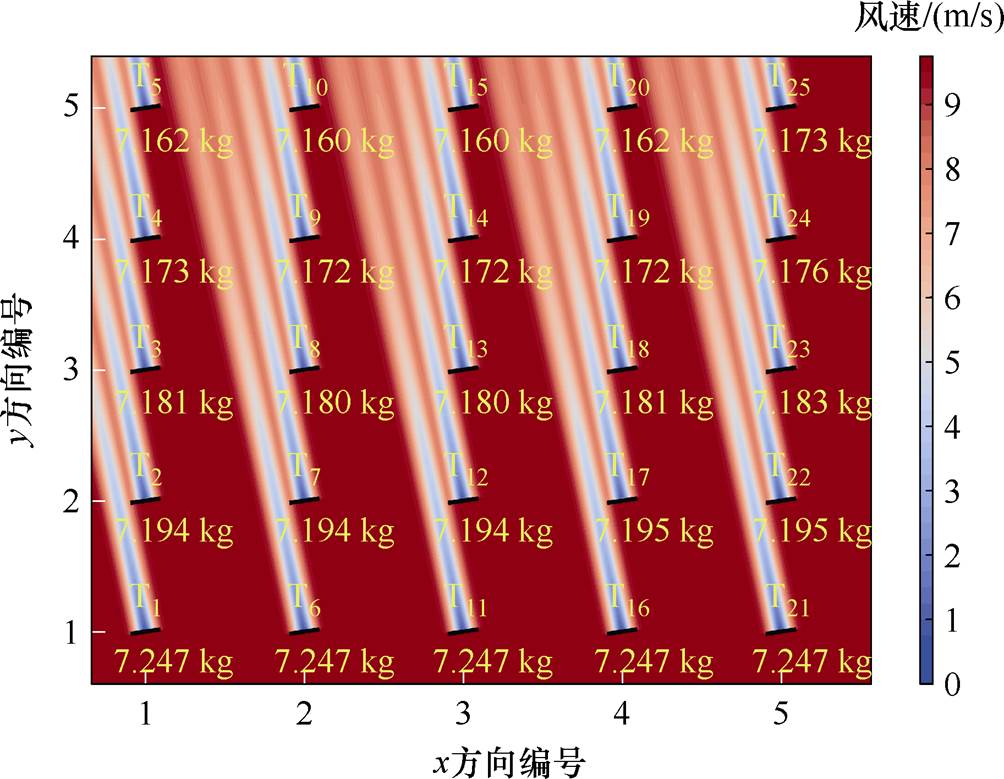
图6 算例1在12 00—12
00—12 15时段的尾流分布情况
15时段的尾流分布情况
Fig.6 Wake distribution of calculation example 1during the time period of 12 00—12
00—12 15
15
如图4b所示,算例4通过不断滚动更新下一时段的风速信息,减少了风速不确定性带来的影响,使得各时刻的制氢量均优于算例3。在4 00—5
00—5 00时段第1个15 min内,日前预测风速偏差为13.69%,而滚动预测偏差为-2.14%,算例3海上风电场的制氢情况如图5b所示。可以看到,在将算例3应用于实际风况时,虽然各个风机的轴向诱导因子与偏航角有所调整,但是上游风机尾流仍会对下游风机产生较大的影响,使得制氢量偏低。
00时段第1个15 min内,日前预测风速偏差为13.69%,而滚动预测偏差为-2.14%,算例3海上风电场的制氢情况如图5b所示。可以看到,在将算例3应用于实际风况时,虽然各个风机的轴向诱导因子与偏航角有所调整,但是上游风机尾流仍会对下游风机产生较大的影响,使得制氢量偏低。
4.2.2 累积疲劳系数标准差优化效果分析
据表2,算例4较算例2的制氢量略有提升,且累积疲劳系数下降了约18.21%,上述两个算例的日内累积疲劳系数分布情况如图7所示。由于算例2采用的逐时段单独优化,仅对该时段各风机的疲劳系数进行优化,无法考虑到下一时段风电场的风况,亦即不具有前瞻性,故算例2针对累积疲劳系数标准差的优化结果劣于算例4。
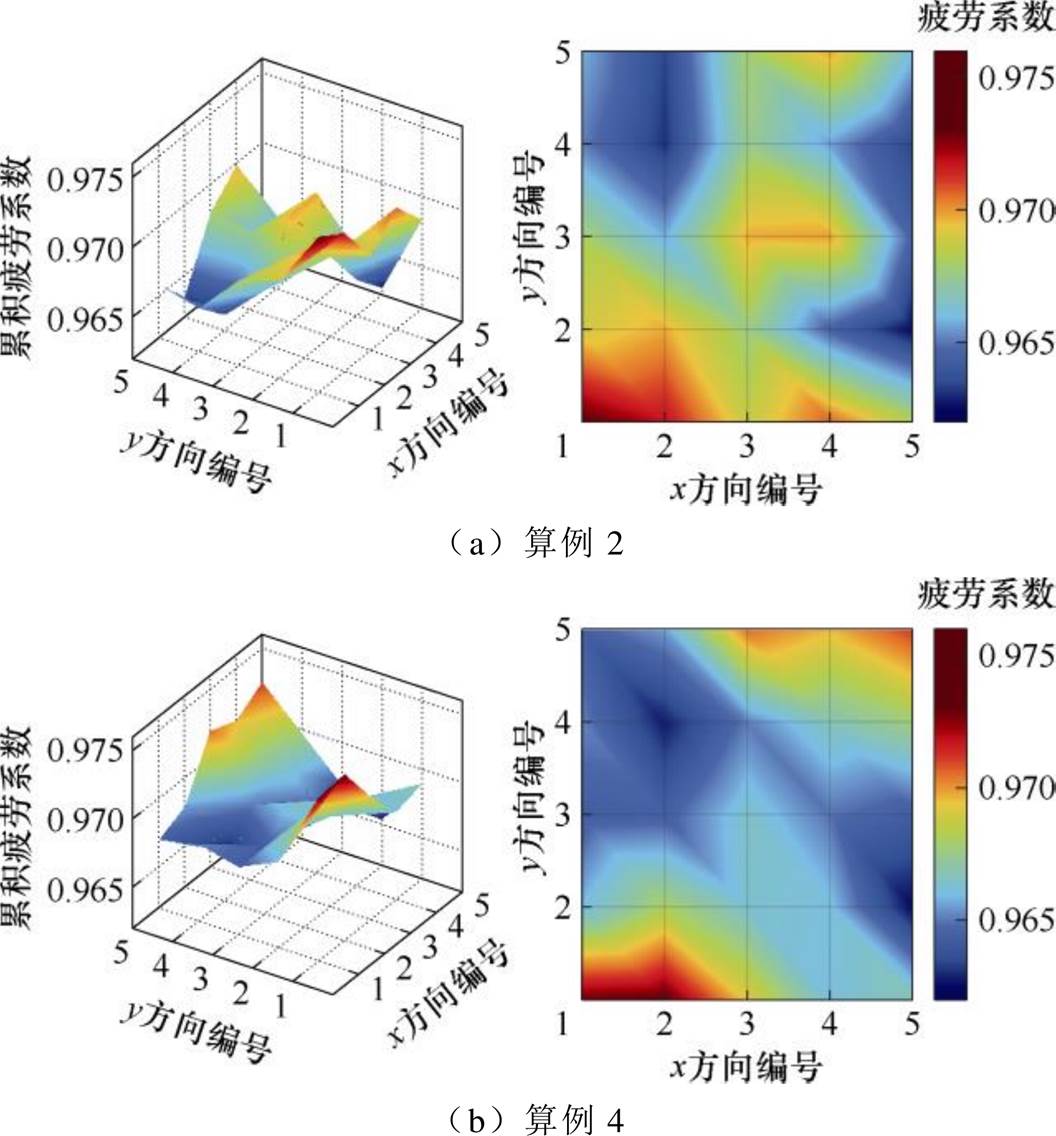
图7 算例2和算例4累积疲劳系数分布情况对比
Fig.7 Comparison of cumulative fatigue coefficient between calculation examples 2 and 4
4.3.1 不同多目标优化算法的优化效果对比
选择00 00—00
00—00 15作为测试时段,图8对比了MO-PSA、MO-PSO、多目标灰狼算法(Multi- objective Grey Wolf Optimization, MO-GWO)、NSGA-Ⅱ算法、多目标樽海鞘算法(Multi-objective Salp Swarm Algorithm, MSSA)、非支配排序的鲸鱼优化算法(Non-dominated Sorting Whale Optimi- zation Algorithm, NSWOA)以及多目标多元宇宙算法(Multi-Objective Multi-Verse Optimization, MO- MVO)求解第3.2节优化问题时得到的Pareto前沿,参数同表1。
15作为测试时段,图8对比了MO-PSA、MO-PSO、多目标灰狼算法(Multi- objective Grey Wolf Optimization, MO-GWO)、NSGA-Ⅱ算法、多目标樽海鞘算法(Multi-objective Salp Swarm Algorithm, MSSA)、非支配排序的鲸鱼优化算法(Non-dominated Sorting Whale Optimi- zation Algorithm, NSWOA)以及多目标多元宇宙算法(Multi-Objective Multi-Verse Optimization, MO- MVO)求解第3.2节优化问题时得到的Pareto前沿,参数同表1。
R1~R7分别是对应算法按照第3.3.2节方法选取得到的OCS。除对目标函数值、计算时长进行比较外,本节还选用附录所示的间距(Spacing, SP)(式(A1))和归一化超体积(Hyper Volume, HV)(式(A3))指标对不同多目标优化算法分布性和延展性进行评价,结果见表3。其中,不同算法各属性的最优值用粗体标出,次优值用下划线标出。
表3 不同优化算法的对比
Tab.3 Comparison of different optimization algorithms
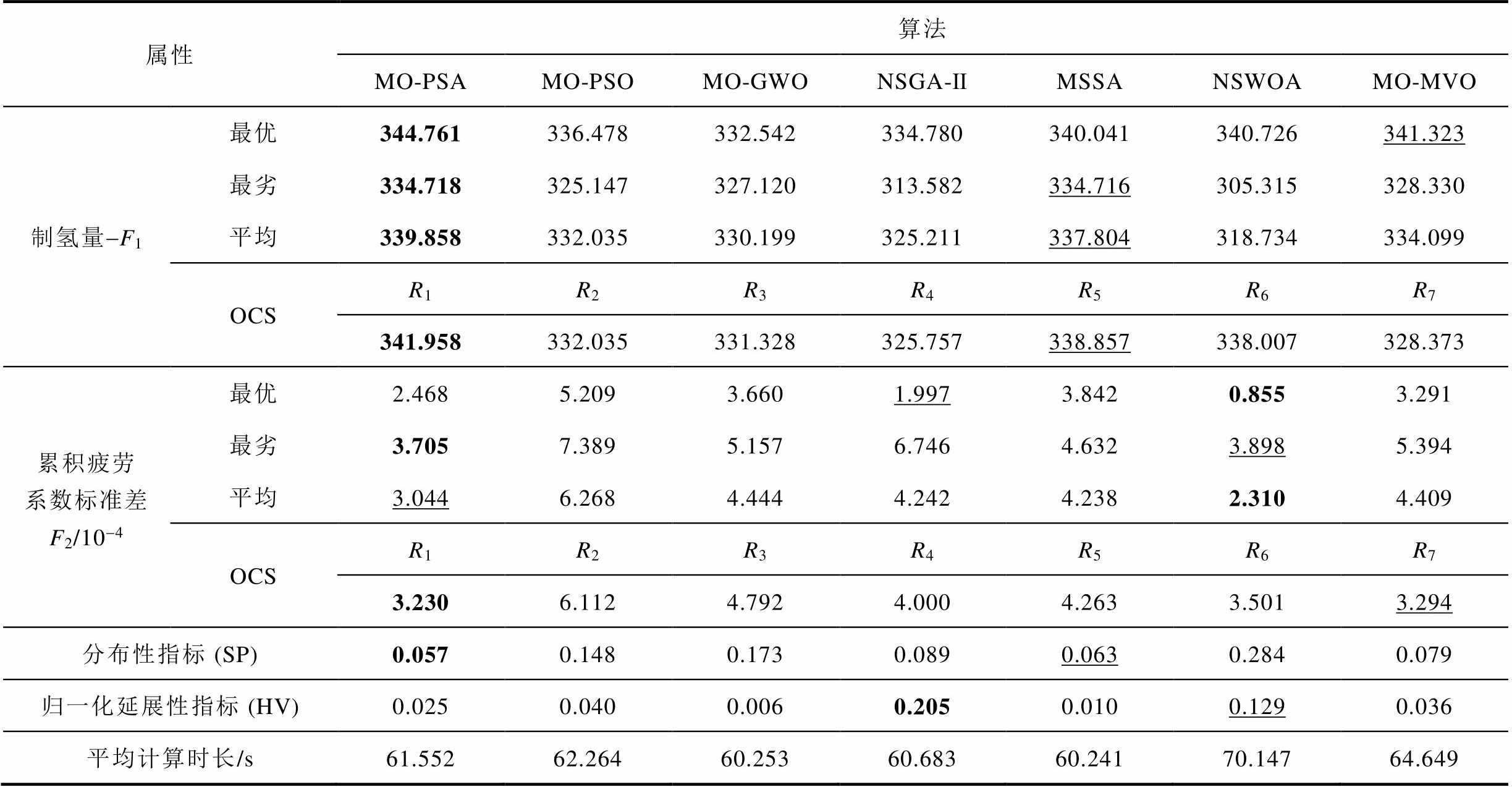
属性算法 MO-PSAMO-PSOMO-GWONSGA-ⅡMSSANSWOAMO-MVO 制氢量-F1最优344.761336.478332.542334.780340.041340.726341.323 最劣334.718325.147327.120313.582334.716305.315328.330 平均339.858332.035330.199325.211337.804318.734334.099 OCSR1R2R3R4R5R6R7 341.958332.035331.328325.757338.857338.007328.373 累积疲劳系数标准差F2/10-4最优2.4685.2093.6601.9973.8420.8553.291 最劣3.7057.3895.1576.7464.6323.8985.394 平均3.0446.2684.4444.2424.2382.3104.409 OCSR1R2R3R4R5R6R7 3.2306.1124.7924.0004.2633.5013.294 分布性指标 (SP)0.0570.1480.1730.0890.0630.2840.079 归一化延展性指标 (HV)0.0250.0400.0060.2050.0100.1290.036 平均计算时长/s61.55262.26460.25360.68360.24170.14764.649
不同算法的Pareto前沿比较如图8所示。由图8可知,相较于其他算法,MO-PSA获得的Pareto前沿更优。据表3,在平均计算时长相近的情况下,MO-PSA多数属性占优。对于优化所得OCS,MO- PSA较NSGA-Ⅱ算法制氢量提升最大,为4.973%,较MSSA制氢量提升最小,为0.915%;MO-PSA较MO-PSO算法风机累计疲劳系数标准差降低最大,为47.153%,较MO-MVO算法风机累计疲劳系数标准差降低最小,为1.943%。MO-PSA的SP值与MSSA接近,说明这两种算法得到的Pareto前沿分布性相似。MO-PSA的归一化HV值偏低,其延展性与MO-MVO、MO-PSO算法接近,劣于NSGA-Ⅱ、NSWOA,优于MO-GWO、MSSA。由于分布式海上风电制氢实际运行中只能选取一组最优解,该值即本文第3.3.2节选取得到的OCS,从表3可知,MO-PSA得到的OCS在制氢量、累积疲劳系数标准差上均优于其他算法得到的OCS,因而延展性对本文所求解的滚动优化问题并无较大影响。综上所述,可以说明本文建立的MO-PSA具有更好的寻优 效果。
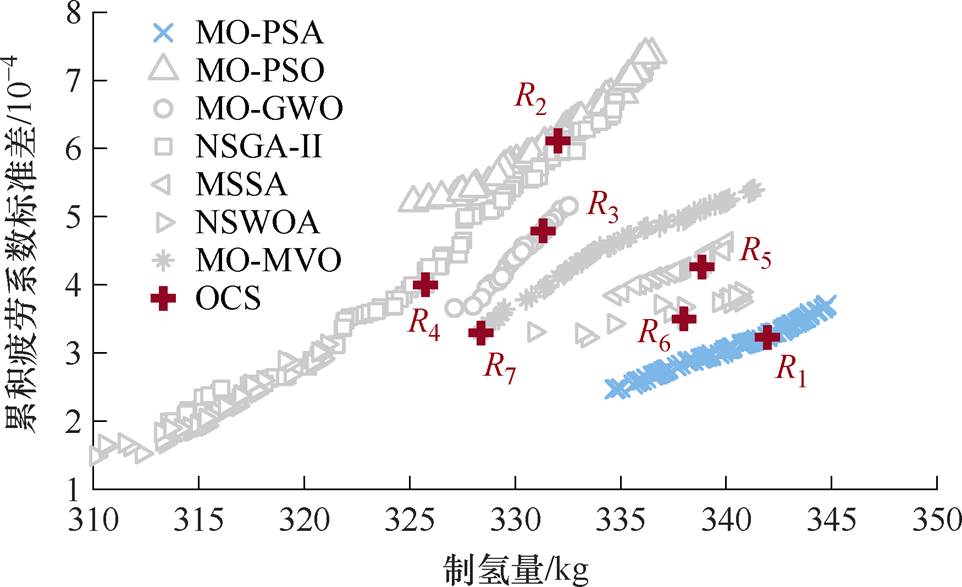
图8 不同算法的Pareto前沿比较
Fig.8 Pareto front comparison of different algorithms
4.3.2 迭代次数对优化结果的影响
选择0 00—0
00—0 15作为测试时段验证迭代次数对MO-PSA算法优化结果的影响。设置种群数为100,最大迭代次数700,重复计算300次,图9展示了MO-PSA求解第3.2节优化问题时OCS所对应两个目标函数值的变化情况,其中实线为平均值,阴影部分为波动域。据图9可知,当迭代次数较少时,优化所得OCS的两个目标函数值平均值随迭代次数增加收敛较快,当迭代次数增加至400次及以上时,平均值虽略有降低但趋于稳定。因而使用MO-PSA求解第3.2节多目标优化问题时,迭代次数在400次及以上时可以得到较为稳定的优化结果。为保证优化结果的准确性,同时兼顾计算成本,本文第4.1节将最大迭代次数设置为400。
15作为测试时段验证迭代次数对MO-PSA算法优化结果的影响。设置种群数为100,最大迭代次数700,重复计算300次,图9展示了MO-PSA求解第3.2节优化问题时OCS所对应两个目标函数值的变化情况,其中实线为平均值,阴影部分为波动域。据图9可知,当迭代次数较少时,优化所得OCS的两个目标函数值平均值随迭代次数增加收敛较快,当迭代次数增加至400次及以上时,平均值虽略有降低但趋于稳定。因而使用MO-PSA求解第3.2节多目标优化问题时,迭代次数在400次及以上时可以得到较为稳定的优化结果。为保证优化结果的准确性,同时兼顾计算成本,本文第4.1节将最大迭代次数设置为400。
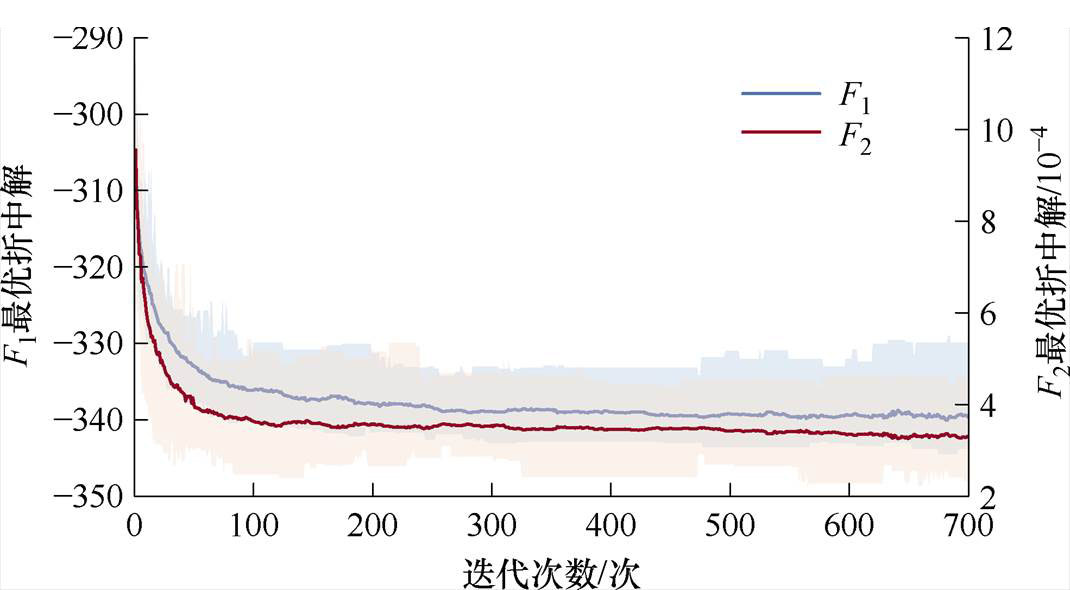
图9 不同迭代次数对优化结果的影响
Fig.9 Impact on optimal results under different iterations
为了分析预测域长度对本文所提滚动优化方法的影响,选择尾流效应影响较大的4 00—5
00—5 00作为测试时段,图10给出了不同预测域长度下制氢量与累积疲劳系数标准差的变化情况。
00作为测试时段,图10给出了不同预测域长度下制氢量与累积疲劳系数标准差的变化情况。
据图10可见,在预测域较短,即预测域长度为2~4个15 min时,由于风速预测误差较小且各时段制氢量相互独立,分布式海上风电制氢量相差不大。此外,风机疲劳为累积量,适当长度的预测域可以前瞻未来一段时间内的风况,即能够在优化中考虑后续时段风况对风机疲劳分布的影响,使得累积疲劳系数标准差降低。但是随着预测域长度继续增加,预测时间范围变长,风速预测精度变低,风速预测误差随之增大,优化所得运行策略在实际风况下难以较好地缓解上游风机尾流对下游风机的影响,导致分布式海上风电制氢量下降较大。同样地,虽然预测域长度的增加可以在优化中考虑到未来更长时间内的风况,但风速预测误差带来的不利影响凸显,未来风况难以为当前优化时段提供有效参考,风机累积疲劳系数标准差也呈增加趋势,优化效果变差。因此,为了兼顾制氢量与风机疲劳的优化结果并考虑到计算时间成本,本文将预测域长度选为4个15 min。
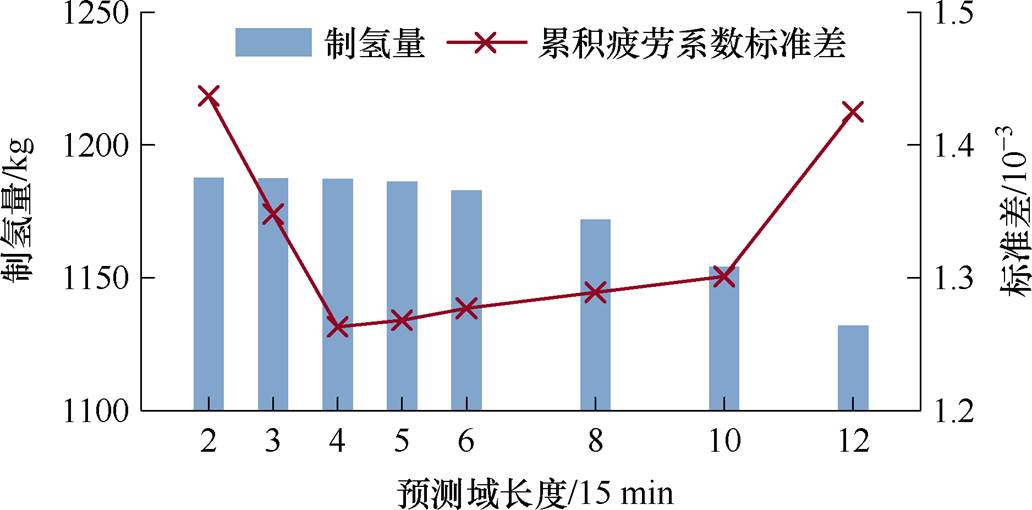
图10 预测域长度对优化结果的影响
Fig.10 Impact of the length of prediction domain on optimized results
为了在应对风速不确定性的同时实现海上风电场制氢量提升与疲劳均匀分布,本文提出一种同时考虑尾流效应与疲劳分布的分布式海上风电制氢滚动优化运行方法,可以为海上风电场内风机运行提供参考,针对该方法提出的MO-PSA多目标优化算法具有较好的寻优效果。基于包含25台风机的5×5海上风电场仿真结果,结论如下:
1)部分风况下,尾流效应会导致下游风机处风速亏损较大,降低风电场的制氢量。与贪婪策略相比,本文考虑尾流效应与疲劳分布后能够在提升5.12%的分布式海上风电制氢量的同时平衡风机疲劳,降低风机累积疲劳系数标准差。
2)风机疲劳为累积量,本文所提滚动优化运行方法具有一定的前瞻性,能够保证未来一段时间内风电场内风机疲劳的均匀分布,累积疲劳系数标准差较每时段单独优化下降了18.21%。
3)为应对风速不确定性,本文所提滚动优化运行方法可以使用精度更高的日内风速预测值,在制氢量与累积疲劳系数标准差的优化上均优于使用日前预测风速的全时段统一优化方法。
4)相比于MO-PSO、MO-GWO、NSGA-Ⅱ等多种多目标优化算法,在相同的种群数与迭代次数下,所提MO-PSA在本文多目标优化问题上可提升0.915%~4.973%的制氢量,降低1.943%~47.153%风机累积疲劳系数标准差,具有更好的寻优效果。
在后续工作中,针对规模更大的分布式海上风电制氢优化问题需要研究更加高效的优化求解算法,例如,将人工智能模型与群体智能算法结合应用,提高求解效率。此外,还可将浮式风电场纳入,进一步探索浮式风机可移动性对制氢优化的影响。
致谢:感谢徐衍会对文章内容给予的建议。
附 录
1. 模型参数
附表1 PEM电解槽参数
App.Tab.1 Parameters of PEM electrolyzer

参 数数 值 串联电解槽数量NEL1 500 理想气体常数R/(J/mol·K)8.31 氧气压力1 阴极电荷转移系数ac/(A/cm2)0.25 交换膜厚度tm/cm0.05 氢气摩尔质量2 c2-0.001 711 c41 变流器损耗占比kloss(%)3 电解槽运行温度TEL/K323 极限电流密度Jlim/(A/cm2)2 氢气高热值HHV/(MJ/kg)141.9 Gibbs自由能变化DG/J2.33×105 氢气压力20 水压力0.2 阳极电荷转移系数aa/(A/cm2)0.8 交换膜电导率sm/(S/cm)0.35 c1-0.0 034 c3-1 反渗透海水淡化电量占比kdes(%)0.07 交换膜面积S/(cm2)500 阴极转移电流密度J0,c/(A/cm2)0.1 阳极转移电流密度J0,a/(A/cm2)1×10-7
附表2 NREL 5 MW风机参数
App.Tab.2 Parameters of NREL 5 MW wind turbine

参 数数 值 转子直径D/m126 额定功率PN/MW5 切入风速vcut-in/(m/s)3 切出风速vcut-out/(m/s)25
附表3 Gauss尾流模型参数
App.Tab.3 Parameters of Gauss wake model
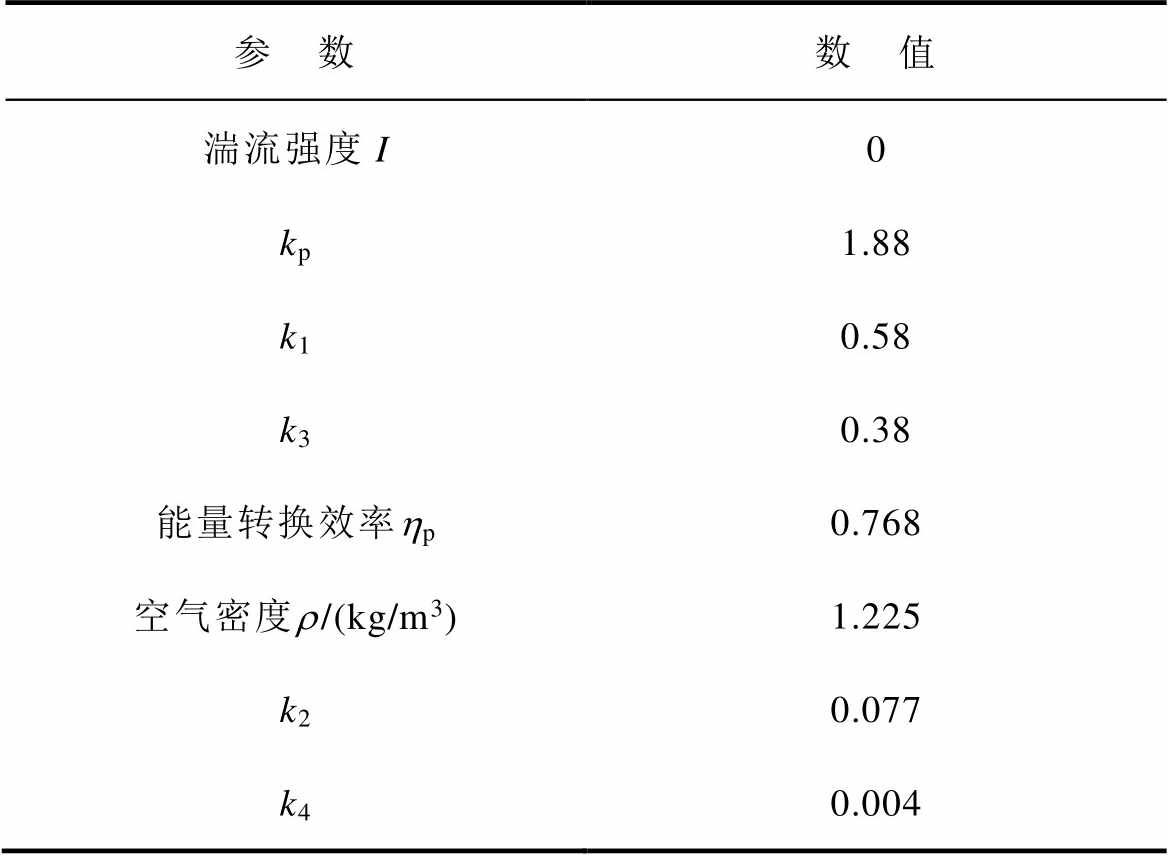
参 数数 值 湍流强度I0 kp1.88 k10.58 k30.38 能量转换效率hp0.768 空气密度r/(kg/m3)1.225 k20.077 k40.004
附表4 风机疲劳系数计算参数
App.Tab.4 Parameters of wind turbine fatigue coefficients calculation
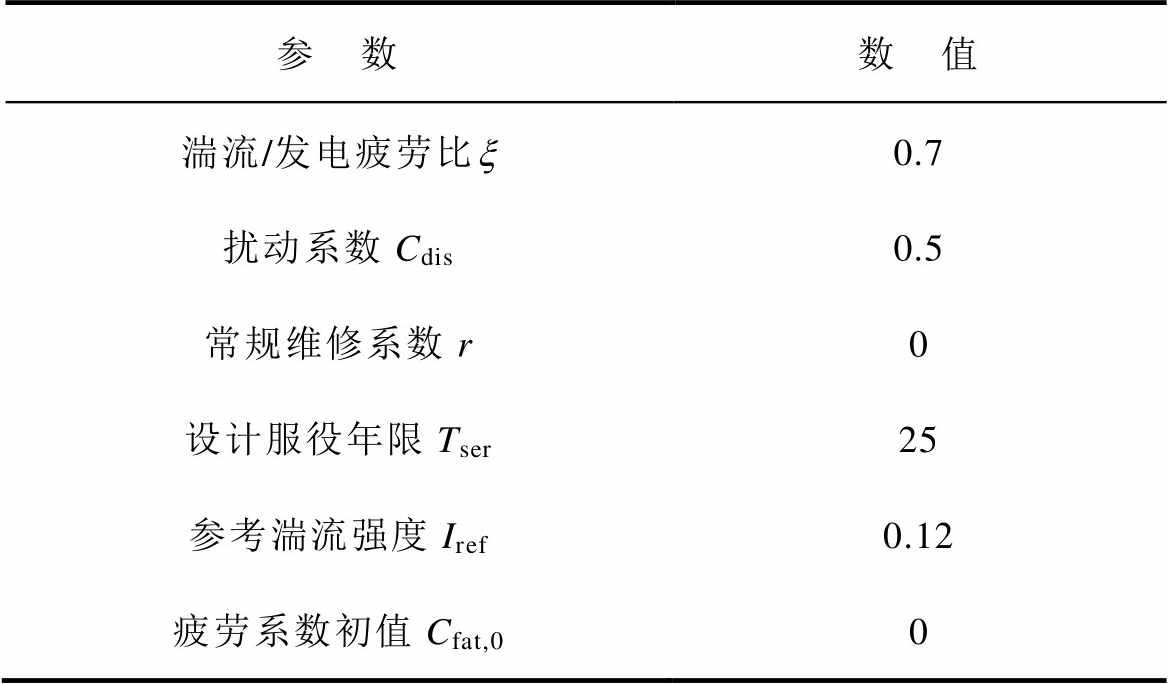
参 数数 值 湍流/发电疲劳比x0.7 扰动系数Cdis0.5 常规维修系数r0 设计服役年限Tser25 参考湍流强度Iref0.12 疲劳系数初值Cfat,00
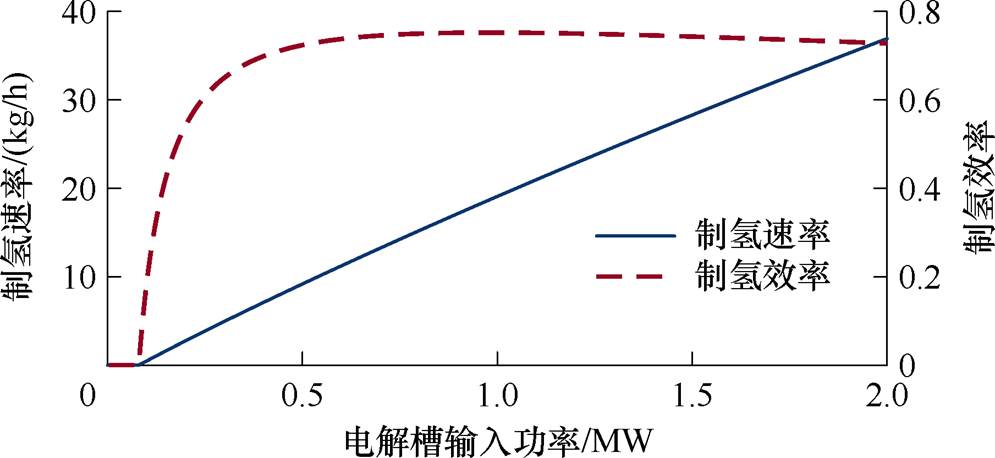
附图1 PEM电解槽输入功率与制氢速率和效率的关系
App.Fig.1 Relationship between PEM electrolyzer input power and hydrogen production rate and efficiency
2. MO-PSA流程及评价指标
附图2 MO-PSA流程
App.Fig.2 Flow chart of MO-PSA
以下提供部分用于评价多目标优化算法的指标。
1)分布性指标(SP)
SP衡量Pareto前沿中每个解到其他解最小距离的标准差,SP值越小说明解在Pareto前沿中分布越均匀,算法的分布性越好,其计算方式为
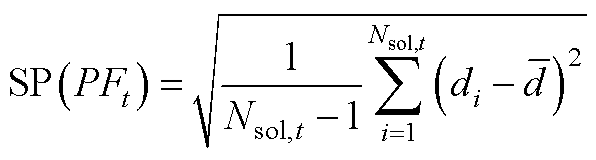 (A1)
(A1)
式中,PFt为第t次迭代计算得到的Pareto前沿;Nsol,t为PFt中解的数量;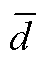 为di的均值,di的计算方式为
为di的均值,di的计算方式为
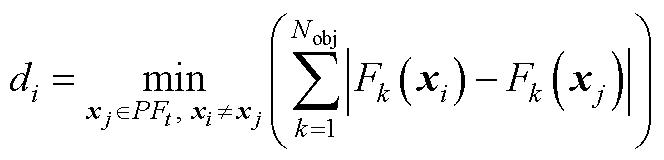 (A2)
(A2)
式中,Nobj为目标函数的数量。
2)延展性指标(HV)
HV衡量算法计算得到的Pareto前沿与所选参照点在目标空间围成的超立方体的体积,HV值越大说明算法的延展性越好。本文对HV值进行了归一化处理,即
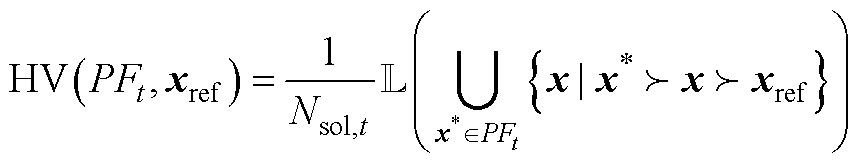 (A3)
(A3)
式中,xref为参照点;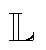 表示Lebesgue测度。
表示Lebesgue测度。
3. 海上风电场参数
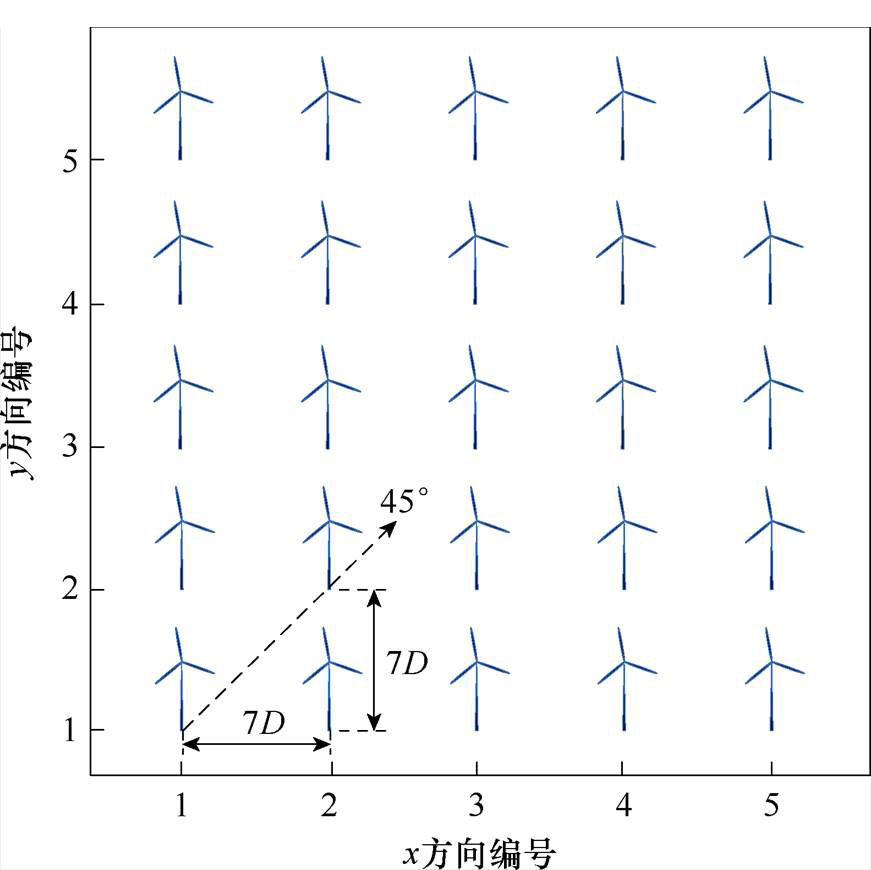
附图3 海上风电场布局
App.Fig.3 Layout of offshore wind farm
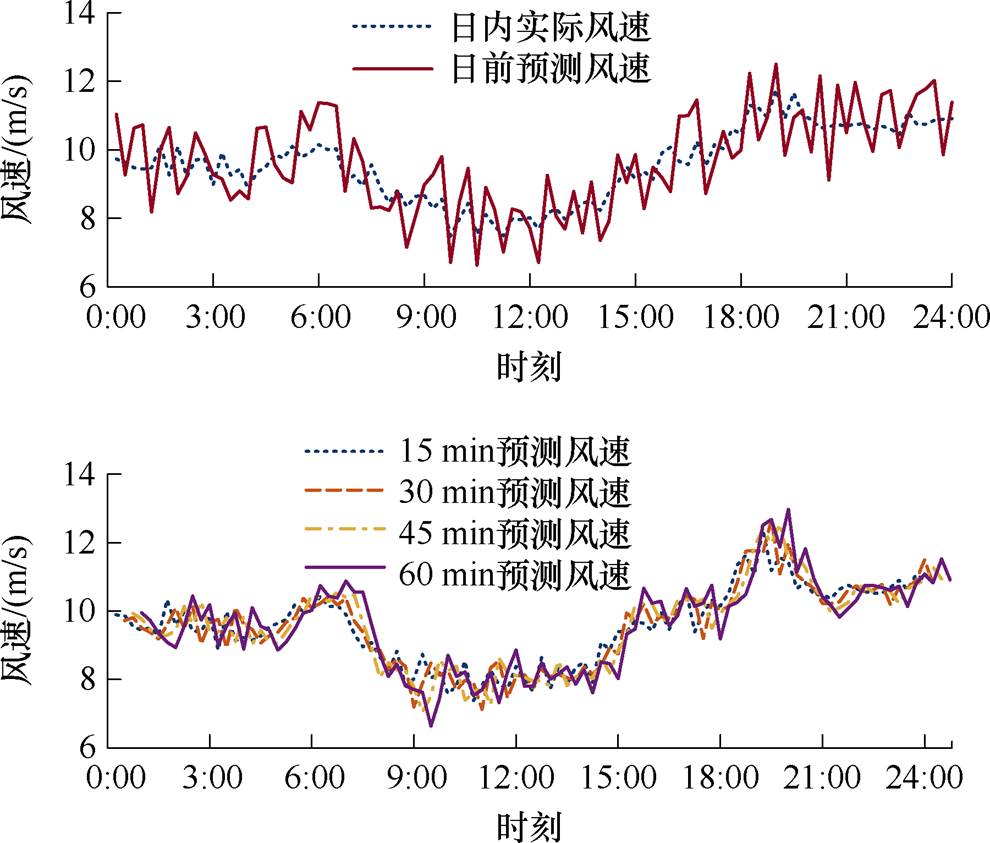
附图4 风速数据
App.Fig.4 Wind speed data
附图5 风速风向概率分布玫瑰图
App.Fig.5 Rose figure of probability distribution of wind direction and windspeed
参考文献
[1] 何俊佳, 宋丽, 周本正, 等. ZnO压敏电阻微观结构调控与性能提升研究综述[J]. 电工技术学报, 2023, 38(20): 5605-5619.
He Junjia, Song Li, Zhou Benzheng, et al. Review on microstructure control and performance improvement of ZnO varistors[J]. Transactions of China Electro- technical Society, 2023, 38(20): 5605-5619.
[2] 刘逸凡, 邹明, 王焱, 等. 面向海上风电仿真的永磁同步发电机电磁暂态等效建模方法[J]. 电工技术学报, 2024, 39(8): 2400-2411.
Liu Yifan, Zou Ming, Wang Yan, et al. Equivalent modeling method for electromagnetic transient of permanent magnet synchronous generator for offshore wind power simulation[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2400-2411.
[3] 严新荣, 张宁宁, 马奎超, 等. 我国海上风电发展现状与趋势综述[J]. 发电技术, 2024, 45(1): 1-12.
Yan Xinrong, Zhang Ningning, Ma Kuichao, et al. Overview of current situation and trend of offshore wind power development in China[J]. Power Generation Technology, 2024, 45(1): 1-12.
[4] d’Amore-Domenech R, Leo T J, Pollet B G. Bulk power transmission at sea: life cycle cost comparison of electricity and hydrogen as energy vectors[J]. Applied Energy, 2021, 288: 116625.
[5] 孔令国, 史立昊, 石振宇, 等. 基于交替方向乘子法的园区电-氢-热系统低碳优化调度[J]. 电工技术学报, 2023, 38(11): 2932-2944.
Kong Lingguo, Shi Lihao, Shi Zhenyu, et al. Low- carbon optimal dispatch of electric-hydrogen-heat system in park based on alternating direction method of multipliers[J]. Transactions of China Electro- technical Society, 2023, 38(11): 2932-2944.
[6] 谭洪, 王宇炜, 王秋杰, 等. 基于氢能固态运输的电-氢综合能源系统双层调度模型[J]. 电工技术学报, 2025, 40(3): 744-758.
Tan Hong, Wang Yuwei, Wang Qiujie, et al. A bi-level dispatching model for electricity-hydrogen integrated energy system based on hydrogen solidity transport[J]. Transactions of China Electrotechnical Society, 2025, 40(3): 744-758.
[7] 郜捷, 宋洁, 王剑晓, 等. 支撑中国能源安全的电氢耦合系统形态与关键技术[J]. 电力系统自动化, 2023, 47(19): 1-15.
Gao Jie, Song Jie, Wang Jianxiao, et al. Form and key technologies of integrated electricity-hydrogen system supporting energy security in China[J]. Automation of Electric Power Systems, 2023, 47(19): 1-15.
[8] Kakoulaki G, Kougias I, Taylor N, et al. Green hydrogen in Europe-a regional assessment: sub- stituting existing production with electrolysis powered by renewables[J]. Energy Conversion and Management, 2021, 228: 113649.
[9] Franco B A, Baptista P, Neto R C, et al. Assessment of offloading pathways for wind-powered offshore hydrogen production: Energy and economic analysis[J]. Applied Energy, 2021, 286: 116553.
[10] Luo Zhibin, Wang Xiaobo, Wen Heng, et al. Hydrogen production from offshore wind power in South China[J]. International Journal of Hydrogen Energy, 2022, 47(58): 24558-24568.
[11] 罗魁, 郭剑波, 马士聪, 等. 海上风电并网可靠性分析及提升关键技术综述[J]. 电网技术, 2022, 46(10): 3691-3702.
Luo Kui, Guo Jianbo, Ma Shicong, et al. Review of key technologies of reliability analysis and improve- ment for offshore wind power grid integration[J]. Power System Technology, 2022, 46(10): 3691- 3702.
[12] 刘一格, 赵振宙, 马远卓, 等. 基于鲸鱼优化算法的串列风力机主动尾流控制策略[J]. 中国电机工程学报, 2024, 44(9): 3702-3709.
Liu Yige, Zhao Zhenzhou, Ma Yuanzhuo, et al. Active wake control strategy of tandem wind turbines based on whale optimization algorithm[J]. Pro- ceedings of the CSEE, 2024, 44(9): 3702-3709.
[13] 宋冬然, 沈旭涛, 黄朝能, 等. 基于代理模型辅助改进标准粒子群算法的浮式风电场功率优化[J]. 中国电机工程学报, 2023, 43(S1): 217-228.
Song Dongran, Shen Xutao, Huang Zhaoneng, et al. Power optimization of floating offshore wind farm based on surrogate-assisted standard particle swarm algorithm[J]. Proceedings of the CSEE, 2023, 43(S1): 217-228.
[14] Shu Tong, Song Dongran, Joo Y H. Non-centralised coordinated optimisation for maximising offshore wind farm power via a sparse communication architecture[J]. Applied Energy, 2022, 324: 119705.
[15] Li Baoliang, He Jia, Ge Mingwei, et al. Study of three wake control strategies for power maximization of offshore wind farms with different layouts[J]. Energy Conversion and Management, 2022, 268: 116059.
[16] 房方, 梁栋炀, 刘亚娟, 等. 海上风电智能控制与运维关键技术[J]. 发电技术, 2022, 43(2): 175-185.
Fang Fang, Liang Dongyang, Liu Yajuan, et al. Key technologies for intelligent control and operation and maintenance of offshore wind power[J]. Power Generation Technology, 2022, 43(2): 175-185
[17] Liao Hao, Hu Weihao, Wu Xiawei, et al. Active power dispatch optimization for offshore wind farms considering fatigue distribution[J]. Renewable Energy, 2020, 151: 1173-1185.
[18] Cai Wei, Hu Yang, Fang Fang, et al. Wind farm power production and fatigue load optimization based on dynamic partitioning and wake redirection of wind turbines[J]. Applied Energy, 2023, 339: 121000.
[19] Xu Jian, Yi Xiankun, Sun Yuanzhang, et al. Stochastic optimal scheduling based on scenario analysis for wind farms[J]. IEEE Transactions on Sustainable Energy, 2017, 8(4): 1548-1559.
[20] 李长霖, 贾燕冰, 石俊逸, 等. 考虑风电集群效应的风储系统一次调频容量配置策略[J]. 中国电机工程学报, 2025, 45(8): 2969-2981.
Li Changlin, Jia Yanbing, Shi Junyi, et al. Capacity optimization of wind farms-energy storage parti- cipation in primary frequency regulation considering wind power cluster effect[J]. Proceedings of the CSEE, 2025, 45(8): 2969-2981.
[21] 张智, 周明, 朱凌志, 等. 风电场协同参与的电力系统发电-备用鲁棒优化运行方法[J]. 电网技术, 2022, 46(4): 1316-1325.
Zhang Zhi, Zhou Ming, Zhu Lingzhi, et al. Robust optimal operation method of wind farms synergetic participation in generation-reserve in power systems[J]. Power System Technology, 2022, 46(4): 1316-1325.
[22] Zhang Jingrui, Li Zhuoyun, Wang Beibei. Within-day rolling optimal scheduling problem for active distribution networks by multi-objective evolutionary algorithm based on decomposition integrating with thought of simulated annealing[J]. Energy, 2021, 223: 120027.
[23] 梁睿, 袁乐童, 黄宏旭, 等. 变温影响下乡村生物质能发电系统跨周期滚动优化运行方法[J]. 中国电机工程学报, 2025, 45(8): 3067-3079.
Liang Rui, Yuan Letong, Huang Hongxu, et al. Multi- hydraulic retention time rolling optimal operation method for rural biomass power generation system under uncertain temperature[J]. Proceedings of the CSEE, 2025, 45(8): 3067-3079.
[24] Gao Yuansheng. PID-based search algorithm: a novel metaheuristic algorithm based on PID algorithm[J]. Expert Systems with Applications, 2023, 232: 120886.
[25] Bastankhah M, Porté-Agel F. Experimental and theoretical study of windturbine wakes in yawed conditions[J]. Journal of Fluid Mechanics, 2016, 806: 506-541.
[26] Zhao Rongyong, Shen Wenzhong, Knudsen T, et al. Fatigue distribution optimization for offshore wind farms using intelligent agent control[J]. Wind Energy, 2012, 15(7): 927-944.
[27] Rogeau A, Vieubled J, de Coatpont M, et al. Techno- economic evaluation and resource assessment of hydrogen production through offshore wind farms: a European perspective[J]. Renewable and Sustainable Energy Reviews, 2023, 187: 113699.
[28] Jang D, Kim K, Kim K H, et al. Techno-economic analysis and Monte Carlo simulation for green hydrogen production using offshore wind power plant[J]. Energy Conversion and Management, 2022, 263: 115695.
[29] 郭志远, 朱玉婷, 叶青, 等. 离子污染对质子交换膜电解制氢的影响研究进展[J]. 全球能源互联网, 2023, 6(3): 325-330.
Guo Zhiyuan, Zhu Yuting, Ye Qing, et al. Research progress on the effect of ion pollution on proton exchange membrane electrolysis for hydrogen pro- duction[J]. Journal of Global Energy Interconnection, 2023, 6(3): 325-330.
[30] 韩鹏飞, 徐潇源, 王晗, 等. 基于功率-温度自适应控制的多堆质子交换膜电解制氢系统效率优化[J]. 电工技术学报, 2024, 39(7): 2236-2248.
Han Pengfei, Xu Xiaoyuan, Wang Han, et al. Operational efficiency enhancement of multi-stack proton exchange membrane electrolyzer systems with power-temperature adaptive control[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2236- 2248.
[31] 李佳蓉, 林今, 陈凯旋, 等. 考虑尾流效应的分布式海上风电制氢集群容量优化配置[J]. 电力系统自动化, 2023, 47(11): 9-17.
Li Jiarong, Lin Jin, Chen Kaixuan, et al. Optimal capacity configuration of distributed offshore wind power-to-hydrogen cluster considering wake effect[J]. Automation of Electric Power Systems, 2023, 47(11): 9-17.
[32] Abomazid A M, El-Taweel N A, Farag H E Z. Optimal energy management of hydrogen energy facility using integrated battery energy storage and solar photovoltaic systems[J]. IEEE Transactions on Sustainable Energy, 2022, 13(3): 1457-1468.
Firstly, to better characterize the wake effect caused by wind turbines, the Gauss wake model is established for wind speed deficit and wake deflection calculation. Then, the sum of square free stream superposition (SOSFS) method is applied to superpose the wake effect caused by multiple upstream wind turbines. Therefore, the output power of each wind turbine can be obtained. The fatigue coefficient is introduced to measure the fatigue due to the power generation of each wind turbine.
Secondly, the hydrogen production power relationship of a single wind turbine unitis analyzed. The distributed hydrogen production by the offshore wind power model, including proton exchange membrane (PEM) electrolyzer modeling, is established to calculate the amount of hydrogen production with a given wind turbine output power.
Based on the Gauss wake model, wind turbine fatigue coefficient, and distributed hydrogen production model, a multi-objective rolling optimal operation method that considers the wake effect and fatigue distribution is put forward. The hydrogen production during each time period is independent of the optimization of distributed hydrogen production by offshore wind power, and the fatigue of wind turbines is a cumulative quantity. Therefore, to balance the cumulative fatigue of each wind turbine while increasing the intra-day hydrogen production amount, the two objectives are set to maximize the total amount of hydrogen production and minimize the standard deviation of each wind turbine’s fatigue coefficient. With the purpose of solving multi-objective optimization problem as well as promoting optimization effectiveness, a Multi-objective PID-based search algorithm (MO-PSA) is consequently proposed.
Finally, four case studies involving (1) greedy operation, (2) optimizing each time period in turn,
(3) optimizing all time periods globally, and (4) rolling optimization are proposed. Simulation and verification are conducted in the 5×5 square layout offshore wind farm with25 wind turbines. The results show that the proposed rolling optimization method can improve hydrogen production amount by 5.12% and 19.16% compared to greedy operation and global optimization, respectively. Moreover, the rolling optimization method lowers the standard deviation of the cumulative fatigue coefficient of each wind turbine by 18.21% compared with case (2). As for the proposed multi-objective optimization algorithm, under a similar calculation time, MO-PSA improves the amount of hydrogen production by 0.915%~4.973% and decreases the standard deviation of wind turbine fatigue coefficients by 1.943%~47.153% compared to several existing optimization algorithms in solving the multi-objective optimization problem in this paper.
Abstract Distributed hydrogen production by offshore wind power and centralized delivery mode is an important route for efficiently utilizing offshore wind resources and achieving low-carbon and clean hydrogen production. The wake effect will cause a loss in hydrogen production by offshore wind power. Nevertheless, only taking the wake effect as the optimization objective to increase hydrogen production can lead to wind turbines’ unevenly distributed fatigues, adding maintenance costs to wind farms. Meanwhile, the accuracy of wind speed prediction is closely related to the offshore wind power’s hydrogen production optimization problem. Insufficient prediction accuracy increases wind speed uncertainty and further affects optimization.
keywords:Hydrogen production by offshore wind power, wake effect, wind turbine fatigue balancing, multi-objective optimization, rolling optimization
DOI: 10.19595/j.cnki.1000-6753.tces.240959
中图分类号:TM614
国家重点研发计划资助项目(2021YFB4000104)。
收稿日期 2024-06-03
改稿日期 2024-08-21
周 帅 男,2000年生,博士研究生,研究方向为新能源电力系统优化运行。E-mail: 15600463955@163.com
艾 欣 男,1964年生,教授,博士生导师,研究方向为新能源电力系统及微网。E-mail: aixin@ncepu.edu.cn(通信作者)
(编辑 郭丽军)