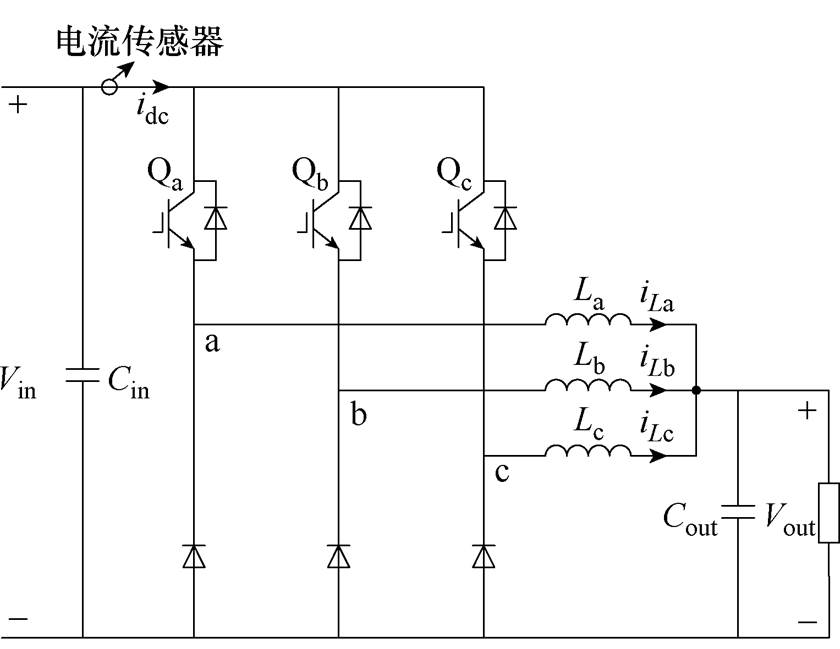
图1 三相交错并联DC-DC降压变换器拓扑
Fig.1 Three phase interleaved DC-DC buck converter
摘要 针对交错并联DC-DC变换器相电感值偏差导致现有电流重构方法精度下降的问题,该文提出一种新型单电流传感器重构策略,实现在全占空比范围内交错电感偏差时各相电流的准确重构。首先,该文量化分析了相电感偏差对现有电流重构方法的影响,分析结果表明,20%的电感偏差将导致重构电流产生高达18%的偏差。因此,该文进一步提出一种电感在线估算方法,通过在一个开关周期内对直流母线电流多次采样,实时计算各相交错电感值。在此基础上,基于直流母线电流的采样值和估算电感值,构建在电流连续导通模式(CCM)和断续导通模式(DCM)下相电流重构的数学模型,实现相电流的准确重构。最后,搭建一套三相交错并联变换器样机,实验对比分析了在相电感偏差时所提出的电流重构策略和已有的电流重构方法的重构效果,通过实验验证了该文所提出的重构策略的准确性和有效性。
关键词:交错并联变换器 电流重构 电感偏差 单电流传感器
当前,世界能源危机加剧以及国家提出“双碳”目标,新能源行业受到高度关注[1-3]。其中多相交错并联DC-DC变换器因其高功率密度、低电流纹波等优势在储能、新能源汽车等领域应用广泛[4-9]。然而,由于设计和制造工艺误差以及器件老化等因素,导致各相电流存在不均衡问题,进而引发相电感饱和、功率管热应力不均等问题,这不仅降低了变换器的可靠性和输出功率,甚至可能损坏变换器[10]。因此如何实现多相交错并联DC-DC变换器各相电流的均衡成为保障其安全可靠运行的关键[11-12]。
目前,均流控制方法主要分为下垂均流控制和有源均流控制两大类[13-14]。下垂均流控制通过调节输出阻抗来实现多个电源的并联均流,但无法解决线路阻抗差异导致的电流不平衡问题[15];有源均流控制通过对每相电流设置独立的PI控制器实现每相电流的均衡控制[16]。然而,以上方法均需要多个电流传感器来获取每相电流值,增加了系统的成本和体积[17]。因此,无电流传感器的均流方案受到了国内外学者的广泛关注。文献[18]引入等效串联电阻表征各相电流不均衡度,通过改变各相占空比调节各交错支路的等效串联电阻实现电流均衡。但等效串联电阻的测量较为复杂,且该电阻对温度变化较为敏感。文献[19]以相邻输入电容电压纹波的峰值之差表征各相电流不均衡度,通过调节各相占空比使电容电压纹波峰值之差为零,实现电流均衡。但该策略对直流电容的等效串联电阻参数较为敏感,且忽略了各相交错电感的感值差异[20]。
因此,相关学者进一步提出了单电流传感器均流方案,其基本思想是根据单电流传感器的采样数据重构各相电流,然后针对每相电流设置独立的控制器实现相电流均衡,有效地克服了无电流传感器对参数敏感的缺点。文献[21]针对交错并联DC-DC变换器,提出了一种电流连续导通模式(Continuous Conduction Mode, CCM)下基于单电流传感器的电流重构策略。通过对每相载波谷值时刻的直流母线电流进行采样重构相电流。但该方法成立的前提是必须确保在采样时刻,只能有一相开关管导通,其他相的开关管必须关断。否则采样值将包含其他相电流的瞬时值,导致该重构方法失效。比如,在三相交错并联Buck变换器中,当占空比D<2/3时,存在直流母线电流等于相电流的时刻,通过采样该时刻的直流母线电流可重构得到相电流;但当D≥2/3时,直流母线电流在任意时刻均不止包含一相电流,因此该重构方法失效。文献[22]利用单个电流传感器对直流母线进行多次采样,构建不同采样点直流母线电流与相电流的数学模型,实现了在CCM下的准确重构,但在电流断续导通模式(Dis- continuous Conduction Mode, DCM)下无法重构相电流。此外,该重构方法未考虑实际应用中金属粉芯电感的偏差问题,导致在电感偏差时该重构方法的精度降低。
因此,针对多相交错并联DC-DC变换器,本文提出了一种考虑电感偏差的单电流传感器重构策略,实现了在CCM和DCM下全占空比范围内的各相电流的准确重构,解决了传统重构方法未考虑电感偏差,且不能在全占空比范围内实现重构的问题,同时,弥补了DCM下电流重构算法的缺失。首先,本文详细分析了在不同占空比下直流母线电流与相电流的关系,建立了不同采样点直流母线电流与相电流的数学模型,讨论了电感值的影响因素,量化分析了相电感偏差对传统电流重构策略重构电流精度的影响。其次,基于电感电流的变化特性,建立了电感在线估算模型。以此为基础,分别构建了在CCM和DCM下相电感偏差时的电流重构策略。最后,搭建了一台三相交错并联DC-DC变换器实验平台,通过实验验证了本文所重构方法的准确性和有效性。
考虑到一般性原则,本文以三相交错并联DC- DC降压变换器为例,其拓扑结构如图1所示。
图1中,Vin、Vout分别为输入电压和输出电压。Cin、Cout分别为输入滤波电容和输出滤波电容。Qn(n=a, b, c,下同)为功率开关管,a、b、c为三相支路,Ln为滤波电感,iLn为输出相电流,idc为直流母线电流。该变换器的工作原理是通过高频开关管Qn将输入电压Vin斩波为PWM电压,该PWM电压与输出电压Vout之差作用在滤波电感上产生期望的输出相电流。设流过开关管Qn的电流为iQn,当开关管Qn开通时,iQn等于对应的输出相电流iLn;当Qn关断时,iQn=0。若定义开关管Qn的开关函数为Sn(当Qn开通,Sn=1;当Qn关断,Sn=0),根据基尔霍夫电流定律可得直流母线电流为

图1 三相交错并联DC-DC降压变换器拓扑
Fig.1 Three phase interleaved DC-DC buck converter
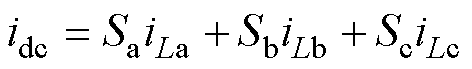 (1)
(1)
由式(1)可知,直流母线电流由高频开关管对输出相电流进行斩波得到,为一系列PWM脉冲。因此,通过在一个开关周期内对直流母线电流进行多次采样,可以得到各相输出电流,即为电流重构。
根据占空比D的大小将变换器分为三个工作区域:①D<1/3;②1/3≤D<2/3;③D≥2/3。不同工作区域下开关管的开关状态与载波对应关系如图2所示。
由图2可知,在D<1/3内,同一时刻最多只有一个开关管导通,此刻直流母线电流只由导通相的电感电流组成;在1/3≤D<2/3内,同一时刻最多有两个开关管导通,当只有一个开关管导通时,直流母线电流只由导通相的电感电流组成;在D≥2/3工作区域下,同一时刻至少有两个开关管导通,此时直流母线电流至少由两相的导通电流组成。综上所述,在不同工作区域,变换器的直流母线电流可以反映相电流变化情况。因此,通过分析在不同工作区域下直流母线电流与输出相电流的关系,可以建立输出相电流的重构模型。
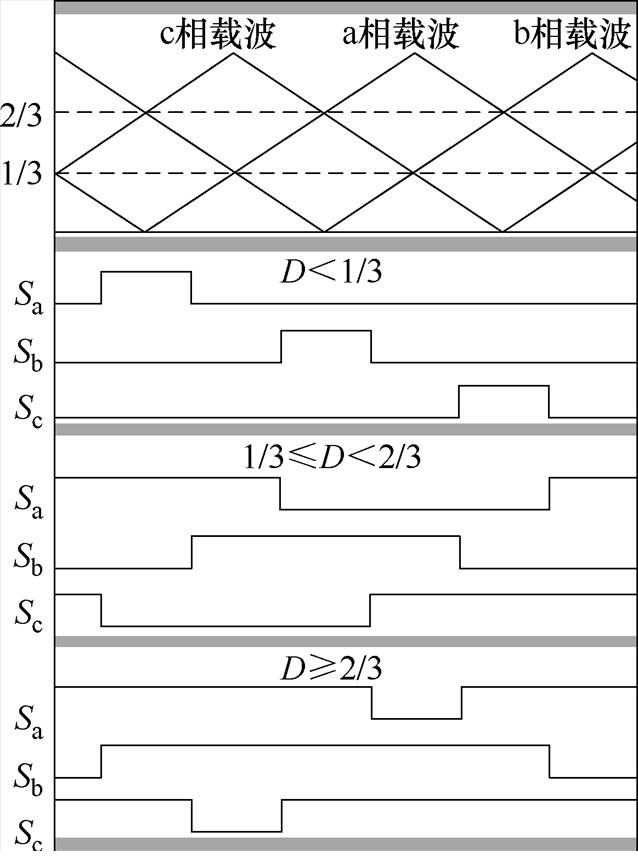
图2 不同工作区域下开关信号与载波对应关系
Fig.2 Correspondence between switch signals and carrier waves in different working areas
基于1.1节所述的电流重构原理,文献[22]提出一种针对三相交错并联DC-DC变换器在CCM下的电流重构方法。当占空比在0<D<2/3时,存在直流母线电流等于相电流平均值的采样点,此时得到的直流母线电流就是对应相的相电流平均值。当 D≥2/3时,三相电流与直流母线电流关系如图3所示(黑色圆点表示该时刻与直流母线电流相关的相电流)。
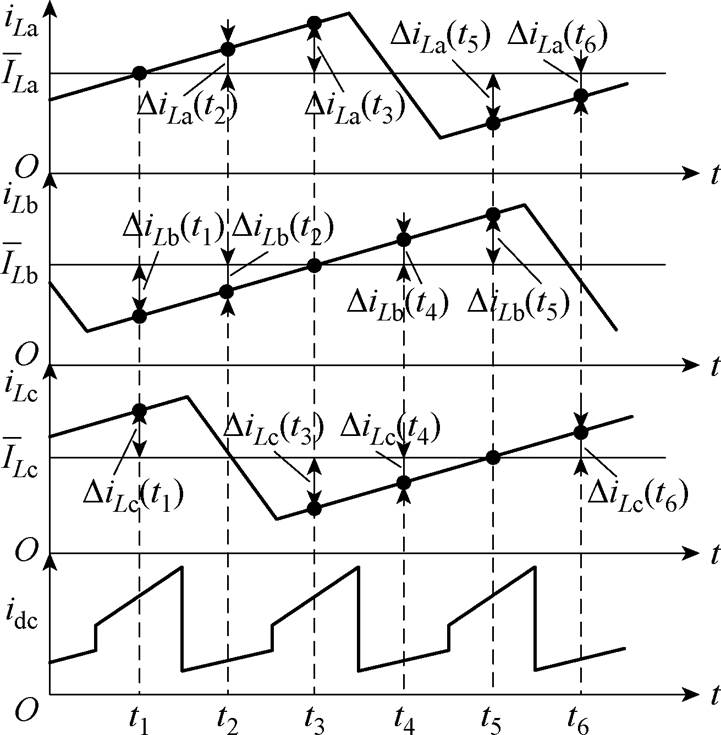
图3 D≥2/3时三相电流与直流母线电流对应关系
Fig.3 Corresponding relationship between phase current and DC bus current when D≥2/3
该传统重构方法最终重构得到每相电流平均值表达式如式(2)所示,用相邻两采样点的直流母线电流之差便能直接得到对应相电流平均值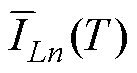 。
。
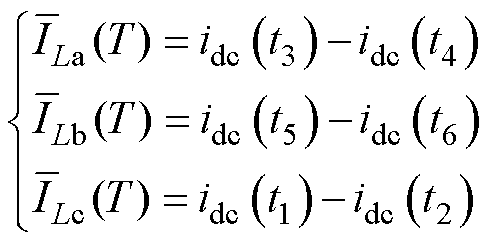 (2)
(2)
式中,idc(tm)(m=1, 2, 3, 4, 5, 6)为不同采样点时刻对应的直流母线电流。式(2)所示的电流重构模型成立的前提是各相交错电感值相等。然而在实际生产应用中,电感值受多方面因素的影响,难以保证其感值相同。当各相交错电感值不等时,该模型将无法对电流进行准确重构。
电感主要由磁心和绕组两部分构成,电感L的参数公式为
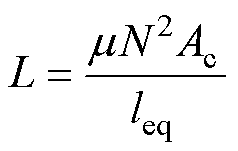 (3)
(3)
式中,Ac为磁心材料的横截面积;m 为磁心材料的磁导率;leq为磁路长度;N为绕组匝数[23]。因此理论上电感值受多个方面因素的影响。在实际生产中,对于同一型号的电感(即采用相同的磁心和绕组匝数制造的电感),尽管其几何参数如Ac、leq以及N均相同,但受限于生产工艺以及制造误差,国内外主要电感磁心厂商(如美磁、东睦科达、天通等)生产的铁硅、铁硅铝磁心的电感系数AL(nH/T2)偏差为±8%。电感系数与电感值的关系式为
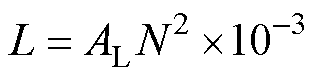 (4)
(4)
考虑到电感生产过程中的非理想因素,结合式(4)可知,同样型号的电感值偏差可能会达到20%。
另一方面,磁导率m(m=B/H)并不是一个固定值。由磁性材料的磁滞回线(即B-H曲线)可知,磁通密度B与磁场强度H的关系是非线性的[24],而磁场强度H与其直流偏置电流成正比,因此磁导率m 会随着直流偏置电流的变化而变化。所以,在多相交错并联变换器中,若重构电流不准确导致各相电感的直流电流不均衡,其不均衡的直流电流会反过来增大各相交错电感值的差异。所以,在多相交错并联变换器中即使采用同一个公司生产的相同型号的电感,其各相交错电感值仍然会存在较大的偏差。
图4给出了在总电流纹波为0.4时,已有电流重构方法在各相电感值不同时的重构电流偏差。由图4可知,重构电流偏差与电感偏差基本呈线性关系。当电感偏差为20%时,传统重构策略无法得到准确的重构电流,其重构偏差高达18%。
为了消除电感偏差对重构电流的影响,需要对各相电感值进行准确计算。然而,受工艺、直流偏置电流等因素的影响,电感值很难直接根据磁心材料参数进行准确计算,尤其是在大规模批量生产时,不可能对每个电感的磁心材料进行测试以获得准确的电感值。因此,本文提出一种新的电感在线计算方法,其基本原理如下:电感两端的电压vL以及流过电感的电流iL的伏安特性始终满足式(5)。因此,在一个开关周期内,式(5)可进一步线性化为式(6)。由式(6)可知,若在某个时间段Dt内,已知电感电流的上升量或下降量DI以及电感两端的电压V,即可准确计算出电感值,从而解决电感值无法准确计算的问题。
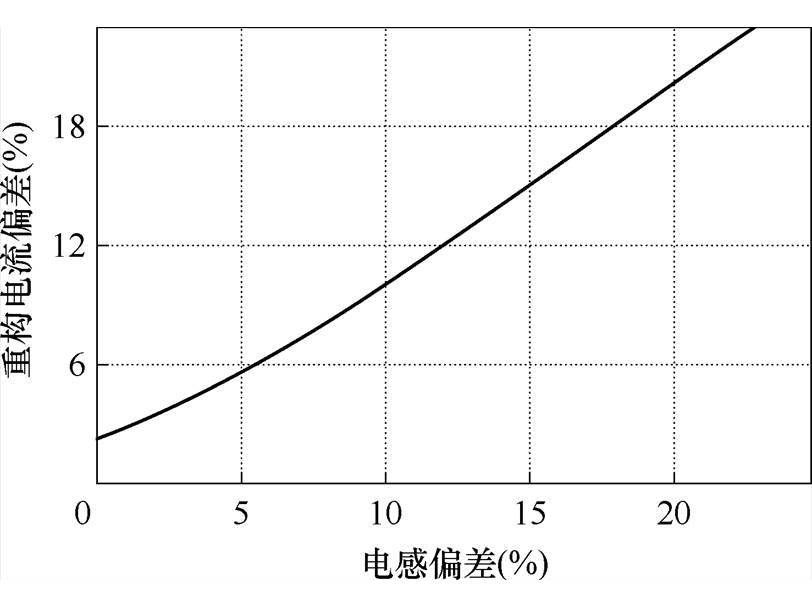
图4 电感偏差对重构电流偏差的影响
Fig.4 The influence of inductance deviation on the reconstruction current deviation
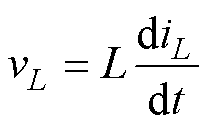 (5)
(5)
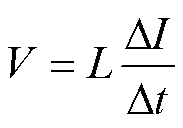 (6)
(6)
综上所述,在各相电感值不一致时传统重构方法已无法对相电流进行准确重构。因此,本文通过实时计算电感值,实现电感值的准确估算,从而消除电感偏差对重构电流的影响,实现电流的准确 重构。
根据不同负载条件,多相交错并联DC-DC变换器可分别工作在CCM和DCM。下面分别详细分析考虑电感偏差时CCM和DCM下的电流重构策略。
针对CCM下不同的工作区域,需对直流母线电流进行多次采样,采样点的设置均满足以下对应规则:采样点t1、t4均对应a相载波的波谷与波峰,采样点t3、t6均对应b相载波的波谷与波峰,采样点t5、t2均对应c相载波的波谷与波峰,如图5所示,在得到不同采样点处的直流母线电流后,通过直流母线电流与相电流的数学模型重构得到相电流平均值。
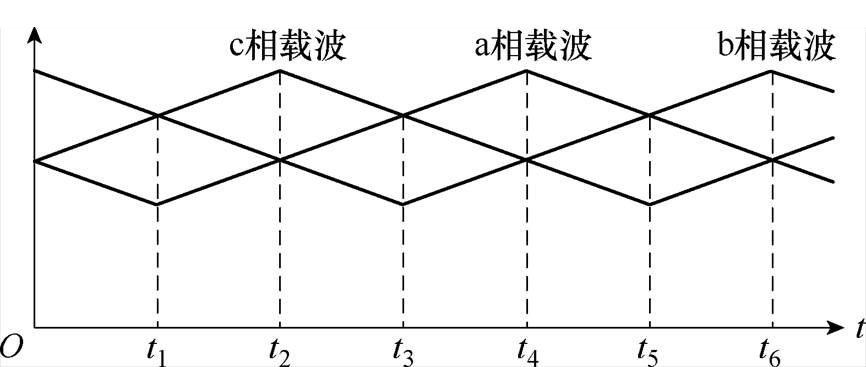
图5 采样点对应规则(CCM)
Fig.5 Sampling point correspondence rules (CCM)
引入相电流重构偏差DiLn(tm),表示某相电流的均值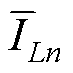 和采样瞬时值之间iLn(tm)的绝对差,即
和采样瞬时值之间iLn(tm)的绝对差,即
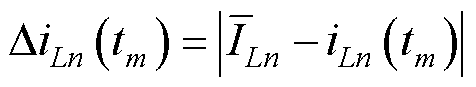 (7)
(7)
由图5可知,采样点t1、t3、t5时刻分别是开关管Qa、Qb、Qc导通时间的中点,所以在t1、t3、t5时刻,对应a相、b相、c相的瞬时电流就是相电流的平均值,三个采样点处对应相的电流重构偏差为零,即
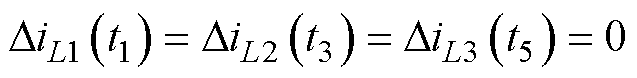 (8)
(8)
2.1.1 D<1/3时的电流重构方法(CCM)
在D<1/3时,直流母线电流等于此刻导通相的相电流,三相电流与直流母线电流对应关系如图6所示。
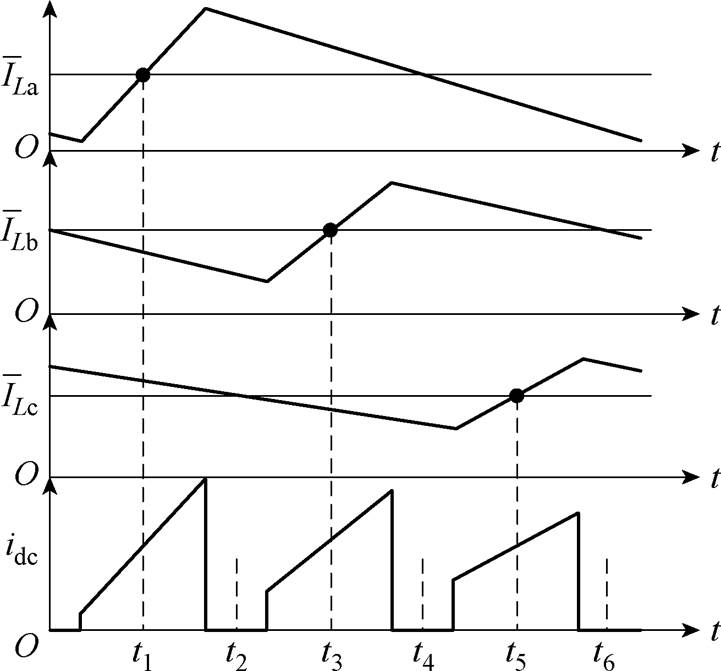
图6 D<1/3时三相电流与直流母线电流对应关系(CCM)
Fig.6 Corresponding relationship between phase current and DC bus current when D<1/3 (CCM)
由式(1)、式(7)可知,不同采样点的直流母线电流可由相电流平均值和相电流重构偏差表示,结合图6,不同采样点处直流母线电流见表1。
所以此工作区域下,结合式(8),相电流平均值可被重构表示为
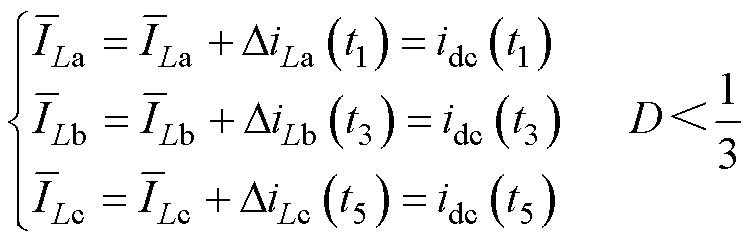 (9)
(9)
表1 不同采样点处的直流母线电流(D<1/3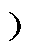
Tab.1 DC bus current at different sampling points (D<1/3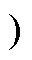

采样点 t1 t20 t3 t40 t5 t60
由式(9)可知,由采样点处直流母线电流便能直接得到每相电流平均值。
2.1.2 1/3≤D<2/3时的电流重构方法(CCM)
当1/3≤D<2/3,有两个开关管导通时,直流母线电流等于导通相电流之和;当只有一个开关管导通时,直流母线电流等于该导通相的电流,三相电流与直流母线电流关系如图7所示。
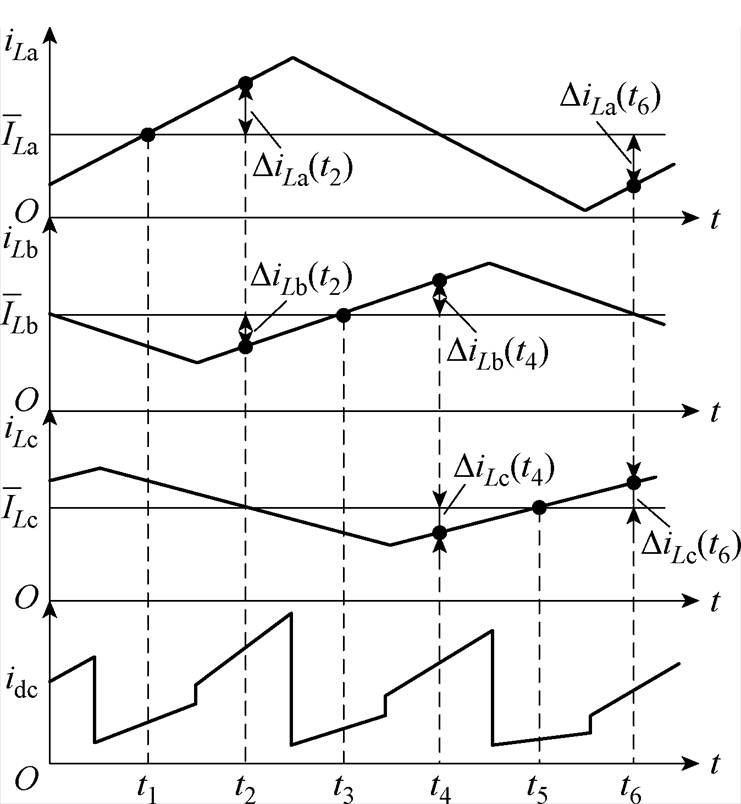
图7 1/3≤D<2/3时三相电流与直流母线电流对应关系(CCM)
Fig.7 Corresponding relationship between phase current and DC bus current when 1/3≤D<2/3 (CCM)
不同采样点处直流母线采样电流用相电流平均值与相电流重构偏差表示,结果见表2。
结合式(8),将相电流平均值重构表示为
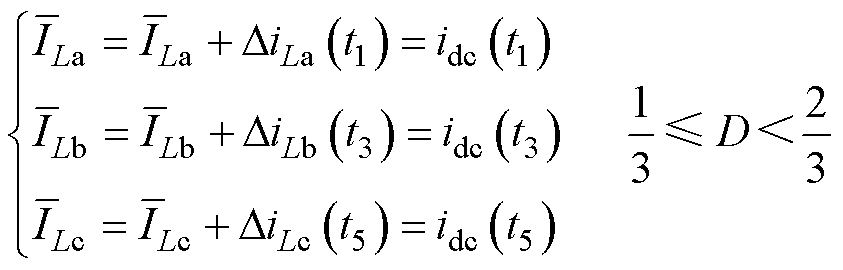 (10)
(10)
表2 不同采样点处的直流母线电流(1/3≤D<2/3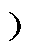
Tab.2 DC bus current at different sampling points (1/3≤D<2/3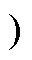

采样点 t1 t2 t3 t4 t5 t6
由式(10)可知,由采样点处直流母线电流便能直接得到每相电流平均值。
2.1.3 D≥2/3时的电流重构方法(CCM)
在D≥2/3时,同一时刻只有两个或三个开关管导通。三相电流与直流母线电流关系如图8所示。
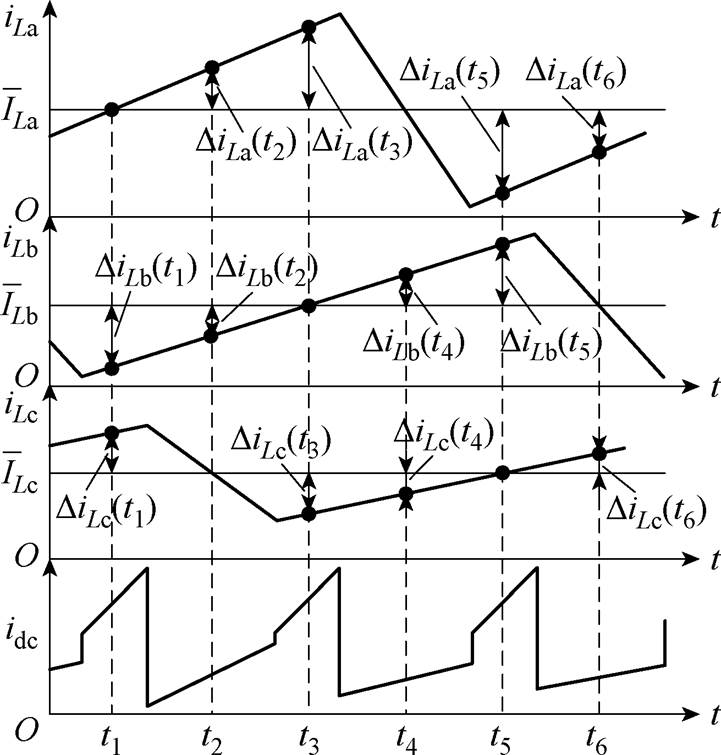
图8 D≥2/3时三相电流与直流母线电流对应关系(CCM)
Fig.8 Corresponding relationship between phase current and DC bus current when D≥2/3 (CCM)
在此工作区域下不存在某个采样点的直流母线电流等于导通相的电流,因此在该工作区域下,无法根据单个采样点的直流母线电流重构得到相电流平均值。
直流母线采样电流用相电流平均值和相电流重构偏差表示,结果见表3。
在采样点t1处,直流母线电流由a、b、c三相导通电流构成,在采样点t2处,直流母线电流由a、b两相导通电流构成。将两采样点处直流母线电流作差,便可得到c相电流平均值的近似值,同理得到其余相电流平均值的近似值,表达式为
表3 不同采样点处的直流母线电流(D≥2/3)
Tab.3 DC bus current at different sampling points (D≥2/3)
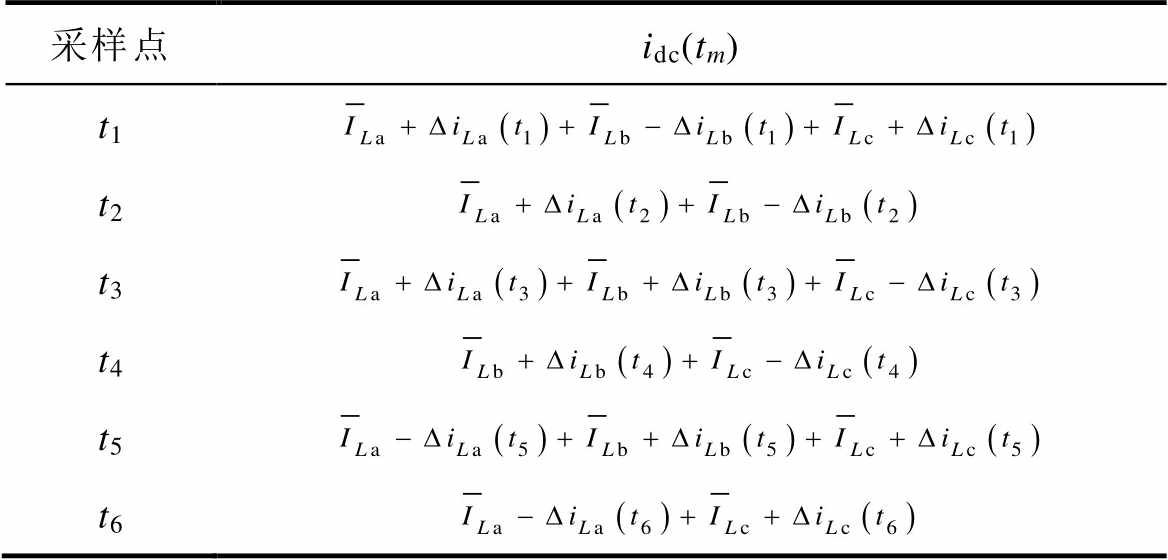
采样点idc(tm) t1 t2 t3 t4 t5 t6
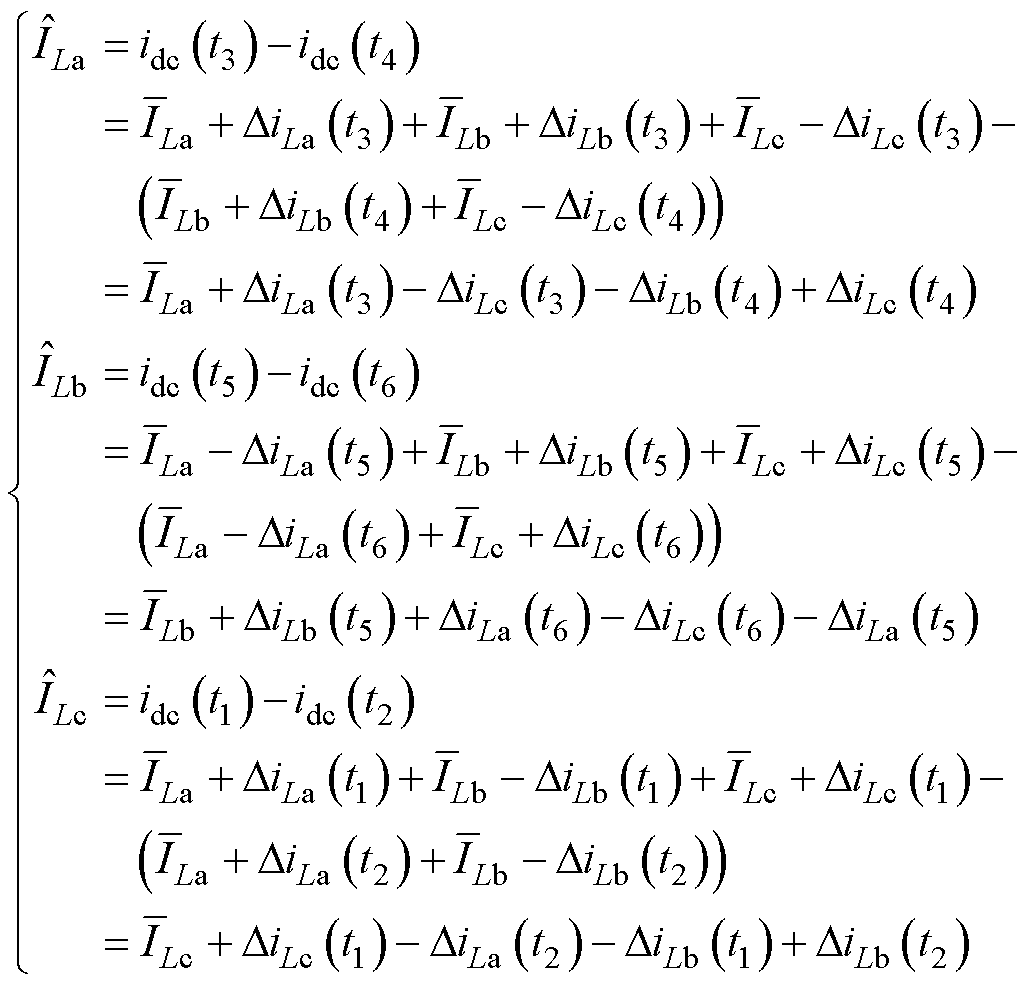 (11)
(11)
式中,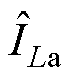 、
、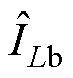 、
、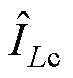 分别为三相电流平均值的近似值,将由相电流重构偏差组成的重构差异值用
分别为三相电流平均值的近似值,将由相电流重构偏差组成的重构差异值用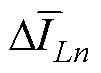
表示,式(11)可归纳为
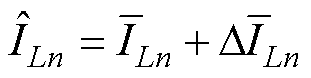 (12)
(12)
由式(12)可知,相电流平均值的近似值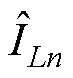 包括相电流平均值
包括相电流平均值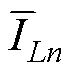 和由相电流重构偏差组成的重构差异值
和由相电流重构偏差组成的重构差异值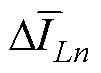 ,近似值
,近似值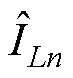 可由两采样点电流作差得到,但无法得到相电流平均值,所以重构相电流平均值的关键为求出各相的重构差异值。
可由两采样点电流作差得到,但无法得到相电流平均值,所以重构相电流平均值的关键为求出各相的重构差异值。
在采样点t2处,直流母线电流由a相、b相电感电流组成,因此直流母线电流的斜率等于电感La上电流的斜率与电感Lb上电流的斜率之和,同理推广至采样点t4、t6处,即
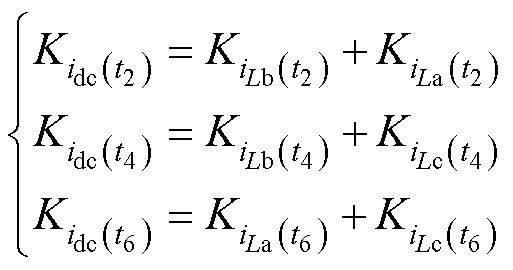 (13)
(13)
式中,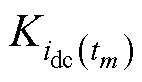 为不同采样点直流母线电流斜率;
为不同采样点直流母线电流斜率;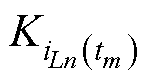 为不同相不同采样点的相电流斜率。采样点t2处的直流母线电流斜率无法通过前述6个采样点得到,需在采样点t2之后增加采样点
为不同相不同采样点的相电流斜率。采样点t2处的直流母线电流斜率无法通过前述6个采样点得到,需在采样点t2之后增加采样点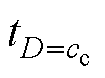 ,即控制开关Qc的载波信号cc与占空比信号D相等处的采样点,然后可通过采样点t2与采样点
,即控制开关Qc的载波信号cc与占空比信号D相等处的采样点,然后可通过采样点t2与采样点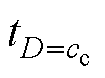 的直流母线电流值得到采样点t2处的直流母线电流斜率,同理得到采样点t4、t6处的直流母线电流斜率为
的直流母线电流值得到采样点t2处的直流母线电流斜率,同理得到采样点t4、t6处的直流母线电流斜率为
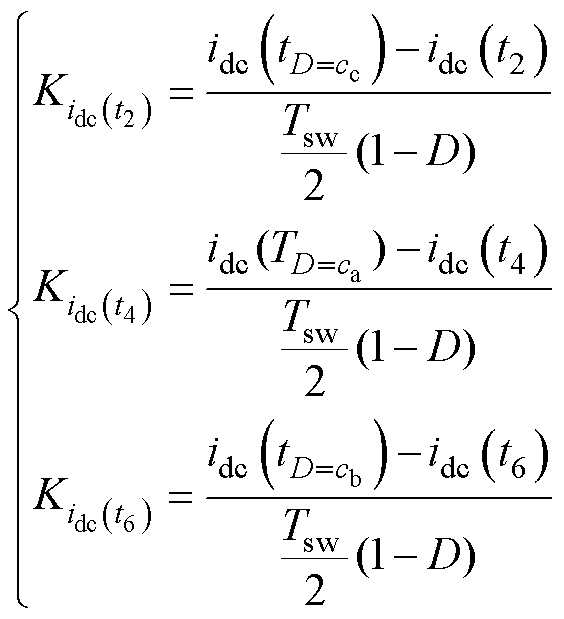 (14)
(14)
式中,ca、cb、cc分别为三相载波;Tsw为开关周期,结合式(14)和采样点的直流母线电流值可以得到每个采样点处的直流母线电流斜率,在同一周期内,同一相电流上升斜率在不同采样点是相同的,即
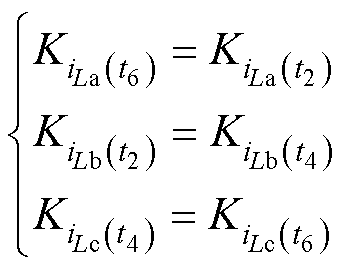 (15)
(15)
将式(15)代入式(13)可解得每一相电流斜率,化简得到
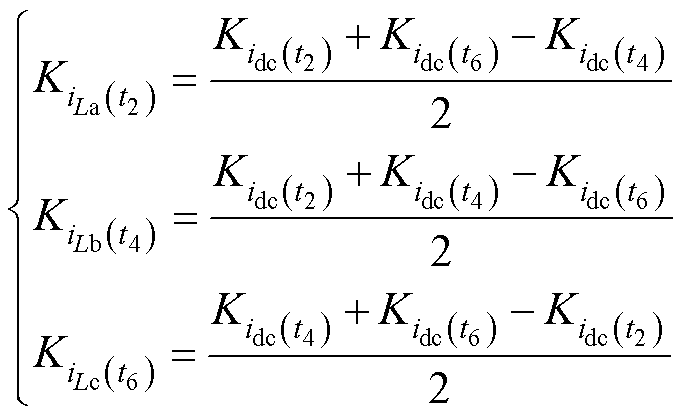 (16)
(16)
根据电感电流变化特性,便能在线计算每相电感值为
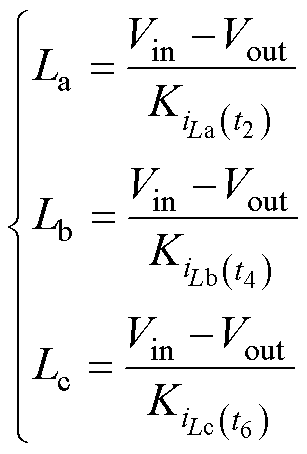 (17)
(17)
采样点t2与采样点t4距采样点t3的时间间隔相等,同一周期内同一相电流斜率相等,因此对电感Lb的电流来说,在采样点t2处的重构偏差等于在采样点t4处的重构偏差,同理可推广到其余相其余采样点,即
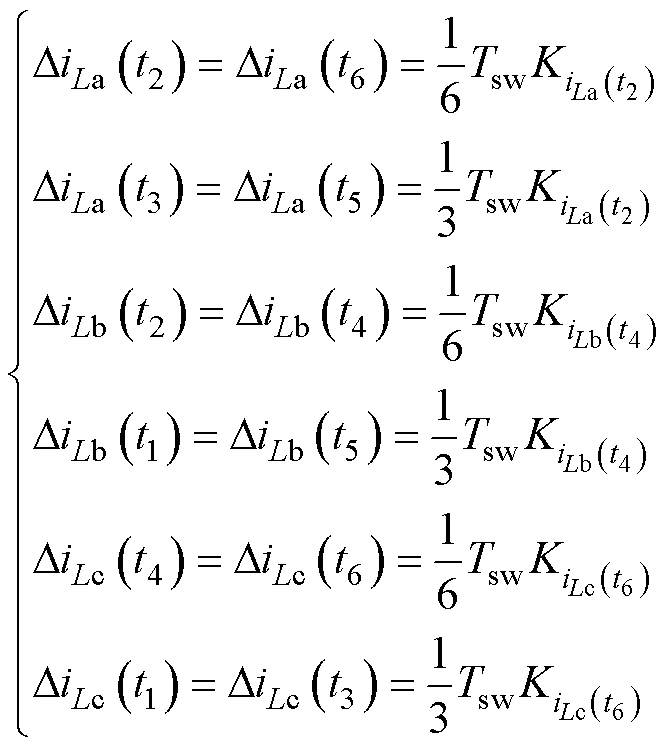 (18)
(18)
由式(18)可得到不同相不同采样点处的电流重构偏差,再将式(18)代入式(11)便可得到近似值中的重构差异值,相电流近似值与重构差异值作差便能重构得到相电流平均值为
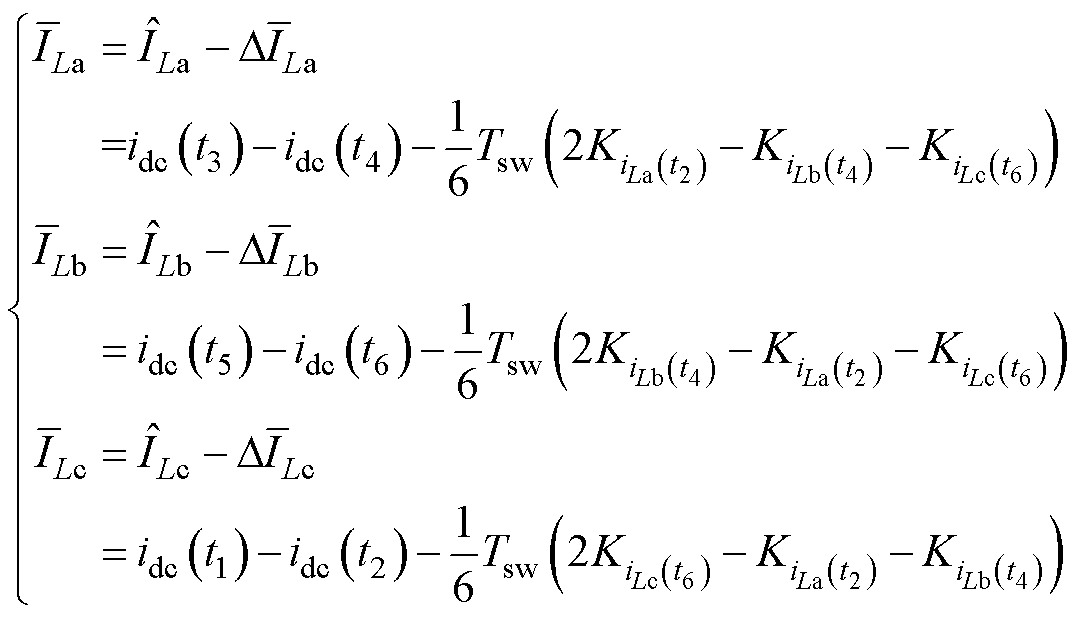 (19)
(19)
在DCM下,电感电流在开关管断开时会下降到零,在开关管导通时会从零开始上升,根据采样点直流母线电流值得到直流母线电流斜率,通过建立直流母线电流斜率与电感电流斜率的数学模型,得到电感电流斜率,再通过电感电流变化特性,得到电感电流峰值和电感值以及电感电流下降持续时间,最后通过电流持续时间、电感电流峰值与相电流平均值的几何关系重构得到相电流平均值。
相较于CCM下的电流重构策略,DCM下电流重构策略采样点的选择发生了变化,仍然选择了a、b、c相载波波谷、波峰的对应时刻作为采样点,也添加了载波信号与占空比相等的时刻作为采样点,在不同的占空比工作区域下,选择不同采样点的采样值进行电流重构。
2.2.1 D<1/3时的电流重构方法(DCM)
在D<1/3时,同一时刻最多只有一个开关管导通,直流母线电流只与导通相的相电流有关,三相电流与直流母线电流关系如图9所示。
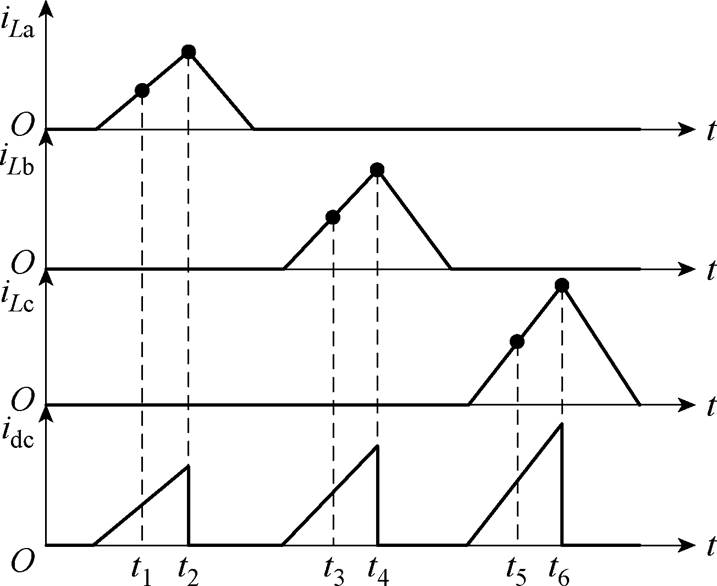
图9 D<1/3时三相电流与直流母线电流对应关系(DCM)
Fig.9 Corresponding relationship between phase current and DC bus current when D<1/3 (DCM)
此工作区域下,采样点t1、t3、t5分别对应a、b、c相载波的波谷,采样点t2、t4、t6分别a、b、c相载波与占空比相等的时刻。通过采样点t1~t6的直流母线电流可得到每相开关管导通时相电流斜率为
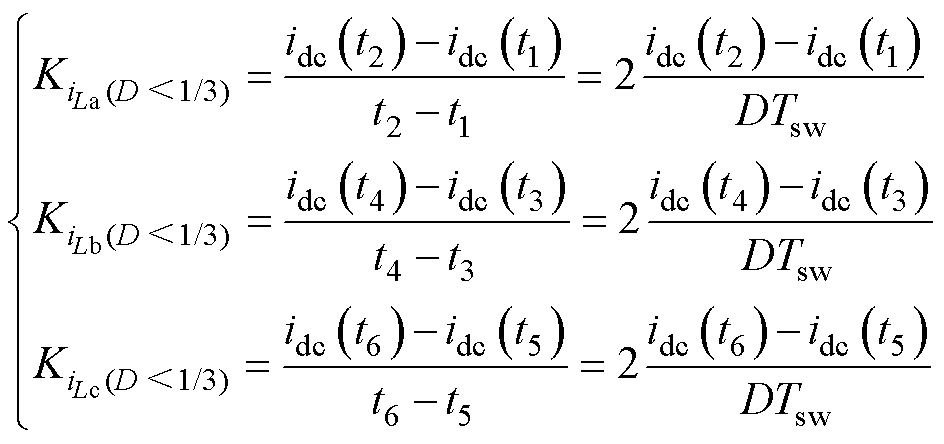 (20)
(20)
电感电流上升时间就是开关管导通的时间,根据电感电流变化特性,可在线计算每相电感值为
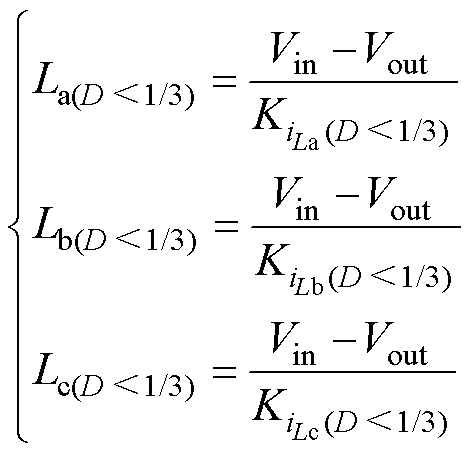 (21)
(21)
在每相开关管关断后,其对应相电感电流会下降到零。且在此工作区域下,t2、t4、t6采样点采样得到的直流母线电流就是每一相电感电流的峰值,可根据电感值、电感电流峰值以及电感上的电压求出电感电流下降持续时间为
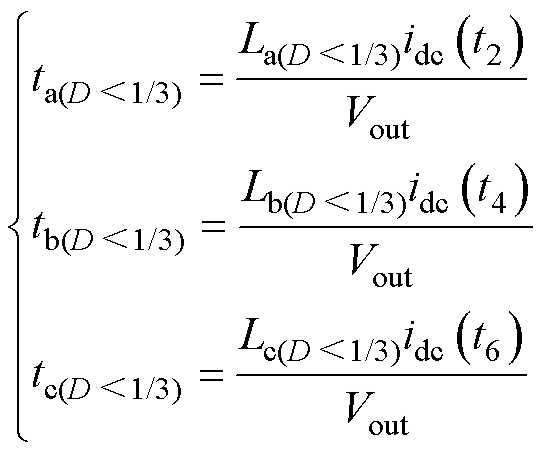 (22)
(22)
式中,ta、tb、tc分别代表三相电感电流从峰值下降到零的时间。
根据电感电流上升持续时间、下降持续时间以及电流峰值重构得到相电流平均值为
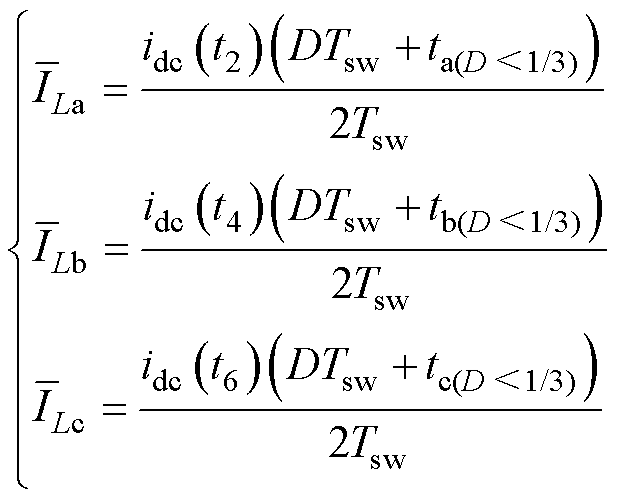 (23)
(23)
2.2.2 1/3≤D<2/3时的电流重构方法(DCM)
在1/3≤D<2/3时,当有两个开关管导通时,直流母线电流等于导通相电流之和;当只有一个开关管导通时,直流母线电流等于该导通相的电流,三相电流与直流母线电流关系如图10所示。
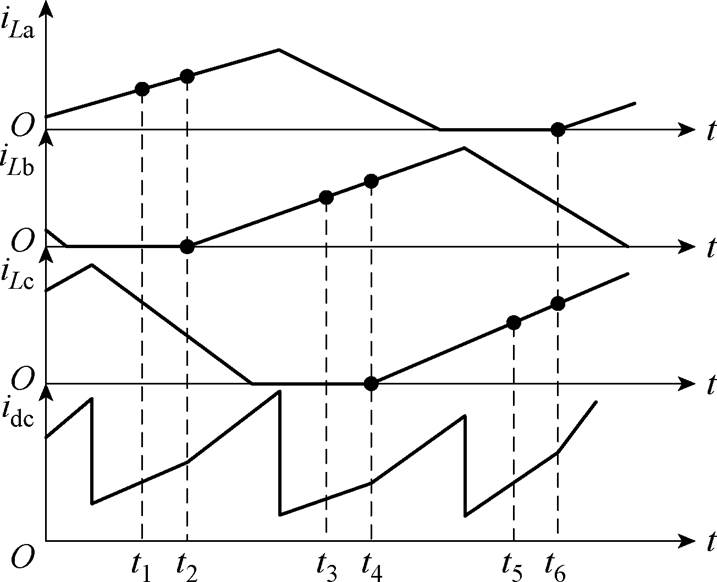
图10 1/3≤D<2/3时三相电流与直流母线电流对应关系(DCM)
Fig.10 Corresponding relationship between phase current and DC bus current when 1/3≤D<2/3 (DCM)
此工作区域下,采样点t1、t3、t5分别对应a、b、c相载波的波谷,采样点t2对应b相载波与占空比相等的时刻,采样点t4对应c相载波与占空比相等的时刻,采样点t6对应a相载波与占空比相等的时刻。由图10可知,在采样点t1、t2时刻采到的直流母线电流均是电感La上的电流,因此根据两个采样点之间的时间间隔与直流母线电流采样值可得到电感La的电流斜率,同理可得到电感Lb、Lc的电流斜率为
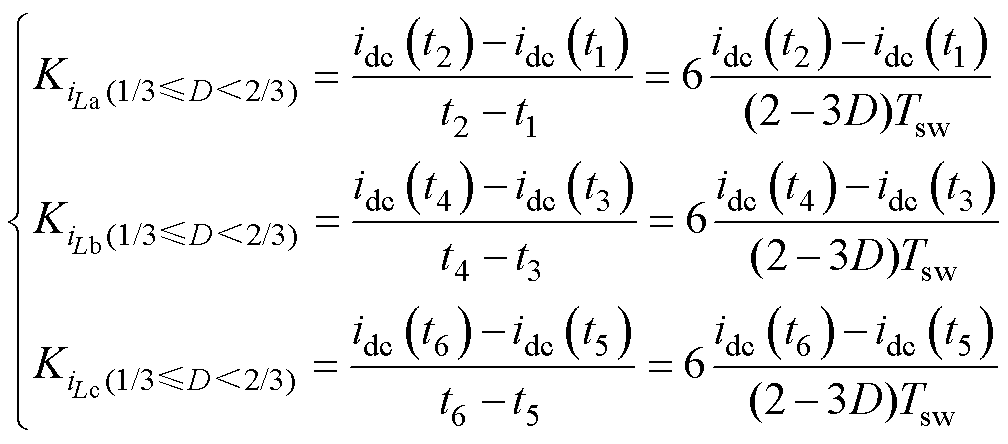 (24)
(24)
通过式(24)可以得到每相电感电流的上升斜率,根据电感电流特性,可在线计算每相电感值为
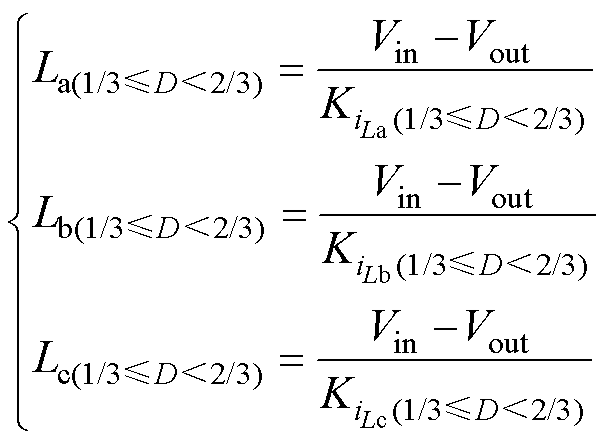 (25)
(25)
同时结合每相电感电流斜率和每相开关管导通时间,可以得到单相电感电流峰值为
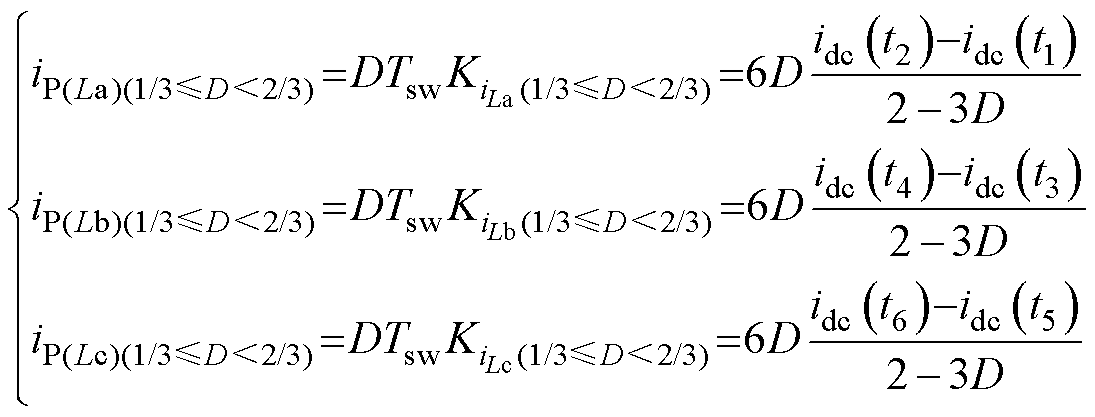 (26)
(26)
式中,iP(Ln)为单相电感电流峰值,在每相开关管关断后,其对应相电感电流会下降到零,可根据得到的电感值、电感电流峰值以及电感上的电压求出电感电流下降时间为
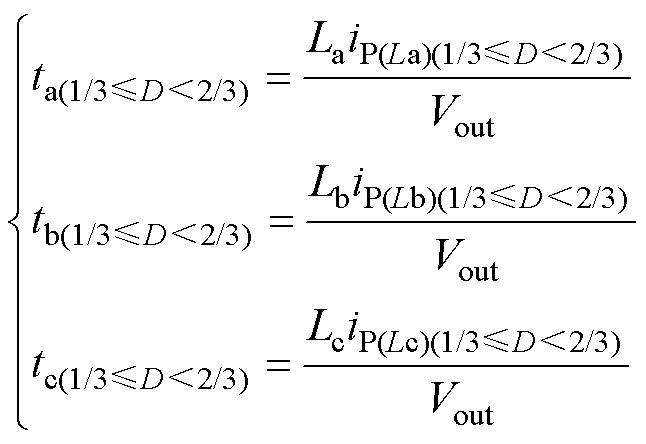 (27)
(27)
然后可根据电感电流持续时间以及电感电流峰值重构得到相电流平均值为
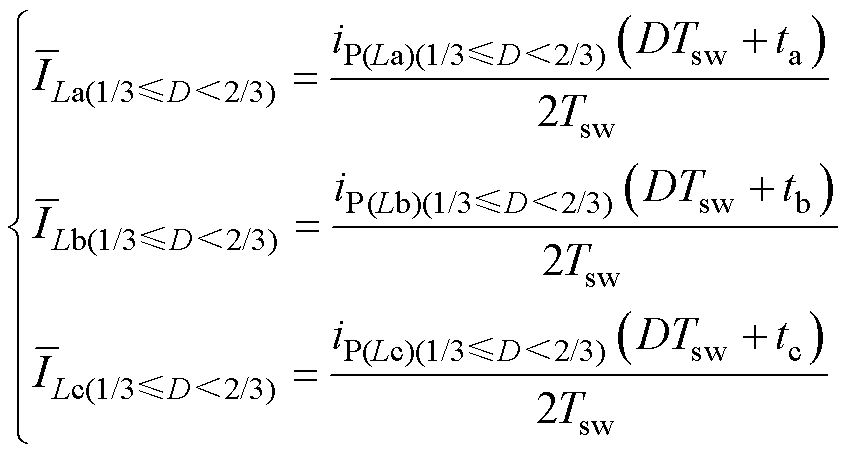 (28)
(28)
2.2.3 D≥2/3时的电流重构方法(DCM)
在D≥2/3时,同一时刻只有两个或三个开关管导通。三相电流与直流母线电流关系如图11所示。
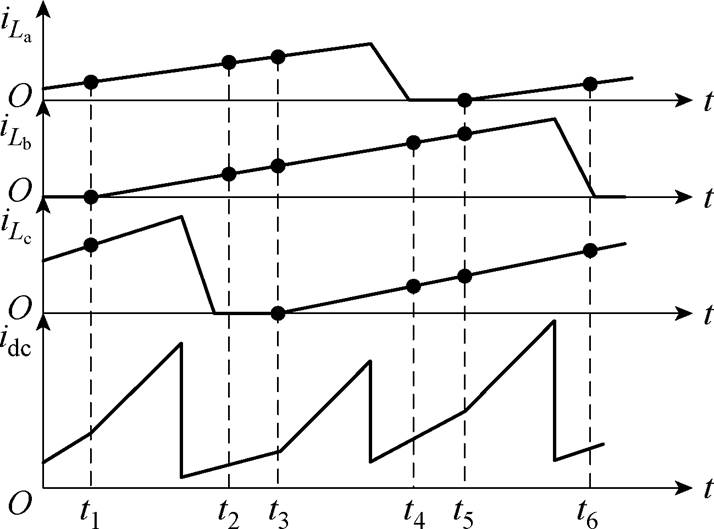
图11 D≥2/3时三相电流与直流母线电流对应关系(DCM)
Fig.11 Corresponding relationship between phase current and DC bus current when D≥2/3 (DCM)
此工作区域下,采样点t2、t4、t6分别对应a、b、c相载波的波峰,采样点t1对应b相载波与占空比相等的时刻,采样点t3对应c相载波与占空比相等的时刻,采样点t5对应a相载波与占空比相等的时刻。由图11可知,在采样点t2、t3时刻均可以采样得到由La和Lb上电流组成的直流母线电流,因此根据两个采样点之间的时间间隔与直流母线电流采样值可得到电感La、Lb的电流斜率之和,同理可以得到电感Lb、Lc的电流斜率之和以及电感La、Lc的电流斜率之和为
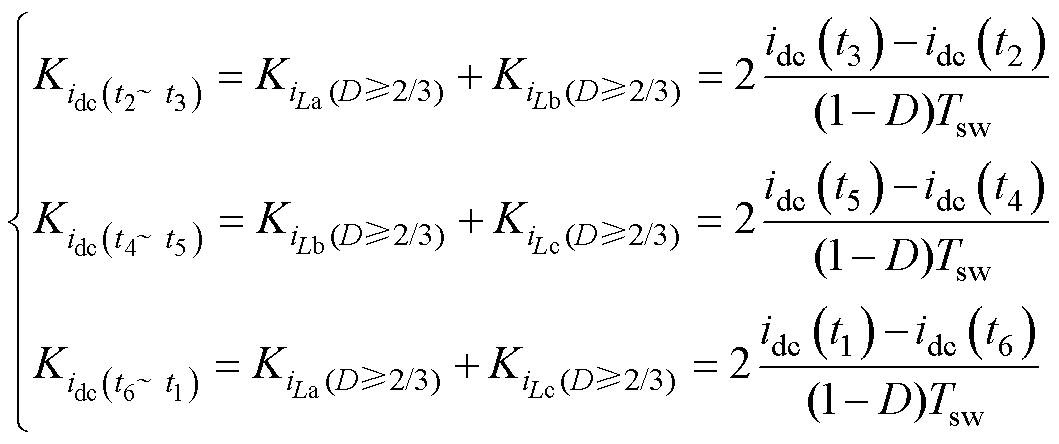 (29)
(29)
得到的直流电流斜率均为不同两相电感电流斜率和,可以解得每相电感电流斜率为
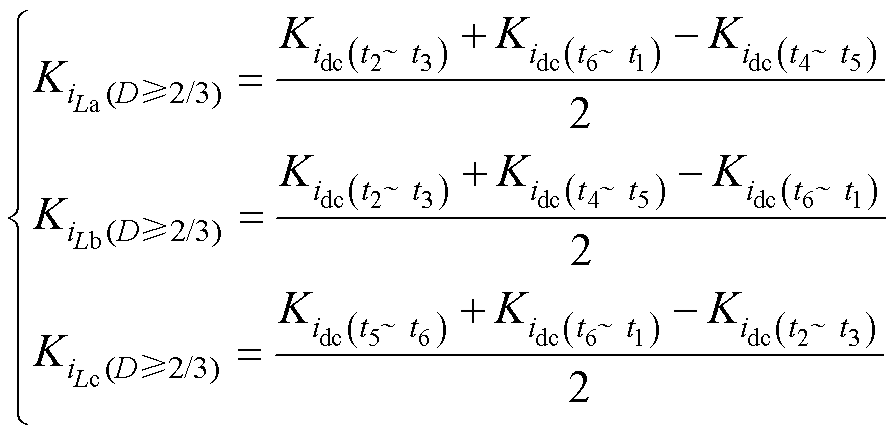 (30)
(30)
得到每相电感电流斜率后,结合每相开关管导通时间,可以得到单相电感电流峰值为
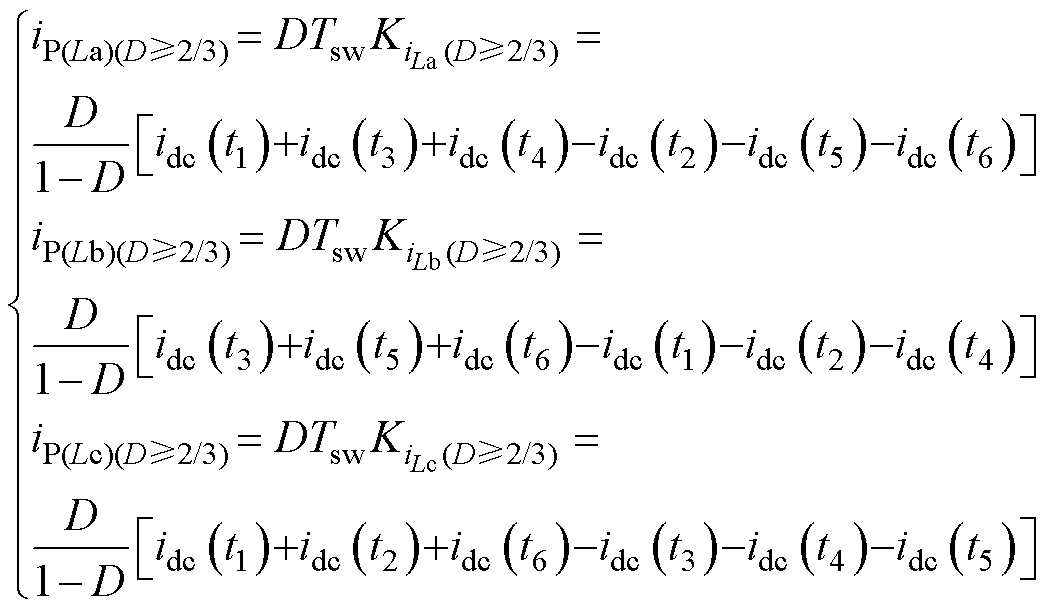 (31)
(31)
同时,根据得到的电感电流斜率,结合电感两端电压,可在线计算每相电感值为
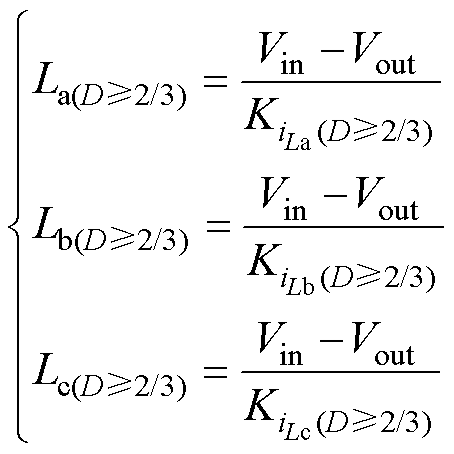 (32)
(32)
在每相开关管关断后,其对应相电感电流下降到0的时间也可得到
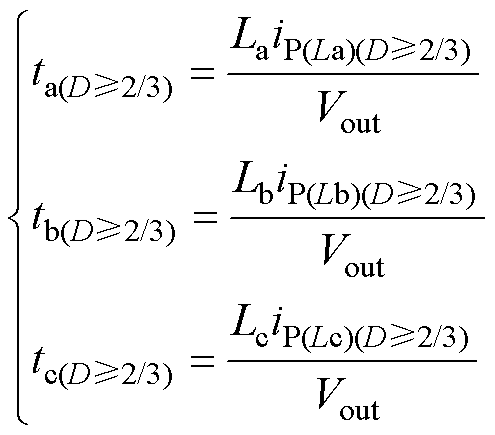 (33)
(33)
因此,可以得到每一相电感电流的持续时间,根据电感电流峰值和电流持续时间便可得到电感电流平均值为
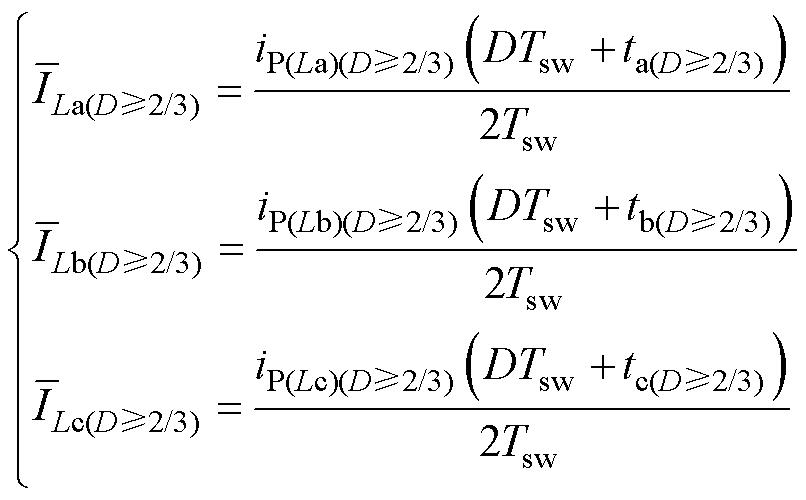 (34)
(34)
通过式(9)、式(10)、式(19)、式(23)、式(28)、式(34)可得到不同模式、不同占空比下的相电流平均值,本文电流重构策略框图如图12所示。首先对直流母线电流进行多次采样,然后在不同模式下进行针对性的电流重构。在CCM下,根据输入电压、输出电压判定占空比所处工作区域,当D<2/3时,通过式(9)、式(10)直接得到相电流平均值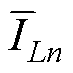 ,实现电流重构;当占空比D≥2/3时,首先利用采样电流通过式(14)得到直流母线电流斜率
,实现电流重构;当占空比D≥2/3时,首先利用采样电流通过式(14)得到直流母线电流斜率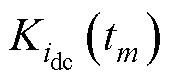 ;其次利用直流母线电流与相电流的数学模型通过式(15)得到每相电流斜率
;其次利用直流母线电流与相电流的数学模型通过式(15)得到每相电流斜率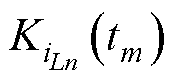 ;再次根据式(17)在线估算每相电感值Ln;然后通过式(18)计算不同相不同采样点处的相电流重构偏差
;再次根据式(17)在线估算每相电感值Ln;然后通过式(18)计算不同相不同采样点处的相电流重构偏差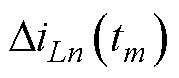 ;最后利用相电流重构偏差通过式(19)消除差异值得到相电流平均值
;最后利用相电流重构偏差通过式(19)消除差异值得到相电流平均值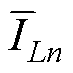 ,实现电流重构。
,实现电流重构。
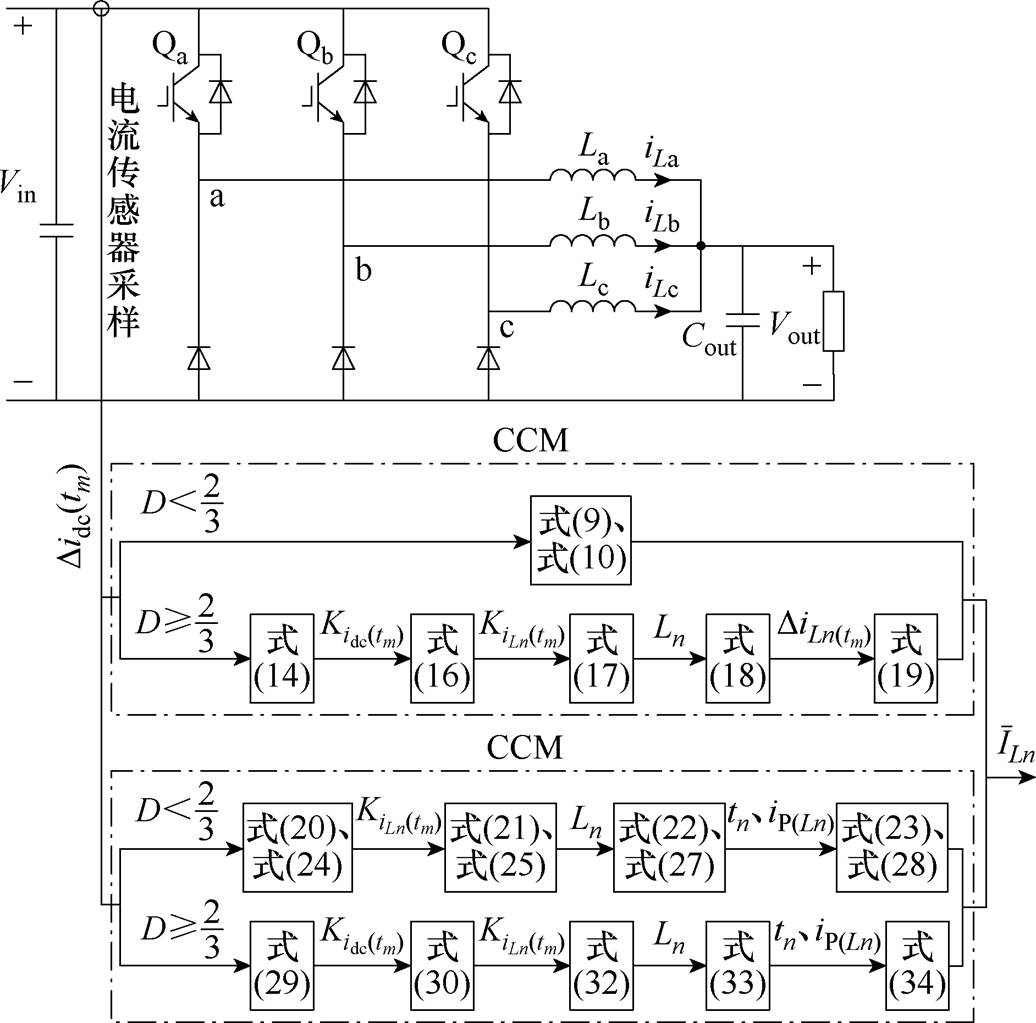
图12 电流重构策略框图
Fig.12 Current reconstruction strategy diagram
在DCM下,当占空比D<2/3时,首先可直接利用采样电流通过式(20)、式(24)得到相电流斜率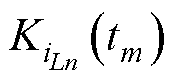 ;然后通过式(21)、式(25)在线计算电感值Ln,根据电感电流特性得到电感电流峰值
;然后通过式(21)、式(25)在线计算电感值Ln,根据电感电流特性得到电感电流峰值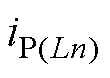 和电流下降持续时间tn;最后根据几何特性通过式(23)、式(28)得到相电流平均值
和电流下降持续时间tn;最后根据几何特性通过式(23)、式(28)得到相电流平均值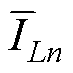 ,实现电流重构。当占空比D≥2/3时,实现电流重构的思路与D<2/3时的电流重构思路稍有区别,不同处在于当D≥2/3时,无法通过采样电流得到每相电流斜率,需要先根据采样电流通过式(29)得到直流母线电流斜率
,实现电流重构。当占空比D≥2/3时,实现电流重构的思路与D<2/3时的电流重构思路稍有区别,不同处在于当D≥2/3时,无法通过采样电流得到每相电流斜率,需要先根据采样电流通过式(29)得到直流母线电流斜率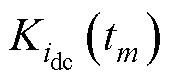 ;然后通过式(30)才能得到每相电流斜率
;然后通过式(30)才能得到每相电流斜率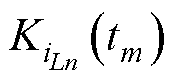 ,其余步骤与D<2/3时求出每相电流斜率后的步骤相同,最终实现电流重构。
,其余步骤与D<2/3时求出每相电流斜率后的步骤相同,最终实现电流重构。
为验证本文提出的重构策略的可行性与准确性,搭建了三相交错并联DC-DC变换器实验平台进行实验验证,实验平台如图13所示,包括实验样机(三相交错并联DC-DC Buck变换器)、可编程直流电源(IT-M3904D-500-24)、直流电阻负载(IT8918A-1200-720)、示波器和电流探头。其中实验样机以TMS320F28376作为主控芯片,功率管型号为 G40T120AK3SD。为了模拟电感偏差的极端情况,实验样机中使用的三相交错电感值偏差约为20%。同时,考虑到在实际应用中,多相交错并联电路中电感电流纹波通常较大以减小电感的体积。因此,在电感值固定的情况下,为了模拟实际应用中较大的电感电流纹波,实验所采用的开关频率为1 kHz。此外,在验证DCM下的电流重构策略时,为了确保变换器工作在DCM,选择小负载进行实验,变换器参数见表4。

图13 系统硬件
Fig.13 System hardware
表4 三相交错并联DC-DC变换器主要参数
Tab.4 Parameters of three-phase interleaved parallel DC-DC converter
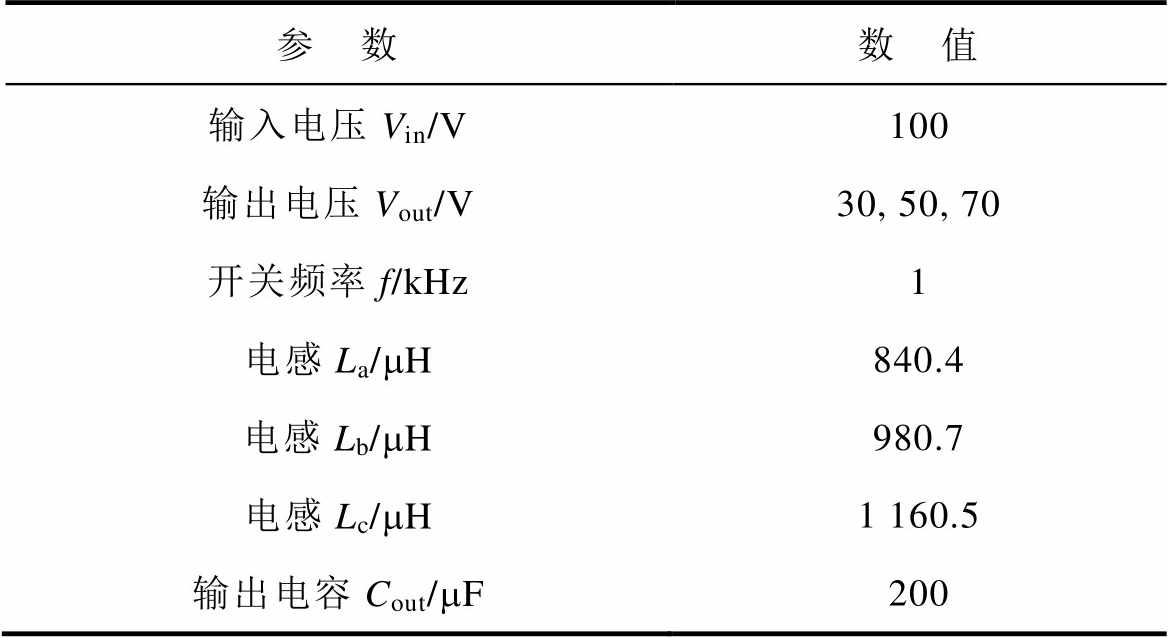
参 数数 值 输入电压Vin/V100 输出电压Vout/V30, 50, 70 开关频率f/kHz1 电感La/mH840.4 电感Lb/mH980.7 电感Lc/mH1 160.5 输出电容Cout/mF200
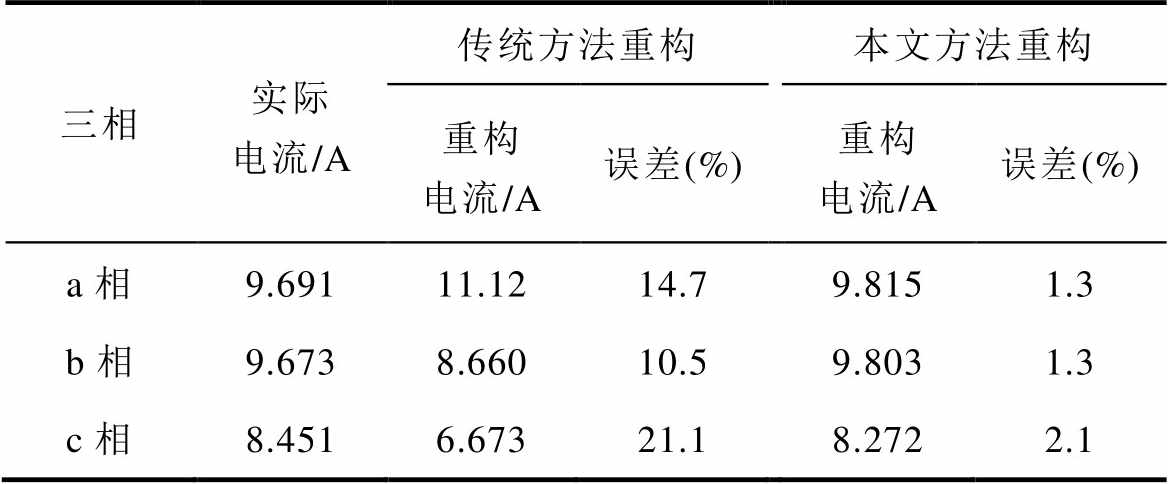
由2.1节分析可知,CCM下,若D<2/3,通过选择合适的采样点可以直接得到相电流平均值,实现电流重构,其重构电流精度与电感值无关。当D≥2/3时,电感偏差会对重构电流产生较大的影响。图14给出了占空比D=0.7时在不同策略下(本文的电流重构策略与传统的电流重构策略)的重构电流波形。由图14可知,当各相交错电感值不等时,传统重构策略的各相重构电流均与实际电流有较大差异,而通过本文提出方法得到的重构电流与实际电流平均值接近。表5给出了在D≥2/3(D=0.7)时本文方法的电流重构误差与传统方法的电流重构误差对比。由表5可知,传统电流重构策略的重构误差最大可达21.1%,而本文的重构策略能将各相电流的重构误差控制在3%以下,消除了电感偏差对重构策略的影响。
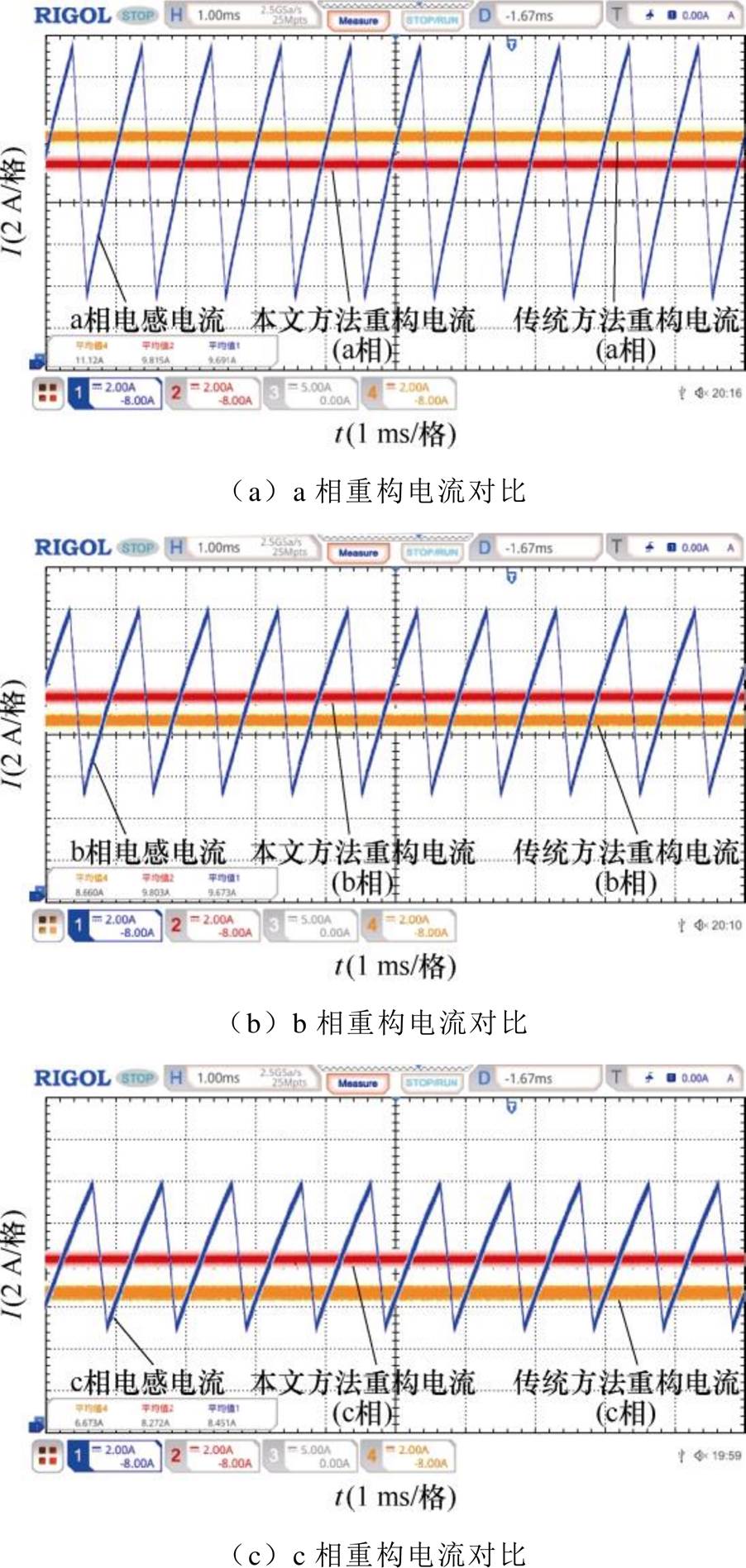
图14 CCM下占空比为0.7时传统重构策略与本文重构策略的实验波形
Fig.14 Experimental waveforms of different reconstruction strategies in CCM (D=0.7)
为了进一步验证本文所提出的重构策略的动态性能,图15给出了负载电流突变时a相的电感电流波形和本文重构策略得到的重构电流波形。由图15可知,当负载电流由15 A阶跃至25 A时以及由25 A下降至15 A时,本文所提出的重构策略均能正确地跟踪动态过程的电流变化。
表5 CCM模式下不同重构策略结果误差对比(D=0.7)
Tab.5 Comparison of error results of different reconstruction strategies in CCM mode (D=0.7)
三相实际电流/A传统方法重构本文方法重构 重构电流/A误差(%)重构电流/A误差(%) a相9.69111.1214.79.8151.3 b相9.6738.66010.59.8031.3 c相8.4516.67321.18.2722.1
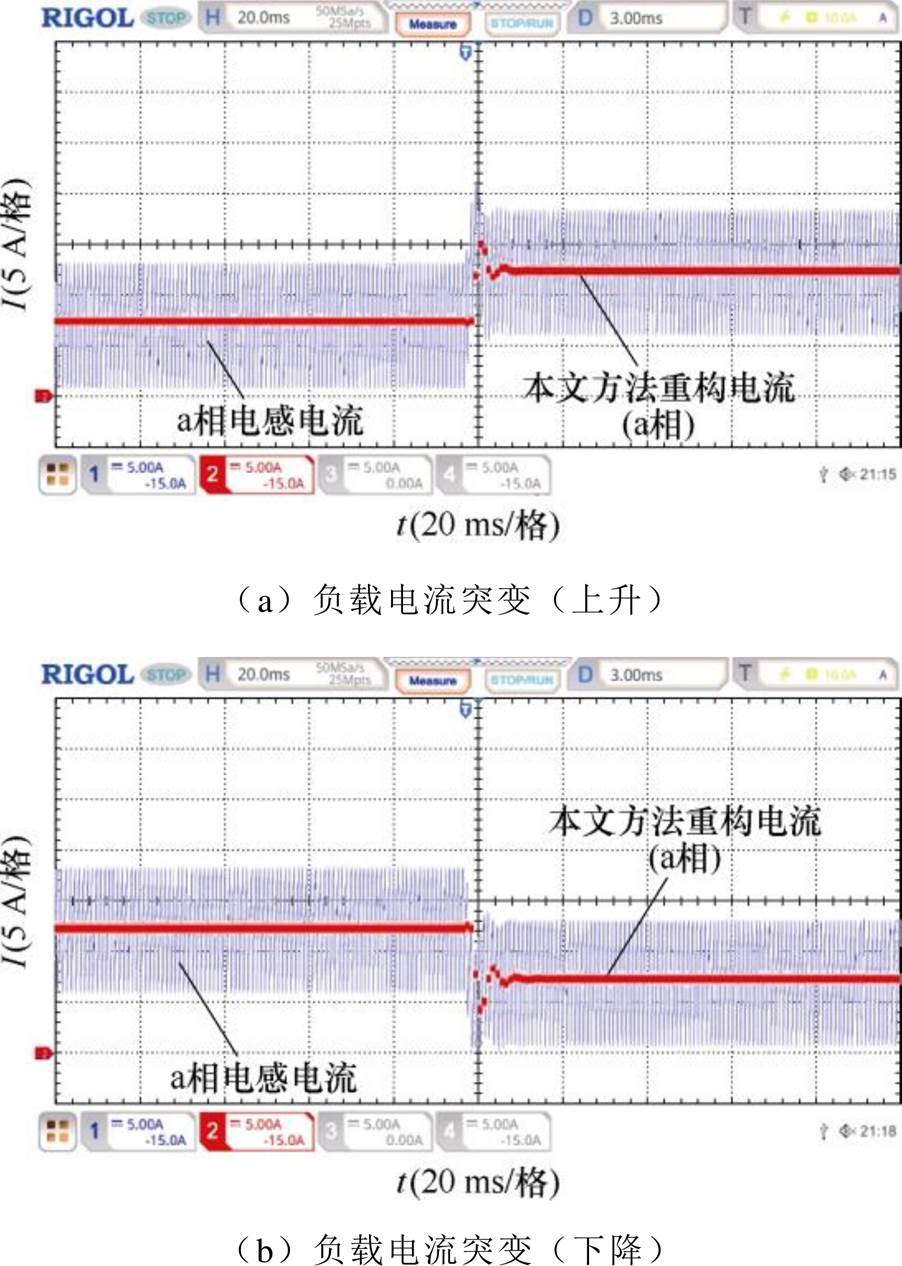
图15 CCM下负载电流突变
Fig.15 Load current sudden change in CCM
针对DCM,本文选取了三种不同占空比(D= 0.3、D=0.5、D=0.7)对所提出的电流重构策略进行验证,三种不同占空比分别代表DCM下变换器的三种工作区域。图16~图18给出了不同占空比下交错相电流的重构波形。由图16~图18可知,在DCM下,所提出的电流重构策略能够准确重构各相电流平均值。其重构误差总结见表6。由表6可知,各相重构电流的误差均在3%以内。图19给出了DCM下负载电流突变时(负载电流由3 A阶跃至5 A时以及由5 A下降至3 A)的a相电感电流波形与本文重构策略得到的重构电流波形。由图19可知,DCM下所提出的重构策略能够准确跟踪电流的阶跃变化。上述一系列实验结果表明,本文提出的电流重构策略在相电感偏差时具有较好的稳态和动态性能,证明了本文所提出方法的有效性和正确性。
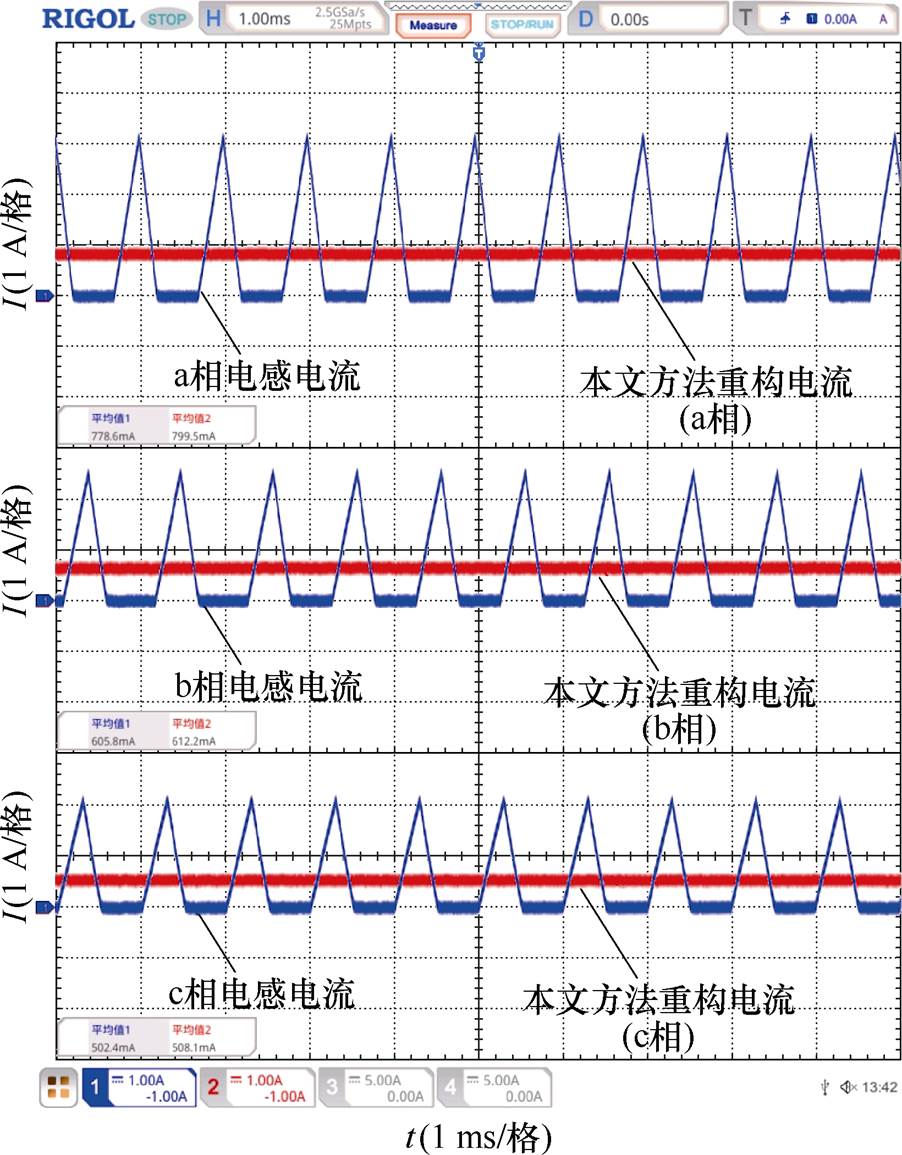
图16 DCM下重构电流波形(D=0.3)
Fig.16 Reconstructing current waveforms in DCM (D=0.3)

图17 DCM下重构电流波形(D=0.5)
Fig.17 Reconstructing current waveforms in DCM (D=0.5)
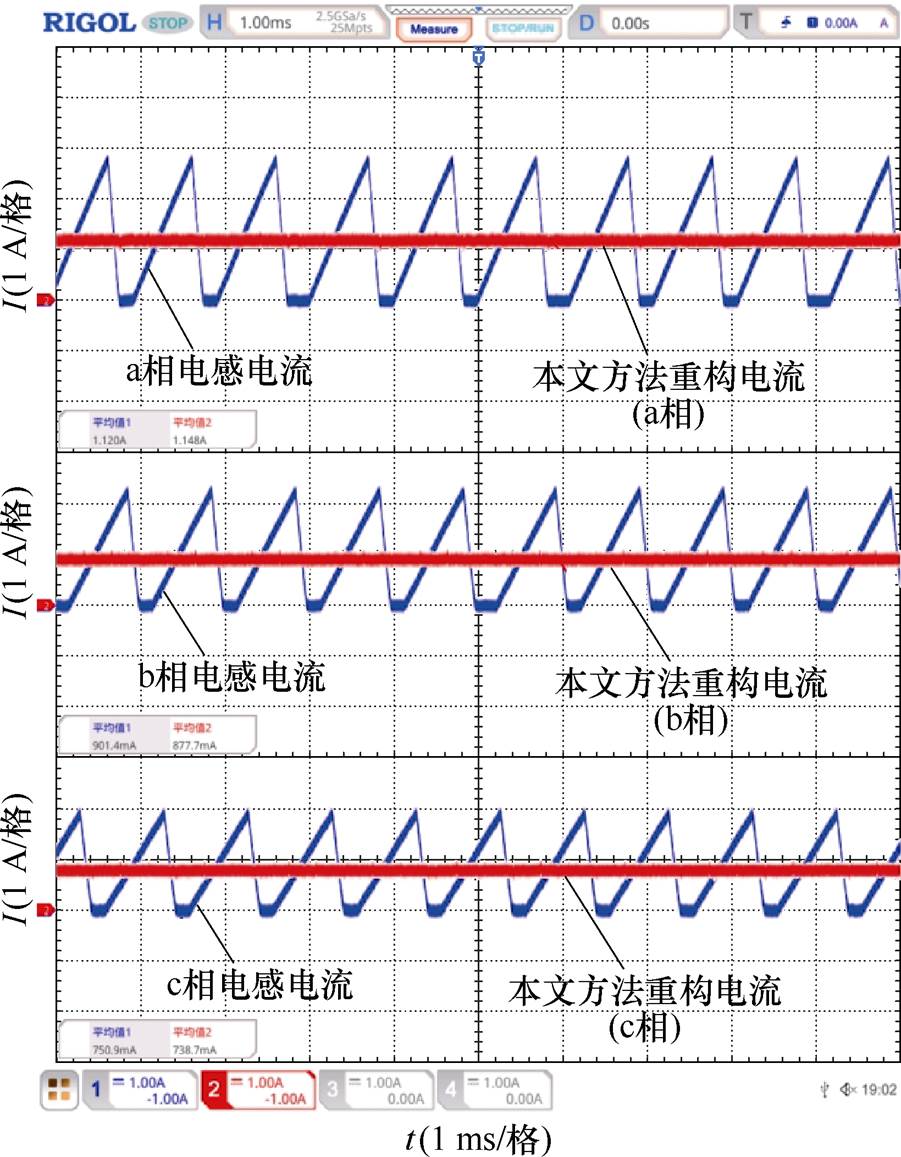
图18 DCM下重构电流波形(D=0.7)
Fig.18 Reconstructing current waveforms in DCM (D=0.7)
表6 DCM下重构电流误差
Tab.6 Reconstructing current error in DCM
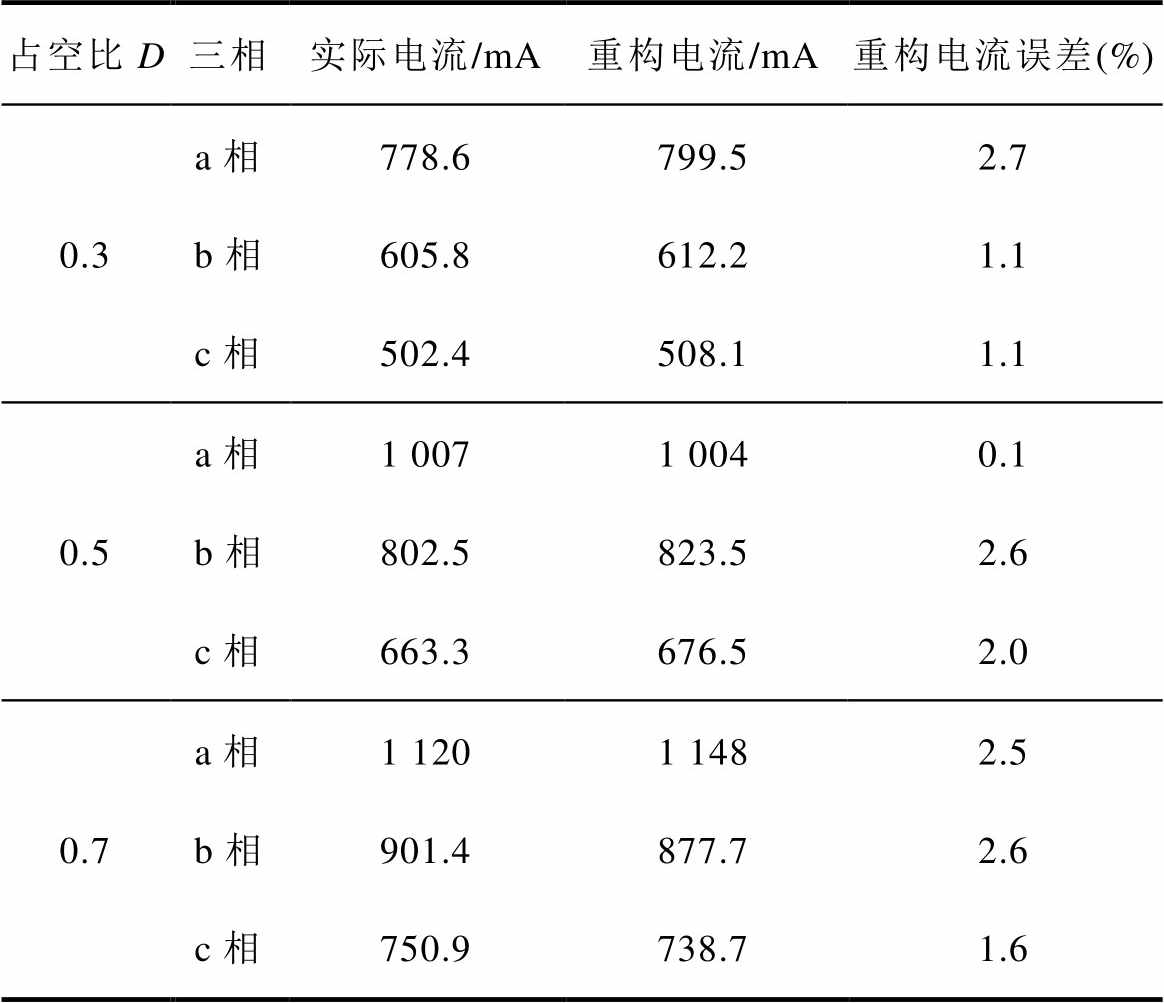
占空比D三相实际电流/mA重构电流/mA重构电流误差(%) 0.3a相778.6799.52.7 b相605.8612.21.1 c相502.4508.11.1 0.5a相1 0071 0040.1 b相802.5823.52.6 c相663.3676.52.0 0.7a相1 1201 1482.5 b相901.4877.72.6 c相750.9738.71.6
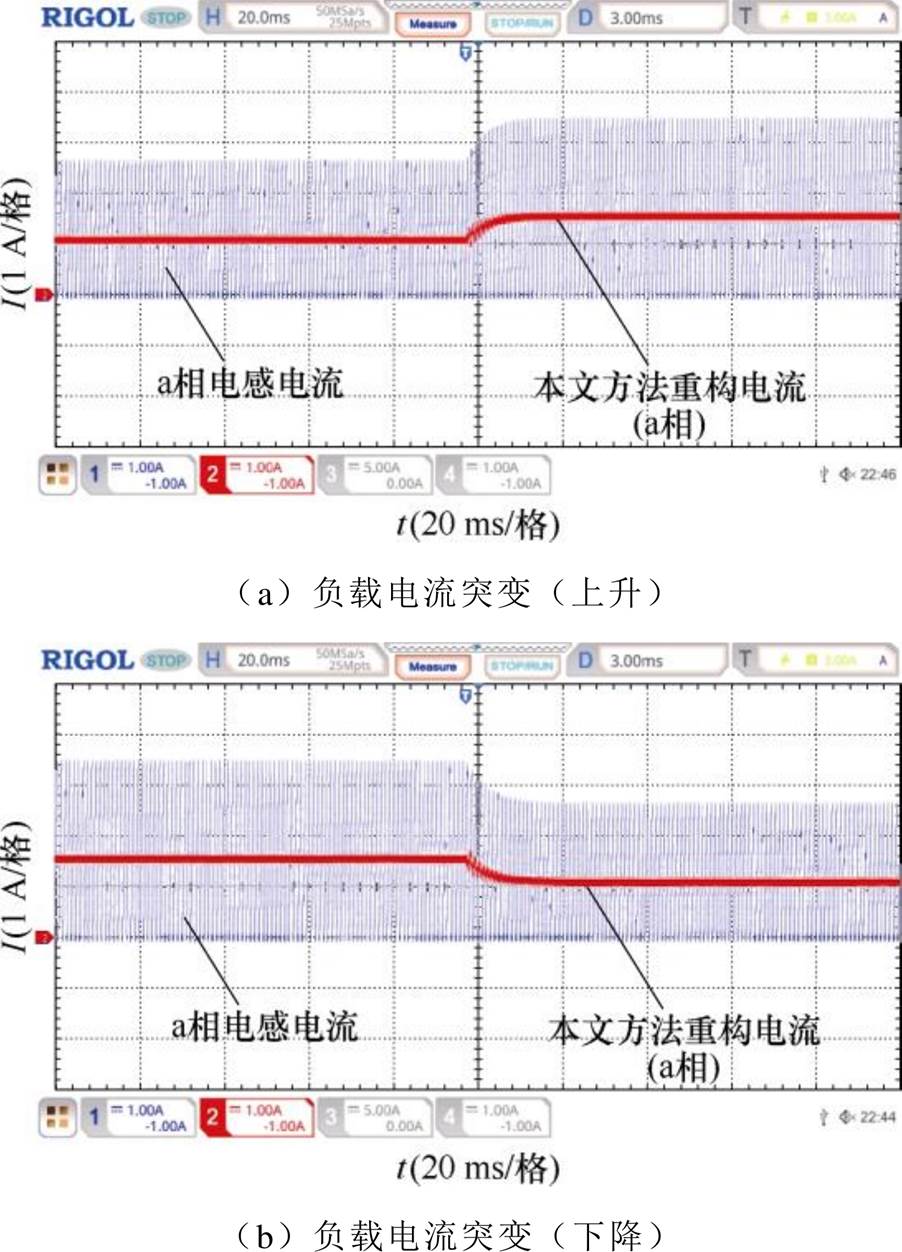
图19 DCM下负载电流突变
Fig.19 Sudden change in load current in DCM
尽管3.1节和3.2节的一系列实验结果证明了本文提出的电流重构策略的准确性和有效性,但由表5和表6可知,电流重构结果和实际值仍然存在一定误差(3%以内)。此外,由于实验平台中的电感较大,为了模拟实际较大的电流纹波,实验中选择的开关频率较低。因此,有必要从开关频率、采样延迟等多方面对本文提出的重构策略的稳定性、实时性以及准确性进行进一步分析。
由图12可知,电流重构策略本质是一个开环算法,其输入是直流母线电流的采样值,输出为各相重构电流。由于直流母线电流的采样值与开关频率无关,且CCM下的电流重构算法核心式(9)、式(10)及式(19)均不依赖开关频率(式(19)可通过简化消除开关频率),而DCM下重构算法的核心公式尽管存在开关频率依赖项,但变换器通常采用固定开关频率控制,开关周期Tsw为一个常数,所以电流重构结果与开关频率无关,开关频率不会影响电流重构策略的稳定性。
另一方面,随着开关频率的提升,留给控制器执行控制算法的时间会变短,如果算法的实际执行时间大于留给控制器执行算法的时间,会对重构算法的实时性产生影响。以CCM为例,占空比为0.8,开关频率为10 kHz,进行电流重构前,需要在一个开关周期内对直流母线电流进行多次采样,待所有采样完成后,留给控制器进行电流重构和闭环控制策略的执行时间变为6.67 ms左右。但目前的控制器性能基本处于过剩状态,其计算能力一般可达上百每秒百万条指令(Million Instruction Per Second, MIPS),以TI公司的低端DSP TMS320F280025PNS为例,计算能力高达100 MIPS(本文采用的是TMS320F28376,计算能力为400 MIPS),完全有能力在该时间内完成该算法,从而使实时性不受影响。此外,目前基于单电流传感器的电流重构算法,均需要对直流母线电流进行多采样实现重构。如文献[21-22]中均需要在一个开关周期内对直流母线电流行6次采样实现三相交错并联变换器的电流重构,其实验结果亦表明开关频率未对重构算法的实时性造成影响。
由于电流重构算法的输入为直流母线电流采样值,因此采样延迟会对电流重构结果产生一定的影响。为了进一步分析采样延迟时间对本文重构策略的影响,定义理论采样时刻为tx,得到采样值时刻记为tx_act,因此tx与tx_act的关系为
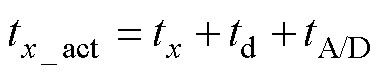 (35)
(35)
式中,td为采样保持时间,tA/D为采样转换时间。CCM下,当D<2/3时,在每个开关周期内,直流母线电流3次不同时刻的采样值即为各相电流平均值。考虑采样延迟等因素,对应的重构电流值为
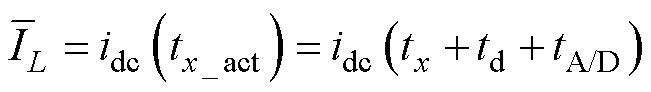 (36)
(36)
以TMS320F28376芯片为例,其ADC时钟频率最高可达200 MHz,根据不同配置采样保持时间、转换时间一共可达数十个时钟周期,其时间尺度在数十到数百ns,而开关周期通常在数十到数百ms。因此尽管实际采样值与理论采样值之间存在一定的延迟,但td与tA/D均非常小,所以CCM下D<2/3时,其产生的采样误差对重构结果的影响很小。对于CCM下D≥2/3的情形,在每个开关周期内,对直流母线电流进行多次采样,然后利用式(14)、式(15)、式(17)~式(19)重构得到相电流平均值。尽管每个实际采样值均会偏离理论采样值,但由于重构策略是对同一个ADC通道进行多次采样,因此不同时刻采样值的采样延迟时间是相同的。而由式(14)可知,直流母线电流斜率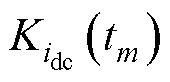 取决于相邻两个采样点之差。而后续式(15)、式(17)~式(19)均是基于式(14)的计算结果进行推导,不再依赖独立的单个采样值,因此CCM下D≥2/3时,采样延迟等非理想因素对重构算法的影响也较小。对于DCM下的重构策略,通过同样的分析也可以得到类似的结论。
取决于相邻两个采样点之差。而后续式(15)、式(17)~式(19)均是基于式(14)的计算结果进行推导,不再依赖独立的单个采样值,因此CCM下D≥2/3时,采样延迟等非理想因素对重构算法的影响也较小。对于DCM下的重构策略,通过同样的分析也可以得到类似的结论。
由于电流重构策略的目的是获得准确的相电流值,以此作为闭环控制的反馈输入,因此理论上重构算法不准确会影响闭环控制的准确性,但闭环控制不会影响重构策略的准确性。如某相电流的实际值为10 A,但重构电流为12 A,均流控制的参考指令为12 A,则此时均流控制器受到了重构电流的“欺骗”,认为该相实际电流已经达到参考值,不会进行额外的调整,导致真正的实际电流与给定电流存在较大的偏差,从而影响均流效果。但由3.1节和3.2节的开环稳态及动态实验结果可知,本文提出的重构策略在各相电感值不一致时仍然可以得到准确的重构电流,从而使均流控制不受影响。为了进一步验证电流重构算法在闭环控制策略下的动态性能,图20给出了在闭环控制策略中负载由3 Ω阶跃至5 Ω以及7 Ω阶跃至5 Ω时的重构电流波形。由图20可知,本文的重构电流在闭环控制策略中仍然能动态跟随实际电流,具有较好的动态性能和准确性。
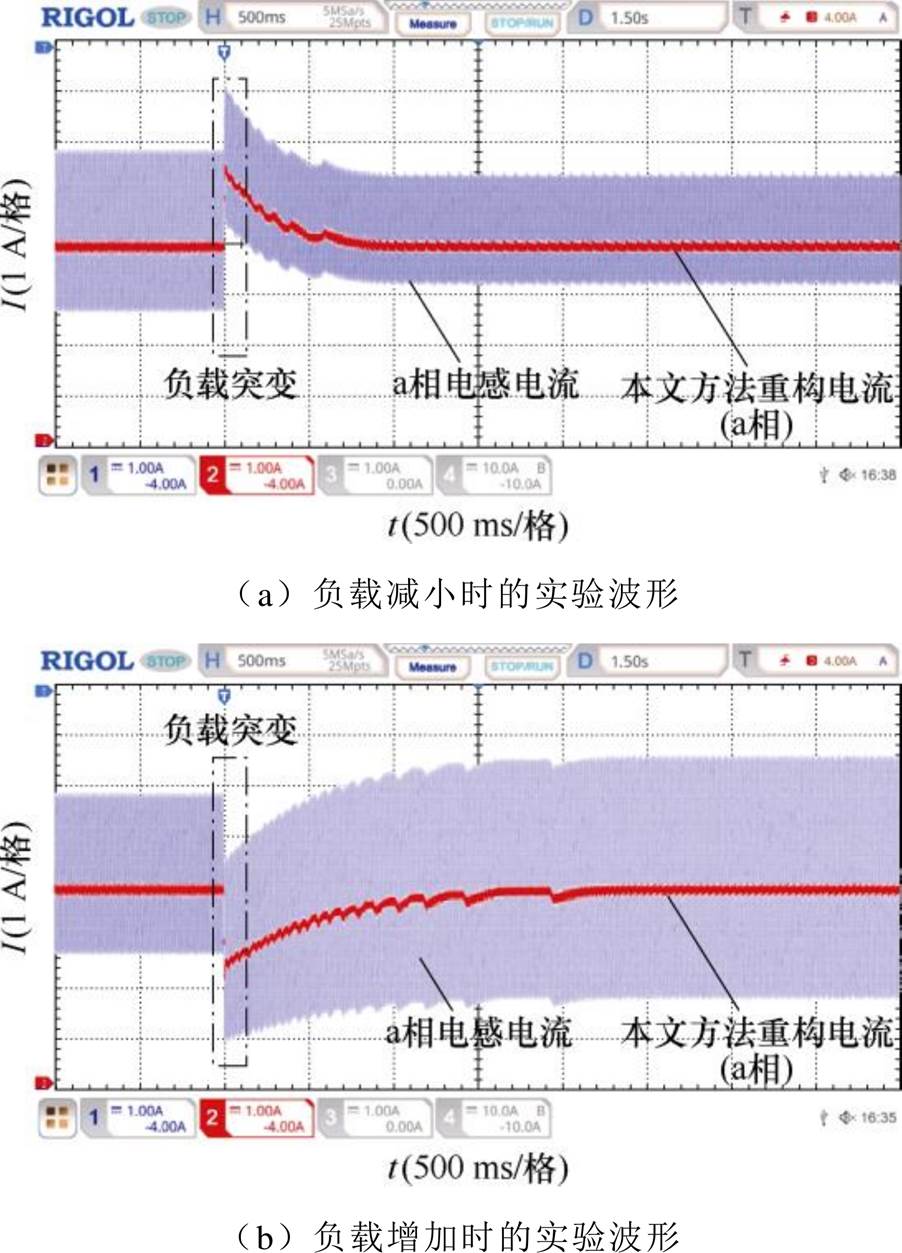
图20 闭环控制策略中负载突变时的实验波形
Fig.20 Current reconstruction waveforms during load mutation in closed-loop control strategy
本文针对多相交错并联DC-DC变换器,考虑电感偏差对电流重构的影响,提出了一种基于单电流传感器的电流重构策略,通过实验结果可以得到以下结论:
1)在CCM下,使用本文重构策略得到的各相电流偏差均在3%以内,与传统电流重构策略相比,消除了电感偏差带来的影响,准确性有较大提高。
2)在DCM下,得到的各相电流偏差均在3%以内,弥补了该模式下的重构策略的缺失。
3)本文提出的电流重构策略在所有占空比下均适用,具有普适性。
参考文献
[1] 刘中华, 舒聪慧, 杨波. 小型风力发电机设计及电磁特性研究[J]. 微电机, 2023, 56(7): 55-58.
Liu Zhonghua, Shu Conghui, Yang Bo. Research on design and electromagnetic characteristics of small wind turbine[J]. Micromotors, 2023, 56(7): 55-58.
[2] 谢宝平, 曾江, 刘佩, 等. 基于改进一阶LADRC光伏逆变器母线电压控制[J]. 电机与控制应用, 2024, 51(4): 1-11.
Xie Baoping, Zeng Jiang, Liu Pei, et al. Bus voltage control of improved first-order LADRC photovoltaic inverter[J]. Electric Machines & Control Application, 2024, 51(4): 1-11.
[3] 郭小龙, 杨桂兴, 张彦军, 等. 构网型储能变流器并网系统SISO环路增益建模与重塑控制[J]. 电气技术, 2023, 24(2): 24-31, 51.
Guo Xiaolong, Yang Guixing, Zhang Yanjun, et al. Modeling and reshaping control of single input and single output loop gain of the grid-forming energy storage converter grid-connected system[J]. Electrical Engineering, 2023, 24(2): 24-31, 51.
[4] 苏冰, 王玉斌, 王璠, 等. 基于耦合电感的多相交错并联双向DC-DC变换器及其均流控制[J]. 电工技术学报, 2020, 35(20): 4336-4349.
Su Bing, Wang Yubin, Wang Fan, et al. Multi-phase interleaved bidirectional DC-DC converter with coupled inductors and current sharing control strategy[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4336-4349.
[5] Dutta S, Johnson B. A practical digital imple- mentation of completely decentralized ripple mini- mization in parallel-connected DC-DC converters[J]. IEEE Transactions on Power Electronics, 2022, 37(12): 14422-14433.
[6] 张理, 韩民晓, 范溢文. 多相堆叠交错并联制氢变换器控制策略与特性分析[J]. 电工技术学报, 2023, 38(2): 485-495.
Zhang Li, Han Minxiao, Fan Yiwen. Control strategy and characteristic analysis of multi-phase stacked interleaved Buck converter for hydrogen produ- ction[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 485-495.
[7] 马小勇, 王萍, 王议锋, 等. 基于交错并联Boost变换器的耦合电感综合建模与多目标优化方法[J]. 电工技术学报, 2022, 37(24): 6399-6410.
Ma Xiaoyong, Wang Ping, Wang Yifeng, et al. Comprehensive modeling and multi-objective opti- mization method for coupled inductors of interleaved Boost converters[J]. Transactions of China Electro- technical Society, 2022, 37(24): 6399-6410.
[8] 桑汐坤, 王懿杰, 徐殿国. 基于输入并联输出串联的高效高升压比DC-DC变换器[J]. 电工技术学报, 2023, 38(20): 5488-5502.
Sang Xikun, Wang Yijie, Xu Dianguo. High- efficiency high voltage gain DC-DC converter based on input parallel and output series connection[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5488-5502.
[9] 王晓姬, 王道涵, 王柄东, 等. 电动汽车驱动/充电一体化系统及其控制策略综述[J]. 电工技术学报, 2023, 38(22): 5940-5958.
Wang Xiaoji, Wang Daohan, Wang Bingdong, et al. A review of drive-charging integrated systems and control strategies for electric vehicles[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(22): 5940-5958.
[10] Cho Y, Koran A, Miwa H, et al. An active current reconstruction and balancing strategy with DC-link current sensing for a multi-phase coupled-inductor converter[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1697-1705.
[11] 黄丫, 田小建, 吴戈, 等. 适用于激光器脉冲驱动系统的低纹波交错并联Boost变换器[J]. 电源学报, 2023, 21(2): 46-54.
Huang Ya, Tian Xiaojian, Wu Ge, et al. Low voltage ripple interleaved parallel Boost converter for pulsed laser driver[J]. Journal of Power Supply, 2023, 21(2): 46-54.
[12] 王庆, 生斌, 同朴超. 一种新型大功率直流电源的均流技术[J]. 电力电子技术, 2023, 57(12): 36-39.
Wang Qing, Sheng Bin, Tong Puchao. A new type of high power DC power supply current sharing tech- nology[J]. Power Electronics, 2023, 57(12): 36-39.
[13] 赵玲玲, 吴云峰, 陈章勇, 等. 全占空比范围电容串接式交错并联Boost变换器均流策略研究[J]. 中国电机工程学报, 2020, 40(7): 2330-2338, 2411.
Zhao Lingling, Wu Yunfeng, Chen Zhangyong, et al. Study on current sharing strategy about series capacitor interleaved Boost converter in full-duty range[J]. Proceedings of the CSEE, 2020, 40(7): 2330-2338, 2411.
[14] 郭强, 李山, 谢诗云, 等. 多相交错并联DC-DC变换器单电流传感器控制策略[J]. 电工技术学报, 2022, 37(4): 964-975.
Guo Qiang, Li Shan, Xie Shiyun, et al. Single-sensor sampling current control strategy of multiphase interleaved DC-DC converters[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 964- 975.
[15] Chen S Y, Yang Bochen, Pu T A, et al. Active current sharing of a parallel DC-DC converters system using bat algorithm optimized two-DOF PID control[J]. IEEE Access, 2019, 7: 84757-84769.
[16] Chiang H C, Jen K K, You G H. Improved droop control method with precise current sharing and voltage regulation[J]. IET Power Electronics, 2016, 9(4): 789-800.
[17] Lin Nan, Zhao Yue, Mantooth H A. An effective current balancing method for inverters with paralleled silicon carbide power modules[J]. IEEE Transactions on Industry Applications, 2023, 59(6): 6986-7000.
[18] Duan Minghang, Duan Jiandong, Sun Li. Sensorless current-sharing scheme for multiphase DC-DC Boost converters[J]. IEEE Transactions on Power Elec- tronics, 2023, 38(2): 1398-1405.
[19] Huang Wangxin, Abu Qahouq J A. Input voltage ripple-based sensorless current sharing autotuning controller for multiphase DC-DC converters[J]. IEEE Transactions on Industry Applications, 2016, 52(5): 4117-4125.
[20] Wang Jianing, Pei Wei, Hu Jiawen, et al. Five-phase LLC resonant DC/DC converter utilizing CLC filter for current sharing[J]. IEEE Transactions on Indu- strial Electronics, 2023, 70(9): 8634-8644.
[21] Kim H, Falahi M, Jahns T M, et al. Inductor current measurement and regulation using a single DC link current sensor for interleaved DC-DC converters[J]. IEEE Transactions on Power Electronics, 2011, 26(5): 1503-1510.
[22] Han J, Song J H. Phase current-balance control using DC-link current sensor for multiphase converters with discontinuous current mode considered[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4020-4030.
[23] 高圣伟, 李永宵, 田金锐, 等. 双频DC-DC变换器的磁集成技术[J]. 电工技术学报, 2024, 39(13): 4025-4036.
Gao Shengwei, Li Yongxiao, Tian Jinrui, et al. Magnetic integration technology of dual-frequency DC-DC converter[J]. Transactions of China Electro- technical Society, 2024, 39(13): 4025-4036.
[24] 申永鹏, 刘迪, 梁伟华, 等. 三相桥式逆变电路电流检测方法综述[J]. 电工技术学报, 2023, 38(2): 465-484.
Shen Yongpeng, Liu Di, Liang Weihua, et al. Review of current detection methods for three-phase bridge inverter circuits[J]. Transactions of China Electro- technical Society, 2023, 38(2): 465-484.
Abstract Current reconstruction strategies based on a single current sensor are critical for achieving current-sharing control in multi-phase interleaved parallel DC-DC converters. Traditional reconstruction methods are effective only within specific duty cycle ranges in continuous conduction mode (CCM), ignoring the impact of phase inductance deviations on reconstruction accuracy. This paper proposes a novel current reconstruction strategy that considers the inductance deviations for multi-phase interleaved parallel DC-DC converters. It achieves the accurate phase current reconstruction in the entire duty cycle range for both CCM and discontinuous conduction mode (DCM), filling the gap in DCM current reconstruction algorithms.
First, this paper analyzes the principles of current reconstruction for multi-phase interleaved parallel DC-DC converters. The relationship between DC-link and phase currents under different duty cycles is discussed, and the impact of phase inductance deviation on existing methods is analyzed. It shows that a 20% inductance deviation can result in up to an 18% reconstruction current error. Consequently, this paper analyzes the factors affecting inductance values, including manufacturing processes and inductance coefficients. Then, the reconstruction strategy for multi-phase interleaved parallel DC-DC converters under both CCM and DCM with phase inductance deviations is investigated. In CCM, when the duty cycle is less than 2/3, there are instances where the DC-link current equals the average phase current. Thus, the reconstruction of the average phase current is directly obtained by sampling the DC-link current at those moments, which is independent of the inductance. When the duty cycle is greater than 2/3, an online inductance estimation model is developed based on the voltage-current characteristics of the inductors. The current reconstruction expression comprises two parts: an inductance- independent term calculated directly from the sampled DC-link current and an inductance-dependent term calculated by the estimated inductance values and sampled DC-link current. In DCM, current reconstruction results in the entire duty cycle range depend on inductance. Hence, an inductance estimation model for DCM is constructed to calculate phase inductances, eliminating the impact of inductance deviations on the reconstructed currents and ensuring the accurate phase current reconstruction under inductance deviations in DCM.
An experimental platform based on a three-phase interleaved parallel DC-DC converter was built. The experimental results indicate that this strategy achieves current reconstruction under 20% inductance deviation in both CCM and DCM, with steady-state errors within 3%. Moreover, the reconstruction strategy shows good dynamic performance in open-loop and closed-loop control. Additionally, this paper analyzes the impact of non-ideal factors, such as switching frequency and sampling delay time, on the real-time performance, stability, and the proposed reconstruction strategy. Analytical and experimental results demonstrate that the proposed method can achieve attractive performance characteristics in current reconstruction, dynamic performance, and current-sharing control for multi-phase interleaved parallel DC-DC converters.
keywords:Interleaved converters, current reconstruction, inductance deviation, single current sensor
DOI: 10.19595/j.cnki.1000-6753.tces.240980
中图分类号:TM46
重庆市教育委员会科学技术研究计划青年项目(KJQN202401152)与重庆理工大学2024年研究生创新项目(gzlcx20242039)资助。
收稿日期 2024-06-07
改稿日期 2024-08-17
王 涛 男,1990年生,博士,讲师,研究方向为功率变换器共性化基础理论技术及大功率、高性能电机控制算法及拓扑等。E-mail: wangtao20190031@cqut.edu.cn(通信作者)
赵丛森 男,1999年生,硕士研究生,研究方向为电力电子变换器拓扑建模及半导体损耗等。E-mail: zhaocongsen@stu.cqut.edu.cn
(编辑 陈 诚)