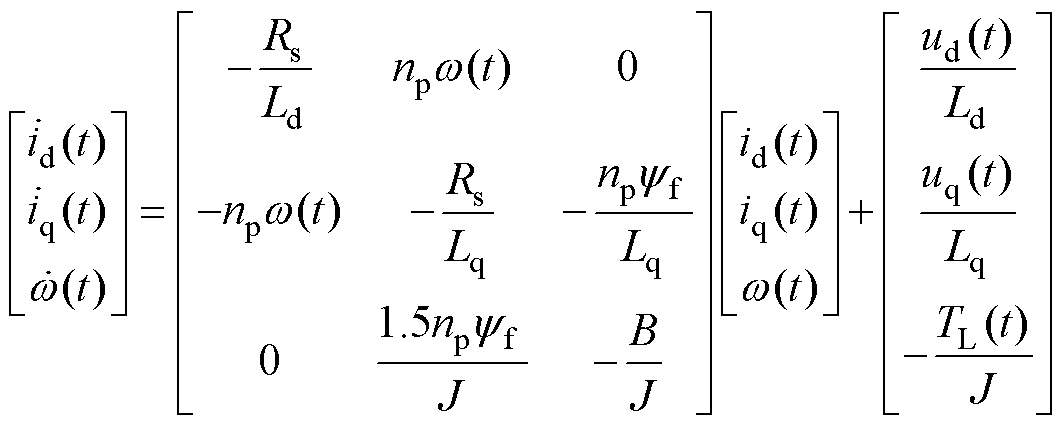 (1)
(1)
摘要 为了提高多永磁同步电机(PMSM)速度调节系统的一致性控制性能,该文提出一种基于预设性能控制(PPC)的多PMSM速度一致性控制方法。首先,将多智能体一致性控制思想引入到多电机速度调节系统中,将每个PMSM调速系统看成一个智能体,利用多智能体系统自组织协同特性来解决多PMSM的速度一致性协同控制问题。其次,设计基于PPC的PMSM多智能体系统速度一致性控制协议,通过预先设置系统的动态和稳态过程,增强多PMSM速度一致性控制系统的同步控制性能。同时,引入超扭扩张状态观测器(STESO)来观测系统中的扰动,并在速度一致性控制协议中进行实时补偿,进而提高系统的鲁棒性。最后,通过一系列对比实验验证了该文所提方法的可行性及优越性。
关键词:多永磁同步电机 多智能体 预设性能控制 超扭扩张状态观测器
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)具有高效、节能、运行速度范围广等优点[1-7],被广泛应用于各种领域,如工业生产[8]、电动汽车[9-12]、风力发电[13]等。但单电机控制系统在实际应用中无法满足在大负载、多操作度加工等场合(如龙门起重机、机械臂、数控机床等)的高性能需求,需要多电机控制系统来弥补其缺陷[14-15]。在多电机控制系统中,如何实现多个永磁同步电机速度的一致性控制成为一个重要且具有挑战性的问题。
经典的多PMSM速度协同控制方法有主从控制、并行控制、交叉耦合、偏差耦合等[16]。主从控制同步时存在着时间差,只适用于同步性要求低的场合。并行控制整个控制结构开环,抗干扰性差,控制精度、同步性能均低于其他各个控制结构[17]。交叉耦合是通过补偿器将两台电机的同步误差反馈给每台电机,使电机之间形成闭环结构。但是该方法仅适用于双电机系统,应用性有限[18]。偏差耦合在交叉耦合的基础上进行了改进。将被控电机转速与其他电机转速作差,然后把速度误差补偿到被控电机中,进一步提升了系统的同步性能。但未考虑其他电机输出转速与系统给定转速值之间的误差,并且系统中具有多台机时,由于补偿器模型较为复杂,设计补偿器的难度将会大大增加,系统运行速度也会变慢[19]。
传统多电机控制方法缺乏全局视角和协作能力,应对复杂任务时可能效率低下。如果系统设计不当,可能出现单机失效导致整体系统故障的风险。当系统受到突发负载冲击或速度需求快速变化时,传统控制方法可能无法快速调整,导致响应时间较长,甚至导致较大的波动,无法确保系统的动态性能和稳态性能[20]。
多智能体系统是多个智能体组成的集合,其目标是将大而复杂的系统分解成小的、彼此互相通信和协调的系统,通过多个子系统之间相互交互可以完成协同控制的任务[21-22]。多智能体系统凭借其灵活性、适应性被广泛应用,如无人机编队[23]、机器人系统[24]。考虑到多智能体系统和多电机系统的相似处,将每个电机系统看成一个智能体,利用多智能体系统的自组织协调特性,将多智能体一致性引入多电机调速系统中。通过设计合适的控制协议,实现多个永磁同步电机速度的一致性控制。
预设性能控制[25](Prescribed Performance Control, PPC)的概念首先由Bechlioulis和Rovithakis提出。PPC的基本思想是将系统响应的误差严格限制在设计者预先设定的范围内,同时还能够设置误差的收敛速度和超调量。相较于传统的控制方法,PPC的核心优势在于其能够主动约束系统的动态响应与稳态精度,同时兼顾抗干扰能力与控制输入平滑性。目前,PPC法已应用于船舶编队[26]、高速飞行器[27]、卫星[28]和机器人系统[29]。PPC法是一种同时保持瞬态和稳态性能的有效方法。因此,引入PPC法可以提高多智能体系统的瞬态和稳态性能[30]。
综上所述,本文将每个PMSM速度控制系统看成一个智能体,提出多PMSM速度一致性的多智能体-预设性能控制(MA-PPC)方法。首先,将单PMSM速度控制系统视为一个智能体,构建多PMSM的多智能体系统分布式一致性控制结构;其次,设计基于PPC的PMSM多智能体系统速度一致性控制协议;然后,设计了基于超扭扩张状态观测器(Super- Twisting Extended State Observer, STESO)的多PMSM速度一致控制系统的扰动观测器,进而实现了多PMSM速度调节系统的一致性协同控制,提高了系统的同步性、灵活性和鲁棒性;最后,通过不同工况下的实验验证了本文方法较偏差耦合控制方法的有效性和优越性。
PMSM系统的动力学模型[31]为
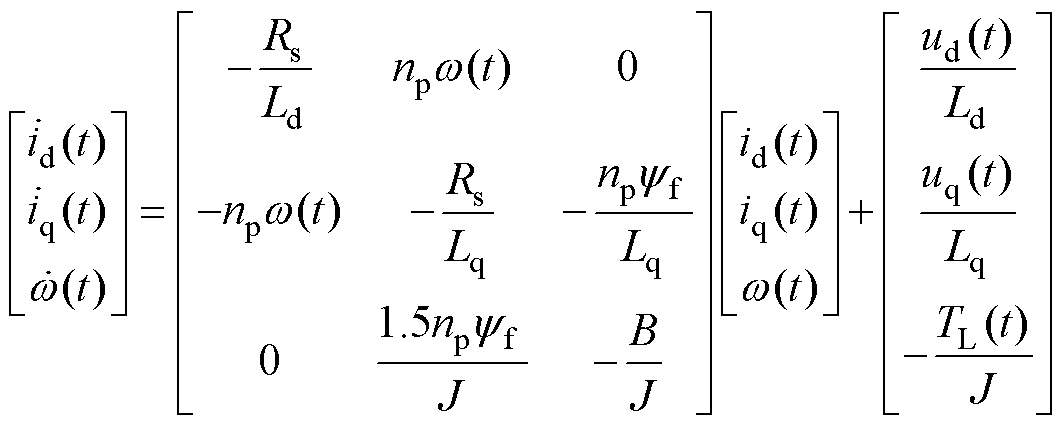 (1)
(1)
式中,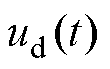 和
和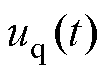 分别为定子d轴和q轴电压;
分别为定子d轴和q轴电压;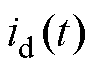 和
和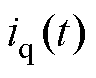 分别为定子d轴和q轴电流;
分别为定子d轴和q轴电流;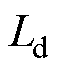 和
和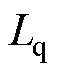 分别为d轴和q轴电感;Rs为定子电阻;
分别为d轴和q轴电感;Rs为定子电阻;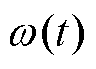 为待控制的转子角速度;
为待控制的转子角速度;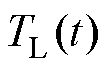 为电机负载转矩;B为摩擦系数;J为转动惯量;
为电机负载转矩;B为摩擦系数;J为转动惯量;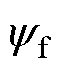 为永磁体磁链;
为永磁体磁链;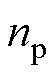 为极对数。
为极对数。
由式(1)得到电机动力学方程为
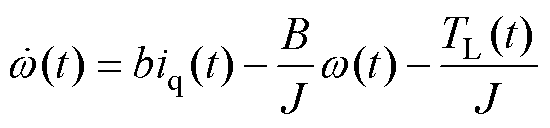 (2)
(2)
其中
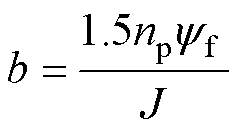
在多智能体系统研究中,通常使用图论来分析智能体之间的通信关系[32]。图论能够将复杂的通信方式抽象为简洁的几何结构,从而使得系统的分析和设计更加直观。用一个图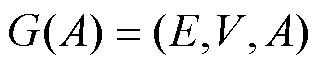 来表示多个智能体所构成的网络。
来表示多个智能体所构成的网络。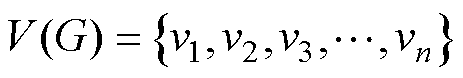 为N个智能体所构成的点集,
为N个智能体所构成的点集, 为图G的边集。由若干节点和边构成的无向图或有向图用于描述信息传递过程。在无向图中,智能体之间可以相互交换获得信息,而在有向图中,信息传递仅能单向进行。本文研究了一类由3个跟随者及1个虚拟领导者的多智能体系统,通信拓扑为有向图。其拓扑结构如图1所示。
为图G的边集。由若干节点和边构成的无向图或有向图用于描述信息传递过程。在无向图中,智能体之间可以相互交换获得信息,而在有向图中,信息传递仅能单向进行。本文研究了一类由3个跟随者及1个虚拟领导者的多智能体系统,通信拓扑为有向图。其拓扑结构如图1所示。
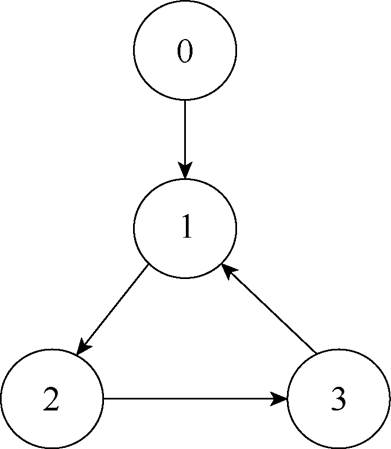
图1 拓扑结构
Fig.1 Topology structure
与图G相关的邻接矩阵记为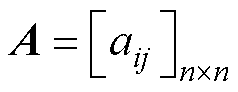 。若智能体
。若智能体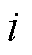 可以获得智能体j(
可以获得智能体j(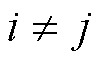 )的信息,则
)的信息,则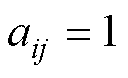 ,否则
,否则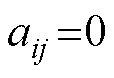 。定义度矩阵为
。定义度矩阵为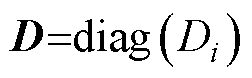 ,
,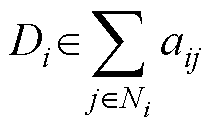 。定义拉普拉斯矩阵为L=D-A,
。定义拉普拉斯矩阵为L=D-A,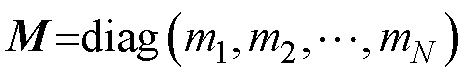 ,如果第i个智能体从领导节点获得信息则
,如果第i个智能体从领导节点获得信息则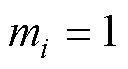 ;否则,
;否则,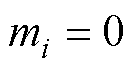 。
。
将每一个电机视为一个智能体,跟随一个虚拟领导者。根据式(2),本文的永磁同步电机多智能体系统运动方程为
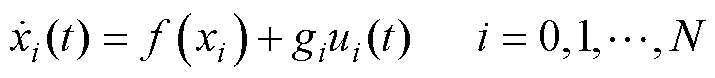 (3)
(3)
其中
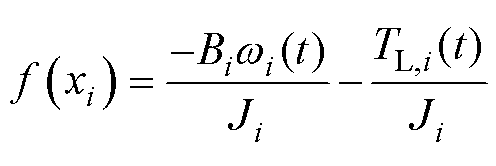
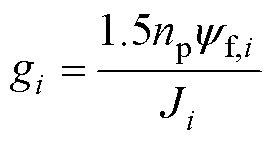
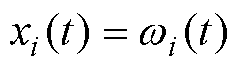
式中,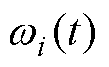 、
、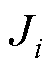 、
、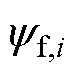 、
、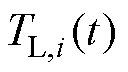 、
、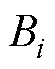 分别为第i台电机的转子角速度、转动惯量、永磁体磁链、负载转矩、摩擦系数。由于采用了虚拟领导者,其状态为
分别为第i台电机的转子角速度、转动惯量、永磁体磁链、负载转矩、摩擦系数。由于采用了虚拟领导者,其状态为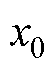 ,令
,令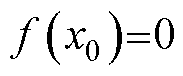 ,
,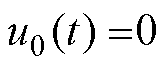 。本文设计的多智能体系统为领导跟随系统,只有一个跟随者与领导者相连,其他跟随者只能获得邻居的信息,所以考虑了具有相对状态信息的分布式控制协议,每个智能体的控制律将基于其邻居误差反馈。将邻居误差定义为
。本文设计的多智能体系统为领导跟随系统,只有一个跟随者与领导者相连,其他跟随者只能获得邻居的信息,所以考虑了具有相对状态信息的分布式控制协议,每个智能体的控制律将基于其邻居误差反馈。将邻居误差定义为
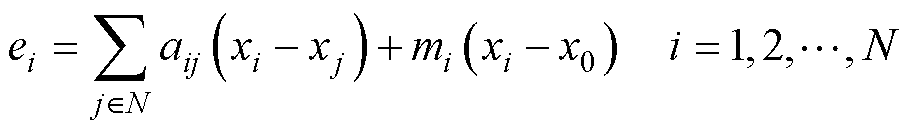 (4)
(4)
将第i个跟随者和领导者的同步误差定义为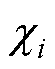 ,有
,有
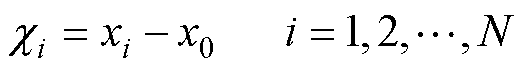 (5)
(5)
由拓扑结构[30]可得
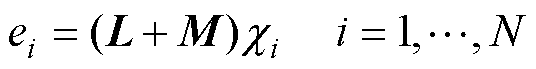 (6)
(6)
当系统趋近稳态,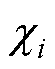 和
和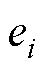 趋近于0,即实现多智能体一致性。
趋近于0,即实现多智能体一致性。
由于永磁同步电机多智能体系统运动方程式(3)与一阶多智能体系统模型一致,所以将多PMSM速度一致性控制问题转化为多智能体一致性控制问题来处理,继而结合多智能体系统理论,本文设计如下的多永磁同步电机速度一致性控制协议。
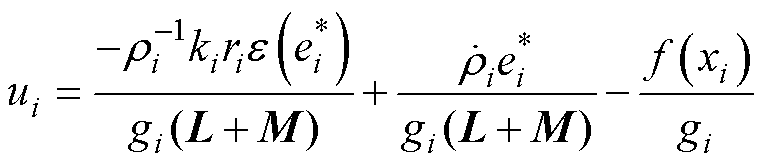 (7)
(7)
式中,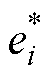 为归一化误差;
为归一化误差;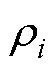 为待设计的性能函数;
为待设计的性能函数;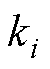 为待设计的正常数增益,需要通过实际的需求来选择,适当增大,可以增强动态性能,但过大会损害静态性能;
为待设计的正常数增益,需要通过实际的需求来选择,适当增大,可以增强动态性能,但过大会损害静态性能;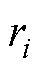 为方便稳定性证明计算设定的函数,定义为
为方便稳定性证明计算设定的函数,定义为
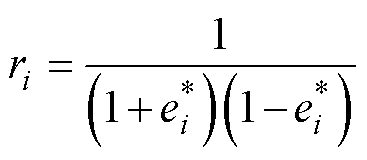 (8)
(8)
ki和ri的紧凑形式为
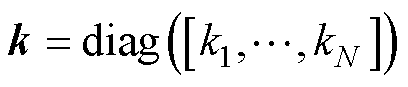 (9)
(9)
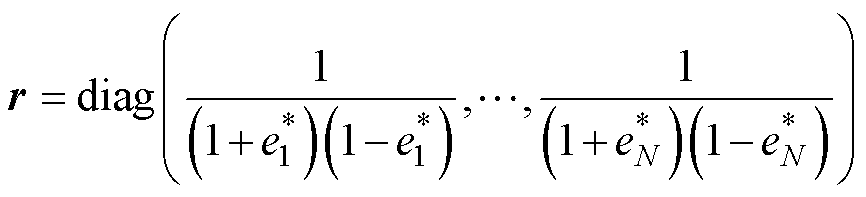 (10)
(10)
本文采用的性能函数[27]为
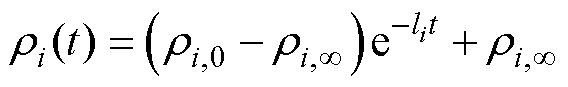 (11)
(11)
式中,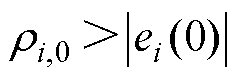 ,
,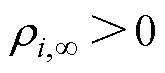 ,
,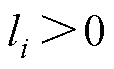 。
。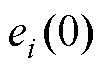 为初始误差。调节
为初始误差。调节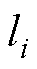 可以调节误差的收敛速率。适当调节
可以调节误差的收敛速率。适当调节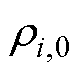 和
和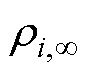 ,可增强系统的动态性能和稳态性能,但
,可增强系统的动态性能和稳态性能,但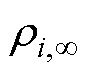 不宜过大或过小,过大会损害系统的动态性能,过小会损害系统的静态性能。
不宜过大或过小,过大会损害系统的动态性能,过小会损害系统的静态性能。
性能函数的紧凑形式为
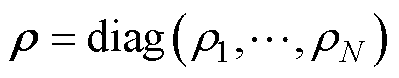 (12)
(12)
当系统的误差处于性能函数约束的区域内,即
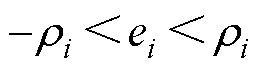
定义归一化误差为
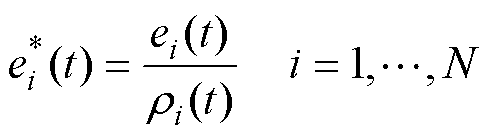 (13)
(13)
可将其写成紧凑形式为
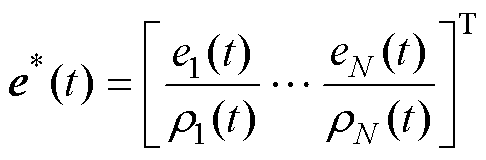 (14)
(14)
由式(14)可知,预设性能的约束为不等式约束,将其转换为等式约束。
采用如下的映射函数
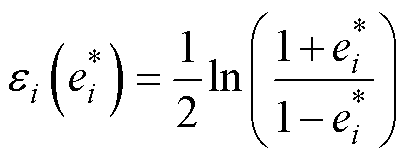 (15)
(15)
其紧凑形式为
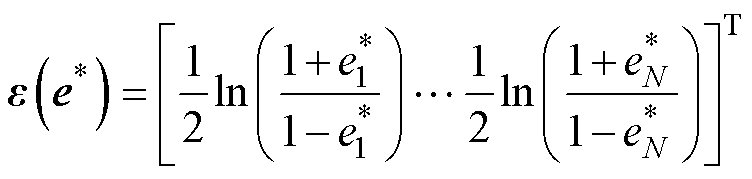 (16)
(16)
由式(3)、式(5)、式(6)可得
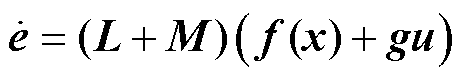 (17)
(17)
由式(14)、式(17)可得
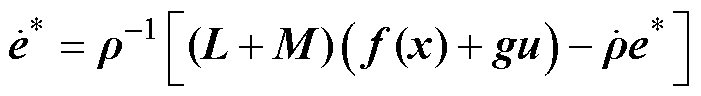 (18)
(18)
由式(16)、式(18)可得
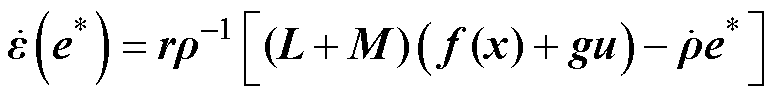 (19)
(19)
定义李雅普诺夫函数
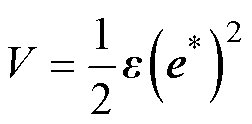 (20)
(20)
对式(20)求导得
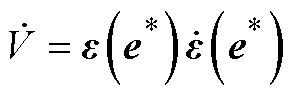 (21)
(21)
代入式(7)、式(19)可得
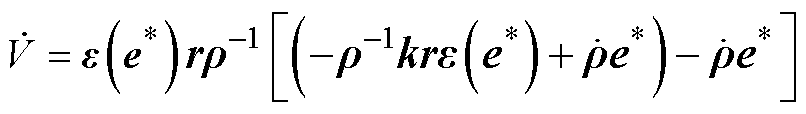 (22)
(22)
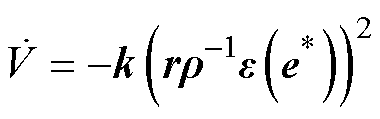 (23)
(23)
即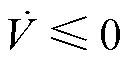 证毕。
证毕。
在永磁同步电机矢量控制的框架下,基于上述设计的多PMSM速度一致性控制协议,本文提出的多PMSM速度一致性控制系统框图如图2所示。
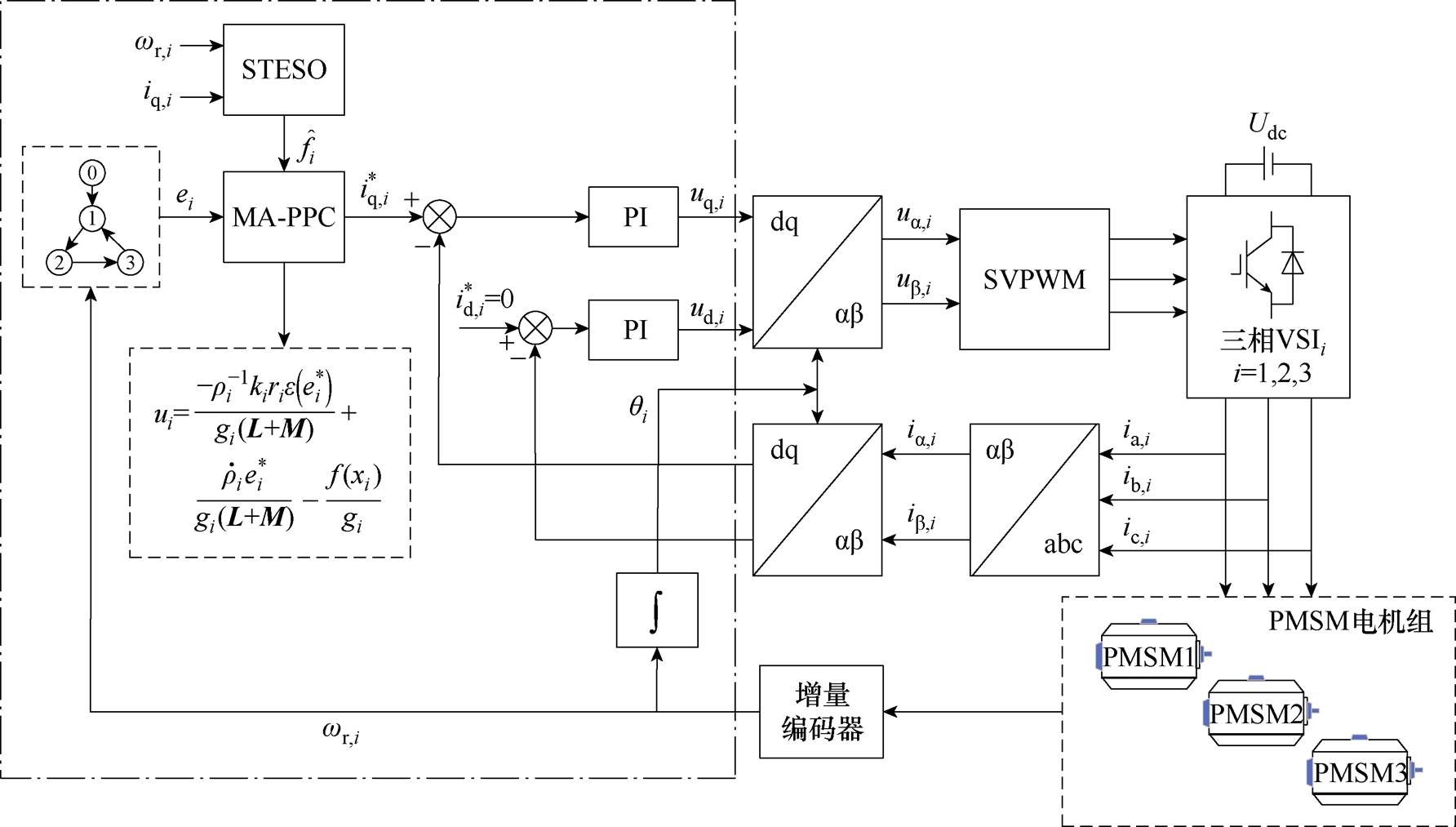
图2 多永磁同步电机多智能体预设性能控制系统框图
Fig.2 Block diagram of MA-PPC control system for multi permanent magnet synchronous motor
在实际运行过程中PMSM会受到各种扰动。这些扰动会影响系统的控制性能。因此,为了保障系统的控制性能,需要对系统扰动进行有效估计。本文采用STESO[33]来观测PMSM调速系统的扰动,并在控制量中进行实时补偿,使系统具有更好的鲁棒性能。
重新定义式(2),有
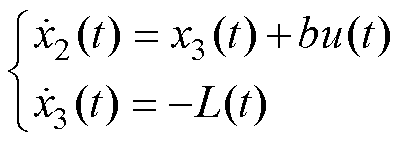 (24)
(24)
其中
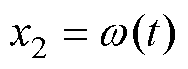
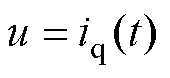
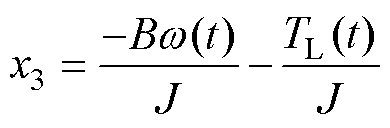
式中,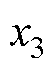 为总扰动;
为总扰动;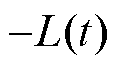 为
为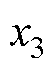 的导数。
的导数。
设计STESO为
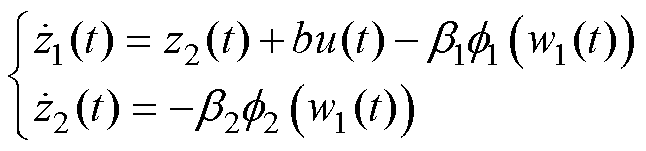 (25)
(25)
其中
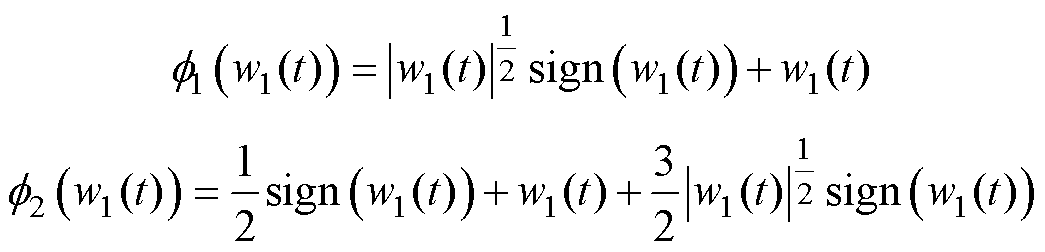
式中,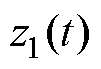 和
和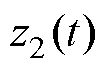 分别为
分别为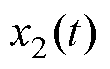 和
和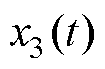 的观测值;
的观测值;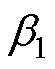 和
和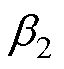 为两个调优参数。
为两个调优参数。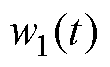 为
为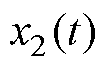 的观测误差。sign(x)为符号函数,定义为
的观测误差。sign(x)为符号函数,定义为
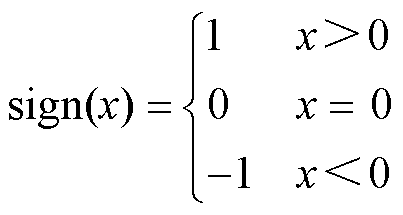
根据式(24)和式(25),得到观测误差系统为
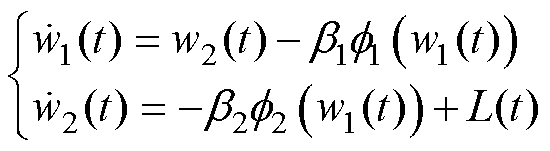 (26)
(26)
其中
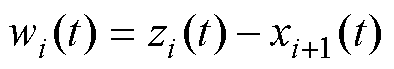 i=1, 2
i=1, 2
式中,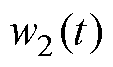 为
为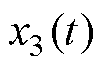 的观测误差。
的观测误差。
为验证本文提出的多PMSM速度一致性MA- PPC方法的优势,在图3所示的多电机实验平台上将其与PI改进的偏差耦合控制进行对比实验。在对比实验中,改进的偏差耦合控制器采用PI控制的补偿器替代了偏差耦合中比例控制的转速补偿,提高了偏差耦合的性能。

图3 多电机实验平台
Fig.3 Multi-motor experimental platform
实验平台中3台电机和3台负载电机的参数相同,见表1。本文提出的速度一致性MA-PPC方法的控制参数见表2,偏差耦合方法的参数见表3。在实验平台中对本文提出的MA-PPC方法和PI改进的偏差耦合方法进行了升降速、加减载以及正反转对比实验验证。
表1 PMSM参数
Tab.1 Parameters of PMSM
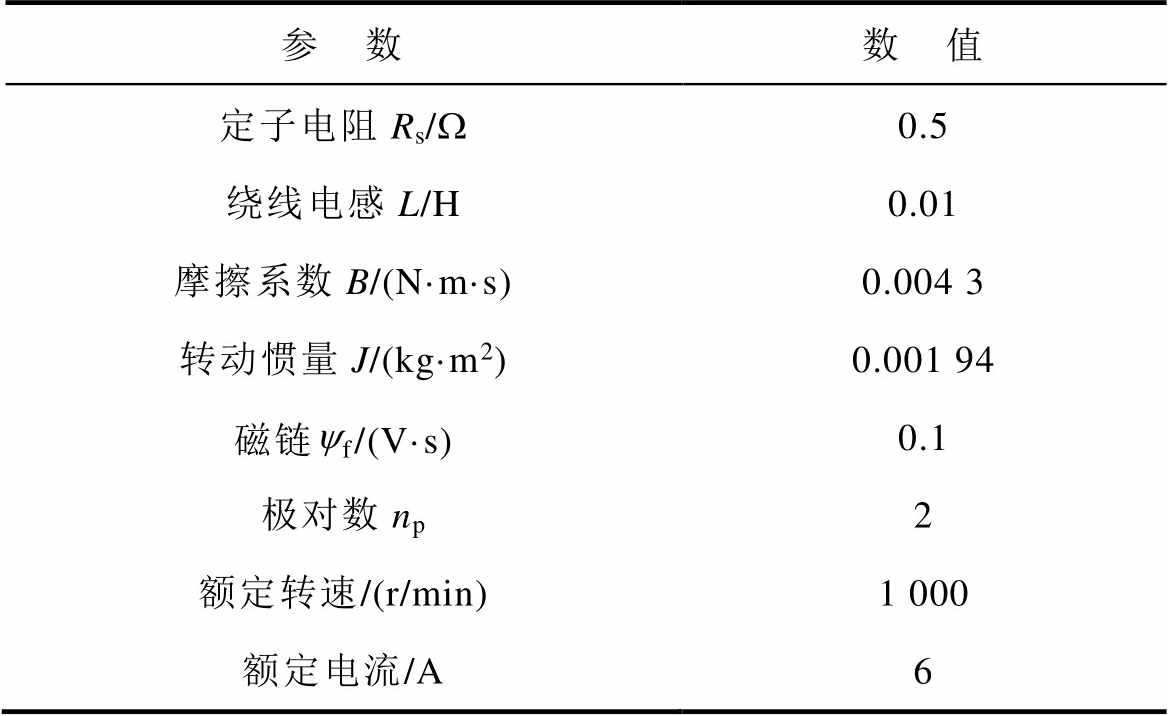
参 数数 值 定子电阻Rs/W0.5 绕线电感L/H0.01 摩擦系数B/(N·m·s)0.004 3 转动惯量J/(kg·m2)0.001 94 磁链yf/(V·s)0.1 极对数np2 额定转速/(r/min)1 000 额定电流/A6
实验平台主要由一台主控计算机、3台工业计算机(操作系统为VxWorks)、6个电机驱动器、3台电动PMSM、3台负载PMSM、3个转矩和速度传感器、一个信号测试箱和必要的配电电路组成。多PMSM控制系统算法在主机上用Simulink搭建并调试成功后,利用Matlab自动代码生成工具将其编译成目标代码并下载到工业计算机上运行,工业计算机通过专门的DSP接口板卡控制电机驱动器,并通过转矩和速度传感器收集PMSM的速度、转矩等数据。
表2 本文控制器参数
Tab.2 Controller parameters in this article

参 数数 值 200 200 200 1 1 1 23 24.5 23 15 4.5 4
表3 PI改进偏差耦合控制参数
Tab.3 Relative coupling controller parameters based on PI
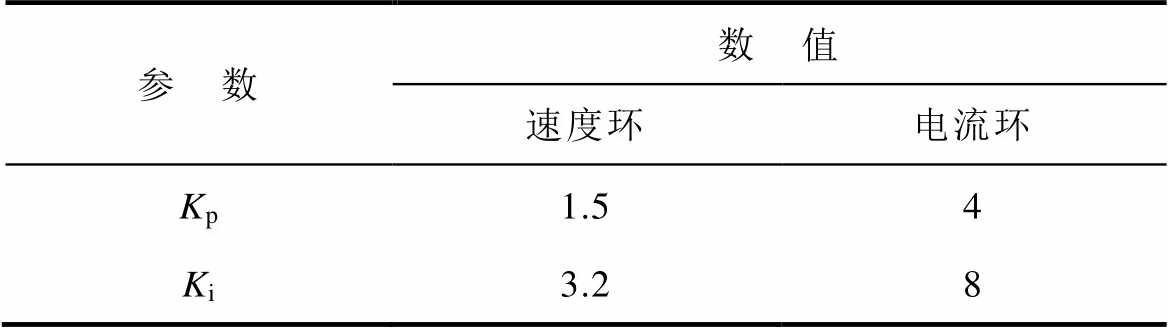
参 数数 值 速度环电流环 Kp1.54 Ki3.28
在多电机实验平台对本文所提方法与偏差耦合方法进行升降速对比实验。将3台PMSM的速度从0 r/min加速到300 r/min,运行平稳后升速到400 r/min,再降速到300 r/min。实验结果如图4所示。
根据图4a所示,采用本文所提MA-PPC方法,多电机系统中的3台PMSM都能准确无误地跟踪上所设定转速。由图4b可知,相较于PI改进的偏差耦合控制方法,本文方法的升降速过程更加平滑,没有超调现象。当多PMSM系统处于稳定运行时,由图4a和图4b可知,本文方法的振幅在0.5 r/min左右,小于PI改进的偏差耦合方法的5 r/min左右的振幅,说明相较于偏差耦合方法有更好的稳态性能。图5c的振幅在0.8 r/min左右,小于图4d 5 r/min左右的振幅。图4e升速前振幅在0.8 r/min左右,小于图4f 6 r/min左右的振幅,图4e升速后振幅在1 r/min左右,小于图4f 8 r/min左右的振幅。本文的控制方法相较于偏差耦合有更好的同步性能和跟踪性能。
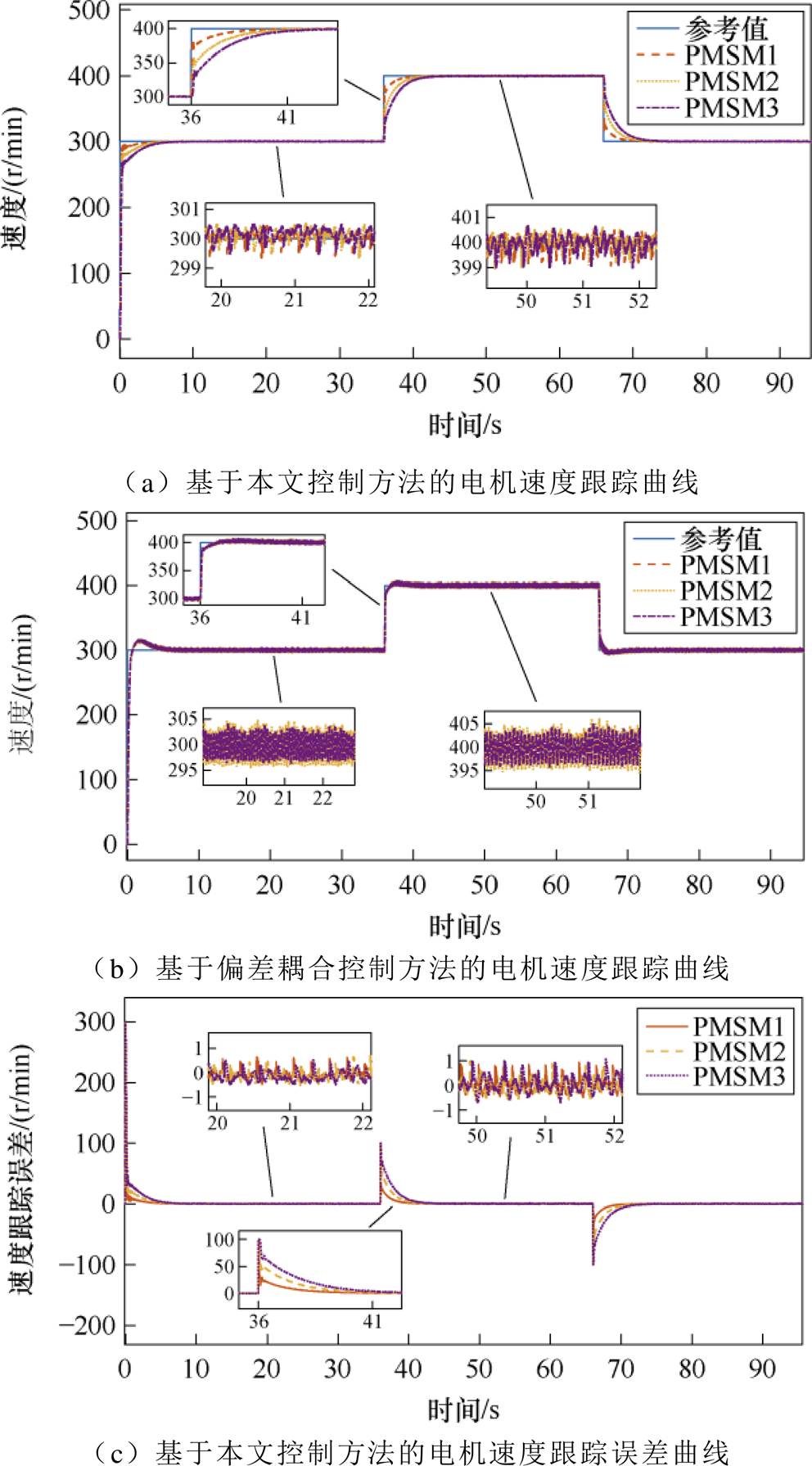
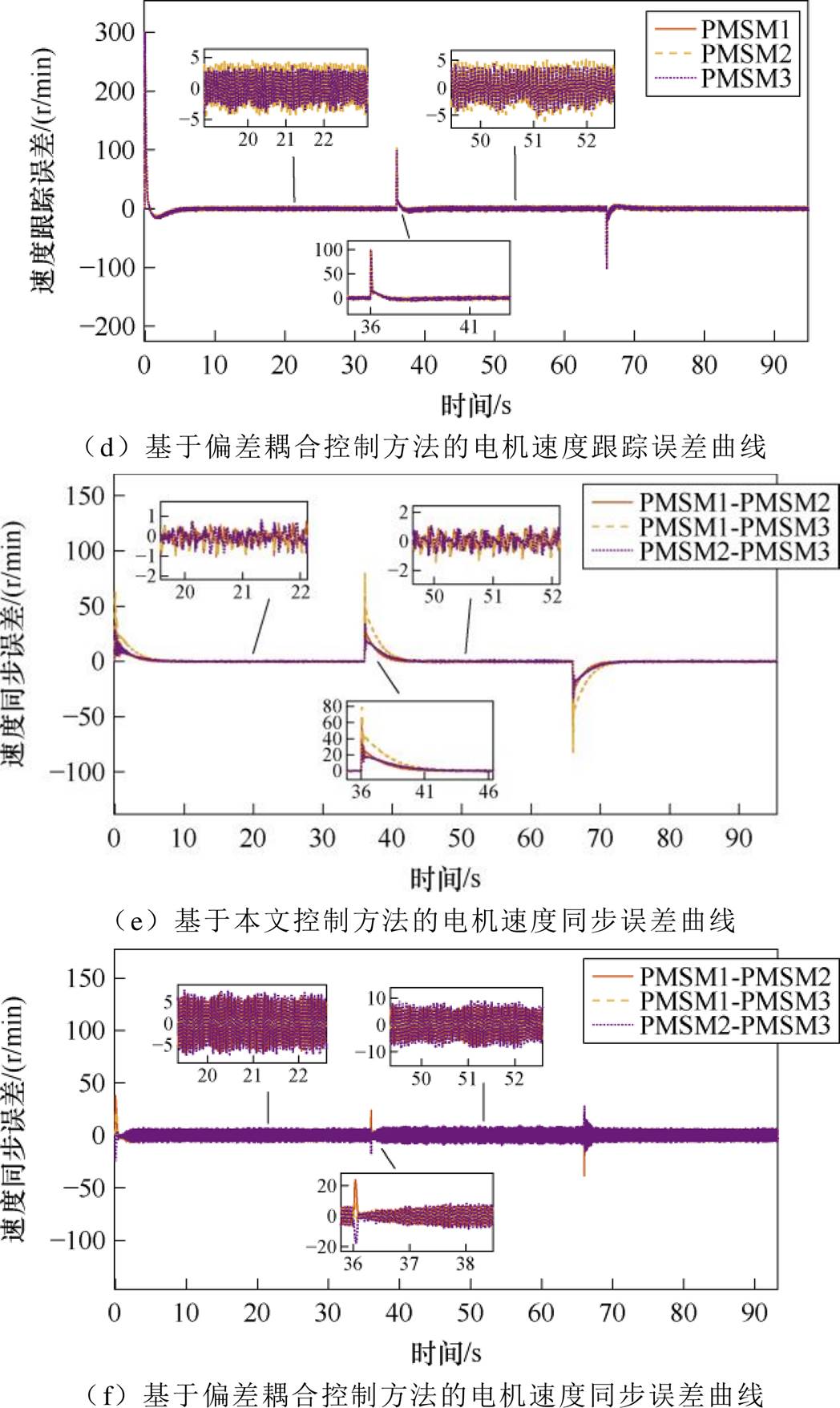
图4 多PMSM升降速实验
Fig.4 Multi-PMSM speed regulation experiments with acceleration and deceleration
在多电机实验平台对本文提出的方法和偏差耦合方法进行加减载对比实验,负载由图3所示的负载电机组所提供,以验证本文所提控制方法的鲁棒性。多电机调速系统从初始速度0 r/min起动,升速到300 r/min。在20、45、70 s分别对3台电机施加7、8、9 N·m的负载,在35、60、85 s移除负载。在95 s向3台电机同时施加7 N·m的负载,在110 s移除负载。实验结果如图5所示。
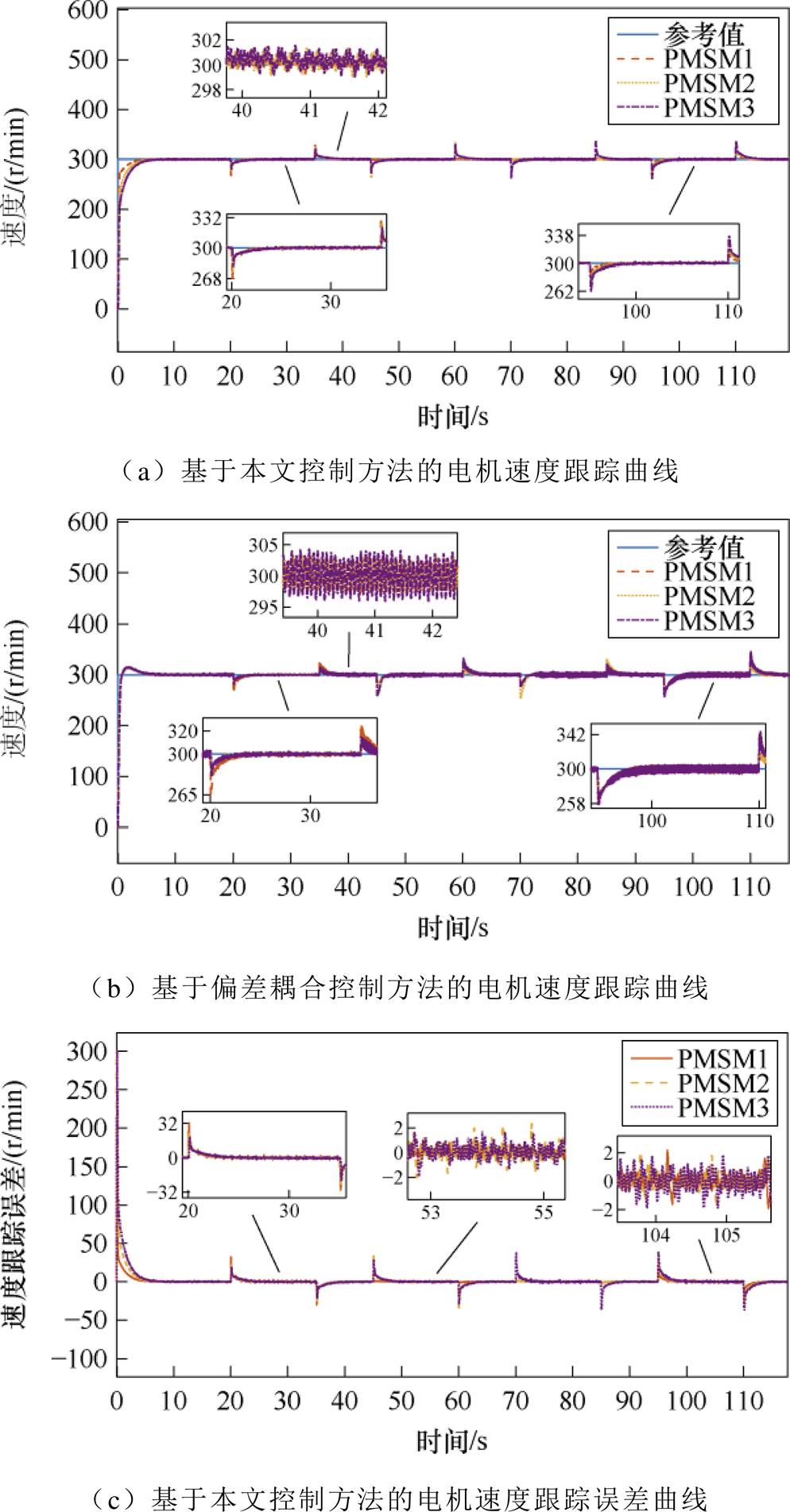
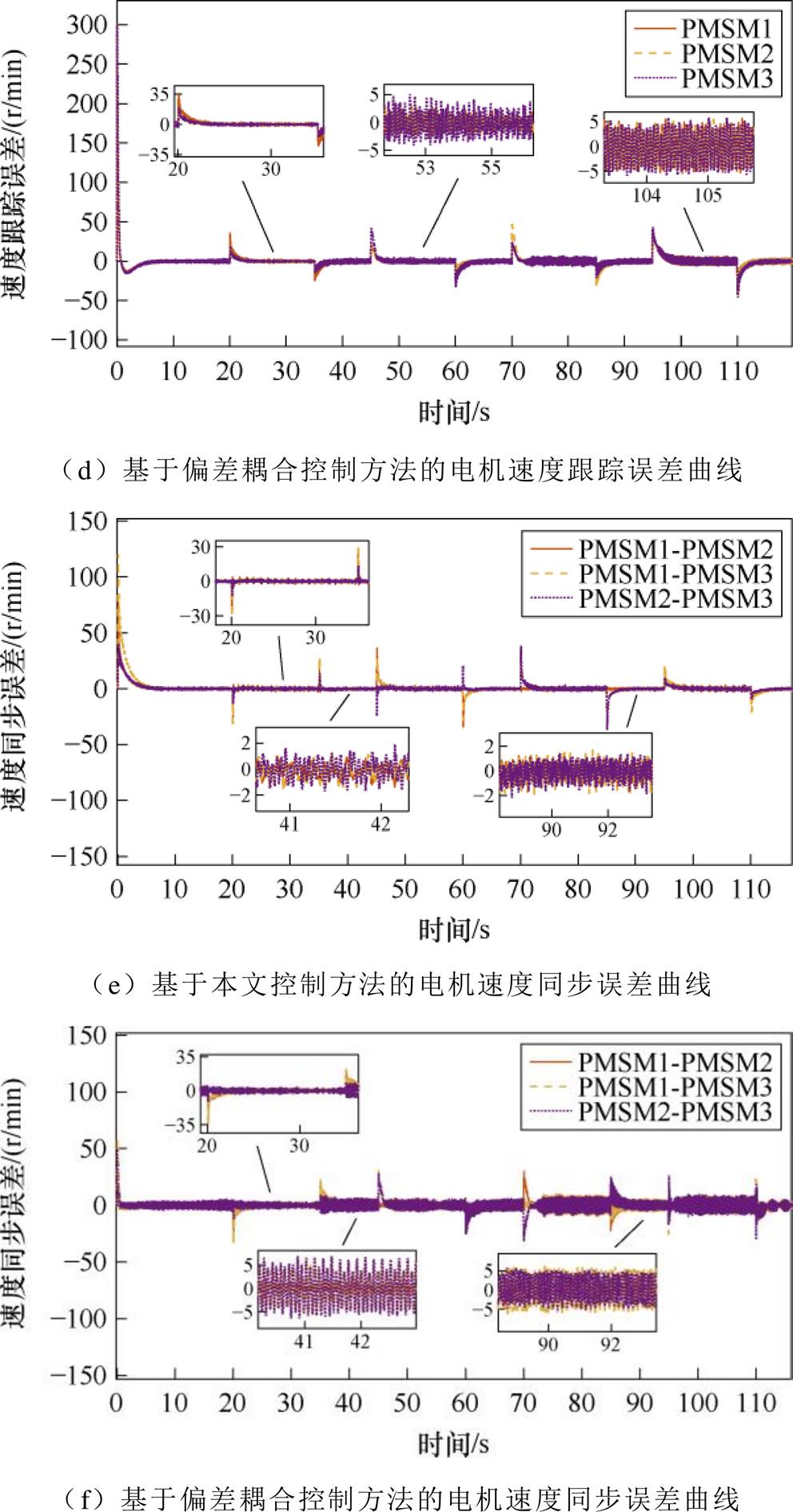
图5 多PMSM加减载实验
Fig.5 Multi-PMSM loading and unloading experiment
如图5所示,当出现负载扰动的情况下,两种控制方法都能在短时间内回到设定的转速。如图5a所示,本文控制方法稳态时振幅为1 r/min左右,小于如图5b所示的PI改进的偏差耦合方法的5 r/min左右的振幅,由此可知,本文所提方法的稳态性能优于偏差耦合方法。当对3台电机在不同时刻施加不同负载扰动时,图5a的转速变化量为32 r/min,而图5b的转速变化量为35 r/min,当向3台电机在相同时刻突加相同负载扰动时,图5a的转速变化量为38 r/min,而图5b的转速变化量为42 r/min,本文所提方法在突加负载时的瞬态性能优于偏差耦合方法。图5c稳态时2 r/min左右的振幅小于图5d稳态时5 r/min左右的振幅。图5e稳态时2 r/min左右的振幅小于图5f稳态时5 r/min左右的振幅。综上所述,本文所设计的控制方法相较于PI改进的偏差耦合方法有更好的鲁棒性。
在多电机实验平台对本文提出的方法和偏差耦合方法进行正反转对比实验,以验证本文所提控制方法的灵活性,将多电机调速系统从初始速度0 r/min起动,升速到300 r/min,然后反转到-300 r/min。从图6a和图6b的对比中可以看到,本文提出的方法没有超调现象,进行反转的过程更加平稳。振幅0.8 r/min,小于振幅4 r/min,说明本文的控制方法的稳态性能优于偏差耦合方法。图6c的稳态误差在0.8 r/min左右,小于图6d 5 r/min左右的稳态误差。图6e的同步误差在1 r/min左右,小于图6f的5 r/min左右的同步误差。说明本文控制方法的跟踪性能和同步性能优于偏差耦合方法。
综上所述,三组对比实验充分验证了本文所提控制方法相较于PI改进的偏差耦合控制方法具有更好的同步性、灵活性和鲁棒性。
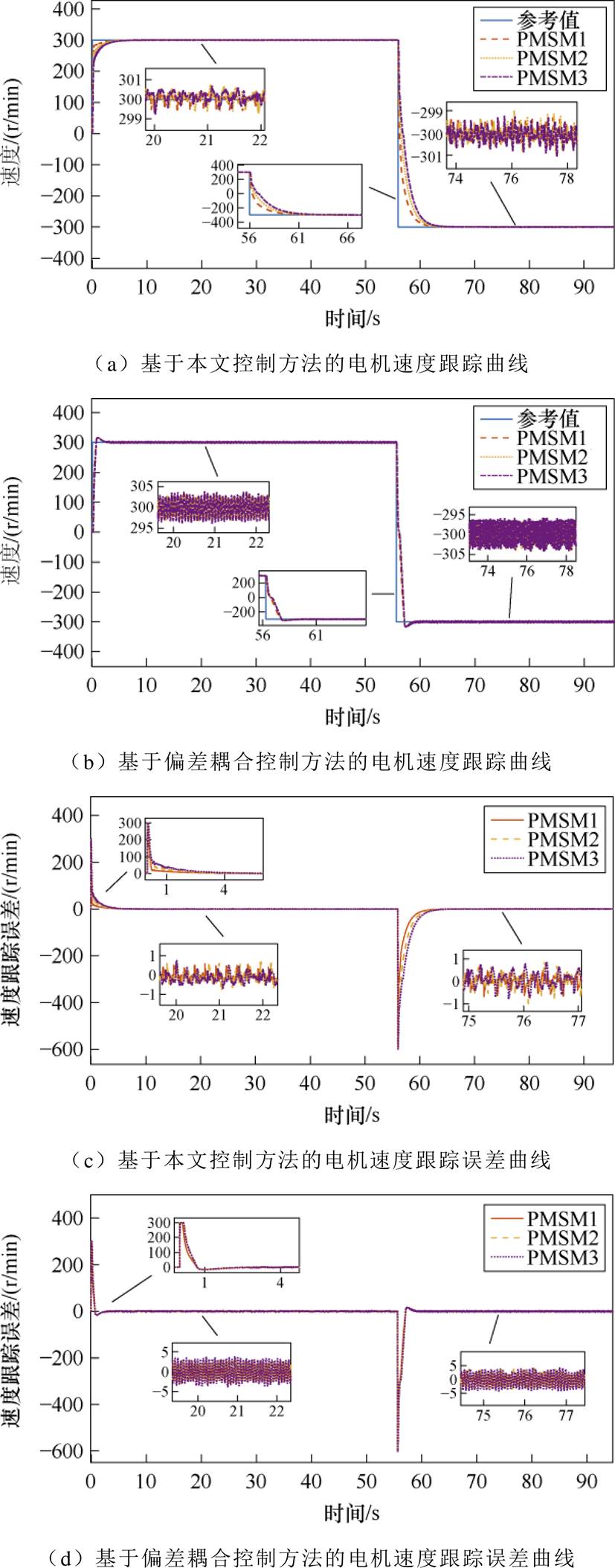
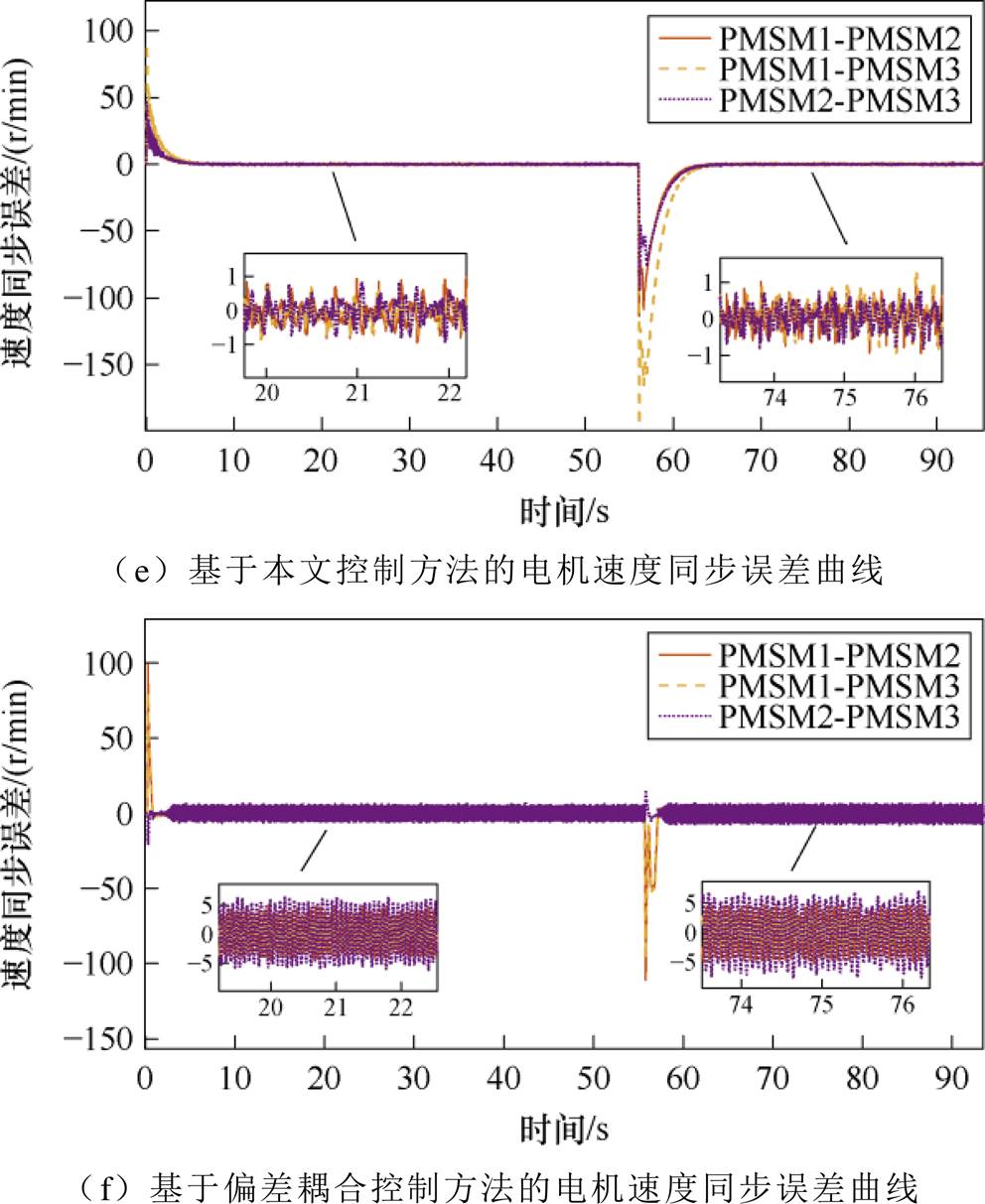
图6 多PMSM正反转实验
Fig.6 Multi-PMSM forward and reverse experiments
本文针对多PMSM调速系统的速度一致性协同控制问题,提出了一种基于PPC的多PMSM速度一致性控制方法。本文的主要贡献如下:
1)相较于传统控制方法,多PMSM的多智能体系统分布式一致性控制结构提高了系统的灵活性和鲁棒性。
2)提出基于PPC的PMSM多智能体系统速度一致性控制协议,提高了系统的瞬态和稳态性能。
3)引入STESO来估计系统干扰,从而使系统更具鲁棒性。
未来的研究工作将考虑当多电机系统出现延时、丢包或者网络拓扑改变情况下的多电机多智能体系统的速度一致性控制问题。
参考文献
[1] 赵凯辉, 刘文昌, 刘智诚, 等. 一种永磁同步电机无模型高阶滑模控制算法[J]. 电工技术学报, 2023, 38(6): 1472-1485.
Zhao Kaihui, Liu Wenchang, Liu Zhicheng, et al. Model-free high sliding mode control for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1472-1485.
[2] 于林鑫, 袁昕, 丁国华, 等. 基于模型预测锁相环的永磁同步电机转子位置估计方法[J]. 电气技术, 2024, 25(8): 18-26, 52.
Yu Linxin, Yuan Xin, Ding Guohua, et al. Research on sensorless control of permanent magnet syn- chronous motor based on model predictive method based phase locked loop[J]. Electrical Engineering, 2024, 25(8): 18-26, 52.
[3] 刘蔚, 李万铨, 王明峤, 等. 复杂工况下的永磁同步电机典型绕组故障在线诊断[J]. 电工技术学报, 2024, 39(6): 1764-1776.
Liu Wei, Li Wanquan, Wang Mingqiao, et al. Online diagnosis of typical winding faults in permanent magnet synchronous motors under complex working conditions[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1764-1776.
[4] 余洋, 张千慧, 余宗哲, 等. 基于反推控制的永磁同步电机稳定性单矢量控制策略[J]. 电工技术学报, 2024, 39(14): 4377-4390.
Yu Yang, Zhang Qianhui, Yu Zongzhe, et al. Stable single vector control strategy of permanent magnet synchronous motor based on backstepping control[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4377-4390.
[5] 倪未希, 刘宇阳, 陈俐. 散热工况下永磁同步电机转子温度的卷积神经网络预测[J]. 电机与控制学报, 2025, 29(1): 15-24, 36.
Ni Weixi, Liu Yuyang, Chen Li. Rotor temperature prediction of PMSM under cooling conditions using convolutional neural network[J]. Electric Machines and Control, 2025, 29(1): 15-24, 36.
[6] 陈瑞, 吴悠, 杜荣华, 等. 一种基于特征模型的永磁同步电机协调控制策略[J]. 电气工程学报, 2025, 20(1): 54-64.
Chen Rui, Wu You, Du Ronghua, et al. A coordinated control strategy for the permanent magnet syn- chronous motor based on the characteristic model[J]. Journal of Electrical Engineering, 2025, 20(1): 54- 64.
[7] 谷鑫, 鲁金月, 王志强, 等. 基于无差拍电流预测控制的永磁同步电机谐波电流抑制策略[J]. 电工技术学报, 2022, 37(24): 6345-6356.
Gu Xin, Lu Jinyue, Wang Zhiqiang, et al. Harmonic current suppression strategy for permanent magnet synchronous motor based on deadbeat current predi- ction control[J]. Transactions of China Electro- technical Society, 2022, 37(24): 6345-6356.
[8] 赵晨辉. 基于永磁同步电机驱动的刮板输送机功率平衡控制[J]. 机械管理开发, 2024, 39(8): 212- 214.
Zhao Chenhui. Power balance control of scraper conveyor based on permanent magnet synchronous motor drive[J]. Mechanical Management and Develop- ment, 2024, 39(8): 212-214.
[9] 崔刚, 熊斌, 黄康杰, 等. 电动汽车用永磁电机的失磁空间分布特性及影响因素[J]. 电工技术学报, 2023, 38(22): 5959-5974.
Cui Gang, Xiong Bin, Huang Kangjie, et al. Spatial distribution characteristics and influencing factors of demagnetization of permanent magnet motor for electric vehicle[J]. Transactions of China Electro- technical Society, 2023, 38(22): 5959-5974.
[10] 关涛, 刘大猛, 何永勇. 永磁轮毂电机技术发展综述[J]. 电工技术学报, 2024, 39(2): 378-396.
Guan Tao, Liu Dameng, He Yongyong. Review on development of permanent magnet in-wheel motors[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 378-396.
[11] 王柄东, 王道涵, 王晓姬, 等. 交流调磁型永磁同步电机磁通协同调控最大转矩铜耗比控制[J]. 电工技术学报, 2024, 39(12): 3630-3645.
Wang Bingdong, Wang Daohan, Wang Xiaoji, et al. A maximum torque per copper loss control for AC flux-regulation permanent magnet synchronous motor with magnetic flux co-regulation[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3630- 3645.
[12] 王力新, 王晓远, 高鹏, 等. 电动汽车用内置式永磁同步电机转矩脉动分析及抑制[J]. 电工技术学报, 2024, 39(20): 6386-6396.
Wang Lixin, Wang Xiaoyuan, Gao Peng, et al. Torque ripple reduction analysis of interior permanent magnet synchronous motor for electric vehicle[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(20): 6386-6396.
[13] 陆秋瑜, 戴耀辉, 杨银国, 等. 适用于孤岛运行的永磁同步电机自动功率平衡控制策略研究[J]. 电工技术学报, 2023, 38(22): 6150-6164.
Lu Qiuyu, Dai Yaohui, Yang Yinguo, et al. Novel autonomous power balance control for PMSG based wind turbine in stand alone operation[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6150-6164.
[14] 夏长亮, 李莉, 谷鑫, 等. 双永磁电机系统转速同步控制[J]. 电工技术学报, 2017, 32(23): 1-8.
Xia Changliang, Li Li, Gu Xin, et al. Speed synchronization control of dual-PMSM system[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 1-8.
[15] 白梓岑, 陈少华. 数控机床伺服驱动系统的多电机同步控制策略[J]. 电机与控制应用, 2024, 51(3): 95-107.
Bai Zicen, Chen Shaohua. Multi-motor synchroni- zation control strategy for servo drive system of CNC machine tools[J]. Electric Machines & Control Appli- cation, 2024, 51(3): 95-107.
[16] 叶宇豪, 彭飞, 黄允凯. 多电机同步运动控制技术综述[J]. 电工技术学报, 2021, 36(14): 2922- 2935.
Ye Yuhao, Peng Fei, Huang Yunkai. Overview of multi-motor synchronous motion control techno- logy[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2922-2935.
[17] 鲍晓明, 林涛, 郑晓翔, 等. 双电机同步控制技术综述[J]. 微特电机, 2024, 52(8): 68-73.
Bao Xiaoming, Lin Tao, Zheng Xiaoxiang, et al. Review of dual-motor synchronous control tech- nology[J]. Small & Special Electrical Machines, 2024, 52(8): 68-73.
[18] 赵宏英, 曾彦, 廖丽. 基于改进交叉耦合的多永磁同步电机速度同步控制[J]. 机床与液压, 2021, 49(22): 44-51.
Zhao Hongying, Zeng Yan, Liao Li. Speed syn- chronous control of multiple permanent magnet synchronous motors based on an improved cross- coupling structure[J]. Machine Tool & Hydraulics, 2021, 49(22): 44-51.
[19] 冯晗, 杜钦君, 徐东祥, 等. 基于均值偏差耦合的多电机同步预测控制[J]. 仪表技术与传感器, 2024(8): 84-92.
Feng Han, Du Qinjun, Xu Dongxiang, et al. Multi- motor synchronized predictive control based on mean deviation coupling[J]. Instrument Technique and Sensor, 2024(8): 84-92.
[20] 李宝, 王鹤, 张勇. 基于狼群优化的偏差耦合结构在多电机速度同步控制仿真[J]. 电子制作, 2024, 32(14): 85-87.
Li Bao, Wang He, Zhang Yong. Simulation of deviation coupling structure based on wolves opti- mization in multi-motor speed synchronization control[J]. Practical Electronics, 2024, 32(14): 85- 87.
[21] 刘凡, 杨洪勇, 杨怡泽, 等. 带有不匹配干扰的多智能体系统有限时间积分滑模控制[J]. 自动化学报, 2019, 45(4): 749-758.
Liu Fan, Yang Hongyong, Yang Yize, et al. Finite- time integral sliding-mode control for multi-agent systems with mismatched disturbances[J]. Acta Auto- matica Sinica, 2019, 45(4): 749-758.
[22] 王卓, 秦博东, 徐雍, 等. 复杂无向网络连通性的一种高效判定算法[J]. 自动化学报, 2020, 46(10): 2129-2136.
Wang Zhuo, Qin Bodong, Xu Yong, et al. An efficient algorithm for determining the connectivity of complex undirected networks[J]. Acta Automatica Sinica, 2020, 46(10): 2129-2136.
[23] Duan Dandan, Liu Chunsheng, Dai Jiao, et al. Neural network-based optimal fault compensation control of the nonlinear multi-agent system and its application to UAVs formation flight[J]. Proceedings of the Insti- tution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2023, 237(9): 1635-1644.
[24] Prieto S A, Giakoumidis N, García de Soto B. Multiagent robotic systems and exploration algo- rithms: applications for data collection in con- struction sites[J]. Journal of Field Robotics, 2024, 41(4): 1187-1203.
[25] 高振宇, 孙振超, 郭戈. 考虑执行器非线性的固定时间全局预设性能车辆队列控制[J]. 自动化学报, 2024, 50(2): 320-333.
Gao Zhenyu, Sun Zhenchao, Guo Ge. Fixed-time global prescribed performance control for vehicular platoons with actuator nonlinearities[J]. Acta Auto- matica Sinica, 2024, 50(2): 320-333.
[26] Liu Haitao, Huang Xiuying, Tian Xuehong, et al. Adaptive intelligent formation control for multiple underactuated surface vessels with prescribed perfor- mance[J]. Ocean Engineering, 2024, 296: 116859.
[27] 马悦萌, 刘明, 杨丁, 等. 热约束下近空间飞行器预设性能抗噪控制[J]. 航空学报, 2023, 44(增刊2): 28-40.
Ma Yuemeng, Liu Ming, Yang Ding, et al. Prescribed performance and anti-noise control of near space vehicle with thermal constraint[J]. Acta Aeronautica et Astronautica Sinica, 2023, 44(S2): 28-40.
[28] Wang Hongwei, Dai Honghua, Yue Xiaokui, et al. Prescribed performance based adaptive model-free control for highly flexible spacecraft detumbling rotating satellites[J]. Advances in Space Research, 2024, 74(5): 2288-2301.
[29] 龚凯, 贾英民. 空间机器人预设性能约束下的鲁棒跟踪控制[J]. 控制理论与应用, 2024, 41(7): 1246- 1254.
Gong Kai, Jia Yingmin. Robust tracking control of space robots with prescribed performance[J]. Control Theory & Applications, 2024, 41(7): 1246-1254.
[30] Bechlioulis C P, Rovithakis G A. Decentralized robust synchronization of unknown high order non- linear multi-agent systems with prescribed transient and steady state performance[J]. IEEE Transactions on Automatic Control, 2017, 62(1): 123-134.
[31] Song Jun, Zheng Wei Xing, Niu Yugang. Self- triggered sliding mode control for networked PMSM speed regulation system: a PSO-optimized super- twisting algorithm[J]. IEEE Transactions on Indu- strial Electronics, 2022, 69(1): 763-773.
[32] 刘伟民, 王永越, 马欣阳, 等. 输入时滞多智能体系统的输入受限一致性控制[J]. 系统工程与电子技术, 2024, 46(9): 3176-3184.
Liu Weimin, Wang Yongyue, Ma Xinyang, et al. Consensus control for input-delay multi-agent system with input constraint[J]. Systems Engineering and Electronics, 2024, 46(9): 3176-3184.
[33] Zhao Ling, Zheng Chengfei, Wang Yingjie, et al. A finite-time control for a pneumatic cylinder servo system based on a super-twisting extended state observer[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(2): 1164-1173.
The proposed method effectively achieves speed consensus control in multi-PMSM regulation systems, demonstrating significant improvements in synchronization accuracy, flexibility, and robustness against external disturbances.
Abstract In the multi-permanent magnet synchronous motor (multi-PMSM), the speed regulation system’s speed synchronization accuracy is critical for production efficiency and equipment stability. To enhance the performance of coordinated speed control in multi-motor systems, this paper proposes a speed consensus control method for multi-PMSM systems based on prescribed performance control (PPC).
Multi-agent systems (MAS) collaborative control, owing to its architectural flexibility, system reconfigurability, and inherent distributed robustness, has shown significant potential in collective decision- making and coordinated optimization for complex industrial systems. Given the marked resemblance between multi-PMSMs coordinated speed regulation mechanisms and MAS collaborative control, this paper innovatively introduces the MAS consensus control paradigm into speed consensus control of multi-PMSMs. Specifically, by conceptualizing each PMSM speed regulation system as an agent and establishing information exchange among motor speed control systems through communication topology networks, the multi-PMSM speed synchronization challenge is transformed into a MAS consensus control problem. A distributed consensus control protocol is designed to guarantee speed coordination convergence across multiple PMSMs.
The paper first formulates the speed consensus control problem for multi-PMSM systems within the theoretical framework of MAS. Subsequently, a PPC-based consensus control protocol is designed for the multi-PMSMs speed consensus control system, in which explicit constraints on transient and steady-state processes are predefined to improve synchronization. Concurrently, a super-twisting extended state observer (STESO) is introduced to estimate system disturbances, with real-time compensation integrated into the consensus control protocol, thereby significantly improving closed-loop robustness. Comparative experimental verification is conducted on a multi-motor speed regulation and loading comprehensive experimental platform under diverse operating conditions.
The experimental protocol includes (1) speed increase and decrease, (2) load addition and subtraction, and (3) forward and reverse rotation. The acceleration and deceleration experiments demonstrate that the proposed method achieves a steady-state amplitude of approximately 0.5 r/min during steady-state operation. The PI-enhanced relative coupling control (RCC) method is around 5 r/min. The tracking error amplitude of the proposed method is approximately 0.8 r/min, significantly smaller than that of the RCC method. Furthermore, the synchronization error amplitudes before and after speed ramping are around 0.8 r/min and 1 r/min, respectively, whereas the RCC method’s synchronization error amplitudes are 6 r/min and 8 r/min. The load variation experiments demonstrate that under the proposed control scheme, the speed variation is approximately 32 r/min when different loads are applied at various times and around 38 r/min when the same load is applied simultaneously. The speed quickly recovers to 300 r/min, with post-recovery tracking and synchronization errors maintained at about 2 r/min. In contrast, under the RCC method, the speed variation is 35 r/min for different loads and approximately 42 r/min for the same load, with post-recovery tracking and synchronization errors around 5 r/min. The forward and reverse experiments show that the proposed method’s stable tracking and synchronization errors are approximately 0.8 r/min, significantly lower than the errors of roughly 5 r/min with the RCC method.
keywords:Multi-permanent magnet synchronous motors (PMSMs), multi-agent, prescribed performance control, super-twisting extended state observer
DOI: 10.19595/j.cnki.1000-6753.tces.242219
中图分类号:TM351
国家自然科学基金项目(52177047, 62173171)和葫芦岛市科技计划项目(2024JH(2)2/05b)资助。
收稿日期 2024-12-10
改稿日期 2025-01-13
李逃昌 男,1983年生,讲师,研究方向为电力电子与电力传动,智能运动与机器人控制。E-mail: litaochang@163.com(通信作者)
丛树源 男,2000年生,硕士研究生,研究方向为电力电子与电力传动、多智能体系统一致性控制。E-mail: csy20000403@163.com
(编辑 崔文静)