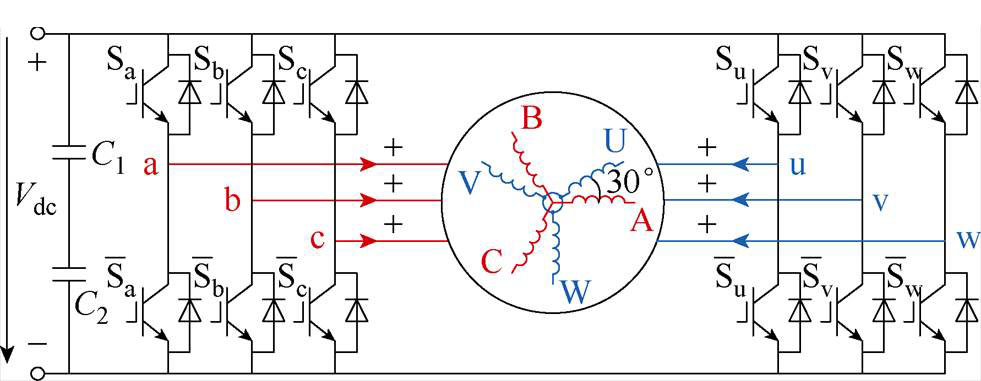
图1 DTP-PMSM驱动系统拓扑结构
Fig.1 Topological structure of dual three-phase permanent magnet synchronous motor drive system
摘要 双三相永磁同步电机(DTP-PMSM)多矢量模型预测电流控制(MPCC)可以解决单矢量MPCC存在的电流和转矩谐波问题。但是传统DTP-PMSM多矢量MPCC仍然具有计算负担重、易受非理想因素影响和xy平面电流谐波大的问题。为此,该文提出一种基于xy平面闭环电流控制的DTP-PMSM改进多矢量MPCC策略。首先采用广义比例积分观测器(GPIO)观测集总扰动并更新预测模型,提高ab 平面电流的控制性能。然后采用ab 平面最外层基本电压矢量合成xy平面的虚拟电压矢量,在不引入额外电压矢量的前提下,实现对xy平面电流的闭环控制,并推导得到脉冲信号的开关序列以及各矢量的作用时间。实验结果表明,所提方法不仅能够减少控制算法的计算时间,提升ab 平面电流的控制性能,还能抑制xy平面谐波电流。同时,该文所提出的xy平面闭环电流控制策略不影响ab 平面MPCC的性能。
关键词:双三相永磁同步电机 模型预测电流控制 谐波电流抑制 多虚拟电压矢量优化
双三相永磁同步电机(Dual Three Phase-Permanent Magnet Synchronous Motor, DTP-PMSM)具有驱动电压低、转矩密度高、容错能力强、转矩纹波小等优点[1-2],在电动汽车、舰船推进、航空航天和风力发电系统等领域具有广泛的应用前景[3-4]。相比于磁场定向控制和直接转矩控制等传统电机控制方法,有限集模型预测电流控制(Model Predictive Current Control, MPCC)具有更快速的动态响应能力,以及多控制目标的处理能力,近几年得到了国内外学者的广泛关注与研究[5-8]。
DTP-PMSM有限集MPCC存在以下问题:①MPCC的离散特性使其难以输出最优的ab平面电压,限制了转矩和电流的控制性能;②电机运行过程中电机参数改变及其他非线性扰动会影响电流的控制性能,导致定子电流出现稳态误差。针对ab平面下最优电压矢量难以输出的问题,国内外学者相继提出了扩展矢量控制集[9-10]、双矢量MPCC[11-12]、多矢量MPCC[13]等方法,以扩大ab平面输出电压范围,提升转矩和电流的控制性能。然而,以上方法不仅计算负担较大,并且控制脉冲的产生过程也较为复杂,难以广泛应用于DTP-PMSM驱动系统。针对参数变化及其他非线性扰动影响电流控制性能的问题,国内外学者提出了参数辨识[14]、相电流测量及电流差更新[15]、机器学习[16-17]等方法,以提升三相电机模型预测电流控制的鲁棒性。但由于计算量大、算法调节过程复杂等原因,以上方法难以应用于DTP-PMSM驱动系统。为此,文献[18]使用扩展状态观测器估计集总干扰,增强了鲁棒性,但由于缺乏模型特征,限制了DTP-PMSM的模型预测电流控制的动态性能。
此外,DTP-PMSM的模型预测电流控制还需要考虑xy平面的电流控制。虽然DTP-PMSM的xy平面电流不影响电机的转矩输出,但会产生额外的损耗并降低系统运行效率。针对这一问题,文献[19]通过引入xy平面电流加权项以实现xy平面电流谐波抑制。但是,该方法需要遍历的控制集元素众多,巨大的计算负担限制了控制频率和系统控制性能。文献[20]提出一种谐波平面平均电压为零的虚拟电压矢量合成方法,通过将几个基本电压矢量合成一个虚拟电压矢量,消除了xy平面电流加权项,简化了电流控制的目标函数。相比于直接使用基本电压矢量的方法,虚拟电压矢量方法不但可以有效减小由xy平面平均电压导致的谐波电流,还可以减少控制算法的计算时间。
然而,DTP-PMSM磁场定向控制中关于谐波电流抑制的研究表明:逆变器非线性、反电动势谐波、绕组不对称性等非理想因素都能够在xy平面产生丰富的谐波电流[21-22]。因此,即便使用虚拟电压矢量后,xy平面依然存在严重的谐波电流。为此,文献[23]研究了反电动势谐波对xy平面电流控制性能的影响,通过调整基本电压矢量的作用时间实现对反电动势谐波的部分补偿。但是该方法不仅需要离线获取准确的反电动势数据,还有庞大的计算量。文献[24]提出动态虚拟矢量的概念,通过不同组别的候选集切换提升了xy平面电流的控制性能。然而,该方法需要三个阶段的成本函数评估以及不少于37次的电流预测,这将耗费大量的计算时间。
综上所述,DTP-PMSM模型预测电流控制存在转矩电流控制性能差、xy平面谐波电流大、控制算法计算量大等问题。为解决上述问题,本文在传统多虚拟电压矢量MPCC的基础上,提出一种基于xy平面电流闭环控制的改进多矢量模型预测电流控制策略。首先,分析影响虚拟电压矢量MPCC性能的主要影响因素及其对dq和xy平面各自的影响程度;其次,引入广义比例积分观测器(Generalized Proportional Integral Observer, GPIO)对集总扰动进行观测,消除逆变器非线性、参数失配等对dq平面电流控制性能的影响;然后,提出一种不引入额外基本电压矢量的xy平面虚拟电压矢量合成方法,进而提出一种计算负担小且实现简单的xy平面电流闭环控制策略,削弱了逆变器非线性、反电动势谐波等因素对xy平面电流的影响;最后,通过实验验证了所提方法的有效性与正确性。
DTP-PMSM的定子绕组由中性点相互隔离的两套星形联结绕组ABC和UVW组成,两套绕组之间存在30°电角度的偏移。DTP-PMSM驱动系统由一套六相电压源型逆变器进行供电,其拓扑结构如图1所示。

图1 DTP-PMSM驱动系统拓扑结构
Fig.1 Topological structure of dual three-phase permanent magnet synchronous motor drive system
根据矢量空间分解(Vector Space Decompo- sition, VSD)理论,电机在自然坐标系下的变量可以变换到三个相互正交的平面:参与机电能量转换的ab平面以及仅产生谐波损耗的xy平面和o1o2平面。由于DTP-PMSM的中性点相互隔离,因此可以忽略电流为零的o1o2平面。对ab平面的变量进行Park变换后,可得本文所研究的表贴式DTP-PMSM在dq平面和xy平面的数学模型为
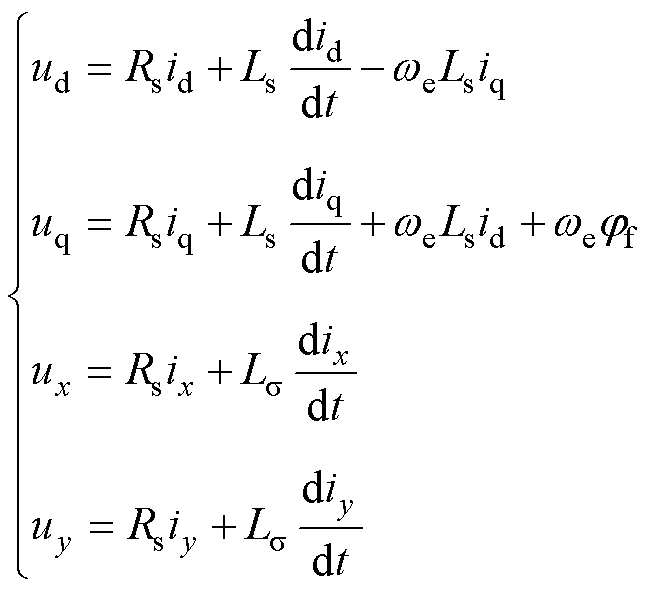 (1)
(1)
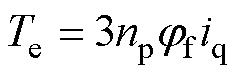 (2)
(2)
式中,ud、uq和id、iq分别为d轴和q轴上的电压和电流;ux、uy和ix、iy分别为x轴和y轴上的电压和电流;Rs为定子电阻;Ls为同步电感;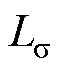 为定子漏感;
为定子漏感;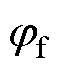 为永磁体磁链;
为永磁体磁链;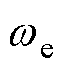 为电角速度;Te为电磁转矩;np为极对数。
为电角速度;Te为电磁转矩;np为极对数。
六相电压源型逆变器共有26=64种开关状态,每种开关状态对应一个基本电压矢量。除去4个零电压矢量(V00、V07、V70、V77),其余60个有源基本电压矢量在ab平面和xy平面的分布和作用效果如图2所示。将有源基本电压矢量按照其在ab平面幅值从大到小的顺序分为P1、P2、P3和P4这四组,当直流母线电压为Vdc时,每组电压矢量在两个空间的幅值见表1,其中P3组拥有24个有源基本电压矢量。
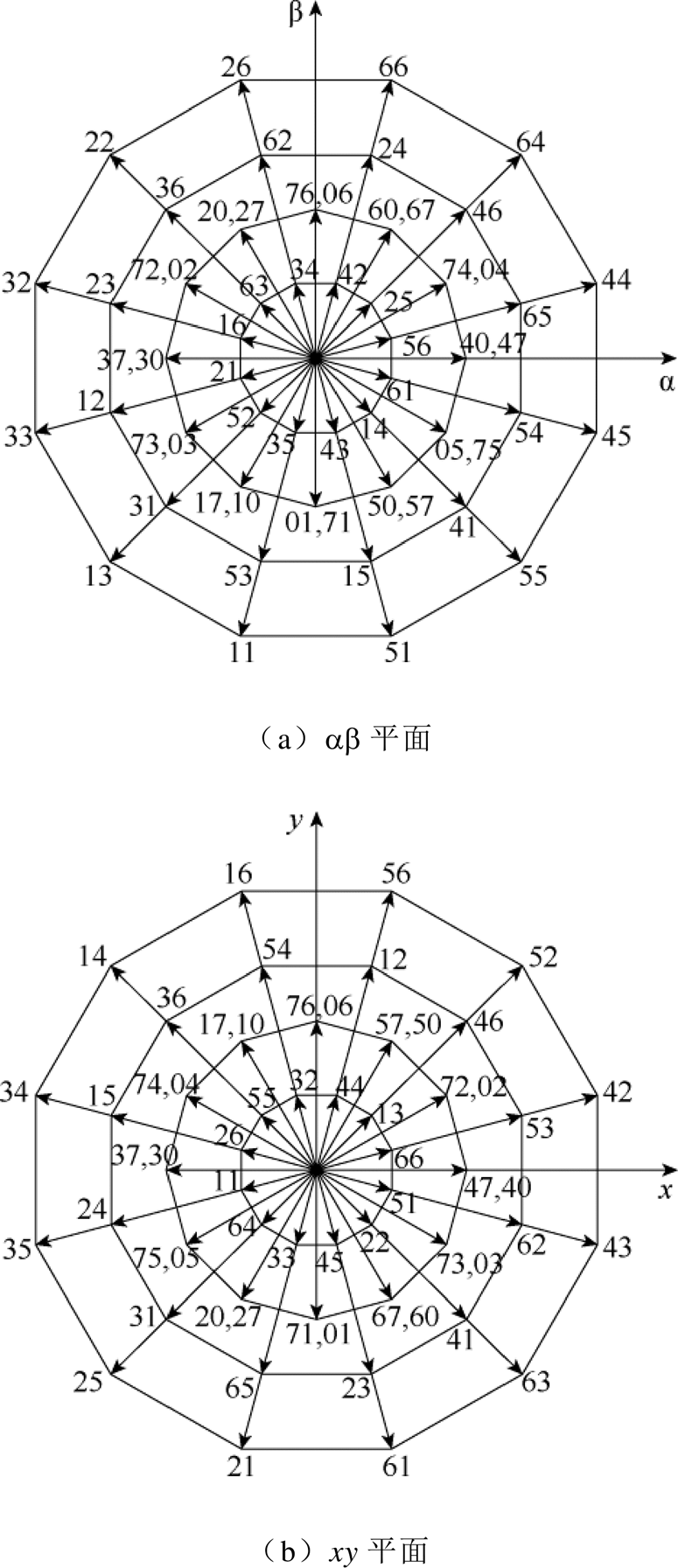
图2 基本电压矢量
Fig.2 Basic voltage vectors
表1 不同平面电压矢量幅值
Tab.1 Amplitudes of different plane voltage vectors
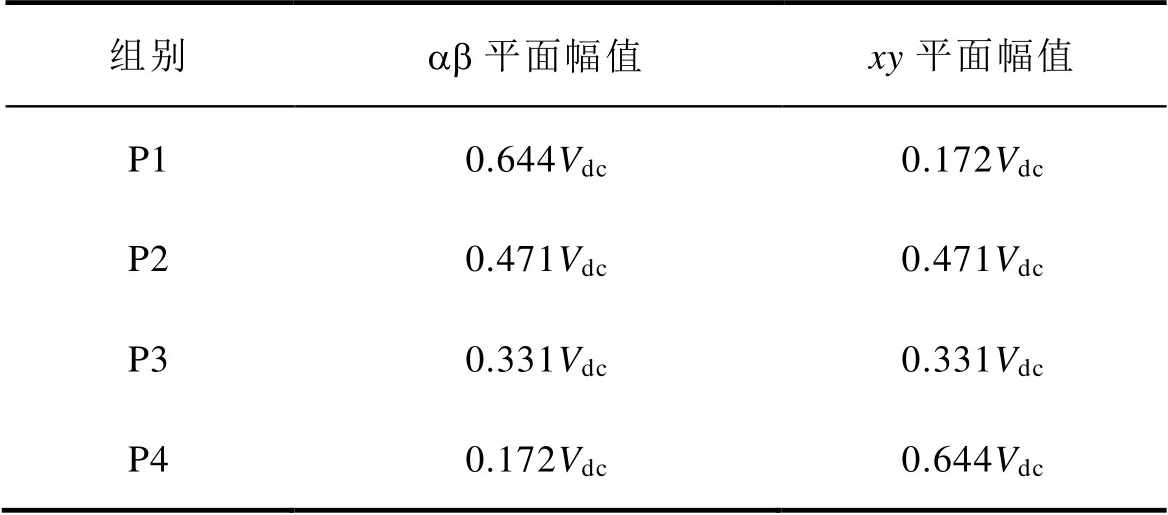
组别ab平面幅值xy平面幅值 P10.644Vdc0.172Vdc P20.471Vdc0.471Vdc P30.331Vdc0.331Vdc P40.172Vdc0.644Vdc
传统DTP-PMSM多虚拟电压矢量MPCC采用虚拟电压矢量作为控制集,对xy平面进行平均电压为零的开环控制。选择图2中ab平面方向相同的P1组和P2组基本电压矢量,根据式(3)可以合成如图3所示的12个虚拟电压矢量。
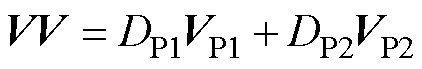 (3)
(3)
式中,VV为所合成的虚拟电压矢量;DP1为P1组矢量的占空比,DP1=0.732;DP2为P2组矢量的占空比,DP2=0.268。由于引入了P2组电压矢量,虚拟电压矢量的幅值降低为0.597Vdc。虚拟电压矢量的使用不仅可以消除xy平面的电流预测项,还可以减少所需遍历元素的数量。
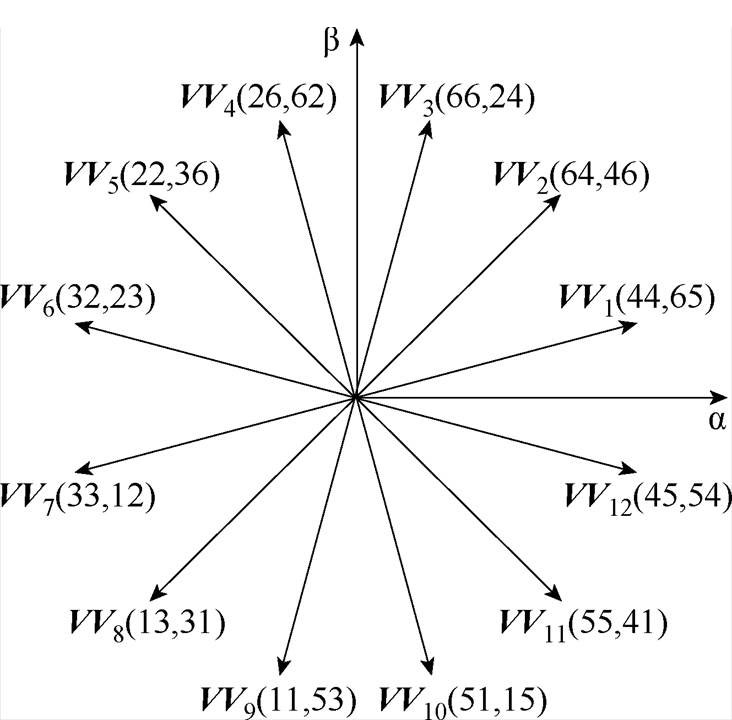
图3 虚拟电压矢量
Fig.3 Virtual voltage vectors
多矢量MPCC被应用于DTP-PMSM以提升dq平面的电压输出精度。其使用两个虚拟电压矢量和一个零电压矢量,能够任意调节输出电压矢量幅值和范围,具有理论最优的dq平面控制性能。
对式(1)中dq平面的电压方程进行前向欧拉离散化处理,可得电流预测模型为
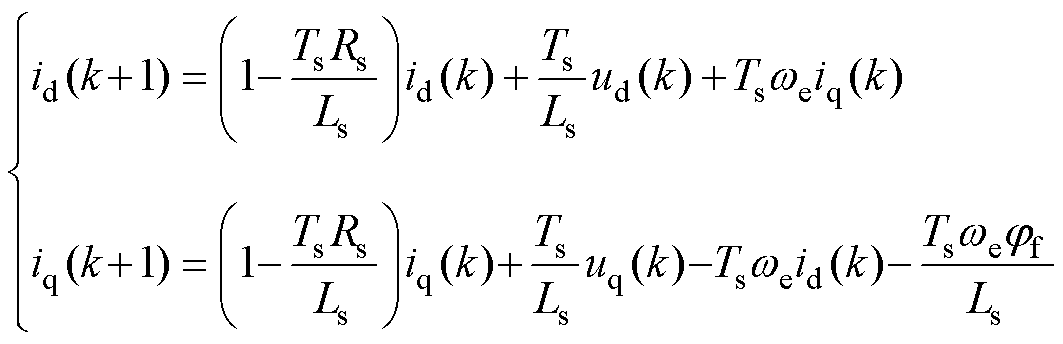 (4)
(4)
式中,id(k), iq(k)、ud(k), uq(k)分别为k时刻的d轴和q轴电流和电压;id(k+1)和iq(k+1)分别为k+1时刻d轴和q轴电流的预测值;Ts为控制周期。
考虑一步延时补偿后,k+1时刻不同电压矢量作用下的电流斜率可以表示为
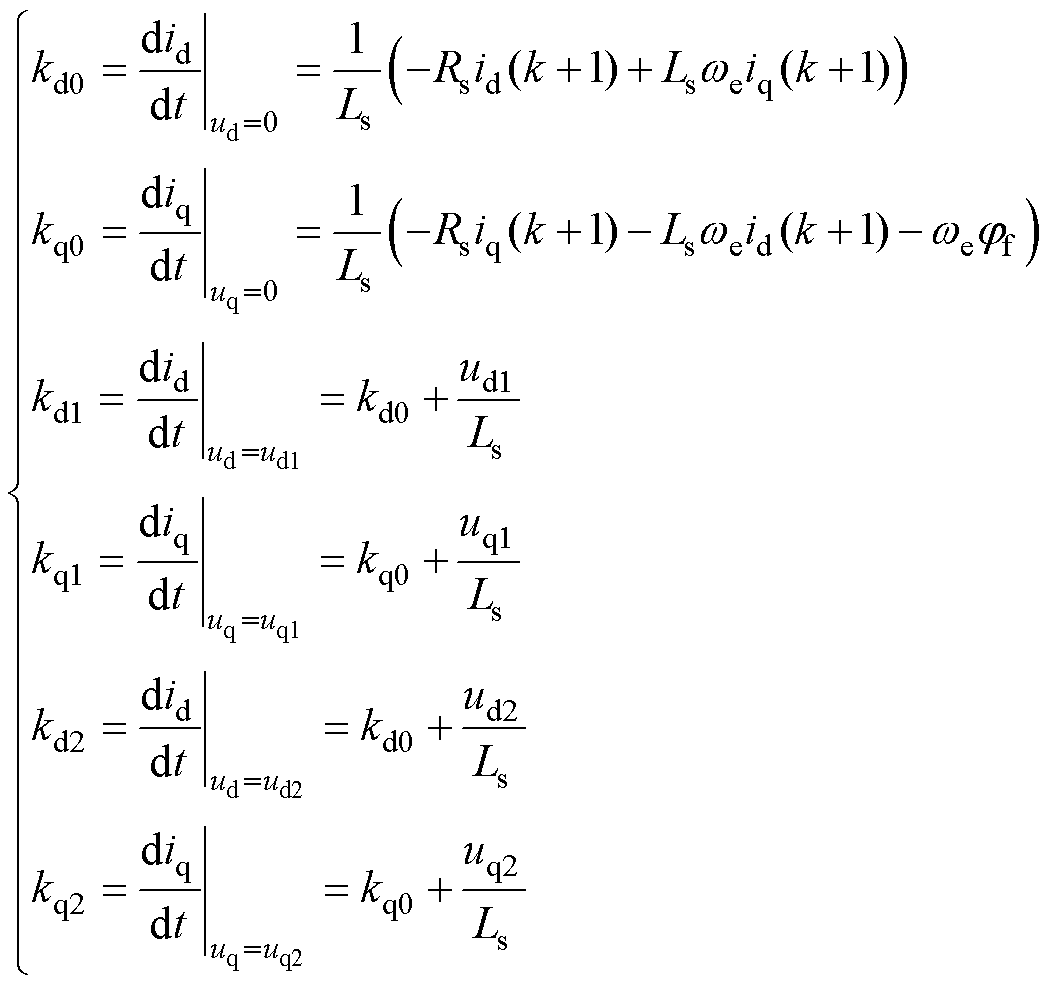 (5)
(5)
式中,ud1, uq1、ud2, uq2分别为所选取的第1、2个虚拟电压在d轴和q轴的投影;kd1, kq1、kd2, kq2、kd0, kq0分别为第1、2个虚拟电压矢量和零矢量作用时d轴和q轴的电流变化率。
以k+2时刻电流反馈等于参考为控制目标,两个虚拟电压矢量的作用时间为
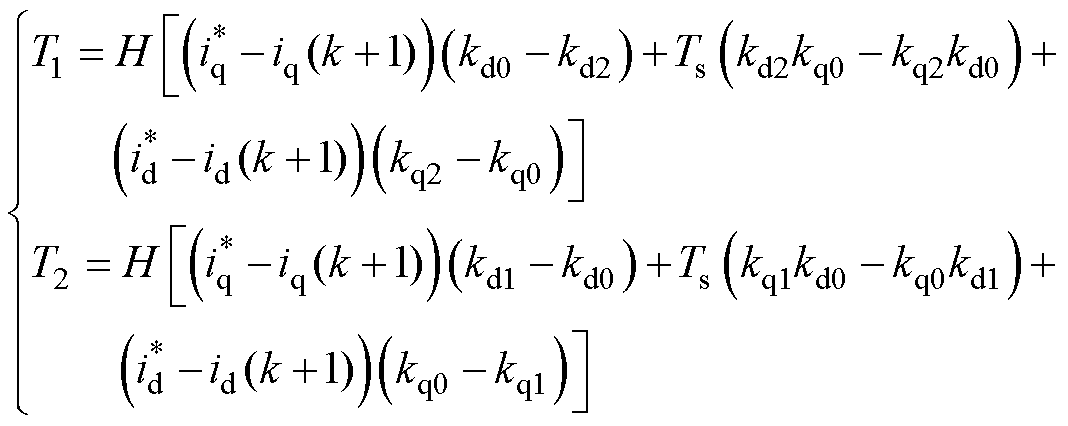 (6)
(6)
其中
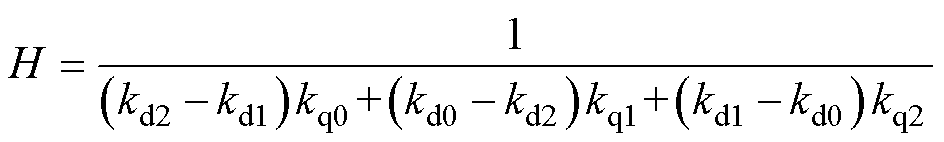
式中,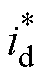 和
和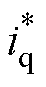 分别为d轴和q轴的参考电流;T1和T2分别为第1、2个虚拟矢量的作用时间。零矢量作用时间为t0=Ts-T1-T2。在T1和T2大于Ts时进行等比例缩小,并舍弃T1和T2计算出现负数的矢量组合方案。
分别为d轴和q轴的参考电流;T1和T2分别为第1、2个虚拟矢量的作用时间。零矢量作用时间为t0=Ts-T1-T2。在T1和T2大于Ts时进行等比例缩小,并舍弃T1和T2计算出现负数的矢量组合方案。
则第k+1个控制周期的dq平面电压可以表示为
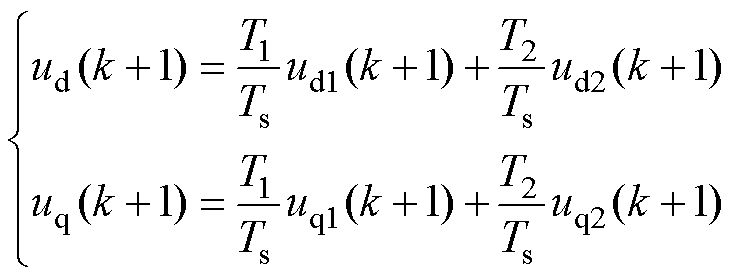 (7)
(7)
式中,ud1(k+1), uq1(k+1)、ud2(k+1), uq2(k+1)分别为在第k+1个控制周期作用的第1、2个虚拟电压矢量在d轴和q轴的电压投影。
通过式(7)可获得不同组合下k+1控制周期的d轴和q轴输出电压。将其代入延时补偿后的预测模型,根据式(8)所示的价值函数获得最佳虚拟电压矢量组合及其作用时间。
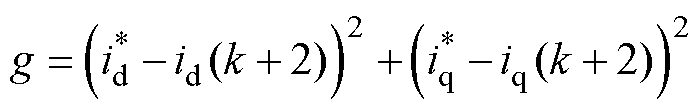 (8)
(8)
式中,id(k+2)和iq(k+2)分别为考虑延时补偿后k+2时刻d轴和q轴的电流预测值。
多矢量模型预测电流控制的控制框图如图4所示。首先,对k时刻d轴和q轴采样电流并进行一步延时补偿预测k+1时刻定子电流,将虚拟电压矢量代入预测模型并利用代价函数得到第一个最优虚拟电压矢量VVopt1。然后将其与所有虚拟电压矢量组合,根据电流斜率获取各种组合下VVopt1和另一个虚拟电压矢量的作用时间,以及合成的dq平面电压。接下来根据不同组合的合成dq平面电压预测k+2时刻电流,并根据价值函数选出最优电压组合VVopt1和VVopt2及其作用时间T1、T2。最后,使用最优电压矢量VVopt1、VVopt2以及一个零电压矢量生成控制逆变器的脉冲信号。
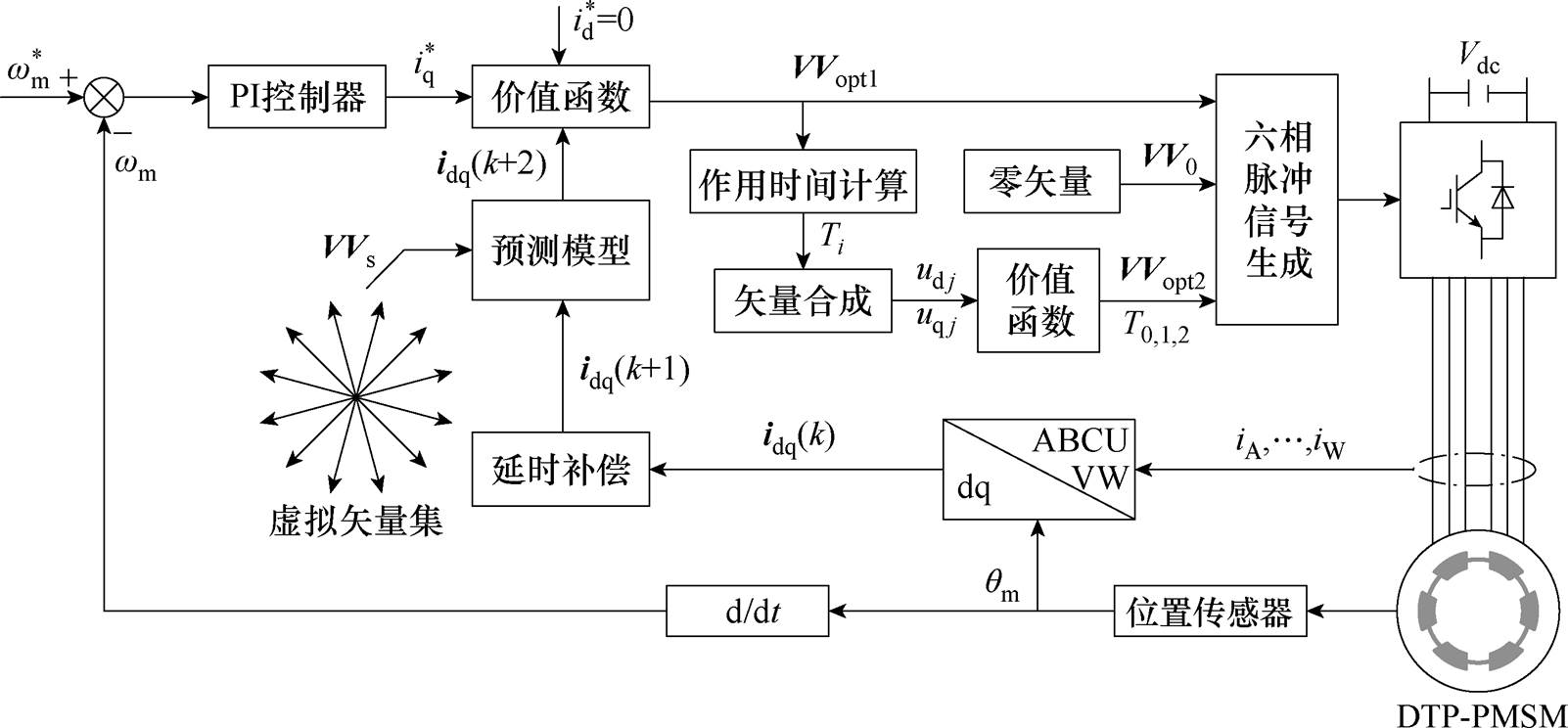
图4 多虚拟电压矢量模型预测电流控制
Fig.4 Multiple virtual voltage vector models predict current control
在实际驱动器中,死区时间、开关器件压降、二极管压降等非线性特性会导致逆变器输出电压发生畸变。DTP-PMSM多虚拟电压矢量MPCC由逆变器非线性引起的电压误差均值可以近似[25]表示为
 (9)
(9)
式中,DVp_dead为p相由逆变器非线性导致的误差电压平均值;ip为p相电流值;Vdead为由逆变器非线性引起的畸变电压幅值。通过傅里叶级数展开,DVp_dead可以分解为一系列正弦分量的总和。同时,当采取d轴电流为零的控制策略时,dq平面电流矢量与q轴重合,则p相误差电压均值可以表示为
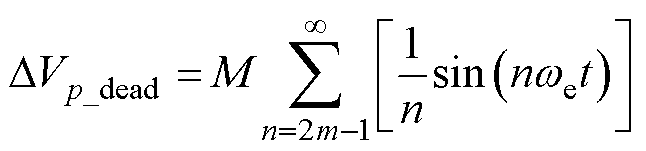 (10)
(10)
其中
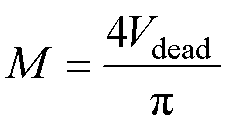
式中,m为正整数。
由式(10)可知,谐波电压幅值和谐波阶次成反比。对各相输出电压误差均值进行VSD变换,可以得到各相输出电压均值在ab平面和xy平面的映射,如式(11)和式(12)所示。
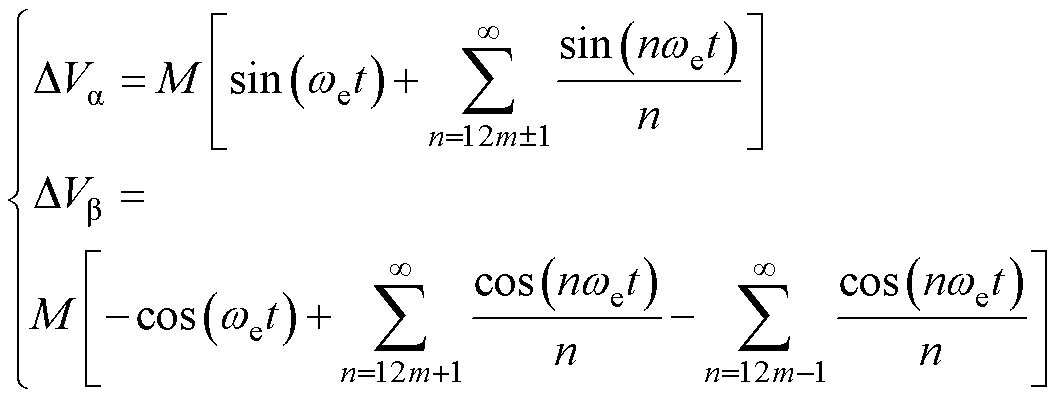 (11)
(11)
式中,m为正整数。
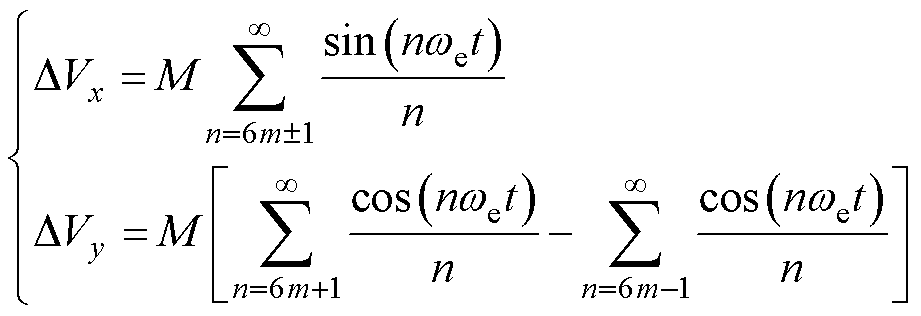 (12)
(12)
式中,m为正奇数。
由式(11)和式(12)可知,逆变器的非线性电压误差对ab平面和xy平面都会产生影响。基波电压误差仅会影响对ab平面的电压输出。ab平面低阶谐波电压的阶次为11和13,xy平面低阶谐波电压的阶次为5和7。这意味着在谐波阻抗更小的xy平面,逆变器的非线性电压误差会在xy平面产生较大的谐波电流。
一般来说,工业应用中DTP-PMSM的反电动势是非正弦的,在DTP-PMSM系统中存在更丰富的反电动势谐波[23]。以A相为例,由于两套三相绕组都采用星形联结,3m(m=1, 3, 5,…)阶的反电动势谐波被忽略,A相反电动势总谐波EAh可以表示为
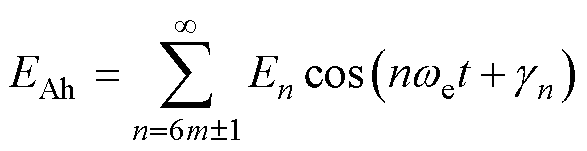 (13)
(13)
式中,En为n阶反电动势谐波幅值;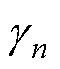 为n阶反电动势谐波的相位。同时,随着反电动势谐波的阶次增大,反电动势幅值会显著降低。因此,可以仅考虑最主要的第5、7阶反电动势对DTP-PMSM多矢量模型预测电流控制的影响,A相反电动势总谐波可以近似为
为n阶反电动势谐波的相位。同时,随着反电动势谐波的阶次增大,反电动势幅值会显著降低。因此,可以仅考虑最主要的第5、7阶反电动势对DTP-PMSM多矢量模型预测电流控制的影响,A相反电动势总谐波可以近似为
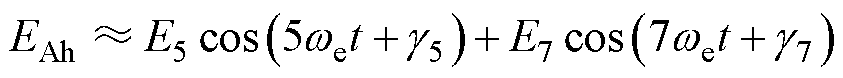 (14)
(14)
将各相的第5、7阶反电动势谐波进行VSD变换,可以获得5、7次反电动势谐波在ab平面和xy平面的作用效果为
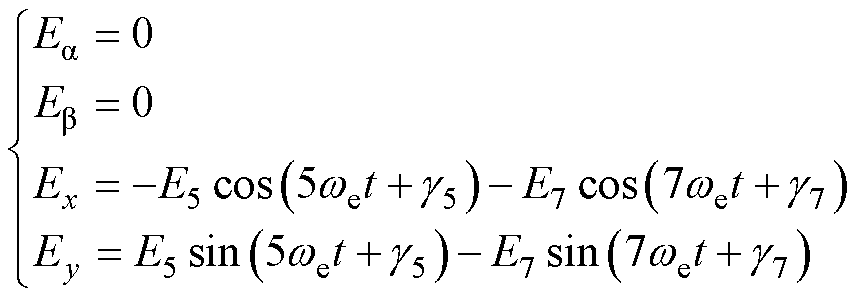 (15)
(15)
由式(15)可知,反电动势中最主要的第5、7阶谐波也仅会作用于xy平面。
在使用虚拟电压矢量的DTP-PMSM多矢量MPCC中,仅在ab旋转后的dq平面进行了模型预测电流控制,而对与ab平面垂直的xy平面采用了平均电压为零的开环控制。因此,理论上模型参数失配仅会影响dq平面的电流控制效果,但不会对采用开环控制且与dq平面垂直的xy平面电流控制产生影响。并且参数失配对DTP-PMSM的dq平面MPCC的影响与对三相永磁同步电机的影响相同。任意参数发生失配均会导致预测电流误差。其中,电感与永磁体磁链的参数失配对预测误差影响较大,电阻失配所造成的影响则相对较小[26]。
由第2节的分析可知,在理想情况下,采用多虚拟电压矢量的DTP-PMSM模型预测电流控制能够获得最优的控制性能。然而,实际驱动系统中的逆变器非线性、反电动势谐波、参数失配等非理想因素会对dq平面和xy平面的电流控制产生影响,降低多虚拟电压矢量MPCC的性能。
为进一步提升多虚拟电压矢量MPCC的性能,本节将提出一种基于xy平面闭环电流控制的改进多虚拟电压矢量模型预测电流控制策略。
3.1.1 ab平面虚拟电压矢量
不同于2.1节所示传统虚拟电压矢量的合成,本文选择ab平面3个最外层的P1组基本电压矢量进行ab平面新虚拟电压矢量合成。以图5a中虚拟电压矢量VV1A的合成为例,选择的3个基本电压矢量分别为V45、V44、V64,其作用时间为
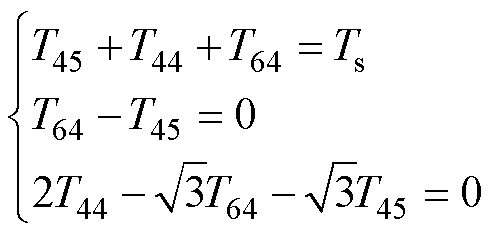 (16)
(16)
式中,T45、T44和T64分别为V45、V44、V64的作用时间,结果为
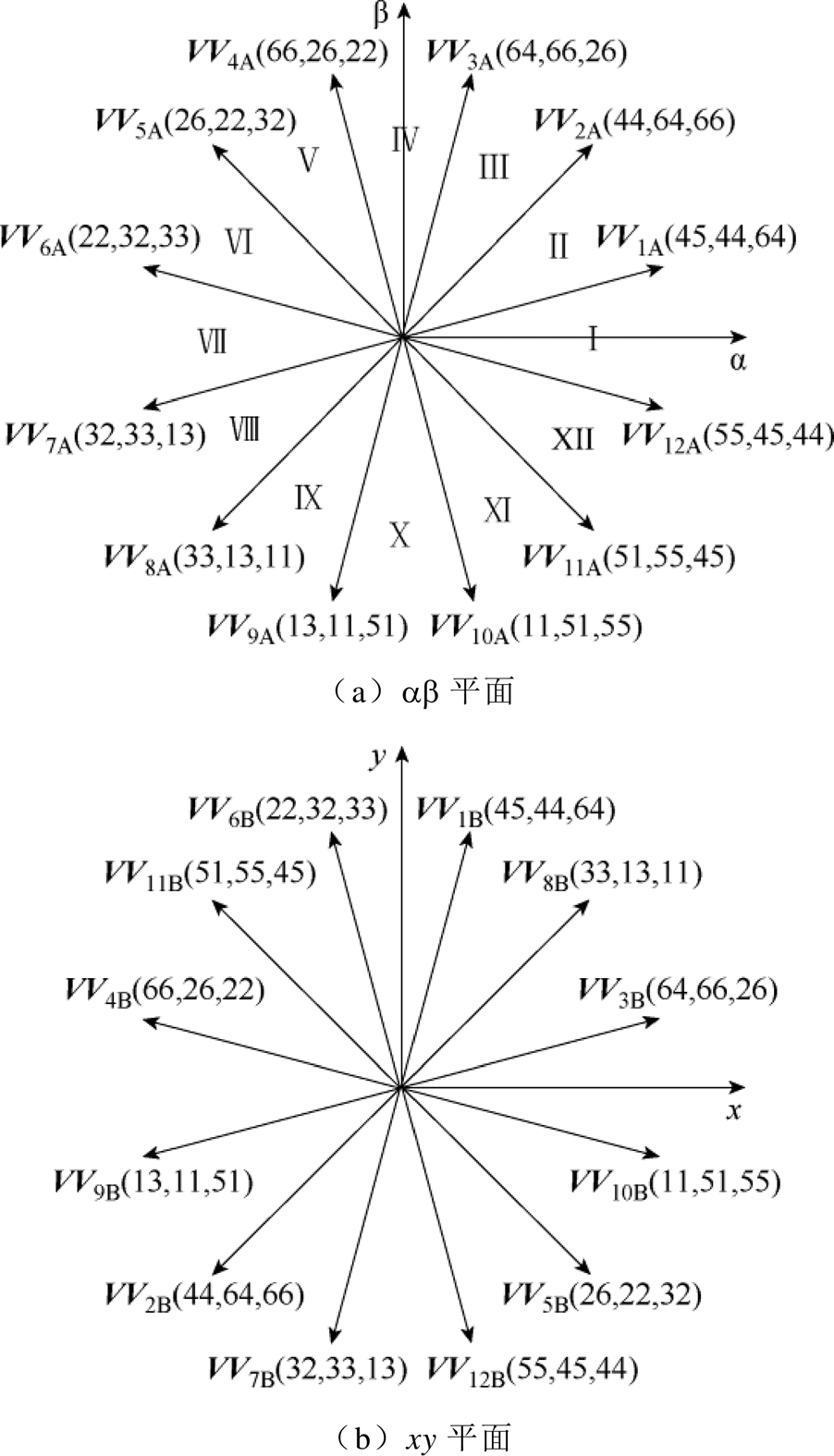
图5 新虚拟电压矢量合成结果
Fig.5 New virtual voltage vector synthesis result
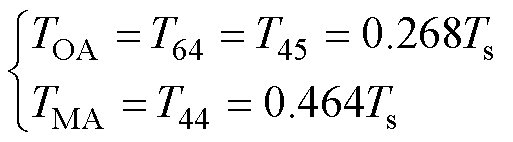 (17)
(17)
式中,TOA为3个基本电压矢量中两侧矢量的作用时间;TMA为中间矢量作用时间。
根据式(17)可以合成其他11个虚拟电压矢量,合成的虚拟电压如图5a所示。新虚拟电压矢量合成所使用的基本电压在xy平面拥有更小的幅值,所合成虚拟电压矢量幅值为0.597Vdc,和第2.1节合成方法幅值相同。但是,各个基本电压矢量在xy平面的幅值对时间积分的最大值相比于第2.1节合成策略降低了37%,这有助于进一步降低xy平面的高频电流谐波。
3.1.2 xy平面虚拟电压矢量
xy平面虚拟电压矢量用于在多虚拟矢量MPCC中实现对xy平面的控制。为保证xy平面电流控制不会对ab平面的MPCC和控制脉冲生成产生影响,xy平面虚拟电压矢量需要以ab平面平均电压为零为合成目标。
理论上,xy平面虚拟电压矢量可以使用任意矢量合成。但是,引入额外矢量会增加脉冲产生的复杂度和驱动器的开关损耗。为此,本文选用第3.1.1节所使用的P1组基本电压矢量进行矢量合成,且每个虚拟电压矢量包含的基本电压矢量和ab平面相同,从而降低xy平面电流控制的实现难度,合成结果如图5b所示。
以图5b中虚拟电压矢量VV1B为例,其选择的基本电压矢量和VV1A相同,都为V45、V44、V64。然后,令ab平面的平均电压为零,各矢量作用时间计算式为
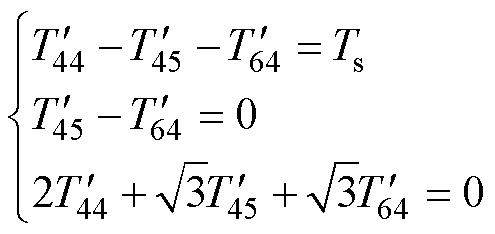 (18)
(18)
式中,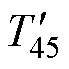 、
、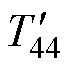 和
和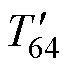 分别为V45、V44、V64的作用时间,其结果为
分别为V45、V44、V64的作用时间,其结果为
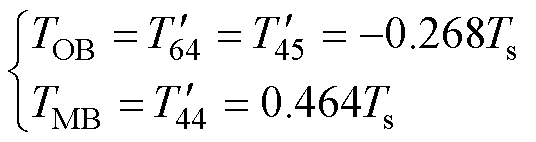 (19)
(19)
式中,TOB为合成xy平面虚拟电压矢量时两侧矢量的作用时间;TMB为合成xy平面虚拟电压矢量时中间矢量的作用时间。
根据式(19)所示的三个矢量的作用时间计算结果,可以合成xy平面另外的11个虚拟电压矢量,如图5b所示。最终合成的xy平面虚拟电压矢量幅值为0.160Vdc。
实际电机中,电机模型参数不匹配、逆变器非线性等都会影响多矢量模型预测电流控制的dq平面电流控制性能。在双闭环控制中,q轴电流跟踪误差会被转速调节器补偿,因此一般情况下不会影响转速跟踪效果。然而,d轴电流跟踪误差会导致电机无法实现每安培最大转矩控制,降低电机运行效率。将所有非理想因素对d轴和q轴电流的影响视为光滑均匀且绝对有界的集总扰动Fd、Fq后,d轴和q轴电流方程可以改写为
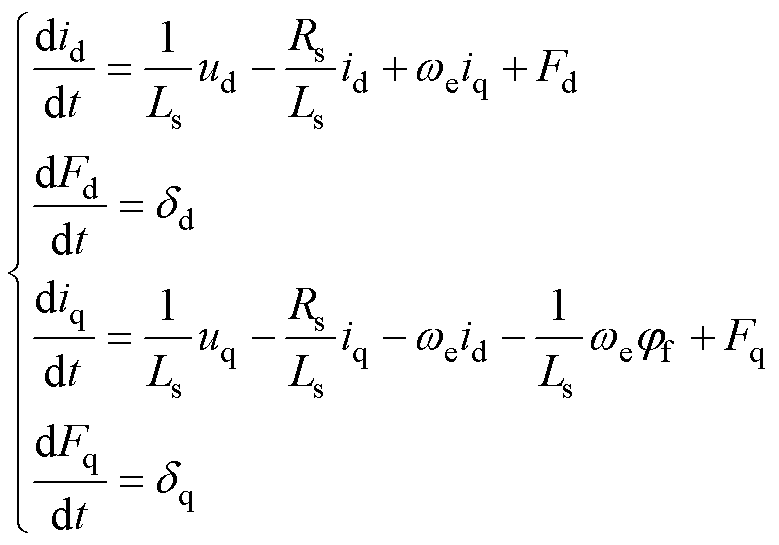 (20)
(20)
式中,dd和dq分别为d轴和q轴集总扰动的一阶导数;Fd、Fq分别为d轴和q轴集总扰动,表达式为
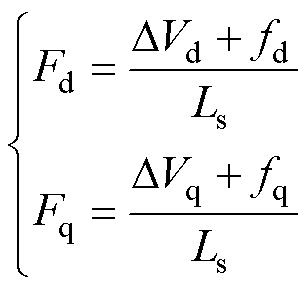 (21)
(21)
式中,DVd和DVq分别为逆变器非线性导致的电压误差在dq平面的映射,由DVa和DVb经Park变换得到;fd和fq分别为参数失配、高阶反电动势谐波和未建模项等变换到dq平面输入电压误差上的扰动。
根据GPIO理论[27],用于观测dq平面集总扰动的GPIO可以设计为
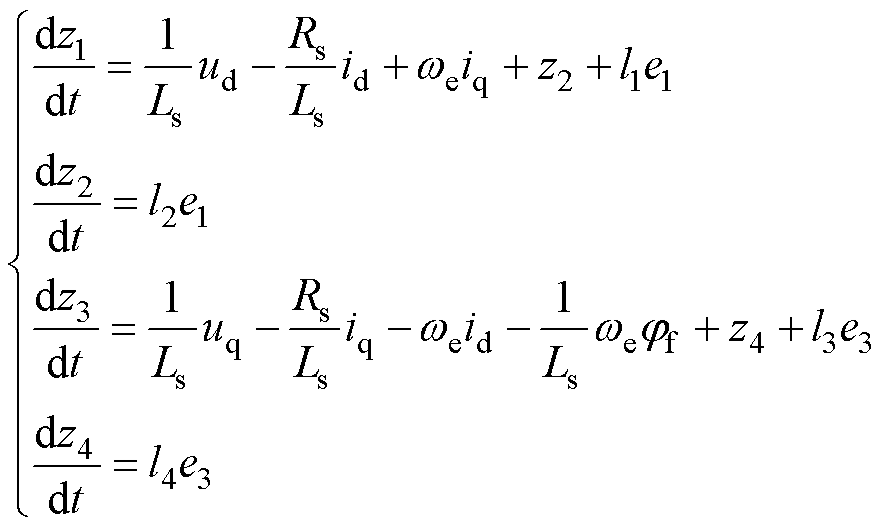 (22)
(22)
式中,z1和z3分别为d轴和q轴定子电流的观测值;z2和z4分别为d轴和q轴集总扰动的观测值;e1为d轴电流观测误差,e1=id-z1;e3为q轴电流观测误差,e3=iq-z3;l1~l4为观测器增益。
式(20)减去式(22)可以得到观测器的误差状态方程。由于d轴和q轴都具有相同结构的状态方程,因此在q轴和d轴采用相同的观测器增益。d轴误差方程可以表示为
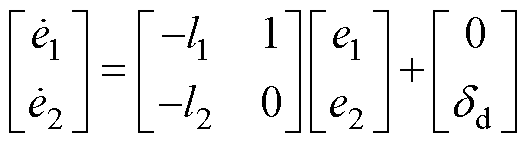 (23)
(23)
式中,e2为d轴集总扰动的观测误差。
当式(23)的两个极点处于左半平面时,观测器稳定。本文将两个极点统一配置在 (-w0, 0) 处,可得观测器的增益l1=l3=2w0,l2=l4=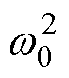 。观测器带宽w0的取值需要综合考虑观测器的动态性能及其对噪声的抑制能力,本文将其配置为3 000 rad/s。
。观测器带宽w0的取值需要综合考虑观测器的动态性能及其对噪声的抑制能力,本文将其配置为3 000 rad/s。
对式(22)进行前向欧拉离散化,可得离散形式的GPIO为
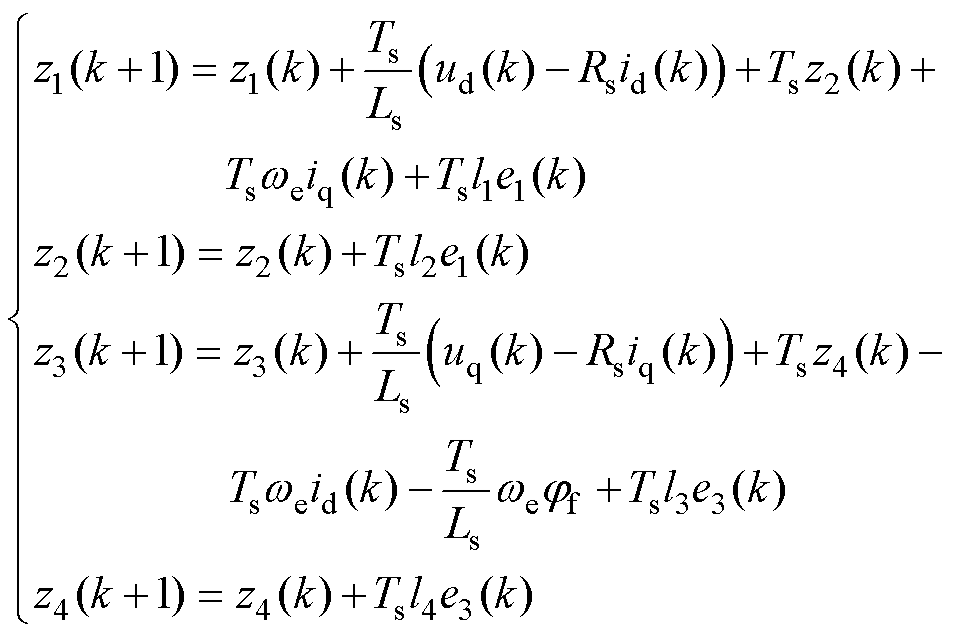 (24)
(24)
式中,e1(k)和e3(k)分别为k时刻d轴和q轴电流观测误差;z1(k)和z3(k)分别为k时刻d轴和q轴电流观测值;z2(k)和z4(k)分别为k时刻d轴和q轴集总扰动Fd、Fq的观测值。
对式(20)中的电流模型进行离散化可以得到随集总扰动更新的可变预测模型,考虑一步延时补偿后,最佳电压参考和电流给定的关系为
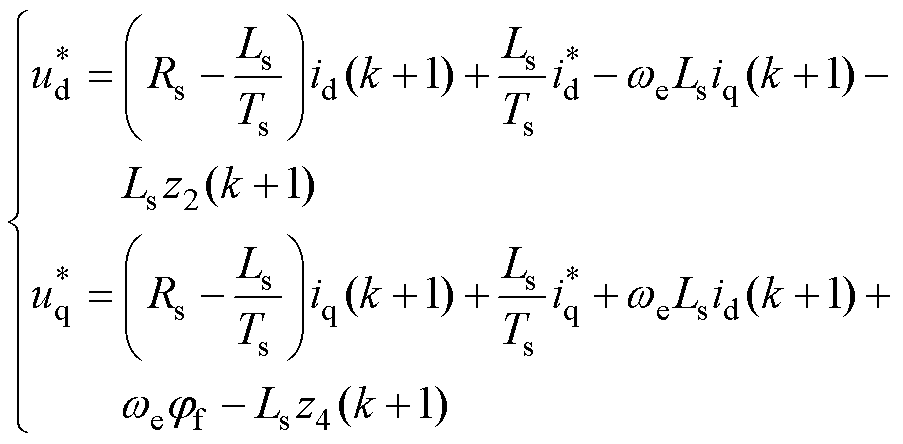 (25)
(25)
式中,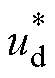 和
和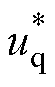 分别为在k时刻计算,但在k+1时刻作用的d轴和q轴最优电压参考。
分别为在k时刻计算,但在k+1时刻作用的d轴和q轴最优电压参考。
第2.2节所述传统多虚拟电压矢量MPCC需要进行24次电流预测和价值函数计算及12次电流斜率计算。为减少计算时间,在使用式(24)的GPIO实现集总扰动观测后,根据式(25)直接计算下一
个控制周期所需的最优输出电压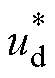 和
和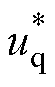 ,并对其进行反Park变换,得到ab平面所需输出的电压为
,并对其进行反Park变换,得到ab平面所需输出的电压为
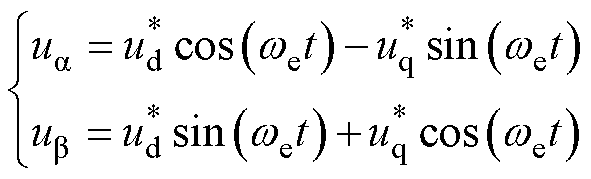 (26)
(26)
根据式(26)计算获得的ab平面电压,计算目标电压所在扇区N为
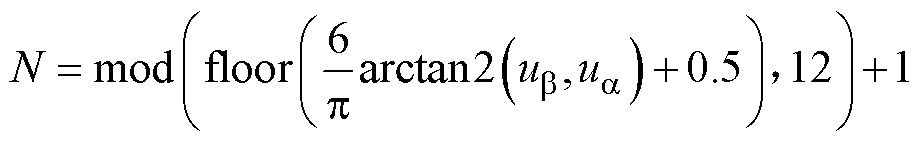 (27)
(27)
式中,mod( )为求余函数;floor( )为向下取整函数;atctan2( )为四象限反正切函数。
最后选择所在扇区边界上的两个虚拟电压矢量作为合成矢量,这不仅有利于产生中心对称的控制脉冲,还能避免遍历无用矢量产生的额外计算。这两个虚拟电压矢量的占空比为
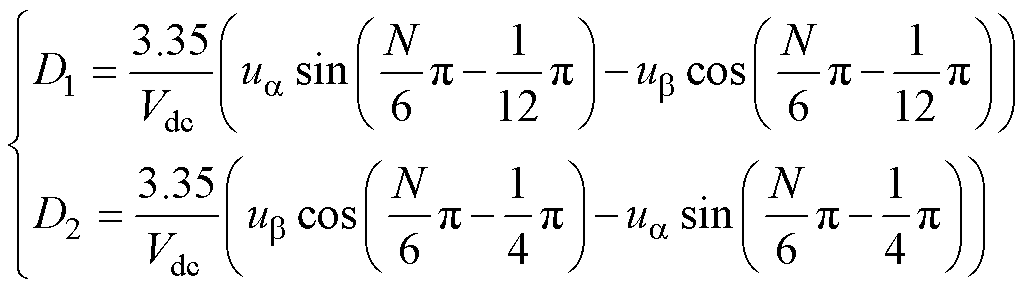 (28)
(28)
式中,D1和D2分别为滞后和超前虚拟电压矢量的占空比。以图5a中第一扇区为例,D1为虚拟电压矢量VV12A的占空比,D2则为虚拟电压矢量VV1A的占空比。当D1与D2之和大于1时,D1与D2等幅缩小。
从第2.3和2.4节的分析可知,在实际控制系统中,使用虚拟电压矢量进行控制时,xy平面的等效作用电压可以表示为
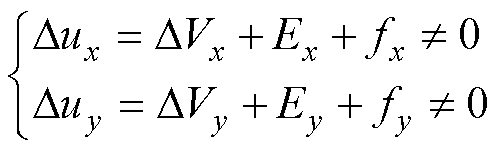 (29)
(29)
式中,Dux和Duy为非理想因素导致的xy平面的电压;fx和fy为其他未建模项在xy平面产生的等效电压。由于xy平面电感小的特性,即使很小的Dux和Duy也很容易产生丰富的电流谐波,降低电机运行效率,影响系统性能。因此,需要采取适当的控制策略实现xy平面电流控制。
综合考虑xy平面闭环电流控制的额外成本和控制性能后,本文选择比例积分控制器作为xy平面闭环电流控制器,在k+1时刻控制器输出ux(k+1)和uy(k+1)可以表示为
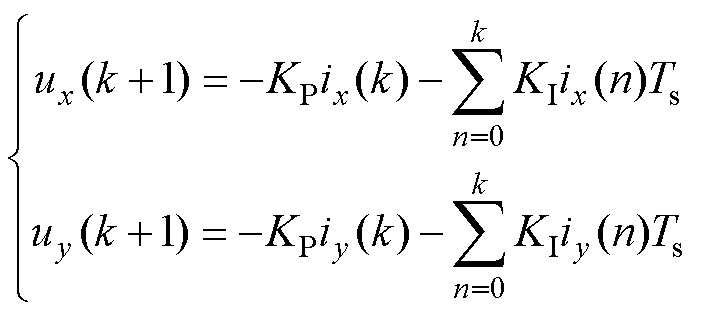 (30)
(30)
式中,KP和KI分别为比例环节系数和积分环节系数;ix(k)和iy(k)分别为k时刻x轴和y轴的电流采样值。
由图5b可知,xy平面第i个虚拟电压矢量VViB与x正半轴的夹角是VViA与a正半轴夹角的5倍。根据式(30)计算出xy平面所需输出电压后,与ab平面第N扇区相邻两个虚拟电压矢量VViA和VVjA所对应的VViB和VVjB占空比为
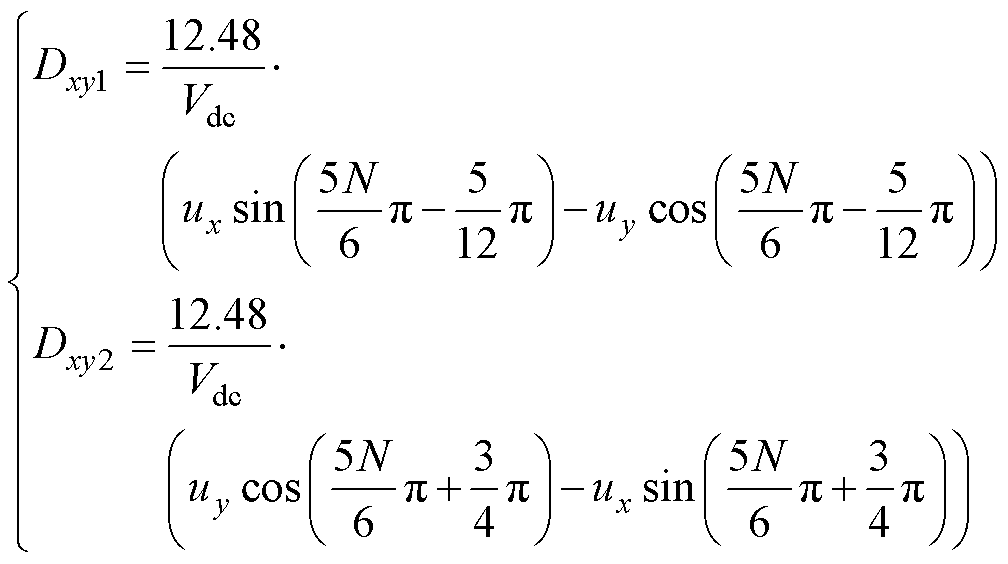 (31)
(31)
式中,Dxy1和Dxy2分别为滞后虚拟电压矢量和超前虚拟电压矢量的占空比。以当N=1时为例,Dxy1和Dxy2分别为VV12B和VV1B的占空比。
由于在第3.1节的矢量合成过程中预先考虑了控制脉冲产生的问题,因此在dq平面使用多矢量优化模型预测电流控制后,再对xy平面进行闭环电流控制不会引入额外的开关状态。
为控制脉冲产生难度,对任意扇区所选择的4个基本电压矢量按照逆时针顺序重命名为V1、V2、V3、V4,零矢量命名为V0。以N=1为例,此时用于dq平面电流控制的虚拟电压矢量为VV1A和VV12A;用于xy平面电流控制的虚拟电压矢量为VV1B和VV12B。这4个虚拟电压矢量所使用的基本电压矢量V1(V45)、V1(V44)、V1(V64)、V1(V66)及零矢量V00各自的作用时间计算为
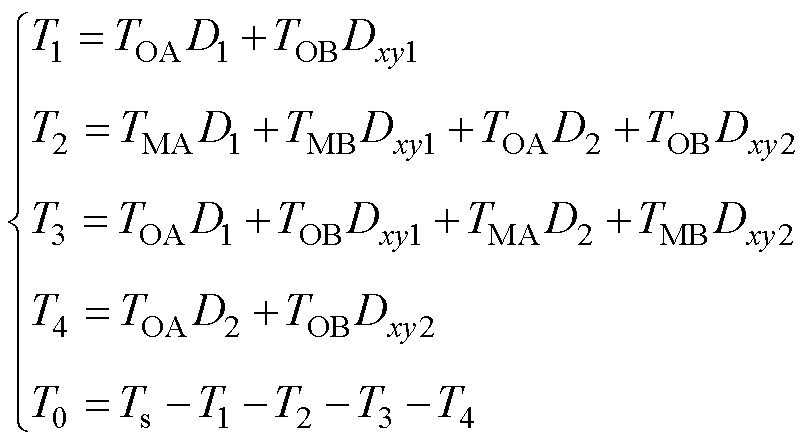 (32)
(32)
式(32)适用于所有扇区的基本电压矢量作用时间计算。对任意扇区所选择的4个基本电压矢量按照逆时针顺序重命名为V1、V2、V3、V4,零矢量命名为V0。
为避免作用时间出现负数和超过Ts的问题,并降低xy平面电流控制的成本,本文限制V1、V2、V3、V4各自作用时间以及所有矢量作用时间的总和都在0~Ts之间。当其中一个或者多个条件不满足时,通过调整对应的Dxy1和Dxy2使其满足所有条件,以避免xy平面谐波电流控制对dq平面电流控制造成影响。尽管在ab平面合成电压与其中一个虚拟电压矢量十分接近或者D1与D2之和接近1时,这种处理方式可能无法输出xy平面所需的全部电压,但是仍然能够输出所需的部分电压。同时,在多数区域逆变器都能够准确输出xy平面闭环控制所需的全部电压。因此,算法仍然可以有效抑制xy平面的电流谐波。
根据所选矢量中4个相邻基本矢量开关状态的规律,选择图6所示的三角波作为载波,以产生中心对称的逆变器控制脉冲。为尽可能减少逆变器开关次数,在第1、4、5、8、9、12扇区采用开关序列V0-V4-V3-V2-V1-V2-V3-V4-V0;其余扇区则采用V0-V1-V2-V3-V4-V3-V2-V1-V0。以第1扇区为例,各相控制脉冲PWM比较寄存器值CPMA和CPMB见表2。
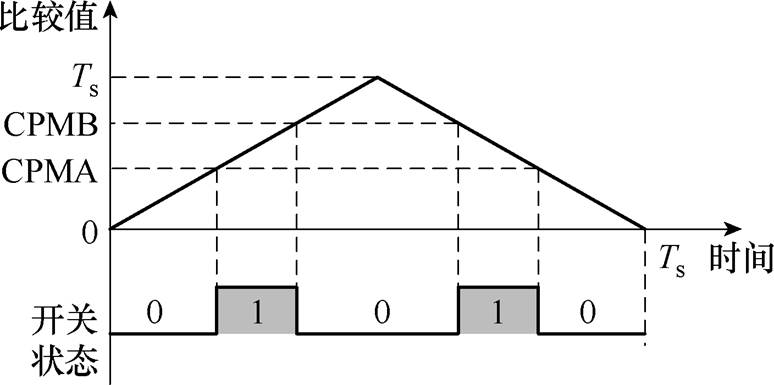
图6 脉冲产生方式
Fig.6 Pulse generation method
当VV12A和VV1A的占空比D1=D2=0.4,VV12B和VV1B的占空比Dxy1=Dxy2=0,T0=0.2Ts时,采用上述方法合成出的控制脉冲如图7所示。一个控制周期总开关次数为6次,作用时间最长的V45(V2)和V44(V3)的单次持续时间为其作用时间的一半。
表2 各相所有比较值
Tab.2 Comparison for all phases
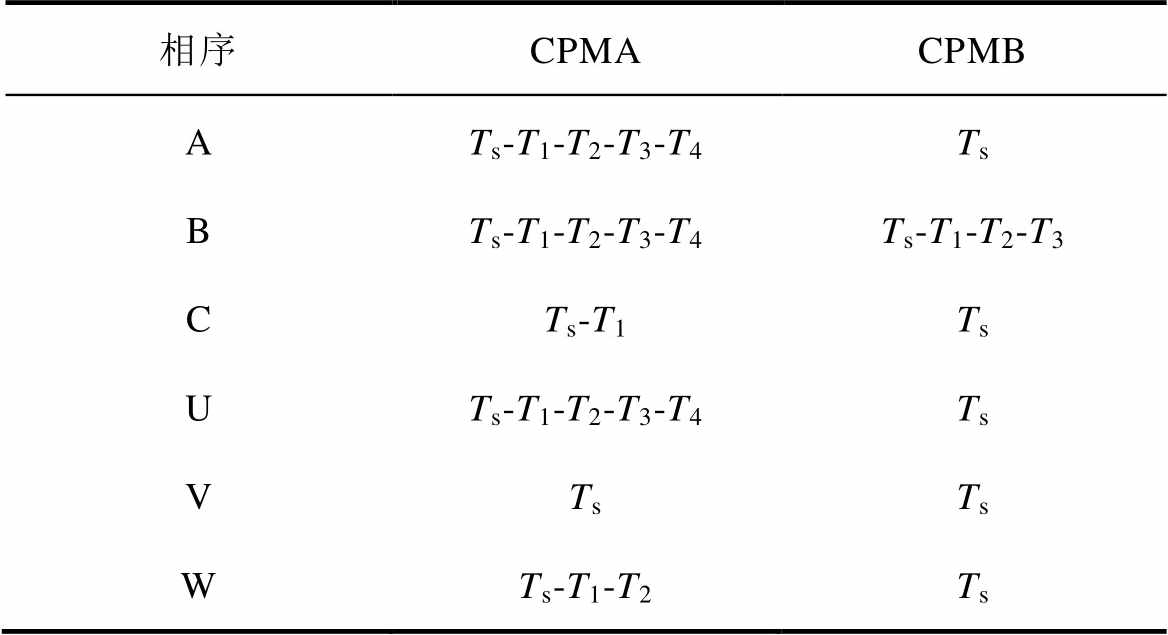
相序CPMACPMB ATs-T1-T2-T3-T4Ts BTs-T1-T2-T3-T4Ts-T1-T2-T3 CTs-T1Ts UTs-T1-T2-T3-T4Ts VTsTs WTs-T1-T2Ts
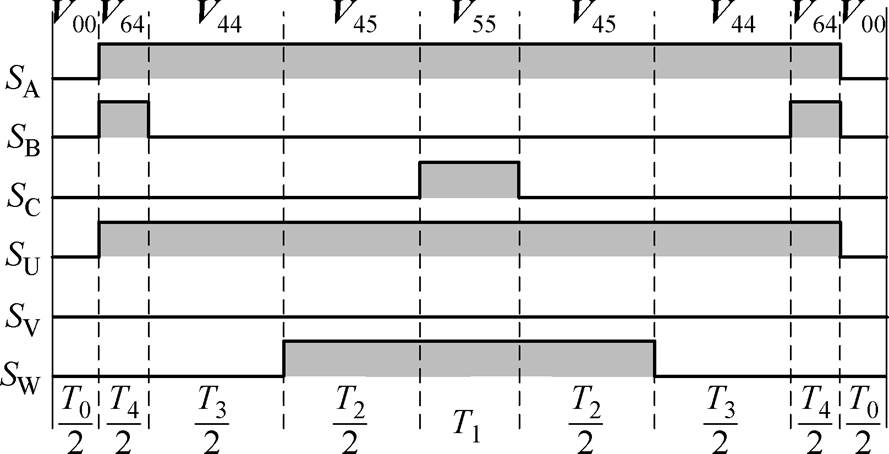
图7 开关序列及控制脉冲
Fig.7 Switching sequence and control pulse
图8为本节所提改进虚拟电压矢量模型预测电流控制方法的流程。首先,采用GPIO对系统在dq平面的集总扰动进行观测并补偿,预测k+1时刻所需电压,计算占空比D1和D2,并记录目标电压所处扇区N。然后,采用比例积分控制器获取xy平面所需输出电压uxy(k),并根据扇区N以及xy平面虚拟电压矢量幅值和相位计算占空比Dxy1和Dxy2。最后,根据预先定义的开关序列,产生逆变器所需的脉冲信号,实现xy平面低计算成本的闭环谐波电流抑制。
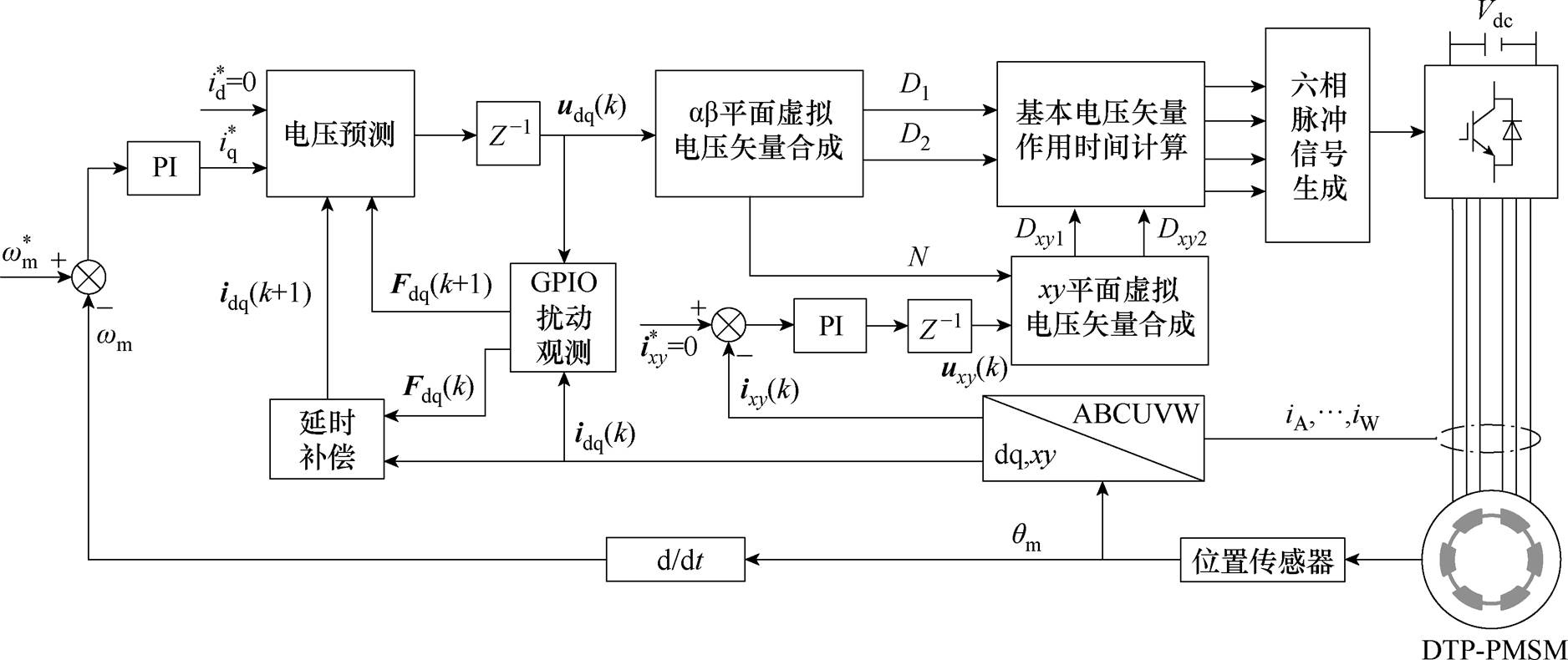
图8 改进虚拟电压矢量模型预测电流控制方法流程
Fig.8 Improved virtual voltage vector model for predicting current control method flow
为验证所提方法的有效性,本文搭建以TMS320F28375D为主控芯片的实验平台,如图9所示。实验电机参数见表3,直流母线电压为48 V,控制频率和采样频率设置为10 kHz。另一个永磁同步电机用作负载电机,通过联轴器连接到实验电机。实验数据由微控制器的集成DAC模块以每100 ms一个数据帧的速率输出到示波器。转速控制器KP和KI参数分别设置为0.02和0.28;xy平面电流控制器KP和KI参数分别设置为30和120。

图9 实验平台
Fig.9 Experimental platform
表3 实验电机参数
Tab.3 Experimental motor parameters
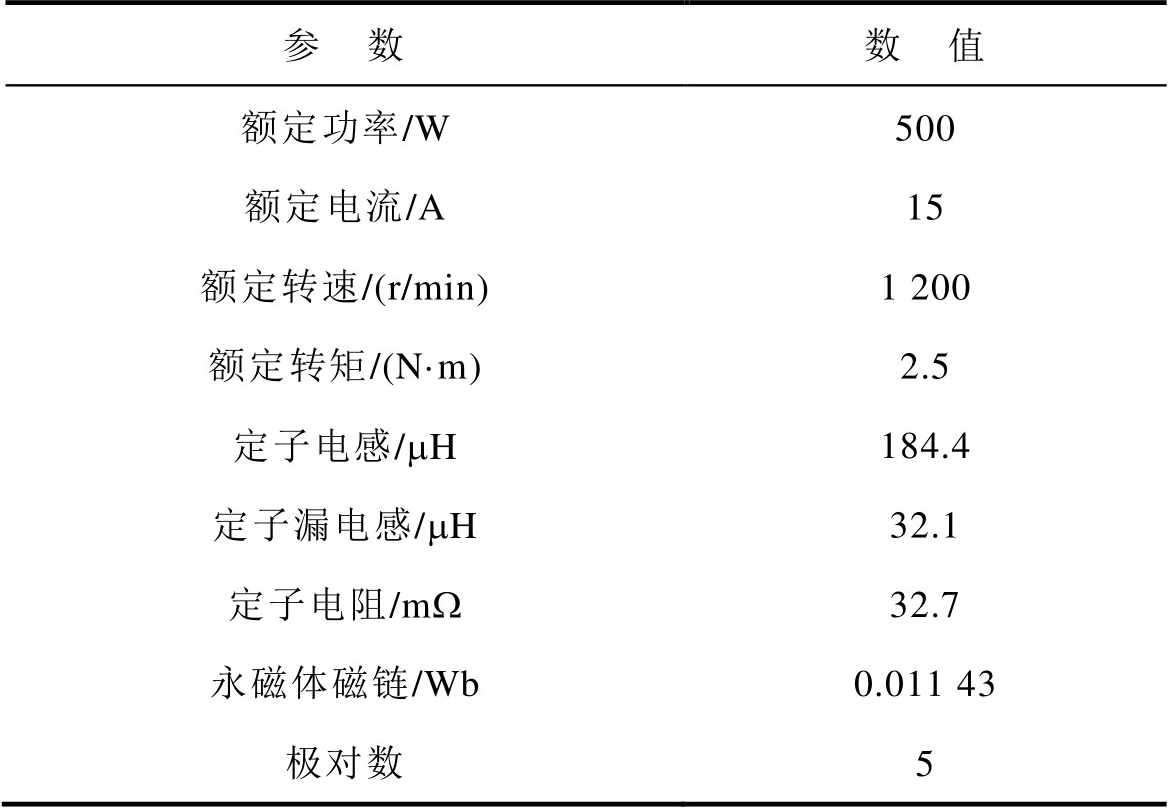
参 数数 值 额定功率/W500 额定电流/A15 额定转速/(r/min)1 200 额定转矩/(N·m)2.5 定子电感/mH184.4 定子漏电感/mH32.1 定子电阻/mW32.7 永磁体磁链/Wb0.011 43 极对数5
为充分验证所提方法的有效性,本文进行完全基于电机模型的多虚拟电压矢量模型预测电流控制(MPCC1)、基于GPIO但不考虑xy平面电流控制的多虚拟电压矢量模型预测控制(MPCC2)和本文所提基于GPIO并考虑xy平面电流控制的多矢量模型预测电流控制(MPCC3)的多组对比实验。
在实验电机转速给定为600 r/min,负载给定为2.5 N·m的工况下进行了稳态实验,实验相电流达到15 A左右,实验结果如图10所示。虽然MPCC1采用了虚拟电压矢量,但是xy平面中仍然存在丰富的电流谐波。同时A、U相电流也存在严重的电流畸变,其中A相电流第5、7阶电流谐波的含量分别为8.99%和4.00%,A相电流的总谐波畸变率(Total Harmonics Distortion, THD)为10.52%。这是因为逆变器非线性、反电动势谐波和未建模项等非理想因素的作用导致xy平面的平均电压并不为零。同时,xy平面的电感(也即是漏电感)很小,导致xy平面产生严重的谐波电流。
MPCC2使用GPIO观测由非理想因素导致的dq平面集总扰动,提升了dq平面稳态电流跟踪性能。但是dq平面和xy平面是两个相互垂直的平面,同时MPCC2采用了虚拟电压矢量的组合。因此,MPCC2相电流和xy平面电流的实验结果和MPCC1相似,xy平面存在丰富的谐波电流,A相电流第5、7阶电流谐波的含量分别为9.11%和4.03%,A相电流的THD=10.67%。在本文所提MPCC3的实验结果中,xy平面谐波电流得到明显抑制,A、U相电流质量也显著提高。A相电流的THD降低至5.31%,第5、7阶电流谐波的含量也减小为3.73%和2.21%。综上所述,图10所示的实验波形证明了本文所提策略的有效性。
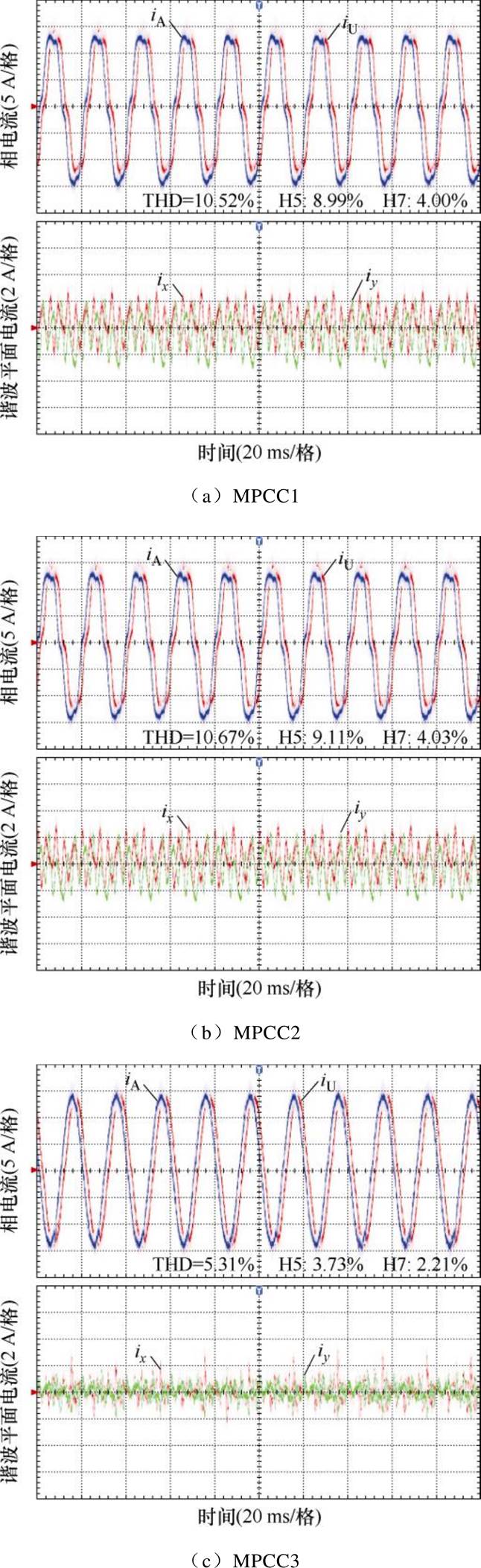
图10 600 r/min稳态实验结果
Fig.10 600 r/min steady-state experimental results
接下来在转速给定为1 200 r/min,负载给定为2.5 N·m工况下进行了稳态实验,并分析MPCC1、MPCC2和MPCC3在不同转速下的性能,实验结果如图11所示。各阶次的谐波系统阻抗和非理想因素导致的总电压误差均会随转速升高而增大。然而,由逆变器非线性引起的电压误差幅值几乎不随转速变化,所以非理想因素导致的总电压误差增加速度低于谐波阻抗的增加速度。因此,从图11可以看出,当转速增加后,MPCC1和MPCC2的相电流质量均有所提高,A相电流THD与600 r/min时相比各自降低了3.51%和4.11%,xy平面的谐波电流幅值也明显减小。本文所提MPCC3的A相电流THD= 5.20%,与MPCC1和MPCC2相比,仍具有最优的稳态性能。
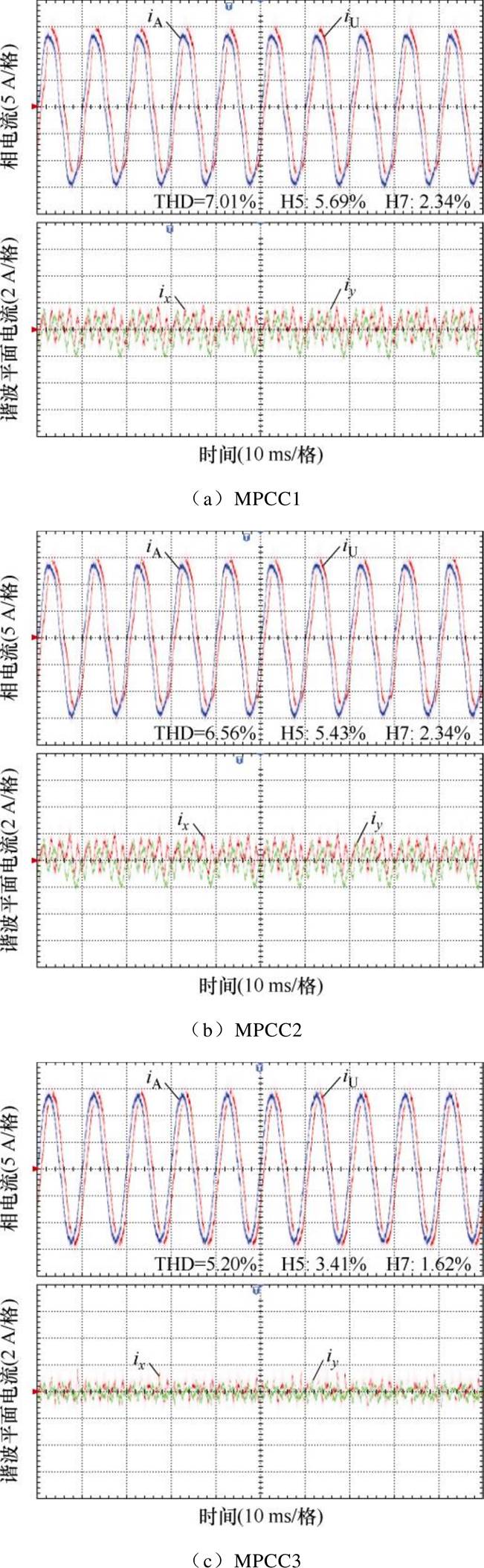
图11 1 200 r/min稳态实验结果
Fig.11 1 200 r/min steady-state experimental results
然后,为验证稳态运行时本文所提xy平面电流控制是否会影响的dq平面电流控制性能,在转速600 r/min、转矩2.5 N·m的工况下进行了MPCC2切换到MPCC3的实验,实验结果如图12所示。从图中可以看出,当xy平面闭环控制被引入后,xy平面的电流谐波幅值显著减小,相电流输出质量明显提升。同时,q轴电流在xy平面闭环控制算法接入瞬间并没有发生改变。这证明了本文所提xy平面电流控制不会对稳态运行时的dq平面电流控制产生影响。
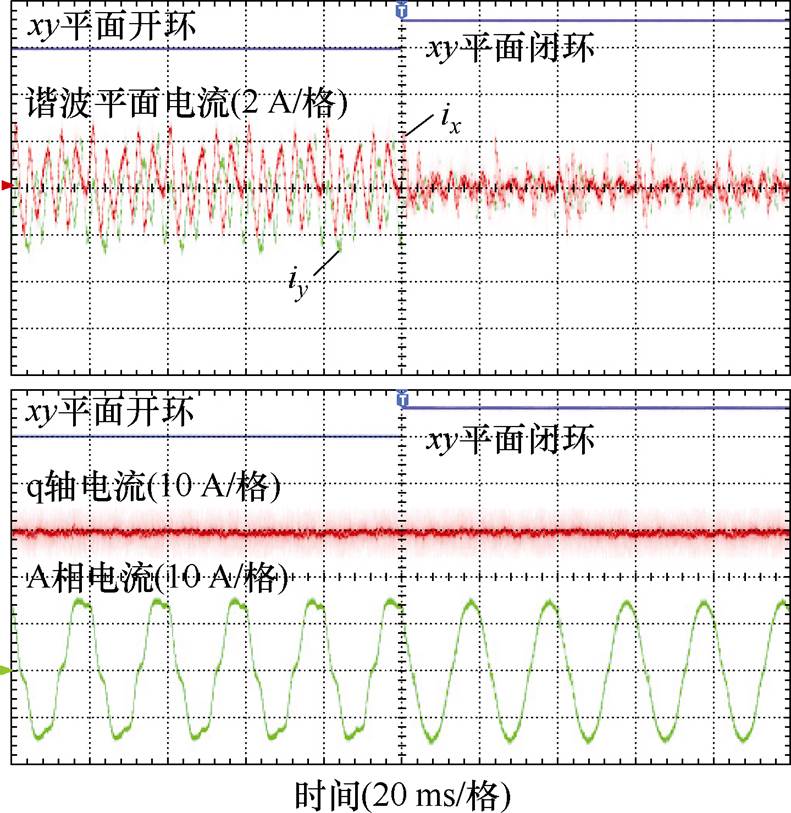
图12 xy平面闭环控制前后实验结果
Fig.12 Experimental results before and after xy plane closed-loop control
从图10c、图11c和图12可以看出,采用MPCC3算法后,xy平面的谐波电流得到显著减少,但是仍然存在少量的谐波电流尖峰。此现象的产生原因有两个:①本文在xy平面所采用的电流比例积分控制器对交流量的控制能力有限;②当输出电压靠近ab平面的虚拟电压矢量时,xy平面的电压输出能力有限。然而,实验结果表明,尽管在少部分时间能够输出的xy平面电压范围有限,所提策略仍然可以显著提升电机的相电流质量,抑制xy平面的谐波电流。
为进一步验证MPCC3所采用的xy平面电流闭环控制策略是否会影响dq平面模型预测电流控制的性能,本文进行了参考电流阶跃变化的对比实验。首先让电机在转速400 r/min、转矩1.2 N·m的工况下稳定运行。然后突加转速参考为1 000 r/min,使速度调节器在一个周期内达到饱和并保持一段时间,通过示波器观测q轴电流控制性能,结果如图13所示。从图13可知,MPCC1、MPCC2和MPCC3都能在两个控制周期后准确跟踪电流参考。但是MPCC1存在0.8 A左右电流跟踪误差,由于逆变器非线性和电机长时间运行后电机参数发生变化引起的。从图13中还可以看出,MPCC2和MPCC3的q轴电流跟踪性能得到了明显提升,且二者具有相同的dq平面电流控制性能。由于电机运行状态变化后扰动也发生了变化,而GPIO对扰动的估计需要时间。因此,当q轴电流参考突变后,出现了较小的q轴电流跟踪误差,这部分误差将在GPIO实现对扰动的准确跟踪后被消除。
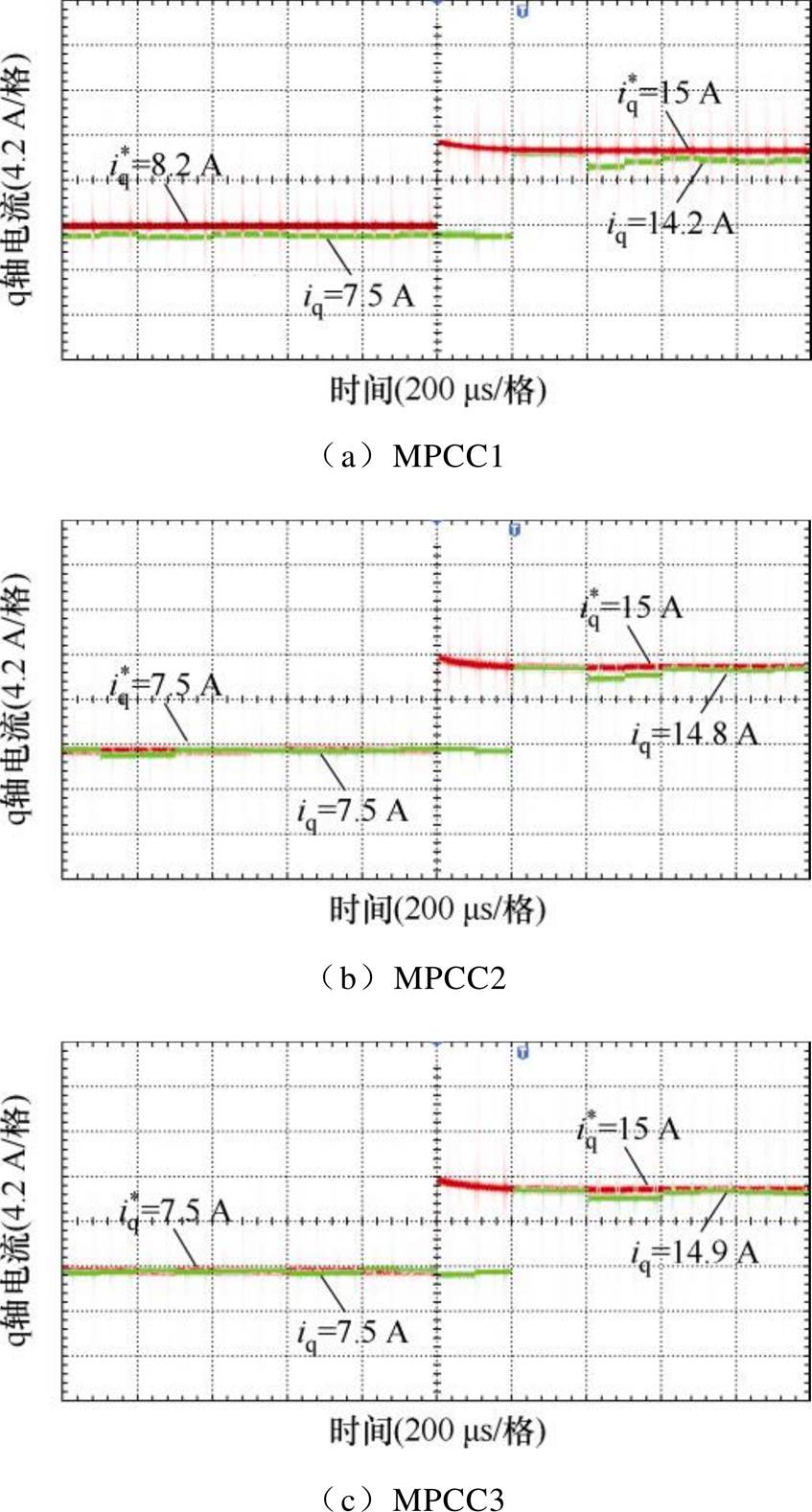
图13 动态实验结果
Fig.13 Dynamic experimental results
在算法首尾改变DAC转换模块的输出值,用示波器测量不同算法的计算时间,结果见表4。由于不需要多次遍历候选集,MPCC2和MPCC3相比于MPCC1在计算时间上具有明显优势。另外,增加xy平面闭环电流控制的MPCC3的计算时间相比于MPCC2仅增加了3.20 ms,证明了本文所提xy平面电流闭环控制策略的高效性。
表4 不同算法计算时间
Tab.4 Calculation time of different algorithms

名 称计算时间/ms MPCC161.2 MPCC227.8 MPCC331.0
本文针对DTP-PMSM多虚拟电压矢量模型预测电流控制电流和转矩控制性能差、xy平面谐波电流大和计算量大的问题,提出了一种基于xy平面电流闭环控制的多虚拟电压矢量模型预测电流控制策略,且通过实验验证了所提方法的有效性及理论分析的正确性,主要研究成果如下:
1)分析了逆变器非线性、反电动势谐波、参数失配等非理想因素对DTP-PMSM多矢量模型预测电流控制性能的影响。
2)针对非理想因素导致ab平面电流控制性能降低的问题,采用GPIO对集总扰动进行观测并更新预测模型,并通过先计算目标电压后选择矢量的方法取代了遍历寻优,在提高鲁棒性的同时可以有效降低控制算法的计算量。
3)针对xy平面谐波电流大的问题,在不需额外增加基本电压矢量的条件下合成了xy平面的虚拟电压矢量,且有效抑制了xy平面的谐波电流。
然而,考虑到计算成本和xy平面有限的电压输出能力,本文在xy平面采用了比例积分控制器,导致xy平面的谐波电流并不能完全消除。对不同工况设计更加多样的矢量选择方案,以扩大xy平面所能合成电压范围,同时结合预测电流控制可进一步提升xy平面谐波电流抑制能力。
参考文献
[1] 宋战锋, 毛丰羽, 崔严谨, 等. 参考跟踪和扰动抑制解耦的双三相永磁同步电机容错控制策略[J]. 电工技术学报, 2023, 38(2): 435-450.
Song Zhanfeng, Mao Fengyu, Cui Yanjin, et al. An fault-tolerant control strategy based on decoupling between reference tracking and periodic disturbance attenuation for dual-three-phase permanent magnet synchronous machine[J]. Transactions of China Elec- trotechnical Society, 2023, 38(2): 435-450.
[2] 孙全增, 张志锋. 双三相永磁同步电机低共模电压模型预测电流控制[J]. 电工技术学报, 2023, 38(14): 3708-3722.
Sun Quanzeng, Zhang Zhifeng. Low common-mode voltage model predictive current control for dual three-phase permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3708-3722.
[3] 刘伟, 刘磊. 基于电流预测及谐波抑制的双三相永磁同步电动机容错控制研究[J]. 电气技术, 2023, 24(7): 20-25, 33.
Liu Wei, Liu Lei. Research on fault-tolerant control of dual three-phase permanent magnet synchronous motor based on current prediction and harmonic suppression[J]. Electrical Engineering, 2023, 24(7): 20-25, 33.
[4] 周长攀, 刘海峰, 景国秀, 等. 双三相永磁同步电机缺相容错运行虚拟矢量间接修正方法及其在直接转矩控制中应用[J]. 电工技术学报, 2023, 38(2): 451-464.
Zhou Changpan, Liu Haifeng, Jing Guoxiu, et al. The indirect correction method of virtual vectors for dual three-phase permanent magnet synchronous motors under the open-phase fault and its application in the direct torque control[J]. Transactions of China Elec- trotechnical Society, 2023, 38(2): 451-464.
[5] 刘忠永, 范涛, 何国林, 等. 高性能永磁同步电机显式模型预测控制算法研究[J]. 电工技术学报, 2023, 38(22): 6039-6058.
Liu Zhongyong, Fan Tao, He Guolin, et al. Research on high-performance explicit model predictive control algorithm for permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6039-6058.
[6] 苗轶如, 宋鹏云, 吕铭晟, 等. 表贴式永磁同步电机预测转矩控制的无权重代价函数设计方法[J]. 电工技术学报, 2023, 38(12): 3141-3150.
Miao Yiru, Song Pengyun, Lü Mingcheng, et al. Design of cost function without weighting factor for predictive torque control of surface-mounted per- manent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3141- 3150.
[7] Rodriguez J, Garcia C, Mora A, et al. Latest advances of model predictive control in electrical drives: part I: basic concepts and advanced strategies[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 3927-3942.
[8] 汪逸哲, 黄晟, 廖武, 等. 基于新型虚拟矢量调制方法的IPMSM模型预测电流控制方法[J]. 电工技术学报, 2024, 39(8): 2422-2433.
Wang Yizhe, Huang Sheng, Liao Wu, et al. IPMSM model predictive current control method based on a novel virtual vector modulation method[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(8): 2422-2433.
[9] Cui Jia, Tao Tao, Zhao Wenxiang. Optimized control set model predictive control for dual three-phase PMSM with minimum error duty cycle regulation[J]. IEEE Transactions on Power Electronics, 2024, 39(1): 1319-1332.
[10] Gonzalez O, Ayala M, Romero C, et al. Model predictive current control of six-phase induction motor drives using virtual vectors and space vector modulation[J]. IEEE Transactions on Power Elec- tronics, 2022, 37(7): 7617-7628.
[11] Aciego J J, González Prieto I, Duran M J. Model predictive control of six-phase induction motor drives using two virtual voltage vectors[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(1): 321-330.
[12] 宋文祥, 任航, 杨煜, 等. 双三相永磁同步电机的双矢量模型预测转矩控制[J]. 电机与控制学报, 2022, 26(9): 97-107.
Song Wenxiang, Ren Hang, Yang Yu, et al. Two vectors based model predictive torque control of dual three phase permanent magnet synchronous motor[J]. Electric Machines and Control, 2022, 26(9): 97-107.
[13] Luan Tianjiao, Wang Zhichao, Long Yang, et al. Multi-virtual-vector model predictive current control for dual three-phase PMSM[J]. Energies, 2021, 14(21): 7292.
[14] Brosch A, Hanke S, Wallscheid O, et al. Data-driven recursive least squares estimation for model predi- ctive current control of permanent magnet syn- chronous motors[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 2179-2190.
[15] Carlet P G, Tinazzi F, Bolognani S, et al. An effective model-free predictive current control for synchronous reluctance motor drives[J]. IEEE Transactions on Industry Applications, 2019, 55(4): 3781-3790.
[16] Schenke M, Kirchgässner W, Wallscheid O. Con- troller design for electrical drives by deep reinforcement learning: a proof of concept[J]. IEEE Transactions on Industrial Informatics, 2020, 16(7): 4650-4658.
[17] Schenke M, Wallscheid O. A deep Q-learning direct torque controller for permanent magnet synchronous motors[J]. IEEE Open Journal of the Industrial Electronics Society, 2021, 2: 388-400.
[18] Agoro S, Husain I. Model-free predictive current and disturbance rejection control of dual three-phase PMSM drives using optimal virtual vector modu- lation[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 11(2): 1432- 1443.
[19] Duran M J, Prieto J, Barrero F, et al. Predictive current control of dual three-phase drives using restrained search techniques[J]. IEEE Transactions on Industrial Electronics, 2010, 58(8): 3253-3263.
[20] Gonzalez-Prieto I, Duran M J, Aciego J J, et al. Model predictive control of six-phase induction motor drives using virtual voltage vectors[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 27-37.
[21] 宋战锋, 毛丰羽, 崔严谨, 等. 基于多级滞环控制器的表贴式双三相永磁同步电机低电流谐波直接转矩控制策略[J]. 中国电机工程学报, 2023, 43(11): 4410-4421.
Song Zhanfeng, Mao Fengyu, Cui Yanjin, et al. Low current harmonic direct torque control strategy for surface-mounted dual-three-phase permanent magnet synchronous machine based on multi-level hysteresis controller[J]. Proceedings of the CSEE, 2023, 43(11): 4410-4421.
[22] Li Yonggang, Hu Yashan, Zhu Z Q. Current harmonics and unbalance suppression of dual three- phase PMSM based on adaptive linear neuron controller[J]. IEEE Transactions on Energy Con- version, 2023, 38(4): 2353-2363.
[23] Shao Bo, Zhu Z Q, Feng J H, et al. Improved direct torque control method for dual-three-phase permanent- magnet synchronous machines with back EMF harmonics[J]. IEEE Transactions on Industrial Elec- tronics, 2021, 68(10): 9319-9333.
[24] Aciego J J, González P I, Duran M J, et al. Model predictive control based on dynamic voltage vectors for six-phase induction machines[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 9(3): 2710-2722.
[25] Agoro S, Husain I. Model predictive control with double virtual vector modulation for suppressing common mode voltages in dual three-phase drives[J]. IEEE Transactions on Industrial Electronics, 2023, 71(9): 10018-10028.
[26] Yang Ming, Lang Xiaoyu, Long Jiang, et al. Flux immunity robust predictive current control with incremental model and extended state observer for PMSM drive[J]. IEEE Transactions on Power Elec- tronics, 2017, 32(12): 9267-9279.
[27] Chen Wenhua, Yang Jun, Guo Lei, et al. Disturbance- observer-based control and related methods: an overview[J]. IEEE Transactions on Industrial Elec- tronics, 2015, 63(2): 1083-1095.
Abstract The dual-three-phase permanent magnet synchronous motor (DTP-PMSM) features low drive voltage, high torque density, strong fault tolerance, and minimal torque ripple. It is ideal for electric vehicles, ship propulsion, aerospace, and wind power systems.
The finite set model predictive control (MPCC) offers fast dynamic response and multi-objective control, drawing widespread attention and research in recent years. However, applying MPCC to DTP-PMSM presents challenges such as poor torque-current control due to the limited d-q subspace voltage range and steady-state current tracking errors caused by motor parameter mismatches. Additionally, the equivalent input voltage caused by inverter nonlinearity and back EMF harmonics, particularly the 5th and 7th harmonics, acts on the lower-impedance x-y subspace. It is prone to generating harmonic currents that reduce motor efficiency.
Therefore, this paper proposes an improved multi-vector model predictive current control (MPCC) method for DTP-PMSM based on closed-loop current control in the x-y subspace. The proposed method mainly consists of four steps. Firstly, the virtual voltage vectors in the a-b and x-y subspaces are synthesized using the same combination of basic voltage vectors, simplifying the control of currents in both subspaces. Secondly, a generalized proportional-integral observer is used in the d-q subspace to detect and compensate for aggregated disturbances, enhancing current control accuracy. Then, a proportional-integral controller and virtual voltage vectors in the x-y subspace are used to implement closed-loop control of the x-y subspace. Finally, a fast voltage vector selection method for simultaneous control in both subspaces and an inverter pulse generation method to reduce current ripple by shortening individual voltage vector durations are proposed.
A comparative experiment was conducted to analyze the traditional multi-vector model predictive current control (MPCC1), the GPIO-based multi-virtual voltage vector MPCC (MPCC2), and the proposed method (MPCC3). Steady-state tests were conducted, and the A-phase current was analyzed using a fast Fourier transform. At 600 r/min and 2.5 N·m, the total harmonic distortion (THD) for MPCC1, MPCC2, and MPCC3 were 10.52%, 10.67%, and 5.31%, respectively. The 5th harmonic distortion rates were 8.99%, 9.11%, and 3.73%; the 7th were 4.00%, 4.03%, and 2.21%. The results demonstrated that the proposed method effectively suppresses harmonic currents while maintaining the current control performance in the d-q subspace. Dynamic tests were then conducted. When the reference speed was suddenly increased, the GPIO-based method showed smaller current tracking errors, while all three methods exhibited similar dynamic performance.
The following conclusions are drawn. (1) The proposed method suppresses x-y subspace harmonic currents with a lower computational burden than traditional multi-vector MPCC. (2) The proposed method maintains dynamic and steady-state current tracking performance. (3) The proposed method suppresses harmonic currents in the x-y plane, and the proportional-integral controller limits the elimination.
keywords:Dual three-phase permanent magnet synchronous motor, model predictive current control, harmonic current suppression, multi-virtual voltage vector optimization
DOI: 10.19595/j.cnki.1000-6753.tces.L11052
中图分类号:TM351
中央高校基本科研业务费项目(2024CDJGF-004)、重庆市自然科学基金项目(CSTB2022NSCQ-MSX0430)和贵州省科技支撑项目(黔科合支撑[2024] 一般 037)(202466295699220662)资助。
收稿日期 2024-07-16
改稿日期 2024-11-12
徐奇伟 男,1983年生,副教授,博士生导师,研究方向为特种电机设计与控制、电动汽车电驱动系统、混合动力的控制与仿真。E-mail: xuqw@cqu.edu.cn
夏 波 男,1990年生,博士后,讲师,研究方向为交流电机无传感器与模型预测控制。E-mail: xiabo@hnu.edu.cn(通信作者)
(编辑 崔文静)