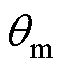 为位置传感器测得的转子机械角度。本文定义当实际转子d轴与定子A轴对齐时,位置传感器机械角度读数
为位置传感器测得的转子机械角度。本文定义当实际转子d轴与定子A轴对齐时,位置传感器机械角度读数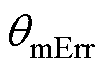 为零位偏差校正值。
为零位偏差校正值。摘要 在航空起动/发电系统中,永磁辅助同步磁阻起/发电机兼具高功率密度和抗短路容错性能,有着良好的应用前景。由于该电机具有永磁磁链小、磁阻转矩大的特点,使用预定位法标校其位置传感器零位时,会出现转子稳定平衡点偏离电流矢量方向的现象。预定位法还存在易受摩擦转矩等干扰的问题。该文分析了磁阻转矩分量对预定位法的平衡点位置和定位精度的影响,推导了由摩擦转矩产生的角度误差的近似公式,得到了定位点和定位电流的选定依据。根据永磁辅助同步磁阻起/发电机的转矩特点,提出了一种新颖的基于不稳定平衡点的定位方法及其控制律的参数估计方法。所提方法利用PI控制器将转子保持在不稳定平衡点,从而可同时利用永磁转矩和磁阻转矩,有效减小摩擦转矩造成的误差。最后通过实验验证了所提定位误差估算模型和零位标校方法的有效性。
关键词:位置传感器零位标校 永磁辅助同步磁阻起/发电机 转子位置检测 预定位法
作为多电飞机的关键技术,高集成度、高功率密度、高可靠性的一体化起/发电机系统被广泛研 究[1-3]。已有多种类型的电机被应用于航空起发系统中,如无刷电励磁同步电机、开关磁阻电机、永磁同步电机、双凸极电机,永磁辅助同步磁阻起/发电机(Permanent Magnet assisted Synchronous Relu- ctance Starter/Generator, PMaSynRS/G)等[4-6]。其中,PMaSynRS/G相较其他电机有独特优势,应用前景良好。与无刷电励磁同步电机相比,PMaSynRS/G本体及其控制器的结构更加简单可靠;与开关磁阻电机相比,PMaSynRS/G具有更大的功率密度和效率,以及更小的转矩脉动;与永磁同步电机相比,PMaSynRS/G具有更宽的恒功率运行范围、更好的抗短路容错性能[7-12]。在起动/发电系统中,电机需要在低速重载工况下实现对发动机的带载起动,在中高转速下提取发动机能量并高效高质地转化为电能供给机载微电网,基于位置传感器的矢量控制方法被广泛应用于起/发电机系统[13-14]。
受限于制造和安装工艺,实际的位置传感器在安装时与电机转子存在一定的机械角度偏差,称为零位偏差。且电机拆装维修、位置传感器或驱动控制器更换等问题都可能导致位置传感器零位信息失效或丢失,需要重新标定[15-17]。传感器零位偏差会造成dq轴电流偏离期望值,进而降低PMaSynRS/G工作效率和峰值转矩,影响控制系统性能及稳定性,特别是在重载起动和高速弱磁工况下[17-20]。因此,高精度、高可操作性的位置传感器的零位标校方法,对于提高起/发电机控制性能具有重要意义。
文献[21-22]提出基于反电动势的方法,通过反拖电机至特定转速,测量电机反电动势的相位从而获知转子位置,再与位置传感器测量值对比纠正得到零位偏差。该类方法精度较高,但需把电机装在特定测试设备上,并同时要测量反电动势及位置传感器信号,适用范围有限。文献[17-19]提出基于特定工况下电压电流的方法,即通过观测电机在特定工况下运行时的电流及电压来估计位置传感器零位偏差。这类方法能实现在线标定及监测,但需让电机运行于设计工况,且校正精度也受逆变器非线性限制。同时该类方法要求安装的零位偏差不能过大,否则电机将不能顺利起动运行。文献[23-25]提出基于电机的矩角特性的方法,通过向电机定子通入给定的电压或电流,使得电机转子最终保持在特定位置,而后通过读取位置传感器测量值得到其零位偏差。该方法也被称为预定位法,其原理简单,便于实施,应用最广,但估计精度易受摩擦转矩等干扰转矩的影响。文献[26]改进了预定位法,通过主动改变定子电流矢量角度,使之与转子d轴正方向重合,达到在转子微动的情况下完成转子位置定位的目的,但其估计精度仍然受摩擦转矩等干扰转矩的影响。
当起/发电机已安装在实验台上并需要重新标校位置传感器零位误差时,难以使用前述基于反电动势的方法及基于特定工况下电压电流的方法。而将预定位法应用于PMaSynRS/G时,需要考虑到电机的电磁转矩除永磁转矩分量外还有源于交、直轴磁路不对称的磁阻转矩分量。先前的文献多以表贴式永磁同步电机为研究对象,没有涉及含磁阻转矩的电机类型,且未对摩擦转矩的影响进行建模分析[23-26]。
本文首先分析了PMaSynRS/G磁阻转矩分量对预定位法的平衡点位置和定位精度的影响。在此基础上推导了由摩擦转矩产生的角度误差的近似公式,为定位电流的选取提供了参考。考虑到PMaSynRS/G的转矩特点,提出了一种新颖的基于不稳定平衡点的定位法及相应控制器的参数估计方法。该方法无需额外硬件,鲁棒性高,且能有效提高传感器零位偏差校正的精度。最后搭建了相应的实验平台,通过实验验证了所提定位误差估算模型和零位标定方法的有效性。
使用预定位法进行零位偏差校正主要分为两个阶段:第一阶段,在定子绕组中产生恒定电流,牵拉转子至特定位置;第二阶段,待转子稳定后,将位置传感器读数与理论值对比,算得位置传感器零位偏差。本文实验所用2对极PMaSynRS/G定、转子结构如图1a所示。由于电机定转子具有旋转对称性,对于多对极电机,一般在dq轴下建模分析一个电周期内的情况[17-21]。图1b为在dq坐标系下定子、转子及位置传感器的关系示意图,图中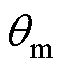 为位置传感器测得的转子机械角度。本文定义当实际转子d轴与定子A轴对齐时,位置传感器机械角度读数
为位置传感器测得的转子机械角度。本文定义当实际转子d轴与定子A轴对齐时,位置传感器机械角度读数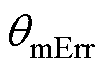 为零位偏差校正值。
为零位偏差校正值。
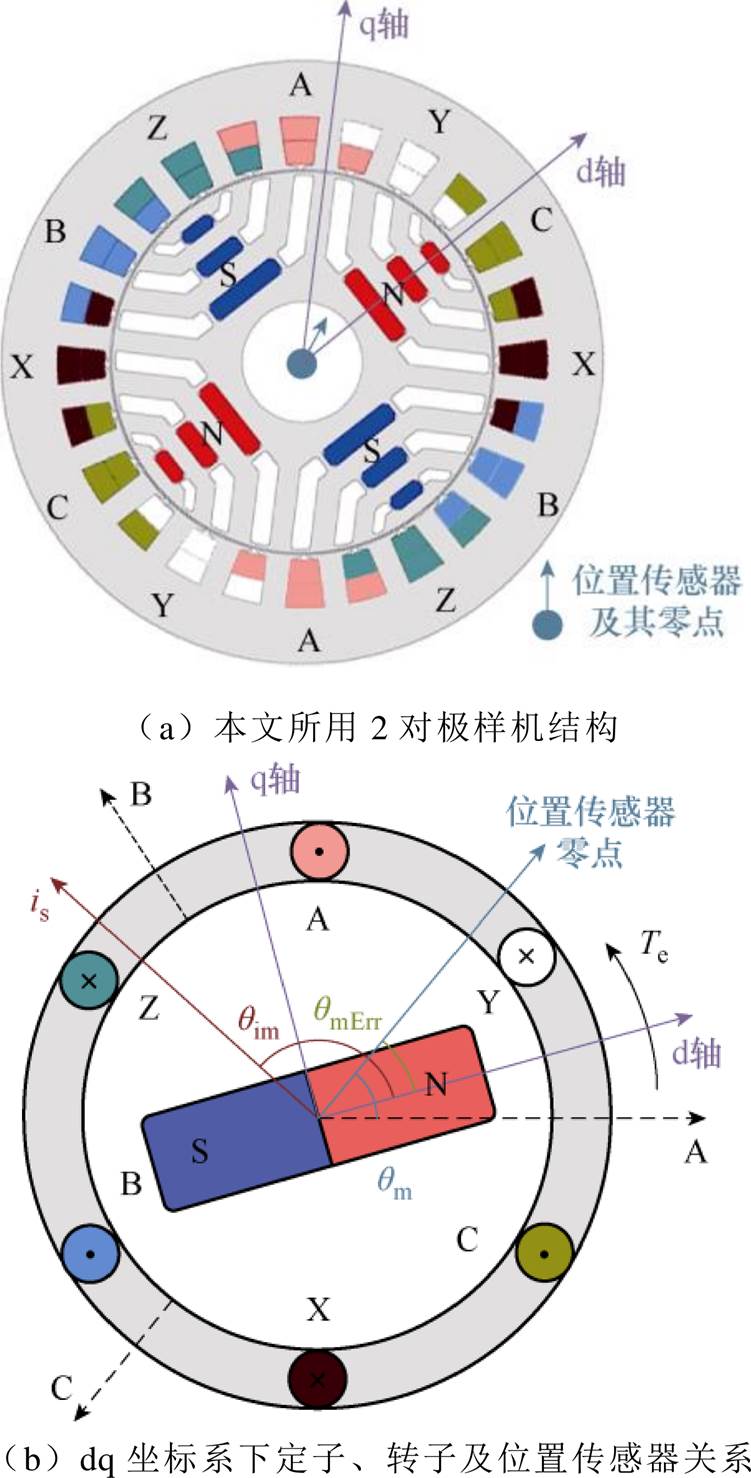
图1 电机定、转子及位置传感器角度关系
Fig.1 Position relationship diagram of stator, rotor and position sensor
由于PMaSynRS/G的磁阻转矩分量较大而永磁转矩分量较小,PMaSynRS/G在预定位的第一阶段的平衡点位置及定位误差特点与表贴式永磁电机有很大不同,下面将对此进行分析。
PMaSynRS/G的电磁转矩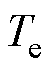 在同步旋转坐标系下可表示[7]为
在同步旋转坐标系下可表示[7]为
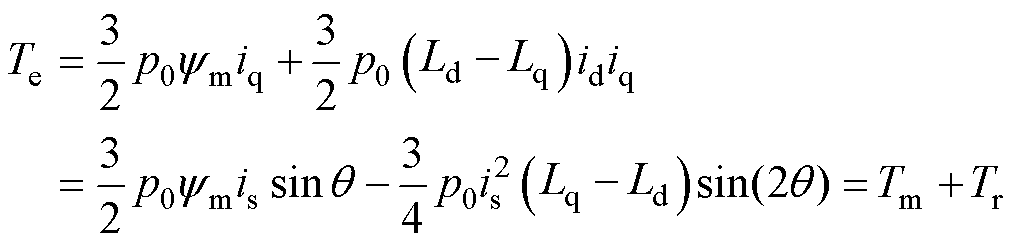 (1)
(1)
式中,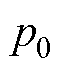 为电机极对数;
为电机极对数;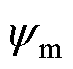 为永磁体磁链;
为永磁体磁链;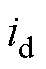 和
和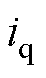 分别为d、q轴电流;
分别为d、q轴电流;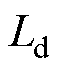 和
和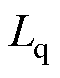 分别为d、q轴电感,且有
分别为d、q轴电感,且有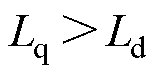 ;
;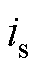 为合成定子电流;
为合成定子电流;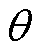 为定子电流矢量超前d轴角度,称为转矩角或负载角,且
为定子电流矢量超前d轴角度,称为转矩角或负载角,且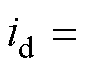
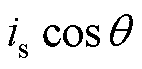 ,
,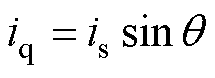 ;
;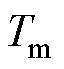 为永磁转矩分量,来源于永磁体与电流作用;
为永磁转矩分量,来源于永磁体与电流作用;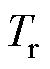 为磁阻转矩分量,来源于dq轴磁路不对称。
为磁阻转矩分量,来源于dq轴磁路不对称。
在使用预定位方法时,设定子中合成电流矢量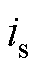 的方向超前于转子实际d轴位置的机械角度值
的方向超前于转子实际d轴位置的机械角度值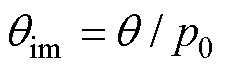 ,如图1b所示。即此时转矩角仍为
,如图1b所示。即此时转矩角仍为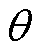 ,式(1)仍然可使用。以实验样机为例,其在不同大小和方向的定子电流下的电磁转矩随
,式(1)仍然可使用。以实验样机为例,其在不同大小和方向的定子电流下的电磁转矩随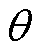 变化的关系如图2所示,该图也被称为矩角特性图。电机进行预定位时所受电磁转矩由永磁分量和磁阻分量组成:永磁分量
变化的关系如图2所示,该图也被称为矩角特性图。电机进行预定位时所受电磁转矩由永磁分量和磁阻分量组成:永磁分量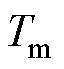 随
随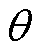 呈正弦变化,其幅值正比于定子电流;磁阻分量
呈正弦变化,其幅值正比于定子电流;磁阻分量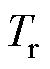 随
随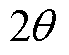 呈正弦变化,其幅值正比于定子电流二次方。当电流较大时,磁阻转矩幅值将超过永磁转矩,且在
呈正弦变化,其幅值正比于定子电流二次方。当电流较大时,磁阻转矩幅值将超过永磁转矩,且在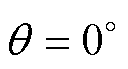 的附近会出现转矩方向改变的现象。
的附近会出现转矩方向改变的现象。
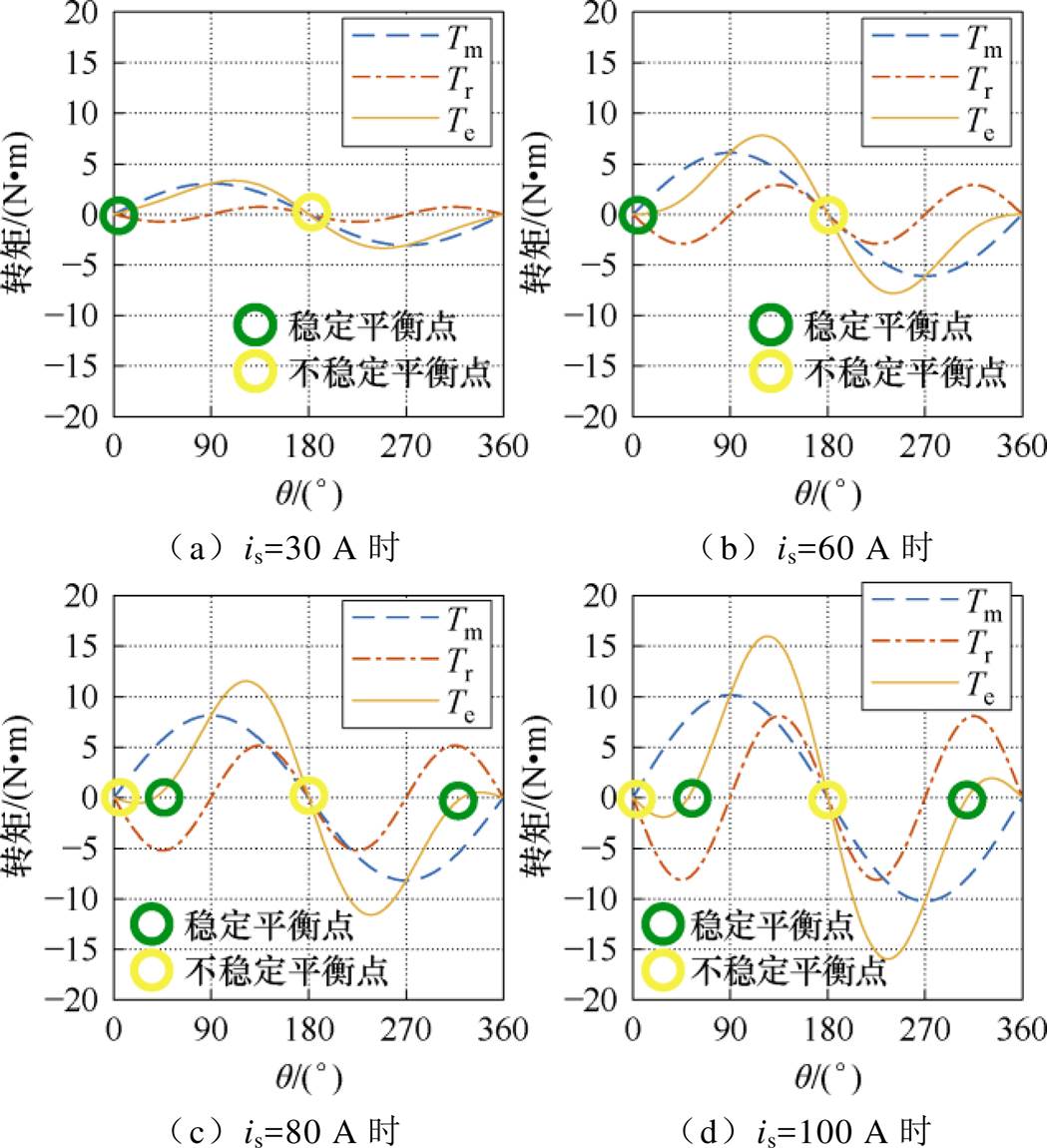
图2 不同定子电流下的转矩随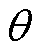 变化的关系
变化的关系
Fig.2 Diagram of the relationship between torque and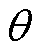 under different stator currents
under different stator currents
表贴式永磁电机只有永磁转矩,在一个电周期中只有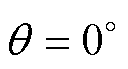 这一个稳定的平衡点。但是,对于PMaSynRS/G而言,这一结论不一定成立。为方便后文表述,定义电流阈值为
这一个稳定的平衡点。但是,对于PMaSynRS/G而言,这一结论不一定成立。为方便后文表述,定义电流阈值为
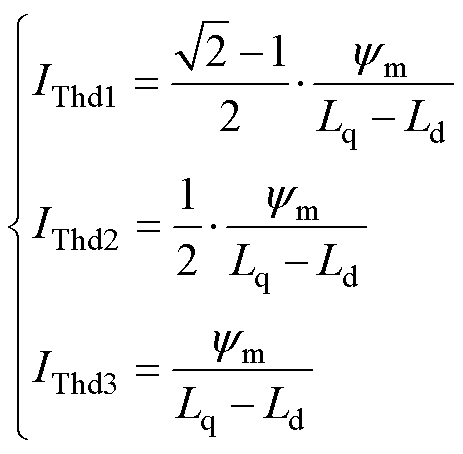 (2)
(2)
先不考虑摩擦转矩的影响,在进行预定位时,若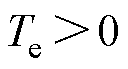 ,则转子受正向转矩,
,则转子受正向转矩,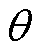 有减小趋势;若
有减小趋势;若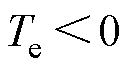 ,则转子受反向转矩,
,则转子受反向转矩,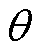 有增大趋势。则当电机处于静止状态时,有
有增大趋势。则当电机处于静止状态时,有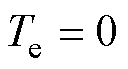 。代入式(1),可得
。代入式(1),可得
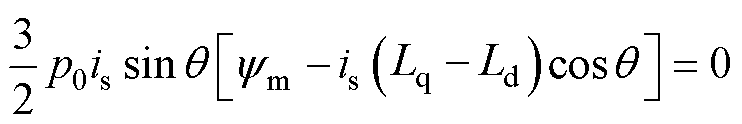 (3)
(3)
可进一步推知,该方程始终有解为
 (4)
(4)
当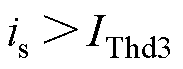 时,有另外的解为
时,有另外的解为
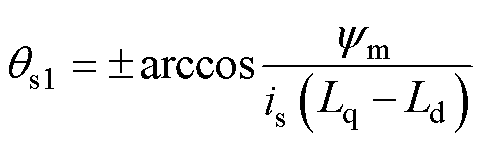 (5)
(5)
式(4)和式(5)只是理论上转矩为零的点,还需要考虑这些平衡点的稳定性。
设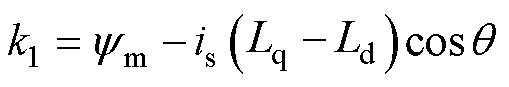 ,则
,则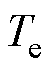 可表示为
可表示为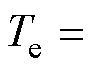
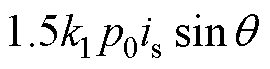 。当
。当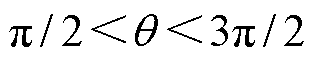 时,有
时,有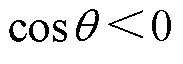 ,通常
,通常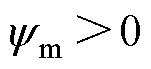 ,
,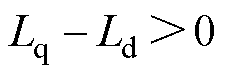 ,则可知
,则可知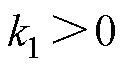 。当
。当
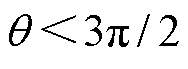 时,
时,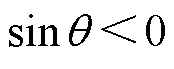 ,可知
,可知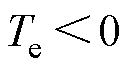 ;当
;当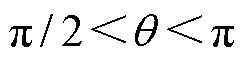 时,
时,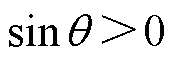 ,可知
,可知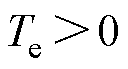 。因此,转子始终有远离原位的趋势,
。因此,转子始终有远离原位的趋势,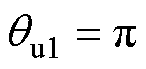 是不稳定平衡点。类似地,当
是不稳定平衡点。类似地,当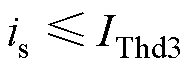 且
且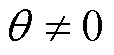 时,有
时,有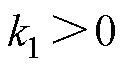 。可知,
。可知,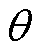 在0附近时,若
在0附近时,若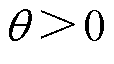 ,则
,则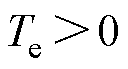 ;若
;若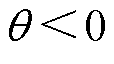 ,则
,则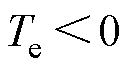 。转子始终有回复到原位的趋势,故
。转子始终有回复到原位的趋势,故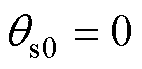 是稳定平衡点。
是稳定平衡点。
将式(1)对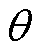 求偏导,可得
求偏导,可得
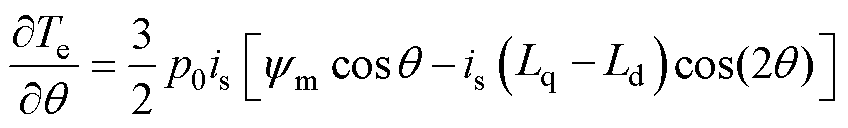 (6)
(6)
若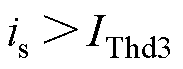 ,则有
,则有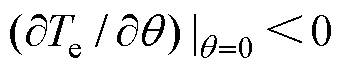 ,故当
,故当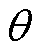 在0附近时,转子始终有远离原位的趋势,稳定平衡点
在0附近时,转子始终有远离原位的趋势,稳定平衡点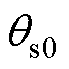 变为不稳定平衡点
变为不稳定平衡点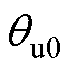 。同理可知,当
。同理可知,当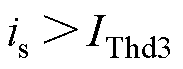 时,
时,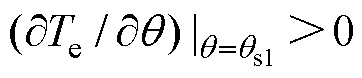 ,
,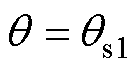 是稳定平衡点。
是稳定平衡点。
综上所述,在不同定子电流下,转子稳定平衡点和不稳定平衡点可分别表示为式(7)和式(8)所示。当定子电流逐渐增大到超过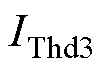 时,稳定平衡点
时,稳定平衡点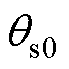 变为不稳定平衡点
变为不稳定平衡点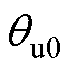 ,并产生电角度关于0对称的两个新的稳定平衡点
,并产生电角度关于0对称的两个新的稳定平衡点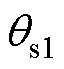 ,如图2所示。实际电机存在电感饱和、永磁磁链随温度变化等非理想因素,这会导致电机的
,如图2所示。实际电机存在电感饱和、永磁磁链随温度变化等非理想因素,这会导致电机的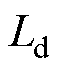 、
、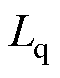 和
和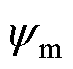 发生变化[27],进而对式(7)中
发生变化[27],进而对式(7)中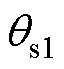 、
、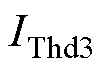 值产生影响。但是,结合不稳定平衡点
值产生影响。但是,结合不稳定平衡点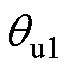 的推导过程和图2可知,
的推导过程和图2可知,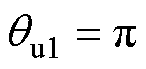 不受影响。
不受影响。
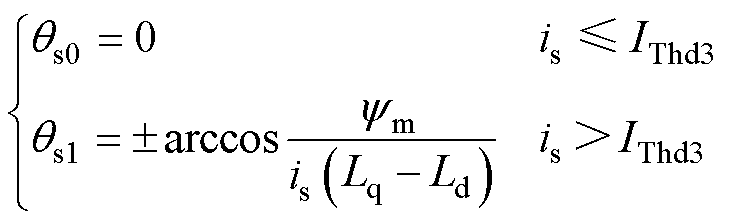 (7)
(7)
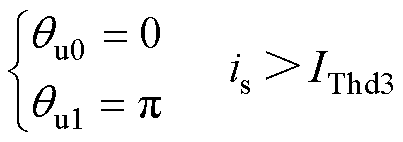 (8)
(8)
考虑摩擦转矩后,在使用预定位法进行转子定位时,其位置可略微偏离稳定平衡点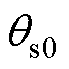 ,出现定位角度误差。电机转子的机械运动方程为
,出现定位角度误差。电机转子的机械运动方程为
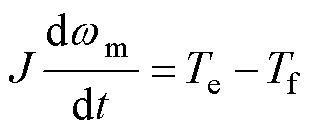 (9)
(9)
式中,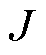 为系统等效转动惯量;
为系统等效转动惯量;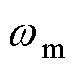 为转子机械角速度;
为转子机械角速度;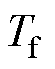 为摩擦转矩。
为摩擦转矩。
根据Stribeck摩擦模型[28],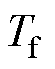 与
与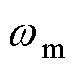 满足
满足
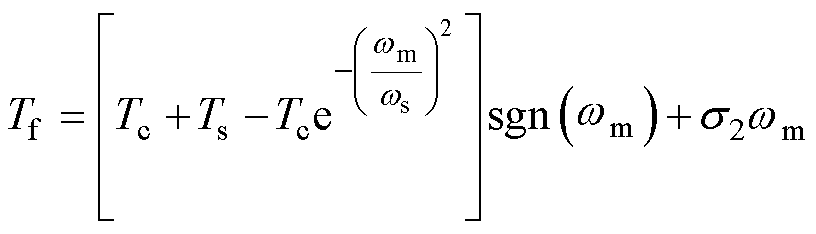 (10)
(10)
式中,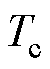 为库仑摩擦力矩;
为库仑摩擦力矩;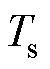 为最大静摩擦力矩;
为最大静摩擦力矩;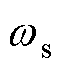 为Stribeck速度;
为Stribeck速度;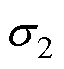 为黏性摩擦系数。
为黏性摩擦系数。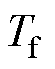 与
与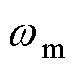 之间关系的非线性较强,如图3所示。
之间关系的非线性较强,如图3所示。
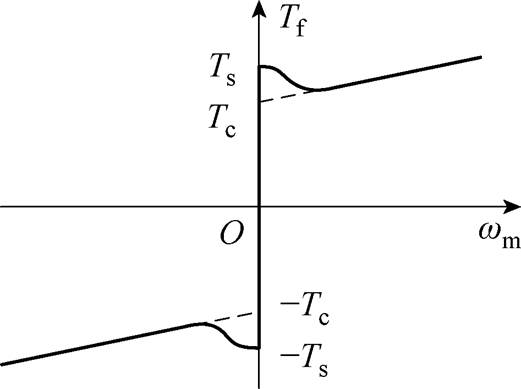
图3 Stribeck摩擦力曲线
Fig.3 Stribeck friction curve
在定子通入电流后,转子将经过一个过渡过程到达平衡位置,最终有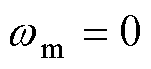 ,
,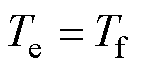 。转子静止时的
。转子静止时的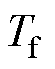 为静摩擦力矩,其值可变,但始终与
为静摩擦力矩,其值可变,但始终与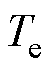 相等,且最大不超过
相等,且最大不超过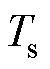 。
。
将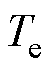 在平衡点附近位置
在平衡点附近位置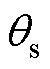 进行泰勒展开可得
进行泰勒展开可得
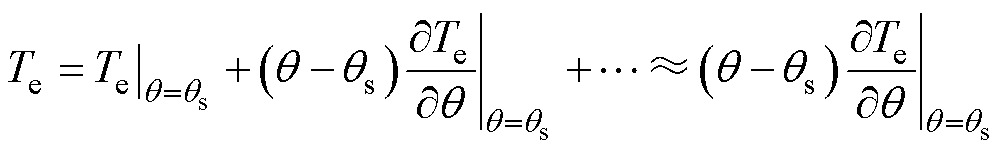 (11)
(11)
将式(11)代入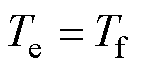 ,得
,得
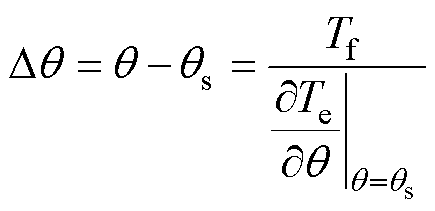 (12)
(12)
式中,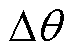 为定位角度误差;
为定位角度误差;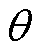 为偏离理想平衡点的电角度近似值。
为偏离理想平衡点的电角度近似值。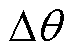 与转子所受摩擦转矩及平衡点处电磁转矩与转矩角的偏导数有关。进而可推知,当
与转子所受摩擦转矩及平衡点处电磁转矩与转矩角的偏导数有关。进而可推知,当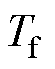 达到最大静摩擦力矩
达到最大静摩擦力矩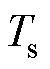 时,
时,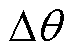 达到最大值,即有
达到最大值,即有
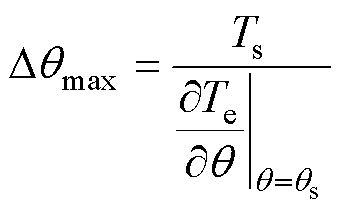 (13)
(13)
将式(6)和式(7)代入式(12),可得转子平衡在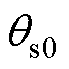 时的角度误差的估计值为
时的角度误差的估计值为
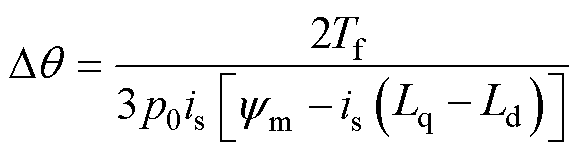 (14)
(14)
式中,分母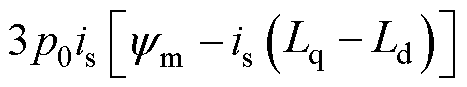 为
为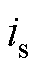 的二次函数,可算得分母在
的二次函数,可算得分母在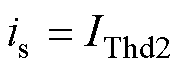 时有最大值。则
时有最大值。则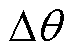 在此
在此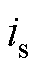 下有最小值为
下有最小值为
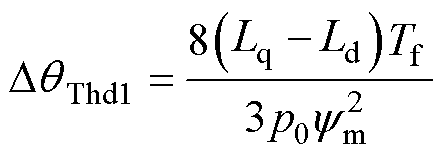 (15)
(15)
也就是说,定位角度误差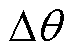 随
随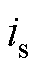 增大而减小,当
增大而减小,当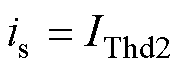 时达到最小值
时达到最小值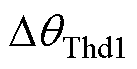 ,而后随
,而后随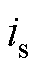 增大而增大;当
增大而增大;当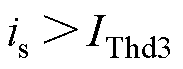 时,转子不能在
时,转子不能在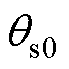 附近保持稳定平衡,表现出趋于新平衡点
附近保持稳定平衡,表现出趋于新平衡点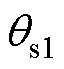 的趋势。
的趋势。
以实验样机(参数见表1)为例,考虑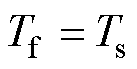 的最坏情况,预定位法的角度误差与定位电流的理论关系如图4所示,实验时
的最坏情况,预定位法的角度误差与定位电流的理论关系如图4所示,实验时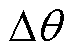 可能为阴影区间内的任何值。预定位法只利用到电机永磁转矩分量,但是在平衡点附近PMaSynRS/G中占比较大的磁阻转矩分量与永磁转矩分量方向相反,这反而会降低预定位法定位的精度。因此,加大定位电流也不一定能减小由于摩擦转矩造成的角度误差,甚至会增大误差,出现转子稳定平衡点偏离电流矢量方向的现象。这说明预定位法不适用于PMaSynRS/G。
可能为阴影区间内的任何值。预定位法只利用到电机永磁转矩分量,但是在平衡点附近PMaSynRS/G中占比较大的磁阻转矩分量与永磁转矩分量方向相反,这反而会降低预定位法定位的精度。因此,加大定位电流也不一定能减小由于摩擦转矩造成的角度误差,甚至会增大误差,出现转子稳定平衡点偏离电流矢量方向的现象。这说明预定位法不适用于PMaSynRS/G。
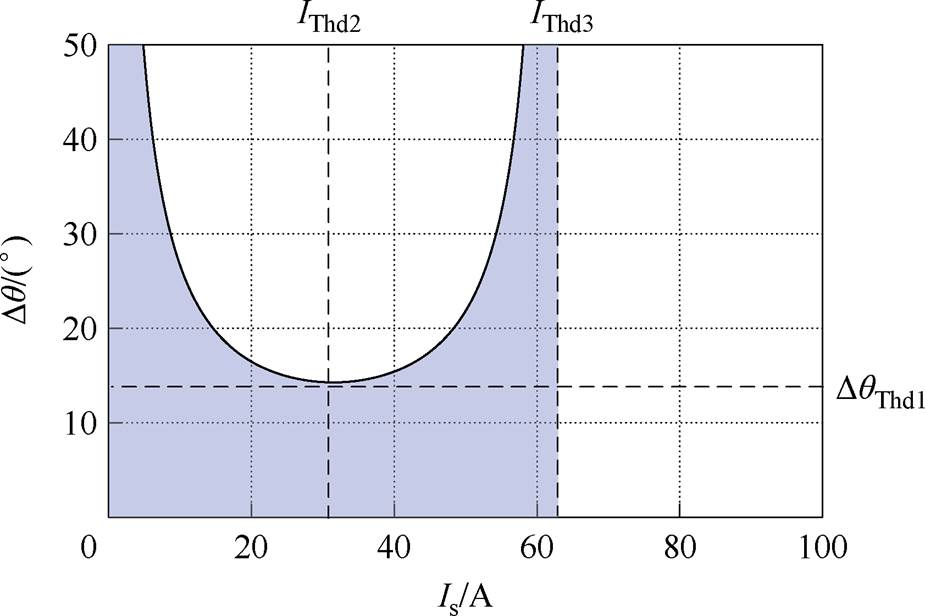
图4 预定位法的角度误差与定子电流关系
Fig.4 Diagram of the relationship between angle error and stator current of the pre-position method
预定位法利用稳定平衡点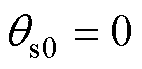 实现转子定位,由第1节分析可知,这并不适用于PMaSynRS/G。
实现转子定位,由第1节分析可知,这并不适用于PMaSynRS/G。
所提方法则加入相应控制算法,实现利用不稳定平衡点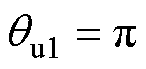 完成转子定位,从而有效降低摩擦转矩影响,提高零位标校精度。该方法结构框图如图5所示,分为控制器参数估计和零位偏差标校两个部分。图5中,
完成转子定位,从而有效降低摩擦转矩影响,提高零位标校精度。该方法结构框图如图5所示,分为控制器参数估计和零位偏差标校两个部分。图5中,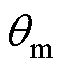 为通过位置传感器直接读取的转子机械角度值,其包含零位偏差。
为通过位置传感器直接读取的转子机械角度值,其包含零位偏差。
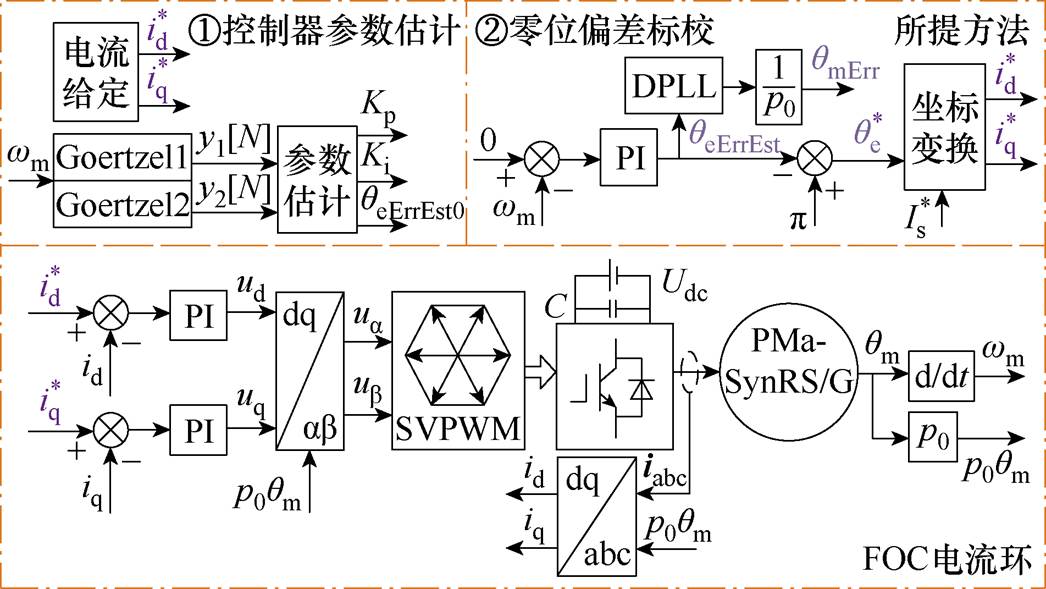
图5 基于不稳定平衡点的零位偏差标校方法结构框图
Fig.5 Structural diagram of zero position deviation correction method based on unstable equilibrium point
基于经典的磁场定向控制(Field Oriented Control, FOC)电流环,向dq轴注入激励电流,其值为
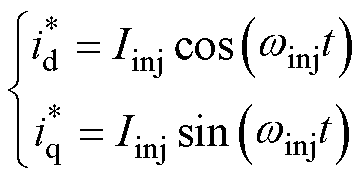 (16)
(16)
式中,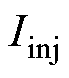 为注入信号的幅值;
为注入信号的幅值;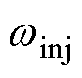 为注入信号的角频率;
为注入信号的角频率;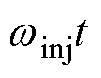 的范围为0~
的范围为0~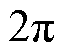 。可得此时
。可得此时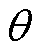 满足
满足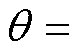
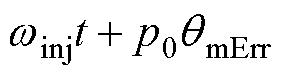 ,其中,
,其中,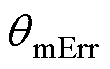 为零位偏差校正值。代入式(1)和式(9)并对
为零位偏差校正值。代入式(1)和式(9)并对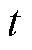 进行定积分,可得转速
进行定积分,可得转速
随时间关系为
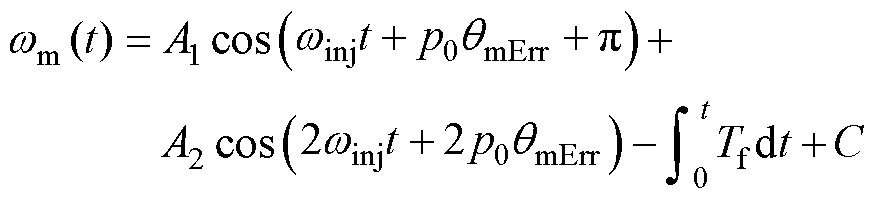 (17)
(17)
式中,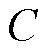 为与初始角速度及定积分运算有关的常数项。
为与初始角速度及定积分运算有关的常数项。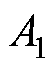 和
和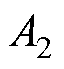 满足
满足
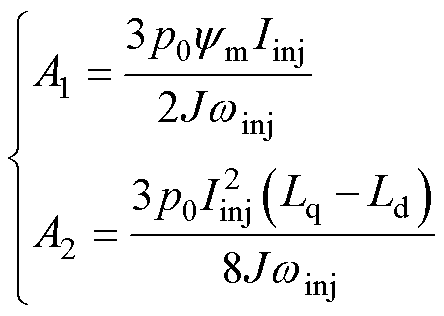 (18)
(18)
由式(17)可知,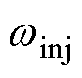 和
和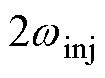 这两个频率转速分量的幅值中含有机电参数的信息,相位中含有
这两个频率转速分量的幅值中含有机电参数的信息,相位中含有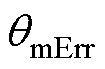 的信息。通过选用较大的
的信息。通过选用较大的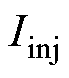 ,可使得执行该步骤时电磁力矩远大于摩擦力矩,在参数估计时可忽略其中的摩擦力矩项。
,可使得执行该步骤时电磁力矩远大于摩擦力矩,在参数估计时可忽略其中的摩擦力矩项。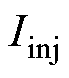 须小于电机和控制器的额定电流。通过选用较小的
须小于电机和控制器的额定电流。通过选用较小的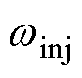 ,可增大
,可增大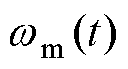 中所需频率分量的幅值,以提高频率分量提取及参数估计的精度。
中所需频率分量的幅值,以提高频率分量提取及参数估计的精度。
本文使用计算离散傅里叶变换(Discrete Fourier Transform, DFT)的格兹尔(Goertzel)算法对转速中相应频率分量进行提取。该算法可简述如下[29]:设以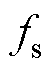 为采样频率得到转速信号序列
为采样频率得到转速信号序列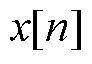 ,其采样长度为
,其采样长度为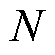 ,待提取转速分量的角频率为
,待提取转速分量的角频率为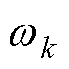 。可推知,
。可推知,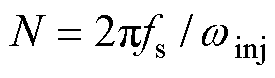 ,
,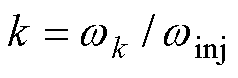 。为避免频谱泄露,
。为避免频谱泄露,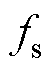 应为
应为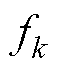 的整数倍。
的整数倍。
Goertzel算法框图如图6所示,图中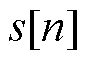 为中间变量,
为中间变量,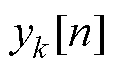 为输出变量。Goertzel算法将DFT视为对输入数据的线性滤波,可分为左边二阶无限脉冲响应(Infinite Impulse Response, IIR)滤波器部分及右边前馈部分,IIR滤波器部分执行N次,而前馈部分只需执行一次,从而可在微处理器中实时执行。可以推知,对角频率为
为输出变量。Goertzel算法将DFT视为对输入数据的线性滤波,可分为左边二阶无限脉冲响应(Infinite Impulse Response, IIR)滤波器部分及右边前馈部分,IIR滤波器部分执行N次,而前馈部分只需执行一次,从而可在微处理器中实时执行。可以推知,对角频率为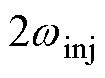 的转速分量,有
的转速分量,有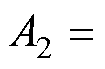
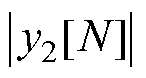 。对角频率为
。对角频率为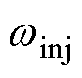 的转速分量有
的转速分量有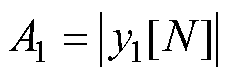 ,并可估计位置传感器零位偏差电角度为
,并可估计位置传感器零位偏差电角度为
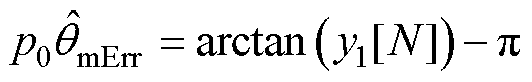 ,其中,
,其中,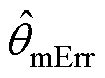 为
为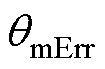 使用Goertzel算法得到的估计值。
使用Goertzel算法得到的估计值。
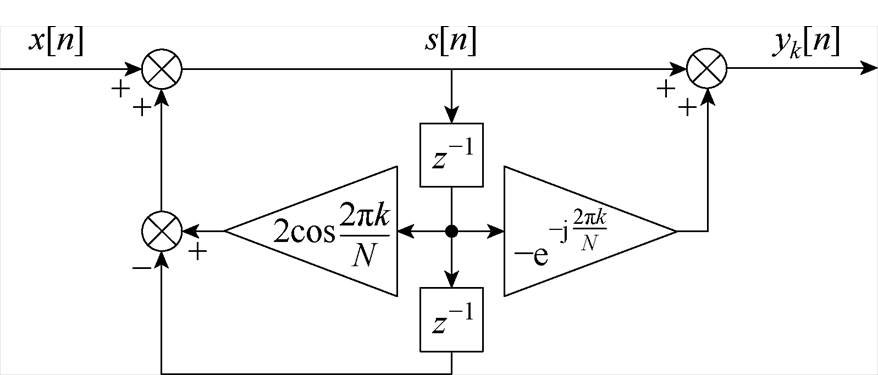
图6 Goertzel算法框图
Fig.6 The block diagram of Goertzel algorithm
通过本节所提步骤可估计出 的初值,使得2.2节所提PI控制器基本工作在预期不稳定平衡点附近。同时,可按照2.2节公式计算出PI控制器参数,从而无需测量电机系统的电感、转动惯量等参数。本节中参数估计的误差只影响零位偏差标校算法的收敛时间,不影响其精度。
的初值,使得2.2节所提PI控制器基本工作在预期不稳定平衡点附近。同时,可按照2.2节公式计算出PI控制器参数,从而无需测量电机系统的电感、转动惯量等参数。本节中参数估计的误差只影响零位偏差标校算法的收敛时间,不影响其精度。
所提位置传感器零位偏差标校方法相当于FOC电流环的外环,其结构如图5右上部分所示。PI控制器的输入为当前转速与零的差,输出为零位偏差电角度的估计值 ,积分初值为2.1节所得
,积分初值为2.1节所得 。定子电流矢量的电角度给定值取为
。定子电流矢量的电角度给定值取为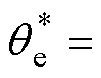
 ,而后经由坐标变换算得dq电流的指令值,即
,而后经由坐标变换算得dq电流的指令值,即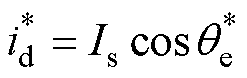 ,
,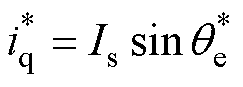 ,其中
,其中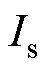 为进行零位偏差标校时定子的电流幅值。可算得此时
为进行零位偏差标校时定子的电流幅值。可算得此时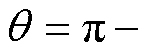
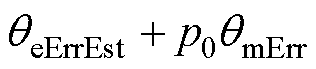 。当
。当 趋于
趋于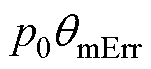 时,
时,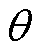 趋于
趋于 ,定子电流矢量方向趋于负d轴方向。
,定子电流矢量方向趋于负d轴方向。
若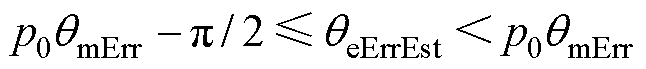 ,可算得此时
,可算得此时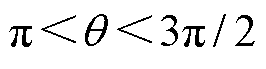 ,由1.2节可知,
,由1.2节可知,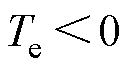 ,结合式(9),可知
,结合式(9),可知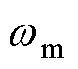 将减小,PI控制器的输入将增大;同理,当
将减小,PI控制器的输入将增大;同理,当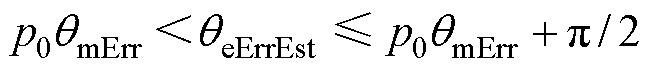 时,有
时,有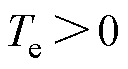 ,则
,则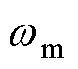 将增大,PI控制器的输入将减小。故当位置传感器存在零位误差时,PI控制器将根据
将增大,PI控制器的输入将减小。故当位置传感器存在零位误差时,PI控制器将根据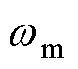 调节
调节 ,使得
,使得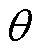 趋于
趋于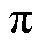 。最终,定子电流矢量方向趋于原不稳定平衡点,且
。最终,定子电流矢量方向趋于原不稳定平衡点,且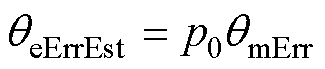 。将
。将 再经过数字锁相环(Digital Phase-Locked Loop, DPLL)平滑滤波处理和极对数换算后,即可得到零位偏差的机械角度值
再经过数字锁相环(Digital Phase-Locked Loop, DPLL)平滑滤波处理和极对数换算后,即可得到零位偏差的机械角度值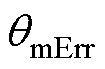 。
。
所提零位偏差标校方法的控制框图如图7所示,图中,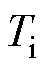 为近似等效为小惯性环节的电流环的时间常数;
为近似等效为小惯性环节的电流环的时间常数;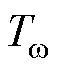 为代表转速测量环节带宽的时间常数;
为代表转速测量环节带宽的时间常数;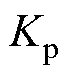 和
和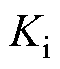 分别为PI控制器的比例和积分系数。将图5模型在平衡点附近进行线性化,可得其开环传递函数为
分别为PI控制器的比例和积分系数。将图5模型在平衡点附近进行线性化,可得其开环传递函数为
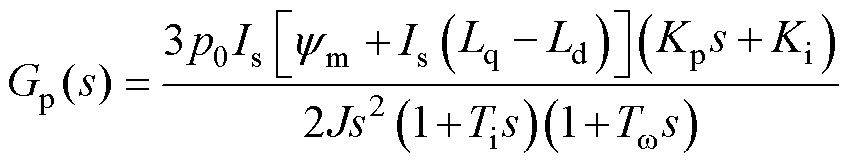 (19)
(19)
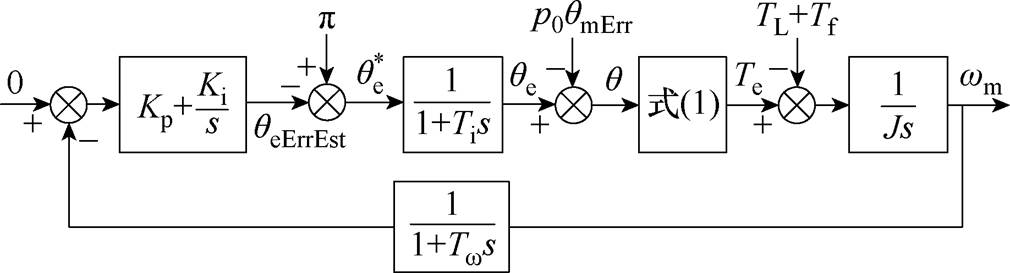
图7 所提方法的控制框图
Fig.7 Control diagram of the proposed method
对式(19)中的小惯性环节进行合并,可将其等效为典型Ⅱ型系统,开环传递函数为
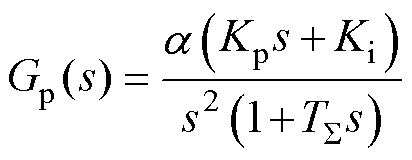 (20)
(20)
式中,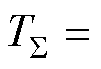
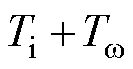 为近似等效的小惯性环节的时间常数;
为近似等效的小惯性环节的时间常数;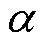 为和线性化工作点相关的系数,有
为和线性化工作点相关的系数,有
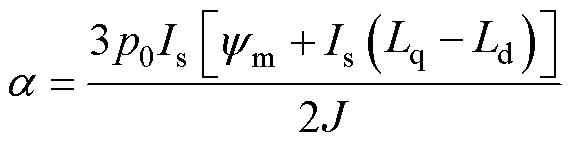 (21)
(21)
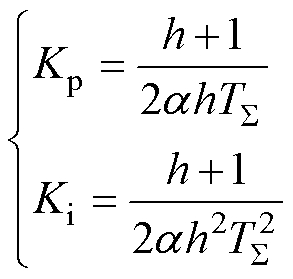 (22)
(22)
式中,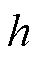 为中频宽,影响控制器带宽和超调。
为中频宽,影响控制器带宽和超调。
根据典型Ⅱ型系统的整定理论,可得PI控制器参数与中频宽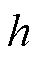 的关系[30]为
的关系[30]为
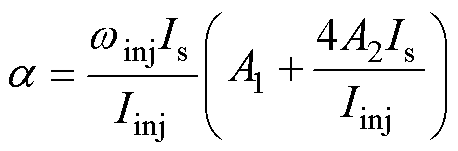 (23)
(23)
可推知,整定PI控制器所需的参数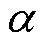 与2.1节算得的
与2.1节算得的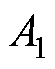 和
和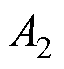 满足式(23)关系。所提算法中PI控制器参数可结合2.1节数据算出,无需额外整定。
满足式(23)关系。所提算法中PI控制器参数可结合2.1节数据算出,无需额外整定。
经过一定的调节时间(根据典型Ⅱ型系统模型,可估计为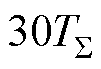 [30])后,PI控制器基本稳定,可将此时所提算法输出的零位偏差校正值
[30])后,PI控制器基本稳定,可将此时所提算法输出的零位偏差校正值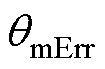 作为最终标校结果。
作为最终标校结果。
由于摩擦转矩的存在,即使定子电流方向略微与d轴负方向有偏移,转子也可能保持静止。同理将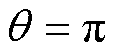 代入式(12),得到由摩擦转矩造成的电角度误差与定位电流的近似关系为
代入式(12),得到由摩擦转矩造成的电角度误差与定位电流的近似关系为
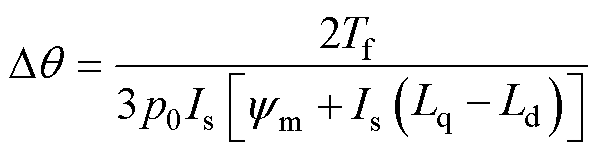 (24)
(24)
以实验样机为例,考虑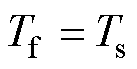 的最坏情况,其角度误差估计值与定子电流关系如图8所示,实验时
的最坏情况,其角度误差估计值与定子电流关系如图8所示,实验时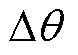 可能为阴影区间内的任何值。对比图4和图8可知,所提方法明显减小了摩擦转矩造成的误差。应用所提方法时,磁阻转矩和永磁转矩方向一致,且定位电流
可能为阴影区间内的任何值。对比图4和图8可知,所提方法明显减小了摩擦转矩造成的误差。应用所提方法时,磁阻转矩和永磁转矩方向一致,且定位电流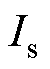 越大,由摩擦转矩造成的误差越小。进一步可算得,当
越大,由摩擦转矩造成的误差越小。进一步可算得,当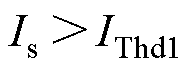 时,
时,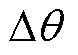 小于预定位法所能实现的最小误差
小于预定位法所能实现的最小误差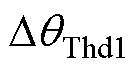 。但由于电机转矩脉动、传感器误差等因素,到一定程度后再增加
。但由于电机转矩脉动、传感器误差等因素,到一定程度后再增加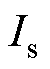 并不能继续提高标校精度,且
并不能继续提高标校精度,且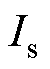 须小于电机和控制器的额定电流。
须小于电机和控制器的额定电流。
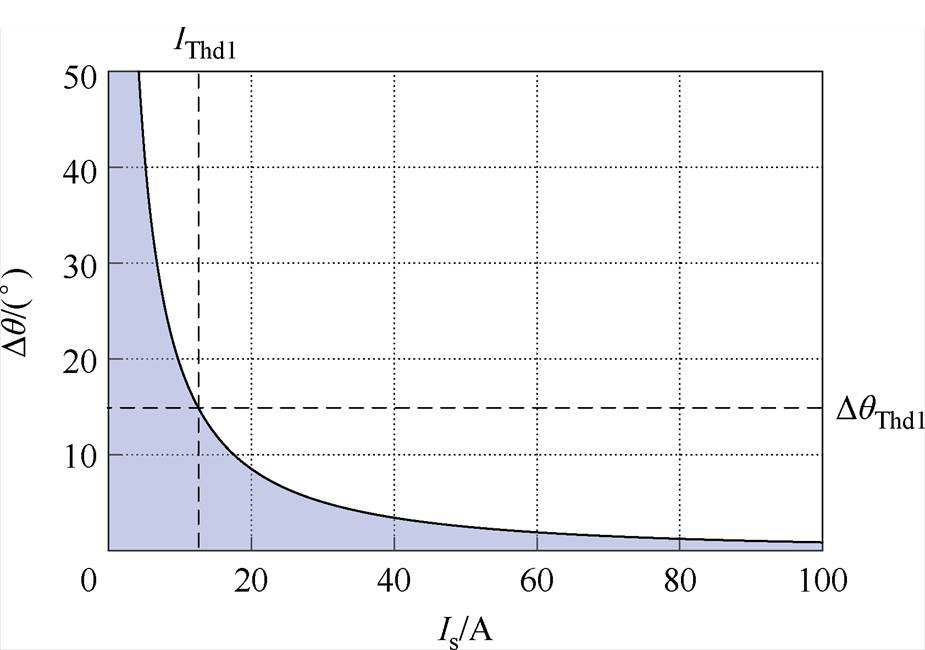
图8 所提方法的角度误差与定子电流关系
Fig.8 Diagram of the relationship between angle error and stator current of the proposed method
综上所述,所提方法的实施步骤如图9所示。图9a需选择的参数中,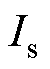 和
和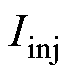 可选择为电机额定电流
可选择为电机额定电流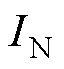 的30%;
的30%;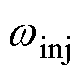 可选择为
可选择为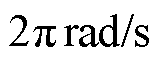 。本文所提方法无需额外硬件,在通用电机驱动器上即可实现。只需选择3个参数即可执行,易于应用,鲁棒性高。该方法可有效减小摩擦转矩造成的误差,提高位置传感器零位标校的精度。
。本文所提方法无需额外硬件,在通用电机驱动器上即可实现。只需选择3个参数即可执行,易于应用,鲁棒性高。该方法可有效减小摩擦转矩造成的误差,提高位置传感器零位标校的精度。
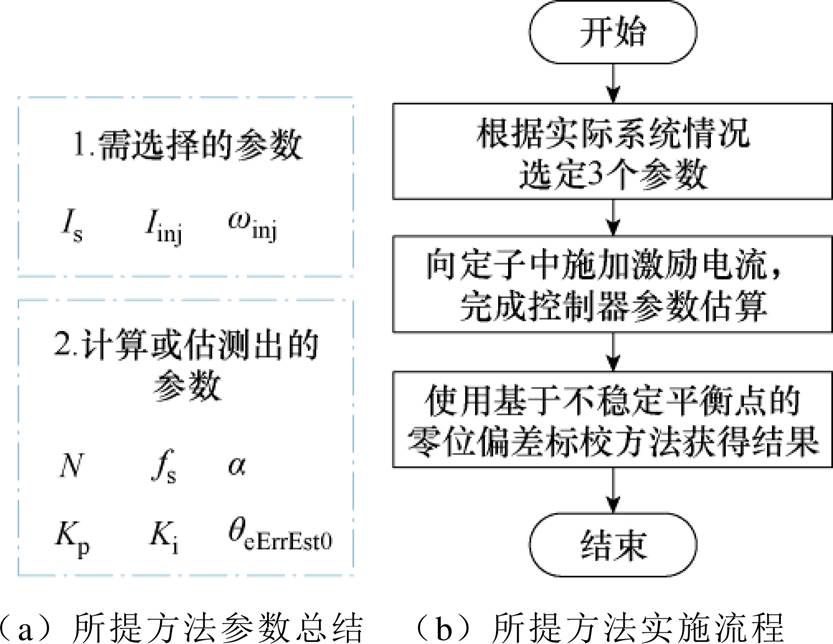
图9 所提方法实施步骤
Fig.9 Implementation steps of the proposed method
为验证本文所提模型及方法的有效性,搭建了如图10所示实验平台,进行了各项验证实验。实验平台主要参数见表1。实验所用位置传感器为一对极旋转变压器,控制器基于TI公司TMS320F28377D芯片搭建,开关频率为15 kHz。为模拟对已安装在系统中的电机进行零位标定的情况,实验时将被测电机连接到了台架测功机(异步电机)上,这使得摩擦转矩和转动惯量增大。

图10 实验平台
Fig.10 Experimental platform
使用预定位法,向电机定子施加方向恒与定子A轴重合,幅值从0缓慢增大至100 A的定位电流矢量。在转子初始机械角度位置分别位于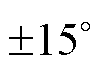 、
、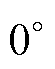 和
和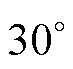 附近时,测得转子机械角度随时间变化关系如图11所示。
附近时,测得转子机械角度随时间变化关系如图11所示。
表1 实验平台主要参数
Tab.1 The parameters of the experimental platform
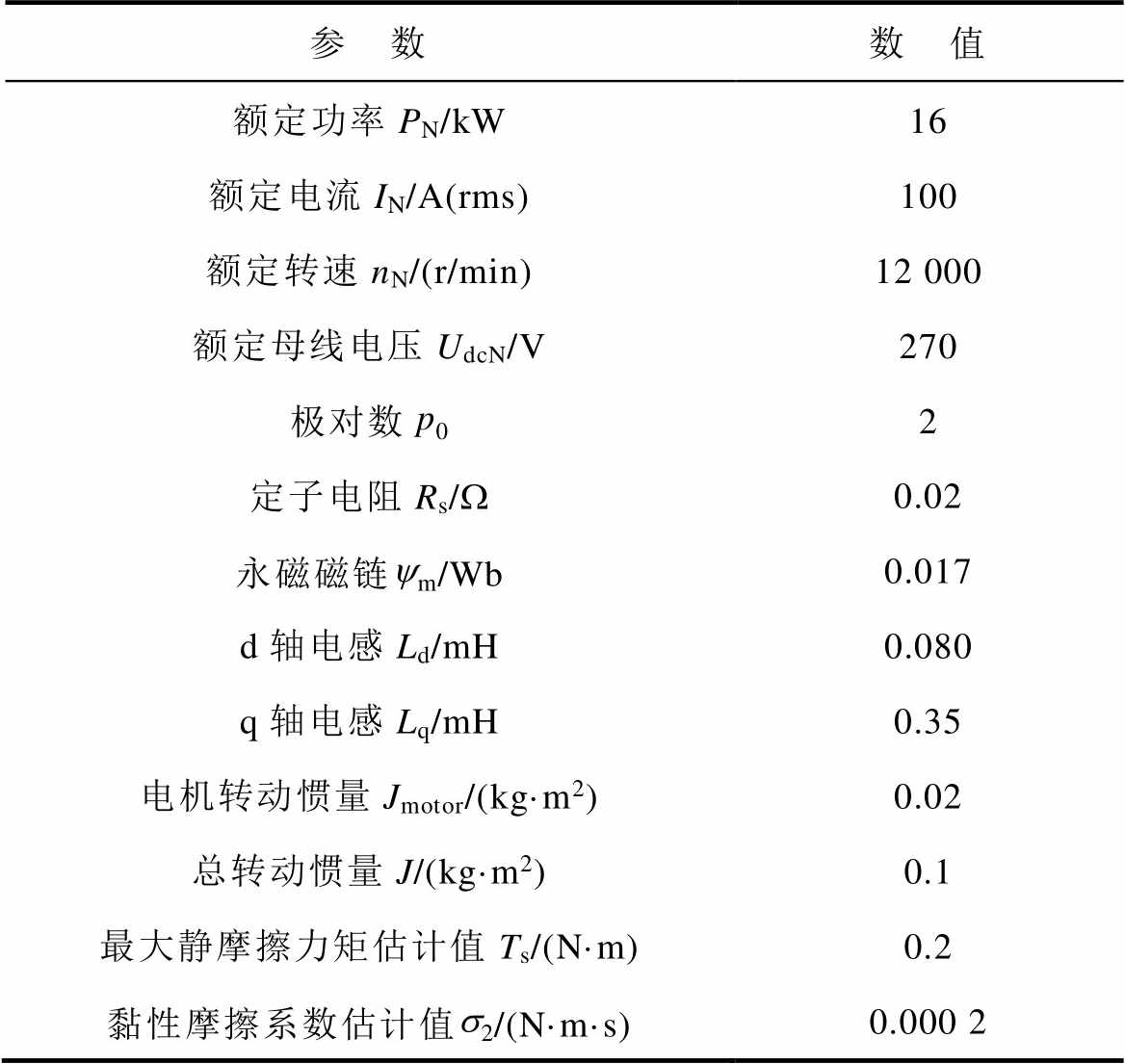
参 数数 值 额定功率PN/kW16 额定电流IN/A(rms)100 额定转速nN/(r/min)12 000 额定母线电压UdcN/V270 极对数p02 定子电阻Rs/W0.02 永磁磁链ym/Wb0.017 d轴电感Ld/mH0.080 q轴电感Lq/mH0.35 电机转动惯量Jmotor/(kg·m2)0.02 总转动惯量J/(kg·m2)0.1 最大静摩擦力矩估计值Ts/(N·m)0.2 黏性摩擦系数估计值s2/(N·m·s)0.000 2
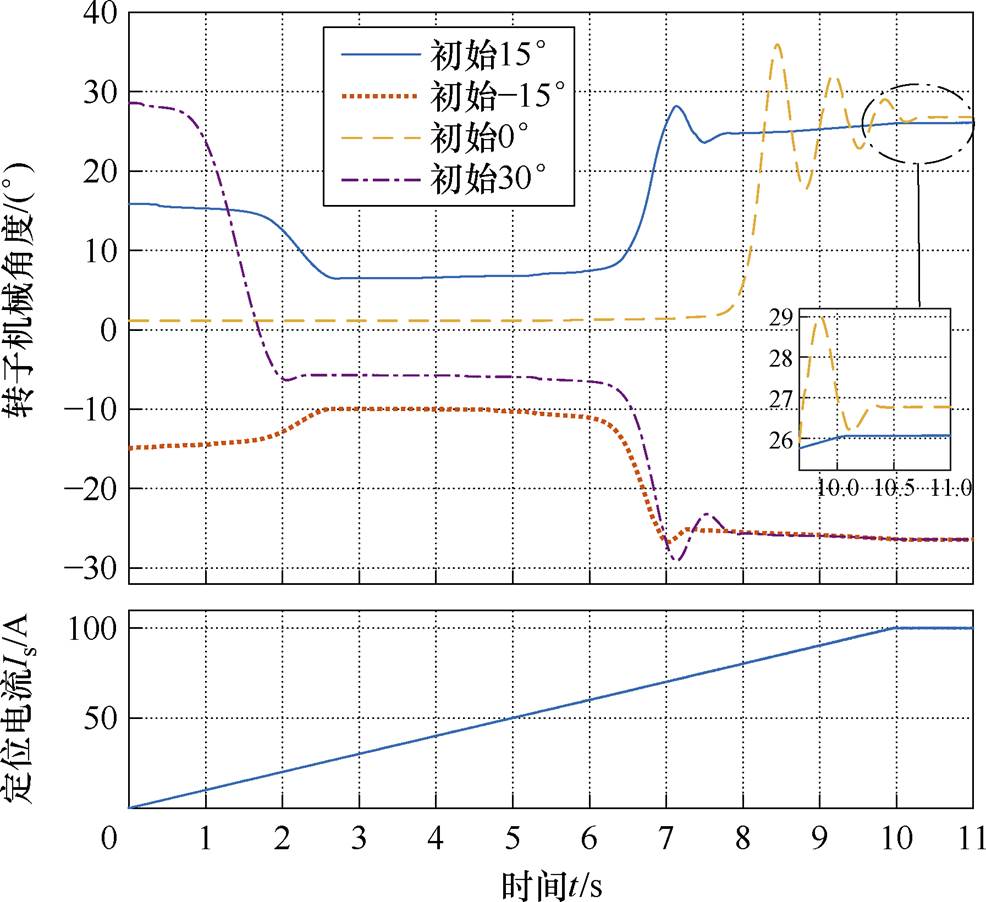
图11 预位法波形
Fig.11 Waveforms of pre-positioning method
当定位电流从0逐渐增大时,转子受电磁力矩作用,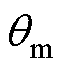 趋于0。但由于摩擦转矩影响,转子d轴不会恰好与A轴重合,即存在较大定位误差。当定位电流增大至约30 A时,定位误差即达到最小值。当电流进一步增大至约60 A时,
趋于0。但由于摩擦转矩影响,转子d轴不会恰好与A轴重合,即存在较大定位误差。当定位电流增大至约30 A时,定位误差即达到最小值。当电流进一步增大至约60 A时,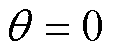 成为不稳定平衡点,转子趋于
成为不稳定平衡点,转子趋于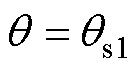 的两个新的稳定平衡点。由图11可得,使用
的两个新的稳定平衡点。由图11可得,使用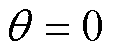 点定位时的误差最大约
点定位时的误差最大约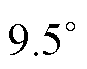 机械角度,合
机械角度,合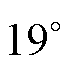 电角度。当定位电流保持在100 A时,新平衡点
电角度。当定位电流保持在100 A时,新平衡点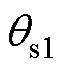 距离原平衡点约
距离原平衡点约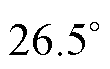 机械角度,合
机械角度,合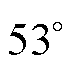 电角度。
电角度。
该实验说明,在PMaSynRS/G上应用预定位法时,由于磁阻转矩方向与永磁转矩方向相反,这会使得总的定位转矩变小,定位精度下降,易受摩擦转矩干扰。当定位电流约为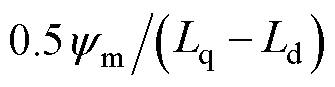 时可获得最小的定位误差。当定位电流超过
时可获得最小的定位误差。当定位电流超过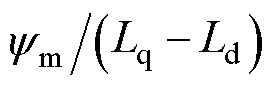 时,转子平衡点又将发生偏移。
时,转子平衡点又将发生偏移。
为研究不同的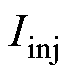 和
和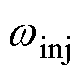 对参数估计步骤精度的影响,使用不同参数值进行实验,测得PI参数估计值与理论值之比及估测
对参数估计步骤精度的影响,使用不同参数值进行实验,测得PI参数估计值与理论值之比及估测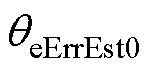 误差随两参数变化关系如图12所示。由图12可知,当
误差随两参数变化关系如图12所示。由图12可知,当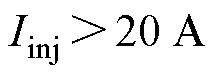 ,
,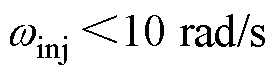 后估计误差基本平稳,可得到足够的参数估计精度。
后估计误差基本平稳,可得到足够的参数估计精度。
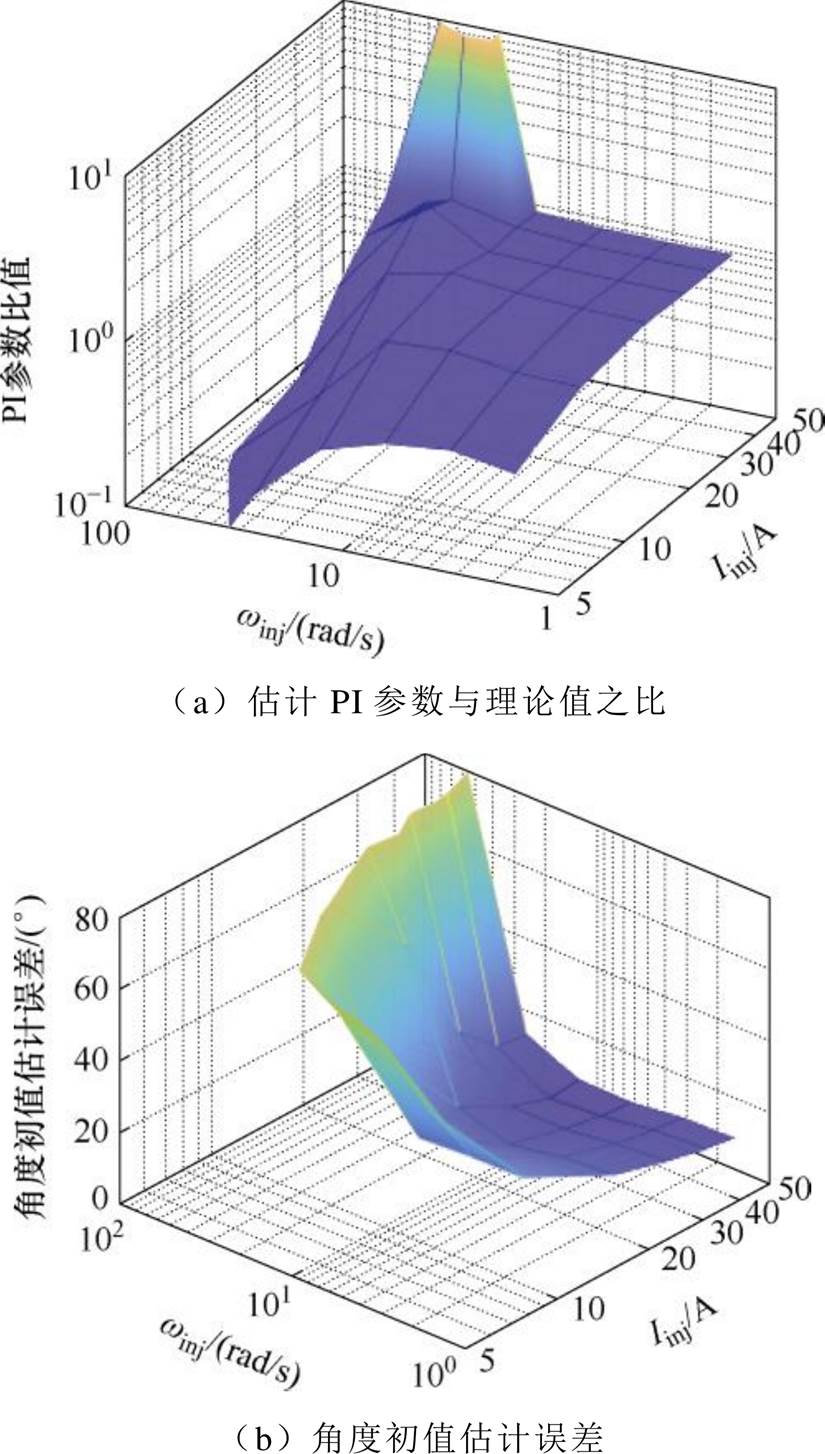
图12 估计误差与选取参数关系
Fig.12 Estimation error and selection parameter relationship diagram
根据实验平台情况,使用表2所提方法参数进行实验。实验所用样机的旋转变压器转子仅靠轴心上一枚螺栓与电机转子固定,因此其出厂时的零位偏差可以是任何值。应用所提方法测得的 、转速及电流波形如图13所示。
、转速及电流波形如图13所示。
所提方法从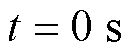 时开始执行,首先进行参数估计步骤,向定子中施加既定激励电流,使用Goertzel算法提取转速信号中的特定频率分量。在
时开始执行,首先进行参数估计步骤,向定子中施加既定激励电流,使用Goertzel算法提取转速信号中的特定频率分量。在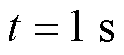 时参数估计完毕,用所得结果设定PI控制器参数及积分初值。判定转速自然归零后,即可开始执行所提零位偏差标校算法,经过0.2~0.3 s后,其标校值基本稳定,可将此时所提方法的输出值作为零位偏差的标校结果。由图13可知,使用所提算法测得零位偏差为
时参数估计完毕,用所得结果设定PI控制器参数及积分初值。判定转速自然归零后,即可开始执行所提零位偏差标校算法,经过0.2~0.3 s后,其标校值基本稳定,可将此时所提方法的输出值作为零位偏差的标校结果。由图13可知,使用所提算法测得零位偏差为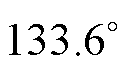 机械角度,而使用反电动势法测得的传感器零位偏差为
机械角度,而使用反电动势法测得的传感器零位偏差为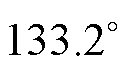 机械角度,相差
机械角度,相差 机械角度。
机械角度。
表2 所提方法参数
Tab.2 Parameters of the proposed method
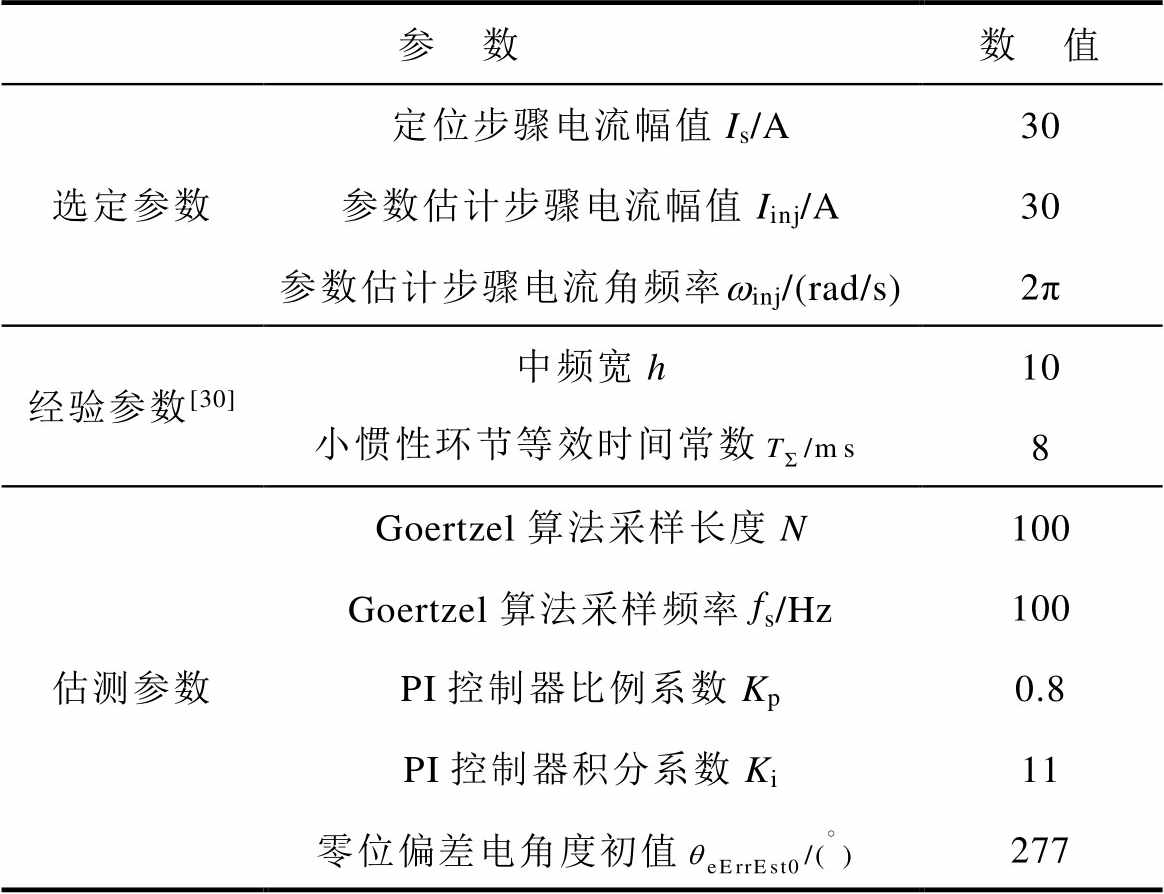
参 数数 值 选定参数定位步骤电流幅值Is/A30 参数估计步骤电流幅值Iinj/A30 参数估计步骤电流角频率winj/(rad/s)2π 经验参数[30]中频宽h10 小惯性环节等效时间常数8 估测参数Goertzel算法采样长度N100 Goertzel算法采样频率fs/Hz100 PI控制器比例系数Kp0.8 PI控制器积分系数Ki11 零位偏差电角度初值277
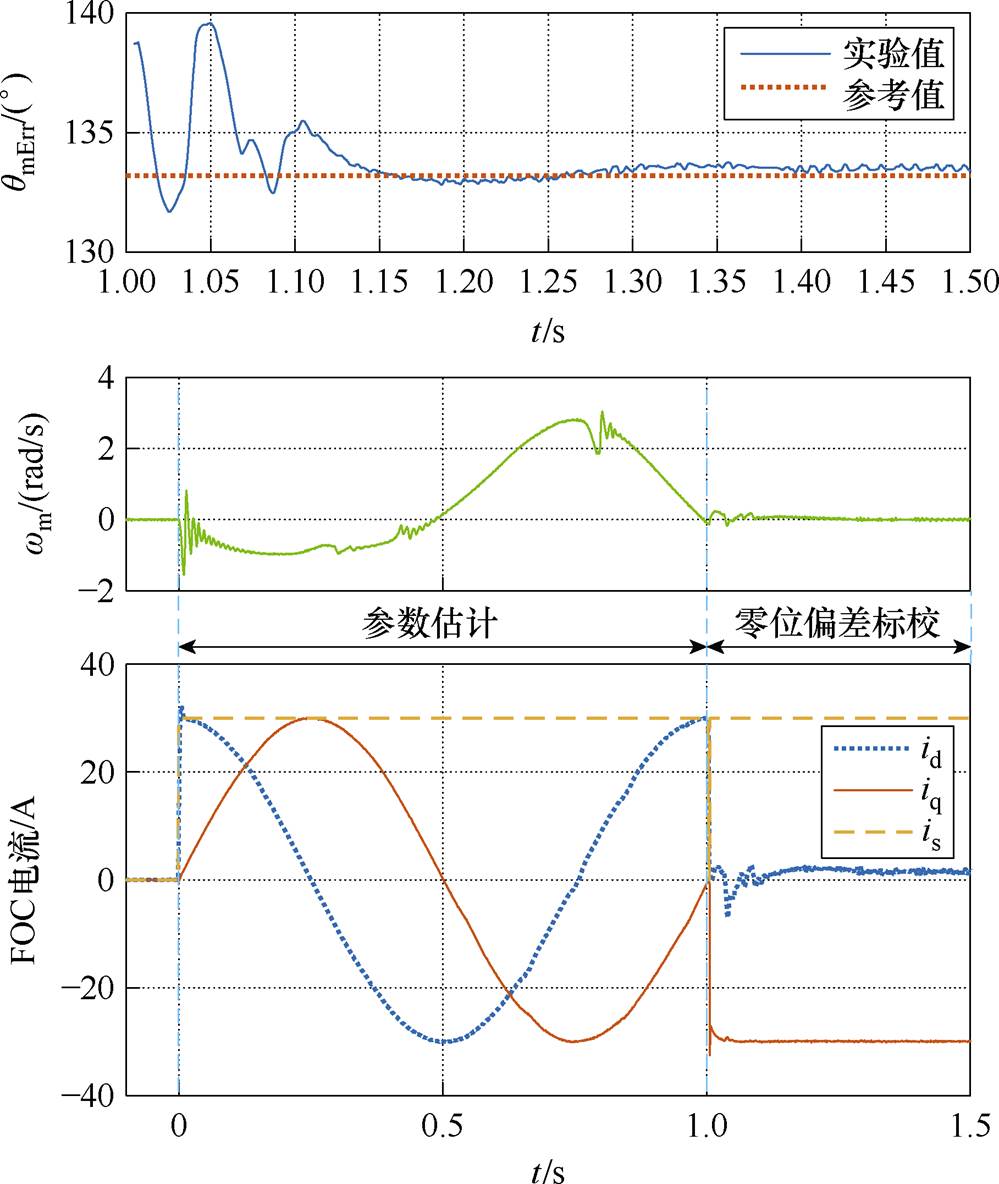
图13 所提方法实验波形
Fig.13 Experimental waveforms of the proposed method
为研究不同的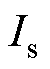 对所提零位偏差标校算法精度的影响,使用不同的
对所提零位偏差标校算法精度的影响,使用不同的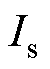 分别进行20次实验,可得20次实验结果中的最大误差随
分别进行20次实验,可得20次实验结果中的最大误差随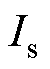 的变化关系如图14所示。实验结果趋势基本与理论推导相符,当定位电流在20 A以上时,所提方法的最大误差可保持在
的变化关系如图14所示。实验结果趋势基本与理论推导相符,当定位电流在20 A以上时,所提方法的最大误差可保持在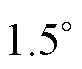 机械角度内,远小于预定位法的
机械角度内,远小于预定位法的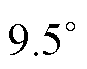 机械角度。当定位电流足够大,受到转矩脉动、位置传感器误差等其他因素影响,再增加定位电流并不能继续提高标校精度。由此可见,使用所提方法能有效减小由摩擦转矩带来的误差影响。
机械角度。当定位电流足够大,受到转矩脉动、位置传感器误差等其他因素影响,再增加定位电流并不能继续提高标校精度。由此可见,使用所提方法能有效减小由摩擦转矩带来的误差影响。
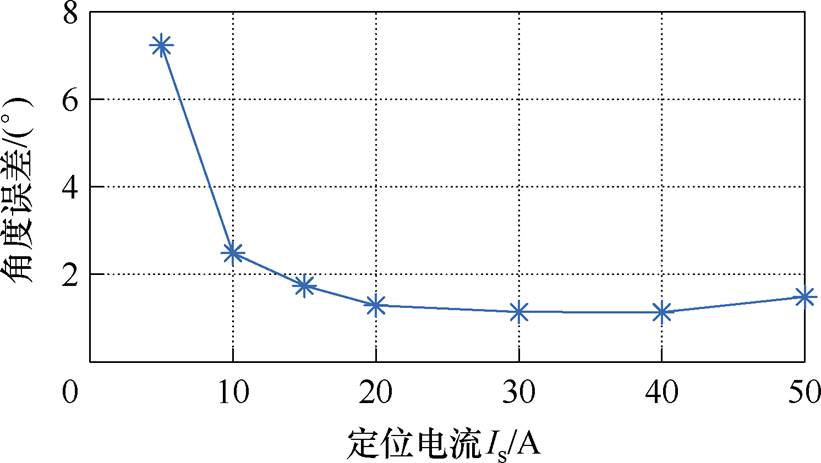
图14 标校误差随定位电流关系
Fig.14 Correction error versus positioning current relationship diagram
针对基于预定位法的位置传感器零位偏差标校方法存在易受摩擦转矩干扰且不适用于PMaSynRS/G的问题,本文分析了预定位平衡点位置和定位精度的影响因素,提出了基于不稳定平衡点的零位偏差标校方法。通过理论分析和实验验证可以得出以下结论:
1)基于本文所提定位角度误差近似的计算方法可知,PMaSynRS/G中占比较大的磁阻转矩分量在稳定平衡点附近与永磁分量方向相反,反而会降低使用预定位方法时的转子定位精度。并且随着定位电流进一步增加,PMaSynRS/G转子平衡点位置及稳定性又将发生变化。
2)所提出的基于不稳定平衡点的位置传感器零位标校方法可同时利用到永磁和磁阻转矩分量,有效减小摩擦转矩带来的误差。本文样机的实验结果表明该方法的零位偏差校正误差小于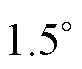 。
。
3)所提方法结构新颖,易于应用,无需额外硬件,标校精度较高。只需选择3个参数即可执行该方法,鲁棒性高。
本文所提方法基于电机固有的矩角特性,需要应用在转子可动的场景,未来研究工作中将进一步提高所提方法的通用性。
参考文献
[1] 蔡正友, 魏佳丹, 胡文枝, 等. 基于改进同步解调方式的三级式同步电机无位置传感器起动控制[J]. 电工技术学报, 2024, 39(14): 4353-4365.
Cai Zhengyou, Wei Jiadan, Hu Wenzhi, et al. Sensorless starting control of three-stage synchronous machines based on improved synchronous demo- dulation scheme[J]. Transactions of China Elec- trotechnical Society, 2024, 39(14): 4353-4365.
[2] 于立, 张卓然, 张健, 等. 多电发动机内装式高速起动发电机研究与实践[J]. 中国电机工程学报, 2020, 40(14): 4615-4628, 4740.
Yu Li, Zhang Zhuoran, Zhang Jian, et al. Study and implementation on high-speed starter/generator for more electric engine application[J]. Proceedings of the CSEE, 2020, 40(14): 4615-4628, 4740.
[3] 赵耀, 沈翀, 李东东, 等. 极端条件下基于特征层面信号融合的电励磁双凸极电机匝间短路故障诊断[J]. 电工技术学报, 2023, 38(10): 2661-2674.
Zhao Yao, Shen Chong, Li Dongdong, et al. Inter-turn short circuit diagnosis of wound-field doubly salient machine based on multi-signal fusion on feature level under extreme conditions[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2661-2674.
[4] Jiao Ningfei, Li Zijie, Mao Shuai, et al. Aircraft brushless wound-rotor synchronous starter-generator: a technology review[J]. IEEE Transactions on Power Electronics, 2023, 38(6): 7558-7574.
[5] Jiang Siyuan, Zhou Bo, Xiong Lei, et al. Analysis and design of embedded high-temperature doubly salient electro-magnetic starter/generator for aviation[J]. IEEE Transactions on Industry Applications, 2023, 59(6): 7126-7136.
[6] Guo Hong, He Xu, Xu Jinquan, et al. Design of an aviation dual-three-phase high-power high-speed permanent magnet assisted synchronous reluctance starter-generator with antishort-circuit ability[J]. IEEE Transactions on Power Electronics, 2022, 37(10): 12619-12635.
[7] 曹恒佩, 艾萌萌, 王延波. 永磁辅助同步磁阻电机研究现状及发展趋势[J]. 电工技术学报, 2022, 37(18): 4575-4592.
Cao Hengpei, Ai Mengmeng, Wang Yanbo. Research status and development trend of permanent magnet assisted synchronous reluctance motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(18): 4575-4592.
[8] 汪波, 徐文翰, 查陈诚, 等. 多三相分布式绕组和集中式绕组永磁磁阻电机对比研究[J]. 电工技术学报, 2024, 39(10): 2984-2994.
Wang Bo, Xu Wenhan, Zha Chencheng, et al. Comparative study on triple 3-phase PMA-SynRM with distributed winding and concentrated winding[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 2984-2994.
[9] 邱建琪, 曾汉, 史涔溦. 永磁辅助式同步磁阻电机自寻优控制及参数辨识[J]. 电机与控制学报, 2022, 26(6): 1-8.
Qiu Jianqi, Zeng Han, Shi Cenwei. Self-optimizing control and parameters identification for permanent magnet assisted synchronous reluctance motor[J]. Electric Machines and Control, 2022, 26(6): 1-8.
[10] 许爱德, 刘鑫, 李新宇, 等. 基于参数辨识的永磁辅助同步磁阻电机电流无差拍控制[J]. 电工技术学报, 2024, 39(18): 5626-5638.
Xu Aide, Liu Xin, Li Xinyu, et al. Current deadbeat control of permanent magnet-assisted synchronous reluctance motor based on parameter identification[J]. Transactions of China Electrotechnical Society, 2024, 39(18): 5626-5638.
[11] 周华伟, 龙顺海, 江光耀, 等. 基于磁链相移原理的不对称交替极永磁辅助同步磁阻电机设计与分析[J]. 电工技术学报, 2024, 39(2): 455-464.
Zhou Huawei, Long Shunhai, Jiang Guangyao, et al. Design and analysis of asymmetric consequent-pole permanent magnet assisted synchronous reluctance motor based on flux linkage phase shifting principle[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 455-464.
[12] Wang Bo, Hu Jiapeng, Hua Wei, et al. Multiple 3-phase PMA-SynRM with delta windings for enhanced fault tolerance[J]. IEEE Transactions on Industrial Electronics, 2023, 70(2): 1094-1104.
[13] Sun Gaoyang, Guo Hong, Ding Xiaofeng, et al. High- performance generation control strategy for aircraft dual-three-phase PM-assisted reluctance starter/ generator system[J]. IEEE Transactions on Power Electronics, 2023, 38(10): 12430-12445.
[14] Tan Yuejin, Cheng Yongjun, Song Kangjian, et al. Capacitor energy based DC-link voltage control method for dual three-phase PM assisted SynR starter/ generator[C]//2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 2023: 4045-4049.
[15] 杨洛鸿, 刘侃, 胡伟, 等. 基于交轴磁链辨识的永磁同步电机位置传感器零位校正方法[J]. 电气工程学报, 2022, 17(4): 163-173.
Yang Luohong, Liu Kan, Hu Wei, et al. A q-axis flux linkage identification based zero-correction for position sensor of permanent magnet synchronous motor[J]. Journal of Electrical Engineering, 2022, 17(4): 163-173.
[16] 吴春, 应王瑞, 郑露华, 等. 一种旋转变压器双采样差分位置解码方法[J]. 电工技术学报, 2024, 39(15): 4896-4908.
Wu Chun, Ying Wangrui, Zheng Luhua, et al. A dual-sampling differential position decoding method for resolvers[J]. Transactions of China Electro- technical Society, 2024, 39(15): 4896-4908.
[17] Kuruppu S S. Open-loop self-calibration of position sensor offset in SM-PMSM drive systems[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 7502007.
[18] Kim D, Kim J, Lim H, et al. A study on accurate initial rotor position offset detection for a permanent magnet synchronous motor under a no-load con- dition[J]. IEEE Access, 2021, 9: 73662-73670.
[19] Kuruppu S S, Abeyratne S G, Hettiarachchi S. Modeling and detection of dynamic position sensor offset error in PMSM drives[J]. IEEE Access, 2023, 11: 36741-36752.
[20] Lian Chuanqiang, Xiao Fei, Liu Jilong, et al. Analysis and compensation of the rotor position offset error and time delay in field-oriented-controlled PMSM drives[J]. IET Power Electronics, 2020, 13(9): 1911- 1918.
[21] Kim M H, Kim D Y. Accuracy improvement in resolver offset detection based on angle tracking observer with coordinate transformation[J]. Elec- tronics, 2021, 10(14): 1643.
[22] 何虔恩, 林见辽源, 许秀英. 基于线反电动势的三相PMSM角度传感器零位标校方法[J]. 中国惯性技术学报, 2023, 31(4): 407-412.
He Qianen, Lin Jianliaoyuan, Xu Xiuying. A novel method of angle sensor zero-position calibration based on line back-EMF for three-phase PMSM[J]. Journal of Chinese Inertial Technology, 2023, 31(4): 407-412.
[23] 刘计龙, 肖飞, 沈洋, 等. 永磁同步电机无位置传感器控制技术研究综述[J]. 电工技术学报, 2017, 32(16): 76-88.
Liu Jilong, Xiao Fei, Shen Yang, et al. Position- sensorless control technology of permanent-magnet synchronous motor-a review[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 76-88.
[24] 朱熀秋, 成秋良. 无起动绕组永磁同步电机初始定位及起动策略[J]. 中国电机工程学报, 2008, 28(9): 61-65.
Zhu Huangqiu, Cheng Qiuliang. Initial orientation and starting strategy on PMSM without starting windings[J]. Proceedings of the CSEE, 2008, 28(9): 61-65.
[25] 王要强, 马小勇, 程志平, 等. PMSM转子初始位置检测分析及起动策略[J]. 电力自动化设备, 2016, 36(9): 156-161, 168.
Wang Yaoqiang, Ma Xiaoyong, Cheng Zhiping, et al. PMSM initial rotor position detection and startup strategy[J]. Electric Power Automation Equipment, 2016, 36(9): 156-161, 168.
[26] 杨立永, 陈为奇. 永磁同步电机转子初始位置检测研究[J]. 电气传动, 2012, 42(3): 57-61.
Yang Liyong, Chen Weiqi. Study on initial position detection of PMSM rotor[J]. Electric Drive, 2012, 42(3): 57-61.
[27] Liu Zirui, Kong Wubin, Fan Xinggang, et al. Online multi-parameter observation of IPM machine with reconstructed nonlinear small-signal model based on dual EKF[J]. IEEE Transactions on Industrial Electronics, 2024, 71(2): 1234-1245.
[28] Wang Can, Peng Jiande, Pan Jianfei. A novel friction compensation method based on stribeck model with fuzzy filter for PMSM servo systems[J]. IEEE Transactions on Industrial Electronics, 2023, 70(12): 12124-12133.
[29] Sundararajan P, Sathik M H M, Sasongko F, et al. Condition monitoring of DC-link capacitors using Goertzel algorithm for failure precursor parameter and temperature estimation[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 6386-6396.
[30] 阮毅, 杨影, 陈伯时. 电力拖动自动控制系统: 运动控制系统[M]. 5版. 北京: 机械工业出版社, 2016.
Abstract A permanent magnet-assisted synchronous reluctance starter/generator (PMaSynRS/G) has high power density and short-circuit fault tolerance characteristics. It has a promising application in the aviation starter/generator system. Due to the small permanent magnet flux and large reluctance torque, zero position drifting and stability distortion of the rotor equilibrium point exist when using the pre-positioning method to calibrate its zero position. Besides, the pre-positioning method suffers from interference such as frictional torque. The previous research mainly focused on surface-mounted permanent magnet synchronous motors without involving motors with reluctance torque and modeling the impact of frictional torque.
This paper analyzes the influence of the reluctance torque component on the equilibrium point and accuracy of the pre-positioning method. An approximate formula is derived for the angle error generated by frictional torque. Additionally, a reference for the selection of the positioning current is provided. Due to the torque characteristics of the PMaSynRS/G, this paper proposes a novel positioning method based on unstable equilibrium points and a parameter estimation method for the control algorithm. The proposed positioning method utilizes a PI controller with permanent magnet torque and reluctance torque to keep the rotor at an unstable equilibrium point, effectively reducing errors from frictional torque. The proposed method is based on motors’ inherent torque angle characteristics and needs to be applied in scenarios where the rotor is movable.
The effectiveness of the proposed positioning error estimation model and zero calibration method is verified through experiments with a PMaSynRS/G prototype. A dynamometer is connected to the prototype to simulate the zero calibration of the machine installed in the system, which increases the frictional torque and inertia. Experimental results show that when the stator current gradually increases to over 60 A in the pre-positioning method, the original stable equilibrium point becomes unstable, and two new symmetrical stable equilibrium points are generated. The zero-position deviation is below 1.5 degrees of mechanical angle using the proposed method, while the pre-positioning method is about 9.5 degrees.
The following conclusions can be drawn. (1) Based on the proposed approximate calculation method of positioning angle error, the reluctance torque component, which accounts for a large proportion of PMaSynRS/G total torque, is in the opposite direction of the permanent magnet component near the stable equilibrium point. The pre-positioning method decreases the positioning accuracy of the rotor. As the positioning current increases, the position and stability of the PMaSynRS/G rotor equilibrium points also change. (2) The proposed calibration method based on unstable equilibrium points uses the permanent magnet torque and reluctance torque, reducing the impact of frictional torque on calibration accuracy. (3) The proposed method does not require additional hardware, is easy to apply, and has high calibration accuracy. Only three parameters are needed, exhibiting high robustness.
keywords:Position sensor zero-position calibration, permanent-magnet-assisted synchronous reluctance starter/generator, rotor position detection, pre-positioning method
DOI: 10.19595/j.cnki.1000-6753.tces.241021
中图分类号:TM341
国家自然基金资助项目(52377050)。
收稿日期 2024-06-17
改稿日期 2024-09-27
谭越瑾 男,2000年生,硕士研究生,研究方向为起/发电机控制。E-mail: yuejintan@hust.edu.cn
孔武斌 男,1986年生,教授,博士生导师,研究方向为航空高温高功率密度控制器、多电飞机伺服驱动控制、电动汽车驱动控制。E-mail: wbkong@hust.edu.cn(通信作者)
(编辑 崔文静)