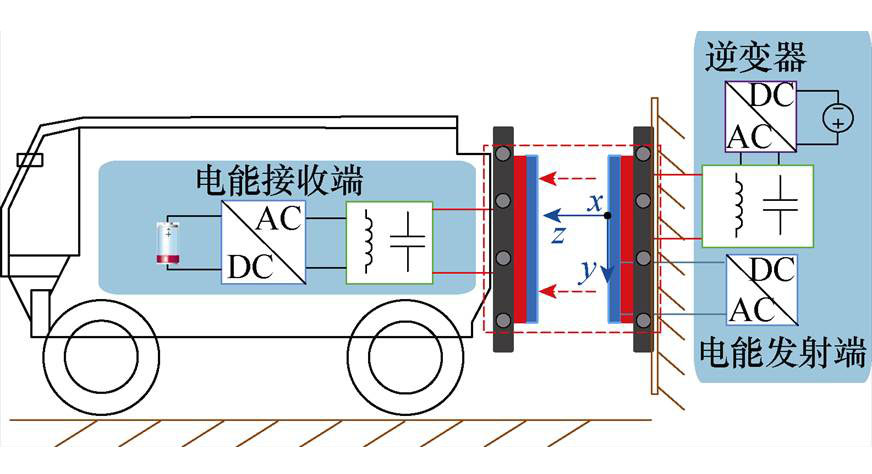
图1 AGV无线充电系统结构示意图
Fig.1 Schematic structure of AGV wireless charging system
摘要 为了解决自动导向车(AGV)无线充电系统中互感与负载变化导致系统输出电流和系统效率变化的问题,该文提出一种基于互感与负载识别的AGV无线电能传输系统闭环恒流与效率优化控制方法。首先,该文进行系统电路分析,给出互感与负载的识别原理。其次,阐述了基于该互感与负载识别原理的系统闭环恒流与效率优化控制方法。在闭环恒流控制方面,对基于移相控制的闭环系统进行分析,说明该系统利用反馈检测电压进行输出电流闭环控制的基本原理;在效率优化控制方面,针对LCC-LCC和SS谐振补偿拓扑建立效率数学模型,对两种补偿拓扑工作模式下的效率负载临界点(即两种拓扑下系统效率相等时的临界负载取值)进行分析,给出可通过识别负载以优化系统效率方法的理论依据,得到基于互感与负载识别的系统效率优化控制流程。最后,搭建了实验装置样机平台,分别对互感与负载识别方法、系统闭环恒流控制方法和效率优化控制方法进行了实验验证,结果表明了该文所提方法的可行性和有效性。
关键词:自动导向车(AGV) 无线电能传输(WPT)系统 闭环恒流 参数识别 效率优化
自动导向车(Automated Guided Vehicle, AGV),是一种能够自主运行的无人驾驶车辆。AGV属于轮式移动机器人的范畴,通常采用激光导航、磁性导航、视觉导航等技术,能够根据预先设定的路径和任务,自主完成物料的搬运和分拣等操作,并具有自动避障、排除问题等功能[1]。AGV在物流仓储、汽车制造、电子制造、食品饮料等行业得到广泛应用,能够提高生产效率、降低人工成本、减少工业事故和错误率等,极大地提高了工业自动化生产的质量和效率[2]。
随着科学技术的飞速发展,AGV将在未来工业中承担更多且更繁重的任务。在AGV的实际应用过程中,当电池电量耗尽时,AGV如若能够自主完成电能的补给,以便能够持续、稳定地参与自动化生产,则会进一步提升工业生产效率。因此,AGV自主充电技术的研发和应用显得尤为重要[3]。
目前,随着无线电能传输(Wireless Power Transfer, WPT)技术的蓬勃发展,应用WPT技术对AGV进行电能补给逐渐成为了企业和科研单位的研究热点[4-8]。与传统有线充电方式相比,无线充电系统省去了充电线缆的束缚,可以更加有效地实现AGV的自主充电技术,从而使AGV更高效、更方便。
AGV无线充电系统的负载对象通常是锂离子动力电池,为了确保锂电池使用过程的安全性得到全面保障,优化其充电性能,同时有效地利用锂电池充放电的有限循环次数,在锂电池的充电过程中一般采用恒流(Constant Current, CC)和恒压两个核心阶段,并且恒流阶段通常占据了锂电池充电的大部分时间[9]。因此,对于给锂电池充电的WPT系统来说,对输出端的恒流控制具有重要意义。实现系统恒流输出的一种方法是设计与负载无关的恒流输出谐振补偿拓扑[10],但由于AGV停车位置的偏移,可能会导致系统输出电流的变化,因此开环控制方法的抗干扰能力较差。
为了增加系统的抗干扰能力,可以采用闭环控制,根据闭环控制器所在位置的不同,可以分为副边闭环控制方法和原边闭环控制方法。对于副边闭环控制方法,实现系统闭环恒流输出可以通过采用DC-DC变换器[11]或有源整流器[12]的方式实现,对于原边闭环控制方法,通常将副边信息通过无线通信的方式反馈到原边,然后通过控制原边DC-DC变换器[13]或者改变逆变器的驱动信号相位差[14]或频率[15]实现闭环恒流输出。原边闭环控制方法可以避免在AGV接收端使用更多的电路模块,因此,原边闭环控制方法更适合AGV无线充电系统的闭环控制。
另外,效率作为无线充电系统的重要指标之一,对其优化和控制也是WPT系统的重要研究方向。在AGV进行无线充电时,由于每次停车位置的不精确,会造成发射线圈与接收线圈之间的互感系数在每次充电时不一致[16];锂电池充电过程中等效内阻也会发生较大变化[17],互感和负载的变化会影响无线充电系统的输出电流和效率,因此,如何解决系统互感和负载变化导致的输出电流与系统效率变化的问题对于AGV无线充电系统来说显得尤为重要。
针对AGV无线充电系统互感与负载变化导致系统输出和系统效率变化的问题,本文提出一种基于互感与负载识别的AGV无线电能传输系统闭环恒流与效率优化控制方法。该方法可以实现AGV充电前互感系数的识别,从而应对AGV停车位置的偏移,并且能够实现无需建立原副边通信回路的闭环恒流控制。该方法通过检测原边逆变电流的有效值以识别负载,结合已提前识别得到的互感系数,用LCC-LCC拓扑与SS拓扑的适时切换以实现AGV无线充电过程中的效率优化控制。
本文主要研究的AGV无线充电系统结构示意图如图1所示。从图中可以看出,在y方向上因车身高度限制,只要AGV无线充电系统耦合机构的接收端线圈安装牢固则可以视为不会发生y方向的偏移。由于AGV停车位置的偏差,仅可能会产生x和z方向的偏移。
本文提出的WPT系统整体结构如图2所示,主要由全桥逆变电路、谐振补偿电路、整流电路、检测电路和原副边控制器组成。谐振补偿电路采用LCC-LCC拓扑结构,S1和S2为一对可同时开闭的交流开关,系统可通过S1和S2的开闭实现LCC-LCC拓扑与SS拓扑的切换,即系统可工作在LCC-LCC拓扑和SS拓扑两种工作模式下。LT和LR分别为发射端线圈和接收端线圈的补偿电感,RT、RP、RS和RR分别为LT、LP、LS和LR上的寄生电阻。CT、CP和CS、CR分别为原边线圈和副边线圈谐振补偿电容。MP为发射端线圈和接收端线圈之间的互感系数,MD为副边补偿电感LR与原边检测电路中线圈电感LD之间的互感系数,其中MP用于保证功率的无线传输,MD用来将副边的输出电流反馈到原边控制器。UD为反映输出电流的检测直流电压,Udc为直流电压源,Uin和IT分别为逆变器输出电压和电流,IP和IS分别为经过原边和副边线圈的电流,IR和US分别为整流器输入电流和电压,IL和UL分别为负载电流和电压,Req为整流器及负载的等效阻抗,ID为经过线圈LD的电流,ILref为参考输出电流,d 为逆变器导通角。

图1 AGV无线充电系统结构示意图
Fig.1 Schematic structure of AGV wireless charging system
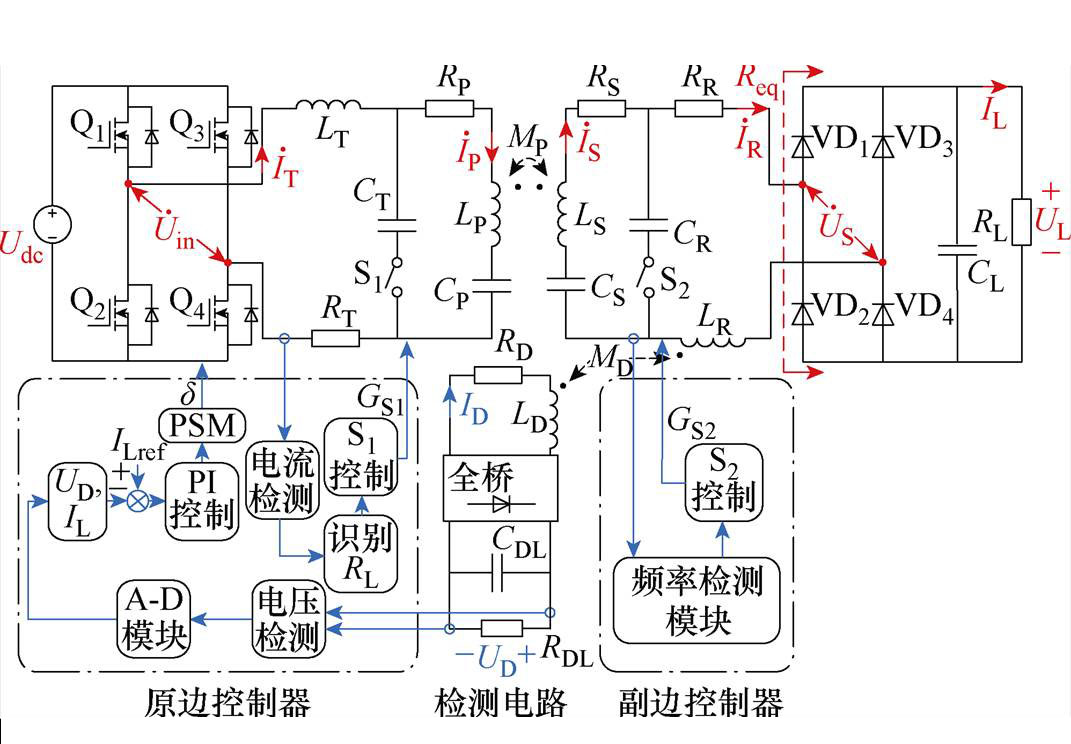
图2 无通信环节的AGV无线电能传输系统整体结构
Fig.2 Overall structure of AGV wireless power transfer system without communication links
如图3a所示为该系统采用的DD-Q组合型磁耦合机构示意图,图中LP和LS分别为发射端DD线圈电感和接收端DD线圈电感,LR为位于接收端的补偿Q线圈电感,LD为位于原边的检测Q线圈电感。由于DD线圈与Q线圈之间的自然解耦特性,当DD线圈和Q线圈重叠时,它们之间的耦合系数可以视为零。LD与LP重叠,LS与LR重叠,实现了磁耦合机构与补偿电感之间的集成设计,减少了AGV接收端的补偿元件所占电路板体积。根据图3a所示的特定位置关系并结合如图1所示的AGV实际应用场景,在线圈因AGV停车位置精准度有限而发生偏移的情况下,接收端能量线圈LS与发射端检测线圈LD和接收端补偿线圈LR与发射端能量线圈LP在x和z方向的偏移情况下均不会产生交叉耦合,所以后文的理论分析均考虑该DD-Q组合型耦合线圈在理想情况下的解耦关系,即仅考虑MP和MD两个互感系数的变化对系统的影响。
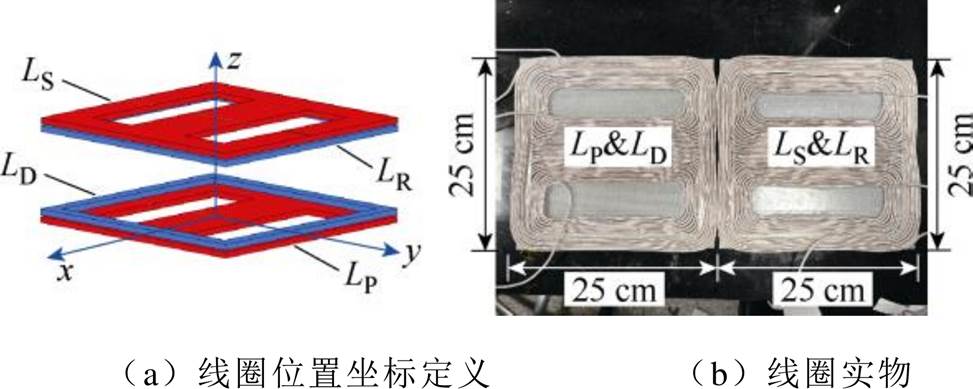
图3 DD-Q组合型磁耦合机构
Fig.3 DD-Q combined type magnetic coupling mechanism
实验绕制了如图3b所示的磁耦合机构发射端与接收端线圈,原边能量发射DD线圈与检测Q线圈重叠绕制,外尺寸为25 cm×25 cm,DD线圈匝数为13匝,Q线圈为5匝,线径均为3 mm;副边能量接收DD线圈与补偿Q线圈重叠绕制,其外尺寸、匝数和线径均与原边相同。
由于AGV停车定位精度的偏差,在每次充电前,其停车位置可能会有所不同。因此,要使用UD控制输出电流,需要首先识别出MD。S1和S2是两个交流开关,用于实现双边LCC和SS拓扑之间的切换,通过检测系统在这两个拓扑下的直流电压UD来识别互感系数。
当S1和S2闭合时,系统工作在LCC-LCC谐振补偿拓扑工作模式下,该拓扑的等效电路如图4所示。
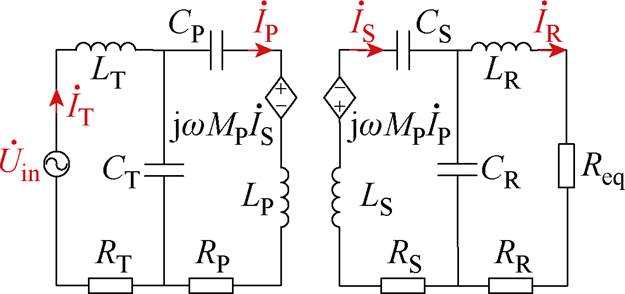
图4 LCC-LCC谐振补偿拓扑等效电路
Fig.4 LCC-LCC resonance compensation topology equivalent circuit
图4中,CT、CP、CS和CR满足
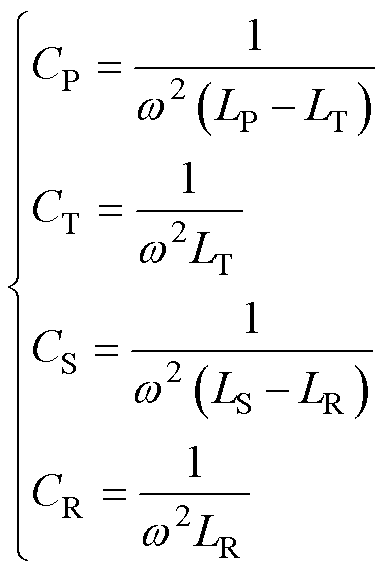 (1)
(1)
式中,w 为LCC-LCC谐振补偿拓扑下系统的工作角频率,w=2p f,f为LCC-LCC补偿拓扑下系统的工作频率,f =125 kHz。
移相控制模块(Phase Shift Modulation, PSM)用于控制逆变器,并且逆变器的基波输出电压的相量形式为
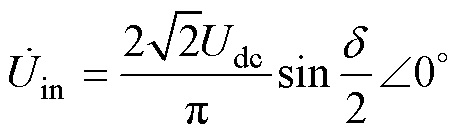 (2)
(2)
根据基尔霍夫电压定律(Kirchhoff Voltage Laws, KVL)和整流电路输入输出电压的关系,可以列出
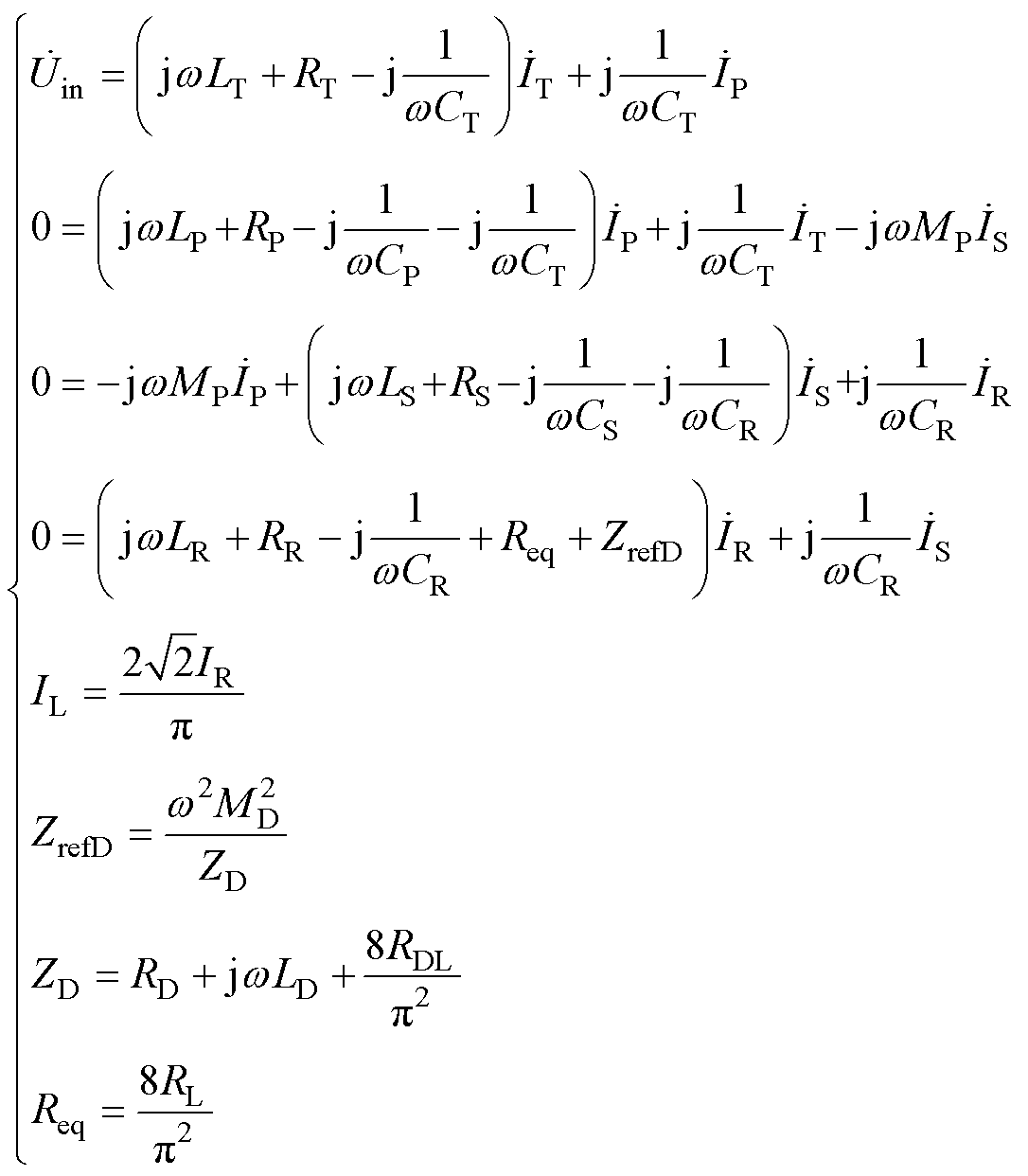 (3)
(3)
式中,IR为输出电流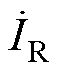 的方均根;ZrefD为检测电路在LR支路上的反射阻抗;ZD为检测电路的阻抗。
的方均根;ZrefD为检测电路在LR支路上的反射阻抗;ZD为检测电路的阻抗。
为了简化分析,假设检测电阻RDL wLD并且
wLD并且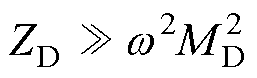 ,因此ZrefD→0,检测电压可以表示为
,因此ZrefD→0,检测电压可以表示为
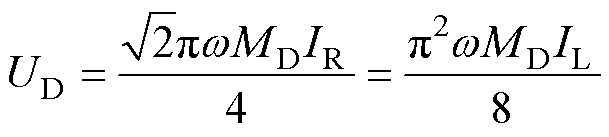 (4)
(4)
此外,在图3b所示的特定线圈尺寸下,实验测量得到频率为125 kHz下的交流寄生电阻RD、RP、RS和RR分别为0.07、0.09、0.09和0.07 W。为了简化分析,可以忽略这些电阻值,将式(1)、式(2)和式(4)代入式(3),可以得到
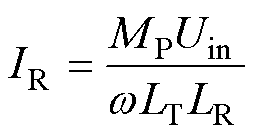 (5)
(5)
当S1和S2断开时,系统工作在如图5所示的SS谐振补偿拓扑工作模式下,并且应满足谐振电容
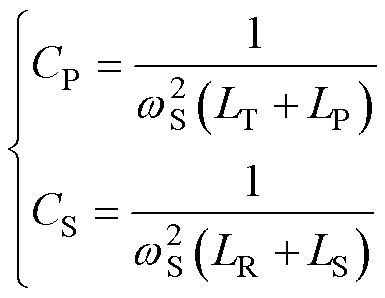 (6)
(6)
式中,wS为SS补偿拓扑下系统的工作角频率,wS= 2p fS,fS为SS补偿拓扑下系统的工作频率,fS= 100 kHz。
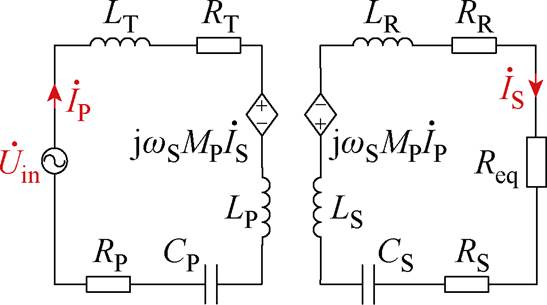
图5 SS谐振补偿拓扑等效电路
Fig.5 SS resonance compensation topology equivalent circuit
根据KVL和整流电路输入输出电压,可以列出SS谐振补偿拓扑系统如式(7)所示,因100 kHz和125 kHz频率下实验测量得到的交流寄生电阻几乎无差异,同理为了简化分析,可以忽略式(7)中各交流寄生电阻值。
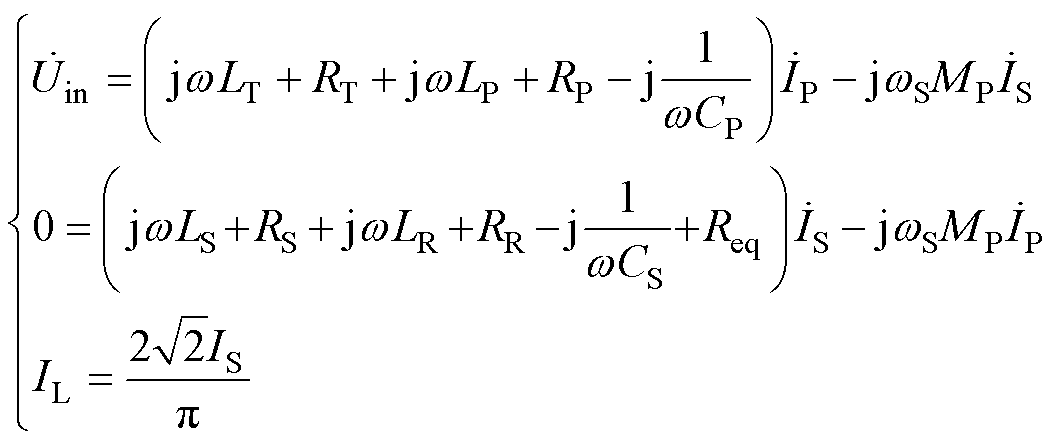 (7)
(7)
将式(2)和式(6)代入式(7),解得IS(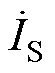 的方均根)为
的方均根)为
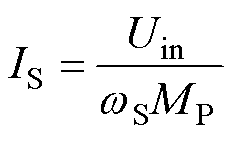 (8)
(8)
最后,可以解得SS谐振补偿拓扑系统下的检测电压UD为
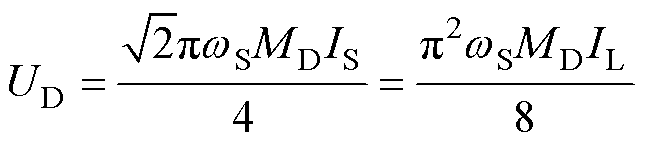 (9)
(9)
2.3.1 互感识别原理
在AGV停车后,系统首先进入互感识别模式,如图6所示为互感识别的具体流程。首先,S1和S2闭合,系统工作在LCC-LCC谐振补偿拓扑下,工作频率为f,逆变器导通角设置为d0_LCC以产生少量能量用于互感识别,可以采样得到检测电压为UD0_LCC。然后,将S1断开,同时将逆变器的输出频率设置为fS,导通角设置为d0_SS,当副边控制器中的频率检测模块检测到频率变化后,S2也切换为断开状态,该时间差可忽略不计,此时系统工作在SS谐振补偿拓扑下,此时同样可以得到检测电压UD0_SS。最后,将以上参数分别代入式(2)、式(4)和式(9),并联立式(2)、式(4)、式(5)、式(8)和式(9),可以解得MP和MD分别为
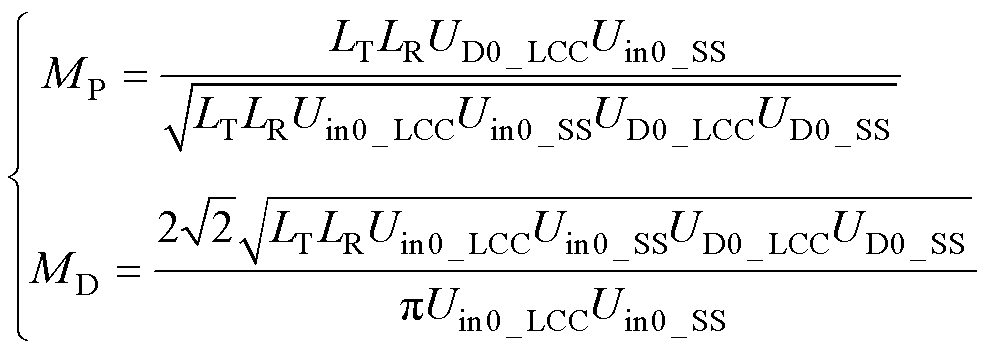 (10)
(10)
其中
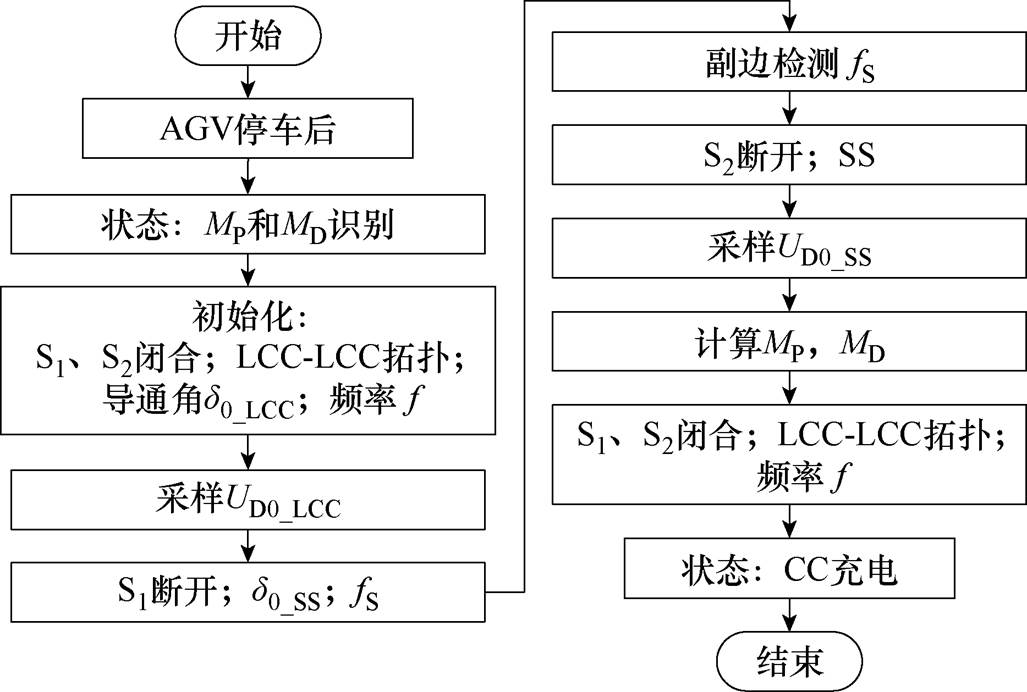
图6 AGV充电前系统互感识别流程
Fig.6 Flow chart of mutual inductance identification of the system before AGV charging
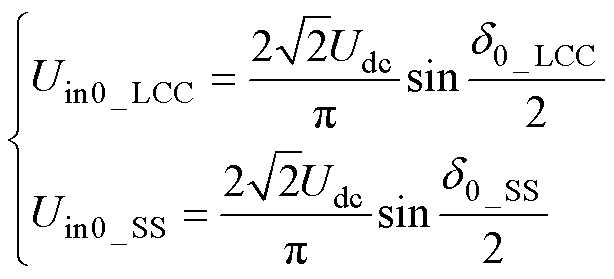
由式(10)可以看出,在设计系统时可以确定Udc、d0_LCC、d0_SS、LT和LR。通过检测直流电压UD0_LCC和UD0_SS便可识别得到MP和MD的具体参数值。值得注意的是,互感的识别流程仅在AGV停车后进行充电前运行一次,即互感系数的识别仅在AGV停车后进行识别确认。
2.3.2 负载识别原理
根据图4中LCC-LCC谐振补偿拓扑等效电路,通过KVL列出的方程式(3)和谐振关系式(1),可解得LCC-LCC补偿拓扑的逆变电流关系式为
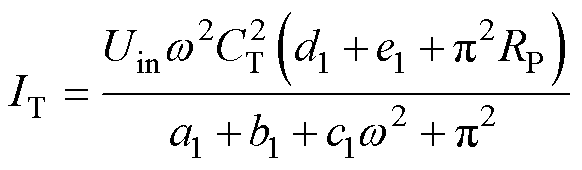 (11)
(11)
其中
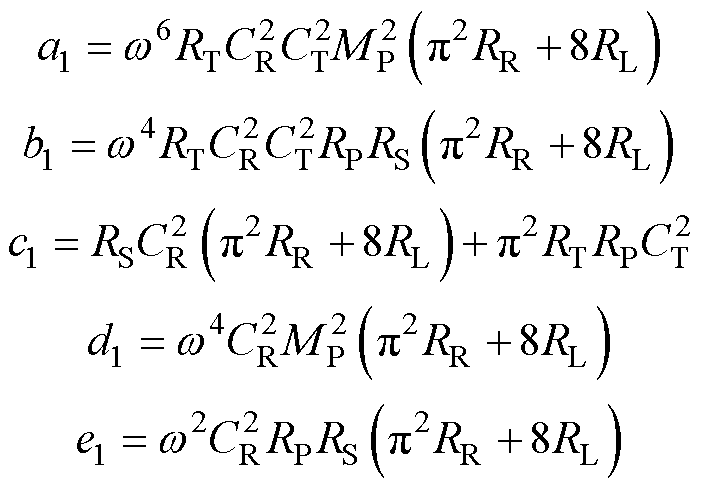
通过式(11)解得负载RL识别公式为
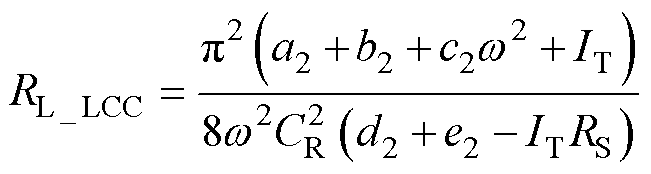 (12)
(12)
其中
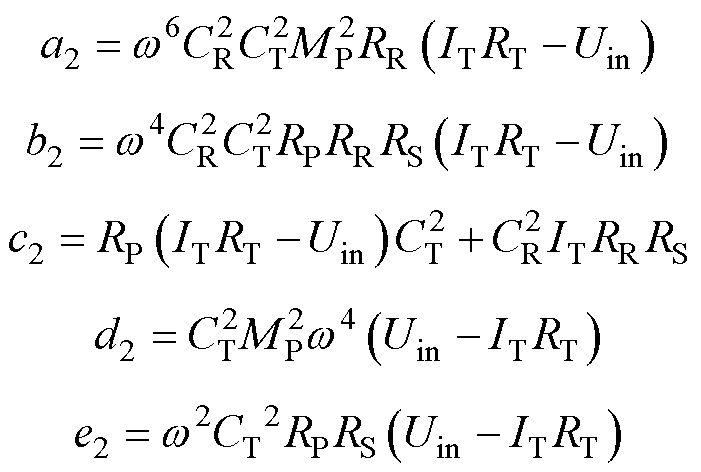
由式(12)可知,LCC-LCC补偿拓扑下的负载RL_LCC在系统参数确定后,只与逆变电压Uin、互感MP和逆变电流IT有关,逆变电压与当前原边控制器输出的d_LCC有关。在通过所述方法识别得到MP后,再通过采样IT便可计算得到负载RL_LCC的值。
根据图5中SS谐振补偿拓扑等效电路,通过KVL列出的谐振关系式(6)和方程式(7)可解得SS补偿拓扑的逆变电流关系式为
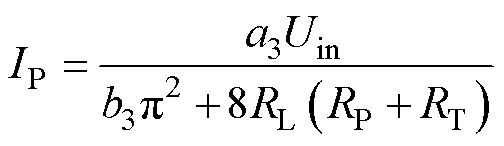 (13)
(13)
其中
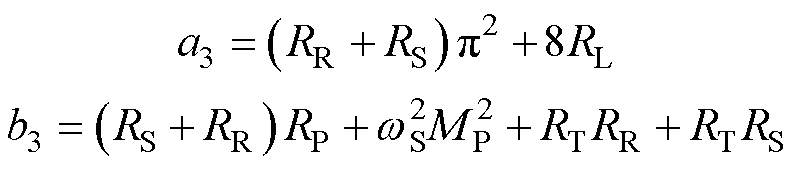
通过式(14)解得负载RL识别公式为
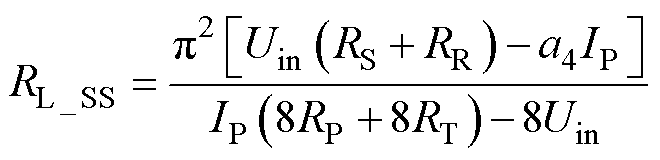 (14)
(14)
其中
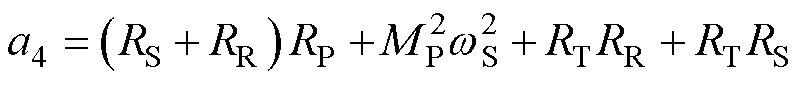
由式(14)可知,SS补偿拓扑下的负载RL_SS在系统参数确定的情况下,只与逆变电压Uin、互感MP和逆变电流IP有关,逆变电压与当前原边控制器输出的d_SS有关。在通过图6所述方法识别得到MP后,再通过采样IP便可计算得到负载RL_SS的值。负载的识别与互感的识别运行流程有所区别,负载的识别需要建立在互感参数识别得到后的基础之上。并且为了后文的效率优化控制,负载的识别需要实时采样逆变电流以得到负载的实时值。该负载辨识即用于后文进行效率优化时的拓扑切换判断标准。
在AGV进行正式充电前通过上述原理识别到了互感系数后,系统即可进入正常闭环恒流充电模式。通过反馈检测回路采样得到的电压信息计算得到输出电流并与设定电流参考值比较,从而实现系统的恒定电流输出。通过识别得到互感系数值,并结合实时检测逆变电流有效值得到负载识别值,从而通过谐振补偿拓扑的适时切换,以完成AGV无线充电时的系统效率优化控制。
在系统将互感MP与MD识别完成后,将进行LCC-LCC谐振补偿拓扑下的恒流充电,如图7所示。原边控制器通过反馈检测电路、电压检测和A-D模块测量得到直流电压UD,并根据式(4)或式(9)可以得到输出电流IL,然后将IL与参考值ILref之间的误差发送到比例积分(Proportional Integral, PI)控制器,将得到后的结果传递到PSM移相控制器进行导通角计算,从而驱动全桥逆变电路,进而调节系统的输出电流IL。
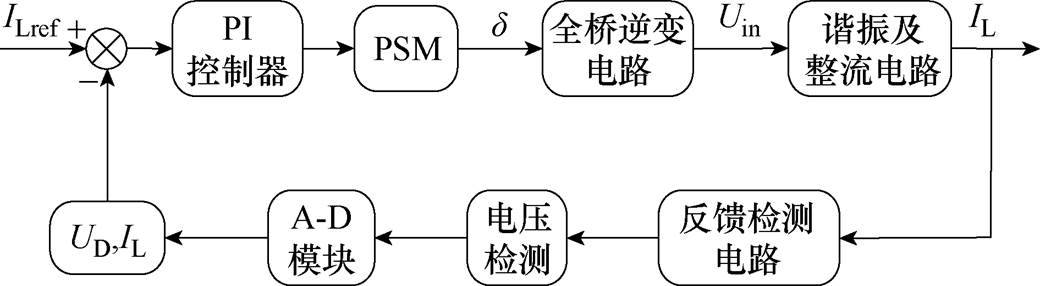
图7 基于移相控制的闭环系统方框图
Fig.7 Block diagram of closed-loop system based on phase-shift control
3.2.1 双边LCC与SS谐振补偿拓扑效率负载临界点分析
根据图4所示LCC-LCC谐振补偿拓扑等效电路可知,其输入、输出功率为
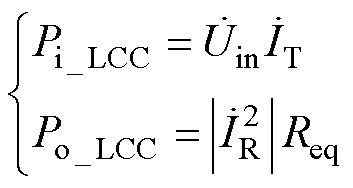 (15)
(15)
LCC-LCC谐振补偿拓扑效率为
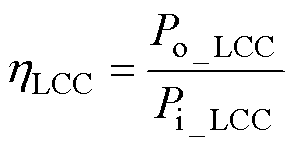 (16)
(16)
由式(15)和式(16)可得出LCC-LCC谐振补偿拓扑下的WPT系统效率为
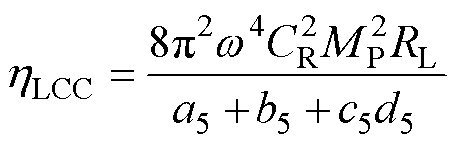 (17)
(17)
其中
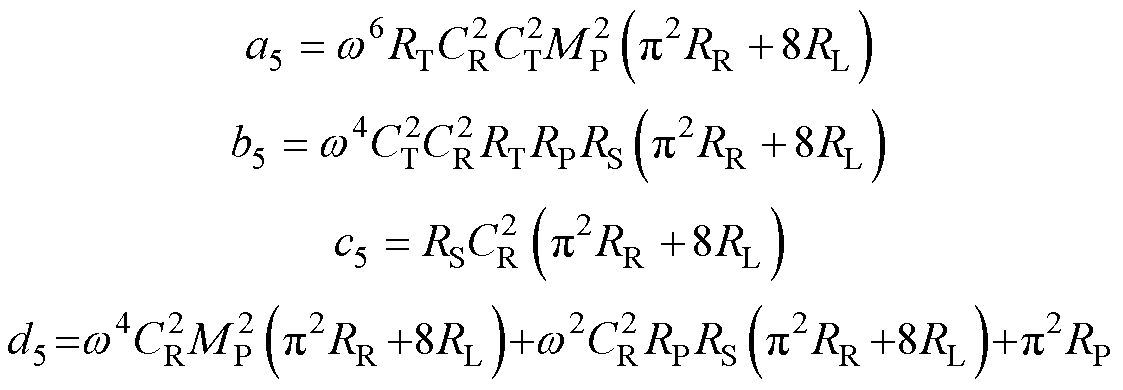
根据图5所示SS谐振补偿拓扑等效电路可知,其输入、输出功率为
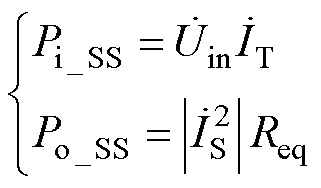 (18)
(18)
SS谐振补偿拓扑下的WPT系统效率为
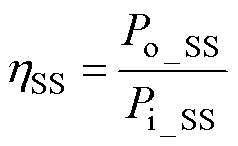 (19)
(19)
由式(18)和式(19)可得出SS谐振补偿拓扑下的效率公式为
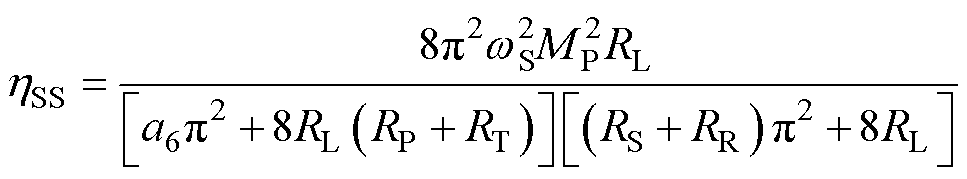 (20)
(20)
其中
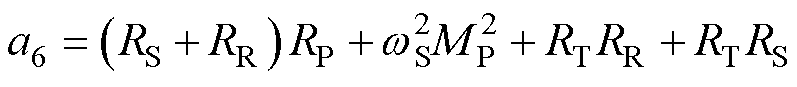
为了研究双边LCC与SS谐振补偿拓扑的效率负载临界值(即两种拓扑下系统效率相等时的临界负载取值)与互感的关系,将式(17)和式(20)作差得
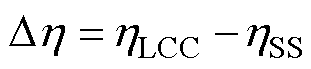 (21)
(21)
令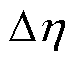 =0,即双边LCC与SS谐振补偿拓扑效率相等时,可以解得
=0,即双边LCC与SS谐振补偿拓扑效率相等时,可以解得
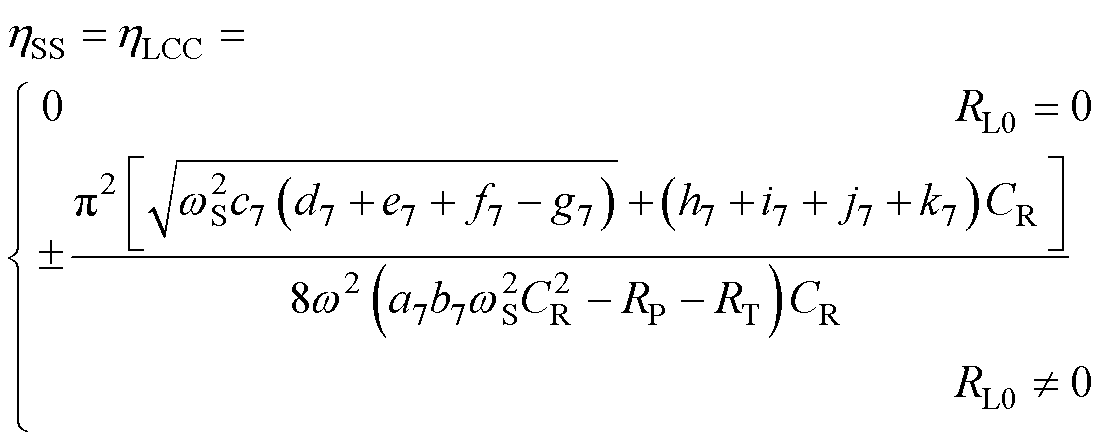 (22)
(22)
其中
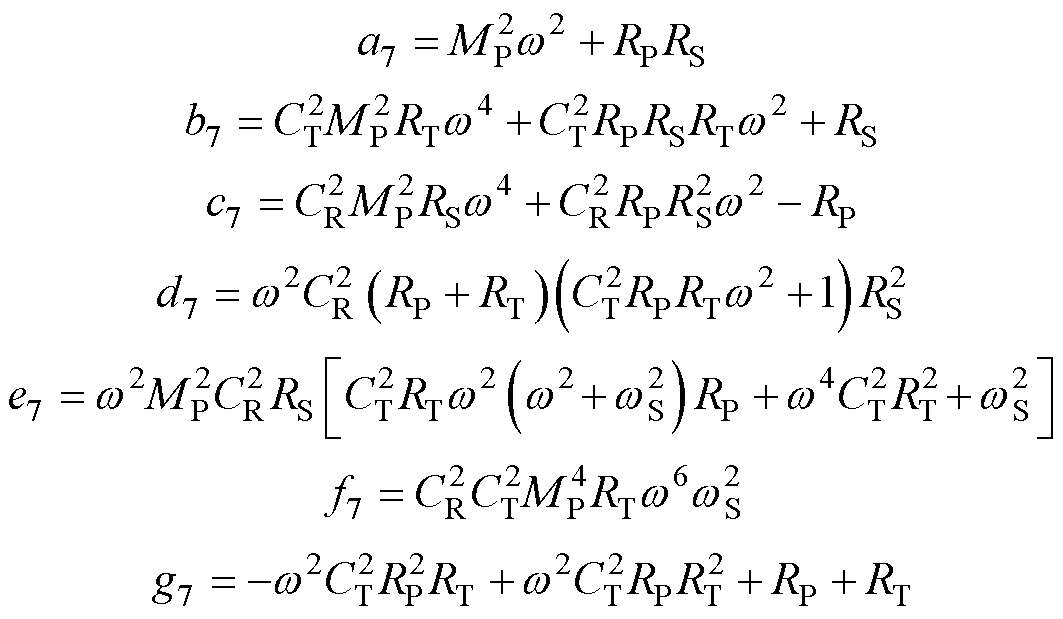
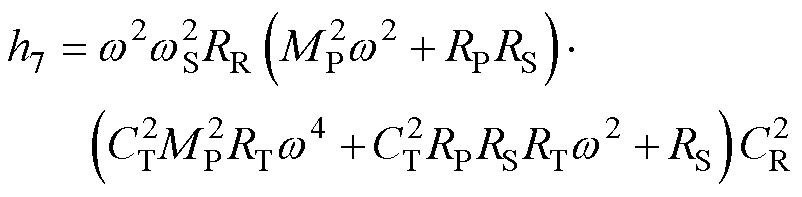
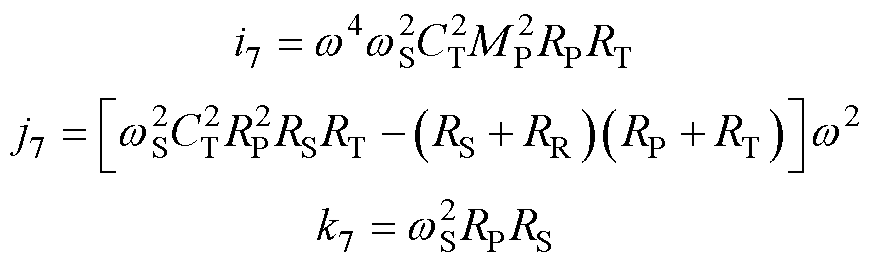
舍去RL0=0,由RL0的非零解作出其随互感MP的变化曲线如图8所示。可以看出,当互感在0~20 mH变化时,负载临界值RL0从11 W 逐渐减小至0 W;当互感在20~40 mH变化时,负载临界值RL0由25 W 逐渐减小至8 W。
3.2.2 基于互感与负载识别的系统效率优化控制流程
如图9所示为基于互感与负载识别的系统效率优化控制流程。在AGV停车后,首先进入互感MP和MD识别流程,根据互感MP和MD的理论公式(10)可以得到AGV停车后的MP和MD识别值。MP、MD识别完成后,系统保持LCC-LCC拓扑下的恒流充电模式。然后检测原边逆变电流的有效值,根据式(12)或式(14)计算出负载电阻值RL,将识别出的MP和RL代入效率公式(式(17)和式(20))得到hLCC和hSS,判断hLCC和hSS的大小进行相应的拓扑选择,保持相应补偿拓扑下的恒流充电。为了实现系统的实时效率跟踪,系统在SS和LCC-LCC补偿拓扑下的恒流充电模式中都应保持持续的逆变电流采样并判断是否进行拓扑切换。
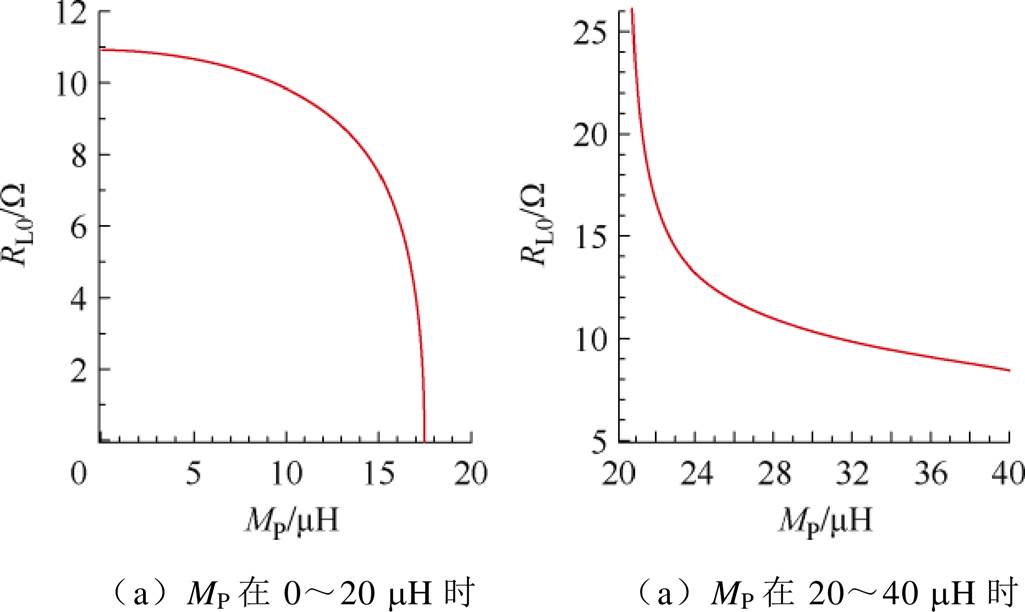
图8 负载临界值RL0随互感MP变化曲线
Fig.8 Variation curves of load threshold RL0 with mutual inductance MP
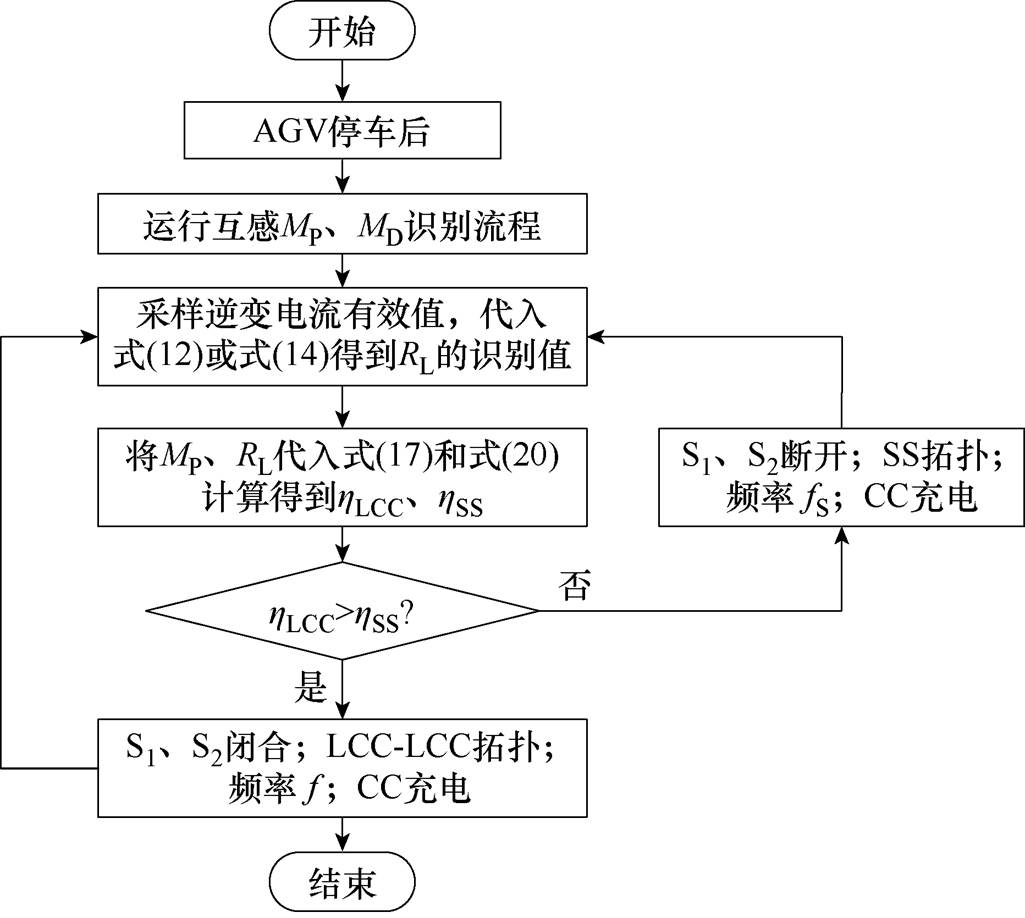
图9 基于互感与负载识别的系统效率优化控制流程
Fig.9 Flow chart of system efficiency optimization control based on mutual inductance and load identification
图10为本文搭建的WPT系统实验装置样机,主要由示波器、直流电源、电子负载、逆变器、原边控制器、发射端谐振电路(LT、CT、CP)、检测电路、磁耦合机构(LP和LD、LS和LR)、接收端谐振电路(CS、CR)、交流开关S1和S2、副边控制器、整流器和滤波电容CL组成。

图10 本文搭建的WPT系统实验装置样机
Fig.10 The prototype of the experimental setup of WPT system built in this thesis
测量实际使用的磁耦合机构、谐振电容和电感参数,并结合实际的输入电压和工作频率等,得到图10所示实验装置样机实测系统参数见表1。
表1 系统参数
Tab.1 System parameters
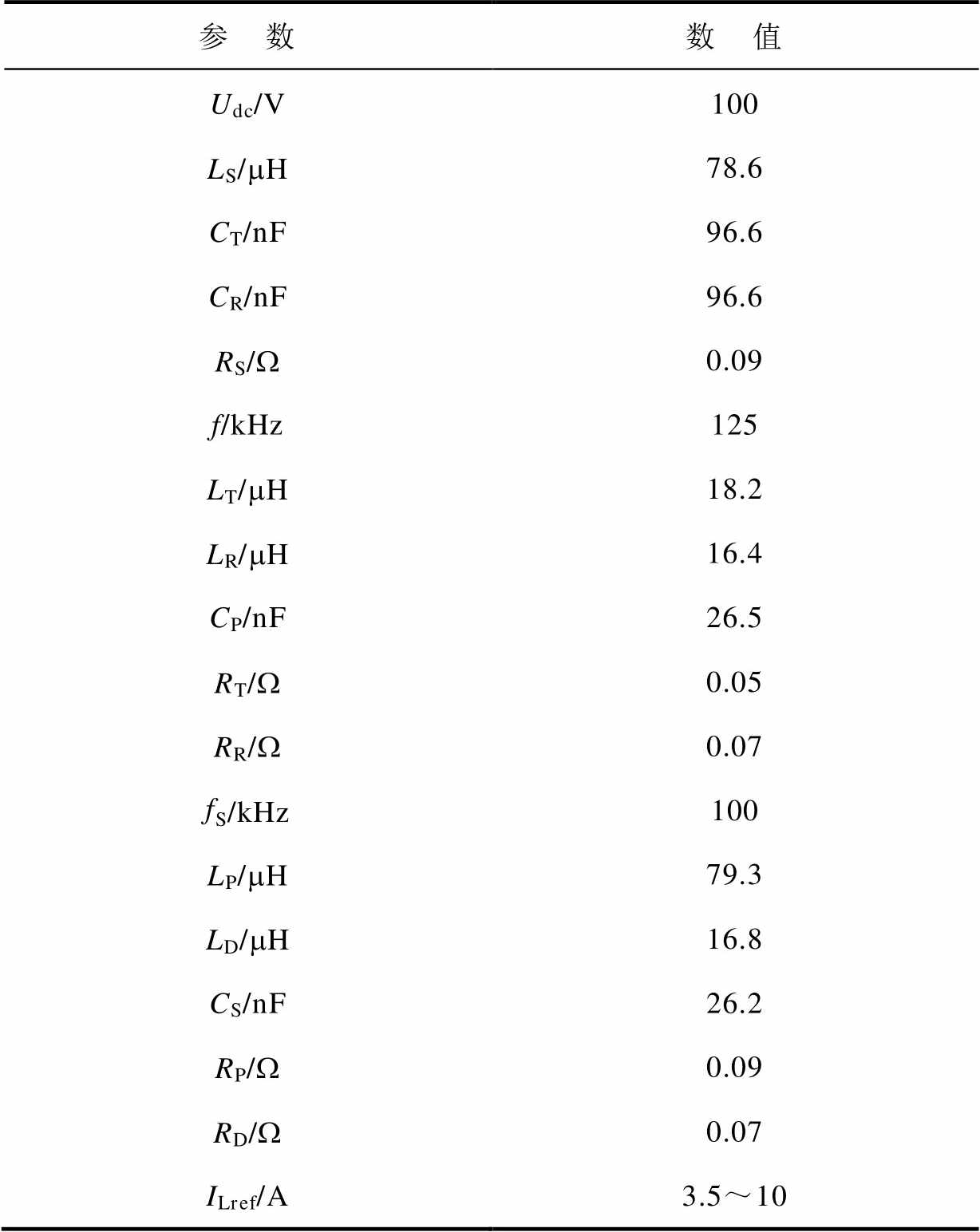
参 数数 值 Udc/V100 LS/mH78.6 CT/nF96.6 CR/nF96.6 RS/W0.09 f/kHz125 LT/mH18.2 LR/mH16.4 CP/nF26.5 RT/W0.05 RR/W0.07 fS/kHz100 LP/mH79.3 LD/mH16.8 CS/nF26.2 RP/W0.09 RD/W0.07 ILref/A3.5~10
利用实验测量得到的检测电压UD与实验设定的初始导通角d=45°并结合表1所示的实验参数值,由互感识别式(10)计算得到各x方向偏移量情况下的互感识别值。将互感识别值与互感实测值进行对比如图11所示。图中,MP-ES和MP-RE分别为互感MP的识别值和实测值,MD-ES和MD-RE分别为互感MD的识别值和实测值。从图中可以看出,MP和MD的实测值与式(10)计算得到的识别值符合度良好。经计算,z=3 cm时,MP的最大识别误差率出现在x=10 cm时,为1.84%,MD的最大识别误差率出现在x=10 cm时,为6.62%;z=4 cm时,MP的最大识别误差率出现在x=10 cm时,为2.59%,MD的最大识别误差率出现在x=10 cm时,为5.95%。以上数据验证了本文所提出的互感参数识别方法的有效性。
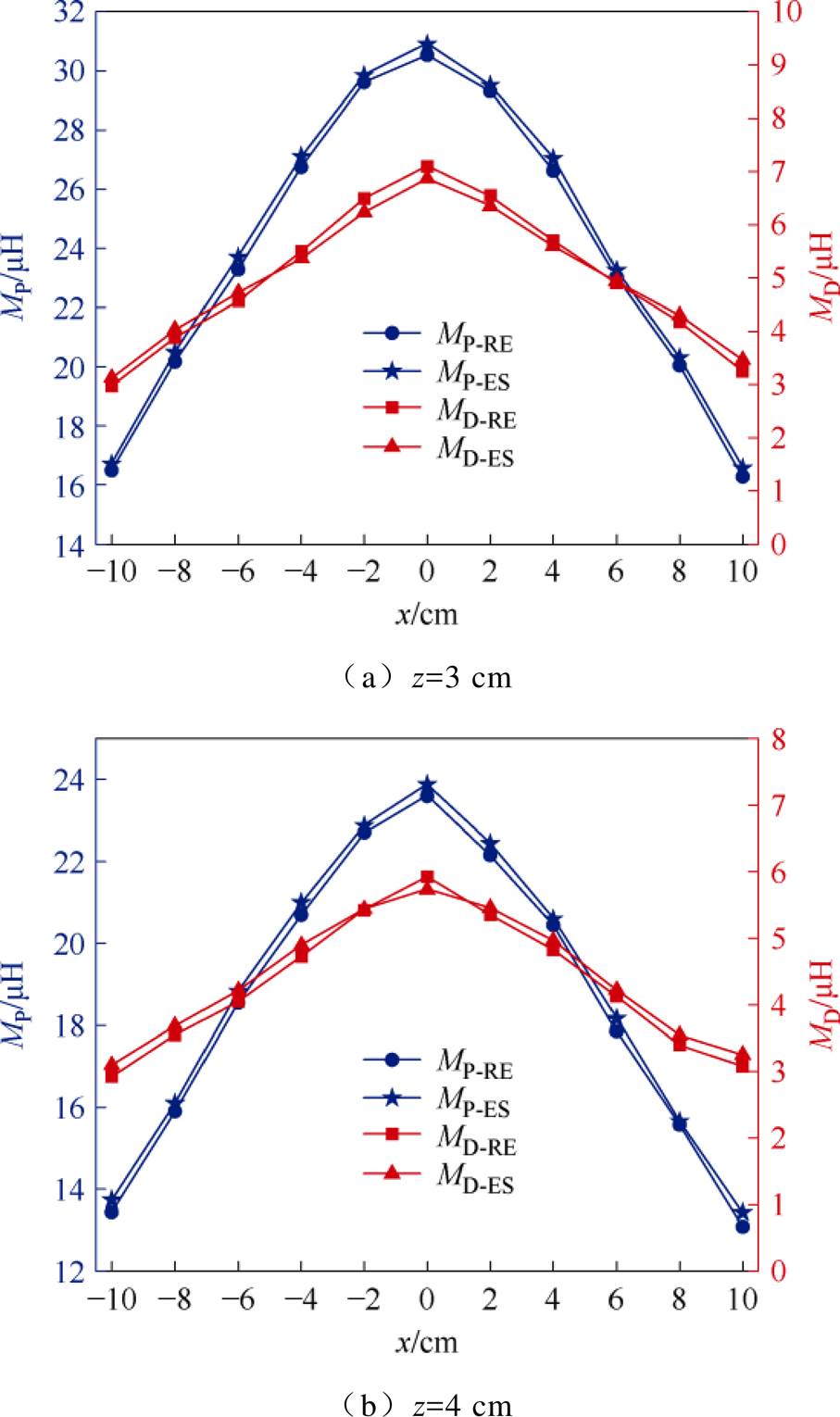
图11 x方向偏移情况下互感识别值与实测值对比
Fig.11 Comparison of mutual identification values and measured values in x-direction offset case
为了进一步验证负载识别方法的有效性,实验选取了耦合机构在z=3 cm、x=0 cm位置情况下的测量参数,通过负载识别所需的系统测量参数导通角d_LCC、逆变电流IT有效值、导通角d_SS和逆变电流IP有效值,结合图11中识别到的此位置情况下的互感MP识别值30.7 mH,代入式(12)和式(14)中分别得到双边LCC和SS谐振补偿拓扑下的负载识别值,如图12所示,双边LCC和SS谐振补偿拓扑下的负载识别值与负载实际值误差均在1 W 以内,验证了负载识别方法的有效性。
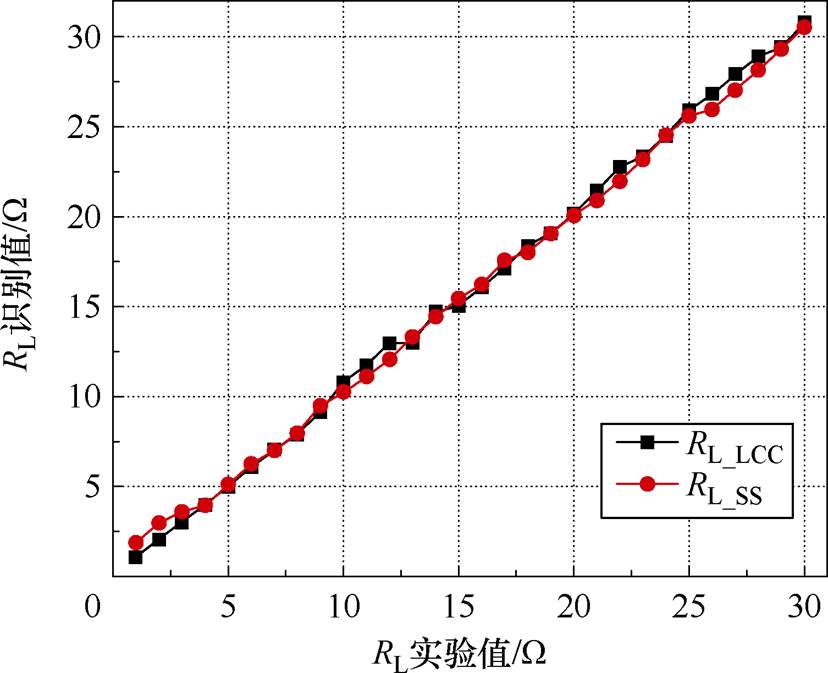
图12 z=3 cm,x=0 cm时负载识别值与实验值对比
Fig.12 Plot of load identification values vs. experimental values for z=3 cm, x=0 cm
图13为系统从SS拓扑切换到LCC-LCC拓扑的关键波形,图中左半部分为SS拓扑工作状态,右半部分为LCC-LCC拓扑工作状态,在0时刻系统进行拓扑切换。从图中上半部分的两个放大图可以看出,切换前系统工作频率为100 kHz,逆变器导通角为45°,切换后系统工作频率变为125 kHz,逆变器导通角保持为45°。检测电压UD和输出电流IL在拓扑切换后均增大,并且在切换时刻产生了一定的电压和电流尖峰,系统工作频率也发生了突变。
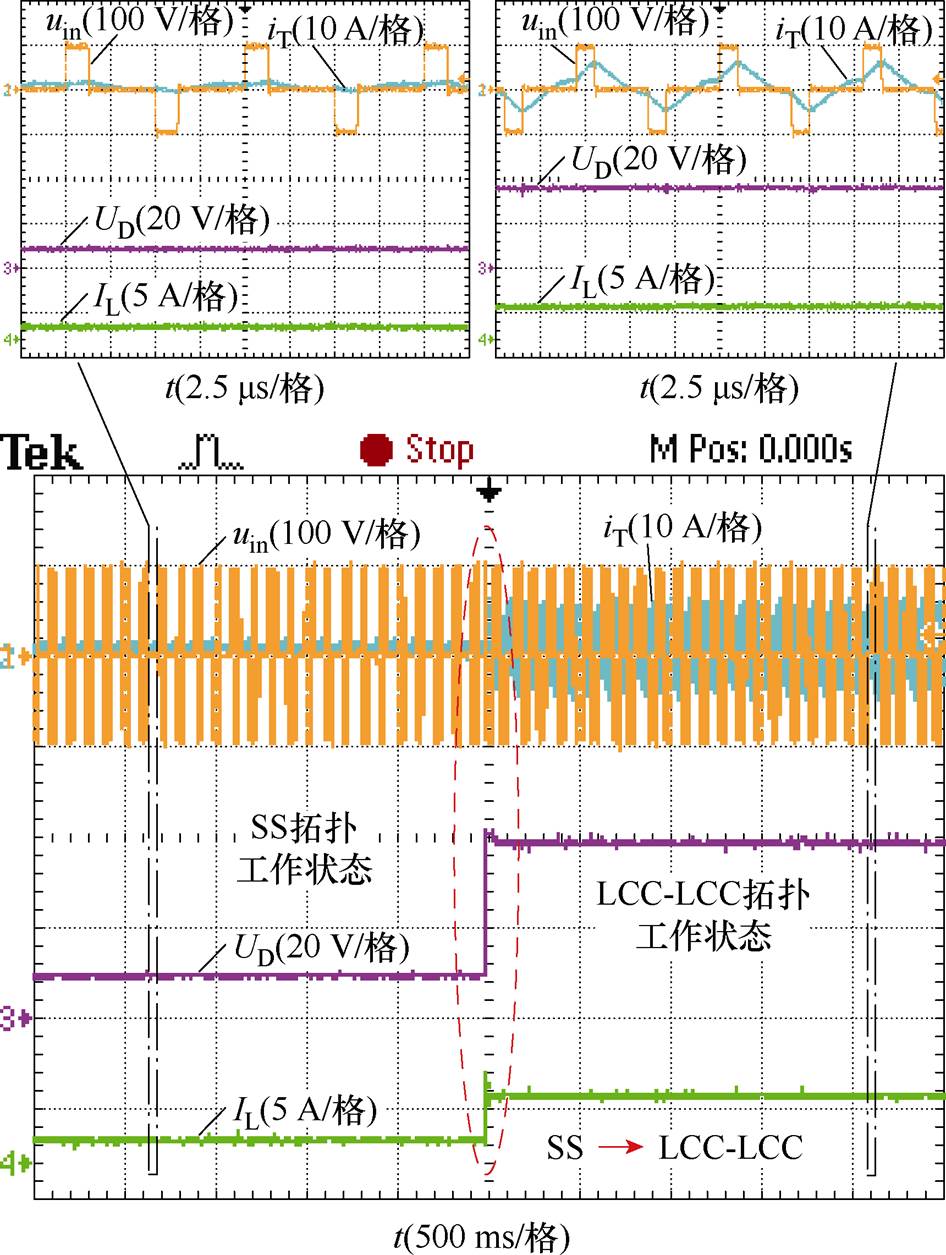
图13 系统从SS拓扑切换到LCC-LCC拓扑的关键波形
Fig.13 Key waveforms when the system switches from SS topology to LCC-LCC topology
图14为系统在LCC-LCC拓扑工作模式下,负载RL从3.6 W 变化到4.8 W,再由4.8 W 变回3.6 W 时的动态响应波形。从图中可以看出,负载切换前后的输出电流IL和检测电压UD均保持稳定,并且通过图中上方的3个放大图可知,逆变器工作频率为125 kHz,在负载切换前后逆变电压的导通角会随系统的改变进行调节,输出电压UL由36 V变为48 V,再由48 V变为36 V,系统的稳态性能和动态性能良好。
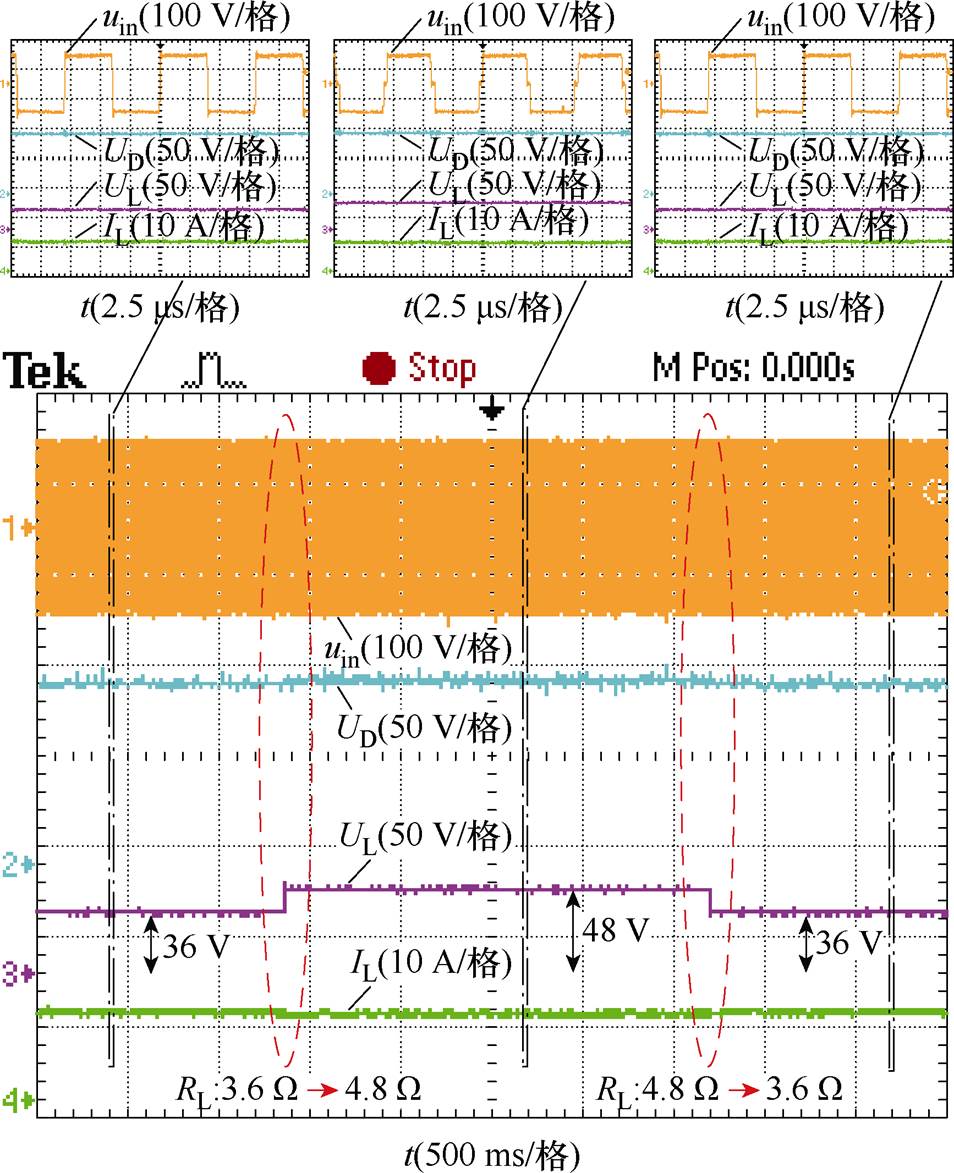
图14 RL从3.6 W 变化到4.8 W,再变回3.6 W 时的动态响应(LCC-LCC拓扑)
Fig.14 Dynamic response when RL changes from 3.6 W to 4.8 W and back to 3.6 W (LCC-LCC topology)
图15为系统在SS拓扑工作模式下,参考值ILref从10 A变化到8 A,再变回10 A时的系统动态响应波形。由图可知,当输出电流参考值ILref由10 A变化到8 A时,检测电压UD、输出电压UL和输出电流IL均减小,输出电压由36 V变化为28.8 V,检测电压UD与输出电流IL同步;当输出电流参考值ILref由8 A再变回到10 A时,检测电压UD、输出电压UL和输出电流IL均增大,检测电压UD与输出电流IL同步。由图中上方的3个放大图可以看出,逆变器工作频率为100 kHz,逆变电压导通角随参考电流的变化先减小后增大,系统的控制稳定性良好。
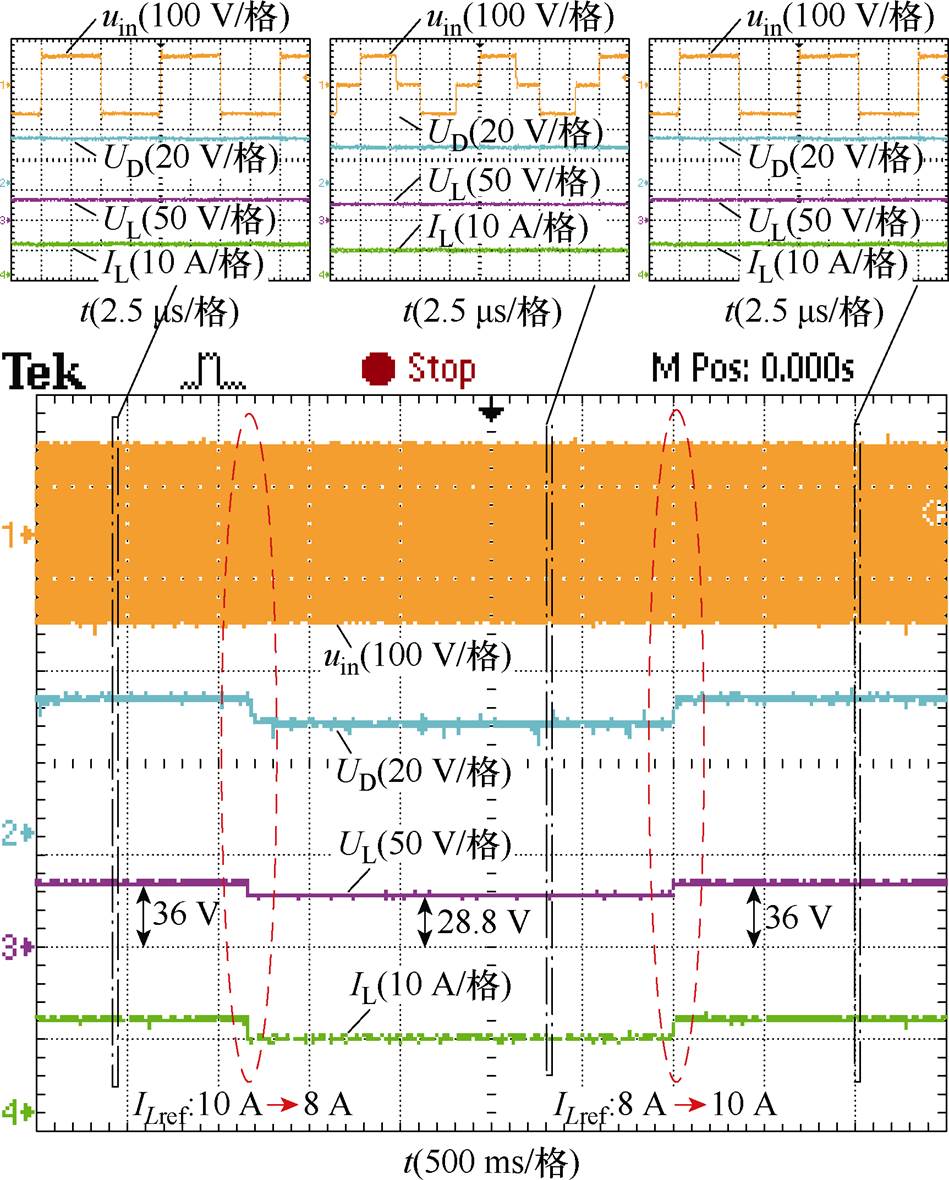
图15 ILref从10 A变化到8 A,然后再回到10 A时的动态响应(SS拓扑)
Fig.15 Dynamic response of ILref changes from 10 A to 8 A and back to 10 A (SS topology)
综上所述,验证了LCC-LCC和SS拓扑工作模式下,通过切换负载RL或输出参考电流ILref的方式,利用示波器截取的系统关键波形进行分析,进而验证了本文提出的闭环恒流控制方法的有效性。
为了验证本文提出的效率优化控制方法,本节实验测试了z=3 cm和z=4 cm传输距离下的系统效率曲线。z=3 cm时,测试了x=0 cm正对情况下的效率曲线,z=4 cm时,测试了x=-10 cm和x=10 cm偏移情况下的系统效率曲线,z=3 cm和z=4 cm时的输出电流IL分别控制为3.5 A和4 A,负载RL变化范围均为1~30 W,即最大输出功率分别为367.5 W和480 W。
图16为系统在1~30 W 负载变化时,记录的电子负载功率变化情况。z=3 cm时,最大输出功率在370 W左右,z=4 cm时,系统最大输出功率为480 W。两条功率曲线大致呈线性变化,系统恒流输出特性良好。
z=3 cm时的实验测量效率曲线如图17所示,图中红色曲线为LCC-LCC拓扑工作模式下系统实验效率测量值曲线,蓝色曲线为SS拓扑工作模式下系统实验效率测量值曲线。x方向为x=0 cm时的正对情况,耦合系数为0.39,负载临界值约为9.5 W,在负载RL大于负载临界点后,SS拓扑大于LCC- LCC拓扑下的系统效率。
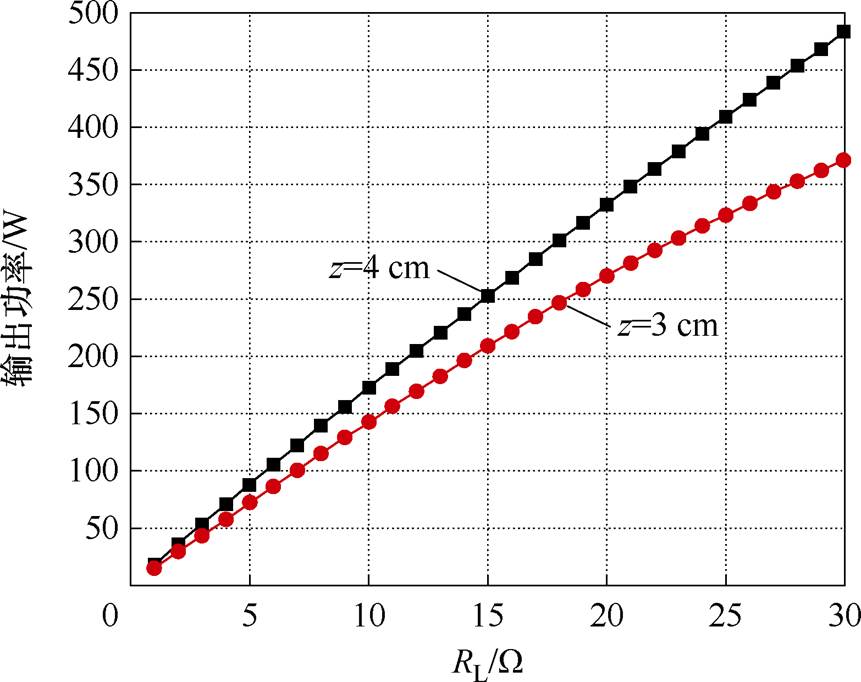
图16 系统在1~30 W 负载变化时输出功率变化情况
Fig.16 Changes in output power of the system when the load changes from 1 W to 30 W
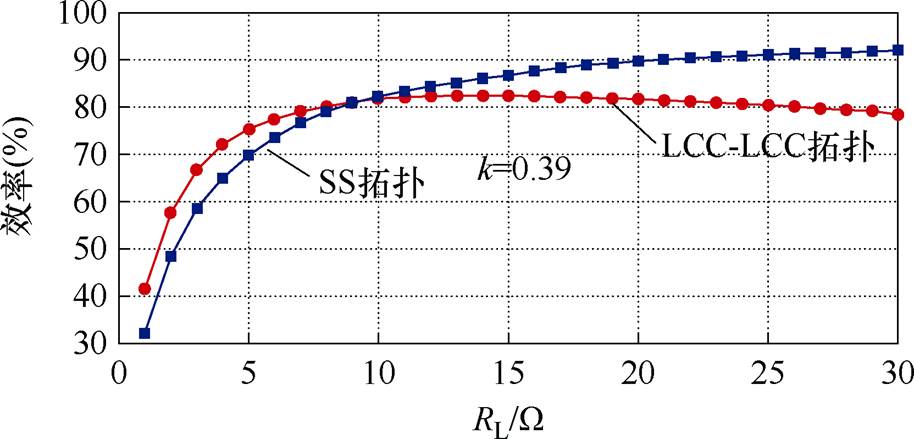
图17 z=3 cm,x=0 cm时系统效率随负载变化曲线
Fig.17 System efficiency changes with load when z=3cm, x=0 cm
z=4 cm时的实验测量效率曲线如图18和图19所示。x方向偏移量分别为x=-10 cm和x=10 cm,对应的耦合系数分别为0.17和0.16,负载临界值分别约为9.0 W 和10.0 W,在负载RL大于负载临界点之后,LCC-LCC拓扑大于SS拓扑下的系统效率。
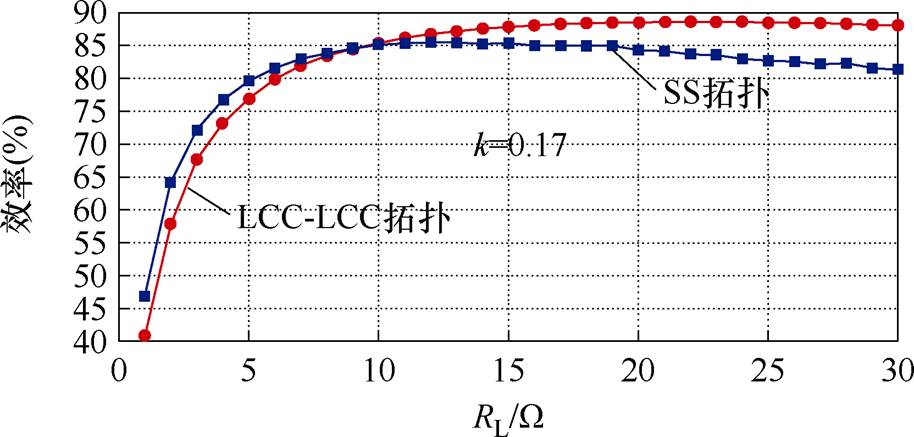
图18 z=4 cm,x=-10 cm时系统效率随负载变化曲线
Fig.18 System efficiency changes with load when z=4 cm, x=-10 cm
图20为负载RL在10 W 状态下,输出电流IL为4 A时,系统从LCC-LCC拓扑切换为SS拓扑工作模式的系统关键波形变化情况。从图中可以看出,在拓扑切换时刻,输出电压UL和输出电流IL均先减小后增大,输出电流IL仅有短时间的尖峰,之后便继续保持4 A的输出电流。从图中上方的两个放大图可知,拓扑切换前逆变器工作频率为125 kHz,切换后逆变器工作频率改变为100 kHz,在切换时刻发生了频率突变。
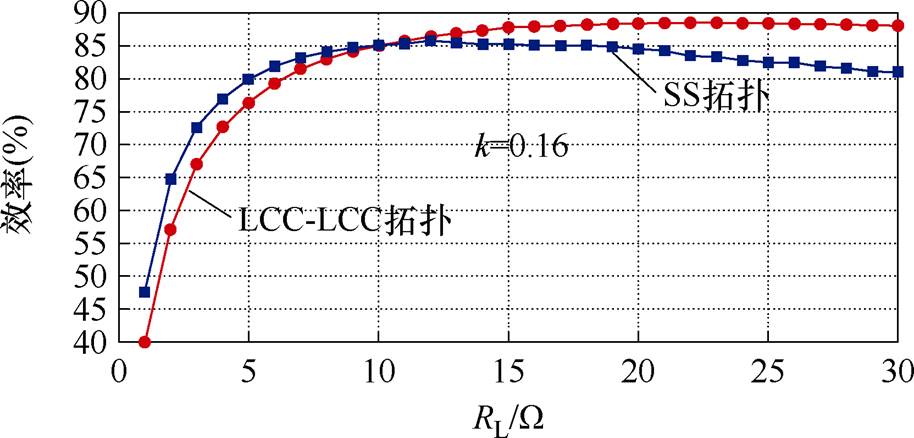
图19 z=4cm,x=10cm时系统效率随负载变化曲线
Fig.19 System efficiency changes with load when z=4 cm, x=10 cm
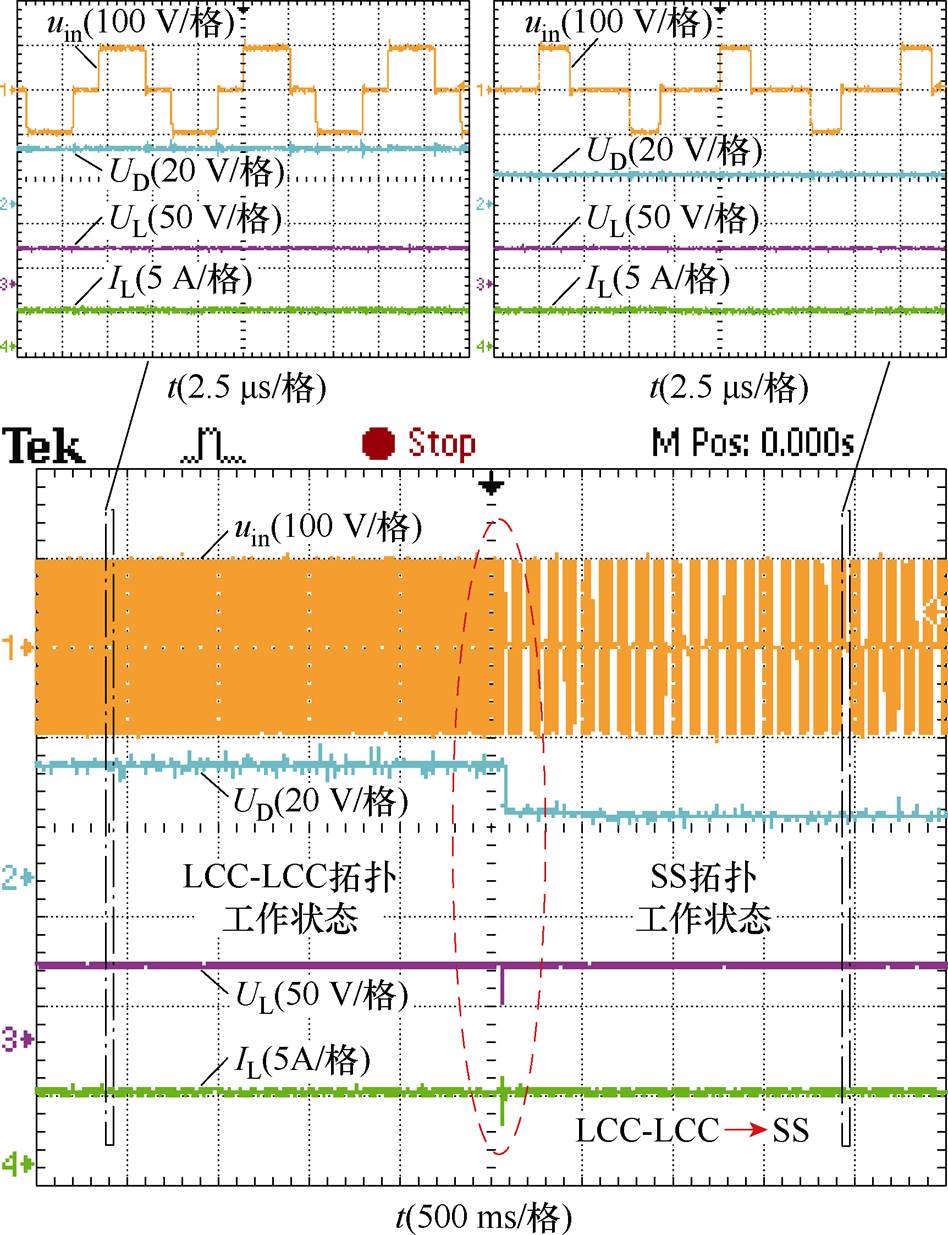
图20 系统从LCC-LCC拓扑切换为SS拓扑的关键波形
Fig.20 Key waveforms when the system switches from LCC-LCC topology to SS topology
以上效率优化控制实验验证波形与实验测量效率曲线验证了本文提出的基于互感与负载识别的系统效率优化控制方法的合理性与可行性。
针对AGV静态无线充电系统中存在互感与负载参数变化导致系统输出电流与系统效率变化的问题,本文提出了一种基于互感与负载识别的AGV无线电能传输系统闭环恒流与效率优化控制方法,该方法同时具有系统互感与负载识别和闭环恒流控制的能力,并能利用识别的参数通过拓扑切换的方式进行充电过程中的效率优化控制,为解决AGV无线充电应用中的该类问题提供了新的解决思路,具有一定的理论价值和实用意义。得到结论具体如下:
1)提出了一种无通信环节的系统闭环恒流控制方法。实验通过切换负载和输出电流参考值的方式验证了LCC-LCC和SS拓扑下的系统动态响应波形,结果表明系统具有较好的稳态和动态性能,验证了该闭环控制方法的有效性。
2)提出了一种基于互感与负载识别的效率优化控制方法。为了验证效率优化控制方法的可行性,实验测量了三组系统效率随负载变化的曲线,结果表明三组效率曲线均存在负载临界值,使得在临界值前后两个拓扑下的系统效率存在高低反转,并且给出了系统从LCC-LCC拓扑切换到SS拓扑并保持恒定电流输出的关键波形,由此证明了通过识别负载来判断是否切换拓扑以优化系统效率的方法的可 行性。
参考文献
[1] 苏庆华, 张娣娣, 吴昊, 等. AGV导航技术综述[J]. 计算机科学与应用, 2022, 12(8): 1990-1997.
Su Qinghua, Zhang Didi, Wu Hao, et al. Overview of AGV navigation technology[J]. Computer Science and Application, 2022, 12(8): 1990-1997.
[2] 蒋金橙, 王佩月, 冯天旭, 等. 基于准双向三态协同调度的无人车和无人机逐级式无线充电应用[J]. 电工技术学报, 2024, 39(22): 6965-6979.
Jiang Jincheng, Wang Peiyue, Feng Tianxu, et al. AGV and UAV stepwise wireless charging appli- cation based on quasi bidirectional three-state collaborative progressive method[J]. Transactions of China Electrotechnical Society, 2024, 39(22): 6965- 6979.
[3] 冯鸿运, 林飞, 杨中平, 等. 应用于自动导引小车无线充电系统的导航与供电一体化线圈研究[J]. 电工技术学报, 2024, 39(14): 4294-4304.
Feng Hongyun, Lin Fei, Yang Zhongping, et al. A research on a navigation and power supply integrated coil for automatic guided vehicle wireless power transfer system[J]. Transactions of China Electro- technical Society, 2024, 39(14): 4294-4304.
[4] Pan Shuaishuai, Xu Yefei, Lu Yuanfang, et al. Design of compact magnetic coupler with low leakage EMF for AGV wireless power transfer system[J]. IEEE Transactions on Industry Applications, 2022, 58(1): 1044-1052.
[5] 荆锐, 张耀, 刘顺攀, 等. 自动导引车动态无线供电系统无通信自动分段切换技术研究[J]. 电工技术学报, 2024, 39(17): 5344-5353.
Jing Rui, Zhang Yao, Liu Shunpan, et al. Research on automatic segment switching without communication in AGV dynamic wireless power transfer system[J]. Transactions of China Electrotechnical Society, 2024, 39(17): 5344-5353.
[6] 童湛安心, 苏建徽, 张健, 等. AGV无线充电全波同步整流尖峰电压抑制方法[J]. 电气传动, 2023, 53(3): 22-27.
Tong Zhan’anxin, Su Jianhui, Zhang Jian, et al. Suppression method of spike voltage of AGV wireless charging by full-wave synchronous rectification[J]. Electric Drive, 2023, 53(3): 22-27.
[7] Li Xiaofei, Wang Cheng, Wang Heshou, et al. A robust wireless power transfer system with self- alignment capability and controllable output current for automatic-guided vehicles[J]. IEEE Transactions on Power Electronics, 2023, 38(10): 11898-11906.
[8] Matsumoto H, Kanazawa H, Uwai H, et al. Segment switching method of three-phase wireless power transmitter for AGV[J]. IEEE Transactions on Industrial Electronics, 2024, 71(7): 6490-6500.
[9] Iam I W, Choi C K, Lam C S, et al. A constant-power and optimal-transfer-efficiency wireless inductive power transfer converter for battery charger[J]. IEEE Transactions on Industrial Electronics, 2024, 71(1): 450-461.
[10] 杨云虎, 贾维娜, 梁大壮, 等. LCC-LCC/S自切换恒流-恒压复合型无线电能传输系统[J]. 电工技术学报, 2023, 38(18): 4823-4837, 4852.
Yang Yunhu, Jia Weina, Liang Dazhuang, et al. A self-switching wireless power transfer system based on hybrid topology of LCC-LCC/S with constant current and constant voltage[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4823-4837, 4852.
[11] Luo Jialin, Xiao Wenxun, Zhang Bo, et al. Design of magnetic coupling resonant wireless charging system for cable tunnel inspection robot[C]//2018 IEEE Wireless Power Transfer Conference (WPTC), Montreal, QC, Canada, 2018: 1-4.
[12] Colak K, Asa E, Bojarski M, et al. A novel phase-shift control of semibridgeless active rectifier for wireless power transfer[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6288-6297.
[13] Dai Xin, Li Xiaofei, Li Yanling, et al. Maximum efficiency tracking for wireless power transfer systems with dynamic coupling coefficient esti- mation[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5005-5015.
[14] Berger A, Agostinelli M, Vesti S, et al. A wireless charging system applying phase-shift and amplitude control to maximize efficiency and extractable power[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6338-6348.
[15] Chen Yang, Li Mingxuan, Yang Bin, et al. Variable- parameter T-circuit-based IPT system charging battery with constant current or constant voltage output[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 1672-1684.
[16] 谢诗云, 杨奕, 李恋, 等. 基于双极性耦合磁场调控的高抗偏移偏转无线电能传输系统[J]. 电工技术学报, 2023, 38(18): 4838-4852.
Xie Shiyun, Yang Yi, Li Lian, et al. Wireless power transfer system with high misalignment tolerance based on bipolar coupling magnetic-field control[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4838-4852.
[17] 姚若玉, 曲小慧, 郁继栋, 等. 自适应电池充电曲线的三线圈电池无线充电器[J]. 电力系统自动化, 2022, 46(7): 170-177.
Yao Ruoyu, Qu Xiaohui, Yu Jidong, et al. Three-coil wireless battery charger with self-adaptation to battery charging curve[J]. Automation of Electric Power Systems, 2022, 46(7): 170-177.
Abstract With the widespread application of AGV in intelligent manufacturing and logistics, a stable and efficient power supply is essential. Enterprises and researchers have proposed applying WPT technology to AGV wireless charging. However, the mutual inductance and load parameter changes lead to system output current and efficiency variations. This paper proposes a closed-loop constant current and efficiency optimization control method for the AGV wireless power transfer system based on mutual inductance and load identification.
Firstly, this paper gives the overall structure of the closed-loop constant current AGV wireless power transfer system without a communication link. According to the topological structure of the system, the LCC-LCC and SS resonant compensation topology circuits are analyzed, the parameter identification formulas of mutual inductance MP and MD are derived, and the principle and identification process of the mutual inductance and load are obtained. Since the mutual inductance MP has been identified in advance, the corresponding load RL in the two topological working modes can be further identified by sampling the inverter current.
Secondly, according to the mutual inductance and load identification principle, the closed-loop constant current and efficiency control method of the AGV wireless power transfer system is obtained based on mutual inductance and load identification. The closed-loop system structure based on phase-shift control is analyzed, and the specific implementation method of closed-loop control of the output current IL using the feedback detection voltage UD is explained. The load critical points under the LCC-LCC and SS resonant compensation topologies are analyzed, and the load critical point has a one-to-one correspondence with the mutual inductance. A flow chart of system efficiency optimization control based on mutual inductance and load identification is given, and the specific control process of efficiency optimization is elaborated.
Finally, an experimental setup is built. The experimental results show that the maximum identification error rates of mutual inductance MP and MD are 2.59% and 6.62% under the two transmission distances of z=3 cm and z=4 cm, and the identification errors of the load identification method under LCC-LCC and SS resonant compensation topologies are both within 1 W. The system dynamic response waveforms are tested under LCC-LCC and SS topologies by switching the load and output current reference values. The results show that the system has good steady-state and dynamic performance. A total of three experimental efficiency curves varying with loads are measured. The results show that a load critical value exists, which reverses the system’s efficiency under the two topologies before and after the critical value. The key waveform of the system switching from LCC-LCC topology to SS topology and maintaining constant current output is given, which proves that topology switch determination through load identification is feasible to optimize the system efficiency.
keywords:Automated guided vehicle (AGV), wireless power transfer (WPT) system, closed-loop constant current, parameter identification, efficiency optimization
DOI: 10.19595/j.cnki.1000-6753.tces.240790
中图分类号:TM724
国家自然科学基金(51777162)和中央高校基本科研业务费专项资金(xzy012019022)资助项目。
收稿日期 2024-05-14
改稿日期 2024-05-28
李小飞 男,1987年生,副教授,研究方向为无线电能传输、电力电子建模与控制。E-mail: xiaofei.li@cqu.edu.cn(通信作者)
蒋光利 男,1998年生,硕士研究生,研究方向为无线电能传输、电力电子建模与控制。E-mail: jgl_545@163.com
(编辑 陈 诚)