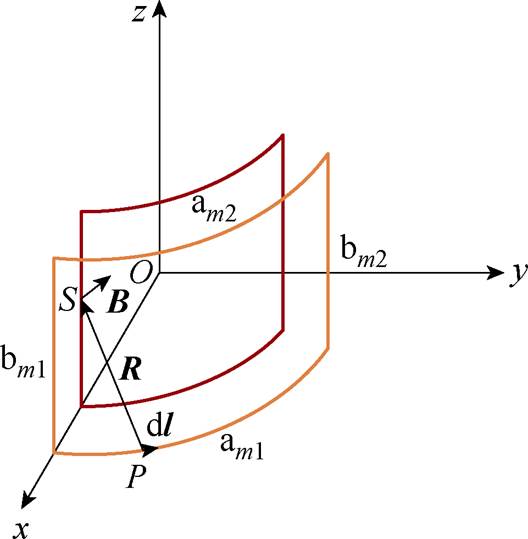
图1 弧形线圈互感计算示意图
Fig.1 Schematic diagram of arc-shaped coil mutual inductance calculation
摘要 海底洋流易造成水下自动潜航器(AUV)的无线充电系统耦合机构出现多方向偏移,导致供电效率和功率均下降,甚至影响系统正常工作。为此,该文围绕适用于AUV的弧形耦合线圈展开抗偏移性能研究与设计。首先提出弧形线圈的互感解析模型。然后通过对弧形线圈的空间磁场分布展开分析,得到对应分布情况,并结合结构参数变化对空间磁场分布的影响,提出单线圈情况下的抗偏移优化策略,考虑到单线圈结构的抗偏移性能有限,基于磁场叠加定理和弧形线圈的空间磁场分布,提出一种新型错位补偿式弧形线圈结构,建立了互感M、匝数Np1(2)与错位距离l的关系模型,实现了线圈关键结构参数的优化设计。最后搭建实验平台验证了互感解析模型的正确性,并验证了错位补偿式弧形线圈具有良好的抗偏移性能:当线圈水平偏移80 mm时,该线圈结构互感保持能力提升19.23%,且抗旋转偏移范围能够达到[-15°, 15°];在线圈水平偏移30 mm时,错位补偿弧形线圈的感应式电能传输(IPT)系统输出电压波动率为0.78%,而单极性弧形线圈电压波动率为7.7%。
关键词:水下感应式电能传输(IPT)系统 弧形线圈 互感计算 抗偏移
我国海洋范围辽阔、资源丰富,而对海洋资源的探索具有战略意义,海洋资源探索离不开水下自动潜航器(Autonomous Underwater Vehicle, AUV)的使用[1-3]。尽管AUV拥有众多优点,但在复杂的海洋环境下为其供电却十分困难。采用传统的接触式充电,电线裸露容易出现漏电、腐蚀等隐患问题,电线的长度也制约了AUV工作的灵活性[4-6]。因此安全、可靠的充电方法是AUV应用急需解决的问题。非接触式电能传输技术成为解决该问题的关键[7-15]。
对于感应式电能传输(Inductive Power Transfer, IPT)系统,与空气介质相比,海水介质环境更加复杂,海底洋流的不可控因素使得AUV设备耦合结构更容易发生偏移进而影响功率传输的稳定性[16-18]。而弧形线圈作为AUV无线电能传输中的唯一能量通道,其对于提升IPT抗偏移能力起着最为直接的影响,因此研究适应海洋环境和AUV稳定充电需求的新型线圈势在必行。
针对水下IPT系统的磁耦合机构设计,文献[19]引入同轴线圈结构,该结构与AUV船体契合度良好,具有良好的旋转抗偏移性能,但同轴线圈结构会使得线圈中心区域磁场过强,严重威胁AUV的正常使用。文献[20]提出一种偶极子线圈结构,该结构有效地降低了耦合机构漏感,但其抗偏移性能较差。文献[21]提出一种原边三相发射线圈,能够较好地将磁场约束在线圈附近,且在旋转偏移时能够保持两线圈间耦合,但对水平偏移的实用性较差。文献[22-23]提出了一种DDQ型线圈,减少了漏磁通量,提高了线圈的抗偏移能力,然而该结构仅考虑了水平方向上的偏移情况,对旋转方向的偏移情况未进行验证。文献[24]对水下单极和双极曲面线圈进行了优化设计,分析了双极曲面线圈的电磁场辐射对AUV内部电子元件的影响,然而并未对曲面线圈的抗偏移性能开展深入研究。
综上所述,本文针对适用于AUV船体,兼顾水平及旋转方向抗偏移性能的弧形线圈结构展开深入研究。在理论方面,建立弧形线圈的空间磁场解析模型,分析其磁场分布,并利用Ansys Maxwell有限元仿真软件进行验证,同时对磁场分布均匀性对抗偏移能力的关系进行探究。在结构设计方面,基于磁场分布提出了新型错位补偿式弧形线圈结构,并对该结构进行优化设计,给出设计方法。此外,文中将所设计的线圈与常见的抗偏移线圈结构进行了性能比较,验证了其在海洋环境中优异的抗偏移性能。
在柱坐标系下以同轴单匝弧形线圈进行磁场分析,进一步根据磁场叠加定理推广多匝情况。
弧形线圈互感计算示意图如图1所示,初级线圈导线上任意点坐标为P(rpcosjp, rpsinjp, zp),次级线圈弧面上任意点坐标为S(rscosjs, rssinjs, zs)。其中rp、rs为初级、次级线圈弧半径,jp、js为初级、次级线圈对应的极角,zp、zs为初级、次级纵坐标。am1、am2为初级、次级弧形导线,bm1、bm2为初级、次级直导线,m为匝数。

图1 弧形线圈互感计算示意图
Fig.1 Schematic diagram of arc-shaped coil mutual inductance calculation
基于毕奥-萨法尔定律,对初级线圈在次级线圈任意点S处的磁感应强度表示为
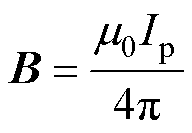
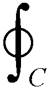
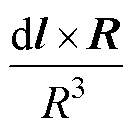 (1)
(1)
式中,m0为真空磁导率;Ip为初级电流;C为由am1、am2、bm1、bm2所组成的闭合曲线;Ipdl为初级电流元;R为初级电流元到点S的距离矢量;R为初级电流元到点S的距离。
am1、am2、bm1、bm2各边微元dl表示为
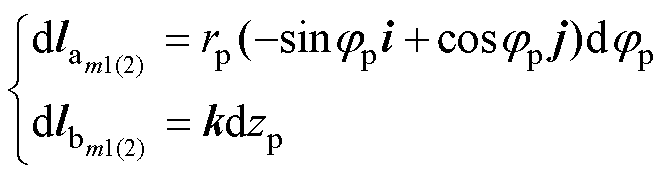 (2)
(2)
式中,i、j、k分别为三维直角坐标系内,与x轴、y轴和z轴方向相同的单位向量。
初级线圈上电流元到点S的距离矢量为
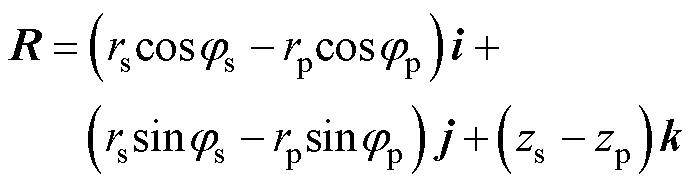 (3)
(3)
对式(3)求模
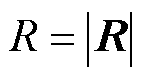 (4)
(4)
将式(2)~式(4)代入式(1)得到第m匝初级线圈各边am1、am2、bm1、bm2在点S处的磁感应强度矢量表达式为
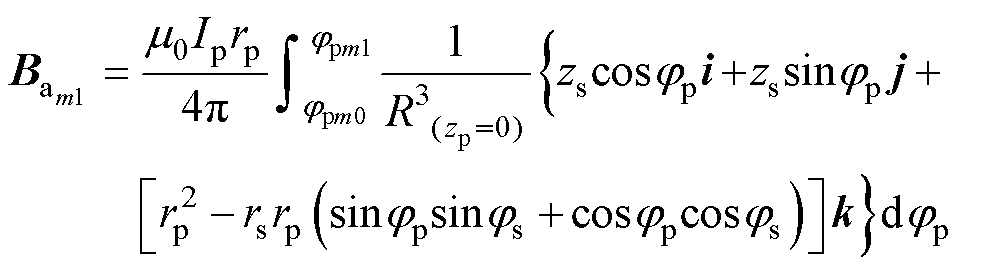 (5)
(5)
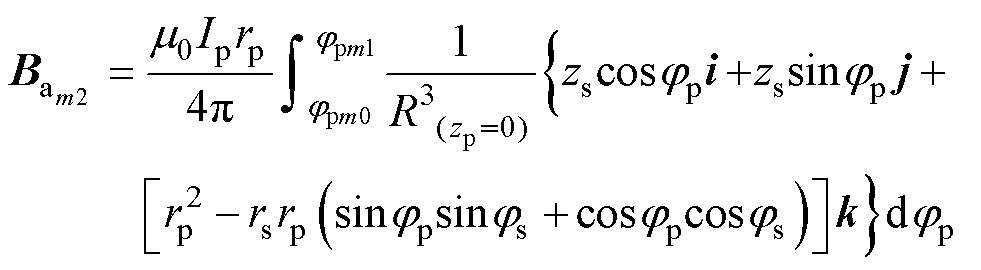 (6)
(6)
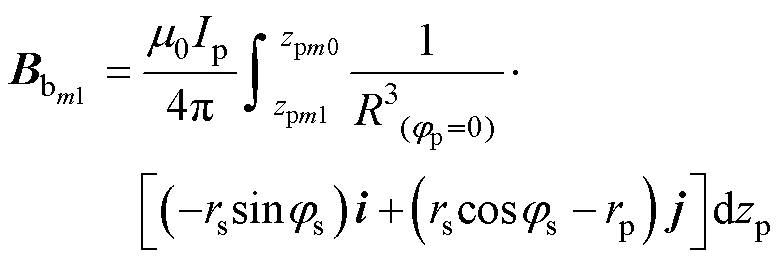 (7)
(7)
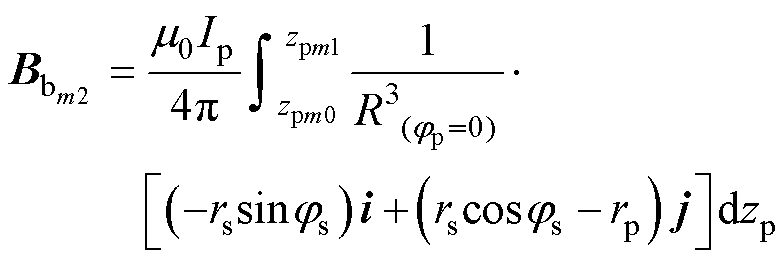 (8)
(8)
式中,zpm0、zpm1为第m匝初级线圈的直导线在z方向的首尾坐标点,其差值等于第m匝直导线长度;jpm0、jpm1为第m匝初级线圈的弧形导线首、尾坐标弧度,其差值等于第m匝弧导线弧度。
次级弧面微元法向量为
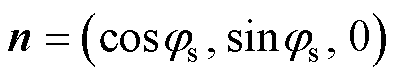 (9)
(9)
将式(9)分别与式(5)~式(8)相乘,得到磁感应强度通过次级弧面元的垂直分量为
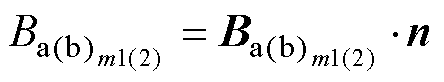 (10)
(10)
则式(5)~式(8)可化简为
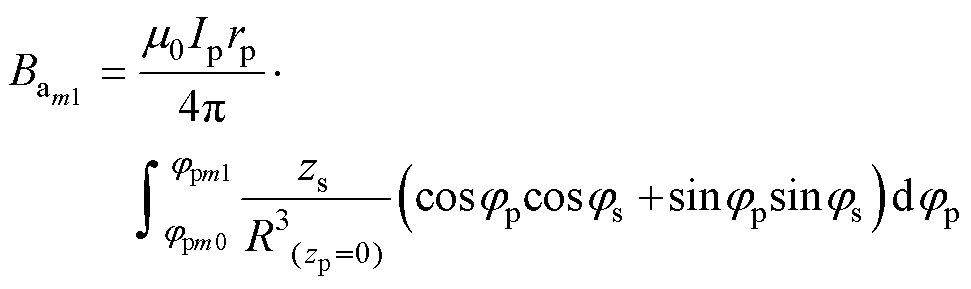 (11)
(11)
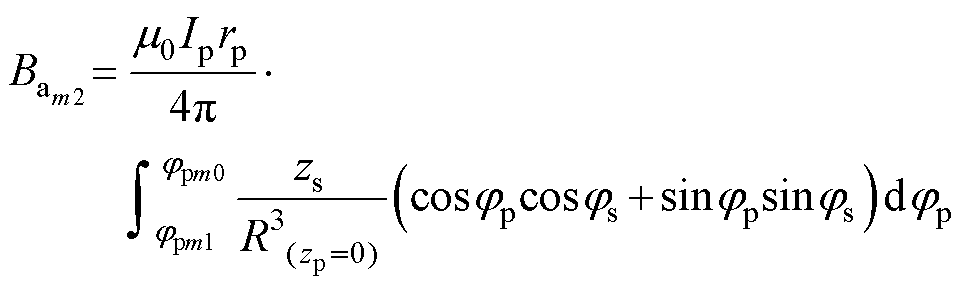 (12)
(12)
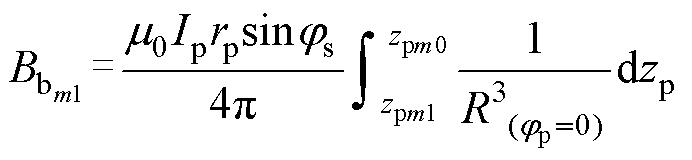 (13)
(13)
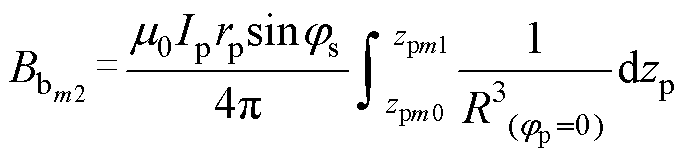 (14)
(14)
将式(11)~式(14)相加得到初级弧形单匝线圈在次级任意点处的磁感应强度为
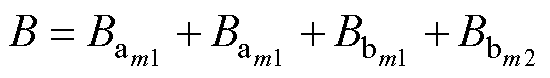 (15)
(15)
结合式(11)~式(15)即可得到初级第m匝线圈穿过次级第n匝线圈的磁通表达式为
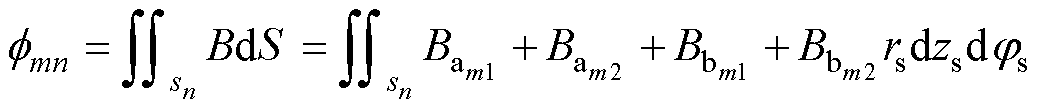 (16)
(16)
式中,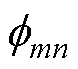 为初级第m匝线圈穿过次级第n匝线圈的磁通量;sn为次级线圈所在区域。
为初级第m匝线圈穿过次级第n匝线圈的磁通量;sn为次级线圈所在区域。
结合式(3)~式(16),对式(16)中的积分表达式进行求解,即可得到弧形线圈在任意空间位置点的磁场分布,接下来针对弧形线圈的磁场分布与互感计算开展进行进一步探究。
对1.1节单匝情况,进行多匝迭代,初始条件:m=1,n=1,对应初级、次级最外匝的参数为
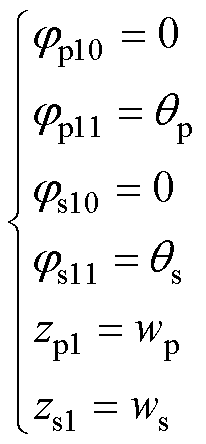 (17)
(17)
式中,qp、qs分别为初级、次级最外匝线圈开角;zp1表示m=1时zpm1与zpm0的差;zs1表示n=1时zsn1与zsn0的差;wp、ws分别为初级、次级最外匝线圈外宽。
初级线圈第m匝参数即可表示为
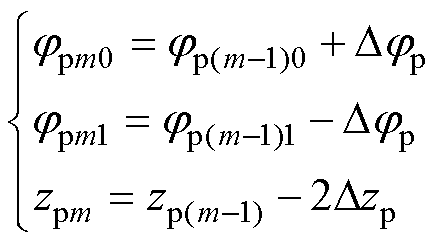 (18)
(18)
同理,次级线圈第n匝参数可表示为
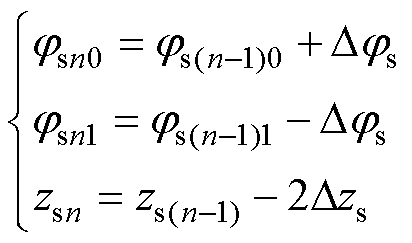 (19)
(19)
式中,Dzp、Dzs分别为初级、次级匝间距;Djp、Djs分别为初级、次级匝弧度间距,可由匝间距Dzp、Dzs与线圈弧半径rp、rs计算得到。
根据互感定义,并代入式(17)~式(19),得到同轴情况下互感表达式为
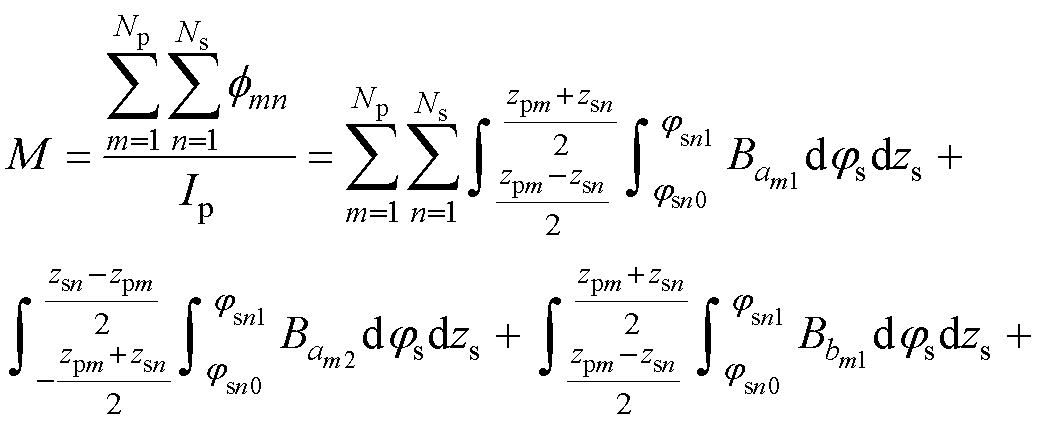
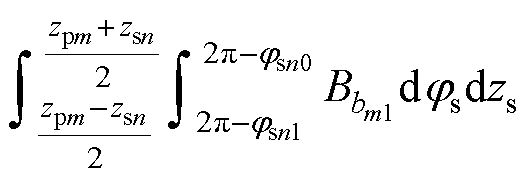 (20)
(20)
由式(20)可以看出,互感能够等价为初级、次级线圈对应的磁通量与初级电流的比值,该值与电流无关,是两线圈间固有性质。
弧形线圈结构如图2所示,设置初级、次级弧形线圈模型参数如下:初级线圈弧半径rp=420 mm,外宽wp=240 mm,线圈开角qp=60°,匝数np=12,匝间距dp=4 mm;次级线圈弧半径rs=390 mm,外宽ws=180 mm,线圈开角qs=60°,匝间距ds=4 mm,匝数ns=10。
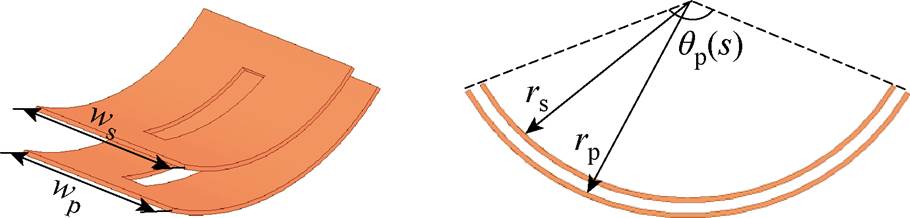
图2 弧形线圈结构
Fig.2 Curved coil structure
如图3所示为初级弧形线圈穿过次级弧形线圈的磁场分布随空间位置变化的趋势。
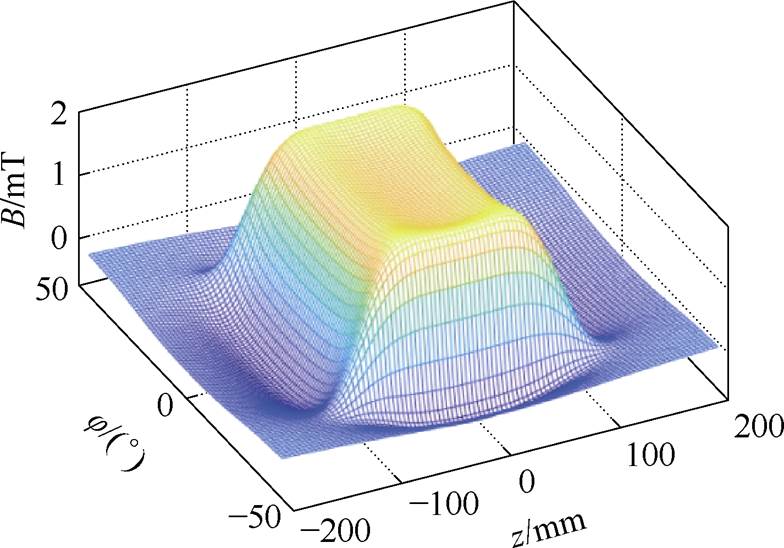
图3 弧形线圈空间磁场分布
Fig.3 Spatial magnetic field distribution of arc coils
由图3可以看出:①在线圈正对中心区域磁场感应强度整体处于峰值,其中仍存在一个相对较小的区域,磁场分布相对均匀;②随着z以及j 的增大,会在一定范围内出现“临界区域”磁场随空间位置变化显著,磁场迅速降低,随着与中心距离的进一步增加,磁力线出现回归,磁场方向发生翻转,进入负磁通区。
由式(20)可知,互感M为对应范围内磁场感应强度对应的曲面积分值,如图4所示,两线圈正对情况下对应范围磁场最强,互感为峰值,而随着偏移的发生,对应范围发生改变,磁场显著降低,对应互感随之减小。
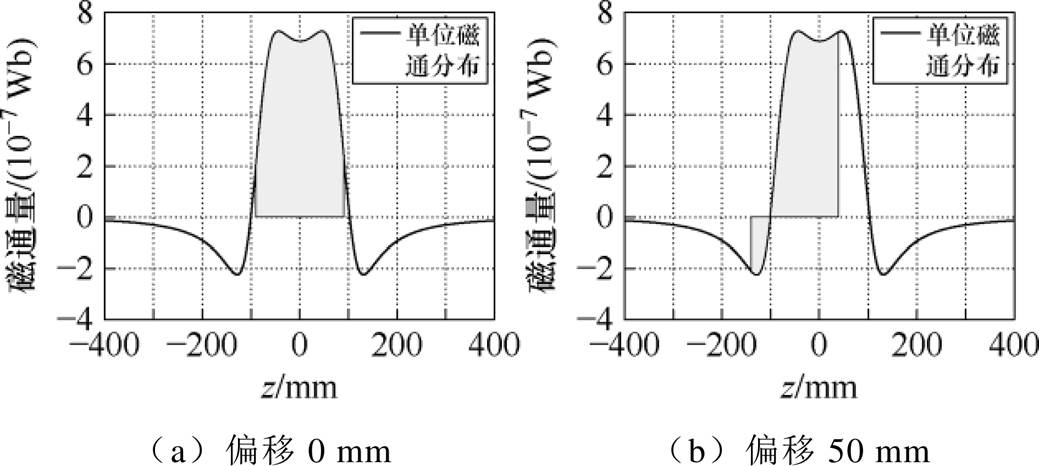
图4 互感计算示意图
Fig.4 Schematic diagram of the calculation of the mutual inductance factor
进一步地,本文分别对初级线圈不同结构参数匝间距、外宽、匝数、开角的沿z方向的磁场分布进行了分析,不同结构参数对弧形线圈磁场分布的影响如图5所示。
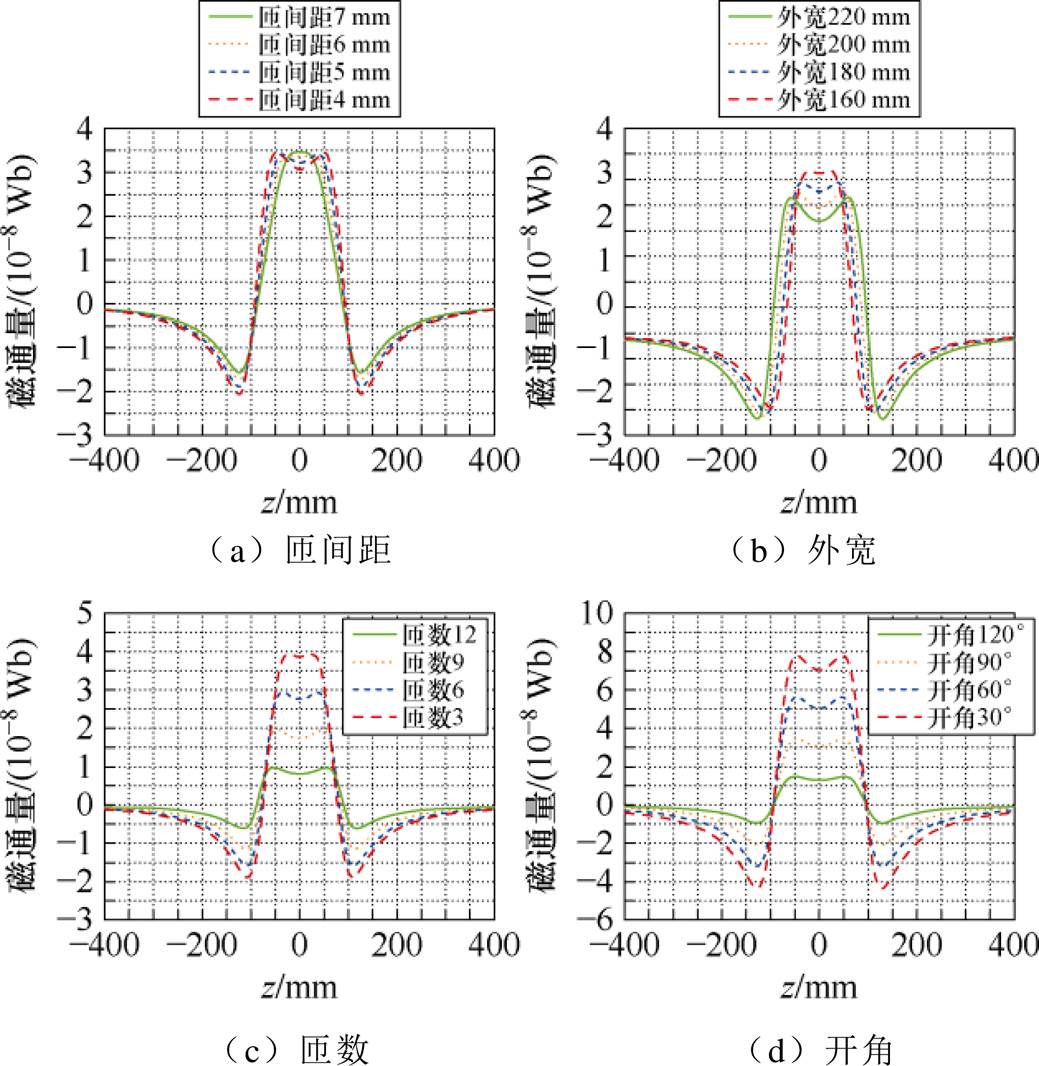
图5 不同结构参数对弧形线圈磁场分布的影响
Fig.5 Influence of different structural parameters on the magnetic field distribution of arc coils
由图5a可知,当匝间距dp=4、5、6、7 mm,随着dp增大,中心区域磁场变化增大,临界区域磁场变化减小。由图5b可知,当外宽wp=160、180、200、220 mm时,随着wp增大,中心区域磁场变化减小,临界区域磁场变化增大。由图5c可知,当匝数Np=3、6、9、12时,随着Np增大,中心区域磁场变化减小,临界区域磁场变化同样减小。由图5d可知,当开角qp=30°、60°、90°、120°时,随着qp增大,中心区域磁场变化增大,临界区域磁场变化同样增大。综上所述,中心区域互感稳定性与匝间距成反比、与外宽成正比。而在全区域内互感稳定性与匝数均成反比、与开角均成正比。
为验证上述分析及结论的正确性,利用有限元仿真软件Ansys Maxwell对弧形线圈进行建模分析,磁感应强度云图如图6所示。
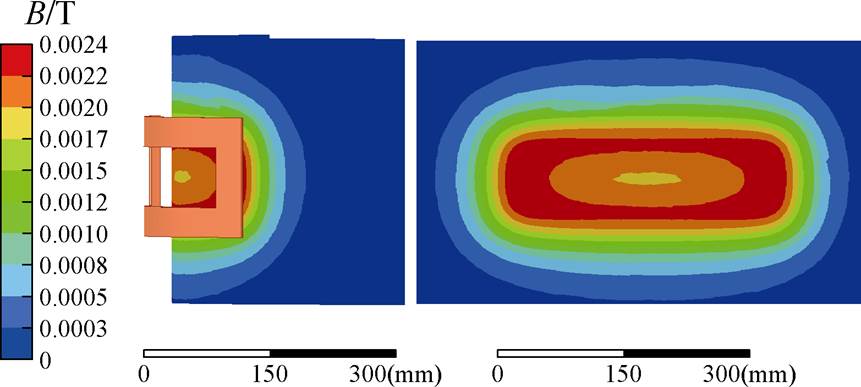
图6 弧形线圈磁感应强度云图
Fig.6 Contour of the magnetic induction intensity of the arc coil
图6中,弧形线圈磁场分布主要集中于中心区域,同时存在磁场强度相对较低的区域,随着z以及j 的增大,磁场分布逐渐减小,并趋向于零。为全面反映磁场方向及负磁通区域问题,本文分别对中心区域z=0 mm与临界区域z=120 mm处的磁感应强度矢量进行截面分析,如图7所示。
由图7中可看出,在中心区域z=0 mm磁场方向由原边穿过副边,而在临界区域z=120 mm处磁场方向则转为了由次级线圈到初级线圈。磁场方向发生了翻转,证明了负磁通区域的存在。
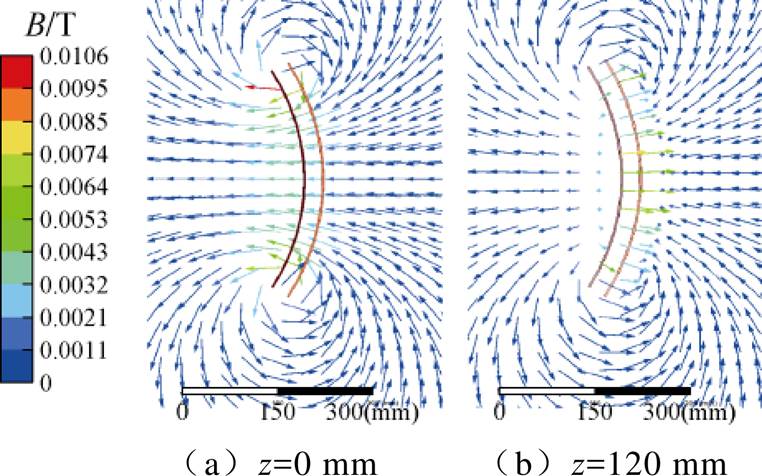
图7 磁感应强度矢量
Fig.7 Vector illustration of magnetic induction intensity
为展开各结构参数对弧形线圈互感稳定性的分析,定义互感保持系数X为
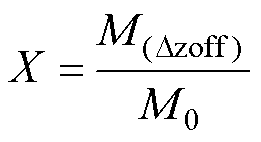 (21)
(21)
式中,M(Dzoff)为偏移后的互感值;M0为正对时的互感值。不同偏移情况下互感保持系数越大则对应线圈结构互感稳定性越好,即可完成不同线圈结构抗偏移特性的量化表征。针对1.2节中初级线圈具有不同匝间距、匝数、开角、外宽的情况下,当线圈发生偏移时,系统的互感保持系数变化曲线如图8所示。
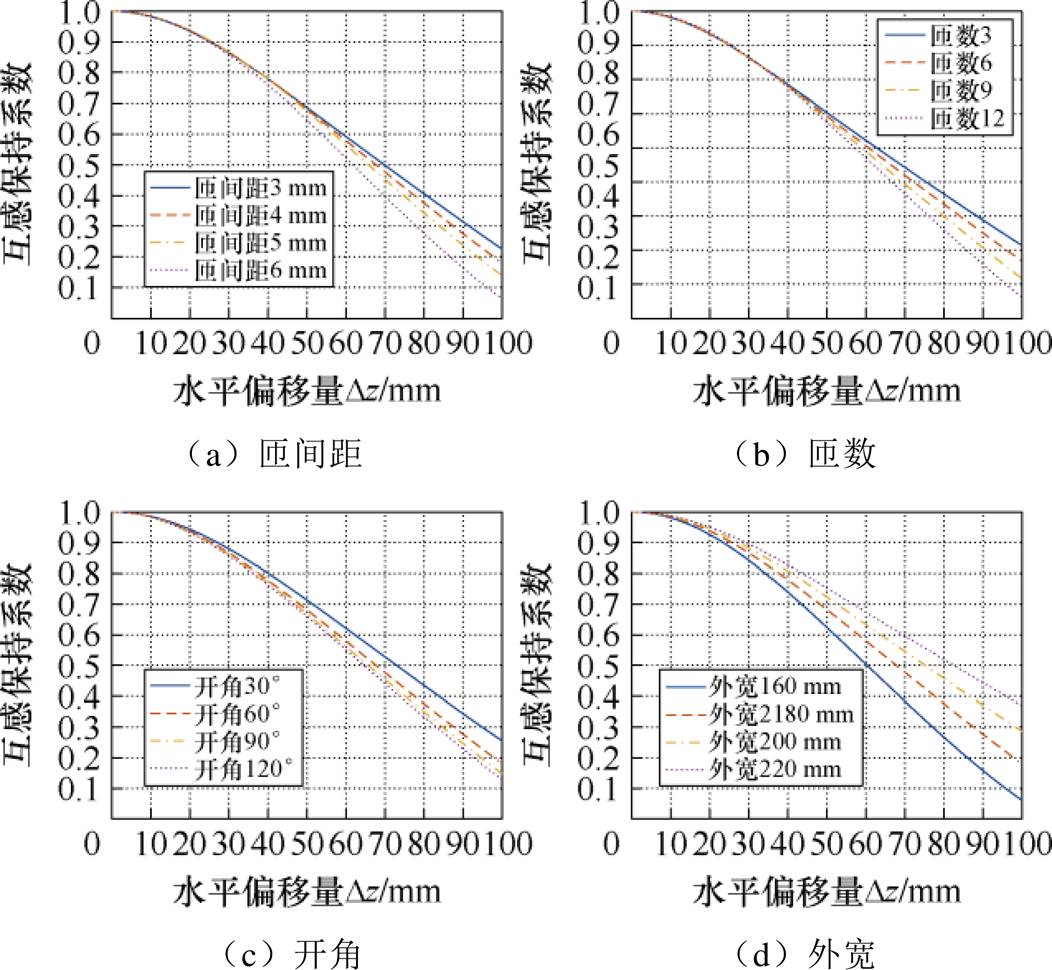
图8 线圈结构参数对抗偏移性能的影响
Fig.8 Effect of coil construction parameters on offset performance
由图8可知,两弧形线圈间水平方向的互感稳定性受各结构参数影响,其中与匝间距、匝数、开角成反比,与外宽成正比,与1.2节磁场分布所得结论相对应,表明通过改变线圈结构参数能够对线圈磁场分布进行调节,进而提升线圈的抗偏移性能。结合图5分析可知,单线圈的“临界区域”磁场变化显著,严重影响其抗偏移能力。因此,为获得更佳的抗偏移特性,文中采用多线圈组合来完成磁场的重新构造,提出互感稳定性更佳的组合式弧形线圈设计。
在对磁场以及互感关系的分析过程中发现,线圈的磁场主要集中在线圈的中心区域,而在边缘处的临界区域出现的负磁通将会大大降低互感稳定性,利用这一磁场特性,在磁场变化较大的区域添加新的组合线圈,用其磁场中心来对原有线圈的临界区域进行填补,能够取得较原有线圈更加均匀的磁场分布,同时进一步扩展了磁场分布范围,因此能够获得更好的抗偏移特性。
错位补偿式弧形线圈结构如图9所示,次级仍采用单线圈结构,能够保证副边质量小、安全性高以及其较低的复杂度。初级在单线圈结构基础上添加对称组合线圈进行磁场补偿。
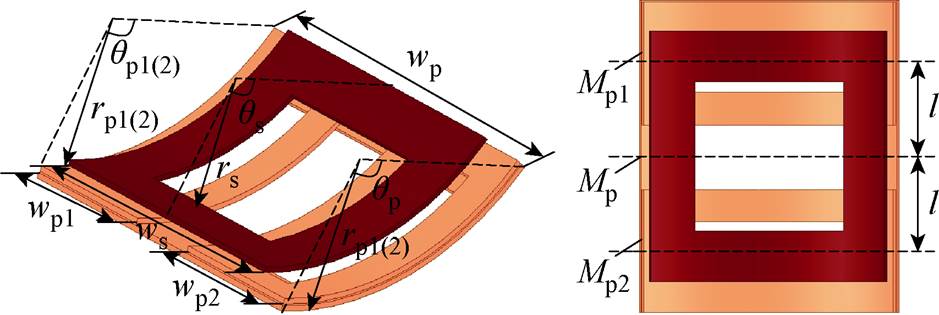
图9 错位补偿式弧形线圈结构
Fig.9 Misalignment compensation arc coil structure
对互感关系以及设计方法展开进一步研究。从互感角度,当线圈正对时,初级主线圈p与次级线圈s正对,而初级错位补偿双线圈与次级线圈存在错位,因此Mp在M中占据主导,Mp1、Mp2趋近为零;而当发生水平偏移时,互感Mp减小,Mp1或Mp2增大,使互感的变化减缓,完成抗偏移能力的提升。偏移情况下总互感变化可表示为
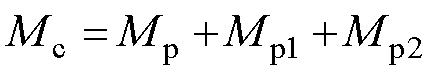 (22)
(22)
式中,Mc为初级、次级线圈间的互感;Mp为初级主线圈与次级线圈间的互感;Mp1、Mp2为初级错位补偿线圈与次级线圈间的互感。
在错位补偿式弧形线圈结构设计当中,其抗偏移能力主要受错位辅助线圈p1、p2对应参数匝数Np1、Np2以及错位距离l的影响。
设定初级主线圈p与次级线圈s结构参数如下:初级线圈弧半径rp=420 mm,外宽wp=240 mm,线圈开角qp=60°,匝间距dp=4 mm,匝数np=12;次级线圈弧半径rs=390 mm,外宽ws=180 mm,线圈开角qs=60°,匝间距ds=4 mm,匝数ns=10。对错位补偿式弧形线圈结构互感保持系数与匝数Np1、Np2以及错位距离l之间的关系进行分析。
错位补偿式弧形线圈抗偏移性能随错位参数变化如图10所示,给出了不同匝数Np1、Np2和错位距离l情况下错位补偿式弧形线圈结构偏移50 mm时对应互感保持系数。
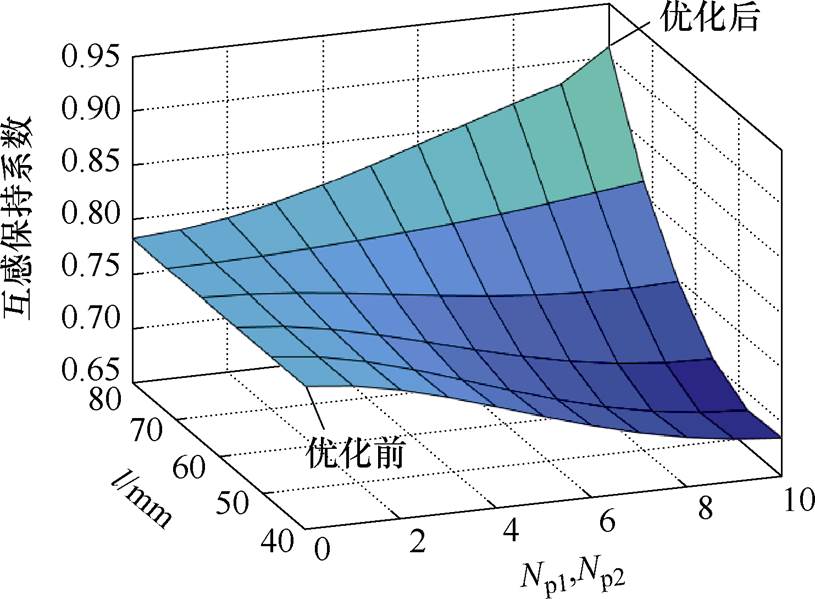
图10 错位补偿式弧形线圈抗偏移性能随错位参数变化
Fig.10 The anti-offset performance of the misalignment compensation arc coil varies with the misalignment parameters
由图10可得,互感保持系数随着错位距离l的增加而增加。互感保持系数受到的影响随着匝数Np1、Np2增加而增强。从上述分析可知,适当的增大错位距离l和增加匝数Np1(2),能够使得错位补偿式弧形线圈结构取得更佳的抗偏移能力。
针对匝数Np1、Np2以及错位距离l的设计,本文采用的错位补偿式弧形线圈设计流程如图11所示。
首先,设定初级主线圈p与次级线圈s结构参数如下:弧半径rp(s)、外宽wp(s)、开角qp(s)、匝数Np(s)、匝间距dp(s),其中弧半径主要由AUV船体结构决定。
其次,设定错位辅助线圈p1、p2初始结构参数如下:弧半径rp1=rp2=rp-dp、外宽wp1=wp2=wp/2、开角qp1=qp2=qp、匝数Np1=wp1/(2dp1), Np2=wp2/(2dp2)、匝间距dp1=dp2=dp、错位距离l=wp/2-w1(2)/2,能够保证错位线圈起到足够的补偿作用。依据参数可计算得到各偏移位置互感值M(Doff)以及互感保持系统曲线X(Doff),用于表征其抗偏移能力。
最后,对匝数Np1、Np2以及错位距离l进行遍寻求解,同理根据对应结构参数计算得到错位补偿式线圈结构各偏移位置互感值,进而得到对应互感保持系数曲线Xc(Doff),然后与X(Doff)进行比较,当X(Doff)<Xc(Doff)时,储存当前结构参数,并令X(Doff)=Xc(Doff)。对条件awp<wp1(2)进行判断,其中a为经验参数,本文设定为0.2,以保证错位线圈拥有足够的补偿能力。循环结束后即可得到当前初级主线圈p与次级线圈s结构参数的最优解。
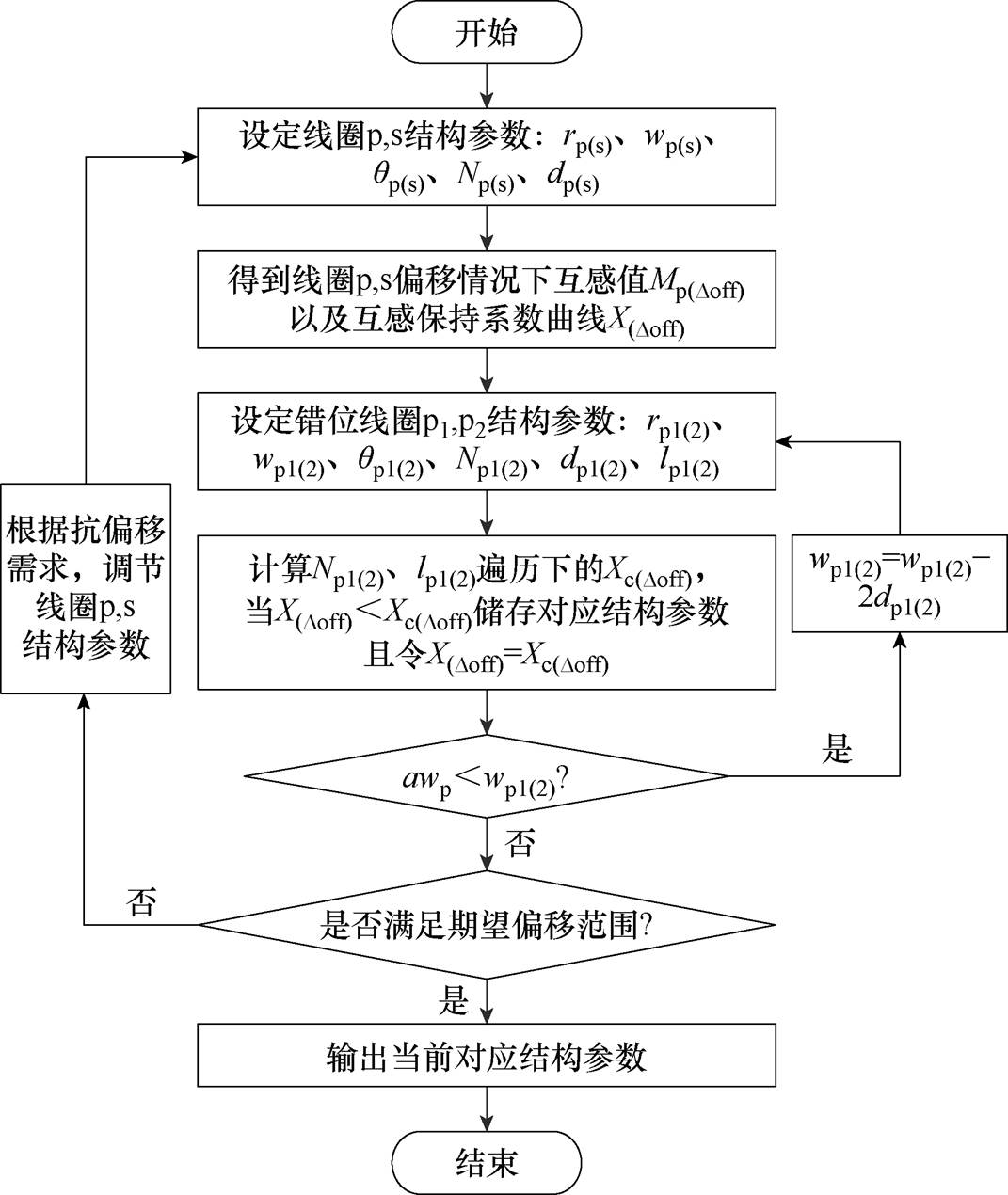
图11 错位补偿式弧形线圈设计流程
Fig.11 Flow chart of the design of the misalignment compensated arc coil
根据图11的设计流程,所得的一组最优尺寸参数见表1,对其抗偏移特性展开具体分析。
表1 线圈设计参数
Tab.1 Coil design parameters
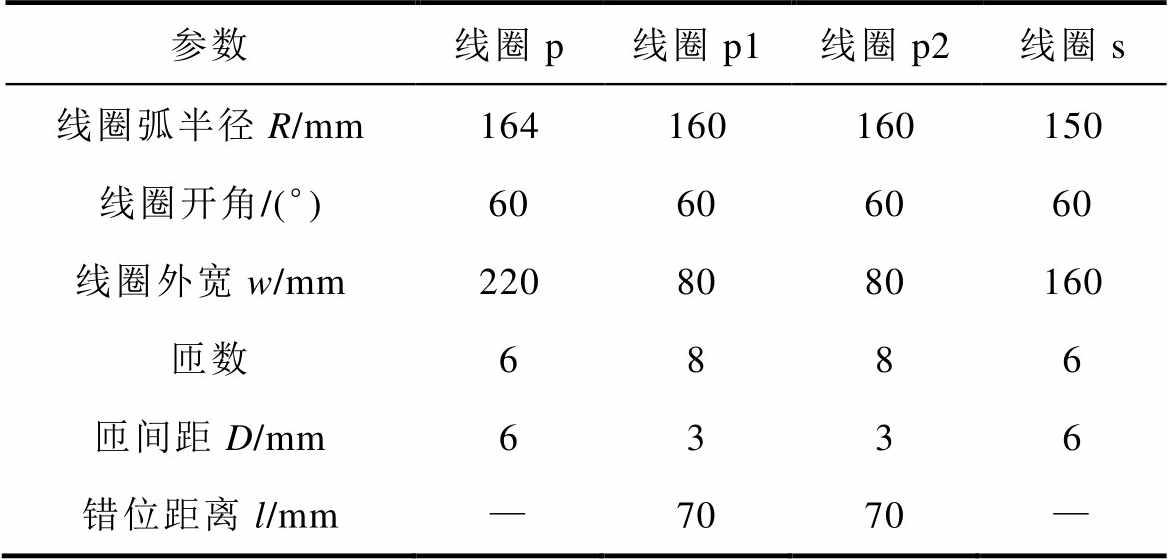
参数线圈p线圈p1线圈p2线圈s 线圈弧半径R/mm164160160150 线圈开角/(°)60606060 线圈外宽w/mm2208080160 匝数6886 匝间距D/mm6336 错位距离l/mm—7070—
图12给出了上述结构参数下添加错位补偿线圈前后空间磁场分布。对比图12a和图12b可知,错位补偿线圈的添加可使其磁场分布在更广的空间范围内,同时避免了磁场集中于中心区域,当发生偏移时,对应磁通变化减小,抗偏移特性更佳。同时,错位补偿线圈的添加可使其磁场分布在更广的空间范围内,同时避免了磁场集中于中心区域,当发生偏移时,对应磁通变化减小,抗偏移特性更佳。
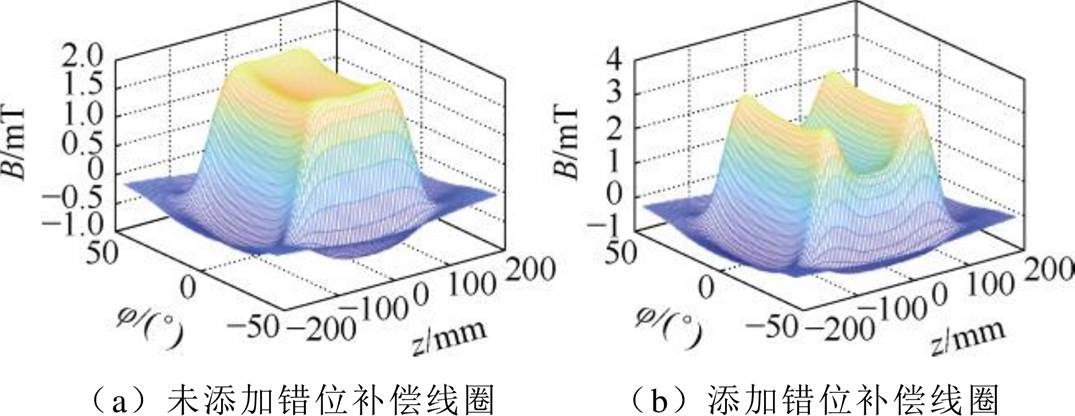
图12 错位补偿式弧形线圈抗偏移性能随错位参数变化
Fig.12 The anti-offset performance of the misalignment compensation arc coil varies with the misalignment parameters
图13为错位补偿式弧形线圈各部分互感值M、Mp、Mp1、Mp2随水平偏移的变化曲线。
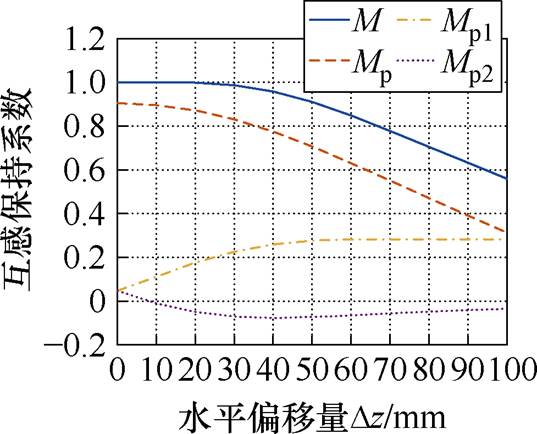
图13 错位补偿式弧形线圈各部分互感值随偏移变化
Fig.13 Diagram of the mutual inductance value of each part of the dislocation compensation arc coil with offset
利用Ansys Maxwell对几种代表性结构进行建模,得到其互感随水平以及旋转偏移的变化情况,计算得到各自对应互感保持系数曲线,结果如图14所示。
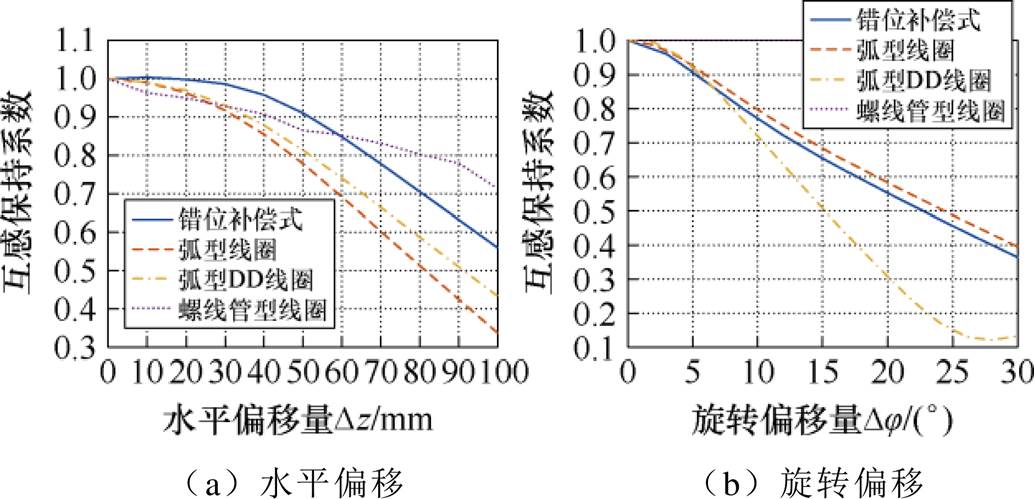
图14 不同结构水平偏移互感保持系数变化
Fig.14 Changes in the horizontal offset mutual inductance retention coefficient of different structures
图14a为各结构互感随水平偏移的变化情况,在[0, 50] mm的范围内,错位补偿式弧形线圈的互感保持系数最高。水平偏移量为100 mm时,错位补偿式弧形线圈互感保持系数依然能够达到0.57,而弧形线圈仅仅能达到0.34,证明了所提错位补偿式弧形线圈结构能够有效提升耦合机构的水平抗偏移能力。图14b给出了各结构互感随旋转偏移的变化情况,其中,螺线管线圈在旋转抗偏移方面占据较大优势,弧形线圈与错位补偿式弧形线圈结构旋转抗偏移能力接近,而弧形DD线圈结构在发生旋转偏移时互感衰减较快不适用于发生旋转偏移的环境。
为验证第1节所求互感解析模型的有效性,本节搭建了仿真模型与实验平台并开展验证工作。在Ansys Maxwell有限元仿真平台进行仿真,仿真模型如图2所示。实验装置如图15所示,整个实验在非磁性木桌上进行,使用阻抗分析仪测量电感,其频率设置为85.0 kHz。

图15 实验装置
Fig.15 Experimental setup
所绕制线圈参数如下:初级线圈弧半径为420 mm,外宽为180 mm,次级线圈弧半径为390 mm,外宽为180 mm,初级、次级线圈开角均为60°,初级、次级匝间距均为4 mm,初级线圈匝数为12,次级线圈匝数为10,初始状态保持同轴,采用400股、单股线径0.1 mm利兹线。
水平偏移量Dz从0 mm变化到90 mm,步长为10 mm,互感计算值、仿真值和实验值及误差见表2,其中Mc为互感计算值,Ms为互感仿真值,Me为互感实验值,仿真误差es、实验误差ee分别表示为
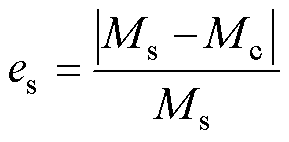 (23)
(23)
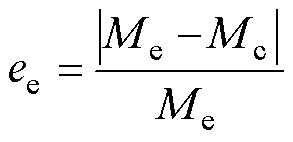 (24)
(24)
从表2可以看出,水平偏移量Dz从0 mm变化到90 mm的过程中仿真误差均小于5%,实验误差均小于5%,计算结果与仿真及实验结果基本保持一致。图16所示为水平偏移时对应的互感变化曲线,互感随水平偏移的增加而逐渐减小,这是由于随着水平偏移,两线圈重合部分减少,线圈耦合减弱,互感减小。
表2 水平偏移时的互感值及误差
Tab.2 Mutual inductance value and error in horizontal offset
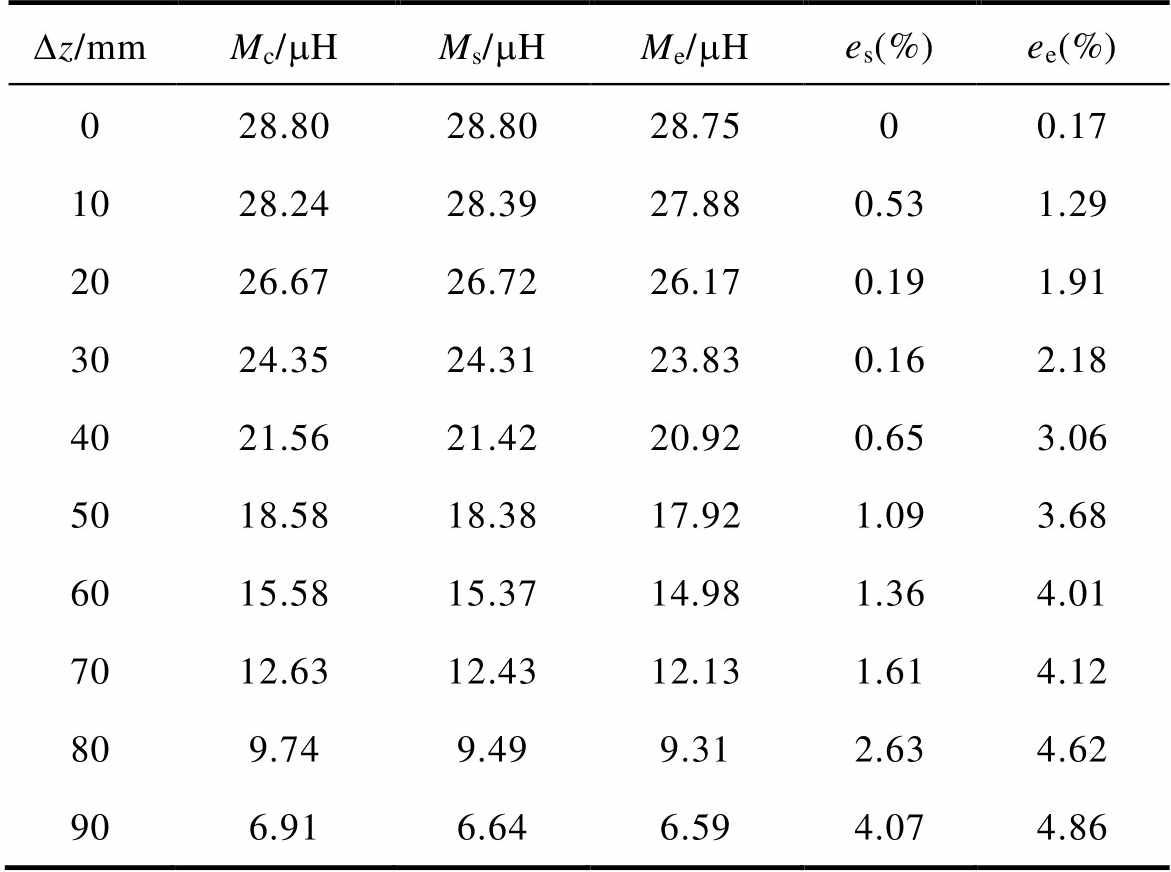
Dz/mmMc/mHMs/mHMe/mHes(%)ee(%) 028.8028.8028.7500.17 1028.2428.3927.880.531.29 2026.6726.7226.170.191.91 3024.3524.3123.830.162.18 4021.5621.4220.920.653.06 5018.5818.3817.921.093.68 6015.5815.3714.981.364.01 7012.6312.4312.131.614.12 809.749.499.312.634.62 906.916.646.594.074.86
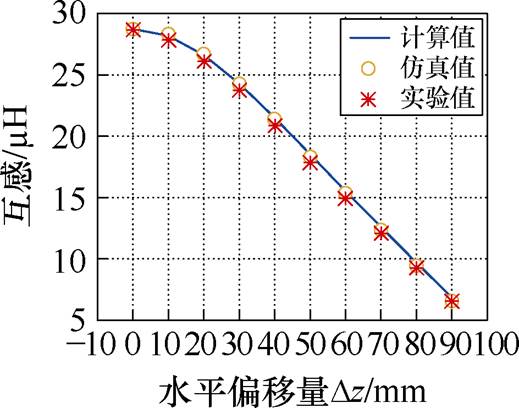
图16 水平偏移时互感变化曲线
Fig.16 Variation curve of mutual inductance in horizontal offset
角度偏移量Dj 从0°变化到15°,步长为3°,互感计算值、互感仿真值和互感实验值及误差见表3。
表3 角度偏移时的互感值及误差
Tab.3 Mutual inductance value and error in angle offset
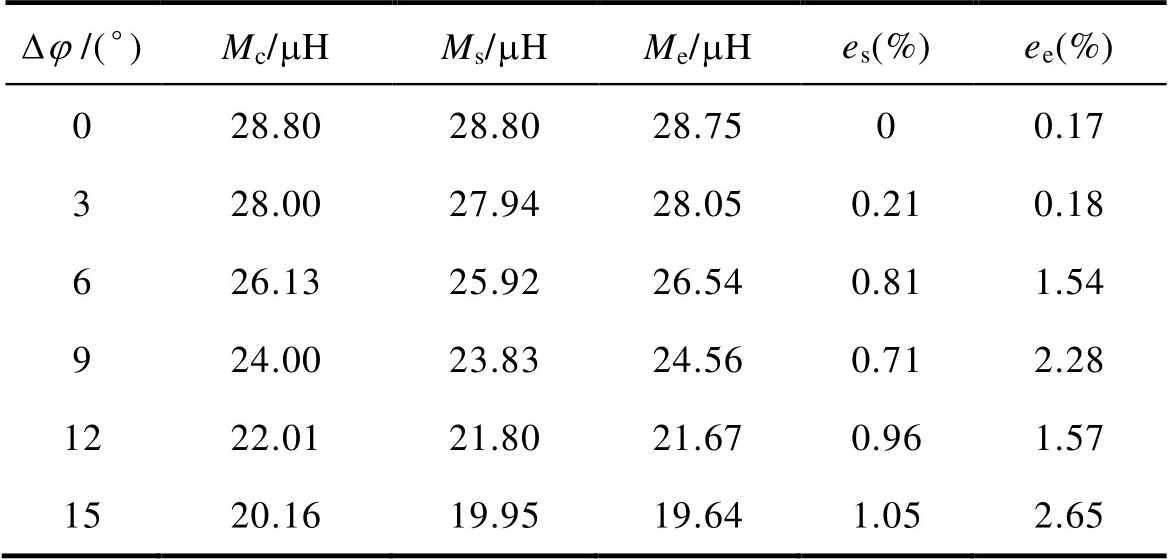
Dj /(°)Mc/mHMs/mHMe/mHes(%)ee(%) 028.8028.8028.7500.17 328.0027.9428.050.210.18 626.1325.9226.540.811.54 924.0023.8324.560.712.28 1222.0121.8021.670.961.57 1520.1619.9519.641.052.65
从表3可以看出,角度偏移量Dj 从0°变化到15°的过程中计算与仿真及实验结果误差均小于3%,计算结果与仿真及实验结果基本保持一致。互感变化曲线如图17所示。
图17中,互感随角度偏移的增加而逐渐减小,原因与水平偏移类似,随着角度偏移,两线圈重合部分减少,耦合减弱,互感减小。
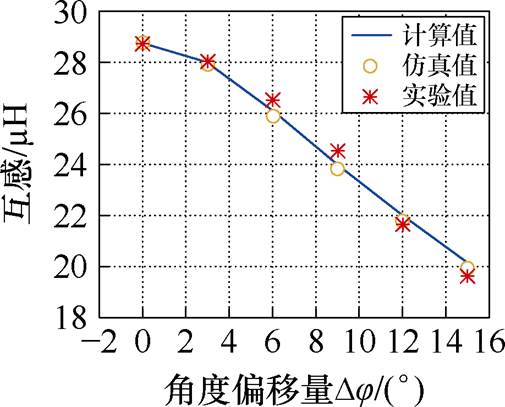
图17 角度偏移时互感变化曲线
Fig.17 Variation curve of mutual inductance in angle offset
垂直偏移量Dh从0 mm变化到30 mm,步长为3 mm,互感计算值、互感仿真值和互感实验值及误差见表4。
表4 垂直偏移时的互感值及误差
Tab.4 Mutual inductance value and error in vertical offset
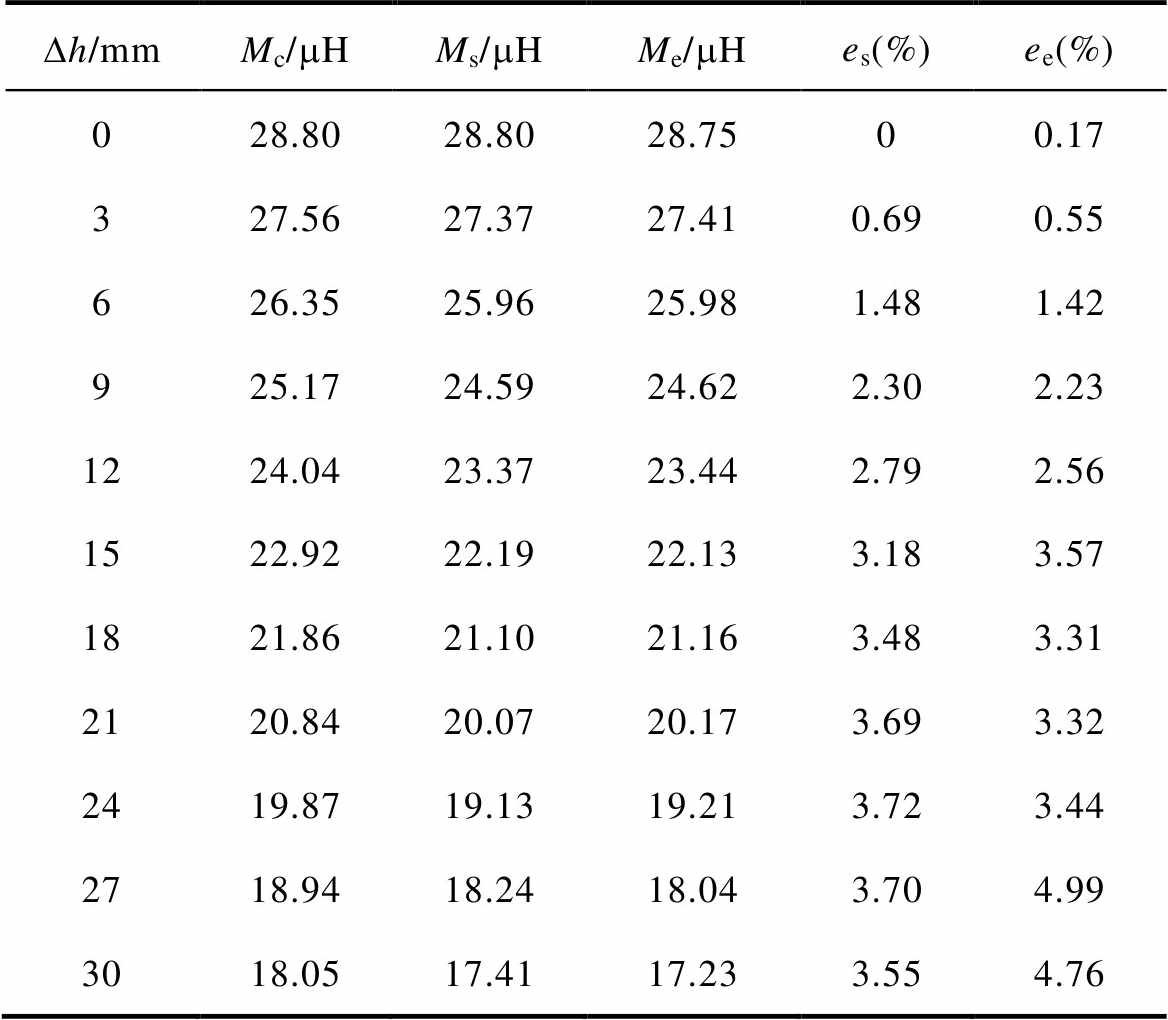
Dh/mmMc/mHMs/mHMe/mHes(%)ee(%) 028.8028.8028.7500.17 327.5627.3727.410.690.55 626.3525.9625.981.481.42 925.1724.5924.622.302.23 1224.0423.3723.442.792.56 1522.9222.1922.133.183.57 1821.8621.1021.163.483.31 2120.8420.0720.173.693.32 2419.8719.1319.213.723.44 2718.9418.2418.043.704.99 3018.0517.4117.233.554.76
从表4可以看出,垂直偏移量Dh从0 mm变化到30 mm的过程中计算与仿真及实验结果误差均小于5%,计算结果与仿真及实验结果基本保持一致。
图18为表4对应互感变化曲线,互感随垂直偏移的增加而逐渐减小,这是由于随着垂直偏移,两线圈距离增加,磁链减小,线圈耦合减弱,互感减小。
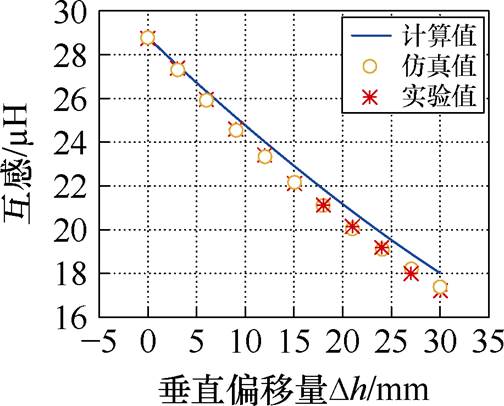
图18 垂直偏移时互感变化曲线
Fig.18 Variation curve of mutual inductance in vertical offset
表5和表6分别为角度偏移6°和12°,水平偏移量Dz从0 mm变化到100 mm,步长为20 mm,互感计算值、仿真值和实验值及误差。
表5 角度偏移6°加水平偏移时的互感值及误差
Tab.5 Mutual inductance values and errors for an angular offset of 6° plus a horizontal offset
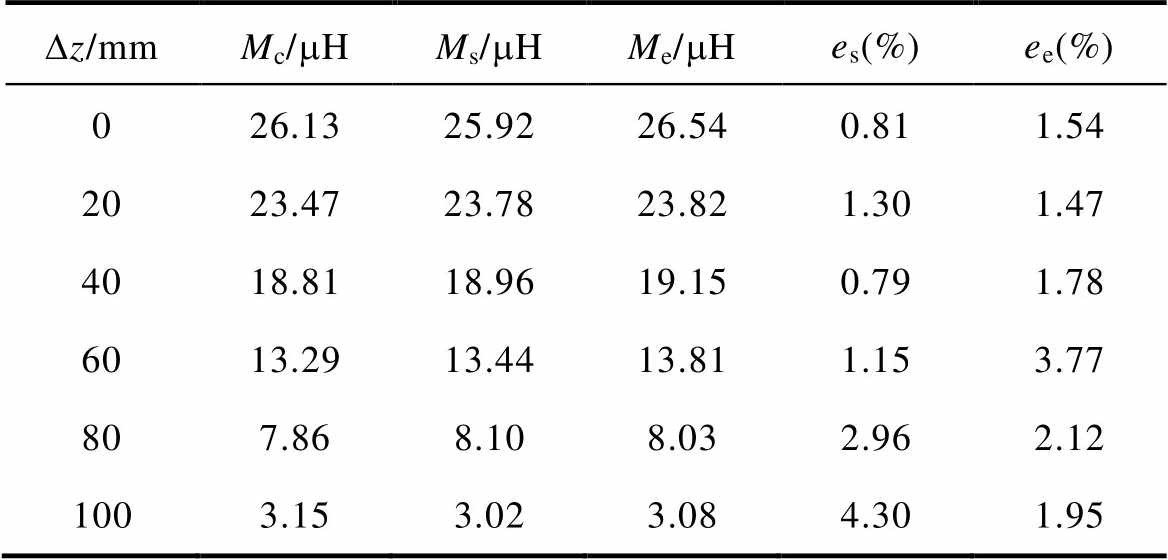
Dz/mmMc/mHMs/mHMe/mHes(%)ee(%) 026.1325.9226.540.811.54 2023.4723.7823.821.301.47 4018.8118.9619.150.791.78 6013.2913.4413.811.153.77 807.868.108.032.962.12 1003.153.023.084.301.95
表6 角度偏移12°加水平偏移时的互感值及误差
Tab.6 Mutual inductance values and errors for an angular offset of 12° plus a horizontal offset
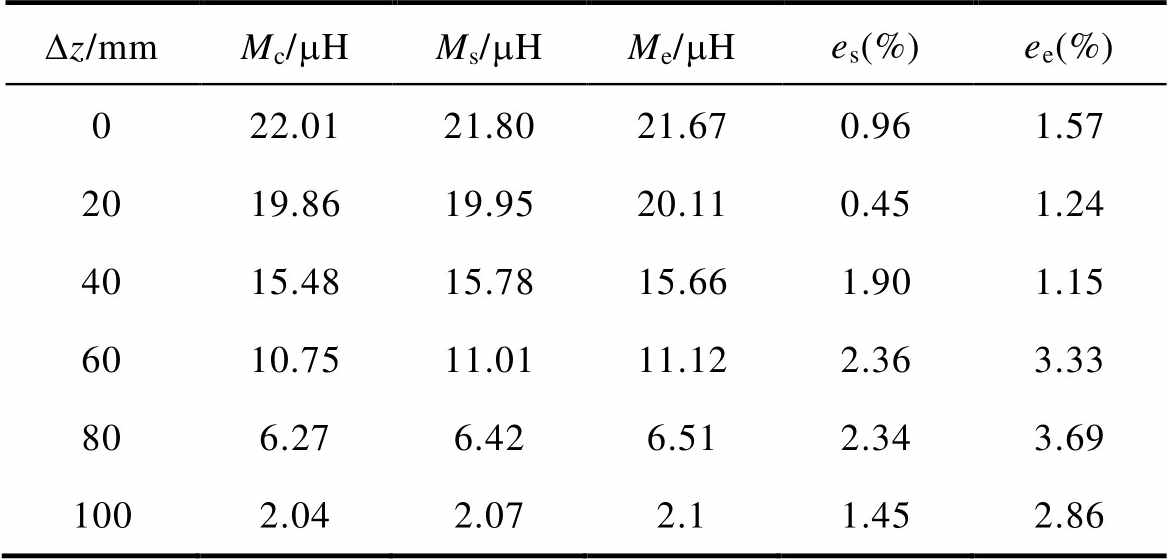
Dz/mmMc/mHMs/mHMe/mHes(%)ee(%) 022.0121.8021.670.961.57 2019.8619.9520.110.451.24 4015.4815.7815.661.901.15 6010.7511.0111.122.363.33 806.276.426.512.343.69 1002.042.072.11.452.86
从表5可以看出,当角度偏移为6°,水平偏移量Dz从0 mm变化到100 mm的过程中计算与仿真及实验结果误差均小于5%,计算结果与仿真及实验结果基本保持一致。
从表6可以看出,当角度偏移为12°,水平偏移量Dz从0 mm变化到100 mm的过程中计算与仿真及实验结果误差均小于5%,计算结果与仿真及实验结果基本保持一致。
图19为表5和表6互感变化曲线,互感随水平偏移的增加而逐渐减小,且角度偏移6°的互感值大于角度偏移12°的互感值。
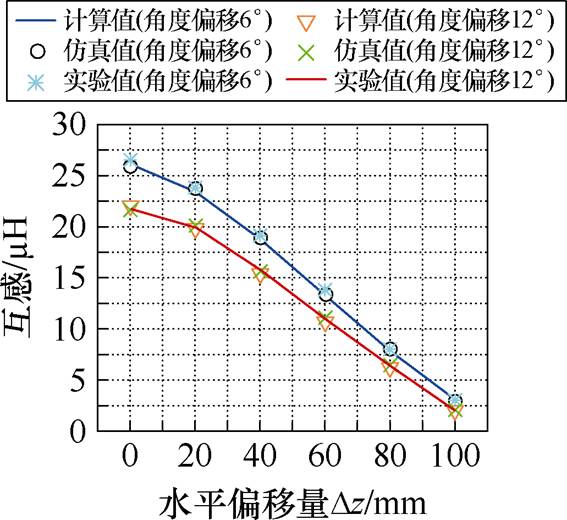
图19 角度偏移加水平偏移时互感变化曲线
Fig.19 Mutual inductance change curves at angular offset plus horizontal offset
通过仿真建模分析与实验验证,文中对弧形线圈结构水平、角度、垂直以及角度加水平四种偏移情况下互感计算进行了验证,其中仿真误差与实验误差均小于5%,结果表明了互感解析计算模型的准确性。
基于2.2节所提出的错位补偿式弧形线圈设计流程,完成对应的耦合机构错位补偿式弧形线圈结构如图20所示,具体参数见表1。

图20 错位补偿式弧形线圈结构
Fig.20 Misalignment compensation arc coil structure
图20中,初级为三线圈结构,由主线圈以及错位补偿线圈组成,错位补偿线圈与主线圈同向串联,保证两者产生的磁场方向一致;次级为单线圈结构,均采用线径为3 mm的利兹线,两线圈间距为3 cm。为保证耦合机构的稳定型与防水性,在耦合机构表面用环氧树脂进行浇灌。经实验测量,发射线圈自感为194.15 mH,发射线圈内阻为0.28 W;接收线圈自感为47.04 mH,接收线圈内阻为0.15 W。初级线圈和次级线圈无偏移时互感为33.59 mH。
基于式(20),并结合错位补偿式弧形线圈耦合机构偏移情况下互感变化测量结果,得到结论如图21所示,可看出实测结果与仿真结果一致。
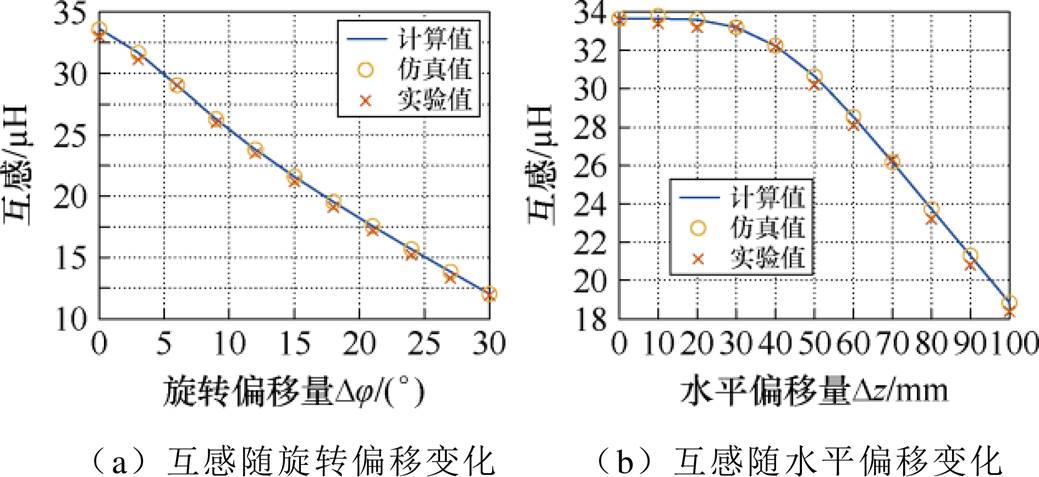
图21 互感实验值与仿真值对比
Fig.21 Comparison of the experimental and simulated values of mutual inductance
结合3.1节中的典型耦合结构,对不同位置互感随偏移变化情况展开对比研究,结果见表7。
由表7可知,当水平偏移50 mm(X50)时,错位补偿式弧形线圈结构互感保持系数为0.910 9,相较普通弧形线圈结构互感保持系数0.778 0提升了13.29%,当其水平偏移80 mm(X80)时,错位补偿式弧形线圈结构互感保持系数为0.705 2,相较普通弧形线圈结构的互感保持系数0.512 9提升了19.23%。互感保持系数变化范围在0.65~1之间时,弧形线圈允许水平偏移范围为[-65 mm, 65 mm],旋转偏移范围为[-17°, 17°];而采用错位补偿式弧形线圈结构容许水平偏移范围可达到[-95 mm, 95 mm],旋转偏移范围为[-15°, 15°]。水平容许偏移范围提升了31.7%,证明了错位补偿式弧形线圈大大提升了耦合机构的水平抗偏移能力,同时较好地维持了其相应的旋转抗偏移特性。
表7 各类型线圈结构水平抗偏移能力对比
Tab.7 Comparison of the anti-offset ability of different structures
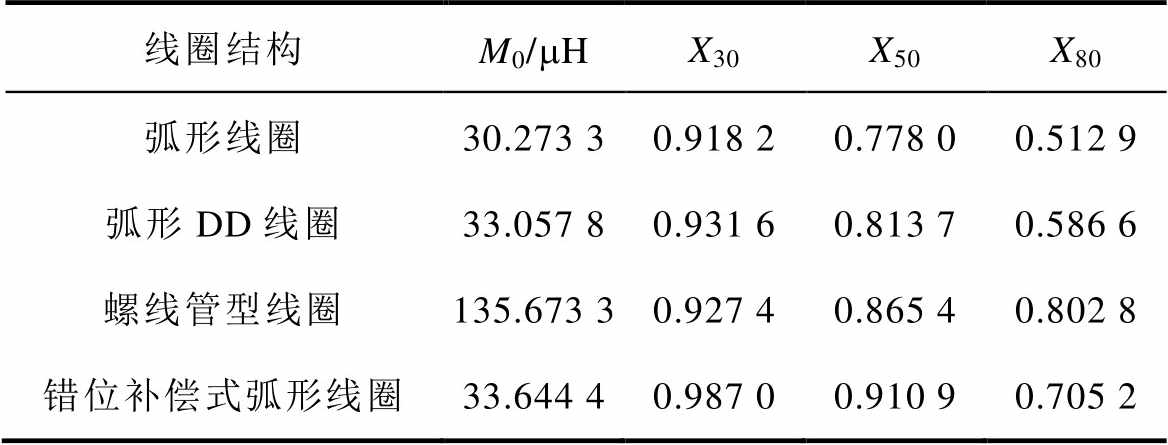
线圈结构M0/mHX30X50X80 弧形线圈30.273 30.918 20.778 00.512 9 弧形DD线圈33.057 80.931 60.813 70.586 6 螺线管型线圈135.673 30.927 40.865 40.802 8 错位补偿式弧形线圈33.644 40.987 00.910 90.705 2
为验证所设计错位补偿式弧形线圈的实际抗偏移性能,本文搭建了基于错位补偿式弧形线圈的IPT系统实验平台,系统原理如图22所示,系统实验装置如图23所示。实验装置主要包括:直流电源、逆变器、发射端谐振网络、耦合机构、接收端谐振网络、整流电路、滤波电容以及负载,外加测量设备Pico示波器。
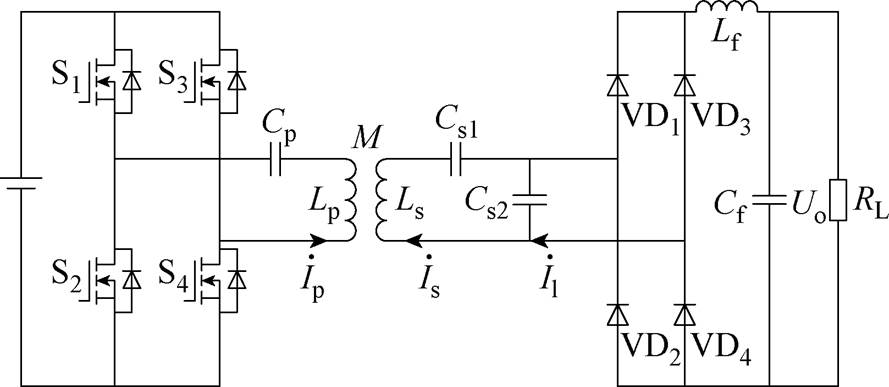
图22 系统原理
Fig.22 System schematic

图23 系统实验装置
Fig.23 System experimental setup diagram
设置系统主要参数见表8。
表8 系统参数
Tab.8 System parameters
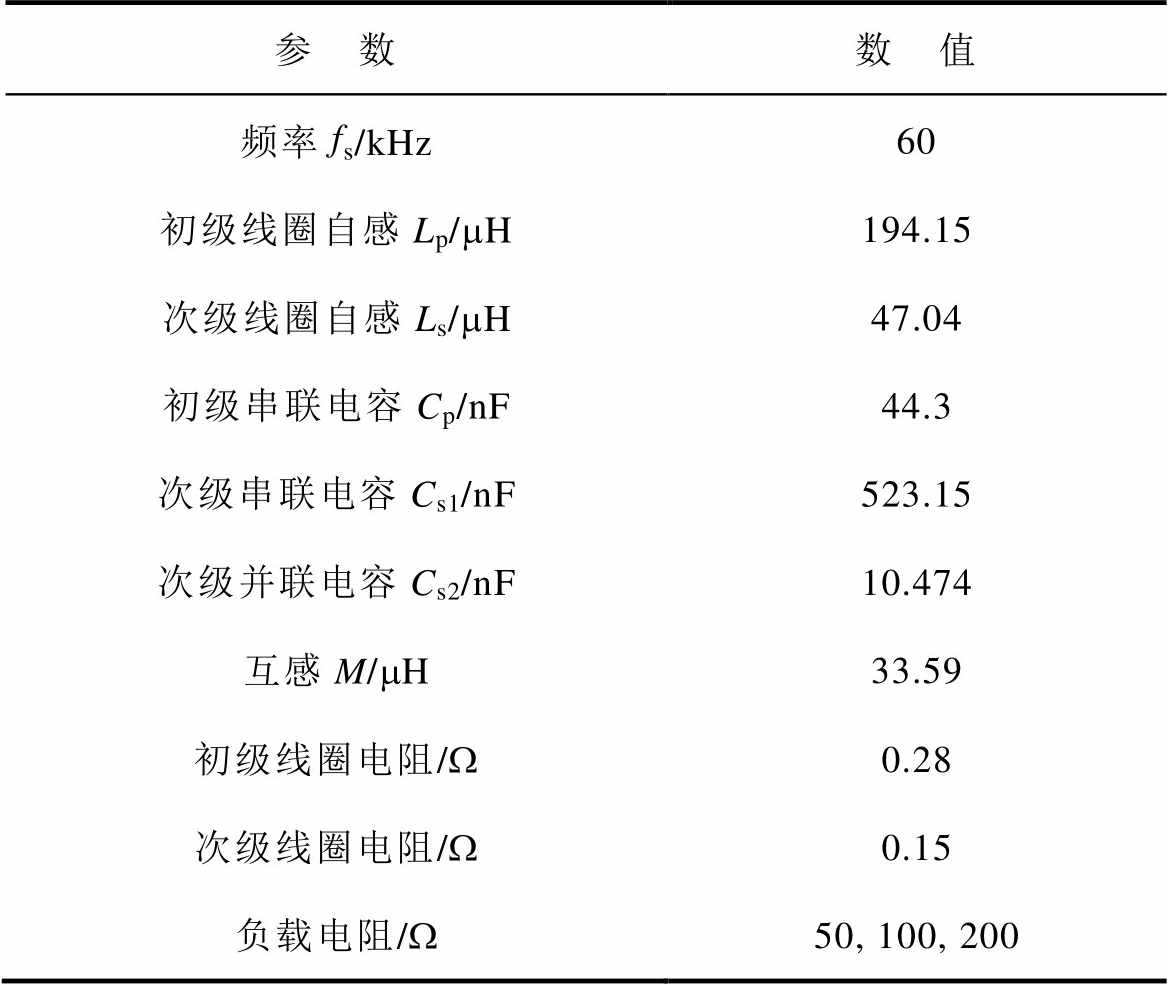
参 数数 值 频率fs/kHz60 初级线圈自感Lp/mH194.15 次级线圈自感Ls/mH47.04 初级串联电容Cp/nF44.3 次级串联电容Cs1/nF523.15 次级并联电容Cs2/nF10.474 互感M/mH33.59 初级线圈电阻/W0.28 次级线圈电阻/W0.15 负载电阻/W50, 100, 200
为量化输出电压波动,表征系统输出电压稳定性,定义输出电压波动率so为
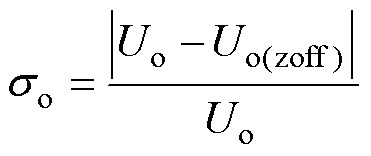 (25)
(25)
式中,Uo为正对情况下输出电压;Uo(zoff)为发生轴向偏移时对应输出电压。
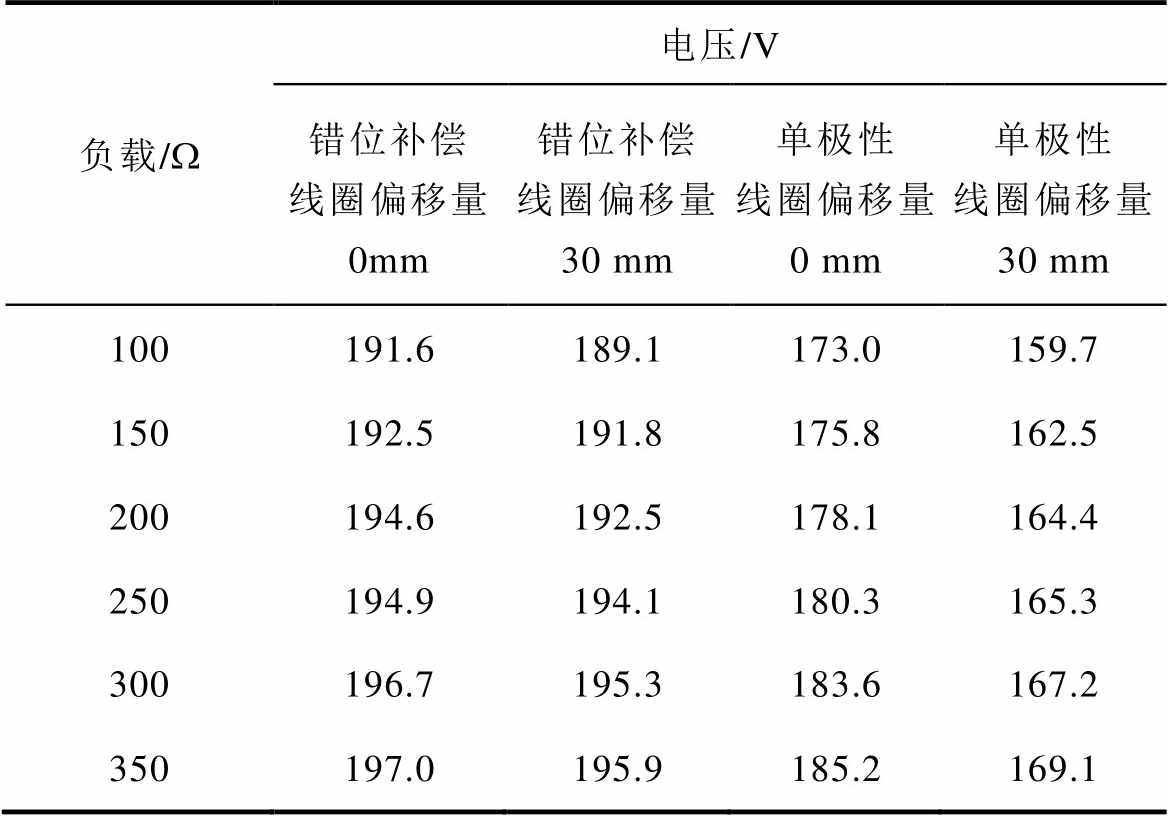
在全负载范围下,保持输入电压不变,改变线圈的偏移距离和负载阻值,测得错位补偿弧形线圈和单极性弧形线圈水平偏移0 mm和水平偏移30 mm的输出电压见表9。
表9 全负载范围不同线圈偏移0 mm和30 mm输出电压
Tab.9 Full load range different coil offsets 0 mm and 30 mm output voltage
负载/W电压/V 错位补偿线圈偏移量0mm错位补偿线圈偏移量30 mm单极性线圈偏移量0 mm单极性线圈偏移量30 mm 100191.6189.1173.0159.7 150192.5191.8175.8162.5 200194.6192.5178.1164.4 250194.9194.1180.3165.3 300196.7195.3183.6167.2 350197.0195.9185.2169.1
图24为输出电压随负载变化曲线。当线圈发生30 mm的水平偏移时,负载的输出电压波动率so= 0.78%,而无补偿弧形线圈在相同条件下的电压波动率so=7.7%。
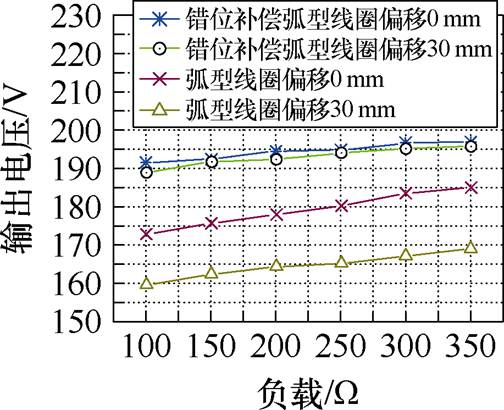
图24 输出电压随负载变化曲线
Fig.24 Output voltage variation curves with load
综上所述,本文所设计基于错位补偿式弧形线圈结构的水下IPT系统,具有良好的抗偏移性能,
在处于偏移状态下输出电压保持稳定,且在宽负载范围内均可适用。
本文基于空间磁场分布所提的错位补偿式弧形线圈结构,具有较好的抗偏移特性,结合理论推导和实验分析可以得到以下结论:
1)弧形线圈磁场分布主要集中于中心区域,随着与中心位置距离的增加会出现磁场迅速减小的区域,然后随着与中心位置距离的进一步增加,空间磁场将趋近于零,这也是偏移对互感影响的原因。
2)分析了弧形线圈在不同偏移方向的情况,互感计算值、仿真值和测量值的各种误差均小于5%,证明了互感解析模型的正确性。
3)本文所提出的错位补偿式弧形线圈结构对临界区域进行错位补偿,获得更佳的抗偏移特性,并与单极性弧形线圈、双极性弧形线圈以及螺线管型进行对比,验证了其具有优越的抗偏移性能。
4)搭建实验平台验证了在全负载范围内,当线圈水平偏移为30 mm时,错位补偿弧形线圈比单极性弧形线圈的输出电压波动率更低,抗偏移性能更好。
参考文献
[1] 刘宇鑫, 高飞, 刘鑫, 等. 深海无人航行器双向无线充电系统的涡流损耗分析与效率优化[J]. 电工技术学报, 2024, 39(18): 5599-5609.
Liu Yuxin, Gao Fei, Liu Xin, et al. Eddy current loss analysis and efficiency optimization of two-way wireless charging system for deep-sea unmanned aerial vehicle[J]. Transactions of China Electro- technical Society, 2024, 39(18): 5599-5609.
[2] Sun Yushan, Chai Puxin, Zhang Guocheng, et al. Sliding mode motion control for AUV with dual- observer considering thruster uncertainty[J]. Journal of Marine Science and Engineering, 2022, 10(3): 349.
[3] Kan Tianze, Mai Ruikun, Mercier P P, et al. Design and analysis of a three-phase wireless charging system for lightweight autonomous underwater vehicles[J]. IEEE Transactions on Power Electronics, 2018, 33(8): 6622-6632.
[4] 何克成, 贾宏杰, 穆云飞, 等. 基于信息间隙决策理论的卡车式移动充电站协同调度策略[J]. 电力系统自动化, 2024, 48(15): 44-53.
He Kecheng, Jia Hongjie, Mu Yunfei, et al. Collaborative scheduling strategy of truck mobile charging station based on information gap decision theory[J]. Automation of Electric Power System, 2024, 48(15): 44-53.
[5] 顾文超, 丘东元, 张波, 等. 水下无线输电技术研究综述[J]. 电源学报, 2023, 21(3): 125-138.
Gu Wenchao, Qiu Dongyuan, Zhang Bo, et al. Review of underwater wireless power transfer technologies[J]. Journal of Power Supply, 2023, 21(3): 125-138.
[6] Li Wanjing, Zhu Jinwei, Wang Yadong, et al. Modeling and characteristic analysis of magnetic coupling mechanism in seawater environment[J]. IEEE Transactions on Magnetics, 2022, 58(9): 8402006.
[7] 程志远, 宋晓逸, 吴晓婷, 等. 无线充电系统旋转式电磁耦合器损耗计算及热点温度研究[J]. 电工技术学报, 2024, 39(7): 1932-1942, 1956.
Cheng Zhiyuan, Song Xiaoyi, Wu Xiaoting, et al. Loss calculation and hot spot temperature research of rotary electromagnetic coupler in wireless charging system[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 1932-1942, 1956.
[8] 唐丁源, 周玮, 黄亮, 等. 具有恒压输出特性的电场耦合式动态无线电能传输技术[J]. 电工技术学报, 2023, 38(20): 5385-5397.
Tang Dingyuan, Zhou Wei, Huang Liang, et al. Dynamic electric-filed coupled wireless power transfer system with constant voltage output characte- ristics[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5385-5397.
[9] 谢诗云, 杨奕, 李恋, 等. 基于双极性耦合磁场调控的高抗偏移偏转无线电能传输系统[J]. 电工技术学报, 2023, 38(18): 4838-4852.
Xie Shiyun, Yang Yi, Li Lian, et al. Wireless power transfer system with high misalignment tolerance based on bipolar coupling magnetic-field control[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4838-4852.
[10] 杨云虎, 贾维娜, 梁大壮, 等. LCC-LCC/S自切换恒流-恒压复合型无线电能传输系统[J]. 电工技术学报, 2023, 38(18): 4823-4837, 4852.
Yang Yunhu, Jia Weina, Liang Dazhuang, et al. A self-switching wireless power transfer system based on hybrid topology of LCC-LCC/S with constant current and constant voltage[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4823-4837, 4852.
[11] 张杰, 赵航, 许知博, 等. 磁耦合谐振式无线电能传输系统变电容调谐控制方法研究[J]. 电源学报, 2023, 21(6): 102-110.
Zhang Jie, Zhao Hang, Xu Zhibo, et al. Variable capacitance tuning control method for magnetically coupled resonant wireless power transfer system[J]. Journal of Power Supply, 2023, 21(6): 102-110.
[12] 李中启, 张晨曦, 王建斌, 等. 基于变频重构S/SP拓扑的无线电能传输系统恒流恒压研究[J]. 电工技术学报, 2024, 39(15): 4718-4732.
Li Zhongqi, Zhang Chenxi, Wang Jianbin, et al. Research on constant current and constant voltage of WPT system based on variable frequency recon- figuration S/SP topology[J]. Transactions of China Electrotechnical Society, 2024, 39(15): 4718-4732.
[13] 张鹏飞, 龚立娇, 马欣欣, 等. 具有可变增益恒压特性的双线圈无线电能传输系统补偿网络设计与分析[J]. 电工技术学报, 2024, 39(5): 1256-1269, 1283.
Zhang Pengfei, Gong Lijiao, Ma Xinxin, et al. Analysis and design of compensation network for two-coil wireless power transfer system with variable constant voltage gain characteristics[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1256- 1269, 1283.
[14] 闫争超, 胡谦宇, 赵晨旭, 等. 水下航行器感应式无线电能传输技术研究综述[J]. 中国电机工程学报, 2023, 43(24): 9668-9682.
Yan Zhengchao, Hu Qianyu, Zhao Chenxu, et al. Review on inductive wireless power transfer technology for underwater vehicles[J]. Proceedings of the CSEE, 2023, 43(24): 9668-9682.
[15] 林志远, 李中启, 胡昌轩, 等. 无线电能传输带凸字环形有界磁屏蔽任意位置圆形线圈互感计算方法[J]. 电工技术学报, 2024, 39(16): 4918-4930.
Lin Zhiyuan, Li Zhongqi, Hu Changxuan, et al. Mutual inductance calculation method of arbitrarily positioned circular coils with convex ring type finite magnetic shielding in wireless power transfer[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 4918-4930.
[16] 张滨山, 张泽恒, 杨斌, 等. 基于钳位电路的LCC-S补偿型感应电能传输系统抗偏移方法[J]. 电工技术学报, 2024, 39(8): 2388-2399.
Zhang Binshan, Zhang Zeheng, Yang Bin, et al. LCC-S compensated inductive power transfer system against misalignment with a clamp circuit[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2388-2399.
[17] Yang Lei, Zhang Yuanqi, Li X, et al. Comparison survey of effects of hull on AUVs for underwater capacitive wireless power transfer system and under- water inductive wireless power transfer system[J]. IEEE Access, 2022, 10: 125401-125410.
[18] Wu Shuai, Cai Chunwei, Wang Aobo, et al. Design and implementation of a uniform power and stable efficiency wireless charging system for autonomous underwater vehicles[J]. IEEE Transactions on Industrial Electronics, 2023, 70(6): 5674-5684.
[19] Shi Jianguang, Li Dejun, Yang Canjun. Design and analysis of an underwater inductive coupling power transfer system for autonomous underwater vehicle docking applications[J]. Journal of Zhejiang University SCIENCE C, 2014, 15(1): 51-62.
[20] Cai Chunwei, Zhang Yanyu, Wu Shuai, et al. A circumferential coupled dipole-coil magnetic coupler for autonomous underwater vehicles wireless charging applications[J]. IEEE Access, 2020, 8: 65432-65442.
[21] Kan Tianze, Zhang Yiming, Yan Zhengchao, et al. A rotation-resilient wireless charging system for light- weight autonomous underwater vehicles[J]. IEEE Transactions on Vehicular Technology, 2018, 67(8): 6935-6942.
[22] Budhia M, Boys J T, Covic G A, et al. Development of a single-sided flux magnetic coupler for electric vehicle IPT charging systems[J]. IEEE Transactions on Industrial Electronics, 2013, 60(1): 318-328.
[23] Zaheer A, Covic G A, Kacprzak D. A bipolar pad in a 10-kHz 300-W distributed IPT system for AGV applications[J]. IEEE Transactions on Industrial Electronics, 2014, 61(7): 3288-3301.
[24] Yan Zhengchao, Zhang Yiming, Zhang Kehan, et al. Underwater wireless power transfer system with a curly coil structure for AUVs[J]. IET Power Electronics, 2019, 12(10): 2559-2565.
Abstract Submarine currents are prone to cause multi-directional offsets in the coupling coils of the wireless charging system for AUVs, leading to a decrease in efficiency and power value, and even affecting the normal operation of the system. Recently, some offset-resistant coupling coils have been proposed to solve with these issues, but these methods have certain defects. To address these issues, this paper proposes a misalignment-compensated arc coil structure. By compensating the magnetic field, the anti-offset performance of the coil is effectively improved.
Firstly, the analytical model for the spatial magnetic field of the arc coil was built based Biot-Savar law, and the analytical equation of the mutual inductance of the arc coil was obtained. Secondly, a simulation model of the arc coil was developed. An anti-offset optimization strategy for a single coil was designed based on the analysis of the spatial magnetic field of the arc coil. The influence of structural parameter changes on the spatial magnetic field distribution was also considered in the design process. Furthermore, a misalignment compensation structure for the arc coil was designed using the superposition theorem of magnetic fields, along with the spatial magnetic field distribution of the arc coil. Finally, a flowchart for the misalignment compensation arc coil was developed, taking into account the effects of the turn numbers Np1, Np2 and the misalignment distance l on mutual inductance. Through an iterative search of different values for the turn numbers and misalignment distance, the optimal parameter design was determined.
Under various offsets, the calculated values of mutual inductance of the arc coil are compared with the experimental and simulated values, and the errors are less than 5%. From the simulation results, when the horizontal offset is 100 mm, the mutual inductance retention coefficient of the misalignment-compensated arc coil still reaches 0.57. In contrast, the arc coil only achieves a retention coefficient of 0.34. The arc coil also demonstrates strong offset resistance under rotating offsets. From the experimental results, the misalignment-compensated arc coil structure shows significant improvements in mutual inductance retention. When the horizontal offset is 50 mm, its retention coefficient increases by 13.29% compared to the ordinary arc coil structure. At an 80 mm horizontal offset, the retention coefficient rises by 19.23% relative to the ordinary design. The output voltage fluctuation of the load is 0.78% when the coil is horizontally offset by 30 mm, while the voltage fluctuation of the uncompensated arc coil is 7.7% under the same condition. These findings demonstrate the effectiveness of the misalignment-compensated design in maintaining mutual inductance under varying offset conditions.
The following conclusions are drawn from calculations, simulations and experimental analyses: (1) The magnetic field distribution of the arc coil is mainly concentrated in the central region. The spatial magnetic field approaches zero as the distance from the center increases. (2) The proposed analytical model of mutual inductance is correct in all dimensions of the offsets. (3) The misalignment-compensated arc coil structure effectively compensates for misalignment in critical regions and demonstrates better offset resistance than other coil designs. (4) The proposed misalignment-compensated arc coil structure has lower output voltage fluctuation than the unipolar arc coil when the coils are subjected to the same offsets in a wireless power transmission system.
keywords:Underwater inductive power transfer (IPT) system, arc coil, mutual inductance calculation, resistance to offset
DOI: 10.19595/j.cnki.1000-6753.tces.241577
中图分类号:TM724
国家自然科学基金项目(52307006、52401402)和烟台市重大创新科技项目(2023ZDCX015)资助。
收稿日期 2024-09-06
改稿日期 2024-10-23
白龙雷 男,1991年生,博士,副教授,研究方向为无线电能传输、先进电力电子技术等。E-mail: longlei0107@hrbeu.edu.cn
游 江 男,1977年生,博士,教授,研究方向为电机驱动、高性能电力电子变换器等。E-mail: youjiang@hrbeu.edu.cn(通信作者)
(编辑 陈 诚)