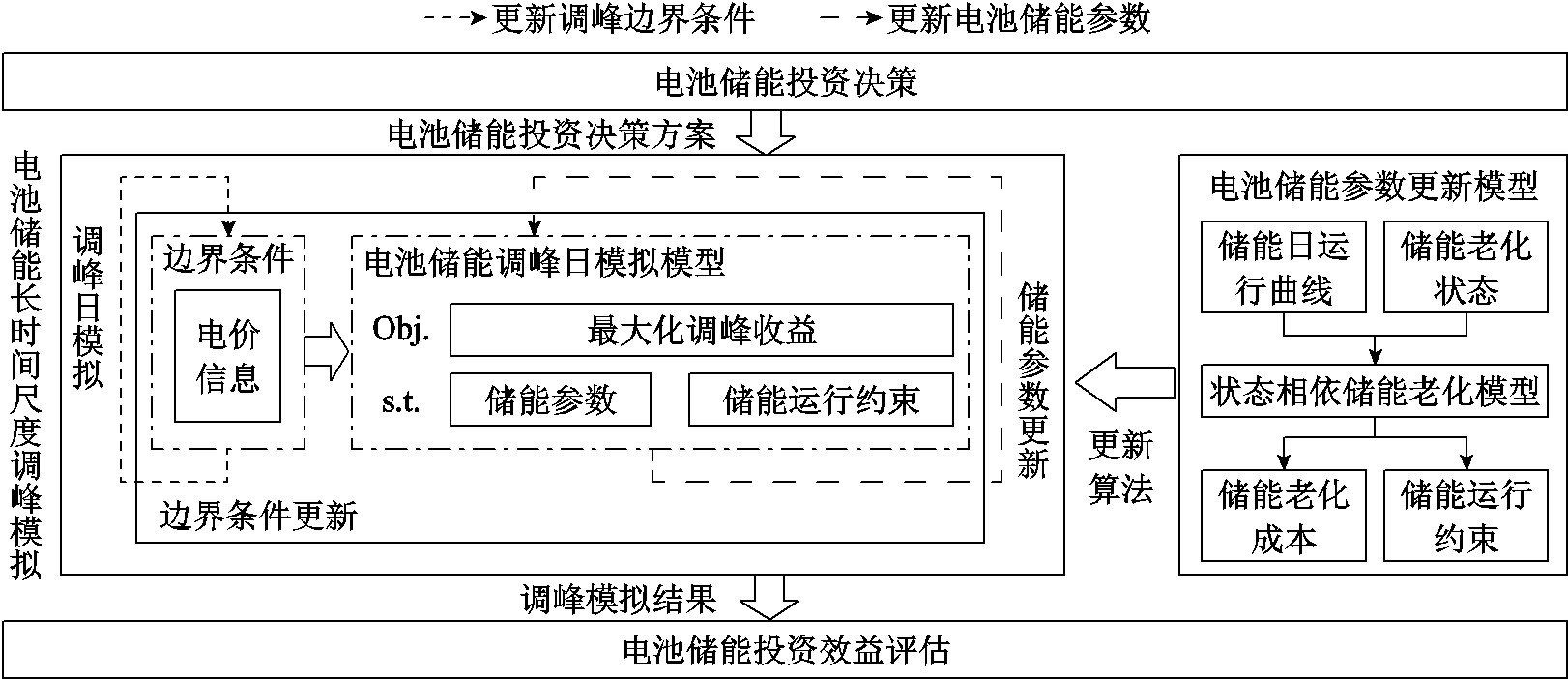
图1 考虑状态相依老化特性的电池储能参与调峰投资效益评估框架
Fig.1 Evaluation framework for the investment benefits of battery energy storage participating in peak shaving considering the state-dependent aging characteristics
摘要 参与电力系统调峰是当前电池储能的重要应用之一。电力市场环境下,电池储能在电价信号的引导下进行充放电获取收益,但同时将造成老化损失,产生相应老化成本。现有固定参数的电池储能老化模型无法在长时间模拟中考虑储能老化参数随寿命的变化。该文基于阿伦尼乌斯经验模型,建立了考虑电池储能老化特性受寿命变化影响的状态相依老化模型,实现电池储能全寿命周期老化特性建模;构建该模型的离散形式以适应电力系统的应用需求;将模型嵌入调峰优化模型中并对其进行线性化以便于模型求解。进一步地,将该方法应用于长时间尺度调峰模拟中,通过动态计算并滚动更新电池储能老化参数,精准地刻画了电池储能全寿命周期老化过程,实现了考虑电池储能状态相依老化特性的调峰投资收益测算,提升了电池储能参与调峰投资效益评估的有效性。
关键词:电力系统调峰 电池储能 阿伦尼乌斯经验模型 状态相依老化模型 投资效益评估
近年来,以锂离子电池为代表的电池储能技术得到快速发展[1],单位成本不断降低,装机容量爆发式增长,在电力系统的各个环节都得到了规模化应用推广[2-4]。当前电力市场环境下,参与电力系统调峰仍是电池储能获取收益的重要途径之一[5]。电池储能在电价信号的引导下开展充放电、获取价差收益的同时,不可逆的老化过程也造成了自身可用容量的损失[6-7],降低了电池储能的使用效率和年限,产生相应的老化成本。对于电池储能投资主体而言,需进行电池储能参与电力系统调峰的长时间尺度收益与成本分析,从而评估投资效益,辅助投资决策[8]。其中,建立电池储能老化模型是模拟其参与电力系统调峰行为、开展投资效益评估的基础[9-10]。并且,准确的电池储能老化模型是提高电池储能全寿命周期调峰投资收益的有效途径[11-12]。
当前,已有许多学者对电池储能老化特性的刻画进行了研究。其中,固定电池储能老化参数的模型具有较为广泛的应用。该模型将电池储能投资建设成本分摊到全寿命周期每单位电量释放量上[13],并设置基于电池储能全寿命周期总能量计算得到的储能老化损失率[14]。然后将储能老化损失率作为固定老化参数应用到电力系统优化模型中[15]。文献[16]将此模型引入多能源微电网规划模型中。但是,受到时变的运行工况和使用频率影响,电池储能的老化参数在动态变化。因此,固定老化参数的模型虽然易于嵌入电池储能参与调峰优化模型,但是该模型没有考虑电池储能的实际运行状态,在长时间尺度调峰模拟和投资效益分析中,具有较大的累积误差。考虑到电池储能的实际运行状态,基于电池储能循环深度的老化模型开始受到关注[17-18]。该模型基于电池储能寿命周期数与循环深度的对应关系[19],建立拟合多项式来近似表征以循环深度为变量的电池储能老化损失[20]。对于电池储能循环深度的计算,现有研究通常使用雨流计数算法来实现[21]。雨流计数算法通过对电池储能运行过程的荷电状态(State of Charge, SOC)进行峰谷判断,然后提取局部循环,实现对电池储能循环深度的计数[22]。文献[23]基于雨流计数算法建立了以循环深度为变量的幂函数形式电池储能老化模型。但是雨流计数算法无法解析表达,需要初始化电池储能运行工况,计算循环深度并进行迭代求解,因此无法直接嵌入电池储能参与调峰优化模型,增加了求解过程的复杂度。
此外,上述研究均忽略了电池储能的老化特性受电池储能寿命变化的影响。对于同一型号的电池储能,在寿命初期和临近退役的状态下以同样的工况进行充放电,造成的电池储能老化损失并不相同[24]。本文将电池储能的老化过程受寿命变化影响的现象称之为“状态相依老化特性”。在电池储能参与调峰的投资效益评估中,需要进行长时间尺度的调峰模拟和收益测算,涵盖电池储能的全寿命周期,因此电池储能的状态相依老化特性不可忽略。
在锂离子电池电化学机理研究领域,阿伦尼乌斯经验模型是描述化学反应速率的经典模型,受到广泛认可[25]。通过该模型,可将电池储能老化过程描述为时间的函数。在此基础上,相关研究对于阿伦尼乌斯经验模型进行了拓展。文献[26]改进了阿伦尼乌斯经验模型,建立了以放电倍率和累积放电量为参数的电池储能老化模型。文献[27]应用阿伦尼乌斯经验模型计算了电池储能参与配电网运行的老化损失。文献[28]将阿伦尼乌斯经验模型改进为半经验组合因子模型,探究了电池储能老化特性对直流微电网能量管理的影响。但上述改进模型中,电池储能外特性参数与电力系统对于电池储能的建模变量没有直接对应,仅能实现电池储能老化程度的事后估计。同时,上述改进模型高度非线性,无法嵌入电池储能参与调峰优化模型。
为在电池储能参与调峰投资效益评估中考虑电池储能的状态相依老化特性,本文首先基于阿伦尼乌斯经验模型提出了适用于电力系统建模的状态相依离散化电池储能老化模型;然后,将所提出的老化模型嵌入电池储能参与调峰优化模型中,并通过线性化方法获得可求解的优化模型;最后,通过考虑电池储能状态相依老化特性的电力系统长时间尺度调峰模拟,实现电池储能投资效益的精准评估。本文主要贡献总结如下:
(1)提出了适用于电力系统调峰模拟优化建模的电池储能状态相依老化特性离散化刻画方法。
(2)将电池储能状态相依老化特性模型嵌入电池储能参与调峰优化模型中,并提出基于线性化的求解方法。
(3)在电池储能投资效益分析中依据状态相依老化特性滚动更新储能参数,动态刻画电池储能全寿命周期的老化特性,进而评估电池储能投资效益。
首先获取电池储能投资决策方案,投资决策方案可来源于优化规划模型[29-30]或方案比选,并将其作为本文方法的输入条件;其次对于获得的电池储能投资规划方案进行调峰模拟;最后基于调峰模拟结果,对电池储能投资效益进行评估。其中,对于投资规划方案的调峰模拟需建立电池储能参与调峰的优化模型,以电力系统电价信号作为输入条件,求解电池储能运行约束下的收益最大化问题[31]。通过在不同场景下的调峰模拟,获取投资规划方案对应在不同调峰场景下的模拟结果,并应用于投资效益评估分析[32]。
现有研究通常采用固定的储能老化参数建立调峰模拟优化模型,求解某一场景完成后仅更新场景边界条件,即开展下一场景的调峰模拟[33]。然而,投资效益评估是在电池储能配置方案确定后,基于给定的规划方案边界条件,进行长时间的调峰运行模拟(通常为数年)[34]。在此过程中,电池储能状态相依老化特性随着运行时间的增加和不同调峰场景的更替逐渐显现,采用固定参数的电池储能老化模型造成的累积误差将不可忽略,导致电池储能的老化损失计算失真,进一步影响电池储能投资效益评估结果的可信度,无法精准支撑电池储能投资决策。
为此,本文提出考虑状态相依老化特性的电池储能参与调峰投资效益评估框架,如图1所示。首先,输入电池储能投资规划方案。其次,对于投资规划方案开展调峰模拟。相比于现有研究,根据电池储能日运行曲线和老化状态建立了状态相依老化模型,动态计算电池储能参数,并应用于调峰日模拟。在调峰日模拟中,某一调峰场景求解完成后不仅更新场景边界条件,同时更新电池储能参数,将其应用于下一场景的优化求解。最后,统计长时间尺度的调峰模拟结果,评估电池储能参与调峰投资效益。

图1 考虑状态相依老化特性的电池储能参与调峰投资效益评估框架
Fig.1 Evaluation framework for the investment benefits of battery energy storage participating in peak shaving considering the state-dependent aging characteristics
电池储能的老化过程具有状态相依特性。本节首先介绍描述电池储能状态相依老化特性的经典模型,即阿伦尼乌斯经验模型。然而,该模型在时间尺度上是连续的,无法适应电力系统运行优化中通常将时间尺度离散成多个时段的模式。为此,本节提出离散化阿伦尼乌斯经验模型,使之适应于电力系统应用。进一步地,本节给出基于实测数据的离散化阿伦尼乌斯经验模型的参数整定方法。
阿伦尼乌斯经验模型的具体形式为
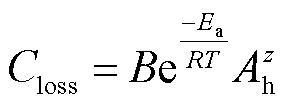 (1)
(1)
式中,![]() 为电池储能累积老化损失;B为指前因子,与放电倍率相关;
为电池储能累积老化损失;B为指前因子,与放电倍率相关;![]() 为反应活化能,与电池储能的类型和放电倍率相关;R为常量,在常规运行工况时保持不变;T为电池储能运行环境的热力学温度;z为幂律因子,通过实测数据集拟合得到;
为反应活化能,与电池储能的类型和放电倍率相关;R为常量,在常规运行工况时保持不变;T为电池储能运行环境的热力学温度;z为幂律因子,通过实测数据集拟合得到;![]() 为累积放电量,计算公式为
为累积放电量,计算公式为
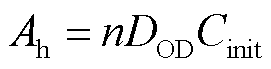 (2)
(2)
式中,n为循环次数;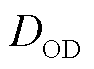 为循环深度;
为循环深度;![]() 为电池储能初始可用容量。
为电池储能初始可用容量。
基于桑迪亚国家实验室实测磷酸铁锂电池储能数据集[35],比较在不同放电倍率完整循环运行工况下使用阿伦尼乌斯经验模型计算的电池储能老化损失与实测老化损失的变化情况,对比结果如图2所示。从图2可以看出,阿伦尼乌斯经验模型可以较为准确地描绘电池储能在不同放电倍率(Crate)运行工况和累积老化程度下的老化过程。
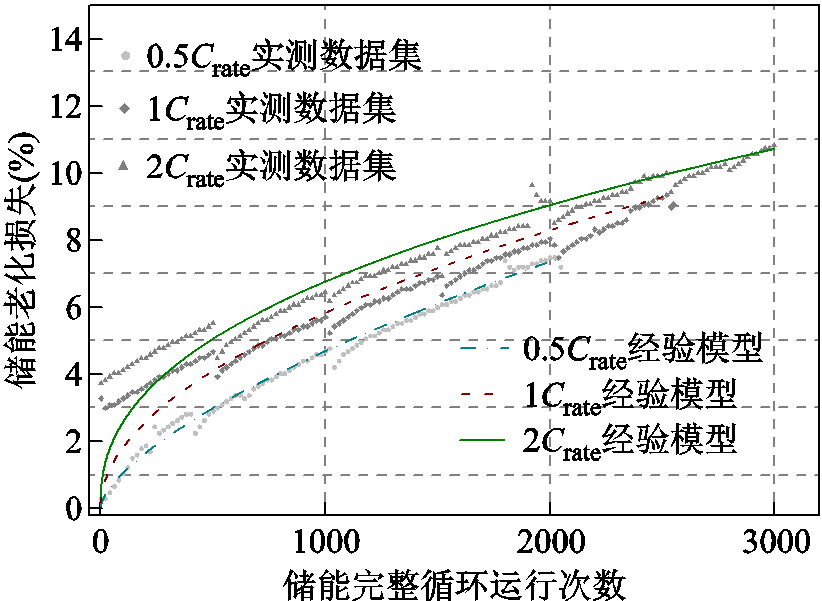
图2 阿伦尼乌斯经验模型计算结果
Fig.2 Calculation results of the Arrhenius empirical model
基于式(1)的阿伦尼乌斯经验模型的局限性在于此模型仅能依据电池储能的历史运行曲线进行储能老化损失的后评估,无法将其应用于电池储能参与调峰优化模型中对电池储能老化损失进行计算。为实现考虑状态相依老化特性的电池储能老化建模,必须依据调峰模拟所对应优化模型的建模形式,提出与之相适应的电池储能老化损失刻画方法。调峰模拟优化模型将时间轴离散为多个时段,并以每个时段中的充放电功率来表示电池储能的调峰行为。因此,本文基于阿伦尼乌斯经验模型提出离散化刻画电池储能状态相依老化特性的模型,从而计算每个时段电池储能的充放电行为所对应的老化损失。
首先,将式(1)对![]() 求偏导计算
求偏导计算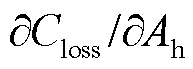 ,得到
,得到
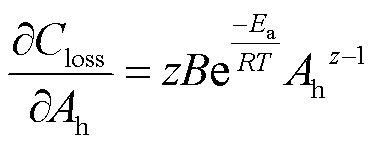 (3)
(3)
然后,将式(1)变形为
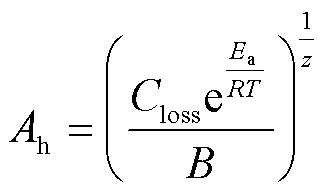 (4)
(4)
最后,将式(4)代入式(3)得到离散化阿伦尼乌斯经验模型为
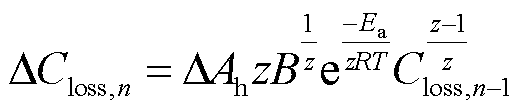 (5)
(5)
式中,![]() 为电池储能投入后第n次调峰时相应的老化损失;
为电池储能投入后第n次调峰时相应的老化损失;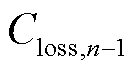 为电池储能已经累积的老化损失;
为电池储能已经累积的老化损失;![]() 为电池储能参与调峰时的电量释放量,计算公式为
为电池储能参与调峰时的电量释放量,计算公式为
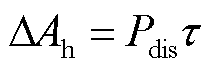 (6)
(6)
式中,![]() 为电池储能的放电功率;
为电池储能的放电功率;![]() 为电池储能放电持续时间。这里认为电池储能的老化过程仅与电池储能放电过程相关,在许多研究中已经证明了这样的假设是正确的[36-37]。
为电池储能放电持续时间。这里认为电池储能的老化过程仅与电池储能放电过程相关,在许多研究中已经证明了这样的假设是正确的[36-37]。
本节进一步提出指前因子B、反应活化能![]() 和幂律因子z的整定方法。反应活化能
和幂律因子z的整定方法。反应活化能![]() 与电池储能的类型和电池储能的放电倍率相关[26],
与电池储能的类型和电池储能的放电倍率相关[26],![]() 的整定通常采用式(7)形式。
的整定通常采用式(7)形式。
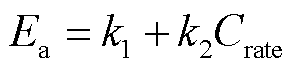 (7)
(7)
式中,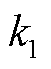 、
、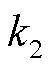 根据实测数据集拟合得到。
根据实测数据集拟合得到。
关于指前因子B和幂律因子z的整定,通过将式(1)取对数得到
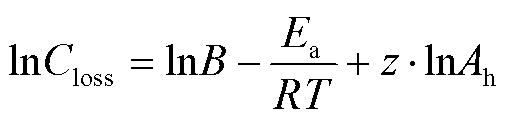 (8)
(8)
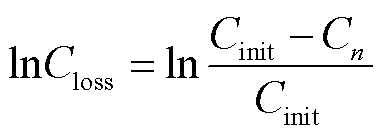 (9)
(9)
式中,![]() 为电池储能第n次完整循环时的可用容量。
为电池储能第n次完整循环时的可用容量。
对式(2)取对数得到式(8)中的![]() ,根据电池储能标准运行工况实测数据集放电倍率和环境温度可确定反应活化能
,根据电池储能标准运行工况实测数据集放电倍率和环境温度可确定反应活化能![]() 、R和T。对式(8)移项得到
、R和T。对式(8)移项得到
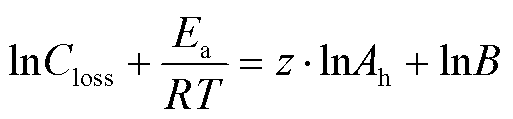 (10)
(10)
基于式(10)对标准运行工况不同放电倍率实测数据集进行线性回归,得到不同放电倍率下的指前因子B。将指前因子B和放电倍率![]() 拟合为
拟合为
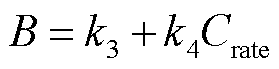 (11)
(11)
在上述参数整定过程中,![]() 和B都建立为放电倍率
和B都建立为放电倍率![]() 的解析表达式。但是电池储能参与电力系统调峰时的外部特性通常表现为放电功率,因此可以通过式(12)将上述参数转换为以放电功率表达的形式。
的解析表达式。但是电池储能参与电力系统调峰时的外部特性通常表现为放电功率,因此可以通过式(12)将上述参数转换为以放电功率表达的形式。
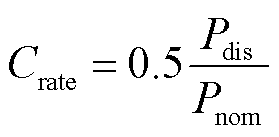 (12)
(12)
式中,![]() 为电池储能的额定功率。将式(6)、式(7)、式(11)、式(12)代入式(5),得到以放电功率
为电池储能的额定功率。将式(6)、式(7)、式(11)、式(12)代入式(5),得到以放电功率![]() 为决策变量的离散化阿伦尼乌斯经验模型为
为决策变量的离散化阿伦尼乌斯经验模型为
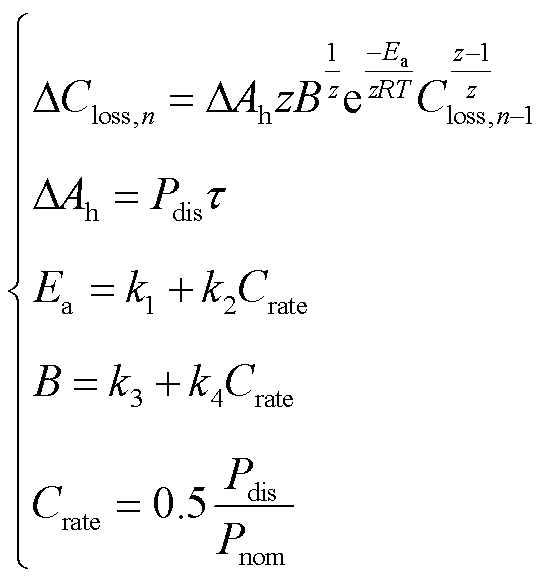 (13)
(13)
选取10次、20次和30次完整循环电量释放量作为离散步长,验证离散化阿伦尼乌斯经验模型的计算精度,结果如图3所示。
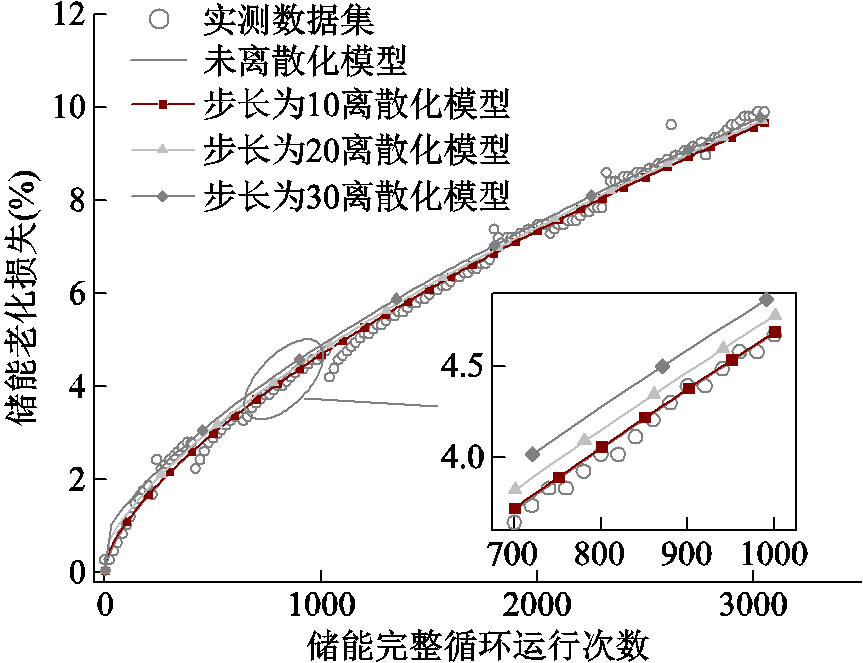
图3 离散化阿伦尼乌斯经验模型计算精度验证
Fig.3 Calculation accuracy verification of the discretized Arrhenius empirical model
从图3可以看出,当离散步长逐渐增大时,离散化经验模型计算误差也呈微小增长趋势,但在调峰模拟中,电池储能单时段电量释放量远小于10次完整循环电量释放量,因此离散误差较小,可以保证离散化经验模型的计算精度。
本节建立了在电价信号引导下的电池储能参与调峰优化模型,并针对电池储能老化模型的复杂非线性特性设计了线性化方法,将考虑电池储能状态相依老化特性的调峰优化模型转换为线性规划模型。在长时间尺度调峰模拟中,建立了电池储能参数动态更新机制,准确地刻画了电池储能不同寿命阶段充放电运行情况下的储能老化损失。
将最大化调峰日模拟净收益作为电池储能参与调峰优化模型的目标函数![]() ,即
,即
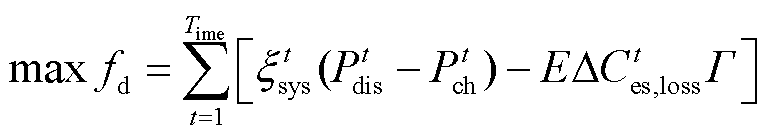 (14)
(14)
式中,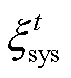 为t时段电池储能参与电力系统调峰时的电价;
为t时段电池储能参与电力系统调峰时的电价;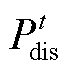 和
和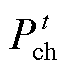 分别为t时段电池储能的放电和充电功率;E为电池储能的额定可用容量;
分别为t时段电池储能的放电和充电功率;E为电池储能的额定可用容量;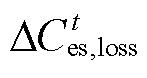 为电池储能t时段参与调峰产生的相应老化损失,其具体含义为电池储能额定可用容量损失的百分比;
为电池储能t时段参与调峰产生的相应老化损失,其具体含义为电池储能额定可用容量损失的百分比;![]() 为电池储能每MW·h容量建设成本;Time为总时段数。将电池储能的建设成本分摊到储能运行的全生命周期中,电池储能参与调峰时由于老化导致的使用寿命缩减,其分摊的建设成本即为老化成本,在调峰优化模型目标函数中电池储能老化成本体现为
为电池储能每MW·h容量建设成本;Time为总时段数。将电池储能的建设成本分摊到储能运行的全生命周期中,电池储能参与调峰时由于老化导致的使用寿命缩减,其分摊的建设成本即为老化成本,在调峰优化模型目标函数中电池储能老化成本体现为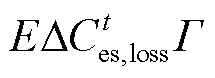 。
。
电池储能运行约束包括充放电互斥约束、充放电功率约束、能量守恒约束和荷电状态约束,具体叙述如下。
1)充放电互斥约束
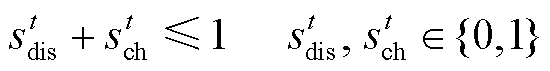 (15)
(15)
式中,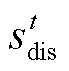 和
和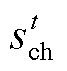 分别为t时段电池储能放电和充电状态的0-1变量。
分别为t时段电池储能放电和充电状态的0-1变量。
2)充放电功率约束
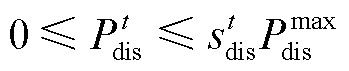 (16)
(16)
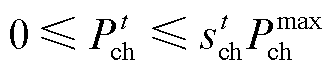 (17)
(17)
式中,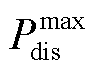 和
和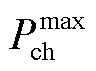 分别为t时段电池储能放电功率
分别为t时段电池储能放电功率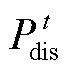 和充电功率
和充电功率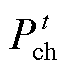 的上限。
的上限。
3)能量守恒约束
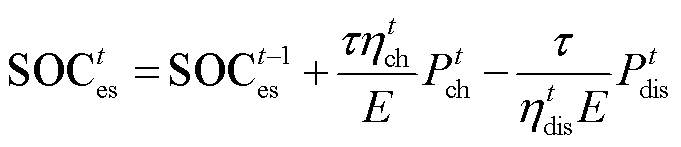 (18)
(18)
式中,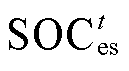 为t时段电池储能的荷电状态;
为t时段电池储能的荷电状态;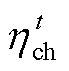 和
和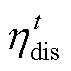 分别为t时段电池储能的充电和放电效率。
分别为t时段电池储能的充电和放电效率。
4)荷电状态约束
为了避免电池储能产生过充和过放行为,引入电池储能荷电状态上下限约束
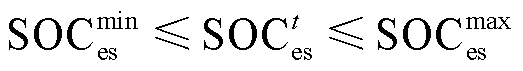 (19)
(19)
式中,![]() 和
和![]() 分别为电池储能荷电状态的下限和上限。
分别为电池储能荷电状态的下限和上限。
在本文建立的式(14)~式(19)调峰优化模型中,精细地刻画了状态相依的电池储能老化特性,而针对模型中的其他要素进行了适当的简化和线性建模。因此在构建的调峰优化模型中,仅有电池储能老化成本项存在非线性,这是由于式(13)极为复杂,给调峰优化模型目标函数式(14)引入了高度非线性,导致求解较为困难。为了便于优化模型求解,需研究电池储能老化特性的线性化方法。为此,分别选取电池储能累积老化损失为0.05%、0.5%、5%和10%的四个阶段,探究通过离散化阿伦尼乌斯经验模型计算的电池储能老化损失与放电功率之间的关系,计算结果如图4所示。
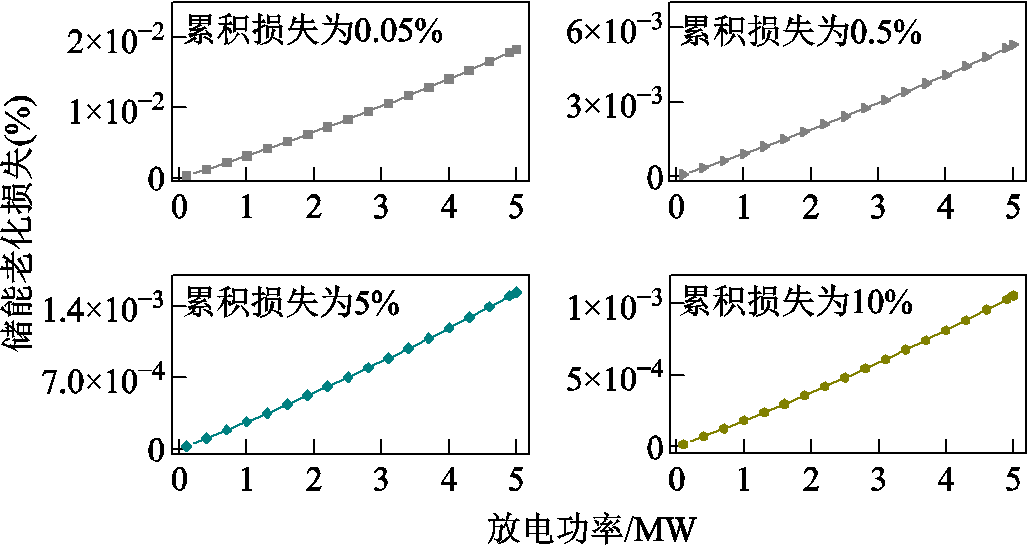
图4 不同累积损失阶段储能老化损失与放电功率关系
Fig.4 Relationship between energy storage aging loss and discharge power at different stages of cumulative loss
在不同累积老化损失阶段,随着电池储能放电功率的增加,储能老化损失的加剧过程都近似为线性形式,并且随着累积老化损失的增加,在相同放电功率下,电池储能老化损失逐渐减小。为了降低调峰优化模型求解的复杂度,根据线性回归结果将式(13)简化为
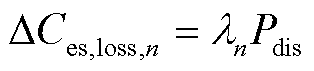 (20)
(20)
式中,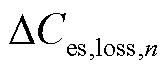 为线性回归后的电池储能离散老化损失;
为线性回归后的电池储能离散老化损失;![]() 为累积老化损失达到
为累积老化损失达到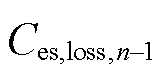 时电池储能参与调峰的储能老化损失率,其具体含义为当前时段电池储能参与调峰每MW·h放电量造成的老化损失。将线性化后的电池储能老化模型替代原模型嵌入调峰优化模型进行调峰模拟。
时电池储能参与调峰的储能老化损失率,其具体含义为当前时段电池储能参与调峰每MW·h放电量造成的老化损失。将线性化后的电池储能老化模型替代原模型嵌入调峰优化模型进行调峰模拟。
通过上述对考虑电池储能状态相依老化特性的建模,获得了目标函数为式(14),约束条件为式(15)~式(19)的调峰优化模型。随着电池储能寿命的增长,其老化特性逐渐变化。本节提出电池储能参数动态更新方法,即电池储能可用容量E、累积老化损失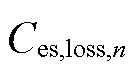 和储能老化损失率
和储能老化损失率![]() 的动态更新方法。首先,根据电池储能日运行曲线和老化状态计算电池储能日运行老化损失
的动态更新方法。首先,根据电池储能日运行曲线和老化状态计算电池储能日运行老化损失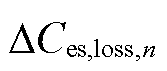 ,将其与已累积老化损失
,将其与已累积老化损失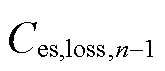 加和得到更新后的累积老化损失
加和得到更新后的累积老化损失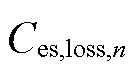 。
。
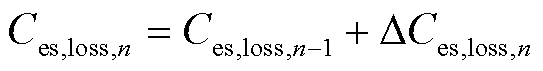 (21)
(21)
然后,将更新后的累积老化损失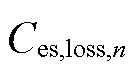 代入离散化阿伦尼乌斯经验模型,在电池储能理论放电功率范围内,计算不同放电功率下累积老化损失为
代入离散化阿伦尼乌斯经验模型,在电池储能理论放电功率范围内,计算不同放电功率下累积老化损失为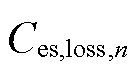 时的电池储能离散老化损失,得到式(20)的线性化结果,将储能老化损失率更新为
时的电池储能离散老化损失,得到式(20)的线性化结果,将储能老化损失率更新为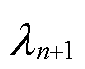 。将调峰优化模型约束(18)中的电池储能可用容量更新为
。将调峰优化模型约束(18)中的电池储能可用容量更新为
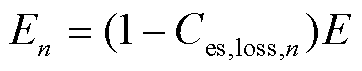 (22)
(22)
式中,En为电池储能第n次调峰后的可用容量。至此,完成电池储能参数动态更新。
本文提出的储能老化模型在电力系统调峰中的适用过程如图5所示。通过2.2节和3.3节所述的储能老化模型离散化过程和线性化过程,储能老化模型可以直接嵌入电力系统长时间尺度调峰模拟中,建立优化求解器可稳定求解的模型,并获得储能参与调峰收益最大化的充放电运行情况;然后通过储能参数动态更新机制,获得下一次调峰日模拟的储能参数。
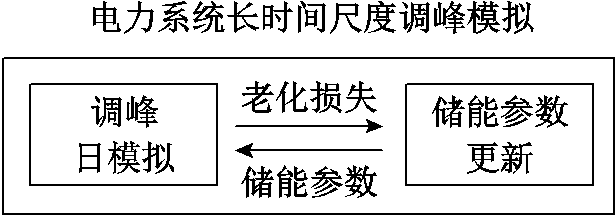
图5 储能老化模型在电力系统调峰中的适用过程
Fig.5 Application process of the energy storage aging model in power system peak shaving
状态相依的储能老化模型相比于已有改进阿伦尼乌斯经验模型而言,解决了模型与电力系统优化建模不适配、无法嵌入调峰优化模型的问题;相比于固定参数模型而言,解决了模型无法刻画储能老化过程随寿命变化的问题。
电池储能参与调峰投资效益受到收益模式、市场电价、建设成本、使用寿命和老化特性等因素的综合影响。收益模式和市场电价方面,本文电池储能参与调峰的收益模式为通过充放电行为获取峰谷价差收益,市场电价水平决定了峰谷价差下电池储能的调峰收益。建设成本方面,建设成本被分摊到电池储能的全生命周期,从而建立电池储能运行行为-寿命损失-建设成本分摊的映射关系,电池储能参与调峰时由于老化导致的寿命损失,其相应分摊的建设成本表现为老化成本。本文建立的储能老化模型可以考虑不同使用寿命阶段的老化特性,更为精细地刻画电池储能充放电运行行为到寿命损失的映射关系。电池储能老化特性是本文研究的重点,因此在众多影响因素中重点考虑,同时也对收益模式、市场电价、建设成本和使用寿命等因素进行了综合考虑。本节基于第3节提出的调峰优化模型,应用考虑电池储能状态相依老化特性的长时间尺度调峰模拟结果,进一步提出电池储能投资效益评估方法。
电池储能在电价信号的引导下优化充放电行为,参与电力系统调峰。不同市场环境下,电池储能执行相应的价格机制。本文提出的模型适用于固定充放电价格、分时电价、电力现货市场价格等多类型电价形式,并在算例研究中基于电力现货市场价格进行分析。需要指出的是,电力现货市场价格由每日的供需情况决定,难以提前预知。因此,本文采用历史电价数据来反映电价的变化趋势和统计特性。此外,该方式也暗含了电池储能被作为价格接受者的假设,这也是相关研究中的常用方式[38-39]。基于历史电价数据[40-41],使用第3节提出的调峰优化模型和电池储能参数动态更新方法,可序贯地对于给定年度的每一日开展电池储能调峰模拟。将第d日的调峰净收益记为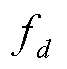 ,则对于总天数为D的第
,则对于总天数为D的第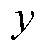 年开展的调峰模拟,年度电池储能调峰收益
年开展的调峰模拟,年度电池储能调峰收益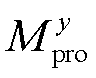 为
为
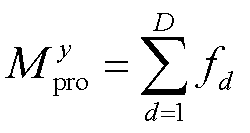 (23)
(23)
本文通过净现值(Net Present Value, NPV)来评估电池储能投资效益。NPV越大代表投资潜力越大,NPV的计算方法如下。
设置折现率为r,电池储能年度调峰收益为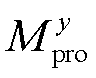 ,则电池储能参与调峰投资效益的年度NPV为
,则电池储能参与调峰投资效益的年度NPV为
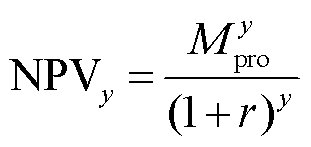 (24)
(24)
则总运行年限为Y年的电池储能参与调峰投资效益的累积NPVtotal为
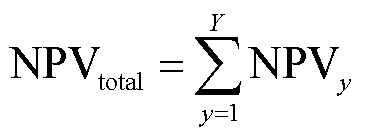 (25)
(25)
第2节离散化阿伦尼乌斯经验模型中的参数![]() 和B与电池储能放电倍率
和B与电池储能放电倍率![]() 相关,需要根据电池储能不同运行工况下的实测数据集拟合得到。本文采用了Battery Archive数据网站(http://www. batteryarchive.org)中桑迪亚国家实验室建立的电池储能数据集[35]。此数据集中包含多类型电池储能在不同标准运行工况下的完整循环实测数据。当前电池储能中依然以磷酸铁锂电池为主,因此本文使用了该数据集中磷酸铁锂电池在0.5
相关,需要根据电池储能不同运行工况下的实测数据集拟合得到。本文采用了Battery Archive数据网站(http://www. batteryarchive.org)中桑迪亚国家实验室建立的电池储能数据集[35]。此数据集中包含多类型电池储能在不同标准运行工况下的完整循环实测数据。当前电池储能中依然以磷酸铁锂电池为主,因此本文使用了该数据集中磷酸铁锂电池在0.5![]() 、
、![]() 、2
、2![]() 等不同放电倍率和25℃测试温度下的数据,该运行条件下的常量R为8.314。由此数据集拟合得到的不同放电倍率工况下
等不同放电倍率和25℃测试温度下的数据,该运行条件下的常量R为8.314。由此数据集拟合得到的不同放电倍率工况下![]() 与
与![]() 的关系如图6所示,图中,
的关系如图6所示,图中,![]() =31 900,
=31 900,![]() =-970。
=-970。
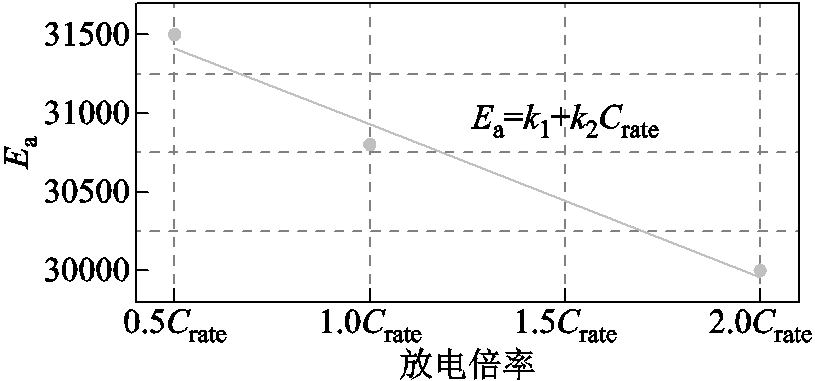
图6 ![]() 与
与![]() 拟合结果
拟合结果
Fig.6 Fitting results of ![]() and
and ![]()
由此数据集拟合得到的不同放电倍率工况下B与![]() 的关系如图7所示,图中,k3=183.5,k4=-41。
的关系如图7所示,图中,k3=183.5,k4=-41。
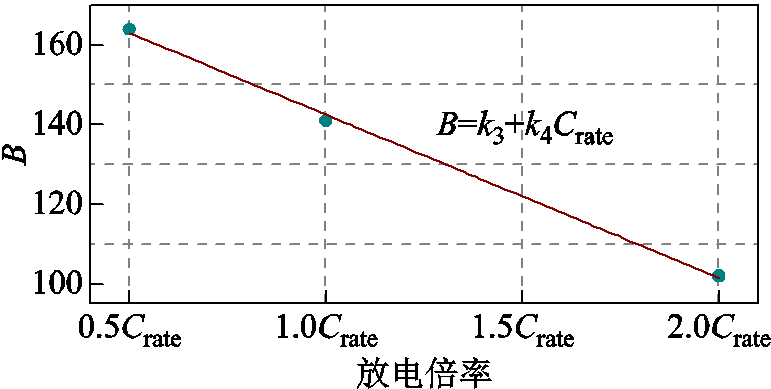
图7 B与![]() 拟合结果
拟合结果
Fig.7 Fitting results of B and ![]()
本文首先通过实测数据集验证了阿伦尼乌斯经验模型的准确性,然后对该模型进行了离散化和线性化处理。为评估对阿伦尼乌斯经验模型改进的效果,通过对比以下储能老化模型(M0~M2)在电池储能0.5![]() 、
、![]() 、2
、2![]() 等不同放电倍率完整循环运行工况下的累积老化损失和相对误差,验证本文提出的状态相依储能老化模型准确性,对比结果见表1。表1中M0代表阿伦尼乌斯经验模型;M1代表本文所提离散化阿伦尼乌斯经验模型;M2代表本文所提内嵌电池储能参数动态更新机制的线性化阿伦尼乌斯经验模型。
等不同放电倍率完整循环运行工况下的累积老化损失和相对误差,验证本文提出的状态相依储能老化模型准确性,对比结果见表1。表1中M0代表阿伦尼乌斯经验模型;M1代表本文所提离散化阿伦尼乌斯经验模型;M2代表本文所提内嵌电池储能参数动态更新机制的线性化阿伦尼乌斯经验模型。
表1 储能老化模型验证
Tab.1 Validation of the energy storage aging model (%)
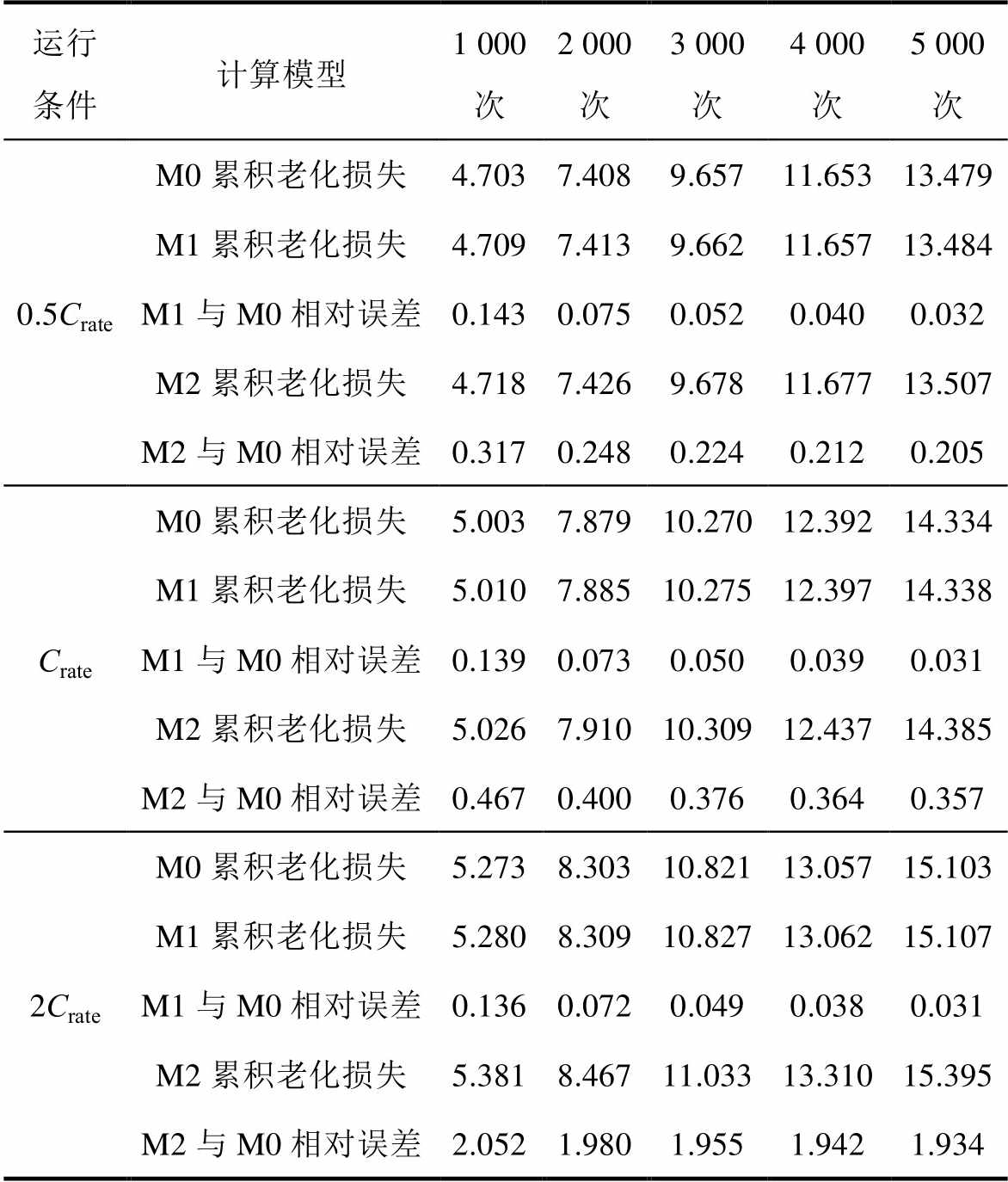
运行条件计算模型1 000次2 000次3 000次4 000次5 000次 0.5M0累积老化损失4.7037.4089.65711.65313.479 M1累积老化损失4.7097.4139.66211.65713.484 M1与M0相对误差0.1430.0750.0520.0400.032 M2累积老化损失4.7187.4269.67811.67713.507 M2与M0相对误差0.3170.2480.2240.2120.205 M0累积老化损失5.0037.87910.27012.39214.334 M1累积老化损失5.0107.88510.27512.39714.338 M1与M0相对误差0.1390.0730.0500.0390.031 M2累积老化损失5.0267.91010.30912.43714.385 M2与M0相对误差0.4670.4000.3760.3640.357 2M0累积老化损失5.2738.30310.82113.05715.103 M1累积老化损失5.2808.30910.82713.06215.107 M1与M0相对误差0.1360.0720.0490.0380.031 M2累积老化损失5.3818.46711.03313.31015.395 M2与M0相对误差2.0521.9801.9551.9421.934
储能老化模型验证结果表明,基于本文所提基于阿伦尼乌斯经验模型进行离散化和线性化处理后的状态相依储能老化模型,在不同寿命阶段仍具有较好的计算精度,可以有效地支撑电池储能参与调峰投资效益评估。
设置调峰优化模型中的电池储能可用容量为10 MW·h,每MW·h的建设成本为120万元,电池储能的老化特性基于5.1节中的参数进行设定。模型输入的电价信号采用SPP(Southern Power Pool)电力市场的历史节点边际电价。以电价信号作为输入条件,对电池储能参与电力系统调峰进行日模拟。根据日模拟结果,通过电池储能参数动态更新机制获得下一次日模拟电池储能参数,并计算电池储能的调峰收益。然后更新边界条件,实现长时间尺度的调峰模拟。直至电池储能累积老化损失达到20%,电池储能退役,计算在电池储能运行年限内,投资电池储能参与调峰的累积净现值。
为了说明本文设计方法的合理性和有效性,与固定参数模型方法进行对比。设置固定参数模型方法中储能老化损失率为4×10-6,其具体含义为,电池储能在每次完整充放电行为后,会损失额定容量的0.004%。在固定参数模型方法和本文方法中均添加日历老化过程,将日历老化损失率设置为2.5×10-5,电池储能每经历一个自然日都会损失额定容量的0.002 5%。
基于单日模拟结果对电池储能运行情况进行分析。选取SPP电力市场2018年第327天的电价作为输入,其变化如图8a所示;电价信号引导下的电池储能日调峰模拟充放电和SOC变化情况如图8b、图8c所示。在电力市场价格信号引导下,电池储能在高峰电价时放电,低谷电价时充电,在最大化自身收益的同时,电池储能充放电行为也帮助电力系统实现了调峰需求。
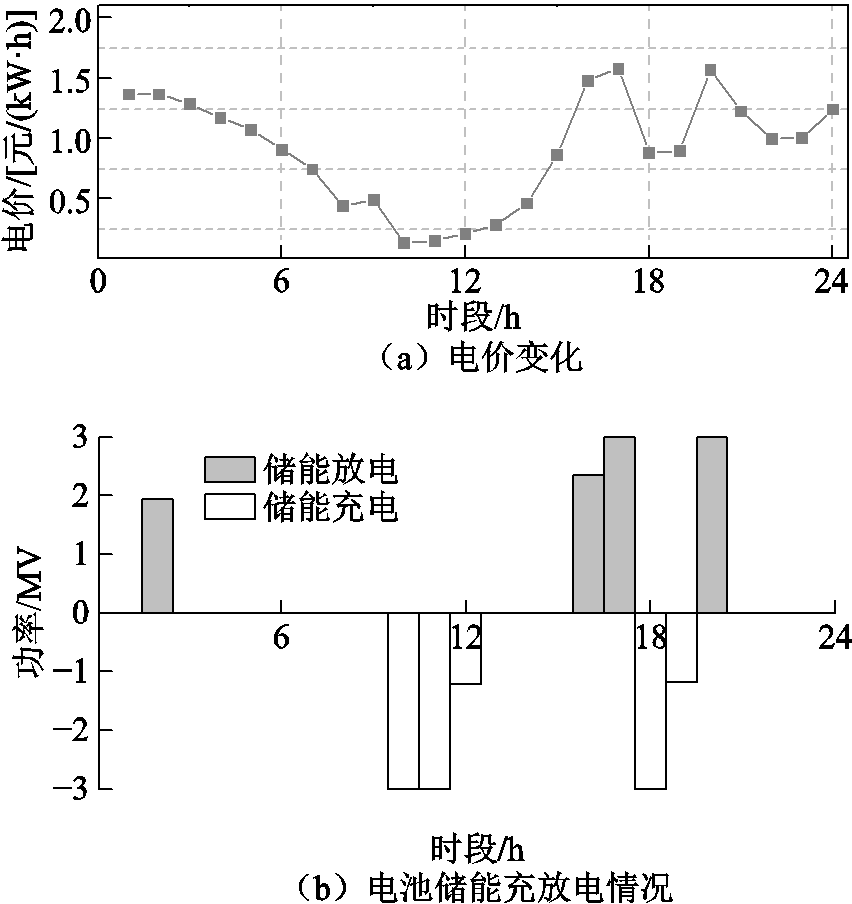
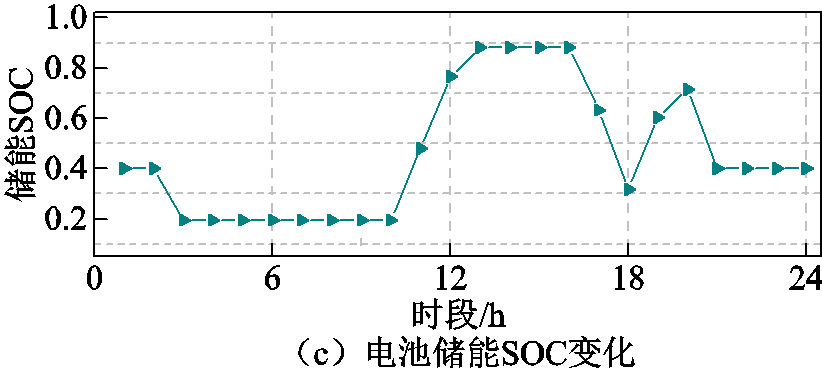
图8 日调峰模拟输入条件和电池储能运行状态
Fig.8 Input conditions for daily peak shaving simulation and operating states of battery energy storage
比较本文方法在不同年度调峰模拟中电池储能年度电量释放量。在运行年限内电池储能年度电量释放量如图9所示。电池储能参与电力系统调峰是市场环境下的综合行为,为实现调峰收益的最大化,电池储能需要根据电价信号和自身运行成本决策充放电行为。其中,调峰收益由电力市场价格信号等参数决定;自身运行成本受到储能老化特性的影响。在本文进行的电池储能全寿命周期年调峰模拟中,以年为时间尺度的电价信号是不变的。但随着年调峰模拟的持续进行,电池储能的老化特性不断发生变化,单位电量释放量所产生的老化损失减小,其对应的老化成本降低。因此,电池储能可以在更多的峰谷价差水平下获取收益,电池储能参与调峰的次数逐渐增加,在年调峰模拟中电量释放量相应地逐渐增大。
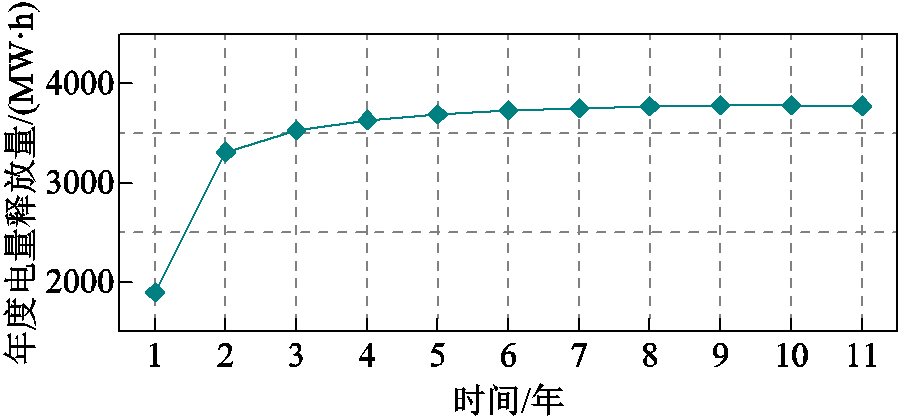
图9 电池储能年度电量释放量
Fig.9 Electricity release of battery energy storage in different years
在本文方法下,投入运行的第1年、第6年和第11年,电池储能的年度电量释放量分别为 1 896.58、3 731.76和3 775.05 MW·h。而对于固定参数模型方法,由于储能参数与电池储能的累积老化损失程度无关,因此,在相同电价信号边界条件和储能参数的年调峰模拟中,电池储能的年度电量释放量是相同的,都为3 257.04 MW·h。应用本文方法,能够在电池储能全寿命周期参与调峰投资效益评估中考虑储能老化损失率随储能寿命增长而发生的变化,反映状态相依老化特性对于电池储能参与调峰模拟结果的影响。
根据电池储能长时间尺度调峰模拟,对于每个日模拟结果进行分年度统计,计算所模拟时间尺度内每个年度的老化损失和调峰收益,并进一步累加获得不同年度的累积老化损失和调峰收益。在模拟中,将电池储能在本文方法和固定参数模型方法下的结果进行对比。由于电池储能的投资效益与总运行年限相关,因此首先分析电池储能的总运行年限。在本文方法和固定参数模型方法下参与调峰的电池储能年老化损失和累积老化损失情况如图10所示。固定参数模型方法仅考虑调峰收益,忽略了电池储能在不同寿命阶段储能老化损失率的变化,因此在老化成本较高时依然频繁调峰,造成每年的老化损失都高达2.38%,以累积老化损失20%为退役阈值,电池储能使用年限为8年。对于本文方法,在长时间尺度调峰模拟第1年,电池储能年老化损失为2.26%,在退役年限的老化损失为1.52%,电池储能使用年限为11年。
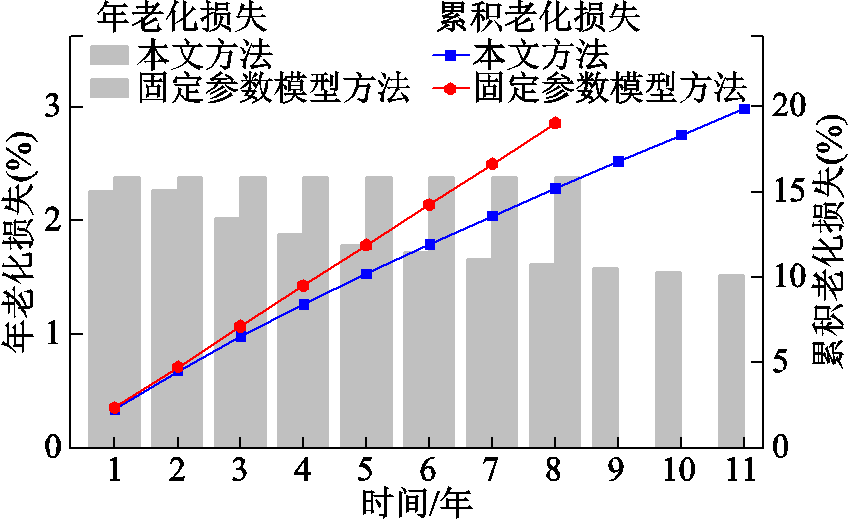
图10 电池储能年老化损失和累积老化损失
Fig.10 Annual aging loss and cumulative aging loss of battery energy storage
进一步地使用本文方法对固定参数模型方法下的电池储能运行决策老化损失进行计算,计算结果如图11所示。在固定参数模型方法下,电池储能的累积老化损失计算误差在运行中后期逐渐增大,累积老化损失的计算误差最大为4.35%。而本文方法能够更加精准地刻画电池储能在不同寿命阶段的老化特性,从而在电池储能长时间尺度调峰模拟中准确地反映老化特性变化对于运行决策的影响,进而有效地评估电池储能参与调峰投资效益。
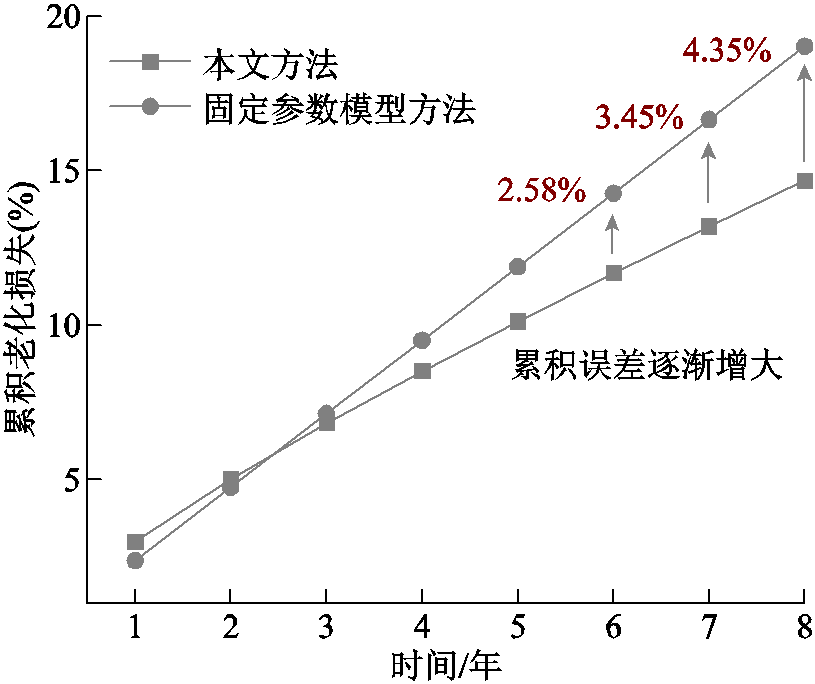
图11 固定参数模型方法误差
Fig.11 Error of the fixed-parameter model method
将本文所提状态相依储能老化模型嵌入调峰优化模型中进行长时间尺度的调峰模拟后,根据第4节电池储能参与调峰投资效益评估方法测算投资效益。设置折现率r为6%,电池储能年度调峰收益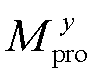 、年度投资
、年度投资![]() 与累积投资
与累积投资![]() 见表2。本文方法在电池储能运行年限内的年度调峰收益和年度投资
见表2。本文方法在电池储能运行年限内的年度调峰收益和年度投资![]() 动态变化,总调峰收益为1 344.483万元,累积
动态变化,总调峰收益为1 344.483万元,累积![]() 为934.960万元。固定参数模型方法在电池储能运行年限内的年度调峰收益为定值93.198万元,总调峰收益为745.584万元,累积
为934.960万元。固定参数模型方法在电池储能运行年限内的年度调峰收益为定值93.198万元,总调峰收益为745.584万元,累积![]() 为578.740万元。本文方法能够精准地测算随电池储能寿命变化的调峰收益,实现电池储能投资效益的准确评估。
为578.740万元。本文方法能够精准地测算随电池储能寿命变化的调峰收益,实现电池储能投资效益的准确评估。
表2 电池储能参与调峰的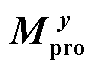 、
、![]() 与
与![]()
Tab.2 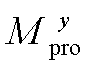 ,
, ![]() and
and ![]() of battery energy storage participating in peak shaving
of battery energy storage participating in peak shaving
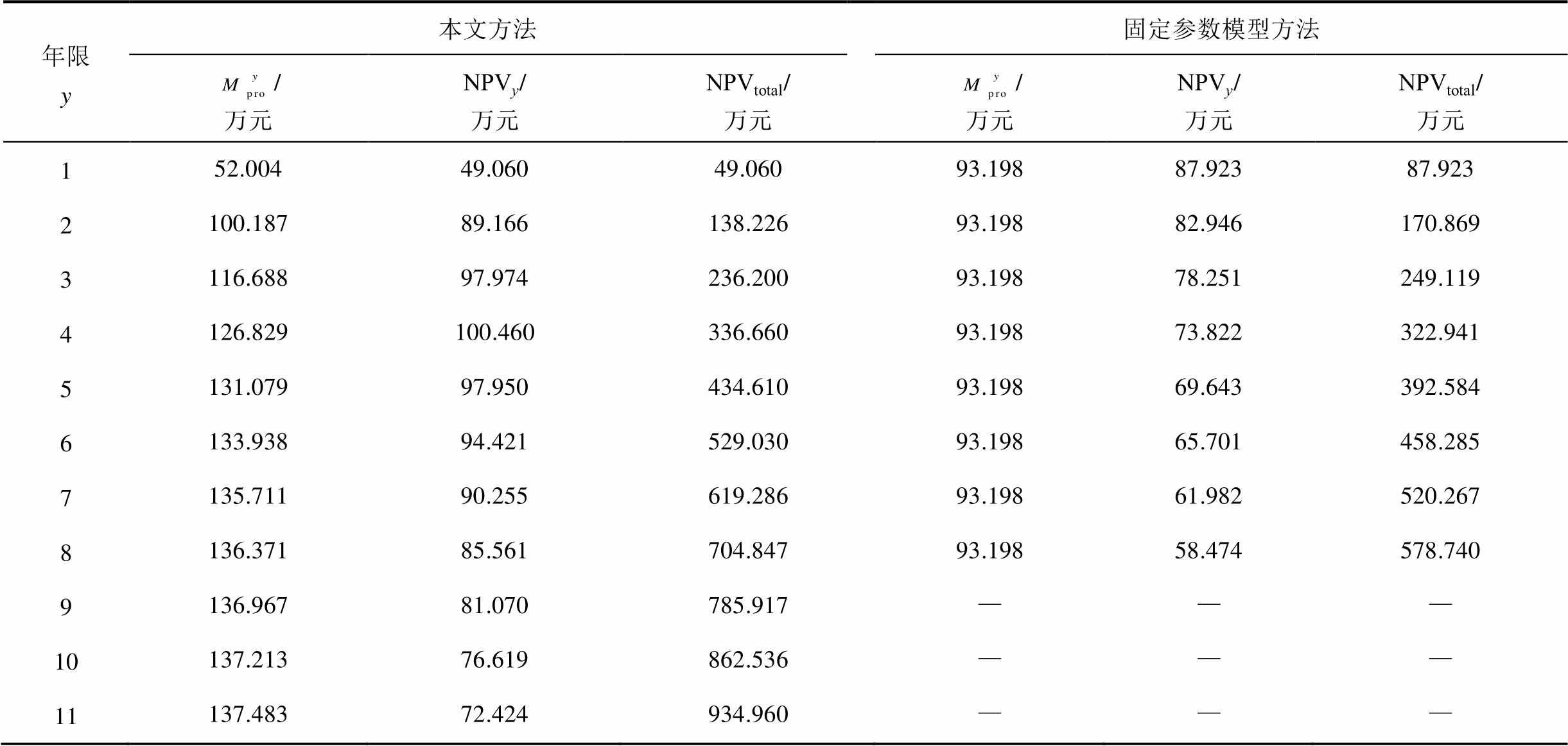
年限y本文方法固定参数模型方法 /万元/万元/万元/万元/万元/万元 152.00449.06049.06093.19887.92387.923 2100.18789.166138.22693.19882.946170.869 3116.68897.974236.20093.19878.251249.119 4126.829100.460336.66093.19873.822322.941 5131.07997.950434.61093.19869.643392.584 6133.93894.421529.03093.19865.701458.285 7135.71190.255619.28693.19861.982520.267 8136.37185.561704.84793.19858.474578.740 9136.96781.070785.917——— 10137.21376.619862.536——— 11137.48372.424934.960———
为在电池储能参与调峰投资效益评估中精准地刻画电池储能老化成本,充分考虑电池储能老化特性受寿命变化的影响,本文建立了适用于电力系统优化建模的状态相依电池储能老化模型,将其嵌入调峰模拟框架中,并提出相应的求解方法。在此基础上,序贯地进行了长时间尺度调峰模拟,并测算了电池储能运行年限内的调峰收益,实现了电池储能投资效益的准确评估。本文的贡献在于以下三个方面:
1)建立了考虑状态相依老化特性的电池储能老化模型,并实现此模型与电力系统优化建模的变量适配,基于模型特点设计了对应的求解方法。
2)在长时间尺度调峰模拟中量化了电池储能老化损失,根据累积老化程度动态更新电池储能参数,刻画了电池储能全寿命周期状态相依老化特性。
3)在电池储能运行年限内精准地计算了电池储能的调峰收益和老化成本,实现了电池储能投资效益的准确评估。
本文提出的状态相依电池储能老化模型同样可以应用在电池储能的优化配置和运行阶段。通过本文提出的基于阿伦尼乌斯经验模型进行离散化和线性化,形成了易于嵌入优化的电池储能老化特性刻画方法。基于此,后续研究将进一步探究如何将状态相依的老化特性建模应用到电池储能的规划和运行模型中,从而增强决策的有效性,提升电池储能的收益。
参考文献
[1] 程曹阳, 杨知方, 余娟, 等. 面向全场景安全的储能投资高效规划方法[J]. 电工技术学报, 2025, 40(1): 63-78. Cheng Caoyang, Yang Zhifang, Yu Juan, et al. An efficient method for energy storage planning considering full-scenario security[J]. Transactions of China Electrotechnical Society, 2025, 40(1): 63-78.
[2] 朱宗耀, 王秀丽, 吴雄, 等. 复合储能参与电能量及辅助服务市场的运行策略[J]. 电力系统自动化, 2023, 47(18): 80-90. Zhu Zongyao, Wang Xiuli, Wu Xiong, et al. Operation strategy for composite energy storage participating in electric energy and ancillary service markets[J]. Automation of Electric Power Systems, 2023, 47(18): 80-90.
[3] 王灿, 张羽, 田福银, 等. 基于双向主从博弈的储能电站与综合能源系统经济运行策略[J]. 电工技术学报, 2023, 38(13): 3436-3446, 3472. Wang Can, Zhang Yu, Tian Fuyin, et al. Economic operation of energy storage power stations and integrated energy systems based on bidirectional master-slave game[J]. Transactions of China Electro-technical Society, 2023, 38(13): 3436-3446, 3472.
[4] 郝艺, 周瑀涵, 刘晨曦, 等. 含跟网型储能的新能源多馈入系统小扰动电压支撑强度分析[J]. 电工技术学报, 2024, 39(11): 3569-3580. Hao Yi, Zhou Yuhan, Liu Chenxi, et al. Small-disturbance voltage support strength analysis for renewable multi-infeed system with grid-following energy storage[J]. Transactions of China Electro-technical Society, 2024, 39(11): 3569-3580.
[5] 李军徽, 安晨宇, 李翠萍, 等. 计及调峰市场交易的储能-新能源-火电多目标优化调度[J]. 电工技术学报, 2023, 38(23): 6391-6406. Li Junhui, An Chenyu, Li Cuiping, et al. Multi-objective optimization scheduling method considering peak regulating market transactions for energy storage-new energy-thermal power[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6391-6406.
[6] 夏向阳, 陈贵全, 刘俊翔, 等. 储能系统直流侧纹波电流对锂离子电池寿命影响分析及优化控制策略[J]. 电工技术学报, 2023, 38(22): 6218-6229. Xia Xiangyang, Chen Guiquan, Liu Junxiang, et al. Analysis of the impact of DC-side ripple current on lithium-ion battery life in energy storage systems and optimal control strategies[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6218-6229.
[7] 刘萍, 李泽文, 蔡雨思, 等. 基于等效电路模型和数据驱动模型融合的SOC和SOH联合估计方法[J]. 电工技术学报, 2024, 39(10): 3232-3243. Liu Ping, Li Zewen, Cai Yusi, et al. Joint estimation method of SOC and SOH based on fusion of equivalent circuit model and data-driven model[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3232-3243.
[8] 姜欣, 郑雪媛, 胡国宝, 等. 市场机制下面向电网的储能系统优化配置[J]. 电工技术学报, 2019, 34(21): 4601-4610. Jiang Xin, Zheng Xueyuan, Hu Guobao, et al. Optimization of battery energy storage system locating and sizing for the grid under the market mechanism[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4601-4610.
[9] Fallahifar R, Kalantar M. Optimal planning of lithium ion battery energy storage for microgrid applications: considering capacity degradation[J]. Journal of Energy Storage, 2023, 57: 106103.
[10] Collath N, Winner H, Frank A, et al. Suitability of late-life lithium-ion cells for battery energy storage systems[J]. Journal of Energy Storage, 2024, 87: 111508.
[11] Collath N, Cornejo M, Engwerth V, et al. Increasing the lifetime profitability of battery energy storage systems through aging aware operation[J]. Applied Energy, 2023, 348: 121531.
[12] Alic A, Trovato V, De Paola A. Revenue maximization for a battery storage with optimal capacity revamping due to cyclic fade[J]. IEEE Transactions on Smart Grid, 2024, 15(5): 4779-4791.
[13] Bahloul M, Daoud M, Khadem S K. Optimal dispatch of battery energy storage for multi-service provision in a collocated PV power plant considering battery ageing[J]. Energy, 2024, 293: 130744.
[14] Collath N, Tepe B, Englberger S, et al. Aging aware operation of lithium-ion battery energy storage systems: a review[J]. Journal of Energy Storage, 2022, 55: 105634.
[15] Muqbel A, Al-Awami A T, Parvania M. Optimal planning of distributed battery energy storage systems in unbalanced distribution networks[J]. IEEE Systems Journal, 2022, 16(1): 1194-1205.
[16] Cardoso G, Brouhard T, DeForest N, et al. Battery aging in multi-energy microgrid design using mixed integer linear programming[J]. Applied Energy, 2018, 231: 1059-1069.
[17] Kwon K B, Zhu Hao. Reinforcement learning-based optimal battery control under cycle-based degradation cost[J]. IEEE Transactions on Smart Grid, 2022, 13(6): 4909-4917.
[18] 商立群, 张建涛. 计及储能电池寿命衰减的居民小区光储优化配置[J]. 电气技术, 2024, 25(2): 1-11, 20. Shang Liqun, Zhang Jiantao. Optimal configuration of photovoltaic energy storage systems in residential communities taking into account energy storage battery life decay[J]. Electrical Engineering, 2024, 25(2): 1-11, 20.
[19] Fagerström J, Das S, Klyve Ø S, et al. Profitability of battery storage in hybrid hydropower–solar photovoltaic plants[J]. Journal of Energy Storage, 2024, 77: 109827.
[20] Amini M, Sanjareh M B, Nazari M H, et al. A novel model for battery optimal sizing in microgrid planning considering battery capacity degradation process and thermal impact[J]. IEEE Transactions on Sustainable Energy, 2024, 15(3): 1435-1449.
[21] Rouholamini M, Wang Caisheng, Nehrir H, et al. A review of modeling, management, and applications of grid-connected Li-ion battery storage systems[J]. IEEETransactions on Smart Grid, 2022, 13(6): 4505-4524.
[22] Shi Yuanyuan, Xu Bolun, Tan Yushi, et al. Optimal battery control under cycle aging mechanisms in pay for performance settings[J]. IEEE Transactions on Automatic Control, 2019, 64(6): 2324-2339.
[23] Diao Rui, Hu Zechun, Song Yonghua. Subgradient of cycle-based aging cost function and its application in optimal operation of battery energy storage system with multiple subsystems[J]. IEEE Transactions on Energy Conversion, 2024, 39(1): 625-643.
[24] Severson K A, Attia P M, Jin N, et al. Data-driven prediction of battery cycle life before capacity degradation[J]. Nature Energy, 2019, 4: 383-391.
[25] Bloom I, Cole B W, Sohn J J, et al. An accelerated calendar and cycle life study of Li-ion cells[J]. Journal of Power Sources, 2001, 101(2): 238-247.
[26] Wang J, Liu Ping, Hicks-Garner J, et al. Cycle-life model for graphite-LiFePO4 cells[J]. Journal of Power Sources, 2011, 196(8): 3942-3948.
[27] Song Ziyou, Nazir M S, Cui Xiaofan, et al. Benefit assessment of second-life electric vehicle lithium-ion batteries in distributed power grid applications[J]. Journal of Energy Storage, 2022, 56: 105939.
[28] Wang Shuoqi, Guo Dongxu, Han Xuebing, et al. Impact of battery degradation models on energy management of a grid-connected DC microgrid[J]. Energy, 2020, 207: 118228.
[29] Pulazza G, Zhang Ning, Kang Chongqing, et al. Transmission planning with battery-based energy storage transportation for power systems with high penetration of renewable energy[J]. IEEE Transactions on Power Systems, 2021, 36(6): 4928-4940.
[30] 卞一帆, 谢丽蓉, 鲁宗相, 等. 基于多主体投资的双储能系统分层优化配置方案[J]. 电力系统自动化, 2023, 47(1): 63-73. Bian Yifan, Xie Lirong, Lu Zongxiang, et al. Multi-agent investment based hierarchical optimal configuration scheme for dual energy storage system[J]. Automation of Electric Power Systems, 2023, 47(1): 63-73.
[31] Yang Zhifang, Yong Pei, Xiang Mingxu. Revisit power system dispatch: Concepts, models, and solutions[J]. iEnergy, 2023, 2(1): 43-62.
[32] 李军徽, 陈国航, 马腾, 等. 高风电渗透率下液流电池储能系统调峰优化控制策略[J]. 发电技术, 2024, 45(3): 434-447. Li Junhui, Chen Guohang, Ma Teng, et al. Optimal control strategy of peak shaving of flow battery energy storage system under high wind power permeability [J]. Power Generation Technology, 2024, 45(3):434-447.
[33] 朱睿, 胡博, 谢开贵, 等. 含风电-光伏-光热-水电-火电-储能的多能源电力系统时序随机生产模拟[J]. 电网技术, 2020, 44(9): 3246-3253. Zhu Rui, Hu Bo, Xie Kaigui, et al. Sequential probabilistic production simulation of multi-energy power system with wind power, photovoltaics, concentrated solar power, cascading hydro power, thermal power and battery energy storage[J]. Power System Technology, 2020, 44(9): 3246-3253.
[34] 李建林, 牛萌, 周喜超, 等. 能源互联网中微能源系统储能容量规划及投资效益分析[J]. 电工技术学报, 2020, 35(4): 874-884. Li Jianlin, Niu Meng, Zhou Xichao, et al. Energy storage capacity planning and investment benefit analysis of micro-energy system in energy interco-nnection[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 874-884.
[35] Preger Y, Barkholtz H M, Fresquez A, et al. Degradation of commercial lithium-ion cells as a function of chemistry and cycling conditions[J]. Journal of the Electrochemical Society, 2020, 167(12): 120532.
[36] Xu Bolun, Zhao Jinye, Zheng Tongxin, et al. Factoring the cycle aging cost of batteries participating in electricity markets[J]. IEEE Transactions on Power Systems, 2018, 33(2): 2248-2259.
[37] 王荔妍, 陈启鑫, 何冠楠, 等. 考虑电池储能寿命模型的发电计划优化[J]. 电力系统自动化, 2019, 43(8): 93-100. Wang Liyan, Chen Qixin, He Guannan, et al. Optimization of generation scheduling considering battery energy storage life model[J]. Automation of Electric Power Systems, 2019, 43(8): 93-100.
[38] Li Jianlin, Fang Zhijin, Wang Qian, et al. Optimal operation with dynamic partitioning strategy for centralized shared energy storage station with integration of large-scale renewable energy[J]. Journal of Modern Power Systems and Clean Energy, 2024, 12(2): 359-370.
[39] Liu Jichun, Chen Xue, Xiang Yue, et al. Optimal planning and investment benefit analysis of shared energy storage for electricity retailers[J]. International Journal of Electrical Power & Energy Systems, 2021, 126: 106561.
[40] Yong Pei, Zhang Ning, Hou Qingchun, et al. Evaluating the dispatchable capacity of base station backup batteries in distribution networks[J]. IEEE Transactions on Smart Grid, 2021, 12(5): 3966-3979.
[41] Grimaldi A, Minuto F D, Brouwer J, et al. Profitability of energy arbitrage net profit for grid-scale battery energy storage considering dynamic efficiency and degradation using a linear, mixed-integer linear, and mixed-integer non-linear optimization approach[J]. Journal of Energy Storage, 2024, 95: 112380.
Abstract Battery energy storage (BES) is widely used in various applications in the power system as a flexible regulation resource. One of the key applications is peak shaving. BES can charge and discharge to capture the price difference between peak and valley periods in the electricity market. However, due to the inherent operational characteristics of BES, peak shaving behavior results in irreversible aging loss, leading to a reduction in lifespan and available capacity. Establishing an accurate aging model for BES is fundamental for simulating its peak shaving behavior and evaluating investment benefits. The aging characteristics of BES are state-dependent at different stages of its lifespan. However, aging models with fixed parameters fail to consider the variation in aging parameters over time during long-term peak shaving simulations.
A state-dependent aging model for BES is proposed, based on the Arrhenius empirical model, which accounts for the impact of lifespan on aging characteristics. This model can represent the full aging behavior of BES throughout its lifespan. A discrete form of the model is developed to meet the application requirements of power system optimization. The discrete variables are adapted to those of the power system, enabling their integration. Furthermore, the discrete aging model is embedded in a peak shaving optimization model. To address the challenge of solving the highly nonlinear discrete aging model, linearization techniques are employed to facilitate model computation. A dynamic parameter updating mechanism for BES is also designed and incorporated into the discrete aging model, enabling dynamic updates of the aging loss rate and available capacity during long-term peak shaving simulations, thus accurately capturing the full aging process throughout the lifespan.
To validate the effectiveness of the proposed method in investment benefits evaluation, historical locational marginal prices from the Southern Power Pool (SPP) electricity market are used as inputs to simulate the daily peak shaving operations of BES. The results of the daily simulations are used to update BES parameters via the dynamic updating mechanism, and the peak shaving benefits are then calculated. By updating boundary conditions, long-term peak shaving simulations of BES throughout its lifespan are performed, and the cumulative net present value (NPV) of investing in BES for peak shaving is computed. The results show that the proposed method allows for considering aging loss variation over time, reflecting the impact of state-dependent aging characteristics on the peak shaving performance of BES. This method enables accurate evaluation of BES investment benefits.
From the analysis, the following conclusions can be drawn: (1) The state-dependent aging model of BES, based on the Arrhenius empirical model and after discretization and linearization, can accurately capture the aging characteristics throughout the entire lifespan of BES. It also facilitates effective application in power system peak shaving simulations. (2) The state-dependent aging characteristics influence the charge and discharge behavior decisions of BES under electricity price signals. Using the state-dependent aging model allows for precise quantification of the aging costs arising from BES’s peak shaving behavior, enabling accurate evaluation of the investment benefits of BES in peak shaving applications.
Keywords:Power system peak shaving, battery energy storage, Arrhenius empirical model, state-dependent aging model, investment benefits evaluating
DOI: 10.19595/j.cnki.1000-6753.tces.241171
中图分类号:TM732
国家电网有限公司科技项目资助(SGCQDK00DWJS2400058)。
收稿日期 2024-07-04
改稿日期 2024-10-21
郭 飞 男,1996年生,博士研究生,研究方向为电化学储能建模、优化运行与配置。E-mail:guofei@stu.cqu.edu.cn
雍 培 男,1995年生,副教授,研究方向为电力系统运行优化与分析、分布式资源协同、可再生能源。E-mail:peiyong@cqu.edu.cn(通信作者)
(编辑 赫 蕾)