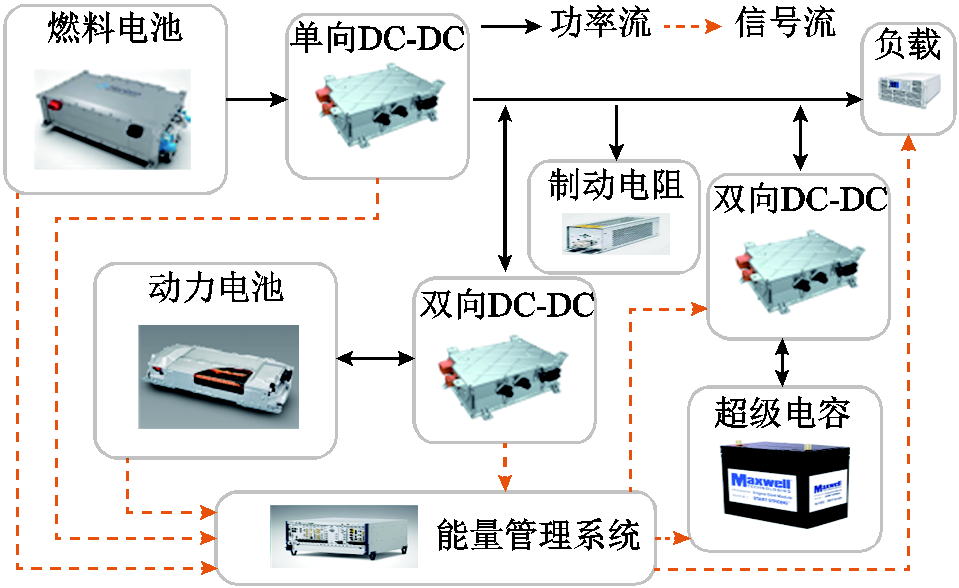
图1 燃料电池混合动力系统结构
Fig.1 Fuel cell hybrid power system structure
摘要 燃料电池混合动力系统中燃料电池和动力电池衰变过程高度不一致,仅考虑单电源寿命衰减,无法保证系统的耐久性和燃料经济性兼优,为此提出一种基于工况预测和动力源寿命衰减协同的优化策略。首先,上层根据历史工况建立马尔可夫链蒙特卡洛(MCMC)预测模型对有轨电车工况进行预测;其次,在下层能量管理策略中分析等效氢耗,建立燃料电池和动力电池的寿命衰减连续表征模型,引入优化目标并配置权重,优化多目标函数;最后,将所提策略与传统等效氢耗最小化策略(ECMS)、外部能耗最大化能量管理策略(EEMS)进行对比。结果表明:在整个工况结束时,所提策略比ECMS下的燃料经济性和系统效率分别提高了13.46%和5.2%,比EEMS下的双动力源寿命衰减率差值减小了95.42%、系统效率提升了2.4%,证明所提策略能在保证燃料经济性的前提下,实现双动力源寿命衰减协同控制效果,延长系统运行生命周期。
关键词:燃料电池有轨电车 工况预测 能量管理 寿命衰减协同
近几十年来,质子交换膜燃料电池(Proton Exchange Membrane Fuel Cell, PEMFC)作为新型绿色动力系统,发展迅速、成本逐渐降低[2-3],且PEMFC 具有零污染、运行性能优异等优点,被广泛应用于如电动汽车、固定式发电站、移动充电等各种场合[4]。然而,PEMFC本身具有动态响应慢、难以适应交通系统的多工况用能需求等缺陷,因此,在使用时往往需要与电池(Battery, BAT)和超级电容(Supercapacitor, SC)结合构成混合牵引动力系统[5]。
电气化铁路通过提高能量管理策略(Energy Management Strategy, EMS)的智能化以提高其电能质量并降低成本[6]。基于优化的能量管理策略可分为全局优化和瞬时优化[7]。动态规划是全局优化中的典型算法,其需要全部工况信息而无法在线应用,往往作为评价其他方法优劣的标准[8]。文献[9]提出一种基于动态规划的混合动力汽车能量管理策略,与基于规则的控制策略相比,减少了油耗。基于瞬时优化的方法是一种在线优化策略,包括等效氢耗最小化策略(Equivalent Consumption Minimization Strategy,ECMS)、庞特里亚金最小原理(Pontryagin's Minimum Principle, PMP)策略和模型预测控制器(Model Predictive Control, MPC)[10]。文献[11]提出了在线自适应优化控制的系统能量管理策略,利用改进Lyapunov优化将随机优化问题转换为确定性问题,相较于现有实时能量管理方法,可有效削减整体用能成本。文献[12]提出多阈值能量管理策略,对容量配置进行优化,从而提高了经济性。文献[13]提出一种改进的PMP策略,能够有效地降低燃料电池(Fuel Cell, FC)启停次数,实现全局和实时最优功率分配。文献[14]提出外部能耗最大化能量管理策略(External Energy Maximization Strategy, EEMS),比ECMS的氢耗量降低17.68 g,峰值电流降低21.81 A。对于车用PEMFC混合电源系统,PEMFC的寿命决定了整个双电源系统的寿命,将抑制PEMFC的寿命损失作为最优控制策略的优化对象是目前主要研究热点[15]。文献[16]在MPC框架下提出了一种基于PMP 的新型 EMS。该方法在成本函数中考虑FC功率的动态变化,从而提高了FC的使用寿命。文献[17]提出了一种退化自适应EMS,即可以利用FC的健康状态自适应地改变动力源功率分配,这种策略具有很强的自适应能力。文献[18]将FC衰减纳入目标函数,设计了具有优先经验重放的深度Q网络EMS,有效地抑制了FC衰减,提高了燃料经济性。文献[19]提出基于状态识别的双电源寿命衰减协同控制的能量管理策略,实现了燃料电池和动力电池寿命衰减的一致性,提高了系统的耐久性。
综上所述,现有的EMS的主要目标是减小燃料消耗,或者最大限度地减少单个电源的寿命损失来提升系统耐久性,却忽略了燃料电池和动力电池的衰变过程高度不一致性,一种动力源的过度消耗和寿命的提前结束,会破坏动力源系统的平衡,预支另一个动力源的性能,造成动力源极速老化,从而影响车辆的经济性,导致系统的整体耐久性降低,无法实现燃料经济性与系统耐久性的兼优。
为解决上述不足,所提策略(Proposed Energy Management Strategy, PEMS)提出一种双层控制结构,上层对工况进行预测,将预测结果输入下层,为能量管理在线优化提供条件;下层能量管理策略综合考虑燃料经济性、燃料电池和动力电池寿命这三个优化目标,并自适应地调整权重,对多目标进行优化。为了验证PEMS的有效性和优越性,通过仿真实验验证,并与ECMS和EEMS下的结果进行对比。
燃料电池混合动力系统结构如图1所示,此结构结合了“FC + BAT ”和“FC + SC ”结构的优点:辅助动力源提供初始动力,弥补燃料电池动态响应性能和冷启动性能差的缺陷。

图1 燃料电池混合动力系统结构
Fig.1 Fuel cell hybrid power system structure
由于超级电容的功率密度和能量转换效率较高,而动力电池的能量密度较高,所以配置结构的工况适应性更强。当机车遇到加速或上坡等工况时,超级电容和动力电池对燃料电池系统进行能量补偿,更好地吸收或释放负载突变时的峰值电流。当机车进入回馈制动工况时,燃料电池无法吸收能量,辅助电源实现制动能量回收,从而降低燃料电池的工作压力,延长燃料电池的循环寿命。同时,当系统出现故障时,动力电池还可作为备用动力源,确保车辆的运行安全。这种结构的设计充分发挥了各动力源的优势,提高了能源利用效率,也增强了系统的稳定性和可靠性。
在Matlab/Simulink中利用SimPowerSystems工具箱建立的燃料电池系统模型如图2所示。
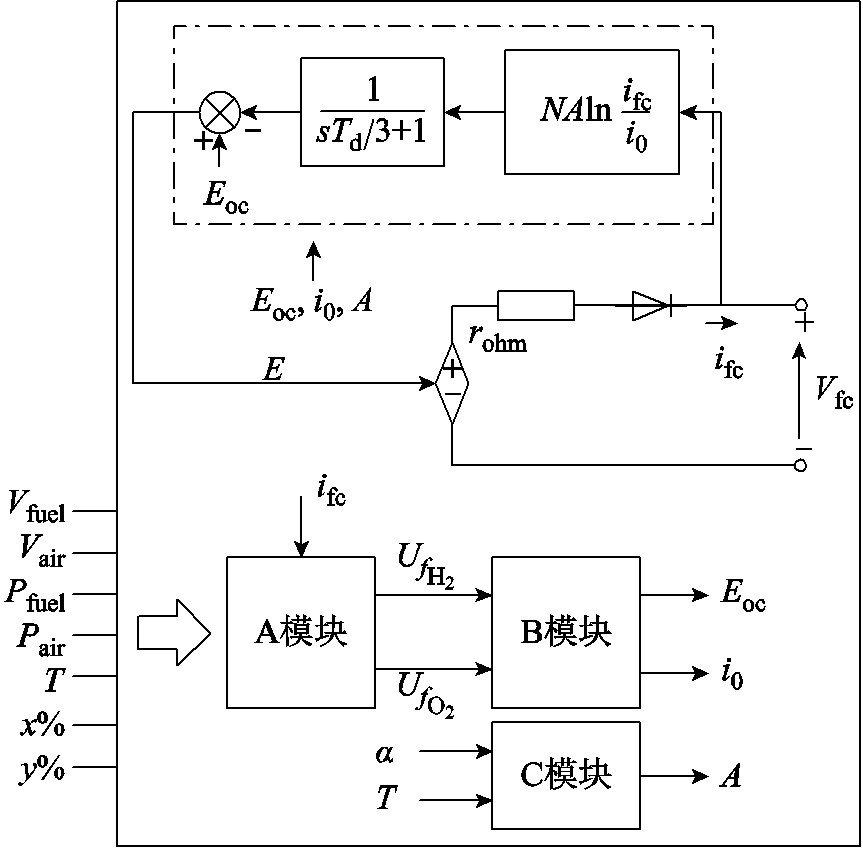
图2 燃料电池模型
Fig.2 Fuel cell model
该模型综合了化学模型和电气模型的特点,考虑激活电压损耗和欧姆损耗,忽略浓差极化电压损耗,能够表征运行参数对燃料电池的影响,即当燃料和空气的压力、温度、成分及流速等参数发生变化时,会影响塔菲尔斜率(A)、交换电流(i0)和开路电压(Eoc),从而影响输出端电压,如式(1)~式(4)所示。
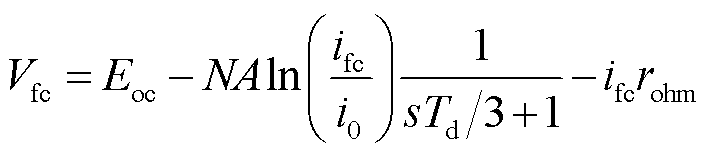 (1)
(1)
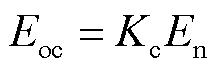 (2)
(2)
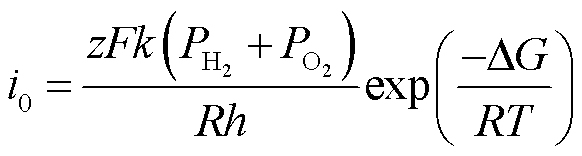 (3)
(3)
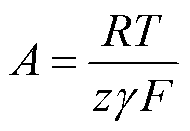 (4)
(4)
式中,Kc为额定条件下的电压常数;Td为反应时间;En为能斯特电压;N为燃料电池单体数量;T为燃料电池的工作温度;z为转移电子数,z=2;F为法拉第常数,F=96 485 C/mol;R为摩尔气体常数,R=8.3145 J/ (mol·K);k为玻耳兹曼常数,k=1.38×10–23 J/K;h为普朗克常数,h=6.626×10–34J·s;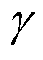 为电荷转移系数;ΔG为吉布斯自由能;
为电荷转移系数;ΔG为吉布斯自由能;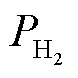 和
和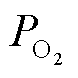 分别为氢气和氧气的供给压力;ifc和rohm分别为燃料电池电流和内阻。
分别为氢气和氧气的供给压力;ifc和rohm分别为燃料电池电流和内阻。
利用A、B模块更新Eoc、i0的值。在A模块中确定氢气和氧气的转换率分别为
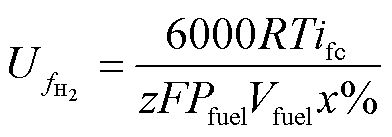 (5)
(5)
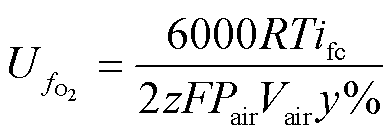 (6)
(6)
式中,Pfuel与Pair分别为燃料和空气的供给压力;Vfuel和Vair分别为燃料和空气的流量;x%和y%分别为燃料中氢气和氧气的占比。
分压和能斯特电压在B模块的确定过程为
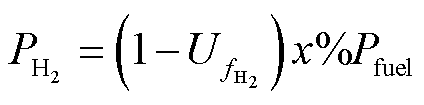 (7)
(7)
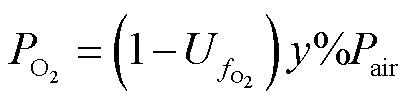 (8)
(8)
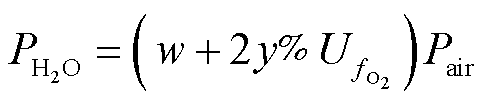 (9)
(9)
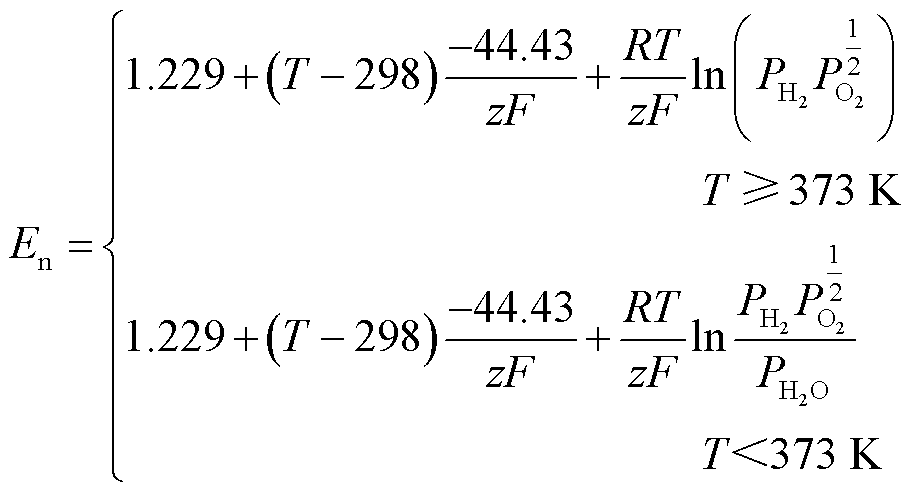 (10)
(10)
式中,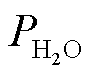 为水蒸气分压;w为氧气中水蒸气百分比。
为水蒸气分压;w为氧气中水蒸气百分比。
为了验证模型的稳态和瞬态输出特性,对燃料电池单体进行极化测试,将模型直接与可编程负载连接,测试在阶跃放电电流下的电压和功率,拟合出极化测试曲线如图3所示。
为了验证所搭建模型的精确度,在额定条件下对电堆进行放电测试,并与Hpower公司提供的同一条件下的测试数据进行对比分析。燃料电池模型精度测试结果如图4所示,误差在±0.2 V以内,所建模型精度高,能够很好地反映PEMFC的运行特性。
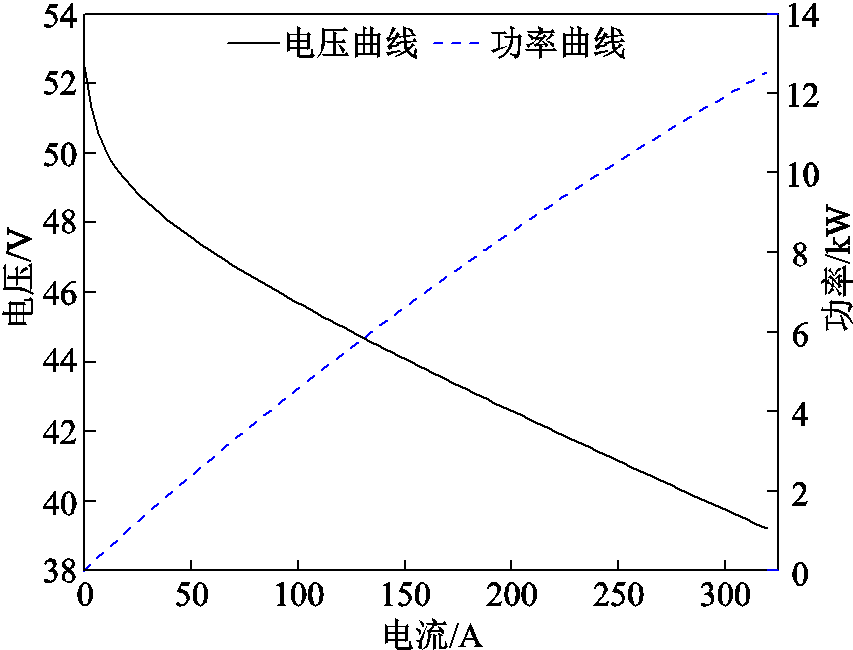
图3 燃料电池单体极化测试曲线
Fig.3 Polarization test curve of fuel cell monomer
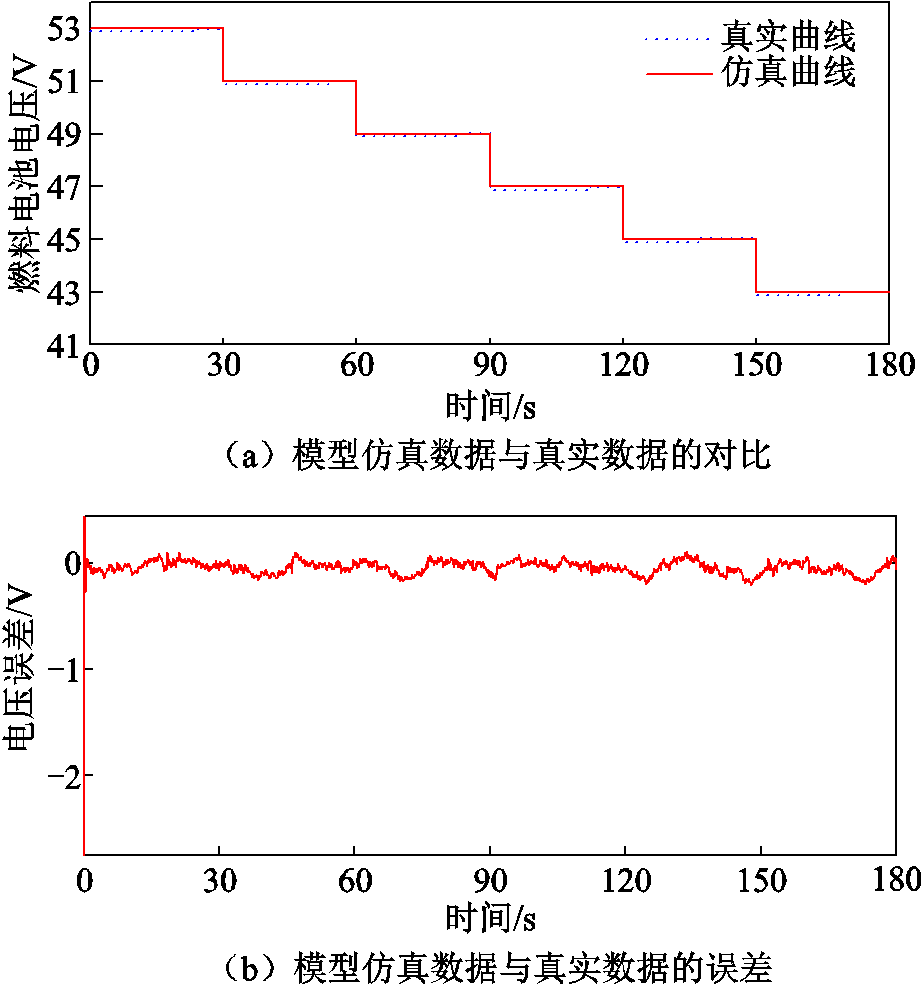
图4 燃料电池模型精度测试结果
Fig.4 Results of fuel cell model accuracy test
动力电池的搭建基于改进后的 Shepherd 模型,如图5所示。为了更好地表示电池充电状态对性能的影响,在电池放电电压的表达式中加入了电压极化,即电池内部电压只与电池充电状态有关,
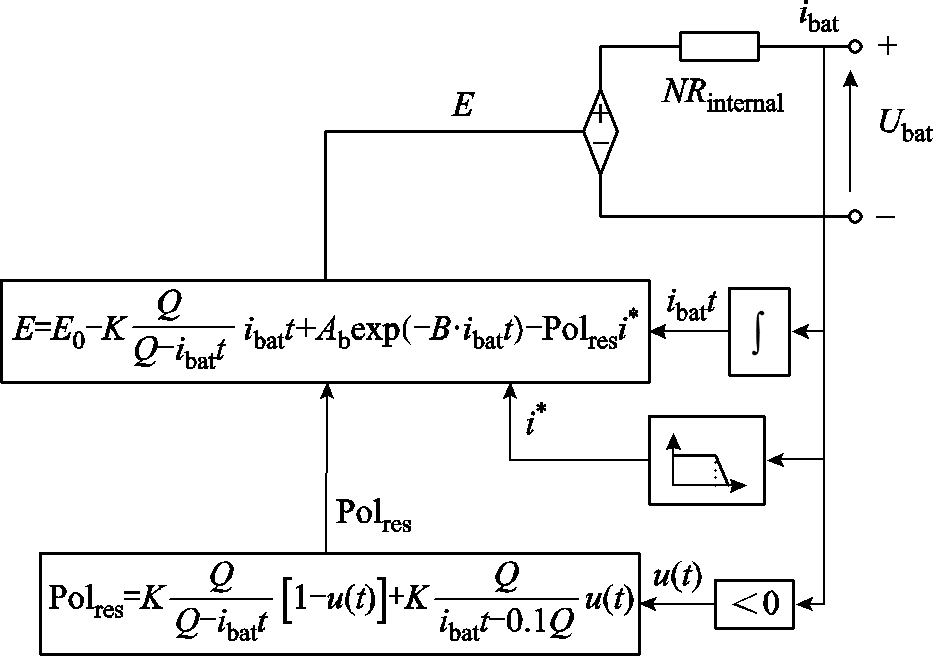
图5 动力电池模型
Fig.5 battery model
与电流无关。同时,为了确保模型的稳定运行,使用滤波电流来计算电池的极化内阻,解决了仿真过程稳定性与代数环问题。
电池输出端电压为
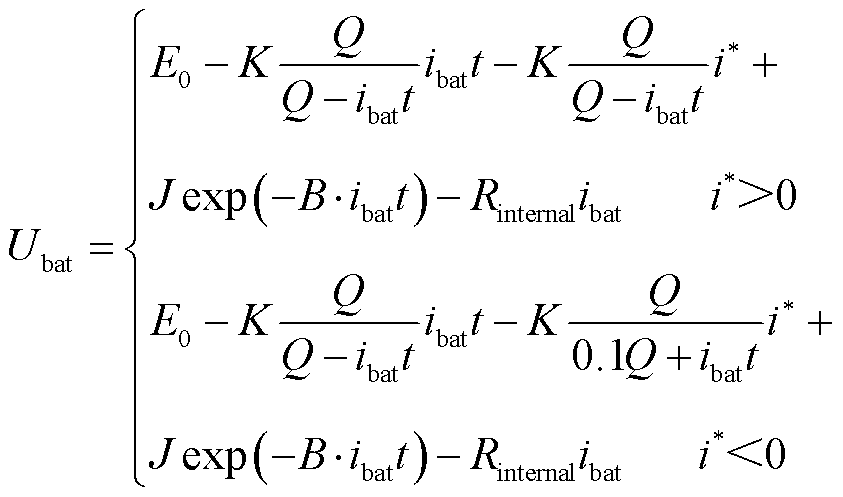 (11)
(11)
式中,E0为电池单体端电压;K为极化常数;Q为电池容量;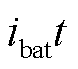 为电池充放电容量;
为电池充放电容量;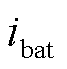 为电池电流;i*为滤波后的输出电流;J为指数电压系数;B为指数容量系数;Rinternal为电池内阻。
为电池电流;i*为滤波后的输出电流;J为指数电压系数;B为指数容量系数;Rinternal为电池内阻。
动力电池荷电状态(State of Charge, SOC)的定义为
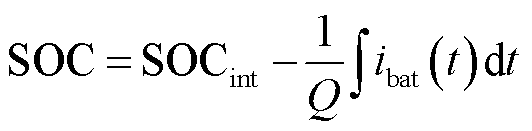 (12)
(12)
式中,SOCint为SOC初始值。
为了验证模型的输出特性,对电池模型单体在额定条件下进行放电测试,结果如图6所示。曲线与苏州星恒公司提供的相同条件下的测试结果基本吻合,说明所建模型可靠,可以在线应用。
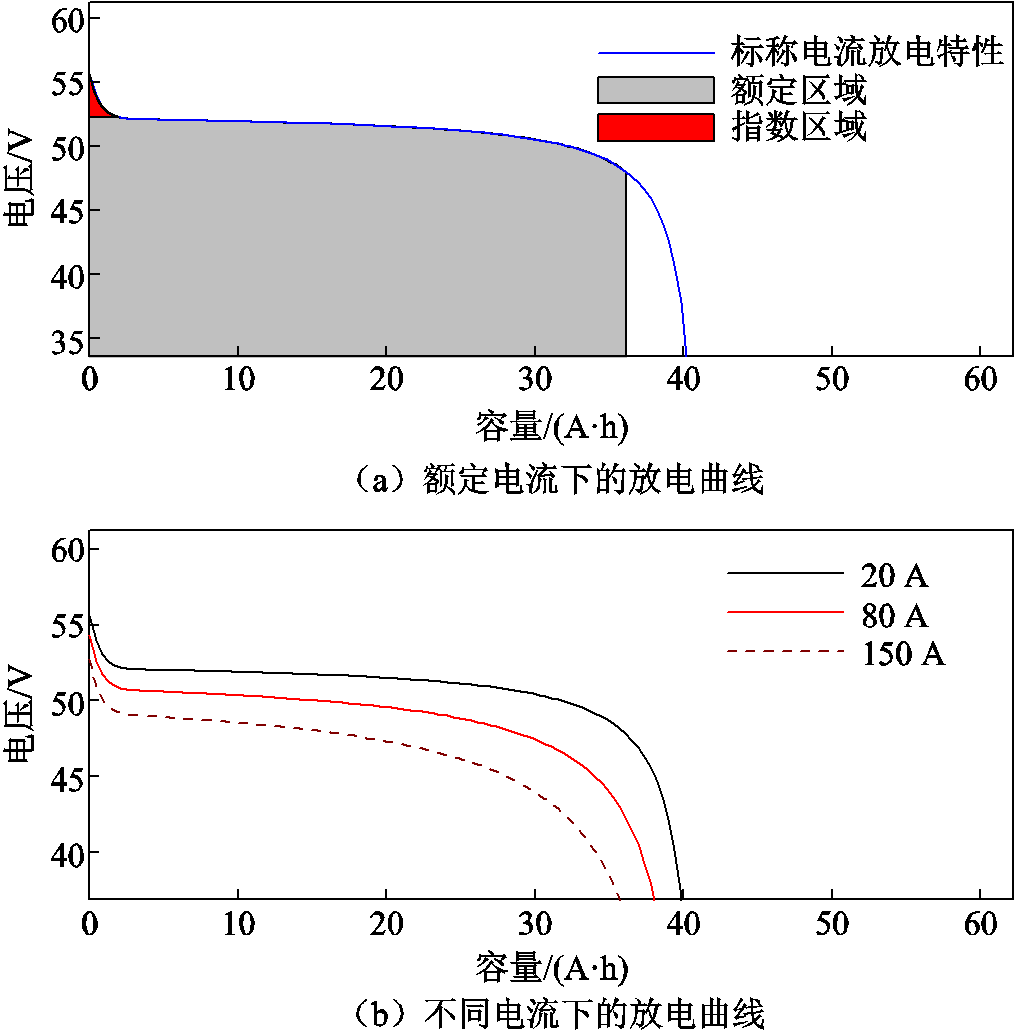
图6 动力电池放电特性仿真曲线
Fig.6 Simulation curves of power battery discharge characteristics
超级电容器主要由两个电极、电解质和多孔碳组成,其性能特点与动力电池的性能特点相辅相成。搭建将Helmholtz模型和Gouy Chapman模型结合的Stern 模型,如图7所示。
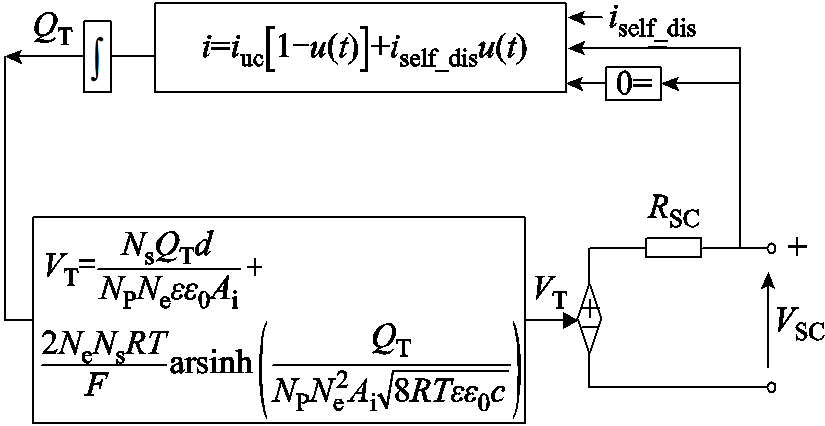
图7 超级电容模型
Fig.7 Supercapacitor model
超级电容的双电层电容是由紧密层电容和扩散层电容构成的,因此电容表示为
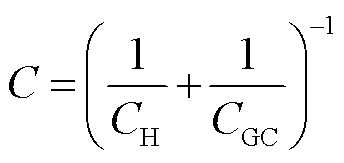 (13)
(13)
式中,CH为紧密层电容;CGC为扩散层电容。
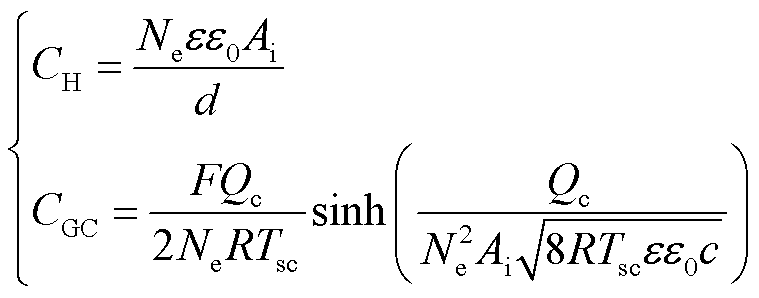 (14)
(14)
式中,Ne为极板层数;ε和ε0分别为电解质材料相对介电常数和真空介电常数;Ai为电极和电解质之间的界面面积;d为双电层距离;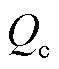 为电量;
为电量;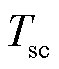 为运行温度;c为体积摩尔浓度。
为运行温度;c为体积摩尔浓度。
对于Ns 个串联电池和Np个并联电池组成的超级电容器模块,总电容值为
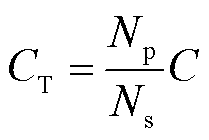 (15)
(15)
考虑到电阻损耗,超级电容器的输出电压表示为
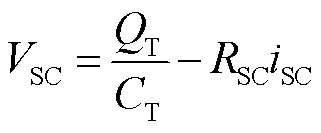 (16)
(16)
其中
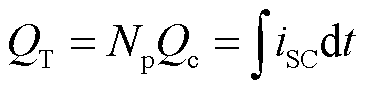 (17)
(17)
式中,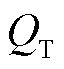 为总电荷;RSC为超级电容的电阻;iSC为超级电容的电流。
为总电荷;RSC为超级电容的电阻;iSC为超级电容的电流。
为了验证模型精度,分别在20、100、200、400 A的条件下进行放电极化测试并与真实数据曲线进行对比。对比结果如图8所示,曲线基本吻合,稳态误差率在2%以内,表明模型能够高精度还原超级电容的输出特性。
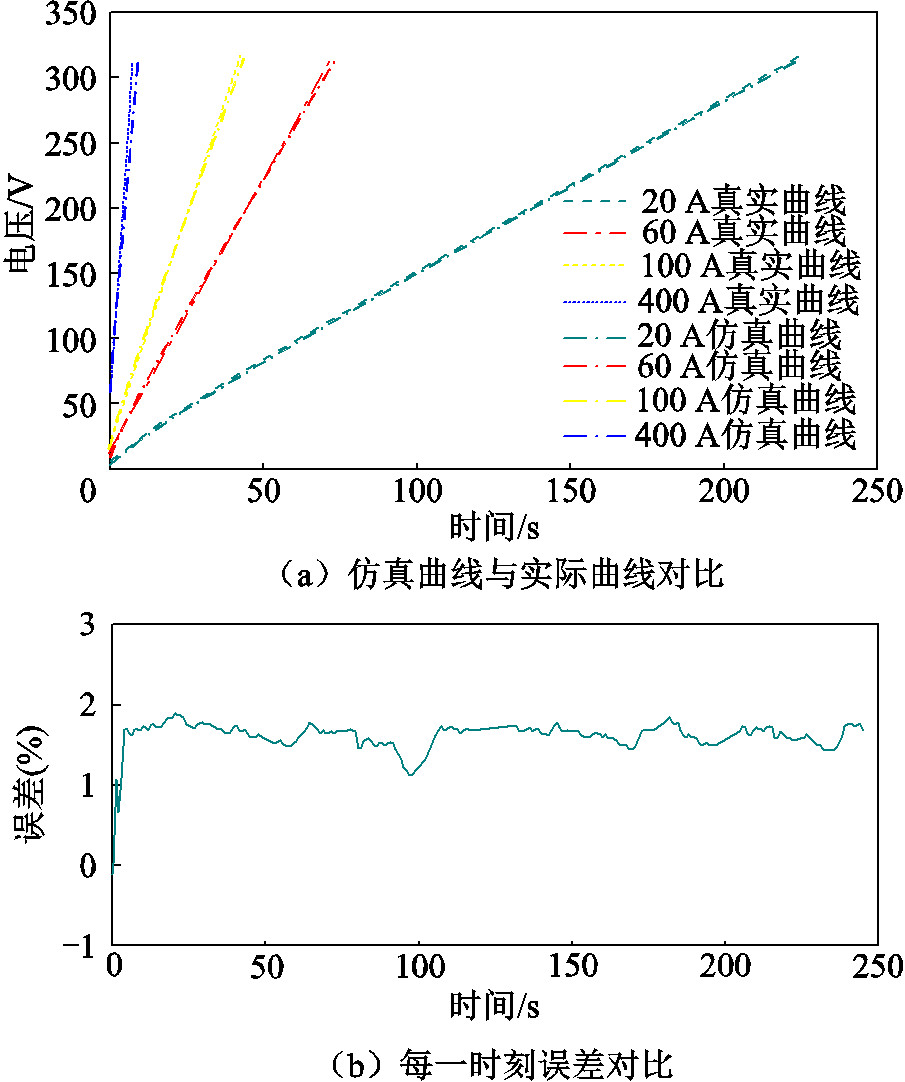
图8 超级电容模型精度测试结果
Fig.8 Results of supercapacitor model accuracy test
ECMS 是一种基于瞬时成本函数的优化策略,其目的是在保证能源平稳运行的情况下,通过最大限度地减少燃料电池消耗的燃料以及维持电池 SOC 所需的等量燃料,将全局优化问题转换为某一时刻等效氢气消耗量最小的瞬时优化问题,从而使混合动力系统的总氢气消耗量最小。ECMS控制示意图如图9所示,其通过输入的负载功率Pload和动力电池当前的SOC,实时优化燃料电池系统的输出功率Pfc,从而使系统瞬时氢耗量最优,最终达到全局最优。
ECMS优化算法的目标函数为
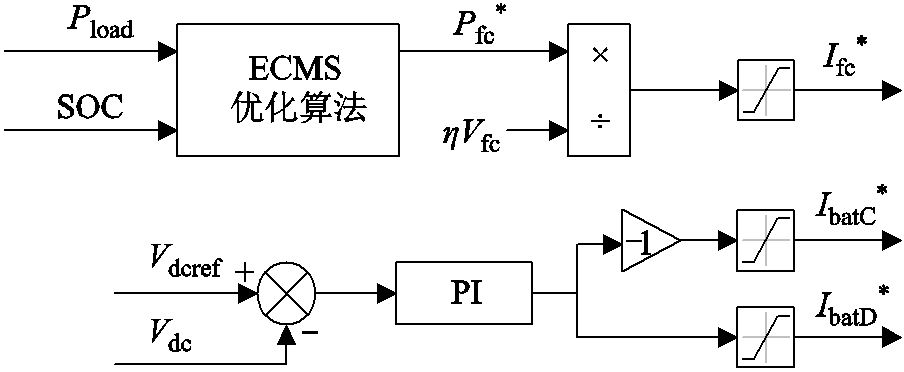
图9 ECMS控制示意图
Fig.9 Control schematic of ECMS
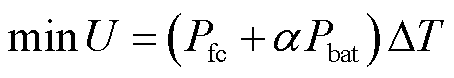 (18)
(18)
约束条件为
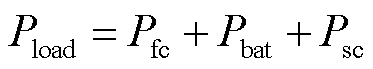 (19)
(19)
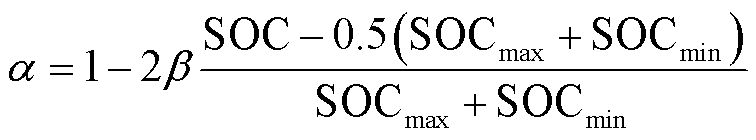 (20)
(20)
边界条件为
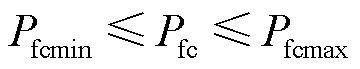 (21)
(21)
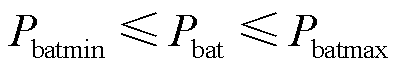 (22)
(22)
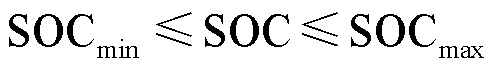 (23)
(23)
式中,Pfc、Pbat、Psc、Pload分别为燃料电池功率、动力电池功率、超级电容功率、负载功率;α为惩罚系数;ΔT为采样时间;Pfcmin和Pfcmax分别为燃料电池的最小功率和最大功率;Pbatmin和Pbatmax分别为动力电池的最小功率和最大功率;SOCmin和SOCmax分别为动力电池SOC的最小值和最大值;β为SOC的平衡系数。
由于直流母线电压由电池转换器控制,因此优化问题中不考虑超级电容器功率。也就是说,一旦超级电容器放电,它们就会被电池系统以相同的能量重新充电。所以,在给定的负载周期内,总负载能量仅由燃料电池和动力电池共享。
马尔可夫链可用于描述离散的随机过程。根据一阶马尔可夫假设,可以根据当前时刻的状态值预测下一时刻的状态值,而且主要的统计特征不会随时间变化,这意味着马尔可夫链是一个平稳分布[20]。因此,从贝叶斯统计的角度来看,可以通过在支持后验分布的样本空间中使用蒙特卡洛方法得到这个随机过程的下一个可能状态,即可以通过在平稳分布中采样预测马尔可夫链的状态,因此采用马尔可夫链蒙特卡洛(Markov Chain Monte Carlo, MCMC)模型进行工况预测。
在车辆实际行驶过程中,工况的变化具有马尔可夫特性。因此,根据历史行驶周期的数据,可以建立运行工况的马尔可夫模型[21]。在确定转移概率矩阵时,以需求功率为状态,建立需求功率的概率转移矩阵。不同状态之间的转移概率可以通过式(24)的最大概率来估算。
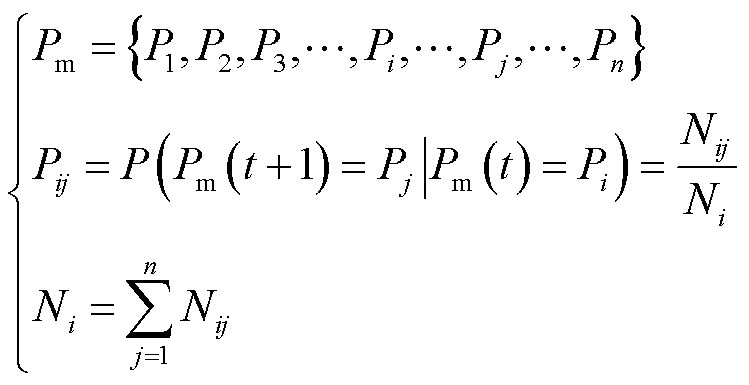 (24)
(24)
式中,Pm为需求功率分为n个状态的集合;Pij为在某一速度下从功率 Pi到Pj的转移概率;Nij为从Pi到Pj的次数;Ni 为状态Pi产生的总次数。
根据驾驶工况下的需求功率变化,需求功率转移概率矩阵的计算流程如图10所示。
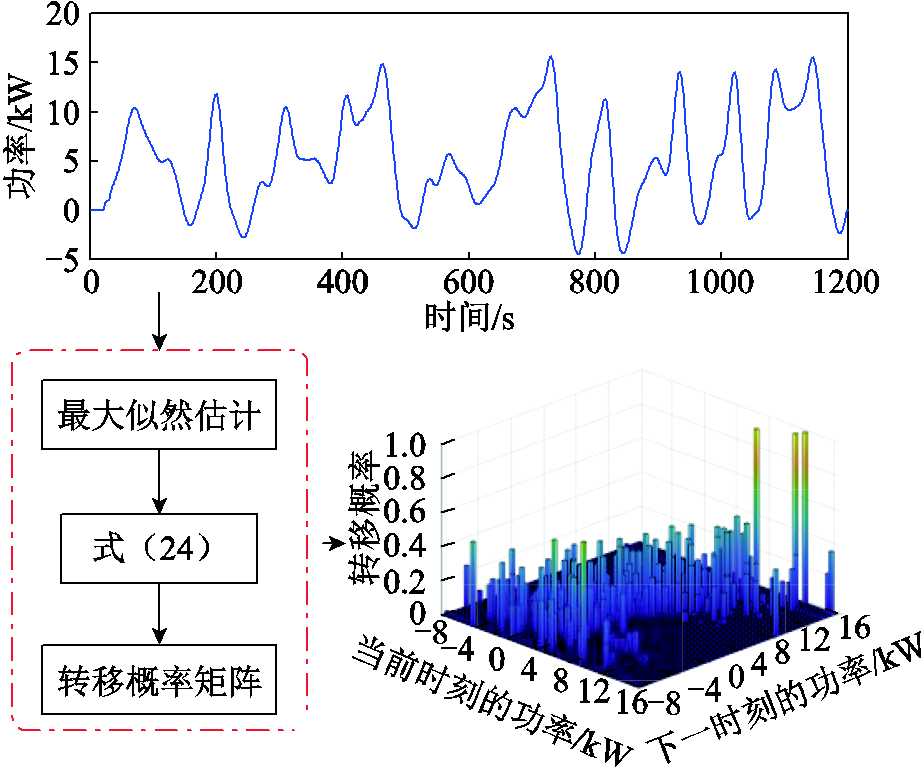
图10 负载功率转移概率矩阵计算流程
Fig.10 Process of calculating the demand power transition probability matrix
为了提高预测的准确性,将工况分为三个具有代表性的工况:低速、中速和高速。需求功率与工况类型的对应关系见表1。通过对输入的需求功率进行逻辑判断,确定需求功率的值属于哪一区间,进而确定工况类型。
表1 需求功率与工况类型对应关系
Tab.1 Relationship between demand power and operating conditions

工况类型速度/(km/h)需求功率/kW 低速0~20-5~4 中速20~404~10 高速40~6010~16
在不同工况下的预测仅基于当前状态,当前状态可模拟为静态马尔可夫链。因此,将工况的变化视为需求功率的变化,从而通过MCMC方法预测几秒钟内的需求功率。三种典型工况下的转移概率矩阵如图11所示。
通过获得的需求功率状态转移概率矩阵可以预测未来行驶过程中的功率需求。由于MCMC预测模型的收敛特性,当预测的时间长度达到一定步长时,就会出现连续预测的稳定分布,所以预测精度有所提高。
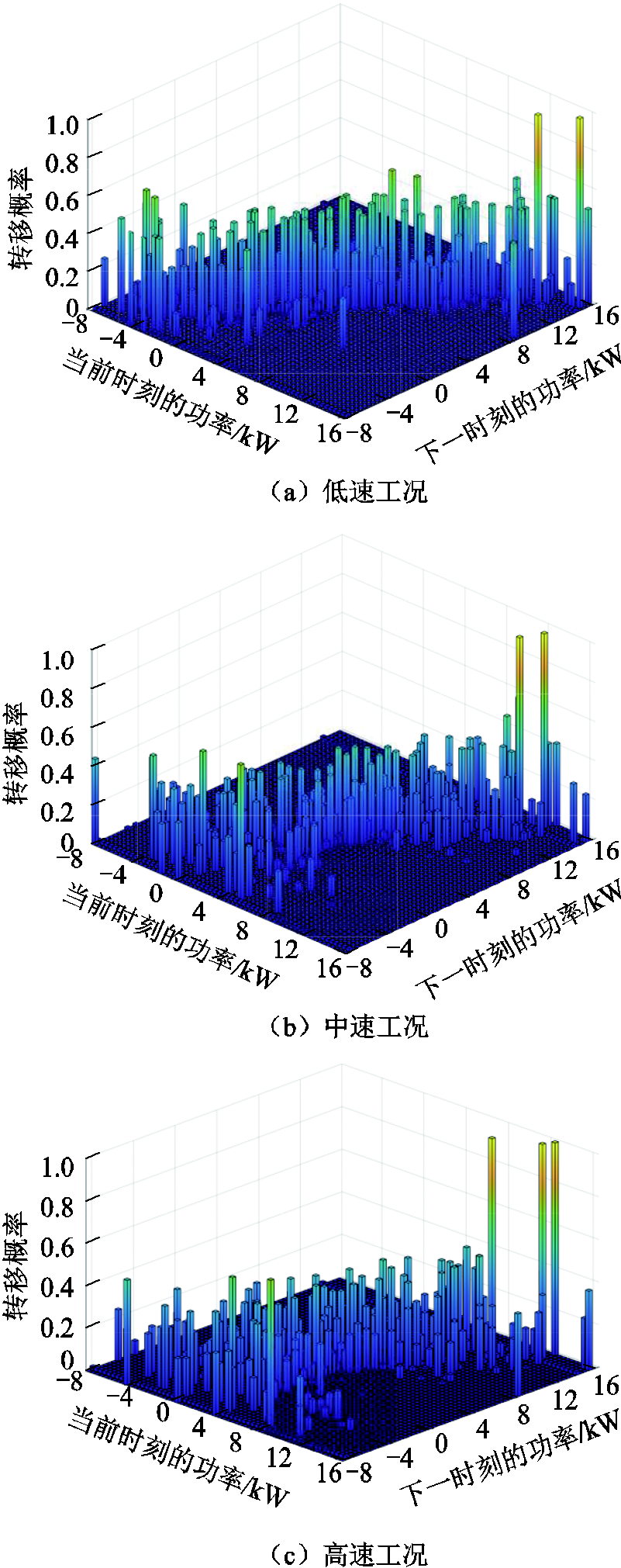
图11 不同工况下的转移概率矩阵
Fig.11 Transition probability matrixes under conditions
车辆在行驶过程中,当前时刻需求功率为P0,下一时刻需求功率Pm(1)的条件分布为
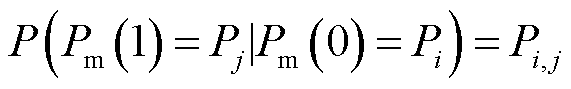 (25)
(25)
在满足均匀分布的条件下,生成一个随机数r1,若满足式(26),则按式(27)取下一刻预测电机需求功率P1,即Pm(1)=P1。以此类推,分别取随机数r2,…,rK。最后,K时刻预测的需求功率为PK。预测流程如图12所示。
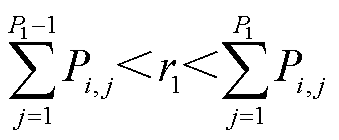 (26)
(26)
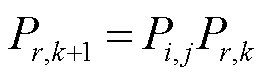 (27)
(27)
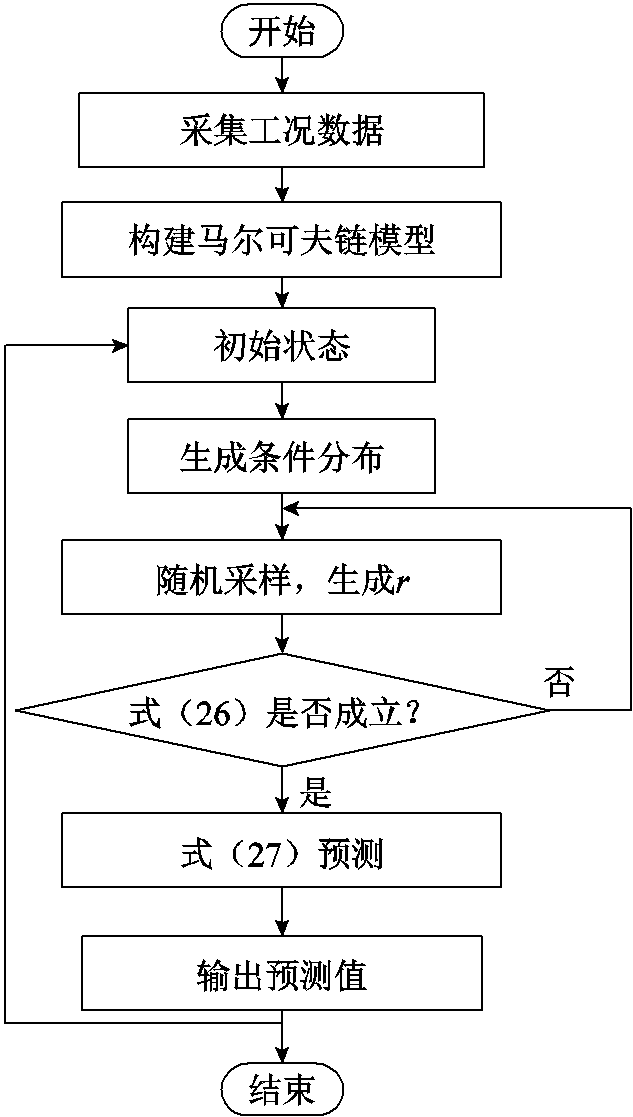
图12 预测模型流程
Fig.12 Predictive modeling flow chart
进行工况预测的最终目的是为有轨电车能量管理策略做铺垫,对工况进行多步预测从而为优化系统能量分配提供更多信息。预测精度将直接影响能量管理策略的性能,随着预测时域的增加,预测精度会越来越低[22]。考虑有轨电车工况的适应性,选取国内某有轨电车工况,采样时间为1 s,分别对预测时域为2、5、10 s进行预测,预测瞬态误差范围分别为±2%、±5%和±7.5%,因此选择预测时域为2 s进行预测,预测结果对比分析如图13所示。
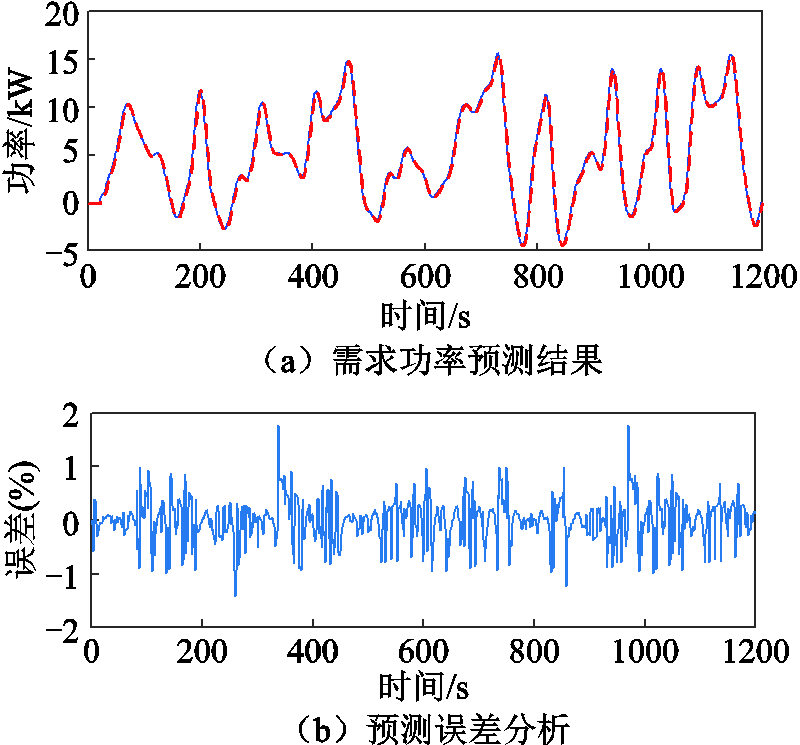
图13 预测结果对比分析
Fig.13 Comparative analysis of forecast results
从图13中可以看出,需求功率预测曲线与实际需求功率曲线比较贴合,并且预测瞬态误差在±2%以内,说明MCMC预测模型可以较准确地对需求功率进行预测,为后续能量管理策略的实际应用提供保障。
在瞬时优化控制策略的优化过程中,可以通过加权因子引入燃料消耗、燃料电池寿命、动力电池寿命等多个目标进行多方面的折中综合优化,同时建立了一个包括经济模型和寿命模型的系统模型,兼顾多目标进行优化以提高燃料电池的耐用性并最大限度地降低成本,构建了整车能量管理策略框架。
2.4.1 氢气消耗模型
燃料电池氢气消耗计算式为
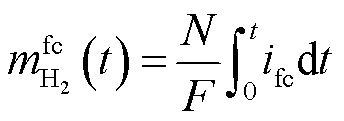 (28)
(28)
根据等效氢耗理论,动力电池等效氢耗的计算式为
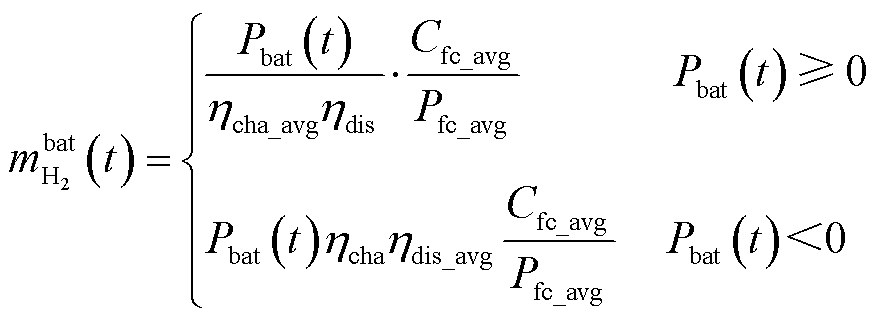 (29)
(29)
式中,Cfc_avg为单位时间内燃料电池平均等效氢气消耗量;Pfc_avg为单位时间内燃料电池平均功率;𝜂dis、𝜂chg、𝜂chg_avg、𝜂dis_avg分别为动力电池的放电、充电、平均充电、平均放电效率。
系统总氢耗量为
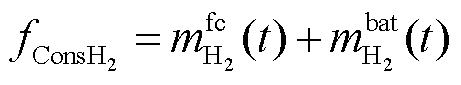 (30)
(30)
2.4.2 燃料电池性能衰退模型
FC的性能衰退主要取决于FC的运行功率和启停次数,运行功率越小,启停次数越多,FC的性能衰退也越快,其连续表征模型计算公式[23]为
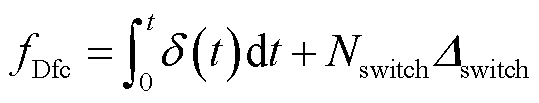 (31)
(31)
其中
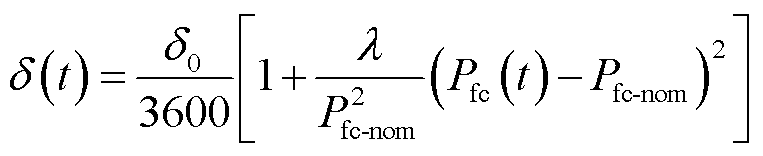 (32)
(32)
式中,Nswitch为FC的启动次数;Δswitch为启停降解系数;δ0和λ为负载系数;Pfc-nom为FC的额定功率。性能衰退函数fDfc取值范围在0(寿命开始)~1(寿命结束)之间。
2.4.3 动力电池性能衰退模型
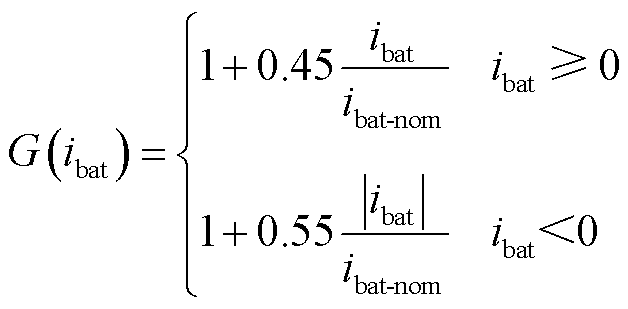
动力电池的性能衰退取决于其SOC和瞬态功率。电池中的大电流,尤其是大充电电流会缩短其使用寿命。SOC变化越大,动力电池性能衰退也越快,其半经验计算公式[24]为
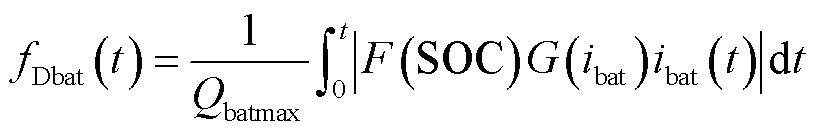 (33)
(33)
式中,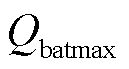 为电池最大容量;F(SOC)为一个加权函数,用于惩罚过多使用SOC导致的电池退化;G(ibat)为一个加权函数,用于惩罚过多瞬态功率导致的电池退化。
为电池最大容量;F(SOC)为一个加权函数,用于惩罚过多使用SOC导致的电池退化;G(ibat)为一个加权函数,用于惩罚过多瞬态功率导致的电池退化。
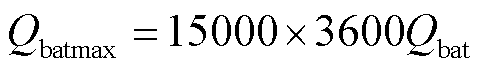 (34)
(34)
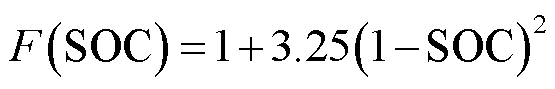 (35)
(35)
 (36)
(36)
式中,Qbat为电池的额定容量;ibat-nom为电池的额定电流。性能衰退函数fDbat取值范围在0(寿命开始)~1(寿命结束)之间。
对等效氢耗量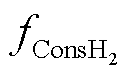 、燃料电池性能衰退
、燃料电池性能衰退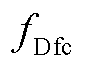 和动力电池性能衰退
和动力电池性能衰退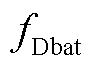 三个目标分别分析定义,最终优化目标为
三个目标分别分析定义,最终优化目标为
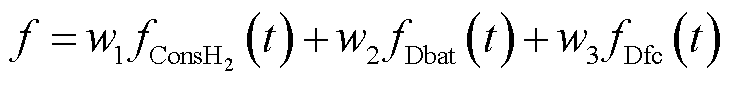 (37)
(37)
式中,w1、w2、w3分别为等效氢耗量、动力电池性能衰退、燃料电池性能衰退三个目标的权重。
目标权重对能量管理策略优化结果的影响较大,不当的权重系数难以使车辆的综合使用性能达到最优。因此,在优化过程中选择在线自适应调整权重的方法,此方法具有较好的灵活性与自适应性,能更好地平衡多目标并进行实时响应和调整,实现更优解。权重动态调整流程如图14所示。
PEMS优化控制原理流程如图15所示,可分为两层,上层进行功率预测,下层进行能量管理。
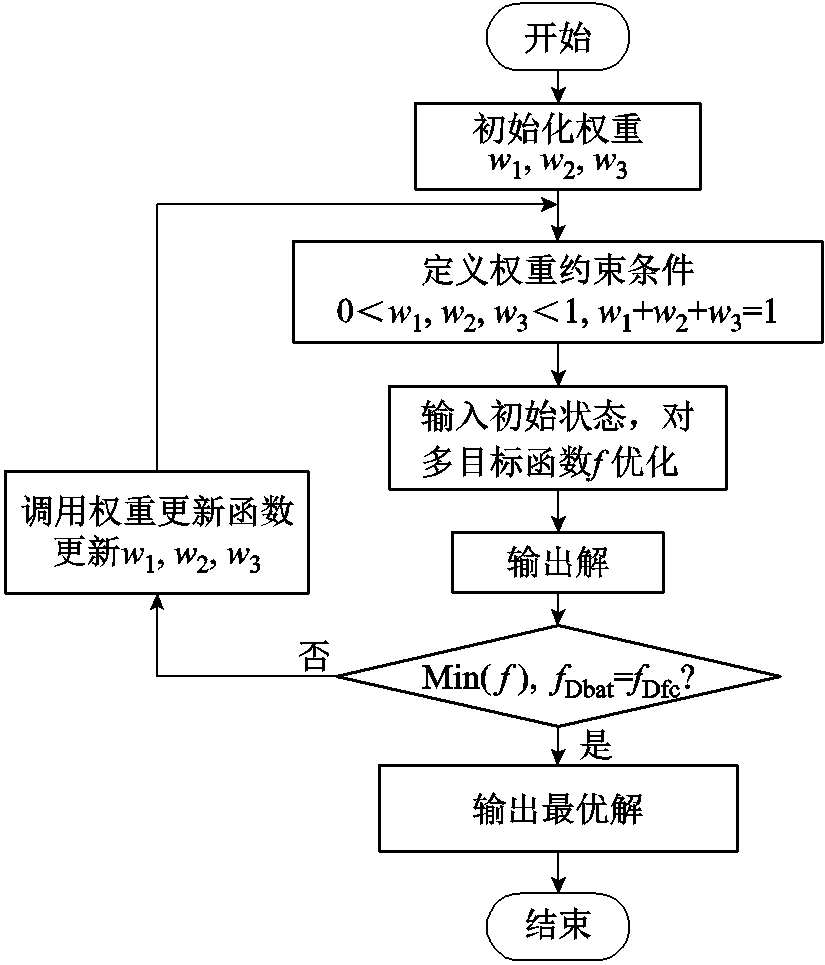
图14 权重动态调整流程
Fig.14 Flow chart for dynamic adjustment of weights
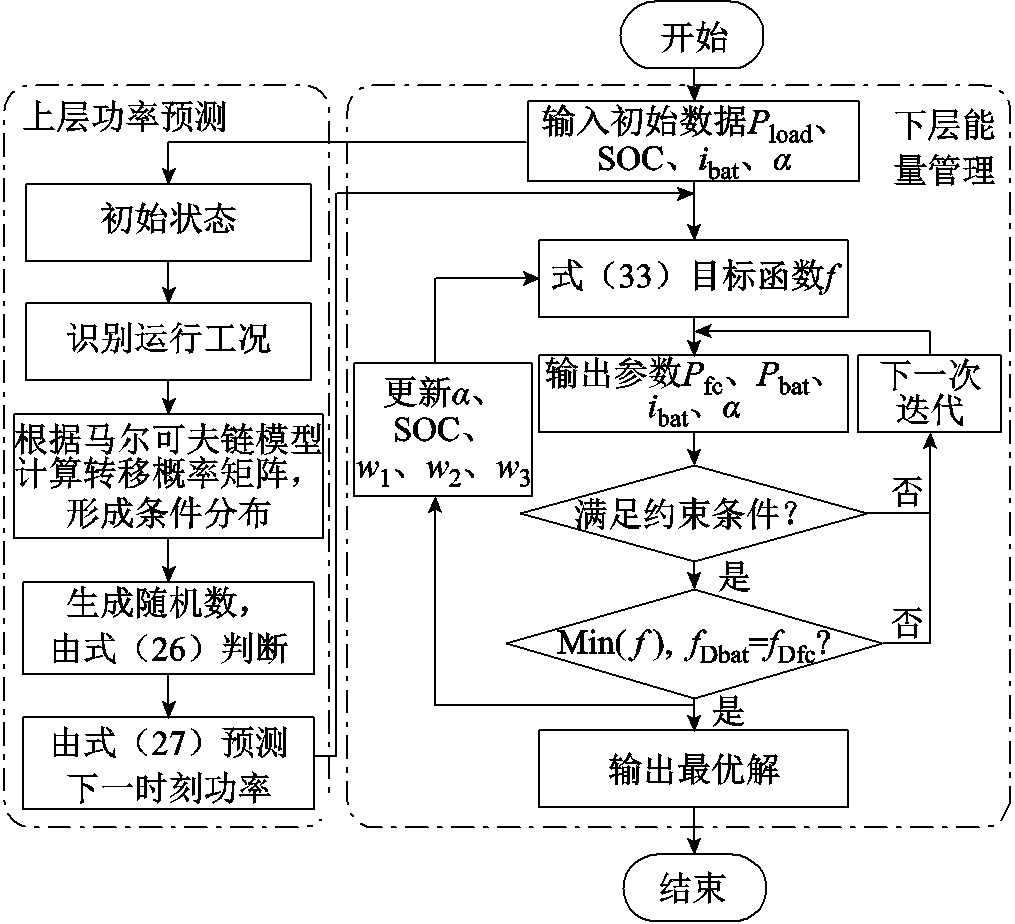
图15 PEMS优化控制原理流程
Fig.15 PEMS optimization control principle flow chart
为了验证所提能量管理策略的有效性和优越性,利用Matlab/Simulink中的Simpowersystem 工具箱搭建如图1所示系统。在相同的仿真参数配置下(见表2),将所提策略与传统ECMS以及EEMS能量管理策略进行仿真验证对比。表2中,1bar=105 MPa。
表2 车载复合电源核心仿真参数
Tab.2 Core simulation parameters of vehicle hybrid power supply

参数数值 燃料电池单体数量/个735 燃料电池堆额定电压/V540
(续)

参数数值 燃料电池堆最大放电电流/A240 燃料电池堆燃料供给压力/bar1.16 燃料电池堆空气供给压力/bar1 燃料电池堆额定效率(%)50 燃料电池堆运行温度/K318.15 动力电池单体数量/个144串2并 动力电池组额定电压/V331 动力电池组最大放电电流/A120 动力电池组初始SOC(%)70 动力电池组额定容量/(A·h)100 超级电容单体数量/个108串1并 超级电容组额定电压/V750 超级电容组运行温度/K298 超级电容组初始SOC(%)85 超级电容组最大电流/A98(持续),1 900(1 s)
负载功率在燃料电池、动力电池和超级电容之间的分配如图16所示。燃料电池提供主功率需求,动力电池和超级电容用于吸收系统制动功率并提供瞬时功率需求。三种策略下各动力源均能满足工况需求,使动力源功率得到合理分配。
如图16a所示,在ECMS下,FC为了兼顾辅助电源的SOC,所以出力较多,导致功率变化率更大,氢气消耗较大,无法保证燃料经济性。如图16b所示,在EEMS中,最大化了辅助电源的出力,虽然这会对燃料经济性有一定的提升,但会导致动力电池在大功率下的工作时间较长,功率波动大且频繁,过度消耗动力电池,造成的衰减更加严重,和燃料电池的衰减程度相差过大,无法保证系统的耐久性。将图16c与图16a、图16b对比可知,PEMS使燃料电池功率曲线更加平滑,有利于延长燃料电池的使用寿命。在整个工况运行期间,燃料电池绝大部分时间处于功率跟随的状态,出力更加合理高效,减小了氢耗量,并且避免了对辅助电源的频繁充放电,进而辅助电源功率变化率及幅值减小,曲线更加平滑,减小了对辅助动力源的伤害。
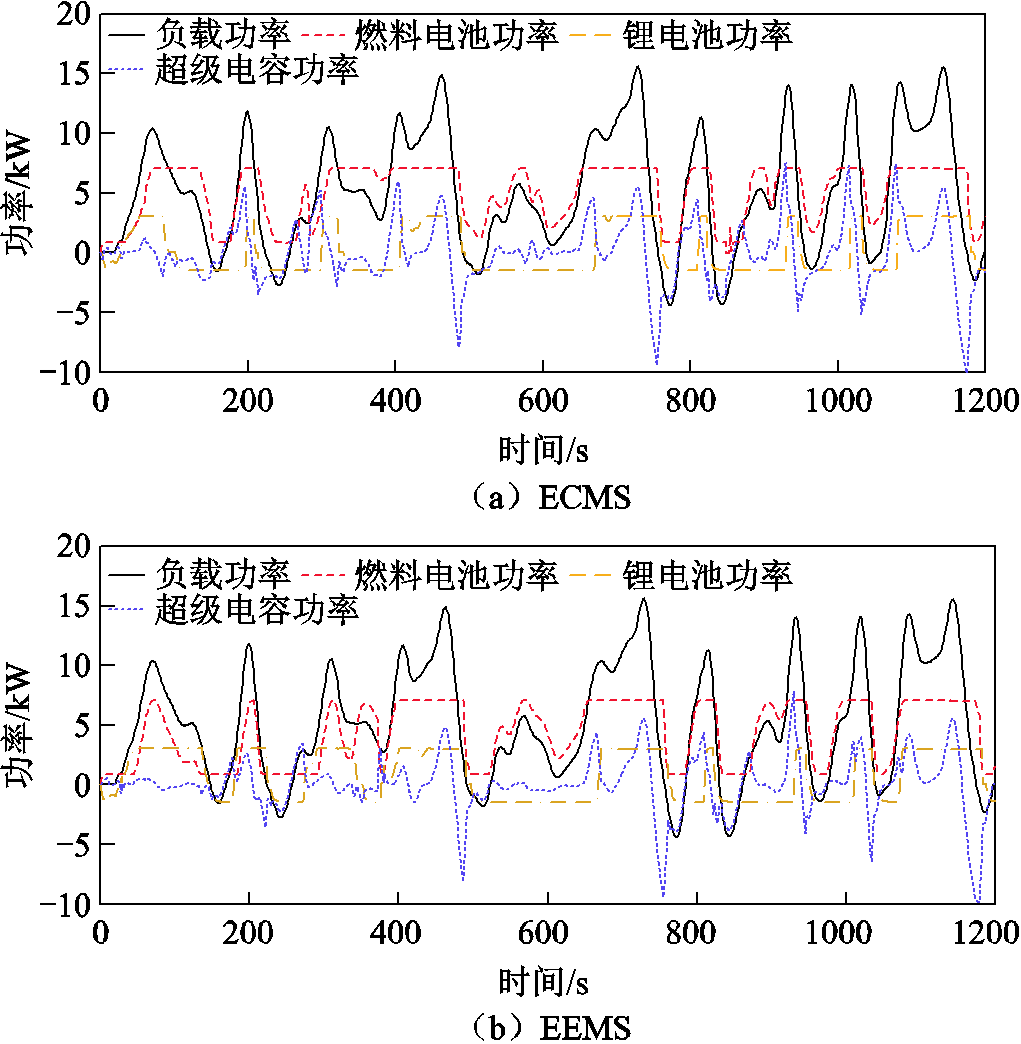
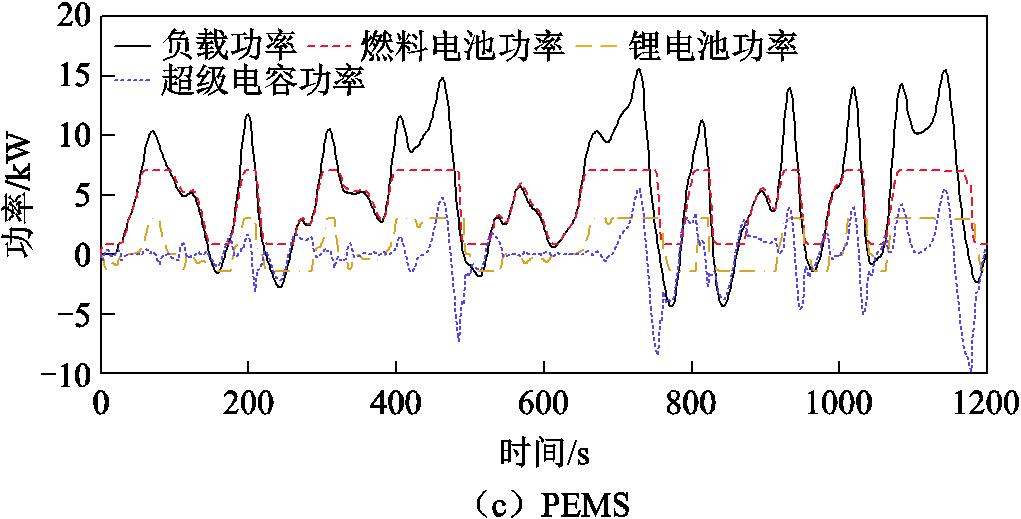
图16 三种能量管理策略下的功率分配对比
Fig.16 Comparison of power allocation under three energy management strategies
综上所述,所提策略能更高效地分配动力源功率,使功率曲线更加平滑,减小各动力源性能的衰退,在提升燃料经济性的同时保证系统耐久性。
各策略下的总体耗氢量和动力电池SOC变化如图17所示。在ECMS、EEMS和PEMS下,整个工况运行结束时,总氢耗量分别为115.1、98.61、99.61 g,最终SOC值分别为58.59%、46.66%、50.05%。
PEMS的燃料经济性相较于ECMS提高了13.46%,但SOC的变化范围增加了8.54个百分点,这是因为ECMS策略具有最小化动力电池和超级电容等效能耗的特点,导致辅助电源出力不足,不能给予燃料电池足够的支持,并且由于α的存在,使得燃料电池为了维持动力电池的SOC要多出力,因此燃料电池内部能耗较大,动力电池SOC变化小。PEMS汲取了EEMS的优点,实现了燃料经济性的提高,和EEMS燃料经济性接近,并且克服了EEMS最大的缺点,使动力电池SOC变化范围减小了14.5个百分点。这是由于EEMS的主旨是最大化动力电池和超级电容消耗,从而减小了燃料电池消耗,动力电池SOC变化更大,这会使得两者性能衰减出现两极分化的情况。
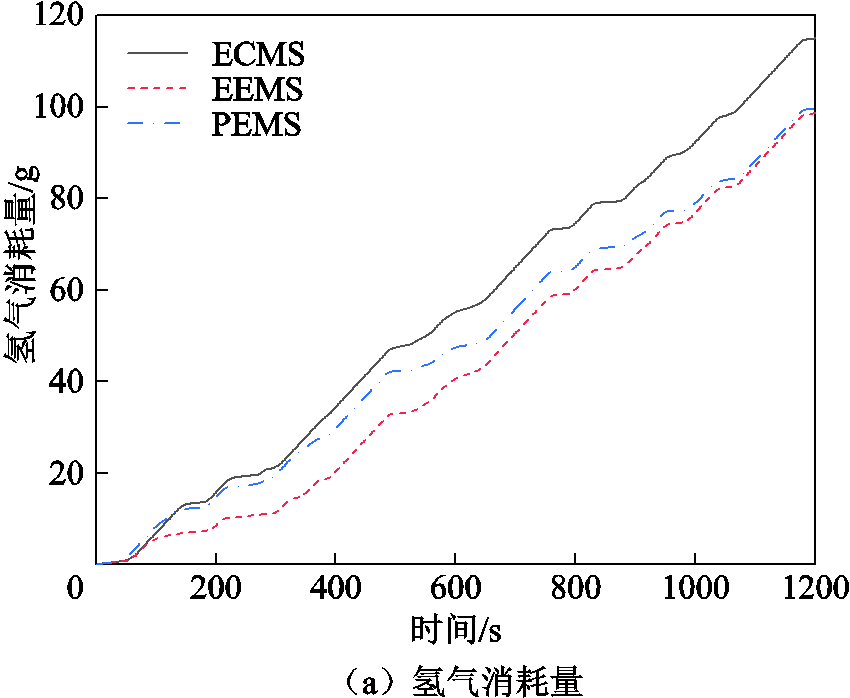
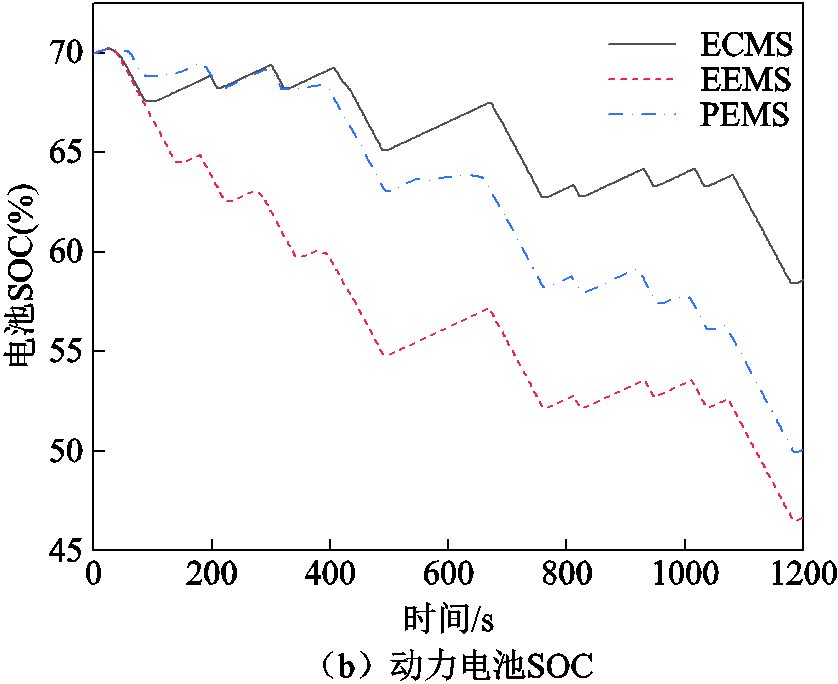
图17 三种策略下的氢气消耗量和锂电池SOC对比
Fig.17 Comparison of hydrogen consumption and SOC of lithium battery under three strategies
综上所述,PEMS可以在确保燃料经济性的同时使得动力电池SOC的变化范围减小,使其保持在合理的范围。
三种能量管理策略下的双主出力电源寿命衰减率如图18所示。在工况结束时,ECMS、EEMS和PEMS下双动力源寿命衰减率差值分别为0.000 55%、0.014 4%、0.000 66%。
PEMS、ECMS与EEMS相比,双动力源寿命衰减率差值分别减小了约95.42%和96.18%,主要原因就是EEMS下对动力电池的消耗太大,而忽略了燃料电池,造成两者使用的程度相差过大,因此使衰减率相差过大。ECMS下衰减率差最小,这是在牺牲燃料经济性的基础之上实现的。为了避免动力电池的过度使用,燃料电池会为动力电池进行充电,因此燃料消耗量大,造成燃料经济性和动力源寿命协同衰减不能兼优。
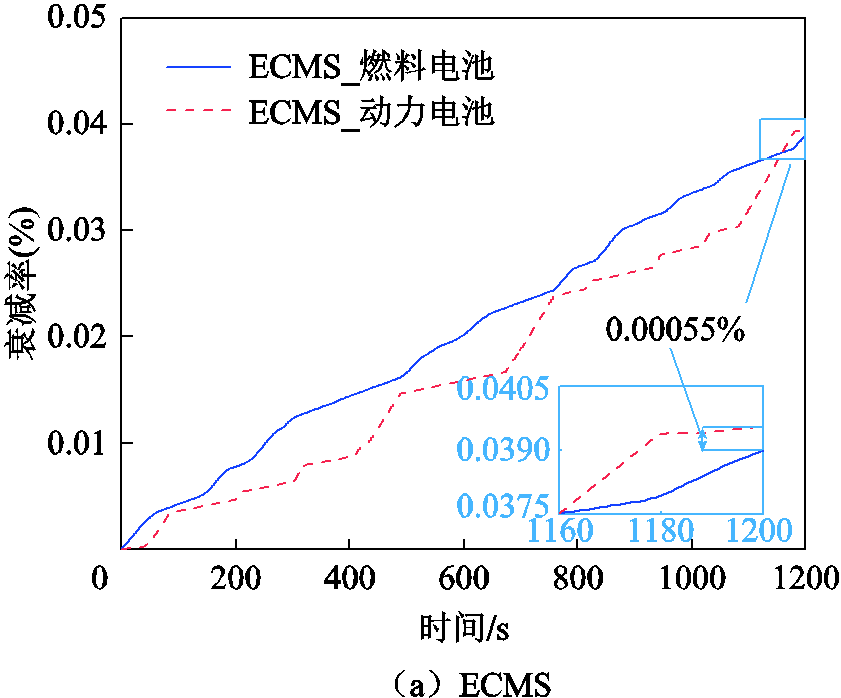
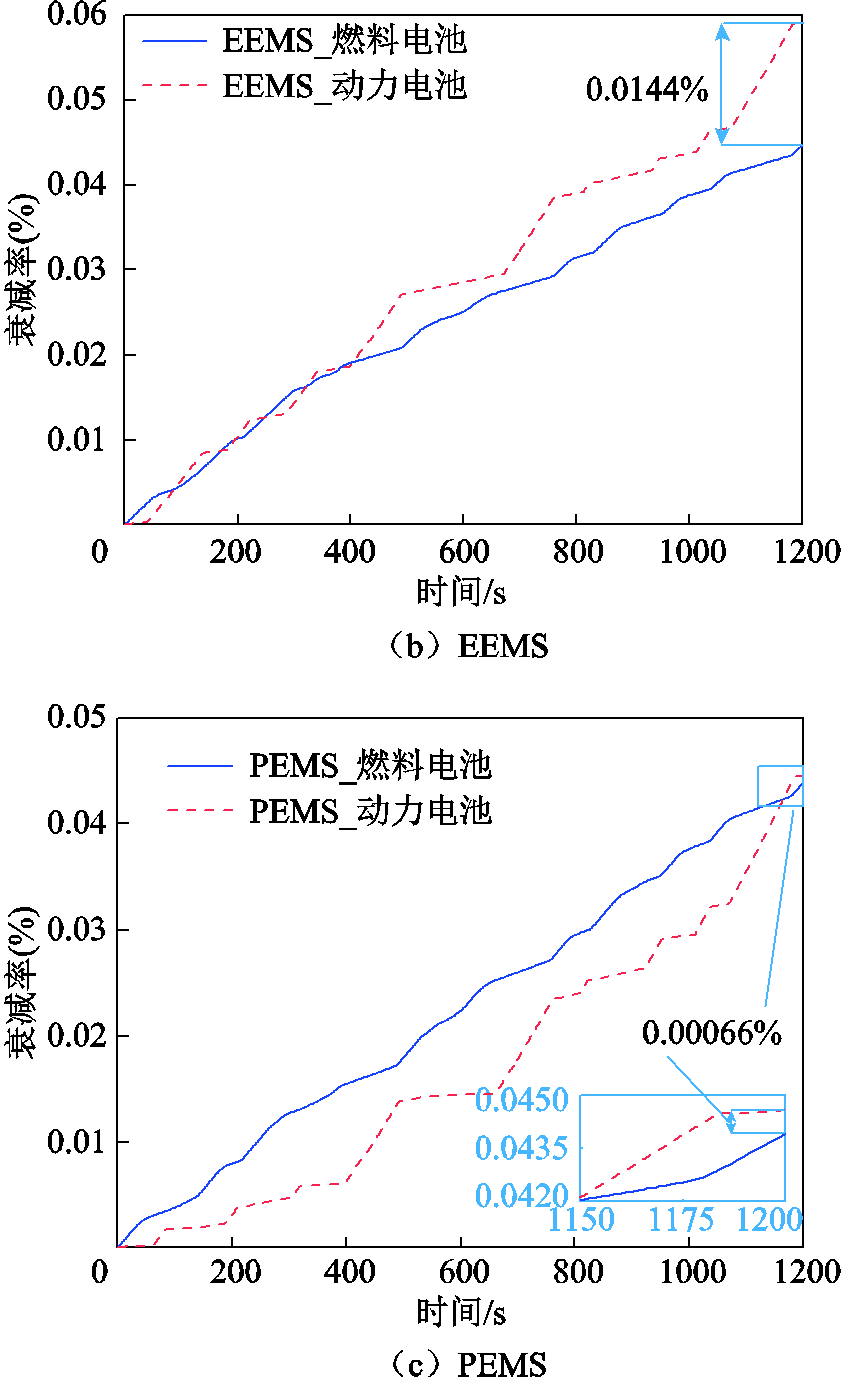
图18 三种策略双动力源寿命衰减率对比
Fig.18 Comparison of dual power source decay rates under three energy management strategies
综上所述,PEMS中考虑了燃料经济性与燃料电池和动力电池的衰减协同,可以使燃料电池和动力电池的寿命衰减趋于一致,以上结果证明了PEMS在实现燃料电池混合动力系统双主出力动力源衰减协同管控方面具有较好的控制效果,能够实现燃料经济性与动力源寿命衰减协同的兼优。
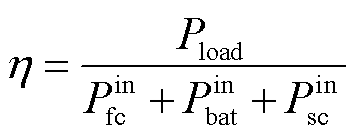
为了验证不同策略下系统的效率,采用功率转换度的思想,将其定义为
 (38)
(38)
式中,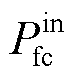 、
、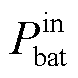 和
和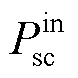 分别为输入燃料电池、动力电池DC-DC 变换器的功率及超级电容的功率。
分别为输入燃料电池、动力电池DC-DC 变换器的功率及超级电容的功率。
ECMS、EEMS和PEMS下系统效率对比如图19所示。系统平均效率分别为77.64%、79.77%、81.66%,PEMS下平均效率最高,相较于ECMS和EEMS分别提高了5.2%、2.4%,证明PEMS策略能够保证整个系统的高效运行。
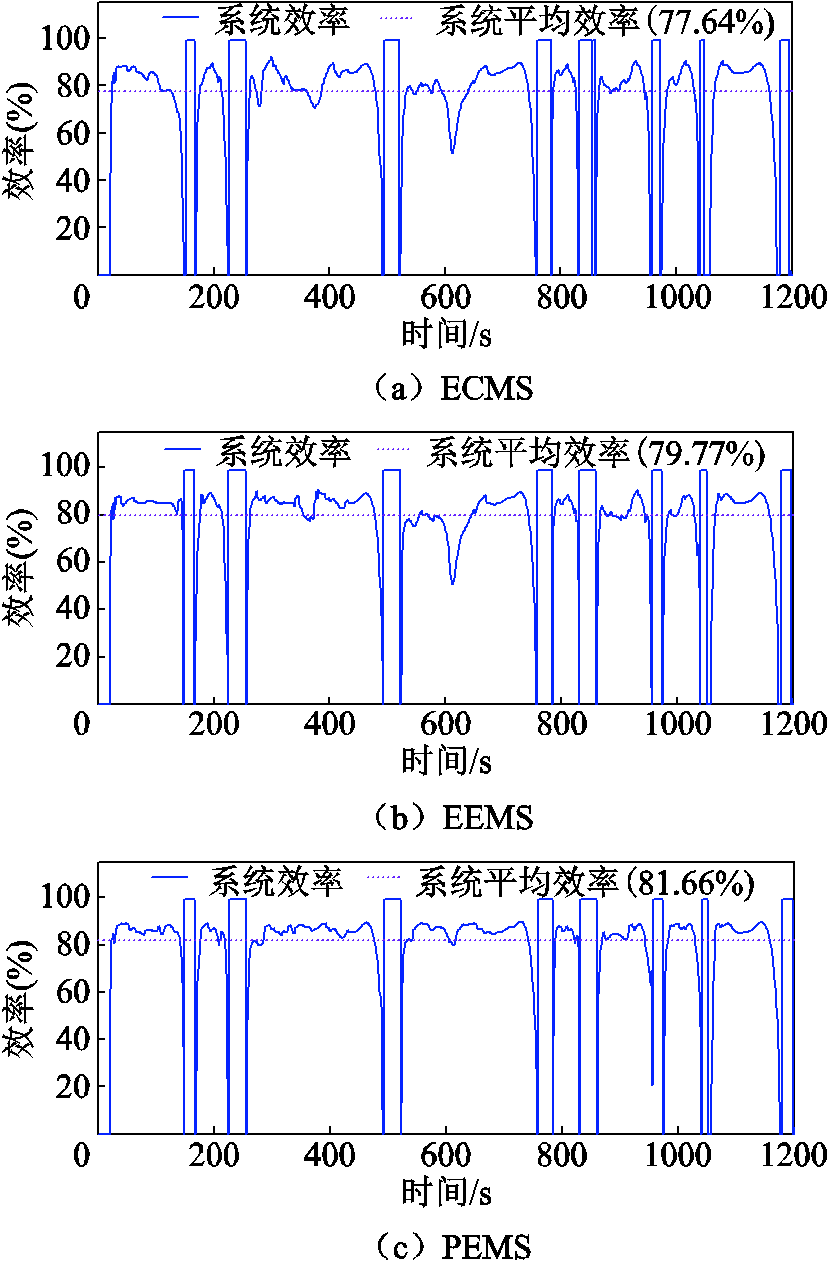
图19 各策略下系统效率对比
Fig.19 Comparison of system efficiency under strategies
电源工作应力越低,输出功率波动的频率和幅度越小,越有利于保持电源的性能[25]。因此,根据Harr小波变换得到的高频分量的标准差σ,可以有效地表示动力源应力。
各策略下动力源应力分析对比如图20所示。PEMS下的动力源功率波动范围为-800~800 W,而ECMS和EEMS下功率波动范围为-1 000~ 1 000 W,说明所提策略可以更好地减小功率波动,提高动力源的耐久性。如图20所示各策略下的动力源应力,PEMS、ECMS和EEMS下BAT的应力分别为117.5、156.6、156.8,SC应力分别为176.4、215、226.6。PEMS下辅助动力源的应力相较于ECMS和EEMS均减小,并且FC和BAT的应力差值减小,这说明所提策略可以有效地降低输出功率波动的频率和幅值,有利于减缓动力源性能的衰退,降低等效氢耗,有助于FC和BAT的寿命衰减趋于一致,从而提升燃料经济性和系统耐久性。
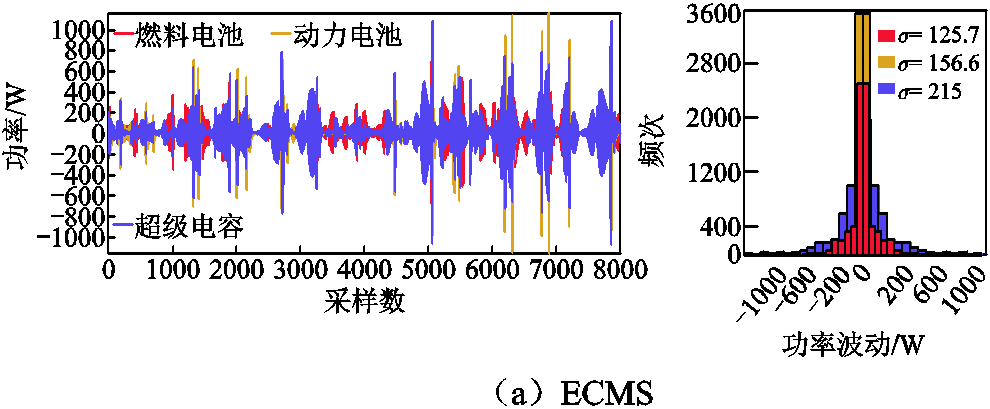
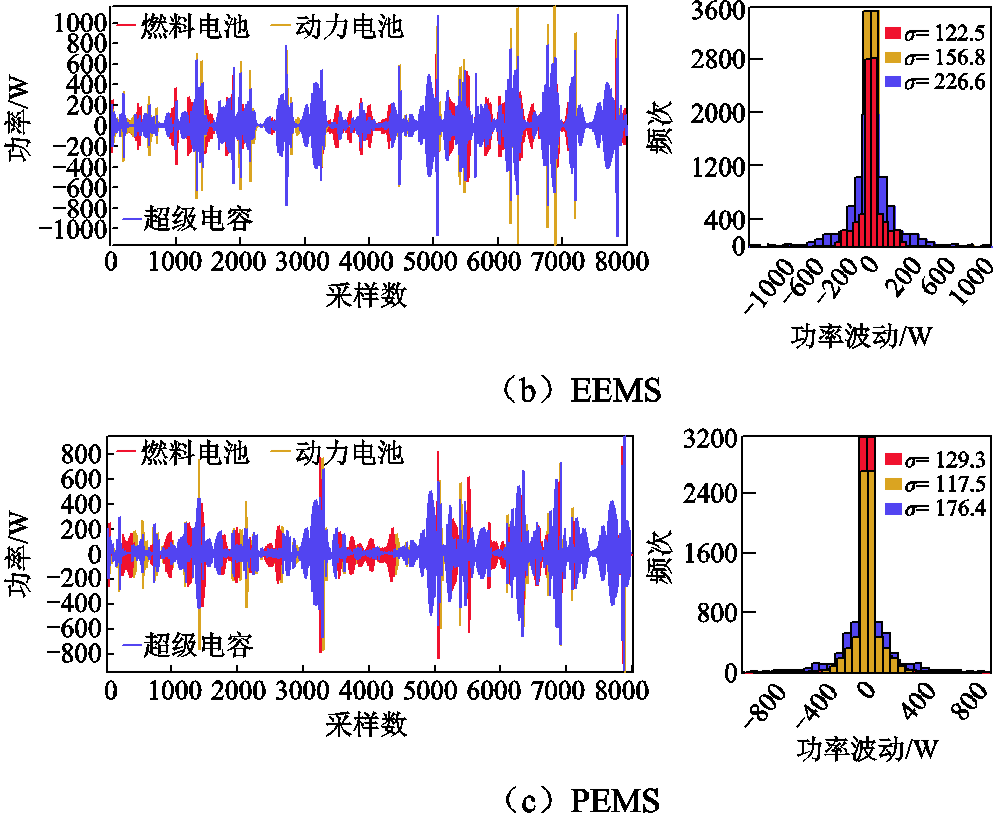
图20 各策略下动力源应力分析对比
Fig.20 Comparison of power sources stress analysis under each strategy
各策略主要结果对比见表3。由表3可知,PEMS解决了ECMS燃料经济性不佳与EEMS动力源衰减不一致导致系统耐久性变差的问题,实现了系统效率的提升,燃料经济性与系统耐久性兼优。
表3 各策略结果对比
Tab.3 Comparison of results by strategies
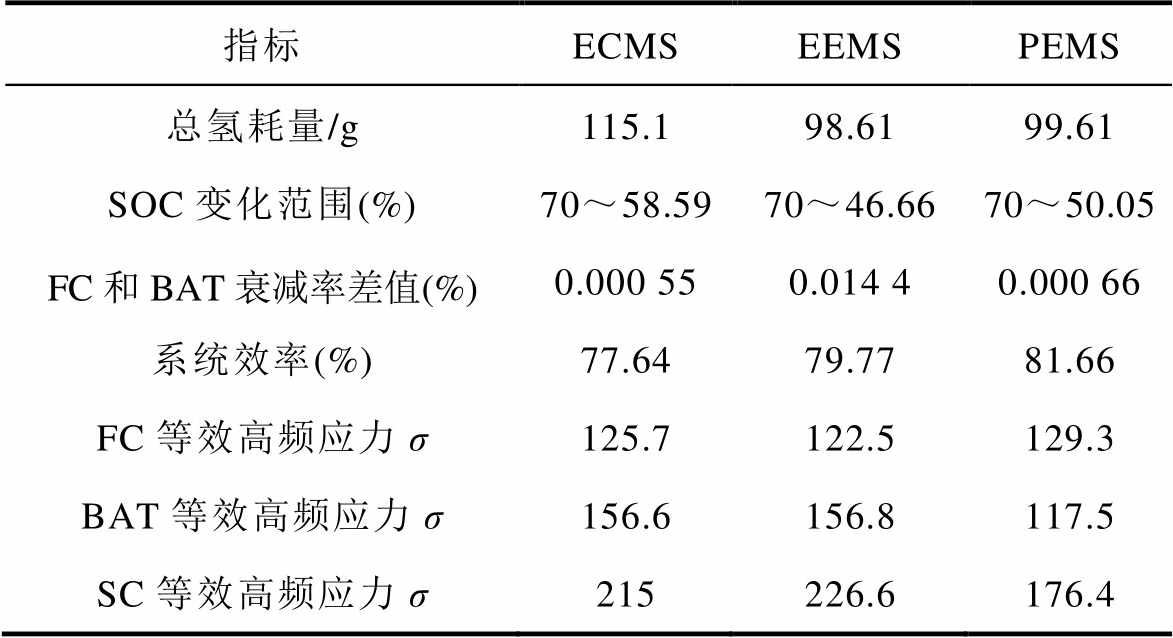
指标ECMSEEMSPEMS 总氢耗量/g115.198.6199.61 SOC变化范围(%)70~58.5970~46.6670~50.05 FC和BAT衰减率差值(%)0.000 550.014 40.000 66 系统效率(%)77.6479.7781.66 FC等效高频应力σ125.7122.5129.3 BAT等效高频应力σ156.6156.8117.5 SC等效高频应力σ215226.6176.4
为实现燃料电池混合动力系统的燃料经济性和整体耐用性的兼优,提出了基于工况识别与动力源寿命衰减协同的燃料电池混合动力有轨电车系统能量管理策略,结论如下:
1)PEMS通过上层工况预测与下层能量管理的结合,克服了传统策略燃料经济性不佳和动力源性能衰减高度不一致的缺点,实现了燃料经济性的提升、动力源寿命衰减协同和系统效率的提升。
2)与ECMS相比,燃料经济性和系统效率分别提升了13.46%和5.2%;与EEMS相比,经济性接近,双动力源寿命衰减率差值减小了95.42%,系统效率提升了2.4%。
所提策略控制结构简单、易于实现,通过仿真在线验证了其有效性和优越性,具有一定的工程实际应用价值,可以为燃料电池混合动力机车系统设计及能量管理优化提供参考。后续将基于此开展多车协同、V2V(vehicleto vehicle)环境下的能量管理策略研究,实现智能网联环境下“人-车-路-云”的车辆多模式、多场景交互综合优化控制。
参考文献
[1] 严锐浩, 许亮.基于模糊控制优化小波分解的FCHEV能量管理策略[J/OL]. 电源学报, 1-12[2025-07-01].http://kns.cnki.net/kcms/detail/12.1420.tm. 20240425.1853.034.html.Yan Ruihao, Xu Liang. Fuzzy control based optimized wavelet decomposition for FCHEV energy management strategy[J/OL]. Journal of Power Supply, 1-12[2025-07-01]. http://kns.cnki.net/kcms/ detail/12.1420.tm. 20240425.1853.034.html.
[2] 陈杰, 陆宇鑫, 王雪钰, 等. 燃料电池/锂电池混合供电系统的分散式鲁棒滑模复合控制[J/OL].中国电机工程学报, 1-12[2025-07-07]. https://doi.org/10. 13334/ j.0258-8013.pcsee.240718. Chen Jie , Lu Yuxin, Wang Xueyu, et al.Decentralized robust sliding mode composite control for the fuel cell/lithium batteryhybrid power supply system [J/OL]. Proceedings of the CSEE, 1-12 [2025-07-07]. https://doi.org/10.13334/j.0258-8013.pcsee.240718.
[3] 李奇, 刘鑫, 孟翔, 等. 基于近端策略优化算法的燃料电池混合动力系统综合价值损耗最小能量管理方法[J]. 中国电机工程学报, 2024, 44(12): 4788-4799. Li Qi, Liu Xin, Meng Xiang, et al. Comprehensive value depletion minimization energy management method for fuel cell hybrid systems based on proximal policy optimization algorithm[J]. Proceedings of the CSEE, 2024, 44(12): 4788-4799.
[4] 蔡良东, 李奇, 刘强, 等. 考虑系统氢耗和耐久性的多堆燃料电池优化控制方法[J]. 中国电机工程学报, 2022, 42(10): 3670-3680. Cai Liangdong, Li Qi, Liu Qiang, et al. Optimal control method for multi-stack fuel cells considering system hydrogen consumption and durability[J]. Proceedings of the CSEE, 2022, 42(10): 3670-3680.
[5] 敖文杰, 陈家伟, 陈杰, 等. 燃料电池-锂电池混合供电系统的无源控制策略及参数设计方法[J].电工技术学报, 2024, 39(2): 580-594. Ao Wenjie, Chen Jiawei, Chen Jie, et al. Passivity-based control strategy and parameter design method forfuel cell-lithium battery hybrid power supply system[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 580-594.
[6] 高锋阳, 宋志翔, 高建宁, 等.计及光伏和储能接入的牵引供电系统能量管理策略[J]. 电工技术学报, 2024, 39(3):745-757. Gao Fengyang, Song Zhixiang, Gao Jianning, et al. Energy management strategies for traction power systems with PV and energy storage access[J]. Transactions of China Electrotechnical Society, 2024, 39(3):745-757.
[7] Zhao Xiuliang, Wang Lei, Zhou Yinglong, et al. Energy management strategies for fuel cell hybrid electric vehicles: classification, comparison, and outlook[J]. Energy Conversion and Management, 2022, 270: 116179.
[8] Kandidayeni M, Macias A, Boulon L, et al. Investigating the impact of ageing and thermal management of a fuel cell system on energy management strategies[J]. Applied Energy, 2020, 274: 115293.
[9] 项鸿博, 裴晓飞, 刘杏, 等. 基于DP的混合动力汽车单踏板控制策略研究[J]. 武汉理工大学学报, 2023, 45(11): 122-131. Xiang Hongbo, Pei Xiaofei, Liu Xing, et al. Research on single pedal control strategy of hybrid electric vehicle based on dynamic programming algorithm[J]. Journal of Wuhan University of Technology, 2023, 45(11): 122-131.
[10] Peng Hujun, Chen Zhu, Deng Kai, et al. A comparison of various universally applicable power distribution strategies for fuel cell hybrid trains utilizing component modeling at different levels of detail: from simulation to test bench measurement[J]. eTrans-portation, 2021, 9: 100120.
[11] 陈恺, 付宇, 孙毅, 等. 基于计算热点转移的5G车联网能量实时协同管理策略[J]. 电工技术学报, 2024, 39(23): 7481-7497. Chen Kai, Fu Yu, Sun Yi, et al. Online energy management strategy for 5g-vehicle network basedon computing hotspot transfer[J]. Transactions of China Electrotechnical Society, 2024, 39(23): 7481-7497.
[12] 高锋阳, 高智山, 强雅昕, 等.计及容量配置优化的有轨电车多阈值能量管理策略[J/OL]. 电源学报, 1-12[2025-07-01].http://kns.cnki.net/kcms/detail/12. 1420.TM.20231219.1227.006.html. Gao Fengyang, Gao Zhishan, Qiang Yaxin, et al. Multi-threshold energy management strategy for trams with capacity configuration optimization[J/OL]. Journal of Power Supply, 1-12[2025-07-01].
[13] 高锋阳, 高翾宇, 张浩然, 等. 全局与瞬时特性兼优的燃料电池有轨电车能量管理策略[J]. 电工技术学报, 2023, 38(21): 5923-5938. Gao Fengyang, Gao Xuanyu, Zhang Haoran, et al. Management strategy for fuel cell trams with both global and transient characteristics[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5923-5938.
[14] 高锋阳, 张浩然, 王文祥, 等. 氢燃料电池有轨电车混合储能系统的节能运行优化[J]. 电工技术学报, 2022, 37(3): 686-696. Gao Fengyang, Zhang Haoran, Wang Wenxiang, et al. Energy saving operation optimization of hybrid energy storage system for hydrogen fuel cell tram[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 686-696.
[15] Song Ke, Wang Xiaodi, Li Feiqiang, et al. Pontryagin’s minimum principle-based real-time energy management strategy for fuel cell hybrid electric vehicle considering both fuel economy and power source durability[J]. Energy, 2020, 205: 118064.
[16] Deng Kai, Peng Hujun, Dirkes S, et al. An adaptive PMP-based model predictive energy management strategy for fuel cell hybrid railway vehicles[J]. eTransportation, 2021, 7: 100094.
[17] Song Ke, Ding Yuhang, Hu Xiao, et al. Degradation adaptive energy management strategy using fuel cell state-of-health for fuel economy improvement of hybrid electric vehicle[J]. Applied Energy, 2021, 285: 116413.
[18] Tang Xiaolin, Zhou Haitao, Wang Feng, et al. Longevity-conscious energy management strategy of fuel cell hybrid electric vehicle based on deep reinforcement learning[J]. Energy, 2022, 238: 121593.
[19] Lu Dagang, Yi Fengyan, Hu Donghai, et al. Online optimization of energy management strategy for FCV control parameters considering dual power source lifespan decay synergy[J]. Applied Energy, 2023, 348: 121516.
[20] Xie Shanshan, He Hongwen, Peng Jiankun. An energy management strategy based on stochastic model predictive control for plug-in hybrid electric buses[J]. Applied Energy, 2017, 196: 279-288.
[21] Lin Xinyou, Xia Yutian, Huang Wei, et al. Trip distance adaptive power prediction control strategy optimization for a plug-in fuel cell electric vehicle[J]. Energy, 2021, 224: 120232.
[22] Zhang Man, Shi Shuming, Lin Nan, et al. High-efficiency driving cycle generation using a Markov chain evolution algorithm[J]. IEEE Transactions on Vehicular Technology, 2019, 68(2): 1288-1301.
[23] Pereira D F, da Costa Lopes F, Watanabe E H. Nonlinear model predictive control for the energy management of fuel cell hybrid electric vehicles in real time[J]. IEEE Transactions on Industrial Electronics, 2021, 68(4): 3213-3223.
[24] Ghaderi R, Kandidayeni M, Soleymani M, et al. Online health-conscious energy management strategy for a hybrid multi-stack fuel cell vehicle based on game theory[J]. IEEE Transactions on Vehicular Technology, 2022, 71(6): 5704-5714.
[25] Wang Tianhong, Li Qi, Wang Xiaotong, et al. A power allocation method for multistack PEMFC system considering fuel cell performance consistency[J]. IEEE Transactions on Industry Applications, 2020, 56(5): 5340-5351.
Abstract In fuel cell hybrid systems, the degradation processes of fuel cells and power batteries are highly inconsistent. The excessive consumption and premature end of life of one power source can disrupt the balance of the power system, deplete the performance of the other power source, accelerate the aging of the entire power system, and negatively affect vehicle economy and system durability. Consequently, it becomes challenging to achieve optimal fuel economy and system durability simultaneously. To address this issue, an optimization strategy based on condition prediction and coordinated power source life degradation is proposed.
Firstly, to improve prediction accuracy, operating conditions are categorized into three typical states: low-speed, medium-speed, and high-speed. An upper-level Markov Chain Monte Carlo (MCMC) prediction model is established based on historical conditions to predict the tram's operating conditions. This prediction provides more information for the lower-level energy management strategy to optimize system energy distribution. Secondly, in the lower-level energy management strategy, the hydrogen consumption of the fuel cell and the equivalent hydrogen consumption of the auxiliary power source are analyzed. A continuous degradation model for the fuel cell and power battery is established, introducing optimization objectives and adaptively adjusting the weights of each objective online to optimize the multi-objective function. Finally, the proposed strategy is compared with the traditional equivalent consumption minimization strategy (ECMS) and the external energy maximization strategy (EEMS).
Results show that at the end of the entire operating condition, the proposed strategy's hydrogen consumption is 99.61 g, the degradation rate difference between the dual power sources is 0.000 66%, the system efficiency is 81.66%, the power fluctuation range is -800 W to 800 W, and the stress on the power battery and supercapacitor is 117.5 and 176.4 respectively. Compared to the ECMS strategy, with a hydrogen consumption of 115.1 g and system efficiency of 77.64%, the proposed strategy improves fuel economy and system efficiency by 15.6% and 5.2% respectively. Compared to the EEMS strategy, with a dual power source degradation rate difference of 0.014 4% and system efficiency of 79.77%, the proposed strategy reduces the degradation rate difference by 21.82 times and improves system efficiency by 2.4%. Additionally, the power fluctuation range under the proposed strategy is significantly reduced compared to the -1 000 W to 1 000 W range under both the ECMS and EEMS strategies, resulting in a smoother power source power curve. Under the ECMS strategy, the stress on the power battery and supercapacitor is 156.6 and 215 respectively, while under the EEMS strategy, the stress is 156.8 and 226.6 respectively. The proposed strategy reduces the stress on the auxiliary power source compared to the ECMS and EEMS strategies, decreasing excessive consumption and resulting in a more reasonable power distribution.
Comprehensive simulation analysis reveals the core advantages of the proposed strategy: (1) Establishing an MCMC prediction model for condition prediction improves the adaptability of the energy management strategy to operating conditions, achieving more reasonable, precise, and efficient energy control and reducing damage to the hybrid power system. (2) Overcoming the poor fuel economy of traditional ECMS and the high inconsistency in power source degradation of EEMS. (3) Achieving superior fuel economy and system durability, thereby extending the lifecycle of fuel cell hybrid systems.
Keywords:hybrid tram, driving cycle prediction, energy management, lifespan decay synergy
DOI: 10.19595/j.cnki.1000-6753.tces.240996
中图分类号:TM92
中车“十四五”科技重大专项计划资助项目(2021CXZ021)。
收稿日期 2024-06-11
改稿日期 2024-07-03
高锋阳 男,1970年生,教授,博士生导师,研究方向为燃料电池有轨电车混合储能系统能量管理策略。E-mail:ljdgaofy@lzjtu.edu.cn(通信作者)
苏红宇 男,1997年生,硕士研究生,研究方向为燃料电池混合动力系统能量管理策略。E-mail:2318562098@qq.com
(编辑 赫 蕾)