
图1 动力电池包三维结构示意图
Fig.1 Schematic diagram of the three-dimensional structure of the power battery pack
摘要 动力电池组温度场用复杂的偏微分方程来描述,由于其中大量的参数未知,且很多模型参数表现出较强的时变性,传统基于物理建模方法在实现动力电池组温度场在线建模方面难度较大。基于深度学习的方法虽然不依赖物理模型,然而在训练过程中需要大量的实验数据,模型训练时间较长,温度场预测的实时性较差。针对以上问题,该文提出一种基于长短期记忆网络的动力电池组温度场时空建模。首先利用时空分离方法提取离线条件下的空间特征和时间特征。空间特征在增量学习的帮助下不断进行更新,长短期记忆(LSTM)网络用于时间动力学的建模。最后,将更新后的空间特征和时间模型进行整合,得到动力电池组温度场的预测模型。在一个由24节电池单体组成的动力电池包上对所提出的方法进行验证,结果表明,无论在正常条件下还是有气流干扰条件下,所提方法都能对动力电池包的温度场进行准确预测。在有气流干扰下,所提方法的单点温度预测误差小于0.07℃,在测试集上的方均根误差为0.014 7℃。
关键词:动力电池组 时空建模 长短期记忆网络 特征提取
动力电池组是新能源电动汽车的核心部件之一,负责存储和释放电能以驱动电动汽车[1]。其主要组成部分包括电池单体、电池管理系统和散热系统。锂离子电池(Li-Ion Battery, LIB)由于其高能量密度、高比能量和高库仑效率而被广泛用于组成电动汽车的动力电池组[2-5]。然而,充放电过程中动力电池组的热量分布并不均匀,会严重影响动力电池组的充电效率、寿命和安全性[6-8]。因此,在对动力电池组进行优化、控制、故障诊断和热管理之前,有必要对电池组的热过程进行精确建模[9-10]。
电池单体的电化学模型或物理模型[11]能够准确地描述电池单体内发生的物理化学反应。其中,电池单体的温度模型是一个涉及热传导、热对流以及内部热源项的多物理场耦合偏微分方程。2021年,S. Sattarzadeh等[12]利用有限差分方法和传感器布放优化算法对方形锂离子电池单体的温度分布进行建模;2023年,Zhou Yu等[13]利用伽辽金谱方法对方形锂离子电池单体的温度场进行建模。虽然这些模型的精度很高,但推导过程相对复杂,且组成它们的耦合非线性微分方程很难获取,在求解时需要消耗大量的计算资源[14]。
同时,国内外研究团队在动力电池组建模方面已开展相关研究工作。Li Jianwei等[15]在2013年开发了一个电池包电路替代模型对电池包的端电压进行建模。S. Castano等[16]在2015年通过大量充放电实验数据辨识电池模型参数,在此基础上对一个由56个电池单体组成的电池包的电压进行建模。2019年,M. D. Kharisma等[17]利用改进电池单体的等效电路模型对整个电池包进行建模。通过综合考虑电化学模型、热模型、电解质固体界面(Solid Electrolyte Interface, SEI)形成模型、流体动力学模型和串并联电路模型,Xia Quan等[18]在2020年提出了通用的电池包寿命建模方法。通过考虑电流的不一致性,Fan Xinyuan等[19]在2021年提出了一种基于等效电路模型的简化算法,适用于非均匀串联和并联电池包。
由于动力电池组中单体温度场相互耦合,与动力电池组电特性方面的建模工作相比,动力电池组温度场建模方面的研究相对较少。2012年,Sun Hongguang等[20]开发了三维热模型用于模拟驾驶循环工况下的电池组中单体的热行为。2013年,Zhu Cong等[21]基于多孔电极和浓溶液理论建立了锂离子电池单体的热模型,并基于该模型的热生成和热耗散预测电池包内每个电池单体的温度变化。2016年,J. Jaguemont等[22]首先对电池单体温度进行建模,然后通过考虑单体之间的热传导对电池包温度场进行仿真。这些方法本质上是单体温度模型的拓展,首先需要对单体温度场进行精确建模,最终电池包温度场的精度高度依赖单体模型的准确性。因此,这些方法同样存在物理方程难以获取和资源消耗量大的特点。
长短期记忆(Long Short-Term Memory,LSTM)网络[23]是一种用于处理序列数据的深度学习模型,特别适用于处理长序列数据和解决梯度消失或爆炸的问题。LSTM网络由一个单元的重复结构组成,每个单元内部包含输入门、遗忘门、输出门和记忆细胞,通过保存这些门的控制信息及信息流动,以解决长序列数据中存在的长距离依赖关系的问题[24]。LSTM网络能够有效地捕捉序列数据中的上下文信息,适用于语言建模、机器翻译、语音识别等领域[25]。其独特的记忆细胞结构使其在处理时序数据时表现出色,被广泛应用于自然语言处理和时间序列预测等任务中[26]。因此,可利用LSTM网络擅长处理时间序列的特性对动力电池组的时间特征进行动力学建模。
为了降低对准确物理模型的依赖,本文提出了一种基于时空分离的动力电池组温度场建模方法。无论正常工况还是有气流干扰的工况,该方法都能准确预测动力电池组的温度场。所提方法可以通过增量学习实时更新空间特征,从而降低方法的计算复杂度。该方法是一种纯数据驱动的方法,不依赖精确的偏微分方程,因此适合应用于实际动力电池组的温度场建模。
图1所示的动力电池包广泛用于新能源电动汽车的动力系统。可用二阶偏微分方程对动力电池包的热过程进行描述,即

图1 动力电池包三维结构示意图
Fig.1 Schematic diagram of the three-dimensional structure of the power battery pack
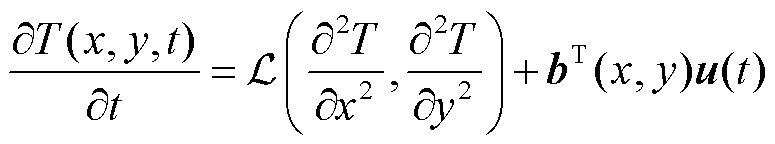 (1)
(1)
满足边界条件
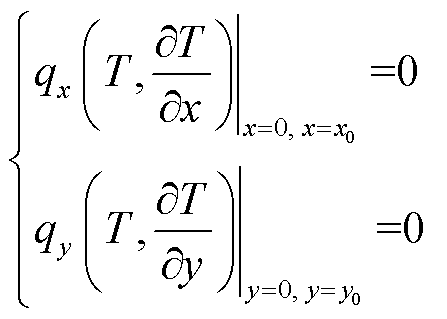 (2)
(2)
和初始条件
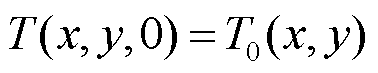 (3)
(3)
其中,热产生速率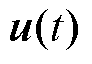 和空间分布函数
和空间分布函数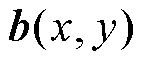 定义为
定义为
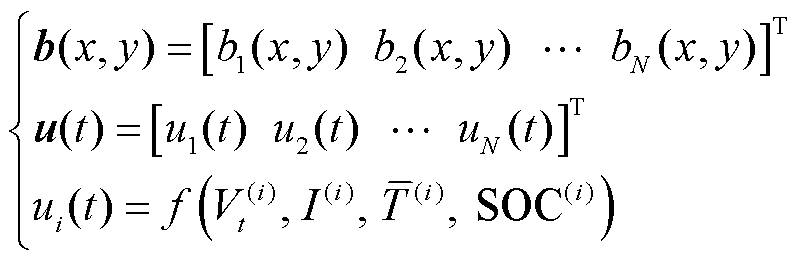 (4)
(4)
式中,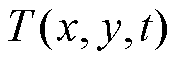 为温度场的时空状态,
为温度场的时空状态,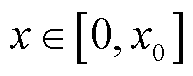 和
和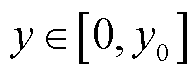 表示空间坐标,
表示空间坐标,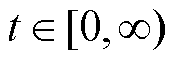 代表时间变量;
代表时间变量;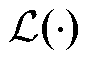 为空间偏导数
为空间偏导数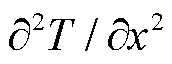 和
和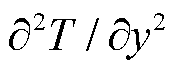 的非线性函数;
的非线性函数;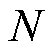 为电池包中电池单体的数量;
为电池包中电池单体的数量;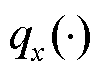 和
和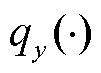 为两个未知的非线性函数;
为两个未知的非线性函数;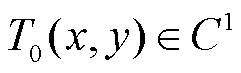 表示在
表示在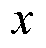 和
和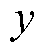 方向上都具有连续一阶偏导的初始条件;
方向上都具有连续一阶偏导的初始条件;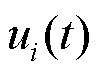 为第
为第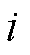 个电池单体的热产生速率;
个电池单体的热产生速率;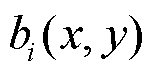 为第
为第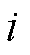 个电池单体热产生速率对应的空间分布函数;
个电池单体热产生速率对应的空间分布函数;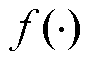 为一个未知非线性函数;
为一个未知非线性函数;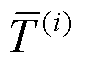 为第
为第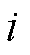 个电池单体的平均温度;
个电池单体的平均温度;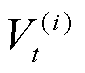 、
、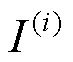 和
和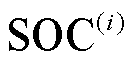 分别为第
分别为第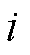 个电池单体的端电压、负载电流和荷电状态(State of Charge, SOC)。
个电池单体的端电压、负载电流和荷电状态(State of Charge, SOC)。
图2描述了动力电池单体等效电路模型,其中,开路电压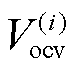 是荷电状态
是荷电状态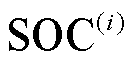 的未知函数,
的未知函数,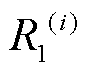 和
和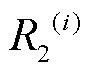 分别为第
分别为第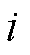 个电池单体的溶液电阻和电荷转移电阻。
个电池单体的溶液电阻和电荷转移电阻。
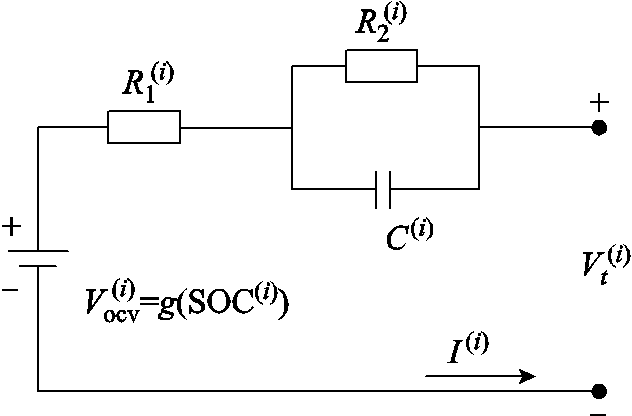
图2 动力电池单体等效电路模型
Fig.2 Equivalent circuit model of a power battery cell
动力电池组温度场偏微分方程式(1)的求解关键在于推导出温度状态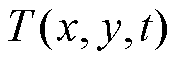 的解析解或者数值解。这些求解方法可分为基于物理的方法和基于数据的方法,其中基于物理的方法主要包括有限元法、有限差分法、谱方法。有限元法通过将连续域离散化为有限数量的小单元进行近似计算,当前大量数值仿真软件都用该方法进行求解,如Ansys、COMSOL Multiphysics;有限差分法通过在预定的网格点上离散化偏微分方程,用差分方程近似求解原偏微分方程;谱方法将偏微分方程降阶为若干个常微分方程后,再对常微分方程进行求解。这些基于物理的方法求解精度高,但是要求原有偏微分方程的参数完全已知,且计算量大、计算时间长,一般不适合在线建模。
的解析解或者数值解。这些求解方法可分为基于物理的方法和基于数据的方法,其中基于物理的方法主要包括有限元法、有限差分法、谱方法。有限元法通过将连续域离散化为有限数量的小单元进行近似计算,当前大量数值仿真软件都用该方法进行求解,如Ansys、COMSOL Multiphysics;有限差分法通过在预定的网格点上离散化偏微分方程,用差分方程近似求解原偏微分方程;谱方法将偏微分方程降阶为若干个常微分方程后,再对常微分方程进行求解。这些基于物理的方法求解精度高,但是要求原有偏微分方程的参数完全已知,且计算量大、计算时间长,一般不适合在线建模。
当前也有研究利用基于数据的方法对动力电池组温度数据进行预测,从而近似求解温度场偏微分方程。这些方法首先采集大量的电池组实验数据(电压、电流、温度等),并利用深度学习等人工智能算法对这些数据进行特征提取和模型预测。这些方法的优势在于不依赖原有偏微分方程,也不需要对偏微分方程具体参数进行辨识,但是其需要大量实验数据对神经网络参数进行学习,同时训练过程漫长、对计算资源的需求较高。
电池包温度场建模对动力电池组的状态估计、结构设计和故障诊断都至关重要。通过以上分析可知,利用当前方法对动力电池包温度场进行建模的主要难点在于:
1)模型(1)(见式(1))中很多参数是未知的,利用基于物理的方法进行参数辨识需要大量的实验数据,且随着电池的老化,很多模型参数表现出较强的时变性,传统基于物理建模方法在实现动力电池组温度场在线建模方面难度较大。
2)基于深度学习的方法虽然不依赖物理模型,然而在训练过程中需要大量的实验数据,模型训练时间较长,温度场预测的实时性较差。
3)传统基于数据的方法往往只考虑单个电池的温度变化,忽略了电池单体之间温度场相互耦合的特性,导致这些方法对温度场的预测精度不足。
为了克服以上困难,本文提出了一种基于时空分离的动力电池组温度场建模方法。该方法基于分布式参数系统建模理论,首先采集电池组充放电数据;随后对分布式温度数据进行时间特征和空间特征提取,并利用非线性辨识方法对时间特征进行动力学建模;最后将空间模型和辨识后的时间模型进行整合,得到动力电池组温度场的时空模型。该方法计算量小、不依赖准确的偏微分方程、实时性好,同时考虑了电池单体之间的相互耦合特性,能从整体上对温度场数据进行特征分析和建模。
图3描述了所提动力电池组温度场建模方法。首先通过时空分离方法提取离线条件下的空间特征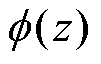 和时间特征
和时间特征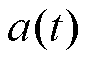 。空间特征
。空间特征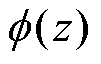 通过增量学习的方式不断更新。长短期记忆网络用来对时间动力学进行建模。最后,将更新后的空间特征和时间模型进行整合,得到动力电池组温度场的预测模型
通过增量学习的方式不断更新。长短期记忆网络用来对时间动力学进行建模。最后,将更新后的空间特征和时间模型进行整合,得到动力电池组温度场的预测模型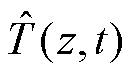 。
。
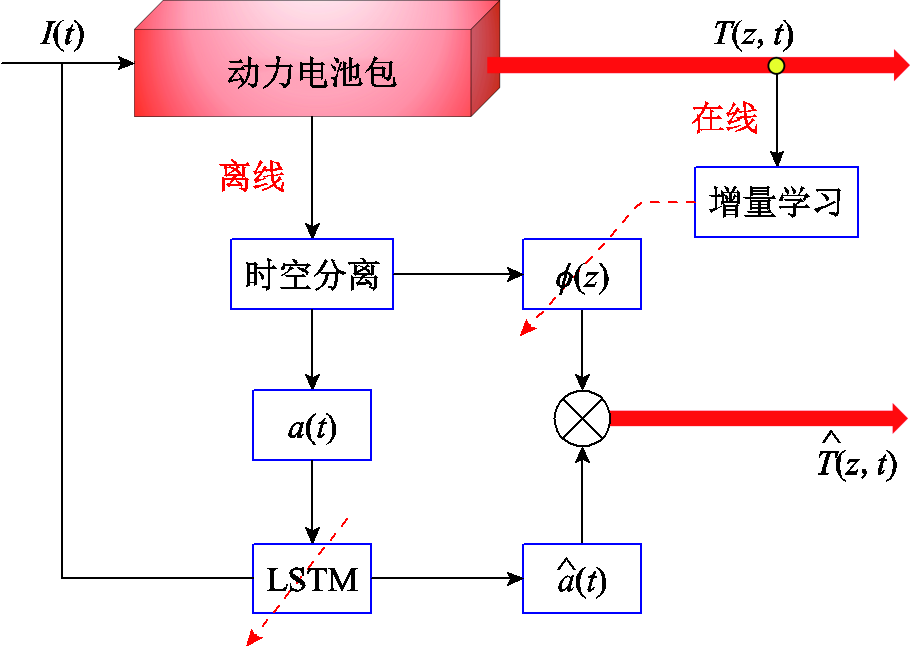
图3 所提出建模方法框图
Fig.3 Framework of the proposed modeling method
与傅里叶级数类似,动力电池组温度场的时空状态可由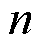 个主要空间基函数
个主要空间基函数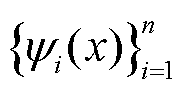 来逼近[27]。
来逼近[27]。
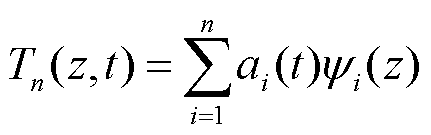 (5)
(5)
式中,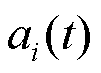 为空间基函数
为空间基函数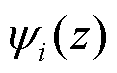 的系数,空间复合坐标
的系数,空间复合坐标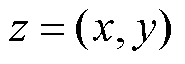 。
。
模型的前n个主要空间基函数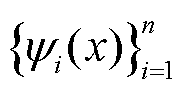 可通过优化以下目标函数得到。
可通过优化以下目标函数得到。
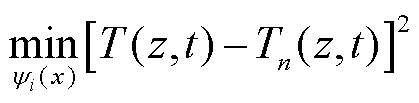 (6)
(6)
约束条件为
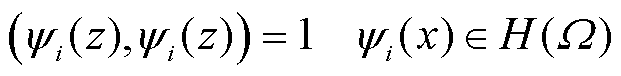 (7)
(7)
约束条件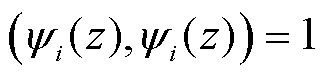 用来保证空间基函数
用来保证空间基函数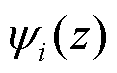 在希尔伯特空间
在希尔伯特空间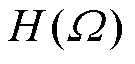 中的唯一性。内乘的定义为
中的唯一性。内乘的定义为
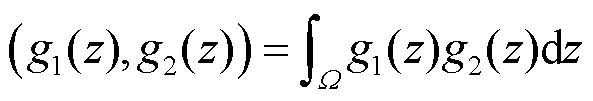 (8)
(8)
则以上约束优化问题可转换为如下特征提取问题:
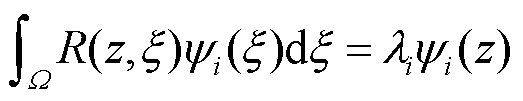 (9)
(9)
式中,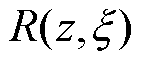 为空间中两点的相关函数;
为空间中两点的相关函数;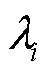 为对应的特征值。
为对应的特征值。
以上特征提取过程在分布式参数系统建模领域也被称为KL分解(Karhunen-Loève decomposition)。在实际应用过程中,由于测量数据在空间和时间上都是离散的,KL分解通常以离散的形式来实现。假设由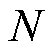 个传感器收集了
个传感器收集了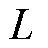 组实验快照
组实验快照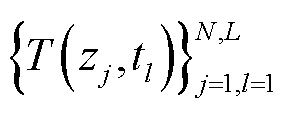 ,这些数据构成了测量矩阵
,这些数据构成了测量矩阵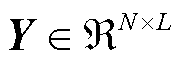 。式(9)可离散表达为
。式(9)可离散表达为
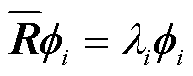 (10)
(10)
其中
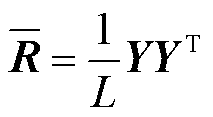
式中,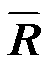 为空间相关矩阵;
为空间相关矩阵;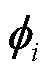 为第
为第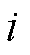 个离散的空间基函数。这里的空间基函数
个离散的空间基函数。这里的空间基函数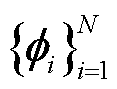 可通过矩阵的特征值分解得到。利用不同位置温度的相关性来提取空间基函数,从而考虑电池单体之间温度的相互耦合特性。
可通过矩阵的特征值分解得到。利用不同位置温度的相关性来提取空间基函数,从而考虑电池单体之间温度的相互耦合特性。
完成空间特征提取后,可通过式(5)的矩阵表达形式完成时间特征的提取。式(5)的矩阵表达形式为
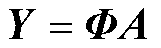 (11)
(11)
式中,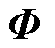 为空间基函数矩阵,
为空间基函数矩阵,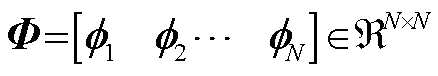 ;A为时间系数矩阵,
;A为时间系数矩阵,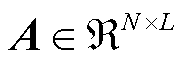 。根据式(11),时间系数可表示为
。根据式(11),时间系数可表示为
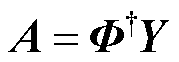 (12)
(12)
式中,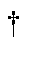 表示矩阵的逆运算。
表示矩阵的逆运算。
增量学习在历史计算结果的基础上通过增量的方式完成结果的更新,而不需要历史数据参与最新结果的更新[28]。假设历史数据矩阵为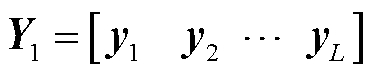 ,其中
,其中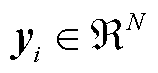 为第
为第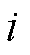 时刻采集的实验数据,增量数据矩阵为
时刻采集的实验数据,增量数据矩阵为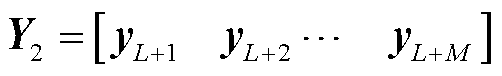 ,
,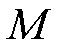 为增量窗口大小。在实际应用过程中,空间基函数和时间系数可通过如下矩阵奇异值(Singular Value Decomposition, SVD)分解得到。
为增量窗口大小。在实际应用过程中,空间基函数和时间系数可通过如下矩阵奇异值(Singular Value Decomposition, SVD)分解得到。
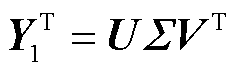 (13)
(13)
空间基函数矩阵可以表示为
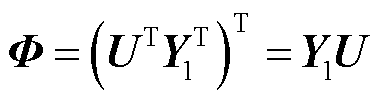
式中,U为左奇导矩阵;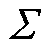 为奇异值矩阵,
为奇异值矩阵,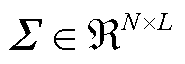 ;V为右奇异矩阵,
;V为右奇异矩阵,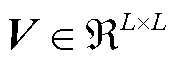 。
。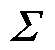 和V可通过矩阵奇异值分解得到。
和V可通过矩阵奇异值分解得到。
根据式(12),时间系数矩阵可以表示为
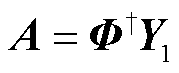 (14)
(14)
随着数据量的积累,测量矩阵的维度将不断增大,矩阵奇异值的运算量也将不断增加,非常不利于模型的在线更新和应用。可通过如下增量学习的方式对空间特征进行在线更新。
所有数据的奇异值分解可以表示为
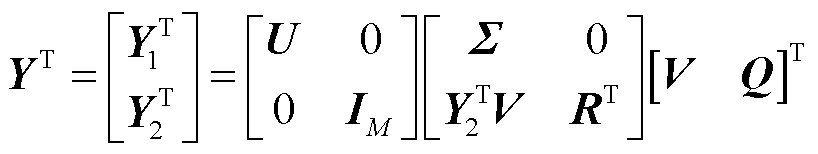 (15)
(15)
式中,矩阵Q和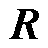 可通过矩阵
可通过矩阵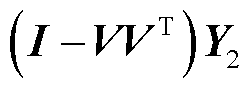 的QR分解得到,即
的QR分解得到,即
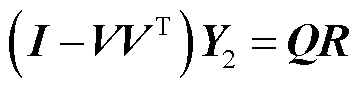 (16)
(16)
式中,Q为正交矩阵;R为上三角矩阵;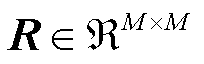 ,
,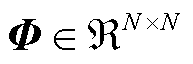 。
。
进一步对式(15)的中间矩阵进行奇异值分解可以得到
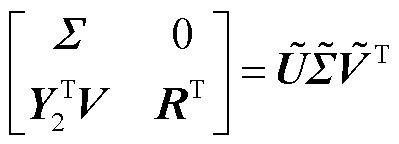 (17)
(17)
则全局空间基函数的最新形式[29]可以表示为
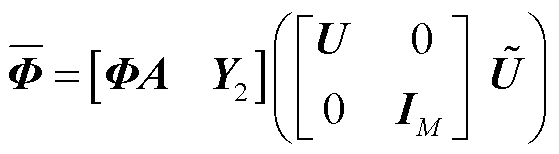 (18)
(18)
经过以上的计算,空间基函数在更新时不再需要历史数据的参与,仅需要从历史数据中提取到的空间基函数矩阵和式(17)、式(18)的矩阵运算,有效地降低了计算复杂度。
联立式(12)和式(18),全局时间系数矩阵可以表示为
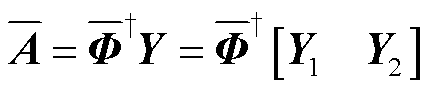 (19)
(19)
式中,时间稀疏矩阵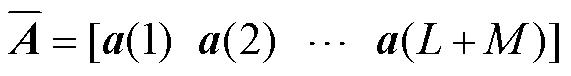
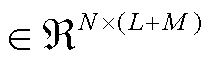 ,
,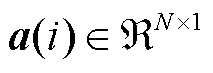 代表第
代表第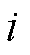 时刻的时间系数,
时刻的时间系数,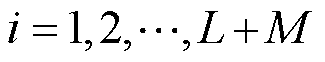 。在线阶段,时间系数可通过以下非线性模型进行辨识。
。在线阶段,时间系数可通过以下非线性模型进行辨识。
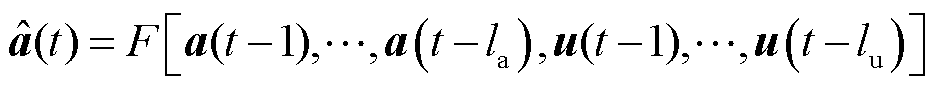 (20)
(20)
式中,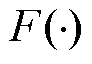 为描述系统时间动力学的非线性函数;
为描述系统时间动力学的非线性函数;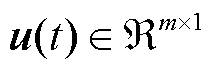 为系统输入向量;
为系统输入向量;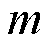 为输入元素的数量;
为输入元素的数量;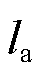 和
和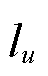 分别为系统输出和输入时滞。
分别为系统输出和输入时滞。
长短期记忆网络属于循环神经网络(Recursive Neural Network, RNN),链式的结构使其天然适合处理序列类型的数据。由于时间系数中的数据高度相关,这里使用LSTM网络对时间动力学进行建模。LSTM网络结构如图4所示,LSTM网络的输入向量记为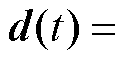
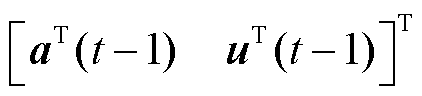 ,输出向量记为
,输出向量记为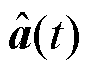 。
。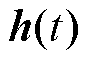 、
、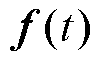 、
、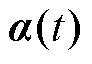 、
、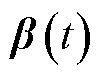 和
和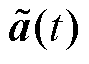 分别代表隐含状态、遗忘门激励、输入门激励、输出门激励和潜在的输出候选向量。LSTM网络的详细推导可参考文献[27-28]。
分别代表隐含状态、遗忘门激励、输入门激励、输出门激励和潜在的输出候选向量。LSTM网络的详细推导可参考文献[27-28]。
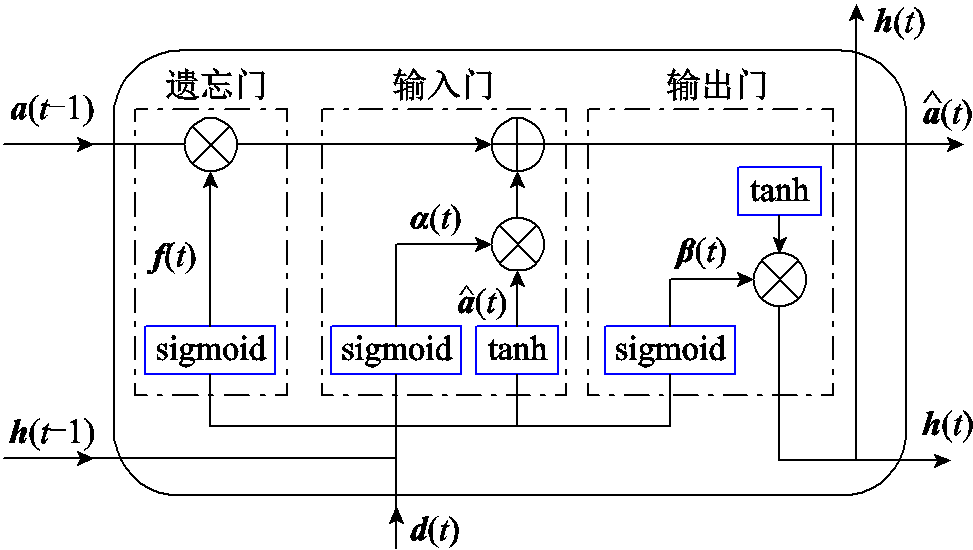
图4 长短期记忆网络结构
Fig.4 Structure of the LSTM network
根据以上推导的空间基函数和时间动力学模型,动力电池的温度场模型可以表示为
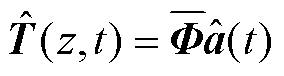 (21)
(21)
其中,全局空间基函数已通过历史数据的增量式学习得到,时间系数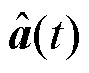 可通过LSTM网络进行预测。
可通过LSTM网络进行预测。
该建模方法的主要流程见表1。
电池包三维结构示意图如图5所示,采用由24节圆柱形锂离子电池组成的电池包来验证所提方法的有效性。首先将四个电池单体并联,然后将六组并联组合串联在一起。每个电池单体的序列号都标记在其顶部。为了更好地模拟实际情况,采用文献[30]中的参数辨识方法来辨识电池单体的主要参数。
表1 算法流程与伪代码
Tab.1 Algorithm pseudo code

算法1:建模方法流程 输入:温度传感器测量数据。输出:式(21)中动力电池温度场预测模型。 (1)空间特征提取:通过矩阵特征值求解,得到式(10)中的空间基函数,并形成空间基函数矩阵。(2)时间特征提取:根据式(12)计算时间系数矩阵A。(3)时间动力学建模:通过式(19)计算全局时间系数矩阵,并利用长短期记忆神经网络得到式(20)中的时间动力学预测模型。(4)时空特征合成:基于全局空间基函数矩阵和时间动力学预测模型得到式(21)中的动力电池温度场预测模型。(5)模型在线更新:当获取到组新数据时,通过式(18)更新得到全局空间基函数矩阵;通过式(20)更新时间动力学预测模型。(6)预测模型输出:输出温度场预测模型,并重新进入步骤(5)的模型在线更新

图5 电池包三维结构示意图
Fig.5 Schematic diagram of the three-dimensional structure of the battery pack
电池单体为高比能21700电池,直径为0.021 m,高度为0.070 m。本次实验采用文献[31]中的电池组仿真方法来产生电池组在不同条件下的温度数据,用于验证所提出建模方法的有效性。产生仿真数据所用软件为COMSOL。图5中,电池组左侧的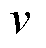 表示气流速度,测试中
表示气流速度,测试中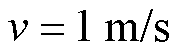 。主要模型参数见表2。温度传感器安装在每个电池单元的顶部电极附近。电池外壁之间的间隙设置为0.002 m,以便达到更好的散热效果[32]。
。主要模型参数见表2。温度传感器安装在每个电池单元的顶部电极附近。电池外壁之间的间隙设置为0.002 m,以便达到更好的散热效果[32]。
表2 主要模型参数
Tab.2 Main model parameters
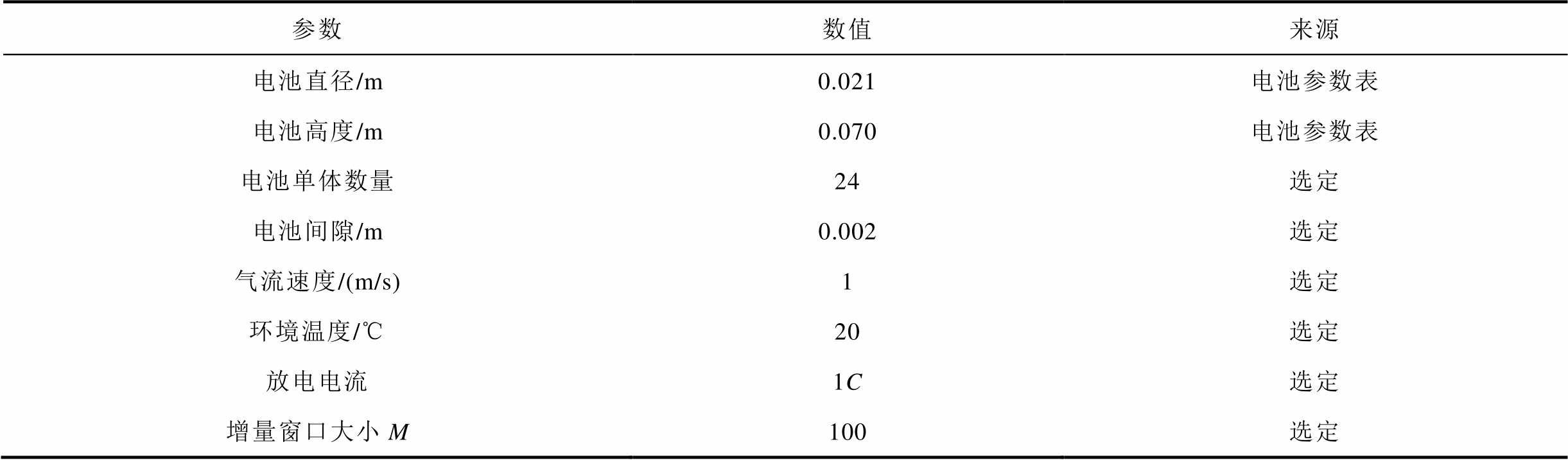
参数数值来源 电池直径/m0.021 电池参数表 电池高度/m0.070电池参数表 电池单体数量24选定 电池间隙/m0.002选定 气流速度/(m/s)1选定 环境温度/℃20选定 放电电流1C选定 增量窗口大小M100选定
本小节实验是在无气流的标准条件下进行的,即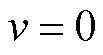 。图6展示了电池包在1 100 s时的温度分布。在没有空气对流的情况下,处于中间区域的电池单体由于散热条件不足,温度比较高。而靠近箱体边缘的电池单体可与周围空气进行充分热交换,温度较低。电池包在标准条件下温度分布变化曲线如图7所示。电池包的起始温度与环境温度相同,随着放电不断进行,电池包的整体温度也在不断上升。
。图6展示了电池包在1 100 s时的温度分布。在没有空气对流的情况下,处于中间区域的电池单体由于散热条件不足,温度比较高。而靠近箱体边缘的电池单体可与周围空气进行充分热交换,温度较低。电池包在标准条件下温度分布变化曲线如图7所示。电池包的起始温度与环境温度相同,随着放电不断进行,电池包的整体温度也在不断上升。
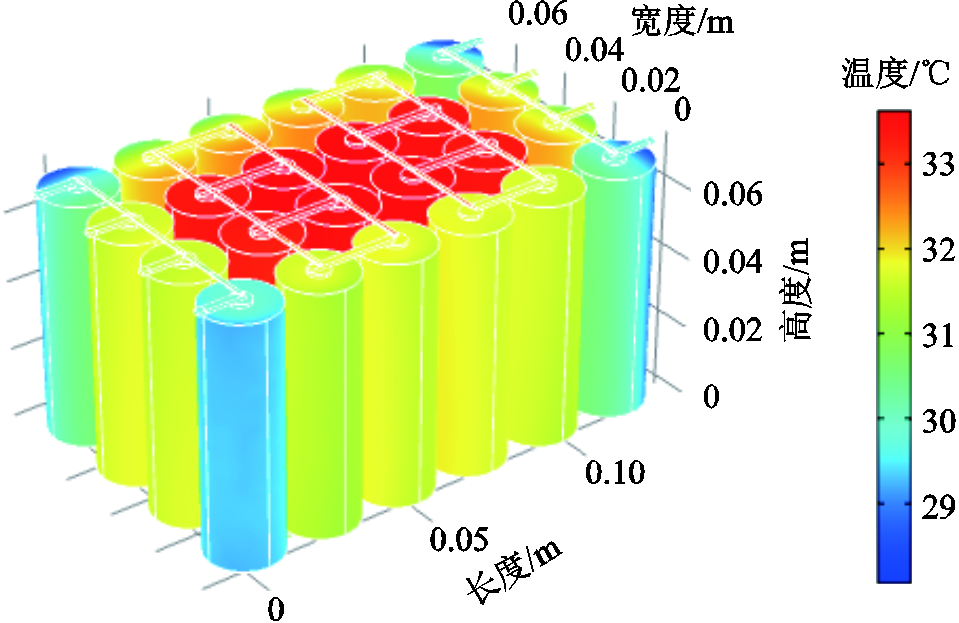
图6 电池包在标准条件下1 100 s时的温度分布
Fig.6 Temperature distribution of battery pack at 1 100 s under the standard condition
每个电池单体顶部的电极附近布置1个温度传感器(热电偶)。如图7所示,共收集了1 600组电池包的温度数据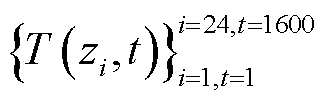 ,采样频率为1 Hz,其中前800组温度数据
,采样频率为1 Hz,其中前800组温度数据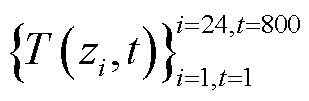 用于模型训练,后800组温度数据
用于模型训练,后800组温度数据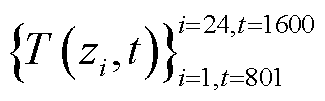 用于模型更新和测试。本研究所用软件为Matlab R2023b,该软件可实现算法1的全部流程,并输出温度场预测结果和预测误差。
用于模型更新和测试。本研究所用软件为Matlab R2023b,该软件可实现算法1的全部流程,并输出温度场预测结果和预测误差。
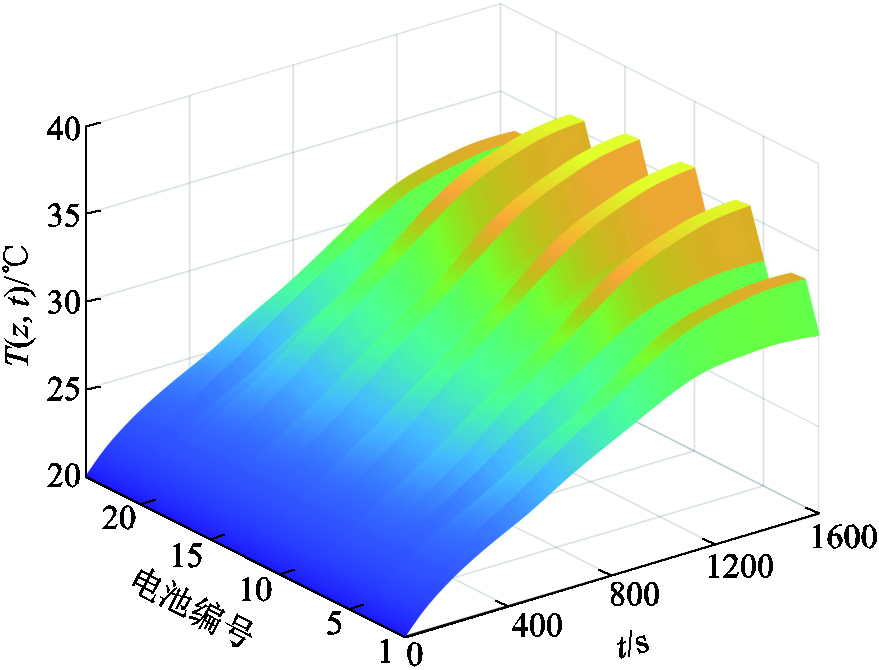
图7 电池包在标准条件下温度分布变化曲线
Fig.7 Temperature distribution curves of battery pack under the standard condition
根据表1中算法的主要流程,前800组温度数据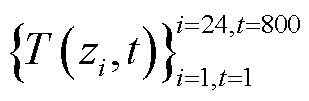 首先用来提取空间基函数矩阵
首先用来提取空间基函数矩阵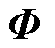 和时间系数矩阵
和时间系数矩阵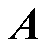 ,并利用长短期记忆网络训练时间动力学预测模型
,并利用长短期记忆网络训练时间动力学预测模型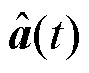 ,再根据式(21)得到温度场预测模型
,再根据式(21)得到温度场预测模型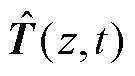 ;800 s之后,每间隔100 s(增量窗口大小
;800 s之后,每间隔100 s(增量窗口大小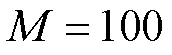 s)利用采集到的新数据完成全局空间基函数矩阵
s)利用采集到的新数据完成全局空间基函数矩阵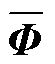 和时间动力学模型
和时间动力学模型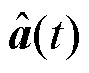 的更新,最后根据式(21)得到温度场预测模型
的更新,最后根据式(21)得到温度场预测模型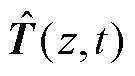 ,并利用该模型对电池温度进行预测。所提方法在动力电池包上的建模误差如图8所示,整体上单点绝对预测误差小于0.4℃,在测试集上的预测方均根误差(Root-Mean-Square Error, RMSE)为0.095 1℃。
,并利用该模型对电池温度进行预测。所提方法在动力电池包上的建模误差如图8所示,整体上单点绝对预测误差小于0.4℃,在测试集上的预测方均根误差(Root-Mean-Square Error, RMSE)为0.095 1℃。
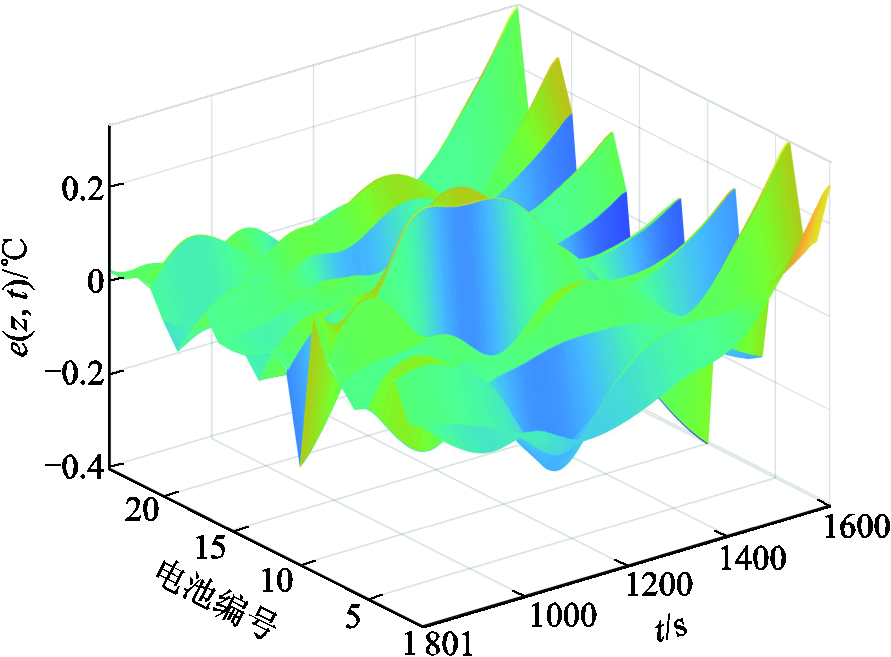
图8 所提出方法在动力电池包温度场上的建模误差
Fig.8 Temperature field modeling error of the proposed method for power battery pack
电池包在气流干扰下1 100 s时的温度分布如图9所示。本小节实验是在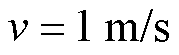 的气流条件下进行的,在气流条件下,靠近气流的电池单体温度较低,远离气流的电池单体温度较高。与没有气流条件下的电池组温度分布相比,在气流干扰下,电池组温度变化梯度更小。电池包在气流干扰下温度分布变化曲线如图10所示,与没有气流干扰条件下类似,电池包的起始温度与环境温度相同,随着不断放电不断进行,电池包的整体温度也在不断上升。
的气流条件下进行的,在气流条件下,靠近气流的电池单体温度较低,远离气流的电池单体温度较高。与没有气流条件下的电池组温度分布相比,在气流干扰下,电池组温度变化梯度更小。电池包在气流干扰下温度分布变化曲线如图10所示,与没有气流干扰条件下类似,电池包的起始温度与环境温度相同,随着不断放电不断进行,电池包的整体温度也在不断上升。
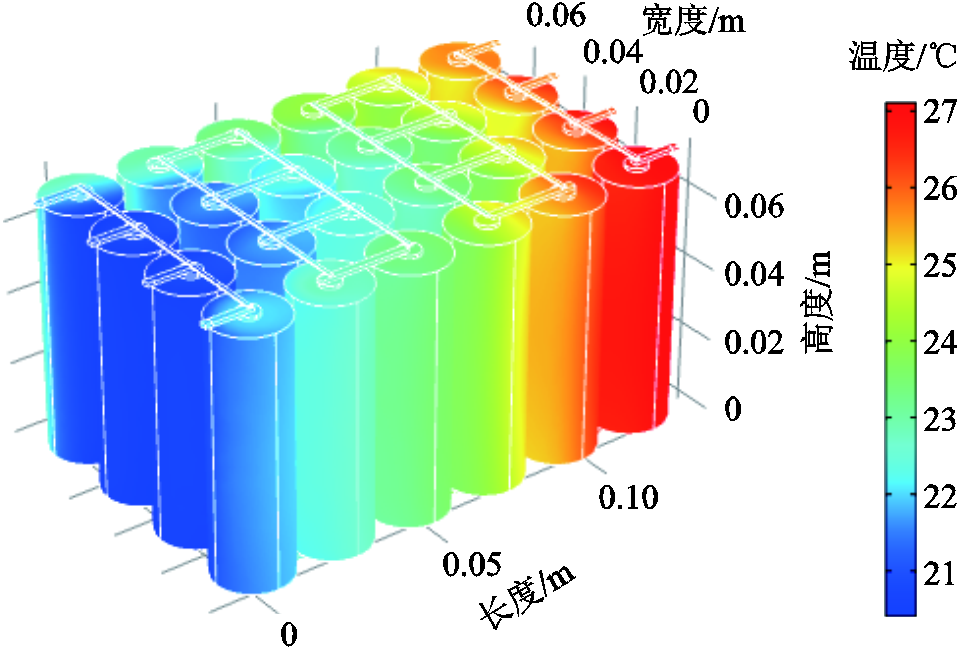
图9 电池包在气流干扰下1 100 s时的温度分布
Fig.9 Temperature distribution of battery pack at 1 100 s under airflow condition

图10 电池包在气流干扰下温度分布变化曲线
Fig.10 Temperature distribution curves of battery pack under air flow interference
在气流干扰下,数据采集和建模流程与3.2节相同。所提方法在动力电池包上的建模误差如图11所示,整体上单点绝对预测误差小于0.07℃,在测试集上的预测方均根误差(RMSE)为0.014 7℃。将图8和图11进行对比可以发现,有气流的条件下,所提出方法的建模误差更小。这是由于在气流干扰条件下,动力电池包在同一时刻的温度在空间上的变化梯度更小,即温度变化更平缓,使得建模时的空间特征更加平滑。
为了比较不同方法的性能,将本文所提方法与文献[33]中基于径向基函数网络的电池温度预测方法,以及利用有限元实现温度仿真的COMSOL软件结果进行了对比,结果见表3。从表3的结果可以看出,虽然所提方法在测试集建模精度上略有损失,但是模型计算效率有明显提升,并且能够实现温度的实时预测。当单步平均预测时间大于1 s时,可认为无法进行实时运算。由于该项研究的实验数据集来源于COMSOL仿真,因此表3中COMSOL有限元仿真无计算误差。
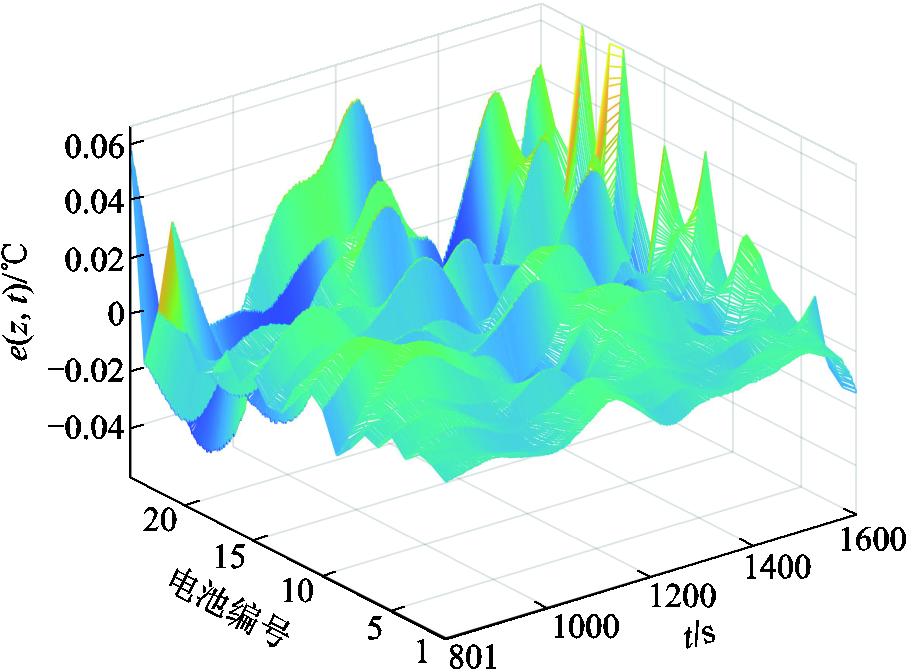
图11 所提方法在气流干扰下对动力电池包温度场进行建模的误差
Fig.11 Temperature field modeling error of the proposed method for power battery pack under air flow interference
表3 不同方法性能对比
Tab.3 Performance comparisons of different methods

方法测试集RMSE℃模型训练时间/s单步平均预测时间/s实时能力 所提方法0.095 1130.14能 径向基函数神经网络模型[33]0.086 3 2742.75否 COMSOL有限元仿真2 9523.69否
研究动力电池组的温度场建模能够揭示动力电池组在工作过程中的温度动力学特征,对于优化电池结构设计、实现健康管理以及提高电池寿命和性能具有重要意义,有利于推动电动汽车技术的发展和应用。本文提出了一种基于时空分离的动力电池组温度场建模方法。
首先利用Karhunen-Loève分解方法对动力电池组温度场数据进行时空特征提取,得到空间基函数和时间系数。为了降低在线建模过程中数据不断增多导致建模计算量不断增大的问题,本文利用空间特征增量式学习的方法来降低空间基函数特征提取的计算量,实现空间基函数的增量更新。进一步利用LSTM网络对提取到的时间特征进行动力学建模,最后将增量学习得到的空间基函数和LSTM网络预测的时间系数进行整合,得到动力电池组温度场的预测模型。
在一个由24节电池单体组成的动力电池包上进行了方法验证,结果表明,无论是在正常条件下还是有气流干扰条件下,所提出的方法都能对动力电池包的温度场进行准确预测。在有气流干扰下,所提出方法的单点温度预测误差小于0.07℃,在测试集上的RMSE为0.014 7℃。
本文所提方法对温度传感器的需求比较高,作者团队目前也在积极解决该问题。一个潜在的解决方案是利用离线模型提供更多的温度场信息,以减少对在线传感器的依赖。
参考文献
[1] 顾菊平, 蒋凌, 张新松, 等. 基于特征提取的锂离子电池健康状态评估及影响因素分析[J]. 电工技术学报, 2023, 38(19): 5330-5342. Gu Juping, Jiang Ling, Zhang Xinsong, et al. Estimation and influencing factor analysis of lithium-ion batteries state of health based on features extraction[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5330-5342.
[2] 孙丙香, 宋东林, 阮海军, 等. 基于自产热和外传热的锂离子电池热学模型参数辨识方法[J]. 电工技术学报, 2024, 39(1): 278-288. Sun Bingxiang, Song Donglin, Ruan Haijun, et al. Parameter identification method of thermal model of lithium-ion battery based on self-generated heat and external heat transfer[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 278-288.
[3] 尹杰, 刘博, 孙国兵, 等. 基于迁移学习和降噪自编码器-长短时间记忆的锂离子电池剩余寿命预测[J]. 电工技术学报, 2024, 39(1): 289-302. Yin Jie, Liu Bo, Sun Guobing, et al. Transfer learning denoising autoencoder-long short term memory for remaining useful life prediction of Li-ion batteries[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 289-302.
[4] 程夕明, 唐宇, 王寿群. 锂离子电池热物性参数测量方法综述[J]. 机械工程学报, 2019, 55(14): 140-150. Cheng Ximing, Tang Yu, Wang Shouqun. Thermo-physical parameter measurements for lithium-ion batteries: a review[J]. Journal of Mechanical Engineering, 2019, 55(14): 140-150.
[5] Zhou Yu, Wang Bingchuan, Li Hanxiong, et al. A surrogate-assisted teaching-learning-based optimization for parameter identification of the battery model[J]. IEEE Transactions on Industrial Informatics, 2020, 17(9): 5909-5918.
[6] 时玮, 韩甜, 赵杨梅, 等. 基于分层电化学热耦合模型的锂电池放电过程研究[J]. 电源学报, 2023, 21(4): 138-147. Shi Wei, Han Tian, Zhao Yangmei, et al. Research on discharging process of lithium battery based on layered electrochemical thermal coupling model[J]. Journal of Power Supply, 2023, 21(4): 138-147.
[7] Feng Xuning, Weng Caihao, Ouyang Minggao, et al. Online internal short circuit detection for a large format lithium ion battery[J]. Applied Energy, 2016, 161: 168-180.
[8] Xu Kangkang, Fan Bi, Yang Haidong, et al. Locally weighted principal component analysis-based multimode modeling for complex distributed parameter systems [J]. IEEE Transactions on Cybernetics, 2022, 52(10): 10504-10514.
[9] Jilte R, Afzal A, Panchal S. A novel battery thermal management system using nano-enhanced phase change materials[J]. Energy, 2021, 219: 119564.
[10] Sattarzadeh S, Roy T, Dey S. Real-time estimation of 2-D temperature distribution in lithium-ion pouch cells[J]. IEEE Transactions on Transportation Electri-fication, 2021, 7(4): 2249-2259.
[11] Li Weihan, Fan Yue, Ringbeck F, et al. Electrochemical model-based state estimation for lithium-ion batteries with adaptive unscented Kalman filter[J]. Journal of Power Sources, 2020, 476: 228534.
[12] Sattarzadeh S, Roy T, Dey S. Real-time estimation of 2-D temperature distribution in lithium-ion pouch cells[J]. IEEE Transactions on Transportation Electrification, 2021, 7(4): 2249-2259.
[13] Zhou Yu, Deng Hua, Li Hanxiong. Control-oriented Galerkin-spectral model for 3-D thermal diffusion of pouch-type batteries[J]. IEEE Transactions on Industrial Informatics, 2023, 19(6): 7508-7516.
[14] Shafiei A, Momeni A, Williamson S S. Battery modeling approaches and management techniques for Plug-in Hybrid Electric Vehicles[C]//2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 2011: 1-5.
[15] Li Jianwei, Mazzola M S. Accurate battery pack modeling for automotive applications[J]. Journal of Power Sources, 2013, 237: 215-228.
[16] Castano S, Gauchia L, Voncila E, et al. Dynamical modeling procedure of a Li-ion battery pack suitable for real-time applications[J]. Energy Conversion and Management, 2015, 92: 396-405.
[17] Kharisma M D, Ridwan M, Ilmiawan A F, et al. Modeling and simulation of lithium-ion battery pack using modified battery cell model[C]//2019 6th International Conference on Electric Vehicular Technology (ICEVT), Bali, Indonesia, 2019: 25-30.
[18] Xia Quan, Yang Dezhen, Wang Zili, et al. Multiphysical modeling for life analysis of lithium-ion battery pack in electric vehicles[J]. Renewable and Sustainable Energy Reviews, 2020, 131: 109993.
[19] Fan Xinyuan, Zhang Weige, Wang Zhanguo, et al. Simplified battery pack modeling considering inconsistency and evolution of current distribution[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(1): 630-639.
[20] Sun Hongguang, Wang Xiaohui, Tossan B, et al. Three-dimensional thermal modeling of a lithium-ion battery pack[J]. Journal of Power Sources, 2012, 206: 349-356.
[21] Zhu Cong, Li Xinghu, Song Lingjun, et al. Development of a theoretically based thermal model for lithium ion battery pack[J]. Journal of Power Sources, 2013, 223: 155-164.
[22] Jaguemont J, Boulon L, Dubé Y. Characterization and modeling of a hybrid-electric-vehicle lithium-ion battery pack at low temperatures[J]. IEEE Transactions on Vehicular Technology, 2015, 65(1): 1-14.
[23] 尹杰, 刘博, 孙国兵, 等. 基于迁移学习和DAE-LSTM的锂离子电池剩余寿命预测[J]. 电工技术学报, 2024, 39(1): 278-288. Yin Jie, Liu Bo, Sun guobing, et al.Transfer learning DAE-LSTM for remaining useful life prediction of Li-ion batteries[J]. Transactions of China Electro-technical Society, 2024, 39(1): 278-288.
[24] 宋显华, 姚全正. 基于片段充电数据和DEKF-WNN-WLSTM的锂电池健康状态实时估计[J]. 电工技术学报, 2024, 39(5): 1565-1576. Song Xianhua, Yao Quanzheng. Real-time state of health estimation for lithium-ion batteries based on daily segment charging data and dual extended kalman filters-wavelet neural network-wavelet long short-term memory neural network. Transactions of China Electrotechnical Society, 2024, 39(5): 1565-1576.
[25] Sherstinsky A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network[J]. Physica D: Nonlinear Phenomena, 2020, 404: 132306.
[26] Huang Ruijie, Wei Chenji, Wang Baohua, et al. Well performance prediction based on Long Short-Term Memory (LSTM) neural network[J]. Journal of Petroleum Science and Engineering, 2022, 208: 109686.
[27] Wei Peng, Li Hanxiong. Two-dimensional spatial construction for online modeling of distributed parameter systems[J]. IEEE Transactions on Industrial Electronics, 2022, 69(10): 10227-10235.
[28] 严璐晗, 林培杰, 程树英, 等. 基于增量学习的CNN-LSTM光伏功率预测[J]. 电气技术, 2024, 25(5): 31-40. Yan Luhan, Lin Peijie, Cheng Shuying, et al. CNN-LSTM photovoltaic power prediction based on incremental learning[J]. Electrical Engineering, 2024, 25(5): 31-40.
[29] Wang Zhi, Li Hanxiong. Incremental spatiotemporal learning for online modeling of distributed parameter systems[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019, 49(12): 2612-2622.
[30] Lao Zizhou, Xia Bizhong, Wang Wei, et al. A novel method for lithium-ion battery online parameter identification based on variable forgetting factor recursive least squares[J]. Energies, 2018, 11(6): 1358.
[31] Saw L H, Ye Yonghuang, Tay A A O, et al. Computational fluid dynamic and thermal analysis of Lithium-ion battery pack with air cooling[J]. Applied Energy, 2016, 177: 783-792.
[32] Wei Peng, Li Hanxiong. A spatio-temporal inference system for abnormality detection and localization of battery systems[J]. IEEE Transactions on Industrial Informatics, 2023, 19(5): 6275-6283.
[33] Wang Yuanlong, Chen Xiongjie, Li Chaoliang, et al. Temperature prediction of lithium-ion battery based on artificial neural network model[J]. Applied Thermal Engineering, 2023, 228: 120482.
Abstract Power battery packs are widely used in new energy electric vehicles and are the core components of electric vehicles. Studying the temperature field modeling of the power battery pack is not only beneficial to understanding its temperature field dynamic characteristics, but is also very important for the structural design and health management of the power battery pack. The temperature field of the power battery pack is described by complex partial differential equations. Since a large number of parameters are unknown and many model parameters show strong time variability, traditional physics-based modeling methods are ineffective in achieving online modeling of the temperature field of the power battery pack. Although methods based on deep learning do not rely on physical models, they require a large amount of experimental data during the training process, the model training time is long, and the real-time performance of temperature field prediction is poor. In response to the above problems, this paper proposes a spatio-temporal modeling of the temperature field of power battery packs based on long short-term memory network.
First, the spatio-temporal separation method is used to extract spatial features and time features under offline conditions. Spatial features are continuously updated with the help of incremental learning, and the long short-term memory (LSTM) network is used to model temporal dynamics. Finally, the updated spatial characteristics and time model are integrated to obtain a prediction model of the power battery pack temperature field.
The proposed method was verified on a power battery pack composed of 24 battery cells. Experimental results show that the proposed method can accurately predict the temperature field of the power battery pack regardless of normal conditions or conditions with air flow interference. Without airflow interference, the single-point temperature prediction error of the proposed method is less than 0.4℃, and the root-mean-square error (RMSE) on the test set is 0.095 1℃. In the presence of airflow interference, the single-point temperature prediction error of the proposed method is less than 0.07℃, and the RMSE on the test set is 0.014 7℃.Under the condition of air flow, the modeling error of the proposed method is smaller. This is because under the condition of air flow interference, the spatial gradient of the temperature change of the power battery pack at the same time is smaller, that is, the temperature change is gentler, making the spatial characteristics of the modeling smoother.
The following conclusions can be drawn from the simulation analysis: (1) the proposed method can accurately predict the temperature field of the power battery pack regardless of normal conditions or conditions with air flow interference. (2) The proposed method can update spatial features in real time through incremental learning, thereby reducing the computational complexity of the method. (3) The proposed method is a purely data-driven method that does not rely on accurate partial differential equations and is therefore suitable for application in temperature field modeling of actual power battery packs.
keywords:Power battery pack, spatio-temporal modeling, long short-term memory network, feature extraction
DOI: 10.19595/j.cnki.1000-6753.tces.241181
中图分类号:TM912
国家自然科学基金(52407250, U24B20103)和中央高校基本科研业务费专项资金(2024IVA044)资助项目。
收稿日期 2024-07-04
改稿日期 2024-08-31
韦 鹏 男,1995年生,博士,研究方向为动力电池系统建模和储能系统健康管理。E-mail:pengwei7@whut.edu.cn
谢长君 男,1980年生,博士,研究方向为新能源汽车电气电控、燃料电池与锂电池管理系统、先进储能科学及应用。E-mail:jackxie@whut.edu.cn(通信作者)
(编辑 郭丽军)