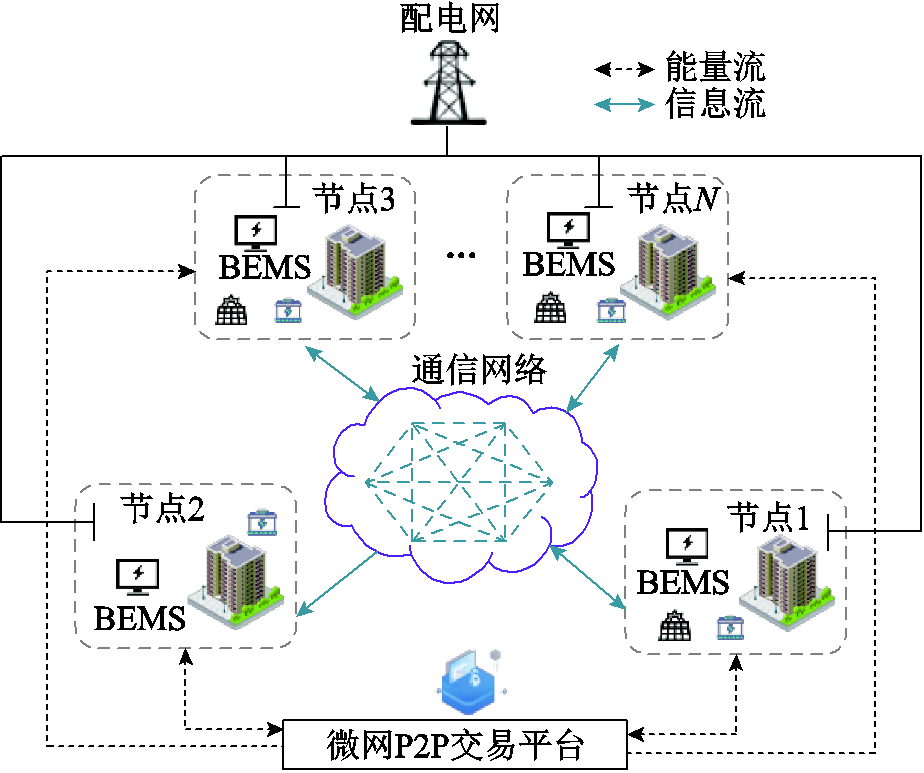
图1 微电网多智能楼宇运行框架
Fig.1 Operation framework of microgrid multi-intelligent building
摘要 随着分布式资源在配电网中渗透率不断提高,兼具产消双重属性的智能楼宇间电能交易为分布式能源就近消纳带来新的机遇和挑战。针对含多智能楼宇的微电网系统,该文提出一种微电网多智能楼宇区间滚动点对点(P2P)电能交易分布式信息交互优化策略。首先,考虑智能楼宇灵活性资源的聚合特性,以聚合功率区间形式表征分布式光伏发电预测区间结果与灵活性资源可行域范围,建立微电网多智能楼宇滚动P2P交易模型;其次,将光伏出力不确定性给P2P交易带来的风险成本进行量化,建立微电网多智能楼宇经济调度模型,在此基础上,将楼宇间P2P交易功率作为一致性变量,基于相邻楼宇间的信息交互进行分布式求解,得出P2P交易功率与交易电价;最后,通过算例验证该文模型可在保证隐私性的同时,有效地提高微电网多智能楼宇系统的经济性。
关键词:微电网 智能楼宇 聚合功率区间 滚动P2P电能交易 分布式信息交互
随着我国能源市场深化改革以及电力系统向低碳化转型,分布式能源在配电网中的占比不断提高,传统电力系统逐渐向新型电力系统转变[1]。作为一种协调能源分配的平台,微电网内兼具电能生产和消费能力的智能楼宇内部聚合了大量可调度资源[2]。多智能楼宇的用能方式具有良好的互补特性和交互关系,可有效提升微电网的运行收益及分布式能源的消纳水平,发挥资源共享互济的优势[3]。这将进一步促使新型利益主体灵活利用其内部柔性资源,提升交易主动性,从而构建售电市场由传统的集中模式向分散自治、异构协同的去中心化趋势发展[4]。
在这种背景下,由去中心化交易机制支撑的点对点(Peer-to-Peer, P2P)交易可以使智能楼宇直接参与批发或零售市场[5],减少楼宇与电网之间频繁交互引起的功率波动,提高多智能楼宇参与市场的主动性、经济性及新能源的消纳率。文献[6]通过P2P电能共享机制和快速交替方向乘子法(Alternating Direction Method of Multipliers, ADMM)求解得到智能楼宇群的最优策略。文献[7]对多楼宇微电网系统提出一种多时间尺度调度方法,能够在日前经济优化调度阶段降低楼宇运行成本,在日内滚动修正阶段平抑由日前预测误差导致的微电网联络线功率波动。然而,楼宇需求侧资源种类丰富且灵活性潜力并非是确定的功率曲线[8],仅对某一种资源进行分析与协同控制会有很大的局限性。因此,需要将楼宇内多种灵活性资源进行量化与聚合。文献[9]基于投影等值理论对配电网/虚拟电厂可行域进行聚合。文献[10]建立了具有鲁棒边界的虚拟电池模型,基于闵可夫斯基求和整合需求侧资源参与日前优化调度。文献[11]引进一种同时结合能源和不确定性的P2P联合市场,将本地交易分为日前市场的预测电力交易和实时市场的不确定性电力交易。文献[12]在P2P能源交易中引入储备市场补偿新能源发电的不确定性,并分配储备成本。文献[13]针对具有不确定性的综合能源系统,采用一种在线预测优化的P2P电氢交易。以上文献均考虑了P2P交易中的不确定性,但无法不断地向前滚动推进P2P交易时段,时效性不足,难有足够能力应对不确定因素的影响。
在应对规模逐渐扩大的微电网多智能楼宇P2P电能交易问题时,传统集中式方法具有通信信息量大、鲁棒性低和涉及用户隐私等缺陷,无法满足电力市场环境下配电网优化调度的需求[14]。分布式优化通过局部信息和相邻通信原则就能实现整个系统的优化调度,更具隐私性与时效性,也符合电力系统去中心化的总体趋势[15]。文献[16]利用对偶一致性交替方向乘子法,实现了所建立模型预测控制问题的完全分布式求解。文献[17]提出基于改进的一致性算法实现无园区层能量管理系统(Energy Management System, EMS)下的分布式综合需求响应。文献[18]将分布式与集中式相结合,利用ADMM对园区电-氢-热系统进行分布式优化。上述文献中虽然采用了分布式求解方法,但提到的ADMM方法需要通过中心机构进行信息传递,个人隐私安全难以得到保障,而一致性算法可能导致系统逐渐集中化,违背了分布式系统去中心化的初衷。文献[19]基于共识算法实现了各市场主体完全平等的去中心化交易,但该算法在一次迭代中需要分两次传递信息。文献[20]采用保密通信策略解决微电网的隐私保护分布式经济调度问题。上述研究实现了分布式信息交互的去中心化问题,但存在运算处理速度慢和收敛性较差等问题。
综上所述,本文基于灵活性资源聚合功率区间进行微电网多智能楼宇滚动P2P电能交易,利用楼宇间分布式信息交互策略建立微电网经济调度模型。最后通过仿真算例验证所提模型的可行性与有效性。
考虑一个由多智能楼宇组成的微电网系统,每栋楼宇之间通过电力和通信网络连接。基于楼宇间的通信连接关系将微电网中每栋楼宇视为节点,根据电能和信息的双向流动特性,建立微电网多智能楼宇运行框架如图1所示。各楼宇都配置了储能系统(Energy Storage System, ESS)、光伏(Photovoltaic, PV)等新能源发电和弹性负荷(Elastic Load, EL)等灵活性资源,这些灵活性负荷通过将电力需求从高峰转移到非高峰期,减轻配电网向微电网系统的供电压力。智能楼宇通过微电网P2P交易平台参与滚动P2P电能交易进行电能的购售,同时每栋楼宇配备楼宇能量管理系统(Building Energy Management System, BEMS)控制内部的灵活性资源。

图1 微电网多智能楼宇运行框架
Fig.1 Operation framework of microgrid multi-intelligent building
在滚动P2P交易阶段,智能楼宇根据PV发电预测区间结合自身分布式资源优化情况,通过BEMS上传预测时域内预交易电量区间至通信网络,更新P2P交易电价并反馈给BEMS,进行预测时域内分布式资源的优化,直到交易功率不再变化时达到均衡状态,得到P2P交易电价和楼宇间交易电量的最优值,在微电网P2P交易平台完成购售电量的交付并进行下个时段的计算。
作为微电网中参与电能交易的实体,各楼宇通过对灵活性资源进行量化,建立P2P交易聚合区间模型,进而结合自身购售电策略参与滚动P2P电能交易。
对于参与P2P电能交易的智能楼宇,其光伏出力、储能系统及弹性负荷都会对楼宇的交易电量产生影响。本节基于灵活性资源的聚合特性分别对楼宇中调度资源的可行域区间进行描述。
1)分布式光伏发电预测区间模型
本文中智能楼宇间P2P交易的电能来自分布式光伏,而光伏出力不确定性可以通过光伏出力预测值在不同置信水平下的基准出力转换为预测分位数进行区间建模[21]。进而,利用不同置信水平下分位数结果中包含的不确定性信息将由光伏预测误差引起的光伏出力所在区间表示为
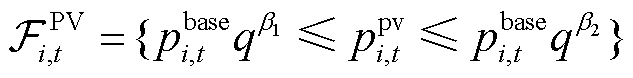 (1)
(1)
式中,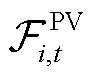 为楼宇
为楼宇 在
在 时段光伏出力的灵活性可行域;
时段光伏出力的灵活性可行域;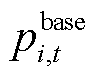 为楼宇
为楼宇 在
在 时段光伏预测出力;
时段光伏预测出力;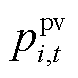 为楼宇
为楼宇 在
在 时段光伏实际出力;
时段光伏实际出力;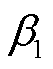 和
和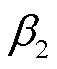 分别为光伏出力低于预测值和高于预测值时对应的置信水平;
分别为光伏出力低于预测值和高于预测值时对应的置信水平;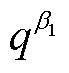 和
和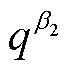 分别为在置信水平
分别为在置信水平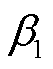 和
和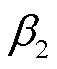 下概率预测的分位数。
下概率预测的分位数。
2)储能系统充放电功率区间模型
智能楼宇中储能系统的充放电功率可以根据预定计划进行调整。储能系统功率调整区间具有确定性,但会受到储能容量和充放电功率上限的影响,因此储能系统充放电功率区间可表示为
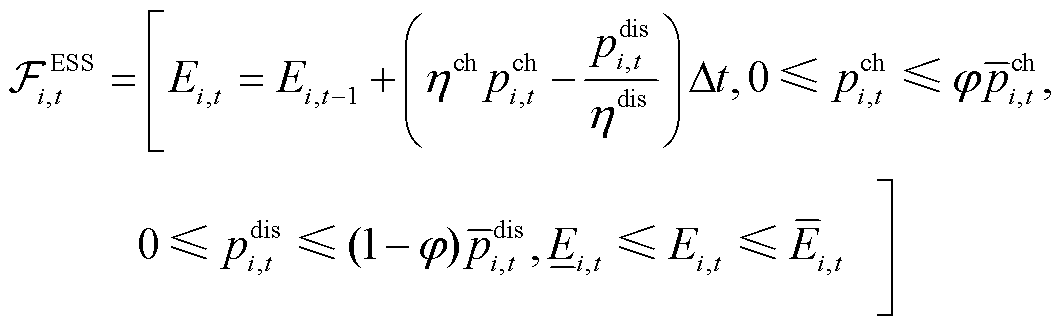 (2)
(2)
式中,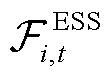 为楼宇
为楼宇 在
在 时段储能系统的灵活性可行域;
时段储能系统的灵活性可行域;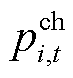 和
和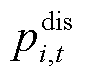 分别为楼宇
分别为楼宇 在
在 时段储能系统充、放电功率;
时段储能系统充、放电功率;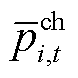 和
和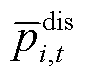 分别为楼宇
分别为楼宇 储能充、放电功率的上限;
储能充、放电功率的上限;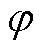 为布尔变量,
为布尔变量,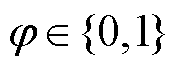 ,为保证储能不可同时充放电,储能充电取1,储能放电取0;
,为保证储能不可同时充放电,储能充电取1,储能放电取0;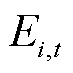 为楼宇
为楼宇 在
在 时段储能容量值;
时段储能容量值;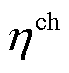 和
和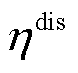 分别为储能系统的充、放电效率;
分别为储能系统的充、放电效率;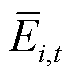 和
和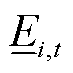 分别为楼宇
分别为楼宇 在
在 时段储能系统荷电状态的最大值和最小值;Dt为两个交易时刻的时间间隔,本文设定为15 min。
时段储能系统荷电状态的最大值和最小值;Dt为两个交易时刻的时间间隔,本文设定为15 min。
3)弹性负荷功率调整区间模型
根据P2P交易中的功率需求,智能楼宇中弹性负荷可在一定区间范围内调整其自身功耗,实现楼宇的经济运行。弹性负荷功率调整区间可表示为
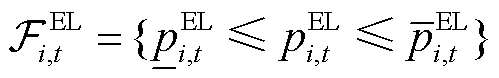 (3)
(3)
式中,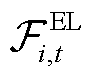 为楼宇
为楼宇 在
在 时段弹性负荷的灵活性可行域;
时段弹性负荷的灵活性可行域;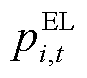 为楼宇
为楼宇 在
在 时段弹性负荷功率;
时段弹性负荷功率;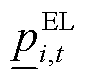 和
和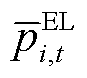 分别为楼宇
分别为楼宇 在
在 时段负荷调整后的最小值和最大值。
时段负荷调整后的最小值和最大值。
受到光伏出力预测区间的影响,楼宇间P2P交易功率也在一定区间范围内波动。智能楼宇由各种分布式资源等值聚合而成,采用闵可夫斯基求和理论[22]对光伏发电预测区间和可控灵活性资源功率区间进行有效整合,将智能楼宇P2P交易功率区间量化为
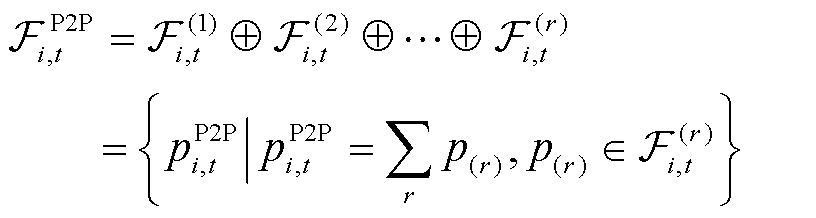 (4)
(4)
式中,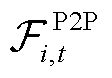 为通过闵可夫斯基求和后进行P2P交易的聚合功率区间;
为通过闵可夫斯基求和后进行P2P交易的聚合功率区间;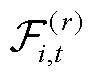 为第
为第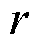 种需求侧资源的可行域空间;
种需求侧资源的可行域空间;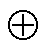 为闵可夫斯基求和符号;
为闵可夫斯基求和符号;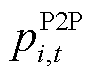 为楼宇
为楼宇 在
在 时段的P2P净交易功率,
时段的P2P净交易功率,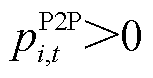 表示楼宇
表示楼宇 在
在 时段购买功率,
时段购买功率,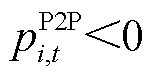 表示楼宇
表示楼宇 在
在 时段出售功率;
时段出售功率;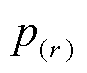 为第
为第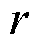 种需求侧资源的功率值。由此,聚合后的P2P交易功率可行域通过功率区间形式表征,以此量化资源的灵活性调控能力,使楼宇内多类别小容量且分散的分布式资源平等地参与到交易中。
种需求侧资源的功率值。由此,聚合后的P2P交易功率可行域通过功率区间形式表征,以此量化资源的灵活性调控能力,使楼宇内多类别小容量且分散的分布式资源平等地参与到交易中。
其中,整合的P2P交易区间在满足上述可行域空间的同时,也应满足如下功率限制约束:
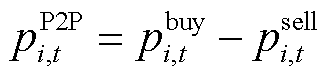 (5)
(5)
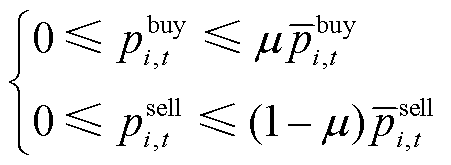 (6)
(6)
式中,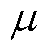 为布尔变量,
为布尔变量,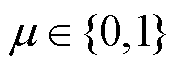 ,为保证楼宇购售电不同时发生,购买功率取1,出售功率取0;
,为保证楼宇购售电不同时发生,购买功率取1,出售功率取0;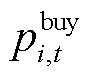 和
和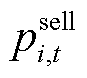 分别为楼宇
分别为楼宇 在
在 时段购买和出售的功率;
时段购买和出售的功率;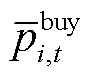 和
和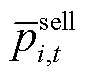 分别为楼宇
分别为楼宇 在
在 时段购买和出售功率的最大值。
时段购买和出售功率的最大值。
在对P2P交易聚合区间建模过程中,考虑到光伏出力区间是在一定置信度水平下表示的,基于式(4)得出楼宇 在调度时段
在调度时段 内交易功率可行范围为
内交易功率可行范围为
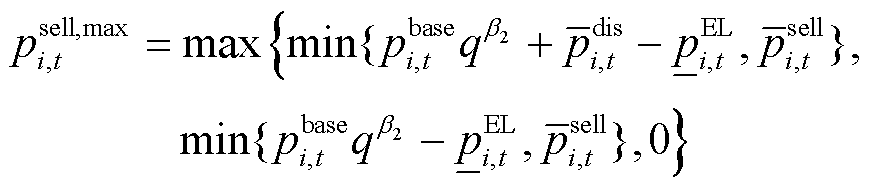 (7)
(7)
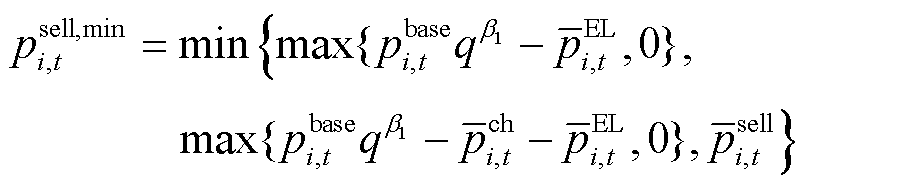 (8)
(8)
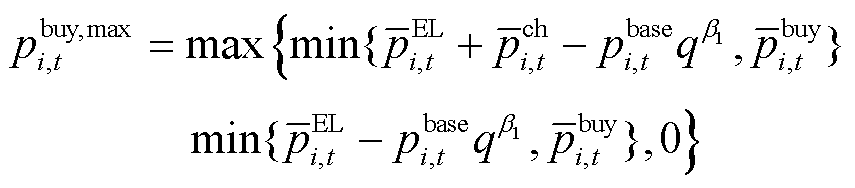 (9)
(9)
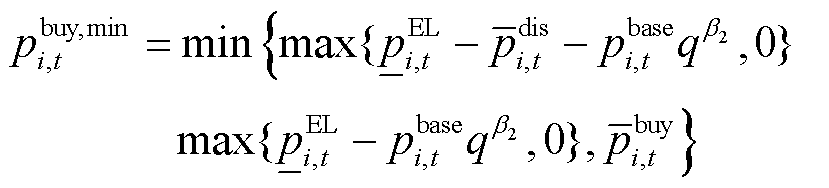 (10)
(10)
式中,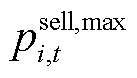 和
和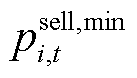 分别为楼宇
分别为楼宇 在
在 时段出售量的最大、最小功率;
时段出售量的最大、最小功率;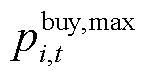 和
和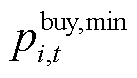 分别为楼宇
分别为楼宇 在
在 时段购买量的最大、最小功率。
时段购买量的最大、最小功率。
智能楼宇根据自身资源调度的灵活性描述其可行域范围,通过闵可夫斯基求和理论聚合成一个整体,在P2P能源交易期间以聚合功率区间形式参与滚动P2P电能交易,交易框架如图2所示。
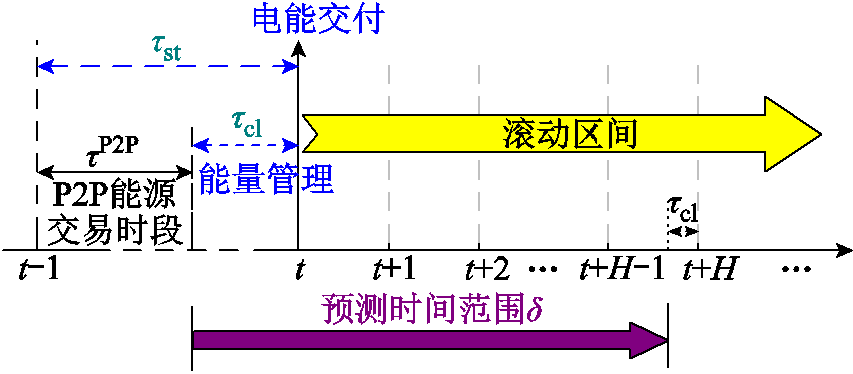
图2 区间滚动P2P电能交易框架
Fig.2 Interval rolling P2P energy trading framework
图2中,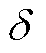 为预测时间范围的长度,
为预测时间范围的长度,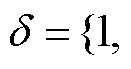
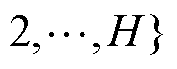 ,将系统的整个优化周期划分为H个时段。P2P能源交易在电能交付时段
,将系统的整个优化周期划分为H个时段。P2P能源交易在电能交付时段 之前的
之前的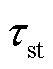 开放,并在电能交付之前的
开放,并在电能交付之前的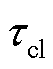 关闭。因此,P2P能源交易时段可表示为
关闭。因此,P2P能源交易时段可表示为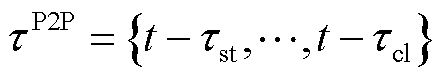 。在此过程中,各楼宇结合自身聚合区间可行域范围与购售电策略在微电网P2P交易平台上寻找相匹配的交易对象进行交互协商,最终完成购售电并达成交易。电能交付后,各楼宇在能量管理时段
。在此过程中,各楼宇结合自身聚合区间可行域范围与购售电策略在微电网P2P交易平台上寻找相匹配的交易对象进行交互协商,最终完成购售电并达成交易。电能交付后,各楼宇在能量管理时段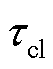 中不断获取新的预测信息并更新自身需求情况,降低不确定性因素的影响,动态调整自身聚合功率区间以参与下一个时段的电能交易。此时滚动区间向前移动到下一运行时段
中不断获取新的预测信息并更新自身需求情况,降低不确定性因素的影响,动态调整自身聚合功率区间以参与下一个时段的电能交易。此时滚动区间向前移动到下一运行时段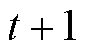 的能量管理开始时刻
的能量管理开始时刻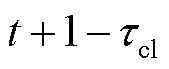 ,并重复上述操作,如此不断迭代直到满足微电网内所有智能楼宇的要求。
,并重复上述操作,如此不断迭代直到满足微电网内所有智能楼宇的要求。
本文在区间滚动P2P电能交易框架的基础上,通过相邻楼宇间的分布式信息交互对微电网经济调度模型进行转换,进而实现多智能楼宇的并行优化。
对于微电网智能楼宇自身而言,其参与P2P交易的主要目的是为减少购电成本以获取更大的收益。在考虑楼宇自身负荷调整及储能系统运维成本的同时,还需考虑光伏出力不确定性给P2P交易带来的风险成本。因此微电网多智能楼宇的总运行成本函数为
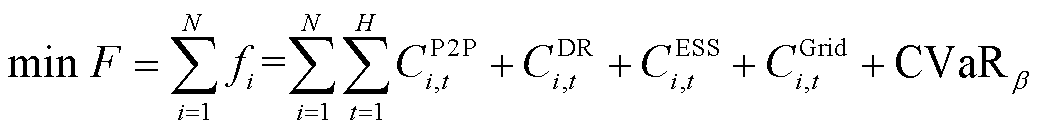 (11)
(11)
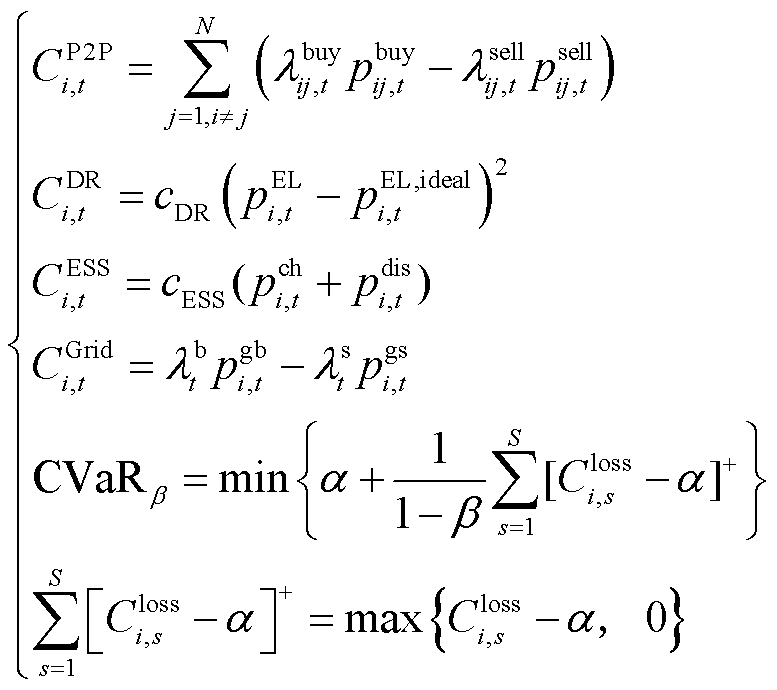 (12)
(12)
式中,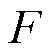 为微电网多智能楼宇在预测时间范围
为微电网多智能楼宇在预测时间范围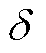 内的总运行成本;
内的总运行成本;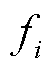 为楼宇
为楼宇 在预测时间范围
在预测时间范围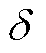 内的总运行成本;
内的总运行成本;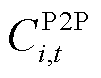 为楼宇
为楼宇 在
在 时段向其他楼宇购电产生的P2P电能交易成本;
时段向其他楼宇购电产生的P2P电能交易成本;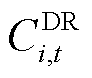 为楼宇
为楼宇 在
在 时段需求响应成本;
时段需求响应成本;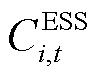 为楼宇
为楼宇 在
在 时段的储能运维成本;
时段的储能运维成本;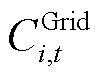 为楼宇
为楼宇 在
在 时段与主网进行功率交互成本;
时段与主网进行功率交互成本;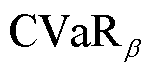 为风险度量成本;
为风险度量成本;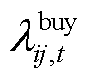 和
和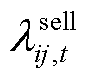 分别为楼宇
分别为楼宇 在
在 时段向楼宇
时段向楼宇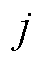 购买和出售功率的价格;
购买和出售功率的价格;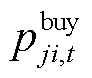 和
和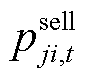 分别为楼宇
分别为楼宇 在
在 时段向楼宇
时段向楼宇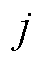 购买和出售功率;
购买和出售功率;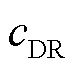 为楼宇
为楼宇 需求响应系数;
需求响应系数;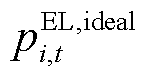 为楼宇
为楼宇 在
在 时段理想用电功率;
时段理想用电功率;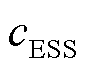 为储能系统运维成本系数;
为储能系统运维成本系数;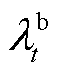 和
和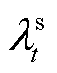 分别为
分别为 时段楼宇分时电价和上网电价;
时段楼宇分时电价和上网电价;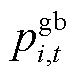 和
和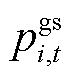 分别为楼宇
分别为楼宇 在
在 时段从主网的购、售功率;
时段从主网的购、售功率;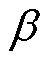 为置信水平;
为置信水平;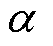 为辅助变量,最优值即为
为辅助变量,最优值即为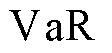 ;S为场景数量;
;S为场景数量;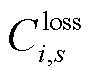 为楼宇
为楼宇 在
在 时段的成本损失值;N为微电网内楼宇总数量;H为总优化时段。
时段的成本损失值;N为微电网内楼宇总数量;H为总优化时段。
光伏出力的不确定性会导致楼宇在P2P交易中出现不同的收益水平,具有一定的风险性。当出售功率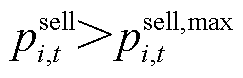 或
或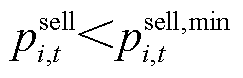 时,将带来收益损失;当
时,将带来收益损失;当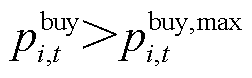 或
或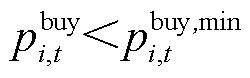 时,将带来购电成本损失。在一定置信水平下光伏出力不确定性给楼宇P2P交易带来的损失值
时,将带来购电成本损失。在一定置信水平下光伏出力不确定性给楼宇P2P交易带来的损失值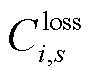 为
为
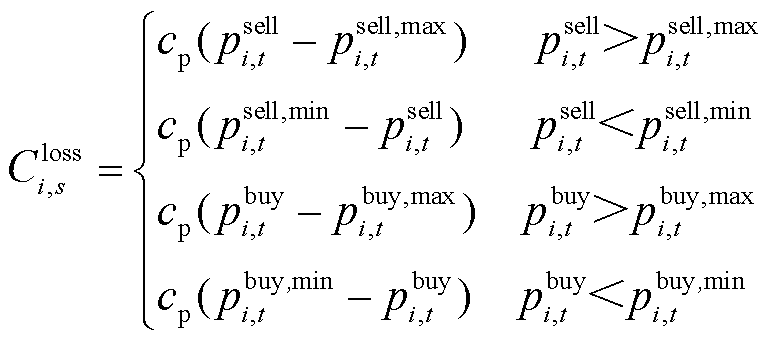 (13)
(13)
式中,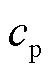 为风险惩罚单位成本。
为风险惩罚单位成本。
式(13)为非线性模型,其线性化处理的详细过程见附录。
为保证微电网的安全稳定运行,需要满足以下约束条件。
1)智能楼宇功率平衡约束
在交易过程中要保证各楼宇内的功率平衡,在忽略网络损耗的情况下要满足的约束为
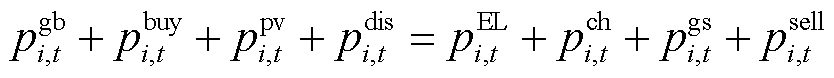 (14)
(14)
2)主网购售电约束
楼宇允许在光伏发电盈余时出售多余电能或在电量短缺时从主网购买电能。但在某调度时刻的购售电量不宜过高,应该在确定的范围内变化,即
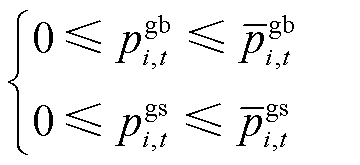 (15)
(15)
式中,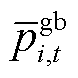 和
和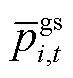 分别为楼宇
分别为楼宇 在
在 时段向主网购、售功率的最大值。
时段向主网购、售功率的最大值。
3)P2P电能交互约束
楼宇间P2P电能交互功率应满足
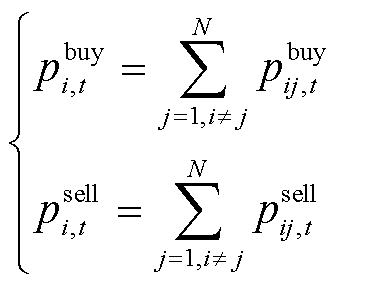 (16)
(16)
本节设定微电网P2P交易平台保留有所有楼宇的交易功率信息。将交易功率作为楼宇间P2P交易的一致性变量,每栋楼宇根据其他楼宇的交易功率进行内部能量管理,更新自身购售电需求,通过BEMS上传预测时间范围内的预交易功率区间至通信网络。在确定各交易对的P2P交易电价并完成P2P交易后,将能源交易时段向后滚动推进并重复上述过程。
将图1含有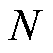 栋智能楼宇的微电网采用无向图模型
栋智能楼宇的微电网采用无向图模型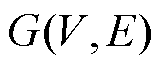 描述。其中V为各个楼宇节点集合,
描述。其中V为各个楼宇节点集合,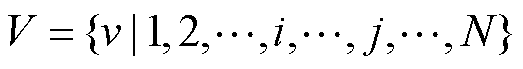 ,P2P交易中的交易功率由节点注入功率表示,节点间通信网络中的通信链路视为无向边,则通信拓扑图的边点关联矩阵可以表示为
,P2P交易中的交易功率由节点注入功率表示,节点间通信网络中的通信链路视为无向边,则通信拓扑图的边点关联矩阵可以表示为
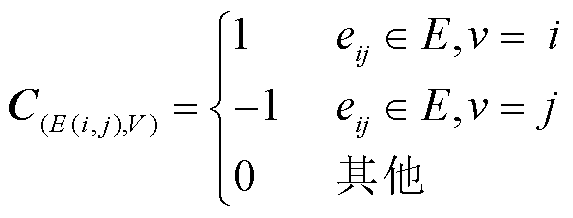 (17)
(17)
式中,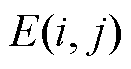 为由楼宇
为由楼宇 和楼宇
和楼宇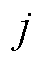 组成的通信链路。无向图
组成的通信链路。无向图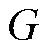 的拉普拉斯矩阵
的拉普拉斯矩阵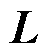 =
=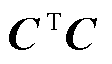 是对称半正定矩阵,其第
是对称半正定矩阵,其第 行表示第
行表示第 个智能楼宇节点对其他所有节点交易功率产生扰动时所产生的增益累积。
个智能楼宇节点对其他所有节点交易功率产生扰动时所产生的增益累积。
定义1:将交易功率作为楼宇间P2P交易的一致性变量,同时满足微电网整体的交易功率平衡条件。
1)一致性变量矩阵
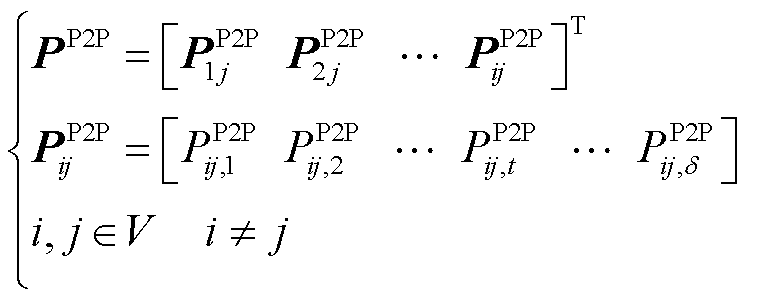 (18)
(18)
2)单个调度时段交易对-交易量系数矩阵和功率平衡条件可表示为
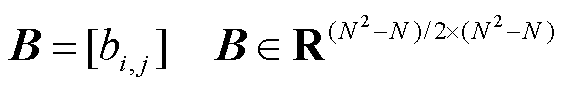 (19)
(19)
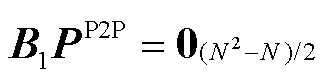 (20)
(20)
式中,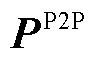 为在预测时间范围
为在预测时间范围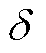 内的交易电量信息;
内的交易电量信息;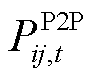 为在
为在 时段楼宇
时段楼宇 向楼宇
向楼宇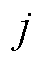 交易的电量;在楼宇
交易的电量;在楼宇 和楼宇
和楼宇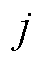 组成的交易对中,涉及楼宇
组成的交易对中,涉及楼宇 和楼宇
和楼宇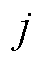 交易时
交易时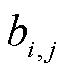 为1,其余情况为0;
为1,其余情况为0;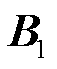 为交易对系数矩阵与单位矩阵的克罗克内积;
为交易对系数矩阵与单位矩阵的克罗克内积;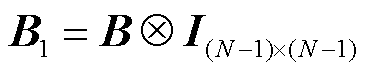 ,其中
,其中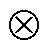 表示克罗内克积,I为单位矩阵。
表示克罗内克积,I为单位矩阵。
根据定义1将微电网多智能楼宇调度问题式(11)转换为矩阵形式,通过辅助变量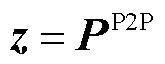 构建拉格朗日函数为
构建拉格朗日函数为
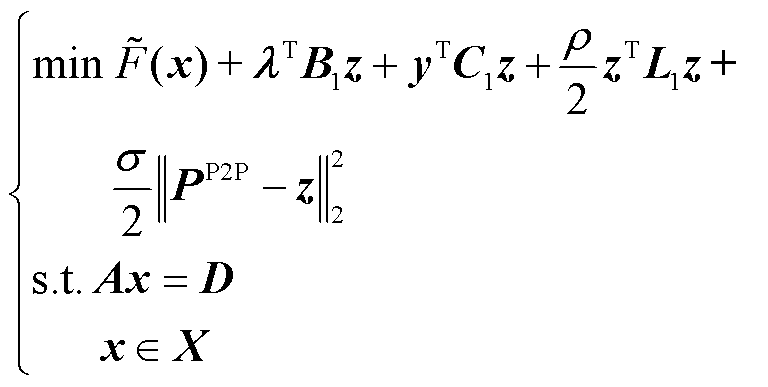 (21)
(21)
式中,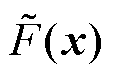 为去除
为去除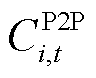 后微电网内多智能楼宇在
后微电网内多智能楼宇在 时段的目标函数;x为微电网多智能楼宇调度中的决策变量,
时段的目标函数;x为微电网多智能楼宇调度中的决策变量,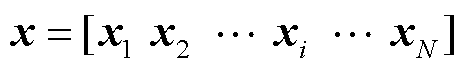 ,xi为楼宇
,xi为楼宇 在预测时间内各个时段的决策变量,
在预测时间内各个时段的决策变量,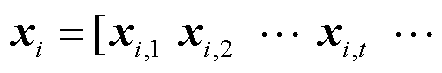
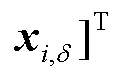 ;
; 和
和 分别为系数矩阵和参数矩阵;
分别为系数矩阵和参数矩阵;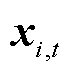 为楼宇
为楼宇 在t时段内决策变量的向量形式,
在t时段内决策变量的向量形式,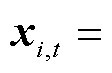
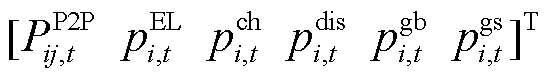 ;
;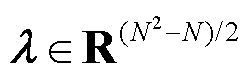 为关于楼宇间交易功率平衡的拉格朗日乘子,可以表示楼宇间进行P2P交易时的价格信息;y为一致性变量的拉格朗日乘子,
为关于楼宇间交易功率平衡的拉格朗日乘子,可以表示楼宇间进行P2P交易时的价格信息;y为一致性变量的拉格朗日乘子,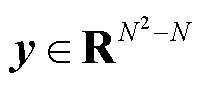 ;
;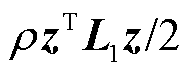 为违反一致性限制的惩罚项,
为违反一致性限制的惩罚项,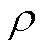 为该项惩罚系数;
为该项惩罚系数;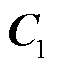 为边点关联矩阵与单位矩阵的克罗克内积,
为边点关联矩阵与单位矩阵的克罗克内积,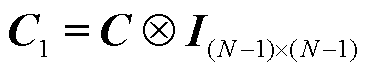 ;
;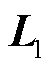 为拉普拉斯矩阵与单位矩阵的克罗克内积,
为拉普拉斯矩阵与单位矩阵的克罗克内积,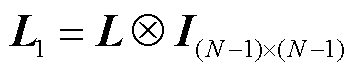 ;
;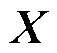 为由式(12)~式(16)构成的楼宇本地决策变量可行域;
为由式(12)~式(16)构成的楼宇本地决策变量可行域;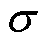 为惩罚系数。
为惩罚系数。
定义2: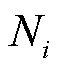 表示楼宇
表示楼宇 的相邻楼宇集合,
的相邻楼宇集合,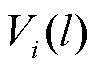 表示至少
表示至少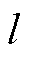 次信息交互与楼宇
次信息交互与楼宇 建立通信的楼宇集合,
建立通信的楼宇集合,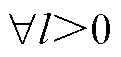 且
且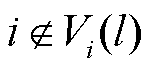 。多楼宇间信息交互内容定义为
。多楼宇间信息交互内容定义为
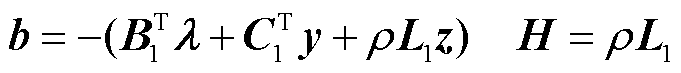 (22)
(22)
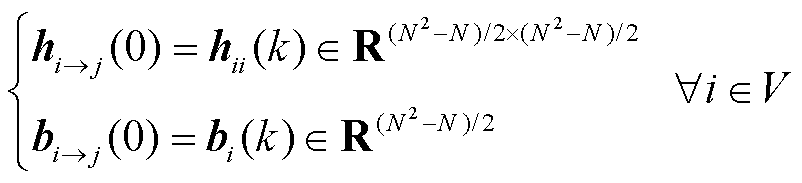 (23)
(23)
式中,信息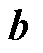 包括购售电量和电价信息;
包括购售电量和电价信息;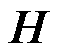 为楼宇间内部电价趋同惩罚信息;
为楼宇间内部电价趋同惩罚信息;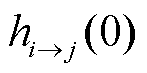 为初始时刻楼宇
为初始时刻楼宇 向楼宇
向楼宇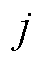 传递的购售电量和电价信息;
传递的购售电量和电价信息;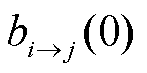 为初始时楼宇
为初始时楼宇 向楼宇
向楼宇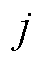 传递的趋同惩罚信息;
传递的趋同惩罚信息;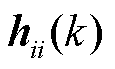 为第
为第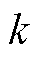 次迭代时
次迭代时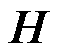 中楼宇
中楼宇 本地购售电量和电价信息;
本地购售电量和电价信息;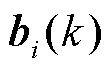 为第
为第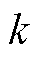 次迭代时
次迭代时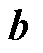 中楼宇
中楼宇 本地趋同惩罚信息。
本地趋同惩罚信息。
楼宇 根据第
根据第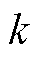 次迭代中预交易电量信息
次迭代中预交易电量信息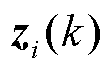 更新自身决策变量
更新自身决策变量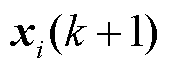 ,进而计算拉格朗日乘子变量
,进而计算拉格朗日乘子变量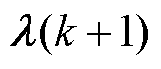 作为P2P交易电价,表达式为
作为P2P交易电价,表达式为
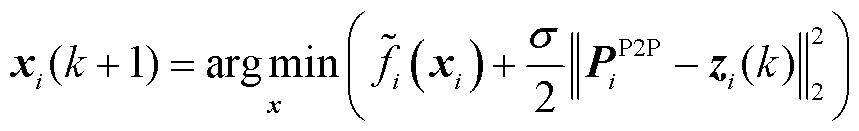 (24)
(24)
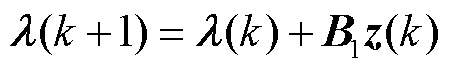 (25)
(25)
式中,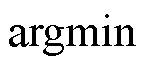 为使目标函数达到最小值时变量的取值。
为使目标函数达到最小值时变量的取值。
对于每个楼宇 ,在信息交互过程中逐步不重复搜集
,在信息交互过程中逐步不重复搜集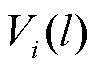 中的信息,楼宇
中的信息,楼宇 传递给楼宇
传递给楼宇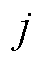 的信息除了自身信息外,还有
的信息除了自身信息外,还有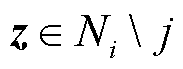 的信息。通过分布式信息交互过程,对原问题式(21)的计算过程可分解为N栋楼宇的子问题。令
的信息。通过分布式信息交互过程,对原问题式(21)的计算过程可分解为N栋楼宇的子问题。令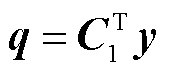 作为新对偶迭代变量,更新预交易电量信息
作为新对偶迭代变量,更新预交易电量信息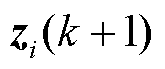 ,楼宇间基于信息交互求解过程为
,楼宇间基于信息交互求解过程为
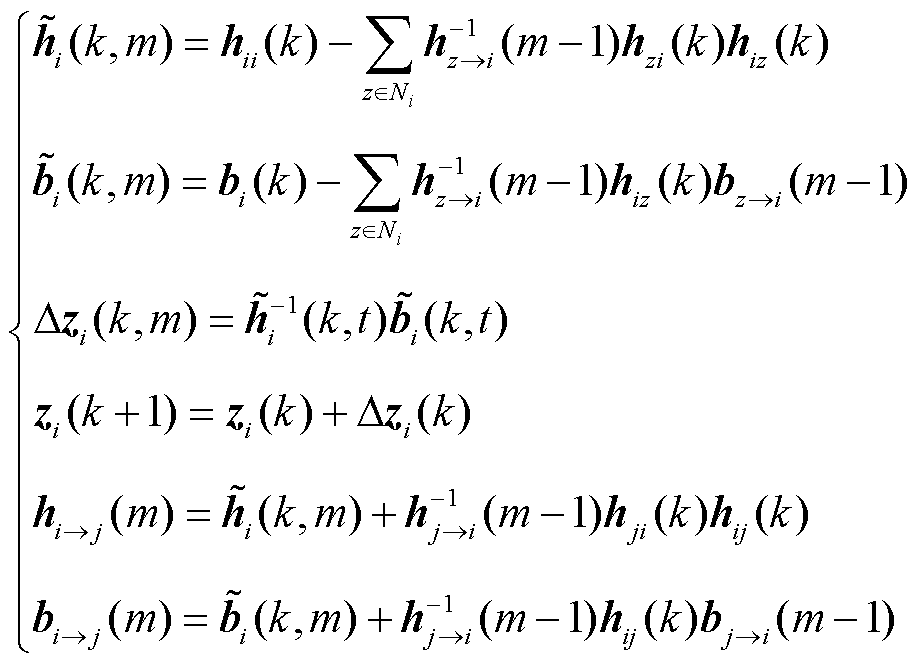 (26)
(26)
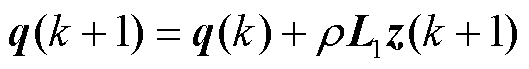 (27)
(27)
式中,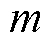 为信息交互次数。
为信息交互次数。
通过上述信息交互策略,可以将原本的耦合矩阵变为分布式计算的形式,其中每栋楼宇的本地分布式计算过程只用了矩阵中的一行或一列进行计算,楼宇 在确定自身P2P购售电量后,通过一定迭代次数后其P2P交易功率与其他楼宇达成一致。
在确定自身P2P购售电量后,通过一定迭代次数后其P2P交易功率与其他楼宇达成一致。
本文采用残差e作为收敛标准,收敛阈值为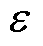 ,残差e定义为
,残差e定义为
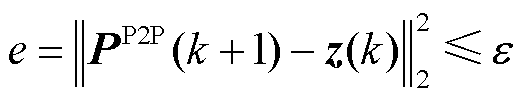 (28)
(28)
基于分布式信息交互的微电网多智能楼宇并行优化调度策略更新的步骤为:
(1)初始化各楼宇间交易对的内部交易电价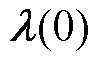 ,制定各楼宇内部预购售电量及储能充放电方案
,制定各楼宇内部预购售电量及储能充放电方案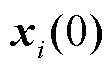 。
。
(2)各楼宇BEMS根据初始交易电价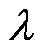 (0)通过式(25)、式(26)信息交互策略更新每组交易对的交易功率,并得出交易电价信息
(0)通过式(25)、式(26)信息交互策略更新每组交易对的交易功率,并得出交易电价信息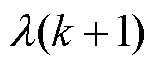 。
。
(3)根据式(28)判断是否满足收敛条件,若不满足则返回步骤(2),直至满足收敛条件。
上述计算过程中,楼宇间P2P交易策略更新过程是通过分布式并行计算完成的。在满足收敛条件时,各楼宇的交易功率不再发生变化,交易电价也随之统一。同时,各楼宇仅通过主体间传递交易功率和交易电价等信息来实现P2P交易,而不需要分享光伏、储能和负荷的功率数据,以此保护智能楼宇的隐私性并减轻计算压力。
为了验证所提区间滚动P2P电能交易模型,本文采用IEEE 13节点配电网系统进行仿真分析。微电网系统由同时配备光伏和储能系统的光伏楼宇1~5和只配备储能系统的一般楼宇6~13组成。分布式发电、各楼宇中负荷、分时电价上网电价等数据来源于文献[23]。分布式光伏系统装机容量为250 kW·h;储能系统充放电效率为0.95,储能容量上、下限分别为600 kW·h、60 kW·h,最大充放电功率为60 kW,充放电成本为0.1元/kW。优化周期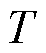 分为96个时段,间隔周期
分为96个时段,间隔周期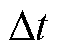 为15 min,预测时间范围
为15 min,预测时间范围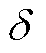 为16个时段。相邻楼宇之间信息交互次数
为16个时段。相邻楼宇之间信息交互次数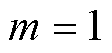 ,收敛阈值
,收敛阈值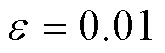 ,楼宇子问题采用Yalmip+Cplex求解。为验证所提模型的可行性与有效性,设置以下三个算例进行验证。
,楼宇子问题采用Yalmip+Cplex求解。为验证所提模型的可行性与有效性,设置以下三个算例进行验证。
算例1:不考虑智能楼宇间P2P电能交易,各楼宇独自安排用能与储能充放电计划。
算例2:考虑智能楼宇间集中式P2P电能交易,楼宇间根据统一P2P交易电价进行内部交易,各楼宇独立安排用能和储能的充放电计划。
算例3:考虑基于聚合功率的区间滚动P2P电能交易,采用本文分布式信息交互策略求解。
本文置信水平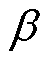 =0.9,在不同置信水平下,光伏发电预测区间范围有所差异[24]。各楼宇BEMS通过求解灵活性资源聚合功率区间,获取楼宇在P2P交易中能够提供的可调度能力范围。由于需求侧灵活性资源特性有所不同,其聚合得到的可调度能力范围均有所不同。以光伏楼宇1为例,给出不同置信水平下光伏楼宇1聚合模型的最优上、下界和
=0.9,在不同置信水平下,光伏发电预测区间范围有所差异[24]。各楼宇BEMS通过求解灵活性资源聚合功率区间,获取楼宇在P2P交易中能够提供的可调度能力范围。由于需求侧灵活性资源特性有所不同,其聚合得到的可调度能力范围均有所不同。以光伏楼宇1为例,给出不同置信水平下光伏楼宇1聚合模型的最优上、下界和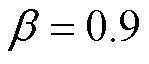 时P2P交易功率情况如图3所示。
时P2P交易功率情况如图3所示。
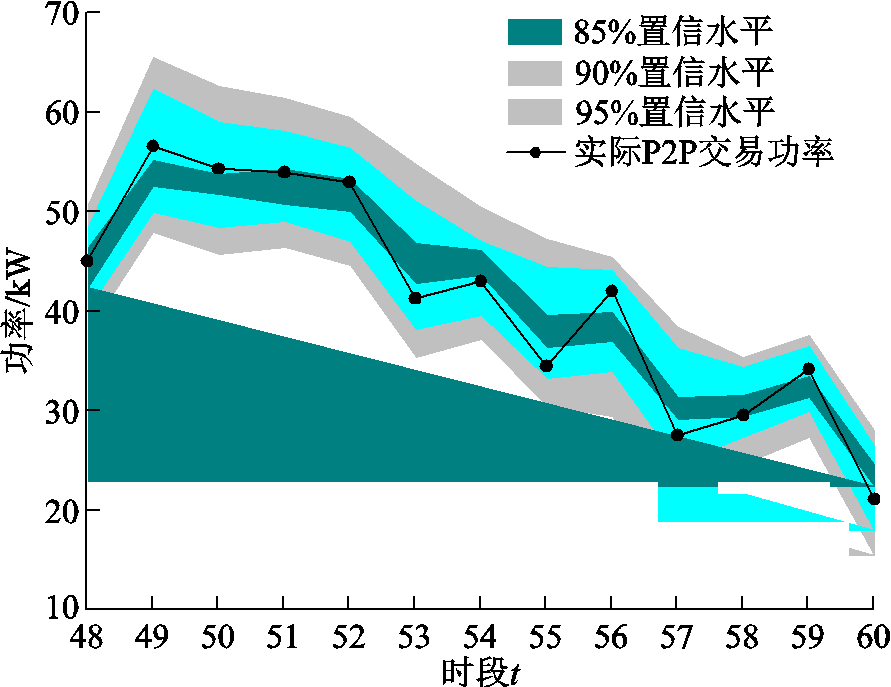
图3 光伏楼宇1聚合区间可调节功率域
Fig.3 Photovoltaic building 1 aggregation interval adjustable power domain
从图3可以看出,聚合区间的功率边界表征楼宇可调度资源在某一时段可以向P2P交易平台提供的最大、最小可交易功率。在t =48~60时段,分布式光伏出力较大,随着置信水平的增加,聚合区间可调节功率域也增大,此时P2P交易功率超过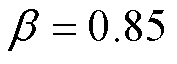 时的聚合区间,并在
时的聚合区间,并在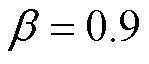 聚合区间内。该聚合功率区间既考虑了不同置信度下的光伏预测出力,又可以对楼宇内多类别小容量且分散的资源进行整合协调,提高了资源的利用率,以应对P2P交易中光伏出力带来的不确定性。
聚合区间内。该聚合功率区间既考虑了不同置信度下的光伏预测出力,又可以对楼宇内多类别小容量且分散的资源进行整合协调,提高了资源的利用率,以应对P2P交易中光伏出力带来的不确定性。
为了进一步分析智能楼宇间的交易情况并验证滚动P2P电能交易的有效性,分别给出算例1~3中光伏楼宇1的调度结果如图4所示。从图4a可以看出,算例1中光伏楼宇1在1:00—8:00期间,通过参与需求响应将负荷转移到谷时段,向主网购买低价电能,在满足自身需求的前提下向储能充电作为备用,可降低在峰时段的购电量。在9:00—18:00期间通过光伏发电以满足自身用电需求,并通过储能装置将多余光伏储存或是出售给主网以提高自身收入。在19:00—24:00期间,通过储能放电降低向主网的购电量,提高自身的经济性。
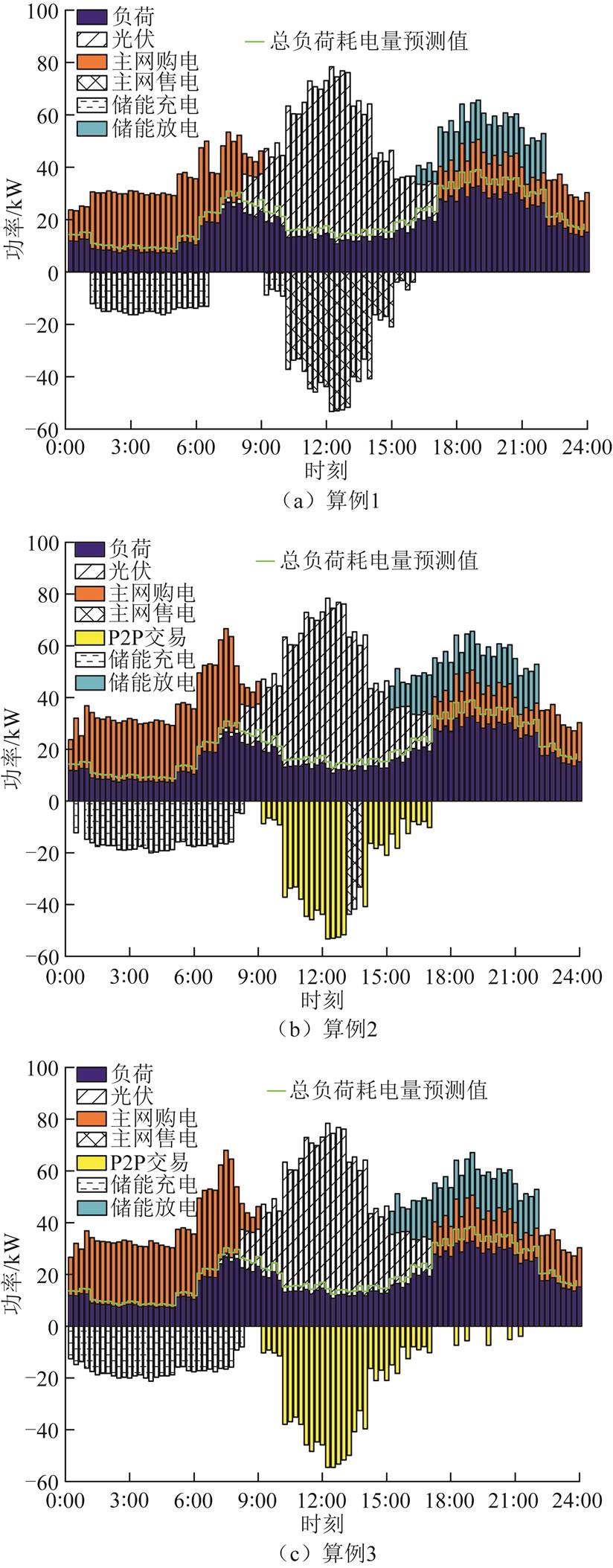
图4 不同算例下光伏楼宇1优化调度结果
Fig.4 The optimal scheduling results of typical photovoltaic building 1 under different examples
如图4b所示,由于考虑了楼宇间的P2P交易,与算例1相比,算例2中光伏楼宇1在1:00—8:00期间的主网购电量有明显提升,在峰时段18:00—23:00分时电价较高时通过储能放电出售给相邻楼宇以提高收益。在9:00—18:00光伏发电时段,楼宇间交易电价低于上网电价,各楼宇更倾向于参与P2P交易以降低自身运行成本。
如图4c所示,算例3在算例2的基础上考虑灵活性资源的聚合特性,以功率区间形式进行滚动P2P电能交易。由仿真结果可以看出,智能楼宇之间更倾向于在更大功率可行域区间的激励下进行交易。但由于光伏出力的不确定性,楼宇需要不断调整自身出力与P2P交易功率以满足供需平衡。光伏楼宇1在18:00—6:00非光伏发电时段各聚合区间可行域弹性较大,这是因为需求侧负荷受价格激励的影响可将负荷功率平移至晚间时段,同时在6:00—18:00期间光伏发电量较高,光伏发电预测区间的不确定性也较大,虽然面临光伏出力不确定性的风险成本,在楼宇之间交易电价的影响下电能出售量也在增加,有效地提高了智能楼宇间P2P交易的积极性,在促进PV发电消纳的同时提升了微电网的灵活性。
为体现本文调度策略的优越性,不同算例下智能楼宇及微电网的运行成本见表1。
表1 不同算例下优化成本
Tab.1 Energy consumption costs under different calculation examples

算例光伏楼宇1总成本/元一般楼宇6总成本/元微电网总成本/元 1398.661 91 054.997 610 437.942 3 2367.578 1963.264 39 567.796 4 3342.876 8890.730 58 878.915 1
表1中分析了不同算例下光伏楼宇1与一般楼宇6的优化成本。算例2较算例1光伏楼宇1成本降低了7.79%,一般楼宇6成本降低了8.6%。算例3在聚合区间模型上考虑了滚动P2P交易特性,同时将风险因素纳入其中,使得光伏楼宇1成本较算例2降低了6.72%,一般楼宇6成本降低了7.53%。在微电网整体层面上,算例2和算例3总运行成本分别以8.3%和14.9%的幅度缩减。这表明本文所提聚合区间滚动P2P交易模式能够有效地利用楼宇内分散、单体容量小的资源的可调度能力参与P2P交易,充分挖掘了微电网多智能楼宇的交易潜力。
置信水平反映了决策者对风险的偏好程度和保守度,表2以算例3为例分析了不同置信水平对光伏楼宇1售电收益的影响。
表2 不同置信水平下光伏楼宇1售电收益
Tab.2 Electricity sales revenue of photovoltaic building 1 under different confidence levels

置信水平P2P收益/元风险成本/元光伏楼宇1总收益/元 0.85256.726 540.107 3216.619 2 0.90276.474 737.600 6238.874 1 0.95301.608 834.836 9266.771 9
结合图3中P2P交易功率可行域聚合区间可知,实际P2P交易功率有可能超过该置信水平下聚合区间的功率边界,此时便会产生风险成本。但随着置信水平的不断提高,聚合区间可行域范围增大,风险成本逐渐降低,P2P交易电量提升,光伏楼宇1总收益随之增加。虽然在一定程度上增加了智能楼宇总运行成本,但微电网的整体收益得到提升,说明了本文所提方法的可行性和经济性。
各楼宇P2P电能交易对之间功率形成的迭代过程如图5所示。每一条曲线对应每栋楼宇交易功率更新过程。在迭代开始时,楼宇根据自身功率聚合区间情况和购售电策略设定P2P预交易电量,在微电网P2P交易平台上分别寻找相匹配的交易对象进行交互。在形成一致性交易电量的过程中,随着信息交互次数的增加每个交易对的交易功率逐渐趋于一致并完成交易,此时交易电价也会随迭代过程完成收敛。参与P2P交易的购售方可以同时进行多次交易,直到满足自身需求为止,在提高交易效率的同时兼顾了楼宇的经济性。
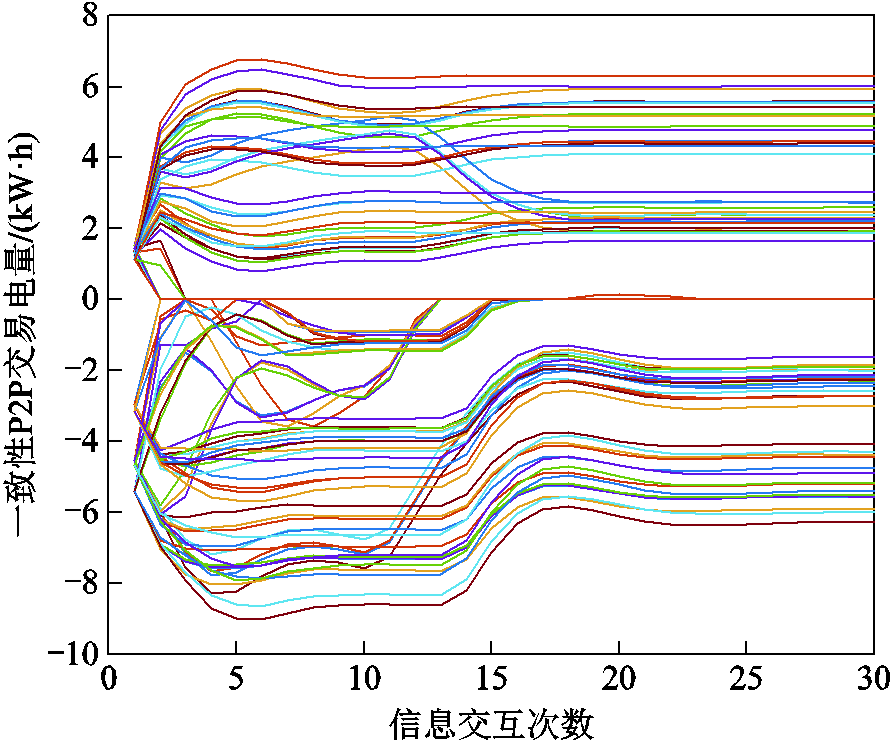
图5 P2P交易功率形成过程
Fig.5 P2P transaction power formation process
图6为不同分布式优化方法的一致性误差收敛曲线,并通过均方误差平方根(Square root of Mean Square Error, SMSE)体现不同算法下交易功率趋于最终优化结果的过程。从图6可以看出,本文分布式信息交互方法交易功率一致性变量的SMSE在第26次收敛。随着信息交互次数的增大,搜集到相邻楼宇交易功率的信息增多,楼宇自身进行本地计算时效率提高,其收敛速度要快于一致性算法和ADMM算法,说明本文所提分布式信息交互策略在解决楼宇间P2P电能交易问题时具有较好的性能和收敛精度。多智能楼宇中所有的更新计算都是通过其自身信息及所接收的相邻楼宇信息进行本地处理和并行计算来完成的,因此整体计算时间较短,同时兼顾了隐私性和计算效率,对于楼宇间P2P交易过程中交易功率的形成有良好的适配性。
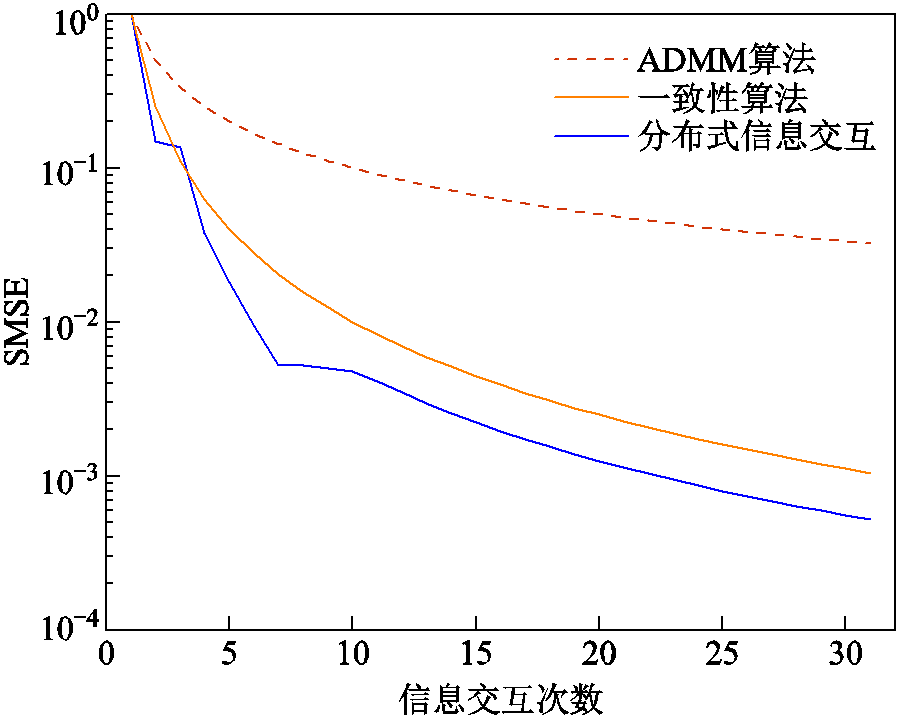
图6 一致性误差收敛曲线
Fig.6 Consistency error convergence curves
T=52时楼宇间P2P交易电价形成过程如图7所示。由图7可知,在初始交易电价的基础上,微电网内智能楼宇P2P交易电价在信息交互26次完成收敛,说明交易功率和交易价格已经确定,楼宇间满足交易功率平衡并完成交易。此时光伏出力较大,负荷需求量较小,光伏楼宇间互相不进行交易,电价下降趋势最为明显,最后稳定在0.443元/(kW·h)。同理,一般楼宇间不进行P2P交易,电价逐渐上升,最后稳定在0.79元/(kW·h)左右。而光伏楼宇与一般楼宇间P2P交易电价介于两者之间,以此激励楼宇间P2P电能交易。
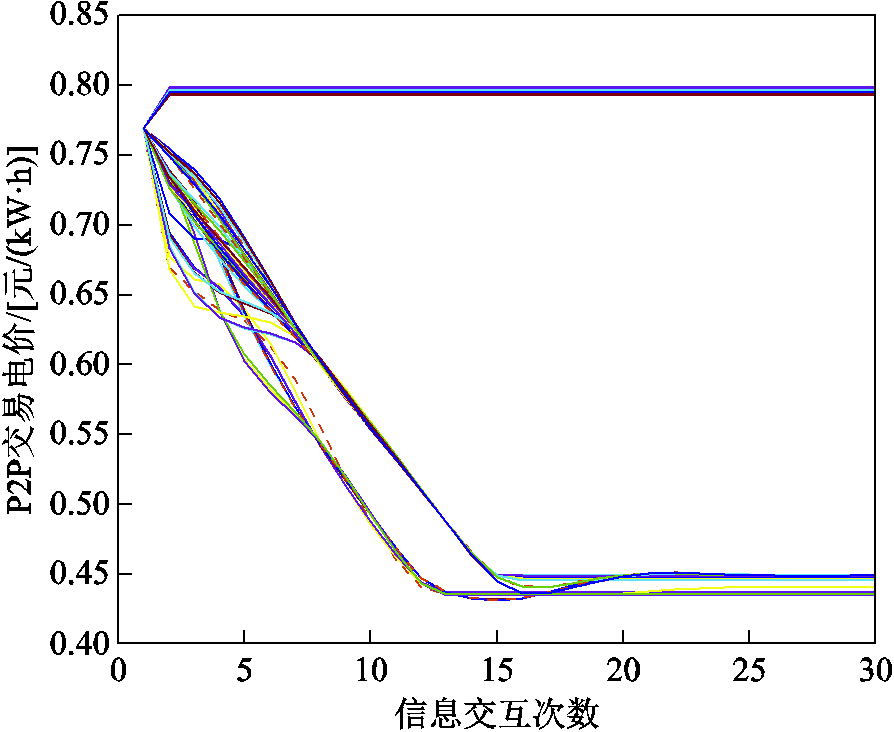
图7 t =52时楼宇间P2P交易电价形成过程
Fig.7 The formation process of P2P transaction price between buildings when t =52
为了验证本文所提分布式信息交互策略的有效性,本节选取某智能楼宇在不同信息交互次数下残差收敛情况如图8所示。可以看出,随着信息交互次数m的增加,迭代次数逐渐降低。所用算法在本文多楼宇问题中在信息交互9次并迭代6次时达到收敛条件,验证了P2P交易中该算法的收敛性。由于微电网经济调度策略更新过程是通过并行计算完成的,因此信息交互次数越多,楼宇间分布式求解速度越快,也说明所提算法对求解这类问题具有较好的性能,更适用于大规模微电网多智能楼宇优化调度问题。
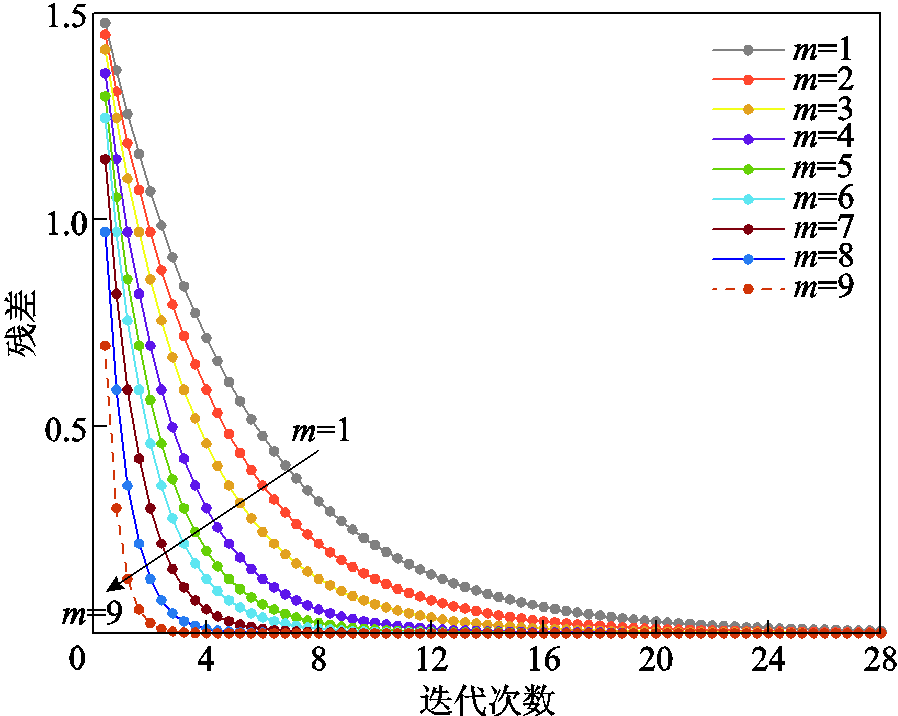
图8 不同信息交互次数下残差收敛过程
Fig.8 Residual convergence process under different information interaction times
算例3中不同算法的优化结果对比见表3。分别使用集中式优化、一致性算法、标准ADMM算法和本文所提分布式信息交互策略进行优化和对比分析,同时给出了本文方法中不同信息交互次数与计算速度的关系。
表3 算例3中不同算法优化结果对比
Tab.3 Comparison of optimization results of different algorithms in Example 3

优化方法微电网总成本/元信息交互次数迭代次数计算时间/s 集中式优化8 752.011 01120.89 一致性算法8 796.520 911353 257.20 标准ADMM算法8 821.562 71321 002.56
(续)

优化方法微电网总成本/元信息交互次数迭代次数计算时间/s 分布式信息交互8 878.915 18 880.243 78 879.642 78 880.873 6126812.62 318631.58 512423.74 78294.23
由表3可知,在计算时间方面,传统集中式方法只需计算一次且算例规模相对较小,所以时间最短;而在分布式优化方法对比中,分布式信息交互策略整体计算时间最短且迭代次数最少,避免了一致性和标准ADMM算法只能信息交互一次的弊端,当进一步增加信息交互次数时,分布式信息交互策略在迭代次数与计算速度上的优势会更加明显。本文所提算法充分结合了一致性算法和标准ADMM算法的特性,在总成本增加甚微的情况下,提升了运算处理速度且具有较好的收敛性。
下面继续探究本文所提算法的实用性,随着未来智能楼宇大规模接入配电网,将楼宇所在节点数从10增长至40,分析不同楼宇规模下算法的迭代次数情况如图9所示。
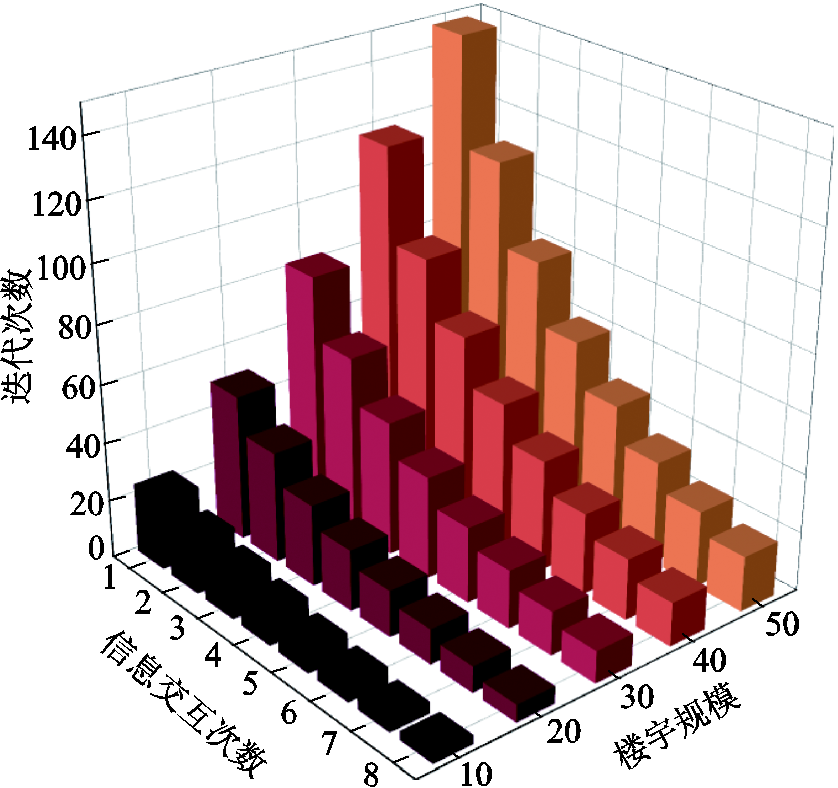
图9 不同楼宇规模迭代次数情况
Fig.9 The number of iterations of different building sizes
由图9可知,随着楼宇数量不断增加,迭代次数呈现近似正相关特性;而在楼宇数量相同的情况下,迭代次数随信息交互次数的增大而减小。数据结果显示,所提方法在更大规模的微电网多智能楼宇调度问题上仍具备良好的扩展性,且求解效率可以满足实际工程的需要。
本文以微电网内兼具电能生产和消费能力的多智能楼宇为研究对象,构建考虑灵活性资源聚合区间的滚动P2P能源交易框架,基于相邻楼宇间的信息交互建立微电网多智能楼宇分布式调度模型,并通过算例分析得到以下结论:
1)本文基于闵可夫斯基求和将楼宇内分布式资源进行等值聚合,得到P2P交易功率可行域,以聚合区间形式参与楼宇间电能交易,充分挖掘了楼宇内灵活性资源的调度潜力,提高了微电网多智能楼宇协调调度的灵活性。
2)针对智能楼宇间电能交易的协调优化问题,提出了一种滚动P2P能源交易框架。与普通P2P交易方式相比,微电网整体运行成本降低了7.2%。在兼顾系统运行经济性的同时,提高了智能楼宇参与P2P电能交易的积极性和分布式能源的自消纳水平。
3)所提出的分布式信息交互策略使微电网多智能楼宇间只需交互预期交易量信息,同时并行求解自身优化问题,与滚动P2P交易方式有较好的契合度。该策略规避了计算压力大、隐私泄露等问题,并提高了分布式信息交互的收敛速度,具有良好的扩展性,可有效解决大规模智能楼宇优化迭代问题。
最后,本文所提模型以智能楼宇作为研究对象,后续可进一步研究P2P市场中楼宇间的竞价策略,建立更有序的市场化交易。
附 录
式(13)的非线性模型是通过引入大M法和0-1变量进行线性化处理的,详细过程如下。
首先对条件风险价值(Conditional Value at Risk, CVaR)的形式引入0-1变量进行线性化,有
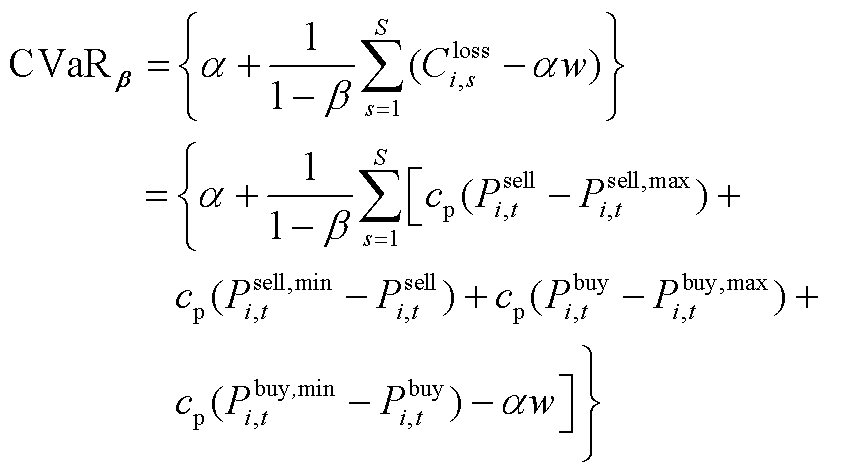 ( A1)
( A1)
式中,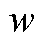 为0-1变量。
为0-1变量。
由于文中式(6)~式(10)的处理,出售和购买功率在同一调度时刻至少一方为0,且任一功率为0的情况下对应的边界条件也为0,不会影响最终的结果,因此将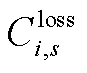 写为上述形式。
写为上述形式。
根据式(13),可将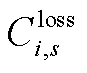 写为以下分段函数形式
写为以下分段函数形式
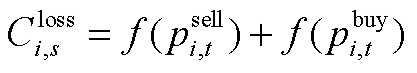
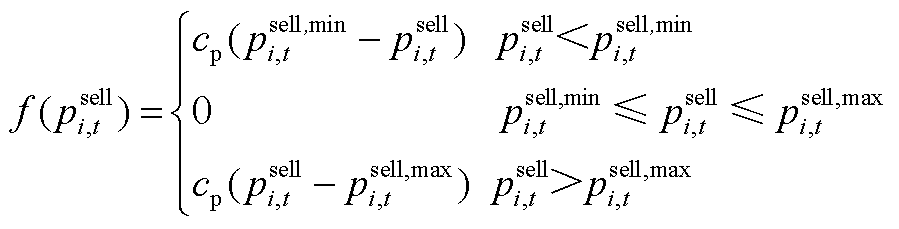 (A2)
(A2)
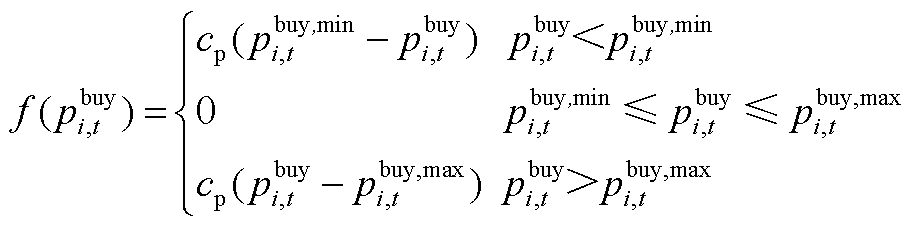 (A3)
(A3)
引入三个0-1变量w1、w2、w3,将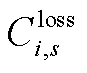 进一步转换为
进一步转换为
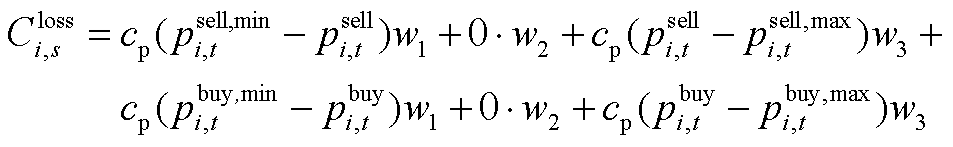 (A4)
(A4)
引入大M法,这里M是一个很大的数。由此,目标函数中关于CVaR的问题线性转换为
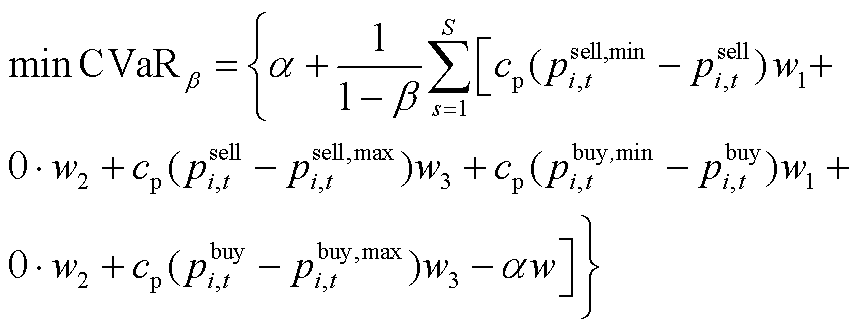 (A5)
(A5)
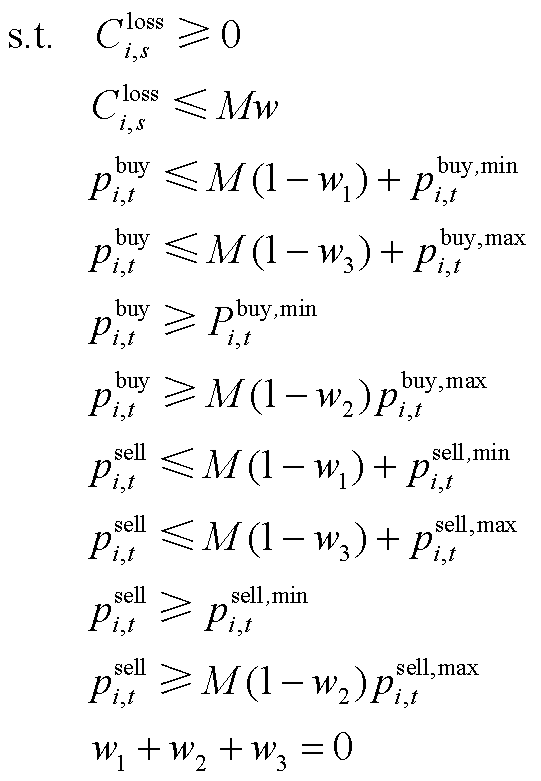 (A6)
(A6)
参考文献
[1] 谢小荣, 马宁嘉, 刘威, 等. 新型电力系统中储能应用功能的综述与展望[J]. 中国电机工程学报, 2023, 43(1): 158-169. Xie Xiaorong, Ma Ningjia, Liu Wei, et al. Functions of energy storage in renewable energy dominated power systems: review and prospect[J]. Proceedings of the CSEE, 2023, 43(1): 158-169.
[2] Chakraborty S, Modi G, Singh B. A cost optimized-reliable-resilient-realtime-rule-based energy management scheme for a SPV-BES-based microgrid for smart building applications[J]. IEEE Transactions on Smart Grid, 2023, 14(4): 2572-2581.
[3] Cui Shichang, Wang Yanwu, Shi Yang, et al. A new and fair peer-to-peer energy sharing framework for energy buildings[J]. IEEE Transactions on Smart Grid, 2020, 11(5): 3817-3826.
[4] Jia Yanbo, Wan Can, Yu Peng, et al. Security constrained P2P energy trading in distribution network: an integrated transaction and operation model[J]. IEEE Transactions on Smart Grid, 2022, 13(6): 4773-4786.
[5] 杜将武, 唐小强, 罗志伟, 等. 面向综合能源园区的丰枯电价定价方法[J]. 发电技术, 2023, 44(2): 261-269. DU Jiangwu, TANG Xiaoqiang, LUO Zhiwei, et al. Pricing method for season of use in integrated energy park[J].Power Generation Technology,2023,44(2):261-269.
[6] 周军, 李佳旺, 马鸿君, 等. 考虑点对点电能共享的智能楼宇群分布式优化调度[J]. 电力自动化设备, 2021, 41(10): 113-121. Zhou Jun, Li Jiawang, Ma Hongjun, et al. Distributed optimal scheduling for smart building clusters considering peer-to-peer electric energy sharing[J]. Electric Power Automation Equipment, 2021, 41(10): 113-121.
[7] Rezaei E, Dagdougui H, Rezaei M. Distributed stochastic model predictive control for peak load limiting in networked microgrids with building thermal dynamics[J]. IEEE Transactions on Smart Grid, 2022, 13(3): 2038-2049.
[8] Nikkhah S, Allahham A, Royapoor M, et al. Optimising building-to-building and building-for-grid services under uncertainty: a robust rolling horizon approach[J]. IEEE Transactions on Smart Grid, 2022, 13(2): 1453-1467.
[9] 张天策, 李庚银, 王剑晓, 等. 基于可行域投影理论的新能源电力系统协同运行方法[J]. 电工技术学报, 2024, 39(9): 2784-2796. Zhang Tiance, Li Gengyin, Wang Jianxiao, et al. Coordinated operation method of renewable energy power systems based on feasible region projection theory[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2784-2796.
[10] 边晓燕, 孙明琦, 董璐, 等. 计及灵活性聚合功率的源-荷分布式协调调度[J]. 电力系统自动化, 2021, 45(17): 89-98. Bian Xiaoyan, Sun Mingqi, Dong Lu, et al. Distributed source-load coordinated dispatching considering flexible aggregated power[J]. Automation of Electric Power Systems, 2021, 45(17): 89-98.
[11] Zhang Zhong, Li Ran, Li Furong. A novel peer-to-peer local electricity market for joint trading of energy and uncertainty[J]. IEEE Transactions on Smart Grid, 2020, 11(2): 1205-1215.
[12] Guo Zhenwei, Pinson P, Chen Shibo, et al. Chance-constrained peer-to-peer joint energy and reserve market considering renewable generation uncertainty[J]. IEEE Transactions on Smart Grid, 2021, 12(1): 798-809.
[13] Zhang Rongquan, Bu Siqi, Li Gangqiang. Multi-market P2P trading of cooling–heating-power-hydrogen integrated energy systems: an equilibrium-heuristic online prediction optimization approach[J]. Applied Energy, 2024, 367: 123352.
[14] 倪萌, 王蓓蓓, 朱红, 等. 能源互联背景下面向高弹性的多元融合配电网双层分布式优化调度方法研究[J]. 电工技术学报, 2022, 37(1): 208-219. Ni Meng, Wang Beibei, Zhu Hong, et al. Study of two-layer distributed optimal scheduling strategy for highly elastic multi-resource fusion distribution network in energy interconnection environment[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 208-219.
[15] 王建元, 李南南. 基于一致性算法的直流微电网分布式储能系统能量控制策略[J]. 东北电力大学学报, 2023, 43(2): 73-81. Wang Jianyuan, Li Nannan. Energy control strategy of DC microgrid distributed energy storage system based on consensus algorithm[J]. Journal of Northeast Electric Power University, 2023, 43(2): 73-81.
[16] 梁栋, 邱馨洁, 刘琪, 等. 电动汽车与直流配电网协同的分布式自适应滚动预测调度[J]. 电力系统自动化, 2023, 47(24): 90-99. Liang Dong, Qiu Xinjie, Liu Qi, et al. Distributed adaptive rolling predictive scheduling based on coordination of electric vehicles and DC distribution networks[J]. Automation of Electric Power Systems, 2023, 47(24): 90-99.
[17] 徐成司, 董树锋, 华一波, 等. 基于改进一致性算法的工业园区分布式综合需求响应[J]. 电工技术学报, 2022, 37(20): 5175-5187. Xu Chengsi, Dong Shufeng, Hua Yibo, et al. Distributed integrated demand response of industrial park based on improved consensus algorithm[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5175-5187.
[18] 孔令国, 史立昊, 石振宇, 等. 基于交替方向乘子法的园区电-氢-热系统低碳优化调度[J]. 电工技术学报, 2023, 38(11): 2932-2944. Kong Lingguo, Shi Lihao, Shi Zhenyu, et al. Low-carbon optimal dispatch of electric-hydrogen-heat system in park based on alternating direction method of multipliers[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2932-2944.
[19] Abdella J, Tari Z, Mahmud R, et al. HiCoOB: hierarchical concurrent optimistic blockchain consensus protocol for peer-to-peer energy trading systems[J]. IEEE Transactions on Smart Grid, 2023, 14(5): 3927-3943.
[20] Chen Wei, Liu Lu, Liu Guoping. Privacy-preserving distributed economic dispatch of microgrids: a dynamic quantization-based consensus scheme with homomorphic encryption[J]. IEEE Transactions on Smart Grid, 2023, 14(1): 701-713.
[21] Wan Can, Zhao Changfei, Song Yonghua. Chance constrained extreme learning machine for nonparametric prediction intervals of wind power generation[J]. IEEE Transactions on Power Systems, 2020, 35(5): 3869-3884.
[22] Yi Zhongkai, Xu Yinliang, Gu Wei, et al. Aggregate operation model for numerous small-capacity distributed energy resources considering uncertainty[J]. IEEE Transactions on Smart Grid, 2021, 12(5): 4208-4224.
[23] 张虹, 闫贺, 申鑫, 等. 面向能源社区能量管理的配网产消者分布式优化调度[J]. 中国电机工程学报, 2022, 42(12): 4449-4459. Zhang Hong, Yan He, Shen Xin, et al. Distributed optimal scheduling for prosumer in distribution network for energy community energy management[J]. Proceedings of the CSEE, 2022, 42(12): 4449-4459.
[24] 徐询, 谢丽蓉, 梁武星, 等. 考虑风电预测误差时序性及风电可信度的双层优化模型[J]. 电工技术学报, 2023, 38(6): 1620-1632, 1661. Xu Xun, Xie Lirong, Liang Wuxing, et al. Bi-level optimization model considering time series characteristic of wind power forecast error and wind power reliability[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1620-1632, 1661.
Abstract In recent years, with the in-depth reform of the electricity market and the continuous improvement of the penetration rate of distributed resources in the distribution network, the energy trading between intelligent buildings with dual attributes of production and consumption has brought new opportunities and challenges to the nearby consumption of distributed energy. However, for the microgrid system with multi-intelligent buildings, there are defects such as large amount of communication information, low robustness and user privacy in the process of power trading. At the same time, it will also be affected by various uncertain factors such as the access of new energy and the lack of timeliness of transactions. In order to solve the above problems, this paper proposes a rolling P2P energy trading optimization strategy based on distributed information interaction for multi-intelligent buildings in microgrid.
Firstly, considering the aggregation characteristics of various flexible resources in intelligent buildings, the prediction interval results of distributed photovoltaic power generation and the feasible range of flexible resources are characterized in the form of aggregation power interval by Minkowski summation theory, and the aggregation interval model of P2P transaction is established. Among them, the distributed photovoltaic prediction interval is modeled by transforming the benchmark output at different confidence levels into the prediction quantile for the feasible region. At the same time, an interval rolling P2P energy trading framework is constructed. During the energy management period, each building participates in the rolling P2P energy trading by combining the aggregated power interval with its own electricity purchase and sale strategy. Secondly, the risk cost brought by the uncertainty of photovoltaic output to P2P transactions is quantified by CVaR, and an economic dispatch model with the minimum total operating cost of microgrid multi-intelligent buildings is established. On this basis, the P2P transaction power between buildings is used as a consistency variable, and the P2P transaction power and transaction price are obtained based on the distributed solution of the information interaction between adjacent buildings, and the energy transaction period is continuously pushed backward until it meets the requirements of all intelligent buildings in the microgrid.
In the case analysis, the scheduling results of different buildings in the microgrid and the optimization results of different algorithms are compared respectively, which verifies the effectiveness of the interval rolling P2P energy trading model proposed in this paper. At the same time, the practicability and solution efficiency of the distributed information interaction algorithm in this paper have also been reflected. Through the example analysis, the following conclusions can be drawn: (1) Participating in the energy transaction between buildings in the form of aggregation interval fully taps the scheduling potential of flexible resources in buildings and improves the flexibility of coordinated scheduling of multi-intelligent buildings in microgrid. (2) Compared with the ordinary P2P trading, the rolling P2P energy trading improves the enthusiasm of intelligent buildings to participate in energy trading and the self-consumption level of distributed energy while taking into account the economy of system operation. (3) The distributed information interaction strategy proposed in this paper makes the multi-intelligent buildings in the microgrid only need to interact with the expected transaction volume information, and at the same time solve their own optimization problems in parallel, which has a good fit with the rolling P2P transaction mode. It avoids the problems of high computational pressure and privacy leakage, and improves the convergence speed of distributed information interaction. It has good scalability and can effectively solve the optimization iteration problem of large-scale intelligent buildings.
keywords:Microgrid, intelligent buildings, aggregation power interval, rolling P2P energy trading, distributed information interaction
DOI: 10.19595/j.cnki.1000-6753.tces.241031
中图分类号:TM732
吉林省科技厅科技发展计划重点科技研发资助项目(20240302094GX)。
收稿日期 2024-06-17
改稿日期 2024-10-09
张 虹 女,1973年生,博士,教授,硕士生导师,研究方向为新能源并网发电技术、电力系统稳定与控制。E-mail:jdlzh2000@126.com(通信作者)
张泽熙 男,1999年生,硕士研究生,研究方向为分布式发电系统运行优化调度。E-mail:zhangzexi0414@126.com
(编辑 赫 蕾)