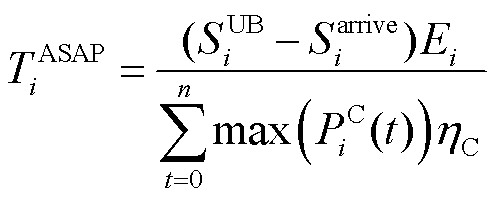 (1)
(1)
摘要 电动汽车集群(EVA)在不同区域中的可调度潜力往往难以准确量化,现有的调控系统也未能充分考虑电力系统的整体性。为解决上述问题,该文首先提出一种考虑用户决策依赖特性的多时段电动汽车可调度域(MEVDR)构建方法,该方法将可调度域划分为可调度能量域(DER)和可调度功率域(DPR),从而全面反映了EVA在特定时间段内的能量与功率调度特性;其次,利用高斯混合模型(GMM)对不同区域和时段的电动汽车数据进行聚类分析,拟合出各类数据的概率密度函数,构建并探讨了不同区域和时间段内EVA MEVDR的差异及其对电力系统的潜在影响;然后,为进一步优化调控策略,考虑MEVDR模型和车-库-网等多个层级的特征,构建了车-库-网多层级协调调控系统(VGGMCCS);最后,将所提方法与对比策略进行了对比,结果表明,VGGMCCS能在保障电力系统长期稳定运行的同时,有效降低用户用车成本,提高车库的经济收益和电网运行效率,实现用户、车库运营商和电网公司的多方共赢。
关键词:电动汽车 车辆到电网 可调度域 有序调控 多区域 调度策略
加快电动汽车(Electric Vehicle, EV)发展,不仅是实现“双碳”目标的迫切任务,更是优化城市能源结构的关键举措[1-3]。然而,EV的大规模普及也带来了一系列新问题和挑战[4]:大量EV的接入将对电网的稳定性和可靠性产生显著影响[5-6]。为应对这些挑战,有必要对电动汽车集群(Electric Vehicle Aggregation, EVA)的聚合特性进行高精度建模,并结合有序调控和车辆到电网(Vehicle-to-Grid, V2G)等技术,实现对EV充放电行为的精准控制,以降低其对电网的潜在影响[7-10]。因此,构建一个能准确评估EVA可调度潜力的模型[11],并设计与之匹配的有序调控方法,对于确保电力系统的安全稳定运行至关重要[12-13]。
在构建EVA聚合模型时,通过假设单台EV的充放电行为是可预测的,能够对EVA的可调度容量进行评估[14]。然而,由于EV的实际充放电行为受到多种因素影响,实际值往往与预测值存在较大偏差。与此相比,尽管EVA的充放电行为也存在波动,但在时间尺度上更具规律性。因此,评估EVA的可调度容量通常更加可行[15-16]。
文献[17]通过将EVA中的汽车划分为以私家车和运营车辆为代表的两大类别,并基于这一分类对集群的可调度容量进行了评估,为EV充放电负荷优化政策的制定以及市场机制的构建提供了重要的参考依据。文献[18]根据电池种类对EVA进行了划分,并指出EV的每日行驶里程会影响其充电习惯和可调度容量。然而,这些方法未能充分考虑不同区域中EV分布的多样性以及用户行为模式的差异,因此存在一定的应用局限性。文献[19]采用高斯分布针对EV驾驶模式及其聚合状态的不确定性进行建模与分析。然而,该模型将EV视为一个统一整体,未能充分考虑各辆EV之间的个体差异,这使得其模型未能真实反映单台EV在实际应用中表现出的随机性和动态充电行为。
为解决上述问题,研究者们提出了一套符合最优化策略的集群负载分布方案[20-21]。华北电力大学的周明教授团队进一步探索,提出了一种EV可调度域形成方法,以有效捕捉EVA在微电网竞标过程中展现的灵活性,为大规模EV融入电力系统提供了解决方案[22]。然而,该方法仅对由两台EV组成的集群进行了可调度域的评估,缺乏一定的普适性。通过结合数据驱动与机器学习技术,文献[23]提出了一种双层聚类EV聚合可调度容量评估模型,该模型融合了EV电量在时间上的分布特性和充电桩在空间上的布局特点,较好地评估了EV的可调度潜力。但该模型未充分考虑用户实际行驶需求的电量预留。综上所述,当前针对EV可调度潜力的评估方法仍存在一些问题:一方面,许多方法忽视了EV的可调度潜力应由功率和能量调度潜力共同构成;另一方面,针对不同区域EV行为的特征差异对其可调度潜力影响的研究仍较为匮乏。
在调控策略方面,许多学者对车-库-网系统进行了广泛研究。文献[24]分析了EV的充电行为特性,从电动汽车聚合商的角度出发,确保了聚合商收益的最大化;文献[25]则基于高置信度的风电场景,从电网的角度进行研究,为大规模EV接入电网后的最优调度提供了解决方案。这些研究为优化调控方案提供了思路,但所涉及的系统层级较为单一,且在用户和EV层面的研究仍显不足。
考虑EV的可调度潜力,许多学者构建了多阶段、多层级的有序调控策略[26]。文献[27]针对EV的可调特性,提出了电动汽车集中管理器参与电网互动模型,从电动汽车聚合商和电网两个角度对车-库-网系统进行了分析;文献[28]构建了基于长短期记忆网络的多阶段调度策略;文献[29]提出了EV参与调峰定价策略的区域电网两阶段优化调度策略,也都从电动汽车聚合商和电网的角度对车-库-网系统进行了深入研究。
上述方法从车-库-网系统的多个层级出发,较为全面地考虑了电力系统的复杂性,但仍存在一些考虑不周之处:①虽然将EV的可调度潜力纳入考虑,但分析较简单,未能结合电网调度深入探讨不同区域中EV可调度潜力的变化及其对实际调度策略制定和调控效果可能产生的影响;②现有研究所提出的有序调控策略多侧重于电网和车库层级的分析,而针对EV和用户层级的研究则相对较为简略。
综上所述,当前相关研究仍存在一定不足,主要体现在EV可调度潜力评估和车-库-网系统调控策略构建两个方面。
1)现有的EV可调度潜力评估方法尚不完善,缺乏系统化的构建与分类方法,忽略了EV可调度潜力应由功率和能量调度潜力共同表征这一关键特性。同时,EV在不同区域内的行为特征差异对其可调度潜力的影响也尚未得到充分研究。因此,有必要深入研究EV可调度潜力的具体构建方法,并系统地分析区域差异性对EVA可调度特征的影响规律,为EV参与电力系统调度提供更为精准的理论支撑。
2)现有研究在构建多层级有序调控策略时,尚未实现对车-库-网系统的全面考量,尤其是未能将EV在不同时空的功率与能量调度潜力纳入调度策略的制定中。为实现更高效的协同调控,亟须构建一个兼顾多维度、多主体的系统性框架,以协调用户需求、EV特性、车库运营约束及电网调度目标等多重因素,在保障各方利益的同时,实现系统整体运行效能的最优化。
针对上述问题,本文首先基于用户行为特性和韧性评估的思想,提出了一种多时段电动汽车可调度域(Multi-stage Electric Vehicle Dispatchable Region, MEVDR)的构建方法,该方法将EV的可调度域划分为可调度功率域和能量域,并对不同场景下EVA的可调度特征进行了系统分析,在全面反映EV可调度潜力的同时,提升了车网互动过程中集群状态的可理解性与直观性;其次,基于聚类分析思想,从不同时空维度分析了配电网调度过程中EVA的决策特性与机理,实现了EVA可调度潜力实时表征能力的提升,为构建车-库-网协同多层级协调调控系统(Vehicles-Garage-Grid Multi-level Coordinated Control System, VGGMCCS)奠定了基础;最后,基于多时段电动汽车可调度域模型,建立了车-库-网多层级协调调控系统。通过将EV的功率和能量可调度潜力纳入调度策略的制定中,实现了车-库-网系统的多层级协同优化;通过引入修正线性单元(Rectified Linear Unit, ReLU)和模型分解迭代方法,在兼顾多方利益的同时提高了求解效率,为可转移负荷参与电力系统调度提供了有益的探索。具体工作可概括如下:
1)提出了电动汽车多时段可调度域的构建方法。
2)使用高斯混合模型(Gaussian Mixture Model, GMM)拟合不同区域和时段各聚类中心的EV数据,构建并讨论了不同区域和时间段内EVA MEVDR的差异。
3)构建了一种基于MEVDR的车-库-网多层级协调控制系统。该系统涵盖用户、车库运营商和电网等多个层级,并能通过商业求解器进行求解。
4)基于改进的IEEE 33节点系统和车库模型进行了仿真,验证了基于MEVDR的VGGMCCS的有效性。
通过电网到车辆(Grid-to-Vehicle, G2V)和V2G技术,EV能够与电网进行双向能量交换,成为灵活的储能系统。为更好地描述EV作为储能系统的特性,本文基于EV入网时间、离网时间、初始电池荷电状态(State of Charge, SOC)、目标SOC、额定电池容量和用户能够接受的SOC下限共六个变量,构建了MEVDR模型。该模型仅在EV接入时采集数据,无需后续维护且不涉及用户隐私。本文同时做出如下假设。
假设1:MEVDR的刻画以午夜12点为界限,不考虑充放电时间跨度跨越这一界限的情况。对于跨夜充电的电动汽车,在午夜12点之前,仍按照前一天的调度策略进行管理;而在午夜12点后,将其视为一个新的调度单元,保留现有数据并重新接入电网,在新的一天重新进行调度。
假设2:将一天划分为96个时间段,针对MEVDR的评估在每个时间段(即15 min)进行一次。
假设3:EV一天只接入一次电网,且充放电过程被视为连续的。
基于上述假设,本文建立了EV的MEVDR模型,用于评估单台EV在特定时间段的调度潜力。MEVDR又可细分为可调度能量域(Dispatchable Energy Region, DER)和可调度功率域(Dispatchable Power Region, DPR),分别刻画EV在能量和功率调度上的特点。单台EV运行特性建模详见附录中式(A1)~式(A8)。
1.2.1 EV-DER的建立
EV-DER反映了EV在特定时间段内可提供的能量总量,为构建DER,结合用户需求限制,本文建立最快需求响应(As Soon As Possible, ASAP)约束和最迟响应(Latest Response, LR)约束。
1)ASAP约束
ASAP指标能够反映EV的可调度能量潜力,其由时间约束和能量约束共同组成。EV的ASAP时间约束(EV ASAP Time constraint, EV-ASAPT)满足
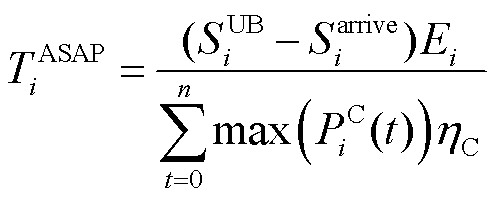 (1)
(1)
式中,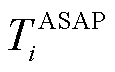 为第i辆EV在接入电网后,充电至用户可接受的最高SOC时所需的最短充电时间;
为第i辆EV在接入电网后,充电至用户可接受的最高SOC时所需的最短充电时间;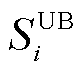 为在调控过程中第i辆EV的用户所能接受的最高SOC;
为在调控过程中第i辆EV的用户所能接受的最高SOC;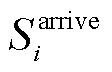 为第i辆EV接入电网时的SOC;Ei为第i辆EV的额定电池容量;
为第i辆EV接入电网时的SOC;Ei为第i辆EV的额定电池容量;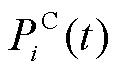 为第i辆EV在时段t的充电功率;
为第i辆EV在时段t的充电功率;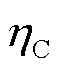 为EV的充电效率;n为时间段索引上限。
为EV的充电效率;n为时间段索引上限。
在ASAPT的基础上,EV的ASAP能量约束(EV ASAP Energy constraint, EV-ASAPE)为
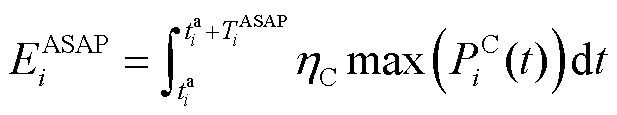 (2)
(2)
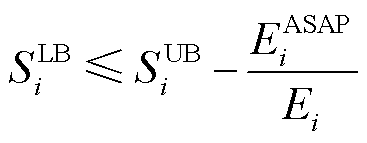 (3)
(3)
式中,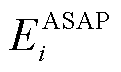 为第i辆EV在其ASAPT内所能从电网中获得的最大能量;
为第i辆EV在其ASAPT内所能从电网中获得的最大能量;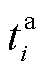 为第i辆EV的入网时间;
为第i辆EV的入网时间;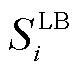 为在调控过程中第i辆EV的用户所能接受的最低SOC。
为在调控过程中第i辆EV的用户所能接受的最低SOC。
为体现用户的行为特点,SiUB和SiLB分别为
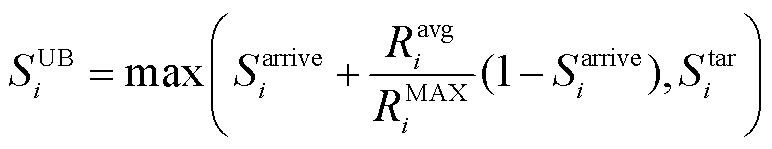 (4)
(4)
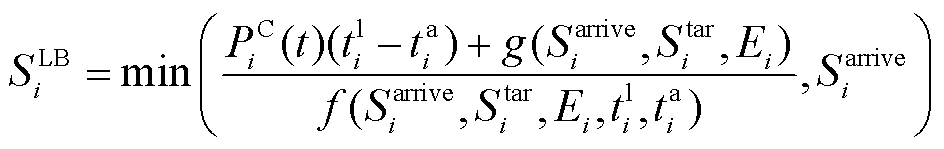 (5)
(5)
式中,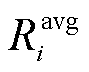 为预计第i辆EV的平均每日行驶距离;
为预计第i辆EV的平均每日行驶距离;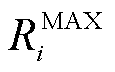 为第i辆EV的满电续航里程;
为第i辆EV的满电续航里程; 为用户设定的第i辆EV的目标SOC;
为用户设定的第i辆EV的目标SOC;![]() 为第i辆EV的离网时间;g(
为第i辆EV的离网时间;g(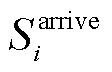 ,
, ,
,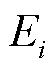 )和f(
)和f(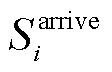 ,
, ,
,![]() ,
,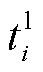 ,
,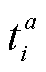 )为经验函数,需要基于用户实际数据调整。在本文中,经数据集测试,式(5)可转换为
)为经验函数,需要基于用户实际数据调整。在本文中,经数据集测试,式(5)可转换为
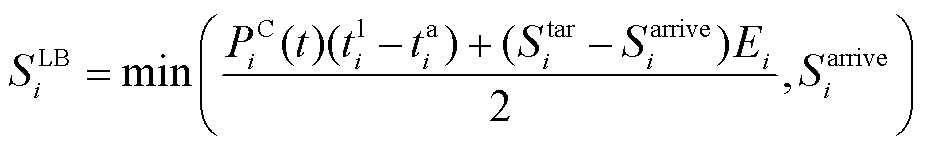 (6)
(6)
2)LR约束
LR指标反映了当前EV所能提供的最大输出能量,EV的LR时间约束(EV LR Time constraint, EV-LRT)满足
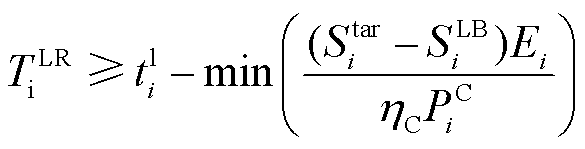 (7)
(7)
式中,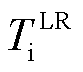 为满足用户需求第i辆EV所能接受的最晚充电时间点。
为满足用户需求第i辆EV所能接受的最晚充电时间点。
在EV-LRT的基础上,本文建立LR能量约束(EV LR Energy constraint, EV-LRE)为
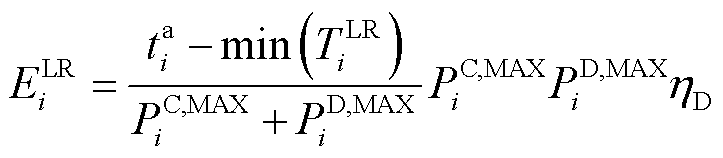 (8)
(8)
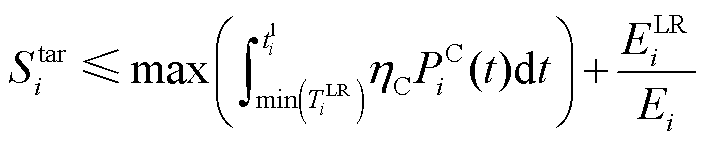 (9)
(9)
式中,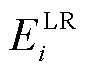 为第i辆EV所能提供的最大输出能量;
为第i辆EV所能提供的最大输出能量;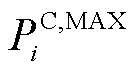 和
和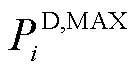 分别为第i辆EV所被允许的最大充、放电功率;
分别为第i辆EV所被允许的最大充、放电功率;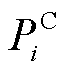 为第i辆EV的充电功率;
为第i辆EV的充电功率;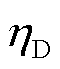 为EV的放电效率。
为EV的放电效率。
在EV-LRE建立后,EV-LRT为
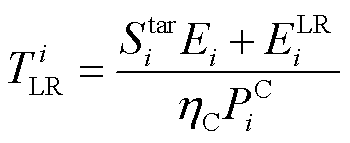 (10)
(10)
式(1)~式(10)量化了DER的边界条件。假设电动汽车各项数据见表1,则基于这些数据生成的DER图像如图1所示。
表1 电动汽车参数
Tab.1 Parameters of EV

参数数值 Sarrive(%)0.3 Star(%)0.8 PC,MAX/kW2 PD,MAX/kW2 E/(kW·h)80 ta4:50 tl19:45
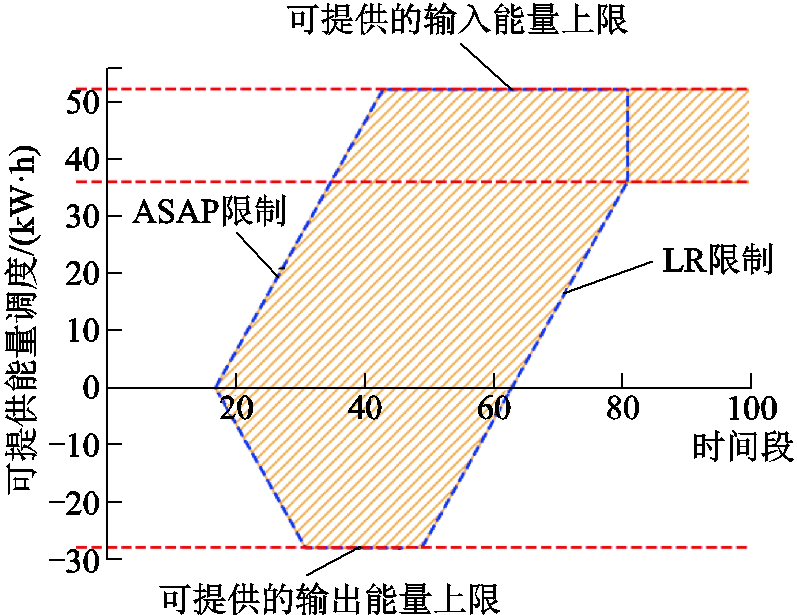
图1 单台EV的DER
Fig.1 DER of a single EV
图1中,蓝色虚线包围的阴影部分即为该EV能提供的能量调度范围。最下和最上两条红色虚线分别代表ELR和EASAP,位于两者之间的红色虚线代表当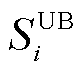 设定为
设定为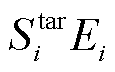 时EV的可调度能量上限。对于负责电力调度的管理者而言,只需要确保EV的能量数据始终维持在阴影区域内,便可以在满足用户需求的前提下,安全地调度该汽车。
时EV的可调度能量上限。对于负责电力调度的管理者而言,只需要确保EV的能量数据始终维持在阴影区域内,便可以在满足用户需求的前提下,安全地调度该汽车。
1.2.2 EV-DPR的建立
基于能源市场价格及电网负载情况等参数的实时变化,电动汽车能够智能决策充放电时机并灵活调整功率大小,以适应不同的能源需求情况[30-31]。然而,如何评估并量化这种能源调度能力依然是个难题。
梯形面积缺失法是韧性评估的传统方式,即计算系统性能曲线在极端事件发生后的面积缺失[32]。
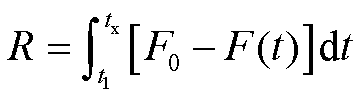 (11)
(11)
式中,R为韧性指标;![]() 为系统的基准性能;F(t)为系统在时段t的实时性能值;tx为系统完全恢复到正常性能
为系统的基准性能;F(t)为系统在时段t的实时性能值;tx为系统完全恢复到正常性能![]() 所用时间。
所用时间。
该方法能够在一定程度上反映系统的恢复能力以及系统的鲁棒性,R值越大,表明电力系统的韧性越弱[33]。基于该思想,为量化EV的可调度功率潜力,本文提出了DPR的构建方法,并引入可调度灵活性(Dispatchable Flexibility, DF)约束如下。
1)DF约束
DF指标能够反映EV的能源调度能力。DF上约束(DF Upper bound, DFU)为
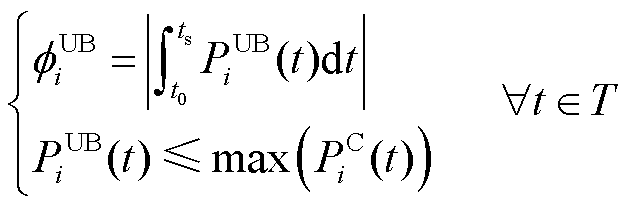 (12)
(12)
式中,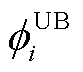 为第i辆EV的DF上约束;t0为第i辆EV可提供功率发生变化或进入稳定状态的起始时间;ts为第i辆EV可提供功率达到稳定状态或发生变化的时刻;
为第i辆EV的DF上约束;t0为第i辆EV可提供功率发生变化或进入稳定状态的起始时间;ts为第i辆EV可提供功率达到稳定状态或发生变化的时刻;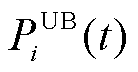 为第i辆EV在时段t的可调度输入功率;T为设定的可调度时间集合。
为第i辆EV在时段t的可调度输入功率;T为设定的可调度时间集合。
相似地,DF下约束(DF Lower bound, DFL)为
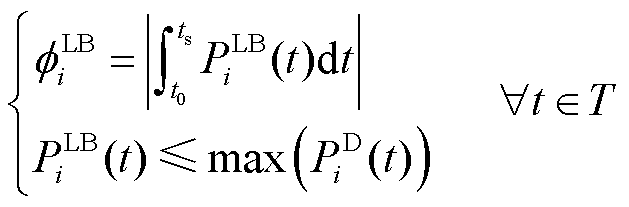 (13)
(13)
式中,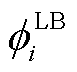 为第i辆EV的DF下约束;
为第i辆EV的DF下约束;![]() 为第i辆EV在t时段的可调度输出功率。式(12)和式(13)定义了EV在执行充放电调度时的灵活性指标。
为第i辆EV在t时段的可调度输出功率。式(12)和式(13)定义了EV在执行充放电调度时的灵活性指标。
2)充放电功率约束
目前,为了实现快速充电,电动汽车多采用直流快充的充电方式[34]。依据相关文献研究[23,35-38],本文设定EV的充电功率为
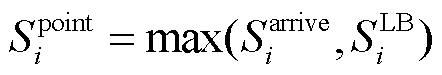 (14)
(14)
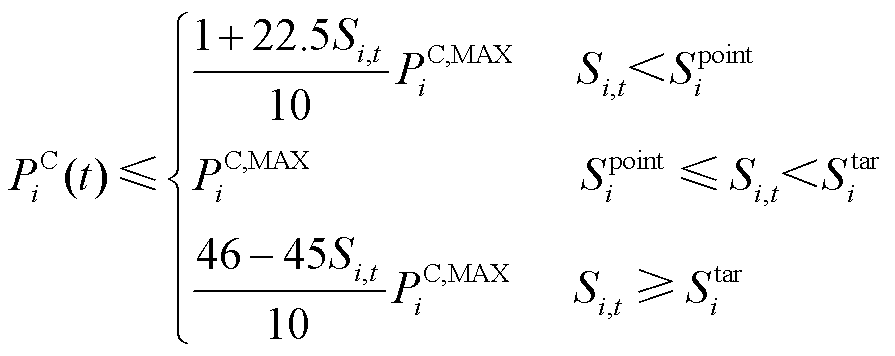 (15)
(15)
式中,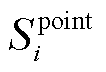 为第i辆EV的SOC阈值;Si,t为第i辆EV在时段t的SOC。
为第i辆EV的SOC阈值;Si,t为第i辆EV在时段t的SOC。
基于上述原理,假设电动汽车各项数据满足表1,根据这些数据生成的DPR图像如图2所示。
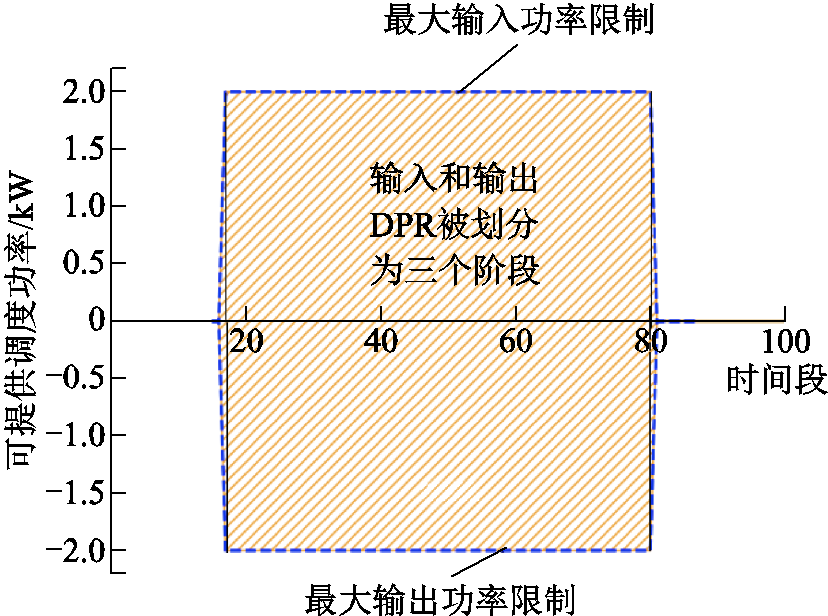
图2 单台EV的DPR
Fig.2 DPR of a single EV
图2中,橙色阴影区域代表EV的DF约束,其中处于y轴正半轴的部分对应DFU,而处于负半轴的部分对应DFL;蓝色虚线则为EV的充放电功率约束。从图2中可以清晰地看到,以两条黑色实线作为分界,EV的DPR被划分为三个不同的部分,分别代表不同阶段下EV的可调度功率潜力。
1.3.1 EVA的运行特性模型
在单台电动汽车运行特性模型的基础上,本文构建了式(16)所示的EVA运行特性模型。
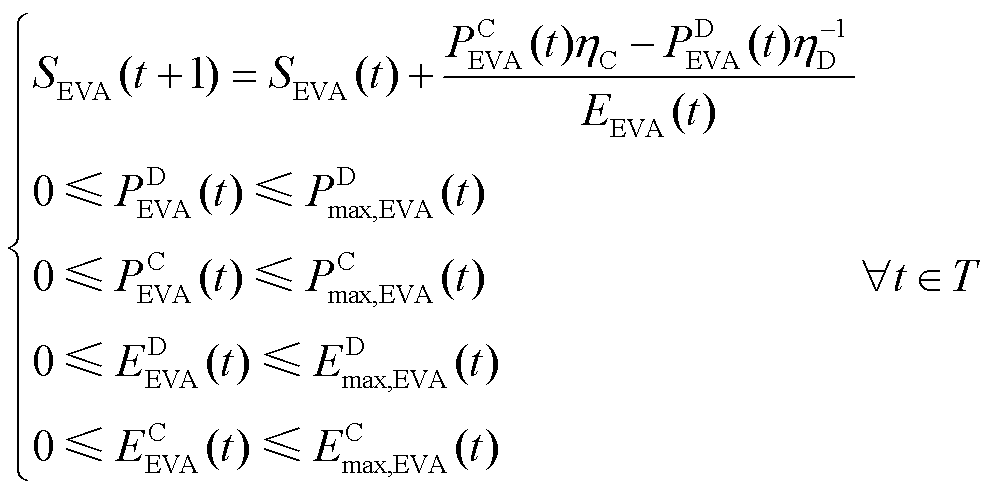 (16)
(16)
式中,SEVA(t)为EVA在时段t时的集群SOC;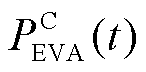 、
、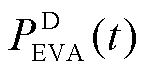 分别为EVA在时段t时的集群充、放电功率;EEVA(t)为EVA在时段t时的集群能量;
分别为EVA在时段t时的集群充、放电功率;EEVA(t)为EVA在时段t时的集群能量;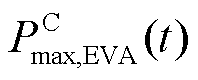 、
、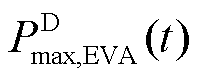 分别为EVA在t时段时的最大集群充、放电功率;
分别为EVA在t时段时的最大集群充、放电功率;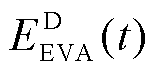 、
、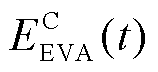 分别为EVA在时段t时的可供调度的集群充、放电能量;
分别为EVA在时段t时的可供调度的集群充、放电能量;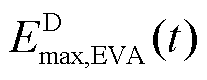 、
、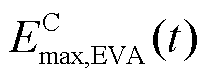 为EVA在时段t时的集群可调度能量边界。这一模型能够准确反映特定区域内电动汽车的整体行为趋势,是MEVDR建立和分析的重要基础。该模型的详细推导过程见附录中式(A9)~式(A31)。
为EVA在时段t时的集群可调度能量边界。这一模型能够准确反映特定区域内电动汽车的整体行为趋势,是MEVDR建立和分析的重要基础。该模型的详细推导过程见附录中式(A9)~式(A31)。
1.3.2 EVA-DER的建立
通过引入单位阶跃函数u(x),建立EVA的ASAP约束和LR约束。
1)ASAP约束
对于EVA,由于每台EV的入网和离网时间各不相同,其时间关系难以直接建立。因此,为了构建EVA的ASAP时间约束(EVA ASAP Time constraint, EVA-ASAPT),需先建立集群的ASAP能量约束(EVA ASAP Energy constraint, EVA-ASAPE),即
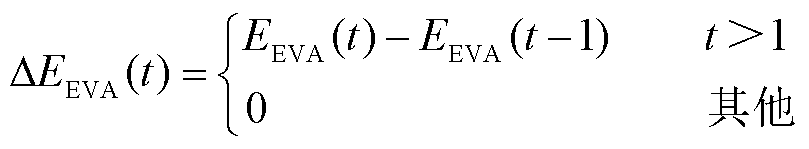 (17)
(17)
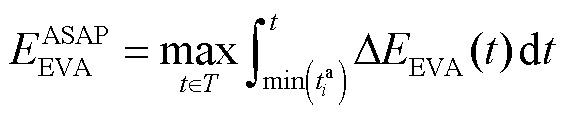 (18)
(18)
式中,ΔEEVA(t)为EVA在两个相邻时段的能量差; 为电动汽车集群的ASAP能量约束;EEVA(t)为EVA在时段t时的集群能量。
为电动汽车集群的ASAP能量约束;EEVA(t)为EVA在时段t时的集群能量。
基于式(17)和式(18)建立的EVA-ASAPE,EVA-ASAPT表示为
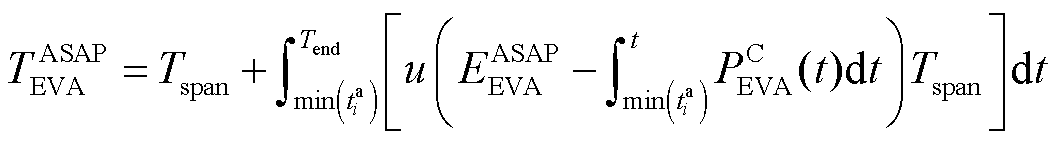 (19)
(19)
式中,![]() 为电动汽车集群的ASAP时间约束;Tend为可调度时间集合的尾值;Tspan为可调度域更新的步长,根据1.1节的假设3,本文Tspan设定为15 min。
为电动汽车集群的ASAP时间约束;Tend为可调度时间集合的尾值;Tspan为可调度域更新的步长,根据1.1节的假设3,本文Tspan设定为15 min。
2)LR约束
首先建立集群的LR能量约束(EVA LR energy constraint, EVA-LRE)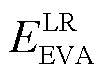 为
为
 (20)
(20)
式中,ci,t为第i辆EV在t时段的入网状态;φEV为所有电动汽车的集合。
基于EVA-LRE,集群的LR时间约束(EVA LR Time constraint, EVA-LRT)可进一步被定义为
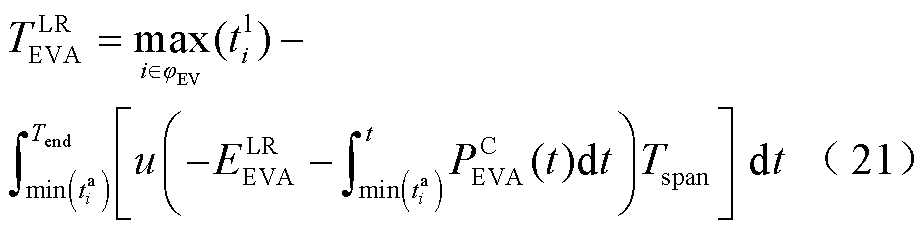
式中,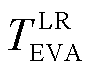 为电动汽车集群的LR时间约束;式(16)~式(21)定义了建立EVA-DER所必须遵循的边界条件。
为电动汽车集群的LR时间约束;式(16)~式(21)定义了建立EVA-DER所必须遵循的边界条件。
此外,由于EVA中的EV均遵循式(3)~式(6)和式(9)所定义的SOC约束,因此EVA的SOC约束已自动得到满足,无需再为EVA额外设定SOC约束。
假定一个电动汽车集群中包含20辆电动汽车,每台汽车的各项数据均符合表2中的分布,则该集群的DER如图3所示。表2中,δa、μa分别为电动汽车集群接入电网时间正态密度函数对应的方差和均值;![]() 、
、![]() 分别为电动汽车集群离开电网时间正态密度函数对应的方差和均值。
分别为电动汽车集群离开电网时间正态密度函数对应的方差和均值。
表2 电动汽车集群参数
Tab.2 Parameters of electric vehicle aggregations

参数数值 SOCarrive(%)0.3 SOCtarget(%)0.8 /kW2 /kW2 E/(kW·h)80 δa/h20.5 μa/h5, 10 δl/h20.5 /h20, 22
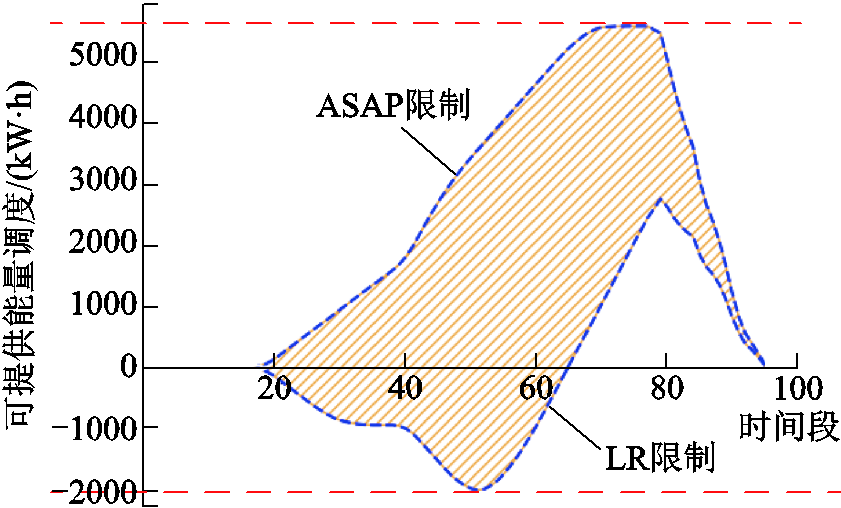
图3 电动汽车集群的DER
Fig.3 DER of EVA
蓝色虚线所包围的阴影部分即为EVA可提供的能量调度;最下和最上两条红色虚线则分别代表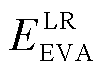 和
和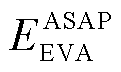 。值得注意的是,在时间段80前后(大约20:00),EVA的DER发生了突变。此时,集群所能提供的能量调度范围明显缩小。这是因为邻近调度时间段末期,EVA中的大部分EV已经完成了充电任务,集群的调控策略逐渐稳定,可调度灵活性显著降低。随着大量EV相继离网,集群可提供的能量调度大幅缩减。
。值得注意的是,在时间段80前后(大约20:00),EVA的DER发生了突变。此时,集群所能提供的能量调度范围明显缩小。这是因为邻近调度时间段末期,EVA中的大部分EV已经完成了充电任务,集群的调控策略逐渐稳定,可调度灵活性显著降低。随着大量EV相继离网,集群可提供的能量调度大幅缩减。
对于电力调度管理者而言,只要确保EVA的能量数据保持在预设的阴影区域内,就可在满足所有EV需求的前提下进行安全的能量调度。
1.3.3 EVA-DPR的建立
由于EVA中的每台EV均已满足式(14)与式(15),因此无需再为EVA制定充放电功率约束,下文只给出DF约束。
EVA-DPR的DF约束可被表述为集群内EV相应约束的闵可夫斯基和。EVA-DFU约束(EVA DF Upper bound)和EVA-DFL约束(EVA DF Lower bound)可由式(22)、式(23)计算而得。
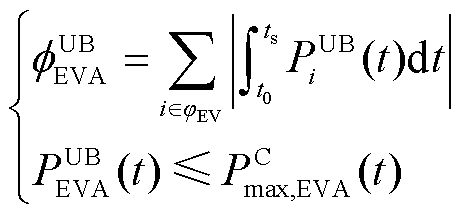 (22)
(22)
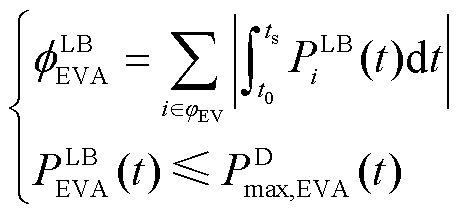 (23)
(23)
式中,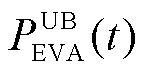 为EVA在时段t的可调度输入功率;
为EVA在时段t的可调度输入功率;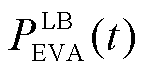 为EVA在时段t的可调度输出功率;
为EVA在时段t的可调度输出功率;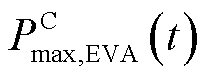 、
、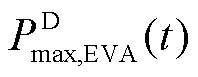 分别为EVA在t时段时的最大集群充、放电功率。式(22)和式(23)定义了建立EVA-DPR所必须遵循的边界条件。假定EVA的各项数据与前文一致,则该集群的DPR如图4所示。
分别为EVA在t时段时的最大集群充、放电功率。式(22)和式(23)定义了建立EVA-DPR所必须遵循的边界条件。假定EVA的各项数据与前文一致,则该集群的DPR如图4所示。
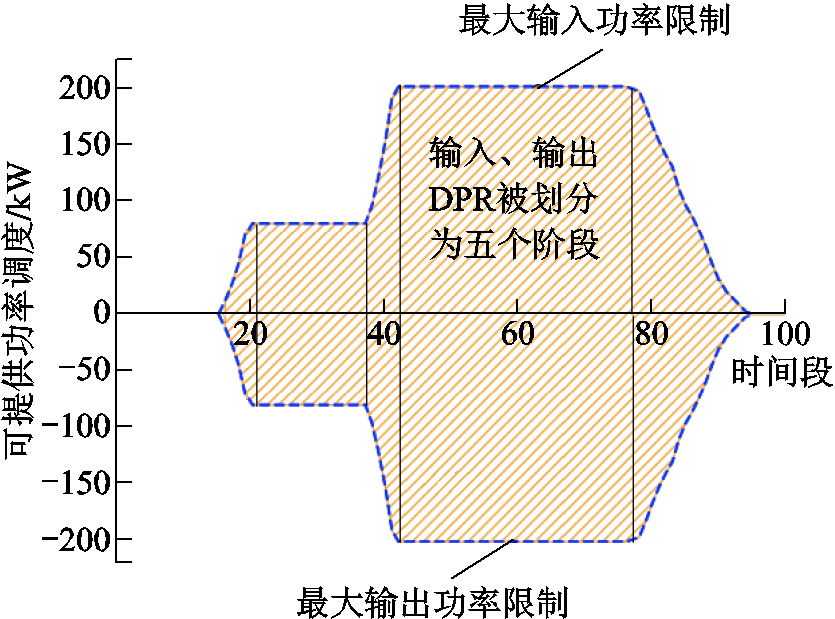
图4 电动汽车集群的DPR
Fig.4 DPR of EVA
图4中,橙色阴影区域代表EVA的DF约束,其中处于y轴正半轴的部分对应EVA-DFU,处于负半轴的部分对应EVA-DFL;蓝色虚线则为集群的充放电功率约束。可以看到,由于集群内含多种行为特征不同的EV,以四条黑色实线作为分界,EVA-DPR被划分为五个不同的阶段。
通过与EVA-DER图像结合分析可以发现,在各个时段内EVA的可调度能量和可调度功率均呈现高度一致性:当DPR图像稳定在某一阶段时,DER展现出一种相对稳定的变化模式;而当DPR进入下一个阶段时,DER的变化模式便会发生一次较为明显的变化。以DER在第80个时间段前后的变化为例,随着DPR进入新的阶段,DER也同步发生了变化。
唯一的例外出现在时间段40~60内。在这个时间段中,尽管DPR没有发生阶段性的变化,DER却出现了异常的降低。这是因为随着离网时间的逼近,为了确保每台电动汽车在离网时均能满足用户的实际需求,集群的最迟响应约束限制了集群能够提供的输出能量,导致了这一异常现象的发生。
电动汽车的行为特征受其所处的区域和时间段影响。为更准确地量化电动汽车集群的可调度潜力,应当分区域、分时间段地建立并分析电动汽车集群的MEVDR。罗平等[39]证明了GMM-4在EV行为聚类中的优越性。在此基础上,本文首先采用高斯混合模型(GMM),通过数据准备、初始化参数以及使用期望最大化(Expectation Maximization, EM)算法进行参数估计等基本步骤,拟合得到了不同区域和时段下各聚类中心EV数据的概率密度函数。随后,基于拟合结果,绘制了相应的EVA-MEVDR图像。GMM的相关公式如式(24)所示,有关GMM聚类的详细内容可参见附录第2节。
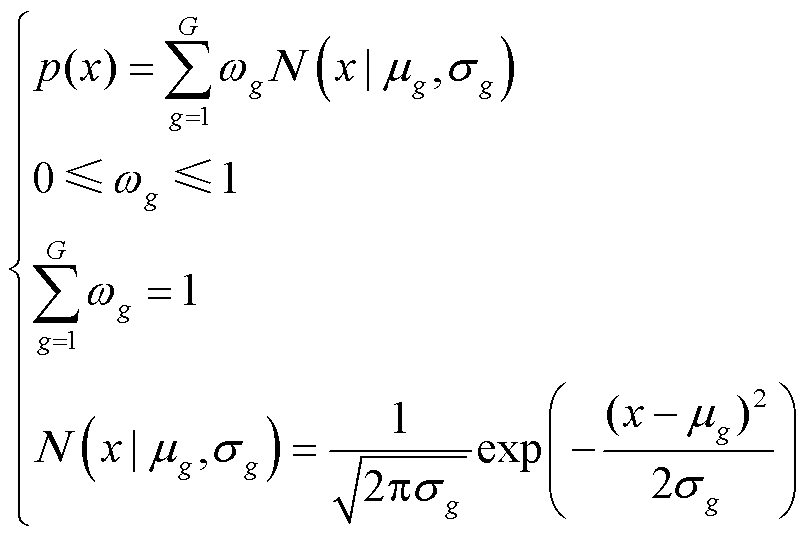 (24)
(24)
式中,G为分量的数量;Wg为第g个分量的混合权值;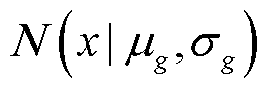 为第g个分量的单变量正态密度函数;
为第g个分量的单变量正态密度函数;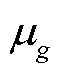 和
和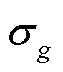 分别为第g个分量的单变量正态密度函数对应的均值和方差。
分别为第g个分量的单变量正态密度函数对应的均值和方差。
本文挑选出了现实中最为普遍,且EV行为特征差异较为明显的三个场景——办公区场景、商业区场景和居民区场景。并在此基础上提出一种“3区域,2状态”的划分方法,将各个区域进一步按照时间划分为工作日和休息日两种状态,以便更细致地分析和描述电动汽车集群在不同条件下的可调度潜力。
由GMM聚合所得的办公区内电动汽车集群在工作日和休息日的行为分布满足附表3,集群内电动汽车的种类分布及其充放电功率满足附表4。所有EV的目标SOC均设定为100%,当出现EV停留时间较短,无法在规定时间段内充满电的情况时,充电目标更改为最大化EV离开时的SOC。依据式(1)~式(22)、式(A1)~式(A31)以及上述设置,办公区EVA在工作日和休息日的DER与DPR图像如图5和图6所示。
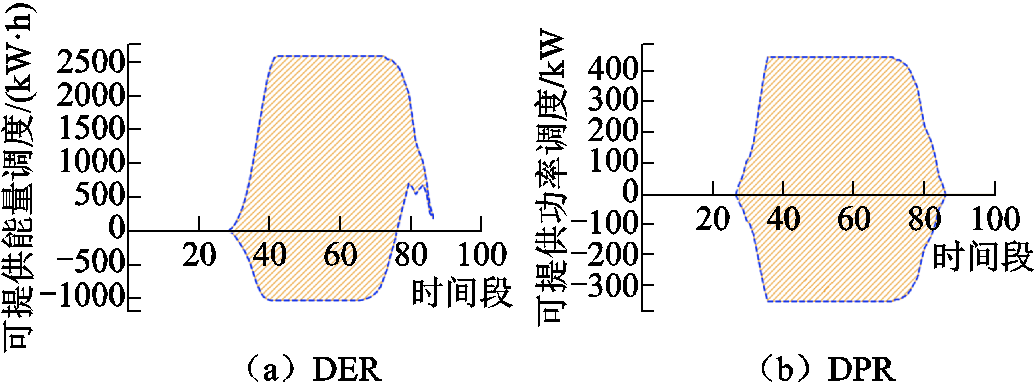
图5 办公区工作日电动汽车集群的MEVDR
Fig.5 MEVDR of EVA in office area on weekdays
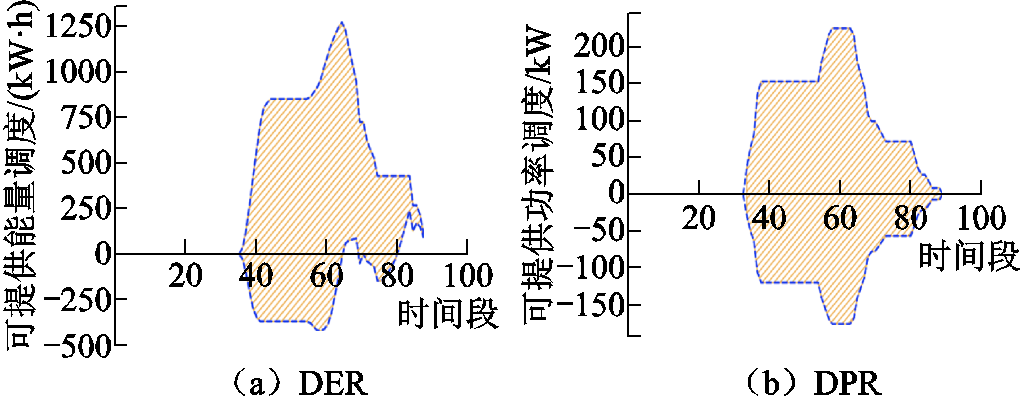
图6 办公区休息日电动汽车集群的MEVDR
Fig.6 MEVDR of EVA in office area on weekends
办公区EVA在工作日上班时段的MEVDR较为连贯,DER和DPR均保持在较高水平,此时段内的EVA展现出了参与大规模电网调度的能力。而在非工作时段,由于汽车数量减少,集群规模随之缩小,集群MEVDR的上下限较低且波动剧烈,此时EVA的调控能力相较于工作时段明显减弱。
在休息日,由于办公区内的EVA规模相对较小,且EV的行为分布相对随机,集群MEVDR的波动幅度显著增大,导致EVA的可调度空间明显减小。此时的EVA并不具备大规模调控能力。
假设商业区内电动汽车集群于工作日和休息日的行为分布满足附表5,集群内电动汽车的各项数据和分布与办公区相同。商业区内集群于工作日和休息日的DER、DPR图像分别如图7、图8所示。
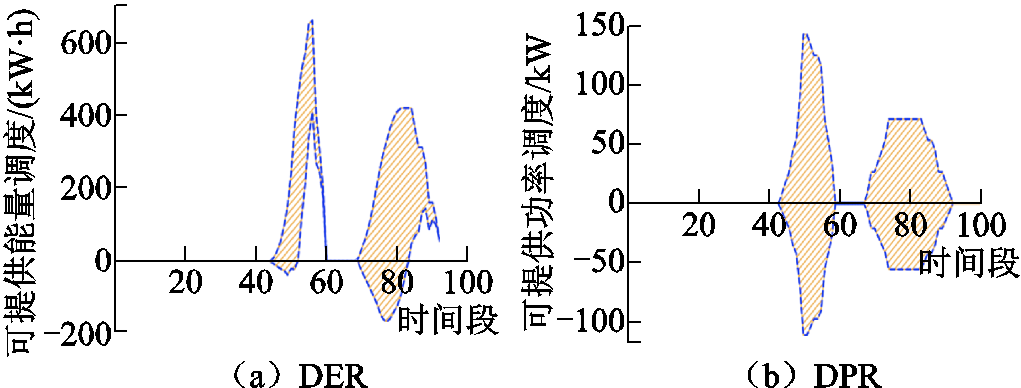
图7 商业区工作日电动汽车集群的MEVDR
Fig.7 MEVDR of EVA in commercial area on workdays
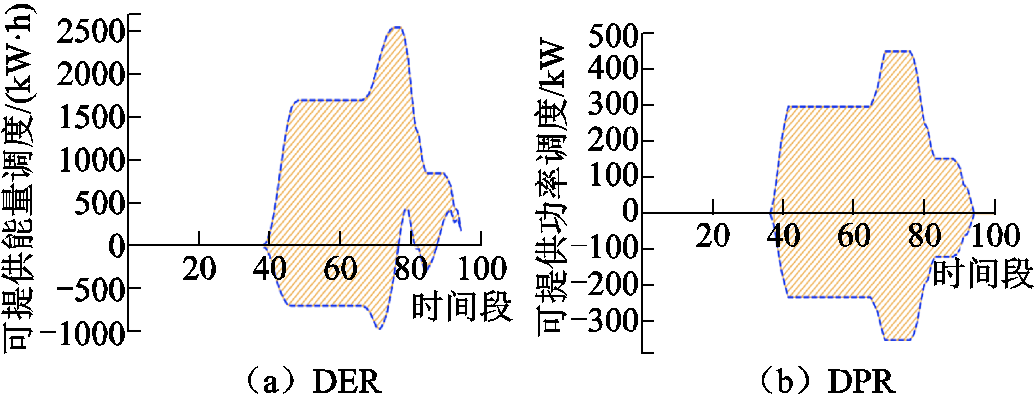
图8 商业区休息日电动汽车集群的MEVDR
Fig.8 MEVDR of EVA in commercial area on weekends
由于商业区内EVA的规模大小受时间等因素影响严重,因此与办公区相比,其MEVDR波动更为剧烈。在特定时间段内,商业区会迎来车辆停放和充电需求的激增,此时该区域内EVA的可调度潜力较高,展现出一定的大规模调节能力。而在其他时间段内,集群的MEVDR会急剧下降,EVA的可调度灵活性较差,难以提供稳定的可调度能量。因此,在这些时段内EVA的大规模调节能力较弱。
假设居民区内电动汽车集群于工作日和休息日的行为分布满足附表6,集群内电动汽车的各项数据和分布与办公区相同。居民区内集群于工作日和休息日的DER、DPR图像分别如图9、图10所示。
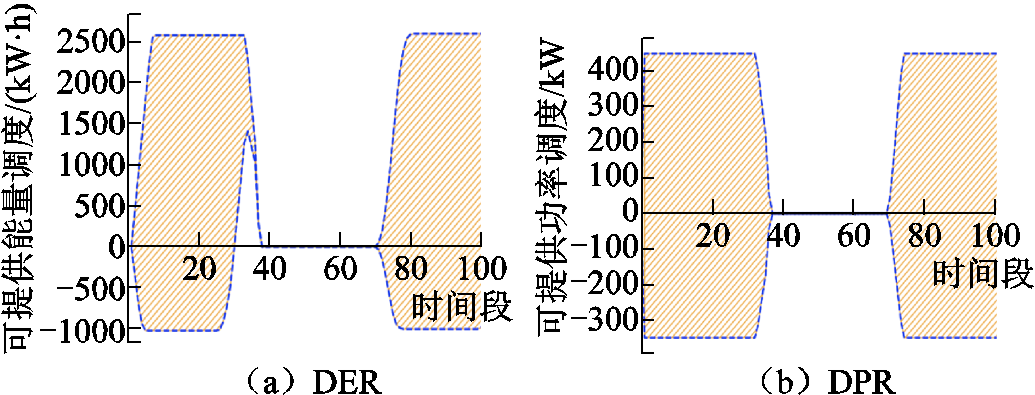
图9 居民区工作日电动汽车集群的MEVDR
Fig.9 MEVDR of EVA in residential area on workdays
在休息日,居民区中EVA的MEVDR上限较高,且整体相对稳定。少数几次波动主要出现在居民出行需求增加的时段,如用餐时段。居民区中的EVA在休息日展现出了良好的可调度潜力。
在工作日,EVA的MEVDR在非工作时段中较为稳定,而在上班时段中下降明显。总的来说,居民区EVA的MEVDR在休息日的绝大部分时间和工作日的非上班时间段内较为稳定,而在其余时段不具备明显规律且波动较大。

图10 居民区休息日电动汽车集群的MEVDR
Fig.10 MEVDR of EVA in residential area on weekends
综上所述,EVA-MEVDR可准确反映处于不同状态下的电动汽车集群的储能和调度特征。这一特点使得管理者能够跨区域、跨时间段地对EVA进行横向对比,从而准确把握各区域、各时间段在可调度潜力上的长处与短板,为优化调度策略提供有力依据。
此外,这样的可视化表证亦为电力调度提供了便利。管理者只需保持EVA的能量和功率数据始终维持在阴影区域内,即可在不违背用户需求的前提下进行安全、可靠的调度。
第1、2节中所得到的不同区域中EVA的MEVDR模型可进一步用于构建多时段约束,进而建立基于MEVDR的VGGMCCS。
VGGMCCS包括上层电网模型和下层车库模型两个层级。下层车库模型位于上层电网模型的一个节点中,通过对上层电网模型提供的宏观调控指令进行分解,制定包括车辆的充放电行为等在内的运行计划,并将其反馈给上层电网模型。上层电网模型则根据这些反馈重新调整宏观调度方案,确保最终策略能够兼顾电网公司、用户和车库运营商等多方利益。VGGMCCS的系统调度关系架构和实时分级响应流程分别如图11、图12所示。
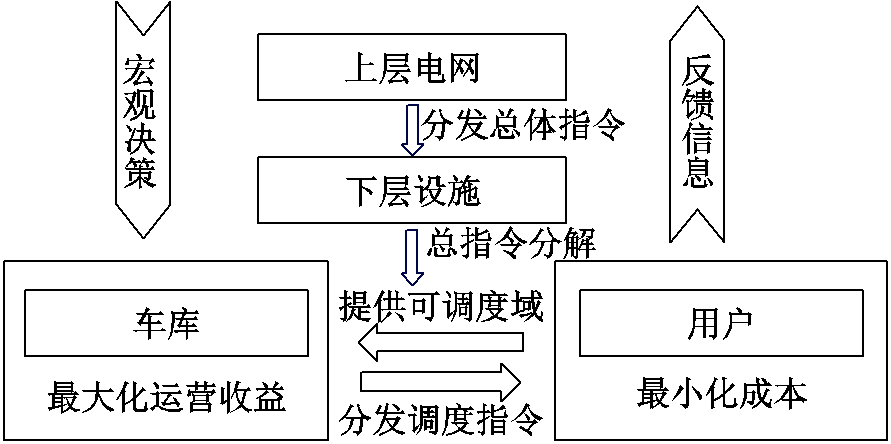
图11 系统调度关系架构
Fig.11 Architectural of system scheduling relationships
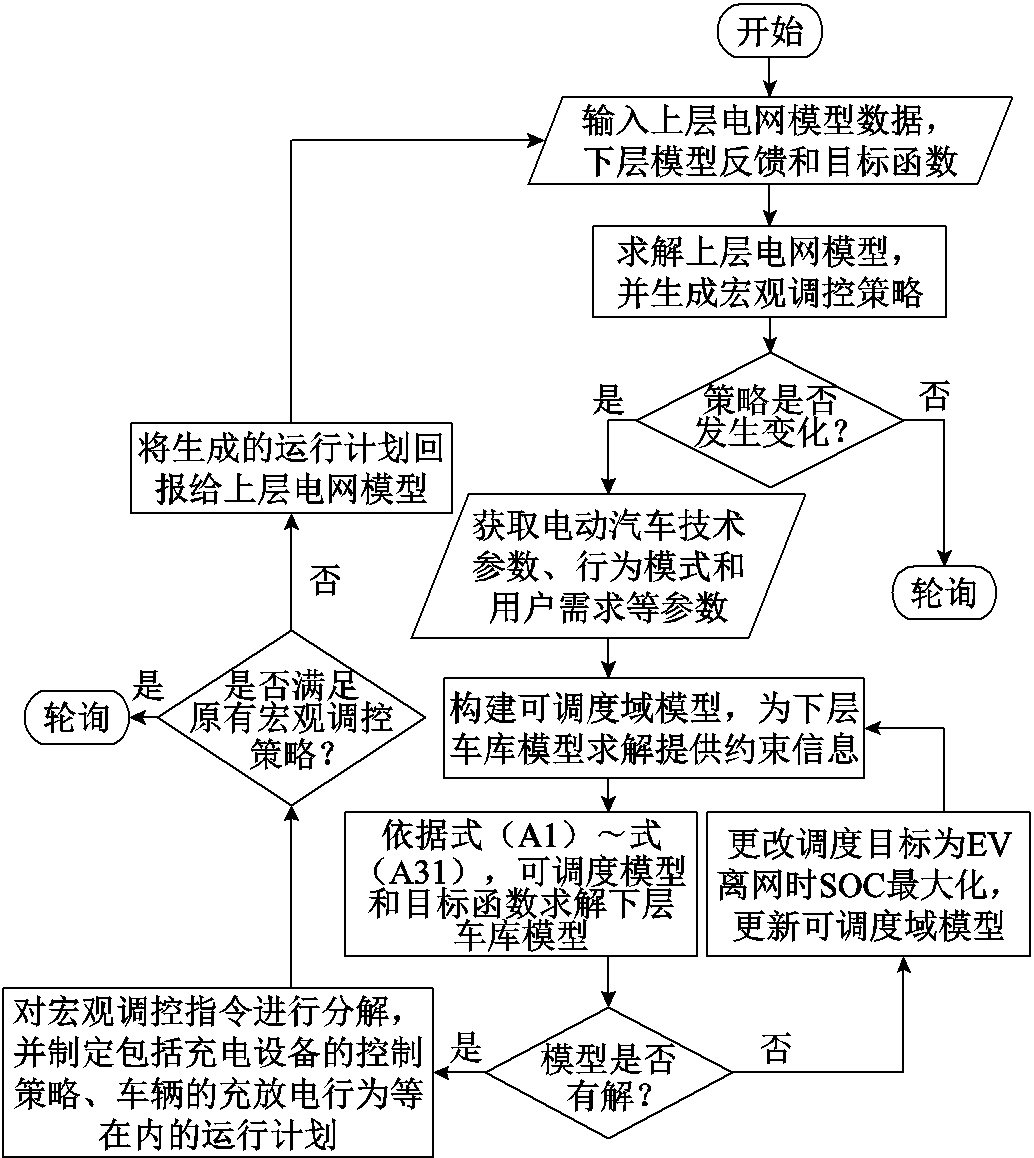
图12 实时分级响应流程
Fig.12 Flow chart of real time hierarchical response
上层电网模型基于IEEE 33节点网络构成,满足以下基本约束。
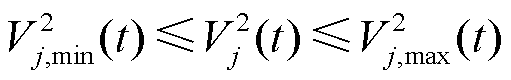 (25)
(25)
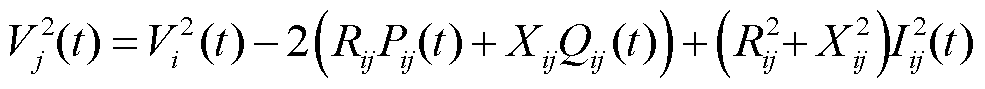 (26)
(26)
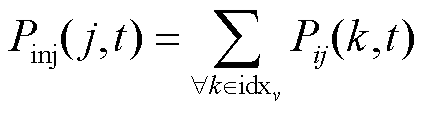 (27)
(27)
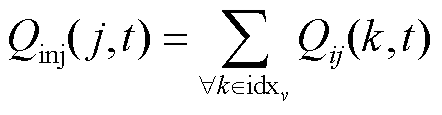 (28)
(28)
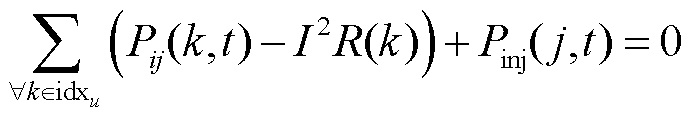 (29)
(29)
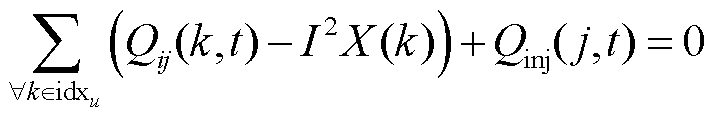 (30)
(30)
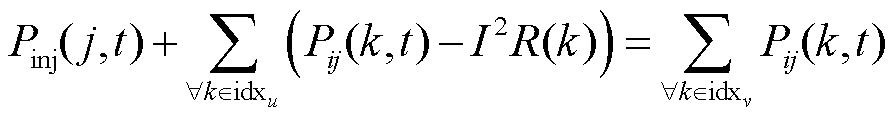 (31)
(31)
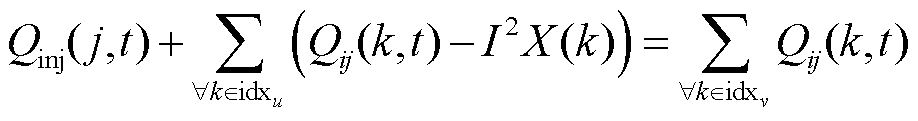 (32)
(32)
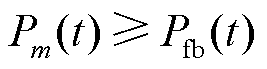 (33)
(33)
式中,Vj(t)为在时段t时母线j的电压幅值;Vi(t)为母线i的电压值;Rij和Xij分别为支路ij的电阻和电抗;Pij(t)和Qij(t)分别为支路ij的有功功率和无功功率;Iij(t)为时间t时支路ij的电流大小;idxu为以节点j为接收端的支路索引;idxv为以节点j为发送端的支路索引;Pinj(j,t)为节点j在时间t的有功功率注入;Qinj(j,t)为节点j在时间t的无功功率注入;Pij(k,t)为从节点i通过支路k传输到节点j的有功功率流;Qij(k,t)为从节点i通过支路k传输到节点j的无功功率流;Pm(t)为节点m在时段t时的有功功率;Pfb(t)为下层模型提供的反馈信息;I为时段t时线路上的电流;R(k)和X(k)分别为支路k的电阻和电抗。
下层模型的目标为最小化电网网损和电压幅值波动,目标函数为
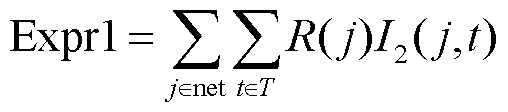 (34)
(34)
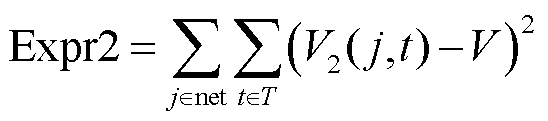 (35)
(35)
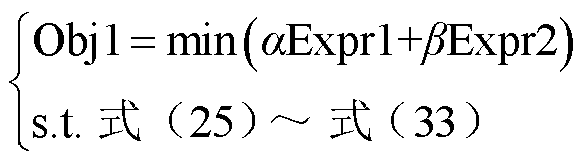 (36)
(36)
式中,j为电网中的支路,R(j)为第j条支路的电阻;I2(j,t)为t时段,第j条支路上通过的电流大小的二次方;V2(j,t)为第j条支路在时段t的电压大小的二次方;V为期望电压的二次方;α和β分别为式(34)和式(35)的权重。
上层电网模型以式(25)~式(33)为目标生成宏观调控指令,并据此为下层车库的具体决策提供指导。
下层模型是对车库内部运行情况的模拟。除式(A1)~式(A31)外,下层车库模型还应满足
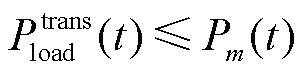 (37)
(37)
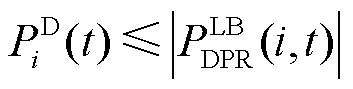 (38)
(38)
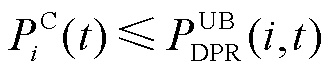 (39)
(39)
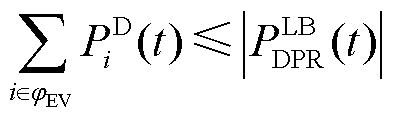 (40)
(40)
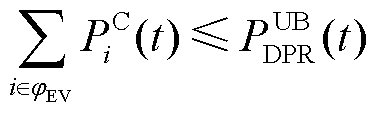 (41)
(41)
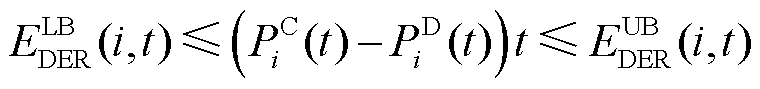 (42)
(42)
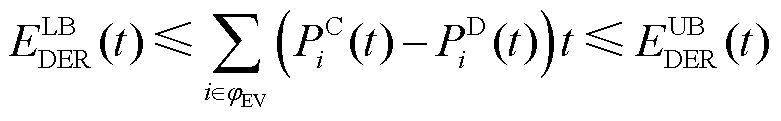 (43)
(43)
式中, 为车库节点处变压器在时段t的负荷;
为车库节点处变压器在时段t的负荷;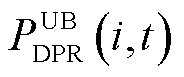 、
、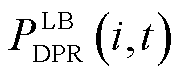 和
和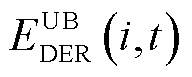 、
、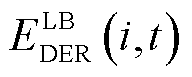 分别为EV i在时间段t时DPR和DER的上、下限;
分别为EV i在时间段t时DPR和DER的上、下限;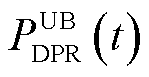 、
、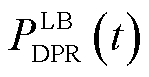 和
和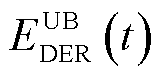 、
、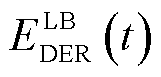 分别为该区域中的EVA在时间段t时DPR和DER的上、下限。式(37)为上层电网模型提供给下层车库模型的宏观调控限制。式(38)~式(43)为MEVDR模型限制。
分别为该区域中的EVA在时间段t时DPR和DER的上、下限。式(37)为上层电网模型提供给下层车库模型的宏观调控限制。式(38)~式(43)为MEVDR模型限制。
下层车库模型以用户成本最小化和车库收益最大化为目标,其中用户成本最小化的优先级更高,即
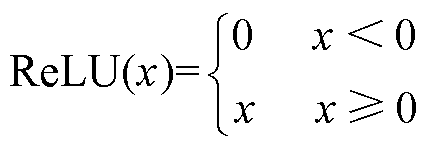 (44)
(44)
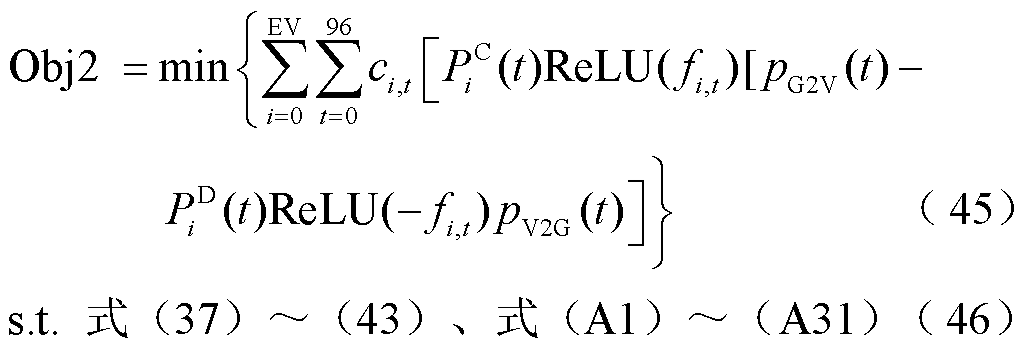
式中,p(t)为时段t时的电价;pG2V(t)、pV2G(t)分别为EV在时段t时进行充放电服务的费用;EV为电动汽车的数量;fi,t为第i辆EV的充放电状态;ReLU为深度学习中常用的激活函数。本文引入ReLU函数的主要目的是简化相关目标函数的表达式,以便于后续求解器的求解。式(45)和式(46)分别为用户成本和车库收益目标函数,在引入ReLU函数之后,这两个目标函数均为混合整数规划(Mixed Integer Programming, MIP)问题。在fi,t确定以后,式(46)的优化问题实际上属于简单的规划问题,因此,下层车库模型的双目标函数可转换为
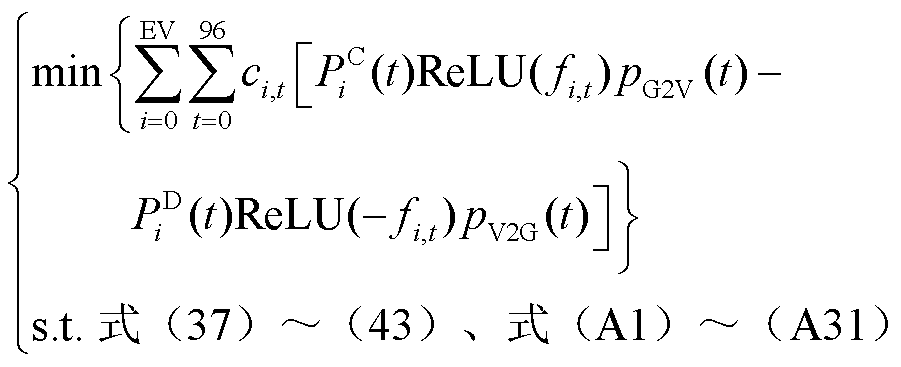 (47)
(47)
显然,式(47)为MIP问题。
进一步地,式(36)可写为
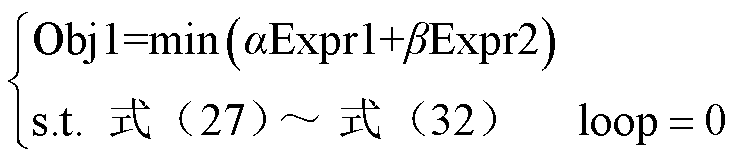 (48)
(48)
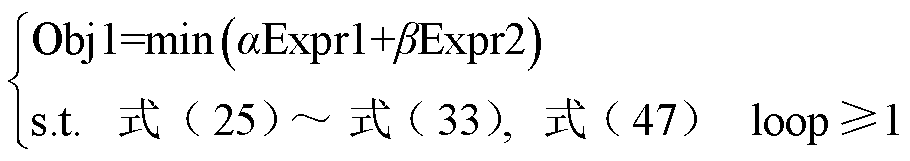 (49)
(49)
式中,loop代表多层级模型所经历的求解阶段。显然,式(48)可解。在loop≥1时,由于上下层模型是分开且按顺序进行求解的,因此在处理上层模型时,式(47)及其他相关变量已经完成求解过程。因此,式(49)同样可解。
综上所述,VGGMCCS的上下层模型均可以采用商业求解器进行快速求解。
选取由国网江苏电科院提供的相关数据构造算例,验证所提基于MEVDR的VGGMCCS的有效性。在该算例系统中,上层电网模型由IEEE 33节点网络构成,下层车库位于上层电网模型的28节点。该节点处变压器容量设定为500 kV·A,常规负荷最高占配电变压器容量的50%。车库位于交通主干道附近的办公区中,最多可为50辆EV提供G2V和V2G服务,支持单台EV最高充电功率36 kW、放电功率28 kW、充放电效率为0.92。算例中的每辆EV均配置一套电池系统,EVA的行为特征分布和EV种类分布符合第2节中办公区工作日时段的分布。
车库从电网购电的电价为分时电价(参照江苏省南京市标准):8:00—12:00、17:00—21:00电价为1.769 7元/(kW·h),12:00—17:00、21:00—24:00电价为1.341 8元/(kW·h),0:00—8:00电价为1.013 9元/(kW·h)。考虑到充电车库内充电设备的建设成本和车库运营维护成本,当向用户提供G2V服务时,车库收取当前电价15%的服务费;当向用户提供V2G服务向电网供电时,车库需向用户提供包含电池折旧费等补偿在内的V2G服务补偿。二者基于分时电价设定为
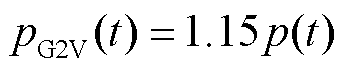 (50)
(50)
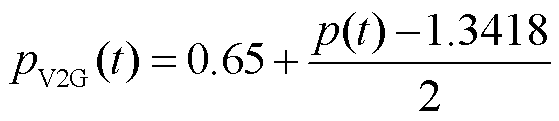 (51)
(51)
为了更好地验证基于MEVDR的VGGMCCS的有效性,本文基于文献[22, 26]中提出的调度策略构建了两套对比系统(以下简称对比策略1和对比策略2)。通过对这两套对比系统进行仿真,并将结果与基于MEVDR的VGGMCCS进行对比分析,研究它们对车-库-网系统各个层级的影响。
仿真在CPU为Intel Core i5-8300H 2.30 GHz,16 G内存的计算机上通过gurobi求解器完成,计算结果见表3。本节将从电网侧、车库侧、经济效益和求解效率方面对仿真结果进行分析。
表3 不同策略下的仿真结果
Tab.3 Simulation results under different strategies
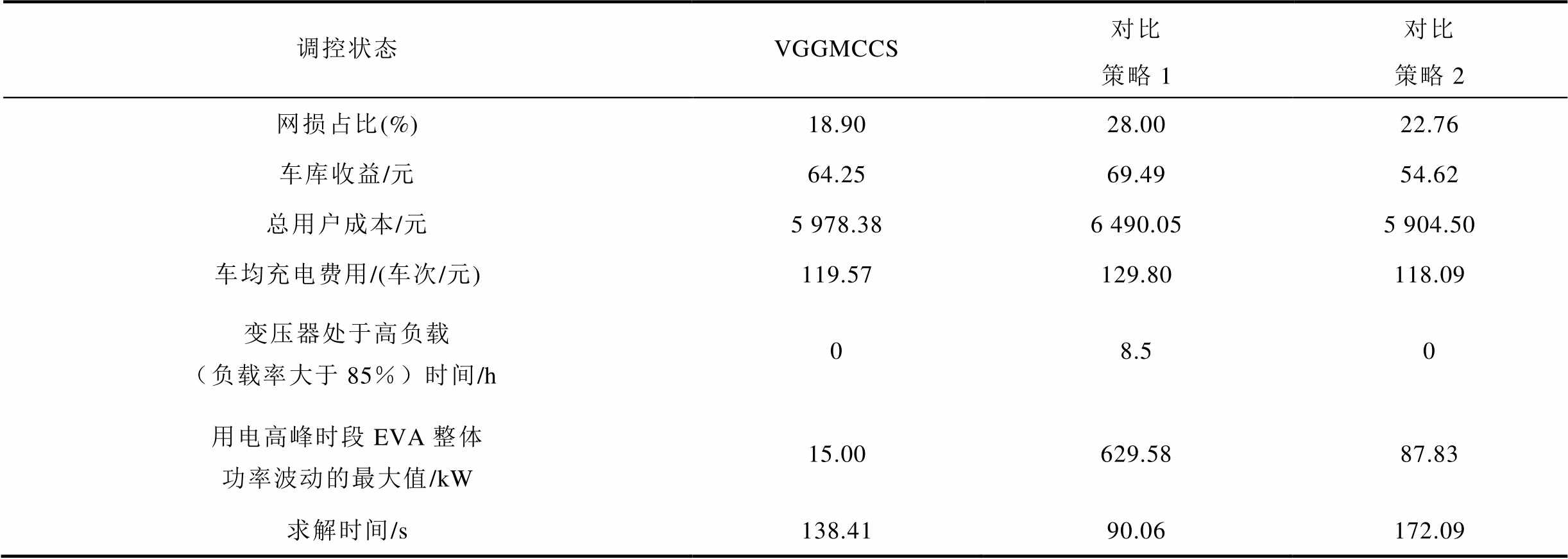
调控状态VGGMCCS对比策略1对比策略2 网损占比(%)18.9028.0022.76 车库收益/元64.2569.4954.62 总用户成本/元5 978.386 490.055 904.50 车均充电费用/(车次/元)119.57129.80118.09 变压器处于高负载(负载率大于85%)时间/h08.50 用电高峰时段EVA整体功率波动的最大值/kW15.00629.5887.83 求解时间/s138.4190.06172.09
4.3.1 电网侧分析
基于电网模型的实际运行数据,绘制了基于MEVDR的VGGMCCS与对比策略下电网网损占比的日变化曲线,如图13所示。相较于对比策略,本文所提方法可有效改善电网运行状况。与对比策略1和对比策略2相比,全天电网网损占比分别下降9.1%和3.86%。在时间段32~84(用电高峰期,对应8:00—21:00)内,电网网损占比较对比策略1下降了12.17%,较对比策略2下降了8.69%。这表明,基于MEVDR的VGGMCCS能够有效改善电网的运行状态。

图13 不同策略下电网网损占比变化曲线
Fig.13 Variation curves of power grid loss proportion under different strategies
4.3.2 车库侧分析
为详尽分析VGGMCCS和对比策略对下层车库模型运行状态的影响,将常规负荷和EV充放电负荷叠加,所得节点变压器日负荷曲线如图14所示。
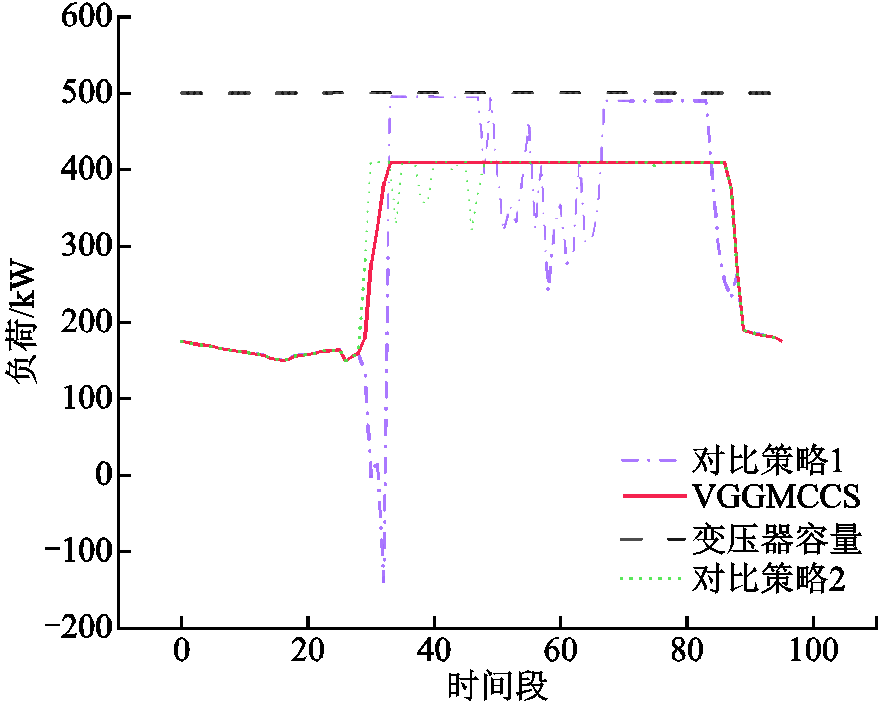
图14 不同策略下的变压器负载曲线
Fig.14 Transformer load curves under different control strategies
可以看出,相较于对比策略1和对比策略2,VGGMCCS显著改善了变压器的运行状态。一方面,在VGGMCCS调度下,变压器处于高负载状态的运行时间显著减少,与对比策略1相比,变压器在高负荷下的运行时间减少了100%;另一方面,在VGGMCCS调度下,变压器的负荷波动幅度显著降低。与其他两种对比策略相比,VGGMCCS下变压器的功率波动极小,特别是在用电高峰期(时间段32~84,对应8:00—21:00),调控效果尤为明显。在该时间段内,VGGMCCS下变压器的功率波动较对比策略1下降了96.36%,较对比策略2下降了82.59%,变压器的运行状态得到了显著改善。
为了更准确地分析上述结果的成因,本文提取了下层车库模型的日调度策略,并做出VGGMCCS和对比策略的EVA日调控策略,如图15所示。通过比较分析可以发现,当大量电动汽车接入电网时,相较于对比策略,VGGMCCS能够根据每个时间段内EVA的总充电功率,更加合理地安排电动汽车的充放电任务。通过这种方法,VGGMCCS在EVA的充电与放电功率之间实现了平衡,使得EVA在每个时间段内的功率波动极小,从而显著减轻了变压器的运行压力。此外,同对比策略1相比,VGGMCCS策略通过上下层模型间的信息传递,有效地约束了EVA在时段40~50和70~90内的充电行为,并将短时间段内的高负荷充电任务均匀地转移至长时间段(50~70)内完成。这有效地避免了变压器长时间满载情况的发生,确保了变压器的安全可靠运行。
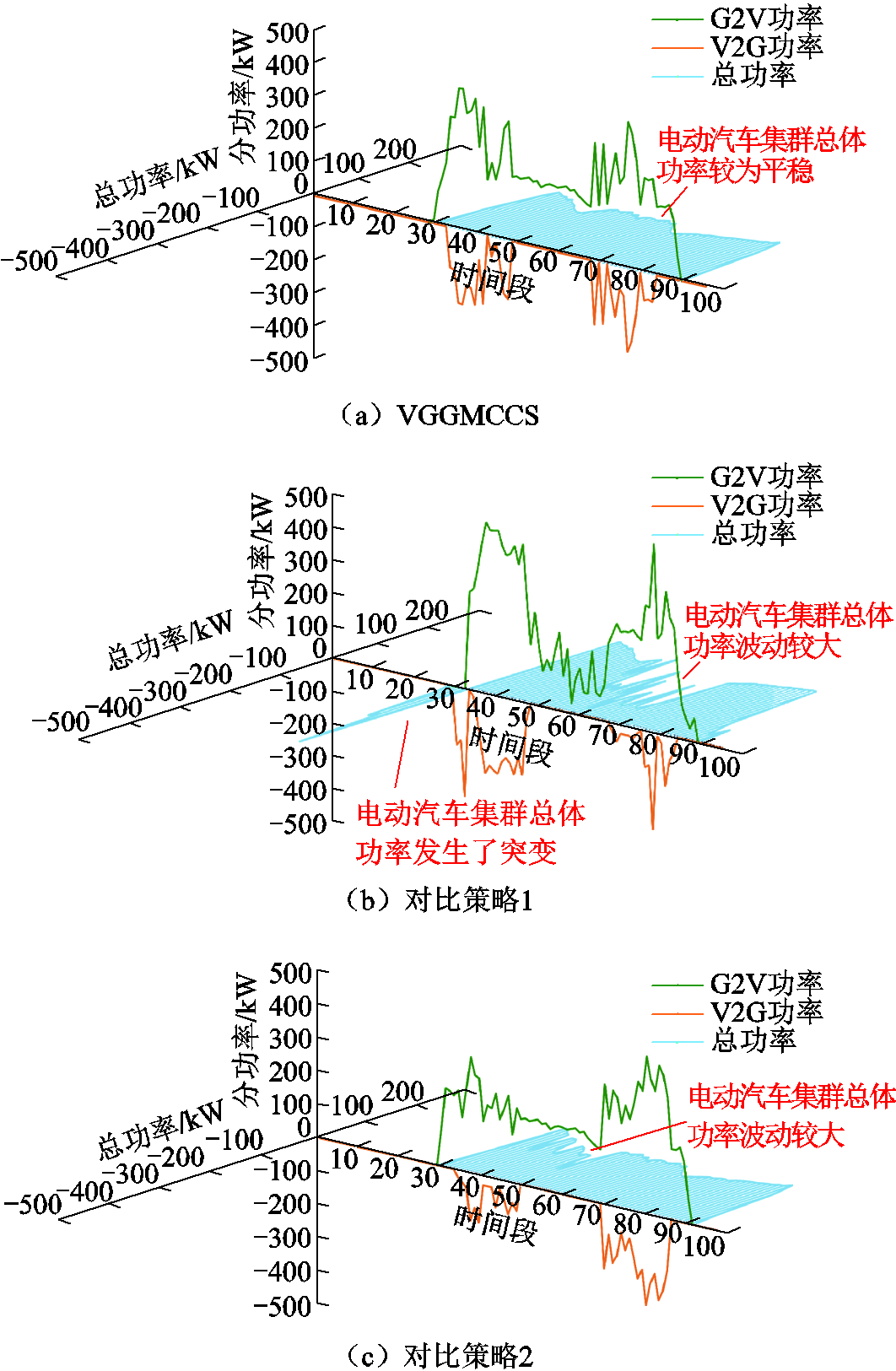
图15 不同策略下电动汽车集群的日调度策略
Fig.15 Daily scheduling strategies for electric vehicle aggregations under different control strategies
4.3.3 EV侧分析
为进一步分析三种方法对EV调度策略的具体影响,本文从车库一天内所服务过的EV中抽取了编号为17和39的两辆EV,并将其在三种控制方法下的具体调控策略可视化,如图16、图17所示。
与两种对比策略相比,VGGMCCS对EV的调度显然更加激进。特别是在用电较多的时段内(时间段32~64,对应8:00—16:00),VGGMCCS下17号EV参与电网调度的时长相较对比策略1增加了10%,相较对比策略2增加了175%;39号EV参与电网调度的时长相较对比策略1增加了25%,相较对比策略2增加了66.67%。这表明VGGMCCS能够更加充分地发挥EV灵活的能源调度能力,在电网需要时提供更多的调度支持。

图16 不同策略下17号电动汽车的调控策略
Fig.16 Control strategies for EV 17 under different strategies
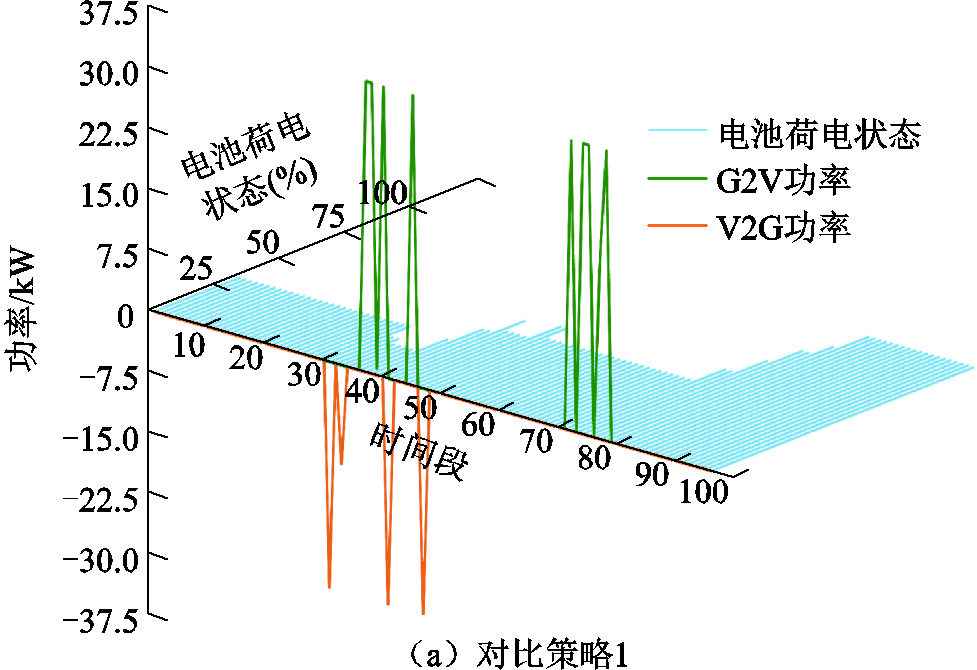
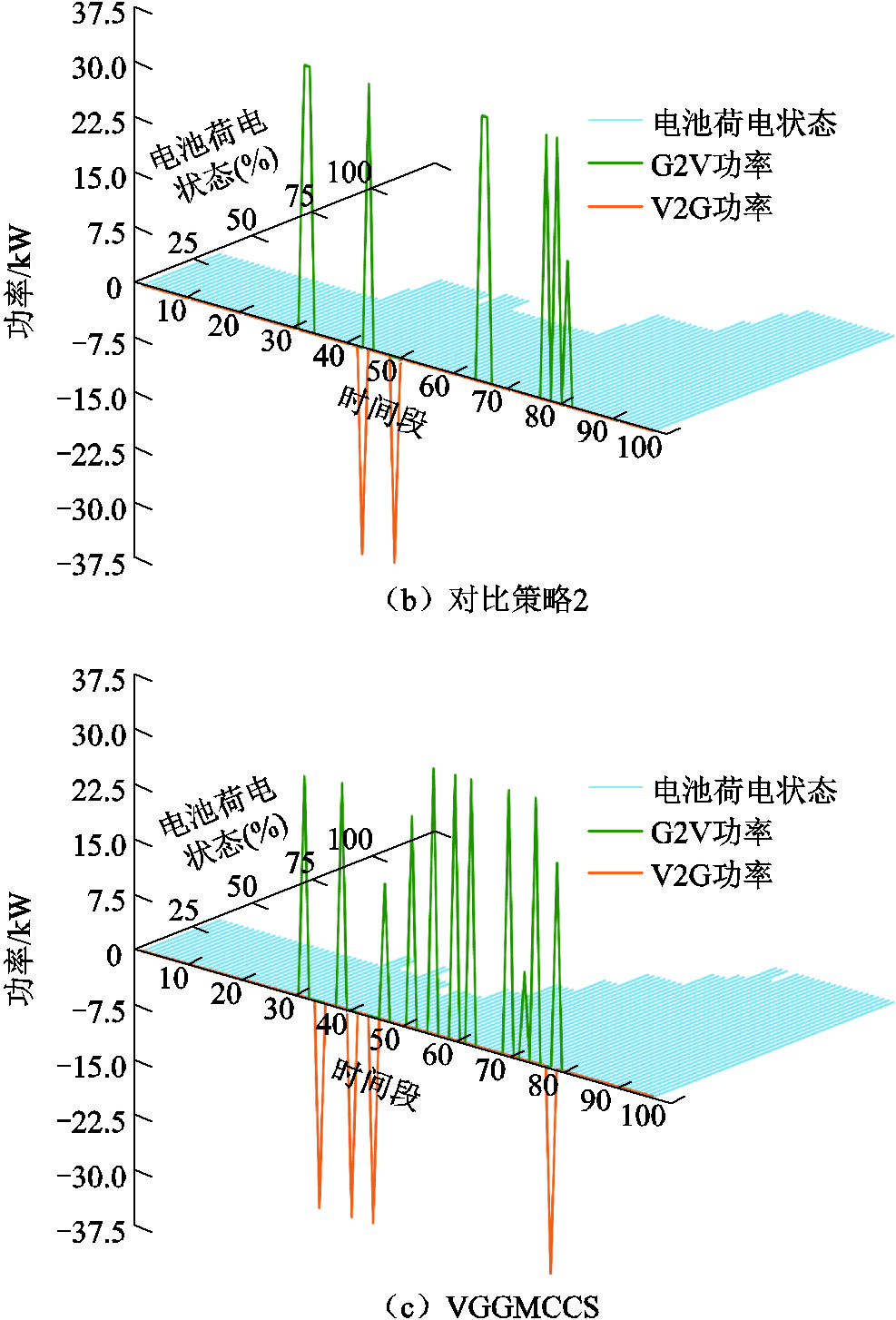
图17 不同策略下39号电动汽车的调控策略
Fig.17 Control strategies for EV 39 under different strategies
此外,在VGGMCCS的调控下,与对比策略1相比,EV17和EV39的SOC超过60%的时间分别增加了11.54%和65.22%;与对比策略2相比,EV 17和EV 39的SOC超过60%的时间分别增加了7.41%和15.15%。这提升了EV在紧急情况下的可靠性,有效地避免了因SOC不足而影响用户即时用车需求的状况。
然而,激进的调度策略也会使得EV的输入输出功率变化更为频繁。若缺乏合理的引导和安排,甚至可能加剧电网中的波峰波谷,影响电网的整体运行。尽管如此,从图15可以看出,相较于一般有序调控方式,VGGMCCS控制下的EVA在用电高峰时间段对外所表现出的整体功率反而更加平稳:在用电高峰期,VGGMCCS控制下的EVA总功率波动和最大功率波动分别比对比策略1及对比策略2减少了83.58%和59.89%,以及90.97%和82.92%,这有助于减少变压器负荷的波动,为电网的稳定运行提供了有力保障。
4.3.4 经济收益分析
从经济收益角度来看,基于MEVDR的VGGMCCS较好地维持了多方利益的平衡。与对比策略1相比,VGGMCCS优先保障了用户利益:用户的日均充电成本下降了7.88%,车均充电成本从129.80元降至119.57元,这与该策略优先考虑用户利益的理念相符;与对比策略2相比,VGGMCCS更好地兼顾了多方利益:车库运营商的收益增长了17.63%,而用户的充电成本仅上涨了1.25%。这表明,VGGMCCS在保障车库运营商收入的同时,最大限度地降低了用户的充电费用,实现了车库运营商与用户之间的利益平衡。
4.3.5 求解效率
如表3所示,在车、库、网各层级调控效果优异且确保了多方利益的前提下,VGGMCCS依然保持了较快的求解速度。与同样需要进行多阶段求解的对比策略2相比,VGGMCCS的求解速度是它的1.24倍。此外,在实际调控过程中,由于电动汽车接入与脱离,下层车库模型的调度策略需要进行频繁调整,因此需要模型具备快速响应能力以应对这些变化。尽管与不需要多阶段求解的对比策略1相比,VGGMCCS的整体求解速度较慢,但其对下层车库的求解速度却极为迅速,仅需3.16 s。这表明,VGGMCCS能够在保证决策准确性的同时,快速响应下层车库的调度需求,进而有效减少因电动汽车接入电网后需要重新调度所带来的时间成本和经济损失。因此,具备快速决策能力的VGGMCCS在实际应用中具有较大的潜力和很强的应用价值。
总体而言,基于MEVDR的VGGMCCS在优化电网能量利用和提高系统收益等方面表现出明显优势。通过共享上下层模型的信息,该系统能够更快速地生成更有效的决策方案,不仅提高了电网运行效率,还降低了车库运营成本,为用户带来了可观的收益,实现了电网公司、用户和车库运营商的多方共赢。
针对电动汽车集群可调度潜力评估尚未形成系统化的构建与分类方法,且现有研究较少考虑电动汽车可调度潜力由功率调度潜力和能量调度潜力共同构成的情况,本文提出了一种多时段电动汽车可调度域(MEVDR)的构建方法。该方法将电动汽车的可调度域划分为可调度功率域和可调度能量域,更全面地反映了电动汽车的可调度潜力。同时,本文深入分析了不同区域和时间段的MEVDR,实现了跨区域、跨时间段的电动汽车可调度潜力的横向对比,显著提高了调控过程中电动汽车集群可调度潜力的可读性。此外,为解决多层级有序调控策略在车-库-网系统中考虑不全面的问题,本文提出了基于电动汽车可调度域的车-库-网多层级协调控制系统(VGGMCCS),将电动汽车的可调度潜力纳入调控策略的构建过程,并对用户和电动汽车层级进行了详细分析。为应对模型参数众多、求解速度较慢的问题,本文将模型拆分为上下两层:上层模型负责宏观调度,下层模型则对调度结果进行详细解释。为提高求解准确性,本文还引入了模型迭代算法,以兼顾多方利益并提升解决方案精度。通过算例仿真对比分析,得出以下主要结论:
1)本文基于用户行为特性和可视化思想,提出了MEVDR的构建方法。该方法将电动汽车的可调度域划分为可调度能量域(DER)和可调度功率域(DPR),不仅能够较为精确地捕捉电动汽车在特定时间段内的能量和功率调度特征,而且可读性较好,适用于大规模电动汽车可调度潜力的预测与分析。
2)本文采用了分区域和分时段的方式对电动汽车集群进行划分,使得不同电动汽车集群的可调度潜力能够在较短的时间跨度内得到展示。这一方法有助于电力调度管理者更加准确地把握各区域、各时间段的电动汽车集群在可调度潜力方面的优势与不足,从而为制定更精准的调度策略提供有力支持。
3)本文提出的基于MEVDR的VGGMCCS能够显著降低用户使用成本、提高车库的经济收益和电网运行效率,在保障电力系统长期稳定运行的同时,实现了用户、车库运营商和电网公司之间的多方共赢。与两种对比策略相比,该方法展现出了一定的优势,为大规模电动汽车集群参与电网调度提供了有益的探索。
附 录
1. 电动汽车运行特性建模
电动汽车个体的数学模型如式(A1)~式(A8)所示。式(A1)为本文所设定的可调度时间集合;式(A2)、式(A3)为EV的充放电功率约束;式(A4)为EV的入网状态约束;式(A5)为EV的充放电状态约束;式(A6)表示EV在实际充电动态过程中的SOC变化;式(A7)、式(A8)为用户需求约束。
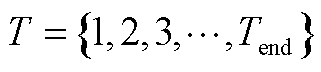 (A1)
(A1)
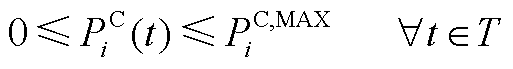 (A2)
(A2)
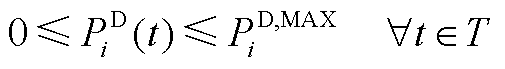 (A3)
(A3)
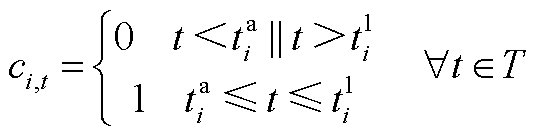 (A4)
(A4)
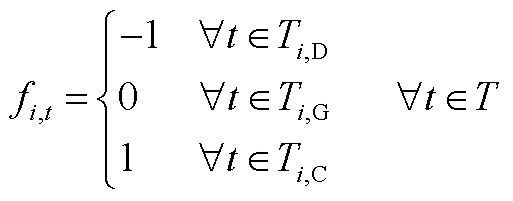 (A5)
(A5)
式中,![]() 、
、![]() 、
、![]() 分别为第i辆EV处于放电、空闲和放电状态的时间集合。
分别为第i辆EV处于放电、空闲和放电状态的时间集合。
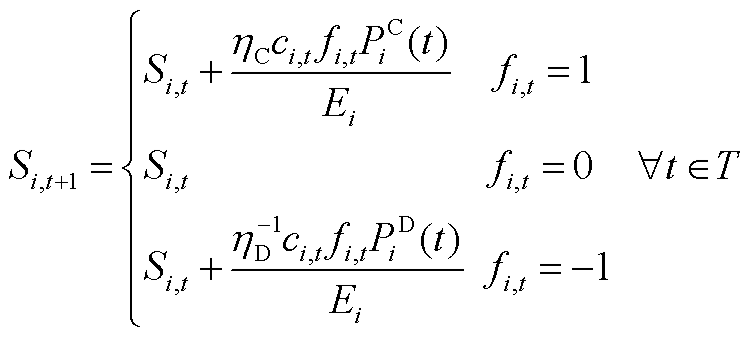 (A6)
(A6)
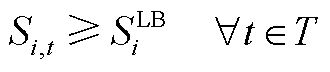 (A7)
(A7)
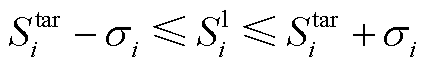 (A8)
(A8)
式中,σi为用户可接受的最终充电结果误差;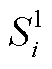 为离网时刻EV的实际SOC。
为离网时刻EV的实际SOC。
EVA数学模型建立如式(A9)~式(A31)所示。
分析上述公式,可以发现,式(A4)、式(A5)的加入使得EV在每个时间段的状态均可被表达为二元向量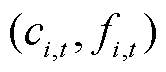 的形式。假设一天被划分为K个时间段,系统中的EV的全天实时状态可被表达为一个2×K的矩阵,有
的形式。假设一天被划分为K个时间段,系统中的EV的全天实时状态可被表达为一个2×K的矩阵,有
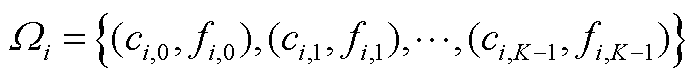 (A9)
(A9)
式中,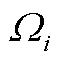 为第i辆EV在一天内的实时状态集合。
为第i辆EV在一天内的实时状态集合。
通过式(A9),EV在一天内任意时段内的状态均可被准确确定,无需为每台EV都定义一个不同的调度时间集合![]() ,不同EV调度时间的定义域可被归纳至相同的调度时间集合T[40]。
,不同EV调度时间的定义域可被归纳至相同的调度时间集合T[40]。
根据前述推论,可以认为式(A2)、式(A3)和式(A7)均具有闵可夫斯基可加性。然而,对于式(A6)而言,由于其在不同情境下的表达式存在差异,因此需要进行适当的转换处理。修正线性单元(ReLU)即是深度学习中常用的激活函数[41],为了整合式(A6)并确保其在不同情境下的适用性,本文借助ReLU函数进行必要的转换处理。
基于ReLU函数,式(A6)中的三种状态可被整合为式(A10),这一整合后的表达式同样具有闵可夫斯基可加性。
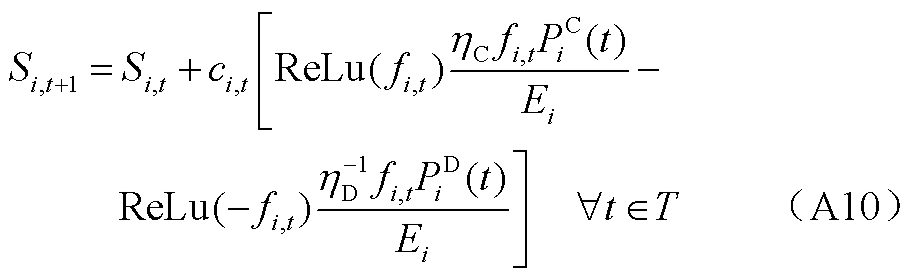
由于EV在一天内的实时状态可被式(A9)表示,式(A2)、式(A3)实际上隐含了类似于式(A6)的EV状态约束条件。但为了便于描述EVA的充放电功率约束,基于ReLU函数,式(A2)、式(A3)可被转换为式(A11)、式(A12)。同式(A2)、式(A3)相同,式(A11)、式(A12)同样具备具有闵可夫斯基可加性。
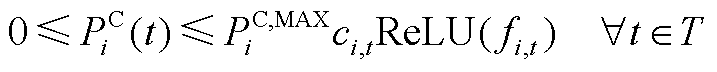 (A11)
(A11)
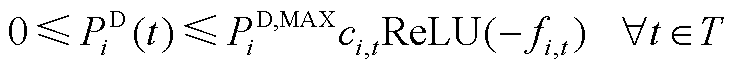 (A12)
(A12)
利用闵可夫斯基加法处理式(A10)~式(A12)得到对应包络空间式(A13)~式(A15)。
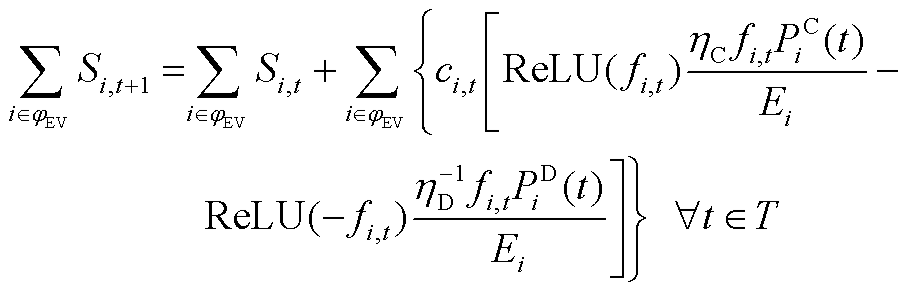 (A13)
(A13)
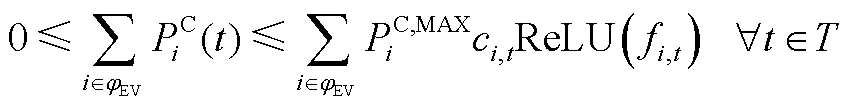 (A14)
(A14)
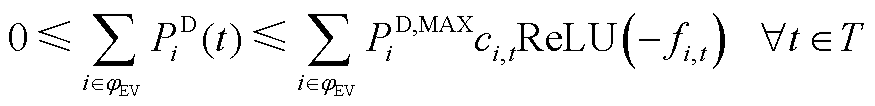 (A15)
(A15)
进一步地,定义![]() 、
、![]() 、
、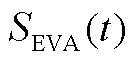 分别为
分别为
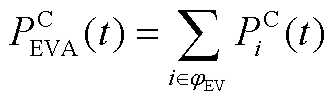 (A16)
(A16)
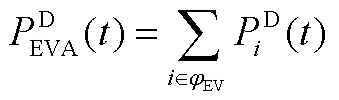 (A17)
(A17)
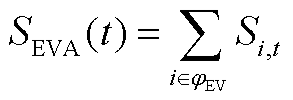 (A18)
(A18)
利用式(A16)~式(A18),EVA能量约束为
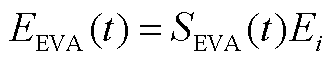 (A19)
(A19)
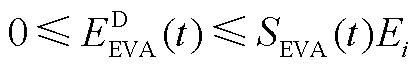 (A20)
(A20)
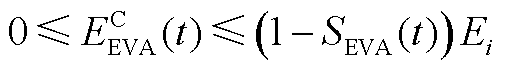 (A21)
(A21)
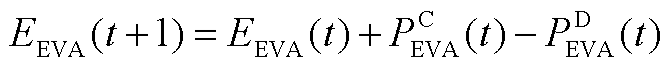 (A22)
(A22)
随后,定义EVA边界参数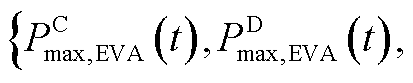
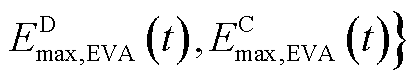 ,可由式(A23)~式(A26)计算得到。
,可由式(A23)~式(A26)计算得到。
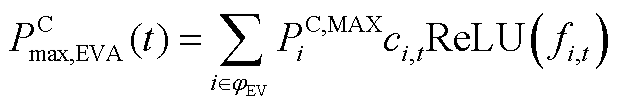 (A23)
(A23)
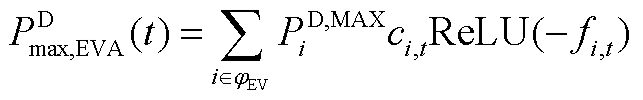 (A24)
(A24)
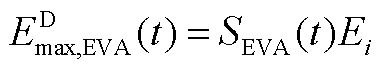 (A25)
(A25)
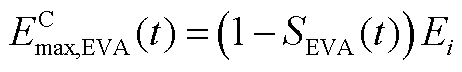 (A26)
(A26)
通过将式(A16)~式(A19)、式(A23)~式(A26)代入式(A13)~式(A15)、式(A20)~式(A22),建立EVA的运行特性模型如式(A27)~式(A31)所示。
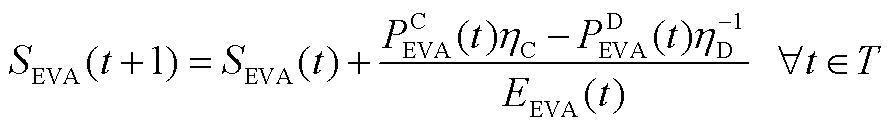 (A27)
(A27)
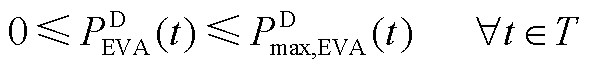 (A28)
(A28)
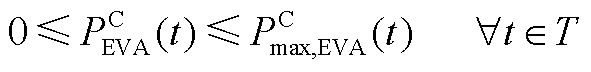 (A29)
(A29)
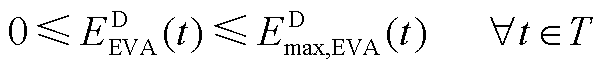 (A30)
(A30)
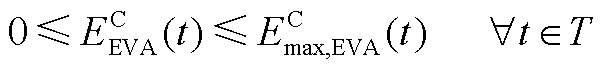 (A31)
(A31)
2. 高斯混合模型
GMM是一种概率模型,它通过多个高斯分布的加权组合来近似描述具有复杂概率分布的随机变量。其聚类过程的基本步骤如附图1所示,概率密度可以通过式(24)进行计算。
通过使用EM算法,式(24)得以求解[42]。为了测试该聚合算法的有效性,从具有预定义参数的两个已知混合分布中各抽取1 000个数据创建两个合成数据集,并通过GMM对该数据集进行拟合,结果如附图2、附图3所示。
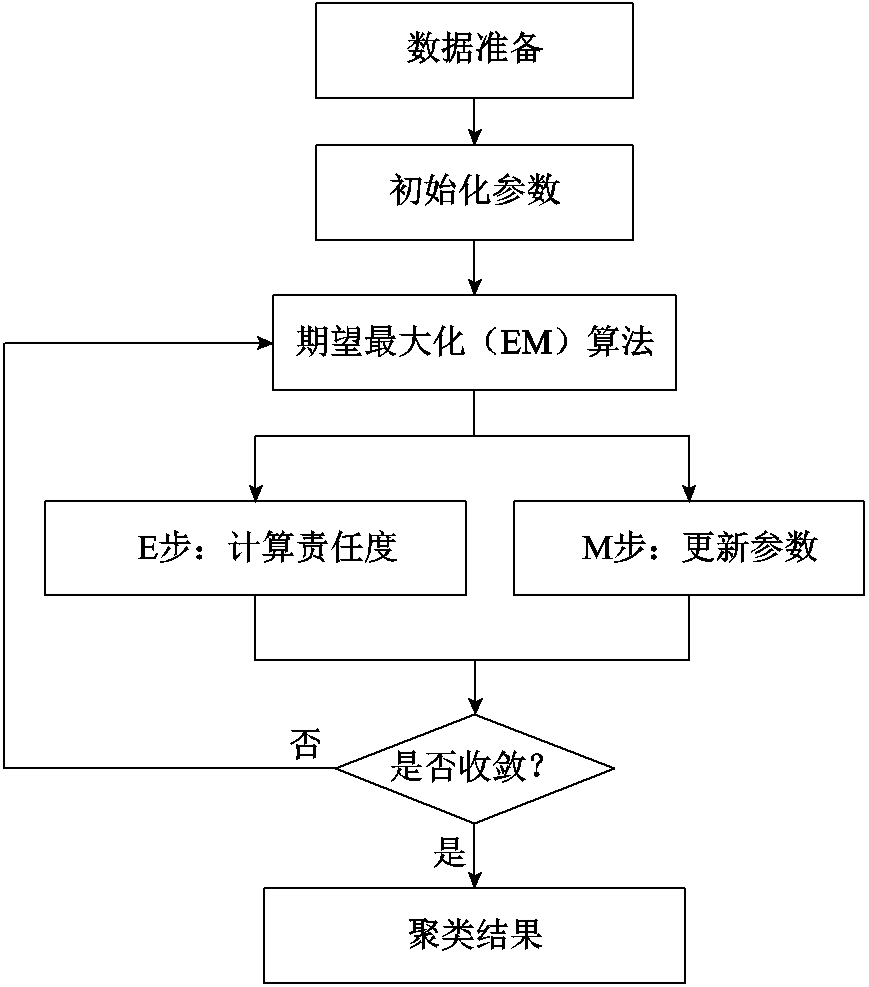
附图1 GMM聚类基本过程流程
App.Fig.1 Flow chart of the basic GMM clustering process
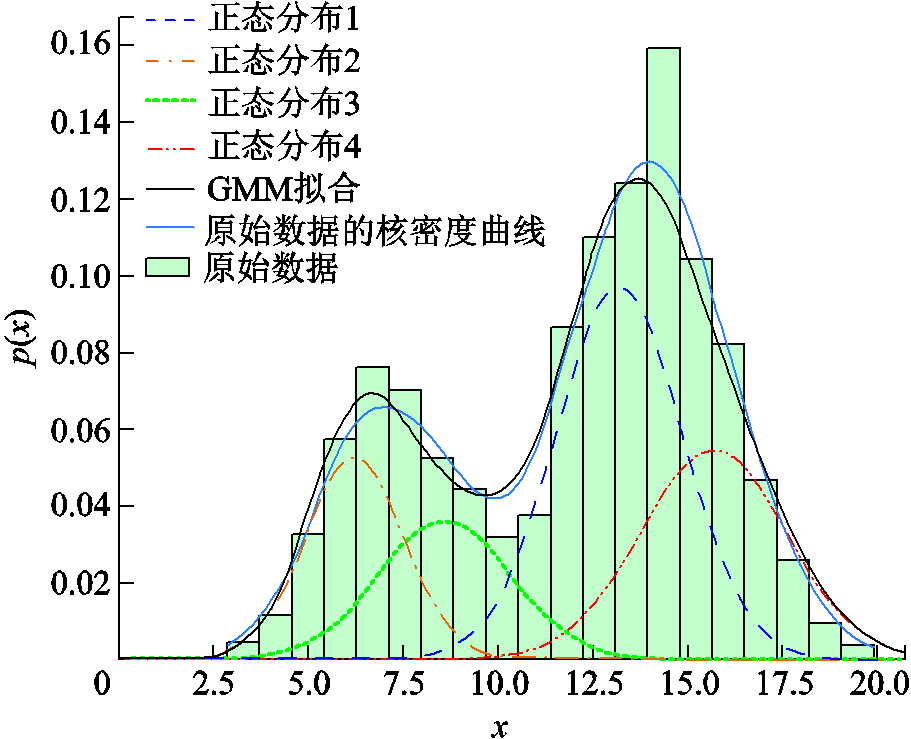
附图2 GMM拟合结果(Ⅰ)
App.Fig.2 Fitting results of GMM (Ⅰ)
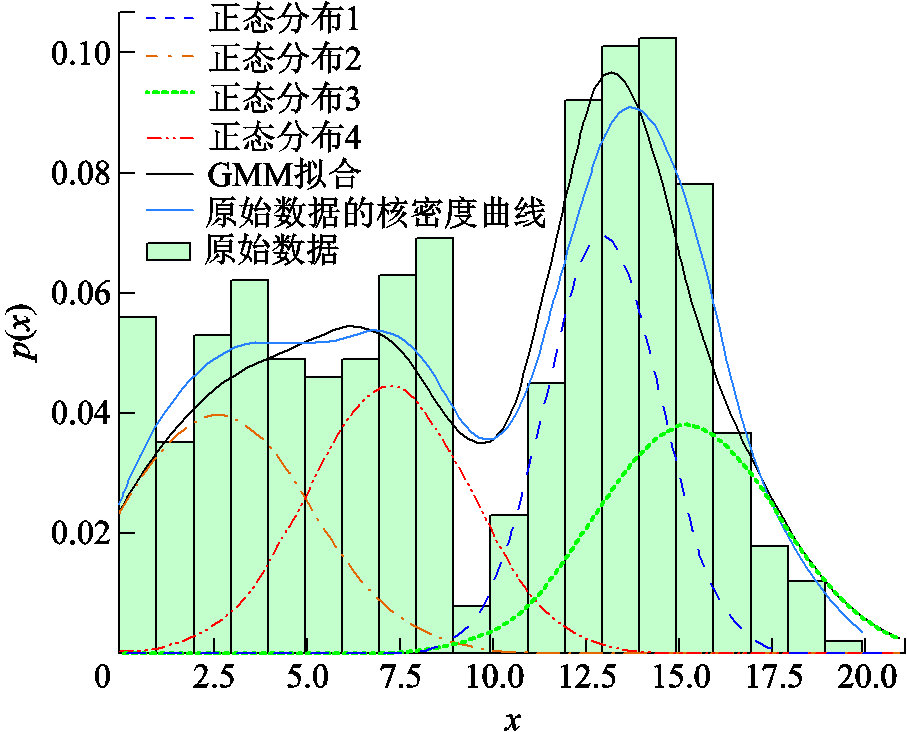
附图3 GMM拟合结果(Ⅱ)
App.Fig.3 Fitting results of GMM (Ⅰ)
可以看出,拟合的分布与数据点的直方图匹配良好,可被视作由多个高斯分布以一定权重组合而成(在附图2、附图3中分别以彩色虚线标示,相关数据见附表1、附表2)。基于上述分析和相关论文研究[39],可以认为不同区域中的EV的行为特征在聚类之后可被近似视为由一个或多个高斯分布以一定权重组合而成。在本文后续的研究中,所使用的关于EVA的行为特征分布数据,均基于GMM聚类后所得到的拟合正态分布,以确保分析的准确性和可靠性。
附表1 附图2的相关数据
App.Tab.1 Dataset specifications of App.Fig.2

正态分布1正态分布2正态分布3正态分布4 权重0.406 40.172 50.158 60.262 5 均值13.236.268.6415.72 方差1.671.311.751.92
附表2 附图3的相关数据
App.Tab.2 Dataset specifications of App.Fig.3

正态分布1正态分布2正态分布3正态分布4 权重0.269 70.252 50.232 60.245 1 均值13.022.6415.297.28 方差1.542.552.452.20
附表3 办公区内电动汽车集群的行为分布
App.Tab.3 Behavioral distribution of EVA in office area

时间段SarriveSl 工作日0.580.520~U (0.2, 0.4)1或 max(SOC) 休息日0.490.417 1421
附表4 电动汽车集群的参数
App.Tab.4 Parameters of EVA
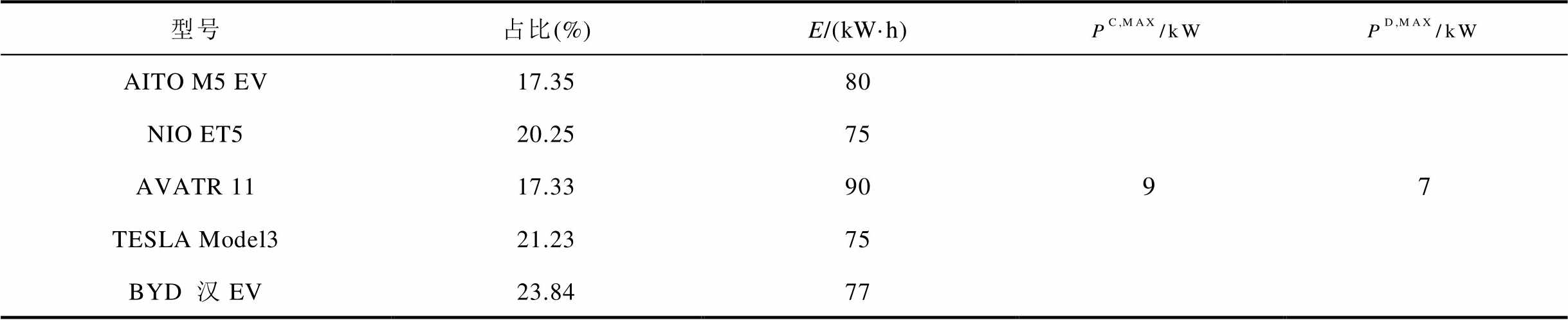
型号占比(%)E/(kW·h) AITO M5 EV17.358097 NIO ET520.2575 AVATR 1117.3390 TESLA Model321.2375 BYD 汉EV23.8477
附表5 商业区内电动汽车集群的行为分布
App.Tab.5 Behavioral distribution of EVA in commercial area

时间段SarriveSl 休息日0.5100.520~U (0.2, 0.4)1或 max(SOC) 0.5170.523 工作日0.4120.414 1822
附表6 居民区内电动汽车集群的行为分布
App.Tab.6 Behavioral distribution of EVA in residential area

时间段SarriveSl 休息日0.500.511~U (0.2, 0.4)1或max(SOC) 1318 2024 工作日0.400.48 1824
参考文献
[1] Song Yonghua, Yang Xia, Lu Zongxiang. Integration of plug-in hybrid and electric vehicles: experience from China[C]//IEEE PES General Meeting, Minneapolis, MN, USA, 2010: 1-6.
[2] 刘动, 孟晨旭, 潘正阳, 等. 居民小区经营性电动汽车充电站投资建设研究[J]. 电气技术, 2022, 23(6): 104-108. Liu Dong, Meng Chenxu, Pan Zhengyang, et al. Research on investment and construction of commercial electric vehicle charging station in housing estate[J]. Electrical Engineering, 2022, 23(6): 104-108.
[3] 王晓姬, 王道涵, 王柄东, 等. 电动汽车驱动/充电一体化系统及其控制策略综述[J]. 电工技术学报, 2023, 38(22): 5940-5958. Wang Xiaoji, Wang Daohan, Wang Bingdong, et al. A review of drive-charging integrated systems and control strategies for electric vehicles[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 5940-5958.
[4] Wang Bo, Dehghanian P, Wang Shiyuan, et al. Electrical safety considerations in large-scale electric vehicle charging stations[J]. IEEE Transactions on Industry Applications, 2019, 55(6): 6603-6612.
[5] 孙立明, 杨博. 基于充电需求时空分布预测的电动汽车充电站最优规划[J/OL]. 发电技术, 1-12[2025-07-02].http://kns.cnki.net/kcms/detail/33.1405.TK. 20240914.1014.002.html. Sun Liming, Yang Bo. Optimal planning of electric vehicle charging station based on spatio-temporal distribution prediction of charging demand[J/OL]. PowerGeneration Technology, 1-12[2025-07-02]. http: //kns.cnki.net/kcms/detail/33.1405.TK.20240914.1014.002.html.
[6] 徐潇源, 李佳琪, 王晗, 等. 城市电力-交通系统韧性研究综述及展望[J]. 电力系统自动化, 2024, 48(23): 1-15. Xu Xiaoyuan, Li Jiaqi, Wang Han, et al. Review and prospect of research on urban power-transportation system resilience[J]. Automation of Electric Power Systems, 2024, 48(23): 1-15.
[7] 范培潇, 杨军, 温裕鑫, 等. 基于可进化模型预测控制的含电动汽车多微电网智能发电控制策略[J]. 电工技术学报, 2024, 39(3): 699-713. Fan Peixiao, Yang Jun, Wen Yuxin, et al. A multi microgrid intelligent generation control strategy with electric vehicles based on evolutionary model predictive control[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 699-713.
[8] 韩丽, 陈硕, 王施琪, 等. 考虑风光消纳与电动汽车灵活性的调度策略[J]. 电工技术学报, 2024, 39(21): 6793-6803. Han Li, Chen Shuo, Wang Shiqi, et al. Scheduling strategy considering wind and photovoltaic power consumption and the flexibility of electric vehicles[J]. Transactions of China Electrotechnical Society, 2024, 39(21): 6793-6803.
[9] 杨祺铭, 李更丰, 别朝红, 等. 台风灾害下基于V2G的城市配电网弹性提升策略[J]. 电力系统自动化, 2022, 46(12): 130-139. Yang Qiming, Li Gengfeng, Bie Zhaohong, et al. Vehicle-to-grid based resilience promotion strategy for urban distribution network under typhoon disaster [J]. Automation of Electric Power Systems, 2022, 46(12): 130-139.
[10] Jin Yuwei, Yu B, Seo M, et al. Optimal aggregation design for massive V2G participation in energy market[J]. IEEE Access, 2020, 8: 211794-211808.
[11] 王飞, 李美颐, 张旭东, 等. 需求响应资源潜力评估方法、应用及展望[J]. 电力系统自动化, 2023, 47(21): 173-191. Wang Fei, Li Meiyi, Zhang Xudong, et al. Assessment methods for demand response resource potential and their application and prospect[J]. Automation of Electric Power Systems, 2023, 47(21): 173-191.
[12] Sarker M R, Dvorkin Y, Ortega-Vazquez M A. Optimal participation of an electric vehicle aggregator in day-ahead energy and reserve markets[J]. IEEE Transactions on Power Systems, 2016, 31(5): 3506-3515.
[13] 张谦, 邓小松, 岳焕展, 等. 计及电池寿命损耗的电动汽车参与能量-调频市场协同优化策略[J]. 电工技术学报, 2022, 37(1): 72-81. Zhang Qian, Deng Xiaosong, Yue Huanzhan, et al. Coordinated optimization strategy of electric vehicle cluster participating in energy and frequency regulation markets considering battery lifetime degradation[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 72-81.
[14] Pertl M, Carducci F, Tabone M, et al. An equivalent time-variant storage model to harness EV flexibility: forecast and aggregation[J]. IEEE Transactions on Industrial Informatics, 2019, 15(4): 1899-1910.
[15] Bhattarai B, de Cerio Mendaza I D, Myers K, et al. Optimum aggregation and control of spatially distributed flexible resources in smart grid[C]//2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 2018: 1-1.
[16] Wang Xiaofei, Li Fangxing, Dong Jin, et al. Tri-level scheduling model considering residential demand flexibility of aggregated HVACs and EVs under distribution LMP[J]. IEEE Transactions on Smart Grid, 2021, 12(5): 3990-4002.
[17] 罗卓伟, 胡泽春, 宋永华, 等. 大规模电动汽车充放电优化控制及容量效益分析[J]. 电力系统自动化, 2012, 36(10): 19-26. Luo Zhuowei, Hu Zechun, Song Yonghua, et al. Coordinated charging and discharging of large-scale plug-in electric vehicles with cost and capacity benefit analysis[J]. Automation of Electric Power Systems, 2012, 36(10): 19-26.
[18] Qian Kejun, Zhou Chengke, Allan M, et al. Modeling of load demand due to EV battery charging in distribution systems[J]. IEEE Transactions on Power Systems, 2011, 26(2): 802-810.
[19] O’Malley C, Badesa L, Teng Fei, et al. Frequency response from aggregated V2G chargers with uncertain EV connections[J]. IEEE Transactions on Power Systems, 2023, 38(4): 3543-3556.
[20] Said D, Mouftah H T. A novel electric vehicles charging/discharging management protocol based on queuing model[J]. IEEE Transactions on Intelligent Vehicles, 2020, 5(1): 100-111.
[21] Shen Jiaming, Wang Laili, Zhang Jialei. Integrated scheduling strategy for private electric vehicles and electric taxis[J]. IEEE Transactions on Industrial Informatics, 2020, 17(3): 1637-1647.
[22] Zhou Ming, Wu Zhaoyuan, Wang Jianxiao, et al. Forming dispatchable region of electric vehicle aggregation in microgrid bidding[J]. IEEE Transactions on Industrial Informatics, 2021, 17(7): 4755-4765.
[23] 王杨洋, 茆美琴, 杨铖, 等. 面向多场景辅助服务的大规模电动汽车聚合可调度容量建模[J]. 电力系统自动化, 2024, 48(7): 103-115. Wang Yangyang, Mao Meiqin, Yang Cheng, et al. Aggregated and schedulable capacity modeling of large-scale electric vehicles for multi-scenario auxiliary services[J]. Automation of Electric Power Systems, 2024, 48(7): 103-115.
[24] 徐俊俊, 程奕凌, 张腾飞, 等. 计及充电行为特征与可调性的电动汽车集群优化调度[J]. 电力系统自动化, 2023, 47(23): 23-32. Xu Junjun, Cheng Yiling, Zhang Tengfei, et al. Optimal scheduling of electric vehicle clusters considering characteristics and adjustability of charging behavior[J]. Automation of Electric Power Systems, 2023, 47(23): 23-32.
[25] Yin Wanjun, Qin Xuan. Cooperative optimization strategy for large-scale electric vehicle charging and discharging[J]. Energy, 2022, 258: 124969.
[26] 王雨晴, 王文诗, 徐心竹, 等. 面向低碳交通的含新能源汽车共享站电-氢微能源网区间-随机混合规划方法[J]. 电工技术学报, 2023, 38(23): 6373-6390. Wang Yuqing, Wang Wenshi, Xu Xinzhu, et al. Hybrid interval/stochastic planning method for new energy vehicle sharing station-based electro-hydrogen micro-energy system for low-carbon transportation[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6373-6390.
[27] 师景佳, 袁铁江, Saeed Ahmed Khan, 等. 计及电动汽车可调度能力的风/车协同参与机组组合策略[J]. 高电压技术, 2018, 44(10): 3433-3440. Shi Jingjia, Yuan Tiejiang, Khan S A, et al. Unit commitment strategy considering cooperated dispatch of electric vehicles based on scheduling capacity and wind power generation[J]. High Voltage Engineering, 2018, 44(10): 3433-3440.
[28] 史文龙, 秦文萍, 王丽彬, 等. 计及电动汽车需求和分时电价差异的区域电网LSTM调度策略[J]. 中国电机工程学报, 2022, 42(10): 3573-3587. Shi Wenlong, Qin Wenping, Wang Libin, et al. Regional power grid LSTM dispatch strategy considering the difference between electric vehicle demand and time-of-use electricity price[J]. Proceedings of the CSEE, 2022, 42(10): 3573-3587
[29] 杨镜司, 秦文萍, 史文龙, 等. 基于电动汽车参与调峰定价策略的区域电网两阶段优化调度[J]. 电工技术学报, 2022, 37(1): 58-71. Yang Jingsi, Qin Wenping, Shi Wenlong, et al. Two-stage optimal dispatching of regional power grid based on electric vehicles′ participation in peak-shaving pricing strategy[J]. Transactions of China Electro-technical Society, 2022, 37(1): 58-71.
[30] Karfopoulos E L, Panourgias K A, Hatziargyriou N D. Distributed coordination of electric vehicles providing V2G regulation services[J]. IEEE Transactions on Power Systems, 2016, 31(4): 2834-2846.
[31] Peng Chao, Zou Jianxiao, Lian Lian. Dispatching strategies of electric vehicles participating in frequency regulation on power grid: a review[J]. Renewable and Sustainable Energy Reviews, 2017, 68: 147-152.
[32] 邓荣楠, 宋梦, 高赐威, 等. 考虑用户负荷决策依赖特性的配电网灾后恢复方法对比分析[J]. 电工技术学报, 2024, 39(23): 7447-7462. Deng Rongnan, Song Meng, Gao Ciwei, et al. Comparative analysis of distribution system load restoration considering decision-dependent behaviors of customers[J]. Transactions of China Electro-technical Society, 2024, 39(23): 7447-7462.
[33] 陈磊, 邓欣怡, 陈红坤, 等. 电力系统韧性评估与提升研究综述[J]. 电力系统保护与控制, 2022, 50(13): 11-22. Chen Lei, Deng Xinyi, Chen Hongkun, et al. Review of the assessment and improvement of power system resilience[J]. Power System Protection and Control, 2022, 50(13): 11-22.
[34] 翟志气. EV直流快充场景的动力电池组冷却技术研究[D]. 长春: 吉林大学, 2024. Zhai Zhiqi. Research on cooling technology of power battery pack in EV DC fast charging scene[D]. Changchun: Jilin University, 2024.
[35] Serhan H A, Ahmed E M. Effect of the different charging techniques on battery life-time: Review[C]// 2018 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2018: 421-426.
[36] Gao Yizhao, Zhang Xi, Cheng Qiyu, et al. Classification and review of the charging strategies for commercial lithium-ion batteries[J]. IEEE Access, 2019, 7: 43511-43524.
[37] 刘向军, 牟明亮, 黄绍模, 等. 考虑充电功率衰减的电动汽车两阶段优化调度策略[J]. 电网技术, 2021, 45(7): 2656-2666. Liu Xiangjun, Mu Mingliang, Huang Shaomo, et al. Two-stage optimal scheduling strategy of electric vehicle considering charging power decay[J]. Power System Technology, 2021, 45(7): 2656-2666.
[38] 孙丙香, 李凯鑫, 荆龙, 等. 锂离子电池不同工况下充电效果对比及用户充电方法选择研究[J]. 电工技术学报, 2023, 38(20): 5634-5644. Sun Bingxiang, Li Kaixin, Jing Long, et al. Comparison of charging effect of lithium-ion battery under different working strategies and study on user charging method selection[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5634-5644.
[39] 罗平, 杨泽喆, 张嘉昊, 等. 考虑多场景充电需求预测的电动汽车充电站规划[J]. 高电压技术, 2025, 51(1): 368-378. Luo Ping, Yang Zezhe, Zhang Jiahao, et al. Electric vehicle charging station planning considering multi-scene charging demand forecasting[J]. High Voltage Engineering, 2025, 51(1): 368-378.
[40] 詹祥澎, 杨军, 韩思宁, 等. 考虑电动汽车可调度潜力的充电站两阶段市场投标策略[J]. 电力系统自动化, 2021, 45(10): 86-96. Zhan Xiangpeng, Yang Jun, Han Sining, et al. Two-stage market bidding strategy of charging station considering schedulable potential capacity of electric vehicle[J]. Automation of Electric Power Systems, 2021, 45(10): 86-96.
[41] Yarotsky D. Error bounds for approximations with deep ReLU networks[J]. Neural Networks, 2017, 94: 103-114.
[42] 钟金琴, 辜丽川, 檀结庆, 等. 基于分裂EM算法的GMM参数估计[J]. 计算机工程与用, 2012, 48(34): 28-32, 59. Zhong Jinqin, Gu Lichuan, Tan Jieqing, et al. Estimating parameters of GMM based on split EM[J]. Computer Engineering and Applications, 2012, 48(34): 28-32, 59.
Abstract As electric vehicles (EV) grow more popular and vehicle-to-grid (V2G) technology advances, large-scale EV aggregations (EVA) have become integral to the power system. However, effectively capturing the distinct idle energy storage characteristics of EVAs across regions and integrating them seamlessly into power system operations remains a challenge.The shortcomings of existing research can be summarized as the follows: Firstly, current methods for assessing the dispatchable regions (DR) of EVs remain inadequate, lacking systematic frameworks and classification methods. Secondly, current multi-level coordinated control strategy often overlooks the holistic nature of coordinated control, which spans multiple levels, including the power grid, garage, and users. Merely considering factors related to EVs and their users is insufficient, as it fails to provide a comprehensive guidance for all coordinated control participants, such as the power grid and garage.
This paper addresses the aforementioned issues by conducting the following works. Firstly, methods for establishing multi-stage electric vehicle dispatchable region (MEVDR) for both EV and EVA are proposed and further investigated. Secondly, the probability density functions of various EV data in different regions and time periods of clustering centers are captured using Gaussian mixture model (GMM). Thirdly, the MEVDR of EVAs in different regions and time periods are established and comprehensively analyzed. Furthermore, the proposed MEVDR model can be used to construct multi-period constraints. Based on this, a vehicles-garage-grid multi-level coordinated control system (VGGMCCS) based on MEVDR can be constructed, which consists of two levels and can therefore be considered a bi-level model. After a thorough analysis, VGGMCCS incorporates two mixed integer programming (MIP) problems, allowing the use of commercial solvers for rapid and efficient problem solving. Finally, in order to provide further validation of the effectiveness of the VGGMCC system based on MEVDR, a comparison was made between the proposed method and the contrasting strategies.
The case study shows that, when compared to two contrasting strategies, the proposed VGGMCCS has been demonstrated to reduce the grid network loss by 12.17% compared to comparative strategy 1 and by 8.69% compared to comparative strategy 2 during peak electricity demand periods. And to reduce users′ average daily charging costs by 7.88% compared to comparative strategy 1, and to increase operators′ revenues by 17.63% compared to comparative strategy 2. Meanwhile, the load fluctuation amplitude of the transformer at the garage node has been significantly reduced. During peak electricity consumption periods, the power fluctuation of transformers under VGGMCCS decreased by 96.36% compared to comparative strategy 1 and by 82.59% compared to comparative strategy 2. Last but not least, VGGMCCS also has a high solution speed, ensuring decision accuracy while quickly responding to dispatching requests from lower-level garages, effectively reducing both the time and economic losses caused by rescheduling requests after EVs are integrated into the power grid. The results show that VGGMCCS can effectively reduce users′ costs, improve the economic benefits of the garage and enhance the operational efficiency of the power grid, while ensuring the long-term stable operation of the power system, thus achieving a win-win situation for users, garage operators and power grid companies.
In summary, this paper provides a thorough establishment and analysis of EVA′s MEVDR across a diverse range of geographical and temporal contexts. Furthermore, when compared to the contrasting strategies, the proposed VGGMCCS promises to enhance both the economic benefits and operational efficiency of the power system significantly.
keywords: Electric vehicle, vehicle-to-grid, dispatchable region, coordinated control, multi-region, scheduling strategy
DOI: 10.19595/j.cnki.1000-6753.tces.241173
中图分类号:TM715
国家自然科学基金项目(52037002, 52107079)和国网江苏省电力有限公司科技项目(J2022088)资助。
收稿日期 2024-07-04
改稿日期 2025-02-21
张睿骐 男,2000年生,硕士研究生,研究方向为人工智能在电力系统调度运行中的运用等。E-mail:220225911@seu.edu.cn
阳 辉 男,1988年生,副教授,博士生导师,研究方向为电动汽车车网互动技术等。 E-mail:huiyang@seu.edu.cn(通信作者)
(编辑 赫 蕾)