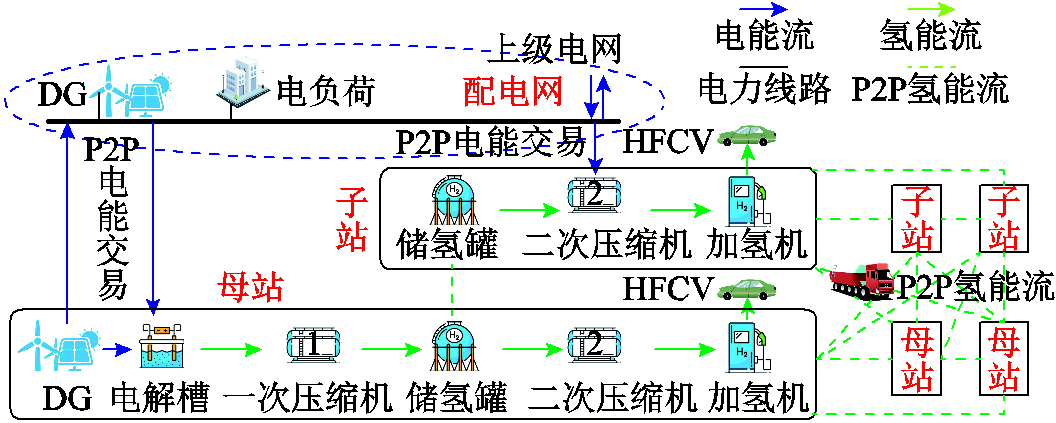
图1 子母站-配电网P2P协同模式
Fig.1 The P2P collaboration mode for on-site/off-site stations and the power distribution network
摘要 分布式供氢网与配电网的耦合日益紧密,电、氢源荷的高维不确定性给两网安全经济运行带来了挑战。为此,基于压缩稀疏-任意多项式混沌展开法,提出电-氢概率最优能量流计算方法。首先,为发挥电-氢能源时空协同潜力,提出子母站-配电网点对点(P2P)协同模式。基于此,构建考虑时滞性和离散性的P2P氢能流约束,基于纳什谈判理论提出电-氢概率最优能量流模型,优化能源价格决策和多主体收益分配。针对电、氢源荷高维不确定性导致概率求解负担大且稳健性不足的问题,对传统多项式混沌展开法进行改进,提出电-氢概率最优能量流的解析求解算法。所提算法基于高斯正交规则和稀疏网格构建配点压缩判据,通过对配点空间快速降维,提升求解效率,并给出了算法精度和效果的数学证明。最后,采用2个仿真系统验证所提方法的有效性。
关键词:电-氢耦合系统 多项式混沌展开 概率最优能量流 多主体博弈 点对点协同
氢能,作为推动可持续能源转型的核心战略资源,对于电力与交通等领域实现深度脱碳目标具有重要意义[1-2]。氢燃料电池汽车(Hydrogen Fuel Cell Vehicles, HFCVs)因其充能快、续航长等优点而备受关注 [2-3]。截至2023年11月,中国氢燃料电池汽车保有量为18 895辆,同时,全国范围内已建成加氢站398座,约占全球总量的40%[4]。预计到2035年,我国加氢站将达到5 000座[5]。
分布式供氢网(Distributed Hydrogen Supply Network, DHSN),作为一种先进的城市供氢解决方案,其核心在于就地实施制氢加氢策略[6]。在DHSN中,母站从配电网或站内分布式电源(Distributed Generators, DG)取电制氢,可就地加氢或通过氢长管拖车(Hydrogen Tube Trailer, HTT)灵活转运到子站以满足更广泛的加氢需求。DHSN所展现的紧密耦合结构,不仅极大地丰富了电力与氢能系统的互动层次,还为电-氢能源系统的协同优化提供了前所未有的机遇[7-8]。然而,氢负荷的波动性与分布式电源出力的不确定性等复杂性问题,共同对DHSN及配电网安全、经济运行的构成挑战。
鉴于此,深入探索电-氢概率最优能量流(Electricity Hydrogen-Probabilistic Optimal Energy Flow, EH-POEF)的研究显得尤为重要。通过这一研究,旨在充分挖掘电-氢协同的潜在优势,为DHSN与配电网耦合下的优化调度、安全经济运行以及长期规划提供坚实的理论支撑与科学依据。
与传统能量流研究相比,EH-POEF研究面临以下核心挑战:第一,EH-POEF研究需跨越不同运营主体的界限,即子站、母站与配电网往往由不同的实体管理运营[9]。这种运营主体的异质性,加之HTT运输所固有的离散性和时滞特性[10-11],使得电-氢系统的能量流动变得更为复杂。在计算电-氢最优能量流时,必须考量这些异质能源收益如何在不同主体间相互交织、影响,以促进跨主体的深度协同与共赢。第二,EH-POEF计算不仅涉及电负荷和新能源随机性,还需要考虑氢负荷随机波动性以及电氢协同对最优能量流分布的影响[13]。这一计算任务本质上属于大规模概率优化问题,其计算量相当庞大,因此,探索高效、稳定的求解算法显得尤为重要。
下面从EH-POEF模型的构建和求解算法两方面进行研究现状综述。
现有的EH-POEF模型主要分为单主体和多主体两类。在单主体视角下,基于因果序图(Causal Ordering Graph, COG)建立了面向控制的制-储-氢发电一体化电站运行动态模型。文献[14-15]将电-氢能源运营商视为同一主体,针对连续性的管道运输氢能流,提出EH-POEF模型。文献[16]利用电解槽等灵活性资源参与配电网运行,以提升私有加氢站运营收益。在多主体视角下,文献[10]将子母站与配电网视为不同主体,基于纳什谈判理论,实现了子母站主体与配电网主体在规划成本上的协调优化。然而,为了更准确地反映现实情况中的主体差异性,文献[17]引入双边Shapley值提升配电网及加氢站P2P电力能源交易公平性,并有效降低了整体运营成本。但文献[17]的P2P协同策略主要聚焦于电力线路,而未能充分利用HTT运输在氢能流调度中的时空协同优势,且其“即时性假设”忽略了HTT运输所固有的离散性和时滞性特征,这在一定程度上限制了模型在实际应用中的有效性和可行性。
在概率能量流问题的求解领域,广泛采用的方法可归结为模拟法与解析法两大类别。模拟法,以蒙特卡洛模拟(Monte Carlo Simulation, MCS)为代表,MCS法通过大量随机抽样实现迭代计算的策略,获得较高的计算精度[14]。然而,MCS方法因其庞大的计算量带来的局限性,在处理复杂系统时尤为突出。解析法作为另一大类方法,主要包括半不变量法和任意多项式混沌展开(arbitrarily Polynomial Chaos Expansion, aPCE)。半不变量法依赖Gram-Charlier级数展开来近似概率分布,但这一过程中可能引入较大的计算误差,影响了结果的准确性[18]。aPCE法是一种历史数据驱动的非线性逼近算法,可用于替代原有的非线性程度高、计算量大且含有随机变量的模型,解析计算模型输出的期望和均值等概率特征,在概率潮流[19]、稳定性分析[20]和风险评估[21]等问题中展现出速度快、精度高等优异性能。然而,在高维电-氢能量流问题中,aPCE法的计算量随维度指数增长,面临严重的“维数灾”问题。
目前处理高维aPCE计算量庞大的问题主要有三种思路:预降维[20,22-24]、输入-输出降维[25-26]和中间降维[27-29]。预降维法在数据处理的初步阶段介入,利用主成分分析[20,22]、奇异值分解[23]和单变元降维法[24]等手段对随机输入变量进行预处理,以剔除或合并非关键变量。然而,此类方法仅基于数据本身的统计特性进行降维,未充分考虑其对模型输出的具体影响,因此降维效果往往有限。输入-输出降维技术,以灵敏度分析为代表,通过评估输入变量对模型输出(即响应函数)的敏感程度来识别并保留关键变量[25]。这种方法虽能有效聚焦于对输出结果影响显著的变量,但采样点选择的主观性和不确定性可能导致分析结果的稳健性不足,从而影响最终的计算精度。中间降维法则是一种更为灵活且针对性强的策略,它深入分析aPCE计算过程中导致“维数灾”的关键环节,并据此采用线性无关[27]、各向异性[28]和对称合并[29]等策略实现降维。尽管这些方法在理论上能够有效降低计算复杂度,但在实际应用中,如何在高维问题中精确识别并处理这些关键环节,同时保持足够的计算精度与求解效率,仍是一个亟待解决的难题。
针对氢能协同潜力挖掘不充分、概率求解算法难以兼顾精度和效率的问题,本文提出基于压缩稀疏-任意多项式混沌展开(Compressed Sparse- arbitrarily Polynomial Chaos Expansion,CS-aPCE)的电-氢概率最优能量流计算方法,主要贡献如下:
(1)为调动氢能时空协同潜力,提出考虑站间氢能点对点(Peer-to-Peer, P2P)协同的电-氢最优能量流建模方法。考虑站间氢能流和双向电能P2P耦合,提出子母站-配电网P2P协同模式。基于纳什谈判理论构建电-氢概率最优能量流模型,考虑时滞性和离散性构建站间氢能P2P约束,协调多主体收益分配及电-氢价格决策,提升可行性和公平性。
(2)基于CS-aPCE提出子母站-配电网概率最优能量流求解算法,以提升高维概率计算的效率和精度。该算法的核心在于利用历史数据驱动生成配点,进而通过解析方法计算期望、标准差等关键统计指标,而无须依赖先验概率信息。为进一步优化计算性能,CS-aPCE算法融合了高斯正交规则以构建高频配点,并结合压缩稀疏网格技术,提出了有效的压缩判据,并对算法的降维效果与计算精度进行了理论证明,确保了算法在高维问题中的高效性与稳健性。
本节提出考虑站间氢能P2P协同的电-氢最优能量流建模方法。首先,为发挥氢能协同潜力,提出子母站与配电网P2P协同模式。然后,模拟时滞效应下的P2P氢能流约束,构建子母站主体统一最优能量流模型、配电网主体最优能量流模型。最后,基于纳什谈判模型协调电-氢能流分布和价格,并基于等效转换和松弛技术建立所提模型的线性化高效求解方法。
为充分利用电-氢能量的时空协同潜力,本文提出了子母站-配电网P2P协同模式,如图1所示。该模式考虑子站、母站通过HTT形成P2P氢能交易,且各站通过电力线路与配电网形成P2P电能交易。子母站含有大量灵活运行设备,母站包含站内DG发电、制氢、储氢、两级压缩和加氢设备,而子站无制氢设备,仅包括功率交互、储氢、二次压缩和加氢设备。因此,母站和子站与配电网分别形成双向和单向的电能交互。此外,由于氢长管拖车的离散性和运输延迟,站间P2P氢能交易具有离散且时滞的特点。因此,电-氢-交通系统多主体利益交互的形式多样且交互特性十分复杂。

图1 子母站-配电网P2P协同模式
Fig.1 The P2P collaboration mode for on-site/off-site stations and the power distribution network
1.2.1 考虑P2P协同的子母站主体统一概率最优能量流模型
1)目标函数
子站主体和母站主体的最优能量流模型均以各自日运行收益最大为目标函数,包括P2P收益、向HFCV供氢的收益、外购氢成本、站内DG弃电成本,如式(1)所示。母站主体的概率能量流优化模型将氢负荷和站内DG出力作为随机输入变量,子站主体的概率能量流优化模型仅涉及氢负荷不确定性,故随机输入变量仅为氢负荷。根据随机变量的不同取值,迭代计算可得到目标函数和网络状态变量的概率特征。
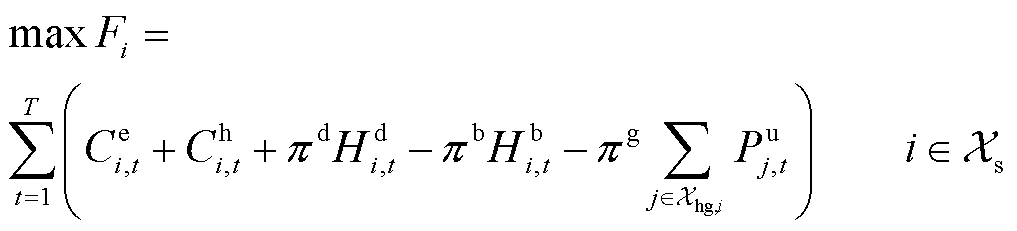 (1)
(1)
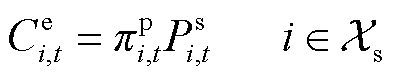 (2)
(2)
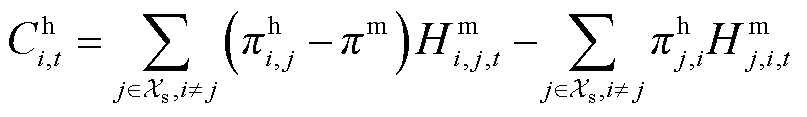 (3)
(3)
式中,Fi(iÎXs)为加氢站i的目标函数,Xs为子母站集合;Ce i,t和Ch i,t分别为t时刻站i与配电网和其他站的P2P交易收益;Hm i,j,t和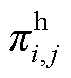 分别为t时刻站i向站j的售氢量和售氢价格;Ps i,t和
分别为t时刻站i向站j的售氢量和售氢价格;Ps i,t和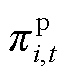 分别为t时刻站i向配电网的售电量和价格;常数p m为单位运氢成本;Hd i,t和p d分别为t时刻站i向HFCV的供氢量和供氢价格,pd为常数;Hb i,t和
分别为t时刻站i向配电网的售电量和价格;常数p m为单位运氢成本;Hd i,t和p d分别为t时刻站i向HFCV的供氢量和供氢价格,pd为常数;Hb i,t和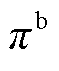 为t时刻站i的购氢量和购氢价格;Pu j,t为t时刻站内第j个DG的弃电功率;pg为单位弃电成本;Xhg,i为站i内的DG集合,子站内不含DG,即当站i为子站时,Xhg,i=Æ;T为时刻数,本文取T =24 h。
为t时刻站i的购氢量和购氢价格;Pu j,t为t时刻站内第j个DG的弃电功率;pg为单位弃电成本;Xhg,i为站i内的DG集合,子站内不含DG,即当站i为子站时,Xhg,i=Æ;T为时刻数,本文取T =24 h。
电-氢多主体最优能量流模型涉及耦合的电能流和氢能流。考虑子母加氢站并网,基于二阶锥电力潮流模型建立配电网潮流模型,详见附录第1节。氢能流包括站内氢能流和站间氢能流两部分。考虑HTT在子母加氢站的装卸行为,建立子母加氢站氢能流模型,详见附录第2节。运氢环节的氢能流依托于氢长管拖车,具有离散特征,下面详细介绍运氢能量流的建模。
2)考虑时滞的P2P氢能流约束
考虑到基于HTT运输的P2P氢能流具有离散、时滞的特点,本节根据装卸时间和最短路径,构建P2P时间颗粒度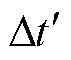 及氢能流约束,见式(4)~式(11)。
及氢能流约束,见式(4)~式(11)。
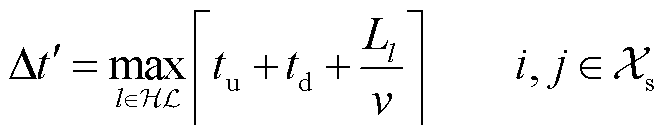 (4)
(4)
式中,é·ù表示向上取整;HL为交通网中两个两两加氢站间最短路径;Ll为路径l的长度;tu和td分别为HTT一次装、卸氢时间;v为氢长管拖车的平均行驶速度。一般有Dt¢>1 h。
P2P氢能与系统仿真时间颗粒度的转换约束为
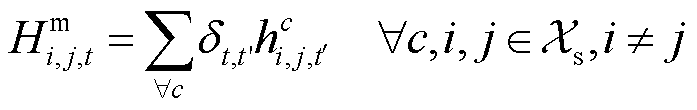 (5)
(5)
状态唯一性和连续性约束为
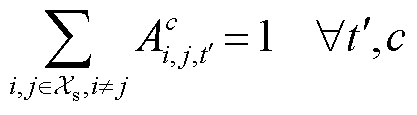 (6)
(6)
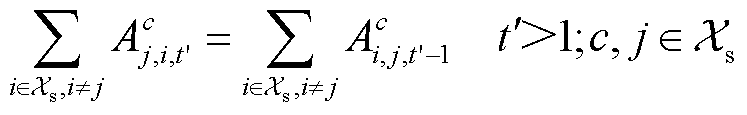 (7)
(7)
运输量的上、下限为
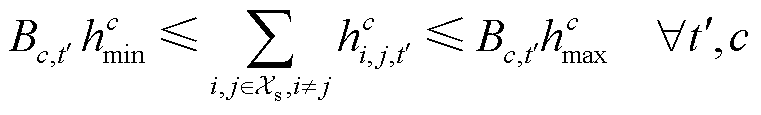 (8)
(8)
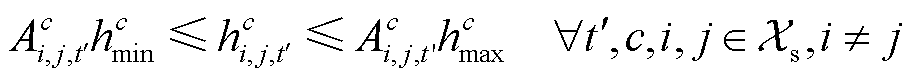 (9)
(9)
式中,hc i,j,t¢为第c辆氢长管拖车在 时刻从加氢站i运输到加氢站j的氢气量;二进制变量dt,t¢=1表示时刻
时刻从加氢站i运输到加氢站j的氢气量;二进制变量dt,t¢=1表示时刻 对应系统仿真时刻t,反之,不对应该时刻; Ac i,j,t¢为氢长管拖车c的位置状态二进制变量,Ac i,j,t¢=1表示第c辆车在
对应系统仿真时刻t,反之,不对应该时刻; Ac i,j,t¢为氢长管拖车c的位置状态二进制变量,Ac i,j,t¢=1表示第c辆车在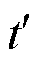 时刻从加氢站i驶向加氢站j,Ac i,j,t¢=0表示不处于该状态;Bc,t¢为工作状态二进制变量,Bc,t¢=1表示运输状态,Bc,t¢=0表示非运输状态;hc max和hc min分别为第c辆车运氢量的最大、最小值。
时刻从加氢站i驶向加氢站j,Ac i,j,t¢=0表示不处于该状态;Bc,t¢为工作状态二进制变量,Bc,t¢=1表示运输状态,Bc,t¢=0表示非运输状态;hc max和hc min分别为第c辆车运氢量的最大、最小值。
从子母站向HTT的装氢量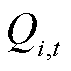 为
为
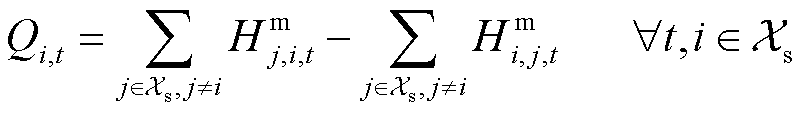 (10)
(10)
氢长管拖车工作时间约束为
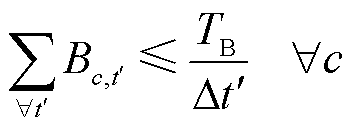 (11)
(11)
式中,TB为一辆HTT每日最长工作时间。参考文献[10, 30]建立子母站内储氢平衡约束、加氢约束、DG出力约束和电解槽三状态热电耦合约束。令Xos为母站集合,具有随机性的、标幺氢负荷和DG发电功率表示为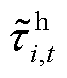 (iÎXs, "t)和
(iÎXs, "t)和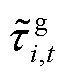 (iÎXos, "t)。
(iÎXos, "t)。
1.2.2 考虑P2P协同的配电网主体概率最优能量流模型
考虑子母站并网构建配电网主体最优能量流模型。模型以日运行收益最大为优化目标,并计及电负荷及DG出力的随机性。配电网主体能量流优化考虑电负荷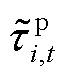 (iÎXrp, "t)及DG出力
(iÎXrp, "t)及DG出力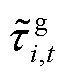 (iÎXpg, "t)的不确定性。日运行收益由供电收益、向加氢站和上级电网的购电成本、DG弃电成本计算,即
(iÎXpg, "t)的不确定性。日运行收益由供电收益、向加氢站和上级电网的购电成本、DG弃电成本计算,即
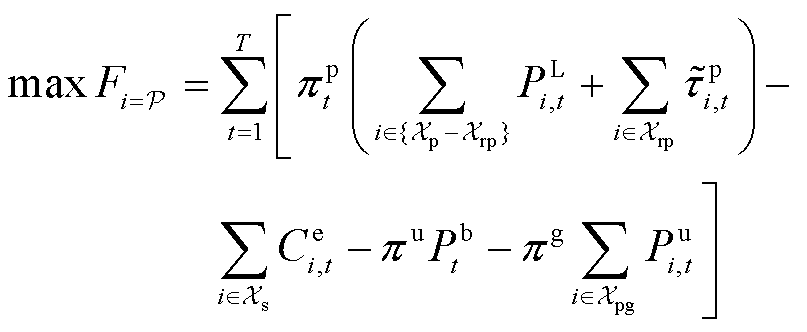 (12)
(12)
式中,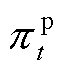 为t时刻除子母站以外负荷的购电价格;
为t时刻除子母站以外负荷的购电价格;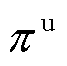 为配电网向上级电网的购电成本;Xp为配电网节点集合;
为配电网向上级电网的购电成本;Xp为配电网节点集合;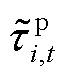 为随机节点负荷;Xrp为随机负荷节点集合;Xpg为配电网的DG集合;P为配电网主体。采用文献[31]所提二阶锥潮流模型对配电网能量流建模,用Cons-配电网表示。
为随机节点负荷;Xrp为随机负荷节点集合;Xpg为配电网的DG集合;P为配电网主体。采用文献[31]所提二阶锥潮流模型对配电网能量流建模,用Cons-配电网表示。
针对传统模型对子母站氢能流协调性不足的问题,建立了考虑站间氢能P2P协同的电-氢多主体纳什谈判模型。该模型以各主体收益的纳什乘积最大为优化目标,并计及子母站P2P协同运行约束、P2P氢能约束及配电网潮流等约束。
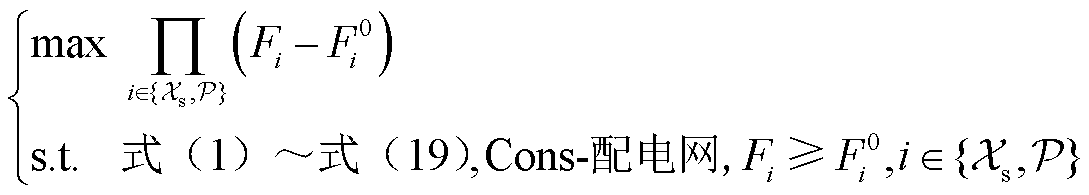 (13)
(13)
式中,F0 i为各主体参与合作前的收益。所提模型是非线性、非凸优化问题,将其等效转换为两个子问题[32]:子母站-配电网协同收益最大化子问题SP1和主体收益谈判子问题SP2。
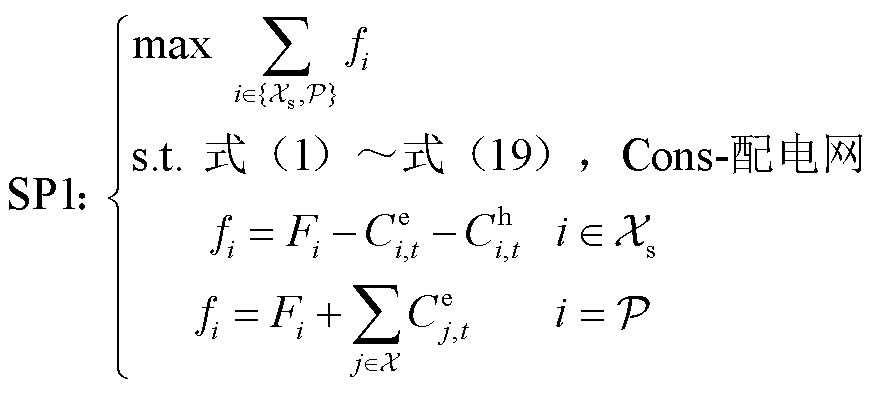 (14)
(14)
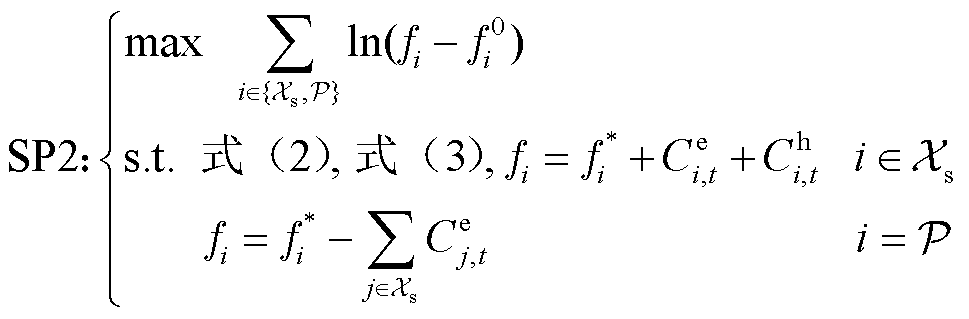 (15)
(15)
式中,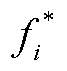 为SP1最优解时主体i的收益。
为SP1最优解时主体i的收益。
SP2的目标函数式(2)和非线性约束式(3)导致SP2非凸,需采用SOS-2序列进行线性化松弛处理[32]。但SP1涉及大量电-氢负荷和新能源出力等随机因素,即随机变量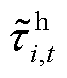 (iÎXs, "t)、
(iÎXs, "t)、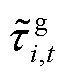 (iÎ{Xos, Xpg}, "t)和
(iÎ{Xos, Xpg}, "t)和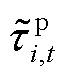 (iÎXrp, "t),属于高维概率计算问题。基于MCS等抽样方法[18]求解存在计算量大、计算时间长的问题。为此,第2节将基于CS-aPCE提出快速解析求解算法,计算能量流的概率特征(期望、标准差、概率密度等)。
(iÎXrp, "t),属于高维概率计算问题。基于MCS等抽样方法[18]求解存在计算量大、计算时间长的问题。为此,第2节将基于CS-aPCE提出快速解析求解算法,计算能量流的概率特征(期望、标准差、概率密度等)。
传统aPCE在高维问题中存在计算量庞大和精度稳健性不足的问题。为此,本文提出CS-aPCE算法,提升电-氢概率最优能量流的求解效率和精度。所提算法通过高斯正交规则和稀疏网格构建压缩判据,通过保留高频配点,实现配点空间的快速、高精度降维。
图2展示了CS-aPCE算法的主要思路。将第1节电-氢最优能量流模型的主体收益或网络状态变量(配电网节点电压、线路电流等)作为响应函数Y(z),将随机变量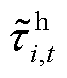 、
、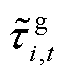 和
和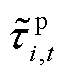 的独立变量记为 z =[z1 ···zN],采用多项式混沌展开逼近Y(z),即
的独立变量记为 z =[z1 ···zN],采用多项式混沌展开逼近Y(z),即
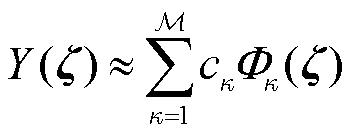 (16)
(16)
式中,ck为展开项Fk的系数;M为展开项数,第一项展开项的系数即表示期望值。
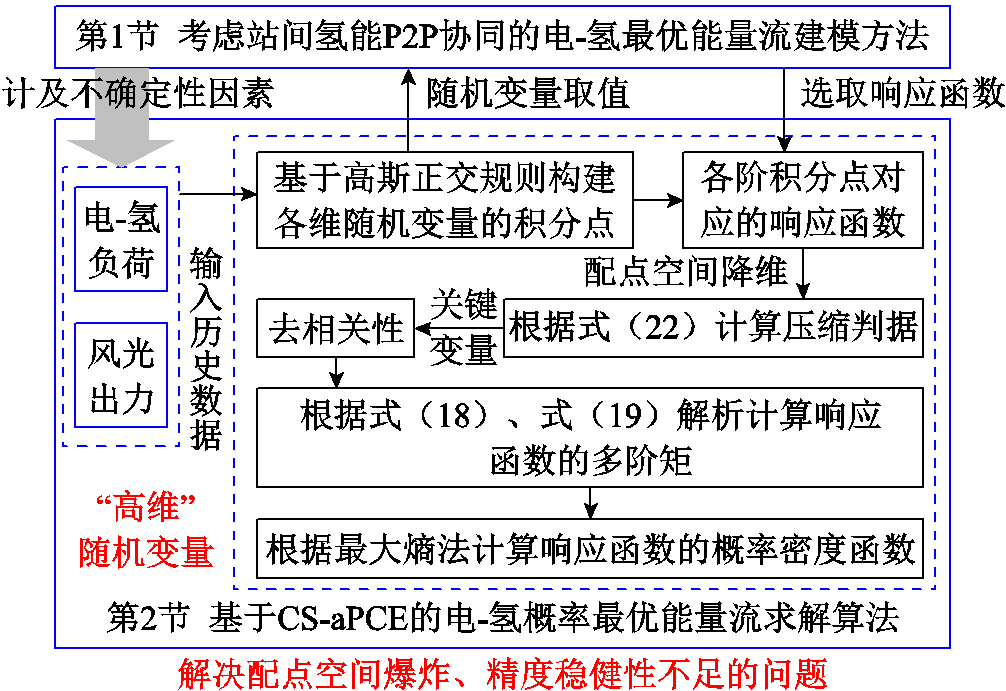
图2 CS-aPCE算法的主要思路
Fig.2 The main idea of the CS-aPCE algorithm
利用Galerkin投影法[33]将Y(z)投影到正交多项式F1上,则响应函数Y(z)的期望m计算式为
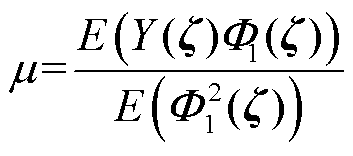 (17)
(17)
根据正交多项式的正交性,式(17))中分母为常数,用J表示。令分子中的函数为G(z )=Y(z )F1(z),采用G(z)的多维数值积分[33]计算m,有
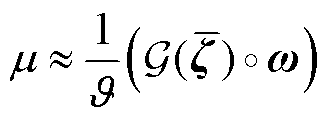 (18)
(18)
式中,°表示内积;` 为多维随机变量的积分点(也即为aPCE的配点);w为积分点权重。根据响应函数的期望m,可进一步采用式(19)递推计算响应函数的k阶矩E[Y(z )k],进而采用最大熵法[34]求得Y(z)的概率密度函数。
为多维随机变量的积分点(也即为aPCE的配点);w为积分点权重。根据响应函数的期望m,可进一步采用式(19)递推计算响应函数的k阶矩E[Y(z )k],进而采用最大熵法[34]求得Y(z)的概率密度函数。
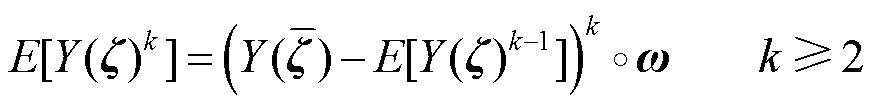 (19)
(19)
虽然基于aPCE的解析计算具有较高的精度,但电-氢概率最优能量流涉及数百维随机变量,为计算式(18)的配点需调取数万次模型,计算效率低。为此,在2.2节中提出压缩稀疏网格,基于高斯正交规则[15, 29]构建压缩判据,以减少配点数量。
配点降维存在两个关键挑战:①随机变量的高斯积分点均为高频点,采用主成分分析[16, 18]等方法舍去某个变量的积分点可能导致非常大的误差;②降维过程不应涉及大量采样计算,应满足快速、计算负担小的要求。为了兼顾降维精度和效率,本文提出压缩稀疏网格法。该方法通过高斯正交规则获取高频配点并筛选关键变量,同时将非关键变量固定在最高频配点,避免大量采样计算且有利于提升精度。本节基于高斯正交规则和稀疏网格[15, 29],提出高斯响应函数及压缩判据,将积分平稳变量作为关键变量,实现降维。
定义高斯响应函数为响应函数在高斯积分点处函数值的加权,权重根据高斯积分点的权重计算。
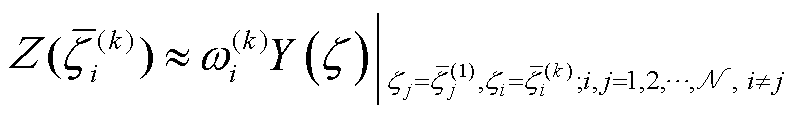 (20)
(20)
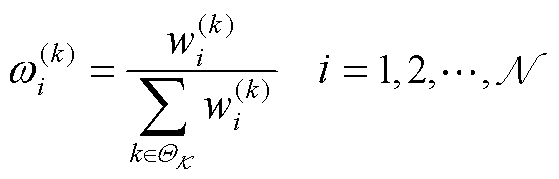 (21)
(21)
式中, N为随机变量维度;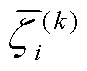 为第i维随机变量的第k个单维高斯型积分点,根据高斯正交规则选为多项式基的特征根[35];
为第i维随机变量的第k个单维高斯型积分点,根据高斯正交规则选为多项式基的特征根[35];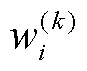 为单维积分点对应的权重。根据正交多项式的三项递推关系,计算对称三角矩阵的归一化特征向量[35],其第一分量即为单维积分点的权重ω(k) i;K为稀疏网格的准入基q+1≤|i|≤q+N 下随机变量的最高阶次,设H为PCE阶数,则K=min {q+1, H};|i|为阶次向量i={i1, ···, iN}的模;q为稀疏网格的级数;QK为阶次K的所有积分点集合。
为单维积分点对应的权重。根据正交多项式的三项递推关系,计算对称三角矩阵的归一化特征向量[35],其第一分量即为单维积分点的权重ω(k) i;K为稀疏网格的准入基q+1≤|i|≤q+N 下随机变量的最高阶次,设H为PCE阶数,则K=min {q+1, H};|i|为阶次向量i={i1, ···, iN}的模;q为稀疏网格的级数;QK为阶次K的所有积分点集合。
若随机变量zi的平稳度ε低于平稳度阈值ε0时,则该变量zi可被压缩,且zi=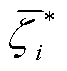 ,
,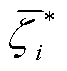 为高斯加权响应函数的中心。满足压缩判据的变量称为积分平稳变量。
为高斯加权响应函数的中心。满足压缩判据的变量称为积分平稳变量。
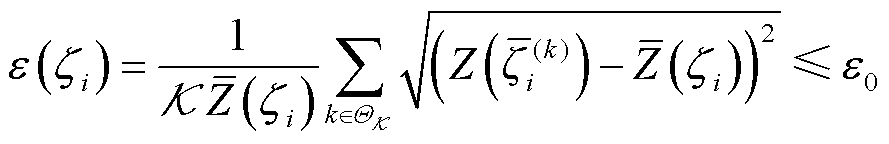 (22)
(22)
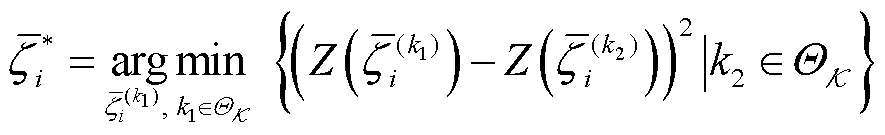 (23)
(23)
式中,平稳度ε为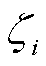 的高斯响应函数值的标幺标准差;
的高斯响应函数值的标幺标准差;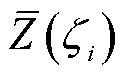 为
为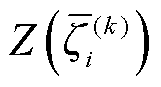 (kÎQK)的均值。
(kÎQK)的均值。
根据压缩条件,可从理论上推导降维前后配点数量的关系及误差边界,证明过程见附录第3和第4节。
推论1:(CS-aPCE算法的降维效果)定义压缩率DTG%为压缩后与压缩前相比积分维度的降低率。定义平稳率r为积分平稳变量维度N*与输入随机变量维度Nint相比的降低率,如式(24)所示。则对于阶次H的aPCE,选择级数为q的稀疏网格计算多维积分,积分点数量为TG,q=N min {q, H},采用压缩降维法后,压缩率为平稳率r的min{q, H}次方,即DTG,q%=rmin {q, H}。推论1的理论证明过程见附录第3节。
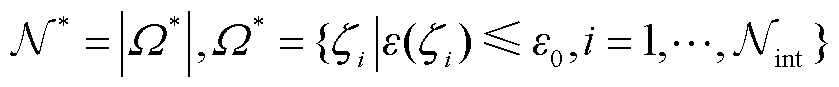 (24)
(24)
式中,W*为积分平稳变量集合。
图3分别以q=2, 3为例展示了CS-aPCE算法的降维效果与平稳率r的关系,说明对低级数网格的降维效果更加明显。
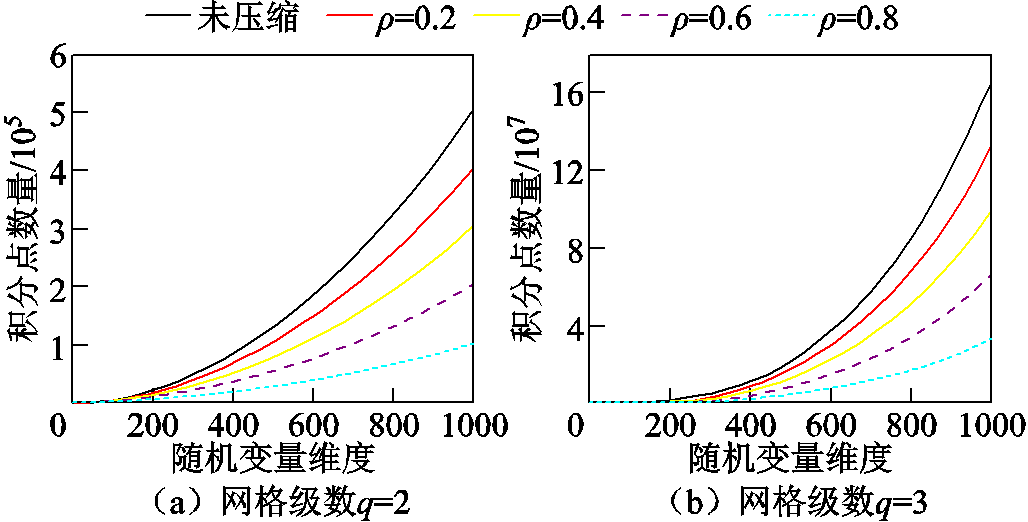
图3 不同网格级数和平稳率下的压缩率(H=q+1)
Fig.3 Compression rate under different grid level and stationarity rate (H=q+1)
推论2:(降维误差边界)定义降维误差为平稳变量的高斯响应函数与压缩后积分点处加强函数值的欧式距离之和,如式(25)所示。则有CS-aPCE的降维误差小于等于N*(q+1)ε0。推论2的理论证明过程见附录第4节。
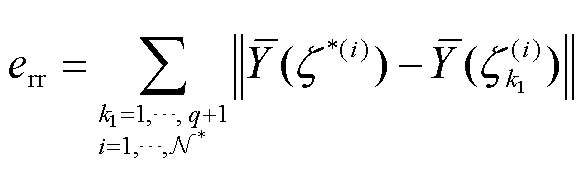 (25)
(25)

算法1:基于CS-aPCE的子母站-配电网概率最优能量流求解算法 步骤1:(输入数据)输入Nint维随机变量(DG出力、电-氢负荷),每维变量有Mp个采样点,组成输入变量Xp=(X(1), …, 。步骤2:(压缩降维)(2.1)根据Xp计算Nint维随机变量0到2l阶矩,计算高斯型积分点`z(k) i和权重w(k) i(kÎQK, i=1, 2,…, Nint)。令i=1。
(续)

(2.2)令,,i, j=1,…,N,i ≠ j计算确定性子母站-配电网P2P协同最优能量流模型式(14)和式(15),根据式(20)和式(21)计算随机变量zi的高斯响应函数。(2.3)若满足压缩判据式(22),则=反之,执行2.4。(2.4)令i=i+1,若i>Nint,统计积分平稳变量为N*维,执行步骤3;反之,返回2.2。步骤3:(去相关性)基于相关系数[22]将N*维变量转换为N 维独立变量。步骤4:(计算多维积分点)基于稀疏网格法计算多维积分。 步骤5:(解析计算响应函数概率特征)根据式(18)和式(19)解析计算Y多阶矩,进而基于最大熵法[34]求解Y的概率密度函数。
本节分别以图4所示的2个子母站-配电网耦合测试系统进行概率能量流仿真分析,以验证所提模型和求解算法的有效性。其中,系统A由2个母站、2个子站和18节点配电网组成[36],系统B由4个母站、6个子站和69节点配电网组成[37]。子母站储氢罐容量为20 kg、50 kg,加氢机额定加氢速率为7.2kg/h、14.4 kg/h,,母站配有1 MW光伏、1 MW风电机组及10个电解单元,每个单元的额定功率为291.66 kW[38]。向HFCV的售氢价格为48元/kg。电负荷满足正态分布,风电、光伏出力历史数据来自文献[39]的数据集。本节仿真均在Matlab2016a和Cplex环境下进行,计算机配置为Intel i7-8700 (3.20GHz),16GB RAM。
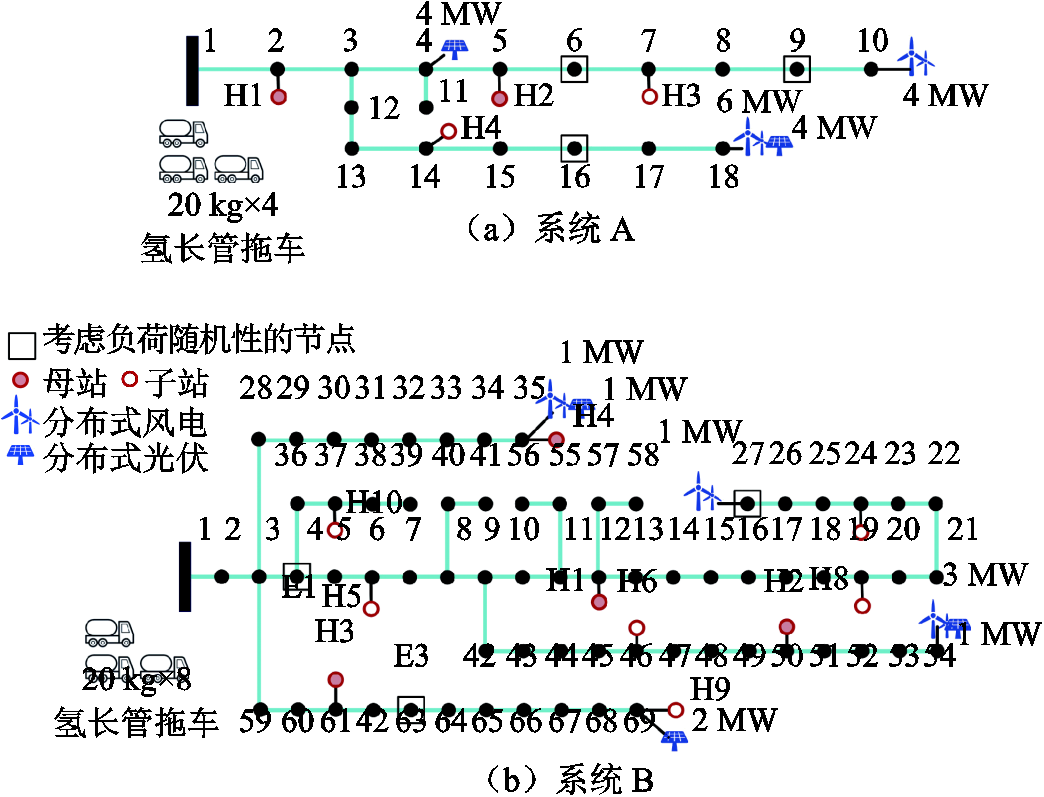
图4 测试系统拓扑
Fig.4 Topology of test systems
为验证本文建立的CS-aPCE算法的有效性,分别采用蒙特卡洛模拟法(模拟法,记为方法1)及四种降维aPCE法(解析法)进行对比,包括奇异值分解法(“预降维”,记为方法2)[23]、对称降维法(“中间降维”,记为方法3)[29]、灵敏度法(“输入-输出降维”,记为方法4)[25]以及本文所提压缩稀疏法(方法5),求解系统的概率最优能量流。方法1作为概率计算准确性的判断标准。方法5与方法2~4对比说明本文所提CS-aPCE的效果。
3.1.1 不同方法的计算精度对比
表1对比了不同方法得到的配电网收益的误差率。由于方法2所需的配点数量约为20万个,超过MCS的模拟次数,计算负担过大导致难以计算。采用方法3对系统A的计算结果比MCS偏低23.86%。由于方法3在系统B中所需配点数超过10万个,计算负担过大导致难以求解。两个系统中,方法4的期望值误差分别为7.10%和8.41%,方法5的期望值误差分别为3.09%和4.21%,降低了56.48%和49.94%。对比3阶和4阶原点矩结果发现,方法4对4阶矩的误差高达29.30%,而方法5的最大误差为17.96%,高阶矩精度提升156.98%~160.67%。同时,图5展示了系统A的站1(母站)和站3(子站)主体收益的概率密度函数。对比发现,方法5的曲线最接近MCS的结果。这是由于方法5采用多阶高斯积分点构建压缩判据,更准确地反映了各维高频点对响应函数的影响。
表1 配电网收益的误差率对比 (%)
Tab.1 The error comparisons for profits of the distribution power network
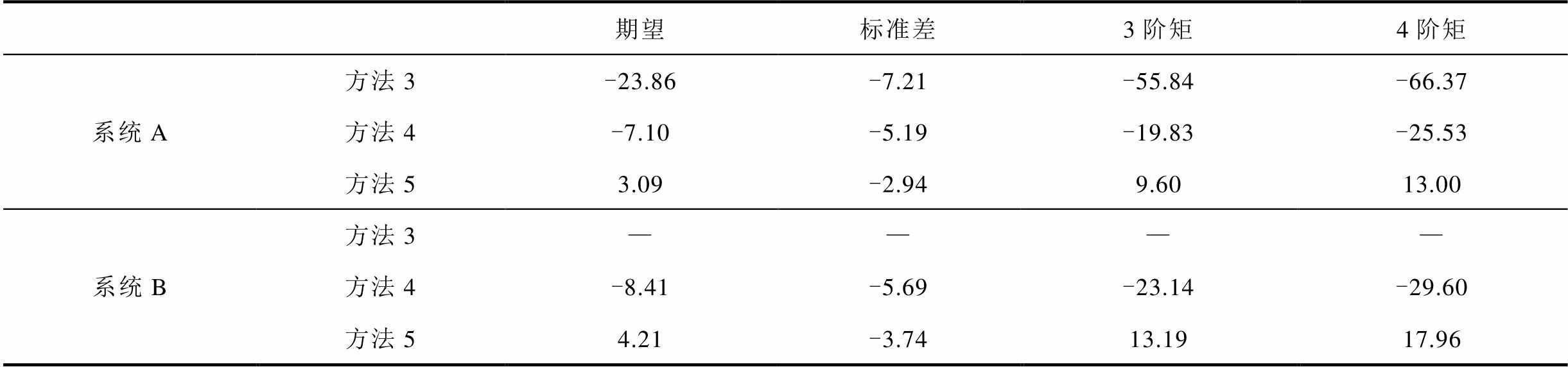
期望标准差3阶矩4阶矩 系统A方法3-23.86-7.21-55.84-66.37 方法4-7.10-5.19-19.83-25.53 方法53.09-2.949.6013.00 系统B方法3———— 方法4-8.41-5.69-23.14-29.60 方法54.21-3.7413.1917.96
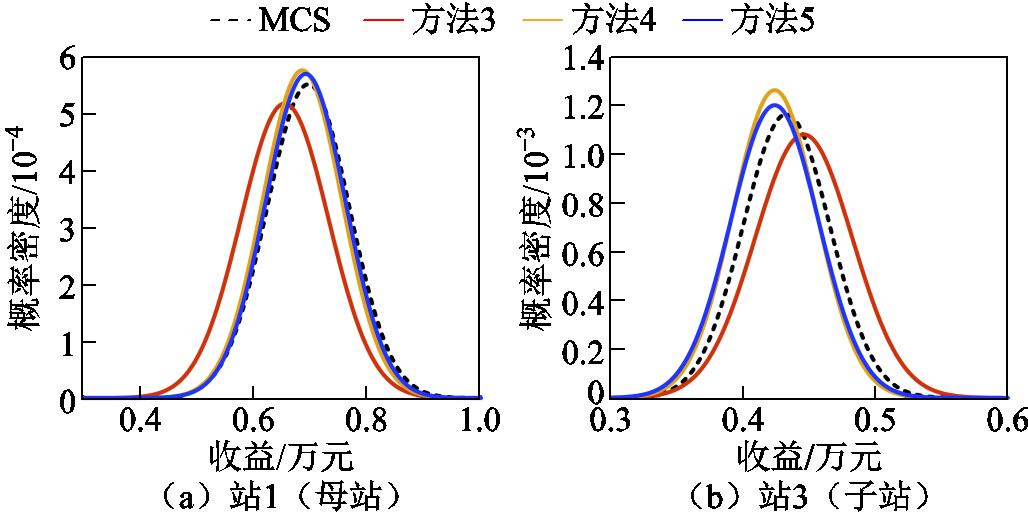
图5 子母站收益的概率密度对比
Fig.5 Probabilistic profits comparisons of the on-site and off-site hydrogen refueling stations
3.1.2 不同方法的降维效果对比
表2对比了不同方法的降维效果。方法2和3的维度最高降低40.18%(系统A)。方法4和5的降维效果最明显,维度下降约90%。方法5对系统A和B降维后,分别比方法4的维度高7维、低9维。由此可见,本文所提方法不一定比方法4维度低,但表1显示方法5的误差比方法4降低更低。下面详细分析原因。
表2 降维前后变量维度对比
Tab. 2 Comparisons of the dimensions of random variable before and after dimension reduction

变量维度系统 A系统B 初始维度N336648 方法2和3维度N201466 方法4维度N43572 方法5 维度N54263
方法2:为了分析方法2的降维效果,图6展示了系统B中随机变量的奇异值分布,奇异值重要度门槛值为0.01[23]。随机变量从648维降为466维,维度降低28.09%。由图6可知,光伏和氢负荷的各维度差异明显,且大部分奇异值小于0.01,因而维度下降明显。但风电出力奇异值下降趋势缓慢,且大部分奇异值在1~30,因而风电出力维度未下降,这导致方法2降维后维度仍然高达466维(见表2),所需配点约为20万个,采样计算负担巨大,需进一步降维。
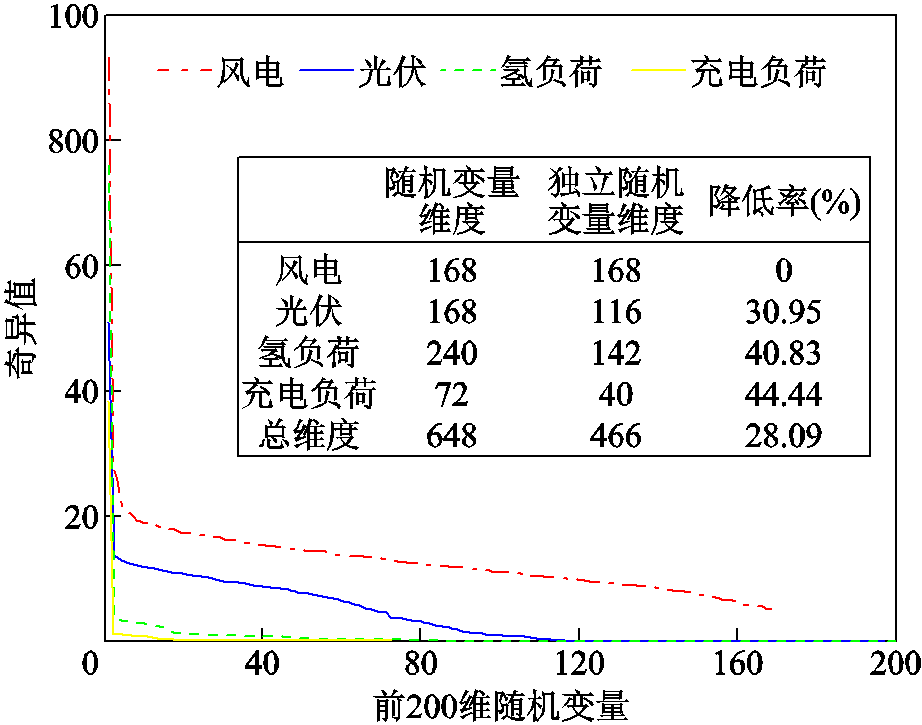
图6 随机变量的奇异值
Fig.6 The singular values of random variables
方法3:图7展示了不同阶次的单维积分点。方法3基于对称分布的假设将二阶积分点合并,但对称分布的随机变量的2个二阶积分点(黄色和红色曲线)的均值应等于一阶积分点(深蓝色曲线)。然而,由于分布的非对称性,风电出力的3个积分点不满足此关系,对称转换将引入误差。此外,由于方法3仅考虑前二阶积分点,而风光出力的三阶积分点与前二阶差异明显,导致表1中方法3计算误差高达23.86%。
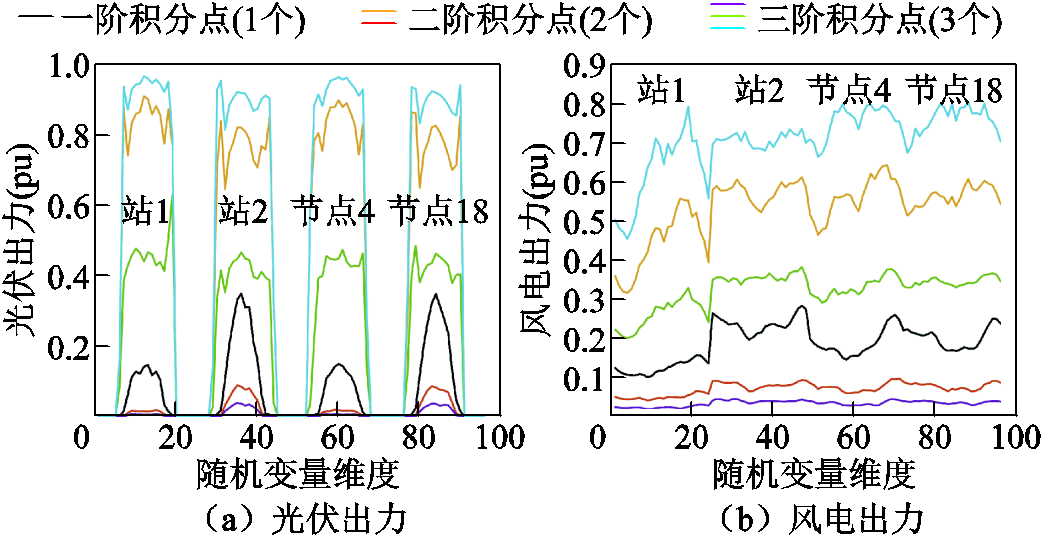
图7 不同阶次的积分点
Fig.7 Integration points of different degrees
方法4和方法5:图8对比了方法4和方法5的降维判据,图9和图10对比了不同采样点(方法4)和积分点(本文所提方法、方法5)对应的配电网收益。从图8中可看出,方法5的积分点和降维判据能够更好地反映风电出力随机性的影响,因而方法5的降维效果和精度与方法4相比有明显提升的。
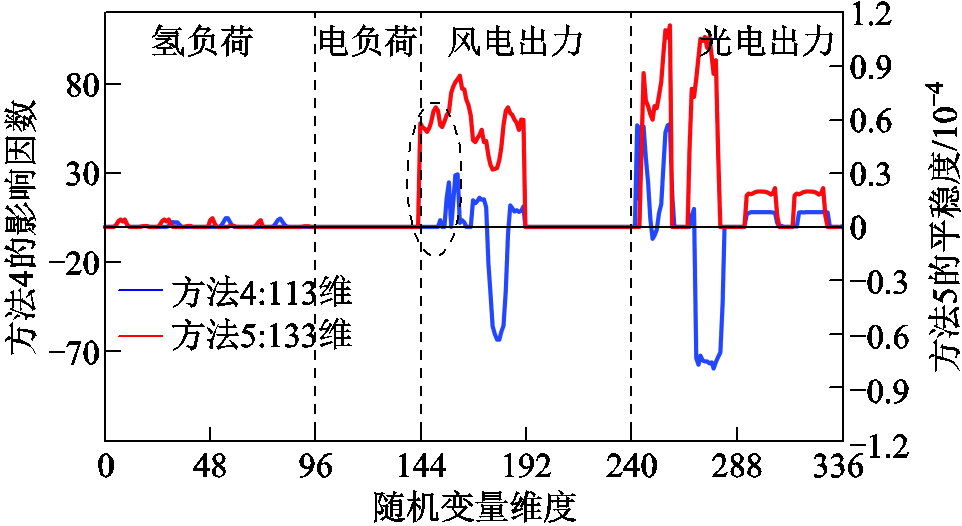
图8 方法4和方法5的降维判据对比
Fig.8 Comparison of dimensionality reduction criteria of Method 4 and Method 5
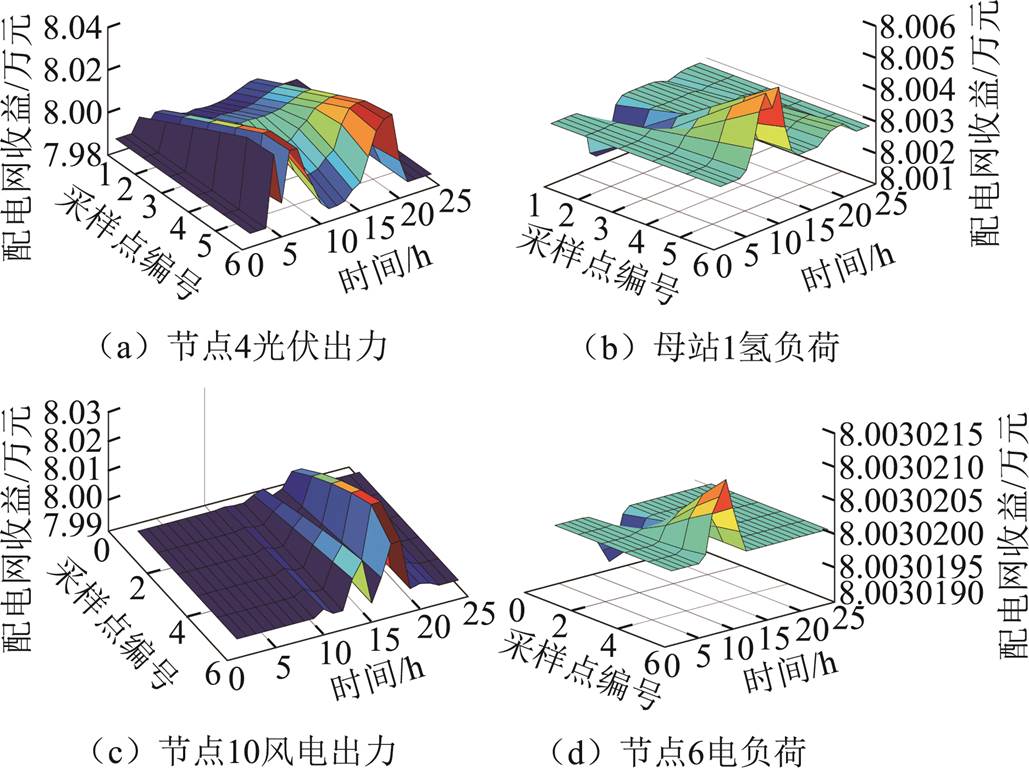
图9 配电网收益的灵敏度分析(方法4)
Fig.9 The sensitivity analysis of profits of distribution power network (Method 4)
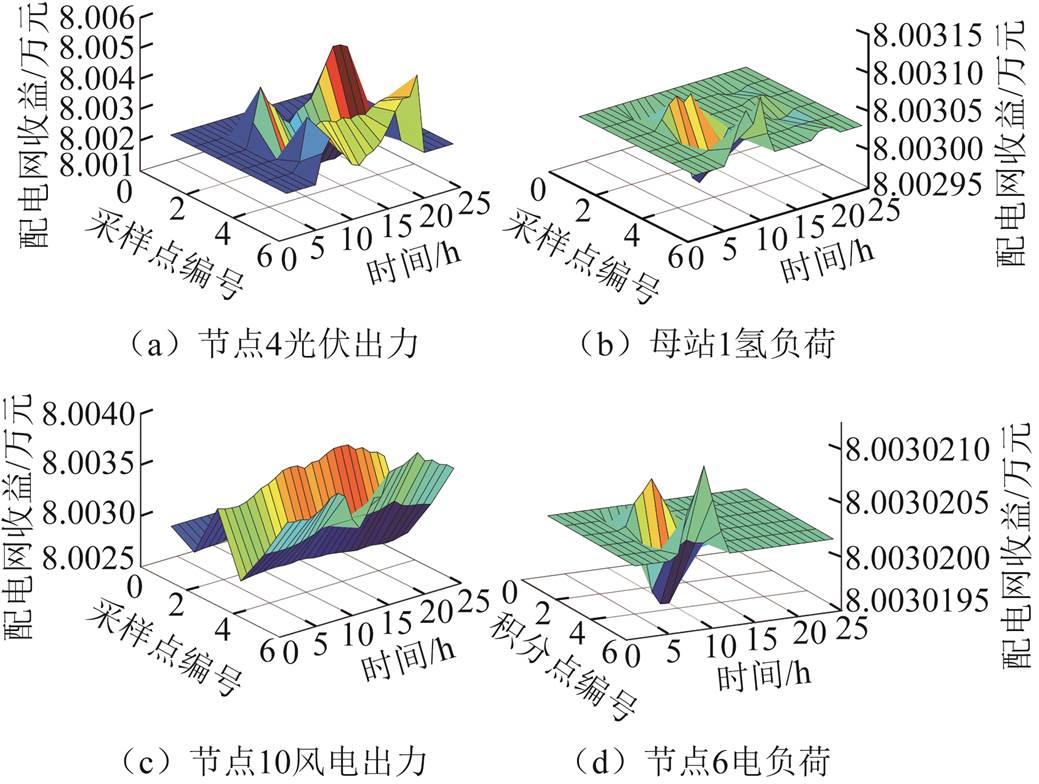
图10 积分点的配电网收益(方法5)
Fig.10 The profits of distribution power network at integration nodes (Method 5)
具体而言,方法4采用一元线性回归得到的影响因素大于0.01作为降维判据,筛选出113维变量,去除相关性后最终为35维变量(见表2)。而方法5采用平稳度大于10-5作为判据,比方法4多保留了7维风电出力随机变量。根据图9,风光出力对总收益的影响均在0.01万元量级,上下波动几百元,且集中在10:00—20:00时段,故方法4仅保留了该时段的风电出力。根据图10,配电网收益在各个时段风电出力的6个积分点处的波动情况相似,因而方法5保留几乎所有时段的风电出力随机变量。方法4的均匀采样点可能是风光出力的低频点(采样点编号值越大,表示随机变量取值越大),而方法5的6个积分点是高频点,因而方法5的降维精度更高。
3.1.3不同方法的计算时间对比
表3给出了MCS法(方法1)的计算时间。系统A和B均需要约20 000次MCS模拟才能收敛,单次计算时间平均为26.38 s和35.11 s,因此MCS求解的计算总时间为146.56 h和195.06 h,难以满足日前概率计算时间要求,需提升求解效率。
表3 MCS法计算时间
Tab.3 Computation time of the MCS method

系统连续变量0-1变量单次计算时间/s次数总时间/h A35 84248 72126.3820 000146.56 B95 87716 36835.1120 000195.06
表4对比了方法3~方法5的计算时间。设获取配点的时间为ts,总时间为ttotal。由于获取配点需要多次调取原模型计算,而因为网格积分均为线性计算,计算速度非常快,几乎不受变量规模影响,因此,表4中获取配点时间ts在总时间中占比97.80%以上,这说明配点数量是决定aPCE法计算效率的关键,这导致不同降维方法的ts差异明显。
表4 不同方法的计算时间对比
Tab.4 Comparisons of the computation time by different method

系统A系统B ts/httotal/httotal/tmcs(%)ts/httotal/httotal/tmcs(%) 方法3148.02148.23101.15——— 方法46.256.394.369.289.424.83 方法58.348.485.7912.5712.716.52
由于方法3对系统A和B降维后仍有201维和466维随机变量,分别需要约2万个和10万个配点。因此,方法3对系统A的计算时间几乎与MCS相等,且由于计算负担过大无法获得系统B的结果。方法4和5的总计算时间大致为MCS的4.36%~6.52%,方法5比方法4增加约1%。这是由于方法4所需配点数量为1 225个,方法5所需配点数量为1 764个,配点数量增加44.00%,因而ts增加约25.06%。
3.1.4 平稳度阈值ε0对CS-aPCE性能的影响
本节采用系统A分析CS-aPCE在不同平稳度阈值ε0下的性能,见表5。平稳度阈值ε0从3´10-5增加到5´10-5,压缩率DTG%、计算时间和精度几乎不变,这是由于几乎没有随机变量的平稳度在3´10-5~5´10-5范围(见图8)。当ε0从6´10-5增加到8´10-5,压缩率DTG%逐步提升,计算时间也显著下降,但计算误差逐步增大,这是由于过多的随机变量被压缩。因此,应综合考虑随机变量的平稳度分布特征选取阈值ε0,保留平稳度有明显差异的随机变量,从而保证压缩降维的精度和计算效率。
表5 不同平稳度阈值ε0下CS-aPCE法性能
Tab.5 Performance of for the CS-aPCE method with different smoothness thresholds ε0

e01´10-53´10-55´10-57´10-59´10-5 维度4231231514 DTG%87.50%90.77%93.15%95.54%95.83% Dm%3.09%4.57%9.57%10.16%16.74% Ds%-2.94%-5.03%-10.22%-17.29%-25.68% ttotal/tmcs(%)4.363.593.262.932.24
为了分析本文所提P2P协同对主体收益的影响,设置以下四种场景,基于本文方法求解系统B的概率最优能量流。不同场景下主体收益的期望值对比见表6和表7,每日能流总量的累积概率分布如图11所示。
表6 系统A在不同场景下的收益期望对比
Tab.6 The expected profits comparisons of system A under different scenarios (单位:元)
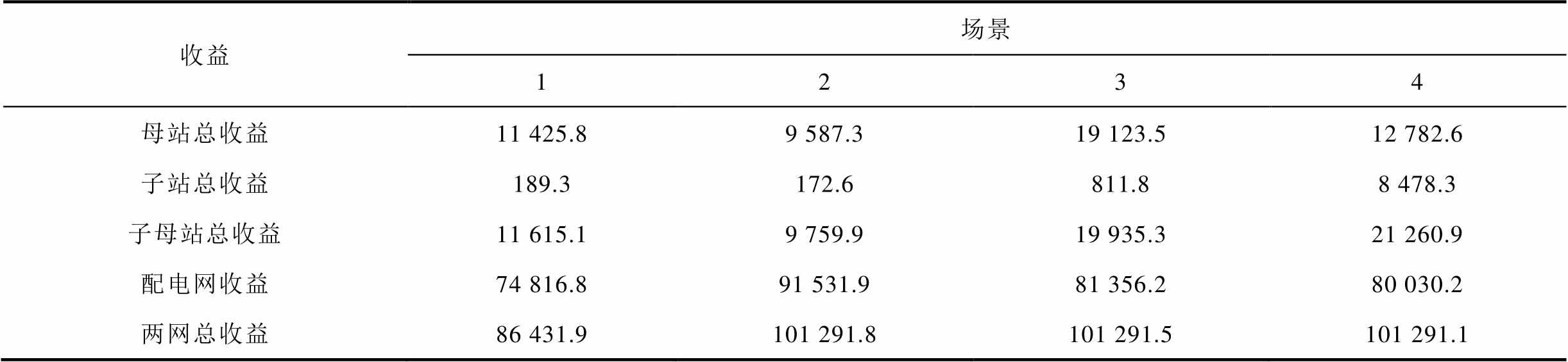
收益场景 1234 母站总收益11 425.89 587.319 123.512 782.6 子站总收益189.3172.6811.88 478.3 子母站总收益11 615.19 759.919 935.321 260.9 配电网收益74 816.891 531.981 356.280 030.2 两网总收益86 431.9101 291.8101 291.5101 291.1
表7 系统B在不同场景下的收益期望对比
Tab.7 The expected profits comparisons of system B under different scenarios (单位:元)
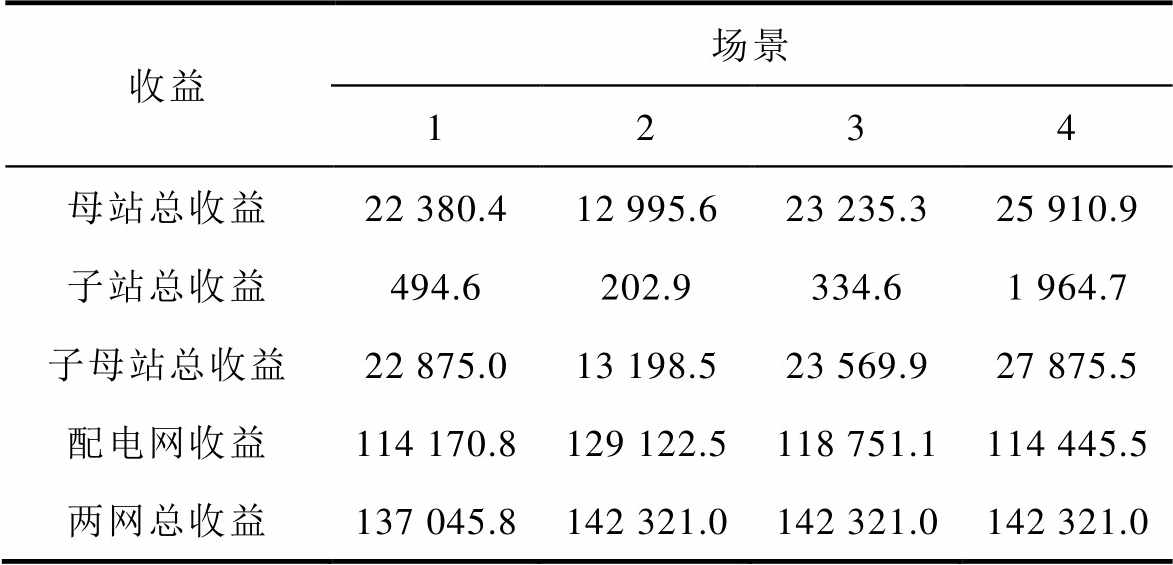
收益场景 1234 母站总收益22 380.412 995.623 235.325 910.9 子站总收益494.6202.9334.61 964.7 子母站总收益22 875.013 198.523 569.927 875.5 配电网收益114 170.8129 122.5118 751.1114 445.5 两网总收益137 045.8142 321.0142 321.0142 321.0
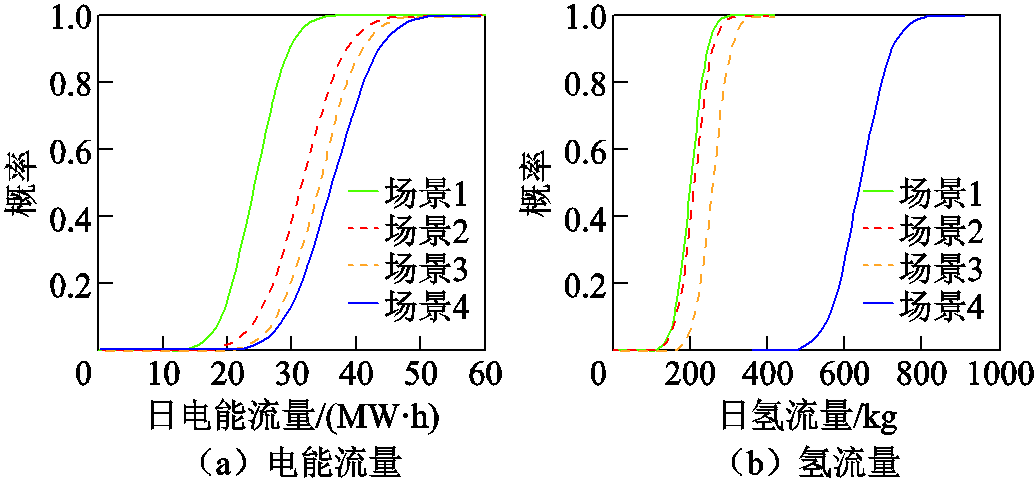
图11 不同场景下每日能流总量的累积概率分布
Fig. 11 Cumulated probability distribution of daily total quantity of energy flows under different scenarios
场景1(非协同):采用给定电价和氢价,基于纳什谈判模型,构建以配电网、子站及母站主体收益的纳什乘积最大为目标函数,优化电-氢能量流。
场景2(同主体协同):采用给定电价和氢价,以配电网、子站及母站主体收益之和最大为目标函数优化电-氢能量流[10]。
场景3(电能P2P协同):考虑电价优化决策(采用给定氢价),基于纳什谈判模型,构建以配电网、子站及母站主体收益的纳什乘积最大为目标函数,优化电-氢能量流[17]。
场景4(本文方法):考虑电价和氢价决策,基于纳什谈判模型,构建配电网、子站及母站主体收益的纳什乘积最大为目标函数,优化电-氢能量流。
场景2和场景1对比,验证协同优化对不同主体的提升效果。场景3与场景1、2对比说明考虑电价优化决策对不同主体收益的影响。场景4与场景3对比说明考虑氢价优化决策,对不同主体收益的影响。
3.2.1 不同场景的收益对比
表6和表7展示了系统A和B在不同场景下的各主体收益的期望值。由于场景2的配电网收益提升22.34%和13.1%,同主体协同(场景2)的总收益相比于场景1增加17.19%(系统A)和3.85%(系统B)这说明DHSN的大量灵活性资源参与了联盟整体的协同从而提升了总收益,两网具有构建合作联盟潜力。在同主体协同的运作模式下,尽管系统整体表现出一定的协同效益,但收益的增量却主要集中在了配电网一侧。具体而言,分布式氢能供应网络(DHSN)的总收益相较于协同前出现了显著的下滑,具体降幅分别达到了15.97%与42.30%。这一结果不仅揭示了当前收益分配机制的不均衡性,更凸显了对子母加氢站主体而言的不公平性。
场景3下,系统A的子母站总收益相比于场景2提升10 175.6元,而配电网收益减少10 175.7元。这说明考虑电能P2P协同后,场景3更有利于收益公平分配。由于场景3和4的子问题SP1即为场景2,因而收益总和基本相等。场景4下,子母站总收益提升6.65%,其中,子站收益增加,母站收益减少。主要原因在于子站储氢罐的灵活调度能力为母站在制氢过程及电力利用方面提供了更为宽广的运行弹性空间。这一特性,在氢能点对点协同框架内尤为显著,因为它促进了系统资源的优化配置与高效利用。因此,从公平性与系统整体效能提升的双重角度出发,为子站分配更多的协同收益是合理且必要的,不仅是对子站提供额外灵活性的合理补偿,也是激励各主体积极参与协同、共同促进电-氢综合能源系统健康发展的重要手段。综上所述,本文所提的考虑站间氢能P2P协同的电-氢最优能量流模型有利于发挥DHSN灵活性资源协同潜力,促进多主体收益公平分配。
图11对比了不同场景的每日能流总量。由图11a可知,场景2~4的电能流量累积概率曲线均相对于场景1后移,这说明场景2~4的电能流量显著提升。主要原因是电能P2P协同促进了DHSN与配电网的电能交互,发挥了电能协同潜力。由图11b可知,场景1~3氢能流量累积概率曲线非常接近,而场景4的曲线后移,这说明场景4显著提升了氢流量,促进了子母站间的氢能交互,从而发挥了氢能协同潜力。
本文基于CS-aPCE提出了电-氢概率最优能量流计算方法。所提方法基于纳什谈判模型和P2P协同模式,充分发挥DHSN的协同潜力,促进了收益公平分配。所提CS-aPCE算法基于高斯正交规则实现配点快速降维,能够高效求解高维电-氢概率最优能量流。本文通过算例验证了所提方法的有效性,结论如下:
1)本文所提CS-aPCE算法能够快速、高精度地求解高维电-氢概率能量流。计算时间仅为MCS法的10%,期望值和标准差误差低于4.21%,且高阶矩的计算精度比传统aPCE法提升60.28%~156.98%。
2)平稳度阈值对CS-aPCE算法的精度和效率有一定影响。应综合考虑随机变量的平稳度分布特征选取合理的阈值。
3)考虑站间氢能P2P协同的电-氢最优能量流模型能够调动DHSN灵活性资源协调潜力,协同站间氢能流分布,并实现多主体收益公平分配。
附 录
1. 考虑子母站并网的配电网潮流模型
考虑子母加氢站的电负荷和站内分布式电源出力,建立考虑子母站并网的配电网潮流模型,如式(A1)~式(A9)所示。
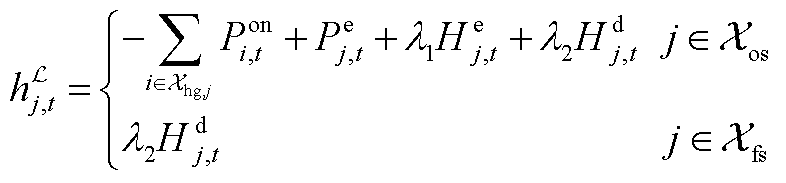 (A1)
(A1)
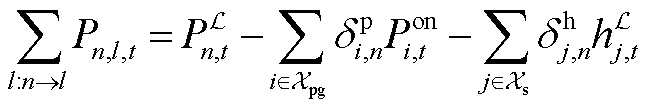 (A2)
(A2)
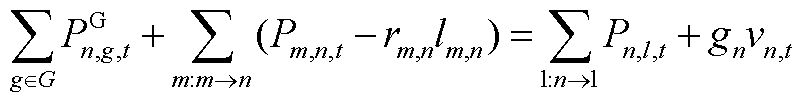 (A3)
(A3)
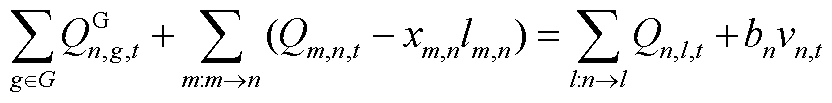 (A4)
(A4)
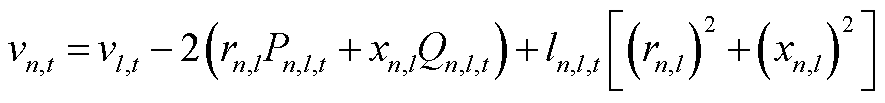 (A5)
(A5)
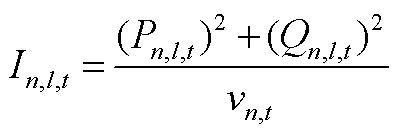 (A6)
(A6)
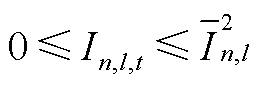 (A7)
(A7)
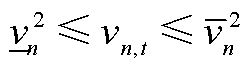 (A8)
(A8)
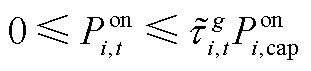 (A9)
(A9)
式中,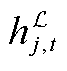 为t时刻子母站j的等效电负荷。母站电负荷(jÎXos)由站内DG的并网功率、电解功率Pe j,t和一次压缩机功率计算。Pon i,t为t时刻站内第i个DG的并网功率。二次压缩机是子站(jÎXfs、Xfs为加氢子站节点集合)的主要电负荷。压缩机功率与压缩的氢气质量线性相关,l1和l2分别为一次和二次压缩机的功率系数。式(A2)为配电网节点n的等效负荷,包括子母站等效负荷
为t时刻子母站j的等效电负荷。母站电负荷(jÎXos)由站内DG的并网功率、电解功率Pe j,t和一次压缩机功率计算。Pon i,t为t时刻站内第i个DG的并网功率。二次压缩机是子站(jÎXfs、Xfs为加氢子站节点集合)的主要电负荷。压缩机功率与压缩的氢气质量线性相关,l1和l2分别为一次和二次压缩机的功率系数。式(A2)为配电网节点n的等效负荷,包括子母站等效负荷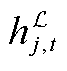 、传统电负荷PL n,t和DG并网功率PD n,t。其中,d h j,n为子母站和配电网的耦合系数,d h j,n=1表示子母站j并入配电网节点n,d h j,n=0表示二者不耦合;d p j,n为DG与配电网的耦合系数,d p j,n=1表示第j个DG并入配电网节点n,
、传统电负荷PL n,t和DG并网功率PD n,t。其中,d h j,n为子母站和配电网的耦合系数,d h j,n=1表示子母站j并入配电网节点n,d h j,n=0表示二者不耦合;d p j,n为DG与配电网的耦合系数,d p j,n=1表示第j个DG并入配电网节点n,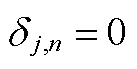 表示二者不耦合。式(A3)和式(A4)分别为配电网有功和无功功率平衡方程,
表示二者不耦合。式(A3)和式(A4)分别为配电网有功和无功功率平衡方程,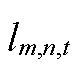 和
和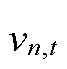 分别为支路电流和节点电压的平方,二者满足约束式(A5)~式(A8)。Pm,n,t和Qm,n,t分别为从节点m流向节点n的有功功率和无功功率;
分别为支路电流和节点电压的平方,二者满足约束式(A5)~式(A8)。Pm,n,t和Qm,n,t分别为从节点m流向节点n的有功功率和无功功率;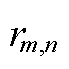 和
和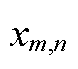 分别为支路mn的电阻和电抗;
分别为支路mn的电阻和电抗;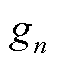 和
和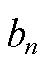 分别为支路mn的电导和电纳;
分别为支路mn的电导和电纳;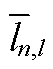 为节点电流In,l,t的最大值;
为节点电流In,l,t的最大值;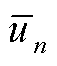 和
和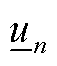 分别为节点电压
分别为节点电压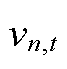 的上、下限;PN为节点电压集合。式(A9)为配电网和母站内DG的并网功率上下限约束,其中Ponj,cap为母站内第j个DG的额定容量;
的上、下限;PN为节点电压集合。式(A9)为配电网和母站内DG的并网功率上下限约束,其中Ponj,cap为母站内第j个DG的额定容量;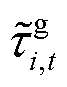 为DG的标幺发电功率;Xpg、Xhg,j分别为配电网DG集合和母站j的DG集合,Xdg=XpgÈ{Xhg,j, jÎXos}。
为DG的标幺发电功率;Xpg、Xhg,j分别为配电网DG集合和母站j的DG集合,Xdg=XpgÈ{Xhg,j, jÎXos}。
2. 子母站氢能流模型
考虑HTT在子母加氢站的装卸行为,建立子母加氢站氢能流模型,如式(A10)~式(A15)所示。
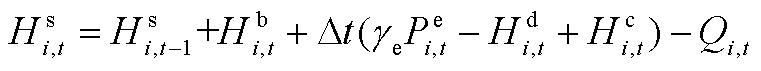 (A10)
(A10)
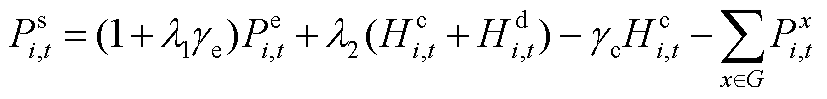 (A11)
(A11)
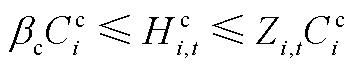 (A12)
(A12)
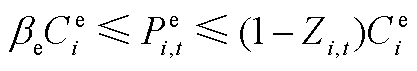 (A13)
(A13)
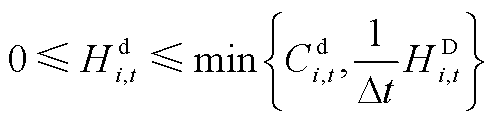 (A14)
(A14)
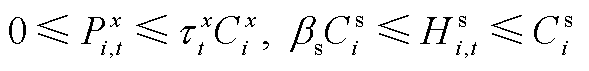 (A15)
(A15)
式中,式(A10)为子母加氢站的统一氢平衡方程,表示t时刻加氢站i的储氢量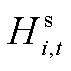 与电解槽制氢功率
与电解槽制氢功率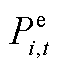 、购氢量
、购氢量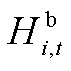 、加氢速率
、加氢速率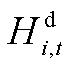 、氢转电速率
、氢转电速率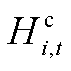 以及向所有HTT的装卸总量Qi,t有关,ge为电解槽电转氢系数。式(A11)表示t时刻加氢站i的电负荷
以及向所有HTT的装卸总量Qi,t有关,ge为电解槽电转氢系数。式(A11)表示t时刻加氢站i的电负荷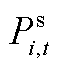 ,包含电解槽功率
,包含电解槽功率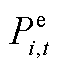 、压缩机功率、氢燃料电池发电功率和站内DG出力
、压缩机功率、氢燃料电池发电功率和站内DG出力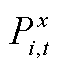 ;l1和l2分别为一次和二次压缩机的功率比;G为DG类型集合(风电、光伏等分布式电源;
;l1和l2分别为一次和二次压缩机的功率比;G为DG类型集合(风电、光伏等分布式电源;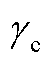 为氢燃料电池的氢转电系数。式(A12)和式(A13)保证电-氢能量转换的非同时性,0-1变量Zi,t表示氢燃料电池和电解槽是否同时工作。Zi,t=1表示前者工作,后者不工作;反之,后者工作,前者不工作;
为氢燃料电池的氢转电系数。式(A12)和式(A13)保证电-氢能量转换的非同时性,0-1变量Zi,t表示氢燃料电池和电解槽是否同时工作。Zi,t=1表示前者工作,后者不工作;反之,后者工作,前者不工作;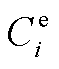 和
和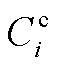 分别为电解槽额定功率和氢燃料电池额定耗氢速率;bc和be为二者的运行下限系数。式(A14)表示加氢速率
分别为电解槽额定功率和氢燃料电池额定耗氢速率;bc和be为二者的运行下限系数。式(A14)表示加氢速率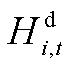 受额定值
受额定值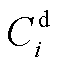 和氢负荷
和氢负荷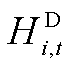 限制。式(A15)为站内DG和储氢罐的运行上下限约束。bs为储氢罐的取气率,
限制。式(A15)为站内DG和储氢罐的运行上下限约束。bs为储氢罐的取气率,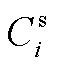 为储氢罐的额定容量;
为储氢罐的额定容量;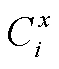 、
、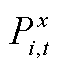 分别为加氢站i内x类型(风电/光伏)的DG额定容量和时刻t的出力。
分别为加氢站i内x类型(风电/光伏)的DG额定容量和时刻t的出力。
3. CS-aPCE算法降维效果的理论证明
定义压缩率DTG%为压缩后与压缩前相比积分维度的降低率。定义平稳率r为积分平稳变量维度N*与输入随机变量维度Nint相比的降低率,即
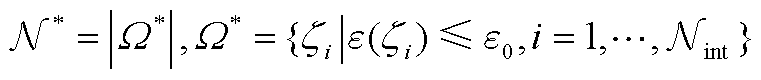 (A16)
(A16)
式中,W*为积分平稳变量集合。
根据准入条件q+1≤|i|≤q+N可知,多维积分点的最高阶次为q+1阶,但单维积分点的最高阶次为H阶,需根据q+1和PCE阶次H的大小关系进行分类讨论。由于级数更高的证明过程类似,且一般1~4级网格即可满足精度要求,下面证明1~4级网格的压缩效果。
1)当q+1≤H时,稀疏网格点数量TG,q复杂度为随机变量维度的q次方,即
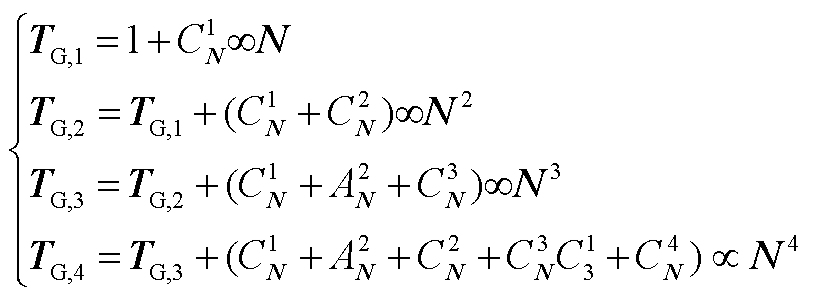 (A17)
(A17)
2)当q+1>H时,多维积分点的最高阶次为H,则准入条件退化为q+1≤|i|≤H-1+N,则网格点数量TG,q的复杂度为N的q次方。当H=2~4时,级数大于H的网格点数量均相等,复杂度为NH,有
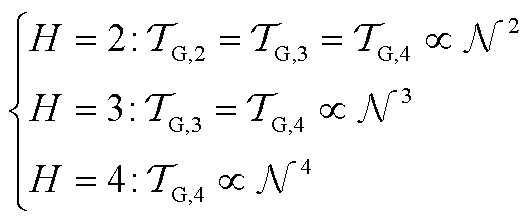 (A18)
(A18)
上述两种情况的网格点数量可统一写为TG,q=N min {q, H}。下面证明压缩率DTG,q%=rmin {q, H}。
将N*=(1-r)N代入式(A18),并计及压缩过程需要的配点数(q+1) N*,化简可得
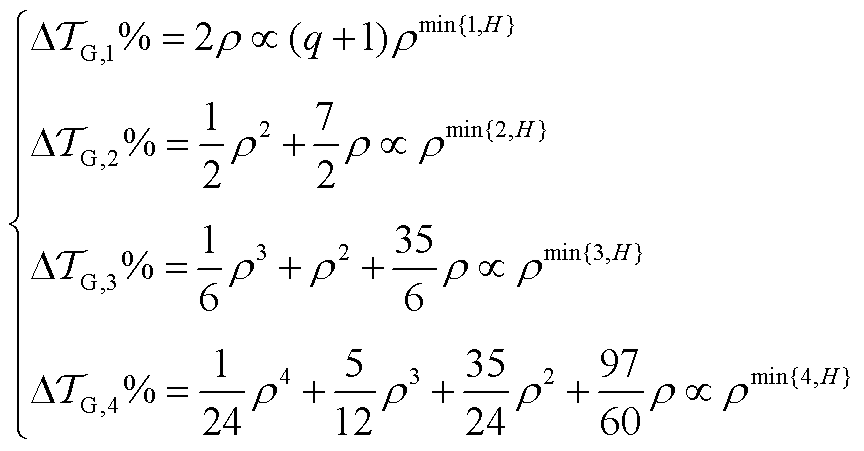 (A19)
(A19)
由式(A19)可知,压缩降维法的压缩率为平稳率r的min{q, H}次方,即DTG,q%=rmin {q, H}。证毕。
4. CS-aPCE算法的降维精度证明
定义:(降维误差)降维误差定义为平稳变量的高斯响应函数与压缩后积分点处加强函数值的欧式距离之和。
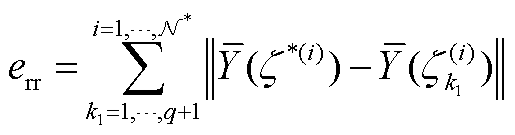 (A20)
(A20)
推论2:(降维误差边界)CS-aPCE的降维误差小于等于N*(q+1)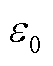 。
。
证明:根据压缩条件得
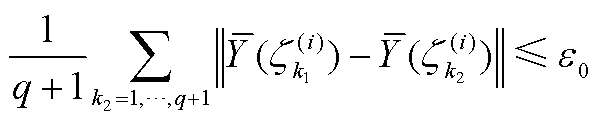 (A21)
(A21)
则
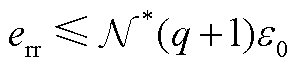 (A22)
(A22)
参考文献
[1] 徐钢, 薛小军, 张钟, 等. 一种基于电解水制氢及甲醇合成的碳中和能源技术路线[J]. 中国电机工程学报, 2023, 43(1): 191-201.
Xu Gang, Xue Xiaojun, Zhang Zhong, et al. A new carbon neutral energy technology route based on electrolytic water to hydrogen and methanol synthesis [J]. Proceedings of the CSEE, 2023, 43(1): 191-201.
[2] 陈逸文, 赵晋斌, 李军舟, 等. 电力低碳转型背景下氢储能的挑战与展望[J]. 发电技术, 2023, 44(3): 296-304.
Chen Yiwen, Zhao Jinbin, Li Junzhou, et al. Challenges and prospects of hydrogen energy storage under the background of low-carbon transformation of power industry[J].Power Generation Technology, 2023, 44(3): 296-304.
[3] Klatzer T, Bachhiesl U, Wogrin S, et al. Ramping up the hydrogen sector: an energy system modeling framework[J]. Applied Energy, 2024, 355: 122264.
[4] 香橙会氢能数据库[EB/OL]. [2024-07-18]. http:// www.xch3.com/#/DefaultReport?name=second.
[5] 中国汽车工程学会. 节能与新能源汽车技术路线图2.0[M]. 北京: 机械工业出版社, 2024.
[6] Zhao Tian, Liu Zhixin, Jamasb T. A business model design for hydrogen refueling stations: a multi-level game approach[J]. International Journal of Hydrogen Energy, 2024, 52: 577-588.
[7] 蒙军, 任洲洋, 王皓. 氢能交互下的多区域电氢综合能源系统可靠性提升策略[J]. 电工技术学报, 2024, 39(16): 5011-5027.
Meng Jun, Ren Zhouyang, Wang Hao. Reliability improvement strategies of multi-region electricity-hydrogen integrated energy systems considering hydrogen interaction between different regions[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 5011-5027.
[8] 程欢, 任洲洋, 孙志媛, 等. 电能-甲醇跨区协同输运下的电-氢耦合系统调度[J]. 电工技术学报, 2024, 39(3): 731-744.
Cheng Huan, Ren Zhouyang, Sun Zhiyuan, et al. A dispatching for the electricity-hydrogen coupling systems considering the coordinated inter-region transportation of electricity and methanol[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 731-744.
[9] Najafi A, Homaee O, Jasiński M, et al. Integrating hydrogen technology into active distribution networks: The case of private hydrogen refueling stations[J]. Energy, 2023, 278: 127939.
[10] 夏威夷, 任洲洋, 潘珍. 考虑子母站灵活互联的分布式供氢网和配电网多主体协调规划方法[J]. 中国电机工程学报, 2024, 44(23): 9187-9200.
Xia Weiyi, Ren Zhouyang, Pan Zhen. A multi-agent cooperative planning method for the distributed hydrogen supply network and the power distribution network considering the flexible interconnections between on-site and off-site hydrogen refueling stations[J]. Proceedings of the CSEE, 2024, 44(23): 9187-9200.
[11] Sun Qirun, Wu Zhi, Gu Wei, et al. Multi-stage co-planning model for power distribution system and hydrogen energy system under uncertainties[J]. Journal of Modern Power Systems and Clean Energy, 2023, 11(1): 80-93.
[12] 马利波, 赵洪山, 余洋, 等. 基于因果序图的氢能一体化电站运行过程建模及能量流控制策略[J]. 电工技术学报, 2024, 39(16): 5220-5237.
Ma Libo, Zhao Hongshan, Yu Yang, et al. Operation process modeling and energy flow control strategy of integrated hydrogen energy power station based on causal ordering graph[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 5220-5237.
[13] 胡俊杰, 童宇轩, 刘雪涛, 等. 计及精细化氢能利用的综合能源系统多时间尺度鲁棒优化策略[J]. 电工技术学报, 2024, 39(5): 1419-1435.
Hu Junjie, Tong Yuxuan, Liu Xuetao, et al. multi-time-scale robust optimization strategy for integrated energy system considering the refinement of hydrogen energy use[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1419-1435.
[14] 王博斐, 肖浩哲, 李国豪, 等. 基于控制目标的氢-电混动系统能量管理策略综述[J]. 发电技术, 2023, 44(4): 452-464.
Wang Bofei, Xiao Haozhe, Li Guohao, et al. A review of energy management strategy for hydrogen-electricity hybrid power system based on control target[J]. Power Generation Technology, 2023, 44(4): 452-464.
[15] 姜云鹏, 任洲洋, 陈志君, 等. 基于交叉项解耦随机响应面的电–气互联系统低碳化概率最优能量流[J]. 中国电机工程学报, 2023, 43(16): 6205-6218.
Jiang Yunpeng, Ren Zhouyang, Chen Zhijun, et al. A low-carbon probabilistic optimal energy flow analysis method for integrated electricity and natural gas systems based on stochastic response surface method improved by decoupling cross-terms[J]. Proceedings of the CSEE, 2023, 43(16): 6205-6218.
[16] Jiang Yuewen, Liu Jianshu, Zheng Hongqi. Optimal scheduling of distributed hydrogen refueling stations for fuel supply and reserve demand service with evolutionary transfer multi-agent reinforcement learning[J]. International Journal of Hydrogen Energy, 2024, 54: 239-255.
[17] Li Yuanzheng, Yu Chaofan, Liu Yun, et al. Collaborative operation between power network and hydrogen fueling stations with peer-to-peer energy trading[J]. IEEE Transactions on Transportation Electrification, 2023, 9(1): 1521-1540.
[18] Singh V, Moger T, Jena D. Probabilistic load flow for wind integrated power system considering node power uncertainties and random branch outages[J]. IEEE Transactions on Sustainable Energy, 2023, 14(1): 482-489.
[19] Shen Danfeng, Wu Hao, Xia Bingqing, et al. Arbitrarily sparse polynomial chaos expansion for high-dimensional parametric problems: parametric and probabilistic power flow as an example[J]. IEEE Systems Journal, 2022, 16(3): 4950-4961.
[20] 申丹枫. 高维稀疏全局多项式逼近方法及其在电力系统参数化小扰动稳定问题中的应用[D]. 杭州: 浙江大学, 2022.
Shen Danfeng. High-dimensional sparse global polynomial approximation method and its applications to power system amall signal stability[D]. Hangzhou: Zhejiang University, 2022.
[21] 姜涛, 李春晖, 张儒峰, 等. 基于多项式混沌展开的电力系统概率可用输电能力评估[J]. 中国电机工程学报, 2024, 44(2): 489-504.
Jiang Tao, Li Chunhui, Zhang Rufeng, et al. Probabilistic available transfer capacity evaluation of power systems using polynomial chaos expansion[J]. Proceedings of the CSEE, 2024, 44(2): 489-504.
[22] 胡潇云. 考虑概率和模糊不确定性的区域电-气联合系统能流及最优能流分析[D]. 重庆: 重庆大学, 2020.
Hu Xiaoyun. Energy flow and optimal energy flowanalysis of regional integrated electricity and gas system considering probabilistic and possibilistic uncertainties[D]. Chongqing: Chongqing University, 2020.
[23] 孙鑫. 计及风电不确定性的可用输电能力计算方法研究[D]. 武汉: 华中科技大学, 2019.
Sun Xin. Research on available transfer capability calculation considering wind power uncertainty[D]. Wuhan: Huazhong University of Science and Techno-logy, 2019.
[24] 侯慧, 朱韶华, 俞菊芳, 等. 基于高效数据降维的配电网风灾停电用户数量预测模型[J]. 电力系统自动化, 2022, 46(7): 69-76.
Hou Hui, Zhu Shaohua, Yu Jufang, et al. prediction model for user number in power outage caused by wind disaster for distribution networks based on high-efficient data dimensionality reduction[J]. Automation of electric power systems, 2022, 46(7): 69-76.
[25] Wu Jinhui, Tao Yourui, Han Xu. Polynomial chaos expansion approximation for dimension-reduction model-based reliability analysis method and application to industrial robots[J]. Reliability Engineering & System Safety, 2023, 234: 109145.
[26] 胡潇云, 赵霞, 冯欣欣. 基于稀疏多项式混沌展开的区域电-气联合系统全局灵敏度分析[J]. 电工技术学报, 2020, 35(13): 2805-2816.
Hu Xiaoyun, Zhao Xia, Feng Xinxin. Global sensitivity analysis for regional integrated electricity and gas system based on sparse polynomial chaos expansion[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2805-2816.
[27] Jiang Yunpeng, Ren Zhouyang, Sun Zhiyuan, et al. A stochastic response surface method based probabilistic energy flow analysis method for integrated electricity and gas systems[J]. IEEE Transactions on Power Systems, 2022, 37(3): 2467-2470.
[28] Wang Xiaoting, Wang Xiaozhe, Sheng Hao, et al. A data-driven sparse polynomial chaos expansion meth-od to assess probabilistic total transfer capability for power systems with renewables[C]//2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 2022: 1.
[29] Bai Jinjun, Zhang Gang, Duffy A P, et al. Dimension-reduced sparse grid strategy for a stochastic collocation method in EMC software[J]. IEEE Transactions on Electromagnetic Compatibility, 2018, 60(1): 218-224.
[30] Zheng Yi, You Shi, Bindner H W, et al. Optimal day-ahead dispatch of an alkaline electrolyser system concerning thermal-electric properties and state-transitional dynamics[J]. Applied Energy, 2022, 307: 118091.
[31] 许康平, 王程, 毕天姝. 基于气网动态代理模型的电–气综合能源系统最优能流计算[J]. 中国电机工程学报, 2023, 43(9): 3415-3429.
Xu Kangping, Wang Cheng, Bi Tianshu. Optimal energy flow calculation of integrated electric-gas systems based on gas network dynamic surrogate model[J]. Proceedings of the CSEE, 2023, 43(9): 3415-3429.
[32] Zhong Weifeng, Xie Shengli, Xie Kan, et al. Cooperative P2P energy trading in active distribution networks: an MILP-based Nash bargaining solution [J]. IEEE Transactions on Smart Grid, 2021, 12(2): 1264-1276.
[33] Van Acker T, Geth F, Koirala A, et al. General polynomial chaos in the current-voltage formulation of the optimal power flow problem[J]. Electric Power Systems Research, 2022, 211: 108472.
[34] Sobczyk K, Trcebicki J. Approximate probability distributions for stochastic systems: maximum entropy method[J]. Computer Methods in Applied Mechanics and Engineering, 1999, 168(1/2/3/4): 91-111.
[35] Golub G H, Welsch J H. Calculation of Gauss quadrature rules[J]. Mathematics of Computation, 1969, 23(106): 221.
[36] Grady W M, Samotyj M J, Noyola A H. The application of network objective functions for actively minimizing the impact of voltage harmonics in power systems[J]. IEEE Transactions on Power Delivery, 1992, 7(3): 1379-1386.
[37] Xie Shiwei, Xu Yan, Zheng Xiaodong. On dynamic network equilibrium of a coupled power and transportation network[J]. IEEE Transactions on Smart Grid, 2022, 13(2): 1398-1411.
[38] Raju M, Khaitan S K. System simulation of compressed hydrogen storage based residential wind hybrid power systems[J]. Journal of Power Sources, 2012, 210: 303-320.
[39] Belgium Elia Transmission. Wind power generation [M/OL]. Belgium, 2024. https://www.elia.be/en/grid-data/.
Abstract Addressing the issues of inadequate exploitation of hydrogen energy collaboration potential and the challenge in balancing accuracy and efficiency of probabilistic solution algorithms, this paper proposes a calculation method for the probabilistic optimal energy flow of electricity-hydrogen systems based on compressed sparse arbitrarily polynomial chaos expansions (CS-aPCE).
Firstly, to harness the spatial-temporal collaboration potential of hydrogen energy, a modeling approach for electricity-hydrogen optimal energy flow is introduced incorporating peer-to-peer (P2P) hydrogen collaboration between on-site and off-site hydrogen refueling stations (HRSs). Considering the P2P coupling of inter-station hydrogen flows and bidirectional electricity flows, a P2P collaboration mechanism is proposed for between on-site and off-site HRSs and the power distribution network. Based on Nash bargaining theory, a probabilistic optimal electricity-hydrogen energy flow model is constructed, which incorporates time-delay and discreteness constraints for inter-station hydrogen P2P transactions. This model coordinates multi-stakeholder benefit allocation and electricity-hydrogen price decisions, enhancing feasibility and fairness.
Secondly, a probabilistic optimal energy flow solution algorithm for on-site and off-site HRSs and power distribution networks is proposed based on CS-aPCE, aiming to improve the efficiency and accuracy of high-dimensional probability calculations. The core of this algorithm lies in leveraging historical data to drive the collocation points, subsequently calculating key statistical metrics such as expectations and standard deviations through analytical methods, without reliance on prior probabilistic information. To further optimize computational performance, the CS-aPCE algorithm integrates Gaussian quadrature rules to construct high-frequency collocation points and incorporates compressed sparse grid techniques. Effective compression criteria are proposed, and the dimensionality reduction effect and computational accuracy of the algorithm are theoretically proven, ensuring its efficiency and robustness under high-dimensional randomness.
The effectiveness of the proposed method is validated through numerical examples, leading to the following conclusions: firstly, the CS-aPCE algorithm presented in this paper can solve high-dimensional and probabilistic electricity-hydrogen energy flow problems rapidly and with high precision. The computation time is merely 10% of that required by the Monte Carlo simulation method, while the errors in expected values and standard deviations are below 4.21%. Furthermore, the computational accuracy for higher-order moments is improved by 60.28% to 156.98% compared to the traditional aPCE method. Secondly, the stationarity threshold exerts a certain influence on the accuracy and efficiency of the CS-aPCE algorithm. A reasonable threshold should be selected by comprehensively considering the stationarity distribution characteristics of random variables. Finally, the electricity-hydrogen optimal energy flow model considering P2P hydrogen collaboration between stations can mobilize the coordination potential of flexible resources within the distributed hydrogen supply network, coordinate the distribution of inter-station hydrogen flows, and achieve fair allocation of benefits among multiple stakeholders.
keywords:Electricity-hydrogen coupling system, polynomial chaos expansions, probabilistic optimal energy flow, multi-agent game, peer-to-peer collaboration
DOI: 10.19595/j.cnki.1000-6753.tces.240729
中图分类号:TM732
国家自然科学基金项目(52277080)和中央高校基本科研业务费项目(2023CDJYXTD-004)资助。
收稿日期 2024-05-07
改稿日期 2024-07-19
夏威夷 女,1996年生,博士后,研究方向为电-氢-交通智慧系统运行与规划。E-mail:wy-xia@mail.tsinghua.edu.cn
任洲洋 男,1986年生,副教授,博士生导师,研究方向为电力能源系统低碳运行及规划、人工智能等。 E-mail:rzhouyang1108@163.com(通信作者)
(编辑 郭丽军)