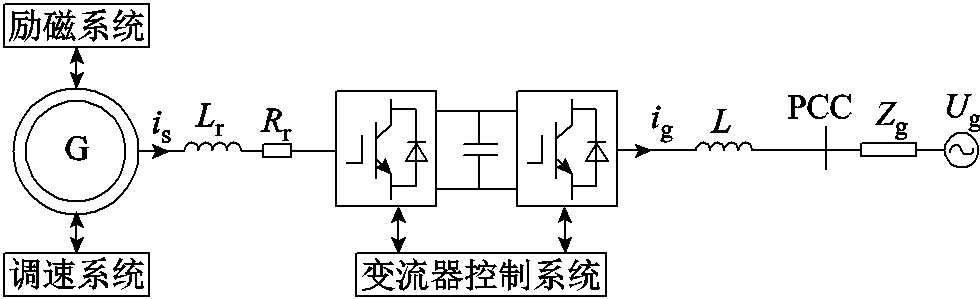
图1 全功率变速抽水蓄能机组结构
Fig.1 Structural diagram of the variable-speed pumped storage unit with full-size converter
摘要 全功率变速抽水蓄能机组通过电力电子装置接入电网，可为电网运行提供调峰、调频、电压频率支撑等服务，然而电力电子装置的多时间尺度控制呈现的复杂频域特性易与电网发生交互作用，引发振荡现象。该文首先以全功率变速抽水蓄能机组为研究对象，建立了水电侧机组以及全功率变流器装置的阻抗模型，进一步推导了计及频率耦合效应的全功率变速抽水蓄能机组的等效阻抗模型；然后基于阻抗判据，分析了全功率变速抽水蓄能机组接入不同电网阻抗下的稳定性，研究了水轮机和调速器的关键参数，以及全功率变流器控制环中锁相环、直流电压环及电流环参数对机组阻抗特性和系统稳定性的影响规律；最后基于Matlab搭建了其系统电磁暂态模型，验证了所建全功率变速抽水蓄能机组阻抗模型的准确性和稳定性分析结果的有效性。
关键词：全功率变速抽水蓄能 阻抗建模 频率耦合 稳定性分析
随着新能源装机容量的逐年攀升，电网的调峰调频以及电力系统对新能源的消纳面临着巨大的挑战，储能可以平衡能源供需差异，成为解决该问题的有效手段[1-5]。在现有的储能系统中，抽水蓄能机组具有容量大、运行灵活、启停迅速等优点，不仅具备调峰、填谷、调频等多种功能[6-7]，而且在促进清洁能源消纳、构建新型电力系统以及实现“双碳”目标中发挥着重要作用[8-10]。
宽频振荡问题给电力系统的安全稳定运行带来了巨大的威胁。开展针对全功率变速抽蓄系统中宽频振荡问题的研究，对实现新能源发电与电网的稳定运行有着重大意义。目前对于全功率变速抽水蓄能机组的研究主要集中在机组自身控制策略[11-12]、功率优化[13-14]、频率支撑[15-17]等方面，对于其并网稳定性的研究相对较少。然而全功率变速抽水蓄能机组的多时间尺度控制呈现的复杂频域特性易与电网发生交互作用，可能诱发系统振荡失稳。文献[18-19]在dq坐标系下，建立了变速抽水蓄能与新能源联合并网系统的数学模型，采用特征值法分析了联合系统的小干扰稳定性，研究发现联合系统间的控制环节存在一定程度的相互作用，有失稳的风险。文献[20]建立了全功率变速抽水蓄能机组快速功率模式小信号模型，包含水轮机、发电机、励磁调速系统及变流器等部分建模，模型较为全面，同样采用特征值法研究了系统存在的振荡风险。基于状态空间模型的特征值分析法主要优点是可以根据系统特征根的分布情况分析潜在的振荡模态，但系统中部分参数或结构发生改变，则需要重新建立状态模型，建模过程依赖系统结构和参数，拓展性差[21-22]。相比于特征值法，阻抗分析法具有扩展性强的优点，降低了系统建模的难度，且可通过测量方式获取对象阻抗[23-25]。
目前，对于全功率变速抽水蓄能机组阻抗建模及其基于阻抗判据的稳定性分析鲜有研究。开展全功率变速抽水蓄能机组阻抗模型及其分析，对于未来大规模抽蓄机组接入电网后从阻抗视角下进行稳定性分析具有重要的意义。
鉴于此，本文主要进行了以下研究工作：
1）建立了水轮机侧在dq坐标系下的阻抗模型，在此基础上建立了机侧以及网侧变流器的阻抗模型，依据整个机组扰动电压激励与电流响应间的关系，得到了全功率变速抽水蓄能机组的自导纳和伴随导纳模型。
2）考虑电网阻抗的影响，推导得到整个抽蓄机组计及频率耦合效应的等效阻抗模型，并采用频率扫描法对其准确性进行了验证。
3）基于阻抗分析法对全功率变速抽水蓄能机组接入不同电网阻抗下的并网稳定性问题进行分析，并研究了水轮机和调速器参数及全功率变流器控制环参数对机组阻抗特性和并网稳定性的影响。
全功率变速抽水蓄能机组结构如图1所示，原动机采用可逆式水泵水轮机，通过带动可变速凸极同步电机发电，发电机组由励磁系统、调速系统组成。抽水蓄能机组通过全功率变流器实现交直流侧的解耦，其中机侧变流器通过功率外环实现对输出功率的控制，网侧变流器通过电压外环实现直流侧电压的稳定。本文中励磁部分采用恒定励磁，因此在建立水电侧机组的阻抗模型时只需考虑水轮机及调速系统和同步电机的影响。图1中，Lr、Rr分别为同步电机的等效电感及电阻；L为网侧变流器滤波电感；Zg为电网阻抗。
图1 全功率变速抽水蓄能机组结构
Fig.1 Structural diagram of the variable-speed pumped storage unit with full-size converter
水轮机非线性数学模型的传递函数框图如图2所示。
图2 水轮机非线性数学模型的传递函数框图
Fig.2 Transfer function block diagram of nonlinear mathematical model for hydraulic turbine
由图2水轮机非线性数学模型的传递函数框图可知水力学方程为
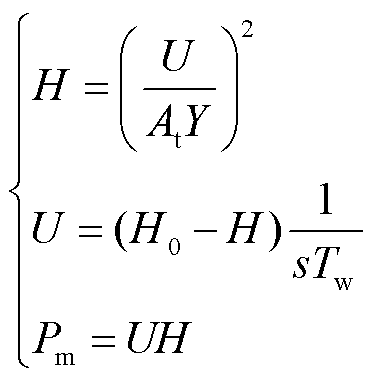（1）
式中，H为水轮机的净水头；U为水流速；Y为导水叶开度；由于导水叶从关闭到打开最初一段需要克服水轮机的静摩擦力，必须将理想开度Y用实际开度u表示，故有u=AtY，At表征导水叶实际开度与理想开度之间的关系；Tw为水锤效应时间常数；H0为水头的初始稳态值；Pm为水轮机输出机械功率。对水力学方程进行小信号线性化可得
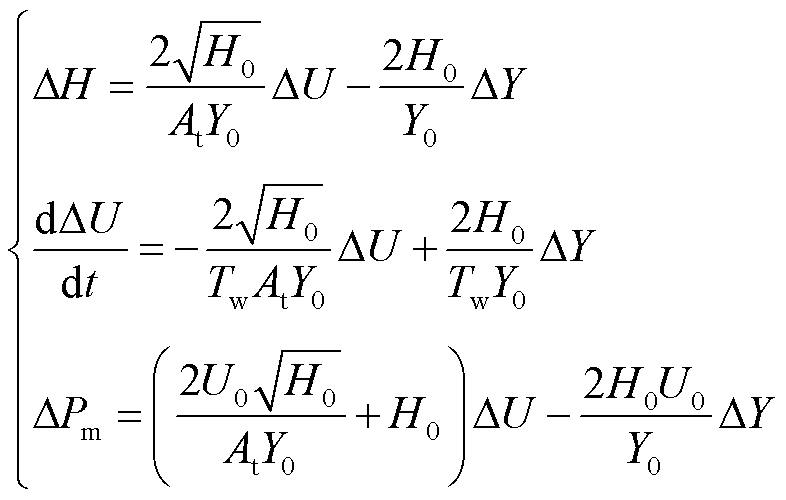（2）
式中，Y0、U0分别为水叶开度、水速的初始稳态值。
调速系统通过检测角速度和输出功率的变化对导叶开度进行控制，进而影响水流速度。调速器由PI控制器和液压伺服系统构成，其数学模型的传递函数框图如图3所示。
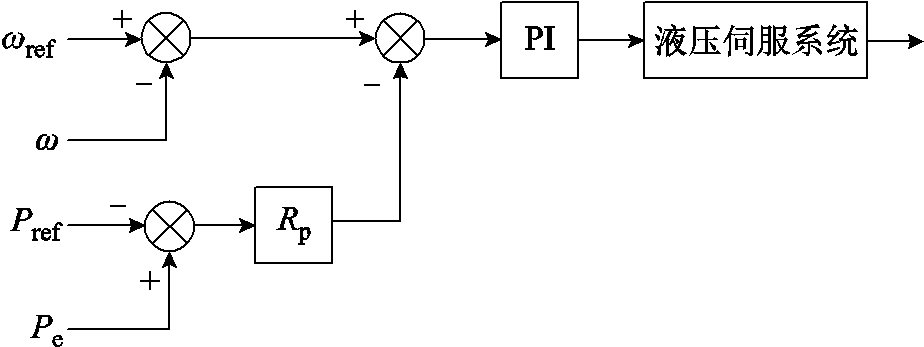
图3 水轮机调速器数学模型的传递函数框图
Fig.3 Transfer function block diagram of mathematical model for hydraulic turbine governor
根据图3可以得到调速器的方程为
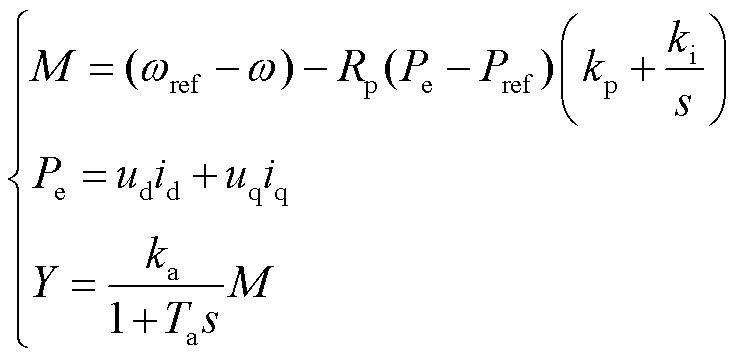（3）
式中，wref和w分别为额定角速度和电角速度；Pref和Pe分别为额定功率和电磁功率；ud和uq、id和iq分别为同步电机d轴和q轴的电压、电流；Rp为功率调节下垂系数；kp和ki分别为PI控制器的比例积分系数；ka和Ta分别为液压伺服系统的增益和时间常数；M为中间状态变量。
将调速器方程进行小信号线性化可得
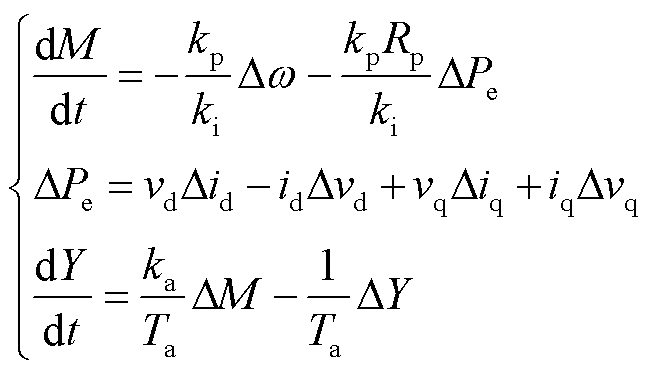（4）
水轮机及其调速器系统与同步电机通过转子运动方程将水轮机输出机械功率与电磁功率联系起来，转子运动方程小信号线性化后得到
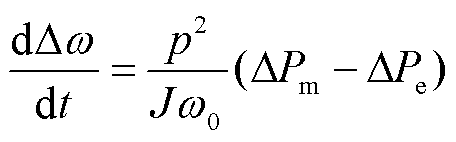（5）
式中，J为转动惯量；p为水轮机的极对数。
同步电机在dq坐标系下的电压方程及磁链方程为
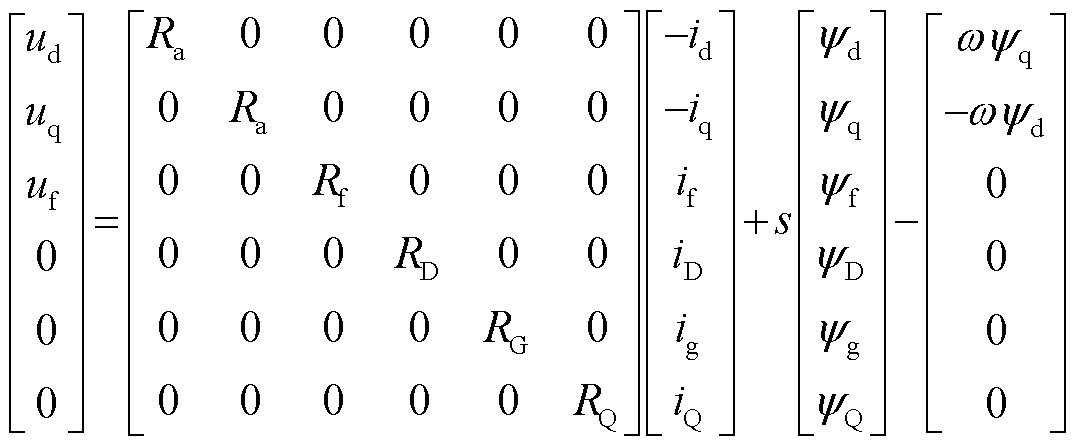（6）
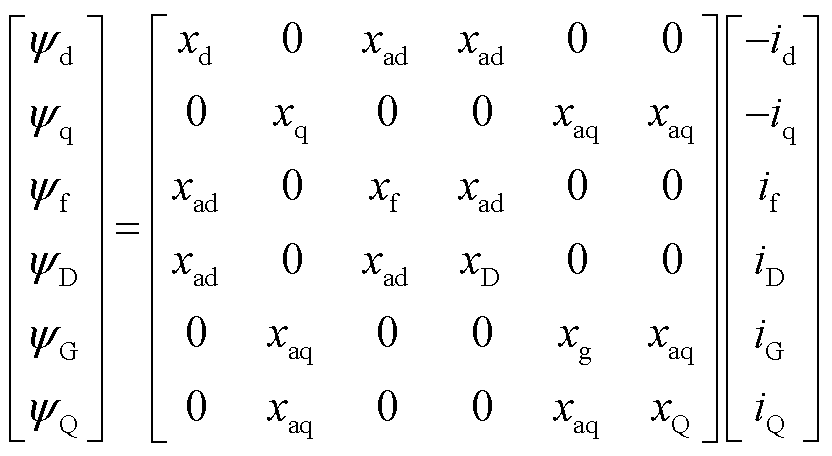（7）
式中，Ra为定子电阻；Rf为励磁绕组电阻；RD、RG、RQ为阻尼绕组电阻；xd为d轴同步电抗；xq为q轴同步电抗；xad和xaq分别为d轴与q轴电枢反应电抗；yx为绕组磁链；uf、if分别为励磁电压和电流；iD、iG、iQ对应三个绕组电流。同步电机模型中认为d轴和q轴定子电阻相等，同轴上各绕组互感相等。
为了得到同步电机的小信号模型，需要对方程式（6）和式（7）进行小信号线性化并且联立，为保证方程的统一性，所有变量均进行标幺化处理。
综合以上分析，同步电机的转子转速w和式（5）中的Δw将水轮机调速系统及同步电机的小信号模型联系为一个整体。选取输入为水轮发电机dq坐标系下的定子电压，输出为dq坐标系下的定子电流，整理可得到水轮发电机的状态空间方程为
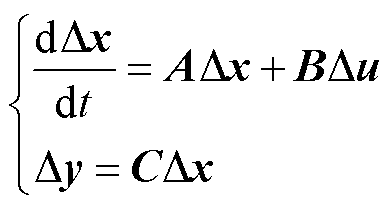（8）
其中
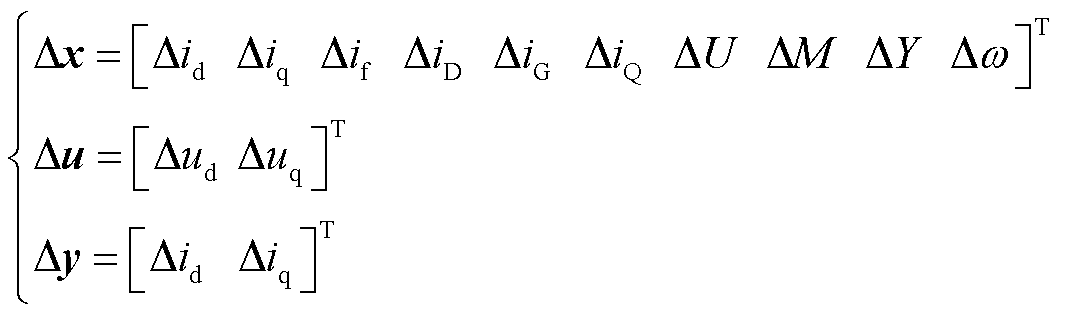（9）
式中，A、B、C为状态空间方程系数矩阵；I为单位矩阵。
根据式（8）中的小信号模型，可以得到水轮发电机系统在dq坐标系下的阻抗模型为
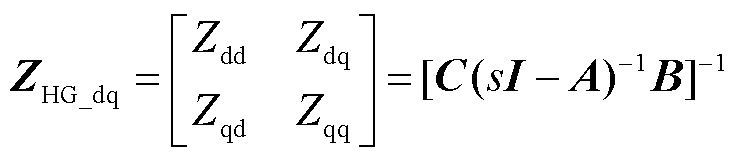（10）
全功率变速抽水蓄能机组通过全功率变流器接入电网，机侧变流器控制框图如图4所示，采用外环功率内环电流控制。
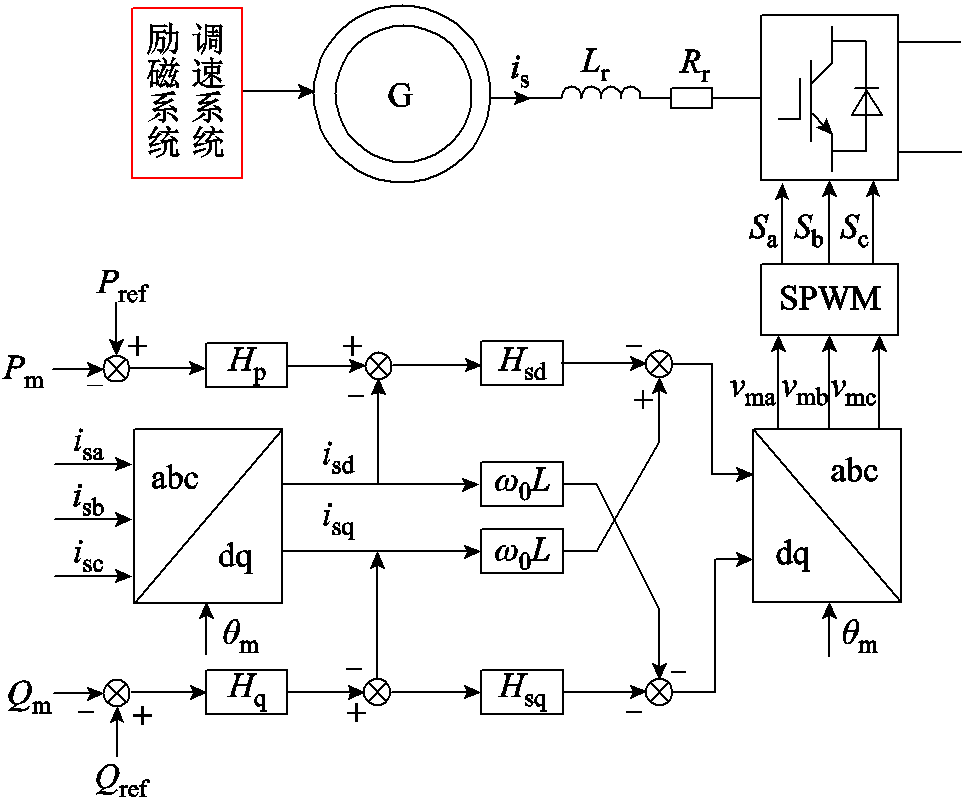
图4 机侧变流器控制框图
Fig.4 Control block diagram of machine-side inverter
同步发电机与机侧变流器中阻抗模型的建立均在dq坐标系下进行，然而同步电机和机侧变流器所对应的dq坐标系相差90°，因此有
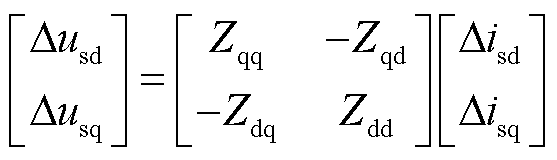（11）
式中，Δusdq和Δisdq分别为机侧变流器所对应的d、q轴电压、电流小信号变化量。根据图4可得机侧变流器在dq坐标系下的主电路方程为
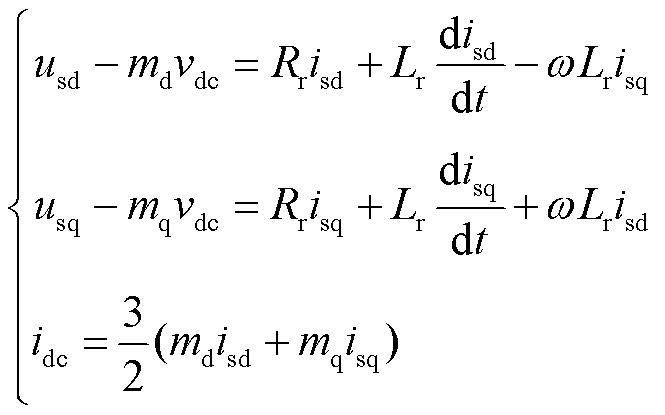（12）
式中，md、mq分别为dq坐标系下d、q轴机侧变流器占空比；Lr、Rr分别为发电机端口到机侧变流器之间的线路等效电感、等效电阻；vdc、idc分别为直流侧电压与电流。根据变流器的控制结构可以得到占空比方程为
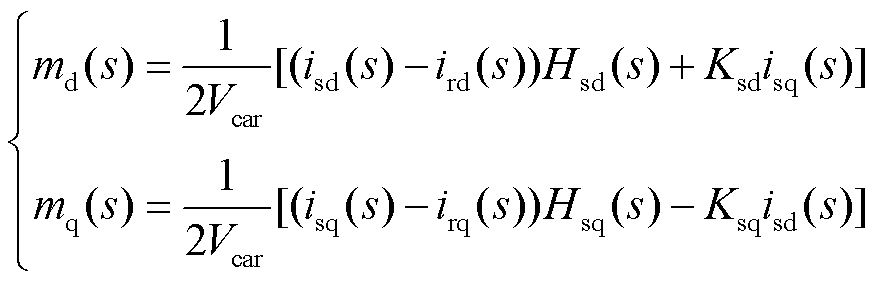（13）
式中，Ksd=Ksq =w0Lr；Vcar为载波幅值；q轴同理，ird(s)、irq(s)为电流内环参考输入扰动，由功率外环引起，其表达式分别为
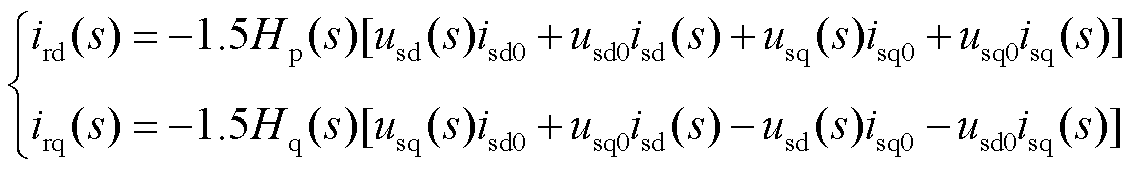（14）
结合式（11）～式（14）得出机侧变流器频域下的小信号模型为
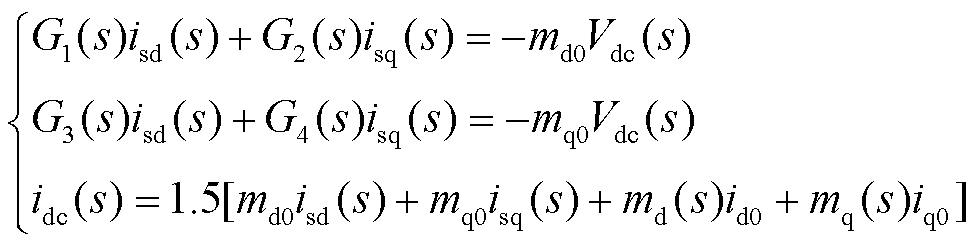（15）
其中
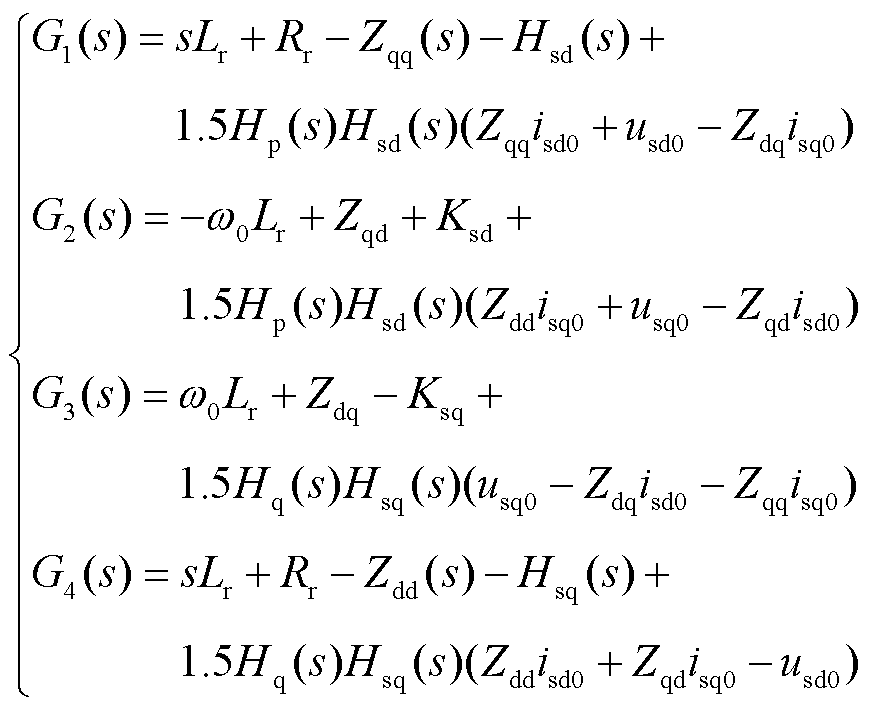（16）
式中，md0、mq0为调制系数md、mq的稳态量。
综上所述，可以得到idc(s)与vdc(s)之比，即为包含水轮发电机以及机侧变流器的直流侧导纳为
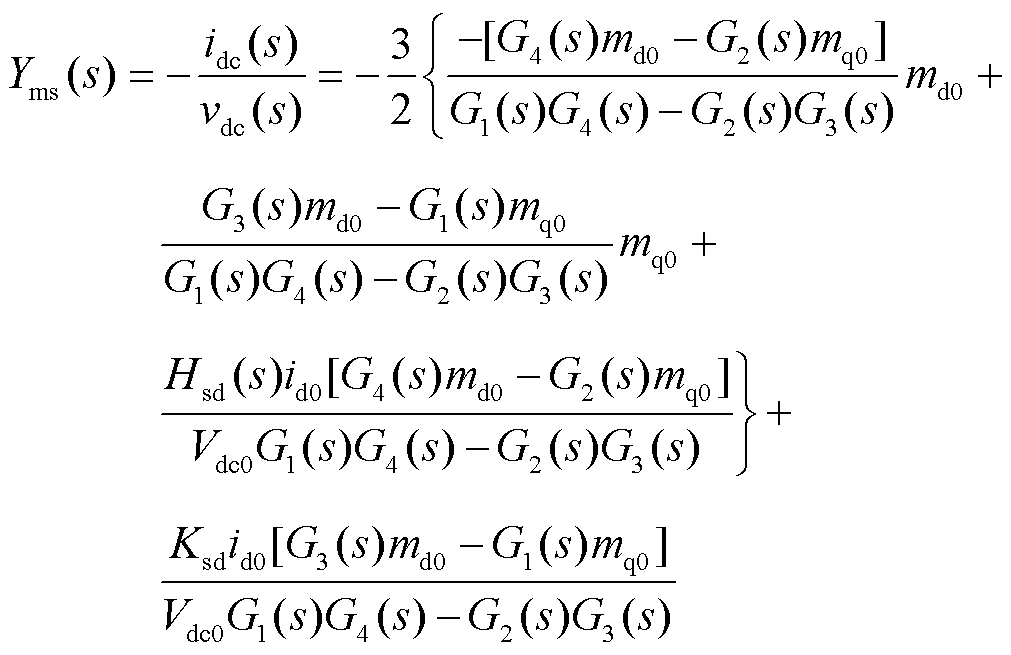(17)
网侧变流器采用外环电压内环电流控制方式，控制器根据实际直流电压与直流电压参考值之间的偏差调节电流环参考值，进而调节输出电流大小，维持直流电压稳定。网侧变流器的控制结构如图5所示。
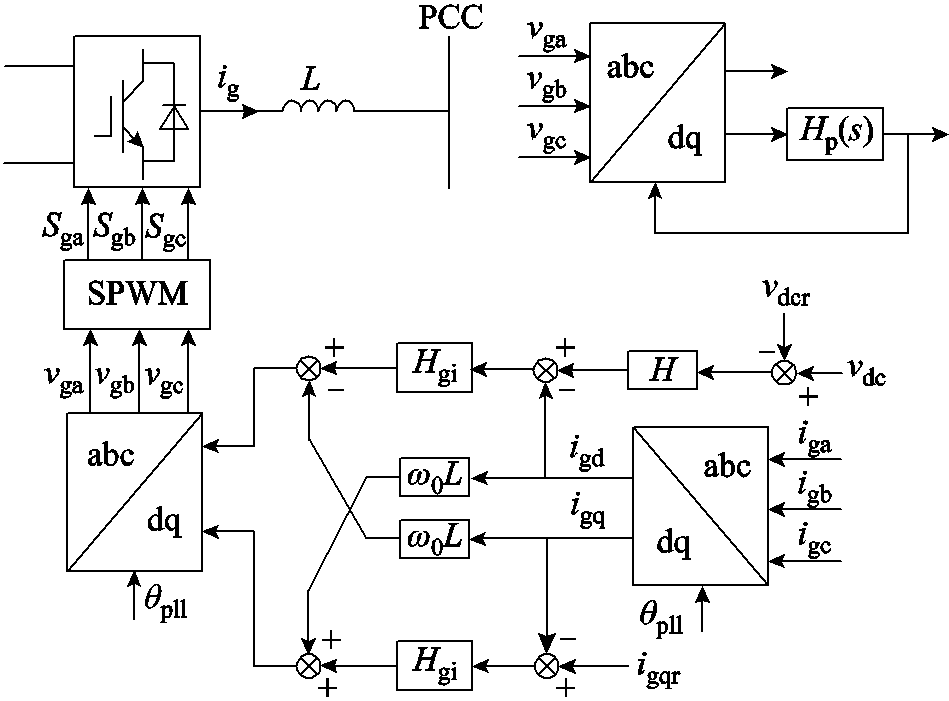
图5 网侧变流器控制框图
Fig.5 Control block diagram of grid-side inverter
由于锁相环的存在导致控制结构不对称，因此在并网点添加小信号扰动的时候，会出现单频率输入双频率输出（Single-frequency Input and Double-frequency Output, SIDO）的现象，即输入fp的扰动频率时，系统会输出fp和2f1-fp的电流响应，同时还会在直流侧产生f1-fp的分量；当在直流侧施加频率为fp的小扰动分量时，会在直流侧产生fp的电流响应，同时会在交流侧产生f1+fp和f1-fp的电流响应。因此在交流测引入频率为fp小扰动分量时，需计及交直流侧的相互耦合。文献[26]对该结构变流器的阻抗模型进行了详细推导，这里不再赘述，直接给出分别在网侧变流器交流侧以及直流侧施加扰动时得到的导纳为
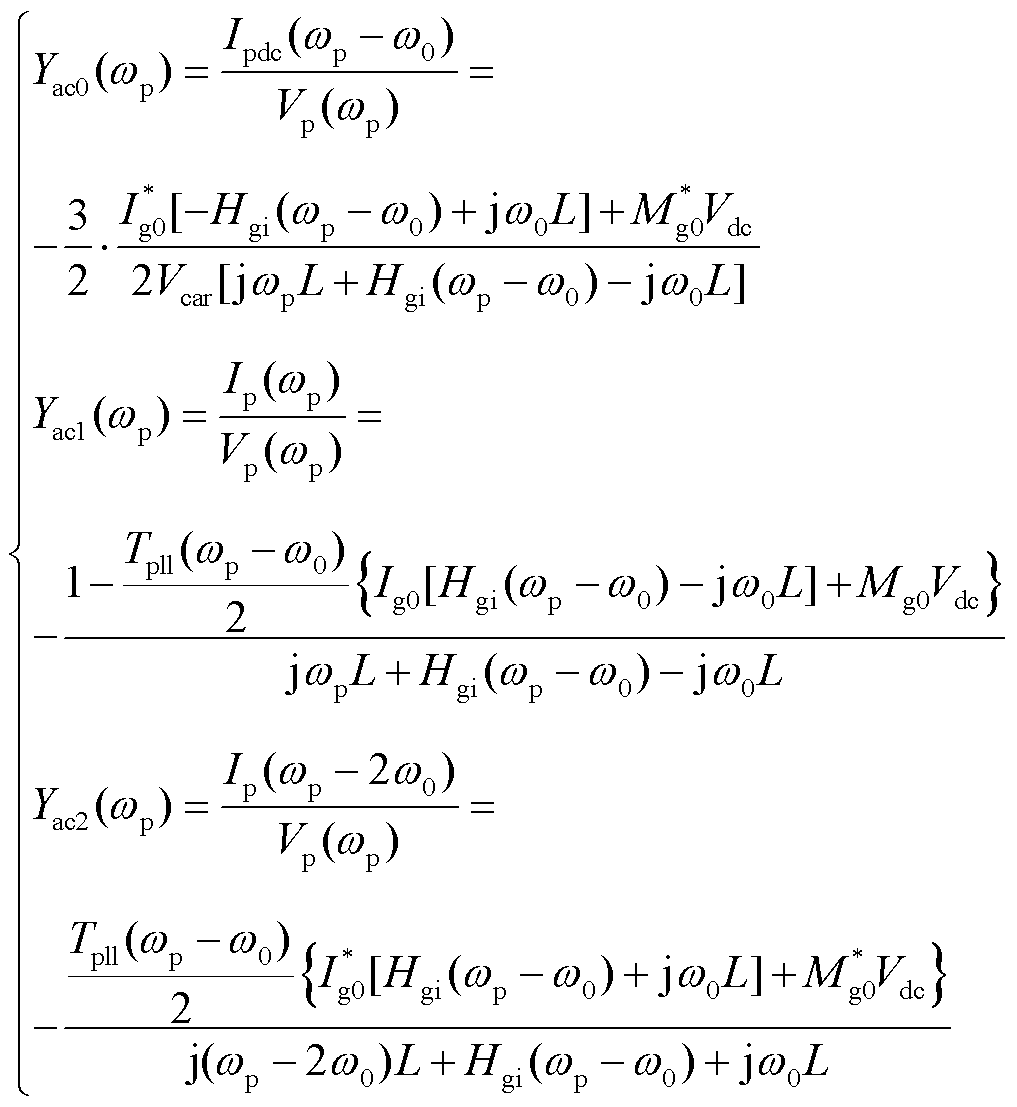（18）
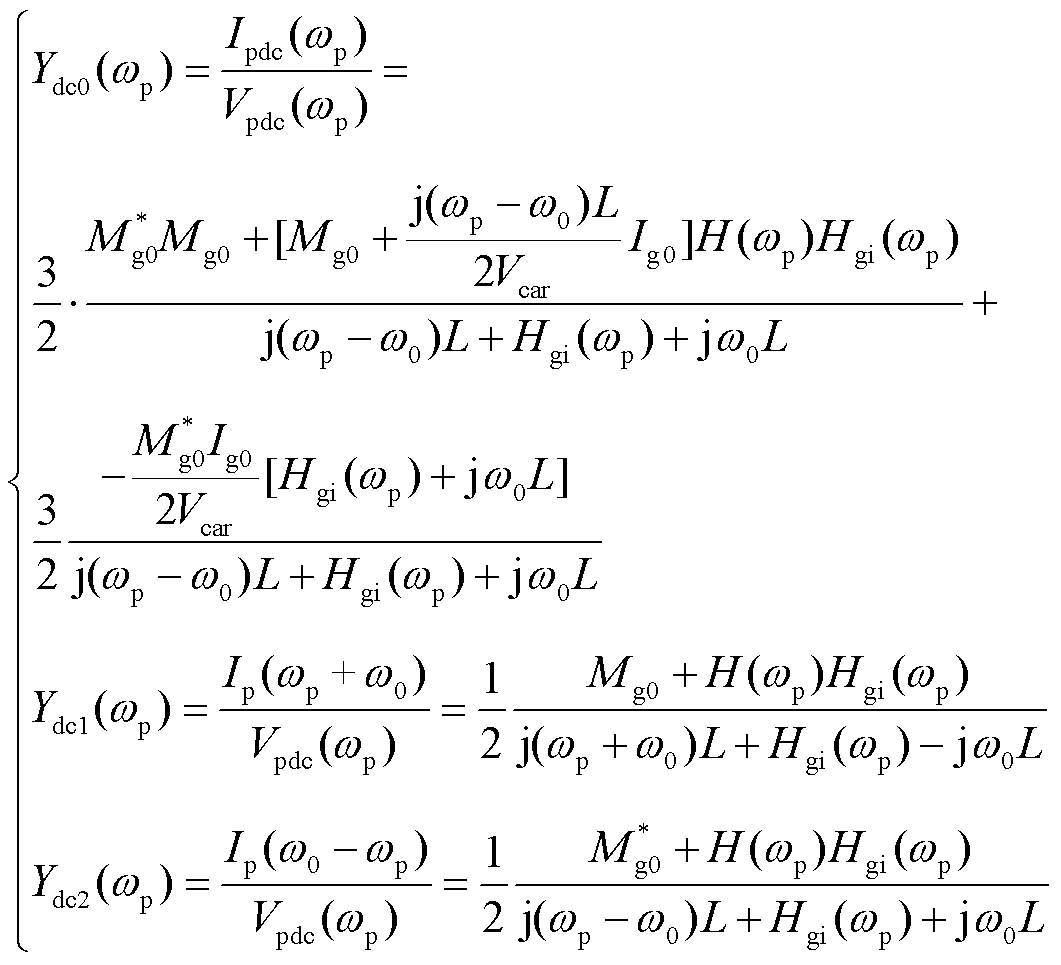（19）
式中，Yac0,1,2为交流侧施加扰动得到的导纳；Ydc0,1,2为直流侧施加扰动得到的导纳；H(wp)和Hgi(wp)分别为直流电压环PI控制器、电流环PI控制器的传递函数；Mg0、Ig0分别为网侧变流器调制系数和交流电流稳态值；Tpll为锁相环的闭环传递函数；“*”表示共轭。
根据式（18）、式（19）可知，对于整个全功率变速抽水蓄能机组，在其并网点处施加fp频率的电压扰动，机组中的扰动电压激励与电流响应之间的关系如图6所示。
图6中Zdc为直流侧电容与机侧变流器并联后的等效阻抗。
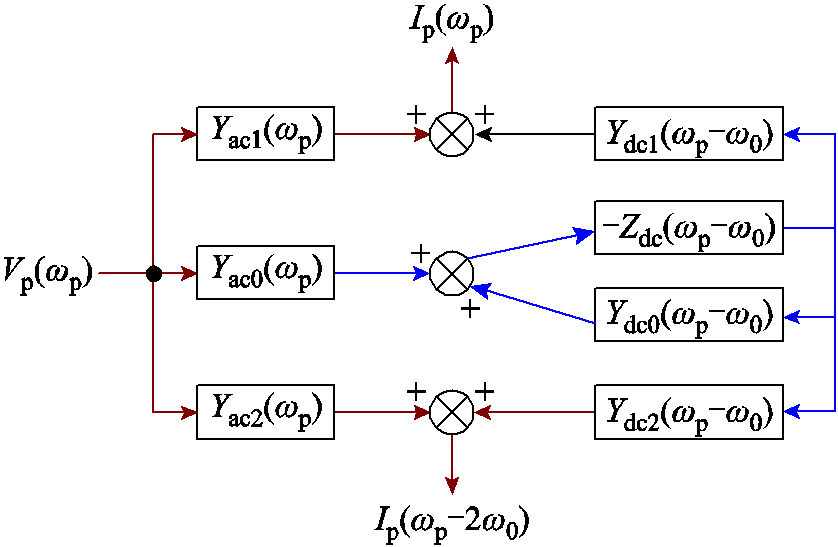
图6 全功率变速抽蓄机组扰动电压与电流响应之间的关系
Fig.6 The relationship between disturbance electricity and current response of the variable-speed pumped storage unit with full-size converter
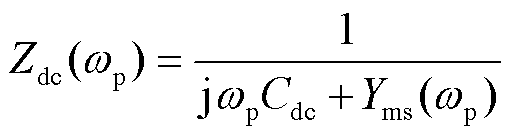（20）
式中，Cdc为机组直流母线电容。
根据图6所示的传递关系可以得到机组的自导纳Ysa(wp)和伴随导纳Yaa(wp)为
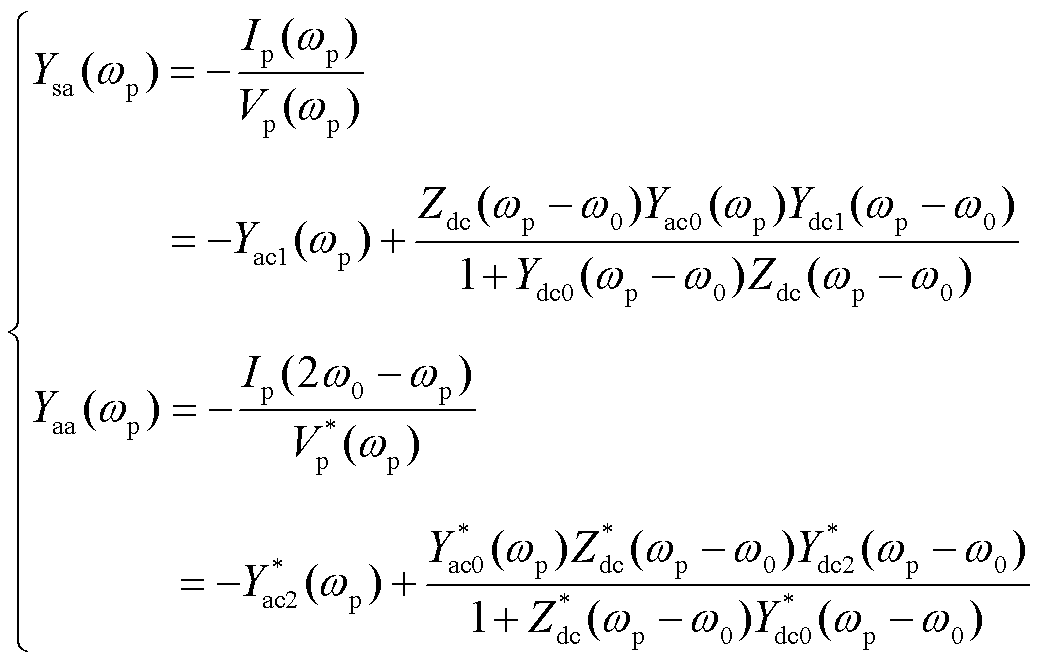（21）
对全功率变速抽水蓄能并网系统中的电网电压施加wp频率的扰动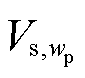
，会产生wp和2w0-wp频率的并网扰动电流Is,wp和Is,2w0-wp。两个频率下的扰动电流通过电网阻抗将产生相应频率下的扰动电压Vpcc,wp和Vpcc,2w0-wp。因此，并网扰动电压以及扰动电流可表示为
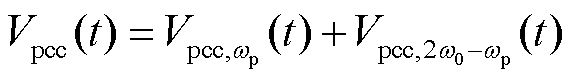（22）
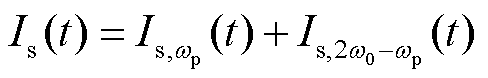（23）
机组扰动电压与扰动电流的关系为
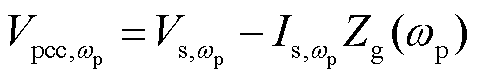（24）
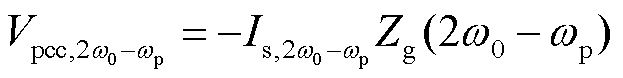（25）
结合1.4节机组自导纳与伴随导纳的解析式可以得到
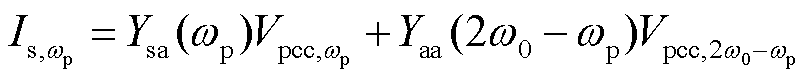（26）
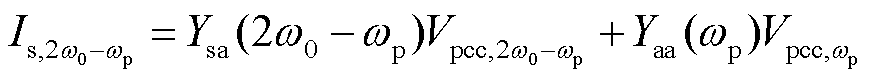（27）
根据式（24）～式（27）可得全功率变速抽水蓄能机组的小信号模型框图如图7所示。
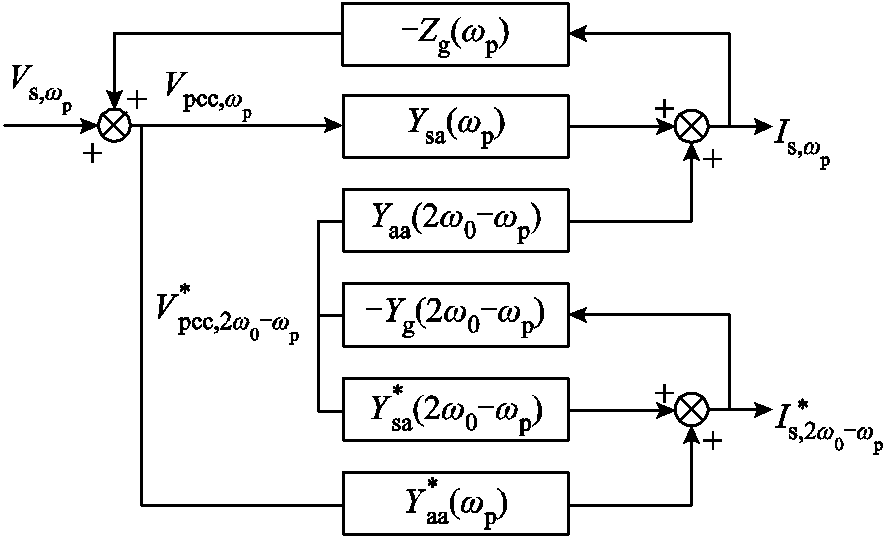
图7 全功率变速抽水蓄能机组小信号模型框图
Fig.7 Block diagram of small signal model for variable-speed pumped storage unit with full-size converter
由图7可推导出机组并网点电流满足
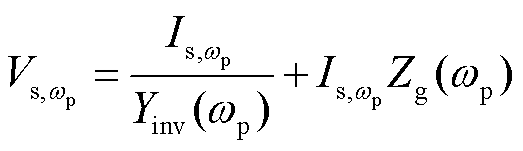（28）
式中，Yinv(wp)为wp频率下机组的等效导纳，表达式为
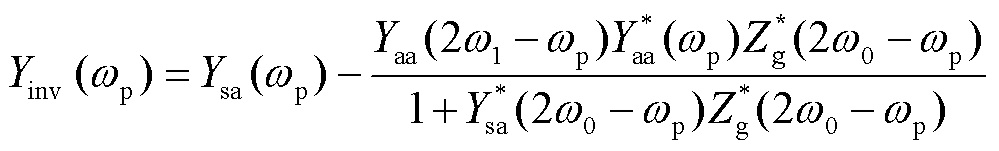（29）
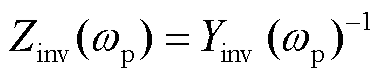（30）
式（29）、式（30）给出了考虑频率耦合影响后的全功率变速抽水蓄能机组的等效导纳（阻抗）模型。
为了验证机组等效阻抗的正确性，在Matlab中搭建了图1所示的全功率变速抽蓄机组并网仿真模型，仿真参数见表1、表2。在抽蓄机组电网侧注入三相小信号扰动电压，对并网电压和并网电流进行快速傅里叶变换（Fast Fourier Transform, FFT）分析，提取并网电压和并网电流wp频率下的分量进行计算，得到等效阻抗。电网电感值Lg设为1.5 mH，其表达式为
表1 水轮机仿真参数
Tab.1 Parameters of hydraulic turbine parameters
参数数值 水头H0/m1 导叶开度Y0(pu)0.725 水的流速U0(pu)0.752 常数At1.036 下垂系数Rp0.05 水锤效应时间常数Tw/s2.67 液压伺服系统增益ka/s10/3 液压伺服系统时间常数Ta/s0.07
表2 全功率变流器仿真参数
Tab.2 Parameters of full-size converter
参数（函数）数值（表达式） 额定功率Sn/MW6 电网电压Vg/kV3 直流母线电压Vdc/kV5.2 滤波电感L/mH2 线路电感Lr/mH2 线路电阻Rr/Ω0.04 直流侧电容Cdc/μF2 000 电网侧电容Cg/μF8 电网侧电阻Rg/Ω0.2 机侧电流控制Hsd(s)9.7+194/s 直流电压控制Hv(s)1.28+11.53/s 网侧电流控制Hgdq(s)23.71+189.68/s 锁相环控制Hpll(s)0.59+96/s
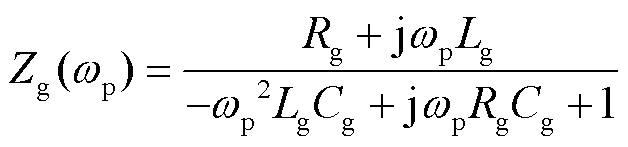（31）
图8为抽蓄机组等效阻抗解析模型与仿真测量结果，蓝色实线为解析模型，红色圆圈为各个频率下的测量结果。由图8可知，等效阻抗仿真测量结果与解析模型吻合度较好，验证了全功率变速抽水蓄能机组阻抗建模的正确性。
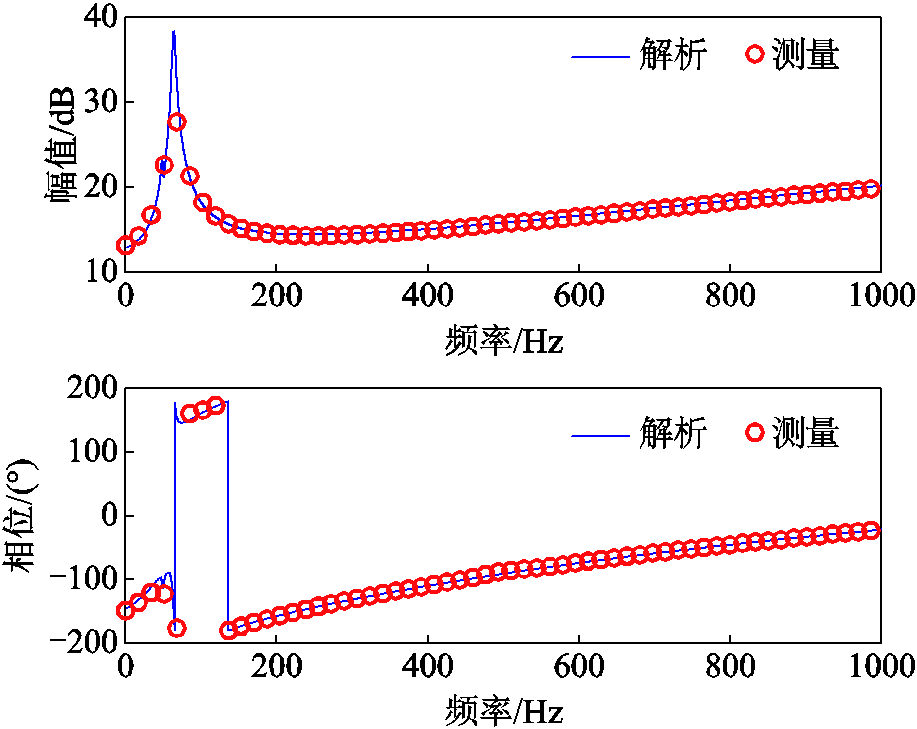
图8 全功率变速抽蓄机组阻抗验证结果
Fig.8 Impedance verification result of the variable-speed pumped storage unit with full-size converter
在第2节已经验证了全功率变速抽水蓄能机组等效阻抗Zinv(wp)的准确性，本节将利用阻抗分析法对抽蓄机组并网系统进行稳定性分析。在阻抗分析法中，系统的开环增益为全功率变速抽蓄机组等效导纳与电网阻抗的乘积Yinv(wp)Zg(wp)。因此利用奈奎斯特判据，分析Yinv(wp)Zg(wp)就可以判断系统的稳定性。
当电网电感值Lg=1.5 mH时，在复平面中画出Yinv(wp)Zg(wp)对应的奈奎斯特曲线，如图9所示。由图可知，奈奎斯特曲线不包围(-1，j0)点，由此判断出此时全功率变速抽蓄机组稳定。仿真中并网电流波形以及FFT分析结果如图10所示，分析结果与仿真验证一致。
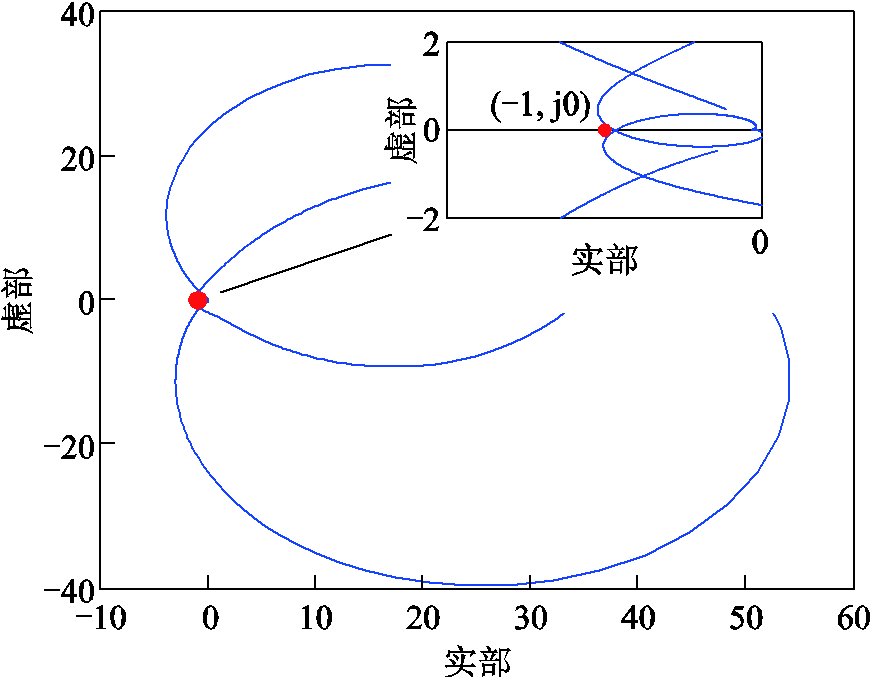
图9 Lg为1.5 mH时对应的奈奎斯特曲线
Fig.9 The corresponding Nyquist curve when Lg=1.5 mH
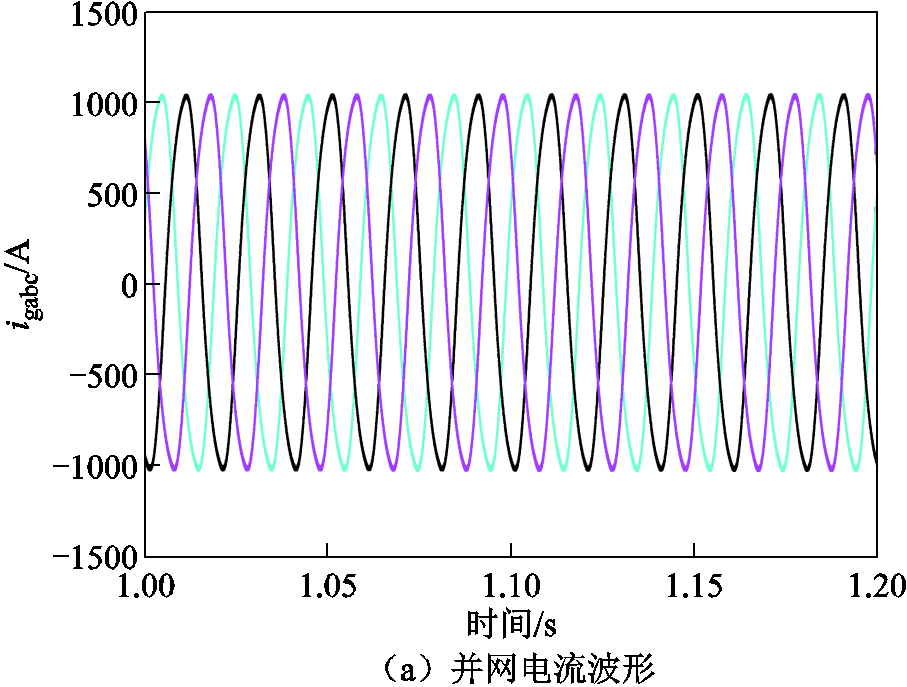
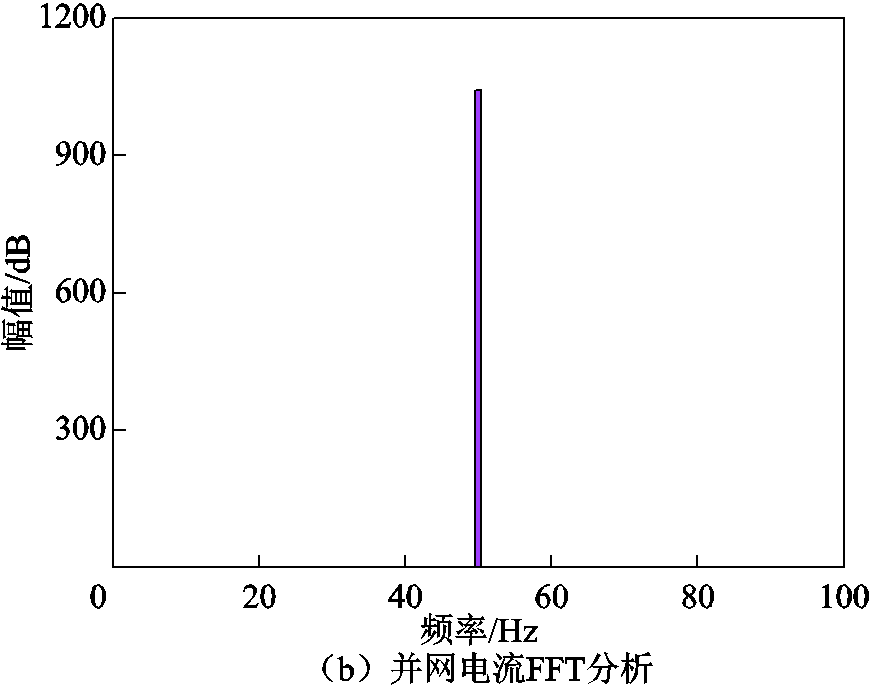
图10 Lg为1.5 mH时对应的并网电流波形及其FFT分析
Fig.10 The corresponding grid connected current waveform and FFT analysis when Lg=1.5 mH
当电网电感为1.8 mH时，Yinv(wp)Zg(wp)对应的奈奎斯特曲线如图11所示。此时奈奎斯特曲线包围(-1，j0)点，说明此时系统不稳定。图12给出了电网电感为1.8 mH时系统的电流波形以及FFT分析结果。由图12可知，此时系统出现了振荡现象，分析结果与仿真结果相吻合。因此随着电网阻抗的增大，系统稳定性变差。
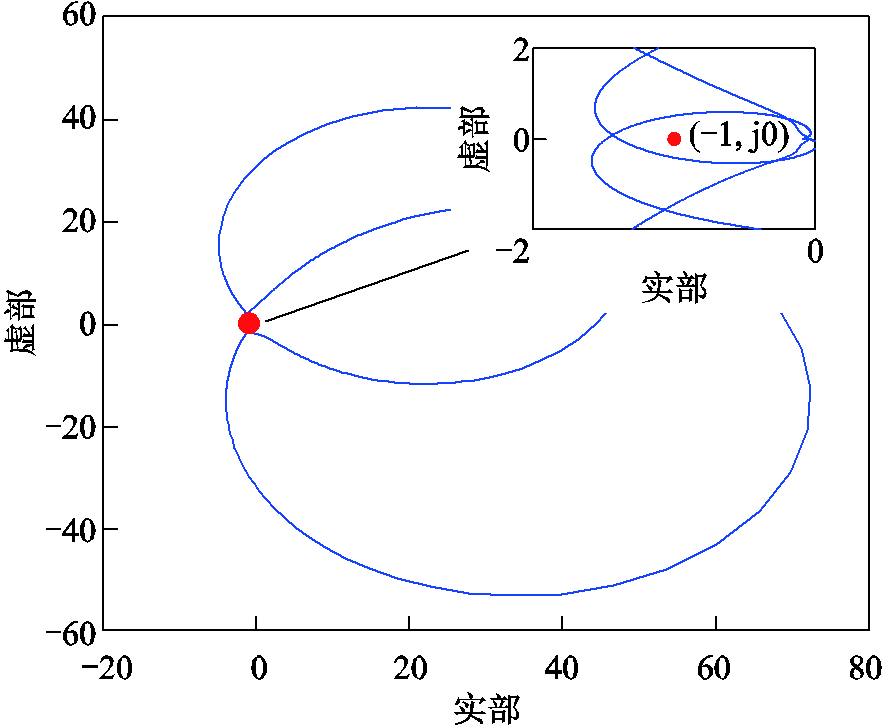
图11 Lg为1.8 mH时对应的奈奎斯特曲线
Fig.11 The corresponding Nyquist curve when Lg=1.8 mH
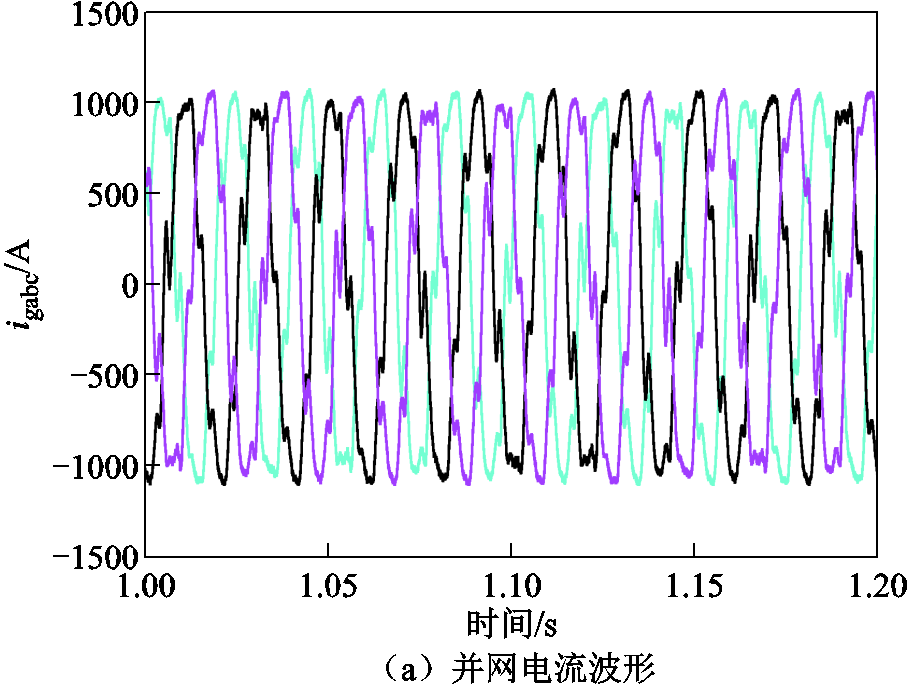
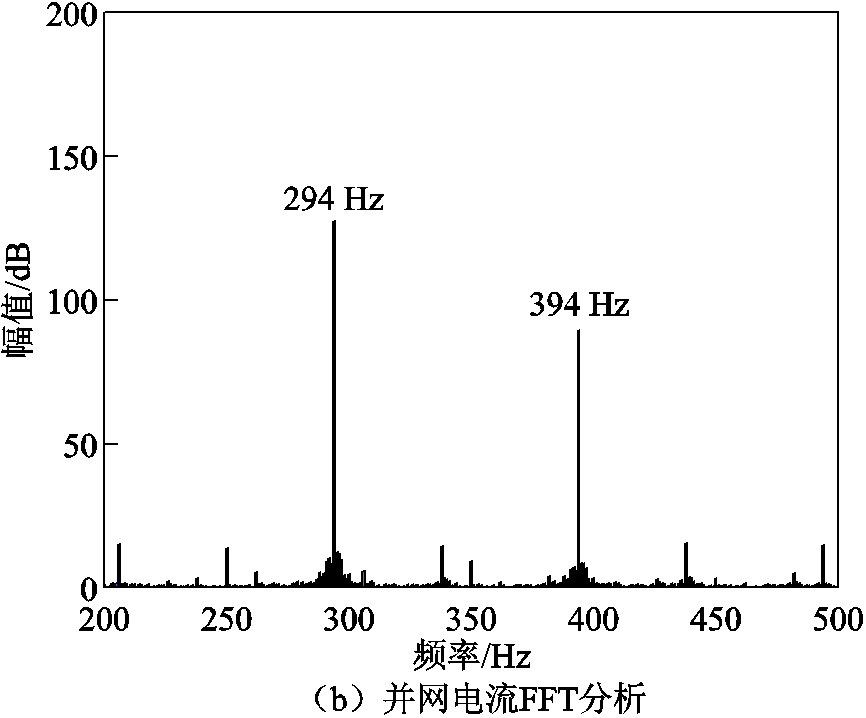
图12 Lg为1.8 mH时对应的并网电流波形及其FFT分析
Fig.12 The corresponding grid connected current waveform and FFT analysis when Lg=1.8 mH
3.2.1 水轮机及调速器关键参数的影响
在本小节中将分析水轮机及调速器关键参数对全功率变速抽蓄系统阻抗特性的影响，主要包括水锤效应时间常数Tw、功率调节下垂系数Rp、液压伺服系统增益系统ka及时间常数Ta对系统阻抗的影响。图13分别给出了对应参数取不同值时所对应的系统阻抗，参数取值以IEEE给出的水轮机控制模型参数[27]为基准。
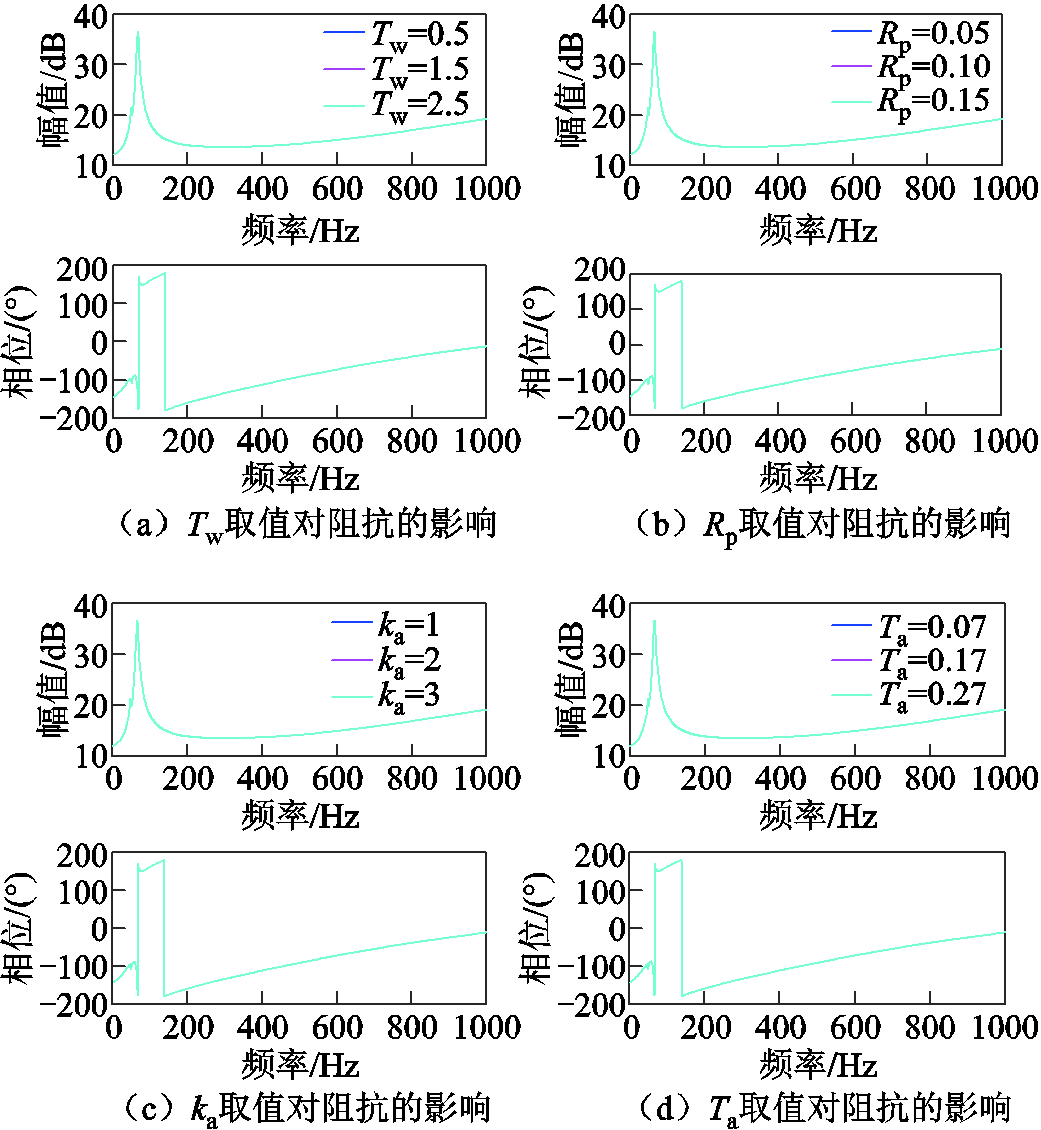
图13 水轮机及调速器关键参数对系统阻抗的影响
Fig.13 Influence of key parameters of hydraulic turbine and governor on system impedance
由图13可知，水轮机以及调速器的关键参数的取值对抽蓄系统的阻抗特性无显著影响，对系统的稳定性影响小。
3.2.2 锁相环的影响
为研究锁相环控制带宽对全功率变速抽蓄机组阻抗特性以及并网稳定性的影响，设置锁相环带宽分别为50、100、200、300 Hz，绘制机组等效阻抗Zinv(wp)与电网阻抗Zg(wp)频率特性曲线，如图14所示。由图14可知，系统锁相环带宽主要影响其高频段的阻抗特性，随着锁相环带宽的增大，高频段阻抗幅值曲线以及相位曲线均降低，导致抽蓄系统在同一电网阻抗下，其等效阻抗与电网阻抗的交点前移，交点处的相位差逐渐增大，系统稳定性变差。因此，为提高抽蓄机组并网系统的稳定性，锁相环带宽设置不宜过大。图15给出了Zinv(wp)与Zg(wp)交点处相位差随锁相环带宽变化的趋势。由图15可知，系统锁相环带宽取253 Hz附近时，二者相位差接近180°，系统近似临界失稳。
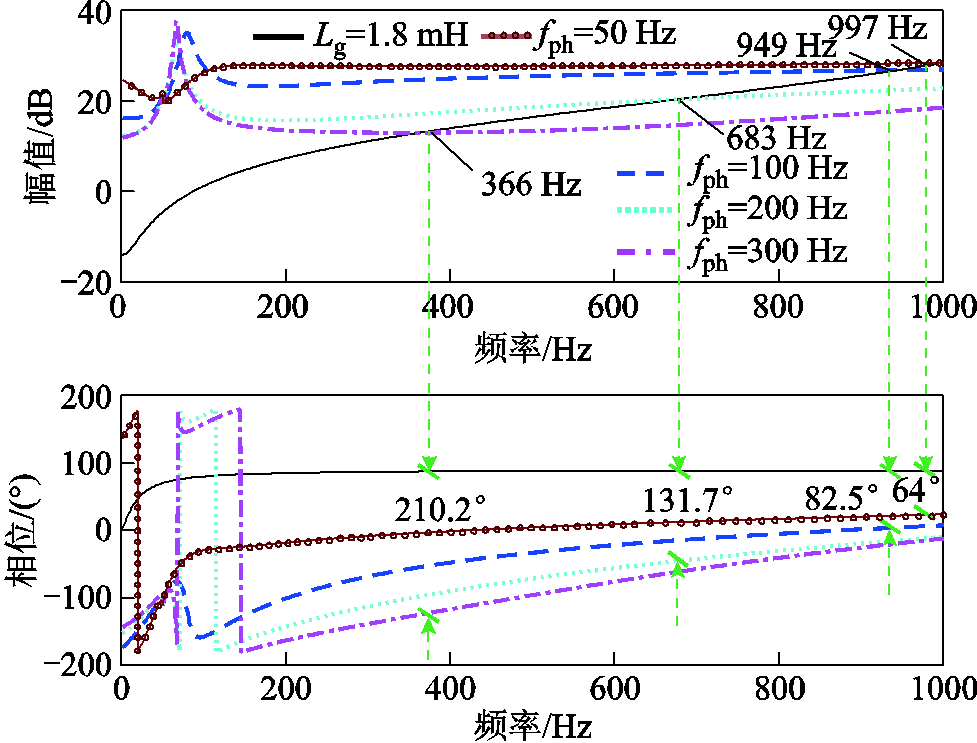
图14 锁相环带宽对系统稳定性的影响
Fig.14 The influence of phase-locked loop bandwidth on system stability
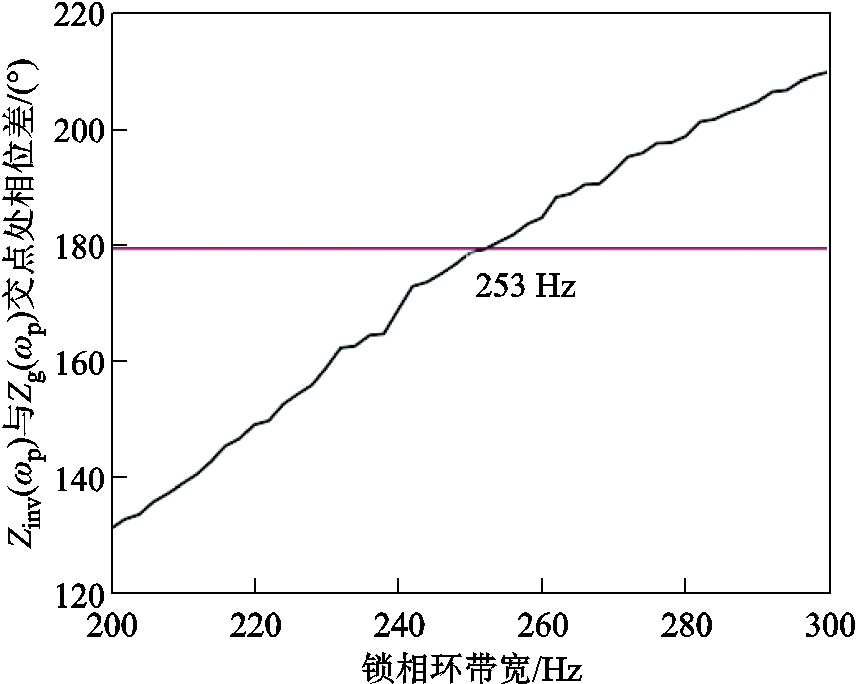
图15 Zinv(wp)与Zg(wp)交点处相位差随锁相环带宽变化趋势图
Fig.15 Trend plot of phase angle difference at the intersection of Zinv(wp) and Zg(wp) with phase-locked loop bandwidth
3.2.3 直流电压环的影响
基于全功率变速抽蓄机组的等效阻抗模型，改变直流电压环带宽分别为20、50、80 Hz，绘制其等效阻抗Zinv(wp)与电网阻抗Zg(wp)的频率特性曲线，如图16所示。由图16可知，直流电压控制环的带宽对系统阻抗特性的影响主要集中在110 Hz以下频段，对高频段的阻抗特性影响甚微。在同一电网阻抗条件下，并没有改变系统的稳定性分析结果。
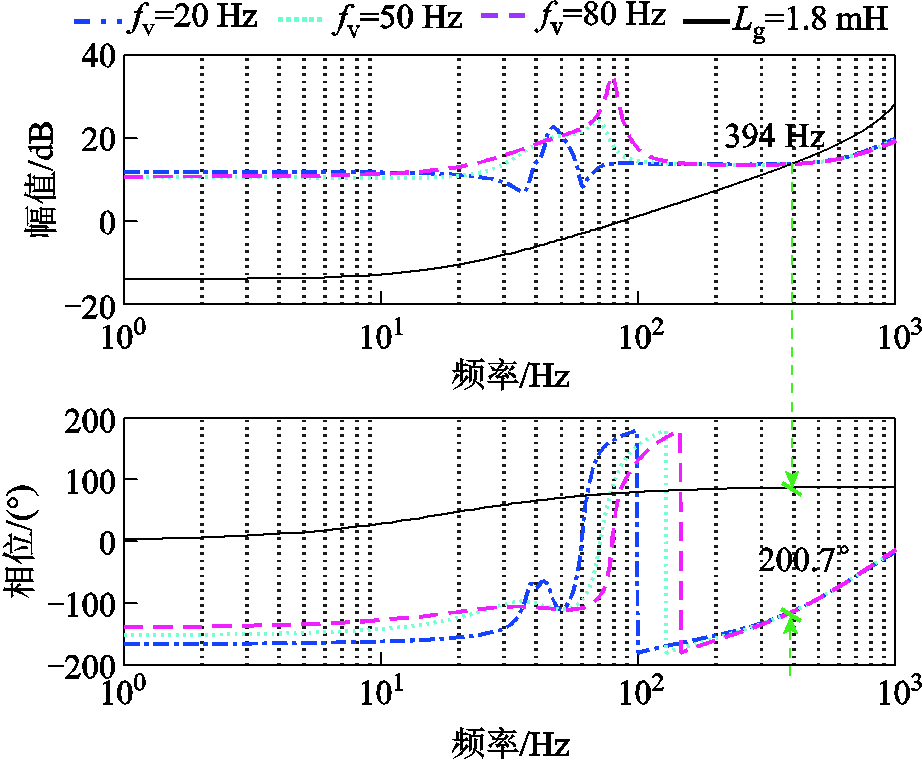
图16 直流电压环带宽对系统稳定性的影响
Fig.16 The influence of DC voltage loop bandwidth on system stability
3.2.4 网侧电流环的影响
设置网侧电流控制环的带宽分别为500、800、1000 Hz，绘制全功率变速抽蓄机组并网系统的等效阻抗Zinv(wp)与电网阻抗Zg(wp)的频率特性曲线，如图17所示。由图17可知，电流控制环的带宽对系统等效阻抗的幅值曲线影响较小，对其在高频段的相位曲线有较大的影响。具体而言，随着电流环带宽的增大，Zinv(wp)与Zg(wp)交点频率分别为401、370、368 Hz，各交点处对应的相位差分别是123.5°、166°、180.3°。由此可以看出电流控制环带宽的增大会导致抽蓄机组并网系统稳定裕度的减小，稳定性变差。且当网侧电流环带宽接近1 000 Hz时，系统接近临界失稳。
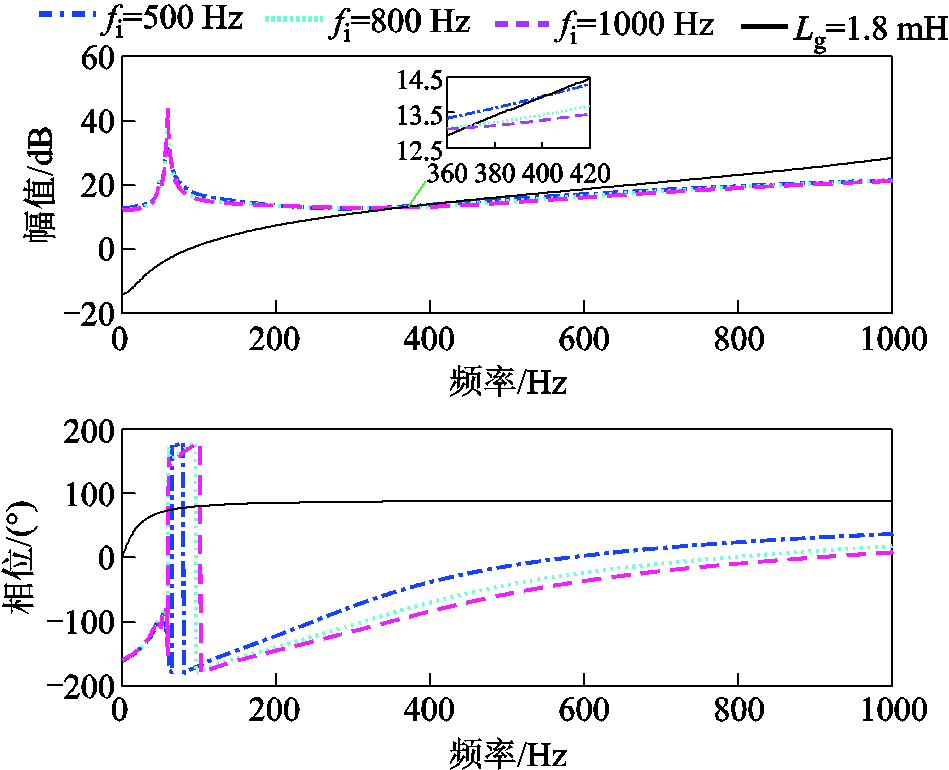
图17 网侧电流环带宽对系统稳定性的影响
Fig.17 The influence of grid-side current loop bandwidth on system stability
综上所述，水轮机和调速器关键参数对系统稳定性影响甚微。在同一电网强度下，锁相环以及电流环的带宽对系统稳定性影响较大，直流电压环带宽对其稳定性影响较小。因此适当减小锁相环以及电流控制环的带宽有利于提高全功率变速抽水蓄能机组的稳定性。
本文建立了全功率变速抽水蓄能机组的阻抗模型，所建立的阻抗模型描述了水轮机及调速系统、直流母线、频率耦合、控制环节等动态特性，同时通过扫频的方式验证了所建模型的准确性。进一步，基于等效阻抗模型对机组的并网稳定性进行了分析。本研究得出以下结论：
1）传统控制方式下的全功率抽水蓄能机组接入电网，随着电网阻抗的增大，稳定性变差。
2）在同一电网强度下，水电侧关键参数对机组阻抗特性以及并网稳定性无显著影响。
3）直流电压环带宽对机组稳定性影响较小，而锁相环及电流环带宽的增大会造成机组稳定性变差。
最后，本文研究结果可以为全功率变速抽水蓄能机组与新能源联合系统稳定性分析提供模型基础，对机组参数设计提供一定的指导意义。
参考文献
[1] 孔令国, 王嘉祺, 韩子娇, 等. 基于权重调节模型预测控制的风-光-储-氢耦合系统在线功率调控[J]. 电工技术学报, 2023, 38(15): 4192-4207. Kong Lingguo, Wang Jiaqi, Han Zijiao, et al. On-line power regulation of wind-photovoltaic-storage-hydrogen coupling system based on weight adjustment model predictive control[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4192-4207.
[2] 张海波, 胡玉康, 李正荣, 等. 负荷高密度地区中计及灵活性不足风险的储能优化配置[J]. 电网技术, 2023, 47(12): 4926-4940. Zhang Haibo, Hu Yukang, Li Zhengrong, et al. Optimal configuration of energy storage considering the risk of insufficient flexibility in high load density areas[J]. Power System Technology, 2023, 47(12): 4926-4940.
[3] 刘畅, 卓建坤, 赵东明, 等. 利用储能系统实现可再生能源微电网灵活安全运行的研究综述[J]. 中国电机工程学报, 2020, 40(1): 1-18, 369. Liu Chang, Zhuo Jiankun, Zhao Dongming, et al. A review on the utilization of energy storage system for the flexible and safe operation of renewable energy microgrids[J]. Proceedings of the CSEE, 2020, 40(1): 1-18, 369.
[4] 张怡静, 李智, 时艳强, 等. 基于储能惯量支撑的受端电网频率优化控制方法[J]. 电工技术学报, 2024, 39(11): 3556-3568. Zhang Yijing, Li Zhi, Shi Yanqiang, et al. Optimal frequency control method of receiving power grid based on energy storage inertia support[J]. Transactions ofChina Electrotechnical Society, 2024, 39(11): 3556-3568.
[5] 石梦舒, 许小峰, 张继广, 等.考虑电-氢市场的虚拟电厂两阶段优化策略研究[J]. 发电技术, 2023, 44(5): 645-655. Shi Mengshu, Xu Xiaofeng, Zhang Jiguang, et al. A two-stage optimization strategy for virtual power plants considering the electricity-hydrogen market[J]. Power Generation Technology, 2023, 44(5): 645-655.
[6] Chen Yahong, Xu Wei, Liu Yi, et al. Modeling and transient response analysis of doubly-fed variable speed pumped storage unit in pumping mode[J]. IEEE Transactions on Industrial Electronics, 2023, 70(10): 9935-9947.
[7] 庄凯勋, 孙建军, 丁理杰, 等. 提升双馈变速抽水蓄能机组频率响应特性的控制策略[J]. 电工技术学报, 2023, 38(23): 6292-6304. Chuang Kaihsun, Sun Jianjun, Ding Lijie, et al. A control strategy with improved frequency response characteristics of variable speed DFIM pumped storage[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6292-6304.
[8] 吴洋, 苏承国, 郭超雨, 等. 考虑风电出力不确定性的风电-抽水蓄能互补系统短期优化调度[J]. 可再生能源, 2023, 41(9): 1222-1231. Wu Yang, Su Chengguo, Guo Chaoyu, et al. Short-term optimal scheduling of wind farms and pumped-storage hydropower plant complementary system considering wind power output uncertainty[J]. Renewable Energy Resources, 2023, 41(9): 1222-1231.
[9] 欧阳晨曦, 赵志高, 李旭东, 等. 海水可变速抽水蓄能与风电联合运行优化研究[J]. 水利水电快报, 2023, 44(5): 65-72. Ouyang Chenxi, Zhao Zhigao, Li Xudong, et al. Operation optimization of combined system of seawater pumped storage with variable-speed units and wind power[J]. Express Water Resources & Hydropower Information, 2023, 44(5): 65-72.
[10] 文劲宇, 周博, 魏利屾. 中国未来电力系统储电网初探[J]. 电力系统保护与控制, 2022, 50(7): 1-10. Wen Jinyu, Zhou Bo, Wei Lishen. Preliminary study on an energy storage grid for future power system in China[J]. Power System Protection and Control, 2022, 50(7): 1-10.
[11] 李辉, 黄樟坚, 刘海涛, 等. 交流励磁抽水蓄能机组快速功率响应控制策略[J]. 电力自动化设备, 2017, 37(11): 156-161, 175. Li Hui, Huang Zhangjian, Liu Haitao, et al. Control strategy of rapid power response for AC excited pump storage unit[J]. Electric Power Automation Equipment, 2017, 37(11): 156-161, 175.
[12] 徐斌, 金龙云, 熊健, 等. 抽水蓄能电站全功率变频控制策略[J]. 电力电子技术, 2020, 54(7): 33-35. Xu Bin, Jin Longyun, Xiong Jian, et al. Control strategy of full power variable in pumping storage power station[J]. Power Electronics, 2020, 54(7): 33-35.
[13] 李文锋, 张健, 卜广全, 等. 抽蓄电站和经多端柔性直流电网接入的大规模新能源间的协调互补优化控制方案[J]. 电力系统保护与控制, 2017, 45(23): 130-135. Li Wenfeng, Zhang Jian, Bu Guangquan, et al. A coordinate complementary optimization control scheme between pumped storage station and large-scale new renewable integrated through VSC-MTDC[J]. Power System Protection and Control, 2017, 45(23): 130-135.
[14] 衣传宝, 梁廷婷, 汪卫平, 等. 全功率变速抽水蓄能机组无功优先控制策略研究[J]. 电力电容器与无功补偿, 2021, 42(1): 25-31. Yi Chuanbao, Liang Tingting, Wang Weiping, et al. Study on reactive power priority control strategy of variable speed pumped storage unit with full-sized converter[J]. Power Capacitor & Reactive Power Compensation, 2021, 42(1): 25-31.
[15] 王廷涛, 苗世洪, 姚福星, 等. 计及频率电压稳定性约束的电力系统多层级储能协同优化运行策略[J]. 电工技术学报, 2024, 39(21): 6759-6777. Wang Tingtao, Miao Shihong, Yao Fuxing, et al. Multi-level energy storage collaborative optimization operation strategy for power systems considering frequency and voltage stability constraints[J]. Tran-sactions of China Electrotechnical Society, 2024, 39(21): 6759-6777.
[16] 朱珠, 潘文霞, 刘铜锤, 等. 变速抽蓄机组频率响应机理模型与性能研究[J]. 电网技术, 2023, 47(2): 463-474. Zhu Zhu, Pan Wenxia, Liu Tongchui, et al. Frequency response mechanism modeling and performance analysis of adjustable-speed pumped storage unit[J]. Power System Technology, 2023, 47(2): 463-474.
[17] 陈超, 汪卫平, 刘海滨, 等. 全功率变速抽水蓄能机组用于提升电网频率稳定性控制策略研究[J]. 水电与抽水蓄能, 2020, 6(5): 68-72. Chen Chao, Wang Weiping, Liu Haibin, et al. Study on the control strategy of FSC-VSPS for improving the frequency stability of power grid[J]. Hydropower and Pumped Storage, 2020, 6(5): 68-72.
[18] Jha P K, Prajapat G P, Bansal S K, et al. Mode identification and small signal stability analysis of variable speed wind power systems[C]//2020 International Conference on Power Electronics & IoT Applications in Renewable Energy and its Control (PARC), Mathura, India, 2020: 286-291.
[19] 王方洲, 谭甜源, 刘开培, 等. 可变速抽蓄机组与直驱风电机组联合运行系统的小信号稳定分析[J]. 电力自动化设备, 2021, 41(7): 65-72. Wang Fangzhou, Tan Tianyuan, Liu Kaipei, et al. Small-signal stability analysis of combined operation system of variable-speed pumped storage unit and direct-drive wind turbine unit[J]. Electric Power Automation Equipment, 2021, 41(7): 65-72.
[20] 史华勃, 王渝红, 滕予非, 等. 全功率变速抽水蓄能机组快速功率模式小信号建模[J]. 电力系统自动化, 2022, 46(4): 162-169. Shi Huabo, Wang Yuhong, Teng Yufei, et al. Small signal modeling of variable-speed pumped storage unit with full-size converter in fast-power mode[J]. Automation of Electric Power Systems, 2022, 46(4): 162-169.
[21] 程佩芬, 李崇涛, 傅闯, 等. 基于状态空间法的高压直流输电系统电磁暂态简化模型的解析算法[J]. 电工技术学报, 2019, 34(6): 1230-1239. Cheng Peifen, Li Chongtao, Fu Chuang, et al. An analytic solution for simplified electromagnetic transient model of HVDC transmission system based on state space method[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1230-1239.
[22] 刘欣, 郭志博, 贾焦心, 等. 基于序阻抗的虚拟同步发电机并网稳定性分析及虚拟阻抗设计[J]. 电工技术学报, 2023, 38(15): 4130-4146. Liu Xin, Guo Zhibo, Jia Jiaoxin, et al. Stability analysis and virtual impedance design of virtual synchronous machine based on sequence impedance[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4130-4146.
[23] 刘俊良, 杜雄, 管勃, 等. 变工作点下的逆变器并网系统建模与稳定性分析[J]. 电网技术, 2022, 46(9): 3642-3650. Liu Junliang, Du Xiong, Guan Bo, et al. Impedance modeling and stability analysis for grid-connected inverter containing operating point variables[J]. Power System Technology, 2022, 46(9): 3642-3650.
[24] 王国宁, 杜雄, 邹小明, 等. 用于三相并网逆变器稳定性分析的自导纳和伴随导纳建模[J]. 中国电机工程学报, 2017, 37(14): 3973-3981, 4275. Wang Guoning, Du Xiong, Zou Xiaoming, et al. Self and accompanying admittance model for three-phase grid-tied inverter stability analysis[J]. Proceedings of the CSEE, 2017, 37(14): 3973-3981, 4275.
[25] 杜程茂, 杜雄, 苏婧媛, 等. 定子电流控制的双馈风机导纳建模与次同步振荡风险分析[J]. 电力系统自动化, 2023, 47(13): 159-167. Du Chengmao, Du Xiong, Su Jingyuan, et al. Admittance modeling and subsynchronous oscillation risk analysis of DFIG-based wind turbine with stator current control[J]. Automation of Electric Power Systems, 2023, 47(13): 159-167.
[26] Vieto I, Du Xiong, Nian Heng, et al. Frequency-domain coupling in two-level VSC small-signal dynamics[C]//2017 IEEE 18th Workshop on Control and Modeling for Power Electronics (COMPEL), Stanford, CA, USA, 2017: 1-8.
[27] Working Group Prime Mover and Energy Supply. Hydraulic turbine and turbine control models for system dynamic studies[J]. IEEE Transactions on Power Systems, 1992, 7(1): 167-179.
Abstract In the existing energy storage system, pumped storage units have the advantages of large capacity, flexible operation, rapid start and stop, etc., and play an important role in the peak frequency regulation of the power system, and pumped storage units and wind power, photovoltaic power generation, etc. with the use of the power system can promote the new energy consumption level. However, the complex frequency domain characteristics presented by the multi-timescale control of the power electronic devices are prone to interacting with the power grid and triggering the oscillation phenomenon. Currently, there are relatively few studies on impedance modeling of the variable-speed pumped storage unit with full-size converter and their stability analysis based on impedance criterion. The impedance modeling of the variable-speed pumped storage unit with full-size converter and its analysis are of great significance for the future stability analysis of large-scale pumped storage units connected to the power grid. Therefore, this paper establishes an impedance model of the variable-speed pumped storage unit with full-size converter taking into account the frequency coupling effect, and analyzes the stability of the grid-connected system of the pumped storage unit based on the impedance model.
In the process of establishing the equivalent impedance model of the variable-speed pumped storage unit with full-size converter, the state-space model of the hydraulic turbine and the synchronous motor are firstly established, and the impedance model in the dq coordinate system is obtained on the basis of the model. After that, the impedance models of the machine-side converter and the grid-side converter are established respectively, and finally the equivalent impedance model of the variable-speed pumped storage unit with full-size converter considering the frequency coupling effect is established taking into account the effect of the grid impedance.
Further, the correctness of the impedance model of the variable-speed pumped storage unit with full-size converter was verified using the frequency scanning method. Based on the established impedance model, the grid-connected stability of the pumped storage unit under different grid impedance conditions is investigated by using Nyquist stability criterion. And the effects of key turbine and governor parameters as well as common control loop parameters such as phase-locked loop, DC voltage outer loop and current loop parameters of the full-power converter on the impedance characteristics of the unit as well as on the grid-connected stability are also investigated.
This study draws the following conclusions: (1) A more accurate equivalent impedance model of the variable-speed pumped storage unit with full-size converter that takes into account the frequency coupling effect is established. (2) As the grid impedance increases, i.e., the grid strength becomes weaker, the stability of the unit deteriorates. (3) Under the same grid strength, the bandwidths of the phase-locked loop and the current loop have a greater impact on the system stability, while the bandwidth of the DC voltage loop has a smaller impact on its stability.In addition, the values of the key parameters of the turbine as well as the governor have no significant effect on the impedance characteristics of the unit and very little effect on the stability of the system.
keywords：The variable-speed pumped storage unit with full-size converter, impedance modeling, frequency coupling, stability analysis
DOI: 10.19595/j.cnki.1000-6753.tces.241060
中图分类号：TM312; TM46
国家电网公司总部科技资助项目（5108-202218280A-2-282-XG）。
收稿日期 2024-06-18
改稿日期 2024-08-15
张 琦 男，1995年生，博士研究生，研究方向为新能源并网系统稳定性分析。E-mail：zhangqi@stu.cqu.edu.cn
杜 雄 男，1979年生，教授，博士生导师，研究方向为新能源并网系统稳定性、电力电子装备可靠性和直流输电系统稳定性。E-mail：duxiong@cqu.edu.cn（通信作者）
（编辑 赫 蕾）