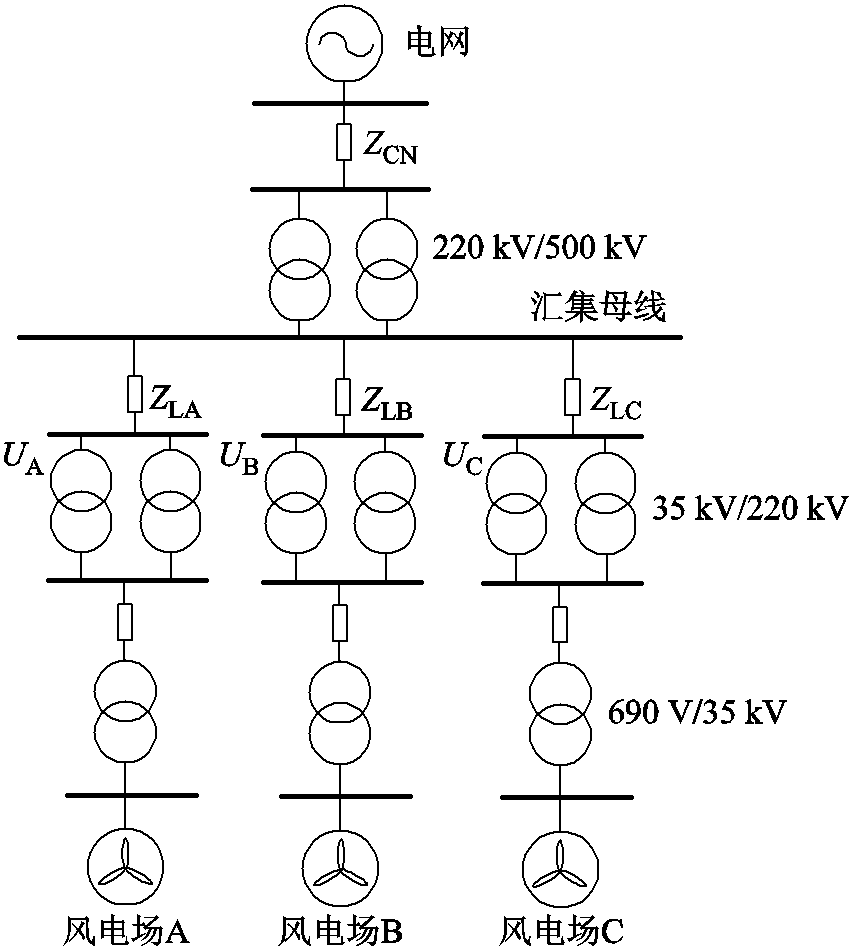
图1 风电场典型拓扑结构
Fig.1 Typical topology of wind farm
摘要 在省调两级电压控制架构下，风电集群中各风电场自动电压控制（AVC）子站在相互间没有通信的情况下独立进行电压控制，导致调节快的风电场无功出力多，调节慢的风电场无功出力少。该文首先分析风电场AVC子站无功调节周期和调节步长对风电场并网点电压控制的影响；然后提出了基于“变步长扰动观测”的风电场AVC子站电压控制策略，通过评估其他风电场电压控制对该风电场并网点电压的影响，动态调节AVC子站无功调节步长，提高风电场电压调节速度；之后，在变步长控制的基础上，考虑风电场无功出力约束，兼顾电压调节速度和风电集群无功功率均衡；最后搭建风电场汇集系统，验证所提策略的有效性。
关键词：自动电压控制（AVC）子站 无功电压控制 变步长 扰动观测 无功约束
为响应“双碳”目标，我国风电规模增长迅速，截至2023年12月底，我国风电装机容量约4.4亿kW，同比增长20.7%[1]。
我国大规模风力发电多采用集中开发方式，并以风电场群形式汇集接入电网[2]。随着风电容量日益增长，大规模风电的集群接入给电网的安全稳定运行造成的威胁也越来越明显[3]。目前，国内外已实现的大电网自动电压控制系统从体系结构上可以分为两类：一类是调度控制中心以协调全网安全性和经济性为目标进行统一决策的三级电压控制模式；另一类是省级调度控制中心从全局层面进行统一决策，控制方案直接下发到控制设备的两级电压控制模式[4]。针对两级电压控制模式，上级调度控制中心直接将电压指令值下发至各风电场的自动电压控制（Automatic Voltage Control, AVC）子站，各风电场AVC独立运行，相互之间无法通信；各风电场AVC子站只能获取本场站的运行数据，无法通过AVC主站进行高效精确的无功调配，使得风电集群电压调节效率低下[5]。另外，当风电场电气距离较近时，风电集群中的各风电场站之间电压耦合明显，电压调节交叉影响显著，给风电集群的电压控制带来了新的挑战[6]。
风电场广泛采用变速恒频风电机组，风电机组作为无功电源参与风电场电压控制已是常态。由于能量管理平台及风电机组的响应时间不同，风电场的电压调节响应速度也不尽相同[7]。在实际运行中响应速度更快的个别风电场将承担更多的无功调节任务，其他响应速度更慢的风电场调节量将更少，导致无功出力不均衡，造成了无功调节能力的浪费[8-9]。
为解决无功不均衡问题，文献[9]以风电场群汇集母线的电压控制为目标，分析了电压指令计算方式和无功调节周期对无功功率均衡性的影响，在此基础上建立了考虑无功均衡性的电压协调优化模型，并提出了改进的无功电压协调控制策略，有效地改善了无功功率的不均衡。文献[10]针对光伏逆变器传统下垂曲线在无功出力自适应性和均衡度方面的不足，提出了一种基于近似电压灵敏度的有源配电网改进下垂曲线无功控制策略，能更好地适应有源配电网的电压控制需求。文献[11]利用虚拟阻抗进行无功功率的反馈，实现了无功功率的精准分配，另外又对传统的下垂控制策略进行改进，有效地抑制了无功环流，但该策略主要是解决多并联逆变器间的环流问题。文献[12]通过分析新能源系统中无功环流产生的原因，在满足电压指标的前提下，对新能源无功出力进行重新分配，从而抑制无功环流。文献[13]提出可变下垂系数改进电压控制策略，同时建立了电网-风电场双层无功优化模型，并以各类损耗和无功不均衡度最小为目标进行求解，以确定各台风机无功出力。但以上研究均是在调度层面通过无功功率控制实现无功均衡的，未能考虑以电压为控制目标的风电场AVC子站的无功功率均衡控制。
国内外学者在风电集群接入区域电压控制方面也开展了较多研究。文献[14]针对有新能源接入的耦合系统中的电压调控问题，基于模型预测控制方法和交替方向乘子法建立网损优化与电压校正双模式自适应切换的滚动时域控制策略，实现了耦合系统的分布式协同电压控制。文献[15]提出了考虑构网型储能电站辅助治理的无功协调优化控制策略，有效地提高了新能源基地安全稳定水平。文献[16]利用模型预测的思想先将多逆变器间的无功电压关系等效为标准预测模型，再利用辅助鲁棒状态反馈控制器将各逆变器间的电压关系进行解耦，从而实现对无功源出力的精确分配，但该方法适用于弱连接电网，较难适用于风电场站间的电压强耦合场景。文献[17]针对大型海上风电系统提出了一种基于一致性控制和中央模型预测控制的混合控制方法，在保证控制系统稳定性的情况下，有效地提升了风电集群汇集母线出口电压质量。为实现无功设备的协调控制，文献[18-19]均采用强化学习的方法进行无功电压优化控制，其中文献[18]侧重于采用多时间尺度的方式统筹考虑无功设备之间的调节差异性，文献[19]侧重于将强化学习进行简化和改进，从而提升各无功设备之间的协同控制效果。文献[20-21]针对风电场群控制周期内有功出力波动对节点电压的影响，提出无功电压分层优化控制策略，减少了场群的电压波动和网损。文献[5, 22]针对风电出力和系统潮流频繁波动的场景，提出了适应频繁多变潮流的无功-电压控制鲁棒分区方法。文献[23]在风机和无功设备的小干扰模型的基础上，分析了AVC无功分配方案对风电场稳定性的影响。文献[24]提出一种基于非线性仿射的风电场电压实时计算和优化方法，能够快速获得系统实时电压状态且有效地防止机端电压越限并减小并网电压波动。但上述研究均未考虑风电集群中各风电场电压调节速度的影响，以及风电场之间没有通信且相互之间电压强耦合的情况下风电场AVC子站的协同控制问题。
针对以上问题，本文在省调二级电压控制模式下，首先分析风电场集群中各场站调节速度对风电场并网点电压控制的影响；为提高风电场AVC子站的电压调节速度，提出了基于“变步长扰动观测法”的风电场AVC子站电压控制策略，AVC先调节风电场输出无功功率，然后测量并网点电压，通过并网点测量电压估计其他场站的运行状态，进而动态调整AVC下次无功调节步长，提升电压调节速度；在此基础上提出考虑无功出力约束的风电场群电压控制策略，在保证电压调节速度的情况下，改善无功不均衡问题。
风电场典型拓扑结构如图1所示。大规模风电集群一般采用放射式接入（如图1中风电场A、B、C所示），运行时无功功率通常由风电场流向电网，补偿沿线无功功率损耗。
图1 风电场典型拓扑结构
Fig.1 Typical topology of wind farm
在省调两级电压控制模式下，上级调度AVC主站下发电压指令至各风电场AVC子站，各场站根据电压偏差和电压无功灵敏度计算无功功率调节量，从而调整风电场内部的无功电源出力，使得风电场并网点电压进入目标电压死区。
以风电场i为例，场站AVC子站测量并网点电压Ui，根据电压指令Uref和电压无功灵敏度Sii，计算无功补偿量ΔQi，即
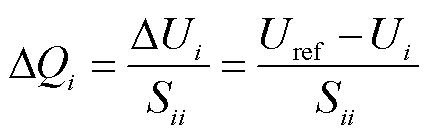（1）
式中，ΔUi为风电场i并网点电压与目标电压的差值。
风电集群中各风电场站间电压调节存在交叉影响，某一场站并网点的电压不仅受本场站输出无功功率的影响，而且也受其他场站输出无功功率的影响。以图1所示风电系统为例，该集群中有三个风电场A、B和C，则A场站的电压变化量可表示为
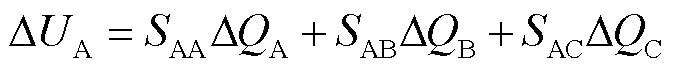（2）
式中，SAB、SAC分别为AB、AC场站之间的电压无功灵敏度；ΔQA、ΔQB、ΔQC分别为风电场A、B、C的无功功率调节量。
因此在场站i的电压调节过程中，由式（1）计算所得的无功补偿量不能直接全部下发至无功电源，通常 AVC子站将计算得到的无功补偿量ΔQi乘以无功调节系数K再下发至无功电源，则每次下发的无功调节量ΔQi1可表示为
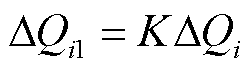（3）
一般地，当风电集群中各风电场容量相同时，无功调节系数K取为
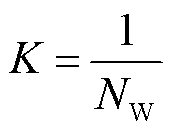（4）
式中，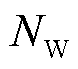
为接入同一汇集母线的风电场数目。
为衡量风电集群的无功不均衡程度，本文定义在t时刻风电集群的无功不均衡系数为
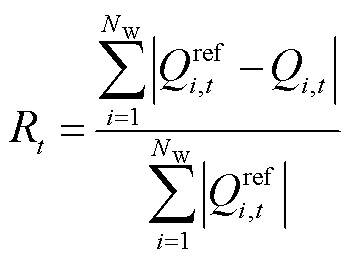（5）
式中，Qi,t为t时刻风电场i的实际无功功率出力；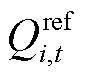
为t时刻风电场i无功功率出力参考值。在同一风电集群中，Rt越小，无功功率越均衡。
由于风电场调节周期由能量管理平台响应时间和调压设备响应速度决定，导致各风电场站无功功率调节周期不同的原因有：
（1）随着风电技术的发展，风电集群中风电场数目逐渐增多，单个风电场容量逐渐增大，当风电机组参与无功调压时，各风电场能量管理平台进行风电场内机组无功出力分配所花费的时间很难统一。
（2）由于风电场的调压设备不同，不同调压设备的响应速度差别较大。
以上情况在风电场集中接入电网时很难规避。在电压控制过程中，风电场调节周期对并网点电压的控制具有明显影响，调节周期不同会使得各风电场电压调节出现相互竞争的现象。以图1的三个风电场为例，假定各场站接收的电压指令相同，风电场A、B调节快，风电场C调节慢。各风电场电压变化量和无功变化量的关系可表示为
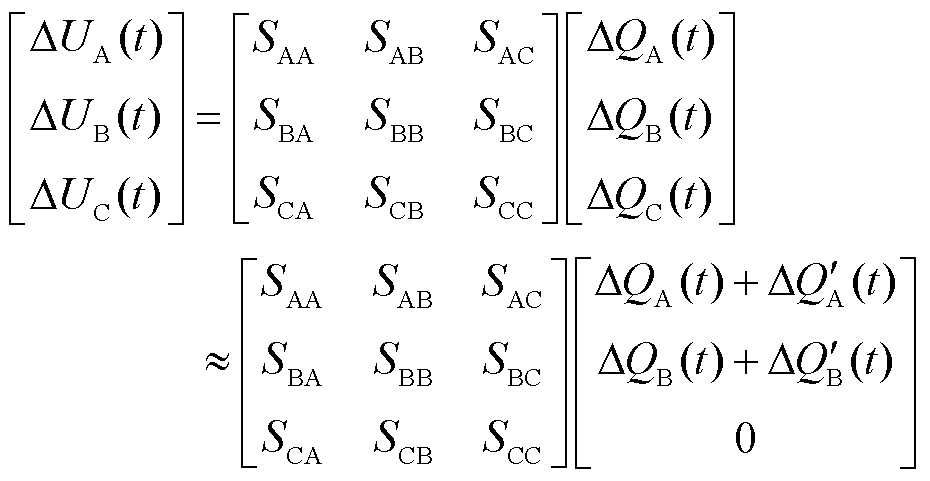（6）
由式（6）可知，在实际运行中，无功调节周期短的风电场站将会明显承担更多的无功调节任务，甚至出现风电场A、B的无功功率流入风电场C中，导致无功分担的不均衡，造成无功调节能力的浪费。同时将会引起变压器过热、线路损耗增加，甚至出现保护整定困难，对风电接入区域的电压稳定性造成不利的影响[12]。
针对各风电场调节周期存在差异的情况，AVC子站在进行电压控制时，为缓解各风电场无功出力的不均衡程度，对于计算所得的无功功率多采用“小步长，多轮次”的方法进行调节。本文首先提出调节周期修正系数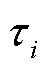
，即
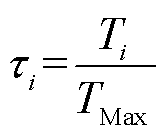（7）
式中，Ti为风电场i的无功调节周期；TMax为接入同一汇集母线风电场的最大无功电压调节周期。
根据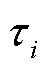对无功调节系数
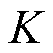进行修正，修正式为
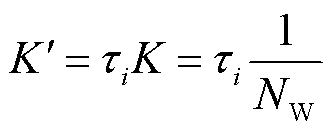（8）
以图1所示的拓扑结构为例进行仿真分析。假定风电场A、B、C内部无功调节周期分别为10、15、20 s；风电场A、B、C的运行状况以及到汇集母线的电气距离完全相同，风电场到汇集母线的线路阻抗见附表1。各风电场AVC子站在0、5、10 min收到的风电场接入点电压参考值分别为1.02(pu)、1.04(pu)、1.06(pu)，电压调节死区为电压参考值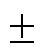 
0.002(pu)，风电场工作于电压指令追踪模式。设置两种场景分别分析无功-电压控制效果。
场景1：风电场A、B、C不考虑调节周期的影响，无功调节系数均为1/3。
场景2：考虑调节周期修正系数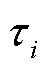，风电场A、B、C无功调节系数分别为1/6、1/4、1/3。
两种场景下，风电场A的并网点电压、三个风电场无功功率及无功不均衡度分别如图2、图3和图4所示。由图2可以看出，两种场景下风电场A并网点电压均能在1 min之内进入死区。两种场景下各风电场的无功出力分别如图3a和图3b所示，由图可知，调节速度快的风电场A无功调节次数多于风电场B、C，而且风电场A的无功调节量明显大于风电场B和C。由图3b和图4可见，考虑了无功调节周期修正系数后，三个场站的无功功率不均衡程度较场景1得到很大改善。同时根据图3a和图3b可知，场景2各场站无功调节次数也比场景1明显增多，风电场并网点电压进入死区时间延长。
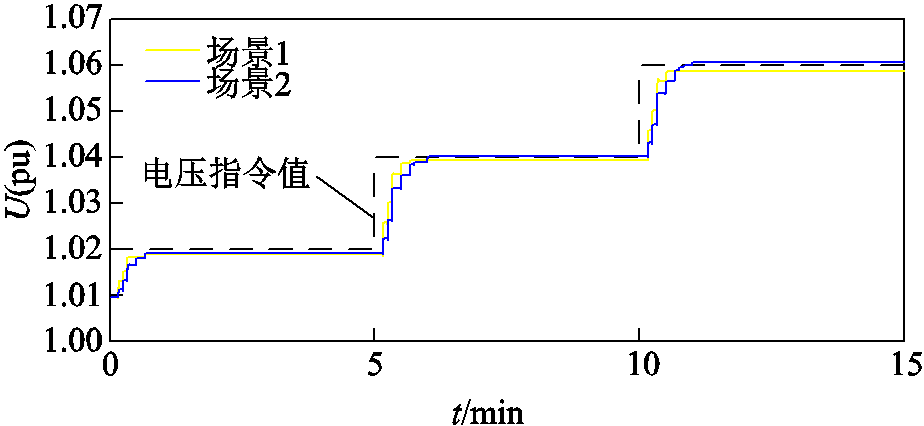
图2 两个场景下风电场A并网点电压控制效果
Fig.2 Voltage control effect of the wind farm grid-connected point in two scenarios
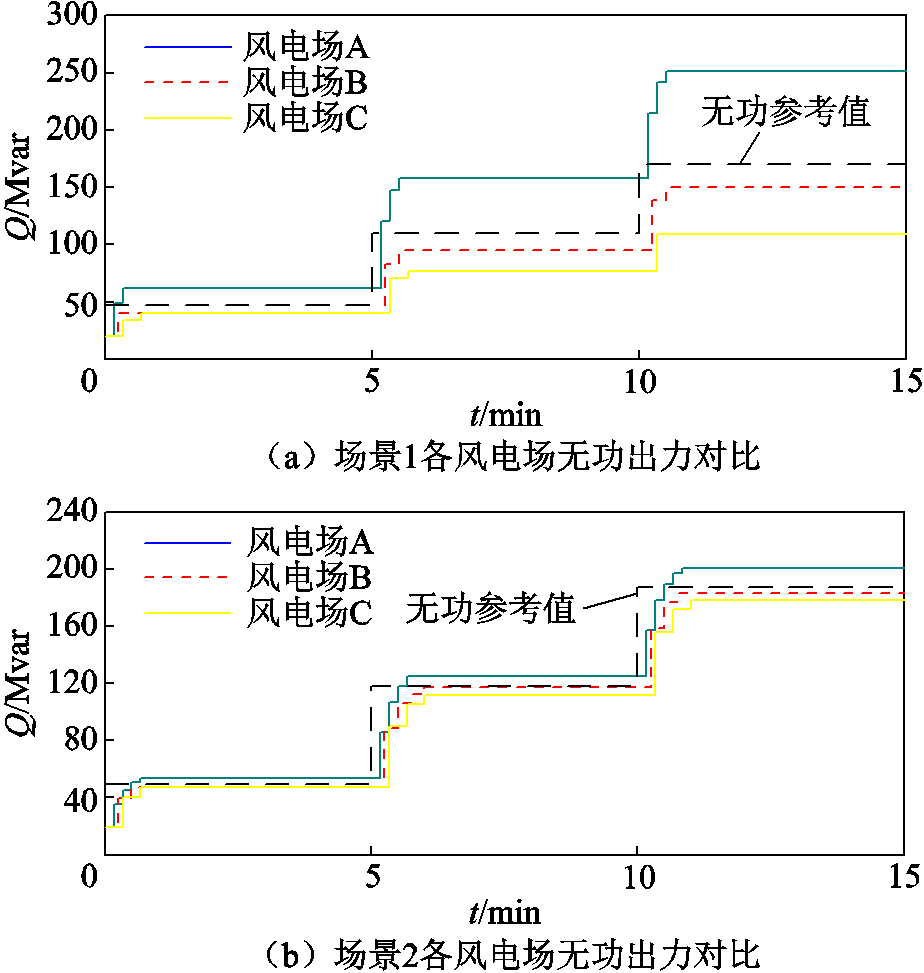
图3 两个场景下风电场无功出力对比
Fig.3 Reactive power output of wind farms in two scenarios
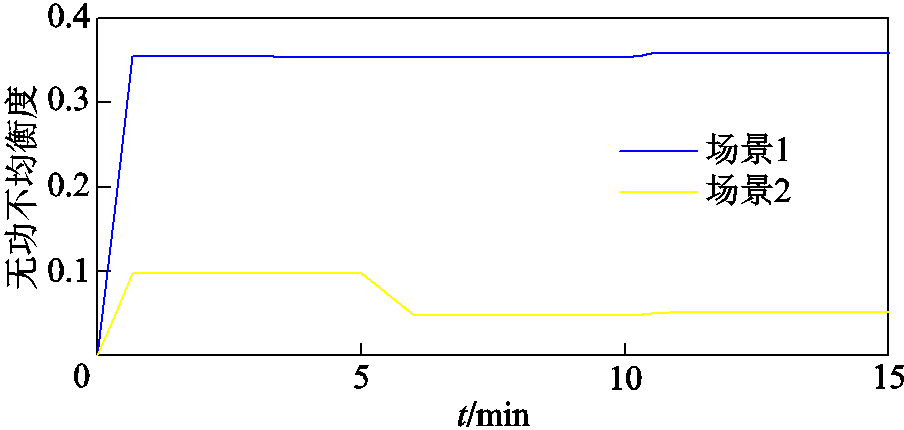
图4 两个场景下无功不均衡度对比
Fig.4 Reactive power imbalance in the two scenarios
由1.2节分析可得，每个调节周期无功功率调节步长取决于无功调节系数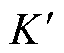
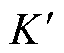，大调节步长大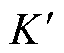，小调节步长小。在每个控制周期，若无功调节步长大，则调节速度快，但会出现电压超调的现象；若无功调节步长小，则调节精度高，但调节速度慢。
仍以图1所示的系统为例进行说明，假定风电场A、B、C内部无功调整周期相同，均设为10 s；设置三个风电场的无功调节系数均相同。当无功调节系数分别为1/2、1/3、1/6时，风电场并网点电压调节效果如图5所示。当K=1/2时，风电场电压第一次调节便出现超调，随后在两次调节后电压逐渐收敛进入死区；当K=1/3时，风电场电压经过一次调节便进入死区，调节时间最短；当K=1/6时，由于调节步长小，风电场电压呈阶梯状调节，在经过4次调节之后电压进入死区。因此，调节步长对风电场电压进入死区的时间有显著影响。
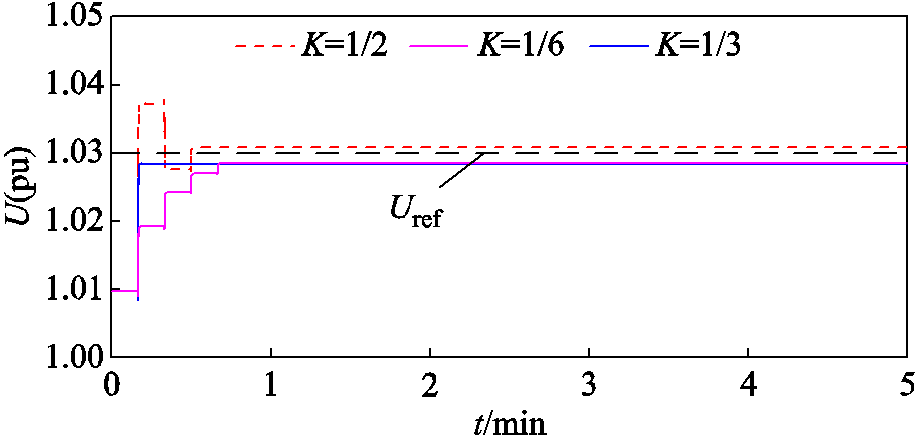
图5 不同调节系数时电压控制效果对比
Fig.5 Comparison of voltage control effect with different adjustable step size
根据以上仿真结果分析可得，无功调节周期和无功调节步长均会影响风电场电压控制。但考虑到实际系统中各场站设备运行参数相对固定，其无功调节周期不易改变，而且固定的比例系数无法兼顾调节速度和调节精度，因此本文侧重通过协调无功调节步长提高电压调节速度。由式（3）可知，当无功补偿量ΔQA和各场站调节周期一定时，通过改变无功调节系数K可以协调场站无功出力大小。同时，在实际系统中，各场站之间没有通信，只能量测到该场站并网点的电压，因此，如何根据有限的量测信息协调AVC子站无功调节步长，使集群中各场站电压尽快进入死区并且无功出力更加均衡至关重要。
为了兼顾调节速度和调节精度，本文提出变步长的风电场电压控制策略。首先通过在并网点施加无功扰动，然后观测电压变化来改变步长，因此称为变步长扰动观测法。变步长扰动观测法的执行架构如图6所示，以风电场i为例，T为风电场i的无功调节周期；n为无功调节周期数。第一次观测是为获取风电场初始电压信息，后续一直按照先扰动后观测的方式进行，扰动量为风电场i的无功出力ΔQi1，观测量为风电场并网点电压实际值Ui。每个控制周期进行一次扰动和一次观测，每次扰动引起的电压变化需要在下一个控制周期的扰动前进行观测。假设其他风电场的无功调节周期为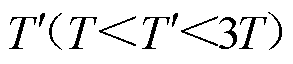
。
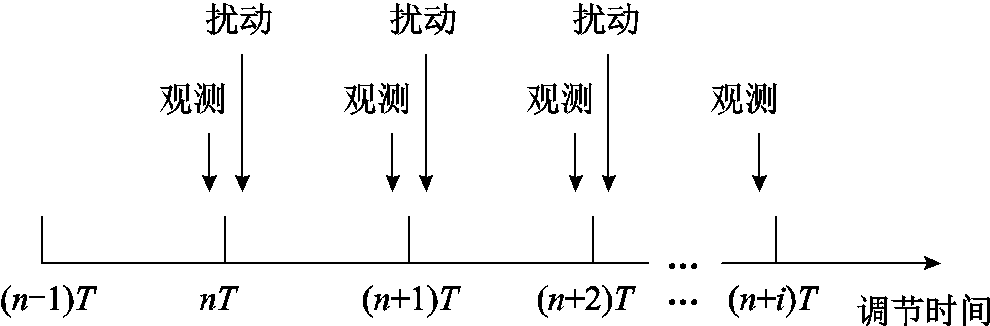
图6 变步长扰动观测法执行架构
Fig. 6 Implementation architecture of variable step size disturbance observation method
变步长扰动观测法流程如图7所示。当AVC子站接收到调度下发的电压参考值指令后，控制周期n=1，由式（1）计算自身场站无功功率初始缺额ΔQi(1)；再由式（3）可根据初始无功调节系数计算第一次的无功扰动量ΔQi1(1)。
在nT时刻进行无功扰动后，观测(n+1)T时刻风电场并网点电压Ui(n+1)，则在一个调节周期内并网点的电压变化量ΔUi(n)为
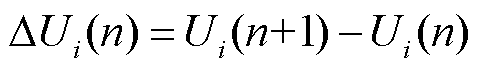（9）
其中，由风电场自己的无功调节引起的电压变化量ΔUiT(n)为
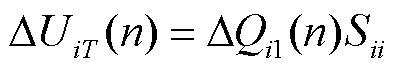（10）
式中，Sii为自身场站电压无功灵敏度。
第n个控制周期内其他场站的无功出力引起的电压变化量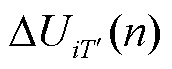
为
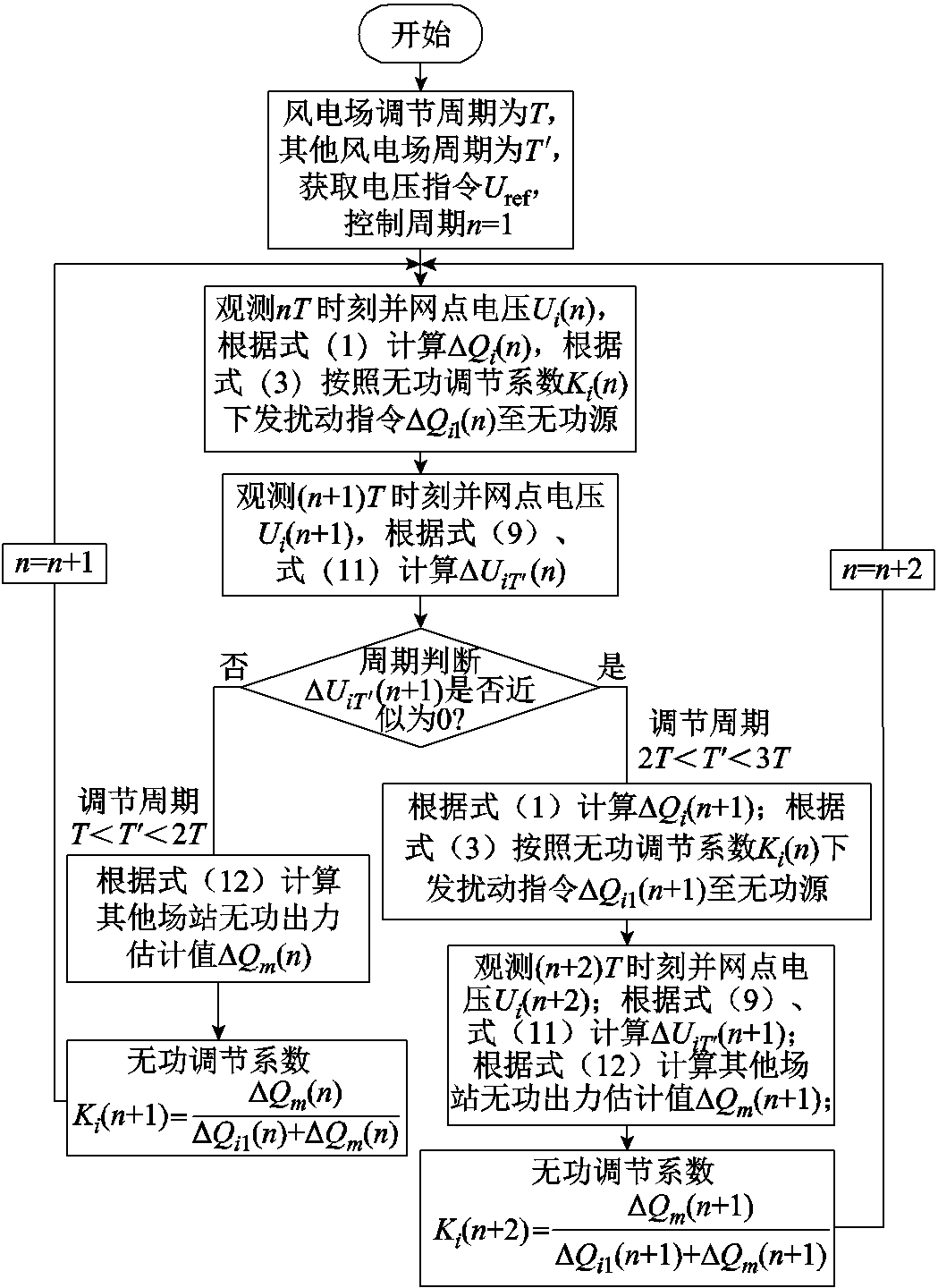
图7 变步长扰动观测法控制流程
Fig.7 Control flow chart of variable step size disturbance observation method
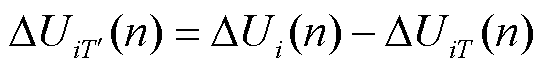（11）
若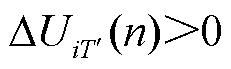
，则其他风电场的无功调节周期为
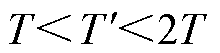；若
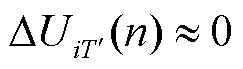，则其他风电场的无功调节周期为
。
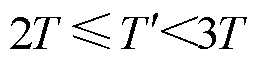在风电场i的第n个控制周期内，其他场站m的无功出力可根据电压变化量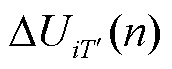和电压无功灵敏度Sim进行计算。然而风电场i无法获得其他场站的电压无功灵敏度，但考虑到同一集群内，场站之间的电压无功灵敏度Sim和场站自己的电压无功灵敏度Sii相差不大，所以采用Sii进行估算，即
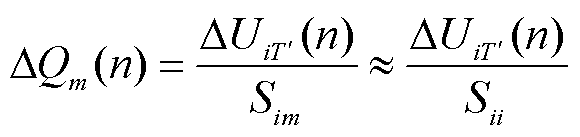（12）
当其他场站周期在T和2T之间时，在第n个控制周期内，风电场i的并网点电压变化量可表示为
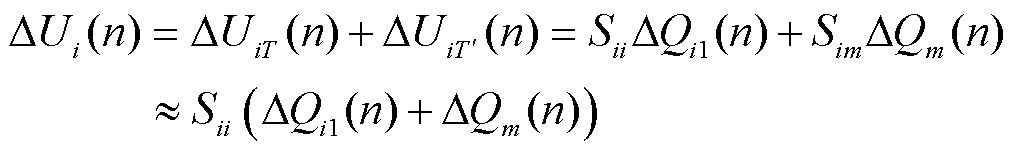(13)
则在第n个控制周期内，风电场自身的无功调节引起的电压变化量和并网点总的电压变化量之间的关系为
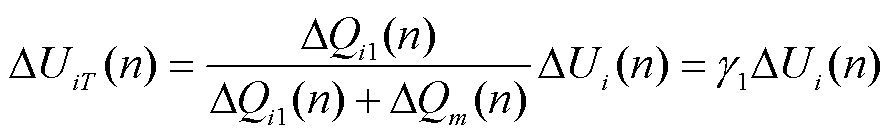（14）
式中，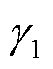
为第n个控制周期内场站自身无功出力占所有风电场总无功出力的比值，同时也是场站自身无功出力引起电压变化量占电压总变化量的比值，表示为
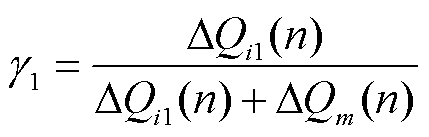
在一个周期之内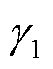，越小，说明该场站无功调节步长越小，电压变化主要由其他场站无功调节引起，在下一个周期应该增大步长，提高电压调节速度；反之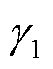，越大，说明该场站无功调节步长越大，电压变化量主要由该场站无功调节引起，在下一个周期应该减小步长，提高电压调节精度。
本文定义其他场站无功出力影响因数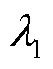
为
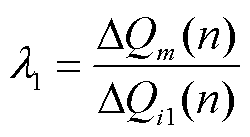（15）
在第n+1个控制周期根据其他场站在第n个周期的无功出力占比对本场站无功调节系数进行修正，从而改变下一控制周期的调节步长，以达到改善并网点电压调节速度的目的。
因此在第n+1个控制周期，场站i的无功调节系数为
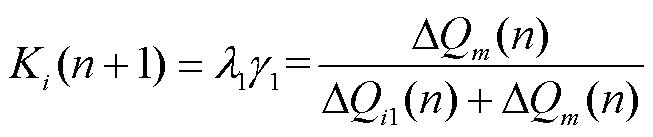（16）
当其他场站调节周期在场站i调节周期的2～3倍之间时，场站i经过2个调节周期才能检测到其他场站无功出力对并网点电压的影响。此时场站i需要根据第n+1个调节周期的无功扰动和检测到的电压变化量，来决定n+2调节周期的无功步长，控制流程详见图7，这里不再赘述。
上述基于变步长扰动观测法的风电场电压控制中，各场站通过动态改变无功调节步长可使各场站并网点电压更快地进入死区，但提高调节速度，可能使各场站无功出力又变得不均衡。因此在变步长控制的基础上，考虑各场站无功出力约束，以改善其无功不均衡现象。
具体地，在同一风电集群中，多个并列运行风电场之间的电压耦合关系可表示为
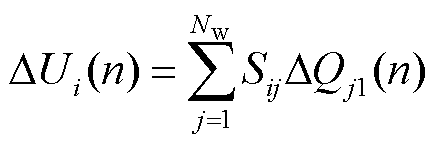（17）
由于各场站间存在强电压耦合，Sij和Sii相差不大，可假定Sij=Sii（i≠j），则可将式（17）化简为
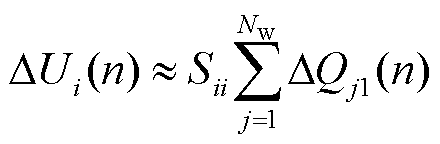（18）
在执行调度下发的某一次指令期间，场站i的电压和无功功率总变化量关系为
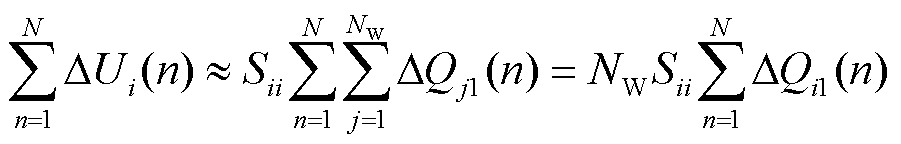（19）
式中，N为调度下发一次指令后AVC子站参与电压调节的次数；另外，在正常调节时每个场站无功调节量相差不大，假定ΔQj1(n)≈ΔQi1(n)。
由式（19）可得
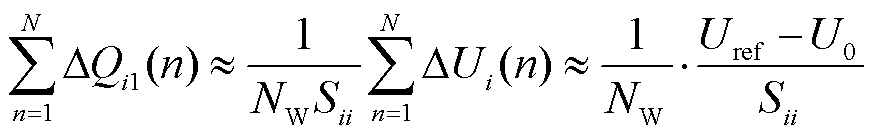（20）
式中，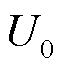
为并网点初始电压。
因此，为保证集群无功出力均衡度，风电场站无功总出力约束关系可表示为
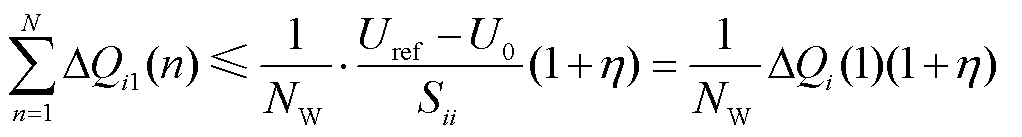（21）
式中，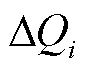
(1)为调度下发一次指令后风电场i在初始电压状态下计算的无功补偿量；
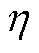为无功总出力裕度（本文设置为10%）。
上述无功总出力约束适用于接入同一汇集母线的各风电场运行状态近似的场景，此时能在保证电压调节速度的基础上，改善集群的无功出力不均衡度；但考虑到实际运行场景各异，当各风电场无功裕度差异较大，一味追求无功出力均衡度可能出现风电场无功出力达到限值时，风电场并网点电压却未进入死区的情况。
基于以上问题，按图8所示对无功总出力约束判定流程进行了完善。首先风电场并网点电压Ui(n)未进入电压死区时，AVC子站根据变步长扰动观测法计算无功指令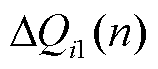
和场站i累计无功出力
。
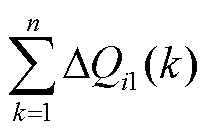当场站i无功累计出力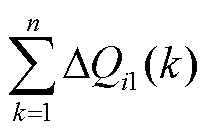小于约束上限时，场站i继续参与无功调节，将根据变步长扰动观测法计算的无功指令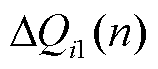下发至风电场无功源，并进入下一调节周期。
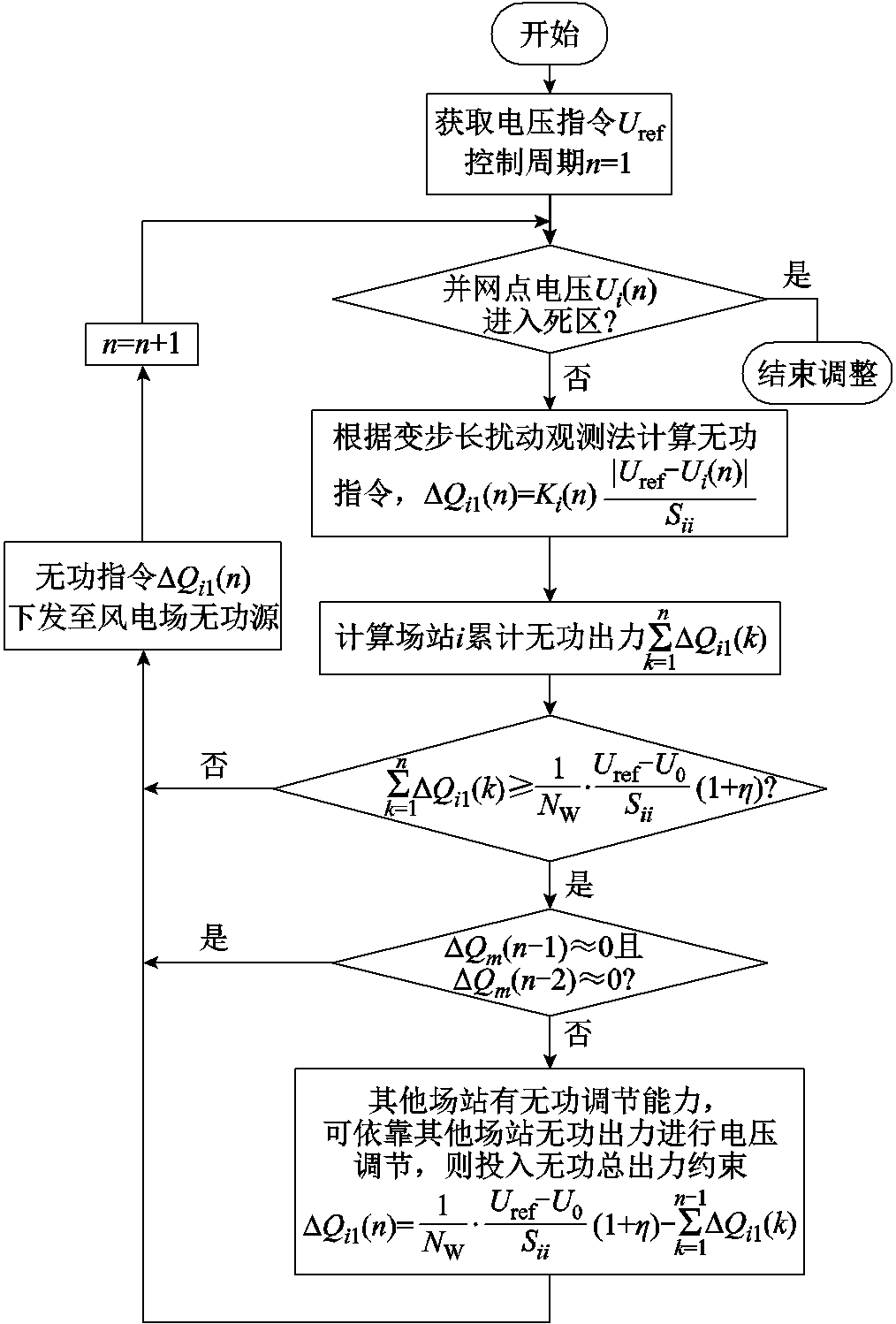
图8 无功总出力约束判定流程
Fig.8 Flow chart of determination using total reactive power output constraint
当场站i无功累计出力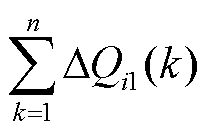
达到约束上限时，判断第n-1和n-2个周期内其他场站的无功出力ΔQm(n-1)和ΔQm(n-2)是否都为零，若为零，则说明其他场站无功出力达到限值，无法依靠其他场站无功出力使风电场i并网点电压进入死区，这时场站i通过自身承担更多的无功出力使风电场并网点电压达到要求；若第n-1和n-2个周期内其他场站无功出力不为0，说明其他场站仍有无功调节能力参与电压调节，这时为改善风电集群无功不均衡程度，采用无功总出力约束限制自身场站的无功出力，后续则依靠其他场站无功出力进行电压调节。在无功总出力约束下，场站i在第n个调节周期的无功指令为
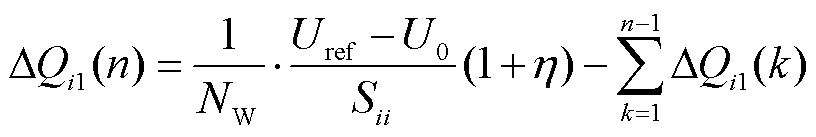（22）
本文以图1所示风电集群为例验证本文所提方法的有效性。该风电集群中各风电场装机容量和变压器容量均相同，风电场容量参数见表1。各风电场所接馈线采用π型电路等效，其参数见表2。电网作为参考节点，电压为1.00(pu)，风电场并网点电压参数见表3。
表1 风电场容量参数
Tab.1 Wind farm capacity parameters
风电场装机容量/(MV·A)变压器容量/(MV·A) A371.8400 B634.5750 C196.4240
表2 风电场馈线阻抗参数
Tab.2 Wind farm feeder impedance
线路起始节点终止节点阻抗r +jx/(pu)接地导纳(pu) ZCN汇集母线电网(1.3+j3.1)×10-30.096 ZLA风电场A汇集母线(6.4+j15.4)×10-40.048 ZLB风电场B汇集母线(5.8+j19.7)×10-40.065 ZLC风电场C汇集母线(12.6+j36)×10-40.099
表3 风电场并网点电压参数
Tab.3 Voltage parameters of wind farm grid-connected point
参数数值 并网点电压基准/kV220 并网点电压指令值(pu)1.03 并网点初始电压U0(pu)1.009 7 并网点电压死区范围(%)±0.2
为验证本文所提基于变步长扰动观测法的风电场群电压控制策略及其改进策略的有效性，假定风电场A、B、C调节周期分别为10 s、15 s、20 s，考虑无功调节周期修正系数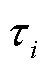
，设置初始无功调节系数分别为1/6、1/4、1/3。考虑以下三个场景：
（1）场景1：采用考虑无功调节周期修正系数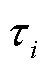的风电场群电压控制策略。
（2）场景2：采用本文的基于变步长扰动观测法的风电场群电压控制策略。
（3）场景3：采用本文所提考虑无功约束的改进风电场电压控制策略。
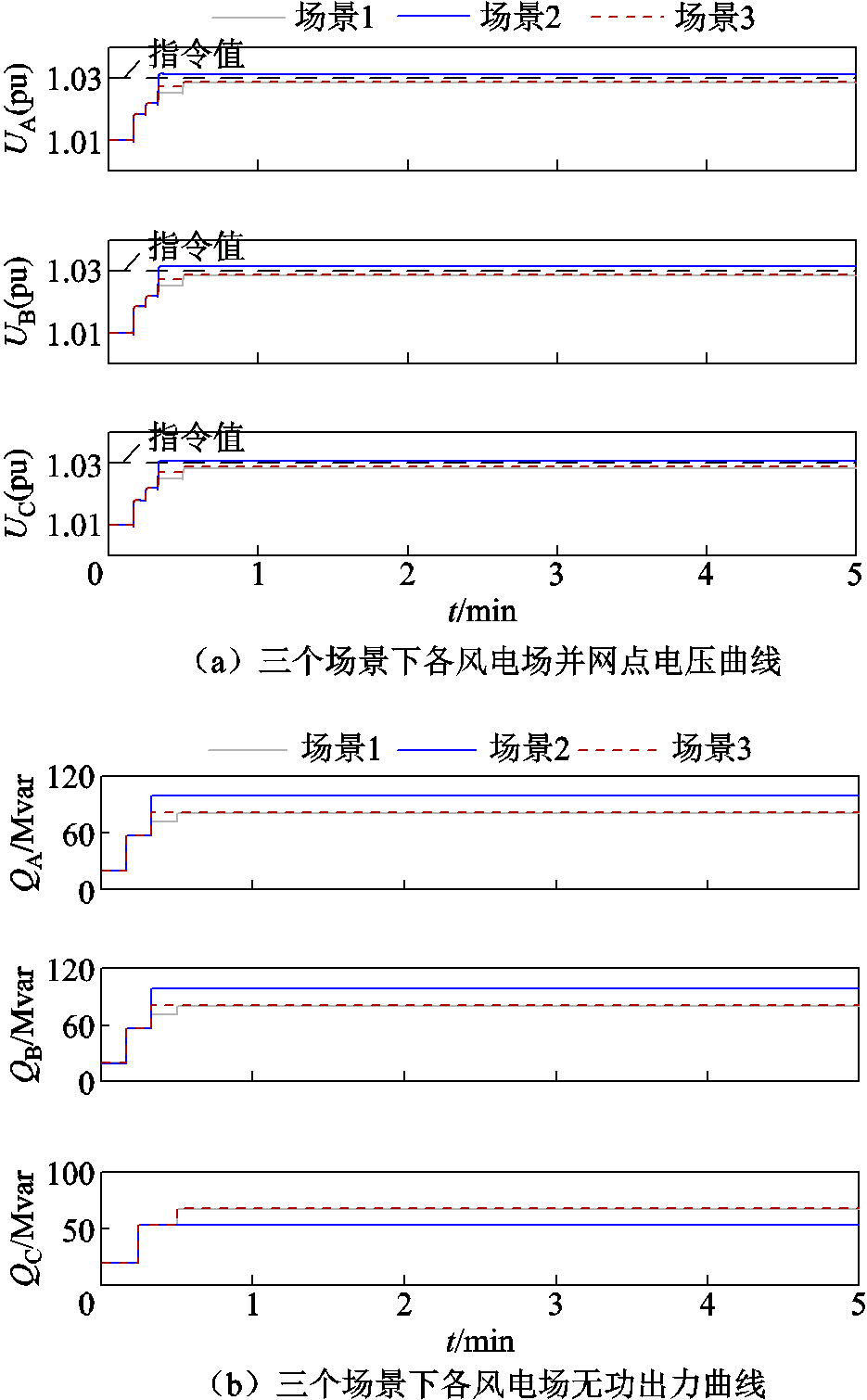
图9为各场站无功裕度充足时三个场景下各风电场并网点电压控制效果对比，其中黑色虚线为风电场接收的电压指令值1.03(pu)。从图9可知，在三个场景下风电场并网点电压都能在1 min内进入电压死区。图10为无功裕度充足时三个场景下各风电场无功出力对比。图11为无功裕度充足时三个场景下各风电场并网点电压进入死区时间对比。图12为无功裕度充足时三个场景下无功不均衡度对比。
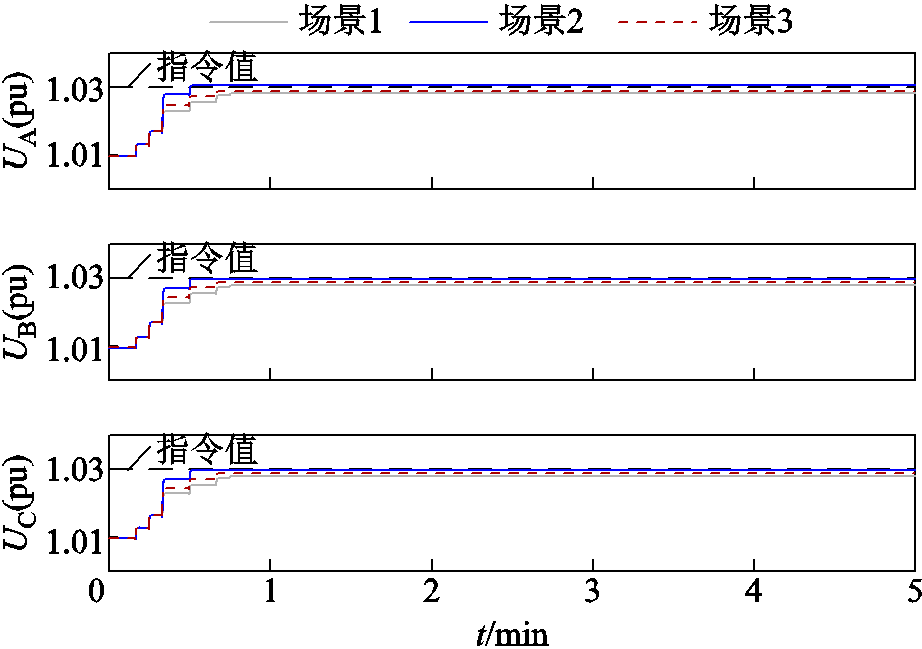
图9 无功裕度充足时三个场景下各风电场并网点电压曲线
Fig.9 Voltage curves of each wind farm grid-connected points under three scenarios when reactive power margin is sufficient
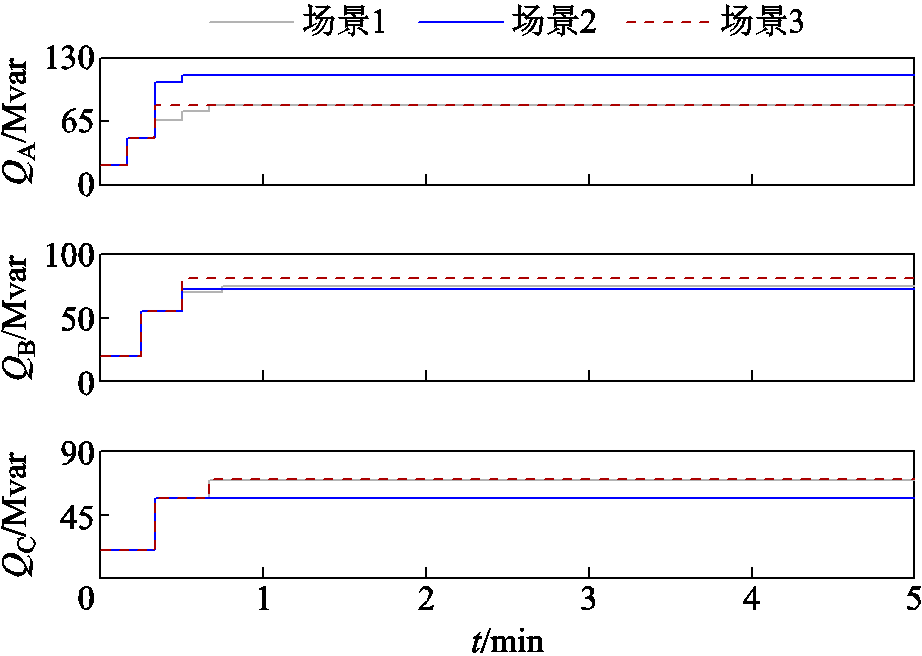
图10 无功裕度充足时三个场景下各风电场无功出力曲线
Fig.10 The reactive power output curves of each wind farm under three scenarios when the reactive power margin is sufficient
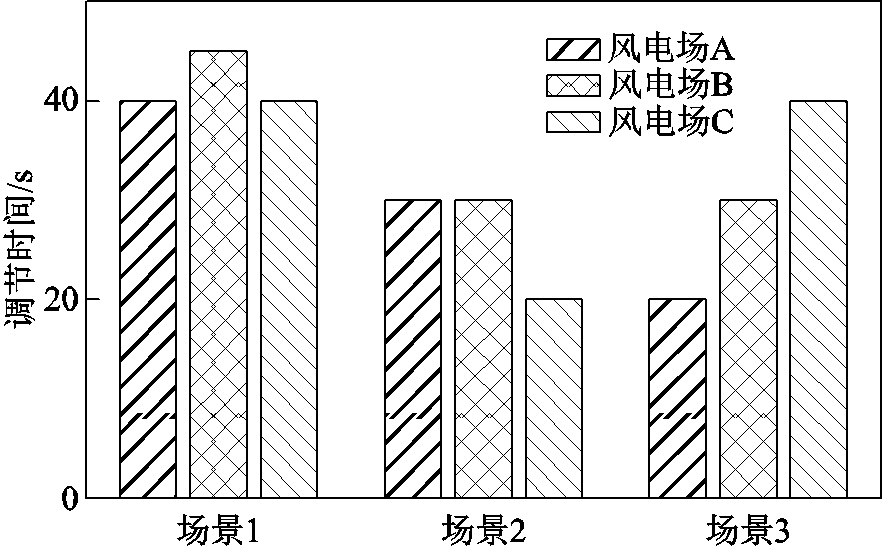
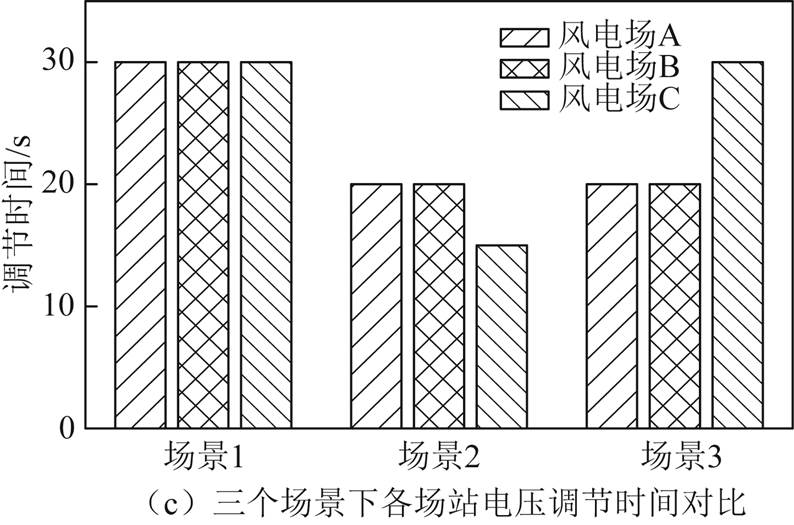
图11 无功裕度充足时3个场景下各场站电压调节时间对比
Fig.11 Comparison of voltage regulation time of each station in three scenarios when reactive power margin is sufficient
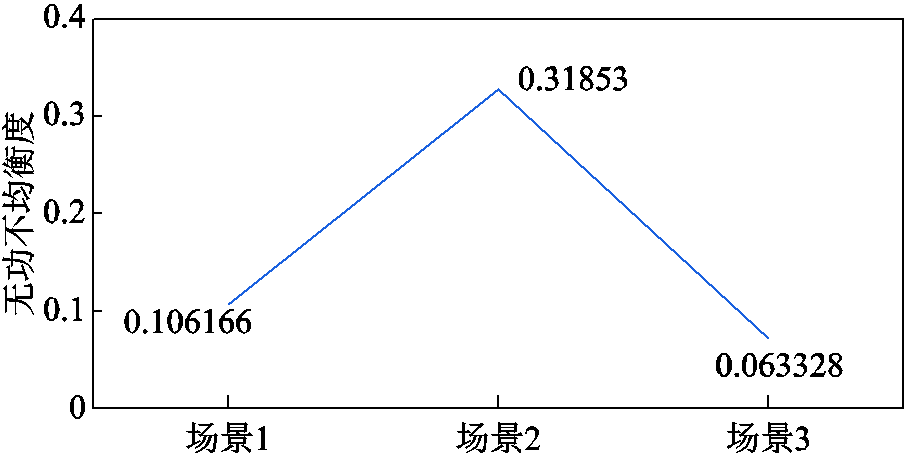
图12 无功裕度充足时三个场景下无功不均衡度对比
Fig.12 Comparison of reactive power imbalance degree in three scenarios when reactive power margin is sufficient
从图10～图12可以看出，场景1考虑固定调节周期修正系数，使调节周期较小的场站A、B对应有较小的固定无功调节系数，从而各风电场无功出力较为均衡，无功不均衡度为0.106 166，但调节时间较长，三个风电场并网点电压进入死区时间均不小于40 s；场景2采用变步长扰动观测法通过“先扰动，后观测”的方式，对其他场站的调节量进行有效评估，从而对无功调节系数进行动态调整，使电压调节速度显著提升，各风电场并网点电压进入死区的时间均小于30 s，但无功不均衡问题较场景1更突出；场景3采用本文所提的考虑无功出力约束的变步长扰动观测法，在考虑无功处理约束之后，各风电场并网点电压进入死区时间较场景2有所增加，但较场景1仍有所改善，场景3下考虑无功出力约束后无功不均衡度为0.063 328，较场景1改善程度显著。
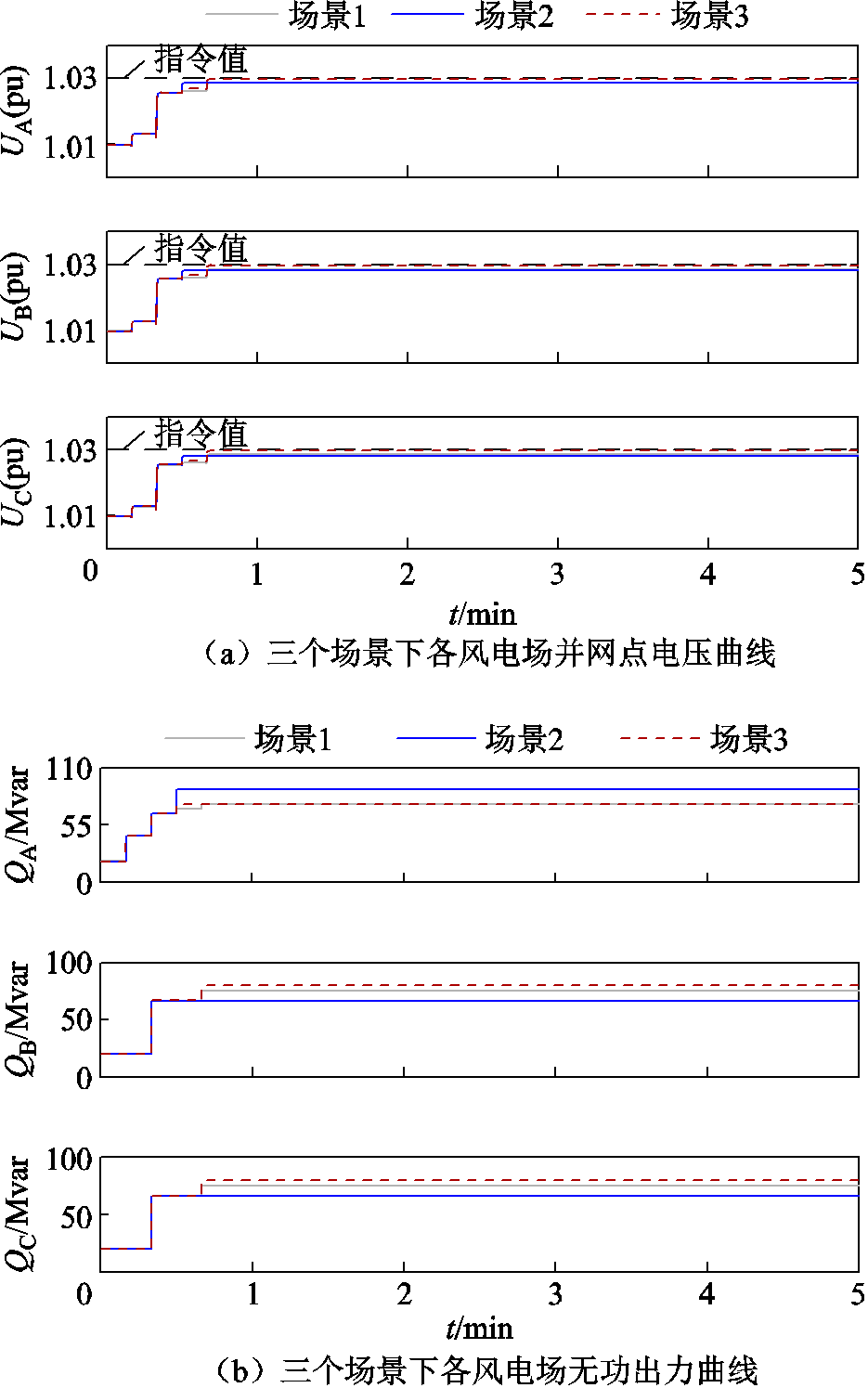
为充分验证无功裕度充足时本文所提电压控制策略的有效性，需考虑在风电场调节周期关系为TA=TB＜TC和TA＜TB=TC两种情况时本文所提策略的控制效果，其控制参数及仿真效果如附图1和附图2所示。通过仿真结果可以看出，在TA=TB＜TC和TA＜TB=TC两种情况时，采用本文提出的基于变步长扰动观测法的风电场群电压控制策略，同样能使风电场电压调节速度得到有效提升，但无功不均衡情况更加明显；而采用本文提出的考虑无功约束的改进风电场群电压控制策略既能提升调节速度又能改善无功不均衡。
综上所述，在各场站无功出力裕度充足时，本文所提的基于变步长扰动观测法的风电场群电压控制策略能够通过观测其他场站的调节状态从而对自身场站调节步长进行动态调整，使各场站调节速度大幅提升，但无功功率不均衡问题更加突出。为有效改善无功功率不均衡问题，本文提出考虑无功功率约束的改进风电场群电压控制策略，在考虑各场站无功出力约束之后，保证电压调节速度的同时，风电场群无功功率不均衡问题得到有效改善，对于提升风电接入区域电压的稳定性具有重要意义。
为验证其他场站无功出力裕度不充足时，本文所提电压控制策略的有效性，设置场站B、C无功出力裕度均为35 Mvar，其他参数不变，三个场景下各场站的电压调节曲线、无功出力曲线和电压调节时间对比分别如图13～图15所示。
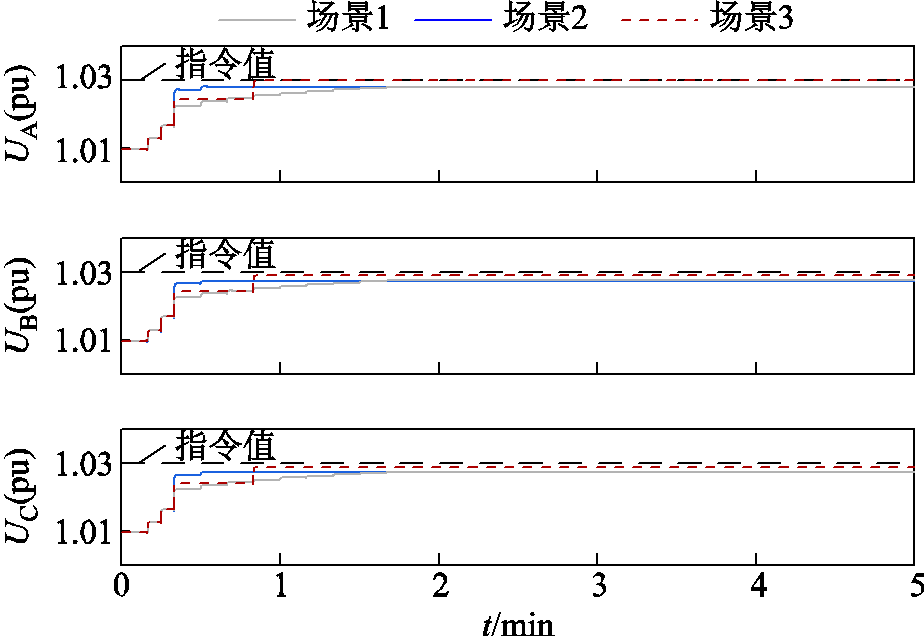
图13 无功裕度不足时三个场景下各风电场并网点电压曲线
Fig.13 Voltage curves of each wind farm grid-connected points under three scenarios when reactive power margin is insufficient
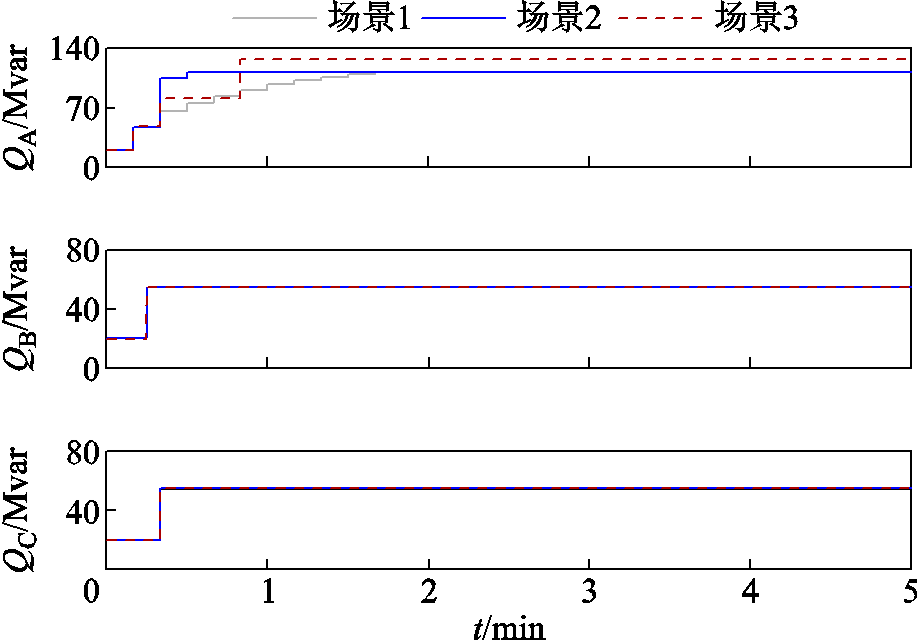
图14 无功裕度不足时三个场景下各风电场无功出力曲线
Fig.14 Reactive power output curves of each wind farm under three scenarios when reactive power margin is insufficient
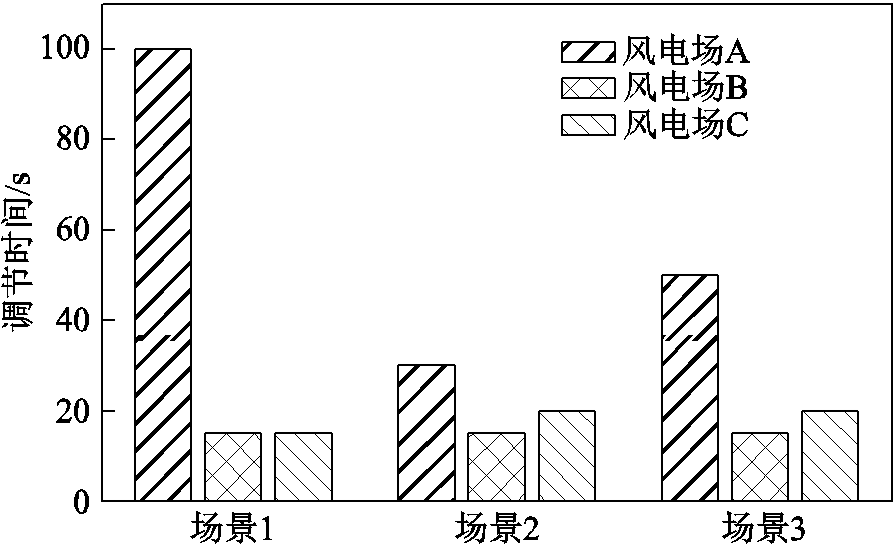
图15 无功裕度不足时3个场景下各场站电压调节时间对比
Fig.15 Comparison of voltage regulation time of each station in three scenarios when reactive power margin is insufficient
由图13～图15可得，场景1下由于场站B、C无功裕度不足，场站A需要提供更多的无功出力，但仅靠无功调节周期修正系数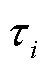只能进行有规律的缓慢调节，这时场站A的并网点电压在第10个调节周期才进入死区，无法满足在1 min内进入死区的要求；场景2下利用变步长扰动观测法对无功调节步长进行动态调整，并网点电压经过3个周期的调节便进入死区，该场景下电压调节速度较场景1有显著提升；场景3下考虑了风电场无功总出力约束，可得场站A在第2个调节周期便达到了无功出力约束上限，此时场站B、C也均经过一次调节便达到无功出力裕度上限。为使风电场并网点电压在规定时间内进入死区，场站A首先对场站B、C的下一周期无功出力进行估计，即估计第3、4个调节周期内其他场站的无功出力情况，然后在判定其他场站没有无功出力后将无功总出力约束解除，最后在变步长扰动观测法的作用下并网点电压在第5个调节周期内进入死区，可得该场景下电压调节速度较场景1同样有明显改善。
由以上仿真结果可知，当风电集群各场站无功裕度充足时，在变步长扰动观测法的基础上考虑无功总出力约束能够使风电场并网点电压调节速度和无功均衡度均得到改善。当风电集群中存在场站无功裕度不足时，由于各风电场AVC子站之间无法通信，应该优先保证并网点电压在规定时间内进入死区，因此设置使用无功总出力约束的判据至关重要。
在省调两级电压控制架构下，风电集群中各风电场AVC子站在相互间没有通信的情况下独立进行电压控制，导致调节快的风电场无功出力多，调节慢的风电场无功出力少。本文提出了一种兼顾电压调节速度和无功均衡度的风电场AVC子站电压控制策略，并进行了算例验证，得到如下结论：
1）无功调节周期和无功调节步长均会影响风电场电压调节速度和集群的无功均衡度。
2）基于变步长扰动观测的风电场AVC子站电压控制策略，通过评估其他场站的无功对并网点电压的影响，动态调节每次无功调节步长，有效地提升了风电场AVC子站的电压调节速度。
3）在变步长扰动观测法电压控制基础上，考虑无功约束，可提升风电场AVC子站的电压调节速度，减小各场站无功不均衡度。
附 录
1. 风电场馈线阻抗参数
附表1 风电场馈线阻抗
App.Tab.1 Wind farm feeder impedance
节点线路阻抗(pu)注入功率/(MV×A)电压幅值(pu) A(6.4+j15.4)´10-4400+j201.009 7 B(6.4+j15.4)´10-4400+j201.009 7 C(6.4+j15.4)´10-4400+j201.009 7
2. 
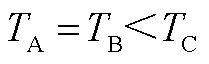及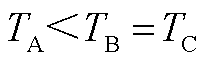
两种周期关系下的仿真参数及结果
附表2 风电场控制参数
App.Tab.2 Wind farm control parameters
参数 A场站无功调节周期/s1010 B场站无功调节周期/s1015 C场站无功调节周期/s1515 A场站AVC初始无功调节系数2/91/6 B场站AVC初始无功调节系数2/91/3 C场站AVC初始无功调节系数1/31/3
附图1 TA=TB＜TC时仿真结果
App.Fig.1 Simulation results when TA=TB＜TC
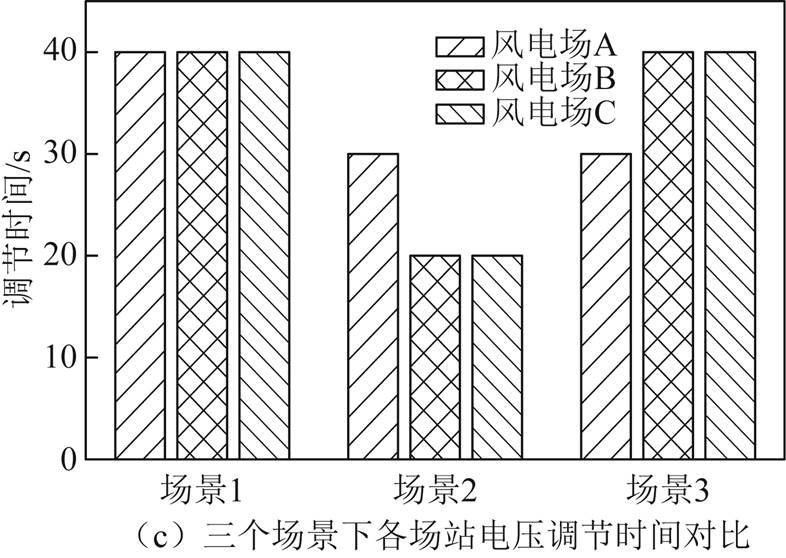
附图2 TA＜TB=TC时仿真结果
App.Fig.2 Simulation results when TA＜TB=TC
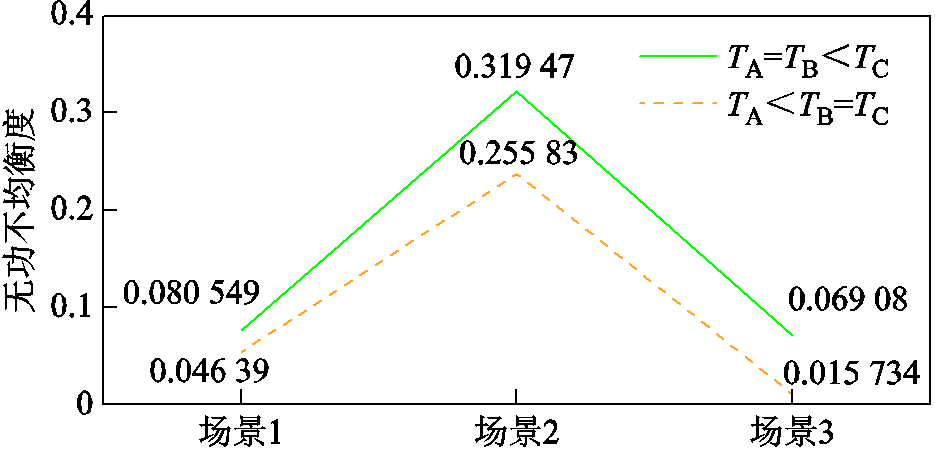
附图3 两种特殊调节周期关系在三个场景下无功不均衡度对比
App.Fig.3 Comparison of reactive power imbalance degree between two special regulation period relations in three scenarios
参考文献
[1] 国家能源局发布2023年全国电力工业统计数据[J]. 电力科技与环保, 2024, 40(1): 95. National Energy Administration released statistical data of national electric power industry in 2023[J]. Electric Power Technology and Environmental Protection, 2024, 40(1): 95.
[2] 王渝红, 宋雨妍, 廖建权, 等. 风电电压主动支撑技术现状与发展趋势[J]. 电网技术, 2023, 47(8): 3193-3205. Wang Yuhong, Song Yuyan, Liao Jianquan, et al. Review and development trends of DFIG-based wind power voltage active support technology[J]. Power System Technology, 2023, 47(8): 3193-3205.
[3] 薛霖, 牛涛, 方斯顿, 等. 计及高比例风电暂态电压安全的主从协同动态无功优化方法[J]. 电力系统自动化, 2023, 47(17): 57-66. Xue Lin, Niu Tao, Fang Sidun, et al. Master-slave cooperative dynamic reactive power optimization method considering transient voltage security of high proportion of wind power[J]. Automation of Electric Power Systems, 2023, 47(17): 57-66.
[4] 孙宏斌, 郭庆来, 张伯明. 电力系统自动电压控制[M]. 北京: 科学出版社, 2018.
[5] Yang Qiuling, Wang Gang, Sadeghi A, et al. Two-timescale voltage control in distribution grids using deep reinforcement learning[J]. IEEE Transactions on Smart Grid, 2020, 11(3): 2313-2323.
[6] 彭啸宇, 沈怡, 陆秋瑜, 等. 考虑风电出力不确定性的电网无功-电压控制鲁棒分区方法[J]. 电网技术, 2023, 47(10): 4102-4111. Peng Xiaoyu, Shen Yi, Lu Qiuyu, et al. Robust var-voltage control partitioning for power grid considering wind power uncertainty[J]. Power System Technology, 2023, 47(10): 4102-4111.
[7] 徐峰达, 郭庆来, 孙宏斌, 等. 基于模型预测控制理论的风电场自动电压控制[J]. 电力系统自动化, 2015, 39(7): 59-67. Xu Fengda, Guo Qinglai, Sun Hongbin, et al. Automatic voltage control of wind farms based on model predictive control theory[J]. Automation of Electric Power Systems, 2015, 39(7): 59-67.
[8] 余达, 武志韬, 陈子文, 等.基于改进近端策略优化算法的双馈风电场站无功裕度优化研究[J/OL].发电技术,1-10[2025-07-01].http://kns.cnki.net/kcms/ detail/33.1405.TK.20250318.1816.002.html. Yu Da, Wu Zhitao, Chen Ziwen. Research on reactive power margin optimization of doubly-fed induction generator wind farm based on improved proximal policy optimization algorithm[J/OL]. Power GenerationTechnology, 1-10[2025-07-01].http://kns.cnki.net/kcms/ detail/33.1405.TK. 20250318.1816.002.html.
[9] 郭嘉庆, 乔颖, 鲁宗相, 等. 风电场群无功不均衡/无功环流抑制研究[J]. 电网技术, 2023, 47(1): 109-121.Guo Jiaqing, Qiao Ying, Lu Zongxiang, et al. Reactive power unbalance/circulation suppression for wind farm group[J]. Power System Technology, 2023, 47(1): 109-121.
[10] 林洪, 唐人, 杨军, 等. 有源配电网改进下垂曲线无功控制策略研究[J]. 自动化仪表, 2024, 45(10): 54-59. Lin Hong, Tang Ren, Yang Jun, et al. Research on reactive power control strategy for improving sag curve in active distribution network[J]. Process Automation Instrumentation, 2024, 45(10): 54-59.
[11] 王俊凯, 牟龙华, 刘鑫. 基于动态虚拟阻抗的多并联逆变器间环流抑制控制策略[J]. 电力自动化设备, 2021, 41(4): 94-100. Wang Junkai, Mu Longhua, Liu Xin. Control strategy based on dynamic virtual impedance to suppress circulating current between multiple parallel inverters[J]. Electric Power Automation Equipment, 2021, 41(4): 94-100.
[12] 吴宇辉, 尚斌, 杨鹏飞, 等. 新能源集群无功环流抑制策略研究[J]. 内蒙古电力技术, 2023, 41(4): 13-19. Wu Yuhui, Shang Bin, Yang Pengfei, et al. Research on reactive circulating current suppression strategies for new energy clusters[J]. Inner Mongolia Electric Power, 2023, 41(4): 13-19.
[13] 李生虎, 章怡帆, 于新钰, 等. 采用改进下垂控制和双层无功优化的风电场无功均衡分配研究[J]. 电力系统保护与控制, 2019, 47(13): 1-7. Li Shenghu, Zhang Yifan, Yu Xinyu, et al. Study on reactive power sharing of wind farms with improved droop control and bi-level reactive power optimi-zation[J]. Power System Protection and Control, 2019, 47(13): 1-7.
[14] 杨浩, 苏文栋, 谷毅, 等. 面向耦合系统的交替方向滚动时域电压分层协同优化控制[J]. 电工技术学报, 2023, 38(21): 5846-5861. Yang Hao, Su Wendong, Gu Yi, et al. Voltage hierarchical cooperative control of coupled system using model predictive control and alternating direction method of multipliers[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5846-5861.
[15] 林俐, 马笑寒, 丁文敏. 计及构网型储能电站的新能源基地无功协调优化控制[J]. 电力系统自动化, 2025, 49(1): 59-68. Lin Li, Ma Xiaohan, Ding Wenmin. coordinated optimal reactive power control of renewable energy base cons-idering grid-forming energy storage station [J]. Automa-tion of Electric Power Systems, 2025, 49(1): 59-68.
[16] Kou Peng, Liang Deliang, Gao Rong, et al. Decentralized model predictive control of hybrid distribution transformers for voltage regulation in active distribution networks[J]. IEEE Transactions on Sustainable Energy, 2020, 11(4): 2189-2200.
[17] Nguyen T T, Kim H M. Cluster-based predictive PCC voltage control of large-scale offshore wind farm[J]. IEEE Access, 2020, 9: 4630-4641.
[18] 马庆, 邓长虹. 基于单/多智能体简化强化学习的电力系统无功电压控制[J]. 电工技术学报, 2024, 39(5): 1300-1312. Ma Qing, Deng Changhong. Single/multi agent simplified deep reinforcement learning based volt-var control of power system[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1300-1312.
[19] 李鹏, 姜磊, 王加浩, 等. 基于深度强化学习的新能源配电网双时间尺度无功电压优化[J]. 中国电机工程学报, 2023, 43(16): 6255-6266. Li Peng, Jiang Lei, Wang Jiahao, et al. Optimization of dual-time scale reactive voltage for distribution network with renewable energy based on deep reinforcement learning[J]. Proceedings of the CSEE, 2023, 43(16): 6255-6266.
[20] 蔡游明, 李征, 蔡旭. 计及控制时间窗内功率波动的风电场群无功电压分层优化控制[J]. 电工技术学报, 2019, 34(6): 1240-1250. Cai Youming, Li Zheng, Cai Xu. Voltage hierarchical optimal control of a wind farm cluster in account of voltage fluctuation in control time window[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1240-1250.
[21] 刘承锡, 张兆毅, 赖秋频. 考虑风电功率短期波动的风电场无功快速跟踪优化[J]. 中国电机工程学报, 2023, 43(15): 5850-5863. Liu Chengxi, Zhang Zhaoyi, Lai Qiupin. Fast-tracking optimization of reactive power for wind farm considering short-term fluctuations of wind generations[J]. Proceedings of the CSEE, 2023, 43(15): 5850-5863.
[22] 李鹏, 王加浩, 徐贤, 等. 面向新型电力系统潮流频繁波动的无功鲁棒分区方法[J]. 电力系统自动化, 2022, 46(11): 102-110. Li Peng, Wang Jiahao, Xu Xian, et al. Robust reactive power partitioning method for frequent power flow fluctuation in new power system[J]. Automation of Electric Power Systems, 2022, 46(11): 102-110.
[23] 朱建华, 何卓林, 闫伟军, 等. 风电场自动电压控制中风机和静止无功发生器的无功分配研究[J]. 电气技术, 2022, 23(4): 31-36. Zhu Jianhua, He Zhuolin, Yan Weijun, et al. Research on reactive power distribution of wind turbine and static var generator in automatic voltage control of wind farm[J]. Electrical Engineering, 2022, 23(4): 31-36.
[24] 张兆毅, 胡浩, 王子江, 等. 基于非线性仿射的风电场电压实时计算和优化方法[J]. 电工技术学报, 2024, 39(13): 3975-3989. Zhang Zhaoyi, Hu Hao, Wang Zijiang, et al. Real-time voltage calculation and optimization method for wind farms based on nonlinear affine transformation[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 3975-3989.
Abstract Under the two-stage voltage control architecture of provincial regulation, the superior dispatching control center directly sends the voltage command value to the automatic voltage control (AVC) sub-stations of each wind farm, and the AVC sub-stations of each wind farm in the wind power cluster independently perform voltage control without communication with each other. In this case, the AVC sub-stations of each wind farm can only obtain the operation data of the local station. The high efficiency and accuracy of reactive power allocation cannot be achieved through AVC master station, which makes the voltage regulation efficiency of wind power cluster low. In addition, due to the different response time of the energy management platform and the wind turbine, the voltage regulation response speed of the wind farm is also different. Wind farms with fast regulation speed bear more reactive power, and wind farms with slow regulation speed bear less reactive power, resulting in unbalanced reactive power and waste of reactive power regulation capacity.
Firstly, this paper analyzes the influence of reactive power regulation period and regulation step of AVC sub-station on the voltage control of wind farm grid-connected point. Considering that the operating parameters of each wind farm equipment in the actual system are relatively fixed, the reactive power regulation period is not easy to change, and the fixed adjustment step cannot take into account the adjustment speed and adjustment accuracy. Therefore, this paper focuses on improving the voltage regulation speed of wind farm by changing the reactive power regulation step length.
Secondly, because the voltage of the wind farm grid-connected point is not only related to the reactive power output of its own station, but also affected by the reactive power output of other stations, this paper proposes a voltage control strategy of the AVC sub-station of wind power plant based on "variable step perturbation observation". This strategy changes the output reactive power of the wind power plant, and then measures the voltage change of the grid-connected point, and evaluate the influence of voltage control of other wind farms on the wind farm grid-connected point, dynamically adjust the reactive power regulation step of AVC sub-station, improve the voltage regulation speed of the wind farm, so that the voltage of the wind farm grid-connected point can enter the voltage dead zone faster.
Thirdly, in order to improve the reactive power imbalance in the wind power cluster, the reactive power constraint relationship of the wind farm stations in the cluster is established by analyzing the voltage reactive power coupling relationship between each wind farm, and considering the difference of the reactive power margin of each wind farm station, the variable step size control strategy is improved, and an improved wind farm voltage control strategy considering reactive power constraint is proposed. The voltage regulation speed and reactive power balance of wind power cluster are considered.
Finally, based on the operating data of a wind power cluster in East China, a simulation model of wind farm convergence system is built to verify the effectiveness of the proposed strategy.
Keywords：Automatic voltage control (AVC) sub-station,reactive voltage control, variable step size, disturbance observation, reactive power constraint
DOI: 10.19595/j.cnki.1000-6753.tces.240956
中图分类号：TM614
国网江苏省电力有限公司科技项目资助（J2023067）。
收稿日期 2024-05-31
改稿日期 2024-10-22
朱晓荣 女，1972年生，副教授，硕士生导师，研究方向为新能源发电及并网技术、直流微电网等。E-mail：xiaorongzhu@ ncepu.edu.cn （通信作者）
刘 伟 男，1999年生，硕士研究生，研究方向为风电并网电压控制技术。E-mail：2311913204@qq.com
（编辑 郭丽军）