基于多光谱卫星遥感的输电网冰灾场景时序建模与韧性提升策略优化
牛 涛1 黄骞谦1 方斯顿1 李晓冬2 廖瑞金1
(1. 输变电装备技术全国重点实验室(重庆大学) 重庆 400044 2. 中国科学院精密测量科学与技术创新研究院 武汉 430071)
摘要 冰灾会对输电网造成严重破坏,提升冰灾天气下的输电网韧性至关重要。不同于台风、地震等极端自然灾害,冰灾因持续时间长且地理覆盖范围受微气象和地形等影响而难以精准预测,目前冰灾的时空演变规律尚不清晰。因此,该文提出一种基于多光谱卫星遥感的冰灾场景时序建模方法,结合多光谱遥感图像融合方法对Sentinel-2卫星遥感图像中的覆冰区域空间分布和时序变化进行高效提取和分析,利用偏微分卷积实现覆冰区域滚动预测,构建冰灾时序模型并基于条件变分自动编码器生成冰灾场景集。基于冰灾场景集,提出一种综合韧性评估指标并构建输电网两阶段鲁棒韧性提升规划模型:第一阶段研究灾前固定储能配置和维修资源的预规划,寻找最优投资决策;第二阶段研究灾中固定储能应急供电,并考虑有限资源的应急维修,保证负荷快速恢复,最大限度地提升系统韧性,减少系统经济损失。最后利用改进IEEE RTS-79输电系统验证所提方法的有效性。
关键词:冰灾 多光谱卫星遥感 图像融合 时序场景 输电网规划 韧性提升
0 引言
随着我国“碳达峰·碳中和”目标的提出,传统电力系统正在向高比例新能源接入的新型电力系统转变,具有较强间歇性和波动性的新能源并网给新型电力系统的稳定运行带来了严重威胁[1]。与此同时,近几十年来的气候变化导致世界范围内极端自然灾害频发,电力供应中断的风险急剧增加[2]。
在各类极端自然灾害中,冰灾发生较为频繁且会给电力系统造成极大的破坏。例如,1998年加拿大东部及美国东北部地区遭遇冰灾袭击,超过1 000座输电杆塔和30 000座配电杆塔倒塌[3];2004年底发生于我国湖南省的一场严重冰灾,导致6条500kV输电线路因发生覆冰闪络而停运,4条 220 kV线路断线[4];2008年一场持续高强度的大规模冰灾袭击了我国南方地区,累计造成12.9万处高压输电线路断线,51.9万基低压线路杆塔倒断,经济损失高达上百亿元[5-7];2011年,我国云南省的冰灾持续了20多天,破坏了78.5 km的线路,造成141.7万元的经济损失[8];2021年,美国得克萨斯州遭遇极端冰灾天气,超过400万户家庭断电[8]。
冰灾下电力系统供电中断的主要原因在于输电线路覆冰的持续积累,最终超过其承受能力,造成输电线路断裂。目前已有相关文献针对输电线路覆冰展开研究,文献[9-13]研究了输电线路覆冰增长模型和预测方法,文献[14-16]对输电线路覆冰闪络进行了研究,文献[17-19]研究了输电线路直流融冰和除冰技术。这些研究从不同角度分析了冰灾的致灾机理,可发现冰灾的灾害特点与台风、地震等灾害具有显著区别。台风、地震灾害持续时间相比冰灾较短,对电网的短时影响强度大,电网伴随灾害运行时间短,电网恢复过程与灾害进程解耦程度高;而冰灾短时影响强度相对较小但持续时间长,影响具有明显的累积效应,电网恢复过程与灾害进程交互影响(如冰灾期间融冰与覆冰的并存拉锯),冰灾发展过程对源、网、荷各侧的影响复杂,难以简单解耦。
在冰灾对输电系统的影响研究方面,文献[20]提出了一种用于输电系统可靠性分析的天气建模方法,能够有效地预测未来冰灾的发展趋势。文献[21]通过分析冰灾天气下架空输电线路所受冰风荷载,基于模糊理论建立了输电线路故障率的预测模型,对停电事故提供预警信息。文献[22-24]基于输电线路覆冰增长物理过程,结合气象因素构建覆冰增长模型,研究覆冰对输电线路故障率的影响。文献[25]基于输电线路冰荷载和风荷载的联合概率分布,结合极值理论提出了冰灾天气下线路故障概率计算方法。文献[26]根据地理和气象环境计算输电线路覆冰厚度,结合实测信息提出输电线路故障率计算方法,并构建灾前停电风险预警模型。
在针对冰灾的输电网韧性提升研究方面,文献[27]提出了一种基于冰灾发展轨迹预测和输电系统元件位置的韧性提升方法,通过准确预测冰灾的时空发展减小其对系统元件的影响,但是忽略了冰灾强度的变化。文献[28]通过直流除冰设备的灾前配置和路径协同优化调度来保证输电系统的安全性,从而提升电网韧性。文献[29]基于气象数据建立了输电系统元件故障概率模型,在时空层面上分析了冰灾对输电系统运行的影响,在通过规划提升系统韧性的同时减少了经济损失。
综上所述,目前计及冰灾影响的输电网韧性提升研究已取得初步成果,但是这些研究均未涉及冰灾的时空演变规律分析。由于冰灾地理覆盖范围受微气象和微地形等影响,难以精准地预测其发展趋势,构建冰灾时序模型较为困难。卫星遥感技术为该难题提供了解决思路。卫星遥感是应用人造地球卫星探测仪器,通过从远处探测研究对象与特定光谱波段的相互作用,记录研究对象的光谱波段特性,进而分析研究对象的特征性质及其变化。经过长时间的发展,目前卫星遥感已能够获得高时空分辨率的遥感图像,被广泛地应用于地质灾害监测。文献[30]利用美国Landsat 7卫星遥感图像,结合随机森林(Random Forest, RF)算法成功地提取了绵远河流域滑坡区域。文献[31]利用高空间分辨率遥感数据成功地识别地裂缝,进而确定某地的地面坍塌范围。文献[32]通过对火山的红外波段遥感图像进行多尺度观测,研究火山活动变化。文献[33]利用美国Landsat TM卫星的历史遥感图像,监测某地区的土壤侵蚀情况,并对侵蚀严重程度进行分级。
在冰灾方面,国内外学者已在该领域开展相关研究,并总结了可用的覆冰监测和时序分析方法。文献[34]利用中分辨率成像光谱仪(Moderate Resolution Imaging Spectroradiometer, MODIS)传感器获取的图像监测覆冰数据,结合气象数据提出基于不同机器学习和深度学习算法的覆冰面积预测方法,并评估了预测精度。文献[35]基于哨兵2号(Sentinel-2)卫星和Landsat-7/8卫星场景、激光雷达和原位数据集,根据不同冠层覆盖度和太阳辐照度试验区记录的现场覆冰深度测量时间序列,评估了覆冰检测的有效性。文献[36]利用MODIS图像和归一化差值积雪指数(Normalized Difference Snow Index, NDSI)阈值法对某流域覆冰面积进行了时空定量分析,但是NDSI阈值的设置对覆冰面积的时序拟合效果影响较大。然而,上述研究仅考虑覆冰面积的监测和时序场景构建,缺乏计及冰灾强度的覆冰区域发展模式时序建模手段。同时,目前针对冰灾下输电网韧性提升的研究都聚焦于灾前预防和灾后维修。而冰灾发展缓慢,持续时间长,对系统特性的影响存在明显的弛豫效应,灾害发展进程与韧性提升措施存在相互作用,可以同时通过灾前预防和灾中维修措施共同增强输电网韧性。本文针对目前冰灾天气下输电网韧性提升研究的不足,提出一种基于多光谱卫星遥感的输电网冰灾场景时序建模与韧性提升策略优化方法。主要贡献如下:
1)提出基于多光谱卫星遥感的冰灾场景时序建模方法,将Sentinel-2卫星遥感图像进行融合,获取高质量覆冰区域提取图像,提高覆冰区域识别精度。基于融合图像,结合偏微分卷积实现覆冰区域图像动态预测,构建冰灾发展时序模型。
2)基于条件变分自动编码器(Variational Auto-Encoder, VAE),结合历史数据生成不同恶劣程度覆冰区域下的风光出力、输电线路传输容量及负荷需求。该方法生成的数据能够准确地反映冰灾下“源-网-荷”的时空特性,且场景生成过程中无需进行概率建模和场景削减。
3)提出基于冰灾场景的输电网两阶段鲁棒韧性提升规划模型:第一阶段以最小化固定储能配置和维修资源成本为目标,在灾害发生前对固定储能配置和维修资源进行预规划,寻找最优投资决策;第二阶段以最大化系统综合恢复为目标,确保固定储能和维修队伍在冰灾发生后快速响应,保证负荷快速恢复,提升输电网韧性,减少经济损失。最后利用可并行计算的列和约束生成(Column and Constraint Generation, C&CG)算法迭代求解该模型。
1 考虑卫星遥感数据的冰灾场景生成
1.1 遥感图像融合
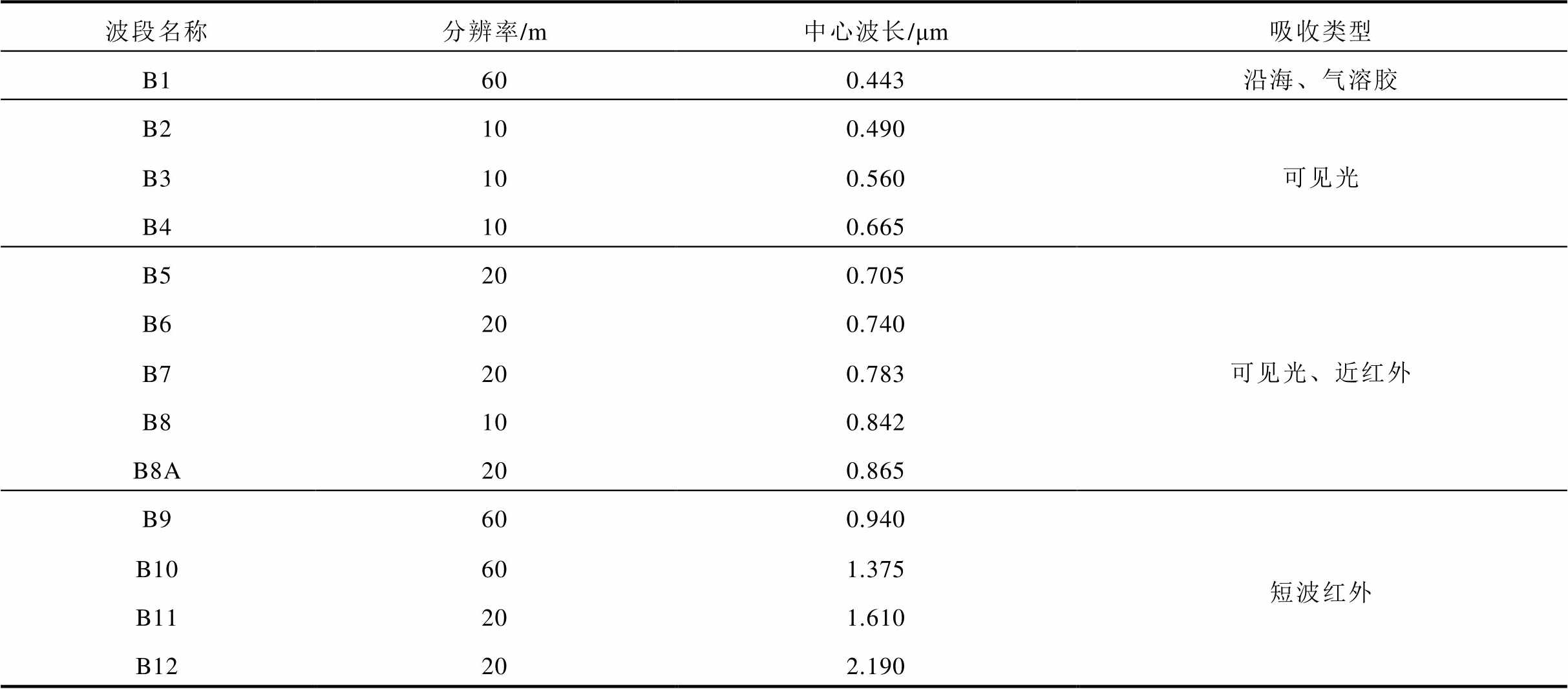
Sentinel-2卫星是欧洲空间局研制的地球观测卫星,配备了最先进的多光谱成像仪,能够捕捉不同尺度光谱波段的图像,提供高分辨率的光学成像,实现对地球表面和大气层的多光谱和多时间尺度观测。Sentinel-2遥感图像的光谱波段和划分见表1。本文将Sentinel-2卫星遥感图像数据的13个光谱波段按照表1中划分为4个吸收类型波段,并在谷歌地球引擎遥感云计算平台(https://earthengine. google.com/)中获取包含不同波段组合的遥感图像。Sentinel-2卫星不同光谱波段组合的遥感图像具有独特的特征优势,可利用波段组合凸显图像中的要素特征,提取特定信息。如自然色波段组合(B4、B3、B2)可直观地监测地表的覆冰区域变化;彩色红外波段组合(B8、B4、B3)可精准地识别植被区域中的覆冰区域;短波红外波段组合(B12、B8A、B4)用于监测各种绿色深浅的植被情况;农业波段组合(B11、B8、B2)用于监测作物的健康状况;地质波段组合(B12、B11、B2)用于寻找断层、岩性和地质构造等地质特征。
表1 Sentinel-2遥感图像的光谱波段和划分
Tab.1 The spectral bands and categories of Sentinel-2 remote sensing images
波段名称分辨率/m中心波长/μm吸收类型 B1600.443沿海、气溶胶 B2100.490可见光 B3100.560 B4100.665 B5200.705可见光、近红外 B6200.740 B7200.783 B8100.842 B8A200.865 B9600.940短波红外 B10601.375 B11201.610 B12202.190
本文采用基于拉普拉斯金字塔分解的图像融合方法对自然色波段组合和彩色红外波段组合的覆冰遥感图像进行融合,增强覆冰区域提取图像质量,提高覆冰区域识别精度,步骤如下。
1)采用拉普拉斯金字塔对多光谱遥感图像进行多尺度分解,通过高斯滤波器将灰度化处理后的不同波段组合原始遥感图像分解成多个不同尺度的细节和近似分量[37],表示为
2)图像融合过程中,融合分量权值由原始图像的显著性水平决定,为在保留各光谱特征优势的同时减少空间特征不匹配的混叠现象,利用导向滤波修正图像融合过程中原始图像的显著性水平[38],融合计算方法为
式中,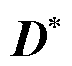 为融合图像;
为融合图像;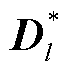 为金字塔第l层的融合分量;
为金字塔第l层的融合分量;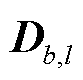 为波段b的金字塔第l层的融合分量;
为波段b的金字塔第l层的融合分量;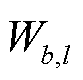 为波段b的金字塔第l层融合分量权值;
为波段b的金字塔第l层融合分量权值;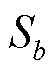 为波段b的显著性水平;
为波段b的显著性水平;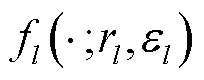 为金字塔第l层导向滤波函数;
为金字塔第l层导向滤波函数;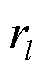 为含参数的导向滤波半径;
为含参数的导向滤波半径;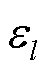 为正则化系数;
为正则化系数;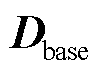 为导向滤波的基底。
为导向滤波的基底。
1.2 基于偏微分特性的覆冰区域图像动态预测
基于1.1节的图像融合结果,可使用卷积神经网络构建覆冰区域图像预测模型,根据历史覆冰区域图像预测覆冰区域的变化。本文结合偏微分网络动态特性[39],构建基于偏微分特性的卷积神经网络覆冰区域图像动态预测模型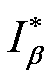 ,如图2所示。
,如图2所示。
当卷积神经网络卷积核C的各阶矩满足特定条件时,可利用偏微分运算作为卷积运算[39]。
式中,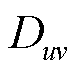 为第u+v阶微分算子;x和y分别表示融合图像的水平和垂直方向。
为第u+v阶微分算子;x和y分别表示融合图像的水平和垂直方向。
在图像滚动预测模型中,利用t+1~t+c-1时间内的预测图像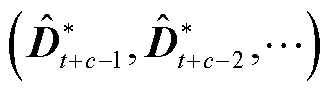 和t时段真实覆冰区域遥感图像
和t时段真实覆冰区域遥感图像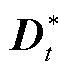 作为模型输入来预测t+c时段的覆冰区域图像
作为模型输入来预测t+c时段的覆冰区域图像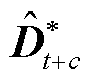 ,预测模型表示为
,预测模型表示为
式中,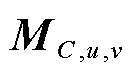 为卷积核C的矩估计;
为卷积核C的矩估计;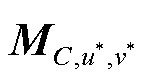 为目标偏微分的矩估计,其中的元素
为目标偏微分的矩估计,其中的元素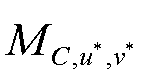 满足式(5);
满足式(5);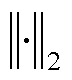 和
和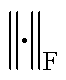 分别为向量2范数和矩阵F范数;β为预测模型
分别为向量2范数和矩阵F范数;β为预测模型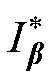 的参数集合。
的参数集合。
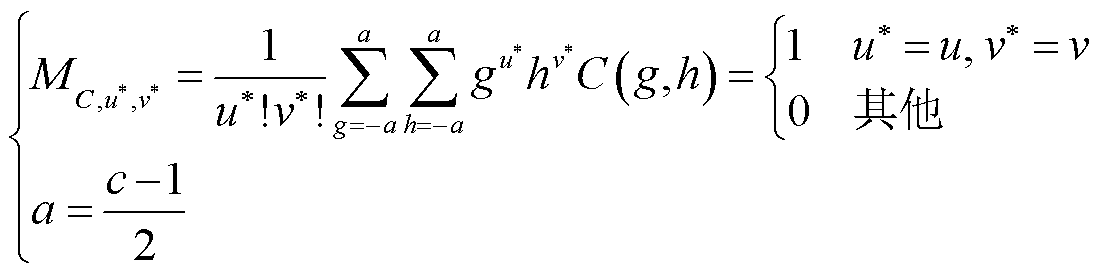 (5)
(5)
式中,C(g, h)为卷积核参数。
1.3 冰灾发展时序模型构建
冰灾对输电网的破坏主要在于对输电网设备的损害,设备故障概率与冰灾恶劣程度Yk直接相关。输电网覆盖区域广,邻近设备故障概率相近,为保证冰灾恶劣程度的实用性,本文利用ArcGIS软件计算1.2节中t时刻某一预测覆冰区域Θ的面积SΘ,t,将该覆冰区域等效为半径为RΘ,t的圆形区域。RΘ,t表达式为
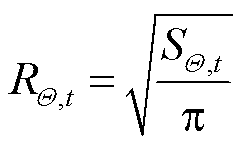 (6)
(6)
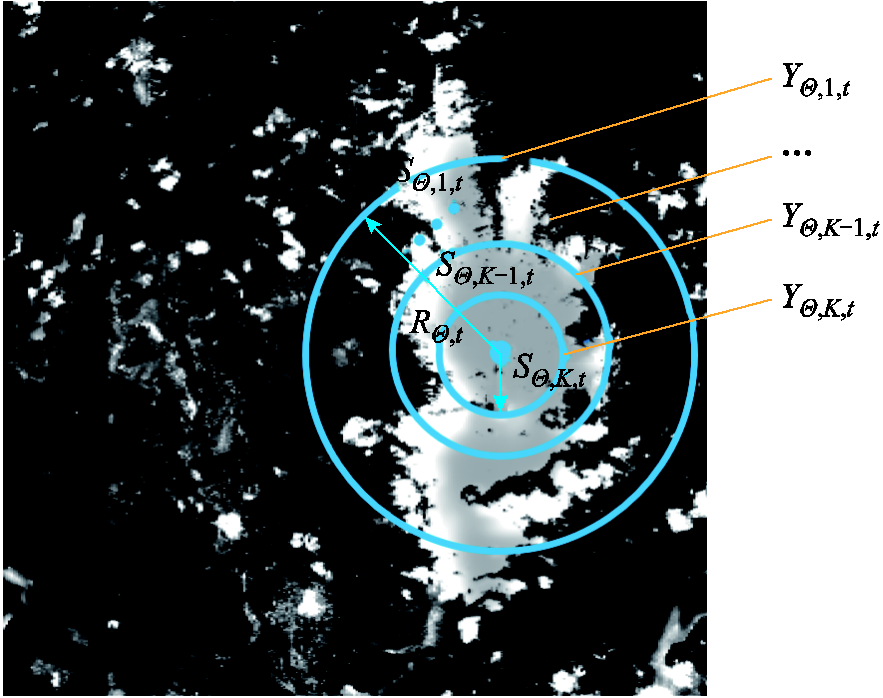
将该覆冰区域均匀地划分为K个子区域,如图3所示。假设在任意时刻t,任意子区域内各点的冰灾恶劣程度相同,距离覆冰区域中心越近的设备故障概率越高,冰灾天气最恶劣,中心子区域SΘ,K,t内各点的冰灾恶劣程度均为YΘ,K,t。随着与覆冰区域中心的距离逐渐增大,冰灾恶劣程度逐渐下降,第k个子区域SΘ,k,t内各点的冰灾恶劣程度为YΘ,k,t,k=1, 2,…, K-1。
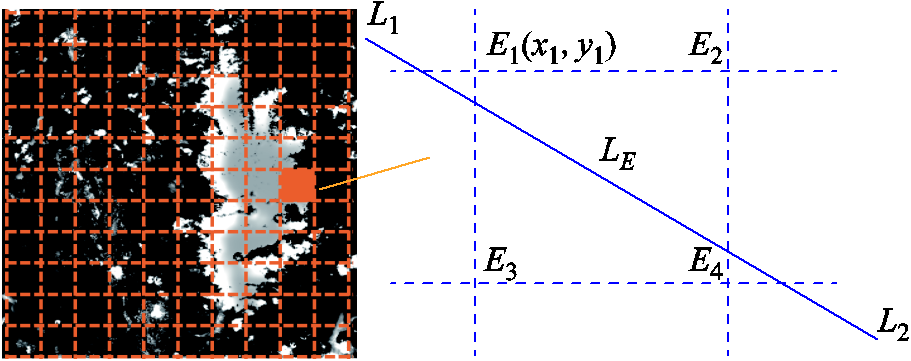
本文通过覆冰区域网格化提高冰灾发展时序模型的预测精度,覆冰区域网格化处理如图4所示。坐标点E1(x1, y1)处的冰灾恶劣程度YΘ,E1,t由其与覆冰区域Θ中心的距离RΘ,E1,t决定,即
同理,E2、E3、E4各点冰灾恶劣程度可由式(7)求得。输电线路L1L2部分线路处于E1、E2、E3、E4组成的区域LE内,区域内冰灾恶劣程度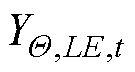 为各顶点的冰灾恶劣程度平均值。
为各顶点的冰灾恶劣程度平均值。
1.4 输电系统故障模型
冰灾天气下,覆冰持续积累导致输电线路断裂,建立网格区域下输电线路覆冰厚度预测模型为
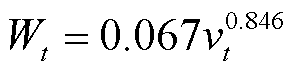 (9)
(9)
式中,Rij,m,t为t时刻线路ij在第m个网格区域内的覆冰厚度;YΘ,m,t为t时刻第m个网格区域内的冰灾恶劣程度;ρ为冰密度;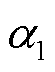 、
、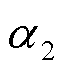 和
和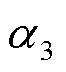 分别为碰撞、捕获和凝结系数;
分别为碰撞、捕获和凝结系数;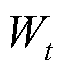 、
、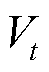 和
和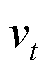 分别为t时刻的空气含水量、风速和降水率。
分别为t时刻的空气含水量、风速和降水率。
然而,输电网沿线普遍存在微地形变化,局部小地形内气象因子(如风速)显著变化,输电线路覆冰增强。本文基于输电线路设计标准,根据地表粗糙度将地表划分为四类,量化微地形与微气象对输电线路覆冰厚度预测的影响。不同地表类别的粗糙度系数见表2。
表2 不同地表类别的粗糙度系数
Tab.2 Roughness coefficient of different landforms

地表类别地表状况粗糙度系数 Ⅰ近海海面、海岸、海岛、开阔水面以及沙漠地区0.12 Ⅱ田野、乡村、丛林以及稀疏低层建筑群地区0.16 Ⅲ树木、密集低层建筑群地区以及平缓的丘陵地区0.22 Ⅳ密集中高层建筑群地区、起伏较大的丘陵地区0.3
不同高度和地表下,距离地表h处的风速为
式中,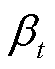 为t时刻风速与输电线路间的夹角;
为t时刻风速与输电线路间的夹角;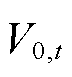 为t时刻距离地表h处的风速;ε为地表粗糙度系数。
为t时刻距离地表h处的风速;ε为地表粗糙度系数。
基于覆冰厚度,得到输电线路的脆弱性模型为
式中,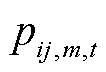 为t时刻线路ij在第m个网格区域内的故障率;
为t时刻线路ij在第m个网格区域内的故障率;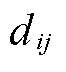 为输电线路ij的最大抗冰厚度。
为输电线路ij的最大抗冰厚度。
线路ij在t时刻的故障率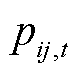 和传输容量
和传输容量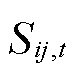 为
为
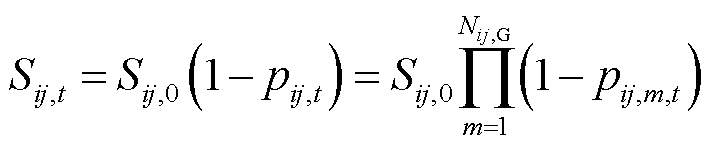 (13)
(13)
式中,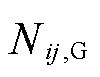 为线路ij所处的网格总数;
为线路ij所处的网格总数;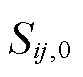 为线路ij正常运行状态下的传输容量。
为线路ij正常运行状态下的传输容量。
冰灾天气下,风力发电机叶片尖端覆冰和光伏组件表面覆冰导致风光机组出力显著下降,风光机组wp覆冰厚度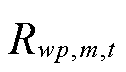 预测模型形式参考式(8)。第m个网格区域内的风光机组wp在t时刻的出力损失
预测模型形式参考式(8)。第m个网格区域内的风光机组wp在t时刻的出力损失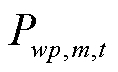 为
为
式中,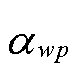 和
和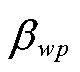 为风光损失系数;
为风光损失系数;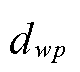 为风光机组的最大抗冰厚度。
为风光机组的最大抗冰厚度。
1.5 基于条件变分自动编码器的冰灾场景生成
在用于输电网韧性提升规划的冰灾场景生成中,关键在于获得不同恶劣程度冰灾天气下覆冰区域的风光出力、输电线路传输容量以及负荷需求概率分布。然而,由于冰灾天气下的“源-网-荷”概率分布模型受冰灾复杂演变过程、风光机组间复杂时空关系、输电线路覆冰积累以及负荷时空特性等因素影响,建立传统概率分布模型的难度大。因此,本文提出一种基于条件变分自动编码器(VAE)的冰灾场景生成方法,利用深度神经网络的强大拟合能力,输入历史覆冰区域的“源-网-荷”数据,变分自动编码器无监督地学习历史数据的统计规律,并基于训练得到的概率分布模型生成符合数据分布特点的全新“源-网-荷”数据。
对传统的VAE进行条件化改进,在VAE模型的训练数据分布拟合阶段加入冰灾天气标签信息,利用one-hot编码表示冰灾的恶劣程度,给每个训练数据添加冰灾标签信息。不同恶劣程度Yk条件下冰灾场景生成所需的“源-网-荷”数据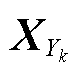 =[XW|Yk XPV|Yk Xline|Yk Xload|Yk]由一系列隐变量Z产生。以风电样本数据为例,记含参数θ的生成模型(解码器)为
=[XW|Yk XPV|Yk Xline|Yk Xload|Yk]由一系列隐变量Z产生。以风电样本数据为例,记含参数θ的生成模型(解码器)为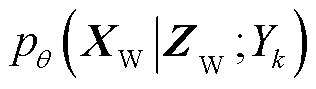 ,假设
,假设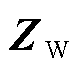 独立同分布,利用对数最大似然估计方法计算生成模型参数为
独立同分布,利用对数最大似然估计方法计算生成模型参数为
式中,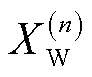 为第n个历史风电出力样本数据,
为第n个历史风电出力样本数据,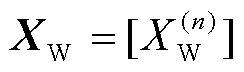 ;N为历史样本数据总数。
;N为历史样本数据总数。
在条件VAE模型中通过识别模型,即含参数f的编码器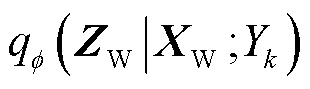 逼近历史样本数据后验概率
逼近历史样本数据后验概率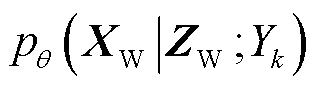 ,利用Kullback-Leibler(KL)距离fKL(·)衡量这两个分布之间的相似程度,表示为
,利用Kullback-Leibler(KL)距离fKL(·)衡量这两个分布之间的相似程度,表示为
使用变分思想优化下界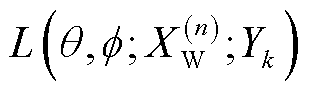 可得
可得
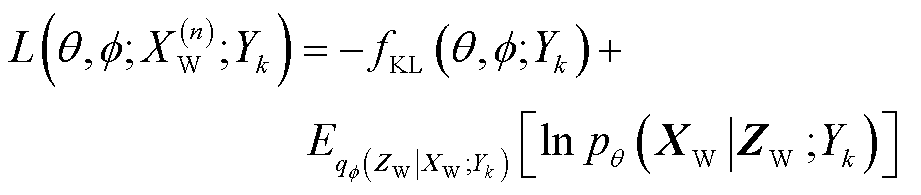 (17)
(17)
对式(17)右侧第一项,令编码器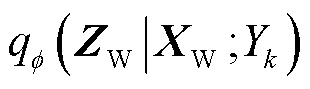 服从独立高斯分布,解码器
服从独立高斯分布,解码器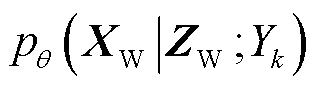 服从标准正态分布,则由KL距离可得
服从标准正态分布,则由KL距离可得
式中,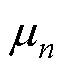 和
和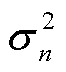 分别为第n个历史风电出力样本数据下编码器
分别为第n个历史风电出力样本数据下编码器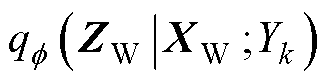 高斯分布的均值和方差。
高斯分布的均值和方差。
对式(17)右侧第二项,其是关于历史样本数据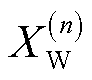 后验概率的对数似然,无法求得解析解,采用蒙特卡洛抽样可得
后验概率的对数似然,无法求得解析解,采用蒙特卡洛抽样可得
式中,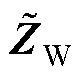 为蒙特卡洛抽样下的隐变量。每次采样总数取1,记此时
为蒙特卡洛抽样下的隐变量。每次采样总数取1,记此时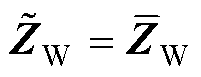 ,则有
,则有
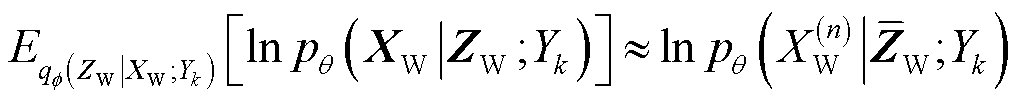 (20)
(20)
式(20)与神经网络损失函数形式相同,令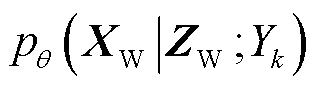 取伯努利分布,则损失函数
取伯努利分布,则损失函数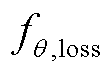 为互熵损失,即
为互熵损失,即
式中,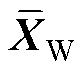 为服从伯努利分布的样本数据。
为服从伯努利分布的样本数据。
综上所述,在本文的冰灾场景生成中,可利用深度神经网络实现对覆冰区域风电数据概率分布的拟合,结合梯度反向传播技术对输入风电数据进行反复训练,解码器即可学习到历史风电数据的映射规律,训练流程如下:
(1)数据编码。输入原始风电数据,通过编码器和高斯分布采样,生成一组特征向量。
(2)数据解码。利用解码器将步骤1)中输出的特征向量还原为原始输入数据形式。
(3)梯度反向传播。通过步骤2)中输出数据与原始输入数据计算损失函数,利用梯度反向传播更新深度神经网络权值。
同理,解码器可学习不同恶劣程度覆冰区域的历史光伏出力、输电线路传输容量及负荷需求数据的映射规律,训练流程同上。提取解码器,将1.3节冰灾发展时序模型中的冰灾恶劣程度Yk以one-hot编码形式和四组符合独立高斯分布的特征向量同时输入,即可生成对应Yk的风电出力、光伏出力、输电线路传输容量以及负荷需求新数据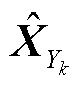 =[
=[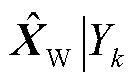
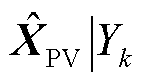
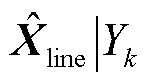
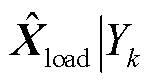 ],该数据集满足历史数据的概率分布。基于条件VAE的冰灾场景生成过程如图5所示。
],该数据集满足历史数据的概率分布。基于条件VAE的冰灾场景生成过程如图5所示。
2 基于冰灾场景的输电网两阶段鲁棒韧性提升规划模型
2.1 目标函数
基于1.5节生成的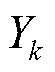 下风光出力、输电线路传输容量以及负荷需求,本节构建基于冰灾场景的输电网两阶段鲁棒韧性提升规划模型。
下风光出力、输电线路传输容量以及负荷需求,本节构建基于冰灾场景的输电网两阶段鲁棒韧性提升规划模型。
目标函数为
式中,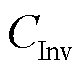 为固定储能配置成本;
为固定储能配置成本;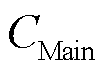 为应急维修投资成本;
为应急维修投资成本;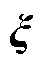 为第一阶段的投资决策变量,包括固定储能的安装位置、配置容量及配置功率;
为第一阶段的投资决策变量,包括固定储能的安装位置、配置容量及配置功率;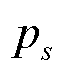 为冰灾场景s出现的概率;S为冰灾场景总数;
为冰灾场景s出现的概率;S为冰灾场景总数;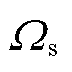 为冰灾场景集合;
为冰灾场景集合;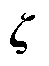 为第二阶段给定投资决策和冰灾场景下的系统运行决策变量,包括固定储能的充放电功率、火电机组出力等;
为第二阶段给定投资决策和冰灾场景下的系统运行决策变量,包括固定储能的充放电功率、火电机组出力等;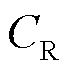 为单位负荷削减的惩罚费用;
为单位负荷削减的惩罚费用;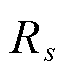 为冰灾场景s下的系统韧性指标。
为冰灾场景s下的系统韧性指标。
1)固定储能配置成本
式中,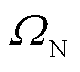 为输电网节点集合;
为输电网节点集合;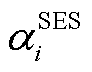 为0-1变量,若取1则表示节点i安装一台固定储能设备,否则取0;
为0-1变量,若取1则表示节点i安装一台固定储能设备,否则取0; 、
、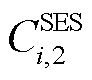 和
和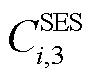 分别为输电网中节点i的固定储能基本配置成本、单位配置容量成本和单位配置功率成本;
分别为输电网中节点i的固定储能基本配置成本、单位配置容量成本和单位配置功率成本;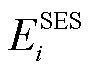 和
和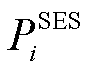 分别为固定储能在输电网节点i的配置容量和功率。
分别为固定储能在输电网节点i的配置容量和功率。
2)应急维修投资成本
式中,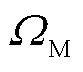 为维修队伍集合;
为维修队伍集合;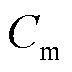 和
和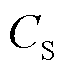 分别为单位维修队伍成本和单位维修资源成本;
分别为单位维修队伍成本和单位维修资源成本;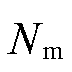 为配备的维修队伍总数;
为配备的维修队伍总数;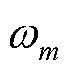 为维修队伍m所能配备的最大维修资源。
为维修队伍m所能配备的最大维修资源。
3)系统韧性指标
基于冰灾对风光出力减小、输电线路传输容量减小以及负荷需求增大的影响,从发电恢复比例、输电恢复比例、负荷恢复比例三个角度出发,构建考虑冰灾发展时序特性的“源、网、荷”多维度系统韧性评估指标体系,为输电系统提供全面的综合韧性评估。
(1)发电恢复比例
式中,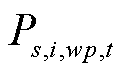 为场景s下节点i在t时刻所连风光机组wp的有功发电功率;
为场景s下节点i在t时刻所连风光机组wp的有功发电功率;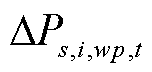 为场景s下节点i在t时刻所连风光机组wp的有功发电功率削减量;T为规划总时间。
为场景s下节点i在t时刻所连风光机组wp的有功发电功率削减量;T为规划总时间。
(2)输电恢复比例
式中,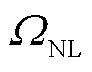 为输电网线路集合;
为输电网线路集合;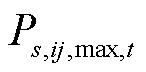 为场景s下t时刻输电线路ij可传递的有功功率最大值;
为场景s下t时刻输电线路ij可传递的有功功率最大值;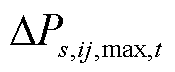 为场景s下在t时刻输电线路ij可传递的有功功率最大值削减量。
为场景s下在t时刻输电线路ij可传递的有功功率最大值削减量。
(3)负荷恢复比例
式中,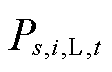 为场景s下t时刻节点i的负荷;
为场景s下t时刻节点i的负荷;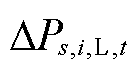 为场景s下t时刻节点i的负荷削减量。
为场景s下t时刻节点i的负荷削减量。
综上所述,系统韧性指标为
式中,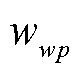 、
、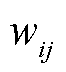 和
和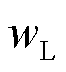 分别为发电恢复比例、输电恢复比例和负荷恢复比例的权重系数,且
分别为发电恢复比例、输电恢复比例和负荷恢复比例的权重系数,且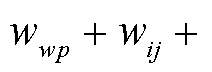
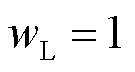 。
。
2.2 约束条件
1)固定储能设备资源约束
假设冰灾发生前储备的固定储能资源有限,并且每台固定储能设备的参数相同,每个节点最多预先配置一台固定储能设备,其数学模型为
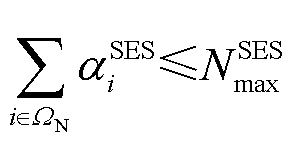 (29)
(29)
式中,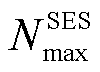 为固定储能设备上限。
为固定储能设备上限。
节点i处固定储能的配置容量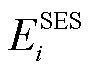 和配置功率
和配置功率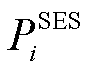 满足约束为
满足约束为
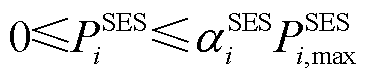 (31)
(31)
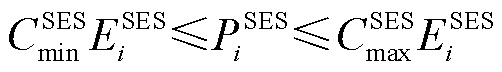 (32)
(32)
式中,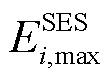 和
和 分别为节点i处固定储能配置容量的最大值、最小值;
分别为节点i处固定储能配置容量的最大值、最小值;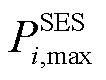 为节点i处固定储能配置功率最大值;
为节点i处固定储能配置功率最大值;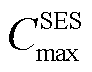 和
和 分别为固定储能最大和最小充电倍率。
分别为固定储能最大和最小充电倍率。
2)固定储能运行约束
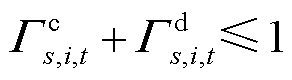 (33)
(33)
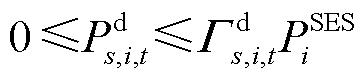 (35)
(35)
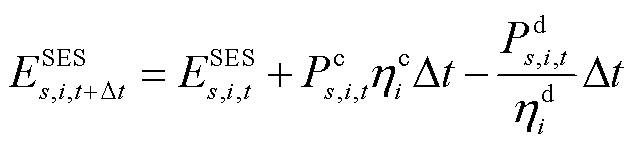 (36)
(36)
式中,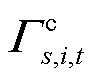 和
和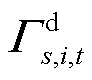 为0-1变量,若取1则分别表示场景s下节点i处的固定储能在t时刻处于充、放电状态,否则取0;
为0-1变量,若取1则分别表示场景s下节点i处的固定储能在t时刻处于充、放电状态,否则取0;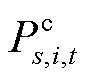 和
和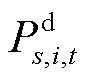 分别为场景s下节点i处的固定储能在t时刻的充、放电功率;
分别为场景s下节点i处的固定储能在t时刻的充、放电功率;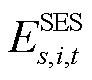 为场景s下节点i处的固定储能在t时刻的存储电量;
为场景s下节点i处的固定储能在t时刻的存储电量;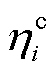 和
和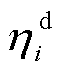 分别为节点i处的固定储能的充、放电效率;
分别为节点i处的固定储能的充、放电效率;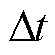 为单个时段的时长;
为单个时段的时长;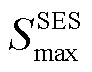 和
和 分别为固定储能荷电状态的上、下限。
分别为固定储能荷电状态的上、下限。
3)输电网直流潮流约束
输电线路ij在场景s下任意时刻t的有功功率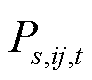 满足
满足
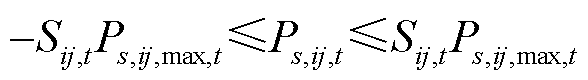 (39)
(39)
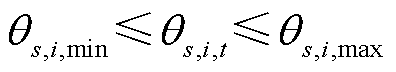 (40)
(40)
式中,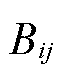 为线路ij的电纳值;
为线路ij的电纳值;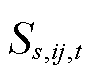 为0-1变量,表示场景s下t时刻输电线路ij的状态,当线路处于故障或维修状态时取0,否则取1;M为一足够大的数;
为0-1变量,表示场景s下t时刻输电线路ij的状态,当线路处于故障或维修状态时取0,否则取1;M为一足够大的数;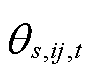 为场景s下节点i与节点j在t时刻的电压相位差,
为场景s下节点i与节点j在t时刻的电压相位差,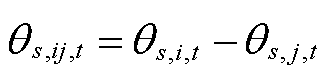 ;
;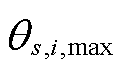 和
和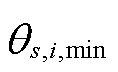 分别为场景s下节点i的电压相位上、下限。
分别为场景s下节点i的电压相位上、下限。
4)节点功率平衡约束
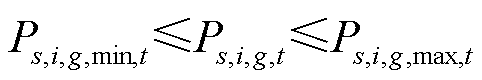 (42)
(42)
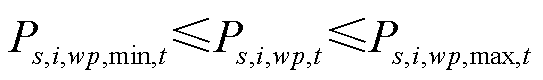 (43)
(43)
式中,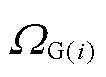 、
、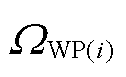 分别为节点i的火电、风光机组集合;
分别为节点i的火电、风光机组集合;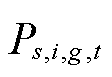 为场景s下t时刻节点i所连火电机组g的有功发电功率;
为场景s下t时刻节点i所连火电机组g的有功发电功率;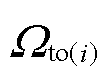 为末节点是i的输电线路集合;
为末节点是i的输电线路集合;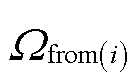 为首节点是i的输电线路集合;
为首节点是i的输电线路集合;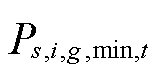 、
、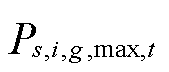 、
、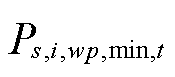 和
和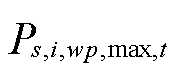 分别为场景s下t时刻节点i所连火电机组和风光机组的最小、最大有功发电功率。
分别为场景s下t时刻节点i所连火电机组和风光机组的最小、最大有功发电功率。
5)灾中维修资源约束
详见附录式(A1)~式(A6)。
3 模型求解
本文构建的输电网两阶段鲁棒韧性提升规划模型为min-max-min三层鲁棒优化问题,采用C&CG算法,将原优化问题分解为主问题和可并行计算的子问题迭代求解。
主问题为在已知冰灾场景下,寻找最优投资决策,具体为
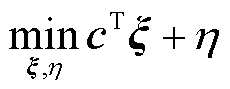 (45)
(45)
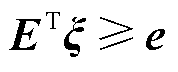 (47)
(47)
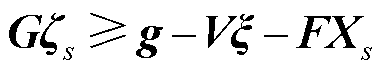 (48)
(48)
式中,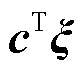 为第一阶段固定储能配置和维修资源投资总成本;
为第一阶段固定储能配置和维修资源投资总成本;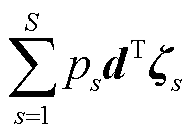 为第二阶段负荷削减损失成本;
为第二阶段负荷削减损失成本;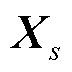 为冰灾场景s下的风光出力、输电线路传输容量及负荷需求;式(47)为投资决策约束,包括式(29)~式(32)及式(A6);式(48)为系统运行约束,包括式(33)~式(44)以及式(A1)~式(A5);E、e、G、g、V、F为相应系数矩阵。
为冰灾场景s下的风光出力、输电线路传输容量及负荷需求;式(47)为投资决策约束,包括式(29)~式(32)及式(A6);式(48)为系统运行约束,包括式(33)~式(44)以及式(A1)~式(A5);E、e、G、g、V、F为相应系数矩阵。
子问题为在给定投资决策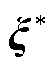 下,寻找最恶劣冰灾场景,表示为
下,寻找最恶劣冰灾场景,表示为
s.t. 式(48) (50)
具体的求解过程如下:
(1)设置初始迭代次数h=0,模型上界UB=+∞,模型下界LB=-∞,模型求解收敛阈值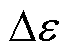 。
。
(2)求解主问题得到最优固定储能配置和维修资源投资决策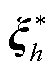 ,更新原问题下界为
,更新原问题下界为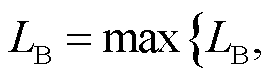
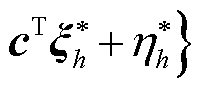 。
。
(3)将主问题解代入子问题中进行求解,获取最恶劣冰灾场景,更新原问题上界为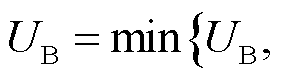
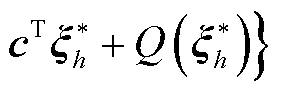 。
。
(4)判断子问题是否存在最优解,若存在,则跳至步骤(6);否则,转向步骤(5)。
(5)令h=h+1,在主问题中新增变量{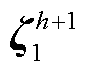 ,
,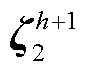 ,…,
,…,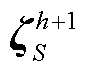 }和式(51)所示可行割,并返回步骤(2)。
}和式(51)所示可行割,并返回步骤(2)。
(6)判断是否满足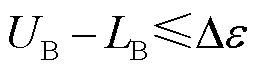 ,若满足,则停止迭代;否则转至步骤(7)。
,若满足,则停止迭代;否则转至步骤(7)。
(7)令h=h+1,在主问题中新增变量{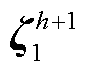 ,
,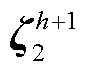 ,…,
,…,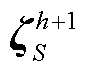 }和式(52)所示最优割,并返回步骤(2)。
}和式(52)所示最优割,并返回步骤(2)。
4 算例分析
4.1 算例设置
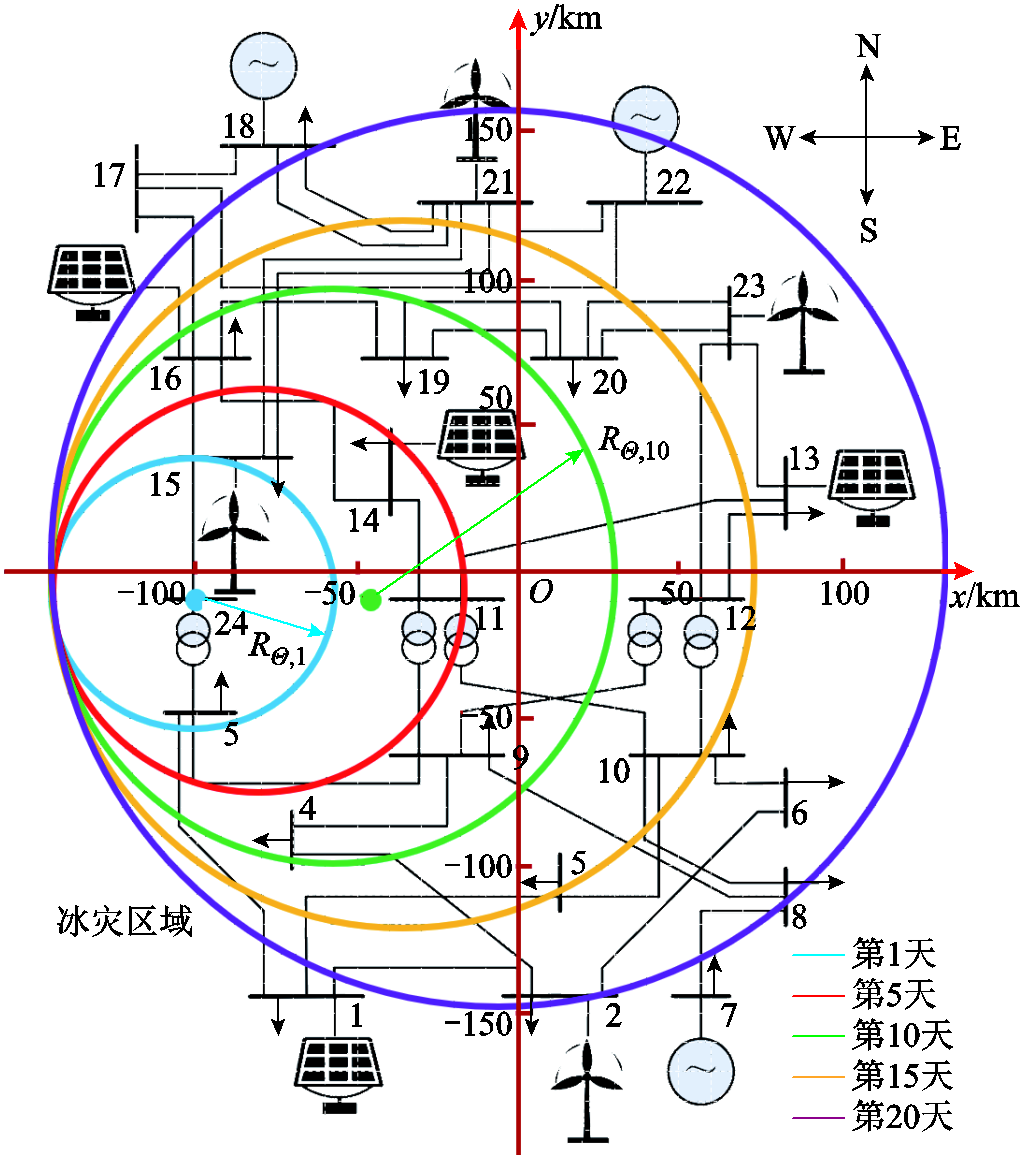
本文以云南某地覆冰遥感数据和改进IEEE RTS-79输电系统作为测试系统进行算例分析,覆冰区域变化如图6所示。
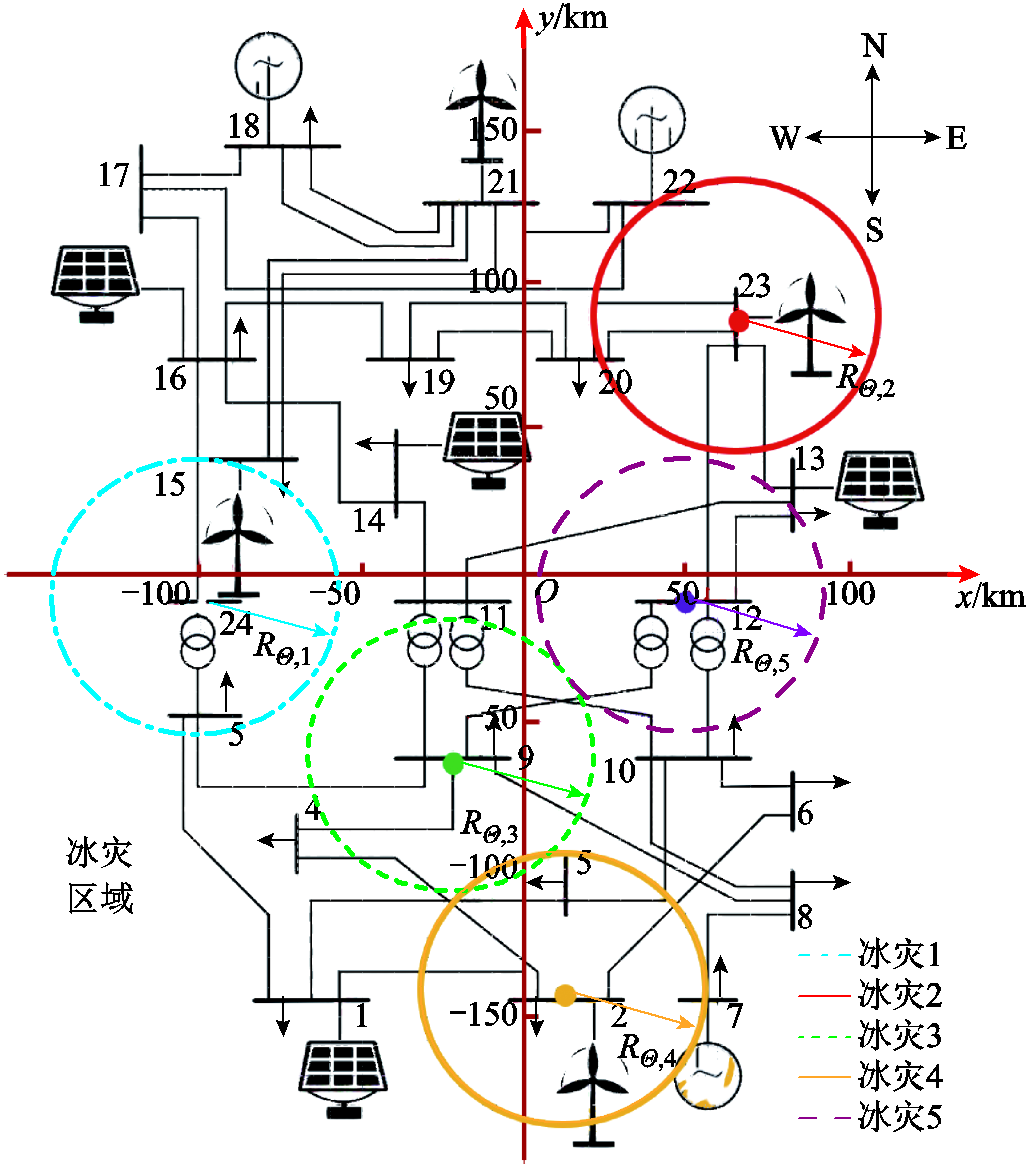
以维修中心O为坐标原点,建立坐标系xOy,单位长度为10 km,改进IEEE RTS-79输电系统示意图如图7所示。
设置K=4,将冰灾恶劣程度划分为四个等级,其对应标签见表3。
表3 冰灾恶劣程度及其对应标签
Tab.3 Ice disasters severity and its corresponding label

冰灾恶劣程度Ykone-hot编码 一般较大重大特大1234[0 0 0 1][0 0 1 0][0 1 0 0][1 0 0 0]
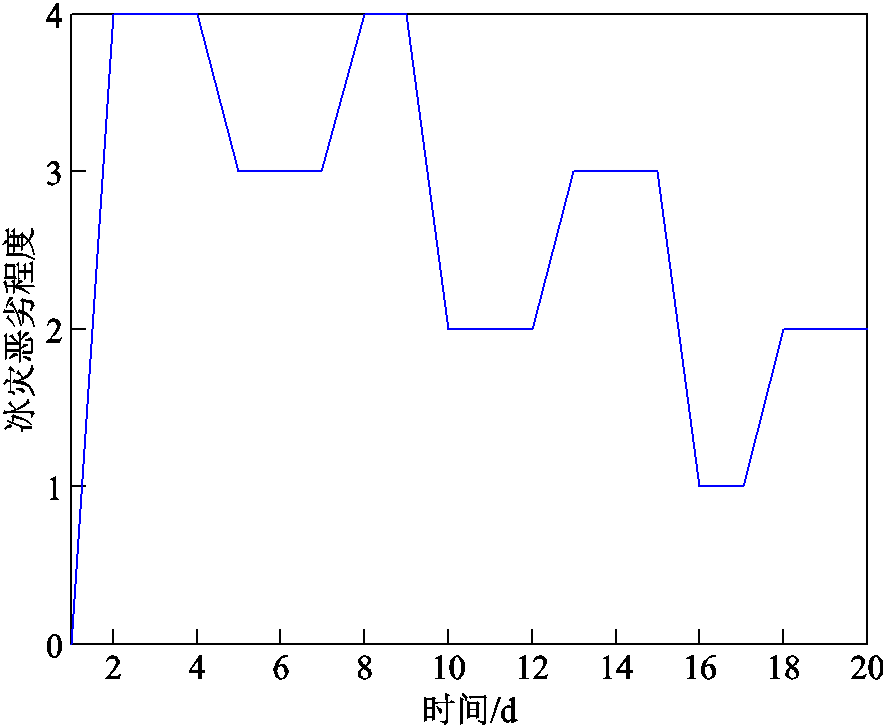
假设规划总时间T为20天,第1天覆冰区域中心位于节点24,区域初始半径RΘ,1=40 km,根据1.3节的冰灾发展时序模型,随着时间的推移,冰灾区域半径逐渐变化,中心逐渐偏移,冰灾区域内各节点的冰灾恶劣程度发生变化,系统中风光机组出力、输电线路容量及负荷需求逐渐变化。节点24的冰灾恶劣程度时序变化如图8所示。同理可分析其他各节点的Yk时序变化。
在节点7、18及22接入火电机组,在节点2、15、21及23接入装机容量相同的风电场,在节点1、13、14及16接入装机容量相同的光伏电站,在节点3、4、19、20接入负荷。风电场与光伏电站出力、输电线路传输容量以及负荷需求由4.3节生成。系统其余参数设置见文献[40]。假设维修队伍的1 km路程理想通行时间为0.1 h,故障元件理想维修时间为2 h,且每个故障元件所需的维修资源相同,均为15。固定储能和维修资源投资参数见表4。
设置储能的荷电状态初始值为0.6,荷电状态的上、下限分别为0.9和0.1,充、放电效率为0.95。设置负荷削减的惩罚费用为5 000元/(MW·h),时间步长为1 h。
表4 固定储能和维修资源投资参数
Tab.4 Investment parameters of energy storage and maintenance resource
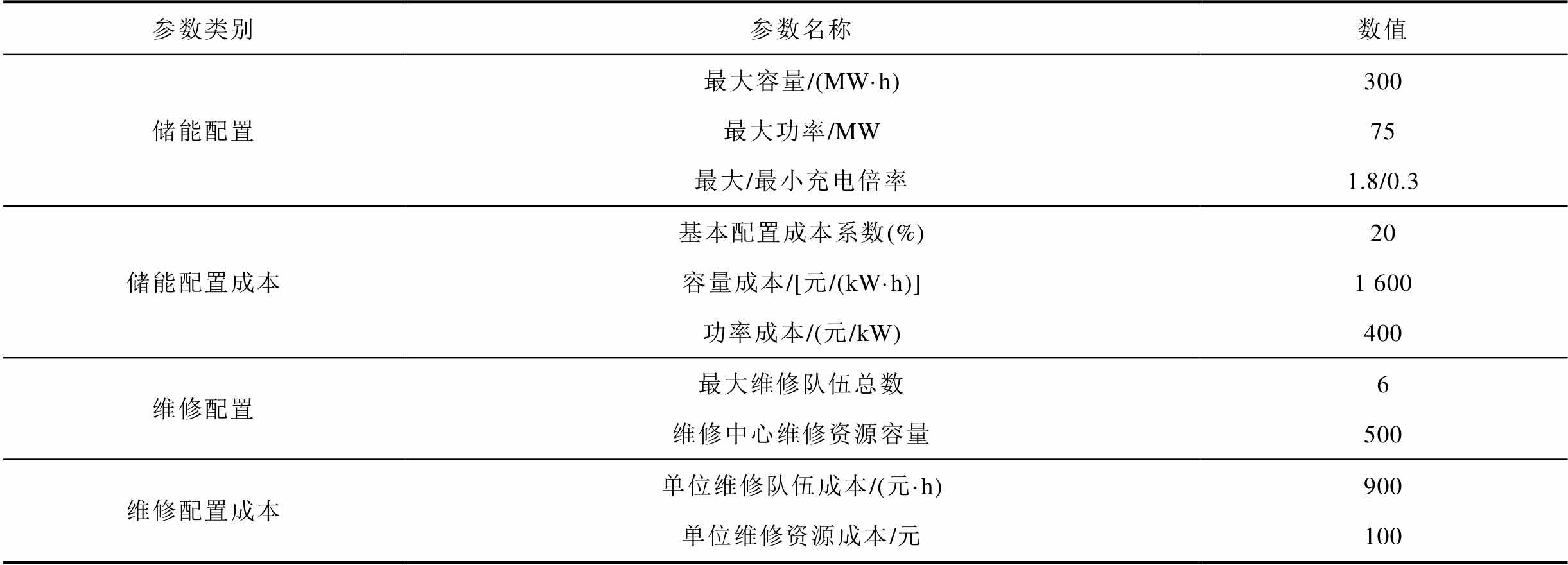
参数类别参数名称数值 储能配置最大容量/(MW·h)300 最大功率/MW75 最大/最小充电倍率1.8/0.3 储能配置成本基本配置成本系数(%)20 容量成本/[元/(kW·h)]1 600 功率成本/(元/kW)400 维修配置最大维修队伍总数6 维修中心维修资源容量500 维修配置成本单位维修队伍成本/(元·h)900 单位维修资源成本/元100
4.2 冰灾时序场景分析
为验证本文所提覆冰区域识别方法和冰灾发展时序模型构建方法的准确性,选取方均根误差(Root Mean Squared Error, RMSE)指标和平均绝对误差(Mean Absolute Error, MAE)指标计算覆冰区域面积误差,表达式分别为
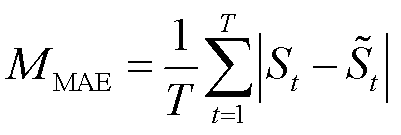 (54)
(54)
式中,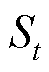 为第t天的覆冰区域实际面积;
为第t天的覆冰区域实际面积;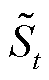 为第t天的覆冰区域提取图中的覆冰面积或第t天的覆冰区域预测面积。
为第t天的覆冰区域提取图中的覆冰面积或第t天的覆冰区域预测面积。
首先,通过与传统的覆冰监测方法如NDSI法、Snowcover法、基于结构注入的空间分辨率增强(ARSIS)法等进行对比,分析比较覆冰区域提取图像中的覆冰面积误差,验证本文所提方法能够有效地提高覆冰区域识别精度。不同方法下的覆冰面积提取误差见表5。
表5 不同方法下的覆冰面积提取误差
Tab.5 Extraction error of ice-covered area under different methods

方法MRMSE/km2MMAE/km2 NDSI法2.8511.336 Snowcover法1.9640.873 ARSIS法2.3711.140 本文方法1.4080.621
然后,通过与传统的机器学习和深度学习算法进行对比,分析比较冰灾发展过程中的覆冰区域面积预测误差,验证本文所提时序模型构建方法的准确性。不同方法下的覆冰面积预测误差见表6。
表6 不同方法下的覆冰面积预测误差
Tab.6 Prediction error of ice-covered area under different methods

方法MRMSE/km2MMAE/km2 支持向量机5.6072.643 多层感知机5.4532.638 长短期神经网络5.3232.470 本文方法4.2702.039
由覆冰面积提取和预测误差比较结果可知,相较于传统的覆冰监测方法以及机器学习和深度学习算法,本文所提图像融合方法能准确地提取覆冰区域,提高覆冰区域识别精度,有效地监督冰灾演变过程,结合偏微分卷积构建的冰灾发展时序模型能准确地预测覆冰面积的发展趋势。
4.3 冰灾场景生成
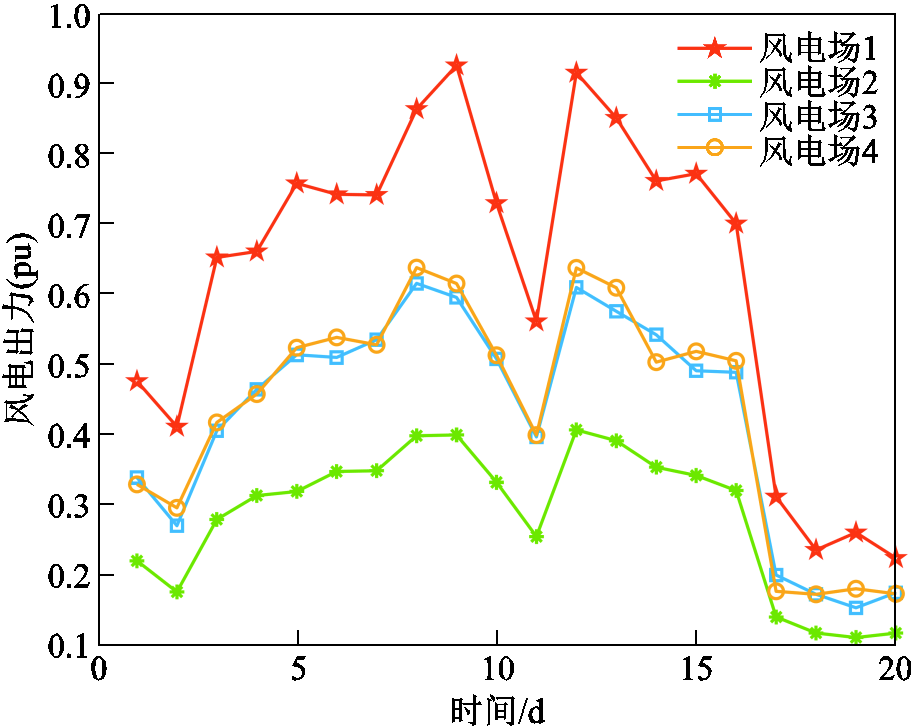
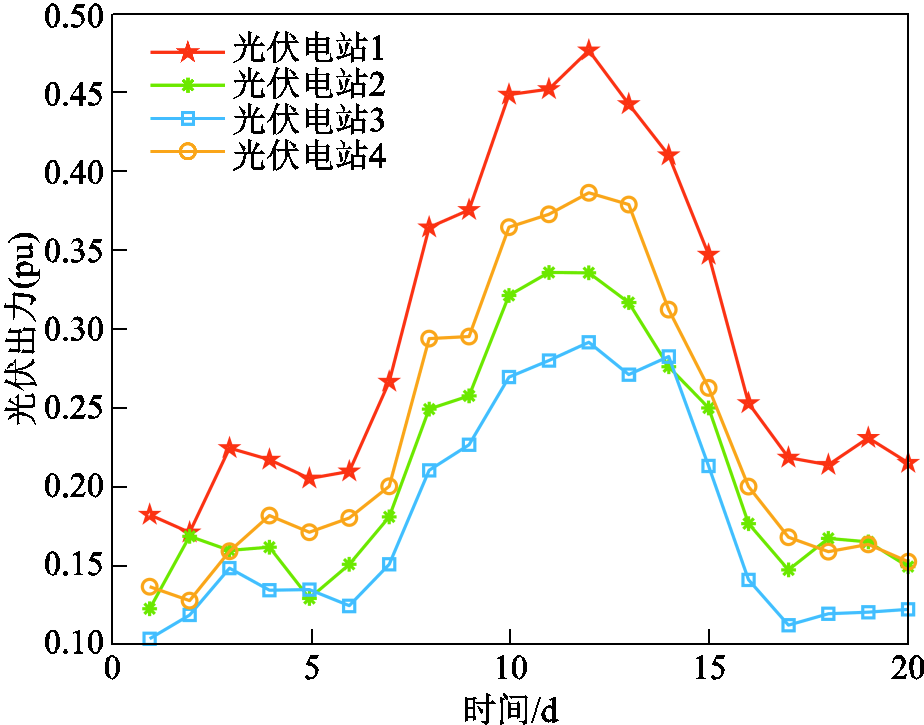
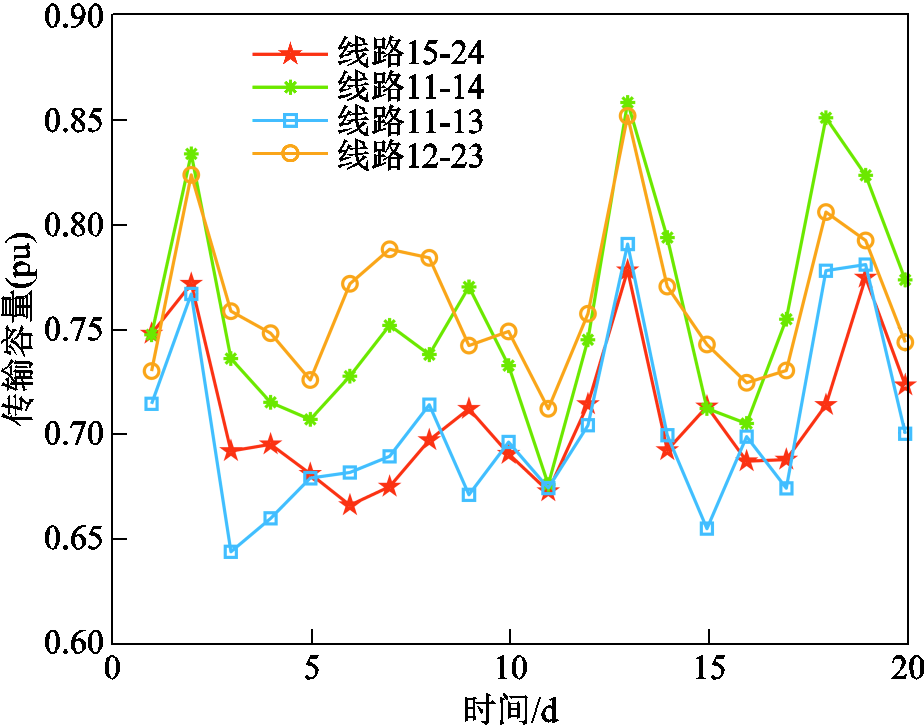
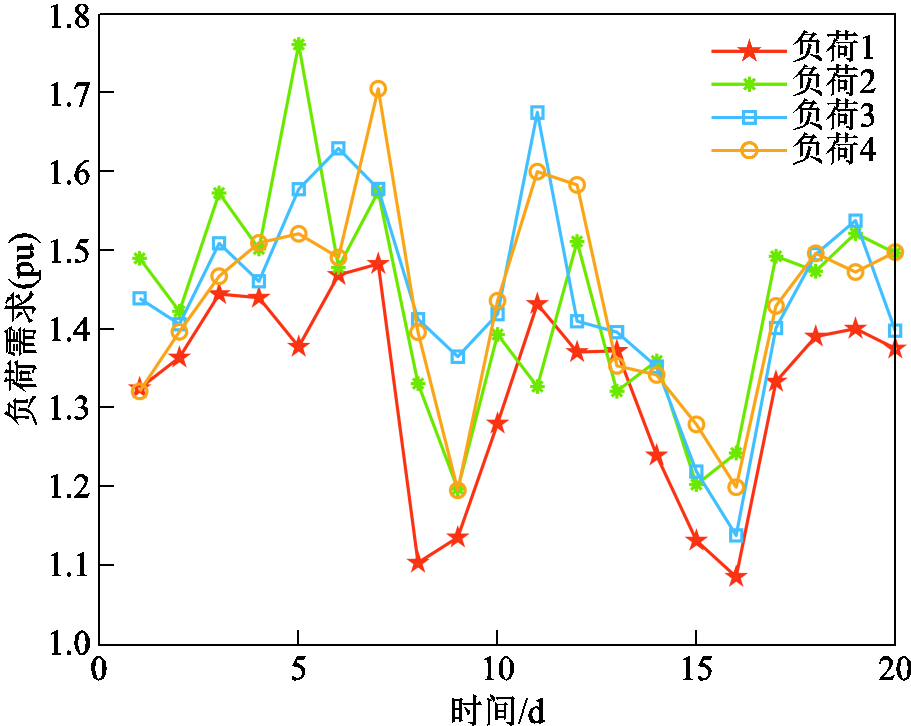
本文采用实际气象数据,结合某地的风电场和光伏电站发电量、输电线路传输容量以及负荷需求,模拟图7中覆冰区域的历史“源-网-荷”数据,分别指定所述的四种冰灾恶劣程度对应的one-hot编码,在训练好的解码器中输入24×20个维度为4的特征向量,因此对于每种冰灾恶劣程度均能产生24×20组“源-网-荷”数据。结合冰灾发展时序模型得到系统的风电场、光伏电站日平均出力,得到部分输电线路日平均传输容量及负荷日平均需求曲线,如图9~图12所示。
由图9和图10可知,随着冰灾恶劣程度的加剧,风光出力整体呈逐渐减小的趋势,且变化趋势相似。当图7中覆冰区域面积变化时,不同地理位置的风电场和光伏电站可能处于覆冰区域中的同一个子区域,与冰灾中心区域的距离相同,冰灾恶劣程度的变化相同,风光机组受冰灾影响的程度相同,因此日平均出力变化趋势相似。
由图11和图12可知,当风光出力逐渐减小时,输电线路传输容量较小,负荷需求较大,可能出现负荷削减的情况,此时需要通过固定储能放电及派出维修队伍应急维修,保障负荷的快速恢复供电,减少经济损失。
4.4 韧性提升规划结果分析
冰灾灾前的固定储能配置与维修资源投资决策为在节点5、14、19接入固定储能,配置容量为73.5 MW·h,配置功率为35.8 MW,配备的维修队伍总数为4,每个队伍配备的最大维修资源为80。
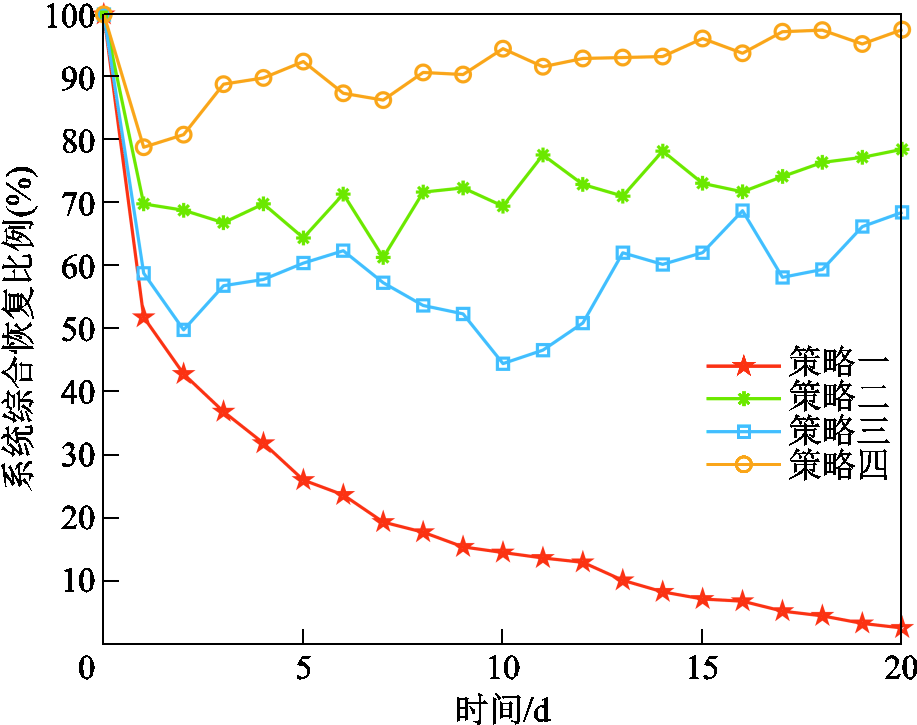
为验证本文所提输电网两阶段鲁棒韧性提升规划策略的优势,设置四种韧性提升策略对比分析:策略一不采取任何措施;策略二仅考虑灾前固定储能配置;策略三仅考虑灾中维修队伍应急维修;策略四为本文所提策略,同时考虑灾前固定储能配置与灾中维修队伍应急维修。不同韧性提升策略下的系统综合恢复比例曲线如图13所示。
由图13可知,当不采取任何措施时,由于冰灾的持续侵蚀作用,系统发电、输电能力以及负荷会逐渐削减。相较于单个韧性提升措施,策略四通过固定储能与应急维修资源协同规划可以最大程度地加快系统综合恢复速度,减少供电负荷削减量。在系统综合韧性提高方面,策略四相较于策略一、二、三分别提高了90.97%、62.69%、82.98%。策略二仅考虑灾前固定储能配置,忽略了灾中输电线路传输容量逐渐下降的情况,持续的覆冰积累过程导致输电线路故障率逐渐增大,传输功率受限,无法充分发挥储能的电源支撑作用。策略三仅考虑灾中应急维修,缺少储能提供必要的功率支撑,当维修队伍处于移动和应急维修状态时,系统供电负荷削减量较大。策略四通过固定储能供电与应急维修的协调配合,能够有效地保证冰灾期间电能的供应以及传输,在冰灾后期系统综合恢复比例达到了96%以上。
四种韧性提升策略下的总成本见表7。由表7可知,虽然策略四的投资成本较高,但在总成本方面,策略四相较于策略一、二、三分别降低了43.19%、24.14%、20.16%。考虑灾前固定储能配置和灾中应急维修的韧性提升规划策略的系统负荷削减损失及总成本均最少,在保证电力安全供应的同时具有更优的经济效应。
表7 不同韧性提升策略下的总成本 (单位:万元)
Tab.7 Total cost under each resilience enhancement strategy

韧性提升策略投资成本负荷削减损失总成本 策略一037 436.1737 436.17 策略二18 974.909 059.6328 034.53 策略三6 772.3619 862.5526 634.91 策略四17 886.403 379.8521 266.25
4.5 不同冰灾发生位置下的韧性提升规划结果分析
本文在图7中设置不同的冰灾区域中心,表示不同的冰灾发生位置。考虑冰灾发生位置的改进IEEE RTS-79输电系统示意图如图14所示。
冰灾2~5的发生位置分别位于节点23、9、2及12,演化过程和系统参数设置与冰灾1相同。不同冰灾发生位置下,本文所提韧性提升策略的投资成本、系统综合韧性提高比例和总成本降低比例见表8。
表8 不同冰灾发生位置下的韧性提升总成本
Tab.8 Total resilience enhancement cost under different ice disaster locations
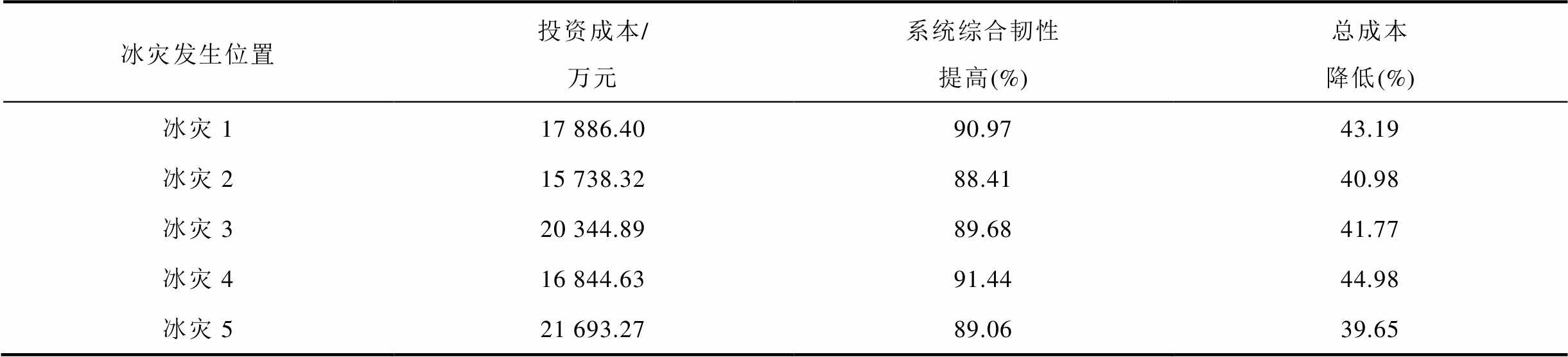
冰灾发生位置投资成本/万元系统综合韧性提高(%)总成本降低(%) 冰灾117 886.4090.9743.19 冰灾215 738.3288.4140.98 冰灾320 344.8989.6841.77 冰灾416 844.6391.4444.98 冰灾521 693.2789.0639.65
由表8可知,对于不同发生位置的冰灾,本文所提方法均能够有效地保障输电系统恢复供电,提高系统韧性,减少负荷削减损失和总成本。
5 结论
针对冰灾的时空演变建模困难及其对输电网的严重破坏,本文提出了基于多光谱卫星遥感的输电网冰灾场景时序建模与韧性提升策略优化方法,构建了冰灾场景时序模型和输电网两阶段鲁棒韧性提升规划模型,并通过算例分析验证了其对输电网韧性提升的有效性,所得结论如下。
1)本文所提的图像融合方法能够将多光谱卫星Sentinel-2不同尺度光谱波段的遥感图像进行特征融合,获取高质量覆冰区域提取图像,并结合偏微分卷积实现覆冰区域的滚动预测,构建冰灾发展时序模型。
2)基于条件变分自动编码器,结合历史数据生成的冰灾场景,能够准确地反映冰灾天气下“源-网-荷”时空特性。
3)利用C&CG算法求解本文所提的基于冰灾场景的输电网两阶段鲁棒韧性提升规划模型,得到的灾前固定储能配置和灾中应急维修方案能够加快冰灾期间系统综合恢复,提高系统韧性。通过与其他韧性提升策略对比可知,本文所提韧性提升策略能同时兼顾经济性与韧性。但本文所提系统韧性评估指标的最优权重系数尚不清晰,如何寻找并自适应不同结构输电网的系统韧性评估指标最优权重系数是未来需要进一步深入研究的问题。
附录 灾中维修资源约束
本文考虑冰灾场景s对路程交通状况的影响,维修队伍m由故障点i到故障点j的时间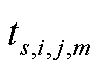 存在不确定性,假设服从偏移伽马分布,即
存在不确定性,假设服从偏移伽马分布,即
式中,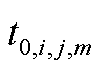 为维修队伍m从i点到j点的理想路程时间;λ和
为维修队伍m从i点到j点的理想路程时间;λ和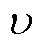 分别为伽马分布的形状与尺度参数;
分别为伽马分布的形状与尺度参数;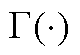 为伽马函数算子;
为伽马函数算子;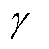 为一正实数。
为一正实数。
同时考虑冰灾天气对维修时间的不确定性影响,假设维修队m在故障点i对故障元件进行维修所需的时间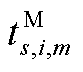 服从正态分布,表示为
服从正态分布,表示为
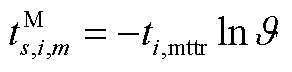 (A2)
(A2)
式中,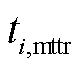 为故障元件的理想维修时间;
为故障元件的理想维修时间;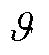 为0~1的随机数。
为0~1的随机数。
设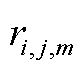 为维修路径决策0-1变量,若维修队m从i点到j点,则
为维修路径决策0-1变量,若维修队m从i点到j点,则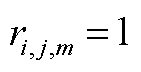 ,否则取0。维修队m从维修中心O出发,在完成所有维修任务后返回维修中心,有
,否则取0。维修队m从维修中心O出发,在完成所有维修任务后返回维修中心,有
式中,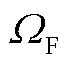 为故障点集合。
为故障点集合。
维修完某一故障元件后,前往维修下一故障元件,维修队m到达第n个故障点i的时间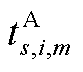 为
为
在任意时刻,每个故障元件只能由一个维修队修复,表示为
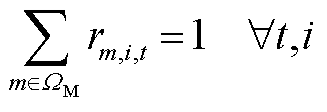 (A5)
(A5)
式中,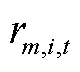 为维修队m是否对故障元件进行维修的0-1变量,取1表示进行维修,否则取0。
为维修队m是否对故障元件进行维修的0-1变量,取1表示进行维修,否则取0。
假设故障点i所需维修资源为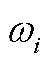 ,则有
,则有
参考文献
[1] 辛保安, 单葆国, 李琼慧, 等. “双碳”目标下“能源三要素”再思考[J]. 中国电机工程学报, 2022, 42(9): 3117-3126. Xin Baoan, Shan Baoguo, Li Qionghui, et al. Rethinking of the “three elements of energy” toward carbon peak and carbon neutrality[J]. Proceedings of the CSEE, 2022, 42(9): 3117-3126.
[2] 安学民, 孙华东, 张晓涵, 等. 美国得州“2·15”停电事件分析及启示[J]. 中国电机工程学报, 2021, 41(10): 3407-3415, 3666. An Xuemin, Sun Huadong, Zhang Xiaohan, et al. Analysis and lessons of Texas power outage event on February 15, 2021[J]. Proceedings of the CSEE, 2021, 41(10): 3407-3415, 3666.
[3] 黄慧. 电力系统冰灾风险评估建模研究[D]. 广州: 华南理工大学, 2011. Huang Hui. Study on risk evaluation model of ice storm in power system[D]. Guangzhou: South China University of Technology, 2011.
[4] 黄新波, 孙钦东, 程荣贵, 等. 导线覆冰的力学分析与覆冰在线监测系统[J]. 电力系统自动化, 2007, 31(14): 98-101. Huang Xinbo, Sun Qindong, Cheng Ronggui, et al. Mechanical analysis on transmission line conductor icing and application of on-line monitoring system[J]. Automation of Electric Power Systems, 2007, 31(14): 98-101.
[5] 中国电力科学研究院. 湖南电网2008年冰雪灾害初步调研报告[R]. 北京: 中国电力科学研究院, 2008.
[6] 国网北京电力建设研究院. 2008电网冰灾技术分析报告[R]. 北京: 国网北京电力建设研究院, 2008.
[7] 胡毅. 电网大面积冰灾分析及对策探讨[J]. 高电压技术, 2008, 34(2): 215-219. Hu Yi. Analysis and countermeasures discussion for large area icing accident on power grid[J]. High Voltage Engineering, 2008, 34(2): 215-219.
[8] Niu Tao, Huang Qianqian, Fang Sidun, et al. Multistage condition-based resilient maintenance scheduling for power systems during ice storms[J]. IEEE Transactions on Industry Applications, 2024, 60(2): 2201-2213.
[9] 庄文兵, 祁创, 熊小伏, 等. 计及气象因素时间累积效应的输电线路覆冰预测[J]. 电力系统保护与控制, 2019, 47(17): 6-13. Zhuang Wenbing, Qi Chuang, Xiong Xiaofu, et al. Transmission line icing forecast considering the time cumulative effect of meteorological factors[J]. Power System Protection and Control, 2019, 47(17): 6-13.
[10] 蒋兴良, 周文轩, 董莉娜, 等. 基于旋转圆柱三电极阵列的覆冰测量方法[J]. 电工技术学报, 2024, 39(5): 1524-1535. Jiang Xingliang, Zhou Wenxuan, Dong Lina, et al. Research on icing measurement method based on rotating cylindrical three-electrode array[J]. Transa-ctions of China Electrotechnical Society, 2024, 39(5): 1524-1535.
[11] 吴海涛, 韩兴波, 蒋兴良, 等. 基于水滴碰冻效率的扩径导线防冰特性分析[J]. 电工技术学报, 2023, 38(11): 3033-3040, 3051. Wu Haitao, Han Xingbo, Jiang Xingliang, et al. Analysis of anti-icing characteristics of expanded diameter conductor based on water droplet collision and freezing efficiency[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 3033-3040, 3051.
[12] 杨国林, 蒋兴良, 廖乙, 等. 输电线路单导线自由扭转覆冰动态仿真研究[J]. 电工技术学报, 2024, 39(13): 4079-4089. Yang Guolin, Jiang Xingliang, Liao Yi, et al. Simulation study of the free torsional icing on single conductors of transmission lines[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 4079-4089.
[13] 赵建坤. 架空输电线路覆冰厚度预测模型研究[D]. 北京: 华北电力大学, 2016. Zhao Jiankun. Research on icing thickness prediction model of overhead transmission lines[D]. Beijing: North China Electric Power University, 2016.
[14] 蒋兴良, 董冰冰, 张志劲, 等. 绝缘子覆冰闪络研究进展[J]. 高电压技术, 2014, 40(2): 317-335. Jiang Xingliang, Dong Bingbing, Zhang Zhijin, et al. Research and development on flashover of ice-covered insulators[J]. High Voltage Engineering, 2014, 40(2): 317-335.
[15] 舒立春, 汪诗经, 叶开颜, 等. 风速对复合绝缘子覆冰增长及其闪络特性的影响[J]. 中国电机工程学报, 2015, 35(6): 1533-1540. Shu Lichun, Wang Shijing, Ye Kaiyan, et al. Influence of wind velocity on ice accretion and flashover performance of composite insulators[J]. Proceedings of the CSEE, 2015, 35(6): 1533-1540.
[16] 常彦. 超高压输电线路防覆冰及防冰闪研究[D]. 北京: 华北电力大学, 2015. Chang Yan. Ultra high voltage transmission line anti icing and ice melting flashover research[D]. Beijing: North China Electric Power University, 2015.
[17] 杨国林, 蒋兴良, 王茂政, 等. 输电线路单导线覆冰形状对直流大电流融冰时间的影响[J]. 电工技术学报, 2024, 39(9): 2916-2924. Yang Guolin, Jiang Xingliang, Wang Maozheng, et al. The impact of ice accumulation shape on the DC high current ice-melting time for a single conductor on power transmission line[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2916-2924.
[18] 蒋兴良, 孟志高, 张志劲, 等. OPGW临界融冰电流及其影响因素[J]. 电工技术学报, 2016, 31(9): 174-180. Jiang Xingliang, Meng Zhigao, Zhang Zhijin, et al. Critical ice-melting current of ice-covered OPGW and its impacting factors[J]. Transactions of China Electrotechnical Society, 2016, 31(9): 174-180.
[19] 曾伟, 蒋兴良, 杨国林, 等. 基于记忆合金双程形状记忆效应的导线雾凇防冰方法及现场试验[J]. 电工技术学报, 2024, 39(7): 2174-2183. Zeng Wei, Jiang Xingliang, Yang Guolin, et al. Research on anti-icing method for fog freezing and field test of wires based on two-way shape memory effect of memory alloy[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2174-2183.
[20] 章坚民, 王雨宽, 薛禹胜, 等. 自然灾害-电力系统-碳排放变化的贝叶斯网络建模与估计[J]. 电力系统自动化, 2023, 47(7): 1-11. Zhang Jianmin, Wang Yukuan, Xue Yusheng, et al. Bayesian network modeling and estimation of natural disaster-power system-carbon emission change[J]. Automation of Electric Power Systems, 2023, 47(7): 1-11.
[21] 孙羽, 王秀丽, 王建学, 等. 架空线路冰风荷载风险建模及模糊预测[J]. 中国电机工程学报, 2011, 31(7): 21-28. Sun Yu, Wang Xiuli, Wang Jianxue, et al. Wind and ice loading risk model and fuzzy forecast for overhead transmission lines[J]. Proceedings of the CSEE, 2011, 31(7): 21-28.
[22] 潘斌, 张勇军, 黄慧. 多因子电网冰灾风险评估建模[J]. 电网技术, 2012, 36(5): 102-106. Pan Bin, Zhang Yongjun, Huang Hui. Modeling for multi-factor risk assessment on ice disaster of power system[J]. Power System Technology, 2012, 36(5): 102-106.
[23] 张勇军, 许亮, 吴成文. 计及多因素的电网冰灾风险评估模型研究[J]. 电力系统保护与控制, 2012, 40(15): 12-17. Zhang Yongjun, Xu Liang, Wu Chengwen. Research on ice disaster risk evaluation model of power system considering multi-factors[J]. Power System Protection and Control, 2012, 40(15): 12-17.
[24] 王建学, 张耀, 吴思, 等. 大规模冰灾对输电系统可靠性的影响分析[J]. 中国电机工程学报, 2011, 31(28): 49-56. Wang Jianxue, Zhang Yao, Wu Si, et al. Influence of large-scale ice disaster on transmission system reliability[J]. Proceedings of the CSEE, 2011, 31(28): 49-56.
[25] 徐文军, 杨洪明, 赵俊华, 等. 冰风暴灾害下电力断线倒塔的概率计算[J]. 电力系统自动化, 2011, 35(1): 13-17. Xu Wenjun, Yang Hongming, Zhao Junhua, et al. Probability calculation of broken transmission lines and collapsed towers under ice storms[J]. Automation of Electric Power Systems, 2011, 35(1): 13-17.
[26] 谢云云, 薛禹胜, 文福拴, 等. 冰灾对输电线故障率影响的时空评估[J]. 电力系统自动化, 2013, 37(18): 32-41, 98. Xie Yunyun, Xue Yusheng, Wen Fushuan, et al. Space-time evaluation for impact of ice disaster on transmission line fault probability[J]. Automation of Electric Power Systems, 2013, 37(18): 32-41, 98.
[27] Lu Jiazheng, Guo Jun, Jian Zhou, et al. Dynamic assessment of resilience of power transmission systems in ice disasters[C]//2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 2018: 7-13.
[28] Yan Mingyu, Ai Xiaomeng, Shahidehpour M, et al. Enhancing the transmission grid resilience in ice storms by optimal coordination of power system schedule with pre-positioning and routing of mobile DC de-icing devices[J]. IEEE Transactions on Power Systems, 2019, 34(4): 2663-2674.
[29] Lu Jiazheng, Guo Jun, Jian Zhou, et al. Resilience assessment and its enhancement in tackling adverse impact of ice disasters for power transmission systems[J]. Energies, 2018, 11(9): 2272.
[30] 龙玉洁, 李为乐, 黄润秋, 等. 汶川地震震后10 a绵远河流域滑坡遥感自动提取与演化趋势分析[J]. 武汉大学学报(信息科学版), 2020, 45(11): 1792-1800. Long Yujie, Li Weile, Huang Runqiu, et al. Automatic extraction and evolution trend analysis of landslides in Mianyuan River Basin in the 10 years after Wenchuan earthquake[J]. Geomatics and Information Science of Wuhan University, 2020, 45(11): 1792-1800.
[31] 周学珍. 遥感技术在矿山地质灾害监测中的应用: 以陕西神府煤矿区为例[J]. 能源环境保护, 2013, 27(1): 52-55. Zhou Xuezhen. Application of remote sensing technology to the monitoring of mine geological disaster: an example in Shenfu Coal Mine Region in Shaanxi[J]. Energy Environmental Protection, 2013, 27(1): 52-55.
[32] Heap M J, Villeneuve M, Albino F, et al. Towards more realistic values of elastic moduli for volcano modelling[J]. Journal of Volcanology and Geothermal Research, 2020, 390: 106684.
[33] Zhu Xiaoyan, Zhang Renzhi, Sun Xuwei. Spatiote-mporal dynamics of soil erosion in the ecotone between the Loess Plateau and Western Qinling Mountains based on RUSLE modeling, GIS, and remote sensing[J]. Arabian Journal of Geosciences, 2021, 14(1): 33.
[34] Aghelpour P, Guan Yiqing, Bahrami-Pichaghchi H, et al. Using the MODIS sensor for snow cover modeling and the assessment of drought effects on snow cover in a mountainous area[J]. Remote Sensing, 2020, 12(20): 3437.
[35] Muhuri A, Gascoin S, Menzel L, et al. Performance assessment of optical satellite-based operational snow cover monitoring algorithms in forested landscapes[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 7159-7178.
[36] Ali S, Cheema M J M, Waqas M M, et al. Changes in snow cover dynamics over the Indus Basin: evidences from 2008 to 2018 MODIS NDSI trends analysis[J]. Remote Sensing, 2020, 12(17): 2782.
[37] Ma Jiayi, Ma Yong, Li Chang. Infrared and visible image fusion methods and applications: a survey[J]. Information Fusion, 2019, 45: 153-178.
[38] Gan Wei, Wu Xiaohong, Wu Wei, et al. Infrared and visible image fusion with the use of multi-scale edge-preserving decomposition and guided image filter[J]. Infrared Physics & Technology, 2015, 72: 37-51.
[39] Long Zichao, Lu Yiping, Ma Xianzhong, et al. PDE-Net: learning PDEs from data[C]//Proceedings of the 35th International Conference on Machine Learning (ICML), Stockholm, Sweden, 2018: 3208-3216.
[40] Subcommittee P M. IEEE reliability test system[J]. IEEE Transactions on Power Apparatus and Systems, 1979, PAS-98(6): 2047-2054.
Temporal Modeling of Ice Disaster Scenarios and Optimization of Resilience Enhancement Strategies in Power Transmission Network Based on Multispectral Satellite Remote Sensing Data
Niu Tao1 Huang Qianqian1 Fang Sidun1 Li Xiaodong2 Liao Ruijin1
(1. State Key Laboratory of Power Transmission Equipment Technology Chongqing University Chongqing 400044 China 2. Innovation Academy for Precision Measurement Science and Technology Chinese Academy of Sciences Wuhan 430071 China)
Abstract Ice disasters can cause serious damage to power transmission network, it is crucial to enhance the resilience of power transmission network during ice disasters. Unlike extreme natural disasters such as hurricanes or earthquakes, ice disasters develop slowly and last long time. It is difficult to predict the development trend of ice disaster accurately due to the influence of microclimate and terrain on their geographic coverage. Currently, the spatiotemporal evolution patterns of ice disasters are not clear. The existing research on improving the resilience of power transmission networks considering the impact of ice disasters have not involved the temporal modeling of ice disaster scenarios. Therefore, the paper proposes a method for temporal modeling of ice storm scenarios based on multispectral satellite remote sensing. By combining multispectral remote sensing image fusion methods based on Laplacian pyramid decomposition, efficient extraction and analysis of the spatial distribution and temporal changes of ice-covered areas in Sentinel-2 satellite remote sensing images are achieved. Using partial differential convolution, ice-covered areas are predicted dynamically based on the fused images, and an ice disaster temporal model is constructed. Additionally, a conditional variational autoencoder is used to generate a set of ice disaster scenarios, which accurately reflect the spatiotemporal characteristics of "source-network-load" during ice disasters.
Considering the interaction between the disaster development process and resilience enhancement measures, the power transmission system resilience can be simultaneously enhanced through both pre-disaster prevention and in-disaster repair measures. This paper proposes a comprehensive resilience evaluation index and constructs a two-stage robust resilience enhancement planning model for power transmission networks based on the set of ice disaster scenarios. The first stage focuses on pre-disaster fixed energy storage configuration and pre-planning of maintenance resources to find the optimal investment decision. The second stage focuses on in-disaster power supply through fixed energy storage and emergency maintenance considering limited maintenance resources, ensuring rapid response from fixed energy storage and maintenance teams after the occurrence time of the ice disaster, which aims to ensure rapid load recovery, maximize system resilience, and minimize system economic losses. The model is iteratively solved using a parallelizable column-and-constraint generation algorithm.
Finally, case studies are conducted using ice-covered remote sensing data from a region in Yunnan and a modified IEEE RTS-79 power transmission system as the test system. The results show that the coordination of fixed energy storage power supply and emergency maintenance can effectively ensure power supply and transmission during ice disasters, as the system resilience improved by 90.97% and total system losses decreased by 43.19% during the ice disasters. Compared with other resilience enhancement strategies, the proposed strategy in this paper balances both economic efficiency and resilience. What’s more, different ice disaster center locations are set in the case study considering the inherent uncertainty of ice disasters. The results demonstrate that for ice disasters with multiple origins, the proposed method effectively ensures power restoration in the transmission system, enhances system resilience, reduces load shedding losses and total costs.
Keywords:Ice disaster, multispectral satellite remote sensing, image fusion, temporal scenarios, power transmission network planning, resilience enhancement
DOI: 10.19595/j.cnki.1000-6753.tces.241008
中图分类号:TM715
中国南方电网有限责任公司总部管理科技项目资助(0500002023030301 GH00107)。
收稿日期 2024-06-13
改稿日期 2024-08-1
作者简介
牛 涛 男,1992年生,博士,特聘研究员,博士生导师,研究方向为交直流混联大电网运行控制与优化。E-mail:niutthu@qq.com
方斯顿 男,1991年生,博士,教授,博士生导师,研究方向为综合能源系统、能源交通融合。E-mail:fangston@cqu.edu.cn(通信作者)
(编辑 李 冰)

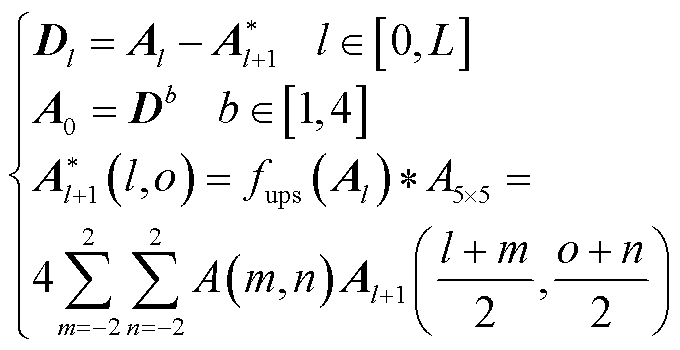 (1)
(1)
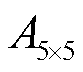 为高斯滤波器;*表示卷积运算;A(m, n)为5×5高斯滤波卷积核在(m, n)的参数。分解后对不同尺度分解层的细节和近似分量分别进行融合,最后通过拉普拉斯逆变换得到融合图像。图1展示了b=1, 2、L=1的覆冰区域遥感图像融合过程,融合图像中白色区域即为覆冰区域。
为高斯滤波器;*表示卷积运算;A(m, n)为5×5高斯滤波卷积核在(m, n)的参数。分解后对不同尺度分解层的细节和近似分量分别进行融合,最后通过拉普拉斯逆变换得到融合图像。图1展示了b=1, 2、L=1的覆冰区域遥感图像融合过程,融合图像中白色区域即为覆冰区域。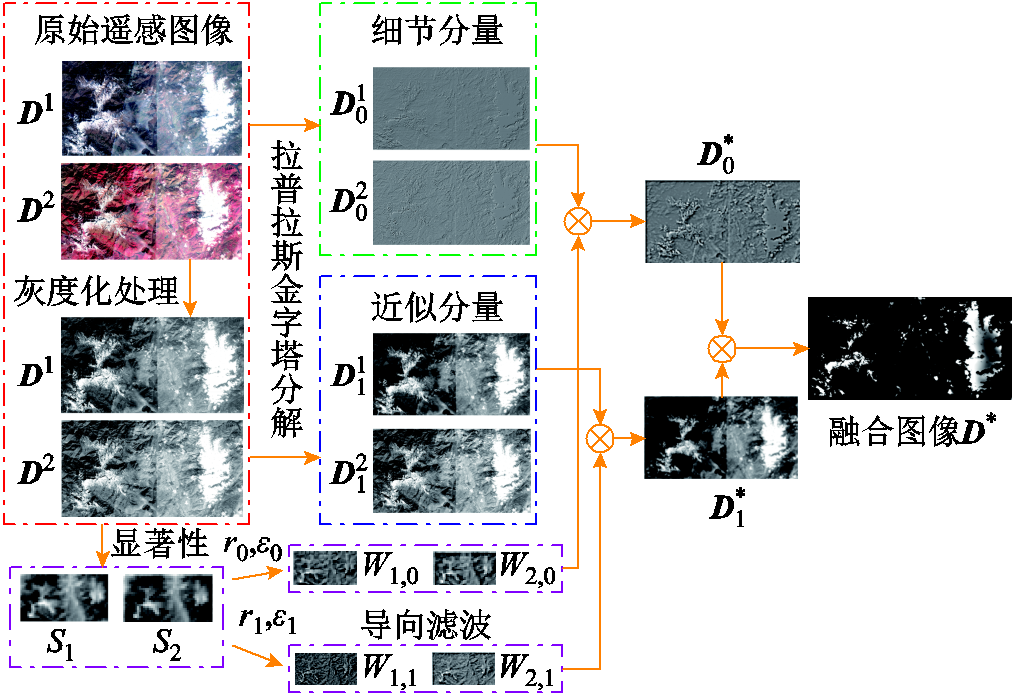
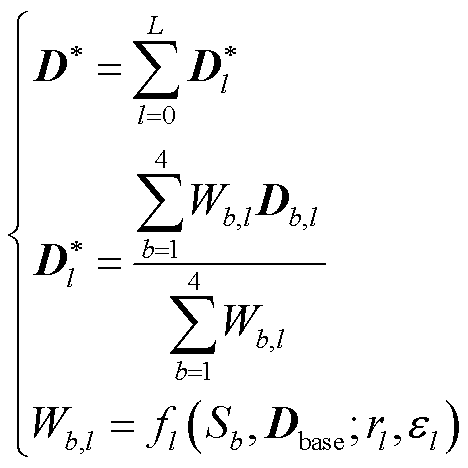 (2)
(2)
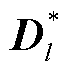 为金字塔第l层的融合分量;
为金字塔第l层的融合分量;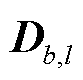 为波段b的金字塔第l层的融合分量;
为波段b的金字塔第l层的融合分量;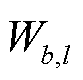 为波段b的金字塔第l层融合分量权值;
为波段b的金字塔第l层融合分量权值;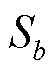 为波段b的显著性水平;
为波段b的显著性水平;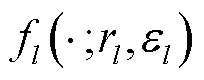 为金字塔第l层导向滤波函数;
为金字塔第l层导向滤波函数;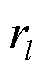 为含参数的导向滤波半径;
为含参数的导向滤波半径;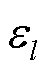 为正则化系数;
为正则化系数;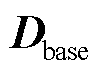 为导向滤波的基底。
为导向滤波的基底。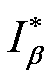 ,如图2所示。
,如图2所示。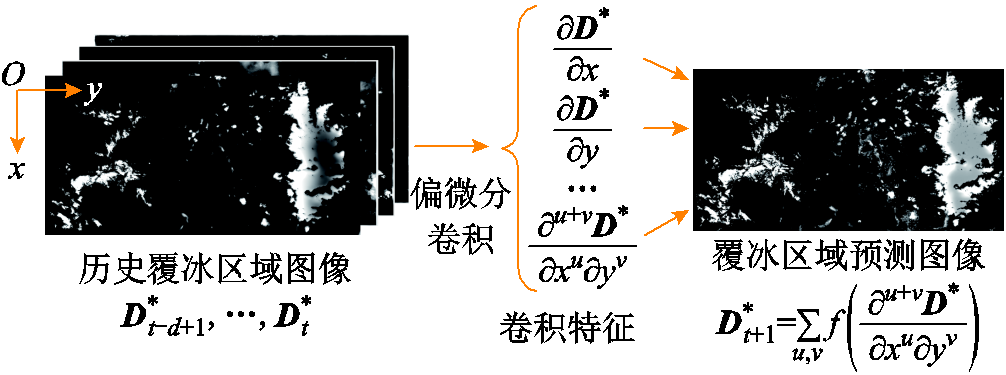
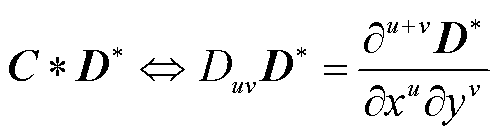 (3)
(3)
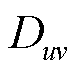 为第u+v阶微分算子;x和y分别表示融合图像的水平和垂直方向。
为第u+v阶微分算子;x和y分别表示融合图像的水平和垂直方向。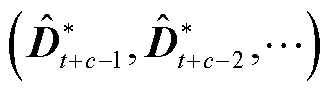 和t时段真实覆冰区域遥感图像
和t时段真实覆冰区域遥感图像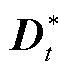 作为模型输入来预测t+c时段的覆冰区域图像
作为模型输入来预测t+c时段的覆冰区域图像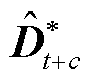 ,预测模型表示为
,预测模型表示为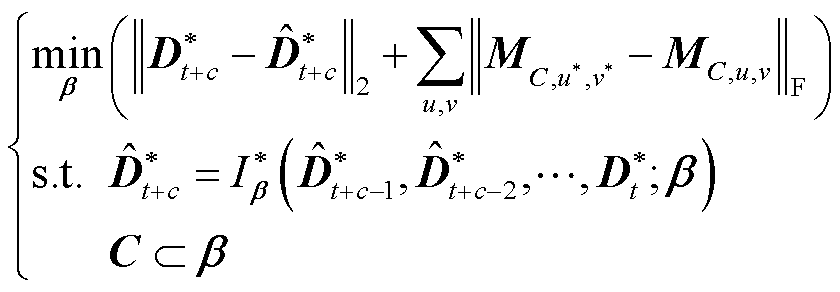 (4)
(4)
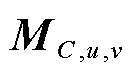 为卷积核C的矩估计;
为卷积核C的矩估计;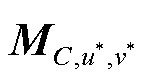 为目标偏微分的矩估计,其中的元素
为目标偏微分的矩估计,其中的元素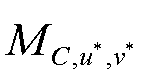 满足式(5);
满足式(5);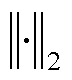 和
和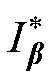 的参数集合。
的参数集合。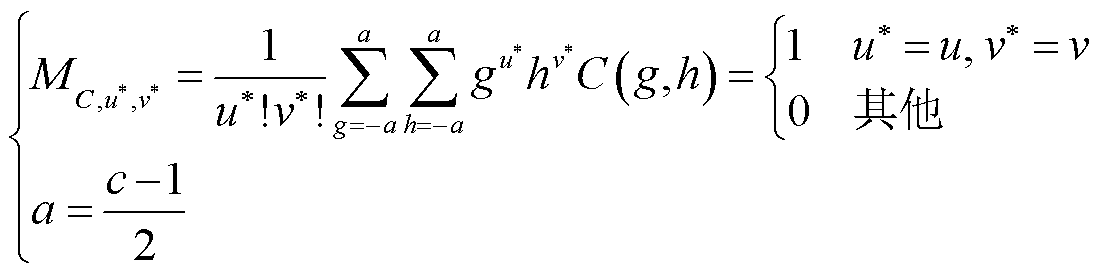 (5)
(5)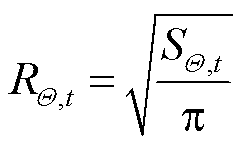 (6)
(6)
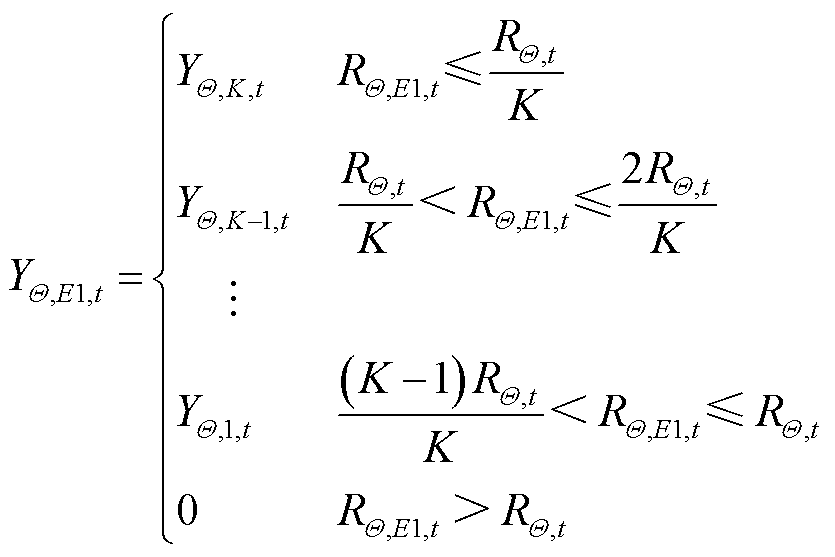 (7)
(7)
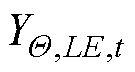 为各顶点的冰灾恶劣程度平均值。
为各顶点的冰灾恶劣程度平均值。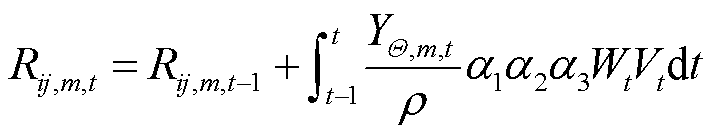 (8)
(8)
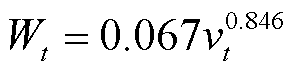 (9)
(9)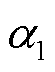 、
、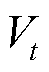 和
和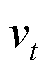 分别为t时刻的空气含水量、风速和降水率。
分别为t时刻的空气含水量、风速和降水率。
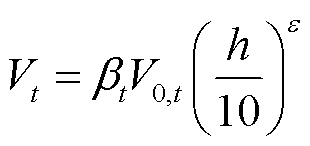 (10)
(10)
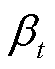 为t时刻风速与输电线路间的夹角;
为t时刻风速与输电线路间的夹角;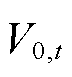 为t时刻距离地表h处的风速;ε为地表粗糙度系数。
为t时刻距离地表h处的风速;ε为地表粗糙度系数。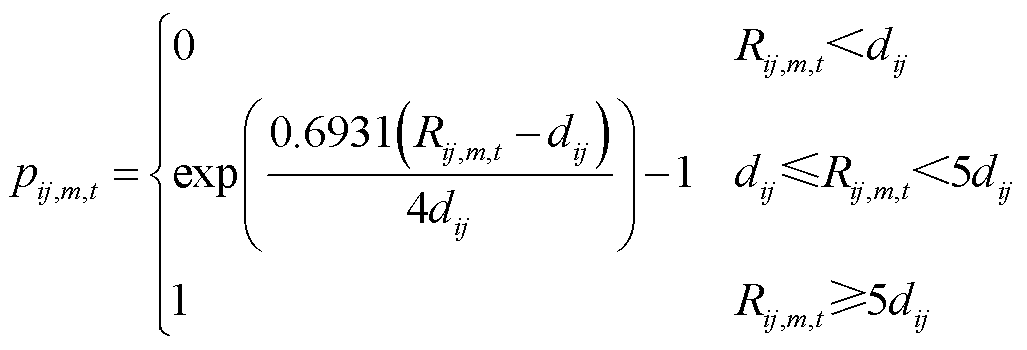 (11)
(11)
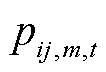 为t时刻线路ij在第m个网格区域内的故障率;
为t时刻线路ij在第m个网格区域内的故障率;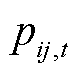 和传输容量
和传输容量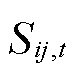 为
为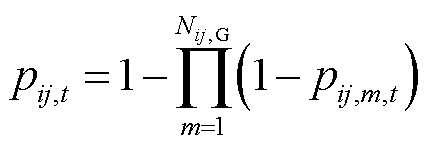 (12)
(12)
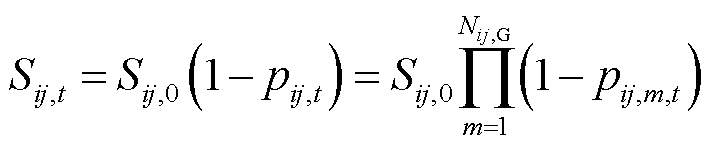 (13)
(13)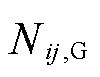 为线路ij所处的网格总数;
为线路ij所处的网格总数;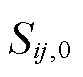 为线路ij正常运行状态下的传输容量。
为线路ij正常运行状态下的传输容量。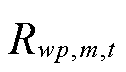 预测模型形式参考式(8)。第m个网格区域内的风光机组wp在t时刻的出力损失
预测模型形式参考式(8)。第m个网格区域内的风光机组wp在t时刻的出力损失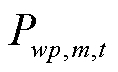 为
为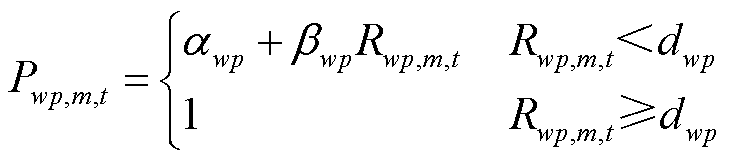 (14)
(14)
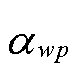 和
和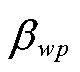 为风光损失系数;
为风光损失系数;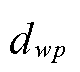 为风光机组的最大抗冰厚度。
为风光机组的最大抗冰厚度。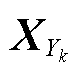 =[X
=[X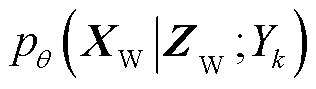 ,假设
,假设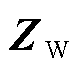 独立同分布,利用对数最大似然估计方法计算生成模型参数为
独立同分布,利用对数最大似然估计方法计算生成模型参数为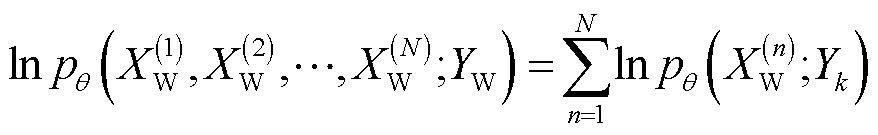 (15)
(15)
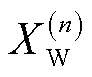 为第n个历史风电出力样本数据,
为第n个历史风电出力样本数据,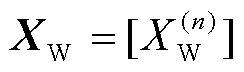 ;N为历史样本数据总数。
;N为历史样本数据总数。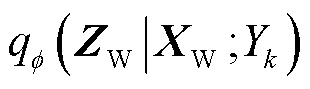 逼近历史样本数据后验概率
逼近历史样本数据后验概率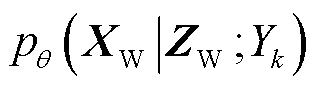 ,利用Kullback-Leibler(KL)距离f
,利用Kullback-Leibler(KL)距离f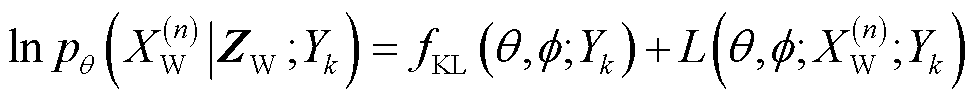 (16)
(16)
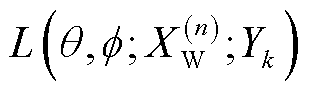 可得
可得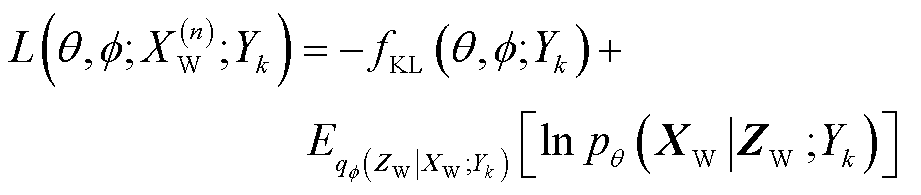 (17)
(17)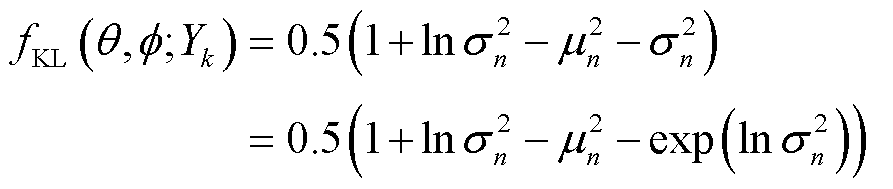 (18)
(18)
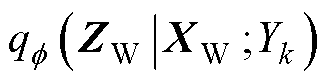 高斯分布的均值和方差。
高斯分布的均值和方差。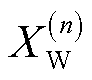 后验概率的对数似然,无法求得解析解,采用蒙特卡洛抽样可得
后验概率的对数似然,无法求得解析解,采用蒙特卡洛抽样可得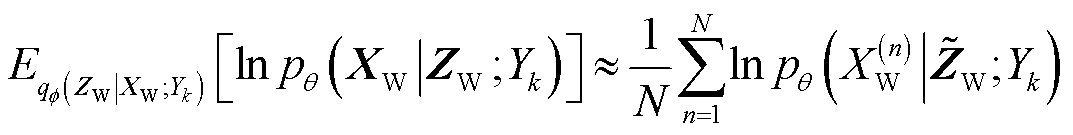 (19)
(19)
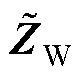 为蒙特卡洛抽样下的隐变量。每次采样总数取1,记此时
为蒙特卡洛抽样下的隐变量。每次采样总数取1,记此时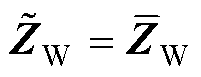 ,则有
,则有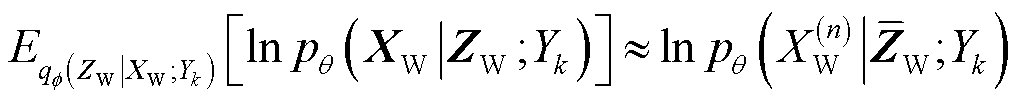 (20)
(20)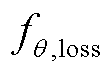 为互熵损失,即
为互熵损失,即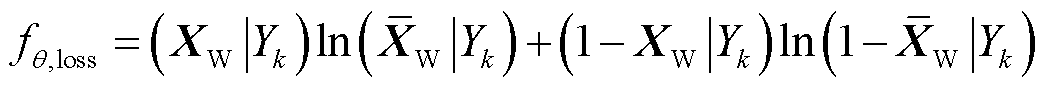 (21)
(21)
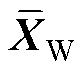 为服从伯努利分布的样本数据。
为服从伯努利分布的样本数据。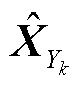 =[
=[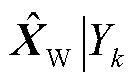
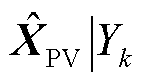
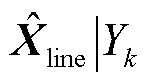
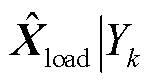 ],该数据集满足历史数据的概率分布。基于条件VAE的冰灾场景生成过程如图5所示。
],该数据集满足历史数据的概率分布。基于条件VAE的冰灾场景生成过程如图5所示。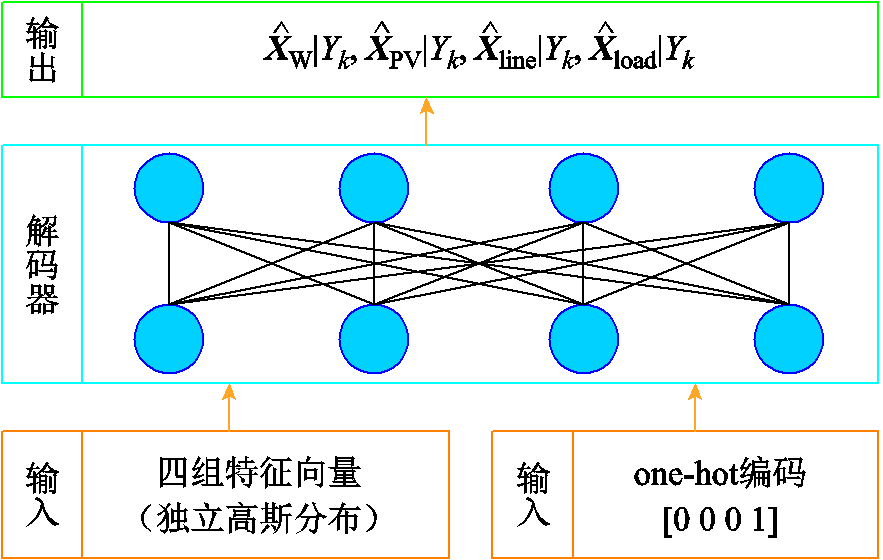
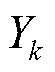 下风光出力、输电线路传输容量以及负荷需求,本节构建基于冰灾场景的输电网两阶段鲁棒韧性提升规划模型。
下风光出力、输电线路传输容量以及负荷需求,本节构建基于冰灾场景的输电网两阶段鲁棒韧性提升规划模型。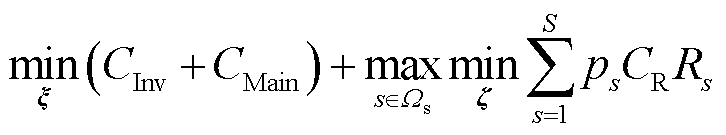 (22)
(22)
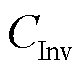 为固定储能配置成本;
为固定储能配置成本;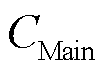 为应急维修投资成本;
为应急维修投资成本;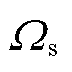 为冰灾场景集合;
为冰灾场景集合;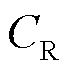 为单位负荷削减的惩罚费用;
为单位负荷削减的惩罚费用;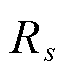 为冰灾场景s下的系统韧性指标。
为冰灾场景s下的系统韧性指标。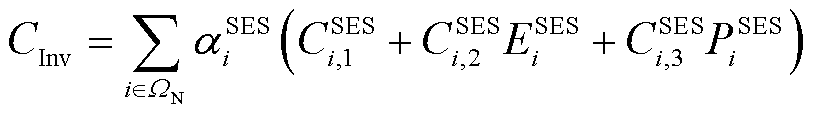 (23)
(23)
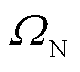 为输电网节点集合;
为输电网节点集合;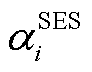 为0-1变量,若取1则表示节点i安装一台固定储能设备,否则取0;
为0-1变量,若取1则表示节点i安装一台固定储能设备,否则取0; 、
、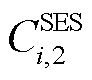 和
和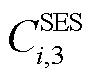 分别为输电网中节点i的固定储能基本配置成本、单位配置容量成本和单位配置功率成本;
分别为输电网中节点i的固定储能基本配置成本、单位配置容量成本和单位配置功率成本;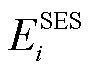 和
和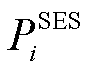 分别为固定储能在输电网节点i的配置容量和功率。
分别为固定储能在输电网节点i的配置容量和功率。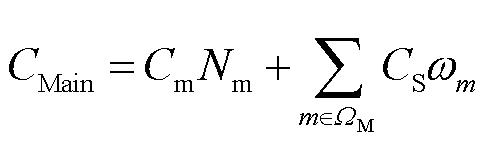 (24)
(24)
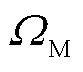 为维修队伍集合;
为维修队伍集合;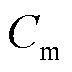 和
和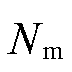 为配备的维修队伍总数;
为配备的维修队伍总数;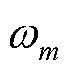 为维修队伍m所能配备的最大维修资源。
为维修队伍m所能配备的最大维修资源。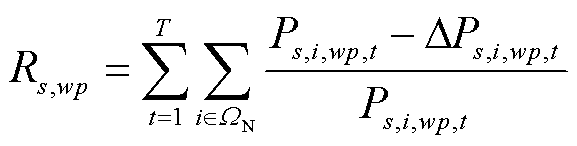 (25)
(25)
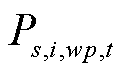 为场景s下节点i在t时刻所连风光机组wp的有功发电功率;
为场景s下节点i在t时刻所连风光机组wp的有功发电功率;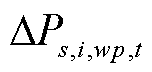 为场景s下节点i在t时刻所连风光机组wp的有功发电功率削减量;T为规划总时间。
为场景s下节点i在t时刻所连风光机组wp的有功发电功率削减量;T为规划总时间。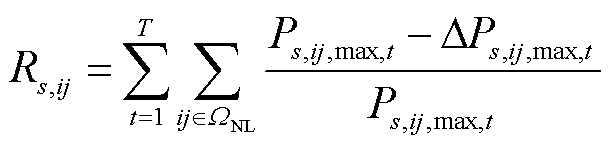 (26)
(26)
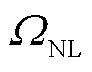 为输电网线路集合;
为输电网线路集合;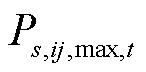 为场景s下t时刻输电线路ij可传递的有功功率最大值;
为场景s下t时刻输电线路ij可传递的有功功率最大值;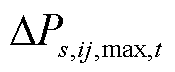 为场景s下在t时刻输电线路ij可传递的有功功率最大值削减量。
为场景s下在t时刻输电线路ij可传递的有功功率最大值削减量。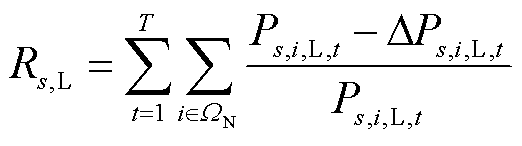 (27)
(27)
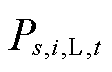 为场景s下t时刻节点i的负荷;
为场景s下t时刻节点i的负荷;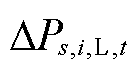 为场景s下t时刻节点i的负荷削减量。
为场景s下t时刻节点i的负荷削减量。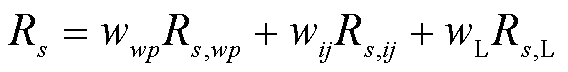 (28)
(28)
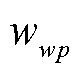 、
、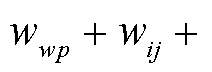
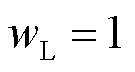 。
。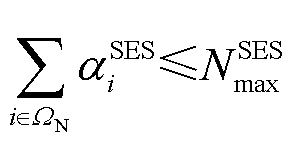 (29)
(29)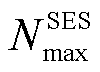 为固定储能设备上限。
为固定储能设备上限。 (30)
(30)
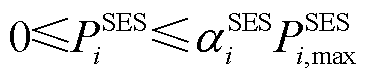 (31)
(31)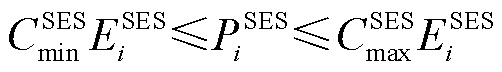 (32)
(32)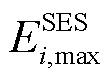 和
和 分别为节点i处固定储能配置容量的最大值、最小值;
分别为节点i处固定储能配置容量的最大值、最小值;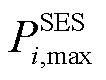 为节点i处固定储能配置功率最大值;
为节点i处固定储能配置功率最大值;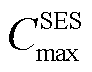 和
和 分别为固定储能最大和最小充电倍率。
分别为固定储能最大和最小充电倍率。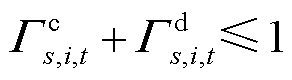 (33)
(33)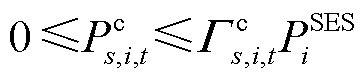 (34)
(34)
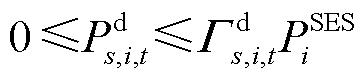 (35)
(35)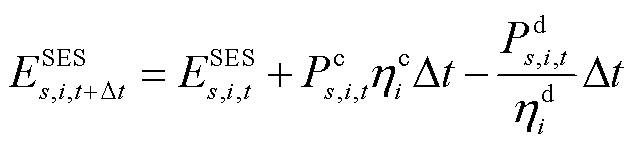 (36)
(36)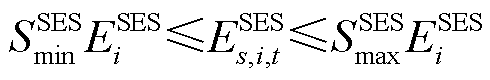 (37)
(37)
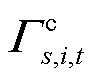 和
和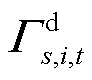 为0-1变量,若取1则分别表示场景s下节点i处的固定储能在t时刻处于充、放电状态,否则取0;
为0-1变量,若取1则分别表示场景s下节点i处的固定储能在t时刻处于充、放电状态,否则取0;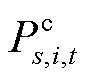 和
和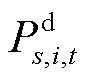 分别为场景s下节点i处的固定储能在t时刻的充、放电功率;
分别为场景s下节点i处的固定储能在t时刻的充、放电功率;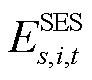 为场景s下节点i处的固定储能在t时刻的存储电量;
为场景s下节点i处的固定储能在t时刻的存储电量;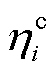 和
和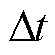 为单个时段的时长;
为单个时段的时长;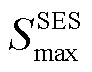 和
和 分别为固定储能荷电状态的上、下限。
分别为固定储能荷电状态的上、下限。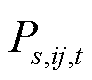 满足
满足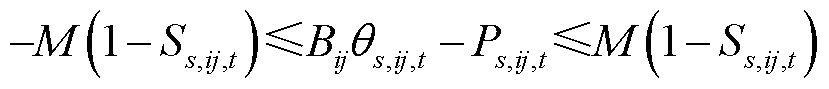 (38)
(38)
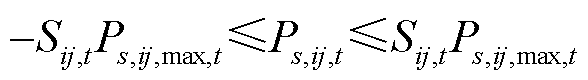 (39)
(39)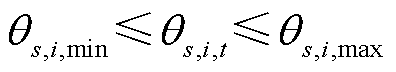 (40)
(40)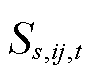 为0-1变量,表示场景s下t时刻输电线路ij的状态,当线路处于故障或维修状态时取0,否则取1;M为一足够大的数;
为0-1变量,表示场景s下t时刻输电线路ij的状态,当线路处于故障或维修状态时取0,否则取1;M为一足够大的数;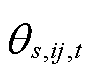 为场景s下节点i与节点j在t时刻的电压相位差,
为场景s下节点i与节点j在t时刻的电压相位差,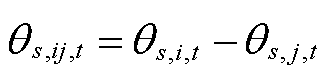 ;
;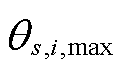 和
和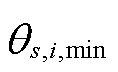 分别为场景s下节点i的电压相位上、下限。
分别为场景s下节点i的电压相位上、下限。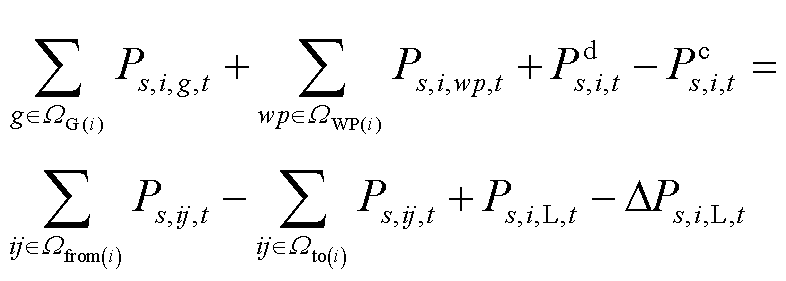 (41)
(41)
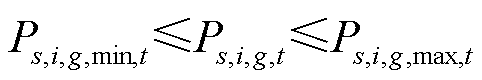 (42)
(42)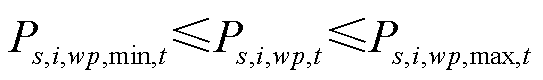 (43)
(43)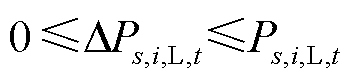 (44)
(44)
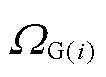 、
、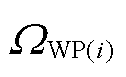 分别为节点i的火电、风光机组集合;
分别为节点i的火电、风光机组集合;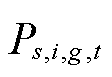 为场景s下t时刻节点i所连火电机组g的有功发电功率;
为场景s下t时刻节点i所连火电机组g的有功发电功率;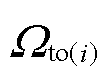 为末节点是i的输电线路集合;
为末节点是i的输电线路集合;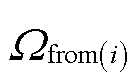 为首节点是i的输电线路集合;
为首节点是i的输电线路集合;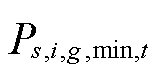 、
、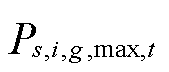 、
、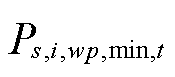 和
和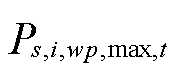 分别为场景s下t时刻节点i所连火电机组和风光机组的最小、最大有功发电功率。
分别为场景s下t时刻节点i所连火电机组和风光机组的最小、最大有功发电功率。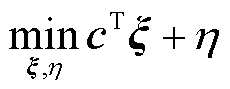 (45)
(45)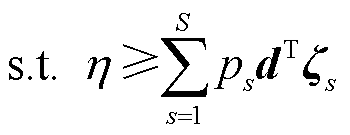 (46)
(46)
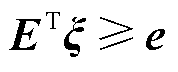 (47)
(47)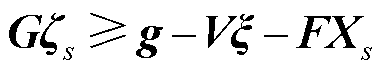 (48)
(48)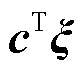 为第一阶段固定储能配置和维修资源投资总成本;
为第一阶段固定储能配置和维修资源投资总成本;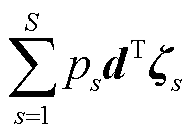 为第二阶段负荷削减损失成本;
为第二阶段负荷削减损失成本;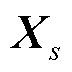 为冰灾场景s下的风光出力、输电线路传输容量及负荷需求;式(47)为投资决策约束,包括式(29)~式(32)及式(A6);式(48)为系统运行约束,包括式(33)~式(44)以及式(A1)~式(A5);E、e、G、g、V、F为相应系数矩阵。
为冰灾场景s下的风光出力、输电线路传输容量及负荷需求;式(47)为投资决策约束,包括式(29)~式(32)及式(A6);式(48)为系统运行约束,包括式(33)~式(44)以及式(A1)~式(A5);E、e、G、g、V、F为相应系数矩阵。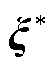 下,寻找最恶劣冰灾场景,表示为
下,寻找最恶劣冰灾场景,表示为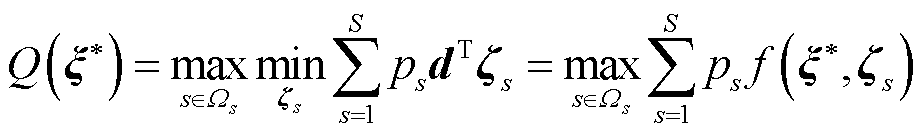 (49)
(49)
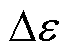 。
。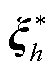 ,更新原问题下界为
,更新原问题下界为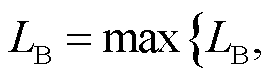
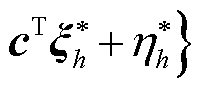 。
。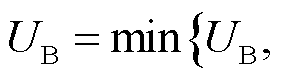
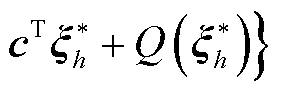 。
。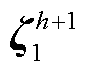 ,
,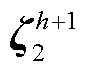 ,…,
,…,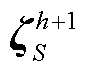 }和式(51)所示可行割,并返回步骤(2)。
}和式(51)所示可行割,并返回步骤(2)。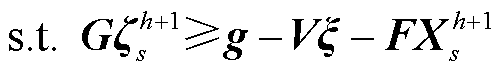 (51)
(51)
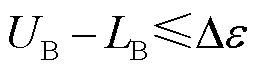 ,若满足,则停止迭代;否则转至步骤(7)。
,若满足,则停止迭代;否则转至步骤(7)。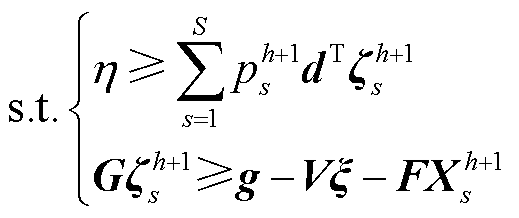 (52)
(52)



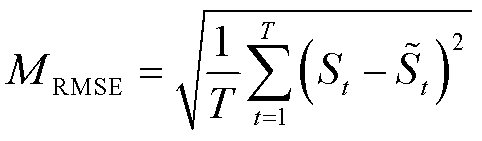 (53)
(53)
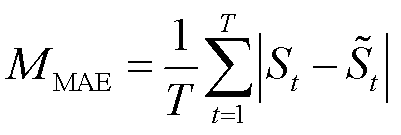 (54)
(54)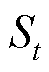 为第t天的覆冰区域实际面积;
为第t天的覆冰区域实际面积;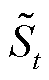 为第t天的覆冰区域提取图中的覆冰面积或第t天的覆冰区域预测面积。
为第t天的覆冰区域提取图中的覆冰面积或第t天的覆冰区域预测面积。



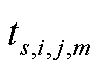 存在不确定性,假设服从偏移伽马分布,即
存在不确定性,假设服从偏移伽马分布,即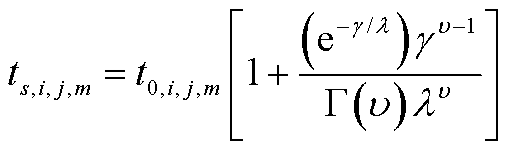 (A1)
(A1)
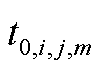 为维修队伍m从i点到j点的理想路程时间;λ和
为维修队伍m从i点到j点的理想路程时间;λ和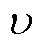 分别为伽马分布的形状与尺度参数;
分别为伽马分布的形状与尺度参数;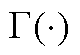 为伽马函数算子;
为伽马函数算子;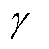 为一正实数。
为一正实数。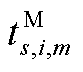 服从正态分布,表示为
服从正态分布,表示为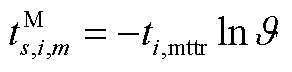 (A2)
(A2)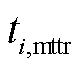 为故障元件的理想维修时间;
为故障元件的理想维修时间;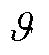 为0~1的随机数。
为0~1的随机数。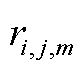 为维修路径决策0-1变量,若维修队m从i点到j点,则
为维修路径决策0-1变量,若维修队m从i点到j点,则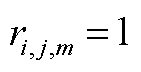 ,否则取0。维修队m从维修中心O出发,在完成所有维修任务后返回维修中心,有
,否则取0。维修队m从维修中心O出发,在完成所有维修任务后返回维修中心,有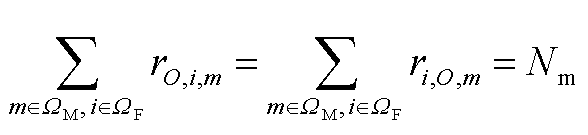 (A3)
(A3)
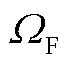 为故障点集合。
为故障点集合。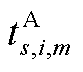 为
为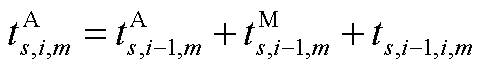 (A4)
(A4)
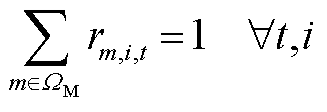 (A5)
(A5)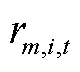 为维修队m是否对故障元件进行维修的0-1变量,取1表示进行维修,否则取0。
为维修队m是否对故障元件进行维修的0-1变量,取1表示进行维修,否则取0。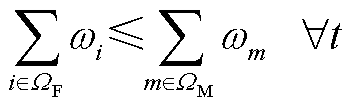 (A6)
(A6)