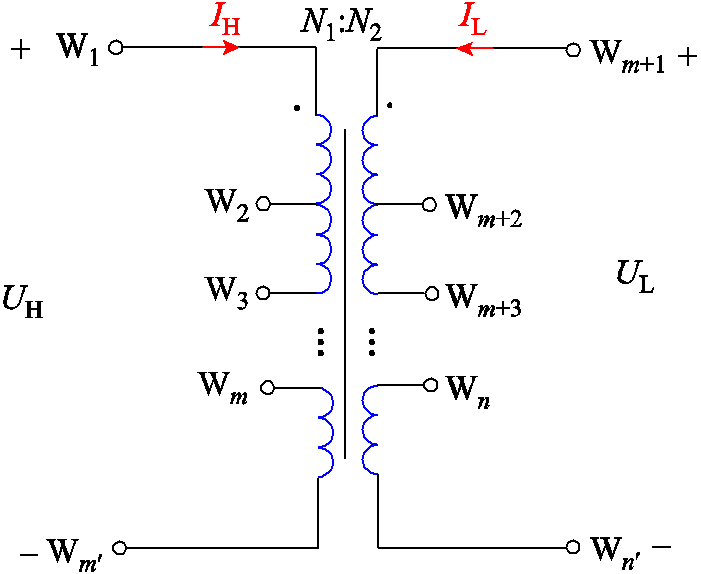
图1 单相双绕组变压器结构
Fig.1 Structure of single-phase double winding transformer
摘要 内部短路是变压器面临的严重故障之一，会导致故障能量在短时间内迅速攀升，极易引发设备内部高能放电爆燃。然而，变压器潜在的内部短路工况组合极多，现有电路模型存在绕组多尺度耦合表征和参数辨识困难的问题。因此，该文瞄准变压器短路故障分析的迫切需求，将变压器绕组轴向虚拟分割为多个子绕组，提出可表征子绕组间漏磁特性的耦合漏感矩阵辨识方法，建立基于耦合漏感矩阵的变压器多尺度故障分析电路模型。该模型无需开展工程测试，直接利用有限元法进行参数化扫描即可提取电路参数。最后开展有限元模型和电路模型对比仿真，证明了该模型可满足多尺度、多工况的变压器内部短路仿真研究的精度要求，且显著提高了仿真效率。该方法能够为装备事故分析、溯源和故障防御等研究提供基础支撑。
关键词：单相变压器 多尺度电路模型 内部短路 耦合漏感矩阵 有限元法
变压器（含换流变压器）是电力系统的高价值核心装备，关乎整个电网的安全稳定运行[1-6]。近年来，国内外已出现多起变压器内部短路事故，造成设备结构失稳和爆燃，变压器和电网安全运行面临重大风险[7-8]。据国际大电网会议工作组CIGRE A2.33统计，约10%的油浸式变压器内部故障会引发爆裂起火[9]，极易引起连锁事故，造成重大经济损失和社会影响[10]。
内部短路是变压器面临的严重故障之一，具有初期故障特征不明显、故障发展迅速、故障电流极大的特点[11-14]，必须通过差流保护进行快速隔离。然而，近年来在运行中发现，部分事故出现了发展性内部短路故障（即短时间内短路匝数迅速增加），导致故障差流二次谐波占比持续大于国家能源局发布的DL/T 684—2012《大型发电机变压器继电保护整定计算导则》中的整定值[15]，引起保护出口显著延迟，故障能量在短时间内迅速攀升，造成爆燃等重大事故[13,16]。因此，亟须提出变压器内部短路故障分析方法，揭示变压器故障电流、故障能量等暂态特性及其对保护的影响规律，为装备制造与继电保护性能的提升提供基础支撑。
由于变压器内部短路试验属于破坏性试验，无法开展真型试验，因此变压器装备制造企业普遍采用场路耦合法对故障进行仿真，以研究变压器内部短路故障的电磁暂态特性，支撑变压器设计校核和事故分析[17]。场路耦合法根据变压器的物理尺寸和材料属性建立有限元模型，并根据短路类型和位置在电路中设置故障，能够较好地对变压器内部故障进行电磁特性分析。但是暂态计算时，该方法在每个时间步长内需对由变压器及其周围场域构成的求解区域的所有网格进行求解，以每个网格所有顶点数值的多项式插值函数作为网格内任一点物理量的值[18]；并且，变压器内部具有显著的多尺度特性，实际短路故障中可能同时涉及单匝、单饼、多饼等尺度的线圈。例如，±800 kV换流变压器网侧绕组具有上百饼共1 000余匝线圈，匝间、饼间、匝地等短路工况组合极多。因此，对于大容量且内部结构复杂的变压器，场路耦合法耗费计算资源过大、仿真时间过长，难以遍历全部潜在短路工况[19-20]。更重要的是，变压器的场路耦合仿真模型难以与外部电网进行联合建模，模型适配性差。例如，换流变压器内部短路仿真需将换流变压器模型与换流阀、电源、负载等模型进行耦合，在有限元仿真软件中难以实现。
为了提高仿真效率并改善模型与外部电网连接的适配性，可建立变压器电路模型，开展内部短路故障分析。当前，用于变压器内部短路故障分析的电路模型主要有电磁暂态仿真软件的内置模型、RLC模型、网格化电路模型等。电磁暂态仿真软件中内置的变压器模型[21-23]开放端口数量较少，如EMTP-RV中最多仅存在三绕组模型；PSCAD中最多仅存在四绕组模型，且元件集成度和封装度较高，仅能仿真极少数特定短路工况。同时，针对不同的短路工况需要对模型参数重新设定，难以对复杂短路的发展过程进行仿真。Matlab中的多绕组变压器模块仅能引出单一绕组的中间节点，各抽头等距分布，绕组电阻和漏感沿抽头均匀分布，且忽略了漏感间的互感。EMTP-RV中的多绕组变压器模型则为理想变压器，仅能反映绕组电压比，而无法表征绕组间的耦合关系。为扩展端口数量以实现绕组的多分段并调用绕组内部节点，可通过串联变压器模型实现多尺度建模，但绕组各段之间的磁耦合关系仍难以被准确表征。RLC模型为多级网络电路，通常每一级由该级绕组的自阻、自感、电导、等值纵向电容、对地电容、绕组间互感等参数构成，根据应用场景不同可适当忽略部分参数以简化模型。RLC模型中目前应用于变压器内部短路故障分析的主要有多导体传输线（Multiconductor Transmission Line, MLT）模型[24-25]、梯形网络模型（详细模型）[26-28]、漏感因子模型[29-30]。其中，MLT模型是基于绕组匝间建模的分布参数模型，而梯形网络模型则是针对饼式绕组建模的集总参数模型[31]。MLT模型将变压器绕组每一匝近似视为一根传输线，整个绕组被模拟成多根相互耦合并且首尾相连的多导体传输线，利用单位长度的电阻、电感、电导、电容矩阵基于频域方程通过编程或在电磁暂态软件中实现。梯形网络模型则通过解析公式或基于有限元模型的静电场和静磁场模块计算变压器每饼的参数，并串联构成多级互耦的梯形网络。上述两种模型目前多应用于研究脉冲输入的行波特性、频率响应特性等变压器高频行为，因此在求解参数时通常忽略铁心的影响，将其等效为空心线圈。基于漏感因子法构建的变压器内部短路故障模型，以N绕组变压器故障前的N阶电阻矩阵R与电感矩阵L为原始数据，通过计算漏感因子求解方程组进而计算故障绕组电感，得到故障后的R、L矩阵，进而根据多绕组变压器端口电压电流暂态计算方程建立模型。但通常需要根据短路类型和短路位置重新计算矩阵，参数求解基于估算或计算过程较为复杂，目前主要用于分析单次匝间短路故障或静态短路故障。RLC模型在变压器工频内部短路计算中通常可省略对仿真准确性影响较小的电容和电阻参数，即为基于绕组自感-互感矩阵的模型。但是对于等尺寸划分的绕组其电感矩阵元素接近，对参数计算结果的精度要求较高，可能造成矩阵行列式为0，在暂态仿真时由于在时域解中阻抗矩阵无法求逆而不能运行。有学者在采用漏感因子法计算故障后参数矩阵的基础上，将基于自感-互感矩阵的多绕组变压器端口方程转换为故障绕组仅分为故障和非故障两部分的形式，并推导计算等效电路参数，但该方法仍需根据不同短路情况重新推导计算电路参数[32]。也有学者通过变压器匝间故障时的磁路，基于对偶原理，得到基于拓扑的变压器匝间故障电路模型，但该方法在激励为理想源时不适用于仿真激励侧的匝间故障[33]。另有学者提出了一种新的网格化变压器建模方法，使基于电路的模型尽可能地类似于有限元，以实现对变压器的精确建模，但计算精度仍与模型复杂程度呈正相关[34]。因此，目前用于变压器内部短路故障分析的电路模型均存在绕组多尺度耦合表征困难的问题，难以适用于分析多尺度、多工况的变压器内部短路故障过程。
现有变压器电路模型中，负电感模型、BCTRAN模型[35-36]和端口对偶模型（Terminal-Duality Model, TDM）[37]能够表征多绕组间的磁耦合关系，具备应用于内部短路故障分析的能力。负电感模型采用星形联结的电感表示绕组间的漏感，但同心式结构的中间绕组等值漏感通常为负，无物理意义，且可能出现仿真失稳发散的问题[38]；而对于三绕组以上或各绕组高度不同的变压器可能存在较大误差，因此，负电感模型主要用于研究三绕组变压器的稳态特性[39]。BCTRAN模型利用矩阵表征变压器绕组间的磁耦合关系，在1 kHz以下具有较高的工程仿真精度，且对于多绕组变压器具有优异的扩展性。矩阵元素通常利用设计公式或基于有限元法、试验法的短路试验结果计算，但由于设计公式只适用于绕组磁场垂直交链的情况，所以对于距离较远的绕组之间的参数计算误差较大[37]。基于端口短路测试的参数求解方法适用于多绕组变压器，但若将绕组视为多个子绕组级联，实际变压器绕组内部无抽头，无法进行端口试验，即使通过有限元仿真代替试验，对于变压器饼级甚至线匝级的小尺度模型，涉及绕组间的短路试验排列组合极多，对单相N绕组变压器也需进行至少N(N-1)/2次试验，工作量和计算量极大，难以获得模型矩阵参数。TDM模型统一了端口模型与电磁对偶模型，具备内部磁耦合表征能力，但存在与BCTRAN模型相同的参数辨识困难问题。
综上所述，现有变压器电路模型均存在绕组多尺度耦合表征和参数辨识困难等问题，难以用于分析多尺度、多工况内部短路故障电气量的暂态特性。因此，亟须构建能精准复现变压器内部短路故障过程，尤其是发展性内部短路的变压器故障分析模型。
综上所述，本文提出一种变压器内部短路多尺度故障分析模型构建方法，首先，以某80 MV·A单相变压器为研究对象，通过求解多饼级联绕组耦合漏感矩阵，构建其饼级尺度电路模型；然后，与有限元模型开展对比仿真，验证电路模型在多工况下的准确性；最后，将发展性匝间短路故障差流二次谐波占比与现有方法分析结果进行对比，证明本文所提电路模型对变压器复杂内部短路二次谐波特性仿真的准确性。
为使单相变压器模型具有多尺度的磁耦合特性表征能力，将单相变压器各绕组拆解为n个子绕组进行建模，每个子绕组可以为单匝、多匝、单饼、多饼线圈，根据短路情况或故障分析需求确定，理论上拆分越精细的模型表征能力越强。考虑到短路匝数对端口暂态电流的影响和构建有限元模型的复杂度，按饼拆分已能够较好地表征多种内部短路情况。以单相双绕组变压器为例，其结构如图1所示。图1中，k为各子绕组编号（k=1, 2,…, n），Wk为第k个子绕组顶端引出端子，N1、N2分别为高压、低压绕组匝数，UH、UL分别为高压、低压绕组电压，IH、IL分别为高压、低压绕组电流。
图1 单相双绕组变压器结构
Fig.1 Structure of single-phase double winding transformer
变压器各子绕组间的磁耦合关系可利用一组相互耦合的电感串联表示，由于各子绕组端口励磁阻抗远大于绕组间μH级的漏感，且漏感之间的互感更小，因此为了在尽量保证电路模型准确性的条件下对模型进行简化，忽略对电路仿真结果准确性影响较小的励磁支路，只在计算绕组自感-互感矩阵时考虑铁心的影响[40]。变压器漏感等效电路如图2所示[37]。图2中，i, j为节点编号，i, j=1, 2,…, n；Ui-1为第i-1个电感产生的电压降；Ii-1为流过第i-1个电感的电流；Lc_i-1, i-1为第i-1个电感的自感，表示第i-1个子绕组与第i个子绕组之间的漏感；Lc_i-1, j-1为第i-1个电感和第j-1个电感之间的互感。该模型本质上是利用电磁对偶原理将子绕组的磁耦合特性用电感电路表示。
首先，将表示各子绕组间磁耦合关系的漏感及互感以耦合漏感矩阵Lc表征，并将该部分电路封装
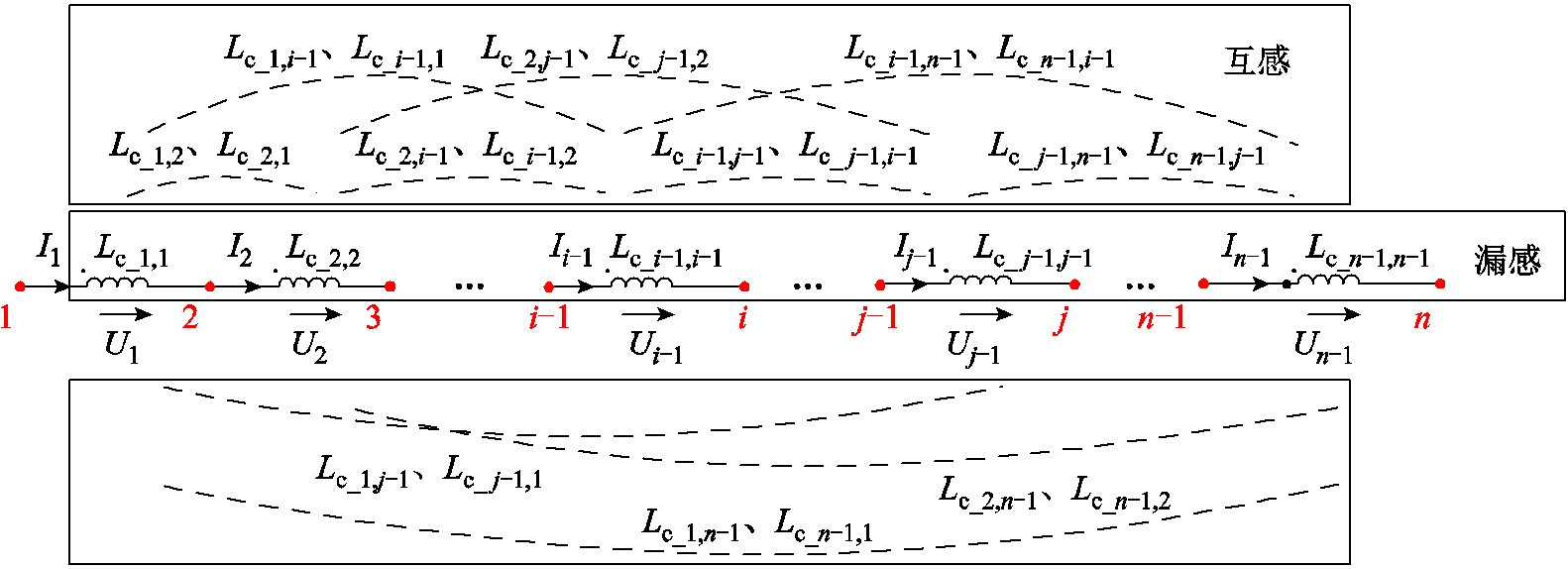
图2 变压器漏感等效电路
Fig.2 Equivalent circuit of transformer leakage inductance
形成模块A。为方便计算和外电路连接，耦合漏感矩阵中的元素均归算至同一匝数，因此需在等效电路各节点与公共节点间接入理想变压器，以实现内部磁特性和外部电路的耦合，同时表示各子绕组的真实匝数。然后，将子绕组电阻与理想变压器相连，再根据变压器各子绕组的电气连接关系，将高压、低压各子绕组分别首尾相接，并引出各子绕组端子，以实现对绕组内部节点的调用，方便后续故障接线。最后，建立变压器多尺度电路模型如图3所示（模块A中任意两电感间均存在互感，图中未表示），并接入激励电源及负载以方便模型测试。图3中，Rk为各子绕组电阻；Nk为各子绕组匝数；Us为电源电压；ZL为低压侧等效负载。
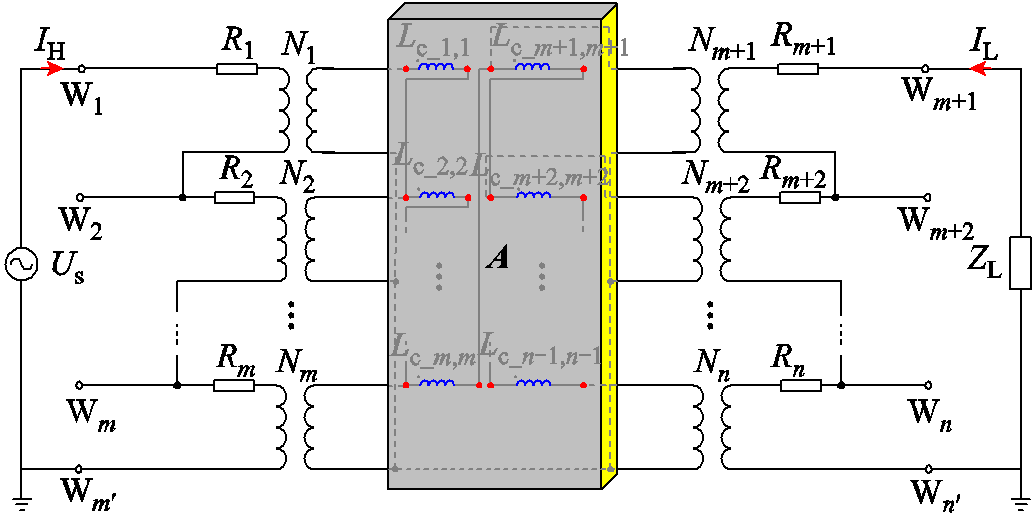
图3 变压器多尺度电路模型
Fig.3 Multi-scale circuit model for transformer
在图3建立的变压器多尺度电路模型的基础上，根据单相变压器电磁连接关系及内部短路物理过程，连接各子绕组端子，即可得到变压器匝间短路、发展性匝间短路、匝地短路、绕组间短路等不同内部短路工况的变压器多尺度故障分析模型。
构建变压器多尺度电路模型及其故障分析模型的关键是核心参数辨识。本文基于有限元法，采用参数化扫描计算得到各子绕组的电阻矩阵R及自感-互感矩阵L，并提出将自感-互感矩阵转换为反映子绕组间漏磁特性的耦合漏感矩阵Lc的参数辨识方法，具体推导过程如下。
当一侧绕组与激励源连接后，由于电磁感应会在其他绕组中产生感应电压，如图1所示，具有n个子绕组的变压器端口电压电流关系满足
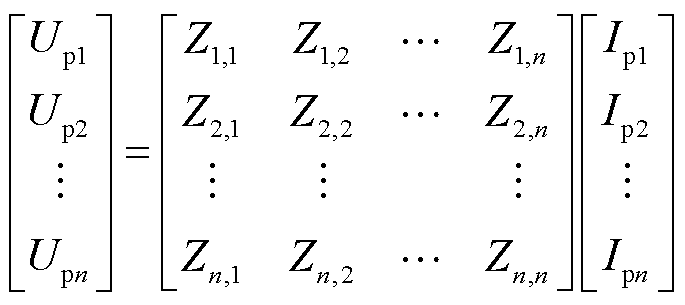（1）
式中，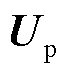
为端口电压向量；
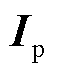为端口电流向量；Z为阻抗矩阵。对于瞬态计算，式（1）可改写为
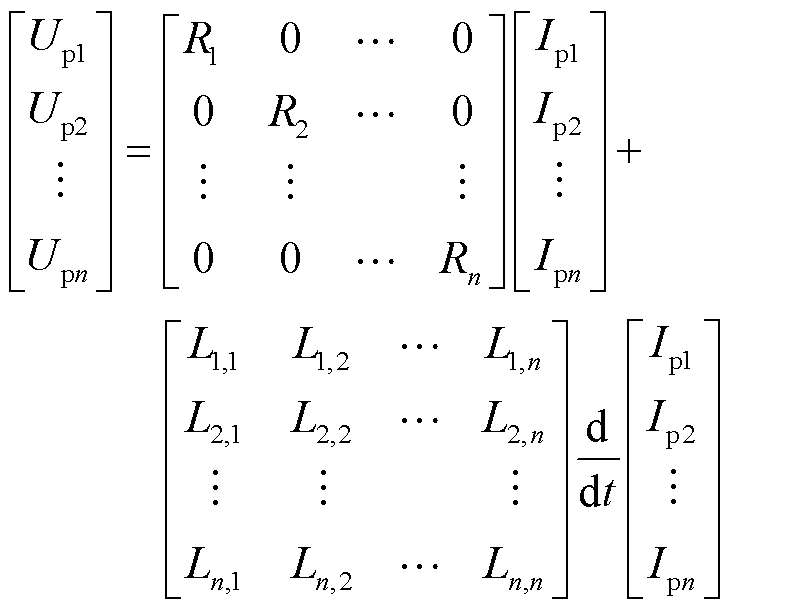(2)
式中，R为电阻矩阵，表示阻抗矩阵Z的实部；L为自感-互感矩阵，表示阻抗矩阵Z的虚部除以角频率ω。
因此，端口电压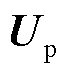可以表示为两部分的串联，其中电感部分导致的压降
可以表示为
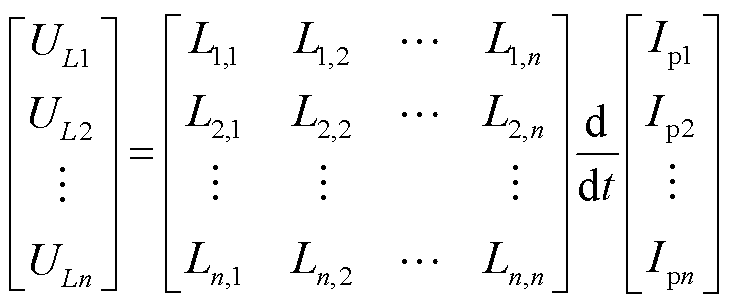（3）
忽略励磁电流[41]，根据基尔霍夫电流定律（Kirchhoff’s Current Law, KCL）可得
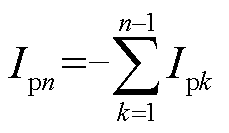（4）
为方便实现对内部任意位置故障进行短路电路连接，一般需根据实际单相变压器将绕组拆分为等尺寸的子绕组，但其自感-互感矩阵的元素值相近，具有病态特征，一般无法利用式（3）进行计算。因此，本文提出将自感-互感矩阵转换为耦合漏感矩阵，具体转换方法如下。
首先，将自感-互感矩阵转换为降阶电感矩阵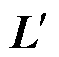
[42]。将式（3）第1～n-1行元素均减去第n行元素，并结合式（4）化简，得到第a（a=1, 2,…, n-1）个子绕组与最后一个子绕组n之间压降的表达式，进而得到关于原自感-互感矩阵的n-1阶降阶电感矩阵，具体为
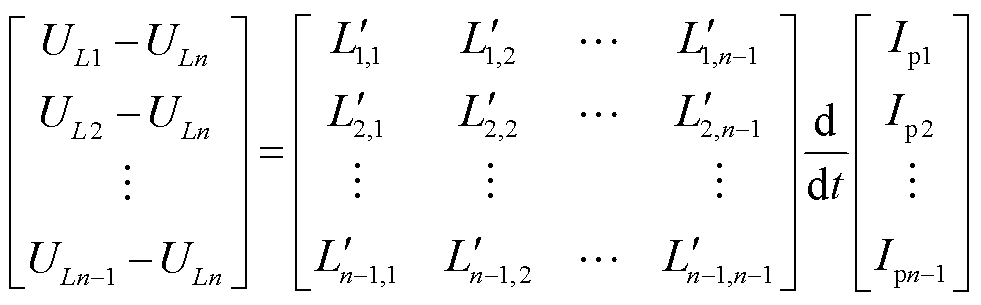（5）
其次，推导短路电感矩阵Ls元素与降阶电感矩阵元素的关联关系。激励第a个子绕组，第n个子绕组短路的短路实验示意图如图4所示。图4中，Wsa表示子绕组编号，ULa表示激励电源电压，Ipa表示激励子绕组端口电流，Ipn表示短路子绕组端口电流。因此，式（5）的电流向量中只有Ipa不为零，且ULn=0，则第a个和第n个子绕组之间的短路电感Ls_a,n的计算方法为
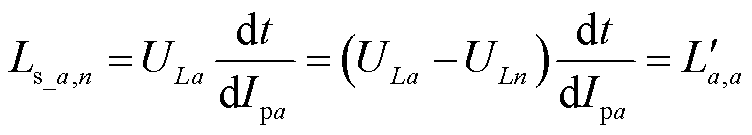（6）
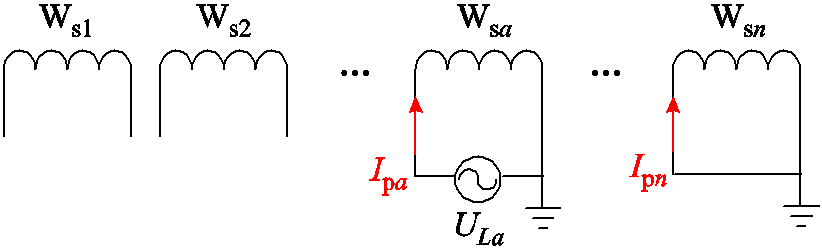
图4 短路实验示意图
Fig.4 Schematic diagram of short-circuit test
同理，第a个和第b（b=1, 2,…, n-1）个子绕组之间的短路电感Ls_a, b的计算方法为
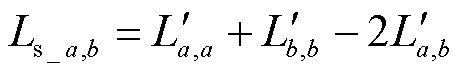（7）
然后，求解耦合漏感矩阵。在图2所示的变压器漏感等效电路中，节点i与节点j（i, j=1, 2,…, n）之间的电压Ui, j为
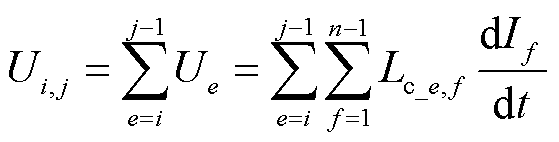（8）
对节点i施加激励，并将节点j接地短路，则在节点i与节点j之间的短路实验中，仅包含在节点i与节点j之间的电感有电流通过，即
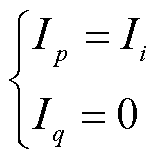（9）
式中，p=i+1,…, j-2, j-1；q=1, 2,…, i-1, j, j+1,…, n-1。将式（9）代入式（8）得
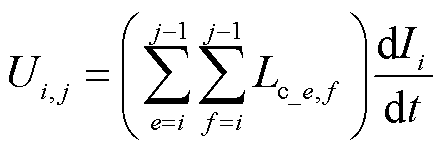（10）
则节点i与节点j之间的短路电感可以表示为
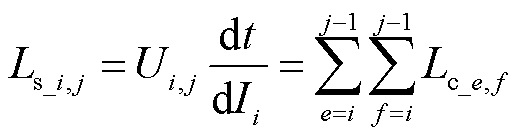（11）
当j=i+1时，耦合漏感矩阵中主对角线元素为
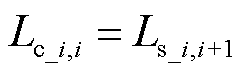（12）
由于耦合漏感矩阵的对称性，得到矩阵中非对角线元素为
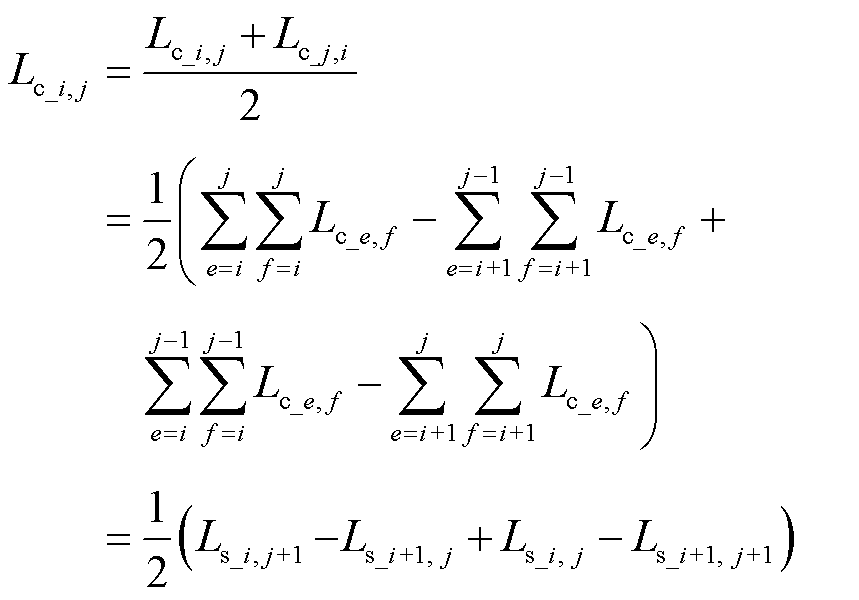(13)
从而可实现将自感-互感矩阵转换为耦合漏感矩阵。其中，自感-互感矩阵可通过有限元仿真快速得到，然后即可利用图3所示的电路模型开展仿真；该模型及其参数辨识方法不需要开展端口短路试验即可获得，解决了现有多绕组变压器模型的参数辨识难题[37]；同时，该模型为电路模型，计算效率大幅提高，且可以与外部电路模型进行联合仿真，解决了基于场路耦合法故障分析模型的效率低和电路适配性差的问题。
目前变压器制造企业大多采用有限元软件开展设计校核及事故分析等工作，与实际产品相比，通过有限元方法计算得到的漏抗误差可控制在±0.5%以内，满足国家电网有限公司电力变压器采购要求[43]。因此，本文为提取构建变压器多尺度电路模型所需参数，并对比验证模型的准确性，根据某变压器装备制造企业提供的实际结构尺寸，在有限元仿真软件中建立了一台80 MV·A、127 kV（即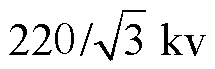
）单相变压器有限元模型，其额定参数见表1。其中高压绕组为78饼结构，共436.094匝，自上而下编号为高压第1～78饼；低压侧为84饼结构，共240匝；调压绕组为52饼结构，共44匝，变压器有限元模型如图5所示。
表1 80 MV·A、127 kV单相变压器额定参数
Tab.1 Rated parameters of the 80 MV·A, 127 kV single-phase transformer
参数数值 额定容量SN/(MV·A)80 高压侧额定电压UNH/kV127 低压侧额定电压UNL/kV70 额定频率fN/Hz50
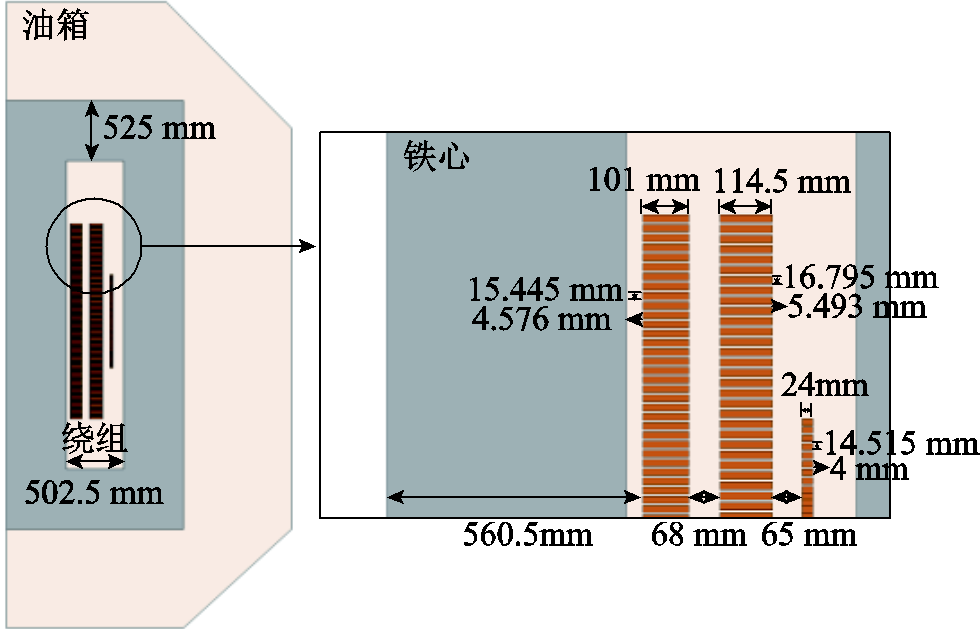
图5 80 MV·A、127 kV单相变压器有限元模型
Fig.5 Finite element model of the 80 MV·A, 127 kV single-phase transformer
本文采用磁场和电路接口建立变压器场-路耦合模型：磁场接口中，线圈采用电路（电流）方式激励；电路接口中，各元件按照图6所示的等效电路连接，并设置部分绕组在某时刻短路，以模拟不同匝间短路工况。图6中，SWr为高压绕组第r次短路部分对应短路环上的开关，tr为高压绕组第r次短路部分发生匝间短路的时间，IW为故障绕组电流，IS为故障绕组对应短路环电流。由图6可知，随着故障的发展，绕组未短路部分的匝数减小，短路部分的等效匝数也减小。
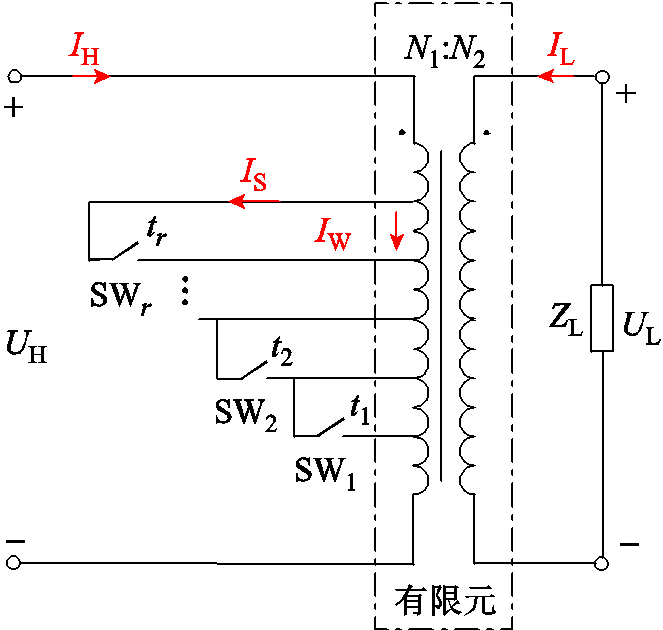
图6 高压绕组匝间短路等效电路
Fig.6 Equivalent circuit of inter-turn short circuit fault in the high-voltage winding
为获取变压器各子绕组的自感-互感矩阵及电阻矩阵，基于变压器有限元模型进行参数提取。能否准确地建立本文所提出的电路模型主要取决于有限元模型计算自感和互感参数的精细程度。由于匝间短路常发生在高压绕组，本文以高压绕组匝间短路故障为例进行模型的构建与验证。为提高仿真效率、降低模型复杂程度，将低压绕组与调压绕组分别视为一个整体，只将高压绕组分饼进行参数提取。计算第k个子绕组的自感及其与其他子绕组之间的互感参数时，对第k个子绕组施加电流激励，其他子绕组保持开路。禁用电路接口，使用参数化扫描进行稳态计算，对各子绕组依次施加电流激励，扫描矩阵为
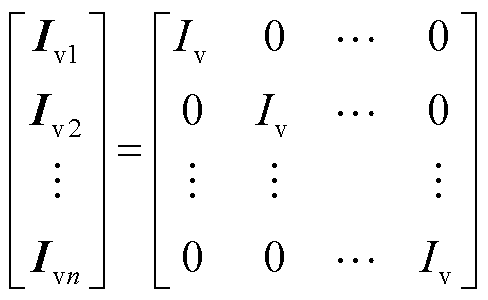（14）
式中，矩阵行向量Ivk表示扫描中对应子绕组每次计算时所施加的电流激励；列向量表示该次计算中各子绕组所施加的电流激励。
从而可推导出关于变压器子绕组的n×n阶自感-互感矩阵和电阻矩阵，其中每次扫描计算结果对应该次扫描中激励子绕组的电阻。
本文80 MV·A变压器为连续式绕组，因此可基于其二维轴对称有限元模型开展参数计算，若变压器包含螺旋式绕组，则应用其三维有限元模型计算，且其与纠结式绕组的参数提取均依赖较高精度的有限元模型参数计算。基于上述参数提取方法，结合1.2节所述耦合漏感矩阵辨识方法，将计算得到的关于变压器绕组的80×80阶自感-互感矩阵转换为79×79阶耦合漏感矩阵，其中，矩阵第1～4阶元素为
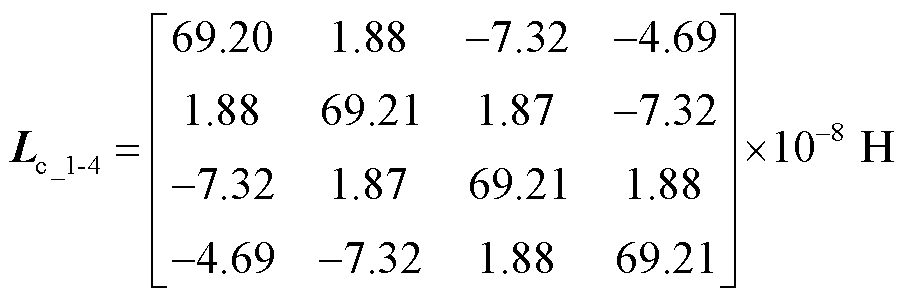（15）
进而计算得到绕组电阻矩阵，其中矩阵第77～80阶元素为
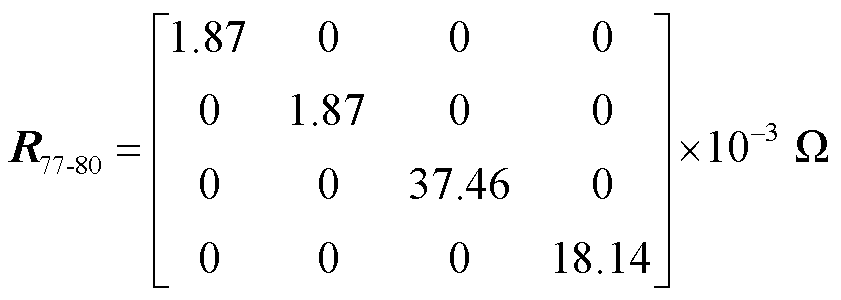（16）
基于上述参数，结合图3构建单相变压器饼级尺度电路模型。
2.3.1 短路阻抗验证
为验证本文构建电路模型的正确性，对有限元模型及电路模型分别进行短路阻抗仿真测试，并计算短路阻抗开展对比验证。基准阻抗ZB的计算公式为
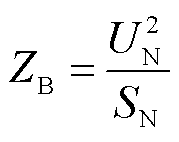（17）
式中，UN为额定电压；SN为额定容量。
改变有限元模型电路接口中的连接方式，只对高压第k饼施加额定电压127 kV激励。磁场接口中，将低压绕组设置为0 V的电压激励方式，从而使低压绕组短路；并将除高压第k饼及低压绕组以外的其他绕组设置为0 A的电流激励方式，使其他绕组保持开路。电路模型的短路阻抗实验等效电路如图7所示。
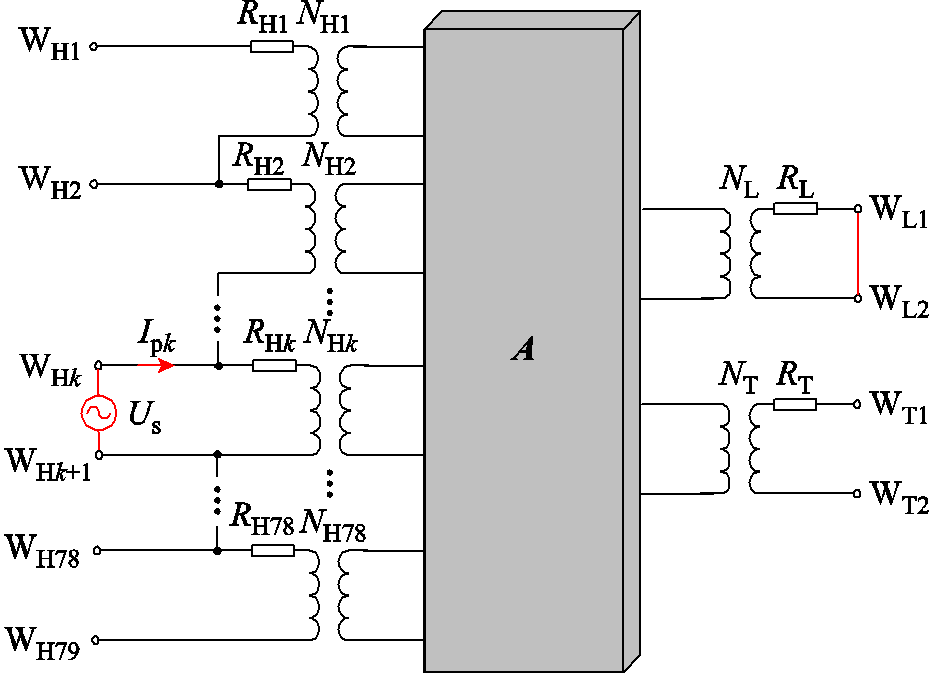
图7 电路模型短路阻抗实验等效电路
Fig.7 Equivalent circuit of short circuit impedance test of circuit model
高压第k饼与低压绕组之间的短路阻抗Zs_k,L（k = 1, 2,…, 78）的计算公式为
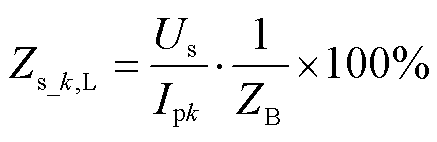（18）
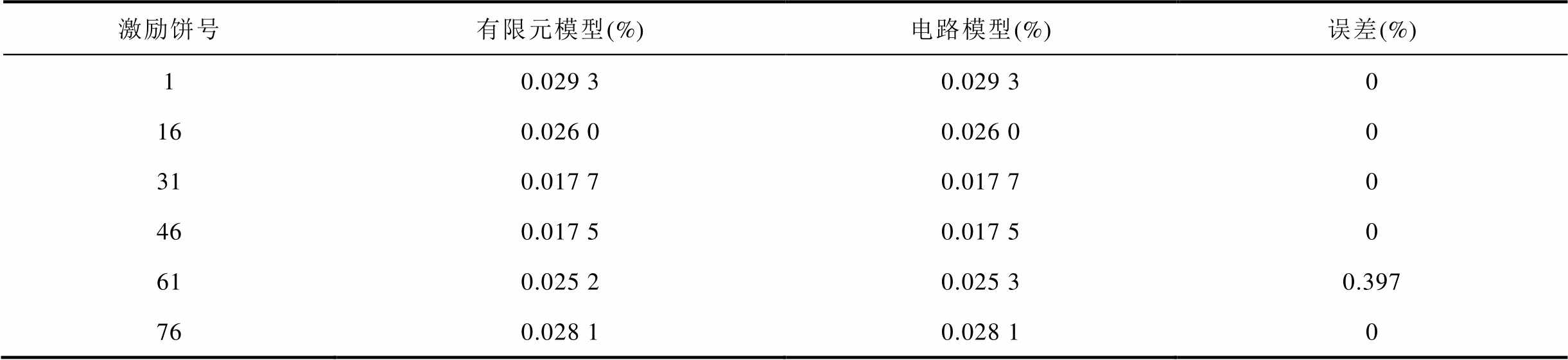
对有限元模型和电路模型开展相同条件的短路阻抗仿真实验，得到短路阻抗计算结果对比见表2，可见两者间基本不存在误差，证明了电路模型的准确性。
表2 短路阻抗计算结果对比
Tab.2 Comparison of short circuit impedance calculation results
激励饼号有限元模型(%)电路模型(%)误差(%) 10.029 30.029 30 160.026 00.026 00 310.017 70.017 70 460.017 50.017 50 610.025 20.025 30.397 760.028 10.028 10
2.3.2 额定工况验证
为进一步验证本文提出的电路模型对变压器端口数据的模拟精度，对有限元模型及电路模型开展额定工况下的对比仿真分析。对两模型高压侧均施加127 kV激励，低压侧接入60.49 Ω的阻性负载。以10-4 s的时间步长进行瞬态仿真，得到高压侧、低压侧端口电流波形对比结果如图8所示。有限元模型高压侧端口电流峰值为0.894 kA，低压侧为1.618 kA。电路模型高压侧端口电流峰值为0.891 kA，与有限元模型相比误差为-0.336%；低压侧端口电流峰值为1.619 kA，误差为0.062%，电路模型与有限元模型在额定工况下的仿真波形高度重合。并且有限元模型仿真时长为873 s，而电路模型仅需0.229 s，仿真耗时缩短约99.98%，在保证模拟精度的同时显著地提高了仿真效率。
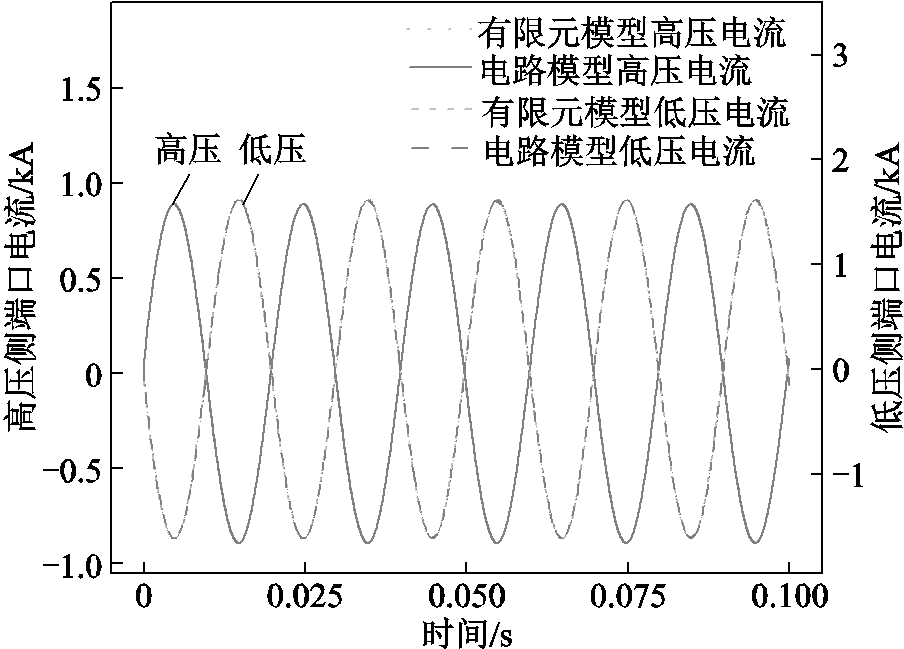
图8 额定工况端口电流对比
Fig.8 Comparison of port currents at rated operating condition
本节进一步验证本文提出的电路模型对变压器发生内部短路故障时暂态特性仿真的准确性。
对变压器有限元模型和电路模型分别施加与2.3.2节额定工况相同的激励，并接入相同的负载。设置高压第49～68饼（共113.625匝）在20 ms时发生匝间短路，有限元模型在电路接口中完成设置，电路模型通过连接各端口完成短路接线，变压器多饼匝间短路故障模型如图9所示。
仿真得到高压侧、低压侧端口电流波形对比如图10所示，其中短路后首峰值的对比见表3（本文均取正峰值）。由于短路饼电流产生的磁通方向与主磁通相反，且高压绕组有效匝数减小，将导致高压侧端口电流增大[3, 44]。发生匝间短路后，两模型高压侧端口电流首峰值的误差为0.620%，低压侧首峰值的误差仅为0.061%。
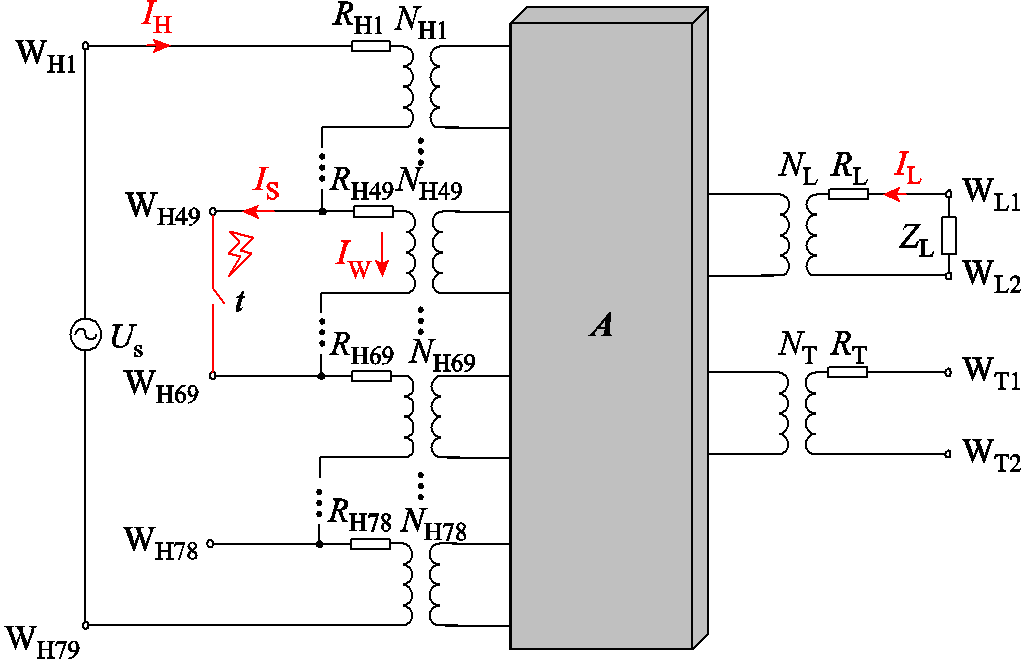
图9 变压器多饼匝间短路故障模型
Fig.9 Model of multi-disk inter-turn short circuit fault in transformer
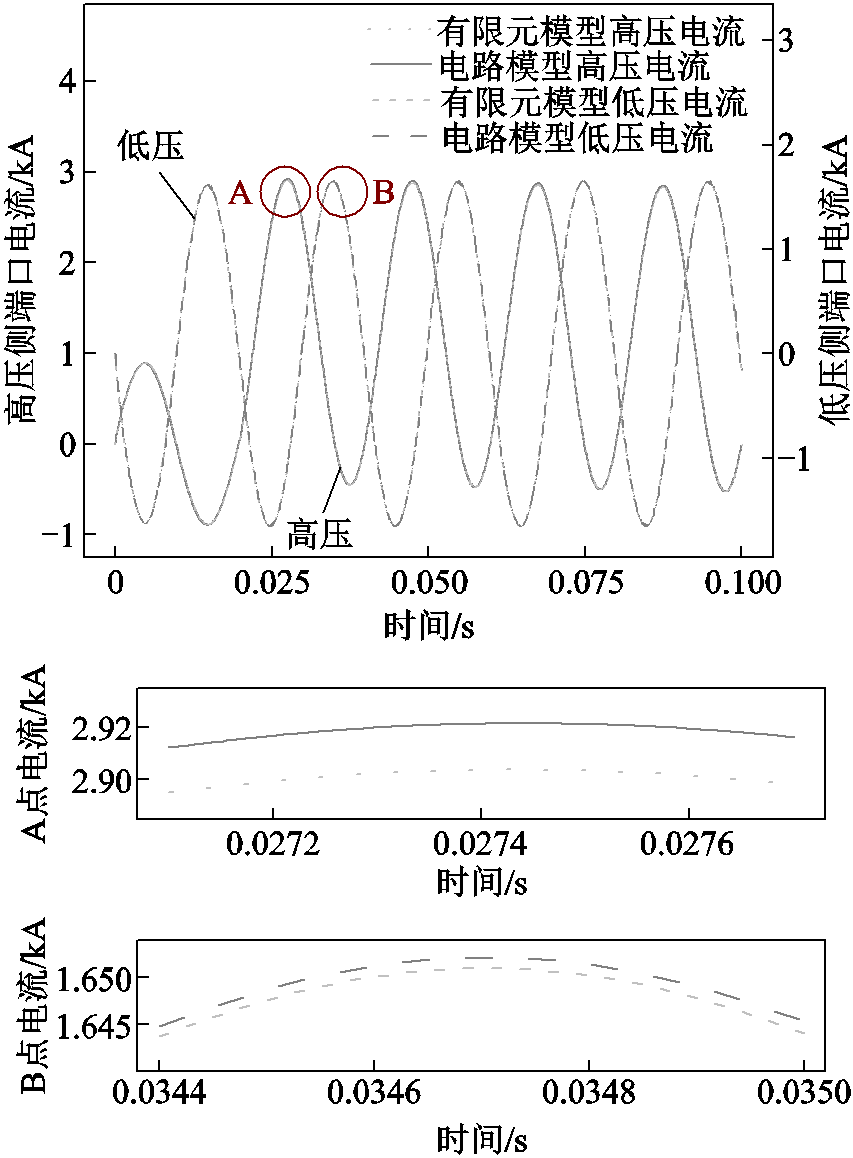
图10 多饼匝间短路故障端口电流对比
Fig.10 Comparison of port currents with multi-disk inter-turn short circuit fault
表3 多饼匝间短路故障电流首峰值对比
Tab.3 Comparison of the first peak values of currents with multi -disk inter-turn short circuit fault
数据类型电流/kA误差(%) 有限元模型电路模型 高压侧端口电流2.9042.9220.620 低压侧端口电流1.6511.6520.061 短路饼电流0.1580.1580 短路环电流9.6109.7020.957
获取两模型高压绕组短路饼流过的电流仿真数据，及其对应短路环电流的仿真数据，绘制两模型的波形对比如图11所示，其中短路后首峰值的对比见表3，短路环电流IS为端口电流IH与短路饼电流IW之差，即
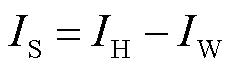（19）
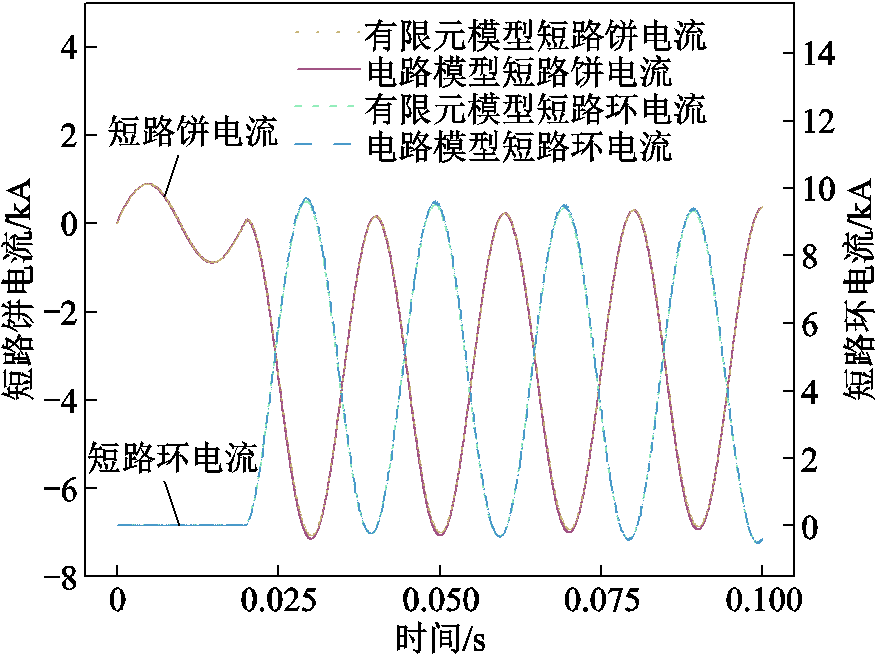
图11 多饼匝间短路故障短路电流对比
Fig.11 Comparison of short-circuit currents with multi-disk inter-turn short circuit fault
发生匝间短路后，有限元模型与电路模型短路饼电流首峰值的误差几乎为0，对应短路环电流首峰值的误差为0.957%。
仍对两模型分别施加与2.3.2节额定工况相同的激励，并接入相同的负载。设置高压第49饼（5.875匝）在20 ms时发生匝间短路，仿真得到的短路后故障电流首峰值对比见表4。发生匝间短路后，两模型高压侧端口电流首峰值的误差为0.846%，低压侧端口电流首峰值的误差为0.608%，短路饼电流首峰值的误差为2.202%，对应短路环电流首峰值的误差为1.039%。由于电路模型忽略了励磁支路，且用于暂态仿真的有限元模型高压绕组采用以多饼为单位的多分段方式建模，电路模型参数基于以饼为单位建模的有限元模型提取，两种模型绕组的划分尺度不同，同时有限元模型的网格剖分、求解器设置、计算步长等仿真设置也会对其仿真结果产生影响，因此在单次匝间短路故障工况下两模型的计算结果会产生误差，但端口电流及短路电流首峰值的误差仍均小于2.5%。仿真结果表明，本文电路模型对变压器匝间短路暂态仿真具有较高的模拟精度。
表4 单饼匝间短路故障电流首峰值对比
Tab.4 Comparison of the first peak values of currents with single-disk inter-turn short circuit fault
数据类型电流/kA误差(%) 有限元模型电路模型 高压侧端口电流2.3642.3840.846 低压侧端口电流1.6461.6560.608 短路饼电流28.29128.9142.202 短路环电流137.309138.7351.039
实际工程中已发生由于变压器发展性匝间短路造成设备爆燃的重大事故，其主要是由于故障差流的二次谐波占比长时间大于整定值（一般取15%～20%），致使保护无法快速出口而引发，存在保护漏洞。因此，还需探究本文电路模型对变压器发展性匝间短路故障暂态仿真的适用性，并对故障差流的二次谐波特性进行分析。
仍对变压器有限元模型与电路模型分别施加与2.3.2节额定工况相同的激励，并接入相同的负载，高压绕组发展性匝间短路等效电路如图6所示。由于工程事故波形数据保密，仅能基于本文建立的变压器有限元模型依照工程事故进行类比仿真。基于某实际工程事故的故障发展过程，设置各开关动作时序如图12所示（1为闭合状态，0为断开状态）。图中，SW1、SW2、SW3、SW4分别对应高压第49～68、34～48、32～33、22～31饼短路环上的开关。
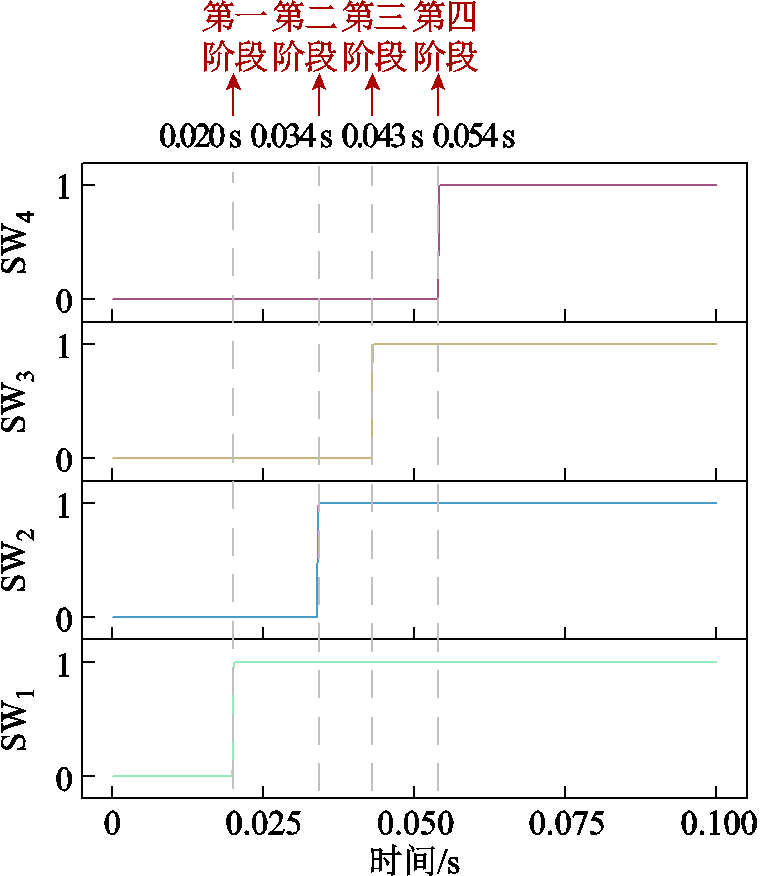
图12 短路环开关动作时序
Fig.12 Timing sequence of short circuit loop switch
获取发生连续发展性匝间短路的高压侧、低压侧端口电流波形对比如图13所示，其中故障后首峰值的对比见表5。发生最后一阶段匝间短路（开关SW4动作）后，两模型高压侧端口电流首峰值的误差为2.646%，低压侧首峰值的误差则为1.814%。进而，将短路发展过程中（0～80 ms）高压侧端口电流局部峰值进行对比，结果见表6，波形前4个峰值中最大误差为2.646%。
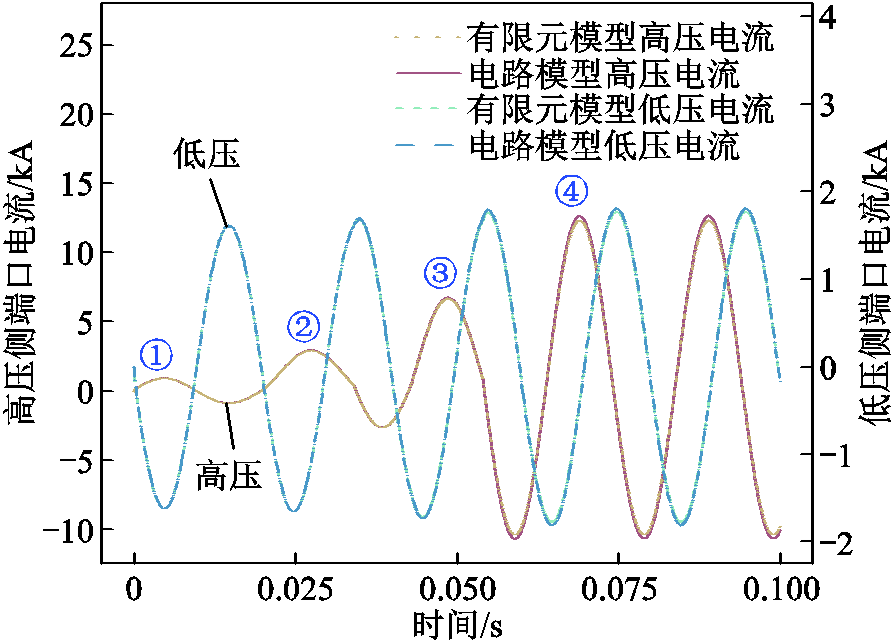
图13 发展性匝间短路故障端口电流对比
Fig.13 Comparison of port currents with developmental inter-turn short circuit fault
表5 发展性匝间短路故障电流首峰值对比
Tab.5 Comparison of the first peak values of currents with developmental inter-turn short circuit fault
数据类型电流/kA误差(%) 有限元模型电路模型 高压侧端口电流12.32212.6482.646 低压侧端口电流1.7641.7961.814 短路饼电流2.1112.2255.400 短路环电流21.30221.7992.333
表6 高压侧端口电流局部峰值对比
Tab.6 Comparison of local peak values of port current on high voltage side
峰值编号电流/kA误差(%) 有限元模型电路模型 ①0.8940.891-0.336 ②2.9042.9220.620 ③6.6686.7391.065 ④12.32212.6482.646
将两模型高压第49～68短路饼流过的电流波形及其对应的短路环电流波形进行对比，如图14所示，其中故障后首峰值的对比见表5。发生最后一阶段匝间短路后，有限元模型与电路模型短路饼电流首峰值的误差为5.400%，对应短路环电流首峰值的误差为2.333%。各故障电流暂态波形均可视为正弦稳态分量及直流衰减分量两项的叠加。进而，将短路发展过程中（0～70 ms）短路饼电流和短路环电流的局部峰值对比见表7。由于累计误差的影响，误差在发展性匝间短路工况下有所增大，但均小于5.5%，仍满足变压器内部短路事故分析要求。对比结果证明了本文所建电路模型可用于分析变压器发展性匝间短路故障。故障发展后端口电流和短路电流的变化主要由电流包含的衰减分量、绕组短路和未短路部分的等效匝数变化、故障位置、以及绕组短路部分附近磁场的“自屏蔽”现象[45]四种因素共同影响。
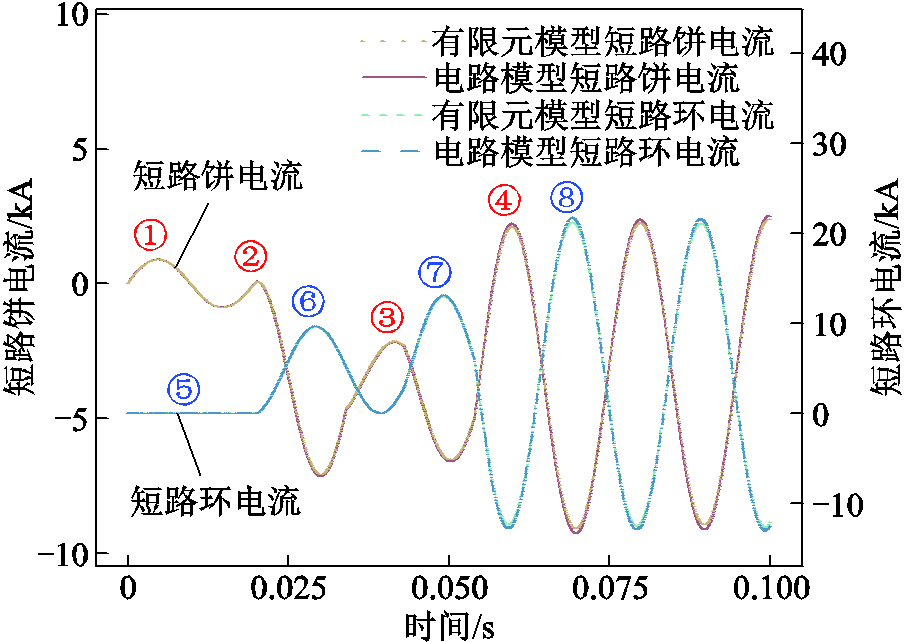
图14 发展性匝间短路故障短路电流对比
Fig.14 Comparison of short-circuit currents with developmental inter-turn short circuit fault
表7 短路电流局部峰值对比
Tab.7 Comparison of local peak values of short-circuit currents
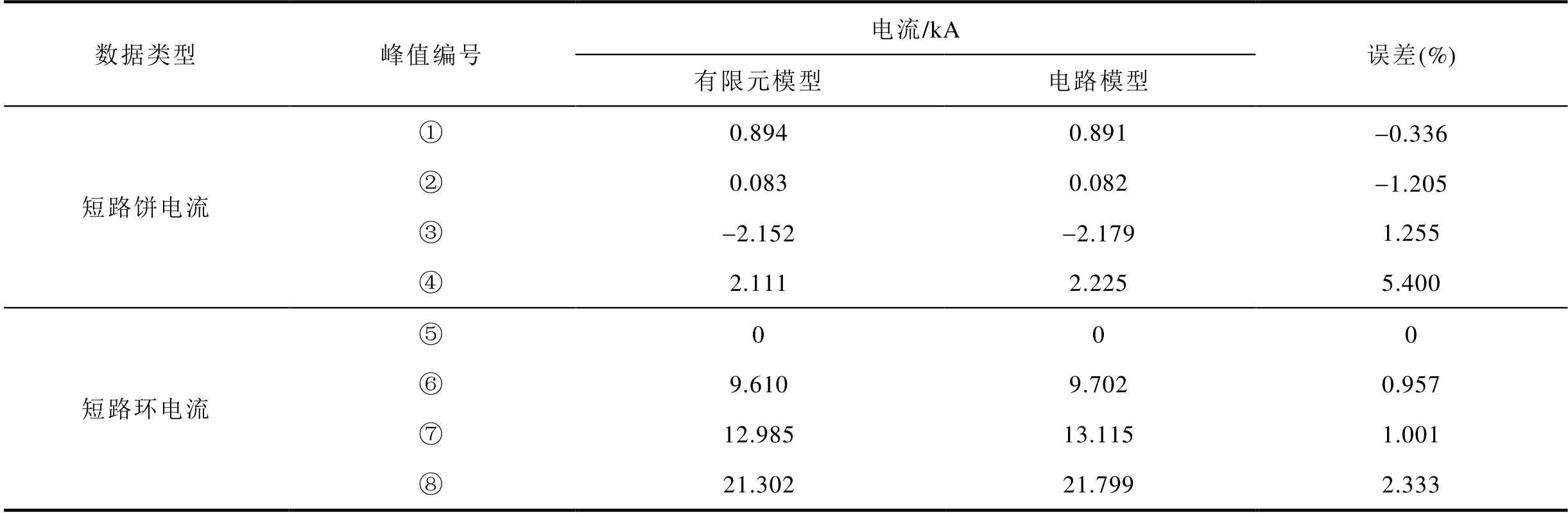
数据类型峰值编号电流/kA误差(%) 有限元模型电路模型 短路饼电流①0.8940.891-0.336 ②0.0830.082-1.205 ③-2.152-2.1791.255 ④2.1112.2255.400 短路环电流⑤000 ⑥9.6109.7020.957 ⑦12.98513.1151.001 ⑧21.30221.7992.333
现有电路模型受限于绕组多尺度耦合表征和参数辨识困难的问题，难以用于分析短路匝数逐渐增加的发展性匝间短路过程。其通常将发生匝间故障的绕组视为互耦的三个独立线圈，即将短路部分看作一个整体（以下简称“现有方法”）。因此计算现有方法（高压第22～68饼单次全部短路）及本文第4.1节发展性匝间短路故障的有限元模型和电路模型的高压侧、低压侧差流ID为
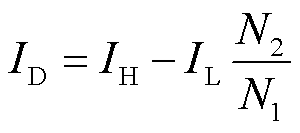（20）
由此得到故障差流对比如图15所示。故障前差流基本为0，故障后现有方法得到的差流迅速增大，而有限元模型及本文电路模型得到的差流则随着故障发展逐渐增大。
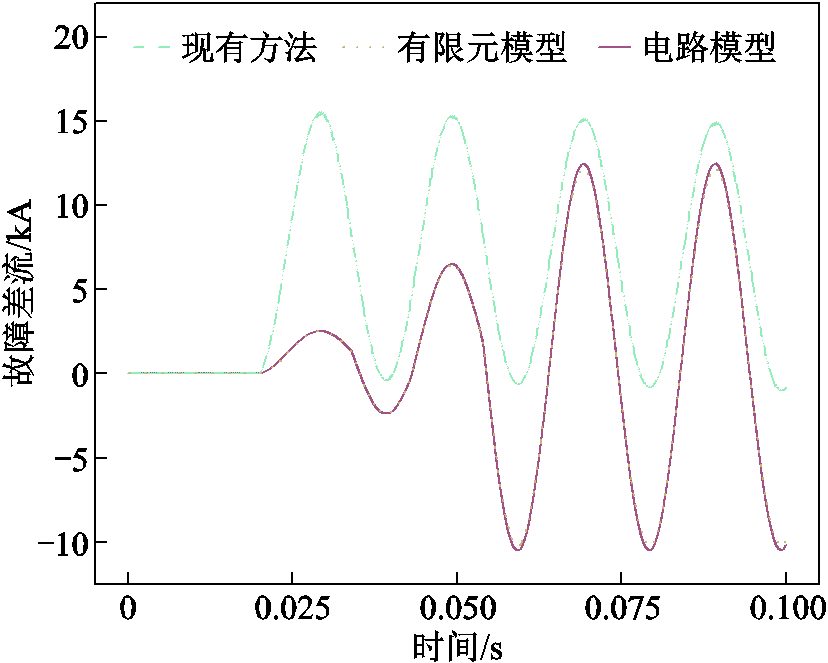
图15 故障差流对比
Fig.15 Comparison of fault differential currents
采用20 ms滑动时间窗，对故障差流进行实时傅里叶变换分析，得到差流的二次谐波占比时域波形如图16所示，并将有限元模型及本文电路模型故障差流的二次谐波占比局部峰值进行对比，结果见表8，可知误差均不超过2.5%。
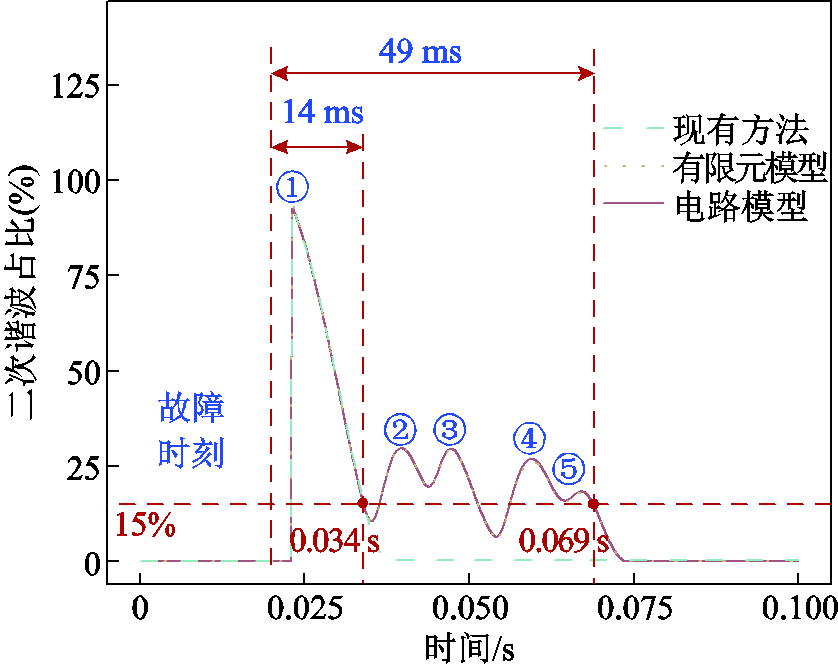
图16 故障差流二次谐波占比对比
Fig.16 Comparison of second harmonic percentage of fault differential currents
表8 发展性匝间短路二次谐波占比局部峰值对比
Tab.8 Comparison of local peak values of second harmonic percentage with developmental inter-turn short circuit
峰值编号二次谐波占比(%)误差(%) 有限元模型电路模型 ①95.02793.251-1.869 ②29.72029.682-0.128 ③29.45129.5760.424 ④26.42926.9481.964 ⑤18.02418.4022.097
其中，现有方法得到的差流二次谐波占比呈持续衰减趋势，自故障发生时刻起，二次谐波占比15%以上的持续时间为14 ms；而发展性匝间短路工况下，有限元模型与电路模型二次谐波占比均随着故障发展呈振荡衰减趋势，自故障发生时刻起，二次谐波占比15%以上的持续时间均为49 ms，即发生最后一阶段短路后15 ms。与现有方法计算结果相比，电路模型发展性匝间短路的差流二次谐波占比持续高于整定值，与有限元模型计算结果相符，会导致差动保护长时间制动。因此，基于本文电路模型可准确地复现现有方法难以得到的发展性内部短路故障差流的二次谐波特性，从而支撑保护方案优化。
针对现有电路模型绕组多尺度耦合表征和参数辨识困难的问题，为揭示变压器内部短路暂态特性、防御设备故障爆燃，本文提出单相变压器内部短路多尺度故障分析模型，并得到结论如下：
1）将变压器绕组轴向分割为多尺度子绕组，基于有限元法计算各子绕组电阻矩阵及自感-互感矩阵，并将自感-互感矩阵转换为耦合漏感矩阵，建立变压器多尺度故障分析模型。
2）构建某80 MV·A单相变压器饼级尺度电路模型，与有限元模型开展对比仿真验证。其中，短路阻抗和额定工况端口电流峰值误差几乎为0；发生单次匝间短路后，其端口电流及短路电流首峰值的误差均不超过2.5%，验证了本文电路模型对变压器进行仿真可达到与有限元模型相似的较高精度，且相对于有限元模型大大缩短了计算耗时，具备模拟变压器内部短路故障的能力。
3）基于某工程事故开展发展性匝间短路类比仿真分析，故障后有限元模型和电路模型端口电流及短路电流首峰值、故障发展过程中局部峰值的误差均不超过5.5%。计算得到电路模型差流二次谐波占比15%以上的持续时间为49 ms，与有限元模型计算结果相符，而现有方法则为14 ms，证明了本文电路模型可仿真现有方法难以得到的变压器内部复杂的短路暂态特性，具有一定的工程应用价值。
综上所述，本文提出了一种单相变压器内部短路多尺度故障分析模型构建方法，能够准确地模拟多尺度、多工况的变压器内部短路暂态特性，为实际工程中内部短路事故分析、继电保护性能和电力装备制造水平的提升提供基础模型和关键数据。下一步将继续基于本文所提出的变压器多尺度电路模型开展故障快速溯源、故障能量计算等方面的研究。
参考文献
[1] 郑玉平, 郝治国, 薛众鑫, 等. 大型电力变压器安全运行与主动保护技术探索[J]. 电力系统自动化, 2023, 47(20): 1-12. Zheng Yuping, Hao Zhiguo, Xue Zhongxin, et al. Exploration of safe operation and active protection technology for large-capacity power transformers[J]. Automation of Electric Power Systems, 2023, 47(20): 1-12.
[2] 胡应宏, 李雨, 李阳, 等. 面向柔直换流站高频谐振问题的换流变压器建模与参数辨识[J]. 电工技术学报, 2024, 39(22): 7154-7166. Hu Yinghong, Li Yu, Li Yang, et al. Modeling and parameter identification of converter transformer for high-frequency resonance problem of flexible DC converter station[J]. Transactions of China Electro-technical Society, 2024, 39(22): 7154-7166.
[3] Asadi N, Kelk H M. Modeling, analysis, and detection of internal winding faults in power transformers[J]. IEEE Transactions on Power Delivery, 2015, 30(6): 2419-2426.
[4] 周利军, 员秀程, 王东阳, 等. 基于电压阻尼振荡的变压器故障绕组识别方法[J]. 电工技术学报, 2024, 39(10): 3218-3231. Zhou Lijun, Yun Xiucheng, Wang Dongyang, et al. Transformer fault winding identification method based on voltage damped oscillation[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3218-3231.
[5] 江涛, 杨传凯, 王荆, 等. 基于健康指数的电力变压器绝缘状态评估方法研究[J]. 高压电器, 2024, 60(5): 124-129. Jiang Tao, Yang Chuankai, Wang Jing, et al. Research on insulation state assessment method of power transformer based on health index[J]. High Voltage Apparatus, 2024, 60(5): 124-129.
[6] 罗文萱. 基于胶囊神经网络的电力变压器故障诊断方法研究[J]. 高压电器, 2024, 60(5): 92-98. Luo Wenxuan. Research on fault diagnosis method of power transformer based on capsule networks[J]. High Voltage Apparatus, 2024, 60(5): 92-98.
[7] 潘超, 石文鑫, 孟涛. 单相变压器匝间短路电磁特性研究[J]. 高电压技术, 2020, 46(5): 1839-1856. Pan Chao, Shi Wenxin, Meng Tao. Study on electromagnetic characteristics of interturn short circuit of single-phase transformer[J]. High Voltage Engineering, 2020, 46(5): 1839-1856.
[8] 闫晨光, 张芃, 徐雅, 等. 换流变压器有载分接开关级间短路故障差动保护动作特性[J]. 电工技术学报, 2023, 38(21): 5878-5888, 5912. Yan Chenguang, Zhang Peng, Xu Ya, et al. Differential protection performance for converter transformer intertap short-circuit faults in on-load tap changers[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5878-5888, 5912.
[9] CIGRE Working Group A2.33. Guide for transformer fire safety practices[R]. Paris: CIGRE, 2013.
[10] 刘云鹏, 黎晏霖, 李欢, 等. 基于布里渊光时域峰值边沿分析的变压器绕组局部热点检测[J]. 电工技术学报, 2024, 39(11): 3486-3498. Liu Yunpeng, Li Yanlin, Li Huan, et al. Local hot spot detection of transformer windings based on Brillouin optical time domain peak edge analysis[J]. Transa-ctions of China Electrotechnical Society, 2024, 39(11): 3486-3498.
[11] 唐起超, 王赞基, 王维俭. 多绕组电力变压器内部短路稳态分析(一)建模与仿真[J]. 电力系统自动化, 2006, 30(10): 44-47, 74. Tang Qichao, Wang Zanji, Wang Weijian. Steady-state analysis of internal short circuits of multi-winding power transformer part I modeling and simulations[J]. Automation of Electric Power Systems, 2006, 30(10): 44-47, 74.
[12] Ahmadi S A, Sanaye-Pasand M, Abedini M, et al. Online sensitive turn-to-turn fault detection in power transformers[J]. IEEE Transactions on Industrial Electronics, 69(12): 13555-13564.
[13] Farzin N, Vakilian M, Hajipour E. Transformer turn-to-turn fault protection based on fault-related incremental currents[J]. IEEE Transactions on Power Delivery, 2019, 34(2): 700-709.
[14] 邓祥力, 朱宏业, 严康, 等. 基于光纤漏磁场测量的变压器磁平衡保护研究[J]. 电工技术学报, 2024, 39(3): 628-642. Deng Xiangli, Zhu Hongye, Yan Kang, et al. Magnetic balance protection of transformers based on optical fiber leakage magnetic field measurement[J]. Tran-sactions of China Electrotechnical Society, 2024, 39(3): 628-642.
[15] 国家能源局. 大型发电机变压器继电保护整定计算导则: DL/T 684—2012[S]. 北京: 中国电力出版社, 2012.
[16] 张宗成. 基于小波分析的变压器绕组匝间短路检测方法研究[D]. 北京: 华北电力大学, 2015. Zhang Zongcheng. Study on the methodology of diagnosis for transformer inter-turn short circuit based on wavelet analysis[D]. Beijing: North China Electric Power University, 2015.
[17] Prasad U R, Vyjayanthi C, Jaison K. Modeling and detection of inter-turn faults in distribution transformer [C]//2019 8th International Conference on Power Systems (ICPS), Jaipur, India, 2019: 1-6.
[18] Biro O, Koczka G, Leber G, et al. Finite element analysis of three-phase three-limb power transformers under DC bias[J]. IEEE Transactions on Magnetics, 2014, 50(2): 565-568.
[19] Liu S, Liu Z, Mohammed O A. FE-based modeling of single-phase distribution transformers with winding short circuit faults[J]. IEEE Transactions on Magnetics, 2007, 43(4): 1841-1844.
[20] 司马文霞, 孙佳琪, 杨鸣, 等. 计及铁心非线性的变压器空间动态磁场加速计算方法[J]. 电工技术学报, 2025, 40(5): 1559-1574. Sima Wenxia, Sun Jiaqi, Yang Ming, et al. Research on accelerated calculation method of space dynamic magnetic field of transformer considering core nonlinearity[J]. Transactions of China Electrotechnical Society, 2025, 40(5): 1559-1574.
[21] 曾麟钧, 林湘宁, 黄景光, 等. 特高压自耦变压器的建模和电磁暂态仿真[J]. 中国电机工程学报, 2010, 30(1): 91-97. Zeng Linjun, Lin Xiangning, Huang Jingguang, et al. Modeling and electromagnetic transient simulation of UHV autotransformer[J]. Proceedings of the CSEE, 2010, 30(1): 91-97.
[22] 李姗姗, 张建华. 基于等效电流法的变压器匝间短路故障分析[J]. 变压器, 2020, 57(4): 43-46. Li Shanshan, Zhang Jianhua. Fault analysis of interturn short-circuit in transformer based on equivalent current method[J]. Transformer, 2020, 57(4): 43-46.
[23] 韩金华. 一起220kV变压器匝间短路故障分析及仿真计算[J]. 变压器, 2018, 55(9): 70-74. Han Jinhua. Analysis and simulation of 220kV transformer interturn short circuit fault[J]. Transformer, 2018, 55(9): 70-74.
[24] 李卓昕, 彭敏放, 黄清秀, 等. 行波反射法在变压器绕组匝间短路故障定位中的应用[J]. 电力系统保护与控制, 2016, 44(21): 84-89. Li Zhuoxin, Peng Minfang, Huang Qingxiu, et al. Application of the traveling-wave reflection method in inter-turn short fault location for transformer[J]. Power System Protection and Control, 2016, 44(21): 84-89.
[25] 彭磊, 程养春, 郑丹阳, 等. 可外接分布参数元件的变压器绕组多导体传输线暂态模型及其模块化封装[J]. 高电压技术, 2022, 48(10): 3955-3965. Peng Lei, Cheng Yangchun, Zheng Danyang, et al. Attachable transient model and its modular packaging of transformer winding multi-conductor transmission lines with external distributed parameter components [J]. High Voltage Engineering, 2022, 48(10): 3955-3965.
[26] Moradzadeh A, Pourhossein K, Mohammadi-Ivatloo B, et al. Locating inter-turn faults in transformer windings using isometric feature mapping of frequency response traces[J]. IEEE Transactions on Industrial Informatics, 2021, 17(10): 6962-6970.
[27] 姚陈果, 胡迪, 赵仲勇, 等. 基于有限元法的电力变压器绕组集总参数电路仿真建模[J]. 高电压技术, 2018, 44(11): 3517-3523. Yao Chenguo, Hu Di, Zhao Zhongyong, et al. Simulation modeling of lumped parameter circuit for power transformer winding based on the finite element method[J]. High Voltage Engineering, 2018, 44(11): 3517-3523.
[28] Nurmanova V, Ahangar R A, Aliakhmet K, et al. Simulation and analysis of transformer winding inter-disk and inter-turn faults for online diagnosis[C]// 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/ I&CPS Europe), Genova, Italy, 2019: 1-5.
[29] Bastard P, Bertrand P, Meunier M. A transformer model for winding fault studies[J]. IEEE Transactions on Power Delivery, 1994, 9(2): 690-699.
[30] 张杰, 罗隆福, Aggarwal R K, 等. 基于多线圈耦合的新型换流变压器仿真模型设计[J]. 电工技术学报, 2010, 25(11): 68-79. Zhang Jie, Luo Longfu, Aggarwal R K, et al. Simulation model’s design of a new converter transformer based on multi-coil coupling[J]. Transactions of China Electrotechnical Society, 2010, 25(11): 68-79.
[31] 刘豪, 刘溪, 王婵, 等. 基于终端测量梯形网络的变压器绕组内部局部放电定位方法[J]. 变压器, 2019, 56(3): 55-61. Liu Hao, Liu Xi, Wang Chan, et al. Method for PD location inside transformer windings based on terminal measurement in ladder network[J]. Transformer, 2019, 56(3): 55-61.
[32] Gholami M, Hajipour E, Vakilian M. A single phase transformer equivalent circuit for accurate turn to turn fault modeling[C]//2016 24th Iranian Conference on Electrical Engineering (ICEE), Shiraz, Iran, 2016: 592-597.
[33] Zhuang Liman, Johnson B K, Chen Xusheng, et al. A topology-based model for two-winding, shell-type, single-phase transformer inter-turn faults[C]//2016 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Dallas, TX, USA, 2016: 1-5.
[34] Pordanjani S R, Naidjate M, Bracikowski N, et al. Electromagnetic modeling of transformers in EMT-type software by a circuit-based method[J]. IEEE Transactions on Power Delivery, 2022, 37(6): 5402-5413.
[35] Yang Ming, Kazemi R, Jazebi S, et al. Retrofitting the BCTRAN transformer model with nonlinear magnetizing branches for the accurate study of low-frequency deep saturating transients[J]. IEEE Transactions on Power Delivery, 2018, 33(5): 2344-2353.
[36] 杨鸣, 龙洋, 汪可, 等. 考虑铁芯深度饱和特性的三相三柱变压器改进BCTRAN模型[J]. 中国电机工程学报, 2023, 43(2): 819-831. Yang Ming, Long Yang, Wang Ke, et al. An improved BCTRAN model for three-phase three-limb transformers considering deep saturation of iron core[J]. Proceedings of the CSEE, 2023, 43(2): 819-831.
[37] Alvarez-Marino C, de Leon F, Lopez-Fernandez X M. Equivalent circuit for the leakage inductance of multiwinding transformers: unification of terminal and duality models[J]. IEEE Transactions on Power Delivery, 2012, 27(1): 353-361.
[38] Henriksen T. How to avoid unstable time domain responses caused by transformer models[J]. IEEE Transactions on Power Delivery, 2002, 17(2): 516-522.
[39] Jazebi S, Zirka S E, Lambert M, et al. Duality derived transformer models for low-frequency electromagnetic transients: part I: topological models[J]. IEEE Transactions on Power Delivery, 2016, 31(5): 2410-2419.
[40] Martinez J A, Mork B A. Transformer modeling for low- and mid-frequency transients: a review[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 1625-1632.
[41] de Leon F, Semlyen A. Efficient calculation of elementary parameters of transformers[J]. IEEE Transactions on Power Delivery, 1992, 7(1): 376-383.
[42] Dommel H W. Electromagnetic Transients Program. Reference Manual (EMTP Theory Book)[M]. Portland: Bonneville Power Administration, 1986.
[43] 国家电网有限公司. 220kV三相三绕组电力变压器采购标准第26部分：220 kV/240 MVA三相三绕组电力变压器（高-中阻抗14%、高-低阻抗24%，中压69，有载）专用技术规范: Q/GDW 13009.26—2018[S].北京: 国家电网有限公司, 2018.
[44] Oliveira L M R, Marques Cardoso A J. Leakage inductances calculation for power transformers interturn fault studies[J]. IEEE Transactions on Power Delivery, 30(3): 1213-1220.
[45] Kulkarni S V, Khaparde S A. Transformer Engineering: Design and Practice[M]. New York: CRC Press, 2004.
Abstract Internal short circuit is one of the most serious faults in transformers, which can lead to a rapid increase in fault energy in a short period of time and easily cause high-energy discharge and explosion inside the equipment. However, there are many potential combinations of internal short circuit conditions in transformers. The analysis method of field-circuit coupling commonly used by transformer manufacturing enterprises has the problems of excessive time and resource consumption. And it is difficult to model jointly with the external power grid. Existing circuit models face difficulties in multi-scale coupling characterization and parameter calculation of windings.
This article focused on the urgent need for transformer short circuit fault analysis. A construction method of multi-scale fault analysis model for single-phase transformer with internal short circuit was proposed. Firstly, based on the multi-scale characteristics of transformer windings and internal short circuit faults, the transformer windings were virtually divided into several sub-windings using axial segmentation. By parametrically scanning the finite element model of the transformer, the self-mutual inductance matrix and resistance matrix of sub-windings was calculated. Secondly, an calculation method was proposed to transform the self-mutual inductance matrix into the coupled leakage inductance matrix, which could effectively characterize the leakage magnetic characteristics between sub-windings. This parameter calculation method could be carried without port short circuit tests, which solved the problem of parameter calculation for existing multi-winding transformer models. Finally, a multi-scale circuit model for transformers was established based on the coupled leakage inductance matrix. By connecting the terminals of each sub-winding based on the electromagnetic connection relationship and the physical process of internal short circuit, transformer fault analysis models for different internal short circuit conditions could be obtained. The problems of low efficiency and poor circuit adaptability in the fault analysis model based on field-circuit coupling were solved.
Furthermore, a disk-scale circuit model of an 80 MV·A single-phase transformer was constructed. A comparative simulation was conducted with the finite element model. The results indicated that the errors of the short-circuit impedance and the peak value of the port current at rated operating condition were almost zero. And the simulation time was reduced by about 99.98%. After single inter-turn short circuit faults, the errors of the first peak values of the port currents and short-circuit currents did not exceed 2.5%. The simulation efficiency was improved while ensuring simulation accuracy. Then, based on a certain engineering accident, a developmental inter-turn short circuit analogy simulation analysis was carried out. The errors of the first peak values of the port currents and short-circuit currents after the fault, as well as the local peak values during the fault development process, did not exceed 5.5%. And the duration of the second harmonic percentage of fault differential current accounting for more than 15% of the circuit model was calculated to be 49 ms. It was consistent with the finite element model calculation results. The existing method was 14ms. Therefore, the proposed construction method of multi-scale fault analysis model for single-phase transformer with internal short circuit can accurately simulate the transient characteristics of transformers with internal short circuit under multiple scales and operating conditions. This method provides a basic model for research on equipment accident analysis, traceability, and fault defense.
keywords：Single-phase transformer, multi-scale circuit model, internal short circuit, coupled leakage inductance matrix, finite element method
DOI: 10.19595/j.cnki.1000-6753.tces.241007
中图分类号：TM41
国家电网公司科技项目资助（5108-202218280A-2-365-XG）。
收稿日期 2024-06-13
改稿日期 2024-10-21
杨 鸣 男，1987年生，教授，博士生导师，研究方向为高电压输变电技术及电力系统过电压。E-mail：cqucee@cqu.edu.cn
司马文霞 女，1965年生，教授，博士生导师，研究方向为电力系统的防雷与过电压防护、特殊环境中外绝缘放电特性及机理。E-mail：cqsmwx@cqu.edu.cn（通信作者）
（编辑 李 冰）