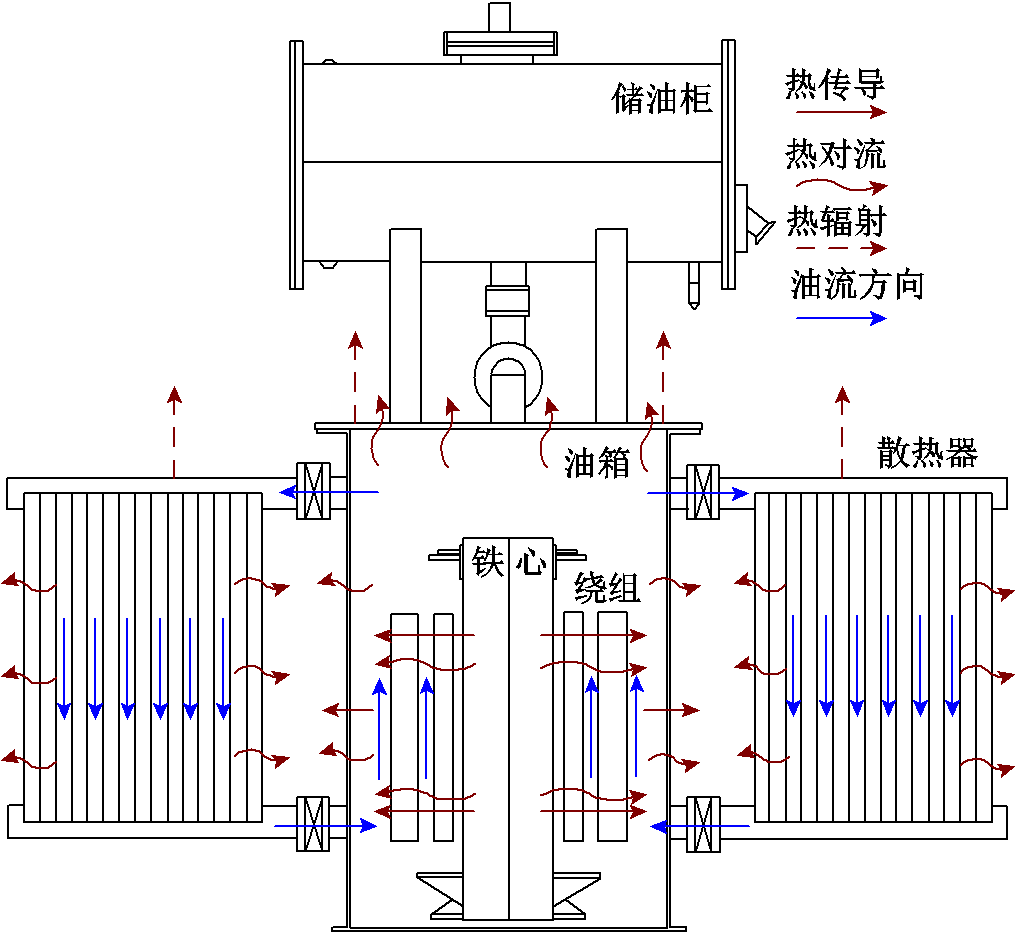
图1 ONAN换流变压器散热方式
Fig.1 Cooling method of ONAN converter transformer
摘要 数字孪生是推动电力设备领域数字化和智能化发展的关键技术之一。构建电力变压器的数字孪生模型有助于保证其运行可靠性、维护效率和故障预测能力。然而，基于模型驱动的数字孪生模型常因计算速度较慢而在应用中受到限制。对此，该文基于Modelica语言，构建了变压器的等效热流计算场路耦合简化模型以降低计算复杂度。模型结合本征正交分解（POD）对场计算部分进行降阶以提高计算效率。为验证所构建模型的有效性，该文对35 kV油浸式自冷（ONAN）换流变压器开展温升实验。结果表明：计算时是否考虑散热器对绕组温升的大小和热点位置均有显著影响。在达到稳态时，所提模型与实验结果的最大绝对误差为1.37 K；所提模型在温升工况下的计算与三维全阶模型相比效率提升258.65倍，与全阶场路耦合模型相比速度提升5.1倍，证明所提模型在保证数字孪生模型计算精度的同时显著提高了计算效率。
关键词：数字孪生 Modelica语言 场路耦合 绕组温升 降阶模型
伴随工业4.0的推进，电力能源行业的智能化与数字化转型快速发展，电力设备领域的数字孪生技术应运而生[1-2]。数字孪生技术在电力设备领域的应用为其全生命周期管理提供了全新的技术路径：通过数字孪生技术，可以建立物理空间和信息空间之间的连接，实现电力设备实体与其数字孪生体之间的交互映射[3]；通过状态感知、物理模拟和数据分析，能够掌握设备的运行状况，并基于结果对设备进行干预，以实现对电力设备全生命周期的监测和控制[4]。油浸式电力变压器作为高压电力系统的关键一次设备，其绕组热点温度是影响绝缘热寿命和瞬态电场分布的关键因素[5]。因此，研究油浸式电力变压器绕组温升计算的数字孪生模型具有重要意义。
数字孪生具备等价映射、实时交互、共生演进、预测优化等特点[6]。当前，基于物联网（Internet of Things, IoT）平台的数字孪生架构一般由基础支撑层、数据互动层、建模仿真层和功能应用层四部分组成[7]。在建模仿真层，构建数字孪生模型的方法包括模型驱动和数据驱动[8]。模型驱动是通过物理机理和过程反映设备实体的状态参量，如电压、电流、温度、损耗等，具有误差和不确定性可控等优点。然而，变压器等电力设备的三维多物理场仿真由于结构复杂、计算量大，仿真时间常为h级甚至d级[9]，这与数字孪生的实时性要求不符。为解决模型计算复杂和成本高的问题，通常采用简化模型法[10]、投影法[11-12]和数据拟合法[13]等模型降阶方法。简化模型法相较投影法和数据拟合法能更直接地反映系统的本质特征。
简化模型法通过充分理解研究问题的物理和数学本质，对设备的三维模型进行低维等效，或者在有限元等数值模拟中对方程或边界进行近似，忽略了非线性项。文献[14]通过将磁滞回线近似为椭圆，并对变压器进行分相简化，从而能够通过有限的信息预测变压器的热点温度和寿命。文献[15]采用全尺寸的二维轴对称数值热传递模型，研究了换流变压器单侧阀绕组的热和流体性能，减少了计算量。投影法通过数学推导，选择合适的基进行截断来形成低阶子空间，然后将原问题投影到该子空间以实现降阶，例如特征正交分解方法和Krylov子空间法等。文献[16]提出了一种结构保留的本征正交分解（Proper Orthogonal Decomposition, POD）和离散经验插值方法相结合的二维瞬态温升快速计算方法，通过引入降阶技术，显著地提升了模型的计算速度。文献[17]提出了一种基于POD和LDEIM-Q的新型降阶模型，有效地减少了非线性热电耦合问题的计算量，同时保持了求解的精度和稳定性。数据拟合法是利用物理模型的大量输入和输出数据，建立黑箱模型以拟合原物理模型的方法。这类方法包括响应面法、支持向量回归、神经网络等。文献[18]通过开发一种基于嵌入机制的级联网络的非侵入式降阶模型，显著提升了变压器绕组三维稳态温度场的计算速度。
为进一步提高油浸式电力变压器绕组瞬态温升计算速度以满足实时性要求，本文基于Modelica语言将换流变压器的三维瞬态温度场模型简化为二维耦合一维的等效模型[19-20]。该模型在二维空间中描述了绕组与油流的热流耦合过程，同时将绝缘油在散热器冷却管道中的热流耦合过程等效为一维计算模型。通过Modelica实现了场模型和路模型的高效耦合求解，其中场模型使用二维有限元法（Finite Element Method, FEM）进行求解，路模型使用热路模型进行描述，通过结合本征正交分解技术进一步降低了二维模型的计算自由度。为验证模型的有效性，对一台35 kV的油浸式自冷（Oil Natural Air Natural, ONAN）换流变压器样机进行了温升实验。通过对比测点温升数据，验证了所建模型的准确性，并通过与该变压器的三维全尺寸温度场计算模型进行对比，验证了所建模型的时效性。
油浸式自冷换流变压器内部温度分布由产热和散热的相互作用决定。绕组内流经的负载电流会在铁心和两侧绕组分别产生空载损耗和绕组损耗，是换流变压器运行时的主要热源。热量通过热传导和热对流的方式传递到周围的变压器油中，变压器油受热升温后，在热浮升力的作用下流向油箱出口，再通过散热器冷却后流入底部油箱入口。ONAN换流变压器散热方式、换流变压器内散热方式及散热路径如图1所示，可以看出，ONAN换流变压器在油箱中的结构具有对称性。
图1 ONAN换流变压器散热方式
Fig.1 Cooling method of ONAN converter transformer
变压器油通过管道离开油箱后，主要在固定的油道中流动。相比绕组内部结构，油道更简单和规则，变压器油在其中的流动速度在一个方向上远大于其他方向。因此，可将三维温升计算模型分为油箱部分和散热器部分。油箱部分的模型等效为二维轴对称模型（场模型），散热器部分的模型等效为一维计算模型（路模型）。模型简化方法和等效思路如图2所示。通过将换流变压器的三维全尺寸模型简化为二维轴对称场模型和一维路模型，显著降低了模型的复杂程度。为了实现场模型与路模型之间的数据传输，基于Modelica语言构建换流变压器温升计算的场路耦合模型。图3展示了模型的实现方法和封装形式。整个模型和资源文件通过包（Package）的方式进行封装，其中资源类文件包括数据、图片及文档等。在仿真过程中，模型会读取和调用这些资源文件。使用OpenModelica平台加载该Package，通过计算可以获得温度场和流场的瞬态节点数据以及一维模型的各变量数据。此外，该模型还可以导出为功能模型单元（Functional Mockup Units, FMU），通过编译和调试后即可部署到物联网（IoT）平台。
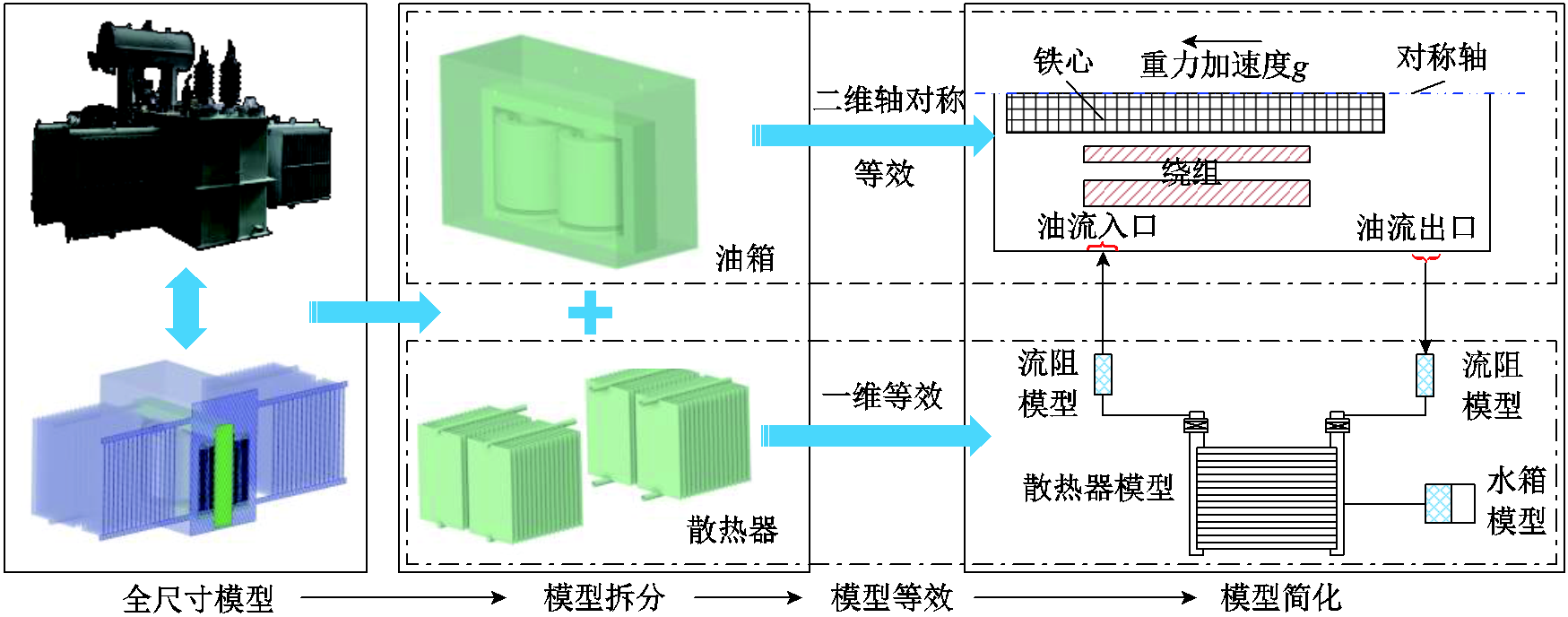
图2 模型简化方法和等效思路
Fig.2 Model simplification methods and equivalent approaches
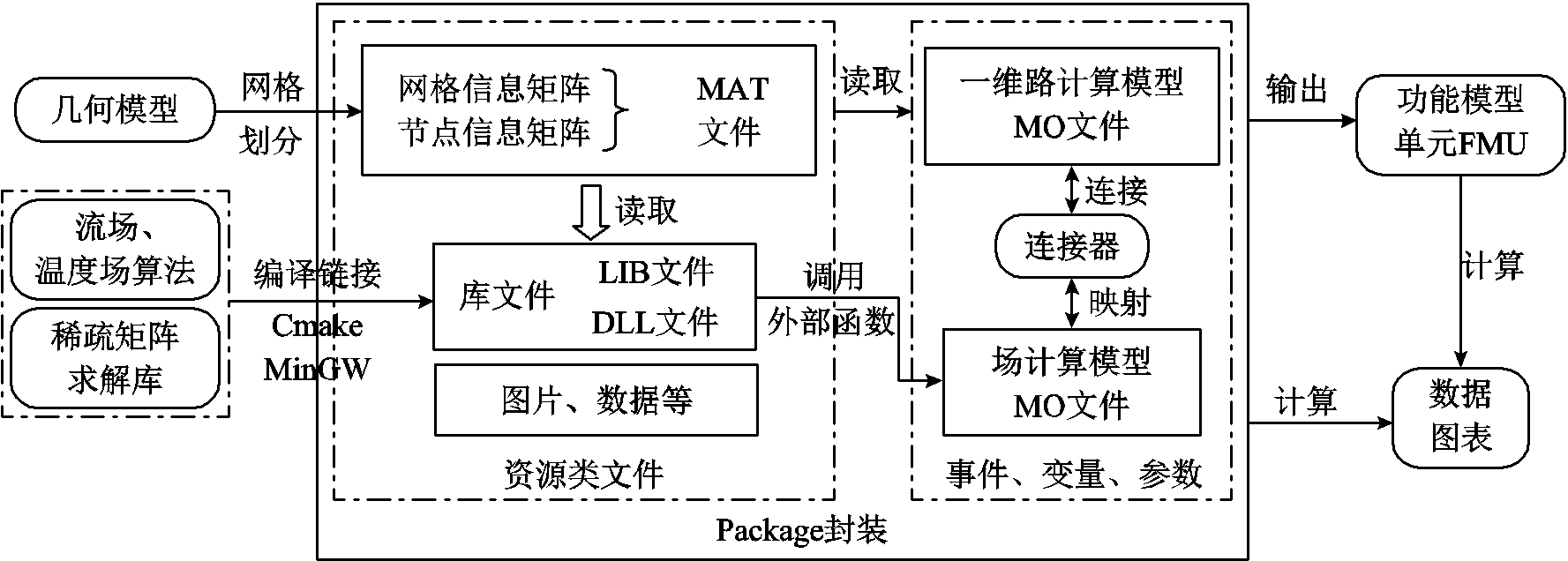
图3 Modelica模型的实现方法和封装形式
Fig.3 Implementation method and encapsulation form of the modelica model
在Modelica语言中，模型间的数据传输可以通过定义连接器来实现。连接器基于广义基尔霍夫定律进行定义，其目的是确保不同模型之间的数据传输遵循特定的守恒关系。连接器主要由三类元素构成：势变量、流变量和参数。其中，势变量描述系统不同部分之间的潜在差异；流变量表示在某个界面上的流动量；而参数则定义系统行为的固定量，并提供必要的静态信息。通过连接器，保证了系统的物理一致性和守恒关系。本文所定义的连接器见表1。
表1 连接器定义
Tab.1 Definition of connector
名称元素类型 流体类型参数 压力p势变量 质量流量流变量 比焓h势变量 焓流率流变量
连接器描述的变量为一维变量，场模型将出口与入口交界面上的数据映射为连接器变量，再与一维路模型进行连接以实现场模型与路模型之间的数据传递[21]。设场在交界面处的物理量为边界单元平均法向流速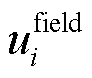
、边界单元平均温度
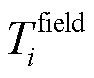、边界单元平均压力
。
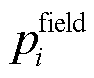在出口交界面上场到路的传递公式为
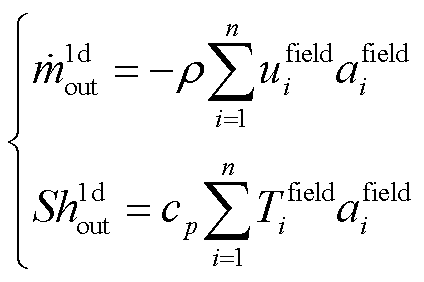（1）
式中，n为出口交界面上的单元数；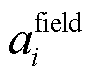
为交界面单元边界长；
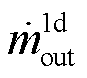为出口连接器质量流量；
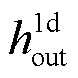为出口连接器比焓；ρ为流体密度；
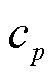为比定压热容；S为交界面边长。
在入口交界面上路到场的传递公式为
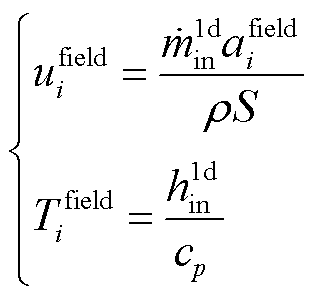（2）
式中，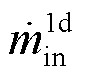
为入口连接器质量流量；
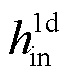为入口连接器比焓。压力传递满足
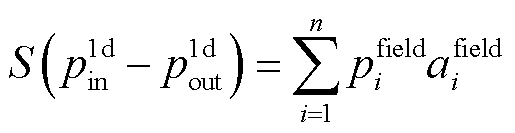（3）
式中，
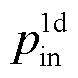与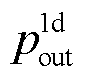
分别为入口和出口连接器压力。为使系统正定，补充场模型的守恒方程为
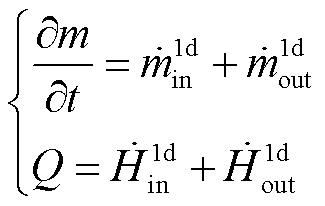（4）
式中，m为场模型中的流体质量；Q为外部热流率；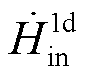
为入口连接器焓流率；
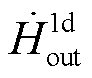为出口连接器焓流率。
如图2所示，散热器部分的一维等效模型包括流阻模型、散热器模型和水箱模型。流阻模型用于模拟由于集油管截面变化和阀门孔处摩擦导致的温度和压力变化。模型两端的压力变化为
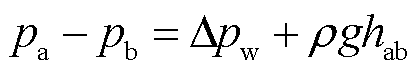（5）
式中，
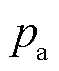与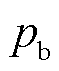
为两端连接器压力；g为重力加速度；hab为管道两端高度差；
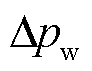为流经管道产生的压力变化[22]，表示为
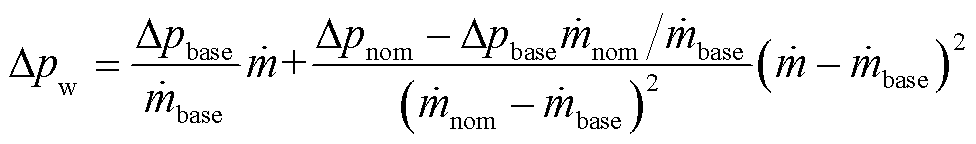（6）
式中，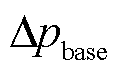
为基线压损；
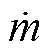为油流侧质量流量；
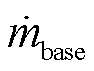为基线质量流量；
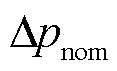为标称压损；
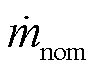为标称质量流量。流动摩擦产生的热量耗散表示为
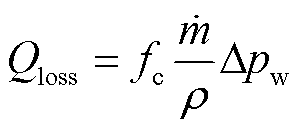（7）
式中，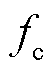
为耗散系数。
水箱模型用于模拟变压器中的储油柜，主要功能是管理变压器油的膨胀和收缩。为了简化计算，忽略了其换热过程。水箱模型的连接器处的压力为环境大气压加上水箱中液体带来的压力，其给予了系统压力定解条件，有助于平滑压力变化和维持系统压力恒定。
散热器模型模拟了变压器油与外界环境的热交换过程以及油流经散热翅片时带来的压力变化[23]。其中，表面传热产生的热流率可以表示为
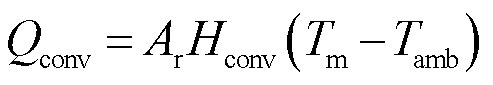（8）
式中，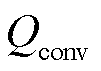
为表面传热热流率；Ar为有效传热面积；Tm为散热器中流体平均温度；Tamb为环境温度；Hconv为等效表面传热系数，表示为[24]
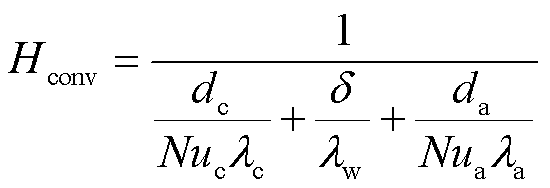（9）
式中，dc和da分别为油流侧和空气侧的特征尺寸；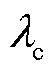
、
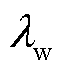和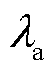
分别为油流侧、壁面和空气侧的导热系数；
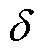为散热管道壁厚；
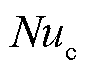和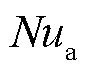
分别为油流侧和空气侧的努塞尔数，其与流体的质量流量、空气的平均流速以及散热器的结构和参数均有关[25]。努塞尔数可以通过经验公式得出，也可以通过实验数据进行回归。
对于ONAN油浸式变压器，式（9）可以写为
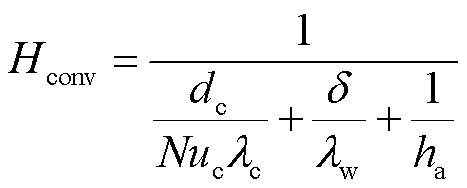（10）
式中，ha为空气侧平均自然表面传热系数。
换流变压器绝缘油在绕组油道中的流动可视为不可压缩层流，控制方程为[26]
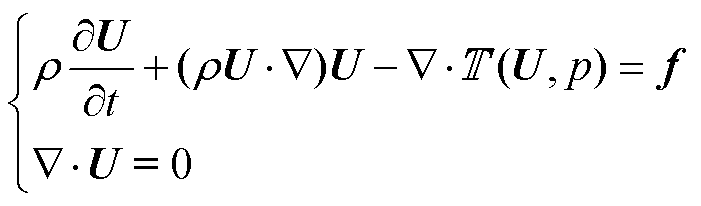（11）
式中，U为速度矢量；f为外力密度矢量，此处为重力密度矢量；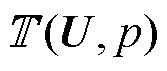
为应力张量，定义为
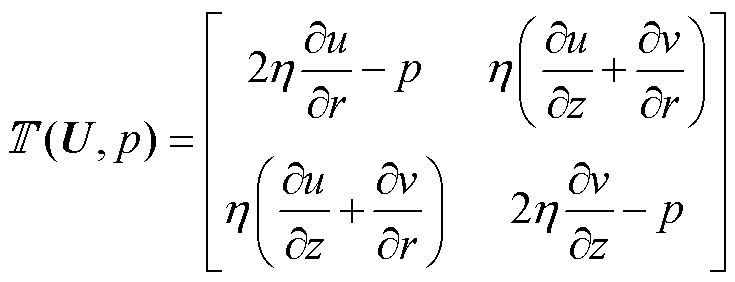（12）
式中，η为流体动力黏度；u、v分别为辐向速度分量和轴向速度分量；p为压力。使用加权余量法将微分形式转换为积分形式，并在方程两边乘以测试函数，通过分部积分将二阶偏微分项转换为一阶项。在二维情况下，式（11）的弱形式为
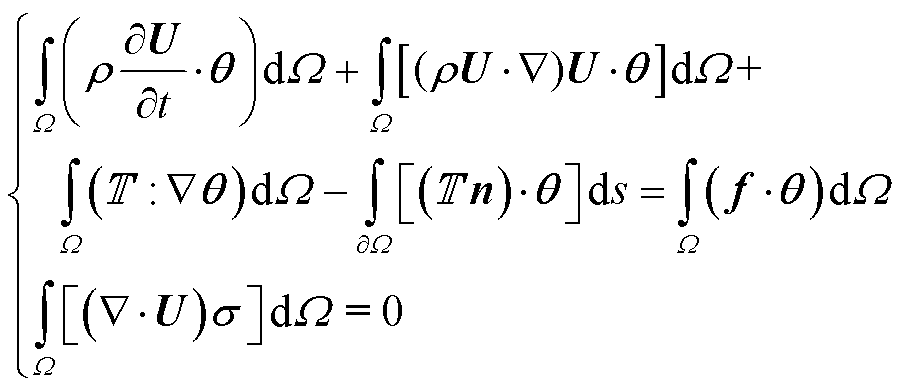（13）
式中，Ω为计算域；∂Ω为计算域边界；n为边界法向量；θ和σ为测试函数。使用三角单元对计算区域进行离散，对速度项使用二阶单元插值，对压力项使用一阶单元插值，单元内速度和压力表示为
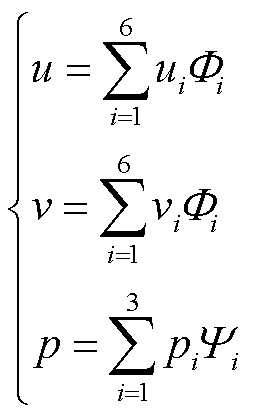（14）
式中，Фi为二阶单元插值基函数；Ψi为一阶单元插值基函数。
使用逐次迭代的方法处理非线性对流项[27]，即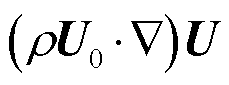
。其中U0为前次非线性迭代得到的流速矢量。为计算热浮升力并减少计算量，使用Boussinesq近似，将除重力项外的其他项密度视为常数。本文流场计算边界均为第一类边界。使用后向欧拉法对时间项进行离散，将测试函数替换为相应的插值函数后，经过推导可以得到瞬态流场计算矩阵方程为
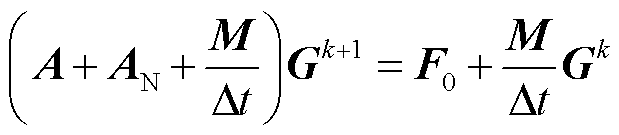（15）
具体矩阵组装形式见附录式（A1）和式（A2）。
温度场控制方程由能量守恒方程[28]得到
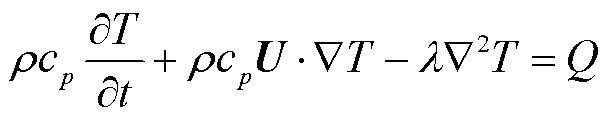（16）
式中，T为温度；U为速度矢量，固体中U为零矢量；λ为所属材料导热系数；Q为所属材料热源密度。
使用加权余量法将式（16）转换为积分形式并在方程两边乘以测试函数，使用分部积分将二阶偏微分项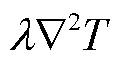
转换为一阶偏微分项，弱形式为
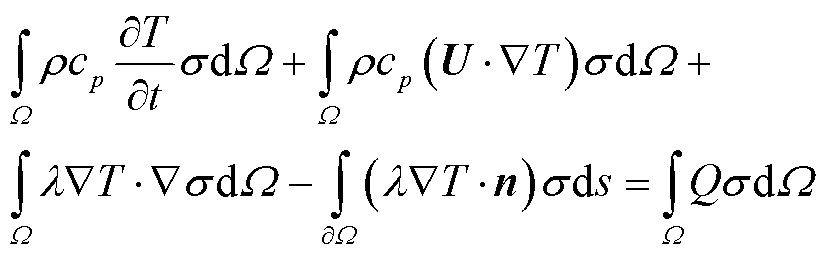（17）
对温度项使用一阶单元进行插值，单元内一点的温度表示为
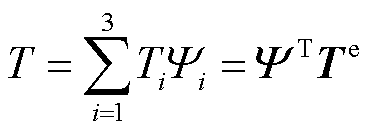（18）
式中，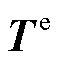
为单元内节点温度列向量。为消除对流项引起的数值振荡，测试函数使用迎风有限元格式[26]，即
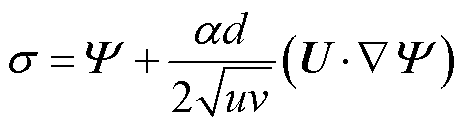（19）
式中，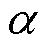
为迎风因子；d为单元特征尺寸。对于每个单元有
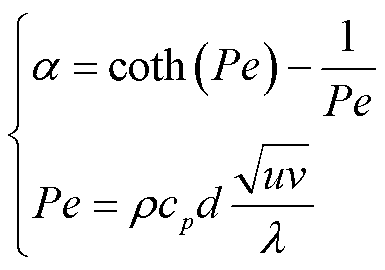（20）
式中，Pe为佩克莱数。温度场计算边界条件为
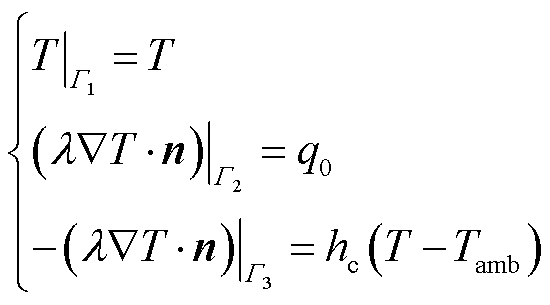（21）
式中，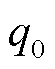
为第二类边界热流密度；hc为表面传热系数。液固分界面的温度和热流密度连续性条件均自动满足。使用Crank-Nicolson法对时间项进行离散，得到瞬态温度场计算矩阵方程为
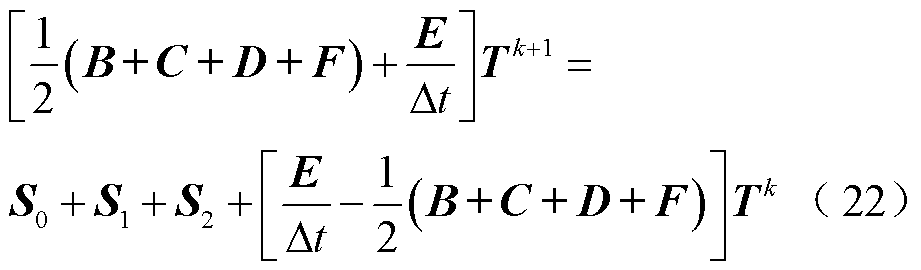
具体矩阵组装形式见附录式（A3）。
为进一步加快计算速度，本文采用基于奇异值分解的本征正交分解（POD）方法对流场和温度场进行降阶处理。
3.3.1 降阶原理
假设某场通过计算得到的快照矩阵为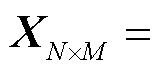
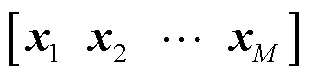，其中N为场节点数，M为离散时间步。设降阶子空间为L维（L
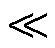N），则需要选取L个反映原系统特征较多的正交基构建子空间。此时原样本数据投影至子空间的解可以表示为
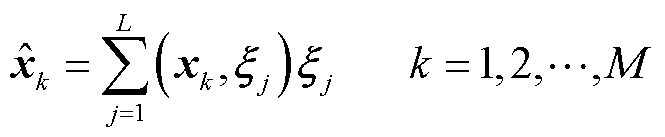（23）
式中，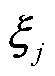
为特征向量，
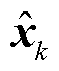为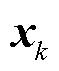
的近似值，为使最小二乘误差最小，需满足约束条件[29]
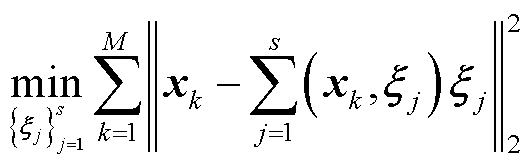（24）
式（24）可通过拉格朗日乘子法转换为特征值问题
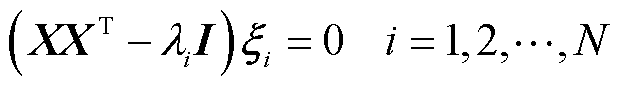（25）
式中，XXT为N´N谁的协方差矩阵；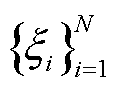
为特征向量；
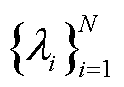为对应的特征值；I为单位矩阵。对矩阵X进行奇异值分解有
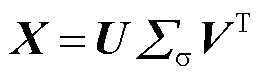（26）
式中，U为N´N维的正交矩阵，其列向量为特征向量；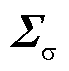
为N´M维的矩阵，其对角线上包含X的奇异值，特征值与奇异值存在二次方关系；V为M´M维的正交矩阵。由式（26）得到一组正交基向量后，截取前L个向量作为降阶正交基矩阵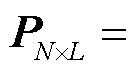
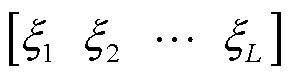，此时i时刻的近似场值
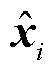为
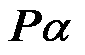，其中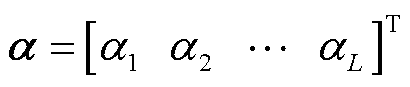
为系数向量。使用截断误差χ作为选取特征向量的标准，表示形式为
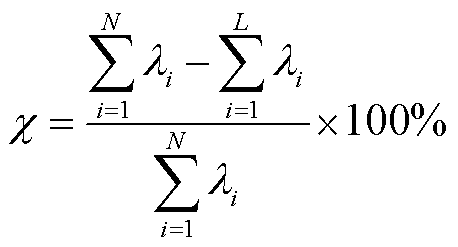（27）
3.3.2 瞬态流场和温度场的降阶模型
对于流场，通过计算得到横向速度、纵向速度和压力快照矩阵，按照截断误差小于0.01%的标准选择特征向量，得到正交基矩阵分别为
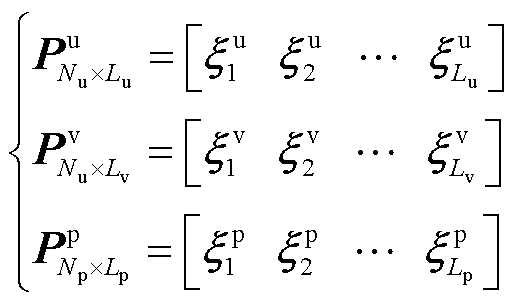（28）
式中，Nu为速度单元节点数；Np为压力单元节点数；Lu、Lv、Lp分别为各场量对应的降阶正交基数量。在第k个时间步有[30]
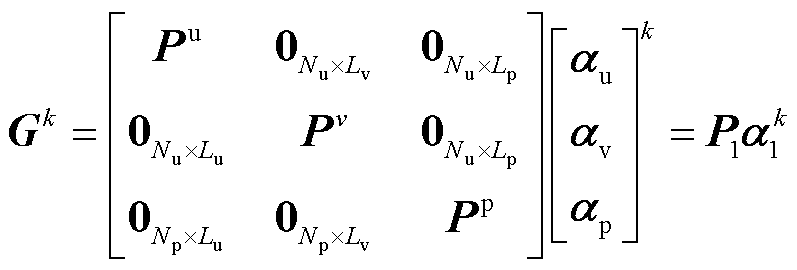（29）
式中，
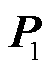和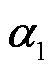
为流场降阶正交基矩阵和系数向量。此时可以得到流场的降阶计算方程为
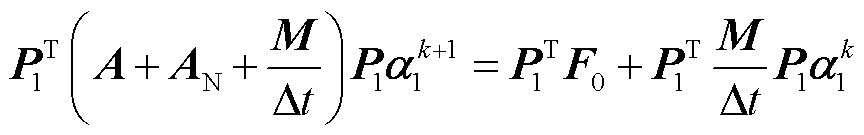（30）
对于温度场，通过温度快照矩阵得到温度正交基矩阵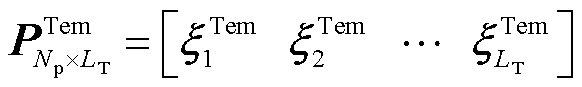
。第k个时间步有
，
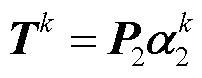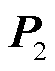和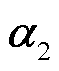
分别为温度场降阶正交基矩阵及系数向量。温度场降阶计算方程为
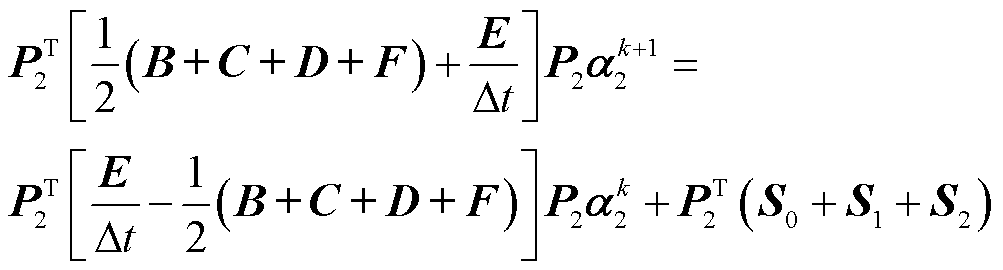（31）
为验证所述模型的适用性，本文使用一台35 kV、800 kV·A缩比换流变压器样机进行了温升实验。该样机内部两列高压绕组并联，同时两列低压绕组串联。由于低压绕组上施加的电流较大，温升现象较为明显，因此本文选取低压绕组作为温升研究对象。样机绕组油道通过三个绕组垫圈被划分为四个导向分区。缩比样机温升实验平台如图4所示。
图4 缩比样机温升实验平台
Fig.4 Scaled model temperature rise experiment platform
换流变压器样机和散热器的基本参数见表2。样机基本结构参数见表3。
表2 换流变压器样机和散热器基本参数
Tab.2 The basic parameters of experimental transformer and radiator
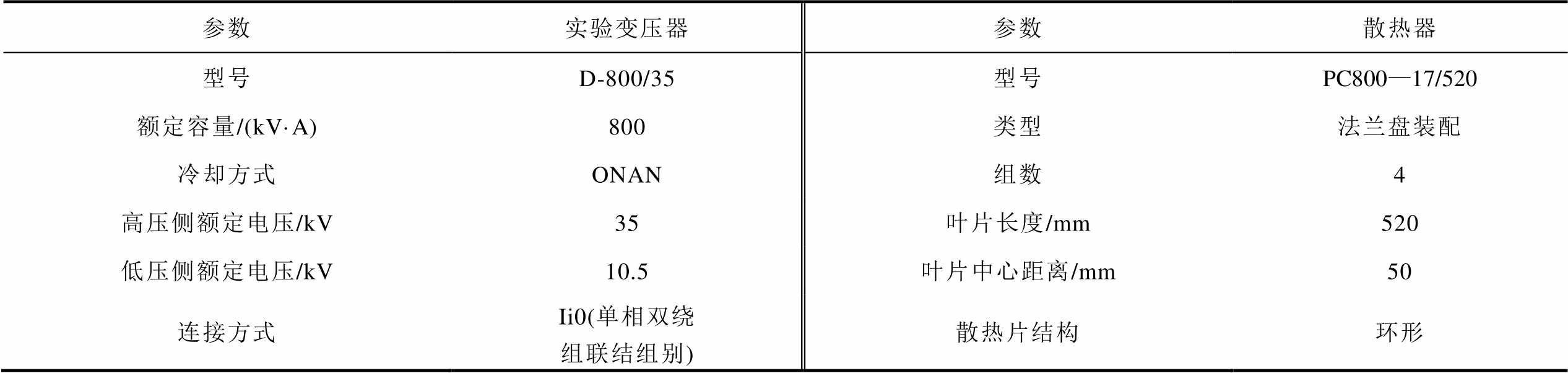
参数实验变压器参数散热器 型号D-800/35型号PC800—17/520 额定容量/(kV·A)800类型法兰盘装配 冷却方式ONAN组数4 高压侧额定电压/kV35叶片长度/mm520 低压侧额定电压/kV10.5叶片中心距离/mm50 连接方式Ii0(单相双绕组联结组别)散热片结构环形
表3 换流变压器样机基本结构参数
Tab.3 Basic structural parameters of transformer
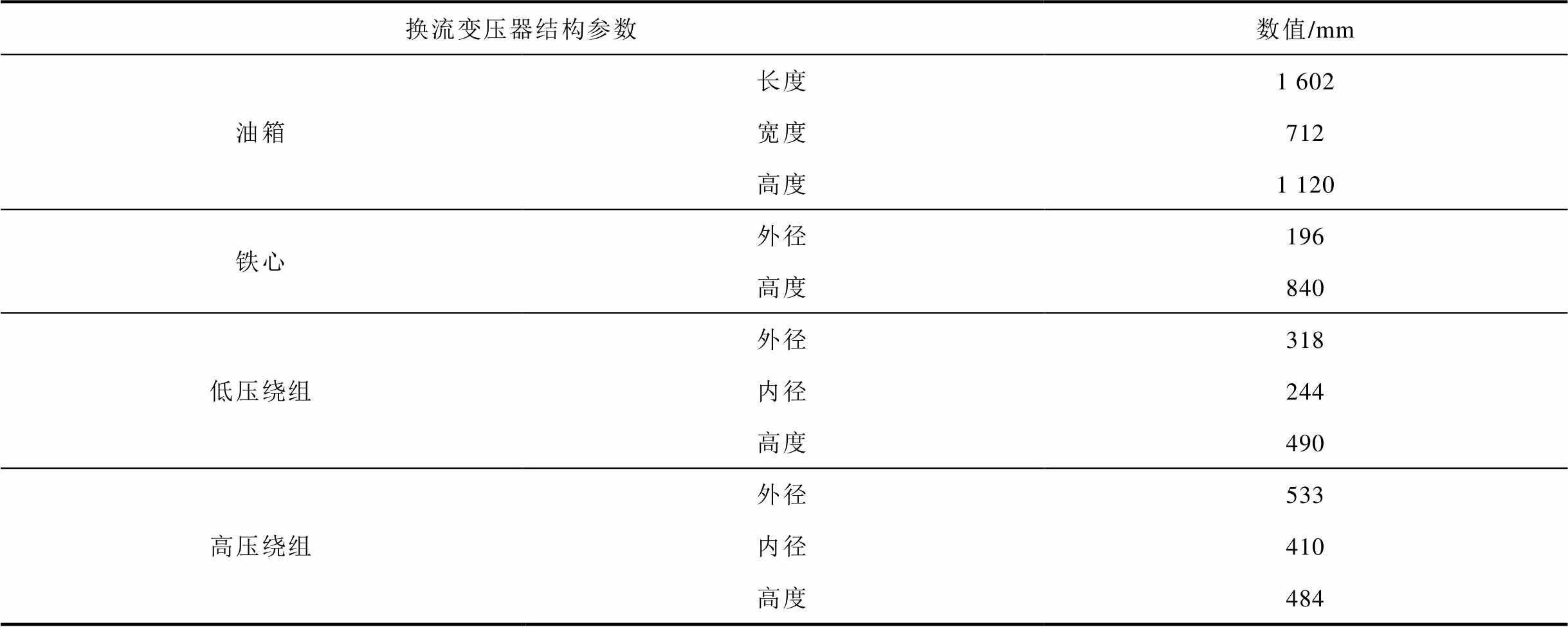
换流变压器结构参数数值/mm 油箱长度1 602 宽度712 高度1 120 铁心外径196 高度840 低压绕组外径318 内径244 高度490 高压绕组外径533 内径410 高度484
样机组装前需将光纤传感器安装在绕组油道内部，当光纤探头监测到信号后，温度数据会通过内部光缆传输至固定在法兰盘上的外部光缆。随后，通过信号调节器和测温装置对温度信号进行存储和分析，实验测温系统接线示意图如图5所示。
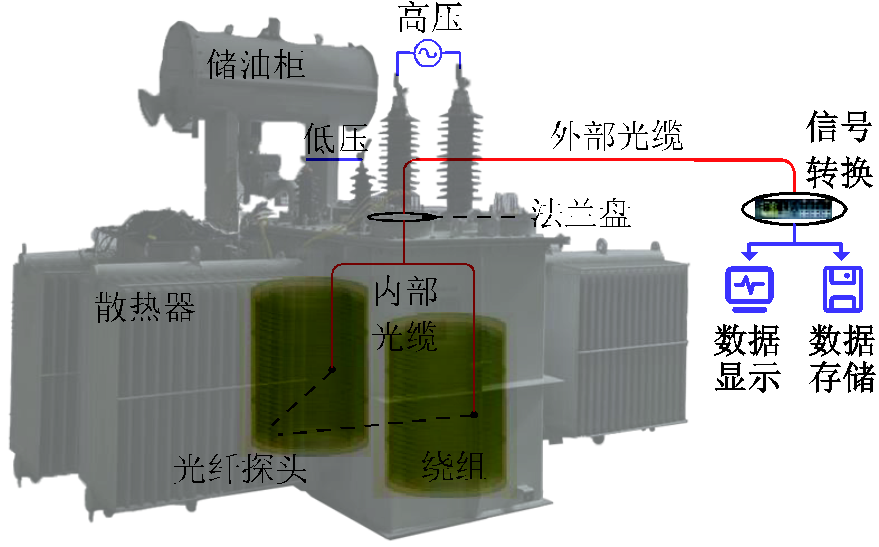
图5 实验测量系统接线示意图
Fig.5 Schematic diagram of experimental temperature
根据标准IEC60076-2[31]，采用短路法进行温升实验，即将低压绕组短路，而高压绕组连接一个合适大小的电容负载以改善电压波形并提高功率因数，然后施加额定电压。实验开始后，传感器每30 s记录一次温度数据，当顶层油温每小时的温升小于1 K时，认为测量状态已达到动态稳定。实验总共记录480 min。
实验选取低压绕组轴向高度4%（底部）、54%（中部）、96%（顶部）作为特征点分别沿圆周方向布置4个光纤探头。监测点示意图如图6所示。
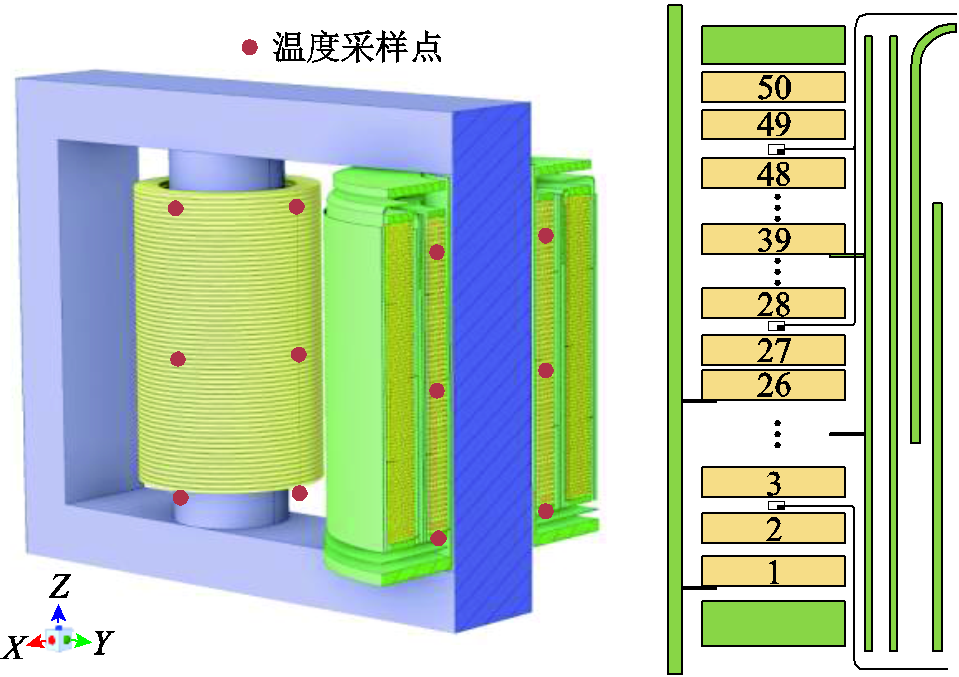
图6 低压绕组中光纤探头的位置
Fig.6 Position of optical fiber probe in low voltage windings
4.2.1 物性参数及边界条件
模型计算中使用的主要材料包括绝缘油、油浸纸板、绕组铜和铁心硅钢等。绝缘油的密度、比热和黏度受温度影响，其中密度膨胀系数较小，可视为不可压缩流体。纸板、铜、硅钢等材料参数受温度影响较小，设为常数。相关物性参数见表4。
表4 材料物性参数
Tab.4 Material parameters
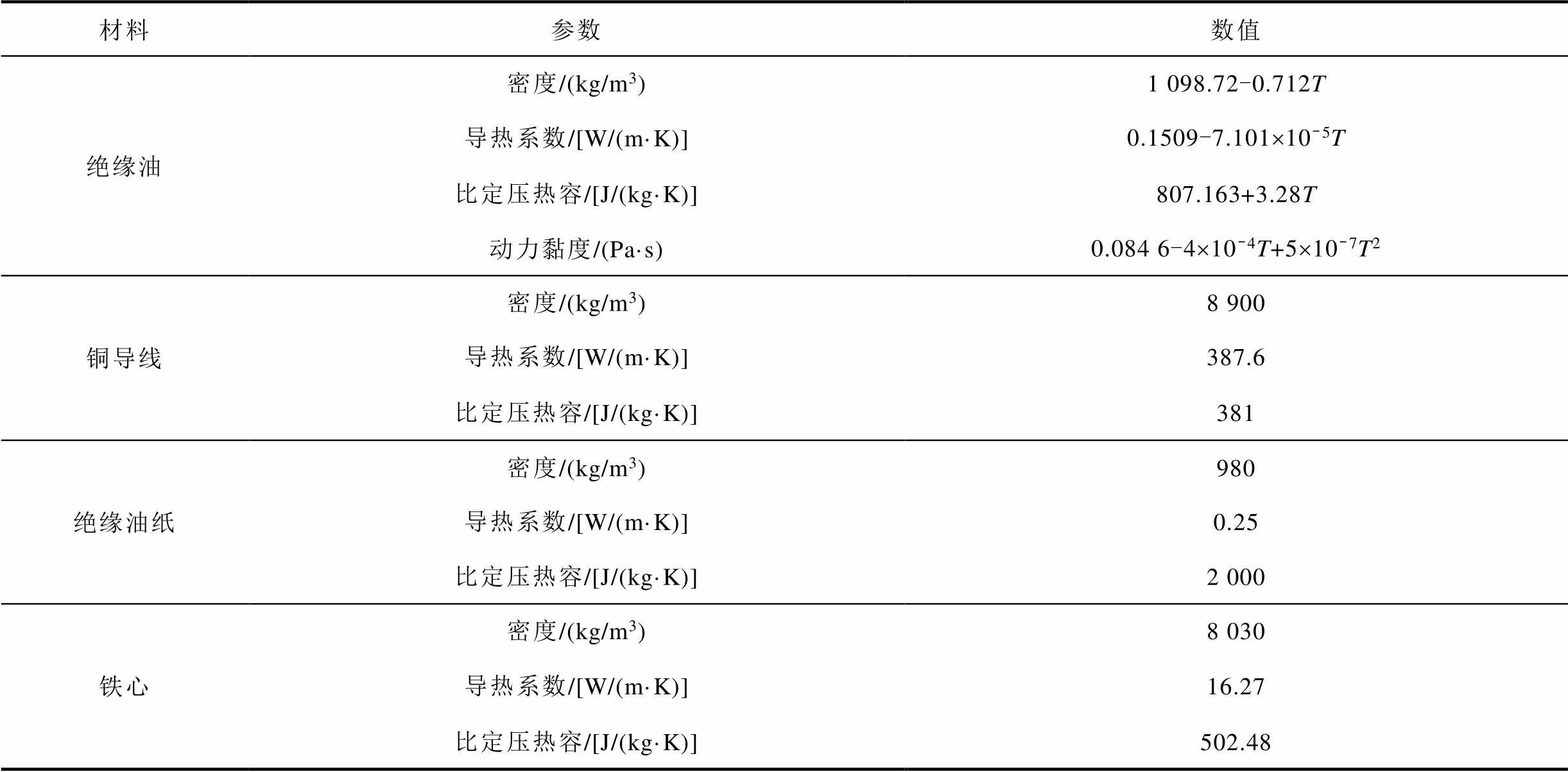
材料参数数值 绝缘油密度/(kg/m3)1 098.72-0.712T 导热系数/[W/(m·K)]0.1509-7.101´10-5T 比定压热容/[J/(kg·K)]807.163+3.28T 动力黏度/(Pa·s)0.084 6-4´10-4T+5´10-7T2 铜导线密度/(kg/m3)8 900 导热系数/[W/(m·K)]387.6 比定压热容/[J/(kg·K)]381 绝缘油纸密度/(kg/m3)980 导热系数/[W/(m·K)]0.25 比定压热容/[J/(kg·K)]2 000 铁心密度/(kg/m3)8 030 导热系数/[W/(m·K)]16.27 比定压热容/[J/(kg·K)]502.48
场路耦合模型的边界条件仅在场模型中设置。固体表面设为与液体接触的无滑移边界。绝缘油通过油箱壁进行表面传热，绕组和铁心作为热源。
4.2.2 结果分析
为构建降阶模型，首先通过场计算结果生成横向速度、纵向速度、压力和温度的快照矩阵，再使用POD方法计算其特征向量和特征值，然后计算各样本数据在子空间中的相对截断误差。相对截断误差的分布曲线如图7所示。
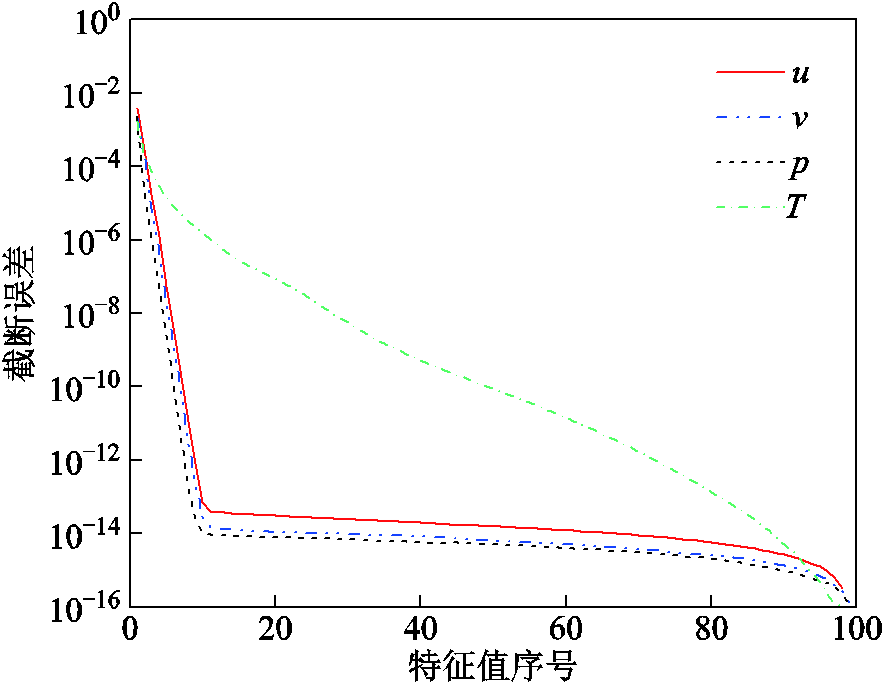
图7 相对截断误差曲线
Fig.7 Relative truncation error curves
按照截断误差小于0.01%的标准选取3个横向流速特征向量、2个纵向流速特征向量、2个压力特征向量和2个温度特征向量构成降阶正交基矩阵，通过式（30）及式（31）建立降阶模型。定义第k个时步的降阶误差为
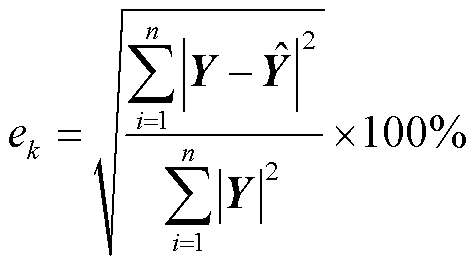（32）
式中，n为节点数量；Y为全阶计算结果；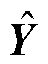
为降阶计算结果。
前100个时步的降阶误差如图8所示。计算过程中，最大降阶误差为0.535%，计算精度处于可接受范围内。
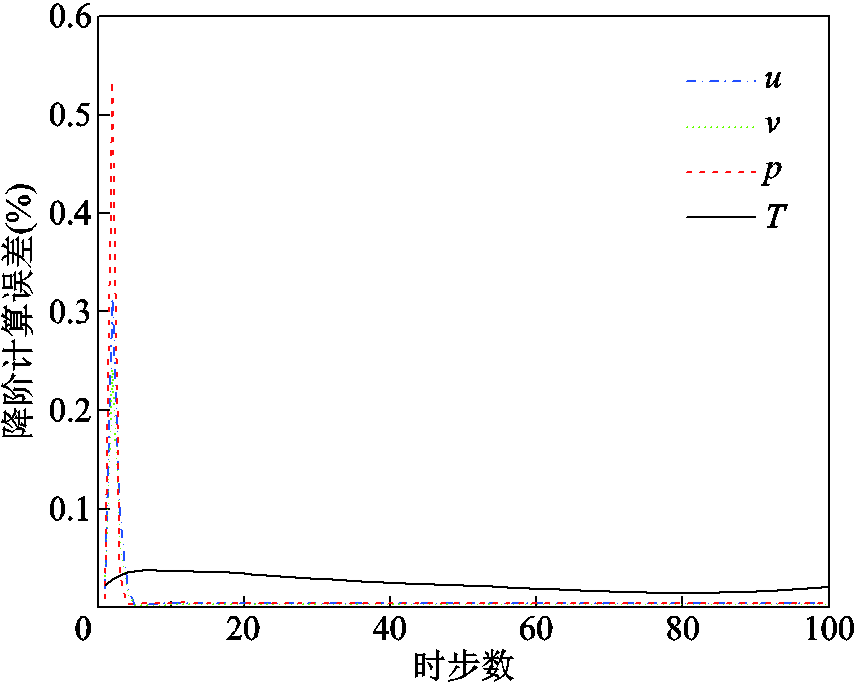
图8 降阶计算误差
Fig.8 Reduced-order computational error
为了比较不同模型的计算时间和准确性，本节将分析以下三个模型：①基于Modelica的换流变压器温升场路耦合与降阶模型；②使用Fluent构建的换流变压器温升全阶模型；③不考虑散热器，仅考虑换流变压器油箱本体温升的模型。
模型①的边界条件主要包括入口和出口边界条件，以及油箱壁的表面传热边界条件。入口和出口边界条件与一维路模型相关。油箱上壁面的平均表面传热系数由经验公式计算后设置为5.67 W/(m2·K)。油箱侧壁面的平均表面传热系数由经验公式计算后设置为4.54 W/(m2·K)。变压器油箱底部由于与基座通过固体散热且总换热量较小，设置为绝热边界。模型②与模型③的油箱上壁面、侧壁面和底部平均表面传热系数均与模型①保持一致。此外，模型②散热片表面传热系数设置为4.79 W/(m2·K)。
提取图6中采样点的瞬态温度变化过程如图9所示。可以看出，采样点温度随着换流变压器运行时间增大而增大，本文所述模型计算结果与实验测得数据之间在0.5～2 h范围内存在较大差异。如顶部采样点，本文所述模型与实验结果最大相差9.8 K。不采用降阶的场路耦合模型与模型①由式（32）得到的温度降阶计算误差如图10所示，可以看到在计算过程中，最大计算误差不超过2%。
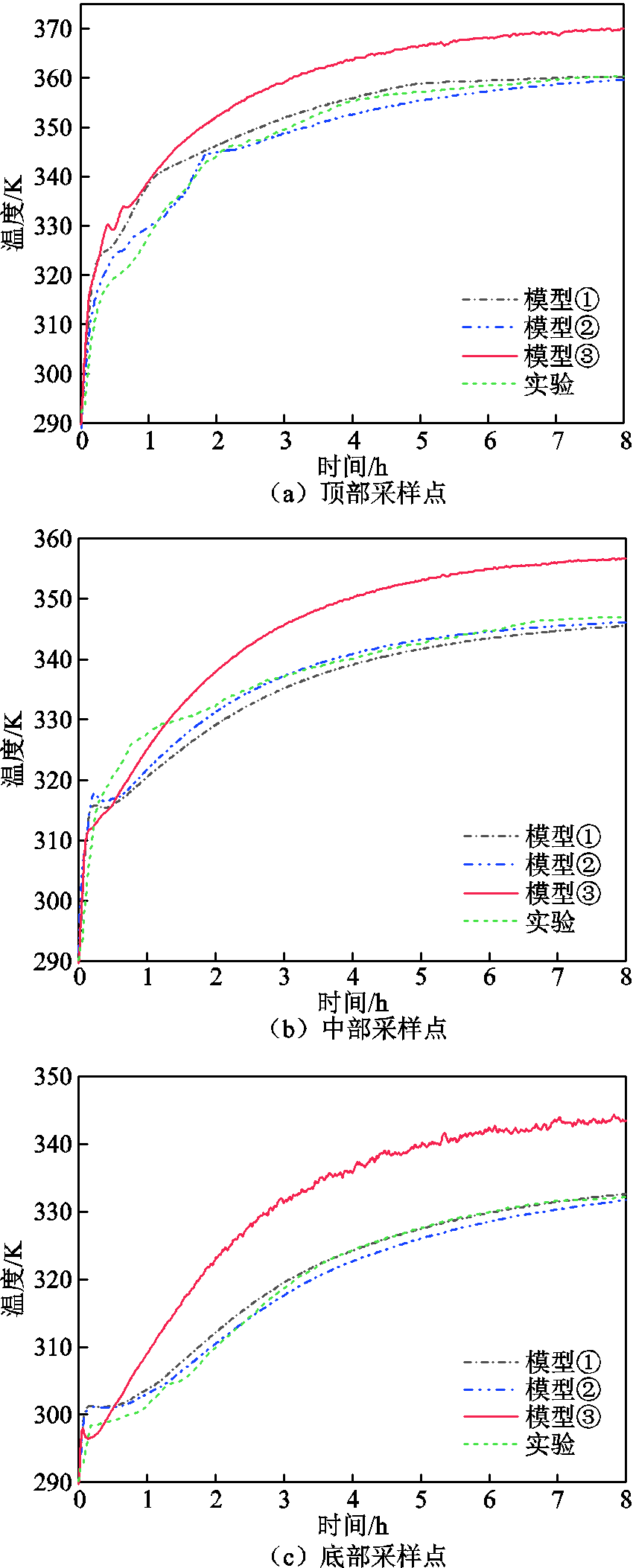
图9 瞬态温度变化过程
Fig.9 Transient temperature variation process
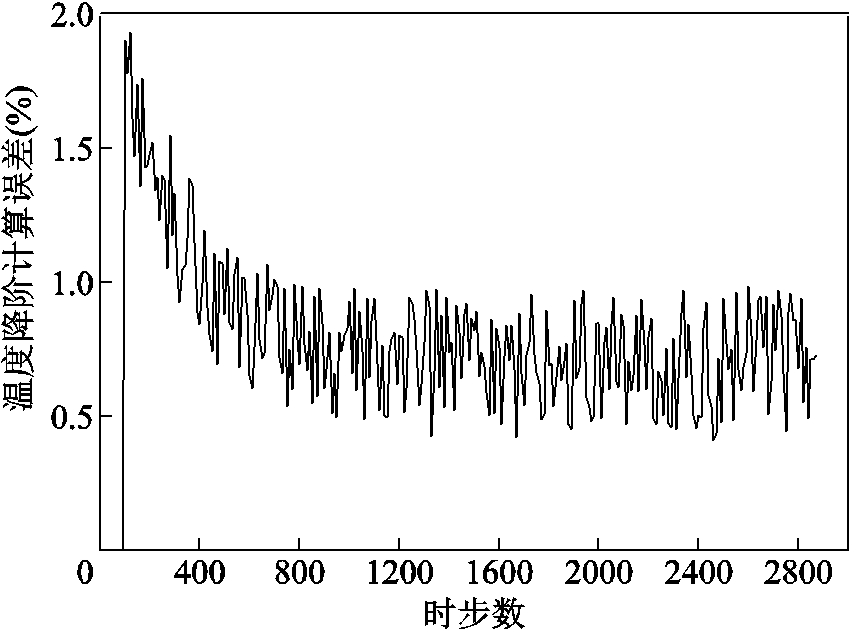
图10 不同时步下温度降阶计算误差
Fig.10 Reduced-order calculation error of temperature at different time steps
随着运行时间的增加，温升差异逐渐减小。稳态时，温度基本一致。稳态时各模型与实验数据的温升及误差见表5。可见，达到稳态后，全阶模型计算结果与实验结果温度最大误差为0.82 K，本文所述模型计算结果与实验结果温度最大误差为1.37 K。模型③由于不考虑散热器，整体计算温升大于考虑散热器的模型①及模型②，与实验结果温度最大误差为11.39 K。本文所述模型与模型③计算得出的油流速度分布云图如图11所示，温度分布云图如图12所示。
表5 稳态温度对比
Tab.5 Comparison of steady-state temperature
名称温度/K 顶部测点中部测点底部测点最大误差 模型①360.16345.56332.621.37 模型②359.61346.11331.690.82 模型③369.99356.71343.5011.39 实验360.35346.93332.11
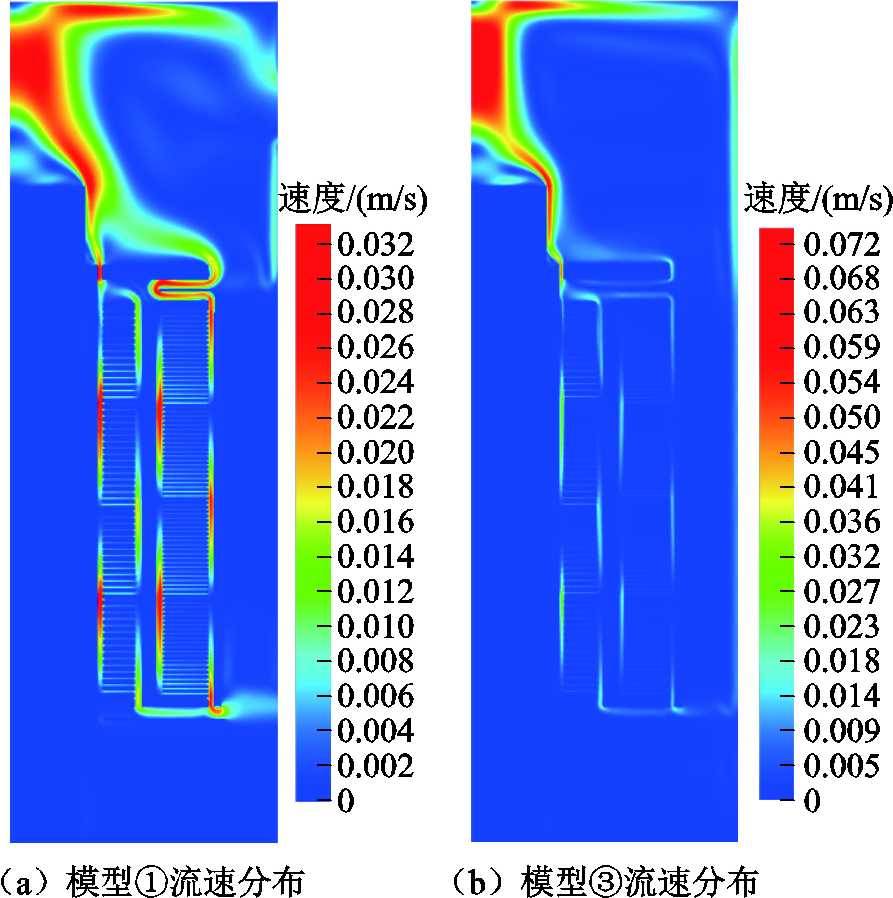
图11 油流速度分布云图对比
Fig.11 Comparison of oil flow velocity distribution
换流变压器温升计算三维全阶模型计算得出的温度云图如图13所示。可见模型整体温度分布具有一定的对称性，且绕组温度分布规律与本文所述场路耦合模型一致。由于绕组垫圈和油浸纸板的影响，绕组线饼的温度并未随轴向高度增加而线性增加。
考虑一维冷却管道影响的模型①与不考虑散热器、仅考虑油箱本体的模型③相比，流速和温度分布存在显著差异。仅考虑油箱本体的模型可能会导致计算的热点大小和位置与实际情况存在较大偏差。
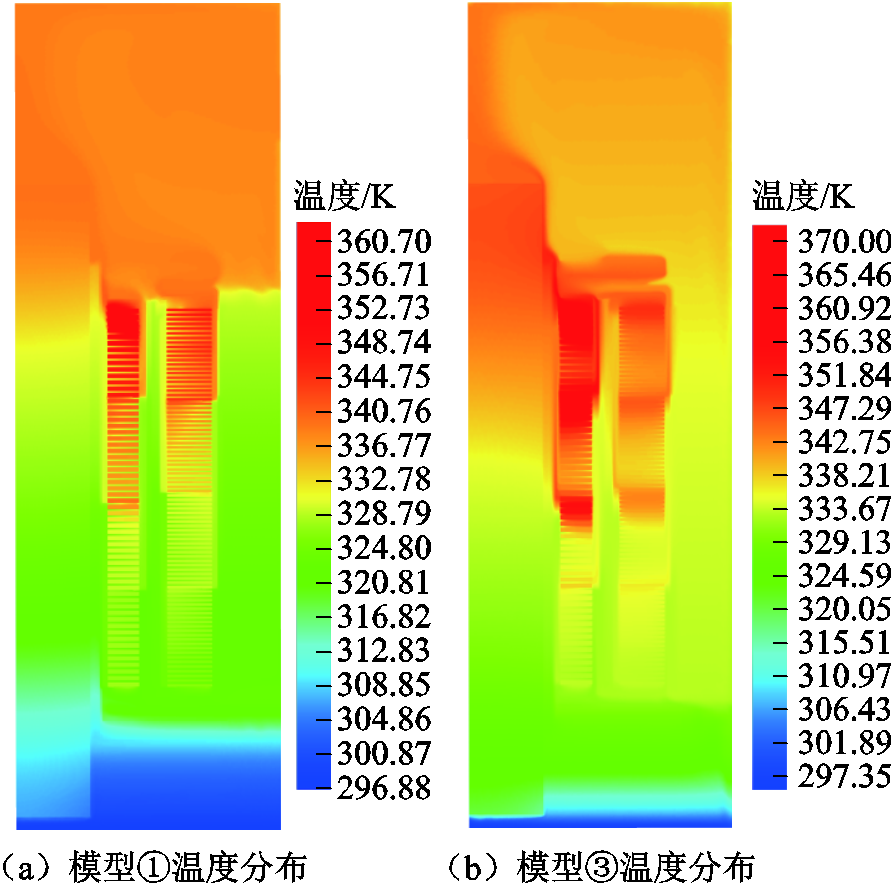
图12 温度分布云图对比
Fig.12 Comparison of temperature distribution
图13 换流变压器全阶模型温度分布
Fig.13 Temperature distribution of model 3
计算效率方面，计算平台配置为：CPU Intel Core i7-14700 K，内存128 GB，主频3.40 GHz。结果表明，模型②计算总耗时860.8 h，全阶场路耦合模型计算总耗时16.97 h，计算速度相较模型②提升至50.72倍。而模型①由于模型简化及模型降阶，计算复杂度大幅降低，总耗时3.328 h。计算速度相较模型②提升至258.65倍，相较全阶场路耦合模型提升至5.1倍。
本文针对油浸式变压器温升过程，基于Modelica语言建立了绕组温升场路耦合及降阶模型。通过场路耦合模型，结合了热路法与FEM的优点，对需要获取详细温度分布的油箱、绕组等部分使用FEM方法计算，而对于不需要详细温度分布但对整体温升计算有影响的散热器部分使用热路法计算，以提高计算效率。为了验证模型的适用性，分别采用本文所述模型、全阶三维模型以及不考虑散热装置的模型对瞬态温升实验工况进行了分析，并与实验数据进行对比，得出结论如下：
1）达到稳态时，全阶模型与实验结果温度最大误差为0.82 K，本文所述模型与实验结果温度最大误差为1.37 K。该模型适用于油浸式变压器温升计算和绕组热点分析。
2）对于油浸式自冷换流变压器，在温升计算中不考虑包含散热装置的完整油流循环可能会导致计算的绕组热点温升大小和热点位置与实际情况出现较大偏差。
3）本文所述模型通过场路耦合及POD降阶法，有效地减少了计算成本。与全阶三维模型相比，计算速度提升了258.65倍，与全阶场路耦合模型相比，计算速度提升了5.1倍，更好地满足了数字孪生模型对于时效性的要求。
附 录
1. 瞬态流场矩阵方程具体形式
式（15）具体矩阵组装形式为
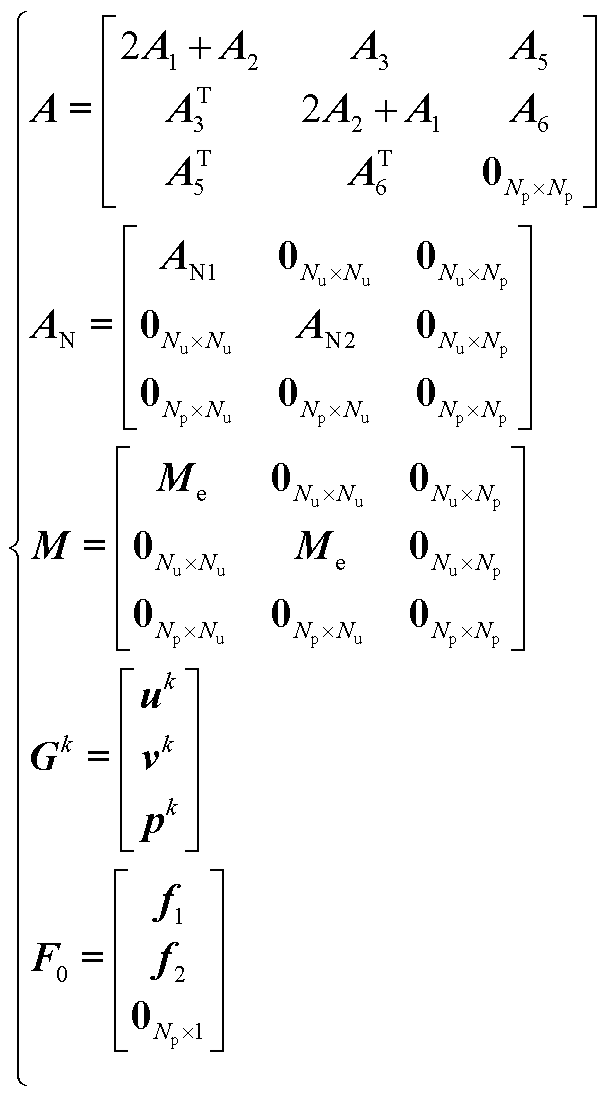（A1）
其中子矩阵的组装形式为
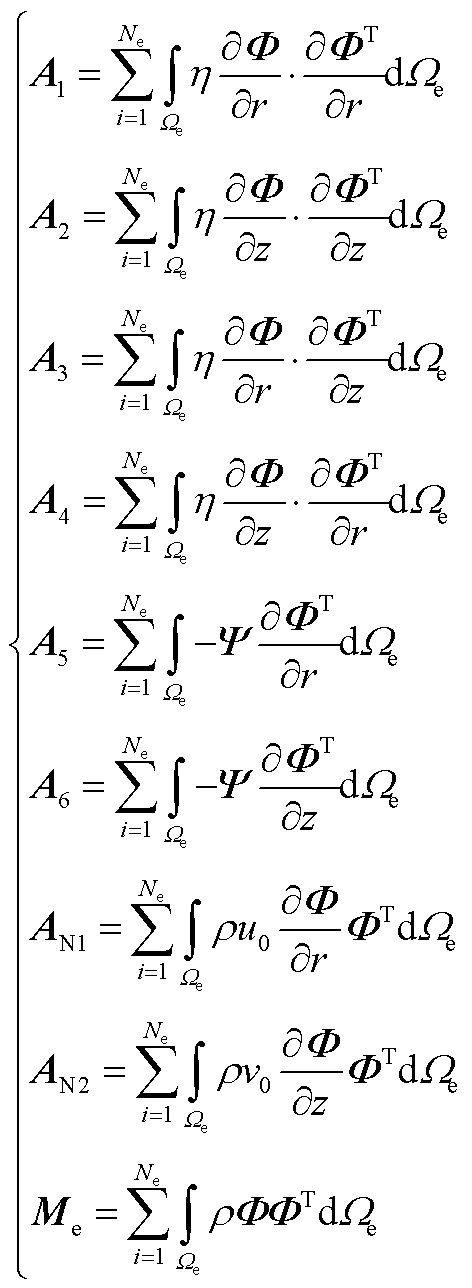（A2）
式中，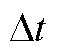
为时间离散步长；Ne为单元总数；Ωe为单元计算域；
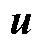为节点横向速度列向量；
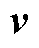为节点纵向速度列向量；
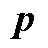为节点压力列向量。
2. 瞬态温度场矩阵方程具体形式
式（22）具体矩阵组装形式为
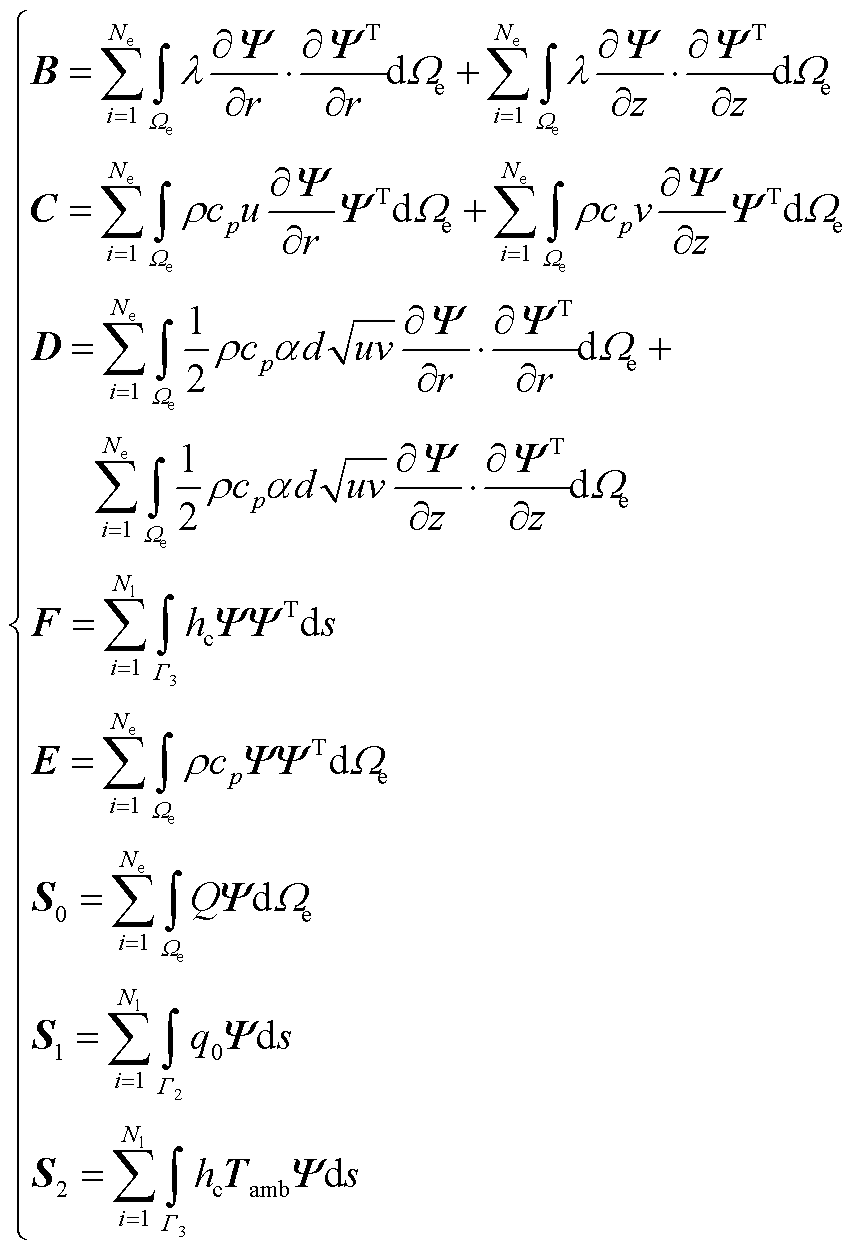（A3）
式中，Nl为边界单元数量。
3. Modelica计算模型和相关参数
本文采用OpenModelica作为计算平台，Modelica计算模型如附图1所示。图中，场模型和散热器模型为自定义组件模型，其余模型为Modelica库中的模型。
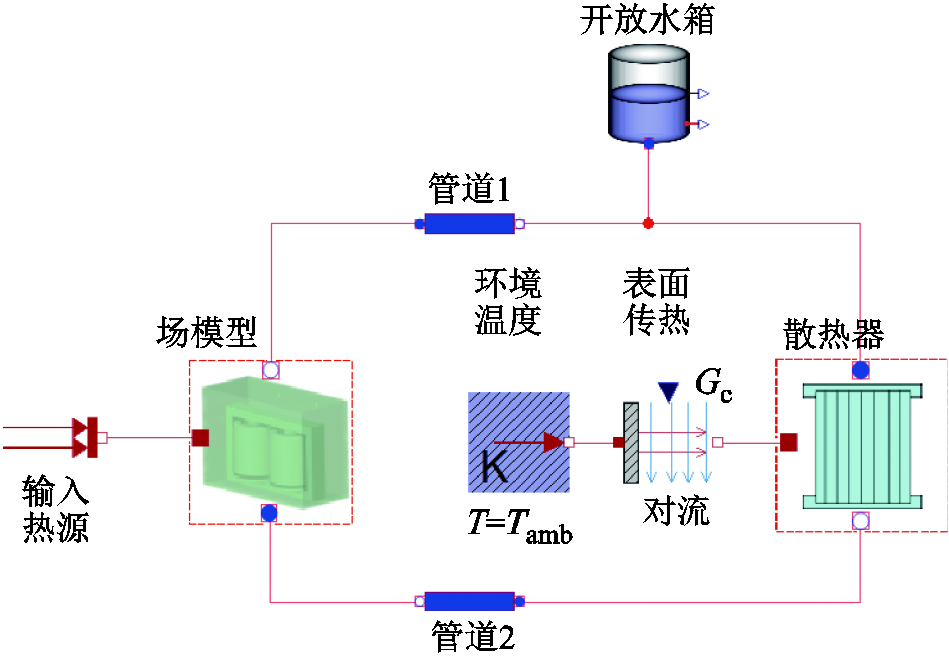
附图1 Modelica计算模型
App.Fig.1 Modelica computational model
本文计算模型中，铁心损耗密度设定为9 340.04 W/m3，阀侧绕组损耗密度设定为136 178.49 W/m3，网侧绕组损耗密度设定为196 573.01 W/m3。等效表面传热系数按式（10）设定为
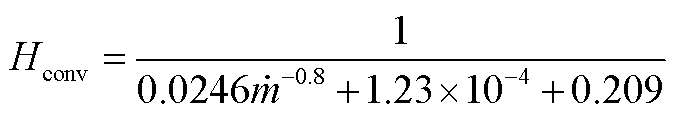（A4）
散热器有效散热面积设定为64.5 m2。
参考文献
[1] 罗豪, 成立, 杨丽君, 等. 虚实融合的变压器内绝缘状态孪生方法[J]. 电工技术学报, 2024, 39(23): 7628-7638. Luo Hao, Cheng Li, Yang Lijun, et al. The state twinning method of transformer internal insulation by virtual-real fusion[J]. Transactions of China Electro-technical Society, 2024, 39(23): 7628-7638.
[2] 王伟杰, 雍明超, 黄金魁, 等. 高压设备数字孪生体构建及状态分析技术研究[J].高压电器, 2023, 59(11): 119-128. Wang Weijie, Yong Mingchao, Huang Jinkui, et al. Research on construction of condition analysis technology of digital twin for high voltage equipment [J]. High Voltage Apparatus, 2023, 59(11): 119-128.
[3] 刘云鹏, 刘一瑾, 刘刚, 等. 电力变压器智能运维的数字孪生体构想[J]. 中国电机工程学报, 2023, 43(22): 8636-8651. Liu Yunpeng, Liu Yijin, Liu Gang, et al. Digital twin conception of intelligent operation and maintenance of power transformer[J]. Proceedings of the CSEE, 2023, 43(22): 8636-8651.
[4] 许剑冰, 冯霄峰, 徐海波, 等. 基于数字孪生的安全稳定控制系统试验验证展望[J]. 电力系统自动化, 2024, 48(5): 1-10.
XuJianbing, Feng Xiaofeng, Xu Haibo, et al. Prospects for experimental verification of safety and stability control systems based on digital twins[J]. Automation of Electric Power Systems, 2024, 48(5): 1-10.
[5] 刘刚, 郝世缘, 朱章宸, 等. 基于动态模态分解-自适应变步长油浸式电力变压器绕组瞬态温升快速计算方法[J]. 电工技术学报, 2024, 39(12): 3895-3906. Liu Gang, Hao Shiyuan, Zhu Zhangchen, et al. Research on rapid calculation method of transient temperature rise of winding of dynamic mode decom-position-adaptive time stepping oil-immersed power transformer[J]. Transactions of China Electrotec-hnical Society, 2024, 39(12): 3895-3906.
[6] 中国电力企业联合会科技开发服务中心. 电力行业数字孪生技术应用白皮书[R/OL].(2022-07-02)[2024-06-10]. https://www.thepaper.cn/newsDetail_forward_ 19289460.
[7] 和敬涵, 张佳宝, 李猛, 等. 基于孪生模型的模块化多电平换流器保护[J]. 电力系统自动化, 2023, 47(21): 119-126. He, Jinghan, Zhang, Jiabao, Li, Meng, et al. Protection of modular multilevel converters based on twin models[J]. Automation of Electric Power Systems, 47(21): 119-126.
[8] 杨帆, 吴涛, 廖瑞金, 等. 数字孪生在电力装备领域中的应用于实现方法[J]. 高电压技术, 2021, 47(5): 1505-1521. Yang Fan, Wu Tao, Liao Ruijin, et al. Application and implementation method of digital twin in electric equipment[J]. High Voltage Engineering, 2021, 47(5): 1505-1521.
[9] 张重远, 刘迪程, 高成龙, 等. 基于Twin Builder的110 kV油浸式变压器3维磁场降阶模型及损耗分析[J]. 高电压技术, 2024, 50(3): 941-951. Zhang Zhongyuan, Liu Dicheng, Gao Chenglong, et al. Three-dimensional magnetic field model order reduction and loss analysis of 110 kV oil-immersed transformer based on Twin Builder[J]. High Voltage Engineering, 2024, 50(3): 941-951.
[10] 王源, 李兴宝, 杨明月, 等. 基于热电类比理论的光纤复合低压电缆温度分布特性研究[J]. 电气技术, 2021, 22(3): 44-51. Wang Yuan, Li Xingbao, Yang Mingyue, et al. Research on temperature distribution characteristics of optical fiber composite low voltage cable based on thermoelectric analogy theory[J]. Electrical Engineering, 2021, 22(3): 44-51.
[11] Jiang Genghui, Kang Ming, Cai Zhenwei, et al. Online reconstruction of 3D temperature field fused with POD-based reduced order approach and sparse sensor data[J]. International Journal of Thermal Sciences, 2022, 175: 107489.
[12] Pla F, Herrero H. Reduced basis method applied to eigenvalue problems from convection[J]. International Journal of Bifurcation and Chaos, 2019, 29(3): 1950028.
[13] 张宇娇, 赵志涛, 徐斌, 等. 基于U-net卷积神经网络的电磁场快速计算方法[J]. 电工技术学报, 2024, 39(9): 2730-2743. Zhang Yujiao, Zhao Zhitao, Xu Bin, et al. Fast calculation method of electromagnetic field based on U-net convolutional neural network[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2730-2742.
[14] Rommel D P, Di Maio D, Tinga T. Transformer hot spot temperature prediction based on basic operator information[J]. International Journal of Electrical Power and Energy Systems, 2021, 124: 106340.
[15] Tan Youbo, Yu Xiaoling, Zang Ying, et al. Improving the flow and thermal uniformities of transformer disc-type windings using a self-blocking oil circuit[J]. International Communications in Heat and Mass Transfer, 2023, 148: 107083.
[16] 刘刚, 胡万君, 郝世缘, 等. 油浸式变压器绕组瞬态温升降阶快速计算方法[J]. 电工技术学报, 2024, 39(3): 643-657. Liu Gang, Hu Wanjun, Hao Shiyuan, et al. Reduced order calculation method of steady temperature rise of oil immersed power transformer[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 643-657.
[17] Chi Cheng, Yang Fan, Ren Zhuoxiang, et al. Reduced order model based on combined POD/LDEIM-Q for nonlinear thermoelectric coupling[J]. IEEE Transactions on Magnetics, 2022, 58(9): 7402304.
[18] Liu Yunpeng, Zhao Qingxian, Liu Gang, et al. A real-time solution method for three-dimensional steady temperature field of transformer windings based on mechanism-embedded cascade network[J]. Case Studies in Thermal Engineering, 2024, 58: 104444.
[19] Delussu F, Manzione D, Meo R, et al. Experiments and comparison of digital twinning of photovoltaic panels by machine learning models and a cyber-physical model in Modelica[J]. IEEE Transactions on Industrial Informatics, 2022, 18(6): 4018-4028．
[20] Masoom A, Mahseredjian J, Ould-Bachir T, et al. MSEMT: an advanced Modelica library for power system electromagnetic transient studies[J]. IEEE Transactions on Power Delivery, 2022, 37(4): 2453-2463.
[21] Nobile F. Coupling strategies for the numerical simulation of blood flow in deformable arteries by 3D and 1D models[J]. Mathematical and Computer Modelling 2009, 49(11-12): 2152-2160.
[22] Fritzson P. Principles of Object-Oriented Modeling and Simulation with Modelica 3. 3: A Cyber-Physical Approach[M]. 2nd ed. Piscataway: IEEE Press, 2015.
[23] 徐天光, 王永庆, 朱超, 等. 变压器用片式散热器散热性能数值模拟及试验研究[J]. 电力工程技术, 2020, 39(5): 178-184. Xu Tianguang, Wang Yongqing, Zhu Chao, et al. Numerical simulation and experimental study on heat transfer performance of panel-type radiators of transformers[J]. Electric Power Engineering Technology, 2020, 39(5): 178-184.
[24] Chi Cheng, Yang Fan, Xu Chong, et al. A multi-scale thermal-fluid coupling model for ONAN transformer considering entire circulating oil systems[J]. Inter-national Journal of Electrical Power and Energy Systems, 2022, 135: 107614.
[25] 王路伽, 蔡镇潞, 邱亚博, 等. 计及风量损耗的油浸风冷外置冷却系统散热效率优化方法[J]. 电工技术学报, 2023, 38(17): 4767-4778. WangLujia, Cai Zhenlu, QiuYabo, et al. Heat dissipation efficiency optimization method for ONAF external cooling system taking into account airflow losses[J]. Transactions of China Electrotechnical Society, 2023 38(17): 4767-4778.
[26] Zienkiewicz O C, Taylor R L, Nithiarasu P. The Finite Element Method for Fluid Dynamics[M]. 6th ed. Builington, MA: Butter-worth-Heinemann, 2005.
[27] 谢裕请. 油浸式电力变压器流场及温度场耦合有限元方法研究[D]. 北京: 华北电力大学, 2017. Xie Yuqing. Study on flow field and temperature field coupling finite element methods in oil-immersed power transformer[D]. Beijing: North China Electric Power University, 2017.
[28] 陶文铨. 数值传热学[M]. 西安: 西安交通大学出版社, 2001.
[29] Wang Yi, Yu Bo, Cao Zhizhu, et al. A comparative study of POD interpolation and POD projection methods for fast and accurate prediction of heat transfer problems[J]. International Journal of Heat and Mass Transfer, 2012, 55(17-18): 4827-4836.
[30] 刘刚, 荣世昌, 武卫革, 等. 基于混合有限元法和降阶技术的油浸式变压器绕组2维瞬态流-热耦合场分析[J]. 高电压技术, 2022, 48(5): 1695-1705. Liu Gang, Rong Shichang, Wu Weige, et al. Two-dimensional transient flow-thermal coupling field analysis of oil-immersed transformer windings based on hybrid finite element method and reduced-order technology[J]. High Voltage Engineering, 2022 48(5): 1695-1705.
[31] International Electrotechnical Commission. Power transformers-part 2: temperature rise for liquid-immersed transformers: IEC 60076-2[S]. Geneva: IEC, 2011.
Abstract As the advancement of Industry 4.0 continues, the power and energy sectors are rapidly undergoing intelligent and digital transformation, leading to the emergence of digital twin technology in the field of electrical equipment. As critical primary equipment, power transformers greatly benefit from the development of digital twin models, which enhance operational reliability, maintenance efficiency, and fault prediction capabilities. However, model-driven digital twin models are often constrained by slow computation speeds. To address this issue, this paper constructs a simplified field-circuit coupled model for oil-immersed power transformers using Modelica, aimed at reducing computational complexity. Additionally, to further enhance computational efficiency, the proper orthogonal decomposition (POD) method is applied to the field computation section for order reduction.
Firstly, we investigate the heat generation, heat dissipation mechanisms, and oil flow circulation of a 35 kV, 800 kV·A scaled-down oil-immersed self-cooled (Oil Natural Air Natural, ONAN) converter transformer prototype. Based on this, a simplified method for coupling thermal and circuit calculations and an equivalent modeling approach for the temperature rise of the converter transformer are proposed. Subsequently, the implementation method and encapsulation form of the thermal circuit coupled model using Modelica are discussed. POD is then employed to reduce the order of the field computation section. Finally, temperature rise experiments on the converter transformer are conducted, and the model's computational data is compared with the experimental results.
The comparison between the model’s computational data and the experimental results reveals significant differences in the range of 0.5 to 2 hours, with the maximum discrepancy reaching 9.8 K at the top sampling point. As the operating time increases, the temperature rise difference gradually diminishes, and the temperatures converge in the steady state. Whether the radiator is considered significantly impacts both the magnitude of the winding temperature rise and the hotspot location. In the steady state, excluding the radiator results in a maximum temperature error of 11.39 K between the model’s calculations and the experimental data, whereas the proposed model's maximum temperature error is 1.37 K, and the full-order model's maximum temperature error is 0.82 K. In terms of computational efficiency, the proposed model takes a total of 3.328 hours under the temperature rise condition, which is 258.65 times faster than the full-order three-dimensional model. Compared to the full-order field-circuit coupled model, the computational speed is increased by 5.1 times.
From the analysis of the model's computational results and the experimental data, the following conclusions can be drawn: (1) The proposed model has a maximum temperature error of 1.37 K compared to the experimental results, making it suitable for temperature rise calculations and winding hotspot analysis of converter transformers. (2) For oil-immersed self-cooled converter transformers, excluding the complete oil flow circulation with the radiator in temperature rise calculations may lead to significant deviations in both the magnitude and location of the winding hotspot temperature rise compared to actual conditions. (3) The proposed model effectively reduces computational costs through the thermal circuit coupling and POD order reduction methods. Compared to the full-order three-dimensional model, the computation speed is increased by 258.65 times, and compared to the full-order field-circuit coupled model, the computation speed is increased by 5.1 times, better meeting the timeliness requirements of digital twin models.
keywords：Digital twin, Modelica, field-path coupling, winding temperature rise, reduced-order model
DOI: 10.19595/j.cnki.1000-6753.tces.241111
中图分类号：TM411
国家重点研发计划资助项目（2021YFB2401700）。
收稿日期 2024-06-26
改稿日期 2024-08-08
杨 帆 男，1980年生，教授，博士生导师，研究方向为输变电设备多物理场计算，电力装备数字孪生。E-mail：yangfan@cqu.edu.cn
王鹏博 男，1994年生，博士，助理研究员，研究方向为多物理场数值计算，太赫兹波产生和调控技术。E-mail：wangpb@cqu.edu.cn（通信作者）
（编辑 郭丽军）