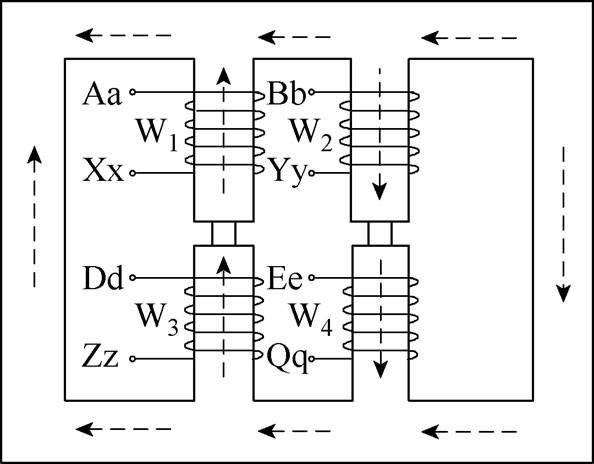
图1 MSCR结构示意图
Fig.1 MSCR structure diagram
摘要 针对电力设备状态动态实时变化的物理实体,构建高效数学模型,是实现电力系统系统级仿真和大型电磁设备一体化分析设计的重要环节。该文以磁饱和式可控电抗器(MSCR)为分析对象,提出一种兼顾计算准确度和计算速度的电磁参数计算新方法——非线性动态电磁网络模型。首先,基于网络图论和区域离散化思想,考虑铁心非线性与磁阀漏磁,建立MSCR二维磁网络模型。其次,根据MSCR的电磁耦合关系,采用受控源的方式建立其电磁耦合等效电路,并生成MSCR非线性动态电磁网络模型。基于此,对MSCR不同磁饱和度下的绕组电流与铁心磁通进行计算。最后,将计算结果与三维有限元模型和实验测量结果比较,验证该模型的有效性。结果显示,与三维有限元模型相比,MSCR的非线性动态电磁网络模型的计算速度为其50~240倍,存储空间仅为其1/10 000~1/7 000,在满足计算精度的要求下有效地提高了计算效率,在可控电抗器的初期设计以及电力系统的系统级仿真方面具有独特的优势。
关键词:磁饱和式可控电抗器 电磁网络模型 电磁参数计算 有限元法
近年来,伴随着高比例分布式电源、大规模电气化交通、电力电子化等特征的新形态电网形 成[1-3],谐波、闪变、电压波动等电能质量问题日益严重。为了应对剧烈的潮流变化,实现电网的动态无功补偿,电力系统对可控电抗器在技术上和性能上提出了更高的要求[4]。随着城市电网规模的日益庞大以及各种先进设备的应用,电力系统综合效能的发挥取决于各设备间的相互配合与协同作用[5],这使得以可控电抗器为代表的电磁设备在优化设计和性能分析方面对计算方法准确性和快速性的需求更加突出。磁饱和式可控电抗器(Magnetically- Saturated Controllable Reactor, MSCR)作为一种通过改变铁心磁饱和度来实现容量平滑输出的新型无功补偿设备,集中涵盖了电力设备出现的直流偏磁、磁饱和特性、复杂铁心磁路建模等亟待解决的难 题[6-8]。因此,本文以MSCR为分析对象,对构建电磁设备高效数学模型进行研究。
在MSCR的建模仿真与参数计算方面,文献[9]建立了800 kV MSCR的二维有限元模型,对其铁心磁场分布与绕组电流进行计算与分析;文献[10]建立MSCR三维场路耦合有限元模型,并对不同工况下的谐波、损耗和电流进行计算;文献[11]基于有限元软件建立MSCR的场路耦合模型并结合电磁暂态模型提出一种电磁参数计算新方法;文献[12]优化MSCR磁阀结构,分别建立单级和多级MSCR有限元模型,并对其磁场分布和功率损耗进行对比分析,得出多级磁阀结构损耗更低的结论;文献[13]分别基于磁路分解法和有限元法建立500 kV MSCR的仿真模型,并计算和分析不同磁饱和度下的绕组漏感。显然,以上文献均采用“场”概念的电磁场数值计算法来建立MSCR的物理场域模型,这种方法更符合实际,具有计算精度高且磁场分布直观的特点;但由于网格剖分复杂、方程组阶数高,使其计算量大、计算时间长,难以适应于含多个、多种电磁设备的电力系统的分析。
为了提高MSCR计算速度,文献[14]基于磁场分割原理建立MSCR非线性饱和等效磁路模型,并对其直流偏磁下的绕组电流进行计算;文献[15]提出考虑磁滞和涡流效应的改进磁路段磁滞模型,并基于电容-回转器模型建立MSCR电磁暂态模型;文献[16]建立多级磁阀的MSCR磁化特性和电流特性的数学模型,并对n级磁阀与MSCR主要参数间的关系进行定量分析,确定最优的磁阀级数及设计方案;文献[17]建立60 MV·A MSCR的电磁数学模型,并对其谐波特性进行研究;上述文献均采用“路”概念的等效分析法来建立MSCR等效数学模型。这种方法基于磁路理论,对MSCR计算模型进行了有效的简化,具有计算简单、方便、速度快的特点;但同样由于模型不同程度的简化,降低了计算精度。
为了在提高电磁设备计算精度的同时大大提高计算速度,文献[18]提出多节点三维磁网络模型,并将其应用于三相电力变压器漏磁场的快速近似计算,对其漏磁分布及热点定位进行分析与实验。磁网络模型以等效磁通管(片)为基本单元对电磁设备场域模型进行网格划分,并根据各支路连接关系采用网络方程法对复杂网格参数进行求解,其基本思想类似于有限元的区域离散化思想,但本质仍为等效磁路模型。因此,磁网络模型兼顾了有限元模型的准确性和磁路模型的快速性[19-22]。
综上所述,为了提高MSCR的计算精度且降低计算代价,本文提出一种兼顾理论分析准确性与参数计算高效性的MSCR计算新方法。首先,借鉴区域离散化思想对MSCR求解域进行网格划分,采用磁通管原理计算非线性网格参数,基于回路电流法建立MSCR等效磁网络模型。其次,根据MSCR的电磁耦合关系,采用受控源的方式建立其电磁耦合等效电路,生成MSCR电磁网络模型,并对其不同磁饱和度下的绕组电流与铁心磁通进行计算。最后,通过有限元仿真和实验测量验证该模型的有效性,从计算准确度、计算速度等方面对其进行对比分析。希望为以MSCR为代表的复杂电磁设备的高效参数计算与结构设计提供一种新方法。
等效磁网络模型的建立是根据区域离散化思想和等效磁通管原理,将求解对象的求解域生成多个求解单元,对求解单元进行磁通管等效,并将磁路连接生成等效磁网络模型,最后对磁路参数进行计算[23]。图1和图2所示分别为他励式MSCR的结构示意图及其绕组端子接线图。其中,铁心结构与绕组排布情况见图1,各绕组端子接线情况见图2,这里需要说明的是,各绕组均采用双根并绕的方式,一套为工作绕组,另一套为控制绕组。根据MSCR的结构特点与磁场分布特点,对其求解域进行网格划分,MSCR求解域网格划分示意图如图3所示。图3中,以MSCR铁轭边沿为求解域边界,且考虑到铁心漏磁与边缘效应,共划分为41个网格。

图1 MSCR结构示意图
Fig.1 MSCR structure diagram
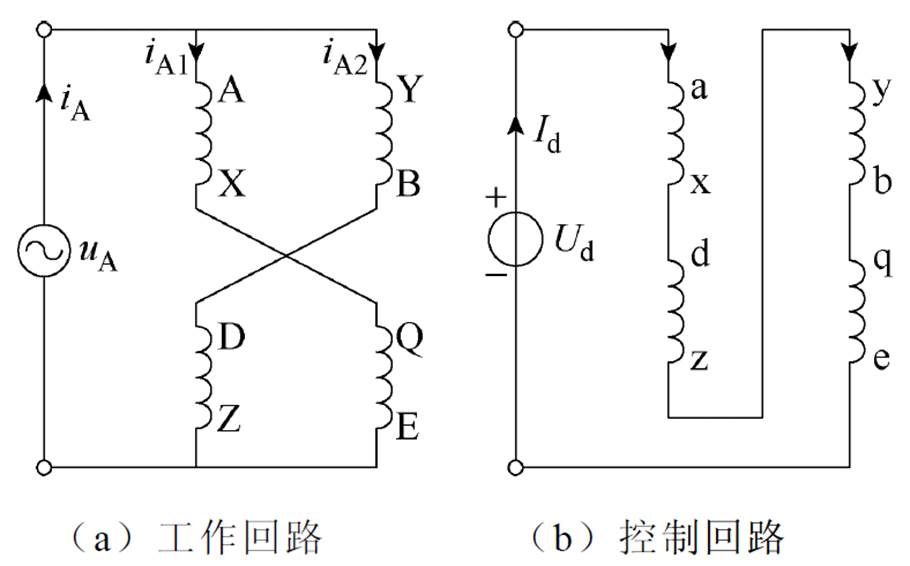
图2 MSCR绕组端子接线图
Fig.2 MSCR winding terminal wiring diagram
在MSCR等效磁网络模型的网格划分过程中,通常将求解域分解为多个磁路段,每个磁路段为一个网格单元。在磁路分析中,采用磁通管法来分析磁路段,即每个磁路段用一个磁通管来代替。图4所示为磁通管的结构示意图,对于一个横截面积为s、磁路长度为l的磁通管,假设其管内磁通均匀且恒定,管两端面s1和s2为等势面。
对于矩形、半圆形、梯形、环形等任意形状规则的磁通管,其磁阻上的磁场能W为
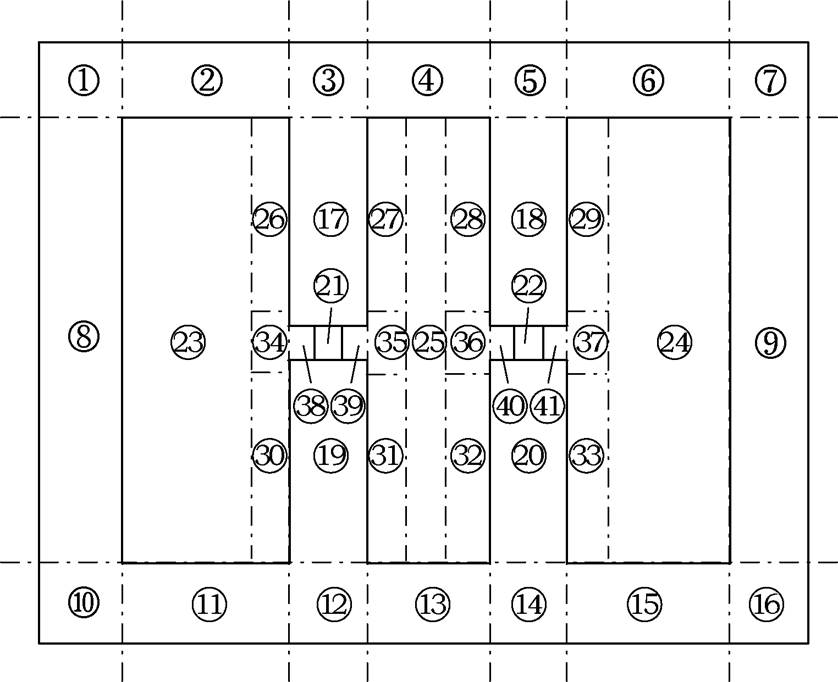
图3 MSCR求解域网格划分示意图
Fig.3 Schematic diagram of MSCR domain meshing
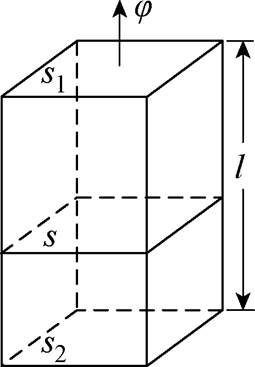
图4 磁通管的结构示意图
Fig.4 Structure diagram of flux tube
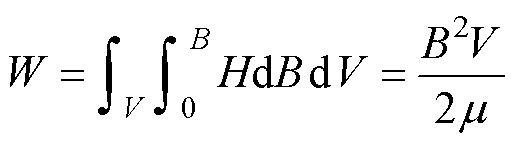 (1)
(1)
式中,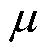 为磁通管的磁导率;H为磁通管的磁场强度;B为磁通管磁通密度;V为磁通管体积。
为磁通管的磁导率;H为磁通管的磁场强度;B为磁通管磁通密度;V为磁通管体积。
假设MSCR采用矩形磁通管,且其磁通流向为x和y两个方向。二维磁网络网格单元示意图如图5所示。根据能量守恒定律,磁通管磁场能的计算公式为
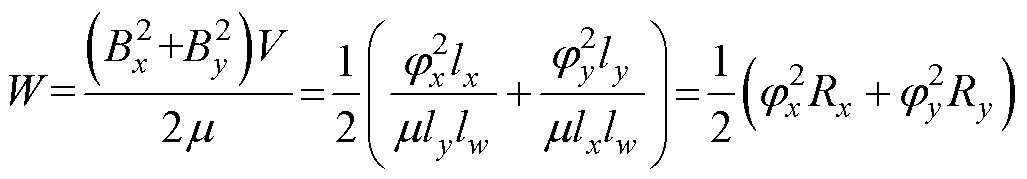 (2)
(2)
式中,Bx、By分别为磁通管在x、y轴方向的磁通密度;lx、ly、lw分别为磁通管结构的长度、宽度、高度;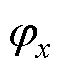 、
、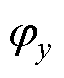 分别为x、y轴方向上的等效磁通;
分别为x、y轴方向上的等效磁通;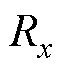 、
、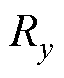 分别为磁通管中x、y轴方向上的磁阻,其表达式为
分别为磁通管中x、y轴方向上的磁阻,其表达式为
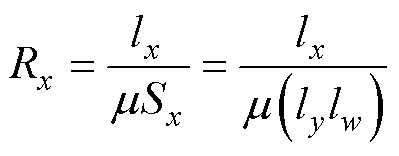 (3)
(3)
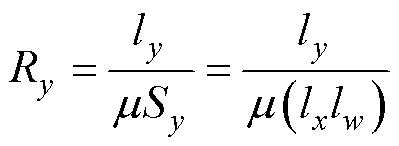 (4)
(4)
磁化曲线作为铁磁材料的基本特性曲线,代表着铁磁材料的磁属性[24]。描述铁心磁饱和特性的模型和方法有多种[24-26],图6所示为铁磁材料磁化曲线模型的两种典型代表。
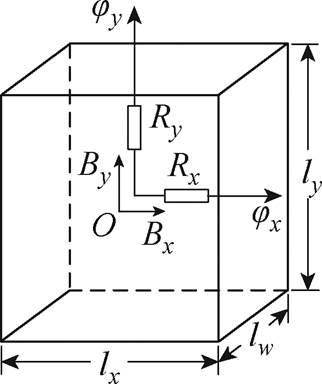
图5 二维磁网络网格单元示意图
Fig.5 Schematic diagram of 2D magnetic network subdivision unit
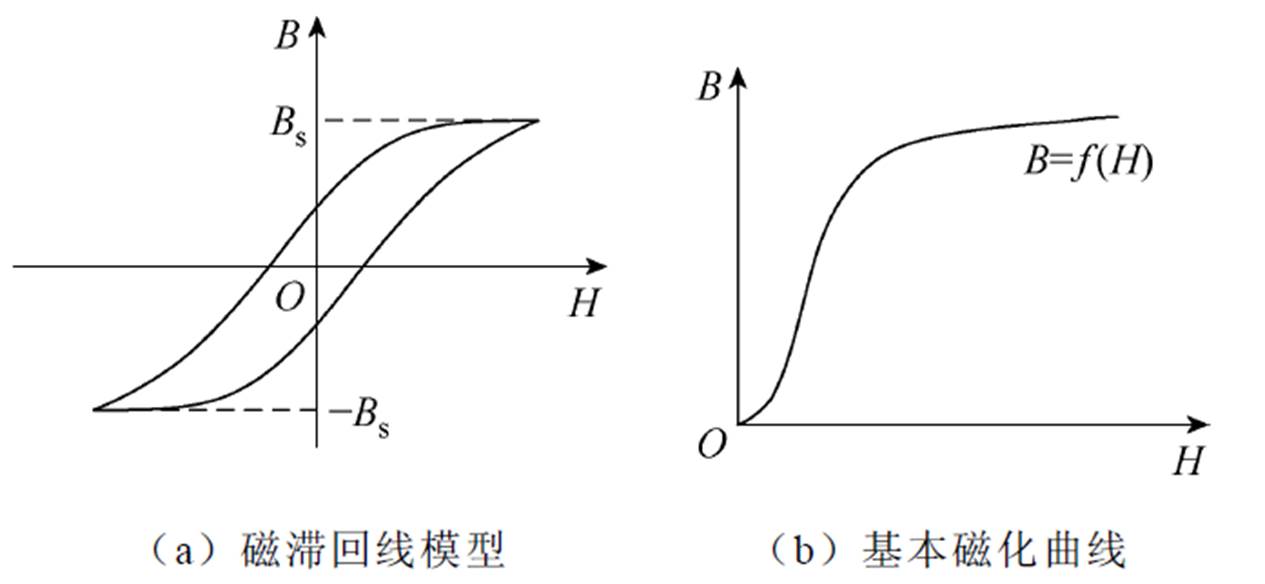
图6 铁磁材料磁化曲线模型
Fig.6 Magnetization curves model of ferromagnetic material
图6a所示为具有多值磁化特性的磁滞回线模型,其不仅能够体现铁心的饱和特性,还反映了磁滞特性与涡流特性,更符合实际。然而,磁滞回线模型的参数辨识基于大量的实验测试,通常难以获得,使其拟合过程较为复杂。为了方便计算,若忽略铁磁材料的磁滞特性,可得到如图6b所示具有单值磁化特性的基本磁化曲线。为了提高计算效率,本文选用单值磁化曲线来描述MSCR铁心的磁特性。磁化曲线的模拟,除了可以根据实验测量数据采用查表插值的方式获取以外,常常通过函数表达式进行拟合。曲线拟合最基本的两种拟合方法分别是插值法和最小二乘法,其中,插值法可以得到较高的拟合精度,而最小二乘法得到的曲线更加光滑。为了提高MSCR磁通管参数计算的精度,本文采用分段插值法建立MSCR的磁化曲线模型,其表达式为
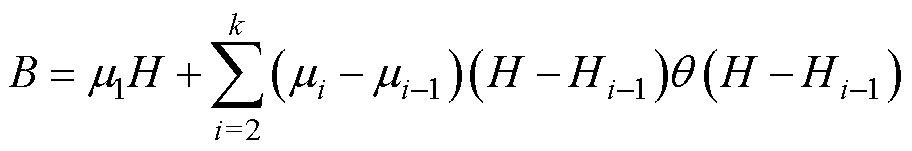 (5)
(5)
式中,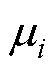 为在分段区间
为在分段区间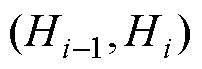 内,铁心磁化曲线的斜率,
内,铁心磁化曲线的斜率,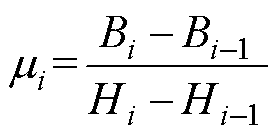 ;
;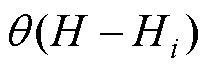 为单位阶跃函数;k为连续磁化曲线所划分的段数。
为单位阶跃函数;k为连续磁化曲线所划分的段数。
对于磁通支路较多的复杂电磁设备磁路,往往需要借助电路分析中的复杂网络参数求解方法。根据基尔霍夫电流定律和基尔霍夫电压定律,复杂网络参数计算与分析通常采用网络方程法来实现,主要包括节点电压法和回路电流法。其中,节点电压法数学方程组的建立较为简单,扩展性强;而回路电流法在解决非线性问题中更具优越性[27]。MSCR铁心材料磁化特性的非线性使其电磁参数计算模型具有非线性的特征,因此,本文选择回路电流法来建立MSCR的等效磁网络模型。
根据图3所示的MSCR求解域网格划分及网格连接情况,结合图5所示的网格单元二维磁阻示意图,可得到MSCR的二维等效磁网络模型,如图7所示。

图7 MSCR的二维等效磁网络模型
Fig.7 2D equivalent magnetic network model of MSCR
假设MSCR二维等效磁网络模型中的磁通回路数为n。根据磁路的基尔霍夫电压定律,可列出任意磁通回路m(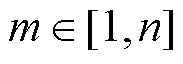 )的磁通回路方程为
)的磁通回路方程为
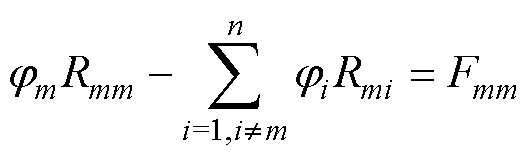 (6)
(6)
式中,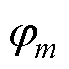 和
和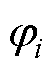 分别为磁通回路m和磁通回路i的回路磁通;
分别为磁通回路m和磁通回路i的回路磁通;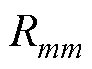 为磁通回路m上的所有磁阻之和;
为磁通回路m上的所有磁阻之和;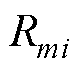 为磁通回路m和磁通回路i共有支路上的磁阻之和;
为磁通回路m和磁通回路i共有支路上的磁阻之和;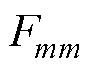 为磁通回路m上的所有磁势源之和。
为磁通回路m上的所有磁势源之和。
同理,根据图7所示的MSCR等效磁网络模型,可列出其等效磁网络矩阵,即
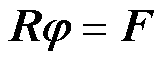 (7)
(7)
式中,R为等效磁网络模型的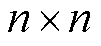 维磁阻矩阵;
维磁阻矩阵;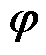 为回路磁通的n维列向量;F为磁势源的n维列向量。
为回路磁通的n维列向量;F为磁势源的n维列向量。
为了实现MSCR的全面分析与设计,需对其进行电场-磁场耦合计算。因此,在建立反映MSCR磁场的等效磁网络模型的同时,还需建立反映MSCR电场的电网络模型,并根据其电-磁耦合关系生成MSCR电磁网络模型。
假设MSCR铁心磁通正方向如图1所示,且将4个绕组分别编号为W1~W4。为了分析电路与磁路的耦合关系,本文以图3中的网格17为例,建立其电场和磁场分离的电路-磁路耦合示意图,如图8所示。
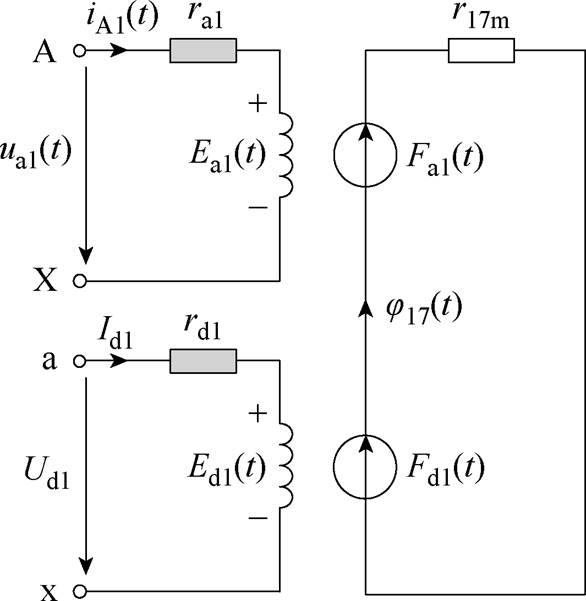
图8 网格单元17的电路-磁路模型
Fig.8 Circuit-magnetic circuit model of grid 17
图8中,ra1、rd1分别为绕组W1的工作回路电阻和控制回路电阻;j17(t)为网格17的磁通;r17m为网格17的磁阻;ua1(t)、iA1(t)分别为绕组W1工作回路端电压和电流,Ud1、Id1分别为绕组W1控制回路端电压和电流;Ea1、Fa1分别为工作回路的感应电动势和磁动势,即
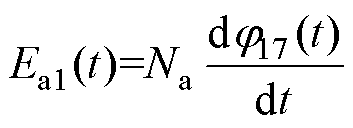 (8)
(8)
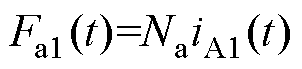 (9)
(9)
式中,Na为工作绕组匝数。
Ed1、Fd1分别为控制回路中绕组W1的感应电动势和磁动势,表示为
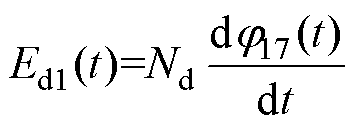 (10)
(10)
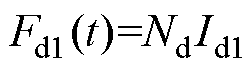 (11)
(11)
式中,Nd为控制绕组匝数。
显然,式(8)和式(10)为微分方程,可采用离散化数值解法进行求解处理,如欧拉法、梯形法、抛物线法等,其中,欧拉法最为简洁。因此,本文采用欧拉法对微分方程进行离散化处理。若将式(8)采用后退欧拉公式进行离散,则可写成
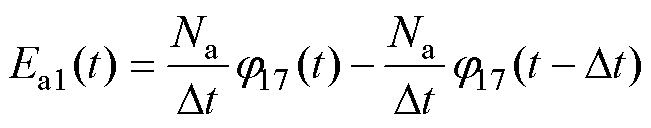 (12)
(12)
若令
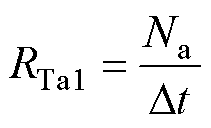
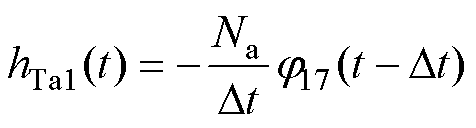
则式(12)可以写成
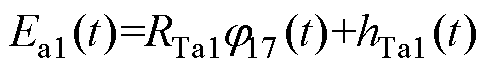 (13)
(13)
式中,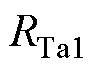 和
和 为网格17的工作绕组电磁耦合部分的等效电阻和等效电源。若将式(13)所示的电-磁耦合关系采用电路形式表示,如图9所示。
为网格17的工作绕组电磁耦合部分的等效电阻和等效电源。若将式(13)所示的电-磁耦合关系采用电路形式表示,如图9所示。
根据图8所示网格单元17的电路-磁路模型以及图9所示的耦合部分等效电路,采用受控源方式实现电路和磁路间的耦合连接,在其电路和磁路之间通过电磁耦合部分等效电路(如图9所示)进行连接,得到网格单元17的电磁耦合等效电路,如图10所示。同理,可分别得到网格单元18~20的电磁耦合等效电路。
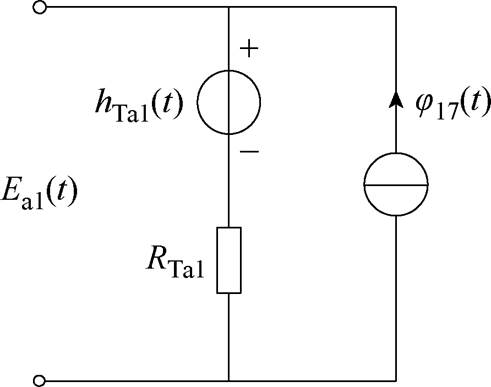
图9 网格单元17工作绕组耦合部分等效电路
Fig.9 Equivalent circuit of electromagnetic coupling part of grid 17
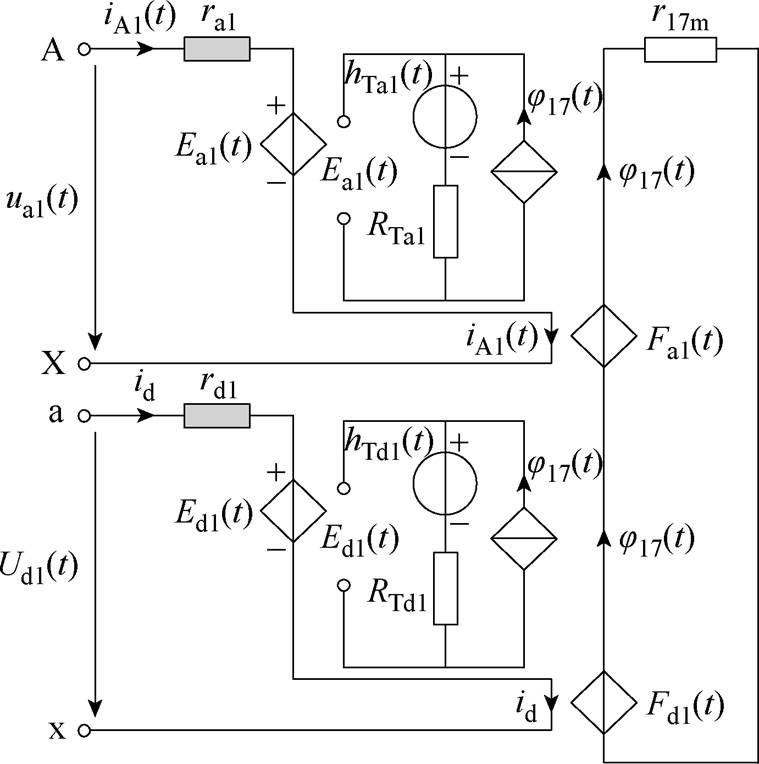
图10 网格单元17的电磁耦合等效电路
Fig.10 Electromagnetic coupling equivalent circuit of grid 17
根据如图10所示的MSCR网格单元电磁耦合等效电路,将网格17~20其按照图2所示的绕组连接关系进行连接,可得到MSCR的电磁耦合电路,如图11所示。
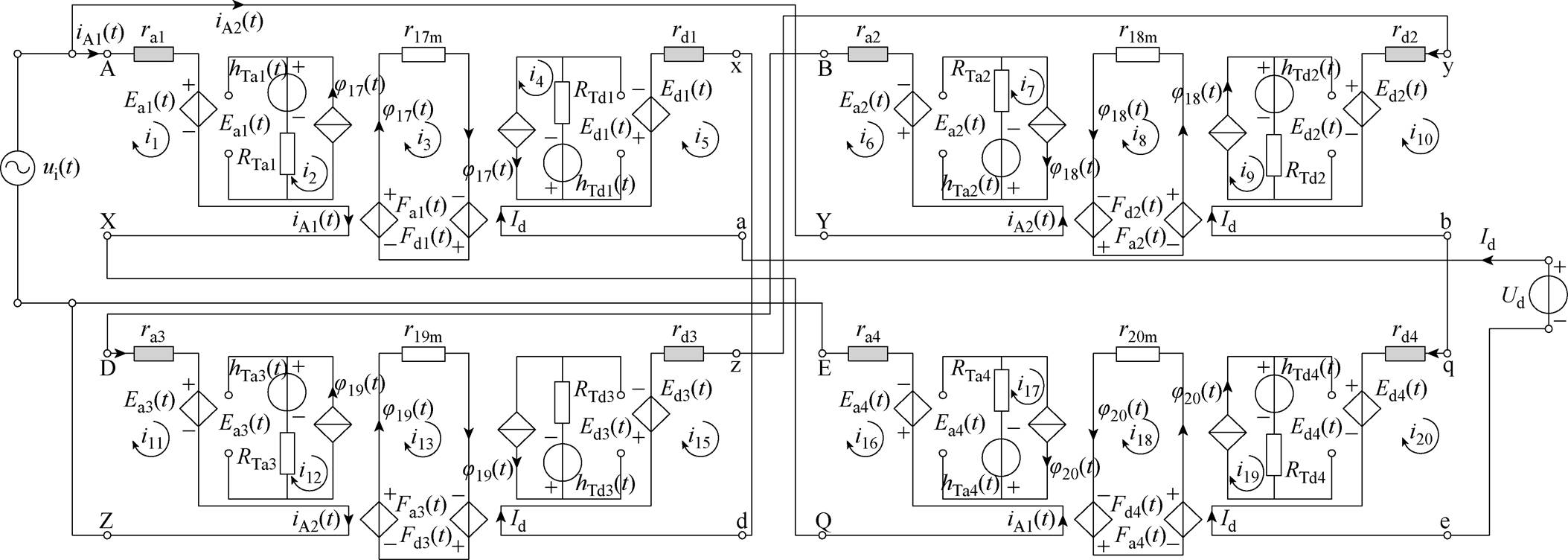
图11 MSCR的电磁耦合模型
Fig.11 Electromagnetic coupling model of MSCR
为求解MSCR电磁耦合模型,本文基于回路电流法建立其回路电压方程组。图11中,有
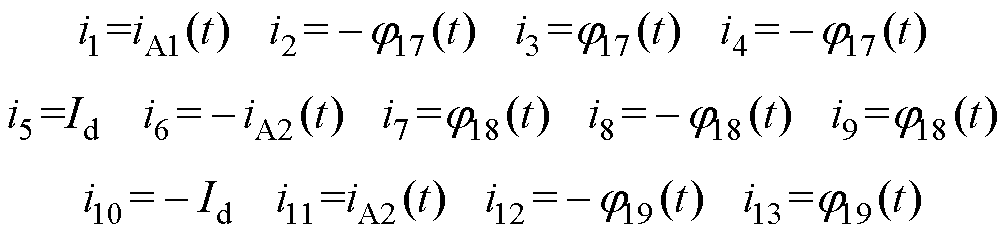
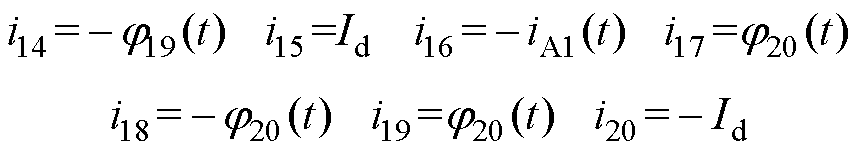
结合式(9)、式(11)、式(13)以及等效磁网络方程式(7),可列出的MSCR电磁网络方程组,即
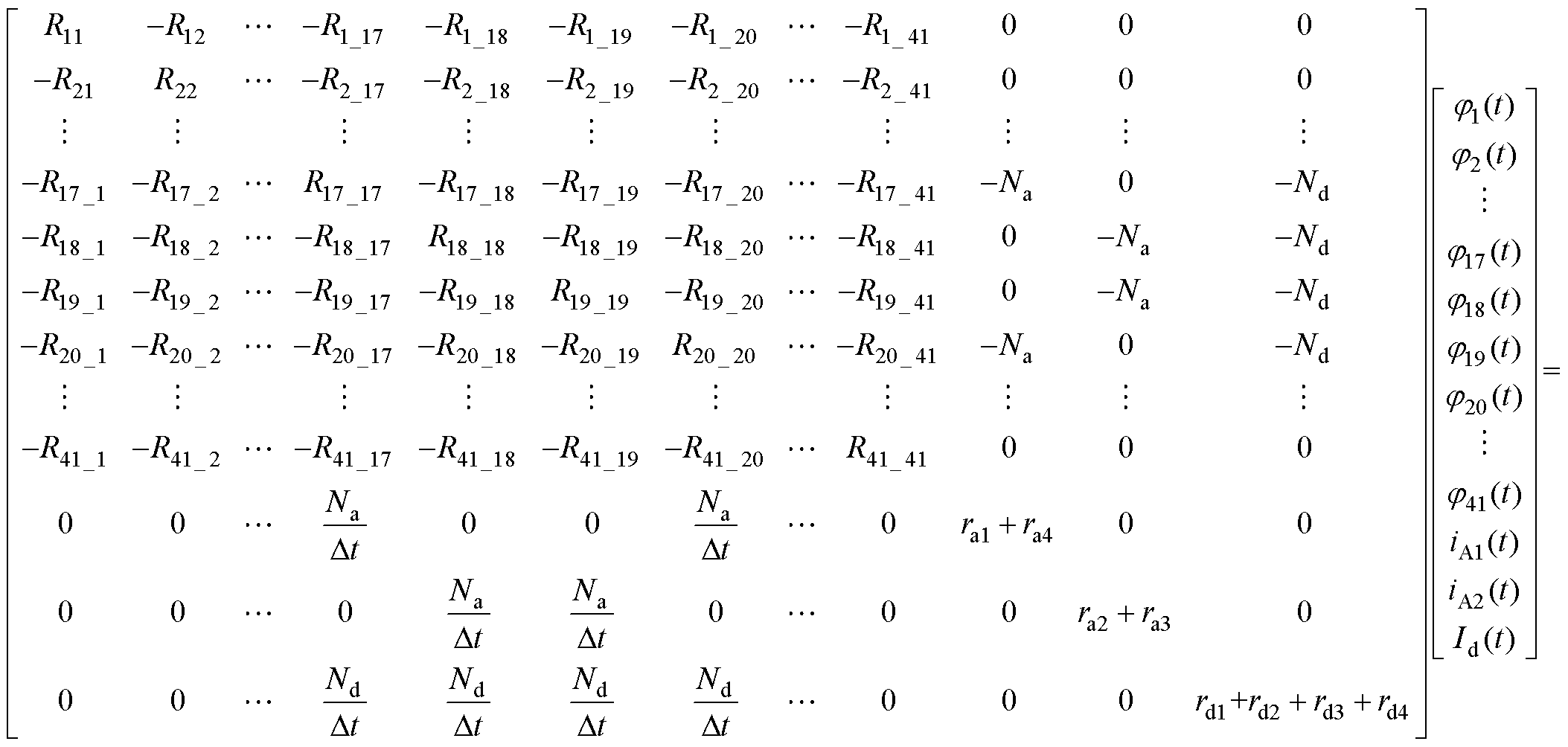
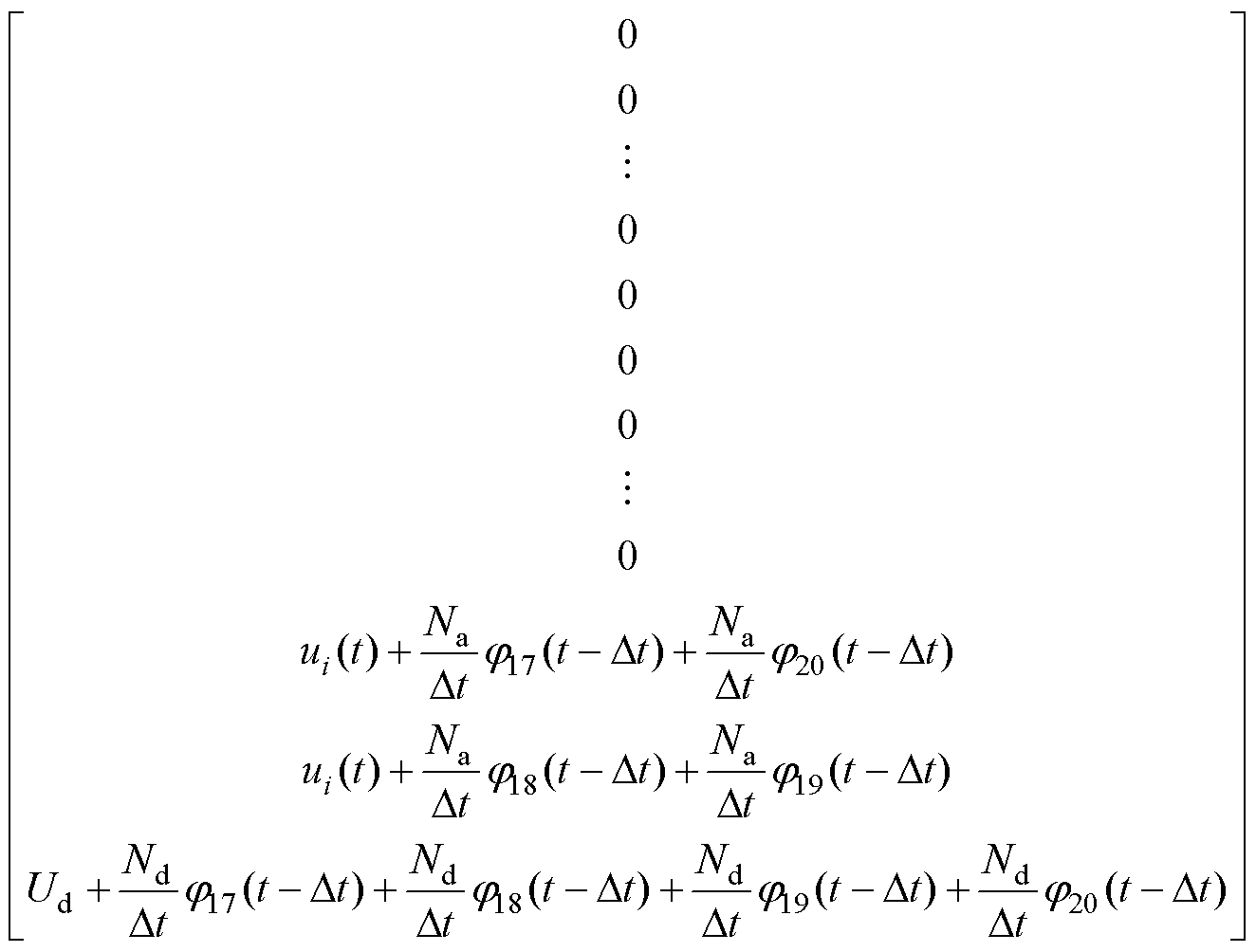 (14)
(14)
需要说明的是,MSCR直流励磁根据励磁电源的不同可采用直流电压源激励和直流电流源激励两种形式。若采用直流电流源励磁,则式(14)中的直流励磁电流Id为已知常数。
若将式(14)记为矩阵形式,则有
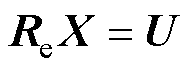 (15)
(15)
MSCR磁化曲线模型的非线性,使各磁通管磁阻的磁导率呈现动态实时变化的特征。为了对MSCR的非线性电磁网络方程式(15)进行求解,本文采用弦割法来解决磁通管磁导率的非线性问题[27]。图12所示为弦割法迭代求解原理示意图。
设第m-1次迭代求解的磁导率mm-1和Xm-1,则根据式(3)、式(4)和式(14),在第m次的迭代计算中,可得到磁通密度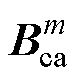 ,进而可得到对应的磁场强度Hm为
,进而可得到对应的磁场强度Hm为
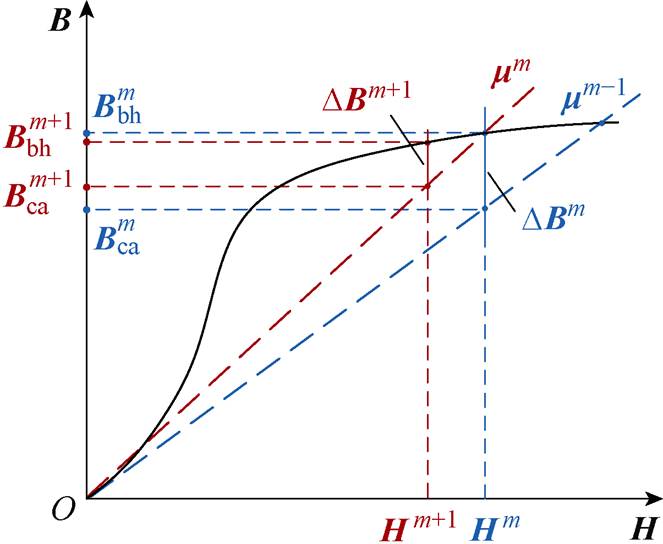
图12 弦割法迭代求解原理示意图
Fig.12 Schematic diagram of iterative solution principle based on chord secant method
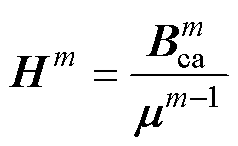 (16)
(16)
若将Hm代入式(5),可得到磁通密度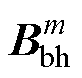 为
为
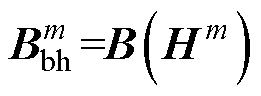 (17)
(17)
对于非线性动态电磁网络模型求解的理想结果是,寻求磁导率mm-1,使电磁网络方程计算得到的磁通密度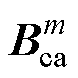 与其所对应的磁化曲线上的磁通密度
与其所对应的磁化曲线上的磁通密度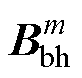 相等,因此,其非线性求解的迭代收敛判别条件为
相等,因此,其非线性求解的迭代收敛判别条件为
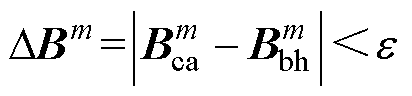 (18)
(18)
式中,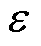 为预设误差。
为预设误差。
若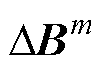 满足式(18),则停止迭代过程;否则,令
满足式(18),则停止迭代过程;否则,令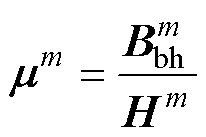 ,重复式(16)~式(18)。这里需注意的是,尽管将式(18)作为磁通管非线性参数计算迭代收敛的判别条件,但为了防止迭代计算因达不到迭代收敛条件而无限循环,还需对迭代次数加以限制。图13所示为MSCR电磁网络模型求解流程。
,重复式(16)~式(18)。这里需注意的是,尽管将式(18)作为磁通管非线性参数计算迭代收敛的判别条件,但为了防止迭代计算因达不到迭代收敛条件而无限循环,还需对迭代次数加以限制。图13所示为MSCR电磁网络模型求解流程。
为了对MSCR电磁网络模型的有效性进行验证,本文以一台220 V/2.2 kvar的他励式MSCR实验样机为分析对象,建立其场路耦合有限元模型,分别基于电磁网络(Electromagnetic Network, EMN)模型、有限元法(Finite Element Method, FEM)模型对不同磁饱和度下MSCR的绕组电流及磁通进行计算,并与实验测量结果进行对比分析。
图14所示为MSCR实验样机及爱泼斯坦方圈磁测量装置。MSCR铁心材料采用30Q130硅钢片叠装,采用图14b所示的爱泼斯坦方圈磁测量装置对铁心材料磁化曲线进行测量,并根据式(5)对其进行拟合。MSCR铁心截面为正方形,铁心磁阀位于铁心高度的中间位置,磁阀宽度为铁心宽度的1/3,绕组材料采用铜导线,且绕组匝数均为200匝。MSCR的额定电压为220 V,实测额定电流为13 A。在MSCR调节过程中,选取5个工况点进行实验测量,各工况的直流励磁电流与MSCR磁饱和度[28]的对应关系见表1。
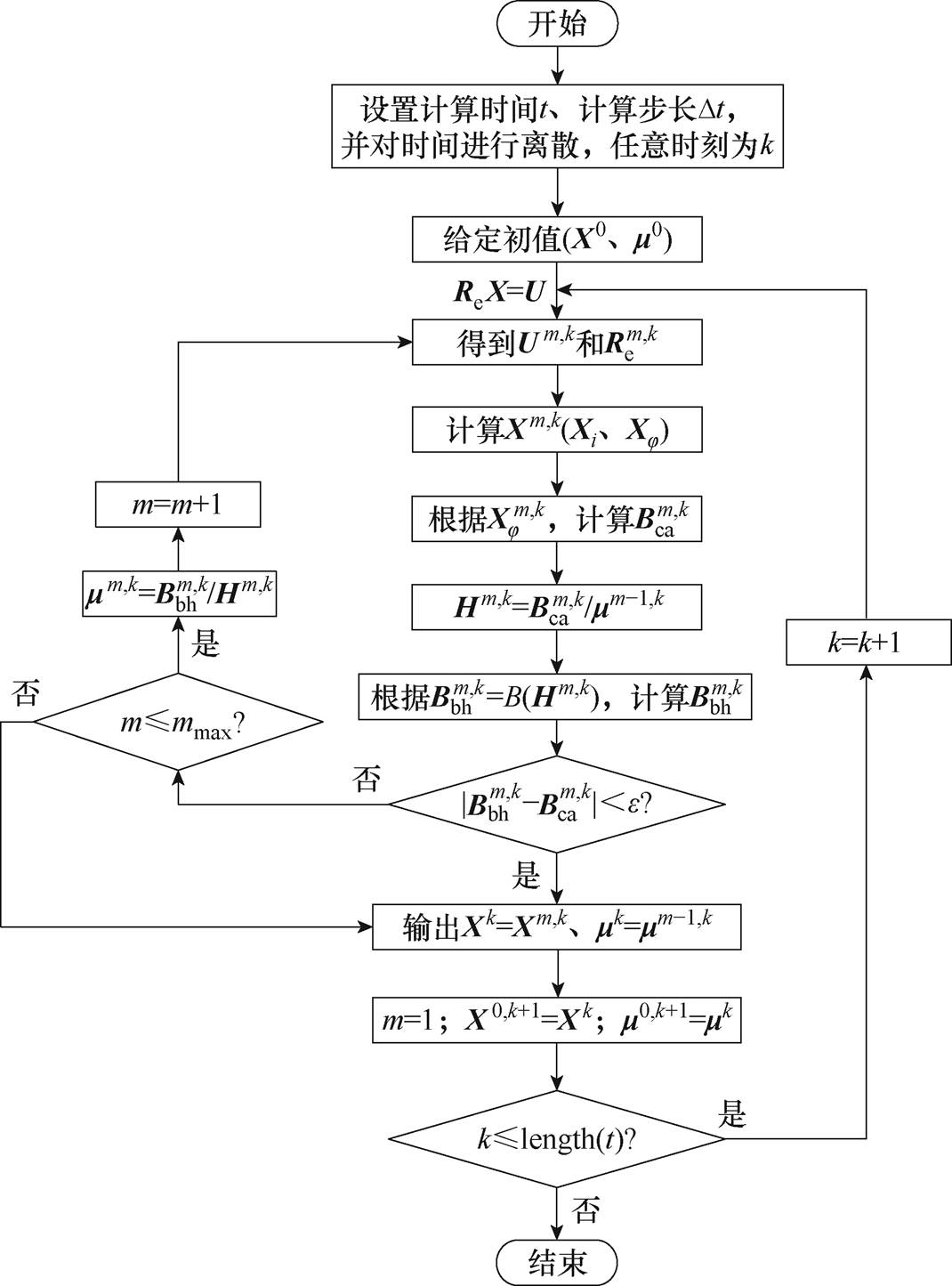
图13 MSCR电磁网络模型求解流程
Fig.13 The solution flowchart of the MSCR electromagnetic network model

图14 MSCR实验样机及磁测量装置
Fig.14 MSCR experimental prototype and magnetic measurement device
表1 直流励磁电流与MSCR磁饱和度对应关系
Tab.1 The relationship between DC excitation current and MSCR magnetic saturation
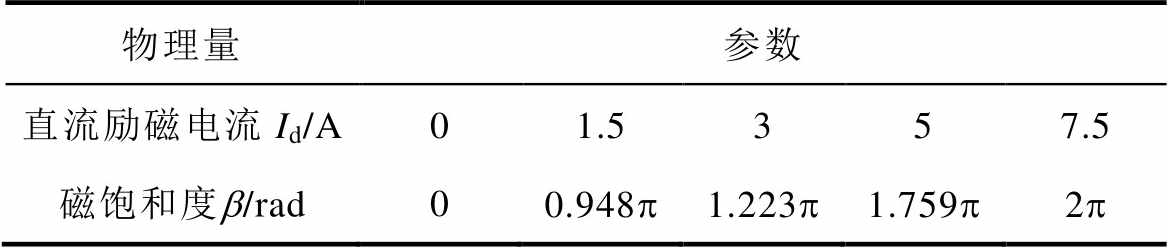
物理量参数 直流励磁电流Id/A01.5357.5 磁饱和度b/rad00.948p1.223p1.759p2p
为了对MSCR电磁参数进行有限元计算与分析,本文建立MSCR的有限元模型,如图15所示,并对其进行场路耦合联合仿真。这里需要说明的是,为了保证MSCR有限元模型的磁场正方向与图1一致,绕组W1、W3的电流正方向设置为逆时针旋转方向,绕组W2、W4的电流正方向设置为顺时针旋转方向。
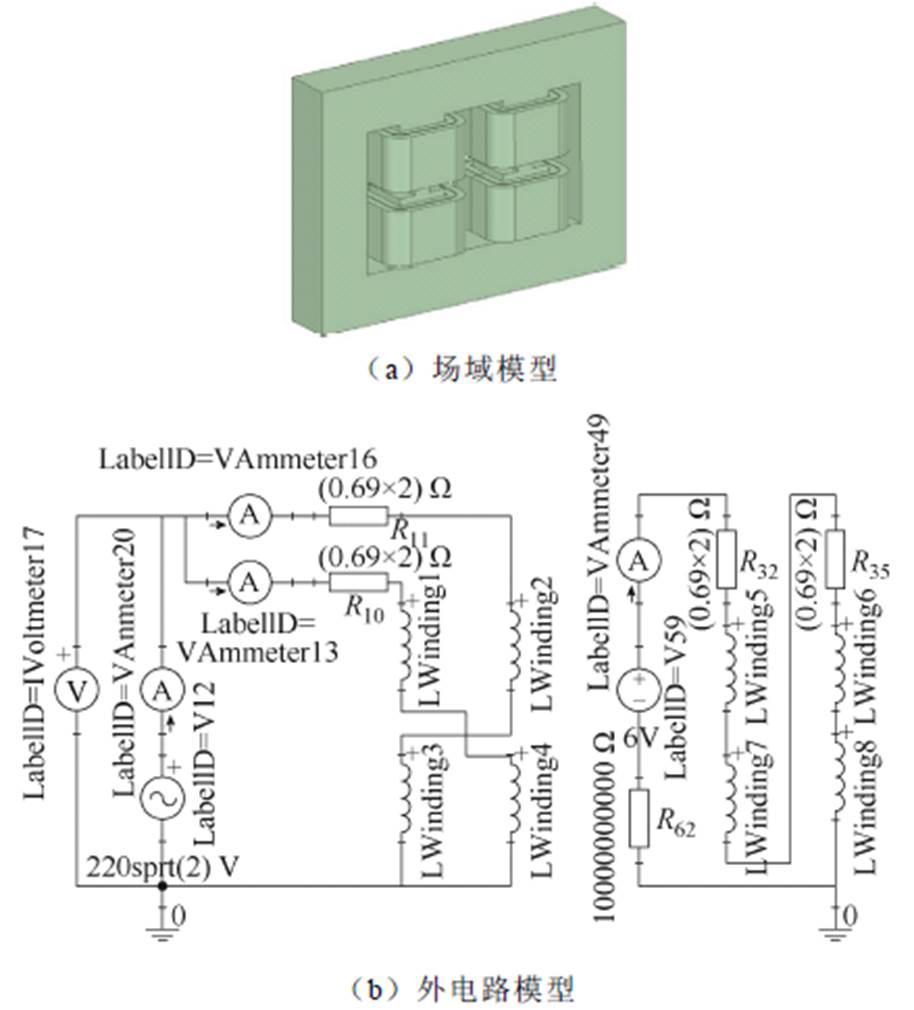
图15 MSCR场路耦合有限元模型
Fig.15 MSCR field-circuit coupled finite element model
为了验证MSCR电磁网络模型与有限元模型在绕组电流计算方面的有效性,本文基于两种模型计算了五种不同磁饱和度下的MSCR稳态工作电流波形,如图16所示,图中也一并给出了实验测量波形。
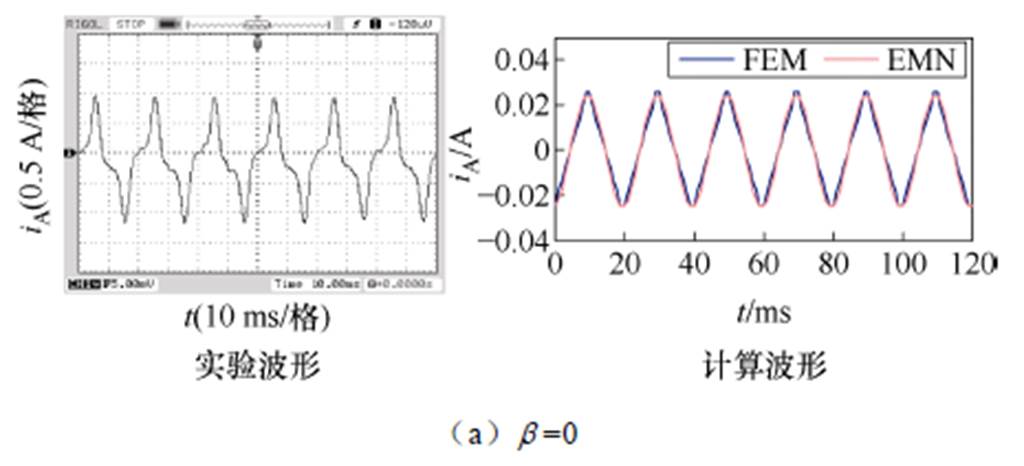
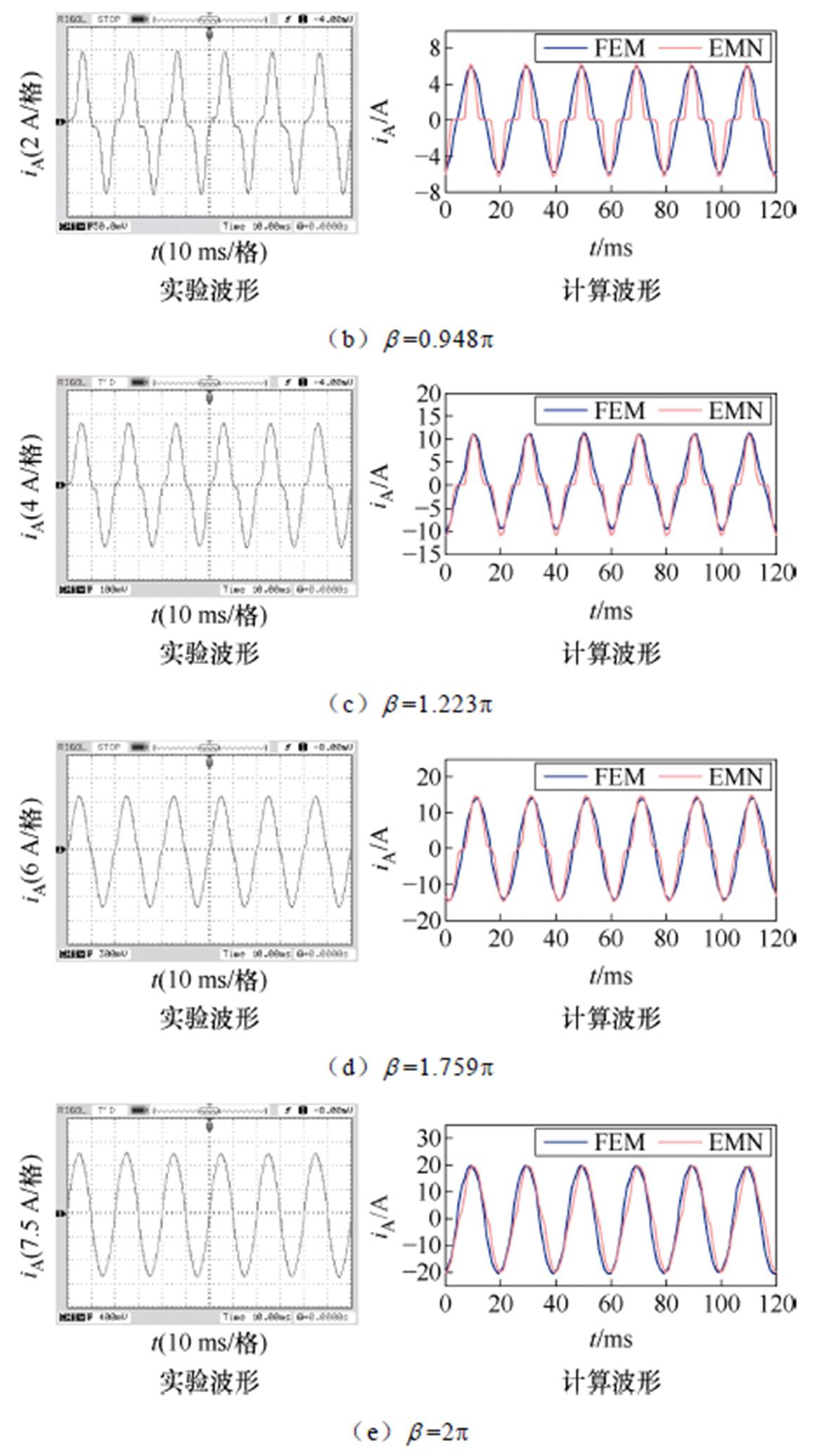
图16 不同磁饱和度下MSCR工作绕组电流波形
Fig.16 Current waveforms of MSCR working winding under different magnetic saturations
从图16a所示的MSCR空载工作电流实验波形可以看出,空载状态下,MSCR工作电流发生了畸变,而并非理论上的正弦波。这是由于MSCR铁心实际上存在磁滞效应、涡流效应以及叠片效应等特征,使其空载电流呈现为尖顶波;而在MSCR电磁网络模型和有限元模型中,为了简化计算、便于分析,铁心的磁化曲线模型尽管考虑了饱和非线性,但却忽略了磁滞效应等特性,因此,MSCR空载电流近似为正弦波。从图16b~图16e中可以看出,在MSCR调节过程中,不同磁饱和度下,基于电磁网络模型和有限元模型的MSCR工作电流波形与实验波形具有良好的一致性,由此可说明,MSCR非线性动态电磁网络模型在绕组电流计算方面的有效性,以及有限元模型的有效性。
为了验证MSCR电磁网络模型在磁场计算方面的有效性,本文以磁阀位置处(即网格21)为代表,对不同磁饱和度下的磁阀磁通进行计算与分析,如图17所示,为了便于对比,图中也一并给出了有限元模型的计算结果。
由图17可看出,在MSCR调节过程中,不同磁饱和度下,基于电磁网络模型的磁阀位置处磁通波形与有限元模型基本一致,由此说明MSCR非线性动态电磁网络模型在磁场计算方面的有效性。
计算耗时与计算精度是评价计算模型优劣的重要指标[29]。不同磁饱和度下,基于电磁网络模型和有限元模型的MSCR磁场计算与工作电流计算的计算精度见表2,计算耗时与计算存储空间见表3。其中,计算耗时和计算存储空间主要指计算模型完成50个计算周期(1 s)所消耗的计算时长和所占用的计算存储空间,计算精度主要从计算波形的峰值和有效值两个方面来分析,工作电流和磁阀磁通的误差计算公式为
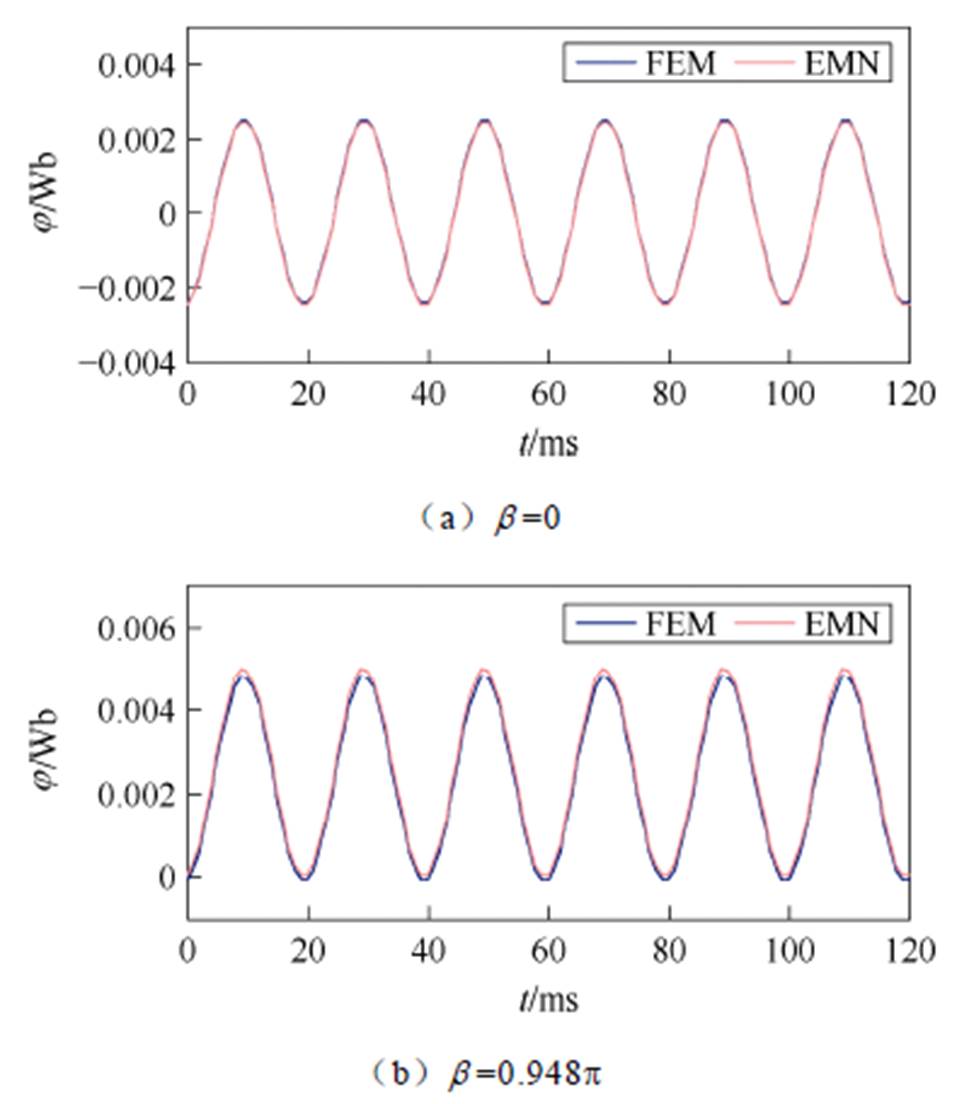
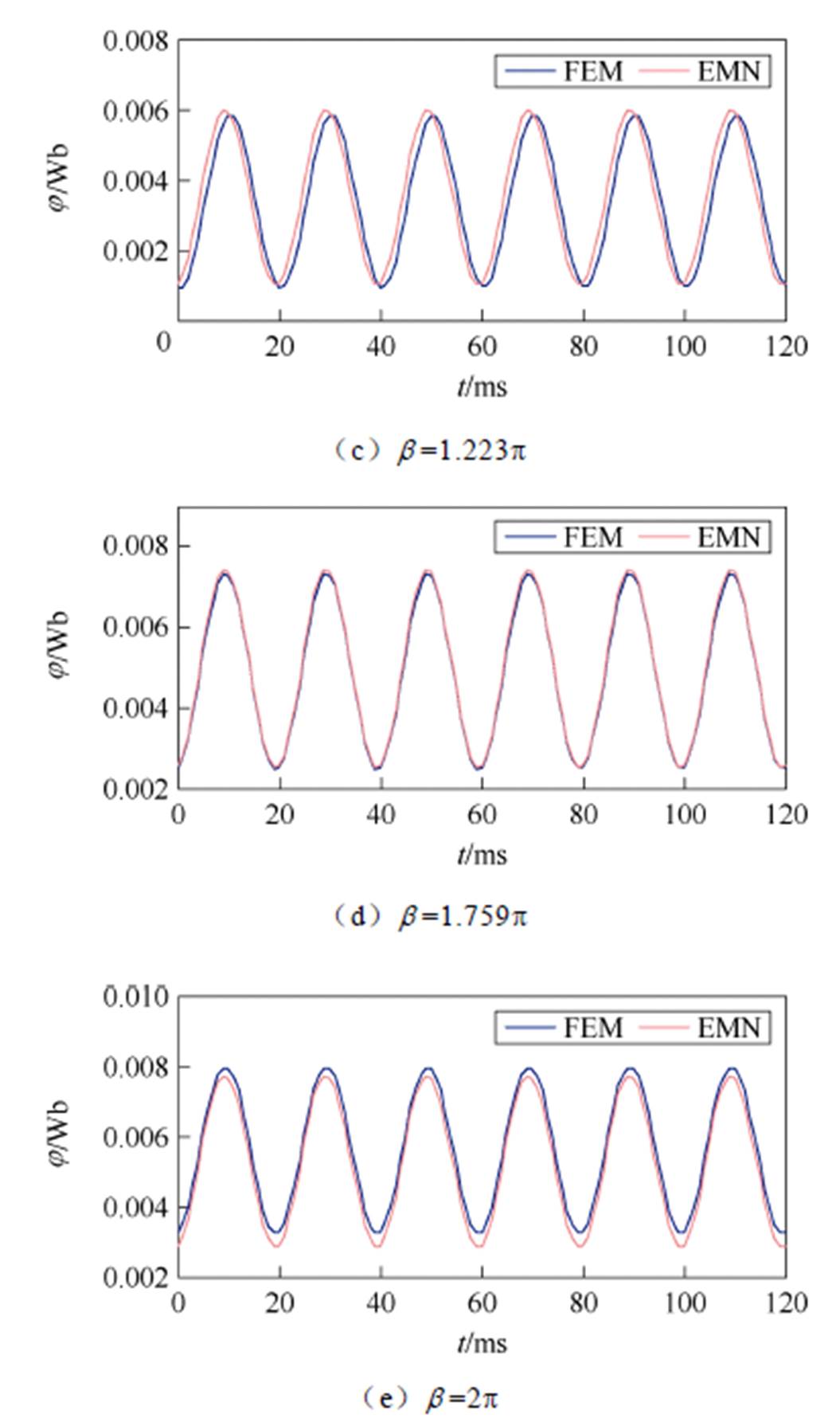
图17 不同磁饱和度下MSCR磁阀磁通波形
Fig.17 Magnetic flux waveforms at MSCR magnetic valves under different magnetic saturations
表2 MSCR计算模型的计算精度
Tab.2 Calculation accuracy of MSCR calculation model
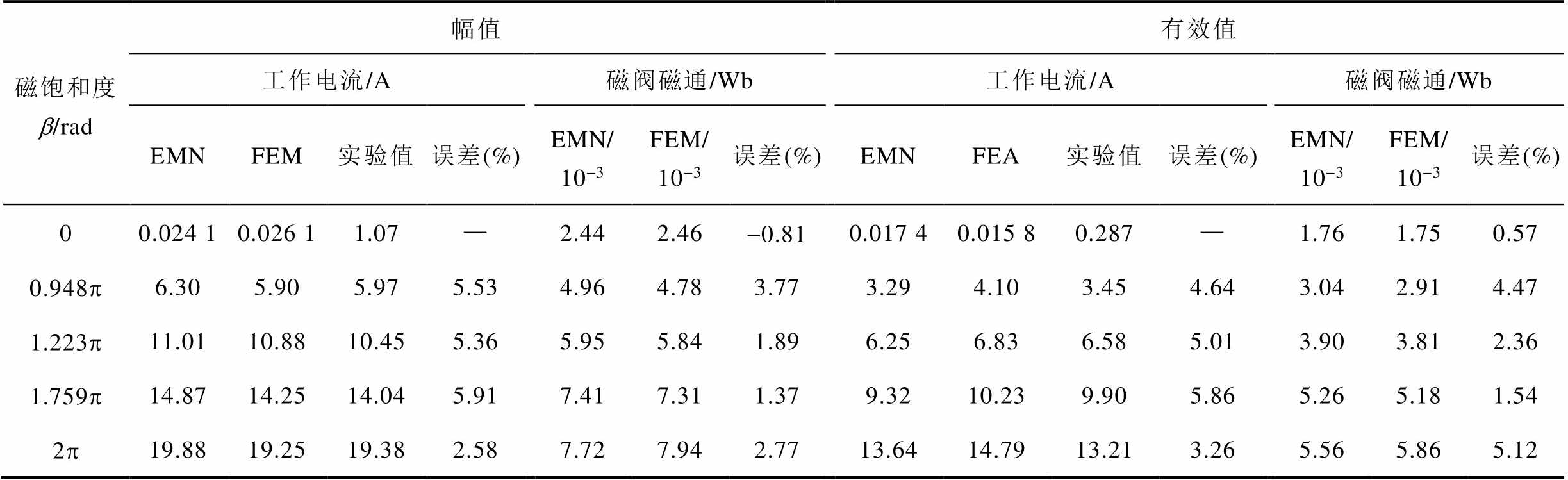
磁饱和度b/rad幅值有效值 工作电流/A磁阀磁通/Wb工作电流/A磁阀磁通/Wb EMNFEM实验值误差(%)EMN/10-3FEM/10-3误差(%)EMNFEA实验值误差(%)EMN/10-3FEM/10-3误差(%) 00.024 10.026 11.07—2.442.46-0.810.017 40.015 80.287—1.761.750.57 0.948p6.305.905.975.534.964.783.773.294.103.454.643.042.914.47 1.223p11.0110.8810.455.365.955.841.896.256.836.585.013.903.812.36 1.759p14.8714.2514.045.917.417.311.379.3210.239.905.865.265.181.54 2p19.8819.2519.382.587.727.942.7713.6414.7913.213.265.565.865.12
表3 MSCR计算模型的计算耗时与计算存储
Tab.3 Calculation time and storage of MSCR calculation model
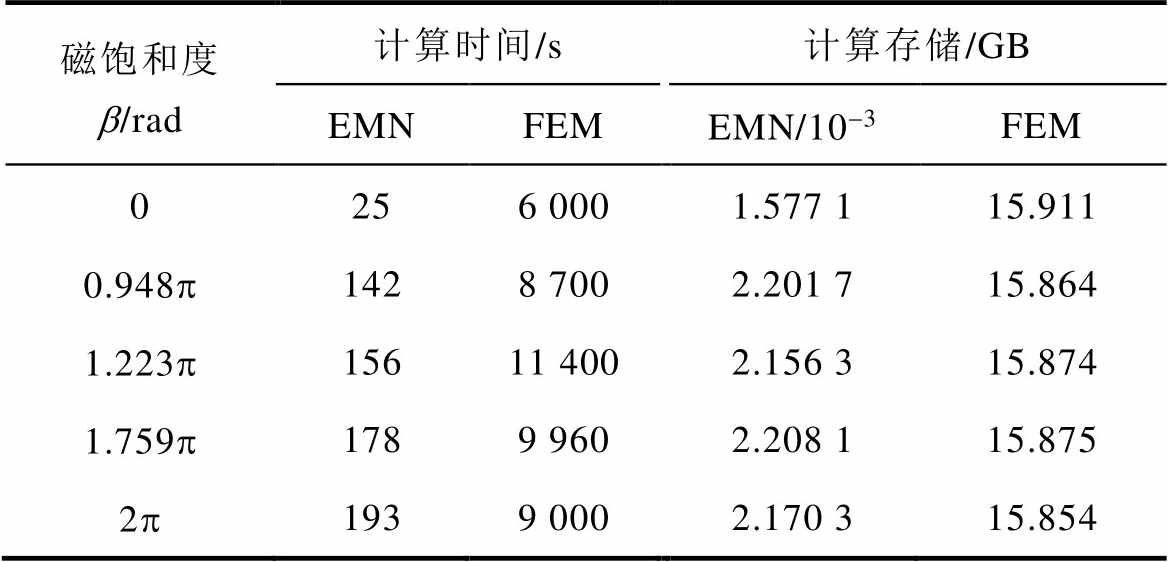
磁饱和度b/rad计算时间/s计算存储/GB EMNFEMEMN/10-3FEM 0256 0001.577 115.911 0.948p1428 7002.201 715.864 1.223p15611 4002.156 315.874 1.759p1789 9602.208 115.875 2p1939 0002.170 315.854
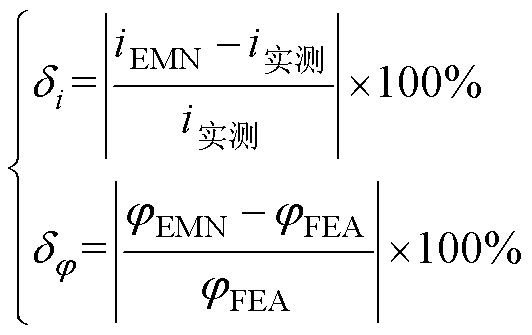 (19)
(19)
式中,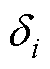 、
、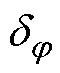 分别为工作电流与磁阀磁通的计算误差;
分别为工作电流与磁阀磁通的计算误差;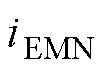 、
、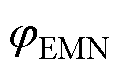 分别为工作电流与磁阀磁通的电磁网络模型计算结果;
分别为工作电流与磁阀磁通的电磁网络模型计算结果;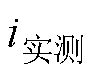 为工作电流的实验测量结果;
为工作电流的实验测量结果;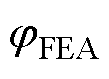 为磁阀磁通的有限元计算结果。
为磁阀磁通的有限元计算结果。
本次计算平台的计算机处理器为Intel(R) Core i7@1.90 GHz四核,计算机内存为16 GB,计算步长均为1 ms。
由于MSCR的电磁网络模型与有限元模型在建模过程中未考虑铁心的磁滞效应、涡流效应以及叠片效应,造成MSCR空载状态下的工作绕组电流计算结果与实验测量存在较大误差。根据表2所示,从计算精度方面来看,在MSCR调节过程中,基于电磁网络模型的MSCR工作绕组电流与实验测量结果的误差均不超过6%,磁阀磁通与有限元模型计算结果误差均不超过5.2%,其计算精度基本满足工程要求。根据表3所示,从计算速度方面来看,基于电磁网络模型的MSCR的电磁参数计算耗时远远小于有限元模型,计算速度约为有限元模型的50~240倍,且随着磁饱和度的增加,基于电磁网络模型的MSCR电磁参数计算耗时有所增加,这是因为铁心磁饱和度的加深导致磁通管在非线性参数计算过程中的迭代次数增加;从计算存储空间来看,基于电磁网络模型的MSCR电磁参数计算所占用的存储空间仅约为电磁网络模型的1/10 000~1/7 000,大大节省了存储空间。综上可知,MSCR电磁网络模型在满足计算精度的情况下有效地提高计算效率,降低计算代价,在可控电抗器的初期设计、理论分析以及电力系统的系统级仿真方面具有独特的优势。
针对MSCR计算模型要么太简单而计算误差大,要么太复杂而计算耗时长,进而无法实现电力系统一体化设计和系统性分析的问题,本文基于网络理论提出一种兼顾理论分析准确性与参数计算高效性的MSCR计算新方法——非线性动态电磁网络模型。基于此,对不同磁饱和度下的MSCR工作电流与铁心磁通进行计算,从计算精度与计算速度、计算存储方面,将计算结果与有限元模型和实验结果进行对比分析,所得结论如下:
1)MSCR的非线性动态电磁网络模型在不同磁饱和度下的工作电流与铁心磁通计算结果,与有限元模型计算结果和实验结果具有良好的一致性,由此可说明MSCR非线性动态电磁网络模型在电磁参数计算方面的有效性。
2)MSCR非线性动态电磁网络模型在电磁参数计算方面的计算速度约为有限元模型的50~240倍,而存储空间仅约为有限元模型的1/10 000~1/7 000,能够大大地节省计算时间和存储空间,在满足计算精度的情况下有效地提高计算效率,降低计算代价,在可控电抗器的初期设计以及电力系统的系统级仿真方面具有独特的优势。
参考文献
[1] 何正友, 李波, 廖凯, 等. 新形态城市电网保护与控制关键技术[J]. 中国电机工程学报, 2020, 40(19): 6193-6207.
He Zhengyou, Li Bo, Liao Kai, et al. Key tech- nologies for protection and control of novel urban power grids[J]. Proceedings of the CSEE, 2020, 40(19): 6193-6207.
[2] 滕贤亮, 谈超, 昌力, 等. 高比例新能源电力系统有功功率与频率控制研究综述及展望[J]. 电力系统自动化, 2023, 47(15): 12-35.
Teng Xianliang, Tan Chao, Chang Li, et al. Review and prospect of research on active power and frequency control in power system with high pro- portion of renewable energy[J]. Automation of Electric Power Systems, 2023, 47(15): 12-35.
[3] 陈冲, 贾利民, 赵天宇, 等. 去碳化导向的轨道交通与新能源融合发展: 形态模式、解决方案和使/赋能技术[J]. 电工技术学报, 2023, 38(12): 3321-3337.
Chen Chong, Jia Limin, Zhao Tianyu, et al. Decarbonization-oriented rail transportation and renewable energy integration development: con- figurations, solutions, and enabling/empowering technologies[J]. Transactions of China Electro- technical Society, 2023, 38(12): 3321-3337.
[4] Shen Shifeng, Wu Xusheng, Yan Sinian, et al. Research on the characteristics of a high-temperature superconducting leakage flux-controlled reactor[J]. IEEE Transactions on Industrial Electronics, 2022, 69(10): 10101-10111.
[5] 马伟明, 王东, 程思为, 等. 高性能电机系统的共性基础科学问题与技术发展前沿[J]. 中国电机工程学报, 2016, 36(8): 2025-2035.
Ma Weiming, Wang Dong, Cheng Siwei, et al. Common basic scientific problems and development of leading-edge technology of high performance motor system[J]. Proceedings of the CSEE, 2016, 36(8): 2025-2035.
[6] Yuan Jiaxin, Zheng Xianfeng, Chen Fan. Analysis and optimized design of a novel compact orthogonal controllable reactor[J]. IEEE Transactions on Power Delivery, 2022, 37(6): 4527-4538.
[7] 袁佳歆, 叶丛韬, 陈鹤冲, 等. 基于非正交解耦原理的紧凑型高压交流磁饱和限流器研究[J]. 高电压技术, 2023, 49(3): 1172-1183.
Yuan Jiaxin, Ye Congtao, Chen Hechong, et al. Research on compact high-voltage saturated core fault current limiter based on non-orthogonal decoupling principle[J]. High Voltage Engineering, 2023, 49(3): 1172-1183.
[8] 田铭兴, 王田戈, 张慧英, 等. 可控电抗器研究综述及展望[J]. 吉林大学学报(工学版), 2023, 53(2): 328-345.
Tian Mingxing, Wang Tiange, Zhang Huiying, et al. Overview and prospect of controllable reactor[J]. Journal of Jilin University (Engineering and Tech- nology Edition), 2023, 53(2): 328-345.
[9] 王青朋, 白保东, 陈德志, 等. 800kV超高压磁饱和可控电抗器的动态特性分析及谐波抑制[J]. 电工技术学报, 2020, 35(增刊1): 235-242.
Wang Qingpeng, Bai Baodong, Chen Dezhi, et al. Dynamic characteristics and harmonic suppression of 800kV extra-high voltage magnetically saturation controlled reactor[J]. Transactions of China Electro- technical Society, 2020, 35(S1): 235-242.
[10] Zhang Huiying, Tian Mingxing, Jing Pei. Effect of magnetization curve model and winding connection mode on magnetically saturated controllable reactor based on ANSYS[C]//2019 22nd International Con- ference on Electrical Machines and Systems (ICEMS), Harbin, China, 2019: 1-5.
[11] Chen Xuxuan, Wang Bin. Optimal design and modeling of the multi-stage saturable magnetically controlled reactor[C]//2017 Progress In Electro- magnetics Research Symposium-Spring (PIERS), St. Petersburg, Russia, 2017: 76-81.
[12] Xu Xiangzheng. Research on magnetic valve structure optimization of magnetic controlled reactor[J]. The Open Mechanical Engineering Journal, 2014, 8(1): 655-661.
[13] Liang Yanping, Zhang Fang, Zhang Haiting, et al. Leakage inductance calculation and simulation research of extra-high voltage magnetically controlled shunt reactor[C]//2010 International Conference on Mechanic Automation and Control Engineering, Wuhan, China, 2010: 4025-4028.
[14] Dong Liwei, Tian Mingxing, Zhang Huiying. Magnetic circuit model of magnetic valve controllable reactor considering magnetic flux leakage effect[C]// 2021 International Conference on Mechatronics Tech- nology and Intelligent Manufacturing, Hangzhou, China, 2021: 1-7.
[15] Zhang Huiying, Tian Mingxing, Li Hongchen, et al. Improved gyrator-capacitor model considering eddy current and excess losses based on loss separation method[J]. AIP Advances, 2020, 10(3): 035309.
[16] 田铭兴, 石鹏太, 马亚珍. n级饱和磁阀式可控电抗器结构特性和仿真方法[J]. 电力自动化设备, 2016, 36(2): 95-101.
Tian Mingxing, Shi Pengtai, Ma Yazhen. Structural property and simulation method of n-stage saturable magnetic-valve controllable reactor[J]. Electric Power Automation Equipment, 2016, 36(2): 95-101.
[17] Xing Tianming, Sheng Yuandong, Hong Yan. Harmo- nic characteristic analysis of magnetically saturation controlled reactor[J]. TELKOMNIKA Indonesian Journal of Electrical Engineering, 2013, 11(8): 4214- 4221.
[18] Turowski J, Turowski M, Kopec M. Method of three- dimensional network solution of leakage field of three-phase transformers[J]. IEEE Transactions on Magnetics, 1990, 26(5): 2911-2919.
[19] Worotyński J, Turowski M, Mendrela E A. The accuracy of calculation of magnetic fields, inductance and forces in electromagnetic devices using the reluctance network method (RNM)[J]. COMPEL-the International Journal for Computation and Mathe- matics in Electrical and Electronic Engineering, 1994, 13(1): 159-162.
[20] 夏云彦, 周洲, 邵远亮, 等. 基于动态磁网络法大型感应电机阻抗参数及起动特性计算[J]. 电工技术学报, 2024, 39(14): 4341-4352.
Xia Yunyan, Zhou Zhou, Shao Yuanliang, et al. Calculation of impedance parameters and starting characteristics of large induction motor based on dynamic magnetic network[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4341-4352.
[21] 佟文明, 王萍, 吴胜男, 等. 基于三维等效磁网络模型的混合励磁同步电机电磁特性分析[J]. 电工技术学报, 2023, 38(3): 692-702.
Tong Wenming, Wang Ping, Wu Shengnan, et al. Electromagnetic performance analysis of a hybrid excitation synchronous machine based on 3D equivalent magnetic network[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 692- 702.
[22] 杨云, 徐奇伟, 苗轶如, 等. 磁力提升型CRDM的动态等效磁网络模型建立与多场耦合计算方法[J/OL]. 电工技术学报, 2024: 1-14. (2024-08-27). http://kns.cnki.net/KCMS/detail/detail.aspx? filename= DGJS20240823005&dbname=CJFD&dbcode=CJFQ.
Yang Yun, Xu Qiwei, Miao Yiru, et al. Establishment of dynamic equivalent magnetic network model and multi-field coupling calculation method for magnetic lift CRDM[J/OL]. Transactions of China Electro- technical Society, 2024:1-14. (2024-08-27). http:// kns.cnki.net/KCMS/detail/detail.aspx?filename=DGJS- 20240823005&dbname=CJFD&dbcode=CJFQ.
[23] Jan K Sykulski. Computational magnetics[M]. London, England: Chapman & Hall, 1995.
[24] 田铭兴, 马亚珍, 石鹏太. 磁阀式可控电抗器磁化特性研究[J]. 高压电器, 2019, 55(4): 125-132.
Tian Mingxing, Ma Yazhen, Shi Pengtai. Research on magnetization characteristic of magnetic-valve con- trollable reactor[J]. High Voltage Apparatus, 2019, 55(4): 125-132.
[25] 李永建, 李宗明, 利雅婷, 等. 考虑磁-力耦合效应的混合磁滞模型研究[J]. 电工技术学报, 2024, 39(22): 6941-6951.
Li Yongjian, Li Zongming, Li Yating, et al. Study of hybrid hysteresis model considering magnetic-force coupling effect[J]. Transactions of China Elec- trotechnical Society, 2024, 39(22): 6941-6951.
[26] 刘任, 杜莹雪, 李琳, 等. 解析逆Preisach磁滞模型[J]. 电工技术学报, 2023, 38(10): 2567-2576.
Liu Ren, Du Yingxue, Li Lin, et al. Analytical inverse Preisach hysteresis model[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2567-2576.
[27] Fu Dongshan, Gong Jinlin, Xu Yanliang, et al. Coupled circuit and magnetic model for a transverse flux permanent magnet linear motor[J]. IEEE Access, 2020, 8: 159274-159283.
[28] 陈柏超. 新型可控饱和电抗器理论及应用[M]. 武汉: 武汉水利电力大学出版社, 1999.
[29] Cao Donghui, Zhao Wenxiang, Ji Jinghua, et al. A generalized equivalent magnetic network modeling method for vehicular dual-permanent-magnet vernier machines[J]. IEEE Transactions on Energy Con- version, 2019, 34(4): 1950-1962.
Research on Nonlinear Dynamic Electromagnetic Network Model of Magnetically-Saturated Controllable Reactor
Abstract With the increasing scale of urban power grids and the application of various advanced power equipment, the comprehensive efficiency of the power system depends on the cooperation and synergy between various power equipment. Aiming at the physical entities with dynamic and real-time changes in the state of power equipment, constructing an efficient mathematical model is essential in system-level simulation of power systems and integrated design of large electromagnetic equipment. Taking the magnetically-saturated controllable reactor (MSCR) as the object, this paper proposes a nonlinear dynamic electromagnetic network model, considering the accuracy of theoretical analysis and the efficiency of parameter calculation.
Firstly, according to the structural characteristics and magnetic field distribution characteristics of MSCR, the MSCR solution domain is meshed by domain discretization. Considering the nonlinearity of the iron core, the magnetization curve model of the MSCR iron core is established by the piecewise interpolation method. The nonlinear grid parameters are calculated according to the principle of the flux tube. The MSCR equivalent magnetic network model is generated based on the loop current method.
Secondly, the electromagnetic model of circuit-magnetic circuit separation is established. The electromagnetic coupling equivalent circuit is established using the controlled source to realize the coupling connection between the circuit and the magnetic circuit. The nonlinear dynamic electromagnetic network model of MSCR is generated. Combined with the nonlinear iterative solution of the chord-cut method, the MSCR winding current and the core flux under different magnetic saturations are calculated.
Finally, a three-dimensional finite element model of MSCR is established based on the finite element method, and field-circuit coupling joint simulation is carried out. Experimental measurements are also performed on the MSCR winding current. The MSCR nonlinear dynamic electromagnetic network model is compared with the three-dimensional finite element model and experimental measurements. The MSCR nonlinear dynamic electromagnetic network model is verified.
(1) The proposed model's calculated winding current and core flux agree with the finite element model and experimental results under different magnetic saturations. (2) The calculation speed and the storage space of the proposed model in electromagnetic parameter calculation are approximately 50~240 times and 1/10 000~1/7 000 of the finite element model. The model can improve calculation efficiency and reduce cost while meeting computational accuracy. It has unique advantages in the initial design of controllable reactors and system-level simulation of power systems.
keywords:Magnetically-saturated controllable reactor (MSCR), electromagnetic network model, electro- magnetic parameter calculation, finite element method
中图分类号:TM474
DOI: 10.19595/j.cnki.1000-6753.tces.241468
国家自然科学基金(52167013),甘肃省自然科学基金(22JR5RA320, 24JRRA244),渭南市重点研发计划(2023ZDYFJH-303),陕西省教育厅一般专项科研(24JK0384)资助项目。
收稿日期 2024-08-16
改稿日期2024-09-30
王田戈 女,1993年生,博士研究生,研究方向为可控电抗器电磁场计算、可控电抗器结构设计、磁集成技术应用。
E-mail: tiange6093@163.com
田铭兴 男,1968年生,教授,博士生导师,研究方向为电力系统电能质量分析与控制、电机与电器设计及其控制、电力电子技术及其应用等。
E-mail: tianmingxing@mail.lzjtu.cn(通信作者)
(编辑 郭丽军)