 ;④反向/降压(k<1
;④反向/降压(k<1 ;⑤正向/升压(k>1);⑥反向/升压(k>1)。定义输出、输入电压比为电压调整率k。
;⑤正向/升压(k>1);⑥反向/升压(k>1)。定义输出、输入电压比为电压调整率k。摘要 为了在功率传输或电压波动下实现双有源桥变换器连续且实时的应力优化控制,对其模式间规律以及模式内的优化控制变量间规律进行研究至关重要。现阶段的研究仍还存在应力优化控制变量函数表达式推导复杂等问题。针对此问题,该文运用遗传算法进行应力优化,解析出各个模式的优化变量间规律。基于此,采用三角函数极坐标法推导出相应优化控制变量函数表达式。首先,利用图形分析法从十二种工作模式中筛选出四种局部最优模式,这四种模式在不同功率区间内具备应力或有效值较低的特征;其次,对四种模式进行应力优化并对比分析优化结果,解析出这四种模式在不同功率段下优化变量间的规律;再次,基于此规律运用三角函数极坐标法推导出电流应力函数表达式及其优化控制变量函数表达式;最后,通过对比这四种模式在全功率区间的电流应力,选择各功率段上的最优模式和最优控制变量,从而实现全局应力优化控制。仿真和实验证明了理论分析的正确性以及优化控制策略有效性。
关键词:双有源桥变换器 应力优化 局部最优工作模式 全局最优工作模式 三角函数极坐标法
直流配电网因供电半径大、线路损耗小,并且不涉及相位、频率和无功功率控制问题,已成为国内外研究热点[1-2]。直流变换装备作为直流配电系统的核心设备,成为目前研究的热点与难点。双有源桥(Dual Active Bridge, DAB)变换器因其具有结构对称、能量双向流动、电气隔离、功率密度高等优势,成为目前直流电能变换装备研究的热点[3-5]。
DAB效率优化研究一直是难点与热点。目前DAB的效率优化主要包括三个技术路线:①调制方法优化,由传统单移相(Single-Phase-Shift, SPS)、扩展移相(Extended-Phase-Shift, EPS)、双移相(Dual-Phase-Shift, DPS)调制发展到三重移相(Triple-Phase-Shift, TPS)调制[6-8];②先进开关器件应用;③新型高效高频变压器应用[9-10]。其中,DAB调制方法中三重移相为主流调制方法,三重移相调制虽然控制相对复杂,但其拥有三个控制自由度,进而能更好地进行优化控制,从而达到提升整体效率的目的。
目前DAB在建模、工作模式分类和简化等方面已有大量研究,但在优化变量间的规律总结以及控制函数数学推导方面仍然存在不足。在工作模式分类和规律总结方面,文献[11]对DAB建模,并得到十二种工作模式,利用粒子群算法对各个工作模式进行应力优化并总结优化变量之间规律,但是未能得到全部优化变量间的规律,使得所得优化结果陷于局部最优,有待进一步完善。文献[12]运用图形分析法将DAB三重移相的五种工作模式简化为两种,极大地减少了优化运算量,并通过复杂数学推导得到全工况优化控制量。但是该DAB模式分类仍存在不足,缺乏对优化变量间内在规律的深入分析。在优化算法方面,文献[13-15]从时域角度推导出电压、电流和功率的时域表达式,但是其中应力单目标优化采用KKT条件求解模式全局最优解。采用此方法的前提是目标函数和约束条件均为凸函数,这些要求证明复杂且难以满足。文献[16]采用线下优化和线上查表的方法。虽然此方法精度高、响应速度快,但是查表法需要预存优化数据,尤其当功率和电压都出现波动时,则需保存大量数据,对实时控制器存储容量和处理速度提出了更高要求。
针对以往研究中存在的不足,为了获得优化变量间规律以及相应优化控制变量的函数表达式,本文首先根据图形分析法总结出模式间规律,筛选出局部最优模式;其次通过时域建模,对电流应力进行单目标遗传优化,得到电压调整率k为不同值时的优化结果;再次分析和对比k为不同值的优化结果,解析出不同模式不同功率段的优化变量间规律;最后利用功率约束条件和三角函数极坐标法推导出优化控制变量函数表达式,实现了DAB变换器在全功率范围内的电流应力优化。具体创新点包括:
1)通过对不同电压调整率k下的电流应力优化结果进行分析和对比,解析出四种局部最优模式在不同功率段下优化变量间的规律。
2)基于优化变量间规律,运用功率约束和三角函数极坐标法准确地推导出应力最优控制变量的函数表达式。对比这四种工作模式的电流应力,选出全功率范围内应力全局最优控制变量。
根据DAB的功率流向和端口电压比例关系,可以将其运行工况分为六大类[12]:①正向/匹配(k=1);②反向/匹配(k=1);③正向/降压(k<1 ;④反向/降压(k<1
;④反向/降压(k<1 ;⑤正向/升压(k>1);⑥反向/升压(k>1)。定义输出、输入电压比为电压调整率k。
;⑤正向/升压(k>1);⑥反向/升压(k>1)。定义输出、输入电压比为电压调整率k。
由其结构的对称性可知:正向/匹配(k=1)可等效于反向/匹配(k=1);正向/降压(k<1 可等效于反向/升压(k>1);反向/降压(k<1
可等效于反向/升压(k>1);反向/降压(k<1 可等效于正向/升压(k>1)。等效的两种工况仅是输入和输出端口位置互换,对其分析无任何影响,因此只研究其中一个即可。本文以正向与反向的降压工况 (k<1)为主要研究对象。
可等效于正向/升压(k>1)。等效的两种工况仅是输入和输出端口位置互换,对其分析无任何影响,因此只研究其中一个即可。本文以正向与反向的降压工况 (k<1)为主要研究对象。
DAB拓扑结构如图1所示,由两个H桥组成两个端口,中间部分由电感L和高频变压器构成。C1和C2分别为输入、输出电容,Vi和Vo分别为变换器输入、输出直流电压,uh1和uh2分别为两个H桥输出电压,uL和iL分别为电感电压和电感电流,n为高频变压器电压比。输出端口交流电压uh2通过中间高频变压器折算到一次侧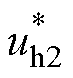 ,即
,即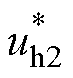 =nuh2。
=nuh2。
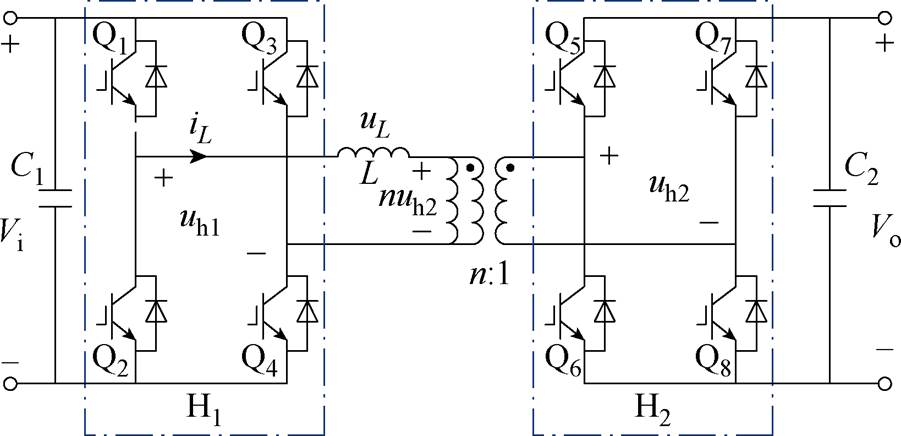
图1 DAB变换器的拓扑结构
Fig.1 Topology of DAB converter
DAB正向和反向传输的波形如图2所示。图2中,Dy1和Dy2分别为两个H桥输出电压高电平在半个周期中的占空比,Da为两个H桥输出电压上升沿相位差在半个周期中的占空比,其方向由输入端指向输出端。DAB通过改变这3个变量来实现功率双向传输。根据伏秒平衡可以得到,稳态下H桥输出电压和电感电流在前后半个周期内大小相等、方向相反。定义输出输入电压比为电压调整率为k,k= nVo/Vi。
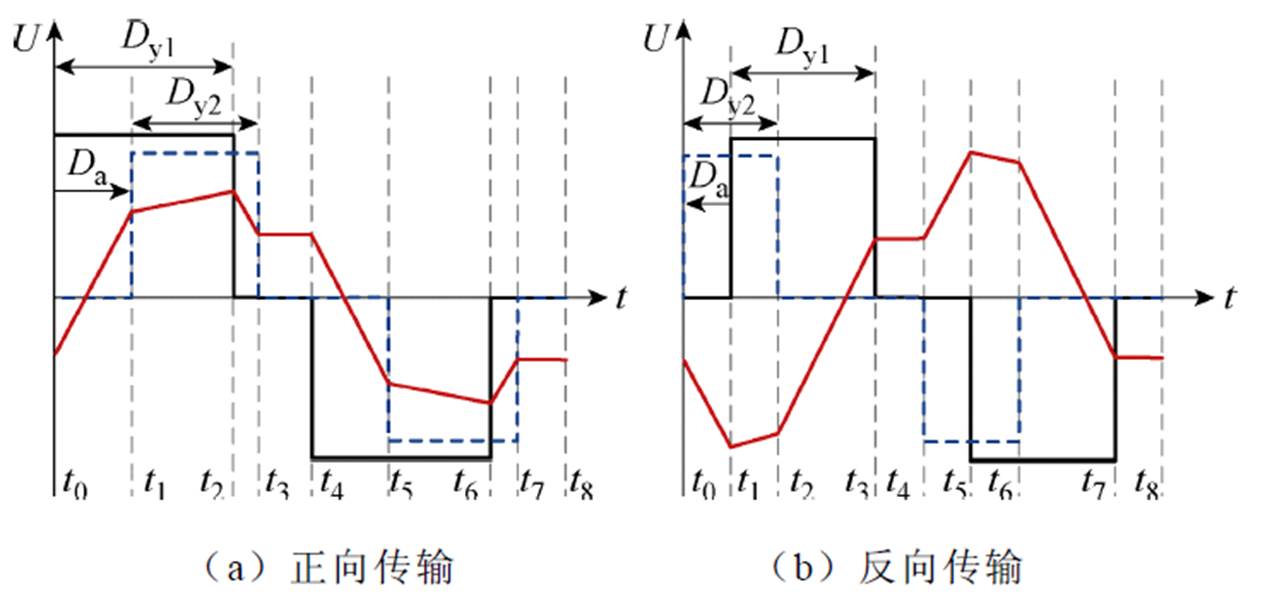
图2 DAB正向和反向传输的波形
Fig.2 DAB waveforms of forward and reverse transmission
根据DAB三重移相控制中Dy1、Dy2和Da的组合方式,可将DAB变换器工作模式分成十二种[11, 17];DAB变换器运行的第三和四种工况(降压工况)对应的工作模式类型见表1,其中工作模式1.2、1.6、2.4和2.6为双向功率传输模式。第五和六种工况(升压工况)和降压工况类似。根据Da是否大于零可将十二种工作模式分成两大类,见表2和附表3。其中工作模式1.1~1.6中Da>0,工作模式2.1~2.6中Da<0。表2中传输功率和功率范围均为标幺值,基准功率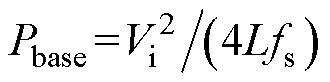 ,fs为开关频率。
,fs为开关频率。
DAB存在着十二种不同的工作模式,逐一优化每一种工作模式将是巨大的工作量。为减少优化工作量,就需减少优化的工作模式的数量。本节对每一种工作模式的波形进行分析并研究其特点,根据图形等效简化法以及波形与能量传输规律,从中筛选出不同功率区间内具备应力或有效值较低特征的工作模式即局部最优工作模式,这样有效地减小了优化模式数量。
表1 DAB降压工况下正反向功率传输的工作模式
Tab.1 Working mode of forward and reverse power transmission under DAB bucking condition

运行工况工作模式 正向/降压1.1、1.2、1.3、1.4、1.5、1.6、2.4、2.6 反向/降压2.1、2.2、2.3、2.4、2.5、2.6、1.2、1.6
表2 DAB变换器四种工作模式特征[11]
Tab.2 Characteristics of four working modes of DAB converter[11]
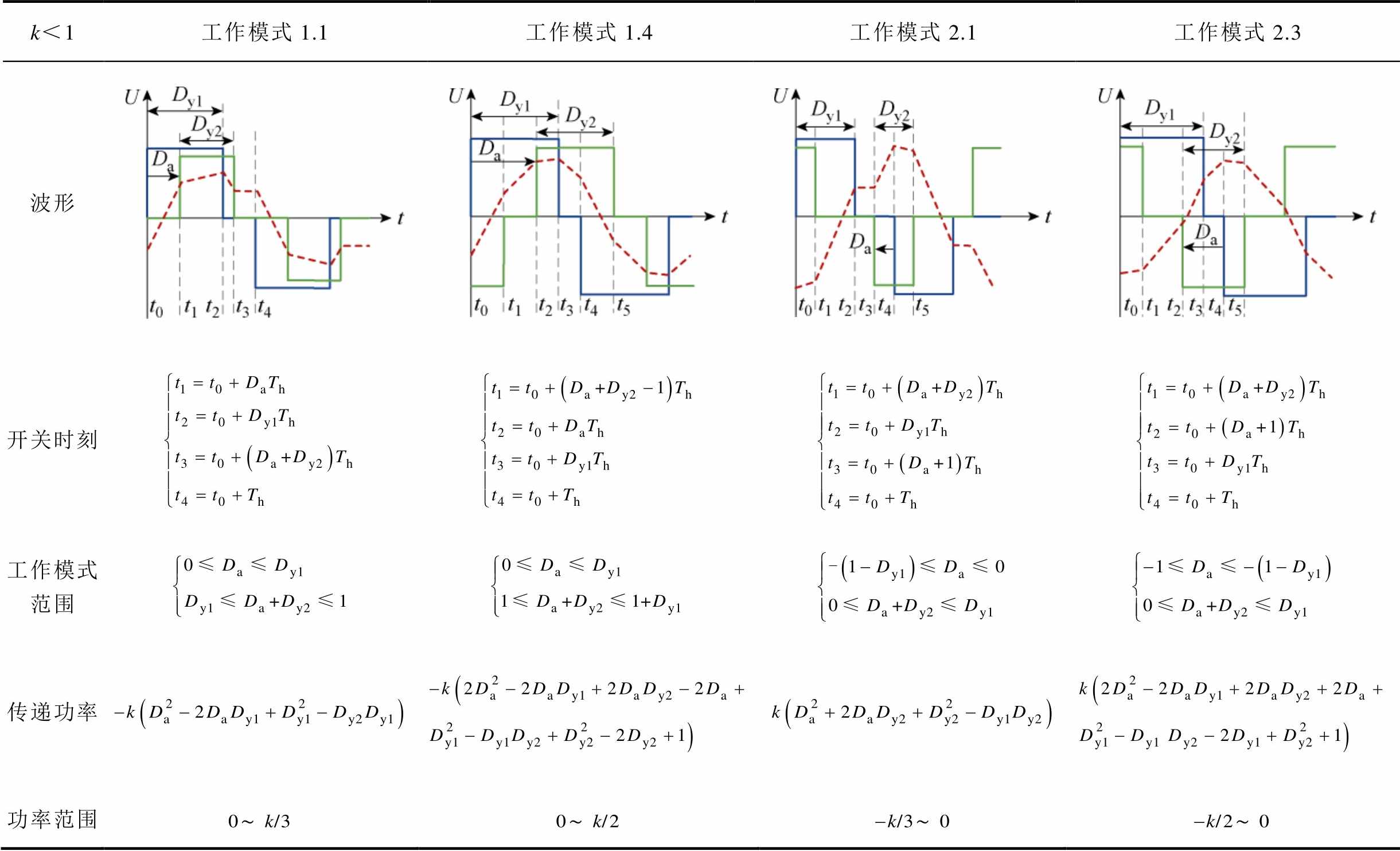
k<1工作模式1.1工作模式1.4工作模式2.1工作模式2.3 波形 开关时刻 工作模式范围 传递功率 功率范围
1)基于图形等效简化法分析
由文献[12]可知图形等效简化法本质:在不改变电压调整率k的前提下,通过对特定时间段波形的合理平移,确保电流曲线与时间轴所围积分面积相等,即等效前后传输功率P保持不变,从而达到降低电流应力或有效值的效果。根据此方法可推导出正向传输功率时工作模式1.2、1.5和2.4均可简化等效为工作模式1.1,如图3所示。
图3a中,模式1.2简化等效为临界模式,此时在相同P和k条件下,其电流有效值和应力均降低。临界模式可视为模式1.1的一种特殊形式,即Dy1= Da+Dy2的情况。
图3b中,模式1.5简化等效为临界模式,此时在相同P和k条件下,其电流有效值降低。临界模式可视为模式1.1的一种特殊形式,即Dy1=Da的情况。
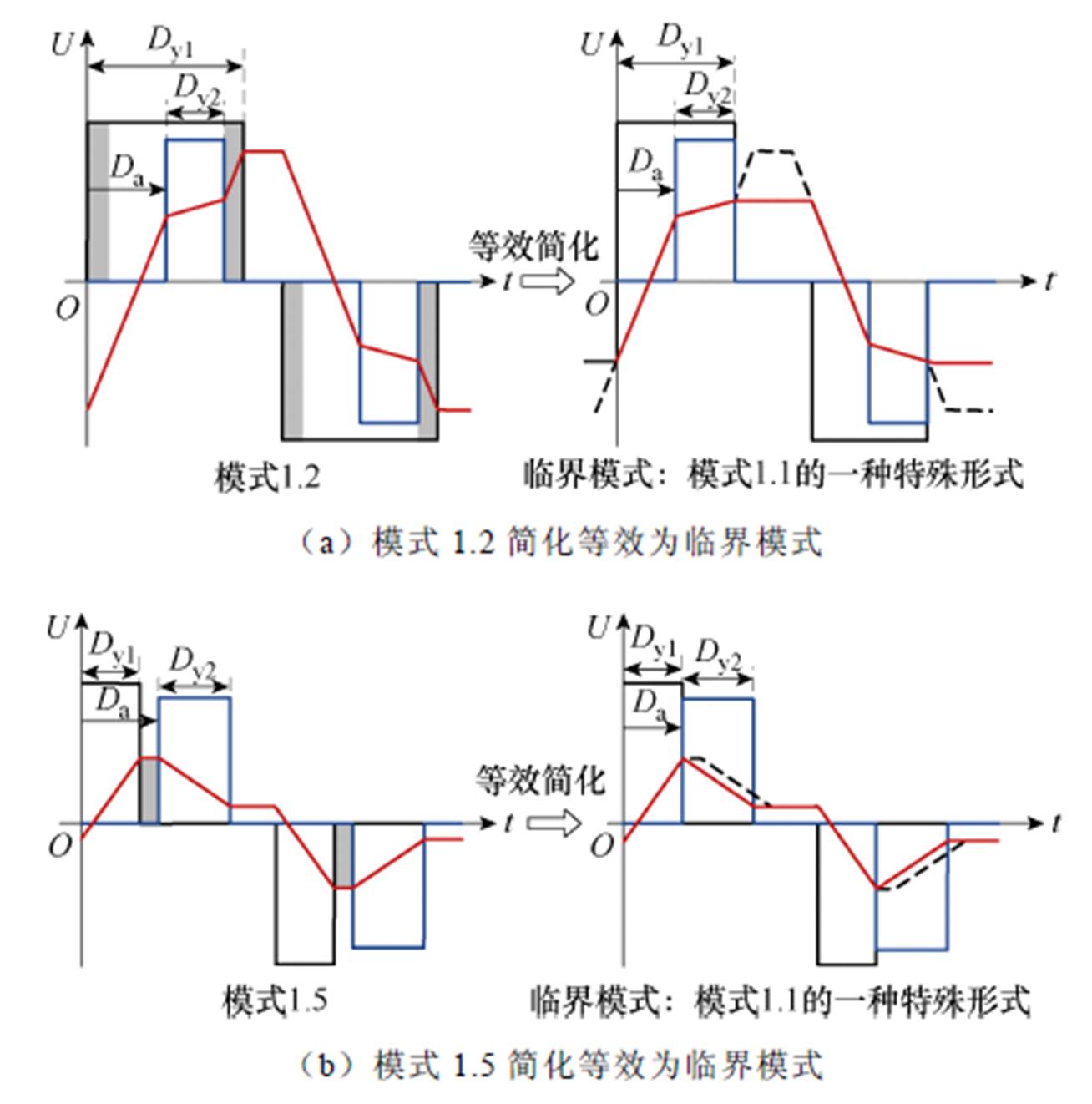
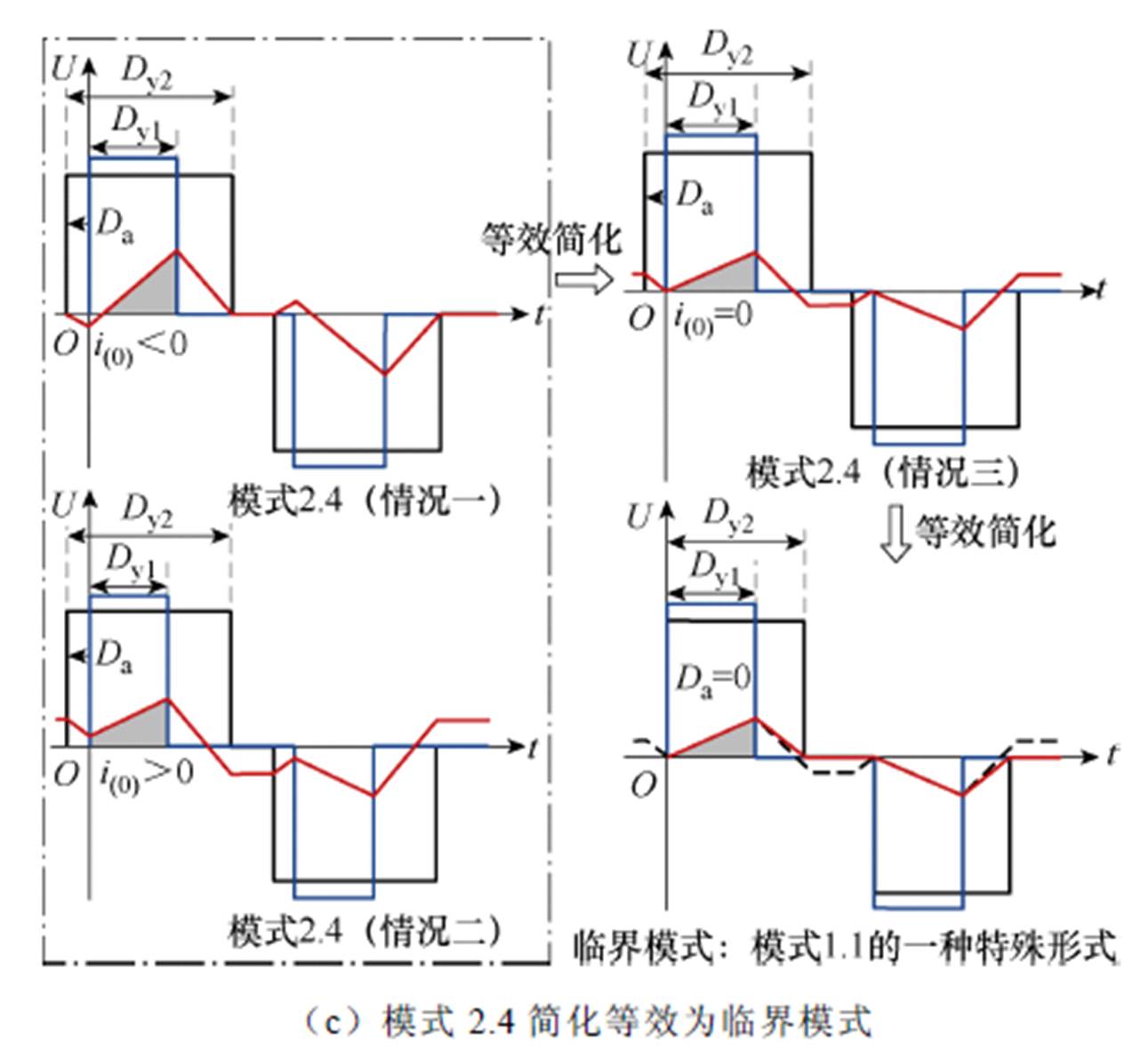
图3 模式1.2、1.5和2.4均可简化等效为模式1.1
Fig.3 Mode 1.2, 1.5 and 2.4 can be simplified and equivalent to Mode 1.1
图3c中,模式2.4的第一、二种情况简化等效为模式2.4第三种情况,在相同的P和k条件下,其电流有效值和应力降低。模式2.4第三种情况可简化等效为临界模式,其电流有效值进一步降低。临界模式视为模式1.1的一种特殊形式,即Da=0的情况。
由以上分析可得:在相同的P和k条件下,临界模式有着更小的电流有效值或电流应力。这些临界模式均可视为模式1.1的特殊形式,所以正向传输功率时,模式1.2、1.5和2.4均可简化等效为模式1.1。同理可证:反向传输功率时,模式2.2、1.2和2.4可简化等效为模式2.1。
2)基于波形与能量传输规律分析
根据文献[18]中波形与能量传输规律可知:正向功率传输时,工作模式1.3、1.5、2.6和1.6由于没有输入电压和输出电压同时为高电平或低电平的时间段,这使得能量不能直接由输入端传到输出端,会暂时存储于变换器的电感之中。电感存储的能量会在端口电平变化后再次从电感释放,并向输出端口传递。能量暂存在电感阶段,会导致电感电流大幅升高从而造成损耗增加[18],即在相同的P和k下,这个过程中电感电流应力和有效值都有较大增加,这也导致损耗增加。综上所述,功率正向传输时,模式1.3、1.5、2.6和1.6相对其他模式有着较大的电流应力和有效值,因此这些模式可以被忽略。同理可证明:功率反向传输时,模式2.2、2.5、1.6和2.6也可以被忽略。
综上所述,十二种工作模式可等效简化为四种局部最优工作模式,其中工作模式1.1和1.4为正向传输功率,工作模式2.1和2.3为反向传输功率。从表2中看到,工作模式1.1和1.4(2.1和2.3)的功率范围有重叠部分。在功率范围重叠部分,应当对两种工作模式下的电流应力进行对比,从而获得全局最优工作模式。
1)电流应力
电流应力为各个开关器件通断时电感电流绝对值中的最大值,即取4个开关时间节点的电感电流绝对值中的最大值。以工作模式1.1为例,半个周期内各个开关节点电感电流函数表达式为
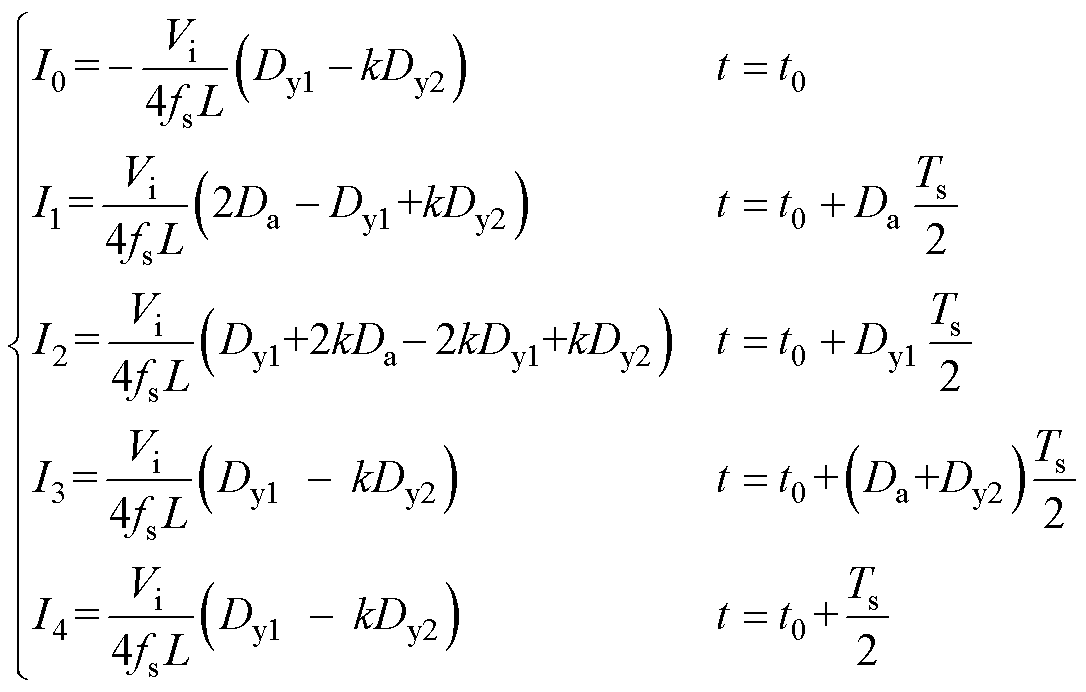 (1)
(1)
模式1.1的电流应力为
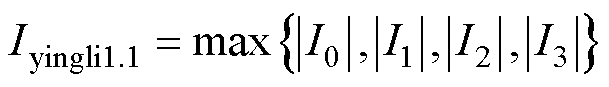 (2)
(2)
为简化计算可将电流应力和有效值转化为标幺值,定义电流基准值为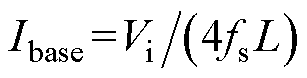 。
。
2)功率函数表达式
工作模式1.1的电感电流平均值为
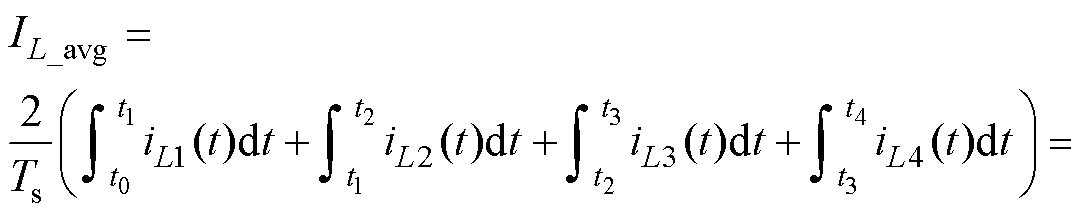
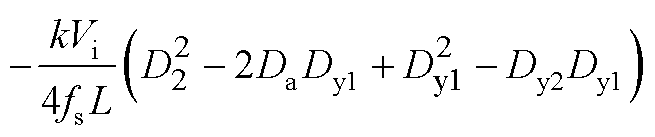 (3)
(3)
其输出功率为
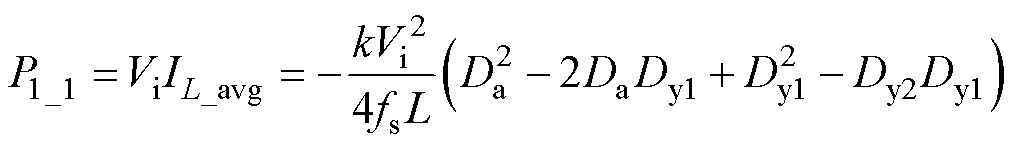 (4)
(4)
对DAB变换器进行时域建模后,本节将运用遗传算法对应力进行优化。单目标遗传算法不要求函数连续、可导和可微,很适合强耦合和非线性系统模型求解[19]。通过对优化算法设置不同电压调整率k和不同传输功率P的约束条件,从而得到一系列的最优解。优化算法中3个优化变量分别为Dy1、Dy2和Da;约束条件为各个工作模式运行范围内变量约束和传输功率约束。工作模式1.1的应力单目标遗传优化见表3,其他模式的优化流程和模式1.1类似。
表3 应力单目标遗传优化(模式1.1)
Tab.3 Genetic optimization with stress optimization objective (Mode 1.1)

优化方法应力单目标遗传优化算法 目标函数 线性约束工作模式范围约束条件: 变量上下界约束条件: 非线性约束传输功率约束条件:
根据两端口间电压匹配特性,本节对电压不匹配中的降压工况(k<1 进行深入研究。在分析四种局部最优模式的应力优化结果的基础上,从不同k和P出发,总结了各个局部最优模式在不同功率段的优化变量间规律。基于此规律,运用功率约束和三角函数极坐标法分别推导出各个局部最优模式中应力最小的最优控制变量表达式。
进行深入研究。在分析四种局部最优模式的应力优化结果的基础上,从不同k和P出发,总结了各个局部最优模式在不同功率段的优化变量间规律。基于此规律,运用功率约束和三角函数极坐标法分别推导出各个局部最优模式中应力最小的最优控制变量表达式。
在应力优化中,k分别取0.2、0.4、0.6和0.8时,得到优化变量在全功率范围内的变化,如图4所示。通过对图4中每个不同k值下不同传输功率的应力优化结果进行分析,得到在不同功率段的优化变量间规律:低功率段规律为Dy1=kDy2,Da=0,高功率段规律为Da+Dy2=1;然后对k为不同值的优化变量间规律进行对比,得到模式1.1中应力优化在不同k值下优化变量间规律均相同,见表4。通过k取0~1中的任意值时应力优化结果分析和对比,得到模式1.1在不同k值下不同功率段内优化变量间规律都是相同的。
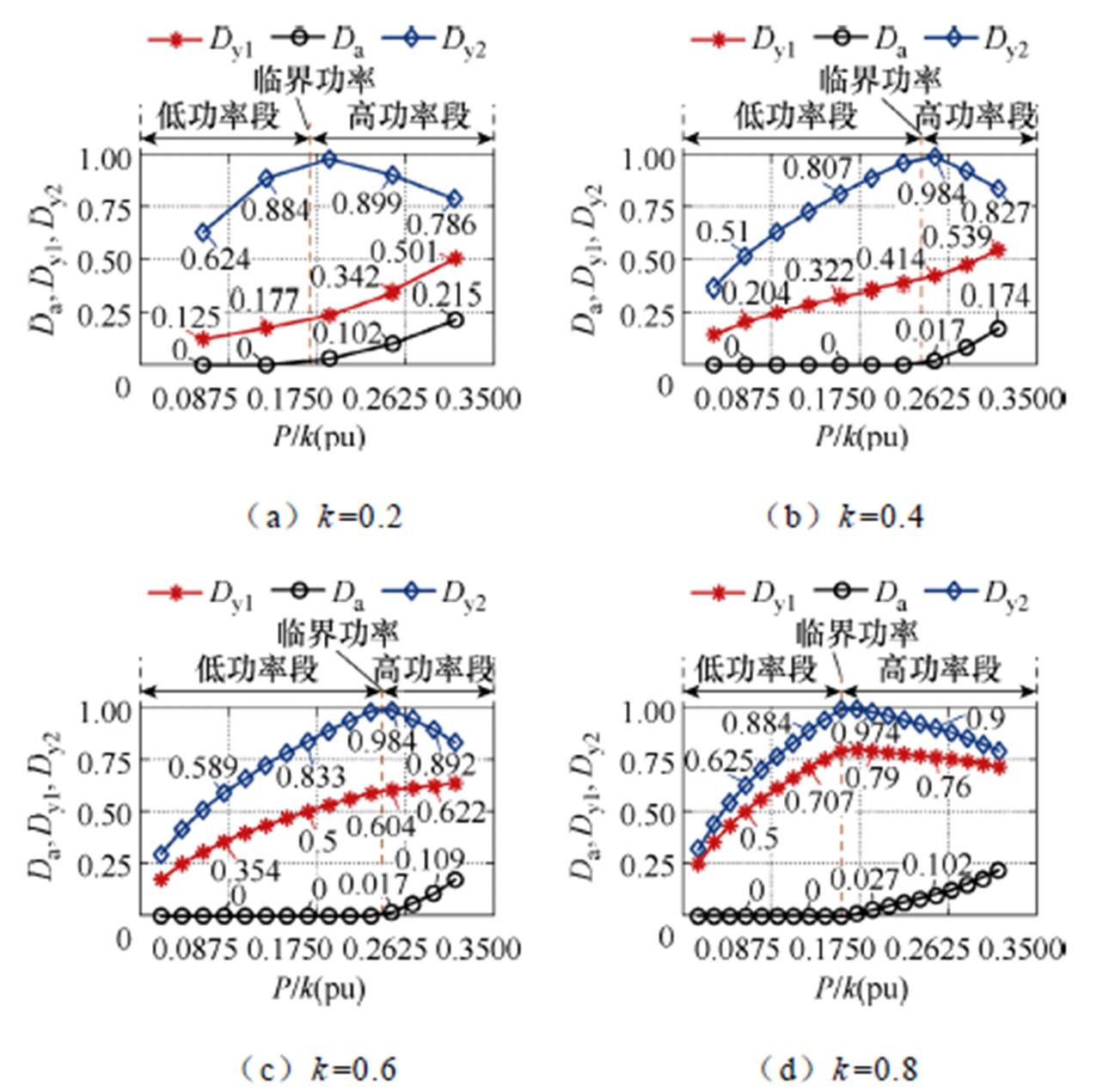
图4 模式1.1在不同k值时全功率范围内应力优化变量
Fig.4 The stress optimization variables of working Mode 1.1 in full power range with different k values
表4 模式1.1应力优化控制变量在不同功率段的规律
Tab.4 Mode 1.1 the law of stress optimization control variables in different power segments

功率范围低功率段临界功率高功率段 优化变量间规律
3.1.1 低功率段应力优化控制变量的计算方法
将表4中低功率段规律Dy1=kDy2、Da=0代入表2中得模式1.1的功率传输表达式为
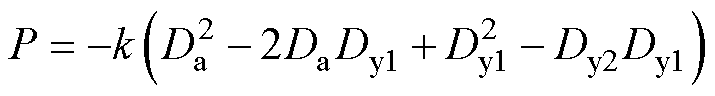 (5)
(5)
得到
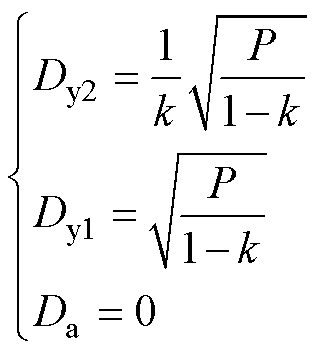 (6)
(6)
将优化控制变量式(6)代入模式1.1低功率段应力函数表达式得到应力最小表达式为
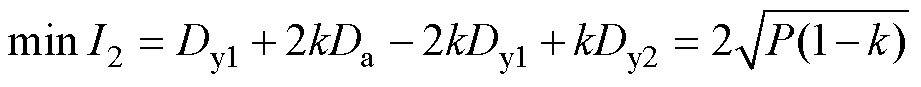 (7)
(7)
3.1.2 高功率段应力优化控制变量的计算方法
根据表4中高功率段规律Da+Dy2=1,运用三角函数极坐标法推导出应力单目标优化控制变量。
表4中高功率段规律为
Da+Dy2=1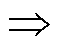 Dy2=1-Da (8)
Dy2=1-Da (8)
将式(8)代入表2中模式1.1的功率传输表达式(5)得到
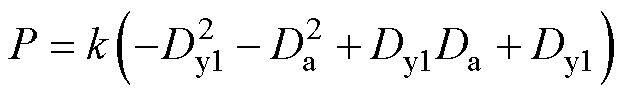 (9)
(9)
进一步简化
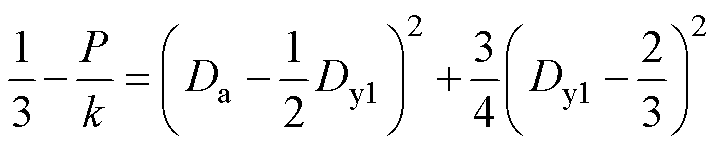 (10)
(10)
令
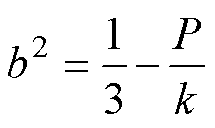 (11)
(11)
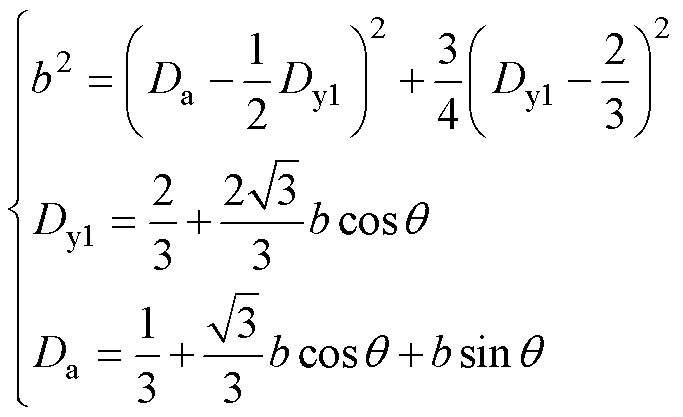 (12)
(12)
将式(8)和式(12)代入应力函数表达式得
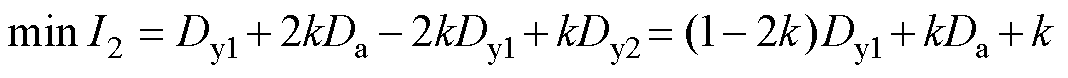 (13)
(13)
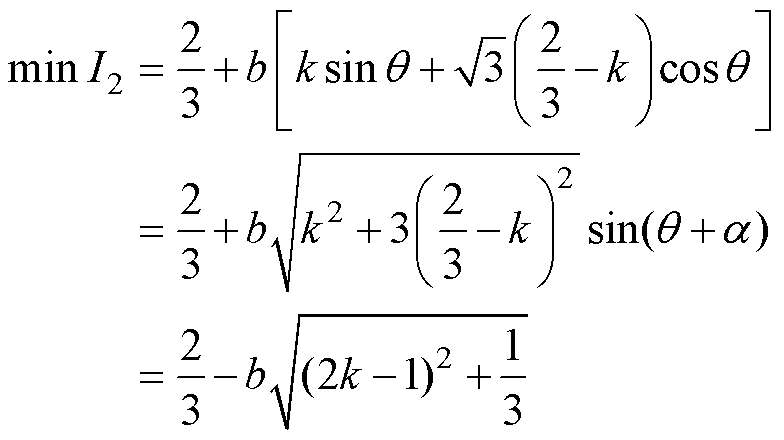 (14)
(14)
其中,满足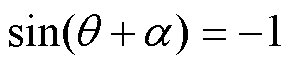 时,I2最小。
时,I2最小。
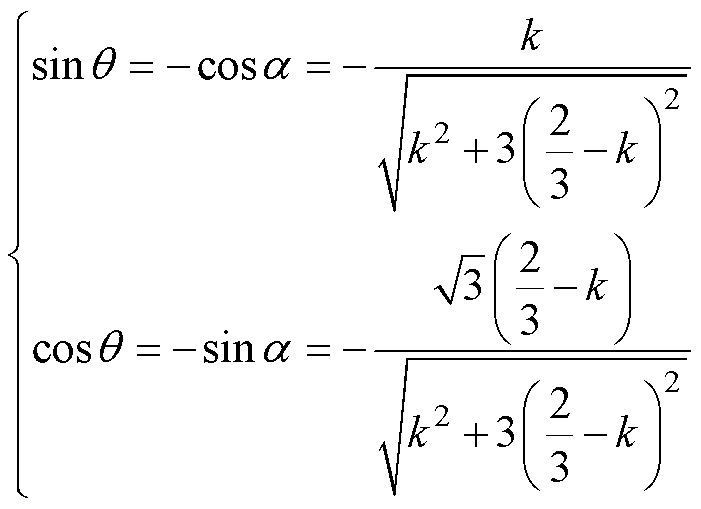 (15)
(15)
将式(11)和式(15)代入式(12)和式(13)得最小应力和优化控制变量的函数表达式为
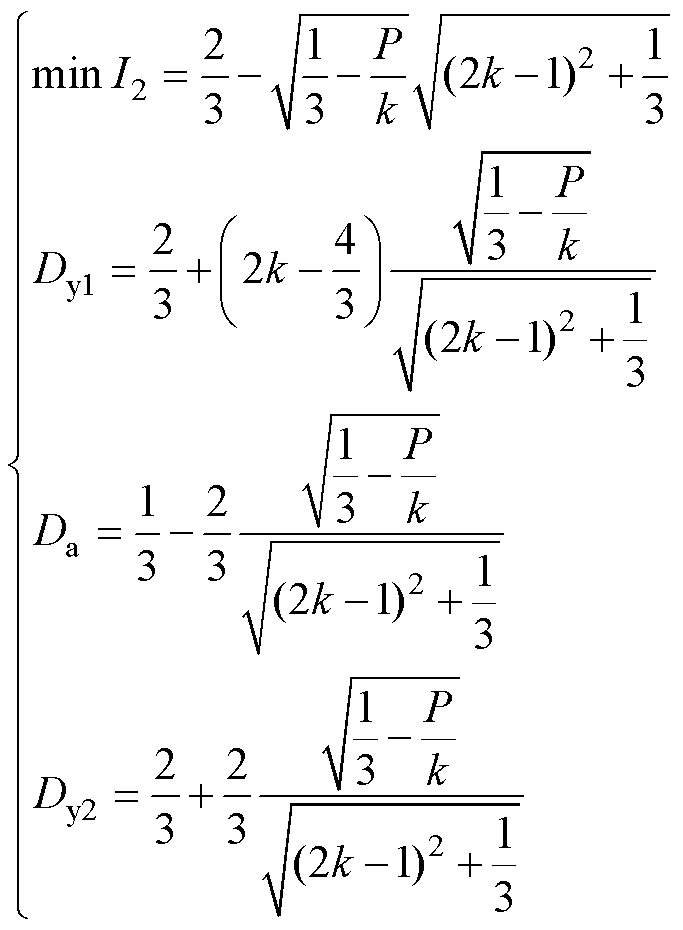 (16)
(16)
3.1.3 模式1.1高、低功率段分界点的优化控制变量计算方法
功率正向传输时,由表4低功率段与高功率段分界点上的优化控制变量之间的规律得到
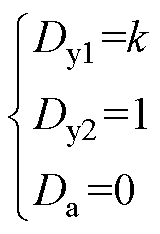 (17)
(17)
将式(17)代入式(5)得高、低功率段分界点的功率P的表达式为
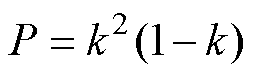 (18)
(18)
将优化控制变量式(17)代入模式1.1低功率段应力函数表达式(13)得到应力最小表达式为
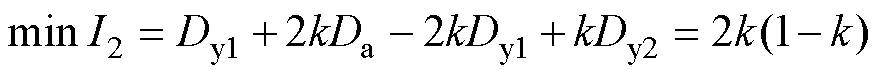 (19)
(19)
模式1.4、2.1和2.3的应力优化和规律总结以及优化控制变量的推导方法和模式1.1类似,其推导流程如图5所示。首先运用应力单目标遗传算法优化出局部最优模式在不同k时全功率范围内的最优解;其次分析和对比不同k值内最优解中优化变量间的关系,总结出不同传输功率段优化变量间的规律;再次对比k为不同值时优化变量间规律之间的差异,得到其规律均相同;然后将这些规律代入相应的功率传输表达式(见表2),并将优化变量转化为三角函数极坐标形式,见附表2;随后将优化变量代入应力函数表达式;最后对应力求最小值并通过运用三角函数最小值法推导出应力优化控制变量函数表达式。
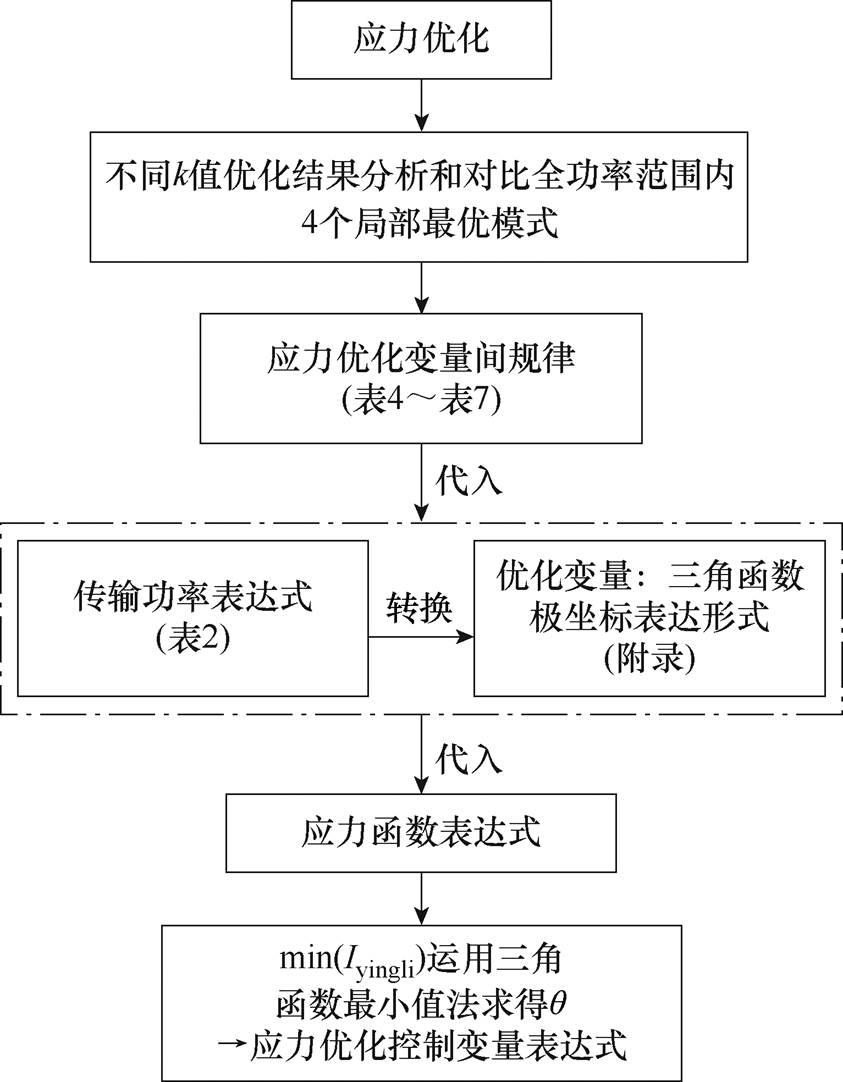
图5 应力优化控制变量推导流程
Fig.5 Derivation flow chart of stress optimization control variables
在应力优化中,k分别取0.2、0.4、0.6和0.8时,得到模式1.4、2.1和2.3的优化变量在全功率范围内的变化,如图6~图8所示。通过对图6~图8中应力优化的优化结果进行分析和对比,得到应力优化在不同功率段有不同的优化变量间规律,见表5~表7。通过对k取0~1中的任何值的优化结
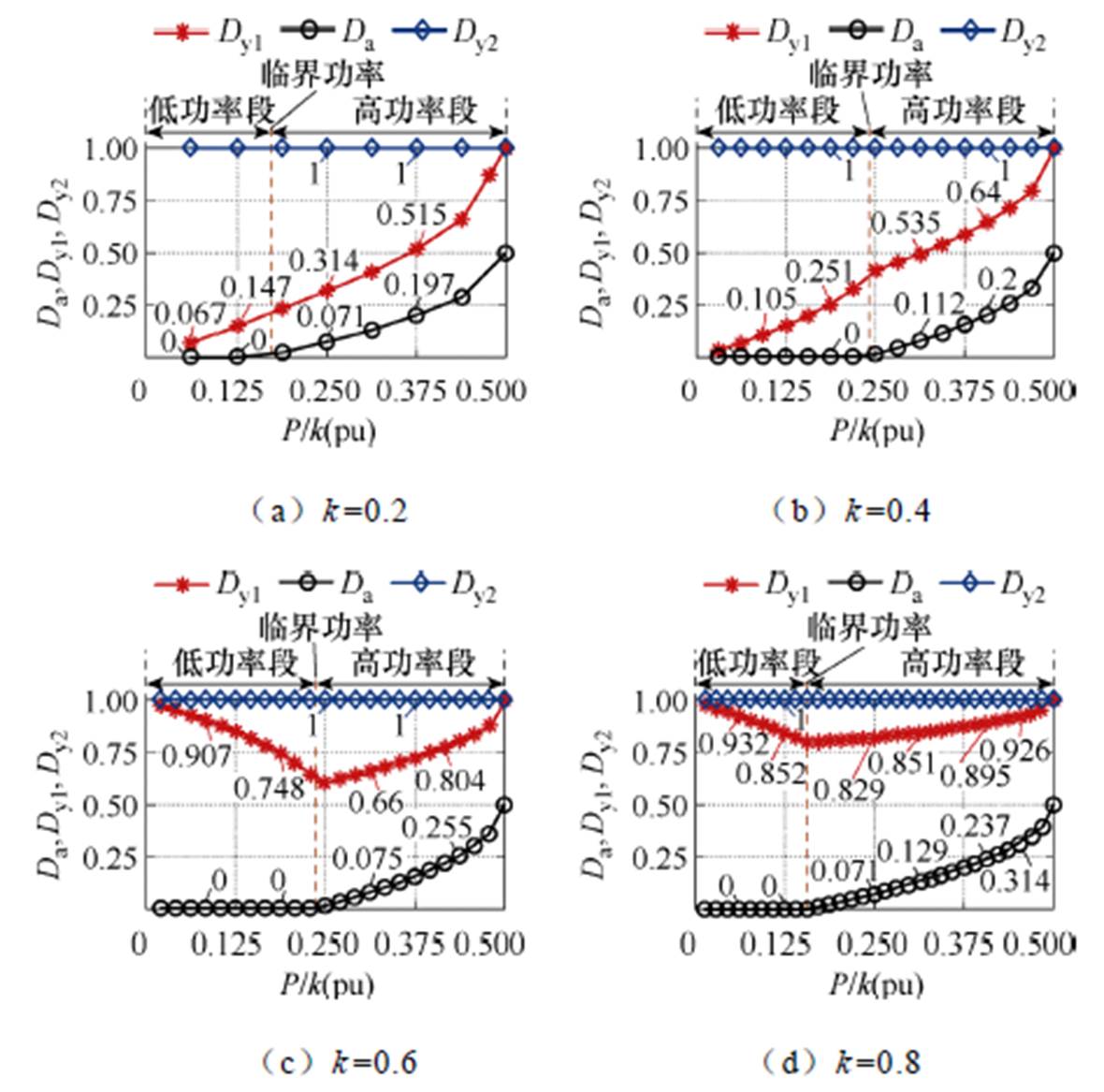
图6 模式1.4在不同k值时全功率范围内应力优化变量
Fig.6 The stress optimization variables of working Mode 1.4 in full power range with different k values
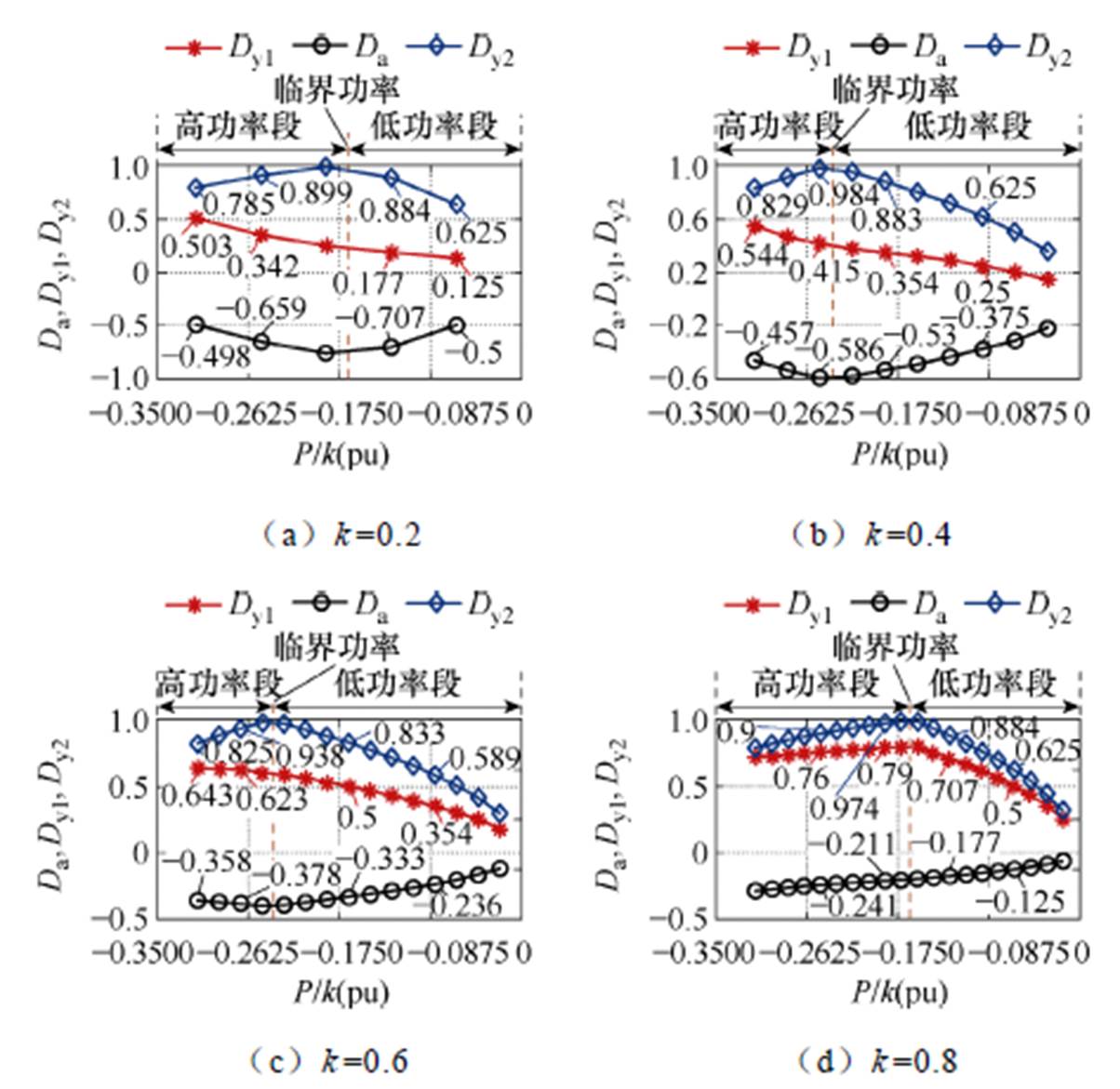
图7 模式2.1在不同k值时全功率范围内应力优化变量
Fig.7 The stress optimization variables of working Mode 2.1 in full power range with different k values
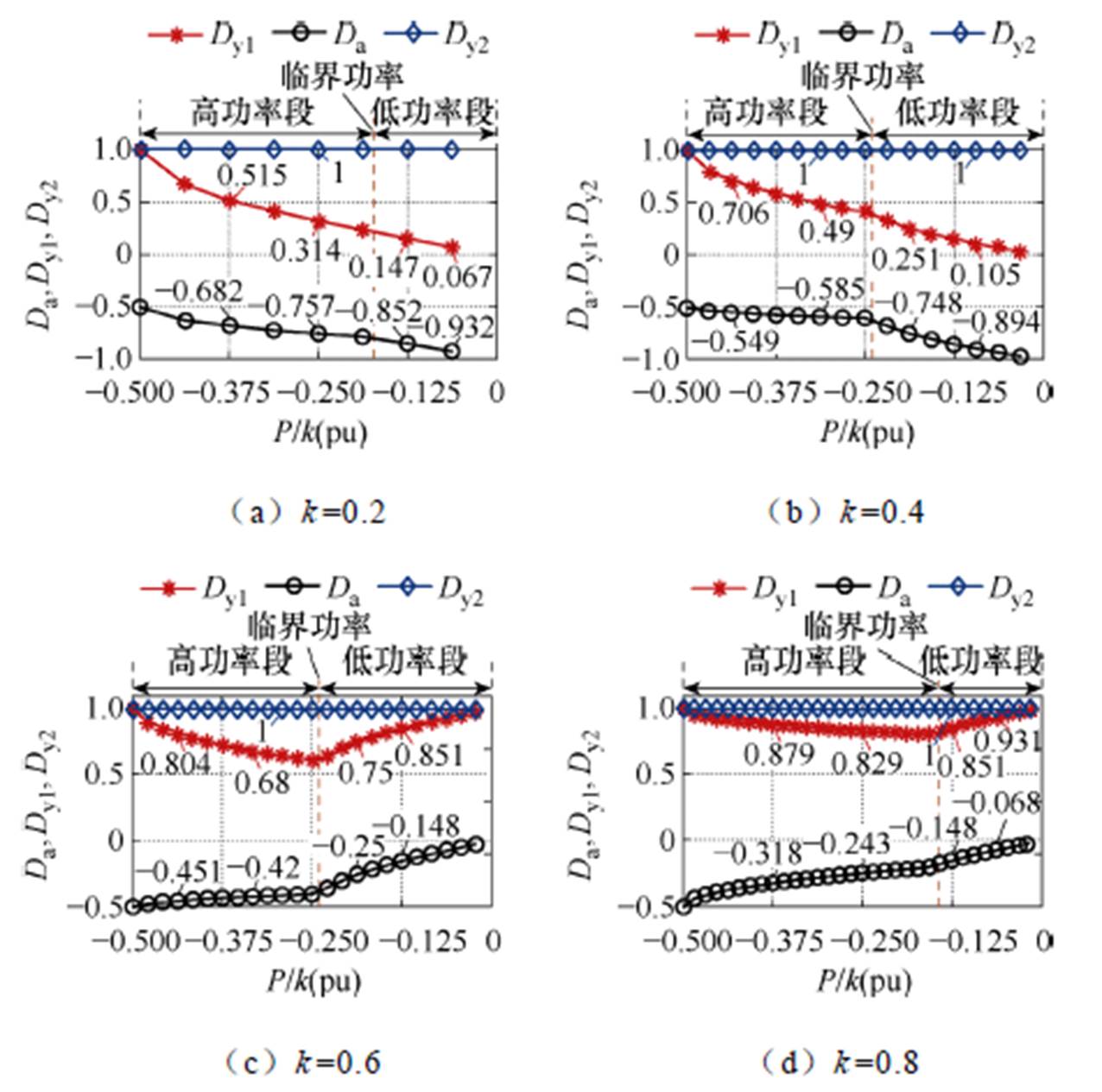
图8 模式2.3在不同k值时全功率范围内应力优化变量
Fig.8 The stress optimization variables of working Mode 2.3 in full power range with different k values
果研究,得到这三个模式中应力优化在不同功率段的优化变量间规律在k(0<k<1 为任意值时均相同。根据优化变量间规律,运用功率约束和三角函数极坐标法分别推导出应力最小的最优控制变量。这三个模式的最优控制变量具体推导过程和3.1节的模式1.1类似,其推导结论见附表1。
为任意值时均相同。根据优化变量间规律,运用功率约束和三角函数极坐标法分别推导出应力最小的最优控制变量。这三个模式的最优控制变量具体推导过程和3.1节的模式1.1类似,其推导结论见附表1。
表5 模式1.4应力优化控制变量在不同功率段的规律
Tab.5 The law of stress optimization control variables in different power segments (Mode 1.4)

功率范围低功率段临界功率高功率段 优化变量间规律
表6 模式2.1应力优化控制变量在不同功率段的规律
Tab.6 The law of stress optimization control variables in different power segments (Mode 2.1)

功率范围低功率段临界功率高功率段 优化变量间规律
表7 模式2.3应力优化控制变量在不同功率段的规律
Tab.7 The law of stress optimization control variables in different power segments (Mode 2.3)

功率范围低功率段临界功率高功率段 优化变量间规律
由于局部最优模式1.1与1.4之间以及模式2.1与2.3之间存在传输功率重叠情况。在功率重叠区间段,本节在第3节所推导得到的最小应力函数表达式和应力优化控制变量的基础上选出全功率范围内全局最优工作模式和应力全局最优控制变量。
对DAB进行全功率范围优化分析时,本节取k分别为0.4和0.8作为具体研究对象,以便进行量化分析。由如图9所示k=0.4时四种工作模式的电流应力优化结果可以看到:在各个模式的功率传输范围内,正向传输的低功率段(0~0.24(pu)),在相同的功率下工作模式1.1的电流应力均低于工作模式1.4,而在高功率段(0.24~0.33(pu))时,则正好相反;反向传输的低功率段(-0.24(pu)~0),在相同的功率下工作模式2.1的电流应力均低于工作模式2.3的,而在高功率段(-0.33~-0.24(pu))时,则正好相反。同理从图10所示的k=0.8时四种工作模式的应力优化可看到,正反传输中高低功率段的应力规律与图9结论类似。
根据表8中应力表达式可利用优化算法比较模式1.1和1.4在低功率段即0<P<k2(1-k)的应力。
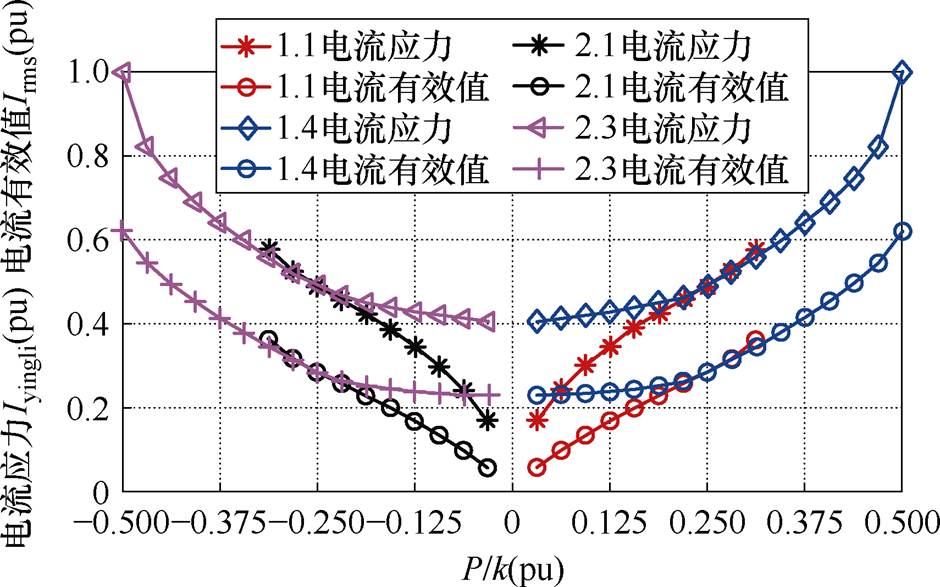
图9 k=0.4时四种工作模式的电流应力优化
Fig.9 Stress optimization: current RMS and stress of four working modes when k=0.4
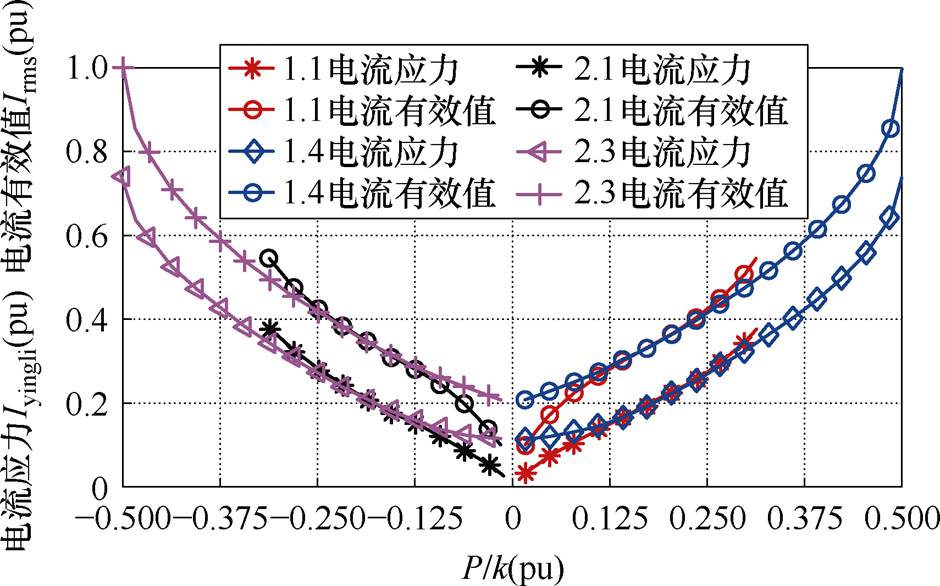
图10 k=0.8时四种工作模式的应力优化
Fig.10 Stress optimization: current RMS and stress of four working modes when k=0.8
目标函数
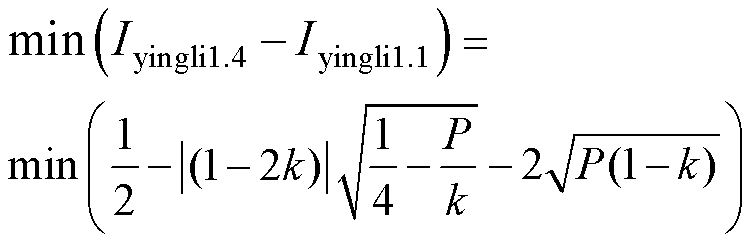 (20)
(20)
式中,约束条件为0<k<1和0<P<k2(1-k)。
通过单目标遗传算法得到min(Iyingli1.4-Iyingli1.1)≥0,则有Iyingli1.4-Iyingli1.1≥min(Iyingli1.4-Iyingli1.1)≥0,得到Iyingli1.4≥Iyingli1.1,所以在正向传输的低功率段0< P<k2(1-k):模式1.1的电流应力低于模式1.4,模式1.1为全局最优。
同理根据表8可证(见附表4):在各个模式功率范围内和不同k值下,正向传输的高功率段:模式1.4的电流应力低于模式1.1的,模式1.4为全局最优。反向传输的低功率段:模式2.1的电流应力低于模式2.3的,模式2.1为全局最优;高功率段:模式2.3的电流应力低于模式2.1的,模式2.3为全局最优。
综上可推导出全功率范围内不同功率上应力全局最优工作模式,见表9。根据上述结论和第3节局部最优工作模式中应力单目标优化结论综合得到,全功率范围内的DAB变换器三重移相调制应力优化控制变量见表10。
表8 四种局部最优工作模式在不同功率段的电流应力表达式
Tab.8 Expressions of current stress for four locally optimal working modes in different power range

无模式2.1高功率段模式2.1低功率段模式1.1低功率段模式1.1高功率段无 模式2.3高功率段模式2.3低功率段模式1.4低功率段模式1.4高功率段
注:P为标幺值,基准值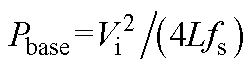 ;Iyingli为标幺值,基准值
;Iyingli为标幺值,基准值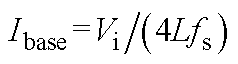 。
。
表9 全功率范围内不同功率段的全局最优工作模式
Tab.9 Global optimal operation modes of different power segments in full power range

功率范围全局最优工作模式 反向/高功率段工作模式2.3 反向/低功率段工作模式2.1 正向/低功率段工作模式1.1 正向/高功率段工作模式1.4
表10 DAB降压条件下全功率内应力最优控制变量
Tab.10 Stress optimal control variables in full power range under DAB buck condition

全局最优模式功率范围应力优化控制变量 模式2.3 临界功率 模式2.1
(续)

全局最优模式功率范围应力优化控制变量 模式1.1 临界功率 模式1.4
为验证所提优化控制方法的正确性和有效性,本文将分别在Matlab/Simulink软件平台与实验平台进行对比和验证,DAB的相关实验参数见表11。
本文所提应力优化控制策略如图11所示,控制输出端电压维持在给定值。未优化控制策略即为SPS单移相控制,其中Dy1和Dy2均为1,只有一个控制自由度Da。
表11 DAB变换器实验参数
Tab.11 Experiment Parameters of DAB converter

参 数数 值 端口1电压U1/V200 端口2电压U2/V160 开关频率/Hz5 000 变压器电压比n11 电感/mH1
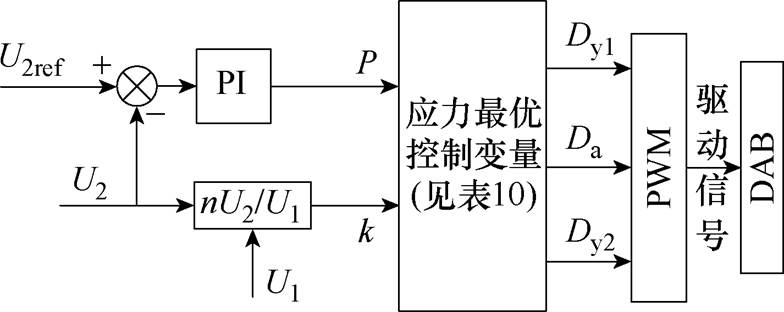
图11 应力优化控制策略
Fig.11 Stress optimization control strategy
本文通过Matlab仿真程序推导出在全功率范围内应力优化控制和SPS控制的电流应力和电流有效值,并在基础上进行分析和对比,如图12所示。从图12中看出:在相应传输功率点上,应力优化控制的电流应力和电流有效值均小于SPS控制。在正和反两个传输方向上传输功率越小,应力优化控制较SPS控制的优化效果越好;相对高功率范围的优化效果,低功率范围的优化效果更为显著。
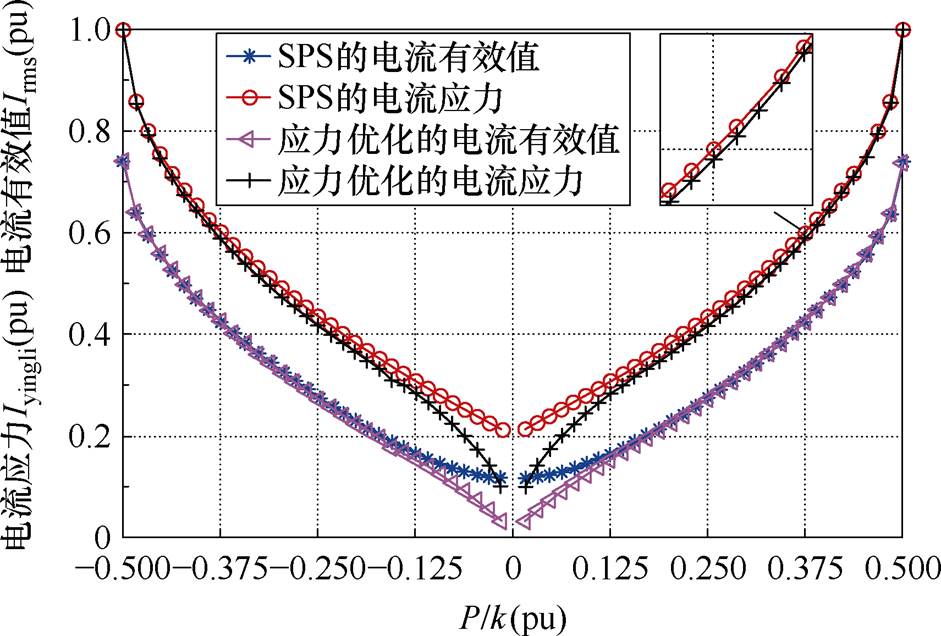
图12 SPS和应力优化的电流应力与有效值对比
Fig.12 Comparison of current stress and RMS value for SPS and stress optimization
本文通过实验平台分别对比应力优化和SPS控制位于正向传输的低和高功率段的两个功率点。未优化和应力优化对比如图13所示,位于正向低功率范围P=0.075(pu)时,SPS控制的电流应力和有效值分别为2.79 A和1.44 A,而应力优化的电流应力和有效值分别为2.45 A和1.24 A,优化的比未优化的明显效果好。未优化和应力优化对比如图14所示,位于正向高功率范围P=0.25(pu)时,未优化的电流应力和有效值分别为5.1 A和3.44 A;应力优化的应力和有效值分别为4.95 A和3.43 A。经优化的较未优化的效果好些但相差不大。综上分析得出,应力优化在全功率范围比未优化SPS的效果好,尤其在低功率段内优化效果更为显著。
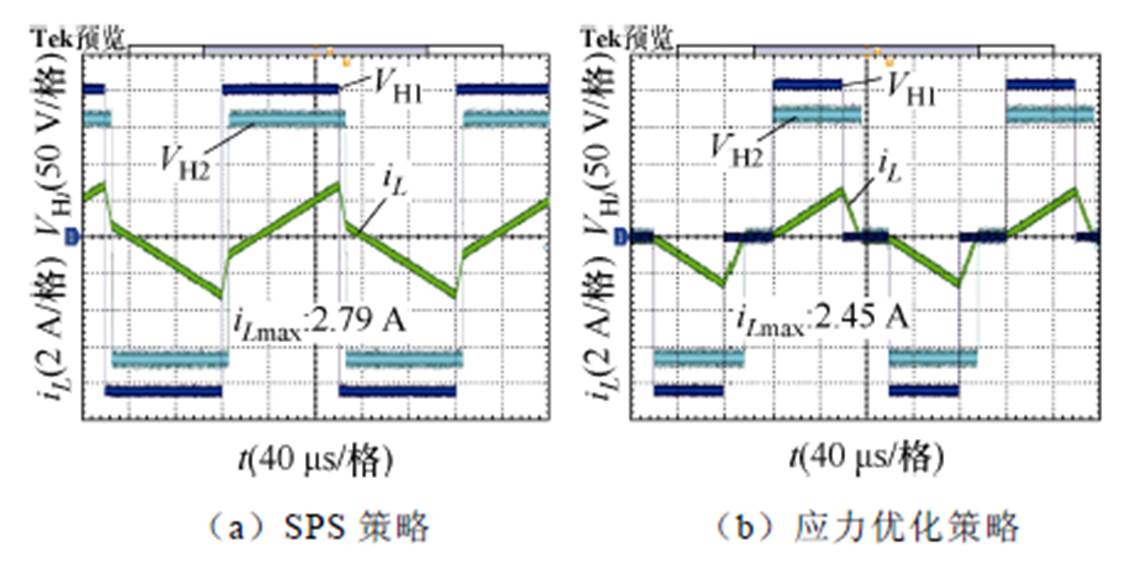
图13 未优化和应力优化对比(P=0.075(pu))
Fig.13 A comparison between non-optimized and stress optimized (P=0.075(pu))
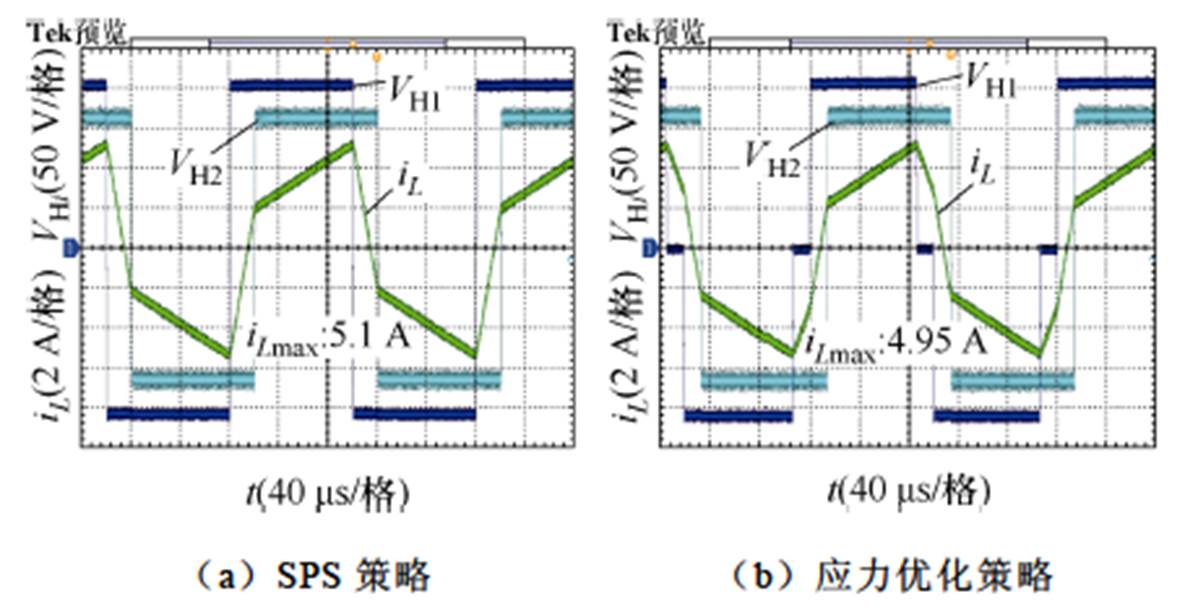
图14 未优化和应力优化对比(P=0.25(pu))
Fig.14 A comparison between non-optimized and stress optimized (P=0.25(pu))
本节通过Matlab程序推导出k=0.8时在全功率范围内各个模式应力优化控制的电流应力,并在此基础上进行对比,如图15所示。图15中,+2.4表示模式2.4正向传输,-2.4表示模式2.4反向传输,其他类似。从图15中看出,在正向传输的功率段工作模式1.1、1.2、+2.4和1.4的应力非常接近,比其他模式应力都小;反向传输的功率段工作模式2.1、1.2、2.3和-2.4的应力非常接近,比其他模式应力都小。这和第2节中图形分析法中选择局部最优模式相一致。
本文再通过实验平台对比两个局部最优模式中位于正向传输的低和高功率段的两个功率点,根据其优化应力值确定此功率点的全局最优工作模式,如图16、图17所示。
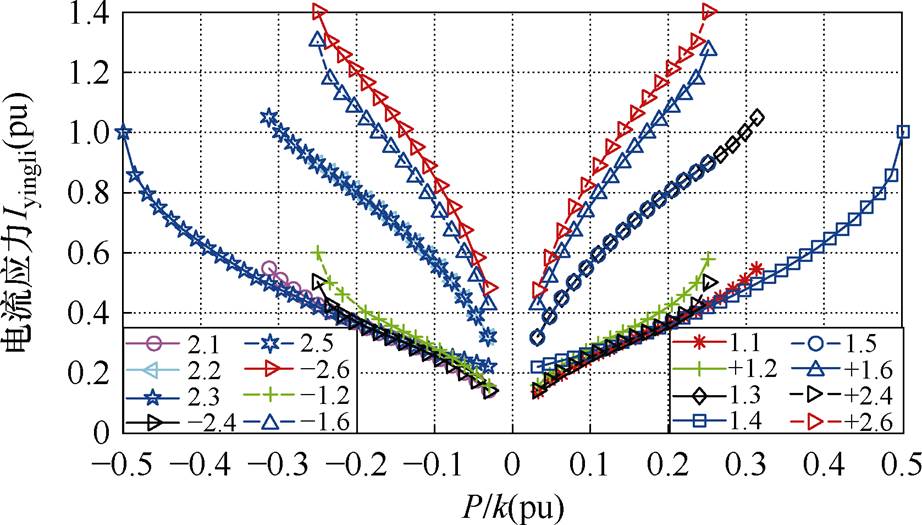
图15 k=0.8不同模式应力优化的电流应力对比
Fig.15 Comparison of current stress for stress optimization with different modes when k=0.8
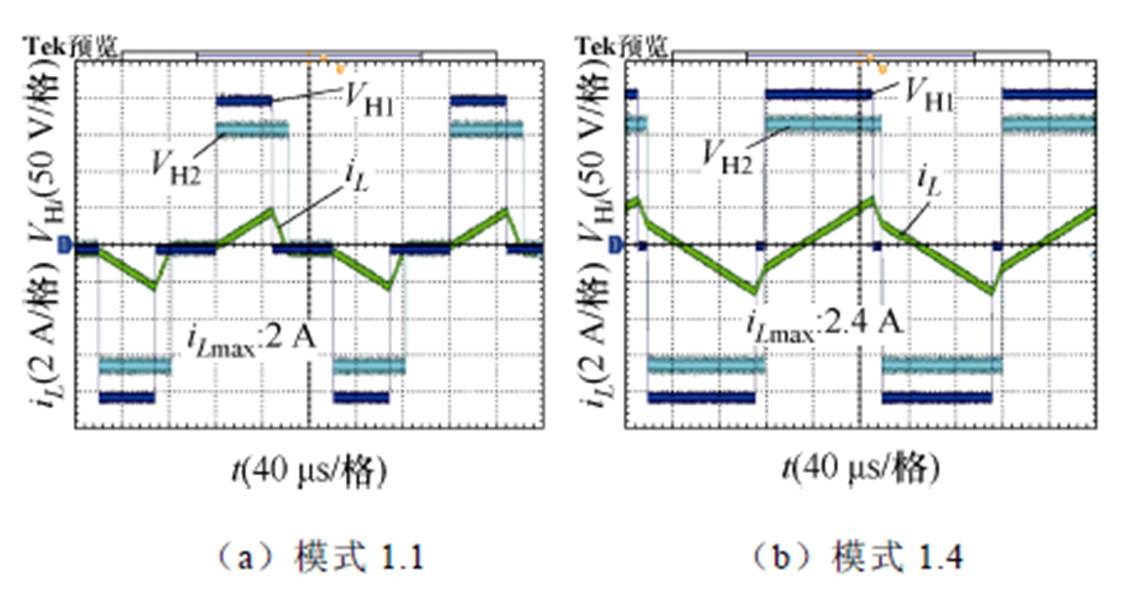
图16 模式1.1和1.4应力优化对比(P=0.05(pu))
Fig.16 Stress optimization comparison for Mode 1.1 and 1.4 (P=0.05(pu))
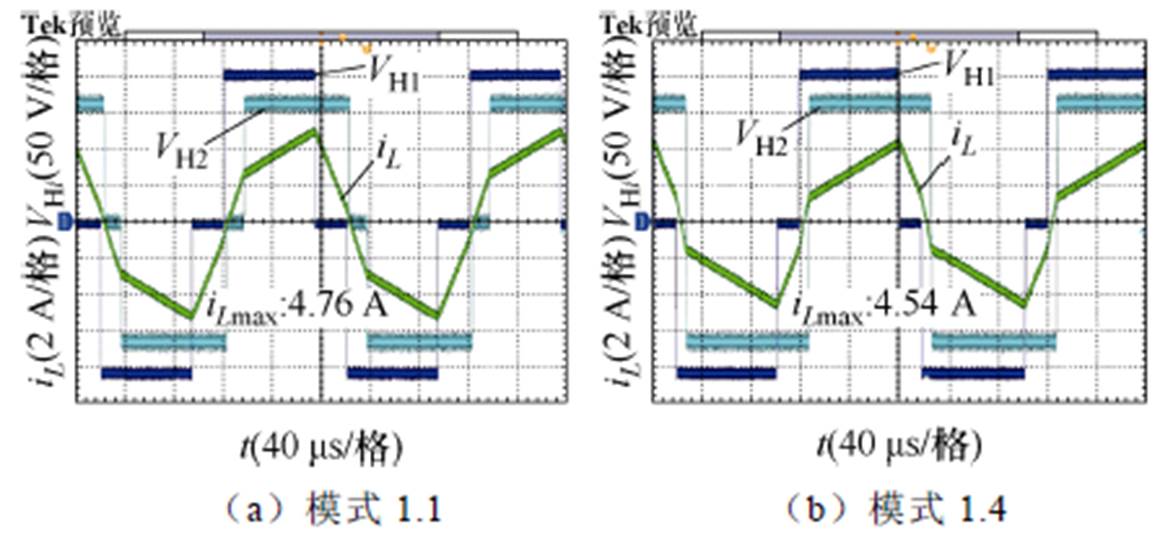
图17 模式1.1和1.4应力优化对比(P=0.225(pu))
Fig.17 Stress optimization comparison for Mode 1.1 and 1.4 (P=0.225(pu))
图16为模式1.1和模式1.4在正向传输下低功率P=0.05(pu)的电流应力和有效值。图16中工作模式1.1的电流应力最大值和有效值分别为2 A和0.91 A;工作模式1.4的电流应力最大值和有效值分别为2.4 A和1.26 A。模式1.1优化效果优于模式1.4。在此低功率点上,模式1.1为全局最优模式。
图17中,模式1.1和模式1.4在正向传输下高功率P=0.225(pu)的应力优化,模式1.4的电流应力最大值和有效值分别为4.54 A和3.06 A;模式1.1电流应力最大值和有效值的4.76 A和3.22 A。模式1.4的应力优化效果优于模式1.1。在此高功率点上,模式1.4为全局应力最优模式。以上实验结果和4.2节应力优化理论分析结果相一致。
本节通过Matlab程序对k=0.4,0.6和0.8在不同调制策略下的应力优化进行了对比,如图18所示。从图18看出,在TPS调制策略下优化的应力较其他调制策略的小。TPS调制下优化的应力和EPS调制下优化的应力在高功率段相同,这与第3节中结论相一致。在低功率段EPS调制下优化的应力高于TPS调制下优化的应力。在低传输功率段或电压不匹配的情况下,TPS调制下应力优化较其他调制策略的效果好。
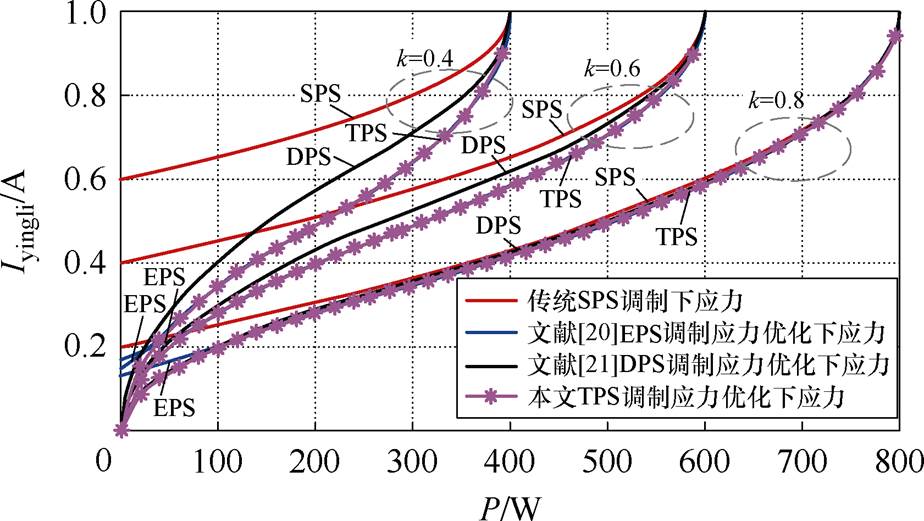
图18 k=0.4,0.6和0.8不同调制策略下应力优化的应力对比
Fig.18 Stress comparison of stress optimization under different modulation strategies for k=0.4, 0.6, and 0.8
在效率方面,本节通过实验平台对k=0.4,0.6和0.8在不同传输功率下应力优化和SPS的传输效率进行对比,如图19所示。从图19看出,三重移相的应力优化在全功率范围内效率均优于SPS,在低功率段较为明显。电压越不匹配即k值越小,三重移相的应力优化效果越好。
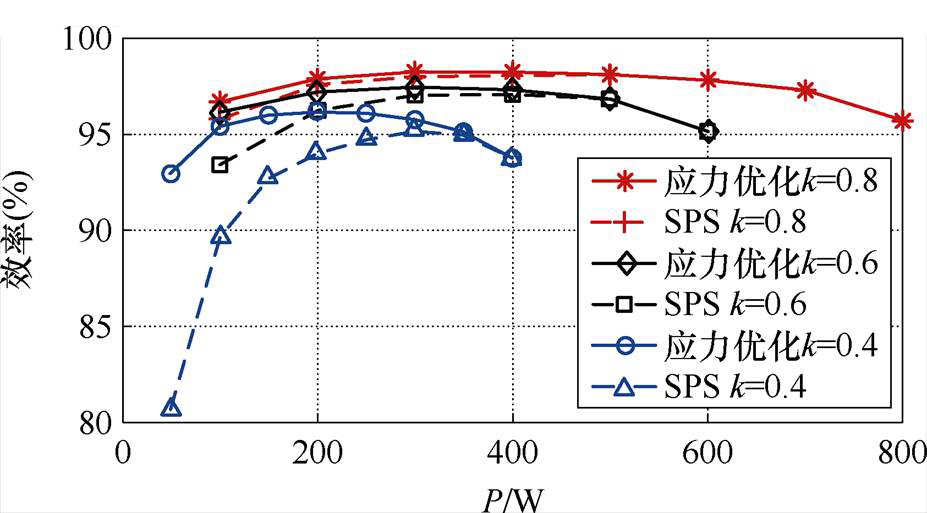
图19 k=0.4,0.6和0.8应力优化和SPS效率对比
Fig.19 Compares the efficiency of stress optimization and SPS for k=0.4, 0.6, and 0.8
本文根据图形分析法把DAB的十二种工作模式简化等效为四种局部最优模式;然后通过遗传算法得到这四种模式在不同功率段的优化变量间的内在规律;再根据此规律和约束条件推导出优化控制变量函数表达式;最后比较不同功率段的应力选出全局最优工作模式,从而得到全功率范围内实时应力优化控制变量函数表达式。理论研究和实验验证可到以下结论:
1)在降压工况下正向和反向传输的全功率范围内:正向低功率段0<P<k2(1-k)模式1.1为全局最优模式,正向高功率段k2(1-k)<P<k/2模式1.4为全局最优模式;反向低功率段k2(k-1)<P<0模式2.1为全局最优模式,反向高功率段-k/2<P<k2(k-1)模式2.3为全局最优模式。
2)通过应力优化控制变量函数能够在功率P或电压调整率k波动条件下实现连续实时应力优化控制。三重移相应力优化控制使得DAB变换器效率较其他调制下的控制在全功率范围上有着整体提升,尤其在低功率段和两端电压不匹配度高情况下提升更为显著。
附 录
附表1 DAB降压条件下三种工作模式全功率范围内不同功率段的应力变量规律和应力最优控制变量
App.Tab.1 The stress variable law and stress optimal control variables of DAB in different power sections in the full power range of 3 working modes under buck conditions

模式()功率范围变量规律应力优化变量和应力最小值的函数表达式 模式1.4低功率段 临界 高功率段 模式2.1低功率段
(续)
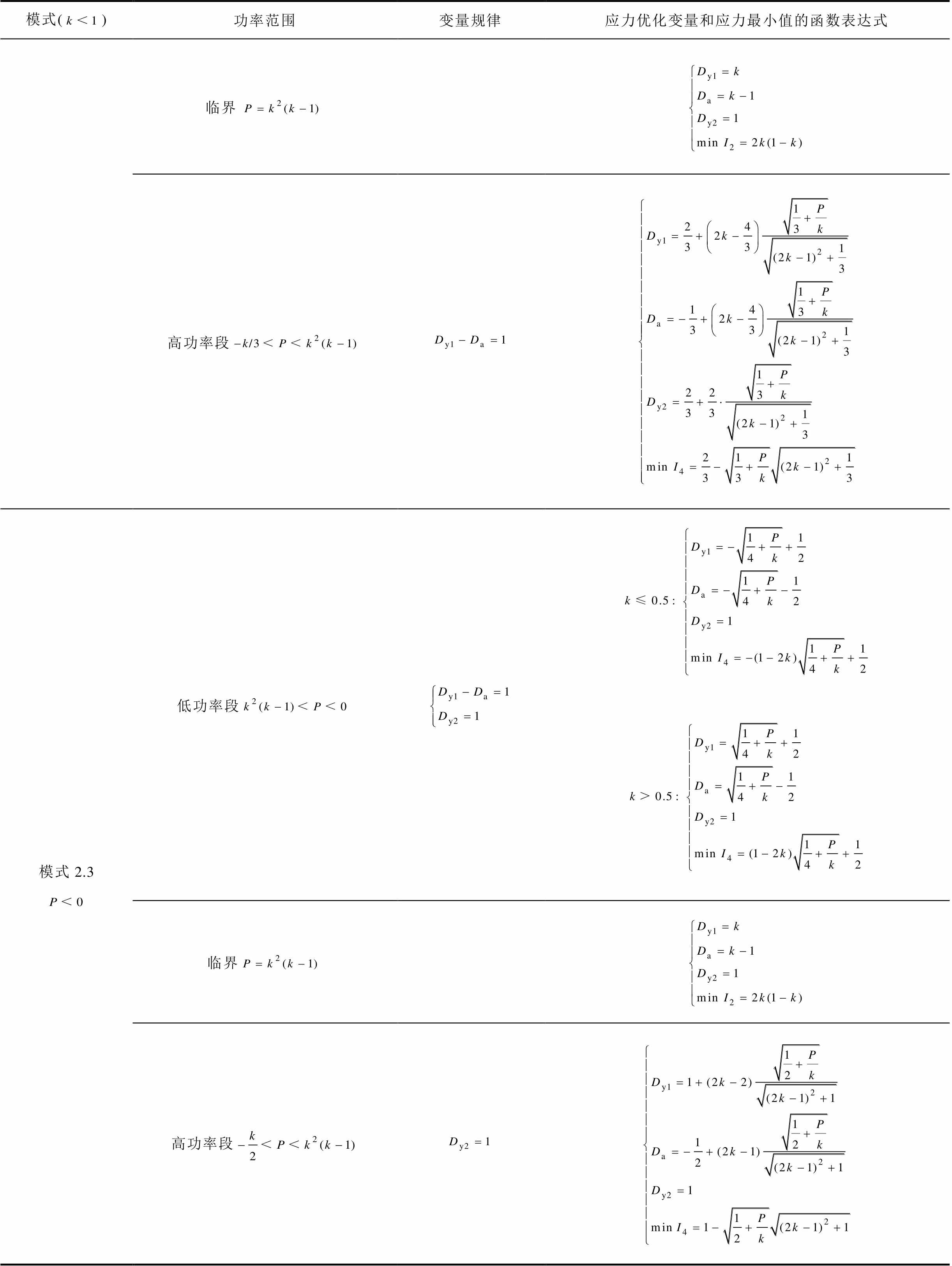
模式()功率范围变量规律应力优化变量和应力最小值的函数表达式 临界 高功率段 模式2.3低功率段 临界 高功率段
注:Ii为标幺值,基准值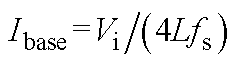 。
。
附表2 工作模式1.4、2.1和2.3高功率段的三角函数极坐标法
App.Tab.2 The trigonometric polar coordinate method in the high power segments of working Modes 1.4、2.1 and 2.3

模式规律三角函数极坐标模式规律三角函数极坐标模式规律三角函数极坐标 1.4令: 2.1令: 2.3令:
附表3 DAB变换器八种工作模式特征[11]
App.Tab.3 Characteristics of eight working modes of DAB converter[11]
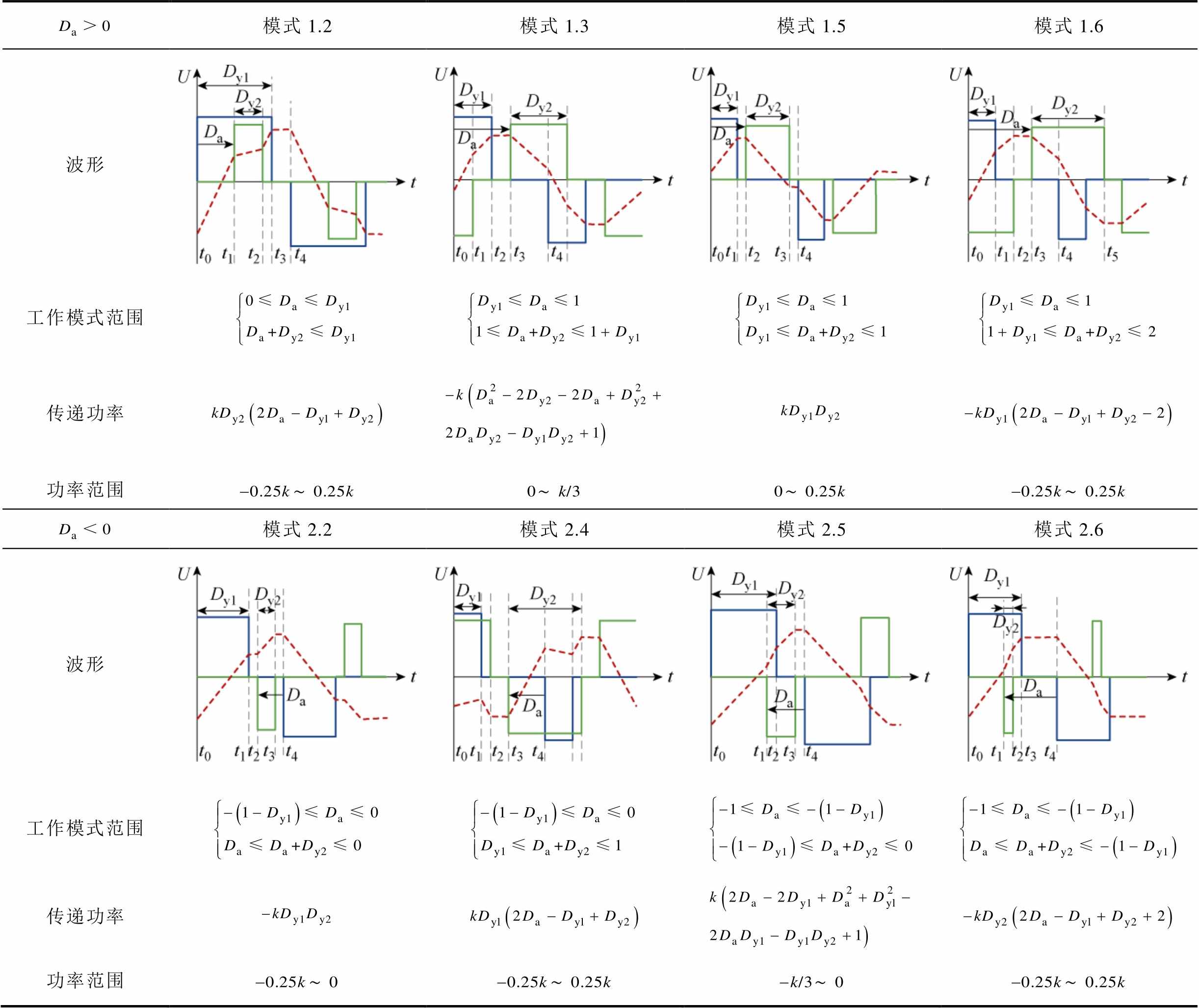
模式1.2模式1.3模式1.5模式1.6 波形 工作模式范围 传递功率 功率范围 模式2.2模式2.4模式2.5模式2.6 波形 工作模式范围 传递功率 功率范围
附表4 运用遗传算法对不同功率段不同局部最优模式的应力进行对比
App.Tab.4 Using genetic algorithm to compare the stress of different locally optimal modes in different power ranges

正向传输高功率段: k2(1-k)<P<k/3反向传输低功率段: k2(k-1)<P<0反向传输高功率段: -k/3<P<k2(k-1) 目标函数 约束条件0<k<1, k2(1-k)<P<k/30<k<1, k2(k-1)<P<00<k<1, -k/3<P<k2(k-1) 结果min(Iyingli1.1-Iyingli1.4)≥0min(Iyingli2.3-Iyingli2.1)≥0min(Iyingli2.1-Iyingli2.3)≥0
参考文献
[1] 宋强, 赵彪, 刘文华, 等. 智能直流配电网研究综述[J]. 中国电机工程学报, 2013, 33(25): 9-19.
Song Qiang, Zhao Biao, Liu Wenhua, et al. An overview of research on smart DC distribution power network[J]. Proceedings of the CSEE, 2013, 33(25): 9-19.
[2] 曾嵘, 赵宇明, 赵彪, 等. 直流配用电关键技术研究与应用展望[J]. 中国电机工程学报, 2018, 38(23): 6790-6801.
Zeng Rong, Zhao Yuming, Zhao Biao, et al. A prospective look on research and application of DC power distribution technology[J]. Proceedings of the CSEE, 2018, 38(23): 6790-6801.
[3] 谷庆, 袁立强, 聂金铜, 等. 基于开关组合规律的双有源桥DC-DC变换器传输功率特性[J]. 电工技术学报, 2017, 32(13): 69-79.
Gu Qing, Yuan Liqiang, Nie Jintong, et al. Transmission power characteristics of dual-active- bridge DC-DC converter based on the switching combination rules[J]. Transactions of China Elec- trotechnical Society, 2017, 32(13): 69-79.
[4] 黄匀飞, 钟启濠, 欧阳有鹏, 等. 双有源桥变换器拓扑结构与控制策略研究综述[J]. 电源学报, 2024, 22(4): 53-65.
Huang Yunfei, Zhong Qihao, Ouyang Youpeng, et al. Overview of topologies and control strategies for dual-active-bridge converter[J]. Journal of Power Supply, 2024, 22(4): 53-65.
[5] 李子欣, 高范强, 赵聪, 等. 电力电子变压器技术研究综述[J]. 中国电机工程学报, 2018, 38(5): 1274-1289.
Li Zixin, Gao Fanqiang, Zhao Cong, et al. Research review of power electronic transformer techno- logies[J]. Proceedings of the CSEE, 2018, 38(5): 1274-1289.
[6] 王攀攀, 徐泽涵, 王莉, 等. 基于三重移相的双有源桥DC-DC变换器效率与动态性能混合优化控制策略[J]. 电工技术学报, 2022, 37(18): 4720-4731.
Wang Panpan, Xu Zehan, Wang Li, et al. A hybrid optimization control strategy of efficiency and dynamic performance of dual-active-bridge DC-DC converter based on triple-phase-shift[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4720-4731.
[7] 竺庆茸. 双有源桥DC-DC的调制方式的研究[J]. 电气技术, 2020, 21(7): 53-56, 68.
Zhu Qingrong. A study of dual active bridge DC-DC modulation mode[J]. Electrical Engineering, 2020, 21(7): 53-56, 68.
[8] 康薇, 肖飞, 任强, 等. 双有源桥DC-DC变换器三移相调制及其死区效应分析和补偿[J]. 电工技术学报, 2024, 39(6): 1907-1922.
Kang Wei, Xiao Fei, Ren Qiang, et al. Three-phase shift modulation of DC-DC converter with dual active bridges and its dead-time effect analysis and com- pensation[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1907-1922.
[9] 刘红晓, 祝丽花, 张俊杰. 宽频下典型高频变压器铁心损耗计算与分析[J]. 电力电子技术, 2022, 56(12): 1-4, 8.
Liu Hongxiao, Zhu Lihua, Zhang Junjie. Typical high-frequency transformer core loss calculation and analysis under wide frequency[J]. Power Electronics, 2022, 56(12): 1-4, 8.
[10] 孙凯, 卢世蕾, 易哲嫄, 等. 面向电力电子变压器应用的大容量高频变压器技术综述[J]. 中国电机工程学报, 2021, 41(24): 8531-8546.
Sun Kai, Lu Shilei, Yi Zheyuan, et al. A review of high-power high-frequency transformer technology for power electronic transformer applications[J]. Proceedings of the CSEE, 2021, 41(24): 8531-8546.
[11] Hebala O M, Aboushady A A, Ahmed K H, et al. Generic closed-loop controller for power regulation in dual active bridge DC-DC converter with current stress minimization[J]. IEEE Transactions on Indu- strial Electronics, 2019, 66(6): 4468-4478.
[12] Shao Shuai, Jiang Mingming, Ye Weiwen, et al. Optimal phase-shift control to minimize reactive power for a dual active bridge DC-DC converter[J]. IEEE Transactions on Power Electronics, 2019, 34(10): 10193-10205.
[13] 关维德, 李涛, 钟健, 等. 电机控制器直流侧前置双有源桥DC-DC变换器的模型预测与应力优化混合控制[J]. 电工技术学报, 2024, 39(12): 3787-3801.
Guan Weide, Li Tao, Zhong Jian, et al. Hybrid control of model prediction and current stress optimization for dual active bridge DC-DC converter in motor drive systems[J]. Transactions of China Electro- technical Society, 2024, 39(12): 3787-3801.
[14] 任强, 艾胜. 全工况范围的DAB三自由度优化控制策略[J]. 中国电机工程学报, 2020, 40(11): 3613- 3621.
Ren Qiang, Ai Sheng. A three degree freedom optimal control strategy of dual-active-bridge converters for full range operations[J]. Proceedings of the CSEE, 2020, 40(11): 3613-3621.
[15] 王仁龙, 李永建, 李珊瑚, 等. 双有源桥变换器电流应力优化的双重移相调制方式[J]. 电源学报, 2023, 21(1): 35-44.
Wang Renlong, Li Yongiian, Li Shanhu, et al. Improved dual phase-shift modulation mode based on current stress optimization of dual active bridge DC-DC converter[J]. Journal of Power Supply, 2023, 21(1): 35-44.
[16] Li Jia, Luo Quanming, Mou Di, et al. A hybrid five- variable modulation scheme for dual-active-bridge converter with minimal RMS current[J]. IEEE Transactions on Industrial Electronics, 2022, 69(1): 336-346.
[17] Gu Qing, Yuan Liqiang, Nie Jintong, et al. Current stress minimization of dual-active-bridge DC-DC converter within the whole operating range[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(1): 129-142.
[18] Tong Anping, Hang Lijun, Li Guojie, et al. Modeling and analysis of a dual-active-bridge-isolated bidi- rectional DC/DC converter to minimize RMS current with whole operating range[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5302-5316.
[19] 王小平, 曹立明. 遗传算法: 理论、应用与软件实现[M]. 西安: 西安交通大学出版社, 2002.
[20] 郭华越, 张兴, 赵文广, 等. 扩展移相控制的双有源桥DC-DC 变换器的优化控制策略[J]. 中国电机工程学报, 2019, 39(13): 3889-3898.
Guo Huayue, Zhang Xing, Zhao Wenguang, et al. Optimal control strategy of dual active bridge DC-DC converters with extended-phase-shift control[J]. Pro- ceedings of the CSEE, 2019, 39(13): 3889-3898,
[21] 曾进辉, 孙志峰, 雷敏, 等. 双重移相控制的双主动全桥变换器全局电流应力分析及优化控制策略[J]. 电工技术学报, 2019, 34(12): 2507-2518.
Zeng Jinhui, Sun Zhifeng, Lei Min, et al. Global current stress analysis and optimal control strategy of dual-active full bridge converter based on dual phase shift control[J]. Transactions of China Electro- technical Society, 2019, 34(12): 2507-2518.
Abstract To achieve continuous and real-time stress optimization control of the dual active bridge converter under power transmission or voltage fluctuations, it is crucial to study the patterns between modes and among optimization control variables in modes. However, current research needs depth, and functional expressions of stress optimization control variables are complex.
This paper employs genetic algorithms for stress optimization. The intrinsic laws among the optimization variables in each mode are elucidated through the optimization results. An innovative trigonometric function polar coordinate method is adopted to derive the corresponding optimization control variable function expressions.
Firstly, based on waveform equivalence simplification and the principle of waveform and energy transmission, the four locally optimal modes are identified from the twelve working modes, which exhibit low stress or effective values in different power ranges. It reduces the number of modes that require optimization, which reduces the optimization burden.
Secondly, the stress of the four modes is optimized, and the optimization results are compared to determine the laws governing the optimization variables in different power ranges with different k values. Through systematic analysis, the laws of four local optimal operating modes in the low/high power section can be obtained.
Thirdly, the expressions with optimization variables are obtained by substituting these laws into the corresponding power transfer expression. The optimized variables are converted into trigonometric polar coordinate forms through the trigonometric function polar coordinate method. The expressions for the minimum current stress function and its optimization control variables are obtained by substituting optimized variables into the stress expression to obtain the minimum stress value.
Compared with the current stress in the full power range for four local operating modes, the optimal mode and optimal control variables for each power segment across the entire power range are selected, thereby achieving global optimization control. The innovations in this study are presented.
(1) Analyze and contrast the current stress optimization results for different voltage adjustment rates k to discern the laws among the optimized variables across the four local optimal modes in various power ranges.
(2) The power constraint and trigonometric polar coordinate methods are utilized to derive a precise expression for the optimal stress control variables. The globally optimal control variables are selected by comparing the current stress of four local optimal modes.
The following conclusions can be drawn. (1) Under the buck operation conditions of stress optimization for both forward and reverse power transfer across the entire power range, mode 1.1 is globally optimal during low forward transmission power when 0<P<k2(1-k); mode 1.4 becomes globally optimal during high forward transmission power in the range k2(1-k)<P<k/2. Similarly, for low reverse transmission power, mode 2.1 is globally optimal in the range k2(k-1)<P<0, and mode 2.3 becomes globally optimal during high reverse transmission power when -k/2<P<k2(k-1). (2) The stress optimization control under TPS modulation improves the efficiency of the DAB converter compared to other modulation strategies. Notably, it exhibits a significant enhancement under the low-power segment and high-voltage mismatch scenarios.
keywords:Dual active bridge converter, stress optimization, local optimal working mode, global optimal working mode, trigonometric function polar coordinate method
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.240701
国家自然科学基金重点资助项目(52130704)。
收稿日期 2024-05-06
改稿日期2024-07-10
张来勇 男,1984年生,博士研究生,研究方向为电力电子装置建模与控制、直流变换器优化和控制。
E-mail: laiyong_zhang@163.com(通信作者)
涂春鸣 男,1976年生,教授,博士生导师,研究方向为电力电子在电力统中的应用、智能配电网、分布式能源与微电网等。
E-mail: chunming_tu@263.net
(编辑 陈 诚)