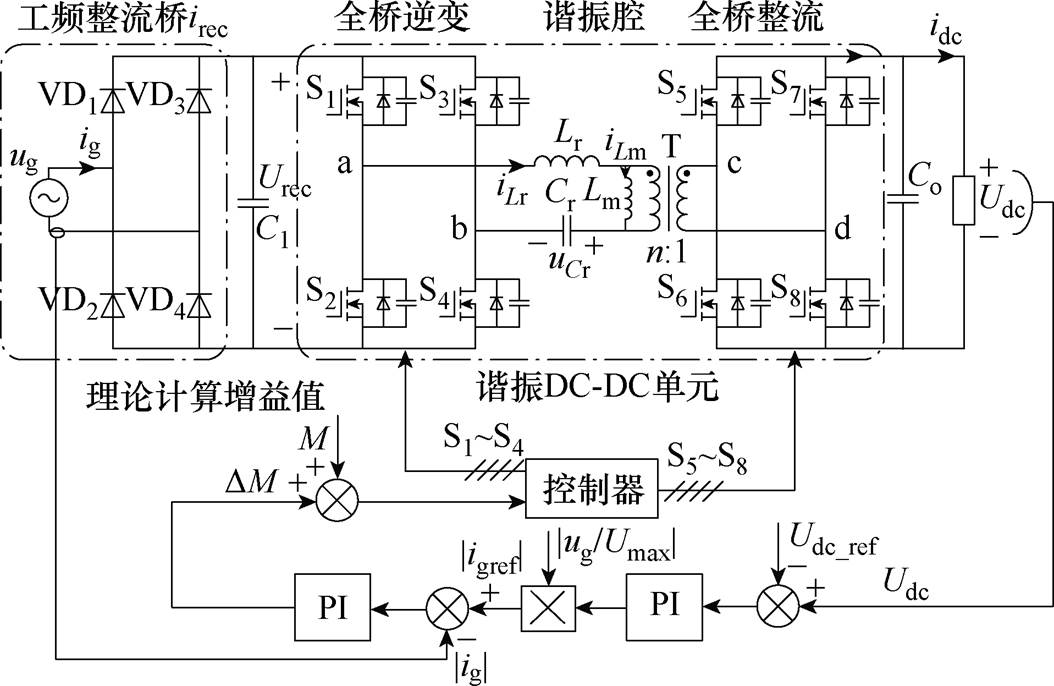
图1 单级式隔离AC-DC变换器的拓扑结构
Fig.1 Topology of single-stage isolated AC-DC converter
摘要 基于串联谐振腔谐振频率点阻抗为零的特点，该文提出基于定频脉冲宽度调制的单级隔离式AC-DC变换器及其优化设计方法。通过调节谐振腔两端高频激励电压脉冲宽度，使得谐振腔两端基波电压相等，实现变换器等效电压增益宽范围连续可调，满足AC-DC变换器交直流侧电压和电流调控需求。该文以AC-DC变换器全功率周期效率优化为目标，建立综合考虑开关损耗和导通损耗的分析模型，并据此给出变换器参数优化设计方法。详细分析AC-DC变换器的工作原理和特性，并制作设计开关频率为300 kHz的实验样机，最后通过实验验证了该文解决方案的有效性。
关键词：单级AC-DC变换器 谐振变换器 脉冲宽度调制 软开关
作为能源转换核心接口的AC-DC变换器，在以新能源为核心的新型电力系统中得到了广泛的应用。随着能源结构的不断改变及优化，各种不同应用场景对AC-DC变换器的效率、功率密度、动态性能、输入电流谐波和功率因数有了更严格、更苛刻的要求[1-3]。由于输入为交流电压，相较于DC-DC变换器，AC-DC变换器也需要更高的调压能力，在实现AC-DC变换器功率因数校正（Power Factor Correction, PFC）的前提下，如何提升其效率、功率密度以及调压范围成为AC-DC变换器需要重点关注和解决的问题[4-9]。
AC-DC变换器通常拥有两种架构：两级式架构和单级式架构[3-5]。相较于两级式AC-DC变换器架构，单级式AC-DC变换器将实现功率因数校正的部分与实现隔离的DC-DC变换器部分集成到一起，从而能够减少更多的开关器件、拥有更高的功率密度。同时通过加入LLC谐振腔可以使单级式AC-DC变换器实现软开关，损耗进一步优化，得到更高的效率[10]。
但是传统的谐振型DC-DC变换器或者谐振型AC-DC变换器通常采用脉冲频率调制（Pulse Frequency Modulation, PFM）[11]。该种调制方法在开关频率偏移谐振频率时，软开关特性会发生改变，在高频下可能会产生较大的开关损耗。并且使用PFM的变换器，电压增益受到功率传输大小改变的影响较大。这两种性质极大地限制了PFM的调压特性，不适用于要求宽范围调压的AC-DC变换器。文献[12]针对直流变换，采用固定频率脉冲宽度调制（Pulse Width Modulation, PWM），实现了串联谐振变换器的升降压宽范围调节，为需要实现宽范围动态调压的单级隔离AC-DC变换提供了可能的解决方案。然而，文献[12]需要额外采用辅助电感实现软开关，电路结构略复杂。此外，针对AC-DC变换器，其参数设计和控制方法也有明显不同[13-16]。
氮化镓器件技术的发展和逐渐成熟为高频、高功率变换提供了新的实现手段。虽然氮化镓器件能够实现更高的开关速度、支持更高的开关频率，但会使开关损耗大大增加，这对于功率开关管的软开关要求也就更加严格了。所以，针对使用氮化镓器件的变换器，需要对其参数以及软开关设计进行进一步优化[17-19]。
本文拟研究一种基于定频控制的谐振型单级隔离AC-DC变换器。并且结合氮化镓器件和AC-DC变换器的运行特性，对变换器的软开关特性、导通损耗特性等进行综合优化设计，不仅使变换器能够在较宽的范围内实现软开关，也避免了一味追求全范围软开关导致的导通损耗过大问题。本文首先对电路的基本拓扑和控制原理进行了分析；其次重点对变换器的控制策略、增益特性分析以及参数优化设计进行了研究；最后对所提出的解决方案进行实验验证。
定频控制谐振型单级式隔离AC-DC变换器的拓扑结构如图1所示，其由工频不控整流桥以及谐振型DC-DC变换器组成。其中工频整流桥由二极管VD1～VD4组成。谐振型DC-DC变换器由一次侧全桥开关管S1～S4，二次侧全桥开关管S5～S8，谐振元件Lr、Cr以及变压器T组成。一次、二次侧全桥通过高频变压器以及谐振元件连接。变换器通过电压外环和电流内环双PI环进行控制。通过电压外环和锁相环得到电流内环参考，然后通过电流内环能够使输入电流对输入电压相位进行跟踪从而实现PFC。图1中，VD1～VD4为二极管，S1～S8为开关管；ug为交流网侧电压，ig为交流网侧电流，irec为工频整流输出电流，Urec为工频整流桥输出电压，iLr为谐振电流，iLm励磁电流，uCr为谐振电容电压，idc为直流输出电流，Udc为直流输出电压；C1为交流侧滤波电容，Lr为谐振电感，Cr为谐振电容，T为变压器，n为变压器变压比，Co为直流输出侧解耦电容；a、b为一次侧全桥桥臂中点，c、d为二次侧全桥桥臂中点；Udc_ref为直流电压参考，Umax为采样所得的交流电压最大值，|igref|为交流电流参考绝对值，|ig|为交流电流采样值绝对值，DM为比例积分控制器（Proportional Integral Controller, PI）所输出的增益误差量，M为前馈的理论计算增益值。
图1 单级式隔离AC-DC变换器的拓扑结构
Fig.1 Topology of single-stage isolated AC-DC converter
为了更直观地分析变换器的增益特性，可以将该变换器等效为如图2所示的谐振腔等效电路。图中，n为变压器电压比，uab、ucd分别为一次、二次侧桥臂中点电压。
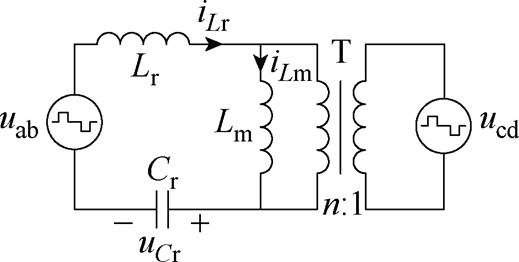
图2 谐振腔等效电路
Fig.2 Resonant tank equivalent circuit
当调节一次、二次侧占空比Dp、Ds时，其波形如图3所示。图中，Urec为输入电压ug经整流后的瞬时电压，Udc为输出直流电压，uab1、ucd1分别为uab、ucd基波分量，iLr为谐振电感电流，iLm为励磁电感电流。
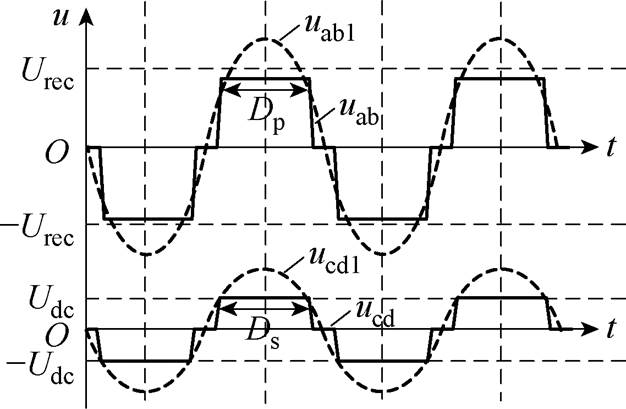
图3 桥臂中点电压波形
Fig.3 Waveforms of bridge arm midpoint voltage
分析谐振腔等效电路可知，当开关频率fs与谐振频率fr相等时，Lr和Cr发生串联谐振，谐振腔阻抗可以对外等效为零，谐振变换器的增益特性因此与负载无关。通过调节桥臂中点电压uab、ucd的基波分量uab1、ucd1的幅值Uab1、Ucd1的大小，即可实现对变换器的调压，对如图3所示的uab、ucd进行傅里叶分解得到基波分量幅值Uab1、Ucd1与占空比的关系分别为
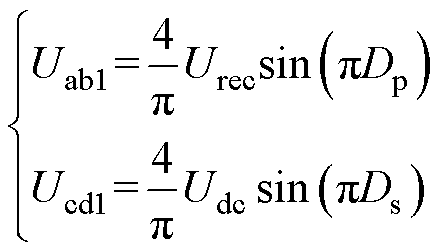（1）
定义变压器的瞬时等效增益为
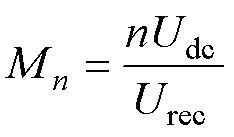（2）
当Mn＞1时，为升压模式；当Mn＜1时，为降压模式。
将式（2）代入式（1），可以得出变压器的瞬时等效增益和占空比的关系为
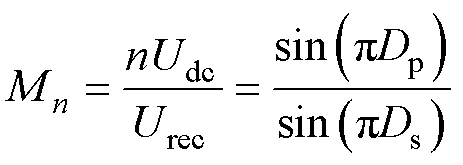（3）
由式（3）得出占空比与增益关系曲线，如图4所示。
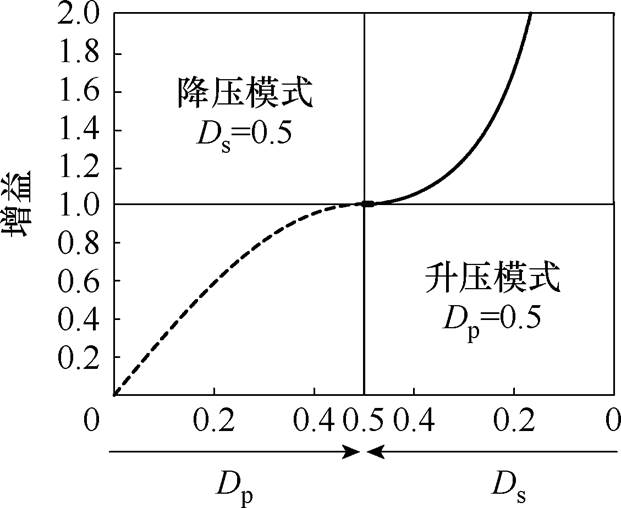
图4 占空比与增益关系曲线
Fig.4 Relationship curves between duty cycle and gain
当变换器工作在升压模式时，需要通过定频调节二次侧开关管占空比Ds以实现升压；当变换器工作在降压模式时，需要通过定频调节一次侧开关管占空比Dp以实现降压。变换器的理论增益调节范围从0到无穷，从而证明了本文使用的定频PWM方法拥有进行整流全范围调压的能力。
图5为所研究变换器的升压模式典型工作波形，由于降压模式的典型工作波形与升压模式一次、二次侧对称，所以本文不再展示，图中，t0～t12为一个开关周期中谐振腔工作模态进行变换的几个关键时间点；uGSx为开关管的驱动波形，x=1,…, 8。
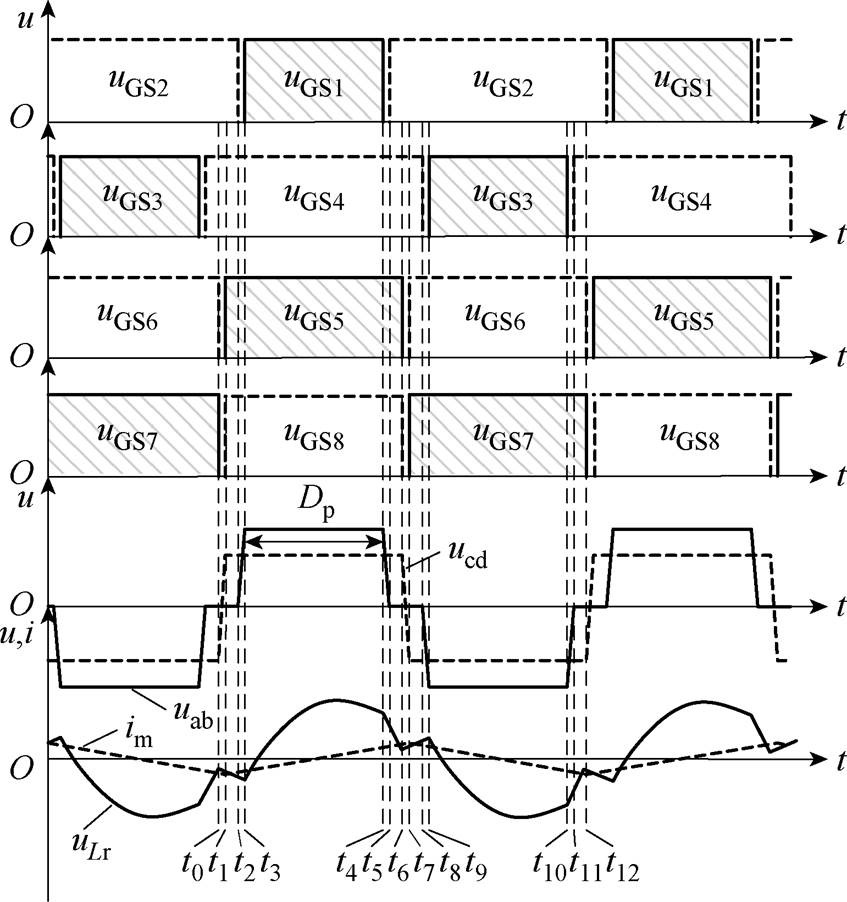
图5 升压模式的典型工作波形
Fig.5 The typical working waveforms of Boost mode
当变换器工作在谐振频率时，谐振电感与谐振电容是没有参与增益调节的，并且考虑到本文所研究的变换器引入了高频氮化镓器件，所以参数优化设计的目标主要在于降低开关损耗以及导通损耗。对变换器软开关特性及谐振腔导通损耗进行数学建模，以在宽电压范围下实现变换器开关管软开关并且控制谐振腔内部导通损耗在合适的范围内。
实现零电压开通（Zero Voltage Switching, ZVS）的等价条件是在死区时间内，开关管的结电容充放电能够顺利完成，以此作为约束条件所列出的不等式为
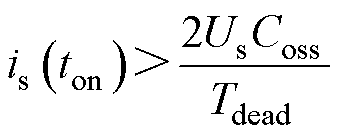（4）
式中，is(ton)为开通时刻开关管的电流；Coss为开关管的结电容；一次侧开关管对应的Us为ug经整流后的瞬时电压Urec；二次侧开关管对应的Us为输出直流电压Udc；Tdead为死区时间。
通过基于图2谐振腔等效电路所列出的谐振腔谐振电流iLr以及谐振电容电压uCr时域表达式，如果要计算出开关管任意开通时刻的电流大小，那么还需要两个初始条件，分别为谐振电感电流初值I0和谐振电容电压初值V0。
定义输入功率因数角为零，此时输入阻抗Rpri为
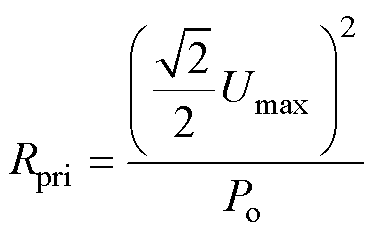（5）
对于升压模式，定义谐振电流初值为I0_Boost，谐振电容电压初值为V0_Boost。根据输入到谐振腔的功率守恒关系并结合图3可以得到
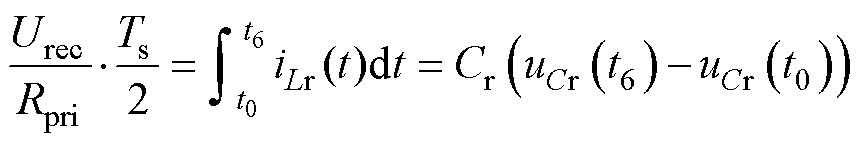
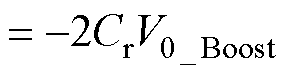（6）
式中，iLr(t)、uCr(t)分别为谐振电流、谐振电容电压；Ts为开关周期。
升压模式谐振电容电压初值为
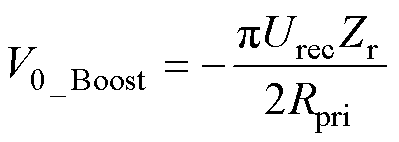（7）
式中，Zr为特征阻抗，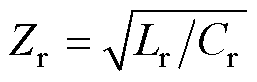
。
如图3所示升压模式工作波形，t0时刻，iLr和iLm基本相等。可以近似得到
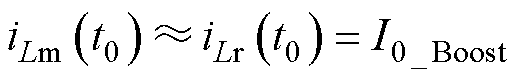（8）
对于降压模式，定义谐振电流初值为I0_Buck，谐振电容电压初值为V0_Buck。根据谐振腔到输出侧的功率守恒关系可以得到
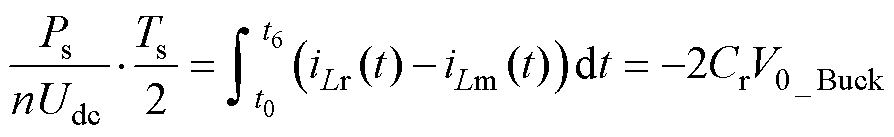（9）
式中，Ps为对应开关周期内一次侧传递到二次侧的平均功率，即
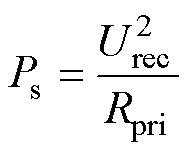（10）
由于半个周期内iLm的积分为0，因此式（9）可以化简为
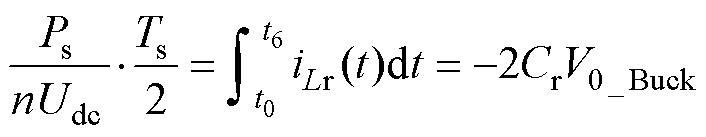（11）
综合式（10）、式（11）可以求解出降压模式的谐振电容电压初值V0_Buck的表达式为
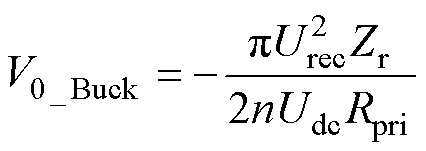（12）
与升压模式类似，t0时刻，iLr和iLm同样近似相等。因此可以认为降压模式谐振电流初值I0_Buck表达式为
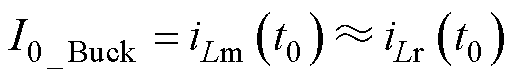（13）
根据求得的初始条件可以求解出各个开关管开通时刻的电流表达式；发现占空比在变化的桥臂对应软开关实现会难于占空比恒定不变的桥臂。
以降压模式一次侧开关管S1为例，其软开关约束条件可以表示为
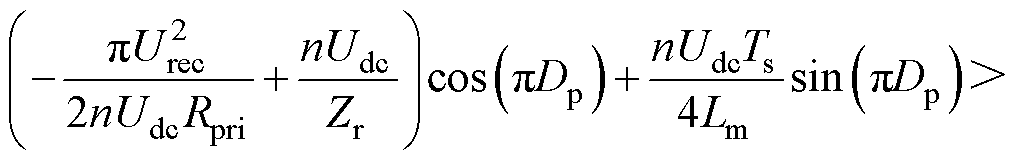
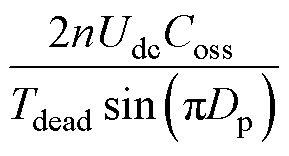（14）
式中，Lm为励磁电感；Coss为开关管的结电容。
通过式（14），可以看到影响软开关的主要参数为Zr与Lm，S1在开通时刻电流大于边界，则开关管S1能实现软开关。
对于同一桥臂的一次侧开关管S2，同样地，可以计算出软开关约束条件为
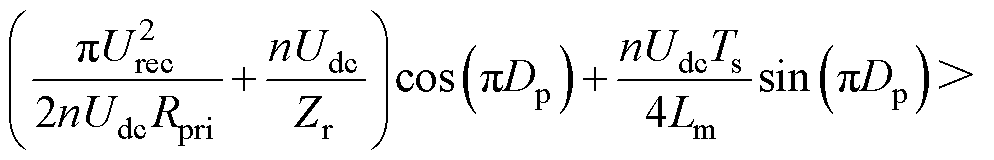
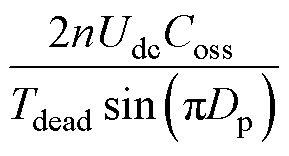（15）
从式（14）与式（15）中可以看到，开关管S2开通时刻的电流一定大于开关管S1，只要S1满足软开关约束，S2就可以实现软开关。一次侧的另外一个桥臂开关管S3和S4，其软开关情况与开关管S1和S2一致，不需要再单独进行分析。对于升压模式，其软开关约束设计方法与降压模式一致，这里不再重复进行分析。
从约束条件中可以看出，变换器在占空比小、输出平均功率大的工作情形下更难实现软开关，所以满载为参数设计时着重考虑的工况。
对谐振腔参数的确定还需进一步考虑谐振腔导通损耗与Zr的关系，即考虑谐振腔电流有效值大小与Zr的关系。以本文所提变换器为例，如图6所示为满载时在不同Zr下半个工频周期内谐振腔电流有效值的变化情况，图中，ws为变换器的开关角频率，ILr_RMS为谐振电流有效值。
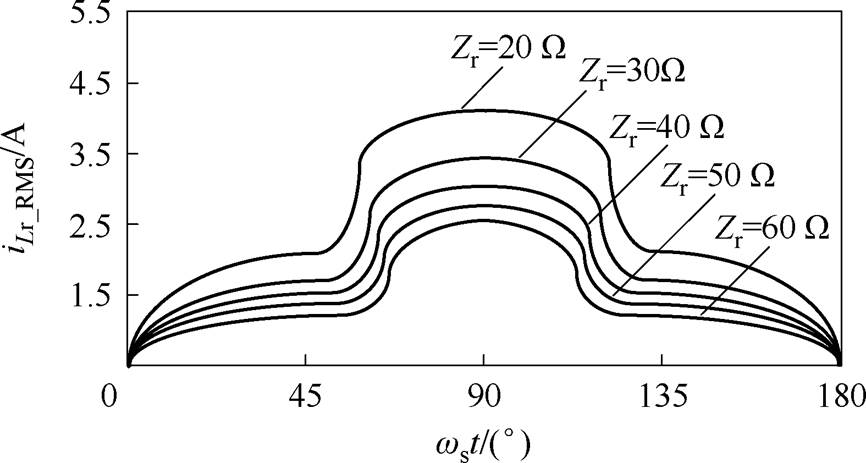
图6 不同Zr下谐振腔电流有效值的变化情况
Fig.6 The RMS value of the resonant current versus time wst with different Zr
对iLr_RMS在半个工频周期的分布曲线再次求有效值，可以得到半个工频周期内ILr_RMS与Zr的关系曲线如图7所示。
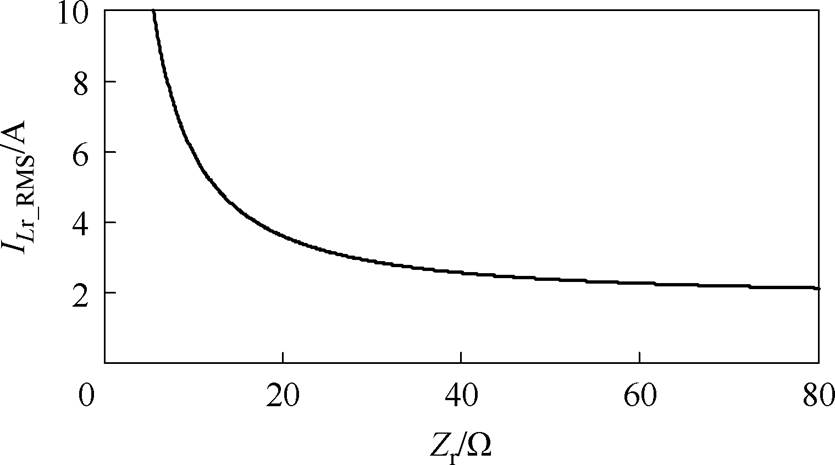
图7 谐振腔电流有效值随Zr变化关系曲线
Fig.7 Curve of ILr_RMS vs. Zr variation
从图7中可以发现，增大Zr有利于减小谐振腔电流有效值从而减小导通损耗，但是Zr增大会导致谐振电容电压有效值增大，在选取Zr时也应考虑谐振电容能够承受的最大电压应力，谐振电容电压有效值UCr_RMS随Zr变化关系曲线如图8所示。
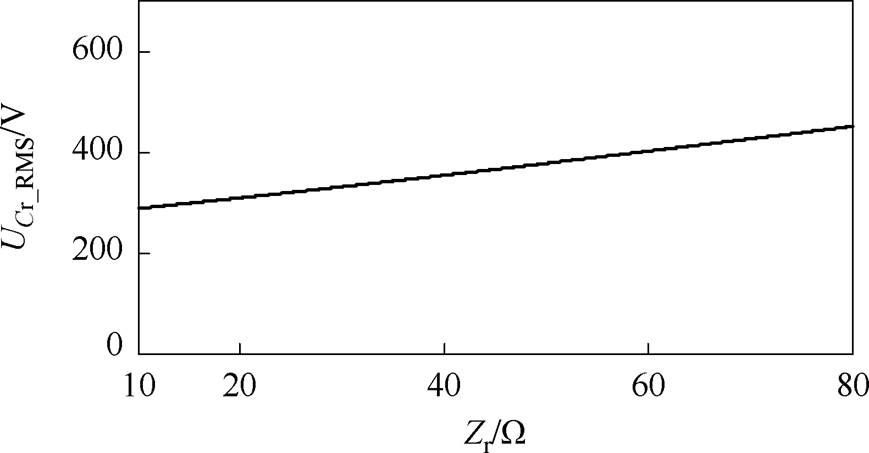
图8 谐振电容电压有效值随Zr变化关系曲线
Fig.8 Curve of UCr_RMSvs. Zr variation
综合图6～图8对Zr进行选取，即变换器在大部分工况下能够实现软开关并且拥有较低的导通损耗。
2.4.1 软开关范围设计
基于2.2节、2.3节所建立的数学模型可以得出，若要实现全交流电压范围的软开关，那么Lm与Zr需取值足够小，但是过小的Lm与Zr会引起谐振腔电流的上升从而提高导通损耗。当电压较小时，谐振腔电流也较小，在设计时可以忽略这一部分的软开关，即保证在工频周期绝大部分功率传输时间内开关管可实现软开关。基于这一特性，设计出变换器软开关的优化设计范围，设需要实现ZVS的功率区间为[q, p-q]，在实现ZVS的电压区间所传输的功率占比如图9所示。图中，Umax为输入交流电压最大值，Imax为输入交流电流最大值，Uz为所设计软开关范围的最小电压，且Uz=Umaxsinq。
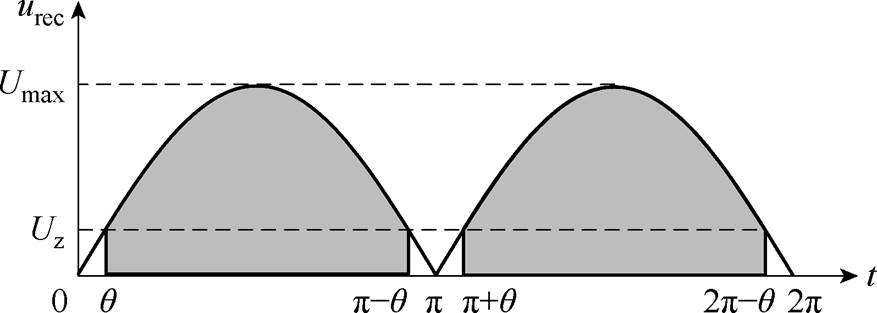
图9 在实现ZVS的电压区间所传输的功率占比
Fig.9 The proportion of power transmitted in the voltage range of achieving ZVS
通过积分计算在实现ZVS的电压区间所传输的功率占比MZVS为
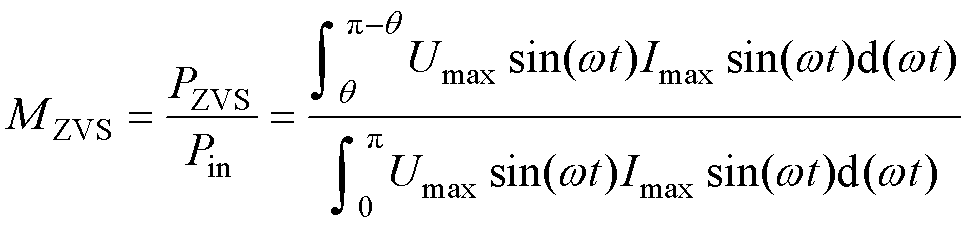
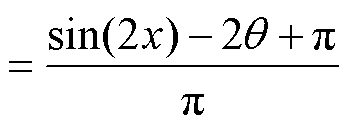（16）
根据实践经验，一般MZVS取70%，当Umax= 311 V时，Uz=250 V。
2.4.2 变压器电压比设计
变压器电压比的设计目标同样是要让所设计的软开关区间发生在功率占比较大的区间。同时，当变换器谐振腔的增益越接近1时，开关管的软开关越容易实现，所以需要配置合适的电压比使谐振腔的增益接近于1时工作在软开关电压范围内，这样才能确保变换器工作在最高的效率。综上所述，将增益为1的点，即Ds=Dp=0.5的时刻设计在软开关[Uz, Umax]电压范围的中点处，根据瞬时等效增益表达式（2）可以得到变压器的电压比n为
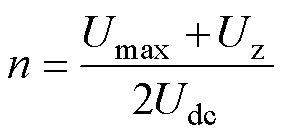（17）
如图10所示为一个工频周期内不同输入电压所对应的电压工作模式划分。t1、t2、t3、t4分别为一个周期内变换器调压模式转换的时刻。
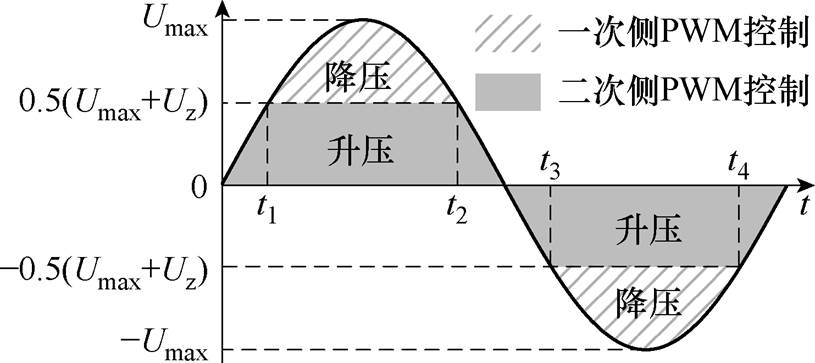
图10 工频周期内工作模式划分
Fig.10 Working mode division in power frequency cycle
基于以上理论所设计变换器输入电压绝对值和一次、二次侧占空比的关系曲线如图11所示。
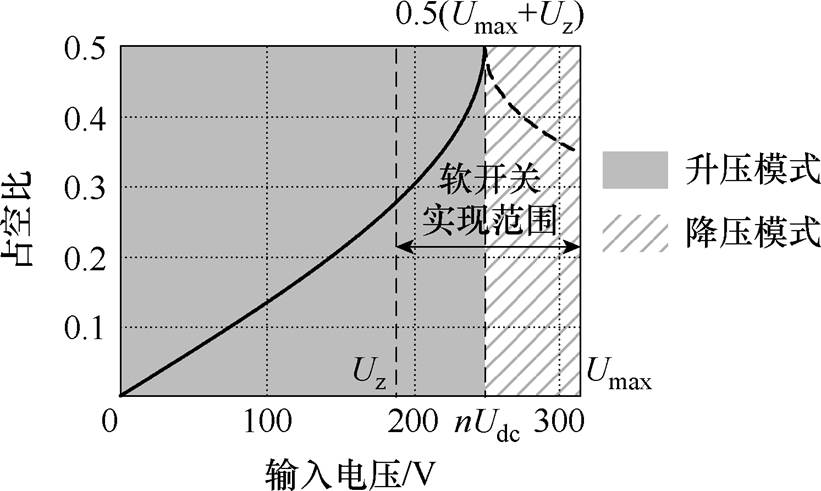
图11 占空比随输入电压变化曲线
Fig.11 Duty cycle curve with input voltage
2.4.3 谐振腔参数选取
以所研究样机为例，通过遍历谐振腔参数Lm、Zr，确保在输入电压绝对值范围在降压模式区间0.5(Umax+Uz)～Umax之内，S1在开通时刻电流大于边界，则开关管S1能实现软开关。如图12所示为遍历后所得出的开关管S1约束平面。以同样方法可以得出S3、S5、S7的软开关约束平面，这里不再重复展示。
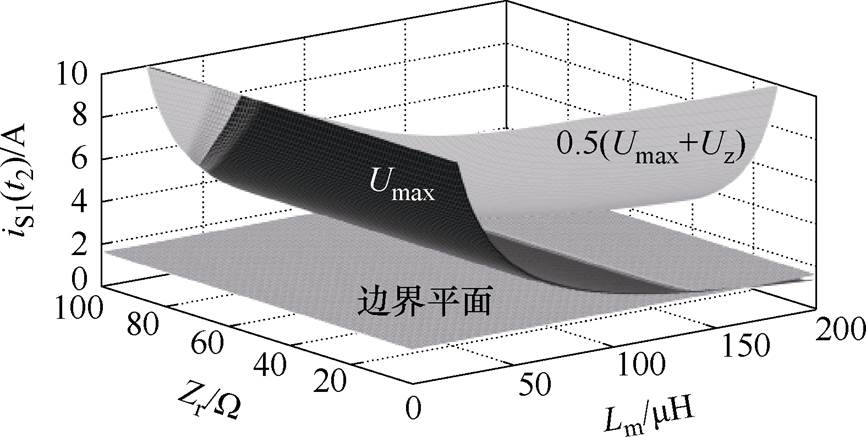
图12 开关管S1软开关约束平面
Fig.12 Soft switch constraint plane of the switch S1
由图7可以得出，当Zr＞20 W 后电流变化减缓，所以Zr应在大于20 W 的区间选取。同时Lm越小越容易实现软开关，但考虑到Lm过小时会带来导通损耗，所以在选取参数时尽量选取边界附近的值，这样可以在最低的开关管导通电流下实现软开关。由图11中可以看到，Zr=60 W 、Lm=120 mH左右时处于三个平面交界处。综合其他开关管的软开关约束条件以及导通损耗数学模型，所研究样机最终选定参数Zr=60 W ，Lm=120 mH。
在实际应用中，由于Lr与Cr在制作和生产中公差的影响，实际的谐振频率会与所设计的值有所偏差，导致谐振腔的谐振状态发生改变。考虑串联谐振腔的阻抗特性，如果开关频率略低于谐振频率，谐振腔将呈容性；如果开关频率略高于谐振频率，谐振腔将呈感性。从软开关的角度，谐振腔呈感性更有利于软开关的实现，此时虽然感性阻抗会略微影响变换器增益，但不会影响变换器软开关特性。因此，实际应用时，考虑到器件的容差，只要确保变换器不会进入谐振腔容性工作区即可，可以选择略高于谐振腔串联谐振频率工作。
为验证本文所研究的单级隔离AC-DC变换器工作原理与特性，制作一台实验样机，其主要参数如下：输入电压ug=AC 220 V；输出电压Udc=28 V；额定输出功率300 W；整流桥VD1～VD4，YBSM6006；一次侧开关管S1～S4，GS66508B；二次侧开关管S5～S8，IAUA180N04S5N012；变压器电压比n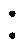
1=10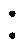1；谐振电感Lr=31.83 mH；谐振电容Cr=8.84 nF；励磁电感Lm=120 mH；开关频率fs=300 kHz。图13为300 W满载稳态实验波形。
图13中，uGS5为二次侧全桥开关管S5的栅源极电压，ig为输入电流。实验波形表明，网侧电流正弦度良好、输出电压稳定。
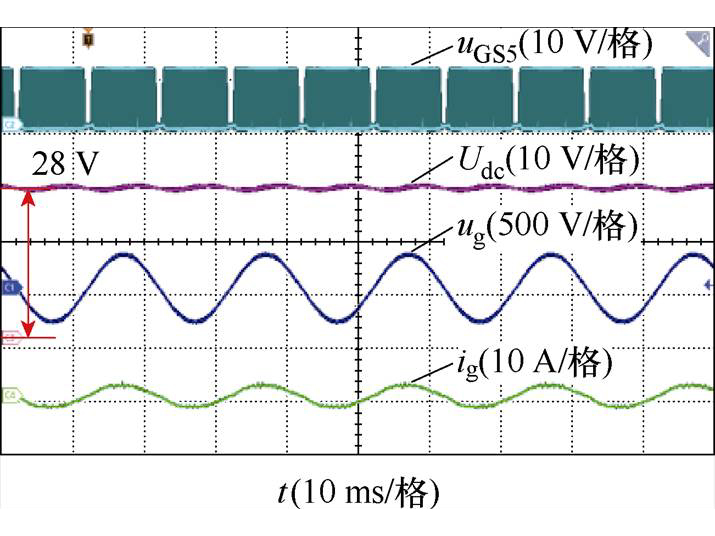
图13 300 W满载稳态实验波形
Fig.13 300 W full load steady-state waveforms
图14为变换器工作在升压模式时上管的软开关波形。图中，uGS3为开关管S3的栅源极电压，uDS3、uDS5为开关管S3、S5的漏源极电压。从图中可以看到，变换器工作于升压模式时，一次侧开关管占空比为0.5，开关管实现了软开关；二次侧开关管的占空比小于0.5，通过调节二次侧开关管占空比实现了谐振腔的升压，开关管实现了软开关。
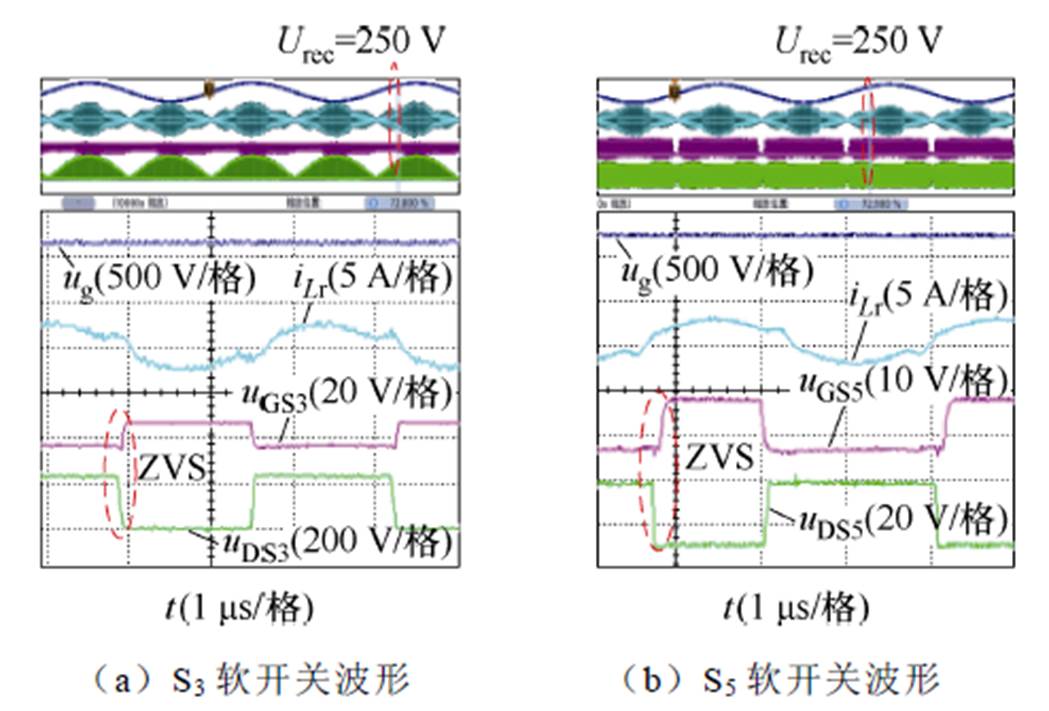
图14 升压模式开关管软开关波形
Fig.14 ZVS waveforms of switches during Boost mode
如图15所示为在降压模式上管的软开关波形。从图中可以看到，变换器工作于降压模式时，一次侧开关管占空比小于0.5，通过调节一次侧开关管占空比实现了谐振腔的降压，开关管实现了软开关；二次侧开关管的占空比为0.5，开关管实现了软开关。
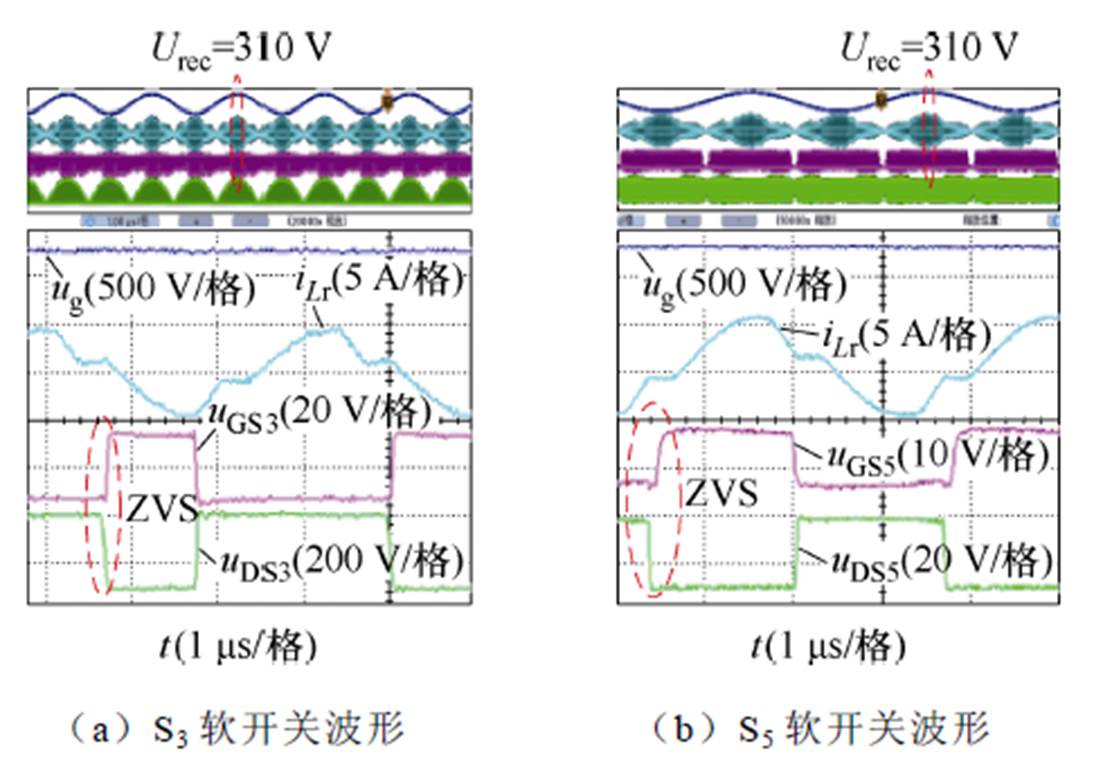
图15 降压模式开关管软开关波形
Fig.15 ZVS waveforms of switches during Buck mode
图16、图17为变换器在稳态情况下的切载实验波形，实验条件为输入电压ug=AC 220 V，输出电压Udc=28 V，输出功率半载和满载之间切换。图16中，Idc为输出电流。从图中可以看到，负载突加突卸时，变换器快速响应，表明变换器具有很好的负载电流响应能力，这是由于变换器等效电压增益与负载无关，变换器输出表现为电压源特性。
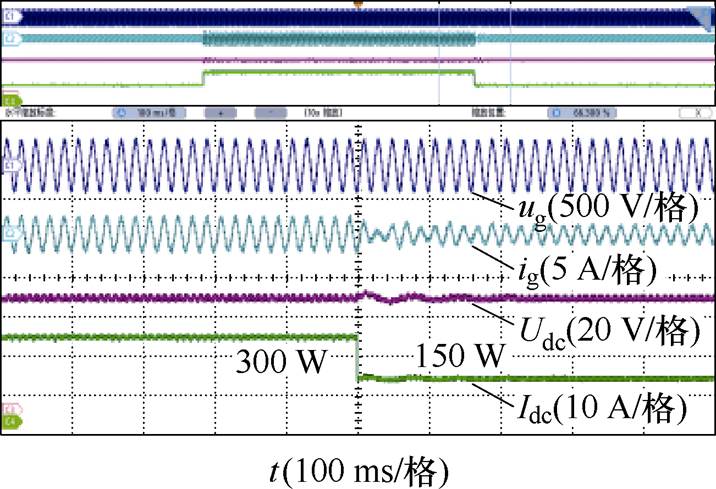
图16 动态实验波形
Fig.16 Dynamic experimental waveforms
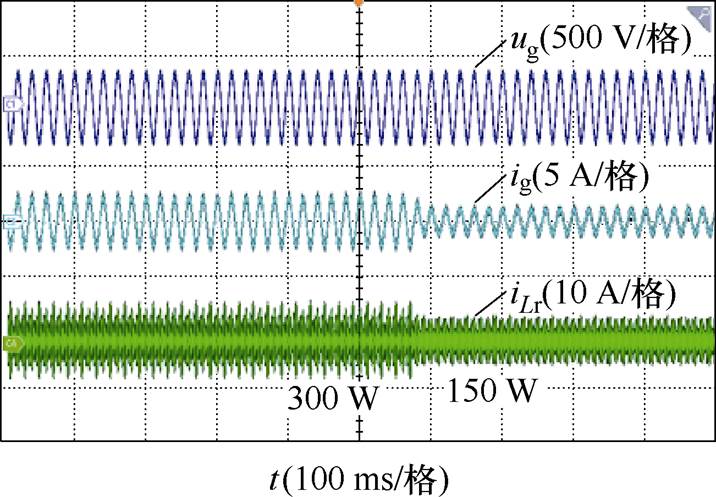
图17 谐振腔动态波形
Fig.17 Dynamic waveforms of resonant tank
图18为变换器效率以及功率因数变化曲线。当fs=300 kHz的时候，变换器的峰值效率为94.2%。在半载以上其功率因数都大于0.98，满载功率因数为0.994，表明变换器可以实现输入端较高的功率因数。
图18 变换器的效率及功率因数变化曲线
Fig.18 Efficiency and PF curves of proposed converter
本文所用定频控制方法与变频、移相调制的对比见表1。
表1 调制策略的对比
Tab.1 Comparison with other modulation
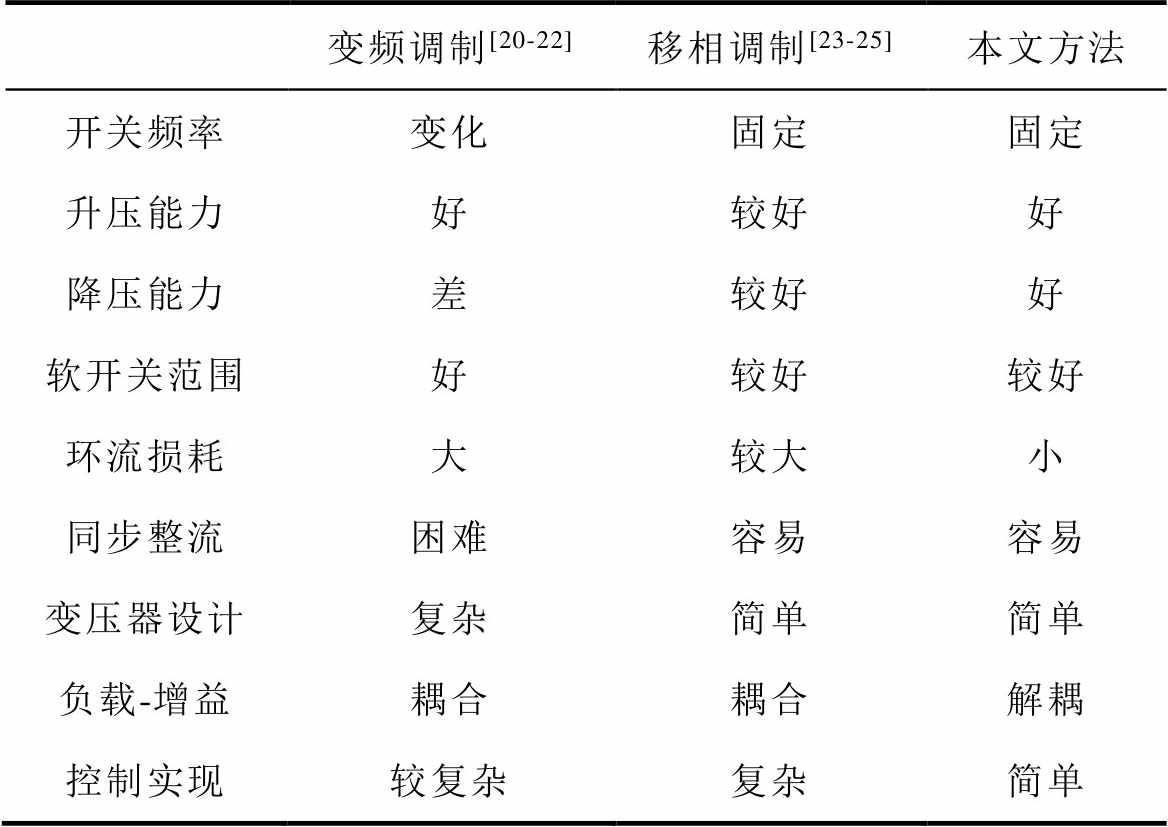
变频调制[20-22]移相调制[23-25]本文方法 开关频率变化固定固定 升压能力好较好好 降压能力差较好好 软开关范围好较好较好 环流损耗大较大小 同步整流困难容易容易 变压器设计复杂简单简单 负载-增益耦合耦合解耦 控制实现较复杂复杂简单
变频调制LLC由于其降压能力受限，通常设计在小于谐振频率的升压区间工作。其具有全范围软开关能力，但为了实现软开关导致的环流损耗增大，变频控制也使得变压器优化设计、二次侧同步整流控制更困难。同时，其负载大小与变换器增益呈强相关，也增加了控制的难度。移相控制虽然也能实现定频工作，但其宽范围调压困难、环流损耗大，且电压增益也受负载大小影响。为了优化效率，需要采用复杂的控制策略，增加了控制的实现难度。本文所提出的方法在电压调节能力、负载调节特性方面具有突出优势，且控制实现非常简单，但考虑到导通损耗等因素，其很难实现整个交流电压范围内的软开关。
本文研究了一种基于定频PWM控制的谐振型单级隔离AC-DC变换器。理论分析和实验结果表明：
1）通过开关管占空比调节能够实现变换器宽范围升压和降压变换，很好地实现交直流侧电压和电流调控。
2）通过参数寻优设计以及合理设置变压器电压比配置，能够兼顾导通损耗并使得变换器所有开关管可以在较宽输入电压范围内实现软开关。
3）实验测试结果表明，变换器具有良好的动稳态性能，且能够实现高功率因数。
参考文献
[1] 董朝阳, 赵俊华, 福拴, 等. 从智能电网到能源互联网: 基本概念与研究框架[J]. 电力系统自动化, 2014, 38(15): 1-11.
Dong Zhaoyang, Zhao Junhua, Fu Shuan, et al. From smart grid to energy internet: basic concept and research framework[J]. Automation of Electric Power Systems, 2014, 38(15): 1-11.
[2] 韩蒙, 吴红飞, 邢岩. 基于隔离升降压变换器的单级软开关功率因数校正变换器[J]. 中国电机工程学报, 2017, 37(8): 2361-2369.
Han Meng, Wu Hongfei, Xing Yan. A single-stage soft-switching power factor correction converter based on an isolated Buck-Boost converter[J]. Pro- ceedings of the CSEE, 2017, 37(8): 2361-2369.
[3] 孟建辉, 吴小龙, 张自力, 等. 三相隔离型AC-DC- DC电源自适应线性自抗扰控制方法及纹波抑制补偿策略[J]. 电工技术学报, 2023, 38(14): 3898-3908.
Meng Jianhui, Wu Xiaolong, Zhang Zili, et al. Adaptive linear active disturbance rejection control method and ripple suppression compensation strategy for three-phase isolated AC-DC-DC power supply[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3898-3908.
[4] 田崇翼, 李珂, 张承慧, 等. 基于切换模型的双向AC-DC变换器控制策略[J]. 电工技术学报, 2015, 30(16): 70-76.
Tian Chongyi, Li Ke, Zhang Chenghui, et al. Control strategy for bi-directional AC-DC converter based on switched system model[J]. Transactions of China Electrotechnical Society, 2015, 30(16): 70-76.
[5] 高敬祥, 张俊洪, 宋庆国, 等. 一种高功率因数低母线电压单级LLC AC/DC变换器[J]. 电源学报, 2023, 21(3): 1-9.
Gao Jingxiang, Zhang Junhong, Song Qingguo, et al. Single-stage LLC AC/DC converter with high power factor and low bus voltage[J]. Journal of Power Supply, 2023, 21(3): 1-9.
[6] 吴红飞, 张炎锋, 杨帆. 宽输出电压范围集成Buck型无桥PFC变换器[J]. 中国电机工程学报, 2018, 38(22): 6655-6661.
Wu Hongfei, Zhang Yanfeng, Yang Fan. Bridgeless power factor correction converter with integrated Buck converter for wide output voltage range appli- cations[J]. Proceedings of the CSEE, 2018, 38(22): 6655-6661.
[7] 王力, 胡佳成, 曾祥君, 等. 基于混合储能的交直流混联微电网功率分级协调控制策略[J]. 电工技术学报, 2024, 39(8): 2311-2324.
Wang Li, Hu Jiacheng, Zeng Xiangjun, et al. Power hierarchical coordinated control strategy for AC/DC hybrid microgrid based on hybrid energy storage[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2311-2324.
[8] 卢伟国, 曹琪, 张婷婷, 等. 基于改进谐波注入的单相Boost功率因数校正变换器直流母线电容参数在线检测[J]. 电工技术学报, 2025, 40(8): 2601- 2614.
Lu Weiguo, Cao Qi, Zhang Tingting, et al. Online detection of DC-link capacitance parameters of single-phase Boost power factor correction converter based on improved harmonic injection[J]. Transac- tions of China Electrotechnical Society, 2025, 40(8): 2601-2614.
[9] Musavi F, Eberle W, Dunford W G. A high- performance single-phase bridgeless interleaved PFC converter for plug-in hybrid electric vehicle battery chargers[J]. IEEE Transactions on Industry Appli- cations, 2011, 47(4): 1833-1843.
[10] 王章毅, 陆道荣, 李想, 等. 基于移相和调频的单级双向AC-DC变换器临界电流调制策略[J]. 电工技术学报, 2023, 38(14): 3888-3897.
Wang Zhangyi, Lu Daorong, Li Xiang, et al. Boundary current modulation strategy of single-stage bidirectional AC-DC converter based on phase-shift and variable-frequency control[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3888- 3897.
[11] 黄何伟, 曹太强, 潘光绪, 等. 考虑回流功率因素的全桥CLL谐振变换器参数优化设计[J]. 电工技术学报, 2023, 38(20): 5503-5514.
Huang Hewei, Cao Taiqiang, Pan Guangxu, et al. Parameter optimal design of full-bridge CLL resonant converter considering backflow power factor[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5503-5514.
[12] Wu Hongfei, Sun Kai, Li Yuewei, et al. Fixed- frequency PWM-controlled bidirectional current-fed soft-switching series-resonant converter for energy storage applications[J]. IEEE Transactions on Indu- strial Electronics, 2017, 64(8): 6190-6201.
[13] Jauch F, Biela J. Single-phase single-stage bidi- rectional isolated ZVS AC-DC converter with PFC[C]//2012 15th International Power Electronics and Motion Control Conference (EPE/PEMC), Novi Sad, Serbia, 2012: LS5d.1-1-LS5d.1-8.
[14] Cheng Chunan, Chang C H, Chung T Y, et al. Design and implementation of a single-stage driver for supplying an LED street-lighting module with power factor corrections[J]. IEEE Transactions on Power Electronics, 2015, 30(2): 956-966.
[15] Li Xiang, Guo Liuniu, Lang Tianchen, et al. Steady- state characterization of LLC-based single-stage AC/DC converter based on numerical analysis[J]. IEEE Transactions on Power Electronics, 2021, 36(9): 9970-9983.
[16] Everts J, Krismer F, Van den Keybus J, et al. Optimal ZVS modulation of single-phase single-stage bidi- rectional DAB AC-DC converters[J]. IEEE Transa- ctions on Power Electronics, 2014, 29(8): 3954-3970.
[17] Krishnamoorthy H S, Garg P, Enjeti P N. A matrix converter-based topology for high power electric vehicle battery charging and V2G application[C]// IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 2012: 2866-2871.
[18] Hou Ruoyu, Xu Jianchun, Chen Di. A multivariable turn-on/turn-off switching loss scaling approach for high-voltage GaN HEMTs in a hard-switching half- bridge configuration[C]//2017 IEEE 5th Workshop on Wide Bandgap Power Devices and Applications (WiPDA), Albuquerque, NM, USA, 2017: 171-176.
[19] Hou Ruoyu, Lu Juncheng, Chen Di. Parasitic capacitance Eqoss loss mechanism, calculation, and measurement in hard-switching for GaN HEMTs[C]// 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 2018: 919-924.
[20] Liu Wenbo, Yurek A, Sheng Bo, et al. A single stage 1.65kW AC-DC LLC converter with power factor correction (PFC) for on-board charger (OBC) appli- cation[C]//2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 2020: 4594-4601.
[21] Forouzesh M, Liu Yanfei, Sen P C. Efficiency improvement of single-stage AC-DC LLC converter using a line cycle synchronous rectifier (SR) driving strategy[C]//2022 24th European Conference on Power Electronics and Applications (EPE'22 ECCE Europe), Hanover, Germany, 2022: 1-10.
[22] Li Xiang, Hu Haibing, Guo Liuniu, et al. A matrix- converter-based single-stage AC-DC converter with a LLC resonant tank to realize soft switching[C]//2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 2020: 1555-1559.
[23] Wang Guangyu, Wen Huiqing. Analysis and reliabi- lity assessment for a bidirectional single-stage DAB- based AC/DC converter[C]//2023 IEEE 14th Inter- national Symposium on Power Electronics for Dis- tributed Generation Systems (PEDG), Shanghai, China, 2023: 5-8.
[24] Liu Bochen, Davari P, Blaabjerg F. A flexible control scheme for single-stage DAB AC/DC converters[C]// 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 2018: 1-6.
[25] Liu W, Zhu D, Yan Q, et al. Simplified peak current optimization of DAB converters with dual-phase-shift control[C]//The 16th IET International Conference on AC and DC Power Transmission (ACDC 2020), Online Conference, 2020: 210-214.
Fixed Frequency Controlled Resonant Single Stage Isolated AC-DC Converter
Abstract AC-DC converters are key equipment to interface the AC grid, DC loads, and renewable generation sources. Efficiency and power density are the main factors in the design and implementation of AC-DC converters. The two-stage power conversion has low system efficiency and high cost. A single-stage AC-DC converter achieves AC-side current regulation, DC-side voltage regulation, and high-frequency galvanic isolation simultaneously through only one stage of high-frequency power conversion, which has the potential advantages of high efficiency and power density. However, the design and implementation of single-stage AC-DC converters are difficult.
This paper presents a resonant single-stage isolated AC-DC converter based on a fixed frequency pulse width modulation strategy. When the switching frequency of the converter is set to the resonant frequency of the series-resonant tank, the impedance of the resonant tank always features zero impedance. Therefore, in steady-state, the total voltage applied on the resonant tank must also be zero, which means the fundamental voltage generated by the primary-side and secondary-side switching bridges must be equal. Following this idea, the converter can operate in both voltage step-down and step-up modes, and the equivalent voltage gain of the converter is continuously adjustable in a wide range by adjusting the pulse width of the high-frequency excitation voltages applied on the resonant tank. Hence, the voltage and current regulation requirements of the single-stage AC-DC converter can be satisfied.Voltage step-down regulation can be achieved by adjusting the primary-side duty ratio Dp, while the voltage step-up regulation can be achieved by adjusting the secondary-side duty ratio Ds.
In order to realize the soft-switching of all switches within a wide voltage range, the soft-switching characteristics of the converter are analyzed in detail. It is found that the magnetizing inductance Lm and quality factor Zr of the resonant tank must be small enough within the entire AC voltage range, leading to much higher conduction losses. When the instantaneous AC voltage is low, the switching losses of switches are also low. Therefore, it is unnecessary to achieve soft-switching within the entire AC voltage range, and trade-offs between switching loss and conduction loss must be made to design the converter’s parameters. Therefore, an optimized parameters design method is proposed for the resonant single-stage AC-DC converter.
An experimental prototype is built and tested. The experimental results indicate that through the fixed-frequency pulse-width modulation strategy, step-up and step-down power conversions, the AC and DC side voltage and current regulation, and high power factor can be realized. With the proposed parameter optimization design method, soft switching of switches can be achieved in a wide input voltage range. The efficiency of the converter is up to 94.2%. In addition, experimental results indicate that the converter has excellent dynamic and steady-state performance.
keywords：Single-stage AC-DC converter, resonant converter, pulse width modulation, soft switching
中图分类号：TM461
DOI: 10.19595/j.cnki.1000-6753.tces.240827
国家自然科学基金资助项目（52122708, U2141227）。
收稿日期 2024-05-21
改稿日期2024-06-30
陈赉阳 男，1999年生，硕士研究生，研究方向为功率电力电子变换技术。
E-mail: chenlaiyangcly@nuaa.edu.cn
吴红飞 男，1985年生，教授，研究方向为功率电力电子变换技术。
E-mail: wuhongfei@nuaa.edu.cn（通信作者）
（编辑 陈 诚）