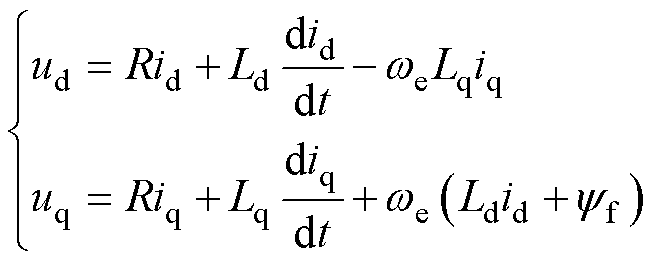（1）
摘要 准确的负载转矩辨识有助于提升复杂非线性负载永磁驱动系统的抗负载扰动能力。滑模观测器具有对噪声高鲁棒性、响应速度快和结构简单等优点，已经成为负载转矩辨识的常用算法。然而，该算法存在高频抖振的缺点，限制了其在电力传动系统中的应用。针对上述问题，该文提出一种新型自适应滑模观测器，在传统滑模观测器模型的基础上，将符号函数替换为饱和函数，设计了一种自适应趋近率，并在反馈回路中引入了一个额外的分量来表示负载转矩的平均估计值，解决了传统滑模观测器趋近时间和系统抖振之间的矛盾。仿真和实验结果表明，所提出的算法相比于传统滑模观测器具有更高的观测精度、更快的响应速度；采用负载转矩观测值作为前馈补偿后提升了驱动系统的响应速度及抗负载扰动能力。
关键词：负载转矩 滑模观测器 永磁同步电机 前馈补偿 抗负载扰动
永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）具有功率密度高、效率高等优点，被广泛应用于机械工业、舰船推进等各领域电力传动系统。当PMSM应用于高精度、复杂非线性电力传动系统时，由于负载转矩的时变特性难以定量刻画，需要对其进行在线辨识[1-4]，从而避免负载转矩的强时变特性造成的转速波动、系统不稳定、传动精度低等问题。
为了实时辨识系统的负载转矩，许多学者已经提出了不同类型的算法。文献[5]中利用降阶Luenberger观测器来估计负载转矩，并用估计值矫正系统的转动惯量。文献[6]采用了全阶Luenberger观测器进行系统参数辨识，利用转子位置观测的误差来估计转动惯量。然而，文献[5-6]的共同问题是Luenberger观测器始终存在稳态误差。文献[7-9]采用模型参考自适应（Model Reference Adaptive System, MRAS）算法对负载转矩进行辨识，通过前馈补偿实现负载扰动的抑制。然而，这些方法依赖于电机的数学模型，鲁棒性较低。文献[10-12]提出了基于扩展卡尔曼滤波（Extended Kalman Filter, EKF）的负载转矩辨识算法，卡尔曼滤波器可根据状态变量的估计误差、测量噪声和系统噪声的统计特性来自动计算最优的反馈增益系数，计算量较大，对数字处理器的要求高，工程实现难度大。
与上述方法相比，滑模观测器（Sliding Mode Observer, SMO）具有鲁棒性高、参数敏感性低、响应速度快和结构简单等优点，因此受到越来越多研究者的关注[13-18]。文献[19-20]提出了基于SMO的负载转矩辨识算法，将负载转矩和转速作为状态变量，将转速的实际值与观测值的偏差作为滑模面，符号函数作为切换函数，理论和实验表明，观测器能准确估计负载转矩。在此基础上，文献[21]分析了转动惯量、摩擦因数等参数失配对负载转矩辨识性能的影响。然而，在上述的传统滑模观测器中，符号函数会引起高频抖振，严重时会引起系统振荡、性能下降，甚至导致系统失稳。与传统的一阶滑模观测器相比，二阶滑模观测器减少了负载转矩识别过程中的抖振。此外，二阶滑模观测器将负载转矩估计误差从指数收敛变为有限时间收敛，有助于提高观测性能和精度。现有的二阶滑模负载转矩辨识算法主要包括超螺旋滑模观测器[22]、终端滑模观测器[23]和快速终端滑模观测器[24]。然而，这些方法往往需要设计的参数更多，并且高阶滑模的设计均需将不确定函数的边界作为已知条件，而该边界在实际中往往是未知的，这极大地限制了高阶滑模算法的工程应用。
综上所述，为了解决传统滑模观测器存在的抖振问题，并兼顾算法的计算量及工程可实现性，本文提出了一种新型自适应滑模负载转矩观测器，解决了传统滑模观测器趋近时间和系统抖振之间的矛盾，可有效抑制传统滑模观测器的抖振问题，同时提高负载转矩观测性能和精度。通过理论、仿真和实验相结合，验证了所提算法的有效性。
为了便于分析永磁同步电机的控制性能，在搭建数学模型时需要进行合理的假设：①转子永磁体磁场与定子电枢磁场在气隙中呈正弦分布，忽略高次谐波的影响；②定子铁心磁路不饱和，磁路为线性且电感参数不变；③不计铁心涡流和磁滞损耗的影响；④转子上无阻尼绕组。基于以上假设，PMSM在dq坐标系下的电压方程可表述为
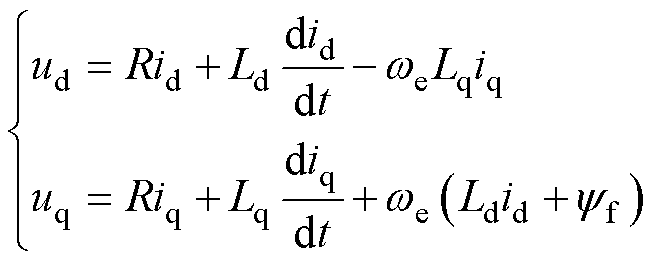（1）
式中，R为定子电阻；ud、uq、id、iq、Ld、Lq分别为定子d轴和q轴的电压、电流和电感；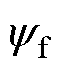
为转子永磁体磁链；we为转子电角速度。
表贴式PMSM的转矩方程为
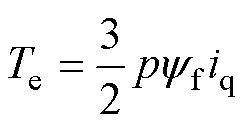（2）
式中，p为电机极对数；Te为电磁转矩。
忽略摩擦力的影响，PMSM的运动方程为
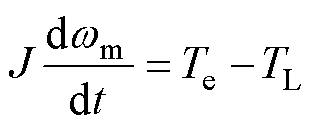（3）
式中，J为转动惯量；TL为负载转矩；wm为转子机械角速度。
根据式（2）、式（3）所示的转矩方程与运动方程，构建PMSM的状态方程为
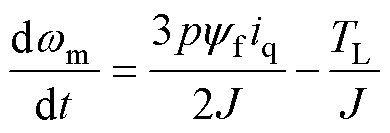（4）
在式（4）的基础上，以电机转速和负载转矩为观测对象，建立滑模负载转矩观测器为
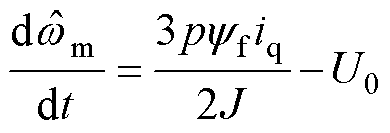（5）
其中
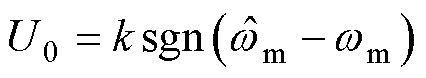
式中，k为滑模增益；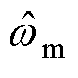
为转子机械角速度估计值；U0为传统趋近率。
定义转速估计误差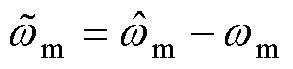
，将式（5）与式（4）相减得到滑模观测误差方程为
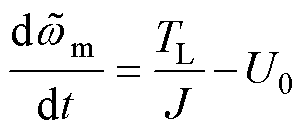（6）
将转速估计误差定义为滑模面，即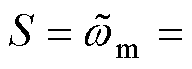
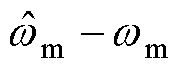。根据滑模控制理论，当系统进入稳态并绕滑模面滑动时，满足
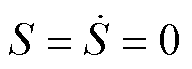。此时，负载转矩可以估计为
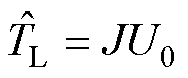（7）
式中，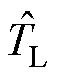
为估计负载转矩。
由于滑模观测器中符号函数的不连续性，由式（7）得到的负载转矩观测值中含有高频噪声，会导致系统的抖振。因此，为了获得无抖振的有效负载转矩观测值，需要采用一阶低通滤波器滤除高次谐波。因此，负载转矩的估计值可以表示为
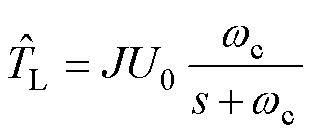（8）
式中，wc为低通滤波器的截止频率；s为拉氏变换中的复变量。传统的滑模负载转矩观测器的结构框图如图1所示。传统滑模观测器反馈回路的滑模中间变量U0中包括了符号函数产生的抖振分量及q轴电流噪声分量，为尽可能削弱抖振和滤除q轴电流噪声，低通滤波器将引入难以接受的观测延迟及误差，影响前馈补偿的效果。
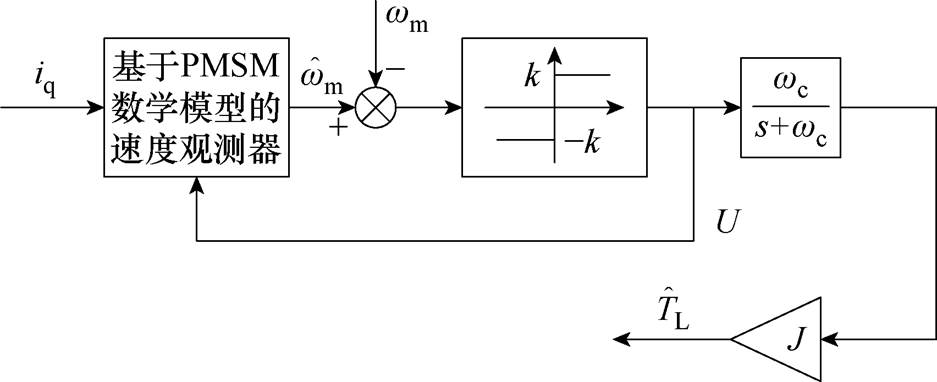
图1 传统滑模负载转矩观测器的结构框图
Fig.1 Block diagram of the traditional sliding mode load torque observer
由于传统SMO采用了不连续的符号函数，导致负载转矩观测结果中含有高频抖振，严重时会引起系统的振荡甚至失稳。引入低通滤波器可以明显缓解抖振现象，但会影响滑模观测器在暂态情况下的准确性和响应速度。
为了解决传统滑模观测器收敛速度和系统抖振之间存在的固有矛盾，本文将传统的符号函数替换为准滑动模态的饱和函数，以抑制负载转矩估计值的高频抖振；设计了一种自适应趋近率，进一步削弱观测器高频抖振的同时加快收敛速度；并对传统负载转矩观测算法进行改进，在传统反馈回路中引入一个表示负载转矩平均估计值的分量，以补偿低通滤波器引入的观测延迟和误差，并根据滑模变结构控制的原理，设计了反馈增益系数的自适应率。改进的自适应滑模负载转矩观测器的结构框图如图2所示。
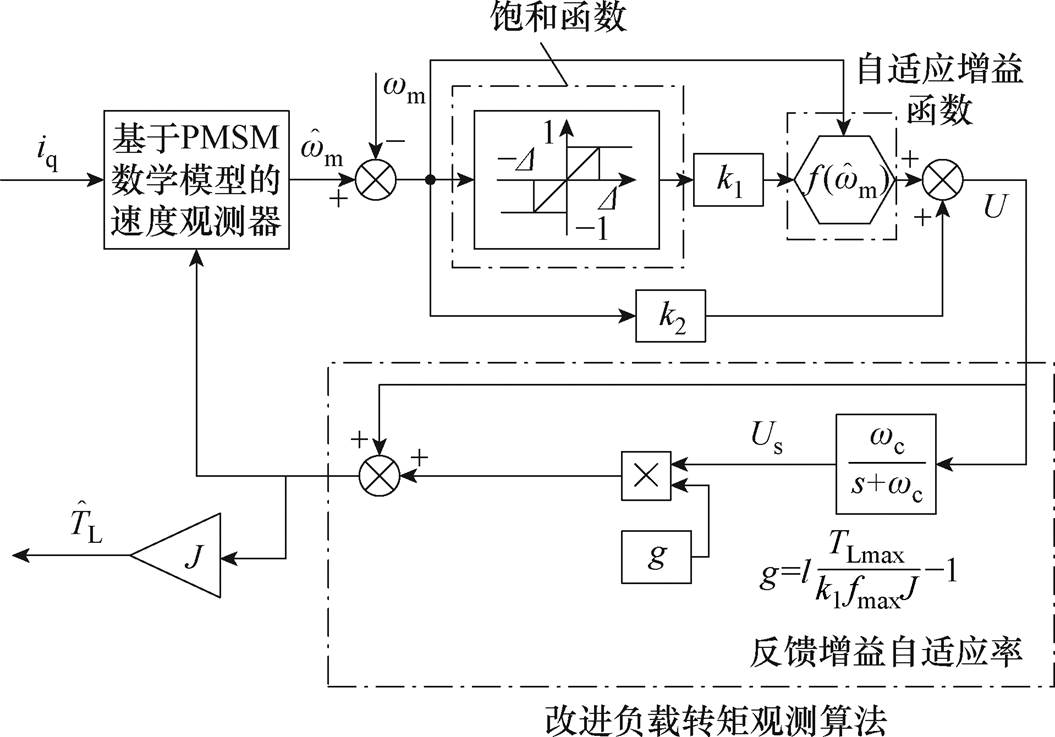
图2 改进的自适应滑模负载转矩观测器结构框图
Fig.2 Improved block diagram of the adaptive sliding mode load torque observer
根据变结构控制原理设计的传统滑模观测器，由于采用的符号函数具有切换开关的特性，虽提高了系统的鲁棒性，但也正是因为这种不连续性，导致抖振现象的产生。为了抑制系统的抖振，可以从准滑动模态的角度出发，在滑模面附近使用连续函数代替不连续的符号函数，从而获得平滑的输出。本文采用式（9）所示的饱和函数代替符号函数。
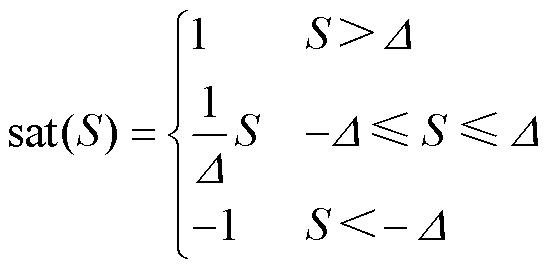（9）
式中，S为所定义的滑模面；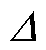
取不同的值对应不同的饱和函数。当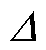值较小时，系统趋近滑模面速度较快，饱和函数趋近于符号函数，负载转矩估计值的抖振较大；当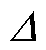值较大时，估计负载转矩抖振较小，但系统到达滑模面的速度会变慢。综上所述，采用饱和函数能有效抑制SMO的抖振现象，但仍无法兼顾收敛速度和观测精度。
传统滑模负载转矩观测器采用等速趋近率，其表达式为
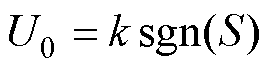（10）
式中，滑模增益k的大小直接影响滑模观测器的收敛速度和观测精度，k值越大，观测器的收敛速度越快，但同时也会增大抖振，降低观测精度。
为了削弱观测器高频抖振的同时加快收敛速度，本文设计了一种自适应趋近率。在传统等速趋近率的基础上，引入了指数趋近项，并设计了等速趋近项的自适应增益，使得滑模观测器随着系统状态的变化自适应地调节收敛速度。结合2.1节所提出的切换函数优化，所设计的自适应趋近率U可以表示为
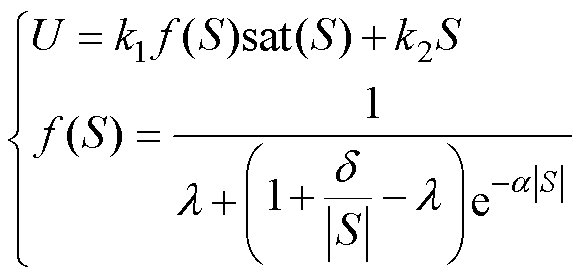（11）
式中，f为等速项自适应增益；k1、k2分别为观测器等速项和指数项的滑模增益，且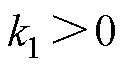
、
；
、
、
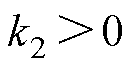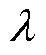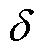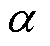为自适应趋近率参数，
，
，
。
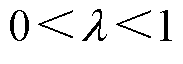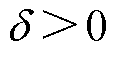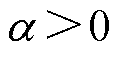通过分析式（11）可知，当滑模观测器轨迹远离滑模面，即
较大时，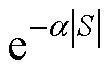
趋近于0，使得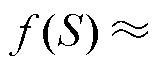
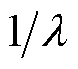，此时滑模观测器等速项的增益
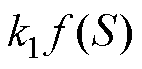大于原始增益
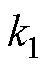，从而保证观测器具有更短的收敛时间和更强的鲁棒性；当滑模观测器轨迹接近于滑模面，即较小时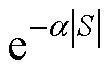，趋近于1，使得
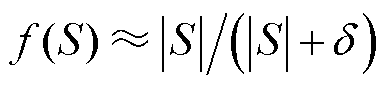，此时滑模观测器等速项的增益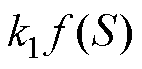始终小于原始增益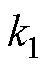，从而抑制稳态下滑模观测器的高频抖振，提升其稳态性能。
为了补偿低通滤波器引入的观测延迟和误差，本文在传统滑模辨识算法中引入了一个额外的分量来表示负载转矩的平均估计值，并将其加入到速度观测器反馈回路中。所提出的改进滑模观测器的运动状态方程可以表示为
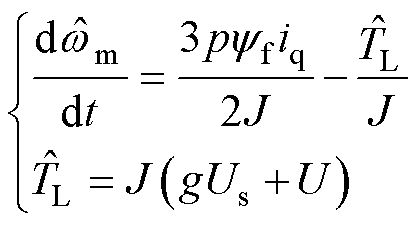（12）
其中
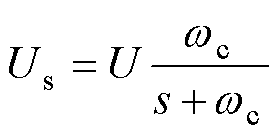
式中，g为Us的反馈增益。
将式（12）与式（4）相减得到转速观测误差方程为
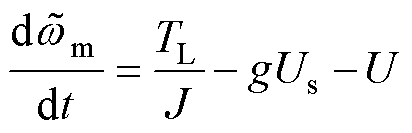（13）
由式（12）可以看出，负载转矩的估计值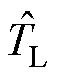由JU和JgUs两部分组成。其中，JU未经过低通滤波器，没有引入额外的延时，保留了饱和函数引起的抖振分量；JgUs经过低通滤波后保留了负载转矩稳态的有效分量。与传统算法相比，改进的负载转矩观测算法在进入迭代计算时就采用了低通滤波后的分量gUs，相当于将低通滤波环节引入反馈回路,并且可以通过调节反馈增益g来抑制抖振和滤除q轴电流噪声，从而降低估计转矩的总谐波含量，由于负载转矩指示信号U可以在没有额外延时的情况下表征负载转矩的变化，并且直接参与转速的估计。因此，所提出的改进负载转矩观测算法可以在瞬态过程中具有更快的响应速度，同时兼顾系统的抖振抑制。
根据滑模变结构控制的原理，设计了反馈增益系数g的自适应率。
根据滑模控制理论可知，广义滑模可达条件为
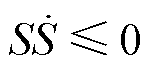（14）
联立式（13）可推得
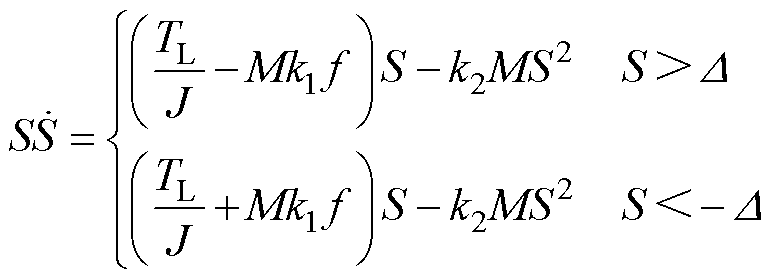（15）
其中
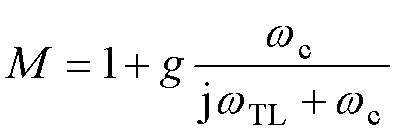
式中，k1和k2均为正实数；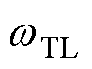
为负载转矩的截止频率，且
，
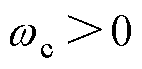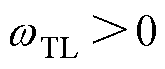。由于反馈增益
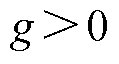，显然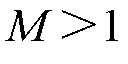
。
分析式（15）可知，当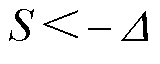
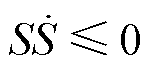时，成立；当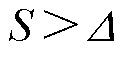
时，为保证广义滑模可达条件，需保证
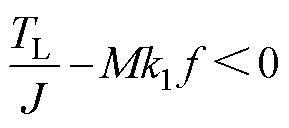，即
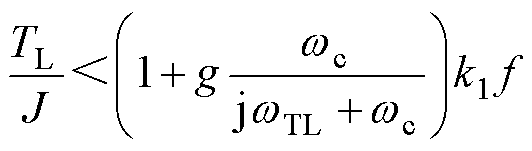（16）
因此，式（16）是滑模观测器稳定的必要条件。令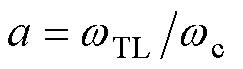
，化简式（16）可得
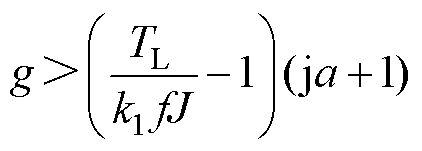（17）
为了满足式（17）的要求并简化计算，式（17）可简化为
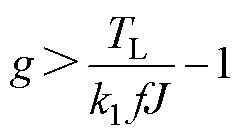（18）
反馈增益系数g以及滑模增益k1的选择必须满足式（18）的要求；否则，观测器无法进入滑动模态。根据式（18）可以设计反馈增益系数g的自适应率。
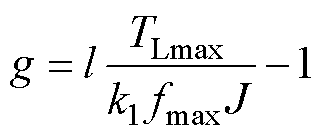（19）
式中，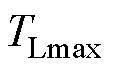
为负载转矩的最大值；fmax为等速项自适应增益最大值；l为常数且
。
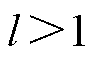利用式（13）观测转速误差方程，对滑模观测器进行稳定性分析。当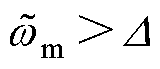
时，饱和函数的输出信号为常数1，此时
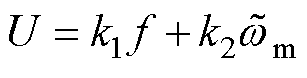，因此U经过低通滤波器的输出信号
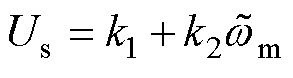。同理可得，当
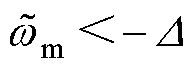时，
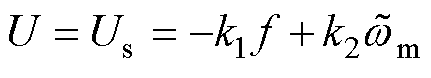。当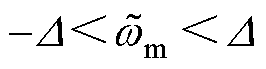
，即观测器运行在滑模面附近时，假设低通滤波器的截止频率
很高，观测信号不受低通滤波影响，则有
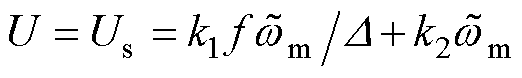。此时，式（13）可改写为
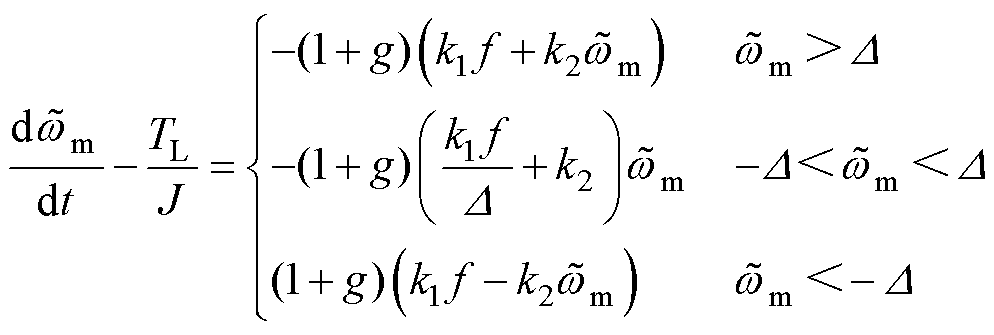（20）
根据Routh-Hurwitz稳定性判据，当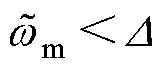
或
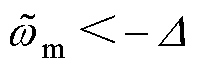时，如果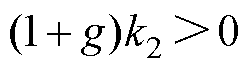
，则系统是稳定的；当
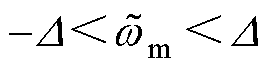时，如果
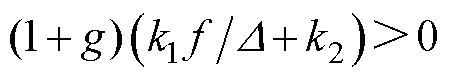，则系统是稳定的，而观测器所有的参数全部为正值，因此，系统始终保持稳定。
观测器运行在滑模面附近时，即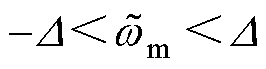
，如果考虑低通滤波对
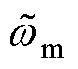的影响，则在频域中的转速误差方程可以表示为
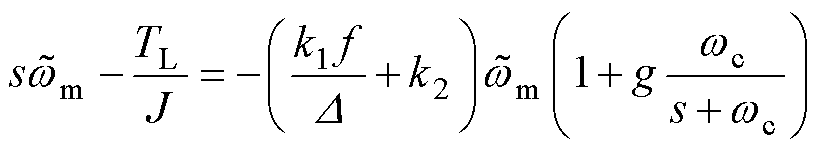（21）
对式（21）进行整理并改写可得
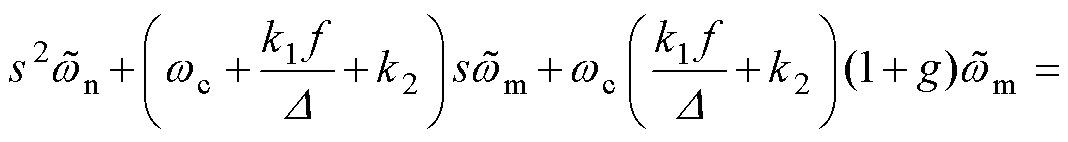
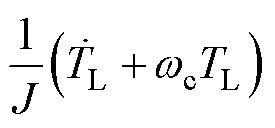（22）
式中，
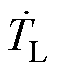为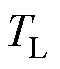
关于时间的微分。根据Routh- Hurwitz稳定性判据，如果
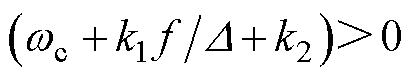且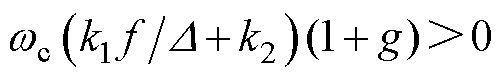
，则系统是稳定的，观测器所有的参数全部为正值，因此，系统始终保持稳定。
在本节中，通过仿真和实验来证明所提出的自适应SMO的有效性。PMSM驱动系统框图如图3
所示。图中，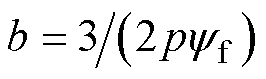
为前馈转矩到参考电流的换算系数。
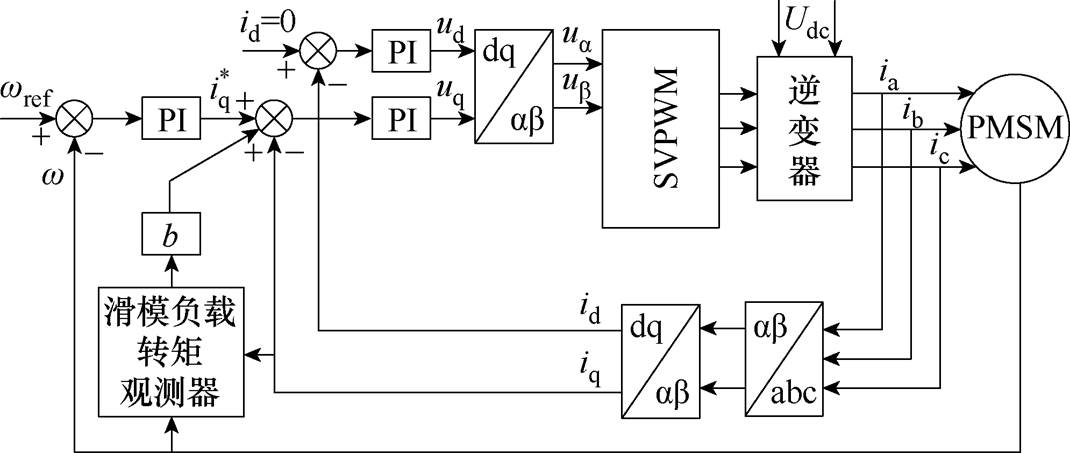
图3 采用滑模负载转矩观测器的PMSM驱动系统框图
Fig.3 Block diagram of a PMSM drive system with a sliding mode load torque observer
在仿真和实验中，将SMO辨识得到的负载转矩作为参考转矩的前馈，提高了系统抗负载扰动的能力。PMSM的设计参数和规格见表1。
表1 仿真和实验用PMSM参数
Tab.1 Parameters of PMSM for simulation and experimentation
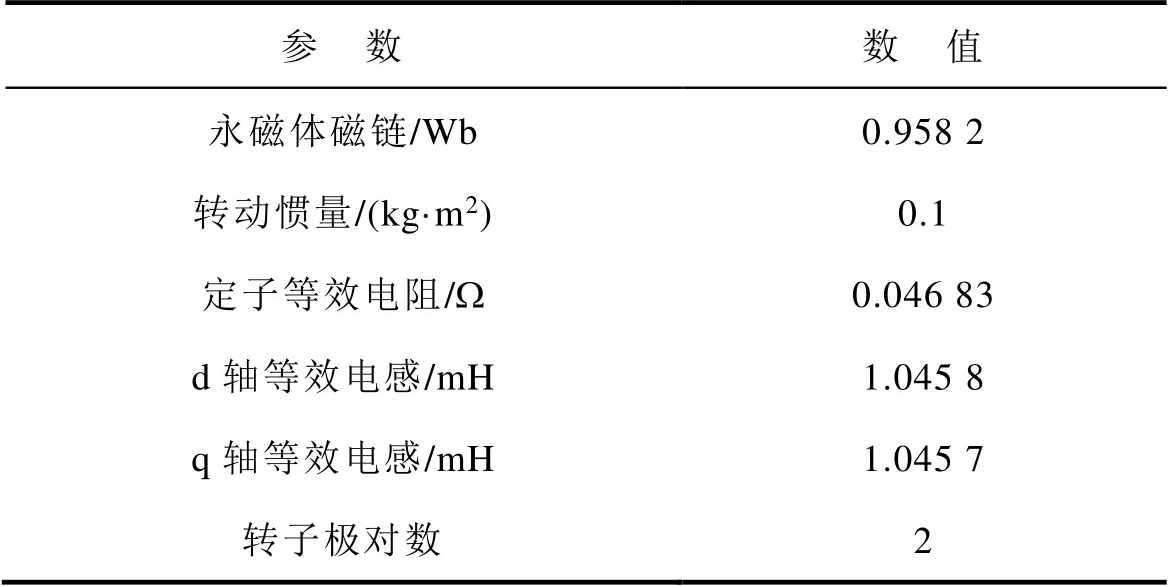
参 数数 值 永磁体磁链/Wb0.958 2 转动惯量/(kg·m2)0.1 定子等效电阻/W0.046 83 d轴等效电感/mH1.045 8 q轴等效电感/mH1.045 7 转子极对数2
为了验证所提方案的正确性和有效性，在Simulink中搭建了仿真模型。首先验证所提出的自适应SMO在抖振抑制方面的有效性，运行状态设置为恒转速恒负载。滑模观测器参数设置为D =10，k1=22.5，k2=70，l=2，自适应趋近率参数设置为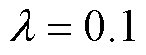
，
，
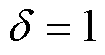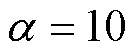，根据以上参数并结合式（19）得到反馈增益系数
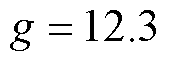。设定参考转速600 r/min、给定负载转矩20 N·m和150 N·m的工况下，对比所提出的自适应滑模观测器与传统滑模观测器的稳态性能，结果如图4所示。
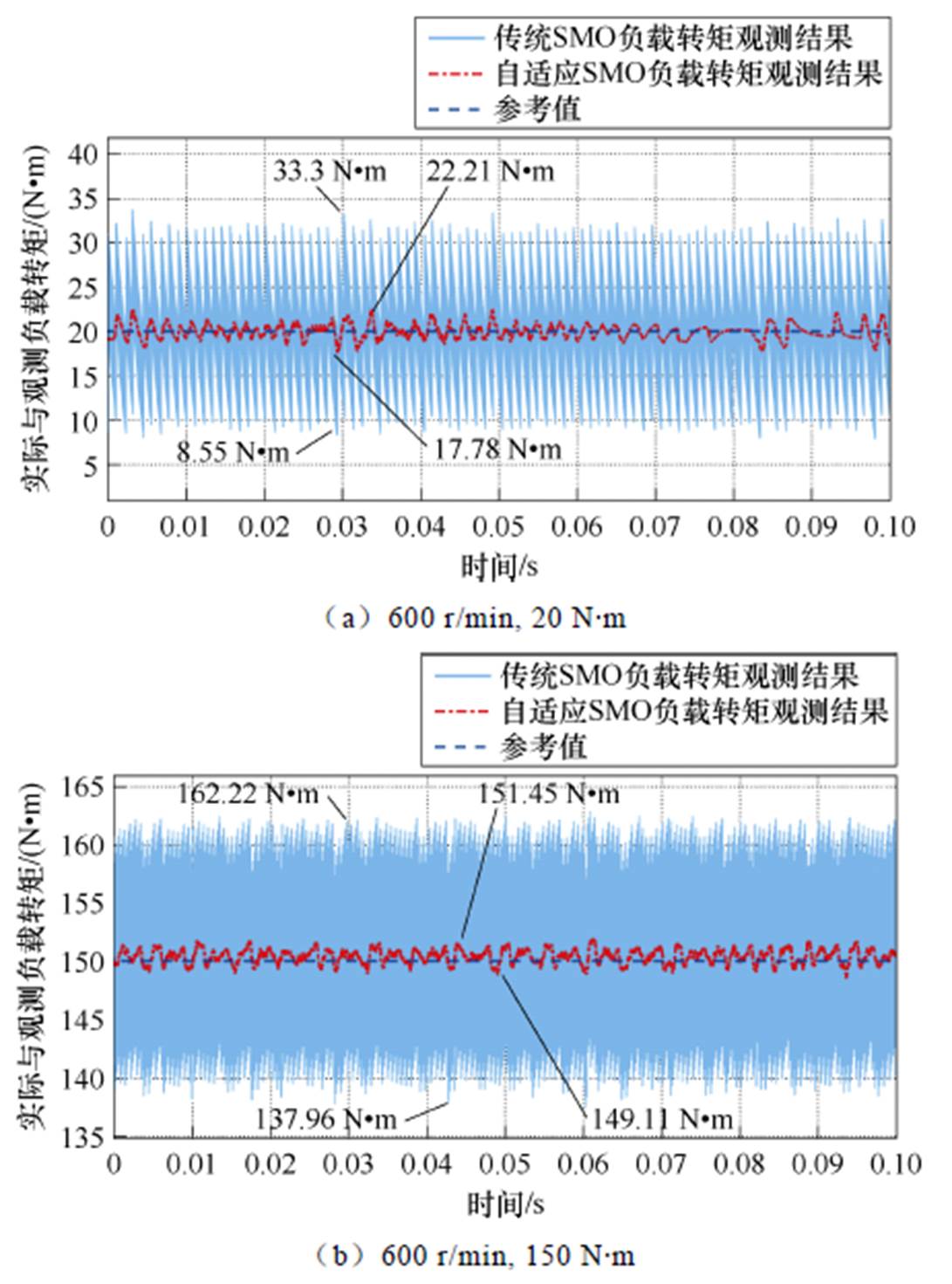
图4 恒转速恒负载工况下负载转矩观测结果对比
Fig.4 Comparison of the observation results of load torque under constant speed and constant load conditions
由图4可以看出，所提出的自适应SMO和传统SMO在不同转速和不同负载的工况下始终可以准确观测负载转矩。由图4a可以得出，在参考转速600 r/min和给定负载转矩20 N·m的工况下，传统SMO和所提出的自适应SMO的负载转矩观测值的最大波动分别为24.75 N·m、4.43 N·m。不同工况下的负载转矩辨识性能比较见表2。
根据表2可以得出，所提出的自适应SMO相较于传统SMO在恒转速恒负载的工况下抖振更小，更小的抖振有利于提高驱动系统的稳定性。
表2 恒转速恒负载工况下负载转矩辨识性能比较
Tab.2 Comparison of load torque identification performance under constant speed and constant load conditions （单位: N·m）
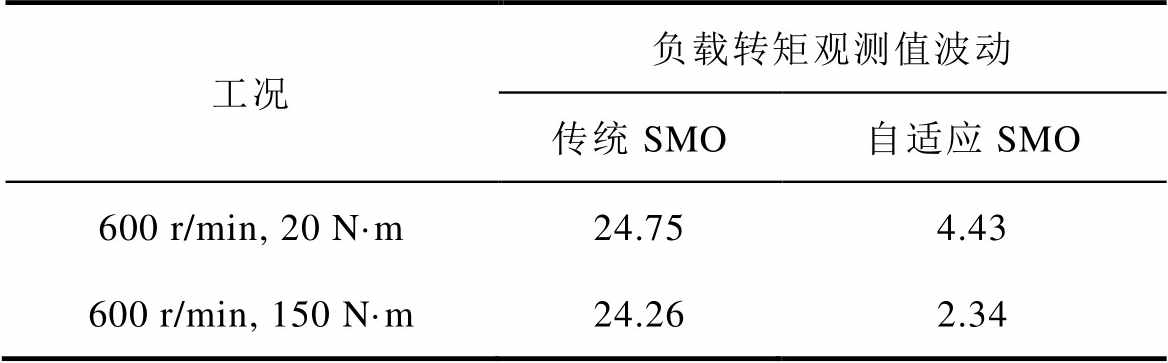
工况负载转矩观测值波动 传统SMO自适应SMO 600 r/min, 20 N·m24.754.43 600 r/min, 150 N·m24.262.34
其次验证所提出的自适应SMO在动态跟踪性能方面的优势，运行状态设置为恒转速突变负载，参考转速600 r/min和800 r/min，负载阶跃突变，对比所提出的自适应SMO和传统SMO的负载转矩动态观测性能，如图5所示。
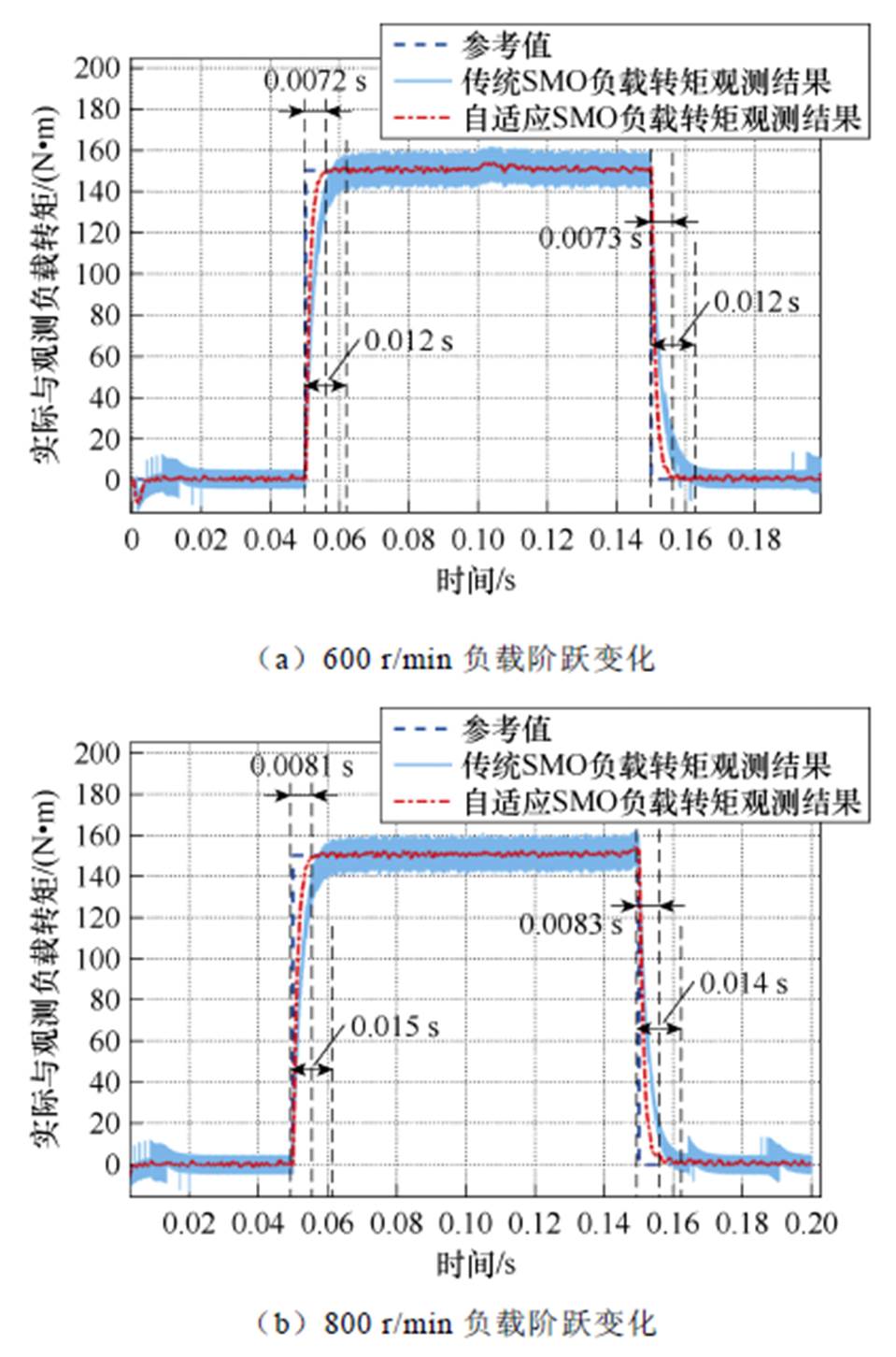
图5 恒转速变负载工况下负载转矩观测结果对比
Fig.5 Comparison of the observation results of load torque under constant speed and variable load conditions
由图5a可以看出，所提出的自适应SMO和传统SMO的观测值可以跟随阶跃变化的负载转矩，并且没有任何超调。电机运行在600 r/min，突加150 N·m负载时，传统SMO响应时间为0.012 s，而自适应SMO响应时间为0.007 2 s。不同工况下的负载转矩辨识性能比较见表3。
表3 恒转速变负载工况下负载转矩辨识性能比较
Tab.3 Comparison of load torque identification performance under constant speed and variable load conditions （单位: s）
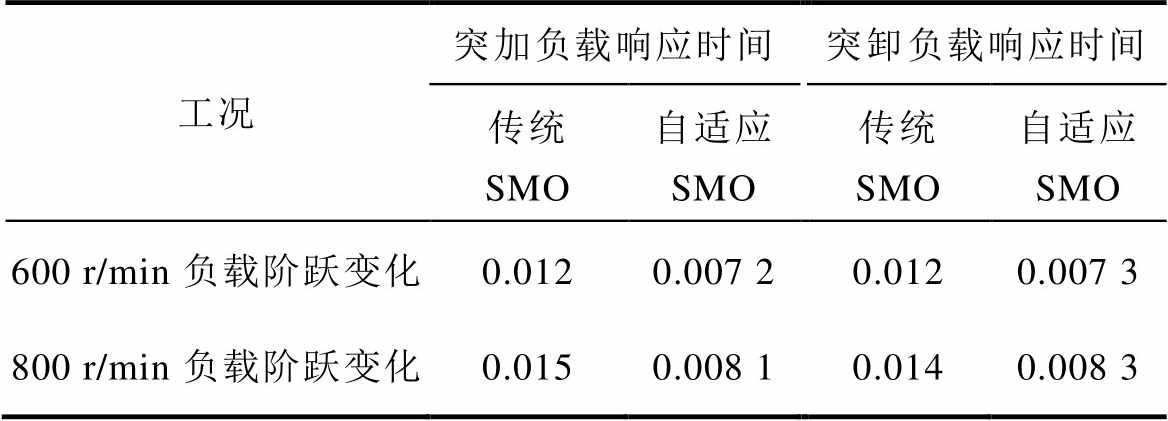
工况突加负载响应时间突卸负载响应时间 传统SMO自适应SMO传统SMO自适应SMO 600 r/min负载阶跃变化0.0120.007 20.0120.007 3 800 r/min负载阶跃变化0.0150.008 10.0140.008 3
从仿真结果可以看出，所提出的自适应SMO相较于传统SMO在恒转速变负载的工况下具有更高的辨识精度和更快的收敛速度。
最后验证采用观测转矩前馈补偿时，系统在负载突变情况下的抗扰动能力。图6、图7分别为给定转速为600 r/min和800 r/min，负载突变时的电机转速仿真结果。
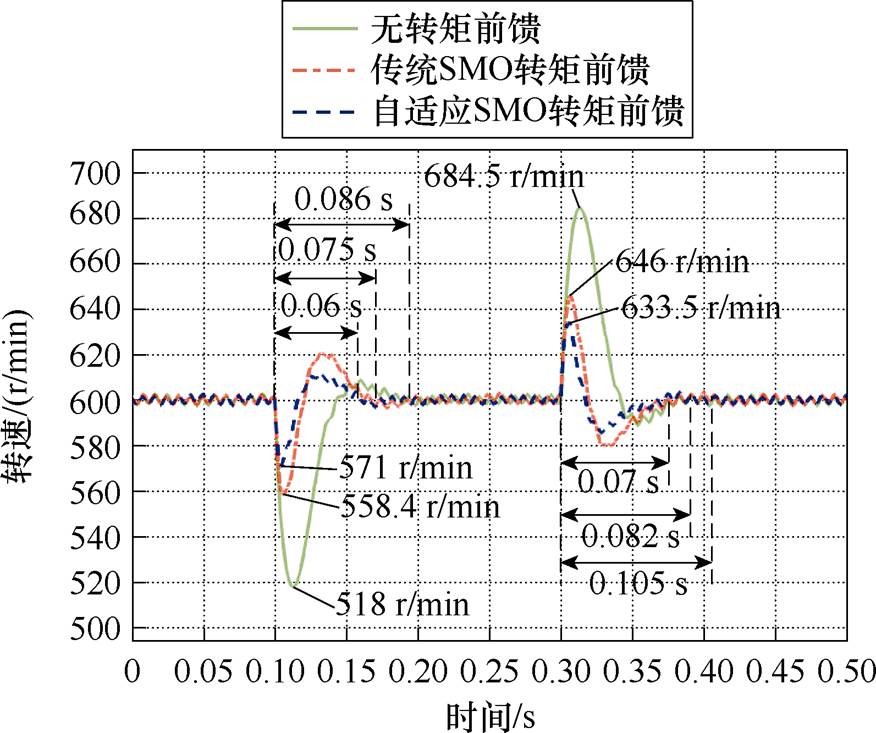
图6 600 r/min时负载突变的实际转速波形
Fig.6 Actual speed waveforms during the sudden load torque changes at 600 r/min
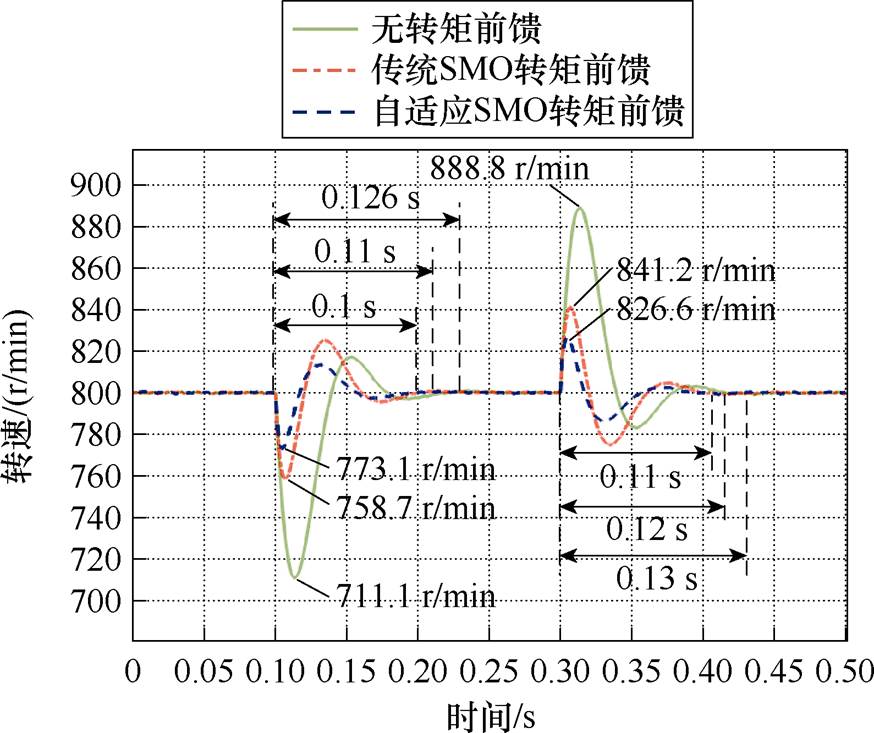
图7 800 r/min时负载突变的实际转速波形
Fig.7 Actual speed waveforms during the sudden load torque changes at 800 r/min
由图6可以看出，未采用转矩前馈时，开始时转速保持在600 r/min，在0.1 s时刻突加150 N·m负载，转速跌落至518 r/min，0.086 s后恢复到600 r/min。相同仿真条件下，采用传统SMO前馈时，在0.1 s时刻突加150 N·m负载，转速跌落至558.4 r/min，0.075 s后恢复到600 r/min；采用自适应SMO前馈时，在0.1 s时刻突加150 N·m负载，转速跌落至571 r/min，0.06 s后恢复到600 r/min。负载突变情况下采用传统SMO和自适应SMO的调速性能比较见表4。
表4 负载突变情况下调速性能比较
Tab.4 Comparison of speed regulation performance under sudden load change
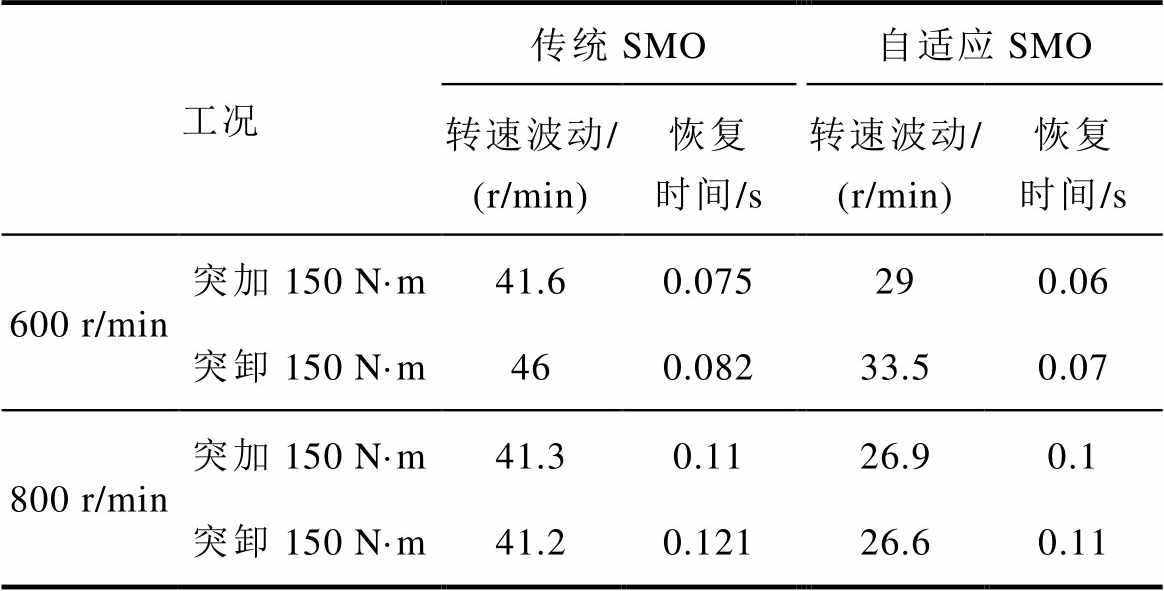
工况传统SMO自适应SMO 转速波动/(r/min)恢复时间/s转速波动/(r/min)恢复时间/s 600 r/min突加150 N·m41.60.075290.06 突卸150 N·m460.08233.50.07 800 r/min突加150 N·m41.30.1126.90.1 突卸150 N·m41.20.12126.60.11
由表4可以得出，相较于传统SMO，使用自适应SMO观测的负载转矩作为前馈补偿时，系统的转速波动更小且恢复时间更快。由此可得，采用所提出的自适应SMO可以大大提高驱动系统的抗扰动能力和动态响应速度。
为了进一步验证所提方案的有效性和相对于传统SMO的优势，搭建了图8所示的实验平台进行实验验证。
图8 实验平台
Fig.8 Experimental platform
4.2.1 所提自适应SMO观测性能对比实验
对传统SMO和所提出的自适应SMO进行负载转矩观测性能比较。图9为给定600 r/min和800 r/min的恒定转速下，分别在空载和负载情况下的负载转矩观测结果。
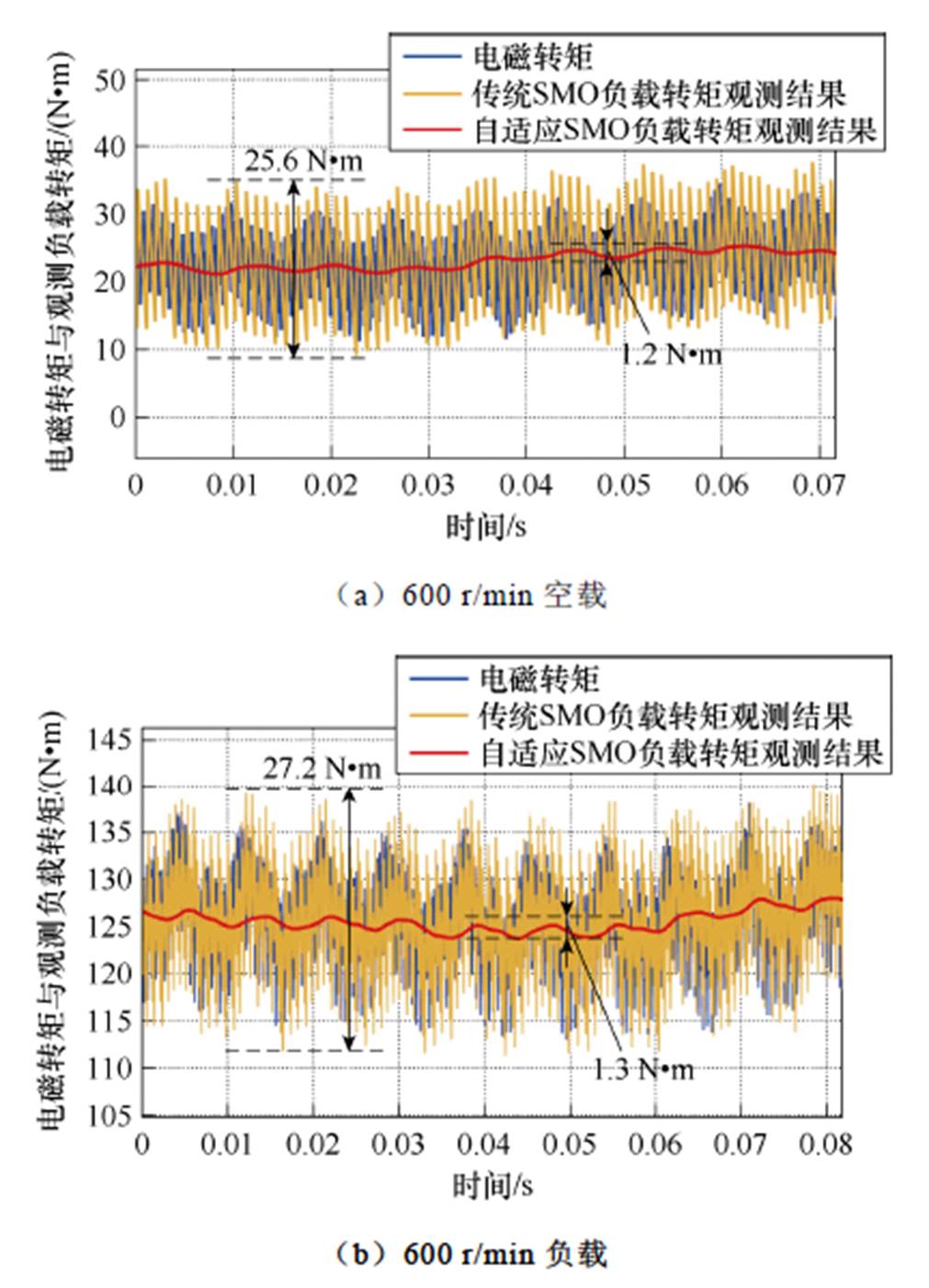
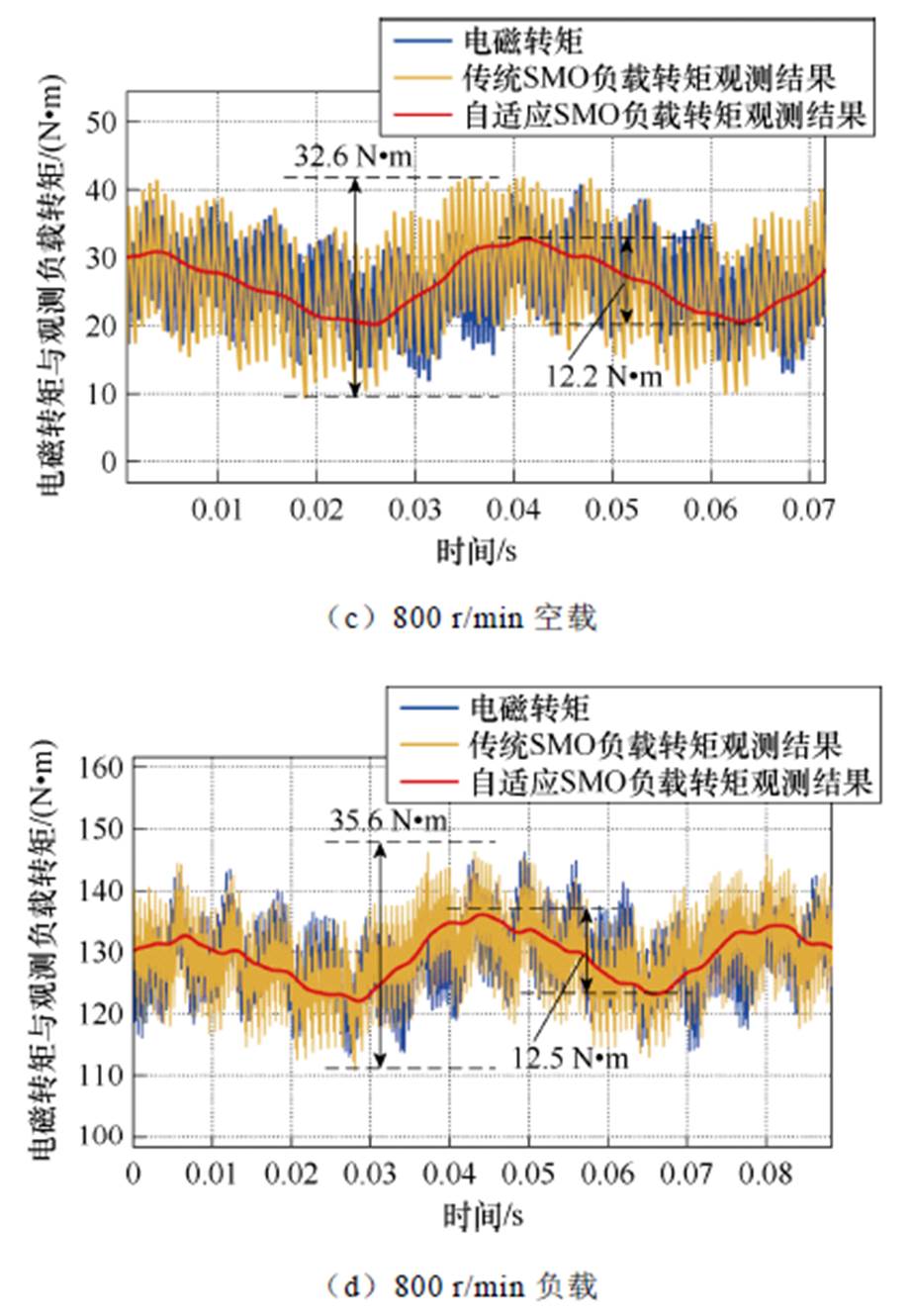
图9 稳态下负载转矩观测性能比较
Fig.9 Comparison of load torque estimation performance at steady state
由图9a可以得出，在参考转速600 r/min空载的工况下，传统SMO和所提出的自适应SMO的负载转矩观测值的最大波动分别为25.6 N·m、1.2 N·m。不同工况下的负载转矩辨识性能比较见表5。
表5 稳态下负载转矩辨识性能比较
Tab.5 Comparison of load torque identification performance at steady state （单位: N·m）
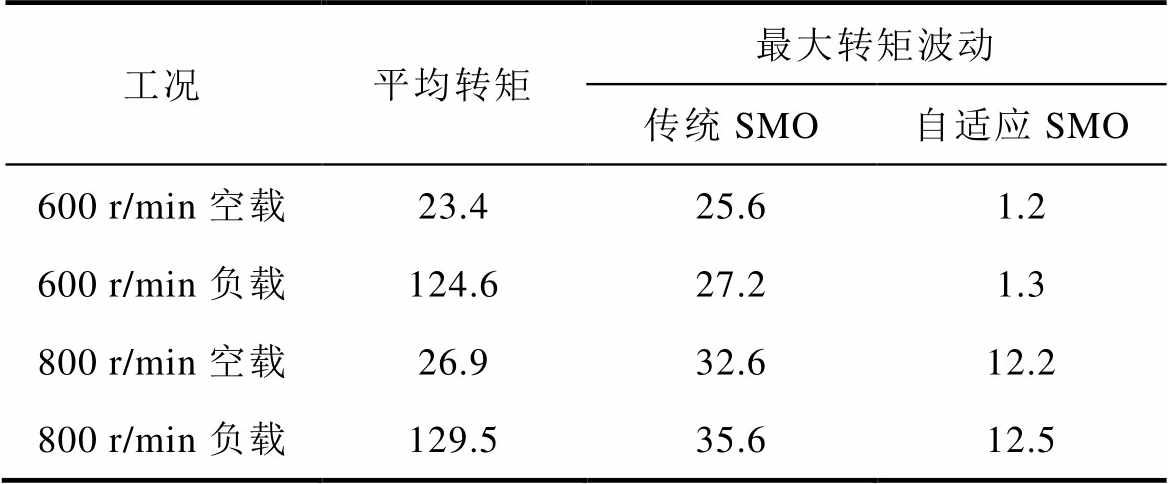
工况平均转矩最大转矩波动 传统SMO自适应SMO 600 r/min空载23.425.61.2 600 r/min负载124.627.21.3 800 r/min空载26.932.612.2 800 r/min负载129.535.612.5
从以上实验结果可以得出，与传统SMO相比，在恒转速恒负载条件下，所提自适应SMO的负载转矩观测结果具有更小的抖振。
其次验证所提出的自适应SMO在动态跟踪性能方面的优势，图10为给定600 r/min和800 r/min的恒定转速，突加负载情况下的负载转矩观测结果。
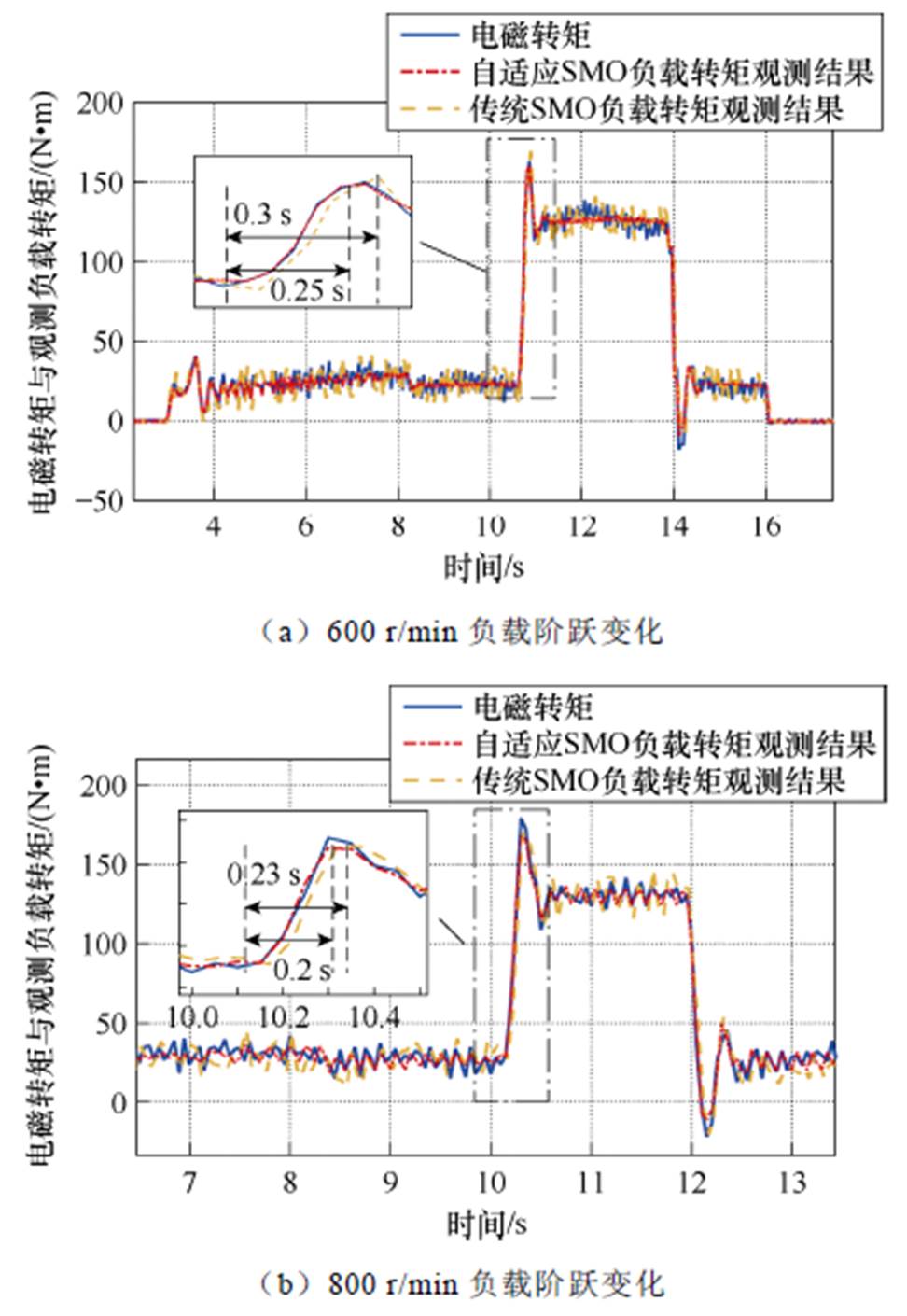
图10 动态下负载转矩观测性能比较
Fig.10 Comparison of load torque estimation performance at dynamic state
由图10a可以看出，在10.6 s处突加130 N·m负载，传统SMO的响应时间为0.3 s，而自适应SMO的响应时间为0.25 s。
从以上实验结果可以得出，与传统SMO相比，在恒转速阶跃变化负载条件下，所提自适应SMO的负载转矩观测结果具有更快的动态响应。
以上实验对比了所提自适应SMO相较于传统SMO的性能提升。为更好地展现所提自适应SMO的优势，验证低速下的观测性能并与高阶滑模观测器进行实验对比，选取应用相对广泛的超螺旋滑模观测器（Super-Twisting SMO, ST-SMO）[22]作为二阶滑模的代表。图11和图12分别为给定20 r/min和600 r/min的恒定转速下，负载转矩观测性能比较。
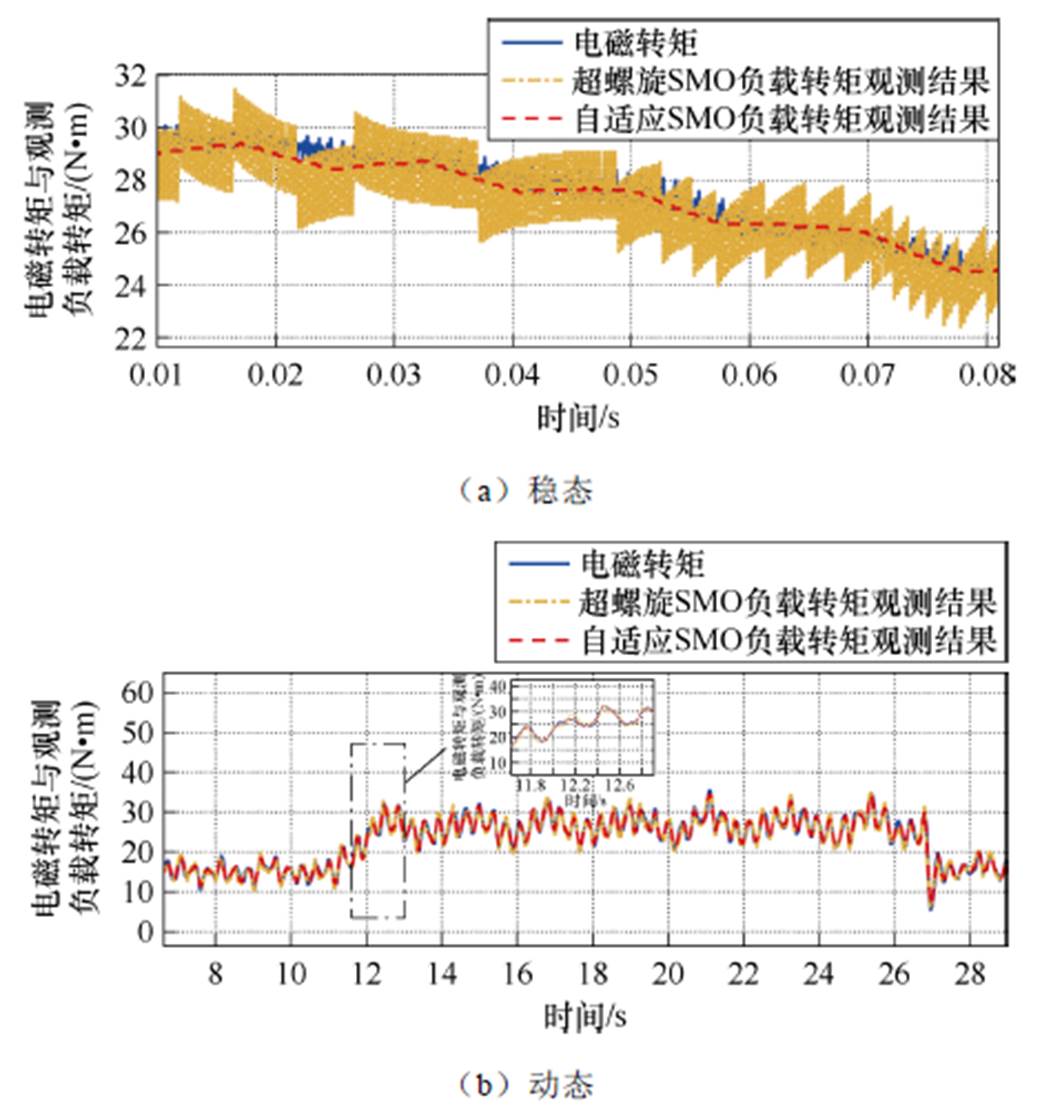
图11 20 r/min负载转矩观测性能比较
Fig.11 Comparison of load torque estimation performance at 20 r/min
由图11可以看出，所提出的自适应SMO在20 r/min的低速状态下仍能对负载转矩进行准确辨识，且相较于ST-SMO负载转矩观测结果具有更小的抖振。由于所提出自适应SMO的输入包括了电机转速，因此自适应SMO可以在低速至额定转速的宽速域下准确观测负载转矩，以上实验结果证明了这一点。
由图12可以看出，所提出的自适应SMO和ST- SMO的负载转矩观测值的最大波动分别为2.1 N·m、11.1 N·m。且所提出的自适应SMO和ST-SMO在负载突变时收敛速度相当。
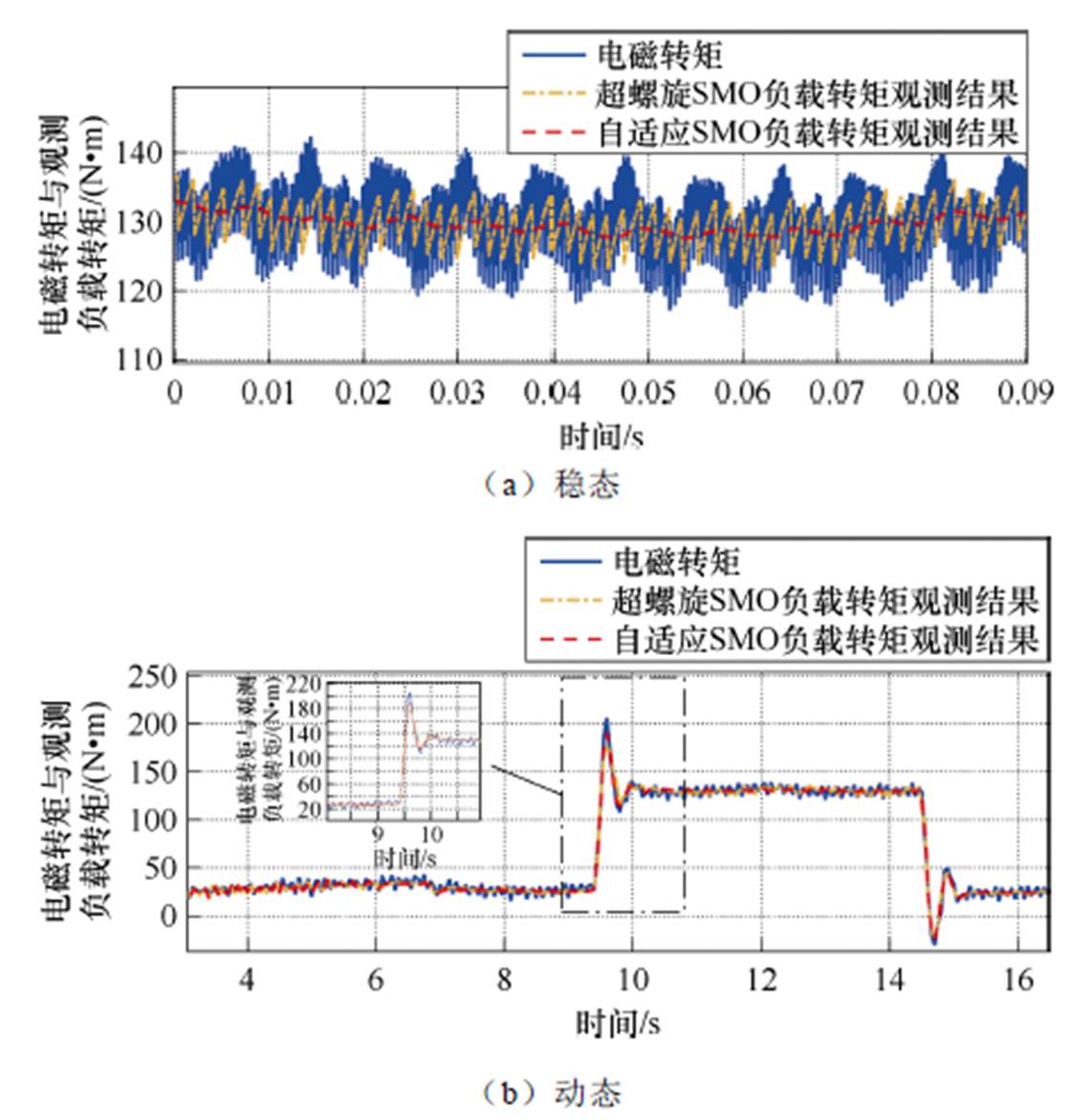
图12 600 r/min负载转矩观测性能比较
Fig.12 Comparison of load torque estimation performance at 600 r/min
根据以上实验结果可知，所提自适应SMO相较于ST-SMO具有更小的抖振和基本相同的收敛速度，并且保留了一阶滑模设计简单、待调节参数少、算法计算负担轻的优势，相较于ST-SMO等高阶滑模观测器更适合实际工程应用。
4.2.2 转动惯量参数变化实验对比
影响所提方法性能的主要参数为电机的转动惯量，下面分析转动惯量失配对所提自适应SMO性能的影响。电机的额定转动惯量为0.1 kg·m2，参考文献[25]的转动惯量辨识策略，给定转速600 r/min并施加幅值100 r/min、周期为1 s的正弦偏执，转动惯量辨识结果如图13所示。
由图13可以看出，转动惯量辨识结果在两个周期后逐渐收敛于0.1 kg·m2，且转动惯量辨识误差在1.7%以内，可以认为辨识结果可靠。当转动惯量变化为额定标称值的2、5、0.5、0.2倍时，所提自适应SMO的负载转矩观测结果如图14所示。
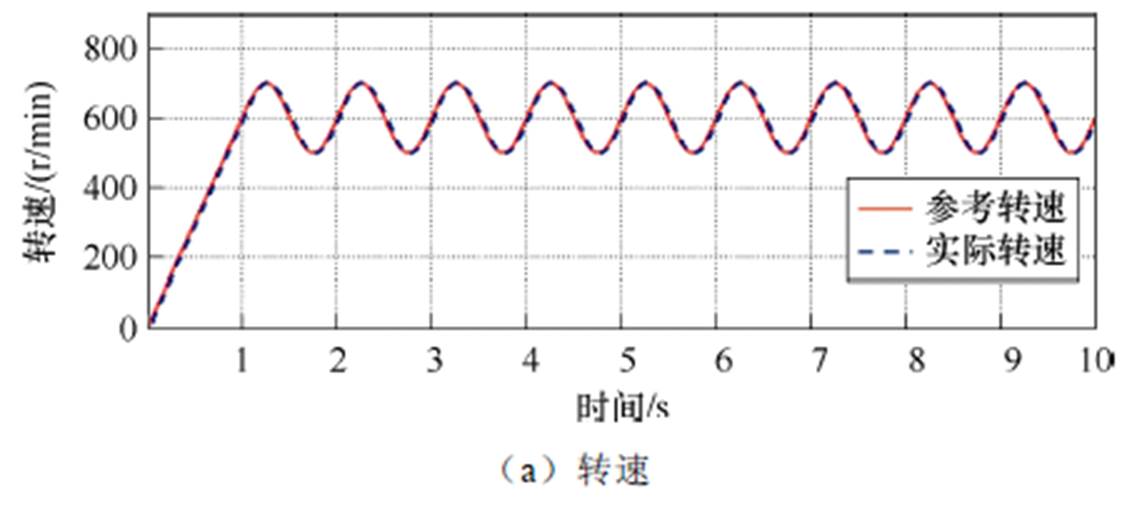
图13 转动惯量辨识结果
Fig.13 Identification results of moment of inertia
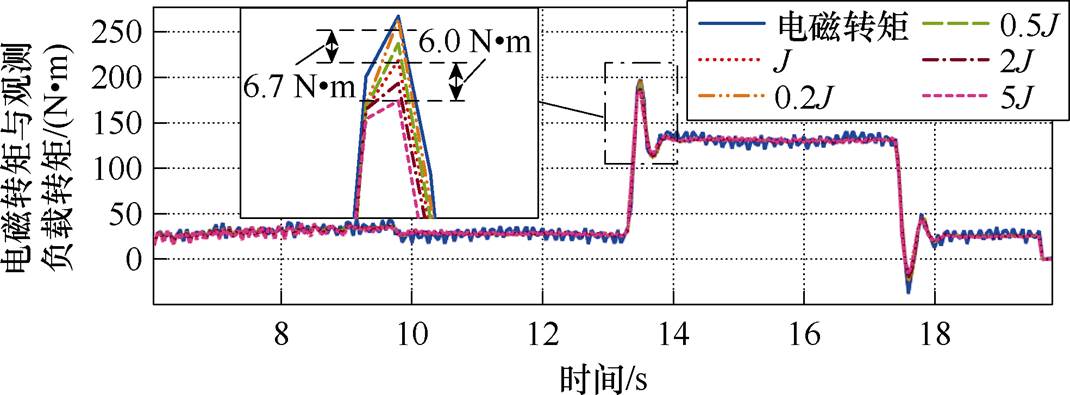
图14 不同转动惯量下负载转矩辨识结果
Fig.14 Identification results of load torque under different moment of inertia
从图14的波形可以看出，当转动惯量在(0.2～5)J之间变化时，负载转矩估计值受转动惯量变化的影响较小，与转动惯量参数匹配时的负载转矩观测结果相比，最大偏差为6.7 N·m。
根据以上分析，所提出的自适应SMO受转动惯量的影响较小，具有良好的鲁棒性。
4.2.3 速度伺服系统驱动性能实验对比
最后验证采用观测转矩前馈补偿时，系统在负载突变情况下的抗扰动能力。图15、图16分别为参考转速600 r/min和800 r/min，负载突变时的实验结果。
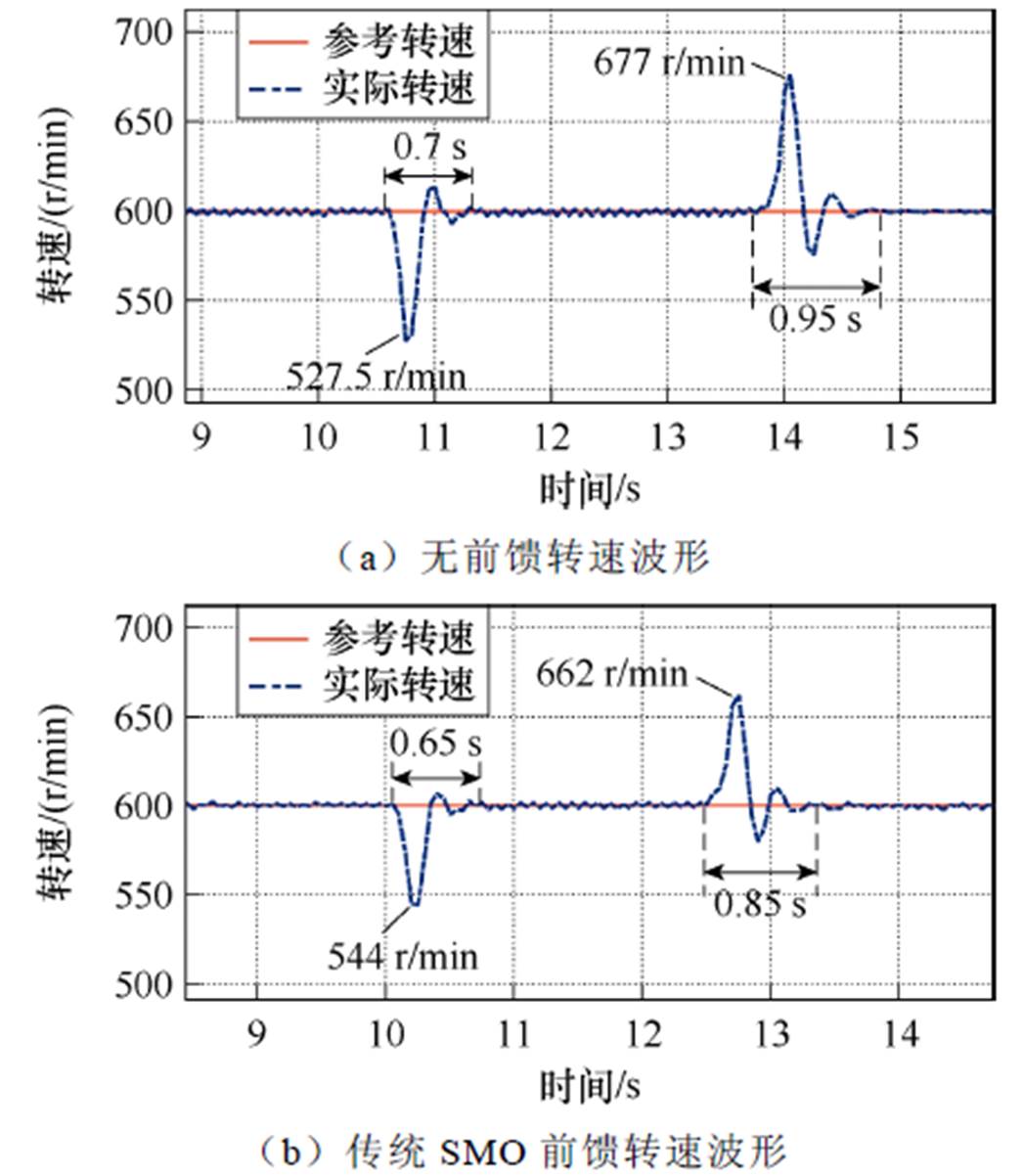
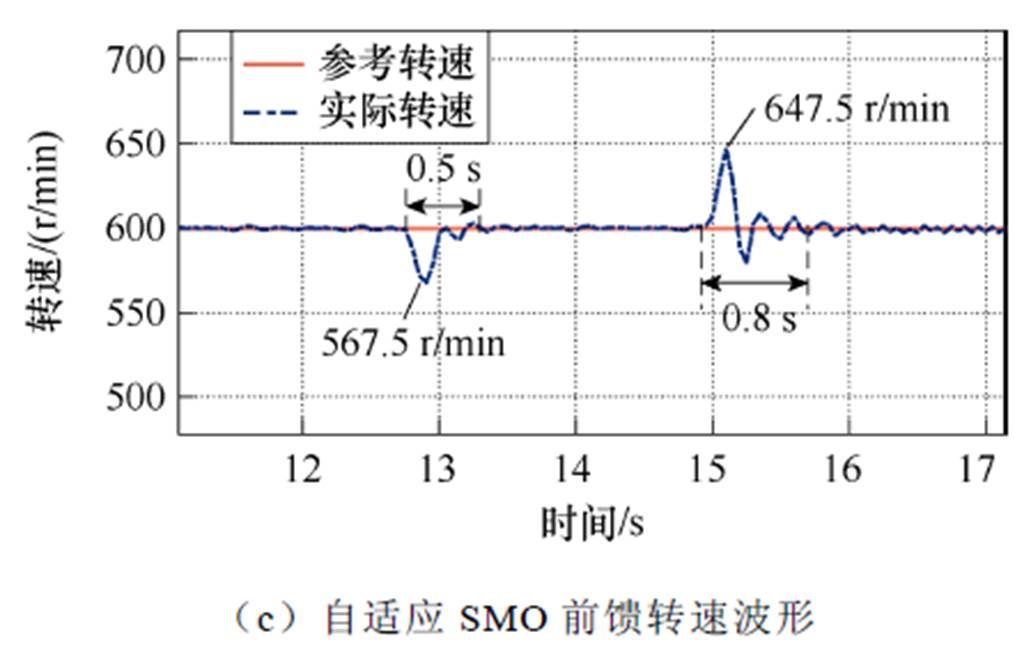
图15 600 r/min负载转矩变化时转速波形
Fig.15 Speed waveforms during the sudden load torque changes at 600 r/min
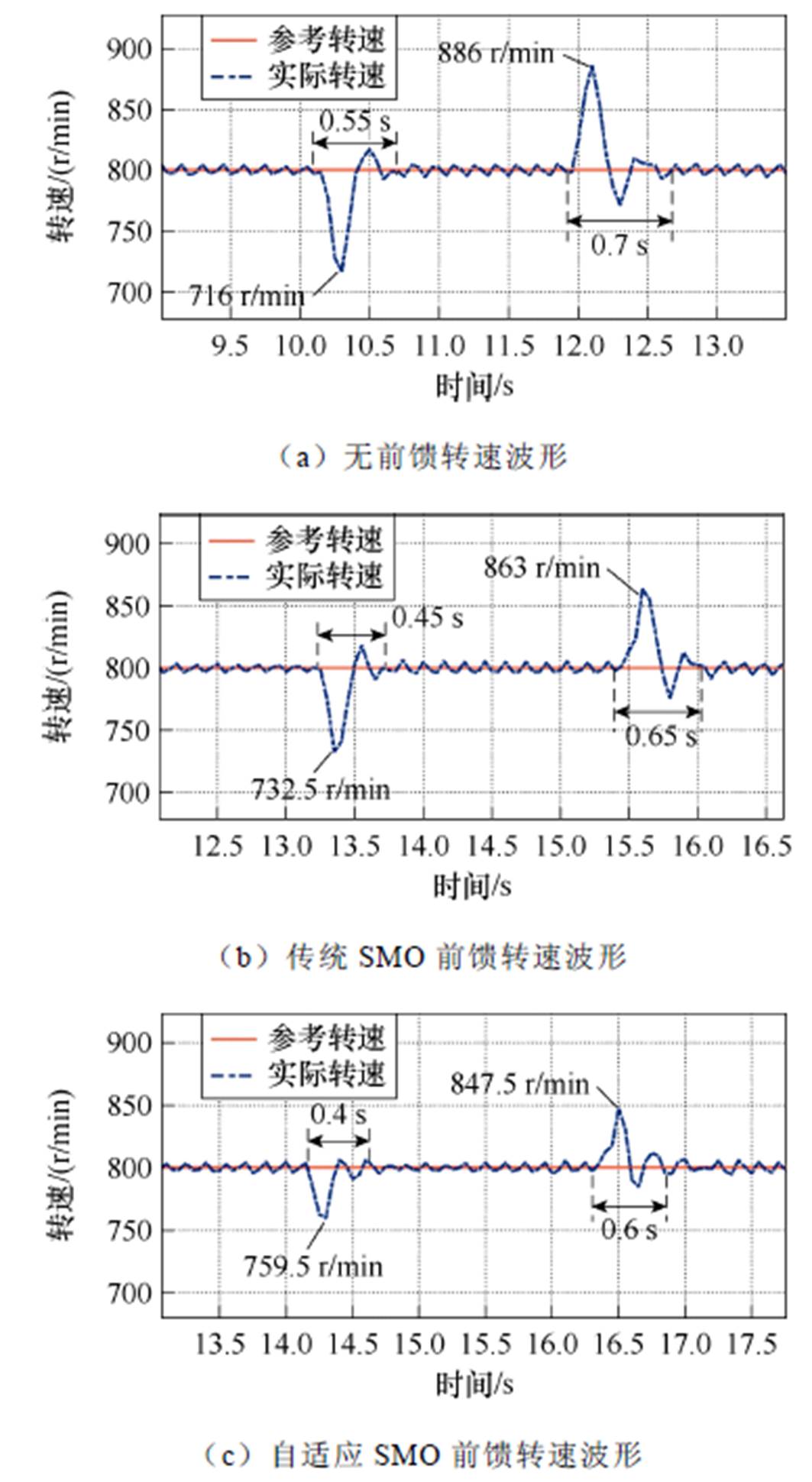
图16 800 r/min负载转矩变化时转速波形
Fig.16 Speed waveforms during the sudden load torque changes at 800 r/min
从图15可以看出，在参考转速600 r/min突加负载时，无转矩前馈、传统SMO转矩前馈和自适应SMO转矩前馈的转速波动分别为72.5、56和35.5 r/min。且系统恢复稳定的时间分别为0.7、0.65和0.5 s。不同工况下的负载转矩辨识性能比较见表6。
由以上实验结果可以得出，引入所提自适应SMO作为转矩前馈补偿时，相较于未前馈和传统SMO前馈，在负载突变时，转速波动更小，恢复时间更快。
表6 负载突变情况下调速性能比较
Tab.6 Comparison of speed regulation performance under sudden load change
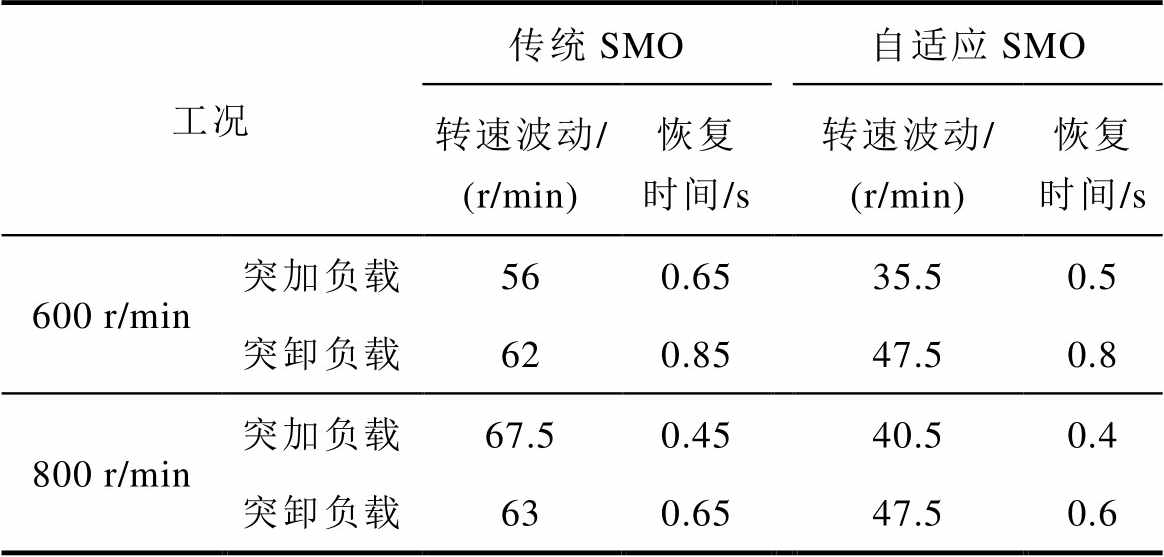
工况传统SMO自适应SMO 转速波动/(r/min)恢复时间/s转速波动/(r/min)恢复时间/s 600 r/min突加负载560.6535.50.5 突卸负载620.8547.50.8 800 r/min突加负载67.50.4540.50.4 突卸负载630.6547.50.6
4.2.4 重载链传动系统驱动性能实验对比
为了进一步验证所提方案在复杂电力传动系统的适用性，将所提方案应用于如图17所示的某环形重载链传动系统。该系统由驱动电机即永磁同步电机、驱动变频器、传动机构、链条和负载组成。其中的永磁同步电机及驱动变频器如图18所示。链传动系统所用PMSM的参数见表7。
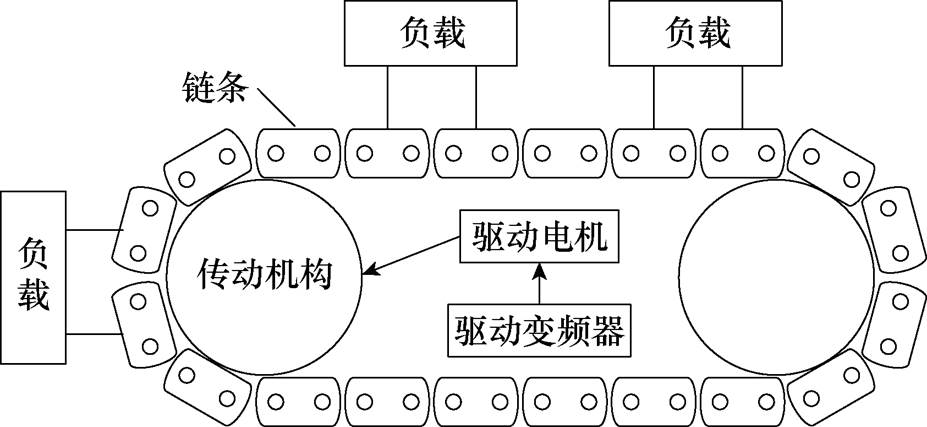
图17 某环形重载链传动系统结构示意图
Fig.17 Schematic structure of ring heavy-duty chain drive system
图18 链传动系统所用永磁同步电机及驱动变频器
Fig.18 PMSM and drive inverter of chain drive system
相较于一般的电力传动系统，实验所用的环形重载链传动系统具有以下特点：
（1）转载状态复杂、快速起停频繁，对负载到位精度要求高。
（2）等效负载转矩多变，系统在运行过程中，链条所带的负载会分别经过直线段和进入齿轮的圆弧段，负载在两段的运行状态及受力情况各有特点。相对而言，负载经过直线段时运动和受力情况比较平缓，进入圆弧段时，由于其自身较大的惯性力，同时受力情况发生突变，此时负载转矩产生剧烈变化，导致整个链传动系统产生速度波动。
表7 链传动系统PMSM参数
Tab.7 Parameters of PMSM for chain drive system
参 数数 值 永磁体磁链/Wb0.95 转动惯量/(kg·m2)10 定子等效电阻/W0.006 1 d轴等效电感/mH0.33 q轴等效电感/mH0.33 转子极对数6
（3）链传动系统中多间隙分布，驱动电机-减速机、减速机-传动轴、链轮-链条之间存在的间隙会导致系统存在传动误差，传动误差的存在会进一步降低系统的响应速度和定位精度。
传统的滑模负载转矩观测器由于存在高频抖振现象，在工程应用中会产生转矩脉动，甚至引起系统失稳。引入低通滤波器后缓解了稳态条件下的抖振问题，但会影响暂态条件下的负载转矩辨识精度。实验所用的环形重载链传动系统的负载转矩时变且无法定量刻画。
为了更好地说明上述问题对链传动机构的影响，首先进行速度爬坡实验。图19为链传动机构驱动电机转速从200 r/min爬升至600 r/min时，实际转速和参考转速的实验波形。
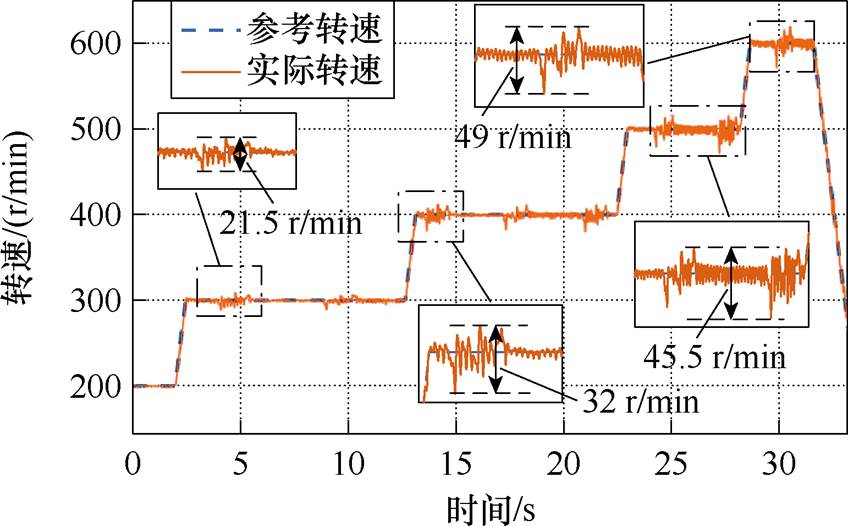
图19 链传动机构转速爬升实验
Fig.19 Speed climbing experiment of chain drive mechanism
由图19实验结果可知，随着转速的升高，由负载带来的扰动更加剧烈，转速的波动逐渐增大，系统的定位精度及运行稳定性逐渐降低。
为解决上述问题，采用本文所提出的自适应SMO对负载转矩进行辨识，利用辨识的负载转矩，对参考转矩进行前馈补偿，从而提高系统的响应速度和抗扰动能力。
为了验证所提出的自适应SMO的有效性，将其负载转矩观测结果作为链传动机构参考转矩的前馈项。图20为链传动机构工作于位置闭环模式、600 r/min工况下的实验结果。
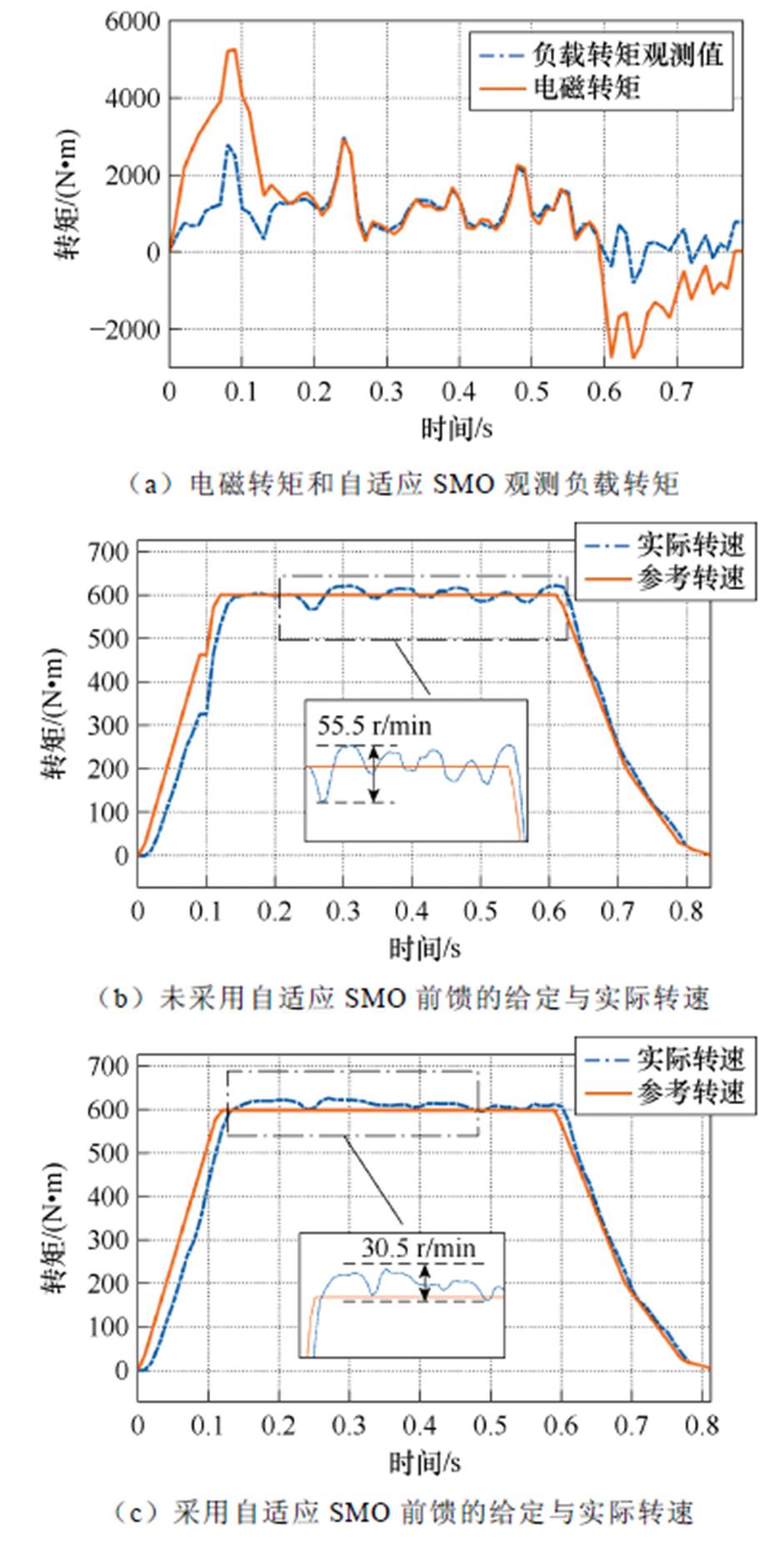
图20 位置闭环模式、600 r/min工况下的实验结果
Fig.20 Experimental results in position closed-loop mode, 600 r/min operating condition
由图20a实验结果可知，当链传动机构工作于位置闭环模式时，驱动电机进入匀速段后，自适应SMO所得负载转矩的观测值与驱动电机输出电磁转矩的波形相吻合，且无明显抖振，从而证明所设计的自适应SMO能够对负载转矩进行准确的观测。
由图20b和图20c对比可知，链传动机构采用自适应SMO前馈补偿后，转速进入匀速段后有轻微超调，最大转速为627.5 r/min，而随后转速的波动逐渐减小，整个匀速段的最大波动值为30.5 r/min。而未采用前馈补偿时，转速进入匀速段后没有超调，但波动剧烈，整个匀速段的最大波动值为55.5 r/min。
根据以上的实验结果可以得出：在不同给定转速的情况下，自适应SMO始终能够很好地跟踪实际负载转矩的变化，验证了本文所提出的自适应SMO的正确性和有效性；此外，引入所提出的自适应SMO前馈算法可以提升链传动机构转运过程的平稳性，在不影响其定位精度的情况下，增强了系统的抗负载扰动能力。
针对现有的滑模负载转矩观测器存在的高频抖振、观测精度不足、响应速度慢等问题，本文对传统的滑模负载转矩观测器的结构进行改进，提出了一种新型自适应滑模负载转矩观测器。通过理论推导、仿真分析和实验验证，得出以下结论：
1）所设计的自适应SMO结构简单、易实现、稳定性高，可以快速准确地对负载转矩进行观测，且其所需参数较少。
2）与传统SMO相比，所提出的自适应SMO在负载转矩瞬态变化的过程中具有更小的抖振和更快的响应速度。
3）所提出的自适应SMO相较于传统SMO更适用于负载转矩多变的场景。实验结果表明，自适应SMO辨识的负载转矩作为参考转矩的前馈项时，可以有效提升重载链传动系统的响应速度及抗负载扰动能力。
参考文献
[1] 张海洋, 许海平, 方程, 等. 基于负载转矩观测器的直驱式永磁同步电机新型速度控制器设计[J]. 电工技术学报, 2018, 33(13): 2923-2934.
Zhang Haiyang, Xu Haiping, Fang Cheng, et al. Design of a novel speed controller for direct-drive permanent magnet synchronous motor based on load torque observer[J]. Transactions of China Electro- technical Society, 2018, 33(13): 2923-2934.
[2] Liu Chunqiang, Li Ziteng, Li Jiahui, et al. Advance- ments in suppressing load disturbances of electric motor drives: an overview[C]//2023 IEEE 6th Student Conference on Electric Machines and Systems (SCEMS), Huzhou, China, 2023: 1-6.
[3] 鲁文其, 胡育文, 梁骄雁, 等. 永磁同步电机伺服系统抗扰动自适应控制[J]. 中国电机工程学报, 2011, 31(3): 75-81.
Lu Wenqi, Hu Yuwen, Liang Jiaoyan, et al. Anti- disturbance adaptive control for permanent magnet synchronous motor servo system[J]. Proceedings of the CSEE, 2011, 31(3): 75-81.
[4] Lu Wenqi, Zhang Zhenyi, Wang Dong, et al. A new load torque identification sliding mode observer for permanent magnet synchronous machine drive system[J]. IEEE Transactions on Power Electronics, 2019, 34(8): 7852-7862.
[5] Niu Li, Xu Dianguo, Yang Ming, et al. On-line inertia identification algorithm for PI parameters optimi- zation in speed loop[J]. IEEE Transactions on Power Electronics, 2015, 30(2): 849-859.
[6] Tuovinen T, Hinkkanen M. Signal-injection assisted full-order observer with parameter adaptation for synchronous reluctance motor drives[C]//2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 2013: 3488-3495.
[7] Masmoudi M L, Etien E, Moreau S, et al. Ampli- fication of single mechanical fault signatures using full adaptive PMSM observer[J]. IEEE Transactions on Industrial Electronics, 2017, 64(1): 615-623.
[8] Wang Shaowei, Wan Shanming. Estimations of load parameters for PMSM by MRAS[C]//2011 Inter- national Conference on Electrical and Control Engineering, Yichang, China, 2011: 657-660.
[9] Prabhakaran K K, Karthikeyan A. Electromagnetic torque-based model reference adaptive system speed estimator for sensorless surface mount permanent magnet synchronous motor drive[J]. IEEE Transa- ctions on Industrial Electronics, 2020, 67(7): 5936- 5947.
[10] Wang Hui, Wang Yunkuan, Wang Xinbo. Speed and load torque estimation of SPMSM based on Kalman filter[C]//2015 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 2015: 808-813.
[11] 郑泽东, 李永东, 肖曦, 等. 永磁同步电机负载转矩观测器[J]. 电工技术学报, 2010, 25(2): 30-36.
Zheng Zedong, Li Yongdong, Xiao Xi, et al. Load torque observer of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2010, 25(2): 30-36.
[12] Shi Tingna, Wang Zheng, Xia Changliang. Speed measurement error suppression for PMSM control system using self-adaption Kalman observer[J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 2753-2763.
[13] 赵文祥, 宋世昌, 周书文, 等. 改进滑模观测器的电流源逆变器驱动PMSM无位置传感器控制[J]. 电工技术学报, 2024, 39(4): 987-995.
Zhao Wengxiang, Song Shichang, Zhou Shuwen, et al. Sensorless control of current source inverter driven PMSM with improved sliding mode observer[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 987-995.
[14] 方馨, 王丽梅, 张康. 基于扰动观测器的永磁直线电机高阶非奇异快速终端滑模控制[J]. 电工技术学报, 2023, 38(2): 409-421.
Fang Xin, Wang Limei, Zhang Kang. High order nonsingular fast terminal sliding mode control of permanent magnet linear motor based on disturbance observer[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 409-421.
[15] 郭科宇, 李耀华, 史黎明. 分段供电双三相永磁同步直线电机电流解耦与扰动抑制[J]. 电工技术学报, 2022, 37(24): 6332-6344.
Guo Keyu, Li Yaohua, Shi Liming. Current decoupling and force disturbance suppression of dual three-phase permanent magnet linear synchronous motors with section power supply[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6332- 6344.
[16] 武志涛, 李帅, 程万胜. 基于扩展滑模扰动观测器的永磁直线同步电机定结构滑模位置跟踪控制[J]. 电工技术学报, 2022, 37(10): 2503-2512.
Wu Zhitao, Li Shuai, Cheng Wansheng. Fixed structure sliding mode position tracking control for permanent magnet linear synchronous motor based on extended sliding mode disturbance observer[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2503-2512.
[17] 许水清, 刘锋, 何怡刚, 等. 基于自适应滑模观测器的新能源汽车驱动系统电流传感器微小故障诊断[J]. 中国电机工程学报, 2023, 43(18): 7277- 7288.
Xu Shuiqing, Liu Feng, He Yigang, et al. Minor fault diagnosis for current sensor of new energy vehicle drive system based on adaptive sliding mode observer[J]. Proceedings of the CSEE, 2023, 43(18): 7277-7288.
[18] 汪凤翔, 杨奥, 于新红, 等. 基于自适应超螺旋滑模观测器的三相Vienna整流器无模型预测电流控制[J]. 电工技术学报, 2024, 39(6): 1859-1870.
Wang Fengxiang, Yang Ao, Yu Xinhong, et al. Model-free predictive current control for three-phase Vienna rectifier based on adaptive super-twisting sliding mode observer[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1859-1870.
[19] 陈天翔, 张辑, 彭彦卿. 基于转矩滑模观测器的抗负载扰动控制方法[J]. 电力系统保护与控制, 2013, 41(8): 114-118.
Chen Tianxiang, Zhang Ji, Peng Yanqing. Anti-load disturbance control method based on torque sliding mode observer[J]. Power System Protection and Control, 2013, 41(8): 114-118.
[20] 张晓光, 孙力, 赵克. 基于负载转矩滑模观测的永磁同步电机滑模控制[J]. 中国电机工程学报, 2012, 32(3): 111-116.
Zhang Xiaoguang, Sun Li, Zhao Ke. Sliding mode control of PMSM based on a novel load torque sliding mode observer[J]. Proceedings of the CSEE, 2012, 32(3): 111-116.
[21] Lian Chuanqiang, Xiao Fei, Gao Shan, et al. Load torque and moment of inertia identification for permanent magnet synchronous motor drives based on sliding mode observer[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5675-5683.
[22] Yang Chengbo, Song Bao, Xie Yuanlong, et al. Adaptive identification of nonlinear friction and load torque for PMSM drives via a parallel-observer-based network with model compensation[J]. IEEE Transa- ctions on Power Electronics, 2023, 38(5): 5875- 5897.
[23] Feng Yong, Yu Xinghuo, Han Fengling. High-order terminal sliding-mode observer for parameter esti- mation of a permanent-magnet synchronous motor[J]. IEEE Transactions on Industrial Electronics, 2013, 60(10): 4272-4280.
[24] Wang Bo, Luo Cheng, Yu Yong, et al. Antidis- turbance speed control for induction machine drives using high-order fast terminal sliding-mode load torque observer[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 7927-7937.
[25] Chen Jiahao, Huang Jin. Alternative solution regarding problems of adaptive observer com- pensating parameters uncertainties for sensorless induction motor drives[J]. IEEE Transactions on Industrial Electronics, 2020, 67(7): 5879-5888.
Load Torque Identification of Permanent Magnet Synchronous Motor Based on Adaptive Sliding Mode Observer
Abstract Accurate load torque identification helps to improve the load disturbance resistance of complex nonlinear loaded permanent magnet drive systems. The sliding mode observer (SMO) has become a commonly used algorithm for load torque identification due to its advantages of high robustness to noise, fast response speed, and simple structure. However, the shortcomings of this algorithm, such as high-frequency chattering and slow response speed, limit its application in electric drive systems. This paper proposes a new adaptive sliding-mode load torque observer to solve the problem of the inherent contradiction between the convergence speed and high-frequency chattering of conventional sliding-mode observers.
Firstly, from the perspective of quasi-sliding mode, the conventional sign function is replaced by the saturation function to suppress the high-frequency chattering of the load torque estimate. The sign function can effectively suppress the chattering phenomenon of SMO, but it still fails to balance the convergence speed and observation accuracy. Second, an adaptive convergence rate is designed to introduce an exponential convergence term based on the conventional isochronous convergence rate. The adaptive gain of the isochronous convergence term is designed to make the sliding-mode observer adaptively adjust the convergence speed along with the change of the system state. Thus, the observer has a short convergence time and strong robustness, and the high-frequency chattering phenomenon of the sliding-mode observer in the steady state is suppressed. Finally, this paper introduces the average estimated value of the load torque in the conventional slip mode identification algorithm and adds it to the feedback loop of the speed observer. The improved load torque observation algorithm can suppress the chattering of the estimated torque by adjusting the feedback gain g. Since the load torque indication signal U can characterize the load torque change without additional delay, it can be directly involved in the speed estimation. Therefore, the proposed algorithm has a fast response speed during transient processes while considering the chattering suppression of the system. Based on the principle of sliding mode variable structure control, the adaptive rate of feedback gain coefficient g is designed.
Simulation and experimental results show that under varying speed and load disturbances, the proposed adaptive SMO has less chattering than traditional SMO and super-twisting SMO. Additionally, the adaptive SMO converges faster than traditional SMO and performs comparably to super-twisting SMO. In load disturbance experiments at a reference speed of 600 r/min, the speed fluctuations for no torque feedforward, traditional SMO with torque feedforward, and adaptive SMO with torque feedforward are 72.5 r/min, 56 r/min, and 35.5 r/min, respectively, with system recovery times of 0.7 s, 0.65 s, and 0.5 s. To further verify the impact of inertia parameter mismatch on the adaptive SMO, inertia was set to 2, 5, 0.5, and 0.2 times the rated value, with the maximum deviation in load torque observation being 6.7 N·m. The results indicate that the impact of parameter mismatch is not significant.
The following conclusions can be drawn. (1) The designed adaptive SMO has a simple structure and high stability, is easy to implement, observes the load torque quickly and accurately, and requires fewer parameters. (2) Compared with the conventional SMO, the proposed adaptive SMO has less chattering and faster response speed during the transient change of the load torque. (3) The proposed adaptive SMO is more suitable for the scenario of variable load torque than the conventional SMO. The experimental results show that when the load torque recognized by the adaptive SMO is used as the feedforward term of the reference torque, the response speed and load disturbance resistance of the heavy-duty chain drive system can be effectively improved.
keywords：Load torque, sliding mode observer, permanent magnet synchronous motor (PMSM), feed- forward compensation, anti-load disturbance
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.240932
收稿日期2024-05-31
改稿日期2024-08-02
石秦赓 男，2000年生，硕士研究生，研究方向为电力电子及电力传动。
E-mail: 220222789@seu.edu.cn
韩 一 男，1990年生，助理研究员，研究方向为电机系统及其控制。
E-mail: frankleonhy@163.com（通信作者）
（编辑 崔文静）