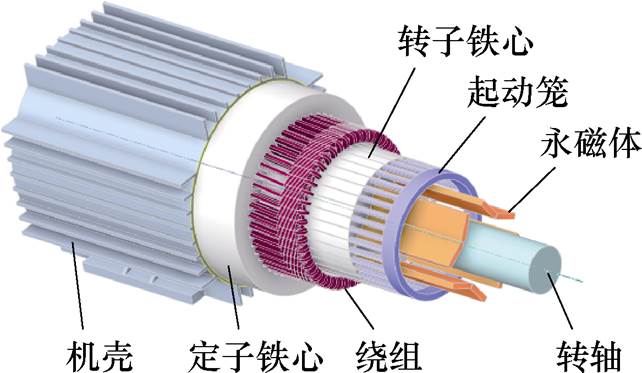
图1 LSPMSM电机3D结构
Fig.1 3D structure of LSPMSM motor
摘要 异步起动永磁同步电机（LSPMSM）区别于其他永磁电机，由于定转子均开槽，其齿槽转矩分析难度增加。该文以异步起动永磁同步电机为研究对象，首先从谐波的角度，建立齿槽转矩与谐波之间的关系；其次在永磁体最大磁能积不变的前提下，确定电机饱和程度与永磁体参数的关系；然后考虑定子是否斜槽和电机的饱和程度将电机分为六种设计情况，将齿槽转矩、效率及转矩脉动作为优化目标，通过响应面法分别建立不同设计情况下优化目标与优化参数的关系；最后采用多目标粒子群算法，对不同的设计情况进行寻优选取出六组最佳优化参数。并通过仿真分析验证齿槽转矩与谐波在不同饱和状态下的关系。搭建实验平台，验证了理论分析与仿真分析的准确性。
关键词：异步起动永磁同步电机 齿槽转矩 谐波 饱和程度 多目标粒子群算法
异步起动永磁同步电机（Line Starting Per- manent Magnet Synchronous Motors, LSPMSM）因具有自起动特性常应用于煤矿及油田等场合[1]。与单边开槽永磁电机不同，其定转子双边开槽结构显著增加了齿槽转矩分析的复杂性。为此，现有分析方法主要包括谐波分析法和基于能量法的气隙磁通密度计算法[2-3]。针对齿槽转矩抑制，山东大学王秀和团队通过调节电枢齿宽、槽口宽度等定转子结构参数减小齿槽转矩[4-5]。合肥工业大学鲍晓华等采用永磁体组合优化其齿槽转矩性能[6]。上海电机学院徐威提出转子分段错开结构以削弱齿槽转矩[7]。在算法层面，众多学者还通过增强灵敏度与动态收敛性实现了多参数的针对性优化[8-10]。此外，通过定转子槽配合的方式改变磁场谐波从而影响永磁电机的电流波形和转矩波动 [11]。而齿槽转矩的削弱会引发效率下降与动态响应灵敏度的降低[12-13]，需多目标协同优化，以实现齿槽转矩抑制与电机综合性能的平衡。
上述文献系统阐述了LSPMSM齿槽转矩抑制方法及多参数协同优化策略，为LSPMSM研究提供了关键理论支撑与设计参考。但现有文献未对LSPMSM的复杂齿槽转矩原理进行深度剖析，且在抑制齿槽转矩性能时仅考虑单一目标，未协同考虑铁心饱和程度、效率等电机电磁性能。因此，亟需一种在优化齿槽转矩的同时，兼顾电机电磁性能的综合设计方法。
本文以LSPMSM为研究对象，构建以铁心饱和程度为约束的电机结构参数多目标协同优化方法，实现电机综合性能的提升。首先确定谐波及齿槽转矩的理论关系。基于永磁体最大磁能积不变的条件，建立气隙磁通密度与永磁体参数的联系及永磁电机饱和峰值的确定方法。根据饱和峰值将电机饱和分为三种状态：未饱和、饱和峰值、过饱和，随后考虑定子是否斜槽，将电机设计方案分为六组：斜槽未饱和、斜槽饱和峰、斜槽过饱和、不斜槽未饱和、不斜槽饱和峰值及不斜槽过饱和。以齿槽转矩、效率、转矩脉动为目标，对转子槽口宽度、转子每极槽数等参数进行多目标多参数优化。通过响应面法对齿槽转矩、效率、转矩脉动率三个优化目标与多参数建立数学模型与响应面。再应用多目标粒子群算法精准寻优得出六组不同状态最佳参数组合，并对优化后的参数组合进行仿真验证。
图1为TBYC180M-4，18.5kW异步起动永磁同步电机结构。表1为样机基础参数。
图1 LSPMSM电机3D结构
Fig.1 3D structure of LSPMSM motor
表1 样机基础参数
Tab.1 Basic parameters of prototypes
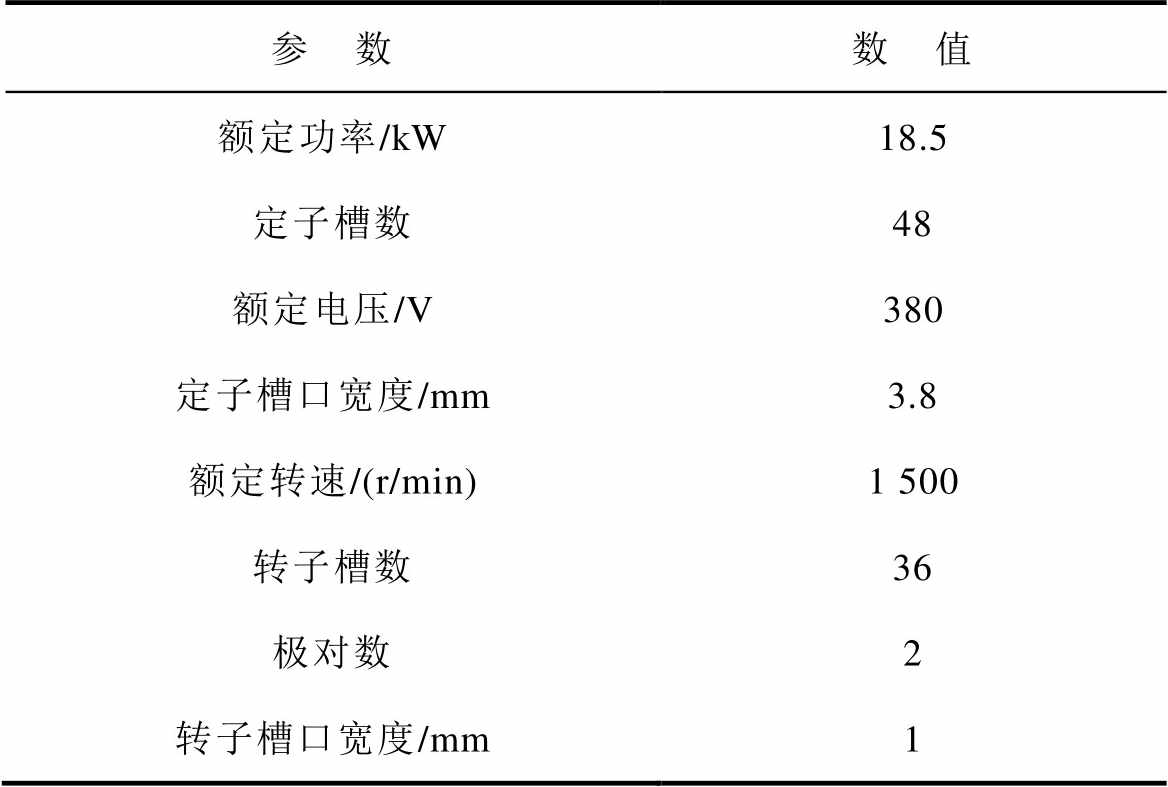
参 数数 值 额定功率/kW18.5 定子槽数48 额定电压/V380 定子槽口宽度/mm3.8 额定转速/(r/min)1 500 转子槽数36 极对数2 转子槽口宽度/mm1
当不考虑定子斜槽时，假设电枢磁导率无穷大，即电机磁场内部能量由气隙磁场储能与永磁体固有磁能构成，因此磁场能量[14]可表示为
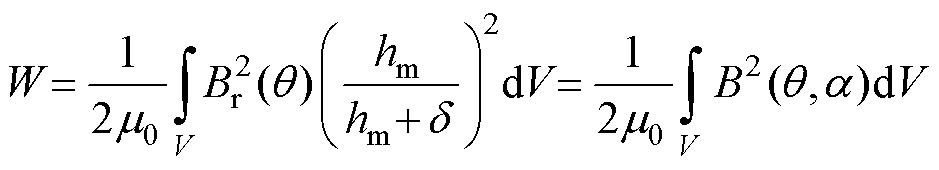（1）
式中，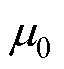
为气隙磁导率；
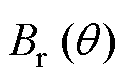为永磁体剩磁；
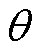为空间变量；
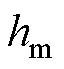为永磁体充磁方向长度；
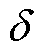为有效气隙长度；V为电机有效气隙体积；
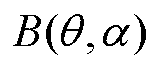为气隙磁通密度；
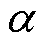为永磁体与定子齿槽之间的相对位置角。
根据磁动势—气隙磁通密度关系，结合式（1）可得
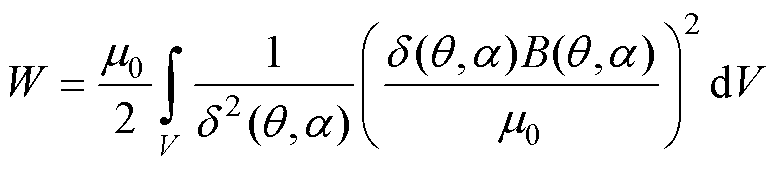（2）
对式（2）中的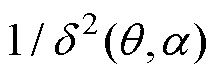
进行傅里叶展开得
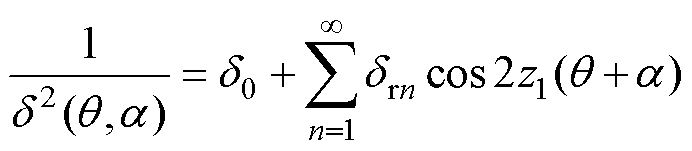（3）
式中，z1为定子槽数；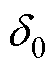
、
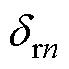分别为径向气隙长度傅里叶分解0次、非0次分量。
气隙磁动势可以表示为
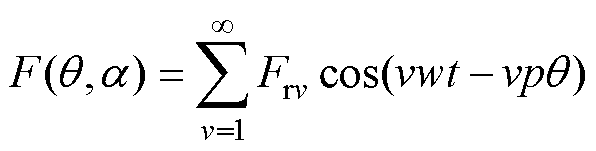（4）
式中，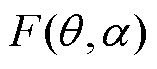
为气隙磁动势；v为谐波次数；Frv为v次谐波磁动势幅值；w为旋转角频率；t为时间变量；p为电机极对数。
将式（2）、式（3）、式（4）代入齿槽转矩-能量关系式Tcog=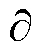
W/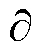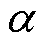中，可以得到谐波磁动势与齿槽转矩关系为
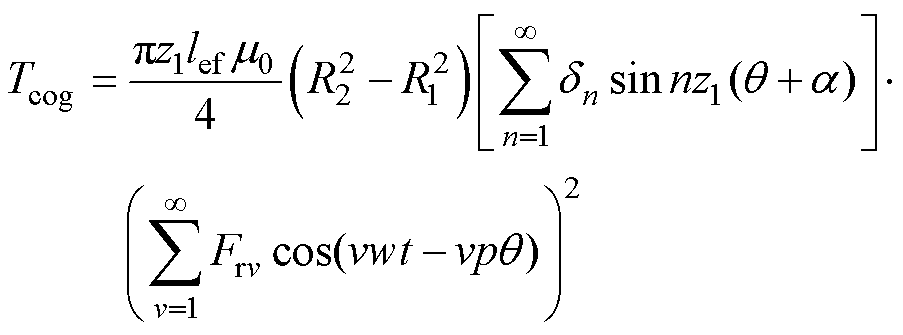（5）
式中，lef为电枢轴向长度；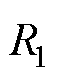
和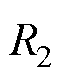
分别为电枢外半径和定子轭内半径。
根据磁动势与磁通密度关系，式（4）中气隙磁动势也可以表示为
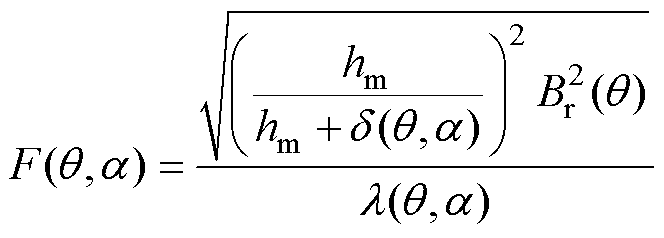（6）
式中，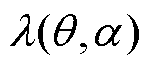
为气隙磁导。因为LSPMSM定转子均开槽，气隙磁导可以近似地表示为
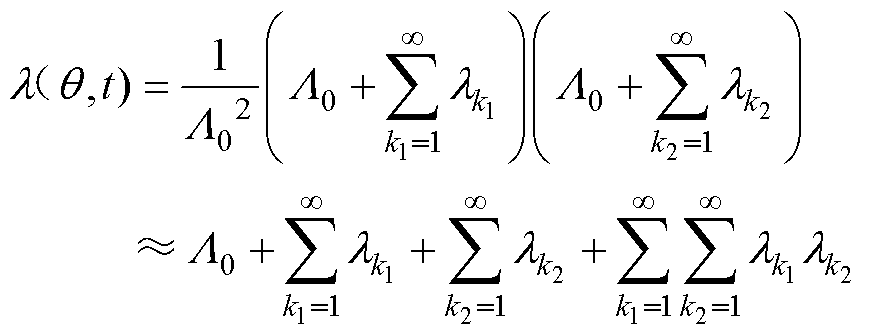（7）
式中，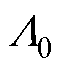
为气隙比磁导；
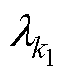和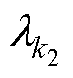
分别为定、转子谐波磁导。将式（5）～式（7）联立可得
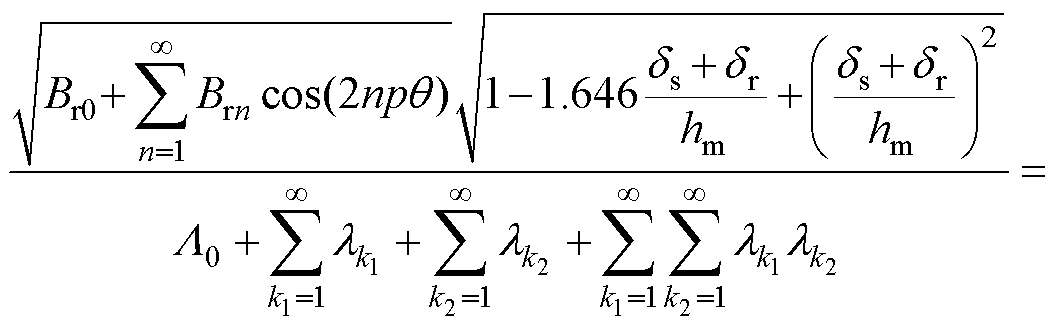
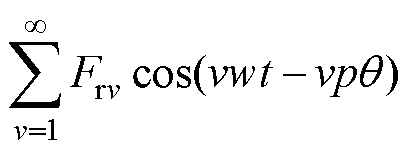（8）
式中，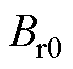
为永磁体基波剩磁；
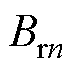为永磁体谐波剩磁展开量；
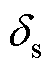和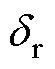
分别为定、转子等效单边气隙。
本文在进行多参数优化时，根据式（8）所建立的齿槽转矩与谐波的关系，结合文献[3]关于异步起动永磁电机气隙磁通密度的傅里叶分解公式以及式（7）中气隙磁导与气隙比磁导的关系，选择转子槽口宽度、转子槽数及永磁体参数作为优化参数。
永磁体厚度与宽度是永磁电机的饱和程度主要影响因素之一。为此，本节通过解析计算建立永磁体尺寸与电机饱和程度的关系，并基于此关系确定电机永磁体参数的选取范围。
永磁体尺寸一般由永磁体最大磁能积来确定。设计永磁体的工作点在最大磁能积处，可以用最少的永磁体得到所需要的磁场。而若永磁体尺寸设计不当，将导致铁心磁饱和，漏磁通增大，效率下降。本文通过磁路法将永磁体与定子电枢等效为两组磁动势与磁阻串联。根据磁动势与等效磁阻即可计算磁通量如式（9），图2为负载情况下等效磁路。
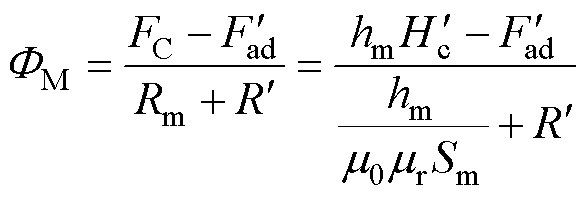（9）
式中，
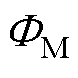为磁通；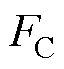
为永磁体内禀磁动势；
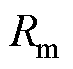为永磁体内磁阻；
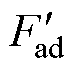为电枢等效磁动势；
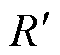为电枢等效磁阻；
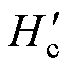为最大磁能积磁场强度；
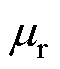为相对磁导率；
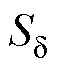为每极气隙面积；
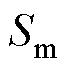为永磁体的面积。
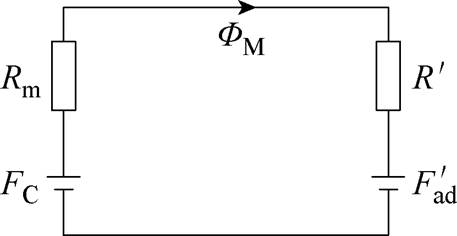
图2 负载情况下等效磁路
Fig.2 Equivalent magnetic circuit under load
假设其外磁路中每极总磁位降为F，每极气隙磁位降为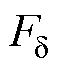
，则
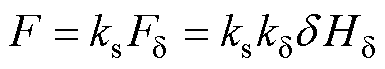（10）
式中，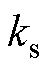
为外磁路饱和系数；
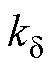为每极气隙磁位降；
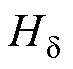为气隙内磁场强度。根据磁路欧姆定律，由永磁体和外磁路组成的闭合磁路满足
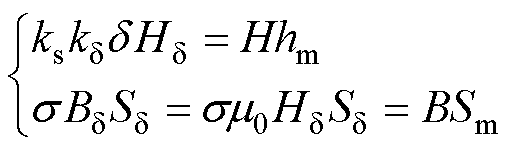（11）
式中，B、H分别为永磁体产生的磁通密度和磁场强度；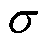
为空载漏磁系数；
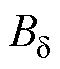为气隙磁通密度。
将式（11）两式相乘可得
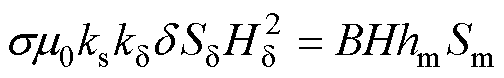（12）
设工作点在最大磁能积点，根据永磁体体积公式结合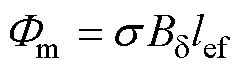
，可得气隙磁通为
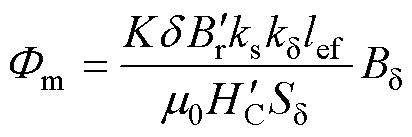（13）
最后得到气隙磁通密度与电机参数关系
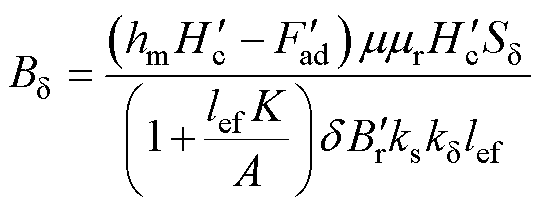（14）
式中，K为永磁体厚度；A为铁心材料横截面积；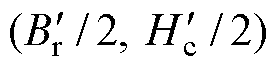
为永磁体最大磁能积工作点；
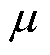为铁磁材料磁导率，其不是一个常数，与铁心磁饱和有关，当磁路饱和后，材料磁导率会急速下降导致电机漏磁增大。
图3所示为有限元仿真与解析法计算得出的永磁体参数对其饱和程度影响。根据最大磁能积关系，逐步增大永磁体厚度，减小其宽度，观察图3中气隙磁通密度幅值随永磁体厚度变化曲线即可准确定位最优尺寸。
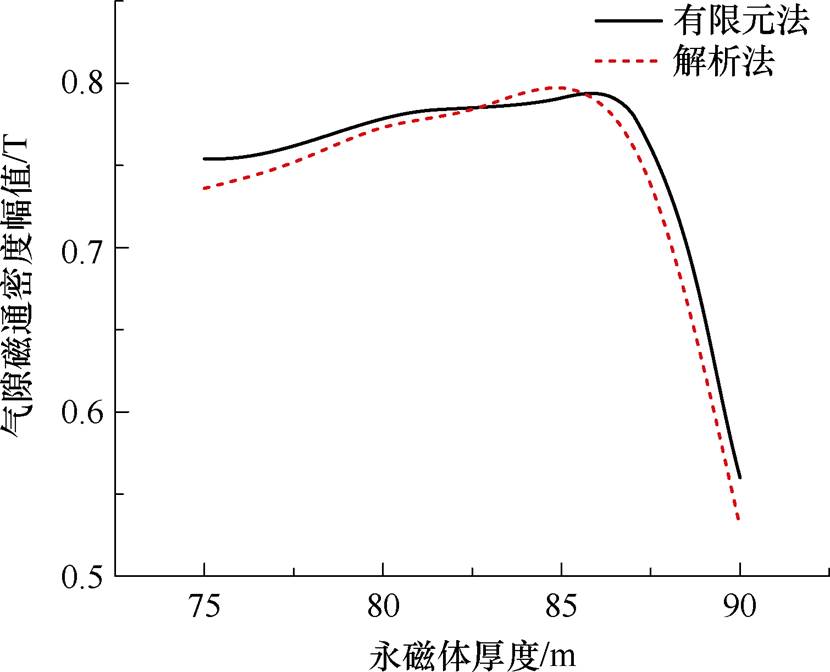
图3 永磁体宽度与厚度对其饱和程度的影响
Fig.3 The influence of permanent magnet width and thickness on its saturation
图3中，有限元法与解析法最大误差为2.4%，该误差产生的主要原因为：解析法假设电机磁导率各向同性，而硅钢片中电磁场为各向异性。并且可以看出，两种方法得到电机永磁体宽度到86mm附近气隙磁通密度幅值最大，将永磁体宽度86mm对应的磁通密度值定义为饱和峰值。因此，在接下来的多参数多目标优化过程中，本文将定义电机三种工作状态：未饱和、饱和峰值、饱和后。并针对三种工作状态进行对应的多目标优化，确保设计结果在全工况范围内的精确性。
响应面法（Response Surface Methodology, RSM）根据可设计的采样点组建立目标与多变量的函数去逐渐逼近一个隐函数。而多目标粒子群优化算法（Multi-Objective Particle Swarm Optimization, MOPSO）则是将粒子群算法与多目标相结合，建立多维空间，在粒子群所在区域搜索最优解[9]。响应面法与粒子群算法的结合的方案可以确保电机性能在多个关键指标上均能达到最优水平。
为了达到电机齿槽转矩、转矩脉动及效率等关键目标的最优化，本文提出了一种融合RSM与MOPSO的综合优化策略。图4为多目标优化流程，其优点在于响应面算法将数群分类，MOPSO基于分区特性自适应调整，缩短算法计算时间，实现全域Pareto前沿的高效探索。
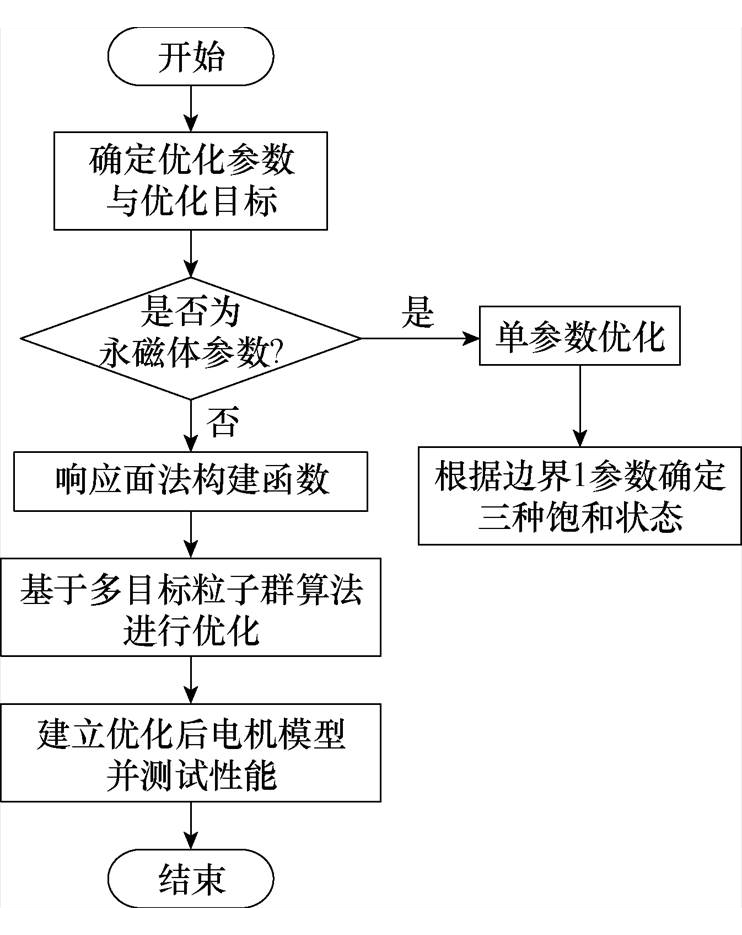
图4 LSPMSM多目标优化流程
Fig.4 LSPMSM multi-objective optimization process
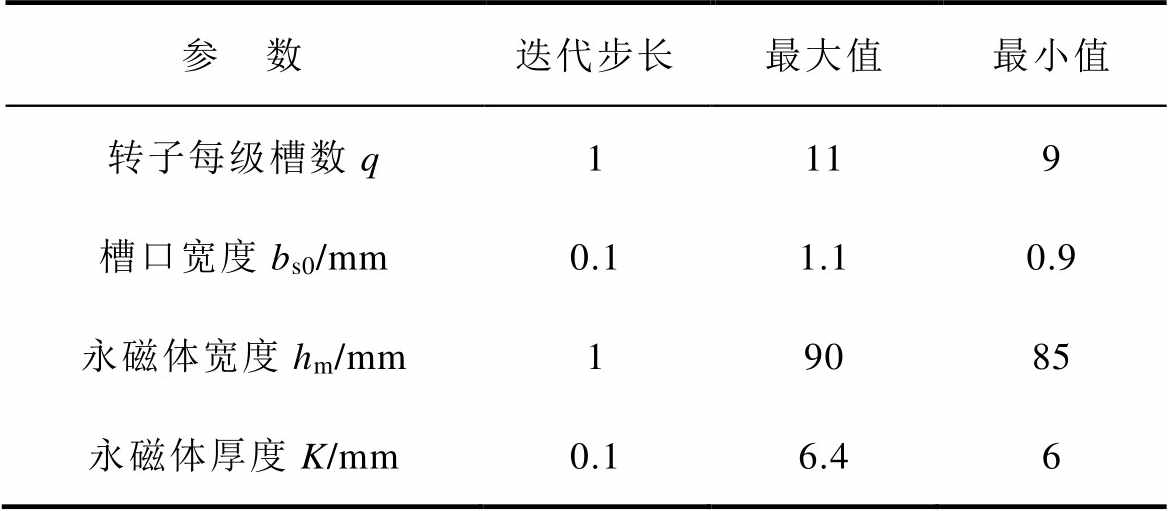
本文将选取电机的齿槽转矩、转距脉动率及效率设置为优化目标，选取转子和永磁体的4个关键参数进行多目标多参数优化设计。表2给出所选优化参数的合理变化范围。其中永磁体厚度与宽度成反比关系，永磁体面积恒定为540 mm2，以保证永磁体设计工作点在最大磁能积点。
基于定子是否斜槽及电机磁路饱和程度两种约束条件，采用Design Expert建立模型[15]。最终获得关于齿槽转距、转距脉动率及效率的数学模型。式（15）为定子添加斜槽的多目标优化函数式，式（16）为定子不添加斜槽对多目标的优化函数式。
表2 LSPMSM转子主要优化参数
Tab.2 Main optimization parameters of LSPMSM rotor
参 数迭代步长最大值最小值 转子每级槽数q1119 槽口宽度bs0/mm0.11.10.9 永磁体宽度hm/mm19085 永磁体厚度K/mm0.16.46
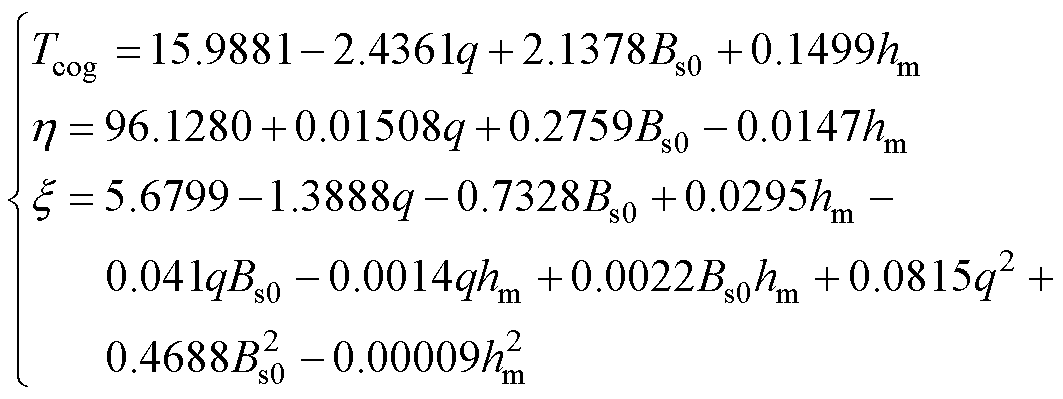（15）
式中，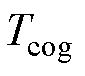
为齿槽转矩峰值；
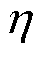为效率；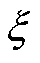
为转矩脉动率；q为转子每级槽数。
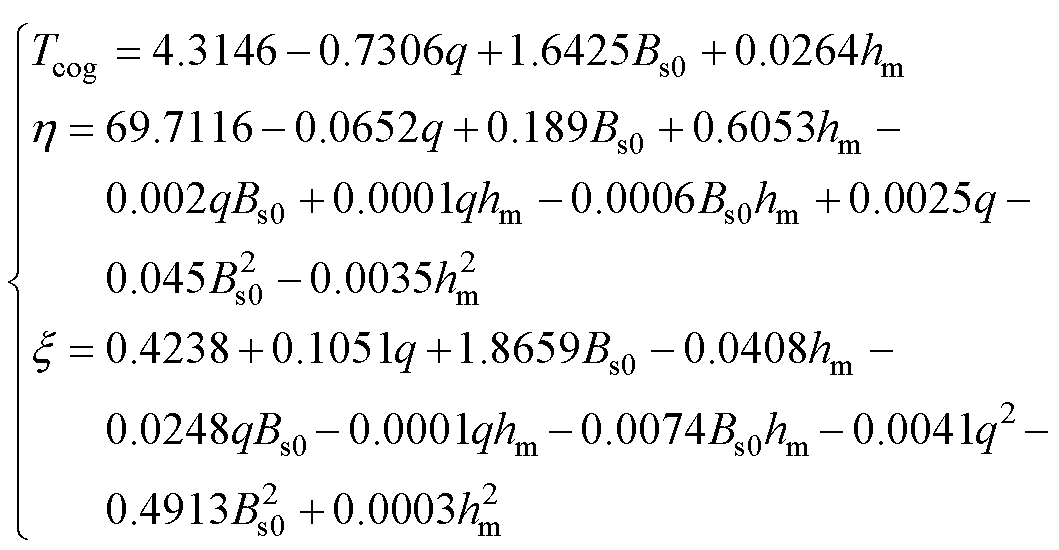（16）
基于式（15）与式（16）目标优化函数，以电机铁心不同饱和程度：未饱和、饱和峰值、过饱和与定子是否添加斜槽两因素为约束条件，构建了18组响应面模型。图5为Tcog关于Bs0、q及饱和状态与定子是否斜槽的响应面。从图5可以看出，无论定子是否斜槽，齿槽转矩最优解均在转子每极槽数为11，转子槽口宽度为1.1mm时，且槽口宽度越小，近槽配合对齿槽转矩影响越大。同时，齿槽转矩幅值随着电机饱和性能的降低而减小。定子斜槽后，当转子每极槽数固定，齿槽转矩幅值随转子槽口宽度变化更加敏感。而定子不斜槽时，齿槽转矩幅值较大，可能影响电机正常运行。
优化目标h 关于Bs0、q及饱和状态与定子是否斜槽的响应面如图6所示。
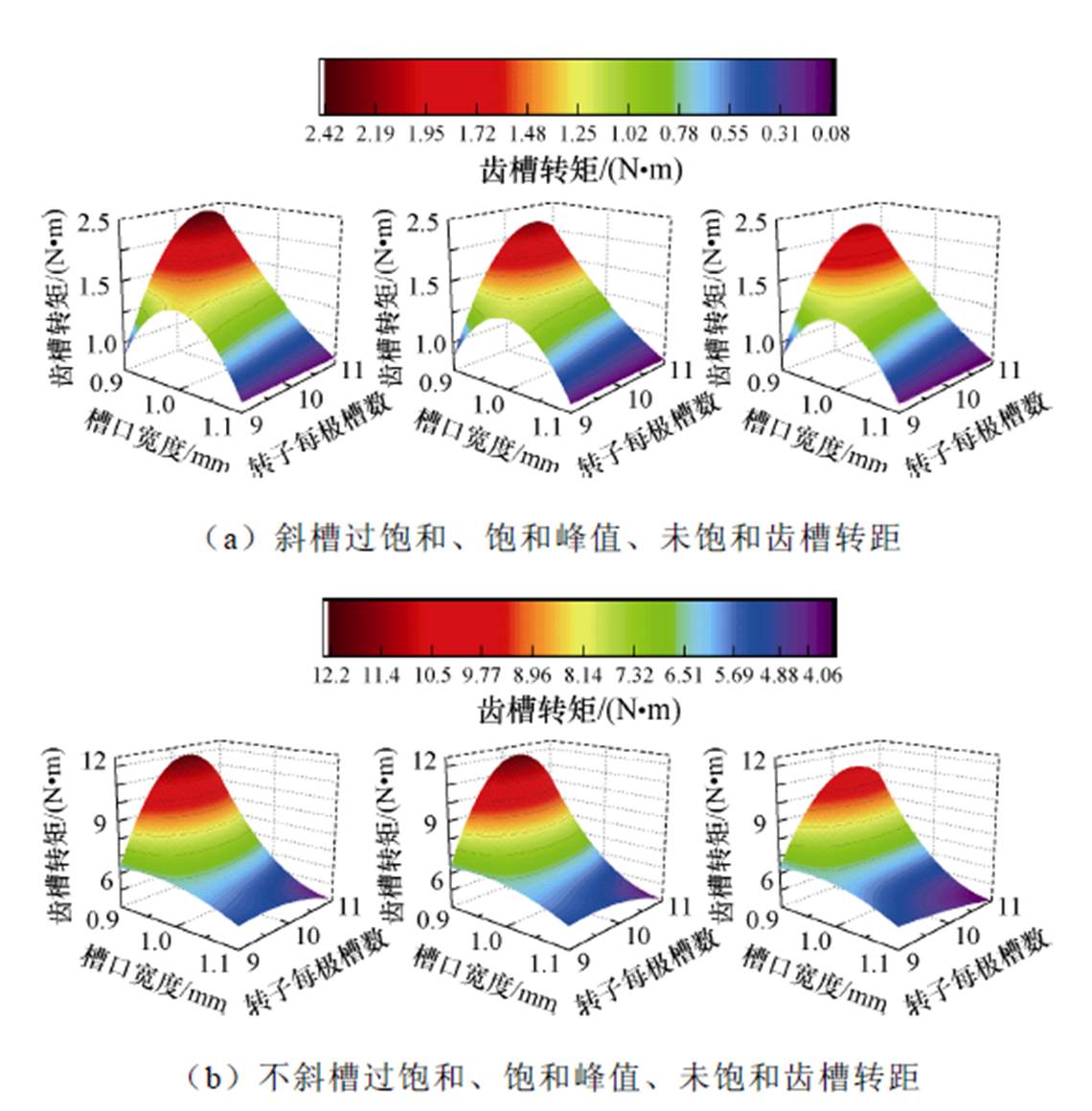
图5 优化目标Tcog关于bs0、q及饱和状态与定子是否斜槽的响应面
Fig.5 Optimization targets Tcog concerning bs0、q and the response surface of the saturation state and whether the stator is chute
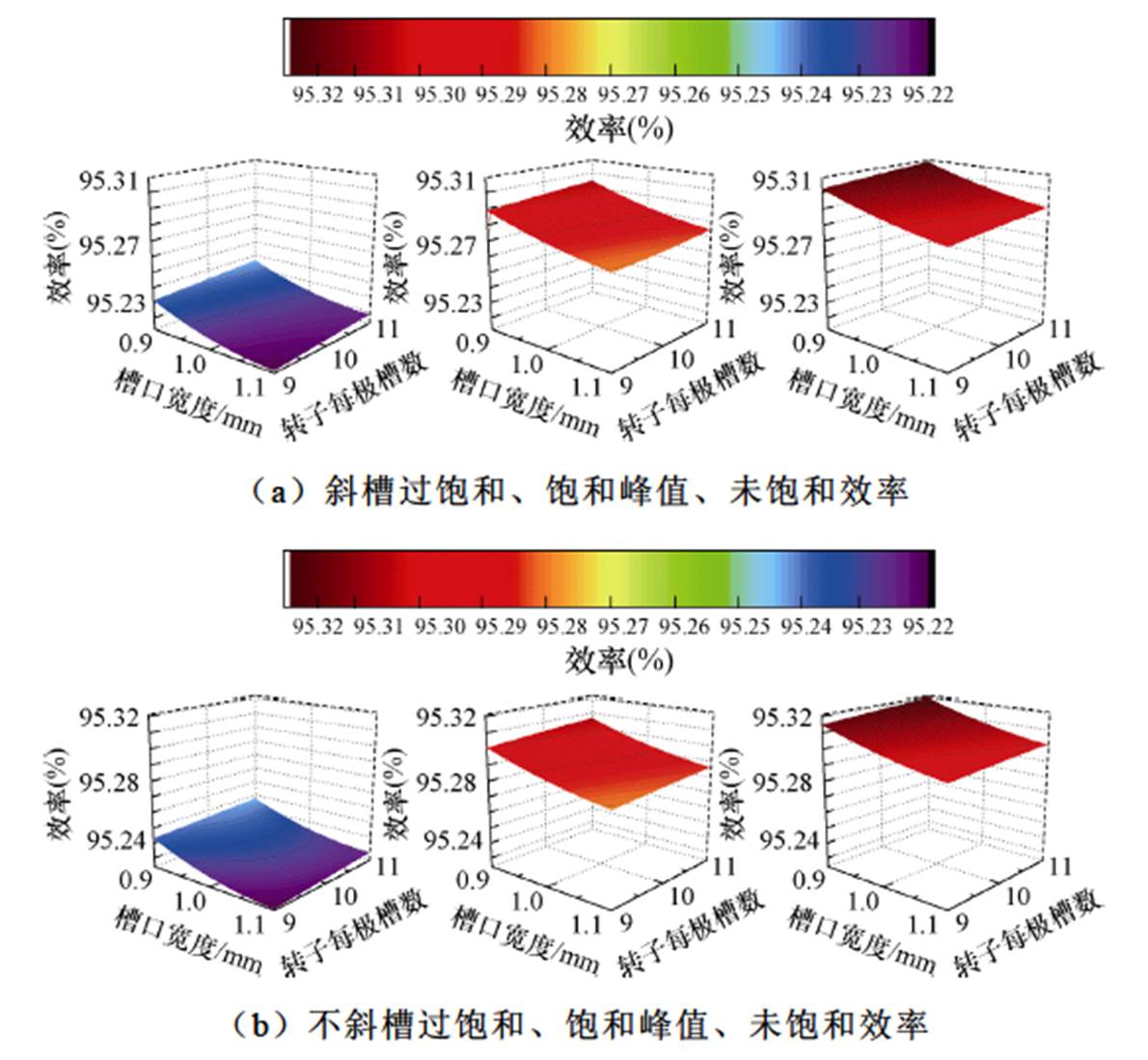
图6 优化目标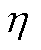
关于Bs0、q及饱和状态与定子是否斜槽的响应面
Fig.6 Efficiency concerning Bs0、q and the response surface of the saturation state and whether the stator is chute
从图6可以看出，定子是否斜槽对效率随优化参数变化趋势影响较小。而效率随着电机饱和程度的降低而提升。从单响应面分析可知，效率最优设计参数区域在0.9≤bs0≤1, 10≤q≤11范围内。其中转子每极槽数为11，槽口宽度为0.9 mm时为效率最优设计参数。
优化目标x 关于Bs0、q及饱和状态与定子是否斜槽的响应面如图7所示。从图7可以看出，当定子不斜槽时，电机不同饱和状态对转矩脉动变化趋势影响不大。当定子斜槽时，电机不同饱和状态对响应面形状影响较大。并且定子是否斜槽会影响转矩脉动最优分布区域，当定子不斜槽时，转矩脉动最优设计参数区域在0.9≤bs0≤1, 9≤q≤11，当定子斜槽时，转矩脉动最优设计参数区域在1≤ bs0≤1.1, 10≤q≤11。最优参数位置出现在定子斜槽且电机饱和峰值，转子每极槽数为11，转子槽口宽度为1.1 mm。
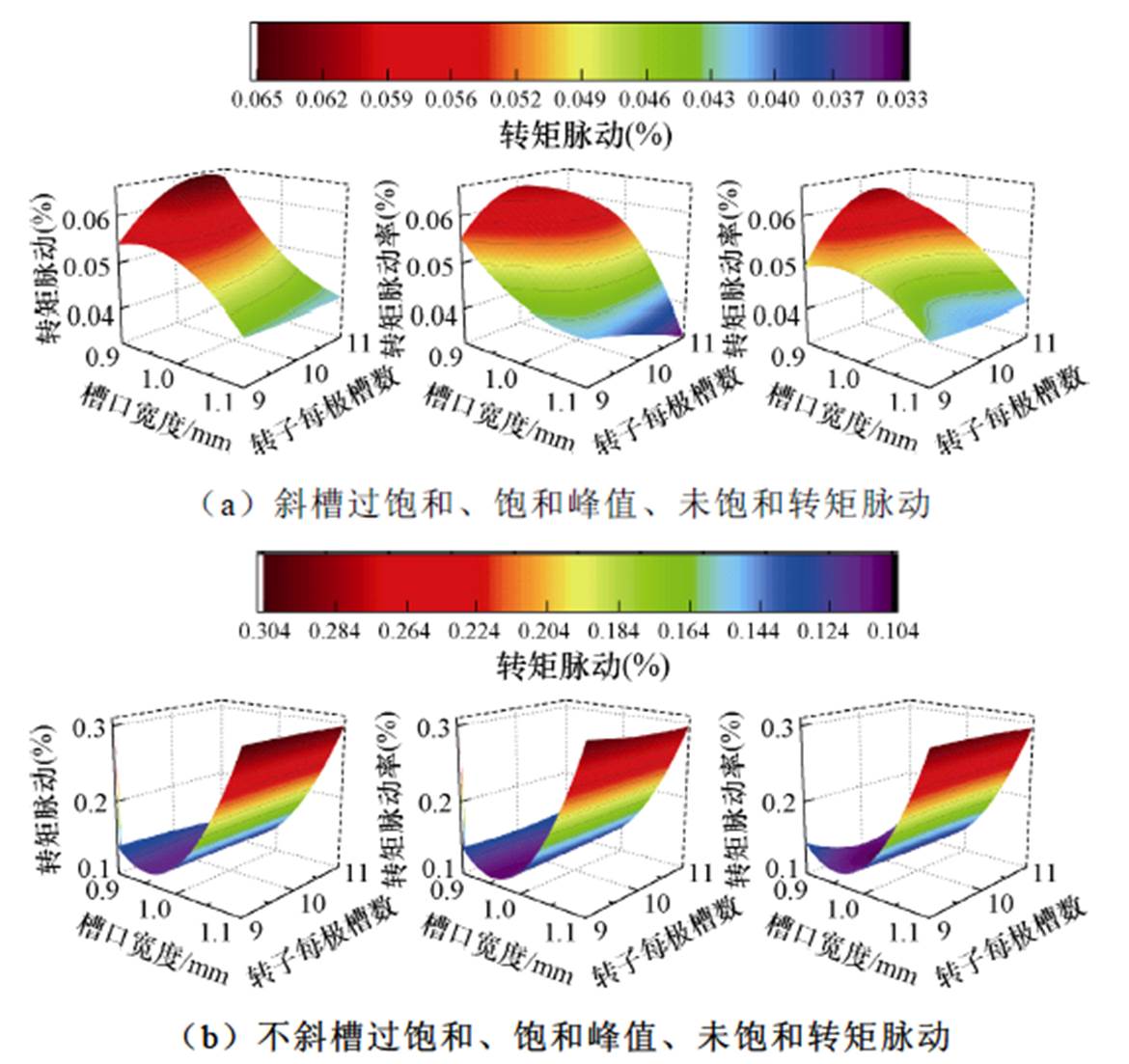
图7 优化目标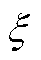
关于Bs0、q及饱和状态与定子是否斜槽的响应面
Fig.7 Optimization targets 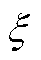concerning Bs0、q and the response surface of the saturation state and whether the stator is chute
通过采用多目标粒子群优化算法，将永磁体参数作为电机饱和程度的变量。并结合电机的三种不同饱和程度及电机定子是否斜槽对电机转矩脉动、齿槽转矩、效率进行寻优以获得最佳优化方案。基于MOPSO对响应面法得到的18组参数组合进行寻优，最终确定6个不同条件下的最优解。最终根据电机转矩脉动最小、齿槽转矩符合要求、效率最佳选择出A、B、D、E、F的6个点作为六种不同条件下的最优解以及最优解参数。粒子群最优解选取如图8所示。图中，最优解用黑色原点展示。
优化点A、B、C、D、E、F分别对应电机六种状态不斜槽过饱和、不斜槽饱和峰值、不斜槽未饱和、斜槽过饱和、斜槽饱和峰值、斜槽未饱和。从六种最优解可以看出，定子不斜槽时，优化方案A、B、C的转子每极槽数均为10。定子斜槽时，优化方案D、E、F的转子每极槽数均为11。根据图8可知，定子斜槽对齿槽转矩幅值及转矩脉动有着极大改善。
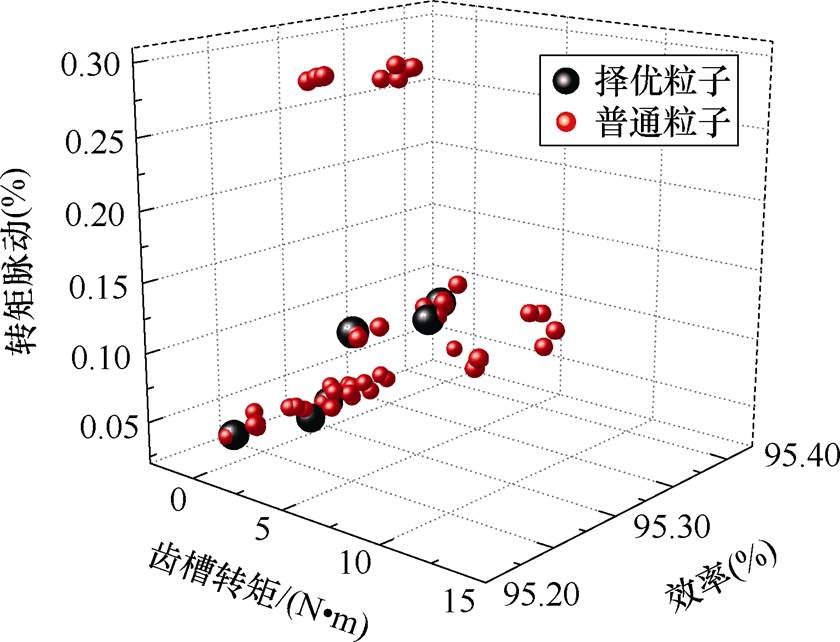
图8 粒子群最优解选取
Fig.8 Optimal solution selection of particle swarms
为探究齿槽转矩及谐波含量与转子每极槽数、转子槽口宽度的关系。本节将从齿槽转矩的幅值、周期与气隙磁通密度谐波关系，以及空载反电动势随转子参数的变化规律两角度进行深度剖析。
优化前电机属于斜槽过饱和设计，其齿槽转矩幅值为2.114 9 N∙m，根据多目标粒子群优化算法所选取的最佳参数所得到的齿槽转矩幅值为0.124 6 N∙m。其齿槽转矩性能大大提升，优化前后齿槽转矩对比如图9所示。
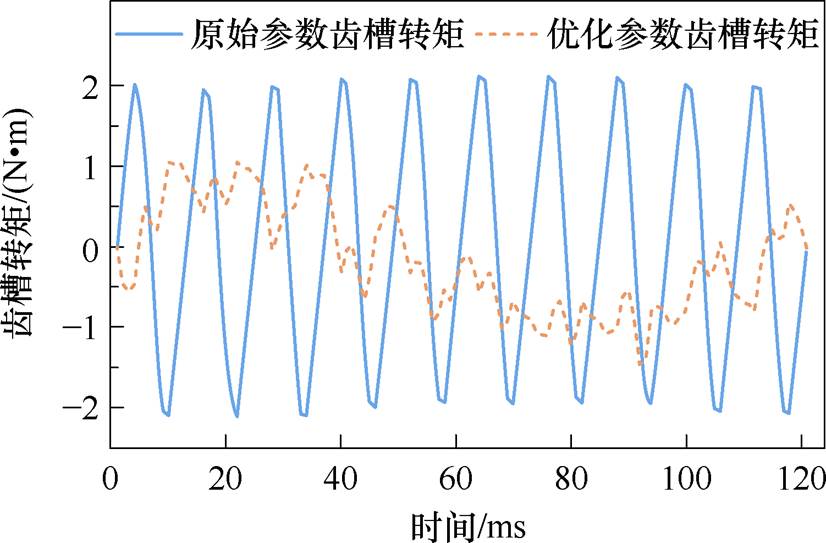
图9 优化前后齿槽转矩对比
Fig.9 Comparison diagram of optimized front and rear cogging torque
从图9中可以看出，尽管齿槽转矩幅值减小，但由于定转子齿槽引起的磁导谐波与永磁体剩磁的相互作用，其周期波动现象仍较为显著。此时齿槽转矩由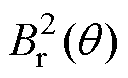
的恒定部分Br0与定子齿槽和转子齿槽引起的磁导谐波共同产生，其可以表示[16]为
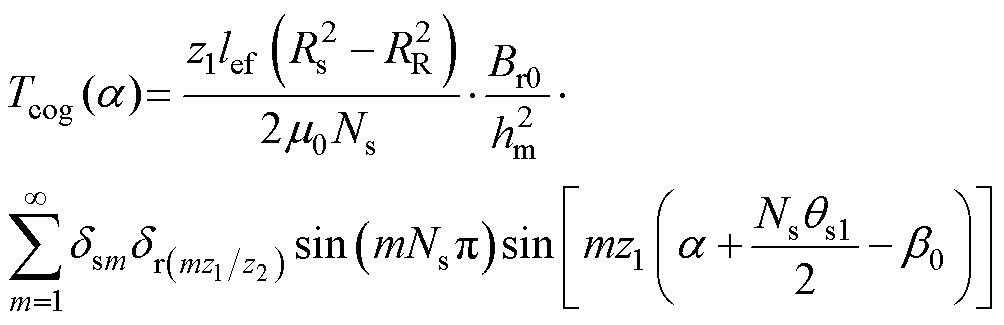（17）
式中，Rs定子内半径；RR转子外半径；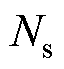
为电机槽数；
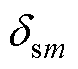为弧度表达的气隙长度；
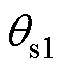为弧度表达的空间变量；z2为转子槽数。当转子每极偶数槽时，
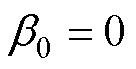，当转子每极奇数槽时，
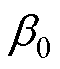等于定子齿距角的1/2。
由式（17）可以看出，齿槽转距波形的周期数取决于定子槽数和转子槽数的配合，周期数应为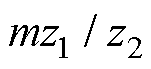
，齿槽转矩周期为定子槽数z1与转子槽数z2之比与相数m乘积。经计算原始数据周期为3，优化后周期为11，因此，图9优化后的齿槽数矩周期发生大幅度变化。
为探究齿槽转矩幅值降低机理，需从定转子侧气隙变化量入手，其关系为
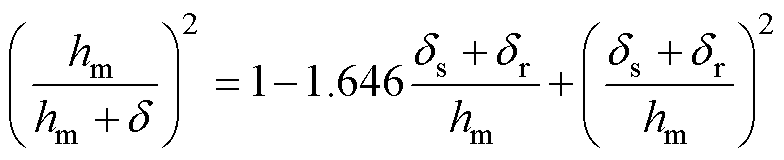（18）
根据式（5）和式（6），齿槽转矩幅值主要与式（18）中(hm/hm+d)2成正比。虽然转子槽数的增加导致转子侧气隙长度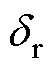
增大，但由于式（18）中(ds+dr/hm)2增量远小于1.646(ds+dr/hm) 减量。因此，随着转子槽数增加，式（18）中(hm/hm+d)2是降低的，从而导致齿槽转矩幅值减小。
针对电机齿槽转矩抑制，当约束电机转子槽数，单方面优化转子槽口宽度[17]满足
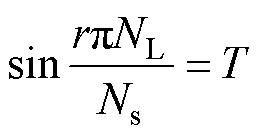（19）
式中，T为齿槽转矩影响系数；r为槽口宽度与槽距的比值；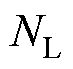
为电机槽数与极数最小公倍数；当T趋近于0时，齿槽转矩越来越好。经计算，当电机转子槽数为36时，随着槽口宽度的升高，电机齿槽转矩幅值升高。当电机转子槽数为40或44时，随着槽口宽度的升高，电机齿槽转矩幅值降低。
图10给出最优化方案的齿槽转矩波形，可以明显地看出，定子不加斜槽的齿槽转矩幅值远高于定子加斜槽的齿槽转距。从过饱和、饱和峰值和未饱和三种情况来看，未饱和的齿槽转矩更优，其主要
原因在于永磁体参数的改变影响了气隙磁通密度幅值。但采用这种优化方案，则需以牺牲其电磁性能为代价。
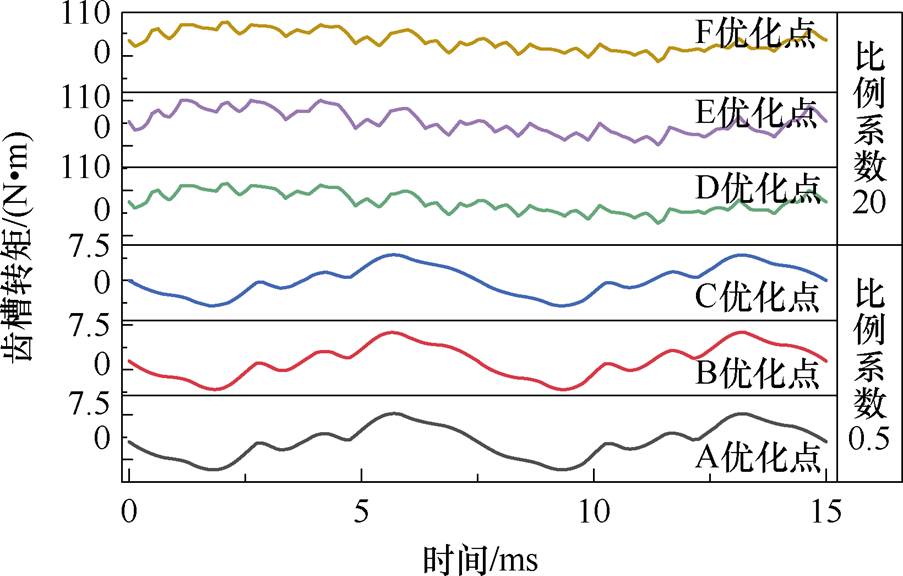
图10 最优解齿槽转矩
Fig.10 Optimal solution cogging torque diagram
基于上述优化方案影响的电磁性能分析，本节主要探究气隙磁通密度及其谐波含量在不同设计方案下的数值。不同优化点气隙磁通密度幅值见表3。
表3 不同气隙磁通密度幅值
Tab.3 Different air gap magnetic density amplitudes
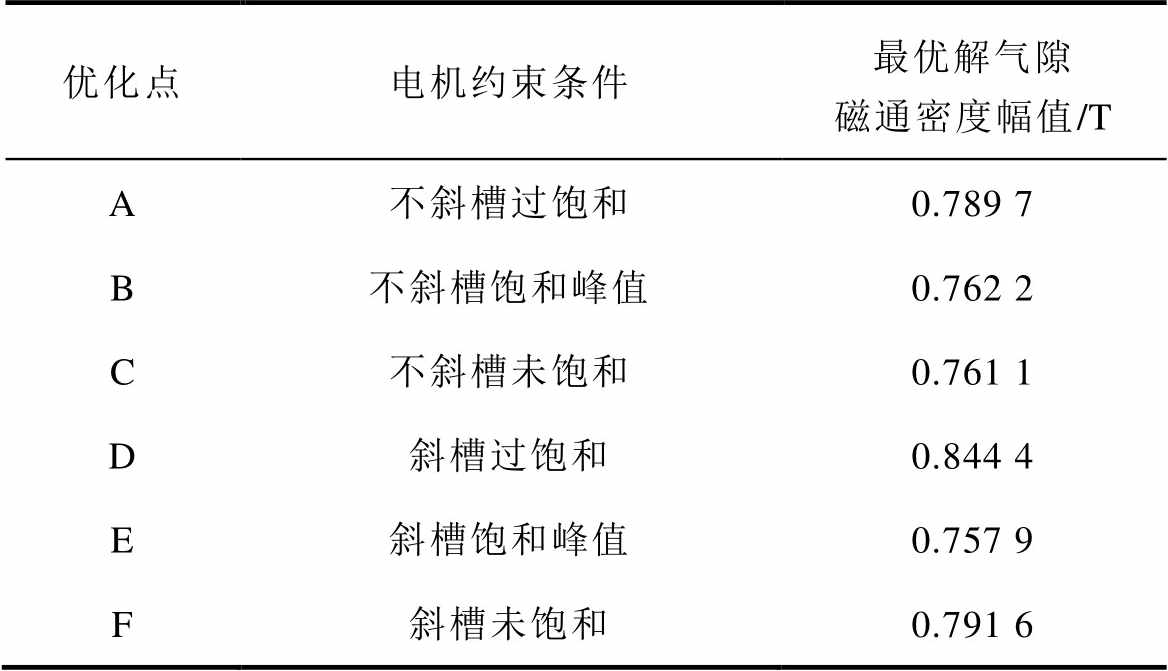
优化点电机约束条件最优解气隙磁通密度幅值/T A不斜槽过饱和0.789 7 B不斜槽饱和峰值0.762 2 C不斜槽未饱和0.761 1 D斜槽过饱和0.844 4 E斜槽饱和峰值0.757 9 F斜槽未饱和0.791 6
为此本文继续分析齿槽转距与谐波之间的关系，图11所示为不同参数方案的空载径向气隙磁通密度的傅里叶分解。
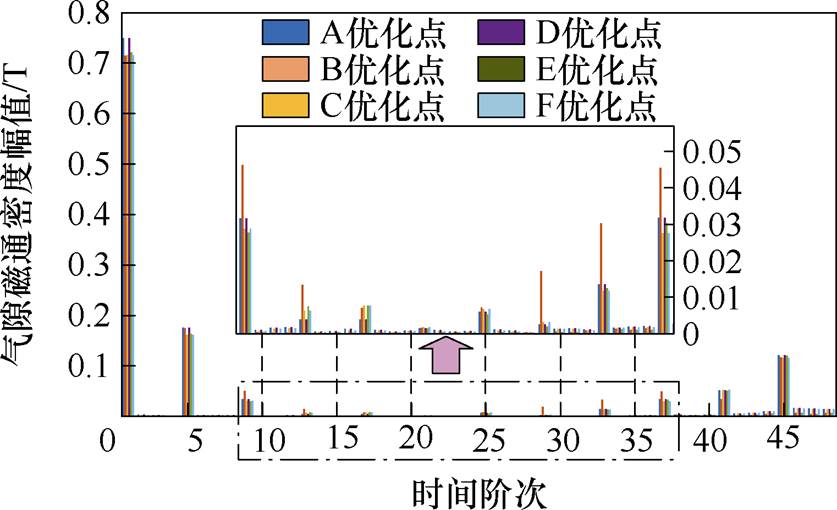
图11 最优解气隙谐波
Fig.11 Optimal solution of air gap harmonics
槽口宽度的增加根据式（7）可知，气隙磁导减小，谐波含量升高；相反，随着转子槽数的升高，气隙磁导升高，谐波含量降低，根据仿真分析得到的数据也能证明理论分析的准确性。谐波含量随优化参数的变化数据见表4。转子每极槽数范围为9～11，优化步长为1。转子槽开口宽度为0.9～1.1 mm，优化步长为0.1 mm。
表4 不同最优解谐波含量
Tab.4 Different optimal solution harmonic content
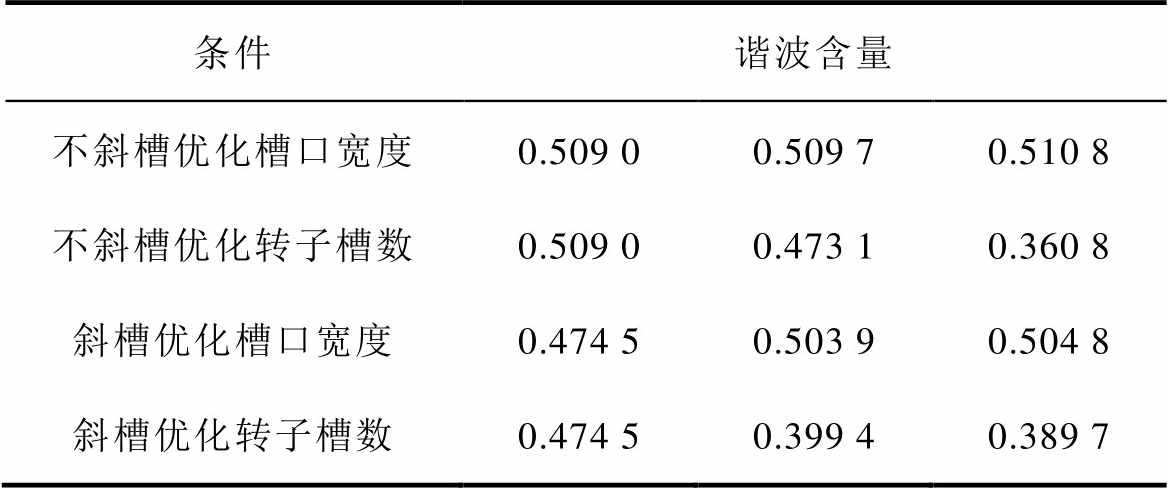
条件谐波含量 不斜槽优化槽口宽度0.509 00.509 70.510 8 不斜槽优化转子槽数0.509 00.473 10.360 8 斜槽优化槽口宽度0.474 50.503 90.504 8 斜槽优化转子槽数0.474 50.399 40.389 7
由表4可知，无论定子是否斜槽，气隙磁通密度谐波含量均随转子槽口宽度的增大而增加，随着转子槽数的增加而减少。此外，齿槽转矩的单参数优化结果与电机饱和程度及转子槽数密切相关，其变化趋势无法单调表征。
空载反电动势也是电机常常关注的指标之一[18]。本文虽以降低齿槽转距为目的，但空载反电动势同样影响电机控制灵敏度，因此可以通过电机空载反电动势进行分析。图12为六组最优参数的空载反电动势。
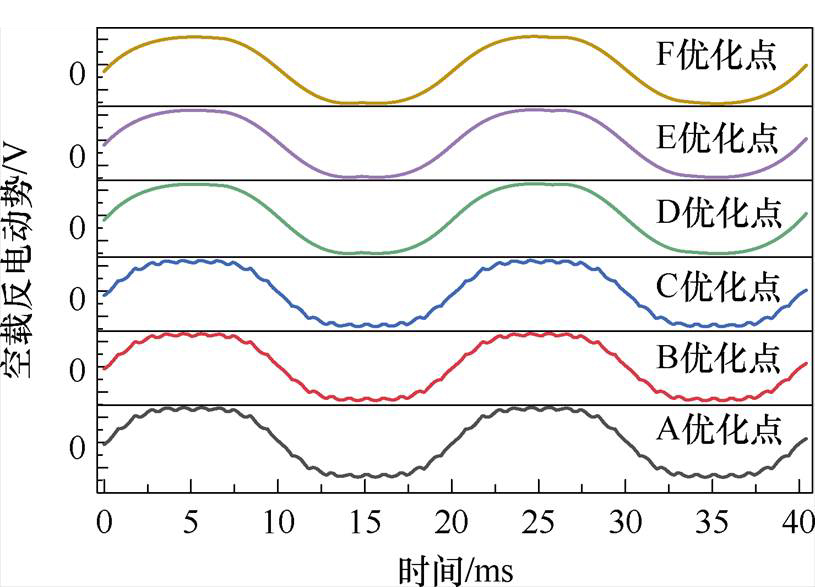
图12 最优解的空载反电动势
Fig.12 No-load back electromotive force for optimal solution
图13为定子不加斜槽电机空载反电动势与转子每极槽数关系。随着转子每极槽数增加，定子不加斜槽的异步永磁电机空载反电动势正弦畸变率明显增加，由图13可知，虽然7次谐波降低，但是62、68高次偶数谐波大大升高。因此，在分析电机运行平稳性与控制灵敏度时，不仅需考虑齿槽转距，还需关注电机空载反电动势波动率，以确保电机整体性能的综合优化。
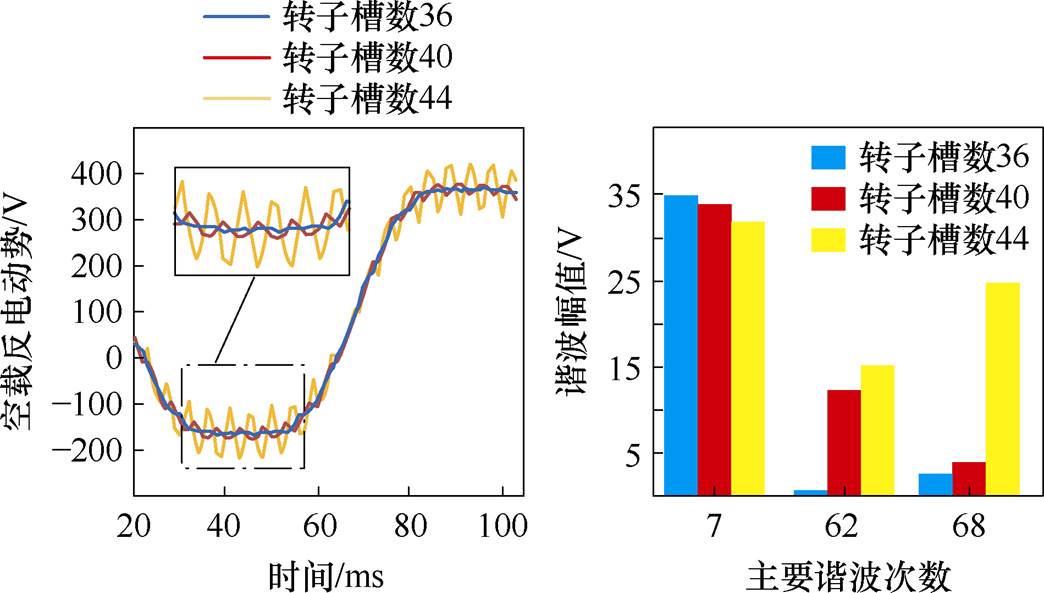
图13 定子不斜槽下转子每极槽数对空载反电动势的影响
Fig.13 Effect of the number of rotor grooves per pole on no-load back EMF in the stator non-chute state
图14为定子加斜槽电机空载反电动势与转子每极槽数的关系。定子是否斜槽对转子每极槽数与空载反电动势的变化规律无显著影响，但定子斜槽后可有效降低空载反电动势波动率。
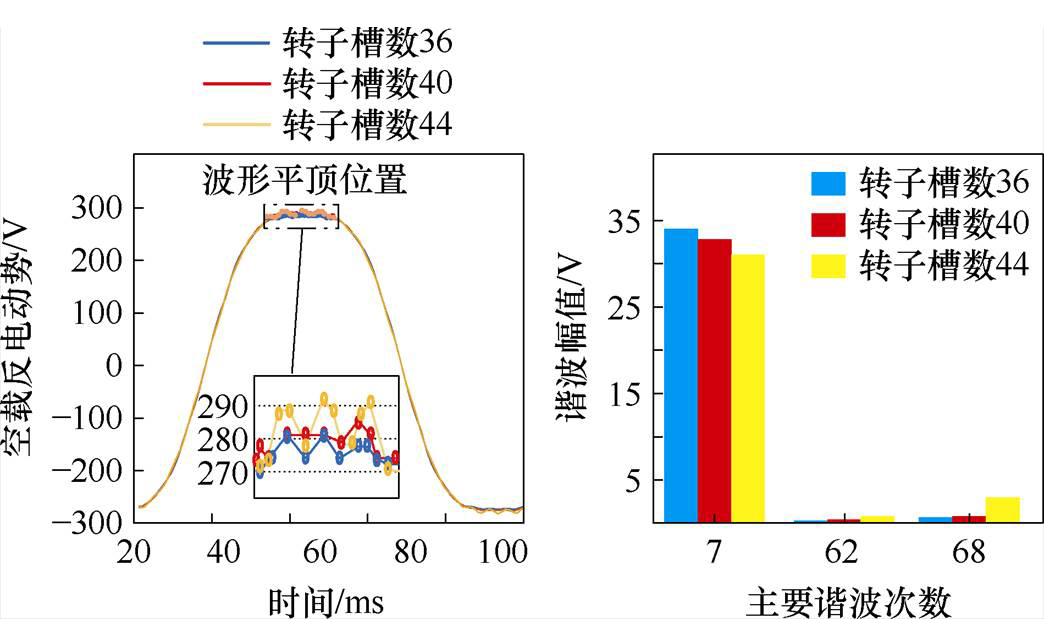
图14 定子斜槽下转子每极槽数对空载反电动势的影响
Fig.14 Effect of rotor grooves per pole on no-load back EMF in stator chute state
为验证本文理论分析的合理性，探究斜槽、极槽配合，槽口宽度对电机转矩的影响。对原始样机结构做出改进。由图5～图8分析可知，极槽配合对电机参数影响较大，因此在原有样机基础上选择48/40和48/44两组参数进行实验对比；基于最优参数，选取一组槽口宽度为1.1mm的饱和峰值电机及饱和峰值斜槽电机，分析斜槽与槽口宽度对电机性能的影响。最终四组优化参数见表5。
根据表5的优化参数，在原有某电机厂样机TBYC180M-4，18.5 kW电机基础上，制造了4台优化参数的实验样机，对5台电机的转矩、效率和空载反电动势的波动率进行测试，实验平台如图15所示。
表5 实验参数选择
Tab.5 Selection of experimental parameters
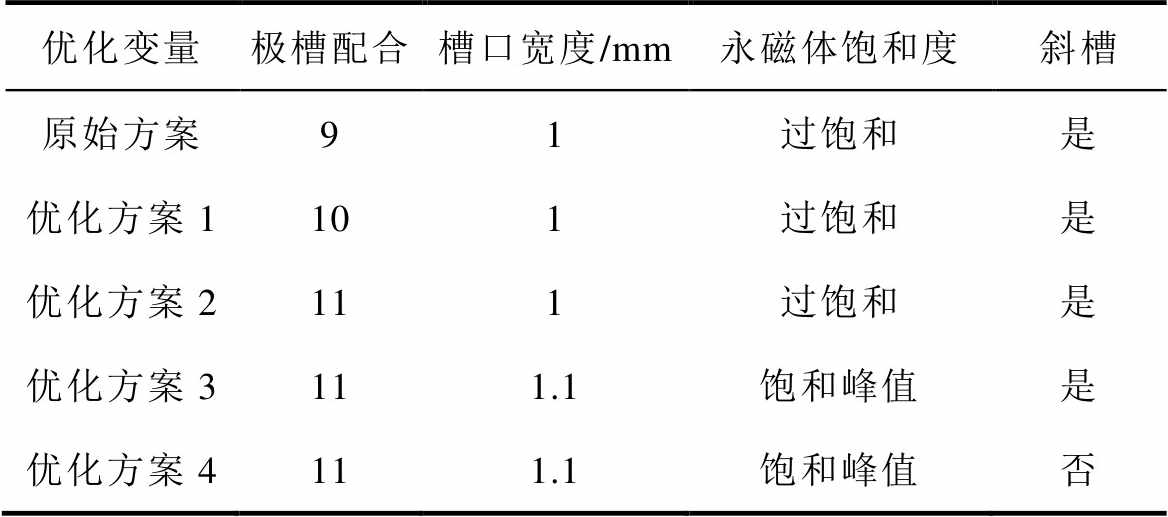
优化变量极槽配合槽口宽度/mm永磁体饱和度斜槽 原始方案91过饱和是 优化方案1101过饱和是 优化方案2111过饱和是 优化方案3111.1饱和峰值是 优化方案4111.1饱和峰值否
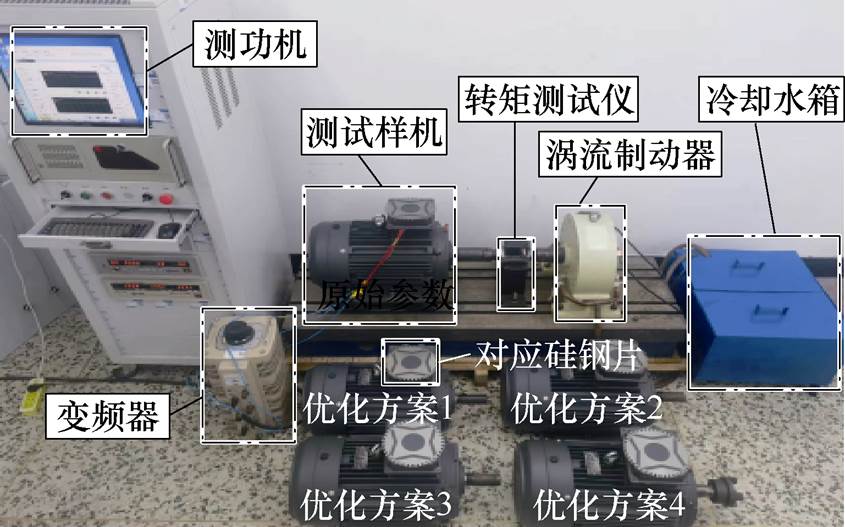
图15 不同转子槽数与定子是否斜槽下的电机目标性能实验
Fig.15 Experimental diagram of the target performance of the motor under different rotor slots and stator or not
对上述样机依次施加额定电压，测功机转矩施加0 N·m负载作空载实验，之后对各电机施加额定电压，测功机施加117 N·m额定转矩进行负载实验实验，数据见表6。
表6 实验结果数据
Tab.6 Experimental results data
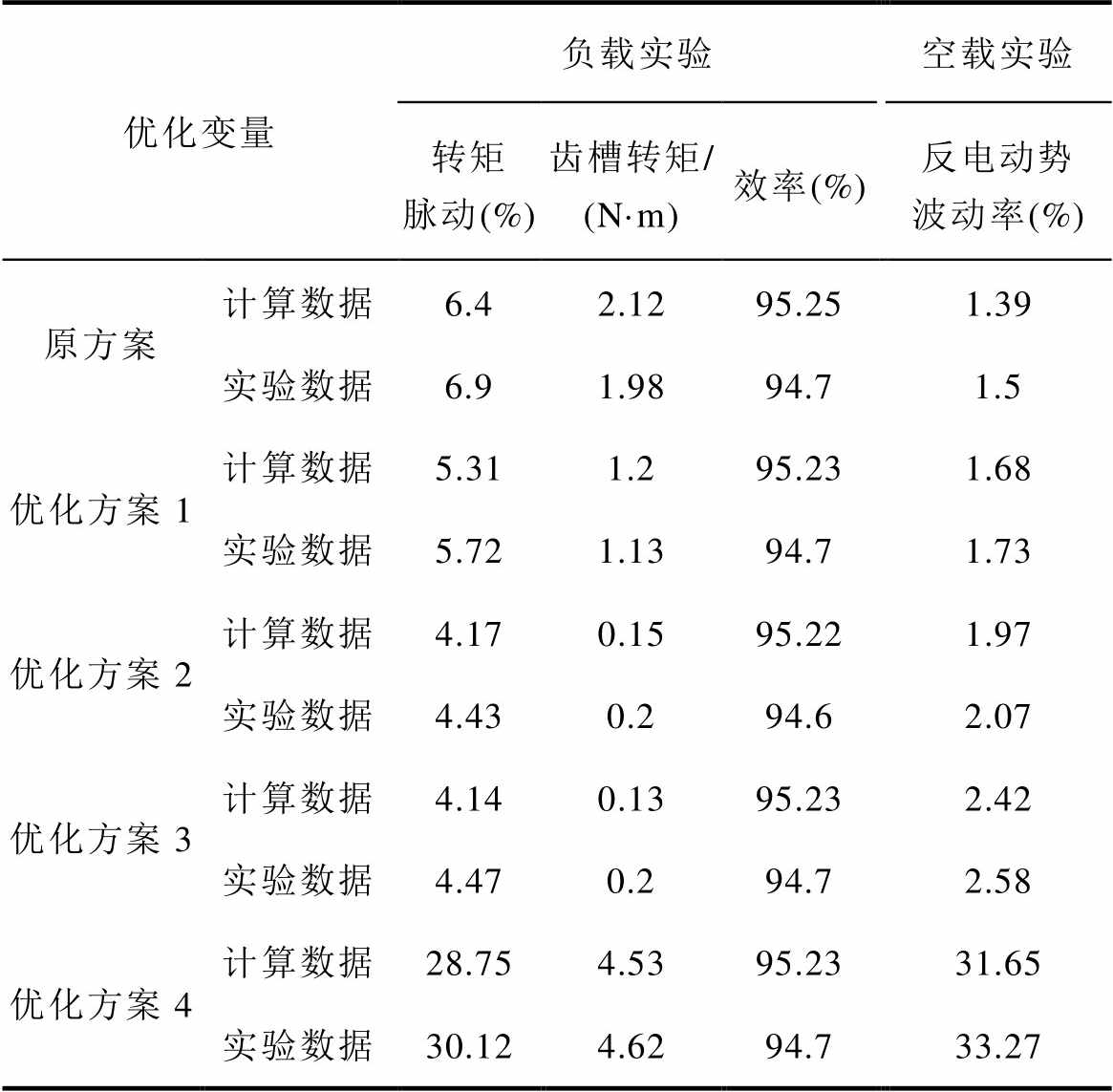
优化变量负载实验空载实验 转矩脉动(%)齿槽转矩/(N·m)效率(%)反电动势波动率(%) 原方案计算数据6.42.1295.251.39 实验数据6.91.9894.71.5 优化方案1计算数据5.311.295.231.68 实验数据5.721.1394.71.73 优化方案2计算数据4.170.1595.221.97 实验数据4.430.294.62.07 优化方案3计算数据4.140.1395.232.42 实验数据4.470.294.72.58 优化方案4计算数据28.754.5395.2331.65 实验数据30.124.6294.733.27
由表6可以看出，效率和优化方案4的误差均在5%以内，而样机原方案与优化方案1、优化方案2和优化方案3其他数据误差在7%左右，这是由于在空载实验时，电源波形输入波形有一定的波动；在负载实验中，受联轴器与设备精度影响，转矩测量数据有一定误差，导致数据普遍偏大[19]。总体来说，表6数据基本验证了仿真准确性，满足工程要求。对比样机原方案、优化方案1和优化方案2，同等条件下，近槽配合的电机转矩脉动、齿槽转矩和效率都远优于远槽配合，空载反电动势在定子斜槽作用下波动较小，证实了图5～图7和图14仿真准确性；对比方案2和方案3，在电机设计成型后，通过细小改变槽口宽度与永磁体参数，电机的性能如齿槽转矩和效率能够有所上升，但并不明显，与图5仿真结果一致；对比优化方案3和优化方案4可知，斜槽对电机性能影响极大，当定子不斜槽时，电机的空载反电动势与转矩波动变化非常明显，证明斜槽对电机的重要性。
综合上述实验数据与图8择优后的仿真数据，优化方案3转子每极槽数11，槽口宽度1.1 mm，定子斜槽、电机铁心处于饱和峰值状态为该样机各项最优的参数方案。
本文建立谐波与齿槽转矩的关系，在保证永磁体最大磁能积不变的情况下，确定电机饱和程度与永磁体参数的关系与定子是否斜槽，将电机分为六种不同设计状态。通过响应面法与多目标粒子群算法计算出六种最优参数，以权衡齿槽转矩幅值、效率及转矩脉动等多目标。最后利用仿真与实验对电机性能进行验证，得到以下结论：
1）通过响应面法与多目标粒子群算法并加以工艺约束，得到了电机不同设计方案下所对应的最优参数。由优化趋势可知，异步起动永磁同步电机其他参数不变，不同饱和状态下，饱和峰值设计方案的性能最优。定子是否斜槽对电机齿槽转矩、转矩脉动和空载反电动势影响较大。通过细小调整槽口宽度，电机性能如齿槽转矩和效率能够有所上升，但并不明显。
2）根据能量法得到的解析公式与有限元仿真同时验证了通过优化气隙磁通密度和谐波含量可以间接改善电机齿槽转矩大小。
3）异步起动永磁同步电机在定转子近槽配合时，齿槽转矩幅值、转矩脉动逐渐降低，齿槽转矩周期增大。空载反电动势高次偶数谐波增大，电动势波动率随之增大。
由于条件所限，本研究未对所有优化方案进行验证，然而，在本文研究的不同饱和工况及相应的电磁性能中，原有TBYC180M-4转子槽数为36时用铝量最少，具有更优的经济性，然而从电机性能方面，转子槽数为44时更优，稳定性更高。为同类电机设计提供了优化方案。
参考文献
[1] 王力新, 王晓远, 高鹏, 等. 电动汽车用内置式永磁同步电机转矩脉动分析及抑制[J]. 电工技术学报, 2024, 39(20): 6386-6396.
Wang Lixin, Wang Xiaoyuan, Gao Peng, et al. Torque ripple reduction analysis of interior permanent magnet synchronous motor for electric vehicle[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(20): 6386-6396.
[2] Mahmoudi A, Roshandel E, Kahourzade S, et al. Bond graph model of line-start permanent-magnet synchronous motors[J]. Electrical Engineering, 2024, 106(2): 1667-1681.
[3] Taravat S, Kiyoumarsi A, Bracikowski N. Mitigation of cogging torque in transverse-flux permanent- magnet machines with flux concentrators by step skewing of stator pole[J]. IET Electric Power Appli- cations, 2020, 14(12): 2378-2388.
[4] 余洋, 余宗哲, 王孟云, 等. 机械弹性储能用永磁同步电机多源谐波提取及统一抑制[J]. 电工技术学报, 2024, 39(4): 1033-1045, 1073.
Yu Yang, Yu Zongzhe, Wang Mengyun, et al. Multi- source harmonic extraction and unified suppression of permanent magnet synchronous motor for mechanical elastic energy storage[J]. Transactions of China Elec- trotechnical Society, 2024, 39(4): 1033-1045, 1073.
[5] 杨玉波, 王秀和, 朱常青. 电枢槽口宽度对内置式永磁同步电机齿槽转矩的影响[J]. 电机与控制学报, 2011, 15(7): 21-25.
Yang Yubo, Wang Xiuhe, Zhu Changqing. Effect of slot opening on the cogging torque of permanent magnet synchronous motor[J]. Electric Machines and Control, 2011, 15(7): 21-25.
[6] 李仕豪, 狄冲, 刘佶炜, 等. 考虑交叉耦合影响的内置式永磁同步电机电感计算及转矩分析[J]. 电工技术学报, 2023, 38(18): 4889-4899, 4931.
Li Shihao, Di Chong, Liu Jiwei, et al. Inductance calculation and torque analysis of interior permanent magnet synchronous machine considering cross- coupling effects[J]. Transactions of China Electro- technical Society, 2023, 38(18): 4889-4899, 4931.
[7] 徐威, 任晓明, 宁银行, 等. 笼型感应电机转子轴向分段错开结构削弱同步附加转矩的研究[J]. 电工技术学报, 2023, 38(20): 5411-5420.
Xu Wei, Ren Xiaoming, Bank of Nanjing, et al Research on weakening synchronous additional torque by axial segmented stagger structure of cage induction motors[J]. Journal of Electrotechnical Technology, 2023, 38(20): 5411-5420.
[8] 刘志赢, 汪友华, 刘成成, 等. 基于多岛遗传算法与响应面法的横向磁通感应加热装置参数优化设计[J]. 电工技术学报, 2024, 39(10): 3180-3191.
Liu Zhiying, Wang Youhua, Liu Chengcheng, et al. Optimization design of parameters for transverse flux induction heating device based on multi-island genetic algorithm and response surface method[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3180-3191.
[9] 傅小利, 顾红兵, 陈国呈, 等. 基于柯西变异粒子群算法的永磁同步电机参数辨识[J]. 电工技术学报, 2014, 29(5): 127-131.
Fu Xiaoli, Gu Hongbing, Chen Guocheng, et al. Permanent magnet synchronous motors parameters identification based on cauchy mutation particle swarm optimization[J]. Transactions of China Elec- trotechnical Society, 2014, 29(5): 127-131.
[10] 华逸舟, 刘奕辰, 潘伟, 等. 基于改进粒子群算法的无轴承永磁同步电机多目标优化设计[J]. 中国电机工程学报, 2023, 43(11): 4443-4452.
Hua Yizhou, Liu Yichen, Pan Wei, et al. Multi- objective optimization design of bearingless per- manent magnet synchronous motor using improved particle swarm optimization algorithm[J]. Pro- ceedings of the CSEE, 2023, 43(11): 4443-4452.
[11] 刘朝华, 李小花, 周少武, 等. 面向永磁同步电机参数辨识的免疫完全学习型粒子群算法[J]. 电工技术学报, 2014, 29(5): 118-126.
Liu Zhaohua, Li Xiaohua, Zhou Shaowu, et al. Comprehensive learning particle swarm optimization algorithm based on immune mechanism for permanent magnet synchronous motor parameter identification[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 118-126.
[12] Rafaq M S, Midgley W, Steffen T. A review of the state of the art of torque ripple minimization tech- niques for permanent magnet synchronous motors[J]. IEEE Transactions on Industrial Informatics, 2024, 20(1): 1019-1031.
[13] Lee T W, Hong D K, Jung T U. High-speed, high- power motor design for a four-legged robot actuator optimized using the weighted sum and response surface methods[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(3): 224-231.
[14] 徐晔鎏, 贾广隆, 张凤阁. 基于代理模型的内置式永磁同步电机多目标优化设计[J]. 电气技术, 2023, 24(5): 23-29.
Xu Yeliu, Jia Guanglong, Zhang Fengge. Multi- objective optimization design of interior permanent magnet synchronous motor based on surrogate model[J]. Electrical Engineering, 2023, 24(5): 23-29.
[15] Gnaciński P, Muc A, Pepliński M. Influence of voltage subharmonics on line start permanent magnet synchronous motor[J]. IEEE Access, 2021, 9: 164275- 164281.
[16] 乔路宽, 张炳义, 李岩, 等. 基于改进粒子群优化算法的外转子永磁同步电机的多目标优化设计[J]. 电机与控制应用, 2023, 50(3): 81-87, 94.
Qiao Lukuan, Zhang Bingyi, Li Yan, et al. Multi- objective optimization design of external rotor per- manent magnet synchronous motor based on improved particle swarm optimization algorithm[J]. Electric Machines & Control Application, 2023, 50(3): 81-87, 94.
[17] Wang Bingdong, Wang Daohan, Peng Chen, et al. Interior permanent magnet synchronous machines with composed T-shaped notching rotor[J]. IEEE Transactions on Industrial Electronics, 2024, 71(6): 5519-5529.
[18] Gnaciński P, Pepliński M, Muc A, et al. Line-start permanent magnet synchronous motor supplied with voltage containing negative-sequence subharmonics[J]. Energies, 2023, 17(1): 91.
[19] 李婕, 杨淑英, 谢震, 等. 基于有效信息迭代快速粒子群优化算法的永磁同步电机参数在线辨识[J]. 电工技术学报, 2022, 37(18): 4604-4613.
Li Jie, Yang Shuying, Xie Zhen, et al. Online parameter identification of permanent magnet syn- chronous motor based on fast particle swarm optimization algorithm with effective information iterated[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4604-4613.
Design of Multi-Objective Particle Swarm Algorithm for Line-Start Permanent Magnet Synchronous Motor Considering Saturation Condition
Abstract Line-starting permanent magnet synchronous motors (LSPMSM) are different from other permanent magnet motors due to their double-sided slotted characteristics of the stator and rotor, making it difficult to analyze the cogging torque. The overall optimization of motor cogging torque and torque ripple rate is also challenging. This paper optimizes the rotor design of the LSPMSM based on multi-objective particle swarm optimization algorithm, considering the saturation performance of the motor.
Firstly, this paper establishes the relationship between harmonic magnetomotive force and cogging torque to predict the cogging torque of the LSPMSM. The cogging torque is analyzed as a dynamic function relationship of various motor parameters, providing corresponding optimization parameters for the subsequent optimization of the prototype. At the same time, under the premise that the maximum magnetic energy product of the permanent magnet remains unchanged, the relationship between the saturation degree of the motor and the parameters of the permanent magnet is determined, and the selection range of the motor's permanent magnet parameters is determined based on this relationship. Define three working states of the motor: unsaturated, peak saturation, and after saturation, to make the analysis and optimization results of the motor more accurate.
Secondly, combined with response surface methodology (RSM) and multi-objective particle swarm optimization algorithm (MOPSO), this paper proposes a comprehensive optimization strategy to optimize key objectives such as motor cogging torque, torque ripple rate, and efficiency. The optimal design solutions in different regions can be obtained by using the response surface algorithm to classify numerical groups and shorten the computation time of the particle swarm optimization algorithm. The optimal solutions under six different conditions are determined after considering whether the stator is skewed and the three working states of the motor.
Finally, simulation analysis verifies the relationship between cogging torque and harmonics under different saturation states, the trend of no-load back electromotive force, and the main harmonic order changing with the number of slots per pole of the rotor. An experimental platform is built to verify the accuracy of theoretical and simulation analysis. This paper provides optimization solutions for the design of motors of the same type.
keywords：Line starting permanent magnet synchronous motors (LSPMSM), cogging torque, harmonic wave, degree of saturation, multi-target particle swarm algorithm
中图分类号：TM343
DOI: 10.19595/j.cnki.1000-6753.tces.240887
国家自然科学基金（52077047）和黑龙江省自然基金（LH2020E092）资助项目。
收稿日期2024-05-27
改稿日期2024-07-31
艾萌萌 男，1991年生，副教授，硕士生导师，研究方向为特种电机设计与大容量高速驱动电机系统匹配。
E-mail: aimengmeng@hrbust.edu.cn
沈 涛 男，1978年生，教授，博士生导师，研究方向为智能感知与光电检测技术。
E-mail: shentao@hrbust.edu.cn（通信作者）
（编辑 崔文静）