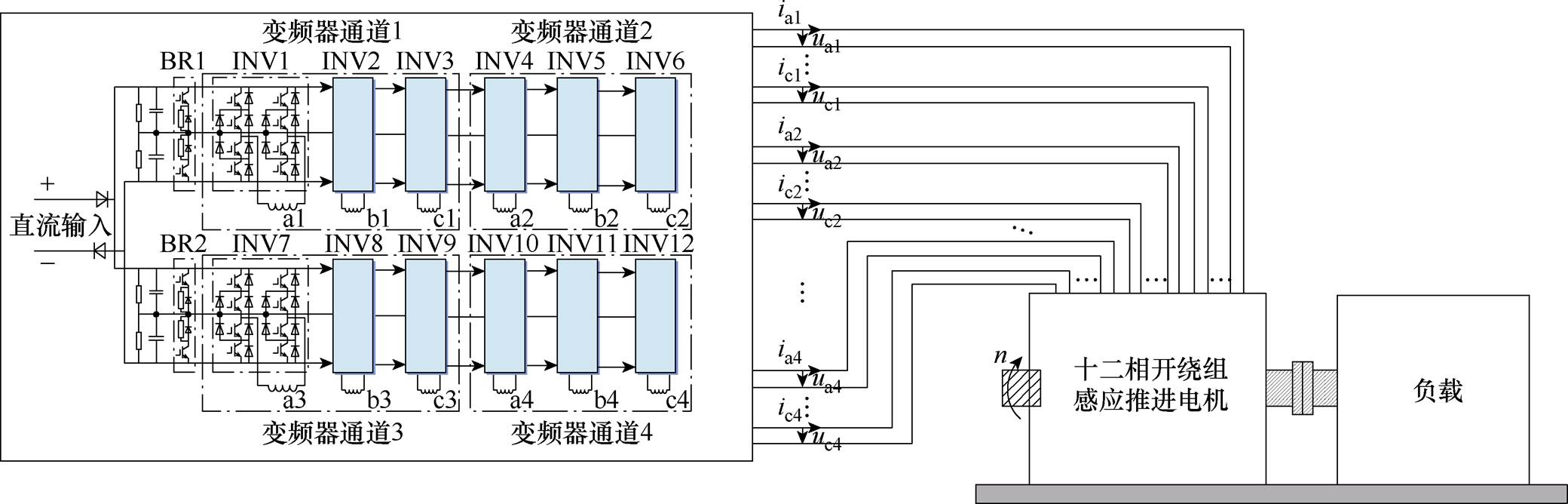
图1 三电平十二相开绕组感应推进系统框图
Fig.1 Block diagram of three-level twelve-phase open-winding induction propulsion system
摘要 全阶观测器因具有控制带宽要求低且观测转速范围宽等优点成为低开关频率电机系统转速估计的优选方案,但与舰船多相开绕组感应电机配套的H桥型大容量变频器开关频率低,不可避免地增加了全阶观测器数字离散化误差。为解决该问题,该文首先结合舰船推进用十二相开绕组感应电机,建立并给出了等效三相全阶观测器模型及其转速估算方法;其次,提出了一种基于四阶Adams方法的全阶观测器离散算法,并利用F范数和极点图对比了全阶观测器不同离散方法的精度及稳定性;最后,搭建十二相/25 kW开绕组感应电机系统仿真模型及试验平台,对全阶观测器转速观测性能予以仿真和试验验证。相比其他离散方法,基于四阶Adams离散方法的全阶观测器电流及转速观测精度明显提高。该文研究结论可为基于全阶观测器的无速度传感器控制技术推广应用于低开关频率多相开绕组感应电机系统提供技术支撑。
关键词:多相开绕组感应电机 全阶观测器 离散算法 低开关频率
在舰船大容量电力推进场合,多相开绕组感应电机及其配套的H桥型多相变频器系统因具有转矩脉动小、故障容错性强、功率容量易拓展等优点得到广泛应用[1-3]。在多相电机高性能矢量控制系统中,转速闭环必不可少。通过电机主轴上的编码器来获得转速的方法不可避免地会带来控制系统体积大、成本与复杂性高等问题,且测速精度易受到环境(船舶环境包括盐雾、油雾、潮湿等)影响,因此亟须开展多相电机无速度传感器控制技术研究。该技术可改善电机驱动系统的可靠性、简化系统硬件结构且降低运行环境要求,具有重要的研究价值[4-5]。
全阶观测器是一种常用的转速估计方法。本文所研究的十二相开绕组感应电机驱动系统需要采用低开关频率(不高于1 kHz)以确保器件结温和开关损耗在安全范围内,同时由于系统相数多、控制复杂,受限于数字控制芯片运算资源限制,数字信号处理器(Digital Signal Processor, DSP)的控制频率一般不高于2 kHz。因此,如何针对十二相开绕组感应电机系统开关频率和控制频率较低的特点改进全阶观测器的离散化误差成为关键问题。针对该问题,国内外学者展开了全阶观测器离散化方法的研究工作,以期改善无速度传感器的转速估计精度。前向欧拉法运算简单,对数字处理器要求不高,缺点是其在高速下离散误差较大,甚至随着转速升高会出现磁链发散现象[6]。双线性法离散精度很高,但是离散观测器存在一个4×4矩阵的逆运算,计算量急剧增加[7]。文献[8]只对状态方程的动态系数矩阵进行离散化,改善了欧拉算法在高速时的离散精度,但需要大量三角函数计算,实现较为困难。文献[9]提出了感应电机特征根离散化模型,在低载波比时仍具有较高的离散化精度,但是运算过程中存在大量矩阵运算,实现难度较高。文献[10]提出一种基于不同参考坐标系下的改进观测器离散化模型,改善了离散精度,但系统的稳定性还需进一步验证。文献[11]提出一种低速区域采用欧拉离散、高速区域采用双线性离散的分段算法来平衡离散精度与运算量,但两种方法之间的切换过程需要进一步探究。文献[12]提出当开关频率较高时,对电流采用欧拉法离散而对磁链采用双线性法离散,当开关频率较低时采用双线性法离散的复合控制策略,但同样没有讨论两种算法的过渡方案。文献[13]在双线性方法的基础上提出一种简化的二阶离散方法,较好地简化了计算量,但是牺牲了一定的离散精度。文献[14]采用的三阶、四阶龙格-库塔算法,精度极高,但运算过于复杂,执行效率较低。
本文针对十二相开绕组电机系统因开关频率、数字控制迭代频率较低而导致的全阶观测器离散化误差加大问题,首先提出一种基于四阶Adams方法的全阶观测器离散算法;其次利用F范数对比不同离散方法的精度;然后在上述基础上对基于不同离散方法的全阶观测器模型进行稳定性分析;最后通过仿真和试验验证了基于Adams方法的离散全阶观测器自适应转速辨识系统的正确性和优越性。
三电平十二相感应电机推进系统如图1所示,十二相推进变频器有四个通道,每个通道由三个H桥逆变单元组成,每个逆变单元采用二极管三电平中性点钳位(Three-Level Neutral-Point-Clamped, 3L- NPC)型H桥主电路,均采用三角载波同相层叠脉宽调制控制算法[15]。十二相开绕组感应电机由四套三相组成,每个通道内三相空间对称,每相互差120°,每两个三相绕组间互差15°,绕组布置如图2所示。

图1 三电平十二相开绕组感应推进系统框图
Fig.1 Block diagram of three-level twelve-phase open-winding induction propulsion system
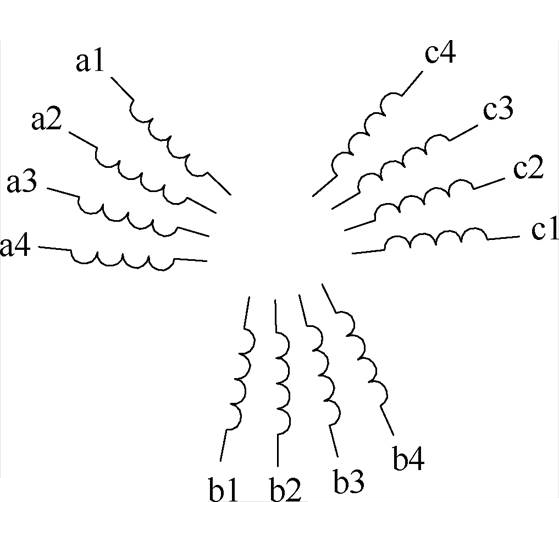
图2 十二相/四通道推进电机绕组布置示意图
Fig.2 Schematic diagram of twelve-phase four-channel propulsion motor winding arrangement
十二相开绕组感应电机的建模与三相电机类似,但其阶数较高,考虑到每个三相绕组是对称供电的且每个三相的设计参数一致,可以将十二相开绕组感应电机等效为三相电机进行简化控制。
假设十二相开绕组电机四个三相输入电压和定子侧电流经坐标变换后对称且相同,如式(1)所示。当忽略dq等效互漏感时,等效三相感应电机模型的数学模型如式(2)~式(4)所示。
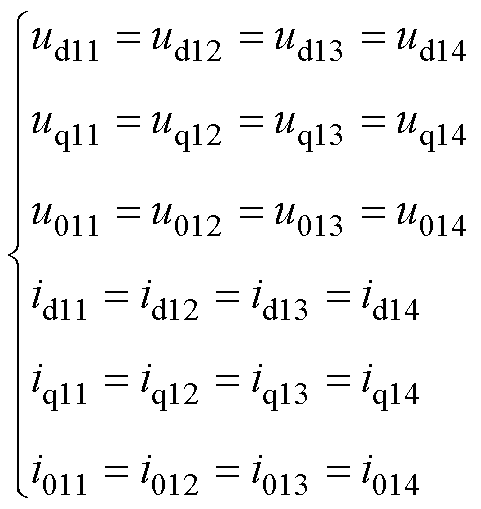 (1)
(1)
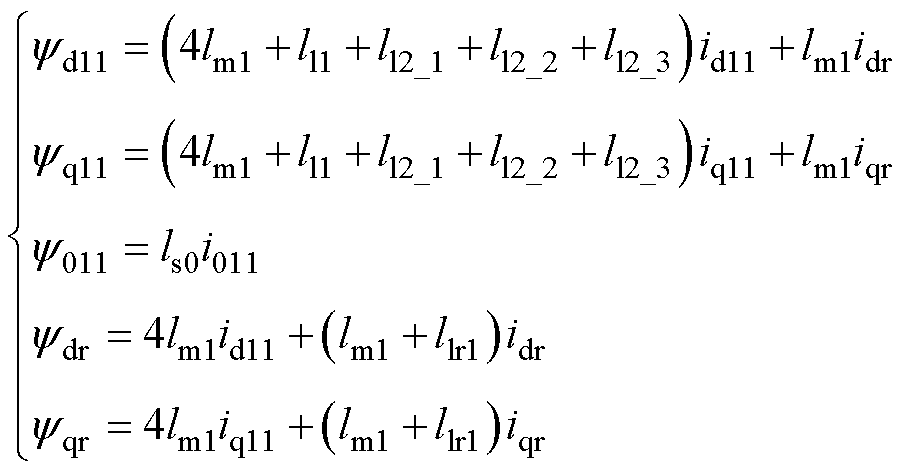 (2)
(2)
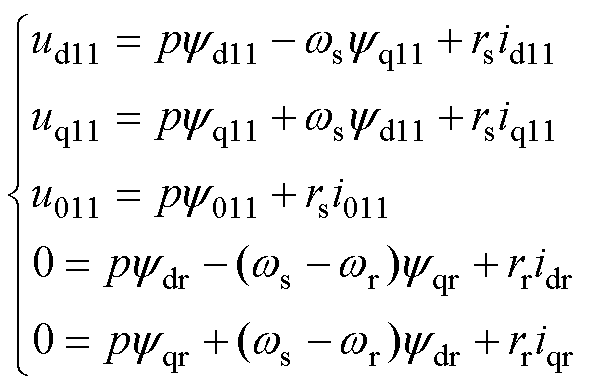 (3)
(3)
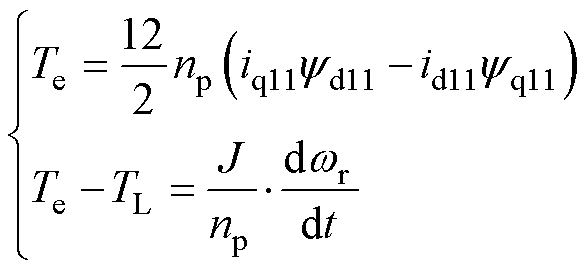 (4)
(4)
其中
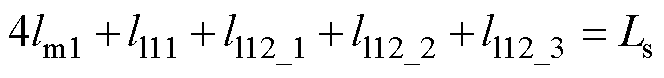
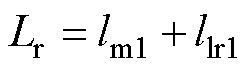
式中,p为微分算子;wr、ws分别为电机转子角速度和同步角速度;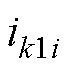 、
、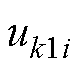 、
、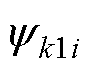 分别为定子电流、电压、磁链,i=1、2、3、4,分别表示通道1~通道4,k=d、q、0,分别表示d、q、0轴分量;
分别为定子电流、电压、磁链,i=1、2、3、4,分别表示通道1~通道4,k=d、q、0,分别表示d、q、0轴分量;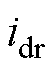 、
、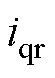 分别为转子电流的d、q轴分量;
分别为转子电流的d、q轴分量;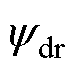 、
、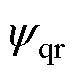 分别为转子磁链的d、q轴分量;ll1为定子等效漏感;ll2_1、ll2_2、ll2_3为相邻两个三相绕组间的基波互漏感;lm1为基波励磁电感;llr1为转子等效基波漏感;ls0为零轴电感;rs、r分别为定子、转子电阻;Ls为等效定子电感;Lr为等效转子电感;np为电机极对数;J为转动惯量;Te为电磁转矩;TL为负载转矩。
分别为转子磁链的d、q轴分量;ll1为定子等效漏感;ll2_1、ll2_2、ll2_3为相邻两个三相绕组间的基波互漏感;lm1为基波励磁电感;llr1为转子等效基波漏感;ls0为零轴电感;rs、r分别为定子、转子电阻;Ls为等效定子电感;Lr为等效转子电感;np为电机极对数;J为转动惯量;Te为电磁转矩;TL为负载转矩。
全阶自适应观测器模型的原理框图如图3所示。图中,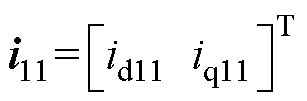 ,
,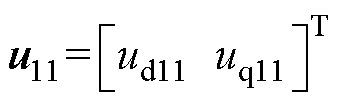 。
。
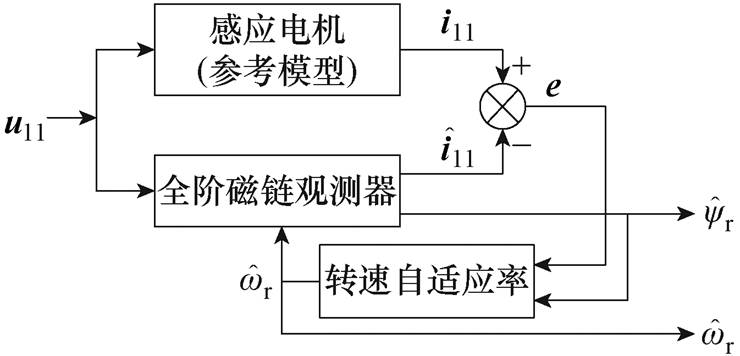
图3 全阶自适应观测器原理框图
Fig.3 Block diagram of the full-order adaptive observer
根据第1节分析得到的等效三相感应电机模型,以定子电流和转子磁链为状态变量,由定子电流观测误差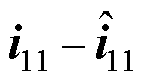 构成校正补偿项,于是全阶状态观测器的状态方程可确定为
构成校正补偿项,于是全阶状态观测器的状态方程可确定为
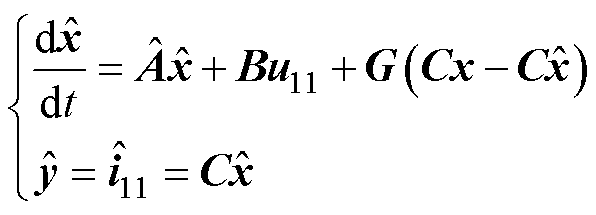 (5)
(5)
其中
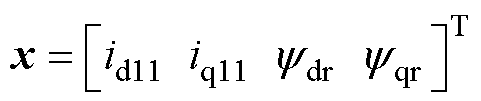
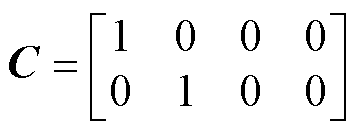
将式(5)展开可得
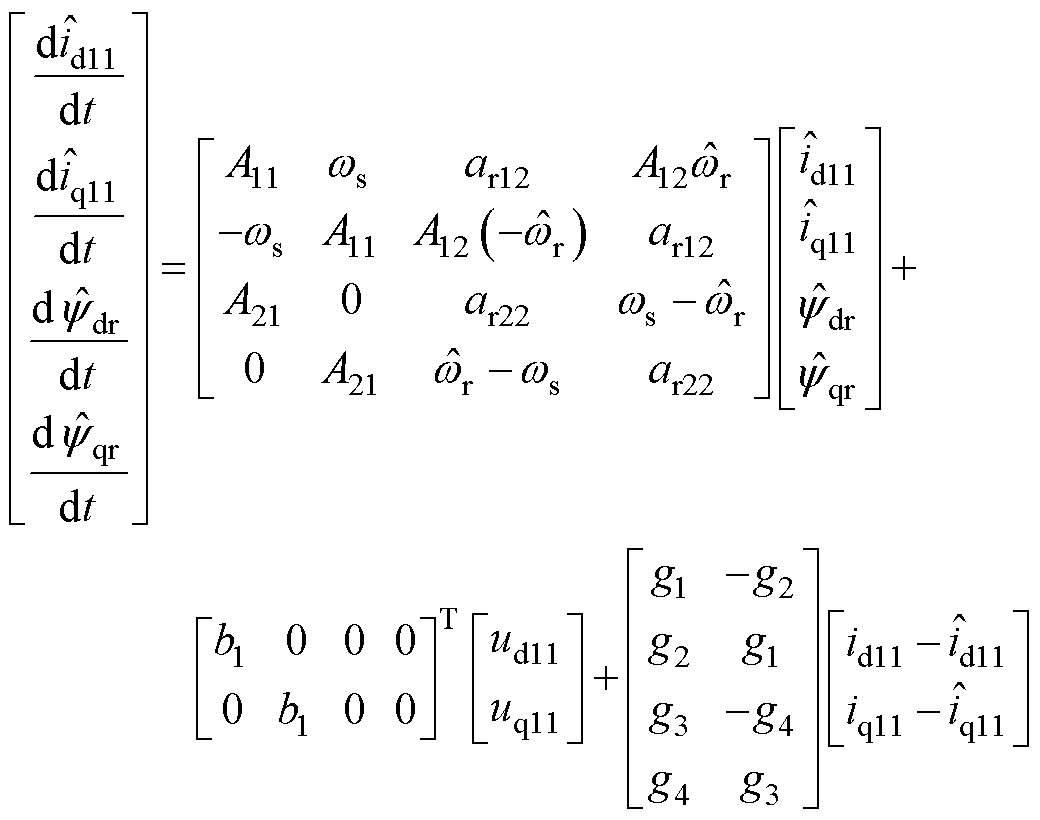 (6)
(6)
其中
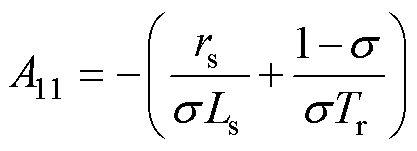
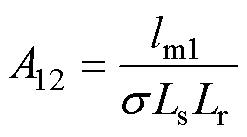
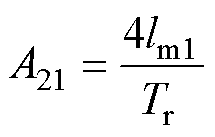
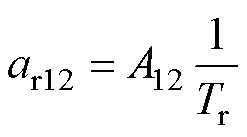
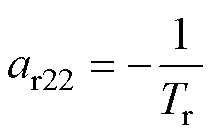
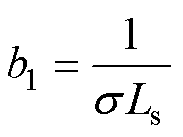
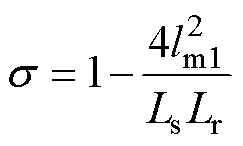
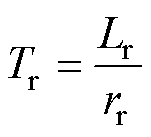
式中,“ ”为观测值;Tr为转子时间常数。
”为观测值;Tr为转子时间常数。
反馈增益矩阵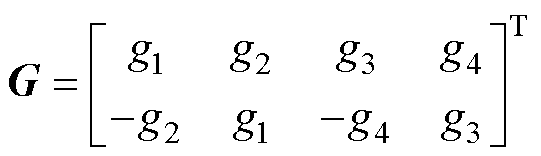 的选择需满足系统稳定性要求[16],全阶观测器中转速自适应律通过李雅普诺夫稳定性定理[17]可推导为
的选择需满足系统稳定性要求[16],全阶观测器中转速自适应律通过李雅普诺夫稳定性定理[17]可推导为
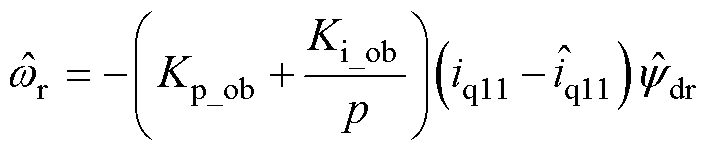 (7)
(7)
式中,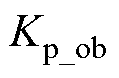 和
和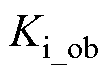 为自适应律PI参数。
为自适应律PI参数。
在实际工程应用中需对全阶观测器进行离散化处理。当不考虑反馈增益矩阵G时,式(5)所示全阶观测器方程为非齐次矩阵方程。令离散化步长即控制周期Ts=0.5 ms,t=(k+1)Ts,可将式(5)离散化为
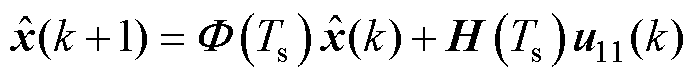 (8)
(8)
式中, 为状态转移矩阵;H为输入矩阵。进一步地,通过求解上述方程的齐次解和非齐次解可得
为状态转移矩阵;H为输入矩阵。进一步地,通过求解上述方程的齐次解和非齐次解可得
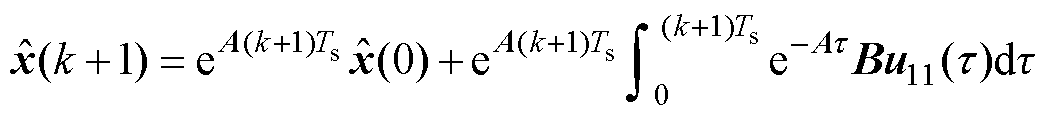 (9)
(9)
经过化简最终可以得到全阶观测器的精确离散模型[7]为
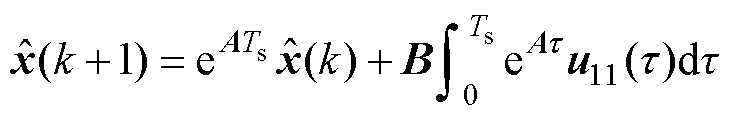 (10)
(10)
其中,矩阵幂指数函数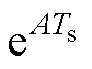 的麦克劳林级数表达式为
的麦克劳林级数表达式为
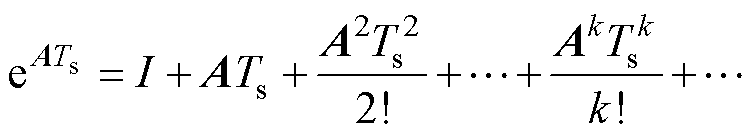 (11)
(11)
由上述分析可知,全阶观测器的精确离散模型中含有极为复杂的矩阵幂指数函数运算,无法应用于数字控制系统。
由于精确离散模型过于复杂,因此采用近似离散化方法来简化分析,常见的方法有前向欧拉法、后向欧拉法和双线性法。三种离散方法的表达式分别为
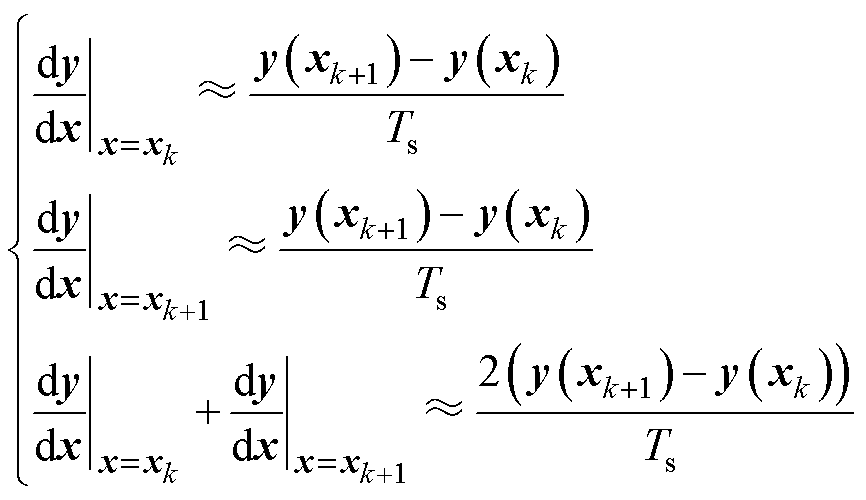 (12)
(12)
当反馈矩阵G=0时,式(5)第一行在ab 静止坐标系下可以展开为
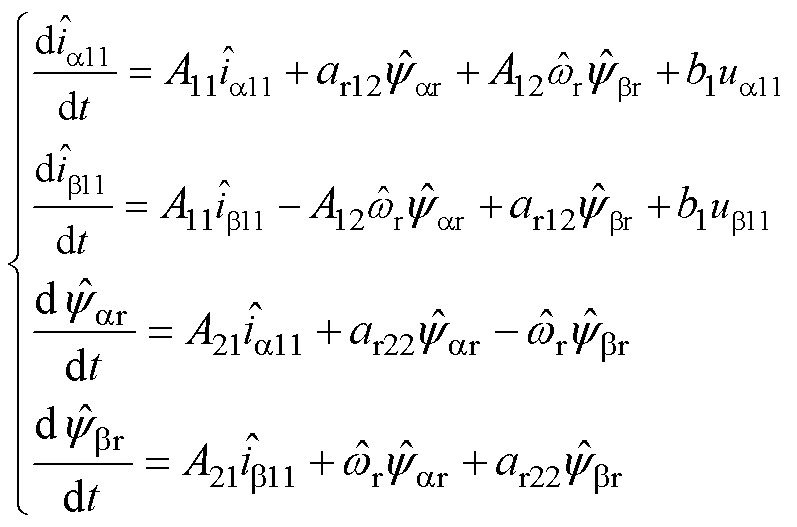 (13)
(13)
结合式(12)、式(13)可得不同离散方法下的全阶观测器离散模型。可以发现,后向欧拉法和双线性法需要计算下一时刻的斜率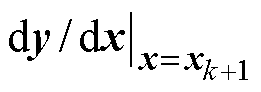 ,所以离散观测器存在一个4×4矩阵的逆运算,实现起来非常复杂。在此基础上文献[13]提出一种简化的二阶离散方法,其与双线性法的离散精度类似,但大大简化了计算量,该离散方法表达式为
,所以离散观测器存在一个4×4矩阵的逆运算,实现起来非常复杂。在此基础上文献[13]提出一种简化的二阶离散方法,其与双线性法的离散精度类似,但大大简化了计算量,该离散方法表达式为
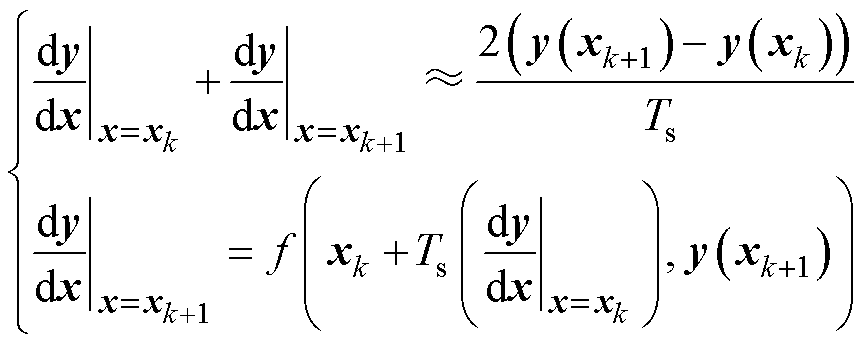 (14)
(14)
结合式(5)和式(14)可得基于简化二阶离散方法的全阶观测器为
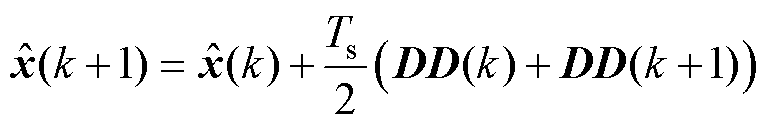 (15)
(15)
式中,DD为状态变量的微分值。根据式(5),当G=0时,DD(k)和DD(k+1)的表达式分别为
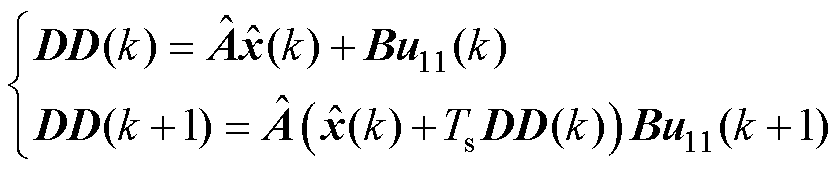 (16)
(16)
由式(16)可知,简化二阶离散方法是通过当前时刻的斜率预测下一时刻的斜率,避免了复杂的四阶矩阵的逆运算。考虑到本文所研究的十二相开绕组感应电机系统应用于大功率场合,其开关频率只有1 kHz,控制系统运算频率只有2 kHz。为了防止因计算频率太低导致的全阶观测器离散误差加大,进而引起转速估计准确性下降的问题,考虑采用四阶离散算法。而传统的四阶龙格库塔运算过于复杂,对控制器要求过高,因此本文基于计算量较少的Adams四阶离散算法[19]对全阶观测器的离散化方法进行改进。其表达式为
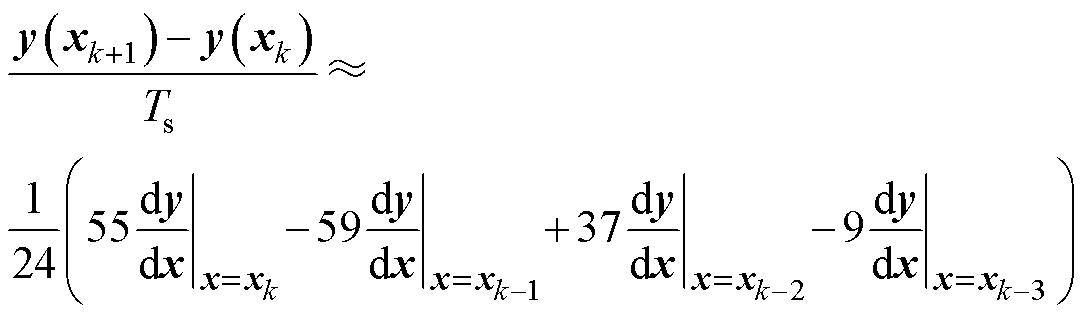 (17)
(17)
由式(17)可知,Adams四阶离散算法不需要计算或者预测下一时刻的斜率,只需要调用t-1、t-2、t-3时刻的斜率即可。结合式(13)可以得到Adams四阶离散算法的全阶磁链观测器模型为
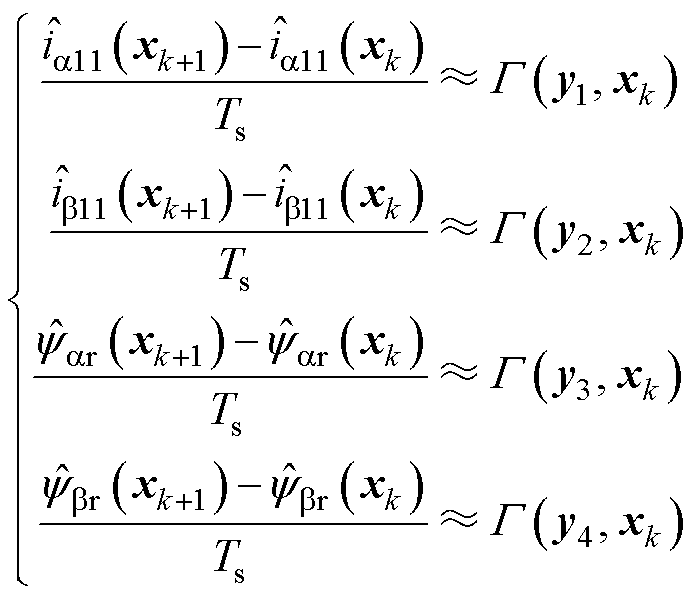 (18)
(18)
其中
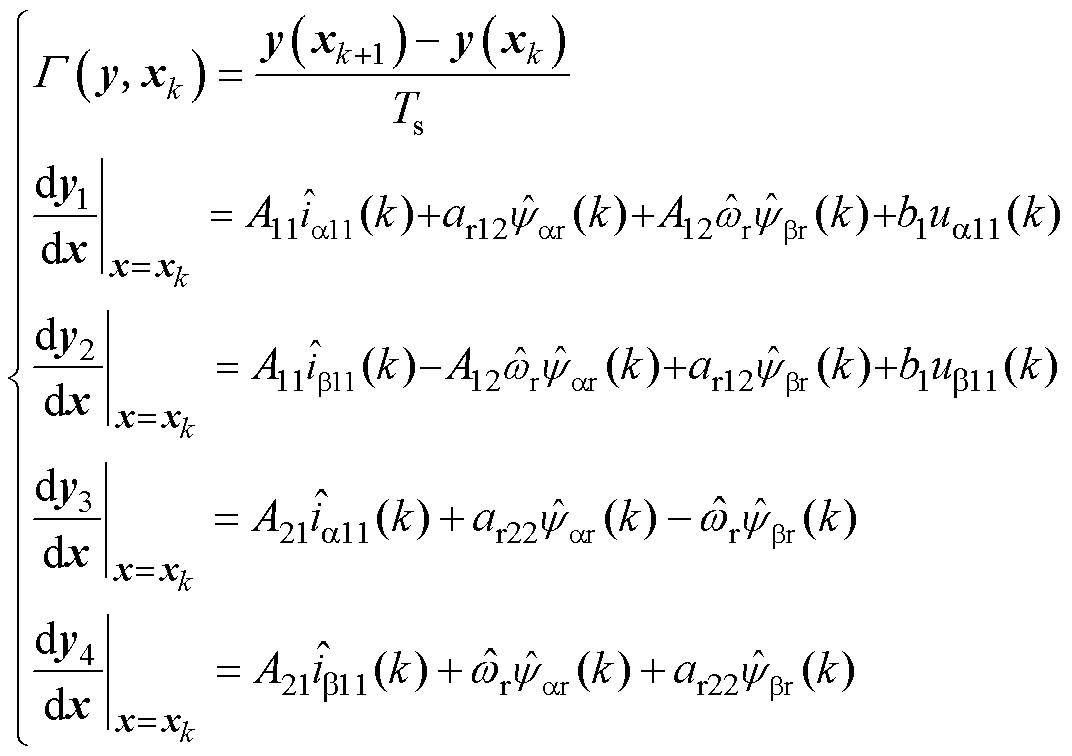 (19)
(19)
而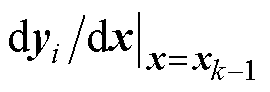 (i=1, 2, 3, 4)的值取控制器中保存的上一时刻状态变量值即可,
(i=1, 2, 3, 4)的值取控制器中保存的上一时刻状态变量值即可,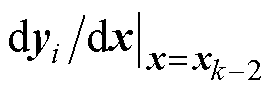 、
、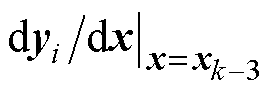 的取值同理,依次类推。由式(19)可以发现,基于Adams四阶离散算法的全阶观测器表达式中四个方程不存在耦合和四阶矩阵的求逆运算,并且相同状态变量前一时刻的值在控制器中可以直接调用,运算的复杂程度并未大幅增加。
的取值同理,依次类推。由式(19)可以发现,基于Adams四阶离散算法的全阶观测器表达式中四个方程不存在耦合和四阶矩阵的求逆运算,并且相同状态变量前一时刻的值在控制器中可以直接调用,运算的复杂程度并未大幅增加。
进一步地,根据式(13)在不同离散化方法下的具体表达式(见附录),全阶观测器不同离散化方法计算量的详细对比见表1。
表1 不同离散化方法整体对比
Tab.1 Overall comparison of different discretization methods (次)

离散化方法前向欧拉法简化二阶法四阶龙格-库塔法四阶Adams法 计算量加减法14406256 乘法205213488
上述几种近似离散方法本质上就是对矩阵幂指数函数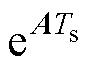 进行近似化处理,其与式(10)和式(11)所示的全阶观测器精确离散模型相比必然存在离散化误差,进而影响转速估算的准确性。下面将对前向欧拉法、简化二阶离散法以及所采用的Adams四阶离散算法的稳态误差进行详细的定性与定量分析。
进行近似化处理,其与式(10)和式(11)所示的全阶观测器精确离散模型相比必然存在离散化误差,进而影响转速估算的准确性。下面将对前向欧拉法、简化二阶离散法以及所采用的Adams四阶离散算法的稳态误差进行详细的定性与定量分析。
将式(12)第一项前向欧拉离散方法代入式 (5)得
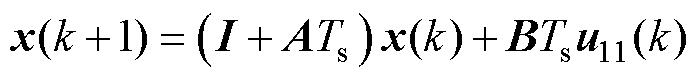 (20)
(20)
前向欧拉离散法、简化二阶离散法、Adams四阶离散法的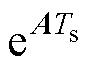 分别近似为式(21)中的A1、A2、A4,其精度分别为一阶、二阶和四阶。
分别近似为式(21)中的A1、A2、A4,其精度分别为一阶、二阶和四阶。
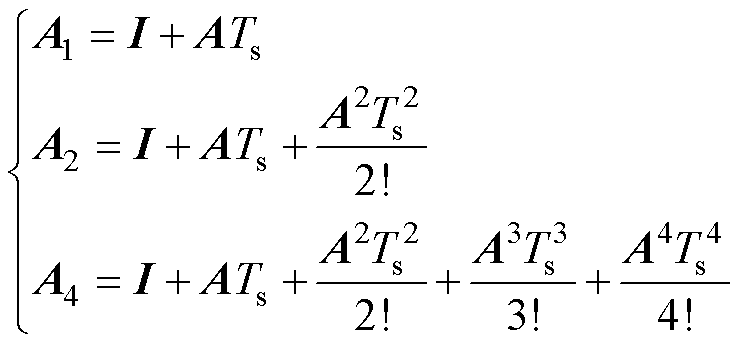 (21)
(21)
图4为200 Hz标准正弦电流采用三种离散方法离散化处理结果,离散化步长为0.5 ms。由图4可以明显发现,Adams离散精度>简化二阶离散精度>前向欧拉法离散精度,这与上述理论分析一致。
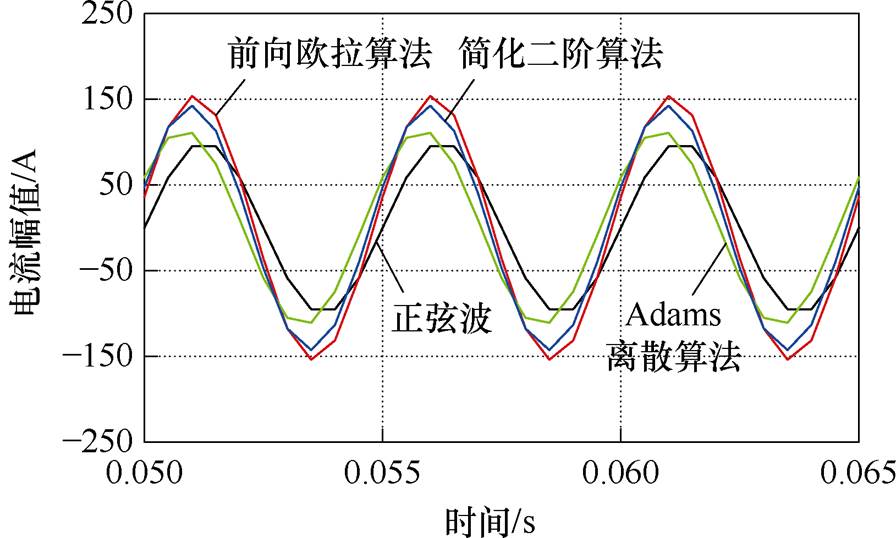
图4 步长为0.5 ms时三种离散方法精度对比
Fig.4 Comparison of the accuracy of three discretization methods at a step size of 0.5 ms
为了更直接地反映出三种离散误差和电机转速的关系,本文采用F范数[8]来表征精确离散模型和近似离散化模型之间的误差,有
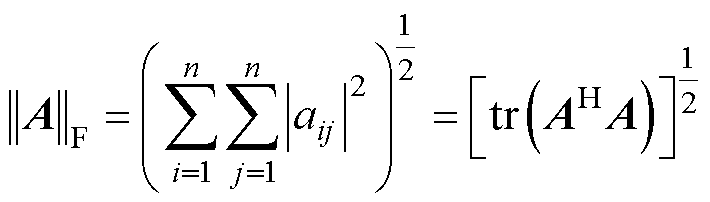 (22)
(22)
式(22)是一个与电机转速有关的函数。为了表征全阶观测器近似离散模型和精确离散模型之间的误差,选取矩阵的F范数为
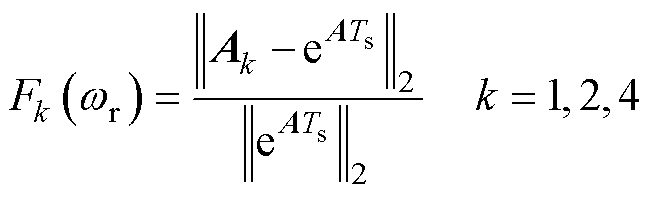 (23)
(23)
分别代入不同种离散方法的Ak值(k=1, 2, 4),离散化步长取0.5 ms,可以得到三种离散方法的误差曲线如图5所示,横坐标是电机转速,转速标幺化的基值是600 r/min,频率是20 Hz。由图5可知,在2 kHz计算频率下,三种离散化方法在额定转速范围(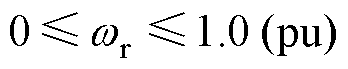 )内的离散误差较小,均在1%以内;在2倍、3倍额定转速范围(
)内的离散误差较小,均在1%以内;在2倍、3倍额定转速范围(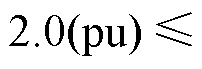
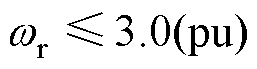 )内,前向欧拉离散法的误差逐渐增大至2%;简化二阶离散算法的误差也随着电机频率的增大而增大;而本文采用的Adams四阶离散算法在全速度范围内的离散误差几乎为0。
)内,前向欧拉离散法的误差逐渐增大至2%;简化二阶离散算法的误差也随着电机频率的增大而增大;而本文采用的Adams四阶离散算法在全速度范围内的离散误差几乎为0。
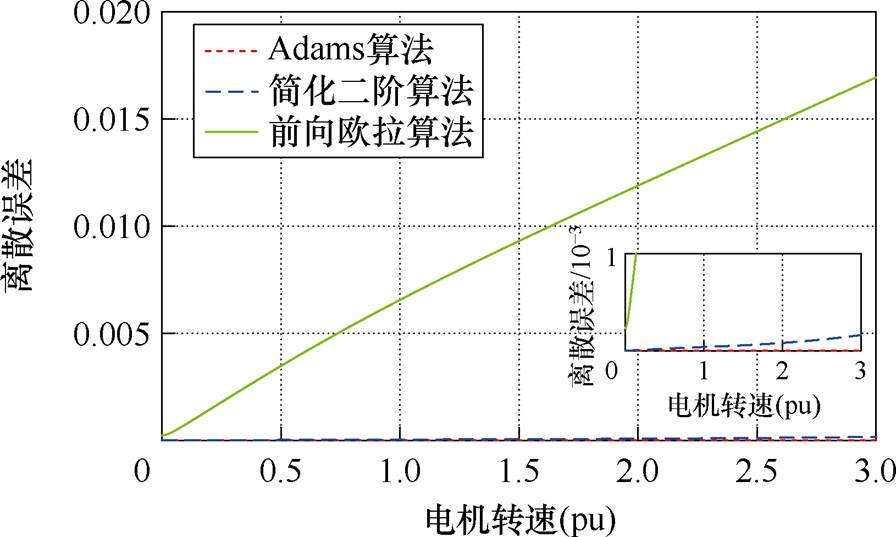
图5 2 kHz频率下三种方法随电机转速wr变化的离散误差
Fig.5 Discrete error of three discretization methods with wr at 2 kHz computational frequencies
结合表1和图5可知,前向欧拉法计算量最小,但该方法精度不高,易导致高速区不稳定;简化二阶离散法计算量较大且高速时离散误差不断增加;四阶龙格-库塔法虽然精度很高,但其计算量剧增,不利于工程实现;而本文采用的Adams离散法相较于传统四阶离散法,在不过多增加数字控制系统计算量的同时保证了最佳的离散精度,更适用于本文所研究的低开关频率大容量电力推进系统。
结合经典控制理论可得欧拉法和简化二阶离散法s域稳定区域如图6所示。
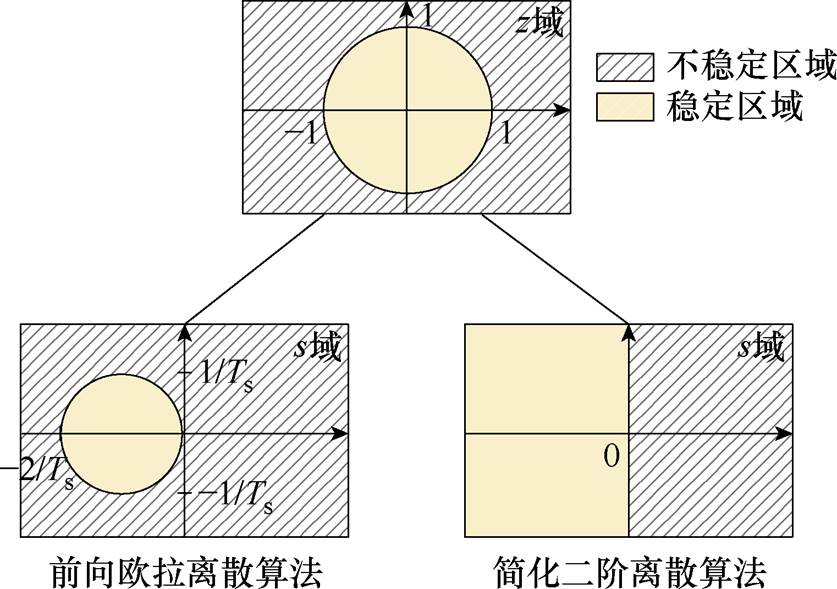
图6 前向欧拉法和简化二阶离散方法的稳定区域
Fig.6 Stabilization region for forward Euler and simplified second-order discretization methods
由式(17)可以得到Adams四阶离散方法的s域和z域的对应关系为
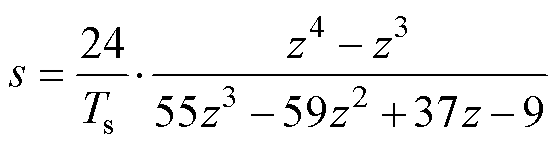 (24)
(24)
Ts=0.5 ms,当z域极点的取值位于z平面单位圆内即满足系统稳定的条件时,通过Matlab软件可求四阶离散算法在s域的稳定区域如图7所示。进而可得考虑三种离散方法稳定区域的离散全阶观测器极点轨迹如图8所示,离散步长为0.5 ms,wr从0变化到2.5(pu)。图8中,①表示等效三相感应电机的极点轨迹[7];②表示左移反馈矩阵的全阶观测器极点轨迹(极点左移距离L=10);③表示K倍极点反馈矩阵的全阶观测器极点轨迹(极点放大倍数K=2);④为前向欧拉法的稳定圆;⑤为简化二阶离散方法的稳定边界;⑥所包括的浅黄色背景为Adams方法稳定区域。
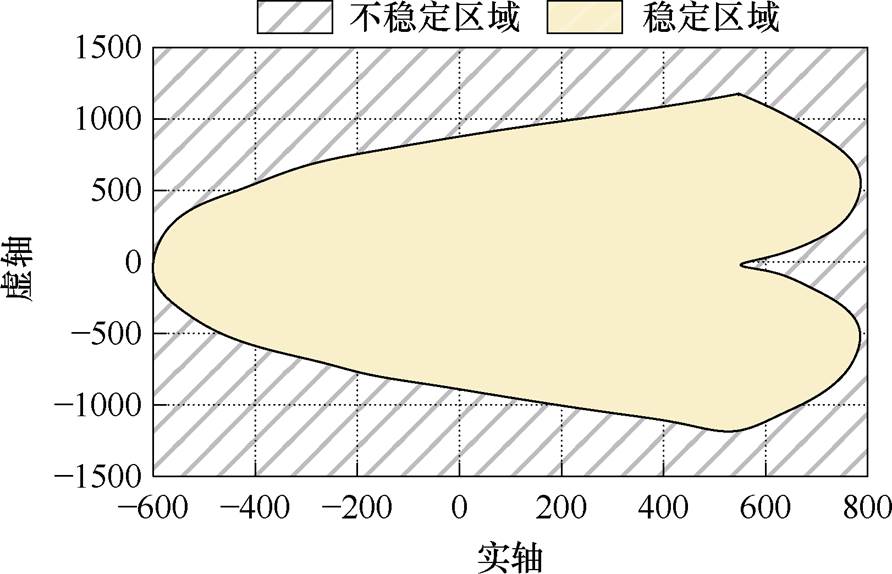
图7 Adams四阶离散方法的稳定区域
Fig.7 Stabilization region for Adams discretization method
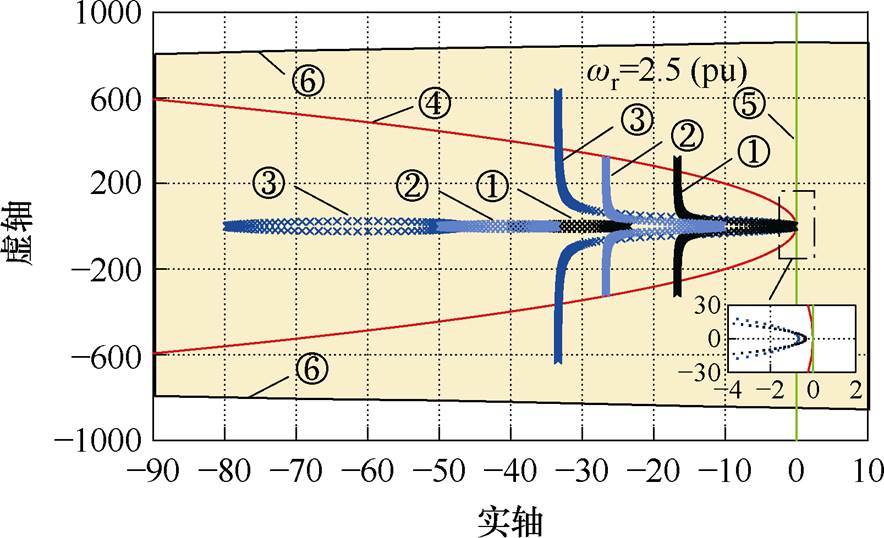
图8 考虑三种离散方法稳定区域的全阶观测器极点轨迹
Fig.8 Pole distribution of full-order observer considering the stabilization region of the three discretization methods
由图8可知,当控制频率为2 kHz、采用前向欧拉法离散时,电机极点轨迹①在电机二倍基频运行时进入不稳定区域;采用K倍(K=2)反馈矩阵设计[17]的全阶观测器极点轨迹③在二倍基频运行时也进入不稳定区域;而采用左移反馈矩阵设计[18]的全阶观测器,可以通过选择合理的左移距离L,使其极点轨迹②均位于前向欧拉法的稳定圆内。而简化二阶离散算法和所提出的Adams离散方法能够保证离散全阶观测器的极点轨迹一直在稳定区间内。
结合3.2节设计的基于Adams离散算法的全阶观测器,图9给出了等效三相感应电机的无速度传感器控制框图。在此基础上通过Matlab/Simulink搭建了等效三相感应电机无速度传感器矢量控制系统仿真模型,对基于三种离散算法的全阶观测器观测性能进行了对比仿真分析,仿真所用电机主要参数见表2。
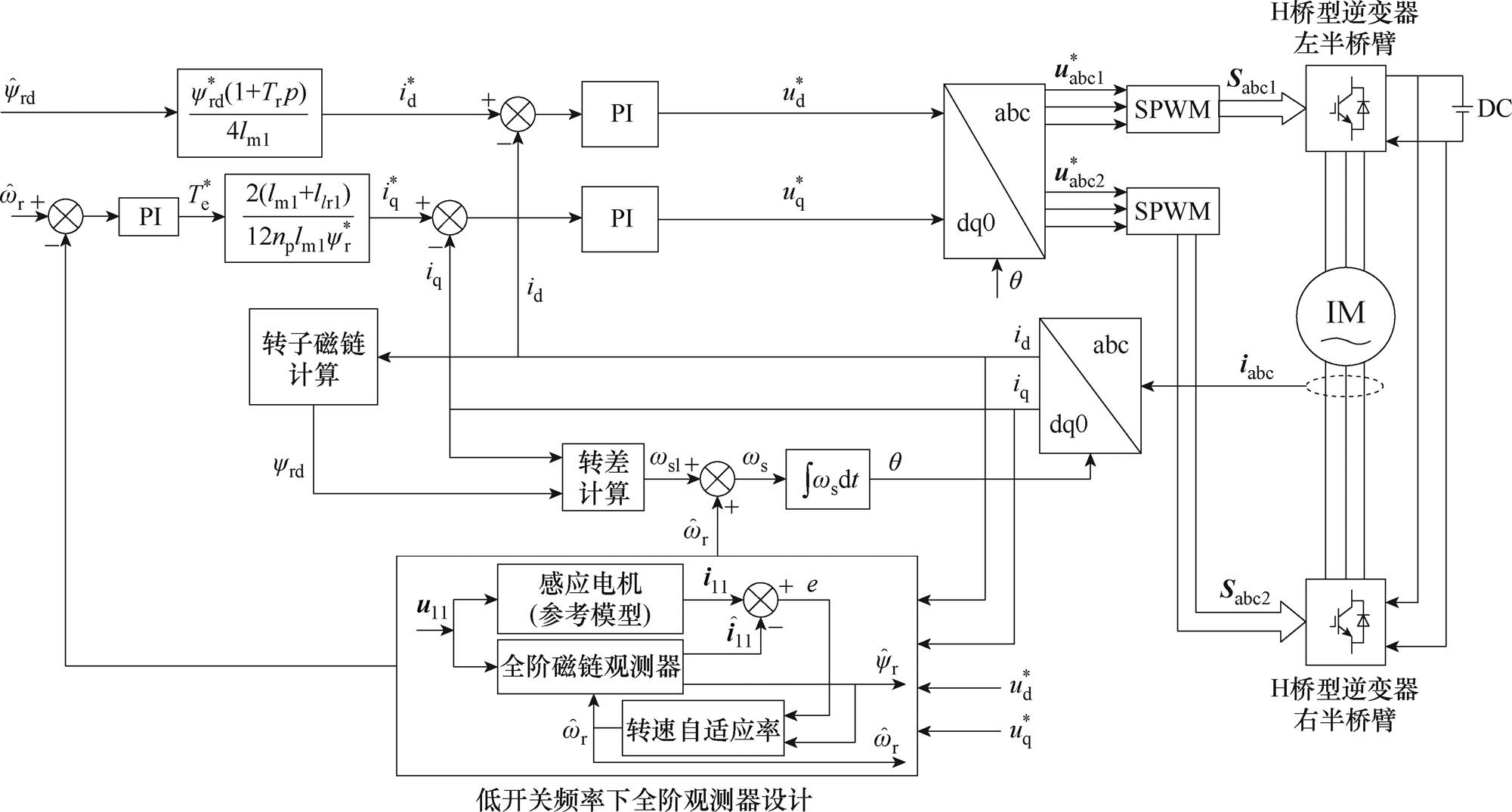
图9 基于离散全阶观测器的无速度传感器闭环矢量控制原理实现框图
Fig 9 Block diagram of speed sensorless control based full-order observer
表2 十二相感应电机主要参数
Tab.2 Main parameters of twelve-phase induction motor
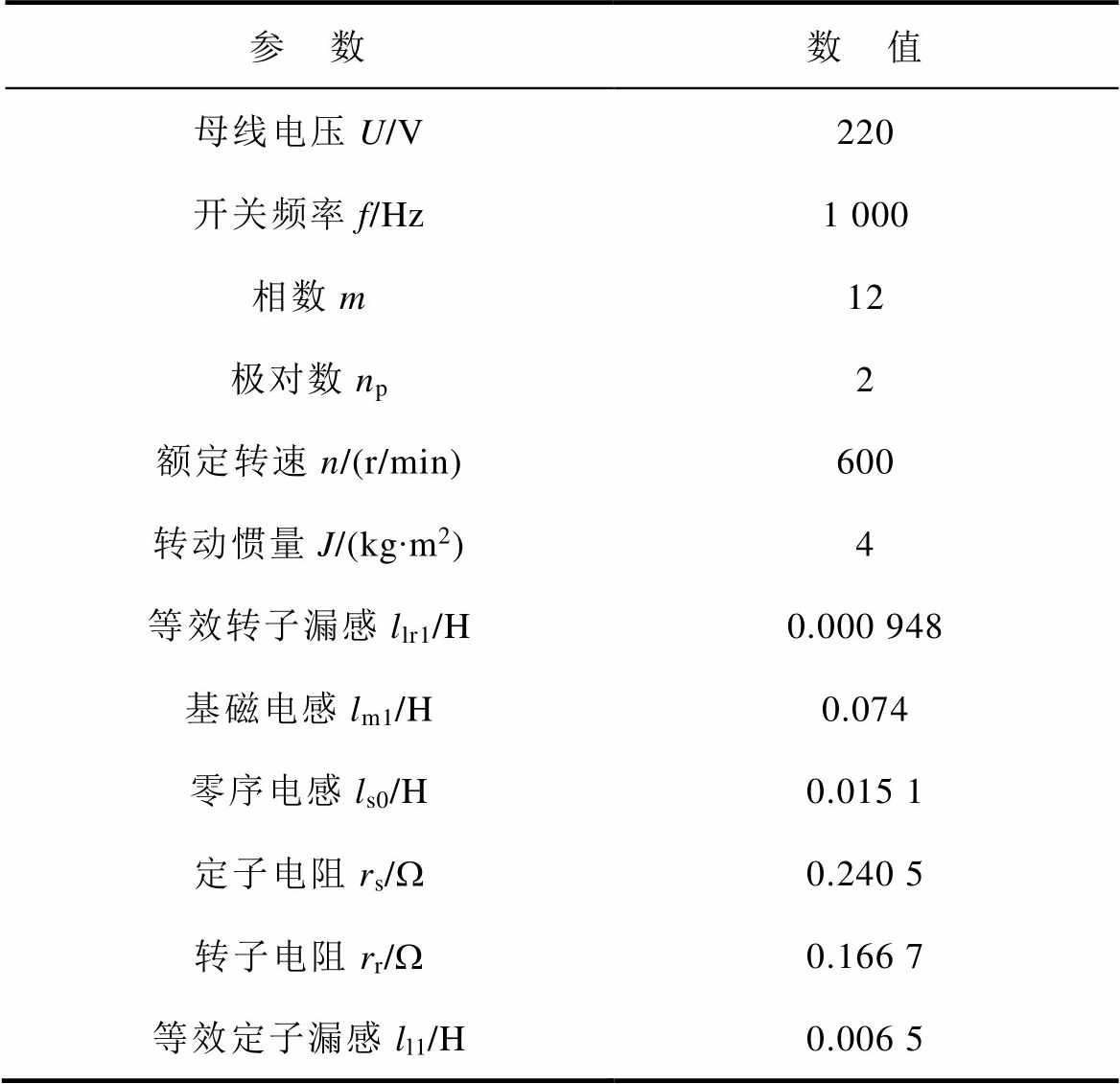
参 数数 值 母线电压U/V220 开关频率f/Hz1 000 相数m12 极对数np2 额定转速n/(r/min)600 转动惯量J/(kg∙m2)4 等效转子漏感llr1/H0.000 948 基磁电感lm1/H0.074 零序电感ls0/H0.015 1 定子电阻rs/W0.240 5 转子电阻rr/W0.166 7 等效定子漏感ll1/H0.006 5
对转速600 r/min电机空载工况进行仿真,三种离散算法仿真对比结果分别如图10~图12所示。图中,iafb、ibfb、icfb为三相反馈电流,iaob、ibob、icob为三相观测电流。
分析图10~图12波形可得,在2 kHz控制频率下,三种离散算法的性能对比见表3。
由表3可知,相比前向欧拉离散法,采用四阶Adams算法时观测定子电流幅值、相位误差分别下降95.5%、99.2%,观测转子磁链幅值、相位误差分别下降93.3%、96.4%,观测转速过程峰值、稳态均值分别下降62.5%、80%;相比简化二阶离散法,采用四阶Adams算法时观测定子电流幅值、相位误差分别下降87.5%、88.5%,观测转子磁链幅值、相位误差分别下降90%、93.6%,观测转速过程峰值、稳态均值分别下降60%、70%。即基于四阶Adams算法的全阶观测器观测定子电流、转子磁链和转速与实际值几乎吻合,观测精度最高。
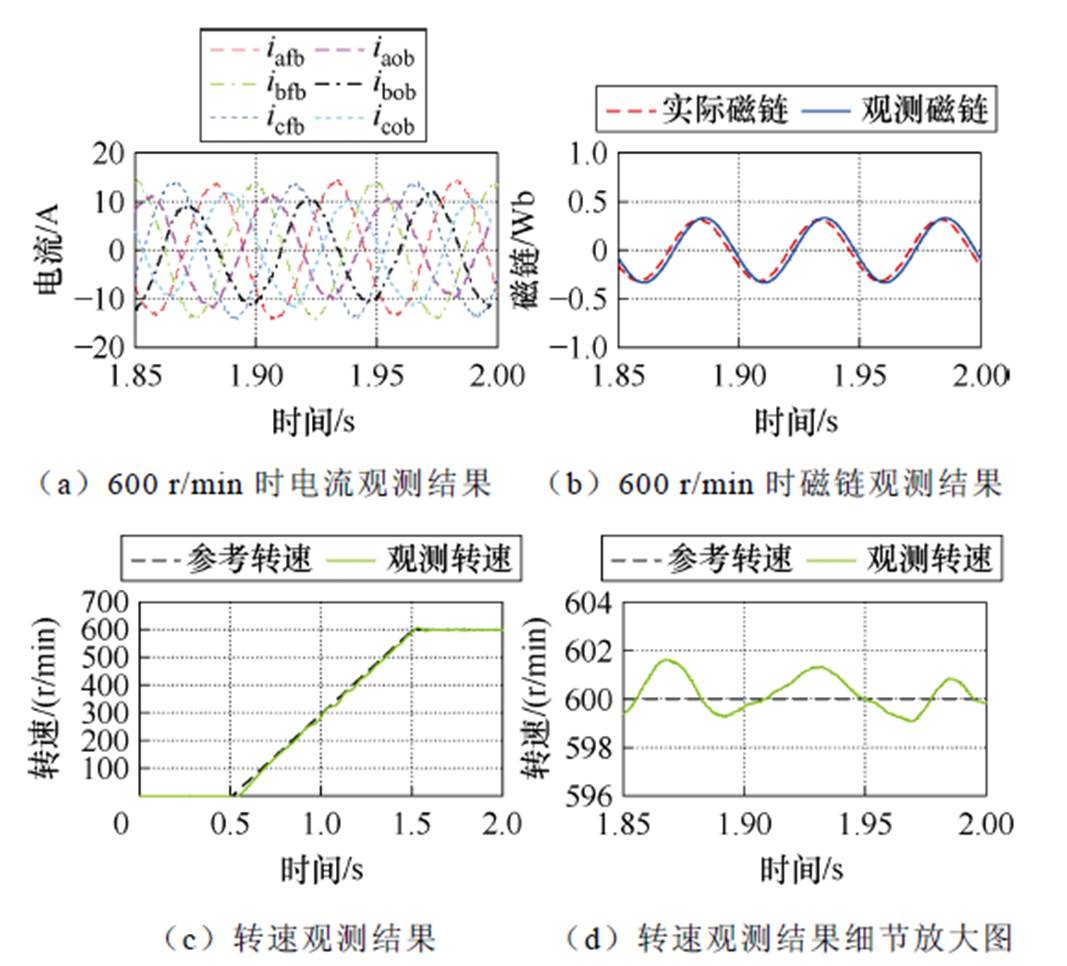
图10 基于前向欧拉离散法的全阶观测器仿真结果
Fig.10 Simulation results of full-order observer based on forward Euler discretization method
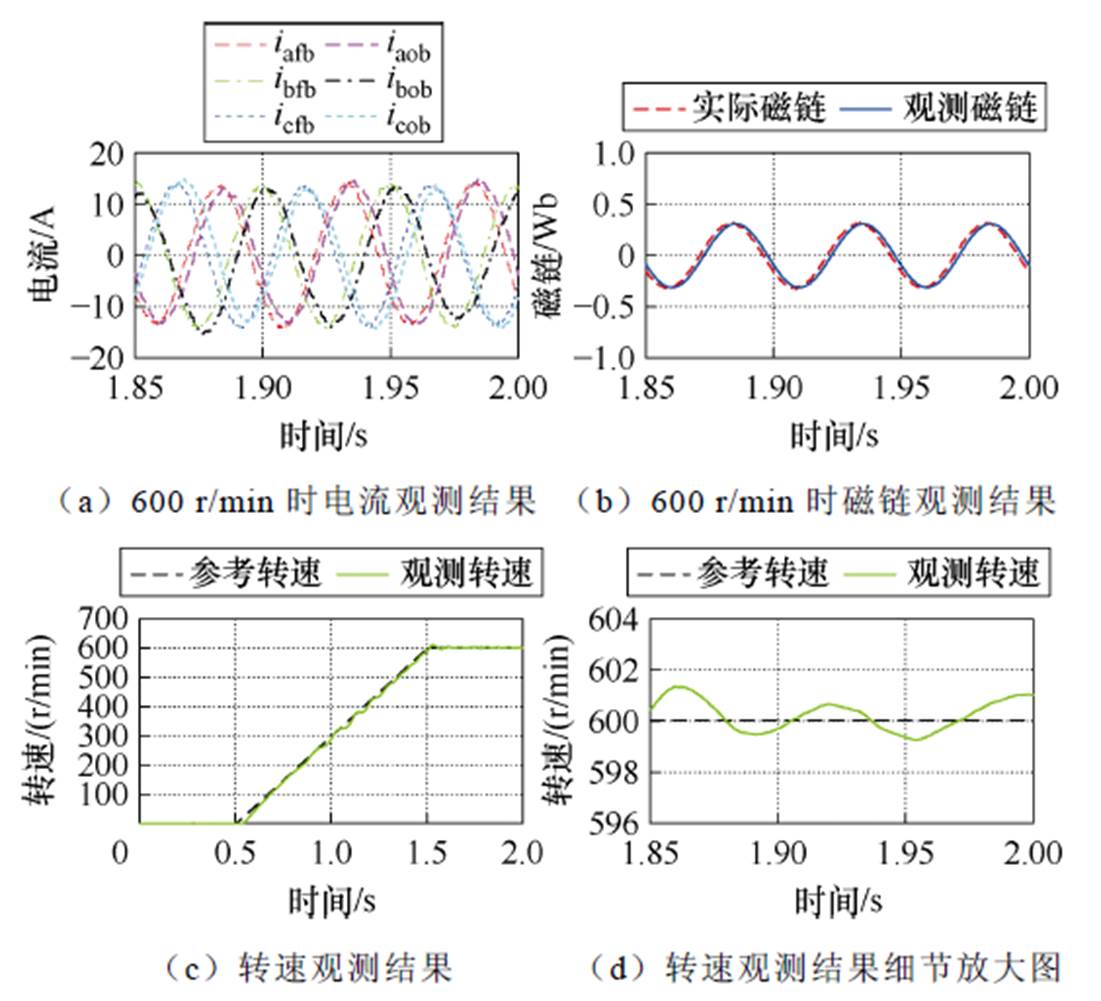
图11 基于简化二阶离散法的全阶观测器仿真结果
Fig.11 Simulation results of full-order observer based on simplified second-order discretization method
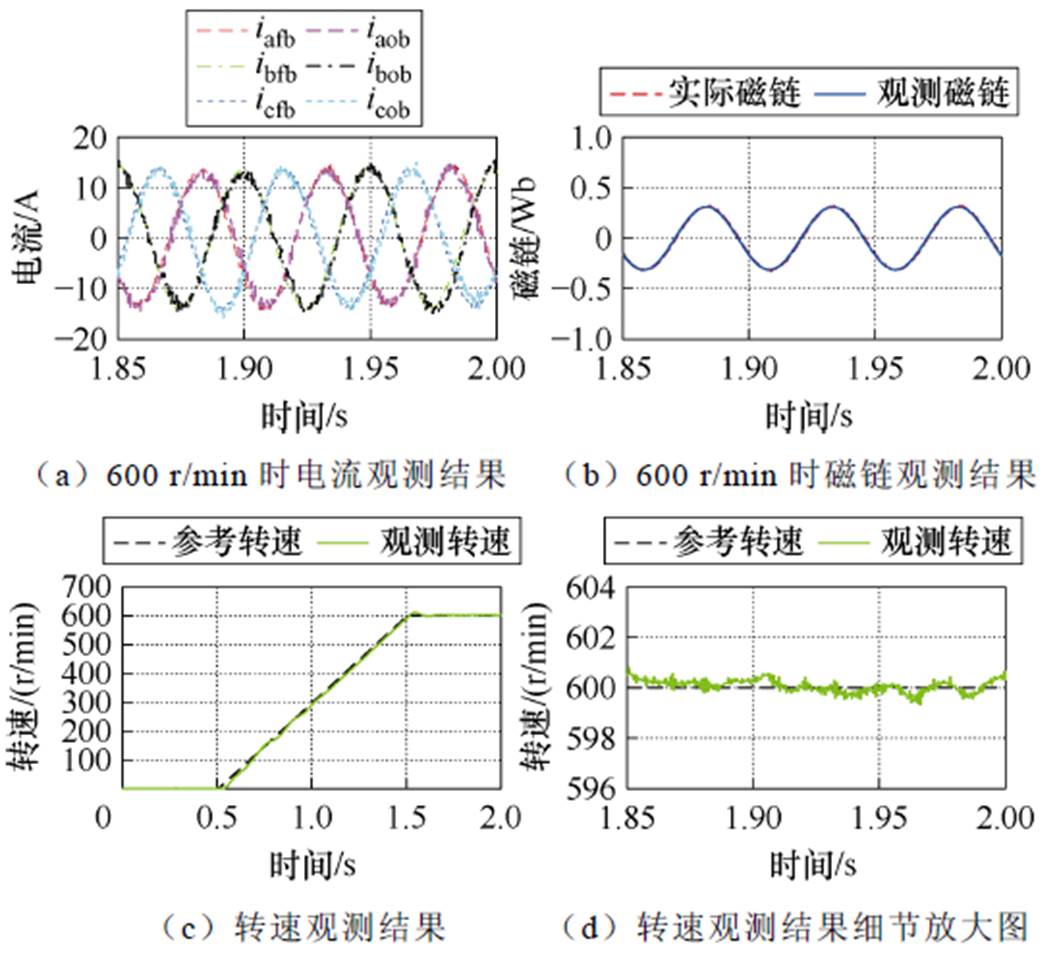
图12 基于Adams四阶离散法的全阶观测器仿真结果
Fig.12 Simulation results of full-order observer based on Adams four-order discretization method
表3 三种离散方法仿真性能对比
Tab.3 Comparison of three discretization methods
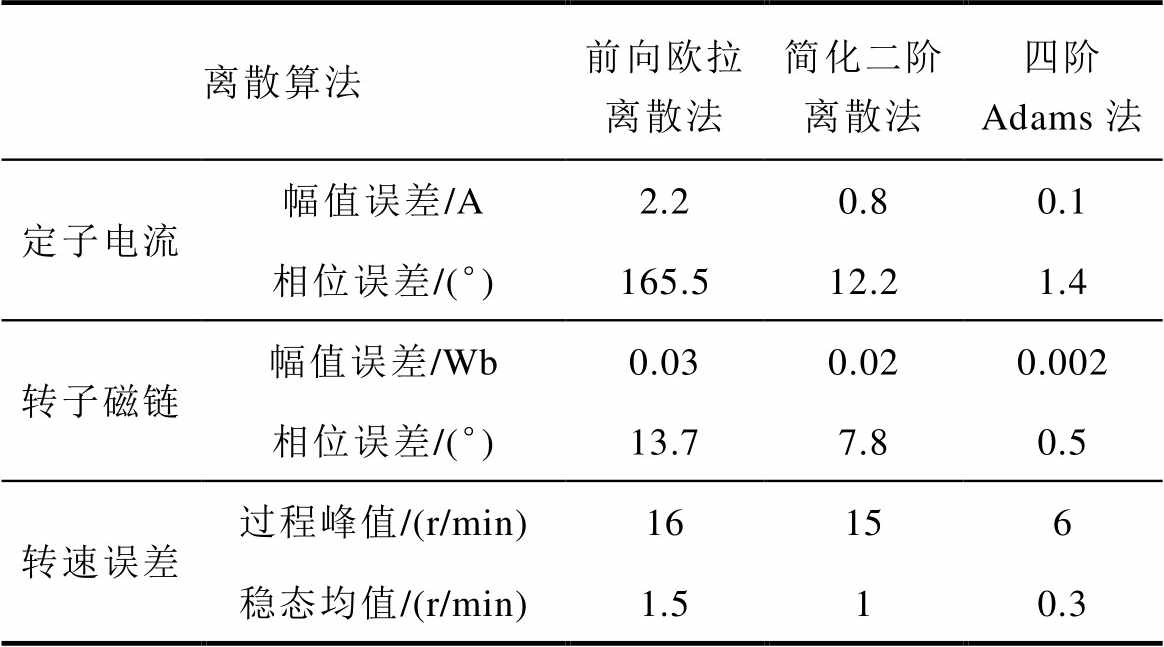
离散算法前向欧拉离散法简化二阶离散法四阶Adams法 定子电流幅值误差/A2.20.80.1 相位误差/(°)165.512.21.4 转子磁链幅值误差/Wb0.030.020.002 相位误差/(°)13.77.80.5 转速误差过程峰值/(r/min)16156 稳态均值/(r/min)1.510.3
为验证本文采用的基于Adams法的离散全阶观测器自适应转速辨识系统的正确性和有效性,搭建了十二相/25 kW级开绕组推进电机及其变频驱动系统试验平台如图13所示,试验所用电机主要参数见表1。

图13 十二相感应电机试验平台
Fig.13 Twelve-phase induction motor test platform
十二相开绕组感应电机试验平台采用“一主+十二从”分布式控制,构架如图14所示。图中,主控制器为DSP+现场可编程门阵列(Field-Programmable Gate Array, FPGA)架构:DSP主要用于十二相开绕组感应电机闭环矢量控制计算,生成调制波;FPGA主要用于载波的生成并与调制波进行比较生成PWM脉冲。从控制器为FPGA架构,其通过接收主控PWM脉冲信号驱动每相功率单元,并汇总各个功率单元电压、电流、温度及IGBT的故障等状态量,通过通信上传至主控制器。
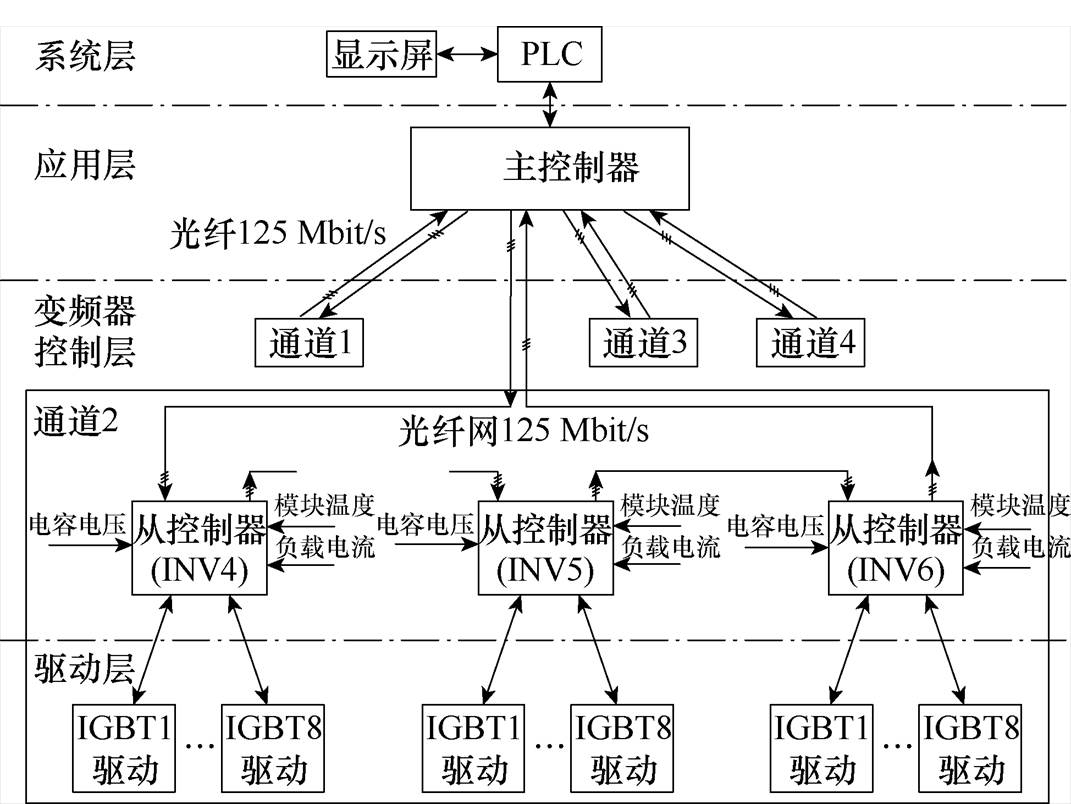
图14 十二相/四套三电平H桥拓扑推进变频器控制构架
Fig.14 Twelve-phase/four sets of three-level H-bridge topology propulsion inverter control architecture
4.2.1 观测转速、磁链不代入闭环运行试验验证
基于第2节所设计的等效三相感应电机的全阶观测器,将其应用于十二相开绕组感应电机任一通道来进行转速观测,以第二通道为例,即将第二通道的三相电压、电流信息输入全阶观测器。在转速600 r/min空载工况对三种离散算法下的电流及磁链观测性能进行对比试验验证,试验参数与仿真保持一致,相关参数观测值与实际值的对比结果如图15~图17所示。
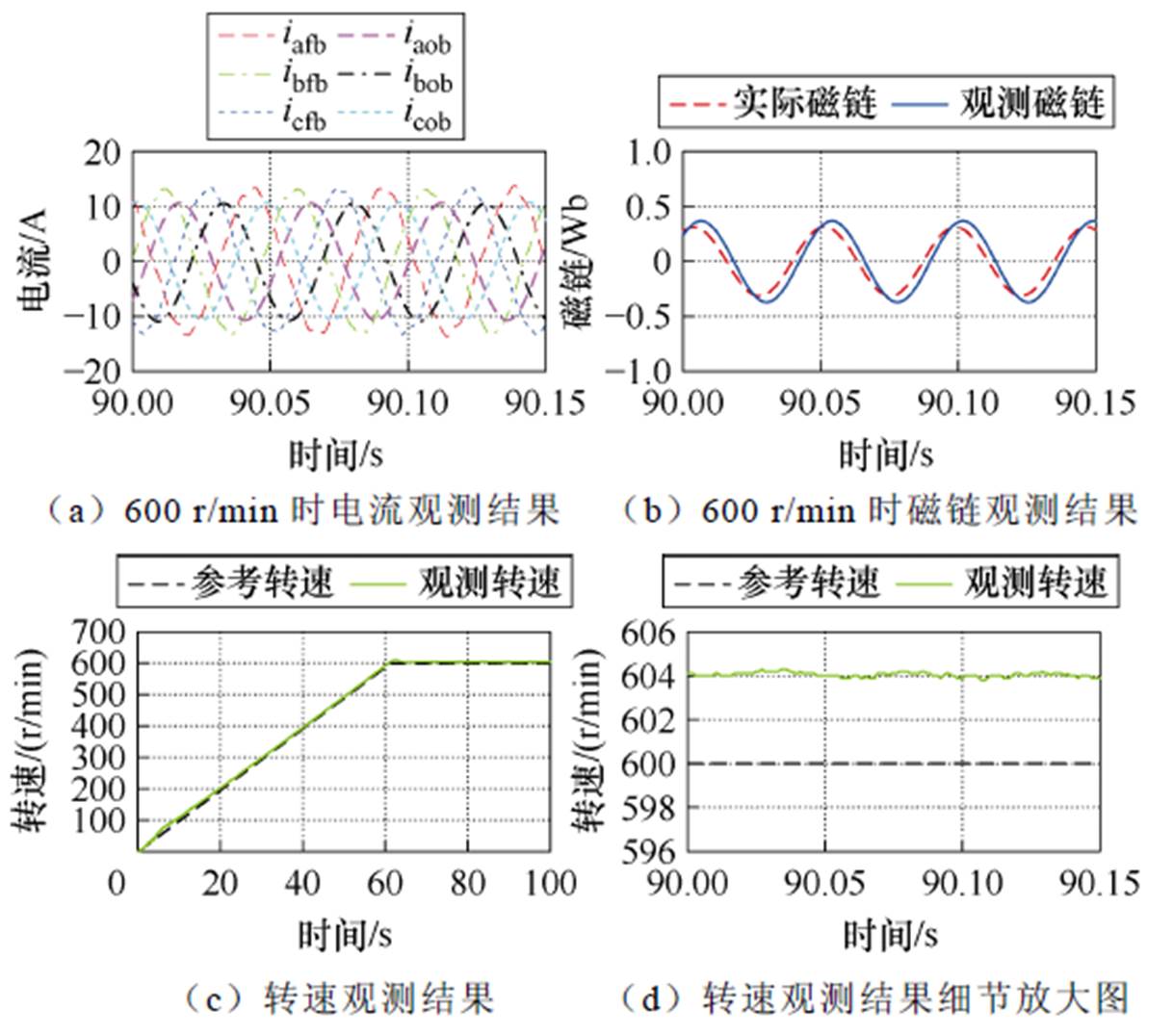
图15 基于前向欧拉离散法的全阶观测器试验结果
Fig.15 Test results of full-order observer based on forward Euler discretization method
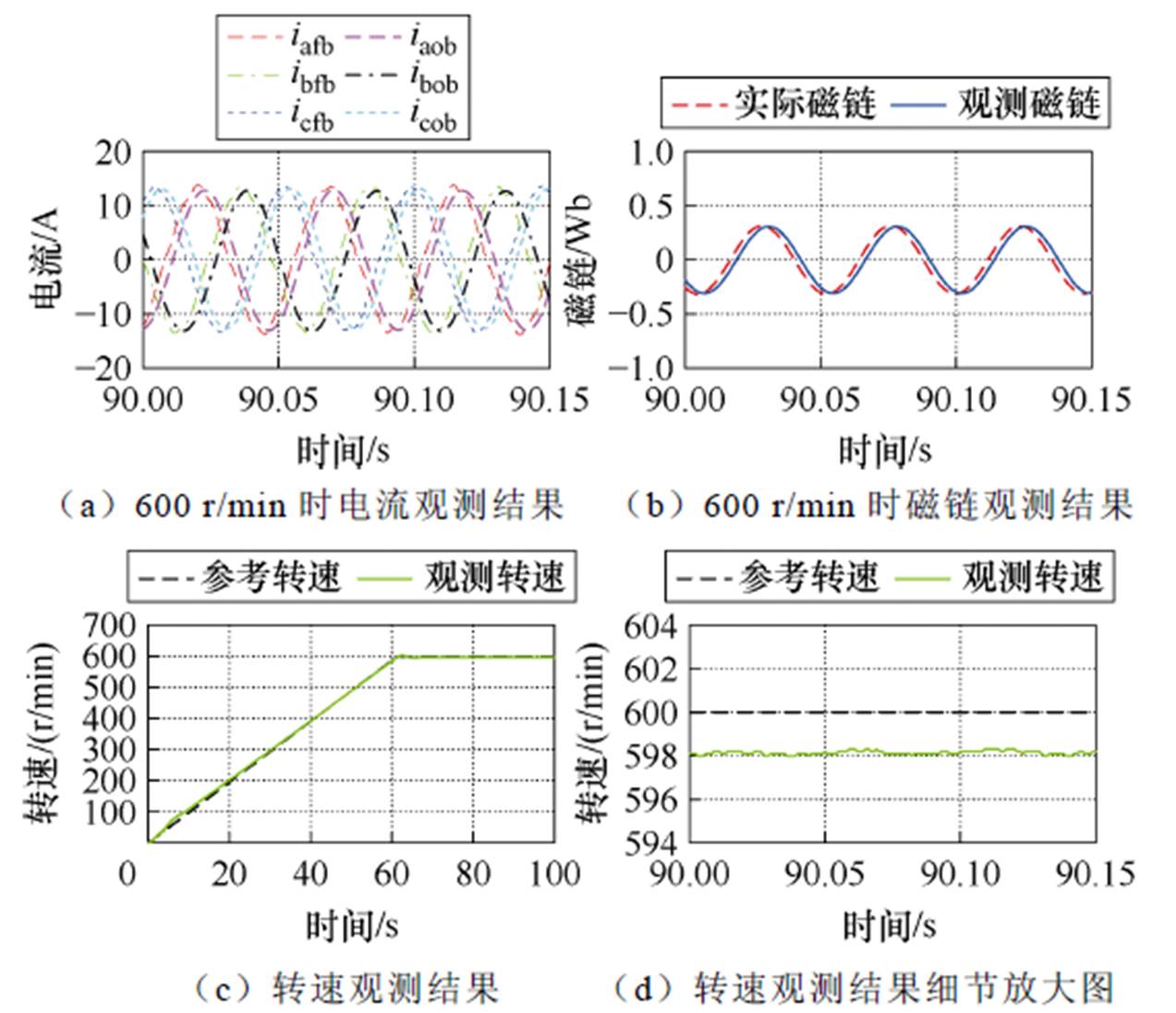
图16 基于简化二阶离散法的全阶观测器试验结果
Fig.16 Test results of full-order observer based on simplified second-order discretization method
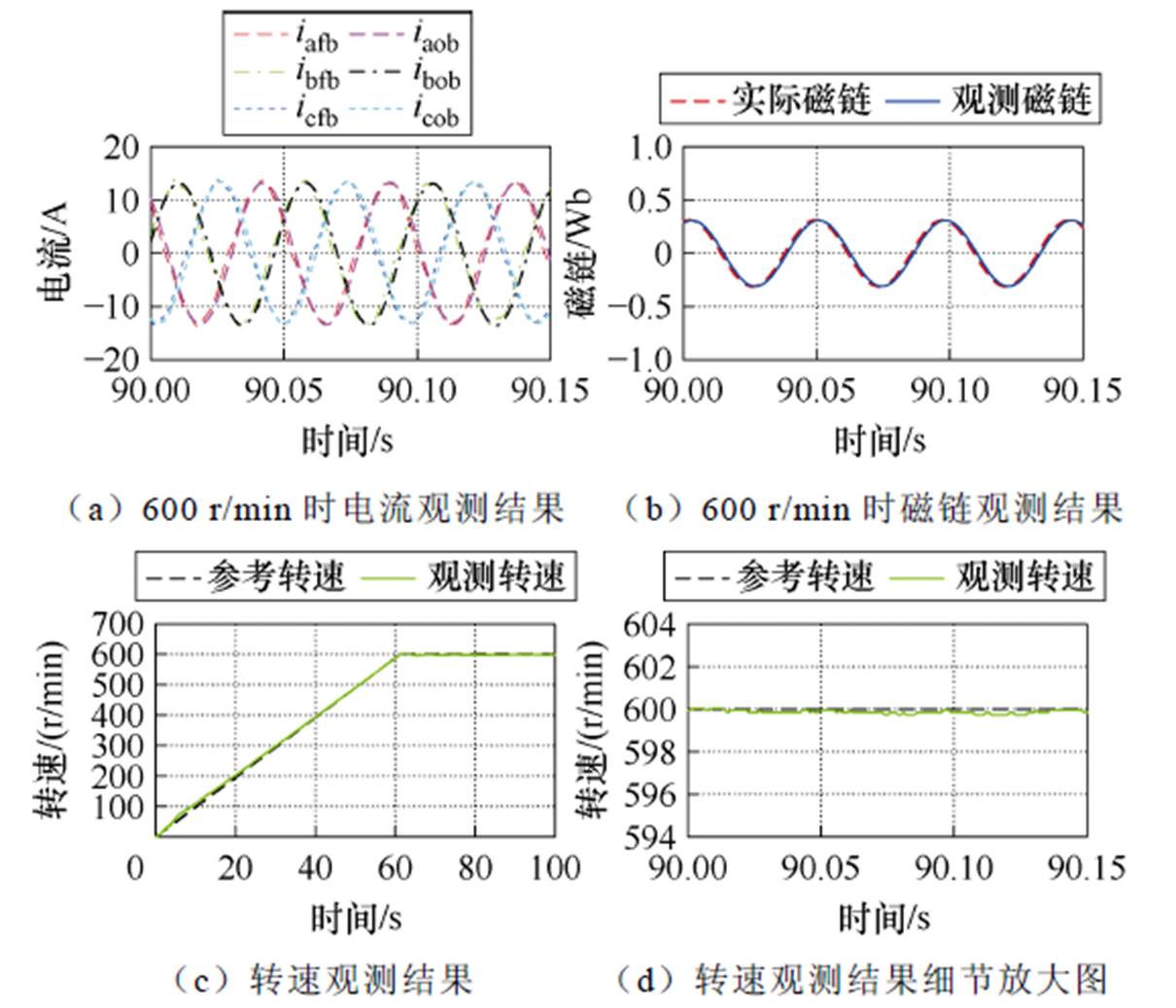
图17 基于Adams四阶离散法的全阶观测器试验结果
Fig.17 Test results of full-order observer based on Adams four-order discretization method
由图15~图17试验波形可得在2 kHz控制频率下,三种离散算法的性能对比见表4。
表4 三种离散方法试验性能对比
Tab.4 Comparison of three discretization methods
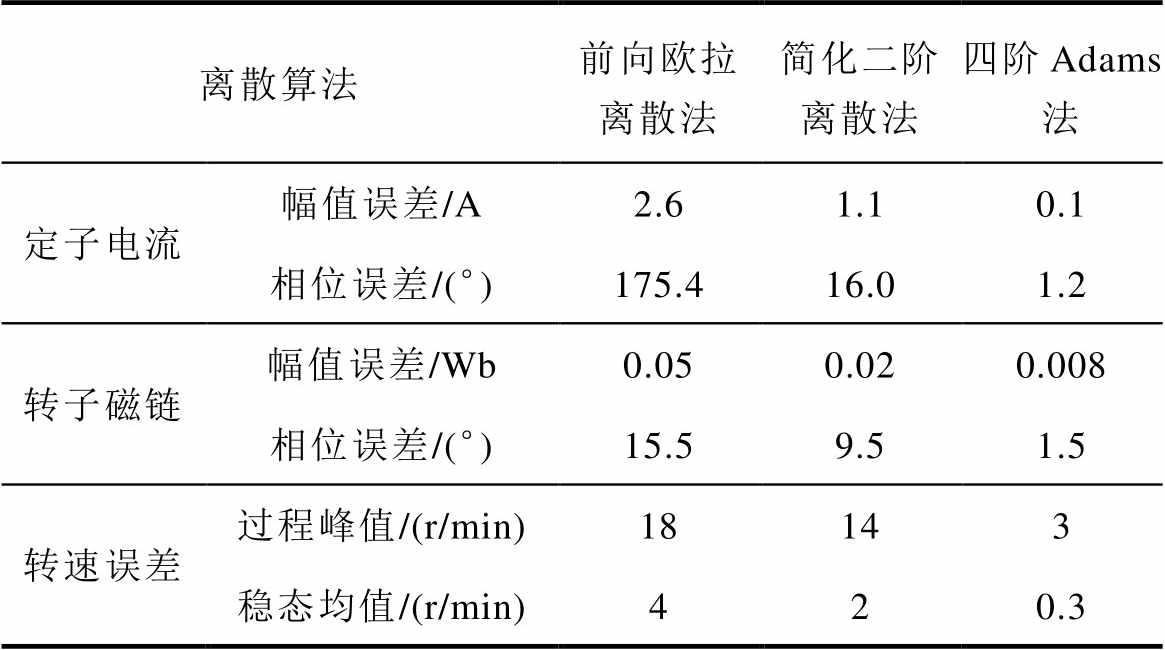
离散算法前向欧拉离散法简化二阶离散法四阶Adams法 定子电流幅值误差/A2.61.10.1 相位误差/(°)175.416.01.2 转子磁链幅值误差/Wb0.050.020.008 相位误差/(°)15.59.51.5 转速误差过程峰值/(r/min)18143 稳态均值/(r/min)420.3
由表4可知,相比前向欧拉离散法,采用四阶Adams算法时观测定子电流幅值、相位误差分别下降96.2%、99.3%,观测转子磁链幅值、相位误差分别下降84%、90.3%,观测转速过程峰值、稳态均值分别下降83.3%、92.5%;相比简化二阶离散法,采用四阶Adams算法时观测定子电流幅值、相位误差分别下降90.9%、92.5%,观测转子磁链幅值、相位误差分别下降60%、84.2%,观测转速过程峰值、稳态均值分别下降78.6%、85%。即基于四阶Adams算法的全阶观测器观测定子电流、转子磁链和转速与实际值几乎吻合,观测精度最高,与仿真分析基本一致。
试验中欧拉法和简化二阶算法观测转速精度与仿真存在些许差异,考虑原因是仿真中观测器参数与被控电机参数一致,而试验中电机参数难以准确获取,随着工况变化还会发生偏移,进而导致离散阶数较低时转速观测幅值存在偏差;退一步来说,即使电机参数偏移,试验结果也依然验证了采用Adams四阶离散算法的全阶观测器的性能优越性。
4.2.2 无速度传感器闭环调速试验
将观测转速与观测磁链代入闭环运行,即采用无速度传感器控制时进行不同转速范围下的调速试验。同样地,仅将第二通道电压、电流信息输入全阶观测器,并将观测转速代入闭环控制,转速试验波形如图18所示,图19为转速动态变化时的电流波形。
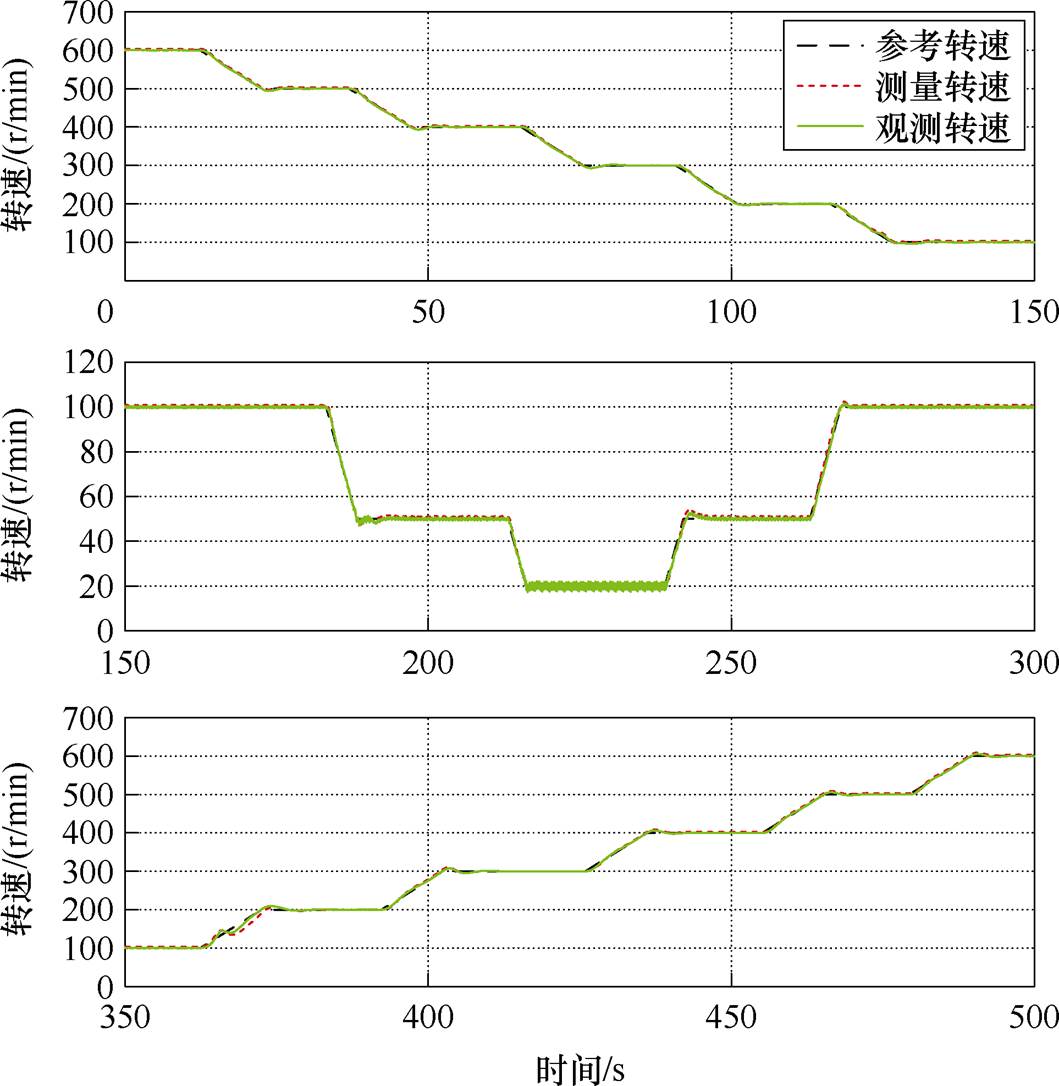
图18 不同转速范围内调速试验结果
Fig.18 Test results in different speed ranges
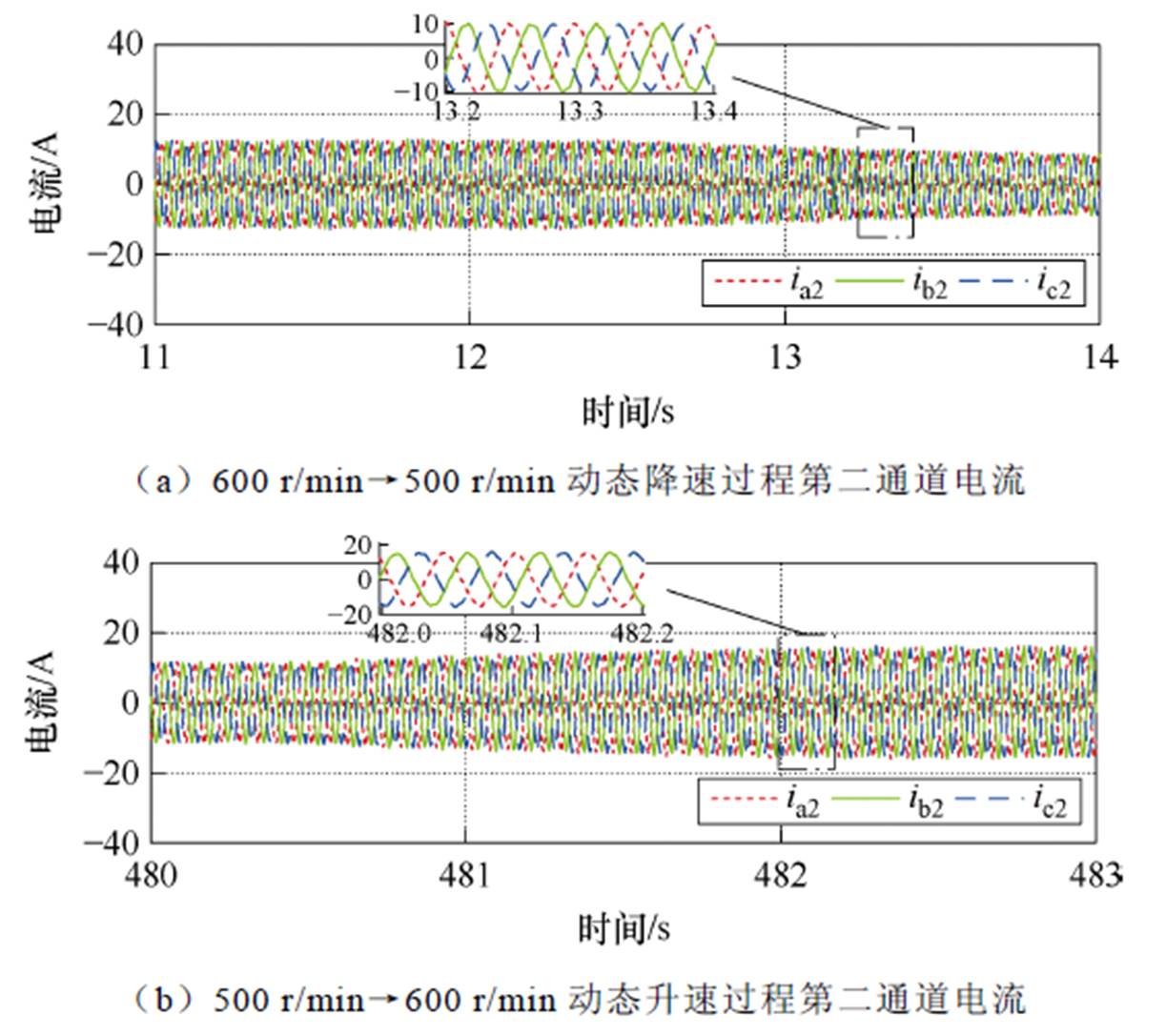
图19 转速动态变化时电流波形
Fig.19 Current waveforms during speed dynamic changes
由图18可知,本文采用基于Adams四阶离散法的全阶观测器在20~600 r/min之间均能实现良好的转速辨识;由图19a、图19b可知,在转速动态变化过程中,第二通道的三相电流依然能保持良好的正弦性和稳定性。
4.2.3 无速度传感器闭环运行加减载试验
为了进一步验证本文所提出的基于Adams四阶离散法的全阶观测器的带载性能,在无速度传感器闭环运行时进行了稳态加减载试验。试验条件为:电机观测转速直接代入闭环由零速起动,至300 r/min稳态运行后,于52 s时刻突加负载3 kW;之后升速至600 r/min稳态运行,于122 s时刻再突加负载6 kW,并于140 s时刻从带载9 kW突卸至空载运行,相关转速及电流、磁链波形如图20、图21所示。
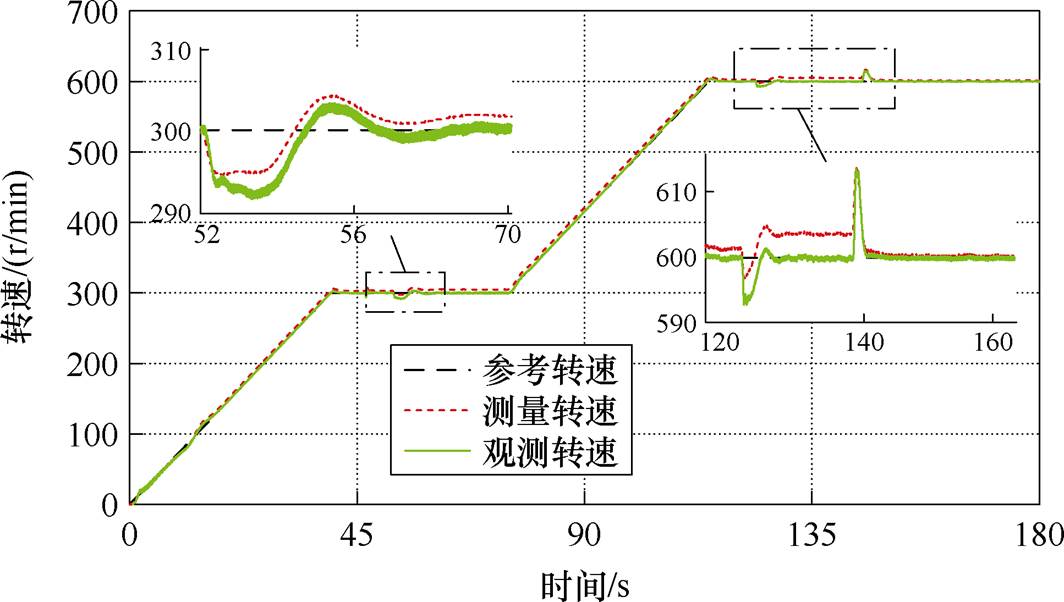
图20 转矩动态变化时的转速波形
Fig.20 Speed waveforms during dynamic changes in torque
由图20可知,无速度传感器闭环运行,在300、600 r/min稳态突加突卸负载时,转速在转矩动态变化时刻会有一定的超调,但能迅速调节至参考转速;由图21a可知,在加减载工况下第二通道的三相电流能够平稳变化;并且由图21b、图21c可知,600 r/min带载9 kW运行时,转子磁链和四个通道电流的正弦性及稳定性很好。本文所提基于Adams四阶离散法的全阶观测器能够保证十二相开绕组感应电机稳定带载运行,并具备较好的动稳态性能。
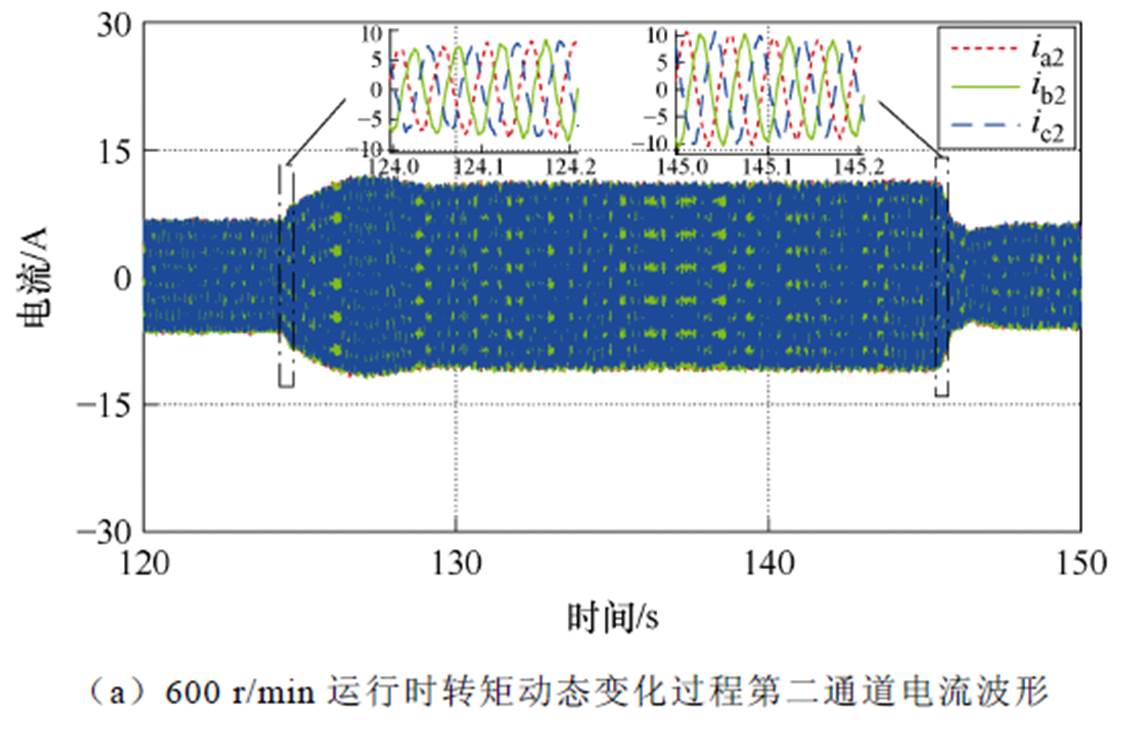
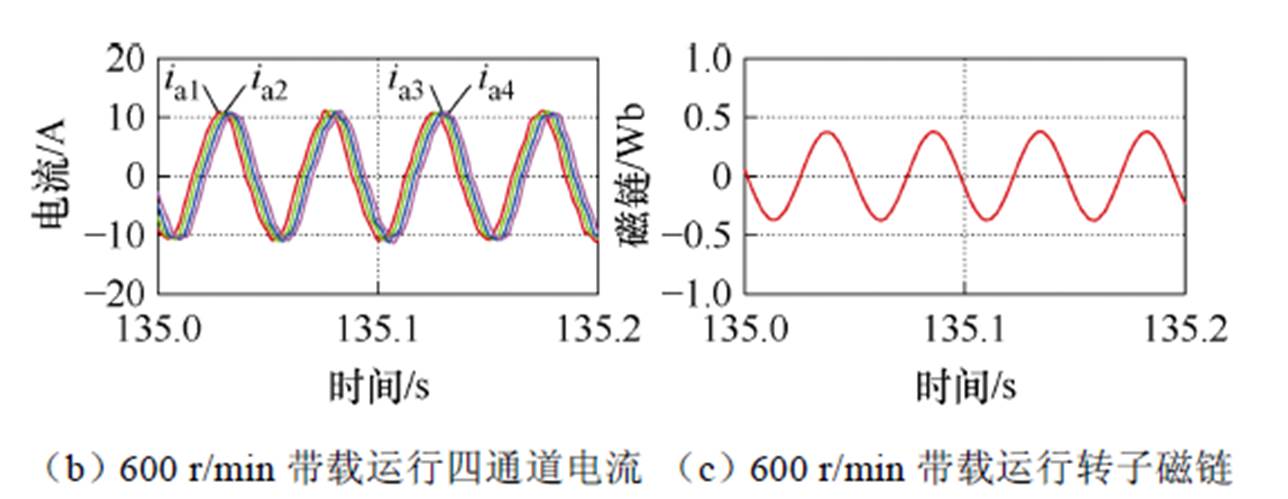
图21 600 r/min稳定运行时转矩动态变化时的电流、磁链波形
Fig.21 Current and magnetic chain waveforms during dynamic change of torque during stable operation at 600 r/min
本文针对舰船大容量电力推进系统低开关频率引起的十二相感应电机全阶观测器离散化误差加大的问题展开了离散化方法优化研究,有以下结论:
1)相比传统的前向欧拉法、二阶离散法,本文所提出的基于Adams高阶离散法的全阶观测器在不过多增加数字控制系统计算量的同时保证了最佳的离散精度,转速、电流及磁链的观测结果与实际值几乎完全吻合;当观测转速代入闭环控制时,即使在转速、转矩动态变化工况下,本文所设计的全阶观测器依然具备良好的调速和带载能力,验证了基于Adams方法的离散全阶观测器自适应转速辨识系统的正确性和优越性。
2)本文研究的多相推进感应电机全阶观测器离散化方法为无速度传感器控制技术推广应用于低开关频率多相开绕组电机系统提供了技术支撑。
附 录
利用式(12)第一式将式(5)展开,可得基于前向欧拉法的开环(G= 0)全阶磁链观测器离散化模型为
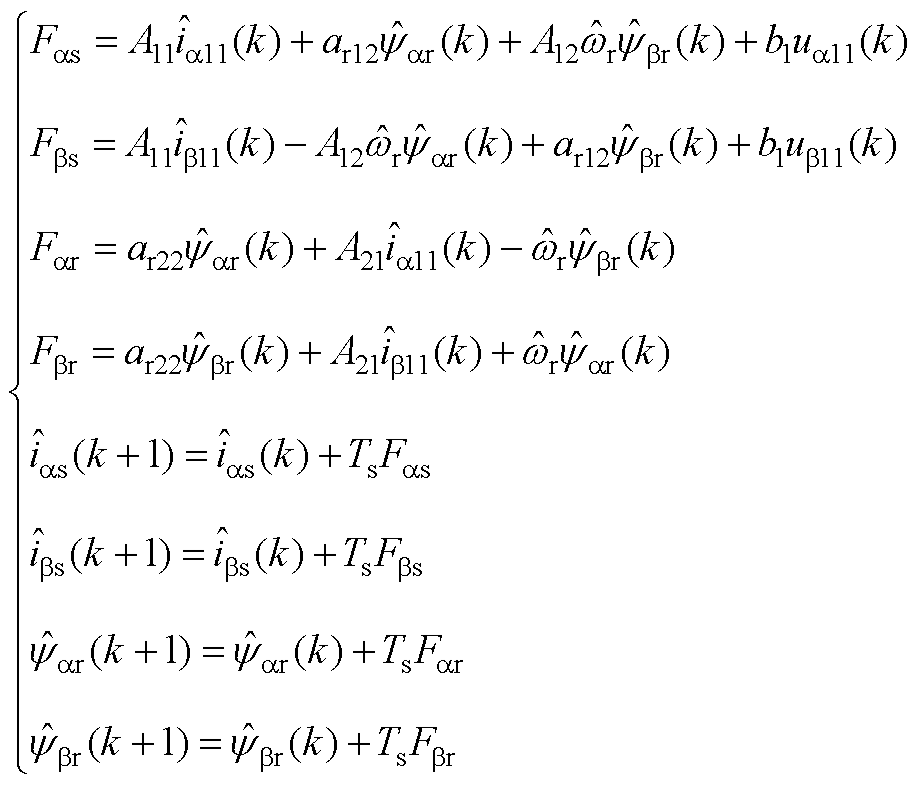 (A1)
(A1)
利用式(15)和式(16)将式(5)展开,可得基于简化二阶离散法的开环(G= 0)全阶磁链观测器离散化模型为
 (A2)
(A2)
四阶龙格-库塔离散法的表达式[12]为
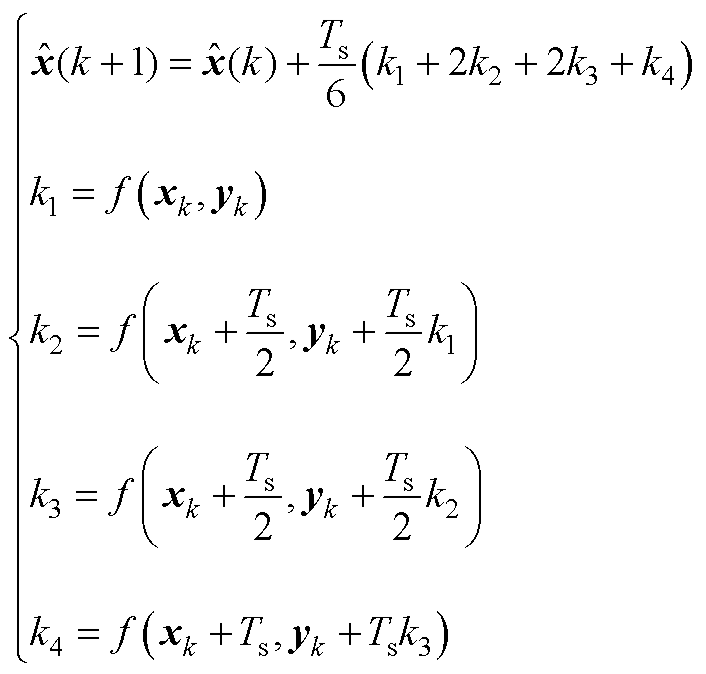 (A3)
(A3)
利用式(A3)将式(5)展开,可得基于四阶龙格-库塔法的开环(G= 0)全阶磁链观测器离散化模型为
 (A4)
(A4)
利用式(17)将式(5)展开,可得基于四阶Adams离散法的开环(G= 0)全阶磁链观测器离散化模型为
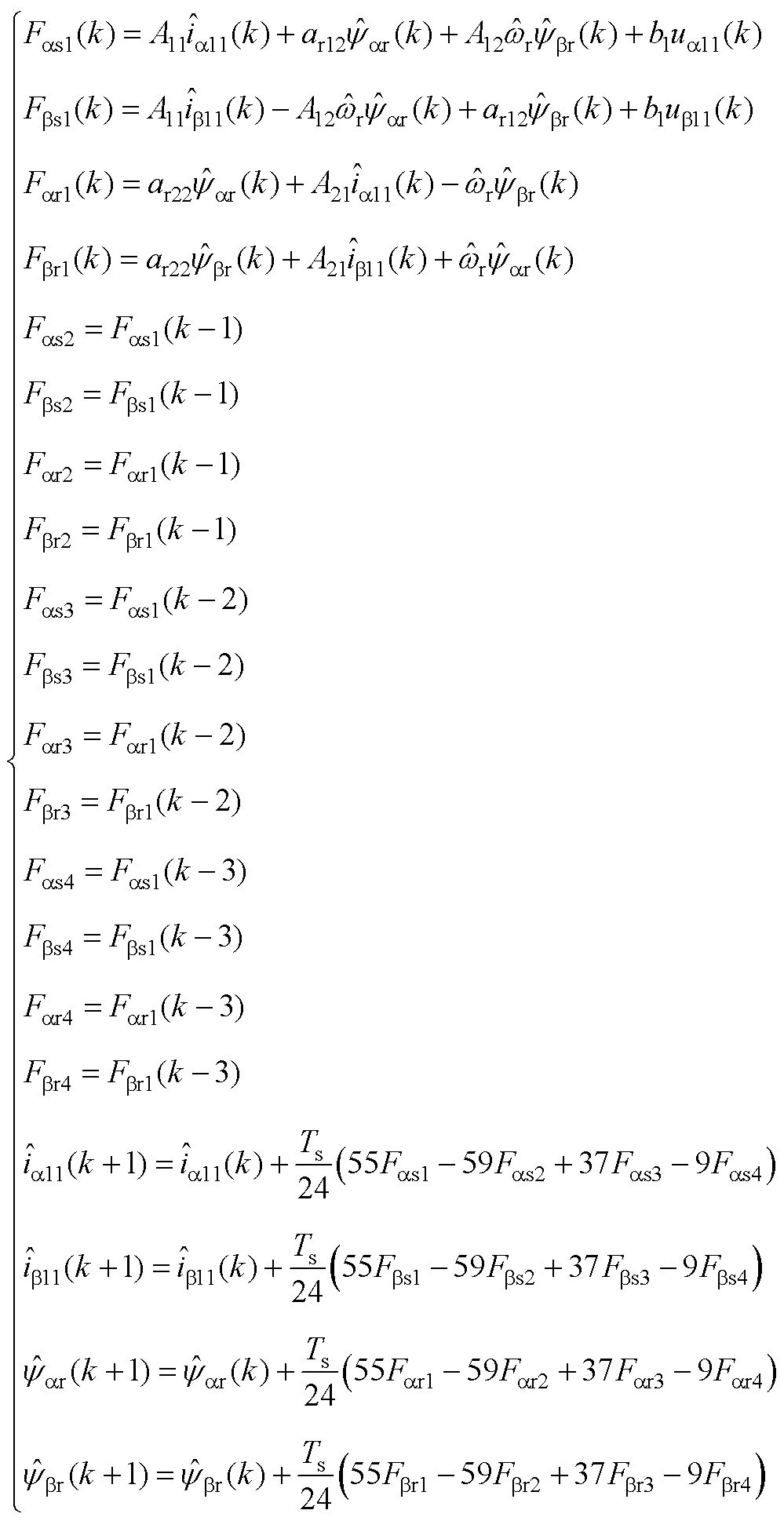 (A5)
(A5)
参考文献
[1] 罗成, 李孺涵, 杨凯, 等. 基于电流优化的无速度传感器感应电机零频穿越策略[J]. 电工技术学报, 2022, 37(19): 4947-4956.
Luo Cheng, Li Ruhan, Yang Kai, et al. Current optimization-based zero frequency ride-through method for speed-sensorless induction motor drives[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4947-4956.
[2] 孙玉华, 赵文祥, 吉敬华, 等. 高转矩性能多相组永磁电机及其关键技术综述[J]. 电工技术学报, 2023, 38(6): 1403-1420.
Sun Yuhua, Zhao Wenxiang, Ji Jinghua, et al. Overview of multi-star multi-phase permanent magnet machines with high torque performance and its key technologies[J]. Transactions of China Electro- technical Society, 2023, 38(6): 1403-1420.
[3] 孙丹, 林斌, 周文志. 开绕组电机系统拓扑及控制技术研究综述[J]. 电工技术学报, 2017, 32(4): 76-84.
Sun Dan, Lin Bin, Zhou Wenzhi. An overview of open winding electric machine system topology and control technology[J]. Transactions of China Elec- trotechnical Society, 2017, 32(4): 76-84.
[4] 杨凯, 李孺涵, 罗成, 等. 负载变化下无传感器感应电机主动零频穿越及脉动抑制策略[J]. 电工技术学报, 2023, 38(18): 4910-4920.
Yang Kai, Li Ruhan, Luo Cheng, et al. Proactive low-frequency ride-through method and its ripple reduction for sensorless induction motor drives under load variations[J].Transactions of China Electro- technical Society, 2023, 38(18): 4910-4920.
[5] 易山, 卢子广, 袁凯南, 等. 中低频轻载工况下引入虚拟电抗的感应电机变频调速系统稳定控制[J]. 电工技术学报, 2022, 37(8): 1959-1971.
Yi Shan, Lu Ziguang, Yuan Kainan, et al. The stability control of induction motor variable frequency speed regulation system injected with virtual reactance under low frequency and light load condition[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 1959-1971.
[6] Harnefors L, Hinkkanen M. Complete stability of reduced-order and full-order observers for sensorless IM drives[J]. IEEE Transactions on Industrial Elec- tronics, 2008, 55(3): 1319-1329.
[7] 罗慧. 感应电机全阶磁链观测器和转速估算方法研究[D]. 武汉: 华中科技大学, 2009.
Luo Hui. Research on full-order flux observer and speed estimation method of induction motor[D]. Wuhan: Huazhong University of Science and Tech- nology, 2009.
[8] 赵雷廷, 刁利军, 董侃, 等. 基于状态空间拆分重组的牵引异步电机闭环离散全阶转子磁链观测器[J]. 电工技术学报, 2013, 28(10): 103-112.
Zhao Leiting, Diao Lijun, Dong Kan, et al. A novel discretized closed-loop full-order rotor flux observer for induction motor based on re-organization of state space[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 103-112.
[9] 张钦培, 李健, 卢阳, 等. 低载波比牵引系统的感应电机特征根离散化模型研究[J]. 电工技术学报, 2024, 39(2): 434-444, 454.
Zhang Qinpei, Li Jian, Lu Yang, et al. Research on discretization model of induction motor for low switching-to-fundamental frequency ratio traction system[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 434-444, 454.
[10] 李杰, 詹榕, 宋文祥. 感应电机低采样频率的磁链观测器离散化模型研究[J]. 电工技术学报, 2019, 34(15): 3136-3146.
Li Jie, Zhan Rong, Song Wenxiang. Improved discrete observer model of induction motor at low sampling frequency[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3136-3146.
[11] 沈凤龙, 满永奎, 王建辉. 基于改进全阶状态观测器的异步电机速度估算系统[J]. 微电机, 2019, 52(6): 34-39, 50.
Shen Fenglong, Man Yongkui, Wang Jianhui. Speed estimation system of induction motor based on improved full order observer[J]. Micromotors, 2019, 52(6): 34-39, 50.
[12] 凌光, 王斯然, 陈斌, 等. 感应电机全阶观测器的一种新型离散方法[J]. 电力电子技术, 2012, 46(4): 78-81.
Ling Guang, Wang Siran, Chen Bin, et al. A new discretization method of full-order observer for induction motor[J]. Power Electronics, 2012, 46(4): 78-81.
[13] Wang Bo, Zhao Yongzheng, Yu Yong, et al. Speed- sensorless induction machine control in the field- weakening region using discrete speed-adaptive full-order observer[J]. IEEE Transactions on Power Electronics, 2016, 31(8): 5759-5773.
[14] 宋文祥, 周杰, 尹赟. 感应电机转速自适应全阶磁链观测器的离散化[J]. 上海大学学报(自然科学版), 2012, 18(6): 582-588.
Song Wenxiang, Zhou Jie, Yin Yun. Discretization of speed adaptive full-order flux observer for induction motors[J]. Journal of Shanghai University (Natural Science Edition), 2012, 18(6): 582-588.
[15] 胡亮灯, 肖飞, 楼徐杰, 等. 基于层叠载波调制的三电平H桥变频器输出电压异常跳变分析研究[J]. 中国电机工程学报, 2019, 39(1): 266-276.
Hu Liangdeng, Xiao Fei, Lou Xujie, et al. Research on output voltage abnormal voltage pulses of three- level H-bridge inverter base on cascaded carrier modulation[J]. Proceedings of the CSEE, 2019, 39(1): 266-276.
[16] 邓歆, 张广明, 王德明, 等. 异步电机全阶磁链观测器反馈矩阵设计[J]. 电机与控制学报, 2015, 19(12): 7-17.
Deng Xin, Zhang Guangming, Wang Deming, et al. Feedback matrix design of full order flux observer for induction motor[J]. Electric Machines and Control, 2015, 19(12): 7-17.
[17] 尹少博. 感应电机无速度传感器控制带速重投方法研究[J]. 电气工程学报, 2022, 17(3): 130-137.
Yin Shaobo. Study on the restarting method of induction motor under speed-sensorless control[J]. Journal of Electrical Engineering, 2022, 17(3): 130- 137.
[18] 胡锦涛, 邵宜祥, 庄圣伦, 等. 基于新型全阶观测器的感应电机无速度传感器控制[J]. 微电机, 2021, 54(5): 79-85.
Hu Jintao, Shao Yixiang, Zhuang Shenglun, et al. Speed sensorless control of induction motor based on new full-order observer[J]. Micromotors, 2021, 54(5): 79-85.
[19] 徐长发, 王邦. 实用计算方法[M]. 武汉: 华中科技大学出版社, 2005.
Research on Full-Order Observer Discretization Method of Multi-Phase Induction Motor at Low Switching Frequency
Abstract The multi-phase open-winding induction motor and its adaptive H-bridge multi-phase inverter system have
receivedextensive attention due to their advantages of small torque ripple, strong fault tolerance, and easy power capacity expansion. This paper analyzes the modeling of the multi-phase open-winding motor system and speed sensorless control technology to achieve high degrees of freedom control and low switching frequency characteristics in a twelve-phase, large-capacity, open-winding motor system. The simulation and experimental verification are conducted to enhance the operating performance of the low-switching-frequency multi-phase open-winding motor system.
The twelve-phase open-winding induction motor system and its equivalent three-phase simplified model are established. The equivalent three-phase full-order observer model and its speed estimation method are presented. The full-order observer used in speed sensorless control has the advantages of low control bandwidth requirements and a wide range of observation speeds. However, the switching frequency of the H-bridge large-capacity inverter supporting the ship’s multi-phase open-winding induction motor is low, which inevitably increases the digital discretization error of the full-order observer. This paper derives the full-order flux observer models based on the forward Euler method, the simplified second-order discretization method, and the proposed Adams fourth-order discretization method. Then, the steady-state error and observer stability are compared using the F-norm and pole diagram. Theoretical analysis reveals that the full-order observer, based on Adams' fourth-order discretization method, achieves the best discrete accuracy and stability of the observation system while minimizing the computational complexity of the digital control system.
A simulation model and a test platform for a twelve-phase, 25 kW open-winding induction motor with speed sensorless control have been developed. The results show that, compared with the forward Euler method and the simplified second-order discretization method, the observation results for speed, current, and flux based on the Adams fourth-order discretization method are almost consistent with the actual values. Through the speed sensorless closed-loop speed regulation test and load mutation test, it is further verified that the full-order observer based on Adams' fourth-order discretization method exhibits good speed regulation and load-carrying capacity, which can achieve better dynamic and steady-state performance under both extremely low and high-speed conditions. The full-order observer discretization method can provide technical support for applying speed sensorless control technology to low switching frequency multi-phase open-winding motor systems.
keywords:Multi-phase open-winding induction motor, full-order observer, discretization algorithm, low switching frequency
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.240819
国防科技基础加强计划资助项目(2022-JCJQ-JJ-0537)。
收稿日期2024-05-19
改稿日期2024-09-09
胡亮灯 男,1986年生,博士,副研究员,博士生导师,研究方向为大容量电力电子变换、高压辅助电源设计和数字有源门极驱动技术。
E-mail: hldhgd@163.com
徐小松 男,2000年生,博士研究生,研究方向为电力电子与电力传动。
E-mail: 3169422144@qq.com(通信作者)
(编辑 崔文静)