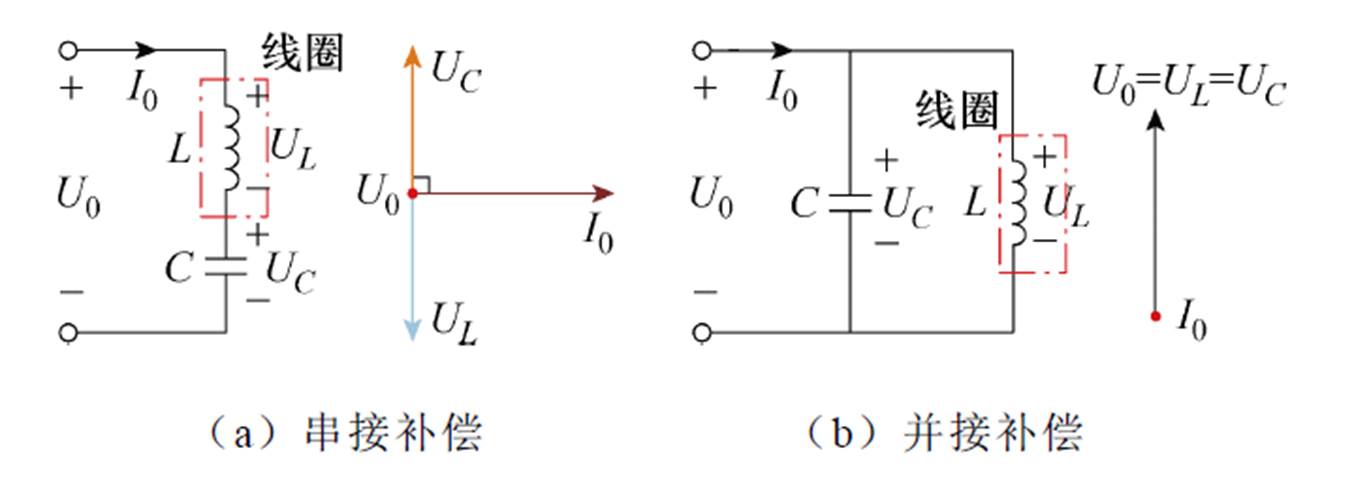
图1 外接电容补偿线圈电路
Fig.1 Equivalent circuit of external capacitor compensation coil
摘要 磁耦合式无线电能传输系统中,线圈的补偿是系统的重要研究内容。通常会外接电容进行补偿,但这不仅增加了系统的尺寸和成本,而且增加了线圈的电压梯度。该文提出一种利用线圈匝间电容实现线圈分段补偿的方法。该方法通过将平面螺旋线圈相邻两匝部分长度的Litz线进行紧密贴合,在高频条件下紧密贴合线圈匝间表现出更明显的电容效应,最终实现对线圈分段补偿的效果。为验证该方法的可行性,搭建一台开关频率500 kHz的实验样机。实验结果表明,匝间电容可实现对线圈的分段补偿,分段补偿线圈最大接收功率比外接电容集中补偿线圈最大功率提高了54.3%,效率提高了27.6%。
关键词:无线电能传输 匝间电容 分段补偿 电压梯度
由于电力电子技术的迅速发展以及无线电能传输(Wireless Power Transfer, WPT)的安全可靠、灵活方便等特点,无线电力传输技术不仅在不断更新迭代的消费电子领域有了更广阔的应用前景,而且在传统领域也产生了深远的影响[1-5]。如电动汽车[6-7]、无人机[8]及自主水下航行器[9]等。无线充电应用场景的特殊性使得传输距离常发生较大变化,若传输距离变长,耦合系数将快速下降并导致传输效率明显降低。为了提高传输效率,常通过添加补偿网络进行阻抗匹配以减小能量损耗并提升系统传输效率[10-12]。
目前,主要有四种外接电容补偿拓扑结构,包括串联-串联(Series-Series, SS)、串联-并联(Series- Parallel, SP)、并联-并联(Parallel-Parallel, PP)和并联-串联(Parallel-Series, PS)[13]。除上述的四种基本补偿拓扑外,还有一些高阶补偿拓扑,如LCL、LCC及LCC/CLC等高阶补偿拓扑[14-16]。在基本补偿网络基础上衍生出LCL补偿拓扑结构[14],该拓扑结构可实现恒流模式与恒压模式的切换。但LCL谐振补偿网络结构传输功率偏小且自由度差。文献[15]提出双边LCC拓扑网络,可解决双边LCL拓扑网络传输功率偏小和自由度差等问题,故在应用中具有较强的适用性。然而对LCC补偿拓扑的基础理论分析进行了理想化处理,并且多个补偿单元增加了线路拓扑的复杂度、成本和功耗以及设计的不稳定性。文献[16]进一步提出LCC/CLC补偿拓扑,该拓扑可实现恒压输出、零输入相位以及零电压软开关(Zero Voltage Switching, ZVS),而且最大输出功率不受耦合参数限制。但这进一步增加了线路拓扑的复杂度以及计算设计的不稳定性。
以上提出的补偿方法均基于外部电容对线圈进行集中补偿。通过外接电容进行线圈补偿,虽然对线圈整体具有较好的补偿效果,但是,外接电容补偿会导致线圈内部电压梯度较大。外接电容补偿线圈电路如图1所示,线圈的最内层和最外层之间具有很大的电压差,增大了线圈的电压损耗以及能量损失。为了克服外接电容集中补偿导致线圈匝间电压过大的问题,文献[17]提出分段补偿线圈的方法,研究了线圈几何参数的影响,并表明分段补偿线圈系统的效率更高,但是没有注意到分段补偿后线圈品质因数的变化。文献[18]采用每匝线圈都串联外接电容的方法使线圈的寄生电容短路,并进一步分析了分段补偿的原理,同时指出减小线圈的寄生电容是提高系统传输效率的关键。但这也增加了线圈补偿的复杂度,使得补偿变得复杂并且需要外接大量的补偿电容。为了避免外接大量的补偿电容,文献[19]利用并联多个多层PCB线圈以获得较大的匝间电容,替代物理补偿电容器,从而减小尺寸和成本,并提高可靠性。文献[20]进一步提出了一种带有集成单开关稳压器的自补偿平面线圈,也是利用线圈匝间电容的方式,实现了对线圈的自补偿,并使自谐振频率低于200 kHz。但这需要并联多个多层PCB线圈,增加了系统的大小和成本。随着拓扑的不断优化改进,增加了线路的复杂度以及器件损耗,同时给对电路拓扑的分析、参数的计算以及后续的硬件实现也带来了一些困难和挑战。

图1 外接电容补偿线圈电路
Fig.1 Equivalent circuit of external capacitor compensation coil
针对以上问题,本文提出了一种利用线圈匝间电容实现线圈分段补偿的方法。利用在高频条件下相邻导线绝缘层相互接触形成电容的原理,将接收线圈相邻两匝的部分线圈紧密贴合,这种线圈绕制方式增加了线圈紧密贴合段的电容大小,进而达到补偿线圈的目的。该方法将线圈划分为若干段,利用匝间电容对线圈各段进行单独补偿,对线圈整体实现了线圈分段补偿的效果。改进后,紧密贴合段的线圈匝间电容显著增大,进而起到代替外接电容以实现补偿的效果。相比于外接电容补偿拓扑,本文所提出的匝间电容分段补偿拓扑能够减小线圈内部的电压梯度、降低电压损耗和能量损失,从而提高线圈的能量接收效率,且该结构更紧凑,尺寸和成本更小。
本文匝间电容补偿线圈的无线电能传输系统电路拓扑分析计算基于以下假设:
(1)电场与磁感应变化率无关,且忽视位移电流。
(2)线圈各匝间距相同,且匝间电压均匀分布。
(3)忽略绝缘材料介电常数的微小变化。
(4)仅考虑紧密贴合线圈部分之间的匝间电容。
考虑匝间电容分段补偿的无线电能传输系统如图2所示,整个无线电能传输系统由E类逆变器、补偿拓扑、负载三部分组成。图2中,E类逆变器包括直流电压源VDD、扼流电感LRFC及型号为IRF740的功率MOSFET管[21]。电容C1包含了MOSFET和LRFC的寄生电容,与电感Lr共同组成了负载网络。补偿拓扑由初级电感线圈L1、次级电感线圈L2及初级电感侧的串接补偿电容CS组成。耦合线圈的初级线圈L1采用串接电容CS补偿的方法,次级线圈L2采用匝间电容分段补偿的方法,Vs为等效电源,I1为初级电流,I2为次级电流,L2i为各分段电感,Mi为各分段互感,CSki为匝间电容,Vgi为分段等效电源,i=1,…, n,即可将该模型分为1~n个电压源。负载部分由逆变桥和稳压电容Cf以及负载R组成,逆变桥臂上的二极管采用肖特基二极管。
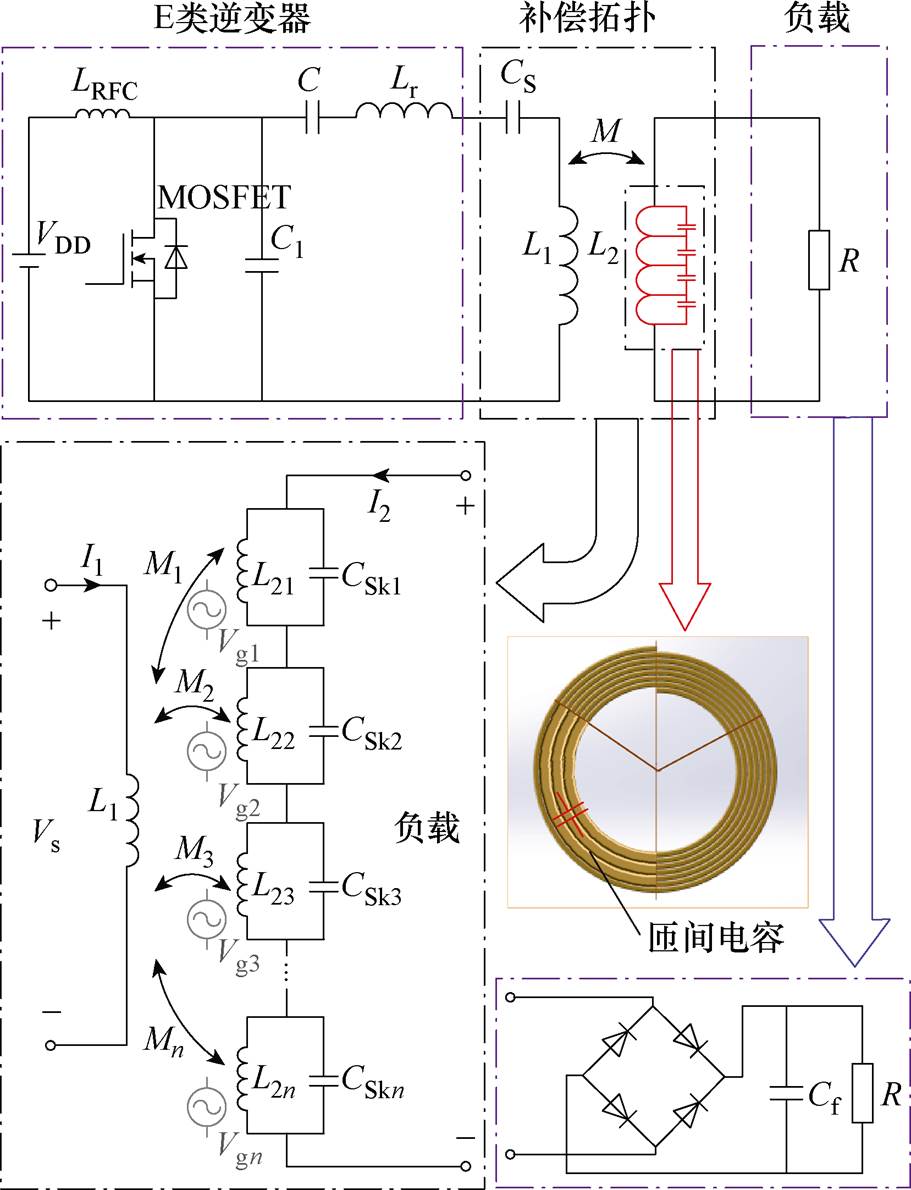
图2 考虑匝间电容分段补偿的无线电能传输系统
Fig.2 WPT system considering segmented compensation of inter-turn capacitance
根据基尔霍夫定律,可列写分段补偿电路拓扑的电压方程为
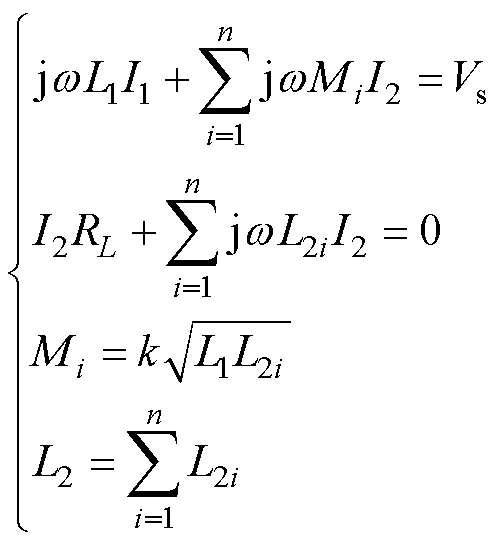 (1)
(1)
每段的等效电压源Vgi为
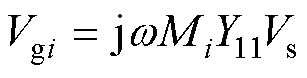 (2)
(2)
式中,k为线圈的耦合系数;RL为线圈的电阻;Y11为初级电导;Mi为分段互感。则分段补偿的等效电源为
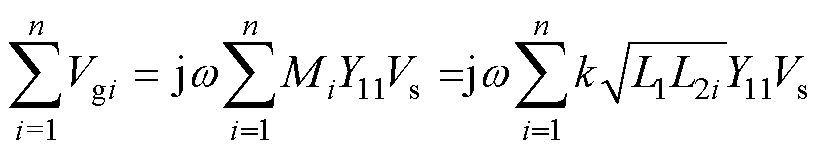 (3)
(3)
当线圈集中补偿时,等效电源为
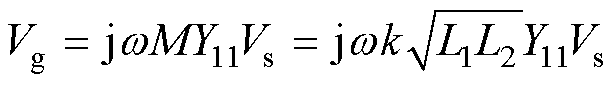 (4)
(4)
显然当分段补偿大于1时,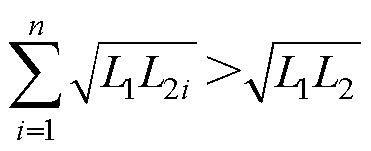 ,则有
,则有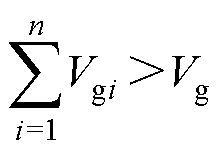 。则其等效电路的各等效电压源之和大于集中补偿的电压源。在同等负载条件下,分段补偿线圈的负载功率更大。
。则其等效电路的各等效电压源之和大于集中补偿的电压源。在同等负载条件下,分段补偿线圈的负载功率更大。
对比于端接电容集中补偿,采用匝间电容补偿线圈电压为
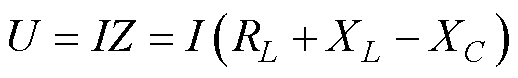 (5)
(5)
式中,U为线圈首末两端的端电压;I为流过线圈的电流;Z为线圈的总阻抗;XL为线圈的感抗;XC为线圈的补偿容抗。则线圈的损耗为
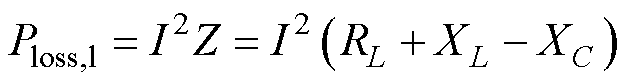 (6)
(6)
因为存在补偿电容,则线圈损耗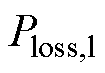 减小。由
减小。由 可知,相同的功率
可知,相同的功率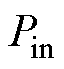 输入条件下,系统的功率损耗小,分段补偿线圈接收到的功率大,进而提高了系统的效率。
输入条件下,系统的功率损耗小,分段补偿线圈接收到的功率大,进而提高了系统的效率。
匝间电容仿真如图3所示,通过仿真可以看到,当线圈紧密贴合时,在贴合处出现明显的电容效应。匝间电容的存在主要归因于绕组中相邻匝之间的电位差。当电流通过绕组时,产生的电动势导致相邻匝之间形成电位差。此外,绕组匝通常缠绕得非常紧密,相邻匝之间的距离极小,这进一步增强了电容效应。绝缘材料不仅可以防止短路,还可作为电介质,进一步增加了电容效应。相邻匝之间的电场效应也是形成匝间电容的重要因素之一。尤其在高频情况下,匝间电容效应更加显著,因为高频电流使得匝间电容的影响更加明显。因此,电位差、紧密间距、绝缘材料和电场效应的共同作用,导致了绕组中相邻匝之间电容的形成,即匝间电容。
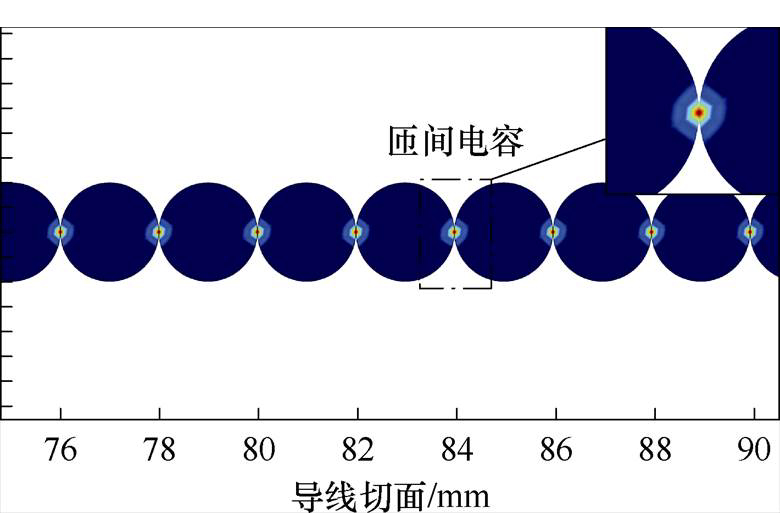
图3 匝间电容仿真
Fig.3 The simulation of inter-turn capacitors
分段匝间电容补偿线圈结构示意图如图4所示,采用多股Litz线绕制线圈。将相邻两匝线圈一段长度紧密贴合以达到增大匝间电容的效果。为简化分析,文献[22]将Litz线等效为带有两层绝缘介质的圆导体,如图5所示。其中第一层绝缘为单股Litz线表面的绝缘涂料,绝缘厚度为dins1,介电常数为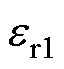 ;第二层绝缘为Litz线外层包裹的绝缘膜,绝缘厚度为dins2,介电常数为
;第二层绝缘为Litz线外层包裹的绝缘膜,绝缘厚度为dins2,介电常数为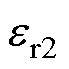 。在等效过程中忽略Litz线单股线最外层导体表面绝缘层和空气间隙的影响,未考虑等效后第一层有效介电常数的变化。
。在等效过程中忽略Litz线单股线最外层导体表面绝缘层和空气间隙的影响,未考虑等效后第一层有效介电常数的变化。
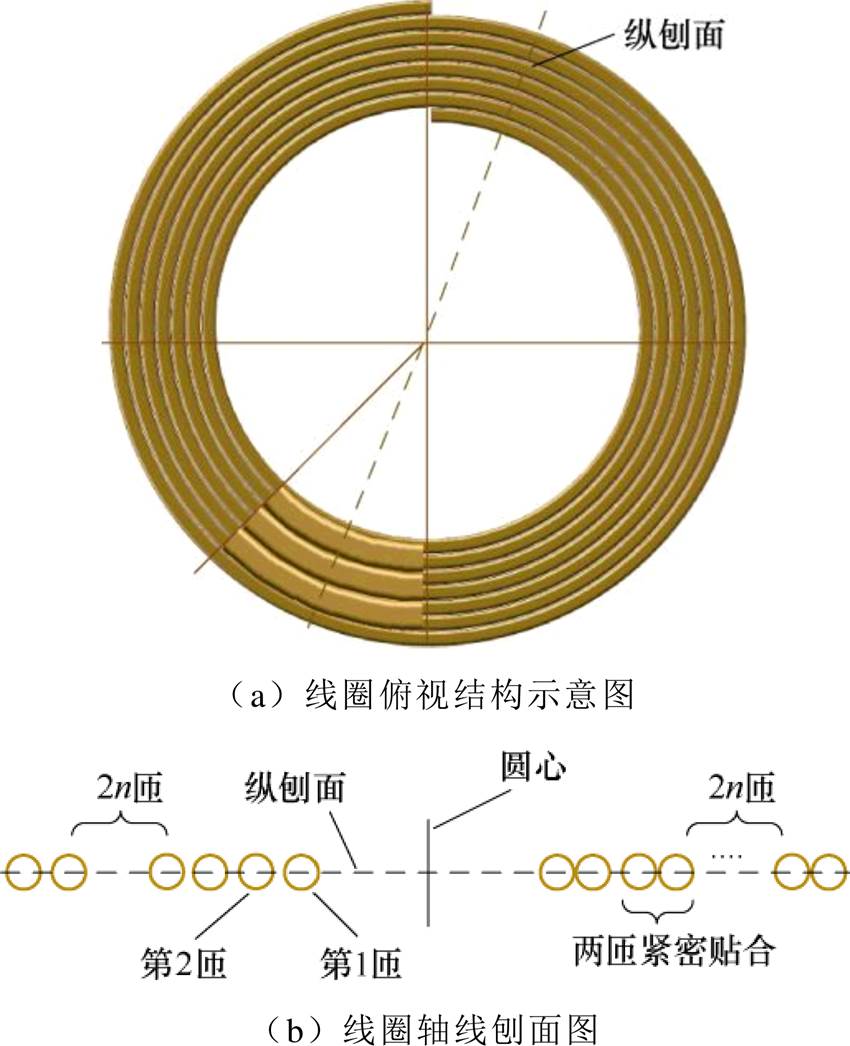
图4 分段匝间电容补偿线圈结构示意图
Fig.4 Structural diagram of segmented inter-turn capacitance compensation coil
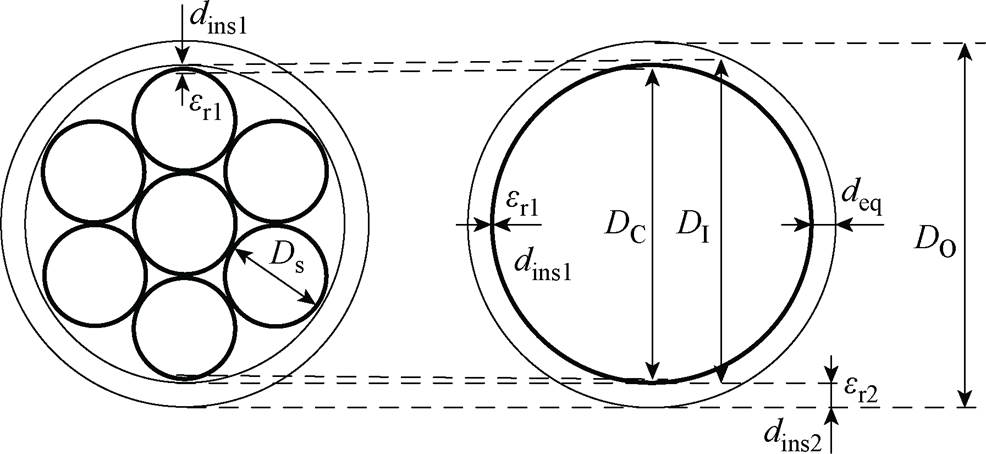
图5 Litz线等效为圆导体结构
Fig.5 The Litz wires is equivalent to the circular conductor structure diagram
为了提高计算精度,将等效后绝缘层的介电常数修正[22]为
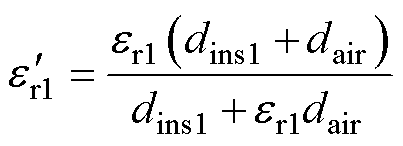 (7)
(7)
式中,dair为空气间隙的平均距离,dair可以用单股Litz线的直径Ds/4进行估算。等效后的圆导体导线外部有两层绝缘层,根据圆柱形电容器对介电常数进行等效计算,计算公式为
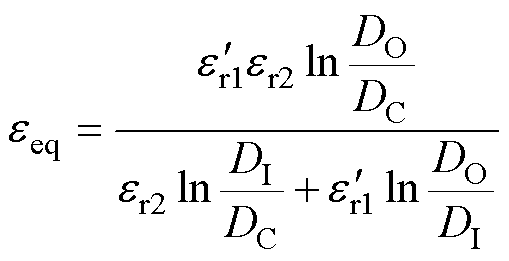 (8)
(8)
等效绝缘距离为外径和导线之间的距离为
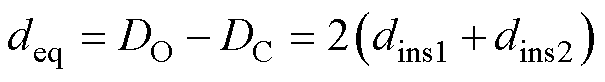 (9)
(9)
选取200股0.1 mm的Litz线的各参数为标准值,则等效绝缘层的介电常数eeq与其他各个变量的变化趋势如图6所示。Litz线的等效介电常数与单股Litz线内径Ds、Litz线外绝缘层膜厚度dins2成反比关系,与单股Litz线绝缘层的介电常数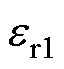 、Litz线外绝缘层的介电常数
、Litz线外绝缘层的介电常数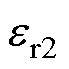 、等效圆导体内径DI、等效圆导体外径DO、单股Litz线绝缘的等效介电常数
、等效圆导体内径DI、等效圆导体外径DO、单股Litz线绝缘的等效介电常数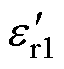 成正比。
成正比。
圆导体匝间电容计算方法如图7所示,有最短路径法、函数法、改进最短路径法[23]等。改进最短路径法结合了函数法和最短路径法的建模思路,使得建模更加精确,故本文采用图7c所示的改进最短路径法计算匝间电容。
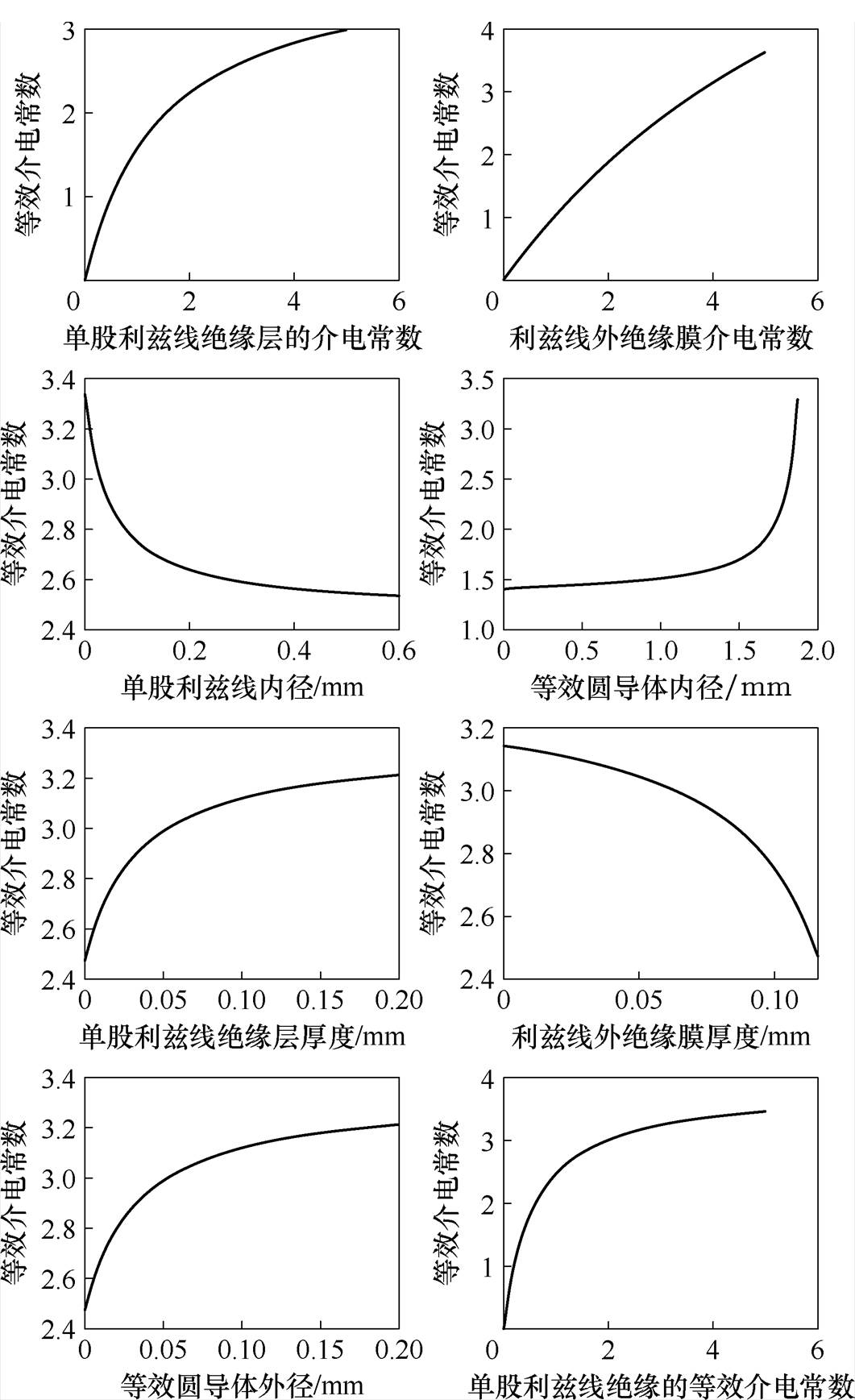
图6 等效介电常数与其他各变量的关系
Fig.6 The relationship between the equivalent dielectric constant and various other variables
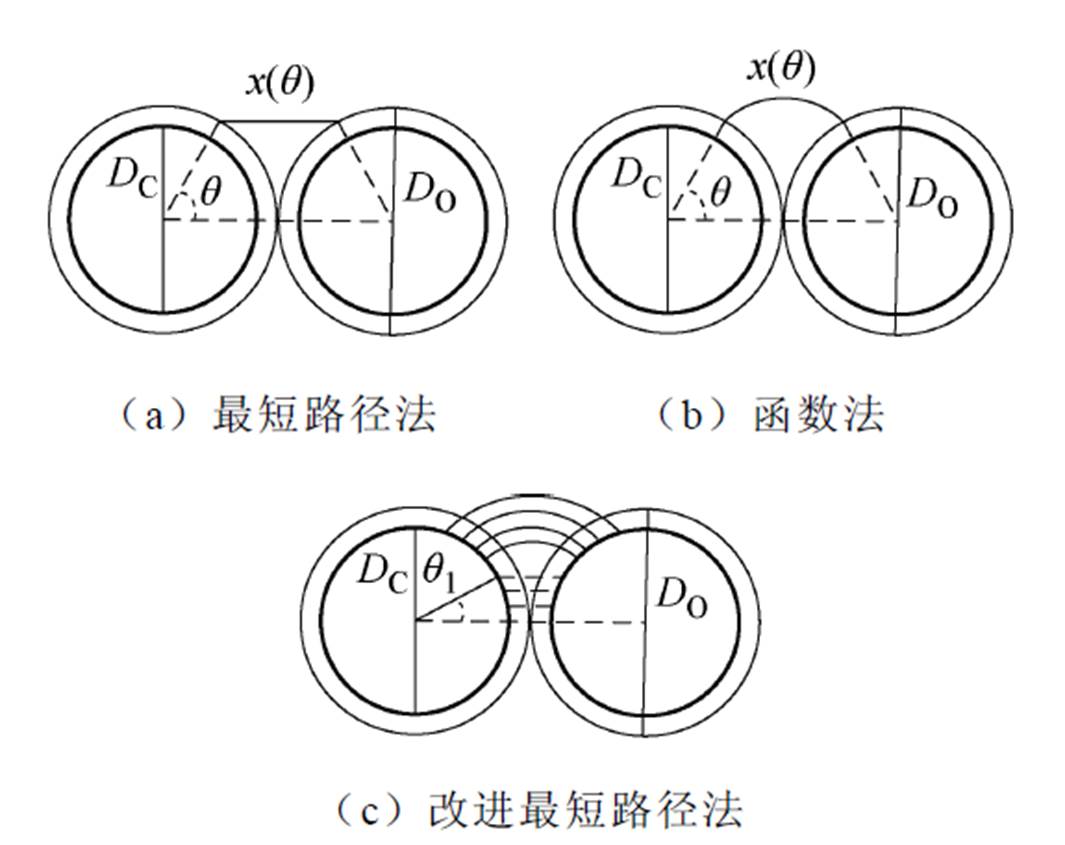
图7 两圆导体间静态电容模型
Fig.7 Static capacitance model between two circular conductors
当Litz线紧密贴合长度为lm时,根据高斯定理可推导出同轴圆柱形电容器的电容为
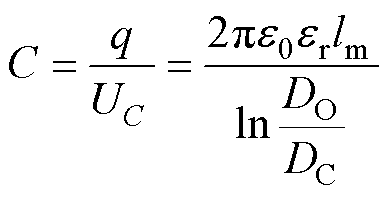 (10)
(10)
式中,UC为线圈间电压;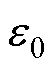 为真空介电常数;
为真空介电常数;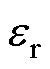 为相对介电常数;q为电荷量。
为相对介电常数;q为电荷量。
则通过圆柱形电容器式(10)得到单位角度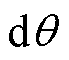 绝缘层中的电容为
绝缘层中的电容为
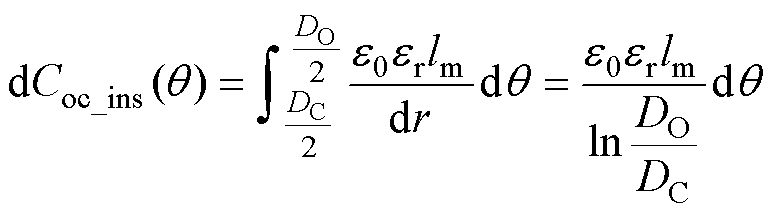 (11)
(11)
式中,q 为总积分角度;r为距离圆导体圆心距离。
空气间隙中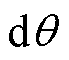 角度对应面积大小为
角度对应面积大小为
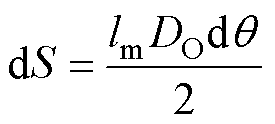 (12)
(12)
根据平行板电容器公式C=e0S/d以及空气间隙长度得到单位角度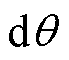 空气间隙电容为
空气间隙电容为
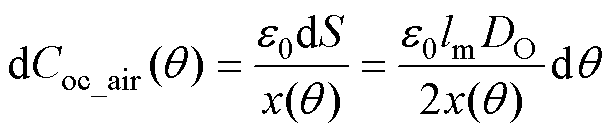 (13)
(13)
式中,x(q)为两导线之间的距离。
根据图7a最短路径法对电场线的定义,利用勾股定理计算可得电场线的长度为
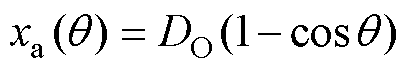 (14)
(14)
将式(14)代入到式(13)中得到图7a最短路径法对应的匝间空气间隙电容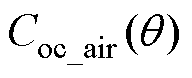 表达式为
表达式为
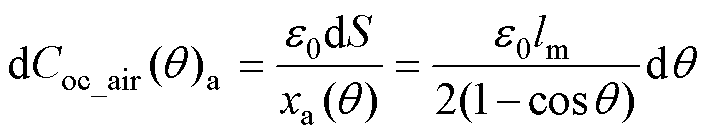 (15)
(15)
根据图7b函数法对电场线的定义,可得电场线长度为
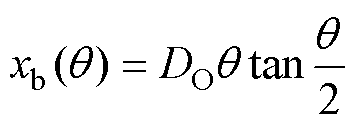 (16)
(16)
将式(16)代入到式(13)中得到图7b函数法对应的匝间空气间隙电容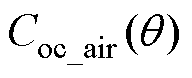 表达式为
表达式为
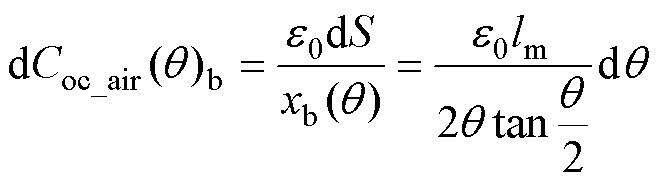 (17)
(17)
图7c所示的改进路径法,在[-q1, q1]区间,可求解得到绝缘层中电场线路径长度为
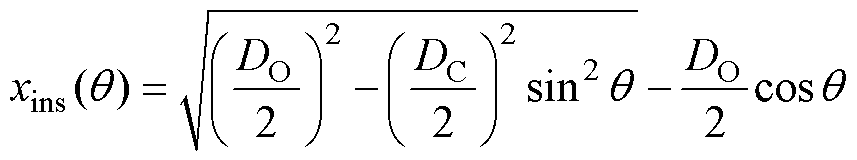 (18)
(18)
可求得此时绝缘层中单位角度分布电容大小为
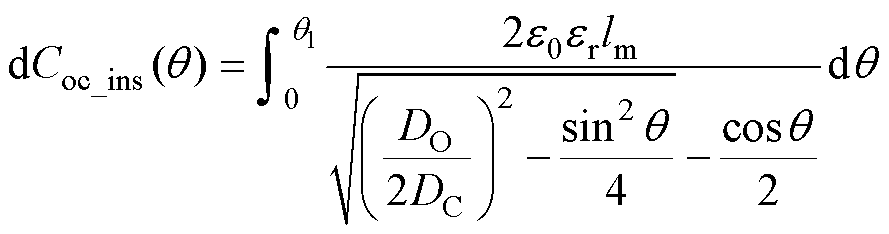 (19)
(19)
空气间隙中电场线路径与式(14)相同,空气间隙电容按照式(13)计算。
在[-qm, -q1 和(-q1, qm
和(-q1, qm 区间,绝缘层的电容可以根据式(11)计算,空气中间隙路径定义可以根据式(16)计算,空气间隙电容根据式(15)计算。根据式(11)和式(19)求解得到绝缘层电容表达式为
区间,绝缘层的电容可以根据式(11)计算,空气中间隙路径定义可以根据式(16)计算,空气间隙电容根据式(15)计算。根据式(11)和式(19)求解得到绝缘层电容表达式为
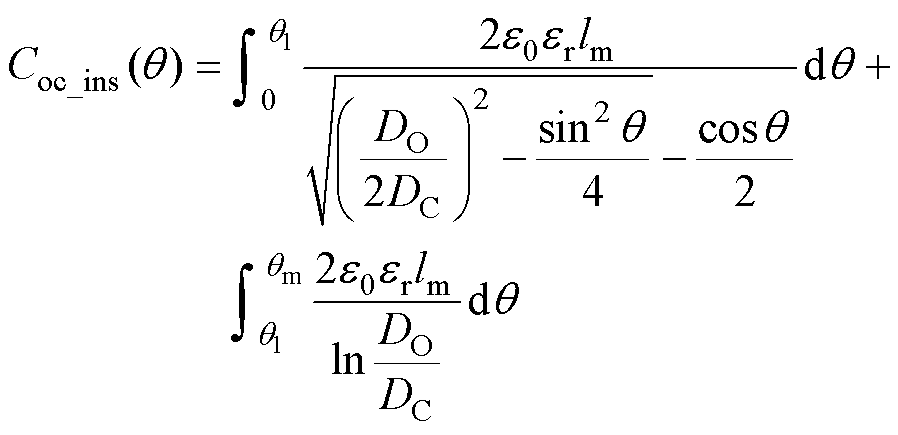 (20)
(20)
式中,qm为积分的最大角度,两根圆导体之间的积分角度qm=p/2。
根据式(15)、式(17)可求解得到空气间隙电容表达式为
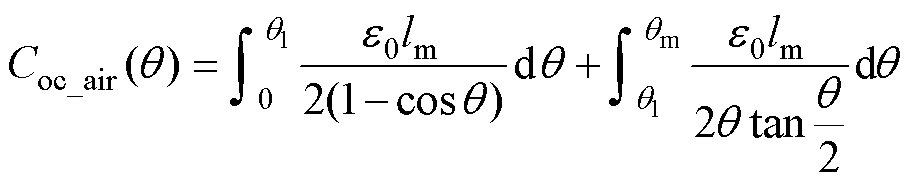 (21)
(21)
两圆导体匝间的电容为绝缘层电容和空气间隙电容串联组成,则两圆导体匝间的电容可求解为
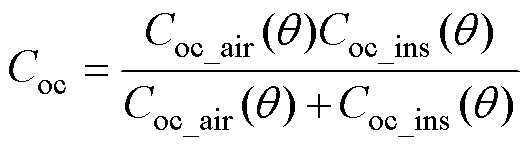 (22)
(22)
匝间电容与紧密贴合长度以及Litz线绝缘层等效介电常数关系如图8所示,匝间电容与紧密贴合距离成正比,与Litz线绝缘层等效介电常数呈正相关。
线圈的品质因数为
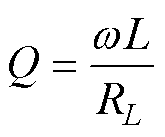 (23)
(23)
在恒定的角频率w 下,线圈的品质因数Q仅取决于线圈的电感和电阻。具体而言,线圈的电感L包括线圈的各匝的自感Lself和各匝间的互感总和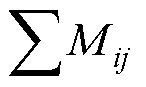 ,而线圈的电阻RL包括直流电阻Rdc、临近效应电阻Rprox以及趋肤效应电阻Rskin。当螺旋线圈采用Litz线绕制时,可以忽略趋肤效应电阻[24]。
,而线圈的电阻RL包括直流电阻Rdc、临近效应电阻Rprox以及趋肤效应电阻Rskin。当螺旋线圈采用Litz线绕制时,可以忽略趋肤效应电阻[24]。
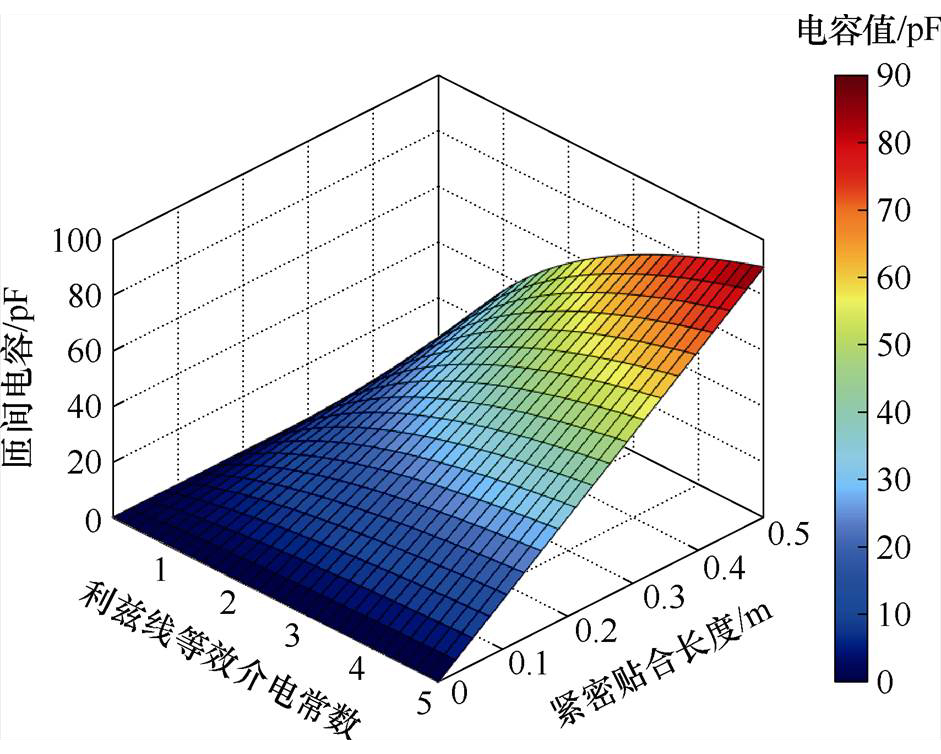
图8 匝间电容与紧密贴合长度和Litz线绝缘层等效介电常数关系
Fig.8 The relationship between inter-turn capacitance and the close fit length, as well as the equivalent dielectric constant of Litz wire insulation
进而线圈的品质因数Q可表示为
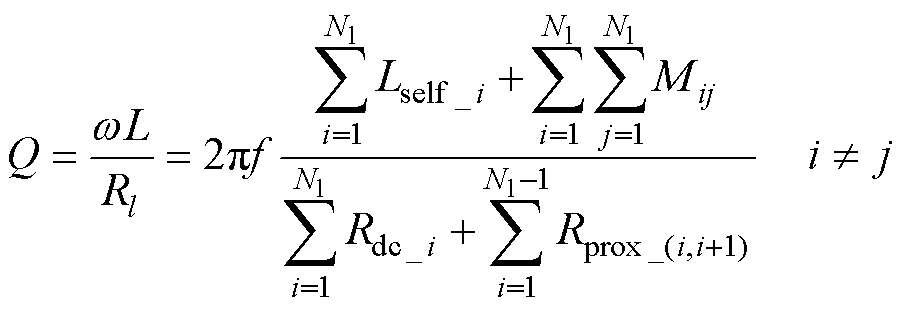 (24)
(24)
由式(24)可知,在一定频率下,线圈的品质因数只与线圈的起始半径DR0、绕制线圈的Litz线直径w和线圈的匝间距s有关。
当选用相同直径w的Litz线以相同的起始半径DR0绕制线圈时,线圈品质因数Q仅与匝间距s相关。线圈匝间距确实会改变线圈的品质因数,但本文只改变了相邻两匝部分长度的匝间距,且匝间距变化的幅度很小,因此对线圈品质因数的影响很小,所以在本文匝间电容的设计过程中可以忽略匝间距对线圈品质因数的影响。
考虑紧密贴合段的电容后,则线圈整体等效电路拓扑如图9所示。图9中,Ln为第n匝线圈未紧密贴合部分自感,Rn为第n匝线圈未紧密贴合部分电阻,LSn为第n匝线圈中紧密贴合部分自感,RSn为第n匝线圈中紧密贴合部分电阻,CSn为剥开绝缘层两匝线紧密贴合段的匝间电容。
当每两匝线圈紧密贴合的长度相同时,为了便于分析计算,忽略各匝间补偿电容的差异,即每段的匝间补偿电容数值相等,则电路可进一步等效为图10所示的拓扑结构。端口阻抗可整理为Z(w)= A+jB的形式,详细推导公式见附录。补偿的目的是使虚部尽可能小。当B=0时,线圈得到完全补偿。
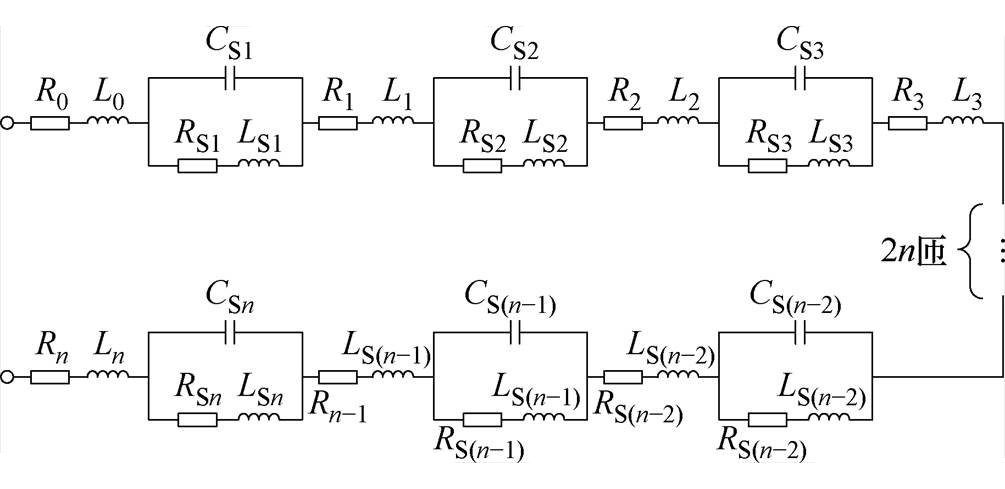
图9 新绕制线圈整体等效电路拓扑
Fig.9 The overall equivalent circuit topology of the newly wound coil
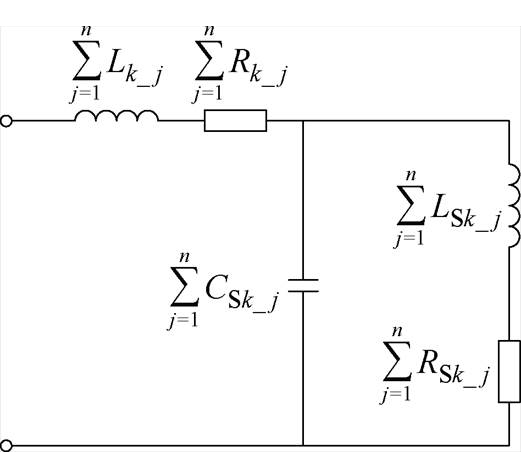
图10 线圈整体串并联电路拓扑等效电路
Fig.10 Equivalent circuit of the overall series-parallel circuit topology of the coil
线圈紧密贴合时,线圈的匝间电容效应明显,利用匝间电容与线圈紧密贴合的长度呈正相关的特性,通过调整两条导线紧密贴合的长度,即可获得相应的匝间电容值,进而实现对线圈的分段补偿。
按照本文所提的设计方法,设计一个接收线圈,使该线圈可以利用匝间电容对线圈本身进行分段补偿,并在频率为500 kHz附近时有较好的补偿效果。线圈的起始半径为7.5 cm,匝数为12,匝间距为1 mm。表1列出了Litz线的具体参数。为了满足线圈分段自补偿的设计要求,将线圈的1/3的弧长进行紧密贴合,以增大两匝导线间的匝间电容值。
表1 Litz线参数
Tab.1 Litz wire parameters
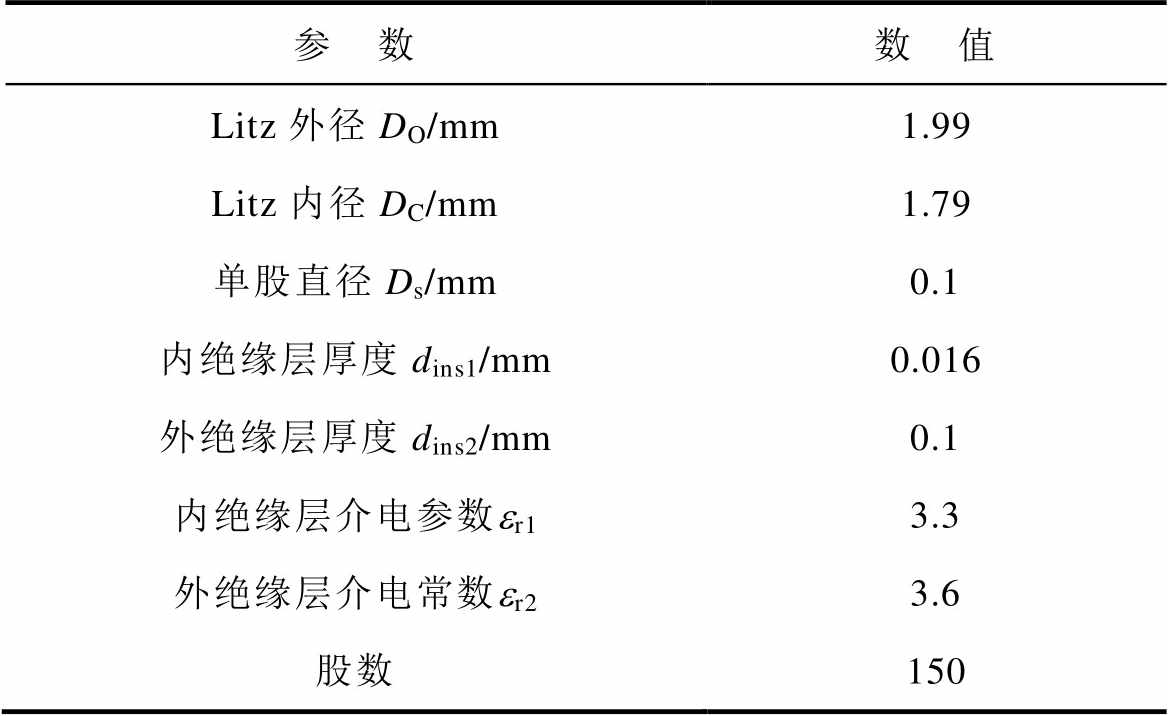
参 数数 值 Litz外径DO/mm1.99 Litz内径DC/mm1.79 单股直径Ds/mm0.1 内绝缘层厚度dins1/mm0.016 外绝缘层厚度dins2/mm0.1 内绝缘层介电参数er13.3 外绝缘层介电常数er23.6 股数150
根据表1中Litz线的具体参数和式(20)可计算出匝间电容值的实际大小和理论值如图11所示。由于紧密贴合的长度不同,各匝间电容值的实际值也略有差异。为了验证匝间电容对线圈的补偿作用,设计了一种对照接收线圈。该线圈采用集中串联电容进行补偿,并实现了全补偿。绕制线圈的材料、规格等各项参数均相同。利用阻抗分析仪对设计的线圈进行阻抗测量,阻抗分析仪型号为nFZGA5920。测量结果如图12所示。由测量结果可知,利用匝间电容可以对线圈进行补偿,在频率为500 kHz附近时有较好补偿效果,说明了本文理论分析的正确性。
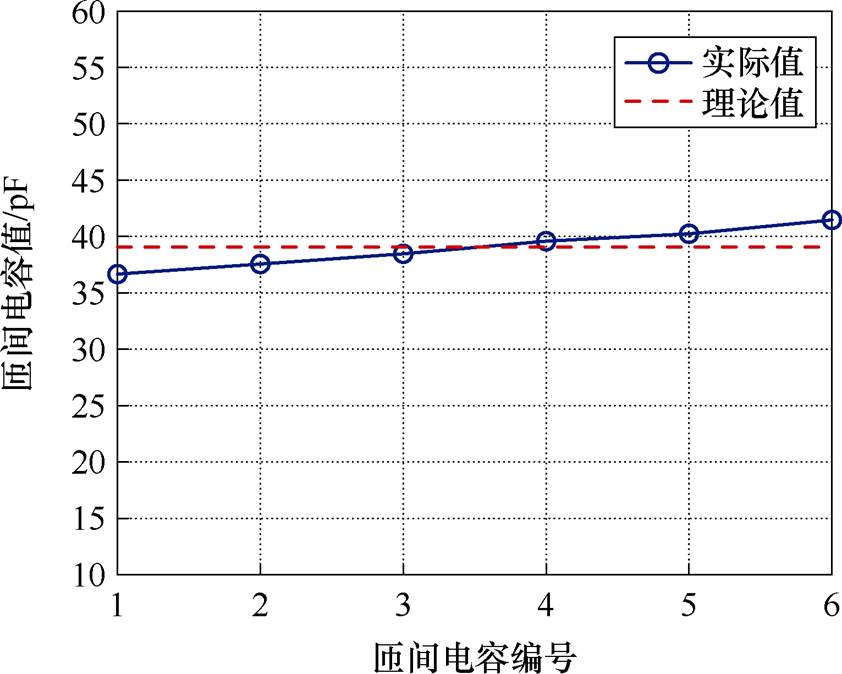
图11 各匝间电容容值
Fig.11 The capacitance of the inter-turn capacitance
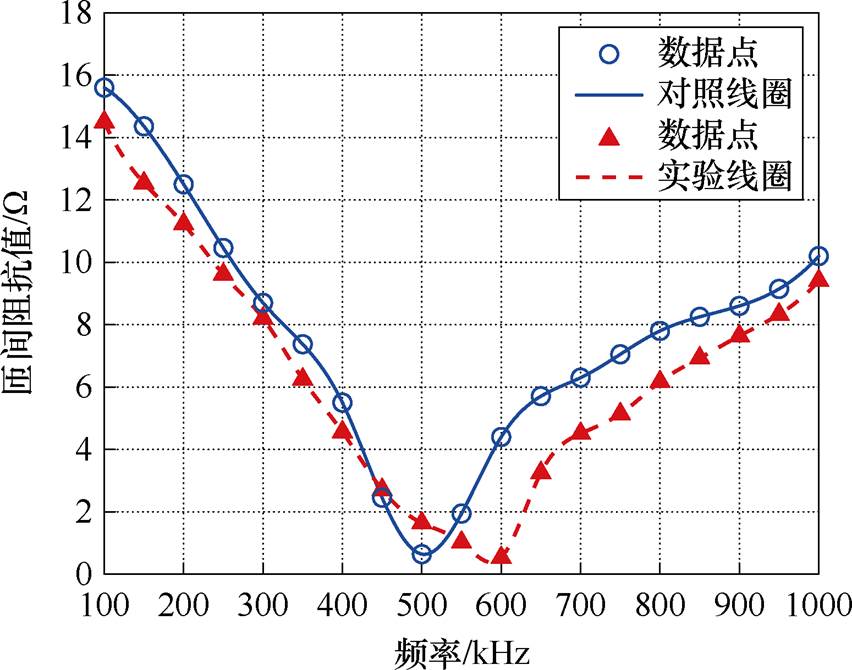
图12 线圈阻抗的测量值
Fig.12 Measured value of coil impedance
为了验证分析方法的正确性,搭建了如图13所示的实验样机。发射线圈被设计成半径为13 cm的圆柱形螺旋线圈,匝数为30。系统采用IRF740作为主功率MOSFET管,系统其他参数见表2。
在相同的输入和负载的条件下,两种补偿方式的线圈在不同距离下的系统的传输效率和接收功率如图14所示。可以看出,匝间电容分段补偿线圈接收到的功率在整个距离范围内均大于外接电容集中补偿线圈的功率。由于分段匝间电容补偿降低了线圈内的电压梯度,使线圈自身的损耗降低,匝间电容分段补偿线圈的传输效率在整个距离范围内也优于外接电容集中补偿线圈的传输效率。
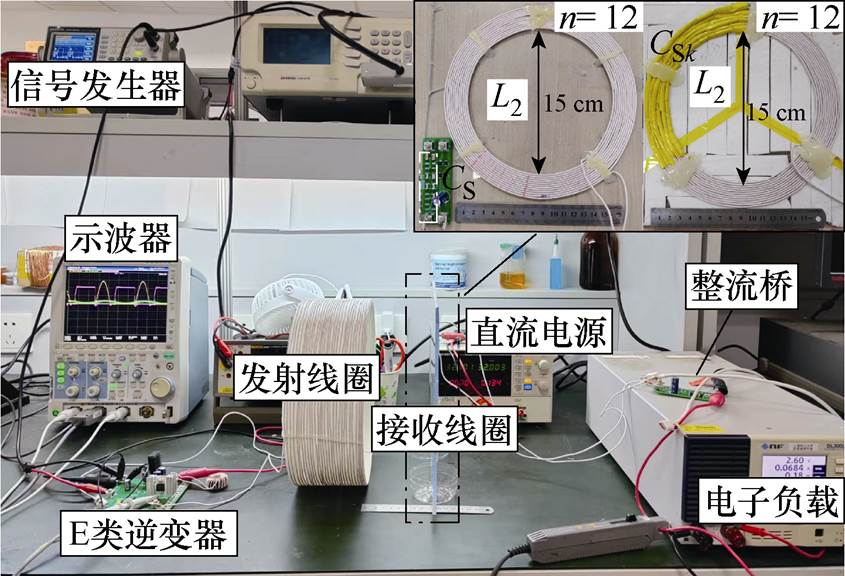
图13 实验原型
Fig.13 Experimental prototype
表2 系统参数
Tab.2 System parameters
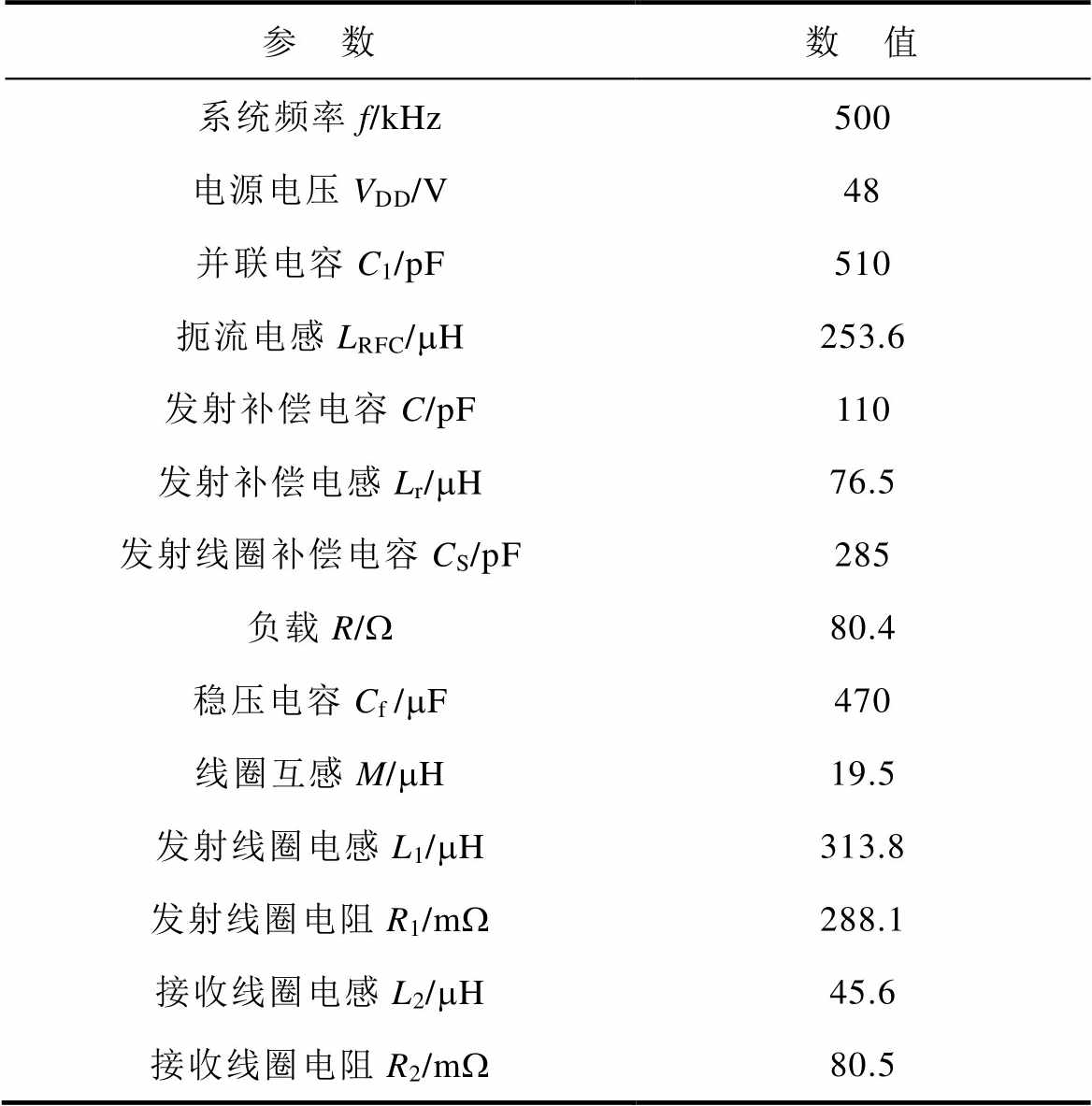
参 数数 值 系统频率f/kHz500 电源电压VDD/V48 并联电容C1/pF510 扼流电感LRFC/mH253.6 发射补偿电容C/pF110 发射补偿电感Lr/mH76.5 发射线圈补偿电容CS/pF285 负载R/W80.4 稳压电容Cf /mF470 线圈互感M/mH19.5 发射线圈电感L1/mH313.8 发射线圈电阻R1/mW288.1 接收线圈电感L2/mH45.6 接收线圈电阻R2/mW80.5
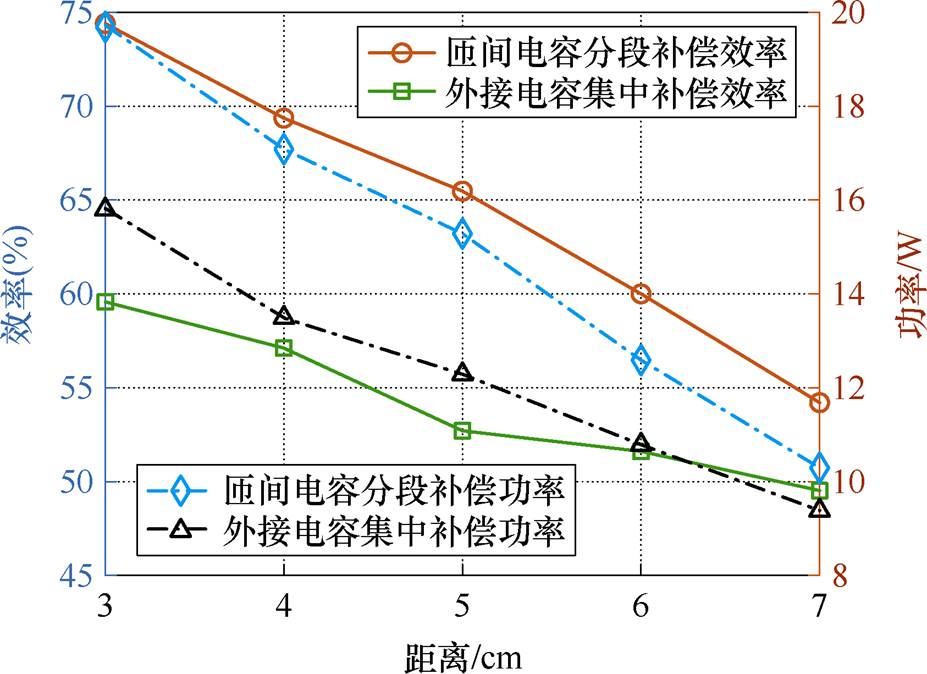
图14 两种补偿方式下系统的效率和功率
Fig.14 System efficiency and power under two compensation methods
在相同的输入和负载条件下,测量了两个线圈的首末两端电压,具体结果如图15所示。由图15可以明显看出,当线圈进行串联电容集中补偿时,导致线圈两端电压显著增大。而采用分段匝间电容补偿时,线圈被分成多个部分进行补偿,线圈首末两端的电压较小。因此,通过分段补偿可以显著降低线圈两端的电压,即降低线圈的电压梯度,从而减少线圈的损耗。
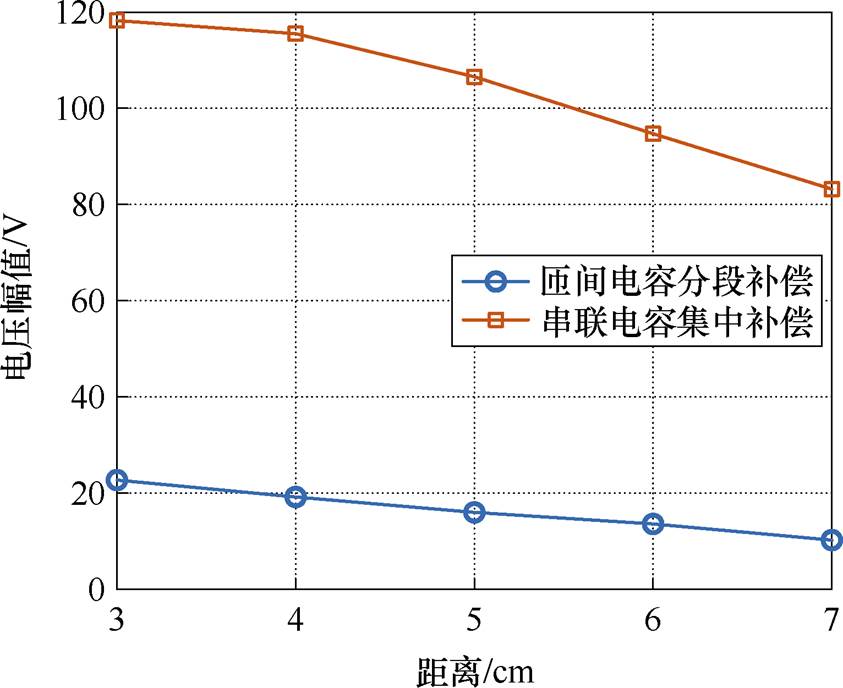
图15 两线圈的首末两端的电压幅值
Fig.15 The voltage amplitude at the beginning and end of the two coils
图16a和图16b分别为外接电容集中补偿和匝间电容分段补偿条件下,传输距离为4 cm时的MOSFET管电压波形。两种补偿方式的实测波形均是在负载为80 W、输入电压为48 V时测量得到。由图16可知,匝间电容分段补偿并不会影响MOSFET管的开关特性,即当利用匝间电容进行分段补偿时,整个系统也处于ZVS状态。这说明利用匝间电容分段补偿在降低线圈匝间电压梯度时,并不会增加其他额外的能量损耗。
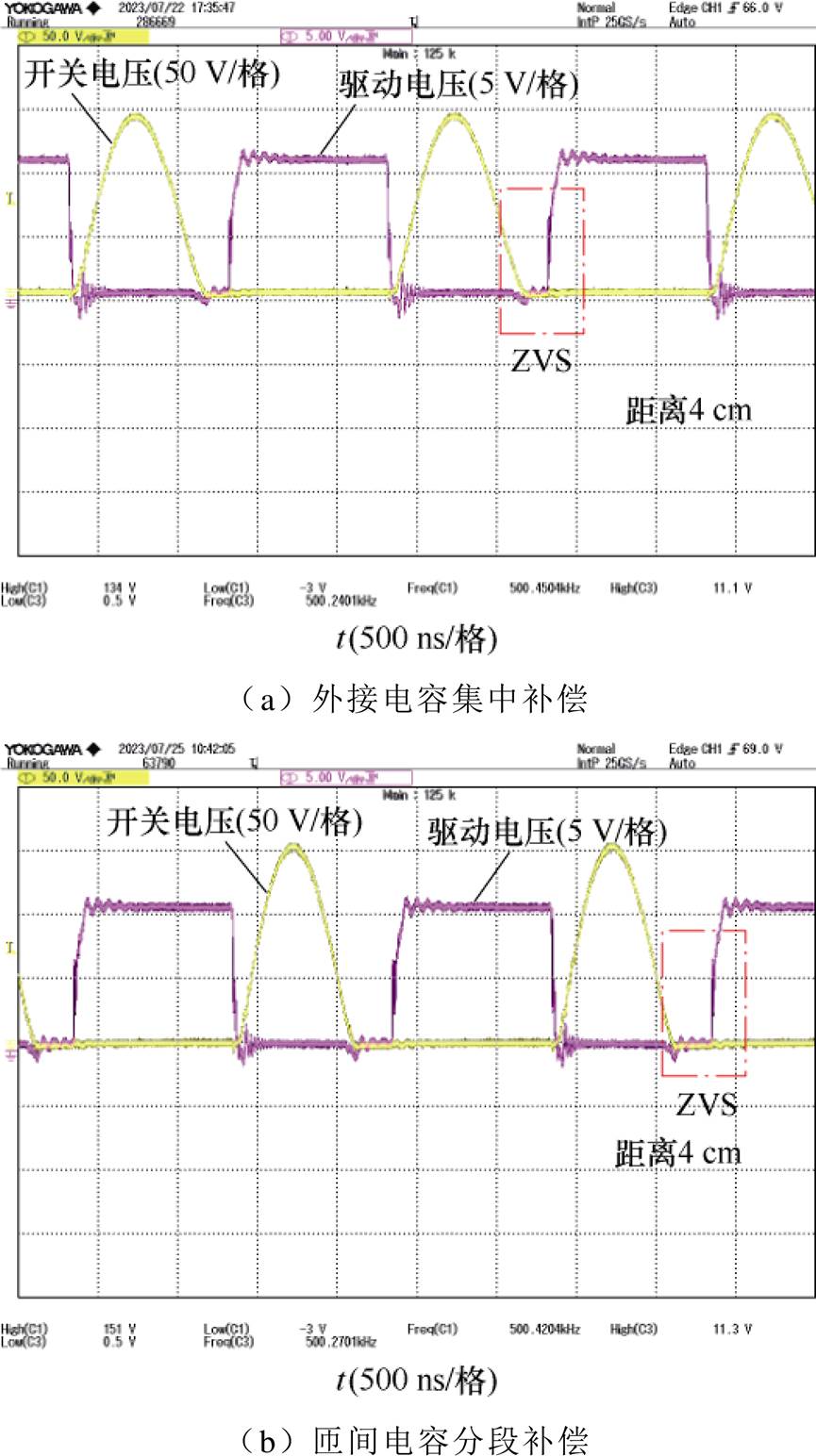
图16 MOSFET管电压波形
Fig.16 MOSFET tube voltage waveforms
图17a和图17b分别展示了外接电容集中补偿接收线圈与匝间电容分段补偿接收线圈系统的损耗占比。分析数据基于实验测量和计算。系统功率损耗来自功率MOSFET管的导通电阻、整流桥二极管的导通压降、线圈的损耗以及其他损耗。由功率损耗分布可知,系统的损耗大部分在两个线圈上,整流桥和功率MOSFET管损耗占比较少。匝间电容补偿由于没有外接电容且采用分段补偿的方式,降低了系统总损耗。
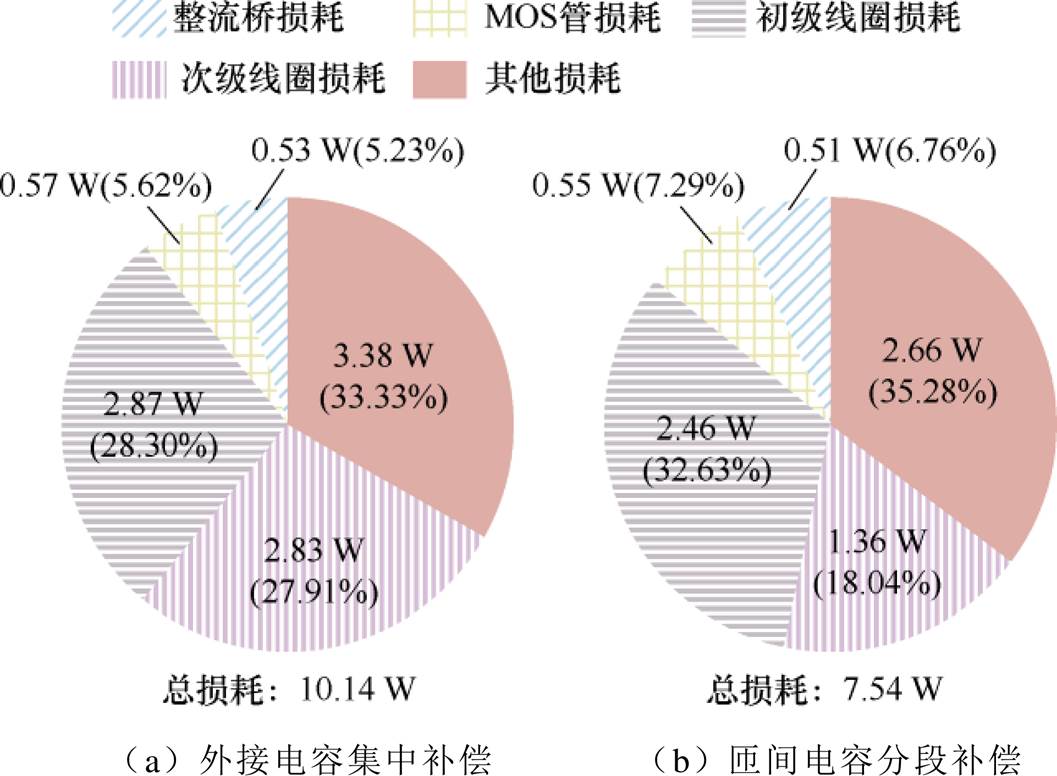
图17 实验系统的功率损耗分布
Fig.17 Power loss distribution of the experiment system
本文针对外接电容导致线圈内部电压梯度较大以及补偿拓扑结构复杂的问题,提出了一种利用匝间电容对线圈分段补偿的方法。利用高频条件下Litz线匝间电容受导线绝缘层介电常数与匝间贴合长度影响明显的特点,通过将部分线圈进行紧密贴合实现线圈匝间电容有效放大,从而使匝间电容可调可控。该方法避免了外接电容带来的拓扑结构复杂性及线圈内部电压梯度较大等问题。对比于外部端接补偿,线圈的匝间分段补偿具有更优的补偿效果。针对本文所提方法进行了定量分析验证并得出以下结论:
1)匝间电容受匝间紧密贴合长度及导线绝缘层介电常数的影响。在导线采用Litz线进行等效分析时,匝间电容在导线紧密贴合长度增加时明显变大,且呈线性增加趋势,匝间电容在绝缘层等效介电常数增大时也显著增加。其匝间电容可实现对线圈的有效补偿。
2)用匝间电容对线圈进行补偿,不仅可以实现对线圈的有效补偿,同时还可以实现对线圈每一匝进行分段补偿的效果。与集中补偿方式相比,分段补偿能够减小线圈内部的电压梯度,降低线圈的电压损耗和能量损失,同时提高线圈的能量接收效率。
附 录
图9中的端口阻抗表示为
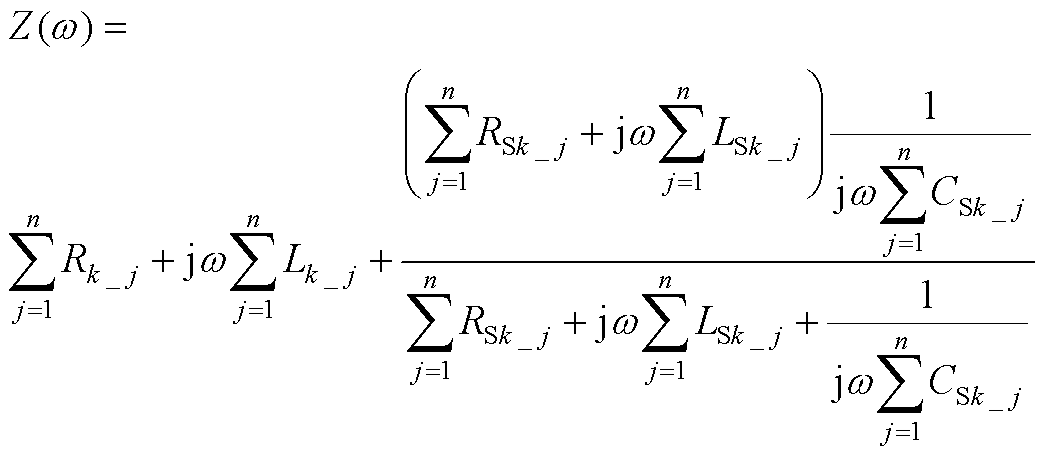 (A1)
(A1)
将其化简为
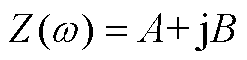 (A2)
(A2)
其中
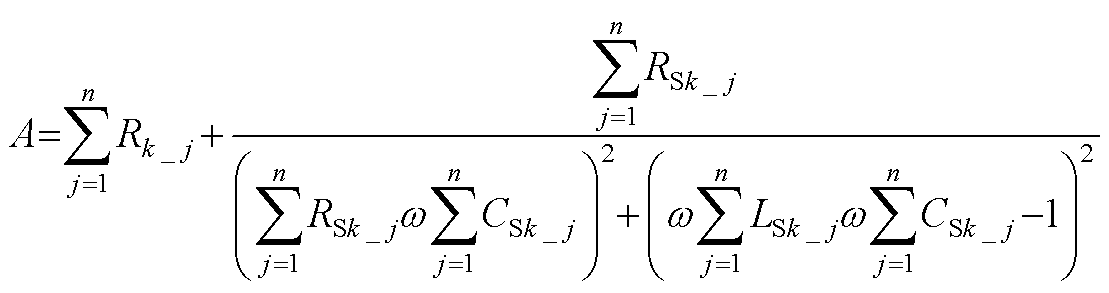 (A3)
(A3)
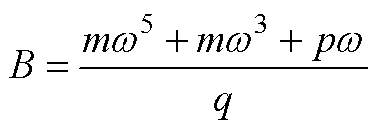 (A4)
(A4)
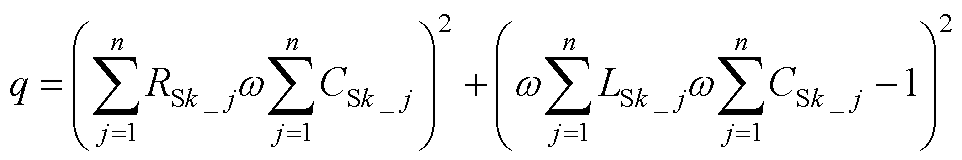 (A5)
(A5)
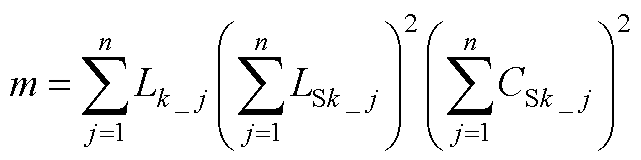 (A6)
(A6)
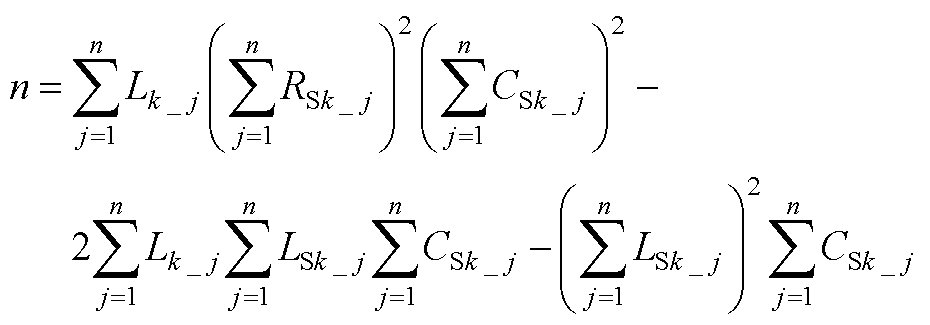 (A7)
(A7)
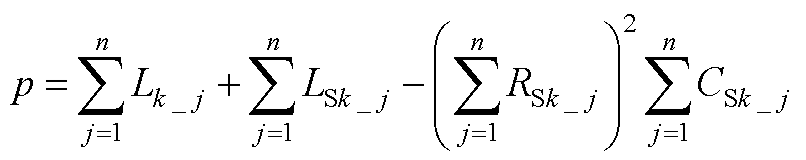 (A8)
(A8)
参考文献
[1] Zhang Zhen, Pang Hongliang, Georgiadis A, et al. Wireless power transfer-an overview[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1044-1058.
[2] 唐丁源, 周玮, 黄亮, 等. 具有恒压输出特性的电场耦合式动态无线电能传输技术[J]. 电工技术学报, 2023, 38(20): 5385-5397.
Tang Dingyuan, Zhou Wei, Huang Liang, et al. Dynamic electric-filed coupled wireless power transfer system with constant voltage output characte- ristics[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5385-5397.
[3] 李争, 唐明磊, 解波, 等. 无线电能传输零电压开关角跟踪和动态电容补偿矩阵复合控制策略[J]. 电工技术学报, 2024, 39(12): 3602-3615.
Li Zheng, Tang Minglei, Xie Bo, et al. Wireless power transmission zero-voltage switching angle tracking and dynamic capacitance compensation matrix compound control strategy[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3602- 3615.
[4] 瓦列里·扎维亚洛夫, 伊琳娜·塞米金娜, 叶夫根尼·杜布科夫, 等. 具有LC串联补偿拓扑结构的无线充电系统的约束效率优化[J]. 电工技术学报, 2024, 39(6): 1627-1642.
Valery Zavyalov, Irina Semykina, Evgeny Dubkov, et al. Constraint efficiency optimization of wireless charging system with LC series compensation topology[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1627-1642.
[5] 田勇, 杨昊, 胡超, 等. 基于毫米波雷达的电动汽车无线充电运动异物检测与跟踪[J]. 电工技术学报, 2023, 38(2): 297-308.
Tian Yong, Yang Hao, Hu Chao, et al. Moving foreign object detection and track for electric vehicle wireless charging based on millimeter-wave radar[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 297-308.
[6] 徐先峰, 吴慧玲, 杨雄政, 等. 空间约束下电动汽车无线充电系统磁耦合结构优化[J]. 电工技术学报, 2024, 39(12): 3581-3588.
Xu Xianfeng, Wu Huiling, Yang Xiongzheng, et al. Optimization of magnetic coupling structure of wireless charging system for electric vehicle under space constraints[J]. Transactions of China Elec- trotechnical Society, 2024, 39(12): 3581-3588.
[7] 陈志鑫, 张献, 沙琳, 等. 基于频率调节的电动汽车无线充电互操作性提升方法研究[J]. 电工技术学报, 2023, 38(5): 1237-1247.
Chen Zhixin, Zhang Xian, Sha Lin, et al. Research on improving interoperability of electric vehicle wireless power transfer based on frequency adjustment[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1237-1247.
[8] 李阳, 安张磊, 孟航, 等. 基于双耦合线圈的无人机轻量化无线充电耦合机构设计[J]. 电源学报, 2023, 21(6): 168-175.
Li Yang, An Zhanglei, Meng Hang, et al. Design of lightweight wireless charging coupling mechanism for UAVs based on dual coupling coils[J]. Journal of Power Supply, 2023, 21(6): 168-175.
[9] 闫争超, 胡谦宇, 赵晨旭, 等. 水下航行器感应式无线电能传输技术研究综述[J]. 中国电机工程学报, 2023, 43(24): 9668-9681.
Yan Zhengchao, Hu Qianyu, Zhao Chenxu, et al. Review on inductive wireless power transfer tech- nology for underwater vehicles[J]. Proceedings of the CSEE, 2023, 43(24): 9668-9681.
[10] Li Weihan, Zhang Qianfan, Cui Chao, et al. A self- tuning S/S compensation WPT system without parameter recognition[J]. IEEE Transactions on Industrial Electronics, 2022, 69(7): 6741-6750.
[11] 田子涵, 张雪莹, 王钰博, 等. 可实现接收端轻量化和抗短路的无线充电系统LCC-S补偿参数配置方法[J]. 中国电机工程学报, 2023, 43(18): 7223-7231.
Tian Zihan, Zhang Xueying, Wang Yubo, et al. LCC-S compensation parameter configuration method for wireless charging system capable of realizing light weight and short circuit resistance at receiving end[J]. Proceedings of the CSEE, 2023, 43(18): 7223-7231.
[12] 刘旭, 宋翔昱, 原熙博, 等. 一种利用可切换补偿电容的三线圈无线电能传输系统互感识别及效率优化方法[J]. 中国电机工程学报, 2022, 42(22): 8309-8320.
Liu Xu, Song Xiangyu, Yuan Xibo, et al. A mutual inductance identification and efficiency optimization method for the three-coil wireless power transfer system by utilizing switchable compensation capacitor[J]. Proceedings of the CSEE, 2022, 42(22): 8309-8320.
[13] Sohn Y H, Choi B H, Lee E S, et al. General unified analyses of two-capacitor inductive power transfer systems: equivalence of current-source SS and SP compensations[J]. IEEE Transactions on Power Elec- tronics, 2015, 30(11): 6030-6045.
[14] 王党树, 董振, 古东明, 等. 基于双边LCL变补偿参数谐振式无线充电系统的研究与分析[J]. 电工技术学报, 2022, 37(16): 4019-4028.
Wang Dangshu, Dong Zhen, Gu Dongming, et al. Research and analysis of resonant wireless charging system based on bilateral LCL variable compensation parameters[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4019-4028.
[15] Fu Na, Deng Junjun, Wang Zhenpo, et al. A hybrid mode control strategy for LCC-LCC-compensated WPT system with wide ZVS operation[J]. IEEE Transactions on Power Electronics, 2022, 37(2): 2449-2460.
[16] Jing Yongzhi, Feng Wei, Qiao Ke, et al. Simultaneous wireless power and data transfer system with full- duplex mode based on LCC/CLC resonant network[J]. IEEE Transactions on Power Electronics, 2023, 38(4): 5549-5560.
[17] Zeng Yufeng, Qiu Dongyuan, Meng Xiangtian, et al. Optimized design of coils for wireless power transfer in implanted medical devices[J]. IEEE Journal of Electromagnetics, RF and Microwaves in Medicine and Biology, 2018, 2(4): 277-285.
[18] Mai Jianwei, Wang Yijie, Zeng Xianrui, et al. A multi-segment compensation method for improving power density of long-distance IPT system[J]. IEEE Transactions on Industrial Electronics, 2022, 69(12): 12795-12806.
[19] Wang Qingsong, Ali Saket M, Troy A, et al. A self- compensated planar coil for resonant wireless power transfer systems[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 674-682.
[20] Lee Y D, Kim K W, Moon G W. A self-compensated planar coil with integrated single-switch regulator for wireless power transfer (WPT) systems[J]. IEEE Transactions on Power Electronics, 2021, 36(10): 10954-10958.
[21] Zhang Junwei, Zhao Jinbin, Mao Ling, et al. ZVS operation of class-E inverter based on secondary side zero compensation switching at variable coupling coefficient in WPT[J]. IEEE Transactions on Industry Applications, 2022, 58(1): 1022-1031.
[22] Biela J, Kolar J W. Using transformer parasitics for resonant converters-a review of the calculation of the stray capacitance of transformers[J]. IEEE Transa- ctions on Industry Applications, 2008, 44(1): 223- 233.
[23] 许伟, 赵争鸣, 姜齐荣. 高频变压器分布电容计算方法[J]. 清华大学学报(自然科学版), 2021, 61(10): 1088-1096.
Xu Wei, Zhao Zhengming, Jiang Qirong. Calculation method for parasitic capacitance of high-frequency transformers[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(10): 1088-1096.
[24] Lu Ming, Ngo K D T. Analytical calculation of proximity-effect resistance for planar coil with Litz wire and ferrite plate in inductive power transfer[J]. IEEE Transactions on Industry Applications, 2019, 55(3): 2984-2991.
Design and Analysis of Segmental Compensation Coils Utilizing Inter-Turn Capacitance in Wireless Power Transfer Systems
Abstract The rapid development of power electronics technology and wireless power transmission (WPT) has broadened application prospects in consumer electronics and traditional fields like electric vehicles, implantable medical devices, and autonomous underwater vehicles. The unique nature of wireless charging scenarios often results in significant variations in transmission distance, causing rapid drops in coupling coefficient and transmission efficiency. Therefore, coil compensation is an important research area of WPT. This paper proposes a segmented coil compensation method using inter-turn capacitance to solve increased internal voltage gradients in coils caused by traditional external capacitor compensation methods. By closely fitting the adjacent turns of the receiving coil, the capacitance of the closely fitting section is increased, thereby achieving coil compensation. The coil is divided into several segments, with inter-turn capacitance to compensate for each segment.
First, the advantages of segmented coil compensation are derived using rigorous circuit theory. Next, equivalent modeling and calculation of the Litz wire wound coil are performed to analyze the factors influencing the size of the inter-turn capacitance. Finally, the overall coil with inter-turn capacitance segmented compensation is modeled, and the port impedance of the entire coil is calculated. The inter-turn capacitance of the closely fitting coil segments increases significantly, effectively replacing the external capacitors for compensation. Compared to external capacitor compensation topologies, the proposed segmented compensation topology can reduce the internal voltage gradient of the coil, voltage loss, and energy dissipation. Accordingly, the energy reception efficiency of the coil is improved. Additionally, this structure is compact, with a small size and cost.
An experimental coil is compared with a coil using external capacitor compensation. Under the same input and load conditions, the receiving power of the coil with the proposed segmented compensation is increased by 54.3%, and efficiency is improved by 27.6%, which verifies the proposed method.
The following conclusions can be drawn. (1) The tight alignment length of the turns and the dielectric constant of the wire insulation layer influence the inter-turn capacitance. When Litz wire is used for equivalent analysis, the inter-turn capacitance increases significantly with the tight alignment length and shows a linear growth trend. The capacitance also increases significantly as the equivalent dielectric constant of the insulation layer increases, effectively compensating the coil. (2) Inter-turn capacitance compensation provides adequate compensation. Compared to traditional concentrated compensation methods, the proposed segmented compensation reduces the internal voltage gradient of the coil, decreases voltage losses and energy dissipation, and enhances the energy reception efficiency of the coil.
keywords:Wireless power transfer, inter-turn capacitance, segment compensation, voltage gradient
中图分类号:TM614
DOI: 10.19595/j.cnki.1000-6753.tces.240951
上海市自然科学基金资助项目(21ZR1425300)。
收稿日期 2024-06-04
改稿日期2024-08-19
孔德乐 男,1999年生,硕士研究生,研究方向为无线充电线圈以及线圈补偿。
E-mail: kdI990619st@mail.shiep.edu.cn
赵晋斌 男,1972年生,教授,博士生导师,研究方向为电力电子电路、装置和系统、智能和模块化控制电力电子电路、能量转换控制和拓扑和可再生能源发电。
E-mail: zhaojinbin@shiep.edu.cn(通信作者)
(编辑 陈 诚)