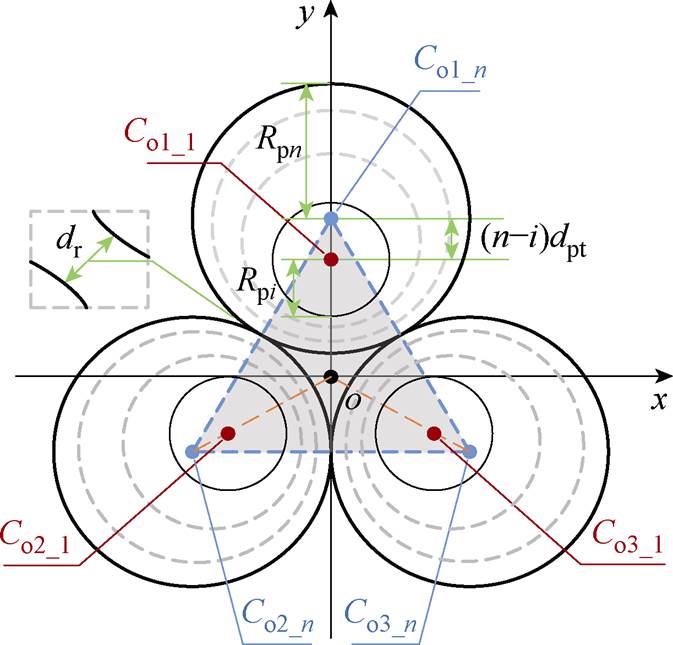
图1 矩阵线圈WPT系统的NEU耦合机构
Fig.1 NEU coupling mechanism structure of matrix coil WPT system
摘要 在近场无线电能传输(WPT)系统中,磁场的紧凑性可以更好地增加能量传输距离。该文以提高中心区域的磁通密度为目标,提出一种基于非中心对称激励单元(NEU)的矩阵耦合机构设计方法,该方法在几乎不削弱自身抗偏移能力的情况下,仅依托二维平面结构增强了磁聚焦性能,而且无需额外的辅助线圈或电路。此外,与传统设计方法相比,在相同尺寸和匝数下该设计方法中的初级线圈自感值更小,其互感利用率更高。该文提出一种基于耦合热度矩阵的空间有效充电面/体积计算方法,用以评估不同矩阵耦合机构的空间供电能力。最后,以LCL-LCC补偿WPT系统作为实例,验证所提出设计方法的可行性,根据提供的磁场仿真和实验结果表明,所提出设计方法相较于传统设计方法在最佳位置处可使感应电压提高24.7%。
关键词:无线电能传输系统 多激励单元 磁聚焦增强 空间传输能力评估方法
当前移动机器人无人机(Unmanned Aerial Vehicle, UAV)/无人车(Automated Guided Vehicle, AGV)/在工业巡检、办公物流、农林植保及军事侦察监视等领域扮演了重要角色[1-4]。目前,有智能园区、工业巡检等场所设计了一套多级多模态供电的示范应用,实现不同无人设备之间的充电对接,但这种示范应用采取的供电方式大多采取定点充电,多级供电方式传能环节较为繁琐,且会面临较多能量流失问题。在野外、水下等特殊充电环境若没有合适的停机充电坪条件,UAV的悬停充电技术则成为最需完善的充电方案,也是构建无线供电传输网应用环境的关键。在空对空、地对地、空对地的无人巡检设备定点悬停、悬停跟随的技术已经十分完善的基础上,悬停补能/对准补能无疑是应用于无人巡检设备的一种非常高效且前沿的设计思路。为进一步提升无线充电系统的灵活性、可靠性,越来越多的无线充电系统基于矩阵线圈进行设计,矩阵式多激励无线充电系统以其发射端对磁场的重构机制以及对电压和电流应力更强的容忍度等特性,获得了更多充电应用产品的青睐[5-7]。
然而,由于线圈数量较多,目前矩阵线圈设计均基于规则版图排布,并未从单元关联及整体传能机制上进一步设计提升传输距离的方法,此外多激励单元背景下的空间供电能力描述及评估尚未完善。利用多线圈的特性来增强能量发射机构的磁聚焦能力显得尤为重要,同时提供成熟的传输能力评估方法是本文的研究目标。当前,提升无线电能传输(Wireless Power Transfer, WPT)系统的近场磁聚焦特性的研究主要集中在以下两个方面:
(1)耦合机构设计[8-11]:文献[8]研究了亚波长聚焦近场阵列与旨在最大化功率传输效率的阵列设计之间的关系;文献[9]提出了一种使用两层平面回路阵列谐振器进行高效近场波束成形的磁共振无线电能传输方法;文献[10]通过将复合谐振中的补偿电感加入磁集成的装置设计中,实现磁通密度的提升;文献[11]通过多物理场软件,对不同类型线圈、不同线圈排列结构的磁场聚焦特性进行仿真,并通过角度、距离、尺寸的逐级优化,分析其磁场聚焦特性,最终得到一种结构简单、可靠性高的线圈结构。
(2)基于传输目标的靶向控制器设计[12-14]:文献[12]提出基于互感识别及移相角优化的全方位WPT系统靶向传能方法,通过互感识别间接判断出“靶”(即接收线圈)的方位,通过移相角优化获得靶向传能所需的激励电流;文献[13]探讨了基于选择性磁共振耦合的无线电能传输系统,该系统能够通过聚焦目标接收器来更好地控制功率分布,同时抑制非目标接收器的能量泄漏;文献[14]通过调控多个初级线圈的激励电流相位,从而使磁场塑形,有效改善系统的效率。以上方法在增强磁聚焦能力方面表现良好,尤其是在使用目标控制器时。然而,当需要植入大量电压和电流检测电路时,系统会变得过于复杂。通过耦合机构优化磁聚焦能力的方法减少了控制复杂度,但大多数方法基于三维结构,这增加了线圈布置的成本和复杂性。总之,当前仍缺乏低成本的解决方案,以显著提升近场磁聚焦效果。
另一方面,对于设计好的系统评估耦合机构的空间充电性能也是影响设计过程的关键步骤。目前,WPT系统构建的综合指标主要集中在传输距离、输出特性、偏移容忍度等方面。文献[15]观察了主线圈电流的谐波分析、传输功率分析以及高速下整体系统性能。文献[16]提出了一种针对感应无线电能传输系统的性能评估程序,重点关注功率和效率,并采用三维有限元模型进行分析。文献[17]则考察了考虑高效率和尺寸的无线电能传输补偿拓扑结构的性能。此外,通过为静态电动车无线充电开发指标体系,构建了一个两步综合评估模型,指标的因素及子因素的权重通过层次分析法得出。当前的评估系统在一定程度上通过构建物理场仿真软件和电路模型反映了系统的电磁特性和输出性能,但尚缺乏计算有效充电空间面积的具体方法。为了扩展充电区域并提高错位容忍度,文献[18-23]提出了各种方法,但往往在同一功率水平下失去了某个充电空间的数据饱和度。因此,基于不同耦合机构设计通用的有效充电区域和有效充电体积计算方法,将极大地改善评估指标体系。
本文提出了一种基于非中心对称激励单元(Non- centrosymmetric Excitation Unit, NEU)的矩阵线圈设计方法,结合耦合热矩阵描述的系统空间场传输能力评估来完善优化设计步骤,以显著增强磁场的聚焦能力。这一设计方法基于二维平面结构,巧妙地在不增加任何辅助线圈或电路的情况下,提升了中心位置的磁通密度。同时,在尽可能避免削弱矩阵线圈自身偏移容忍度的情况下,考虑降低线圈单元的自感值以提升互感利用率。本文描述了系统的构成及其建模过程。深入探讨了非中心对称耦合机构的设计原理,并阐明其如何有效地提升磁场聚焦性能。此外,还提供了的磁场计算结果与对比分析,展示了一种基于耦合热矩阵的空间充电区域估算方法。最后,构建了一个经过精确补偿的LCL-LCC WPT系统,以验证理论分析的可行性。
传统的矩阵线圈布局通常具有均匀性和可重复性。从磁场的角度来看,单元线圈和矩阵线圈构建的磁场深度几乎没有差异。因此,增强单元线圈之间的紧密度是实现磁聚焦的关键。
以三初级线圈架构为例,整个耦合机构呈现出中心对称的特性,内环线圈与传统的均匀绕组方式不同。通过加紧内环线圈,系统中心部分的磁场强度得以增强。根据图1所示的矩阵线圈WPT系统的NEU耦合机构,多个激励线圈矩阵中的每个初级线圈参数相同。系统参数设置如下:n为线圈的匝数,Rpi为第i匝初级线圈的半径(i=1, 2,…, n),dpt为Rp1与Rpn之间的距离,而dst为Rs1与Rsn之间的距离,dr为两个初级线圈之间的距离,dwire为导线直径。Rsi为第i匝次级线圈的半径。Coi为每个圆的中心,其坐标在图1中已标注。与传统矩阵线圈布局相比,所提方法将每个线圈单元的匝数向中心位置紧凑排列。在图1的基础上,建立一个笛卡尔坐标系。对于尺寸已确定的线圈单元,三个中心点Co1_n、Co2_n、Co3_n的坐标可分别表示为

图1 矩阵线圈WPT系统的NEU耦合机构
Fig.1 NEU coupling mechanism structure of matrix coil WPT system
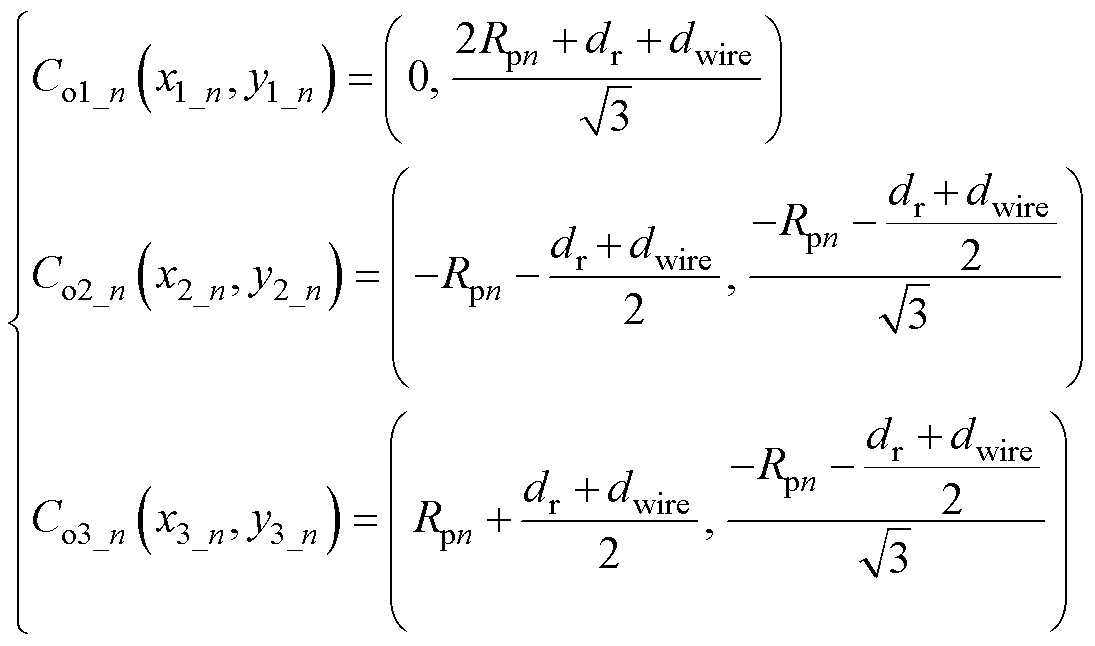 (1)
(1)
为了确保线圈单元中的每一匝都可以以等距内缩的形式排列在初级线圈中,匝间距离为dpt,可以计算得到第i匝线圈单元的中心坐标为

同时,由图1可以看出,中心圆各圆心Coi_1在满足等距离内缩的情况下,存在绕制的极限。对于外径为Rpn的线圈,其第i匝线圈的半径可以表示为
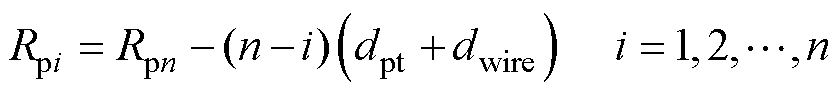 (3)
(3)
为保证中心圆线圈在满足等长dpt内缩的情况下有足够的空间绕制成圆,第一匝线圈的尺寸需要满足
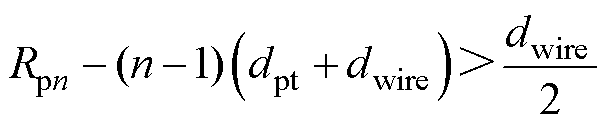 (4)
(4)
每一匝线圈的轨迹方程为
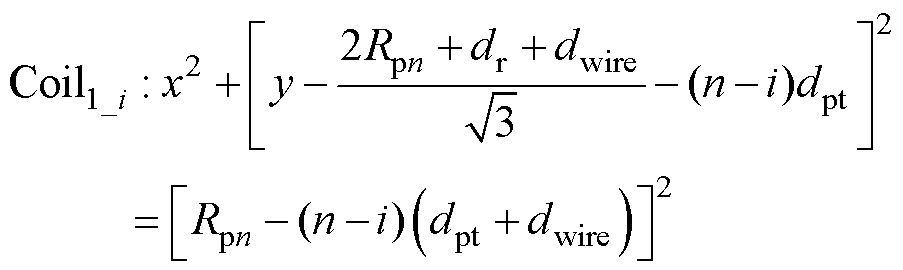 (5)
(5)
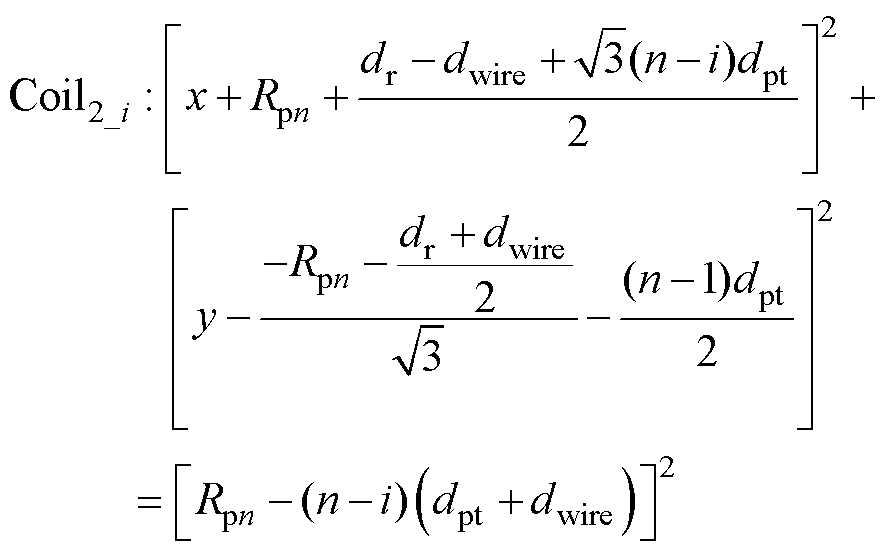 (6)
(6)
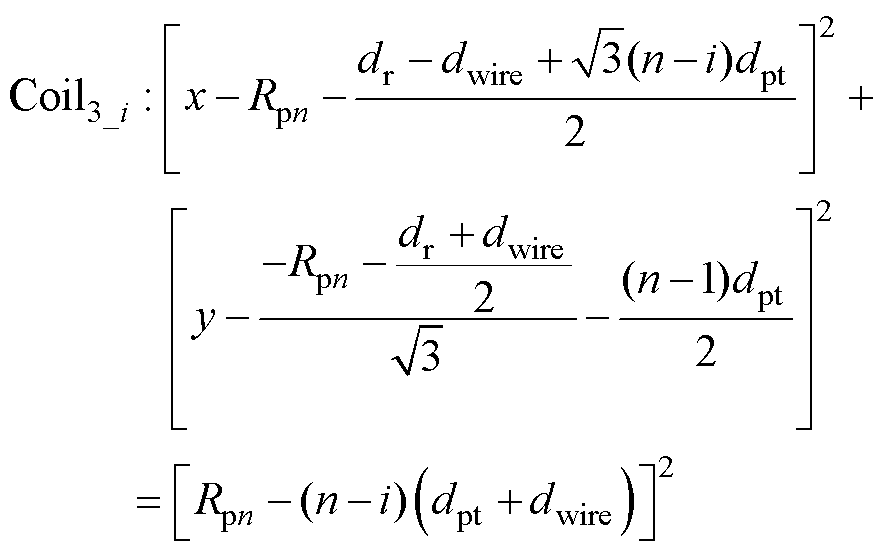 (7)
(7)
式中,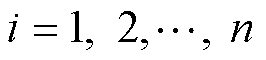 。
。
以线圈1为例,根据纽曼公式,两个不同载流导线间的互感Mij可以表示为
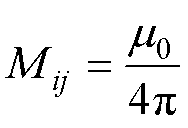
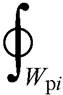
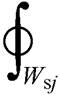
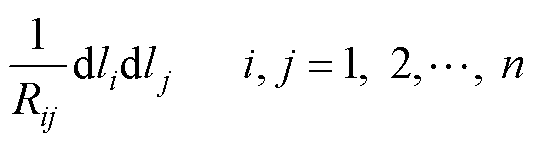 (8)
(8)
式中,Wpi为初级线圈的第i匝;li为线圈Wpi轨迹方程;Wsj为次级线圈的第j匝;lj为线圈Wsj的轨迹方程。线圈1位于xOy平面上,假设次级线圈的高度为z,Rij为li和lj之间的距离,可以表示为
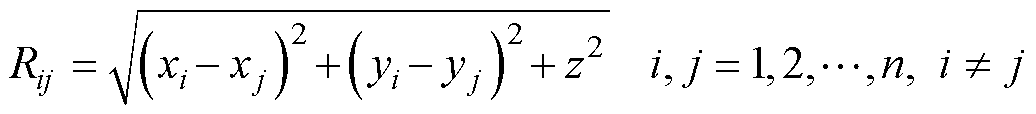 (9)
(9)
系统电路原理如图2所示。图2中,Lpi为初级线圈,Ls为次级线圈,RLpi和RLs分别为它们的内阻,Cpi为初级电容,Cs为次级串联补偿电容,Csr为次级并联补偿电容,Lri为补偿电感,RLri为Lri的内阻,Lsr为次级补偿电感,RLsr为其内阻,S1~S4为全桥逆变器的开关。ipi和is分别为流经初级线圈和次级线圈的电流,isr为整流桥的输入电流,uin为逆变器输出的方波电压,us为整流电路的输入电压,Cr为滤波电容,Ro为负载。
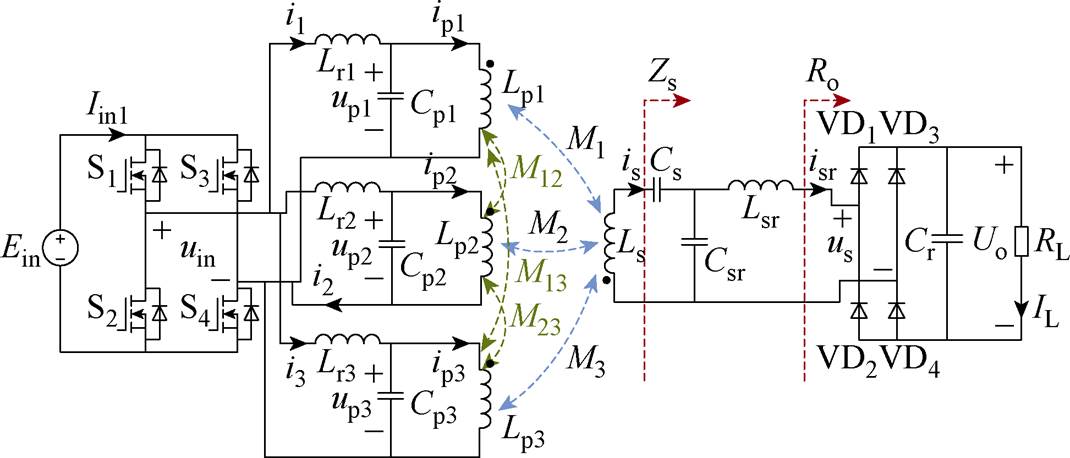
图2 系统电路原理
Fig.2 System circuit schematic
为了平衡磁场分布,每个初级线圈在多激励线圈矩阵中具有相同的参数。系统参数设定为:Cp1=Cp2=Cp3,Lp1=Lp2=Lp3,RLp1=RLp2=RLp3。以LCL-LCC型拓扑为例,初级和次级工作频率在相同的角频率w 下运行。
根据基尔霍夫电压定律,电流与电压之间的关系可以推导为
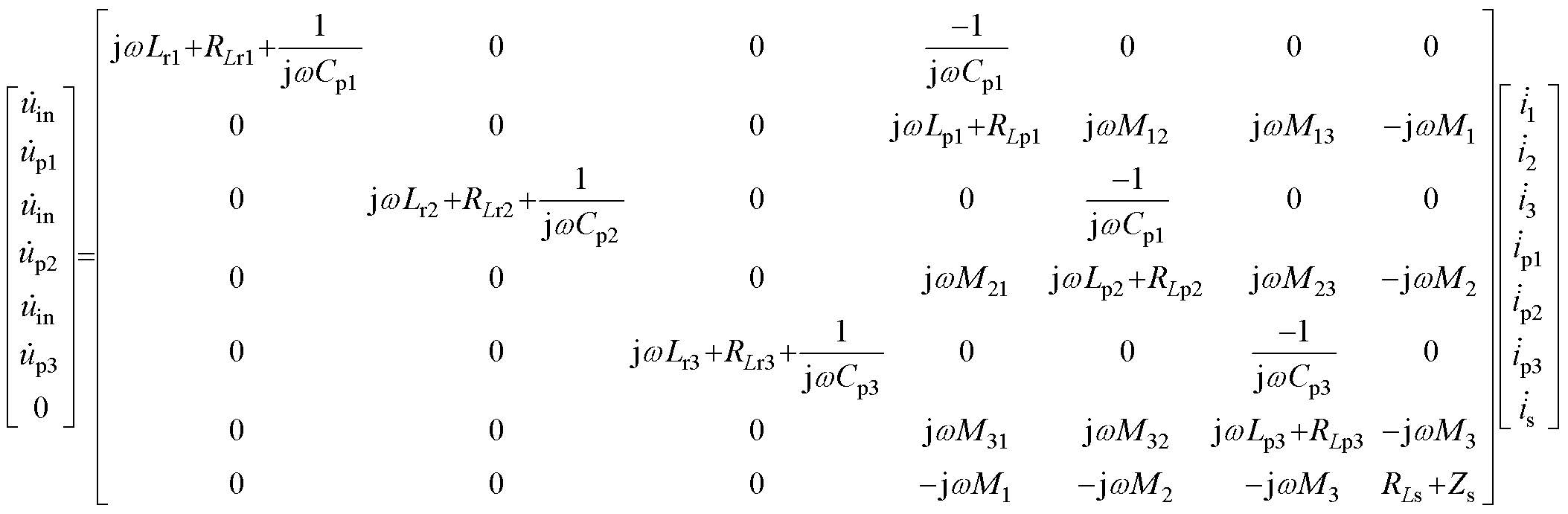 (10)
(10)
式中,Ro=8RL/p2;Zs为次级等效阻抗,Zs=Lsr/Csr·(8RL/p2+RLsr)。初级和次级工作频率在相同的角频率w 下运行,w 为
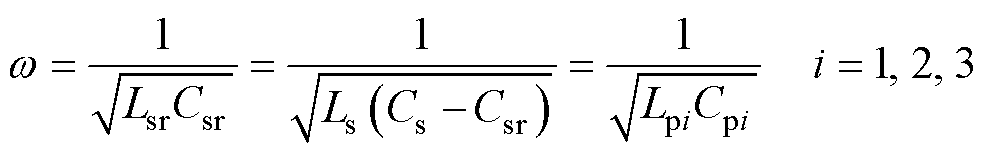 (11)
(11)
由于初级补偿电感的寄生电阻较小,忽略RLr1、RLr2和RLr3以简化方程式(10),可以得到输入电流方程为
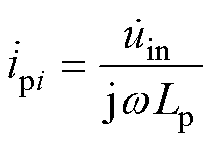 (12)
(12)
LCL复合谐振网络具有较好的鲁棒性,对于负载的动态变化具有良好的恒流特性,因此从系统的整机输出功率角度来说,交叉互感的大小对其几乎无影响,因此初级谐振电流is可表示为
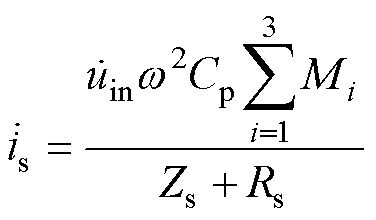 (13)
(13)
可以观察到在参数匹配良好的情况下,次级的感应电压随着激励单元的增加而增加。对于方程式(12)和式(13),当激励单元的输入电压一致时,谐振电流是相等的。在确保同相激励电流的条件下,可以得到系统功率Pout的表达式为
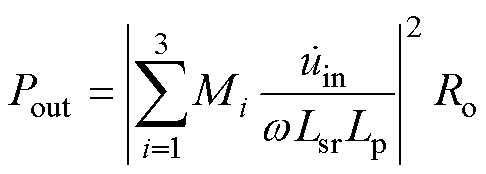 (14)
(14)
根据互感方程式(8)和图1,可以推断互感函数Mi与可变空间位置相关。设第i个初级线圈的坐标为 (xi, yi, 0),次级线圈的坐标为 (xs, ys, zs)。可以通过使用感应电压方程式(13)获得任意位置的功率分布面函数P(xs, ys, zs)为
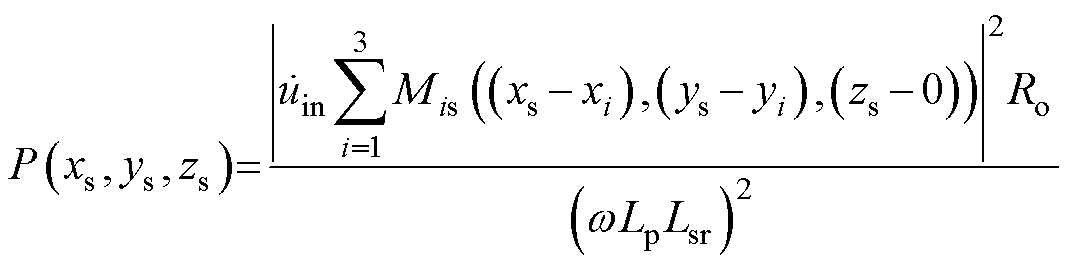 (15)
(15)
在传统设计方法中,为了降低使用导线的成本,初级线圈通常采用中空圆形结构,每个单元线圈呈现中心对称形状。实际上,传统设计方法导致空间中的磁场分布不够紧凑。为了获得更好的磁聚焦性能,需要对线圈的每一匝进行重新优化,确保其在二维平面上的合理布局。所提方法的设计流程如图3所示。
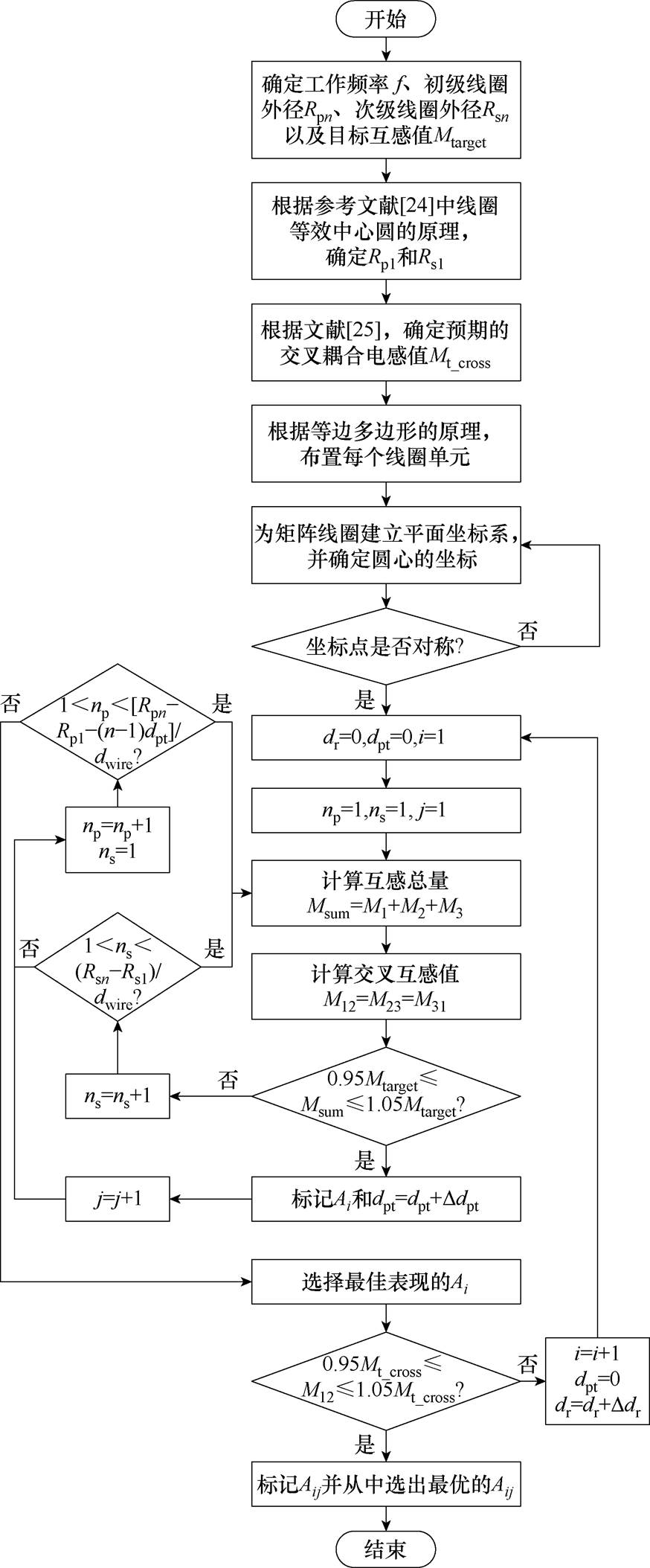
图3 NEU矩阵线圈设计流程
Fig.3 Flowchart for the design of NEU matrix coils
所提设计方法的优化步骤如下:
(1)根据充电环境和工作指标,确定工作频率f、初级线圈外径Rpn、次级线圈外径Rsn,以及目标互感值Mtarget。
(2)根据文献[24]针对线圈耦合模型的建立以及文献[27-28]对于传输距离和性能调试的研究现状可知,通过传输距离与耦合机构尺寸的比例来评估系统传输能量的舒适圈,对于kHz的WPT系统,径距比在0.7以下为耦合舒适区,当径距比为1时,WPT系统的传输能力达到了极限。通常情况下,当传输距离小于等于初级、次级线圈最小线圈尺寸的时候系统性能较优,以此确定Rp1和Rs1。
(3)考虑基于互建模的交叉耦合影响[25],确定交叉耦合电感Mt_cross的期望值。
(4)以三角形元素为例,根据等边多边形原理布置每个线圈单元。
(5) 为矩阵线圈建立平面坐标系,根据式(3)~式(7)确定圆心坐标。
(6)设置循环变量i、j=1,初始值dr=0、dpt=0、np=1、ns=1,同时确保线圈坐标的对称性。
(7)定义参数Msum为3个线圈互感的总和,作为确定功率指标的基础。此外,计算每个单元线圈与次级线圈之间的互感及初级线圈之间的交叉耦合。通常,对于均匀线圈矩阵,M12=M23=M13。
(8)在指定尺寸内顺序增加初级线圈和次级线圈的匝数。
(9)判断Msum是否在目标的可容忍范围内,如果不满足要求,则返回第(8)步;如果满足,则进行下一步。
(10)统计满足当前指标的情况Ai,改变dpt值,返回第(8)步。重新绕线后,记录符合性能的情况Aij,并从中选择最佳案例。
(11)判断在第(10)步中选择的最佳情况Aij是否满足交叉耦合指标的要求。如果不满足,改变线圈间距dr并返回第(6)步;如果满足要求,则结束优化。
为了更直观地观察基于该设计方法的磁聚焦效果,使用磁场仿真软件COMSOL计算磁通密度。每个初级线圈的激励电流设为1 A,系统参数根据第1节的设计条件和2.1节的设计部分得到,磁场仿真主要参数见表1。通过这些计算,可以评估所提出的设计在增强磁场聚焦能力方面的有效性。
不同设计方法下的磁场分布结果如图4所示。根据六种情况的磁场分布强度结果,可以看出本文提出的方法无论在使用还是不使用铁氧体芯的情况下,都能提供更强的磁聚焦能力。从图4a和图4b可以看出,图4b采用的方法在一定程度上聚集了磁场,图4f和图4d相比于传统方法在中心位置的磁场强度有明显提升。同时,从传输高度的角度来看,所提方法也能够提供更高的功率。
表1 磁场仿真主要参数
Tab.1 Parameters of magnetic field simulation
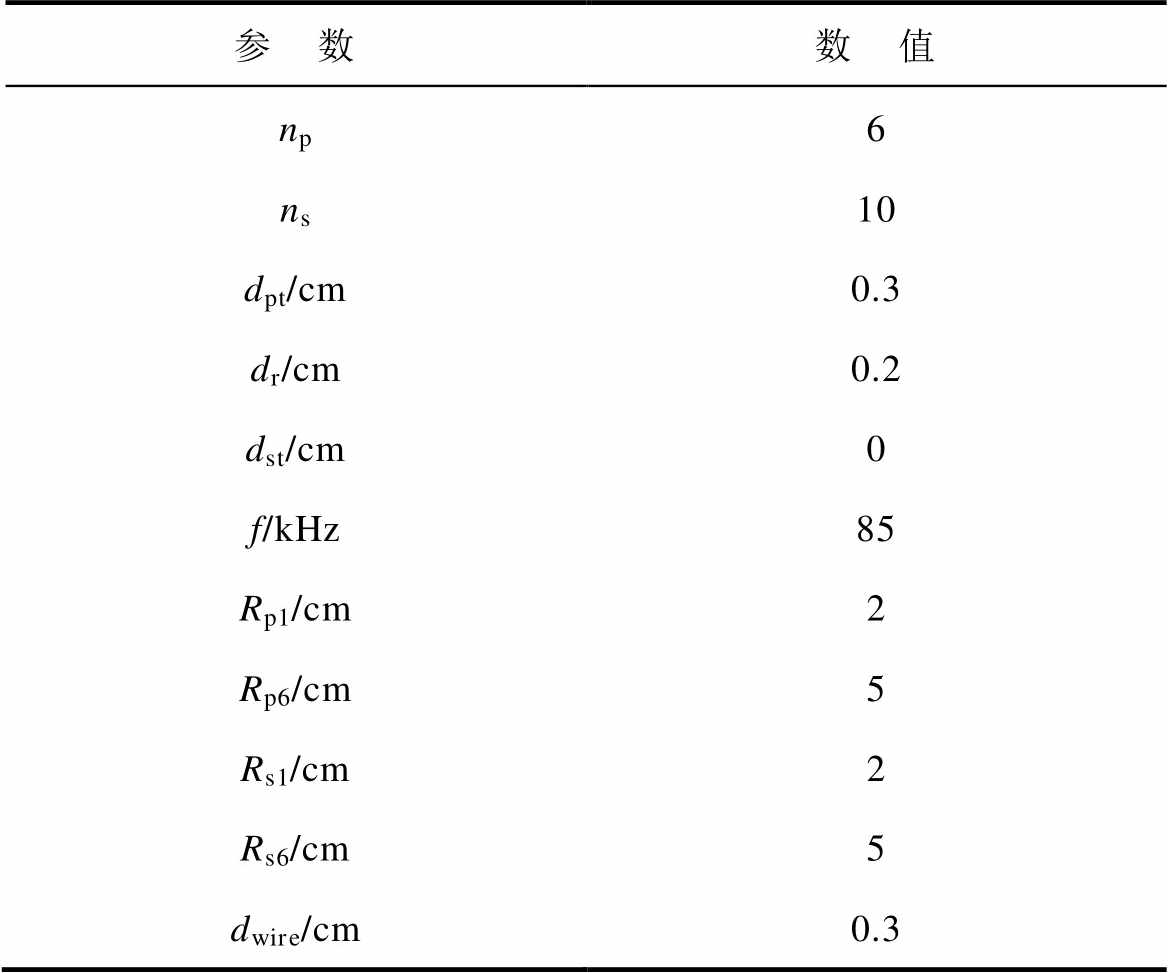
参 数数 值 np6 ns10 dpt/cm0.3 dr/cm0.2 dst/cm0 f/kHz85 Rp1/cm2 Rp6/cm5 Rs1/cm2 Rs6/cm5 dwire/cm0.3
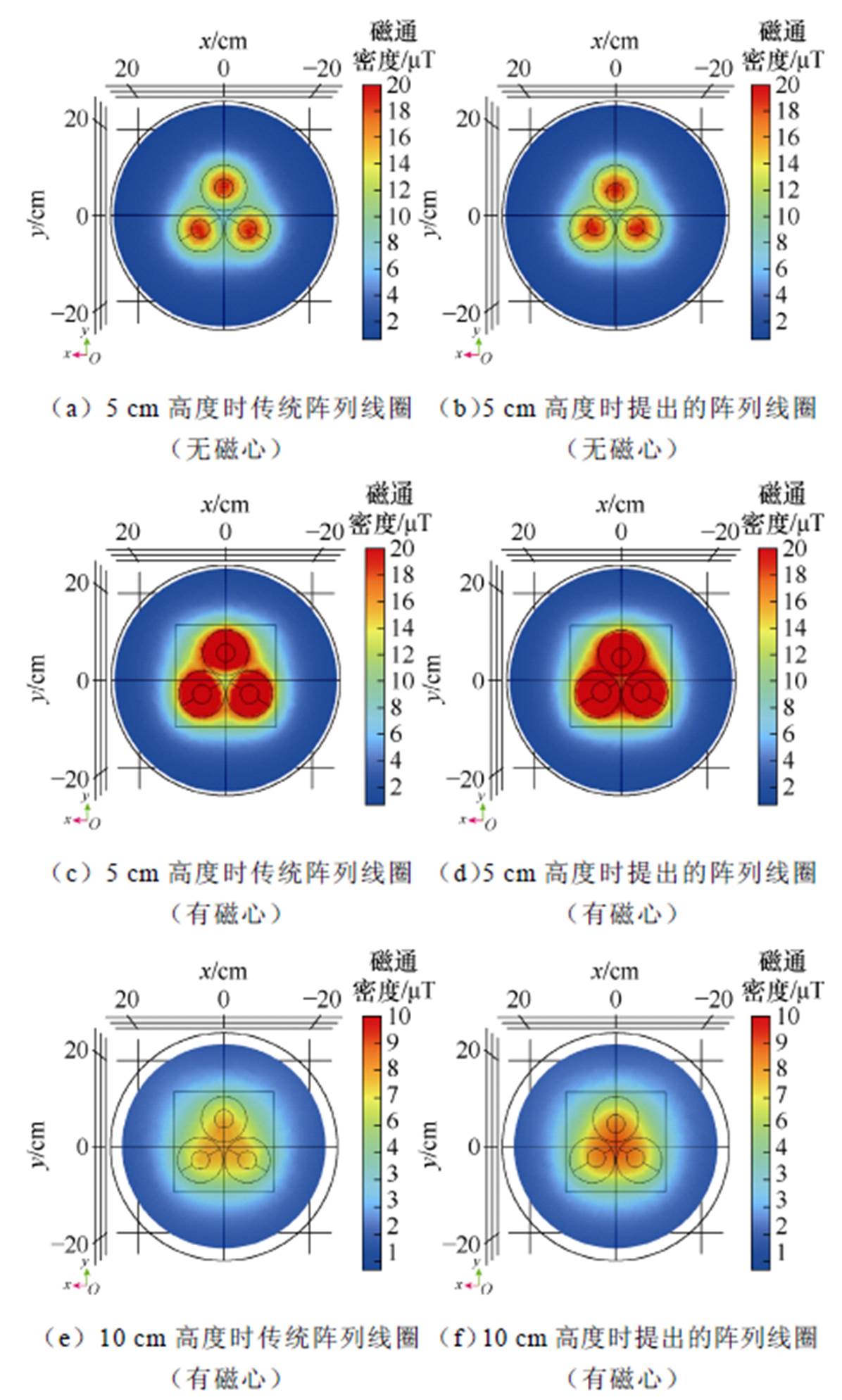
图4 不同设计方法下的磁场分布结果
Fig.4 Magnetic field distribution results with different designed method
图5a展示了在水平移动下的输出特性,比较了在不同高度下使用传统设计(Conventional Design, CD)和所提设计(Proposed Design, PD)时次级线圈的感应电压,且未进行谐振匹配。当系统在最大传输距离(z=10 cm,等于线圈尺寸)下运行时,从图5b可以看出,CD方法在中心位置的感应电压为0.095 V(未使用铁氧体芯),而PD为0.105 V,这意味着PD的性能提升了10.5%。类似地,在使用铁氧体芯的情况下,CD为0.158 V,PD为0.176 V,拾取电压提升了11.4%。当系统的传输距离处于中等范围(z=5 cm)时,从图5c可以看出,CD方法在最佳位置的感应电压为0.212 V(未使用铁氧体芯),而PD为0.260 V,性能提升了22.6%。使用铁氧体芯时,CD方法的感应电压为0.364 V,而PD为0.456 V,性能提升了25.2%。尽管偏移容忍度并不是本文关注的设计指标,但从图5的比较结果来看,所提方法几乎没有削弱传统初级线圈的偏移容忍度。
为了验证1.1节互感分析方法的准确性,将COMSOL仿真和理论推导计算结果进行对比如图6所示。
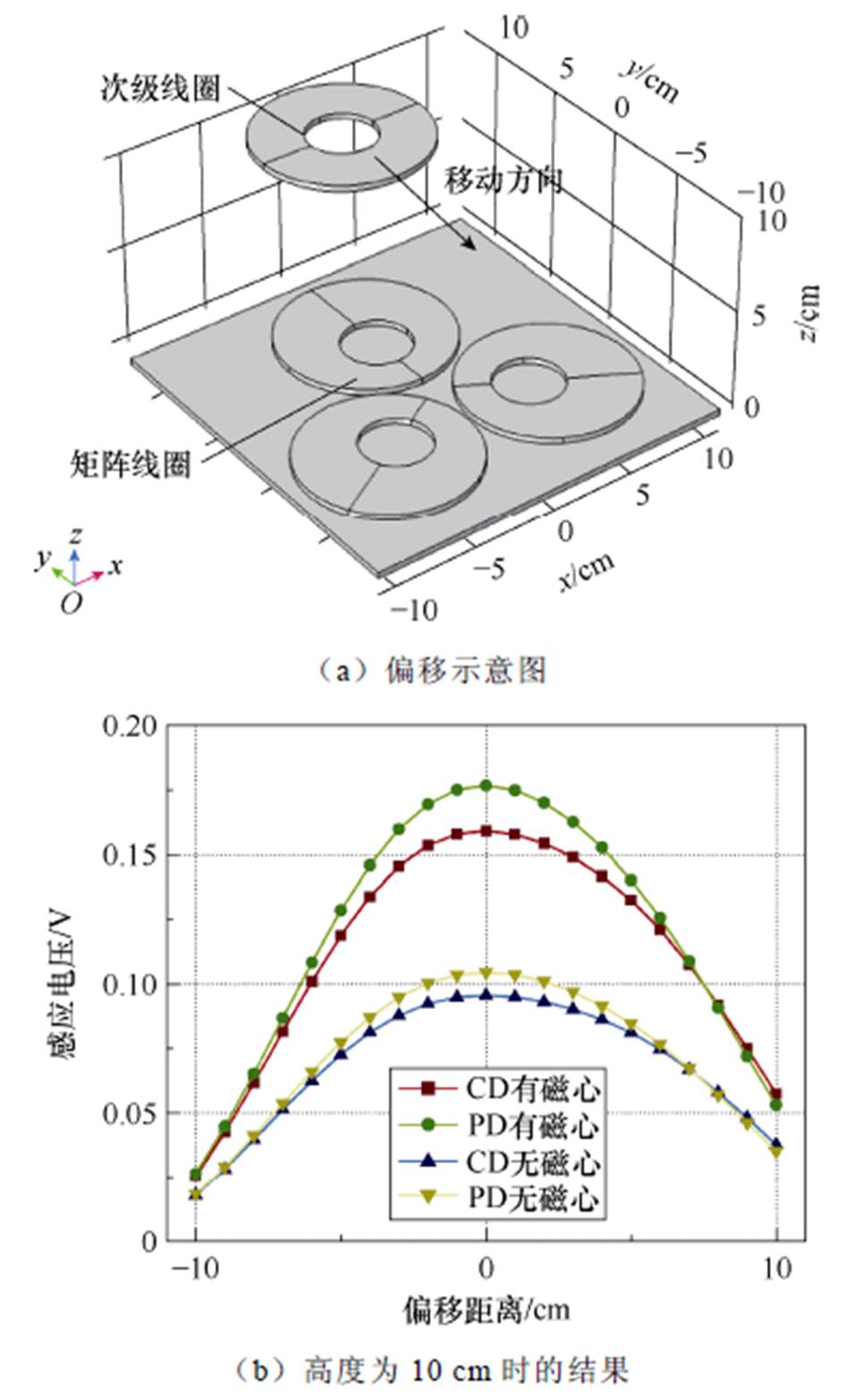
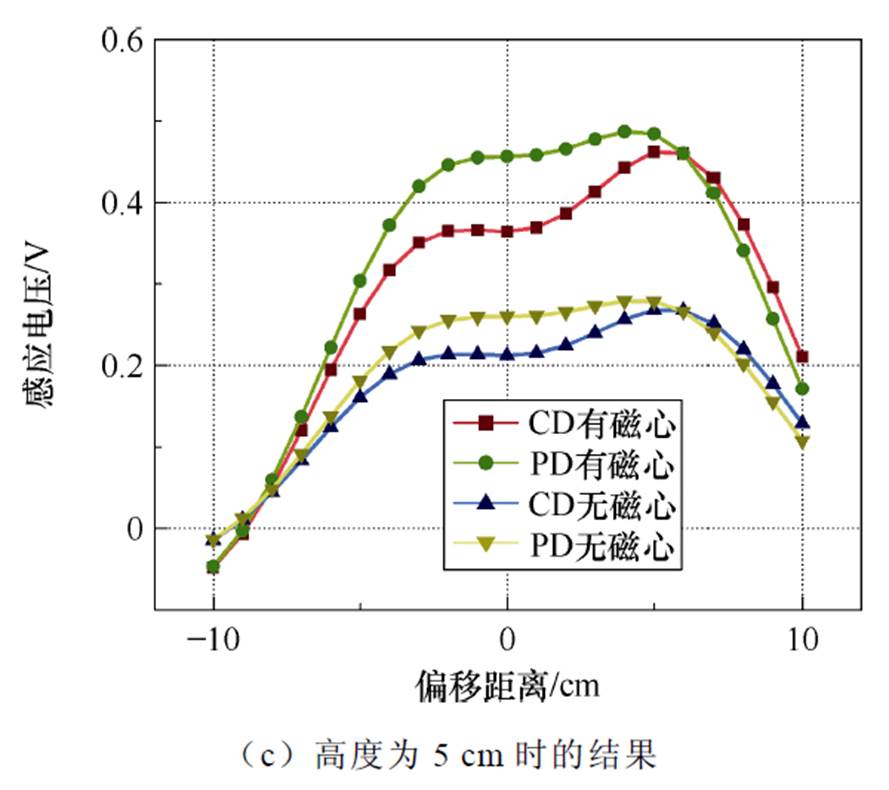
图5 不同设计方法下水平运动的感应电压计算结果
Fig.5 Magnetic field calculation results under horizontal movement with different designed method
参考电路原理图1和图2,M1、M2和M3分别为线圈单元1、2和3对次级线圈的互感。对空间互感值的对比分别选取(x, y, z)坐标为(-9, 0, 5)、(-6, 0, 5)、(-3, 0, 5)、(0, 0, 5)、(-9, 0, 10)、(-6, 0, 10)、(-3, 0, 10)、(0, 0, 10) 8个点,由于M2和M3关于y轴对称,因此其仿真和理论计算数据一致,当次级线圈运动到x=0, y=0时,其位于发射机构中心位置,3个线圈的互感值几乎一样。从图6可以看出,理论计算和磁场仿真的结果在中心区域的耦合计算值误差不大,但随着次级线圈远离中心区域,由于理论推导几乎为拟合的线性叠加运算,相对误差还是有一定提升。同时,从坐标 (0, -3) 至 (0, 0) 的数据可以看出,基于NEU的矩阵线圈在核心区域的耦合能力得到提升。
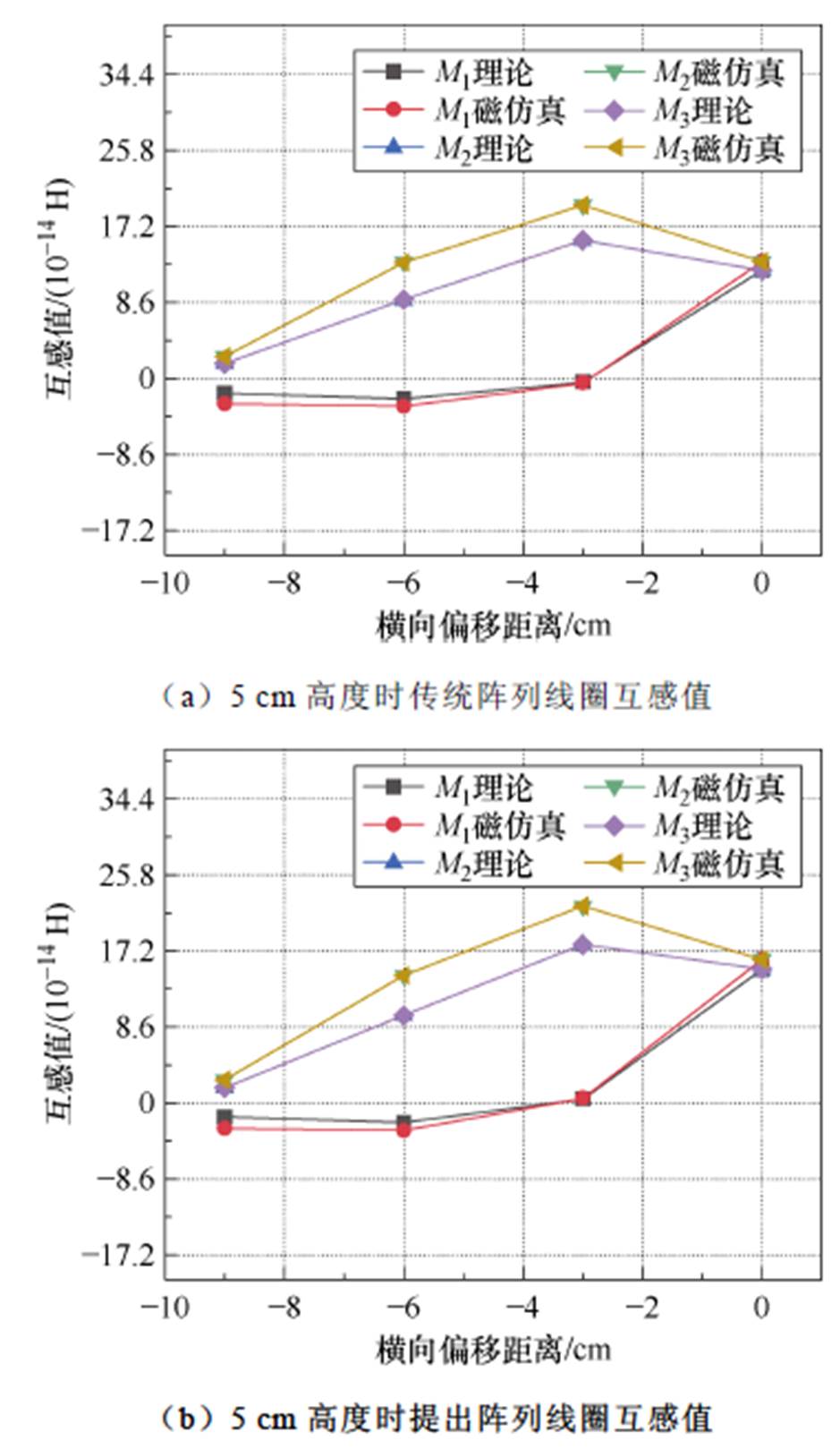
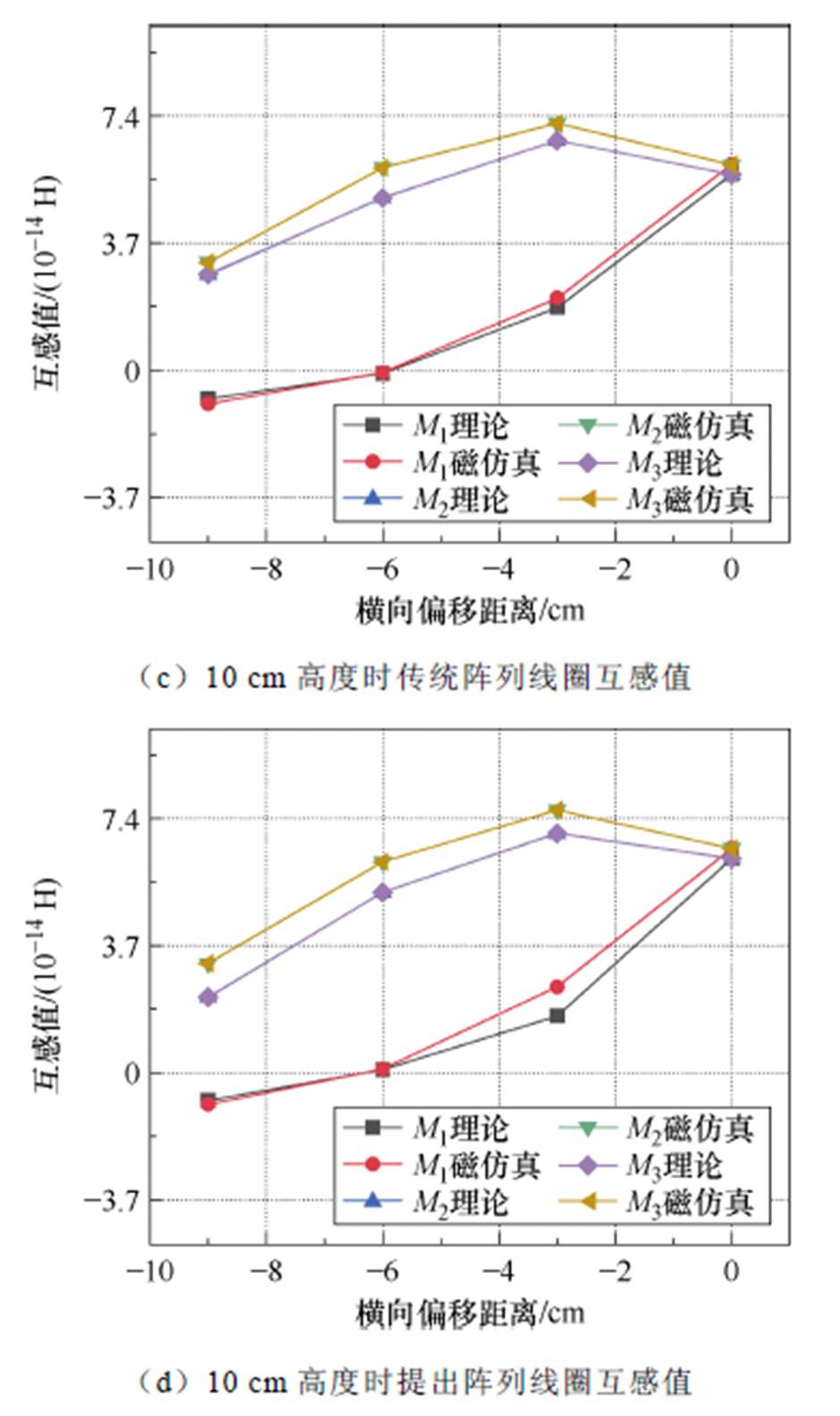
图6 线圈空间定点互感值对比
Fig.6 Comparison of mutual inductance values of matrix coils
实际上,三个空间轴的偏差容忍度是评估耦合机构充电性能的重要指标。为了更准确地描述满足额定功率的三维空间区域的体积,采用基于网格描述的n维矩阵来描述空间耦合热矩阵并优化评估方法。
对于矩阵线圈,当线圈电流同相时,次级线圈获取最大能量,并将Ptarget设定为负载的目标输出功率。在指定的传输高度zs下,在xOy平面上的投影z=Ptarget可以表示为
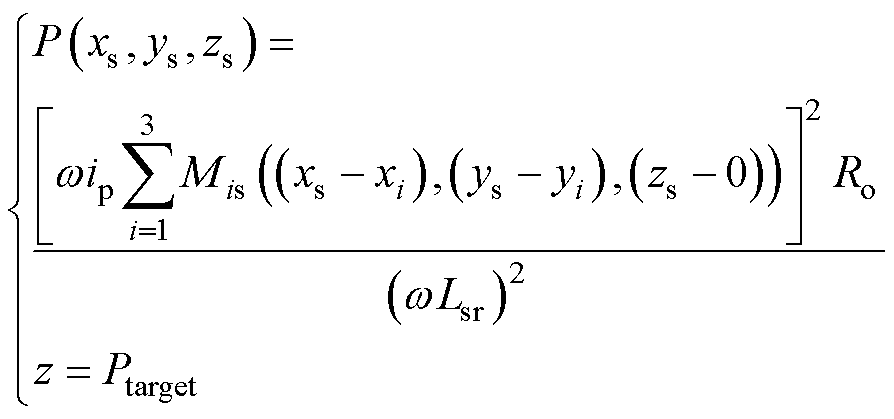 (16)
(16)
次级线圈在空间中任意位置的中心坐标为(xs, ys, zs)。根据给定的线圈尺寸,定义三个n维向量x、y和z,以及空间网格大小s,其中s 为Dx、Dy和Dz的单位增量。
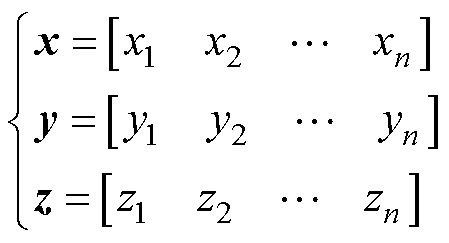 (17)
(17)
其中
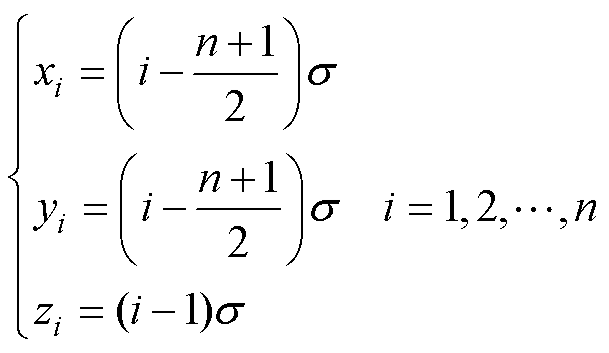 (18)
(18)
可以看出,s(n-1)实际上是线圈在某个轴上的移动距离。
1)传统矩阵线圈的空间充电区域估算
对于传统矩阵线圈,每圈激励单元的中心坐标是一致的,设第m个激励单元的坐标为Com(xm, ym, 0)。在某一传输距离z=zi(i=1, 2,…, n)处,横向位移的描述矩阵Fn×n可表示为
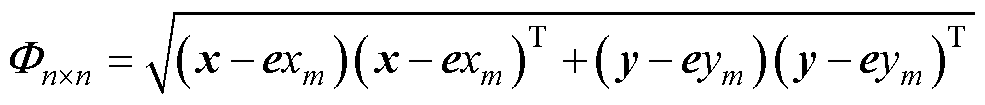 (19)
(19)
式中,e为一个所有元素均为1的n维向量。根据互感式(8)以及参考文献[25-26]中的互感计算拟合函数,设Jn×n为一个所有元素均为1的n阶方阵,初级线圈和次级线圈在任意空间网格中的互感描述耦合热矩阵Mn×n可表示为
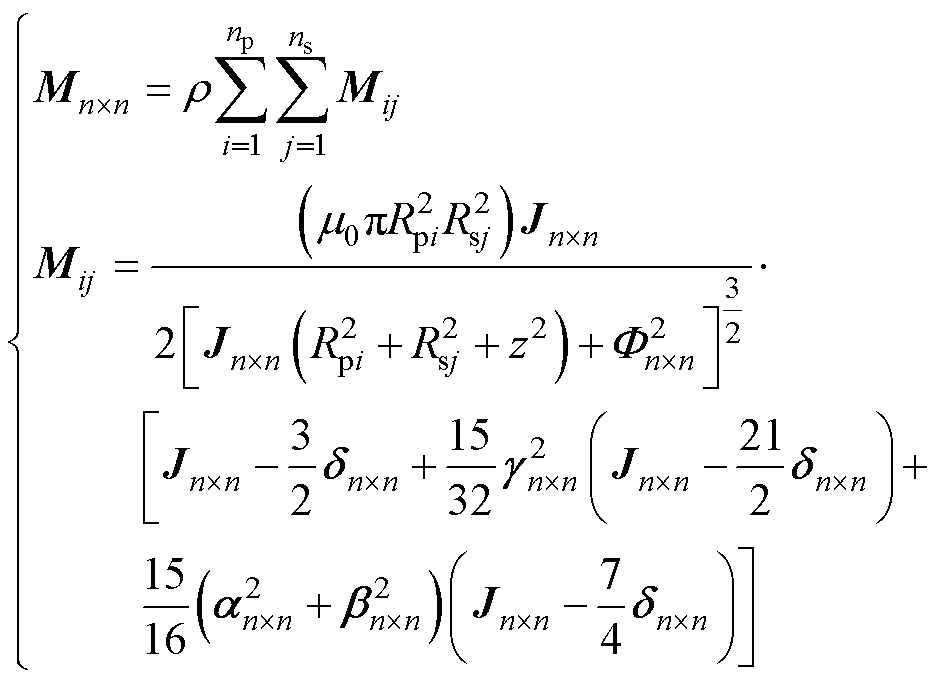 (20)
(20)
式中,r 为线圈的形状系数,当线圈为圆形时,r=1。Mij为在任意空间网格中第i匝初级线圈与第j匝次级线圈之间的n阶互感矩阵。而式(20)中的拟合参数矩阵可以表示为
 (21)
(21)
根据式(20)和式(21),定义函数f ( · ),该函数将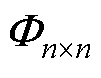 转换为i匝初级线圈与j匝次级线圈之间的互感矩阵Mij为
转换为i匝初级线圈与j匝次级线圈之间的互感矩阵Mij为
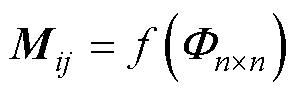 (22)
(22)
根据1.2节的分析,设式(15)为基于互感值的功率映射函数g( · )。将式(20)和式(22)代入式(16),对于m个激励单元,当每个激励单元的电流幅值和相位相同时,传输距离为z=zi时的功率矩阵Pn×n可以表示为
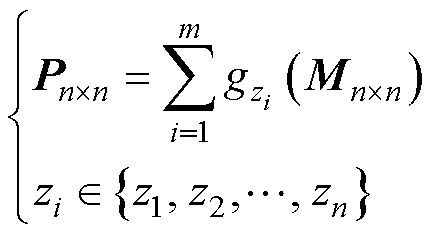 (23)
(23)
2)本文所提出的矩阵线圈的空间充电面积估算
以图1为例,类似地,对于所提出的耦合线圈矩阵,根据1.1节的分析,非中心对称激励单元的每一匝的中心坐标都是变化的。从方程式(2)出发,设定Com_i(xm_i, ym_i, 0) 为第m个激励单元中第i匝线圈的中心坐标(i=1, 2,…, np; m=1, 2, 3)。对于m个激励单元中的第i匝线圈,根据式(19),其与次级线圈的横向偏移矩阵F m_i可表示为
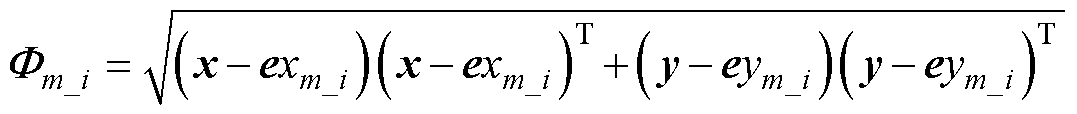 (24)
(24)
因此,可以通过式(22)推导出在固定传输距离z下,所提出的矩阵耦合机构中第m个激励单元
的空间互感矩阵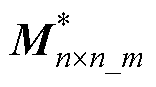 (r=1)为
(r=1)为
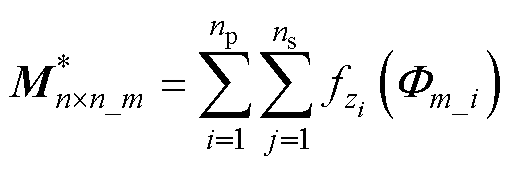 (25)
(25)
根据式(23),可以得到本文提出的耦合机构的功率矩阵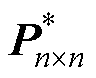 为
为
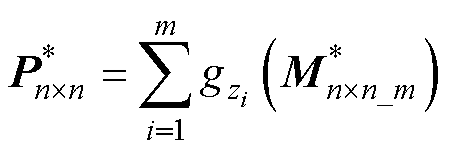 (26)
(26)
实际上,功率矩阵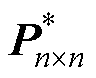 描述了在给定传输距离zi处的功率分布表面。对于给定的zi(zi∈z),定义函数H( · )用于计算功率大于额定功率Ptarget的网格单元数量,即
描述了在给定传输距离zi处的功率分布表面。对于给定的zi(zi∈z),定义函数H( · )用于计算功率大于额定功率Ptarget的网格单元数量,即
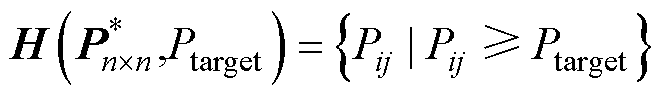 (27)
(27)
式中,Pij为n阶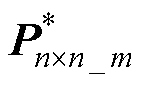 的元素。有效空间充电区域体积V可以表示为
的元素。有效空间充电区域体积V可以表示为
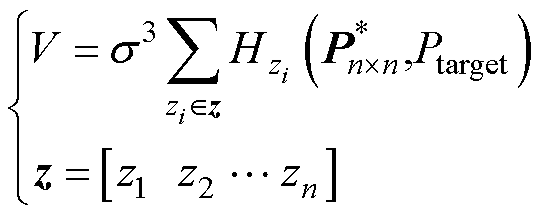 (28)
(28)
本文进一步分析了系统的空间输出功率特性,并根据表2的参数设计系统。为了提升耦合机构的输出功率,初级线圈的电流设定为5 A,次级谐振网络采用LCC恒流源谐振网络,次级补偿电感为1 mH,串联补偿电容为0.551 mF,并联补偿电容为3.51 mF。当次级线圈在空间范围x, y∈[-0.1 m, 0.1 m], z∈[0.03 m, 0.075 m] 内移动时,依据式(23)和式(26),定义z轴的网格单元大小为5 mm,其输出功率的四维可视化场图如图7所示。
表2 主要系统参数
Tab.2 The main parameter of system
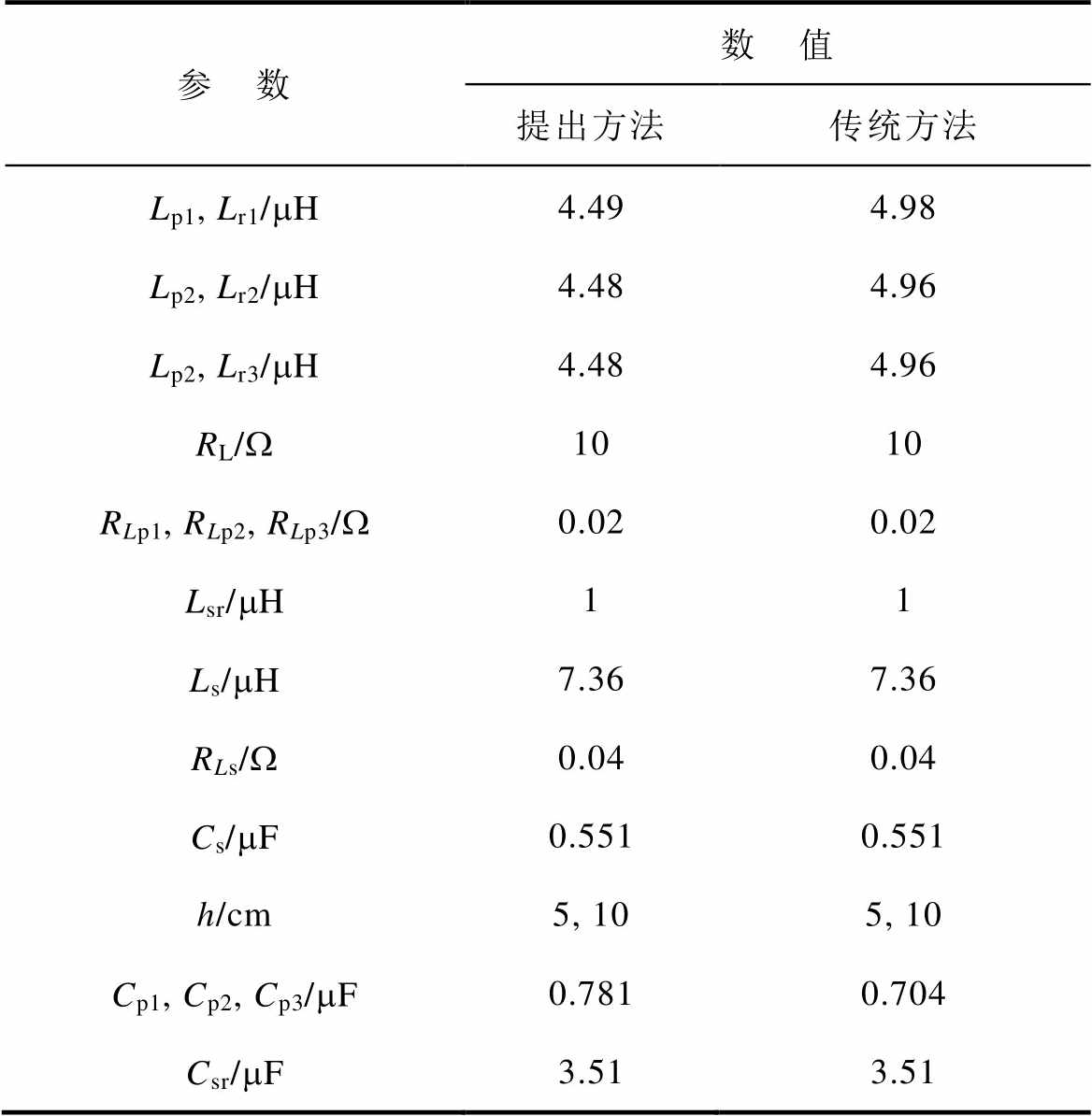
参 数数 值 提出方法传统方法 Lp1, Lr1/mH4.494.98 Lp2, Lr2/mH4.484.96 Lp2, Lr3/mH4.484.96 RL/W1010 RLp1, RLp2, RLp3/W0.020.02 Lsr/mH11 Ls/mH7.367.36 RLs/W0.040.04 Cs/mF0.5510.551 h/cm5, 105, 10 Cp1, Cp2, Cp3/mF0.7810.704 Csr/mF3.513.51
将从7a和图7b可以看出,在传输距离从0.03 m到0.075 m之间,输出功率范围几乎为0~300 W。当传输距离较近时,由于耦合紧密,输出功率较高,但该范围内功率波动较大且衰减迅速,增大次级线圈的尺寸可以减少这种波动。例如,图7a中,当高度为0.03 m时,传统设计方法的线圈矩阵在中心位置的功率场衰减显著,而所提方法的功率波动相对较小。而在图7c和图7d中,当传输距离从0.05 m变为0.075 m时,功率衰减的程度逐渐平坦。从图7每一个对应传输距离的功率切面可以看出,提出方法在同色域的范围有明显的拓展。同时,随着高度的增加,在较远距离的功率切面中,如z=0.045 m, 0.05 m, 0.055 m, 0.06 m, 0.065 m, 0.07 m,中心位置的能量色温块相较于传统方法有明显的聚焦性。所提方法的功率聚合程度高于传统方法。
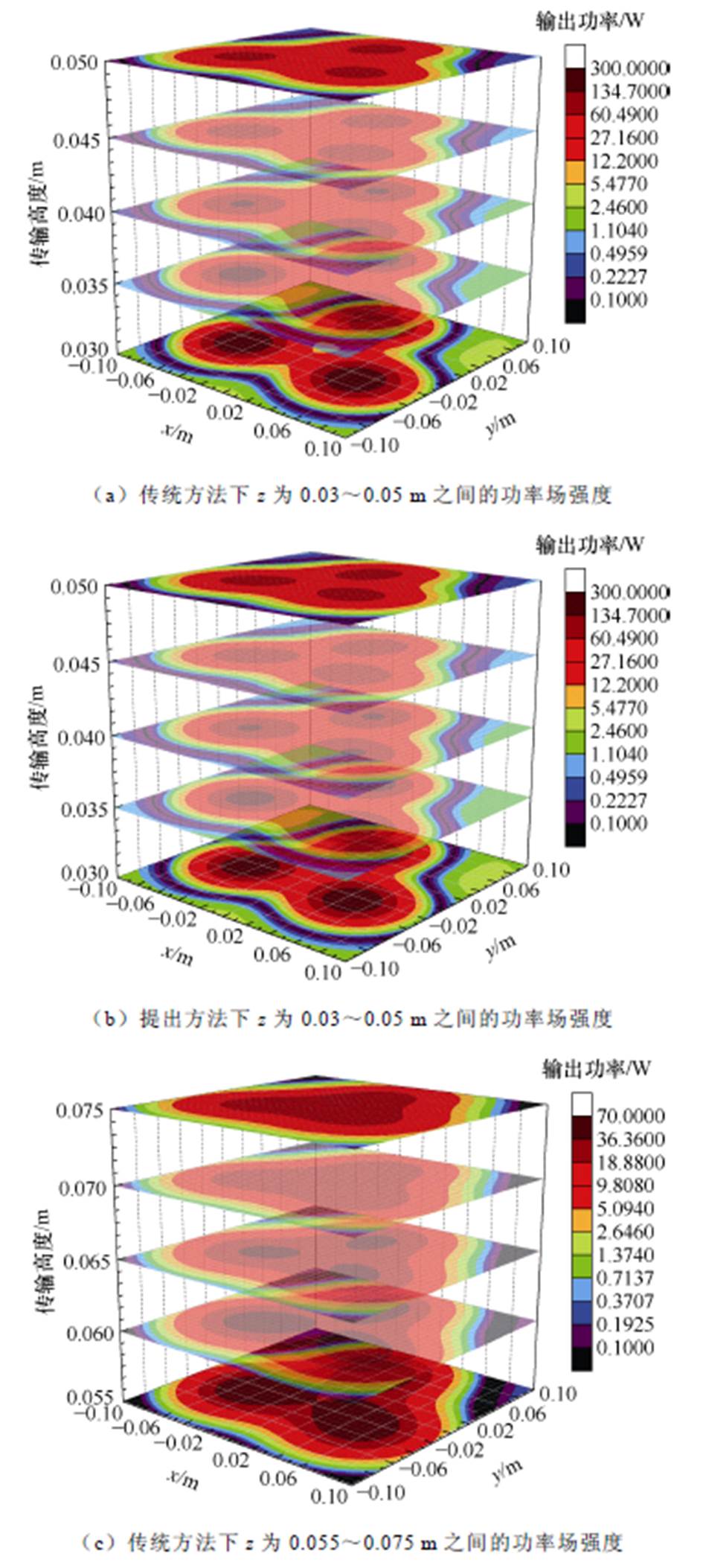
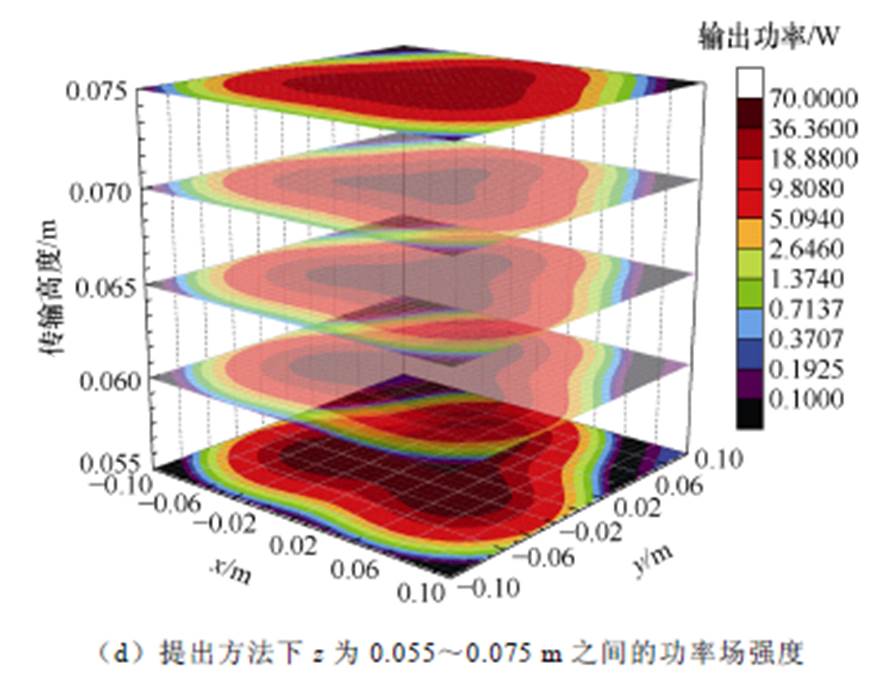
图7 输出功率的四维可视化场图
Fig.7 The four-dimensional visualization field diagram of output power
根据功率场强度的等高线可以看出,所提方法在中央区域聚集的充电范围优于传统方法。基于空间区域内功率场强度的趋势,所设计的耦合机构基于所采用的线圈尺寸具有约40 W的舒适功率传输范围。此外,可以使用式(27)和式(28)计算在特定高度下满足额定充电功率的充电区域和定义空间范围内的体积。参考系统参数和图7中的舒适功率传输范围,各高度的有效充电面积(Effective Charging Area, ECA)及整体有效充电体积(Effective Charging Volume, ECV)如图8所示。
图8展示了根据式(28)在不同传输高度z下所指代的xOy充电平面上,有效充电面积估计的计算结果以及满足目标充电功率的空间有效充电体积。当目标功率为30 W时,PD方法在0.025~0.05 m之间的有效充电面积显著增加,相比于CD方法传输高度增加了12.16%。与此同时,PD方法的空间有效充电体积为896.535 cm3,比CD方法大9.17%。当目标功率为50 W时,PD方法在0.03~0.062 m之间的有效充电面积显著增加,尽管传输距离仅增加了5%。PD方法的空间有效充电体积为539.185 cm3,增加了14.83%。
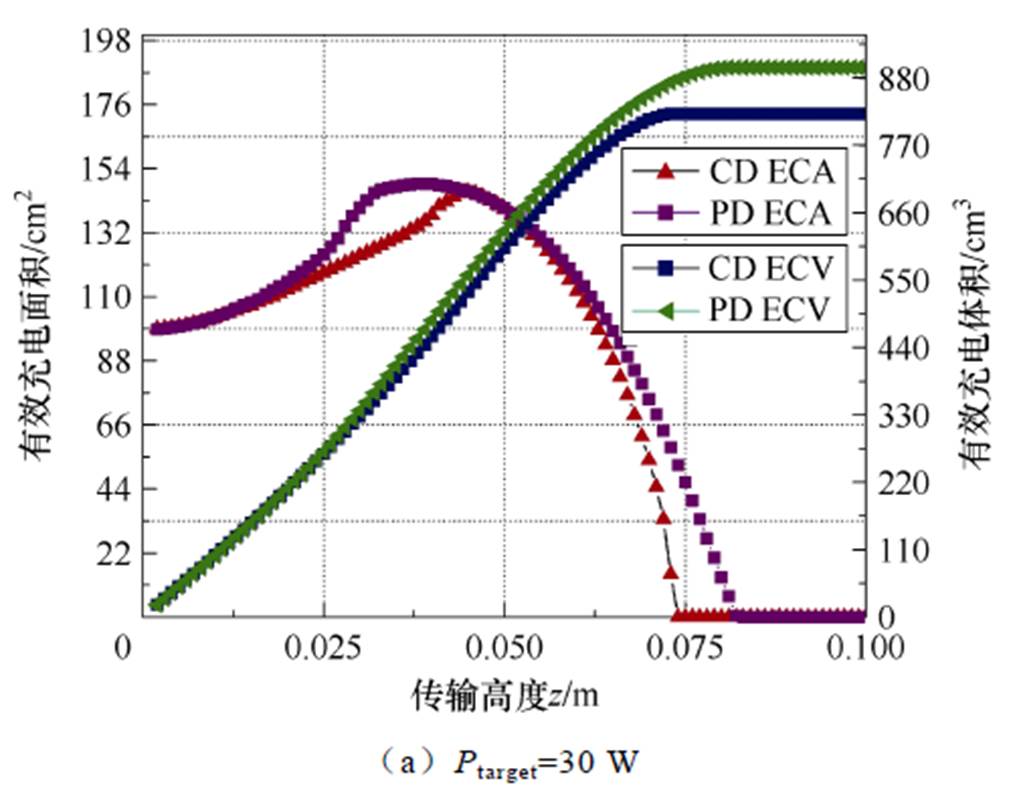
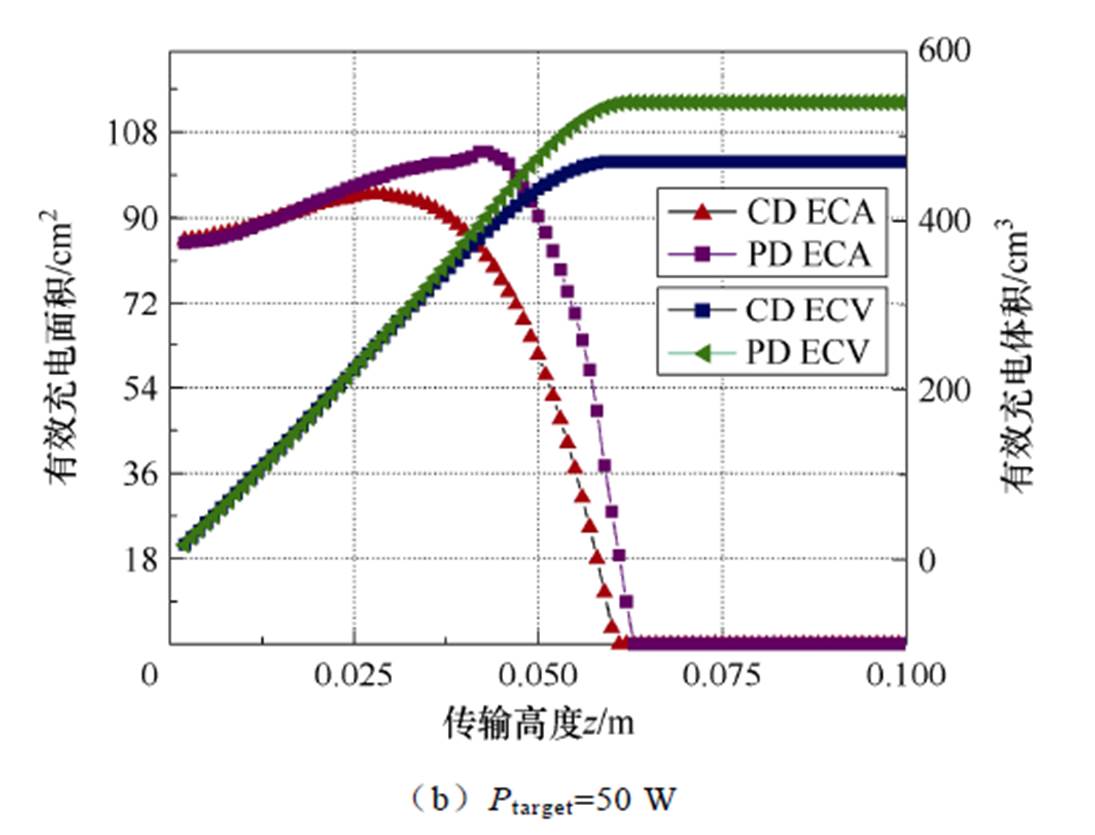
图8 有效充电面积和体积估计
Fig.8 Estimation of ECA &ECV
实验装置如图9所示。设置系统工作频率为85 kHz,其他参数见表2。

图9 实验装置
Fig.9 Experimental set-up
本实验考虑了两种不同的矩阵线圈设计方法,通过在相同输入源15 V的基础上比较磁聚焦性能。一种是传输距离z=5 cm,另一种是传输距离z= 10 cm。测试方法如图10所示。
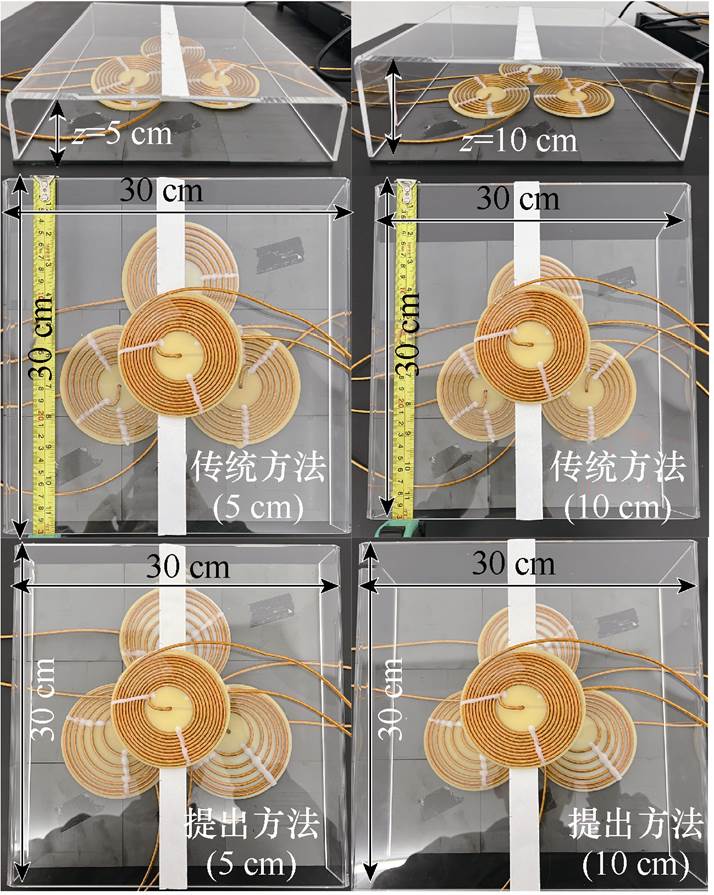
图10 实验装置测试示意图
Fig.10 Schematic diagram of experimental apparatus testing
第一种情况在错位条件下不同设计方法下的实验结果(z=5 cm)如图11所示,其中图11b、图11d、图11f、图11h、图11j、图11l、图11n采用了本文提出的方法,而图11c、图11e、图11g、图11i、图11k、图11m、图11o则采用了传统方法。由于初级采取LCC拓扑,谐振电流几乎为恒流且逆变输出稳定。当错位距离为-9 cm时,PD的输出电压Uo=0.14 V,CD的Uo=0.35 V;当错位距离为-6 cm时,PD的Uo=11.7 V,CD的Uo=10.5 V;当错位距离为-3 cm时,PD的Uo=21.9 V,CD的Uo=18.4 V;当错位距离为0 cm时,PD的Uo=23.7 V,CD的Uo=19.0 V;当错位距离为3 cm时,PD的Uo=24.8 V,CD的Uo=21.5 V;当错位距离为6 cm时,PD的Uo= 23.8 V,CD的Uo=23.7 V;当错位距离为9 cm时,PD的Uo=13.5 V,CD的Uo=14.7 V。
同样地,第二种情况在错位条件下不同设计方法下的实验结果(z=10 cm)如图12所示,其中图12b、图12d、图12f、图12h、图12j、图12l、图12n采用了本文提出的方法,而图12c、图12e、图12g、图12i、图12k、图12m、图12o采用了传统方法。同理,初级采取LCC拓扑,谐振电流几乎为恒流且逆变输出稳定。当错位距离为-9 cm时,PD的输出电压Uo=2.43 V,CD的Uo=2.30 V;当错位距离为-6 cm时,PD的Uo=5.82 V,CD的Uo=5.43 V;当错位距离为-3 cm时,PD的Uo=8.53 V,CD的Uo= 7.79 V;当错位距离为0 cm时,PD的Uo=9.44 V,CD的Uo=8.56 V;当错位距离为3 cm时,PD的Uo=8.68 V,CD的Uo=7.98 V;当错位距离为6 cm时,PD的Uo=6.72 V,CD的Uo=6.51 V;当错位距离为9 cm时,PD的Uo=3.85 V,CD的Uo=4.03 V。
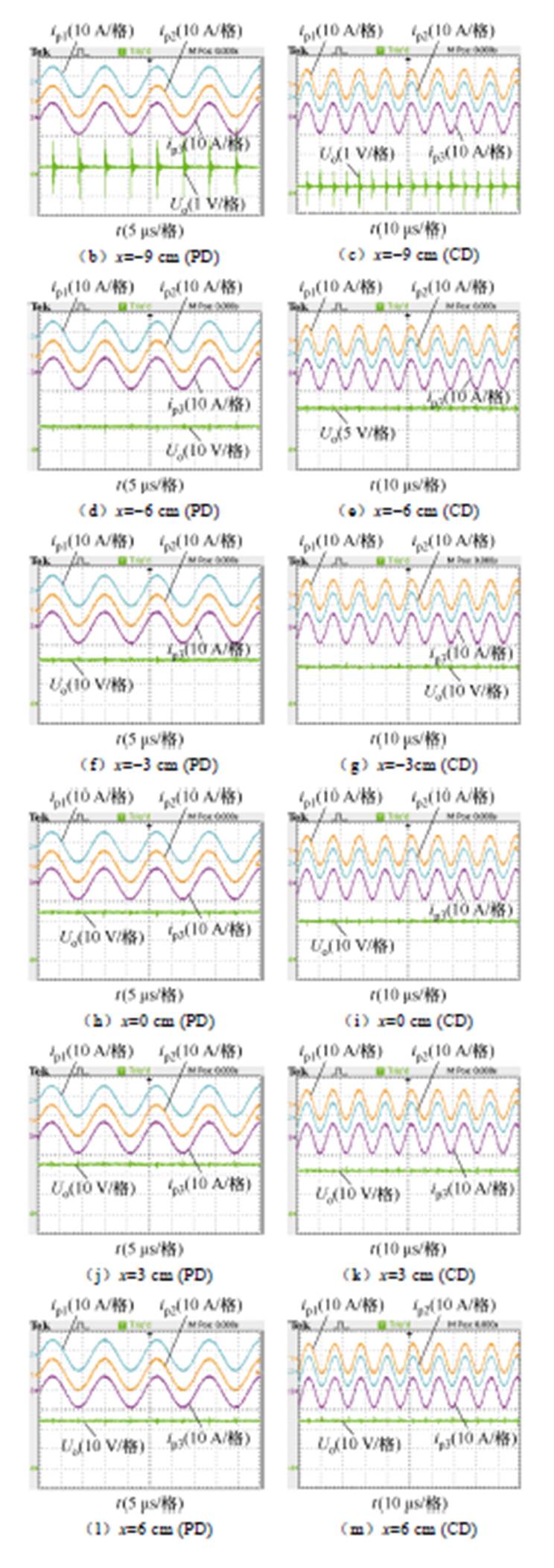
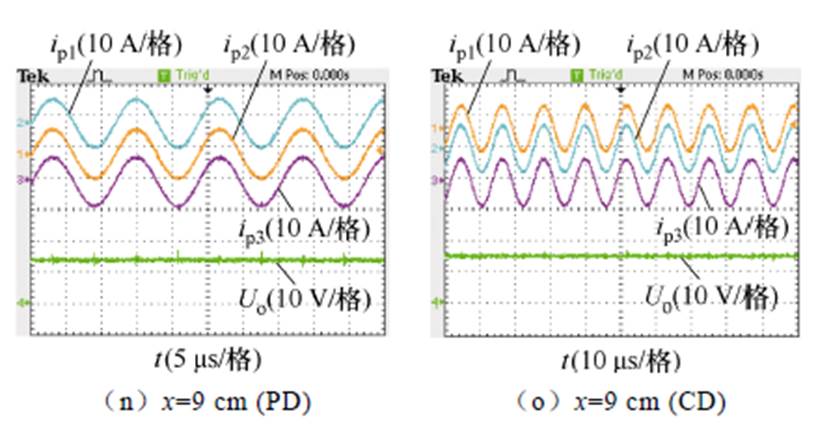
图11 在错位条件下不同设计方法下的实验结果(z=5 cm)
Fig.11 Experimental results under misalignment with different design method (z=5 cm)
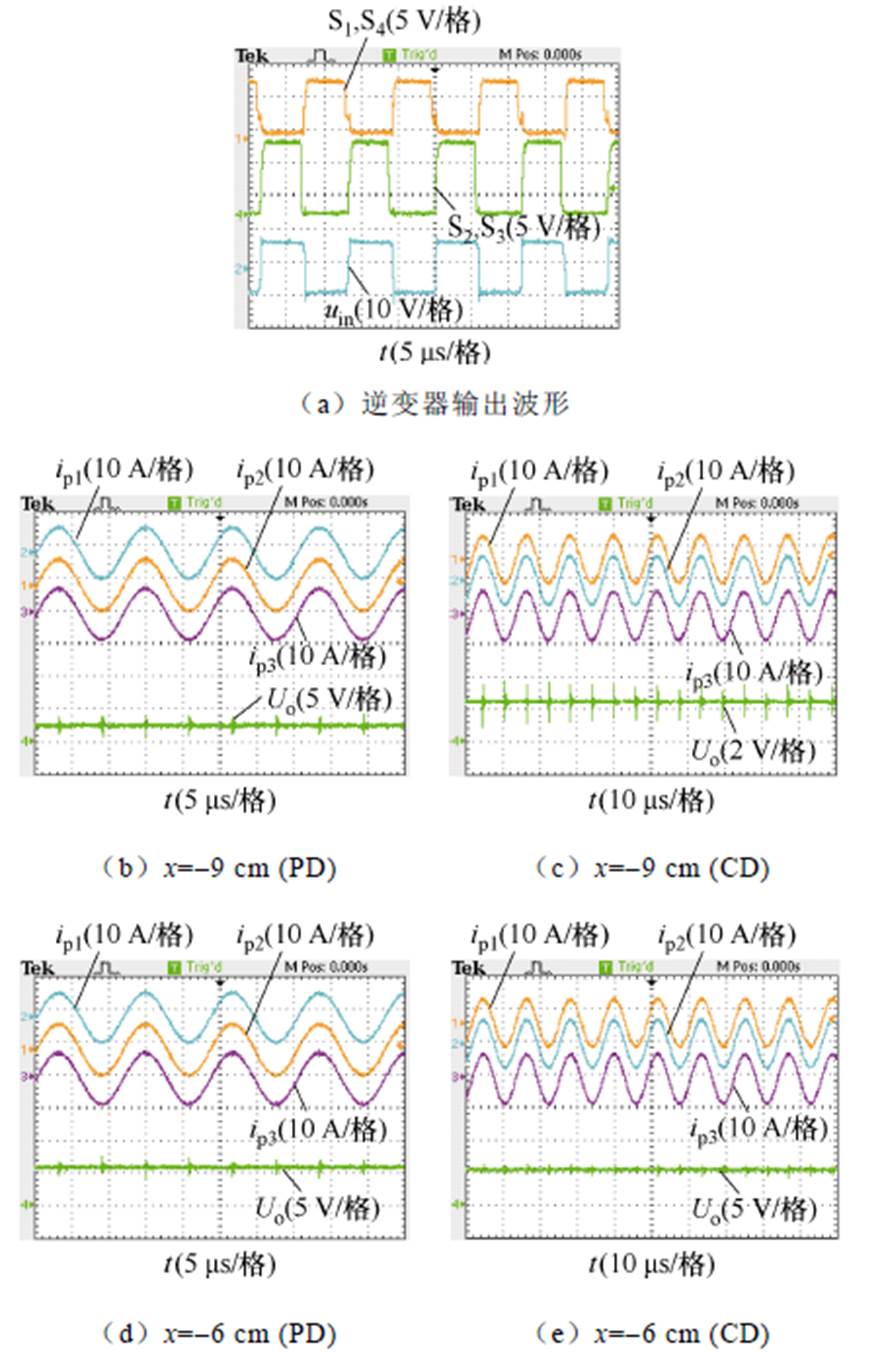
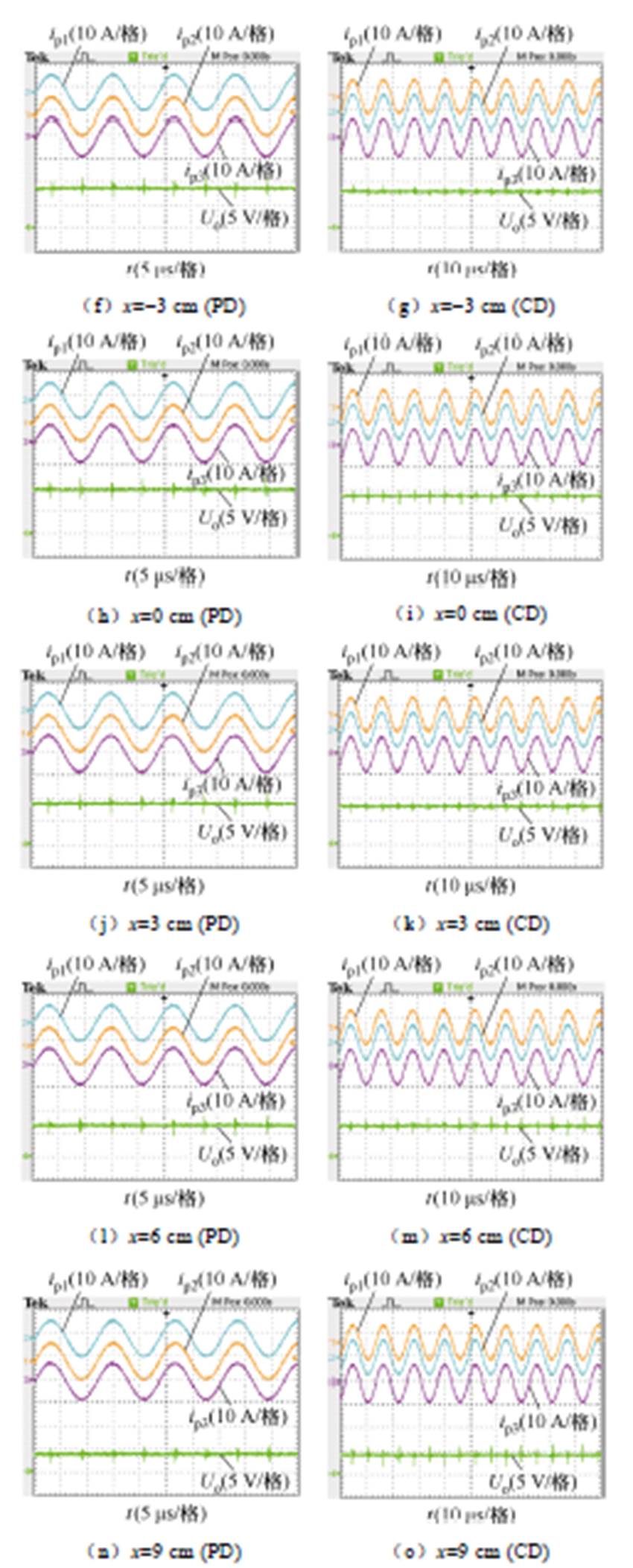
图12 在错位条件下不同设计方法下的实验结果(z=10 cm)
Fig.12 Experimental results under misalignment with different design method (z=10 cm)
本文根据表1绕制了两种类型的线圈。从表2可以看出,基于PD方法的线圈单元的自感值在相同尺寸和匝数下降低了10.9%。图13展示了实验数据与仿真数据的对比。根据本文提出设计方法(PD)和传统设计方法(CD)矩阵线圈的绕制方式,给出了不同传输距离和错位情况下的输出性能测试,其中输入电压为15 V,负载为10 W。可以看出,当传输高度为10 cm时,基于PD方法的耦合机构在中心位置的拾取电压为9.44 V,功率为8.91 W,而CD方法的拾取电压为8.56 V,功率为7.32 W,感应电压性能提高10.2%。当传输高度为5 cm,拾取线圈的错位距离分别为-3、0和3 cm时,基于PD方法的耦合机构的拾取电压分别为21.9、23.7和24.8 V,功率分别为47.96、56.17和61.50 W。而基于CD方法的拾取电压分别为18.4、19.0和21.5 V,功率分别为33.85、36.1和46.22 W,最佳性能提升率为24.7%。此外,在不同情况下,错位容差几乎保持不变。从图13c可以看出,当次级线圈位于舒适区的充电区域时,其工作效率在中心位置可维持在约85%。当传输距离达到线圈单元的尺寸时,功率和效率急剧下降到约54%。提高此系统效率的方法为增加传输功率或改进次级线圈的设计尺寸,以进一步提高耦合系数。
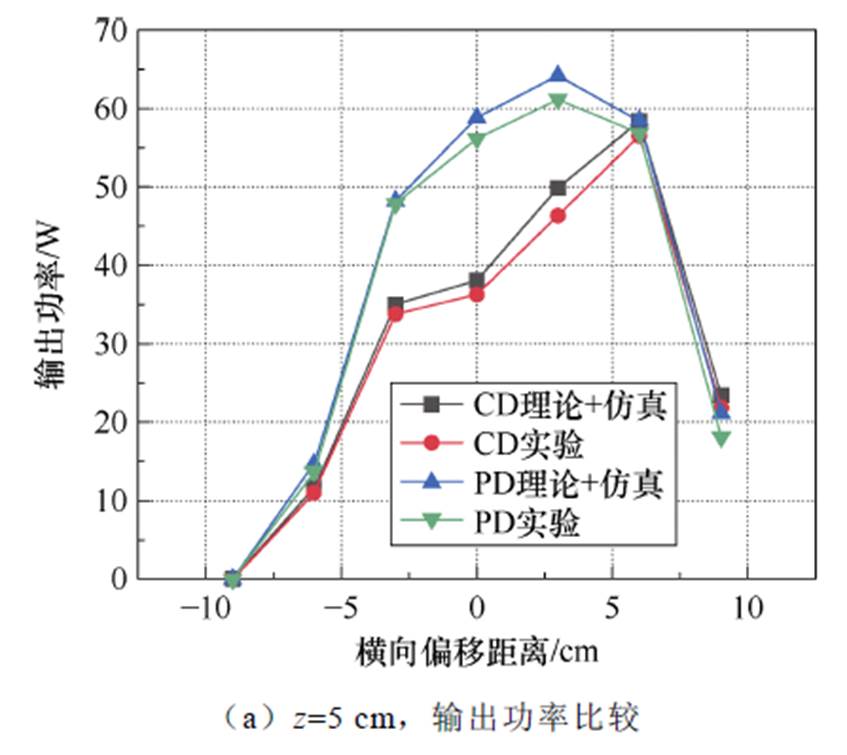
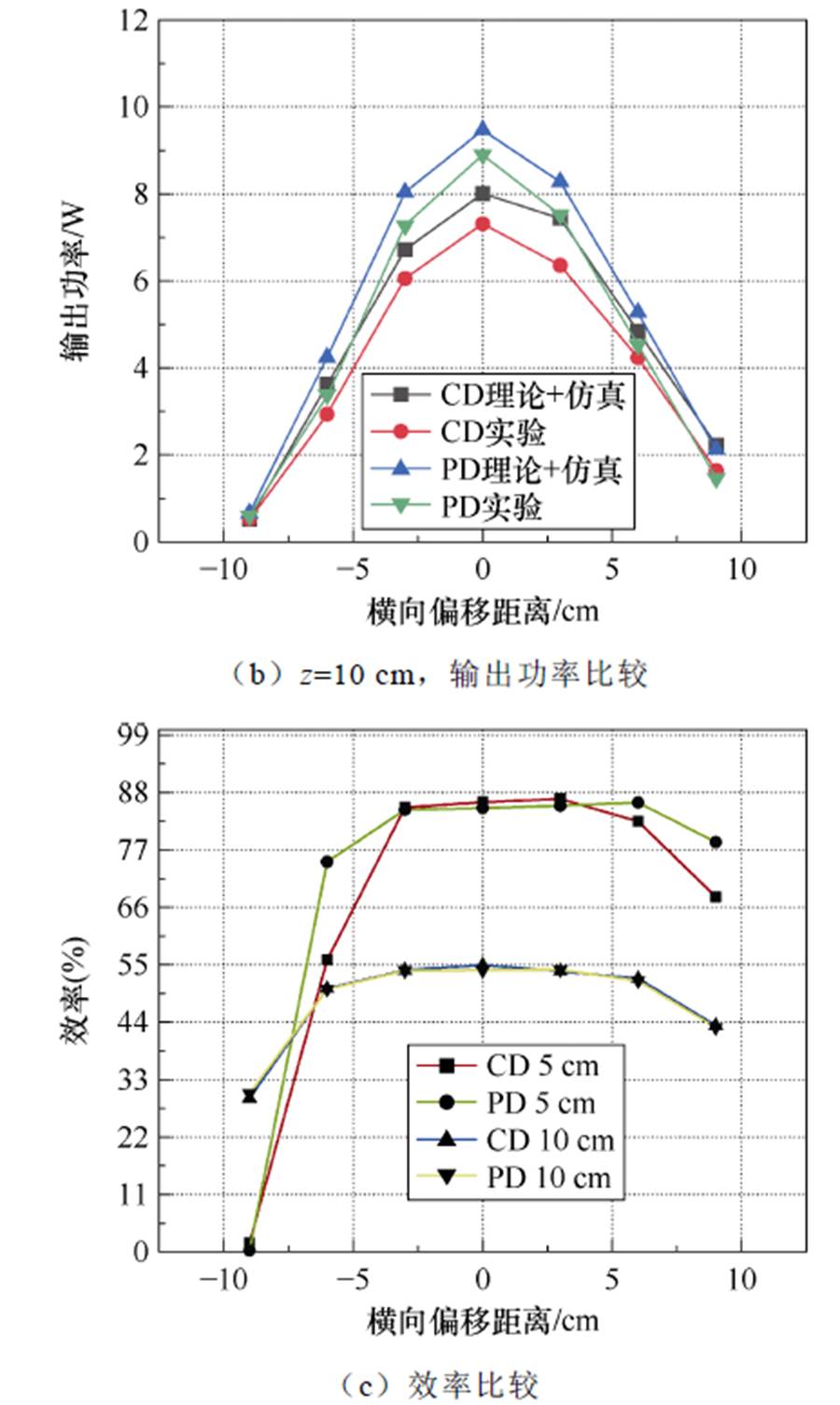
图13 实验结果比较
Fig.13 Experimental results comparison
进一步地,本文以矩阵线圈磁聚焦优化为核心关注点,与相关文献作了一个综合对比,见表3。综上所述,本文提出的方法基于二维线圈对系统磁聚焦性提升具有一定的贡献,不仅降低了系统控制电路和耦合机构设计的复杂度,也在耦合利用率上进行了一定的优化,但抗偏移能力相较于其他文献并不具有突出的设计亮点,将在后续的工作中进行进一步研究探索。
表3 磁聚焦WPT系统性能对比
Tab.3 Performance comparison of magnetic focusing WPT system
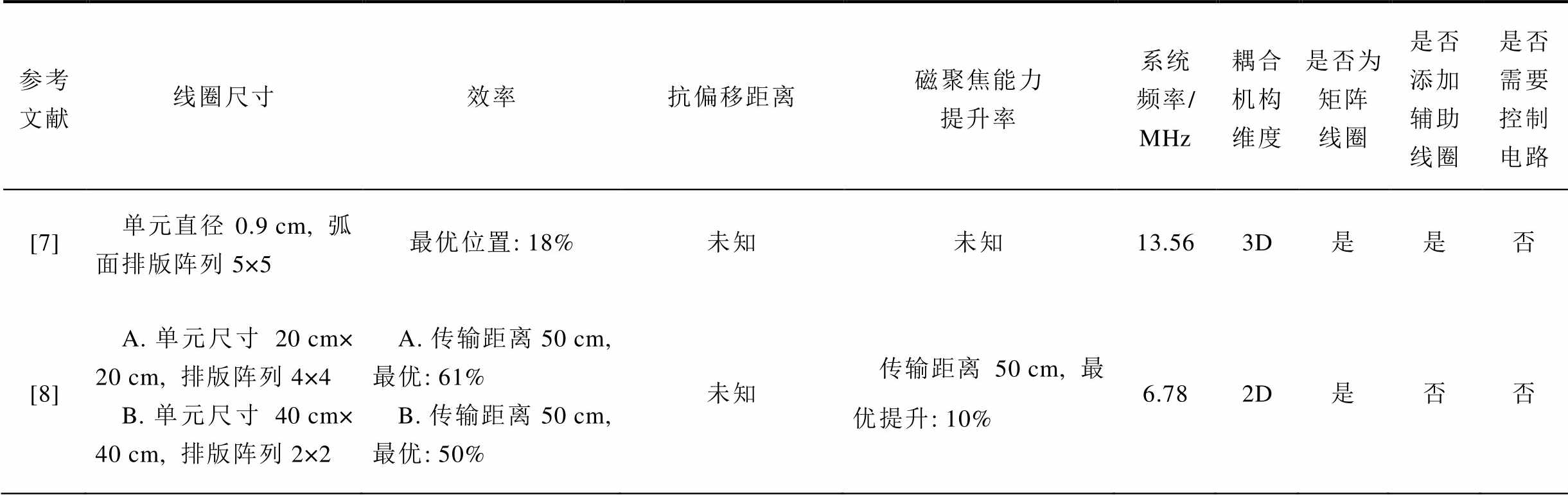
参考文献线圈尺寸效率抗偏移距离磁聚焦能力提升率系统频率/MHz耦合机构维度是否为矩阵线圈是否添加辅助线圈是否需要控制电路 [7]单元直径0.9 cm, 弧面排版阵列5×5最优位置: 18%未知未知13.563D是是否 [8]A. 单元尺寸20 cm× 20 cm, 排版阵列4×4B. 单元尺寸40 cm× 40 cm, 排版阵列2×2A. 传输距离50 cm, 最优: 61%B. 传输距离50 cm, 最优: 50%未知传输距离50 cm, 最优提升: 10%6.782D是否否
(续)

本文提出了一种用于矩阵式无线电能传输(WPT)系统的非中心对称激励单元设计方法,以增强矩阵耦合机构的磁聚焦能力。该方法在考虑了绕组成本和保持偏移容差的同时,不依赖任何辅助线圈或电路使得互感利用率得到提升。此外,基于耦合热矩阵提出了一种空间有效充电区域计算方法,用于评估耦合机构的空间输出特性指标。通过磁场计算和实验验证,结果表明该方法在中心位置能够将接收侧的感应电压提高10%~24.7%,同时每个激励单元的自感值降低了10.9%。
参考文献
[1] 杨庆新, 张献, 章鹏程. 电动车智慧无线电能传输云网[J]. 电工技术学报, 2023, 38(1): 1-12.
Yang Qingxin, Zhang Xian, Zhang Pengcheng. Intelligent wireless power transmission cloud network for electric vehicles[J]. Transactions of China Elec- trotechnical Society, 2023, 38(1): 1-12.
[2] 田勇, 杨昊, 胡超, 等. 基于毫米波雷达的电动汽车无线充电运动异物检测与跟踪[J]. 电工技术学报, 2023, 38(2): 297-308.
Tian Yong, Yang Hao, Hu Chao, et al. Moving foreign object detection and track for electric vehicle wireless charging based on millimeter-wave radar[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 297-308.
[3] 周玮, 郑宇锋, 陈泽林, 等. 基于副边解耦极板的电容式无线电能传输系统拾取端失谐评估[J]. 电力系统自动化, 2024, 48(3): 142-149.
Zhou Wei, Zheng Yufeng, Chen Zelin, et al. Detuning estimation of pickup loop in capacitive wireless power transfer system based on secondary-side decoupled capacitive coupler[J]. Automation of Electric Power Systems, 2024, 48(3): 142-149.
[4] 刘祺, 薛明, 章鹏程, 等. 基于无线充电系统的多模块扩展均压技术研究与设计[J]. 电工技术学报, 2024, 39(22): 6980-6989.
Liu Qi, Xue Ming, Zhang Pengcheng, et al. Modular extensible voltage equalization based on wireless charging system[J]. Transactions of China Electro- technical Society, 2024, 39(22): 6980-6989.
[5] 陈志鑫, 张献, 沙琳, 等. 基于频率调节的电动汽车无线充电互操作性提升方法研究[J]. 电工技术学报, 2023, 38(5): 1237-1247.
Chen Zhixin, Zhang Xian, Sha Lin, et al. Research on improving interoperability of electric vehicle wireless power transfer based on frequency adjustment[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1237-1247.
[6] 孙天, 宋贝贝, 崔淑梅, 等. 电动汽车无线充电系统接收端位置大范围唯一性辨识系统设计[J]. 电工技术学报, 2024, 39(21): 6626-6635.
Sun Tian, Song Beibei, Cui Shumei, et al. Design of accurate position detection system applied to large misalignment range for electric vehicle wireless charging system[J]. Transactions of China Electro- technical Society, 2024, 39(21): 6626-6635.
[7] 程志远, 宋晓逸, 吴晓婷, 等. 无线充电系统旋转式电磁耦合器损耗计算及热点温度研究[J]. 电工技术学报, 2024, 39(7): 1932-1942.
Cheng Zhiyuan, Song Xiaoyi, Wu Xiaoting, et al. Loss calculation and hot spot temperature research of rotary electromagnetic coupler in wireless charging system[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 1932-1942.
[8] Dellabate A, Lazzoni V, Brizi D, et al. Near-field focusing conformal magnetic metasurface for wireless power transfer[C]//2023 IEEE International Sympo- sium on Antennas and Propagation and USNC-URSI Radio Science Meeting (USNC-URSI), Portland, OR, USA, 2023: 531-532.
[9] Nam Y H, Lee J H. Efficient near-field beamforming using two-layer planar loop array for magnetic reso- nance wireless power transfer[J]. IEEE Microwave and Wireless Components Letters, 2020, 30(8): 818- 820.
[10] 陈伟华, 宋宇航, 闫孝姮, 等. 心脏起搏器无线电能传输LCC-LCC磁集成印刷螺旋线圈研究[J]. 电工技术学报, 2024, 39(17): 5289-5299.
Chen Weihua, Song Yuhang, Yan Xiaoheng, et al. Research on wireless power transmission for cardiac pacemakers using LCC-LCC magnetic integrated printed spiral coil[J]. Transactions of China Elec- trotechnical Society, 2024, 39(17): 5289-5299.
[11] 何亚伟, 李阳, 杨庆新, 等. 磁耦合谐振式无线电能传输线圈的磁聚焦仿真[J]. 天津工业大学学报, 2015, 34(2): 75-79.
He Yawei, Li Yang, Yang Qingxin, et al. Simulation of focus magnetic field of magnetically coupled resonant wireless power transfer coil[J]. Journal of Tianjin Polytechnic University, 2015, 34(2): 75-79.
[12] 冯天旭, 史可, 孙跃, 等. 基于互感识别及移相角优化的全方位无线电能传输系统靶向传能方法[J].电工技术学报, 2023, 38(24): 6581-6595.
Feng Tianxu, Shi Ke, Sun Yue, et al. Targeted power transfer method for omnidirectional wireless power transfer system based on mutual inductance identi- fication and phase-shift angle optimization[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(24): 6581-6595.
[13] Jung H, Lee B. Optimization of magnetic field focusing and null steering for selective wireless power transfer[J]. IEEE Transactions on Power Elec- tronics, 2020, 35(5): 4622-4633.
[14] Kang Ning, Shao Yaoxia, Liu Ming, et al. Analysis and implementation of 3D magnetic field shaping via a 2D planar transmitting coil array[J]. IEEE Transa- ctions on Power Electronics, 2022, 37(1): 1172-1184.
[15] Budak A, Durna E. Performance evaluation of inductive wireless power transfer for high-speed non-contact slip ring applications[C]//2022 IEEE Applied Power Electronics Conference and Expo- sition (APEC), Houston, TX, USA, 2022: 500-504.
[16] Hariri A O, Berzoy A, Mohamed A A S, et al. Performance evaluation of a wireless power transfer system using coupled 3D finite element-circuit model[C]//2015 IEEE Wireless Power Transfer Conference (WPTC), Boulder, CO, USA, 2015: 1-4.
[17] Cetin S, Demirci Y E, Yenil V. Performance evaluation of wireless power transfer compensation topologies for active implantable medical devices[C]// 2021 IEEE 19th International Power Electronics and Motion Control Conference (PEMC), Gliwice, Poland, 2021: 798-803.
[18] Xiang Lijuan, Sun Yue, Dai Xin, et al. Evaluation of magnetic coupler for stationary EVs' wireless charging[J]. International Journal of Applied Elec- tromagnetics and Mechanics, 2017, 53(1): 167-179.
[19] 郑小瑶, 江彦伟, 疏许健, 等. 宇称-时间对称电场耦合无线电能传输系统电场分布特性研究[J]. 电源学报, 2024, 22(5): 60-66.
Zheng Xiaoyao, Jiang Yanwei, Shu Xujian, et al. Study on electric-field distribution characteristics of parity-time symmetric electric-field coupled wireless power transfer system[J]. Journal of Power Supply, 2024, 22(5): 60-66.
[20] 赖禹同, 郭锋, 唐自强, 等. 双负载磁谐振S-LCL无线充电系统频率分叉分析[J]. 电气工程学报, 2023, 18(1): 86-93.
Lai Yutong, Guo Feng, Tang Ziqiang, et al. Analysis of frequency bifurcation of dual load magnetic resonance S-LCL wireless charging system[J]. Journal of Electrical Engineering, 2023, 18(1): 86-93.
[21] 王成亮, 潘志新, 翟学锋, 等. 基于改进粒子群算法的无线充电系统参数优化[J]. 电气传动, 2023, 53(3): 64-69.
Wang Chengliang, Pan Zhixin, Zhai Xuefeng, et al. Parameter optimization of wireless charging system based on improved PSO algorithm[J]. Electric Drive, 2023, 53(3): 64-69.
[22] Wen Feng, Cheng Xingchen, Li Qiang, et al. A strong misalignment tolerance dual-channel coupler for wireless power transfer system[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(8): 0601005.
[23] Feng Jing, Wei Guo, Zhang Jiantao, et al. An LCCC- LCC compensated dual-coupled WPT system with MI enhancement and high misalignment tolerance[J]. IEEE Transactions on Power Electronics, 2023, 38(12): 15162-15167.
[24] Shi Ke, Feng Tianxu, Jiang Jincheng, et al. A highly magnetic integrated method of LCC-compensated IPT system with excellent misalignment tolerance[J]. IEEE Transactions on Power Electronics, 2023, 38(12): 16256-16268.
[25] Raju S, Wu Rongxiang, Chan Mansun, et al. Mode- ling of mutual coupling between planar inductors in wireless power applications[J]. IEEE Transactions on Power Electronics, 2014, 29(1): 481-490.
[26] Zhong W X, Liu Xun, Ron Hui S Y. A novel single-layer winding array and receiver coil structure for contactless battery charging systems with free- positioning and localized charging features[J]. IEEE Transactions on Industrial Electronics, 2011, 58(9): 4136-4144.
[27] Zhu Lei, Wang Laili, Wu Min, et al. Precise modeling and design of self-resonant for high-efficiency mid- range wireless power transfer system[J]. IEEE Transactions on Power Electronics, 2023, 38(6): 7848-7862.
[28] 陈雨晨, 陈凯楠, 郑树轩, 等. 无线电能传输磁耦合机构磁心解析模型与设计方法[J]. 电气技术, 2022, 23(6): 83-92.
Chen Yuchen, Chen Kainan, Zheng Shuxuan, et al. Analytical model and design method of magnetic core for wireless power transfer magnetic coupler[J]. Electrical Engineering, 2022, 23(6): 83-92.
Magnetic Focusing Enhancement with Non-Centrosymmetric Excitation Unit for Matrix Coil in Wireless Power Transfer System
Abstract The magnetic field's compactness can better increase energy's transmission distance in a near-filed wireless power transfer (WPT) system. This paper proposes a non-centrosymmetric excitation unit (NEU) design method for the WPT system with a matrix coupling mechanism to improve the magnetic flux density in the central region. The proposed method enhances the magnetic focusing performance with a flat two-dimensional structure while maintaining its misalignment tolerance without any other auxiliary coil or circuit. The self-inductance value of the transmitting coil in this design method is even smaller than that of the conventional design method under the same size and number of turns. In addition, the proposed method is applicable to all regular matrix coils. Then, a detailed design method of the coupler is given based on the circuit analysis. Finally, taking the LCL-LCC compensation WPT system as an example, the feasibility of the proposed design method is verified. Compared to traditional design methods, the proposed design method can increase the induced voltage by 24.7% at the optimal position.
The current mobile robot UAV (unmanned aerial vehicle)/AGV (automated guided vehicle) plays an important role in industrial inspection, office logistics, agricultural and forestry plant protection, and military reconnaissance and surveillance fields. A multi-level, multi-modal power supply demonstration application has been designed in intelligent parks and industrial inspections to achieve charging docking between unmanned devices. However, most power supply methods are fixed-point charging, which is complicated in the energy transmission process and faces energy loss problems. In special charging environments such as wilderness and underwater, if there is no suitable parking charging platform condition, UAV hovering charging technology has become the most necessary and perfect charging solution, and it is also the key to building wireless power transmission network environments. Based on the well-established technology of fixed-point hovering and hovering following for unmanned inspection equipment in the air-to-air, ground-to-ground, and air-to-ground scenarios, hovering and alignment energy replenishment is undoubtedly a highly efficient and cutting-edge design concept applied to unmanned inspection equipment. Nowadays, to further enhance the flexibility and reliability of wireless charging systems, more and more wireless charging systems are designed based on matrix coils. The matrix-based multi-excitation wireless charging system has gained more favor in charging applications due to its reconstruction mechanism of the magnetic field at the transmitting end and strong tolerance for voltage and current stress.
In summary, a matrix coil design method based on non-centrosymmetric excitation units is proposed, combined with an evaluation of the system's spatial field transmission capability to improve the optimization design steps and the focusing ability of the magnetic field. This design method, which has a two-dimensional planar structure, enhances the magnetic flux density at the center position without any auxiliary coils or circuits, avoiding the offset tolerance weakening of the matrix coil itself as much as possible. It reduces the self-inductance of the coil unit to improve mutual inductance utilization.
keywords:Wireless power transfer system, multi excitation units, magnetic focusing enhancement, assessment method for spatial transmission capability
中图分类号:TM724
DOI: 10.19595/j.cnki.1000-6753.tces.241765
国家重点研发计划项目(2022YFF0604200)、重庆市教委科技项目(KJQN202201630, KJZD-K202401604)和重庆市自然科学基金面上项目(CSTB2024NSCQ-MSX0812)资助。
收稿日期 2024-10-11
改稿日期2024-12-09
蒋金橙 男,1993年生,博士,讲师,研究生导师,研究方向为电力电子、嵌入式系统及无线电能传输技术。
E-mail: jiangjinc@cqupt.edu.cn
邓棚亓 男,1992年生,博士,研究方向为非线性建模及分析,电磁干扰抑制和无线电能传输技术。
E-mail: dengpq@cqupt.edu.cn(通信作者)
(编辑 陈 诚)