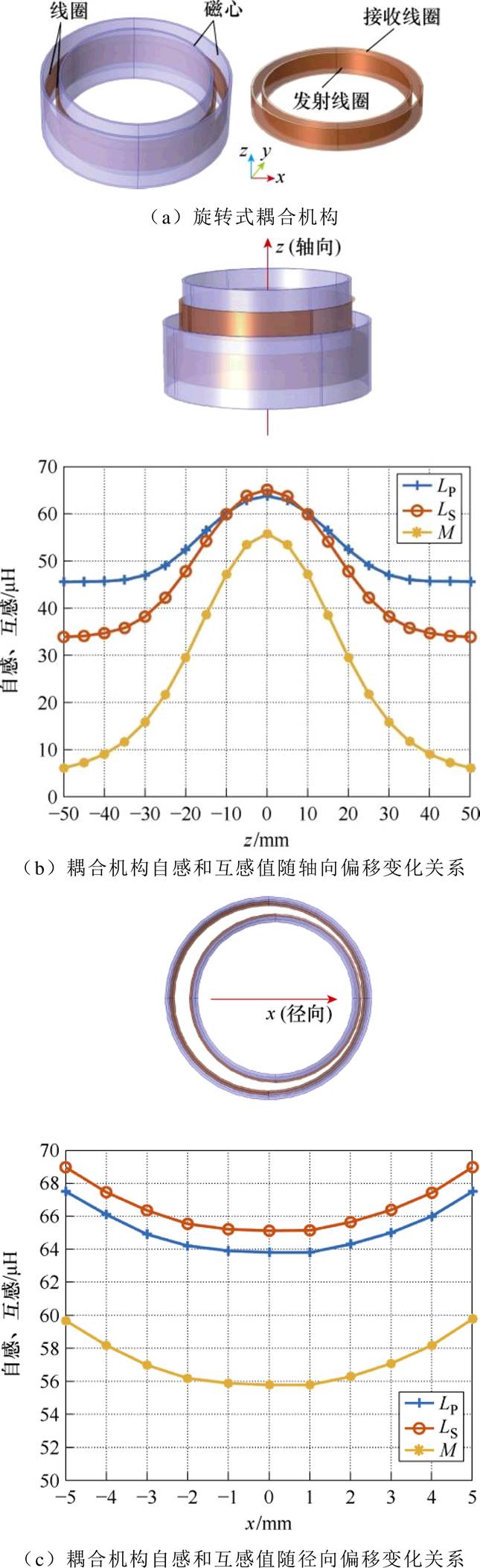
图1 旋转式耦合机构及其参数变化规律
Fig.1 The rotating coupling mechanism and its parameter variation rule
摘要 无线电能传输(WPT)技术可有效解决旋转设备的稳定供电问题。然而,由于铁氧体磁心的存在,旋转侧和静止侧的相对偏移会显著影响磁耦合机构自感和互感参数,从而引起输出功率波动和效率降低。该文提出一种考虑线圈参数变化的失谐型WPT系统抗偏移方法,利用线圈自感变化构造失谐WPT系统,从而抵消互感变化带来的输出功率波动。通过推导接收端失谐程度与互感变化的恒压输出条件,结合粒子群优化算法对系统补偿参数进行优化,旋转式WPT系统具备了良好的轴向和径向抗偏移能力。该方法利用了旋转式耦合机构自身参数变化相互平衡抵消的特性,无需额外的无线通信和闭环控制以及DC-DC环节,实现更为简单可靠。实验结果表明,所提方法能够在耦合系数0.39~0.89、互感变化74%和自感变化48%的范围内,实现近似恒定输出,输出电压波动最大仅为9.5%(轴向)和2.8%(径向),系统效率最高达到93%。
关键词:无线电能传输 参数变化 抗偏移 失谐 粒子群优化算法
为旋转设备供电问题普遍存在于航空航天、石油钻井、水下航行器等领域[1-5]。而传统接触式供电方式存在易磨损老化、故障率高等问题,导致设备的可靠性降低、使用寿命受到限制。无线电能传输(Wireless Power Transfer, WPT)技术因采用非接触的电能传输方式,具有安全可靠、灵活便捷和免维护等优点,为解决旋转设备的稳定供电问题提供了有效途径。
然而,在实际应用中,旋转侧和静止侧的相对偏移不可避免[6-7]。例如,在石油钻采设备中,移动的钻杆和静止的筒壁之间存在一定的轴向和径向偏移。同时在WPT系统工程应用中,由于铁氧体磁心的存在,耦合机构偏移会显著影响线圈自感和互感参数,从而引起输出功率波动和效率降低[8-10]。因此,提升系统在线圈参数变化下的抗偏移能力至关重要。
根据线圈自感是否变化,WPT系统的抗偏移技术可分为只有互感变化和自感互感同时变化两种。关于线圈偏移引起的互感变化问题,解决思路大致可分为三种:耦合机构设计[11]、补偿网络优化[12]和控制策略提升[13]。而自感变化往往会引起失谐,使系统分析变得更为复杂,传统的抗偏移方法不再适用[14]。
为解决自感和互感同时变化的问题,从磁耦合机构设计出发,文献[15]提出一种自感与气隙无关的线圈结构,利用铁磁性材料和金属材料对线圈自感的反作用规律,实现了气隙变化下近似的恒功率输出。文献[16]采用“大发射小接收”的设计思想,实现了原边线圈自感与气隙变化无关。然而文献[15-16]仅实现了单侧自感变化且不明显,其适用范围受限。在补偿拓扑参数优化方面,文献[17]基于粒子群优化(Particle Swarm Optimization, PSO)算法提出了考虑线圈参数变化的串联-串联(Series- Series, SS)补偿拓扑WPT系统参数设计方法,实现了气隙变化下的恒流输出。文献[18]提出了基于T/S补偿拓扑的抗偏移WPT系统,实现了气隙和负载变化下的恒流输出和高效率运行。文献[19]提出了基于S/SP补偿拓扑的强抗偏移WPT系统,实现了在变耦合变自感和变耦合不变自感两种情况下均能保证较小的输出电压波动和较高的传输效率。然而这些方法所适应的参数变化范围较为受限。从闭环控制的角度,文献[20]提出了零电压开关角跟踪和动态电容补偿矩阵复合控制策略,显著降低了由于系统参数变化引起的传输功率和传输效率的下降。文献[21]提出WPT系统的零相位频率跟踪策略,实现了参数变化下的零相位快速跟踪,提升了系统输出功率和传输效率。文献[22]利用自感变化实现了WPT系统宽范围零电压软开关运行,在恒定输出的同时提升了系统效率。然而,上述基于闭环控制的方法需引入新的控制变量,使系统更为复杂,从而降低其可靠性。
为提升WPT系统在线圈参数变化下的抗偏移能力并简化控制,本文提出一种失谐型WPT系统参数配置方法。首先,总结了旋转式耦合机构在轴向与径向偏移下的参数变化规律,提出了利用自感变化动态调整系统失谐程度以抵消互感变化引起输出波动的思想。其次,推导了接收端失谐程度与互感变化的恒压输出条件,并基于PSO算法对电感-电容-电容-串联(Inductor-Capacitor-Capacitor-Series, LCC-S)补偿拓扑参数进行优化,实现了旋转式WPT系统良好的轴向和径向抗偏移能力。最后,搭建了170 W的实验装置验证所提方法的有效性。实验结果表明,在轴向偏移±30 mm、径向偏移±5 mm范围内,旋转式耦合机构最大互感变化为74%、自感变化为48%、耦合系数为0.39~0.89,输出电压波动最大仅为9.5%(轴向)和2.8%(径向),系统效率最高达到93%。本方法利用了耦合机构自身参数变化相互平衡抵消的特点,其显著优势在于结构简单有效、无DC-DC环节、无通信及闭环控制,系统更为稳定可靠,特别适用于井下高温、高压、高频振动等恶劣环境中的无线供电,降低供电系统故障率,提升供电可靠性。
本文选取如图1a所示的旋转式耦合机构进行研究,其外形为套筒式结构。其中,内筒为能量发射侧,外筒为能量接收侧,发射线圈与接收线圈内外侧分别装有铁氧体磁心,以增强耦合并减少电磁泄漏,铁氧体磁心材质为PC40。定义沿z轴方向偏移为轴向,沿x或y轴方向偏移为径向,同时由于耦合机构的对称性,为简化分析,以下径向偏移均指沿x轴方向偏移。

图1 旋转式耦合机构及其参数变化规律
Fig.1 The rotating coupling mechanism and its parameter variation rule
以表1所示旋转式耦合机构参数为例,利用有限元仿真软件COMSOL研究耦合机构自感和互感值随轴向和径向偏移的变化关系,如图1所示。图中,LP、LS和M分别为原、副边线圈自感和互感。当耦合机构发生轴向偏移时,线圈自感和互感均会显著减小,偏移到一定程度后自感趋于稳定而互感仍然减小。在轴向偏移±60%范围(Dz=±30 mm)内,互感变化达到71.7%,自感变化达到41.3%,耦合系数变化达到56.9%。当耦合机构发生径向偏移时,线圈自感、互感和耦合系数均会增大。总体而言,耦合机构自感和互感变化趋势相同,在一定偏移范围内变化程度相似。因此,在系统设计过程中有必要考虑线圈参数变化带来的影响。
表1 旋转式耦合机构参数
Tab.1 The rotating coupling mechanism parameters
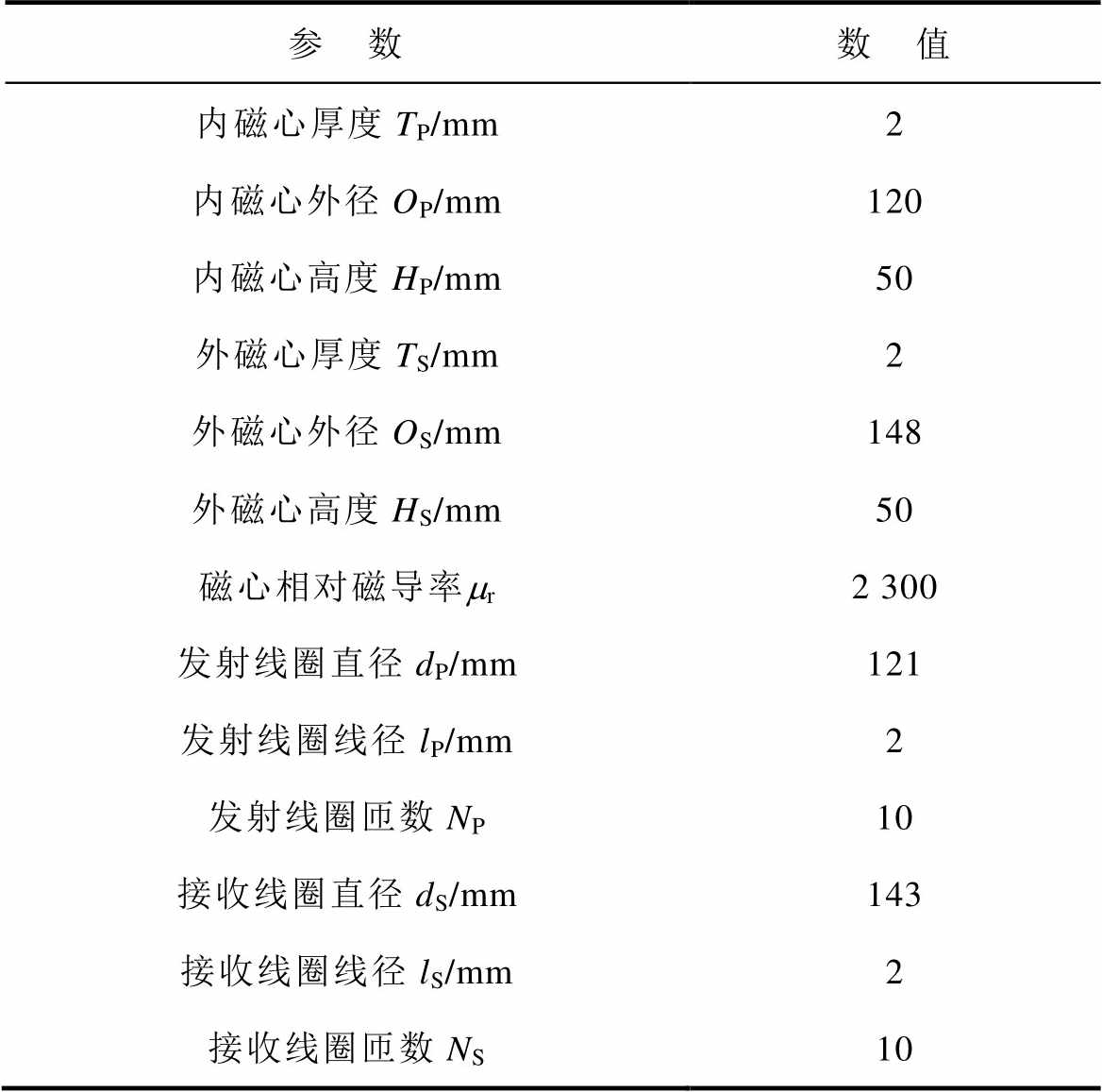
参 数数 值 内磁心厚度TP/mm2 内磁心外径OP/mm120 内磁心高度HP/mm50 外磁心厚度TS/mm2 外磁心外径OS/mm148 外磁心高度HS/mm50 磁心相对磁导率mr2 300 发射线圈直径dP/mm121 发射线圈线径lP/mm2 发射线圈匝数NP10 接收线圈直径dS/mm143 接收线圈线径lS/mm2 接收线圈匝数NS10
图2给出了耦合机构偏移情况下的磁场分布情况。可以看到,旋转式耦合机构内外套筒之间磁场分布最强,铁氧体磁心有效屏蔽了磁场,但同时,磁场强度分布也随耦合机构的偏移而变化。
根据上述分析,建立基于LCC-S补偿拓扑的变参数WPT系统如图3所示。图中,Udc与UL分别为输入、输出直流电压,MOSFET Q1~Q4组成全桥逆变电路,肖特基二极管VD1~VD4组成不控整流电路,Cd为滤波电容,LT、CT、CP和CS组成LCC-S补偿拓扑,RT、RP、RS为线圈等效串联电阻(Equivalent Series Resistance, ESR),RL为负载电阻。在实际应用中,线圈ESR通常很小,为简化分析可将其忽略,得到如图4所示的等效电路。
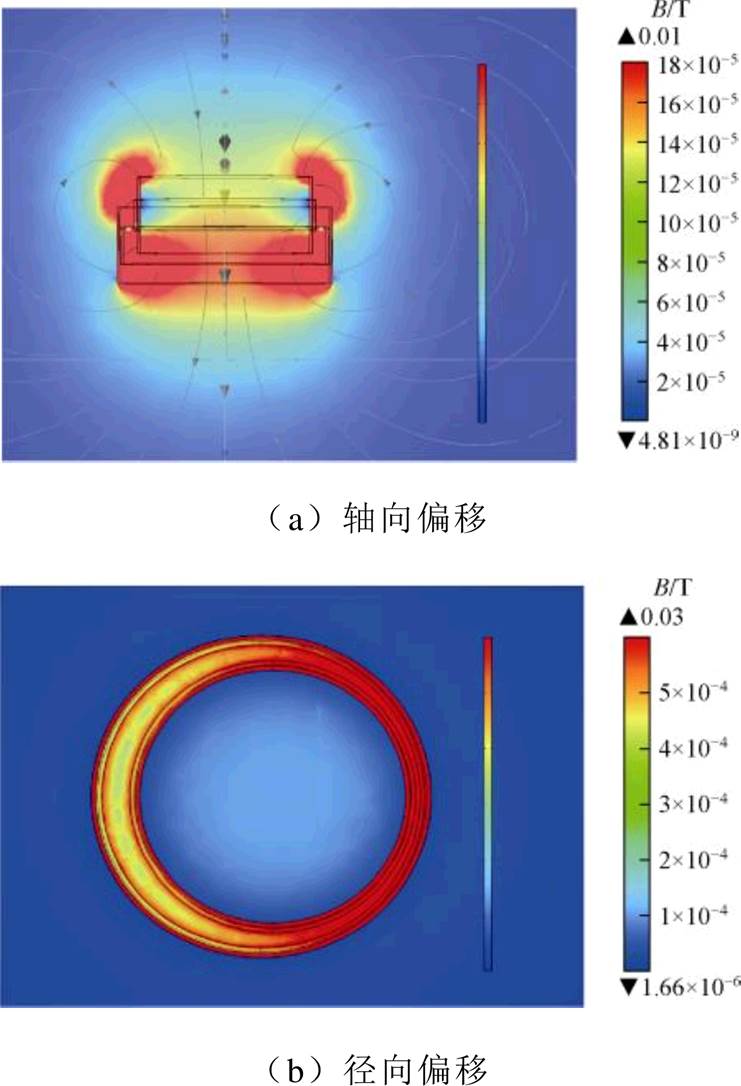
图2 旋转式耦合机构磁场分布情况
Fig.2 Magnetic field distribution of rotary coupling mechanism
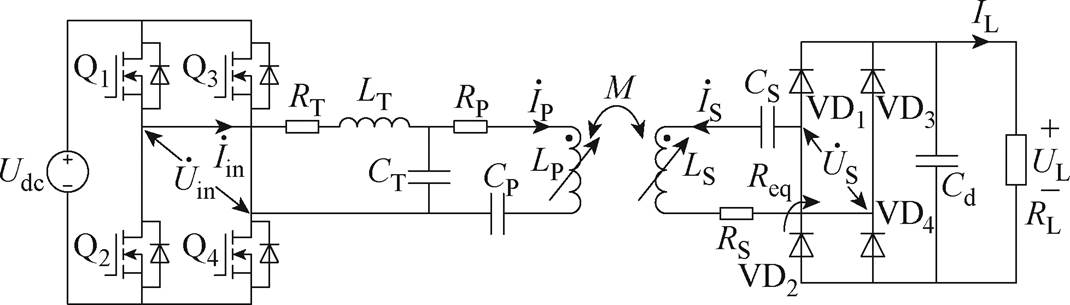
图3 基于LCC-S补偿拓扑的变参数WPT系统
Fig.3 Variable parameter WPT system based on LCC-S compensation topology
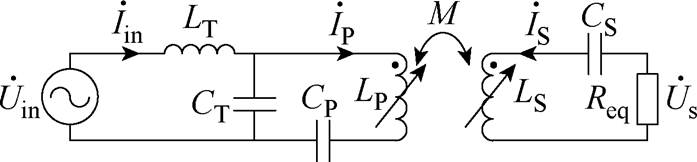
图4 等效电路
Fig.4 Equivalent circuit
图4中,LP、LS和M均为变量,自感可表示为
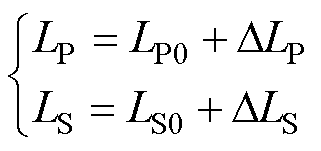 (1)
(1)
式中,LP0、LS0为初始值;DLP、DLS分别为其变化量。
等效负载电阻Req可表示为
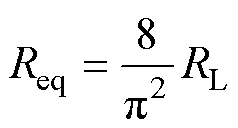 (2)
(2)
补偿电容CT、CP和CS满足
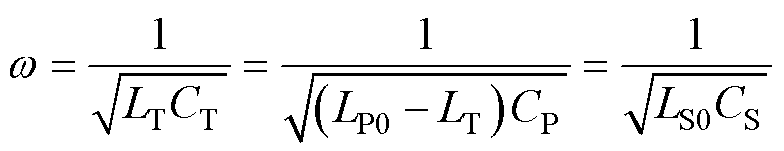 (3)
(3)
式中,w 为系统工作角频率。
根据基波近似分析,逆变器输出电压Uin及整流器输入电压US可分别表示为
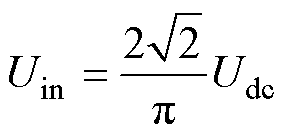 (4)
(4)
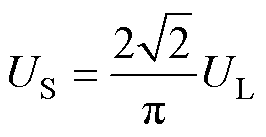 (5)
(5)
根据基尔霍夫电压定律可得
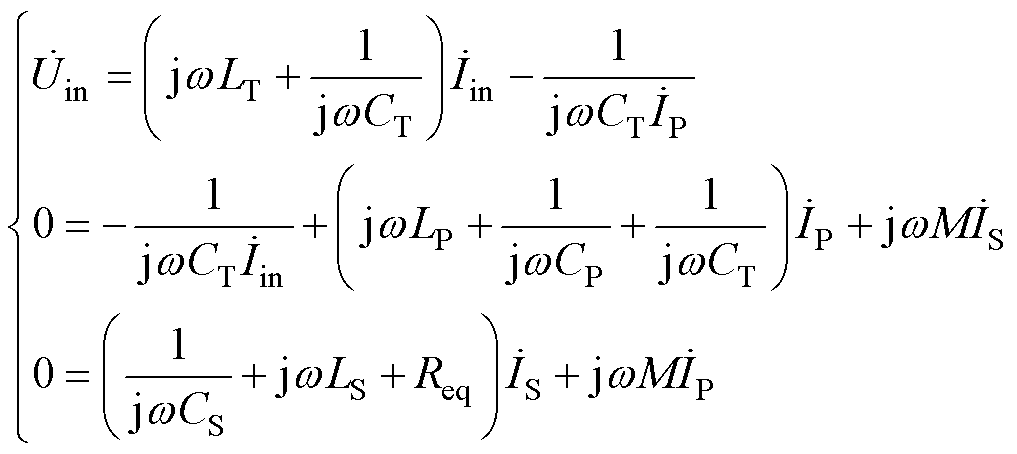 (6)
(6)
式中,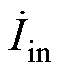 为逆变器输出电流;
为逆变器输出电流;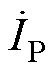 为发射线圈电流;
为发射线圈电流;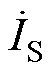 为接收线圈电流。
为接收线圈电流。
联立式(1)~式(6)可得系统输出负载电压UL为
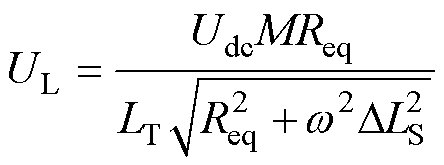 (7)
(7)
由式(7)可知,在负载一定的情况下,输出电压仅与M和DLS有关,而与DLP无关,且M和DLS均与分子和分母呈正相关。根据1.1节所得耦合机构参数变化规律可知,如果参数配置得当时,接收线圈自感变化可抵消互感变化带来的影响,实现恒定输出。将式(7)变换可得系统恒压输出的条件为
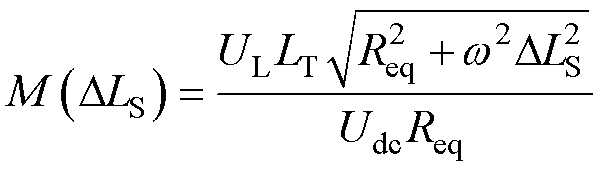 (8)
(8)
系统输入阻抗及其阻抗角为
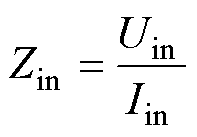 (9)
(9)
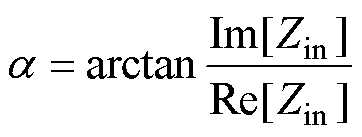 (10)
(10)
联立式(1)、式(3)、式(6)、式(9)可得输入阻抗虚部为
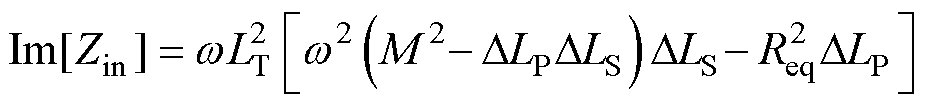 (11)
(11)
由式(11)可知,DLP与Im[Zin]呈负相关,即DLP的增大使输入阻抗趋于容性;而DLS与Im[Zin]的关系取决于耦合机构参数变化特性。
WPT系统功率损耗主要包括逆变器损耗Pinv_loss、谐振网络损耗PESR_loss和整流器损耗Prec_loss三部分[16],可表示为
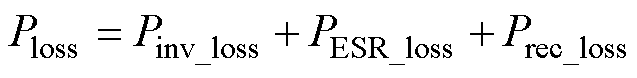 (12)
(12)
逆变器损耗主要包括MOSFET的导通损耗Pmos和开关损耗PSW,即
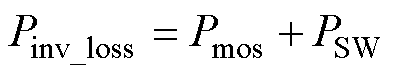 (13)
(13)
导通损耗可表示为
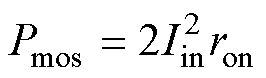 (14)
(14)
式中,ron为MOSFET的通态电阻。
开关损耗可表示为
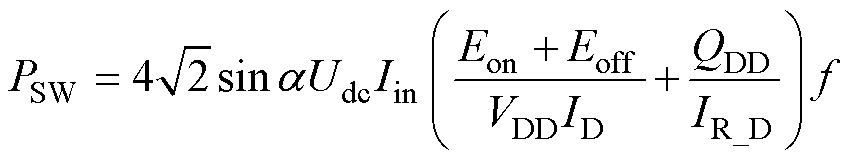 (15)
(15)
式中,Eon和Eoff分别为MOSFET开通和关断能量;VDD和ID分别为其参考漏源电压和电流;QDD和IR_D分别为MOSFET反并联二极管的反向恢复电荷和参考电流;f为系统工作频率。当逆变器实现零电压开通(Zero Voltage Switching, ZVS)时,MOSFET的导通损耗为零,只考虑MOSFET的关断损耗和反并联二极管的开关损耗。
同时,谐振网络损耗可表示为
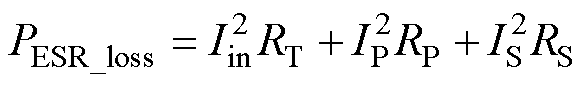 (16)
(16)
整流器的功率损耗主要是由整流器二极管的正向压降和通态电阻引起的,所以其功率损耗可以表示为
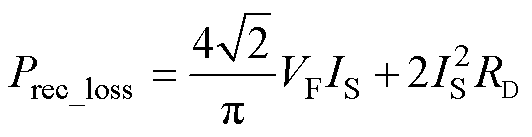 (17)
(17)
式中,VF和RD分别为整流二极管的正向压降和等效通态电阻。
进一步地,结合线圈参数变化规律与电路分析,研究线圈参数对系统运行的影响情况,系统参数见表2。
由式(8)和表2可得不同LT下的系统恒压输出条件,如图5所示。可以看到,恒压输出条件下,补偿电感参数影响了M和DLS的关系。因此,要提升系统抗偏移性能,可通过耦合机构设计和补偿参数优化两种方式结合,来使式(8)的恒压输出条件近似成立。
表2 系统参数
Tab.2 System parameters

参 数数 值 Udc/V80 w/(rad/s)6.28×105 UL/V32 RL/W6
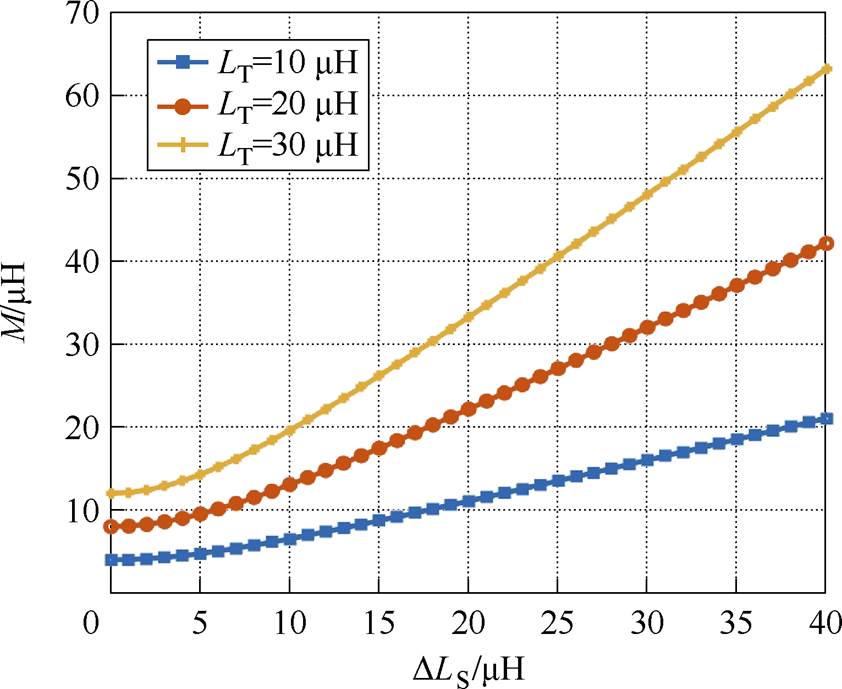
图5 不同LT下的系统恒压输出条件
Fig.5 System constant voltage output conditions at different LT
系统输入阻抗角反映了功率因数的大小,并在很大程度上决定了逆变器ZVS能否实现,从而影响系统效率。一般来说,a>0有利于实现ZVS运行,但过大的阻抗角会使谐振回路无功电流增大,导致效率降低[23]。因此,a 的理想取值应为一个较小的正值。图6所示为LT=20 mH时a 与耦合机构参数变化关系。可以看到,DLP的增大总会使a 减小;而DLS与a 的关系取决于M的取值。因此,可以通过调节耦合机构参数变化规律使a 保持在理想范围内。
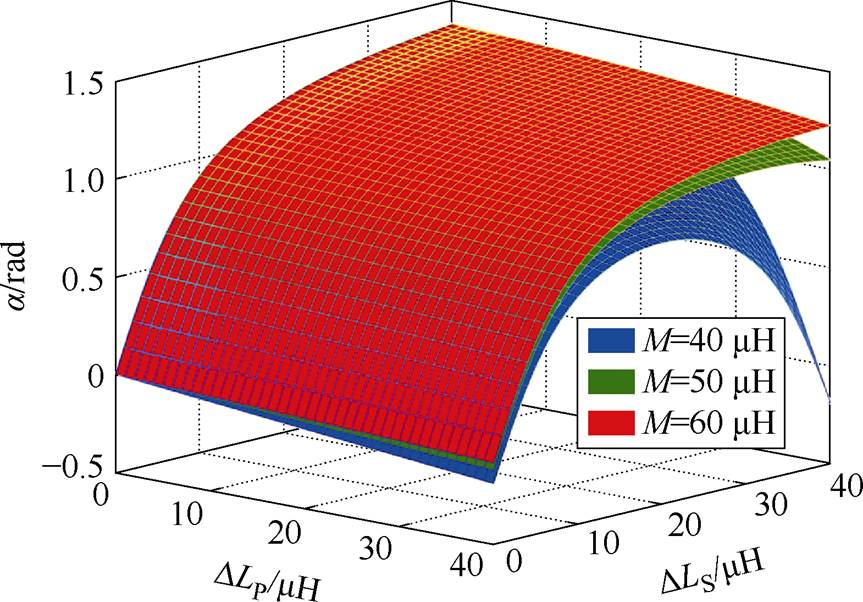
图6 系统输入阻抗角与耦合机构参数变化关系
Fig.6 The relationship between the system input impedance angle and the coupling mechanism parameters
由1.1节可知,旋转式耦合机构自感和互感参数在轴向偏移下变化更为明显,且由于耦合机构的对称性,沿z轴和-z轴偏移时参数变化也完全对称。因此,本节研究主要围绕沿z轴正向偏移时的系统参数设计方法,给定偏移范围为[0, 30 mm]。由式(8)可知,系统恒压输出条件主要取决于M和DLS的关系,所以,为简化分析,耦合机构设计主要针对副边线圈匝数NS展开。基于表1所示的旋转式耦合机构参数,结合图5所示的恒压输出条件,利用COMSOL仿真软件得到不同NS下的参数变化情况如图7所示。
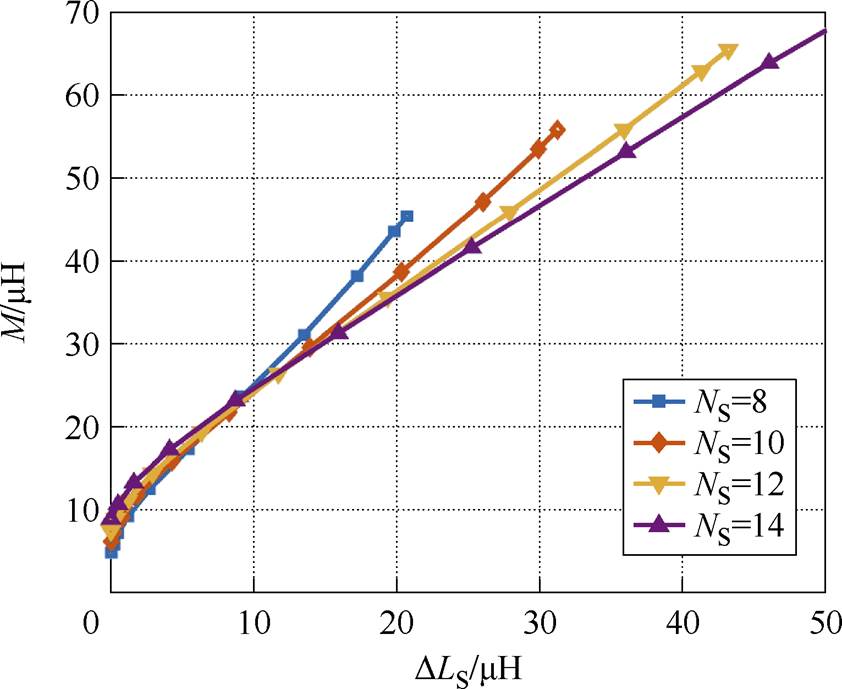
图7 不同NS下的旋转式耦合机构参数变化情况
Fig.7 The parameter variation of rotary coupling mechanism at different NS
图7中,不同NS对应曲线斜率不同,且DLS的变化范围也不同。当NS过小时,DLS的最大变化范围较为受限,也即相应的抗偏移范围有限;同时,考虑到线圈内阻对系统效率的影响,NS也不宜过大。综合上述考虑,选取NS=12。
LCC-S补偿系统谐振参数包括LT、CT、CP和CS 4个参数,由于LT参数选定后不会变化,CT根据式(3)计算即可。由于系统变量较多,且多个变量之间相互耦合,无法直接求出谐振参数的最优显式表达式,因此,谐振参数优化是一个典型的多参数优化问题[24]。
PSO算法是一种基于群体的智能算法,类似于鸟类或鱼类在搜索空间中移动,每个粒子的运动由一个有大小和方向的速度来控制。任何时间点上的每个粒子位置都受其历史最佳位置和问题空间中最佳粒子位置的影响。粒子的性能通过目标函数值来度量,即目标函数越小、性能越好[25-27]。由于PSO算法是一种易于理解、收敛快速、易于实现的寻优算法,本文采用该算法对谐振参数LT、CP和CS进行优化设计,将其转化为一个三维优化问题。
1)目标函数
谐振参数设计以输出恒定和效率提升为目标,首先保证输出电压在理想范围内,其次要保证ZVS运行和较小的无功功率。目标函数包括两个部分,即在轴向偏移z∈[0, 30 mm]范围内,输出电压UL和输入阻抗角a 分别在期望区间内。选取目标函数为
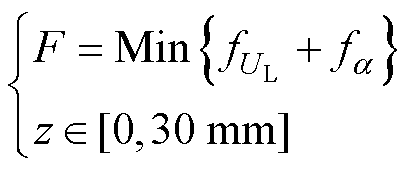 (18)
(18)
其中
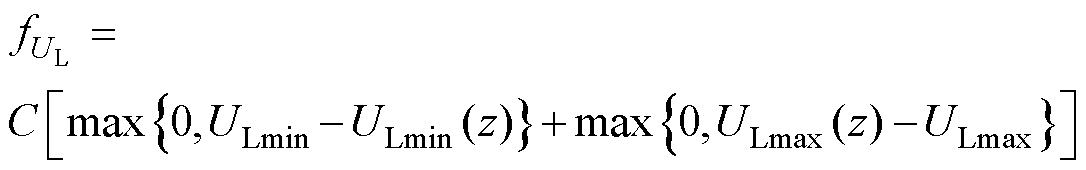 (19)
(19)
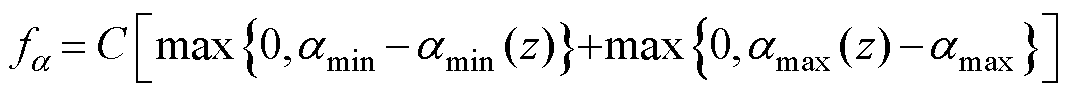 (20)
(20)
式中,C为较大的惩罚常数;max{a, b}表示取a, b之间的最大值;[ULmin, ULmax]和[amin, amax]分别为输出电压与输入阻抗角的期望区间;ULmin(z)、ULmax(z)和amin(z)、amax(z)分别为输出电压和输入阻抗角在轴向偏移[0, 30 mm]区间上的最小值和最大值。当存在任意UL和a 不在期望区间内时,其函数值较大,而目标函数是使两个函数值之和最小,这样可以保证UL和a 尽可能在期望范围内。
2)解空间和粒子速度限制
根据耦合机构参数,可以得到系统恒压输出条件与实际参数变化情况对比如图8所示。M(DLS)为NS=12对应的耦合机构参数变化情况用实线表示;根据式(8)得到不同LT下系统恒压输出条件,用虚线表示。可以看到,当LT=30 mH时,恒压输出条件变化趋势比实际参数变化较陡,随着LT逐渐减小,恒压输出条件整体变化趋势变得平缓,当LT= 20 mH时,恒压输出条件变化趋势比实际参数变化较平缓。因此,选取LT解空间在20~30 mH范围内。
根据传统的完全谐振条件,可以得到补偿电容的参考解空间[28]为
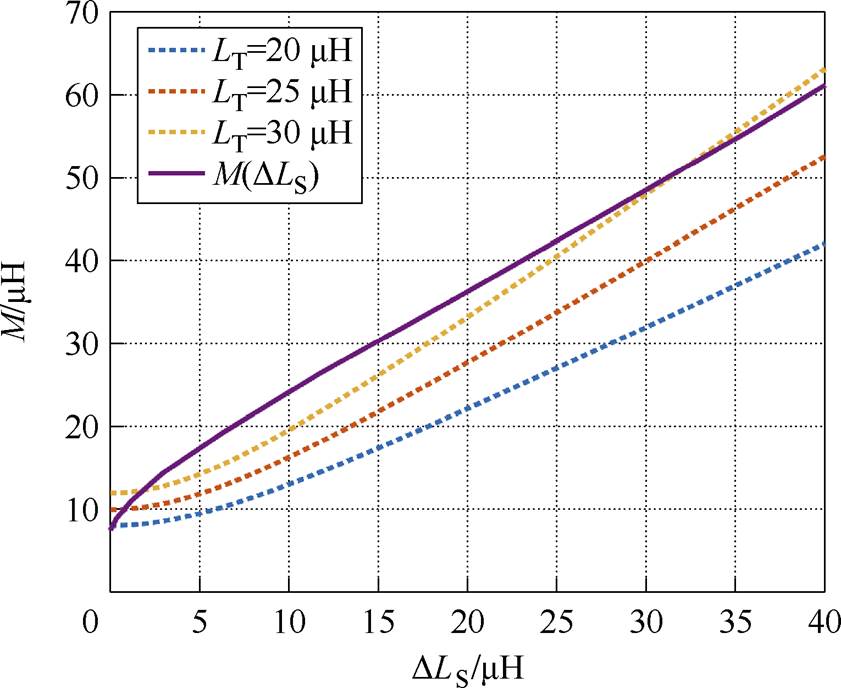
图8 系统恒压输出条件与实际参数变化情况对比
Fig.8 Comparison of system constant voltage output conditions with actual parameters variations
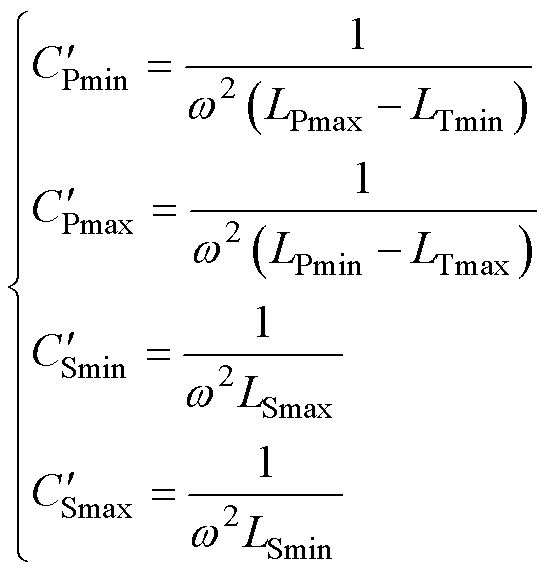 (21)
(21)
式中,LPmax和LPmin分别为LP在偏移情况下的最大值和最小值,其余类似。根据式(21)可得PSO算法的实际解空间为
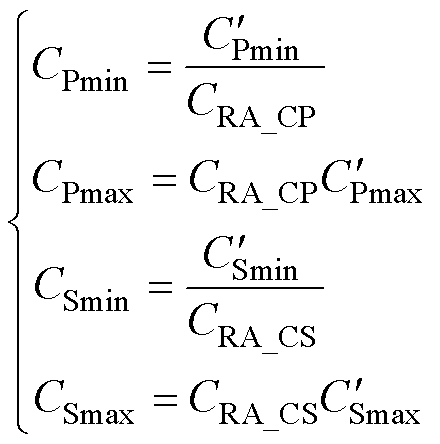 (22)
(22)
式中,CRA_CP和CRA_CS均为定值,代表了补偿参数的放大和缩小系数,主要根据补偿电容的实际限制而定。
一般来说,粒子的最大速度和最小速度设置为相反数,即vmax=-vmin。最大速度与算法的收敛速度和搜索能力有关,最大速度越小,搜索精度越高,但算法的收敛速度越慢。根据解空间可得到最大速度为
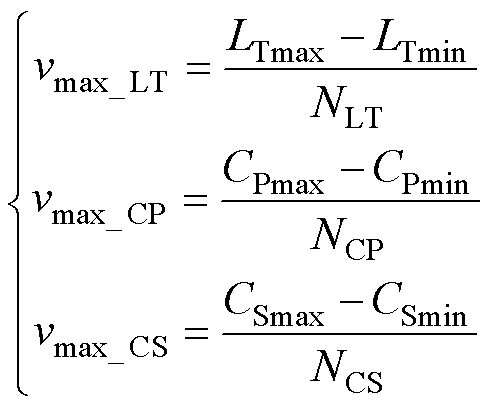 (23)
(23)
式中,NLT、NCP、NCS为3个正整数,为保证算法的搜索精度和收敛速度,其取值应适中。
3)PSO参数优化流程
粒子速度和位置的迭代公式为
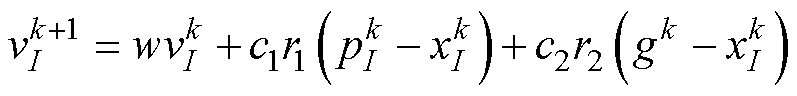 (24)
(24)
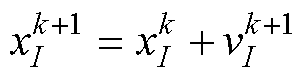 (25)
(25)
式中,w为惯性权重;c1和c2分别为认知加速系数和社会加速系数;r1和r2为独立随机数,均匀分布在[0, 1]上;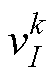 为粒子在第k次迭代中的速度;
为粒子在第k次迭代中的速度;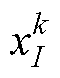 为粒子在第k次迭代中的位置;
为粒子在第k次迭代中的位置;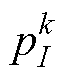 为k次迭代中粒子的最优位置;
为k次迭代中粒子的最优位置;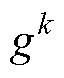 为k次迭代后群体的全局最优位置。
为k次迭代后群体的全局最优位置。
基于PSO算法的系统参数设计流程如图9所示。首先,输入系统基本设计参数和线圈参数以及期望的输出电压范围[ULmin, ULmax]和输入阻抗角范围[amin, amax],通过COMSOL仿真并拟合LP、LS和M与轴向偏移z的关系。
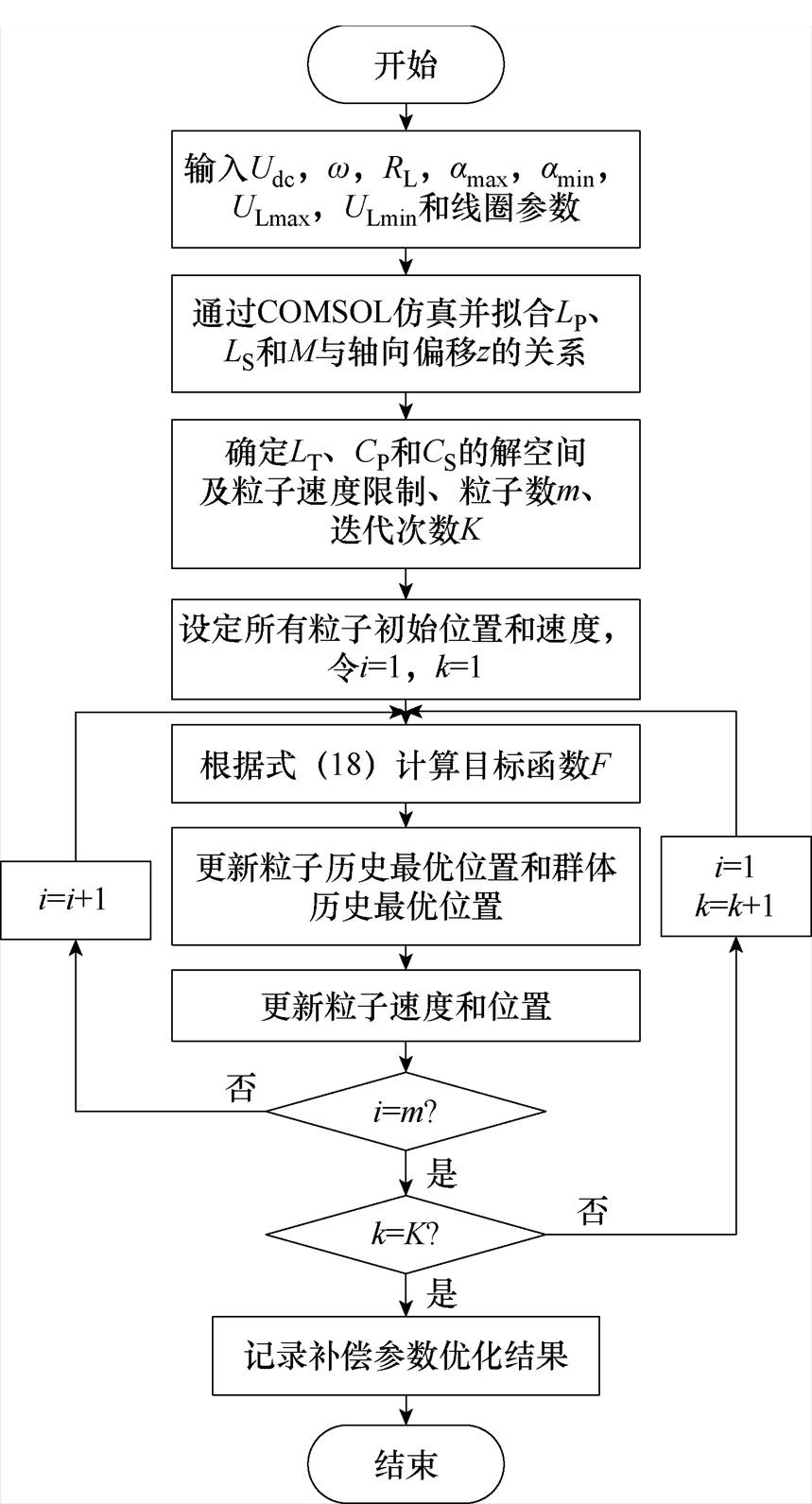
图9 参数设计流程
Fig.9 Parameter design flowchart
其次,确定补偿参数解空间和粒子速度限制及粒子数m和迭代次数K,并初始化所有粒子位置和速度。
然后,根据式(18)计算目标函数,并更新粒子和群体历史最优位置以及粒子的速度和位置。
最后,重复上述步骤并记录最优粒子位置,即补偿参数的最优解。
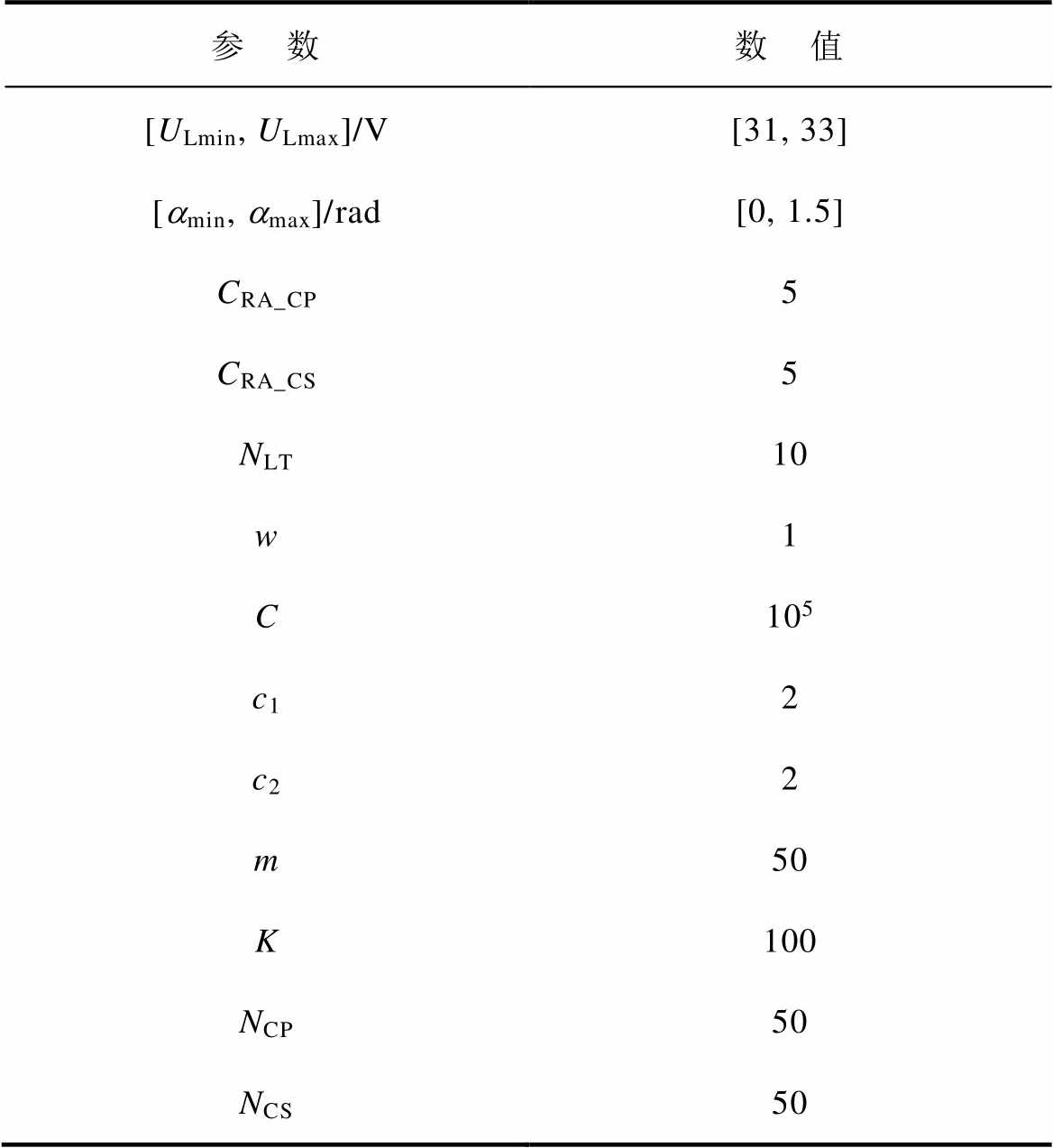
PSO算法参数见表3,得到目标函数与迭代次数的关系如图10所示。可以看到,初始目标函数值为2.5×105,迭代后逐渐收敛至2.2×104,表明补偿参数得到了显著优化,此时补偿参数值分别为LT= 22 mH,CP=508 nF,CS=61 nF。
表3 PSO算法参数
Tab.3 PSO algorithm parameters
参 数数 值 [ULmin, ULmax]/V[31, 33] [amin, amax]/rad[0, 1.5] CRA_CP5 CRA_CS5 NLT10 w1 C105 c12 c22 m50 K100 NCP50 NCS50
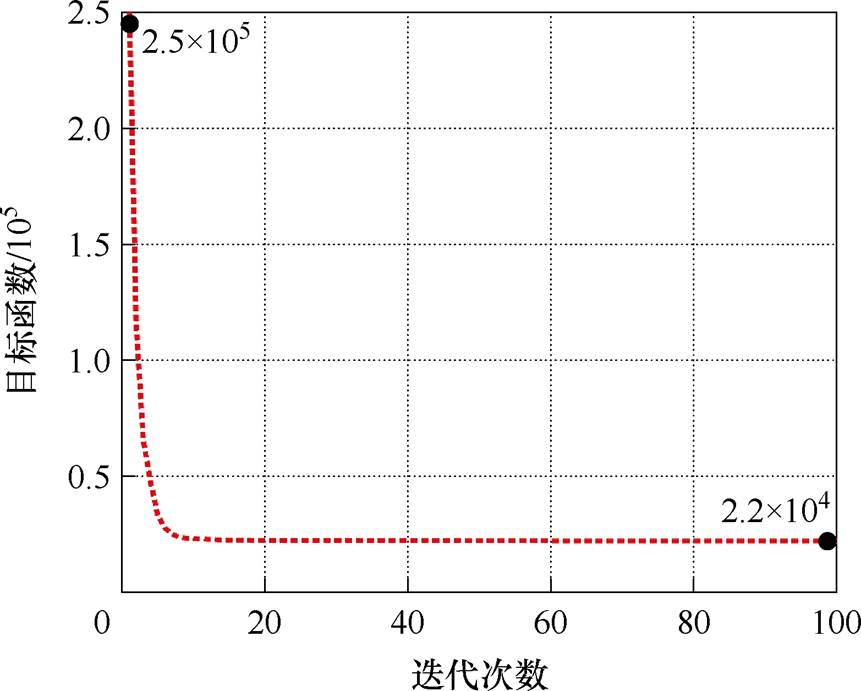
图10 目标函数与迭代次数的关系
Fig.10 Profile of optimization function with respect to particle generation
根据PSO算法优化结果,得到系统在参数优化后UL与a 随轴向偏移和径向偏移的变化情况如图11所示。随着轴向偏移增加,输出电压先增大后减小,但整体波动较小,能够保持在期望范围内;输入阻抗角逐渐减小,同样保持在期望范围内,意味着系统ZVS运行和较小的无功电流能够同时实现。随着径向偏移的增加,输出电压与输入阻抗角均减小,但能够保持在期望范围内。
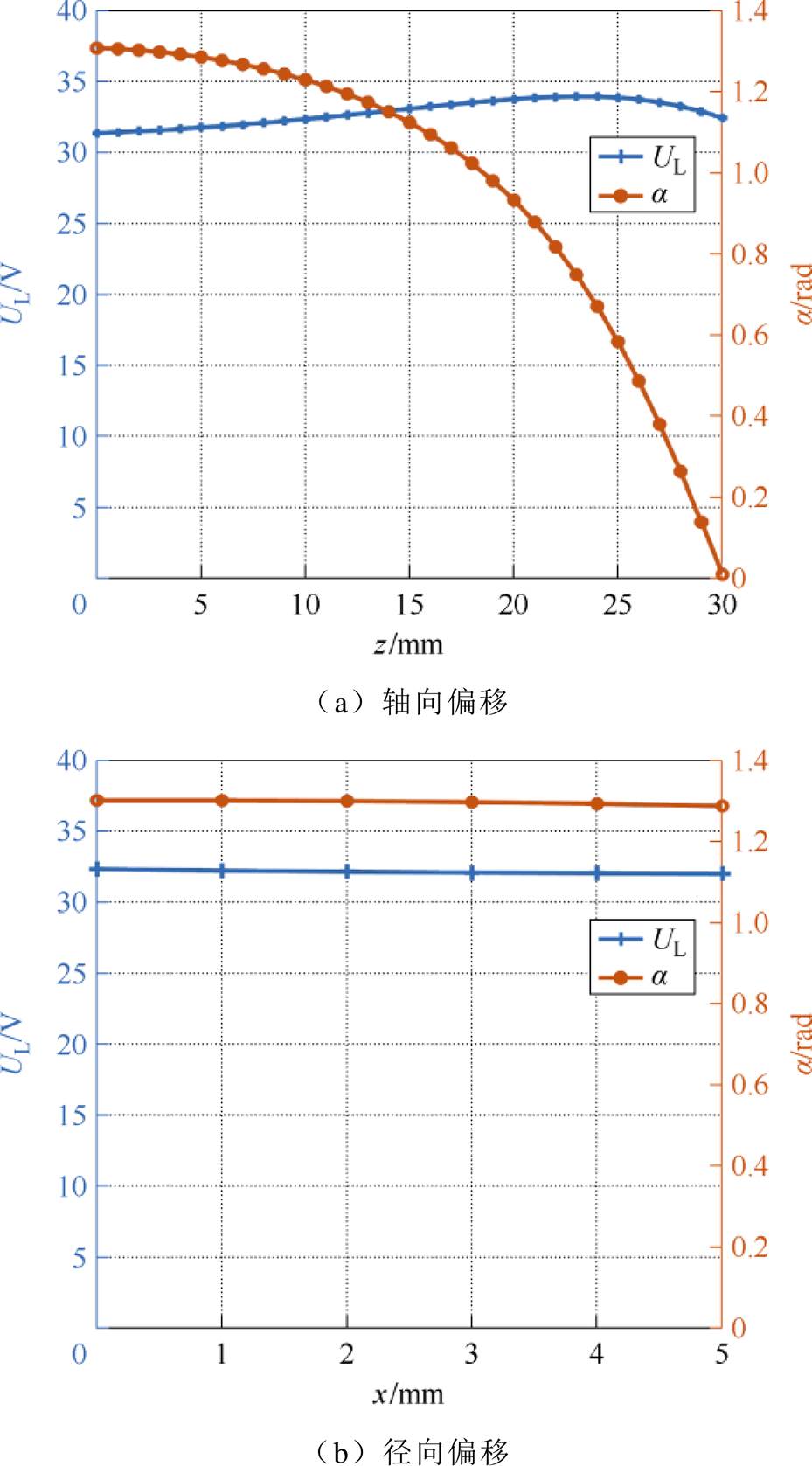
图11 参数优化后UL与a 随轴向偏移变化情况
Fig.11 Changes of UL and a with axial misalignment after parameter optimization
为验证所提方法的有效性,搭建了如图12所示的实验装置。其中,耦合机构参数和系统输入输出参数与理论分析保持一致,MOSFET Q1~Q4型号为TPW65R044MFD,肖特基二极管VD1~VD4型号为SL1045DS,直流电源IT6514D作为系统输入源,直流电子负载IT8514B作为输出负载。使用LCR电桥测试得到了旋转式耦合机构在轴向偏移±30 mm、径向偏移±5 mm范围内的实际参数和谐振电容参数见表4。

图12 实验装置
Fig.12 Experimental setup
表4 实验参数
Tab.4 Experimental parameters

参 数数 值 LP/mH[48.1, 71.0] RP/mW[95, 135] LS/mH[50.7, 96.6] RS/mW[132, 165] M/mH[19.1, 73.3] 耦合系数[0.39, 0.89] LT/mH21.9 CT/nF115.4 CP/nF508.3 CS/nF60.8 ron/mW39 Eoff/mJ40 VDD/V650 ID/A20 QDD/mC1.45 IR_D/A12 VF/V0.42 RD/mW42 f/kHz100 RT/mW68
图13所示为耦合机构不同轴向偏移下原边逆变器和副边直流输出电压电流波形,图13a~图13d为轴向偏移逐渐增大的过程,可以看到,系统输出电压电流基本保持不变,而逆变器输出电流滞后于输出电压角度(即系统输入阻抗角a)逐渐减小,但始终大于零,这与理论分析保持一致。
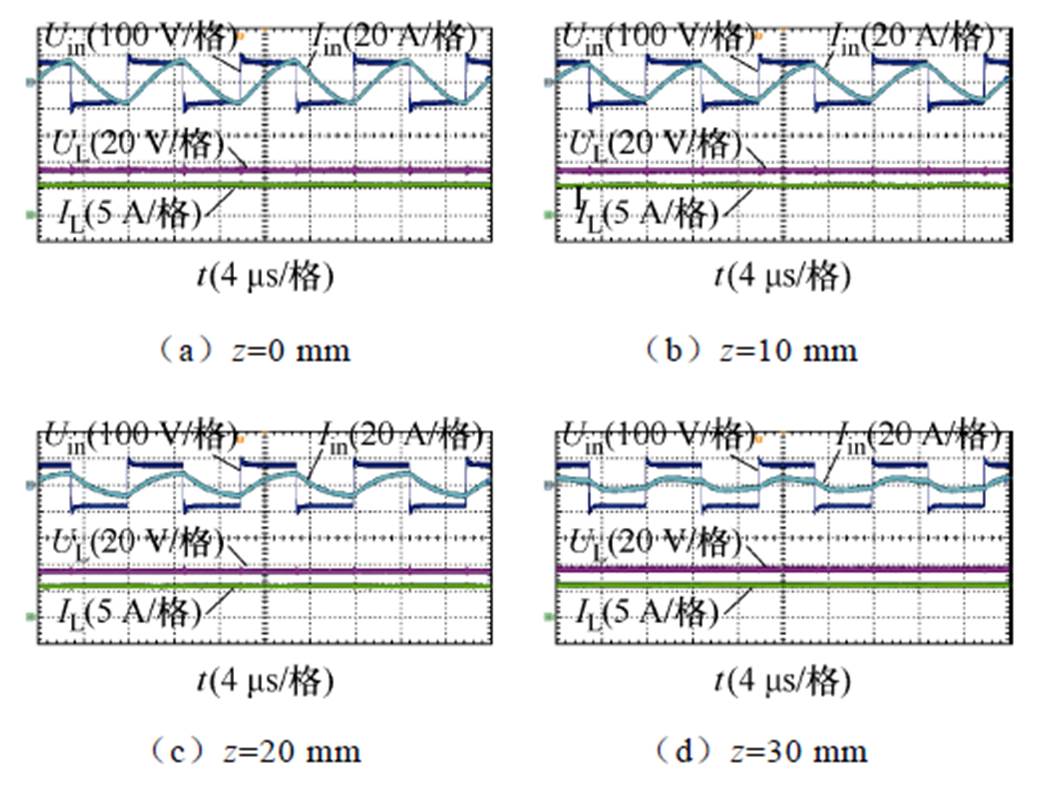
图13 不同轴向偏移下原边逆变器和副边直流输出电压电流波形
Fig.13 Output voltage and current waveforms of primary inverter and secondary at different axial misalignment
实验测得轴向偏移±30 mm范围内的系统输出电压和效率变化曲线如图14所示。可以看到,输出电压基本平稳,保持在[31.5, 34.8] V内,最大波动小于9.5%。系统效率先减小后增加,最高达到93%。在正对情况下,系统效率较低,是因为此时输入阻抗角过大引起的。
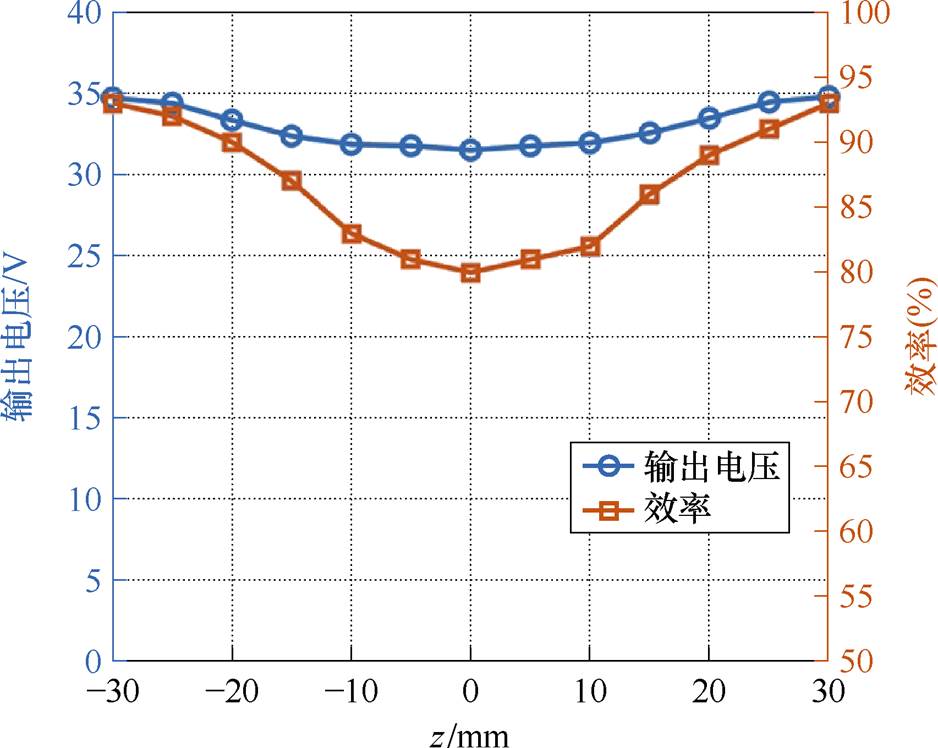
图14 系统输出电压和效率随轴向偏移实测值
Fig.14 The measured values of system output voltage and efficiency with axial misalignment
为验证系统抗径向偏移能力,实验测得径向偏移±5 mm范围内的原边逆变器和副边直流输出电压电流波形及系统输出电压和效率分别如图15、图16所示。输出电压同样波动较小,最大波动率小于2.8%。
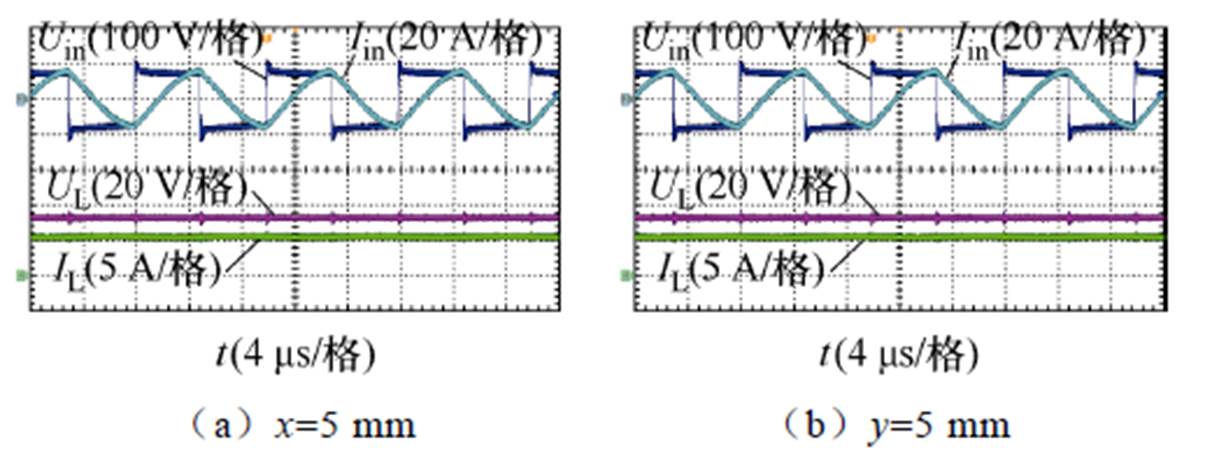
图15 不同径向偏移下原边逆变器和副边直流输出电压电流波形
Fig.15 Output voltage and current waveforms of primary inverter and secondary at different radial misalignment
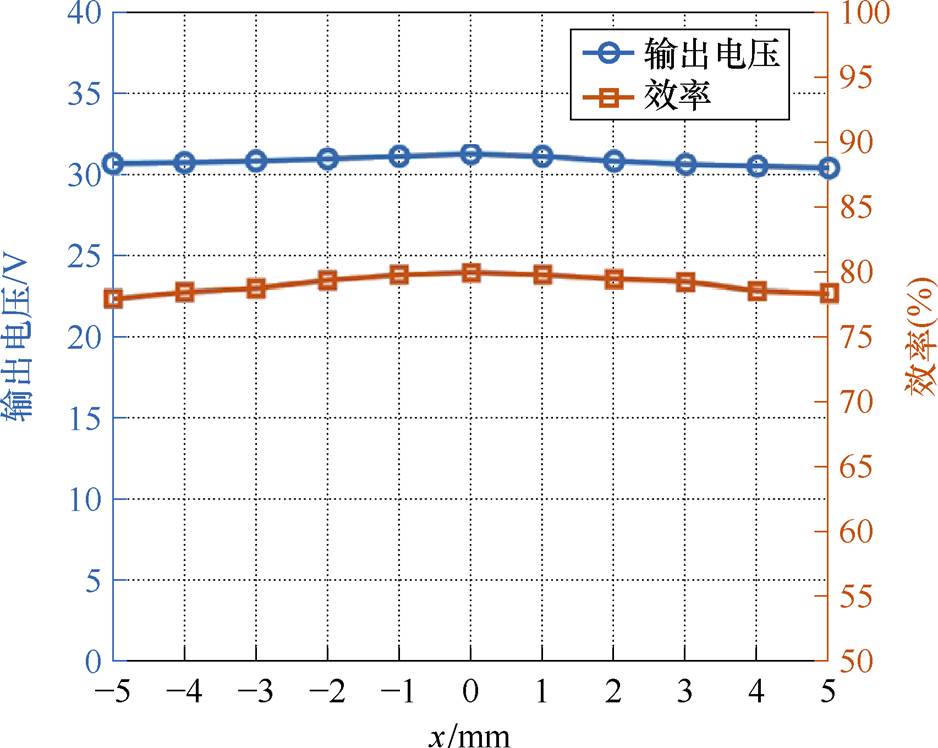
图16 系统输出电压和效率随径向偏移实测值
Fig.16 The measured values of system output voltage and efficiency with radial misalignment
图17给出了不同轴向偏移下逆变器MOSFET Q1的实验波形,图中,Uds为漏极-源极电压,Ugs为栅极-源极电压,可以看到,在栅极驱动信号置高前,MOSFET两端电压降为零,保证了系统全范围处于ZVS状态运行。
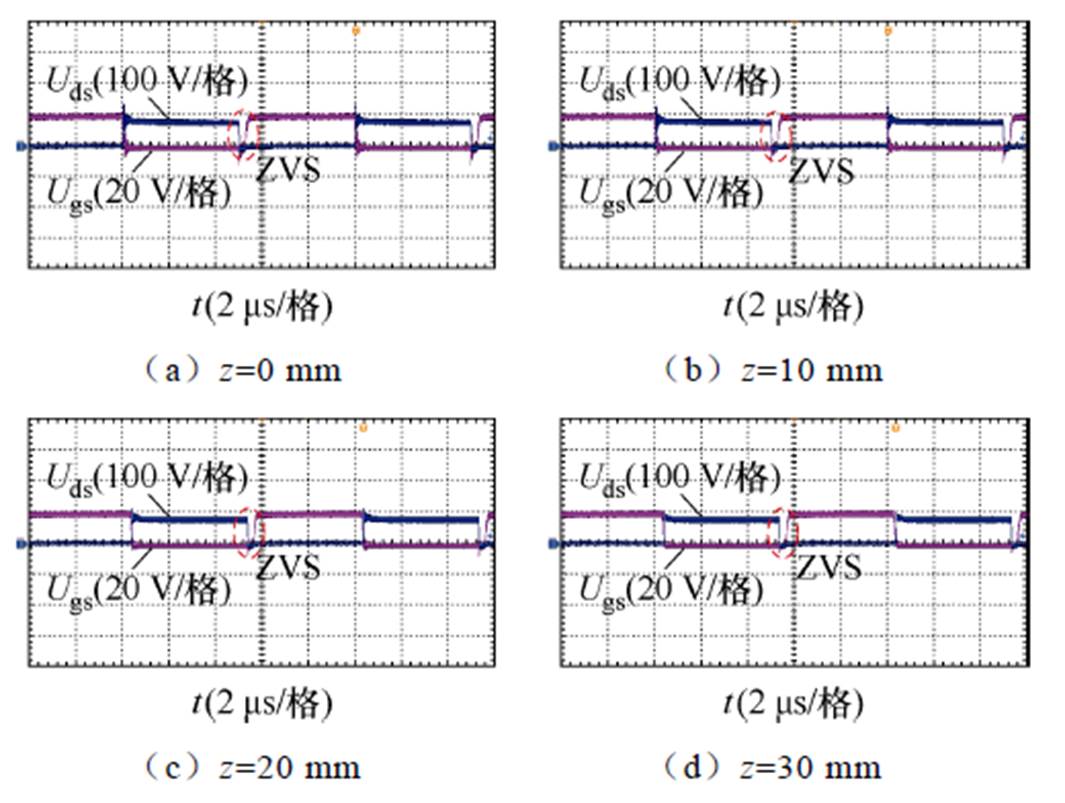
图17 不同轴向偏移下MOSFET实验波形
Fig.17 Experimental waveforms of MOSFET at different axial misalignment
图18和图19分别给出了耦合机构轴向与径向偏移切换下原、副边输出电压、电流波形,可以看到,输出电压变化比较平稳,逆变器始终处于ZVS状态运行。因所提方法依靠耦合机构自身参数变化实现抗偏移特性,无需复杂的闭环控制或其他功率变换环节,系统响应更快,可靠性更高。
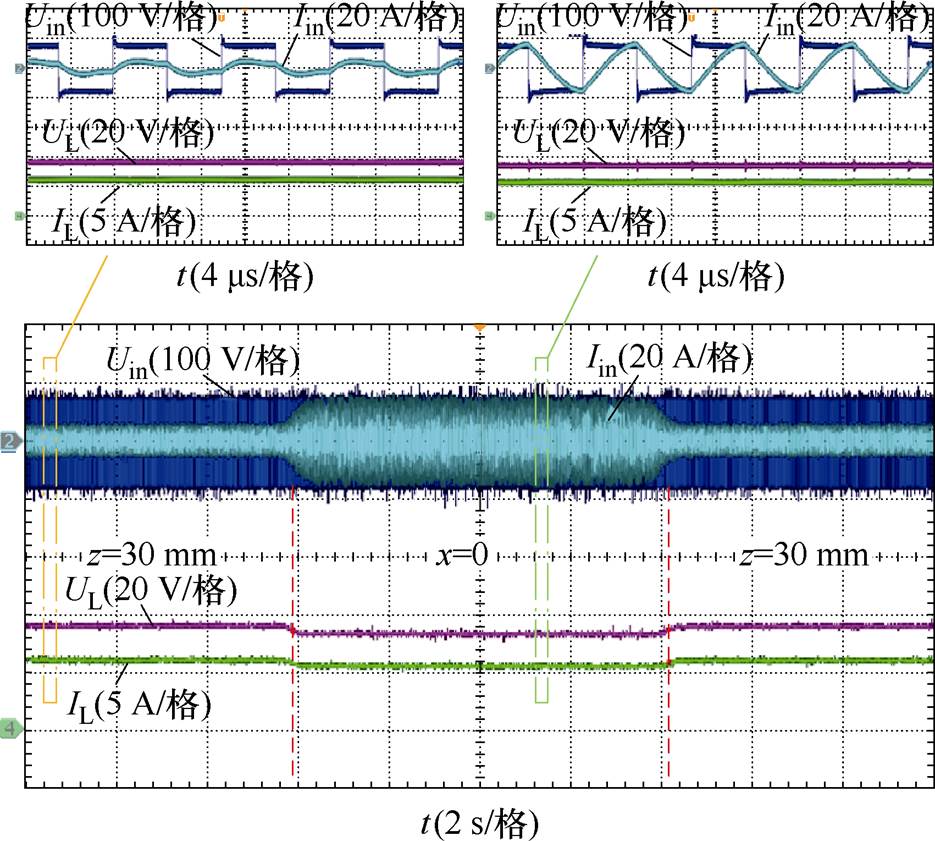
图18 轴向偏移切换下原副边输出电压电流波形
Fig.18 Output voltage and current waveforms of primary and secondary side under axial misalignment switching
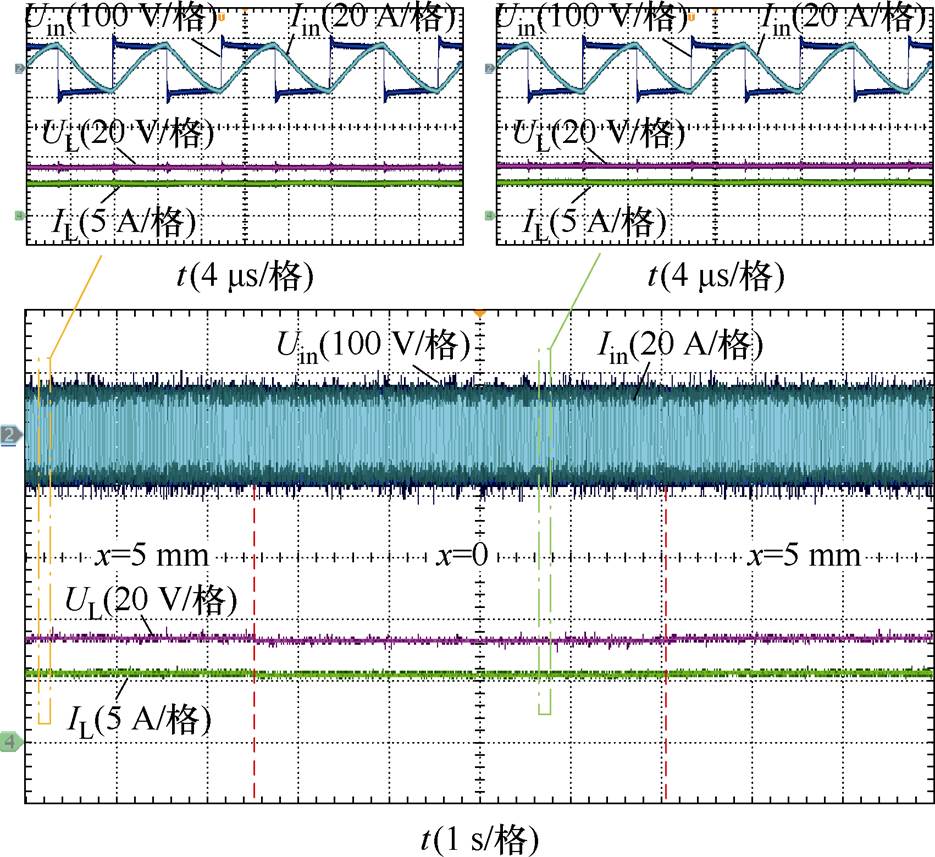
图19 径向偏移切换下原副边输出电压电流波形
Fig.19 Output voltage and current waveforms of primary and secondary side under radial misalignment switching
图20所示为耦合机构无偏移时测得的系统功率损耗分布情况。根据实际测量的电路参数,结合线圈参数和所选的MOSFET和肖特基二极管参数,可按式(12)~式(17)计算出各部分的功率损耗。可以看出,逆变器损耗所占比例最大,其次是整流器损耗和谐振网络损耗,而全桥驱动电路等其他损耗所占比例最小。提高系统效率主要应从降低逆变器关断损耗和提高系统功率因数入手。
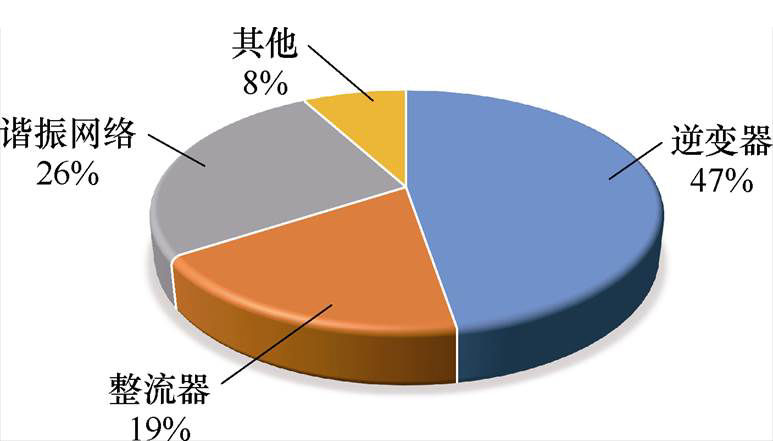
图20 功率损耗分布
Fig.20 Power loss distribution
表5对比了近年来相关文献中的主要技术参数,其中,文献[11-13]实现了较好的横向抗偏移效果,但其并未考虑线圈自感变化。文献[18-19]综合考虑了线圈自感和耦合系数变化,但其所适应的偏移范围有限,相应的耦合系数和线圈自感变化范围较小。相比之下,本文所提方法针对旋转式耦合机构参数变化情况,所能适应的偏移范围更宽,耦合系数和自感变化范围更大,且实现了较为稳定的输出。
表5 相关文献对比
Tab.5 Comparison of relevant literature
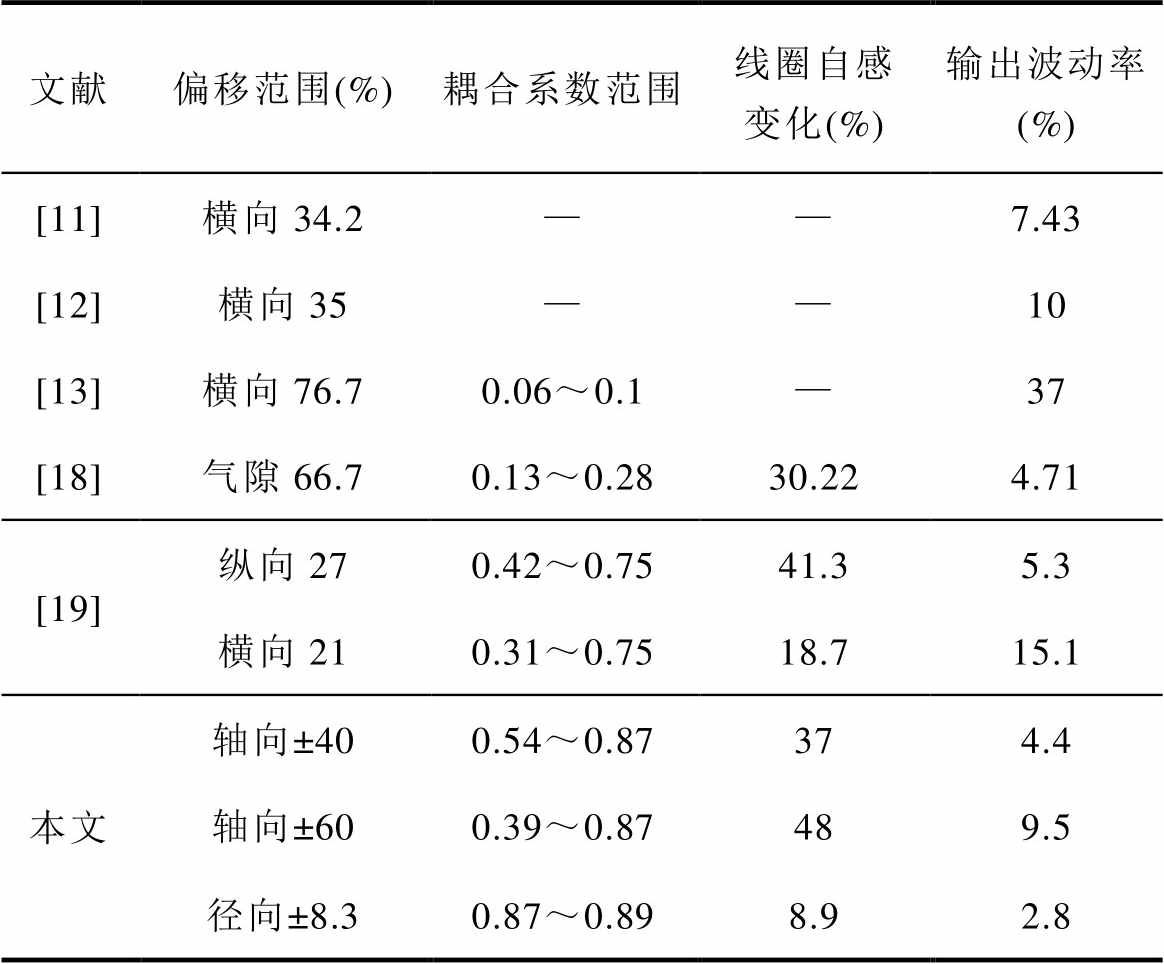
文献偏移范围(%)耦合系数范围线圈自感变化(%)输出波动率(%) [11]横向34.2——7.43 [12]横向35——10 [13]横向76.70.06~0.1—37 [18]气隙66.70.13~0.2830.224.71 [19]纵向270.42~0.7541.35.3 横向210.31~0.7518.715.1 本文轴向±400.54~0.87374.4 轴向±600.39~0.87489.5 径向±8.30.87~0.898.92.8
注:输出波动率=(最大输出电压-最小输出电压)/最大输出电压。
本文提出了一种考虑线圈参数变化的失谐型WPT系统抗偏移方法,其核心思想在于利用线圈自感变化构造失谐WPT系统,来抵消互感变化引起的输出波动。通过总结旋转式耦合机构在轴向与径向偏移下的参数变化规律,给出了失谐型WPT系统的恒压输出条件,并在此基础上利用PSO算法对补偿参数进行优化,以实现参数大范围变化时的稳定输出。实验结果表明,在互感变化74%、自感变化48%和耦合系数变化0.39~0.89范围内,系统实现近似恒压输出,输出电压波动最大仅为9.5%(轴向)和2.8%(径向),系统实现全范围ZVS运行,效率最高达到93%。
此外,本文所提方法只适用于恒定负载,主要考虑了应用于石油钻采设备WPT系统等负载变化不大的场景,下一步将研究负载变化较大的情况。
参考文献
[1] 孙远航, 王永松, 孙习武, 等. 航天用导电滑环失效建模与工艺优化研究[J]. 机械工程学报, 2020, 56(16): 1-12.
Sun Yuanhang, Wang Yongsong, Sun Xiwu, et al. Research on failure modeling and process opti- mization of transmission conductive slip ring for aerospace[J]. Journal of Mechanical Engineering, 2020, 56(16): 1-12.
[2] 张莲, 杨洪杰, 经廷伟, 等. 井下磁耦合无线电能传输系统的全谐振特性分析[J]. 工矿自动化, 2022, 48(2): 83-92.
Zhang Lian, Yang Hongjie, Jing Tingwei, et al. Analysis of full resonance characteristics of under- ground magnetic coupling wireless power transfer system[J]. Industry and Mine Automation, 2022, 48(2): 83-92.
[3] 苏玉刚, 钱林俊, 刘哲, 等. 水下具有旋转耦合机构的电场耦合无线电能传输系统及参数优化方法[J]. 电工技术学报, 2022, 37(10): 2399-2410.
Su Yugang, Qian Linjun, Liu Zhe, et al. Underwater electric-filed coupled wireless power transfer system with rotary coupler and parameter optimization method[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2399-2410.
[4] Rouse C D, Cove S R, Salami Y, et al. Three-phase resonant capacitive power transfer for rotary appli- cations[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(1): 160-169.
[5] 程志远, 宋晓逸, 吴晓婷, 等. 无线充电系统旋转式电磁耦合器损耗计算及热点温度研究[J]. 电工技术学报, 2024, 39(7): 1932-1942, 1956.
Cheng Zhiyuan, Song Xiaoyi, Wu Xiaoting, et al. Loss calculation and hot spot temperature research of rotary electromagnetic coupler in wireless charging system[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 1932-1942, 1956.
[6] 程志远, 陈坤, 李东东, 等. 旋转式无线充电系统偏移特性研究[J]. 电工技术学报, 2021, 36(22): 4648-4657.
Cheng Zhiyuan, Chen Kun, Li Dongdong, et al. Research on offset characteristics of rotary wireless charging system[J]. Transactions of China Electro- technical Society, 2021, 36(22): 4648-4657.
[7] Ji Li, Ge Fuchen, Zhang Chi. Design of wireless power transmission coupling structure based on rotary steerable drilling[J]. IEEE Transactions on Power Electronics, 2023, http://ieeexplore.ieee.org/document/ 10321715.
[8] Zhang Hailong, Chen Yafei, Kim D H, et al. Variable inductor control for misalignment tolerance and constant current/voltage charging in inductive power transfer system[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(4): 4563-4573.
[9] Zhu Gangwei, Dong Jianning, Grazian F, et al. A parameter recognition-based impedance tuning methodfor SS-compensated wireless power transfer systems[J]. IEEE Transactions on Power Electronics, 2023, 38(11): 13298-13314.
[10] Zhang Renjie, Yuan Huan, Rong Mingzhe, et al. Self-tuning WPT system with constant voltage output under resonance frequency shift[J]. IEEE Transa- ctions on Power Electronics, 2024, 39(1): 1713- 1722.
[11] 庄廷伟, 姚友素, 袁悦, 等. 基于DDQ/DD耦合机构的强抗偏移电动汽车用无线充电系统[J]. 中国电机工程学报, 2022, 42(15): 5675-5685.
Zhuang Tingwei, Yao Yousu, Yuan Yue, et al. A DDQ/DD-coupler-based wireless power transfer system for electric vehicles charging featuring high misalignment tolerance[J]. Proceedings of the CSEE, 2022, 42(15): 5675-5685.
[12] 谢文燕, 陈为, 陈庆彬, 等. 双耦合SP-S补偿紧凑型抗偏移WPT系统[J]. 中国电机工程学报, 2024, 44(2): 714-724.
Xie Wenyan, Chen Wei, Chen Qingbin, et al. Compact anti-offset WPT system with dual-coupled SP-S compensation[J]. Proceedings of the CSEE, 2024, 44(2): 714-724.
[13] 王懿杰, 陆凯兴, 姚友素, 等. 具有强抗偏移性能的电动汽车用无线电能传输系统[J]. 中国电机工程学报, 2019, 39(13): 3907-3917.
Wang Yijie, Lu Kaixing, Yao Yousu, et al. An electric vehicle (EV)-oriented wireless power transfer system featuring high misalignment tolerance[J]. Proceedings of the CSEE, 2019, 39(13): 3907-3917.
[14] Kim D H, Ahn D. Self-tuning LCC inverter using PWM-controlled switched capacitor for inductive wireless power transfer[J]. IEEE Transactions on Industrial Electronics, 2019, 66(5): 3983-3992.
[15] Choi J S, Jeong S Y, Choi B G, et al. Air-gap- insensitive IPT pad with ferromagnetic and con- ductive plates[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 7863-7872.
[16] Jia Yahui, Wang Zhihui, Tang Chunsen, et al. An efficiency improvement method for the small air gap wireless power transfer system with variable para- meters[J]. IEEE Transactions on Power Electronics, 2023, 38(11): 13443-13453.
[17] 陆远方, 黎祎阳, 杨斌, 等. 考虑线圈参数变化的SS型动态无线电能传输系统参数优化设计方法[J]. 电工技术学报, 2022, 37(18): 4537-4547.
Lu Yuanfang, Li Yiyang, Yang Bin, et al. Parameter design method for SS compensated dynamic wireless power transfer system considering coils' parameters variations[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4537-4547.
[18] Yang Bin, Lu Yuanfang, Peng Yuner, et al. Analysis and design of a T/S compensated IPT system for AGV maintaining stable output current versus air gap and load variations[J]. IEEE Transactions on Power Electronics, 2022, 37(5): 6217-6228.
[19] 麦建伟, 曾宪瑞, 刘治钢, 等. 基于S/SP补偿拓扑的强抗偏移感应式无线电能传输系统[J]. 中国电机工程学报, 2023, 43(4): 1525-1536.
Mai Jianwei, Zeng Xianrui, Liu Zhigang, et al. An IPT system based on S/SP compensation topology with high misalignment tolerance[J]. Proceedings of the CSEE, 2023, 43(4): 1525-1536.
[20] 李争, 唐明磊, 解波, 等. 无线电能传输零电压开关角跟踪和动态电容补偿矩阵复合控制策略[J]. 电工技术学报, 2024, 39(12): 3602-3615.
Li Zheng, Tang Minglei, Xie Bo, et al. Composite control strategy of zero voltage switch angle tracking and dynamic capacitance compensation matrix for wireless power transfer[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3602-3615.
[21] 金卓航, 武晋德, 韩晓霞, 等. 无线电能传输系统中零相角频率跟踪策略研究[J]. 中国电机工程学报, 2025, 45(2): 725-736.
Jin Zhuohang, Wu Jinde, Han Xiaoxia, et al. Study of zero-phase angle frequency tracking strategy in wire- less power transfer system[J]. Proceedings of the CSEE, 2025, 45(2): 725-736.
[22] 贾亚辉, 王智慧, 肖静, 等. 磁耦合无线电能传输系统宽范围零电压开关实现方法[J]. 电工技术学报, 2024, 39(22): 6952-6964.
Jia Yahui, Wang Zhihui, Xiao Jing, et al. Imple- mentation method of wide range zero voltage switching in magnetic coupling wireless power transfer system[J]. Transactions of China Electro- technical Society, 2024, 39(22): 6952-6964.
[23] Wang Xiaoqiang, Xu Jianping, Leng Minrui, et al. A hybrid control strategy of LCC-S compensated WPT system for wide output voltage and ZVS range with minimized reactive current[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9): 7908-7920.
[24] 焦超群, 杨旭, 杨俊峰, 等. 基于多目标优化理论的耦合无关恒压输出型LCC/S补偿感应电能传输系统[J]. 电工技术学报, 2023, 38(24): 6565-6580.
Jiao Chaoqun, Yang Xu, Yang Junfeng, et al. Coupling-independent constant-voltage output LCC/S compensation inductive power transfer system based on multi-objective optimization theory[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(24): 6565-6580.
[25] Jia Yahui, Zhao Lei, Wang Zhihui, et al. Integrated LCC-LCC topology for WPT system with CC output regarding air gap and load variations[J]. IEEE Transa- ctions on Power Electronics, 2024, 39(10): 11904- 11915.
[26] 王佩月. WPT系统双向信号并行传输技术与拓扑研究[D]. 重庆: 重庆大学, 2021.
Wang Peiyue. Research on parallel transmission technology and topology of bidirectional signals in WPT system[D]. Chongqing: Chongqing University, 2021.
[27] Gong Zhaowei, Zhao Lei, Zhang Ningchao, et al. Analysis and design of an air-gap-insensitive hybrid inductive power transfer system with constant voltage output[J]. IEEE Transactions on Power Electronics, 2024, 39(8): 10496-10505.
[28] Yao Yousu, Wang Yijie, Liu Xiaosheng, et al. Particle swarm optimization-based parameter design method for S/CLC-compensated IPT systems featuring high tolerance to misalignment and load variation[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5268-5282.
Anti-Misalignment Method of Detuned Wireless Power Transfer System Considering Coil Parameters Variations
Abstract Wireless power transfer (WPT) technology provides an effective way to solve the problem of stable power supply for rotating equipment. However, in practical applications, the relative misalignment between the rotating side and the stationary side is inevitable. In the practical application of WPT system, due to the presence of ferrite cores, the misalignment of the coupling mechanism will significantly affect the self-inductance and mutual inductance parameters of the coils, resulting in output power fluctuations and efficiency reduction. In order to enhance the anti-misalignment capability of WPT systems under changes in coil parameters, this paper proposes a detuned WPT system anti-misalignment method that considers changes in coil parameters. The detuned WPT system is constructed using changes in coil self-inductance to counteract the output power fluctuations caused by changes in mutual inductance.
Firstly, using the finite element simulation software, the parameter variation laws of the rotary coupling mechanism under axial and radial offsets were summarized. The study found that the self-inductance and mutual inductance of the coupling mechanism have the same trend of change, and the degree of change is similar within a certain offset range. And based on this, the idea of using self-inductance changes to dynamically adjust the degree of system detuning to offset output fluctuations caused by mutual inductance changes was proposed.
Secondly, the influence of parameter changes on system operation was obtained through circuit analysis, and the constant voltage output conditions for the degree of receiver detuning and mutual inductance changes were derived, providing a theoretical basis for the coupling mechanism design and compensation parameters optimization. The coupling mechanism design revolves around the number of turns on the secondary side, and the compensation parameters optimization is based on the particle swarm optimization (PSO) algorithm. With the goal of constant output and efficiency improvement, the compensation topology parameters of the inductor-capacitor-capacitor-series (LCC-S) are comprehensively optimized to achieve good axial and radial anti-misalignment capabilities of the rotary WPT system.
Finally, a 170 W experimental setup was constructed to validate the effectiveness of the proposed method. The experimental results show that within the range of axial offset ±30 mm and radial offset ±5 mm, the maximum mutual inductance change of the rotary coupling mechanism is 74%, the self-inductance change is 48%, and the coupling coefficient is 0.39 to 0.89. The maximum output voltage fluctuation is only 9.5% (axial) and 2.8% (radial), and the maximum efficiency of the system is 93%. This method utilizes the equilibrium characteristic of the parameter changes for the coupling mechanism itself. Its significant advantages lie in simple and effective structure, no DC-DC converter, no communication and closed-loop control, and a more stable and reliable system. It is particularly suitable for WPT system in harsh environments such as high temperature, high voltage, and high-frequency vibration underground, reducing the failure rate of the system and improving power supply reliability.
keywords:Wireless power transfer (WPT), parameters variations, anti-misalignment, detuning, particle swarm optimization (PSO) algorithm
中图分类号:TM724
DOI: 10.19595/j.cnki.1000-6753.tces.240847
国家自然科学基金资助项目(62073246)。
收稿日期 2024-05-22
改稿日期2024-07-01
贾亚辉 男,1996年生,博士研究生,研究方向为无线电能传输技术、电力电子技术。
E-mail: 20153965@cqu.edu.cn
陈丰伟 男,1986年生,博士,副教授,研究方向为无线电能传输技术、系统辨识和参数估计。
E-mail: fengwei.chen@cqu.edu.cn(通信作者)
(编辑 陈 诚)