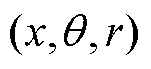表示的圆柱壳的轴向、切向和径向位移分别用
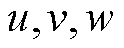表示，R为壳体半径，h为壳体厚度，l为壳体长度。壳体两端边界条件以假设分布的弹性约束为表征从而模拟多种工况下的壳体条件。灵活边界条件下圆柱壳振动分析模型如图1所示，沿径向、切向、轴向分别设置三套线性弹簧和一套旋转弹簧，其弹性系数分别为
、
、
、
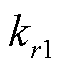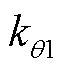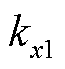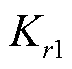，并通过设置不同的弹簧刚度来对应不同的边界条件。例如，当设置边界弹簧刚度为无穷大时，表示该边界为刚性支撑；当设置边界弹簧刚度为零时，则表示该边界端自由[23]。摘要 气体绝缘开关设备（GIS）带电操作后故障频发，据统计，GIS带电操作后故障占总故障的比例超过60%。GIS带电操作产生的强烈冲击振动，不仅会产生金属污染物，还会激活潜伏微粒，严重影响GIS的绝缘安全。为厘清球形金属微粒在GIS内受冲击振动后的运动机理，该文首先研究了振动在腔体内的传播过程，在灵活边界三维圆柱振动模型的基础上进行了受迫修正，提升了与实际工况的等价性。其次对腔体和微粒受振后的能量传递过程进行分析，以能量为纽带，搭建了腔体-微粒动能传递守恒模型，并借助起跳场强界定了微粒激活条件，提出了微粒受振激活判据。然后在前述研究基础上，综合考虑微粒荷电运动特性及碰撞随机特性，建立了振动激励下微粒运动全过程模型，并进行实验验证。在验证基础上进行了考虑微观作用力的修正，并从微观角度对误差进行了分析。模型充分考虑了不同粒径大小和材质对微粒动力学的影响，相比恢复系数定义的方法，与实际工况等价性更高。最后明确了振动激励对微粒运动行为的影响，并结合传播衰减特性，提出了带电工况下微粒的临界激活距离判据，计算了不同因素下微粒临界激活距离的变化情况。研究表明，随着电压幅值和振动强度的增加，临界激活距离呈对数型增大。该文可为解决GIS带电操作后故障频发这一难题提供帮助。
关键词：气体绝缘开关设备（GIS） 带电操作 能量传递守恒 运动特性
气体绝缘开关设备（Gas Insulated Switchgear, GIS）在运行过程中操作断路器及隔离开关时会产生强烈的冲击[1]，不仅会使内部部件磨损、剥离，生成更多的金属污染物，还会激活潜伏微粒，严重影响GIS的绝缘安全。特别是2023年以来，国家电网公司多个超/特高压变电站相继出现GIS带电操作引发的放电故障。据国家电网公司对GIS放电故障的统计，近十年来由微粒引发的放电故障占比达61%，且在带电操作期间及其后30 min内发生的故障占总故障的比例超过60%。因此，对金属异物在带电操作后的运动行为开展深入研究，厘清微粒运动机理，建立振动激励下的微粒运动模型，将为攻克GIS内部放电的难题提供有力支撑，对提升电网整体安全运行具有重大意义[2-7]。
针对GIS内部的金属微粒运动行为，国内外学者进行了大量的研究，且得出了一些结论。A. H. Cookson等对平板电极形成的间隙中的金属微粒运动行为进行研究，引入恢复系数等建立了考虑碰撞反弹的金属微粒在平行电场下的初步运动模型[8-9]；I. A. Metwally等针对自由金属微粒在电场中的受力进行了分析，并仿真证明了交流电压频率对微粒运动行为存在一定的影响[10]；华北电力大学王健等通过对同轴圆柱腔体内的球形金属微粒运动行为展开深入研究，建立了考虑表面粗糙度和旋转矢量的非弹性随机碰撞与混合气体阻力影响下的微粒运动模型，利用流体力学和弹性力学分析了气体阻力及表面粗糙度对微粒运动的影响[11-14]；西安交通大学李晓昂等通过实验对工频电压叠加冲击振动激励下的微粒起跳规律进行研究，结果表明外施冲击振动能够有效地降低微粒起跳场强[15]；同时，李晓昂等还借助真型252 kV GIS实验平台复现了GIS运行过程中微粒在断路器动作产生的冲击振动激励下的运动过程，探究了多微粒被激励起跳后诱发GIS放电故障的机理[16-17]；西安交通大学宋颜峰等通过搭建机械振动与交流电压联合实验平台对不同机-电联合状态下的微粒运动及放电行为进行了研究，结果表明随着机械振动幅值和频率的增加，金属微粒的局部放电起始电压降低且放电活动更为剧烈[18]。
然而，针对振动在GIS内的传播特性大多关注于长期电应力激励下的情况[18-19]，关于腔体受断路器及隔离开关分合闸冲击振动后的传播作用机理，以及受振后的微粒和腔体的相互作用机制鲜有分析。因此，本文通过搭建GIS内振动传播衰减模型和基于能量法的腔体-微粒动能传递守恒模型，借助有限元仿真手段，构建基于能量法和碰撞随机特性的带电操作振动激励下微粒运动的全过程模型，对微粒受振后的一系列运动行为进行分析，并结合实验加以验证，为解决GIS内金属微粒引发绝缘故障这一难题提供支撑。
对于GIS腔体受冲击后的振动特性，以往的研究大多将其视作刚性体的传递，用恢复系数对其进行定义，这存在很大的局限性。因此，对腔体受冲击后的行为进行研究是非常有必要的。以真型设备为基础，构建GIS腔体内冲击振动的作用机理及传播特性的数学和物理模型，通过仿真平台进行详细的微观研究，并用实验加以印证是解决这一问题的必由之路。
根据Love假设条件，当壳体厚度远小于长度和中性面的最小曲率半径等几何参数、壳体中应变和位移足够小时，可将其视为小变形薄壳进行分析，即薄壳振动理论分析的第一假设。在此基础上陆续发展出多种较为成熟的圆柱壳体理论，如Donnell和Flügge等理论[20-22]。
相较于其他理论，Flügge理论的适用范围更广泛，精确度也更高，因此本文以该理论为基础进行建模分析。将圆柱坐标系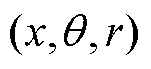表示的圆柱壳的轴向、切向和径向位移分别用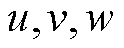表示，R为壳体半径，h为壳体厚度，l为壳体长度。壳体两端边界条件以假设分布的弹性约束为表征从而模拟多种工况下的壳体条件。灵活边界条件下圆柱壳振动分析模型如图1所示，沿径向、切向、轴向分别设置三套线性弹簧和一套旋转弹簧，其弹性系数分别为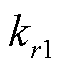、、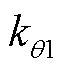、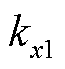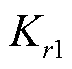，并通过设置不同的弹簧刚度来对应不同的边界条件。例如，当设置边界弹簧刚度为无穷大时，表示该边界为刚性支撑；当设置边界弹簧刚度为零时，则表示该边界端自由[23]。
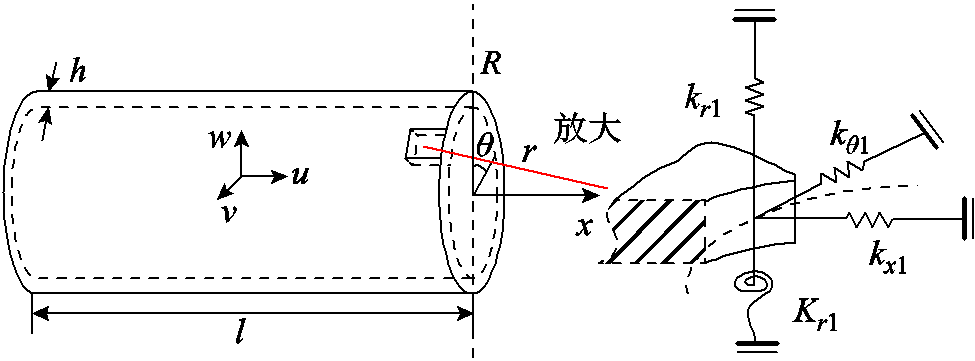
图1 灵活边界条件下圆柱壳振动分析模型
Fig.1 Cylindrical shell vibration analysis model with flexible boundary conditions
可采用基于哈密顿原理的瑞利里兹法，以能量为纽带，获得精确满足圆柱壳体的振动控制方程和边界约束条件，哈密顿原理的表达式为
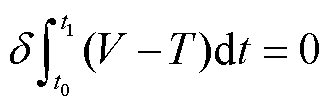（1）
式中，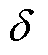
为变分符号；
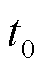和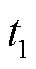
分别为振动开始时刻和结束时刻；V为系统中的总势能；T为系统中的总动能。系统中，总势能包括壳体的应变势能和储存在边界弹簧中的势能，V的表达式由于太过冗长将在附录部分给出。总动能T表达式为
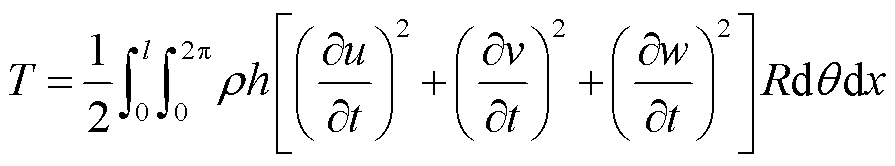（2）
式中，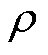
为柱壳密度。
但在工程实际中，圆柱壳结构通常会在内部装置运转的激励下产生结构振动。而本文主要研究的是GIS腔体内断路器合闸操作在内部产生的冲击振动对于壳体的影响，因此本文在上述圆柱壳体基本理论分析的基础上进行受迫振动修正。对于强迫振动计算，可将施加在壳体上的外力所做的功添加至哈密顿方程中，从而得到系统拉格朗日方程为
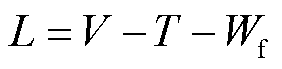（3）
式中，L为振动对系统的作用量；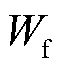
为作用在壳体上的外部激励所做的功，如果添加径向外部激励，则其表达式可写为
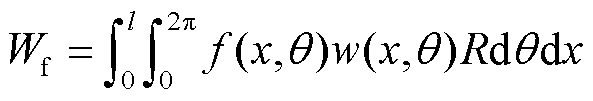（4）
式中，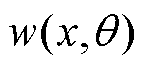
为径向位移；
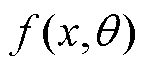为外部激励力的大小及方向，对于施加在壳体表面任一位置(xe, θe)的力而言，其表达式可简化为
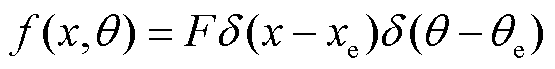（5）
式中，F为冲击激励力的幅值。在模态给定的情况下，壳体上任一点的振动响应情况可由式（6）求得。
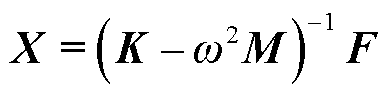（6）
式中，K为系统总刚度矩阵；M为质量矩阵，由材料属性决定；F为外部激励力的向量形式，对径向力而言F=[0 0 Fw]T；X为振动波的传播解矩阵；ω为壳体模态特征频率。在给定的壳体模态特征频率ω下可由式（6）得到X，进而求得地电极任一点的位移、速度以及加速度等各项响应情况。
GIS腔体管道是由SF6气体组成的流体域和以铝合金等金属所组成的固体域构成的。机械振动在固体介质中以应力波的形式传递，在流体域中以声波的形式传递，这两种波都属于机械波的范畴，因此GIS腔体受振后机械波的传播较为复杂。
为简化模型采取以下假设：①认为腔内气体静止且为理想气体，忽略流体黏性和摩擦的影响；②忽略Stokes运动惯性力；③忽略压缩产生的热损耗；④忽略温度影响；⑤振动信号传播衰减以阻尼描述，采用瑞利阻尼模拟壳体阻尼；⑥认为在不同材料传播过程中的阻尼恒定不变，铝的阻尼比在0.000 2～0.002之间，故选定腔体外壳的阻尼比为0.001；⑦忽略固体的受热膨胀作用。即认为GIS中介质均匀，忽略散射衰减，且由于传播距离较短可忽略SF6的吸收衰减。
机械振动产生的机械波，即声波在流体域中的传播运动过程可由其声学波动方程进行表述[24]，即
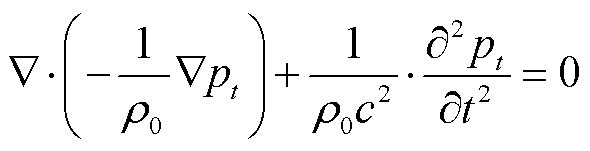（7）
式中，pt为声压，即大气压受振动后的压缩变化量；ρ0为SF6气体密度；c为声波在介质内的传播速度。
基于以上假设，且以国内某真型126 kV GIS气室间隔为参考，建立真型GIS仿真模型如图2所示。模型由外壳、绝缘子、流体域、高压导体四部分构成，壳体两端及高压导体边界条件设为固定刚性连接，以模拟气室间隔。模型几何参数如下：外壳长为600 mm，外半径为140 mm，内半径为120 mm，厚度为20 mm；高压导体长度为600 mm，半径为45 mm。绝缘子为盆式绝缘子，以嵌套方式在高压导体与外壳间固定；壳体与高压导体和绝缘子间差集为流体域。流体域为SF6气体，密度为6.088 6 kg/m3（20℃，0.1 MPa），动力黏度为1.377×10-5 Pa·s；外壳固体域为金属铝，密度为2 700 kg/m3，杨氏模量为7×1010 Pa，泊松比为0.33；绝缘子固体域为环氧树脂，密度为2 300 kg/m3，杨氏模量为3.5×109 Pa，泊松比为0.38。
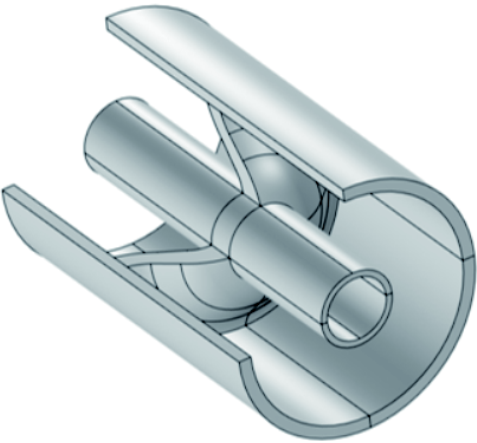
图2 真型GIS仿真模型
Fig.2 Real GIS simulation model
在仿真模型端点施加径向冲击加速度激励，激励大小为50g（本文中的所有加速度均用重力加速度g的倍数来衡量，g≈9.8 m/s2），作用时间为 0.1 ms，产生的振动波形如图3a所示，对比图3b中国内某真型GIS操作产生的振动波形，二者存在较小的差异。差异的主要来源是真型GIS内部具有较复杂的部件和连接机构，会对壳体的振动模态造成一定的影响，但该影响较小，在合理范围内。因此认为振动传播模型的搭建比较贴合实际工况，可借助仿真模型研究断路器操作产生的振动波在GIS腔体内的传播。
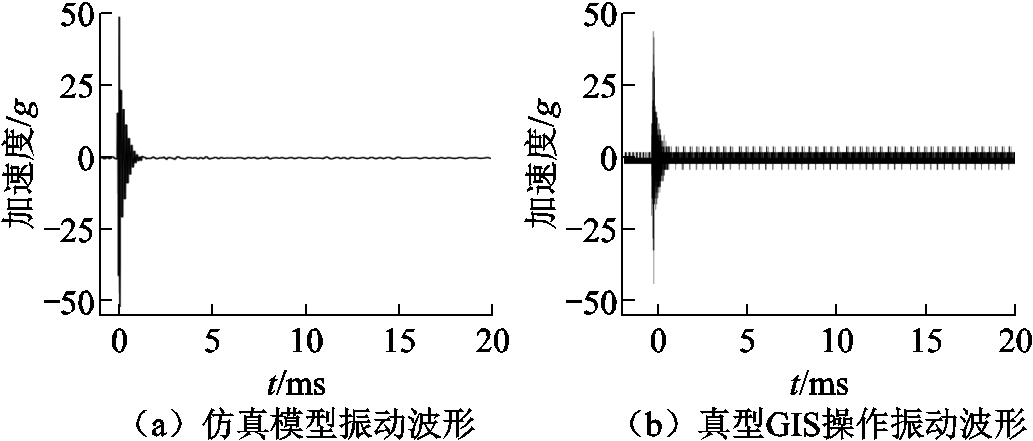
图3 真型设备实测与仿真对比结果
Fig.3 Comparison results of real equipment measurement and simulation
仿真振动波传播云图如图4所示。可见，机械波的传播呈“涟漪”状扩散，且在时域内前方波头为传播速度较快的纵波（P波，与传播方向相同），后方较慢的为横波（S波，与传播方向垂直），纵波和横波的区别随着传播距离的增大而增大[25]。
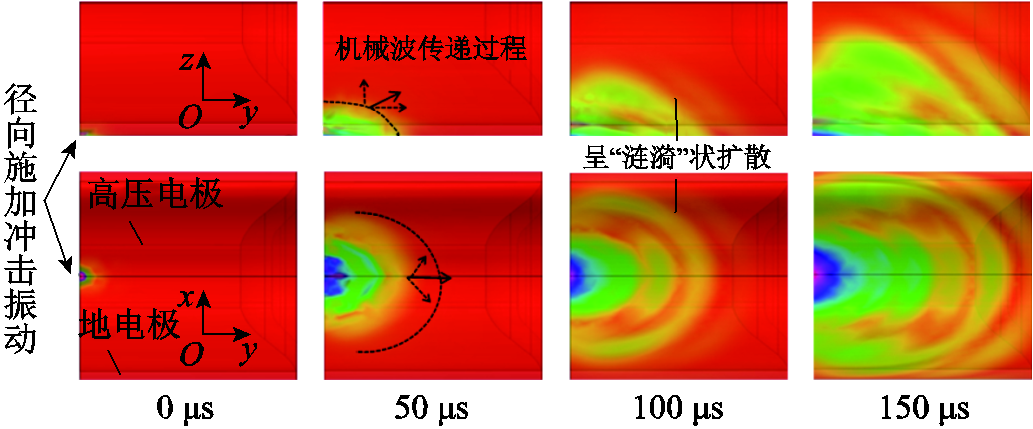
图4 仿真振动波传播云图
Fig.4 Simulated vibration wave propagation cloud
纵波对径向运动的激励作用较横波小，可类比地震的传播预警过程。在地震预测中总是先收到传播速度较快的纵波信号，此时感受到轻微晃动；在数秒后横波到达，此时地动山摇，地震的主要破坏也由横波造成。因此，纵波波速快，作用方向与传播方向一致，对微粒起跳贡献很小；横波传播较慢，作用方向与传播方向垂直，对微粒起跳起主要作用。因此，静止在地电极的微粒主要受到横波的影响，进而起跳。
由于微粒起振运动行为主要受径向振动加速度的影响，且径向振动加速度幅值在腔体固体域中的传播会随着距离的增大而衰减。因此，对传播衰减行为进行研究，总结传播衰减规律，可得到现场快速计算方法，对工程实际应用具有较好的帮助。由于振动随距离的衰减呈现指数型衰减的特点[26]，根据仿真结果对曲线进行指数函数拟合即可得到加速度幅值与传播距离间的经验公式，如图5所示。经验公式为
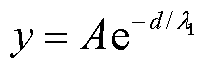（8）
式中，y为距离振动施加点d处的振动加速度幅值；
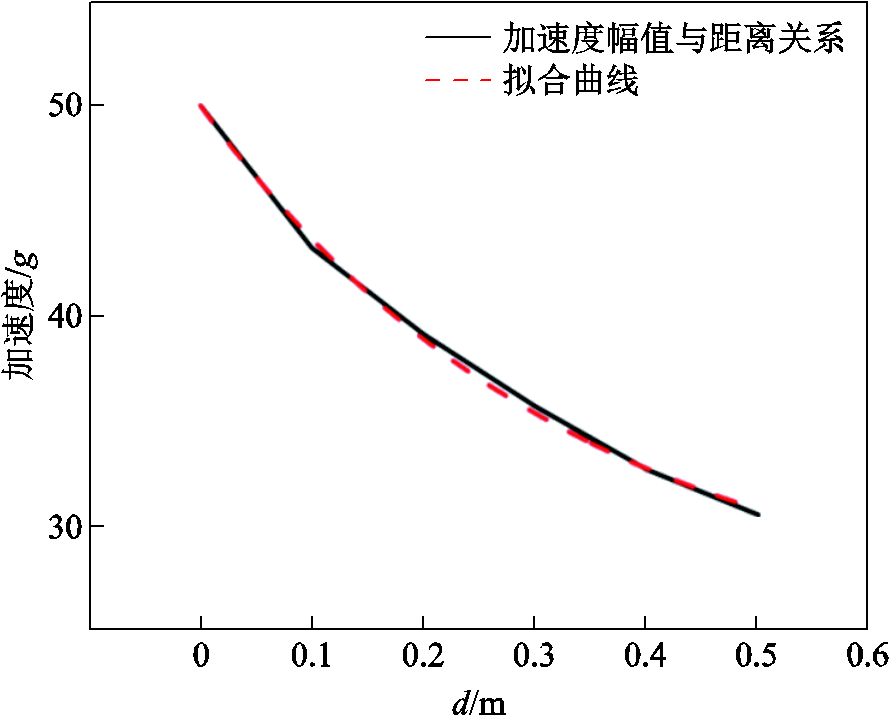
图5 加速度幅值与传播距离经验公式拟合
Fig.5 Acceleration amplitude fitted to an empirical equation for the propagation distance
A为施加的冲击加速度幅值；l1为衰减系数，取值为0.9。由此可快速求得腔体底部轴向分布的任意位置的加速度大小。
本文通过开展大量预实验进行观测，腔体受振后瞬态腔体形变及微粒运动行为如图6所示。在观测中发现，微粒起跳前，地电极底部产生微小形变，形变产生向上抬升的位移和速度，微粒随电极位移的抬升向上运动，在位移达到最大值时脱离地电极继续向上运动，微粒起始运动初速度与地电极最大位移时基本保持一致。详细过程如图7所示。
图6 腔体受振后瞬态腔体形变及微粒运动行为
Fig.6 Transient cavity deformation and particle motion behavior after cavity vibration
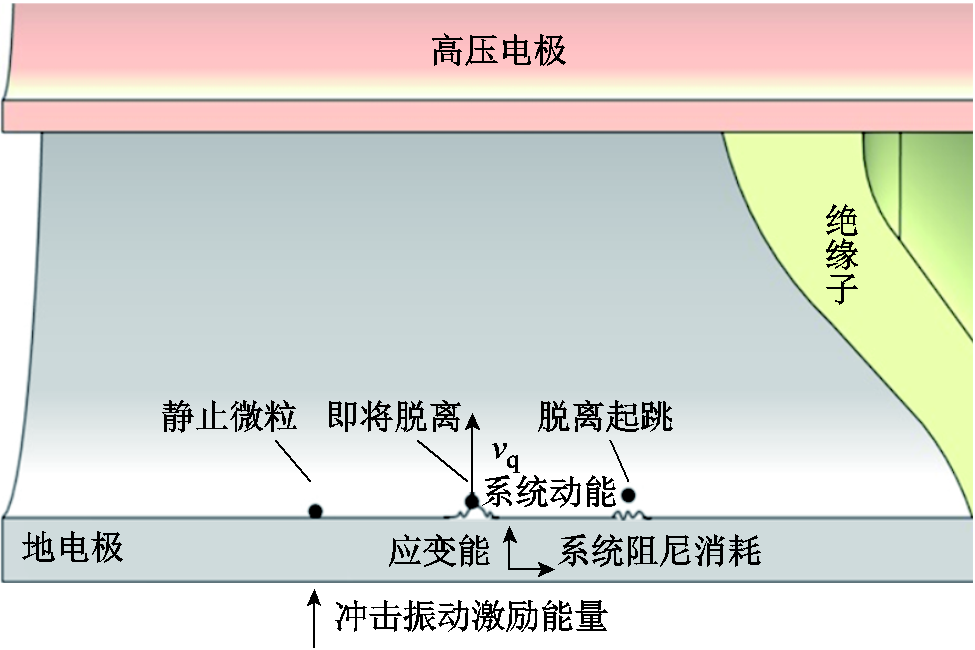
图7 腔体及微粒受振后瞬态行为示意图
Fig.7 Schematic diagram of transient behavior of cavity and particles after vibration
根据预实验观测到的静止微粒受冲击瞬间的运动行为，对冲击振动作用过程进行解析，并建立数学模型。瞬间受冲后的微粒运动行为可由Hunt-Crossley模型给出[27]，基于Hertz接触理论[28]，将阻尼系数Fz描述成迟滞阻尼因子χ与接触形变量σ之间的函数为
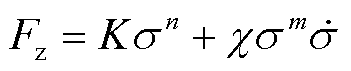（9）
式中，m为接触参数；n为能量指数；K为接触刚度，由材料固有属性和接触面积决定，对于铝球和铝制腔体而言，K ≈ 0.033 8。
对腔体受冲击振动后的行为运用能量法进行分析，外部激励对腔体做功，一部分功被系统阻尼所消耗，另一部分功转化为腔体和金属微粒组成的系统的应变能，剩余部分则转化为系统动能[29-30]。
由碰撞过程能量守恒原则，碰撞过程中的耗散项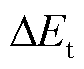
可表示为
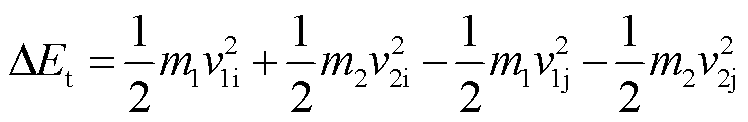（10）
式中，m1与m2为碰撞体的质量；v1i与v2i为碰撞前的初始速度；v1j与v2j为碰撞后的速度。再由碰撞前后动能守恒有
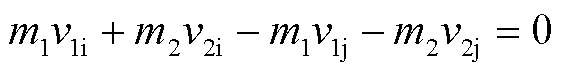（11）
借助恢复系数定义，假设恢复系数ε为初始相对碰撞速度的线性函数，则有
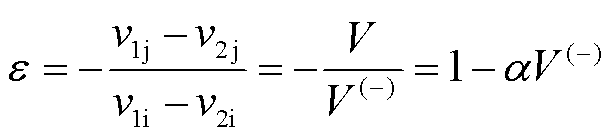（12）
式中，V为碰撞后的相对速度；V(-)为初始相对碰撞速度；a为常数，一般取0.08～0.32[31]，将a代入式（10）可得
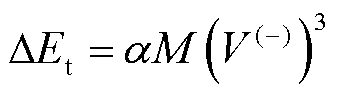（13）
式中，M为系统等效质量，M=m1m2/(m1+m2)，其与碰撞过程是否发生弹塑性形变无关。阻尼消耗的能量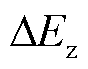
可由对模型中的阻尼项积分得到[32]，表达式为
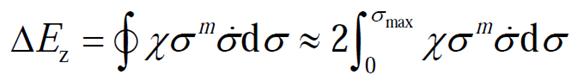（14）
式中，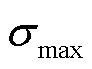
为应变压缩最大深度；阻尼迟滞因子
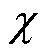由接触参量K和初始相对碰撞速度
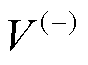共同决定，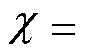
。
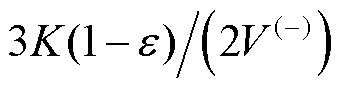虽然压缩结束后应变能可以通过弹性力做功，但金属球形微粒脱离系统起跳后，系统的应变能无法再对微粒做功转化为微粒的动能。而相比初始动能微粒自身的应变能过小，可忽略不计。因此仅需计算系统自压缩开始阶段至临界压缩值时的应变能。该应变能U计算公式为
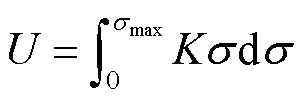（15）
基于式（13）～式（15），以及能量守恒原则，可由能量法得到静止在腔体内壁的球形金属微粒受外部激励后瞬间的起跳速度满足关系为
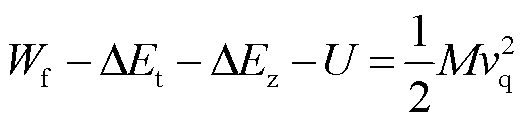（16）
式中，vq为微粒脱离地电极底部的初始速度，即微粒起始运动的初速度。微粒在仅施加电压时会先悬浮，待电场强度达到起跳场强时会向上做抬升运动。因此，当微粒被激励向上运动到达满足起跳电场强度后，微粒被有效激活，进而在电场作用下在地电极和高压电极间往复运动。球形微粒的理论起跳场强表达式[33]为
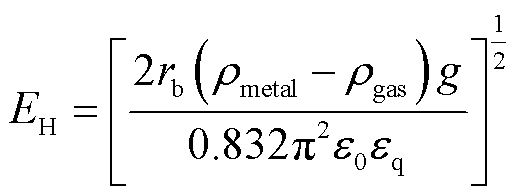（17）
式中，ρmetal、ρgas分别为铝制金属微粒密度和气体密度；ε0为真空介电常数，ε0=8.85×10-12 F/m；εq为气体相对介电常数；rb为球形微粒半径。由此，可借助起跳场强对微粒的有效激活判据进行界定，微粒激活判据可表示为
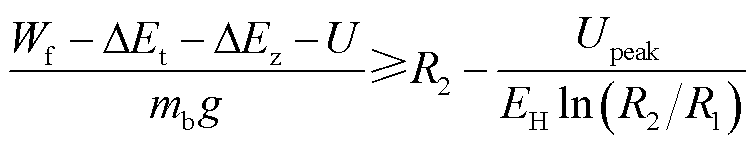（18）
式中，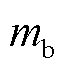
为微粒质量；R1为高压电极外半径；R2为GIS地电极内半径；Upeak为交流电压峰值。对于本文中腔体内半径为1.0 mm的铝制微粒，当交流电压为73 kV，冲击加速度大小为8.7 g时，微粒恰好达到临界激活条件。
GIS内微粒运动行为的随机性很大。微粒的运动行为由受力情况决定，而微粒的荷电机理是分析微粒受力及运动行为的重要前提。对高压导体施加工频交流电压Uac(t)，则同轴圆柱腔体内微粒所在位置的电场强度E(t)可由式（19）求得。
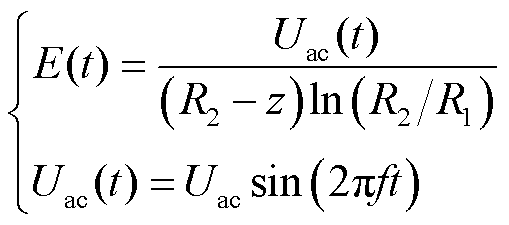（19）
式中，z为微粒距离地电极内壁的径向高度；Uac为交流电压幅值；E为微粒所在位置的电场强度；f为电压频率。交流电压下微粒荷电量q±表达式[34]为
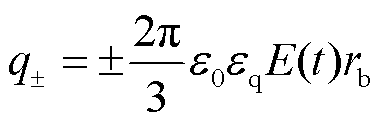（20）
GIS内部微粒在封闭腔体内受多种复杂力的共同作用。特别是在交流电场中，由于电场时刻变化，微粒的受力也是时刻变化的。对GIS内自由金属微粒运动进行简单受力分析，其示意图如图8所示。
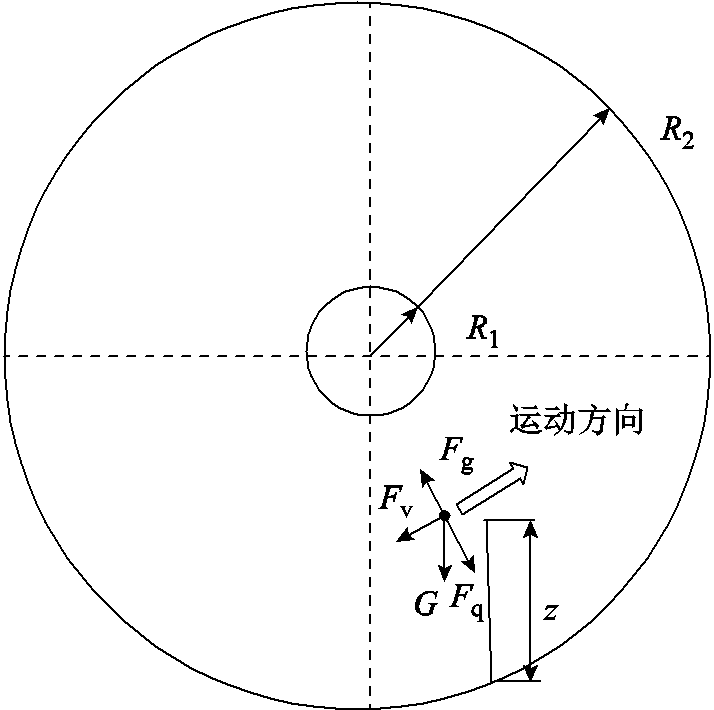
图8 GIS内自由金属微粒运动受力分析示意图
Fig.8 Analysis of forces on the motion of free metal particles within GIS
在交流电场中，库仑力的大小并不恒定，而是随着电场的变化而变化，而且还与微粒的带电量紧密相关。在微粒运动过程中未发生碰撞时，假设微粒的带电量并不发生改变；但微粒碰撞电极时，微粒的带电量发生改变，极性也会与碰撞电极极性保持一致，带电量的变化量与此时碰撞点的电场强度以及微粒的尺寸相关。微粒受到的作用力及其表达式见表1[35-37]。表中，k为镜像电荷引发的修正系数，当微粒悬浮时，k=1，当微粒与电极接触时k=0.832；η为气体黏滞系数，η =1.377×10-5 Pa·s；vball为微粒运动速度。
表1 球形金属微粒受力分析
Tab.1 Spherical metal particle force analysis
受力类型方向表达式 重力+浮力G竖直向下 库仑力Fq随电场变化 电场梯度力Fg电场梯度方向 气体阻力Fv与运动方向相反
金属微粒在GIS三维腔体内的运动方程为
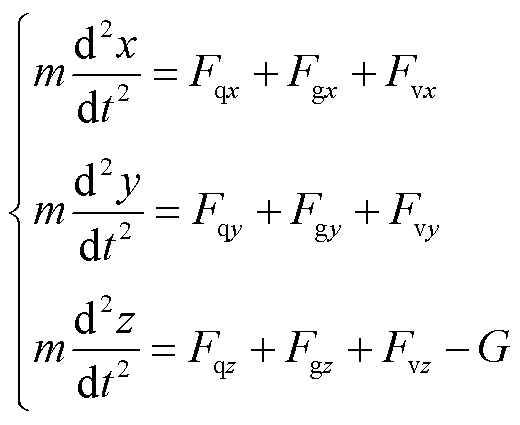（21）
金属微粒在GIS腔体中运动碰撞时总是伴随着能量的损失，相较于碰撞过程而言，微粒在运动过程中的损耗要小得多。为简化分析计算过程，默认在运动过程中不发生碰撞，则微粒能量保持不变。
同时GIS内电场分布呈梯度式，微粒在克服重力后所受库仑力逐渐增大，可认为碰撞前微粒的速度近似垂直于碰撞切面。同时，又因为微粒半径远小于外壳和高压导体半径，因此可将碰撞过程简化为球-板模型的非弹性正碰撞过程，不再考虑斜碰撞引起的剪切形变和摩擦能损。考虑碰撞过程能量损耗，碰撞后微粒动能可由前文式（12）中恢复系数定义，同时由于恢复系数仅与材料的固有属性相关，则碰撞后微粒动能可表示为[11]
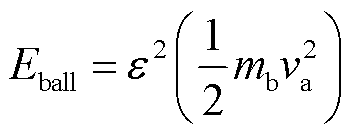（22）
式中，va为微粒碰撞前的速度。
微粒与电极碰撞时，电极表面在微观尺度上并非绝对光滑，存在着表面粗糙度的差异。而表面粗糙度的差异会引起速度反射角的随机变化，因此需要考虑反射角的随机变化，示意图如图9所示。图9中，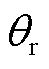
为入射角，则考虑随机碰撞的随机速度反射角q 可表示为
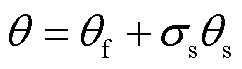（23）
式中，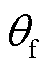
为镜面反射下的反射角；
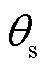为粗糙最大反射角度减去镜面反射角；
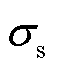为符合粗糙度分布的随机分布数，表面完全光滑时为0。
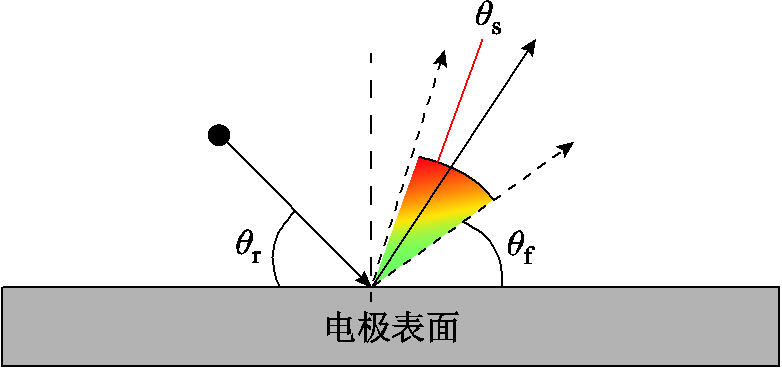
图9 微粒碰撞电极随机反射角示意图
Fig.9 Schematic diagram of random reflection angle of particle collision electrode
基于上述研究，构建基于能量法和考虑微粒碰撞随机特性的微粒运动仿真模型，有助于研究带电操作引发的典型振动对微粒的激励影响。
构建考虑碰撞随机特性的振动激励下的微粒运动仿真计算模型。为简化分析过程，本文分析的基础设定为远离绝缘子端的金属微粒，忽略绝缘子对电场的畸变作用。微粒运动的仿真计算流程如图10所示，借助COMSOL有限元仿真软件，实现球形金属微粒的运动轨迹可视化分析。
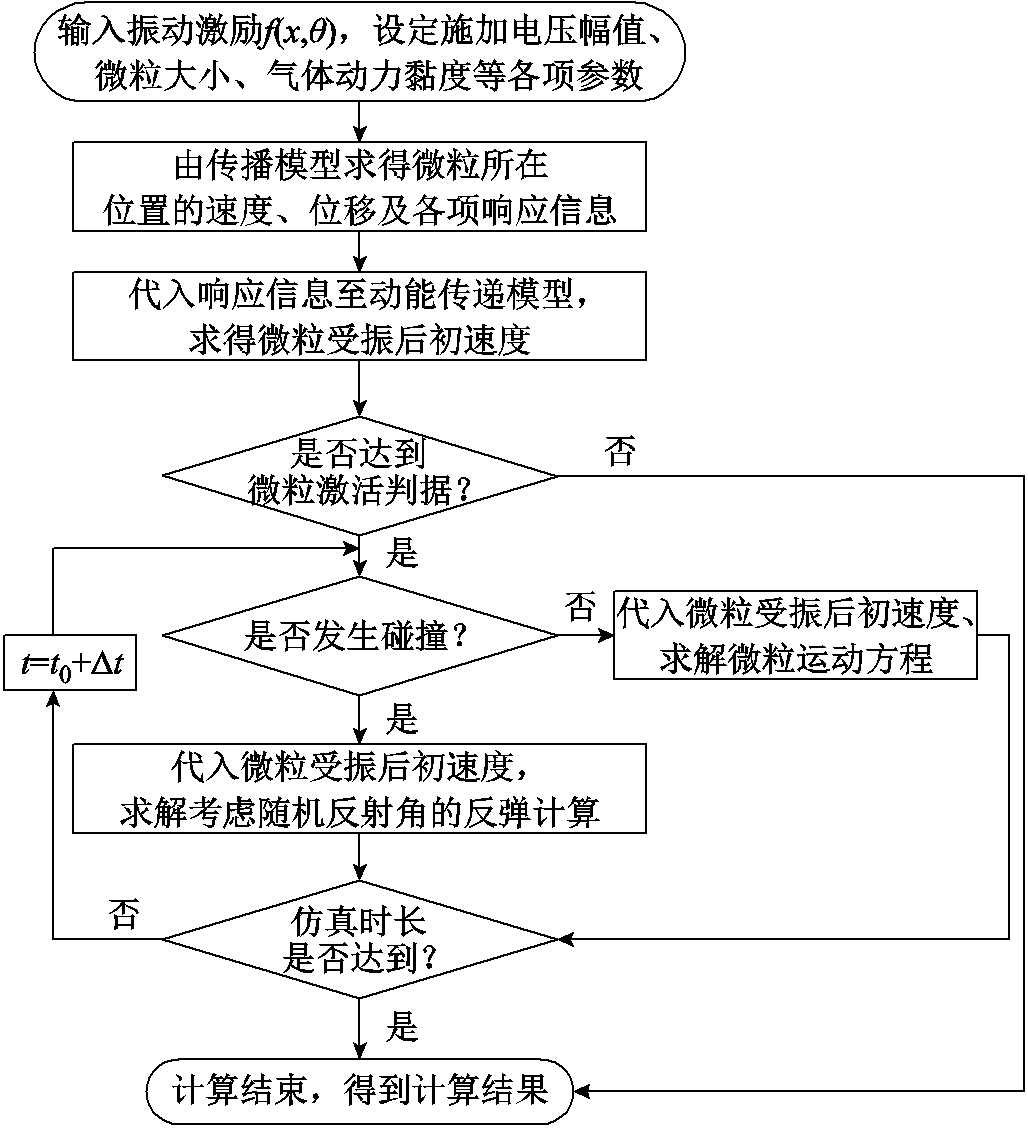
图10 仿真模型计算流程
Fig.10 Flow chart of the simulation model
仿真中，GIS腔体的设置如腔体尺寸、腔内气体气压、动力黏度等沿用前文1.2节中的设置；设定半径分别为0.5、0.7、0.8、1.0 mm的四种铝制金属微粒，密度为2 700 kg/m3；冲击加速度大小取10g、15g、20g、25g、30g；电压幅值取73、110、126 kV（50 Hz，0°）交流电压；随机反射角取10°。
图11为0.5 mm铝制金属微粒在10g冲击作用、126 kV下的受力情况、径向速度以及三维可视化粒子轨迹。微粒被激活后有一定的初速度，在运动初始阶段，微粒以一定的初速度向上运动进入较高电场强度区域，受电场力影响最大。同时由于微粒处于50 Hz交流电场中，微粒所受电场力也以0.02 s为周期交变。重力方向恒定向下，幅值仅与微粒大小有关，对于0.5 mm微粒，重力在10-5 N数量级；同时微粒受10-6～10-5 N数量级的气体阻力的影响，与微粒运动方向相关；电场梯度力作用最小，在10-8～10-7 N数量级；在合力作用下，微粒在腔体地电极与高压电极间做速度时刻改变的简谐往复运动。
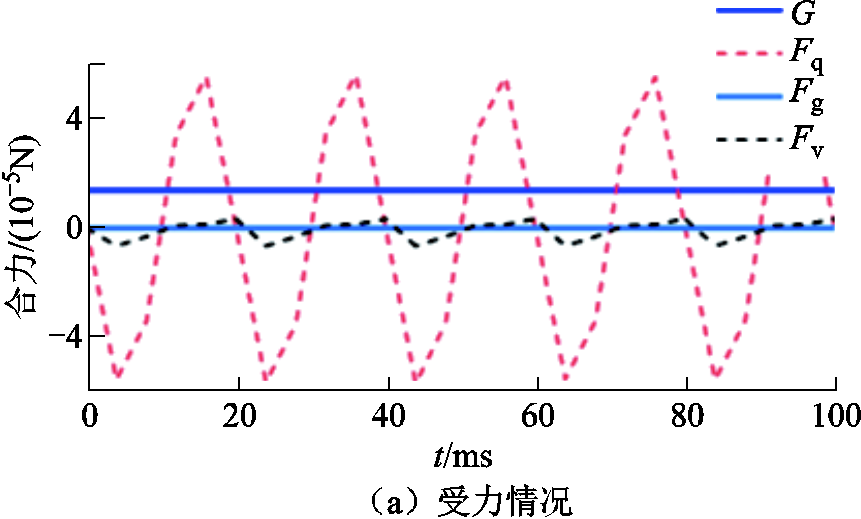
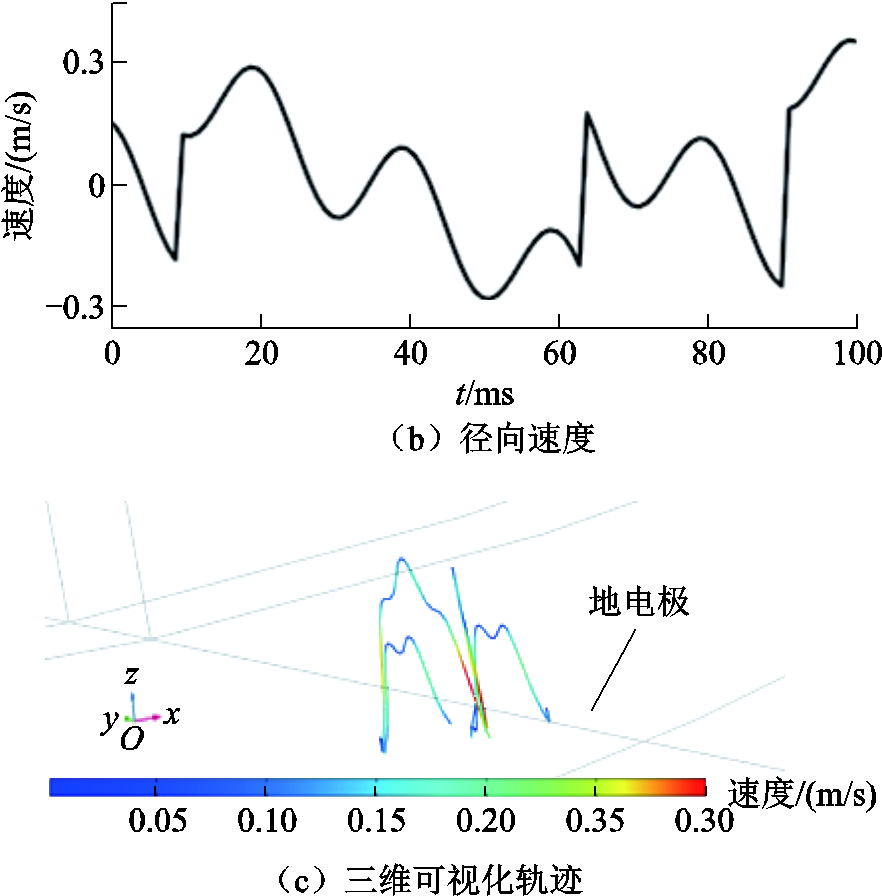
图11 受力、径向速度、三维可视化粒子轨迹
Fig.11 Force, radial velocity, 3D visualization of particle trajectory
为验证仿真的准确性并提高与实际工况的等价性，本文搭建了冲击振动传播及微粒运动观测综合实验平台，对仿真结果进行验证。
3.3.1 实验平台搭建
本文基于国内某真型126 kV GIS腔体，搭建了如图12所示的实验平台。腔体高压导体半径为45 mm，外壳内半径为120 mm，外壳外半径为140 mm。实验平台由126 kV真型GIS腔体、加速度传感器（量程为±250g，灵敏度为20.6 mV/(m/s2)，分辨率为0.04g）、220 V交流电源、集成电路型压电式传感器（Integrated Electronics Piezo-Electric, IEPE）恒流适配器（0.3～105 Hz，误差≤±1.5%)、示波器、冲击振动施加装置、调压器、高速相机（Optronis高速相机，帧率为2 000帧/s，分辨率为1 920×1 080）、强光LED光源、观测计算机、高压电源及控制台组成。
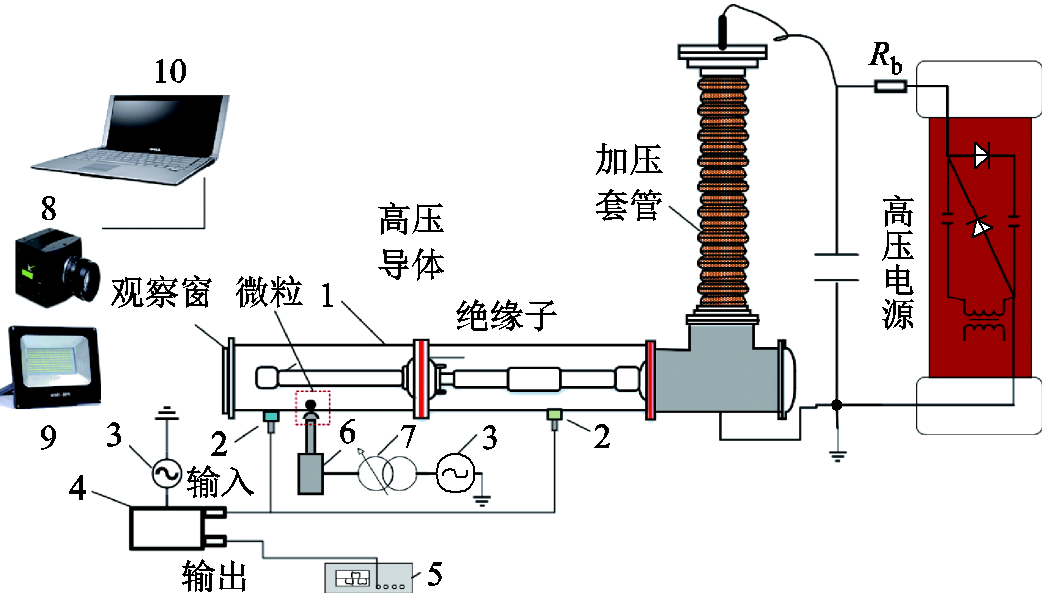
图12 冲击振动下微粒运动综合实验平台 1—126 kV真型GIS腔体 2—加速度传感器 3—220 V交流电源 4—IEPE恒流适配器 5—示波器 6—冲击振动施加装置 7—调压器 8—高速相机 9—强光LED电源 10—观测计算机
Fig.12 Comprehensive experimental platform for particle motion under shock and vibration
冲击振动施加装置通过电磁铁来控制撞击头的击发，电磁铁吸合力度大小与外施电压基本呈线性关系[15]，可通过调压器和动作时间控制冲击振动施加大小和作用时间，该装置可实现0～60g冲击加速度的可控施加。微粒放置在靠近观察窗一端远离绝缘子处，在观察窗外采用强光LED光源对腔体内补光，同时使用高速相机观测记录微粒的运动行为。高压电源及控制台通过加压套管对GIS腔体施加电压，可实现0～300 kV可控电压施加。Rb为保护电阻。
3.3.2 实验方法
加速度传感器通过耦合剂与腔体外壁紧密贴合，先标定冲击加速度幅值大小，在距离施加点位100、200、300、400 mm处布置传感器，以测量传播及衰减情况。取半径为0.5、0.7、0.8、1.0 mm的四种铝制球形金属微粒进行实验，微粒放置在振动施加点及传感器布置点正上方。为避免脏污对微粒起跳产生影响，实验前采用无水乙醇对腔体和微粒进行清洁擦拭，待其挥发后，将金属微粒放置至指定位置，合上密闭盖进行抽真空处理，而后充入SF6气体至0.1 MPa。
图13为实验中某次微粒运动的轨迹观测图。由于实验具有较强的随机性，因此每种条件进行20组重复实验。通过大量预实验发现，电压幅值对微粒初速度的影响不大，这是由于地电极附近的电场强度较低，对微粒受振后初速度的瞬时影响微乎其微。因此在标定每组振动强度后，设置施加126 kV电压（单相运行电压73 kV）进行实验验证。本文忽略相位对微粒运动的影响，因此采用延后触发方式确保冲击振动施加时的电压相位为0°。最后通过统计学对微粒的运动行为进行分析并与仿真结果进行对比。
图13 微粒运动轨迹观测图
Fig.13 Observations of particle trajectories
3.3.3 实验结果分析
微粒初速度仿真结果与实验观测结果对比如图14所示，可明显观察到仿真值与实测值存在差别。并且在实验中发现，同样激励条件下微粒的初速度随着金属微粒半径的增大而增大，因此还需对仿真模型进行修正。
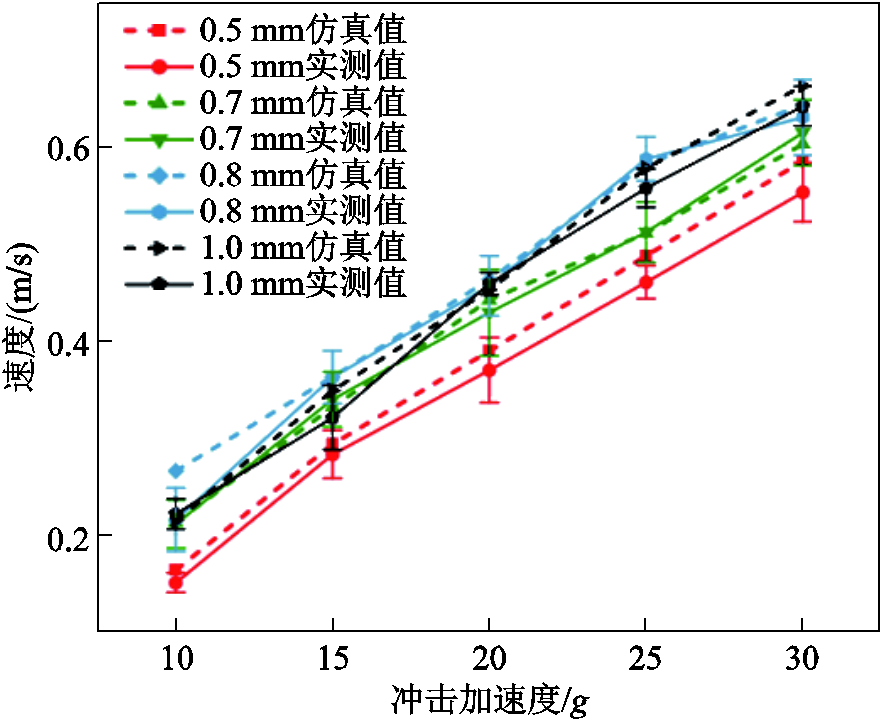
图14 微粒初速度仿真与实验观测对比
Fig.14 Comparison of particle initial velocity simulation and experimental observation
由于球形微粒静止于地电极时与地电极底部呈内切关系，球形微粒半径越大，微粒与地电极的接触面积越大，传递的动能也就越大。同时由Bradley法则可知，对于1 mm以下的微粒，范德华力对于微粒的作用要大于重力对微粒的作用[38-39]。因此需要对模型进行修正，在受冲瞬间考虑范德华力的影响。范德华力原指分子间作用力，在GIS金属微粒方面，逐渐用来指代微粒和接触物体之间由于分子间作用力而表现出的宏观吸引力。范德华力属于近程力，是影响壁面沉积以及微粒接触后行为的主要因素。微粒与腔体间的临界脱离范德华力公式[40-41]可表示为
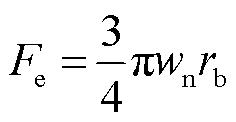（24）
式中，wn为黏附功，取典型值wn=2 mJ/m2。模型修正后，微粒初速度仿真结果与实验观测结果对比如图15所示。
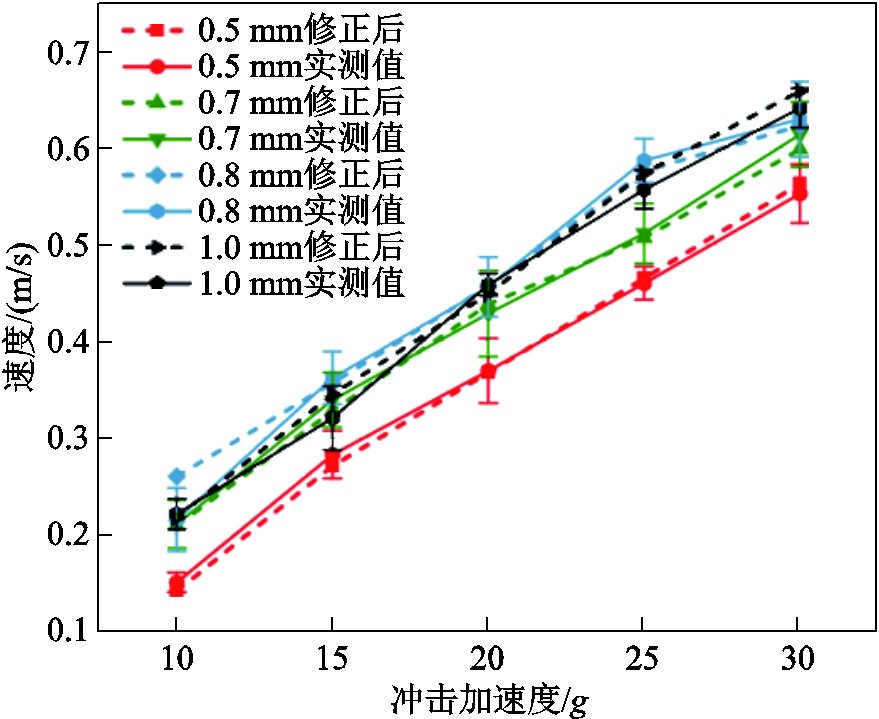
图15 修正后微粒初速度与实验观测对比
Fig.15 Comparison of corrected particle initial velocities with experimental observations
修正后微粒运动模型仿真的微粒受振后初速度与实测值较为吻合，但仍存在一定的误差。这是由于在仿真中设置微粒表面是绝对光滑的，然而实际中金属微粒虽在肉眼观察下是光滑的，但在显微镜下可以观察到微粒表面存在一些不均匀分布的毛刺，这些毛刺会改变微粒与腔体的接触面积。0.5 mm铝制微粒肉眼可见光下与显微镜下放大200倍的形态如图16所示。而毛刺的出现又具有一定的随机性，因此该误差在合理范围之内，可认为仿真的设置和修正与实际工况的对应性较好。
图16 0.5 mm铝制微粒肉眼与显微镜下放大200倍形态
Fig.16 Morphology of 0.5 mm aluminum particles by naked eye and 200× microscope
针对金属微粒在腔体底部受振激励后的起跳行为，已有不少学者进行了相关研究，但大多仅将过程等效为由恢复系数定义的刚性体的速度传递，其碰撞瞬间微粒运动速度表达式为
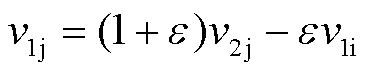（25）
式中，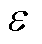
为式（12）中定义的碰撞恢复系数；
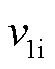和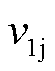
分别为微粒碰撞前后速度，碰撞前微粒速度
；
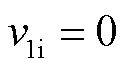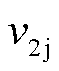为壳体碰撞后速度[15-16]。
经实验得到铝制球形微粒和铝板间的碰撞恢复系数约为0.45，根据式（12）计算恢复系数定义方法的理论值，同时开展大量预实验，得到恢复系数定义的方法、修正模型与实验观测下的微粒起跳初速度对比如图17所示。可发现恢复系数定义的模型与实验观测值差别较大，且在该模型下对于不同粒径大小和材质的微粒在受振后的初速度是完全相同的，有悖于客观实际。而本文模型与实际贴合度较高，该模型能够较为准确地描述带电操作产生的典型振动的传播及对微粒的作用行为。
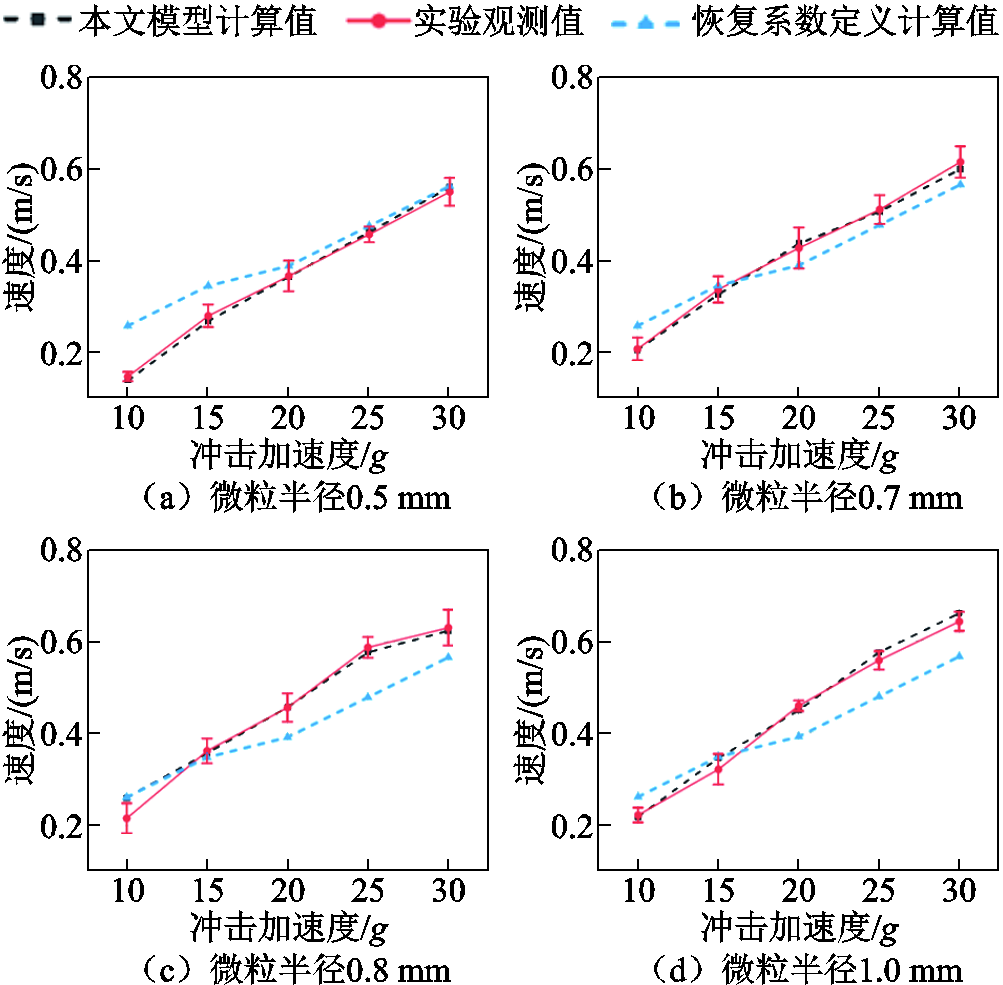
图17 恢复系数定义的方法、修正模型与实验观测下的微粒起跳初速度对比
Fig.17 Comparison of particle jump initial velocities under traditional methods, modified models and experimental observations
将有无振动激励与施加电压的初始边界条件代入基于能量法和碰撞随机特性的带电操作振动激励下微粒全过程运动模型，进行多次仿真，运用统计学工具对影响微粒活跃的因素进行归纳。施加30g冲击振动和126 kV时，三种情况下的运动轨迹对比如图18所示。
在有冲击振动无电压时，由于没有电场作用，微粒初始阶段最大运动高度高于无振动有电压和同时有振动和电压的情况，但微粒由于无电场的作用会做幅值衰减的径向往复运动直至静止。在有电压无振动情况下，由于施加电压远高于起跳电压，微粒在初始阶段会经过短暂的静止过程。当电场力大于重力和浮力的作用时微粒起跳，在腔体底部做简谐往复运动，但幅值较低，对绝缘危害的风险不大。对同时施加电压和振动的情况而言，微粒在0时刻受振向上起跳，初始阶段由于向上运动到达高电场强度区域需克服电场力做功，最大运动高度较无电压有振动时略低，但随后微粒动能逐渐累积，微粒反射后运动高度逐渐变大，微粒较无振动有电压时更为活跃。这表明振动激励能够使GIS内的金属微粒更为活跃，更加危险。
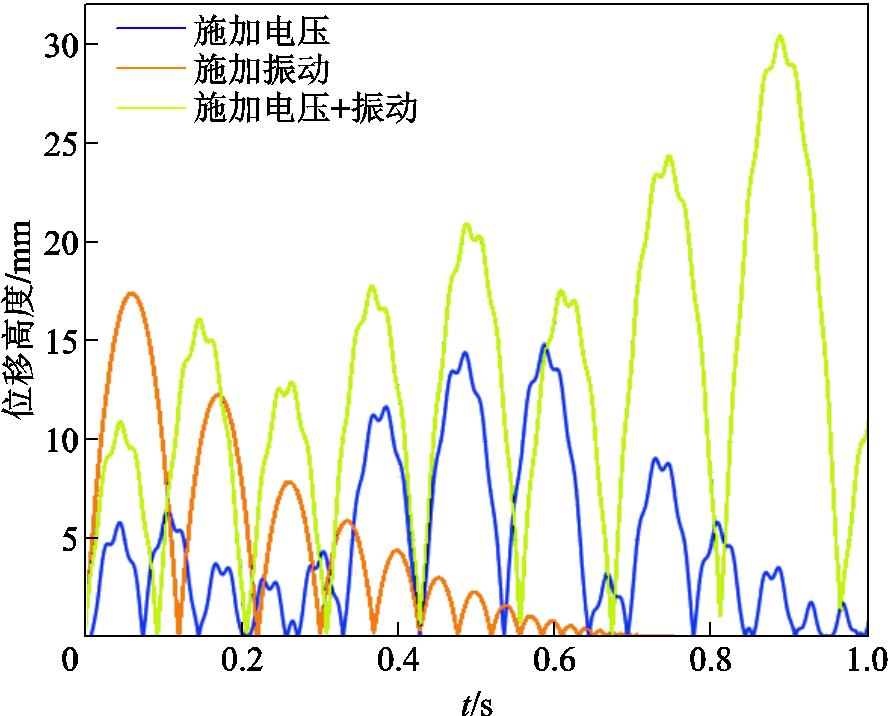
图18 有无电压、有无振动条件下微粒运动轨迹
Fig.18 Particle trajectories with and without voltage, with and without vibration conditions
在正常运行工况下，微粒并不都分布在断路器和隔离开关附近，因此在振动点附近的微粒会被激活，而距离振动点较远的微粒将继续潜伏。为定量分析微粒在多远的距离能够被激活，根据1.3节中研究的衰减行为，定义微粒临界激活距离xc。xc表示随着振动随距离的衰减微粒能够达到临界起跳条件的距离，表达式为
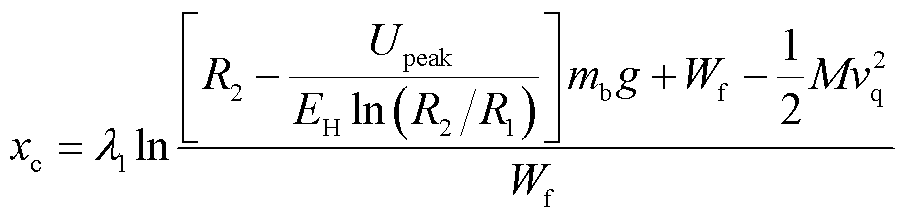（26）
当微粒距振动点距离小于临界激活距离xc时，微粒会被激活；当超出这一距离后，微粒将继续潜伏。微粒临界激活距离随振动强度及电压幅值的变化情况如图19所示。对于本文中腔体内的1.0 mm铝制微粒，在交流电压为73 kV、冲击大小为50g条件下，当微粒距离振动施加点1.573 m外时，微粒继续潜伏。通过计算得到1.0 mm。
对于同样大小、材质的球形金属微粒而言，随着振动强度和电压幅值的增大，冲击振动对系统整体做功增大，传递给微粒的动能也不断增大。同时电压幅值的提高增强了腔体内的电场强度，使得在更远距离的微粒能够起跳。
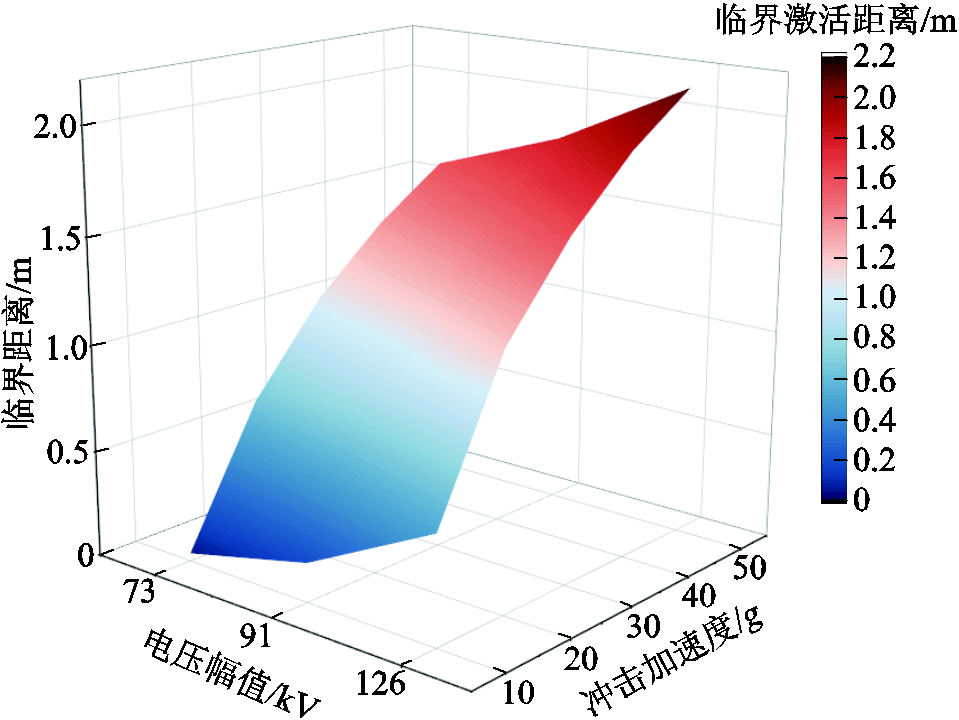
图19 临界激活距离和电压幅值及振动强度关系
Fig.19 Critical activation distance and voltage amplitude and vibration intensity relationships
1）获得了GIS内振动波的传播衰减规律。振动在GIS内以波的形式传播，传播随距离呈指数型衰减，行为呈“涟漪状”，并分化为纵波和横波。纵波的传播和作用方向一致，波速快，对微粒起跳影响小；横波的传播和作用方向垂直，波速慢，会对微粒起跳产生显著影响。在此研究基础上得到了振动幅值随距离衰减关系式。
2）获得了GIS内静止金属微粒受冲击振动后的动力学特性。考虑应变能和系统的阻尼损耗，搭建了腔体-微粒动能传递守恒模型。对微粒在腔体内静止时的受振行为进行分析，提出了微粒受振有效激活判据。
3）建立了带电操作典型振动激励下微粒运动全过程模型，并进行了实验验证和理论修正，修正后的模型与基于恢复系数定义的方法相比，考虑了微粒大小和粒径以及微观作用力对微粒受振运动行为的影响，与实际工况的等价性更高。
4）研究了振动对带电微粒运动行为的影响，考虑实际传播衰减，提出了微粒临界激活距离判据，并计算了不同因素下微粒临界激活距离的变化情况。研究表明，随着电压幅值和振动强度的增加，临界激活距离呈对数型增大。
附录 系统总势能V表达式
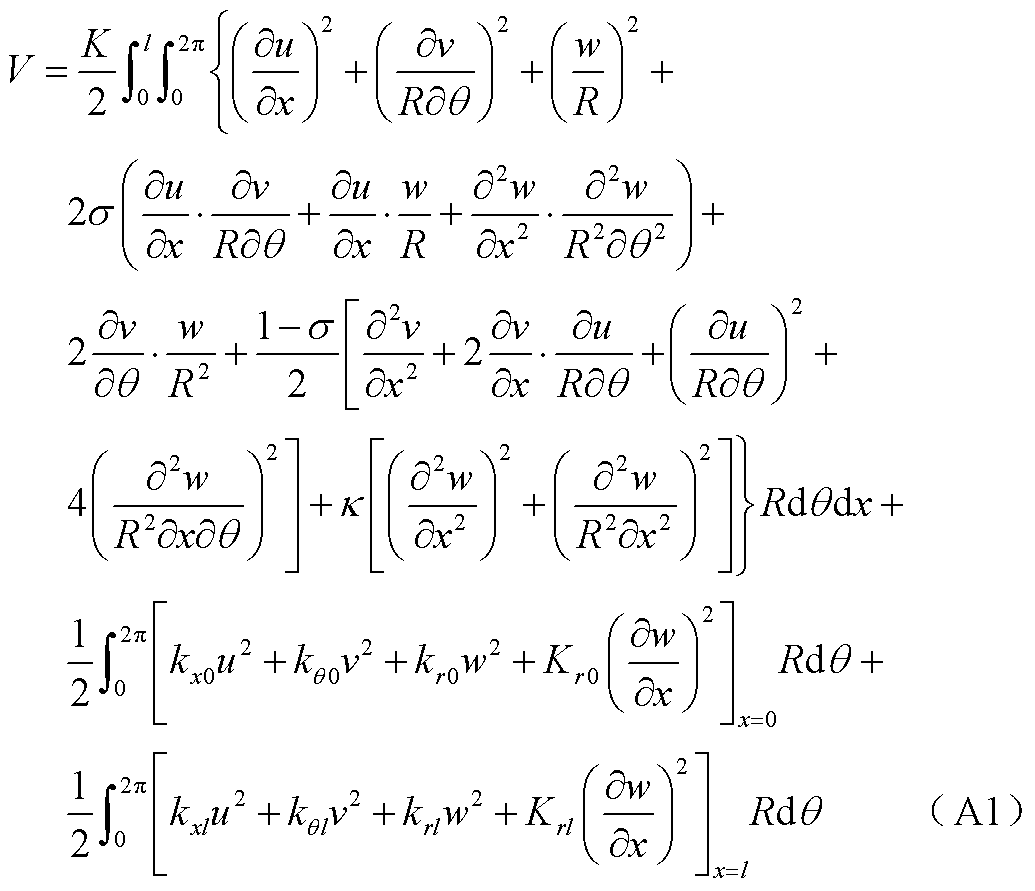
其中
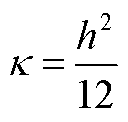（A2）
式中，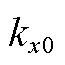
、
、
、
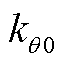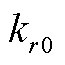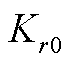为x=0端的弹簧弹性系数；
、
、
、
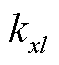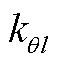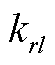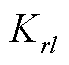为x=l端的弹簧弹性系数。
参考文献
[1] 豆龙江, 何玉灵, 万书亭, 等. 基于振动信号的高压断路器弹簧疲劳程度检测方法[J]. 电工技术学报, 2022, 37(24): 6420-6430.
Dou Longjiang, He Yuling, Wan Shuting, et al. Detecting method of high voltage circuit breaker spring fatigue based on vibration signal[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6420-6430.
[2] 汤广福, 庞辉, 贺之渊. 先进交直流输电技术在中国的发展与应用[J]. 中国电机工程学报, 2016, 36(7): 1760-1771.
Tang Guangfu, Pang Hui, He Zhiyuan. R & D and application of advanced power transmission technology in China[J]. Proceedings of the CSEE, 2016, 36(7): 1760-1771.
[3] 张连根, 路士杰, 李成榕, 等. GIS中线形和球形金属微粒的运动行为和危害性[J]. 电工技术学报, 2019, 34(20): 4217-4225.
Zhang Liangen, Lu Shijie, Li Chengrong, et al. Motor behavior and hazard of spherical and linear particle in gas insulated switchgear[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4217-4225.
[4] 李庆民, 薛乃凡, 王媛, 等. 交直流输电管道绝缘运行安全关键技术[J]. 中国电机工程学报, 2024, 44(4): 1629-1649.
Li Qingmin, Xue Naifan, Wang Yuan, et al. Key technologies for operation safety of AC/DC gas insulated transmission lines[J]. Proceedings of the CSEE, 2024, 44(4): 1629-1649.
[5] 梁芳蔚, 张长虹, 吕金壮, 等. 直流气体绝缘输电线路关键问题及装备研发现状综述[J]. 高压电器, 2023, 59(9): 1-11.
Liang Fangwei, Zhang Changhong, Lyu Jinzhuang, et al. Review of key problems and development status of DC gas insulated transmission line[J]. High Voltage Apparatus, 2023, 59(9): 1-11.
[6] 董曼玲, 臧春艳, 詹振宇, 等. GIL内部金属微粒问题研究进展[J]. 高压电器, 2024, 60(1): 1-14.
Dong Manling, Zang Chunyan, Zhan Zhenyu, et al. Research progress on metal particle issues inside GIL[J]. High Voltage Apparatus, 2024, 60(1): 1-14.
[7] Li Chuanyang, Lin Chuanjie, Yang Yong, et al. Novel HVDC spacers by adaptively controlling surface charges–part ii: experiment[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2018, 25(4): 1248-1258.
[8] Cookson A H, Wooton R E. Movement of filamentary conduct-ing particles under AC voltages in high pressure gases[C]//Proceedings of the International High Voltage Symposium, Zurich, Switzerland, 1975: 416-420.
[9] Cookson A H, Farish O, Sommerman G L. Effect of conducting particles on AC corona and breakdown in compressed SF6[J]. IEEE Transactions on Power Apparatus and Systems, 1972, PAS-91(4): 1329-1338.
[10] Metwally I A, A-Rahim A A. Dynamic analysis of motion of spherical metallic particles in non-uniform electric field[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2002, 9(2): 282-293.
[11] 王健, 李庆民, 李伯涛, 等. 考虑非弹性随机碰撞与SF6/N2混合气体影响的直流GIL球形金属微粒运动行为研究[J]. 中国电机工程学报, 2015, 35(15): 3971-3978.
Wang Jian, Li Qingmin, Li Botao, et al. Motion analysis of spherical conducting particle in DC GIL considering the influence of inelastic random collisions and SF6/N2 gaseous mixture[J]. Proceedings of the CSEE, 2015, 35(15): 3971-3978.
[12] 王健, 李庆民, 李伯涛, 等. 直流GIL中自由线形金属微粒的运动与放电特性[J]. 中国电机工程学报, 2016, 36(17): 4793-4801.
Wang Jian, Li Qingmin, Li Botao, et al. Motion and discharge behavior of the free conducting wire-type particle within DC GIL[J]. Proceedings of the CSEE, 2016, 36(17): 4793-4801.
[13] 王健. 直流GIL金属微粒的荷电运动机制与治理方法研究[D]. 北京: 华北电力大学, 2017.
Wang Jian. Research on the moving mechanisms of charged metal particles in DC GIL and suppressing methods[D]. Beijing: North China Electric Power University, 2017.
[14] 王健, 常亚楠, 王靖瑞, 等. 基于捕捉效用分析的直流GIL微粒陷阱设计与参数优化[J]. 中国电机工程学报, 2020, 40(15): 5050-5061.
Wang Jian, Chang Yanan, Wang Jingrui, et al. Design and optimization of particle traps in DC GIL based on the capture effect analysis[J]. Proceedings of the CSEE, 2020, 40(15): 5050-5061.
[15] 李晓昂, 李杰, 任静, 等. 冲击振动激励下GIS内自由金属微粒起跳特性[J]. 高电压技术, 2022, 48(5): 2005-2012.
Li Xiaoang, Li Jie, Ren Jing, et al. Lift-off characteristics of free metal particles in GIS under shock vibration[J]. High Voltage Engineering, 2022, 48(5): 2005-2012.
[16] 李杰, 李晓昂, 吕玉芳, 等. 正弦振动激励下GIS内自由金属微粒运动特性[J]. 电工技术学报, 2021, 36(21): 4580-4589, 4597.
Li Jie, Li Xiaoang, Lü Yufang, et al. Motion characteristics of free metal particles in GIS under sinusoidal vibration[J]. Transactions of China Electro-technical Society, 2021, 36(21): 4580-4589, 4597.
[17] 胡新文, 李晓昂, 王舒啸, 等. 冲击振动激励下GIS内自由金属微粒运动及其诱发间隙击穿特性[J]. 高电压技术, 2024, 50(1): 339-347.
Hu Xinwen, Li Xiaoang, Wang Shuxiao, et al. Free metal particles movement and its induced gap breakdown characteristics in GIS under impact vibration [J]. High Voltage Engineering, 2024, 50(1): 339-347.
[18] 宋颜峰, 郑中原, 于金山, 等. 机-电联合作用下SF6气体中金属微粒运动行为与局部放电特性研究[J]. 西安交通大学学报, 2023, 57(7): 74-83.
Song Yanfeng, Zheng Zhongyuan, Yu Jinshan, et al. Study on the motion behavior and partial discharge characteristics of metal particles in SF6 gas under the combined action of mechanical and electrical[J]. Journal of Xi’an Jiaotong University, 2023, 57(7): 74-83.
[19] 王扬程, 关向雨, 陈志鹏, 等. 基于结构声强法的GIS机械振动传递特性[J]. 电工技术学报, 2024, 39(16): 5162-5171.
Wang Yangcheng, Guan Xiangyu, Chen Zhipeng, et al. Energy transfer characteristics of GIS mechanical vibration based on structural intensity method[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 5162-5171.
[20] Leissa A W. Vibration of Shells[M]. Washington: Scientific and Technical Information Office, National Aeronautics and Space Administration, 1973.
[21] Qatu M S. Vibration of Laminated Shells and Plates [M]. Amsterdam: Elsevier, 2004.
[22] Lam K Y, Loy C T. Analysis of rotating laminated cylindrical shells by different thin shell theories[J]. Journal of Sound and Vibration, 1995, 186(1): 23-35.
[23] 代路. 复杂边界条件圆柱壳耦合结构动力学特性及声辐射研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
Dai Lu. Study on dynamic behavior and acoustic radiation for the coupling structure of cylindrical shells with complex boundary conditions[D]. Harbin: Harbin Engineering University, 2013.
[24] 杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 3版. 南京: 南京大学出版社, 2012.
[25] 赵翼飞. 基于机械波的结构系统冲击动力学问题研究[D]. 沈阳: 东北大学, 2019.
Zhao Yifei. Research on problems regarding impact dynamics of structural systems based on mechanical waves[D]. Shenyang: Northeastern University, 2019.
[26] 刘晨. 核电站管道振动检测系统设计[D]. 西安: 西安理工大学, 2023.
Liu Chen. Design of pipeline vibration detection system for nuclear power plant[D]. Xi’an: Xi’an University of Technology, 2023.
[27] Hunt K H, Crossley F R E. Coefficient of restitution interpreted as damping in vibroimpact[J]. Journal of Applied Mechanics, 1975, 42(2): 440-445.
[28] Bhushan B. Contact mechanics of rough surfaces in tribology: multiple asperity contact[J]. Tribology Letters, 1998, 4(1): 1-35.
[29] Liu Cheng, Tian Qiang, Hu Haiyan. Dynamics and control of a spatial rigid-flexible multibody system with multiple cylindrical clearance joints[J]. Mechanism and Machine Theory, 2012, 52: 106-129.
[30] Rodrigues da Silva M, Marques F, Tavares da Silva M, et al. A compendium of contact force models inspired by Hunt and Crossley’s cornerstone work[J]. Mechanism and Machine Theory, 2022, 167: 104501.
[31] Carvalho A S, Martins J M. Exact restitution and generalizations for the Hunt-Crossley contact model[J]. Mechanism and Machine Theory, 2019, 139: 174-194.
[32] Corral E, Moreno R G, García M J G, et al. Nonlinear phenomena of contact in multibody systems dynamics: areview[J]. Nonlinear Dynamics, 2021, 104(2): 1269-1295.
[33] Khan Y, Okabe S, Suehiro J, et al. Proposal for new particle deactivation methods in GIS[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2005, 12(1): 147-157.
[34] 张宁, 王鹏, 刘智捷, 等. 流-电耦合场中金属颗粒群的荷电计算及影响因素研究[J]. 电工技术学报, 2024, 39(17): 5534-5544.
Zhang Ning, Wang Peng, Liu Zhijie, et al. Study on the charge calculation and influencing factors of metal particle groups in fluid-electric coupling field [J]. Transactions of China Electrotechnical Society, 2024, 39(17): 5534-5544.
[35] 耿秋钰, 胡智莹, 李庆民, 等. 特高压交流GIS/GIL拔孔型陷阱优化设计与协同布置方法[J]. 电工技术学报, 2023, 38(23): 6539-6552.
Geng Qiuyu, Hu Zhiying, Li Qingmin, et al. Optimal design and synergism arrangement methodology of convex-shaped traps for ultra high voltage AC GIS/GIL applications[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6539-6552.
[36] 王健, 平安, 常亚楠, 等. 直流应力下主动式微粒抑制方法的动态配合研究[J]. 电工技术学报, 2023, 38(10): 2794-2805, 2831.
Wang Jian, Ping An, Chang Yanan, et al. Research on dynamic coordination of active particles suppression methods under DC stress[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2794-2805, 2831.
[37] 胡智莹, 耿秋钰, 魏来, 等. 直流GIS/GIL中驱赶电极与微粒陷阱的协同抑制作用及优化设计方法[J]. 电工技术学报, 2023, 38(12): 3338-3349.
Hu Zhiying, Geng Qiuyu, Wei Lai, et al. Synergistic inhibitory effect and optimal design method of driving electrode and particle trap in DC GIS/GIL[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3338-3349.
[38] 柳冠青. 范德华力和静电力下的细颗粒离散动力学研究[D]. 北京: 清华大学, 2011.
Liu Guanqing. Discrete element methods of fine particle dynamics in presence of van der Waals and electrostatic forces[D]. Beijing: Tsinghua University, 2011.
[39] 崔燕. 微米级固体颗粒的分形及其与界面间粘附力的关系研究[D]. 长沙: 中南大学, 2011.
Cui Yan. Investigation on the relationship between adhesion force and the fractal characteristics of solid micro-particle[D]. Changsha: Central South University, 2011.
[40] 梁瑞雪, 刘衡, 胡琦, 等. GIS/GIL内微米级金属粉尘动力学行为与诱发放电特性研究进展[J]. 中国电机工程学报, 2020, 40(22): 7153-7166.
Liang Ruixue, Liu Heng, Hu Qi, et al. Research advances in the kinetic behavior and induced discharge characteristics of micron metal dust within GIS/GIL[J]. Proceedings of the CSEE, 2020, 40(22): 7153-7166.
[41] 薛乃凡, 李庆民, 刘智鹏, 等. 微纳粉尘运动行为与微弱放电探测技术研究进展[J]. 电工技术学报, 2022, 37(13): 3380-3392.
Xue Naifan, Li Qingmin, Liu Zhipeng, et al. Research advances of the detection technology for kinetic behavior and weak discharge of the micro-nano dust[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3380-3392.
Abstract Gas insulated switchgear (GIS) faults occur frequently after live operation, and according to statistics, the faults after live operation account for 60% of the total. The strong shock vibration generated by GIS live operation not only produces metal contaminants, but also activates latent particles, which seriously affects the insulation safety of GIS. The physical effects generated by GIS live operation are complicated, mainly including shock vibration, overvoltage, residual voltage and other physical effects. The mechanism by which the particles inside the GIS are affected by switching operation is unknown and is extremely dangerous. The mechanism of switching operation on particles in GIS is unknown and extremely dangerous.
In order to solve the problem that particles are prone to discharge after live operation, and to clarify the motion mechanism of spherical metal particles in GIS after impact vibration, this paper carries out the following work: firstly, we study the propagation process of vibration inside the cavity, and then we carry out the forced correction on the basis of the flexible boundary three-dimensional cylindrical vibration model, which improves the equivalence with the actual working conditions. The propagation form and the "ripple" propagation behavior of shock vibration in GIS are revealed, and it is clarified that the vibration wave is divided into P-wave and S-wave during the propagation process, the P-wave propagates faster than the S-wave, and the S-wave plays a major role in the jumping of the particles. And then the energy transfer process of the cavity and particles after being vibrated is analyzed, and the excitation effect of the shock vibration on the system is analyzed in the form of energy as a link. The energy transformation of the system after the vibration work is clarified, the cavity-particle kinetic energy transfer conservation model is constructed, and the activation conditions of the particles are defined with the help of the jumping field strength, and the activation criterion of the particles subjected to vibration is proposed. On the basis of the aforementioned research, the whole process model of particle motion under typical vibration excitation of live operation is established by considering the particle charge motion characteristics and collision random characteristics, and verified by experiments. On the basis of the validation, the correction considering the microscopic force is carried out, and the error is analyzed from the microscopic point of view.
The model fully considers the influence of different particle sizes and materials on the particle dynamics, and is more equivalent to the actual working conditions than the method defined by the recovery coefficient. Finally, it is clarified that the vibration excitation can activate the motion of the particles, and the influencing factors of the motion behavior of the particles are explored. Combined with the propagation and attenuation characteristics of vibration, the criterion of critical activation distance of particles under charged working conditions is proposed, and the changes of critical activation distance of particles under different factors are calculated. The study shows that the critical activation distance increases logarithmically with the increase of voltage amplitude and vibration intensity. This study provides support for solving the problem that particles are very likely to cause discharge faults after GIS live operation.
Keywords：Gas insulated switchgear (GIS), live operation, conservation of energy transfer, kinematic properties
中图分类号：TM84
DOI: 10.19595/j.cnki.1000-6753.tces.240861
国家电网有限公司科技项目资助（5200-202355792A-3-8-KJ）。
收稿日期 2024-05-23
改稿日期 2024-07-11
王 健 男，1985年生，副教授，博士生导师，研究方向为高电压与绝缘技术、放电物理等。
E-mail：wangjian31791@ncepu.edu.cn（通信作者）
秦诚意 男，1998年生，硕士研究生，研究方向为GIS/GIL中金属微粒的运动与放电机理。
E-mail：1048457768@qq.com
（编辑 李 冰）