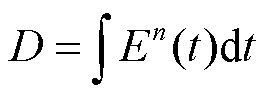（1）
摘要 聚合物材料因其优异的介电性能被广泛应用于电气绝缘设备中。但长期带电运行会使得其内部缺陷处产生的电树枝快速发展，造成材料的绝缘击穿。数值模拟方法能为研究固体绝缘材料内部电击穿过程提供参考，然而现有的模拟方法依旧存在模型参数难以获得和校准的问题，其结果很难得到实际应用。考虑到电树枝损伤累积增长的唯象规律符合反幂定律，该文基于反幂定律建立局部电损伤方程，进一步结合有限元计算建立电树枝模拟方法，研究反幂定律模型参数（电压耐受指数n、累积损伤阈值DC及材料分散性）对模拟结果的影响规律，提出一种模型简单、参数可实验获取的电树枝模拟方法，并开展电树枝老化实验对模拟方法的有效性进行验证。结果表明，该方法能够基于实验获取的材料参数对电树枝进行模拟，对电树枝形态和生长规律的模拟效果良好。
关键词：聚合物 电树枝 反幂定律 绝缘 数值模拟
聚合物材料由于其优良的介电性能，被广泛应用于国内外功率电子器件和输配电系统中[1-3]。然而，绝缘材料内部在机械应力、热效应、电应力等因素的长期耦合作用下，易引起电树枝生长，将造成材料内部损伤劣化，并最终导致贯穿性放电造成危害。因此，抑制固体绝缘材料在设备运行工况下内部的电树枝发展，是保障设备安全稳定运行的重要途径，掌握长期作用下绝缘材料的介电击穿行为及其影响因素，并以此研究分析电气设备绝缘损伤发展规律，对提升系统绝缘的可靠性具有重要意义[4]。
电树枝是材料内部电老化的体现，也是造成材料绝缘失效的重要原因，由于材料制作过程中内部会不可避免地形成气隙、杂质[5]等缺陷，使得其局部电场分布不均，进一步引起树枝状的放电通道。电树枝一旦形成便易快速发展，造成材料绝缘的整体击穿。近些年来，国内外学者对绝缘材料的电树枝生长特性进行了广泛的研究。文献[6-9]探究了温度对绝缘材料中电树枝生长的影响，实验结果表明电树枝的生长速度在高温条件下，相比于低温条件有更明显的优势。杜伯学等[10-11]研究了脉冲激励作用下绝缘材料电树枝的生长特性，并且分别探究了脉冲幅值、重复频率、极性及脉宽对其电树枝生长规律的影响，发现当重复频率增加时，电树枝更易生长且形态往往会发生改变。何东欣和黄路等[12-13]研究发现，脉冲边沿时间对电树枝生长有明显的影响，且脉冲边沿时间越短，越容易产生电树枝。
尽管现有的实验并未系统地解释绝缘材料内部电树枝演化的理论体系，但通过数值模拟方法也能为提升系统绝缘的可靠性提供参考。最早的电树枝模型为L. Niemeyer、L. Pietronero和H. J. Wiesmann提出的基于分形理论的NPW模型，该模型中电树枝的生长是按离散步长进行的，其生长概率与局部电场强度相关，但也会受到材料微观结构和缺陷分布等因素的影响[14]。在NPW模型的基础上，H. J. Wiesmann和H. R. Zeller通过引入生长临界场强和电树通道内部的结构内电场，形成WZ模型，能够更准确地模拟固体电介质中的分形击穿现象和各种放电结构类型[15]。NPW模型和WZ模型将电树枝简化为按离散步长的突变生长模式，这与实际绝缘局部击穿前存在自由基引发电树枝渐进变化的实际不符[16-19]。基于此，Chen Longqing[20]将J. W. Cahn和S. M. Allen等[21-22]提出的相场模型（Phase Field Model, PFM）引入电树枝模拟，使得能够通过能量泛函最小化过程求解电树枝的渐进生长过程[23-26]。然而，相场模型的一些关键参数，如临界能量密度、界面能和动力学系数等，难以从实验中直接获得，仅能通过模型校核实现特定材料的微观电树枝模拟，无法实现从材料参数测试到复杂结构电树枝预测的工程性任务。因此，亟须提出一种模型简单、参数可实验获取的电树枝模拟方法，提升电树枝模拟的工程适用性。
反幂定律是直接根据固体电介质寿命数据建立的唯象电损伤模型[27]，描述了电损伤随时间渐进增长的规律，其模型简单，参数可实验获取。考虑到电树枝渐进生长的本质是局部电损伤的发展过程，电树枝生长动力学方程也应服从反幂定律。因此，本文基于反幂定律建立局部电损伤方程，进一步结合有限元计算建立电树枝模拟方法，分析反幂定律模型参数对模拟结果的影响规律，并开展电树枝实验验证该方法的有效性。本文提出的方法具有模型简单、参数可实验获取的优点，有更加广泛的工程应用价值。
聚合物固体电介质电损伤规律服从反幂定律，表示为
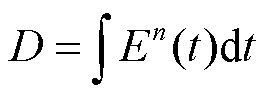（1）
式中，D为累积电损伤；E(t)为随时间变化的电场强度；t为电场持续时间；n为电压耐受指数。
根据式（1）可知，电介质内部D将随着电场持续时间t的增长而增大，D越大则固体电介质的电老化程度越高。当D达到某一失效阈值DC后，电介质绝缘性能完全劣化，电介质发生击穿，达到其寿命末期。假设电场为不随时间变化的恒定电场E，那么根据式（1）可推导电介质的电寿命L服从式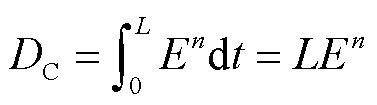（2）。
（2）
式（2）即为学术界常用的绝缘电寿命反幂模型，根据式（2）描绘的聚合物电介质反幂寿命曲线如图1所示。
反幂定律是直接根据固体电介质寿命数据建立的唯象模型，其描述了固体电介质整体电损伤积累直至贯穿性树枝通道产生的物理过程，其中n描述了电损伤增长速度与电场强度间的关系，DC描述了电损伤发展成贯穿性树枝通道所需要累积损伤总量。不同的材料和微观结构具有不同的n和DC，从而产生不同的寿命曲线。聚合物内电树枝发展是未贯穿的局部树枝通道，若将聚合物分为有限个单元方块，则绝缘未贯穿的树枝通道可以看作单元内电损伤累积直至单元内产生贯穿性树枝通道的过程，即每个有限单元的电损伤过程应服从反幂定律，这是反幂定律能够描述电树枝的理论基础。不同的单元由于分子链、化学缺陷等材料差异，以及非晶、结晶、物理缺陷等微观结构差异，从而具有不同的反幂模型。根据反幂定律可知，各单元在相同电场强度下产生树枝通道所需的时间不同，树枝无法一直沿着电场强度最大方向生长，从而产生分叉，引起电树枝老化。
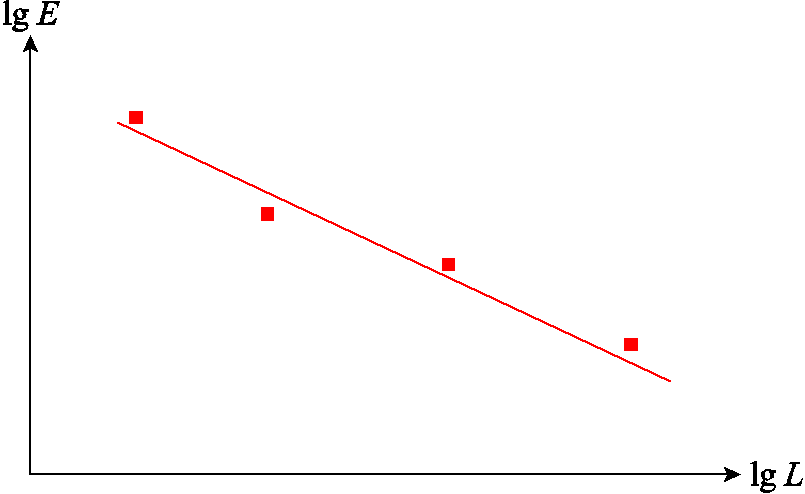
图1 聚合物反幂寿命曲线
Fig.1 Inverse life curve of polymer
根据反幂定律，可将电树枝生长过程作以下描述：固体介质内部可分为若干个有限元，用p表示有限元的空间位置。当外部施加电压时，每个有限元内都承受一定的电场，使得每个有限元内都产生了电损伤D(p, t)。假设D(p, t)生长规律符合式（3）所示的反幂定律，则电场强度E(p, t)越高，D(p, t)增长越快。空间中电场集中位置px的电损伤D(px, t)率先达到材料失效阈值DC，使得该有限元发生相变，从绝缘状态转换为导电或半导电状态，产生局部损伤，萌生电树枝。随后电树枝尖端重复以上过程不断生长。
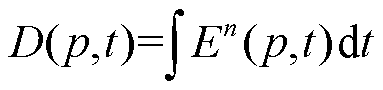（3）
式（3）描述的电损伤增长符合电场越集中的位置越易产生电树枝的规律。同时，式（3）能够描述历史电场对有限元内电损伤的累积规律，满足电树枝生长导致电场分布变化情况下的损伤计算，如图2所示。
引入一个描述有限元区域内相变的变量η(p, t)。当η(p, t)=0时，表示有限元区域内材料处于良好绝缘状态，未进入电树枝区域；当η(p, t)=1时，表示有限元区域内电损伤已达到失效阈值，材料处于导电或半导电状态，完全失效；当0＜η(p, t)＜1时，表示有限元区域内电损伤已开始积累，处于老化但未失效的绝缘或半导电状态，属于过渡区域。符合上述条件的函数很多，本文采用式（4）描述相场变量η(p, t)与电损伤D(p, t)之间的关系[25]。
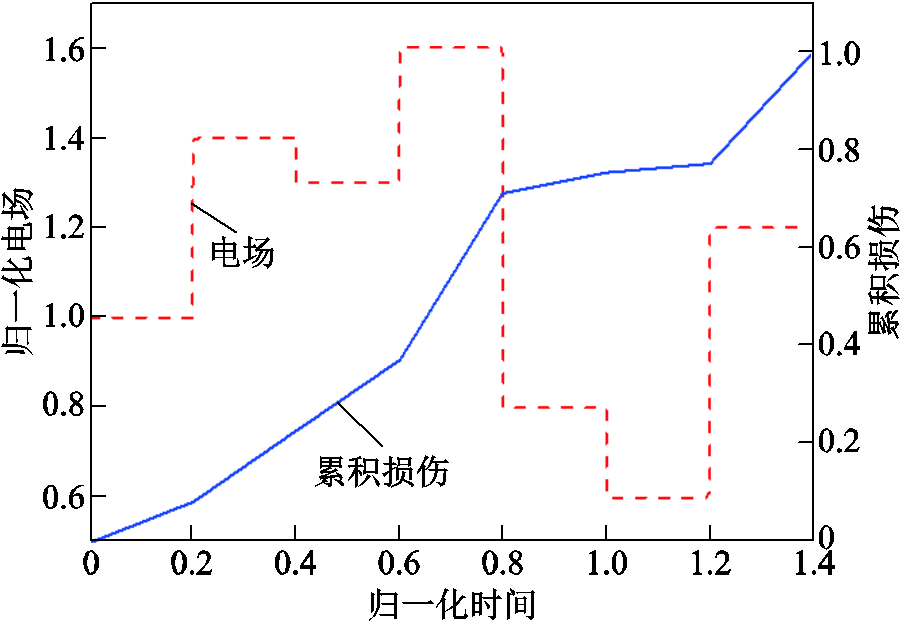
图2 电场分布变化情况下的损伤计算
Fig.2 Damage calculation under varied electric field distribution
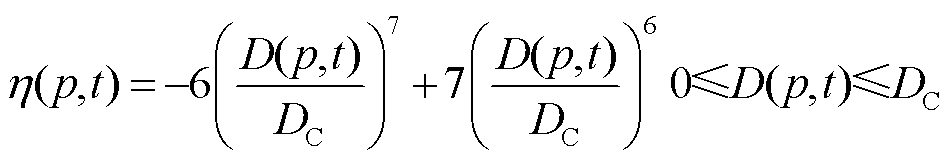（4）
假设完好的有限元区域内部电导率为σI，达到失效阈值区域内的电导率为σD，则建立有限元区域逐渐劣化时的电导率模型为
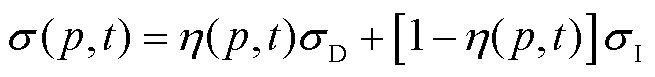（5）
材料的微观性能并非均匀的，例如聚乙烯内部存在晶相、非晶相、缺陷（均匀分布）等多种结构，其中晶相的耐电损伤能力更强，导致电树枝更易在非晶相或缺陷处发展。电树枝发展路径会受到材料微观分散性的影响，因此需要建立方程描述材料电损伤发展的分散性。
失效阈值DC描述了材料失效所需电损伤的总量，微观上易失效的非晶相、界面、缺陷等结构的DC较小；反之，不易失效的晶相、交联网格等结构的DC较大。因此微观上失效阈值是空间变量的分布函数，即DC(p)。由于DC(p)为对数坐标系下的分布[28]，因此本文假设ln[DC(p)]服从正态分布，其概率密度fDC表达式为
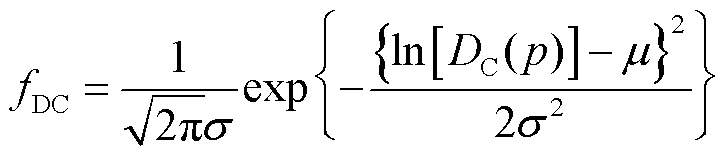（6）
式中，μ和σ分别为ln[DC(p)]的均值和标准差。
考虑电树枝生长过程一般为局部高电场下电损伤缓慢发展的过程，介质内部泄漏电流较低，产生的热效应较小，难以引起介质内的温度分布产生显著变化，因此本文忽略热效应带来的影响，不计算温度场分布，仅计算电场分布。
以准静态电场方程计算介质内电场分布，即
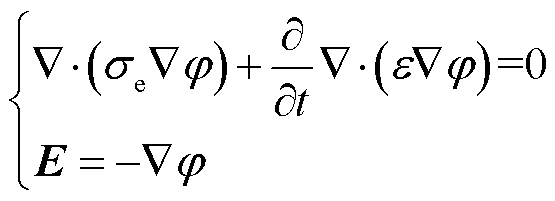（7）
式中，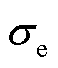
为电导率；ε为介电常数；
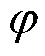为电势；E为电场强度矢量。该方程描述了准静态电荷的电场分布，能够准确地计算交流（静电荷）以及直流（运动电荷）下的电场分布。采用该方程可使电树枝模拟方法能够适用于交流和直流电应力。
联合准静态电场方程组、电树枝模拟方程组、材料分散性方程，建立二维针-板几何模型如图3所示。本仿真中聚合物部分的长度和宽度均为2 mm。聚合物底端接地，顶端中间位置插入针电极。针电极直径为0.01 mm，高度为0.2 mm，其插入聚合物中的高度为0.1 mm，针尖圆角为0.005 mm。
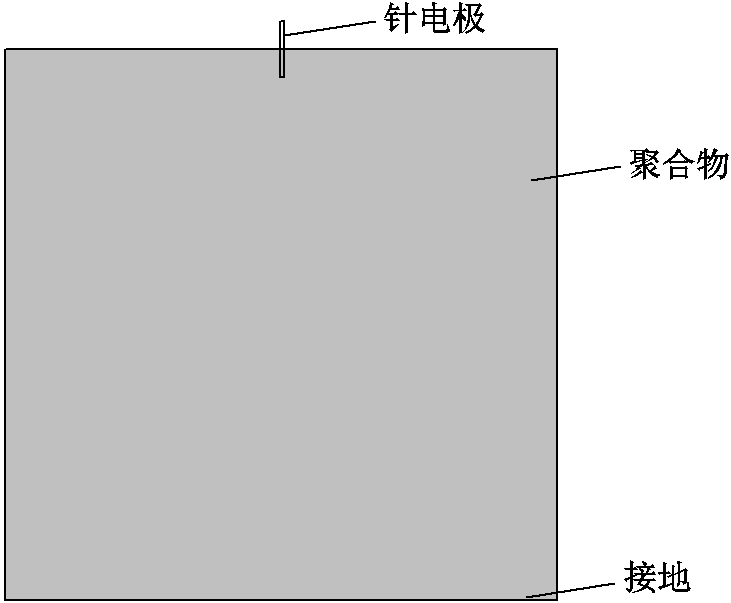
图3 二维几何模型
Fig.3 2D geometric model
进行电树枝仿真模拟时，设定模型边界条件：针电极边界为阳极，电压设置为10 kV；聚合物底端为阴极接地；周围边界设置为电绝缘。聚合物材料仿真介电参数见表1。
表1 材料仿真介电参数
Tab.1 Simulation parameters of materials
参数数值 电导率/(S/m)1×10-12 相对介电常数2.3
基于有限元计算工具即可模拟电树枝的生长过程。采用该方法模拟的电树枝发展过程及其发展过程中对电场线分布的影响过程如图4所示。
图4 电树枝随时间的发展过程
Fig.4 The development process of electrical tree over time
电损伤的增长率g(p, t)可用D(p, t)对时间的偏导表示为
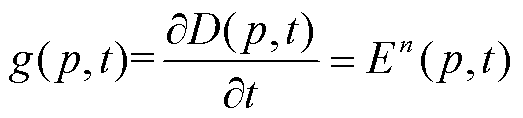（8）
即g(p, t)与n呈指数关系。因此，若失效阈值DC保持不变，n值越大，有限元相变时间越短，则电树枝生长速度越快，电树枝的生长速度也与n呈指数关系。
如图4所示，电树枝某条路径的顶端位置为电场集中点，此处电场强度高，易产生电损伤从而使得电树枝沿着该路径继续生长。若电树枝沿着电场最高的方向生长的能力越强，则其越容易沿着原有路径生长，可称之为顶端优势d。d可以用电树枝顶端损伤增长率gmax与绝缘平均损伤增长率gave的比值表示，即
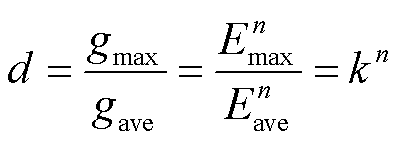（9）
式中，Emax为电树枝顶端的最大电场强度；Eave为绝缘平均电场强度；k为电场畸变率。可见，电树枝顶端优势与k和n值相关，在相同的k作用下，n值越大，电树枝越容易沿着原有路径继续生长，此时其分叉少，树枝纤细；反之，n值越小，电树枝分叉增多，而树枝变粗。
在针-板电极结构下开展不同n值的电树枝模拟仿真如图5所示，其余模型参数与边界条件保持一致。当n=1.5时，树枝枝干粗且分叉多，形态接近水树枝形态；当n≥2时，树枝枝干随着n值增加而变细，且由于顶端优势的不断增强，树枝分叉逐渐减少。
图6为不同n值的电树枝模拟仿真过程中，树枝沿电场方向的增长速率，可见随着n值的增加，电树枝生长速率呈指数级上升。
图5 不同n值的电树枝模拟仿真
Fig.5 Simulation of electrical tree with different n
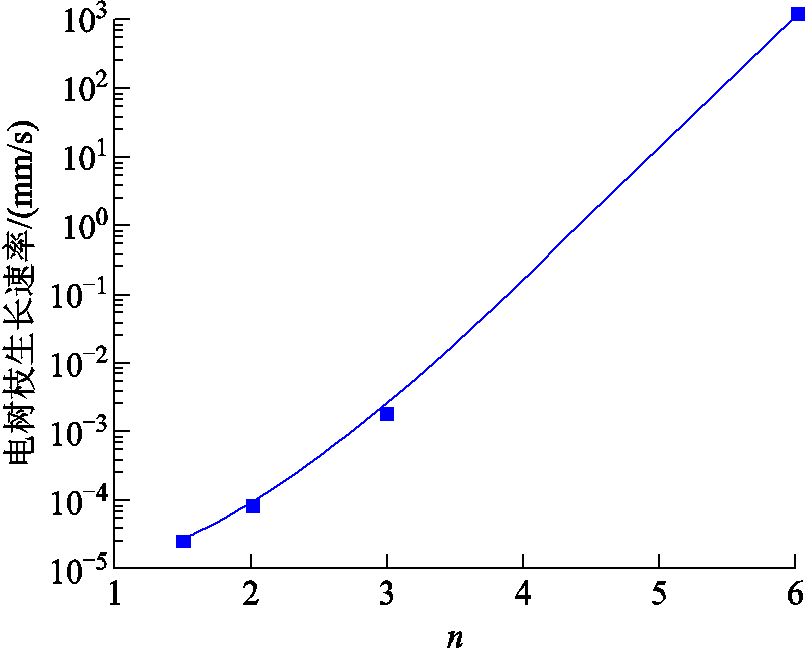
图6 电树枝n值对电树枝生长速率的影响
Fig.6 The influence of the nof electrical tree on the growth rate of electrical tree
综上所述，n值对电树枝生长模拟存在两方面影响：一方面，n值决定了电树枝的生长速率；另一方面，n值影响了电树枝的形态，n值越大，电树枝顶端优势越强。
有限元完成绝缘到半导电状态相变所需时间可定义为其寿命L(p)，则L(p)服从
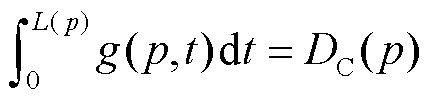（10）
假设g(p, t)不随时间变化，则有限元平均相变速度为
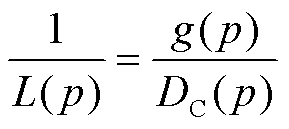（11）
根据DC(p)服从正态分布假设，若其标准差σ不变，均值μ越大，有限元相变速度越慢，电树枝生长越慢，即电树枝生长速度与μ成反比。
在针-板电极结构下，开展不同μ值的电树枝模拟仿真如图7所示，其余模型参数与边界条件保持一致，并提取电树枝平均生长速率与μ的关系如图8所示。可见，μ对电树枝生长形态的影响较小，但对生长速率存在较大的影响，μ与生长速率确为反比关系，μ越大则电树枝生长越慢。
图7 不同μ值的电树枝模拟仿真
Fig.7 Simulation of electrical tree with different μ
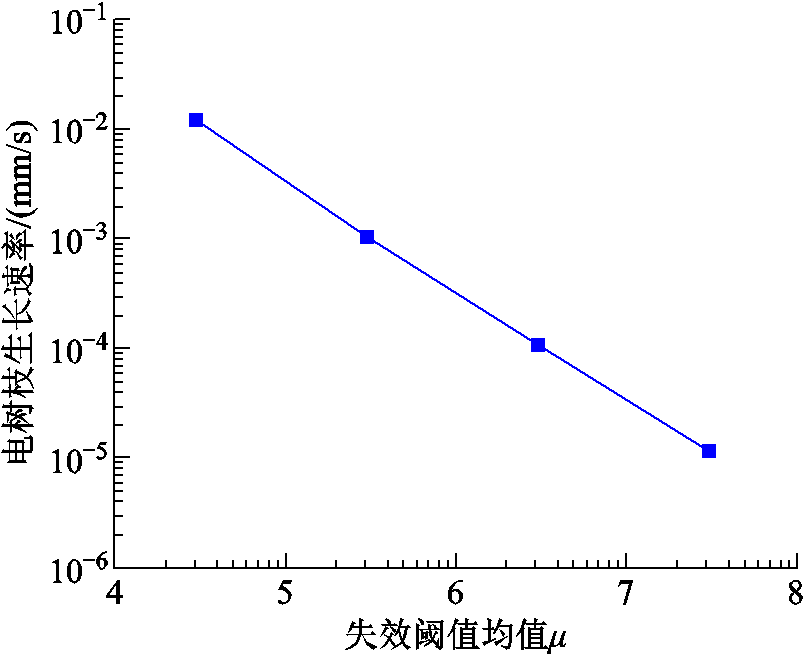
图8 失效阈值均值μ对电树枝生长速率的影响
Fig.8 The influence of mean failure threshold μ on the growth rate of electrical tree
在针-板电极结构下，开展不同σ的电树枝模拟仿真如图9所示，其余模型参数与边界条件保持一致，并提取电树枝平均生长速率与σ的关系如图10所示。可见，σ对电树枝生长形态存在影响，随着σ的增大，电树枝发展随机性增强，电树枝分叉数量逐渐变多，但由于顶端优势并未发生变化，电树枝粗细保持不变。同时σ对电树枝生长速率也存在影响，随着σ的增大，生长速率先下降后增加。这表明当σ较小时，材料分散性的增大能适当地阻碍电树枝的发展，这是由于分散性增大使得材料内的稳定结构增多，并且这些结构致密，电树虽然在薄弱结构内发展但会遇到稳定结构的阻碍；当σ较大时，材料分散性的增大使得内部稳定结构变得越来越稀疏，此时电树枝越来越容易沿着薄弱结构发展。
图9 不同σ值的电树枝模拟仿真
Fig.9 Simulation of electrical tree with different σ
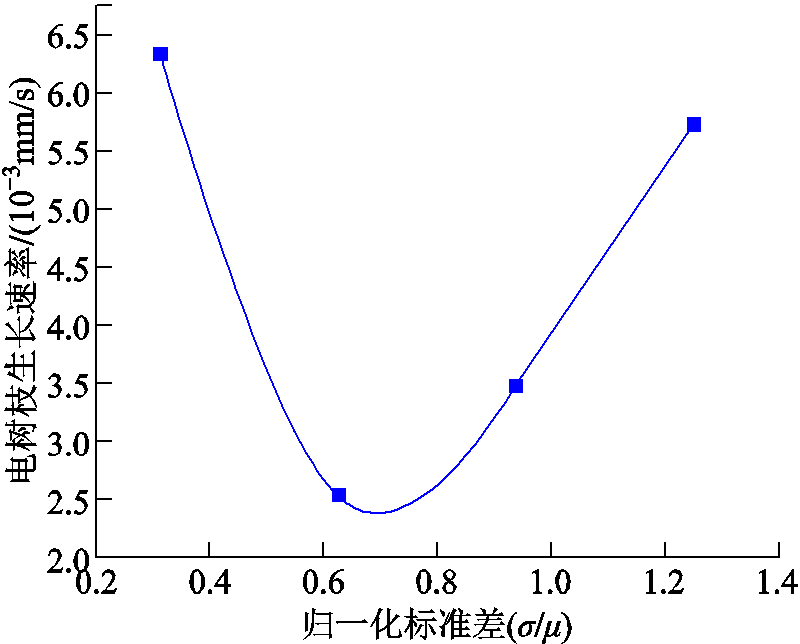
图10 标准差对电树枝生长速率的影响
Fig.10 The influence of standard deviation on the growth rate of electrical tree
为了验证本文提出的电树枝模拟方法的有效性，本节通过寿命实验获取环氧树脂样品的模型参数，进一步采用这些参数进行针-板电极结构下的电树枝模拟，同步开展相同结构下的电树枝老化实验，对比分析实验与模拟的电树枝生长规律的一致性。
为获取电树枝模拟所需要的必要参数，选择环氧树脂为绝缘材料，设计如图11所示的针-板电极样品，针尖曲率半径为5 μm。将针-板电极固定，两者间距设置为1 mm，然后将环氧A、B组分混合并充分搅拌后，浇注到针-板电极模具中，随后在室温下固化24 h，获得环氧树脂针-板电极样品。
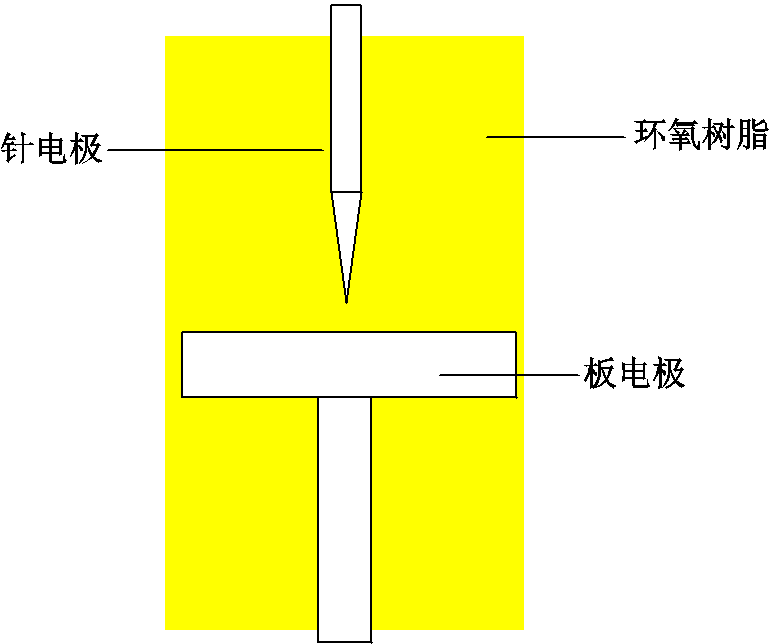
图11 针-板电极样品示意图
Fig.11 Schematic diagram of needle-plate electrode sample
为提高实验效率，采用步进应力寿命实验，获取环氧树脂针板电极样品的n，以及DC的分布参数μ和σ。步进应力实验参数设置见表2，共设计三组步进应力实验，每组实验重复9次。参数设计方法参考文献[28]，三组实验的起始电压U0、升压步长ΔU相同，时间步长Δt不同。
表2 步进应力试验参数
Tab.2 Step stress test parameter
参数数值 起始电压U0/kV5 升压步长ΔU/kV2 时间步长Δt/s10, 100, 1 000
通过步进应力实验，基于文献[28]方法，获得针-板电极环氧树脂样品的寿命曲线如图12所示。从寿命曲线中提取反幂模型参数n=9.01。进一步计算所有样品的累积损伤lnDC，并拟合正态分布如图13所示，获得μ=27.8，σ=1.74。
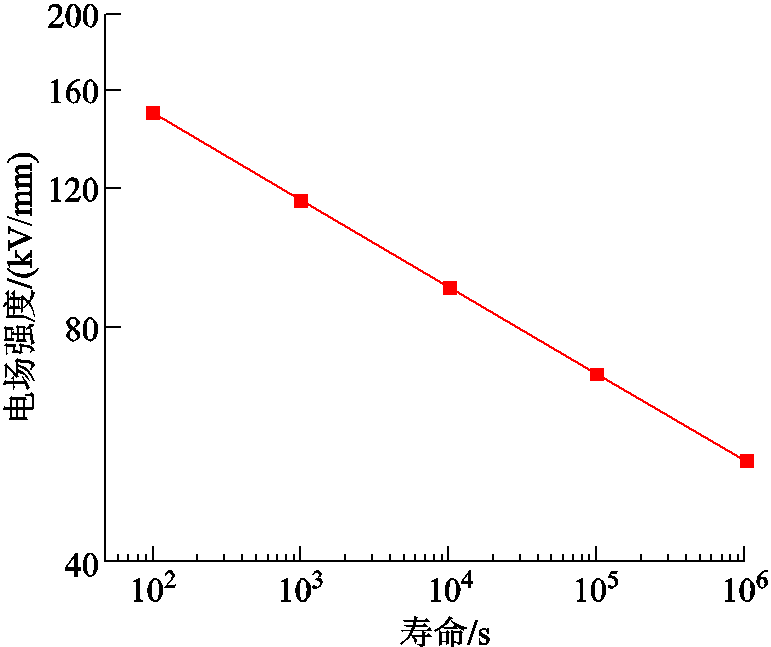
图12 针-板电极样品寿命曲线
Fig.12 Sample life curve of needle-plate electrode
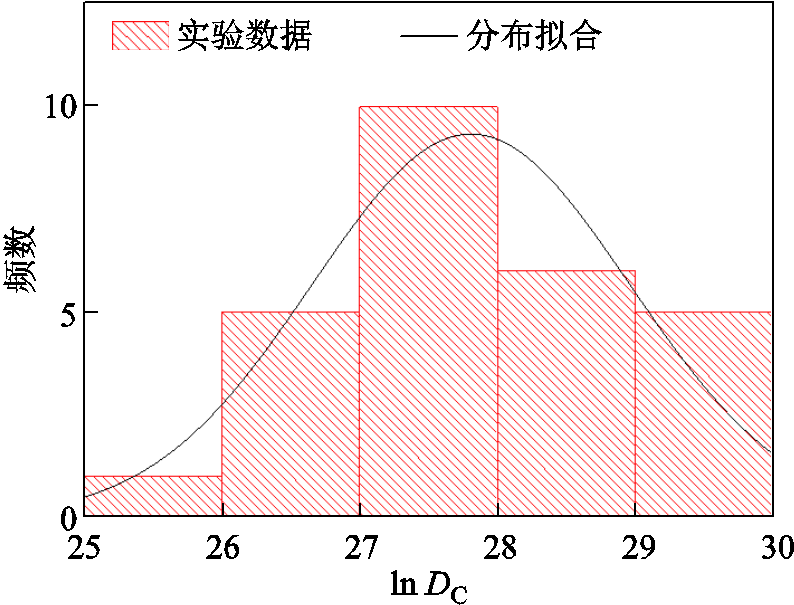
图13 针-板电极样品lnDC分布特性
Fig.13 Distribution characteristics of lnDC in needle-plate electrode samples
建立与图11相同的针-板电极几何模型，基于本文方法和实验获取的模型参数，开展电树枝模拟仿真计算。同时，采用图11所示针-板电极样品，开展电树枝模拟实验。仿真与实验中电压均设置为10 kV。仿真与实验获得的电树枝生长规律分别如图14和图15所示。
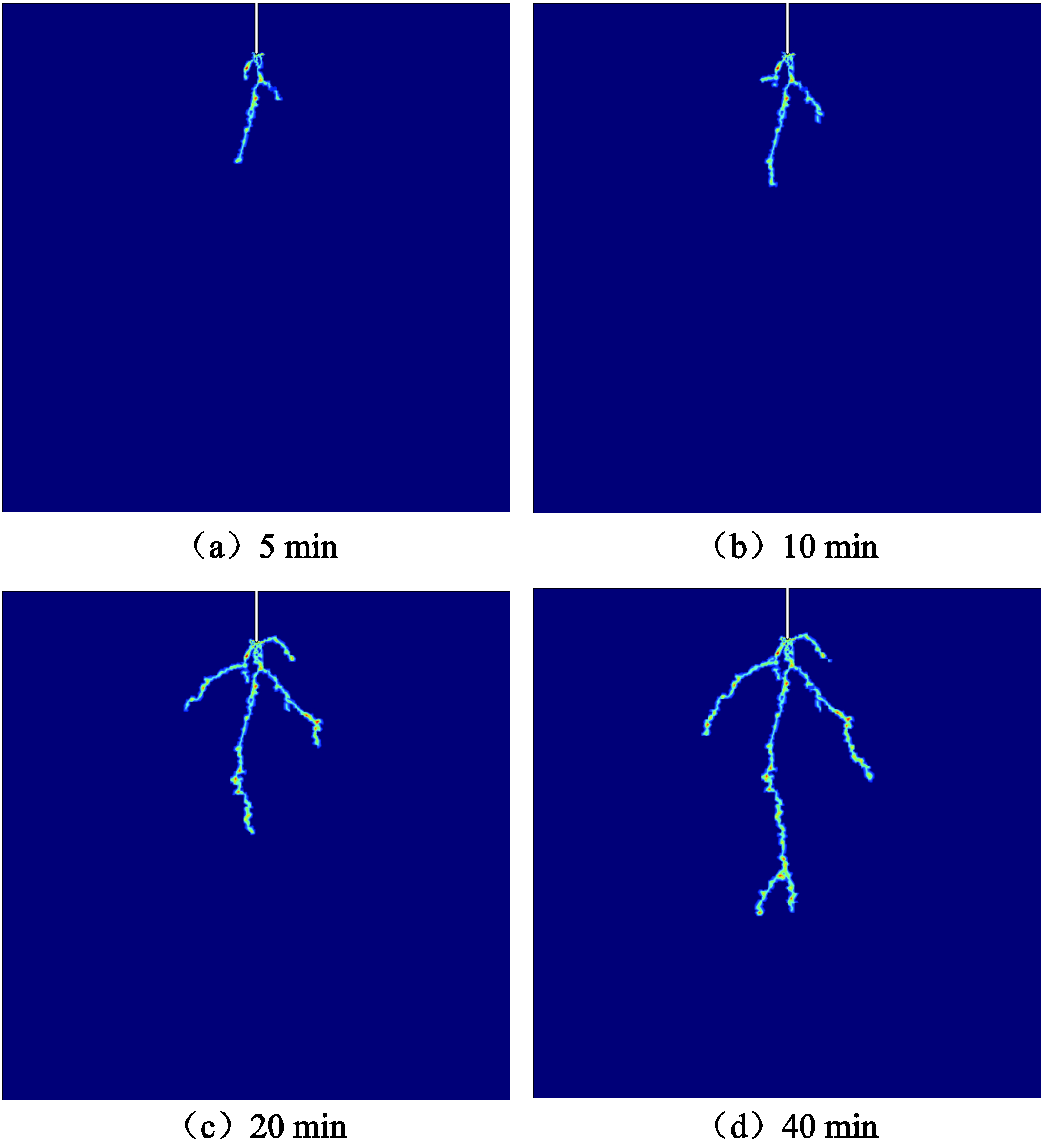
图14 针-板电极样品电树枝模拟规律
Fig.14 Simulation law of electrical tree of needle-plate electrode sample
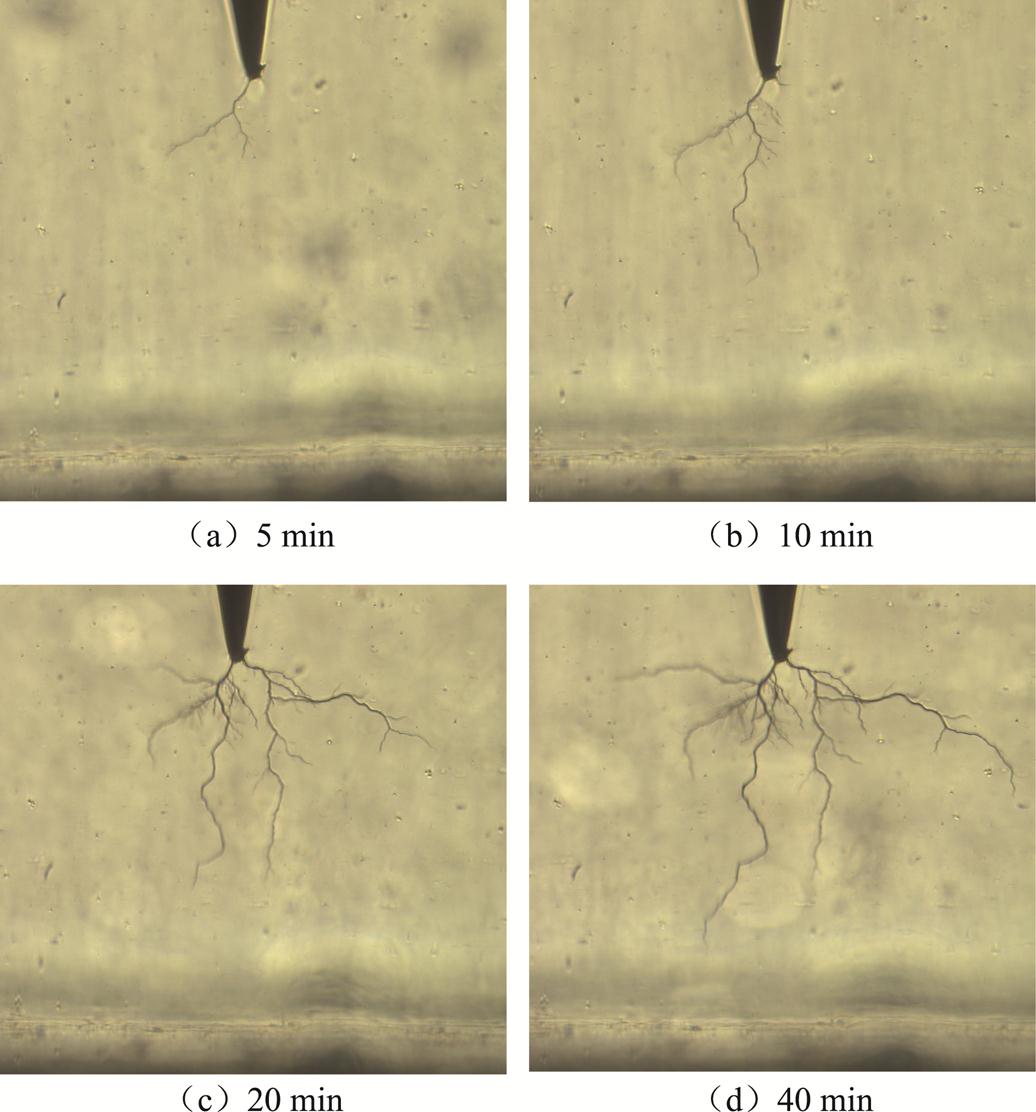
图15 针-板电极样品电树枝实验生长规律
Fig.15 Growth law of electrical tree experiment of needle-plate electrode sample
对比仿真与实验获得的电树枝整体形态可知，实验获得的电树枝枝干纤细且分叉较少，在40 min时共观察到5条树枝主干。仿真获得的电树枝通道同样枝干纤细，分叉较少，在40 min时共观察到4条树枝主干。可见，仿真与实验获得的电树枝整体形态相似，表明仿真能够通过实验参数对电树枝形态进行模拟。
实验过程中，电树枝生长存在平台期，即最先从针尖生长出来的电树枝发展到一定长度后存在停滞现象，随后从针尖或其他位置生长出新的电树枝。如图15中，在0～10 min时，1条电树枝沿着电场方向不断生长，但在10～20 min时，该电树枝并未发生明显生长，而是从针尖新长出更多的电树枝。仿真同样模拟出了这种平台现象，在0～10 min时生长的电树枝，在10～20 min出现停滞，转而其他电树枝开始生长。可见，仿真能够模拟电树枝的生长规律。
图16对比了本文提出的模型和其他典型电树枝仿真模型对于二维微米片复合材料中电树枝发展的仿真结果。由图16可知，三种模型均能够模拟微米片对电树枝的阻挡和诱导作用，但在电树枝生长方式和参数获取方面有一定的区别。
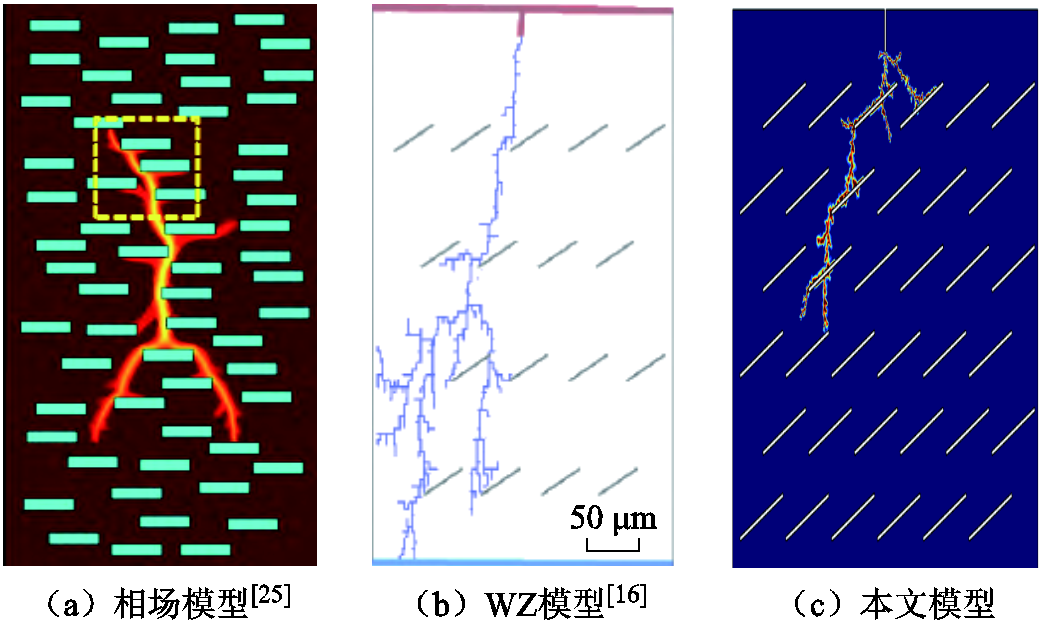
图16 本文提出模型与其他电树枝仿真模型效果对比
Fig.16 Comparison between the model proposed in this paper and other electrical tree simulation models
本文模型和相场模型为连续模型，电树枝在空间区域中连续渐变生长；而WZ模型为离散模型，其电树枝按预设的离散步长突变生长。实际电树枝的产生是一系列物理化学过程演变的结果，一般认为电树枝尖端电场强度高，易引起局部放电或电荷注入/抽出，从而引起此处聚合物分子链断链，自由基逐步累积，降低该区域的密度或引起炭化，进而产生树枝化通道。显然，本文模型和相场模型的渐变生长过程更符合电树枝生长的物理化学机制。
本文模型的关键参数，如电压耐受指数、累积损伤阈值等，都有成熟的实验获取方法，可基于材料参数正向地预测电树枝生长。而相场模型的关键参数，如临界能量密度、界面能和动力学系数等，尚无成熟的实验获取方法，目前仅能通过实际电树枝结果进行模型校核，逆向地进行模拟。因此，本文模型更适用于难以获得电树枝发展规律的情况，如材料透明度低、绝缘结构复杂等，可通过标准样品的材料级测试预测电树枝发展。而相场模型更适用于易获得电树枝发展规律的材料级模拟。
针对当前研究中聚合物绝缘电树枝数值模拟仿真中模型参数难以获得和校准的问题，本文提出了基于反幂定律的聚合物电树枝生长数模拟研究方法。该方法依据寿命数据建立的唯象模型，采用反幂定律描述电树枝的发展规律，建立了基于反幂定律的聚合物电树枝有限元仿真模型，分析了模型参数对聚合物电树枝生长模拟的影响，并开展了相关的实验。可以得出以下结论：
1）建立了一种简单、参数可实验获取的电树枝模拟方法，经过实验验证表明该方法能够实现基于材料参数的电树枝有效模拟。
2）在本文方法中，电树枝形态与电压耐受指数、累积损伤标准差相关，电树枝生长速率与电压耐受指数、累积损伤均值相关。
通过本文提出的方法，能够有效地模拟电树枝的生长，且模型参数能够通过实验获得。后续的研究将结合本文提出的方法聚焦于解释复合电介质和复杂绝缘结构下的电树枝生长机制及其对绝缘可靠性的影响规律。
参考文献
[1] 杜伯学, 张莹, 孔晓晓, 等. 环氧树脂绝缘电树枝劣化研究进展[J]. 电工技术学报, 2022, 37(5): 1128-1135, 1157.
Du Boxue, Zhang Ying, Kong Xiaoxiao, et al. Research progress on electrical tree in epoxy resin insulation[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1128-1135, 1157.
[2] 李进, 赵仁勇, 陈允, 等. 水分含量影响玻璃纤维增强环氧树脂电树枝生长特性研究[J]. 电工技术学报, 2023, 38(5): 1166-1176, 1189.
Li Jin, Zhao Renyong, Chen Yun, et al. Effects of moisture contents on electrical treeing process in glass fiber reinforced epoxy resin[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1166-1176, 1189.
[3] 张雯嘉, 王伟, 袁浩, 等. 接枝聚丙烯电缆绝缘材料的电树枝特性及机理[J]. 电工技术学报, 2024, 39(1): 88-98.
Zhang Wenjia, Wang Wei, Yuan Hao, et al. Electrical tree characteristics and mechanism of grafted polypropylene cable insulation[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 88-98.
[4] 陈向荣, 洪泽林, 朱光宇, 等. 高温下电压稳定剂对交联聚乙烯电树枝化及局部放电特性的影响[J]. 电工技术学报, 2023, 38(3): 577-586.
Chen Xiangrong, Hong Zelin, Zhu Guangyu, et al. Effect of voltage stabilizer on electrical treeing and partial discharge characteristics of crosslinked polyethylene at high temperature[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 577-586.
[5] 巫松桢, 谢大荣, 陈寿田, 等. 电气绝缘材料科学与工程[M]. 西安: 西安交通大学出版社, 1996.
[6] 李志坚, 张莹, 田猛, 等. 直流-温度复合场下环氧树脂内电树枝生长特性研究现状[J]. 绝缘材料, 2021, 54(3): 10-17.
Li Zhijian, Zhang Ying, Tian Meng, et al. Research status of electrical tree growth characteristics in epoxy resin under DC-temperature compound field[J]. Insulating Materials, 2021, 54(3): 10-17.
[7] Jiang Tie, Dai Chao, Hong Zelin, et al. DC electrical tree characteristics in epoxy resin at cryogenic temperature[C]//2020 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Beijing, China, 2020: 1-4.
[8] 杜伯学, 张苗苗, 姜恵兰, 等. 环氧树脂在低温环境下的电树枝生长特性[J]. 高电压技术, 2016, 42(2): 478-484.
Du Boxue, Zhang Miaomiao, Jiang Huilan, et al. Growth characteristics of electrical tree in epoxy resin under low temperature[J]. High Voltage Engineering, 2016, 42(2): 478-484.
[9] Du Boxue, Xue Jushao, Su Jingang, et al. Effects of ambient temperature on electrical tree in epoxy resin under repetitive pulse voltage[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(3): 1527-1536.
[10] Du Boxue, Zhang Miaomiao, Han Tao, et al. Effect of pulse frequency on tree characteristics in epoxy resin under low temperature[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016, 23(1): 104-112.
[11] Du Boxue, Xue Jushao, Zhang Miaomiao. Effect of pulse duration on electrical tree and breakdown process of epoxy resin in LN2[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(1): 359-366.
[12] 何东欣, 张涛, 陈晓光, 等. 脉冲电压下电力电子装备绝缘电荷特性研究综述[J]. 电工技术学报, 2021, 36(22): 4795-4808.
He Dongxin, Zhang Tao, Chen Xiaoguang, et al. Research overview on charge characteristics of power electronic equipment insulation under the pulse voltage [J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4795-4808.
[13] 黄路, 王鹏, 朱英伟, 等. 重复方波电压上升时间对交联聚乙烯电树特性影响研究[J]. 电工电能新技术, 2023, 42(5): 73-80.
Huang Lu, Wang Peng, Zhu Yingwei, et al. Impact of rise time of repetitive square wave voltage on electrical tree characteristics in XLPE[J]. Advanced Technology of Electrical Engineering and Energy, 2023, 42(5): 73-80.
[14] Niemeyer L, Pietronero L, Wiesmann H J. Fractal dimension of dielectric breakdown[J]. Physical Review Letters, 1984, 52(12): 1033-1036.
[15] Wiesmann H J, Zeller H R. A fractal model of dielectric breakdown and prebreakdown in solid dielectrics[J]. Journal of Applied Physics, 1986, 60(5): 1770-1773.
[16] 周远翔, 胡德雄, 张云霄, 等. 二维微米片复合材料取向调控电树枝生长特性的仿真研究[J]. 绝缘材料, 2022, 55(1): 24-31.
Zhou Yuanxiang, Hu Dexiong, Zhang Yunxiao, et al. Simulation study on growth characteristics of electrical tree in two-dimensional microsheet compositeby orientation regulating[J]. Insulating Materials, 2022, 55(1): 24-31.
[17] 薛福明. 基于WZ模型的电树枝生长仿真分析[D].哈尔滨: 哈尔滨理工大学, 2012.
Xue Fuming. Simulation analysis of electrical tree growth based on WZ model[D]. Harbin: Harbin University of Science and Technology, 2012.
[18] Wang Wei, Li Changyun, Dong Jiahua, et al. Numerical simulation of electric trees based on fractal theory[C]//2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 2021: 1-5.
[19] 谷琛, 严萍, 张适昌. 嵌入屏障的绝缘介质中电树生长模型[J]. 高电压技术, 2006, 32(7): 6-9.
Gu Chen, Yan Ping, Zhang Shichang. Electrical treeing model in dielectric with barriers[J]. High Voltage Engineering, 2006, 32(7): 6-9.
[20] Chen Longqing. Phase-field models for microstructure evolution[J]. Annual Review of Materials Research, 2002, 32: 113-140.
[21] Cahn J W, Hilliard J E. Free energy of a nonuniform system. I. interfacial free energy[J]. The Journal of Chemical Physics, 1958, 28(2): 258-267.
[22] Allen S M, Cahn J W. A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening[J]. Acta Metallurgica, 1979, 27(6): 1085-1095.
[23] Zhu Mingxiao, Li Jiacai, Song Henggao, et al. A phase field model for the propagation of electrical tree in nanocomposites[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2020, 27(2): 336-342.
[24] Zhao Liang. A mathematical model for conductive electrical tree growth in dielectrics: part I: theory[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2022, 29(4): 1353-1360.
[25] 张语桐, 吴泽华, 谢宗良, 等. 固体介质内绝缘损伤演化的相场模拟研究[J]. 中国电机工程学报, 2023, 43(17): 6885-6895.
Zhang Yutong, Wu Zehua, Xie Zongliang, et al. Phase field simulation for internal insulation damage evolution in solid dielectric[J]. Proceedings of the CSEE, 2023, 43(17): 6885-6895.
[26] 王雨帆. 温度梯度影响环氧树脂绝缘击穿特性及其相场模拟研究[D]. 天津: 天津大学, 2022.
Wang Yufan. Insulation breakdown characteristics of epoxy resin under temperature gradient and its phase field simulation[D]. Tianjin: Tianjin University, 2022.
[27] 边浩然. 考虑场强和空间电荷的XLPE电寿命指数模型研究[D]. 重庆: 重庆大学, 2021.
Bian Haoran. Electrical life exponent model considering electric field and space charge effect[D]. Chongqing: Chongqing University, 2021.
[28] Bian Haoran, Yang Lijun, Yao Renyun, et al. Method of selecting step stress test parameters for XLPE insulation DC voltage endurance coefficient[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2019, 26(3): 746-753.
Numerical Simulation of Polymer Electrical Tree Growth Based on Inverse Power Law
Abstract Polymer materials are widely used in power electronics and power transmission and distribution systems because of their excellent dielectric properties. However, under the long-term coupling effect of mechanical stress, thermal effect, electrical stress and other factors inside the insulation material, it is easy to cause the growth of electrical trees, which will cause internal damage and deterioration of the material, and eventually lead to the harm caused by penetrating discharge. The numerical simulation method can provide reference for improving the insulation reliability of the system. However, some key parameters of the existing model are difficult to obtain directly from the experiment, and can only be realized through the model verification to achieve the microscopic electrical tree simulation of specific materials, and can not achieve the engineering tasks from material parameter testing to complex structure electrical tree prediction. Therefore, this paper aims to propose a method of electrical tree limb simulation with simple model and parameters that can be obtained by experiment, so as to improve the engineering applicability of electrical tree limb simulation.
The inverse power law is a phenomenological model directly based on the lifetime data of solid dielectric, which describes the physical process of the accumulation of electrical damage in solid dielectric to the generation of penetrating tree channels, and has the theoretical basis for describing the growth of electric treees. Therefore, this paper analyzes the physical relationship between the parameters of the inverse power model and the growth law of electrical trees, establishes the basic equation of local electrical damage based on the inverse power model, and establishes the electric tree simulation method based on the inverse power model combined with the electric field calculation and the material dispersion equation. Further, a sample of pin-plate electrode is used to demonstrate how to simulate the electrical tree by testing the basic parameters of the material. The experimental verification of the simulated results of electric treees is carried out, and the simulated growth law of electric treees is compared with the experimental growth law of electric treees. Finally, the difference between the proposed method and the phase-field simulation and WZ model is compared.
The final results show that the method proposed in this paper can effectively simulate the electrical trees by using the experimental material parameters. The simulated electrical trees in this paper agree with the experimental results in terms of morphology and growth law. In this method, the shape of electrical trees is correlated with voltage tolerance index and cumulative damage standard deviation, and the growth rate of electrical trees is correlated with voltage tolerance index and cumulative damage mean. Compared with the phase-field simulation and WZ model, the proposed method can simulate the gradual growth of electrical trees, and the model parameters can be obtained experimentally.
Keywords：Polymer, electrical tree, inverse power law, insulation, numerical simulation
中图分类号：TM852
DOI: 10.19595/j.cnki.1000-6753.tces.L11021
收稿日期 2024-07-10
改稿日期 2024-09-10
边浩然 男，1994年生，助理研究员，研究方向为高电压器件与绝缘失效机理与寿命预测技术。
E-mail：bhriee@163.com
姚 成 男，1994年生，博士研究生，研究方向为复合材料电寿命预测、老化状态评估。
E-mail：327074925@qq.com（通信作者）
（编辑 李 冰）