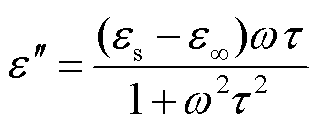 (1)
(1)
摘要 频域介电谱(FDS)技术因其检测精度高、携带绝缘信息丰富等优势,在油纸绝缘电力设备的状态评估中被广泛应用。然而,低温环境会导致FDS测试结果异于常值,严重影响检测的准确性。因此,该文搭建了低温介电响应实验平台,测量不同温度(-40~30℃)下油浸绝缘纸的介电响应。利用等温吸附实验发现,绝缘纸内部存在大量游离水和少量结合水,通过热刺激电流法与衍生对导数法研究了低温下弛豫过程的变化情况。进一步地,基于改进Havriliak-Negami模型对FDS结果进行解谱,探究低温对油浸绝缘纸内部极化与电导过程的作用机理,研究发现低温可能会导致浓差极化消失,界面极化和电导损耗减弱,偶极子极化增强。最后,提出针对低温环境的温度归一化方法,与传统“主曲线”法相比,所提方法可以有效地提高低温下FDS曲线温度归一化的精度,解决了传统校正方法测量精度差、频率数据点不足的问题。
关键词:油纸绝缘 频域介电谱 低温 Havriliak-Negami模型 温度归一化
近年来,我国能源体系发生深刻变革,以电能为载体的绿色能源高度依赖装备安全,如何提高电力设备可靠性、加强系统运维水平,是保障电力系统长期稳定运行、延长设备服役时间的关键[1-3]。频域介电谱(Frequency Domain Spectroscopy, FDS)作为一种无损诊断技术,因其对绝缘劣化检测具有较高的灵敏度,被广泛应用于油纸绝缘电力设备的状态诊断中[4]。然而,其测量结果受温度影响较大[5-7],例如在我国东北、西北地区,冬季气温经常低于-40℃,电力设备经受着严峻的极寒考验[8-10]。当电力设备停运检修时,环境温度会导致油纸绝缘设备内部水分结晶析出,变压器油局部凝固,FDS测量结果出现偏差,无法对电力设备状态进行准确评估。因此,探究低温下油纸绝缘的介电响应特性,提高低温环境下绝缘状态检测的准确性,对于理论研究和工程实践具有重大意义。
温度是影响FDS曲线的主要原因[11]。随着温度的降低,FDS曲线呈现向低频方向移动的趋势,目前对温度的校正一般采用“主曲线”法。然而,在低温环境下,该方法存在误差较大、频点不完整等问题。D. Linhjell等[12]利用“主曲线”法对频域介电谱曲线进行校正时发现,当温度低于0℃后,测量结果会出现明显的偏移,推测可能与低温下电流幅值较小、测量结果受噪声影响较大有关。J. Liu等[13]在对归一化关键参数“活化能”进行研究时发现,活化能同时受温度、水分和老化程度等多种因素影响,传统的单一活化能归一化结果会在高频段出现明显误差。R. Zafar等[14]对环氧树脂进行频域介电谱实验时发现,温度对FDS曲线的影响并不是整体性的,而是会显著地增强或减弱某一弛豫过程,从而导致FDS曲线局部发生移动。
传统“主曲线”法在常温(0~60℃)下具有较好的结果[15],但在极端环境中,特别是在低温下存在明显偏差。为解决这一问题,一些学者提出了不同的方法。S. Chowdhury等[16]基于Debye模型建立了含水量与活化能的关系,从而提高了传统方法的归一化精度。谢佳成等[17-18]通过解谱FDS曲线,获得了不同弛豫过程的势垒能级,并研究了不同温度、水分和老化程度下势垒能级的变化情况,提出了基于势垒能级的温度校正方法。高岩峰等[19]提出利用Kramers-Kronig变换对整个频域进行分段,以实现对介电响应的数值计算,进而计算不同温度的FDS曲线。然而,上述方法并没有提出针对极寒地区的频域介电谱温度归一化方法,缺少低温下介电响应特性的研究。
本文首先从电介质的微观机理出发,研究温度对弛豫过程与电导过程的影响,探究油纸绝缘内部水分存在形式和弛豫极化类型;然后对不同温度的FDS曲线进行解谱分析,研究不同温度(-40~30℃)下不同含水量油浸绝缘纸样品的介电响应特性;最后提出适用于低温环境的温度归一化模型,并与传统“主曲线”法进行对比,证明所提方法具有更高的精度,解决了传统方法误差较大、频点不完整的问题。
电介质极化主要分为瞬时极化和弛豫极化。其中,瞬时极化包括电子极化和原子/离子极化,极化过程时间短,不受温度影响;弛豫极化包括偶极子转向极化、空间电荷极化、界面极化等,极化时间较长,极化过程受温度影响较大。FDS测试频率为1 mHz~5 kHz,主要表征较低频率下的弛豫极化与电导过程。
在电介质内部存在一定固有偶极矩的极性分子,这些分子受到电场作用时会发生定向转动,产生感应电矩和剩余电矩,这种现象称为偶极子极化。根据分子运动势垒能级和克-莫方程可推导出偶极子极化的复介电常数以及介质损耗角正切值的表达式为[20]
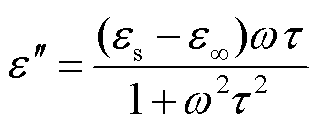 (1)
(1)
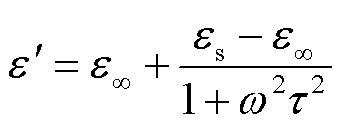 (2)
(2)
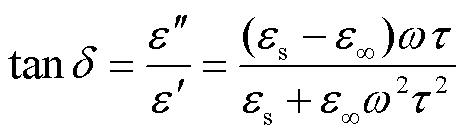 (3)
(3)
式中,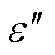 和
和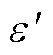 分别为复介电常数虚部和实部;ω为交变电场角频率;εs为静态介电常数,即在恒定电场下的介电常数;ε¥为光频介电常数,其数值只与材料种类有关,不受温度影响;τ为弛豫时间,其与温度的关系可表示为
分别为复介电常数虚部和实部;ω为交变电场角频率;εs为静态介电常数,即在恒定电场下的介电常数;ε¥为光频介电常数,其数值只与材料种类有关,不受温度影响;τ为弛豫时间,其与温度的关系可表示为
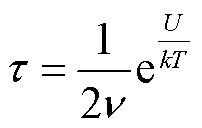 (4)
(4)
式中,n为分子平衡状态的热振动频率;U为分子势垒能级;k为玻耳兹曼常数;T为内部温度。
偶极子极化的介电常数与束缚能级分布有关,其表达式为[21]
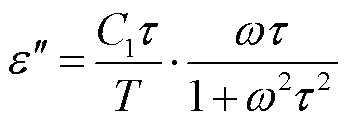 (5)
(5)
 (6)
(6)
式中,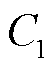 和
和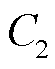 为与
为与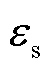 、
、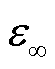 相关的常数。
相关的常数。
FDS曲线高频段主要表现为偶极子极化,这是由于界面极化的弛豫时间大于0.1 s,在高频段,随着频率的逐渐增加,当交流电场一个周期的时间超过界面极化所需的弛豫时间时,载流子无法完全跟随电场变化,极化损耗会减弱,而偶极子极化弛豫时间较短,开始占据主导地位,因此高频段主要表征偶极子极化。同时,温度通过改变束缚能级与弛豫时间来影响介电常数的数值。其中束缚能级的改变会使介电常数整体增加或减少,弛豫时间的改变会导致FDS曲线向高频或低频方向移动。因此在FDS曲线温度归一化中存在水平系数α和垂直系数β两种系数。其中,垂直系数主要表征油纸绝缘内部势垒能级的变化情况,表达式为
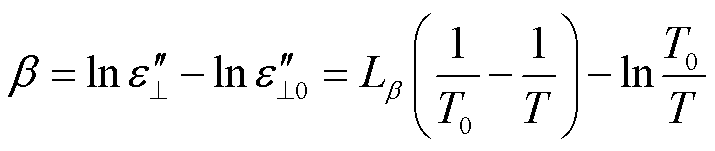 (7)
(7)
式中,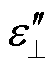 和
和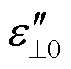 分别为垂直平移后和平移前的复介电常数虚部;
分别为垂直平移后和平移前的复介电常数虚部;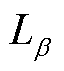 为垂直平移的相关参数;T0为目标温度。偶极子弛豫时间除了受温度影响较大以外,还与水分关系密切,而水平系数主要表征油纸绝缘偶极子极化的弛豫时间的变化,其弛豫时间受水分形态影响较大,因此水平系数需要通过实验计算得出。
为垂直平移的相关参数;T0为目标温度。偶极子弛豫时间除了受温度影响较大以外,还与水分关系密切,而水平系数主要表征油纸绝缘偶极子极化的弛豫时间的变化,其弛豫时间受水分形态影响较大,因此水平系数需要通过实验计算得出。
油纸绝缘内部除偶极子极化以外,还存在由自由电荷载流子(正、负离子等)与油纸内部大分子物质引起的浓差极化和界面极化,由于这两种极化的特性相似,因此可以一起讨论。这两种极化的弛豫时间通常较长,可以达到几秒甚至十几秒,出现在FDS曲线的中低频段(1 mHz~100 Hz)。同时,这两种极化的静态介电常数几乎不受温度影响,温度只会影响弛豫时间,导致FDS发生水平平移,其表达式为
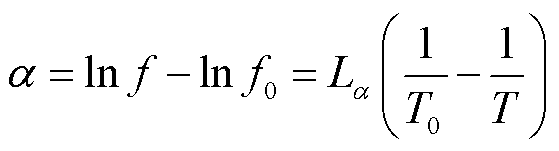 (8)
(8)
式中,f和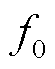 分别为水平平移前和平移后的频率;
分别为水平平移前和平移后的频率;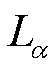 为水平平移的相关参数。
为水平平移的相关参数。
油纸绝缘内部不同于传统本征化合物或单一电介质,其电导过程是由固体绝缘纸的离子电导和液体变压器油的电泳电导共同组成的。
离子电导是绝缘油和纸中杂质离子定向运动导致的,在电场强度E作用下,绝缘纸中离子的平均运动速度可表示为
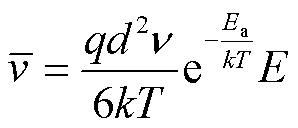 (9)
(9)
式中,q为离子所带电荷;d为离子平均跃迁距离;Ea为分子活化能。此时离子电导率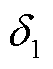 与温度T的关系可表示为
与温度T的关系可表示为
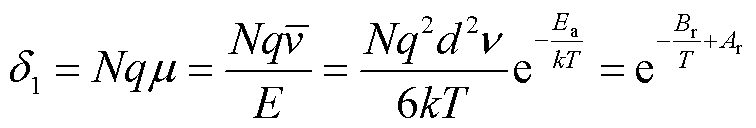 (10)
(10)
其中
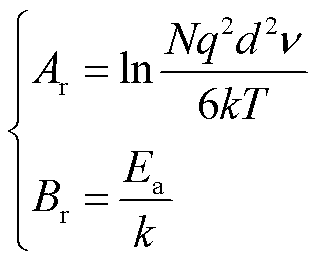 (11)
(11)
式中,N为电介质单位体积内的载流子数;μ为载流子迁移率。
除离子电导外,变压器油中还存在以胶体粒子、小水珠或小冰晶为载流子的电泳电导。电泳电导率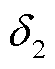 的表达式[22]为
的表达式[22]为
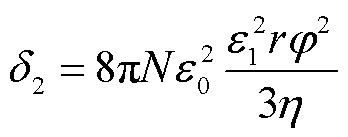 (12)
(12)
式中,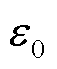 为真空介电常数;
为真空介电常数;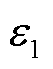 为粒子相对介电常数;r为粒子半径;φ为粒子电动电位;η为变压器油黏度。随着温度的降低,液体黏度逐渐增大,黏度η和温度T很好地服从关系[22]
为粒子相对介电常数;r为粒子半径;φ为粒子电动电位;η为变压器油黏度。随着温度的降低,液体黏度逐渐增大,黏度η和温度T很好地服从关系[22]
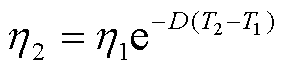 (13)
(13)
式中,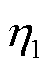 、
、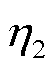 分别为温度T1、T2时的黏度;D为系数。
分别为温度T1、T2时的黏度;D为系数。
因此,根据式(10)与式(12),将两种电导过程相加,得到油纸绝缘的总电导率随温度的变化关系式为
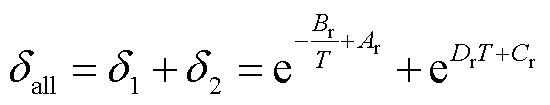 (14)
(14)
式中,Ar、Br、Cr、Dr为与电导分量相关的常数,与材料类型和介电常数有关。其中,含水量和水分形态的改变会显著影响胶体粒子半径r与相对介电常数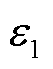 ,在进行温度校正前要基于电导率数值对Cr进行单独计算。
,在进行温度校正前要基于电导率数值对Cr进行单独计算。
为了研究低温环境下油纸绝缘的介电响应特性,在实验室中制备具有不同含水量的油浸绝缘纸样品。绝缘纸采用厚度为0.13 mm的魏德曼(Weidmann)变压器绝缘纸,并裁成50 mm´50 mm的正方形。变压器油选取45号克拉玛依矿物绝缘油。首先将绝缘纸分散直立地放置在真空烘箱中,在85℃/100 Pa下干燥72 h;同时,将变压器油在105℃/100 Pa下干燥48 h,得到干燥好的绝缘纸与变压器油。由于水分主要存在于绝缘纸中,因此将绝缘纸放置在空气中进行自然和人工受潮,并利用卡尔费休水分测定计(KFT831)对受潮后的绝缘纸进行水分标定,得到含水量mc为0.41%、1.10%、2.03%、2.84%、3.91%的绝缘纸,将绝缘纸样品浸入干燥变压器油中密封,静置48 h以排除气泡。油浸绝缘纸样品如图1所示。

图1 油浸绝缘纸样品
Fig.1 Oil paper insulation samples
本文实验所采用的温控系统为北京华测公司生产的Huace650T系列高低温冷热台,其温度范围为-160~600℃,精度控制在±0.25℃,温度变化速度可设定为0.01~10℃/min。频域介电谱测量采用Omicron公司生产的DIRANA介电响应测试仪,测试电压幅值为200 V,在1 mHz~5 kHz的频率内进行扫频测量。测量电极为三电极结构,避免表面电流对实验结果产生影响。实验接线示意图如图2所示。
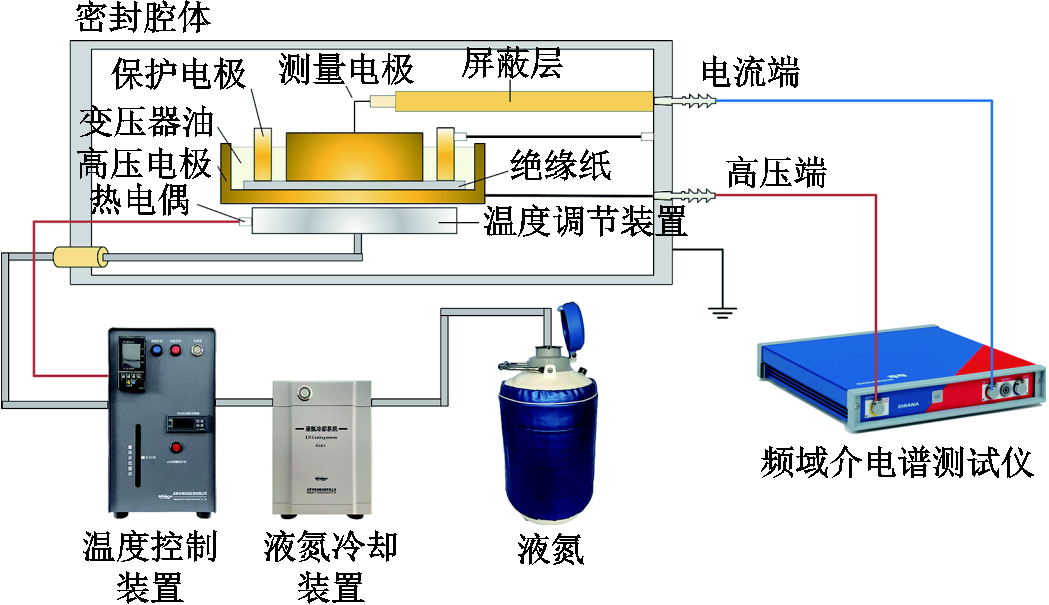
图2 实验接线示意图
Fig.2 Experimental schematic diagram
测试过程中,将油浸纸样品从容器中取出,并快速置于密封腔体中恒定温度1 h以上,以保证整个样品内外温度保持一致,并在测量过程中始终处于保温状态。
为研究不同含水量对油纸绝缘介电响应特性的影响,在所搭建的实验平台上测量不同含水量的油浸绝缘纸频域介电谱,其中不同温度的介电谱曲线如图3所示。
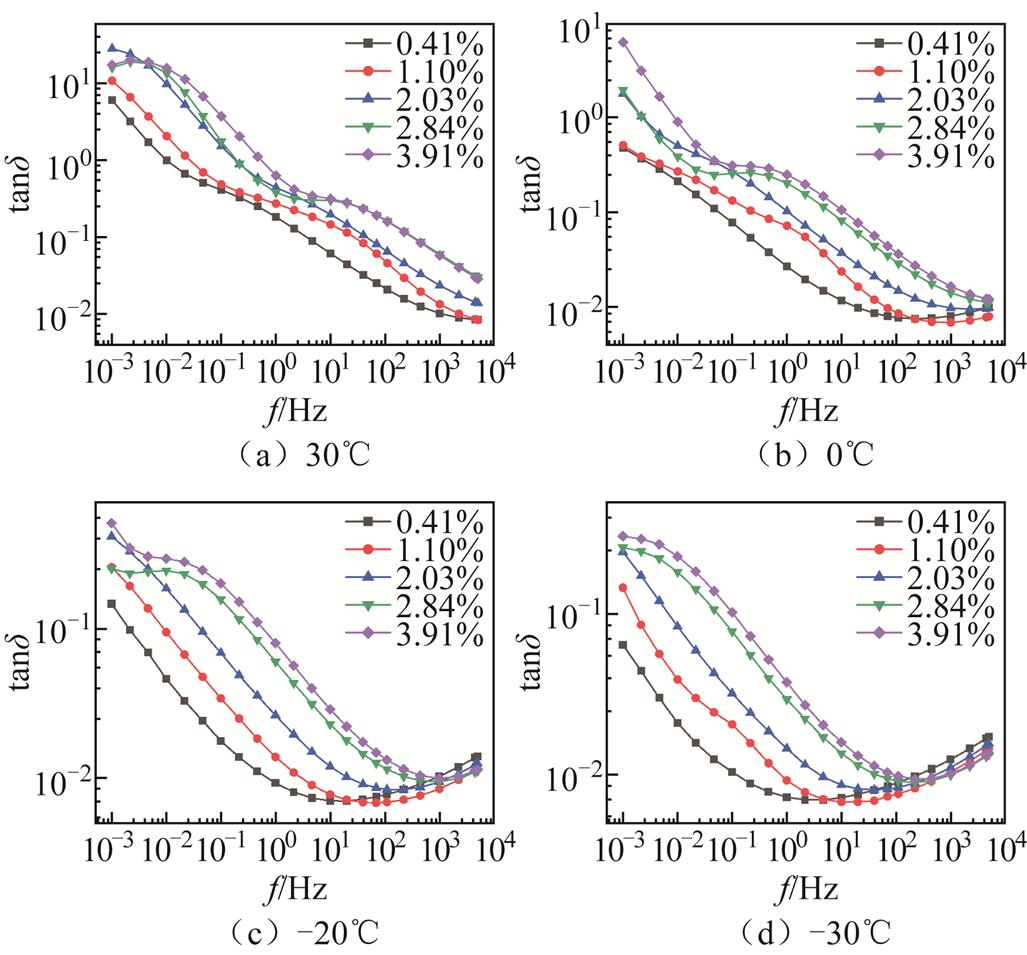
图3 不同含水量下的油浸绝缘纸样本FDS结果
Fig.3 FDS results of oil paper insulation samples with different moisture content
由图3可得,随着含水量的逐渐增加,tan δ不断增大,这是因为含水量的增加会导致油浸纸内部载流子数量增多,从而导致损耗增加。同时,当含水量较大时(mc>2%),会在低频段(1 mHz~0.1 Hz)和中频段(0.1~100 Hz)出现明显的极化峰,这可能是因为含水量的增加显著增强了某些极化过程。此外,温度的降低会导致FDS越来越趋于一致,特别是在高频段(100 Hz~5 kHz),含水量导致的介质损耗差异在低温环境下越来越小,这可能与水分形态变化有关,同时也是低温下传统温度归一化方法出现偏差的原因,“主曲线”法只是对曲线的简单平移,从而导致在高频段出现明显误差。
为研究不同温度下极化过程的变化情况,测量含水量为2%的样本在-40~30℃下的频域介电谱,其随温度的变化规律如图4所示。
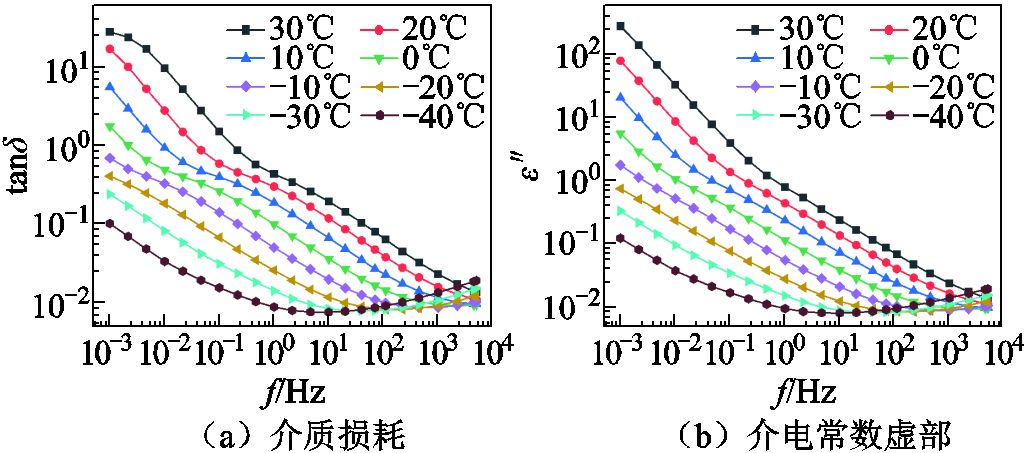
图4 不同温度下含水量2%油浸绝缘纸样本FDS结果
Fig.4 FDS results of oil paper insulation samples with 2% moisture content at different temperatures
由图4a可得,随着温度逐渐降低,曲线基本符合向低频方向移动的趋势,这与弛豫时间减小有关。在中低频段(1 mHz~100 Hz),介质损耗随着温度降低而不断减小,并在温度大于0℃时出现明显的拐点,而在温度小于0℃时弛豫峰消失,低频段逐渐呈一条直线,这可能是因为低温会导致某种极化过程不再显现。在高频段(100 Hz~5 kHz),随着温度降低,介质损耗和介电常数呈先减小后增大的趋势,介电常数虚部主要表征油浸绝缘纸内部的电导损耗和极化损耗,变化趋势与介质损耗变化趋势相同,温度降低使界面极化减弱,在一定程度上减小了损耗;但随着温度的进一步降低,偶极子极化逐渐占据主导地位,高频段极化过程得到加强,导致介质损耗增大。
在分析油纸绝缘内部极化过程前,需要对绝缘纸内部水分的存在形式进行研究,从而推断低温下水分与载流子浓度变化情况。基于标准GB/T 19560—2008《煤的高压等温吸附试验方法》[23],采用多站重量法真空蒸汽吸附仪在25℃下对绝缘纸进行等温吸附实验,通过测量不同水分活度下的含水量,来确定其内部水分存在的方式,其中水分活度aw表示饱和蒸气压与相同温度下纯水的饱和蒸气压的比值。绝缘纸吸附等温曲线如图5所示。
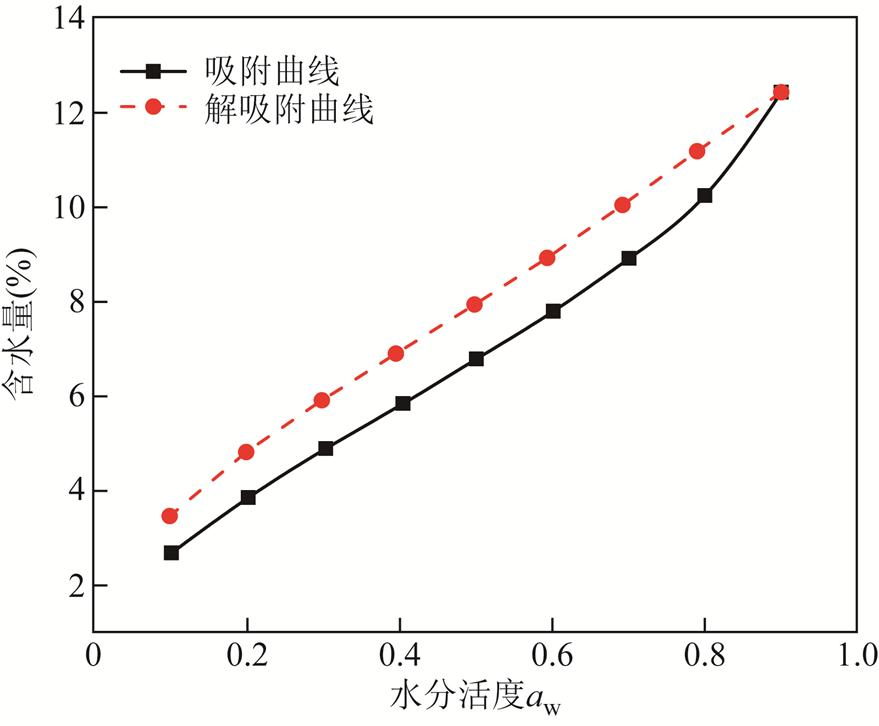
图5 绝缘纸吸附等温曲线
Fig.5 Sorption isotherms of insulating paper
利用GAB方程[24]计算绝缘纸内部水分与氢键的连接情况,从而得到绝缘纸内部水分存在形式。该模型关于平衡含水量h与水分活度aw关系的表达式为
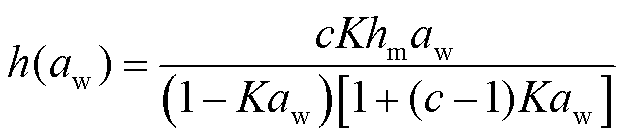 (15)
(15)
式中,hm为直接附着在吸附点的水分子质量分数;c为第一吸附层水分子与连续吸附层水分子之间的能量差相关系数;K为第二吸附层和后续吸附层中吸收的水分子与纯液态水之间的能量差相关系数。其中,各个参数的数值见表1。根据hm可计算吸附位点数量nm,表示为
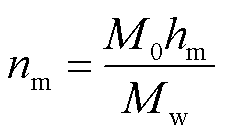 (16)
(16)
式中,M0和Mw分别为纤维素和水的相对分子质量。假设纤维素中1个水分子与2个羟基连接,则每个纤维素链段有3个水分子被吸附,然而计算得到的nm值远小于3,因此说明绝大多数水分以游离水的形态存在于绝缘纸中,而并未与绝缘纸形成羟基,这部分游离水受低温影响易结晶析出,从而对杂质离子的极化过程与频域介电谱的高频段产生影响。
表1 GAB方程的参数
Tab.1 Parameters of the GAB equation

参数数值参数数值 hm0.052 5K0.664 c11.534nm0.472
根据图4a可得,当温度大于0℃时,在低频段和中频段存在两个明显的弛豫过程,同时在高频段还有可能存在偶极子极化过程。因此,为确定油纸绝缘内部极化种类,揭示油纸绝缘频域介电谱曲线所包含的物理机理,通过测量油浸绝缘纸的热刺激电流(Thermally Stimulated Depolarization Current, TSDC)来分析其极化过程。
首先以5℃/min的升温速率将样品升至140℃,释放其中残余电荷;其次,在油纸样品上施加250 V的极化电压并保持60 min;然后,以30℃/min的冷却速率开始快速冷却,到-100℃后撤掉外加电压;最后,将样品以5℃/min的速率加热至160℃,记录该过程中的外电流。通过热刺激电流可计算得到油浸绝缘纸所包含的主要极化过程及相关弛豫参数。去极化过程中的热刺激电流可表示为
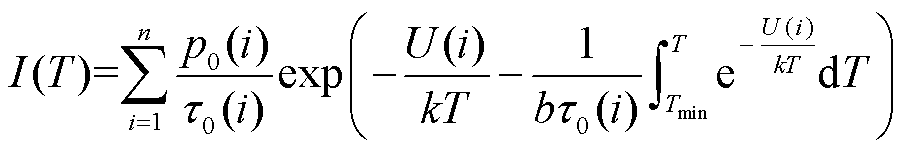 (17)
(17)
式中,p0为极化强度;τ0为极化弛豫时间;b为升温速度;Tmin为开始加热的最低温度;n为极化种类;i代表第i种极化类型。利用式(17)对TSDC进行解谱,结果如图6所示。可以看到曲线有三个明显的峰值,分别设为峰α、β、γ,代表三种极化过程。计算得到每种极化过程的势垒能级、极化强度与弛豫时间,结果见表2。
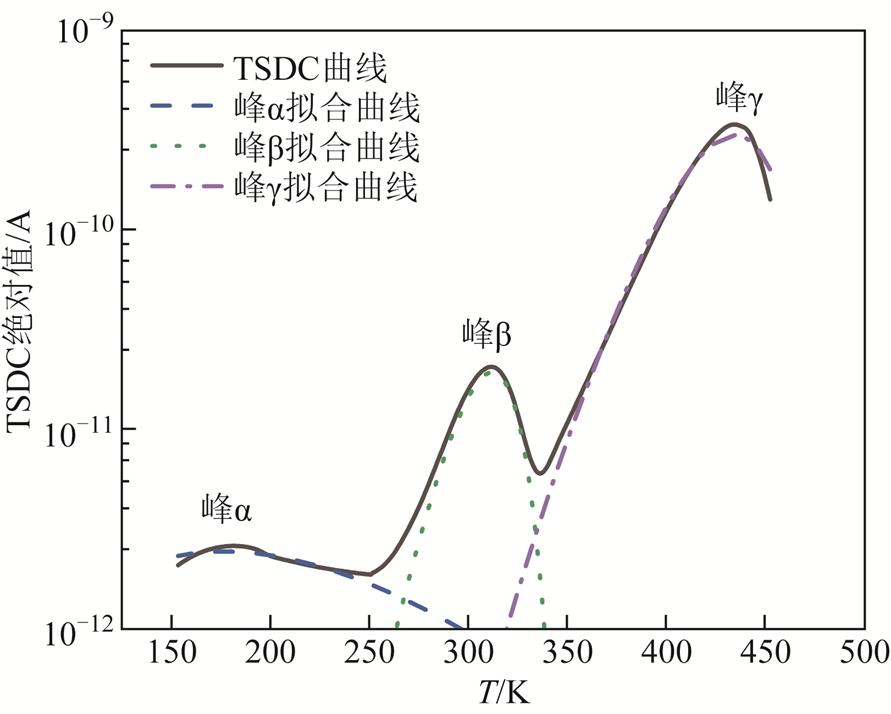
图6 油浸绝缘纸TSDC曲线解谱结果
Fig.6 Oil-paper insulation TSDC curve spectrum analysis results
表2 TSDC各极化过程参数
Tab.2 Parameters of various polarization processes in TSDC

类型势垒能级U/eV极化强度p0/(C/m2)弛豫时间t0/s 峰α0.0291.05´10-105.44 峰β0.5582.42´10-104.88´10-9 峰γ0.6845.79´10-99.09´10-8
其中,峰α势垒能级为0.029 eV,极化强度为1.05´10-10 C/m2,弛豫时间为5.44 s,表明油浸绝缘纸中存在势垒较小、弛豫时间较长的极化过程,应为绝缘油和绝缘纸中杂质离子所造成的浓差极化。对于峰β,因其弛豫时间较短,且势垒能级接近偶极子转向极化,表明峰β为油浸绝缘纸中的偶极子极化过程。峰γ的弛豫时间介于浓差极化与偶极子极化之间,应为大分子物质导致的界面极化。
为了更加清晰地观察温度对极化过程的影响,采用衍生对导数法对复介电常数实部曲线进行处理[25],所得到的求导结果如图7所示,即对e¢关于角频率的对数lnw求导,将复介电常数转换为介电松弛峰,表达式为
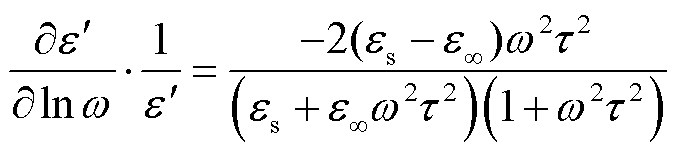 (18)
(18)
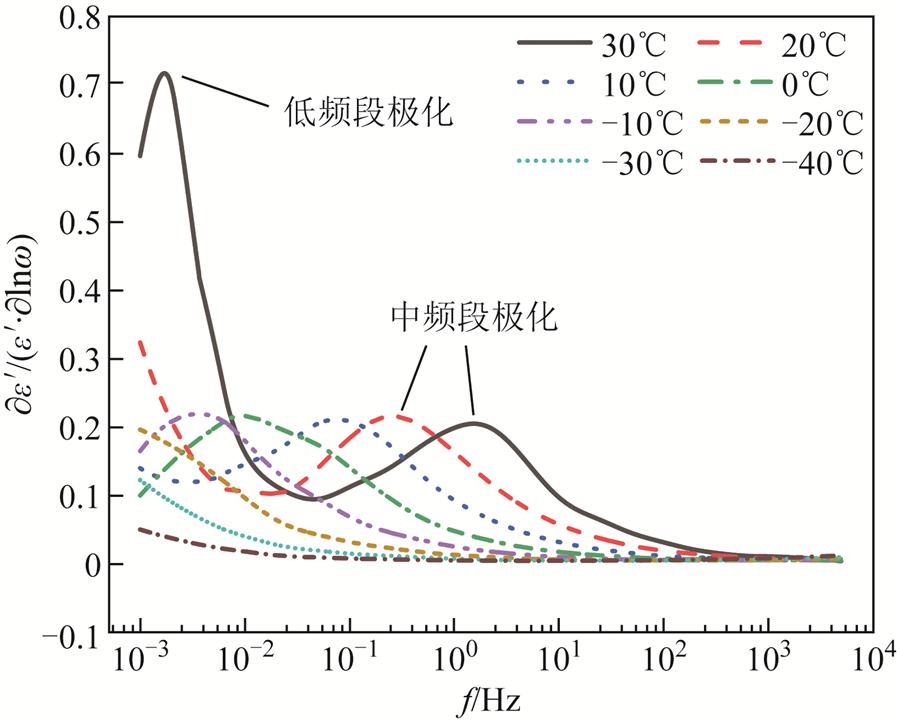
图7 不同温度下衍生对导数法结果
Fig.7 Results of the derivative logarithmic derivative method at different temperatures
随着温度逐渐降低,各弛豫峰向低频方向移动。同时浓差极化峰值随着温度减小逐渐降低,说明低温会改变油浸绝缘纸内部水分形态,进而降低载流子浓度,导致浓差极化强度降低。同时界面极化峰值几乎不变,说明温度只对界面极化的弛豫时间有影响。为进一步验证温度对极化过程的影响,采用改进Havriliak-Negami(H-N)模型对复介电常数进行解谱,研究不同温度下不同极化过程的变化情况。
为描述多种弛豫过程的变化情况,探究不同因素对弛豫过程的影响,通常采用Havriliak-Negami(H-N)模型对弛豫过程进行描述,其中经典H-N模型的表达式为[26]
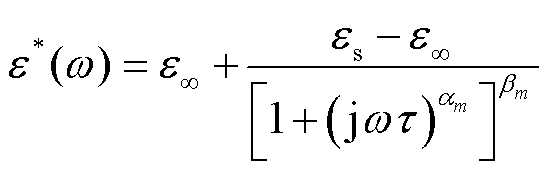 (19)
(19)
式中,αm、βm为H-N模型相关参数。然而一般的介电常数曲线包含多种极化过程,同时考虑到在低频段存在直流电导的影响,因此对经典的H-N模型进行修改,得到改进H-N模型,表达式为
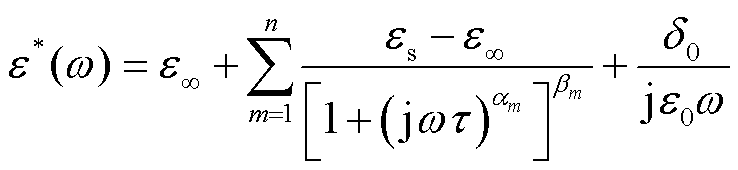 (20)
(20)
式中,δ0为电导率分量。通过TSDC分析可得,整个油纸绝缘极化过程主要包括浓差极化、界面极化与偶极子极化三种,因此设置n=3。根据式(20)可以推导出复介电常数实部和虚部表达式为
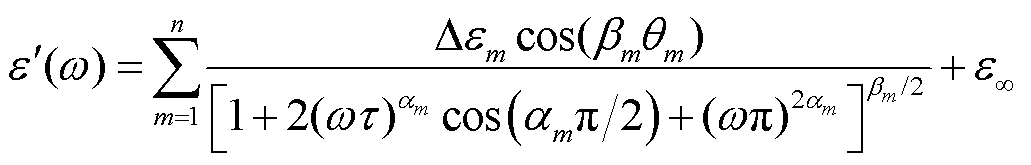 (21)
(21)
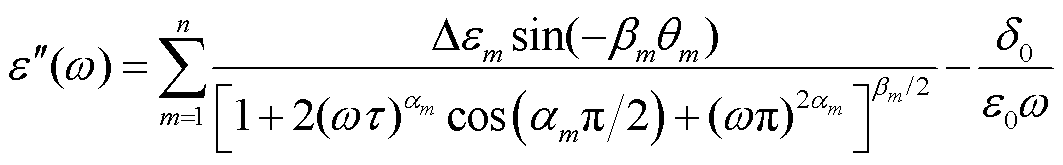 (22)
(22)
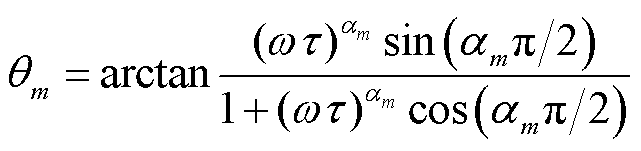 (23)
(23)
式中,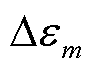 为第m类极化过程中关于
为第m类极化过程中关于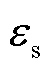 、
、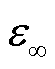 的常数。
的常数。
利用粒子群算法得到不同温度下改进H-N模型的解谱曲线,30℃和-30℃解谱曲线分别如图8、图9所示。当温度小于0℃时,低频段浓差极化过程消失。这可能是因为游离水凝固成小冰晶后,溶于水中的杂质离子消失,导致浓差极化不再显现。
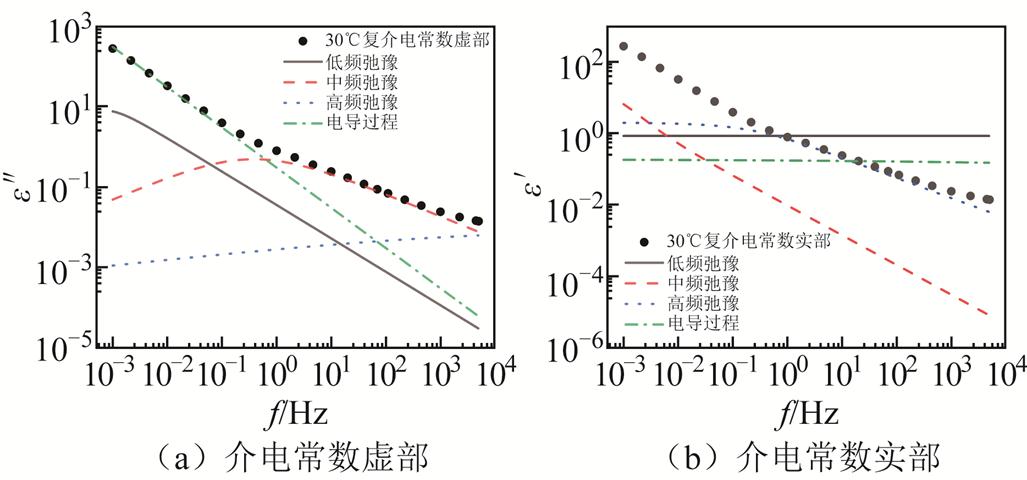
图8 30℃频域介电谱H-N模型解谱结果
Fig.8 Frequency domain dielectric spectrum H-N model analysis results at 30℃
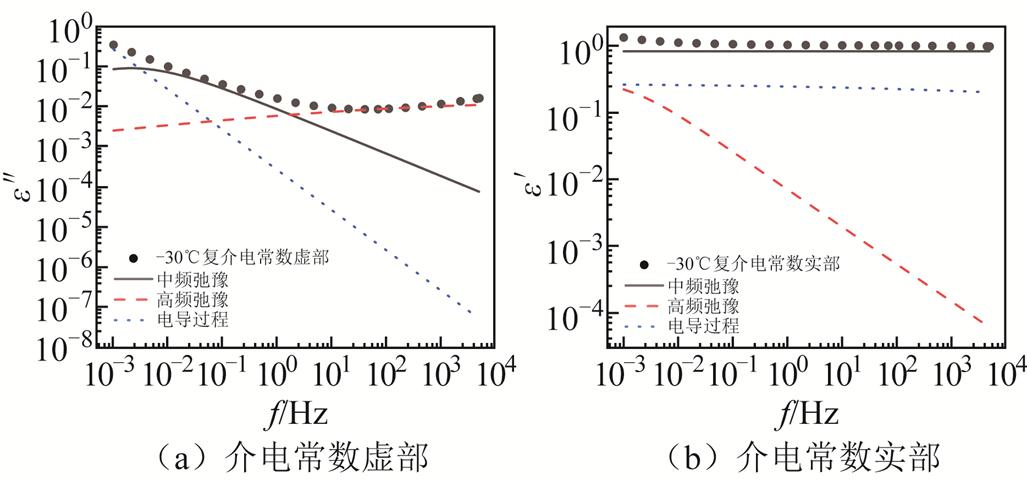
图9 -30℃频域介电谱H-N模型解谱结果
Fig.9 Frequency domain dielectric spectrum H-N model analysis results at -30℃
为研究不同极化和电导过程随温度的变化情况,揭示低温下油纸绝缘的介电响应特性,提取温度特征参量。将三种极化过程与电导过程分离,得到不同极化过程和电导过程随温度变化曲线,其中对介电常数虚部的解谱结果如图10所示。
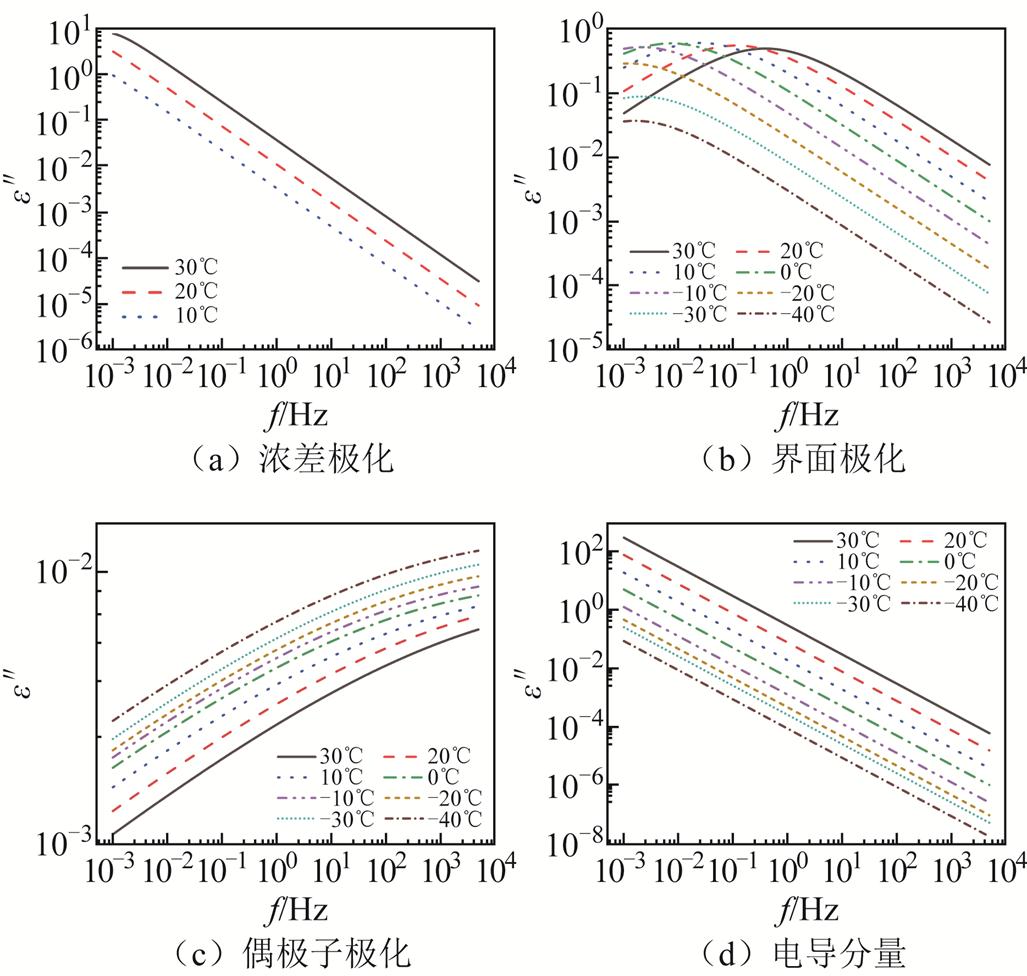
图10 不同温度下介电常数虚部解谱结果
Fig.10 Dielectric constant imaginary part spectrum results at different temperatures
图10a反映浓差极化过程,当温度大于0℃时,浓差极化强度随着温度降低而逐渐减小;当温度小于0℃时,浓差极化消失。由3.1节可知,油纸绝缘内部存在大量的游离水,这部分游离水散布在绝缘纸周围或吸附在纤维素上,而在油纸绝缘系统生产、加工与运行过程中,会引入小分子酸、弱电解质、无机盐等物质,这些物质会在游离水的作用下解离成离子,产生大量的H+、金属阳离子、OH-、CH3COO-等,解离的离子在电场作用下发生定向移动,并在电极附近积聚,形成浓差极化。温度降低使这些离子的迁移速率逐渐减小,离子解离与复合速度减慢,同时低温也会使水中溶解度降低,导致游离水中离子浓度减小,极化损耗减小;随着温度进一步降低,游离水析出凝结成小冰晶,离子不再发生解离反应,浓差极化消失。
图10b反映油纸界面极化过程,主要为油浸绝缘纸内部大分子物质定向排列引起。随着温度降低,界面极化曲线向低频方向移动,低温使分子迁移率降低,导致极化时间逐渐增大,极化曲线整体向低频方向水平移动,而温度并不会改变大分子数量,因此对极化强度没有影响。
图10c主要反映偶极子转向极化,一方面,低温减弱了分子热运动,降低了偶极子极化的难度,使偶极子转向更加充分;另一方面,低温下变压器油的黏度增大,进一步增大了偶极子极化损耗,因此偶极子极化随温度降低而逐渐增大。这也解释了FDS曲线在高频段(100 Hz~5 kHz)随温度的降低先减小后增大的原因。高频段受偶极子极化和界面极化的共同作用,当温度较高时,偶极子极化相对较弱,此时界面极化占据主导地位;随着温度的降低,界面极化损耗减弱,介质损耗减小;随着温度进一步降低,界面极化变得微弱,此时偶极子极化占据主导,温度使偶极子极化损耗增加,最终导致高频段FDS曲线先减小后增大。
图10d反映电导损耗,由式(14)可得,温度的降低使得油浸绝缘纸内部电导率逐渐降低并趋近于恒定,这是因为低温下离子迁移速率减小,通过的电流幅值减弱,最终导致电导损耗降低。
根据上文研究发现,传统的“主曲线”法只是对曲线进行简单平移,忽略了不同极化过程受温度和水分的影响差异,会在低温或含水量较大时出现明显误差。因此,基于改进H-N模型研究不同极化过程的介电常数随温度的变化规律,提取不同极化过程与电导过程的温度校正相关参量,计算不同极化过程的温度平移系数,通过归一化介电常数进而实现对FDS曲线的校正。
浓差极化时间较长,温度主要影响极化的弛豫时间,当温度大于0℃时,只需要关注其水平平移系数。根据水平平移系数计算式(8),得到相关参数为α=12 190。当温度小于0℃,浓差极化消失,不再考虑其温度影响。
温度对油纸界面极化的影响与浓差极化类似,温度的降低只会改变大分子间距,进而改变其弛豫时间,因此只存在水平平移系数。界面极化平移系数随温度的变化关系如图11所示。
偶极子转向极化主要作用于高频段,与油纸界面极化不同,低温除了降低弛豫时间外,还会导致势垒能级的变化,这将导致偶极子极化存在水平和垂直两种温度校正参数。其中,偶极子极化垂直平移系数和水平平移系数拟合结果如图12所示。由于低温会导致水分形态发生变化,使得各个分子之间的间距逐渐增大,势垒能级逐渐增大。同时弛豫时间的减小速率呈现先减小后增大的趋势,拐点出现在0℃附近,这可能是由于冰的弛豫时间远大于水,冰晶的形成减弱了温度对弛豫时间的影响,当温度小于0℃后,游离水几乎全部凝结成冰,此时弛豫时间只受温度影响。
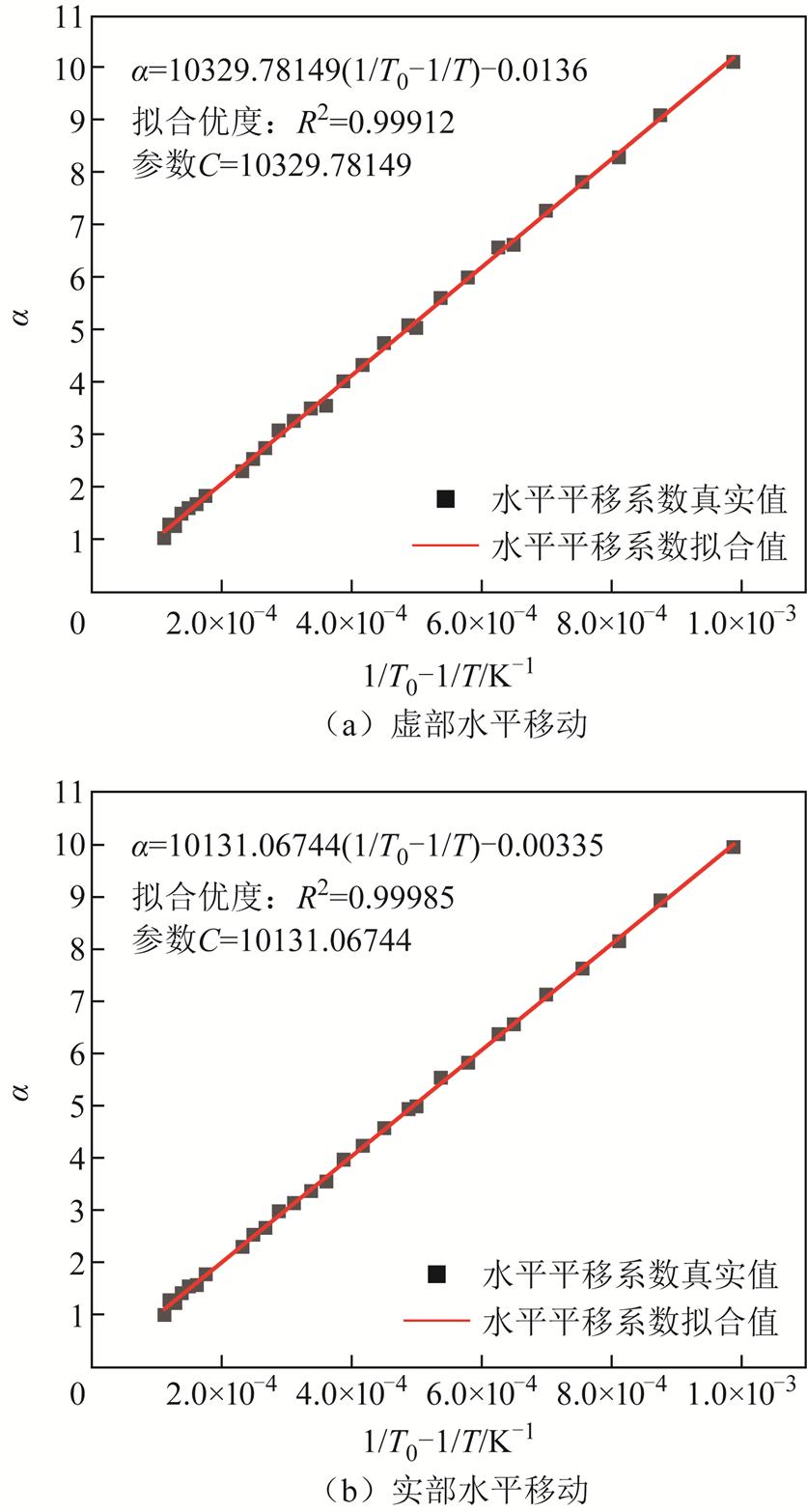
图11 界面极化平移系数
Fig.11 Shift coefficient of interfacial polarization
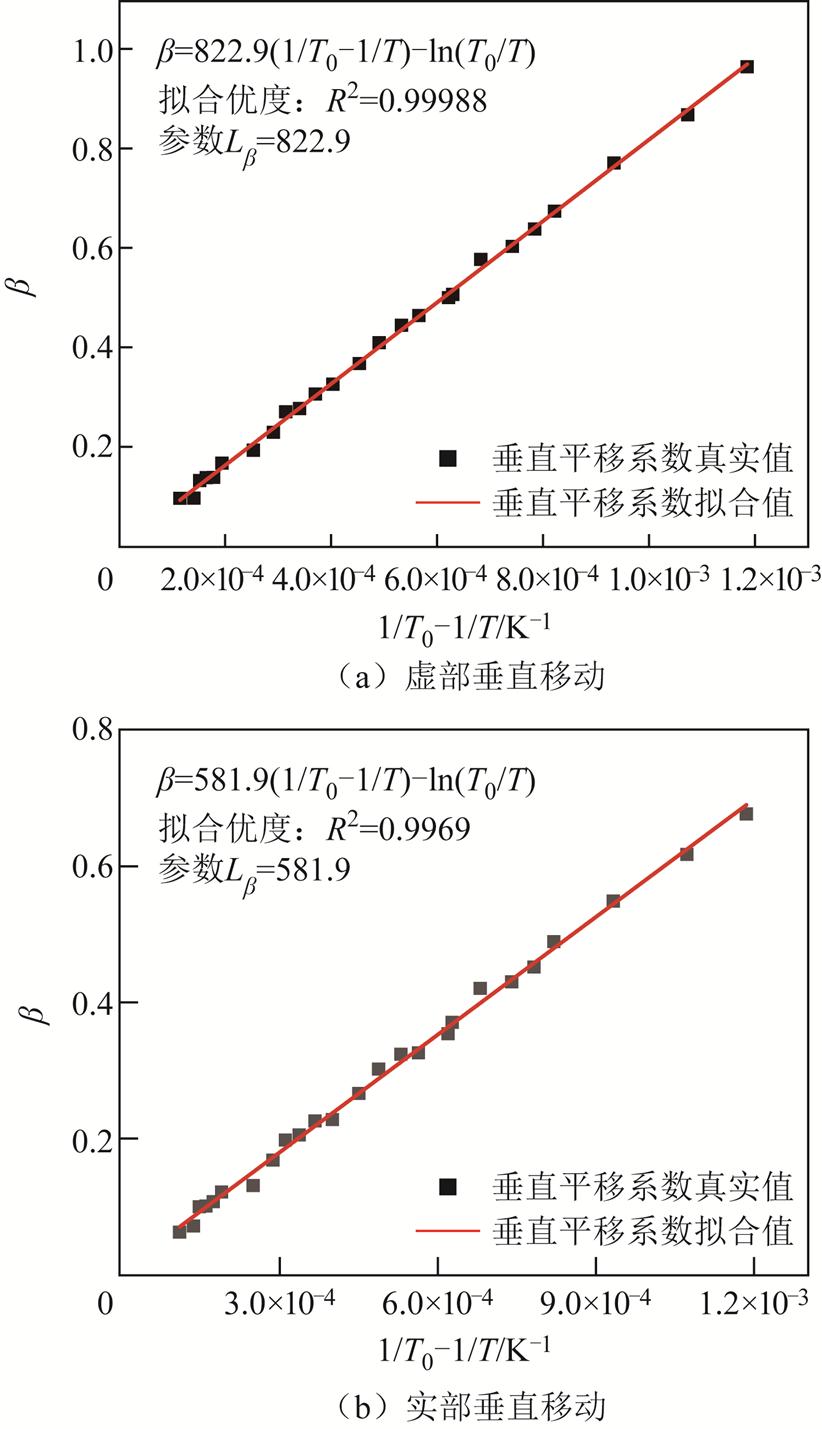
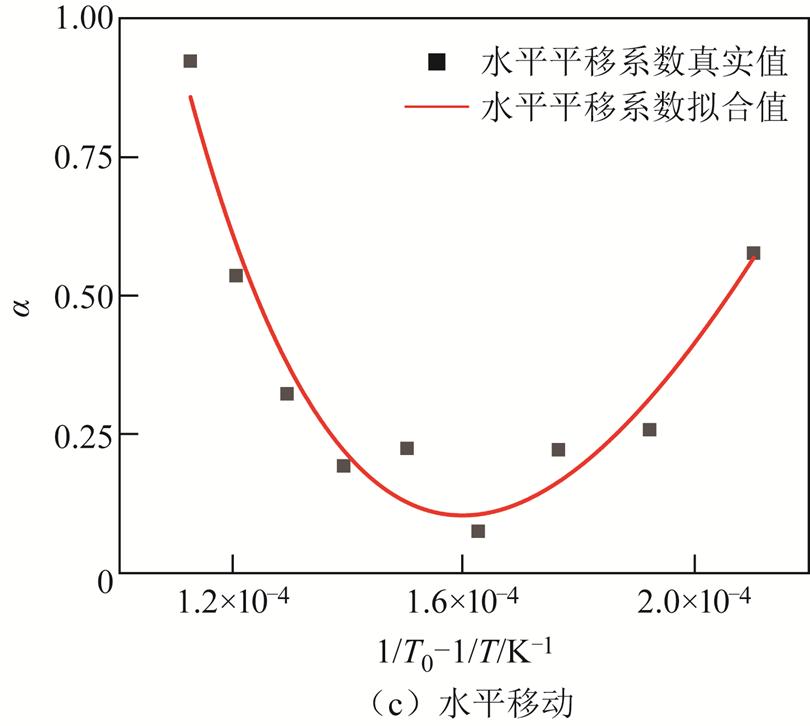
图12 偶极子极化平移系数
Fig.12 Shift coefficient of dipole polarization
电导分量随温度的变化规律与电导率变化规律相同,其中电导分量变化规律如图13所示。由式(14)推导可得,油浸绝缘纸的电导过程由离子电导和电泳电导共同作用。温度较高时,内部溶解离子较多,以离子电导为主,此时电导率变化过程呈一条直线;而随着温度降低,电泳电导占比增大,电泳电导几乎不受温度影响,电导分量逐渐趋于恒定值。
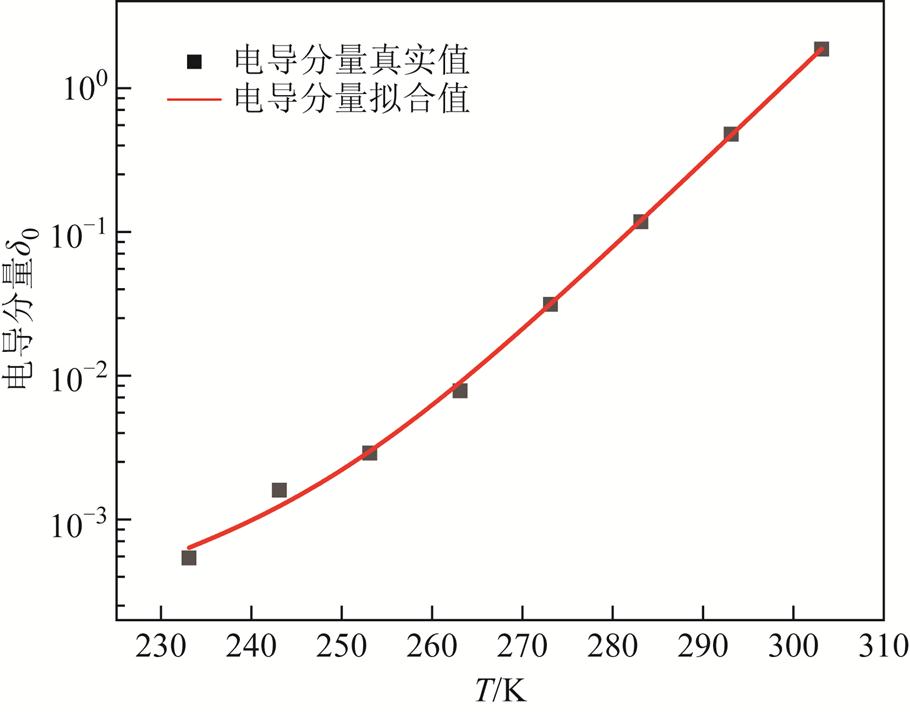
图13 电导分量随温度变化曲线
Fig.13 Conductivity-temperature change curve
综上所述,基于改进H-N模型的不同极化过程温度归一化参数见表3。表中,下标L、M、H分别表示低频、中频、高频极化。
根据所得到的参数,对不同含水量样品的介电常数实部和虚部进行解谱,得到不同极化和电导过程的解谱曲线,分别对其进行低温归一化处理,最终实现FDS曲线归一化。
表3 温度归一化参数
Tab.3 Parameters of temperature normalization
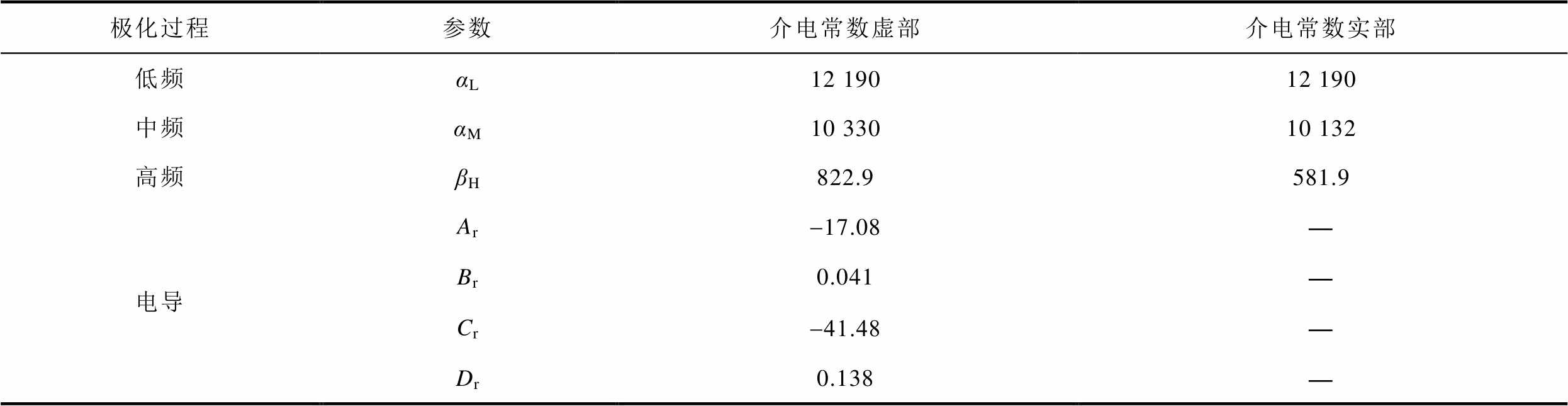
极化过程参数介电常数虚部介电常数实部 低频αL12 19012 190 中频αM10 33010 132 高频βH822.9581.9 电导Ar-17.08— Br0.041— Cr-41.48— Dr0.138—
根据第1节理论推导,极化过程和电导过程并不完全遵从传统Arrhenius模型,而传统“主曲线”法依据Arrhenius模型对不同温度下的tanδ-f曲线进行归一化则不再在低温环境下适用,其中,“主曲线”法公式可表示为
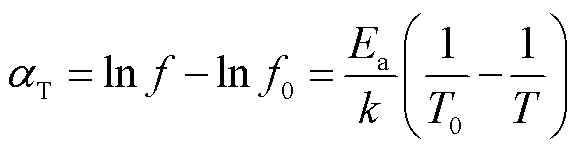 (24)
(24)
式中,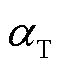 为“主曲线”法温度平移系数;现有研究一般取活化能Ea=0.909 eV[27]。
为“主曲线”法温度平移系数;现有研究一般取活化能Ea=0.909 eV[27]。
结合改进H-N模型低温介电响应特性研究,对每种极化过程进行单独校正。一方面避免了传统方法忽略多种极化的问题,另一方面每种极化过程都对应不同的势垒能级与校正系数,可同时考虑每种极化在低温环境中所表现的特性,使归一化精度得到进一步提升。低温下FDS曲线温度归一化流程如图14所示。
通过将FDS曲线进行解谱,得到不同极化和电导过程的解谱曲线。根据3.4节研究发现,0℃以下会导致油浸绝缘纸内部水分析出结晶,低频段浓差极化消失。因此当目标温度和初始温度差距较大时,需去除浓差极化的影响,最终将所得到的归一化结果代入数据库进行受潮与老化评估。
为验证该方法的准确性,分别对含水量为1.10%、2.84%、3.91%的样品进行温度归一化,探究低温与高水分环境下该方法的精度,得到的归一化结果如图15、图16所示。
通过图15的直观对比可以看到,当目标温度大于0℃时,两种方法均可得到较为理想的结果。如图15a所示,采用所提极化分离的温度校正方法从20℃向10℃进行归一化时,拟合优度为R2=0.987 6。但当目标温度小于0℃时,“主曲线”法出现明显的偏差,特别是在低频段较为明显,其原因是游离的水分子结晶析出,使低频段浓差极化消失,进而导致归一化结果出现较大误差。而所提方法消除了低频极化的干扰,从而得到更为准确的校正曲线,拟合优度为0.975 7,依然保持在较高水平,而“主曲线法”的拟合优度下降到0.952 6,证明本文方法相较于传统方法在低温环境中更有优势。同时传统方法在高频段会丢失5~7个频率数据点,而极化分离法可以实现全频段校正。
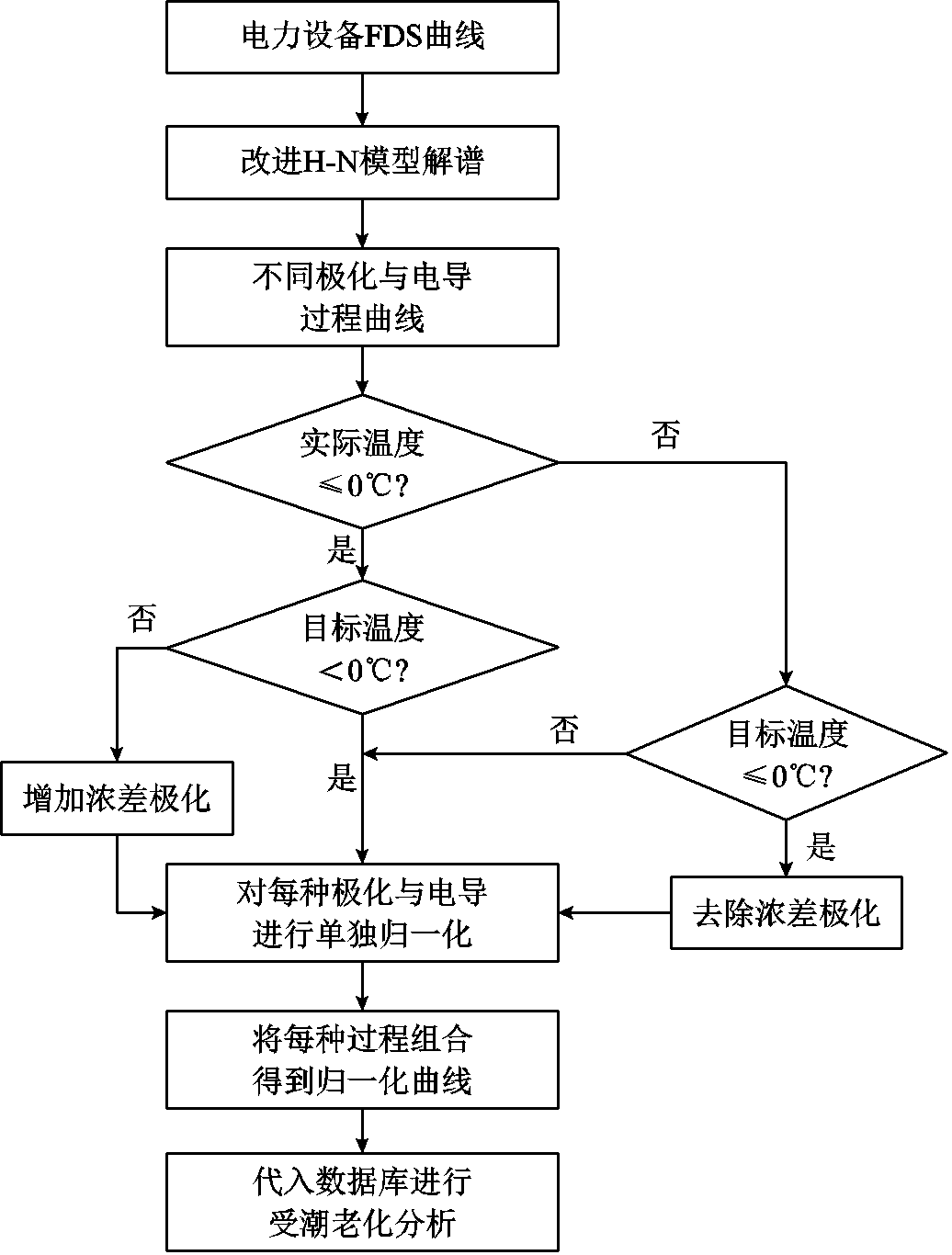
图14 低温下FDS曲线温度归一化流程
Fig.14 Temperature normalization flow chart of FDS curves at low temperature
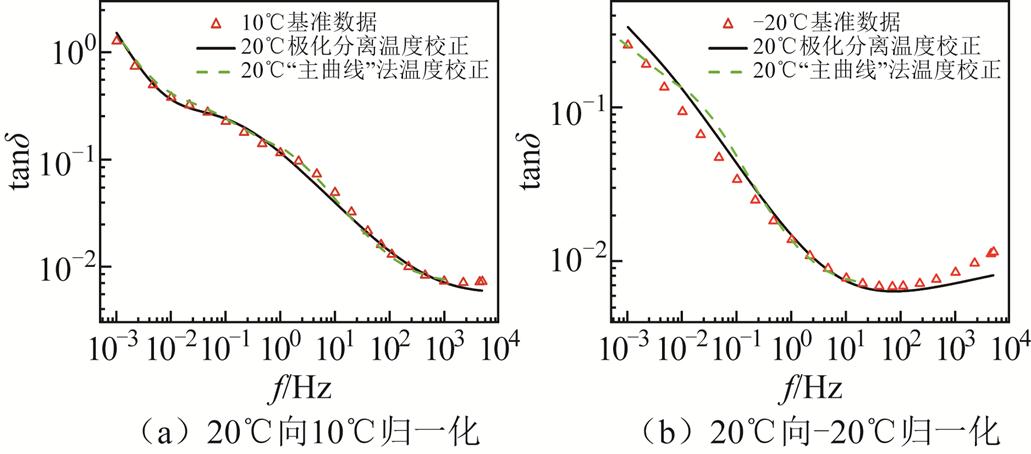
图15 含水量1.10%的样品温度归一化结果
Fig.15 Temperature normalization resultsof samples with 1.10% moisture content
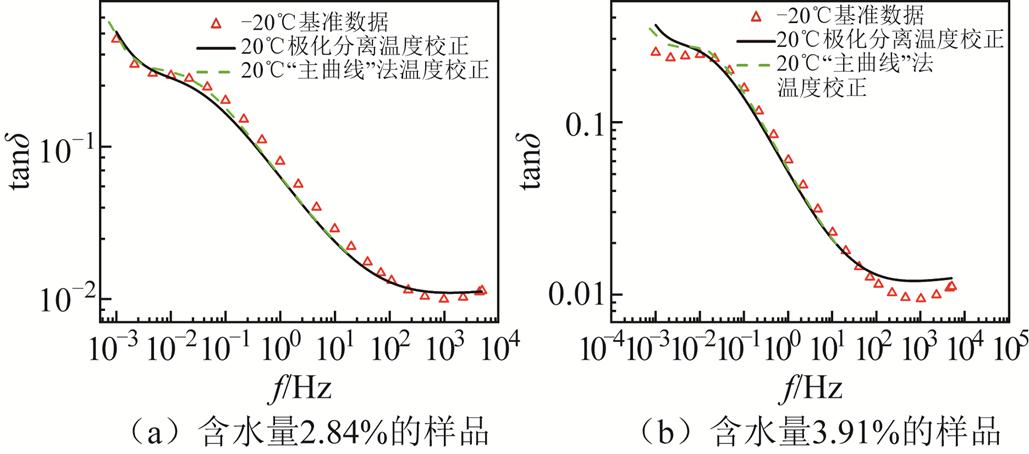
图16 高水分样品温度归一化结果
Fig.16 Temperature normalization resultsof samples with high moisture content
在高含水量下这种差异会更加明显,如图16所示,高含水量下由于其浓差极化与偶极子极化强度增强,使用传统方法进行归一化时会在高频段与低频段同时产生较大的误差,而利用所提方法可以使2.84%含水量的样品温度归一化精度提高到0.982 2,优于传统方法。
本文对不同含水量的油浸绝缘纸样本进行了不同温度下的FDS测试,研究了低温下油浸绝缘纸的介电响应特性,提出了温度校正新方法,所得结论如下:
1)定性研究极化和电导演变规律发现,油浸绝缘纸频域介电谱主要表征浓差极化、油纸界面极化、高频偶极子极化、离子电导和电泳电导过程。由于低温会使游离水析出结晶,导致与水中离子相关的浓差极化过程逐渐消失,同时界面极化与电导过程减弱,偶极子极化增强。
2)利用改进H-N模型提取的温度校正相关参数,提出分离极化和电导的温度校正新方法。相较于“主曲线”法,所提方法在低温和高含水量情况中具有明显的优势。在低温下拟合优度从0.952 6提升到0.975 7,同时在高频段补全了5~7个频率数据点。所提方法解决了“主曲线”法低温校正误差较大、频段数据点不足的问题。
参考文献
[1] Tabor D P, Roch L M, Saikin S K, et al. Accelerating the discovery of materials for clean energy in the era of smart automation[J]. Nature Reviews Materials, 2018, 3: 5-20.
[2] Momete D C. Analysis of the potential of clean energy deployment in the European union[J]. IEEE Access, 2018, 6: 54811-54822.
[3] 陈冲, 贾利民, 赵天宇, 等. 去碳化导向的轨道交通与新能源融合发展: 形态模式、解决方案和使/赋能技术[J]. 电工技术学报, 2023, 38(12): 3321-3337.
Chen Chong, Jia Limin, Zhao Tianyu, et al. Decarbonization-oriented rail transportation and renewable energy integration development—configur-ations, solutions, and enabling/empowering technologies [J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3321-3337.
[4] 张璐, 李洋, 穆海宝, 等. 冲击电压激励下变压器套管介电响应快速测量方法[J]. 高压电器, 2023, 59(6): 147-153.
Zhang Lu, Li Yang, Mu Haibao, et al. Fast measurement method of dielectric response of transformer bushing under impulse voltage excitation [J]. High Voltage Apparatus, 2023, 59(6): 147-153.
[5] Liu Jiefeng, Wang Qingyin, Fan Xianhao, et al. Effects of temperature gradient induced aging and moisture distribution on dielectric response measurement for transformer insulation[J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 1-10.
[6] 陈晓琳, 符小桃, 吴乾东, 等. 基于频域介电谱的油纸绝缘套管局部受潮诊断研究[J]. 电力工程技术, 2022, 41(2): 149-155.
Chen Xiaolin, Fu Xiaotao, Wu Qiandong, et al. Partial damp diagnostic method of oil-paper insulating bushing based on frequency domain spectroscopy[J]. Electric Power Engineering Technology, 2022, 41(2): 149-155.
[7] 邹阳, 林锦煌, 何津, 等. 基于频谱解构法的油纸绝缘扩展德拜模型参数辨识[J]. 电工技术学报, 2023, 38(3): 622-632.
Zou Yang, Lin Jinhuang, He Jin, et al. Parameter identification of oil paper insulation extended Debye model based on spectrum deconstruction method[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 622-632.
[8] 罗子秋, 肖黎, 聂伟峰, 等. 极寒条件下纳米SiO2改性变压器油的导热和绝缘特性[J]. 高电压技术, 2022, 48(9): 3542-3550.
Luo Ziqiu, Xiao Li, Nie Weifeng, et al. Thermal conductivity and insulation of nano-SiO2 modified transformer oil under extremely low temperatures[J]. High Voltage Engineering, 2022, 48(9): 3542-3550.
[9] 池明赫, 陈庆国, 王新宇, 等. 温度对复合电压下油纸绝缘电场分布的影响[J]. 中国电机工程学报, 2015, 35(6): 1524-1532.
Chi Minghe, Chen Qingguo, Wang Xinyu, et al. Influence of temperature on electric field distribution of oil-paper insulation under compound voltage[J]. Proceedings of the CSEE, 2015, 35(6): 1524-1532.
[10] 马御棠, 束洪春, 钱国超, 等. 基于频域介电谱曲线分解的氧化锌避雷器老化状态评估[J]. 电工技术学报, 2024, 39(3): 901-913.
Ma Yutang, Shu Hongchun, Qian Guochao, et al. Method for evaluating the aging state of ZnO arrester based on curve decomposition of frequency domain dielectric spectrum[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 901-913.
[11] 张大宁, 白帆, 牛朝滨, 等. 不同受潮类型下油纸绝缘套管的频域介电谱特性[J]. 中国电机工程学报, 2018, 38(16): 4942-4950, 4998.
Zhang Daning, Bai Fan, Niu Chaobin, et al. Frequency domain spectroscopy characteristics of oil-paper insulated bushings under different damp types[J]. Proceedings of the CSEE, 2018, 38(16): 4942-4950, 4998.
[12] Linhjell D, Lundgaard L, Gafvert U. Dielectric response of mineral oil impregnated cellulose and the impact of aging[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2007, 14(1): 156-169.
[13] Liu J, Fan X, Zheng H, et al. Aging condition assessment of transformer oil-immersed cellulosic insulation based upon the average activation energy method[J]. Cellulose, 2019, 26(6): 3891-3908.
[14] Zafar R, Gupta N. Dielectric spectroscopy of epoxy-based barium titanate nanocomposites: effect of temperature and humidity[J]. IET Nanodielectrics, 2020, 3(1): 20-27.
[15] 王镜然, 王英杰, 庄宏伟, 等. 低压电缆绝缘热氧老化过程中介电响应的Davidson-Cole分析[J]. 电工技术学报, 2023, 38(15): 4030-4039.
Wang Jingran, Wang Yingjie, Zhuang Hongwei, et al. Dielectric response during thermal-oxidative aging of low-voltage cable insulation analyzed by Davidson-Cole[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4030-4039.
[16] Chowdhury S, Haque N, Chatterjee S, et al. Temperature compensation of frequency domain spectroscopy measurement for condition assessment of oil-paper insulation[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2022, 29(1): 255-263.
[17] 谢佳成, 董明, 于泊宁, 等. 宽频带油纸绝缘介电响应的全过程谱图提取和定量分析[J]. 中国电机工程学报, 2021, 41(5): 1547-1557.
Xie Jiacheng, Dong Ming, Yu Boning, et al. Spectra extraction and quantitative analysis for all independent dielectric processes of oil-paper insulation in broad frequency band[J]. Proceedings of the CSEE, 2021, 41(5): 1547-1557.
[18] 谢佳成, 夏昌杰, 董明, 等. 频域介电谱温度归一化微观机理及优化策略研究[J]. 高电压技术, 2021, 47(7): 2416-2424.
Xie Jiacheng, Xia Changjie, Dong Ming, et al. Microscopic mechanism and optimized strategy for temperature normalization process of frequency domain spectroscopy[J]. High Voltage Engineering, 2021, 47(7): 2416-2424.
[19] 高岩峰, 卢毅, 梁曦东, 等. Kramers-Kronig变换在介电响应分析中的数值计算方法、意义及应用[J]. 中国电机工程学报, 2020, 40(1): 318-329, 398.
Gao Yanfeng, Lu Yi, Liang Xidong, et al. Numerical computational method, application and significance of the Kramers-Kronig transform in the analysis of dielectric response[J]. Proceedings of the CSEE, 2020, 40(1): 318-329, 398.
[20] 赵孔双. 介电谱方法及应用[M]. 北京: 化学工业出版社, 2008.
[21] 刘付德, 凌志远, 熊茂仁. 固体介质中电偶极子介电常数温度特性与能级密度分布关系[J]. 物理学报, 1995, 44(8): 1302-1309.
Liu Fude, Ling Zhiyuan, Xiong Maoren. The relationship study between temperature characteristics of dipole permittivities and activation energy density distribution in solid dielectrics[J]. Acta Physica Sinica, 1995, 44(8): 1302-1309.
[22] 钟力生, 李盛涛, 徐传骧, 等. 工程电介质物理与介电现象[M]. 西安: 西安交通大学出版社, 2013.
[23] 国家质量监督检验检疫总局, 国家标准化管理委员会. 煤的高压等温吸附试验方法: GB/T 19560—2008[S]. 北京: 中国标准出版社, 2009.
[24] Liu Tianqi, Aniagor C O, Ejimofor M I, et al. Recent developments in the utilization of modified graphene oxide to adsorb dyes from water: a review[J]. Journal of Industrial and Engineering Chemistry, 2023, 117: 21-37.
[25] 李泉浩, 张大宁, 王谦, 等. 气固复合绝缘变压器聚酯材料老化特性研究[J]. 电机与控制学报, 2023, 27(1): 23-32.
Li Quanhao, Zhang Daning, Wang Qian, et al. Aging characteristics of polyester material of gas-solid composite insulated transformer[J]. Electric Machines and Control, 2023, 27(1): 23-32.
[26] 温福新, 董明, 任明, 等. 基于修正的Havriliak-Negami模型的SiO2纳米改性变压器油宽频介电弛豫特性[J]. 电工技术学报, 2016, 31(7): 166-172.
Wen Fuxin, Dong Ming, Ren Ming, et al. The broadband dielectric relaxation properties of the transformer oil based on SiO2 nanoparticles using modified Havriliak-Negami model[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 166-172.
[27] 黎枝鑫, 王东阳, 温荣婷, 等. 基于时变指前因子和频域介电谱平移系数的油浸纸热老化评估方法[J]. 电工技术学报, 2022, 37(17): 4487-4496, 4516.
Li Zhixin, Wang Dongyang, Wen Rongting, et al. Thermal aging assessment method of oil impregnated paper based on time-varying pre-exponential factor and translation coefficient of frequency domain spectroscopy[J]. Transactions of China Electro-technical Society, 2022, 37(17): 4487-4496, 4516.
Study of Dielectric Response Characteristics and Temperature Normalization of Oil-Paper Insulation in Low Temperature
Abstract Frequency domain dielectric spectroscopy (FDS) is widely used for condition diagnosis of oil-paper insulated power equipment due to its high measurement accuracy and ease of operation. However, in winter in Northeast and Northwest China, the temperatures remain below -40℃ for extended periods, and rapid internal cooling of equipment during maintenance can lead to water crystallization and partial solidification of transformer oil, severely affecting accuracy of FDS results. In order to improve the accuracy of oil-paper insulation condition assessment, it is necessary to perform temperature normalization of the test results. However, traditional "master curve" methods are unsuitable for low-temperature environments as they produce significant errors in high and low frequency ranges. Existing research rarely focuses on the dielectric response characteristics and assessment methods of oil-paper insulation in extremely low-temperature environments. Therefore, this paper studies the FDS results of oil paper insulation at different temperature, and establishes a new temperature normalization model by Havriliak-Negami (H-N) model. This model improves the temperature normalization accuracy, filling the gap in the assessment of oil-paper insulation condition in low-temperature environments.
Firstly, starting from the physics of dielectrics, derive the effects of temperature on the relaxation processes. to obtain the formula for temperature normalization parameters. Samples of oil paper insulation with different moisture contents (0.41%~3.91%) are prepared, and an experimental platform for high and low temperature dielectric response testing is set up. By measuring the frequency dielectric spectra (1 mHz~5 kHz) of samples with different moisture contents at various temperatures (-40~30℃), it is found that as the moisture content gradually increases, the dielectric loss values also increase. Additionally, the decrease in temperature tends to make the high-frequency FDS results more consistent the relaxation peaks less distinct, which increases the difficulty of assessing moisture content. In order to understand the changes in the internal water morphology of oil-paper insulation at low temperatures, the distribution of moisture within insulation paper is studied using isothermal adsorption experiments, revealing a substantial amount of free water attached to cellulose fibers. At low temperature, this part of water crystallizes and precipitates, which affects internal polarization processes of oil paper insulation. Using thermally stimulated depolarization current (TSDC), it is discovered that concentration polarization, interfacial polarization, and dipole polarization are the main three polarization processes in oil-paper insulation. Based on the extended derivative method, it is found that as the temperature decreases, the intensity of concentration polarization gradually weakens, and the relaxation time of interfacial polarization decreases.
In order to study different polarization processes separately, the improved Havriliak-Negami (H-N) model is used to decompose FDS results, extracting characteristic parameters of each relaxation process. It is discovered that as temperature decreases, concentration polarization diminishes and disappears below 0℃, temperature only changes the relaxation time of interfacial polarization without altering its strength, and dipole polarization intensifies due to reduced molecular thermal motion. Moreover, the conductivity process, influenced by both ionic and electrophoretic conductivity, gradually decreases and stabilizes. At the same time, temperature normalization parameters for each relaxation process are extracted.
Finally, a new temperature normalization method is proposed based on the characteristics of each polarization process. Compared to the traditional “master curve” method, this method has higher accuracy in low temperature environments and in conditions with high moisture content. In low temperature, this method maintains high accuracy with a goodness of fit of 0.975 7, compared to 0.952 6 with the traditional method, In samples with high moisture content, the goodness of fit is 0.982 2. At the same time, 5 to 7 more frequency data points are added and full-frequency range correction is achieved, solving the issues of large low-temperature correction errors and insufficient frequency data in the “master curve” method.
Keywords:Oil paper insulation, frequency domain spectroscopy, low temperature, Havriliak-Negami model, temperature normalization
中图分类号:TM855
DOI: 10.19595/j.cnki.1000-6753.tces.240816
国家自然科学基金青年科学基金(52107165)和第71批博士后基金面上资金(2022M712511)资助项目。
收稿日期 2024-05-19
改稿日期 2024-06-20
田文锐 男,1999年生,博士研究生,研究方向为油纸绝缘介电响应。
E-mail:tianwenrui@stu.xjtu.edu.cn
张大宁 男,1989年生,副研究员,研究方向为电力设备的运行状态检测以及电力电子装置等。
E-mail:daningzhang@xjtu.edu.cn(通信作者)
(编辑 李 冰)