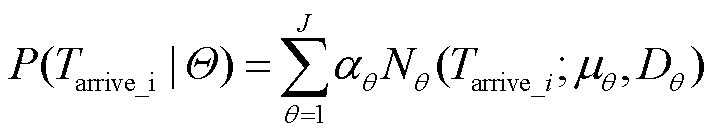（1）
摘要 电动汽车（EV）联网渗透率大幅提高后，可作为移动储能并网提供辅助频率控制。针对电动汽车调频策略较少计及充电行为不确定性而导致调频能力不准确的问题，提出了考虑用户特征与用户意愿的电动汽车调节功率边界刻画模型及频率支撑策略。首先，基于高斯混合分布方法对EV的用户行为模式、电池容量、充电和放电率等电动汽车相关的不确定性进行描述，并采用Logit模型对EV可调度意愿进行预测；其次，刻画了考虑用户特性和用户意愿的EV调节边界，通过改变EV功率波动上下限确定用户的调节方式，并提出一个保证用户荷电状态整体趋势呈现上升以及考虑用户不确定性特征和用户可调度意愿的EV调频策略；最后，对构建的模型和提出的控制策略进行仿真分析，并基于SPSS软件对仿真结果中影响用户可调度意愿的各决策变量进行相关性分析，随后采用T检验对其进行显著性验证，验证了所提方法的有效性。
关键词：电动汽车 用户特征 用户意愿 调频 功率边界
交通电气化是实现“双碳”目标的关键途径之一。电动汽车（Electric Vehicle, EV）使用电力替代传统的碳基化石燃料，从而显著减少化石燃料消耗和温室气体排放。然而，EV用户自身的充放电行为具有随机性和不确定性[1-3]，当EV以高渗透率接入电网时，大规模的EV充放电行为将会给电网带来巨大的威胁[4-7]。采取计及EV不确定性的控制策略是解决问题的关键。
随着电动汽车的普及，电网的实时供电及电功率守恒压力也在增加。准确的负荷预测有助于平衡电网负荷，促进清洁能源的使用，减少对化石燃料的依赖。文献[8]使用正态分布描述EV无序充放电曲线。文献[9]以对数正态分布刻画EV的行驶里程。文献[10]使用正态分布表达EV出行和返回时间。总体来看，在EV参与电网调节的负荷预测方面，相关文献将EV用户的特征大部分近似为正态分布，未能通过指定合理的控制规则在保证用户满意度的前提下充分释放EV富余能量参与电网调节。
文献[11-12]分别提出了基于Ford-Fulkerson最大流算法的主从博弈双层迭代的电动汽车参与负荷频率控制的方法和EV聚合体在负荷频率控制中的优化调度方法，尽管都充分利用了EV的灵活性，但假设用户行为完全可预测，忽略了用户意愿对EV充电行为的影响。文献[13]提出结合EV经济调度与频率调节的协同优化方法，主要通过调度EV的充放电行为调节频率。文献[14]基于策略投标方法，研究了EV聚合体在频率调节中的最优充电调度，虽然建模时考虑了EV充电行为的不确定性，但是并未对用户参与电网调频意愿进行建模，会导致调度结果与实际需求不符，进而影响频率调节效果。文献[15]提出计及电池寿命损耗的电动汽车参与能量-调频市场协同优化负荷频率控制方法，但未充分考虑个体用户的充电需求和满意度，会导致用户参与度较低。文献[16]提出基于粒子群算法的电动汽车有序充放电两阶段优化策略进行负荷频率调节分析，但在出现不符合优化目标的高负荷情况下，系统频率波动问题依然明显。文献[17-18]分别提出了计及车辆限制和EV用户不确定性的电动汽车参与电网频率调节的控制策略，虽然明确规定调频功率的上下限，但在建立约束的过程中并没有考虑用户行为的不确定性和意愿特征。上述文献采取不同方法对EV集群并网进行优化，但在EV数量徒增、充放电功率波动较大的情况下，负荷频率调节策略也会导致调频时段产生新的频率尖峰[19]或难以有效改善频率峰均比[20]，在设计调频策略时，未充分考虑电动汽车用户的充电行为具有不确定性，这可能导致调频能力的不准确。虽然上述文献明确规定调频功率的上下限，但该上下限为较为主观的数值，并没有考虑用户意愿和用户不确定性对约束的影响。
为解决传统调频策略中因未充分考虑用户行为特征和意愿而导致的调频能力不准确的问题，本文首先基于高斯混合模型（Gaussian Mixture Model，GMM）与Logit模型对EV用户的行为模式（包括到达时间、停留时间和初始荷电状态等）进行建模；然后，基于SPSS获得各决策变量用户的可调度意愿相关性分析，并采用T检验对其进行显著性验证；最后，基于用户特征和意愿刻画了EV调节边界，提出一个保证用户荷电状态整体趋势呈现上升前提下计及用户不确定性特征和用户可调度意愿的EV实时功率调节策略及频率支撑策略。
电动汽车用户个体并网的充电功率由充电桩决定，但EVs并网功率往往是由EVs的用户特征决定。表征EVs用户特征的方法通常有以下几种：回归分析、聚类分析、决策树和机器学习算法。当下研究主要通过正态概率分布拟合，而用户出行分布具有早、晚高峰，并且根据峰谷电价的不同并网分布也有所不同，故正态分布无法准确地描述多峰和峰谷电价激励现象。而GMM能准确地描述多峰分布，因此，本文采用GMM根据EV的到达时间Tarrive_i和初始荷电状态SOCi0的实际数据对所建立的概率密度函数Pd进行分类拟合，则第i辆EV到达充电桩时间的具体概率分布函数P(Tarrive_i|Θ)为
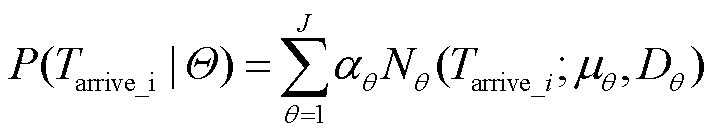（1）
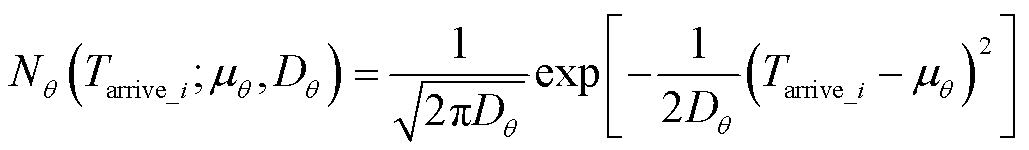（2）
式中，Nθ(Tarrive_i; μθ, Dθ)为θth高斯分量函数；μθ为平均值；Dθ为方差；J为高斯分量的总数；αθ为该高斯分量所占的权重；一维GMM的表达式Θ={θ1,…, θJ}，通过确定Tarrive_i、μθ、Dθ来拟合高斯混合分布，而J是在估计以前通过EV用户自身设定，估计后根据实际的拟合效果对J进行调整。
EV初始能量概率密度函数Pd(Ei0; φθ, Dθ)为
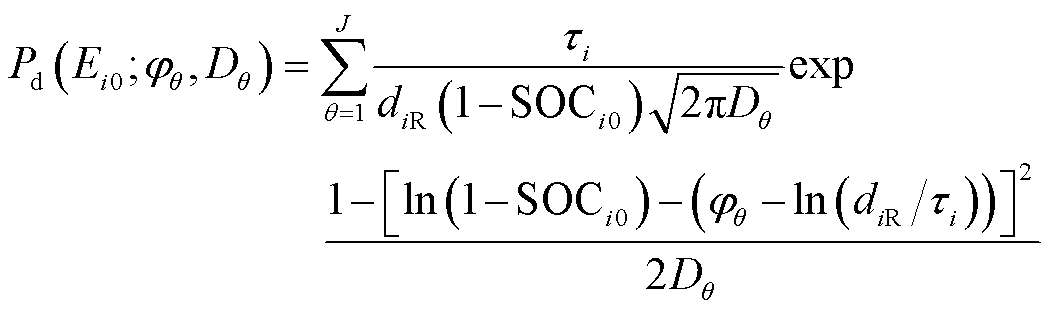（3）
式中，Ei0为第i辆EV的初始能量；φθ为第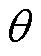
个分布的均值；τi为第i辆EV充电后可行驶天数；diR为第i辆EV的续航里程。
对 EV 初始 SOC 概率密度函数的参数通过历史数据进行估计，将拟合得到的SOCi0和Tarrive_i中的密度函数导出。模拟时分别根据各概率密度通过蒙特卡洛方法抽取随机数，同时根据用户设置的停靠时长得到离开时间Tdeprive（共EV_Number个），刻画出用户特征。
Logit模型主要用于分析和预测 EV 用户在电力市场环境下对不同充电策略和电网需求时的选择行为：根据用户的特征判断其选择是否接受电网调度的意愿，并根据该意愿的大小判断其参与电网调节的模式。
Logit 模型适合表征具有二元结果（接受、拒绝）的场景，可有效呈现充电状态、调度补贴激励、控制灵活性等多个变量对决策过程的影响，以清楚地了解不同因素如何影响决策。使用 Logit 概率模型表征EV可调度意愿主要包括以下步骤：
1）本文考虑EV的荷电状态、电网各时段的调度补贴、EV用户在充电区域停留时间作为影响用户意愿的多个因素，故用户调度意愿的概率模型中的隐变量yi可表示为
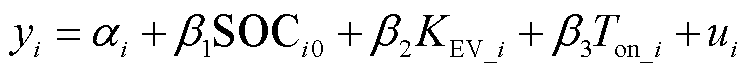（4）
式中，yi为第i辆EV的决策意愿隐变量；ai为基准概率分布函数系数；β1、β2、β3为系数；KEV_i、Ton_i分别为电动汽车调度补贴激励、用户输入的充电桩停留时间；ui为决策意愿的随机误差变量。
在实际应用中，各个解释变量的系数通常使用mnrfit函数对历史数据进行Logit回归分析获得。该函数专用于拟合多项式逻辑回归模型，适用于具有二元结果的参数估计。
2）使用Logit函数将隐变量yi转换为用户的选择概率。EV接受电网调度和不接受调度的概率函数分别用式（5）、式（6）表示，其中调度意愿概率模型中的隐变量yi的取值范围为(-∞, +∞)，调度意愿概率F(yi)的取值范围为(0, 1)。
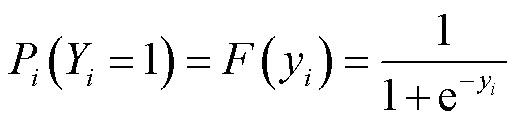（5）
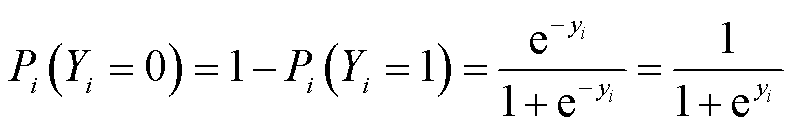（6）
式中，Yi为第i辆EV的决策意愿变量，Yi=1表示用户选择接受电网调度，Yi=0表示用户选择闲置；Pi(Yi=1)表示用户做出的选择决策Y的概率，取值范围为(0,1)。
该决策变量受到荷电状态、电网各时段的调度补贴、EV用户在充电区域停留时间等因素的影响。其中，对意愿选择权重占比最高的为调度补贴，根据EVs中每辆车在各自停留期间各小时段不同的峰谷电价来影响Logit模型中用户参与调节的意愿。
因此，本文首先基于图1考虑用户特征的EV充电日负荷曲线，使用梯形隶属度函数计算的方法对峰谷隶属度进行划分。设Tp为谷值负荷阈值，Tv为峰值负荷阈值，日负荷曲线如图1所示是一组数据L={l1,l2,…,ln}，其中每个li代表一个特定时间点的电网负荷。梯形谷隶属函数通常定义为四个参数，Tpa、Tp、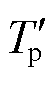
和Tpd，其中[Tp,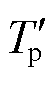]表示隶属度为1的核心区域，而[Tpa,Tp]和[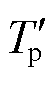,Tpd]为上升沿和下降沿，隶属度从0增加到1，或从1减少到0。梯形峰隶属函数的四个参数为Tva、Tv、
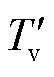和Tvd。对于峰谷划分，峰值负荷与谷值负荷隶属度函数分别为
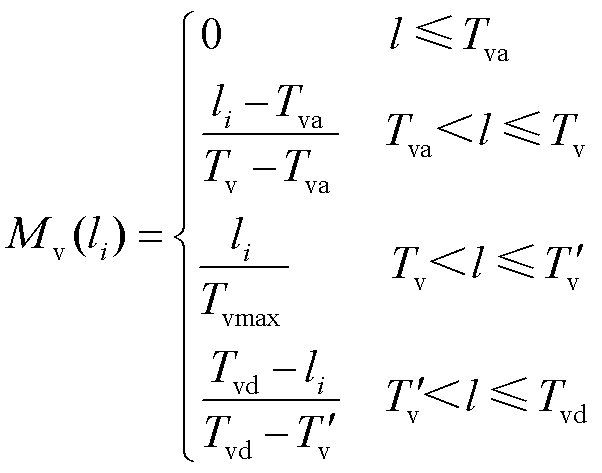（7）
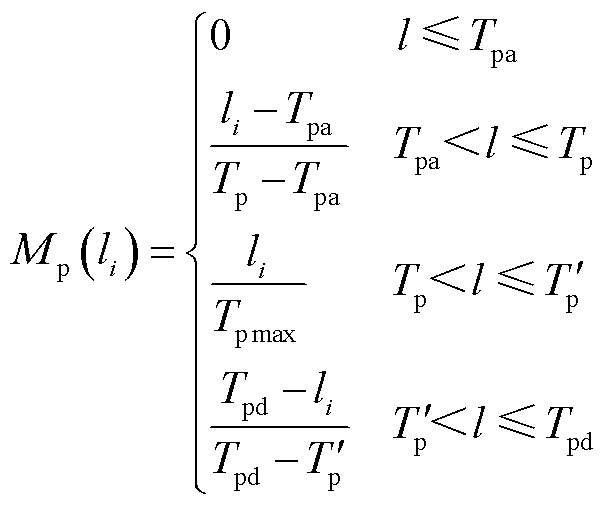（8）
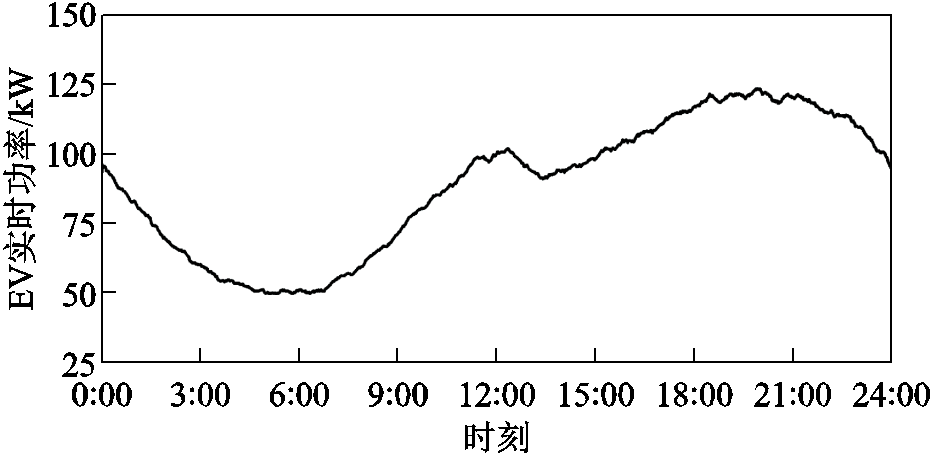
图1 考虑用户特征的EV充电负荷曲线
Fig.1 EV charging load curve considering user characteristics
使用梯形峰谷隶属度函数计算每日各时段负荷的峰谷隶属度，其分布见表1。
表1 基于EVs日负荷曲线的峰谷隶属度分布
Tab.1 Distribution of daily load peak and valley membership degrees
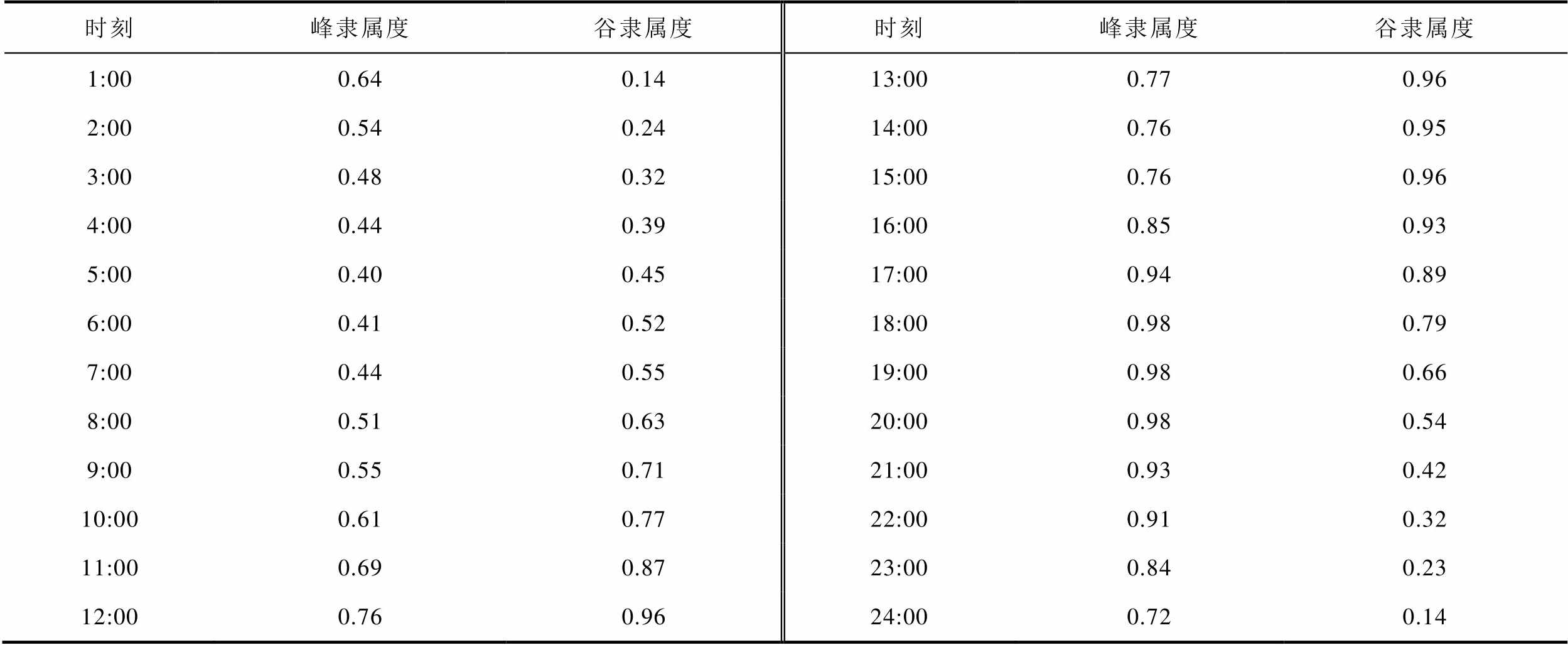
时刻峰隶属度谷隶属度时刻峰隶属度谷隶属度 1:000.640.1413:000.770.96 2:000.540.2414:000.760.95 3:000.480.3215:000.760.96 4:000.440.3916:000.850.93 5:000.400.4517:000.940.89 6:000.410.5218:000.980.79 7:000.440.5519:000.980.66 8:000.510.6320:000.980.54 9:000.550.7121:000.930.42 10:000.610.7722:000.910.32 11:000.690.8723:000.840.23 12:000.760.9624:000.720.14
综上所述，本文通过构建EV日负荷曲线的峰谷隶属度分布，刻画不同时间段的充电负荷特性，并有效识别峰值与谷值负荷时段，从而反映电价的时段性变化。高峰时段电价较高，低谷时段电价较低，这一变化趋势直接影响用户的充电决策与调度意愿。用户更倾向于在低谷时段充电，以避免高峰时段的高电价，从而实现电网负荷的平衡与充电成本的降低。通过Logit模型，将隶属度函数与用户调度意愿相结合，形成用户行为特征与调度意愿的关系模型。在高隶属度时段，用户更愿意响应电网的调度需求，提供调频服务。隶属度函数提供的量化数据，不仅支持电网运营者制定更加科学的调度策略，还能在满足用户充电需求的同时，优化电网的负荷管理和频率调节。
考虑到双向变流器在现实工作中的响应时间通常为ms级，往往忽略电动汽车的电磁暂态过程，EV调频功率可表示为
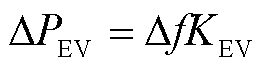（9）
式中：ΔPEV为EV充放电功率变化量；Δf为系统的频率扰动偏差；KEV为EV参与系统频率响应的响应系数。
根据式（9）得EV并网的输出功率波动量与系统频率间存在线性关系。电动汽车功率-频率下垂特性曲线如图2所示。
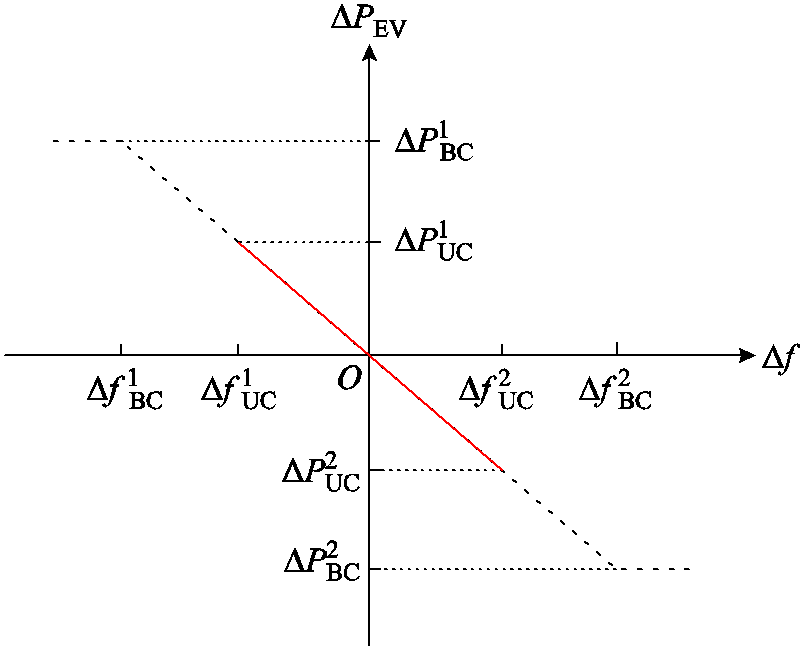
图2 EV参与调频时的下垂特性
Fig.2 Droop characteristic of EV providing FR
图2中，黑色虚线为双向V2G（Bidirectional Charging, BC）模式下的EV并网调频的下垂特性，此模式下EV既可以充电又可以放电；红色实线表示单向V2G（Unidirectional Charging, UC）模式下EV并网调频的下垂特性，两者在系统频率波动时均以KEV为EV系统频率响应系数并网调频。但电网频率波动所需的调节功率往往要大于EV自身功率波动范围，因此，调节功率约束的刻画直接影响EV参与电网调节能力，EV调节功率上下限约束为
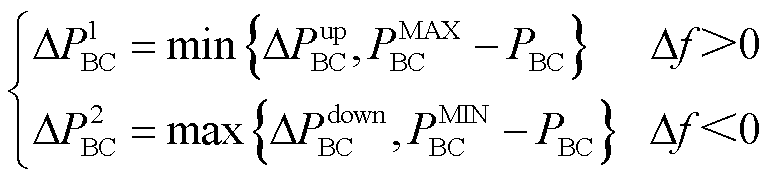（10）
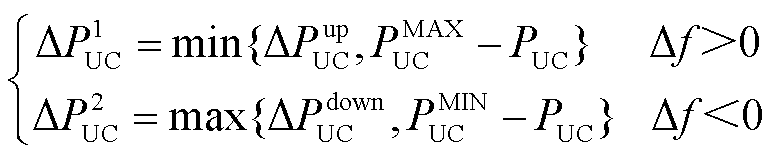（11）
式中，ΔP1 UC和ΔP1 BC分别为单向和双向V2G的功率波动上限，由最大充放电功率PMAX BC、PMAX UC与上一采样时间的充放电功率PBC、PUC的差值及调频功率上限值ΔPup BC、ΔPup UC二者之间的最小值决定；ΔP2 BC、ΔP2 UC为功率波动下限，由上一采样时间的充放电功率PBC、PUC 与最小充放电功率PMIN BC、PMIN UC的差值及调频功率下限值ΔPdown BC、ΔPdown UC二者之间的最大值决定。两者之间的异同点为：BC模式下的ΔPup BC、ΔPdown BC和PMAX BC还有UC模式下PMAX UC的绝对值为EV充放电功率的最大值，而ΔPdown UC、ΔPup UC的绝对值为EV充放电功率的最大值的一半，且PMIN UC为0。根据EV调节功率上下限约束得到EV充放电功率变化量表达式为
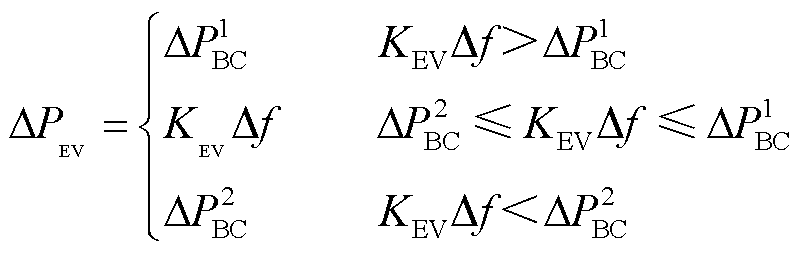（12）
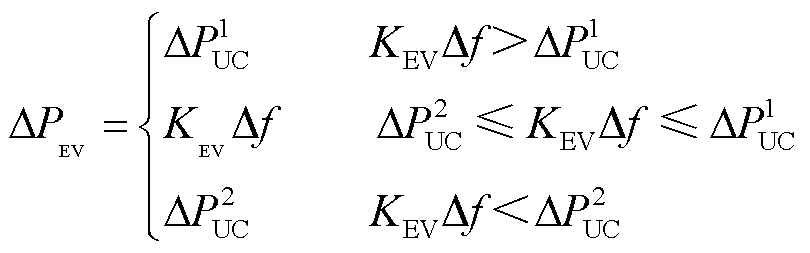（13）
结合考虑用户特性和用户意愿，刻画EV调节边界，约束EV实时调频功率，并通过改变EV功率波动上下限确定用户的调频方式，准确刻画EV调频特性。
为提高EV调频参与度及其调频能力，提出了在保证用户荷电状态整体趋势呈现上升的前提下,考虑不同用户特征和意愿的调频策略。
EV参与电网调频达到用户设置终止充电量SOCie所需的充电时间为
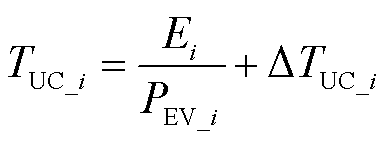（14）
式中，TUC_i为第i辆EV的UC模式下达到设定SOCe所需充电时间；Ei为第i辆EV所需补充的能量；PEV_i为第i辆EV的充放电功率；ΔTUC_i为第i辆EV的UC模式下充电时间裕量，min。该裕量旨在减少使用开路电压（Open Circuit Voltage, OCV）取代EV电池端电压所出现的误差，并且能够补偿实际电网负荷波动均值偏移出现的波动量，从而确保计算得到的充电时间不会被低估。合适的ΔTUC_i值需要电网调度中心根据长期运行数据分析和计算得出。
为精确评估EV用户的充电意愿需求，计及SOCi0、EV电池容量、SOCie、EV电池组类型等信息计算所需补充的电池能量的计算公式为
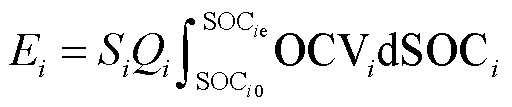（15）
式中，Si为第i辆EV串联的动力电池数量；Qi为第i辆EV的电池组额定容量；OCVi为第i辆EV的单个电池开路电压。SOCi与OCVi之间的函数关系以锰酸锂电池为例表示为
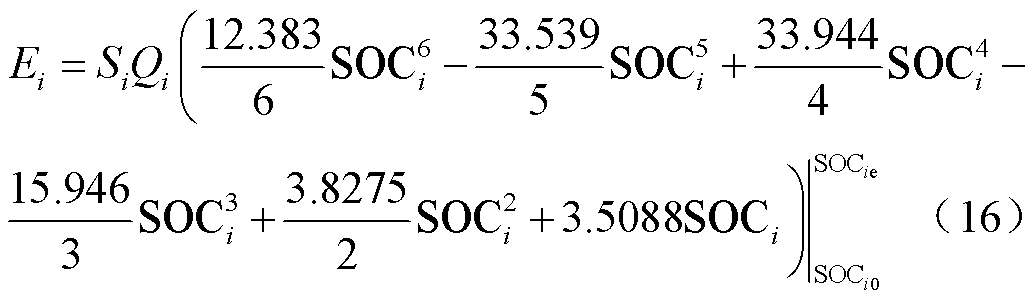
依据式（16）得到的EV所需补充能量的充电时间、实际并网起始时间和设定终止时间确定该车参与电网调频的规则，见表2。表2中，Ton_i为第i辆EV的调频控制时间，即该EV用户设置的终止时间te_i与并网起始时刻tb_i之差；mode=1时表示工作于单向V2G模式，mode=2时表示工作于双向V2G模式。该规则旨在建立一个提高用户满意度的模型，这不仅能够为EV用户提供更为人性化的可靠服务，还可提供刻画得更为精确的调频资源。
表2 EV参与电网调频的规则
Tab.2 Rules for EV participation in FR
规则内容 1如果TUC_i≥Ton_i，则mode=2直到te_i时刻 2如果SOC0＜50%并且TUC_i＜Ton_i，则mode=1直到SOC=50%；然后mode=2持续(Ton_i-TUC_i)h；之后mode=1直到te_i时刻 3如果TUC_i＜Ton_i并且SOC0≥50%，则比对从SOC=50%到SOC0所用的时间是否大于以Pmax/2充电功率从SOC=50%到SOC0的时间，如果T≥Tpmax/2，则mode=2 4如果SOC0≥50%、T≥Tpmax/2并且TUC_i＜Ton_i，则mode=2持续(Ton_i-Tu)h；然后mode=1直到te时刻
为验证EV参与电网调节规则对用户个体提供服务的可靠性、Logit模型对用户意愿的激励效果、GMM模型对用户特征刻画的准确性，以及调节策略控制负荷频率波动的效果，本文提出一种计及用户不确定性特征和用户可调度意愿的EV实时调节功率刻画及频率支撑策略模型。采用Matlab/ Simulink以单区域系统为例进行仿真验证。预测系统总负荷峰值PLOAD_max在实际数据基础上通过GMM方法得到，取模拟电动汽车共3 000辆[17]。EV集群参与电网调频的双向变流器响应速度非常快，3 000辆EV集群的整体响应速度可能会存在一定延迟，其延迟时间可通过惯性环节的时间常数刻画。本文与当前大部分研究一样忽略了EV群响应时间问题，重点放在基于用户不确定性特征和用户可调度意愿对EV实时调节功率进行刻画及辅助调频控制分析。
并网频率调节控制的EV车辆类型为纯电动汽车，动力电池类型为锰酸锂电池。其余的EV参与电网频率控制的相关参数见表3。其中电动汽车实时调节功率刻画参数为单区域电力系统典型值[21]，电动汽车电池参数参考文献[22]。峰时段（11:00—24:00）、谷时段（3:00—9:00）、平时段（24:00—3:00、9:00—11:00）电价分别为：峰时段1.004 4元/(kW·h)、谷时段0.695 0元/(kW·h)、平时段0.453 2元/(kW·h)[23]。
表3 EV参与电网频率控制的相关参数
Tab.3 Relevant parameters for EV participation in grid frequency control
参数数值 系统发电功率PG/MW300 基准功率Pbase/MW300 基准频率fbase/Hz50 调速器时间常数Tg/s0.2 原动机时间常数Tch/s0.3 惯性时间常数M/s10 负荷-阻尼常数D1 机组调差率δ(pu)5 区域频率响应系数B(pu)21 EV电池容量Qi/(A·h)80 动力电池串联数量Si/个80 电池单体内阻R/mΩ0.8 SOC最大值SOCmax(%)100 SOC最小值SOCmin(%)20 EV最大充放功率绝对值Pmax(pu)3×10-5 电网频率波动值上限Δfmax/Hz0.1 电网频率波动值下限Δfmin/Hz-0.1 EV频率响应系数KEV(pu)-3×10-3 EV时间常数TEV/ms0.3
EV实时调节功率刻画主要分为三个场景。场景1：考虑用户特征的EV充电功率刻画；场景2：考虑用户特征及充放电控制策略的EV充放电功率刻画；场景3：考虑用户特征及意愿和充放电控制策略的EV充放电功率刻画。
不同场景下EV实时输出功率如图3所示。图1正常功率输出的负荷曲线与图3a考虑充放电控制策略的EV充放电功率曲线相比，参与电网调频EV集群产生的负荷功率明显变小，降低了41%的负荷功率强度，负荷率提升了5.23%。图3b为考虑用户意愿和充放电控制策略的EV充放电功率曲线，数据结果说明，场景3的充放电控制方式有效地减小了EV集群产生的负荷功率，同时，基于EVs日负荷曲线峰谷充电提供的电价激励，场景3在电网需求高峰时反向提供电能。
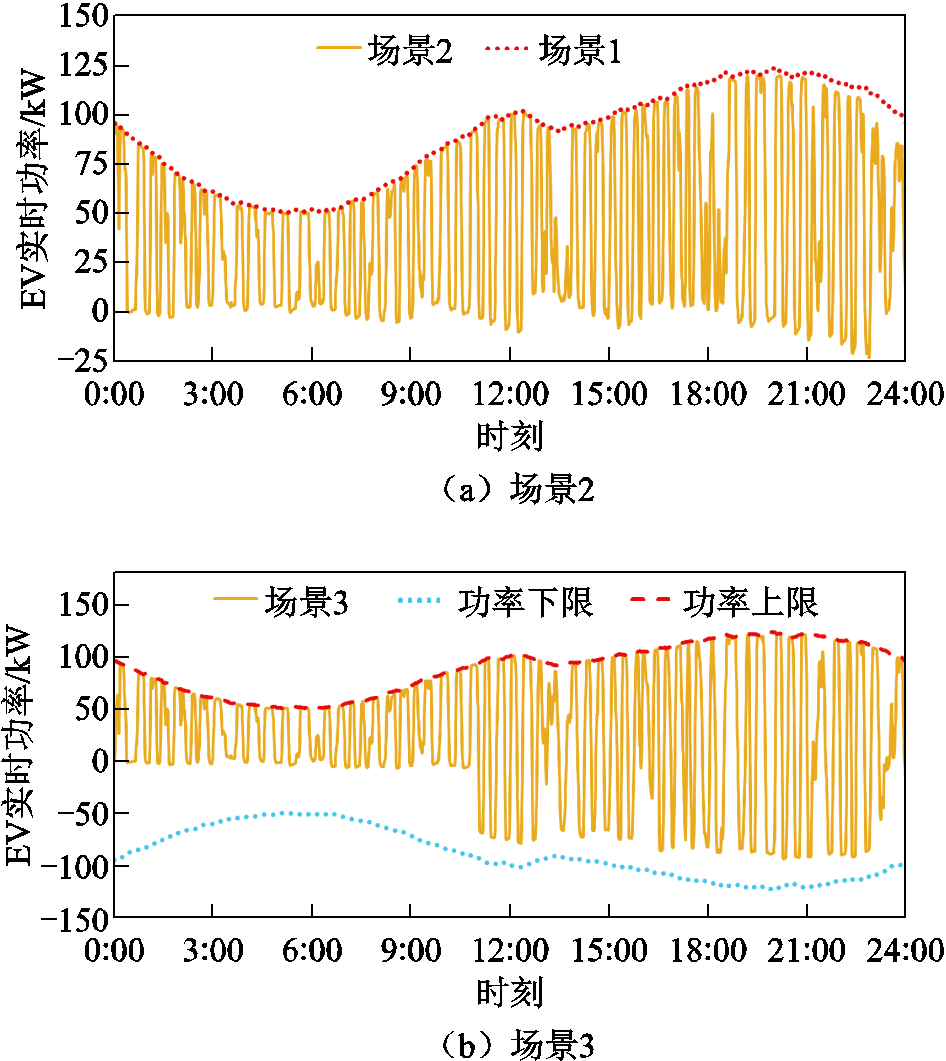
图3 不同场景下的EV输出功率
Fig.3 Characterization of EV output power in different scenarios
场景2和场景3下EVs可调节功率能力刻画如图4所示。图4a和图4c显示，在场景2中，EV调节功率可以在11:00—24:00可再生能源生产过剩的时期提供向上可调节功率，吸收在风力和太阳光辐射强时发出的多余电能。通过对向上调节功率备用的刻画，可以有计划地吸收低谷时段的电能，并在高峰时段释放。因此，这也是对EVs调频能力的一种刻画。其有助于减少需购买的高价峰值电力，从而降低整体运行成本。
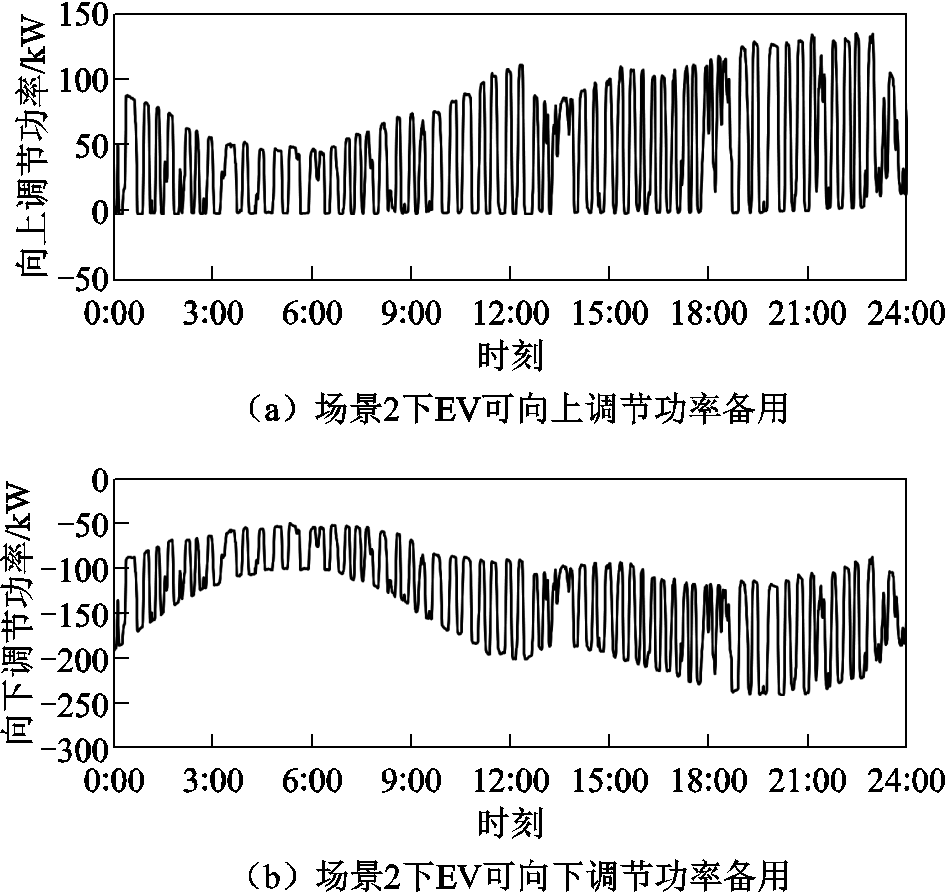
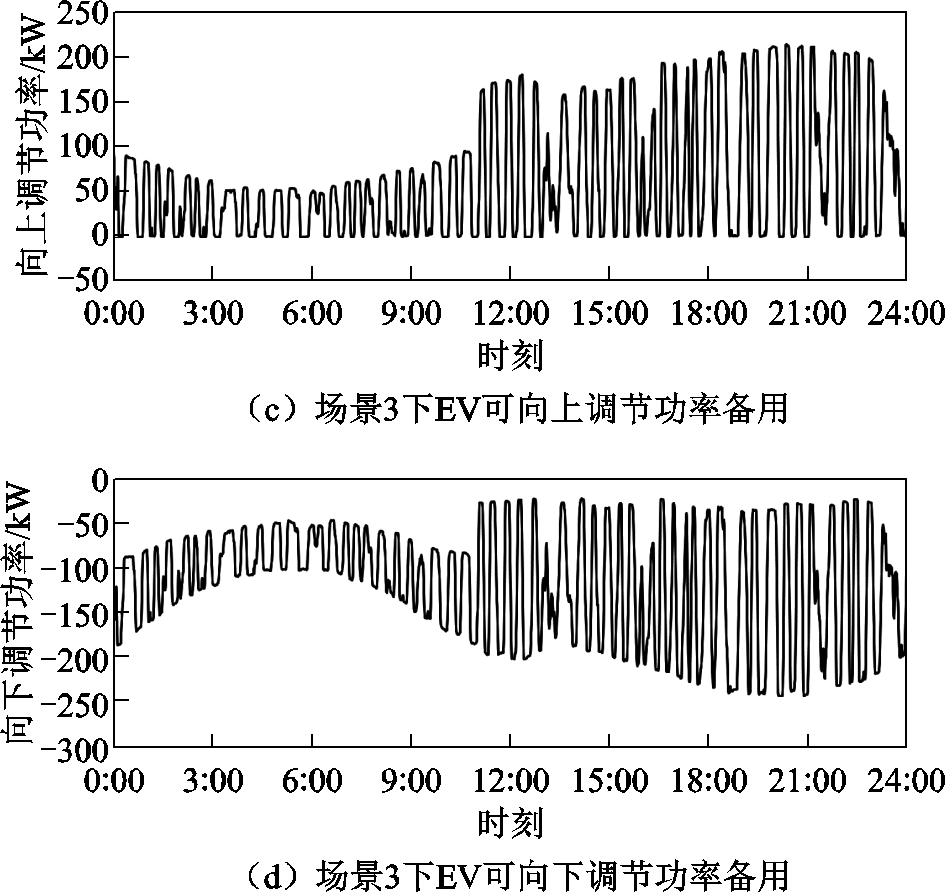
图4 场景2和场景3下EVs可调节功率能力刻画
Fig.4 Characterizations of EVs adjustable power capability in scenarios 2 and 3
图4b和图4d中向下调节功率曲线有两个高峰，分别为午高峰和晚高峰，恰好能在电网负荷需求量高、波动量大的时间段增加EV集群向电网迅速释放储存的电能。因此，可将EV集群看作一个分布式负荷缓冲装置，在实时功率与上下边界的差额内提供功率支撑，平衡供需关系，从而提高电网的稳定性。
图4c和图4d与图4a和图4d的区别主要在于电价激励不同。根据Logit模型的仿真结果，峰谷隶属度较高的时段用户参与电网调节的意愿也相对较高，不仅在实时功率上的调节效果良好，且在向上向下调节功率的备用预留上也有所提高。
图5为计及用户不确定性特征、控制策略和用户可调度意愿的场景下，EV参与调频期间其自身SOC的变化曲线。但不同电价模式下EV参与调频的意愿呈现差异，导致SOC变化趋势略有不同。图中短划线为高电价模式，此时补贴和充电成本都比较高，电动汽车参与电网调频程度较强，但SOC增长较小不符合满足用户基础用车需求前提。点画线和实线为低电价模式，此时补贴和充电成本都比较低，电动汽车参与电网调频程度较弱，SOC增长较大符合满足用户基础用车需求前提。而虚线和长划线为分时电价模式，该模式则能通过Logit模型尽可能地使用户参与电网调频获得相关补贴，低电价充电成本较低的时段充电，高电价充电补贴较高的时段给电网反向充电。在保证用户荷电状态整体趋势呈现上升的前提下实现了计及用户不确定性特征和用户可调度意愿的EV实时功率调节。
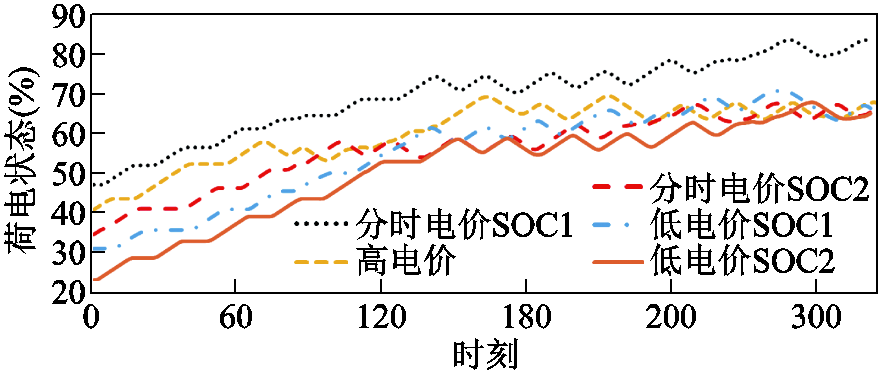
图5 场景3中的EV典型SOC曲线
Fig.5 Typical SOC curves of EV in scenarios 3
对影响电动汽车参与电网调频的主要决策因素进行可视化分析。首先从整体角度出发，通过不同电价分析EV参与电网调频能力边界的影响；然后从个体角度出发，分别研究了EV用户差异化的初始SOC和等待时间对其参与电网调频时间占比的相关性。
1）不同电价激励对EV参与电网调频的影响
场景3下三种不同电价对EV充放电功率边界的影响图6所示。从图6可以看出，本文1.2节提出的Logit模型的权重决策变量电价激励对刻画EV充放电功率边界具有重要意义。低电价时充电需求旺盛，功率上边界较高、下边界较低；高电价时充电需求疲软，EV反向给电网放电，功率下边界较高、上边界较低；而通过峰谷隶属度求解得到的分时电价兼顾了高低电价的优势，在减少功率波动量的同时，保障了电网供电的经济性。
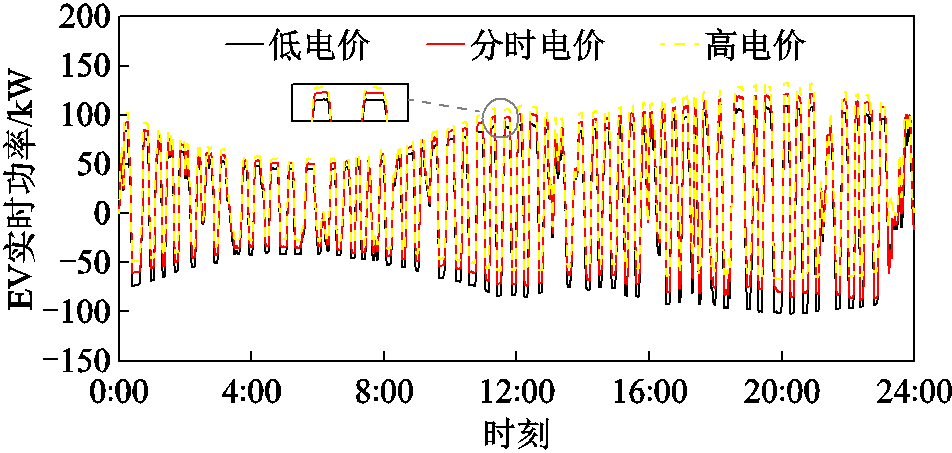
图6 场景3下三种不同电价对EV充放电功率边界的影响
Fig.6 Effects of three different electricity prices on EV charging and discharging power in scenario 3
从用户行为建模和调度策略优化的角度来看，所提规则的有效性在于用户的充放电行为能够提供给用户更高的收益和更低的成本，并通过优化控制策略提高调频的效率。为验证所提规则的有效性，首先根据峰值和谷值隶属度及对应的电价，计算每小时的分时电价；然后结合场景2和场景3的实时功率，通过遍历60 min的数据，分别计算充电成本和调频收益。图7为分时电价模式下场景2和场景3不同控制策略对用户充电成本和调频收益的影响。使用Logit模型表达各决策变量对用户调度意愿的场景3的调频收益更高、充电成本更低，表明在考虑各决策变量影响意愿的调度策略下，用户更积极地参与调频服务，这种策略使得用户能够在满足自己出行需求的同时，提高调频收益，体现了文中所提到的考虑用户满意度的规则的有效性。
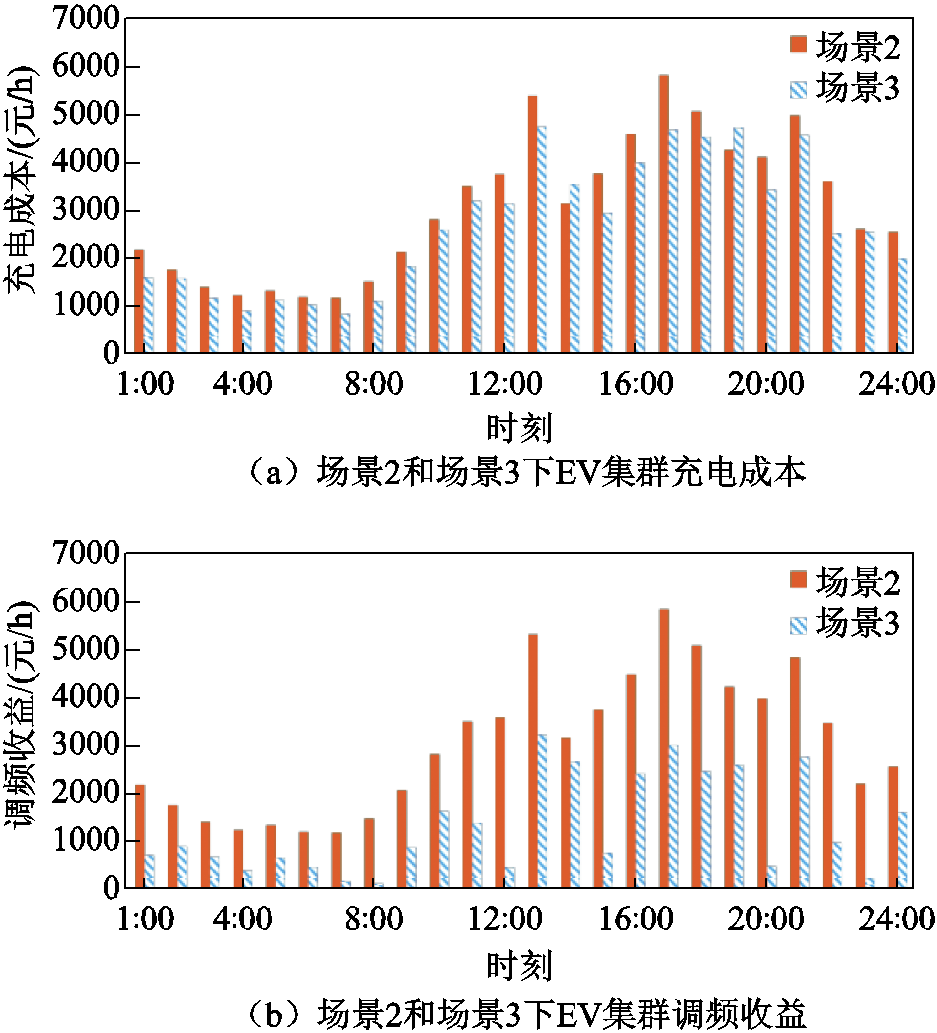
图7 场景2和场景3不同控制策略对用户充电成本和调频收益的影响
Fig.7 Effects of user charging costs and FR benefits under different control strategies in scenarios 2 and 3
2）EV初始SOC对EV参与电网调频的影响
初始SOC对EV参与调频时间相对停靠时间占比的关系如图8所示，其横坐标为初始SOC百分比，纵坐标为该百分比区间内所有EV个体参与调
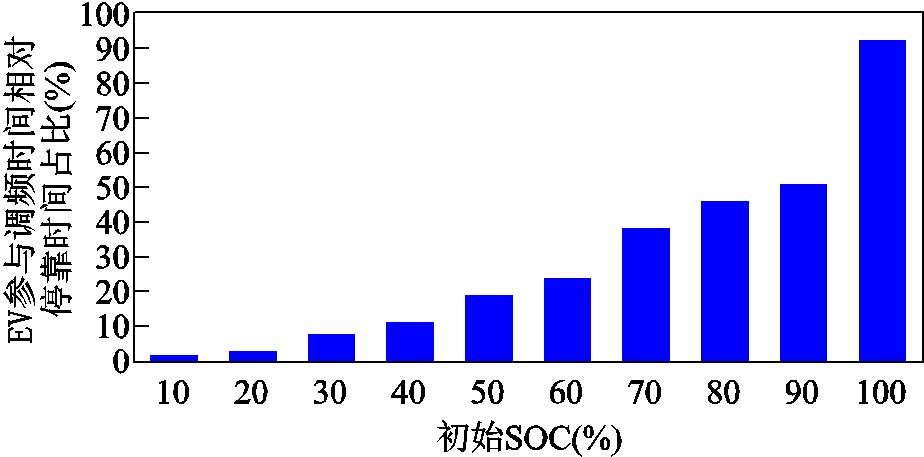
图8 初始SOC对EV参与调频时间相对停靠时间占比的关系
Fig.8 Relationship between the initial SOC and the proportion of EV's participation in FR time relative to the stopping time
频时间相对该个体在充电桩等待时间的比值进行加权平均。图8中初始SOC为100%的EV个体采样较少，参与调频占比特征明显。而其余数据趋势也同样反映初始SOC大小与EV参与电网调频时间占比呈正相关关系，即随着电动汽车初始SOC增加，EV参与电网调频能力显著增加。
3）EV停靠时间对EV参与电网调频的影响
不同停靠时间对EV参与调频时间相对停靠时间占比的关系如图9所示，停靠时间长的EV更可能被纳入调频服务，提供了更大的时间窗口来参与电网的需求响应和调频服务。意味着电池有充足的时间达到理想的充电状态，从而最大化其响应调频信号时的有效性。
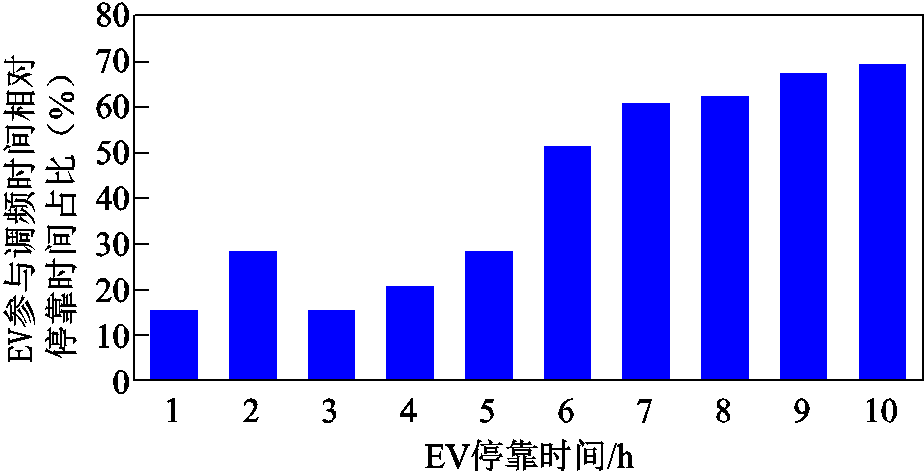
图9 不同停靠时间对EV参与调频时间相对停靠时间占比的关系
Fig.9 Relationship between different stopping times and the relative proportion of EV participation in FR time
4）相关性分析
基于SPSS获得相关性分析结果如图10和图11所示。图10为变量散点图矩阵，其主对角线为3 000辆EV个体在各自决策变量的数量分布占比柱状图，非对角元为各自互相关性散点图。通过第三列前两个图可以直观地分析出，初始SOC和停靠时间与参与调频占比呈现正相关性。图11为矩阵相关性热力图，通过色阶分析可以看出，虽然初始SOC和停靠时间都与参与调频占比呈现正相关性，但是初始SOC的相关系数为0.602 4，高于停靠时间的0.393 7，表现出更强的相关性。
图10 变量散点图矩阵
Fig.10 Matrix of variable scatter plot
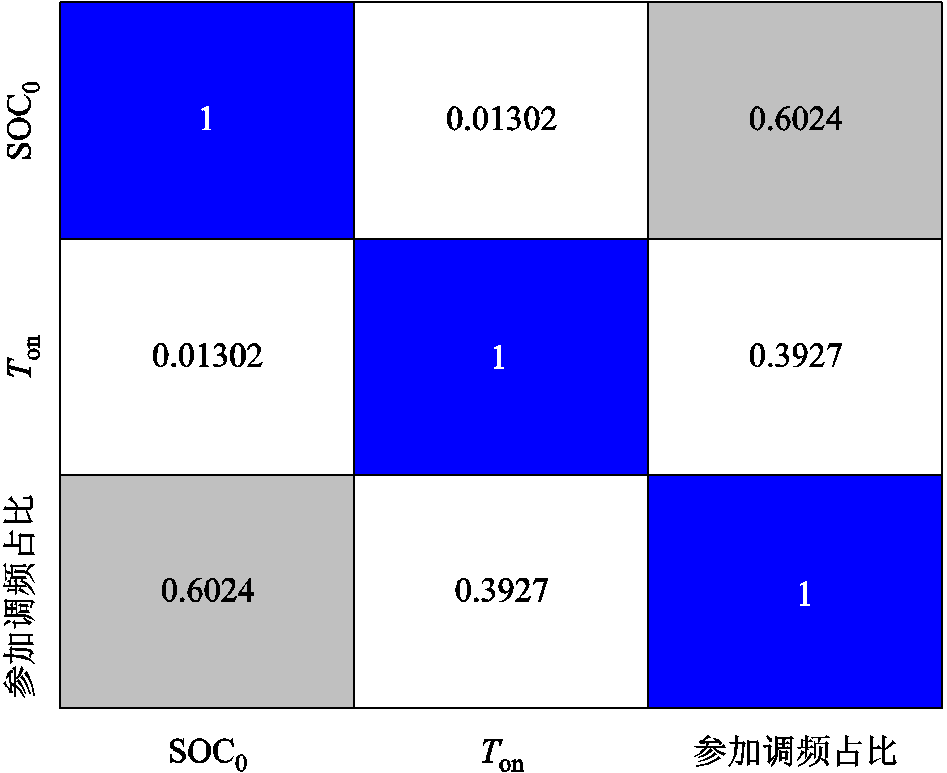
图11 矩阵相关性热力图
Fig.11 Matrix correlation heatmap
5）显著性验证
结合图3的仿真数据，基于T检验结果初始SOC对调频意愿的显著性水平a值为0.005 923，远小于常见的显著性水平（如0.05），表明SOC对用户调频意愿有非常显著的影响，这意味着用户的荷电状态在他们是否愿意参与电网调频中起到关键作用。当SOC较高时，用户不需要维持充电状态，且剩余向下可调节功率增多，使其能够更自由地参与调频活动，从而表现出更高的调频意愿。电价激励对调频意愿的显著性水平a值为0.009 532，表明电价激励也是影响用户调频意愿的关键因素之一。停靠时间对调频意愿的显著性a值为0.0199，小于0.05，表明停靠时间对用户调频意愿有一定的影响，但低于初始SOC及电价激励对调频意愿的影响。
当采用考虑EV辅助调频控制策略时，虽然系统频率及有功出力波动相比常规充电场景得到了一定改善，但与考虑用户意愿的控制策略相比，其调频效果欠佳，原因是单纯的EV辅助控制场景没有考虑电价激励的影响，没有计及用户在充电期间获得的收益会极大地增益用户意愿，制约了EV集群的调频潜力。而本文在EV调频控制策略的设计中，通过实时对用户特征和用户意愿的状态反馈，以及外部扰动的补偿，使EV集群能够更加灵活地响应电网频率的变化，缩减了电网频率偏移范围，平抑了原动机组有功出力的波动。图12a为常规充电、考虑EV辅助调频和考虑用户意愿模型三种场景下EV调节功率对比。从图中可以看出，11:00—23:00的峰时段，场景3和场景2提供调节能力的差值明显高于谷时段和平时段。对照组为文献[14]中的EV调节功率，其模型中EV用户参与电网调频模块设置为聚合模型，即仅刻画一个EV用户的模型，然后以比例系数放大，相较于场景2（考虑用户特征和用户不确定性），忽略了EV用户特征和用户不确定性对调频功率的影响；场景3在场景2的基础上，加入了分时电价激励、初始SOC和停靠时间对用户参与调频的意愿，在低电价充电成本较低的时段充电，在高电价充电补贴较高的时段给电网反向充电，提供优质的调频能力，能够在保证用户荷电状态整体趋势呈现上升的前提下实现计及用户不确定性特征和用户可调度意愿的EV实时功率调节。
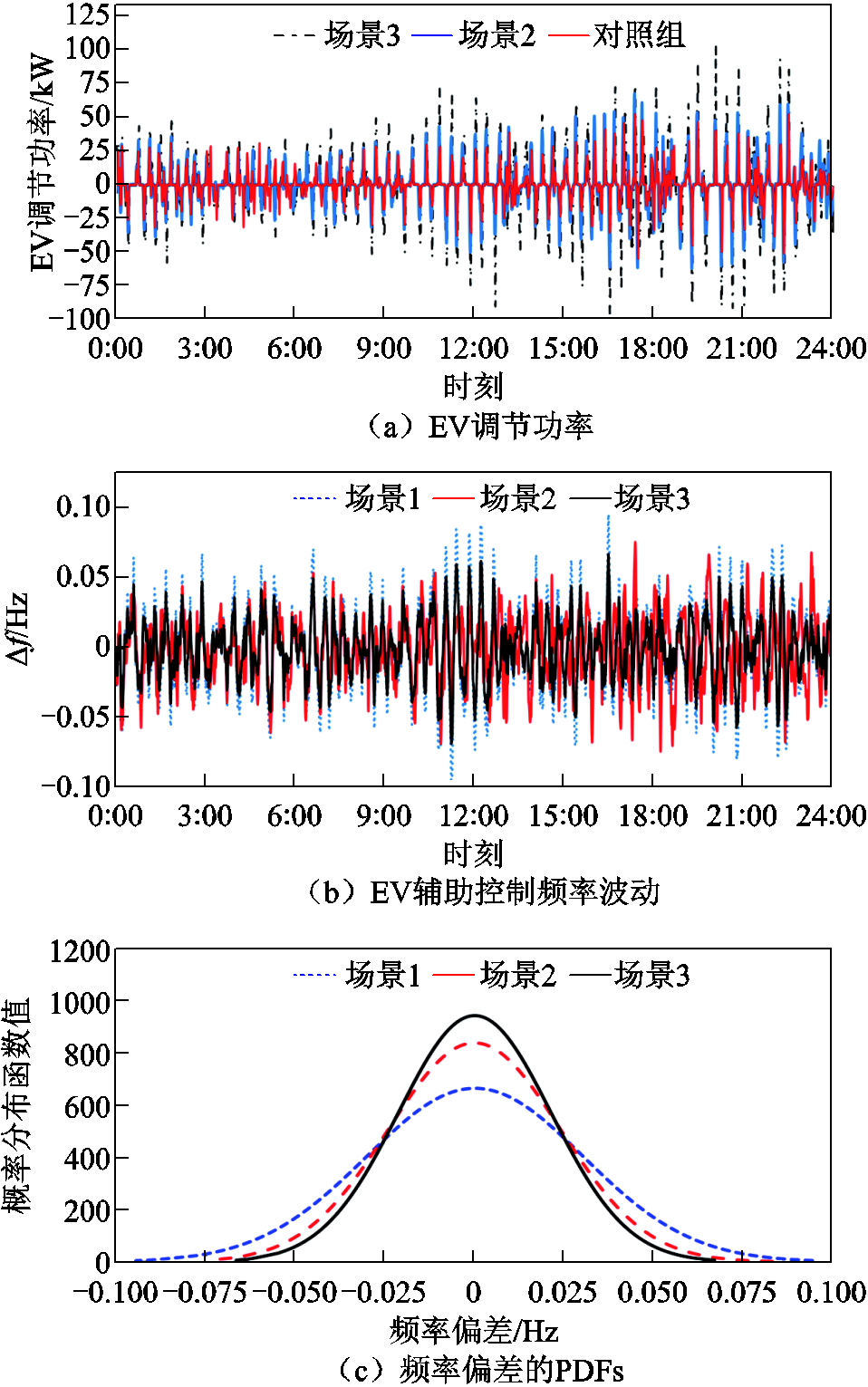
图12 EV常规充电、考虑EV辅助调频和考虚用户意愿下EV辅助调频控制特性分析
Fig.12 Analysis of EV auxiliary frequency regulation control characteristics under conventional charging, considering EV auxiliary frequency regulation, and considering user willingness
图12b为常规充电、考虑EV辅助调频和考虑用户意愿模型三种场景下辅助控制频率波动对比。结合仿真指标计算结果可知，场景3在各项频率指标方面均表现出出色的调频性能，EV集群采用改进方法时，最大频率偏差与最小频率偏差相较于场景2、场景1分别减少了13.91%、和29.27%。此外，从系统频率偏差的方均根来看，改进方法相较于传统EV辅助控制、无调频控制分别减少了11.13%和29.59%；从系统频率偏差在±0.033 Hz持续的时间来看，改进方法表现出最短的持续时间，且相较于其他两种控制方法分别缩短了18.21%、42.69%的频率偏差时间；从系统频率fsys与PEV的协方差来看，改进方法下EV集群有功出力波动导致的系统频率波动程度分别降低了17.76%和41.30%。此外，从图12c所示的频率偏差概率密度函数（Probability Density Functions, PDFs）可知，改进方法的频率偏差集中分布于±0.033 Hz区间的概率大于其他两种控制方法，有效地防止了调频时段产生新的频率尖峰。
本文在考虑不同用户特征和用户需求的前提下，提出一种计及用户不确定性特征和用户可调度意愿的EV实时调节功率刻画及频率支撑策略模型。通过高斯混合分布和Logit模型，制定兼顾辅助频率控制和用户满意度的充电方案，得出如下结论：
1）考虑用户特性和用户意愿，刻画了EV调节边界，约束EV实时调频功率。通过改变EV功率波动上下限确定用户调频方式，准确刻画EV调频边界。
2）基于SPSS对仿真结果中影响用户可调度意愿的各决策变量进行相关性分析，随后采用T检验对其进行显著性验证。发现EV用户的初始SOC、在充电桩的停靠时间和电价激励是影响EV参与电网调频行为重要的三个决策变量。从整体角度出发，本文通过摄动电价研究EV参与电网调频能力边界的影响；从个体角度出发，结合相关系数发现初始SOC相比于停靠时间及电价激励对EV个体参与调频时间占比的相关性更大。
3）提出的在保证用户荷电状态整体趋势呈现上升前提下，计及考虑用户不确定性特征和用户可调度意愿的电动汽车调频策略，保证了EV用户在参与调节过程中SOC的整体上升趋势。并且通过考虑用户意愿优化了快速频率改进控制策略，有效地减小负荷功率的波动，使频率偏差尽可能集中分布于±0.033 Hz区间。
参考文献
[1] 刘明杭, 田书, 梁英达. 考虑电动汽车用户满意度的微电网双层多目标优化调度[J]. 分布式能源, 2022, 7(2): 18-25.
Liu Minghang, Tian Shu, Liang Yingda. Double-level multi-objective optimal scheduling of microgrid considering customer satisfaction of electric vehicles[J]. Distributed Energy, 2022, 7(2): 18-25.
[2] 刘岩, 邓彬, 王瑾, 等. 基于多目标优化模型的电动汽车充电调度策略[J]. 沈阳工业大学学报, 2022, 44(2): 127-132.
Liu Yan, Deng Bin, Wang Jin, et al. Charging scheduling strategy of electric vehicle based on multi-objective optimization model[J]. Journal of Shenyang University of Technology, 2022, 44(2): 127-132.
[3] 王雨晴, 王文诗, 徐心竹, 等. 面向低碳交通的含新能源汽车共享站电-氢微能源网区间-随机混合规划方法[J]. 电工技术学报, 2023, 38(23): 6373-6390.
Wang Yuqing, Wang Wenshi, Xu Xinzhu, et al. Hybrid interval/stochastic planning method for new energy vehicle sharing station-based electro-hydrogen micro-energy system for low-carbon transportation[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6373-6390.
[4] 杨健维, 杨鹤, 张夏霖, 等. 基于换电规则优化与车辆–电池组匹配的电动公交车充换电站充电优化策略[J]. 中国电机工程学报, 2019, 39(8): 2337-2347, 16.
Yang Jianwei, Yang He, Zhang Xialin, et al. A charging optimization strategy on charging and swapping station for electric buses based on optimization of switching rules and matching of buses and batteries[J]. Proceedings of the CSEE, 2019, 39(8): 2337-2347, 16.
[5] 杨镜司, 秦文萍, 史文龙, 等. 基于电动汽车参与调峰定价策略的区域电网两阶段优化调度[J]. 电工技术学报, 2022, 37(1): 58-71.
Yang Jingsi, Qin Wenping, Shi Wenlong, et al. Two-stage optimal dispatching of regional power grid based on electric vehicles' participation in peak-shaving pricing strategy[J]. Transactions of China Electro-technical Society, 2022, 37(1): 58-71.
[6] 徐湘楚, 米增强, 詹泽伟, 等. 考虑多重不确定性的电动汽车聚合商参与能量-调频市场的鲁棒优化模型[J]. 电工技术学报, 2023, 38(3): 793-805.
Xu Xiangchu, Mi Zengqiang, Zhan Zewei, et al. A robust optimization model for electric vehicle aggregator participation in energy and frequency regulation markets considering multiple uncertainties [J]. Transactions of China Electrotechnical Society, 2023, 38(3): 793-805.
[7] 吴珊, 边晓燕, 张菁娴, 等. 面向新型电力系统灵活性提升的国内外辅助服务市场研究综述[J]. 电工技术学报, 2023, 38(6): 1662-1677.
Wu Shan, Bian Xiaoyan, Zhang Jingxian, et al. A review of domestic and foreign ancillary services market for improving flexibility of new power system[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1662-1677.
[8] 朱磊, 黄河, 高松, 等. 计及风电消纳的电动汽车负荷优化配置研究[J]. 中国电机工程学报, 2021, 41(增刊1): 194-203.
Zhu Lei, Huang He, Gao Song, et al. Research on optimal load allocation of electric vehicle considering wind power consumption[J]. Proceedings of the CSEE, 2021, 41(S1): 194-203.
[9] 窦迅, 王俊, 杨志宏, 等. 含交直流混合配网综合能源系统的电动汽车分群调控策略[J]. 中国电机工程学报, 2021, 41(14): 4829-4844.
Dou Xun, Wang Jun, Yang Zhihong, et al. Cluster-based control strategies of electric vehicles for integrated energy system with AC-DC hybrid distribution network[J]. Proceedings of the CSEE, 2021, 41(14): 4829-4844.
[10] 张绍兴. 大规模电动汽车接入后考虑电价激励的配电网优化运行[D]. 北京: 华北电力大学, 2022.
Zhang Shaoxing Optimal operation of distribution network considering price incentive after large-scale electric vehicles are connected[D]. Beijing: North China Electric Power University, 2022.
[11] 黄小庆, 李隆意, 徐鹏鑫, 等. 多主体博弈共赢的电动汽车充电桩共享方法[J]. 电工技术学报, 2023, 38(11): 2945-2961.
Huang Xiaoqing, Li Longyi, Xu Pengxin, et al. Electric vehicle charging pile sharing method based on multi-subject game and win-win[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 2945-2961.
[12] Habibifar R, Aris Lekvan A, Ehsan M. A risk-constrained decision support tool for EV aggregators participating in energy and frequency regulation markets[J]. Electric Power Systems Research, 2020, 185: 106367.
[13] Das S, Acharjee P, Bhattacharya A. Coordinated charging scheduling for electric vehicles and optimal tuning of the controller for frequency regulation under uncertain environment[C]//2021 IEEE Industry Applications Society Annual Meeting (IAS), Vancouver, BC, Canada, 2021: 1-6.
[14] Germanà R, Liberati F, De Santis E, et al. Optimal control of plug-In electric vehicles charging for composition of frequency regulation services[J]. Energies, 2021, 14(23): 7879.
[15] 张谦, 邓小松, 岳焕展, 等. 计及电池寿命损耗的电动汽车参与能量-调频市场协同优化策略[J]. 电工技术学报, 2022, 37(1): 72-81.
Zhang Qian, Deng Xiaosong, Yue Huanzhan, et al. Coordinated optimization strategy of electric vehicle cluster participating in energy and frequency regulation markets considering battery lifetime degradation[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 72-81.
[16] 张良, 孙成龙, 蔡国伟, 等. 基于PSO算法的电动汽车有序充放电两阶段优化策略[J]. 中国电机工程学报, 2022, 42(5): 1837-1852.
Zhang Liang, Sun Chenglong, Cai Guowei, et al. Two-stage optimization strategy for coordinated charging and discharging of EVs based on PSO algorithm[J]. Proceedings of the CSEE, 2022, 42(5): 1837-1852.
[17] 鲍谚, 贾利民, 姜久春, 等. 电动汽车移动储能辅助频率控制策略的研究[J]. 电工技术学报, 2015, 30(11): 115-126.
Bao Yan, Jia Limin, Jiang Jiuchun, et al. Research on the control strategy of electric vehicle mobile energy storage in ancillary frequency regulation[J]. Transactions of China Electrotechnical Society, 2015, 30(11): 115-126.
[18] 吴巨爱, 薛禹胜, 谢东亮, 等. 电动汽车参与电量市场与备用市场的联合风险调度[J]. 电工技术学报, 2023, 38(23): 6407-6418.
Wu Juai, Xue Yusheng, Xie Dongliang, et al. The joint risk dispatch of electric vehicle in day-ahead electricity energy market and reserve market[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6407-6418.
[19] 杨晓东, 张有兵, 蒋杨昌, 等. 微电网下考虑分布式电源消纳的电动汽车互动响应控制策略[J]. 电工技术学报, 2018, 33(2): 390-400.
Yang Xiaodong, Zhang Youbing, Jiang Yangchang, et al. Renewable energy accommodation-based strategy for electric vehicle considering dynamic interaction in microgrid[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 390-400.
[20] 史一炜, 冯冬涵, Zhou Ella, 等. 基于主从博弈的充电服务商充电引导方法及其定价策略[J]. 电工技术学报, 2019, 34(增刊2): 742-751.
Shi Yiwei, Feng Donghan, E Zhou, et al. Charging guidance method and pricing strategy of charging service providers based on master-slave game[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 742-751.
[21] 昆德. 电力系统稳定与控制[M]. 北京: 中国电力出版社, 2002.
[22] 鲍谚, 姜久春, 张维戈, 等. 电动汽车移动储能系统模型及控制策略[J]. 电力系统自动化, 2012, 36(22): 36-43.
Bao Yan, Jiang Jiuchun, Zhang Weige, et al. Model and control strategy of electric vehicle mobile energy storage system[J]. Automation of Electric Power Systems, 2012, 36(22): 36-43.
[23] 刘畅. 电动汽车快充网络运营技术[M]. 北京: 中国电力出版社, 2017.
Adjusting Power Characterization and Frequency Support Strategies for Electric Vehicles Considering Characteristics and Willingness
Abstract As electric vehicles (EVs) achieve higher penetration, their potential as mobile energy storage systems for auxiliary frequency control becomes increasingly evident. However, uncertainties in EV user behaviors, such as irregular charging patterns and diverse preferences, present challenges to fully utilizing their frequency regulation capabilities. This study proposes a power boundary description model and frequency support strategy for EVs, integrating user-specific characteristics and preferences to address these issues.
The research begins with a detailed analysis of uncertainties related to EV user behaviors, battery capacities, and charging/discharging rates. A Gaussian mixture distribution method is employed to model these uncertainties, capturing the probabilistic variability inherent in user behavior. To further refine the model, a Logit framework predicts the schedulability of EVs, accounting for user willingness to participate in grid services based on factors such as charging convenience and state-of-charge (SOC) preferences.
Building on this foundation, the study develops a dynamic EV regulation boundary model that reflects user preferences and behavior characteristics. By adjusting the upper and lower limits of power fluctuations, the model defines flexible boundaries tailored to individual user needs. This approach ensures an upward trend in users’ SOC during participation in grid services, preventing excessive battery depletion and enhancing user satisfaction. The regulation strategy dynamically adjusts to user-defined constraints, enabling effective participation in grid frequency control while respecting user autonomy.
To validate the feasibility of the proposed method, simulations are conducted under various scenarios. The results demonstrate that the regulation strategy significantly improves frequency stability metrics. Compared to conventional methods, the proposed approach reduces maximum and minimum frequency deviations by 13.91% and 29.27%, respectively, and decreases the root mean square frequency deviation by up to 29.59%. The method also shortens the duration of extreme frequency deviations by 42.69%, showcasing its ability to enhance grid frequency stability while minimizing disruptions to user operations.
This study also examines the broader implications of integrating user-specific characteristics into EV frequency regulation. By ensuring a balance between grid stability and user satisfaction, the proposed strategy highlights the potential of EV fleets as flexible and reliable grid resources. The findings emphasize the role of EVs in supporting renewable energy integration, mitigating the challenges posed by the variability of wind and solar power. In conclusion, the study provides a comprehensive framework for characterizing EV power boundaries and developing frequency support strategies. By incorporating user behavior and preferences into the control process, the proposed method offers a practical solution to the challenges of large-scale EV integration. These results contribute to the advancement of smart grid technologies and provide valuable insights for policymakers and grid operators aiming to maximize the benefits of EV participation in modern power systems.
Keywords：Electric vehicles, frequency regulation, user characteristics, user willingness, power boundary
中图分类号：TM614
DOI: 10.19595/j.cnki.1000-6753.tces.240773
吉林省科技厅一般项目资助（YDZJ202401566ZYTS）。
收稿日期 2024-05-14
改稿日期 2024-11-27
杨德健 男，1990年生，博士，副教授，研究方向为风力发电机并网控制技术。
E-mail：yangdejian@neepu.edu.cn
卢学炫 男，2000年生，硕士研究生，研究方向为电动汽车并网控制技术。
E-mail：kayee617@126.com（通信作者）
（编辑 赫 蕾）