图1 省间电力中长期交易出清优化示意图
Fig.1 Schematic of market clearing of inter-provincial medium- and long-term power transaction
摘要 随着全国统一电力市场建设的推进，我国市场规模逐步增长。以省间电力交易为例，当前市场主体已达上千个。由于大量市场主体报价具有相似性，可能导致市场出现多组具有相同社会福利的购售匹配对，使得最大化社会福利的出清问题存在多个最优解。为保障出清的有效性与公平性，多解场景下需开展多层目标顺次寻优，但现有基于多目标优化的方法难以兼顾出清效果和效率。对此，该文以存在多解场景的省间电力交易问题为研究对象，提出多层目标顺次寻优的高效出清方法：构建多层目标顺次寻优出清模型，前序模型的最优目标函数将作为后续模型的约束，以确保高优先级目标函数的最优性；提出基于最优解达界约束的出清问题多解判定模型，以帮助了解出清问题的多解性，同时，将其嵌入顺次寻优出清流程，通过避免无效寻优实现出清进程加速；提出有效利用前序模型求解信息的出清无损加速方法，以满足计算效率要求。基于我国实际交易数据的算例仿真表明，所提方法可在保障首要目标最优性的前提下，有效地提升面向次要目标的出清效果；所提加速策略可将典型场景的出清计算效率无损提高37倍。
关键词：省间电力中长期交易 出清问题多解 多层目标顺次寻优 多解判定 出清加速
发挥电力市场资源配置作用是提升电网新能源消纳水平、推动落实“双碳”目标的重要途径，省间电力中长期市场则是其中关键、基础的环节之一，其通过资源广域优化配置实现新能源的跨区消纳、缓解我国能源供需逆向分布难题[1-2]。
省间电力中长期交易出清以社会福利最大化为目标，在考虑输配电费及网损成本后，根据市场成员报价确定成交的购售匹配对及各匹配对经过的输电路径，可构建为线性规划（Linear Programming, LP）问题形式[3]。相比于省内电力现货交易，省间电力中长期交易的市场成员由各省级电网交易主体组成，规模更加庞大。根据市场组织经验，由于同一地区、相同类型机组具有相似的成本及报价行为，在考虑输电费和网损折价后省间电力中长期交易的市场成员之间常出现报价相同的情形，使得某些购售匹配对具有相同的社会福利，可能导致市场出清问题存在多个最优解，即存在多种能够使社会福利最大的出清方案[4]。随着全国统一电力市场建设目标的推进，省间电力中长期交易将进一步朝着大规模方向发展[5]，届时将更容易出现出清问题存在多解的场景。面向多解场景，市场运营机构需根据市场运营目标，从众多最优解中进一步获取资源配置效果最佳的出清方案。否则，只能从众多满足社会福利最大化的出清方案中随机选取一种作为最终出清方案，无法获取面向其他市场运营目标的最优出清方案，也无法保证可成交电力在社会福利相同购售匹配对间的平等分配，将损失市场出清效果与公平性。
出清问题多解判定可为市场运营机构设计面向多解场景的处理措施提供参考。对于省间电力中长期交易出清这类LP问题，现有研究根据非基变量检验数的取值是否为零来判定其是否存在多解，但文献[6]指出，当出清问题出现退化最优解时，该判定方法可能失效，难以保证多解判定的准确性。此外，文献[7]针对省内能量-备用市场联合出清问题，对可能出现的多解场景进行了探讨，但并未给出多解判定方法。文献[8]针对省内电力市场出清问题，在假定所有发电机报价均不相同的条件下，提出了出清问题多解判定准则。然而，该假设在大规模省间电力中长期交易出清问题中并不成立。因此，尚缺乏适用于省间电力中长期交易出清问题的多解判定方法。
在出清问题多解场景处理方面，有研究提出将可成交电力平均分配至报价相同的市场成员[9]。该方法可确保市场的公平性，但难以保障市场资源配置方案的最优性。为解决该问题，在当前我国省间电力中长期市场出清的工程实践中，除社会福利最大化这一首要目标外，还引入了清洁能源成交量最大化以及总成交量最大化等多层次目标。省间电力中长期交易出清问题由此转换为多目标优化问题，市场运营机构希望通过多层目标的顺次寻优，给出依次满足不同层次优化目标的出清方案，以保障多解场景下市场出清的有效性。现有多目标优化方法主要包括加权法和Pareto解集法。其中，加权法通过加权求和的方式将多目标优化转换为单目标优化，不同目标函数的权重取值可反映市场运营机构对不同层次目标函数的关注程度[10-11]。该方法计算效率较高，是目前国内省间电力中长期市场所实际采用的方法。然而，目标函数权重取值对优化结果的影响较大，不合理的权重设置将影响出清方案对于更重要目标函数的最优性，无法保证多层目标的顺次实现[12]。Pareto解集法旨在获取多目标优化模型的Pareto最优解集，最优解集中每个解至少有一个目标函数是最优的，市场运营机构可从中依次寻找针对各层次优化目标的最优解，进而实现多层目标的顺次寻优[13-14]。然而，Pareto解集的获取难度较高，一般采用智能算法、权重法等策略进行求取，存在计算效率低或参数设置困难等问题[15]，难以应用于工业实际。
综上所述，面向省间电力中长期交易出清问题的多解场景，目前尚缺乏适用的多解判定方法以及保障市场资源配置效果的高效出清方法，难以获得顺次满足多层次寻优目标的最优出清方案。对此，本文提出了多层目标顺次寻优的省间电力中长期交易高效出清方法，主要贡献如下：
1）提出多层目标顺次寻优的省间电力中长期交易出清策略。构建了多层目标顺次寻优出清模型，将前序模型的最优目标函数作为下一层次模型的运行约束，进而在满足高优先级目标函数最优性的条件下展开针对下一层次目标函数的寻优，从而保障市场资源配置效果。提出基于最优解达界约束的出清问题多解判定模型，可帮助市场运营机构了解出清问题的多解性，同时，可判定多层目标顺次寻优过程中出清问题是否存在多解，若不存在多解，则可不再执行后续出清模型的求解，进而简化出清流程，提升出清计算效率。
2）提出了有效利用前序模型求解信息的省间电力中长期交易出清无损加速方法。针对多层目标顺次寻优出清模型，将前序出清模型最优解作为下一层次出清模型的高质量初始可行解，引导后续出清模型的热启动无损加速进程；针对出清问题多解判定模型，基于前序出清模型最优解及计算过程中当前可行解目标函数的取值，建立了多解判定模型求解进程终止判据，在出清问题多解场景下可提前结束求解进程而不影响多解判定的准确性，为后续多解场景的处理预留时间。
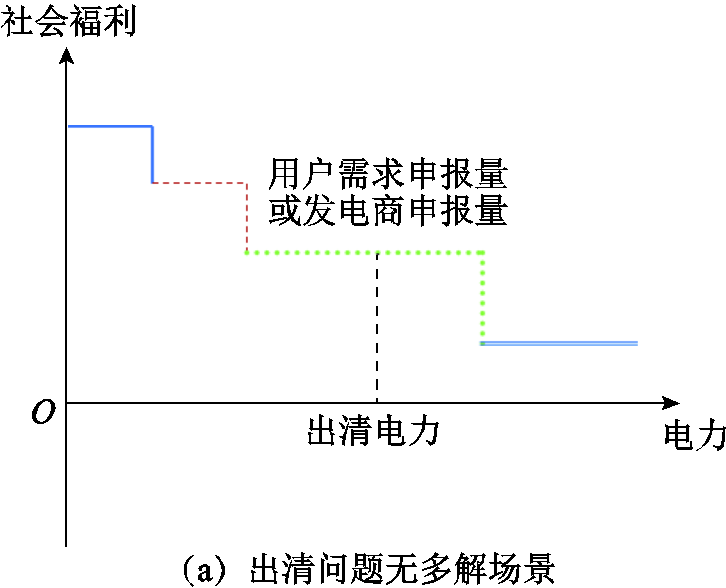
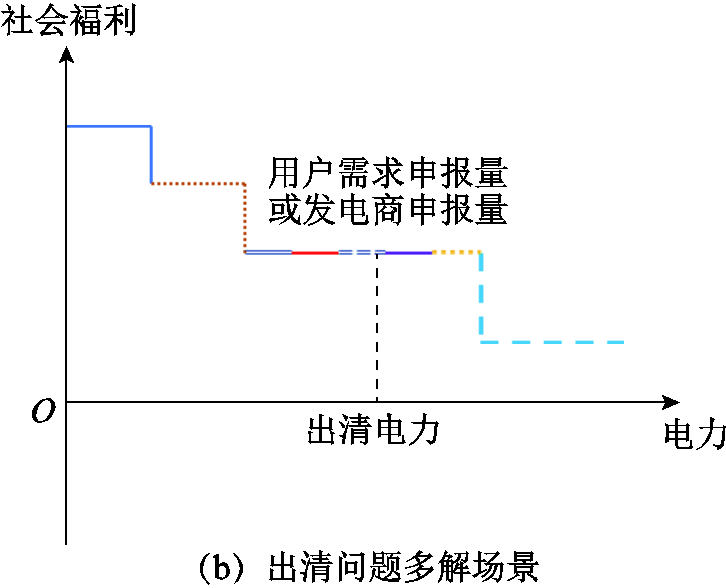
本节将探讨省间电力中长期交易出清问题存在多解的原因。为便于阐述，在假设输电通道传输容量足够的前提下，省间电力中长期交易出清优化问题的示意图如图1所示。图中，不同颜色线段代表不同的购售匹配对，其社会福利包括了输电费和网损折价，详见2.2.1节。值得一提的是，本文研究的省间电力中长期交易出清问题主要关注有功功率的交易，无功功率并不在考虑范畴内。
省间电力中长期交易出清优化示意图如图1所示，图中不同线型线段代表不同购售匹配对。不同购售匹配对将按照其社会福利由高到低的顺序依次中标电力，直至满足用户申报需求或发电商申报电力全部出清。值得一提的是，同一用户可以通过不同输电路径与不同的发电商组成购售匹配对，类似地，同一发电商也可与不同的用户组成购售匹配对。以用户为例，当某一用户与某一发电商所组成的购售匹配对的社会福利较低时，该用户与其他发电商所组成的社会福利较高的购售匹配对将优先中标，当其他发电商能够满足该用户的申报需求时，该用户与该发电商所组成的购售匹配对将无法中标（即图1中出清电力之后的购售匹配对）。
图1 省间电力中长期交易出清优化示意图
Fig.1 Schematic of market clearing of inter-provincial medium- and long-term power transaction
如图1a所示，当不同的购售匹配对具有不同的社会福利时，省间电力中长期交易出清问题将具有唯一解。但当不同购售匹配对具有相同的社会福利时，省间电力中长期交易出清问题将可能存在多个最优解，如图1b所示，图中5个社会福利相同购售匹配对之间任一满足出清电力的中标组合均为出清问题最优解。
如1.1节所述，当出清问题存在多解时，意味着多种购售匹配对的中标组合均满足社会福利最大化这一出清目标。在该场景下，为保障最终出清方案的资源配置效果，应从众多最优解中进一步寻找更优的出清方案。为此，国内工业界在社会福利最大化这一目标的基础上，进一步引入清洁能源成交量最大化、总成交量最大化等其他目标，并通过加权求和形成综合考虑多种目标的单目标优化问题，如图2a所示。在完成出清问题求解后，再进一步将用户与发电商之间的交易量平均分配到不同的可行交易路径上，以提升出清方案的公平性。然而，不合理的目标函数权重设置将使多目标优化方法难以保障出清方案对于重要程度更高目标函数的最优性，影响最终出清方案的资源配置效果。同时，仅计及可行交易路径的中标电力再分配方式无法考虑其他具有相同社会福利但未中标的用户-发电商交易对，难以真正保障出清方案的公平性。此外，该方法只能给出最终的市场出清方案，无法获取出清问题的多解特性，难以为市场运营机构设计应对多解场景的处理措施提供可靠依据。
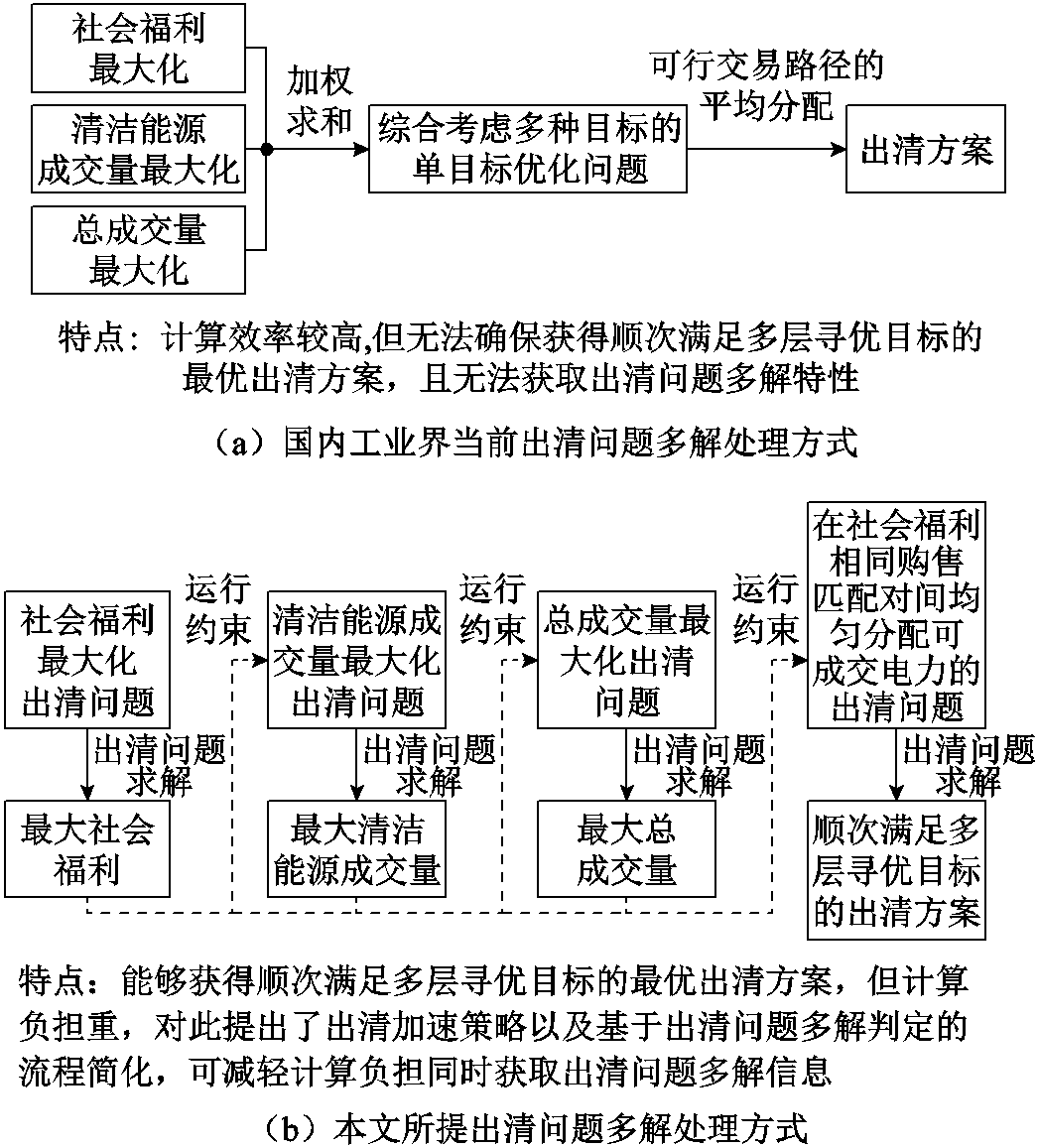
图2 省间电力中长期交易出清问题多解处理方式对比
Fig.2 Method comparison for handling market clearing problem of inter-provincial medium- and long-term power transaction with multiple solutions
针对工业界当前处理方式存在的问题，本文提出了多层目标顺次寻优的省间电力中长期交易出清思路，如图2b所示。通过在满足高优先级目标函数最优性的条件下顺次求解针对各层目标函数的出清问题，可确保最终出清方案的资源配置效果而不依赖参数设置。同时，通过在社会福利相同购售匹配对间均匀分配可成交电力这一目标函数的引入，有力地保障了出清方案的公平性而无需对出清结果进行再调整。然而，省间电力交易出清问题的顺次求解将大幅增加出清计算负担。为此，本文基于出清问题多解判定对多层目标顺次寻优出清流程进行了简化，并提出了有效利用前序模型求解信息的出清无损加速方法。本文所提多层目标顺次寻优的省间电力中长期交易出清策略将在第2节进行详细介绍；所提有效利用前序模型求解信息的省间电力中长期交易出清无损加速方法将在第3节进行详细介绍。
对比当前工业界所采用的多目标优化方法与本文所提方法可以发现，当不同目标函数权重值设置得完全合理时，现有多目标优化方法能够满足多层目标顺次实现需求，此时多目标优化方法与本文所提方法在出清方案资源配置效果方面是等效的。然而，当目标函数权重值设置不合理时，多目标优化方法将无法保证最终出清方案对于更重要目标函数的最优性，此时所提方法将不能被多目标优化方法所替代，本文算例分析部分也对此进行了分析论证。此外，本文所提出清问题多解判定模型可获取出清问题的多解特性，在这一点上所提方法无法被多目标优化方法所替代。
本节所提多层目标顺次寻优的省间电力中长期交易出清流程如图3所示。
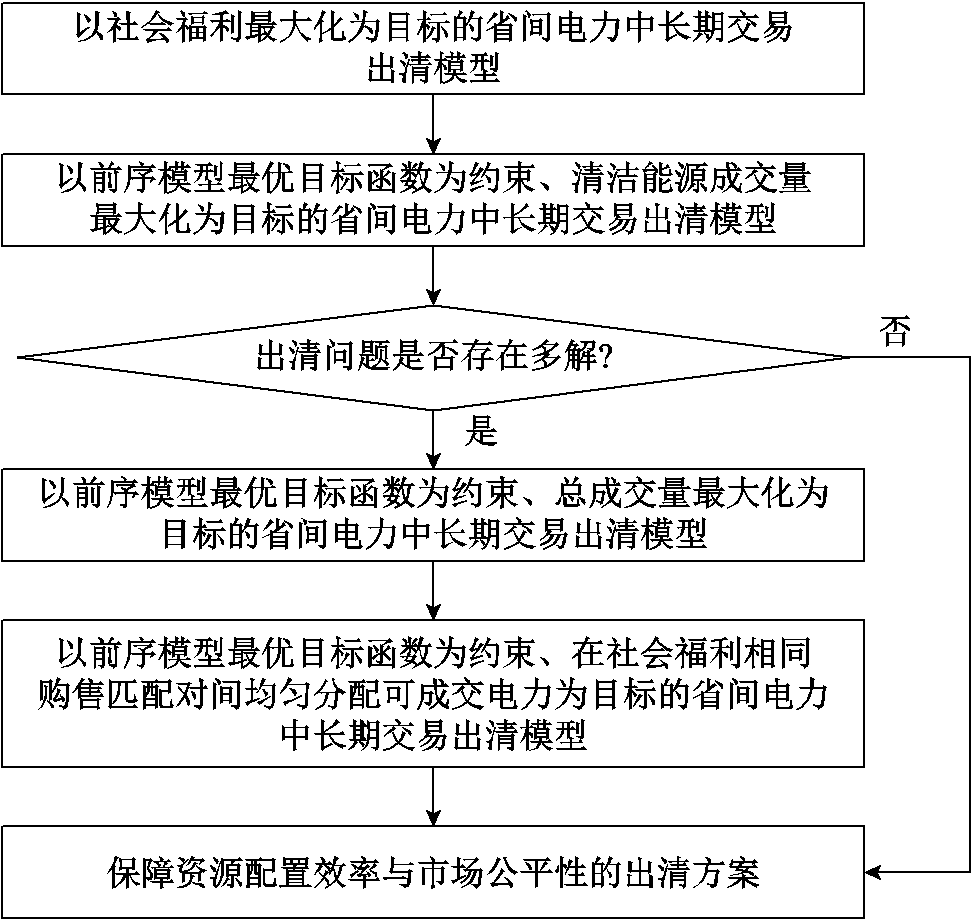
图3 多层目标顺次寻优的省间电力中长期交易出清流程
Fig.3 Market clearing idea of inter-provincial medium- and long-term power transaction with sequential optimization for multi-level objectives
所提多层目标顺次寻优出清策略根据市场资源配置目标建立了多层出清优化目标（社会福利最大化、清洁能源成交量最大化、总成交量最大化及在社会福利相同购售匹配对间均匀分配可成交电力），并顺次开展面向不同层次目标的出清优化。其中，前一层次的最优目标函数将作为下一层次出清模型的运行约束，以确保重要程度更高目标函数的最优性。通过前三个层次目标的顺次寻优，可保障出清方案的资源配置效果，通过第四个层次目标的寻优，则可进一步保障出清方案的公平性。
通过四个层次目标的顺次寻优，可保证即使出清问题存在多解现象，所获取的出清方案也是众多出清解中效果最佳的方案。然而，大规模省间电力中长期交易出清问题面临着较重的计算负担[16]，上述策略中顺次求解四个出清模型的流程较为繁琐，计算负担较重。本文基于我国交易中心实际数据开展了仿真测试，发现通过前两个层次目标的顺次寻优可有效减少出清问题多解场景（以所收集的省间电力中长期交易实际数据为初始场景，假设市场主体报量报价信息的变化服从正态分布，通过抽样生成了100个交易场景，经首要目标寻优后共有20个场景存在多解，占比20%，表明多解场景不可忽视，而经前两个层次目标的顺次寻优后出清问题仍有多解的场景仅占7%）。此外，经出清问题多解判定后，本文发现由省间电力中长期交易实际数据直接构成的出清场景在首要目标寻优后存在多解（经前两个层次目标的顺次寻优后不再存在多解），表明多解现象在我国实际交易过程中真实存在。具体而言，在该场景中，最终得以中标的不同边际购售匹配对具有相同社会福利，且受输电通道传输容量限制，边际购售匹配对未能完全中标，此时可中标电力在不同边际购售匹配对间的任意分配均为出清问题最优解，最终导致出清问题存在多解。同时，值得一提的是，本文所收集的实际数据为众多交易场景中任意挑选的某一普通场景，并非特意挑选的出清问题多解场景。综上可见，出清问题多解场景在我国实际交易中并非极为罕见的特殊场景，而经前两个层次目标的顺次寻优后可有效减少多解场景的数目。
对此，所提策略在第二层次出清模型的求解之后嵌入了出清问题多解判定环节：若此时出清问题仅有唯一解，则不再执行后续两个层次出清模型的求解，直接得到最终出清方案；反之，若出清问题仍存在多解，则继续开展面向后续目标的寻优以获得保障资源配置效果的出清方案。多解判定环节的嵌入可简化大部分场景下省间电力中长期交易的出清流程，提升出清的计算效率。此外，多解判定也可帮助市场运营机构了解出清问题的多解性，为多层目标顺次寻优的出清策略设计提供参考。例如，若经历史数据分析发现在完成前三个层次目标的顺次寻优后，仍存在较多出清多解场景，则可进一步引入售方碳排放量最低等其他目标，以确保出清方案的资源配置效果。
所提策略中面向各层次寻优目标的出清模型以及出清问题多解判定方法将分别在2.2节及2.3节进行详细介绍，所提策略的详细计算流程将在2.4节进行详细介绍。
如2.1节所述，所提多层目标顺次寻优的省间电力中长期交易出清模型由四个以各层次寻优目标为目标函数的出清模型构成，分别阐述如下。
2.2.1 以社会福利最大化为目标的出清模型
1）目标函数
社会福利最大化是市场资源配置的首要目标，也是现有省间电力中长期交易出清模型所普遍采用的目标函数[17]，即
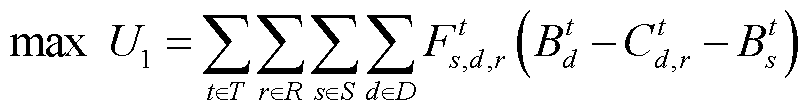（1）
式中，d、s、r、t分别为购方、售方、路径和时段的编号；D、S、R、T分别为购方、售方、路径和时段的集合；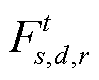
为一对购售匹配对（本文所述购售匹配对包含购方、售方、路径和时段四维信息），即t时段购方d和售方s在路径r上的成交电力；
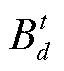和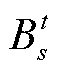
分别为购方和售方申报的价格；
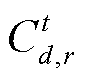为购方d通过路径r购电所需承担的输电费和网损折价，可由式（2）计算得到。
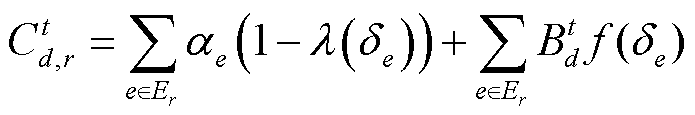（2）
式中，第一项为输电费，e为输电通道或节点的编号，Er为交易路径r所经过的所有输电通道或节点的集合，αe为输电通道或节点的输电价格，δe为输电通道或节点的网损系数，λ(δe)为关于网损系数的折算公式；第二项为网损折价，f(δe)为关于网损系数的折算公式。λ(δe)和f(δe)的具体表达式详见文献[18]。
由式（1）可见，每一购售匹配对的社会福利包括了输电费用和网损折价。
2）运行约束
省间电力中长期交易出清模型的运行约束主要包括[3]：①售方中标电力约束，售方中标电力应不超过其申报量；②购方中标电力约束，考虑网损后的购方中标电力应不超过其申报量；③交、直流输电通道可用输电能力（Available Transfer Capability, ATC）约束，经由输电通道上的潮流应不超过其ATC；④输电通道潮流变化率约束，相邻时段间输电通道的潮流变化量应不超过其限值。
上述模型即为所提多层目标顺次寻优出清模型中的第一层次出清模型，可简化表示为m1。
2.2.2 以清洁能源成交量最大化为目标的出清模型
假设第一层次出清模型m1所求得的最优目标函数为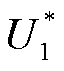
，以此为基础可构建以清洁能源成交量最大化为目标的第二层次出清模型m2，具体如下。
1）目标函数
以清洁能源成交量最大化为目标的目标函数可表示为
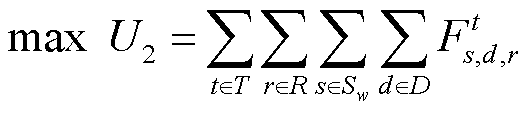（3）
式中，Sw为清洁能源售方主体的集合。
2）运行约束
（1）前序出清模型最优目标函数约束
在多层目标顺次寻优出清策略下，第二层次出清模型m2所获取的出清方案需满足社会福利最大化这一首要目标，即
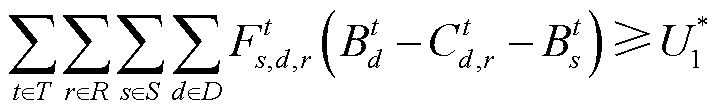（4）
（2）其他常规运行约束
m2所需满足的其他常规运行约束与m1中运行约束相同。
需要说明的是，清洁能源成交量的增大理论上将导致系统对电压支撑电源的需求增大。然而，由于当前国内外市场出清未考虑无功功率、电压的影响，电压支撑电源在出清过程中不会因无功支撑的必要性而获得稳定出清。因此，即便系统无功支撑需求增大，电压支撑电源也无法通过抬高报价来影响市场价格，进而影响市场资源配置效果。此外，即使未来市场出清中考虑了无功影响，数目繁多的电压支撑电源也会因巨大的竞争压力而不敢贸然抬高自身报价。由此可见，以清洁能源成交量最大化为目标的出清模型并不会影响市场中电压支撑电源的配置效果。
2.2.3 以总成交量最大化为目标的出清模型
与第二层次出清模型m2类似，可根据m1所求得的最优目标函数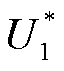以及m2所求得的最优目标函数
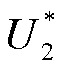，构建以总成交量最大化为目标的第三层次出清模型m3，具体如下。
1）目标函数
以总成交量最大化为目标的目标函数可表示为
（5）
2）运行约束
（1）前序出清模型最优目标函数约束
第三层次出清模型m3需同时满足社会福利最大化以及清洁能源成交量最大化这两个前序出清模型的优化目标，分别如式（4）和式（6）所示。
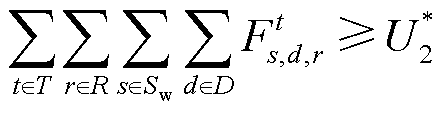（6）
（2）其他常规运行约束
m3所需满足的其他常规运行约束与m1中运行约束相同。
通过m1～m3的顺次求解，可保证即使出清问题存在多解现象，所获出清方案也是众多出清解中资源配置效果最佳的方案。
2.2.4 以在社会福利相同购售匹配对间均匀分配可成交电力为目标的出清模型
通过前述m1～m3的顺次求解可以减少出清方案多解场景的发生次数，但这仍不能保证所获出清方案的唯一性。当出清方案多解现象发生时，秉着市场公平性原则，市场运营机构需从众多出清解中选择相对公平的出清方案。为此，本节进一步引入以在社会福利相同购售匹配对间均匀分配可成交电力为目标的第四层次出清模型m4，进而保障出清方案的公平性，具体如下。
1）目标函数
以在社会福利相同购售匹配对间均匀分配可成交电力为目标的目标函数可表示为
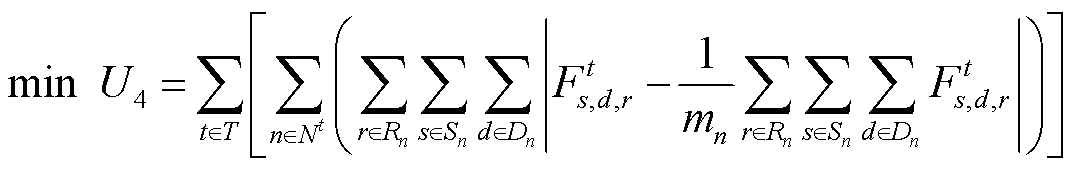（7）
式中，n为具有相同社会福利购售匹配对组别的编号；mn为第n组购售匹配对中购售匹配对的个数；Nt为第t时段具有相同社会福利购售匹配对组别的集合；Rn、Sn和Dn分别为第n组购售匹配对中路径、售方和购方的集合。
式（7）中最小化目标函数里的绝对值项可通过引入非负辅助变量的方式进行线性化处理，详见文献[19]。
2）运行约束
（1）前序出清模型最优目标函数约束
第四层次出清模型m4需同时满足社会福利最大化、清洁能源成交量最大化以及总成交量最大化这三个前序出清模型的优化目标，分别如式（4）、式（6）和式（8）所示。
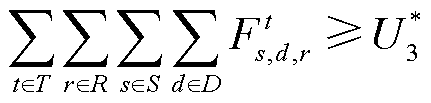（8）
（2）非社会福利相同购售匹配对中标量固定约束
对于不属于某一具有相同社会福利购售匹配对组别的购售匹配对，其中标量无需进行再分配，故其中标量应与第三层次出清模型m3所获最优解保持一致，如式（9）所示。同时，该约束提前固定了部分购售匹配对的中标量，可降低m4的求解负担。
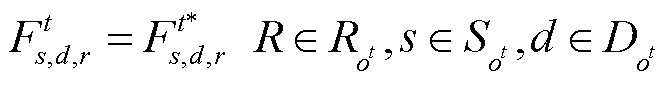（9）
式中，
、
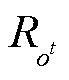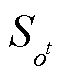和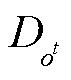
分别为第t时段不属于某一具有相同社会福利购售匹配对组别的路径、售方和购方的集合；
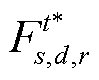为m3所获最优解。
（3）其他常规运行约束
m4所需满足的其他常规运行约束与m1中运行约束相同。
在m4目标函数中的绝对值项经过线性化处理后，前述四个层次的出清模型均为LP问题，通过m1～m4的顺次求解，可确保即使出清问题存在多解，最终获取的出清方案也能够有效保障资源配置效果与市场公平性。
此外，本文所述针对各层目标的出清模型均为LP问题。对于LP问题，只要其存在可行解，采用单纯形等算法便能够求得该问题的全局最优解。而由前序出清模型和后续出清模型的构成可以发现，前序出清模型所求得的最优解一定是后续出清模型的可行解。由此可见，只要前序出清模型求解可行，本文所提方法便能够求得后续出清模型的全局最优解，且该最优解能够同时满足前序目标与后续目标的最优性。
如2.1节所述，在第二层次出清模型完成求解后嵌入多解判定环节可有效避免后续出清模型的求解，从而简化省间电力中长期交易出清流程。本文提出的出清问题多解判定方法详述如下。
如2.2节所述，第二层次出清模型m2为LP问题，为便于后续描述，m2可改写为
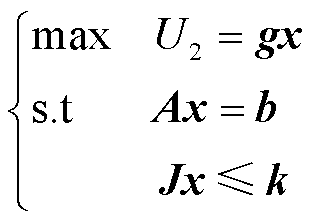（10）
式中，x为决策变量，即购售对的中标电力；g为目标函数系数向量；A为等式约束的系数矩阵；b为等式约束的右端项常数；J为不等式约束的系数矩阵；k为不等式约束的右端项常数矩阵。
假设通过求解器求得的最优出清解为x*，判定出清问题是否有多解即是判定除x*外是否还有其他可行解也能够达到最优目标函数。对于LP出清问题而言，求解器输出的最优出清解x*将是其发现的某一最优基可行解，对应于可行域上的某一顶点，而这一顶点将与一组达界约束唯一对应。因此，可通过寻找是否存在既能达到原出清模型最优目标函数，又能使原出清模型最优解达界约束集合中某些约束不达界的可行解来判定出清问题是否存在多解。基于上述考虑，本节提出基于最优解达界约束的出清问题多解判定模型为
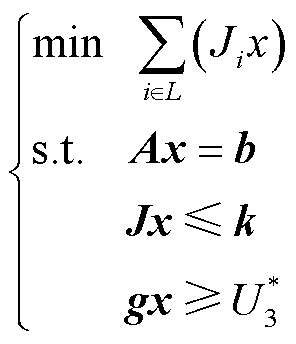（11）
式中，i为不等式约束系数矩阵的行编号；L为根据出清模型式（10）最优出清解x*所获取的不等式约束中达界约束的集合。
由于出清模型式（10）中不等式约束为小于或等于右端项k，故出清问题多解判定模型式（11）的目标函数最大值将为约束集合L中右端项之和（记为K）。若原出清模型式（10）存在多解，则表明除x*外还有其他解能够满足优化模型式（11）的运行约束，这些解中约束集合L里将存在不达界的约束（L全部达界的情况与原出清模型最优解x*唯一对应），由于多解判定模型的目标函数为最小化L中右端项之和，故此时优化模型式（11）的最优目标函数将小于K；若原出清模型式（10）只有唯一解（即x*），则表明只有x*能够满足优化模型式（11）的运行约束，由于x*中不等式约束集合L将全部达界，故此时多解判定模型的目标函数将等于K。综上所述，可根据多解判定模型的目标函数是否小于K来判定原出清模型式（10）是否存在多解。
本文所提多层目标顺次寻优的省间电力中长期交易出清策略的计算流程总结如下：
1）求解以社会福利最大化为目标的出清模型m1，获取最大社会福利。
2）求解以清洁能源成交量最大化为目标、以最大社会福利为约束的出清模型m2，在保障最大社会福利的条件下，获取最大清洁能源成交量。
3）判定当前获取的出清方案是否存在多解，若存在多解，转步骤4）；否则，转步骤6），输出最优出清方案。
4）求解以总成交量最大化为目标、以前序目标最优性为约束的出清模型m3，在满足前序目标最优性的条件下，获取最大总成交量。
5）求解以在社会福利相同购售匹配对间均匀分配可成交电力为目标、以前序目标最优性为约束的出清模型m4，在满足前序目标最优性的条件下，确保可成交电力在社会福利相同购售匹配对间的公平分配。
6）获取省间电力中长期交易最优出清方案，输出结果。
本文所提多层目标顺次寻优的省间电力中长期交易出清策略能够保障出清问题多解场景下所获出清方案的资源配置效果，但所提策略需额外开展面向其他层次目标函数的出清模型求解以及出清问题多解判定模型的求解，将加重出清问题的计算负担。为满足实际市场出清计算效率要求，本文针对多层目标顺次寻优的省间电力中长期交易出清模型及出清问题多解判定模型分别提出了加速方法，可在不损失计算精度的条件下，有效提升计算速度，分别阐述如下。
如2.1节所述，本文所提多层目标顺次寻优的出清策略需依次求解两个（多解判定结果为无多解时）或四个（多解判定结果为存在多解时）出清模型，相比于仅需求解社会福利最大化出清模型的传统方式，将面临更重的计算负担。为此，本小节将利用前序出清模型求解信息实现后续出清模型的无损加速。需要说明的是，本文重点关注完成第一层次出清模型（即社会福利最大化出清模型）的求解之后，如何有效提升后续出清模型的求解效率，对于初始出清模型的加速计算，则不在本文研究范畴。
2.2节中每一层次的出清模型均是一个大规模LP问题，常用求解方法包括单纯形法、Barrier法等，求解思路是：先找出一个初始可行解，并从该初始可行解出发，不断迭代寻找目标函数更优的另一解，直至找到某一符合最优性判别准则的最优解[20]。对于大规模省间电力中长期交易出清问题，由于商用求解器通过预求解生成的初始可行解往往与最优解相差较大，求解算法需要经过大量迭代才能找到最优解。相反，若能从一个接近于最优解的高质量初始可行解开始迭代寻优进程，则可在不影响最优性的条件下有效地减少迭代寻优次数，实现出清问题的热启动无损加速。
对于多层目标顺次寻优出清模型，前一层次出清模型的求解信息可为后一层次出清模型的求解提供有益信息。如2.2节所述，各层次出清模型将以前序出清模型的最优目标函数作为运行约束，这表明后一层次出清模型的最优解与前一层次出清模型的最优解均可在常规运行约束的限制下满足前序目标函数的最优性，因此这两个最优解之间将较为接近。基于上述考虑，本文提出以前一层次出清模型的最优解作为后一层次出清模型的高质量初始可行解，进而实现后一层次出清模型的无损加速计算：若前一层次出清模型已不存在多解，那么所提供的初始可行解即是后一层次出清模型的最优解，因此无需迭代便可寻得最优解；即使前一层次出清模型存在多解，后一层次出清模型也能够从接近于其最优解的初始点开始迭代寻优进程，进而提升寻优速度。
如2.3节所述，本文所提出清问题多解判定模型的目标函数最大值为前序出清模型最优解中达界不等式约束的右端项之和，其通过最小化寻优来评估多解判定模型的目标函数能否小于其最大值，进而判定出清问题是否存在多解。而仅当多解判定模型的决策变量与前序出清模型最优解相等时，多解判定模型的目标函数才能达到最大值。因此，若将前序出清模型最优解作为多解判定模型的初始可行解，则能够使其快速定位目标函数最大值，并沿目标函数最小化方向开始寻优。此外，2.3节中提到，只要多解判定模型的目标函数能够小于其最大值，就可以判定出清问题存在多解，而无需完整地执行多解判定模型的求解进程。
基于上述考虑，本文提出了如下多解判定模型无损加速策略：
1）以前序出清模型的最优解作为多解判定模型初始可行解，使其初始目标函数为目标函数最大值。
2）执行多解判定模型的目标函数最小化寻优，并判断是否已完成多解判定模型的求解，若已完成，转步骤4）；否则，转步骤3）。
3）在寻优过程中不断读取当前可行解目标函数的取值，若当前目标函数小于初始目标函数，则终止多解判定模型的求解，转步骤4）；否则，返回步骤2），继续执行目标函数最小化寻优。
4）判断多解判定模型的最终目标函数是否小于其初始目标函数，若小于，则表明出清问题存在多解，输出判定结果；否则，表明出清问题不存在多解，输出判定结果。
该无损加速策略的伪代码如下：
算法1:多解判定模型无损加速策略 输入：前序出清模型的最优解；输出：出清问题多解判定结果。1: 获取前序出清模型最优解x02: 以x0为初始解3: 开始多解判定模型的最小化寻优4: while 多解判定模型未寻得最优解：5: 读取当前目标函数值6: if 当前目标函数值＜初始目标函数：7: 终止求解，存在多解，输出结果8: break9: end while10: if 求得最优解：11: if 最优解目标函数值＜初始目标函数：12: 存在多解，输出结果13: else:14: 不存在多解，输出结果
在所提多解判定模型加速策略下，若出清问题不存在多解，那么所提供的初始可行解即是多解判定模型的最优解，可使其无需迭代便可寻得最优解，进而有效提升求解效率；若出清问题存在多解，通过求解进程提前终止判据的构建，可提前结束多解判定模型的求解进程，提升模型求解速度。此外，所提策略并不对多解判定模型本身作任何简化处理，因而不会影响多解判定结果的准确性。
本文采用省间电力中长期交易实际运行数据开展算例分析，以验证所提方法的有效性。本文采用商用求解器Gurobi10.0.1对出清问题进行求解，所用计算机硬件环境为Intel(R) Core(TM) i5-12400F CPU @ 2.50 GHz 32GB RAM。
本节将在三个不同算例（S1～S3）上开展出清方法对比分析，各算例（S1～S3）的规模详见表1。
表1 各算例中省间电力交易的问题规模
Tab.1 Problem scale of the inter-provincial power transaction in S1～S3
算例S1S2S3 售方数69274274 购方数262626 路径数378378378 时段数720720720
其中，S1规模较小，将主要用于阐述所提方法在资源配置效果方面的有效性。S2与S3在算例S1的基础上增加了售方数目，以扩大交易规模，将主要用于阐述所提出清加速策略的有效性。S2与S3的规模一致，仅购售方的报量及报价信息存在差异。例如，以第一时段为例，S2与S3的售方平均报价分别为225.6元/MW和231.7元/MW，购方平均报价分别为466.5元/MW和472.1元/MW。两者因报价差异而表现出不同的多解特性（详见4.3节），可验证所提方法在不同多解场景下的有效性。
算例仿真中的对比方法如下：
M1：仅考虑社会福利最大化这一首要目标的出清方法。
M2：基于加权法的多目标出清方法。
M3：本文所提多层目标顺次寻优的出清策略，但未在出清流程中嵌入多解判定环节，也未采用基于前序模型求解信息的无损加速策略。
M4：同M3，但采用基于前序模型求解信息的无损加速策略。
M5：同M3，但在出清流程中嵌入多解判定环节。
M6（本文方法）：同M4，但在出清流程中进一步嵌入多解判定环节。
为验证所提多层目标顺次寻优出清策略在资源配置效果方面的有效性，本小节将以S1和S3为例，对比M1～M3所得出清方案的各个目标函数值，分别见表2和表3。
表2和表3中，Obj1代表社会福利（元），Obj2代表清洁能源成交量（MW），Obj3代表总成交量（MW），Obj4代表社会福利相同购售匹配对间的中标电力差异之和（MW）。M2（W1）、M2（W2）和M2（W3）分别表示三组目标函数权重取值下M2的资源配置效果，M2（W1）中四个目标的权重依次设为0.4、0.3、0.2、0.1，M2（W2）中四个目标的权重依次设为0.9、0.09、0.009、0.001，M2（W3）中四个目标的权重依次设为0.99、0.009、0.000 9、 0.000 1。
表2 S1中M1～M3所得出清方案的各目标函数值
Tab.2 Value of each objective function of market clearing results obtained by M1～M3 in S1
目标函数Obj1Obj2Obj3Obj4 M19 264 217 9374 689 787.241 049 773.3665 445 M2(W1)9 264 005 9116 122 636.341 055 833.8377 270 M2(W2)9 264 197 6366 102 825.141 049 540.2377 804 M2(W3)9 264 200 6296 055 094.441 049 709.3377 354 M39 264 217 9376 094 486.241 049 773.40
表3 S3中M1～M3所得出清方案的各目标函数值
Tab.3 Value of each objective function of market clearing results obtained by M1～M3 in S3
目标函数Obj1Obj2Obj3Obj4 M18 637 868 0584 142 160.741 018 469.3914 697 M2(W1)8 637 866 76413 758 474.341 019 721.7921 734 M2(W2)8 637 868 05813 755 953.341 018 488.5913 784 M2(W3)8 637 868 05813 755 953.341 018 488.5918 257 M38 637 868 05813 756 656.041 018 487.90
由表2和表3可见，M1仅考虑了社会福利最大化这一首要目标，因而能够确保社会福利的最优性，但所得出清方案在其他次要目标上的资源配置效果难以得到保障。
相较于M1，M2通过引入其他次要目标，提升了Obj2～Obj4的效果。然而，对比M2(W1)、M2(W2)和M2(W3)可以发现，各目标函数的权重对M2所得出清方案资源配置效果的影响较大，不合理的权重值设置将影响首要目标的最优性（表2中，M2所得出清方案的社会福利最小）。此外，采用同一套目标函数权重值的M2在不同算例上的资源配置效果也存在差异。以W2为例，M2（W2）在算例S1中难以保证首要目标的最优性（首要目标函数与最优值之间相差20 300元），而在算例S3中，M2（W2）则能够取得最优的首要目标函数。由此可见，目标函数权重值对工业界目前所采用的多目标优化方法M2的资源配置效果影响较大，不合理的权重设置将影响其资源配置效果，且同一套权重在不同算例中的适用性也难以得到保障。
相较于M1和M2，本文所提多层次目标顺次寻优出清方法（M3）能够在不损失前序目标最优性的前提下，有效地提升后序各层目标的资源配置效果。同时，由于所提方法不依赖参数设置，其在不同算例上都具有较好的适用性。具体而言，相较于M1，M3的清洁能源成交量（Obj2）在算例S1和S3中平均提升了131.03%，社会福利相同购售匹配对间的中标电力差异之和（Obj4）在算例S1和S3中由平均790 071 MW大幅下降至0 MW，保证了市场出清的有效性与公平性。由此，验证了所提方法在资源配置效果方面的有效性。
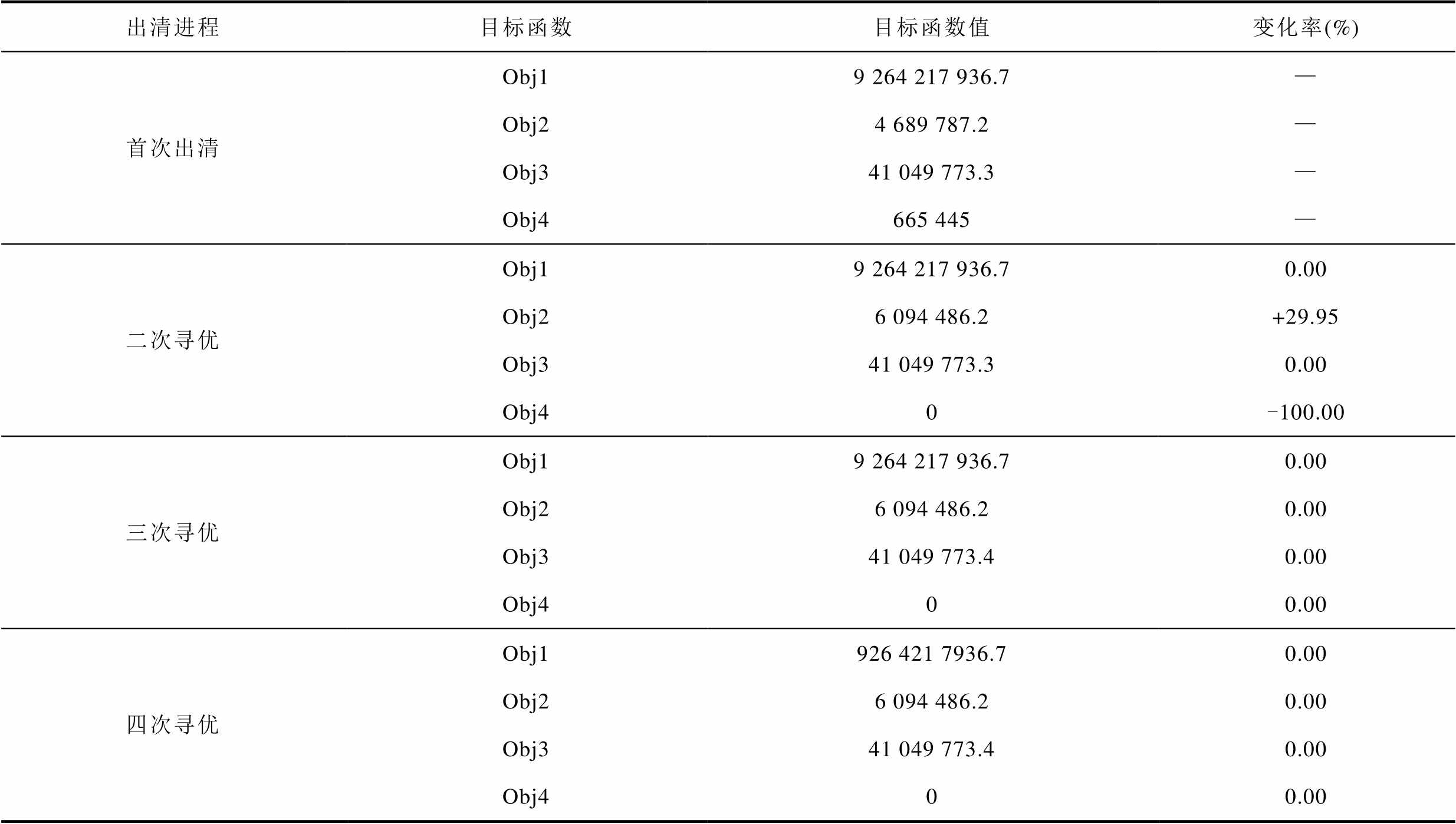
为进一步说明所提方法有效性，算例S1中M3在多层次目标顺次寻优过程中各目标函数值的变化见表4。
表4 多层次目标顺次寻优过程中各目标函数值的变化
Tab.4 Changes of each objective function value during the process of sequential optimization for multi-level objective
出清进程目标函数目标函数值变化率(%) 首次出清Obj19 264 217 936.7— Obj24 689 787.2— Obj341 049 773.3— Obj4665 445— 二次寻优Obj19 264 217 936.70.00 Obj26 094 486.2+29.95 Obj341 049 773.30.00 Obj40-100.00 三次寻优Obj19 264 217 936.70.00 Obj26 094 486.20.00 Obj341 049 773.40.00 Obj400.00 四次寻优Obj1926 421 7936.70.00 Obj26 094 486.20.00 Obj341 049 773.40.00 Obj400.00
由于存在多个满足社会福利最大化这一首要目标的最优出清方案，在执行针对清洁能源成交量最大这一第二层次目标的寻优之后，市场出清方案的资源配置效果较首次出清发生了较大变化。清洁能源成交量这一寻优目标提升了29.95%，同时，社会福利相同购售匹配对间的中标电力差异之和也大幅下降至0。由于此时的出清方案已十分接近满足多层次目标顺次实现需求的最优出清方案，故在执行针对总成交量最大这一第三层次目标的寻优之后，市场出清方案的资源配置效果几乎未发生变化，仅总成交量这一寻优目标提升了0.1 MW。此时的市场出清方案已经满足了多层次目标的顺次实现需求，故在执行社会福利相同购售匹配对间的中标电力差异之和最小这一第四层次目标的寻优之后，市场出清方案的资源配置效果未发生任何变化。由此可见，本文所提出清策略通过顺次执行针对各层目标的寻优进程，可逐步提高所得市场出清方案的资源配置效果。
综上所述，本文所提多层次目标顺次寻优出清策略可有效提升市场出清方案的资源配置效果。然而，M3需顺次求解四个针对不同层次目标函数的出清模型，相较于仅需求解1次市场出清模型的M1和M2而言，计算负担大幅增加。例如，M1和M2在S1中的计算时间仅为98.96 s和68.93 s，而M3的计算时间长达8 512.36 s，难以满足实际市场出清计算效率要求。为此，本文提出了针对多层次目标顺次寻优出清方法的加速策略，其有效性将在4.3节进行详细阐述。
本文从多层目标顺次寻优出清流程简化以及出清模型加速求解两个方面提升多层目标顺次寻优出清效率，为验证其有效性，本文以多解特性不同的大规模算例S2和S3为例开展仿真分析。其中，算例S2在经过前两个层次目标的顺次寻优后已不存在多解（模拟生成的100个场景中，该类场景占比93.00%），而算例S3在经过前两个层次目标的顺次寻优后仍存在多解（模拟生成的100个场景中，该类场景占比7.00%）。
M3～M6在算例S2中的求解性能见表5。
表5 M3～M6在算例S2中的求解性能
Tab.5 Calculation performance of M3～M6 in S2
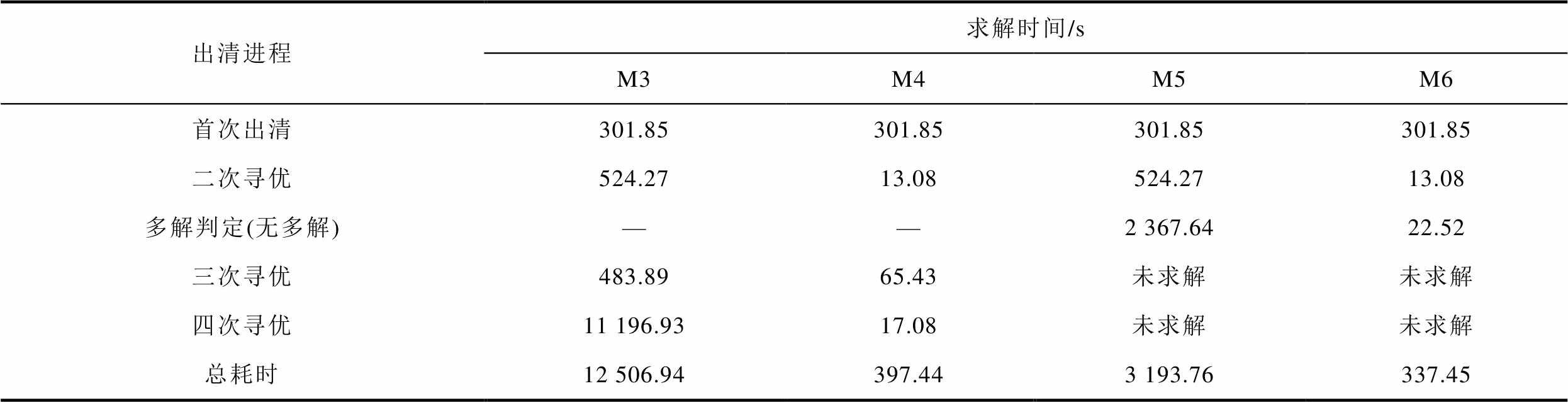
出清进程求解时间/s M3M4M5M6 首次出清301.85301.85301.85301.85 二次寻优524.2713.08524.2713.08 多解判定(无多解)——2 367.6422.52 三次寻优483.8965.43未求解未求解 四次寻优11 196.9317.08未求解未求解 总耗时12 506.94397.443 193.76337.45
对比M3和M4可以发现，在多层目标顺次寻优过程中，以前序出清模型最优解作为后序出清模型初始解可有效引导后序出清模型的热启动进程，进而显著提升模型求解效率，总加速比达31.47。其中，二次寻优的加速比更是高达40.08。算例S2中M3和M4两种方法下二次寻优出清模型相对误差在求解过程中的收敛曲线如图4所示。
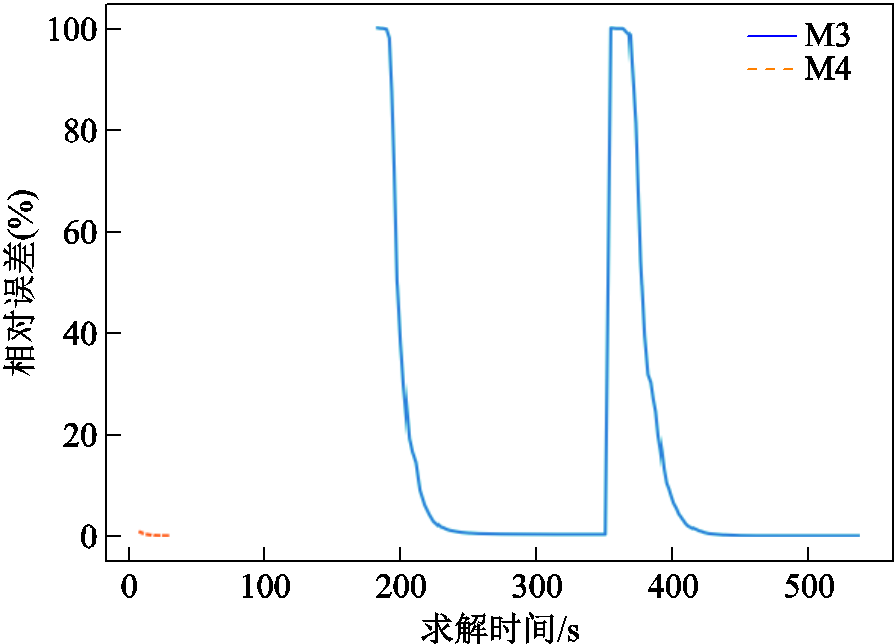
图4 S2中M3和M4两种方法下二次寻优出清模型的相对误差收敛曲线
Fig.4 Relative error convergence curves of M3 and M4 during the optimization for the second-level objective in S2
由图4可见，M3和M4的相对误差最终都收敛至0，M4只是由更接近最优解的初始点开始迭代寻优，并未改变出清模型的约束和变量，因而M4能够在保证出清准确性的条件下大幅减少算法迭代次数，进而有效提升出清计算效率。其中，经求解器自动选择，M3采用求解大规模问题更占优势的barrier算法进行求解，在迭代过程中可能存在迭代路径突变而导致相对误差突然增大的情况。
对比M3和M5可以发现，M3无论出清问题是否存在多解都将执行完整的四次寻优过程，求解时间较长；而M5通过嵌入多解判定环节，可知晓算例S2在经过前两个层次目标的顺次寻优后已不存在多解，因而不再执行针对后序两个层次目标的寻优进程，从而简化出清流程，减少出清计算时间（出清计算时间较M3减少74.46%，加速效果较为明显）。
对比M5和M6可以发现，本文所提多解判定模型无损加速策略利用前序出清模型的最优解信息可显著提升多解判定效率，加速比为9.46。算例S2中M5和M6两种方法下多解判定模型目标函数的变化曲线如图5所示。
由于经过前两个层次目标的顺次寻优后出清问题已不存在多解，故前序出清模型的最优解也是多解判定模型的最优解，且为唯一可行解。此时，M6将前序出清模型最优解作为多解判定模型的初始解，使得初始解即是多解判定模型最优解，可令模型直接寻得最优解（见图5），进而有效地提升求解效率。相反，M5还需执行预求解、单纯形迭代等步骤才能寻得多解判定模型的唯一可行解（见图5），计算时间较M6更长。此外，在无多解场景下，M6仅为多解判定模型提供初始解，将不影响多解判定的准确性。
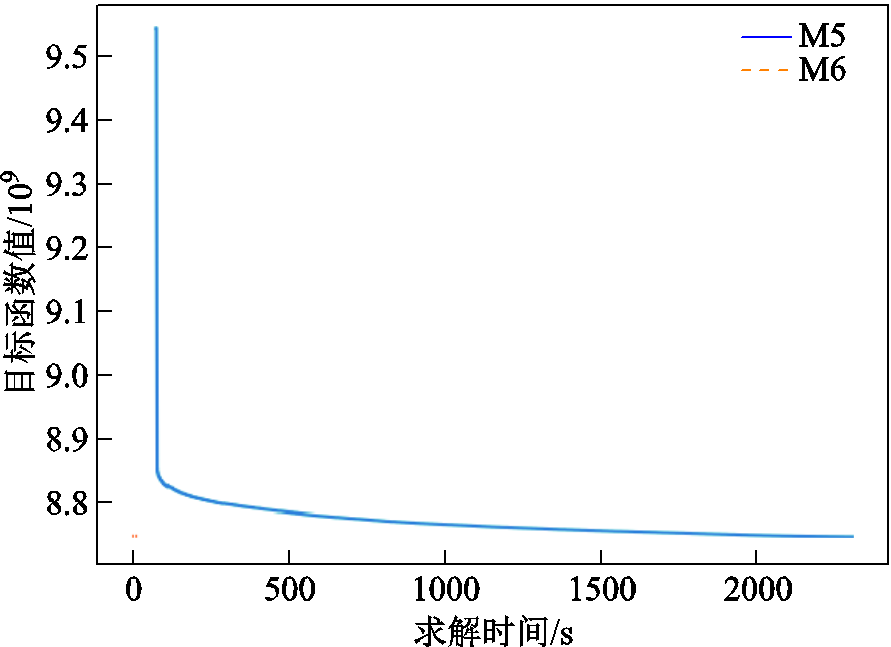
图5 S2中M5和M6两种方法下多解判定模型的目标函数变化曲线
Fig.5 Objective function change curves of multiple solution judgment optimization model under M5-M6 in S2
对比M4和M6可以发现，在考虑出清模型热启动无损加速策略后，嵌入多解判定环节也可有效简化出清流程，进一步提高出清求解效率，求解时间减少了15.09%。
由此可见，本文所提出清无损加速方法能够在不损失计算精度的条件下，有效提升出清模型及多解判定模型的计算效率。同时，在经过前两个层次目标的顺次寻优后已不存在多解的出清场景下（场景占比93.00%），多解判定环节的嵌入能够简化出清流程，进一步提高多层目标顺次寻优出清策略的计算效率（相较未加速的M3，所提方法M6总体加速比达37.06）。
然而，对于在经过前两个层次目标的顺次寻优后仍存在多解的出清场景（场景占比7.00%），多解判定环节的嵌入将反而增加计算时间，下面将以算例S3为例对此进行探讨。
M4和M6在算例S3中的求解性能见表6。
表6 M4和M6在算例S3中的求解性能
Tab.6 Calculation performance of M4 and M6 in S3
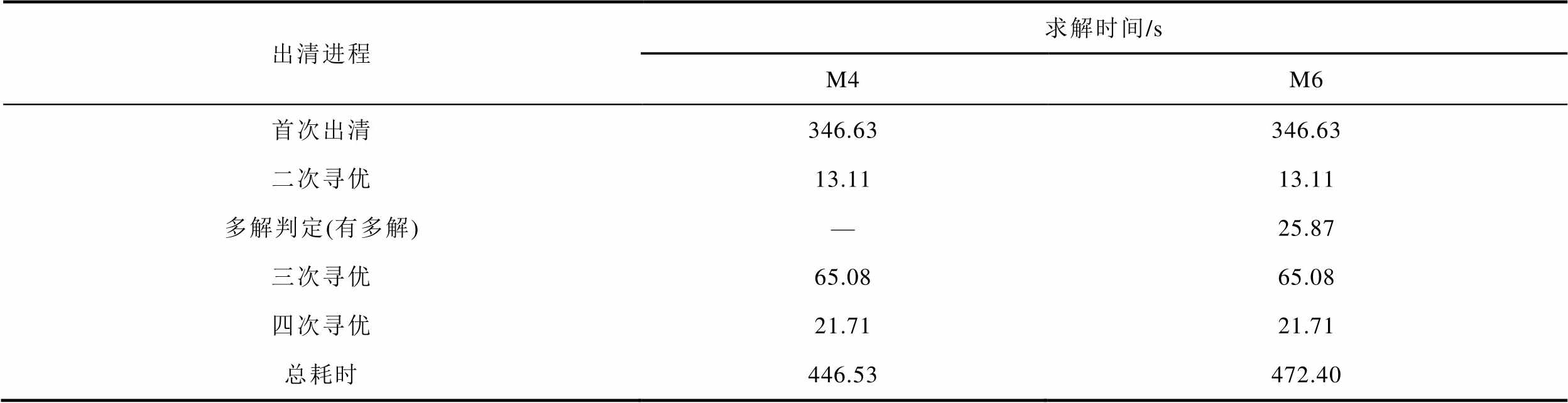
出清进程求解时间/s M4M6 首次出清346.63346.63 二次寻优13.1113.11 多解判定(有多解)—25.87 三次寻优65.0865.08 四次寻优21.7121.71 总耗时446.53472.40
由表6可见，在经过前两个层次目标的顺次寻优后，M6通过多解判定发现该场景仍存在多解，故仍需执行针对后序两个层次目标的寻优进程。相较于直接完整执行四次寻优过程的M4，M6额外执行了多解判定过程，计算时间较M4增加了5.79%。
然而，如前所述，在经过前两个层次目标的顺次寻优后仍存在多解的出清场景较少，而在大部分出清场景下，多解判定环节的嵌入可将出清计算效率提高15%左右。因此，嵌入多解判定环节有利于提高多层目标顺次寻优出清方法的总体计算效率。
此外，为进一步说明本文所提多解判定无损加速策略的有效性，算例S3中M5和M6两种方法下多解判定模型目标函数的变化曲线如图6所示。
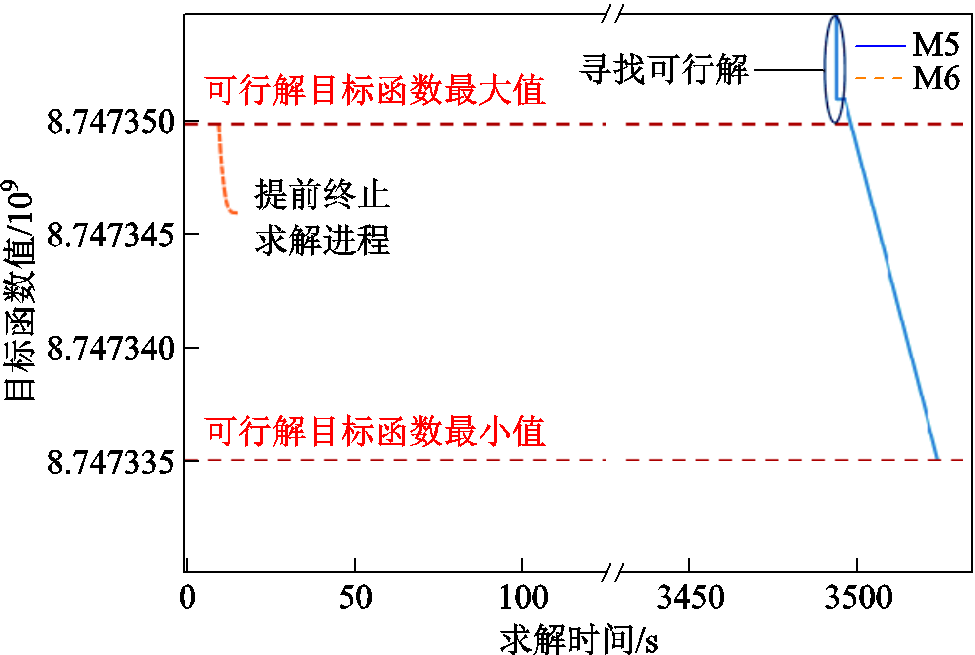
图6 S3中M5和M6两种方法下多解判定模型的目标函数变化曲线
Fig.6 Objective function change curves of multiple solution judgment optimization model under M5 and M6 in S3
在出清问题存在多解的场景下，多解判定模型具有多个可行解，M5需从随机初始解（不一定可行）开始经大量迭代寻到可行的目标函数最小值（即最优目标函数），进而判定出清问题存在多解。而M6将前序出清模型最优解作为多解判定模型的初始解，可令多解判定模型由可行的目标函数最大值（见图6中M6起点）出发向下寻找目标函数最小值，同时，在寻得目标函数取值比初始目标函数小的可行解后便提前终止求解进程（见图6中M6终点），并判定出清问题存在多解，可有效减少多解判定模型的迭代寻优次数，进而提高模型计算效率。如2.3节所述，只要多解判定模型的目标函数小于其最大取值便可判定出清问题存在多解，故M6中多解判定模型求解进程的提前终止并不影响多解判定的准确性。
综上所述，本文所提有效利用前序模型求解信息的出清无损加速方法能够在不损失计算精度的条件下，有效提升多层目标顺次寻优出清方法的总体计算效率。
针对大规模省间电力中长期交易出清问题易出现的多解现象，本文提出了多层目标顺次寻优的高效出清方法，以提升多解场景下省间电力中长期交易出清的资源配置效果。该方法建立了多层目标顺次寻优的省间电力中长期交易出清模型，可在保证高优先级目标函数最优性的条件下开展针对下一层次目标的寻优进程，从而保障市场出清方案的有效性与公平性。同时，提出了出清问题多解判定模型，有助于简化顺次寻优出清流程并帮助市场运营机构了解出清问题多解性。进一步，面向市场出清计算效率要求，提出了有效利用前序模型求解信息的多层目标顺次寻优无损加速方法。基于我国省间电力中长期交易实际运行数据的算例仿真结果表明，本文所提方法通过顺次执行针对各层目标的寻优进程，能够在不影响前序目标最优性的前提下，逐步提高所得市场出清方案的资源配置效果。此外，基于多解判定的出清流程简化策略以及面向出清模型与多解判定模型的加速策略能够在不损失计算精度的条件下，大幅提高出清计算效率（典型场景的出清加速比达37.06）。
参考文献
[1] 国家发展改革委, 国家能源局. 国家发展改革委国家能源局关于加快建设全国统一电力市场体系的指导意见[R/OL]. 北京: 国家发展改革委，国家能源局 [2022-01-18]. https://www.gov.cn/zhengce/ zhengceku/2022-01/30/content_5671296.htm.
[2] 夏清, 陈启鑫, 谢开, 等. 中国特色、全国统一的电力市场关键问题研究(2): 我国跨区跨省电力交易市场的发展途径、交易品种与政策建议[J]. 电网技术, 2020, 44(8): 2801-2808.
Xia Qing, Chen Qixin, Xie Kai, et al. Key issues of national unified electricity market with Chinese characteristics (2): development path, trading varieties and policy recommendations for inter-regional and inter-provincial electricity markets[J]. Power System Technology, 2020, 44(8): 2801-2808.
[3] 陈泓霏, 向明旭, 杨知方, 等. 大规模省间电力中长期交易出清的伴随模型引导加速方法[J/OL]. 中国电机工程学报, 2024: 1-14 [2024-04-09]. http:// kns.cnki.net/kcms/detail/11.2107.tm.20240408.0941.002.html.
Chen Hongfei, Xiang Mingxu, Yang Zhifang, et al. Adjoint model-guided acceleration method for large-scale inter-provincial medium and long-term power transactions clearance[J/OL]. Proceedings of the CSEE, 2024: 1-14 [2024-05-06]. http://kns.cnki.net/ kcms/detail/11.2107.tm.20240408.0941.002.html.
[4] Nemo Committee. EUPHEMIA public description: Single price coupling algorithm[R/OL]. EU: Nemo Committee [2020-10-12]. https://www.nordpoolgroup. com/4adb91/globalassets/download-center/single-day-ahead-coupling/euphemia-public-description.pdf.
[5] 陈熠, 王晗, 严正, 等. 全国统一电力市场演进过程下省间-省内市场出清及定价模型[J]. 电工技术学报, 2024, 39(7): 2116-2131.
Chen Yi, Wang Han, Yan Zheng, et al. Inter-and intra-provincial electricity market clearing and pricing model under the evolution of national unified electricity market[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2116-2131.
[6] 张汉斌. 线性规划多重最优解判别准则刍议[J]. 运筹与管理, 2002, 11(5): 43-46.
Zhang Hanbin. Discussion on the discriminate criterion of multiple optimum solution in the linear programming[J]. Operations Research and Management Science, 2002, 11(5): 43-46.
[7] Gan Deqiang, Litvinov E. Energy and reserve market designs with explicit consideration to lost opportunity costs[J]. IEEE Transactions on Power Systems, 2003, 18(1): 53-59.
[8] Krebs V, Schewe L, Schmidt M. Uniqueness and multiplicity of market equilibria on DC power flow networks[J]. European Journal of Operational Research, 2018, 271(1): 165-178.
[9] Ambrosius M, Grimm V, Kleinert T, et al. Endogenous price zones and investment incentives in electricity markets: an application of multilevel optimization with graph partitioning[J]. Energy Economics, 2020, 92: 104879.
[10] 林雨眠, 熊厚博, 张笑演, 等. 计及新能源机会约束与虚拟储能的电-热系统分布式多目标优化调度[J]. 电工技术学报, 2024, 39(16): 5042-5059.
Lin Yumian, Xiong Houbo, Zhang Xiaoyan, et al. Distributed multi-objective optimal scheduling of integrated electric-heat system considering chance constraint of new energy and virtual storage[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 5042-5059.
[11] 李军徽, 安晨宇, 李翠萍, 等. 计及调峰市场交易的储能-新能源-火电多目标优化调度[J]. 电工技术学报, 2023, 38(23): 6391-6406.
Li Junhui, An Chenyu, Li Cuiping, et al. Multi-objective optimization scheduling method considering peak regulating market transactions for energy storage-new energy-thermal power[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6391-6406.
[12] 徐玖平, 李军. 多目标决策的理论与方法[M]. 北京: 清华大学出版社, 2005.
[13] 张世旭, 李姚旺, 刘伟生, 等. 面向微电网群的云储能经济-低碳-可靠多目标优化配置方法[J/OL]. 电力系统自动化, 2024: 1-14 [2024-01-02]. http://kns.cnki.net/kcms/detail/32.1180.TP.20231123.1059.004.html.
Zhang Shixu, Li Yaowang, Liu Weisheng, et al. Multi-objective optimal configuration method of cloud energy storage for microgrid clusters driven by economy, low-carbon and reliability[J/OL]. Automation of Electric Power Systems, 2024: 1-14 [2024-01-02]. http://kns.cnki.net/kcms/detail/32.1180.TP.20231123.1059.004.html.
[14] 冯陈, 周大庆, 郑源, 等. 基于精细化建模的抽水蓄能机组低水头背靠背启动多目标优化[J]. 中国电机工程学报, 2023, 43(8): 3059-3070, 15.
Feng Chen, Zhou Daqing, Zheng Yuan, et al. Multi-objective optimization of back-to-back starting process for pumped storage units at low head area based on refined model[J]. Proceedings of the CSEE, 2023, 43(8): 3059-3070, 15.
[15] 莫静山. 基于LCC-HVDC的交直流系统电压无功优化方法研究[D]. 重庆: 重庆大学, 2021.
[16] 曾丹, 杨争林, 冯树海, 等. 交直流混联电网下基于ATC的省间交易优化出清建模[J]. 电网技术, 2020, 44(10): 3893-3899.
Zeng Dan, Yang Zhenglin, Feng Shuhai, et al. Inter-provincial power exchange optimization modeling considering ATC constrains of hybrid AC/DC power system[J]. Power System Technology, 2020, 44(10): 3893-3899.
[17] 程海花, 杨辰星, 刘硕, 等. 基于路径组合计及ATC的省间中长期交易优化出清和系统研发[J]. 电网技术, 2022, 46(12): 4762-4770.
Cheng Haihua, Yang Chenxing, Liu Shuo, et al. Optimization clearing and system development of inter-provincial medium and long term trade considering ATC base on path combination[J]. Power System Technology, 2022, 46(12): 4762-4770.
[18] 胡晨旭, 关立, 罗治强, 等. 跨区域省间富余可再生能源现货交易优化出清模型[J]. 电力系统自动化, 2021, 45(13): 110-116.
Hu Chenxu, Guan Li, Luo Zhiqiang, et al. Optimal clearing model for trans-regional and cross-provincial spot trading of surplus renewable energy[J]. Automation of Electric Power Systems, 2021, 45(13): 110-116.
[19] Xiang Mingxu, Yang Zhifang, Yu Juan. Hierarchical AGC dispatch with detailed modeling of energy storage system behaviors[J]. IEEE Transactions on Power Systems, 2023, 38(2): 1689-1701.
[20] 潘平奇. 线性规划计算（下）[M]. 北京: 科学出版社, 2012.
Efficient Sequential Optimization Method for Inter-Provincial Medium- and Long-Term Power Transaction Clearing Problem under Multiple-Solution Scenarios
Abstract With the development of the national unified electricity market, the market scale has gradually increased. Take inter-provincial medium- and long-term power transaction as an example, the number of market participants is over a thousand. The similarity of the bid prices of numerous market participants is likely to lead to multiple purchasing and selling pairs having the same social welfare. As a result, the market clearing problem that maximizes social welfare may have multiple optimal solutions. To ensure the effectiveness and fairness of market clearing, the multi-level objective sequential optimization should be implemented under multiple-solution scenarios. However, the existing methods based on multi-objective optimization cannot balance effectiveness and efficiency. To address this issue, take inter-provincial medium- and long-term power transaction that may have multiple solutions as a research objective, an efficient multi-level objective sequential optimization method is proposed in this paper. The main contributions are illustrated as follows:
First, the market clearing model with multi-level objective sequential optimization is established. Four objective functions are considered according to the industrial practices, including maximizing social welfare, maximizing transaction volume of renewable energy, maximizing total transaction volume, and equally distributing tradable power among purchasing and selling pairs with the same social welfare. Market clearing models considering the aforementioned four objective functions are separately established. The optimal objective functions of the preorder model are used as the operating constraints of the subsequent model to ensure the optimality of the objective functions with high priorities. By sequential solving these four market clearing models, the market clearing effectiveness and fairness can be guaranteed even under multiple-solution scenarios.
Second, the multiple-solution judgment auxiliary optimization model for the market clearing problem is established based on the bound constraints of the optimal solution, according to which the multiple-solution characteristics of market clearing problems can be recognized. The recognized multiple-solution characteristics can provide support for market operators to design the measure for handling multiple-solution scenarios. For instance, more objective functions can be introduced if multiple-solution scenarios cannot be effectively avoided after the sequential optimization of four objective functions. Besides, regarding the computational burden caused by the solution to four market clearing models, the multiple-solution judgment auxiliary optimization model is embedded into the sequential optimization process to simplify the clearing process by avoiding unnecessary optimization.
Third, to meet the calculation efficiency demand, the lossless acceleration method for market clearing based on solution information of the preorder model is proposed. For the market clearing models with multi-level objective functions, the optimal solution of the preorder model is used as the high-quality initial feasible solution of the subsequent model, which can guide the warm-start accelerating process of the subsequent model without the loss of accuracy. For the multiple-solution judgment auxiliary optimization model, the optimal solution of the preorder model is used as the initial feasible solution. Based on this, the termination criterion for the calculation process is established according to the comparison between the initial objective function and the current objective function. In this way, the judgment process can be accelerated without affecting judgment accuracy.
Finally, case studies based on practical inter-provincial medium- and long-term transaction data in China demonstrate that the proposed method can greatly improve the market clearing effect for the subordinate objectives while ensuring the optimality of the primary objective. In addition, benefiting from the proposed model solution acceleration strategy and the sequential optimization process simplification strategy, the market clearing efficiency can be improved by 37 times without the loss of accuracy under the typical scenario.
Keywords：Inter-provincial medium- and long-term power transactions, multiple solutions of market clearing, multi-level objective sequential optimization, multiple solution judgment, market clearing acceleration
中图分类号：TM73; F426.61
DOI: 10.19595/j.cnki.1000-6753.tces.240774
国家电网有限公司科技资助项目（5108-202218280A-2-284-XG）。
收稿日期 2024-05-14
改稿日期 2024-08-17
向明旭 男，1994年生，博士，助理研究员，研究方向为电力市场、电力优化调度等。
E-mail：mxxiang@cqu.edu.cn
杨知方 男，1992年生，博士，教授，研究方向为电力系统优化、电力市场等。
E-mail：zfyang@cqu.edu.cn（通信作者）
（编辑 赫 蕾）