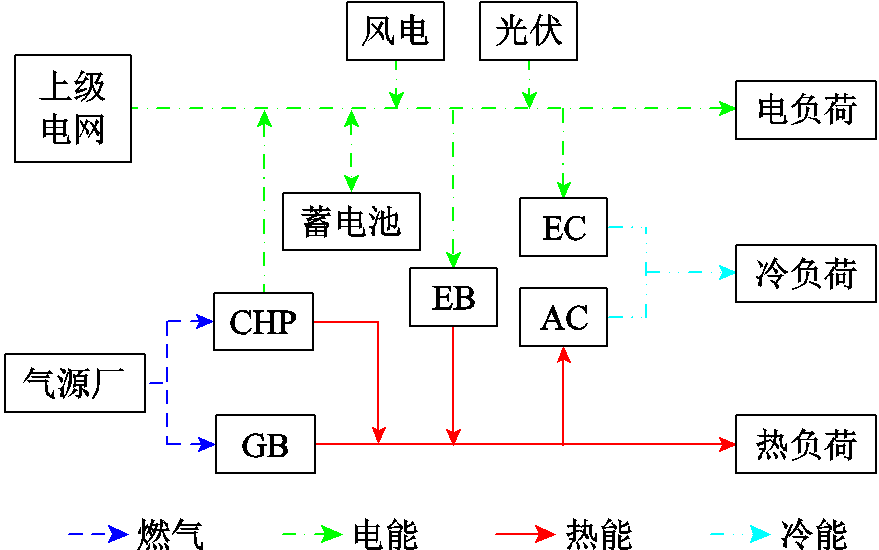
图1 区域综合能源系统结构
Fig.1 Regional integrated energy system structure
摘要 考虑异质能源在网络中的流动时间差异性,提升系统设备在不同时间尺度下调控的灵活性,是实现区域综合能源系统(RIES)多时间尺度优化调度的关键。为此,该文提出一种面向冷-热-电RIES的分布式双层近端策略优化(DBLPPO)调度模型。首先将RIES内部能源的出力、储存和转换构建高维空间的马尔可夫决策过程数学模型;其次基于改进的分布式近端策略优化算法对其进行序贯决策描述,构建内部双层近端策略优化(PPO)的控制模型,局部网络采用“先耦合-再解耦”的求解思路对冷-热力系统和电力系统的设备进行多时间尺度优化决策,最终实现RIES冷-热力系统与电力系统的多时间尺度调度和协同优化运行;最后仿真结果表明,所提模型不仅能克服深度强化学习算法在复杂随机场景下的“维数灾难”问题,实现RIES各能源网络在不同时间尺度下的协同优化管理,还能加快模型的最优决策求解速度,提高系统运行的经济效益。
关键词:区域综合能源系统 多时间尺度 分布式双层近端策略优化 深度强化学习 协同优化管理 经济效益
随着全球气候变化和能源短缺问题的加剧,为维护人类可持续发展,我国在2020年提出“双碳”战略目标,旨在推动能源系统的低碳转型[1]。区域综合能源系统(Regional Integrated Energy System, RIES)聚合冷、热、电等多种异质能源,通过各能源网络间的能源转换与协调运行,有效地实现能源的梯级利用,保证系统的低碳、经济运行[2-3]。
作为现代能源体系的重要一环,RIES因其多能耦合的特性,在提高主网的调控灵活性和新能源消纳潜力等方面具有重大意义[4-5]。目前,国内外学者对RIES安全运行的研究聚焦于灵活调控系统各类能源形式和储能装置,增强系统的调度灵活性与能源互补能力,促进新能源消纳,实现系统安全、绿色、高效运行[6-9]。以上研究往往忽视系统内部异质能源传输的物理差异,由于冷、热能流在供能管道中传输的延时特性,导致传统调度模型不能体现异质能源的动态流通特性,增加了RIES优化运行的管理难度[10-12]。
针对上述问题,现有文献常采用多时间尺度调度方法对RIES进行优化管理[13-15]。文献[16]采用模型预测控制方法,构建两阶段多时间尺度调度模型,有效地提高了系统的运行经济性和供能可靠性。文献[17]构建日前-日内两阶段优化调度模型,利用多场景技术和模糊数学理论对源荷进行精确建模,实现了系统的多时间尺度低碳运行。文献[18-19]建立日前-日内-实时的三阶段综合能源系统优化调度模型,充分考虑min级的需求侧波动响应,保证系统满足不同时间尺度下的调度需求。上述模型驱动的多时间尺度RIES调度方法依赖于准确的源荷预测结果和设备数学建模,并采用凸松弛技术或线性化方法进行模型求解和能源管理[20-22]。然而,日益复杂的RIES内部能源耦合结构提升了其精细化数学建模和求解的难度,复杂的非凸非线性数学模型导致传统松弛优化求解难度陡升,给RIES的实时调度决策和安全优化运行带来了挑战。
深度强化学习(Deep Reinforcement Learning, DRL)采用“数据-经验-智能”的递进学习思想,利用历史数据驱动智能体自寻模型的最优解,克服传统非凸非线性模型的求解困难问题[23]。此外,深度强化学习凭借计算机的强大算力,能够对复杂环境下的RIES优化调度问题进行高效计算[24]。文献[25]引入碳捕集装置,将碳排放流理论与深度确定策略梯度(Deep Deterministic Policy Gradient, DDPG)强化学习算法相融合,实现复杂场景下RIES的碳电协同优化。文献[26]提出一种柔性Actor-critic强化学习算法,能够快速计算风光出力与多元负荷影响下的RIES多目标优化调度问题,提高新能源利用率。文献[27]采用分布式近端策略优化(Distributed Proximal Policy Optimization, DPPO)强化学习算法,实现复杂能源输送结构下的电-热-液协同优化调度,有效地解决新能源发电与负荷多重不确定性带来的决策困难问题。上述研究表明,深度强化学习算法能够高效求解复杂场景下的RIES优化调度问题,无需对源荷预测数据与系统参数进行精确建模。
然而,深度强化学习在处理RIES多时间尺度优化调度问题时具有一定的局限性,主要表现在:①深度强化学习算法与外部环境的每一次交互中,智能体执行的动作变量在维度上都是统一的,这使得传统深度强化学习模型无法实现异质能源设备的多时间尺度调控[28];②RIES内部设备的种类和数量不断增多,导致系统潜在运行方案呈指数倍激增,引发的“维数灾难”会严重影响深度强化学习求解的收敛性[29]。
针对上述问题,本文提出一种分布式双层近端策略优化(Distributed Bi-Layer Proximal Policy Optimization, DBLPPO)强化学习调度模型,实现RIES各能源网络的多时间尺度优化管理。本文主要创新点如下:
1)时间维度方面:所提模型充分考虑冷、热、电三种能源流速的差异性,构建双层深度强化学习模型,分别以1 h和15 min为时间尺度动态调整冷、热能设备和电能设备出力,弥补各能源网络在短时期内的供能缺额,确保系统安全经济运行。
2)计算寻优方面:所提模型的分布式双层模型结构能够有效地对RIES冷-热力系统与电力系统进行解耦分析,减少每层模型的控制变量数量,克服模型在寻优过程中的“维数灾难”问题,提高模型的收敛性能。
3)复杂场景适用性方面:DBLPPO调度模型凭借强化学习算法卓越的自学习能力,能够有效地克服源荷功率的随机波动影响,针对复杂运行场景实时生成最优调度方案。
RIES主要包含冷力、热力、电力三种能源网络[30]。本文中的天然气只作为系统中的冷-热-电联供燃料,不独立成网。RIES结构如图1所示。

图1 区域综合能源系统结构
Fig.1 Regional integrated energy system structure
RIES从上级电网、气源厂、风电以及光伏获取能量,通过热电联产(Combined Heat and Power, CHP)机组、燃气锅炉(Gas Boiler, GB)、电制热(Electric Boiler, EB)机组、吸收式制冷机(Absorption Chiller, AC)、电制冷(Electric Chiller, EC)机组进行能源的相互转换,利用蓄电池(Battery Energy Storage, BES)对电能进行储存/释放,满足冷、热、电负荷的用能需求。
1.2.1 可再生能源发电
RIES新能源发电分为风力机组发电和光伏发电。为减小源侧不确定性与预测误差引起的决策失准,风光发电功率在原基础上增加服从TLS(T location-scale)分布的噪声ξ,其分布函数fξ为
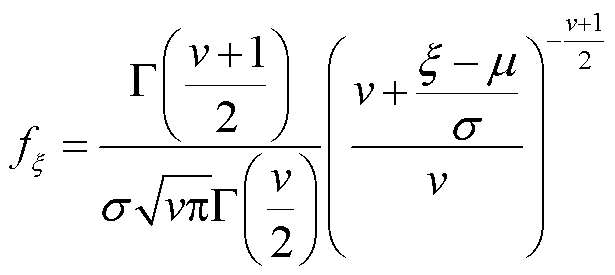 (1)
(1)
式中,v、σ、μ分别为TLS分布的形状参数、尺度参数、位置参数;Γ(·)为伽马函数。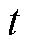 时刻光伏、风力发电功率分别计为
时刻光伏、风力发电功率分别计为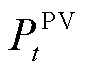 和
和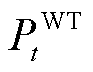 ,其发电功率约束为
,其发电功率约束为
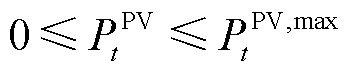 (2)
(2)
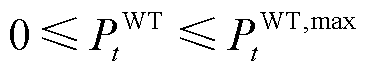 (3)
(3)
式中,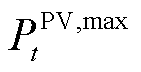 、
、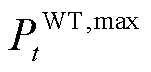 分别为
分别为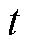 时刻的光伏、风力最大发电功率。
时刻的光伏、风力最大发电功率。
1.2.2 上级电网
RIES通过向上级电网购电,满足内部机组和负荷供能需求,在新能源发电富余时减少购电,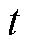 时刻电网的购电功率为
时刻电网的购电功率为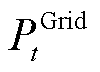 ,其模型约束为
,其模型约束为
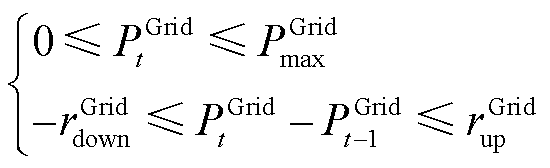 (4)
(4)
式中,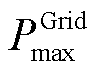 为从上级电网购电的最大功率;
为从上级电网购电的最大功率;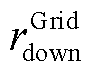 与
与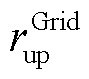 分别为购电功率的最大滑坡率和最大爬坡率。
分别为购电功率的最大滑坡率和最大爬坡率。
1.3.1 热电联产机组
CHP机组能够消耗天然气产生电能和热能,是热电联产场景下重要的能量枢纽设备。在本案例中采用“以热定电”的模式运行,其物理模型为
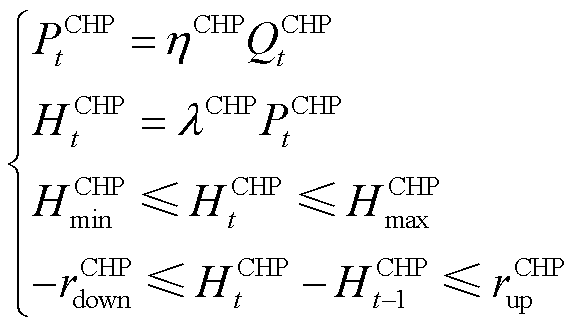 (5)
(5)
式中,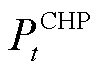 、
、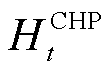 和
和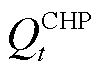 分别为
分别为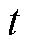 时刻CHP机组产生的电功率、热功率和消耗的天然气等效功率;
时刻CHP机组产生的电功率、热功率和消耗的天然气等效功率;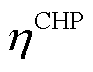 、
、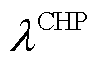 分别为CHP机组的天然气转换效率和热电比;
分别为CHP机组的天然气转换效率和热电比;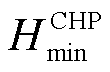 、
、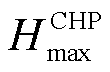 分别为CHP机组产生的最小、最大热功率;
分别为CHP机组产生的最小、最大热功率;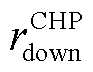 、
、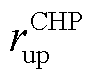 分别为CHP机组的最大滑坡率和最大爬坡率。
分别为CHP机组的最大滑坡率和最大爬坡率。
1.3.2 燃气锅炉
GB机组通过燃烧天然气产生热能,以实现供热系统的负荷平衡,其物理模型为
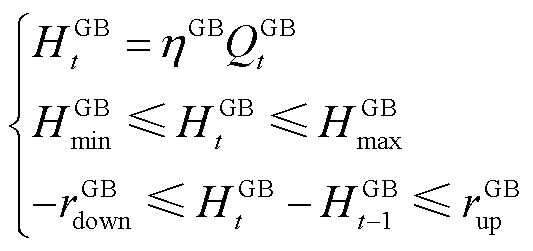 (6)
(6)
式中,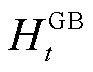 、
、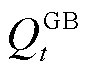 分别为
分别为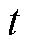 时刻GB机组产生的热功率和消耗的天然气等效功率;
时刻GB机组产生的热功率和消耗的天然气等效功率;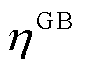 为GB机组的天然气转换效率;
为GB机组的天然气转换效率;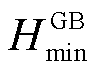 、
、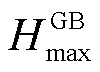 分别为GB机组发出的最小、最大热功率;
分别为GB机组发出的最小、最大热功率;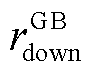 、
、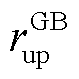 分别为GB机组的最大滑坡率和最大爬坡率。
分别为GB机组的最大滑坡率和最大爬坡率。
1.3.3 电制热机组
EB机组通过消耗电能产生热能,能够灵活调整热能出力,其物理模型为
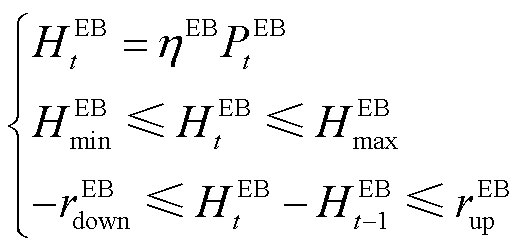 (7)
(7)
式中,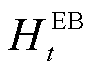 、
、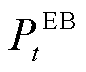 分别为EB在
分别为EB在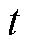 时刻产生的热功率和消耗的电功率;
时刻产生的热功率和消耗的电功率;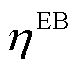 为EB电转热的能源利用效率;
为EB电转热的能源利用效率;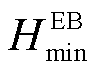 、
、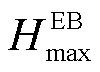 分别为EB机组发出的最小、最大热功率;
分别为EB机组发出的最小、最大热功率;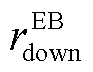 、
、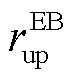 分别为EB机组的最大滑坡率和最大爬坡率。
分别为EB机组的最大滑坡率和最大爬坡率。
1.3.4 电制冷机组
EC机组耗电制冷,能够灵活调整冷能出力,实现供冷系统的负荷平衡,其物理模型为
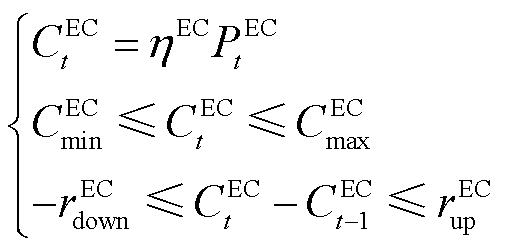 (8)
(8)
式中,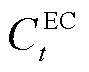 、
、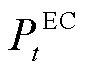 分别为
分别为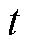 时刻EC机组发出的冷功率和消耗的电功率;
时刻EC机组发出的冷功率和消耗的电功率;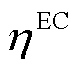 为EC机组的能源转换效率;
为EC机组的能源转换效率;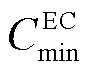 、
、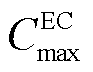 分别为EC机组发出的最小和最大冷功率;
分别为EC机组发出的最小和最大冷功率;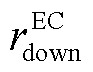 、
、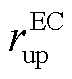 分别为EC的最大滑坡率和最大爬坡率。
分别为EC的最大滑坡率和最大爬坡率。
1.3.5 吸收式制冷机
AC机组可以通过吸收热能释放冷能,是冷热耦合系统中重要的能量转换设备,其物理模型为
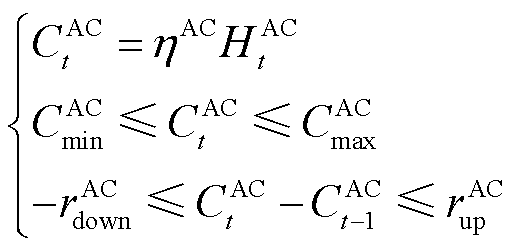 (9)
(9)
式中,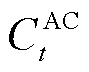 、
、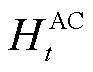 分别为
分别为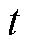 时刻AC机组发出的冷功率和吸收的热功率;
时刻AC机组发出的冷功率和吸收的热功率;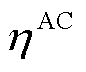 为AC机组的能源转换效率;
为AC机组的能源转换效率;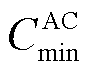 、
、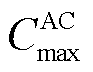 分别为AC机组发出的最小和最大冷功率;
分别为AC机组发出的最小和最大冷功率;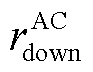 、
、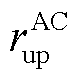 分别为AC机组的最大滑坡率和最大爬坡率。
分别为AC机组的最大滑坡率和最大爬坡率。
RIES储能端为蓄电池,能够对风光发电进行削峰填谷,存储富裕的发电功率,弥补系统供电缺口[31]。蓄电池的动态存储特性一般用荷电状态(State of Charge, SOC)表示,其物理模型为
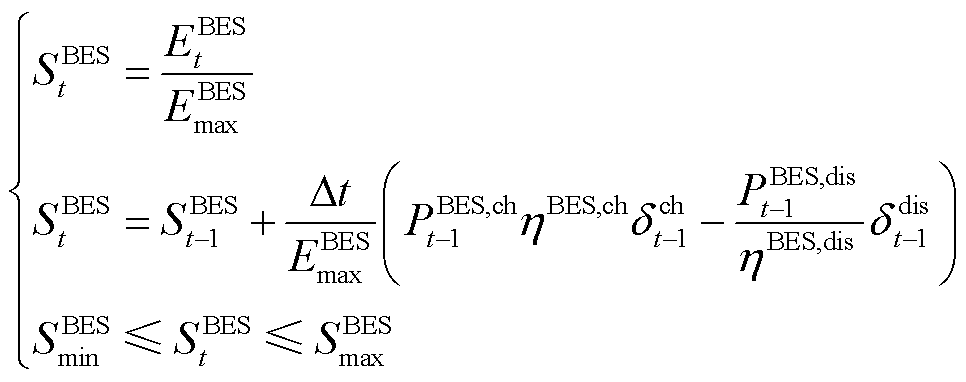 (10)
(10)
式中,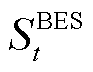 为
为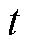 时刻蓄电池的荷电状态;
时刻蓄电池的荷电状态;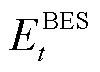 和
和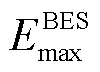 分别为
分别为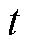 时刻蓄电池的蓄电量和最大蓄电量;
时刻蓄电池的蓄电量和最大蓄电量;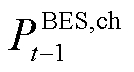 、
、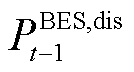 分别为蓄电池在
分别为蓄电池在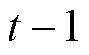 时刻的充、放电功率;
时刻的充、放电功率;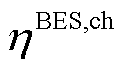 、
、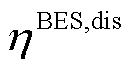 分别为蓄电池充、放电效率;
分别为蓄电池充、放电效率;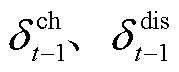 分别为
分别为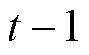 时刻蓄电池的储、放电状态0/1变量;
时刻蓄电池的储、放电状态0/1变量;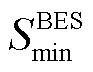 、
、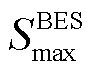 分别为最小、最大荷电状态。
分别为最小、最大荷电状态。
RIES中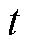 时刻电、热、冷力系统的负荷功率分别用
时刻电、热、冷力系统的负荷功率分别用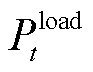 、
、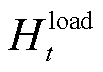 和
和 表示,系统依靠各能源机组之间的相互配合实现各能源网络的供需平衡,并充分考虑每个时段(15 min)之间的负荷需求变化,依靠用电设备弥补该时间尺度下的供能缺口。
表示,系统依靠各能源机组之间的相互配合实现各能源网络的供需平衡,并充分考虑每个时段(15 min)之间的负荷需求变化,依靠用电设备弥补该时间尺度下的供能缺口。
深度强化学习凭借卓越的自学习能力,通过与外部环境的持续性交互试错,自主学习以目标函数为导向的最优行为策略,最终实现序贯决策问题的优化求解[32-35]。上述深度强化学习过程可以描述为一个马尔可夫决策过程(Markov Decision Process, MDP),包含环境空间S、动作空间A、奖励空间R、状态转移概率P和智能体策略π。
RIES优化调度作为一种典型的序贯决策问题,可以利用强化学习模型进行高效求解。本文以前沿DPPO强化学习算法为基础,将RIES内部可调设备的调度指令作为动作空间,将RIES与可调设备的观测状态作为环境空间,将RIES负荷平衡与经济运行作为目标函数,构建分布式双层强化学习优化调度模型。通过智能体在模拟仿真环境中不断探索,自主学习最优策略π*,最终实现各能源设备的协同配合与灵活调控,保证系统的实时负荷需求与全局经济最优。
DPPO算法采用经典的Actor-critic强化学习框架,在梯度函数内部引入一种特殊权重,保证模型在训练过程中具有平滑的收敛趋势[36]。此外,多线程的工作模式能够提高经验数据的收集效率,缩短有效的训练时长。DPPO算法的优化计算过程如图2所示。
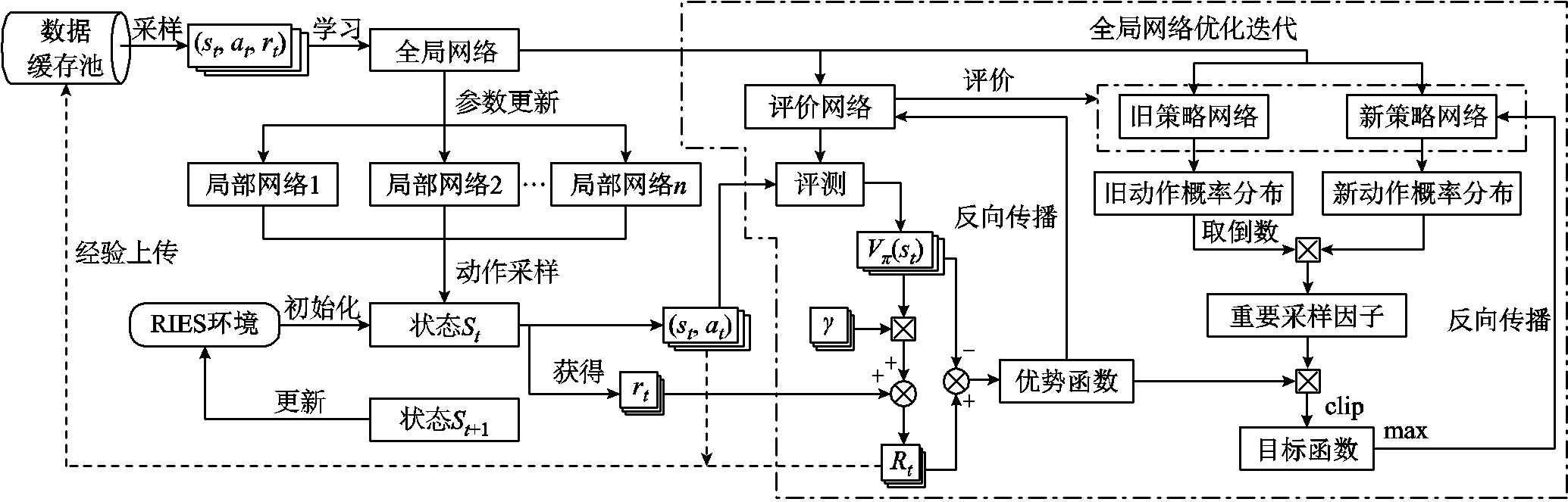
图2 DPPO优化计算过程
Fig.2 The DPPO optimization calculation process
DPPO算法在训练过程中通常采用优势函数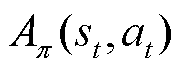 引导策略更新,获取最大回报。优势函数由状态-价值函数
引导策略更新,获取最大回报。优势函数由状态-价值函数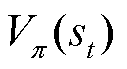 和状态-动作值函数
和状态-动作值函数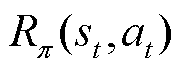 组成,其数学公式为
组成,其数学公式为
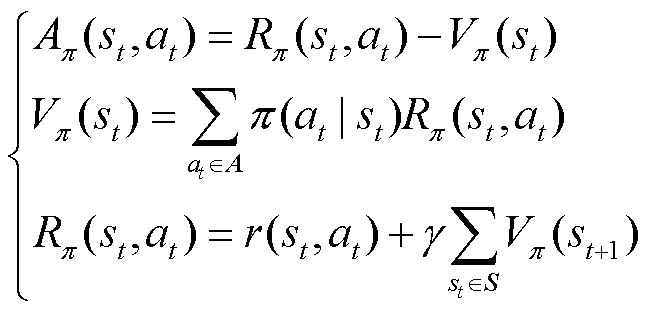 (11)
(11)
式中,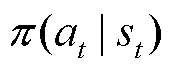 为智能体在观测到环境变量
为智能体在观测到环境变量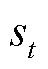 后,做出动作
后,做出动作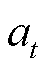 的概率分布;
的概率分布;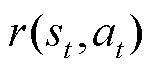 为在t时刻智能体从外部环境中获得的即时奖励;
为在t时刻智能体从外部环境中获得的即时奖励;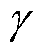 为奖励折旧因子。
为奖励折旧因子。
常规深度强化学习算法在每次参数更新后,需重新与环境互动,获取新的经验样本,并再次对模型进行更新。由于上述训练过程较为繁琐,为简化训练流程,DPPO算法引入重要性采样(Important Sampling)因子,利用旧策略网络收集的经验样本优化新策略网络参数,避免模型每次更新后的重复采样。重要性采样因子为新、旧策略网络动作概率分布的采样比,其数学公式为
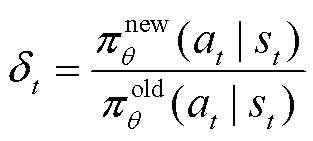 (12)
(12)
式中,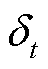 为重要性采样因子;
为重要性采样因子;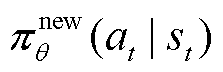 为新策略网络动作概率分布;
为新策略网络动作概率分布;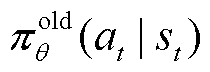 为旧策略网络动作概率分布。
为旧策略网络动作概率分布。
为降低更新步长过大所造成的收敛波动影响,减轻非线性KL约束下的梯度函数计算负担,DPPO算法在目标函数的梯度计算式中引入了裁剪项,数学公式为
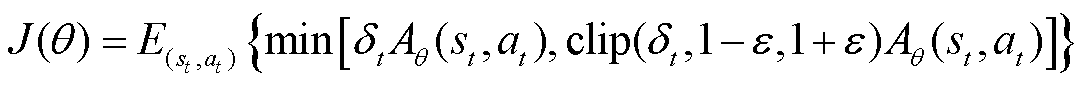 (13)
(13)
式中,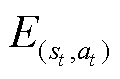 为取更新步长的均值;
为取更新步长的均值;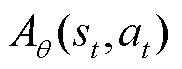 为模型参数为θ时的优势函数;ε为裁剪因子,数值为0.2;clip为裁剪项。策略网络以
为模型参数为θ时的优势函数;ε为裁剪因子,数值为0.2;clip为裁剪项。策略网络以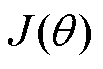 为目标函数进行梯度更新。
为目标函数进行梯度更新。
DPPO算法具有独特的分布式结构,内部包含一个全局网络和多个局部网络。局部网络负责与外部环境互动,将收集到的环境变量、动作变量和奖励变量打包成训练数据储存到经验池中。全局网络负责模型优化,从数据缓存池中小批量抽取样本数据,进行梯度计算和参数更新。全局网络与局部网络神经元结构一致,每次更新完毕后,全局网络将优化后的模型参数传递给局部网络,进行新一轮的互动和更新。模型不断重复上述步骤,向奖励最大化方向不断优化并最终达到收敛。这种分布式结构可以同时让多个局部网络与环境多线程互动,提高样本数据的采集效率;此外,每个局部网络的动作函数均为概率分布函数,面对同一环境状态,各局部网络输出的动作值也存在差异,使得样本数据种类得到提升。DPPO算法分布式结构如图3所示。
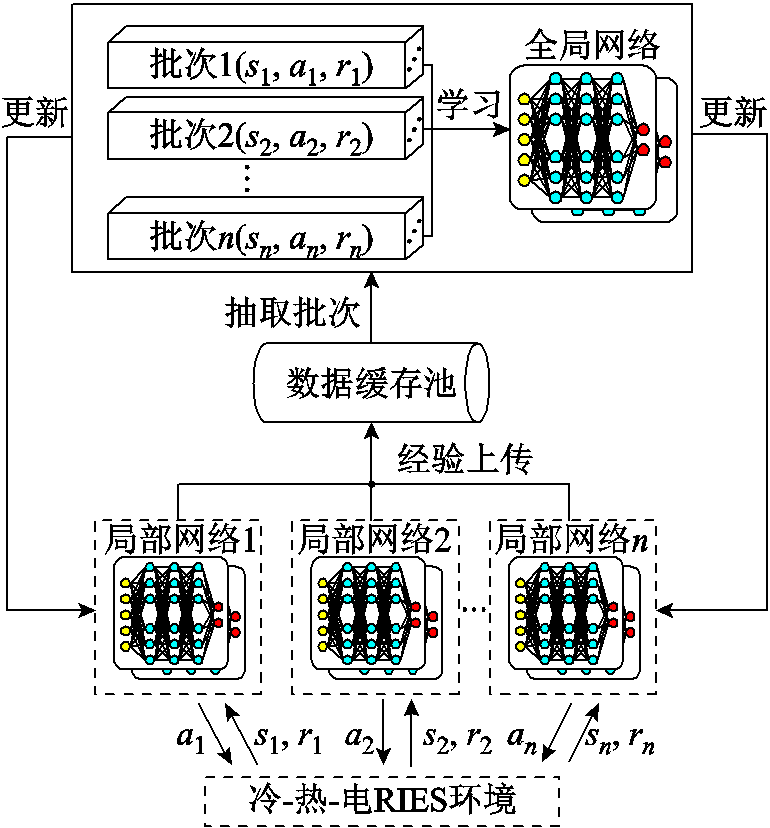
图3 DPPO算法分布式结构
Fig.3 DPPO algorithm distributed structure
在冷-热-电RIES中,为了体现电能流和热、冷能流在供能网络中传输的时间差异性,同时避免在模型训练过程中因控制变量过多导致“维数灾难”,缩短模型有效训练时长。本文基于DPPO强化学习算法,提出一种改进的DBLPPO多时间尺度调度模型。
所提模型的核心思想是在DPPO算法内部建立双层模型,分别对RIES中的冷、热力系统与电力系统进行调控,其中与冷、热力系统进行交互的模型称为DBLPPO内层模型,与电力系统进行交互的模型称为DBLPPO外层模型。全局网络与局部网络均为双层结构,其中,内层模型注重长时间尺度下能源调控策略的更新,外层模型在分布式系统模型中协调所有策略,进行短时间尺度下的能源调控。内、外层模型相互配合,共同实现冷-热-电RIES中异质能源的多时间尺度管理。DBLPPO内、外层模型的神经网络结构一致,以内层模型为例,其网络结构如图4所示。
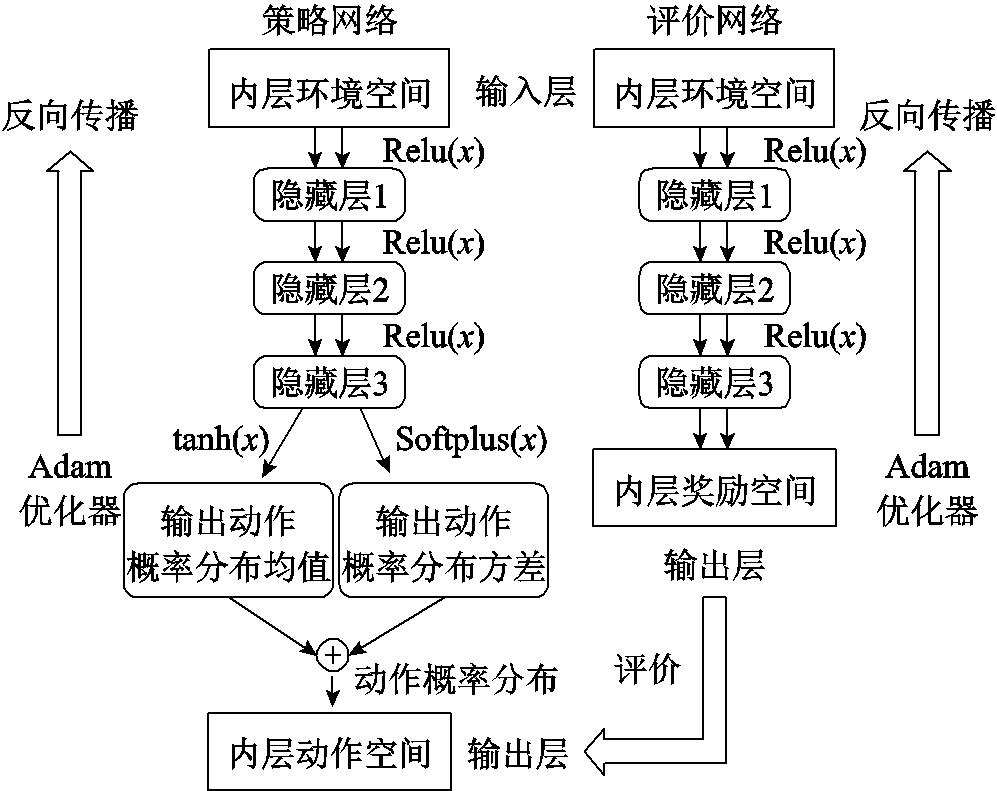
图4 DBLPPO网络结构
Fig.4 The structure of DBLPPO network
DBLPPO内层模型以1 h为调度周期,对冷-热力系统进行设备调控。内层环境状态变量为冷、热负荷功率,供需不平衡度以及EB、EC运行功率。内层动作状态变量为CHP、GB、AC运行功率。在1 h内,内层模型的动作状态变量不发生改变。
DBLPPO外层模型以15 min为调度周期,对电力系统进行设备调控。外层环境状态变量为冷、热、电负荷功率及其供需不平衡度,风电、光伏发电功率,CHP、GB、AC运行功率和蓄电池荷电状态。外层动作状态变量为EB、EC运行功率,上级电网购电功率以及蓄电池储/放电功率。
DBLPPO内层模型调控设备的出力在长周期内保持不变,无法满足短周期内系统冷、热负荷功率波动的需求,因此RIES系统依靠DBLPPO外层模型的灵活调控,动态调整EB、EC机组的运行功率来弥补冷、热负荷的供需缺口。DBLPPO算法多时间尺度优化调度模型结构如图5所示。
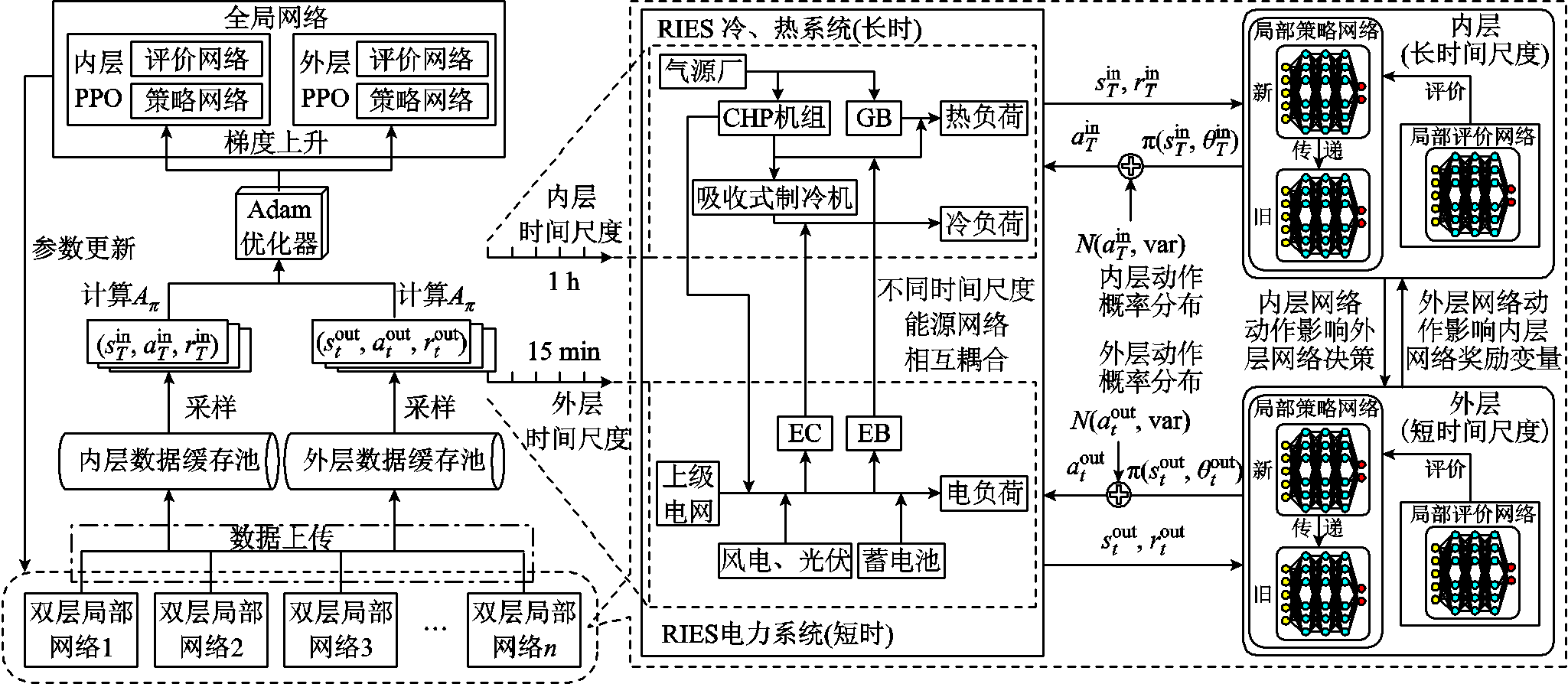
图5 基于DBLPPO算法的RIES多时间尺度优化调度模型结构
Fig.5 The structure of RIES multi-time scale optimization scheduling model based on DBLPPO algorithm
DBLPPO调度模型采用“先耦合-再解耦”的求解思路对RIES进行多时间尺度能源管理。本文中1个长时间尺度(T1)包含4个短时间尺度(t1、t2、t3、t4),在t1内模型采用耦合求解,DBLPPO内、外层模型分别根据当前接收到的环境变量,在各自的约束条件下,以内、外层奖励函数最大化为目标进行权衡优化,最终内、外层奖励函数达到优势平衡,系统实现最优经济运行。
在余下的三个短时间尺度内模型采用解耦求解,在t2内DBLPPO外层模型根据当前外层环境变量,在外层模型约束条件下,以外层奖励函数最大化为目标,基于t1时刻的内层模型调度方案(内层模型的调度方案在T1内不发生变化)灵活制定外层调度方案,满足t2时刻的负荷需求并实现经济运行。t3、t4的外层调度方案求解过程与t2一致。在T1内DBLPPO模型对调度方案求解完毕后,进入下一个调度周期T2,其求解过程与T1一致。基于DBLPPO算法的RIES多时间尺度调度求解过程如图6所示。
3.2.1 DBLPPO内层模型环境空间
DBLPPO内层模型以1 h为调度周期,根据冷、热负荷功率及其供需不平衡度和EB、EC机组的运行功率,对冷-热力系统制定调度方案,内层模型的环境空间为
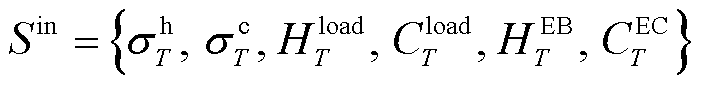 (14)
(14)
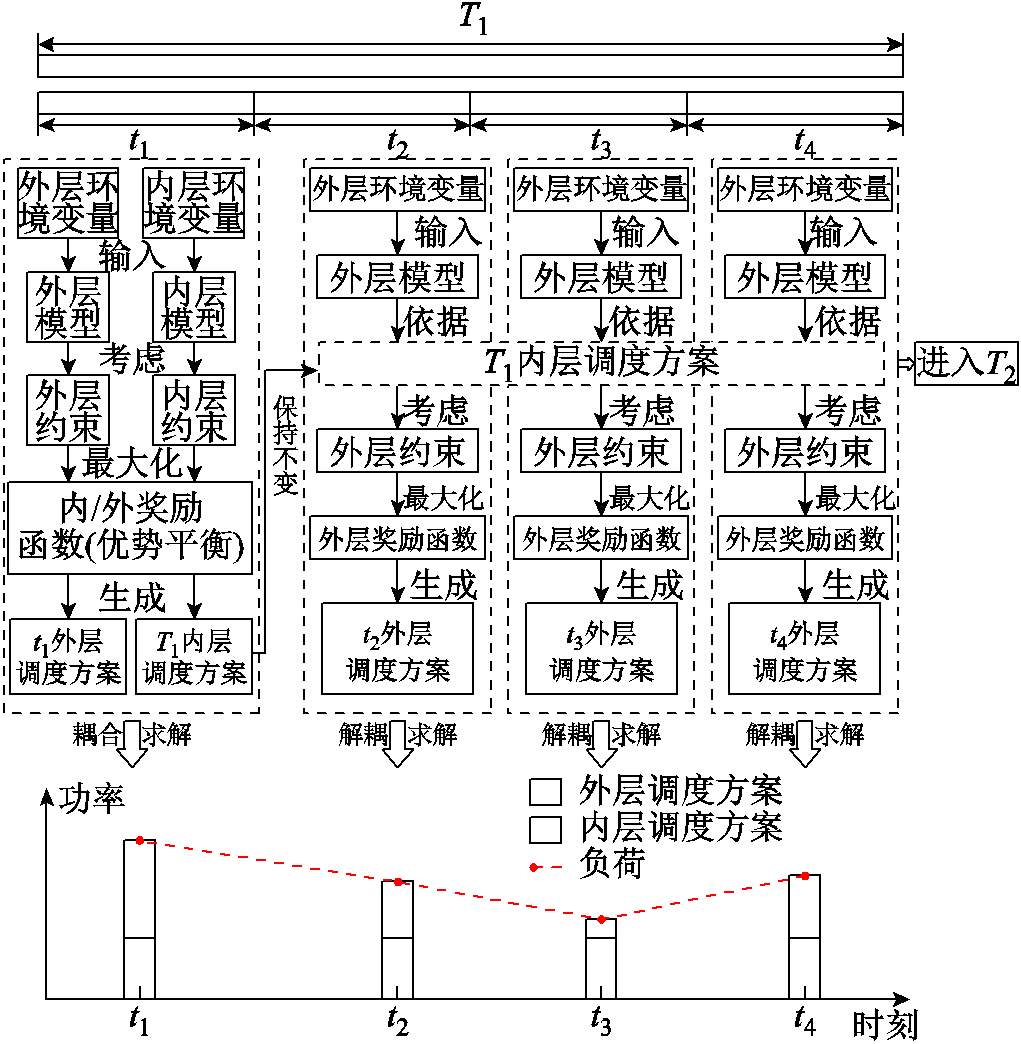
图6 DBLPPO多时间尺度调度求解过程
Fig.6 The solution process of the DBLPPO multi-time-scale scheduling
式中,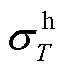 、
、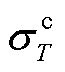 分别为热、冷负荷不平衡度;
分别为热、冷负荷不平衡度;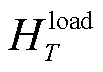 、
、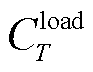 分别为热、冷负荷大小;
分别为热、冷负荷大小;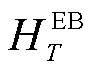 、
、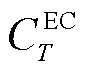 分别为EB、EC机组的热、冷出力功率;下标T为长时间尺度,数值为1 h的倍数。
分别为EB、EC机组的热、冷出力功率;下标T为长时间尺度,数值为1 h的倍数。
3.2.2 DBLPPO内层模型动作空间
DBLPPO内层模型以经济调度、可再生能源消纳为目标,对CHP、GB、AC机组进行功率调控,其动作空间为
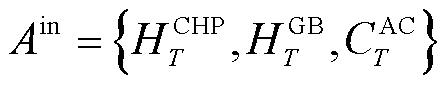 (15)
(15)
式中,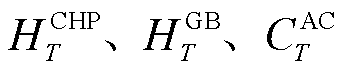 分别为DBLPPO在T时刻CHP、GB机组的产热功率和AC机组冷能的出力功率。
分别为DBLPPO在T时刻CHP、GB机组的产热功率和AC机组冷能的出力功率。
3.2.3 DBLPPO内层模型奖励空间
DBLPPO内层模型调控的目标是以1 h为时间尺度,在满足冷-热负荷功率平衡的情况下,尽可能地减少CHP、GB、AC机组的运行成本,奖励函数公式为
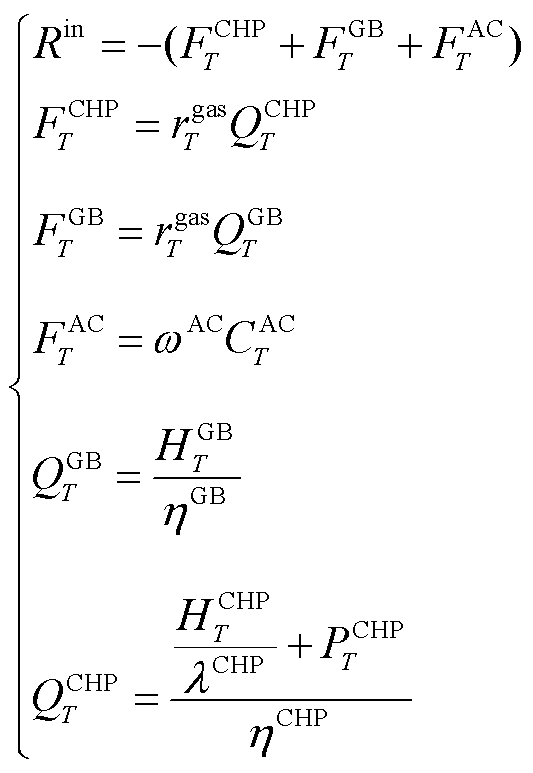 (16)
(16)
式中,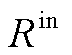 为内层模型奖励函数;
为内层模型奖励函数;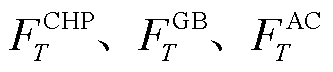 分别为DBLPPO的CHP、GB机组燃料成本和AC机组的运维成本;
分别为DBLPPO的CHP、GB机组燃料成本和AC机组的运维成本;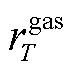 为T时刻天然气的购价;
为T时刻天然气的购价;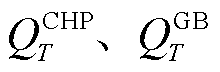 分别为T时刻CHP、GB机组消耗的天然气等效功率;
分别为T时刻CHP、GB机组消耗的天然气等效功率;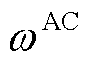 为AC机组的运行维护成本系数;
为AC机组的运行维护成本系数;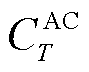 为AC机组在T时刻冷能出力功率。
为AC机组在T时刻冷能出力功率。
3.2.4 DBLPPO内层模型约束
DBLPPO内层模型面向冷、热力系统制定调度方案,需要考虑长时间尺度下各机组出力与负荷功率之间的平衡约束,其数学公式为
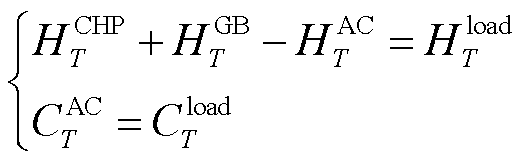 (17)
(17)
除冷、热子系统中的能量平衡约束外,还有CHP、GB、AC机组的出力约束,见式(5)、式(6)、式(9)中不等式约束部分。
3.3.1 DBLPPO外层模型环境空间
DBLPPO外层模型以15 min为调度周期,根据冷、热、电负荷功率及其供需不平衡度,风力、光伏机组发电功率,CHP、GB、AC机组运行功率和蓄电池荷电状态对电力系统制定调度方案,外层模型环境空间为
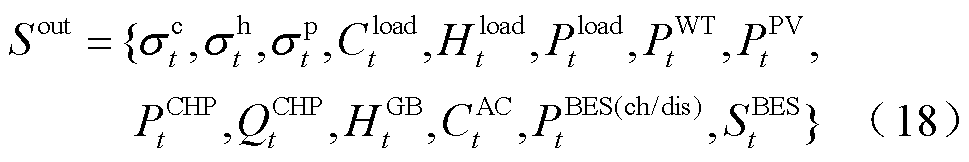
式中,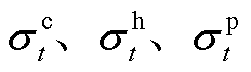 分别为t时刻冷负荷、热负荷与电负荷不平衡度;
分别为t时刻冷负荷、热负荷与电负荷不平衡度;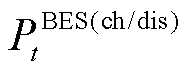 为蓄电池的储/放电功率;下标t为短时间尺度,数值为15 min的倍数。
为蓄电池的储/放电功率;下标t为短时间尺度,数值为15 min的倍数。
3.3.2 DBLPPO外层模型动作空间
DBLPPO外层模型以经济调度、可再生能源消纳为目标,对EB、EC机组运行功率和蓄电池储/放电功率进行调控,并从上级电网购电满足电力负荷平衡,其动作空间为
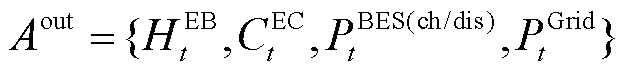 (19)
(19)
3.3.3 DBLPPO外层模型奖励空间
DBLPPO外层模型调控的目标是以15 min为时间尺度,在满足电力负荷功率平衡的基础上,尽可能地减少EB、EC的运行成本、BES的储/放电成本及上级电网的购电成本,数学公式为
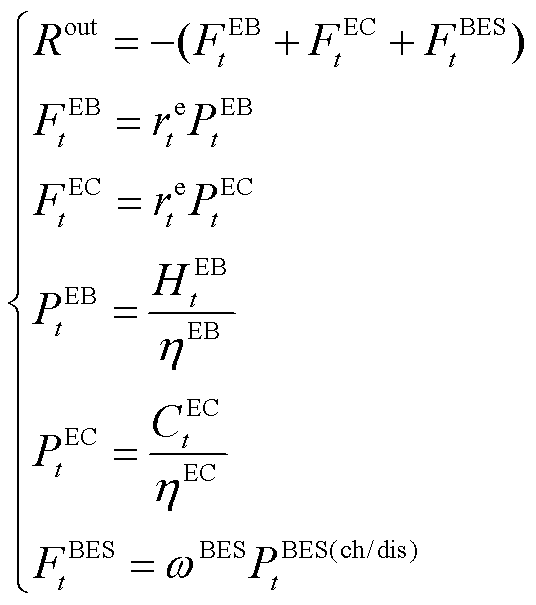 (20)
(20)
式中,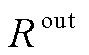 为外层模型奖励函数;
为外层模型奖励函数;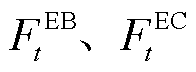 、
、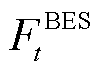 分别为t时刻EB、EC机组运行的耗电成本和蓄电池的运行维护成本;
分别为t时刻EB、EC机组运行的耗电成本和蓄电池的运行维护成本;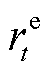 为在t时刻的电价;
为在t时刻的电价;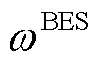 为蓄电池的运维成本系数。
为蓄电池的运维成本系数。
3.3.4 DBLPPO外层模型约束
DBLPPO外层模型面向电、冷、热力系统制定调度方案,在短时间尺度下实现冷、热、电负荷平衡。此外,针对短时间尺度下热、冷负荷波动影响,依靠EC、EB机组的调控灵活性,弥补长时间尺度下的冷、热功率缺额,其功率平衡约束条件为
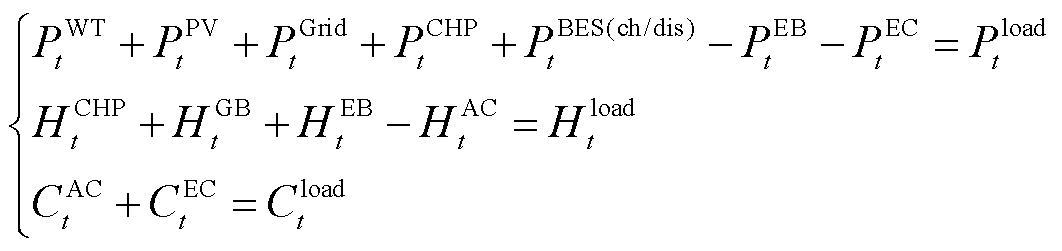 (21)
(21)
热、冷能平衡约束左侧分别加入EB机组的产热功率和EC机组发出的冷功率。
蓄电池的动作约束模型为
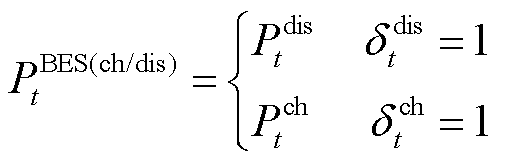 (22)
(22)
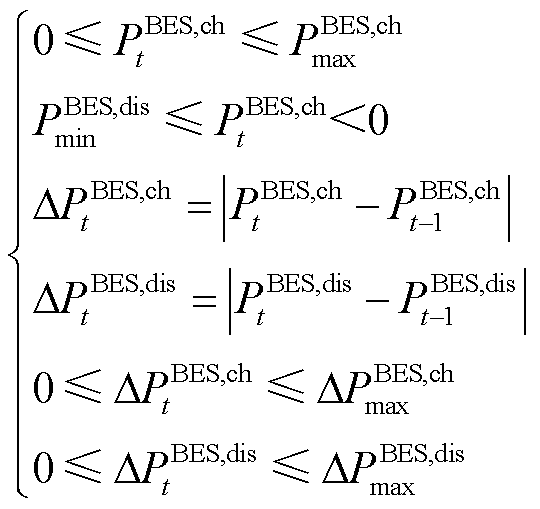 (23)
(23)
式中,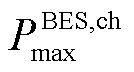 、
、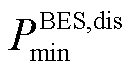 分别为蓄电池储电最大功率、放电最小功率(其值为负);
分别为蓄电池储电最大功率、放电最小功率(其值为负);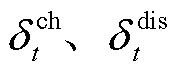 分别为蓄电池储、放电系数;
分别为蓄电池储、放电系数;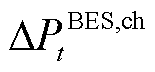 、
、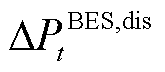 分别为蓄电池储、放电爬坡率;
分别为蓄电池储、放电爬坡率;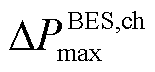 、
、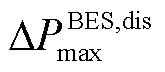 分别为蓄电池储、放电最大爬坡率。此外,在每个短时间尺度下蓄电池都只有储电或放电一种状态,即
分别为蓄电池储、放电最大爬坡率。此外,在每个短时间尺度下蓄电池都只有储电或放电一种状态,即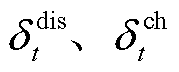 还需满足
还需满足
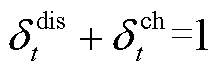 (24)
(24)
除能量平衡约束和蓄电池动作约束外,还有EB、EC机组的出力约束和上级电网购电约束,见式(4)、式(7)、式(8)中不等式部分。
本文以图1所示RIES运行场景为例进行仿真分析。采用美国亚利桑那州立大学2020年第一季度冷、热、电负荷功率作为训练数据,风电、光伏出力如附图1、附图2所示。系统分时电价信息见附表1,天然气价格始终保持为0.4元/(kW·h),系统向上级电网购电功率范围为[0, 850]kW,RIES内各设备相关参数见附表2。
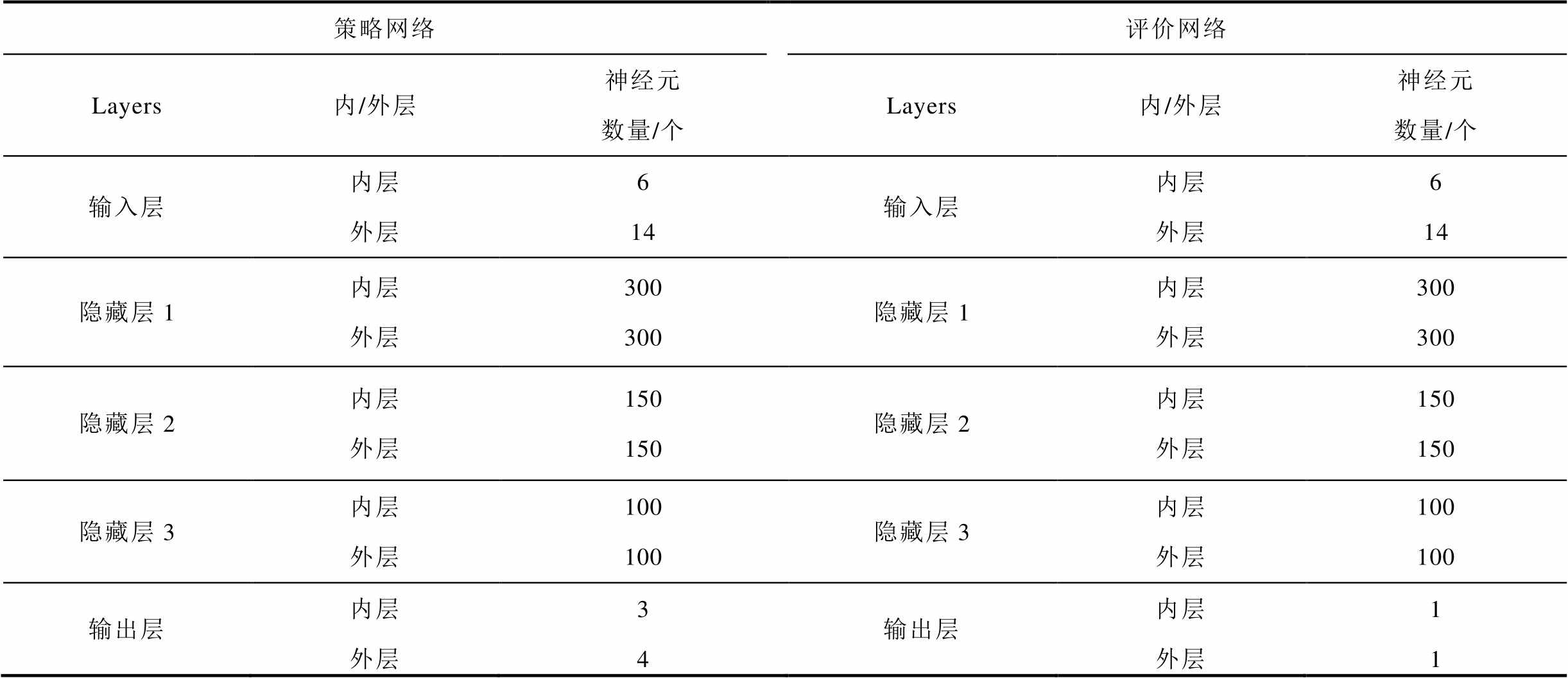
DBLPPO算法基于Pycharm平台进行搭建,编程语言为Python3.5,软件环境为tensorflow1.10.0。策略网络与评价网络均采用Adam优化器进行更新,学习率分别设为5×10-6和2×10-5,折旧因子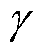 为0.95,每次抓取样本批次为24。策略网络与评价网络的隐藏层结构一致,但参数不同,其神经元参数见附表3。
为0.95,每次抓取样本批次为24。策略网络与评价网络的隐藏层结构一致,但参数不同,其神经元参数见附表3。
本次仿真试验进行10次训练,每次训练包含 7 000个小循环,每个小循环的调度步长为96。DBLPPO内、外层模型训练得到的奖励值变化曲线如图7和图8所示,其中浅色部分表示10次训练过程中奖励函数的波动区间,深色表示10次训练过程中的平均奖励函数值。
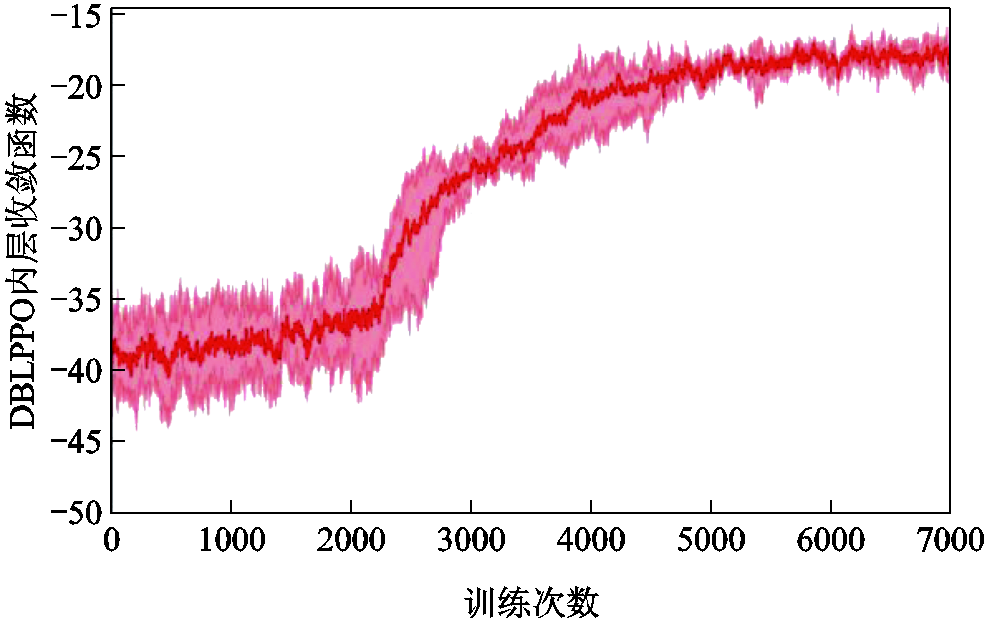
图7 DBLPPO内层奖励函数波动区间和收敛曲线
Fig.7 The fluctuation interval and convergence curve of the inner DBLPPO model’s reward function
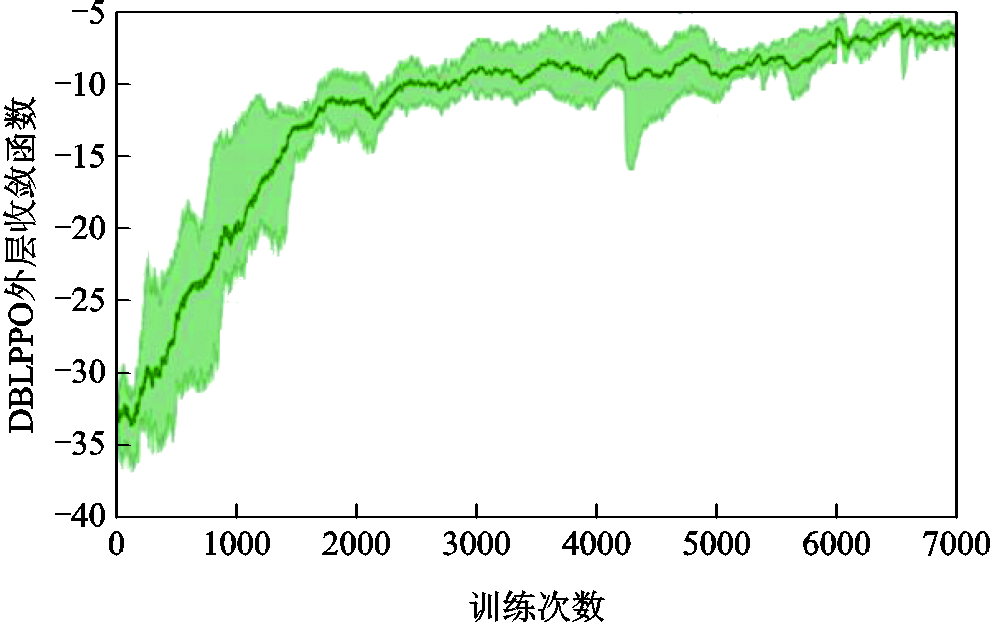
图8 DBLPPO外层奖励函数波动区间和收敛曲线
Fig.8 The fluctuation interval and convergence curve of the outer DBLPPO model’s reward function
内、外层奖励函数分别在6 200次和6 600次收敛,说明DBLPPO优化调度模型能够制定满足各能源网络需求的能量管理方案,实现冷力系统、热力系统与电力系统异质能源间的协同优化管理。由于内、外层奖励函数存在耦合关系,DBLPPO内层模型奖励函数受外层策略影响,DBLPPO外层模型基于内层调度方案统筹全局策略进行优化。所以内、外层奖励函数在最初的相互影响下,向最优化方向波动收敛,最终达到动态平衡。
此外,局部网络数量会影响DBLPPO调度模型的收敛速度。局部网络数量较少时,DBLPPO调度模型的训练时长会随着局部网络数量的增多而减少。当达到阈值后,局部网络数量增多,DBLPPO调度模型的训练时长反而增加。造成上述情况的原因有以下两点:①局部网络过多可能会导致收集到的劣质样本数据增多,阻碍模型向奖励最大化方向收敛;②局部网络过多还会增加全局网络的梯度计算负担,延长奖励函数的收敛时间。不同数量的局部网络与训练时长的关系如附图3所示。
训练完毕,调用已保存的DBLPPO调度模型,选用1月份中某一天的冷、热、电负荷数据进行仿真测试,电力、热力和冷力系统调度结果如图9~图11所示,图中上半部分为能源系统供给功率,下半部分为能源系统需求功率。
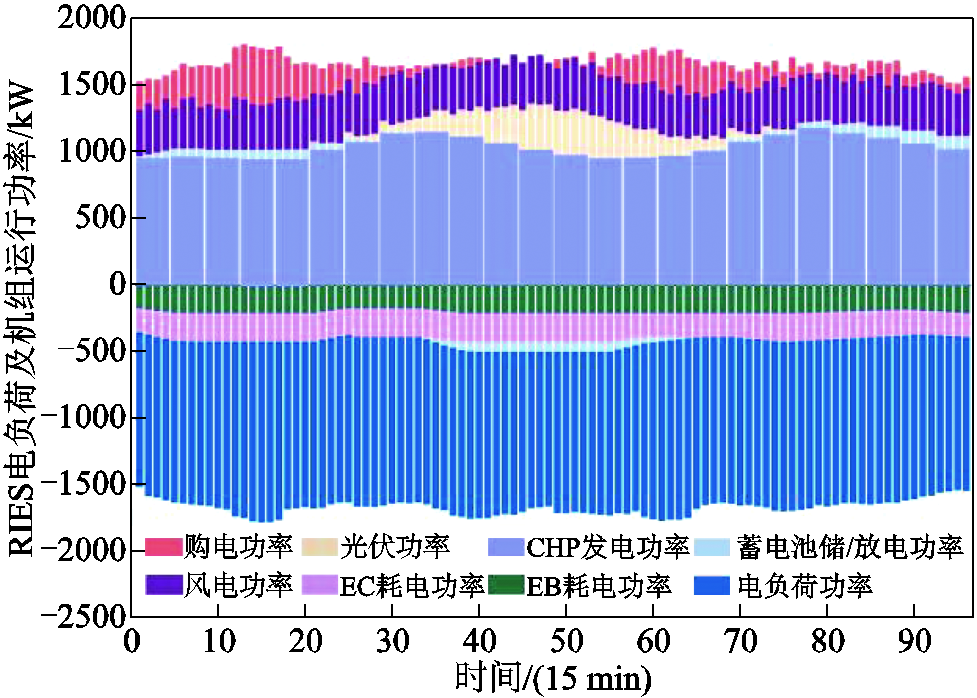
图9 电力系统调度结果
Fig.9 The results of electricity system scheduling
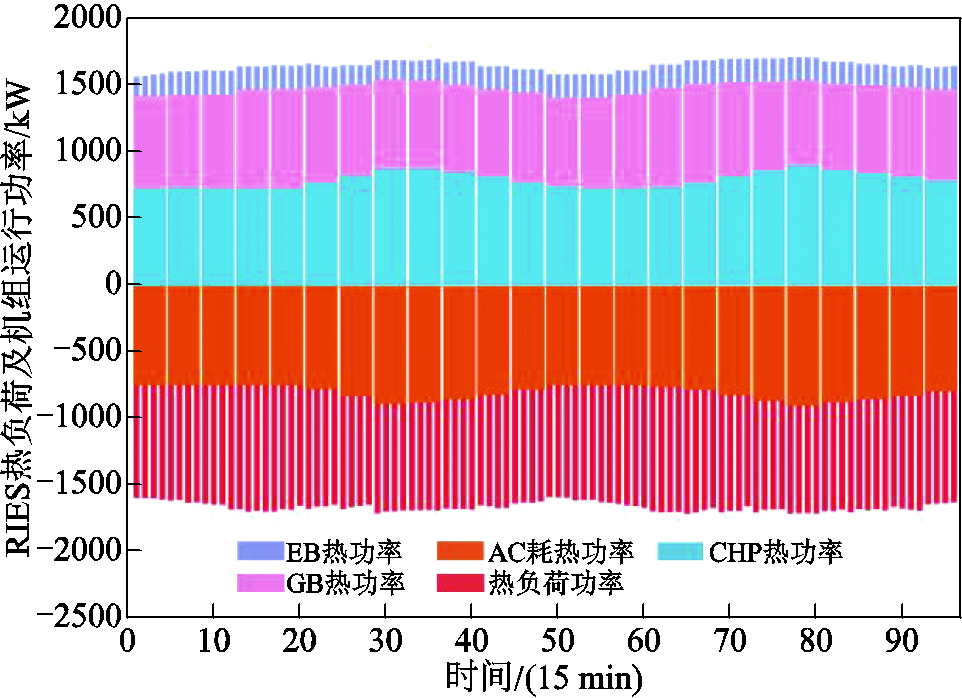
图10 热力系统调度结果
Fig.10 The results of heating system scheduling
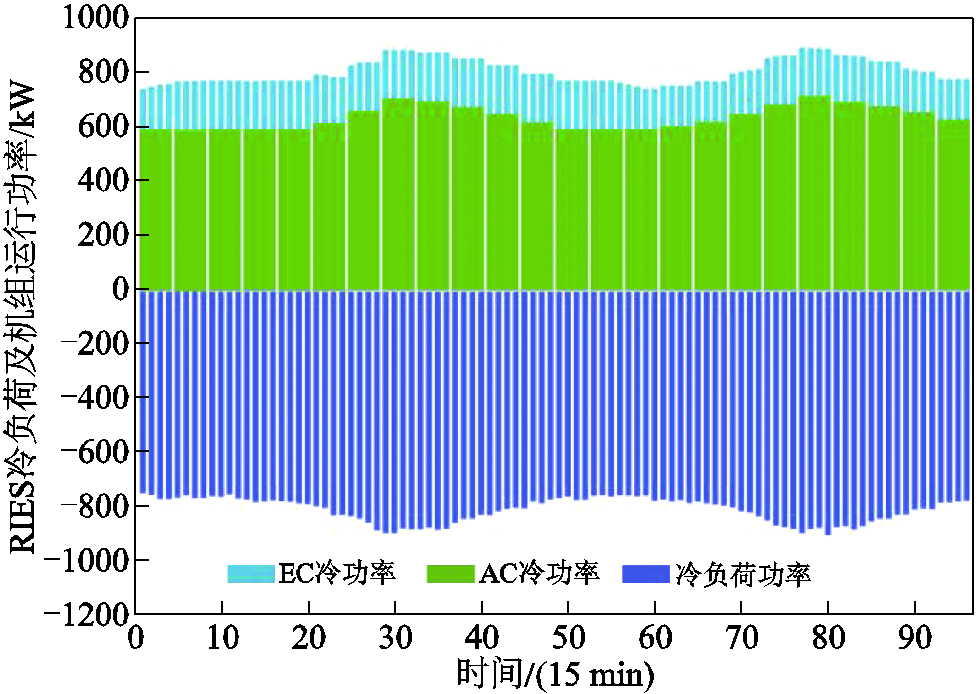
图11 冷力系统调度结果
Fig.11 The results of cooling system scheduling
在0:00—6:00时与23:00—24:00时,电价处于低谷,低于天然气价格。从图9中可以发现,系统向上级电网购电满足电负荷功率需求和EB、EC机组用能需求,EB、EC机组耗电功率增加,RIES的综合用电量升高,为减少上级电网购电成本,蓄电池开始放电。从图10和图11可以看出,冷、热力系统中负荷功率从谷值逐渐升高,为减少系统运行成本,此时AC机组处于最小出力状态,冷负荷功率缺额由EC机组出力弥补。同时为保证AC机组用能需求,CHP机组也处于最低运行状态。GB机组为满足热负荷功率需求,出力平缓增加。
在6:00—10:00时与16:00—20:00时,电价处于平时段,与天然气价格相等。从图10、图11中可以看到,热、冷负荷功率逐渐升高至峰值,CHP机组与AC机组为满足热、冷负荷需求不断增加出力,GB机组为保证热负荷功率平衡降低出力。在6:00—10:00时,电力系统中光伏、风机开始发电,此时为促进系统新能源消纳,配合CHP机组运行出力,系统减小上级电网的购电功率,增加EB、EC机组出力功率,此时蓄电池开始储电,留待备用。在16:00—20:00时,电力系统中光伏出力逐渐消失,为保证用户用电需求,系统从上级电网大量购电,蓄电池不再储电。同时为满足冷、热负荷平衡,EC机组增加出力弥补冷负荷功率缺额,EB机组与CHP、GB机组配合出力,弥补热负荷功率缺额。
在10:00—16:00时与20:00—23:00时,电价处于峰时段,高于天然气价格。从图10、图11中可以看到,冷、热负荷功率从峰值逐渐降低,CHP机组与AC机组迅速减小出力来平衡热、冷负荷功率,同时为满足热负荷功率平衡,减少系统机组运行的耗电成本,GB机组出力增发。在10:00—16:00时,电力系统中新能源发电处于富裕时段,为保证新能源完全消纳,蓄电池开始大量储电,同时系统不再从上级电网购电。当CHP机组电出力功率明显减少时,为满足负荷平衡,系统才从上级电网进行购电。此时,热、冷力系统中,EB、EC机组处于最大功率运行状态,在实现热、冷负荷平衡的同时,最大程度地进行风光消纳。在20:00—23:00时,电力系统中负荷功率下降,为防止系统因上级电网购电过多造成系统运行成本过高,蓄电池开始大量放电,EB、EC机组的耗电功率降低,系统从上级电网的购电行为得到抑制,降低了系统运行成本。
CHP机组采取以热定电的模式运行,其作用为满足AC机组的用能需求。从图10中可以发现,CHP机组能够灵活调整出力,满足AC机组的热能消耗,为冷力系统的能量供需平衡提供支持。同时,其产生的电能与电力系统的机组相互配合,实现电能供需平衡。
通过以上分析可以发现,系统外部购电量、EB、EC机组出力受外部电价影响较大,蓄电池与外部购电可以弥补因源荷不确定性导致的用能缺额,同时蓄电池可以对新能源发电进行削峰填谷,采取价低时储、价高时放的调控策略。由于冷、热力系统无法直接购买外部能量,仅靠电能耦合机组调控出力,其调整的灵活性相对电力系统较弱,所以优先保证自身网络负荷平衡。
此外,本文为验证DBLPPO调度模型运行的经济性,在相同调度环境下建立近端策略优化(Proximal Policy Optimization, PPO)调度模型和DPPO调度模型进行对比,计算三者每个时段的RIES综合运行成本(机组运行成本加负荷不平衡等效成本),对比结果如图12所示。
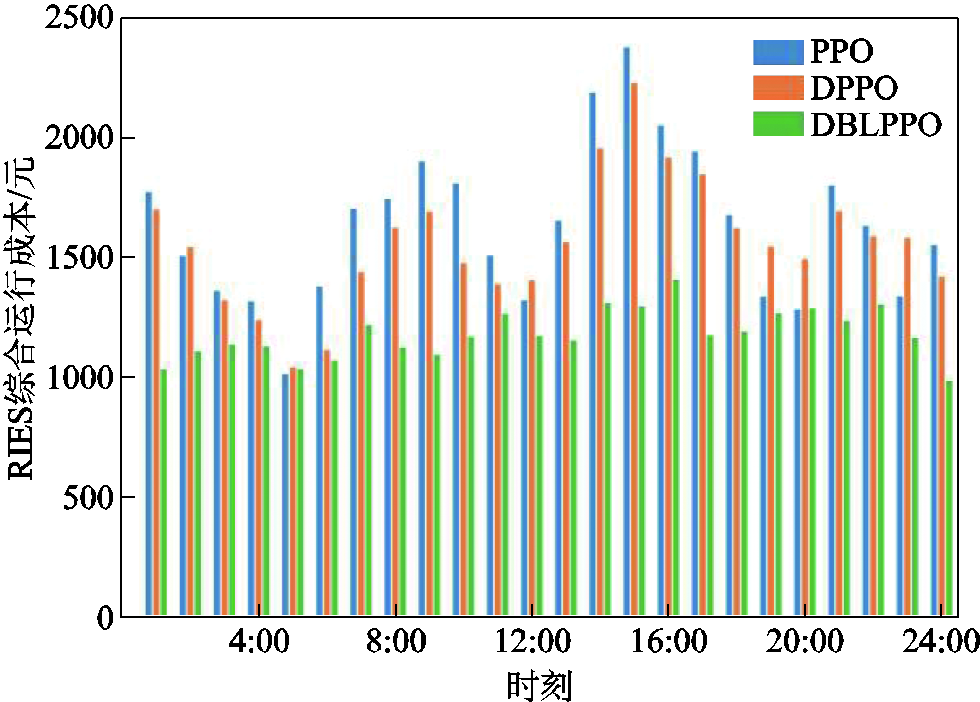
图12 RIES综合运行成本对比
Fig.12 RIES comprehensive operating cost comparison
上述结果表明,相较于PPO、DPPO调度模型,DBLPPO调度模型在每个小时内的综合运行成本基本是最低的。其全天综合运行成本较DPPO调度模型降低了24.47%,较PPO调度模型降低了28.54%。
最后,与其他强化学习模型对比验证本文所提算法模型的综合性能。面向冷-热-电RIES的DBLPPO调度模型与PPO调度模型、DPPO调度模型、双层PPO调度模型和Zhou Suyang等所提出的DPPO热-电联产调度模型[37]进行对比。五种方法在训练时长、RIES综合运行成本及时间尺度方面的对比结果见表1,其中训练时长指相同数据集训练30次的平均时长。
表1 不同调度模型性能比较
Tab.1 Comparison of the performance of different scheduling models
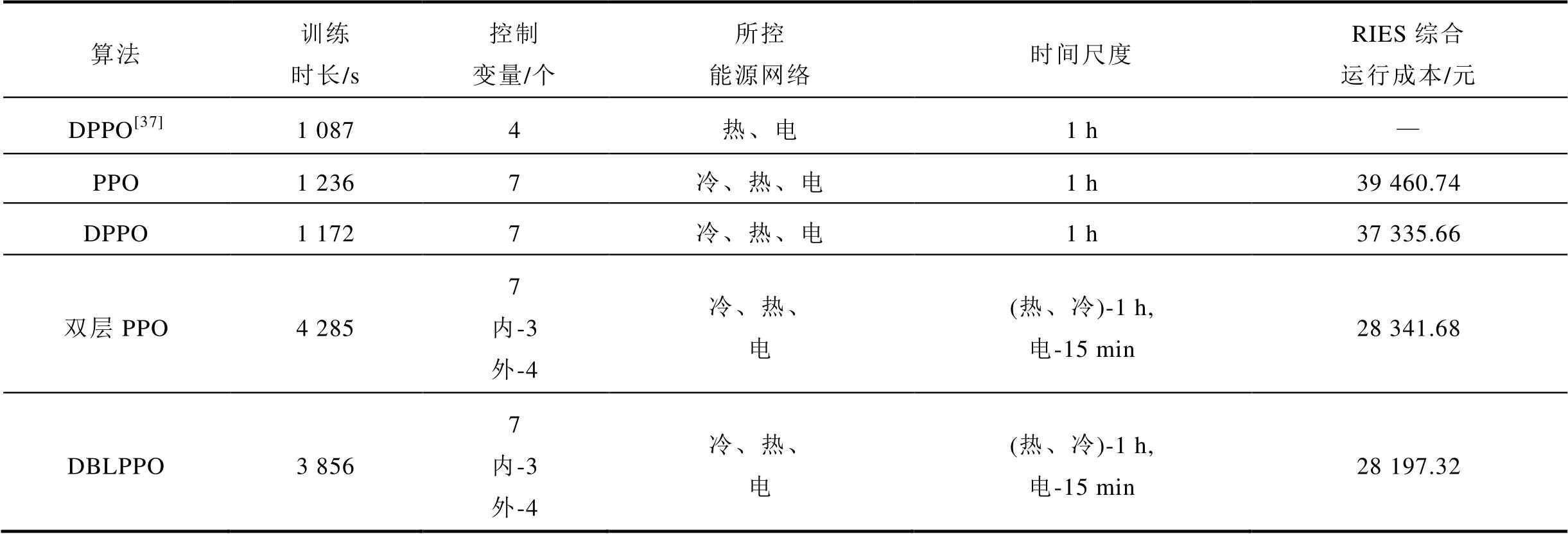
算法训练时长/s控制变量/个所控能源网络时间尺度RIES综合运行成本/元 DPPO[37]1 0874热、电1 h— PPO1 2367冷、热、电1 h39 460.74 DPPO1 1727冷、热、电1 h37 335.66 双层PPO4 2857内-3外-4冷、热、电(热、冷)-1 h,电-15 min28 341.68 DBLPPO3 8567内-3外-4冷、热、电(热、冷)-1 h,电-15 min28 197.32
本文仿真试验中,PPO、DPPO、双层PPO和DBLPPO调度模型的应用场景和机组运行参数一致。其中应用场景均为冷-热-电RIES,且天然气只作为联供燃料,不独立成网。PPO、DPPO调度模型采用单一时间尺度,根据每小时初期的负荷需求进行日内调度,双层PPO、DBLPPO调度模型采用 1 h-15 min多时间尺度,内外双层分别根据每小时初期以及每小时各15 min初期的负荷需求进行日内调度。在计算系统的综合运行成本时,四种调度模型均采用15 min尺度的负荷数据计算负荷不平衡等效成本。综上所述,可以对四种调度模型的经济效益进行有效的对比分析。
为分析控制变量个数对调度模型求解速度的影响,本文引入了文献[37]提出的基于DPPO算法的热-电联产调度模型进行对比分析。与上述四种调度模型相比,此模型在调度场景方面缺失了冷力系统。电、热机组的运行参数与其他模型保持一致,在此不考虑其运行成本的对比。
对比训练时长可以发现,文献[37]所设计的能源网络结构最为简单,控制变量最少,训练时长最短。DPPO调度模型与PPO调度模型对比发现,分布式的网络结构能够缩短单一时间尺度调度模型的训练时长。双层PPO调度模型与PPO调度模型对比发现,双层模型结构提高了模型收敛的难度,增加了模型训练时长。DBLPPO调度模型与双层PPO调度模型对比发现,分布式的网络结构在多时间尺度优化调度中依然能够有效地缩短训练时长,DBLPPO调度模型的训练时长较双层PPO降低了10.01%。
从经济效益方面对比发现,PPO、DPPO调度模型只能进行单一时间尺度优化调度,而双层PPO、DBLPPO调度模型可以采用“先耦合-再解耦”的求解思路对RIES进行多时间尺度优化调度,因此后两者机组的调控灵活性更高,更能满足冷、热、电负荷在15 min内的功率波动需求,降低系统的综合运行成本。此外,PPO、DBLPPO调度模型采用分层控制策略对冷-热力系统和电力系统进行解耦分析,将7个控制变量划分为内层3个和外层4个,有效地提高了模型收敛的鲁棒性,防止在模型训练过程中陷入局部最优或“维数灾难”,保证每次训练的有效性。对双层PPO、DBLPPO调度模型进行多次仿真验证,其调度结果均能兼顾运行成本和多元负荷平衡。DBLPPO调度模型与双层PPO调度模型对比发现,前者凭借多线程的工作模式具有更好的收敛效果,在经济方面表现为系统综合运行成本更低。
综上所述,相较于其他四种方法,本文所提DBLPPO调度模型利用双层模型结构对冷-热-电能源系统进行解耦分析,降低了每层模型的控制变量数量,缓解了控制变量增多引起的“维度灾难”问题。此外,传统强化学习模型如PPO、DPPO等因其动作维度受限,只能以1 h的时间尺度进行能源管理,而本文所提DBLPPO调度模型采用“先耦合-再解耦”的求解思路对机组进行多维时间调控,实现“时-分”互补的能源管理策略,弥补系统在15 min内的供需缺额,提高了系统的综合经济效益。在面对复杂RIES系统时,因其特有的多线程工作模式,能够辅助智能体高效收集大量数据,有效地缩短训练时长,避免多时间尺度优化调度造成的寻优困难。
本文针对冷-热-电区域综合能源系统的多时间尺度优化管理问题,提出了一种基于分布式双层近端策略优化(DBLPPO)的强化学习模型。案例分析结果表明,本文的DBLPPO调度模型能够以两种时间尺度对三种能源网络进行协同优化管理,有效地提升了模型算法的收敛性能和RIES的综合经济效益。本文所得结论如下:
1)本文提出的DBLPPO调度模型通过构建双层模型分别对冷-热力系统和电力系统进行多维时间调控,解决了强化学习算法动作维度与异质能源管理时间尺度不匹配的问题,克服了不同能源系统时间响应差异所造成的调度困难。
2)DBLPPO调度模型能够解耦分析冷、热、电三种能源系统,有效地避免常规强化学习RIES调度模型由于控制变量过多引发的“维数灾难”问题,保证了算法的收敛性。
3)DBLPPO调度模型继承了DPPO算法的分布式结构,通过设计多个局部网络与外部环境多线程互动,提高样本数据的采集效率,减小了训练所需时间。
4)DBLPPO调度模型凭借深度强化学习算法的自学习能力,能够快速地适应环境频繁变化的系统,以应对不断变化的能源需求和供应模式,保证RIES安全、经济运行。
附 录
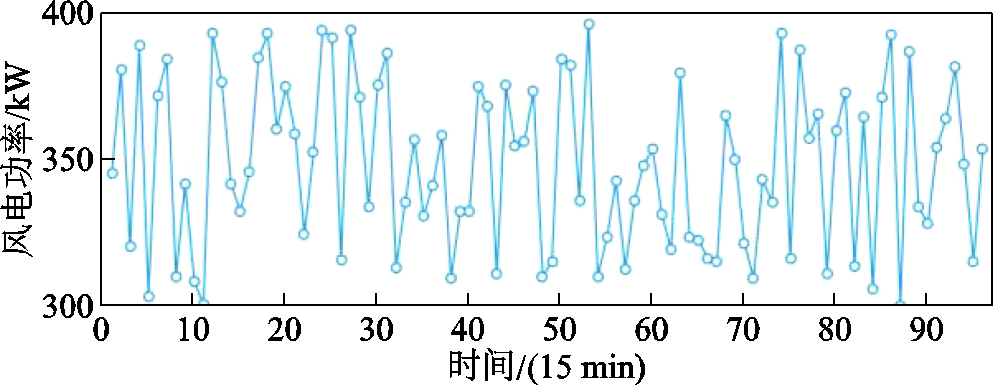
附图1 RIES风力机组发电功率
APP.Fig.1 The power of RIES’s wind turbines
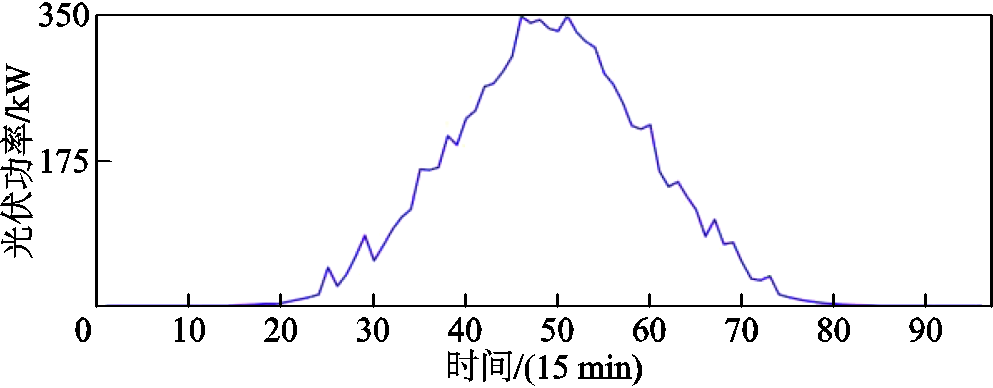
附图2 RIES光伏机组发电功率
APP.Fig.2 The power of RIES’s photovoltaic generators
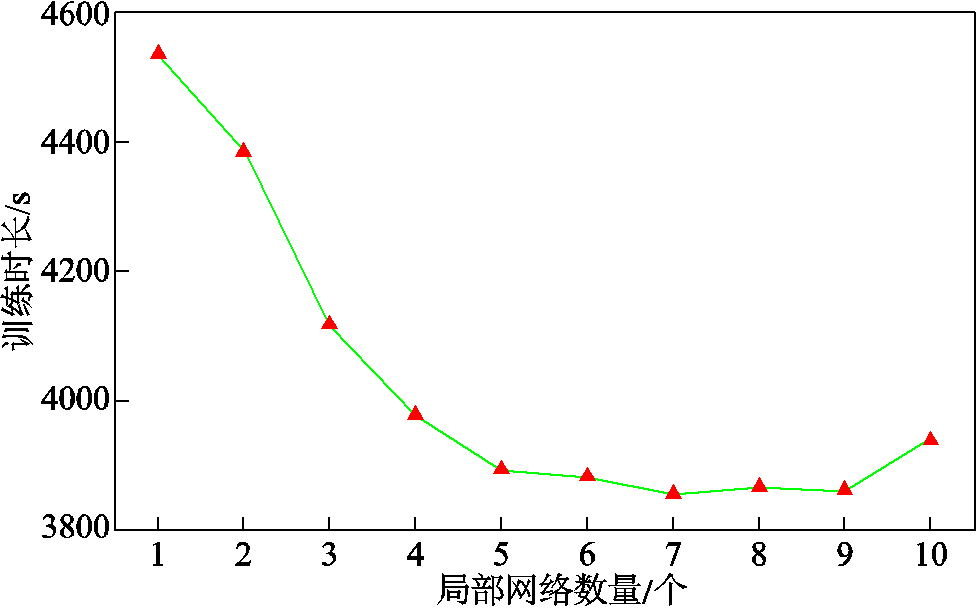
附图3 局部网络数量与训练时长关系
APP.Fig.3 The relationship between the number of local networks and training duration
附表1 分时电价信息
APP.Tab.1 Time-of-use electricity price

时段时刻购电单价/[元/(kW·h)] 峰时10:00—16:0020:00—23:000.68
(续)

时段时刻购电单价/[元/(kW·h)] 平时6:00—10:0016:00—20:000.40 谷时0:00—6:0023:00—24:000.23
附表2 RIES设备相关参数
APP.Tab.2 The parameters of RIES device

参数数值 480, 400 510, 480, 450 710, 1 000 80, 77 150, 150 640, 745 120, 125 100, 240 85, 90 60, 50 150, 270 60, 50 570, 720 90, 80 3 000, 120, 120 20, 80 0.9, 1.05 0.25, 0.05
附表3 DBLPPO模型神经元参数
APP.Tab.3 Neural network parameters of the DBLPPO model
策略网络评价网络 Layers内/外层神经元数量/个Layers内/外层神经元数量/个 输入层内层外层614输入层内层外层614 隐藏层1内层外层300300隐藏层1内层外层300300 隐藏层2内层外层150150隐藏层2内层外层150150 隐藏层3内层外层100100隐藏层3内层外层100100 输出层内层外层34输出层内层外层11
参考文献
[1] 陈艳波, 张宁, 李嘉祺, 等. 零碳园区研究综述及展望[J]. 中国电机工程学报, 2024, 44(14): 5496-5517.
Chen Yanbo, Zhang Ning, Li Jiaqi, et al. Review and prospect of zero carbon park research[J]. Proceedings of the CSEE, 2024, 44(14): 5496-5517.
[2] 高玉, 王琦, 陈严, 等. 考虑需求响应和能量梯级利用的含氢综合能源系统优化调度[J]. 电力系统自动化, 2023, 47(4): 51-59.
Gao Yu, Wang Qi, Chen Yan, et al. Optimal dispatch of integrated energy system with hydrogen considering demand response and cascade energy utilization[J]. Automation of Electric Power Systems, 2023, 47(4): 51-59.
[3] 杨龙, 张沈习, 程浩忠, 等. 区域低碳综合能源系统规划关键技术与挑战[J]. 电网技术, 2022, 46(9): 3290-3304.
Yang Long, Zhang Shenxi, Cheng Haozhong, et al. Regional low-carbon integrated energy system planning: key technologies and challenges[J]. Power System Technology, 2022, 46(9): 3290-3304.
[4] 潘超, 范宫博, 王锦鹏, 等. 灵活性资源参与的电热综合能源系统低碳优化[J]. 电工技术学报, 2023, 38(6): 1633-1647.
Pan Chao, Fan Gongbo, Wang Jinpeng, et al. Low-carbon optimization of electric and heating integrated energy system with flexible resource participation[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1633-1647.
[5] 吴孟雪, 房方. 计及风光不确定性的电-热-氢综合能源系统分布鲁棒优化[J]. 电工技术学报, 2023, 38(13): 3473-3485.
Wu Mengxue, Fang Fang. Distributionally robust optimization of electricity-heat-hydrogen integrated energy system with wind and solar uncertainties[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3473-3485.
[6] Li Canbing, Yang Hanyu, Shahidehpour M, et al. Optimal planning of islanded integrated energy system with solar-biogas energy supply[J]. IEEE Transactions on Sustainable Energy, 2020, 11(4): 2437-2448.
[7] 任洲洋, 王皓, 李文沅, 等. 基于氢能设备多状态模型的电氢区域综合能源系统可靠性评估[J]. 电工技术学报, 2023, 38(24): 6744-6759.
Ren Zhouyang, Wang Hao, Li Wenyuan, et al. Reliability evaluation of electricity-hydrogen regional integrated energy systems based on the multi-state models of hydrogen energy equipment[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6744-6759.
[8] Wang Yudong, Hu Junjie, Liu Nian. Energy management in integrated energy system using energy–carbon integrated pricing method[J]. IEEE Transactions on Sustainable Energy, 2023, 14(4): 1992-2005.
[9] 董雷, 李扬, 陈盛, 等. 考虑多重不确定性与电碳耦合交易的多微网合作博弈优化调度[J]. 电工技术学报, 2024, 39(9): 2635-2651.
Dong Lei, Li Yang, Chen Sheng, et al. Multi-microgrid cooperative game optimization scheduling considering multiple uncertainties and coupled electricity-carbon transactions[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2635-2651.
[10] 曾艾东, 王佳伟, 邹宇航, 等. 考虑供热管网储热的综合能源系统多时间尺度优化调度[J]. 高电压技术, 2023, 49(10): 4192-4202.
Zeng Aidong, Wang Jiawei, Zou Yuhang, et al. Multi-time-scale optimal scheduling of integrated energy system considering heat storage characteristics of heating network[J]. High Voltage Engineering, 2023, 49(10): 4192-4202.
[11] 栗海润, 穆云飞, 贾宏杰, 等. 考虑量化储热的多区域电–热综合能源系统优化调度[J]. 中国电机工程学报, 2021, 41(增刊1): 16-27.
Li Hairun, Mu Yunfei, Jia Hongjie, et al. Optimal dispatching of multi-regional electricity-heat integrated energy system considering quantitative thermal storage[J]. Proceedings of the CSEE, 2021, 41(S1): 16-27.
[12] 徐卫君, 张伟, 胡宇涛, 等. 先进绝热压缩空气储能多能流优化调度模型[J]. 电工技术学报, 2022, 37(23): 5944-5955.
Xu Weijun, Zhang Wei, Hu Yutao, et al. Multi energy flow optimal scheduling model of advanced adiabatic compressed air energy storage[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5944-5955.
[13] 汤翔鹰, 胡炎, 耿琪, 等. 考虑多能灵活性的综合能源系统多时间尺度优化调度[J]. 电力系统自动化, 2021, 45(4): 81-90.
Tang Xiangying, Hu Yan, Geng Qi, et al. Multi-time-scale optimal scheduling of integrated energy system considering multi-energy flexibility[J]. Automation of Electric Power Systems, 2021, 45(4): 81-90.
[14] 韩丽, 王晓静, 鲁盼盼, 等. 考虑风电功率预测误差分时补偿的电热联合系统多时间尺度调度[J]. 电力系统自动化, 2023, 47(1): 74-85.
Han Li, Wang Xiaojing, Lu Panpan, et al. Multi-time-scale dispatching of integrated electricity and thermal system considering time-sharing compensation of wind power forecasting error[J]. Automation of Electric Power Systems, 2023, 47(1): 74-85.
[15] 李勇, 凌锋, 乔学博, 等. 基于网侧资源协调的自储能柔性互联配电系统日前-日内优化[J]. 电工技术学报, 2024, 39(3): 758-773, 923.
Li Yong, Ling Feng, Qiao Xuebo, et al. Day-ahead and intra-day optimization of flexible interconnected distribution system with self-energy storage based on the grid-side resource coordination[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 758-773, 923.
[16] 陈志颖, 温步瀛, 朱振山. 计及风电相关性的区域综合能源系统多时间尺度优化调度[J]. 电力自动化设备, 2023, 43(8): 25-32.
Chen Zhiying, Wen Buying, Zhu Zhenshan. Multi-time scale optimal scheduling of regional integrated energy system considering wind power correlation[J]. Electric Power Automation Equipment, 2023, 43(8): 25-32.
[17] 南斌, 姜春娣, 董树锋, 等. 计及源荷不确定性的综合能源系统日前-日内协调优化调度[J]. 电网技术, 2023, 47(9): 3669-3683.
Nan Bin, Jiang Chundi, Dong Shufeng, et al. Day-ahead and intra-day coordinated optimal scheduling of integrated energy system considering uncertainties in source and load[J]. Power System Technology, 2023, 47(9): 3669-3683.
[18] 陈静, 杨坤漓, 张岩, 等. 多时间尺度下计及综合需求响应和碳捕集-电转气联合运行的综合能源系统优化调度[J]. 电力自动化设备, 2024, 44(6): 68-76.
Chen Jing, Yang Kunli, Zhang Yan, et al. Optimal scheduling of integrated energy system considering integrated demand response and joint operation of carbon capture and power-to-gas under multiple time scales[J]. Electric Power Automation Equipment, 2024, 44(6): 68-76.
[19] 李天格, 胡志坚, 陈志, 等. 计及电-气-热-氢需求响应的综合能源系统多时间尺度低碳运行优化策略[J]. 电力自动化设备, 2023, 43(1): 16-24.
Li Tiange, Hu Zhijian, Chen Zhi, et al. Multi-time scale low-carbon operation optimization strategy of integrated energy system considering electricity-gas-heat-hydrogen demand response[J]. Electric Power Automation Equipment, 2023, 43(1): 16-24.
[20] 崔杨, 曾鹏, 王铮, 等. 计及电价型需求侧响应含碳捕集设备的电-气-热综合能源系统低碳经济调度[J]. 电网技术, 2021, 45(2): 447-461.
Cui Yang, Zeng Peng, Wang Zheng, et al. Low-carbon economic dispatch of electricity-gas-heat integrated energy system with carbon capture equipment considering price-based demand response[J]. Power System Technology, 2021, 45(2): 447-461.
[21] 李壹民, 邵振国, 黄圆皓, 等. 电-热综合能源系统仿射型区间多能流算法[J]. 中国电机工程学报, 2023, 43(9): 3429-3444.
Li Yimin, Shao Zhenguo, Huang Yuanhao, et al. Interval multi-energy flow algorithm for integrated heat and electricity system based on affine arithmetic[J]. Proceedings of the CSEE, 2023, 43(9): 3429-3444.
[22] 林旗斌. 基于模型预测控制的含压缩空气储能微能网多时间尺度优化调度方法[J]. 电气技术, 2023, 24(7): 11-19, 63.
Lin Qibin. Multi-time scale optimal scheduling strategy for micro energy network with compressed air energy storage based on model predictive control[J]. Electrical Engineering, 2023, 24(7): 11-19, 63.
[23] Yi Zonggen, Luo Yusheng, Westover T, et al. Deep reinforcement learning based optimization for a tightly coupled nuclear renewable integrated energy system[J]. Applied Energy, 2022, 328: 120113.
[24] Zhou Kunshu, Zhou Kaile, Yang Shanlin. Reinforcement learning-based scheduling strategy for energy storage in microgrid[J]. Journal of Energy Storage, 2022, 51: 104379.
[25] Li Jifeng, He Xingtang, Li Weidong, et al. Low-carbon optimal learning scheduling of the power system based on carbon capture system and carbon emission flow theory[J]. Electric Power Systems Research, 2023, 218: 109215.
[26] 乔骥, 王新迎, 张擎, 等. 基于柔性行动器-评判器深度强化学习的电-气综合能源系统优化调度[J]. 中国电机工程学报, 2021, 41(3): 819-833.
Qiao Ji, Wang Xinying, Zhang Qing, et al. Optimal dispatch of integrated electricity-gas system with soft actor-critic deep reinforcement learning[J]. Proceedings of the CSEE, 2021, 41(3): 819-833.
[27] Li Yang, Bu Fanjin, Li Yuanzheng, et al. Optimal scheduling of island integrated energy systems considering multi-uncertainties and hydrothermal simultaneous transmission: a deep reinforcement learning approach[J]. Applied Energy, 2023, 333: 120540.
[28] 彭春华, 陈思畏, 徐佳璐, 等. 综合能源系统混合时间尺度多目标强化学习低碳经济调度[J]. 电网技术, 2022, 46(12): 4914-4925.
Peng Chunhua, Chen Siwei, Xu Jialu, et al. Low carbon economic scheduling for integrated energy systems with mixed timescale & multi-objective reinforcement learning[J]. Power System Technology, 2022, 46(12): 4914-4925.
[29] 陈明昊, 孙毅, 谢志远. 基于双层深度强化学习的园区综合能源系统多时间尺度优化管理[J]. 电工技术学报, 2023, 38(7): 1864-1881.
Chen Minghao, Sun Yi, Xie Zhiyuan. The multi-time-scale management optimization method for park integrated energy system based on the bi-layer deep reinforcement learning[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1864-1881.
[30] 李鹏, 王加浩, 黎灿兵, 等. 计及源荷不确定性与设备变工况特性的园区综合能源系统协同优化运行方法[J]. 中国电机工程学报, 2023, 43(20): 7802-7812.
Li Peng, Wang Jiahao, Li Canbing, et al. Collaborative optimal scheduling of the community integrated energy system considering source-load uncertainty and equipment off-design performance[J]. Proceedings of the CSEE, 2023, 43(20): 7802-7812.
[31] 郑诗程, 许浩, 郎佳红, 等. 计及光伏不确定性的多区域综合能源系统多场景分布鲁棒优化调度[J]. 太阳能学报, 2024, 45(3): 460-469.
Zheng Shicheng, Xu Hao, Lang Jiahong, et al. Multi-scenario distributed robust optimal scheduling of multi-area integrated energy systems considering photovoltaic uncertainty[J]. Acta Energiae Solaris Sinica, 2024, 45(3): 460-469.
[32] 冯斌, 胡轶婕, 黄刚, 等. 基于深度强化学习的新型电力系统调度优化方法综述[J]. 电力系统自动化, 2023, 47(17): 187-199.
Feng Bin, Hu Yijie, Huang Gang, et al. Review on optimization methods for new power system dispatch based on deep reinforcement learning[J]. Automation of Electric Power Systems, 2023, 47(17): 187-199.
[33] Duan Jiajun, Shi Di, Diao Ruisheng, et al. Deep-reinforcement-learning-based autonomous voltage control for power grid operations[J]. IEEE Transactions on Power Systems, 2020, 35(1): 814-817.
[34] 周毅斌, 肖浩, 裴玮, 等. 基于纵向联邦学习的微电网群协同优化运行与策略进化[J]. 电力系统自动化, 2023, 47(11): 121-132.
Zhou Yibin, Xiao Hao, Pei Wei, et al. Collaborative optimization operation and strategy evolution of microgrid cluster based on vertical federated learning[J]. Automation of Electric Power Systems, 2023, 47(11): 121-132.
[35] 董雷, 杨子民, 乔骥, 等. 基于分层约束强化学习的综合能源多微网系统优化调度[J]. 电工技术学报, 2024, 39(5): 1436-1453.
Dong Lei, Yang Zimin, Qiao Ji, et al. Optimal scheduling of integrated energy multi-microgrid system based on hierarchical constraint reinforcement learning[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1436-1453.
[36] 蔺伟山, 王小君, 孙庆凯, 等. 计及安全约束的综合能源系统深度强化学习优化调度策略研究[J]. 电网技术, 2023, 47(5): 1970-1983.
Lin Weishan, Wang Xiaojun, Sun Qingkai, et al. Optimal dispatch strategy of integrated energy system based on deep reinforcement learning considering security constraints[J]. Power System Technology, 2023, 47(5): 1970-1983.
[37] Zhou Suyang, Hu Zijian, Gu Wei, et al. Combined heat and power system intelligent economic dispatch: a deep reinforcement learning approach[J]. International Journal of Electrical Power & Energy Systems, 2020, 120: 106016.
Abstract Under the background of the dual carbon goals, the regional integrated energy system (RIES) can achieve interconversion between heterogeneous energy sources due to its multi-energy coupling characteristics, providing new technical support for energy-saving and efficient operation of modern energy systems. Due to the differences in the flow of heterogeneous energy sources in transmission pipelines, existing research usually adopts convex relaxation techniques or linearization methods to model and solve the RIES for multi-time-scale, and relies on high-precision source-load forecasting results and equipment mathematical modeling to improve the reliability of scheduling decisions. However, the increasingly complex internal energy coupling structure of the RIES has increased the difficulty of its refined mathematical modeling and solution, posing challenges to the real-time scheduling decisions and safe optimal operation of the RIES. Therefore, this paper proposes an improved distributed bi-layer proximal policy optimization (DBLPPO) deep reinforcement learning scheduling model. This model can achieve multi-time-scale optimization management of various energy networks in the RIES and avoid the optimization difficulties caused by non-convex nonlinear model structures in scheduling solutions.
Firstly, the power output, storage, and transformation of internal energy in the RIES are constructed into a high-dimensional space Markov decision process mathematical model. Secondly, based on the improved distributed proximal policy optimization (DPPO) algorithm, a sequential decision description is made for it, and a control model of the internal bi-layer proximal policy optimization (PPO) is constructed. The local network adopts the "coupling first, then decoupling" solution approach to carry out multi-time-scale optimization decision-making for the cold-heat system and the power system. In the early stage of long time scale, the inner and outer models perform coupled solutions, and the RIES cold-heat system and power system achieve coordinated optimal operation. In the remaining short time scales, the inner and outer models perform decoupled solutions and carry out short-term flexible regulation of the power system. The inner and outer models interact with each other and fluctuating convergence towards the reward maximization direction, eventually achieving multi-time-scale optimization scheduling of the RIES cold-heat system and power system.
This paper conducts simulation experiments with a cold-heat-electric RIES as the scheduling scenario, and compares the scheduling results of the DBLPPO scheduling model with those of a single time scale scheduling model (PPO, DPPO). The results show that the DBLPPO scheduling model can flexibly regulate the system's adjustable resources in the short time scale, meet the power fluctuation requirements of electricity, heat, and cold loads in the short time scale, and has the lowest comprehensive operating cost, which is 24.47% lower than that of the DPPO scheduling model and 28.54% lower than that of the PPO scheduling model. In addition, simulation experiments are conducted with the DBLPPO scheduling model and the bi-layer PPO scheduling model in the same scenario, and the results show that the distributed structure of the DBLPPO scheduling model still has a significant advantage in improving model training efficiency, which can effectively shorten the training time, 10.01% shorter than that of the dual-layer PPO scheduling model.
Through case analysis, it is verified that the proposed scheduling model can achieve coordinated optimal management of various energy networks in the RIES at different time scales, accelerate the optimal decision-making speed of the multi-time-scale scheduling model, and by virtue of the fast adaptability of the deep reinforcement learning algorithm, efficiently solve random optimization problems in complex RIES scenarios, and improve the economic benefits of system operation. The next step of work will be to improve the model to enhance the environmental awareness ability of the inner model, so that its decision-making scheme is always the optimal scheduling decision in the long time scale.
Keywords:Regional integrated energy system, multi-time-scale, distributed bi-layer proximal policy optimization, deep reinforcement learning, coordinated optimal management, economic benefits
中图分类号:TM73
DOI: 10.19595/j.cnki.1000-6753.tces.240907
国家自然科学基金重点资助项目(52337004)。
收稿日期 2024-05-29
改稿日期 2024-08-08
张 薇 女,1987年生,副教授,研究方向为综合能源系统优化调度,新能源电力系统不确定性预测,人工智能及其电力系统应用。
E-mail:zhangwei@neepu.edu.cn(通信作者)
王浚宇 男,1998年生,硕士研究生,研究方向为综合能源系统优化调度。
E-mail:wjy15639787553@163.com
(编辑 赫 蕾)