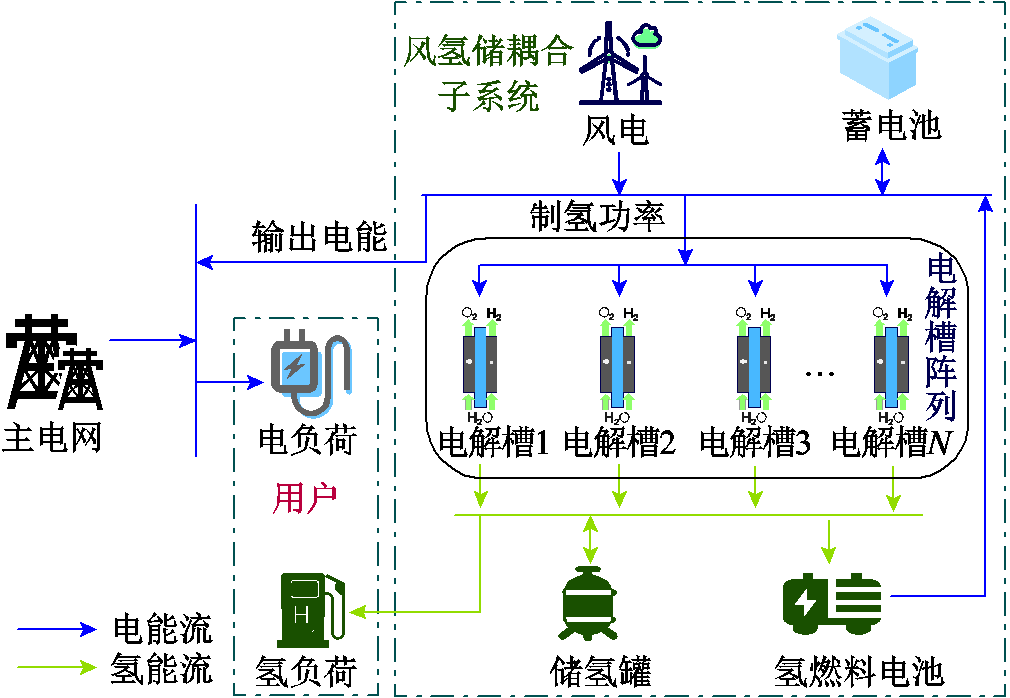
图1 电氢能源系统的结构示意图
Fig.1 The structural diagram of electricity and hydrogen energy systems
摘要 构建电力系统与氢能耦合发展的电氢能源系统是推动碳中和的可行路径。该文在计及新能源不确定性影响下,为实现系统经济与节能的均衡运行,提出了一种基于㶲经济分析的电氢能源系统区间鲁棒优化调度模型。首先,考虑电解槽动态效率特性,利用分段线性化处理功率-效率的动态映射关系引入的非凸项,构建包含制氢功率分配的设备运行模型;其次,精细分析系统的㶲损失分布,提出包含内和外两方面的㶲损失成本核算模型,内部利用成本分摊方法核算设备运行㶲损失成本,外部根据现行电价等政策核算输电线损和弃风惩罚成本;然后,构建最小总㶲损失成本目标下的电氢能源系统优化调度模型,转为基于置信区间不确定集的鲁棒优化形式,并提出模型的对偶转换求解方法;最后,仿真算例表明,所提模型在保障风电消纳能力的同时,可实现电氢耦合利用过程经济效益与㶲损失的平衡,也有利于降低电解槽运行的寿命损耗。
关键词:电氢能源系统 㶲经济分析 㶲损失成本 置信区间 鲁棒优化
氢能作为一种清洁、高效的优质能源,其利用已被视为实现能源系统脱碳和减缓气候变化的重要解决方案[1-3]。电氢能源系统以电和氢为能源载体[4],是实现电力系统与氢能的耦合发展,突破可再生能源的发展限制,有效推动多种能源方式互联互补、源网荷储深度融合的关键途径[5]。
电氢耦合过程是电氢能源系统中氢能价值发挥的主要环节。该过程将氢气作为储能媒介,通过电-氢-电的转换,为全时段源荷匹配提供调节支撑[6]。优化调度是包含电氢耦合过程在内的整个系统安全和经济运行的必要保障。文献[7-9]通过构建优化调度模型,在负荷低谷利用新能源驱动电解槽制氢,峰时以氢燃料电池发电,通过削峰填谷发挥了电氢耦合的经济性和新能源消纳能力提升价值。但上述研究将电制氢效率视为恒定值,未考虑电解槽效率与功率间的动态映射关系[10],将造成调度计划与实际的偏差,不利于系统安全稳定运行。对此,文献[11]通过机理模型与经验模型的结合,仿真出质子交换膜(Proton Exchange Membrane, PEM)电解槽的动态效率曲线,并利用分段线性化将此关系体现在调度模型中。文献[12-14]在动态电解槽效率下,通过多个电解槽的功率分配和轮值,实现了整体制氢效率的进一步提升。以上研究表明电解槽的动态效率特性不可忽略,也为面向效率提升的电解槽阵列能量管理策略提供了切入点。从调度目标来看,上述研究本质上均为经济调度。然而,目前电解槽和燃料电池的转换效率不高[15],导致电氢耦合过程在发挥经济效益的同时,也难免产生大量能源损失,可能需要更多的火电来填补绿电损失引起的负荷缺口,甚至不利于我国节能政策[16]下的能源利用效率提升。在电氢能源系统调度中,需应对能源损失。此外,以上研究均是在数量层面以热效率建立调度模型,忽略了异质能源的品质差异,对能源价值的衡量并不完整。
㶲是衡量能源数量和品质价值的统一指标[17]。目前㶲分析方法已被用于综合能源系统的节能调度中。文献[18]建立了电热综合能源系统的㶲分析模型,并将㶲损失纳入调度目标中,降低了能源贬值。文献[19]将㶲引入多能源枢纽优化调度中,以㶲损失最低为优化目标实现了能源的高效利用。文献[20]提出计及㶲效率的电-气-热综合能源系统多目标调度方法,实现了量质协同运行。以上研究验证了在能源系统运行中引入㶲损失的必要性和可行性,但鲜有研究在电氢能源系统运行中考虑电氢耦合过程的大量㶲损失。另外,电氢耦合过程的经济价值和㶲损失是对立的,其带来的经济效益越大,伴随的㶲损失也越大,如何寻求成本与㶲损失均衡的系统运行方案仍是一个难题。近年来,随着㶲分析理论的进一步发展,基于㶲价格化的㶲经济分析方法[21]逐渐形成,该方法通过将㶲进行成本分摊,实现了对㶲损失所具经济价值的衡量[22]。㶲经济分析已在多能联产系统的设计和评估中得到应用[23-25],核心在于通过㶲经济价值的量化和参数优化达到能效和经济之间的平衡,也为能源系统在经济与节能一致性方面的优化调度和能量管理研究提供了参考。电氢耦合过程的经济与节能均衡运行难题有望依托㶲经济分析得以解决。
另一方面,电氢能源系统的主要特征是高新能源占比和绿电制氢。而新能源出力不确定性引起的较大预测误差将对系统供需平衡、电解槽运行工况等产生不利影响,在优化调度中应充分考虑新能源不确定风险。现有的经济调度模型中,鲁棒优化较为常用[26],但在过于保守缺陷上一直饱受争议。计及概率分布的区间鲁棒优化方法[27]能改善这一问题,且模型求解方式较为简便,为本文研究提供了参考。
针对上述问题,本文面向电氢耦合过程的经济效益与㶲损失均衡运行,提出一种基于㶲经济分析的电氢能源系统优化调度模型,建立其区间鲁棒优化形式,主要工作如下:
1)提出电氢耦合能源系统的架构,考虑电解槽动态效率与制氢功率分配,建立设备运行模型。
2)将系统㶲损失分为内外两部分,基于㶲经济分析方法,提出电氢能源系统㶲损失成本核算模型。
3)建立最小化㶲损失成本的优化调度模型,构造为置信区间不确定集下的鲁棒优化形式,并提出转换求解方法。
电氢能源系统的结构示意图如图1所示。系统可细分为风氢储耦合子系统和用户。子系统包含电解槽阵列、氢燃料电池和电、氢储能设备,主要承担用户氢负荷供应及应对风电出力波动性的任务。而用户电负荷则通过子系统电能输出和主电网购电的协同实现供需平衡。显然,系统的能量源为主电网和风电。对主电网而言,其电能有一定比例的火电,系统购电将带来间接碳排放;对于风电来说,出力波动极易造成制氢功率不平稳,为降低其对电解槽寿命的影响,可通过制氢功率在电解槽阵列中的灵活分配,使单电解槽的运行工况更加稳定。

图1 电氢能源系统的结构示意图
Fig.1 The structural diagram of electricity and hydrogen energy systems
1.2.1 电氢耦合过程
电氢耦合本质上为“以电制氢、氢再发电”[28],具体来说是指在新能源富集时将绿电制氢储存,在负荷高峰时利用所存氢气发电的电-氢-电转换过程。整个过程需要依托电解槽和氢燃料电池两种能源转换设备完成。
1)考虑动态效率与制氢功率分配的电解槽模型
电解槽是电制氢设备,本文选用更适应电源波动的PEM电解槽为研究对象。对于阵列中的单个电解槽来说,其效率呈现随运行功率改变而动态变化的特点。考虑此特性,单电解槽模型表示为
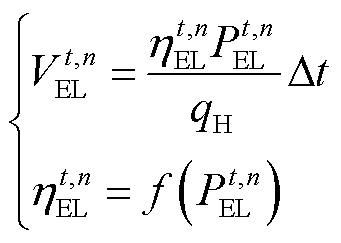 (1)
(1)
式中,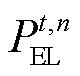 为第n个电解槽在t时刻的用电功率;
为第n个电解槽在t时刻的用电功率;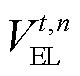 为第n个电解槽在t时刻的产氢体积;
为第n个电解槽在t时刻的产氢体积;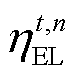 为第n个电解槽在t时刻的效率;
为第n个电解槽在t时刻的效率;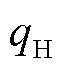 为氢气的热值;
为氢气的热值;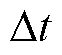 为调度步长;
为调度步长;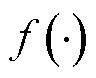 表示效率和功率的动态映射关系。
表示效率和功率的动态映射关系。
式(1)中存在功率与效率乘积的非线性项,给模型求解带来挑战。对此,采用文献[11]的分段线性化方法,先求得电解槽功率与氢气产量的映射曲线,再考虑到电解槽最小运行功率为额定功率的10%[29],将式(1)分段处理为
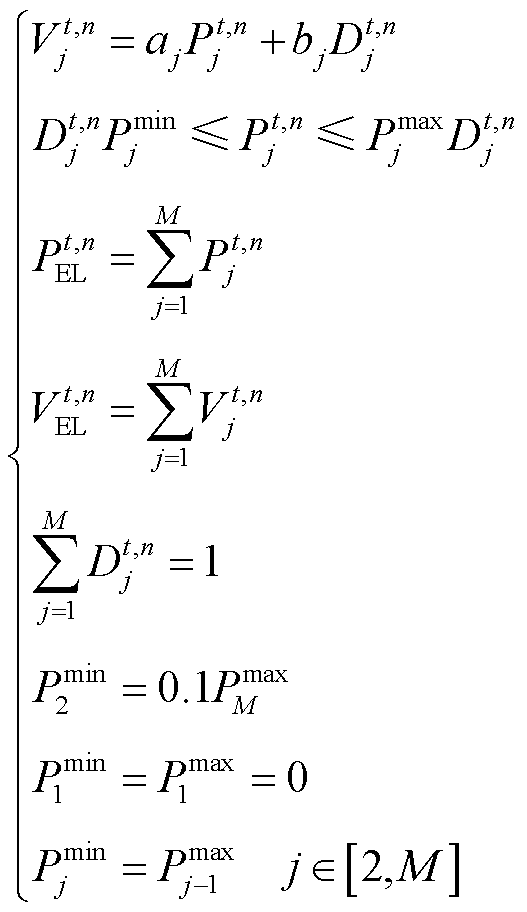 (2)
(2)
式中,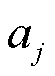 和
和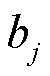 为分段系数,分别对应第j段函数的斜率和截距;
为分段系数,分别对应第j段函数的斜率和截距;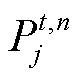 和
和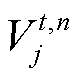 分别为t时刻第n个电解槽在第j段的功率和产量;
分别为t时刻第n个电解槽在第j段的功率和产量;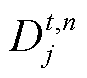 为二进制变量,1代表电解槽功率位于该段之中,0代表不在该段;
为二进制变量,1代表电解槽功率位于该段之中,0代表不在该段;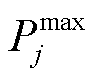 和
和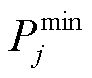 分别为第j段功率的上限和下限;M为分段数量。分段线性化的原理如图2所示,第1段为停机状态,其余段表示运行状态。
分别为第j段功率的上限和下限;M为分段数量。分段线性化的原理如图2所示,第1段为停机状态,其余段表示运行状态。
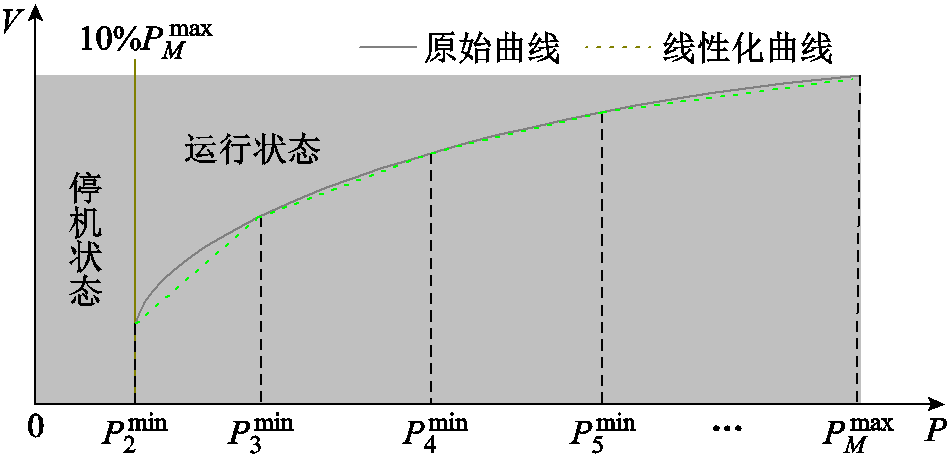
图2 电解槽功率与产量映射曲线的线性化
Fig.2 Linearization of the electrolyzer power versus yield mapping curve
各PEM电解槽的运行功率由整体制氢功率灵活分配得到,表示为
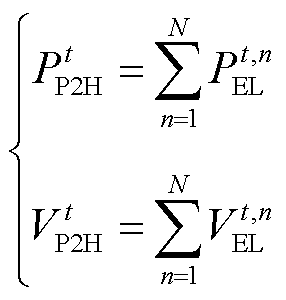 (3)
(3)
式中,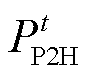 为t时刻电氢能源系统的整体制氢功率;
为t时刻电氢能源系统的整体制氢功率;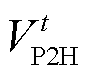 为t时刻的整体氢气产量;N为电解槽的数量。
为t时刻的整体氢气产量;N为电解槽的数量。
2)氢燃料电池发电模型
氢燃料电池消耗氢气发电,模型表示为
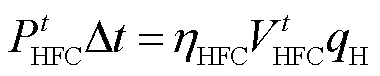 (4)
(4)
式中,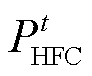 和
和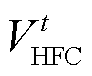 分别为氢燃料电池在t时刻的发电功率和耗氢体积;
分别为氢燃料电池在t时刻的发电功率和耗氢体积;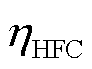 为氢燃料电池的效率。
为氢燃料电池的效率。
1.2.2 电、氢储能设备模型
系统内包含蓄电池和储氢罐两种储能设备,以荷电状态(State of Charge, SOC)的变化来刻画其实时状态,有
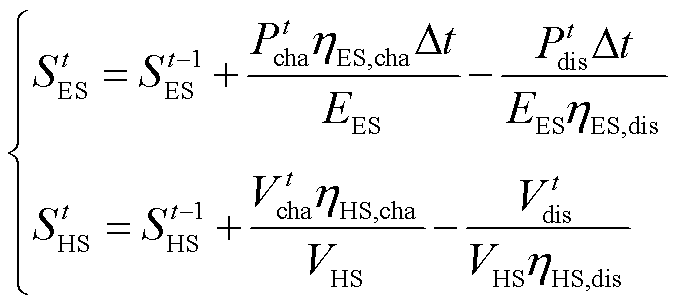 (5)
(5)
式中,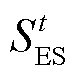 和
和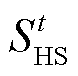 分别为t时刻蓄电池和储氢罐的SOC;
分别为t时刻蓄电池和储氢罐的SOC;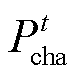 和
和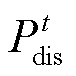 分别为t时刻蓄电池的充、放电功率;
分别为t时刻蓄电池的充、放电功率;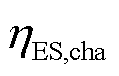 和
和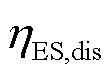 分别为蓄电池的充、放电效率;
分别为蓄电池的充、放电效率;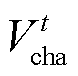 和
和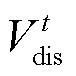 分别为t时刻储氢罐的充、放氢体积;
分别为t时刻储氢罐的充、放氢体积;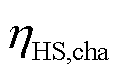 和
和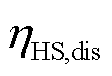 分别为储氢罐的充、放氢效率;
分别为储氢罐的充、放氢效率;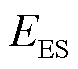 和
和 分别为蓄电池和储氢罐的容量。
分别为蓄电池和储氢罐的容量。
为使电氢能源系统的调度方案既能发挥电氢耦合的经济效益,又能将能源的数量和品质损失维持在较低水平,建立基于㶲经济分析的优化调度模型。首先,在㶲分析的基础上,通过㶲的价格化,实现㶲损失成本的量化。㶲损失成本是结合运行成本和㶲损失从内部机理层面分析得到的㶲经济指标,理论上㶲损失成本的减小需要依托成本和㶲损失的均衡降低。然后,以㶲损失成本最小为目标函数,构建电氢能源系统调度模型。
本文㶲经济分析的框架如图3所示,主要目的在于对整个供能过程产生的㶲损失成本进行核算。㶲损失成本是㶲损失的价格衡量,本文根据系统的㶲损失分布,将其分为内、外两部分进行分别核算。
内部㶲损失成本是系统内部设备运行过程中㶲损失对应的成本,由电解槽、燃料电池在能源转换过程中的㶲损失和储能设备充放过程中的㶲损失引起。该部分的核算需在㶲分布明确的前提下,借助成本分摊方法,实现㶲的价格化;进而以单位㶲损失成本和㶲损失的乘积计算出内部总㶲损失成本。
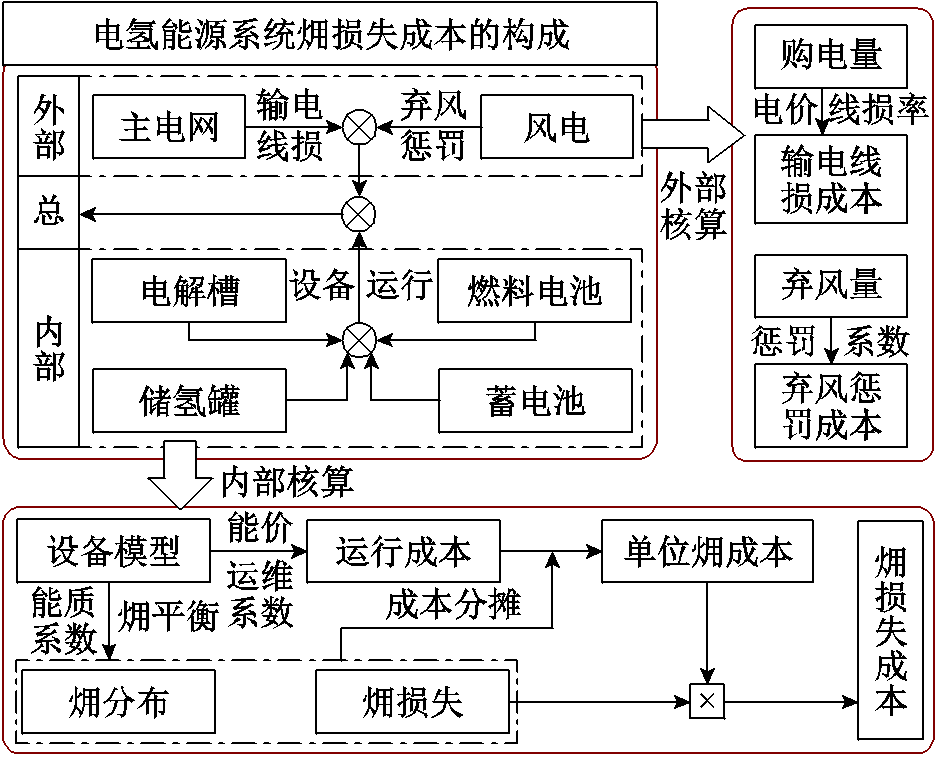
图3 㶲经济分析框架
Fig.3 The framework of exergoeconomic analysis
外部㶲损失成本是与系统内设备运行无直接联系的损失成本,由能源传输损耗和政策性因素产生,在本文的系统框架中主要为主电网的输电线损成本和弃风导致的惩罚成本,可依据相应的线损承担机制和弃风惩罚系数分别核算。
2.1.1 内部㶲损失及其价格化
首先,在设备数学模型的基础上,利用能质系数[30]和㶲平衡理论[31]对系统内部㶲的分布和设备运行的㶲损失进行分析核算,有
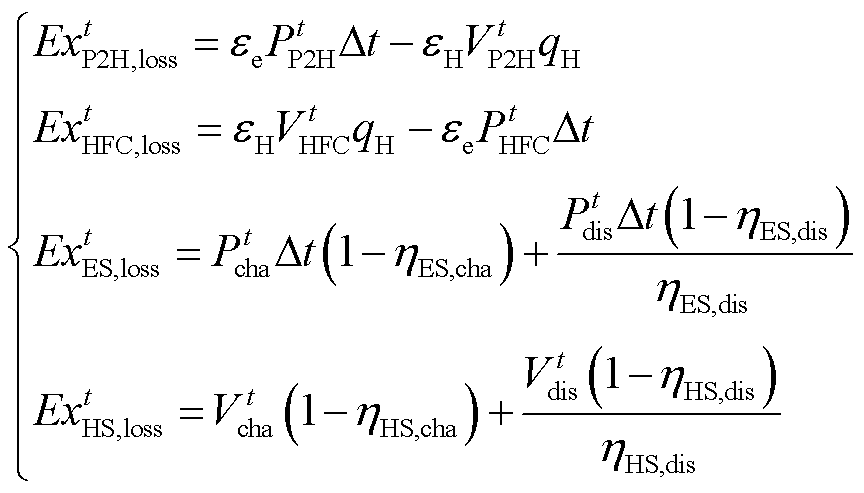 (6)
(6)
式中,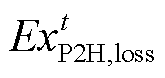 、
、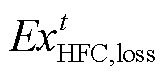 、
、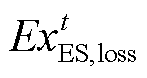 和
和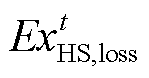 分别为t时刻电解槽阵列、氢燃料电池、蓄电池和储氢罐的㶲损失;
分别为t时刻电解槽阵列、氢燃料电池、蓄电池和储氢罐的㶲损失;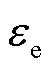 和
和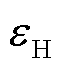 分别为电能和氢能的能质系数,可理解为能源单位能量中的㶲,能质系数越高则代表能源的品位也越高。系统内的两种能源形态中,
分别为电能和氢能的能质系数,可理解为能源单位能量中的㶲,能质系数越高则代表能源的品位也越高。系统内的两种能源形态中,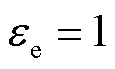 ,氢能的能质系数[31]为
,氢能的能质系数[31]为
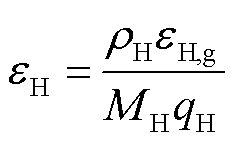 (7)
(7)
式中,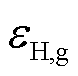 为纯氢单质的标准㶲;
为纯氢单质的标准㶲;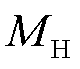 为氢气的摩尔质量;
为氢气的摩尔质量;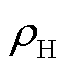 为氢气的密度。
为氢气的密度。
然后,按照同设备输入输出单位㶲成本一致的原则进行成本分摊,即㶲价格化,表示为
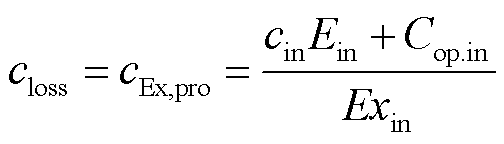 (8)
(8)
式中,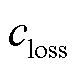 为单位㶲损失成本;
为单位㶲损失成本;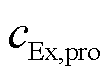 为产物的单位㶲成本;
为产物的单位㶲成本;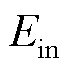 和
和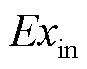 分别为输入能量和输入㶲;
分别为输入能量和输入㶲;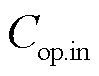 为设备运维成本。具体来说,该原则的本质是能源转换前后㶲的单位经济价值保持一致,输入能量成本和运维成本构成的总运行成本与输入㶲的比值即为单位㶲成本。此原则下,输出能量的单位㶲成本与单位㶲损失成本相同,而单位数量成本与能质系数呈正相关,体现出能源的品位与单位数量经济价值的一致性,可在㶲的视角为能量的合理定价提供科学的依据。
为设备运维成本。具体来说,该原则的本质是能源转换前后㶲的单位经济价值保持一致,输入能量成本和运维成本构成的总运行成本与输入㶲的比值即为单位㶲成本。此原则下,输出能量的单位㶲成本与单位㶲损失成本相同,而单位数量成本与能质系数呈正相关,体现出能源的品位与单位数量经济价值的一致性,可在㶲的视角为能量的合理定价提供科学的依据。
依据式(8)推导出各设备的单位㶲损失成本为
 (9)
(9)
式中,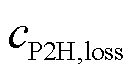 、
、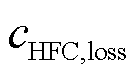 、
、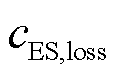 和
和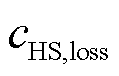 分别为电解槽阵列、氢燃料电池、蓄电池和储氢罐的单位㶲损失成本;
分别为电解槽阵列、氢燃料电池、蓄电池和储氢罐的单位㶲损失成本;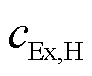 为氢气的单位㶲成本;
为氢气的单位㶲成本;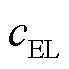 、
、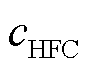 、
、 、
、 和
和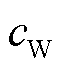 分别为电解槽、氢燃料电池、蓄电池、储氢罐和风电的单位运维成本。
分别为电解槽、氢燃料电池、蓄电池、储氢罐和风电的单位运维成本。
进而,核算t时刻系统内部总㶲损失成本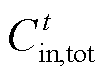 为
为
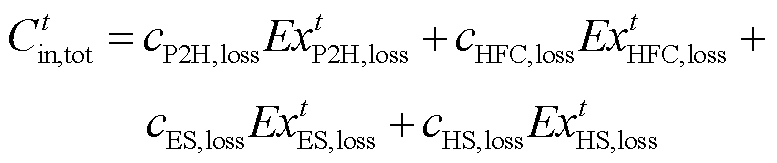 (10)
(10)
2.1.2 外部㶲损失成本
对于主电网的输电线损成本,依据我国现行的输配电价政策[32],电能传输中的线损电量应由用户承担,线损成本按电价和综合线损率计算,表示为
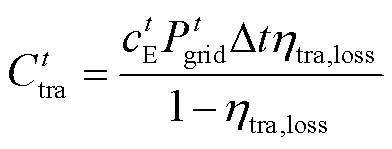 (11)
(11)
式中,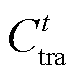 为t时刻系统购电产生的主电网线损成本;
为t时刻系统购电产生的主电网线损成本;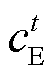 为t时刻的购电价格;
为t时刻的购电价格;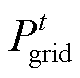 为t时刻系统的购电功率;
为t时刻系统的购电功率;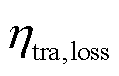 为主电网的综合线损率。考虑到从电网购电的间接碳排放,实际的购电价格由电网电价和碳税单价组成,即
为主电网的综合线损率。考虑到从电网购电的间接碳排放,实际的购电价格由电网电价和碳税单价组成,即
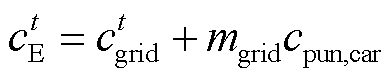 (12)
(12)
式中,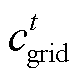 为t时刻的电网电价;
为t时刻的电网电价;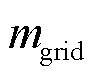 为主电网的碳排放因子;
为主电网的碳排放因子;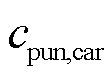 为碳排放惩罚系数。
为碳排放惩罚系数。
对于弃风惩罚成本,其核算[33]为
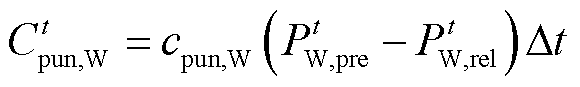 (13)
(13)
式中,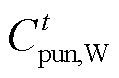 为t时刻系统的弃风惩罚成本;
为t时刻系统的弃风惩罚成本;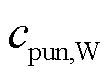 为弃风惩罚系数;
为弃风惩罚系数;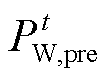 和
和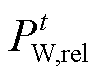 分别为t时刻风电预测功率和实际计划出力功率。
分别为t时刻风电预测功率和实际计划出力功率。
进一步,t时刻系统的外部㶲损失成本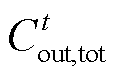 为
为
 (14)
(14)
本文以总㶲损失成本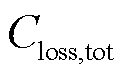 最小为目标函数,即
最小为目标函数,即
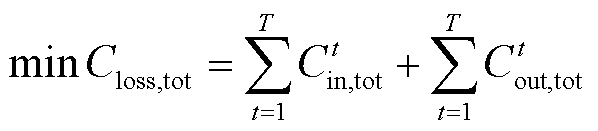 (15)
(15)
式中,T为一个周期内的调度时段总数。
约束条件包括设备运行约束、能量平衡约束、购电及风电约束。
1)设备运行约束
电解槽运行的动态效率约束见式(2)。此外,为降低频繁启停和功率波动对其寿命损耗的加剧程度,电解槽运行还需满足启停次数约束和功率爬坡约束,表示为
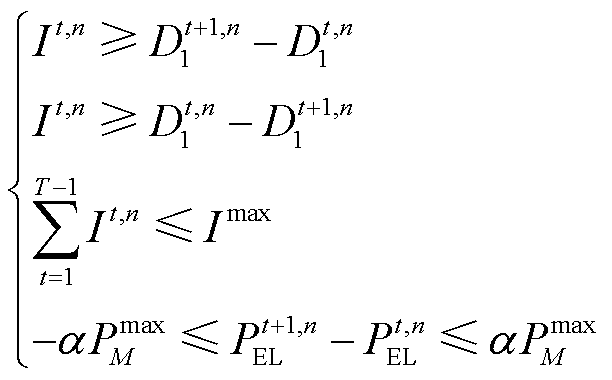 (16)
(16)
式中,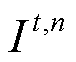 为启停状态;
为启停状态;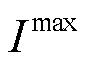 为最大启停次数;
为最大启停次数;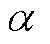 为爬坡限制系数。
为爬坡限制系数。
其余设备运行约束条件较为常规,本文参考文献[12]设置,不再赘述。
2)能量平衡约束
系统供能过程应满足供需平衡,表示为
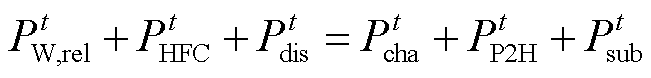 (17)
(17)
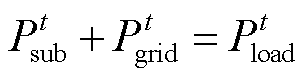 (18)
(18)
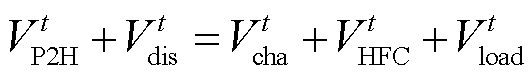 (19)
(19)
式中,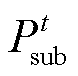 为t时刻风氢储耦合子系统的输出功率;
为t时刻风氢储耦合子系统的输出功率;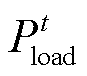 和
和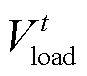 分别为t时刻电氢能源系统的电负荷及氢负荷。
分别为t时刻电氢能源系统的电负荷及氢负荷。
3)购电及风电约束
系统由主电网购电的功率和风电出力应满足
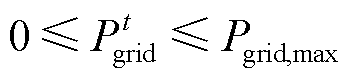 (20)
(20)
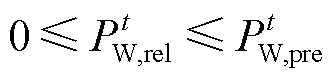 (21)
(21)
式中,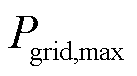 为电网购电功率上限。
为电网购电功率上限。
风电预测与实际值之间往往存在较大误差,带来了风电出力的不确定性,忽略其影响可能会使弃风增加,引起额外的成本和㶲损失。对此,本文将风电预测误差视为不确定变量,构造第2节调度模型的鲁棒优化形式。为克服鲁棒优化的保守缺陷,以置信区间代替传统区间集的历史边界,并提出相应的转换求解方法。
考虑预测误差后,风电最大出力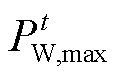 可表示为
可表示为
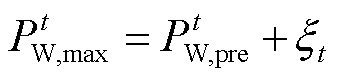 (22)
(22)
式中,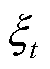 为t时刻的风电预测误差,是不确定变量,以区间集表示其范围,有
为t时刻的风电预测误差,是不确定变量,以区间集表示其范围,有
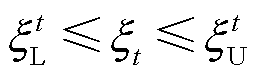 (23)
(23)
式中,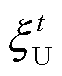 和
和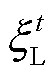 分别为t时刻不确定变量的上界和下界。
分别为t时刻不确定变量的上界和下界。
传统鲁棒优化常采用历史值的边界构造区间集,这种做法较为稳妥,但过于保守。本文考虑历史数据的概率信息,以置信区间作为区间集,将不确定集合理收缩,从而降低鲁棒优化的保守程度。
若t时刻历史样本的均值和标准差分别为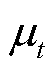 和
和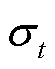 ,那么置信水平为
,那么置信水平为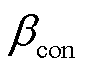 时置信区间的边界[34]为
时置信区间的边界[34]为
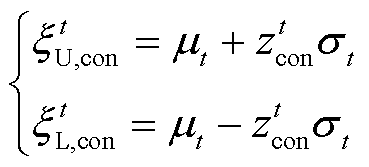 (24)
(24)
式中,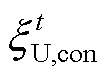 和
和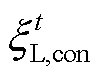 分别为置信区间的上界和下界;
分别为置信区间的上界和下界;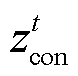 为正态分布的z分位数,可由正态逆累积分布函数
为正态分布的z分位数,可由正态逆累积分布函数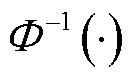 计算得到
计算得到
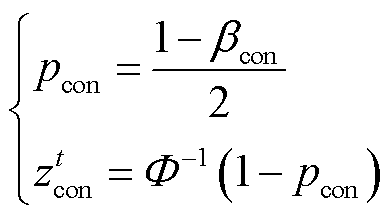 (25)
(25)
式中,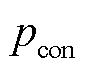 为
为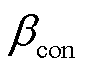 的显著性水平。
的显著性水平。
然后,构造电氢能源系统区间鲁棒优化形式。该形式本质上是min-max的双层零和博弈问题,内层max问题的主体为大自然,目的在于获取风电出力的最恶劣场景;外层min问题的主体为调度决策者,目的在于制定最恶劣场景下的最优计划。模型表示为
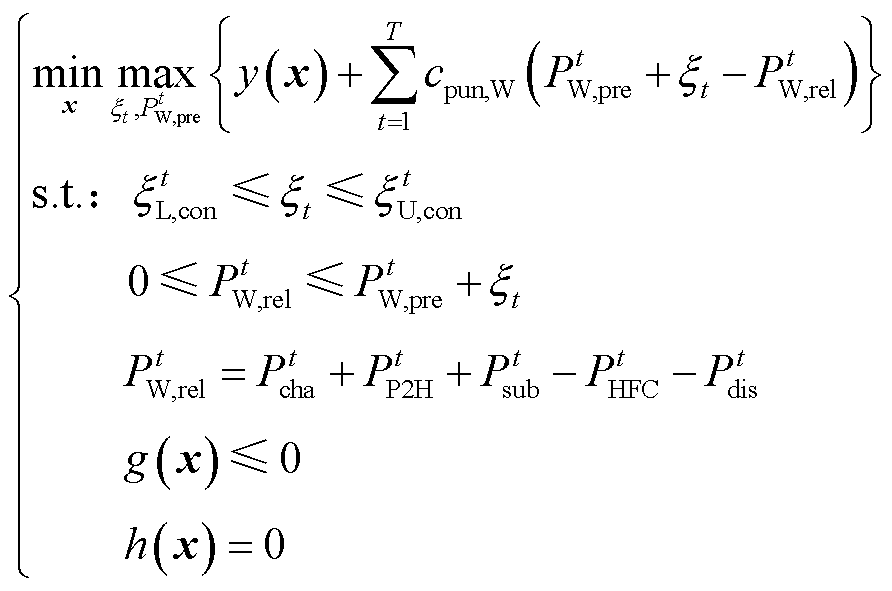 (26)
(26)
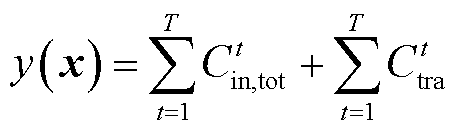 (27)
(27)
式中,x为除风电出力外的设备运行及购电计划;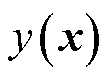 为确定性优化模型目标函数中与x有关的部分;
为确定性优化模型目标函数中与x有关的部分;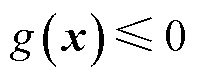 和
和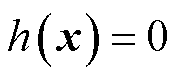 分别为确定性优化模型中除风电相关约束外的不等式和等式约束。
分别为确定性优化模型中除风电相关约束外的不等式和等式约束。
为实现式(26)模型的求解,依据对偶理论,将内层max问题转换为对偶的min形式,即
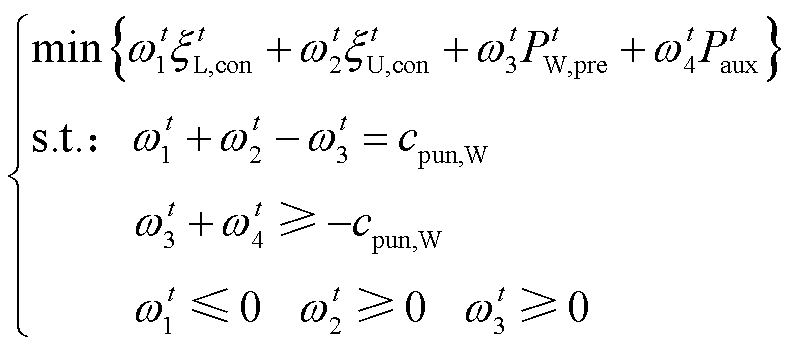 (28)
(28)
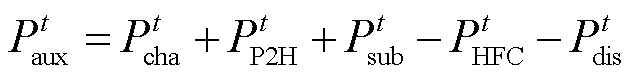 (29)
(29)
式中,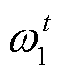 、
、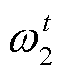 、
、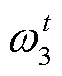 和
和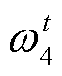 均为原内层问题的对偶变量;
均为原内层问题的对偶变量;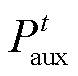 为便于模型推导引入的辅助变量。
为便于模型推导引入的辅助变量。
基于此,原问题转换为单层的min形式,即
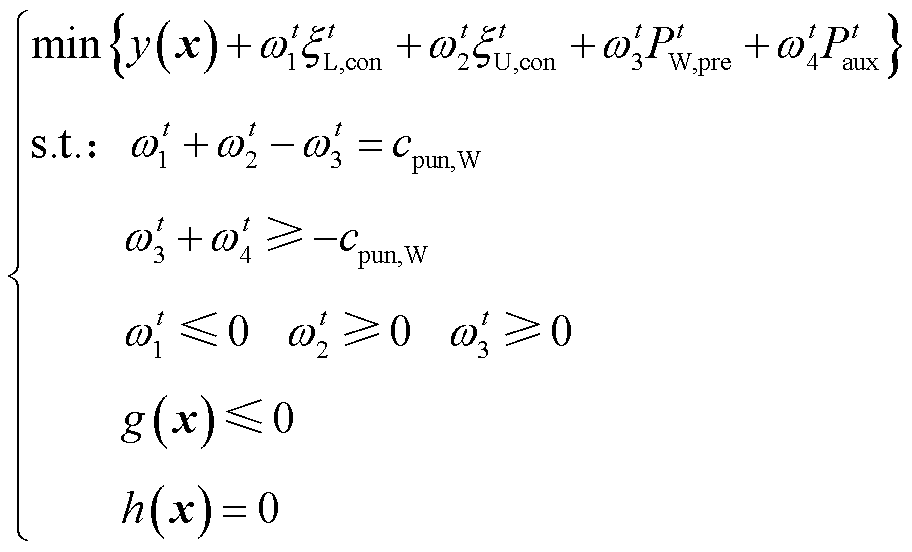 (30)
(30)
式(30)即为最终的单层优化调度模型,可利用商用求解器实现快速简便求解。
为对所提调度模型进行多方面可行性评估,本文构建包含整体制氢㶲效率、购电量、风电消纳量、运行成本、㶲损失及碳排放量六个指标的评估指标体系,各指标的计算方法如下。
1)整体制氢㶲效率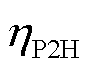 ,即整个周期内生产的氢能㶲与耗电㶲的比值。
,即整个周期内生产的氢能㶲与耗电㶲的比值。
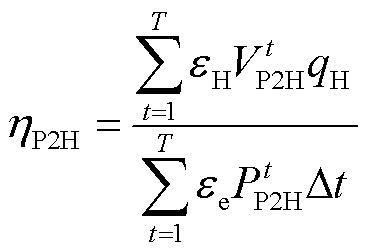 (31)
(31)
2)购电量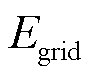 ,即整个调度周期包含主电网线损在内的实际总购电量。
,即整个调度周期包含主电网线损在内的实际总购电量。
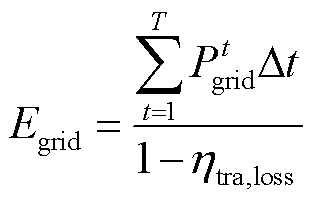 (32)
(32)
3)风电消纳量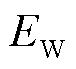 ,即整个调度周期系统的风电消纳总量。
,即整个调度周期系统的风电消纳总量。
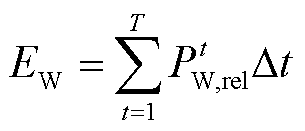 (33)
(33)
4)运行成本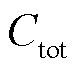 ,即整个调度周期系统的总运行成本,由购电成本、输电线损成本、弃风惩罚成本和设备运维成本构成。
,即整个调度周期系统的总运行成本,由购电成本、输电线损成本、弃风惩罚成本和设备运维成本构成。
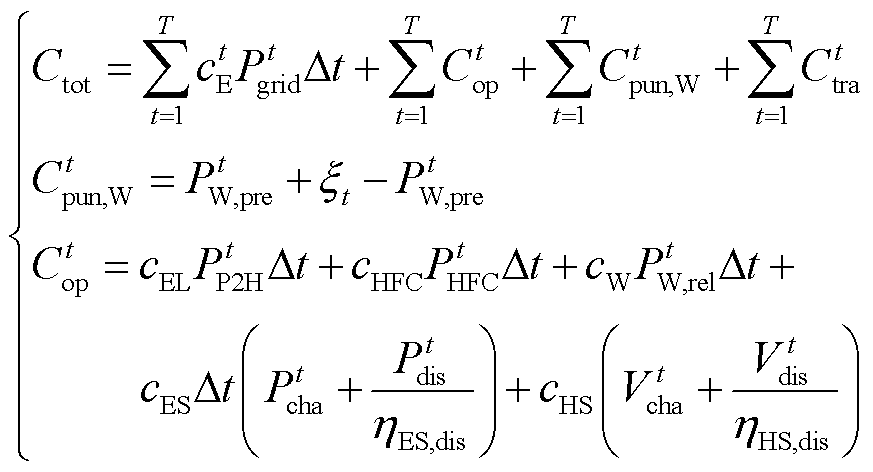 (34)
(34)
式中,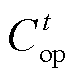 为t时刻设备运维成本之和。另外,式中包含的不确定变量
为t时刻设备运维成本之和。另外,式中包含的不确定变量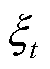 的取值无法通过求解式(30)直接获取,需依据互补松弛定理由对偶变量推导计算,具体过程见附录。
的取值无法通过求解式(30)直接获取,需依据互补松弛定理由对偶变量推导计算,具体过程见附录。
5)㶲损失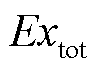 ,即系统在整个调度周期内的总㶲损失。
,即系统在整个调度周期内的总㶲损失。
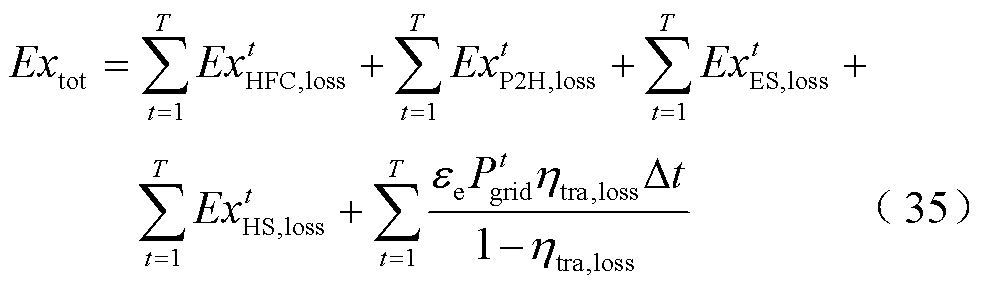
6)碳排放量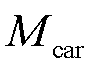 ,即系统因购电产生的间接碳排放总量。
,即系统因购电产生的间接碳排放总量。
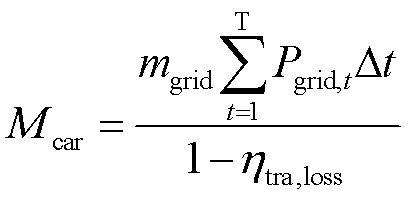 (36)
(36)
为验证所提模型的可行性,设置算例进行仿真分析,仿真平台为Matlab R2022a和Gurobi 11.0.0。
本文以图1所示电氢能源系统为研究对象。系统内设置四个电解槽组成阵列,单电解槽的动态效率及产量曲线如附图1所示,其余运行参数见附表1。风电、负荷预测及分时电价数据如附图2所示。风电预测误差5 000个样本的历史数据如附图3所示。碳排放惩罚系数取0.26元/kg。氢气密度、热值等相关参数取值参考文献[11, 31]。仿真调度步长和周期分别设置为1 h和24 h。
㶲经济分析为本文所提调度模型的基础,为验证其合理性和正确性,同时明确制氢效率提升的重要性,下面对电氢耦合过程进行㶲经济分析。
4.2.1 㶲价格化结果分析
电氢耦合过程的㶲价格化结果如图4所示。分析可得,随着电-氢-电的依次转换,单位㶲成本逐渐升值,与初始风电相比,燃料电池所发电能的单位㶲成本升高了0.07元,这是因为各能源转换过程都伴随设备运维成本的注入,在能源由风电经电解槽、储氢罐和燃料电池供应至负荷的过程中,输入成本不断累积,进而引起过程中单位㶲成本的升高,同时单位㶲损失成本也在随之升值。这表明成本和损失成本存在一致性,能源转换次数越多,付出的损失成本代价实际上也越大,因此在供能过程中因尽可能做到能源的直接利用。
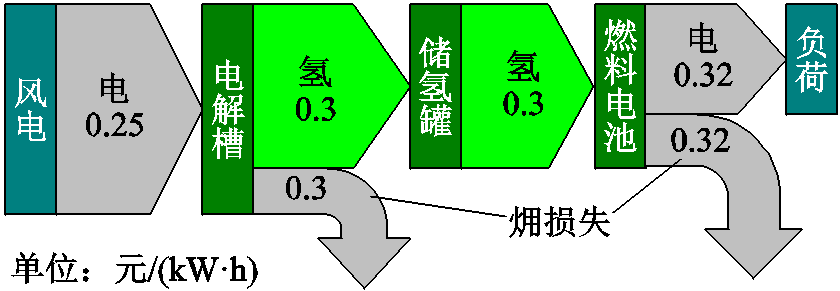
图4 电氢耦合过程的㶲价格化结果
Fig.4 The exergy valorization results of the electro-hydrogen coupling process
4.2.2 制氢效率对电氢耦合可行性的影响分析
电氢耦合过程的利用需具备可行性。本文认为该可行性受制氢效率的影响,包含经济、㶲损失和损失成本方面的综合表现,分别量化为单位电量成本、单位电量㶲损失、单位电量损失成本、单位风电消纳量损失成本四个指标,其计算方法见附表2。单位电量成本和单位风电消纳量损失成本随制氢效率的变化情况如图5所示。
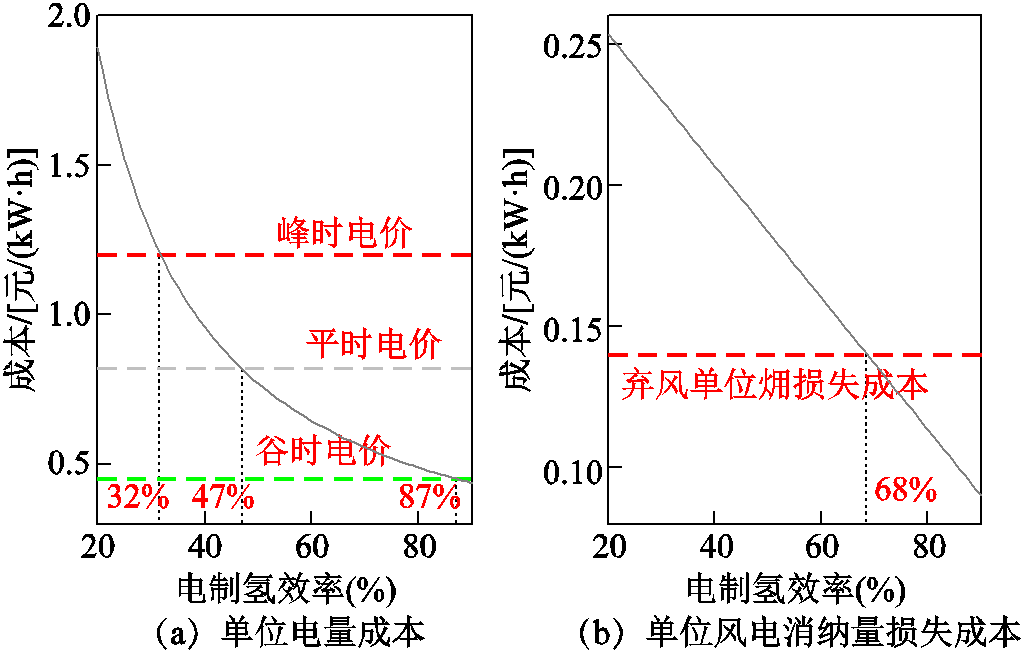
图5 单位电量成本和单位风电消纳量损失成本随制氢效率的变化情况
Fig.5 Changes in unit electricity cost and unit wind power consumption loss cost with hydrogen production efficiency
从经济角度,图5a为单位电量成本随制氢效率的变化情况,可见随制氢效率的升高,电氢耦合过程的发电成本逐渐降低,制氢效率分别大于32%、47%和87%时,单位电量成本将低于峰、平和谷时电价。与购电相比,当电氢耦合过程的单位电量成本低于主电网电价时,其利用将使系统用电成本降低。这是因为制氢效率越高,单位发电量消耗制氢电能降低,进而所需风电成本减少。从㶲损失和损失成本角度,通过指标的计算式可以发现,单位电量㶲损失、单位电量损失成本均随制氢效率的增大而降低。表1为90%制氢效率下电氢耦合过程与峰时主电网购电的两指标对比。可见即便在极高的制氢效率下,电氢耦合过程的㶲损失和损失成本均高于主电网购电,这与其经济可行性形成对立,表明仅考虑经济效益不足以满足节能需求。
从风电消纳的机理上,图5b为单位风电消纳量损失成本随制氢效率的变化情况,可见制氢效率大于68%时,电氢耦合过程的单位风电消纳量损失成本低于单位弃风惩罚成本。此时与弃风相比,消纳风电能降低系统的损失成本。因此在最小化㶲损失成本目标下,即使此时利用电氢耦合消纳风电的㶲损失和㶲损失成本高于购电,系统还是会选择消纳风电来降低弃风带来的损失成本。以上分析表明,制氢效率的提升和弃风惩罚成本的合理取值均会给电氢耦合的利用带来有利影响。而弃风惩罚成本作为保障绿电消纳的政策性参数,其值不应设置太低,同时㶲经济分析也可为其取值提供理论参考。
表1 90%制氢效率下电氢耦合过程与购电的指标对比
Tab.1 Comparison of the indicators between the electro-hydrogen coupling process and power purchase at 90% hydrogen production efficiency

指标电氢耦合主电网购电 单位电量㶲损失/(kW·h)0.3890.053 单位电量损失成本/[元/(kW·h)]0.1250.063
为评估所提基于㶲经济分析调度模型的可行性和优越性,本文设置三个运行方案进行对比分析,各方案鲁棒优化的不确定集均设为90%置信区间。方案1:系统优化调度目标为最小化运行成本;方案2:系统优化调度目标为最小化㶲损失;方案3:系统优化调度目标为最小化㶲损失成本,即本文所提调度模型。
4.3.1 不同方案结果对比分析
不同方案下的系统调度结果见表2。由表2可见,方案3的运行成本和㶲损失均介于方案1和2之间。具体来看,在经济方面,方案3的运行成本比方案2降低了8.66%(748.41元),这是因为方案3消纳风电多而购电更少;在节能方面,与方案1相比,方案3的购电量更少,整体制氢效率也略高,这使其㶲损失降低了3.65%(27.76 kW·h)。以上分析表明,最小化㶲损失成本目标的优化调度能使系统实现经济和节能运行的均衡,具备两方面的可行性,改善了经济调度和㶲损失调度一方最优而另一方最差的极端局面。
表2 不同方案的调度结果
Tab.2 Scheduling results of different cases
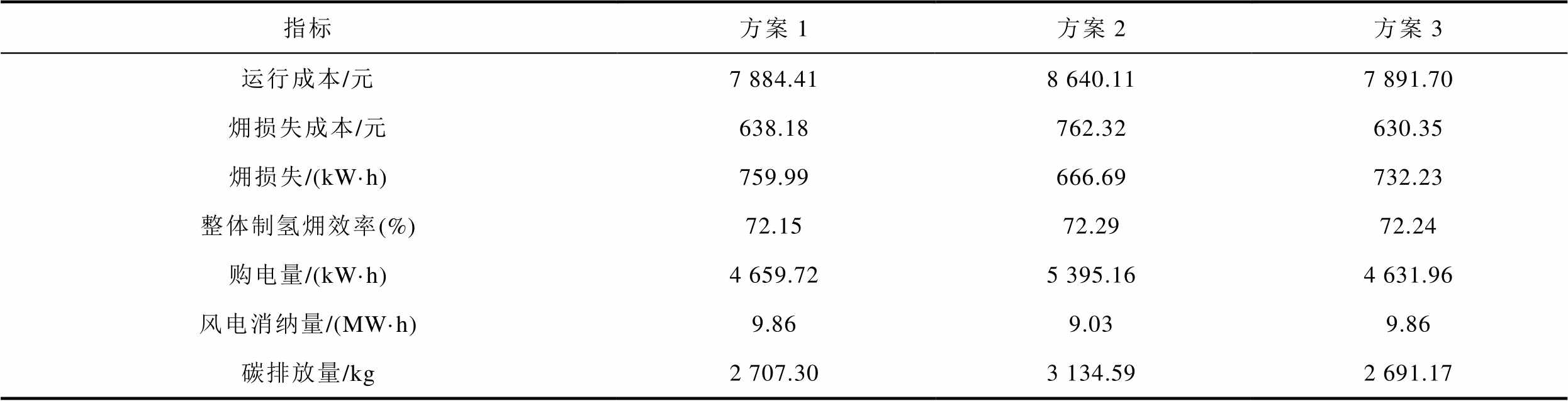
指标方案1方案2方案3 运行成本/元7 884.418 640.117 891.70 㶲损失成本/元638.18762.32630.35 㶲损失/(kW·h)759.99666.69732.23 整体制氢㶲效率(%)72.1572.2972.24 购电量/(kW·h)4 659.725 395.164 631.96 风电消纳量/(MW·h)9.869.039.86 碳排放量/kg2 707.303 134.592 691.17
由表2还可看出,方案3的购电量最低,使得其碳排放量最低,其风电友好性与方案1一致,均优于方案2。这是因为方案3整体制氢效率高于方案1,制氢消耗的风电量更少,使得风电的直接利用量更多,进而减少了外购电量;与方案2相比,4.2节的分析已证明方案3倾向于利用电氢耦合的灵活性调节消纳弃风,而弃风对方案2的目标函数影响较小,直接购电供应负荷的㶲损失最低,因此方案2的风电消纳量更少、外购电更多。
值得注意的是,方案3在与方案1购电更少、风电消纳相同的情况下,运行成本却升高了7.29元;方案2㶲损失最低但㶲损失成本最高。下面结合图6中各方案的分时购电功率和图7各方案的㶲损失成本构成,对此现象的原因进行具体分析。可以看到,方案1与方案2的损失成本差异主要在电解槽和燃料电池,这是因为方案1用电解槽消纳风电制氢再于峰时段用燃料电池供电具有经济效益,因此其电氢耦合的利用规模更大,进而过程中的损失成本更多;而方案与方案3存在数量差异的外部购电部分的㶲损失成本相差却不大,由图6可见,方案3在7:00购电量更少,但在19:00—22:00峰时段的购电量更多,这就解释了购电量少而成本高的原因。
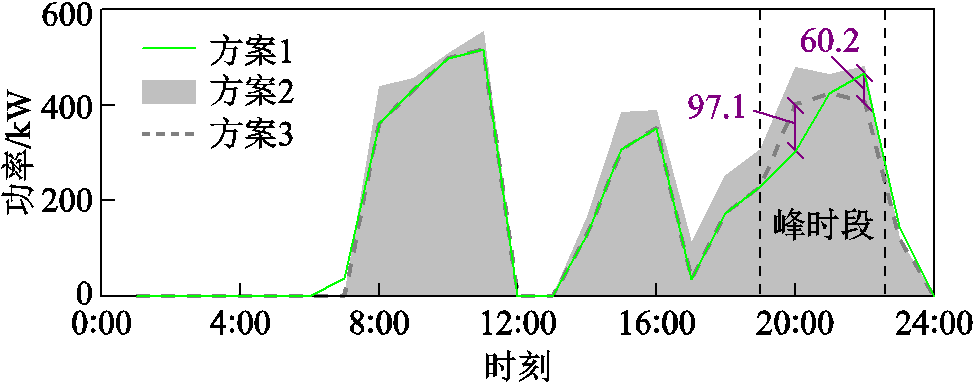
图6 不同方案的分时购电功率
Fig.6 The power purchased at each time of different cases
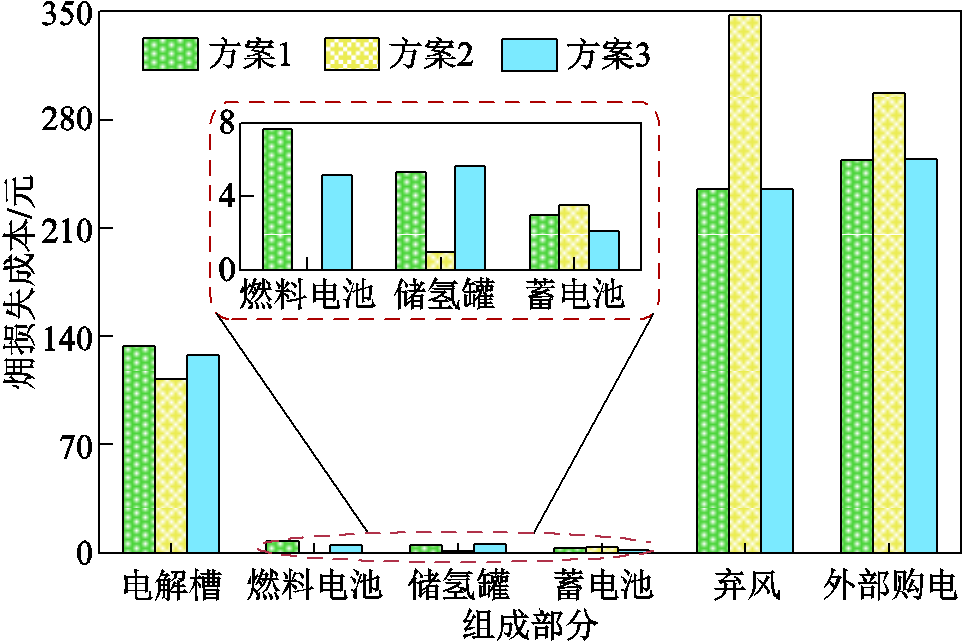
图7 不同方案的㶲损失成本构成
Fig.7 The exergy loss cost components of different cases
对于方案2,电氢耦合过程供电的单位电量㶲损失较大,系统即使选择弃风也不愿将富余风电制氢储存到峰时发电,这导致方案2弃风和外部购电部分的㶲损失成本极高。
综上所述,本文所提模型能同时考虑经济和节能两方面来合理安排电氢耦合过程的运行,并能在机理上保障系统的高新能源消纳能力,对于电氢能源系统的稳步推广和能源的高效利用具有重要意义。
4.3.2 供能计划分析
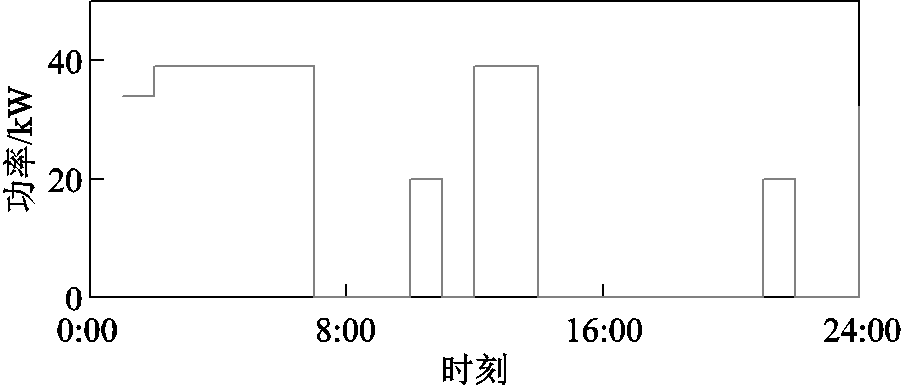
为进一步分析系统以所提模型运行的合理性,对系统的供能计划进行分析。图8和图9分别为方案3的供电和供氢计划,图10为风氢储耦合子系统的运行计划。
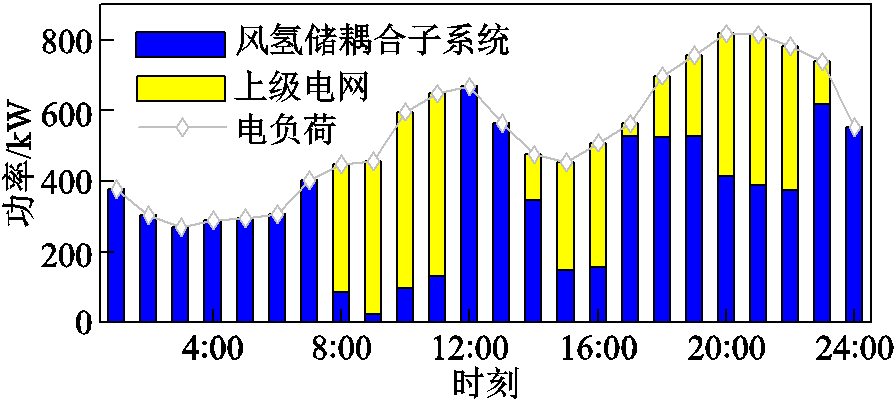
图8 方案3的供电计划
Fig.8 Power supply plan of Case 3
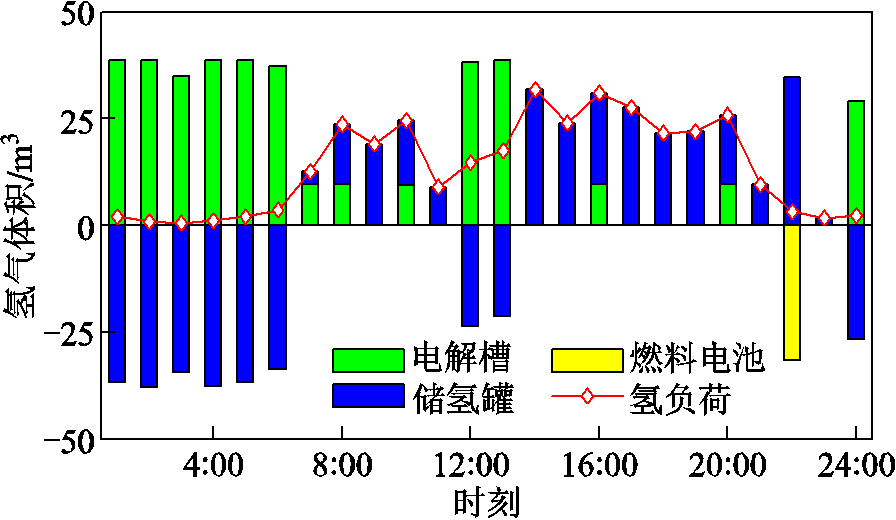
图9 方案3的供氢计划
Fig.9 Hydrogen supply plan of Case 3
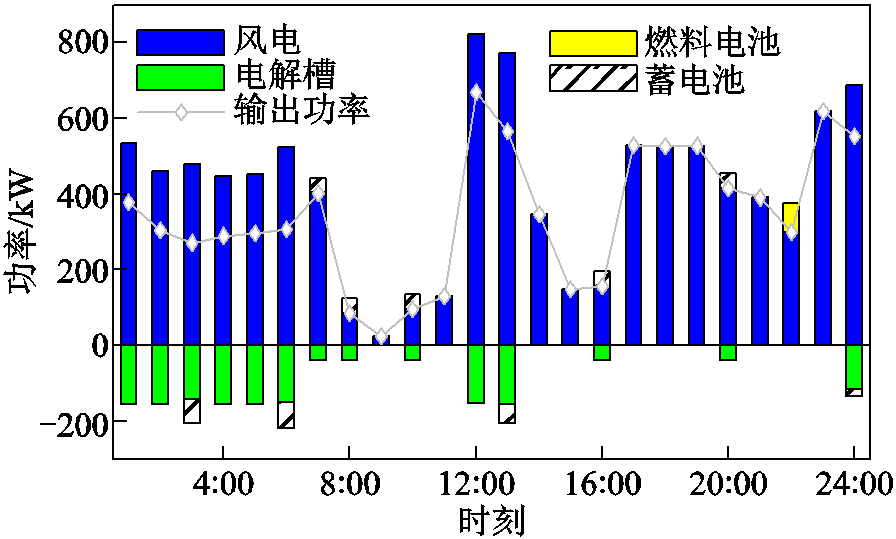
图10 方案3的风氢储耦合子系统运行计划
Fig.10 Wind-hydrogen-storage coupling subsystem operation plan of Case 3
可以看出,系统在1:00—6:00时段通过储氢罐和蓄电池储存富余风电,并于风电出力小的时段释放,尤其是在22:00通过燃料电池耗氢发电,表明所提模型下,储能仍能发挥灵活调节作用。在方案3下,此举是为了使损失成本尽可能低,实际上,这也减小了峰时段购电量,进而降低了运行成本。此外,与附图4中方案1的供氢计划相比,由于考虑到燃料电池发电的单位㶲损失成本较高,方案3燃料电池在峰时段的耗氢量更少,这减小了电氢耦合过程的㶲损失。以上表明,本文所提模型一方面保留了储能利用的经济效益,另一方面也使电氢耦合的利用规模实现了成本与㶲损失降低的平衡,即做到了经济性与能源节省的对立统一。
4.3.3 电氢储能协调价值分析
下面对图11中蓄电池和储氢罐的SOC计划进行分析,以评估所提模型下不同类型储能配合的价值发挥情况。
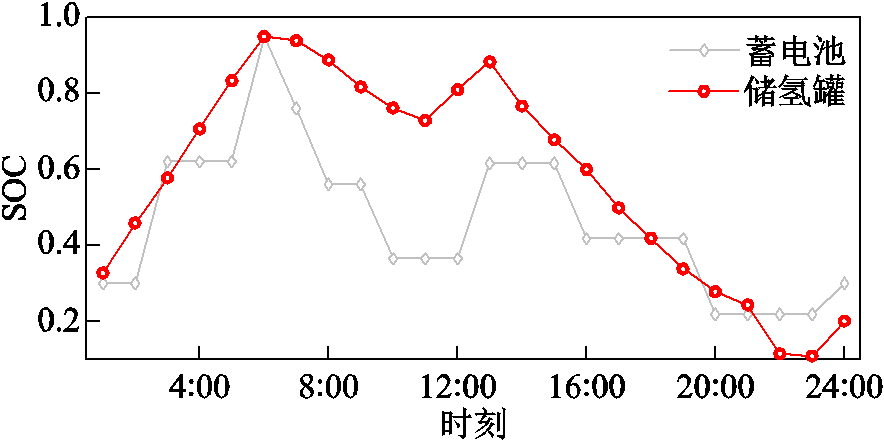
图11 电氢储能的SOC计划
Fig.11 SOC planning curves of electricity and hydrogen energy storage
由图11可见,两种储能的SOC波动趋势大致相同,均为在风电富余时段充能,并在风电不足时段放能,其间的差异在于储氢罐是持续地充放运行,且SOC的爬坡明显更低;而蓄电池则在4:00—6:00、9:00、11:00—12:00、14:00—15:00、17:00—19:00、21:00—23:00几个时段不运行。这是因为氢储能可储存的能量更多,调节能力更大,单次充放对SOC的影响更小;而蓄电池的容量较小,其运行在于发挥对氢储能的配合作用。以上表明,所提模型形成了以氢储能为主、电储能为辅的储能协调运行模式,能充分发挥电氢储能各自分别的灵活调节和大容量优势,为系统提供更为灵活和可靠的储能容量支撑。
为了验证电解槽阵列功率灵活分配的有效性,本文设置不考虑制氢功率灵活分配的方案4进行对比分析,即制氢功率统一调配,所有电解槽运行工况始终保持一致,其余条件与方案3相同,即文献[11]的电解槽阵列运行方法。
方案3与方案4的调度结果对比见表3。显然,方案3的制氢㶲效率比方案4提升了1.15个百分点。得益于制氢效率的提升,系统制氢过程的㶲损失降低,制氢所需风电量更少,风电的直接供能量更多,这带来了运行成本降低33.69元、㶲损失降低6.56 kW·h、㶲损失成本降低6.3元的综合效益。
表3 方案3和4的调度结果对比
Tab.3 Comparison of scheduling results in Case 3 and 4

方案运行成本/元㶲损失/(kW·h)㶲损失成本/元整体制氢㶲效率(%) 37 891.70732.23630.3572.24 47 925.39 738.79636.6571.09
两方案下电解槽阵列的运行计划分别如图12和附图5所示。由图可知,方案3通过制氢功率的灵活分配,使各电解槽运行功率基本位于最大效率点附近,而方案4在10:00—11:00和21:00—22:00时段处于低效率点,这也就是方案3整体制氢效率更高的原因。另外,方案3下各电解槽的启停次数与方案4相比均减少了2次,运行功率也更为平稳,对电解槽寿命的损耗程度更小。
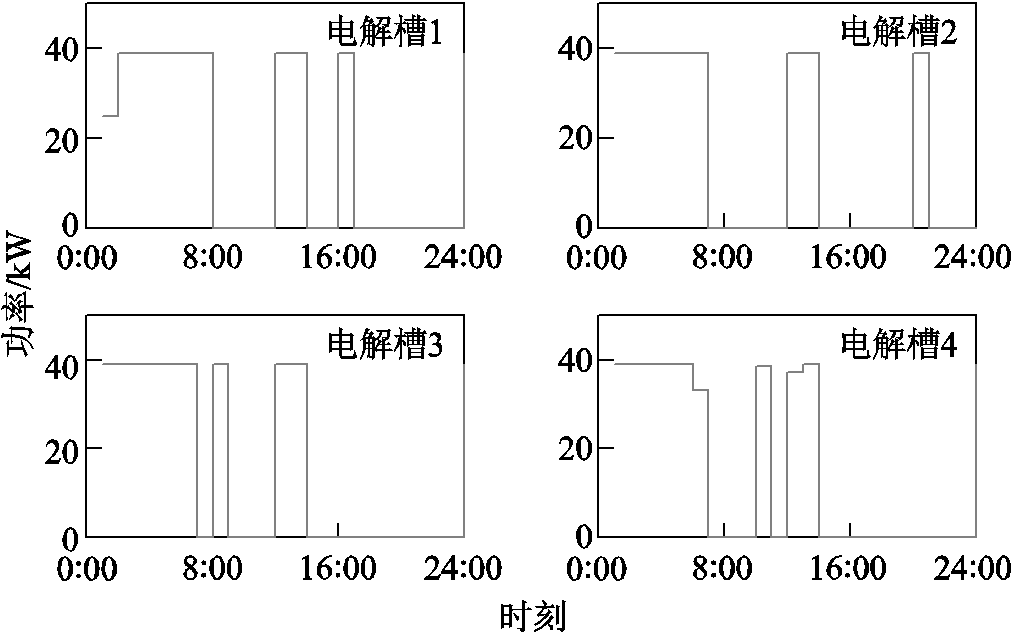
图12 方案3的电解槽阵列运行计划
Fig.12 Operational plan of electrolyzer array at Case 3
综合以上分析,通过电解槽功率灵活分配这一技术手段,能提升整体的制氢效率,同时也更有利于电解槽在波动制氢功率下的延寿运行。
为验证置信区间鲁棒优化的有效性,分别求解确定性、历史值区间鲁棒优化的模型结果,其与90%置信区间结果的对比见表4。
表4 不同模型的结果对比
Tab.4 Comparison of results in different models

模型㶲损失成本/元运行成本/元风电消纳量/(kW·h) 确定性578.677 058.8210.87 历史值区间708.038 750.868.83 90%置信区间630.357 891.709.86
由表4可知,本文模型能克服确定性优化过于乐观的不足,通过减少一部分风电消纳量来增加对新能源出力不确定风险的抵御能力,提升了系统调度的鲁棒性,同时也能改善传统鲁棒的保守性,使运行成本和㶲损失成本大幅下降。结合图13不同置信区间的边界可见,90%置信区间和历史值区间的边界相差较大,但风电预测误差落入这一区域的概率极小,这解释了以历史值区间为鲁棒优化区间集过于保守的原因。而本文所提置信区间鲁棒优化模型则通过概率量化,有依据地缩短了区间集的范围,提升了调度方案的经济可行性。
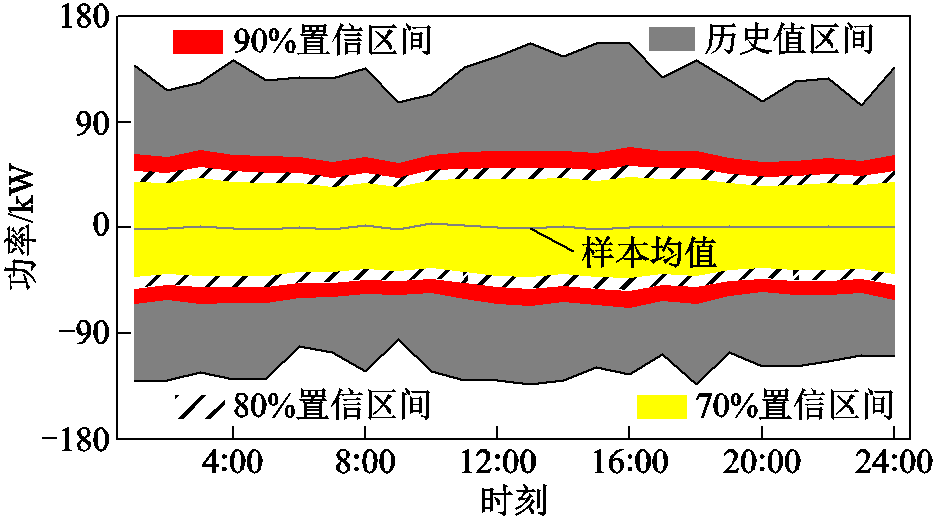
图13 不同置信区间的边界
Fig.13 Boundaries of different confidence intervals
本文模型下,置信区间的设置至关重要。不同置信区间下的调度结果如图14所示。由图14可见,随着置信水平的降低,系统的运行成本和㶲损失成本也逐渐降低,但降低的趋势逐渐减缓。结合图13可发现原因在于区间边界随置信水平降低的缩小程度变化率也是逐渐减小的。这表明,系统运行的经济性随置信区间的收缩而提升,但鲁棒性不断降低。为确保系统能够抵抗风电不确定性的干扰,调度决策者应综合考虑目标函数值低与置信水平高两方面,确定合适的置信水平取值。
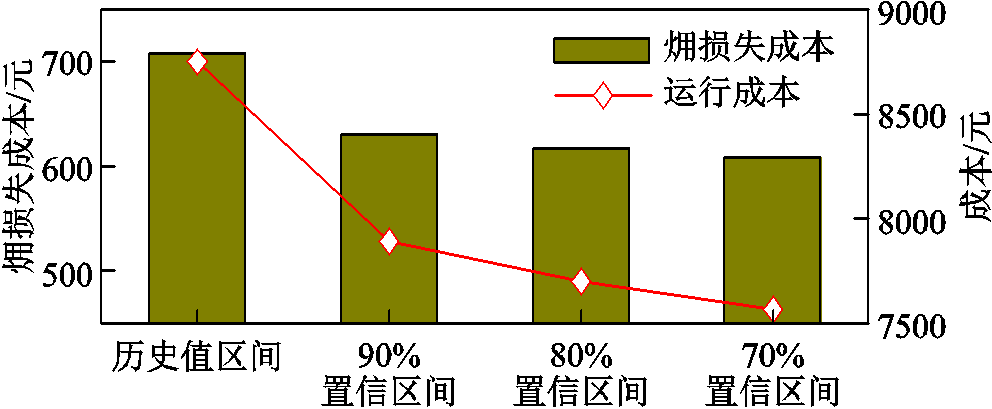
图14 不同置信区间下的调度结果
Fig.14 Scheduling results with different confidence intervals
本文提出基于㶲经济分析的的电氢能源系统优化调度模型,并计及风电不确定性将模型转换为置信区间鲁棒优化形式。通过算例仿真验证了所提模型的可行性和优越性,得到如下结论:
1)从㶲经济的角度,以㶲损失成本最小为优化目标,通过合理设置弃风惩罚系数,可在保障风电消纳能力的同时,实现电氢耦合利用过程中经济效益与㶲损失的平衡。
2)所提模型可以利用制氢功率分配的灵活性,进一步提升电解槽阵列的整体制氢效率,单电解槽运行工况对寿命损耗的不利影响更小,进而提高系统运行的经济性,降低㶲损失。
3)以置信区间作为鲁棒优化不确定集,能考虑到随机变量的概率特征,在确保鲁棒性的前提下,降低系统运行的保守程度。
在后续研究工作中,可考虑电氢储能的不同时间尺度响应特性,在大电网层面通过潮流计算和追踪技术,计及更为具体的能源损耗,建立面向大规模电氢能源系统的㶲经济分析灵活调度模型。
附 录
1. 依据互补松弛定理求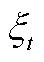 取值
取值
首先,将原内层问题的约束条件标准化为
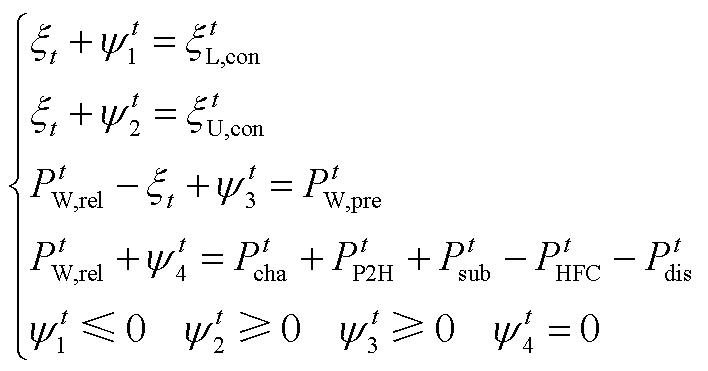 (A1)
(A1)
式中,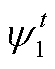 、
、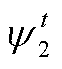 、
、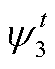 和
和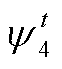 为松弛变量。
为松弛变量。
依据互补松弛定理,对偶变量和原问题的松弛变量满足
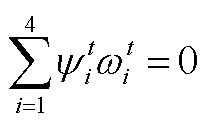 (A2)
(A2)
将对偶问题的最优解视为已知量,代入式(A1)和式(A2)联立后形成的线性方程组,即可求解得到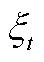 的值。
的值。
2. 电解槽运行特性及算例数据
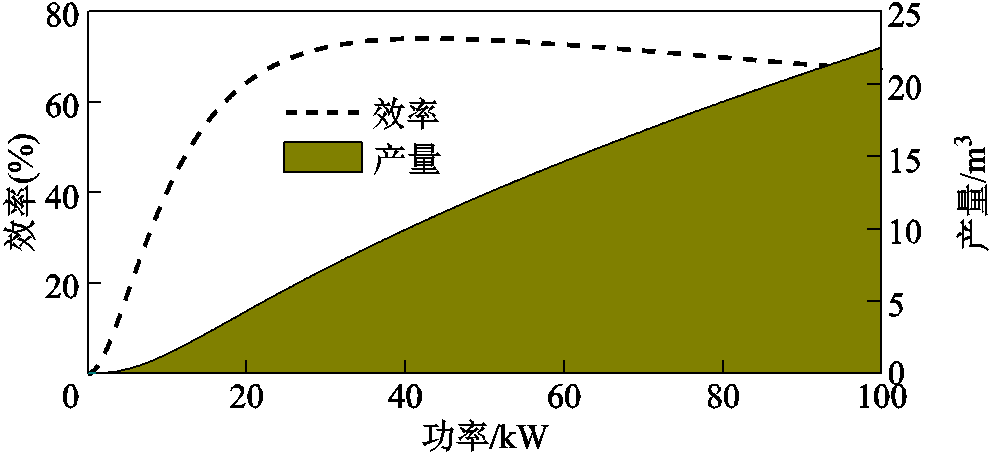
附图1 单电解槽的动态效率及产量曲线
App.Fig.1 Dynamic efficiency and yield curves for a single electrolyzer
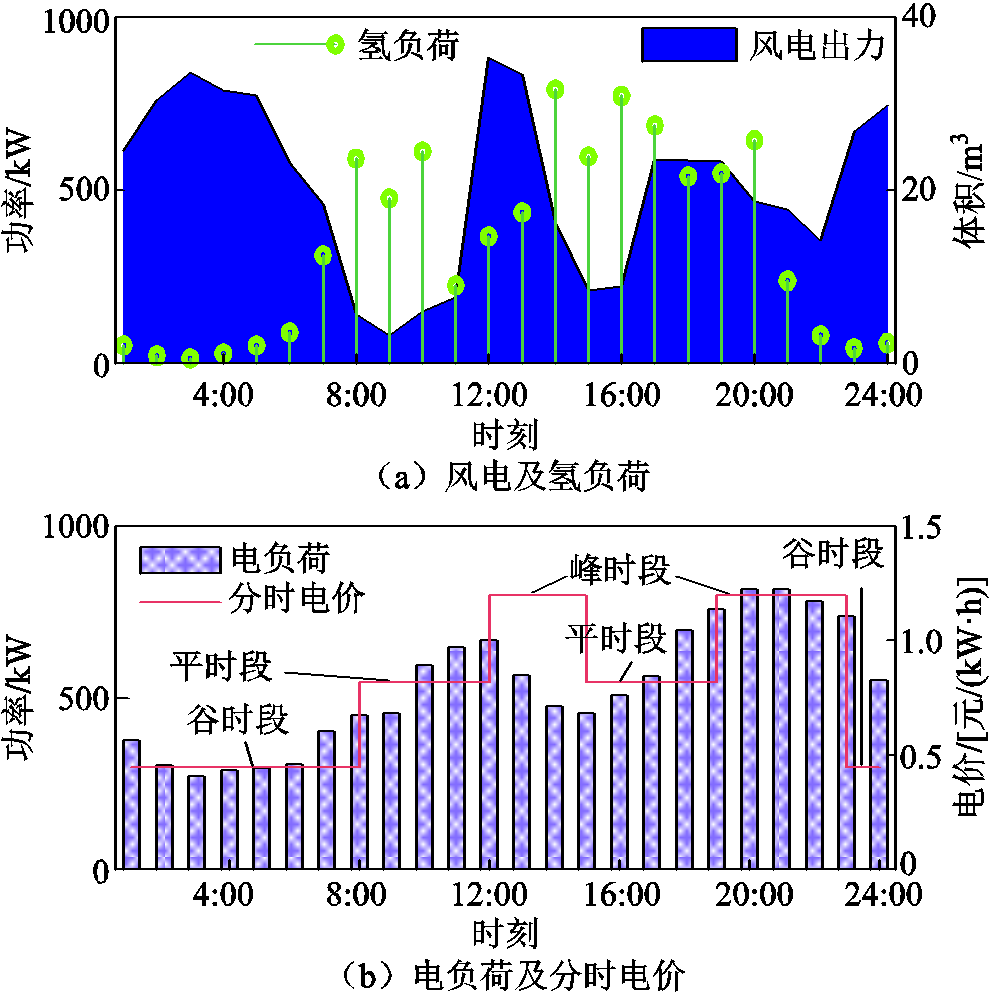
附图2 算例数据
App.Fig.2 Case data
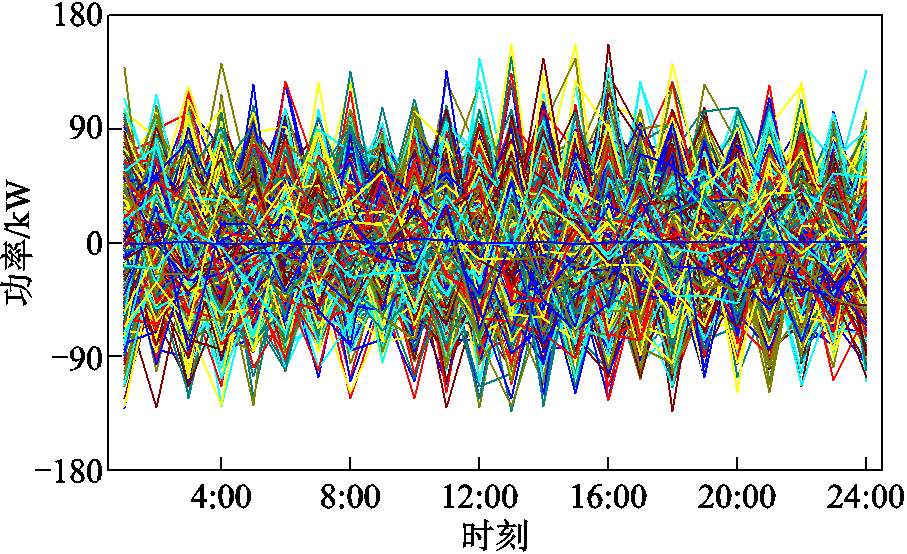
附图3 风电预测误差历史数据
App.Fig.3 Historical data on wind power output prediction errors
3. 系统运行参数的取值
附表1 系统运行参数
App.Tab.1 Operating parameters of the system
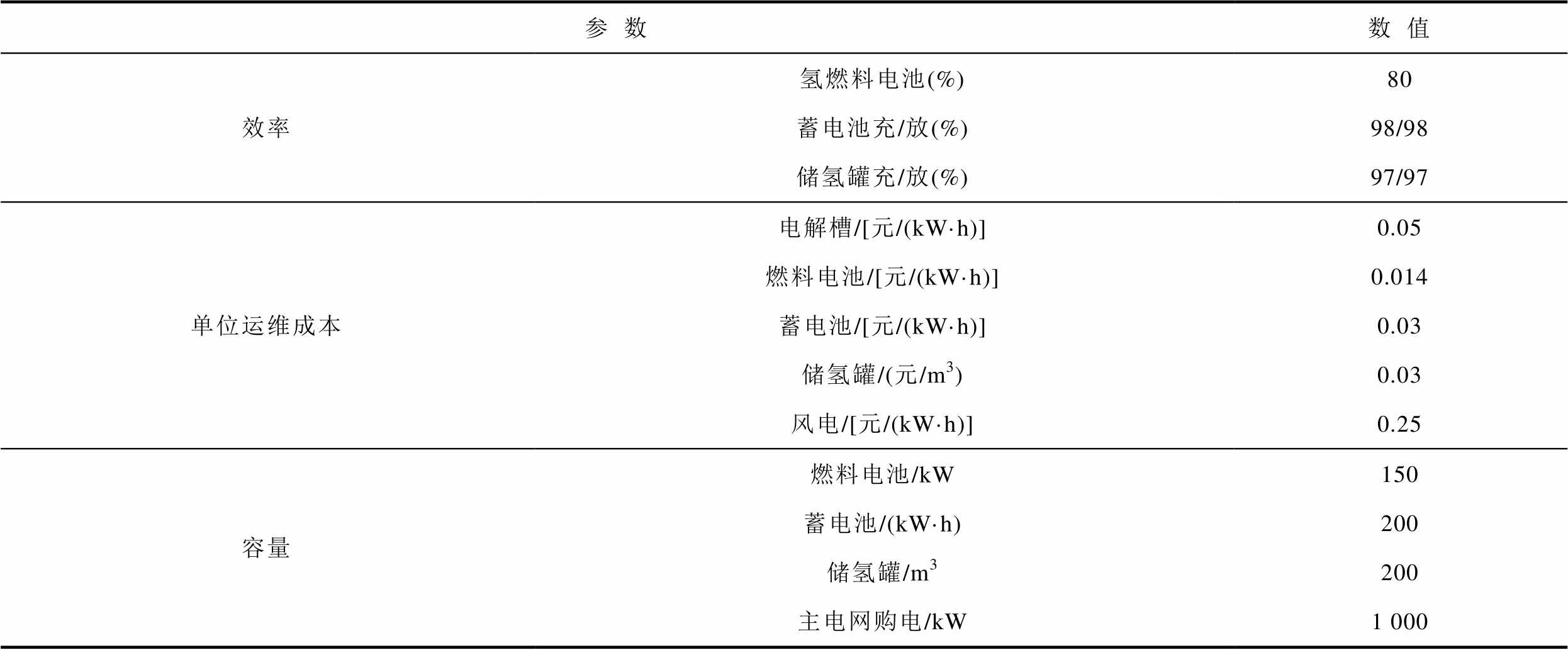
参数数值 效率氢燃料电池(%)80 蓄电池充/放(%)98/98 储氢罐充/放(%)97/97 单位运维成本电解槽/[元/(kW·h)]0.05 燃料电池/[元/(kW·h)]0.014 蓄电池/[元/(kW·h)]0.03 储氢罐/(元/m3)0.03 风电/[元/(kW·h)]0.25 容量燃料电池/kW150 蓄电池/(kW·h)200 储氢罐/m3200 主电网购电/kW1 000
(续)

参数数值 碳排放因子主电网/[kg/(kW·h]0.581 弃风惩罚系数风电/[元/(kW·h)]0.14 综合线损率主电网(%)5 功率爬坡限制系数电解槽0.4 最大启停次数电解槽/次8
4. 电氢耦合㶲经济分析指标
附表2 电氢耦合过程㶲经济分析指标的计算
App.Tab.2 Calculation of indicators for exergoeconomic analysis of electro-hydrogen coupling process

指标计算方法 单位电量成本 单位电量㶲损失 单位电量损失成本 单位风电消纳量损失成本
5. 方案1与方案4的部分调度结果
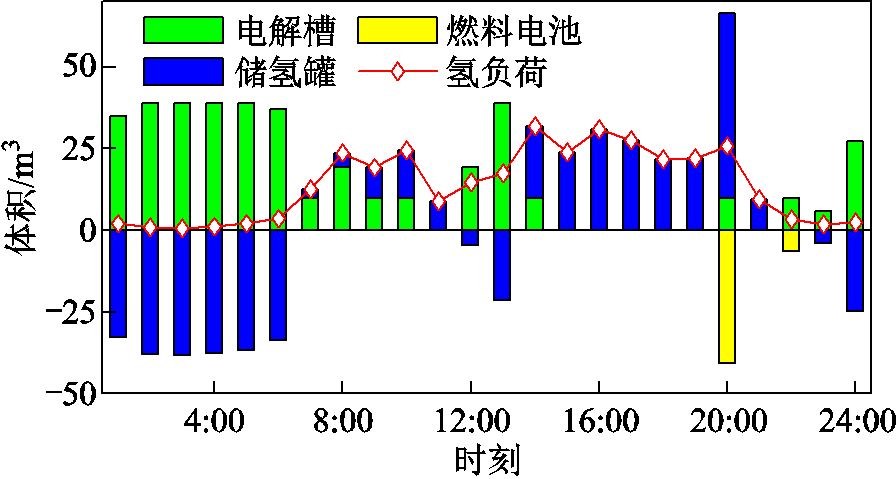
附图4 方案1的供氢计划
App.Fig.4 Hydrogen supply plan of Case 1
附图5 方案4的各电解槽运行计划
App.Fig.5 Operational plan of each electrolyzer at Case 4
参考文献
[1] 中华人民共和国国家发展和改革委员会. 氢能产业发展中长期规划(2021-2035年)[EB/OL]. (2022-03-23). https://zfxxgk.nea.gov.cn/2022-03/23/c_1310525630. htm.
[2] 程欢, 任洲洋, 孙志媛, 等. 电能-甲醇跨区协同输运下的电-氢耦合系统调度[J]. 电工技术学报, 2024, 39(3): 731-744.
Cheng Huan, Ren Zhouyang, Sun Zhiyuan, et al. A dispatching for the electricity-hydrogen coupling systems considering the coordinated inter-region transportation of electricity and methanol[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 731-744.
[3] 清华大学气候变化与可持续发展研究院. 中国的氢能政策和技术现状及发展建议[EB/OL]. (2023-11-27). https://lce.tsinghua.edu.cn/info/1042/1457.htm.
[4] 潘光胜, 顾伟, 张会岩, 等. 面向高比例可再生能源消纳的电氢能源系统[J]. 电力系统自动化, 2020, 44(23): 1-10.
Pan Guangsheng, Gu Wei, Zhang Huiyan, et al. Electricity and hydrogen energy system towards accomodation of high proportion of renewable energy[J]. Automation of Electric Power Systems, 2020, 44(23): 1-10.
[5] 郜捷, 宋洁, 王剑晓, 等. 支撑中国能源安全的电氢耦合系统形态与关键技术[J]. 电力系统自动化, 2023, 47(19): 1-15.
Gao Jie, Song Jie, Wang Jianxiao, et al. Form and key technologies of integrated electricity-hydrogen system supporting energy security in China[J]. Automation of Electric Power Systems, 2023, 47(19): 1-15.
[6] Zhong Zhiyao, Fang Jiakun, Hu Kewei, et al. Power-to-hydrogen by electrolysis in carbon neutrality: technology overview and future development[J]. CSEE Journal of Power and Energy Systems, 2023, 9(4): 1266-1283.
[7] 吴孟雪, 房方. 计及风光不确定性的电-热-氢综合能源系统分布鲁棒优化[J]. 电工技术学报, 2023, 38(13): 3473-3485.
Wu Mengxue, Fang Fang. Distributionally robust optimization of electricity-heat-hydrogen integrated energy system with wind and solar uncertainties[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3473-3485.
[8] 罗潇, 任洲洋, 温紫豪, 等. 考虑氢能系统热回收的电氢区域综合能源系统日前优化运行[J]. 电工技术学报, 2023, 38(23): 6359-6372.
Luo Xiao, Ren Zhouyang, Wen Zihao, et al. A day-ahead dispatching method of regional integrated electric-hydrogen energy systems considering the heat recycle of hydrogen systems[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6359-6372.
[9] Feng Chenjia, Shao Chengcheng, Xiao Yunpeng, et al. Day-ahead strategic operation of hydrogen energy service providers[J]. IEEE Transactions on Smart Grid, 2022, 13(5): 3493-3507.
[10] Hernández-Gómez Á, Ramirez V, Guilbert D. Investigation of PEM electrolyzer modeling: electrical domain, efficiency, and specific energy consumption [J]. International Journal of Hydrogen Energy, 2020, 45(29): 14625-14639.
[11] 李志伟, 赵雨泽, 吴培, 等. 基于制氢设备精细建模的综合能源系统绿氢蓝氢协调低碳优化策略[J]. 电网技术, 2024, 48(6): 2317-2326.
Li Zhiwei, Zhao Yuze, Wu Pei, et al. Low-carbon dispatching strategy of integrated energy system with coordination of green hydrogen and blue hydrogen based on fine modeling of hydrogen production equipment[J]. Power System Technology, 2024, 48(6): 2317-2326.
[12] 胡俊杰, 童宇轩, 刘雪涛, 等. 计及精细化氢能利用的综合能源系统多时间尺度鲁棒优化策略[J]. 电工技术学报, 2024, 39(5): 1419-1435.
Hu Junjie, Tong Yuxuan, Liu Xuetao, et al. Multi-time-scale robust optimization strategy for integrated energy system considering the refinement of hydrogen energy use[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1419-1435.
[13] 李建林, 赵文鼎, 梁忠豪, 等. 基于混合电解槽制氢系统的功率分配技术[J]. 电力系统自动化, 2024, 48(13): 9-18.
Li Jianlin, Zhao Wending, Liang Zhonghao, et al. Power distribution technology based on hybrid-electrolyzer hydrogen production system[J]. Automation of Electric Power Systems, 2024, 48(13): 9-18.
[14] 沈小军, 聂聪颖, 吕洪. 计及电热特性的离网型风电制氢碱性电解槽阵列优化控制策略[J]. 电工技术学报, 2021, 36(3): 463-472.
Shen Xiaojun, Nie Congying, Lü Hong. Coordination control strategy of wind power-hydrogen alkaline electrolyzer bank considering electrothermal characte-ristics[J]. Transactions of China Electro-technical Society, 2021, 36(3): 463-472.
[15] Ding Hongbing, Dong Yuanyuan, Zhang Yu, et al. Energy efficiency assessment of hydrogen recirculation ejectors for proton exchange membrane fuel cell (PEMFC) system[J]. Applied Energy, 2023, 346: 121357.
[16] 中华人民共和国中央人民政府. 2024—2025年节能降碳行动方案[EB/OL]. (2024-05-29). https://www. gov.cn/zhengce/content/202405/content_6954322.htm.
[17] Hu Zhengbiao, He Dongfeng, Zhao Hongbo. Multi-objective optimization of energy distribution in steel enterprises considering both exergy efficiency and energy cost[J]. Energy, 2023, 263: 125623.
[18] Chen Jianrun, Chen Haoyong, Liang Zipeng, et al. An exergy analysis model for the optimal operation of integrated heat-and-electricity-based energy systems[J]. Protection and Control of Modern Power Systems, 2024, 9(1): 1-18.
[19] 何帅, 刘念, 盛超群, 等. 多能源枢纽联合运行的㶲损最小化分布式优化调度[J]. 电力系统自动化, 2021, 45(9): 28-37.
He Shuai, Liu Nian, Sheng Chaoqun, et al. Distributed optimal scheduling for minimizing exergy loss based on joint operation of multiple energy hubs[J]. Automation of Electric Power Systems, 2021, 45(9): 28-37.
[20] 刘帅东, 韩松, 荣娜, 等. 计及㶲效率的电-气-热综合能源系统多目标优化调度方法[J]. 电网技术, 2024, 48(7): 2715-2722.
Liu Shuaidong, Han Song, Rong Na, et al. A multi-objective optimal scheduling method for integrated electricity-gas-heat energy system taking into account the exergy efficiency of the integrated energy system[J]. Power System Technology, 2024, 48(7): 2715-2722.
[21] 亓海青, 韩巍, 张娜, 等. 基于能的品位概念的㶲经济分析方法及其案例分析[J]. 中国电机工程学报, 2016, 36(12): 3223-3231.
Qi Haiqing, Han Wei, Zhang Na, et al. Exergo-economic analysis methodology based on energy level and case study[J]. Proceedings of the CSEE, 2016, 36(12): 3223-3231.
[22] Fu Yidan, Cai Lei, Liu Chunming, et al. Thermodynamic and economic performance comparison of biomass gasification oxy-fuel combustion power plant in different gasifying atmospheres using advanced exergy and exergoeconomic approach[J]. Renewable Energy, 2024, 226: 120290.
[23] 杨俊兰, 高思雨, 李久东. CO2跨临界制冷循环系统 经济分析[J]. 太阳能学报, 2020, 41(1): 60-65.
经济分析[J]. 太阳能学报, 2020, 41(1): 60-65.
Yang Junlan, Gao Siyu, Li Jiudong. Exergoeconomic analysis of CO2 transcritical refrigeration cycle system[J]. Acta Energiae Solaris Sinica, 2020, 41(1): 60-65.
[24] Wang Xi, Henshaw P, Ting D S. Exergoeconomic analysis for a thermoelectric generator using mutation particle swarm optimization (M-PSO)[J]. Applied Energy, 2021, 294: 116952.
[25] Yang Kun, He Yiyun, Du Na, et al. Exergy, exergoeconomic, and exergoenvironmental analyses of novel solar- and biomass-driven trigeneration system integrated with organic Rankine cycle[J]. Energy, 2024, 301: 131605.
[26] 韩子娇, 那广宇, 董鹤楠, 等. 考虑灵活性供需平衡的含电转氢综合能源系统鲁棒优化调度[J]. 电力系统保护与控制, 2023, 51(6): 161-169.
Han Zijiao, Na Guangyu, Dong Henan, et al. Robust optimal operation of integrated energy system with P2H considering flexibility balance[J]. Power System Protection and Control, 2023, 51(6): 161-169.
[27] 王灿, 张雪菲, 凌凯, 等. 基于区间概率不确定集的微电网两阶段自适应鲁棒优化调度[J]. 中国电机工程学报, 2024, 44(5): 1750-1764.
Wang Can, Zhang Xuefei, Ling Kai, et al. Two-stage adaptive robust optimal scheduling based on the interval probability uncertainty set for microgrids[J]. Proceedings of the CSEE, 2024, 44(5): 1750-1764.
[28] 清华大学电机工程与应用电子技术系. 构建新型电力系统的战略构想: 新能源为主、电网配送、电氢融合[EB/OL]. (2021-07-10). https://www.eea.tsinghua. edu.cn/info/1038/2092.htm.
[29] 袁铁江, 万志, 王进君, 等. 考虑电解槽启停特性的制氢系统日前出力计划[J]. 中国电力, 2022, 55(1): 101-109.
Yuan Tiejiang, Wan Zhi, Wang Jinjun, et al. The day-ahead output plan of hydrogen production system considering the start-stop characteristics of electrolytic cell[J]. Electric Power, 2022, 55(1): 101-109.
[30] 张艺晨, 戈志华, 杨勇平, 等. 基于㶲分析的热电联产能耗一致性评价方法[J]. 中国电机工程学报, 2024, 44(2): 642-651.
Zhang Yichen, Ge Zhihua, Yang Yongping, et al. Unified evaluation method of cogeneration energy consumption based on exergy analysis[J]. Proceedings of the CSEE, 2024, 44(2): 642-651.
[31] 国家市场监督管理总局, 国家标准化管理委员会. 能量系统分析技术导则: GB/T 14909—2021[S]. 北京: 中国标准出版社, 2021.
[32] 中华人民共和国国家发展和改革委员会. 关于第三监管周期省级电网输配电价及有关事项的通知[EB/OL]. (2023-05-15). https://www.ndrc.gov.cn/ xxgk/zcfb/tz/202305/t20230515_1355747.html.
[33] 林雨眠, 熊厚博, 张笑演, 等. 计及新能源机会约束与虚拟储能的电-热系统分布式多目标优化调度[J]. 电工技术学报, 2024, 39(16): 5042-5059.
Lin Yumian, Xiong Houbo, Zhang Xiaoyan, et al. Distributed multi-objective optimal scheduling of integrated electric-heat system considering chance constraint of new energy and virtual storage[J]. Transactions of China Electrotechnical Society, 2024, 39(16): 5042-5059.
[34] Li Peng, Yang Ming, Wu Qiuwei. Confidence interval based distributionally robust real-time economic dispatch approach considering wind power accommodation risk[J]. IEEE Transactions on Sustainable Energy, 2021, 12(1): 58-69.
Interval Robust Optimal Scheduling of Electricity and Hydrogen Energy System Based on Exergoeconomic Analysis
Abstract Hydrogen, as a clean, efficient, and high-quality energy source, is recognized as a crucial solution for decarbonizing the energy system and mitigating climate change. The electricity and hydrogen energy system, which uses electricity and hydrogen as energy carriers, represents a key pathway for integrating power systems with hydrogen energy. It helps overcome the developmental limitations of renewable energy, fosters the interconnection and complementarity of multiple energy modes, and promotes deep integration across generation, grid, load, and storage. The electro-hydrogen coupling process, central to this system, can lower operating costs through peak shaving and valley filling. However, the efficiency of electrolyzers and fuel cell remain suboptimal, resulting in significant exergy losses alongside economic benefits during the coupling process. Striking a balance between economic viability and energy saving continues to be a challenging task. Moreover, the substantial forecasting errors caused by the uncertainty of renewable energy outputs can negatively impact the supply-demand balance and the operating conditions of electrolyzers. Therefore, the uncertainty risks associated with renewable energy must be thoroughly considered in optimal scheduling. In response to the above problems, a robust optimal scheduling model based on exergoeconomic analysis is proposed, with the uncertainty set defined by the confidence interval to reduce the conservatism of robust optimization.
Firstly, considering the dynamic efficiency characteristics of the electrolyzer, piecewise linearization was applied to handle the non-convex terms introduced by this relationship. The operation model of the electrolyzer including hydrogen production power allocation and operation models of fuel cell and energy storage equipment were constructed. Secondly, the energy quality coefficients were employed to analyze the exergy loss distribution based on the equipment operation model. A cost accounting method for exergy losses, including both internal and external factors, was proposed. Internally, the cost allocation method was used to price unit exergy losses, enabling the calculation of operational loss costs based on the distribution of exergy losses. Externally, the cost of transmission line losses and penalties of wind curtailment were calculated according to current electricity prices and relevant policies. Thirdly, taking into account constraints such as electrolyzer start-stop cycles, ramping power, and energy balance, an optimal scheduling model was developed with the goal of minimizing total exergy loss costs in the electricity and hydrogen energy system. Then, the model was reformulated into a robust optimization problem based on the uncertainty set of the confidence interval,and a dual transformation method for solving the model was proposed.
In the case simulation, four cases are set up for comparative analysis, leading to the following conclusions: (1) By setting the wind curtailment penalty coefficient appropriately, with the goal of minimizing exergy loss costs, a balance can be achieved between the economic benefits and the exergy losses associated with the electricity-hydrogen coupling process, while ensuring the efficient absorption of wind power. (2) The proposed model can further improve the overall hydrogen production efficiency of the electrolyzer array by taking advantage of the flexibility of hydrogen production power allocation. (3) The confidence interval is used as the uncertainty set of robust optimization, which can take into account the probability characteristics of random variables, and reduce the conservative degree of system operation under the premise of ensuring robustness.
Keywords:Electricity and hydrogen energy system, exergoeconomic analysis, exergy loss cost, confidence interval, robust optimizatio
中图分类号:TM73
DOI: 10.19595/j.cnki.1000-6753.tces.240619
国家自然科学基金(52307098)和中央高校基本科研业务费专项资金(2023MS099)资助项目。
收稿日期 2024-04-22
改稿日期 2024-09-24
李志伟 男,1989年生,硕士生导师,研究方向为电力系统优化调度。
E-mail:zhiwei__li@126.com
赵雨泽 男,2001年生,硕士研究生,研究方向为电力系统优化调度。
E-mail:zyzeenc@163.com(通信作者)
(编辑 赫 蕾)