非介入型LCC-HVDC系统阻抗宽频测量
王 丹1 李 勇1 张 益1, 3 付 颖2 刘泽洪2
(1. 湖南大学电气与信息工程学院 长沙 410082 2. 国家电网有限公司 北京 410006 3. RTDS技术公司温尼伯 R3T 5V6)
摘要 为了在不额外增设一次设备的条件下有效监测电网换相换流器型高压直流输电(LCC-HVDC)系统中馈入受端交流系统的运行动态特性及接入后的宽频振荡风险,提出一种非介入型LCC-HVDC系统阻抗宽频测量方法。所提方法与现有采用单一电压/电流扰动注入或宽频谐波扰动注入等介入型方法不同,无需向高压直流输电系统注入谐波扰动,避免了可能产生的谐振风险。同时所提方法引入了曲线相似度与动态调整时间步长的采样方案。该文首先阐述了LCC系统接入受端交流系统的交互原理;其次以单极大地回线的拓扑结构作为分析对象,采用谐波状态空间(HSS)理论建立了LCC-HVDC系统的HSS阻抗模型;进而提出非介入型阻抗宽频测量方法来观测系统的运行状态,判断宽频振荡风险,剖析LCC系统与受端电网的交互与宽频振荡特性;最后,以CIGRE标准模型算例仿真验证了所提方法的正确性与实用性。
关键词:换相换流器型高压直流输电(LCC-HVDC) 非介入 阻抗宽频测量 谐波状态空间 曲线相似度 动态调整时间步长
0 引言
随着大型风电和光伏基地在沙漠、戈壁及荒漠地区的广泛规划与建设,电网换相换流器型高压直流输电(Line-Commutated Converter based High-Voltage Direct-Current, LCC-HVDC)工程承担了重要使命,负责高容量和远距离的能源输送 [1-3]。然而,随着直流输电规模的不断扩大以及电力系统高电力电子化和高新能源占比的双高特征,电网阻抗呈现非线性化,各种波动性的新能源和电力电子器件接入大电网,深刻改变了电力系统的动态行为[4-5],给系统稳定运行和阻抗测量带来巨大挑战。
近年来,国内外学者针对LCC-HVDC的阻抗建模与稳定性分析已开展了诸多研究,尤其在送出系统的阻抗建模方面颇有深度。文献[6]针对模块化多电平换流器(Modular Multilevel Converter, MMC)场景建立系统输入输出阻抗模型,但侧重于稳定性提升方法的研究。文献[7-8]采用特征值的方法分别基于LCC-HVDC和电压源换流器型高压直流输电(Voltage Source Converter technology based High-Voltage DC, VSC-HVDC)并网系统建立时域模型来分析多频段振荡特性,但其所采用的特征值分析在系统规模较大时分析比较困难。文献[9]采用双傅里叶变换方法建立了LCC-HVDC整流站的序阻抗模型,但建模过程缺乏系统性。文献[10]考虑频率耦合特性建立了LCC整流站的阻抗模型并分析了LCC整流站、直驱风电场和弱电网互联系统的交互稳定性,但未精准刻画逆变站的阻抗特性。文献[11]考虑LCC的换相过程,在dq坐标系下建立了LCC受端系统精确的阻抗模型,但dq域阻抗模型的物理意义不明晰。文献[12]建立计及受端换流站阻抗解析模型,分析换流站交流侧与直流侧间、送端换流站与受端换流站间的阻抗耦合关系,但侧重于送出系统阻抗建模。文献[13-14]分别建立MMC在dq坐标系下的阻抗模型和换流变压器的阻抗模型来分析相关环节的高频振荡特性,但主要面向柔直高压直流系统。文献[15]基于单边调制映射函数在频域上建立直流阻抗数学模型,但其未考虑LCC系统的整体建模。
近年来也有不少学者研究谐波状态空间的阻抗建模方法,例如,文献[16]建立了变流器谐波与阻抗的映射关系,但未针对LCC-HVDC系统展开分析。文献[17]以谐波状态空间(Harmonic State Space, HSS)为底层理论建立LCC-HVDC的耦合阻抗矩阵揭示系统内部的谐波耦合机理,但是未考虑阻抗测量的实现。文献[18]以六脉波换流器开关函数为基础,提出了针对LCC-HVDC系统的一种有效分析交直流系统间的频率耦合关系的HSS建模方法,但未考虑换流器的换相过程且模型截断阶数过低,其精度难以保证。文献[19]计及换流器的开关过程,将系统原始数学模型线性化,并结合线性时不变(Linear Time-varying Periodically, LTP)理论建立了LCC-HVDC整流系统的HSS模型,相较于传统基频动态相量模型具有更高的准确度。文献[20]利用HSS建模方法研究了角型链式静止同步补偿器接入LCC-HVDC弱受端电网下的交互稳定性问题。
与此同时,在阻抗测量方面,国内外已经开展了大量关于电网阻抗测量方面的研究与应用。文献[21]面向±800 kV特高压直流输电工程接地极阻抗开展监测研究,但监测范围仅限于接地极阻抗。文献[22]提出通过变压器将扰动电压串入回路,再通过频率响应分析仪检测响应来测量阻抗。由于变压器串入的扰动信号叠加在流过主回路的电流上,直流电流较大时易使磁心饱和。文献[23]提出通过隔直电容将变压器并联耦合交流扰动电流的方法。因测量仪器功率有限,扰动信号耦合太弱,只适合于100 W以下小功率变换器测量。文献[24]基于串联谐波电压源扰动的方法进行电网阻抗测量,但只应用在有源配电网阻抗。文献[25]采用脉冲信号注入(Pulsed Signal Injection, PSI)和最小二乘(Recursive Least Square, RLS)算法相结合的方法来估计电网连接阻抗,但注入短持续时间电压脉冲有限且主要应用在微电网。文献[26]以新能源并网逆变器的阻抗测量为研究对象,提出了双模式扰动下新能源发电装备的宽频带序阻抗在线精确测量方法,但需在双模式扰动注入方式下实现阻抗的在线测量。文献[27]考虑了电网阻抗和频率耦合效应,实现了逆变器阻抗的精确测量,但未考虑算力和测量步长。文献[28]测量新能源发电基地内大型光伏、风力等新能源发电装备的频域阻抗特性,但仍需设计电压扰动注入单元。文献[29]利用电池的DC-DC变换设备,对其控制系统加入相应的谐波控制环节来测量电池的频域阻抗特性,但引入伪随机二进制序列(Pseudorandom Binary Sequence, PRBS)扰动。文献[30]依靠最大长度二进制序列(Maximum Length Binary Sequence, MLBS)、离散间隔二进制序列(Discrete Interval Binary Sequence, DIBS)信号频谱可控性,尽管这种介入型方法取得了一定的测量效果,但需增加额外的扰动注入设备。文献[31]提出了一种基于数据-模型融合驱动的新能源场站宽频阻抗/导纳在线辨识方法,该方法无需注入扰动,但依赖数据样本及模型训练精度。
为了克服上述阻抗建模及宽频测量的困难,综合考虑LCC-HVDC系统的运行要求,本文从不向系统实际注入扰动的角度,设计一种非介入型的LCC-HVDC阻抗宽频测量方法。基于LCC-HVDC的单极大地回线拓扑结构详细推导了HSS阻抗模型,采用数据+模型驱动的阻抗测量方法监测宽频域阻抗,并通过阻抗分析法剖析了LCC系统与受端电网的交互和宽频振荡特性。首先,介绍了LCC-HVDC单极大地回线的系统拓扑及子系统的交互原理;然后,详细介绍了LCC-HVDC系统阻抗建模并推导了阻抗宽频测量数学模型;最后,通过量测数据和阻抗模型双驱动的方案实现对系统阻抗的“非介入”宽频测量。本文的创新点主要包括:①该测量方法无需向系统注入谐波扰动;②LCC-HVDC的主要阀控器件为晶闸管,换流站建成后其拓扑及参数基本固定,基于拓扑建立HSS模型具有可实施性;③通过改变曲线相似度和采样数据的时间步长可以观测系统运行状态和精准捕捉幅频曲线交点,节省算力和数据存储空间。以CIGRE标准模型算例的参数作为基础,通过Matlab仿真验证了本文所提非介入型阻抗建模与阻抗宽频测量方法的正确性与实用性,为高压直流输电领域的阻抗宽频测量与交直流运行管理部门的运行管理提供设计参考与辅助决策建议。
1 LCC-HVDC的谐波交互原理
常规高压直流输电工程中每个阀组均由12脉波换流器构成,运行模式之一为单极大地回线方式。LCC-HVDC是一个较为庞大且复杂的电力电子系统,从受端系统可将其分为LCC系统和受端交流系统,其中LCC系统包括从受端公共连接点(Point of Common Coupling, PCC)看向直流侧方向的所有系统,受端交流系统包括受端电网及交流滤波系统。为便于阻抗建模与宽频测量及振荡特性分析,本节重点介绍所研究对象LCC-HVDC系统的拓扑结构及谐波在两个子系统之间的交互原理。
1.1 LCC-HVDC拓扑结构
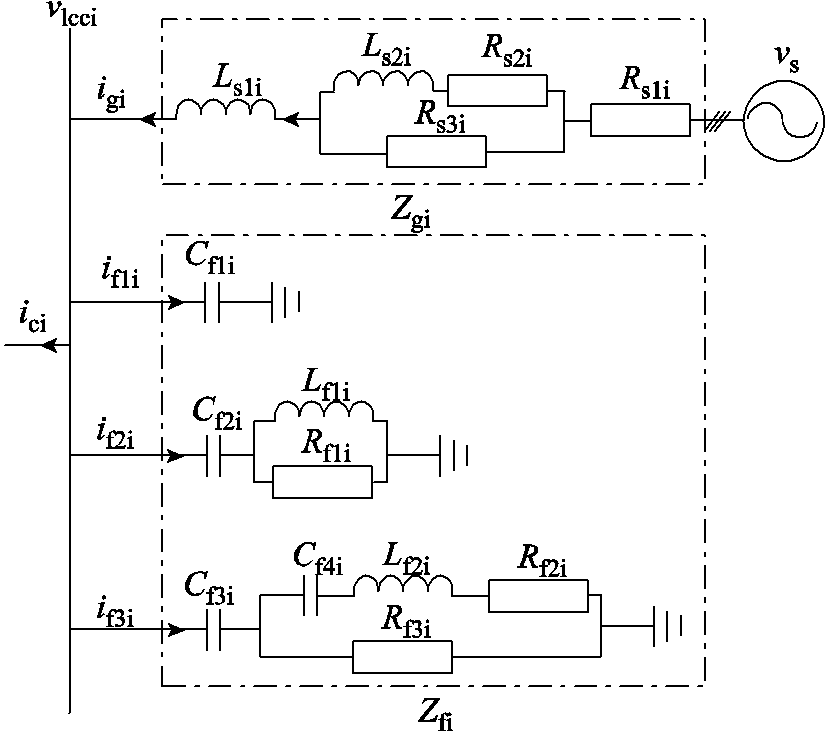
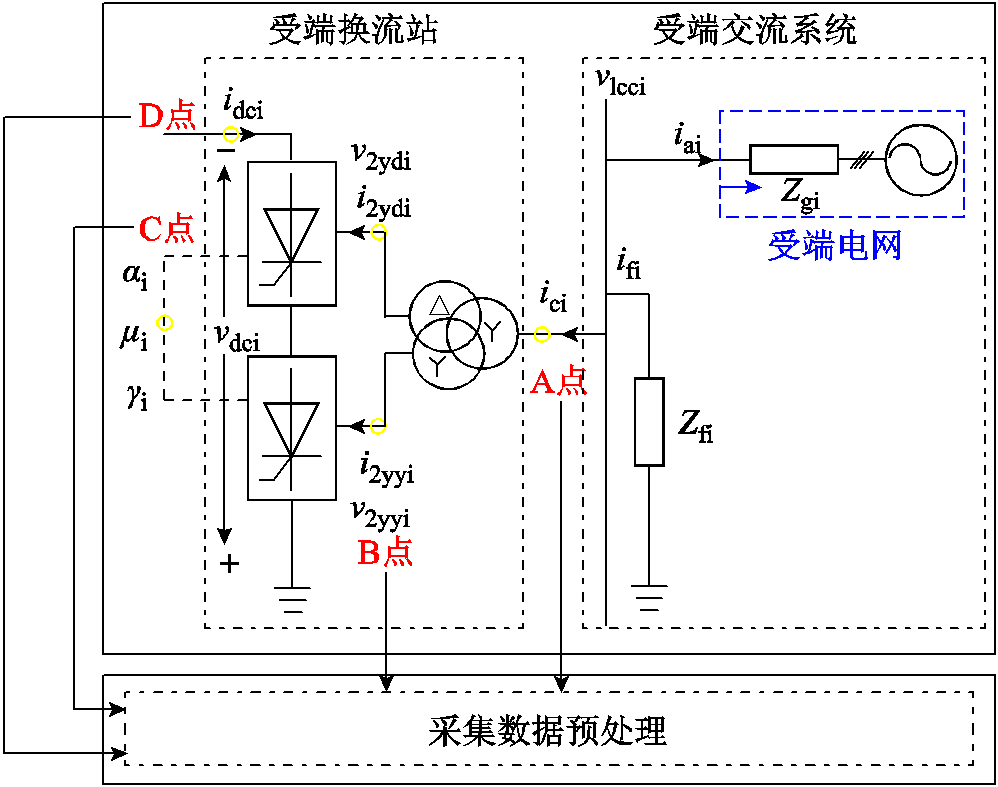
图1所示为LCC-HVDC单极大地回线运行方式的主电路及控制结构,送受端换流站分别采用定电流控制和定电压控制。图1中,下标“r”和“i”分别表示送端和受端;“ ”为LCC-HVDC可采样数据的采样点,可直接从换流站的二次同步量测装置获取;iai和ifi分别为受端交流系统的线路总电流和滤波总电流;vlcci和ici分别为受端换流变压器的一次电压和一次电流;v2ydi、i2ydi和v2yyi、i2yyi分别为受端换流变压器二次三角形侧和星形侧的电压、电流;vdci和idci分别为受端换流站直流电压和电流;Zgi、Zfi分别为受端交流系统的线路总阻抗和滤波总阻抗;αi、μi和γi分别为受端换流站的触发角、换相角、关断角;kti、Lti分别为受端换流变压器的电压比和漏感;Rd、Ld、Cd分别为直流线路的等效电阻、电感、电容;vdc0为直流系统对地电容的电压;Gidc_r和Gvdc_i分别为送、受端换流站控制中直流电流和直流电压的滤波器的传递函数;Hidc_r和Hvdc_i分别为送、受端换流站控制中直流电流和直流电压的PI控制器的传递函数;HPLL_r和HPLL_i分别为送、受端换流站控制中锁相环的PI控制器的传递函数。
”为LCC-HVDC可采样数据的采样点,可直接从换流站的二次同步量测装置获取;iai和ifi分别为受端交流系统的线路总电流和滤波总电流;vlcci和ici分别为受端换流变压器的一次电压和一次电流;v2ydi、i2ydi和v2yyi、i2yyi分别为受端换流变压器二次三角形侧和星形侧的电压、电流;vdci和idci分别为受端换流站直流电压和电流;Zgi、Zfi分别为受端交流系统的线路总阻抗和滤波总阻抗;αi、μi和γi分别为受端换流站的触发角、换相角、关断角;kti、Lti分别为受端换流变压器的电压比和漏感;Rd、Ld、Cd分别为直流线路的等效电阻、电感、电容;vdc0为直流系统对地电容的电压;Gidc_r和Gvdc_i分别为送、受端换流站控制中直流电流和直流电压的滤波器的传递函数;Hidc_r和Hvdc_i分别为送、受端换流站控制中直流电流和直流电压的PI控制器的传递函数;HPLL_r和HPLL_i分别为送、受端换流站控制中锁相环的PI控制器的传递函数。
1.2 LCC-HVDC谐波交互机理
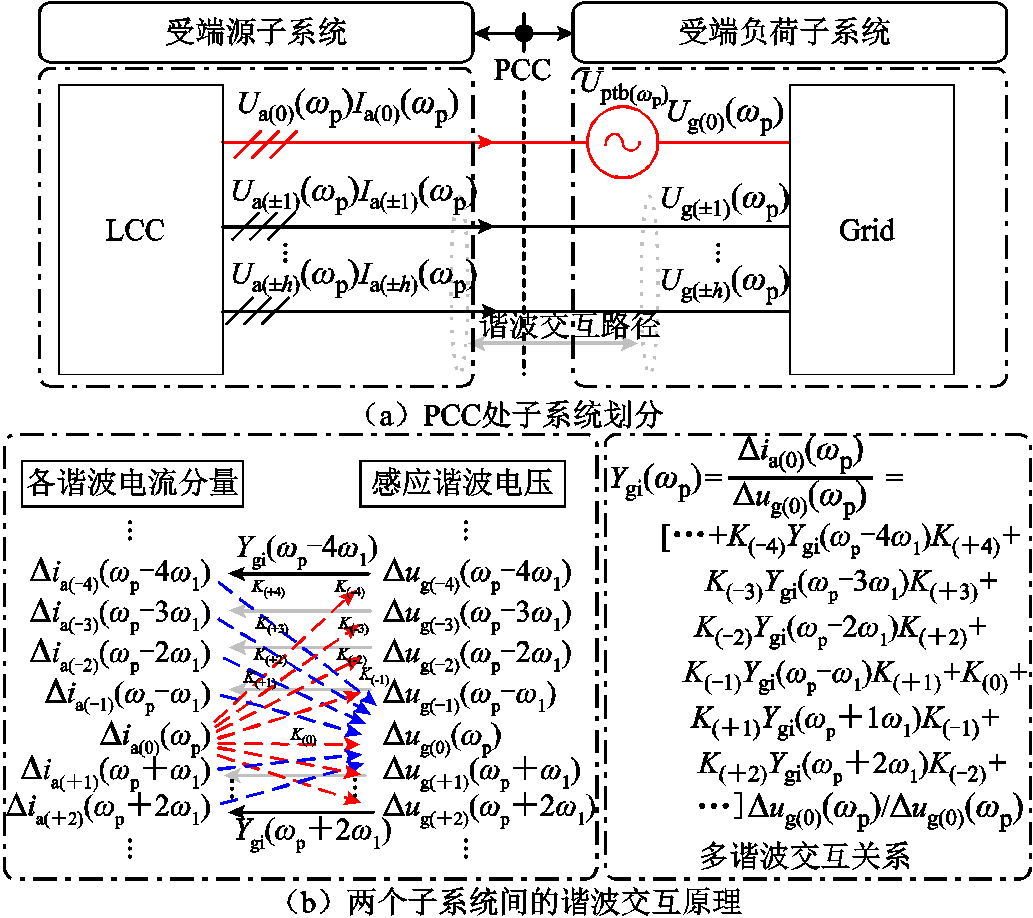
LCC-HVDC是以晶闸管为主要换相器件的直流输电系统,在系统运行时晶闸管换相过程产生丰富的谐波扰动信号,这些信号在LCC系统与受端交流系统之间产生耦合,存在交互行为。LCC-HVDC谐波交互机理如图2所示。
如图2a所示,从受端PCC处将系统划分为源/荷子系统,就可通过电路谐振原理、奈奎斯特定理等方法来分析宽频振荡及源/荷子系统交互机理[8]。单独分析LCC系统和受端交流系统的阻抗特性,它们的端口传递函数是开环的,当两者经PCC连接后就形成了一个封闭系统,两个子系统之间就会发生相互作用。假设LCC系统在虚拟角频率ωp处存在一个独立电压源的虚拟扰动,其产生的电流响应不仅包含虚拟角频率ωp处的分量,还包含ωp+kω1,k=±1,…,±h阶的谐波,从而LCC系统在各谐波阶次产生的分量涌入交流电网时,LCC的电流相应地将在电网侧感应出谐波电压Ugk(ωp),k=0,±1,…,±h。此时LCC系统与受端电网的谐波电压(以a相为例)满足Ua(±k)(ωp)=Ug(±k)(ωp),k≠0,LCC系统与受端电网之间存在交互且谐波关联。图2b为LCC系统和电网间各阶谐波的交互关系,K为各谐波分量对感应谐波电压响应的增益系数,可见各谐波间是存在交互关联的。由此,精准剖析两个子系统之间的交互作用与宽频振荡风险,应先建立一套涵盖多谐波状态的阻抗模型,并准确测量宽频域的阻抗。
2 LCC-HVDC阻抗建模
本节着重介绍LCC-HVDC系统各环节的阻抗建模,先做如下说明。
1)对谐波状态空间理论的应用规则约定。
(1)建立时域小信号模型后进行傅里叶级数展开,得到时域上的周期小信号Δx(t)的数学表达式为
式中,h为谐波阶数;Z为整数集。
(2)通过卷积将时域中的变量Δx(t)及其稳态系数p(t)的乘法转换到频域,对应关系为
其中
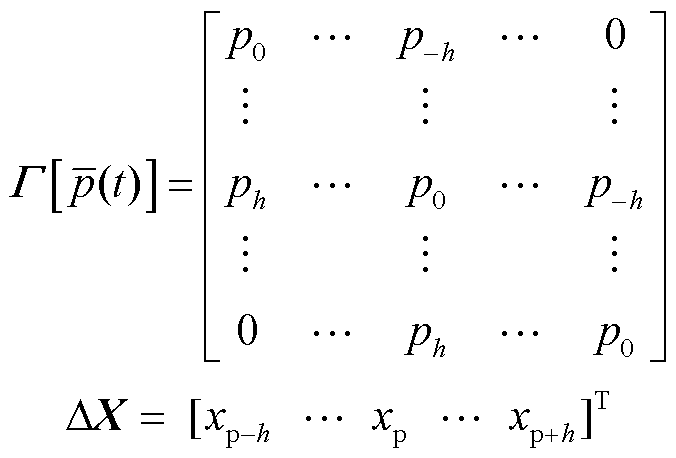
式中,`p(t)为快速傅里叶(Fast Fourier Transform, FFT)分析的各谐波阶数下的稳态分量;Г[`p(t)]为Toepliz频率矩阵;ΔX为对应的谐波阶数的状态变量;上标“-”表示稳态量。
(3)关于Δx(t),通过关系式(3)将其转换为频域。
式中,N = diag(j(ωp-hω1),…, jωp,…, j(ωp+hω1)),ωp=2πfp,fp为虚拟扰动频率。
(4)完成步骤(1)~步骤(3)处理后,再对每一个状态向量和输入向量的元素及系数矩阵的元素扩展至2h+1维,扩展规则为:状态向量和输入向量从fp-hf1到fp+hf1的谐波阶数依次进行排列;按照系数矩阵的常数项元素乘以2h+1维单位矩阵I,对角线位置减去对角矩阵N。
每个环节建立小信号时域模型后,均按照上述规则进行频域转换,得到相应的HSS模型。
2)本文以LCC-HVDC受端为例开展模型推导,送端类似处理,不再赘述。
2.1 受端交流系统的HSS模型
将图1中受端交流系统的线路总阻抗Zgi的内部元素扩展为2h+1维矩阵后求逆为受端交流系统的线路总导纳矩阵Ygi。类似扩展Zfi得到受端交流系统的滤波支路总导纳矩阵Yfi。
本文以CIGRE标准模型参数建模,受端交流系统的线路总阻抗Zgi和滤波总阻抗Zfi的内部结构如图3所示。
令状态变量Δxi = [Δvcf1i Δvcf2i Δvcf3i Δvcf4i Δif1i Δif2i]T,输入变量Δui = [(Δici-Δigi)/Ci1 0 0 0 0 0]T,根据HSS应用规则,受端交流系统线性化后的小信号模型可写为
式中,Ai为元素扩展后的系数矩阵;Bi为单位矩阵。
2.2 受端换流站的HSS模型
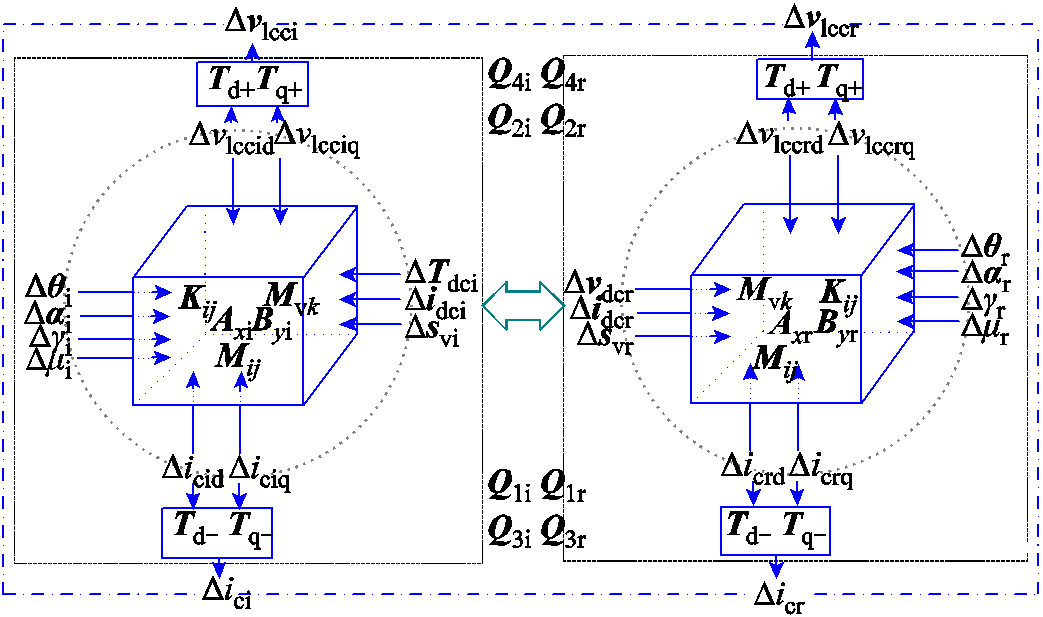
2.2.1 受端变压器一次电流HSS模型
受端换流站的阻抗建模主要包括受端变压器、换流器、LCC直流系统、控制系统的阻抗建模。根据文献[17, 29],考虑LCC-HVDC系统中的换流器通过控制晶闸管的触发角、关断角和换相角来实现直流与交流之间的能量转换,在稳态下存在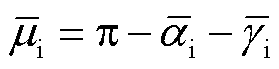 ,三个变化量关系为
,三个变化量关系为
其中
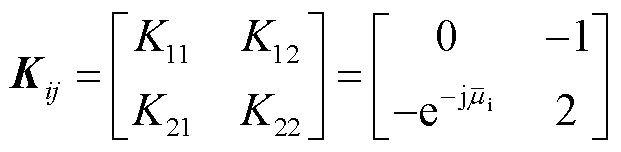
结合谐波状态空间理论的应用规则,受端换流变压器一次电流HSS模型可表示为
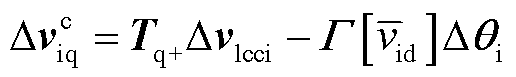 (7)
(7)
其中
式中,Mlcci_a、Midc_a、Mαi_a分别为交流电压变化对交流电流的影响系数、直流电压变化对交流电流的影响系数、相位变化对交流电流的影响系数;Δvciq为控制系统的输入变量;Mij为考虑晶闸管的触发角、关断角和换相角的影响系数;Td+、Tq+、Td-、Tq-为Park变换矩阵与逆Park变换矩阵[32]。
2.2.2 LCC直流系统的HSS模型
LCC-HVDC的换流器开关函数非常复杂,根据文献[4]进行简化处理之后进行HSS规则应用,得到受端交流系统LCC直流电压的HSS模型为
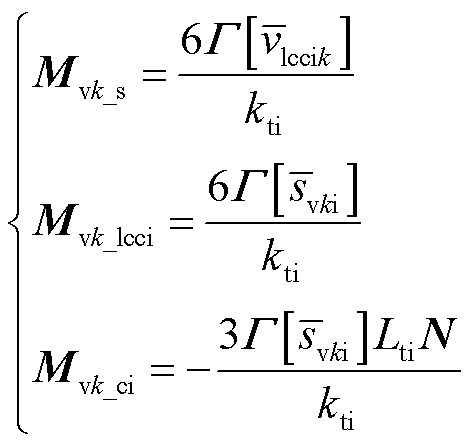 (9)
(9)
式中,Mvk_s、Mvk_lcci、Mvk_ci分别为开关函数变化对直流电压的影响系数、交流电压变化对直流电压的影响系数、交流电流变化对直流电压的影响系数;k为a、b、c三相;sv为开关函数;Lt为换流变压器的漏感。
LCC-HVDC的直流输电线路采用图1所示的T型等效电路,通过电路定理可将送端换流站与受端换流站建立联系,令状态变量Δxdc=[Δidcr ΔidciΔvdc0]T,输入变量Δudc =[Δvdcr/Ld Δvdci/Ld 0]T,根据HSS应用规则,受端交流系统线性化后的小信号模型可写为
式中,Adc为元素扩展后的系数矩阵;Bdc为单位矩阵I。
2.2.3 控制系统的HSS模型
LCC-HVDC采用典型的控制策略,整流侧定电流控制,逆变侧定电压控制。根据文献[20],再结合HSS应用规则,受端交流系统线性化后可直接写为
式中,Ac为元素扩展后的系数矩阵;Bc为单位矩阵;Aαr、Aαi分别为整流、逆变触发角扰动与直流电压电流扰动的影响系数矩阵;状态变量Δxc = [Δxplli Δθplli Δidci Δxidci]T;输入变量Δuc=[Δvlcciq kpllpi/Δvlcciq Δidci/Tidc 0]T,kpllpi和Tidc分别为Hvdc_i传递函数比例常数和Gvdc_i传递函数中的时间常数。
各环节建模中的影响系数Mij、Ax、Bx│x=i、c、dc、α的计算详见文献[33],本文不再赘述。
2.3 LCC-HVDC的整体HSS模型
根据2.2节各环节建立的HSS模型,将模型中的小信号进行对消处理,可得到Δici与Δvlcci的传递函数矩阵YLCCi。该传递函数是关于送受端各扰动影响系数及元素扩展的矩阵,能刻画出LCC-HVDC不含交流滤波支路受端系统多输入多输出(Multiple-Input Multiple-Output, MIMO)导纳模型。小信号的对消逻辑[33]如图4所示,对消后得到的平衡方程为
式中,Q为对消合并后的系数矩阵。
根据基尔霍夫定律,由图1可以写出
式中,YLCCi为LCC-HVDC含交流滤波支路的受端系统MIMO导纳模型,YLCCi= YLCC0i + Yfi;YLCC0i为LCC-HVDC不含交流滤波支路的受端系统MIMO导纳模型。
选定受端系统的电压电流方向为正方向,类似可写出:Δici = -( Ygr +Yfr) Δvlcci。Yfi、Yfr、Ygi、Ygr可由含扩展元素Ax、Bx的HSS模型推导得到。
由式(12)可以推导出导纳矩阵YLCC0i为
LCC-HVDC受端系统MIMO阻抗模型为
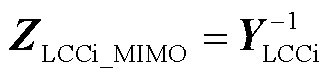 (15)
(15)
LCC-HVDC受端系统馈入电网的MIMO阻抗模型为
3 非介入型阻抗宽频测量方法
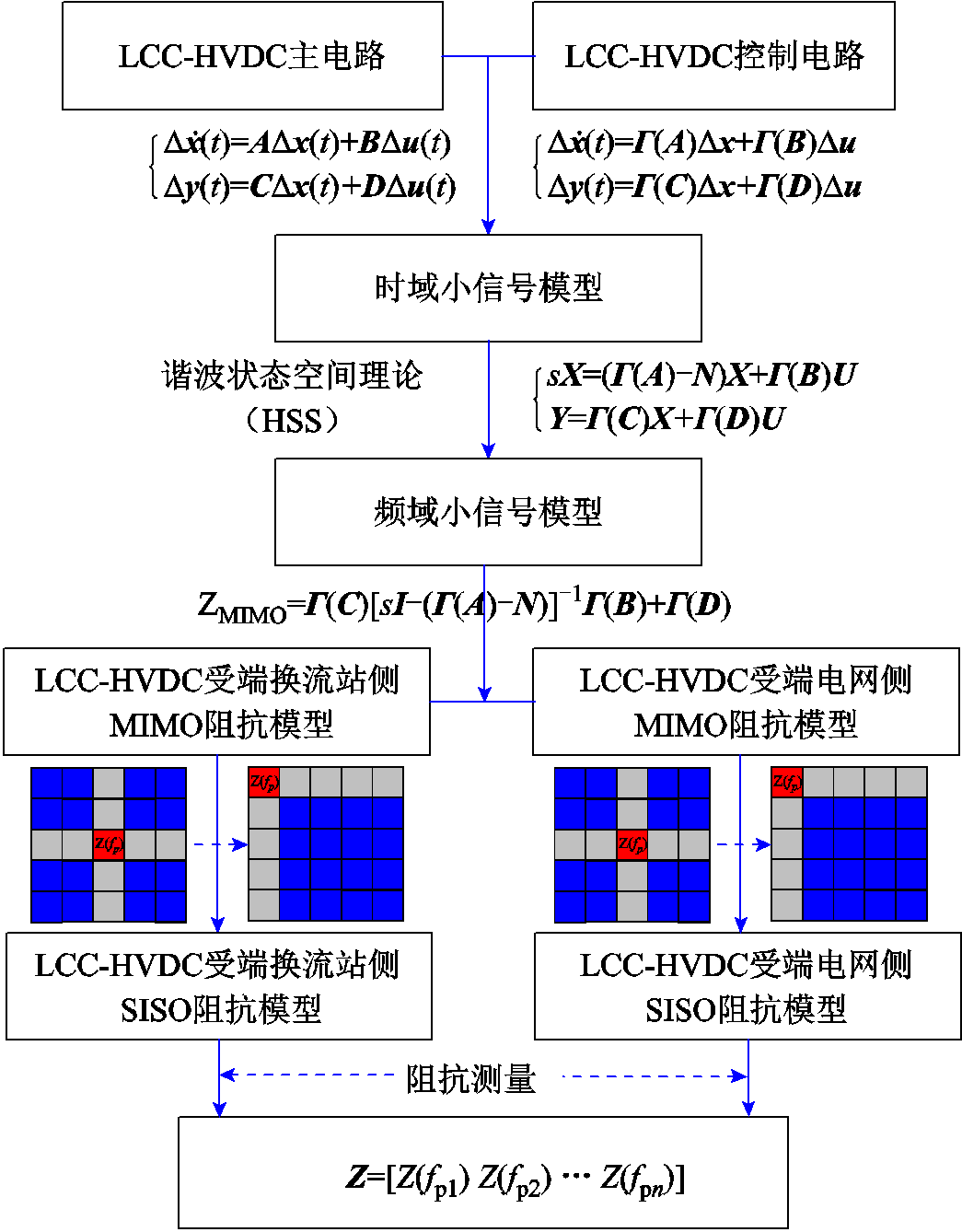
3.1 非介入型阻抗宽频测量原理
本文通过收集LCC-HVDC的系统参数及可采集的运行数据,按照第2节建立的阻抗数学模型,实现LCC-HVDC在宽频尺度下的阻抗测量。
非介入型阻抗宽频测量的基本原理如图5所示。从阻抗测量的角度出发,本文首先采用小信号建模方法建立主电路和控制电路的时域小信号模型;然后基于傅里叶特性和谐波平衡理论,将时域小信号模型转换为频域小信号模型,得到LCC-HVDC多频耦合的谐波状态空间MIMO模型。而HSS模型实际为一个无穷大阶数模型,算力将无穷大,不便于实际测量。第2节中建立HSS模型应用的规则实则是将其截断为谐波h阶,用(2h+1)× (2h+1)维矩阵表示。截断谐波阶数h的选择对模型精度有重要影响,理论上阶数越大,模型精度越高,测量越准。较小的稳态谐波分量可以降低频率耦合的程度,模型降阶可以通过关键稳态谐波分量值来度量。考虑LCC-HVDC受端系统的阻抗测量,应将涵盖所有谐波耦合和正负序耦合的MIMO阻抗模型ZLCC_MIMO和Zgi_MIMO转换为能包含所有耦合项的单输入单输出(Single-Input Single-Output, SISO)阻抗模型ZLCC_SISO和Zgi_SISO。结合文献[34-35]所提出VSC的MIMO模型转换为SISO模型的方法,类比处理:将LCC-HVDC受端系统以PCC为断面看作源荷两个子系统,考虑两个子系统的谐波耦合特性,设定谐波阶数为h,将式(15)、式(16)按照元素重排,LCC与电网的h阶模型可分别写为二端口方程式(17)和式(18)。
由此可以写出两个子系统的SISO阻抗模型分别为
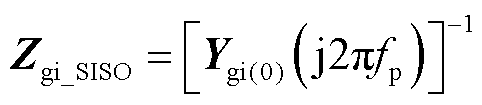 (20)
(20)
上述推导的式(19)和式(20)分别为LCC-HVDC的系统侧与受端电网侧的宽频阻抗测量的数学模型。
3.2 宽频测量的数据采集与输入
根据3.1节推导的SISO阻抗模型,确定阻抗测量模型的详细输入。本文以CIGRE标准模型参数作为基准参数,网架结构参数采取默认值。数据采集点为PCC(A点)、换流变二次侧(B点)、换流站控制器(C点)、换流站直流侧(D点),阻抗测量所需的数据输入为A点的相电压、B点的相电压、C点的触发角、关断角、换相角,D点的电压电流数据采集与监测主要是为实时观测系统传输功率状态。以受端为例测量示意图如图6所示。
3.3 宽频测量的阻抗测量分析
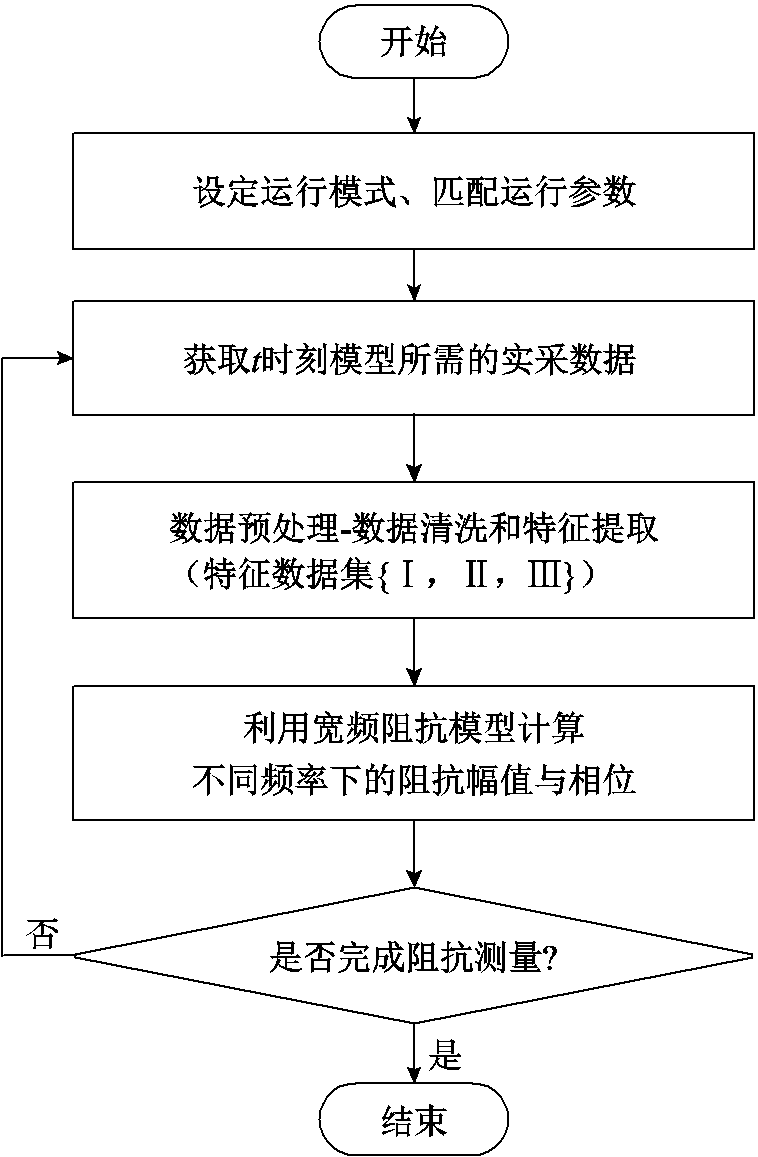
3.1节推导的SISO阻抗模型是以虚拟扰动为离散变量的宽频阻抗计算模型,既包含了各谐波阶次的耦合项也包含与电网交互的耦合项。图7所示为宽频阻抗测量流程。
1)设定运行模式并匹配运行参数,以本文研究对象为例,应设定为单极大地回线运行方式,匹配CIGRE标准参数。
2)获取t时刻模型所需的实采数据,通过采集模块或装置采集图6中的实时信息数据。
3)数据预处理,主要包括数据清洗与特征提取,将采集模块采集的数据进行清洗,检测有无数据缺失、重复、错误等进行补充并修正。特征提取主要是将A点相电压先进行dq变换,再对d轴分量进行FFT分析,提取典型谐波次特征分量的耦合量,并按照时间断面存储数据集Ⅰ;对B点相电压进行FFT分析特征提取典型谐波次特征分量,并按照时间断面存储为数据集Ⅱ;对C点的角度数据按照对应的时间断面存储数据集Ⅲ;特征数据集{Ⅰ,Ⅱ,Ⅲ}作为模型输入。
4)宽频阻抗计算,将预处理后的特征数据集输入SISO阻抗模型进行运算,获取该时间断面的宽频阻抗的幅值与相位。
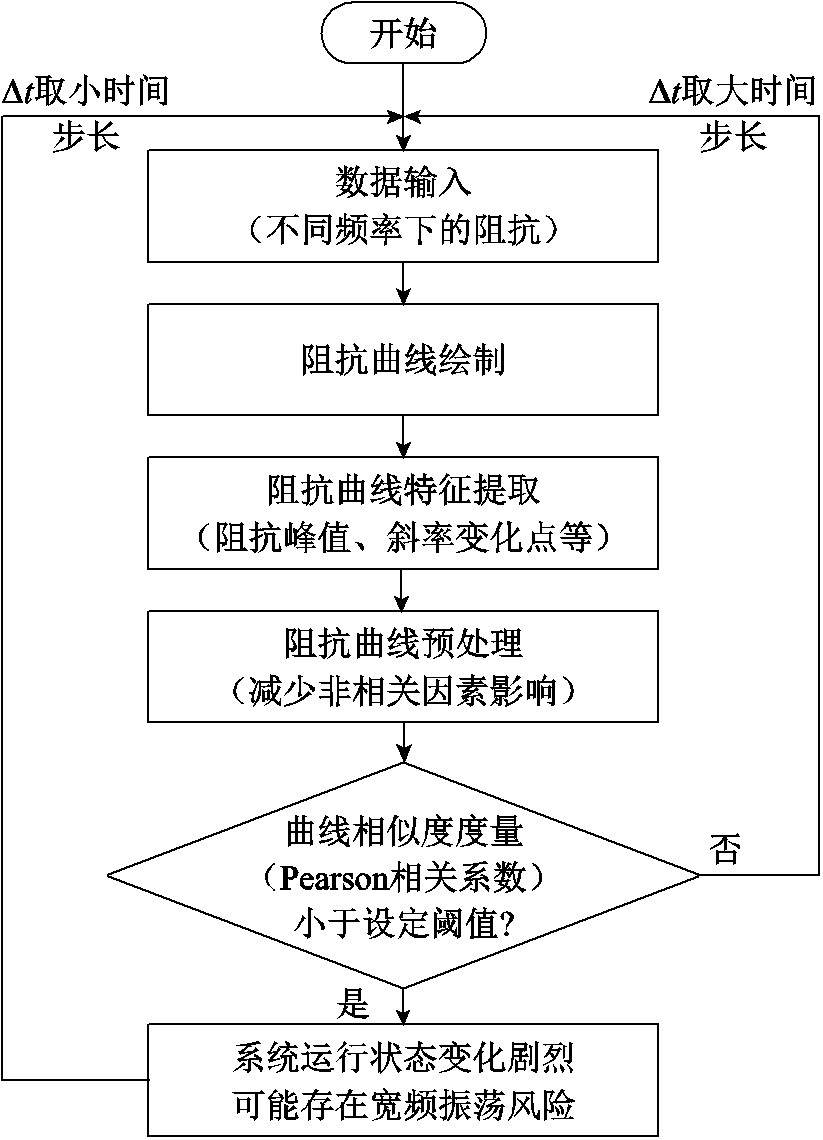
值得注意的是,在第4)步可按照时间断面将预处理后的数据流逐批输入SISO阻抗模型,计算该时间断面下宽频阻抗幅值和相位。具体实施是根据设定固定大步长(50个周波,约1 s)所测量阻抗曲线的相似度与历史最近正常运行的阻抗曲线的相似度作比较,当相似度小于设定阈值(即系统运行状态变化剧烈可能存在宽频振荡风险)时动态调整数据输入的时间步长,如设定阈值为0.99,当相似度<0.99时,从1 s开始递减至0.1 s进行阻抗测量。采用相似度分析法对宽频振荡风险区段进行高颗粒度捕捉的流程如图8所示。可见相似度分析不仅能观测系统运行状态,还能对存在宽频振荡风险区段进行高颗粒度捕捉,进一步通过大小步长的选取还可优化运算算力空间,这在工程应用上具有一定的实用性。
系统绝大部分时间运行在稳定状态。然而,当系统的控制参数、传输功率水平、系统运行强度发生变化引发宽频振荡等稳定性问题时,也会存在因系统自身弹性和自调节能力重新恢复到一种稳定运行状态的情况。考虑系统运行的稳定性及临界状态是否诱发振荡等问题,需预知振荡风险的存在。在阻抗测量与振荡风险预判时会因为量测阻抗宽频曲线的相近或数据采样时间不适配等错过捕捉振荡风险。故而本文引入Pearson相关系数预估曲线相似度,通过计算各不同断面下的量测曲线的相似系数,观测该断面下的振荡风险或运行状态变化。
假设有两组量测阻抗曲线XA(fn)、YB(fn),二者的Pearson相关系数为
式中,µXA、σXA分别为XA的均值、标准差;µXB、σXB分别为XB的均值、标准差;n为样本数量;Ave(·)为求平均值函数。
Pearson相关系数的取值范围[-1,1],接近1表示正相关,表明XA(fn)和YB(fn)的曲线形状接近一致,粗判两者所对应断面的运行状态接近;接近-1表示负相关,表明XA(fn)和YB(fn)的曲线形状对称且呈现极性相反,粗判两者所对应断面的量测信号取反导致模型输入量的符号极性取反,需排查量测装置的互感器接线方式;接近0表示无相关性,表明XA(fn)和YB(fn)的曲线形状不相关,粗判两者所对应断面的运行状态发生了较大的变化,可进一步结合其他条件评估系统运行状态。
由式(21)可知,两条阻抗曲线的相关系数矩阵为对应每个虚拟频率下的阻抗幅值数组组合的相关系数的矩阵为
由于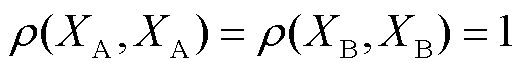 ,即
,即
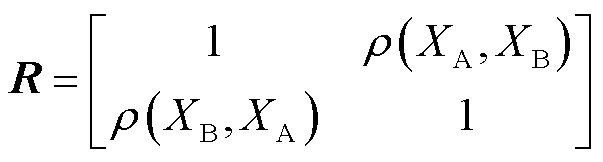 (23)
(23)
通过Pearson相关系数对所量测的阻抗宽频曲线进行高颗粒度捕捉,再结合采样步长的调整,密集或稀疏测量宽频阻抗,精确捕捉幅值交点或交点域,确定对应频率的相位差,精准捕捉系统振荡的频率点或频率段,及时报送给运行人员辅助决策建议,必要时作出应急补救措施。
4 算例分析
4.1 阻抗模型验证
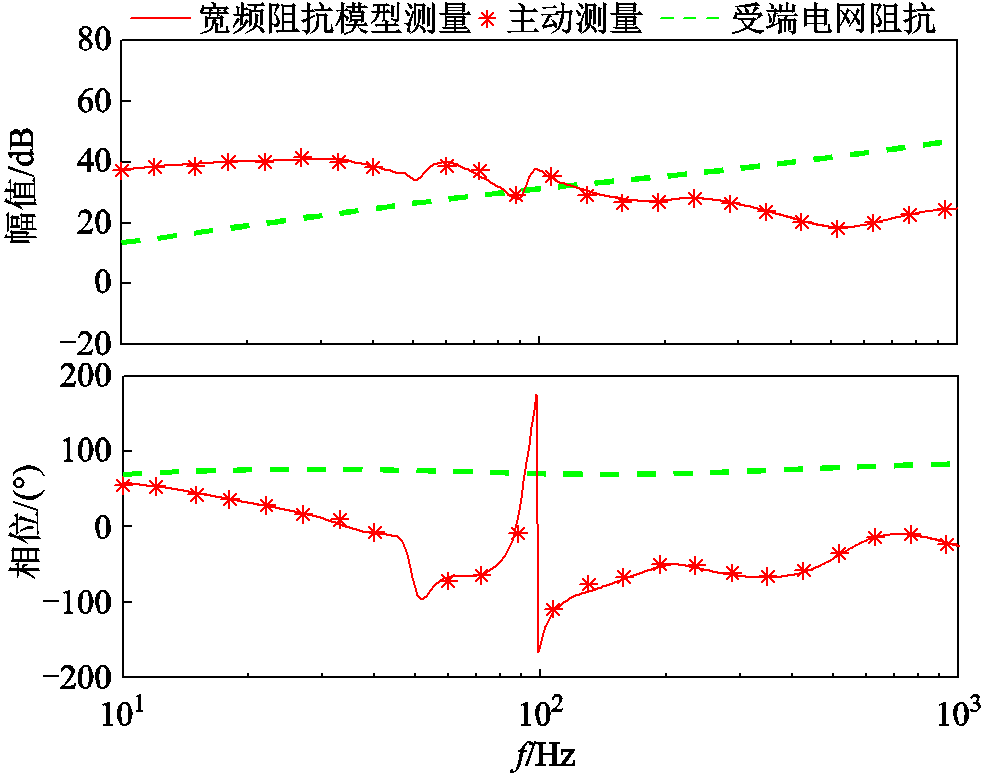
为了验证所推导LCC-HVDC阻抗模型在宽频域下测量的有效性,在Matlab/Simulink中以采用主动测量的方式对LCC-HVDC受端系统阻抗进行测量与验证。单极12脉动LCC-HVDC 模型控制参数见表1。系统运行参数、滤波器参数和无功补偿装置按照CIGRE直流输电第一标准[36-37]。取谐波阶次为13次,图9所示在10~1 000 Hz频段内推导的13阶正序阻抗(红色实线)与主动测量的正序阻抗(红色*号)基本吻合。非介入型的阻抗测量与主动测量的拟合曲线的相关系数为0.998 3(接近于1),即曲线相似度为99.83%,说明所提非介入型的阻抗测量结果的准确度高达99%以上,验证了所推导的宽频域阻抗模型的正确性。
表1 LCC-HVDC控制参数
Tab.1 Control parameters of LCC-HVDC

参数类别整流侧逆变侧 低通滤波器时间增益0.001 20.02 PI控制器比例增益2.995×10-49.012×10-7 PI控制器积分增益1.29×10-23.68×10-5 PLL锁相环控制器比例增益5.68×10-41.135×10-3 PLL锁相环控制器积分增益7.1×10-41.42×10-3
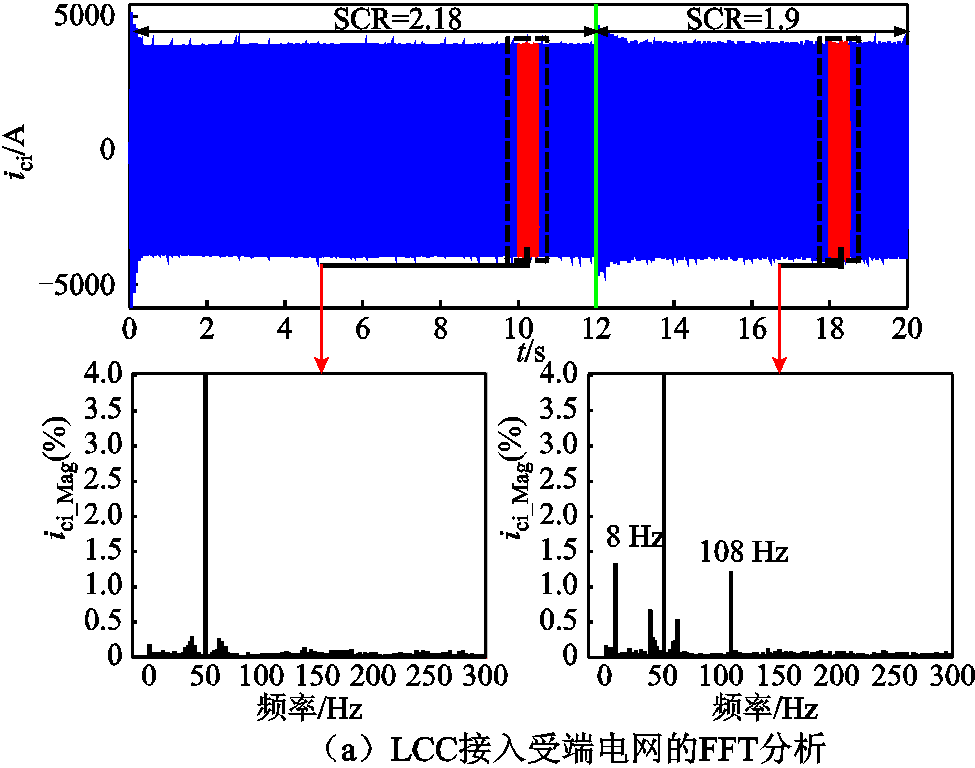
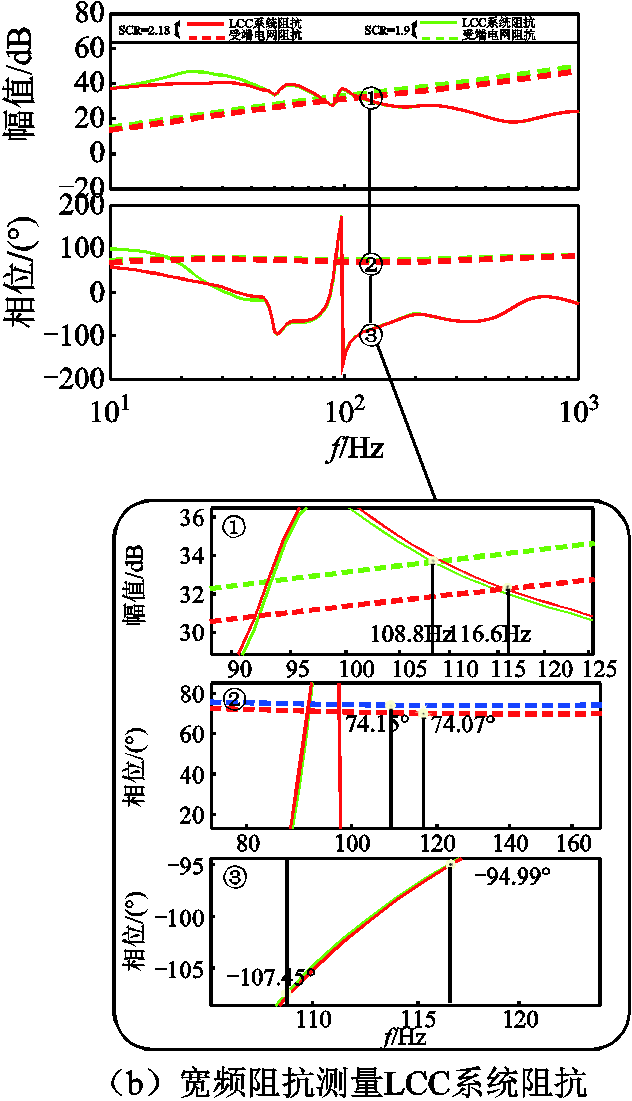
考虑到模型能否捕捉到系统的振荡点,在仿真中改变图3中运行参数Lsli,使短路比SCR由2.18(36.5 mH)减小到1.9(46.5 mH)。FFT分析LCC接入受端电网的PCC电流波形,SCR=1.9时在108 Hz(耦合频率8Hz)出现明显振荡,如图10a所示。通过模型测量,阻抗幅频曲线出现三处交点,SCR=1.9时在第3个交点频率108.8 Hz处存在相位裕度小于0,如图10b所示。由此,双重验证了模型的有效性。
4.2 阻抗测量分析
本文采用谐波状态空间理论建立HSS模型。HSS模型实际为一个无穷大阶数模型,在第2节中描述HSS建模的应用规则就已经将其截断为谐波h阶,用(2h+1)×(2h+1)维矩阵表示。
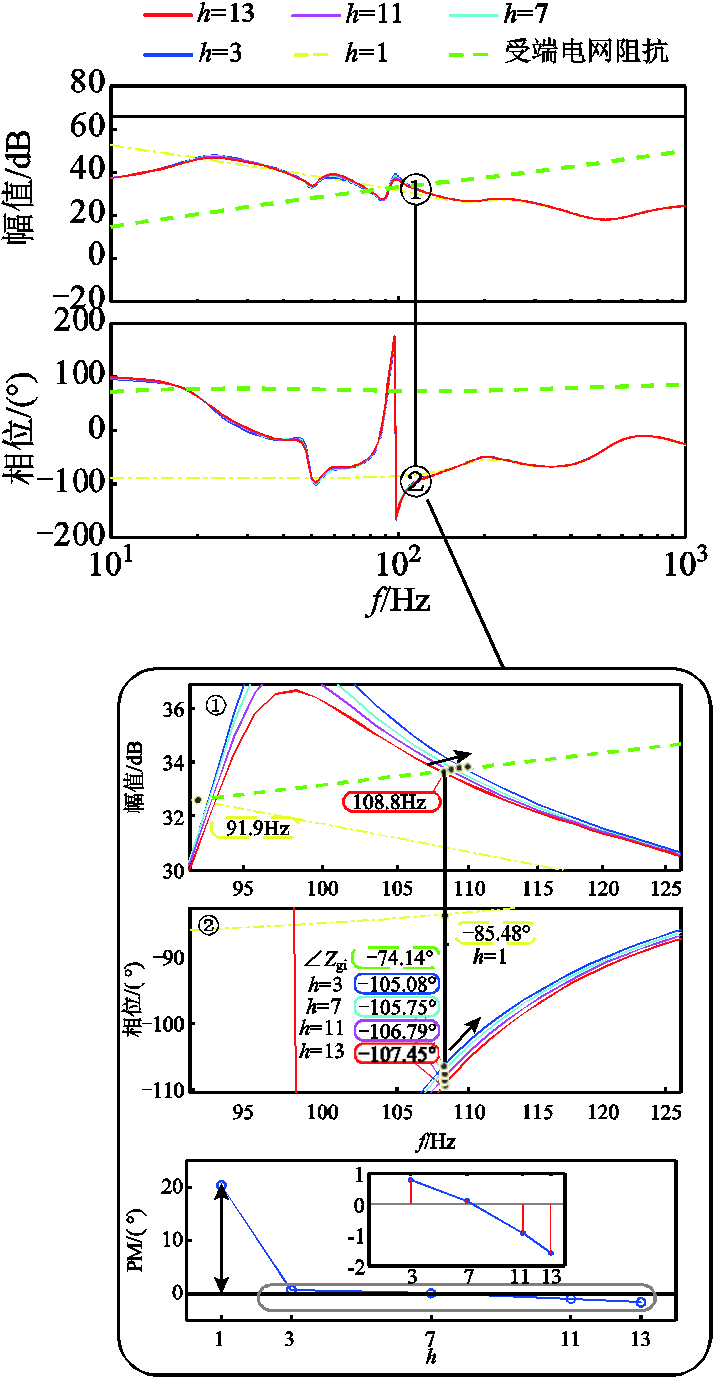
当h=1时不考虑谐波耦合,当h为其他阶次时,考虑谐波耦合。h分别取3、7、11、13时,通过不同谐波阶次的HSS模型来测量LCC-HVDC系统的宽频域阻抗。为了便于分析,取受端电网的短路比SCR=1.9时系统运行的量测曲线如图11所示。
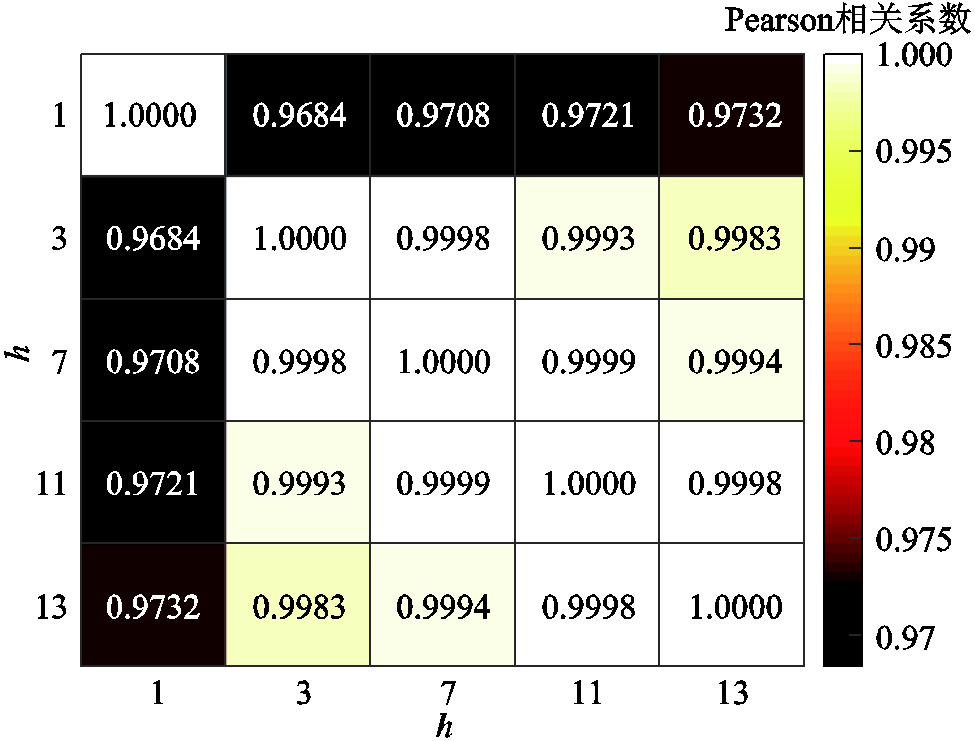
图12所示为不同谐波阶次下的宽频阻抗测量曲线的相似度矩阵热力图。可以看出,当h=1时,测量曲线与其他谐波阶次的Pearson相关系数远离数值1,呈现深蓝色,h=3、h=7与h=11的相应测量曲线的Pearson相关系数很相近,最大误差在0.2%内,呈现深红色。h=13与h=3、7、11的测量曲线的Pearson相关系数按照谐波阶次的递增逐步逼近1,进一步结合图11中的阻抗分析,可见h=13的模型相对更精准。由于h=1的模型未考虑任何频率耦合,而h=3、h=7、h=11的模型仅涵盖了二倍频的谐波耦合,h=13的模型能涵盖十二倍频的谐波耦合,模型阶数更高测量更准,但对计算机的算力要求更高。为便于仿真,后续测量分析模型采用13阶模型。若用于工程实际,还应优先考虑算力的压力,可将幅频交点的误差可行域适当扩大,可采用3≤h<13的低阶测量模型。
1)调整采样时间步长测量
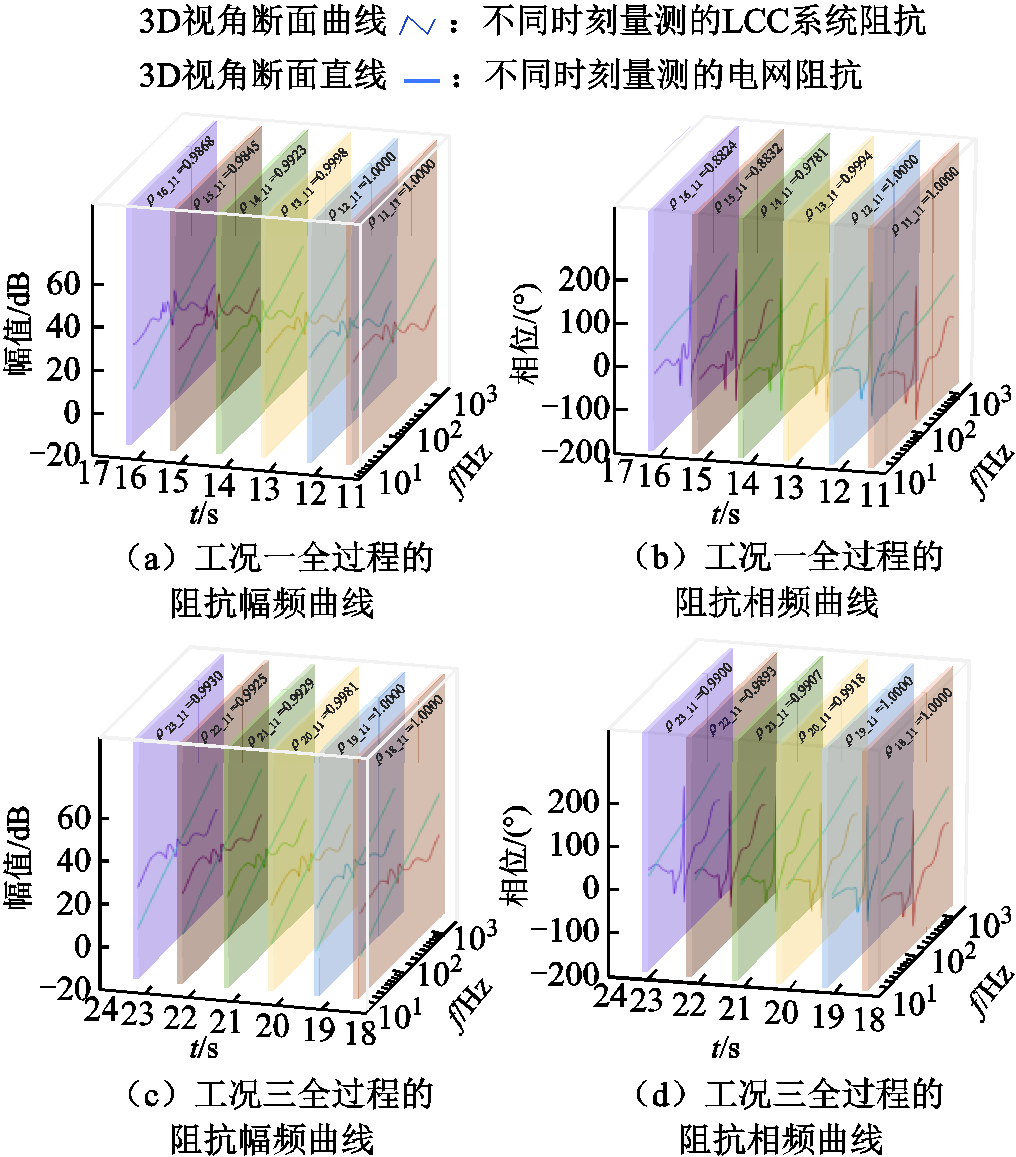
假设在额定状态下稳定运行后,12~16 s调整系统控制参数后振荡(工况一),16~20 s恢复稳定运行(工况二),20~24 s受端电网的短路比减小后系统振荡(工况三)。通过仿真测量模块或量测装置以一定的采样频率实时动态地采集三种工况下不同时间断面的数据,将动态采集的数据进行特征提取后输入宽频阻抗运算模块进行宽频域阻抗运算,量测不同时间断面的阻抗幅频曲线和相频曲线。
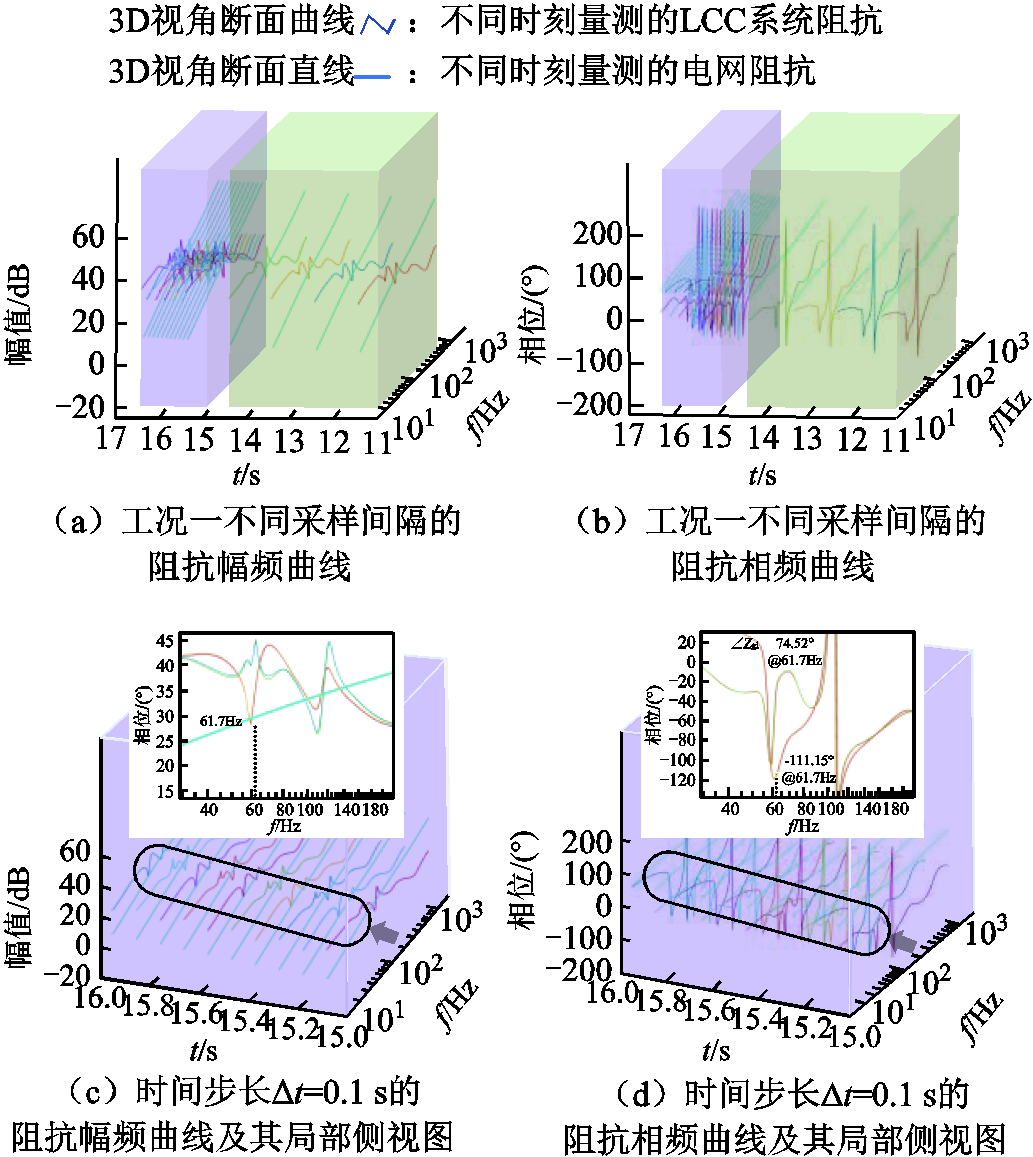
图13a、图13b和图13c、图13d分别为在采样间隔Δt=1 s能涵盖工况一全过程和工况三全过程的宽频阻抗量测曲线,工况二为系统恢复稳定运行过程,其量测曲线作为参考曲线。由图13的量测结果可知,在13~16 s的宽频阻抗曲线形状开始产生显著变化,通过Pearson相关系数的数据亦可预判该时间段系统运行状态发生改变;类似地,在20~23 s的宽频阻抗曲线形状略有变化,Pearson相关系数的数据更清晰明了地体现了该时间段系统运行状态改变。图14在15~16 s按照采样间隔Δt=0.1 s复测一组宽频阻抗曲线,发现10~100 Hz中出现了幅频交点,再通过侧视图观测发现在61.7 Hz处存在相位裕度小于0的现象。由此可见,“大时间步长测量+曲线相似度分析”可对宽频振荡风险区段进行颗粒度捕捉;“小时间步长测量+奈奎斯特判稳分析”可精准捕捉宽频振荡点。关于工况三改变受端短路比使系统运行状态改变的分析在图10中已体现,此处不再赘述。
2)改变传输功率测量
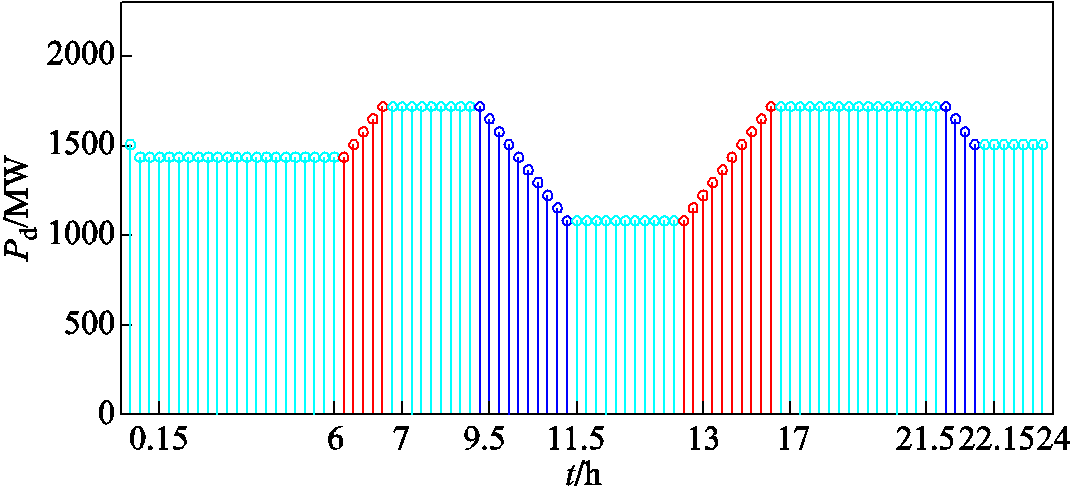
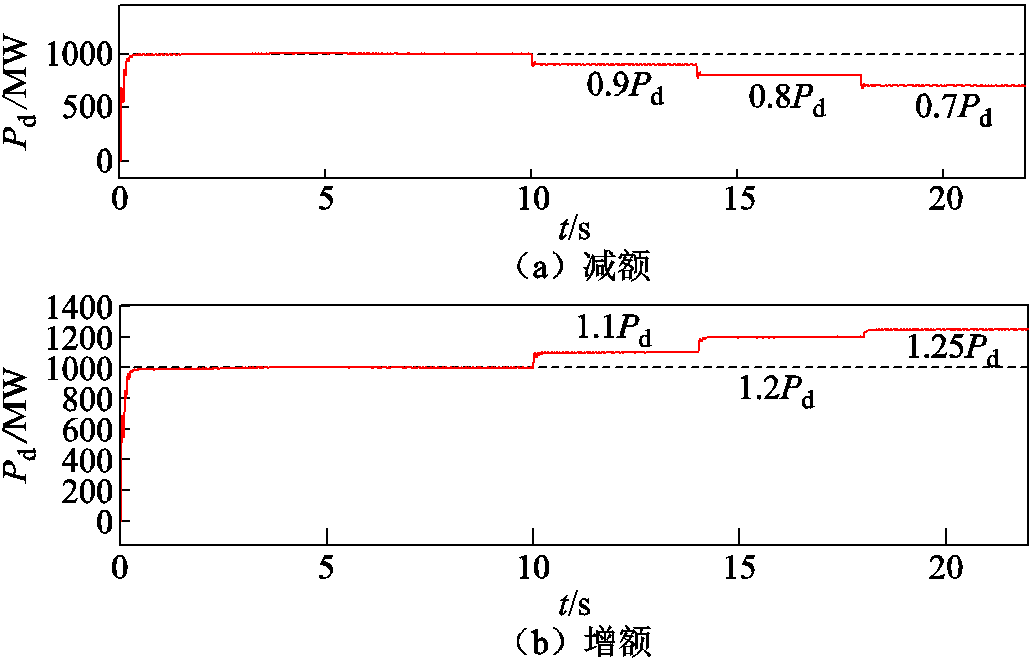
在换流站实际运行中,传输功率会根据用电负荷进行相应调整。实际换流站的日调度电力数据趋势如图15所示,换流站的额定传输功率为2 000 MW。可以看出实际运行存在不同的传输功率的工况且全日未在系统额定传输功率下运行。为了探究传输功率对系统稳定性的影响,仿真测量CIGRE标准系统中传输系统在增额和减额运行条件(额定功率为 1 000 MW)下的宽频域阻抗,并分析其是否会引发系统的稳定性问题。
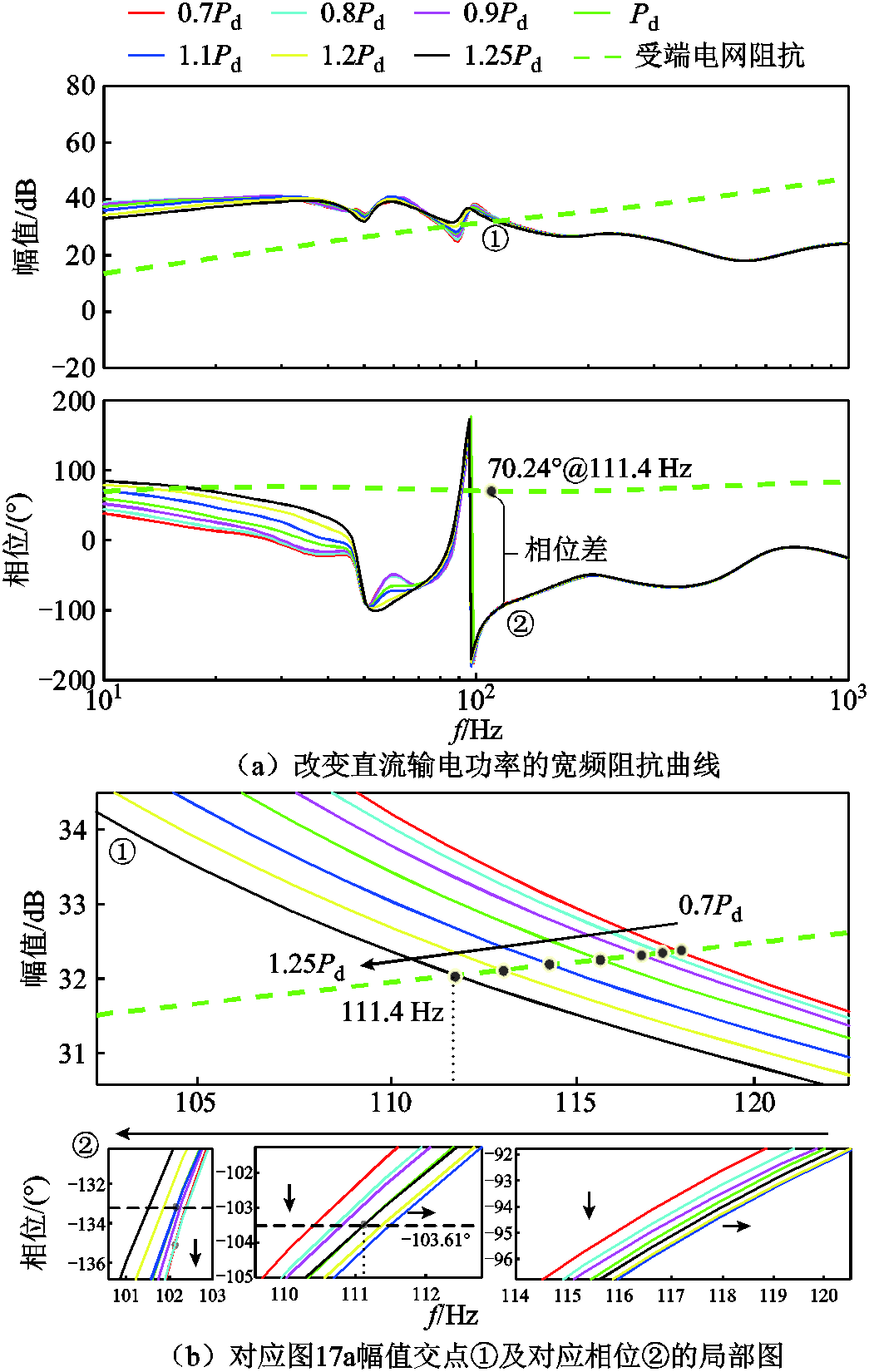
传输功率递减(Pd→0.9Pd→0.8Pd→0.7Pd)和递增(Pd→1.1Pd→1.2Pd→1.25Pd)的功率曲线如图16所示。传输功率变化下对应量测的宽频阻抗曲线如图17所示。可见,随着功率的递增,所测阻抗曲线在100~120 Hz的幅频曲线沿LCC系统与受端电网幅频曲线的交点逐级下移,相位差逐级接近180°。根据幅频曲线沿LCC系统与受端电网幅频曲线交点的运动路径可见传输功率递增,系统失稳风险增大;随着功率递减,系统失稳风险降低。各功率段运行时测量的阻抗曲线与额定功率运行的阻抗曲线的相关系数见表2,功率递减时较功率递增更接近1,也就是更趋于稳定,相频曲线的相关系数更显著。由此可见,上述根据曲线路径推演的系统振荡风险趋势与相关系数的预测结果一致。
表2 传输功率变化的宽频域阻抗曲线Pearson系数
Tab.2 Wideband impedance curves of Pd change Pearson coefficient

曲线Pearson系数 0.7Pd0.8Pd0.9Pd1.0Pd1.1Pd1.2Pd1.25Pd 幅频0.997 40.998 80.999 710.999 20.996 10.992 6 相频0.990 60.995 50.998 810.916 70.911 70.906 8
5 结论
本文提出了一种非介入型的LCC-HVDC系统阻抗建模与阻抗宽频测量方法,旨在不增加一次设备可量测系统宽频阻抗来观测系统的运行状态和判断宽频振荡风险,再剖析LCC系统与受端电网的交互及宽频振荡特性。现将本文的贡献和结论总结如下:
1)设计了一种非介入型的LCC-HVDC阻抗建模与阻抗宽频测量方法,该方法无需向系统注入谐波扰动。该方法下的13阶模型测量阻抗曲线与主动测量的拟合曲线的Pearson相关系数为0.998 3,非常接近于1,验证了本测量模型的正确性。
2)通过分析不同阶模型的测量曲线的相似度矩阵,发现h=3、h=7与h=11的测量曲线的Pearson相关系数很相近,最大误差在0.2%内。由此适当扩大幅频交点的误差可行域,采用3≤h<13的低阶测量模型在综合考虑算力方面具有可实施性。
3)通过调整采样时间步长和改变传输功率的两个条件下所测量的系统宽频阻抗曲线特性可知:时间步长的适配性调整不仅有利于精准捕捉到幅频曲线交点,还能减小算力和节省存储空间,而传输功率的递增会加大系统失稳的风险。
本文所提方法同时适用于离线设计与在线运行,在实际中易于实现,具有一定的工程应用价值。同时值得进一步探索的问题还有很多,如通信同步问题等。
参考文献
[1] 卓振宇, 张宁, 谢小荣, 等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化, 2021, 45(9): 171-191.
Zhuo Zhenyu, Zhang Ning, Xie Xiaorong, et al. Key technologies and developing challenges of power systemwith high proportion of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(9): 171-191.
[2] 高本锋, 王义, 范辉, 等. 基于阻尼路径的新能源经LCC-HVDC送出系统次同步交互作用分析方法[J]. 电工技术学报, 2023, 38(20): 5572-5589.
Gao Benfeng, Wang Yi, Fan Hui, et al. A sub-synchronous interaction analysis method of renewable energy generations integrated with LCC-HVDC system based on damping path[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5572-5589.
[3] 李勇, 常樊睿, 彭衍建, 等. 基于小扰动频率量测数据的电网节点惯量分布评估方法[J]. 电力系统自动化, 2024, 48(13): 71-86.
Li Yong, Chang Fanrui, Peng Yanjian, et al. Evaluation method for node inertia distribution of power grids based on small disturbance frequency measurement data [J]. Automation of Electric Power Systems, 2024, 48(13): 71-86.
[4] 林锦杰, 李勇, 胡斯佳, 等. 计及再生制动能量的铁路潮流控制器功率柔性分配方法[J]. 电工技术学报, 2023, 38(22): 6121-6132.
Lin Jinjie, Li Yong, Hu Sijia, et al. Flexible power assignment method for railway power flow controller considering regenerative braking energy[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6121-6132.
[5] 郑乐, 吴晶, 徐衍会, 等. HVDC送端系统振荡引发受端换相失败的机理分析[J]. 电工技术学报, 2024, 39(9): 2743-2754.
Zheng Le, Wu Jing, Xu Yanhui, et al. Mechanism analysis of commutation failure at receiving end caused by HVDC transmission system oscillation[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2743-2754.
[6] 孙伟君, 夏翔, 刘刚, 等. MMC型级联变换器阻抗建模和稳定性分析[J]. 电力系统保护与控制, 2023, 51(5): 117-127.
Sun Weijun, Xia Xiang, Liu Gang, et al. MMC-based cascaded converter impedance model and stability analysis[J]. Power System Protection and Control, 2023, 51(5): 117-127.
[7] 郭春义, 宁琳如, 王虹富, 等. 基于开关函数的LCC-HVDC换流动态模型及小干扰稳定性[J]. 电网技术, 2017, 41(12): 3862-3870.
Guo Chunyi, Ning Linru, Wang Hongfu, et al. Switching-function fased dynamic model of LCC-HVDC station and small signal stability analysis[J]. Power System Technology, 2017, 41(12): 3862-3870.
[8] 陈宝平, 林涛, 陈汝斯, 等. 直驱风电场经VSC-HVDC并网系统的多频段振荡特性分析[J]. 电工技术学报, 2018, 33(增刊1): 176-184.
Chen Baoping, Lin Tao, Chen Rusi, et al. Characteristics of multi-band oscillation for direct drive wind farm interfaced with VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 176-184.
[9] Liu Hanchao, Jian Sun. Analytical mapping of harmonics and impedance through phase-controlled converters[C]//2012 IEEE 13th Workshop on Control and Modeling for Power Electronics (COMPEL), Kyoto, Japan, 2012: 1-8.
[10] 刘斌, 呼斯乐, 王甲军, 等. 直驱风电场经LCC-HVDC 外送系统阻抗建模及振荡机理分析[J]. 中国电机工程学报, 2021, 41(10): 3492-3504.
Liu Bin, Hu Sile, Wang Jiajun, et al. Impedance modeling and oscillation mechanism analysis of D-PMSG-based wind farms integration through LCC-HVDC system[J]. Proceedings of the CSEE, 2021, 41(10): 3492-3504.
[11] Chen Xiang, Ma Junpeng, Wang Shunliang, et al. An accurate impedance model of line commutated converter with variable commutation overlap[J]. IEEE Transactions on Power Delivery, 2022, 37(1): 562-572.
[12] 肖云涛, 李光辉, 王伟胜, 等. 新能源基地经LCC-HVDC送出系统振荡机理分析与抑制策略(一): 计及受端影响的阻抗建模[J]. 中国电机工程学报, 2023, 43(2): 427-442.
Xiao Yuntao, Li Guanghui, Wang Weisheng, et al. Oscillation mechanism analysis and suppression strategy of renewable energy base connected into LCC-HVDC (part I): impedance modeling with the consideration of receiving-end influence[J]. Proceedings of the CSEE, 2023, 43(2): 427-442.
[13] 郭贤珊, 刘泽洪, 李云丰, 等. 柔性直流输电系统高频振荡特性分析及抑制策略研究[J]. 中国电机工程学报, 2020, 40(1): 19-29.
Guo Xianshan, Liu Zehong, Li Yunfeng, et al. Characteristic analysis of high-frequency resonance of flexible high voltage direct current and research on its damping control strategy[J]. Proceedings of the CSEE, 2020, 40(1): 19-29.
[14] 胡应宏, 李雨, 李阳, 等. 面向柔直换流站高频谐振问题的换流变压器建模与参数辨识[J]. 电工技术学报, 2024, 39(22): 7154-7166.
Hu Yinghong, Li Yu, Li Yang, et al. Modeling and parameter identification of converter transformer for high-frequency resonance problem of flexible DC converter station[J]. Transactions of China Electro-technical Society, 2024, 39(22): 7154-7166.
[15] 汪娟娟, 莫泽, 刘岳坤, 等. 基于单边调制映射函数的LCC-HVDC直流侧阻抗精确建模[J]. 电工技术学报, 2024, 39(13): 3928-3942.
Wang Juanjuan, Mo Ze, Liu Yuekun, et al. Accurate modeling of DC side impedance of LCC-HVDC based on single-side modulated mapping function[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 3928-3942.
[16] Liu Hanchao, Sun Jian. Small-signal stability analysis of offshore wind farms with LCC HVDC[C]//2013 IEEE Grenoble Conference, Grenoble, France, 2013: 1-8.
[17] 王杨, 夏菲, 田旭, 等. 基于谐波状态空间的高压直流输电系统SISO阻抗建模及稳定性分析[J]. 中国电机工程学报, 2024, 44(5): 1985-1998.
Wang Yang, Xia Fei, Tian Xu, et al. SISO impedance modeling and stability analysis of HVDC transmission system based on harmonic state space[J]. Proceedings of the CSEE, 2024, 44(5): 1985-1998.
[18] 周攀, 刘天琪, 王顺亮, 等. 考虑谐波耦合特性的LCC-HVDC换流站小信号建模[J]. 电网技术, 2021, 45(1): 153-161.
Zhou Pan, Liu Tianqi, Wang Shunliang, et al. Small signal modeling of LCC-HVDC station with consideration of harmonic coupling characteristics[J]. Power System Technology, 2021, 45(1): 153-161.
[19] 江克证, 朱建行, 胡家兵, 等. 计及开关过程的LCC-HVDC小信号建模及其对电力系统电磁尺度稳定性分析[J]. 清华大学学报(自然科学版), 2021, 61(5): 395-402.
Jiang Kezheng, Zhu Jianxing, Hu Jiabing, et al. Small-signal modeling of LCC-HVDC systems with switching for electromagnetic timescale stability analyses of power systems[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(5): 395-402.
[20] 刘一锋, 周小平, 洪乐荣, 等. 弱受端场景下角型链式STATCOM接入HVDC系统的阻抗建模及稳定性分析[J]. 电网技术, 2023, 47(3): 1269-1279.
Liu Yifeng, Zhou Xiaoping, Hong Lerong, et al. Impedance modeling and stability analysis for HVDC system with delta-connected cascaded STATCOM in weak receiving grid scenario[J]. Power System Technology, 2023, 47(3): 1269-1279.
[21] 张青伟, 宗万里, 李然, 等. 晋北-南京±800kV特高压直流输电工程接地极阻抗监视系统测量环节干扰问题分析[J]. 电气技术, 2018, 19(4): 108-111.
Zhang Qingwei, Zong Wanli, Li Ran, et al. Analysis of measurement interference of the earth electrode impedance monitoring system in Jinbei-Nanjing ±800kV HVDC transmission project[J]. Electrical Engineering, 2018, 19(4): 108-111.
[22] Venable H. Source-load interactions in multi-unit power system[C]//Intersociety Energy Conversion Engineering Conference, Monterey, CA, 1994: 4235.
[23] Ridley R. Measuring frequency response: tips and methods [J]. Switching Power Magazine, 2002, 3(2): 12-27.
[24] 陶骞, 熊平, 尹志鹏, 等. 有源配电网阻抗特性分析与测量[J]. 科学技术与工程, 2021, 21(1): 215-221.
Tao Qian, Xiong Ping, Yin Zhipeng, et al. Characteristics analysis and measurement of active distribution network impedance[J]. Science Technology and Engineering, 2021, 21(1): 215-221.
[25] Suárez A, Blanco C, García P, et al. Grid impedance estimator for active multisource AC grids[J]. IEEE Transactions on Smart Grid, 2023, 14(3): 2023-2033.
[26] 谢志为, 陈燕东, 伍文华, 等. 双模式扰动下新能源发电装备的宽频带序阻抗在线精确测量方法[J]. 中国电机工程学报, 2020, 40(9): 2903-2913.
Xie Zhiwei, Chen Yandong, Wu Wenhua, et al. A wide-bandwidth sequence-impedance online precise measurement method for renewable energy generation equipment with dual-mode disturbance[J]. Proceedings of the CSEE, 2020, 40(9): 2903-2913.
[27] Liu Junliang, Du Xiong, Shi Ying, et al. A new impedance measurement method and its application to stability analysis of the inverter-grid system[J]. IET Renewable Power Generation, 2021, 15(1): 73-85.
[28] 伍文华, 蒲添歌, 陈燕东, 等. 兆瓦级宽频带阻抗测量装置设计及其控制方法[J]. 中国电机工程学报, 2018, 38(14): 4096-4106.
Wu Wenhua, Pu Tiange, Chen Yandong, et al. Megawatt wide-bandwidth impedance measurement device design and its control method[J]. Proceedings of the CSEE, 2018, 38(14): 4096-4106.
[29] Huang Wangxin, Abu Qahouq J A. An online battery impedance measurement method using DC-DC power converter control[J]. IEEE Transactions on Industrial Electronics, 2014, 61(11): 5987-5995.
[30] Roinila T, Vilkko M, Sun Jian. Online grid impedance measurement using discrete-interval binary sequence injection[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(4): 985-993.
[31] 饶仪明, 吕敬, 王众, 等. 基于数据-模型融合驱动的新能源场站宽频阻抗在线辨识及稳定性评估[J]. 中国电机工程学报, 2024, 44(7): 2670-2684.
Rao Yiming, Lü Jing, Wang Zhong, et al. On-line identification and stability evaluation of broadband impedance of new energy station driven by data-model fusion[J]. Proceedings of the CSEE, 2024, 44(7): 2670-2684.
[32] Xu Zigao, Li Binbin, Han Linjie, et al. A complete HSS-based impedance model of MMC considering grid impedance coupling[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 12929-12948.
[33] Kwon J, Wang Xiongfei, Blaabjerg F, et al. Harmonic interaction analysis in a grid-connected converter using harmonic state-space (HSS) modeling[J]. IEEE Transactions on Power Electronics, 2017, 32(9): 6823-6835.
[34] 郭小龙, 杨桂兴, 张彦军, 等. 构网型储能与跟网型光伏混联发电系统阻抗建模与小扰动稳定机理分析[J]. 电气工程学报, 2025, 20(1): 299-308.
Guo Xiaolong, Yang Guixing, Zhang Yanjun, et al. Impedance modeling and small-signal stability mechanism analysis of grid-forming energy storage and grid-following PV hybrid power generation system[J]. Journal of Electrical Engineering, 2025, 20(1): 299-308.
[35] Zhang Chen, Molinas M, Føyen S, et al. Harmonic-domain SISO equivalent impedance modeling and stability analysis of a single-phase grid-connected VSC[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9770-9783.
[36] 李勇. 感应滤波理论及其在直流输电系统中的应用研究[D]. 长沙: 湖南大学, 2011.
Li Yong. Research on induction filtering theory and its application in DC transmission system[D]. Changsha: Hunan University, 2011.
[37] Jiang Xiao, Gole A M. A frequency scanning method for the identification of harmonic instabilities in HVDC systems[J]. IEEE Transactions on Power Delivery, 1995, 10(4): 1875-1881.
Non-Invasive Impedance Wideband Measurement Method for LCC-HVDC Systems
Wang Dan1 Li Yong1 Zhang Yi1,3 Fu Ying2 Liu Zehong2
(1. College of Electrical and Information Engineering Hunan University Changsha 410082 China 2. State Grid Corporation of China Beijing 410006 China 3. RTDS Technologies Winnipeg R3T 5V6 Canada)
Abstract To monitor the dynamic characteristics of the receiving AC system and assess the risk of wideband oscillation in LCC-HVDC without additional equipment, this paper presents a non-invasive impedance wideband measurement method for LCC-HVDC systems. Unlike existing invasive methods, such as single voltage/current or wideband harmonic disturbance injections, the proposed method does not inject harmonic disturbances into LCC-HVDC, thereby avoiding the potential resonance risk. Furthermore, the proposed method introduces curve similarity and a dynamically adjusted time-step sampling scheme. First, this paper discusses the interaction principles between the LCC system and the receiving AC system. Secondly, this paper establishes the harmonic state space (HSS) impedance model for LCC-HVDC, based on HSS theory, focusing on the unipolar earth loop topology. Subsequently, a non-invasive impedance wideband measurement method is proposed to observe the operating state of the system, judge the risk of wideband oscillation, and analyze the interaction and wideband oscillation characteristics between the LCC system and the receiver network through impedance analysis. Finally, an example of CIGRE standard model is used to verify the correctness and practicality of the proposed method.
Based on the HSS theory and the concept of digital modulus, this paper introduces a non-invasive impedance wideband measurement method. Firstly, the system topology and the interaction principles of the LCC-HVDC unipolar earth loop subsystems are detailed. Then, the impedance modeling of the LCC-HVDC system is elaborated, and the HSS impedance mathematical model for wideband measurement is derived based on the system's topology. Finally, the system model is constructed in MATLAB/Simulink using parameters from the CIGRE standard model, and the impedance calculation model is applied to measure the impedance of the LCC system. Combined with the measured wideband impedance curve, the interaction between the LCC system and the receiving network, as well as the wideband oscillation characteristics, were analyzed using the generalized Nyquist criterion for stability. At the same time, the Pearson correlation coefficient was introduced to capture the similarity of impedance curves with high granularity, thereby exploring the adaptability of impedance models of different orders and the factors influencing the oscillation risk. It offers theoretical support for the measurement methods used in the engineering application of impedance measurement, and appropriately expanding the permissible error range in the amplitude-frequency intersection can enhance the universality of impedance analysis methods.
The main contributions and conclusions of this paper are summarized as follows: (1) A non-invasive LCC-HVDC impedance model and impedance wideband measurement method are designed, which does not require injecting harmonic disturbances into the system. The Pearson correlation coefficient between the measured impedance curve of the 13th-order model and the fitted curve from active measurements is 0.998 3, which is very close to 1. This high value indicates that the accuracy of the measurement model is high, suggesting a close match with the actual impedance characteristics. (2) By analyzing the similarity matrix of measurement curves from models of varying orders, it is observed that the Pearson correlation coefficients for the phase measurement curves are closely matched for orders h=3, h=7, and h=11, with the highest deviation being within 0.2%. Consequently, the acceptable error margin for amplitude-frequency intersection points may be suitably broadened. Considering computational efficiency, a lower-order measurement model within the range of 3 to 13 can be selected. (3) The characteristics of the measured wideband impedance curve of the system can be observed under two conditions: adaptive adjustment of the sampling time step and variation in transmission power. Adaptive adjustment of the time step is not only conducive to accurately identifying the crossover points of the amplitude-frequency response but also reduces the computational load and minimizes storage requirements. Conversely, an increase in transmission power raises the risk of system instability.
Keywords:Line-commutated converter based high-voltage direct-current(LCC-HVDC), non-invasive, impedance wideband measurement, harmonic state space, curve similarity, dynamically adjusted time-step sampling
中图分类号:TM721.1;TM712
DOI: 10.19595/j.cnki.1000-6753.tces.240782
国家重点研发计划政府间国际科技创新合作重点项目(2022YFE0129300)、湖南省科技创新计划项目(2023GK2007,2023RC1038)和宁夏-湖南±800kV特高压直流输电工程科研项目(SGZB0000TGJS2300786)资助。
收稿日期 2024-05-14
改稿日期 2024-08-12
作者简介
王 丹 女,1988年生,博士研究生,研究方向为高压直流输电阻抗建模与量测。
E-mail:807178691@qq.com
李 勇 男,1982年生,教授,博士生导师,研究方向为电力系统运行与控制、电力电子系统与控制。
E-mail:yongli@hnu.edu.cn(通信作者)
(编辑 赫 蕾)
 ”为LCC-HVDC可采样数据的采样点,可直接从换流站的二次同步量测装置获取;iai和ifi分别为受端交流系统的线路总电流和滤波总电流;vlcci和ici分别为受端换流变压器的一次电压和一次电流;v2ydi、i2ydi和v2yyi、i2yyi分别为受端换流变压器二次三角形侧和星形侧的电压、电流;vdci和idci分别为受端换流站直流电压和电流;Zgi、Zfi分别为受端交流系统的线路总阻抗和滤波总阻抗;αi、μi和γi分别为受端换流站的触发角、换相角、关断角;kti、Lti分别为受端换流变压器的电压比和漏感;Rd、Ld、Cd分别为直流线路的等效电阻、电感、电容;vdc0为直流系统对地电容的电压;Gidc_r和Gvdc_i分别为送、受端换流站控制中直流电流和直流电压的滤波器的传递函数;Hidc_r和Hvdc_i分别为送、受端换流站控制中直流电流和直流电压的PI控制器的传递函数;HPLL_r和HPLL_i分别为送、受端换流站控制中锁相环的PI控制器的传递函数。
”为LCC-HVDC可采样数据的采样点,可直接从换流站的二次同步量测装置获取;iai和ifi分别为受端交流系统的线路总电流和滤波总电流;vlcci和ici分别为受端换流变压器的一次电压和一次电流;v2ydi、i2ydi和v2yyi、i2yyi分别为受端换流变压器二次三角形侧和星形侧的电压、电流;vdci和idci分别为受端换流站直流电压和电流;Zgi、Zfi分别为受端交流系统的线路总阻抗和滤波总阻抗;αi、μi和γi分别为受端换流站的触发角、换相角、关断角;kti、Lti分别为受端换流变压器的电压比和漏感;Rd、Ld、Cd分别为直流线路的等效电阻、电感、电容;vdc0为直流系统对地电容的电压;Gidc_r和Gvdc_i分别为送、受端换流站控制中直流电流和直流电压的滤波器的传递函数;Hidc_r和Hvdc_i分别为送、受端换流站控制中直流电流和直流电压的PI控制器的传递函数;HPLL_r和HPLL_i分别为送、受端换流站控制中锁相环的PI控制器的传递函数。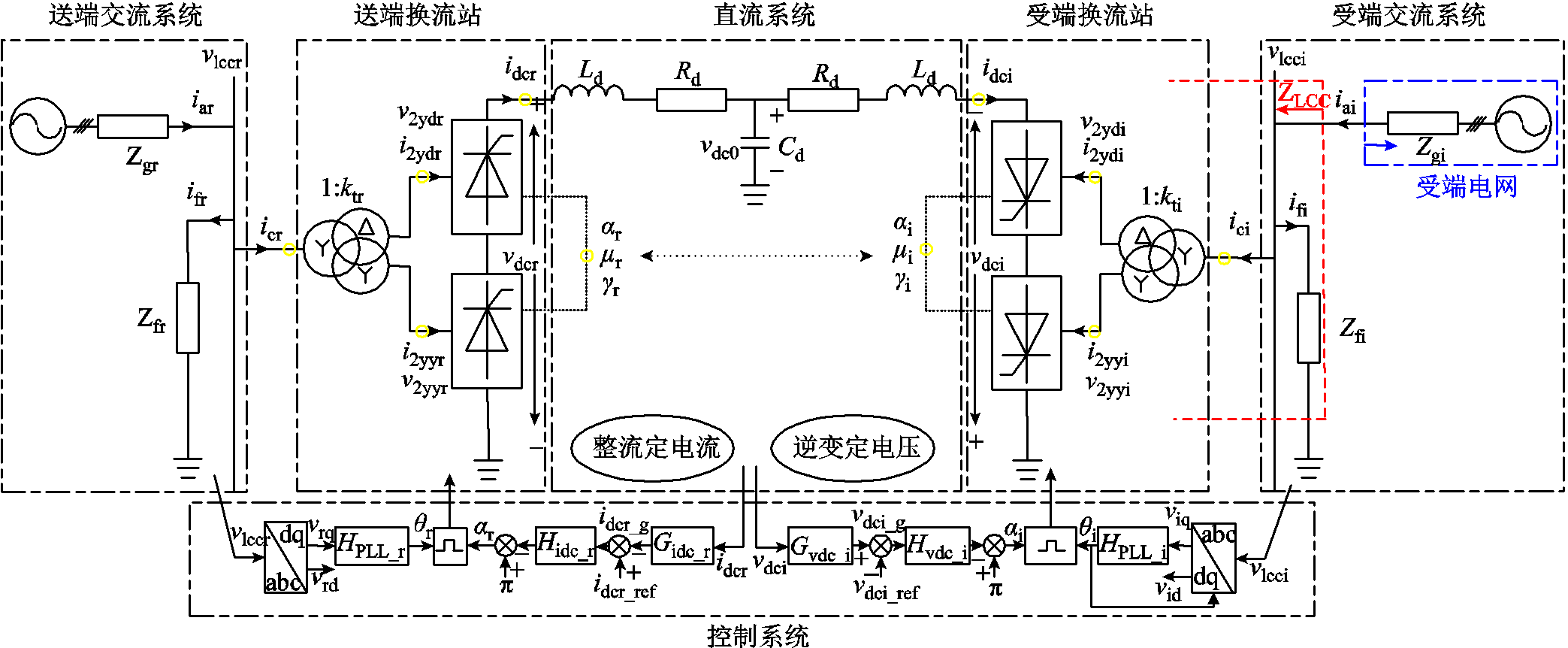
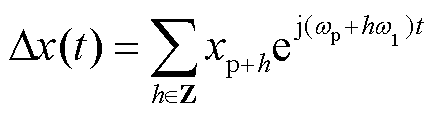 (1)
(1)
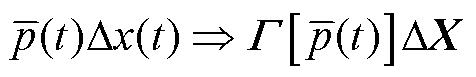 (2)
(2)
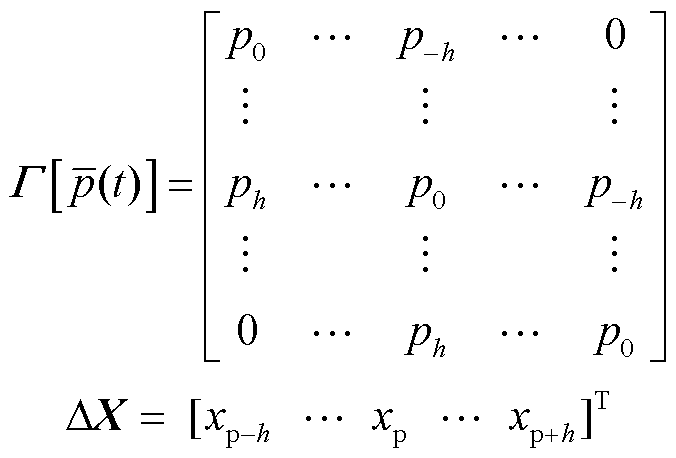
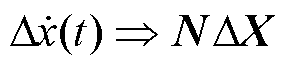 (3)
(3)
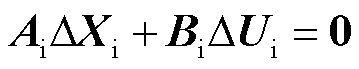 (4)
(4)
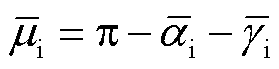 ,三个变化量关系为
,三个变化量关系为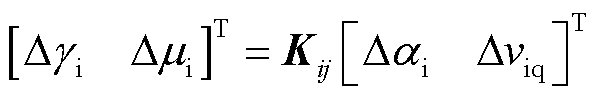 (5)
(5)
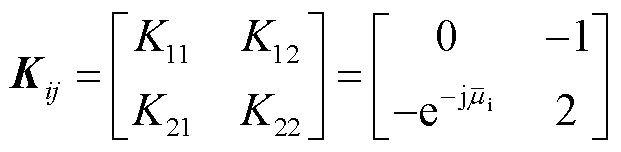
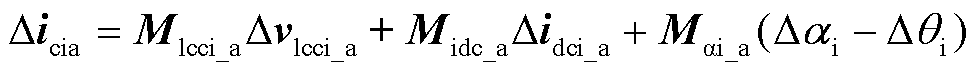 (6)
(6)
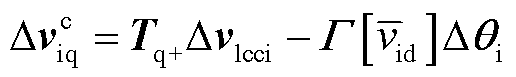 (7)
(7)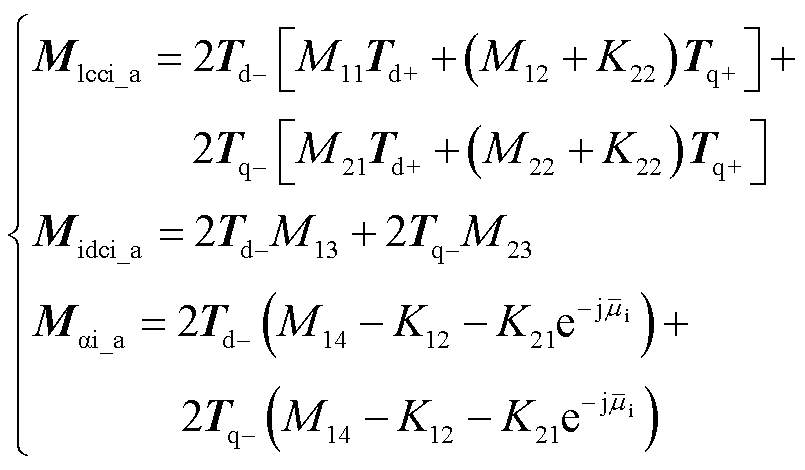
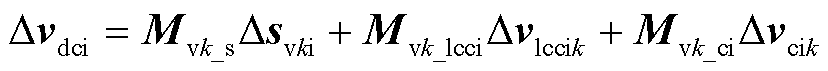 (8)
(8)
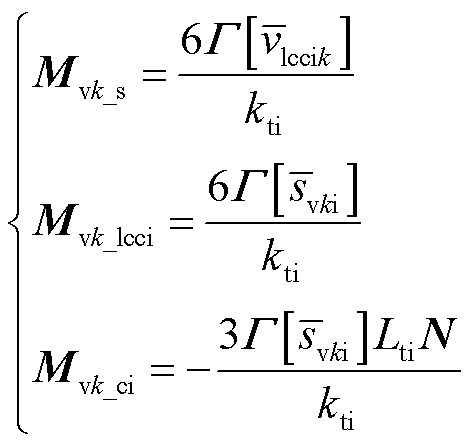 (9)
(9)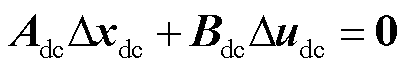 (10)
(10)
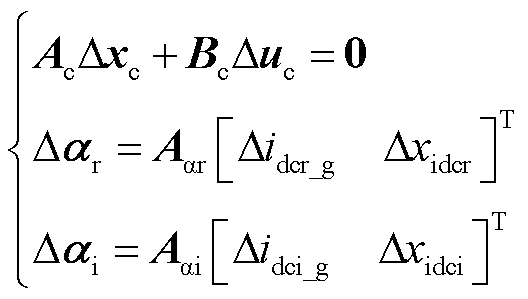 (11)
(11)
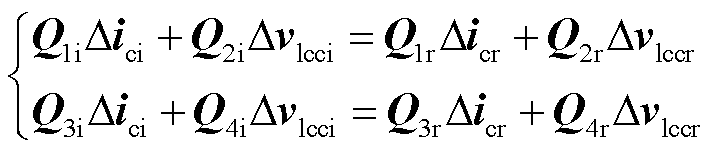 (12)
(12)
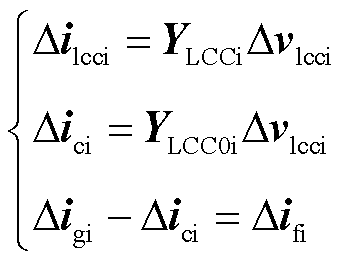 (13)
(13)
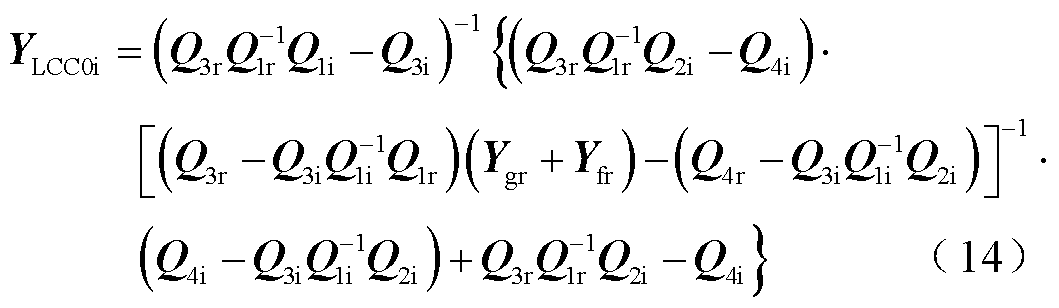
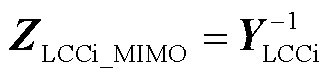 (15)
(15)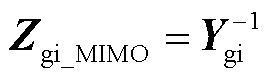 (16)
(16)
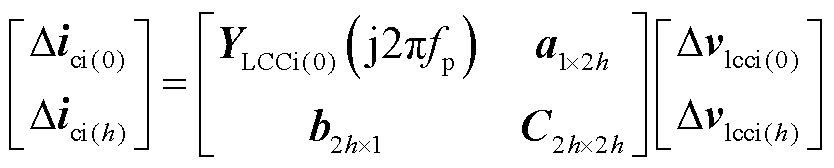 (17)
(17)
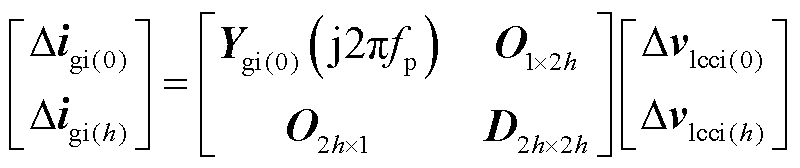 (18)
(18)
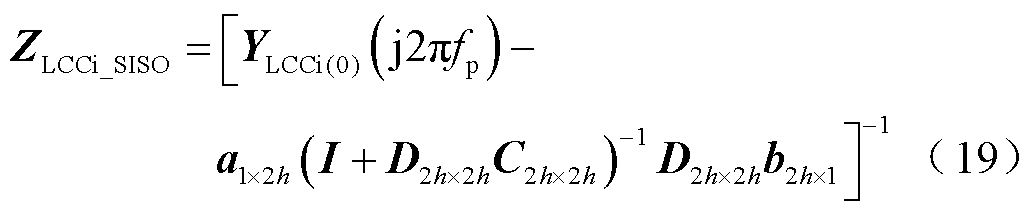
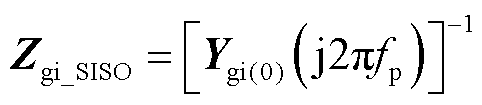 (20)
(20)
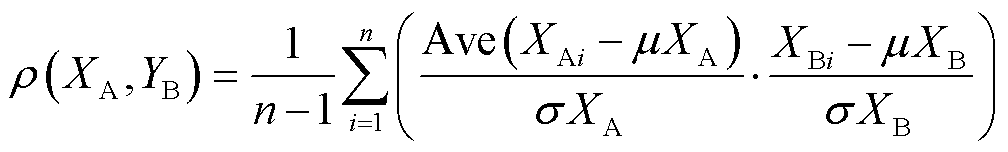 (21)
(21)
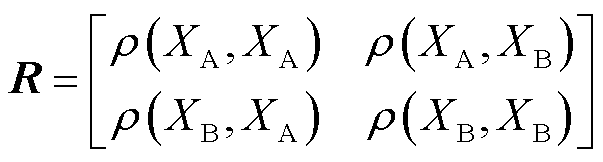 (22)
(22)
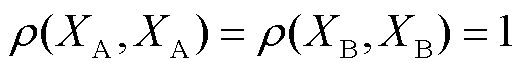 ,即
,即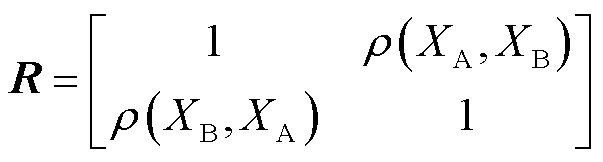 (23)
(23)