图1 电压型三相IGBT变流器
Fig.1 Voltage three-phase IGBT converter
摘要 由于风电机组工作环境恶劣,电力电子设备脆弱,变流器故障成为风电机组的常见故障之一。而变流器在风力发电系统中起到优化运行的作用,因此针对变流器开路故障的检测与识别至关重要。现有的检测方法存在鲁棒性不强及计算复杂的问题,为此该文提出一种同时基于直流母线电压和转子电流的故障识别方法。该方法基于数学形态学提取直流母线电压故障特征实现故障检测;基于Pearson相关系数提取转子侧三相电流波形特征定位故障相;基于电流平均值定位故障桥臂。该方法计算过程简单,可以准确识别变流器功率管的单管和双管故障,理论推导证明了所提方法的有效性和可靠性。仿真算例考虑了风速波动、负载波动和噪声环境的影响,结果表明所提方法具有较高的准确率及较强的鲁棒性。
关键词:变流器 开路故障 故障识别 数学形态学 Pearson相关系数
随着“双碳”目标的提出,对可再生能源的关注度不断升高,风能作为目前应用前景广阔的可再生能源之一,其发电的占比正在不断提高,风电的稳定运行至关重要[1-2]。变流器作为风力发电系统中的关键设备[3],是风力发电与电网的接口,但也是故障频率和停电时长较高的器件之一,每年因为故障产生的维护成本很高[4-7]。相对于网侧变流器,转子侧变流器因承受热载荷更多而导致故障率更高[8],并且其功率管开路故障对系统运行影响较大[9]。变流器功率管故障分为开路故障和短路故障。目前变流器普遍配备了硬件过电流保护,短路故障由于故障后过电流明显易于检测和保护,并且可以将快速断路器串入变流器的电路,使短路故障转变成开路故障,再采用开路故障的诊断方法实施相关措施[10]。开路故障由于不会产生过电流,用硬件保护较难检测[11],因此对开路故障进行故障识别研究有重要意义。
现在对变流器开路故障故障识别的研究方法主要有三种:基于模型的方法、基于数据驱动的方法和基于信号的方法[5]。基于模型的方法利用系统内部的信息,能够有效地反映物理系统故障的本质特征[12]。文献[13]构造了变流器双线性电流观测器,通过电流残差变流器进行故障检测。文献[14]使用卡尔曼滤波器对三相电流进行实时估计,通过平均归一化残差信号进行实时故障诊断。文献[15]设计自适应滑模观测器估计电流值进行故障检测,并根据电流残差定位故障功率管。但由于风力发电机是一个复杂的系统,其参数繁多且各不相同,而基于模型的方法必须构建精确的数学模型和明确的数值表达式,否则识别结果易受到变化的系统参数和模型准确度的影响。
基于数据驱动的方法使用数据挖掘技术或统计方法诊断变流器故障,其典型过程包括数据处理和特征提取、模式训练和识别。文献[16-17]分别使用小波包和变分模态分解提取故障特征,并输入支持向量机进行故障分类。文献[18]使用长短期记忆网络(Long Short-Term Memory, LSTM)检测开路故障。文献[19]通过栈式稀疏自编码网络训练原电流数据构建特征矩阵,使用LSTM进行故障检测和分类。文献[20]基于改进小波包算法提取故障向量,并输入优化随机森林中定位故障功率管。文献[21]利用短时傅里叶变换提取桥臂电压信号的特征参数,通过深度置信网络实现故障检测并基于卷积神经网络定位故障。基于数据驱动的方法训练时间久,需要大量数据,而实际数据难以获取,并且训练过程解释性差。
基于信号的方法通常基于单一的电压或电流信号,直接分析信号,提取信号的幅值、相位、频率等参数,结合波形特征分析故障[22]。文献[23]通过比较正常和故障工作方式下门极信号和交流侧线电压的变化情况,建立故障特征向量。然而门极信号需要增加额外的硬件电路,难以获取。文献[24]通过对比故障前后频谱特征实现故障检测,但由于直流母线电压在不同故障类型下差异小,无法实现故障识别。综上所述,基于单一电压的识别方法存在缺陷,但是直流母线电压受变流器控制及系统干扰影响小,因此有必要利用电压进行故障检测。文献[25]求取电流相位的导数和归一化的相电流平均绝对值作为故障特征向量进行故障定位,其检测精度依赖高采样频率,硬件成本高。文献[26]通过三相网侧相电流及其共轭电流分别绘制Hilbert矢量图,基于矢量图位置进行故障识别,但只能实现单管故障识别。文献[27]基于电流Park矢量模计算归一化电流及其平均值,并构造故障检测特征量;使用电流平均值和电流绝对值平均值定位故障;但其电流Park矢量模计算误差大,可靠性低。文献[28]通过经验模态分解三相电流,使用Hilbert变换计算瞬时频率进行故障检测,并计算转子电流平均值进行故障识别,其诊断阈值固定,鲁棒性差。综上所述,基于单一电流信号的识别方法的阈值固定,受干扰因素多,但是发生开路故障时电流波形特征差异明显,因此有必要利用电流进行故障识别。文献[29]基于直流母线电压实现故障检测,并计算转子电流平均值和绝对平均值进行故障识别,效果较好。
由于直流母线电压信号易获取,独立于负载和控制策略,便于实现故障检测;转子电流信号包含故障特征多,便于实现故障分类。因此本文提出一种同时基于直流母线电压和转子电流的故障识别方法。本文首先阐述了变流器电路工作原理;然后分析故障状态下的电路工作状态和电流波形特征;最后搭建仿真模型验证了所提方法的有效性及鲁棒性。
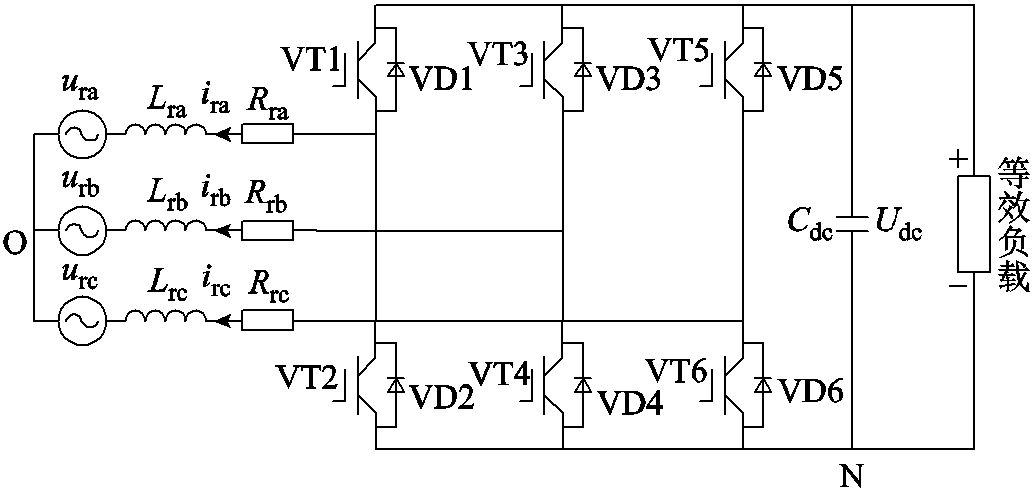
在双馈风机发电系统中,转子侧变流器用于控制发电机的有功和无功输出以及稳定发电机变速恒频运行。变流器能量双向流动,可工作在整流或逆变状态,电压型三相IGBT变流器如图1所示。

图1 电压型三相IGBT变流器
Fig.1 Voltage three-phase IGBT converter
图1中,ura、urb、urc为转子三相电压,ira、irb、irc为转子三相电流,Rra、Rrb、Rrc和Lra、Lrb、Lrc分别为转子各相绕组电阻和电感,VT1~VT6为IGBT功率管,VD1~VD6为反向续流二极管,Cdc为直流母线电容,Udc为直流母线电压。变流器采用正弦脉宽调制(Sinusoidal Pulse Width Modulation, SPWM)SPWM控制,输出为等效面积的脉冲电压波。三相相电压可表示为
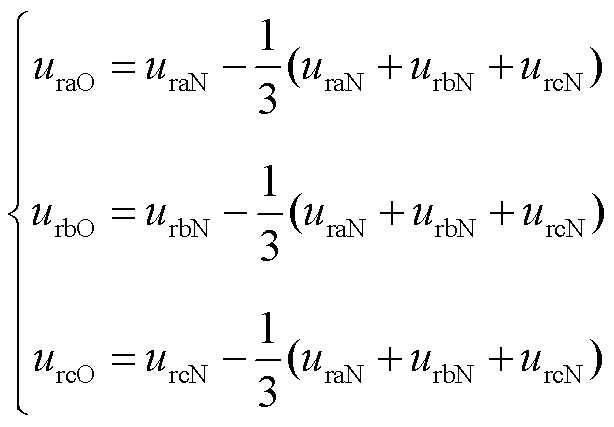 (1)
(1)
式中,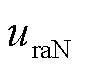 、
、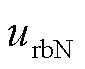 、
、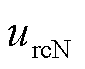 为三相到中点N的电压。
为三相到中点N的电压。
任意时刻同桥臂只有一个桥臂导通,通过定义单极性开关函数s来表征这一特点,有
 (2)
(2)
桥臂导通表示对应的功率管或反向续流二极管导通,则三相到中点N的电压可表示为
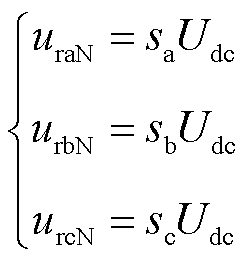 (3)
(3)
相应地,三相电压用开关函数表示可表示为
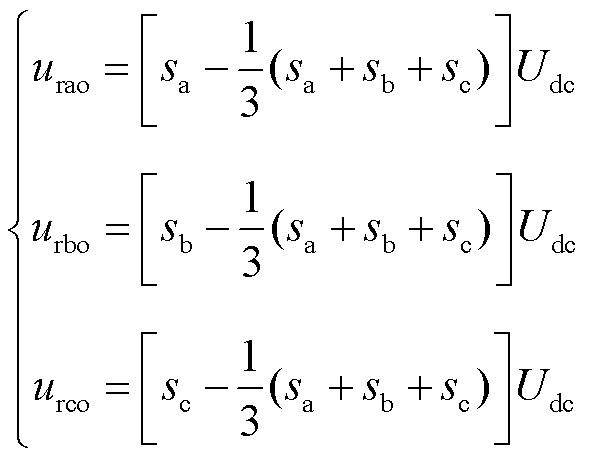 (4)
(4)
根据三相正弦调制信号,可将电压分为六个区间,又根据转子电流可将电流分为六个区间,结合SPWM原理可得无故障状态下各区间的电路开关模式见表1。从表1中可以看出,在一个区间内,变流器工作状态转换过程为电感充能电容放电、电感放能电容充电的交替过程。(0-0-0)和(1-1-1)过程转子侧电感存储能量,直流侧电容放电。其余状态下转子侧电感对负载释放能量,直流侧电容充电。
以VT1发生开路故障为例,给出VT1故障下转子侧变流器工作在超同步运行的开关模式,见表2。对比表1和表2可以发现,故障发生后A相上桥臂VT1关断,区间1~5和12由于A相上桥臂导通期间均为VD1导通,未受到开路故障影响,A相电流负半波正常。区间6~11除(0-0-0)工作模式(电流接近于0)外的工作模式均为A相上桥臂导通,而A相上桥臂导通为VT1导通及二极管VD2续流,故在VT1开路后,VD2续流消失,A相正半波丢失,原正半波电流流向B、C两相。其余故障类型的电路工作过程变化与此类似。
典型故障下的转子电流波形如图2所示,可以发现在转子侧发生单管故障时,故障相电流出现半波缺失,若上桥臂的功率管故障,则对应故障相电流缺失正半波,下桥臂的功率管故障,电流缺失负半波。转子侧发生双管故障时,故障电流波形特征与单管类似,基于基尔霍夫电流定律,在非故障相电流上波形会出现相应变化。根据故障管数量及故障位置不同可分为四种类型,具体见表3。
表1 无故障状态下各区间的电路开关模式
Tab.1 Circuit switching modes in each zone in the no-fault state
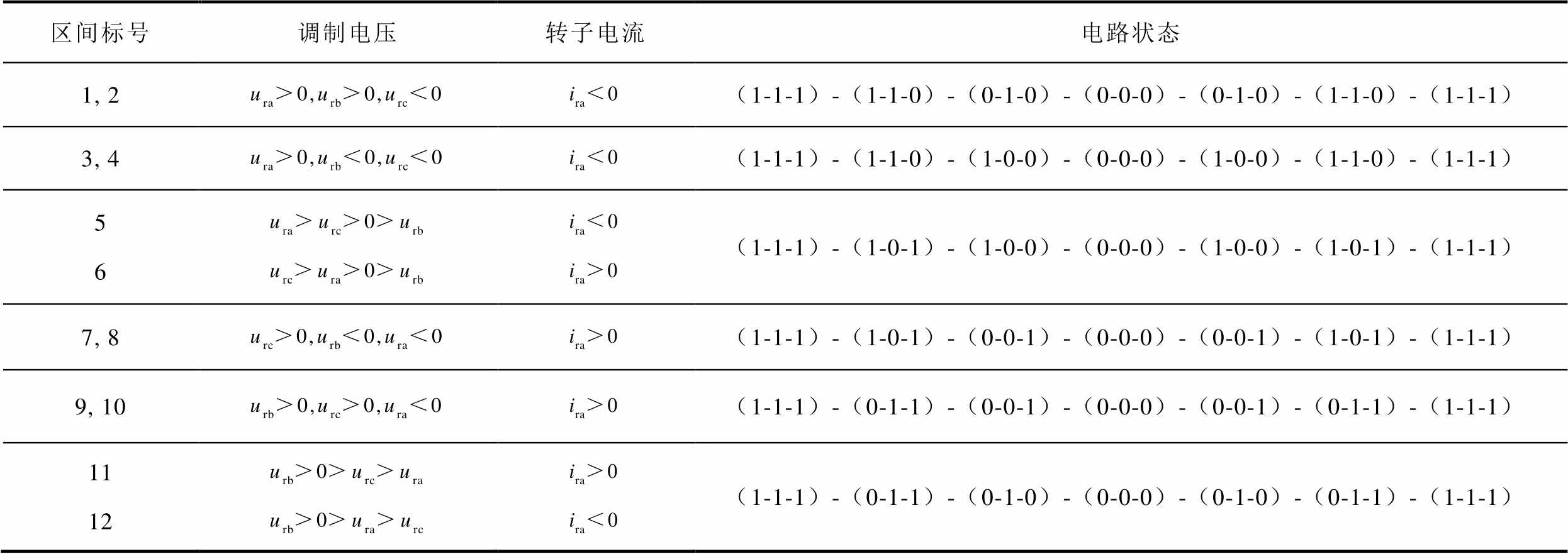
区间标号调制电压转子电流电路状态 1, 2(1-1-1)-(1-1-0)-(0-1-0)-(0-0-0)-(0-1-0)-(1-1-0)-(1-1-1) 3, 4(1-1-1)-(1-1-0)-(1-0-0)-(0-0-0)-(1-0-0)-(1-1-0)-(1-1-1) 56(1-1-1)-(1-0-1)-(1-0-0)-(0-0-0)-(1-0-0)-(1-0-1)-(1-1-1) 7, 8(1-1-1)-(1-0-1)-(0-0-1)-(0-0-0)-(0-0-1)-(1-0-1)-(1-1-1) 9, 10(1-1-1)-(0-1-1)-(0-0-1)-(0-0-0)-(0-0-1)-(0-1-1)-(1-1-1) 1112(1-1-1)-(0-1-1)-(0-1-0)-(0-0-0)-(0-1-0)-(0-1-1)-(1-1-1)
表2 VT1开路故障状态下各区间下的电路开关模式
Tab.2 Circuit switching modes under each interval of VT1 open-circuit fault state
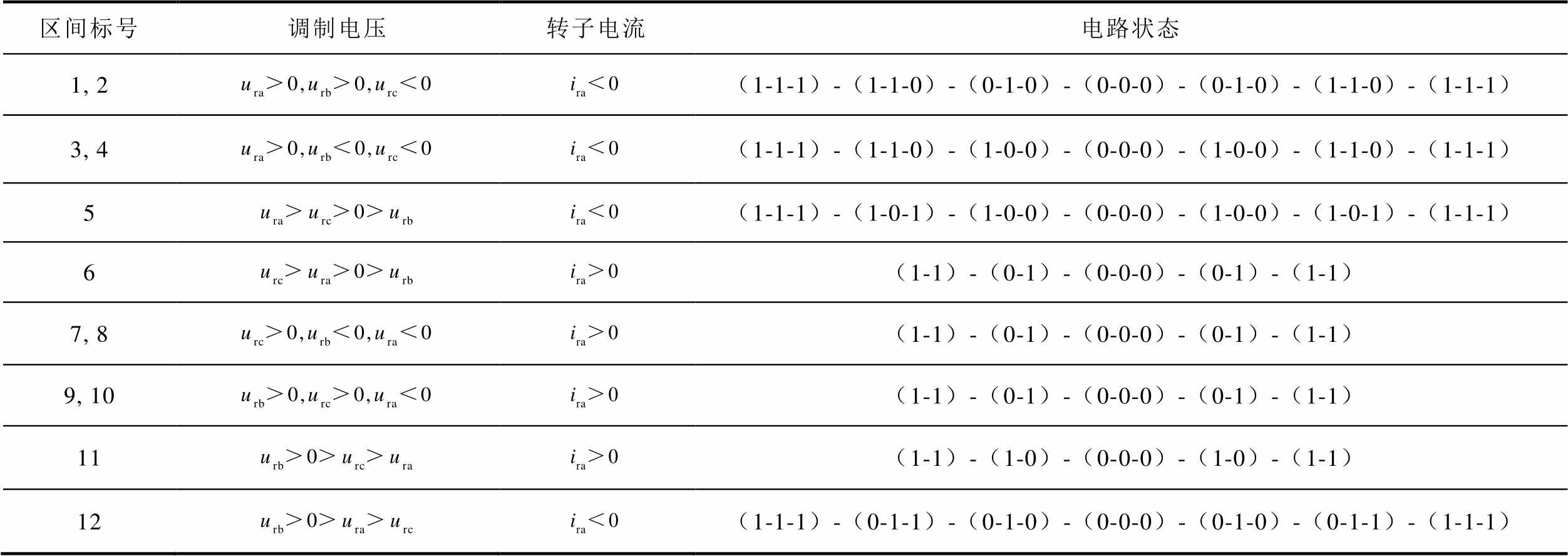
区间标号调制电压转子电流电路状态 1, 2(1-1-1)-(1-1-0)-(0-1-0)-(0-0-0)-(0-1-0)-(1-1-0)-(1-1-1) 3, 4(1-1-1)-(1-1-0)-(1-0-0)-(0-0-0)-(1-0-0)-(1-1-0)-(1-1-1) 5(1-1-1)-(1-0-1)-(1-0-0)-(0-0-0)-(1-0-0)-(1-0-1)-(1-1-1) 6(1-1)-(0-1)-(0-0-0)-(0-1)-(1-1) 7, 8(1-1)-(0-1)-(0-0-0)-(0-1)-(1-1) 9, 10(1-1)-(0-1)-(0-0-0)-(0-1)-(1-1) 11(1-1)-(1-0)-(0-0-0)-(1-0)-(1-1) 12(1-1-1)-(0-1-1)-(0-1-0)-(0-0-0)-(0-1-0)-(0-1-1)-(1-1-1)
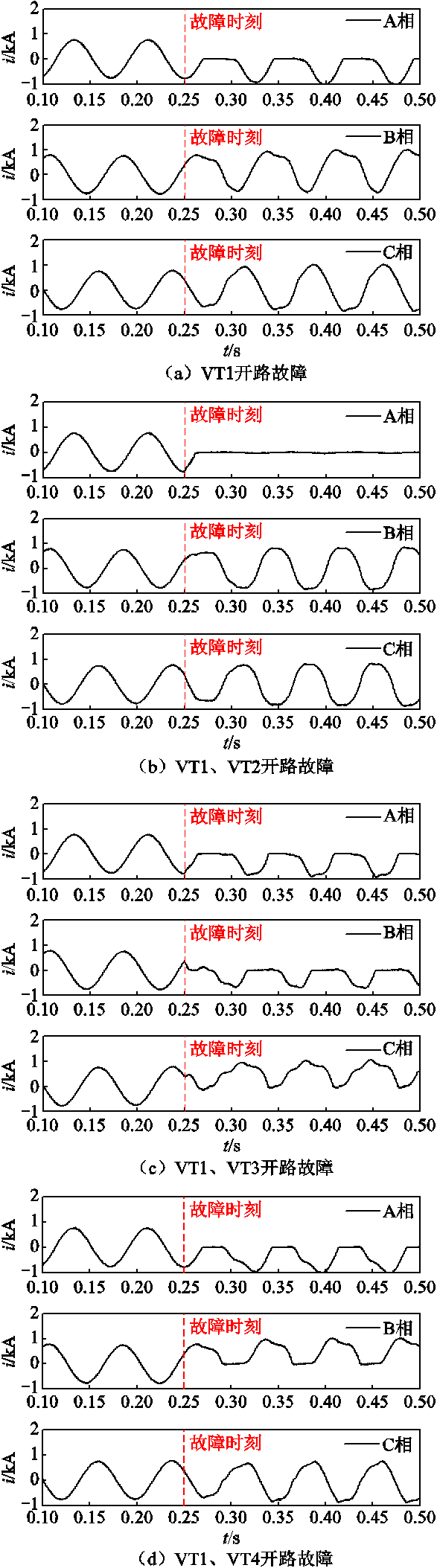
图2 典型功率管开路故障电流波形
Fig.2 Typical power tubes open-circuit fault current waveforms
表3 变流器开路故障类型
Tab.3 Converter open circuit fault types

故障类型故障编号故障描述 —0无故障 Ⅰ1~6单只IGBT管故障 Ⅱ7~9同桥臂两只IGBT管故障 Ⅲ10~15同一半桥两只IGBT管故障 Ⅳ16~21不同桥臂上下两只IGBT管故障
变流器功率管发生开路故障后,直流母线电压出现波动,产生转子基频及其倍频波动。开路前后直流母线电压波形如图3所示。

图3 直流母线电压波形
Fig.3 DC bus voltage waveform
可以发现故障后直流母线电压波形波动明显。由于其电压信号便于测量,能够持续监测其波形变化情况,并且独立于负载和控制策略,因此可通过对直流母线电压进行特征提取实现故障检测。
数学形态学是一种时域信号处理算法,通过对信号进行形态学运算获取信号的时域特征。数学形态学基本运算包括膨胀和腐蚀,设一维离散信号为f(n),结构元素为g(m),其计算公式为
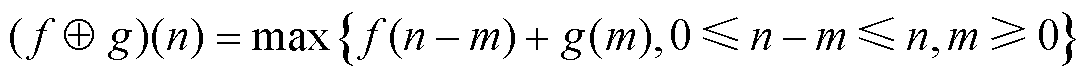 (5)
(5)
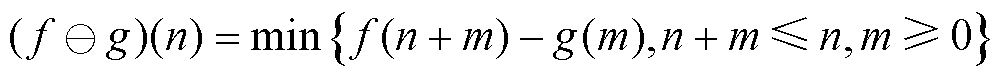 (6)
(6)
式中,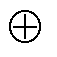 表示膨胀运算;
表示膨胀运算;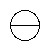 表示腐蚀运算。
表示腐蚀运算。
形态学梯度(Morphological Gradient, MMG)基于数学形态学,可以用作边缘提取[30]。梯度原本是指多元函数的点所取导数最大值的向量,在数学形态学中则指信号的边缘信息。形态学梯度由膨胀腐蚀运算组合得到,即
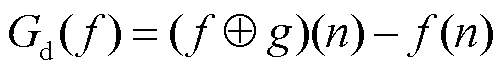 (7)
(7)
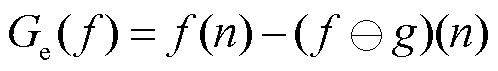 (8)
(8)
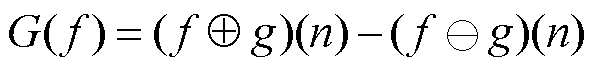 (9)
(9)
式(7)为膨胀梯度,式(8)为腐蚀梯度,式(9)为形态学梯度。对信号求形态学梯度可以提取波形的暂态特征,从而确定故障发生时间。因为结构元素的位置和长度不同会对梯度运算的结果产生影响,所以一般都采用原点位置位于中心的结构元素进行计算。本文采用长度为40的扁平结构元素进行计算,根据转子基频周期提取归一化直流电容电压一次梯度的绝对值D1,寻找极大值,与设定阈值作比较,若满足条件D1>0.009认为有可能发生故障,但为了排除是噪声影响,再计算电压信号的方差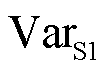 ,若
,若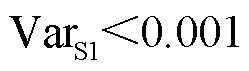 则认为发生故障,并定义故障监测标记为
则认为发生故障,并定义故障监测标记为
 (10)
(10)
检测到故障发生后将采样窗口的结尾时间作为故障发生时间,并传递给故障分类模块。
直流母线电压在不同故障下的波形特征差异小,因此只能用作故障检测。而转子电流的波形特征随着故障类型不同差异明显,可以用作故障分类。根据不同故障类型的波形特征不同,基于Pearson相关系数计算及电流平均值构建了故障特征量,设计了故障管定位方法。Pearson相关系数是一个用于度量两个变量X和Y之间线性相关程度的指标。Pearson相关系数绝对值越大,表明两个变量之间相关程度越高,反映到波形上则表明波形越相似。Pearson相关系数的计算公式为
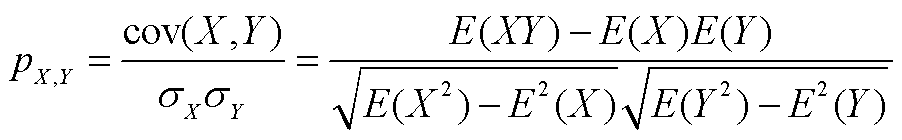 (11)
(11)
式中,p为Pearson相关系数;cov为协方差;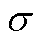 为标准差;E为均值。对三相电流两两之间求取Pearson相关系数绝对值,计算数据长度为一个基频周期,有
为标准差;E为均值。对三相电流两两之间求取Pearson相关系数绝对值,计算数据长度为一个基频周期,有
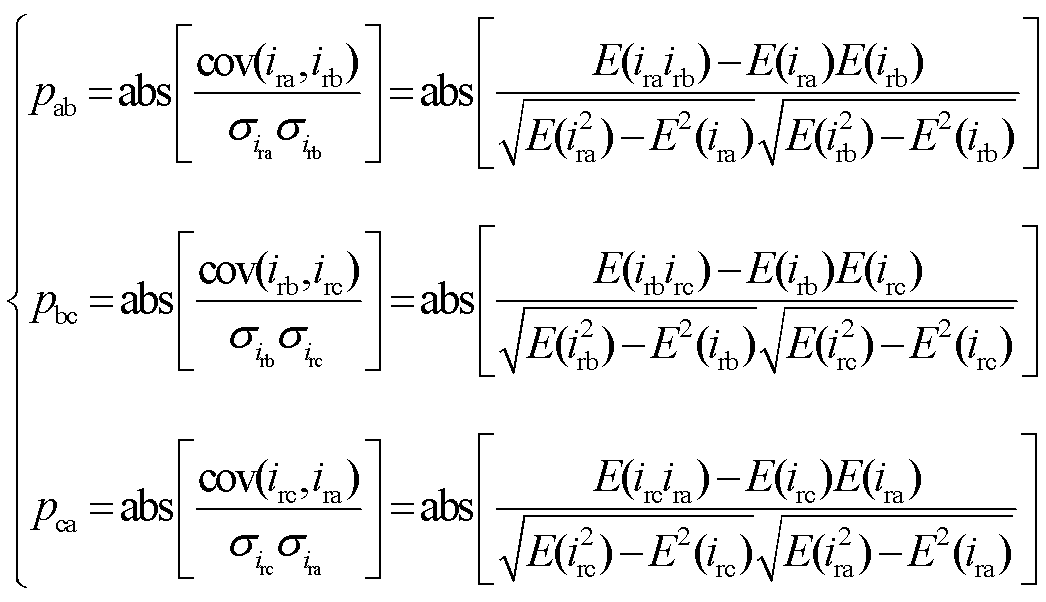 (12)
(12)
经过仿真试验,不同故障类型下的Pearson相关系数绝对值见表4。
表4 不同故障类型的Pearson相关系数绝对值
Tab.4 Absolute values of Pearson correlation coefficient for different fault types

开路故障类型 无故障≈0.5≈0.5≈0.5 Ⅰ(VT1)<0.25>0.65≈0.5 Ⅱ(VT1,VT2)≈0≈0≈1 Ⅲ(VT1,VT3)0.25~0.650.25~0.650.25~0.65 Ⅳ(VT1,VT4)≈0>0.65>0.65
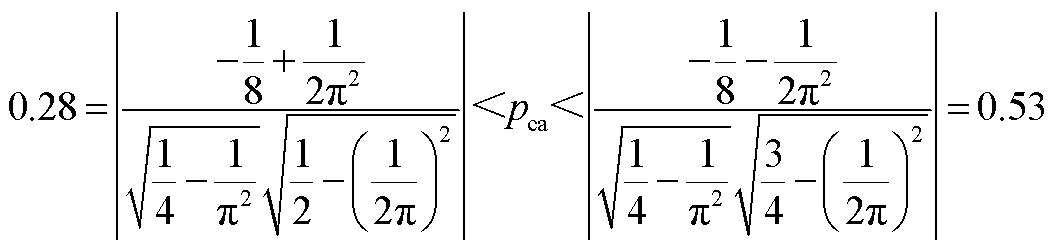
可以发现不同故障状态下,两相电流之间的Pearson相关系数存在显著不同。结合理论分析(见附录),其设定阈值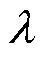 用于故障分类的判据为
用于故障分类的判据为
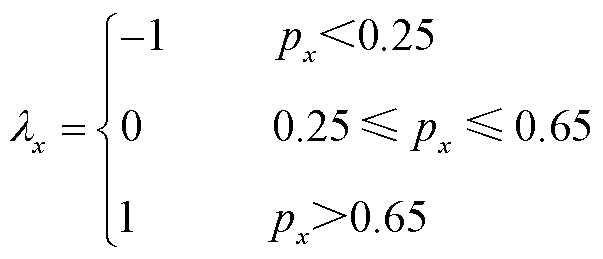 (13)
(13)
式中,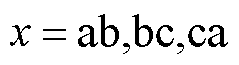 。但Pearson相关系数只能确定故障发生相,不能确定故障桥臂,因此根据变流器输出电流平均值,构建故障特征量为
。但Pearson相关系数只能确定故障发生相,不能确定故障桥臂,因此根据变流器输出电流平均值,构建故障特征量为
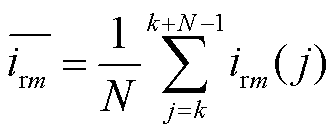 (14)
(14)
式中,m=a, b, c;k为MMG所测得的故障起始采样点;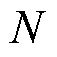 为一周期采样点数量。故障分类判别条件见表5。
为一周期采样点数量。故障分类判别条件见表5。
表5 故障分类判别条件
Tab.5 Fault classification judgment condition
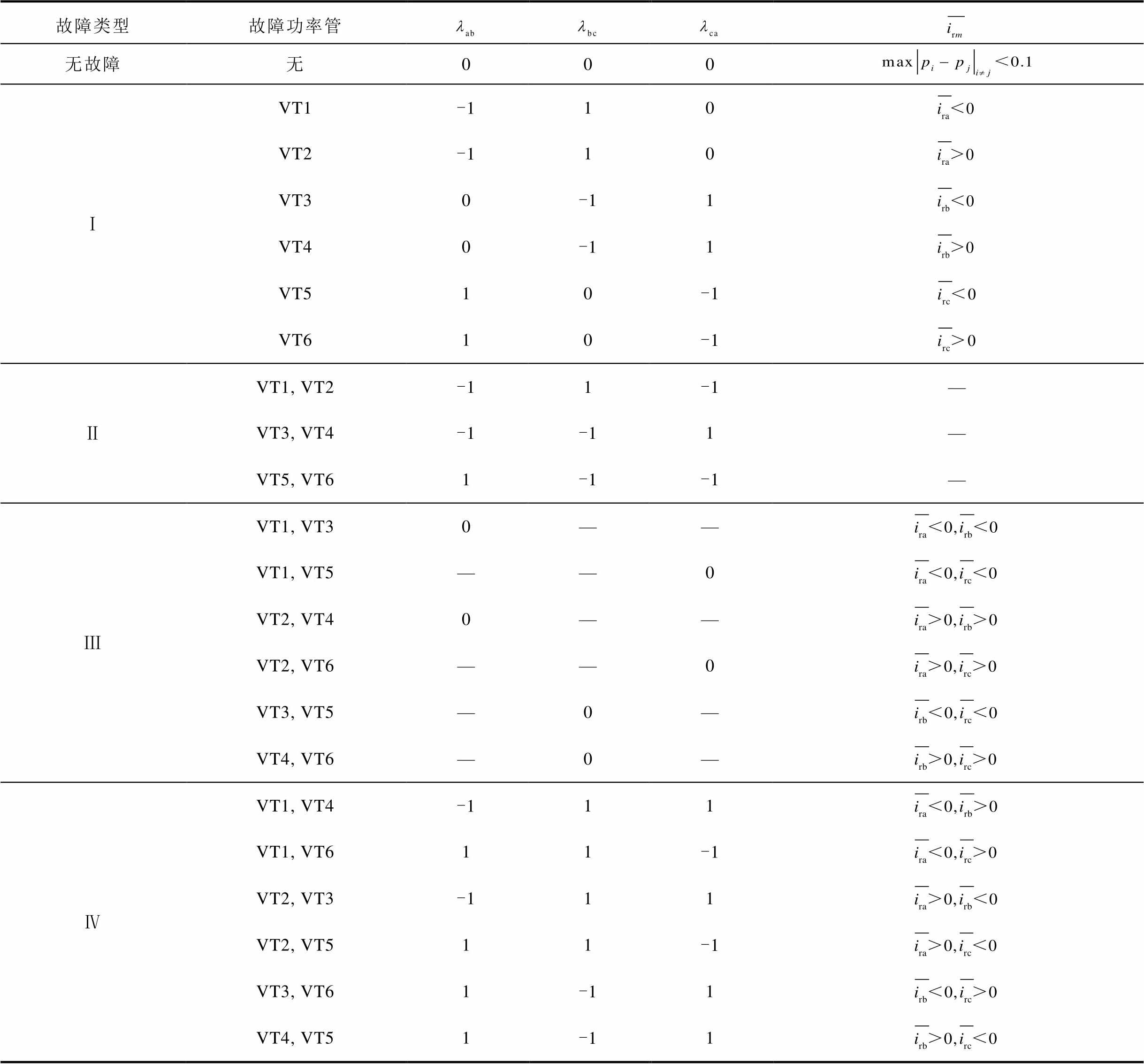
故障类型故障功率管 无故障无000 ⅠVT1-110 VT2-110 VT30-11 VT40-11 VT510-1 VT610-1 ⅡVT1, VT2-11-1— VT3, VT4-1-11— VT5, VT61-1-1— ⅢVT1, VT30—— VT1, VT5——0 VT2, VT40—— VT2, VT6——0 VT3, VT5—0— VT4, VT6—0— ⅣVT1, VT4-111 VT1, VT611-1 VT2, VT3-111 VT2, VT511-1 VT3, VT61-11 VT4, VT51-11
综上所述,先使用MMG监测实时母线电压,提取电压波形的暂态特征,当检测到故障发生时则计算转子侧三相电流两两之间的Pearson相关系数判别故障相,并根据电流平均值判断故障发生桥臂,最终定位故障功率管,实现故障分类。方法流程如图4所示。
为验证本文所提方法的有效性,基于Matlab/ Simulink平台搭建了一个9 MW风力发电系统模型。该系统由6台1.5 MW风力发电机组成,并连接到25 kV配电系统,然后通过30 km、25 kV馈线向120 kV电网输出电力。其中,双馈感应风力发电机组由绕线转子感应发电机和基于AC-DC-AC的三相变流器组成。定子绕组直接连接到60 Hz电网,转子通过AC-DC-AC变流器(变频器)变频供电。其中风机的控制系统使用转矩控制器以保持速度为1.2(pu),额定风速为11 m/s。设置脉冲驱动信号缺失来模拟IGBT功率管开路,其余电路元件正常工作。设置故障发生时间为0.25 s,风速为15 m/s, 采样频率为4 kHz。系统模型主要参数见表6。
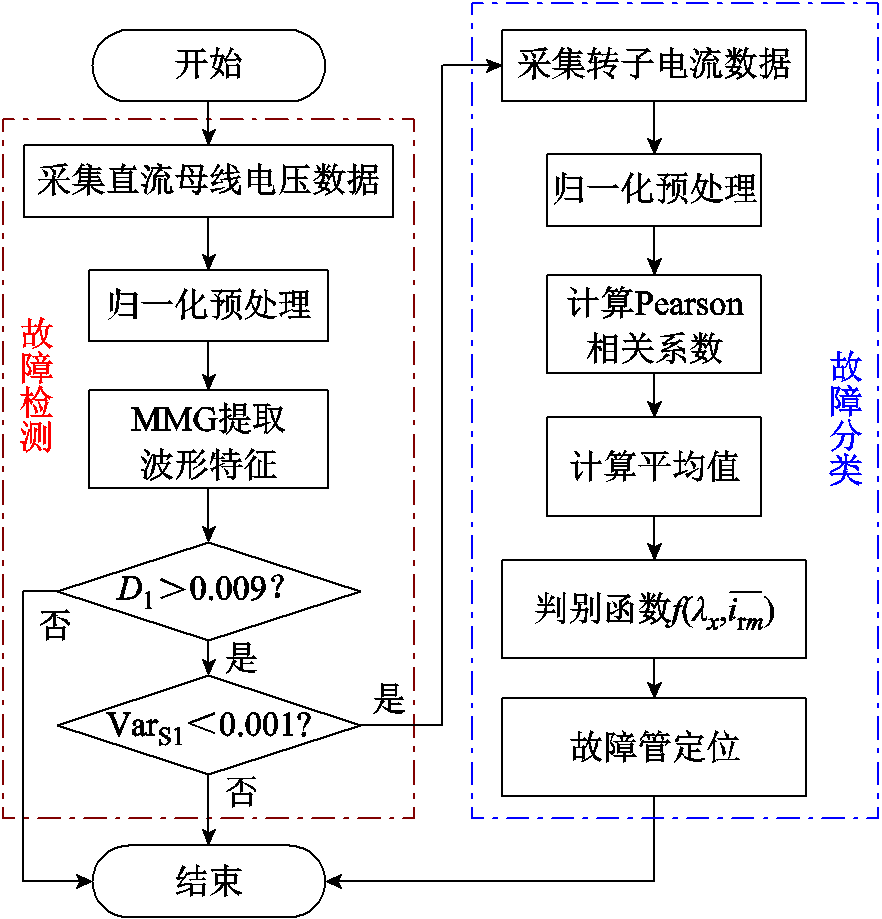
图4 方法流程
Fig.4 Flow chart of the proposed method
表6 系统模型主要参数
Tab.6 Main parameters of the system model

参数数值 直流母线电压/V1 150 额定功率/(MV·A) 1.5 额定电压/V575 涡轮机初始转速(pu)1.2 初始输出转矩(pu)0.83 定子电阻(pu)0.023 定子电感(pu)0.18 转子电阻(pu)0.016 转子电感(pu)0.16 定转子互感(pu)2.9 极对数3
设置VT1的驱动脉冲信号输出为0模拟开路故障,故障识别过程如图5所示。可以看到,在故障发生后,直流母线电压的一次梯度有模极大值点,通过条件判断输出故障标记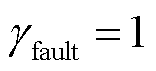 。
。
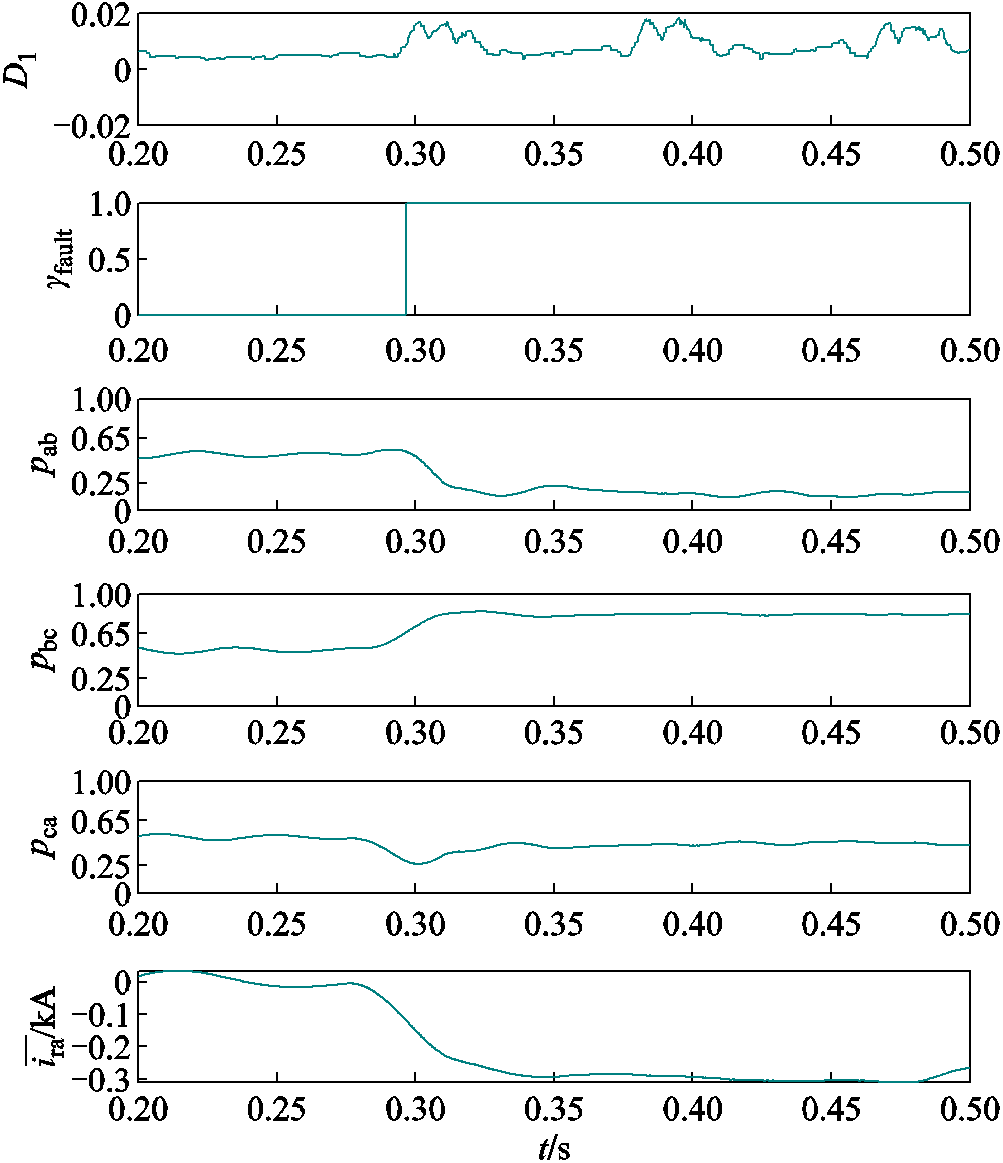
图5 VT1故障识别过程
Fig.5 VT1 fault identification process
对故障标记后一周期内的转子三相电流数据进行计算,发现特征量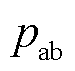 、
、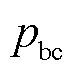 、
、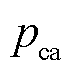 在无故障时值约等于0.5,故障发生后
在无故障时值约等于0.5,故障发生后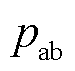 逐渐减小,虽有波动但均小于0.25,
逐渐减小,虽有波动但均小于0.25,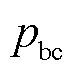 逐渐增大,虽有波动但其值均大于0.65,
逐渐增大,虽有波动但其值均大于0.65,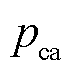 虽有波动但其值稳定在0.5左右,
虽有波动但其值稳定在0.5左右,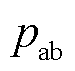 、
、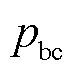 、
、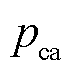 值所在范围与表5第2、3行(文中表格所指的行均为数据行,不包括标题行)相符,判断故障功率管位于A相桥臂。又由于A相正半波消失,A相电流平均值极性为负并远小于0,判断故障功率管为VT1。
值所在范围与表5第2、3行(文中表格所指的行均为数据行,不包括标题行)相符,判断故障功率管位于A相桥臂。又由于A相正半波消失,A相电流平均值极性为负并远小于0,判断故障功率管为VT1。
同理,故障类型Ⅱ中VT1、VT2故障后的识别过程如图6所示。直流母线电压一次梯度模极大值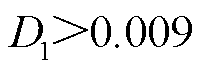 ,因此判断故障发生;故障发生后
,因此判断故障发生;故障发生后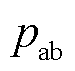 、
、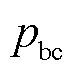 、
、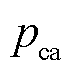 值所在范围与表5第8行相符,故判断故障功率管为VT1、VT2。
值所在范围与表5第8行相符,故判断故障功率管为VT1、VT2。
故障类型Ⅲ中VT1、VT3故障后的识别过程如图7所示。直流母线电压一次梯度模极大值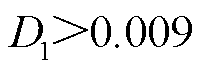 ,因此判断故障发生;故障发生后
,因此判断故障发生;故障发生后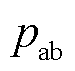 、
、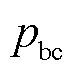 、
、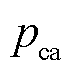 值所在范围与表5第11、13行相符,又因为A、B相电流平均值极性为负并远小于0,故判断故障功率管为VT1、VT3。
值所在范围与表5第11、13行相符,又因为A、B相电流平均值极性为负并远小于0,故判断故障功率管为VT1、VT3。
故障类型Ⅳ中VT1、VT4故障后的识别过程如图8所示。直流母线电压一次梯度模极大值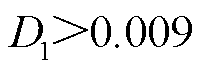 ,因此判断故障发生;故障发生后
,因此判断故障发生;故障发生后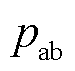 、
、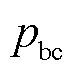 、
、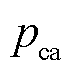 值所在范围与表5第17、19行相符,且A相电流平均值极性为负并远小于0,B相电流平均值极性为正并远大于0,判断故障功率管为VT1、VT4。
值所在范围与表5第17、19行相符,且A相电流平均值极性为负并远小于0,B相电流平均值极性为正并远大于0,判断故障功率管为VT1、VT4。
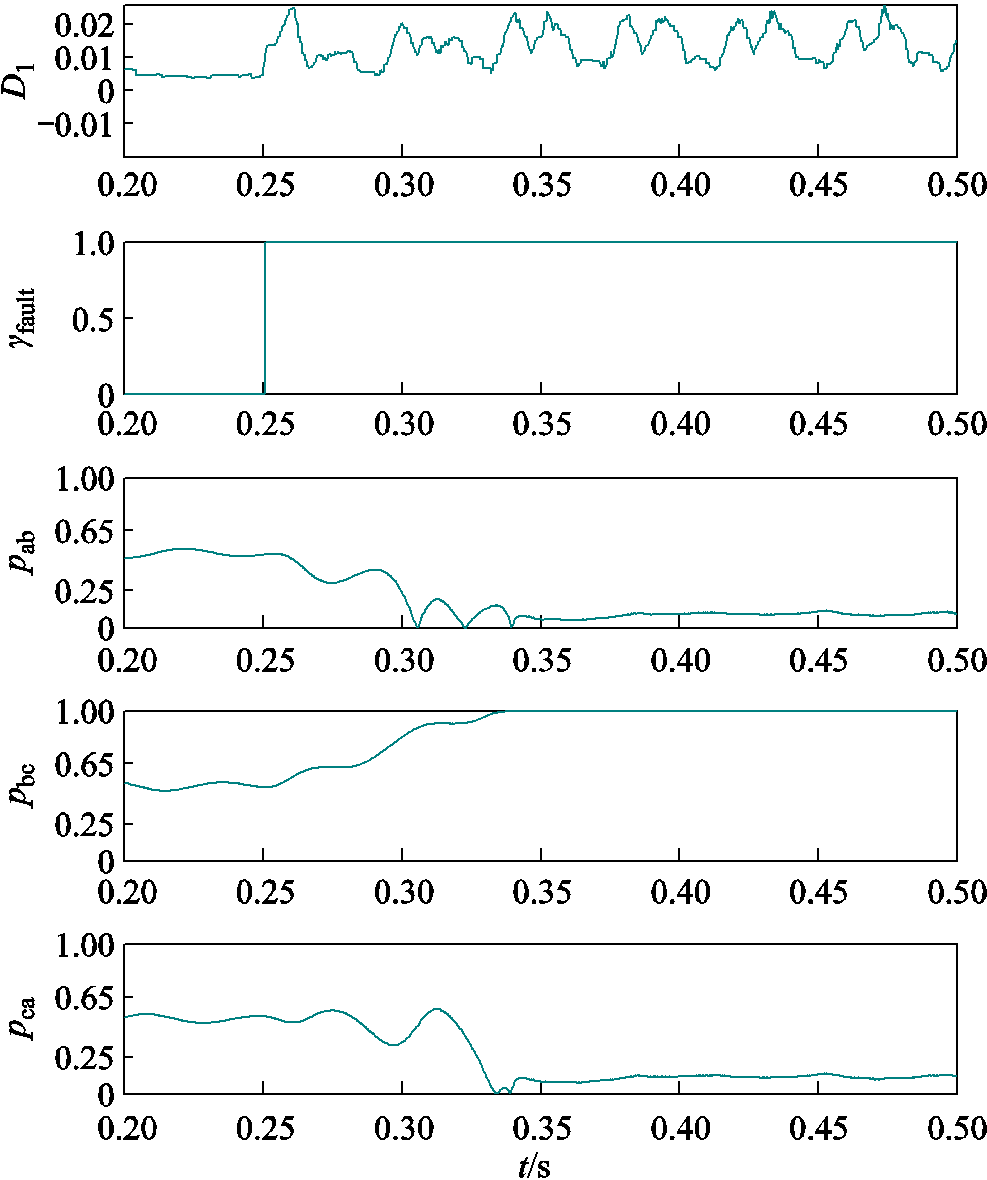
图6 VT1、VT2故障识别过程
Fig.6 VT1, VT2 fault identification process
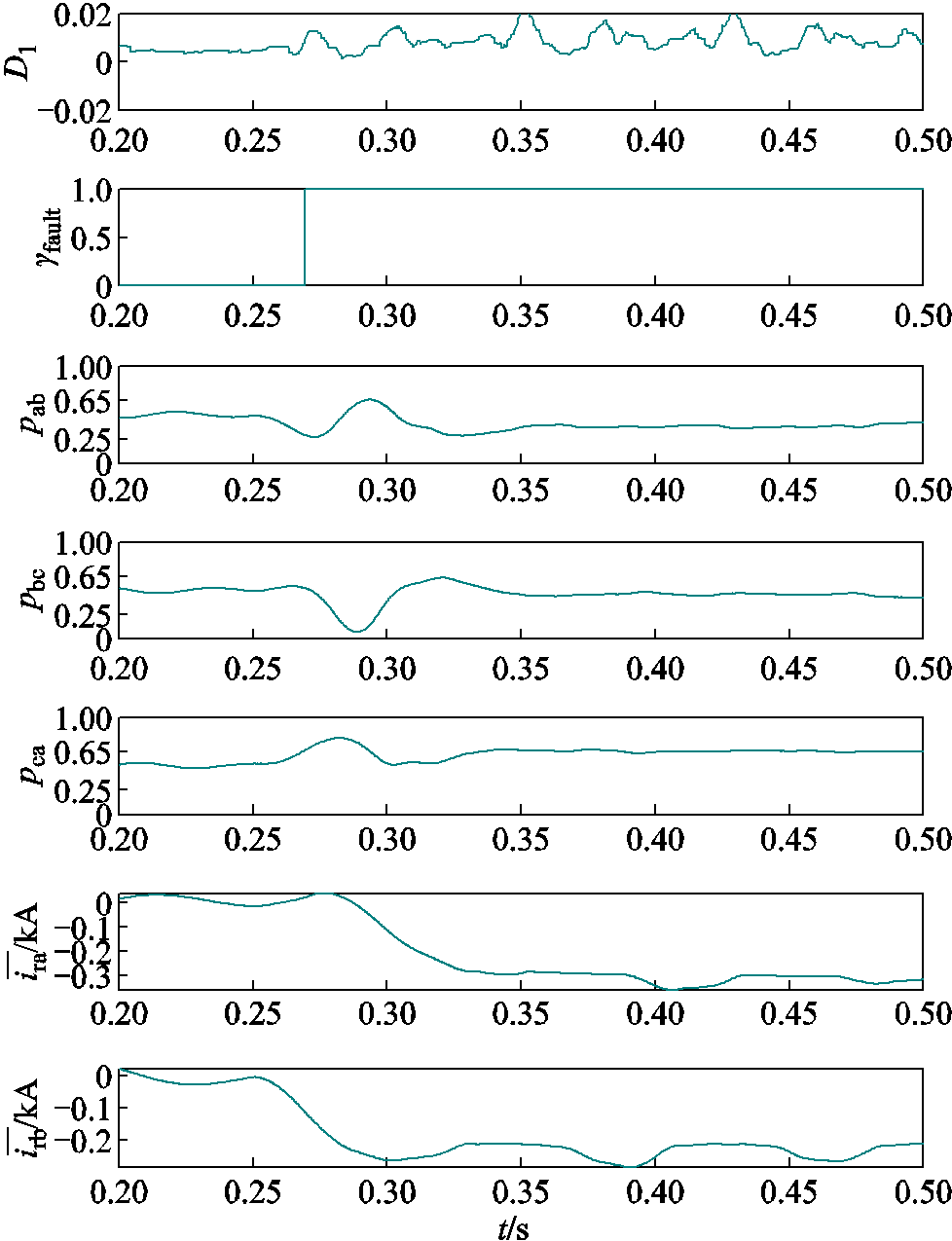
图7 VT1、VT3故障识别过程
Fig.7 VT1, VT3 fault identification process
以上是四种故障类型下的方法演示,可见本文所提方法可以准确地判断故障发生并定位功率管所在位置。
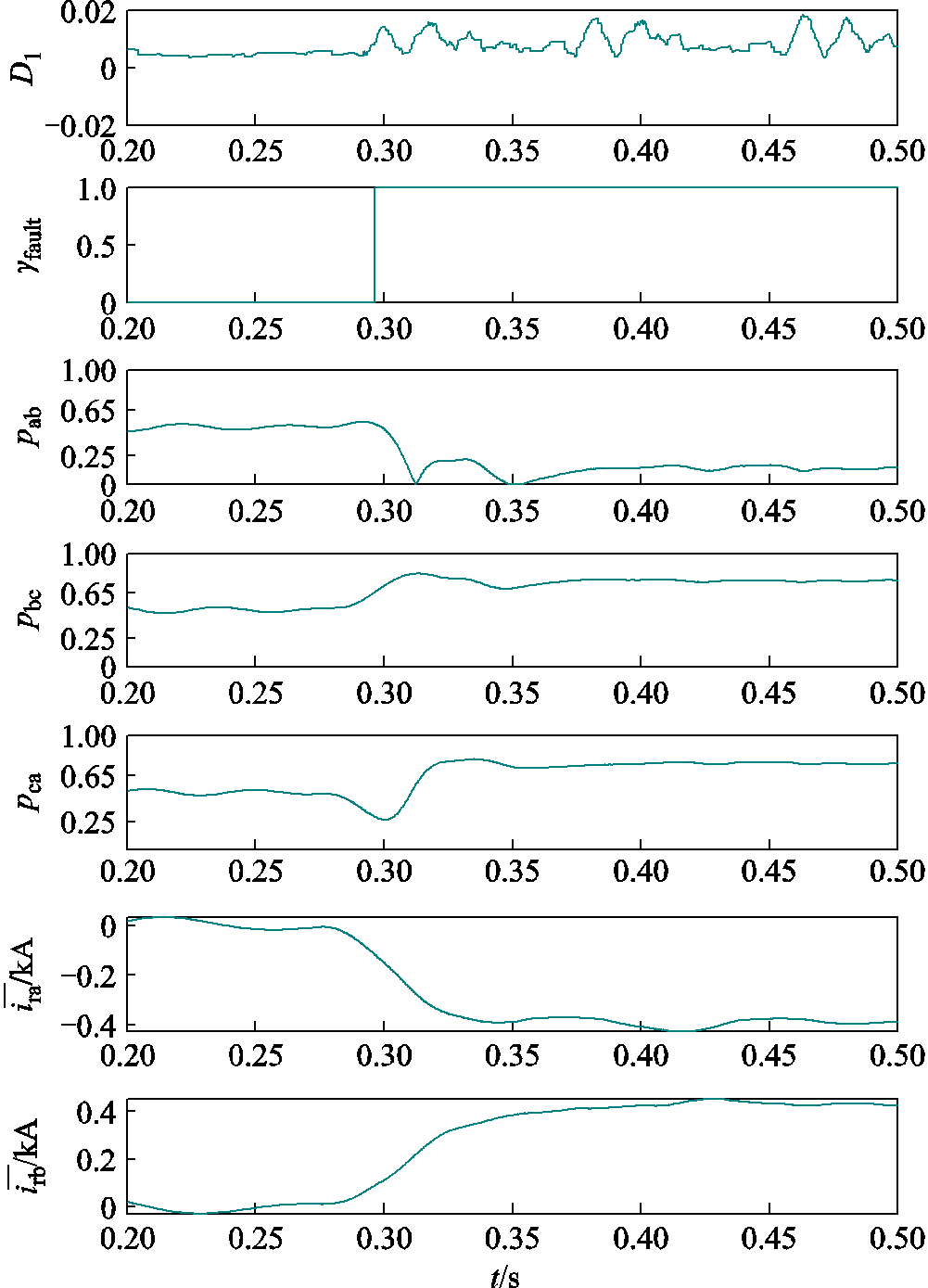
图8 VT1、VT4故障识别过程
Fig.8 VT1, VT4 fault identification process
3.2.1 风速波动
模拟风速波动的情况,设置初始风速等于额定风速,0.2~0.6 s线性减小至7 m/s,0.6~1.0 s内线性增大至15 m/s。仿真数据的检测结果如图9所示,可以发现风速波动对直流母线电压和转子电流的影响可以忽略不计,未检测到故障发生,同时电流特征量稳定在无故障情况下的范围,说明本文方法可以克服风速波动的干扰。
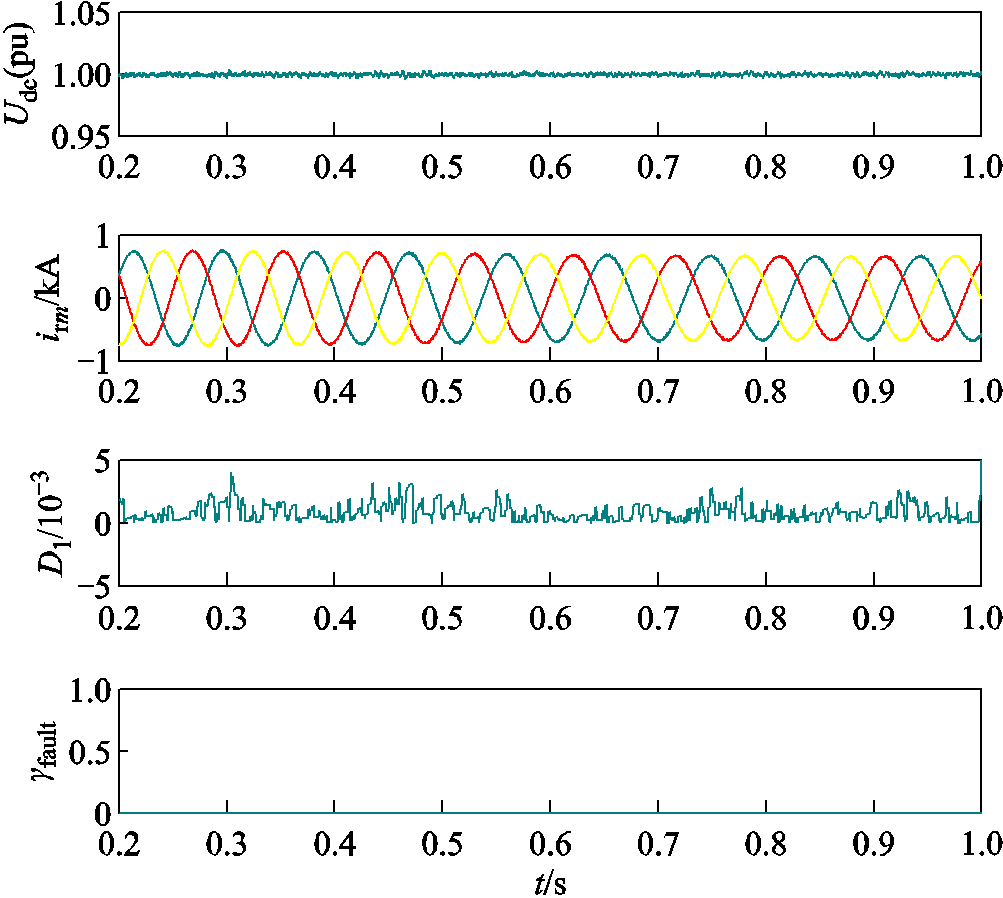
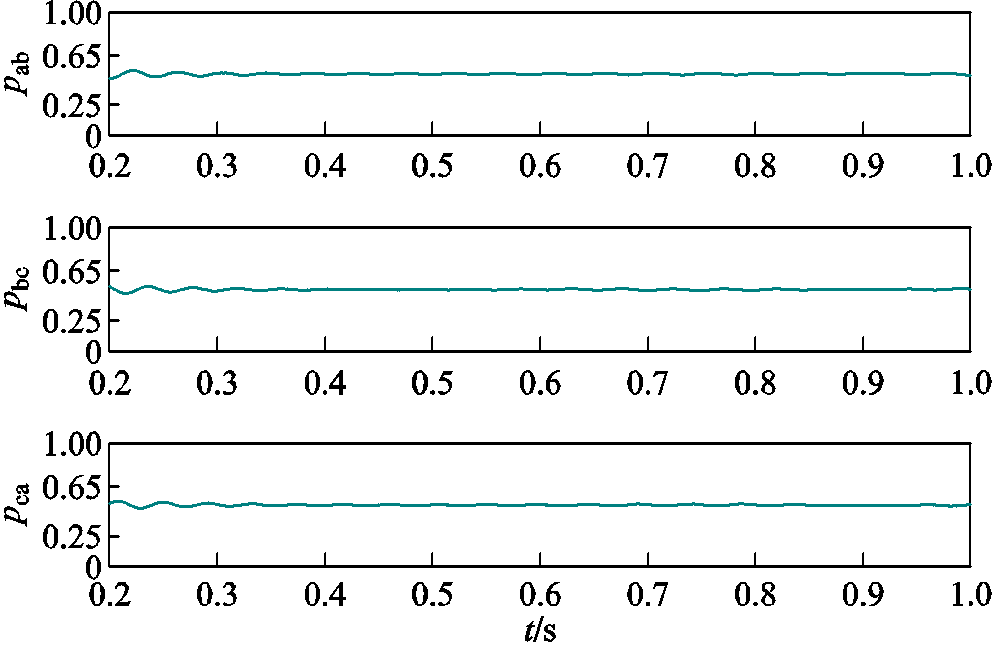
图9 风速波动下的故障识别过程
Fig.9 Fault recognition process under wind speed fluctuation
3.2.2 负载波动
通过仿真电压跌落模拟负载波动的情况。在0.5 s时风机出口电压跌落20%,仿真数据的检测结果如图10所示。可以发现直流母线电压波动明显,故障检测模块误判断发生故障,电流特征量受影响小且大小相近,判断未发生故障,因此故障识别模块可作为故障检测的验证。
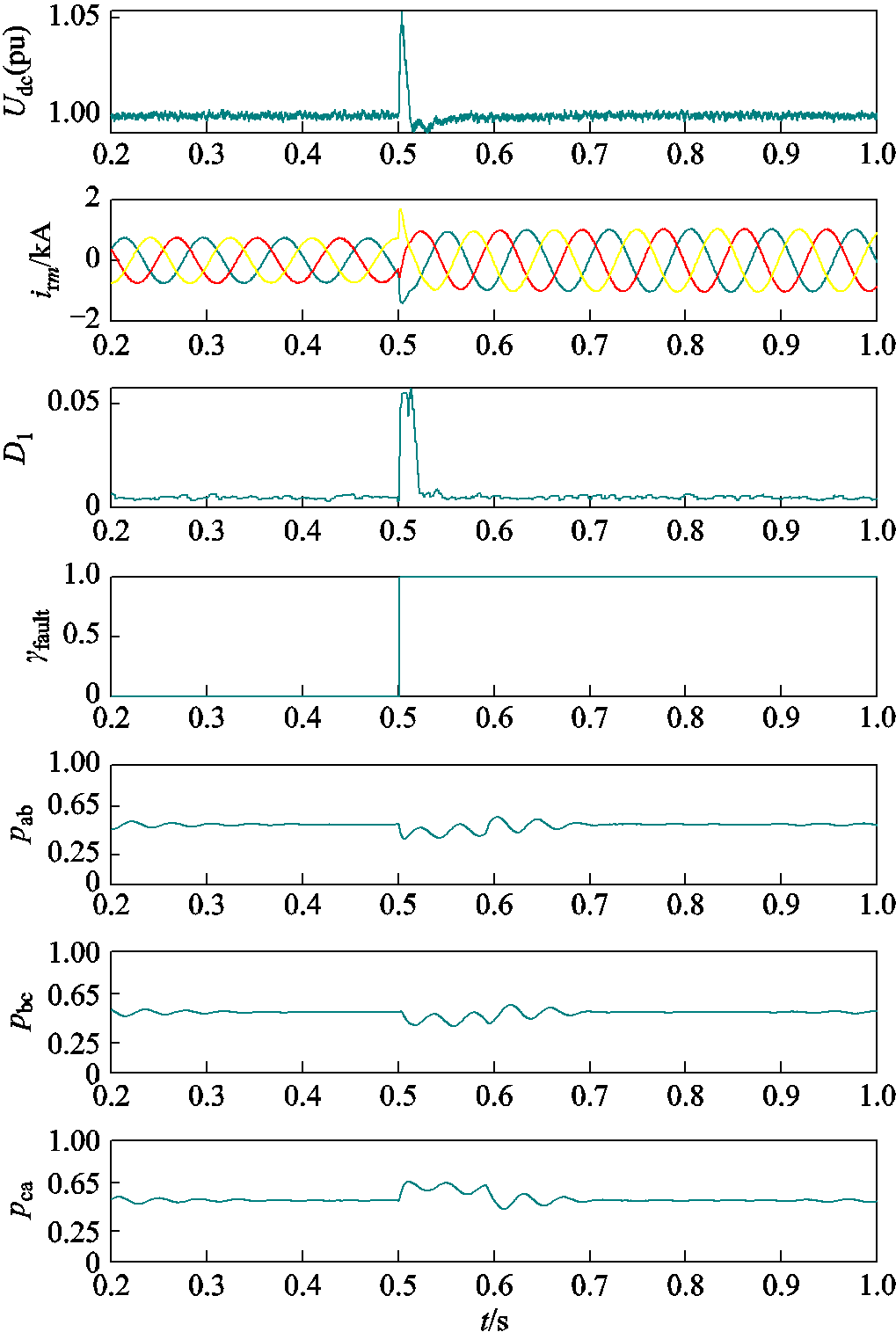
图10 负载波动下的故障识别过程
Fig.10 Fault recognition process under load fluctuation
3.2.3 噪声干扰
向获取到的电压电流数据中添加信噪比为20 dB的高斯白噪声,噪声环境下的故障识别过程如图11所示。从图11可以看出,母线电压和三相电流幅值在噪声影响下波动明显,其一次梯度模极大值符合故障判断条件,但方差超出阈值,因此判断未发生故障,并且电流特征值未受到噪声影响。
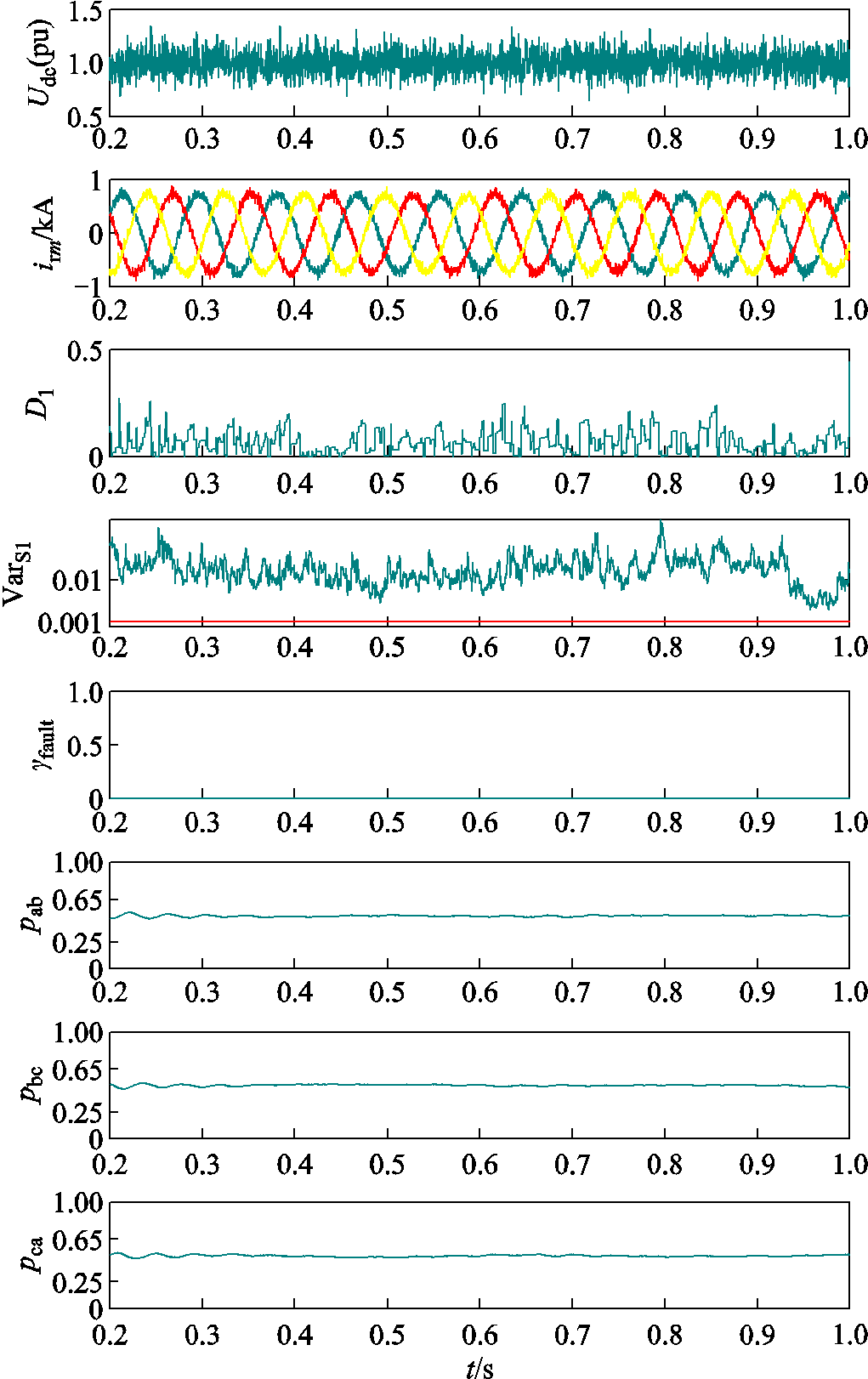
图11 噪声环境下的故障识别过程
Fig.11 Fault recognition process under noise environment
为突出方法的优越性并验证该方法的有效性,采用步长为2的滑动窗口构造不同故障发生时刻的数据,仿真额定风速下无故障和21种故障类型下的80组数据样本,样本总数为22×80=1 760组故障数据,与文献[18,27-29]所提方法进行对比。平均检测时间表示检测到的故障发生时间与实际故障发生时间的平均值,准确率表示检测故障发生并正确分类故障功率管的正确率。所得到结果见表7,本文所提方法对仿真数据具有宽容性,在不同故障发生时间都可以准确判断故障发生并定位故障功率管。文献[18]准确度较高,但是依赖于已经发生的故障事件来构建模型,检测时间长;文献[27]的平均检测时间较长,且准确率较低;文献[28]的平均检测时间较短,但其准确率非常差,并且计算较为复杂;其算法故障识别部分较为简单,未考虑三相电流之间的耦合性,不能区分故障功率管;文献[29]的平均检测时间较长,准确率低于本文所提方法。综上所述,本文提出的方法在提高了准确率的同时保持较短的检测时间,具有更高的实用性和可靠性。
表7 算法验证结果
Tab.7 Algorithm validation results

文献平均检测时间/s准确率(%) [28][27]0.0210.04450.0068.19 [29][18]0.0250.08390.9198.00 本文提出方法0.02499.50
RTDS是由加拿大曼巴托尼直流研究中心推出的电力系统实时数字仿真系统。RTDS同时具备了数值仿真和动态仿真的特性,具有建模周期短、灵活性强、计算精度高等特点,可以较好地模拟现实系统环境。
为对风电变流器故障识别算法进行更真实的验证,本文在RTDS仿真平台上搭建了并网型双馈风力发电系统模型,通过模数转换以物理量输出至上位机,模拟量输出用示波器显示,仿真平台如图12所示。设置VT1、VT4开路故障发生时刻0.25 s,使用上位机处理仿真数据。RTDS仿真故障的识别过程如图13所示,电流产生相应的波形缺失,实验现象与仿真结果基本吻合;同时实验数据分析的故障识别结果与表5第17行一致。表明本文所提方法在更贴近真实状况的实时分析中依旧具有可靠性。
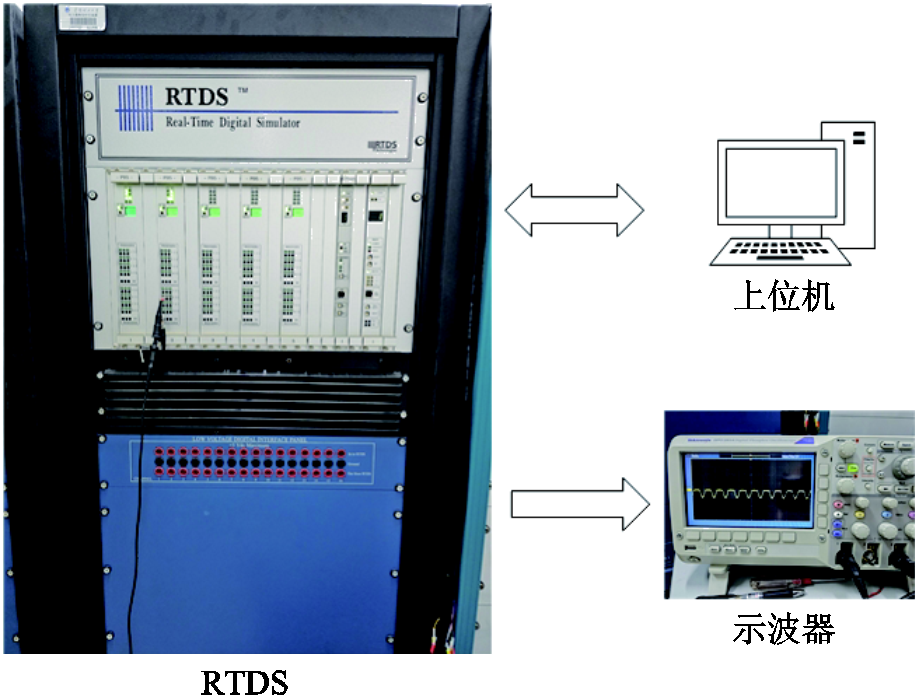
图12 RTDS硬件仿真平台
Fig.12 RTDS hardware simulation platform
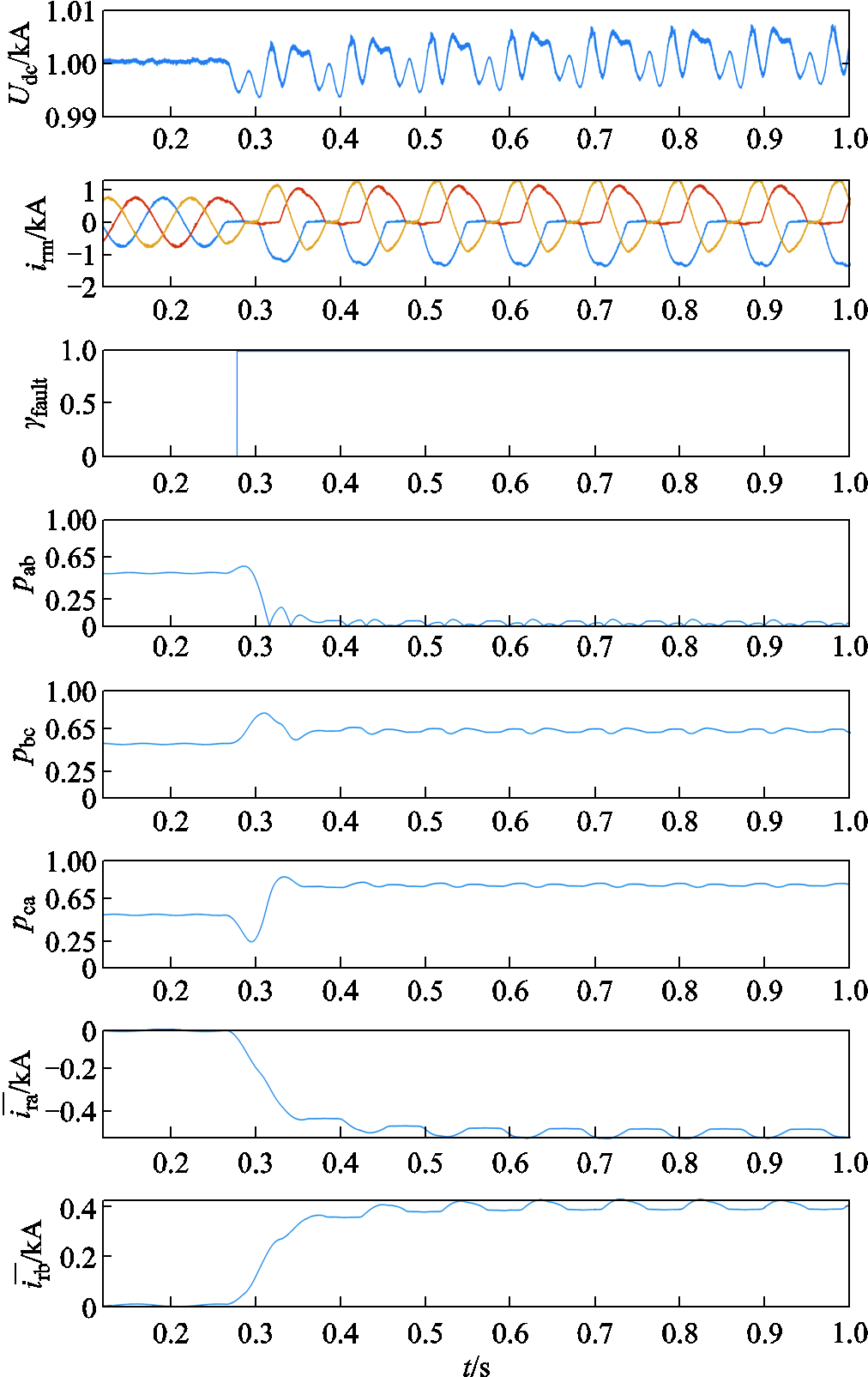
图13 RTDS仿真故障的识别过程
Fig.13 RTDS simulation fault identification process
本文所提方法可以应用在大规模风电场在线检测平台,能防止风电机组遭受严重的损坏,减少故障引发的巨大经济损失,提高风能利用率并提升风电场的经济效益。本文提出的方法在解决风电机组变流器开路故障识别方面具有显著的优势,可以实现故障的快速检测,准确区分变流器功率管单管、双管故障并定位功率管。相较于现有方法,该方法不仅计算简单有效,而且能够在外界干扰和噪声影响下保持良好的性能表现,并得到以下结论:
1)基于MMG的故障检测方法利用直流母线电压,便于获取数据且检测迅速,不受噪声影响。
2)基于Pearson相关系数的故障分类方法根据转子三相电流的波形相关性进行分类,理论与仿真结果的一致性表明该方法有效且具有实际意义,同时该方法有较强的鲁棒性。
附 录
假设风机工作在超同步状态下,转子侧变流器工作在整流模式,VT1发生故障。由本文分析可知A相电流正半波缺失,根据基尔霍夫电流定律B、C相在A相电流正半周期内波形对称。定义三相电流幅值为1,A相初相位为0°,则有
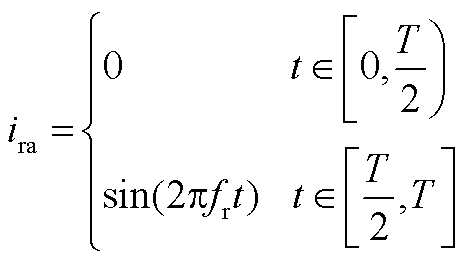
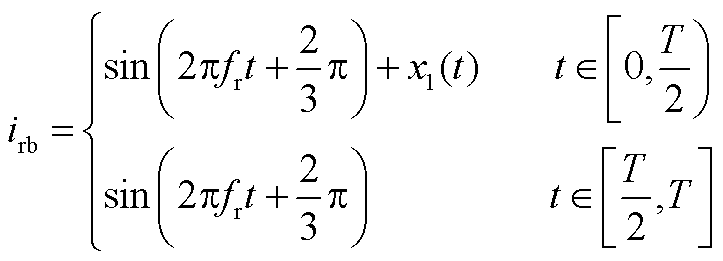
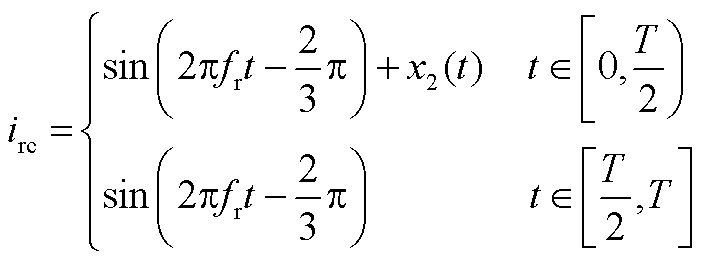
根据B、C相电流幅值相位相同,方向相反可以得到
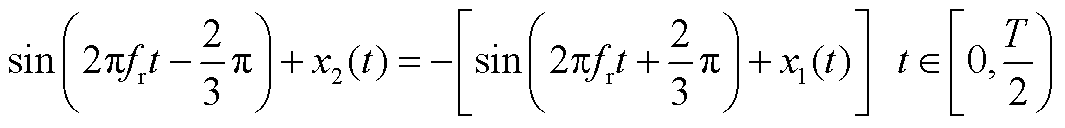
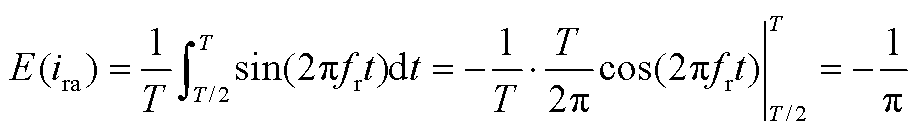
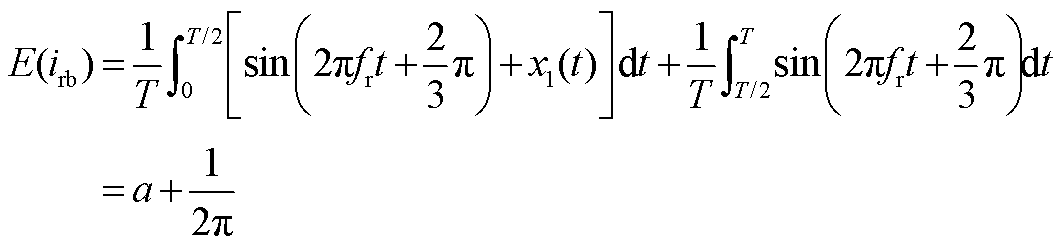
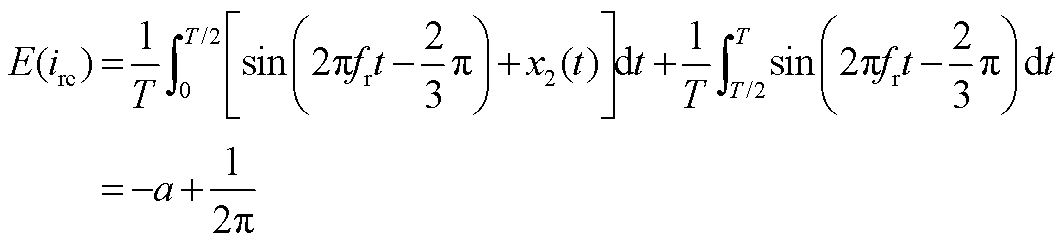
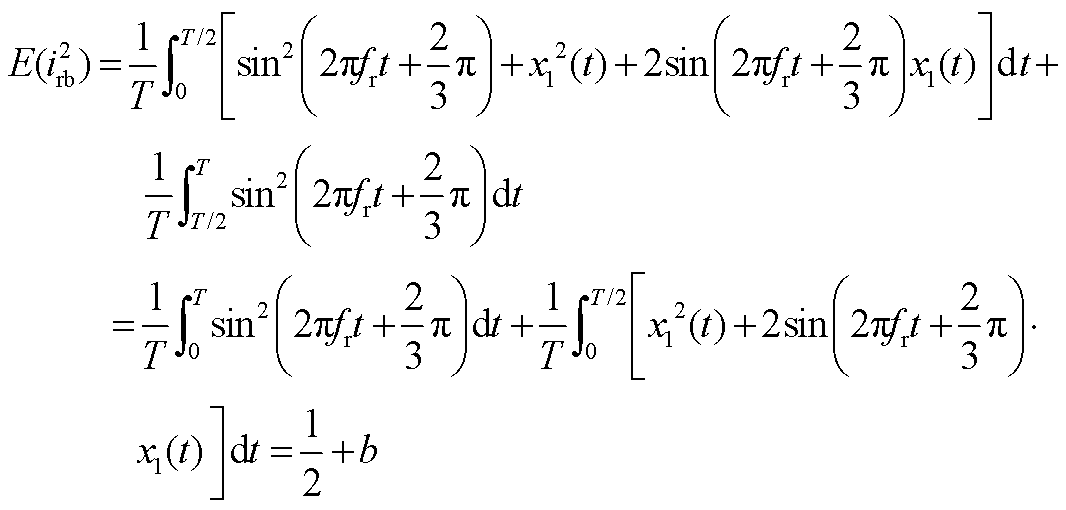
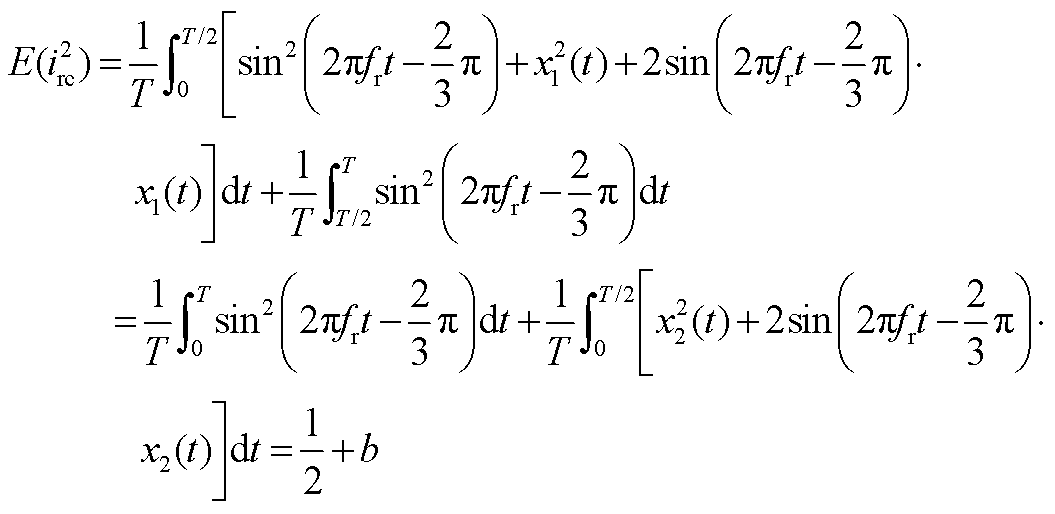
根据仿真波形及基尔霍夫电流定律,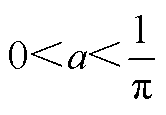 ,
,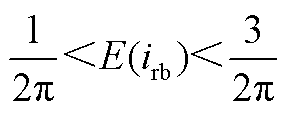 ,
,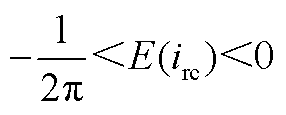 ;
;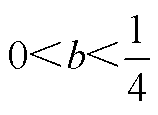 ,
,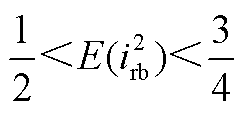 ,
,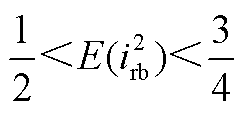 。
。
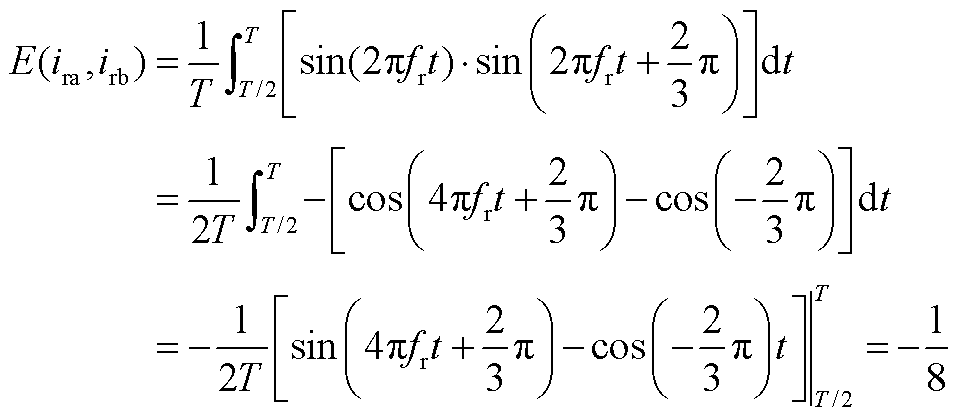
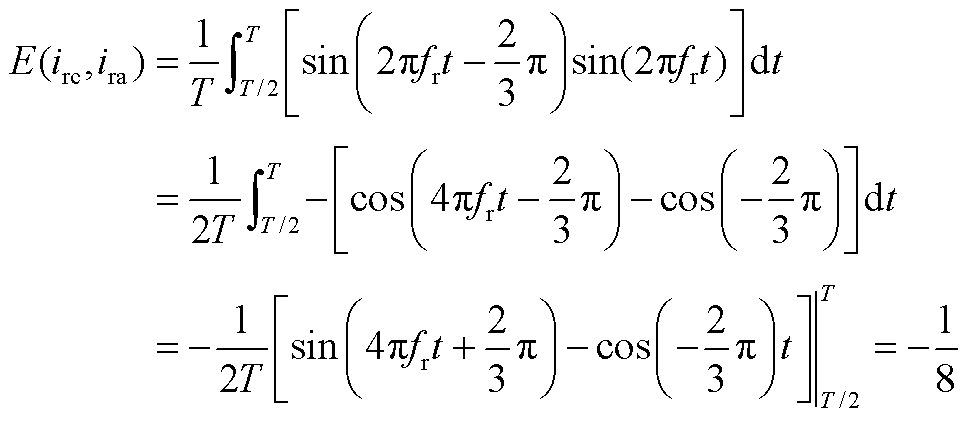
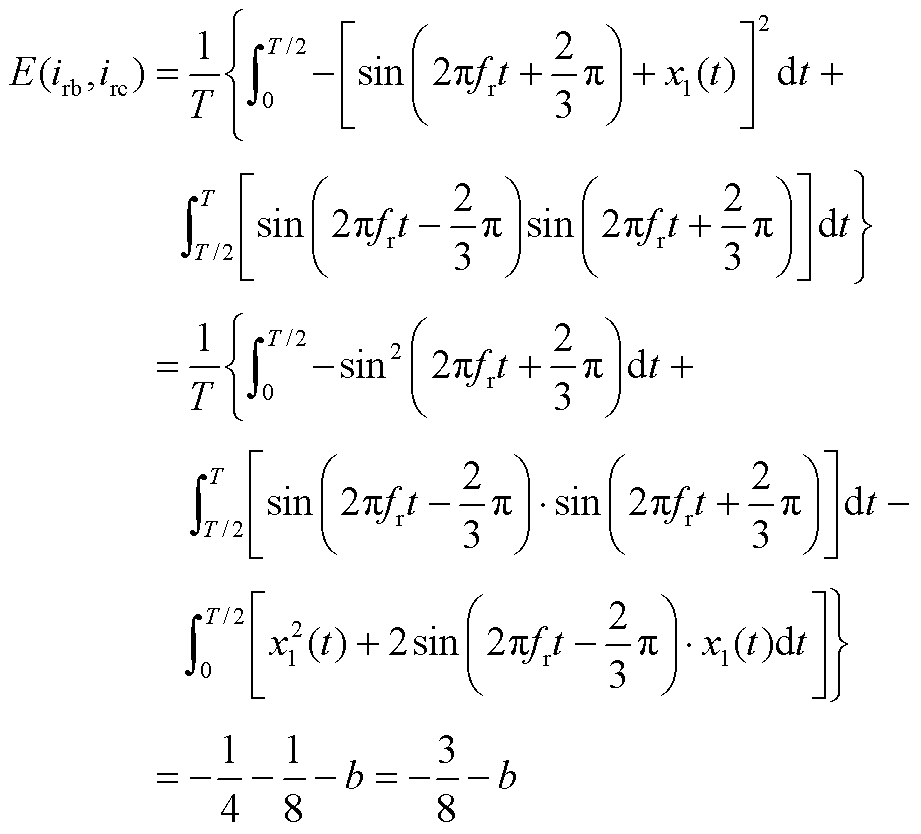
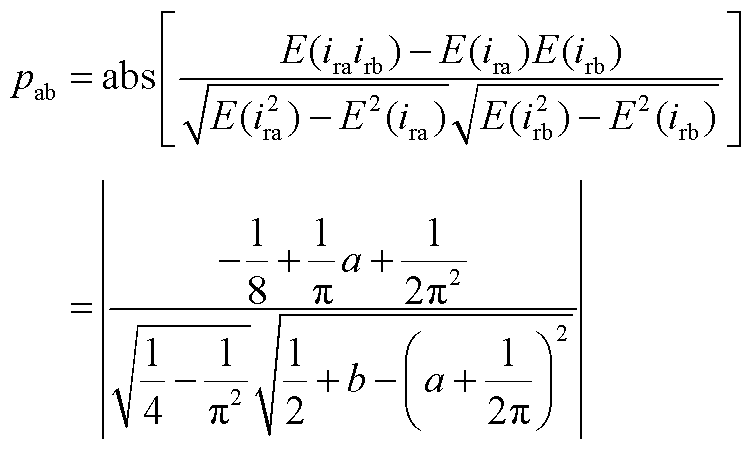
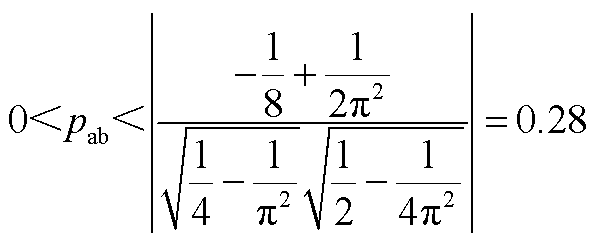
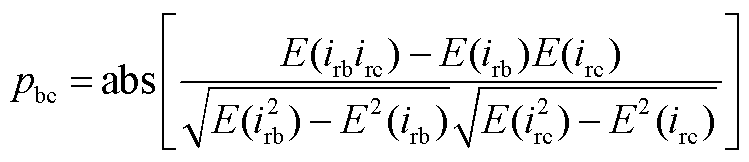
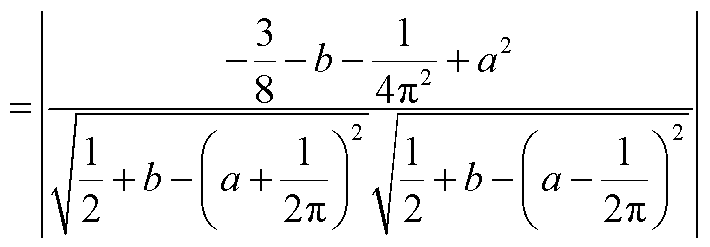
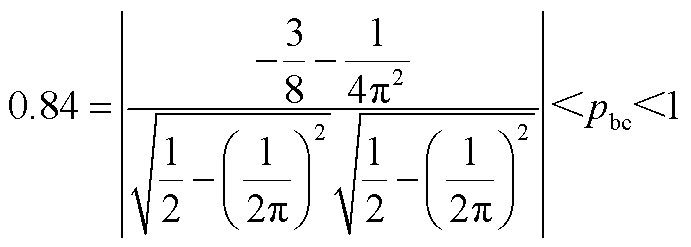
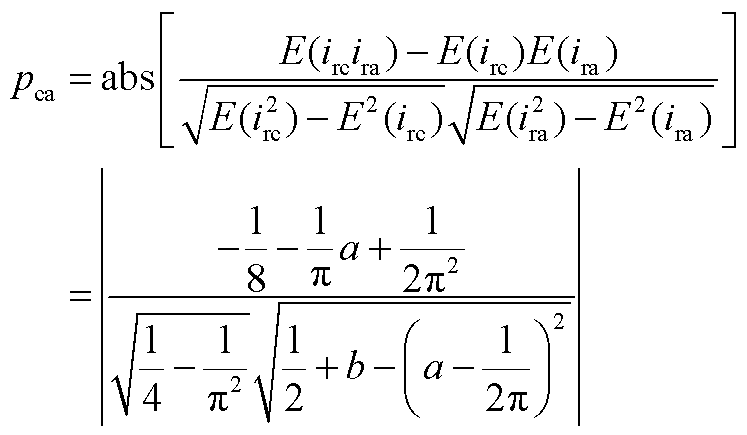
a、b具有正相关性,只能同时取最大或最小值。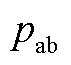 最大值取
最大值取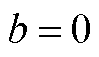 ,
,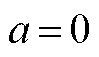 ;
;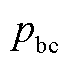 最小值取
最小值取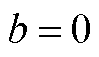 ,
,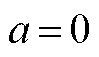 ;
;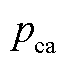 最小值取
最小值取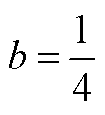 ,
,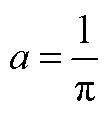 ;
;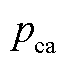 最大值取
最大值取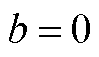 ,
,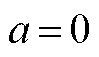 。此为理论计算,根据仿真数据的实际计算结果可以确定
。此为理论计算,根据仿真数据的实际计算结果可以确定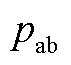 、
、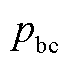 、
、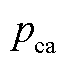 的合适区间。
的合适区间。
参考文献
[1] 刘逸凡, 邹明, 王焱, 等. 面向海上风电仿真的永磁同步发电机电磁暂态等效建模方法[J]. 电工技术学报, 2024, 39(8): 2400-2411.
Liu Yifan, Zou Ming, Wang Yan, et al. Equivalent modeling method for electromagnetic transient of permanent magnet synchronous generator for offshore wind power simulation[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2400-2411.
[2] 潘郑楠, 邓长虹, 徐慧慧, 等. 考虑灵活性补偿的高比例风电与多元灵活性资源博弈优化调度[J]. 电工技术学报, 2023, 38(增刊1): 56-69.
Pan Zhengnan, Deng Changhong, Xu Huihui, et al. Game optimization scheduling of high proportion wind power and multiple flexible resources considering flexibility compensation[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 56-69.
[3] 谢震, 杨曙昕, 代鹏程, 等. 构网型全功率风电机组网侧变流器耦合分析及抑制策略[J]. 电工技术学报, 2023, 38(14): 3745-3758, 3768.
Xie Zhen, Yang Shuxin, Dai Pengcheng, et al. Grid-side coupling analysis and suppression strategy of grid-forming full-power wind turbines[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3745-3758, 3768.
[4] Yang Zhimin, Chai Yi. A survey of fault diagnosis for onshore grid-connected converter in wind energy conversion systems[J]. Renewable and Sustainable Energy Reviews, 2016, 66: 345-359.
[5] Liang Jinping, Zhang Ke, Al-Durra A, et al. A state-of-the-art review on wind power converter fault diagnosis[J]. Energy Reports, 2022, 8: 5341-5369.
[6] Mayilsamy G, Lee S R, Joo Y H. Open-switch fault diagnosis in back-to-back NPC converters of PMSG-based WTS via zero range value of phase currents[J]. IEEE Transactions on Power Electronics, 2024, 39(4): 4687-4703.
[7] Liang Jinping, Zhang Ke, Al-Durra A, et al. A multi-information fusion algorithm to fault diagnosis of power converter in wind power generation systems[J]. IEEE Transactions on Industrial Informatics, 2024, 20(2): 1167-1179.
[8] 尹志豪, 余典儒, 朱家峰, 等. IGBT功率模块封装失效机理及监测方法综述[J]. 电工电能新技术, 2022, 41(8): 51-70.
Yin Zhihao, Yu Dianru, Zhu Jiafeng, et al. Review of IGBT power module packaging failure mechanism and monitoring methods[J]. Advanced Technology of Electrical Engineering and Energy, 2022, 41(8): 51-70.
[9] 程亮亮. 双馈风电机组变流器故障诊断研究[D]. 北京: 华北电力大学, 2017.
Cheng Liangliang. Research on fault diagnosis of doubly-fed wind turbine converter[D]. Beijing: North China Electric Power University, 2017.
[10] Lu Bin, Sharma S K. A literature review of IGBT fault diagnostic and protection methods for power inverters[J]. IEEE Transactions on Industry Applications, 2009, 45(5): 1770-1777.
[11] 李咏秋, 徐晋, 汪可友, 等. 小型固态变压器状态监测及单管开路故障诊断数字孪生方法[J]. 电力系统自动化, 2023, 47(5): 153-161.
Li Yongqiu, Xu Jin, Wang Keyou, et al. Digital twin method for state monitoring and single-tube open-circuit fault diagnosis of small solid-state transformer [J]. Automation of Electric Power Systems, 2023, 47(5): 153-161.
[12] 陈诗灿, 林琼斌, 陈四雄, 等. 电力电子变流器故障诊断的智能方法综述[J]. 电气技术, 2019, 20(3): 6-12.
Chen Shican, Lin Qiongbin, Chen Sixiong, et al. Review on intelligence fault diagnosis in power electronic converters[J]. Electrical Engineering, 2019, 20(3): 6-12.
[13] 赵洪山, 程亮亮. 基于双线性观测器的双馈风电机组变流器功率管开路故障诊断[J]. 电力自动化设备, 2017, 37(3): 72-79.
Zhao Hongshan, Cheng Liangliang. Open-circuit fault diagnosis based on bilinear observer for converter power-switch of doubly-fed wind turbine[J]. Electric Power Automation Equipment, 2017, 37(3): 72-79.
[14] Naseri F, Schaltz E, Lu Kaiyuan, et al. Real-time open-switch fault diagnosis in automotive permanent magnet synchronous motor drives based on Kalman filter[J]. IET Power Electronics, 2020, 13(12): 2450-2460.
[15] 许水清, 黄文展, 何怡刚, 等. 基于自适应滑模观测器的中点钳位型三电平并网逆变器开路故障诊断[J]. 电工技术学报, 2023, 38(4): 1010-1022.
Xu Shuiqing, Huang Wenzhan, He Yigang, et al. Open-circuit fault diagnosis method of neutral point clamped three-level grid-connected inverter based on adaptive sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 1010-1022.
[16] 沈艳霞, 周文晶, 纪志成, 等. 基于小波包与SVM的风电变流器故障诊断[J]. 太阳能学报, 2015, 36(4): 785-791.
Shen Yanxia, Zhou Wenjing, Ji Zhicheng, et al. Fault diagnosis of converter used in wind power generation based on wavelet packet analysis and SVM[J]. Acta Energiae Solaris Sinica, 2015, 36(4): 785-791.
[17] Yuan Yuan, Chai Yi, Qu Jianfeng, et al. Circuit fault diagnosis method of wind power converter with VMD-SVM[C]//2016 35th Chinese Control Conference (CCC), Chengdu, China, 2016: 6564-6569.
[18] Xue Z Y, Xiahou K S, Li M S, et al. Diagnosis of multiple open-circuit switch faults based on long short-term memory network for DFIG-based wind turbine systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(3): 2600-2610.
[19] 张瑞成, 白晓泽, 董砚, 等. 基于SSAE-LSTM神经网络的风电变流器开路故障诊断[J]. 可再生能源, 2023, 41(3): 361-369.
Zhang Ruicheng, Bai Xiaoze, Dong Yan, et al. Wind power converter fault diagnosis based on SSAE-LSTM network[J]. Renewable Energy Resources, 2023, 41(3): 361-369.
[20] 王静, 郑小霞, 叶禹含, 等. 基于LWP和改进RF的风机变流器故障诊断[J]. 电力电子技术, 2023, 57(2): 30-33.
Wang Jing, Zheng Xiaoxia, Ye Yuhan, et al. Fault diagnosis of wind power converter based on LWP and improved RF[J]. Power Electronics, 2023, 57(2): 30-33.
[21] 朱琴跃, 于逸尘, 占岩文, 等. 基于短时傅里叶变换和深度网络的模块化多电平换流器子模块IGBT开路故障诊断[J]. 电工技术学报, 2024, 39(12): 3840-3854.
Zhu Qinyue, Yu Yichen, Zhan Yanwen, et al. IGBT open-circuit fault diagnosis of modular multilevel converter sub-module based on short-time Fourier transform and deep networks[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3840-3854.
[22]  V, de Jesus Rangel-Magdaleno J, Barron-Zambrano J H, et al. Review of fault detection techniques in power converters: fault analysis and diagnostic methodologies[J]. Measurement, 2024, 234: 114864.
V, de Jesus Rangel-Magdaleno J, Barron-Zambrano J H, et al. Review of fault detection techniques in power converters: fault analysis and diagnostic methodologies[J]. Measurement, 2024, 234: 114864.
[23] 高鑫哲, 杜明星, 魏克新. 一种PWM整流器IGBT开路故障诊断方法[J]. 电气传动, 2014, 44(7): 63-67.
Gao Xinzhe, Du Mingxing, Wei Kexin. An diagnosis method for PWM rectifier IGBT open-fault[J]. Electric Drive, 2014, 44(7): 63-67.
[24] 沈艳霞, 周文晶, 纪志成, 等. 基于小波包分析的风力发电系统中变流器的故障识别[J]. 电网技术, 2013, 37(7): 2011-2017.
Shen Yanxia, Zhou Wenjing, Ji Zhicheng, et al. Fault identification of converter used in wind power generation based on wavelet packet analysis[J]. Power System Technology, 2013, 37(7): 2011-2017.
[25] 宋佩云, 肖岚, 许政. 基于电流相角的三相整流器开路故障诊断方法[J]. 电力电子技术, 2016, 50(6): 81-85.
Song Peiyun, Xiao Lan, Xu Zheng. Fault diagnosis method in three-phase rectifier based on the current phase angle[J]. Power Electronics, 2016, 50(6): 81-85.
[26] 陈栋, 刘振兴, 张晓菲. SVPWM整流器IGBT模块的故障诊断技术研究[J]. 华北电力大学学报(自然科学版), 2012, 39(4): 72-76.
Chen Dong, Liu Zhenxing, Zhang Xiaofei. Fault diagnosis of IGBT, odules for SVPWM rectifier[J]. Journal of North China Electric Power University (Natural Science Edition), 2012, 39(4): 72-76.
[27] 程亮亮, 沈伟强, 韦舒天, 等. 双馈风电机组变流器功率管开路故障诊断方法[J]. 可再生能源, 2019, 37(11): 1691-1696.
Cheng Liangliang, Shen Weiqiang, Wei Shutian, et al. Open switch fault diagnostic method of converters for doubly fed wind turbine[J]. Renewable Energy Resources, 2019, 37(11): 1691-1696.
[28] 许水清, 陶松兵, 何怡刚, 等. 基于相电流瞬时频率估计的永磁直驱风电变流器开路故障诊断[J]. 电工技术学报, 2022, 37(2): 433-444.
Xu Shuiqing, Tao Songbing, He Yigang, et al. Open-circuit fault diagnosis for back-to-back converter of PMSG wind generation system based on estimated instantaneous frequency of phase current[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 433-444.
[29] 李辉, 杨甜, 谭宏涛, 等. 基于电压和电流特征的双馈风电变流器功率器件开路故障综合诊断[J]. 电工技术学报, 2021, 36(16): 3433-3445.
Li Hui, Yang Tian, Tan Hongtao, et al. Comprehensive diagnosis of open-circuit fault for power devices of doubly-fed wind power converter based on the features of voltage and current[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3433-3445.
[30] Wu B Q H, Lu Z, Ji T Y. Protective Relaying of Power Systems Using Mathematical Morphology[M]. London: Springer, 2009.
Identification of Open-Circuit Fault in Wind Power Converter Based on Mathematical Morphology and Pearson Correlation Coefficient
Abstract The increasing deployment of wind turbines in challenging environments has led to the prevalent issue of converter faults, which significantly affect the reliability and efficiency of wind power systems. Given the critical role that the converter plays in optimizing the wind power conversion process, detecting and identifying open-circuit fault in wind converter is essential for maintaining operational integrity and maximizing energy output. Current fault identification methods often suffer from limitations related to robustness and computational complexity, necessitating improved solutions. To address these shortcomings, this paper introduces an innovative fault identification method that integrates analysis of the direct current (DC) bus voltage and rotor current characteristics. It can accurately recognize the single and double tube faults of converter power tubes.
Firstly,Fault detection is facilitated by the fact that the DC bus voltage signal is easily accessible, independent of the load and control strategy. Extraction of DC bus voltage edge gradients using mathematical morphology as a feature to detect the occurrence of faults. Secondly, the Pearson correlation coefficients of the rotor side currents are calculated to analyze waveform characteristics. The coupling relationship between the three-phase currents is theoretically deduced, and it is proved that the Pearson correlation coefficients between the two-phase currents are significantly different under different fault conditions, enabling precise identification of the fault phase. Moreover, the location of the fault bridge arm is determined using the average value of the current, enhancing the accuracy of fault identification. Finally, the decision function is used to locate the faulty power tube and realize the fault classification.
Simulation results of the open-circuit fault model of doubly-fed wind power converter show that the proposed method in this paper can accurately determine the occurrence of faults and locate the position of power tubes. By comparing under large data sets, it is found that the proposed method improves the accuracy while maintaining a shorter detection time compared to other methods, which is more practical and reliable. The simulation results show that the wind speed fluctuation has a negligible effect on the DC bus voltage and rotor current, and no fault occurrence is detected, while the current characteristics are stabilized in the range of the fault-free case, which indicates that the proposed method can overcome the interference of wind speed fluctuation. By simulating voltage dips to model the load fluctuations, it is found that the fault detection module misjudges the occurrence of faults, and the current characteristics is small affected but similar in size. It is judged that no faults have occurred, so the fault identification module can be used as a verification of fault detection. A Gaussian white noise with a signal-to-noise ratio of 20 dB is also added to the acquired voltage and current data, and the results show that the proposed method is not disturbed by noise.
The following conclusions can be drawn from the simulation analysis: (1) Compared with existing methods, the method is not only simple and effective in calculation, but also has a higher accuracy rate. (2) The fault detection method based on mathematical morphology utilizes the DC bus voltage, which is easy to obtain data and rapid to detect, and is not affected by noise. (3) The Pearson correlation coefficient-based fault classification method classifies the rotor three-phase currents according to their waveform correlation, and the consistency of theoretical and simulation results shows that the method is effective and of practical significance, and the method has strong robustness.
Keywords: Converter, open circuit fault, fault identification, mathematical morphology, Pearson correlation coefficient
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.240752
国家自然科学基金(52077081)和广东省基础与应用基础研究基金自然科学基金(2022A1515011608)资助项目。
收稿日期 2024-05-10
改稿日期 2024-10-11
卢奥煊 男,2000年生,硕士研究生,研究方向为风电变流器故障诊断及信号处理。
E-mail:202221015205@mail.scut.edu.cn
季天瑶 女,1981年生,教授,博士生导师,研究方向为电力系统信号处理。
E-mail:tyji@scut.edu.cn(通信作者)
(编辑 赫 蕾)