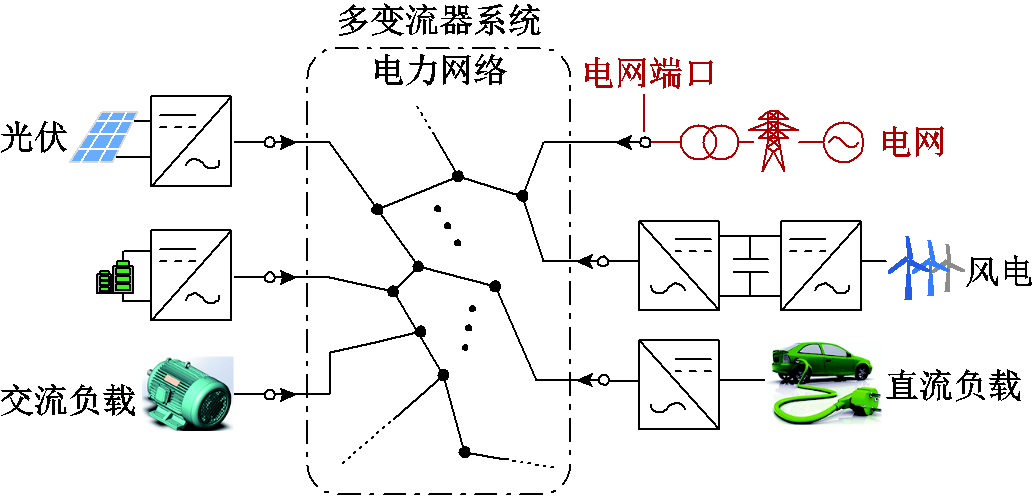
图1 多变流器并网系统示意图
Fig.1 Diagram of multi-converter grid-tied system
摘要 随着新能源渗透率的不断提高,以同步发电机为主的传统电力系统正向以多样化电力电子装备为主的新型电力系统转变,多变流器并网系统的小干扰稳定性问题受到广泛关注。然而,状态空间法和传统阻抗法在分析多变流器系统稳定性时仍存在复杂度高及难以准确评估闭环极点关于各变流器灵敏度的问题。针对上述问题,该文首先提出一种用于分析多变流器并网系统小干扰稳定性的单输入单输出(SISO)dq阻抗判据,该判据可将多输入多输出系统(MIMO)转换为若干SISO系统以简化稳定性分析过程,相比于MIMO系统分析方法,其在避免求解高维矩阵特征值的同时降低了奈奎斯特曲线分析的复杂度,同时该方法还具有从物理角度揭示振荡失稳机理的优点。然后,基于所提出的稳定性判据公式,进一步提出一种用于求取闭环极点关于各变流器阻抗/导纳灵敏度的分析方法,该方法可有效评估系统中不同变流器对振荡模态的影响程度,有助于实现诱发系统振荡的主导变流器的辨识。最后,通过Matlab/Simulink仿真和硬件在环实验验证了所提方法的正确性。
关键词:多变流器并网系统 SISO dq阻抗模型 小干扰稳定性 灵敏度分析
在以新能源为主体的新型电力系统中,电力电子变流器广泛用于发电、输电、用电各个环节,这种以电力电子变流器为主的组网方式,可能诱发系统振荡失稳问题[1-3]。
用于分析变流器并网系统小干扰稳定性的方法主要分为状态空间法[4-5]和阻抗分析法。然而,状态空间法存在如下不足:①需要依赖系统拓扑和参数构建状态方程,但由于厂商技术保密,获得建模所需的详细参数较为困难[6];②难于从物理角度揭示振荡机理[7];③对于拓扑复杂的多变流器并网系统,状态方程规模较大,给特征值计算带来很大的困难[8-9]。相比于状态空间法,阻抗分析法存在以下优势:①当变流器内部参数已知时,可经推导获得阻抗表达式,而当参数未知时,通过测量亦可获得阻抗频率特性;②物理意义明确,可从电路角度对振荡失稳机理作出物理解释;③便于模块化建模,可先对各子系统独立建模,再依据拓扑互联约束构建整个系统模型。鉴于上述原因,阻抗分析法已成为目前分析小干扰稳定性的最为普遍的技术手段。
目前,关于单个变流器并网系统的小干扰稳定性分析、失稳机理揭示及抑制策略已较为成熟,随之多变流器系统的小干扰稳定性问题逐渐成为近年来研究的热点问题[9-12]。文献[10]将整个多变流器系统视为一个多输入多输出(Multiple-Input Multiple-Output, MIMO)的负反馈系统,并基于盖尔圆定理提出了一种稳定性分析方法,但该方法可能对稳定系统给出存在失稳风险的错误评估。在文献[10]的基础上,文献[11]给出了一种稳定性分析的简化手段,但其基本原理仍与文献[10]相同,未能从根本上解决误判问题。文献[12]基于Brauer定理提出了一种估计MIMO负反馈模型开环函数特征值的方法,但该判据具有保守性。相较之,基于奈奎斯特稳定性判据的分析方法仍是目前最为可靠的方法。为了避免开环系统右半平面(Right Half Plane, RHP)极点的判断问题,人们希望沿用单变流器系统的分析方法,即将目标系统分解为若干自身稳定的子网络,仅通过分析奈奎斯特曲线绕(-1, j0)点的圈数判断系统的稳定性。这类方法的基本原理是基于阻抗和[13]或者阻抗比[14-15]传递函数实现稳定性分析。例如,文献[16]中提出了一种基于保守区域的稳定性分析方法,并应用于具有多个电流控制型逆变器(Current Controlled Inverter, CCI)的辐射状配电网,但该方法是以忽略正、负序阻抗之间的耦合为前提。文献[17]提出了合阻抗比判据,但该方法亦忽略了频率耦合效应,且仅适用于共母线系统。文献[18]通过分析各变流器自身在并网点的阻抗比的奈奎斯特图,对由多个电压控制型逆变器(Voltage Controlled Inverter, VCI)和CCI组成的三相网状电力系统的谐波稳定性进行了评估。然而,文献[19]指出该方法对于不同并网点下的稳定性分析结果可能会出现相互矛盾的结果。为解决传统方法分析多变流器的复杂性问题,文献[20]提出了一种具有递归形式的多回路系统稳定性分析方法,简化了多变流器系统的稳定性分析过程。然而,由于该方法是以在开环传递函数不存在右半平面极点为前提,因此仅适用于单一类型的多变流器系统(仅含有CCI或VCI的系统),而难以分析同时含两种类型变流器的混合系统。文献[21]充分考虑了CCI和VCI的RHP极点的数量,分别提出了两种用于分析系统稳定性的方法,其一是首先通过建立整个系统的开环传递函数,然后基于奈奎斯特判据一次性给出稳定性的分析结果;方法二则通过将变流器逐个接入并分步骤实现系统的稳定性评估。本质上,第二种方法与文献[20]思路相一致,这种采用逐步判稳的优点在于可有效降低分析高阶系统大量奈奎斯特曲线的复杂度,且有助于理解各变流器对系统稳定性的影响。但文献[20-21]均忽略了并网逆变器的阻抗/导纳矩阵的耦合项元素,即认为正负序/dq阻抗之间相互解耦,然而研究表明,忽略该耦合项极有可能造成稳定性误判[22-23]。虽然上述方法并不完善,但它们为多变流器并网系统的稳定性分析提供了新的思路。为继承此类方法在稳定性分析上所具有的简便易行的优点,并且弥补它们因忽略耦合项所带来的准确度不足的缺点,亟须提出一种兼具准确性和简便性的方法。同时,考虑基于dq阻抗模型所建立的系统回差矩阵行列式为有理分式形式(序阻抗模型为非有理分式形式),相比序阻抗模型更适于获得闭环极点(即振荡模式),可进一步将阻抗分析法扩展应用于分析关键振荡模式关于分析各个变流器的灵敏度。为实现上述目标,本文提出了一种基于单输入单输出(Single-Input Single-Output, SISO)dq阻抗比判据且具有递归形式的多变流器并网系统小干扰稳定性分析方法。
除了需要实现系统稳定性的准确判定以外,如何评估各变流器对系统稳定性的影响程度并在此基础上实现振荡源辨识也一直是人们所关注的焦点。为实现这一目的,目前的主流技术是通过评估关键振荡模态关于各个变流器的灵敏度来实现。状态空间法在这一方面具有天然优势,其是利用关键模态的特征向量计算某一状态变量的参与因子(本质上,参与因子与灵敏度在概念上是一致的)来实现这一功能。鉴于阻抗分析法在多变流器稳定性分析上更具优势,为了进一步扩展阻抗分析法的功能,近年来学者们对基于阻抗模型的灵敏度分析进行了探索,以期望实现一种兼具稳定性和灵敏度分析功能的系统性方法。文献[24]将节点导纳矩阵的零特征值定义为系统的临界模式,提出了一种基于节点导纳-回路模型的临界模式灵敏度分析方法,但研究表明该临界模式灵敏度相比特征值灵敏度在理论上缺乏严谨性[25]。文献[26-27]通过求解系统节点导纳矩阵或回路阻抗矩阵行列式的零点来获得系统的极点,该极点数值上与状态空间法中状态矩阵的特征值相等,并基于该特征值对应的特征向量引入节点灵敏度和支路灵敏度的概念,用以评估各变流器的灵敏度。上述两种方法的提出为阻抗模型的灵敏度分析提供了新思路,但它们并未阐明阻抗模型中的灵敏度与状态空间模型中的参与因子之间的明确关系。
此外,为简化推导过程,这两种方法均忽略了正负序阻抗/导纳之间的耦合,因此它们无法全面准确地描述系统特性。为丰富上述两种方法的理论基础,文献[28-30]提出了基于全系统阻抗模型的多变流器系统小干扰稳定性分析方法,该方法首先建立包含全部变流器和电力网络的全阻抗模型,然后通过求解闭环极点实现系统稳定性的评估。而且文献[29]还证明了状态空间特征值关于变流器阻抗的灵敏度与该特征值对应的闭环传递函数矩阵的留数具有理论上的对应关系。
在上述方法基础上,文献[25]进一步给出了一种基于全系统阻抗矩阵Zsys(系统节点导纳矩阵的逆矩阵)的多变流器系统特征值灵敏度的分析方法。但上述方法仍是对MIMO系统进行稳定性分析,由于开环传递函数矩阵是阶数为 2n的高阶矩阵(n为系统中变流器的数量),在对该高阶矩阵进行特征值计算时必然存在一定误差,而且由于各频点下的特征值需单独计算,容易造成部分频点下的特征值彼此之间发生跳变,导致奈奎斯特曲线难以观察,分析过程非常复杂;而若采用闭环极点进行分析,则会因难以获得传递函数的解析表达式而在求解闭环极点时引入误差,造成分析结果误判。此外,上述方法均认为Zsys的各元素均具有相同的极点(大小等于整个系统的特征值),并利用矢量匹配法获得Zsys中各元素关于极点的留数,进而实现灵敏度分析。具体实现时,矢量匹配法认为各个元素表达式分子和分母具有相同的阶次,通过对Zsys中元素频率特性进行最小二乘拟合来获得留数,因此欲对闭环极点关于多个变流器的灵敏度进行评估则必须构建包含大量超定方程的方程组,考虑到优化问题仅能保证全局最优以及各个元素的阶次不尽相同(例如构网型和跟网型变流器因控制策略不同,其阻抗表达式阶次并不相同),将会导致计算所得留数存在较大误差,进而影响灵敏度的计算精度。为解决上述问题,本文在推导获得SISO dq阻抗稳定性判据公式的基础上,进一步提出了一种用于评估闭环极点关于各变流器灵敏度的方法,构建了兼具稳定性和灵敏度分析功能的完整框架。
综上所述,现有方法无论在系统稳定性分析的复杂性方面还是在分析振荡模态关于各变流器的灵敏度方面均存在改进空间。首先,本文针对多变流器并网系统的稳定性判据及闭环极点关于各变流器的灵敏度进行了系统研究,提出了一种基于SISO dq阻抗判据的多变流器并网系统稳定性判据,简化了稳定性的分析过程并继承了单变流器阻抗判稳方法所具有的可从物理角度揭示失稳机理的优点;然后,在上述稳定性判稳公式的基础上,提出了一种用于分析闭环极点关于各变流器灵敏度的分析方法,结合判稳方法共同构建了多变流器并网系统小干扰稳定性分析及振荡源辨识的系统性方法;最后,结合仿真算例和硬件在环(Hardware-in-the-Loop, HIL)实验验证了本文所提方法的有效性。
不同于序阻抗模型,建立在dq坐标系下的阻抗模型及据此所建立的传递函数矩阵中各元素的表达式均为有理分式,从而使得其可依靠矢量匹配法获得系统闭环极点。因此,本文选择dq坐标系下的建模方法对系统进行描述。本部分重点给出多变流器系统的dq坐标系下的数学模型的描述方法。
多变流器并网系统示意图如图1所示,其含有n台变流器,新能源电源及储能通过逆变器接入电网,其中部分逆变器采用跟网型控制,另部分采用构网型控制,线路网络可为任意拓扑结构。

图1 多变流器并网系统示意图
Fig.1 Diagram of multi-converter grid-tied system
就CCI而言,由于其前级变流器(如两级式光伏变流器的前级为DC-DC变换器、风机的机侧变流器为AC-DC变流器)一般采用最大功率点跟踪的控制方式,故跟网型变流器的控制策略一般采用直流电压外环控制和电流内环控制,因此,跟网型变流器的外特性主要表现为电流源。这说明该类变流器在连接无穷大电压源时可稳定运行,即其输出导纳不存在RHP极点。鉴于上述原因,跟网型变流器适合采用诺顿等效电路进行描述。式(1)给出了采用定直流电压控制下的跟网型变流器的dq导纳矩阵表达式,即
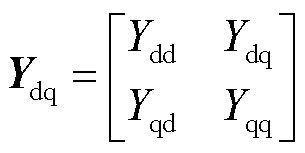 (1)
(1)
式中,Ydd和Yqq分别为d轴和q轴自导纳;Ydq和Yqd为d轴和q轴的耦合项,具体表达式可参见文献[31]。关于该dq导纳的准确性验证将在2.3节给出。
不同于CCI,VCI对外呈现电压源特性,这说明当其连接理想电流源时系统可稳定运行,故其输出阻抗不含有RHP极点,因此适宜采用戴维南等效电路进行描述。本文所选用的构网型逆变器为基于虚拟同步机(Virtual Synchronous Generator, VSG)的控制策略,其dq阻抗的表达式为
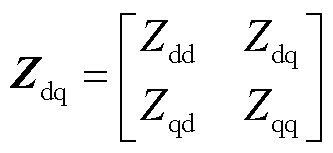 (2)
(2)
式中,Zdd和Zqq分别为d轴和q轴自阻抗;Zdq和Zqd为d轴和q轴的耦合项,具体表达式可参见文献[32]。关于该dq阻抗的准确性验证亦在2.3节给出。
对于不同馈入位置的变流器,其dq坐标系都是建立在自身并网点的局部坐标系之上,但在分析整个系统的小干扰稳定时,必须统一坐标系。该全局坐标系可以任意选择,具体地,本文选择图1中与电网的连接点建立全局坐标系,因此,各变流器在局部坐标系(下标为“local”)下电压和电流的dq分量与全局坐标系(下标为“global”)下的分量映射关系为[33]
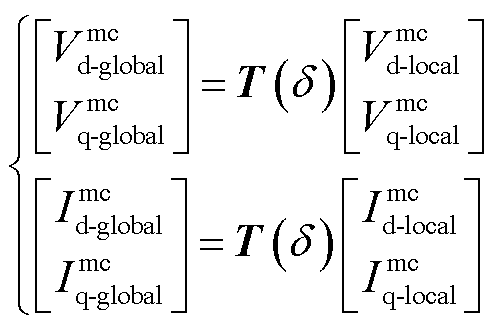 (3)
(3)
其中变换矩阵为
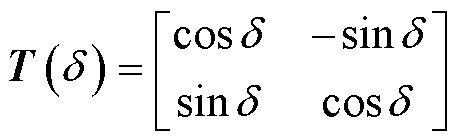
式中,δ为局部坐标系超前于全局坐标系的相位。基于式(3),可将各变流器的dq阻抗/导纳转换至全局坐标系下,即
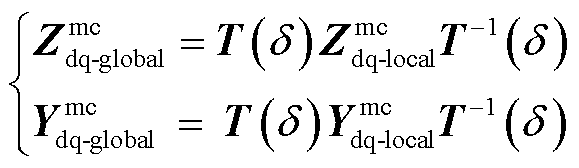 (4)
(4)
为行文简便,下文中所有阻抗/导纳均是建立在全局dq坐标系之下,不再在下标中体现“global”字样。
对图1所示的多变流器并网系统进行分析,可将整个系统分解为含变流器的“变流器有源系统”和不含变流器“电力网络无源系统”。鉴于1.2节和1.3节中关于阻抗/导纳RHP极点的阐述,在小干扰稳定性分析时,宜将CCI视为诺顿电路,同时将VCI视为戴维南电路,因此,对于含有n个变流器的“变流器有源系统”的数学描述为
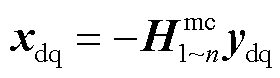 (5)
(5)
其中
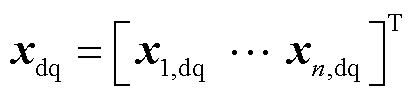
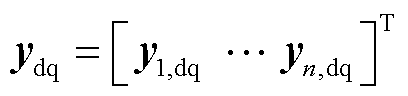
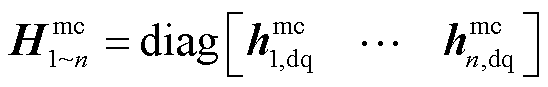
上述向量及矩阵中元素的具体含义为
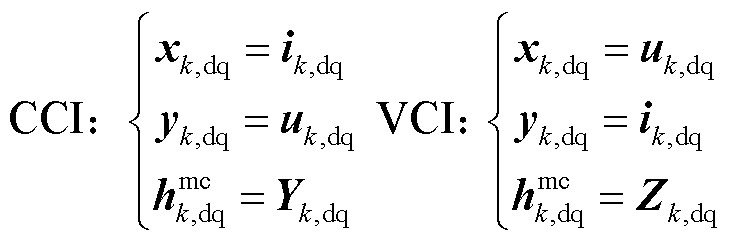 (6)
(6)
采用上述描述方式可避免在基于奈奎斯特稳定性判据时对变流器阻抗/导纳的RHP极点的判断,从而使得稳定性分析过程得以简化。
为与式(5)相适应,“电力网络无源系统”则应采用混合参数进行描述,即
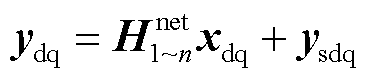 (7)
(7)
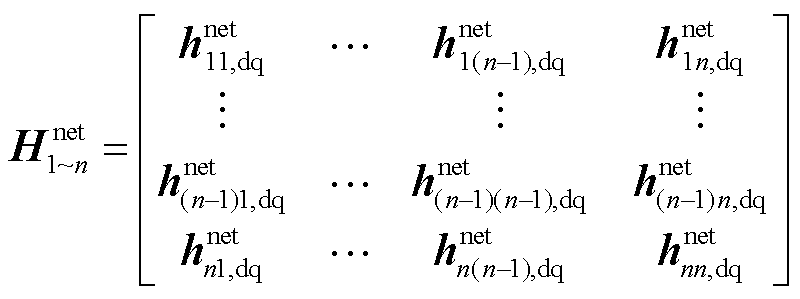
式中,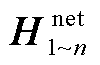 为“电力网络无源系统”的混合参数矩阵;ysdq为外部扰动源矩阵。考虑到直接建立上述混合参数矩阵存在困难,其可由短路导纳参数矩阵间接得到,下面给出具体过程。首先,可基于节点电压法获得“电力网络无源系统”的节点电压方程,即
为“电力网络无源系统”的混合参数矩阵;ysdq为外部扰动源矩阵。考虑到直接建立上述混合参数矩阵存在困难,其可由短路导纳参数矩阵间接得到,下面给出具体过程。首先,可基于节点电压法获得“电力网络无源系统”的节点电压方程,即
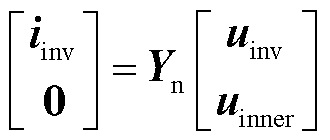 (8)
(8)
其中
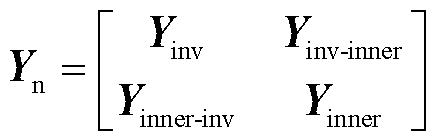
式中,iinv为各变流器注入其所连接端口的电流列向量;uinv和uinner分别为各变流器所连端口的电压列向量和电力网络中内部节点的电压列向量;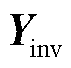 为以变流器dq导纳矩阵作为对角块构成的导纳矩阵;
为以变流器dq导纳矩阵作为对角块构成的导纳矩阵; 为电力网络内部节点的自导纳矩阵;
为电力网络内部节点的自导纳矩阵;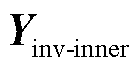 和
和 为变流器连接点与电力网络内部节点之间的互导纳矩阵。
为变流器连接点与电力网络内部节点之间的互导纳矩阵。
式(8)节点导纳矩阵可视为以各个节点相对于系统参考接地点所形成的多端口网络的短路导纳参数矩阵,由于网络中内部节点不与外电路相连,故可以基于“开路抑制”法将其消去,从而得到仅含外部节点的多端口网络的短路导纳参数为
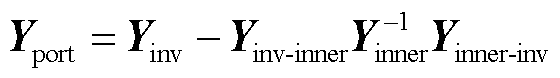 (9)
(9)
在上述基础上,可根据短路导纳参数和混合参数的转换关系获得电力网络的混合参数矩阵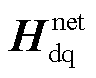 。
。
本部分提出了一种基于SISO dq阻抗比判据的多变流器并网系统稳定性的分析方法。该方法可将整个MIMO系统的稳定性分析转换为对若干SISO系统的稳定性分析,从而有效降低MIMO系统高阶回率矩阵特征值求解的难度及大量奈奎斯特曲线分析的复杂性。需要指出,该方法还继承了SISO阻抗法所具有的从物理角度揭示失稳机理的优点。
对于图1所示的多变流器并网系统,结合式(5)和式(7)所给出的“变流器有源系统”和“电力网络无源系统”二者的数学表达式,可绘制图2所示的等效框图,该系统可视为一个MIMO负反馈系统,从而可利用广义奈奎斯特稳定性判据进行系统稳定性分析。
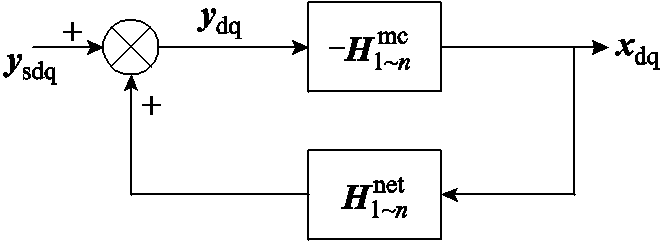
图2 多变流器并网系统等效框图
Fig.2 Equivalent diagram of multi-converter grid-connected system
根据图2,可得其输入输出的闭环传递关系为
 (10)
(10)
其中
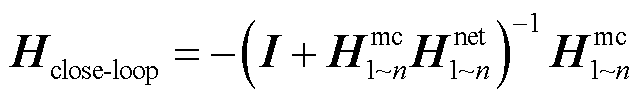
式中,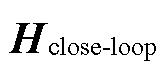 为整个系统的闭环传递函数矩阵,与之对应的回差矩阵和回率矩阵分别为
为整个系统的闭环传递函数矩阵,与之对应的回差矩阵和回率矩阵分别为
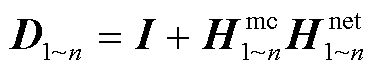 (11)
(11)
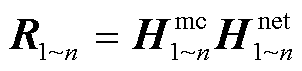 (12)
(12)
根据广义奈奎斯特稳定性判据,图2所示闭环系统的RHP极点个数为
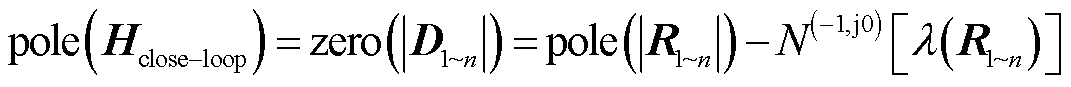 (13)
(13)
式中,zero(·)表示零点个数;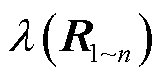 为回率矩阵的特征值;
为回率矩阵的特征值;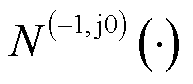 表示
表示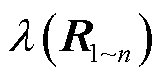 从-∞~+∞的奈奎斯特曲线逆时针围绕(-1, j0)点的圈数。
从-∞~+∞的奈奎斯特曲线逆时针围绕(-1, j0)点的圈数。
考虑到并网稳定性分析的前提为CCI/VCI单独连接理想电压/电流源时可稳定运行,故采用dq导纳/阻抗矩阵对二者进行建模时矩阵元素均不含有RHP极点;同时,由于电力网络无源,其混合参数亦不存在RHP极点。因此,根据式(12)有
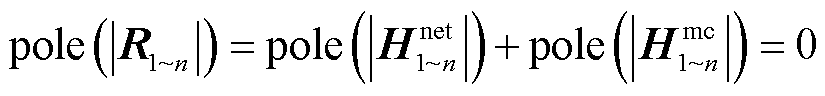 (14)
(14)
将式(14)代入式(13),则有
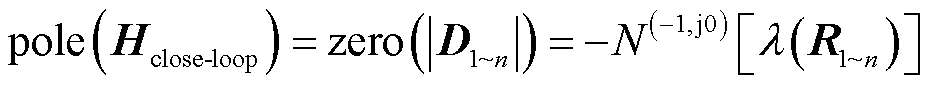 (15)
(15)
虽然理论上可以利用式(15)实现整个系统的稳定性分析,但对于多变流器系统,回差矩阵R1~n的阶次将较高,其特征值计算会存在一定误差。而且,由于各频点下R1~n的特征值需单独计算,容易造成部分频点下的特征值彼此之间发生跳变,因此准确地判断大量的特征值幅相曲线围绕(-1, j0)的圈数并非易事。此外,广义奈奎斯特判据亦不能对振荡失稳机理作出物理解释,因此,式(15)的稳定性分析方法在准确性、实用性及机理揭示功能上仍需改进。
考虑到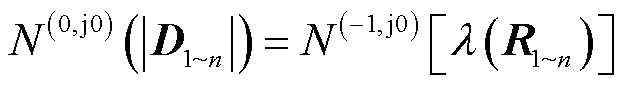 ,式(15)可改写为
,式(15)可改写为
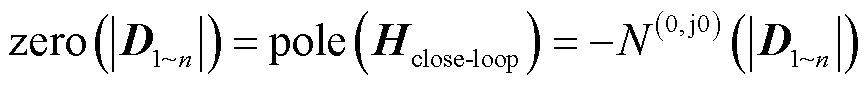 (16)
(16)
相比于式(15),式(16)虽可避免特征值计算及大量的特征值奈奎斯特曲线分析,但该方法丧失了阻抗分析法所具备的从物理角度揭示振荡失稳机理的优势,同时,该方法仅能给出整个系统的稳定性分析结果,无法分析各个变流器对系统稳定性的影响。因此,本文希望提出一种简便易行且具有揭示振荡失稳机理功能的稳定性分析方法。
基于式(5)和式(7),将矩阵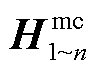 和
和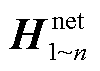 写为
写为
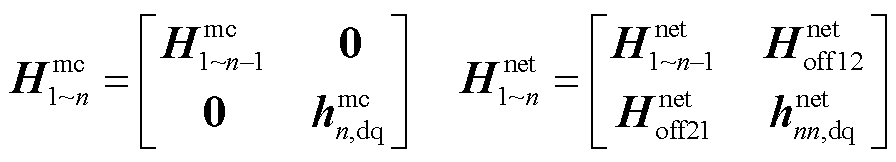 (17)
(17)
其中
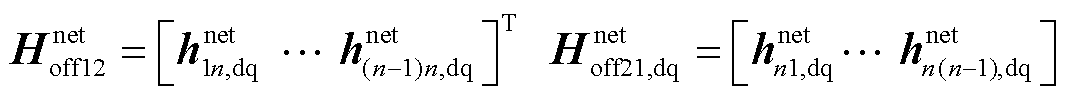
同时将其代入式(11),则回差矩阵行列式可改写为
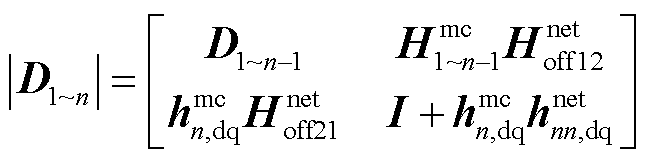 (18)
(18)
经推导,式(18)可写为
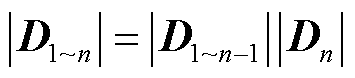 (19)
(19)
其中
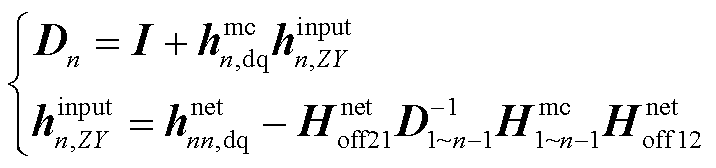 (20)
(20)
可以证明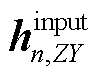 为1~n-1端口连接相应逆变器下从第n个端口看入的输入阻抗或导纳,具体推导过程参见附录式(A1)~式(A5)。
为1~n-1端口连接相应逆变器下从第n个端口看入的输入阻抗或导纳,具体推导过程参见附录式(A1)~式(A5)。
观察式(19),还可发现其具有递归形式,故可以将式(19)进一步写为
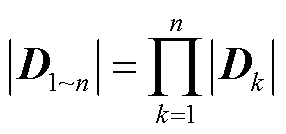 (21)
(21)
其中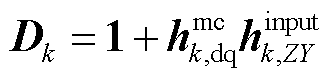 。将式(21)代入式(16),可得
。将式(21)代入式(16),可得
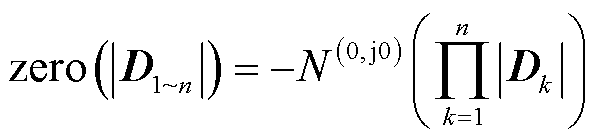 (22)
(22)
根据奈奎斯特稳定性判据,有
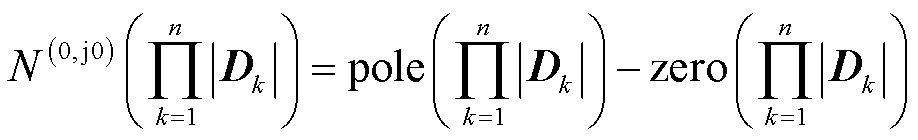 (23)
(23)
考虑到具有连乘形式表达式的零极点具有如下性质
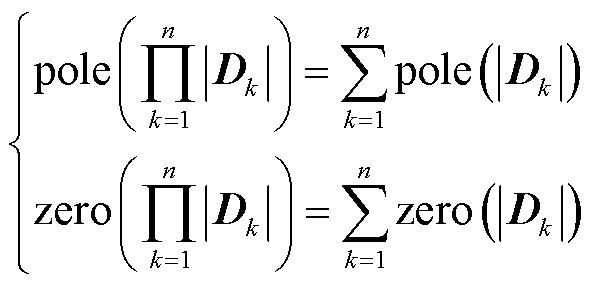 (24)
(24)
将式(24)代入式(23)可得
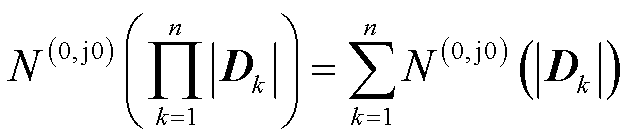 (25)
(25)
所以式(22)可改写为
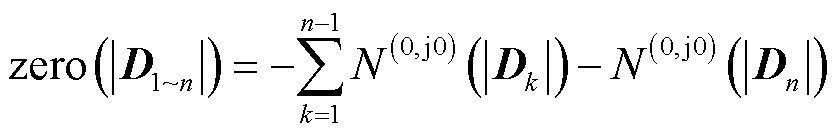 (26)
(26)
结合式(22),式(26)可改写为
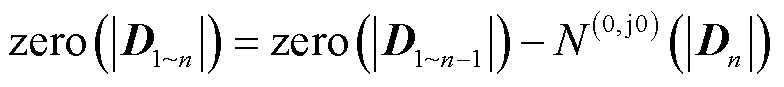 (27)
(27)
由式(20)可知,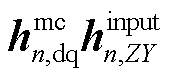 可视为在1~n-1端口接入相应逆变器的基础上在第n个变流器接入系统所对应的回率矩阵,因此,式(27)可进一步表示为
可视为在1~n-1端口接入相应逆变器的基础上在第n个变流器接入系统所对应的回率矩阵,因此,式(27)可进一步表示为
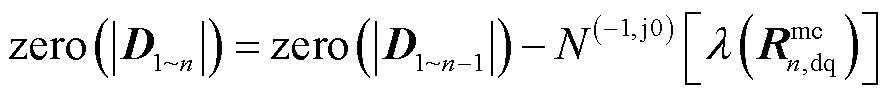 (28)
(28)
式中,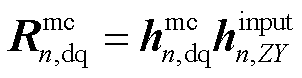 。从式(28)可以看出,整个系统的稳定性不仅取决于变流器n与其外接网络构成回率矩阵特征值,还取决于由1~n-1个变流器构成的有源系统回差矩阵行列式的零点数量,即RHP极点的数量。相比于式(15)中的
。从式(28)可以看出,整个系统的稳定性不仅取决于变流器n与其外接网络构成回率矩阵特征值,还取决于由1~n-1个变流器构成的有源系统回差矩阵行列式的零点数量,即RHP极点的数量。相比于式(15)中的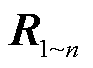 ,式(28)中的
,式(28)中的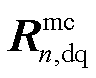 仅为2×2矩阵,其特征值可解析计算且仅需观察两条特征值的奈奎斯特曲线即可实现稳定性分析,分析过程大为简化。
仅为2×2矩阵,其特征值可解析计算且仅需观察两条特征值的奈奎斯特曲线即可实现稳定性分析,分析过程大为简化。
观察式(28)可知,其同样具有递归形式,因此可以分步骤完成整个系统的稳定性分析,具体如图3所示。
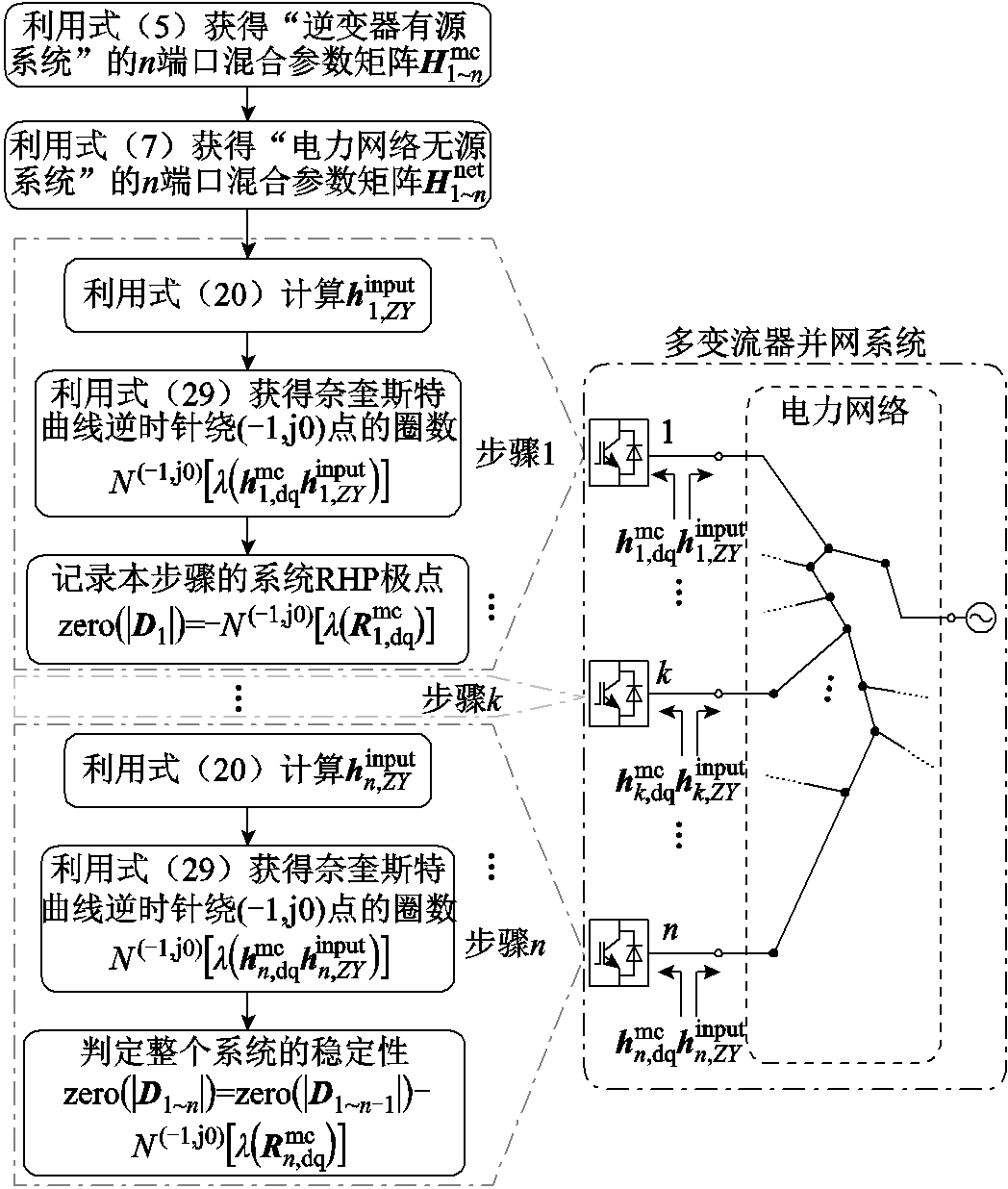
图3 多变流器并网系统的小干扰稳定性分析步骤
Fig.3 Stability analysis procedure for the multi-converters grid-tied system
在图3所示分析流程的每个步骤中,仅需对某个单变流器系统进行分析,相比于基于广义奈奎斯特判据的判稳过程,即式(15),其奈奎斯特曲线绕(-1, j0)点圈数分析的复杂度得以大为简化。
进一步,对于单变流器的稳定性分析可采用SISO等效判据,其奈奎斯特曲线逆时针绕(-1, j0)点的圈数为
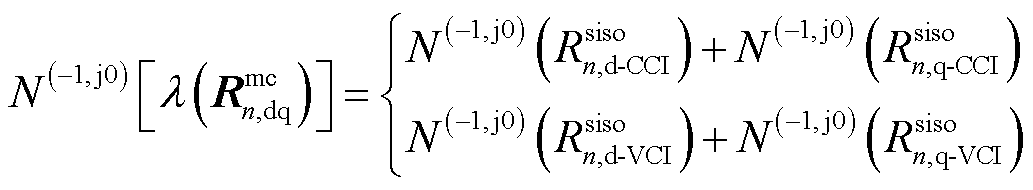 (29)
(29)
其中用于获得CCI和VCI的SISO dq轴阻抗比的计算公式分别为
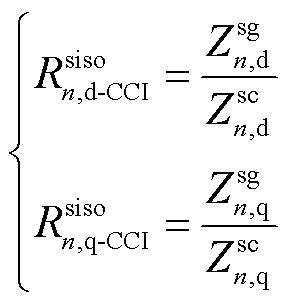 (30)
(30)
和
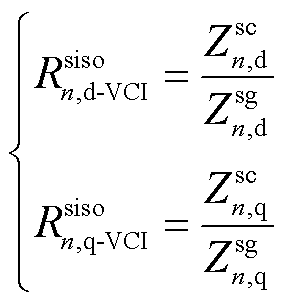 (31)
(31)
相应的d轴和q轴SISO阻抗计算公式[31]为
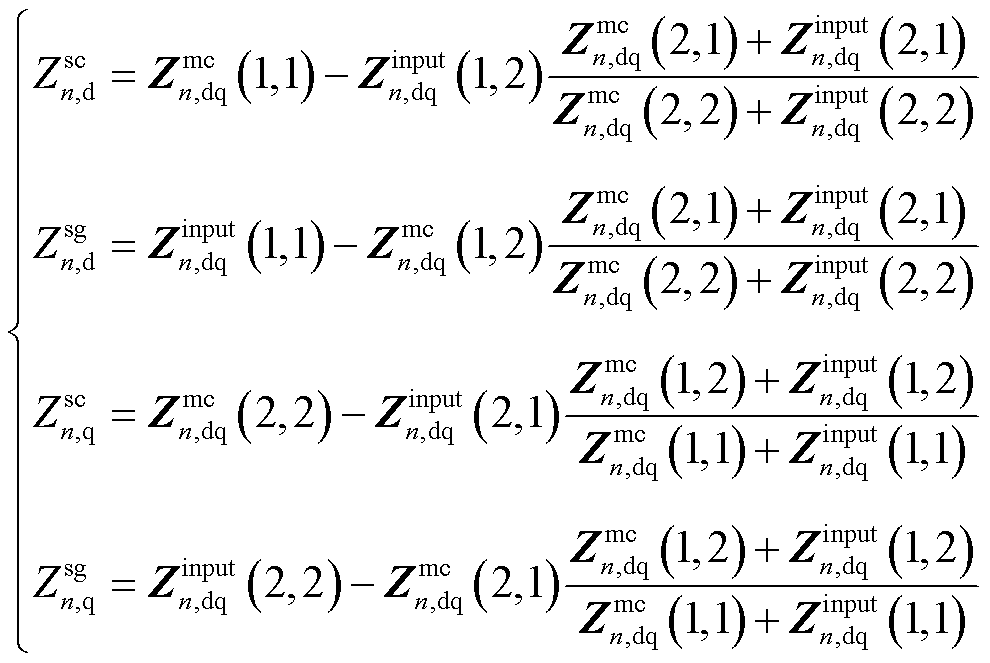 (32)
(32)
其中,对于CCI,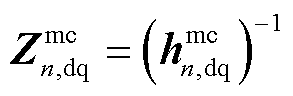 ,
,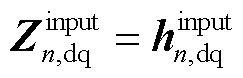 ;对于VCI,
;对于VCI,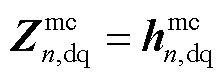 ,
,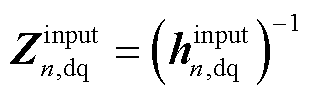 。
。
附录第2节中给出了单个CCI和VCI变流器接入电网的SISO dq阻抗理论公式计算结果和扫频结果,经对比可知,二者吻合良好,说明了本文CCI和VCI的SISO dq阻抗理论计算的正确性。
基于上述推导,最终可利用式(28)和式(29)实现多变流器并网系统的稳定性分析。假设一个由n个变流器所构成的系统,整个稳定性分析步骤可分解为n步,在每个步骤中,仅需绘制两条SISO dq轴阻抗比奈奎斯特曲线或者Bode图即可实现系统的稳定性分析。而且,这种基于SISO dq阻抗比的判稳方法还可对振荡失稳机理给出物理解释。上述所提稳定性分析方法的有效性将在第4节通过算例予以验证。
不同于序阻抗法,基于dq阻抗/导纳法所获得的系统回差矩阵行列式为有理分式,为进一步获得系统闭环极点(振荡模态)创造了条件。由于整个多变流器系统的闭环极点等于系统回差矩阵行列式的零点λ,因此根据式(21)有
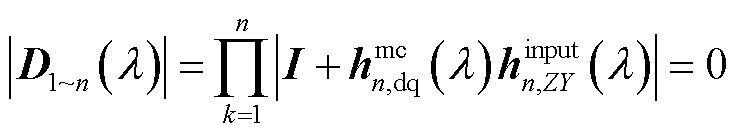 (33)
(33)
数学形式上,式(33)为图3中各步骤所对应的回差矩阵行列式之积,粗略上看,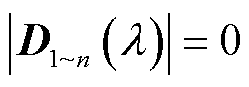 的零点为各步骤中回差矩阵行列式的零点的总和。但如此则意味着判稳过程中,如果先前步骤所对应的系统不稳定,后续接入的变流器也无法使得系统恢复稳定,这显然与事实不符。因此,并不能直接通过式(33)来获得闭环极点,必须进行更进一步的分析。
的零点为各步骤中回差矩阵行列式的零点的总和。但如此则意味着判稳过程中,如果先前步骤所对应的系统不稳定,后续接入的变流器也无法使得系统恢复稳定,这显然与事实不符。因此,并不能直接通过式(33)来获得闭环极点,必须进行更进一步的分析。
根据式(19),闭环极点亦可通过下式计算。
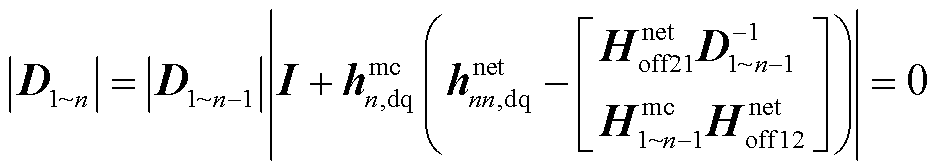 (34)
(34)
根据克莱姆法则,矩阵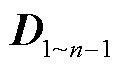 的逆为
的逆为
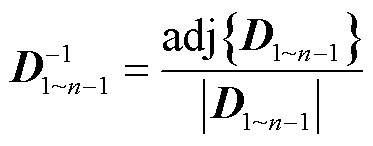 (35)
(35)
式中,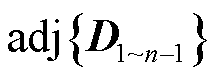 为
为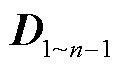 的伴随矩阵。将式(35)代入式(34),可得
的伴随矩阵。将式(35)代入式(34),可得
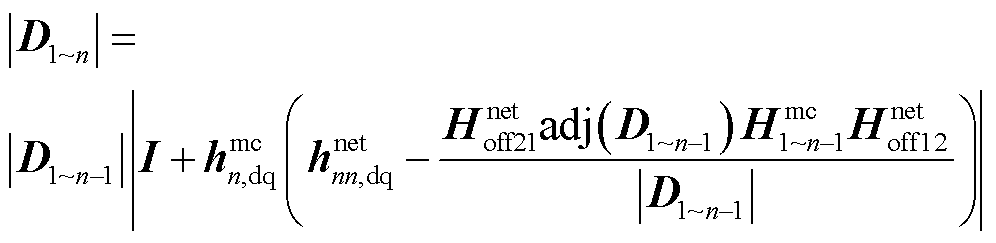 (36)
(36)
从式(36)可以看出,位于分子位置的回差矩阵行列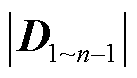 与分母进行了对消,因此,第1~n-1步的回差矩阵行列式的零点并不会在第n步被保留下来,极点将会重新分布。最终,根据式(36)可得用于计算整个系统闭环极点的表达式为
与分母进行了对消,因此,第1~n-1步的回差矩阵行列式的零点并不会在第n步被保留下来,极点将会重新分布。最终,根据式(36)可得用于计算整个系统闭环极点的表达式为
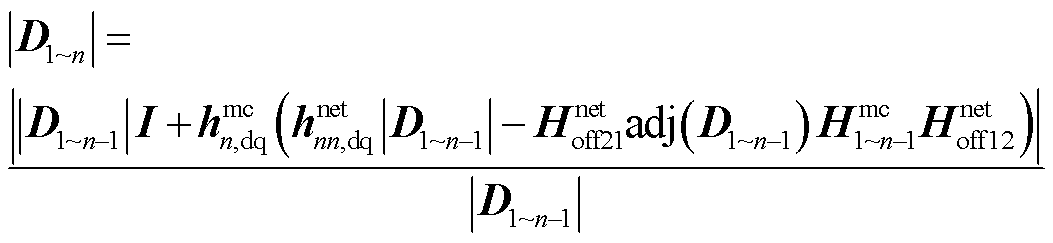 (37)
(37)
因此,可通过对式(37)进行扫频,继而利用矢量匹配法即可获得系统的闭环极点。
本部分以第m个闭环极点λm关于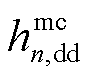 的绝对灵敏度为例进行推导。当第n台变流器的d轴阻抗/ 导纳发生
的绝对灵敏度为例进行推导。当第n台变流器的d轴阻抗/ 导纳发生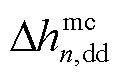 变化时,相应的闭环极点也将发生变化,将其记为
变化时,相应的闭环极点也将发生变化,将其记为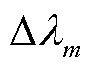 ,因此有
,因此有
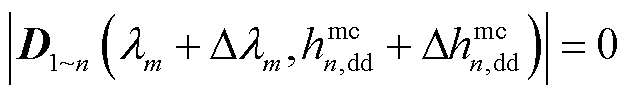 (38)
(38)
将式(38)在点λm进行一阶泰勒级数展开,可得
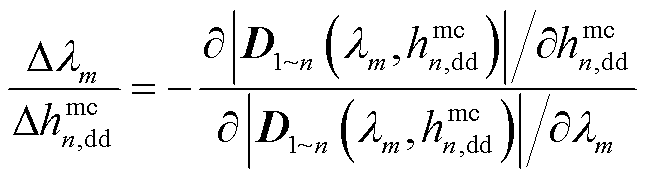 (39)
(39)
借助洛必达法则,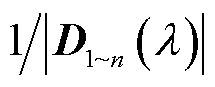 的留数可表达为
的留数可表达为
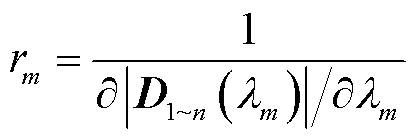 (40)
(40)
将式(40)代入式(39),则第m个系统闭环极点λm关于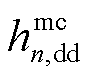 的绝对灵敏度为
的绝对灵敏度为
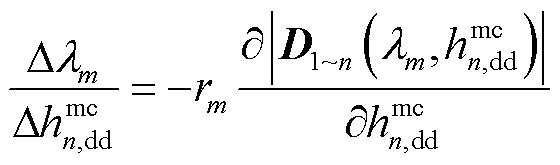 (41)
(41)
将式(21)代入式(41),同时考虑到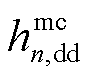 只是
只是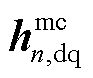 的元素,且由于第n个变流器被最后接入系统,故
的元素,且由于第n个变流器被最后接入系统,故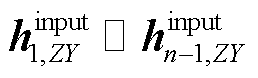 及
及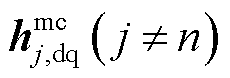 中均不会含有
中均不会含有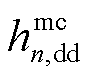 ,故有
,故有
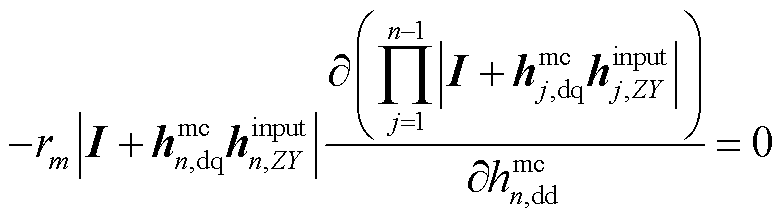 (42)
(42)
所以式(41)可以化简为
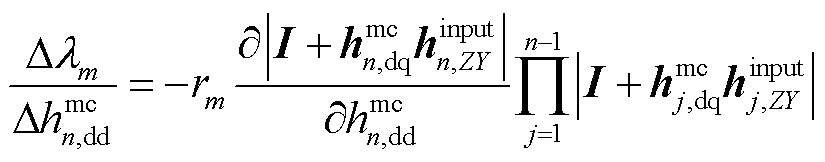 (43)
(43)
进一步,式(43)中的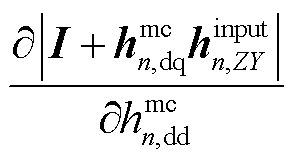 可写为
可写为
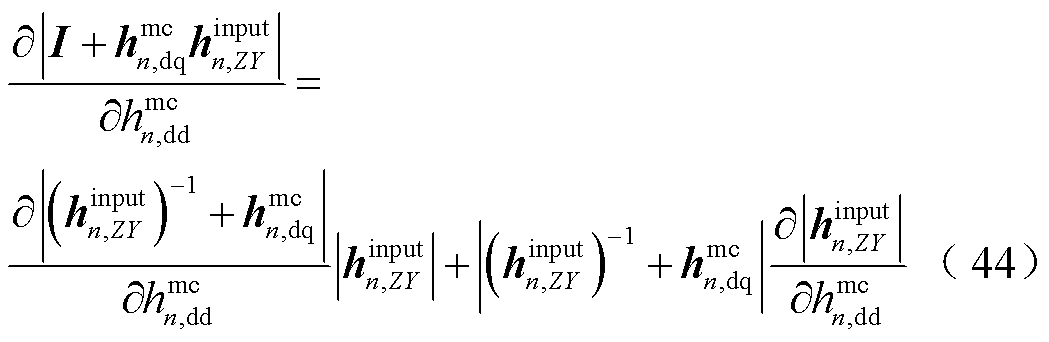
同时考虑到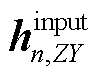 与
与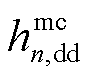 无关,故式(44)中
无关,故式(44)中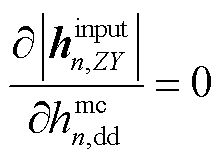 ,则式(44)可最终写为
,则式(44)可最终写为
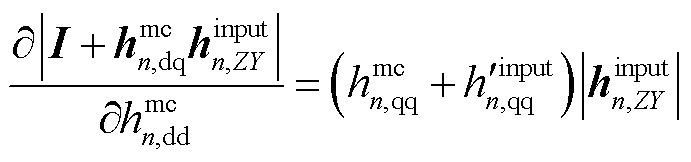 (45)
(45)
式中,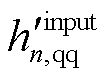 为矩阵
为矩阵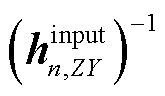 的第2行第2列元素。将式(45)代入式(43),可得第m个系统闭环极点λm关于
的第2行第2列元素。将式(45)代入式(43),可得第m个系统闭环极点λm关于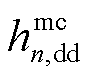 的灵敏度计算公式为
的灵敏度计算公式为
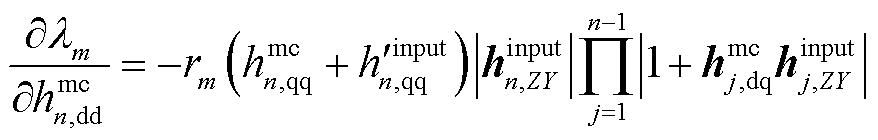 (46)
(46)
同理可得第m个闭环极点λm关于第n个变流器dq阻抗/导纳矩阵中4个元素的灵敏度分别为
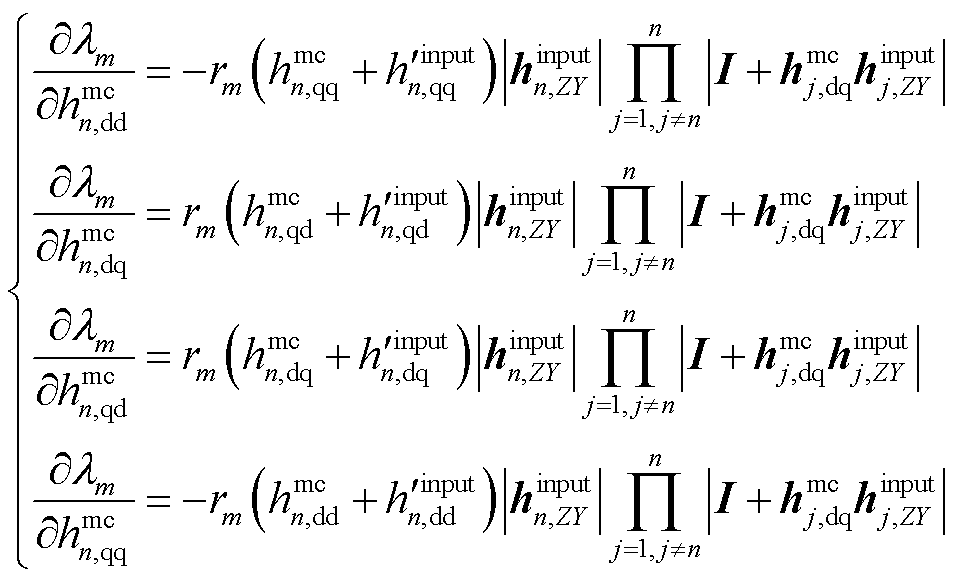 (47)
(47)
具体计算时,可将待分析变流器接入顺序置于最后,利用式(47)即可实现系统闭环极点关于该变流器的灵敏度分析。
本节通过Matlab/Simulink仿真和HIL实验对所提出的稳定性判据及闭环极点关于各变流器dq阻抗灵敏度公式的有效性进行验证。采用的多变流器系统如图4所示,其中电力网络的详细参数列于附录附表1中,各变流器的具体参数将在各算例中给出。需要指出的是,本节算例均基于该拓扑结构,但不同算例中所包含的变流器数量和参数有所不同,以从多种场景验证本文方法的正确性。
图4 多变流器并网系统拓扑结构
Fig.4 Topology of multi-converter grid-tied system
本算例的分析对象为由图4中4个CCI所构成的系统,用以分析仅含跟网型逆变器CCI系统的小干扰稳定性,详细参数列于附表2中。0.1 s前,电网电感为0.6 mH,此阶段系统可以稳定运行。0.1 s时,电网电感增加至0.75 mH,利用所提出的判稳方法得到各步骤中SISO dq阻抗比的奈奎斯特曲线如图5所示,其顺时针绕(-1, j0)点的圈数及系统稳定性分析结果总结于表1中。由图5可以看出,在CCI 1和CCI 2的基础上接入CCI 3所对应的奈奎斯特曲线顺时针绕(-1, j0)两圈(由于此时奈奎斯特曲线近似穿越(-1, j0),故可认为系统近似处于临界稳定状态),此时系统将发生振荡而无法稳定运行。对于同时含有CCI 1~4的多变流器并网系统,根据本文稳定性判据,其RHP闭环极点数量为
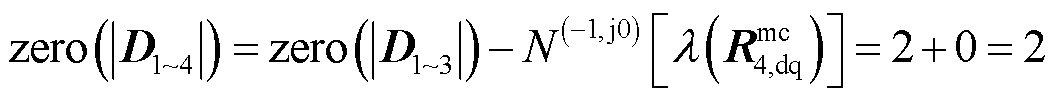 (48)
(48)
故可判定此时系统亦不稳定。
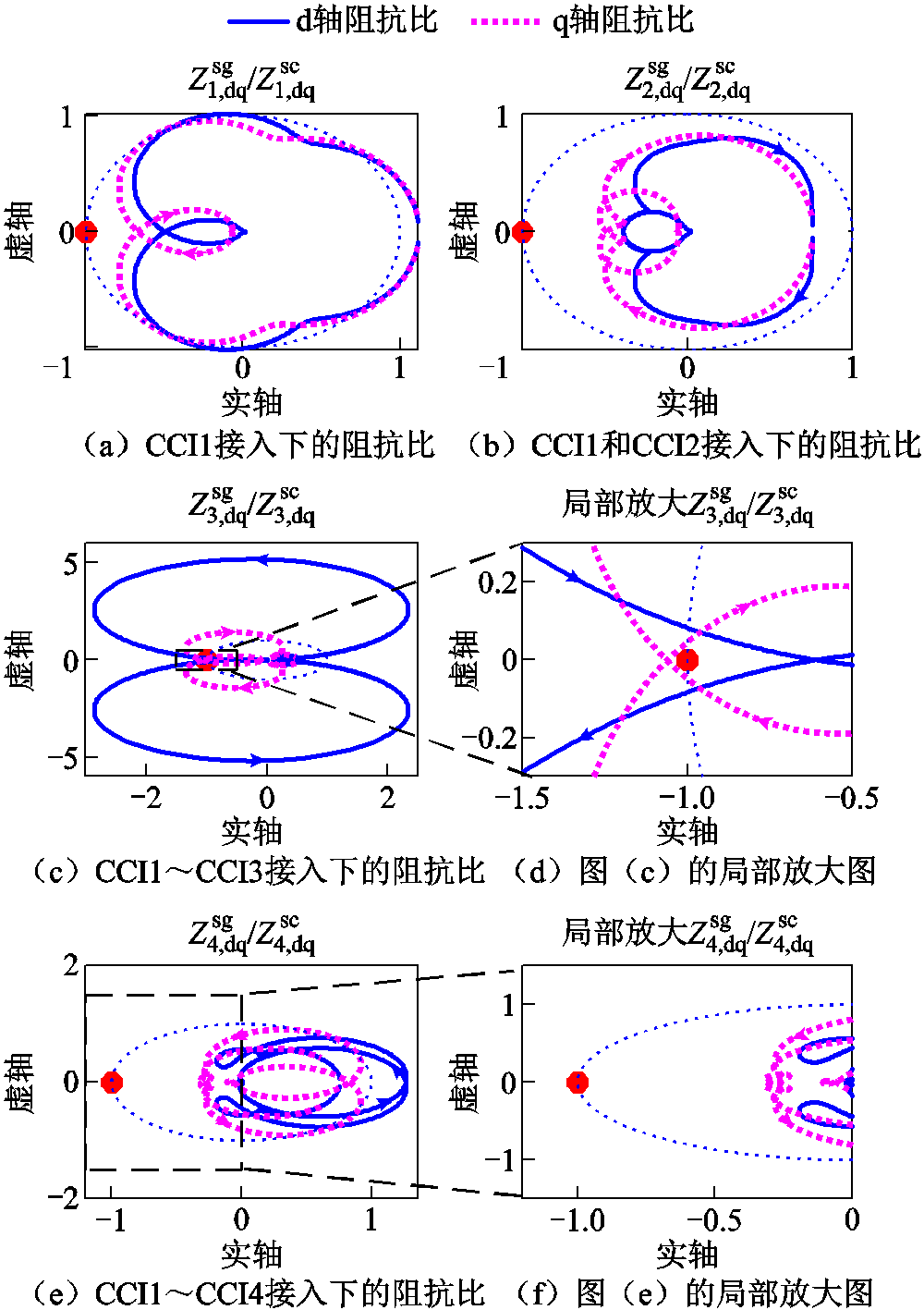
图5 稳定性分析步骤中SISO dq阻抗比的奈奎斯特曲线
Fig.5 Nyquist plots of SISO dq impedance ratio
表1 稳定性分析结果
Tab.1 Results of stability analysis

步骤零点RHP极点数稳定性 100稳定 200稳定 322临界稳定 402不稳定
在Matlab/Simulink中搭建上述系统的仿真模型,电网电感取0.75 mH,分别在0.25 s、0.75 s和1.25 s依次接入CCI 2、CCI 3和CCI 4,所得各变流器输出电流如图6所示。可以看出,在CCI 1和CCI 2接入系统时,系统可稳定运行,继而接入CCI 3后,系统发生振荡,并在CCI 4接入后迅速失去稳定。该仿真结果与表1所给出的稳定性分析结果一致,说明了本文所提出的稳定性判据的正确性。
对包含CCI 1~3共三台变流器系统的并网总电流进行快速傅里叶变换(Fast Fourier Transform, FFT)分析,结果如图7所示,可知系统在21 Hz和79 Hz存在次同步和超同步谐波分量。为了揭示上述振荡现象的机理,图8给出了CCI 3接入系统下的dq轴阻抗比伯德图,可以看出,在29.2 Hz,CCI 3的q轴阻抗与从其所连端口看入的阻抗模值相交截,该频率下对应的相位为182°,且随着频率升高,当二者阻抗比相位为180°时,其模值略大于1,说明在该频率下系统幅值裕度为负,系统振荡失稳。根据频率耦合效应,dq坐标系下的频率29.2 Hz在abc坐标系下所对应的频率为21.8 Hz和79.2 Hz,与图7所给出的电网电流的振荡频率基本一致,定量说明了本文所提出的稳定性判据的正确性。此外,经图8分析还可得出,逆变器SISO dq阻抗在29 Hz附近所呈现的负阻容性与外部系统所呈现的感性相互作用是造成系统振荡失稳的根本原因,说明本文方法保留了传统单变流器阻抗法所具有的从物理角度揭示振荡失稳机理的优点。
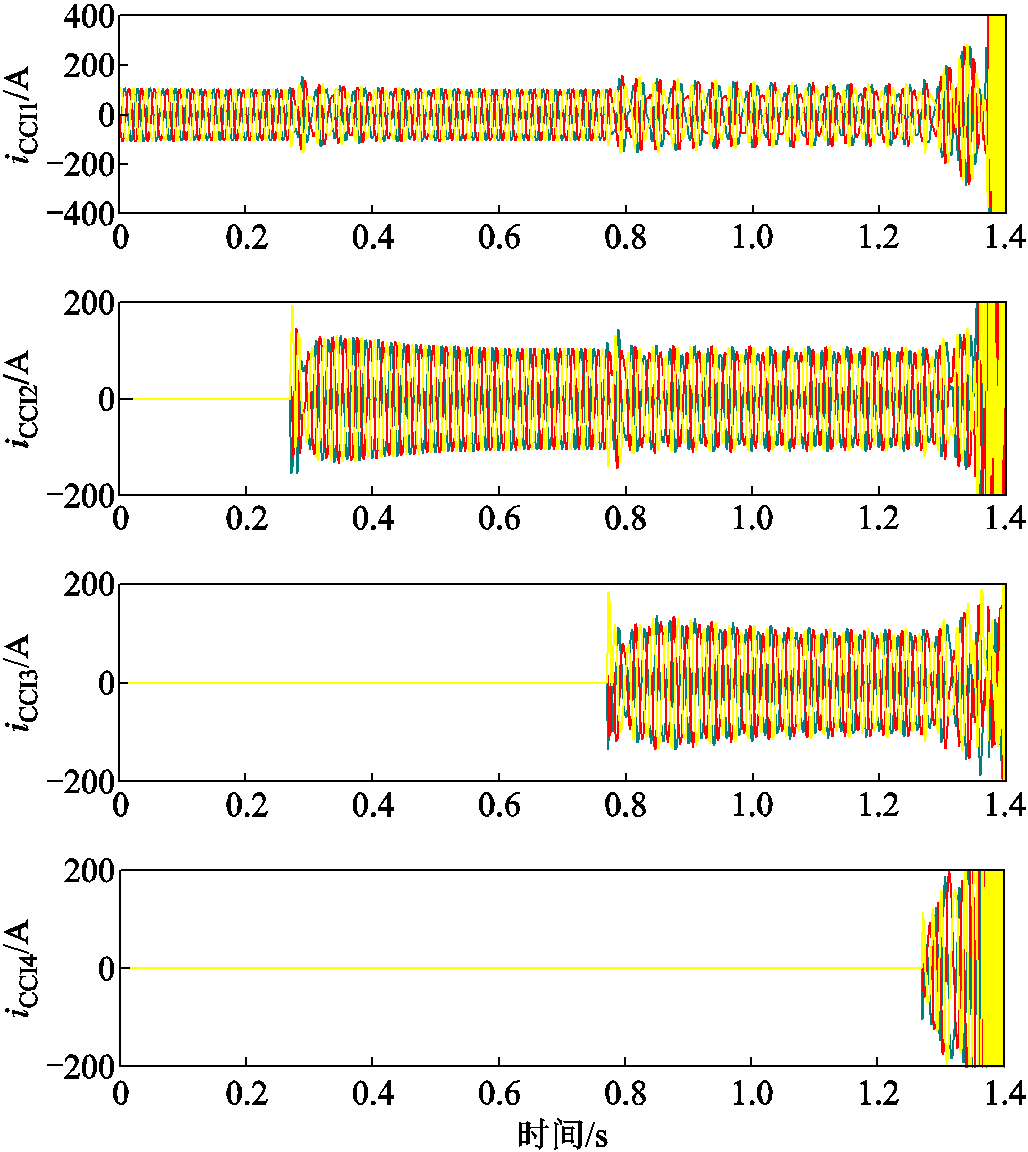
图6 分阶段投入4个CCI时各变流器的输出电流波形
Fig.6 Output current of each CCI when different converter connects to the grid
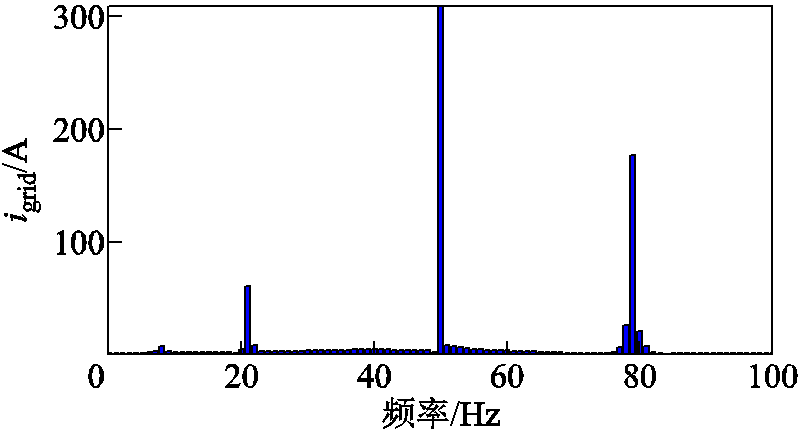
图7 并网电流的FFT分析
Fig.7 FFT analysis of grid current
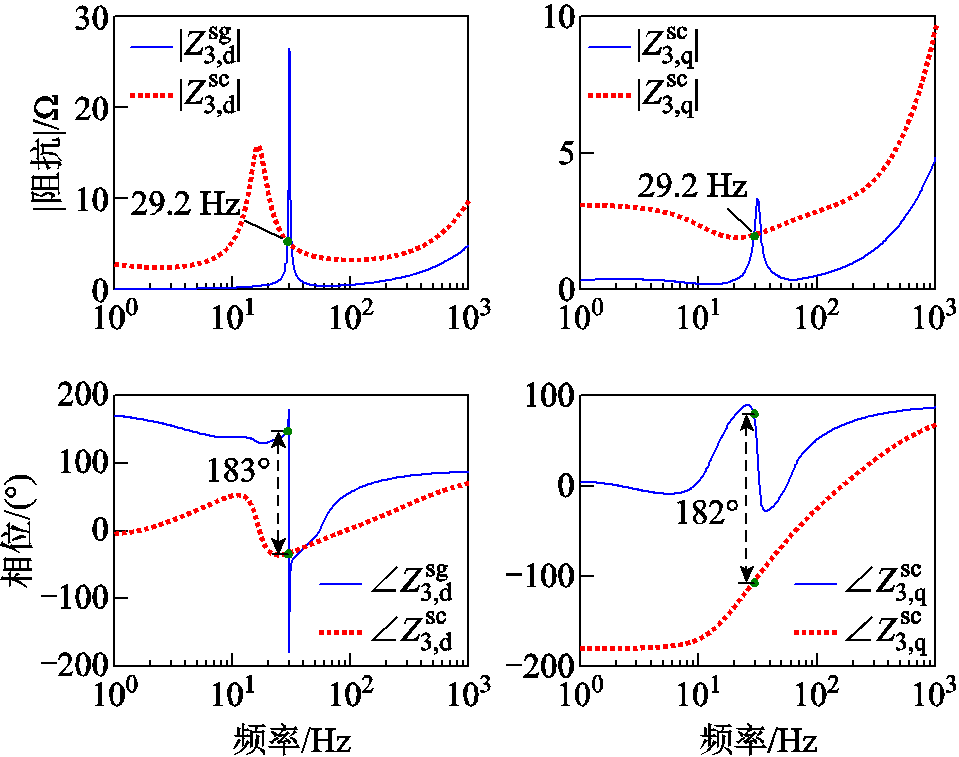
图8 CCI 1~3并网系统的dq阻抗比伯德图
Fig.8 Bode plots of SISO dq impedance ratio of the system containing CCI 1~3
为进一步分析各逆变器对系统稳定性的影响,结合式(37),经矢量匹配法计算可得该系统会存在一对不稳定的共轭闭环极点,大小为7.575± j183.658。利用本文所提灵敏度式(47)计算得到该闭环极点关于各变流器dq导纳的灵敏度如图9所示(以CCI 1的q轴灵敏度为基准进行标幺化)。
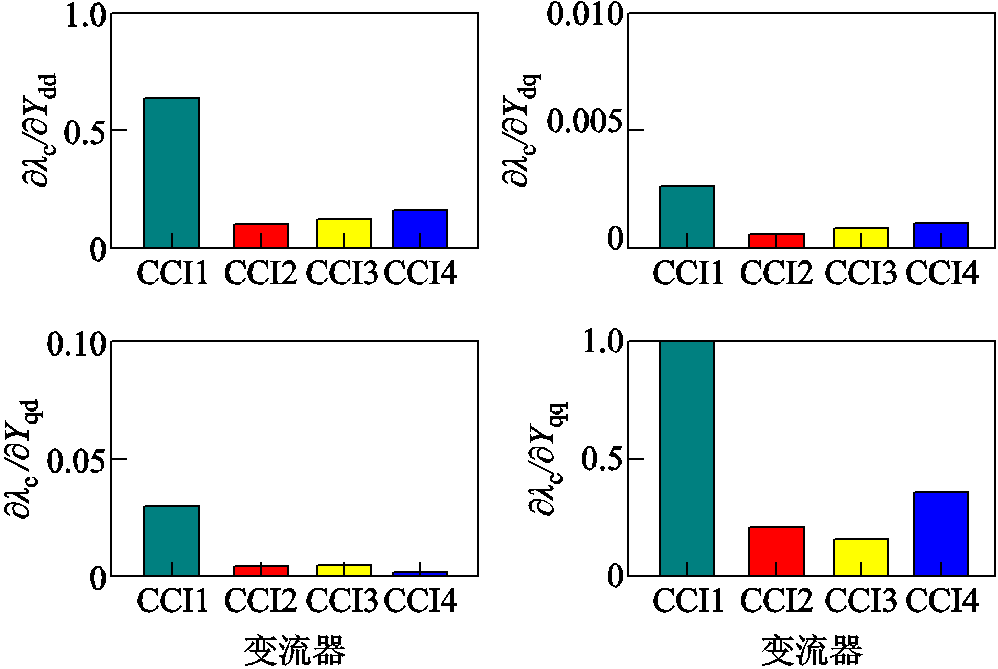
图9 不稳定闭环极点关于四个CCI的dq阻抗灵敏度
Fig.9 Sensitivity of unstable poles with respect to dq admittances of different converters
由图9可知,该闭环极点关于CCI 1的q轴导纳灵敏度最高,说明4个变流器中CCI 1的q轴导纳对系统小干扰稳定性影响最为显著,相比之下,CCI 4次之,CCI 2和CCI 3影响较小。为了验证上述灵敏度分析的正确性,图10给出了包含4台变流器的并网系统发生振荡后0.2 s切除CCI 1时各变流器输出的电流波形,可以看出,此时系统可很快恢复稳定。为进行对比,同样在振荡发生后0.2 s切除CCI 3的仿真结果如图11所示。可以看出,将其切除仍无法使系统恢复稳定,说明CCI 3对系统稳定性的影响明显弱于CCI 1。进一步,对比图11所示的各变流器的输出电流波形可知,CCI 1的电流相较于其他变流器振荡更为剧烈,说明CCI 1是造成系统振荡失稳的主要诱因。
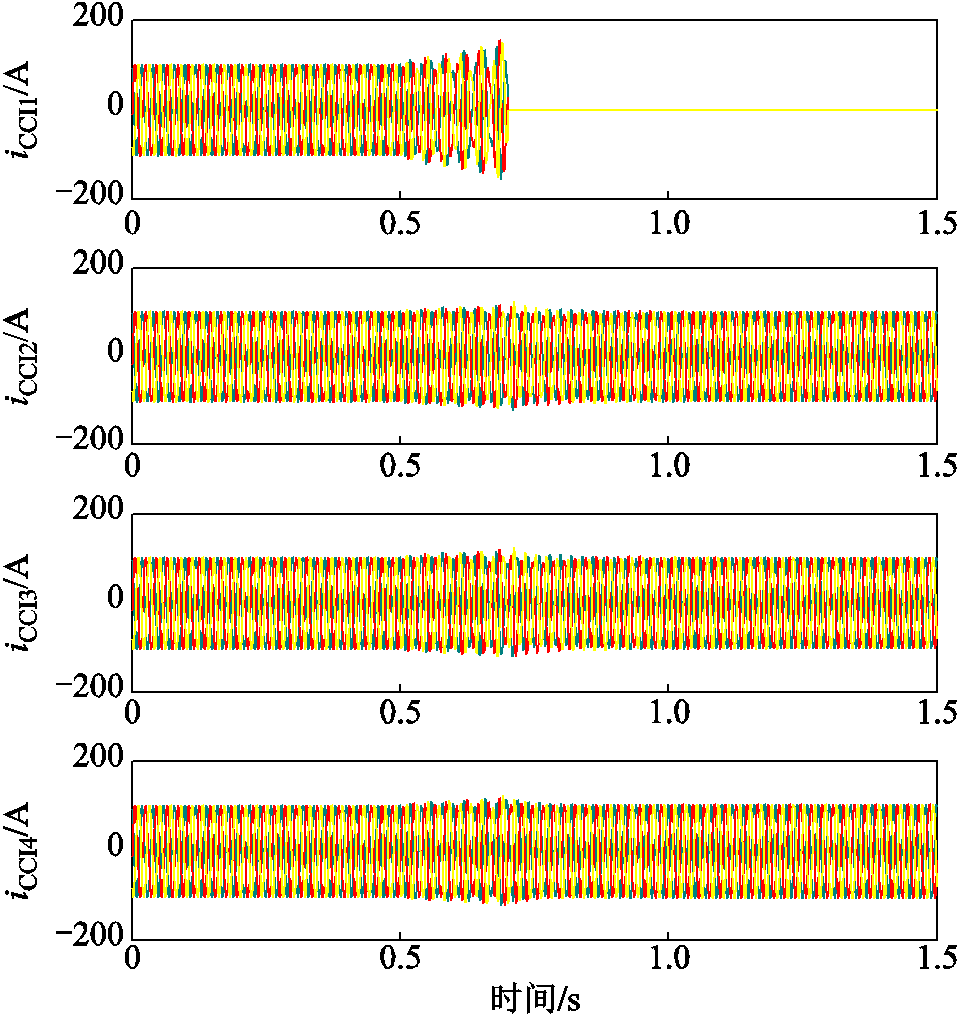
图10 切除CCI 1下的各变流器输出电流波形
Fig.10 Output current of each converter when disconnecting CCI 1
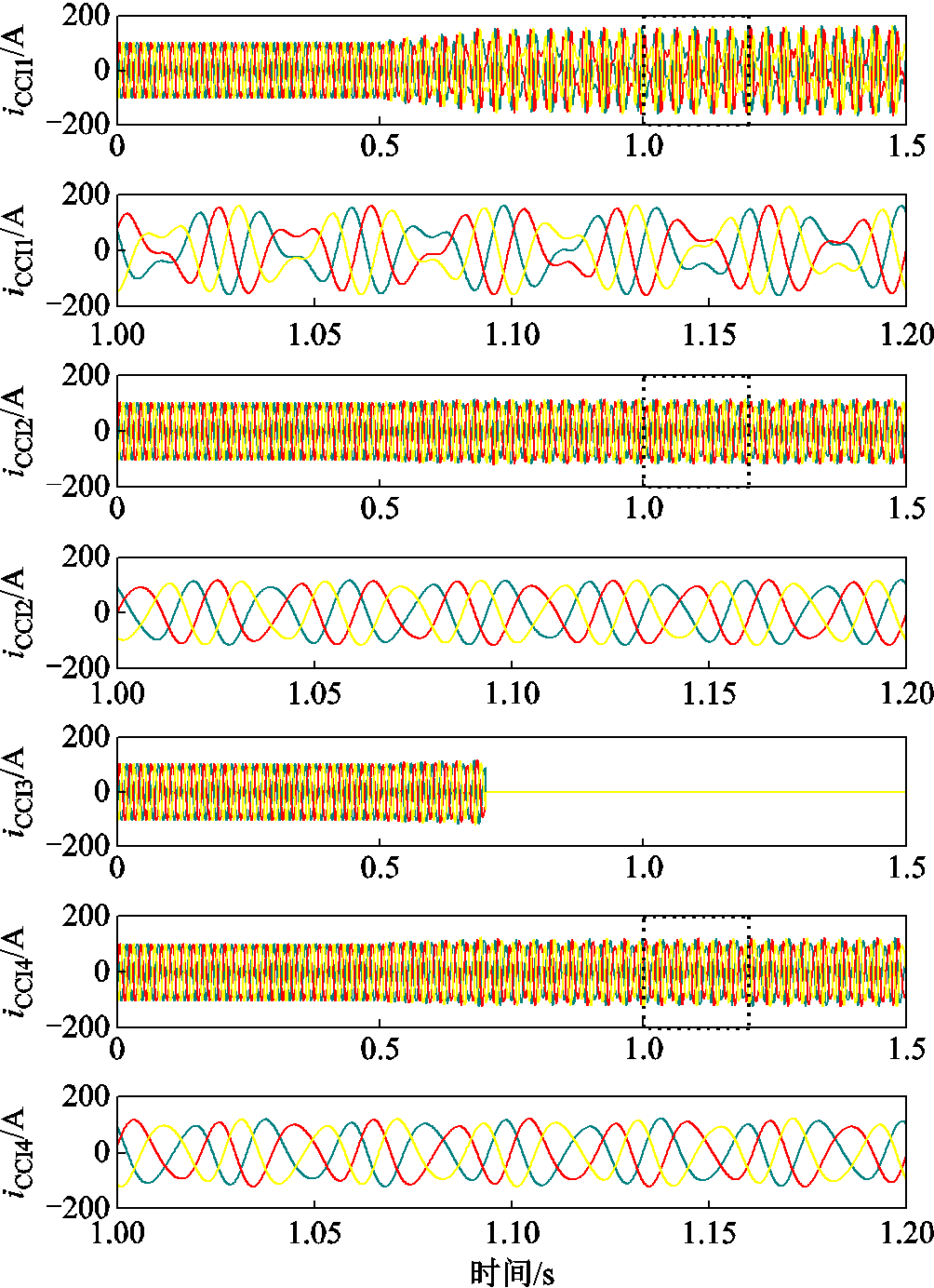
图11 切除CCI 3的各变流器输出电流波形
Fig.11 Output current of each converter when disconnecting CCI 3
图12给出了分别切除变流器CCI 1~4时并网总电流的FFT分析结果。切除CCI 1后,由于系统已恢复稳定,此时电网电流仅含有50 Hz稳态分量,而切除其他变流器,并网电流均在20 Hz和80 Hz左右存在次同步和超同步频率分量,且谐波含量从大到小的工况依次为“切除CCI 3”“切除CCI 2”和“切除CCI 4”,这与图9给出的灵敏度分析结果相吻合,从而验证了本文所提出的闭环极点关于变流器灵敏度分析方法的正确性。
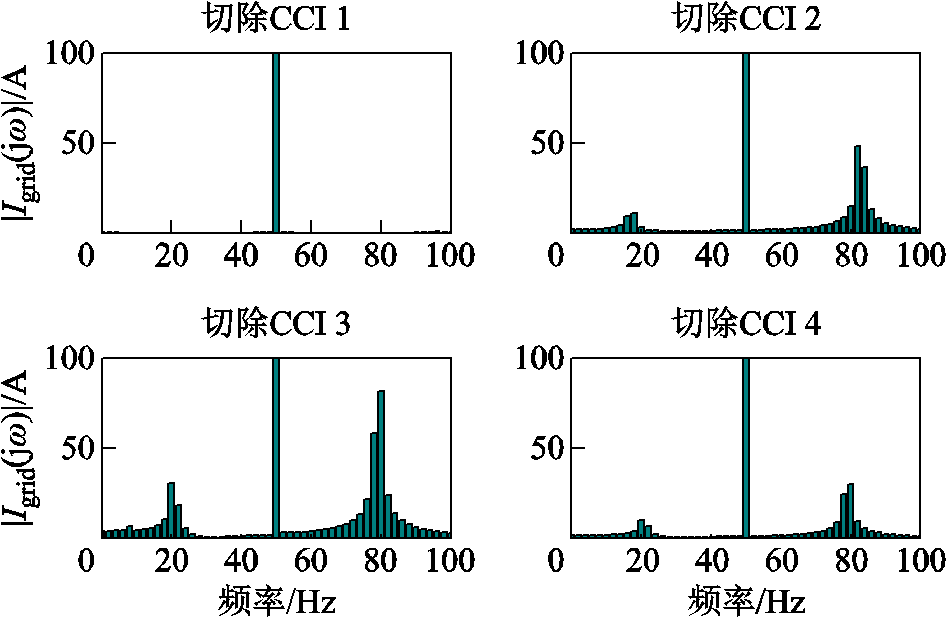
图12 切除各变流器的电网电流FFT分析结果
Fig.12 FFT analysis of grid current when disconnecting different converter
为进一步进行验证,采用同4.1节相同的算例开展HIL实验,实验平台如图13所示。实验平台采用NI PIXe-1082实时仿真机,电气回路仿真步长为1 μs,控制器PWM载波频率和采样频率为10 kHz,相比于Simulink仿真所采用的100 kHz更加符合实际情况。

图13 硬件在环实验平台
Fig.13 HIL simulation platform
需要说明,由于HIL实验和Matlab/Simulink离线仿真存在上述差异,在进行HIL实验时,模型中控制器的PI参数需在Matlab/Simulink模型中相应PI参数基础上略作调整,详细参数列于附表3之中。
为验证各变流器对系统小干扰稳定性的影响程度,图14给出了4台CCI全部接入、仅切除CCI 1、仅切除CCI 3和仅切除CCI 4的四种场景下各变流器A相电流的实验波形。同时,图15给出了4台CCI同时接入场景下电网电流的FFT分析结果,可以看出,当电网阻抗从0.6 mH增加至0.84 mH时,该4台变流器并网系统将发生频率分别为32 Hz和68 Hz的次同步和超同步振荡。在上述系统的基础上,切除 CCI 1,系统可快速恢复稳定;而切除CCI3,系统仍处于振荡失稳状态;若切除CCI 4,系统虽最终可回到稳定状态,但相较于切除CCI 1,需要更长的时间才能恢复稳定,由此说明系统稳定性对CCI 1最为敏感。
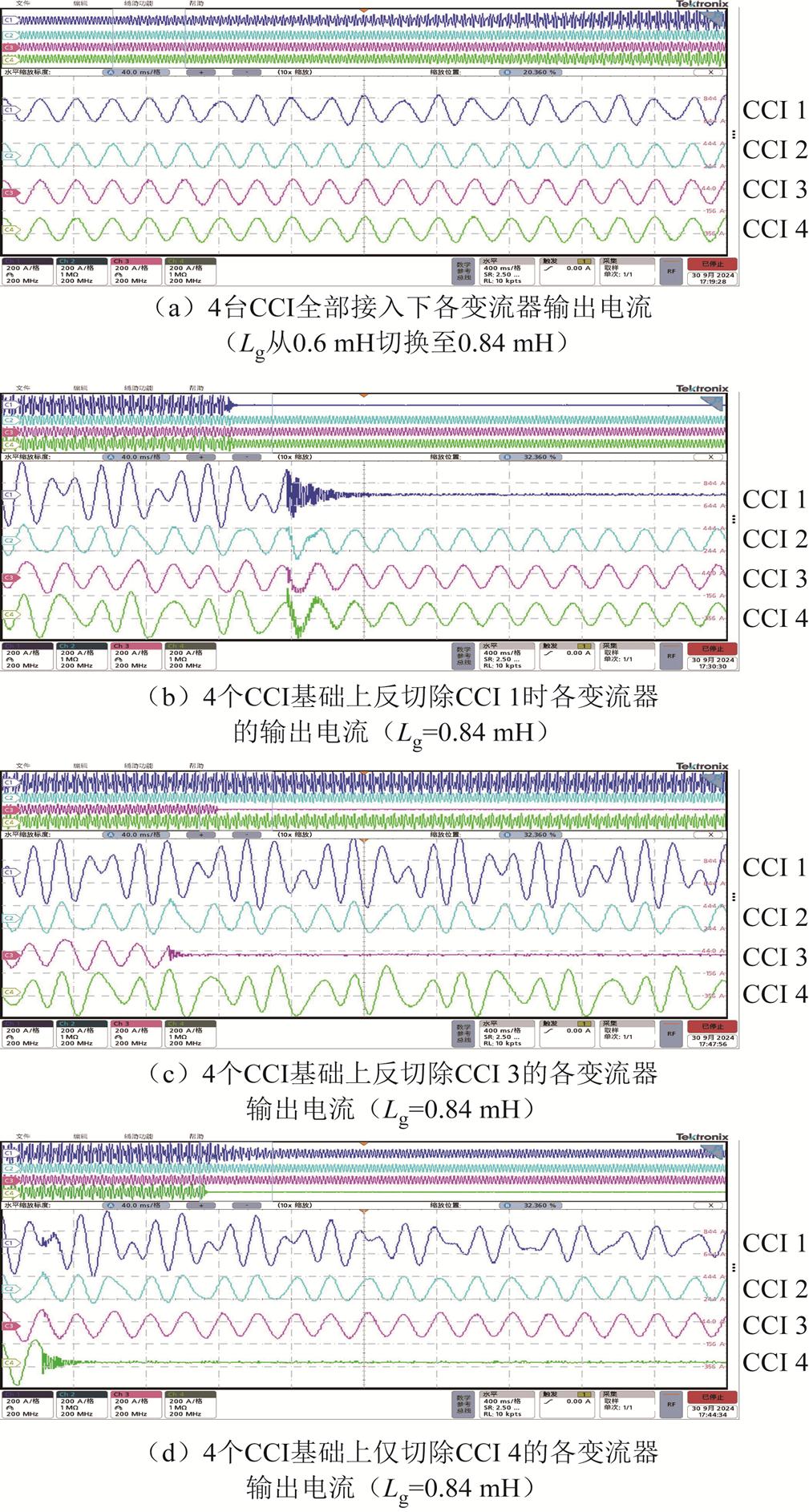
图14 各变流器A相输出电流时域波形
Fig.14 Waveforms of phase A currents of converters
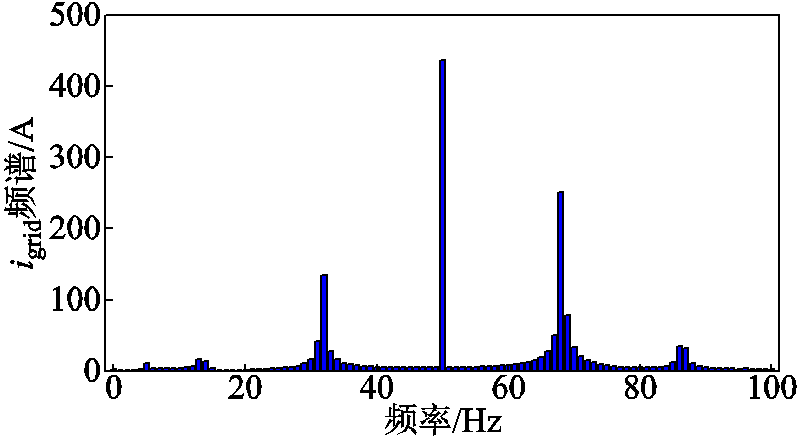
图15 并网电流的FFT分析结果
Fig.15 FFT analysis of grid current
经本文所提灵敏度分析方法计算关键特征值关于各变流器dq导纳的灵敏度如图16所示,可以看出,CCI 1对系统稳定性影响最大,CCI 4次之,该分析结果与图14所给出的实验结果相吻合,进一步从实验角度验证了本文所提方法的正确性。
本算例的分析对象为由图4中4个CCI和2个VSG(基于VSG控制策略的逆变器为构网型变流器,其对外呈现电压源特性,属于VCI)所构成的系统,用以分析同时含跟网型和构网型逆变器的系统小干扰稳定性,各变流器的详细参数列于附表4中。4个CCI和1个VSG最初接入电网,电网电感为0.3 mH时系统可以稳定运行,随着电网强度变弱,当电网电感增加至1.14 mH时,系统发生振荡,如图17a所示。为提升系统强度,增加接入第2台VSG,系统将恢复稳定,如图17b所示。若此时电网电感减小至0.6 mH,系统又会再次发生振荡,如图17c所示。
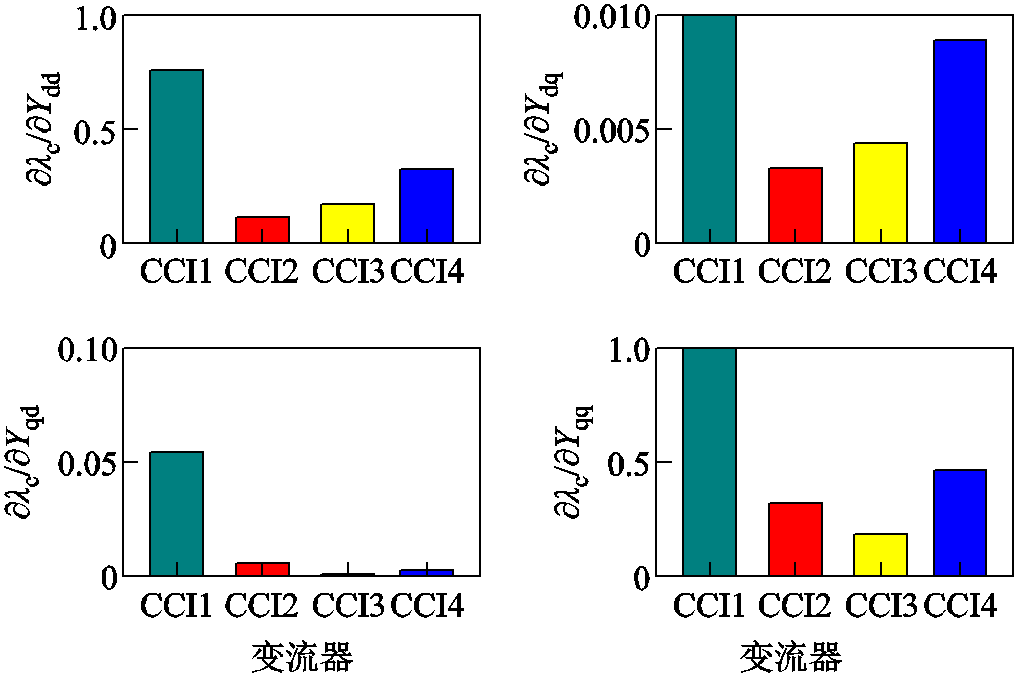
图16 不稳定极点关于4个CCI的dq阻抗的灵敏度
Fig.16 Sensitivity of the unstable pole with respect to dq admittances of different converters
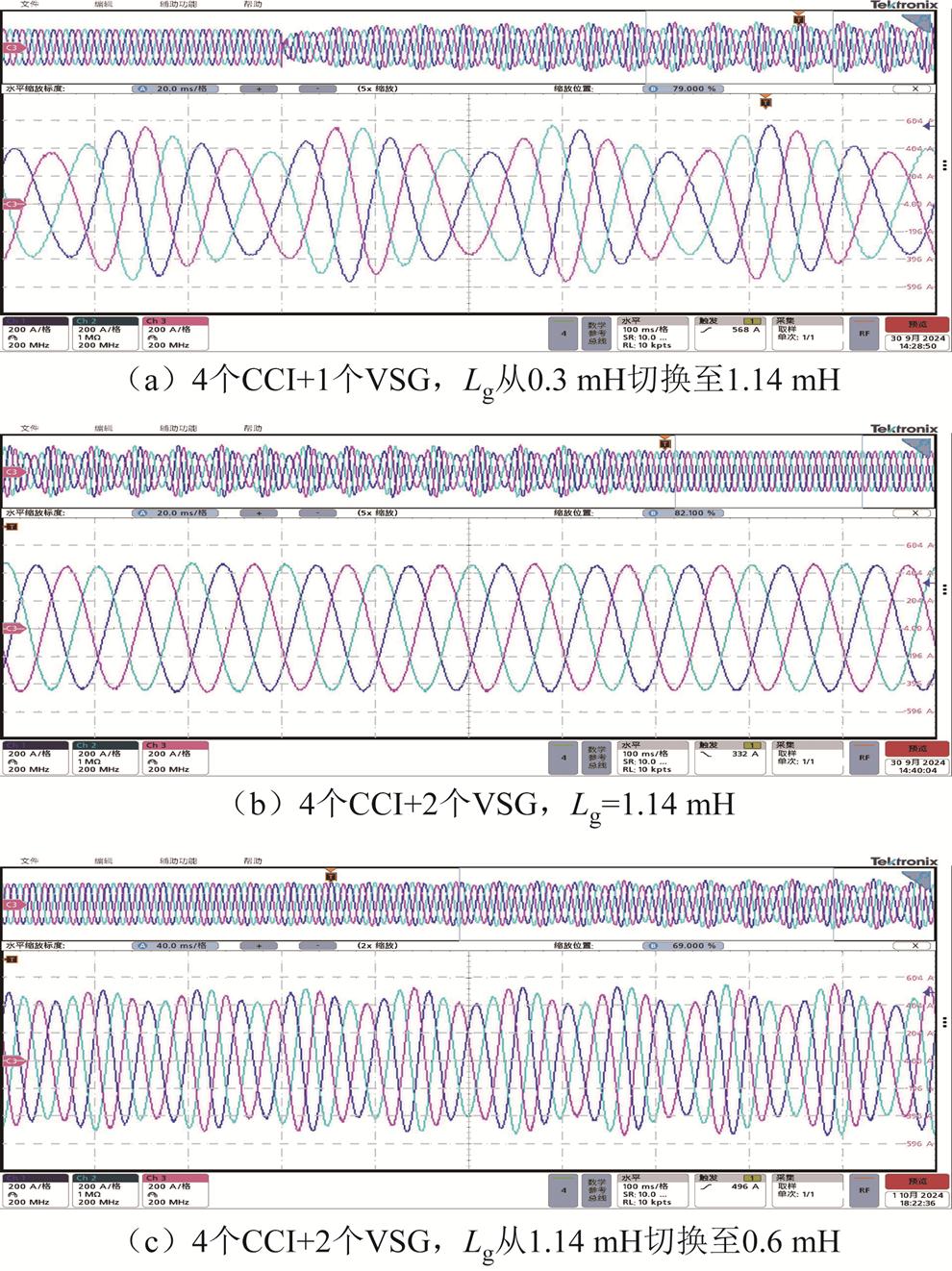
图17 三种场景下的并网电流波形
Fig.17 Waveforms of grid current under three scenarios
利用本文稳定性分析方法对上述各场景进行稳定性分析,所得SISO dq阻抗比奈奎斯特曲线如图18所示,相应的各步骤详细分析结果列于表2中。可以看出,稳定性分析结果与图17给出实验结果相一致,说明了本文所提判据的正确性。
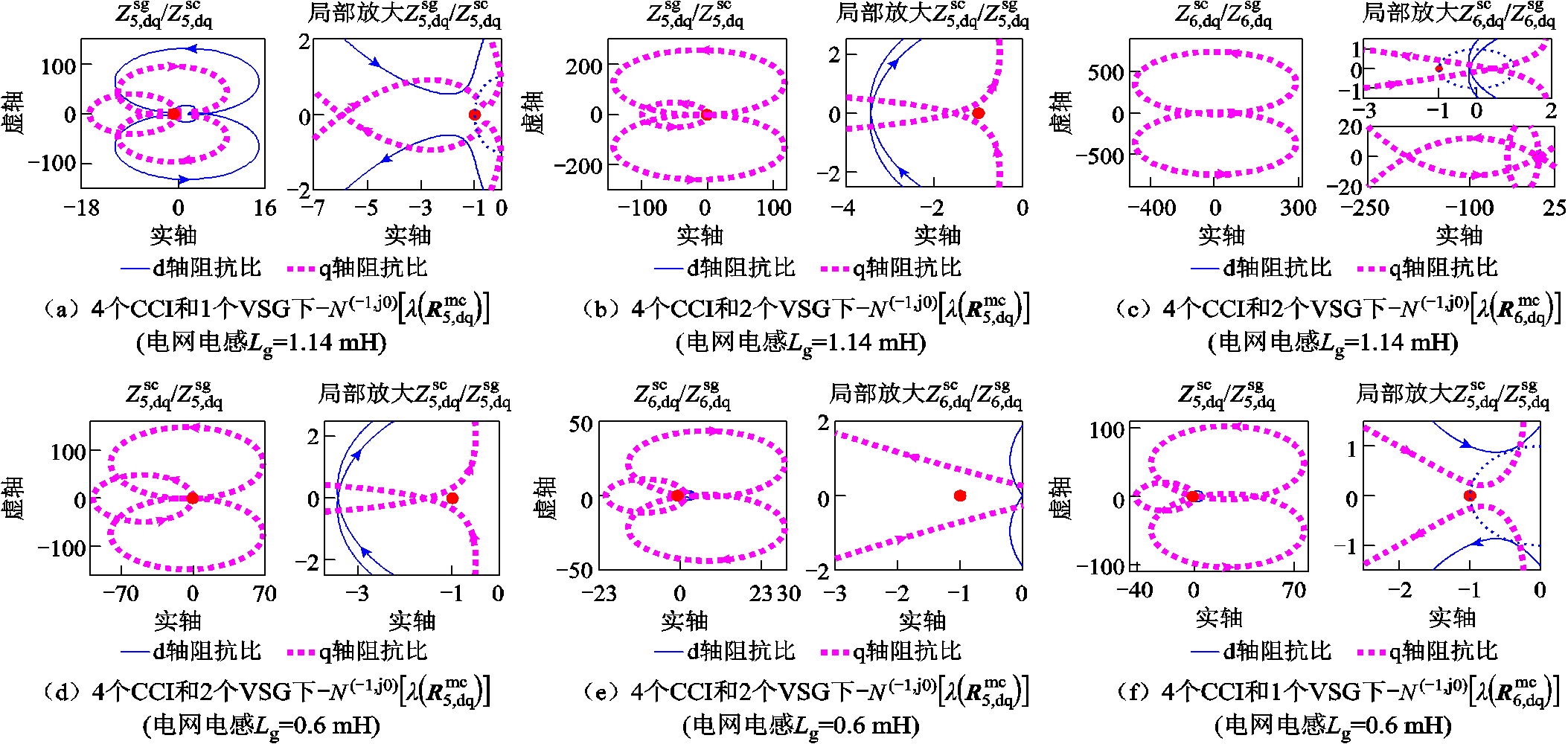
图18 稳定性分析各步骤dq阻抗比奈奎斯特曲线
Fig.18 Nyquist plot of SISO dq impedance ratio in steps of stability analysis
表2 HIL实验2稳定性分析结果
Tab. 2 Results of stability analysis in HIL experiment 2

系统组成电网电感Lg/mH图18中奈奎斯特曲线顺时针绕(-1, j0)圈数闭环极点数量稳定性 zero(|D1~4|) 4个CCI+1个VSG1.1402,对应图18a不稳定 4个CCI+2个VSG1.1402,对应图18b-2,对应图18c稳定 4个CCI+2个VSG0.602,对应图18d0,对应图18e不稳定 4个CCI+1个VSG0.600,对应图18f稳定
为了评估该系统中各变流器对系统小干扰稳定性的影响程度,利用本文方法所获得的关键闭环极点关于各变流器dq导纳/阻抗的灵敏度结果如图19所示。可以看出,相比于CCI,两个VSG对系统稳定性起决定性作用。开展HIL实验,获得的仅切除VSG 2和CCI 1的电网电流时域波形如图20所示。
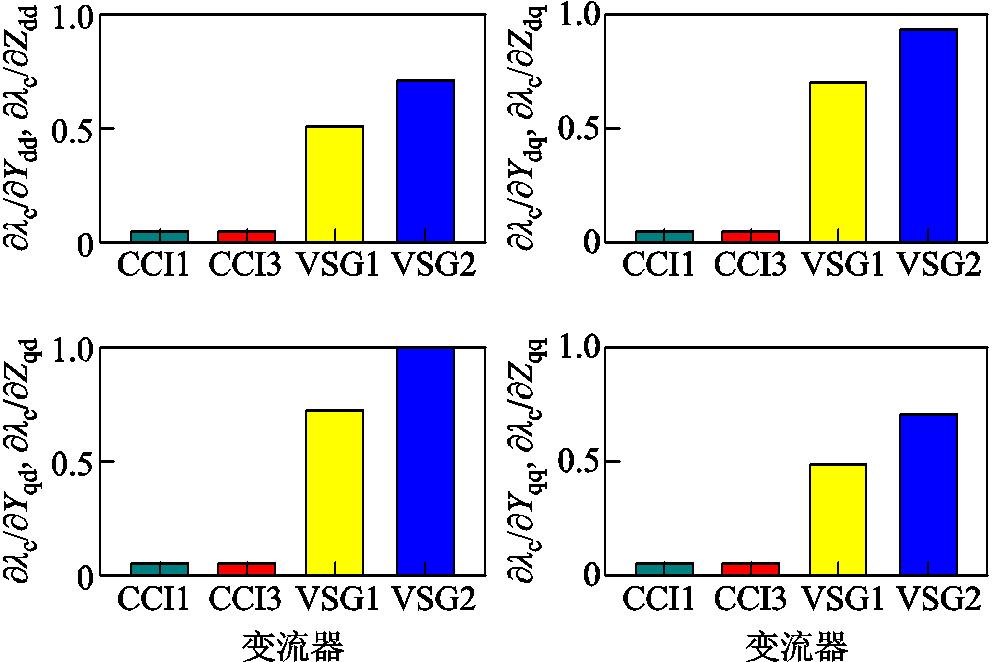
图19 不稳定极点关于4个变流器dq导纳/阻抗的灵敏度
Fig.19 Sensitivity of unstable poles with respect to dq impedances of different converters
可以看出,在未切除任何变流器之前,系统处于振荡失稳状态,若此时切除VSG 2,系统可快速恢复稳定;而若切除CCI 1,由于CCI和VSG关于稳定性的作用恰恰相反,此时系统会发生更严重的振荡而迅速失去稳定。该HIL实验结果与图19所给出的灵敏度分析结果相吻合,再次验证了方法的正确性。造成上述现象的原因可解释为:当电网电感Lg=0.6 mH时,此时为强电网,由于VSG对外呈现电压源特性,其接入强电网容易诱发失稳,因此此时切除1台VSG有助于恢复系统稳定运行;而切除CCI,由于电网强度进一步提升,系统将更加趋于失稳。
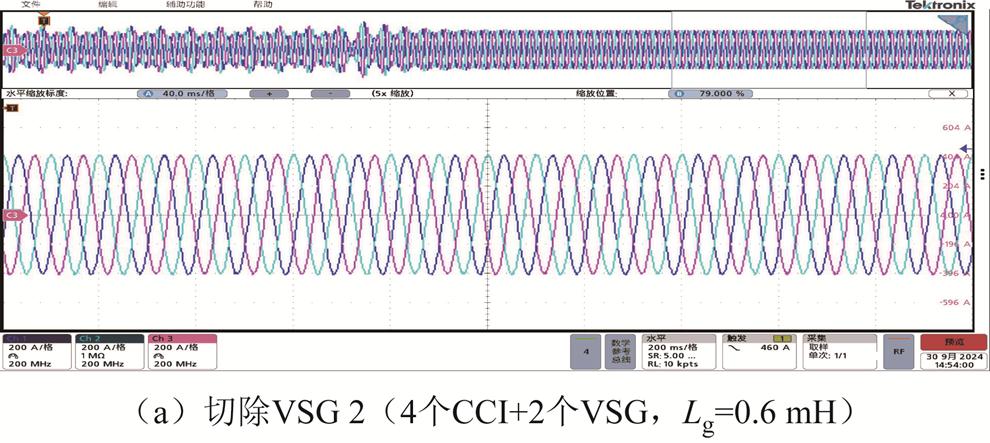
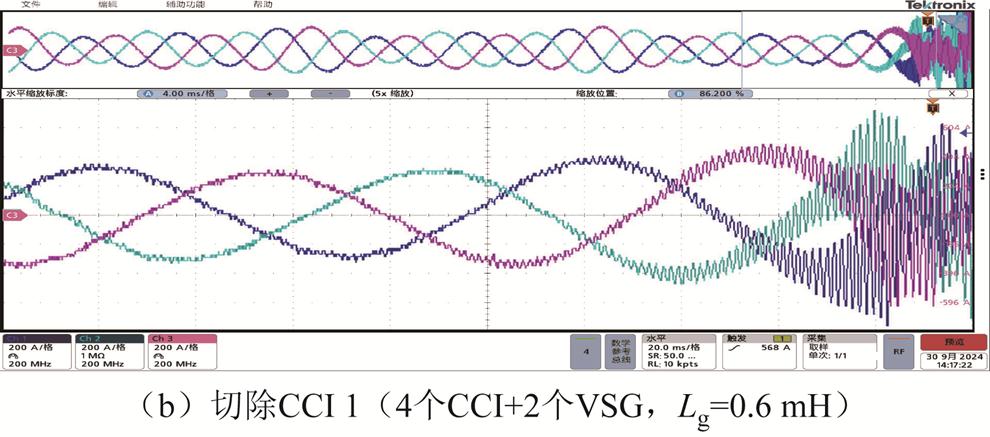
图20 切除VSG 2和切除CCI 1下的并网电流波形
Fig.20 Waveforms of grid current when disconnecting VSG 2 or CCI 1 from system
本文针对多变流器并网系统的小干扰稳定性判据及闭环极点关于各变流器dq阻抗/导纳的灵敏度进行了系统性的研究,所得结论如下:
1)针对多变流器并网系统的小干扰稳定性问题,本文提出了一种基于SISO dq阻抗比的递归小干扰稳定性分析方法,并给出了完整的判稳步骤。该方法与基于广义奈奎斯特判据的判稳方法相比,通过将MIMO系统稳定性分析问题转换为对一系列SISO系统的稳定性分析,判稳过程中仅需d轴和q轴阻抗比即可实现整个系统的稳定性分析。由于采用SISO阻抗比进行稳定性分析,可避免传统方法所需的高阶回率矩阵特征值的求解,同时还有效降低了MIMO系统需要进行大量奈奎斯特曲线分析所带来的复杂度。而且,该方法还保留了传统SISO阻抗法所具有的物理解释功能,可从电路特性角度揭示振荡失稳的机理。结合典型仿真算例和HIL实验,对所提判据的正确性进行了验证。
2)在本文所提出的小干扰稳定性判据公式的基础上,进一步推导并获得了用于求取系统闭环极点的表达式。由于本文采用在dq坐标系下进行建模和推导,相比序阻抗模型,可保证传递函数矩阵元素均为有理分式的形式,故可结合矢量匹配法得到闭环极点。
3)为实现系统闭环极点关于各变流器灵敏度的准确评估,本文经推导获得了系统闭环极点关于系统中变流器dq导纳/阻抗的灵敏度公式,结合矢量匹配法获得的闭环极点的留数,可用于分析系统中各变流器对关键模态的影响程度,有助于实现诱发系统振荡失稳源的辨识。结合典型算例,开展了仿真和HIL实验,验证了本文方法的有效性。
附 录
1. 式(20)中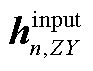 的公式推导
的公式推导
1~n号变流器接入电网,根据式(7)和式(15),有
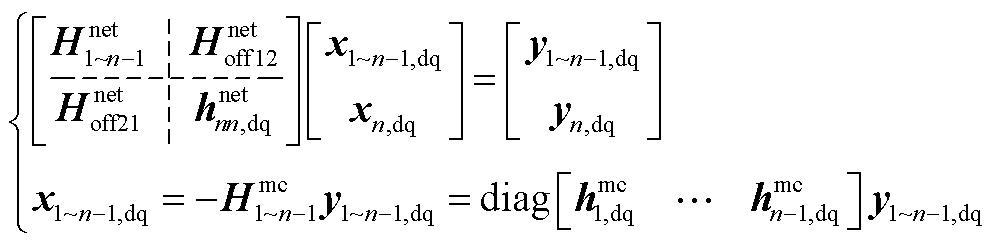 (A1)
(A1)
对于不同控制方式的变流器,式(A1)中各列向量和矩阵中的元素具有不同含义,具体为
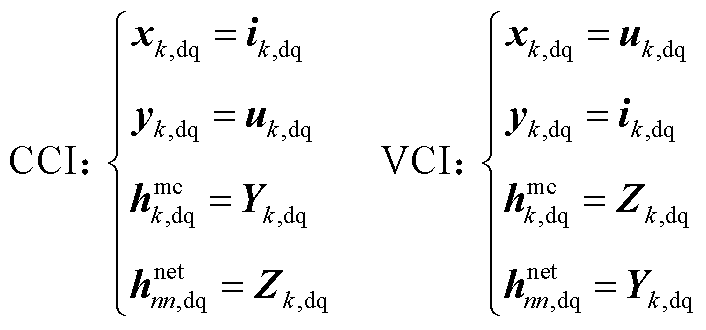 (A2)
(A2)
将式(A1)中第1式代入(A1)第2式,得
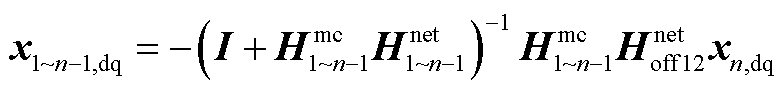 (A3)
(A3)
将式(A3)代入式(A1)中第2式,即可得
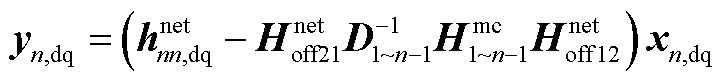 (A4)
(A4)
其中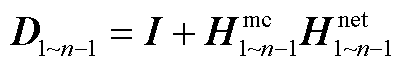 。令
。令
 (A5)
(A5)
式(A5)即为式(20)中 的表达式。若n号变流器为CCI,根据式(A2)中变量的具体含义可知,
的表达式。若n号变流器为CCI,根据式(A2)中变量的具体含义可知, 为从该变流器所连端口看入的输入阻抗;若n号变流器为VCI,
为从该变流器所连端口看入的输入阻抗;若n号变流器为VCI, 则代表从该变流器所连端口看入的输入导纳。
则代表从该变流器所连端口看入的输入导纳。
2. CCI和VCI的SISO dq导纳/阻抗理论公式计算结果与扫频验证
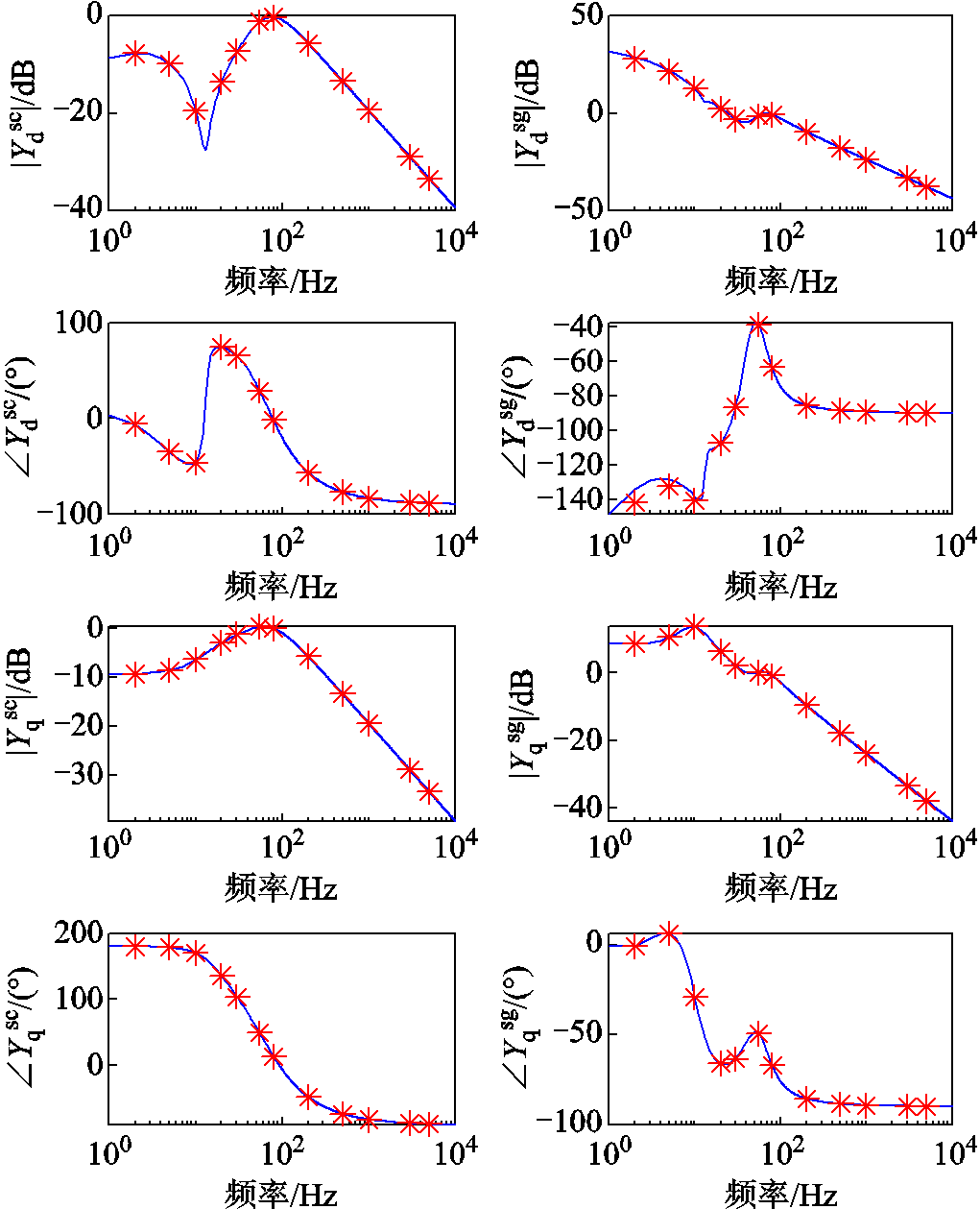
附图1 CCI的SISO dq阻抗理论公式计算及扫频结果
App.Fig.1 Theoretical frequency characteristics and simulation results of SISO dq impedance of CCI
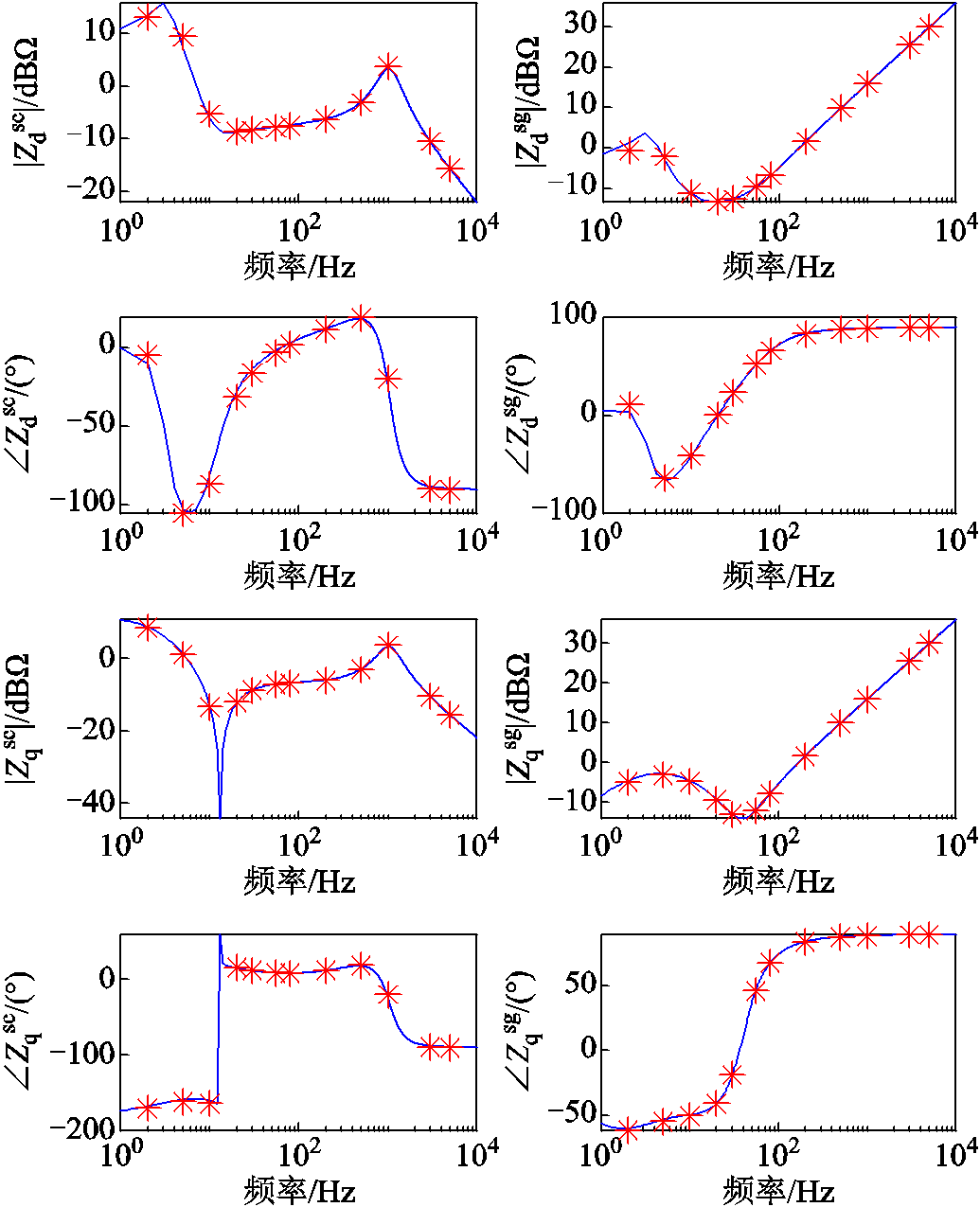
附图2 VCI的SISO dq阻抗理论公式计算及扫频结果
App.Fig.2 Theoretical frequency characteristics and simulation results of SISO dq impedance of VCI
3. 仿真算例和HIL算例中电力网络及各变流器参数
附表1 电力网络线路参数
App.Tab.1 Parameters of power network

电气参数线路阻抗算例4.1中电阻和电感值算例4.2中电阻和电感值算例4.3中电阻和电感值 线路阻抗ZLine1,,, ZLine2,,, ZLine3,,, ZLine4,,, ZLine5——, ZLine6——, ZLine7,,, ZLine8,,, ZLine9,,, ZLine10,,, ZLg具体见正文具体见正文具体见正文
附表2 CCI电气和控制仿真参数
App.Tab.2 Electrical and control parameters of CCI in simulation
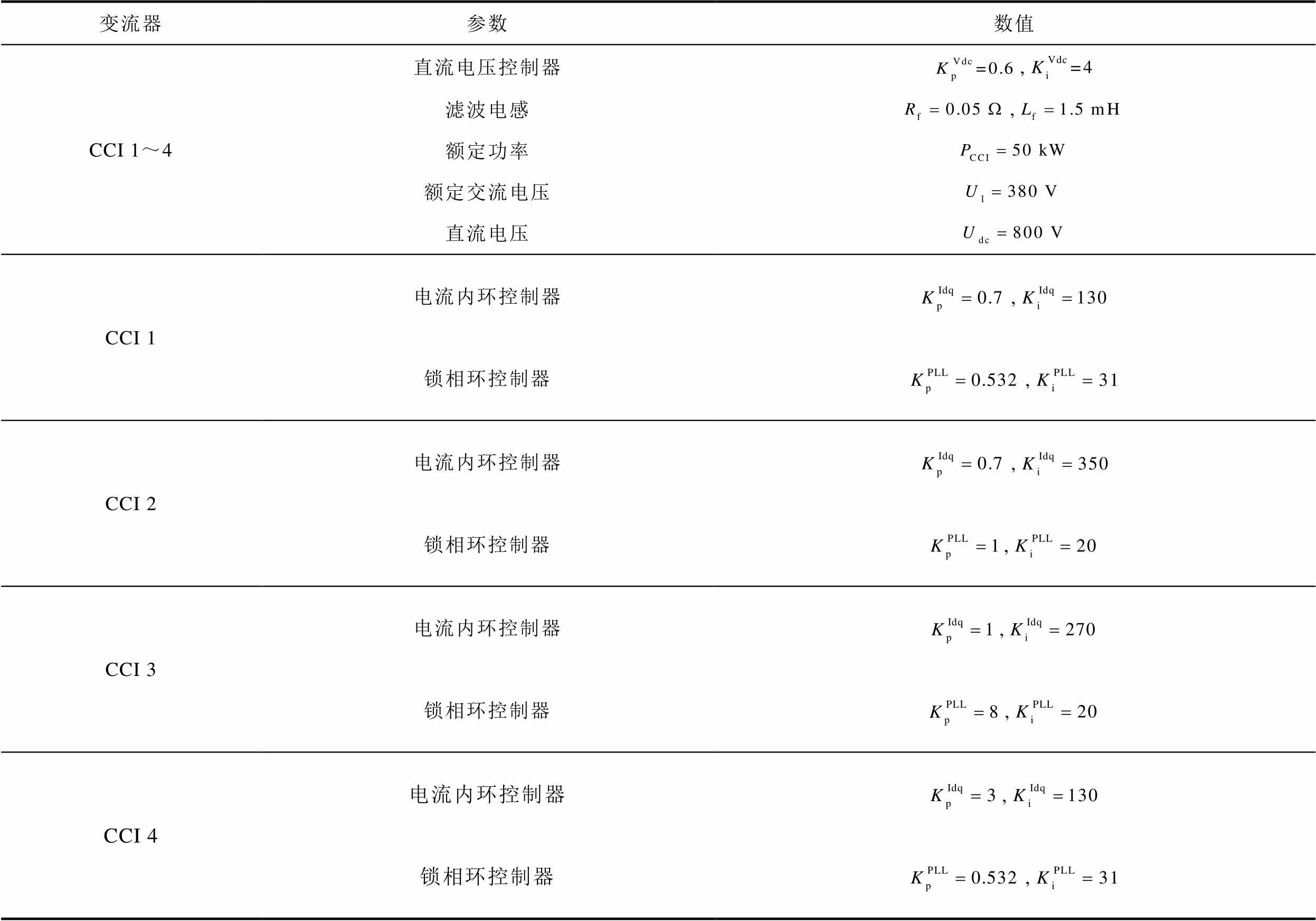
变流器参数数值 CCI 1~4直流电压控制器, 滤波电感, 额定功率 额定交流电压 直流电压 CCI 1电流内环控制器, 锁相环控制器, CCI 2电流内环控制器, 锁相环控制器, CCI 3电流内环控制器, 锁相环控制器, CCI 4电流内环控制器, 锁相环控制器,
附表3 HIL实验1中CCI的电气和控制参数
App.Tab.3 Electrical and control parameters adjustment of CCI in HIL experiment 1
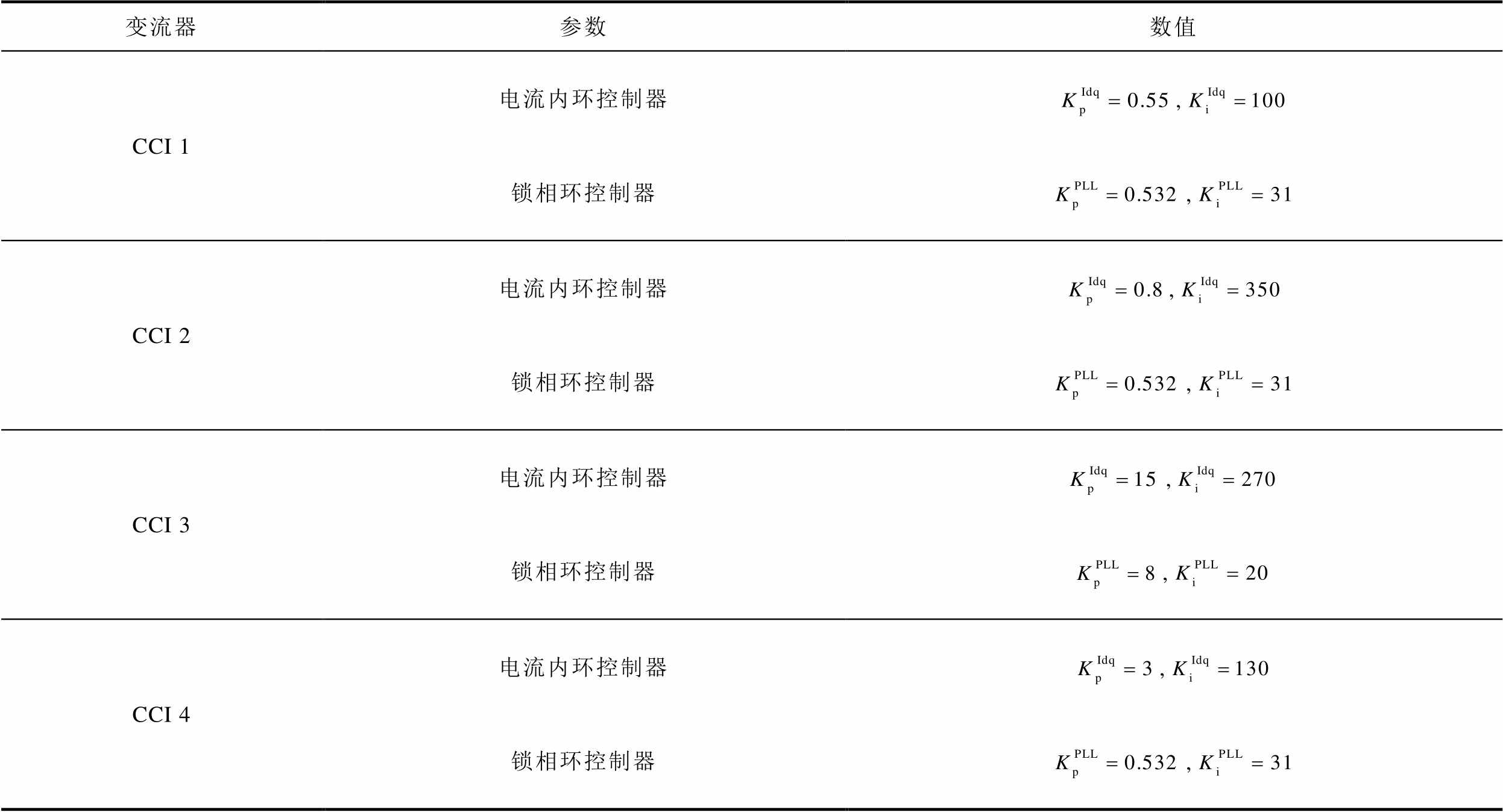
变流器参数数值 CCI 1电流内环控制器, 锁相环控制器, CCI 2电流内环控制器, 锁相环控制器, CCI 3电流内环控制器, 锁相环控制器, CCI 4电流内环控制器, 锁相环控制器,
附表4 HIL实验2中CCI和VSG的电气和控制参数
App.Tab.4 Electrical and control parameters of CCI and VSG in HIL experiment 2

变流器参数数值 CCI 1~4直流电压控制器, 电流内环控制器, 锁相环控制器, 滤波电感, 额定功率 额定交流电压 直流电压 VSG 1~2虚拟惯量 有功阻尼系数 无功功率系数 电压控制系数, 电流控制系数, 滤波电感, 额定功率 额定交流电压 直流电压
参考文献
[1] 吴翔宇, 张晓红, 尚子轩, 等. 基于频域阻抗网络建模分析的交直流微电网振荡问题研究[J]. 电工技术学报, 2024, 39(8): 2294-2310.
Wu Xiangyu, Zhang Xiaohong, Shang Zixuan, et al. Research on the oscillation problem of AC-DC microgrids based on frequency domain impedance network modeling and analysis[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2294-2310.
[2] 高磊, 吕敬, 马骏超, 等. 基于电路等效的并网逆变器失稳分析与稳定控制[J]. 电工技术学报, 2024, 39(8): 2325-2341.
Gao Lei, Lü Jing, Ma Junchao, et al. Instability analysis and stability control of grid-connected inverter based on impedance circuit equivalent[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2325-2341.
[3] 尚佳宇, 虞家骏, 刘增, 等. 构网型与跟网型逆变器并联系统精确频域建模及简化稳定判据[J]. 电力系统自动化, 2025, 49(2): 53-63.
Shang Jiayu, Yu Jiajun, Liu Zeng, et al. Accurate frequency-domain modeling and simplified stability criterion for parallel grid-forming and grid-following inverter system[J]. Automation of Electric Power Systems, 2025, 49(2): 53-63.
[4] 胡光, 庄可好, 高晖胜, 等. 低惯量交流系统并网变流器次/超同步振荡分析[J]. 电工技术学报, 2024, 39(8): 2250-2264.
Hu Guang, Zhuang Kehao, Gao Huisheng, et al. Sub/super synchronous oscillation analysis of grid-connected converter in low inertia AC system[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2250-2264.
[5] Chen Qifan, Bu Siqi, Chung C Y. Small-signal stability criteria in power electronics-dominated power systems: a comparative review[J]. Journal of Modern Power Systems and Clean Energy, 2024, 12(4): 1003-1018.
[6] 申科, 汪万兴, 赵丹. 三有源桥DC-DC变换器广义状态空间平均模型及控制策略研究[J]. 电源学报, 2024, 22(5): 161-169.
Shen Ke, Wang Wanxing, Zhao Dan. Research on generalized state space average model and control strategy for triple active bridge DC-DC converter[J]. Journal of Power Supply, 2024, 22(5): 161-169.
[7] 章艳, 高晗, 张萌. 不同虚拟同步机控制下双馈风机系统频率响应差异研究[J]. 电工技术学报, 2020, 35(13): 2889-2900.
Zhang Yan, Gao Han, Zhang Meng. Research on frequency response difference of doubly-fed induction generator system controlled by different virtual synchronous generator controls[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2889-2900.
[8] 满九方, 谢小荣, 陈垒, 等. 柔性直流输电系统高频振荡建模分析与抑制策略综述[J]. 中国电机工程学报, 2023, 43(9): 3308-3322.
Man Jiufang, Xie Xiaorong, Chen Lei, et al. Overview of modeling analysis and mitigation strategies of high-frequency resonance in MMC-HVDC systems[J]. Proceedings of the CSEE, 2023, 43(9): 3308-3322.
[9] 胡秦然, 巫绍辉, 韩汝帅, 等. 多虚拟同步发电机主导系统稳定性分析方法及提高措施综述[J/OL]. 电力系统自动化, 1-20[2025-01-19].http://kns.cnki. het/kcms/detail132.1180.TR20240905.1916.008.html.
Hu Qinran, Wu Shaohui, Han Rushuai, et al. Review of stability analysis methods and improvement measures for power system dominated by multiple virtual synchronous generators[J/OL]. Automation of Electric Power Systems: 1-20[2025-01-19].http://kns. cnki.het/kcms/detail132.1180.TR20240905.1916.008. html.
[10] 朱宇昕, 赵晋斌, 毛玲, 等. 多变流器并网系统的小干扰稳定性判据与参数灵敏度分析[J]. 中国电机工程学报, 2021, 41(18): 6235-6245.
Zhu Yuxin, Zhao Jinbin, Mao Ling, et al. A small-signal stability criterion and parametric sensitivity analysis for multiple grid-connected-converter system [J]. Proceedings of the CSEE, 2021, 41(18): 6235-6245.
[11] 林鸿彬, 葛平娟, 徐海亮, 等. 异构逆变器并联系统改进Gershgorin圆稳定性判据及其多维谐振特性分析[J]. 电工技术学报, 2024, 39(8): 2265-2280.
Lin Hongbin, Ge Pingjuan, Xu Hailiang, et al. Improved gershgorin-circle stability criterion and multi-dimensional resonance characteristics analysis for heterogeneous inverter paralleled system[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2265-2280.
[12] 刘镇湘, 屈克庆, 赵晋斌, 等. 基于Brauer定理的多变流器并网系统小干扰稳定性分析[J]. 中国电机工程学报, 2022, 42(9): 3363-3373.
Liu Zhenxiang, Qu Keqing, Zhao Jinbin, et al. Analysis of the small-signal stability for multiple grid-connected-converter system based on brauer theorem[J]. Proceedings of the CSEE, 2022, 42(9): 3363-3373.
[13] 饶仪明, 吕敬, 戴金水, 等. 不同控制策略下直驱风电机组的机网耦合特性及稳定性分析[J]. 电力系统自动化, 2024, 48(4): 150-159.
Rao Yiming, Lü Jing, Dai Jingshui, et al. Analysis of generator-grid coupling characteristics and stability for direct-drive wind turbines with different control strategies[J]. Automation of Electric Power Systems, 2024, 48(4): 150-159.
[14] Wen Bo, Dong Dong, Boroyevich D, et al. Impedance-based analysis of grid-synchronization stability for three-phase paralleled converters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 26-38.
[15] Wen Bo, Boroyevich D, Burgos R, et al. Inverse nyquist stability criterion for grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2017, 32(2): 1548-1556.
[16] Yoon C, Bai Haofeng, Wang Xiongfei, et al. Regional modeling approach for analyzing harmonic stability in radial power electronics based power system[C]//2015 IEEE 6th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aachen, Germany, 2015: 1-5.
[17] 李达, 张涛. 基于阻抗法的光储逆变器交直流建模及耦合分析[J]. 电工技术学报, 2024, 39(10): 3038-3048.
Li Da, Zhang Tao. Modeling and coupling analysis of DC and grid side of solar-storage inverter based on impedance method[J]. Transactions of China Electro-technical Society, 2024, 39(10): 3038-3048.
[18] Wang Xiongfei, Blaabjerg F, Wu Weimin. Modeling and analysis of harmonic stability in an AC power-electronics-based power system[J]. IEEE Transactions on Power Electronics, 2014, 29(12): 6421-6432.
[19] Ye Qing, Mo Ran, Shi Yanjun, et al. A unified Impedance-based Stability Criterion (UIBSC) for paralleled grid-tied inverters using global minor loop gain (GMLG)[C]//2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 2015: 5816-5821.
[20] Wang Xiongfei, Blaabjerg F, Loh P C. An impedance-based stability analysis method for paralleled voltage source converters[C]//2014 International Power Ele-ctronics Conference (IPEC-Hiroshima 2014-ECCE ASIA), Hiroshima, Japan, 2014: 1529-1535.
[21] Cao Wenchao, Ma Yiwei, Wang F. Sequence-impedance-based harmonic stability analysis and controller parameter design of three-phase inverter-based multibus AC power systems[J]. IEEE Transactions on Power Electronics, 2017, 32(10): 7674-7693.
[22] Shi Kai, Wang Yu, Sun Yuxin, et al. Frequency-coupled impedance modeling of virtual synchronous generators[J]. IEEE Transactions on Power Systems, 2021, 36(4): 3692-3700.
[23] 刘欣, 郭志博, 贾焦心, 等. 基于序阻抗的虚拟同步发电机并网稳定性分析及虚拟阻抗设计[J]. 电工技术学报, 2023, 38(15): 4130-4146.
Liu Xin, Guo Zhibo, Jia Jiaoxin, et al. Stability analysis and virtual impedance design of virtual synchronous machine based on sequence impedance [J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4130-4146.
[24] Xu Wilsun, Huang Zhenyu, Cui Yu, et al. Harmonic resonance mode analysis[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 1182-1190.
[25] Zhu Yue, Gu Yunjie, Li Yitong, et al. Impedance-based root-cause analysis: comparative study of impedance models and calculation of eigenvalue sensitivity[J]. IEEE Transactions on Power Systems, 2023, 38(2): 1642-1654.
[26] Ebrahimzadeh E, Blaabjerg F, Wang Xiongfei, et al. Bus participation factor analysis for harmonic instability in power electronics based power systems [J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10341-10351.
[27] Zhan Ying, Xie Xiaorong, Liu Huakun, et al. Frequency-domain modal analysis of the oscillatory stability of power systems with high-penetration renewables[J]. IEEE Transactions on Sustainable Energy, 2019, 10(3): 1534-1543.
[28] Zhang Chen, Molinas M, Rygg A, et al. Impedance-based analysis of interconnected power electronics systems: impedance network modeling and comparative studies of stability criteria[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(3): 2520-2533.
[29] Zhu Yue, Gu Yunjie, Li Yitong, et al. Participation analysis in impedance models: the grey-box approach for power system stability[J]. IEEE Transactions on Power Systems, 2022, 37(1): 343-353.
[30] Gu Yunjie, Li Yitong, Zhu Yue, et al. Impedance-based whole-system modeling for a composite grid via embedding of frame dynamics[J]. IEEE Transactions on Power Systems, 2021, 36(1): 336-345.
[31] Xiao Qi, Mattavelli P, Khodamoradi A, et al. Modelling and analysis of equivalent SISO d-q impedance of grid-connected converters[J]. Mathematics and Computers in Simulation, 2021, 184: 5-20.
[32] Guo Jian, Chen Yandong, Wang Lei, et al. Impedance analysis and stabilization of virtual synchronous generators with different DC-link voltage controllers under weak grid[J]. IEEE Transactions on Power Electronics, 2021, 36(10): 11397-11408.
[33] Xiao Qi, Mattavelli P, Khodamoradi A, et al. Analysis of transforming dq impedances of different converters to a common reference frame in complex converter networks[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 342-350.
Abstract As the penetration rate of renewable energy resources continues to increase, the traditional power system based on synchronous generators is evolving into a power system based on diversified power electronic equipment. The small disturbance stability analysis problem of multi-converter grid-connected system has attracted widespread attention. State-space model and impedance-based model are two main small disturbance stability analysis methods. Being as the white-box method, state-space model can be difficult to apply in practice because the differential equations describing the controllers of converters are not generally openly available due to commercial confidentiality. Impedance models have been popular in the field of power electronics for analysis of interactions between grid and converters. However, applying it directly to the stability analysis of multi-converter system will make the analysis process very complicated. Generally, the existing state-space and the impedance method still have room for improvement for the small disturbance stability analysis and sensitivity analysis of the oscillation mode of each converter.
Firstly, this paper proposes a single-input single-output (SISO) dq impedance stability criterion for analyzing the small disturbance stability of the multi-converter grid-connected system. Secondly, based on the formula of the stability criterion proposed, an expression for calculating the closed-loop pole of the system is derived. Because this formula is only a scalar function, the accuracy can be guaranteed for the usage of vector fitting (VF) method. Furthermore, a method for analyzing the sensitivity of oscillation modes to the impedance/admittance of each converter is proposed. This method can effectively evaluate the influence of different converters on the oscillation modes and help identify the dominant converter that causes oscillations. Finally, the accuracy of the proposed method is verified by Matlab/Simulink simulation and hardware-in-the-loop experiment.
The results are as follows: firstly, the proposed multi-converter system model can be used to represent the converter grid-connected system with any network structure and any number of grid-forming and grid-following converters. Based on the proposed method, it can be used to analyze the overall stability of the system as well as the influence of each converter on the system stability. Secondly, the proposed sensitivity analysis method can be used for evaluating which power converters are more sensitive to the close-loop poles and have a significant contribution to the harmonic instability.
The following conclusions can be drawn from the above results: (1) A recursive stability evaluation method for analyzing the stability of the multi-converter grid-connected system based on SISO dq impedance ratio is achieved, and a complete stability evaluation procedure is provided. Compared with the stability analysis method based on generalized Nyquist criterion, the stability analysis problem of a MIMO system is transformed into the stability analysis of a series of SISO systems, and the stability analysis of the whole system can be realized only by the impedance ratio of d-axis and q-axis in the stability analysis process. Because the SISO impedance ratio is used for stability analysis, the solution of the eigenvalues of the high-order return rate matrix required by the traditional method can be avoided, and the complexity of Nyquist plot analysis required for MIMO system can be effectively reduced. (2) In the proposed impedance stability criterion, dq impedance is adopted to model the VCI while dq admittance is used to describe the CCI, so the complicated procedure for obtaining the RHP open loop poles can be avoided. (3) Based on the proposed stability criterion proposed, an expression for calculating the closed-loop pole of the system is derived. Since this paper adopts dq coordinate system for modeling and derivation, compared with the sequential impedance model, the transfer function matrix elements can be guaranteed to be rational fractions, so the closed-loop poles can be obtained by VF method. (4) The sensitivity formula of the system's closed-loop poles on the dq admittance/impedance of the converter in the system is derived in this paper. Combining with the residual of the closed-loop poles obtained by the VF method, it can be used to analyze the influence of each converter on the key modes in the system. Therefore, it is helpful to identify the source that causes oscillatory instability.
Keywords:Multi-converter grid-connected system, SISO dq impedance model, small disturbance stability, sensitivity analysis
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.242081
国家自然科学基金资助项目(52207102)。
收稿日期 2024-11-19
改稿日期 2025-01-20
刘 欣 男,1980 年生,博士,副教授,硕士生导师,研究方向为新能源发电系统建模、控制与稳定性分析。
E-mail:liuxinhust@163.com(通信作者)
吴柳颖 女, 2002 年生,硕士研究生,研究方向为新能源发电系统建模、控制与稳定性分析。
E-mail:18032200286@163.com
(编辑 郭丽军)