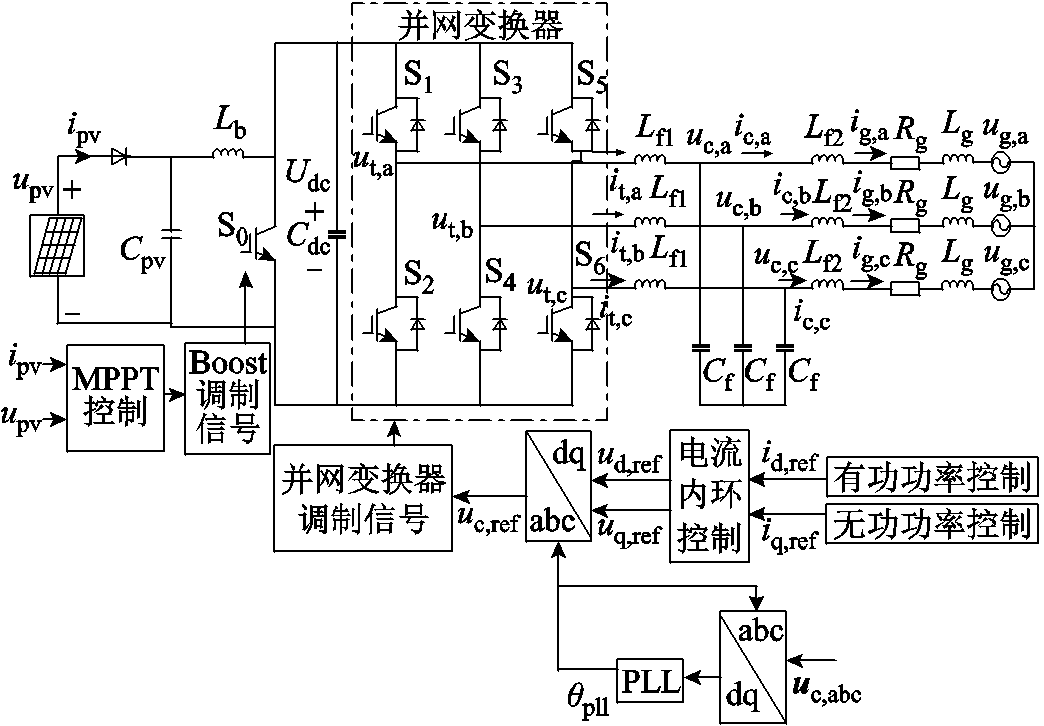
图1 光伏发电系统模型
Fig.1 Photovoltaic generation system model
摘要 光伏电站并网时需要具备一定的无功支撑能力,通常需要配备无功补偿装置,二者之间的相互作用增加了静态同步稳定问题的分析难度。该文首先提出一种含静止同步补偿器(STATCOM)的光伏并网系统静态同步稳定分析方法;然后考虑不同并网变换器dq坐标系间的变换,构建多并网变换器并联系统的等效小信号模型,在阻抗分析方法基础上改进稳定判据,并利用衰减系数指标定量刻画系统的静态同步稳定性能,构建静态同步稳定量化评估指标体系;最后结合改进的判据和量化指标,详细地分析了STATCOM对光伏并网系统静态同步稳定性能的影响,总结了各控制参数对于系统运行零极点分布的影响规律。
关键词:光伏系统 静止同步补偿器(STATCOM) 静态同步稳定 阻抗分析方法 衰减系数
电力系统内各动态元件处于相对静止的安全稳定运行状态,被称为电力系统处于同步状态[1]。风电和光伏等新能源采用电力电子装置作为并网接口,具有非线性、异构性和低惯量等明显特征,导致系统同步方式从以同步发电机为主导的物理同步转变为以并网变换器为主导的控制同步,引起了新型电力系统中的同步机理转变[2-3]。随着新能源装机规模的增加,电网传统物理同步方式的主导特性持续减弱,并网变换器多控制回路间的强耦合特性对电网影响日益显著,新型电力系统静态同步稳定问题机理更加复杂[4-5]。相较于传统电力系统,新型电力系统静态同步稳定问题分析的难点在于并网变换器的应用使得输出特性与控制策略密切相关,亟须对控制策略主导下的新能源静态同步稳定问题开展分析[6-7]。
现有研究大多采用阻抗分析方法评估新能源发电系统的静态同步稳定特性[8]。文献[9]针对多并网变换器系统,给出详细的阻抗分析建模过程,分析系统的稳定性,采用仿真验证了所提方法的准确性。文献[10]针对线性变参数(Linear Parameter-Varying, LPV)控制的功率同步跟网型变流器(Power-Synchronized Grid Following Inverter, PSGFLI),构建输出的阻抗矩阵,分析控制参数运行对系统稳定性能的影响。文献[11]构建含储能多馈入系统的交流电网动态阻抗模型,基于多变量反馈理论实现系统的模态解耦。文献[12]构建模块化多电平变换器(Modular Multilevel Converter, MMC)多输入多输出模型,采用块对角占优理论实现模型降维。阻抗分析方法的难点在于稳定判据的选取,要进一步拓展阻抗分析稳定判据[13-16]。
影响系统静态稳定的因素主要有以下几点:
1)系统的静态同步稳定性受电压影响,在电压较低时,并网变换器输出的电流值上限较低,限制并网变换器输出功率及静态储备系数,不利于系统静态稳定;在发生电压跌落时,并网变换器输出功率急剧下降,系统易同步失稳[17-18]。
2)系统的静态同步稳定性受电网阻抗的影响,在并网变换器接入系统后,较高的电网阻抗值会导致系统整体等效阻尼较小,甚至呈现负阻尼,引发低频振荡[19]。利用电网短路比(Short Circuit Ratio, SCR)表征并网变换器接入电网的相对强度,当构网型(Grid Forming, GFM)装置接入点SCR在1附近时,系统不一定存在稳定工作点,因此短路比较小的系统更容易发生静态同步稳定失稳[20-21]。
3)系统的静态同步稳定性受并网变换器控制方式及参数的影响,利用复转矩系数法分析可得到阻尼传递函数D(s),增加新的控制环节能够增加系统的静态同步稳定裕度[22-23]。文献[24]揭示了各控制参数与特征根间的关系,改变系统的控制参数能够提高扰动振荡过程的衰减速度。文献[25]针对锁相环(Phase Locked Loop, PLL)控制引入线性反馈补偿器,使得跟网型(Grid Following, GFL)装置的静态稳定能力不依赖初始的PLL参数设计,通过改变线性反馈补偿器,实现GFL装置在弱电网下的静态运行能力的提升。文献[26]提出一种基于相位补偿器的改进PLL控制策略,有效地改善了GFM装置在弱电网下的静态稳定性能。
虽然业界已对并网变换器与电网交互系统的静态同步稳定问题开展了系统研究,但对并网变换器间交互机理的研究还不够深入,未区分系统控制环节产生的主导特征值。在实际工程中,新能源机组并网运行时会增设无功补偿装置,以确保并网变换器输出电压稳定[27-28]。但是现有研究尚未分析静止同步补偿器(Static Synchronous Compensator, STATCOM)对光伏发电系统静态稳定机理的影响,缺乏含静止同步补偿器STATCOM的光伏并网系统静态同步稳定判据。相较于现有的研究,本文考虑STATCOM锁相环及电流控制环节对光伏系统静态同步稳定的影响,提出了适用于多并联变换器系统的静态同步稳定分析方法,构建了静态同步稳定判别。相较于现有研究中线性化的参考坐标系确定方法,本文结合基尔霍夫电流定律,建立了电压参考坐标系转换传递函数,减少了分析时的旋转误差。
在变换器同步稳定分析方面,现有研究一般假设并网输出电压等于参考信号,主要考虑控制环节的影响,忽略变换器本身特性对系统同步稳定的影响[8,29]。因此,级联H桥电路、三电平和两电平等不同类型的并网变换器的分析方法和结果是相同的。本文以两电平并网逆变器为例进行分析,光伏发电系统模型如图1所示。其中,光伏由侧Boost两级式升压电路组成,光伏功率输出模式为最大功率跟踪(Maximum Power Point Tracking, MPPT)控制,并网逆变器采用电压电流内外双环控制。

图1 光伏发电系统模型
Fig.1 Photovoltaic generation system model
新能源机组并网控制信号输出主要由电流环和锁相环调节,其余环节通过影响电流环参考值来改变并网变换器的控制信号。多并网变换器系统如图2所示,假设系统中光伏并网变换器数量为M,STATCOM变换器数量为N,总变换器数量为K。
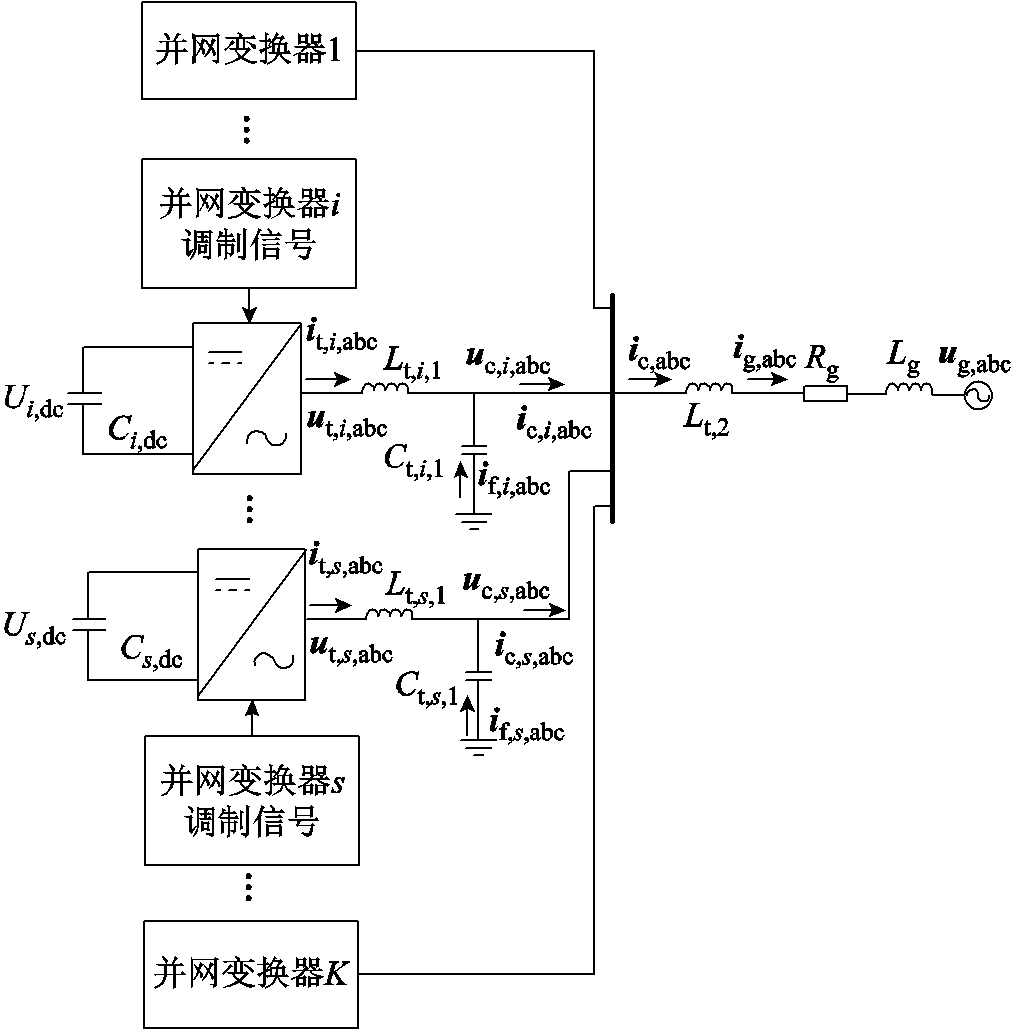
图2 多并网变换器系统
Fig.2 Grid-connected system with multiple converter
在忽略端口电阻的情况下,并网变换器i端口处输出电压ut,i,abc和电流it,i,abc间的关系为
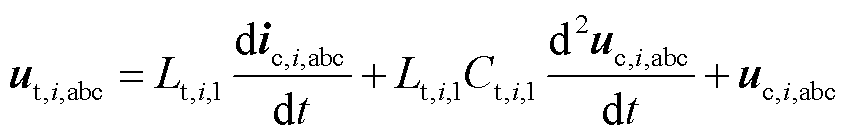 (1)
(1)
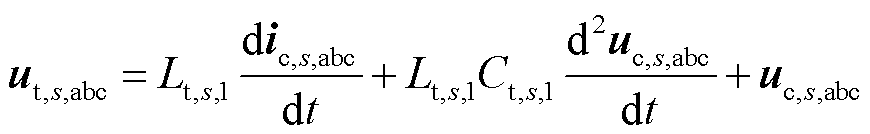 (2)
(2)
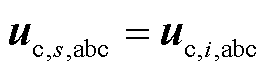 (3)
(3)
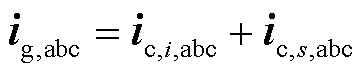 (4)
(4)
式中,下标i为光伏变换器的序号,i=1,2,…,N;下标s为STATCOM装置变换器序号,s=1,2, …,M;Lt,i,1和Lt,s,1分别为并网变换器i和s网侧滤波电感;Ct,i,1和Ct,s,1分别为光伏并网变换器i和s滤波电容;uc,i,abc为并网变换器i网侧滤波电容端电压;uc,s,abc为STATCOM并网变换器s滤波电容端电压;ig,abc为电网输入电流;ic,i,abc为光伏并网变换器i输出电流;if,i,abc为光伏并网变换器i电容电流;ic,s,abc为STATCOM并网变换器s输出电流。
光伏变换器i采用双闭环电压电流矢量控制,实现输出功率的解耦。其中,d轴电流控制采用定直流电压控制,q轴电流控制采用定无功电流控制,并网变换器控制策略和锁相环控制环节分别如图3和图4所示。图中,ut,i,d,ref、ut,i,q,ref分别为光伏系统并网变换器i输出d轴、q轴电压控制信号;ii,d,ref、ii,q,ref分别为变换器i输入d轴、q轴电流控制信号;ω0为电网稳定运行状态下角频率;kp,i,c为并网变换器i电流环比例系数;kin,i,c为并网变换器i电流环积分系数;ui,dc,ref为并网变换器i直流侧电压参考值;ui,dc为并网变换器i直流侧电压值;kp,i,dc为并网变换器i电压环比例系数;kin,i,dc为并网变换器i电压环积分系数;θpll,i为并网变换器i输出相位;ωpll,i为并网变换器i锁相环输出频率。kp,i,pll为并网变换器i锁相环比例系数;kin,i,pll为并网变换器i锁相环积分系数。
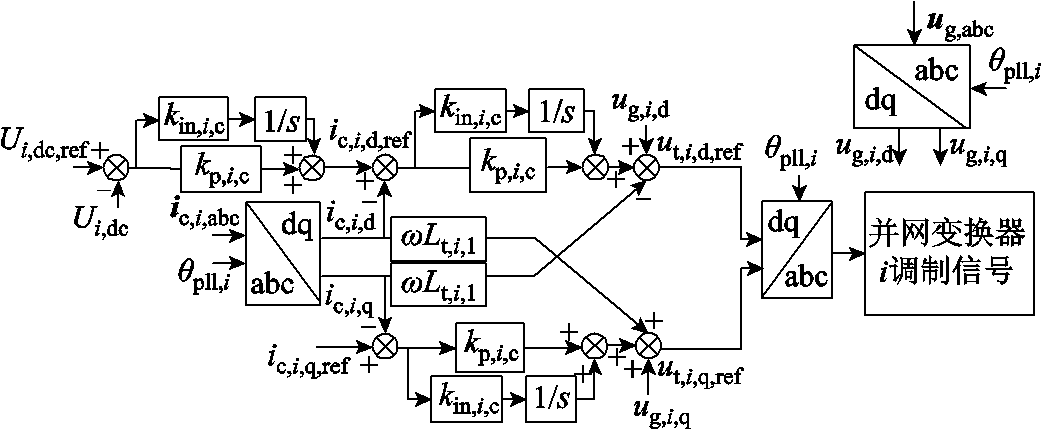
图3 并网变换器控制策略
Fig.3 Control strategy of grid-connected converter
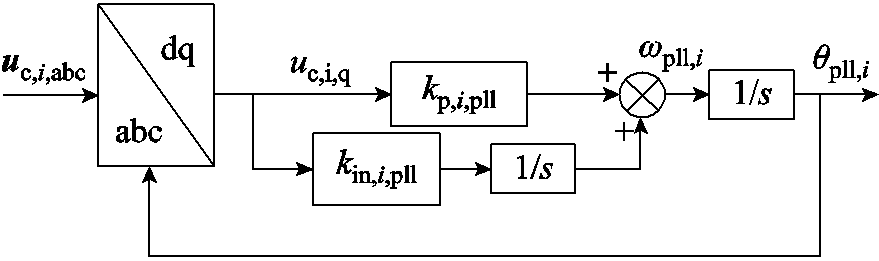
图4 锁相环控制环节
Fig.4 Phase-locked loop control link
STATCOM具备快速调节性能,其拓扑结构如图5所示。STATCOM并网侧的结构与新能源机组相同,其输出电压ut,s,abc和电流it,s,abc间的关系同样与新能源机组相同。
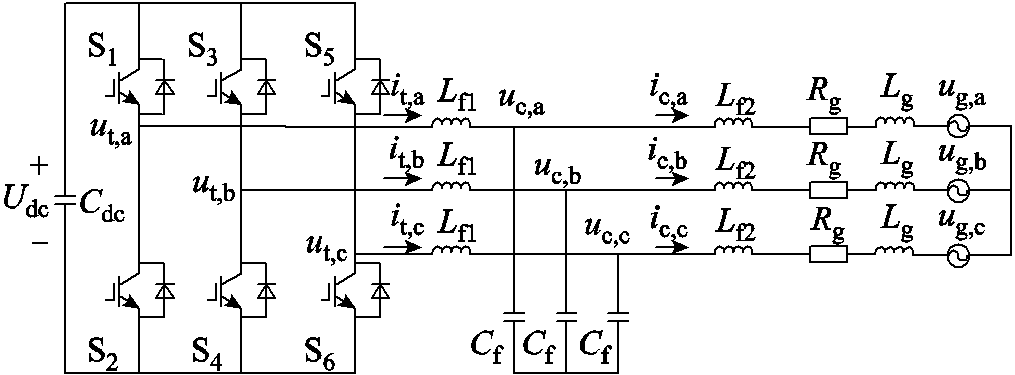
图5 STATCOM拓扑结构
Fig.5 Topological structure of STATCOM
STATCOM锁相环控制方程与光伏并网变换器锁相环控制分析相同,假设在运行过程中无功输出不超过容量限制,其控制策略如图6所示。图中ut,s,d,ref、ut,s,q,ref分别为STATCOM的变换器s输出d轴、q轴电压控制信号;is,d,ref、is,q,ref分别为变换器s输入d轴、q轴电流控制信号;kp,s,c、kin,s,c、us,dc,ref、us,dc、kp,s,dc和kin,s,dc分别为STATCOM的电流环比例系数、电流环积分系数、直流电压参考值、直流电压值、电压环比例系数和电压环积分系数。
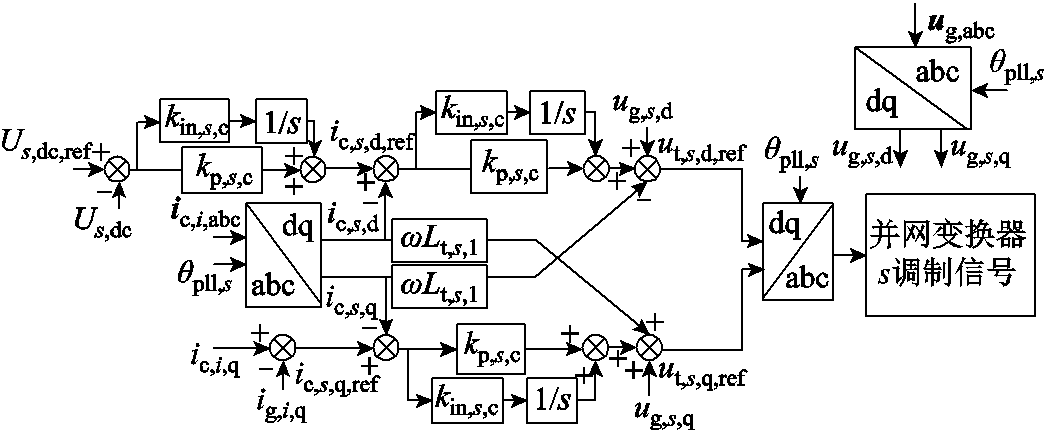
图6 STATCOM控制策略
Fig.6 Control strategy of STATCOM
2.1.1 光伏系统信号建模
当锁相环输出功角发生变化时,Park变换的线性化公式可表示为
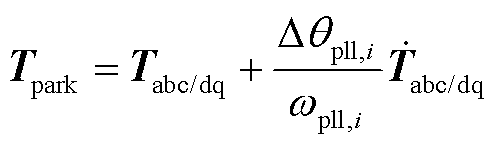 (5)
(5)
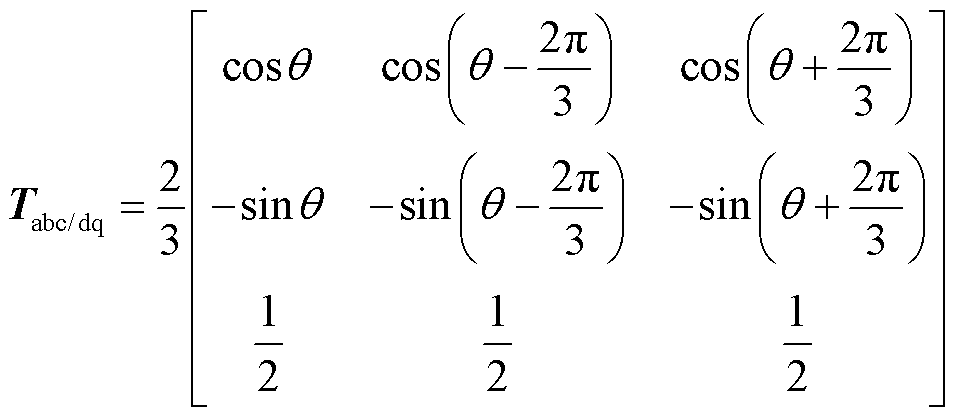 (6)
(6)
将式(1)和式(2)转换至dq坐标系下,线性化可得
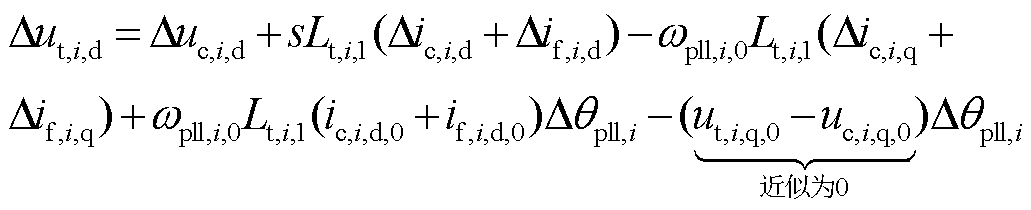 (7)
(7)
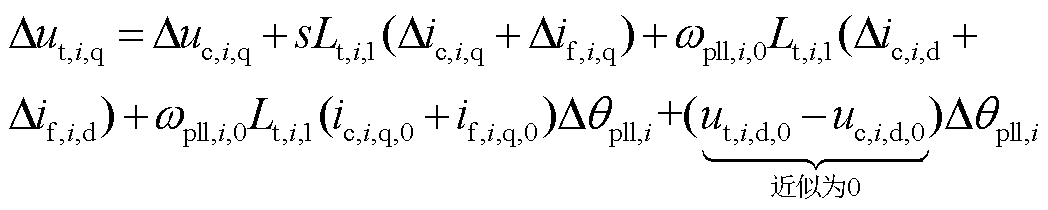 (8)
(8)
式中,ωpll,i,0为并网变换器i锁相环稳态输出频率;uc,i,d,0和uc,i,q,0分别为并网点处d轴和q轴稳态电压;ut,i,d,0和ut,i,q,0分别为变换器i端口处d轴和q轴稳态电压;ic,i,d,0和ic,i,q,0分别为并网点处d轴和q轴稳态电流;if,i,d,0和if,i,q,0分别为滤波电容的d轴和q轴稳态电流;Δuc,i,d和Δuc,i,q分别为并网点处d轴和q轴线性化电压;Δic,i,d和Δic,i,q分别为并网点处d轴和q轴线性化电流;Δut,i,d和Δut,i,q分别为变换器i端口处d轴和q轴线性化电压;Δif,i,d和Δif,i,q分别为滤波电容的d轴和q轴线性化电流。
对滤波电容电流进行分析,可得
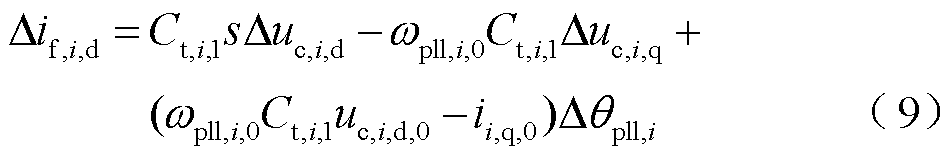
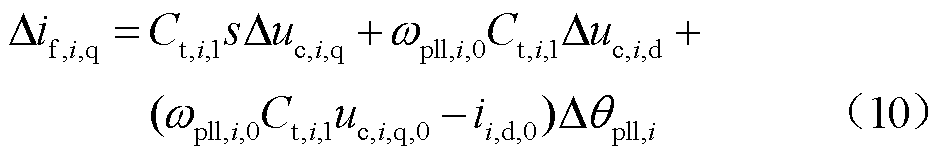
由于滤波器电容通常较小,Lt,i,1、Ct,i,1的值远小于其他参数。因此,将式(9)和式(10)分别代入式(7)和式(8),并转换至频域,整理可得
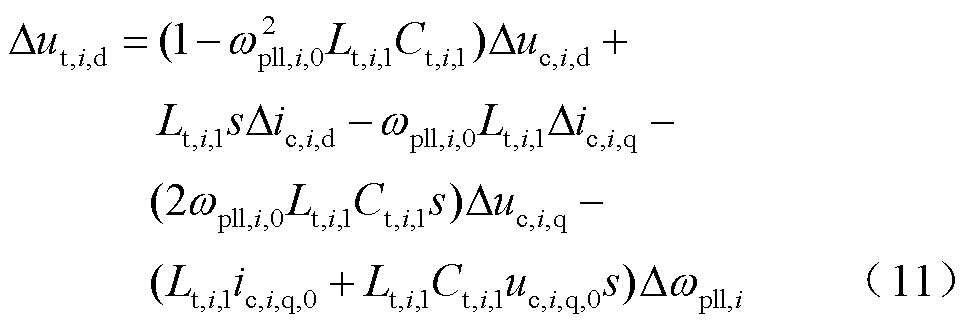
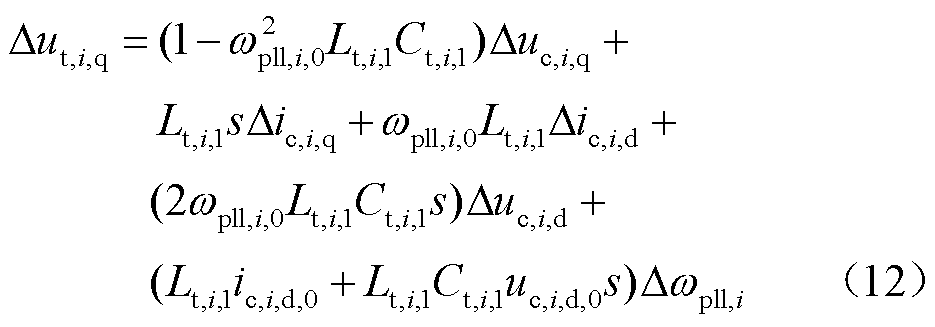
光伏并网变换器的功率关系可表示为
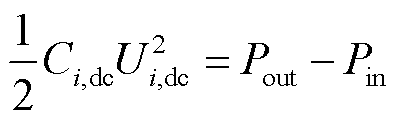 (13)
(13)
式中,Ci,dc为稳压电容;Pout为新能源机组输出功率;Pin为输入电网功率。
在小扰动过程中,假设Pout不发生变化,可得
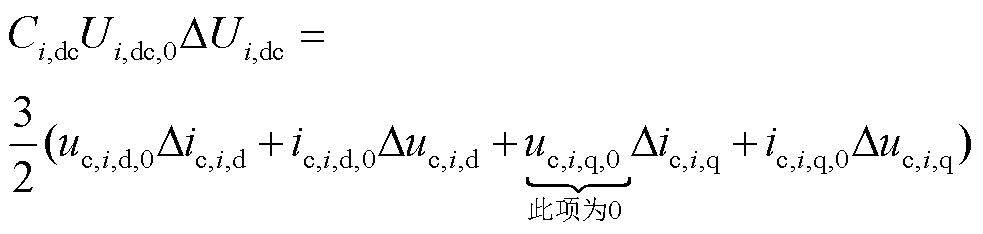 (14)
(14)
对光伏并网系统的电流控制环节进行线性化,并转换至频域,整理可得
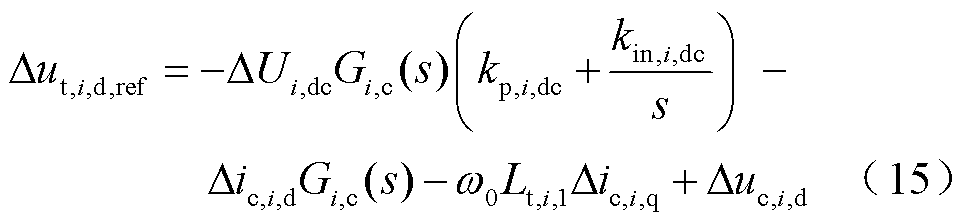
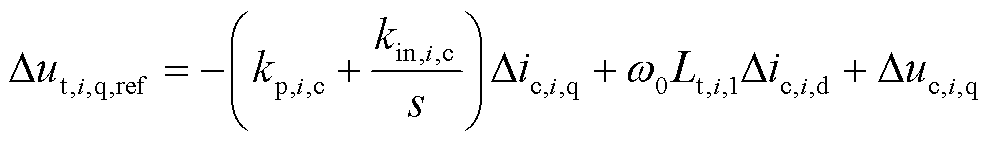 (16)
(16)
式中,Gi,c(s)和Gi,dc(s)分别为电流控制环节和直流电压控制环节PI控制函数,表达式为
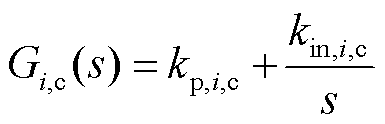
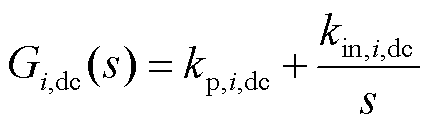
对锁相环控制环节进行线性化,并转换至频域,整理可得
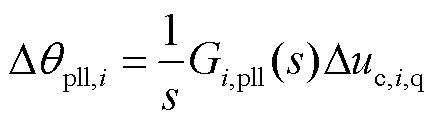 (17)
(17)
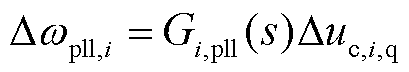 (18)
(18)
式中,Gi,pll(s)为锁相环PI控制函数。
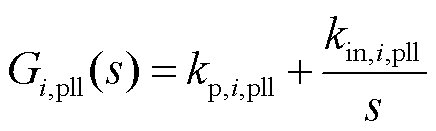
整理式(11)、式(12)、式(15)、式(16)和式(18)可得
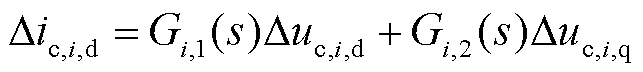 (19)
(19)
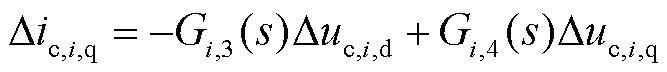 (20)
(20)
式中,Gi,1(s)、Gi,2(s)、Gi,3(s)、Gi,4(s)、gi,1(s)、gi,2(s)、gi,3(s)、gi,4(s)、gi,5(s)和gi,6(s)为中间变量,且
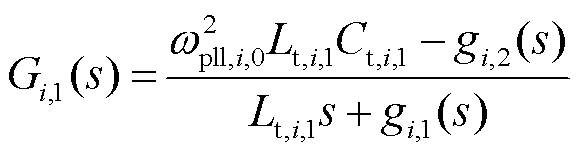
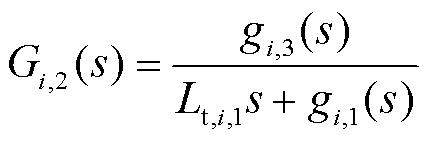
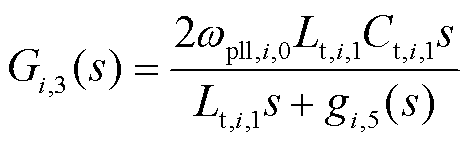
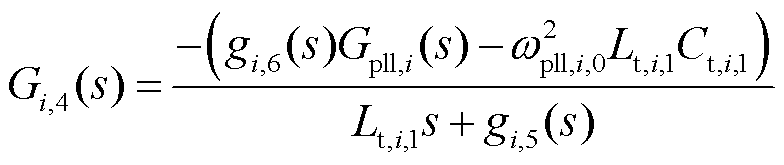
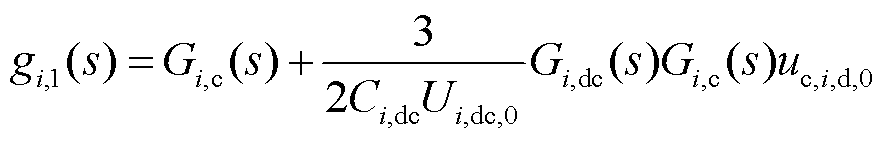
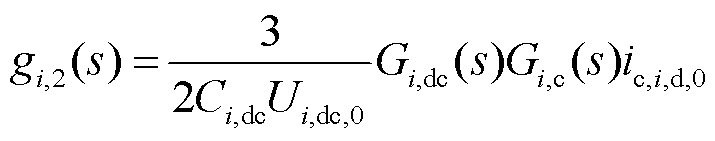
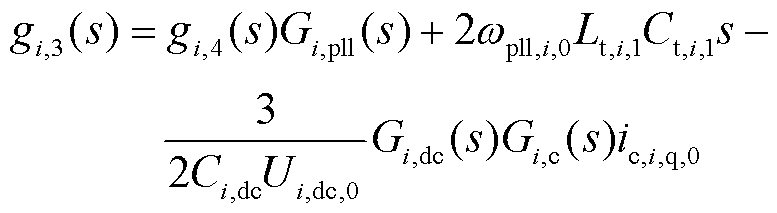
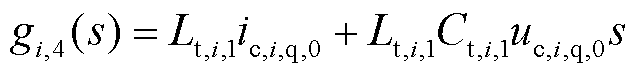
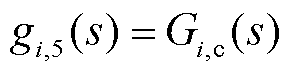
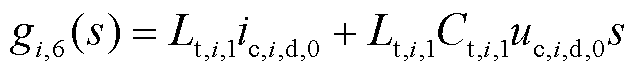
2.1.2 STATCOM小信号建模
假设系统无功功率由各STATCOM平均补偿,且STATCOM在稳态时不提供有功功率,线性化整理可得
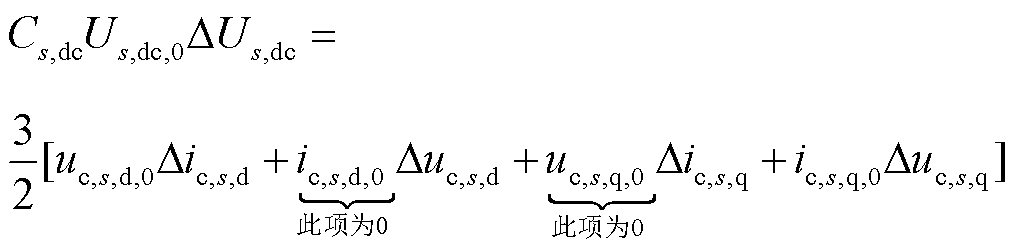 (21)
(21)
对STATCOM电流控制环节进行线性化,并转换至频域,整理可得
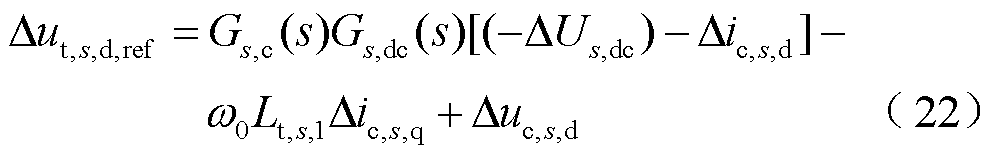
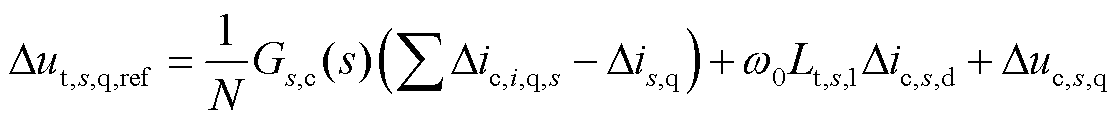 (23)
(23)
式中,Δic,i,q,s为并网变换器i转换至并网变换器s的dq坐标系下的q轴并网点电流。
STATCOM的电路及锁相环控制方程的线性化方式与光伏并网系统相同,结合式(22)和式(23),整理可得d轴电流表达式为
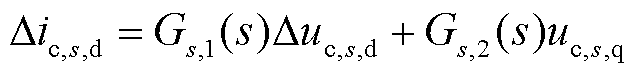 (24)
(24)
式中,Gs,1(s)和Gs,2(s)为中间变量,且
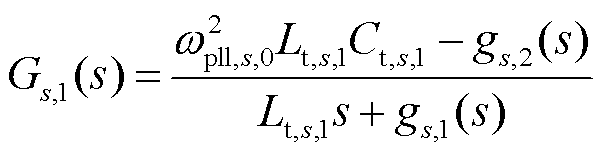
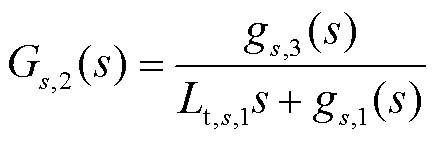
在不同旋转坐标系下的系统电流可表示为
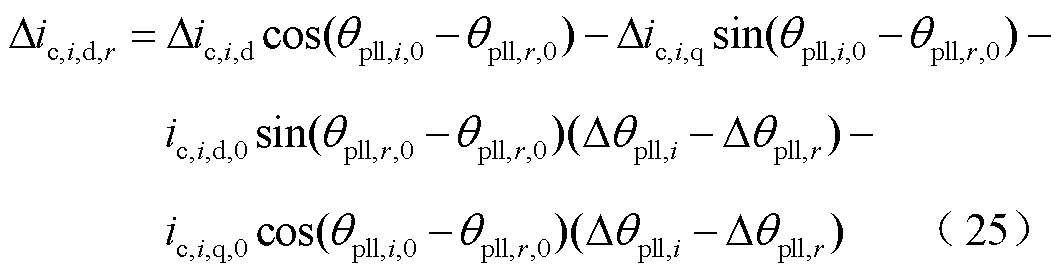
式中,Δic,i,d,r为并网变换器i转换至并网变换器r的dq坐标系下的d轴并网点电流值。
在稳态运行状态下,各并网变换器锁相环输入参考电压相同,输出相角相同,因此有qi,0=qr,0,代入式(25)整理可得
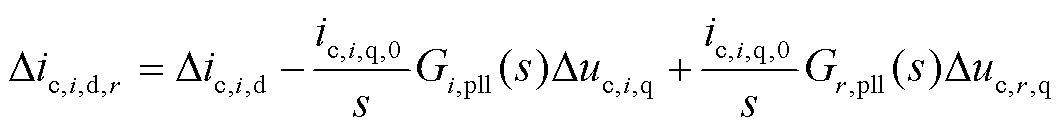 (26)
(26)
同理可得
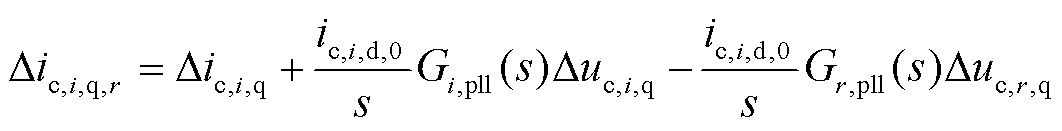 (27)
(27)
式中,Δic,i,q,r为并网变换器i转换至并网变换器r的dq坐标系下的d轴并网点电流值。
因此,在STATCOM旋转坐标系下,整理可得
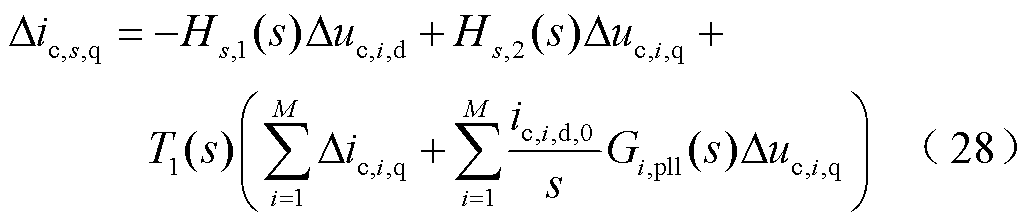
式中,T1(s)、Hs,1(s)、Hs,2(s)为中间变量,且
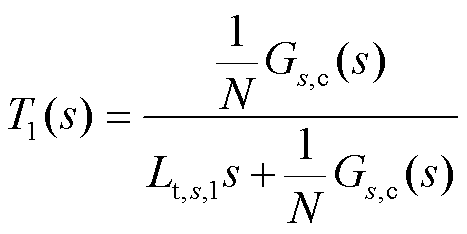
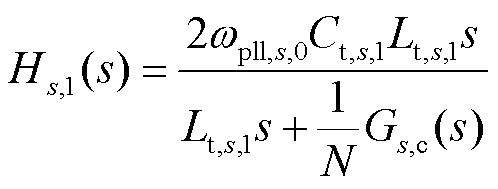
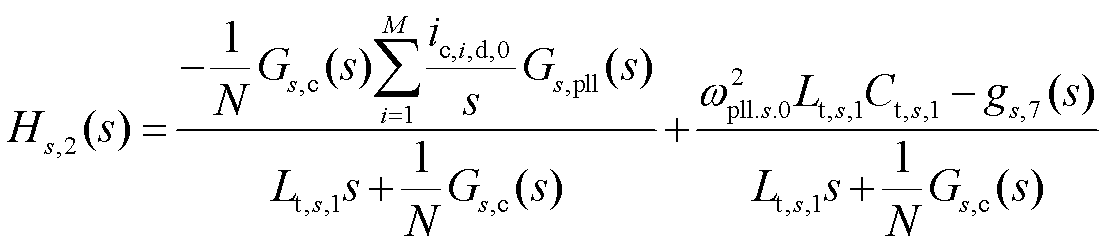
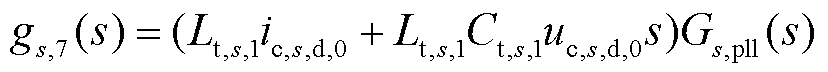
2.1.3 阻抗分析模型
基于基尔霍夫电流定律,对并网点处的电路方程分析可得电压旋转表达式为
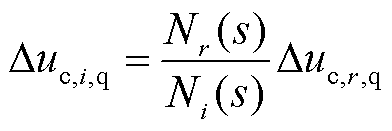 (29)
(29)
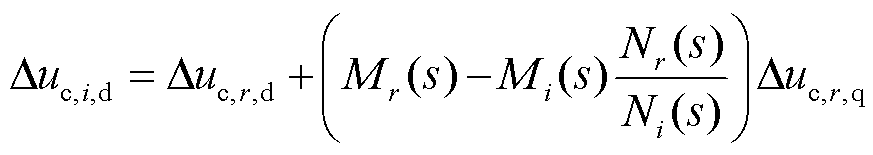 (30)
(30)
式中,Δuc,i,d,r为并网变换器i转换至并网变换器r在dq坐标系下的d轴并网点电压值;Mr(s)和Nr(s)为中间变量,且
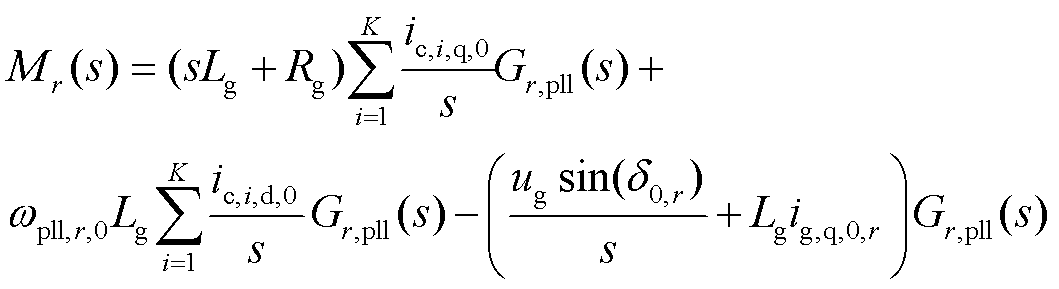
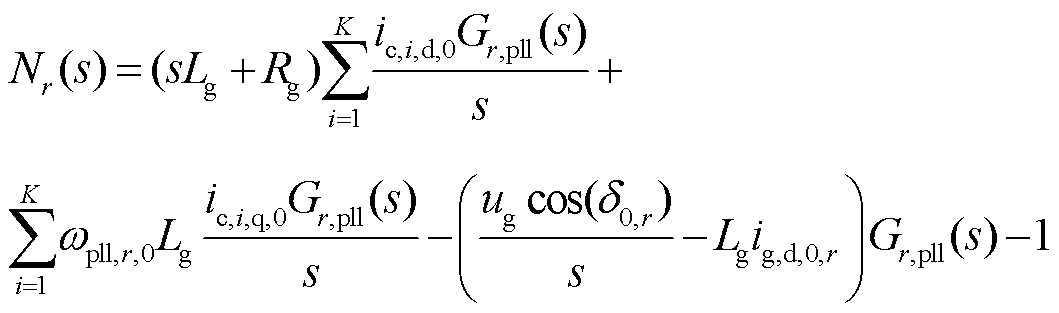
由式(28)~式(30)可得,STATCOM的q轴输出电流可表示为
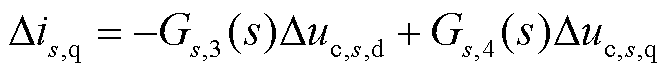 (31)
(31)
式中,Gs,3(s)和Gs,4(s)为中间变量,且
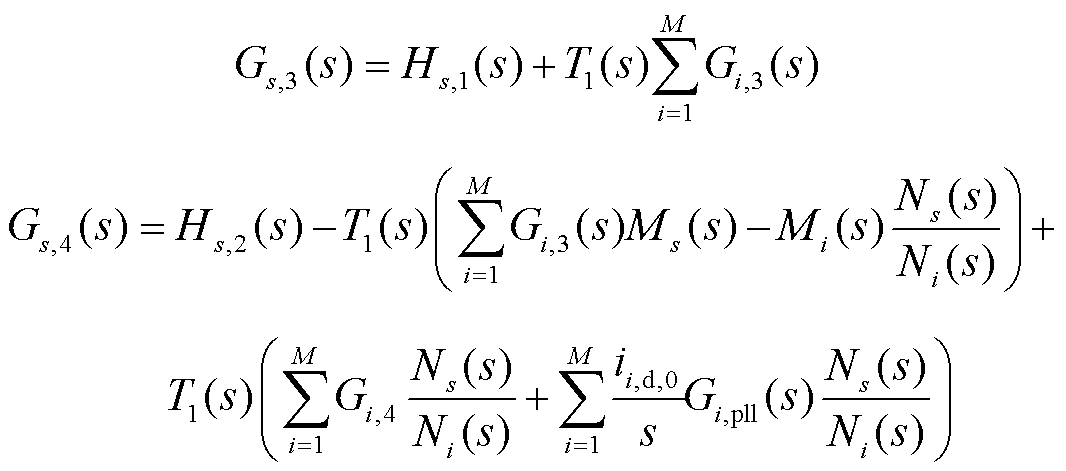
以并网变换器所在dq轴为参考系,可得并网点输出电流可表示为
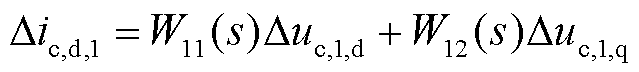 (32)
(32)
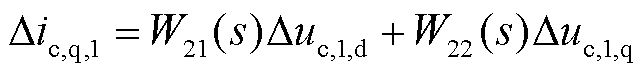 (33)
(33)
式中,W11(s)、W12(s)、W21(s)和W22(s)分别为光伏并网系统的dd、dq、qd和qq通道阻抗模型,且
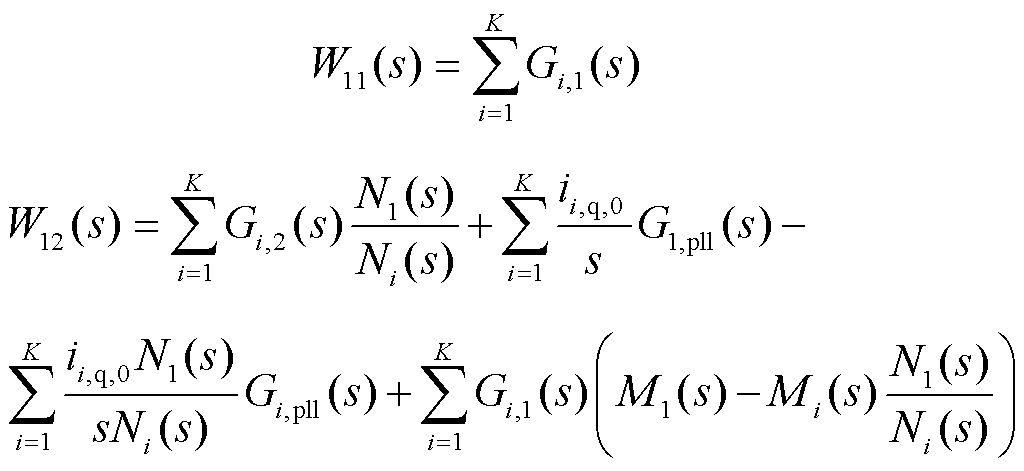
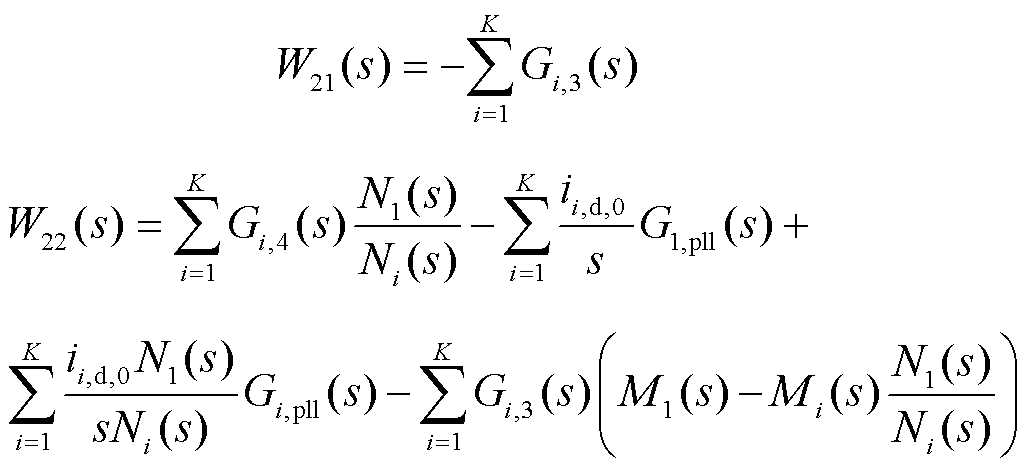
系统的输出阻抗阵可表示为
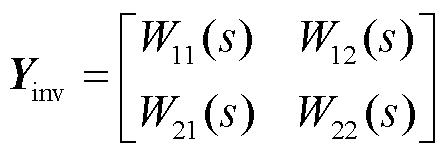 (34)
(34)
同理可得,电网等效输出矩阵可表示为
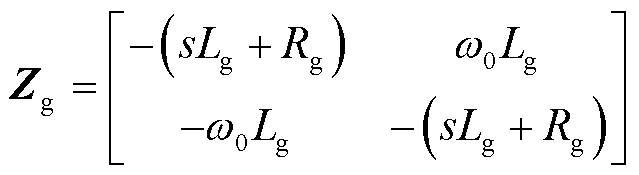 (35)
(35)
式中,Lg为电网等效电感;Rg为电网等效阻抗;ω0为并网点处电网的稳态频率。
GFL变流器并网系统的等效电路如图7所示。
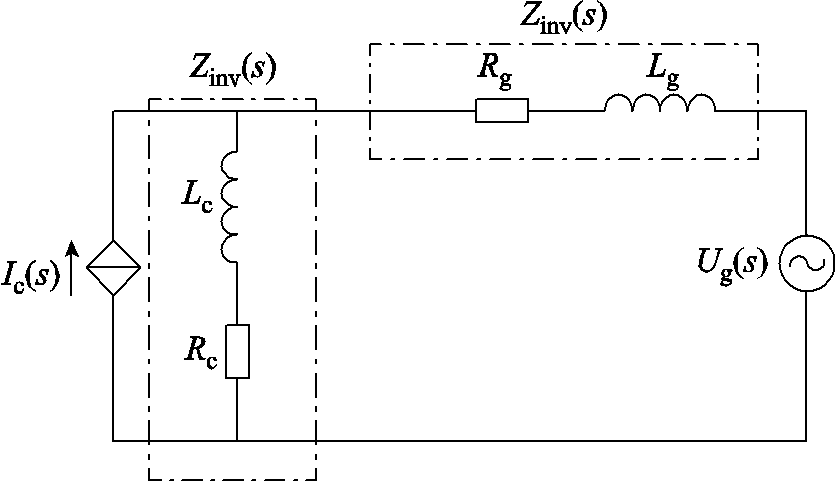
图7 GFL变流器并网系统等效电路
Fig.7 Equivalent circuit of grid-connected system with GFL converter
由图7可得
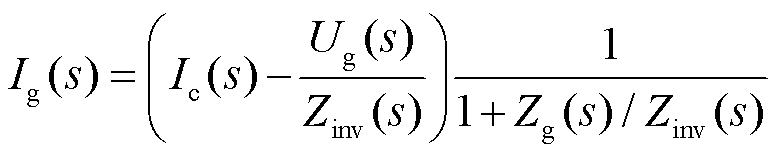 (36)
(36)
假设并网变换器和电网两个子系统都能够独立稳定运行,由式(36)可得,系统的稳定性取决于1+Zg(s)/Zinv(s),该环节可等效为负反馈传递函数,其中,G(s)=1,H(s)=Zg(s)/Zinv(s)。
在dq坐标系下,GFL变流器并网系统还应满足
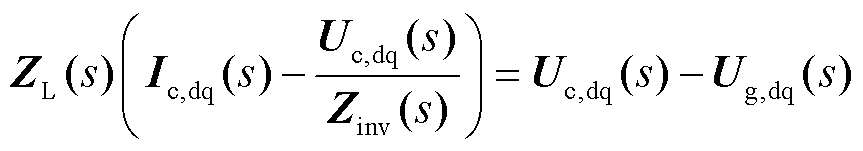 (37)
(37)
因此,以等效电压源分析得到的稳定判据可表示为
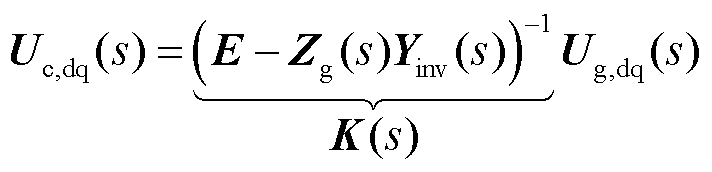 (38)
(38)
式中,E为单位矩阵。
由式(38)可得,系统满足静态同步稳定运行的条件为等效传递函数K(s)的特征根的实数部均为负数。
在对系统的静态同步稳定进行分析时,还需要分析系统在小扰动下的暂态性能,引入超调量s和调节时间ts两项暂态性能指标,可表示为
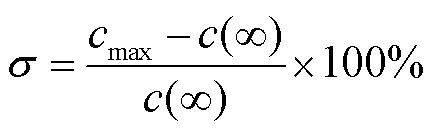 (39)
(39)
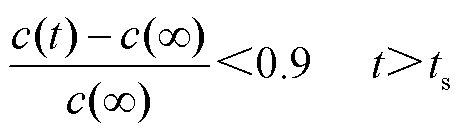 (40)
(40)
式中,c(t)为信号函数t时刻的取值;cmax为信号函数中的最大值;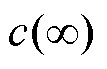 为信号函数在时间无限大时的取值,即信号的稳态值,当信号不稳定时该值不存在。
为信号函数在时间无限大时的取值,即信号的稳态值,当信号不稳定时该值不存在。
为量化分析各极点对系统小扰动振荡过程的影响,引入参与因子指标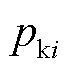 ,可表示为
,可表示为
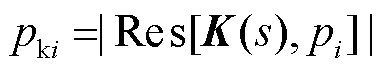 (41)
(41)
式中,Res[K(s), pi]为在pi处的留数;pki为留数的模值,反映极点对系统振荡的影响程度。
此外,引入衰减系数β,以量化系统的小扰动稳定性能,可表示为
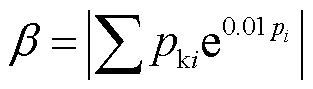 (42)
(42)
在Matlab/Simulink中搭建模型进行仿真验证,其中,单光伏并网变换器系统参数见表1,电流基准值为100 A。
表1 光伏并网系统参数
Tab.1 Grid-connected system parameter
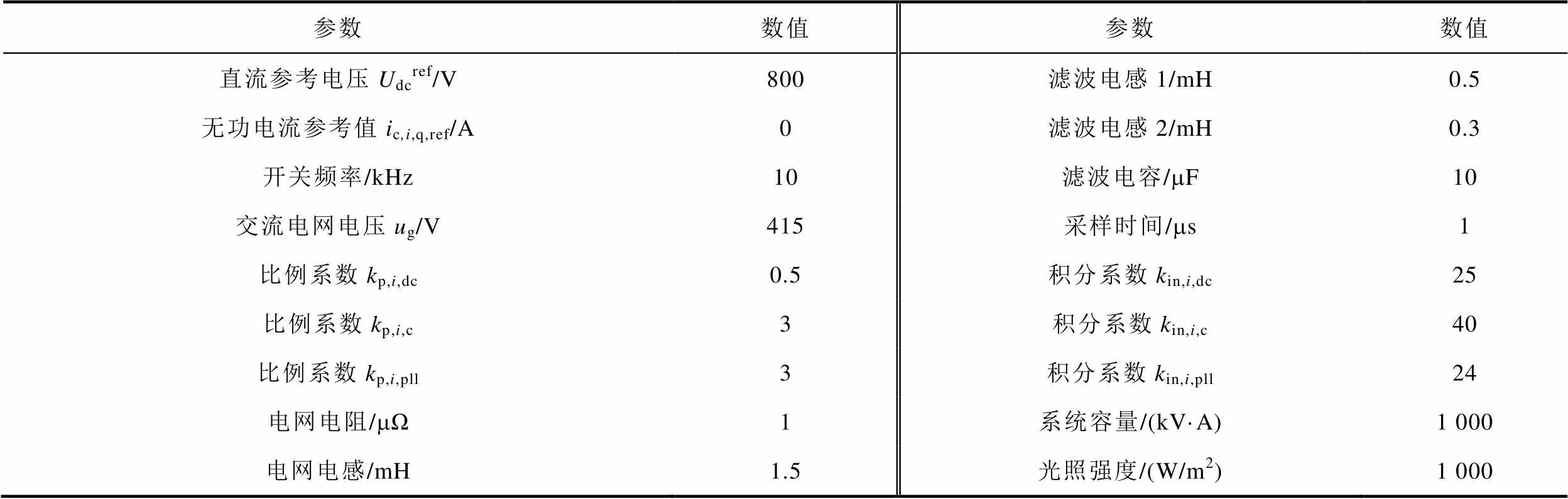
参数数值参数数值 直流参考电压Udcref/V800滤波电感1/mH0.5 无功电流参考值ic,i,q,ref/A0滤波电感2/mH0.3 开关频率/kHz10滤波电容/mF10 交流电网电压ug/V415采样时间/ms1 比例系数kp,i,dc0.5积分系数kin,i,dc25 比例系数kp,i,c3积分系数kin,i,c40 比例系数kp,i,pll3积分系数kin,i,pll24 电网电阻/mΩ1系统容量/(kV·A)1 000 电网电感/mH1.5光照强度/(W/m2)1 000
采用扫频法,通过在变换器端口串联电压源注入不同频率扰动并测量其响应,以获取系统的幅频特性与相频特性,与理论分析结果对比如图8所示。上述结果表明,扫频结果与理论分析模型基本一致,验证了所提模型的准确性。
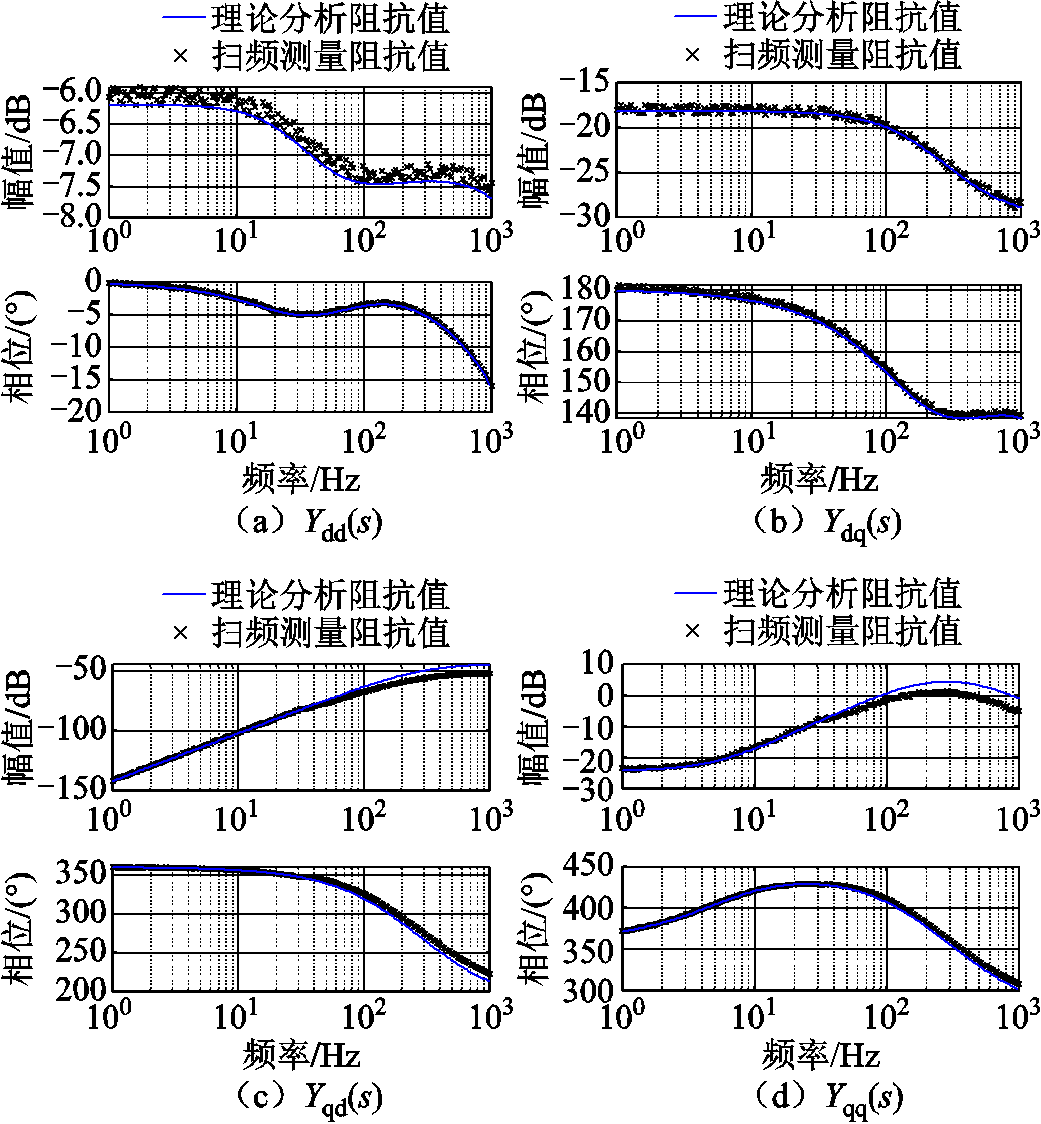
图8 扫频结果对比
Fig.8 Comparison between simulation results and theoretical analysis
在去掉传递函数的零极点对消后,系统的极点分布如图9所示。各通道的极点相同且实部均为负数,表明系统当前位于稳定域中。设置ic,i,q,ref =0,且0.4 s时刻发生扰动故障,0.5 s后故障切除,并网变换器的输出电压与电流如图10所示。
由图10可得,系统在发生小扰动故障时能够保持稳定运行,与理论分析结果相符。设置ic,i,q,ref的变化范围为[-2.5,2.5](pu),以靠近虚轴近极点轨迹为
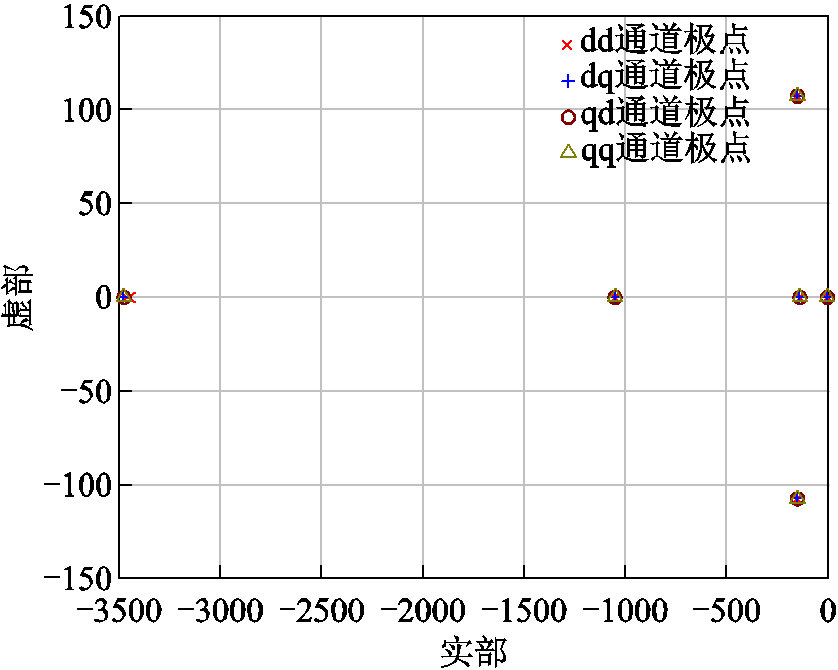
图9 系统极点分布
Fig.9 Pole distribution of system
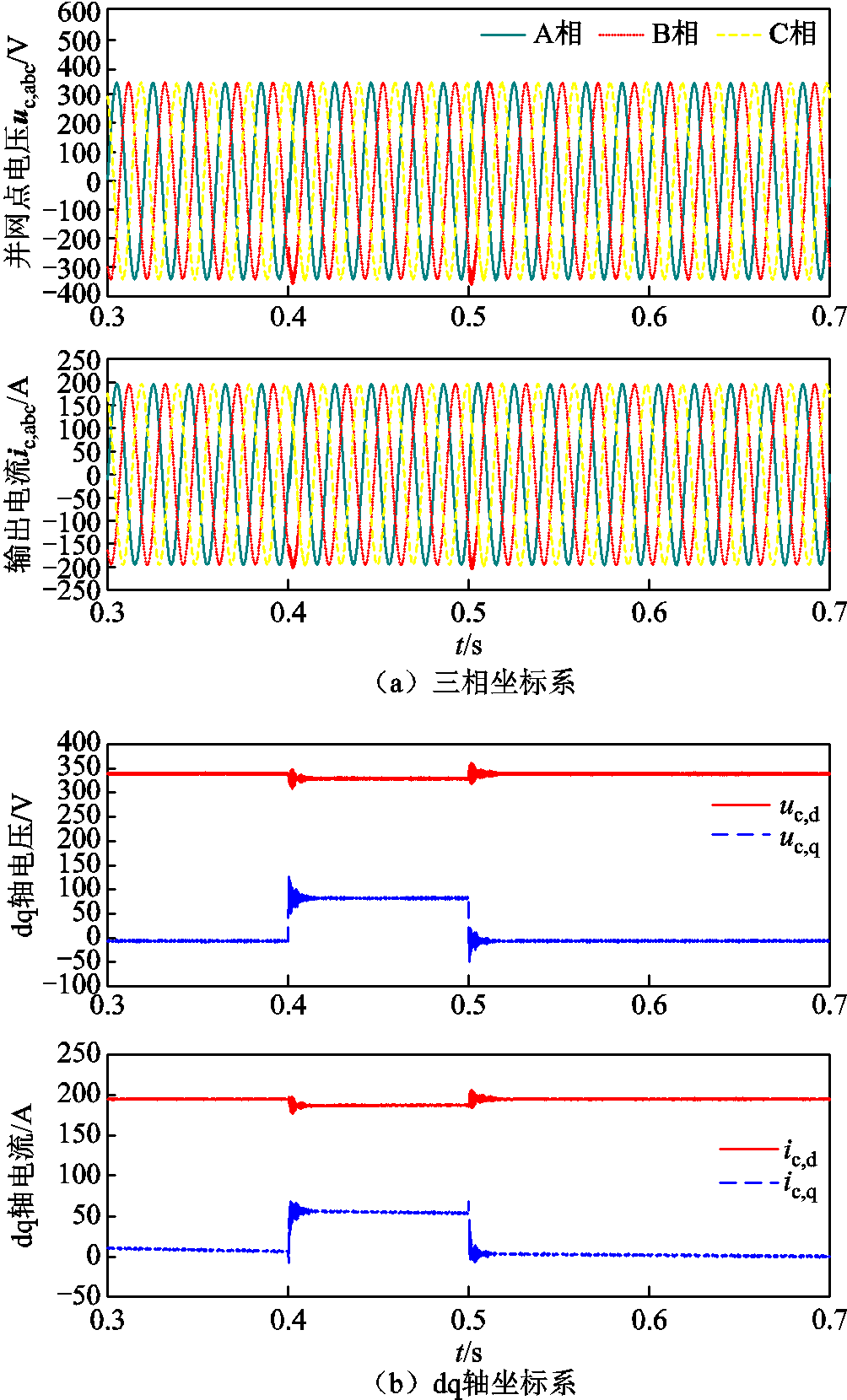
图10 在ic,i,q,ref = 0时光伏系统并网点小扰动故障下电压和电流
Fig.10 Voltage and current of grid-connected point of PV system under small disturbance fault with ic,i,q,ref = 0
例进行分析,临界极点变化轨迹如图11所示。随着并网变换器输出无功功率的增加,系统的p2极点向右半平面偏移。这是因为并网变换器系统输出的无功功率逐渐增加,导致系统静态安全裕度降低,从而使得系统由稳定运行状态转变为不稳定运行状态。同时,计算系统参与因子与衰减系数,其变化轨迹分别如图12和图13所示。
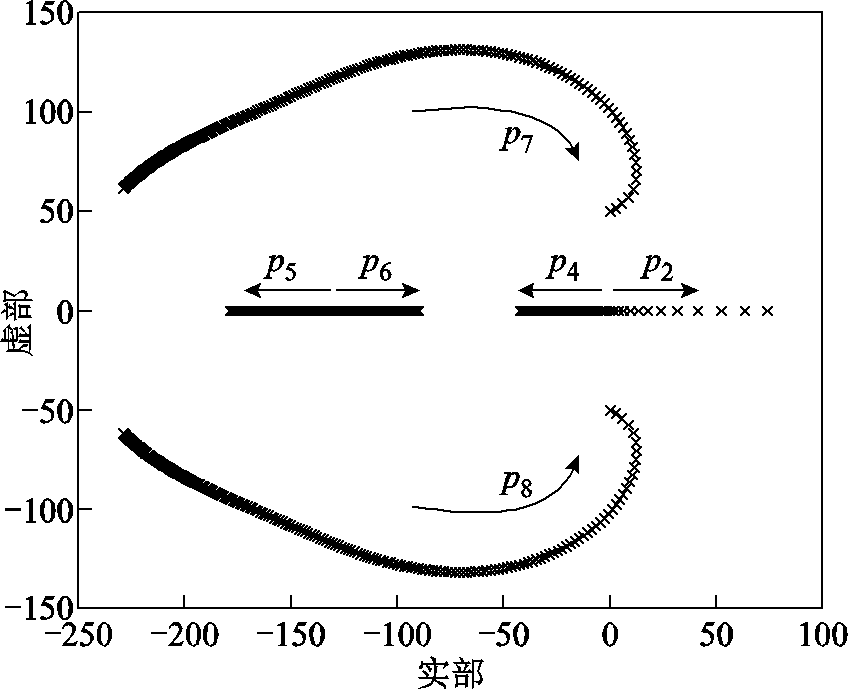
图11 临界极点变化轨迹
Fig.11 Variation trajectory of critical pole
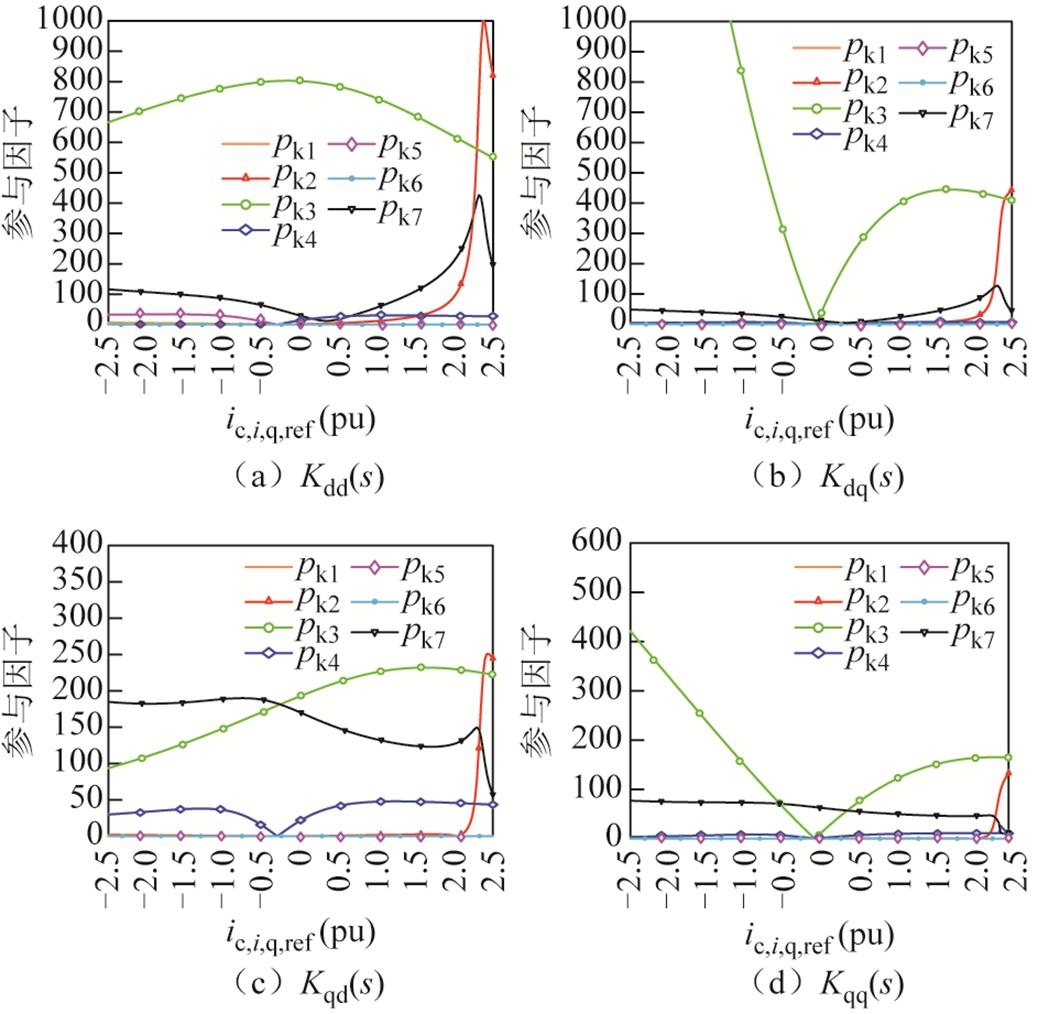
图12 临界极点参与因子变化轨迹
Fig.12 Variation trajectory of critical pole participation factor
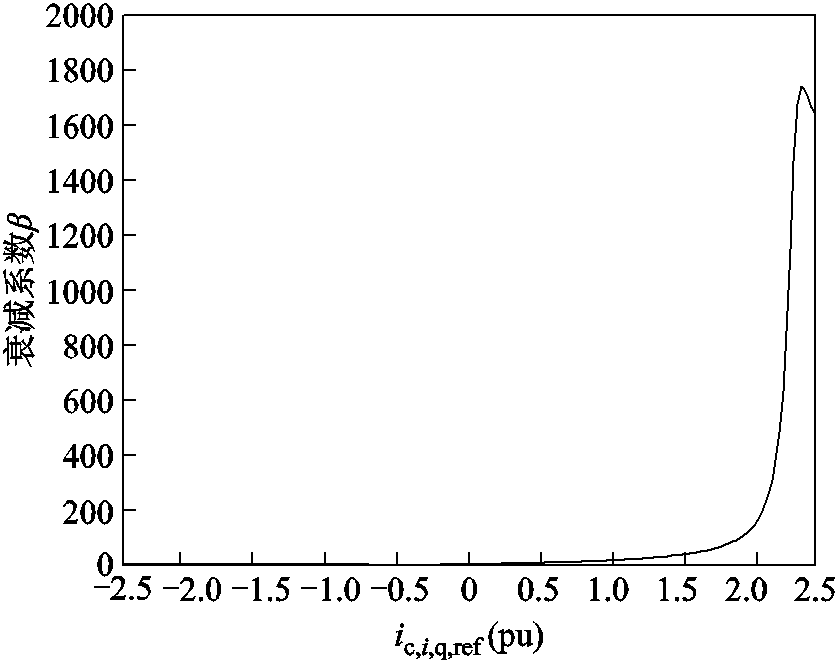
图13 衰减系数变化轨迹
Fig.13 Variation trajectory of attenuation coefficient
由图12和图13可得,当系统处于安全域内时,锁相环控制产生的p3极点占据主导地位,并且通过合理配置锁相环控制参数能够有效提升系统的稳定性能。随着输出无功功率的增加,极点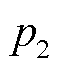 逐渐接近虚轴,同时
逐渐接近虚轴,同时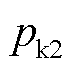 迅速上升,从而使系统的稳定性能主要受到有功功率控制环节的限制。通过对图中结果进行分析可以发现,在系统接近临界稳定运行边界时,衰减系数β会快速上升。因此,β可以作为衡量系统稳定性能的一个重要指标之一,并且应避免其过大。
迅速上升,从而使系统的稳定性能主要受到有功功率控制环节的限制。通过对图中结果进行分析可以发现,在系统接近临界稳定运行边界时,衰减系数β会快速上升。因此,β可以作为衡量系统稳定性能的一个重要指标之一,并且应避免其过大。
图14为光伏并网变换器输出电流为0.6(pu)时小扰动波形。对比图10可得,当光伏并网逆变器向电网输送无功电流时,系统的超调量s%从7.13%增加为12.76%,调节时间从0.017 s增加为0.038 s,静态同步稳定性能下降。上述分析结果与图10相同,光伏逆变器向电网输送无功电流不利于系统的静态同步稳定性能的提升。图15给出了系统小扰动不稳定时输出的电压电流波形,系统发生静态同步失稳现象,此时系统存在实部为正的极点p2=6.27。仿真结果与理论分析相符,验证了本文提出的静态同步稳定分析方法的正确性。
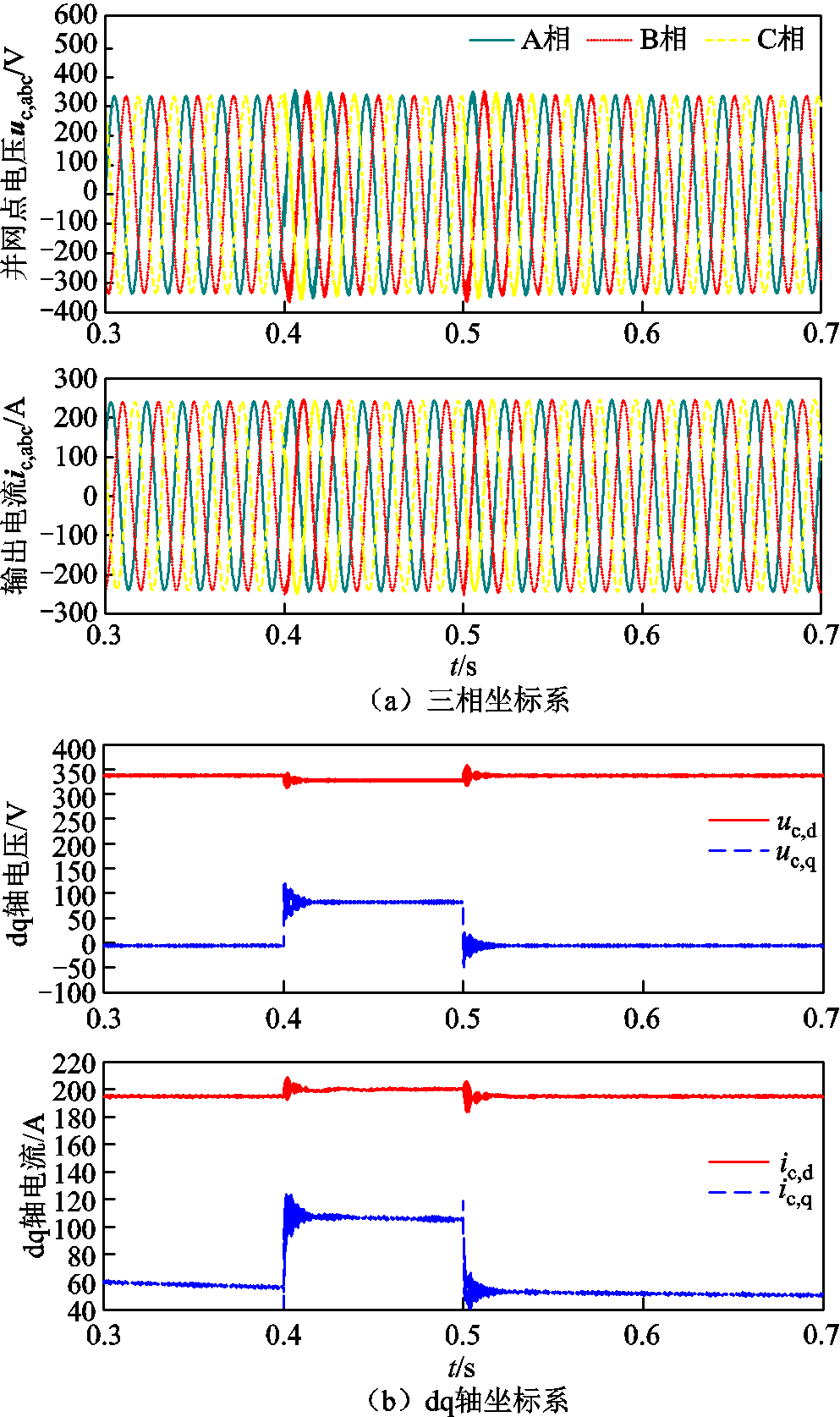
图14 在ic,i,q,ref=0.5时光伏系统并网点小扰动故障下电压和电流
Fig.14 Voltage and current of grid-connected point of PV system under small disturbance fault with ic,i,q,ref=0.5
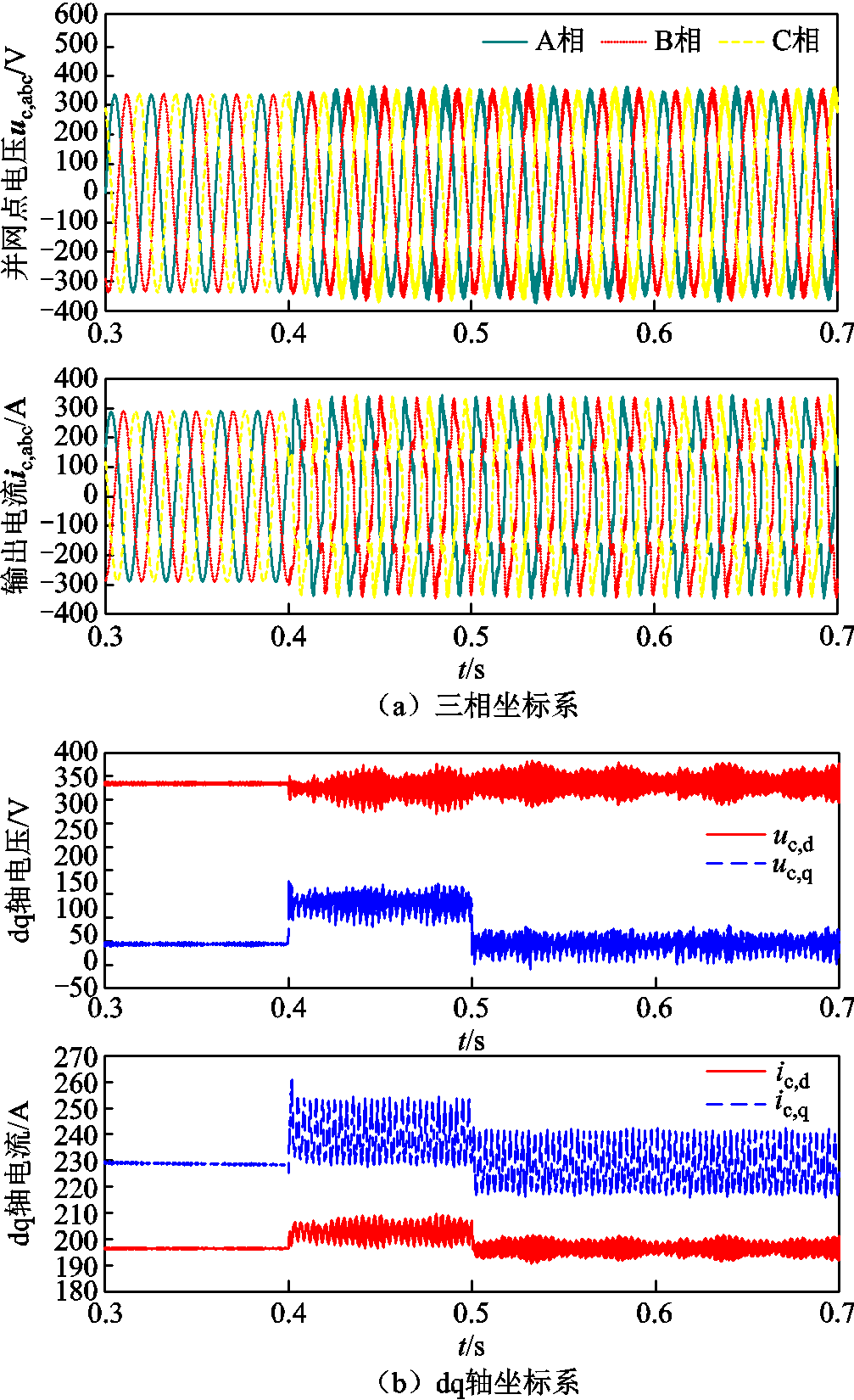
图15 小扰动故障并网点输出电压电流结果(ic,i,q,ref =2.3,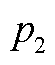 =6.27)
=6.27)
Fig.15 Output voltage and current result of small disturbance fault and grid point(ic,i,q,ref =2.3,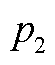 =6.27)
=6.27)
在3.1节光伏并网系统模型的基础上增加STATCOM,其参数见表2。采用扫频法分析模型的准确度,具体结果如图16所示,验证了所提模型的准确性。并网变换器等效导纳矩阵传递函数伯德图对比结果如图17所示。在增加STATCOM后,主要影响并网逆变器q耦合通道,原因在于跟网型并网变换器的同步环节使用锁相环控制策略,同步稳定性能受到并网点q轴电压影响。当系统发生振荡时,由于各并网变换器所属的dq参考坐标系不相同,导致其q轴电压振荡方式不同,在iq控制通道上会额外产生耦合作用效果。
表2 STATCOM参数
Tab.2 Parameters of STATCOM
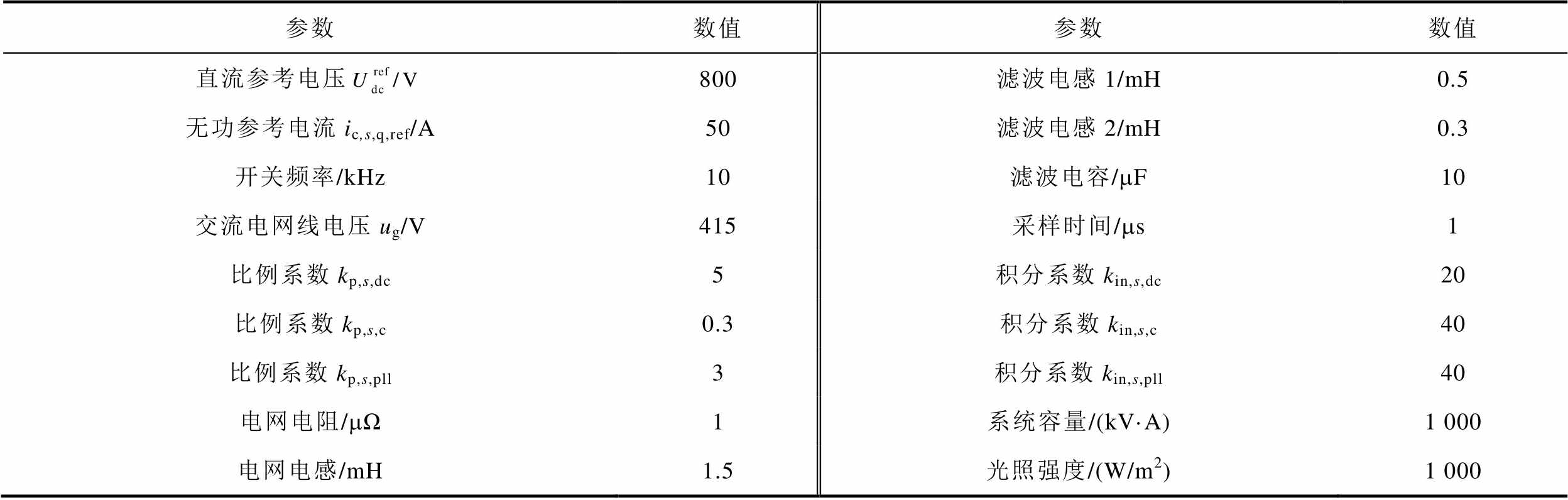
参数数值参数数值 直流参考电压800滤波电感1/mH0.5 无功参考电流ic,s,q,ref/A50滤波电感2/mH0.3 开关频率/kHz10滤波电容/mF10 交流电网线电压ug/V415采样时间/ms1 比例系数kp,s,dc5积分系数kin,s,dc20 比例系数kp,s,c0.3积分系数kin,s,c40 比例系数kp,s,pll3积分系数kin,s,pll40 电网电阻/mΩ1系统容量/(kV·A)1 000 电网电感/mH1.5光照强度/(W/m2)1 000
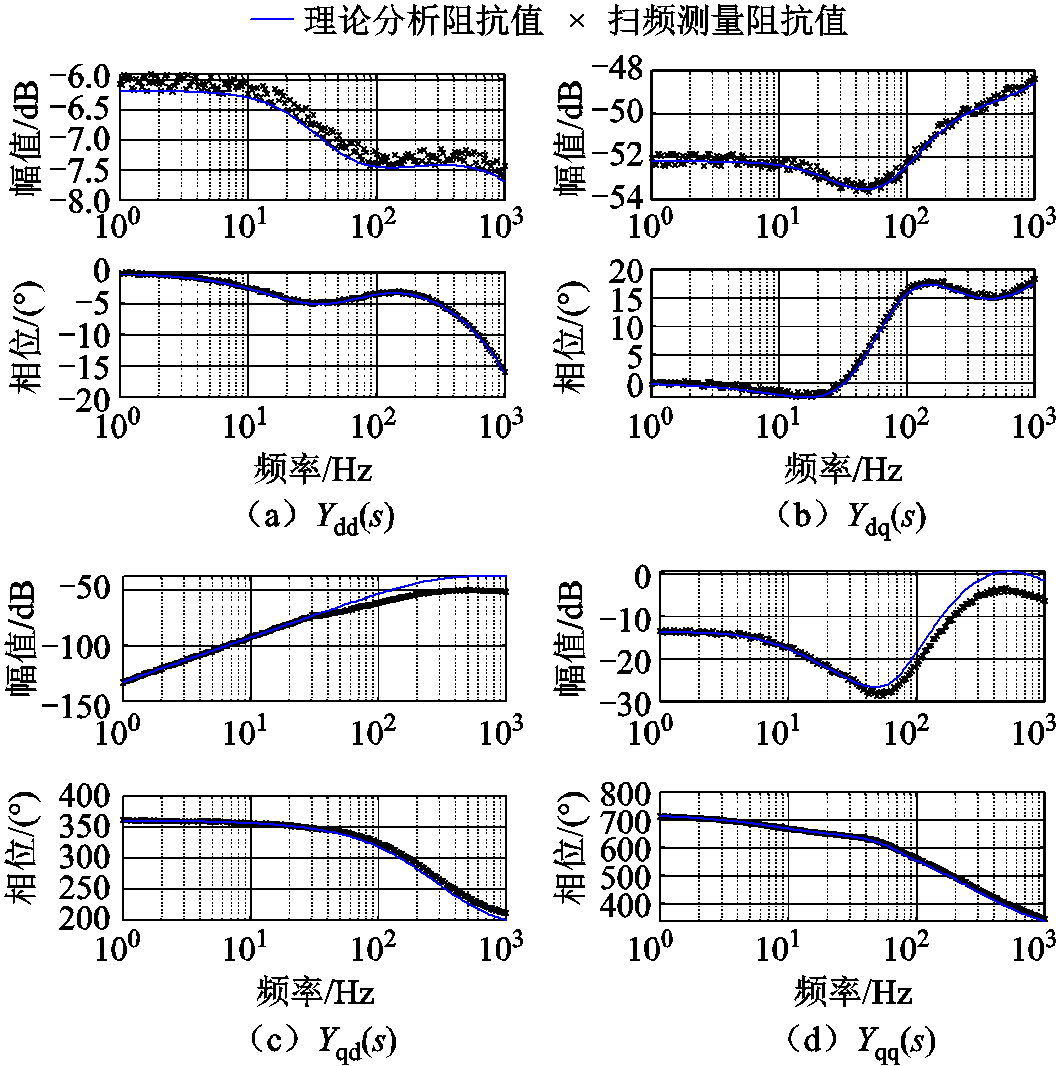
图16 扫频结果对比
Fig.16 Comparison between simulation results and theoretical analysis
系统dd通道传递函数不受影响,因此在部分文献中,将dd通道的导纳值作为跟网型并网变换器同步稳定判据之一[10]。系统极点分布如图18所示,部分关键极点见表3。
对比图9和图18可得,在配置STATCOM后,系统中在dd通道引入了p1、p2和p17极点,在q耦合通道引入了p22、p23、p50、p51、p52和p53极点,其分布更加接近临界稳定运行边界。若按照传统的稳定分析标准,系统的稳定性能应降低。在发生小扰动故障后,并网点处电压和电流如图19所示。
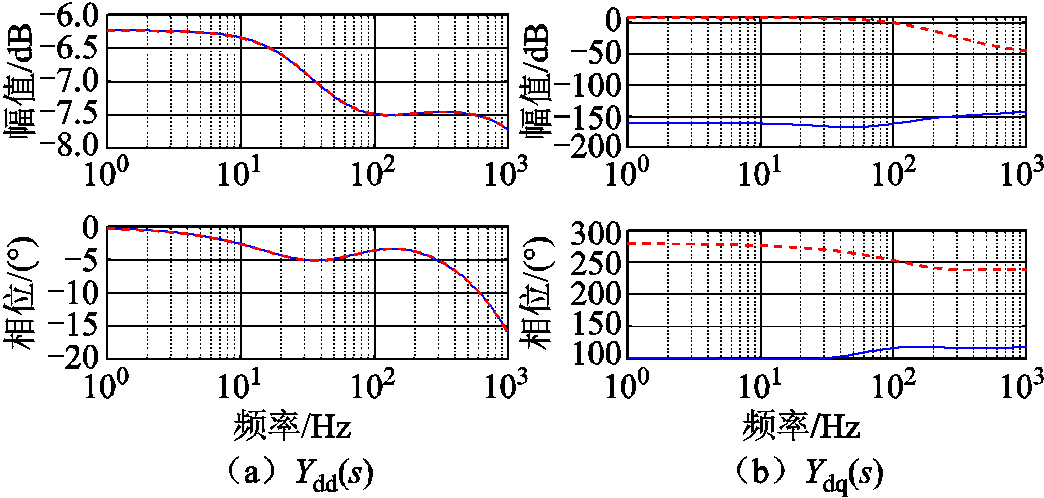
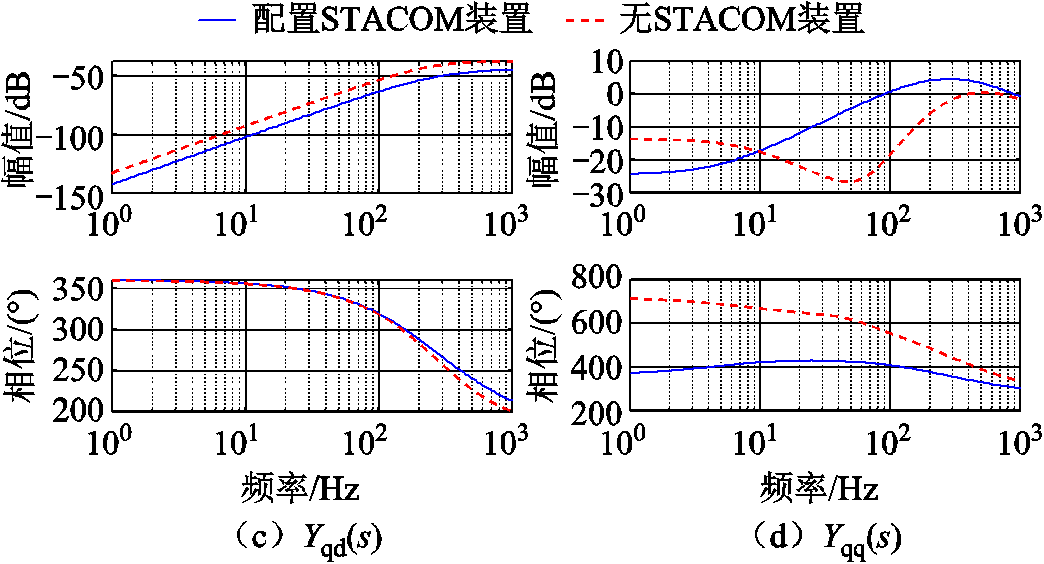
图17 等效导纳矩阵传递函数伯德图
Fig.17 Bode diagram of equivalent admittance matrix transfer function
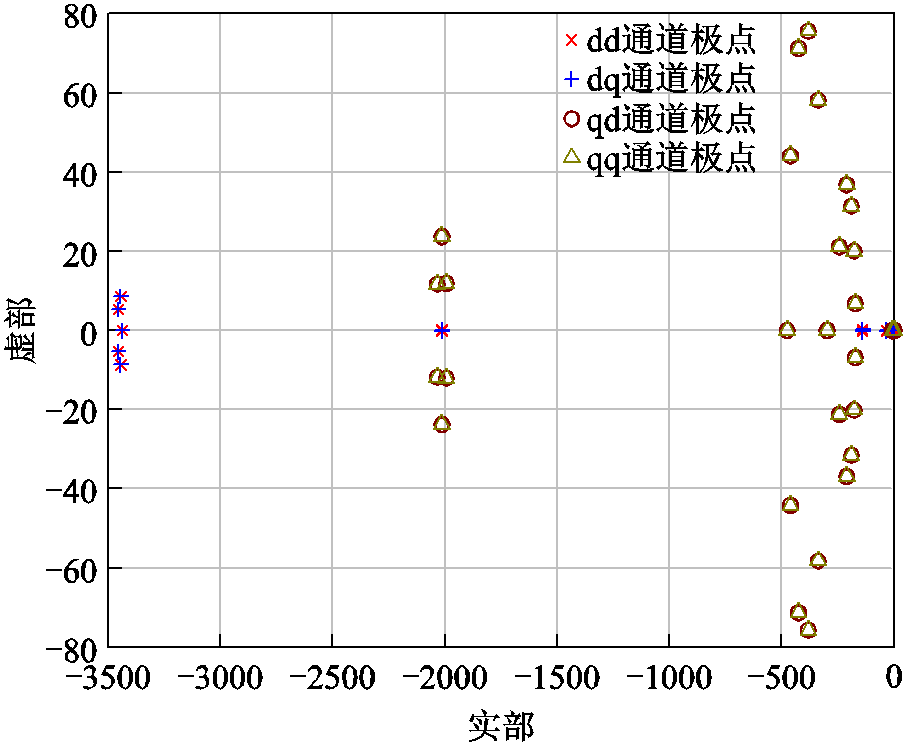
图18 含STATCOM系统极点分布
Fig.18 Pole distribution of system with STATCOM
表3 系统关键极点
Tab.3 Key pole of system

d通道q通道 p1-8.032+0.003ip22-8.032+0.006i p23-8.032-0.006i p2-8.032-0.003ip50-8.038 p51-8.025 p21-3457.421p52-4.812 p53-4.811
对比图14和图19可得,系统的超调量s%从12.76%减少为5.76%,调节时间从0.038 s减少为0.010 s,系统暂态稳定性能反而得到提升。因此,在并网变换器控制参数配置合理的情况下,配置一定容量的无功补偿装置,能够有效提升系统的静态同步稳定性能。仅以极点的实部幅值作为稳定性能评价会致使分析结果偏保守。部分关键极点的参与因子分布见表4。结果表明,STATCOM引入新极点的同时也引入了附近的零点,自身参与因子小且降低了原有临界极点的参与因子,提高了系统的静态稳定性能。
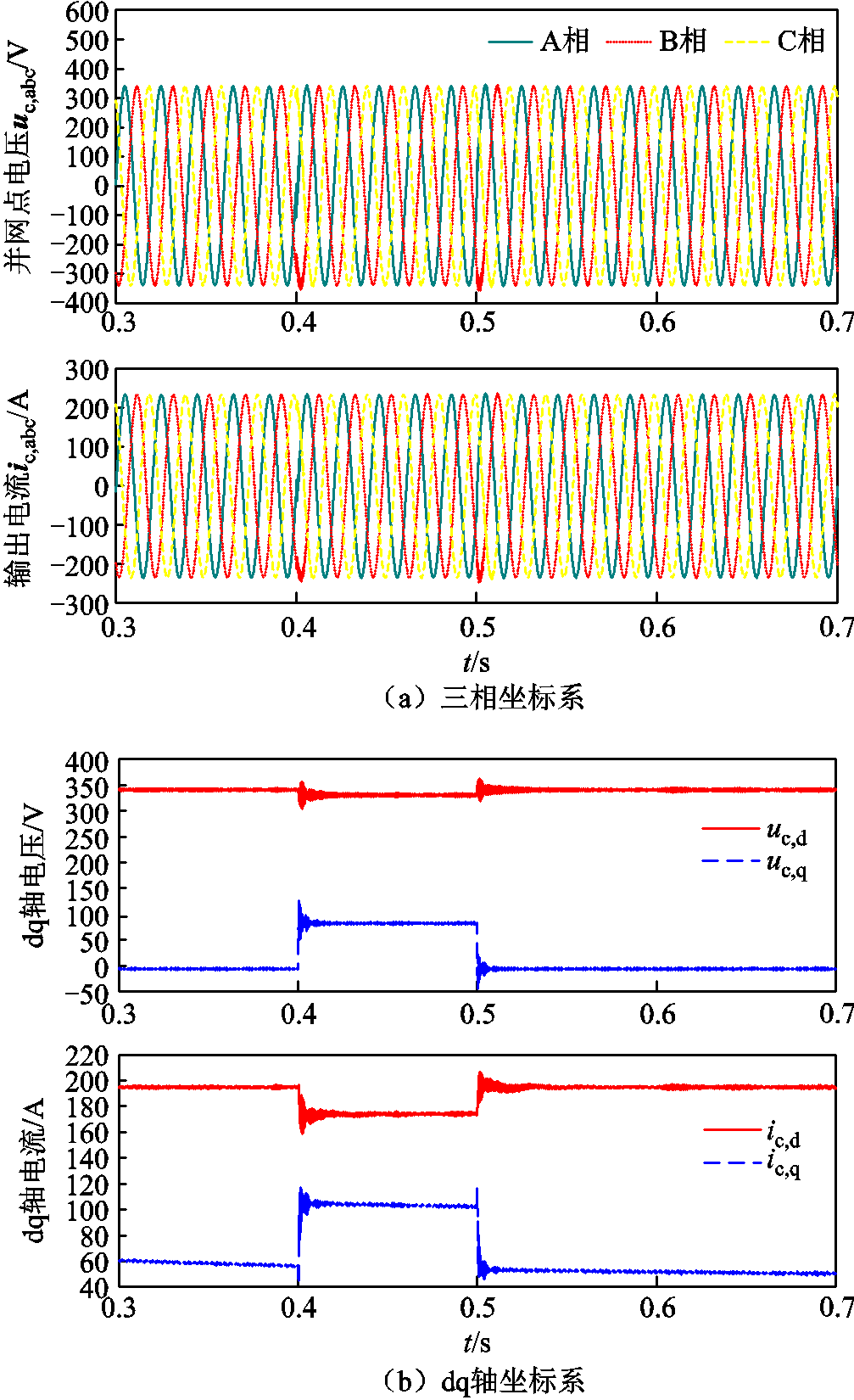
图19 在ic,i,q,ref=0.5时并联系统并网点小扰动故障下电压和电流
Fig.19 Voltage and current of grid-connected point of parallel system under small disturbance fault with ic,i,q,ref=0.5
表4 关键极点参与因子
Tab.4 Participation factors of some key pole

通道参与因子 dpk11.28×10-12 pk21.28×10-12 pk173.32×10-13 qpk226.25×10-12 pk236.25×10-12 pk299.05×10-12 pk309.05×10-12 pk313.32×10-13 pk323.35×10-13
系统的衰减系数β从3.15×10-4变为1.27×10-5,降低了95.97%,其原因为配置STATCOM后改变了系统内零点和极点的分布位置,零点与极点分布更加相近,降低极点在振荡中的影响。图20为闭环传递函数K(s)的伯德图,配置STATCOM能够消除原并网变换器dq通道与qq通道中谐振频率点,从而降低系统在低频至中频段的幅值,并且与衰减系数分析结果相一致。
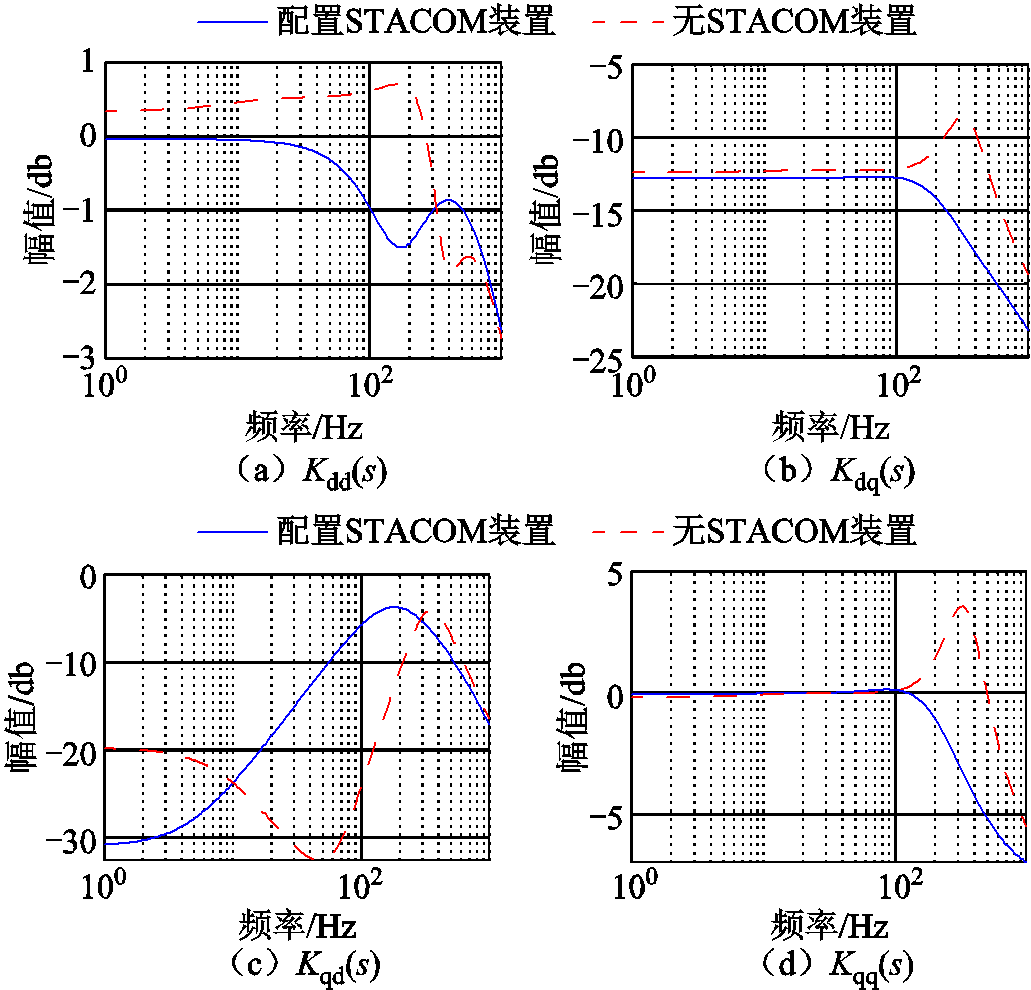
图20 闭环传递函数K(s)伯德图
Fig.20 Bode diagram of closed-loop transfer function K(s)
本节主要分析STATCOM外环控制参数对于并网变换器静态同步稳定性的影响,并以光照强度为2 000、1 000、500 W/m2下的光伏典型运行工况为例进行分析。
3.3.1 比例控制系数kp,s,dc影响
设置直流电压控制环节比例系数kp,s,dc变化范围为[0,7],其余参数不变。在上述三种运行工况下,当kp,s,dc增大时,q通道极点受到影响较小,几乎不发生变化,原因在于STATCOM并网变换器与光伏并网变换器的锁相环参数配置相近,在旋转坐标系下耦合影响进一步削弱。d通道主导极点变化如图21所示,在三种光伏典型运行工况下,随着kp,s,dc的增大,d通道主导极点向远离虚轴移动,光照强度较低运行工况需要设置较大的kp,s,dc才能够保证系统的静态同步稳定性。
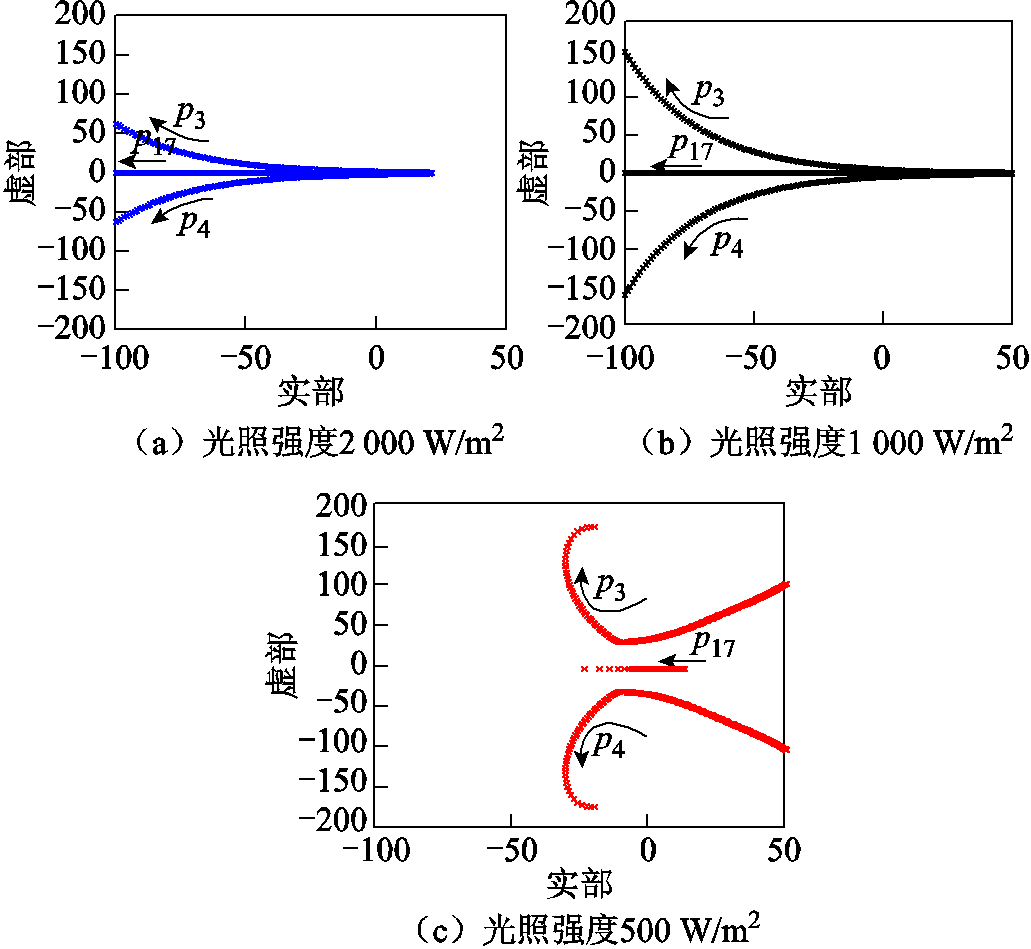
图21 d主导通道极点变化轨迹
Fig.21 Pole of d channel change trajectory
参与因子分析过程与上述分析过程相同,结果过于庞大,此处给出分析结论,结合图21极点分布有如下结论:在kp,s,dc较小时,系统稳定性由极点p3、p4、p17主导影响;当kp,s,dc较大时,系统稳定性主要由中频段极点主导影响。
系统的衰减系数β如图22所示。在稳定运行区域,随着kp,s,dc的增大,系统的衰减系数不断增大,系统静态同步稳定的暂态性能下降,不利于系统的稳定运行;光照强度较高的运行工况设定较小的kp,s,dc便能够满足静态同步稳定性能。由上述分析可得知,在实际工程中,当控制参数不可调整时,可通过调整光伏机组接受的光照强度大小实现静态同步稳定性能的调整。
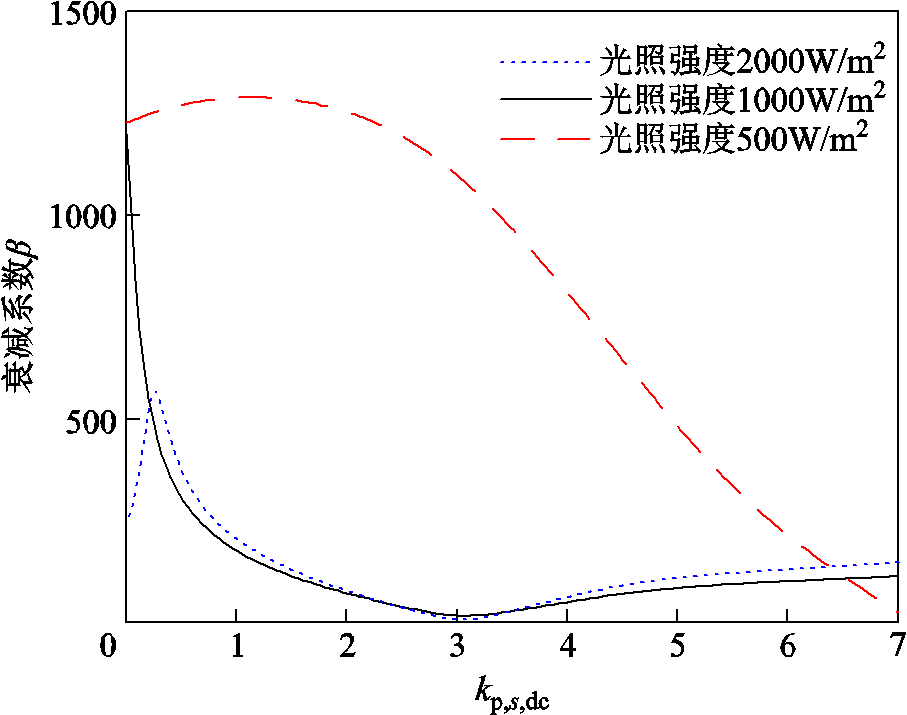
图22 不同kp,s,dc下的衰减系数变化轨迹
Fig.22 Variation trajectory of attenuation coefficient with different kp,s,dc
3.3.2 积分控制系数kin,s,dc影响
设置直流电压控制环节积分系数kin,s,dc变化范围为[0, 30],其余参数不变,可得系统的衰减系数β如图23所示。在光照强度较高的光伏运行工况下,系统的缩减系数β随着积分系数kin,s,dc的增加而增加,较小的积分系数kin,s,dc就能够实现较好的稳定性能。在其他光照强度下,系统的缩减系数β随着积分系数kin,s,dc的增加先减小后增加,其变化轨迹上存在一个极值点。
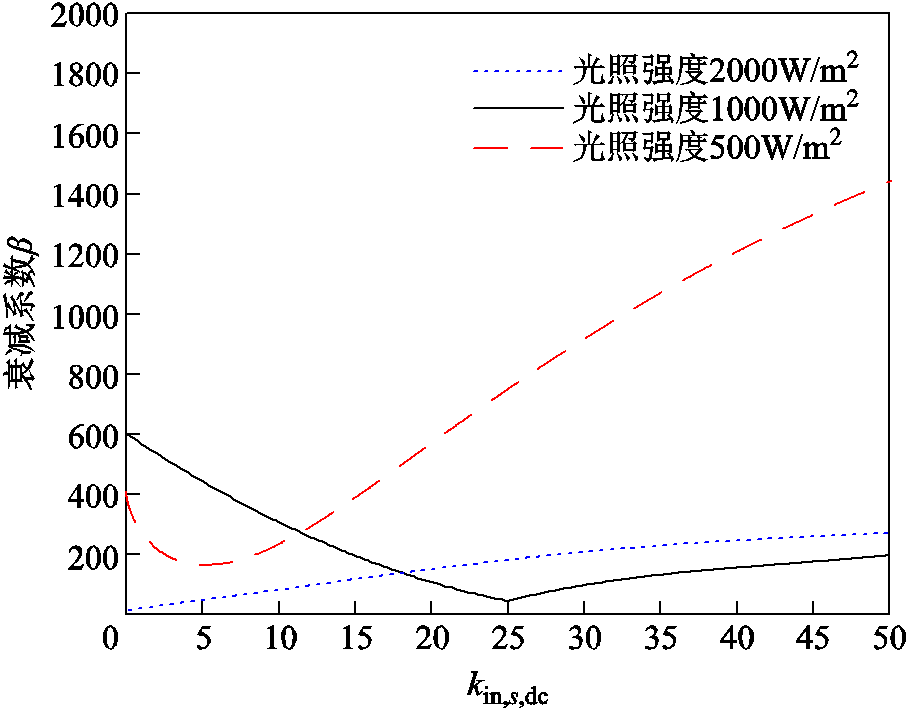
图23 不同kin,s,dc下的衰减系数变化轨迹
Fig.23 Variation trajectory of attenuation coefficient with different kin,s,dc
结合图22直流电压控制环节比例系数kp,s,dc衰减系数变化轨迹,可得:在稳定运行区域内,逐渐减小外环控制的带宽有助于提高系统的静态同步稳定性能;而当外环控制的带宽持续减小至阈值时,关键控制信号可能丢失,从而不利于系统的静态同步稳定性能提升。因此,在配置系统各控制环节的带宽值时需要合理考虑。
本文参数分析验证得到的主要结论如下:
1)在稳定运行区域内部,直流电压控制环节、有功电流控制环节及无功电流控制环节的带宽增大会导致系统的衰减系数增大,系统振荡幅值增大,衰减速度降低。
2)当STATCOM装置的锁相环参数与光伏逆变系统相同时,系统的稳定性能主要受到电网阻抗和各并网逆变器等效导纳传递函数影响,不存在d轴对q轴的耦合作用影响。此时只需满足各并网逆变器均可独立接入电网稳定运行即可保证系统静态同步稳定。
3)在实际工程中,当控制参数不可调整时,可通过调整光伏机组接受的光照强度大小实现静态同步稳定性能的调整。
4)根据本文仿真分析得到的结果,总结规律如下:当光伏系统的衰减系数大于300时,可判定系统出现静态同步失稳现象;当衰减系数指标小于250时,则表明系统处于静态同步稳定状态;当衰减系数指标介于二者间需进一步采用稳定判据进行判别。
由于STATCOM无功容量的输出是通过改变ic,s,q,ref的数值实现的,所以将ic,s,q,ref的变化范围设置为[-2.5 pu, 2.5 pu],以分析不同STATCOM容量占比的影响,如图24所示。对比图13可得,在光照强度为1 000 W/m2的光伏典型运行工况下,由STATCOM向电网提供无功电流相较于光伏并网变换器提供无功电流的静态同步稳定性能更好。
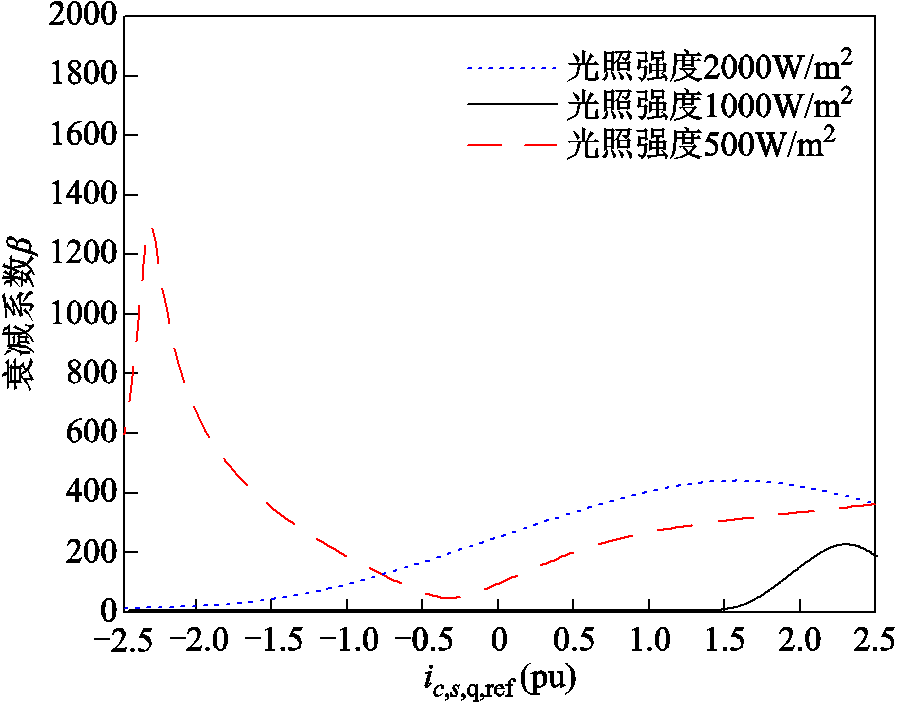
图24 不同STATCOM占比下的衰减系数变化轨迹
Fig.24 Variation trajectory of attenuation coefficient with different STATCOM ratio
由图24可得,当光照强度增加时,适当提高STATCOM容量以向光伏系统提供容性无功支撑,能够有效地提升系统的静态同步稳定性能,原因在于STATCOM向光伏系统提供容性无功支撑可以有效抑制光伏系统有功出力增加导致的电压下降,并为并网点电压稳定性提供保障。在光照强度较低的情况下,过高的无功补偿量会降低系统的静态同步稳定性能,反而不利于系统的稳定运行。因此,在不同的光伏运行工况下需要及时调整STATCOM的无功补偿量。
针对含有STATCOM的光伏并网系统,建立了静态同步稳定分析模型,改进了稳定判据和静态同步稳定评估指标,详细分析了增加STATCOM对光伏并网系统静态同步稳定性影响,主要结论如下:
1)在已知并网变换器控制参数的情况下,合理地优化并网变换器输出的无功功率可以有效提升其静态同步稳定性能;小扰动后振荡模式主要由锁相环控制产生的极点所主导。
2)在并网变换器运行工况接近临界稳定区域时,系统的衰减系数β会迅速增加。因此,在运行过程中,系统需要具备一定的衰减系数裕度。根据本文仿真分析结果表明,当光伏系统的衰减系数大于300时,可以判定系统出现静态同步失稳现象;而当衰减系数小于250时,则表示系统处于静态同步稳定状态。这为系统的静态同步稳定性分析提供了判别标准。
3)光伏并网系统在增加STATCOM后,主要影响了q耦合通道输出的导纳矩阵传递函数,而dd通道则不会受到并网变换器间锁相环耦合振荡的影响。在稳定运行区域内部,直流电压控制环节、有功电流控制环节以及无功电流控制环节的带宽增大,将导致系统衰减系数增加、系统振荡幅值增大,并且降低系统暂态性能中的衰减速度。
4)当STATCOM的锁相环参数与光伏逆变系统相同时,系统的稳定性能主要受到电网阻抗和各并网逆变器等效导纳传递函数影响。在这种情况下,只需确保各并网逆变器能够独立接入电网并实现稳定运行,以保证系统达到静态同步稳定。
5)当光伏系统有功出力较小时,STATCOM倾向于提供较小的容性无功出力或者提供较大的感性无功出力,以提高系统的静态同步稳定性能。然而,在光伏系统有功出力较大时,采用STATCOM来提供容性无功补偿可以更优于光伏并网变换器自身所提供的无功补偿。因此,合理配置STATCOM容量,能够有效地增强系统的静态同步稳定性能。
本文主要针对含STATCOM的光伏并网系统静态同步稳定分析进行研究,下一步将研究更加精细化控制参数的设计方法。
参考文献
[1] 韩应生, 孙海顺, 秦世耀, 等. 电压源型双馈风电并网系统小扰动低频稳定性分析[J]. 电工技术学报, 2023, 38(5): 1312-1324, 1374.
Han Yingsheng, Sun Haishun, Qin Shiyao, et al. Low-frequency stability analysis of voltage-sourced doubly-fed wind power grid-connected system under small disturbance[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1312-1324, 1374.
[2] 汪春江, 孙建军, 宫金武, 等. 并网逆变器与电网阻抗交互失稳机理及阻尼策略[J]. 电工技术学报, 2020, 35(增刊2): 503-511.
Wang Chunjiang, Sun Jianjun, Gong Jinwu, et al. Mechanism and damping strategy of interactive instability between grid-connected inverter and grid impedance[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 503-511.
[3] 曹永吉, 吴秋伟, 张恒旭, 等. 考虑分时电价和最大暂态频率偏移的储能机会约束优化配置[J]. 电力系统自动化, 2023, 47(2): 61-68.
Cao Yongji, Wu Qiuwei, Zhang Hengxu, et al. Chance-constrained optimal configuration for energy storage system considering time-of-use price and maximum transient frequency deviation[J]. Automation of Electric Power Systems, 2023, 47(2): 61-68.
[4] 马睿聪, 邹世豪, 曹永吉, 等. 基于灵敏度分析的同步调相机及其励磁系统参数分类辨识方法[J]. 电力系统保护与控制, 2024, 52(4): 26-37.
Ma Ruicong, Zou Shihao, Cao Yongji, et al. Sensitivity analysis-based classification and identification method of a synchronous condenser and its excitation system parameter[J]. Power System Protection and Control, 2024, 52(4): 26-37.
[5] 罗魁, 郭剑波, 王伟胜, 等. 跟网型新能源附加频率控制对频率稳定及小扰动同步稳定影响分析综述[J]. 中国电机工程学报, 2023, 43(4): 1261-1280.
Luo Kui, Guo Jianbo, Wang Weisheng, et al. Review of impact of grid following variable renewable energy supplementary frequency control on frequency stability and small-disturbance synchronization stability[J]. Proceedings of the CSEE, 2023, 43(4): 1261-1280.
[6] San Guocheng, Zhang Wenlin, Luo Ran, et al. Small-signal multi-frequency model for grid-connected inverter system with PWM effect[J]. CSEE Journal of Power and Energy Systems, 2020, 6(2): 307-317.
[7] Yu Jiale, Qi Yang, Deng Han, et al. Evaluating small-signal synchronization stability of grid-forming converter: a geometrical approach[J]. IEEE Transactions on Industrial Electronics, 2022, 69(9): 9087-9098.
[8] 胡祺, 付立军, 马凡, 等. 弱电网下基于锁相控制并网变换器小扰动同步稳定分析[J]. 中国电机工程学报, 2021, 41(1): 98-108.
Hu Qi, Fu Lijun, Ma Fan, et al. Small signal synchronizing stability analysis of PLL-based VSC connected to weak AC grid[J]. Proceedings of the CSEE, 2021, 41(1): 98-108.
[9] Wen Bo, Dong Dong, Boroyevich D, et al. Impedance-based analysis of grid-synchronization stability for three-phase paralleled converters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 26-38.
[10] Mansour M Z, Mohammed N, Ravanji M H, et al. Output impedance derivation and small-signal stability analysis of a power-synchronized grid following inverter[J]. IEEE Transactions on Energy Conversion, 2022, 37(4): 2696-2707.
[11] 郝艺, 周瑀涵, 刘晨曦, 等. 含跟网型储能的新能源多馈入系统小扰动电压支撑强度分析[J]. 电工技术学报, 2024, 39(11): 3569-3580.
Hao Yi, Zhou Yuhan, Liu Chenxi, et al. Small-disturbance voltage support strength analysis for renewable multi-infeed system with grid-following energy storage[J]. Transactions of China Electro-technical Society, 2024, 39(11): 3569-3580.
[12] 宗皓翔, 张琛, 吕敬, 等. MMC多入多出阻抗及其在不对称小扰动稳定分析中的应用[J]. 中国电机工程学报, 2022, 42(15): 5649-5664.
Zong Haoxiang, Zhang Chen, Lü Jing, et al. MMC MIMO impedance and its application in the asymmetric small-signal stability analysis[J]. Proceedings of the CSEE, 2022, 42(15): 5649-5664.
[13] 艾力西尔·亚尔买买提, 辛焕海, 宫泽旭, 等. 锁相环主导下变流器振荡问题的阻抗分析方法:标称性与鲁棒性[J]. 中国电机工程学报, 2024, 44(15): 6035-6047.
Yaermaimaiti Ailixier, Xin Huanhai, Gong Zexu, et al. Impedance analysis method of oscillation issues in converter caused by phase-locked loop: nominal performance and robustness[J]. Proceedings of the CSEE, 2024, 44(15): 6035-6047.
[14] Zhang Chen, Føyen S, Suul J A, et al. Modeling and analysis of SOGI-PLL/FLL-based synchronization units: stability impacts of different frequency-feedback paths[J]. IEEE Transactions on Energy Conversion, 2021, 36(3): 2047-2058.
[15] 宫泽旭, 艾力西尔·亚尔买买提, 辛焕海, 等. 新能源电力系统并网设备小扰动稳定分析(一): 机理模型与稳定判据适用性[J]. 中国电机工程学报, 2022, 42(12): 4405-4418.
Gong Zexu, Yaermaimaiti Ailixier, Xin Huanhai, et al. Small signal stability analysis of equipment in renewable energy power system (part Ⅰ): mechanism model and adaptation of stability criterion[J]. Proceedings of the CSEE, 2022, 42(12): 4405-4418.
[16] 宫泽旭, 艾力西尔·亚尔买买提, 辛焕海, 等. 新能源电力系统并网设备小扰动稳定分析(二): 导出机理与稳定性分类探讨[J]. 中国电机工程学报, 2022, 42(14): 5126-5139.
Gong Zexu, Yaermaimaiti Ailixier, Xin Huanhai, et al.. Small signal stability analysis of grid-connected equipment in power system (part Ⅱ): discussion on mechanism derivation and classification of stability[J]. Proceedings of the CSEE, 2022, 42(14): 5126-5139.
[17] 康勇, 林新春, 郑云, 等. 新能源并网变换器单机无穷大系统的静态稳定极限及静态稳定工作区[J]. 中国电机工程学报, 2020, 40(14): 4506-4515.
Kang Yong, Lin Xinchun, Zheng Yun, et al. The static stable-limit and static stable-working zone for single-machine infinite-bus system of renewable-energy grid-connected converter[J]. Proceedings of the CSEE, 2020, 40(14): 4506-4515.
[18] 曹永吉, 张恒旭, 施啸寒, 等. 规模化分布式能源参与大电网安全稳定控制的机制初探[J]. 电力系统自动化, 2021, 45(18): 1-8.
Cao Yongji, Zhang Hengxu, Shi Xiaohan, et al. Preliminary study on participation mechanism of large-scale distributed energy resource in security and stability control of large power grid[J]. Automation of Electric Power Systems, 2021, 45(18): 1-8.
[19] 王凯, 原熙博, 王晖, 等. 弱电网下逆变器并网系统失稳的两种诱因[J]. 电网技术, 2023, 47(3): 1230-1241.
Wang Kai, Yuan Xibo, Wang Hui, et al. Two causes of the inverter-based grid-connected system instability in weak grids[J]. Power System Technology, 2023, 47(3): 1230-1241.
[20] 詹长江, 吴恒, 王雄飞, 等. 构网型变流器稳定性研究综述[J]. 中国电机工程学报, 2023, 43(6): 2339-2358.
Zhan Changjiang, Wu Heng, Wang Xiongfei, et al. An overview of stability studies of grid-forming voltage source converters[J]. Proceedings of the CSEE, 2023, 43(6): 2339-2358.
[21] 王冠中, 董炜, 辛焕海, 等. 基于广义短路比的电力电子多馈入系统小干扰概率稳定评估[J]. 电力系统自动化, 2018, 42(18): 17-24.
Wang Guanzhong, Dong Wei, Xin Huanhai, et al. Probabilistic stability evaluation of small disturbances for power electronic multi-infeed system based on generalized short-circuit ratio[J]. Automation of Electric Power Systems, 2018, 42(18): 17-24.
[22] Ni Kai, Gan Chun, Hu Yihua, et al. Input-output small-signal stability analysis of a PLL-free direct power-controlled partially power-decoupled more-electric shipboard propulsion system[J]. IEEE Transactions on Transportation Electrification, 2021, 7(3): 1672-1686.
[23] Chen Yahong, Xu Wei, Liu Yi, et al. Small-signal system frequency stability analysis of the power grid integrated with type-II doubly-fed variable speed pumped storage[J]. IEEE Transactions on Energy Conversion, 2023, 38(1): 611-623.
[24] 曾德银, 姚骏, 张田, 等. 虚拟同步发电机多机并联系统的频率小信号稳定性分析研究[J]. 中国电机工程学报, 2020, 40(7): 2048-2061.
Zeng Deyin, Yao Jun, Zhang Tian, et al. Research on frequency small-signal stability analysis of multi-parallel virtual synchronous generator-based system[J]. Proceedings of the CSEE, 2020, 40(7): 2048-2061.
[25] Mansour M Z, Ravanji M H, Karimi A, et al. Small-signal synchronization stability enhancement of grid-following inverters via a feedback linearization controller[J]. IEEE Transactions on Power Delivery, 2022, 37(5): 4335-4344.
[26] 李红, 梁军杨, 王振民, 等. 跟网型变换器的小扰动同步稳定机理分析与致稳控制[J]. 电工技术学报, 2024, 39(12): 3802-3815.
Li Hong,Liang Junyang,Wang Zhenmin,et al.Small signal synchronization stability analysis and improved control strategy for grid following converter[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3802-3815.
[27] Sajadi A, Zhao Shuang, Clark K, et al. Small-signal stability analysis of large-scale power systems in response to variability of offshore wind power plants[J]. IEEE Systems Journal, 2019, 13(3): 3070-3079.
[28] 马富艺龙, 辛焕海, 刘晨曦, 等. 新能源基地柔性直流送出系统小扰动电压支撑强度评估[J]. 电工技术学报, 2023, 38(21): 5758-5770, 5938.
Ma Fuyilong, Xin Huanhai, Liu Chenxi, et al. Small-disturbance system voltage support strength assessment method for renewables VSC-HVDC delivery system [J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5758-5770, 5938.
[29] 张宇, 张琛, 蔡旭, 等. 并网变换器的暂态同步稳定性分析: 稳定域估计与镇定控制[J]. 中国电机工程学报, 2022, 42(21): 7871-7883.
Zhang Yu, Zhang Chen, Cai Xu, et al. Transient grid-synchronization stability analysis of grid-tied voltage source converters: stability region estimation and stabilization control[J]. Proceedings of the CSEE, 2022, 42(21): 7871-7883.
Static Synchronization Stability Analysis of PV Grid-Connected System with Static Synchronous Compensator
Abstract PV systems are typically equipped with reactive power compensation devices when connected to the grid, and static synchronous compensator (STATCOM) devices are widely employed due to their flexible control capabilities. The increasing utilization of power electronic devices in the power grid has resulted in a shift from physical synchronization to control synchronization as the dominant mode of system operation. Analyzing static synchronization stability problem is more challenging for these systems compared to conventional power systems, as converter output characteristics are influenced by control strategies. Therefore, it is imperative to urgently address the problem of static synchronization stabilization under control strategy dominance.
First, this paper establishes the static synchronous stability analysis model of the grid-connected converter based on the control loop and circuit structure of each converter in a parallel system under the respective dq reference frame. The dq reference frame of the converter is determined by the phase information provided by the control loop in a multiple converter parallel system, thus enabling a unified coordinate system for static synchronization stability analysis. Subsequently, an equivalent small signal model is developed for analyzing multiple grid-connected converters. In comparison with existing coordinate conversion methods, Kirchhoff's current law is incorporated to enhance accuracy and reduce errors.
Then, the stability criterion for impedance analysis is enhance, and the static grid-synchronization performance indices are created. The small perturbation oscillation characteristics are measured using overshooting and regulation time, while the participation factor is employed to analyze the impact of each pole of the system. Finally, the attenuation coefficient is utilized to assess static synchronization stability performance.
The model is developed in Matlab/Simulink for simulation verification. Subsequently, an analysis is conducted on the impact of parameters such as the control loop parameters and STATCOM capacity on static synchronization stability. The main conclusions are summarized as follows:
(1) Optimizing the reactive power output of the grid-connected converter based on known control parameters can significantly enhance static synchronization stability performance, with the dominant influence of small perturbations after oscillation mode being attributed to poles generated by phase-locked loop control.
(2) The attenuation coefficient of the system exhibits a rapid increase in proximity to the critical stability region. Hence, it is imperative for the system to possess a certain margin of attenuation coefficient during operation. Based on the simulation analysis results presented in this study, static synchronous instability phenomena occur when the attenuation coefficient of the PV system exceeds 300. Conversely, when the attenuation coefficient falls below 250, the system remains in a state of static synchronous stability. These findings establish a criterion for analyzing and assessing static synchronization stability within such systems.
(3) The addition of STATCOM to the PV system primarily impacts the conductance matrix transfer function of the q-coupled channel. The phase-locked-loop coupling oscillations between the grid-connected converters do not affect the dd channel. Within the stable operating region, an increase in bandwidth for the DC voltage control loop, active current control loop, and reactive current control loop results in an amplification of both attenuation coefficient and system oscillation amplitude.
(4) When the phase-locked loop parameters of the STATCOM are the same as the PV system, the stability performance of the system is mainly affected by the grid impedance and the equivalent conductance transfer function of each grid-connected converter. And each grid-connected converter can independently connect to the grid and achieve stable operation to ensure that the system achieves static synchronous stability in this case.
(5) In cases where the active output of the PV system is low, STATCOM typically adjusts its capacitive or inductive reactive power provision to improve static synchronization stability performance. Conversely, when compensating for capacitive reactive power, utilizing STATCOM may yield superior results compared to using the PV grid-connected converter alone. Hence, allocating an optimal capacity for STATCOM can significantly enhance static synchronization stability performance.
Keywords:PV system, static synchronous compensator (STATCOM), static synchronization stability, impedance analysis method, attenuation coefficient
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.240754
国家自然科学基金智能电网联合基金集成项目(U22B6008)和山东省自然科学基金项目(ZR2021QE133)资助。
收稿日期 2024-05-10
改稿日期 2024-06-25
马睿聪 男,1999年生,博士研究生,研究方向为电力系统同步稳定分析与紧急控制。
E-mail:202114573@mail.sdu.edu.cn
曹永吉 男,1992年生,副研究员,硕士生导师,研究方向为电力系统稳定分析与控制、可再生能源并网及储能技术应用。
E-mail:yongji@sdu.edu.cn(通信作者)
(编辑 赫 蕾)