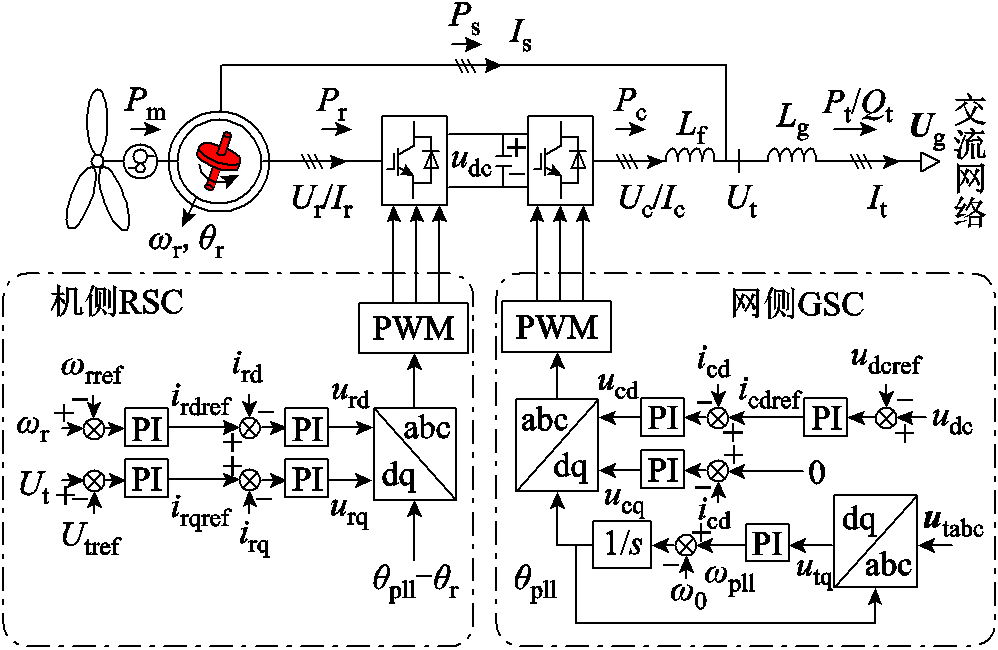
图1 双馈风机单机无穷大系统拓扑与控制框图
Fig.1 Schematic show of the control diagram of the DFIG system
摘要 随着新能源装备占比不断增加,其内在同步稳定机理逐步发生改变。为此,该文对转子转速尺度双馈风机单机无穷大系统的小扰动同步稳定机理进行研究。首先,构建该转子转速尺度下双馈风机的暂态模型,仿真验证了降阶模型的合理性。通过分岔分析,发现随着电网变弱,系统将出现小扰动失稳现象。采用主导模态分析法,确定转子转速尺度下双馈风机小扰动失稳的主导环节为功率平衡环节(转子动态与有功外环)。因此,以功率平衡环节为核心,构建了类Heffron-Phillips模型,并揭示了储能元件状态量与同步环节相位之间的关系。进一步地,基于复转矩系数法,发现锁相环环节对系统同步/阻尼特性影响很小,而端电压环节是引入负阻尼的主要因素。最后,针对有功外环、端电压环节的参数影响进行了分析,为参数优化提供相应指导。上述理论分析均通过了Matlab/Simulink仿真验证和硬件在环实验。
关键词:双馈风机 转子转速 时间尺度 主导模态分析 复转矩系数法
为实现“双碳”目标,我国近年来加速开发和应用新能源,预计在2030年风电/光伏总装机容量将达到12亿kW[1]。由于新能源装备不断增加,导致系统的同步稳定机理逐步演化,为稳定运行及稳定分析带来新的挑战[2-4]。双馈风机(Doubly Fed Induction Generator, DFIG)作为新能源发电装备的主流机型,研究其小扰动同步稳定机理对系统稳定运行具有重要的意义。
传统同步机装备中储能元件状态量表征功率平衡及同步状态,同步稳定问题直接取决于转子是否同步[5]。而双馈风机的储能元件状态量通常作为控制器输入量,经由诸多控制环节共同作用对其进行负反馈调节,从而实现功率平衡。同时,锁相同步环节为其提供参考坐标系,使之与系统保持同步运行[6]。由此可见,双馈风机的功率平衡与同步运行包含多个环节,难以分析其同步稳定机理。
对于双馈风机的小扰动稳定问题,一些研究人员探讨了双馈风机对同步机稳定性的影响。基于特征根分析法,文献[7]认为双馈风机在替换同步机之后,原有同步机的振荡模态消失,将引入新的机电模态;而文献[8]认为双馈风机的接入对系统区域间和局部模态的振荡特性影响并不是十分显著。进一步,文献[9]采用状态空间矩阵法进行推导,发现双馈风机的自身状态量对系统机电模式参与程度为0,认为双馈风机主要通过改变稳态平衡点来影响系统小扰动稳定,可以视为恒功率源。针对含有同步机、双馈风机的多机系统,文献[10]推导了双馈风机对同步机提供的阻尼转矩数学表达式,发现该阻尼受传输线影响很大,因而合理布置风电场对提升阻尼有重要作用。文献[11]针对风火打捆系统,构建了复频域模型,并采用复转矩法分析了双馈风机引起火电机组的多模态次同步谐振机理。而关于双馈风机自身的稳定性问题,也逐渐被人们所关注。文献[12]基于阻尼转矩法,对有功控制回路分析其阻尼特性,发现最大功率跟踪控制引入了负阻尼;而文献[13]则详细推导了电气阻尼转矩表达式,进而分析了风速、发电机参数以及系统控制参数对电气阻尼特性的影响规律。
上述研究通常忽略了锁相环(Phase Locked Loop, PLL)动态,然而锁相环在双馈风机与电网的同步过程中发挥着重要作用,有些工作研究了锁相环动态对双馈风机小扰动稳定性的影响。文献[14]在含有PLL的风机模型中,采用特征根分析法,发现弱电网下主导振荡模态由锁相环引入,当锁相环比例/积分系数增大,将会恶化阻尼特性。文献[15]采用阻抗法,发现锁相环与转子电流动态之间的传递函数会导致频率耦合现象,从而削弱系统稳定性,进而提出阻抗重塑方法来削弱锁相环的影响。由于在物理机理上对状态空间法与阻抗法缺乏直观的理解,因此文献[16]采用阻尼转矩法,忽略外环控制,构建了包含网侧变换器与机侧变换器的小扰动模型,发现锁相环总是提供正的固有阻尼,而变换器的电流内环提供负阻尼。更进一步地,研究人员将双馈风机降阶为锁相环二阶系统,并将其用于多机系统中以分析其稳定性[17]。文献[18]针对同步机双馈风机并联系统,基于摄动理论及模态分析法,揭示了锁相环模态与同步机功角模态间相互作用的机理。而对于计及锁相环及其他控制器动态的多机系统,有研究人员发现多个相似的DFIG集体行为会导致并网风电场的振荡失稳新现象[19]。
此外,在与之类似的同步稳定机理研究方面,针对同步失稳是锁相环自身失稳还是装备整体失稳的问题,文献[20]对计及锁相环动态的直驱风机进行了研究。经过定量计算与仿真分析,发现锁相环相位在系统同步失稳过程中紧紧跟随端电压相位一同摆开,跟踪性能良好,不存在锁相环自身的失稳。因此,锁相环相位主要用于表征大扰动同步失稳与否,功率不平衡或许才是系统失稳的真正根源。为凸显功率环节的重要性,文献[21-22]忽略锁相环动态,初步探索了直流电容电压与同步相位之间的关系,揭示了直流电压尺度下功率环节在同步稳定中的作用。文献[23]发现对于锁相环逆变器系统的大扰动同步稳定,直流电压尺度下锁相环与功率控制环节均起主导作用。文献[24]通过引入异尺度参与因子来量化多时间尺度相互作用,并发现提高锁相环带宽将增强尺度间相互作用。
综上所述,以上研究对于同时计及锁相环动态以及有功环节的同步稳定涉及较少,并且尚未深入分析转子转速尺度下双馈风机的小扰动同步稳定机理。因此,本文首先针对转子转速尺度双馈风机进行暂态建模,通过分岔分析,发现当电网逐渐变弱时,存在小扰动失稳。基于主导模态分析法,发现功率不平衡环节(转子动态、有功外环)在小扰动失稳中为主导环节。接着在工作点附近进行线性化,以功率不平衡环节为核心,得到了用于分析小扰动同步稳定的Heffron-Phillips模型,并建立锁相环相位与储能元件状态量的关系,揭示了系统同步稳定的核心在于储能元件状态量的稳定。进一步采用复转矩系数法,发现锁相环对系统的同步/阻尼特性影响很小,端电压是系统负阻尼引入的主要因素。通过参数影响分析发现,端电压环节比例/积分系数增大将有利于系统稳定;有功外环比例系数增大、积分系数减小将提高系统稳定性,为参数设计提供指导。最终通过硬件在环实验验证了上述理论的正确性。
典型的双馈风机控制框图及单机无穷大拓扑结构如图1所示。双馈风机具有定、转子两条支路,定子支路直接与并网点相连,而转子支路经由“背靠背”逆变器与并网点连接。其中,下标“s”表示定子支路的电气量,下标“r”表示机侧变换器(Rotor Side Converter, RSC)的电气量,下标“c”表示网侧变换器(Grid Side Converter, GSC)的电气量,详细的符号注释见附表1。

图1 双馈风机单机无穷大系统拓扑与控制框图
Fig.1 Schematic show of the control diagram of the DFIG system
RSC与GSC均采用矢量控制,锁相环通过跟踪端电压相位为矢量控制提供dq坐标系。将图1中的控制量与电气量归算至锁相环提供的dq坐标系下,各矢量的坐标变换关系将如图2所示。其中,电网电压Ug默认在公共坐标系x轴上,Fi为各矢量的代表形式,在公共坐标系中其相位表示为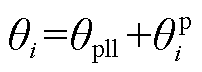 ,其中,
,其中,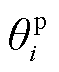 为矢量dq坐标系里的相位。
为矢量dq坐标系里的相位。
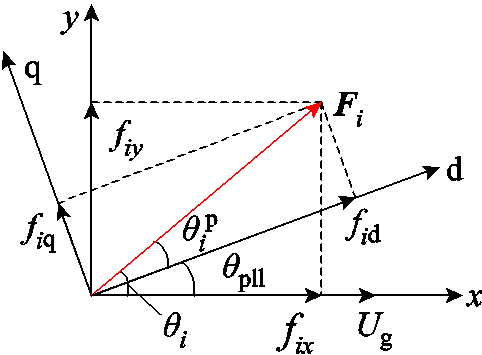
图2 各电气矢量dq坐标系、xy坐标系位置关系
Fig.2 Schematic show of the dq and the xy reference frames
RSC的转速外环控制与端电压外环控制分别生成转子电流指令值irdref/irqref。GSC的d轴外环以直流电容电压为目标值控制生成d轴电流指令值icdref,q轴外环则给定指令值icqref=0。内环则控制电流能够跟踪电流指令值,并生成内电动势调制PWM。从能量角度,RSC与GSC分别保证了转子与电容上的功率平衡。
双馈风机中含有多种形式的储能元件,在动态过程中具有多时间尺度特性。根据储能元件的容量大小及响应速度,可以将装备的时间尺度划分为转子转速时间尺度、直流电压时间尺度、交流电流时间尺度[2]。当系统遭遇扰动事件时,一般是容量最小的储能元件先响应,最后是容量最大的储能元件动作,呈现出多尺度序贯动作特性。各储能元件的状态量都受到控制器调节,控制器的带宽设定通常与对应的储能元件响应速度所匹配,最快的交流电流时间尺度一般为100 Hz左右,直流电压时间尺度一般为10 Hz左右,而转子转速尺度则为1 Hz左右。
针对所研究的问题,通常需要对双馈风机模型进行适当的简化[25]。在转子转速尺度下,重点关注转子动态与控制其动态的机侧变换器,而控制直流电容的网侧变换器动态则忽略不计。同样,也忽略电流内环控制动态,认为电流始终能够快速跟踪指令值。另外,由于锁相环节作为装备与电网的关键同步单元,保留其动态。
双馈风机中的异步发电机除了转子动态以外,定、转子磁链关系是其重要组成部分,包含了定/转子电压、定/转子电流之间的关系。在实际分析中,一般对磁链动态采用准稳态处理[26],详细推导见附录。为方便在同一电路中进行分析,将转子侧磁链方程归算至定子侧,拓扑电路如图3a所示。其中,XIs、XIr分别表示定子、转子漏电抗,Xm表示互感电抗。Rs、Rr分别表示定子、转子电阻,一般认为很小,通常忽略不计。另外,图3中定子电流方向采用发电机惯例,转子电流方向采用电动机惯例,本文建模与之保持一致。其中,转差率sp=(ωs-ωr)/ωs,此处近似考虑电网频率ωs≈1(pu)。
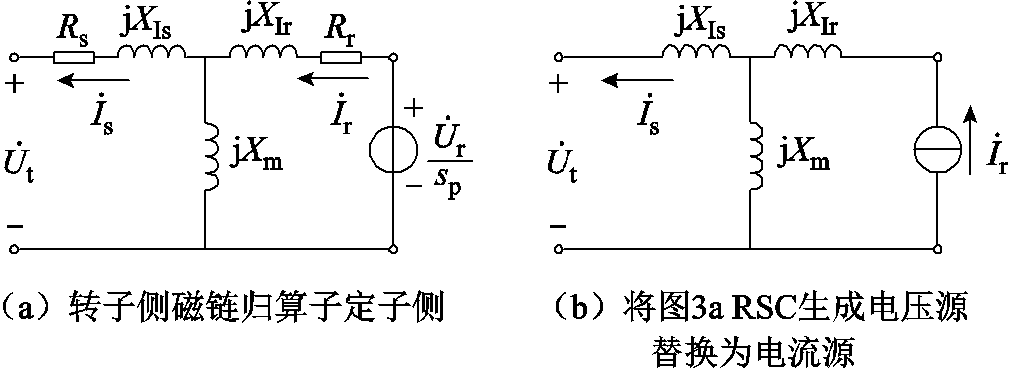
图3 异步发电机准稳态拓扑电路
Fig.3 Quasi-steady state topology diagram of asynchronous machine
由于只考虑RSC的外环控制,图3a中由RSC控制生成的电压源将替换为电流源,进一步简化为图3b的形式,从而得到异步发电机与RSC的拓扑电路。在dq坐标下,定、转子电流关系为
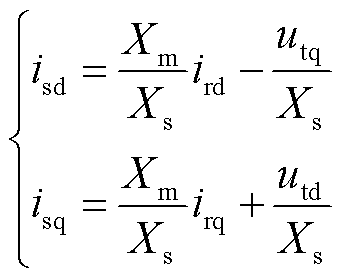 (1)
(1)
考虑GSC动态快速跟踪,将始终满足直流电容两侧的功率平衡,即Pr=Pc。而定子支路功率Ps与转子支路功率Pr成转差倍数关系,即Ps=-spPs。因此定子支路功率Ps与GSC向并网点输出功率Pc同样为转差倍数关系,即Pc=-spPs。进而,变换器支路上的有功电流icd与定子支路上的有功电流isd将始终保持转差倍数关系。因此GSC输出电流:icd=-spisd,icq=0。
进一步地,将GSC所在的变换器支路与图3b的拓扑电路合并,DFIG单机无穷大等效拓扑电路如图4所示。在dq坐标系下,装备整体对外输出电流it的表达式为
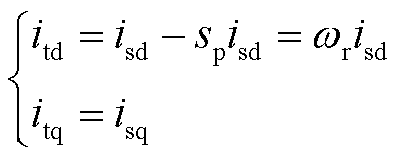 (2)
(2)
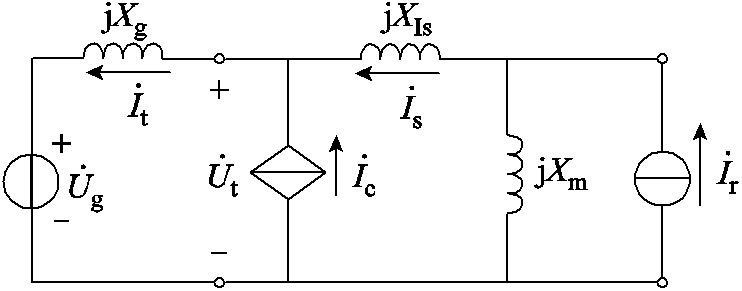
图4 DFIG 单机无穷大等效拓扑电路
Fig.4 Single-machine infinite bus equivalent topology circuit diagram of DFIG
为便于分析,将DFIG整体视为电流源,其简化拓扑电路如图5a所示。DFIG基于简化模型的内部控制框图如图5b所示,状态空间方程的推导详见附录。
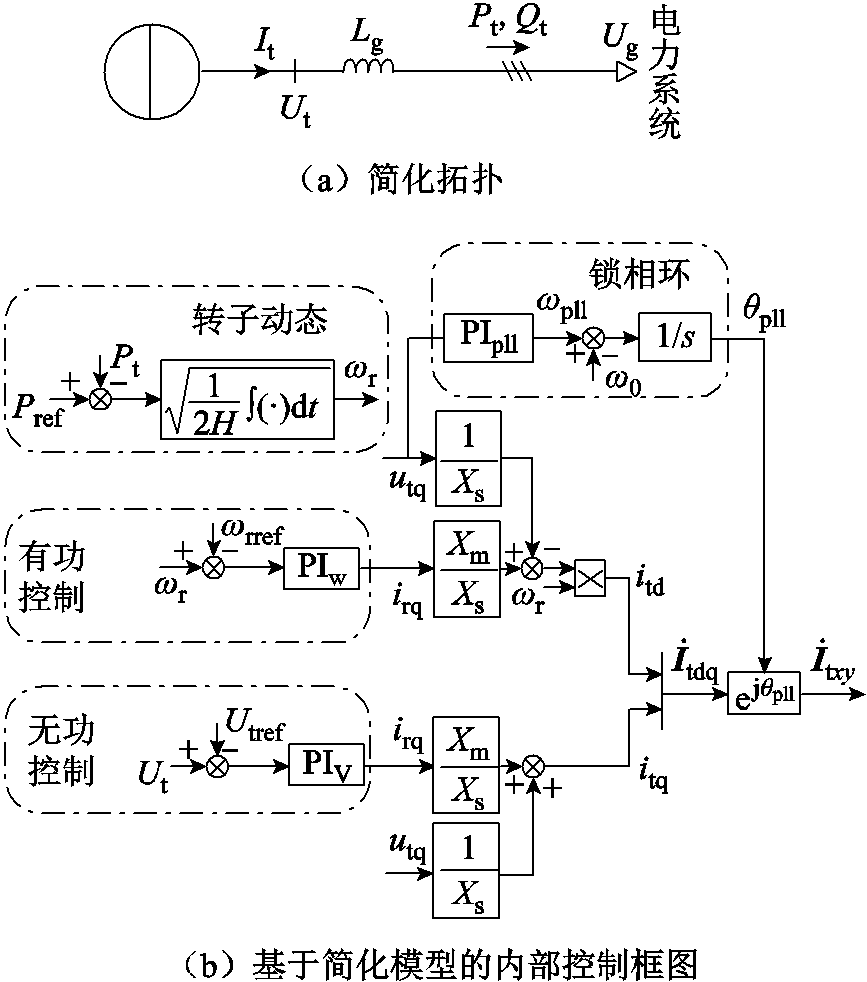
图5 DFIG 转子转速时间尺度下简化模型控制框图
Fig.5 Simplified model control block diagram of DFIG within rotor speed time scale
为验证双馈风机在转子转速尺度下模型简化的合理性,在Matlab/Simulink中搭建双馈风机单机无穷大系统进行仿真,全阶模型拓扑结构与控制方式如图1所示。其中,双馈风机与无穷大电网的连接电抗Xg=0.5(pu),各控制器参数详见附录。仿真设置:在1 s时刻,电网电压骤降至0.8(pu),全阶模型与简化模型的时域仿真对比如图6所示。仿真表明,简化模型与全阶模型在大致趋势上基本吻合。
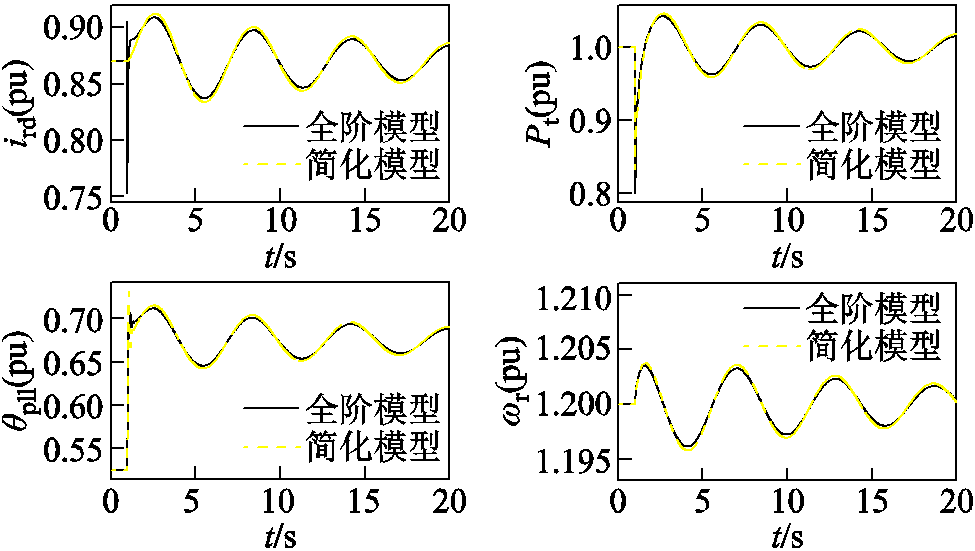
图6 全阶与简化模型的时域仿真对比
Fig.6 Comparison of time-domain simulations between full-order model and simplified model
分岔现象通常指系统参数发生小而连续的变化时,动力学系统产生本质的改变。在电力系统中,常使用分岔分析为研究人员提供一个整体的动力学图像。本文主要研究弱电网下发生的小扰动失稳,因此,绘制了电网电抗连续变化下的分岔图,来分析双馈风机在转子转速时间尺度下的动力学特性。
具体的绘制步骤如下:根据不同的电网电抗计算状态量的平衡解,并针对各分段性质进行判定。其中,判定为非稳平衡点则是红色点画线,判定为小扰动失稳则是蓝色虚线,而黑色实线则判定为小扰动稳定。
随着短路比(SCR=1/Xg)的改变,双馈风机五阶模型的分岔分析图如图7所示。曲线的整体轮廓为不同电抗下相位的平衡解,但是各区域的性质并不相同,其中,红色点画线段表示不稳定工作点;蓝色虚线表示系统存在小扰动失稳;黑色实线表示稳定工作点,系统小扰动稳定。红色点画线与蓝色虚线交界处发生了广义鞍结点分岔,在蓝色虚线与黑色实线交界处发生了亚临界Hopf分岔。系统发生亚临界Hopf分岔时,临界短路比SCR大约为1.163。
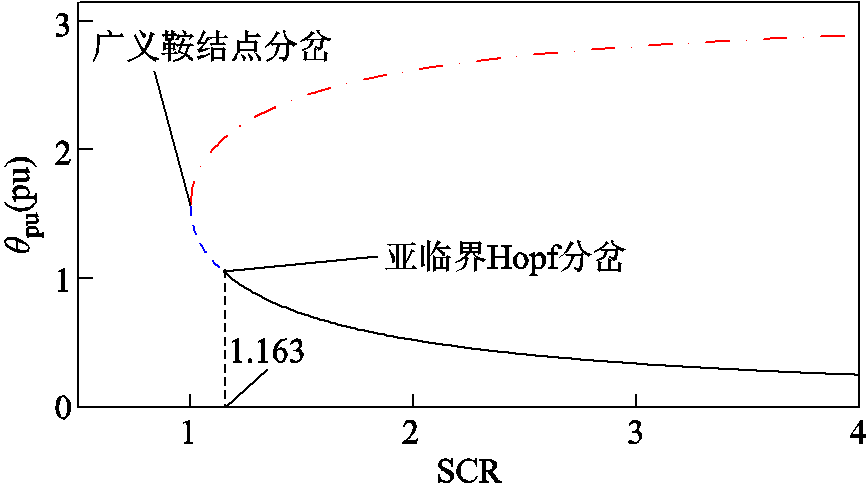
图7 双馈风机五阶模型的分岔分析图
Fig.7 Bifurcation analysis diagram of fifth order model
进一步地,在临界短路比SCR附近进行时域仿真。电网电压初始值为1(pu),分别设置短路比SCR=1.15与SCR=1.17,并于电网电压处施加微小扰动,时域仿真结果如图8所示。仿真结果表明,当短路比SCR较小时,系统存在小扰动失稳风险,表现为低频振荡失稳形式(振荡频率为0.173 Hz)。
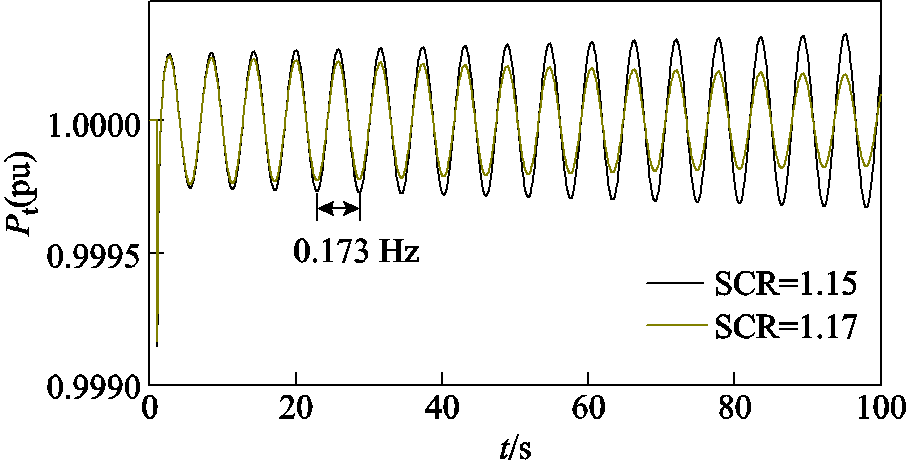
图8 不同SCR下五阶模型的时域仿真结果
Fig.8 Time domain simulation of fifth-order model under different SCR
根据附录给定的状态空间方程,对其绘制特征根轨迹,如图9所示。当短路比SCR不断减小时,存在一对共轭复根将穿过虚轴,且该特征根刚好穿过虚轴时虚部大约为j1.086,与时域仿真出现的低频振荡频率0.173 Hz近似吻合,可以认为这对特征根为主导振荡模态。
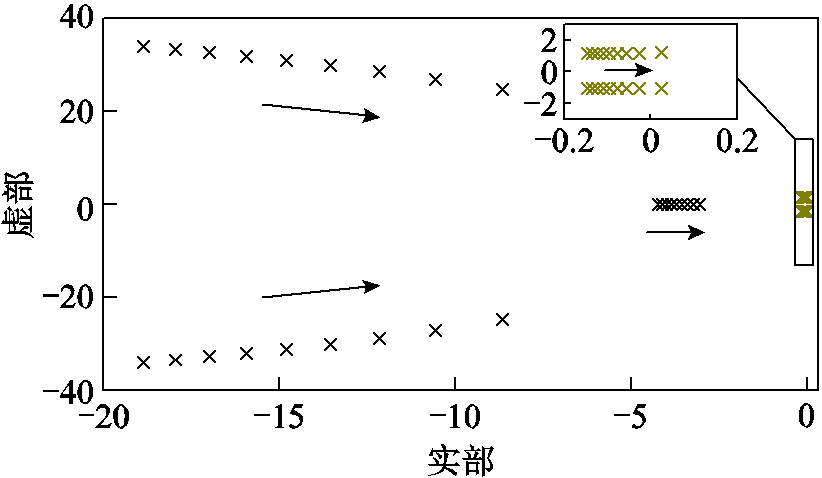
图9 DFIG五阶模型根轨迹
Fig.9 Root locus diagram of fifth-order model of DFIG
主导振荡模态各状态量的参与因子见表1。其中参与程度最高的为转子动态与有功外环的状态量ωr和ird;其次是端电压环节的状态量irq;最后是锁相环环节的状态量ωpll和θpll。主导模态分析结果表明,在转子转速尺度下,转子动态与有功外环为主导失稳环节。
表1 主导振荡模态各状态量的参与因子
Tab.1 The participation factor of the dominant mode

状态量0.009 + 1.086i ωr0.493 ird0.484 irq0.009 ωpll0.000 5 θpll0.000 5
为进一步分析DFIG小扰动同步稳定机理,对上述暂态模型在工作点附近线性化。根据主导模态分析结果,转子动态与有功外环占据主导,因此将功率平衡环节视为核心来构建小扰动同步稳定分析模型。
转子动态及有功外环的原始框图如图10a所示,有功外环小扰动表达式为
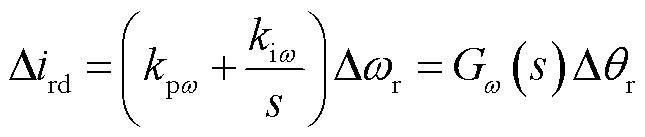 (3)
(3)
式中,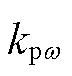 、
、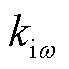 分别为转子转速控制器的比例系数、积分系数。传递函数
分别为转子转速控制器的比例系数、积分系数。传递函数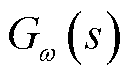 的表达式为
的表达式为
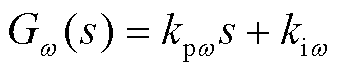 (4)
(4)
由于转子转速∆ωr积分之后为转子相位∆θr,具有实际物理意义。因此为凸显∆ωr/∆θr的重要性,将原始框图变换后如图10b所示。
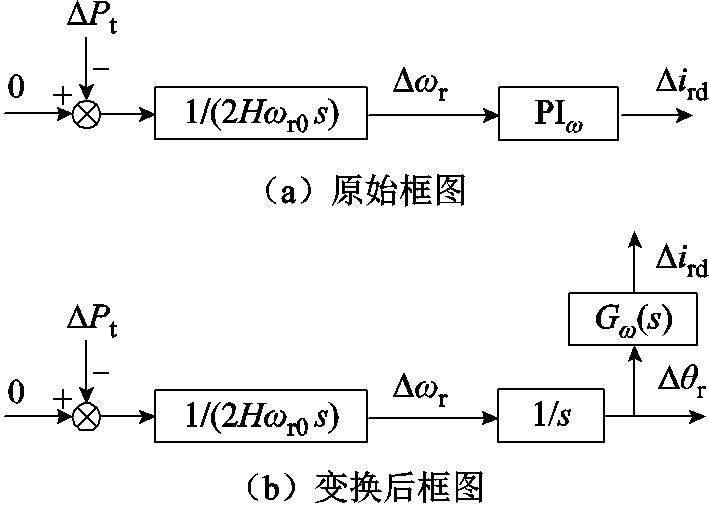
图10 转子动态与有功外环控制框图
Fig.10 Rotor dynamic and active outer loop control diagram
系统的网络方程如附录中式(A9)所示,在平衡点附近对其进行线性化,小信号表达式为
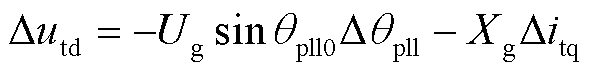 (5)
(5)
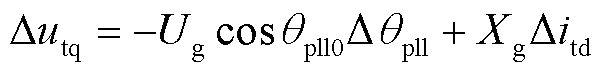 (6)
(6)
双馈风机整体对外输出电流表达式如附录中式(A10)所示。线性化之后,装备整体输出有功、无功电流∆itd、∆itq小信号表达式为
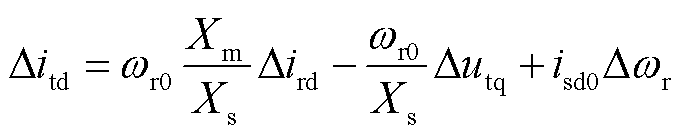 (7)
(7)
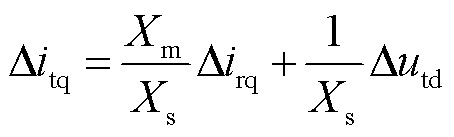 (8)
(8)
因此,结合式(5)~式(8),以及utd0=1(pu)、utq0=0,装备输出电磁功率的小扰动表达式如式(9)所示。由三部分组成。其中∆Pt1可以视为转子动态与有功外环的固有分量,而∆Pt2与∆Pt3视为其他环节引入的附加分量。
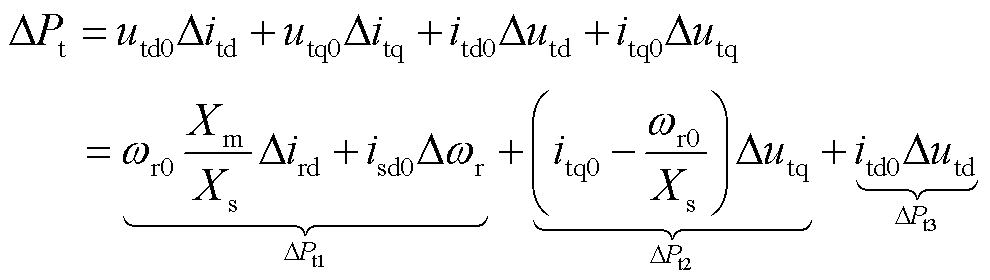 (9)
(9)
由于图10b对外输出的是转子有功电流∆ird,现分别求解∆ird与∆utd、∆utq的传递函数,进而得到∆Pt2与∆Pt3的表达式。
1)∆Pt2的表达式求解
无功控制的小扰动动态表达式为
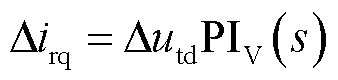 (10)
(10)
式中,传递函数PIV(s)表达式为
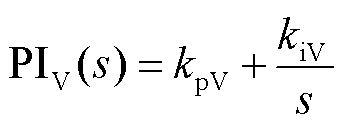 (11)
(11)
式中,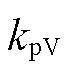 、
、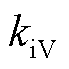 为单电压外环控制器的比例系数、积分系数。
为单电压外环控制器的比例系数、积分系数。
联立式(5)、式(8)、式(10)将得到∆utd的小扰动表达式为
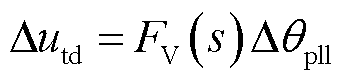 (12)
(12)
其中
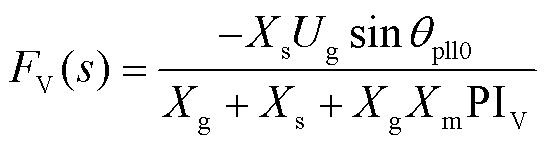 (13)
(13)
同理,联立式(6)、式(7)将得到∆utq的小扰动表达式为
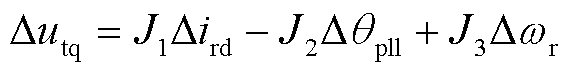 (14)
(14)
其中
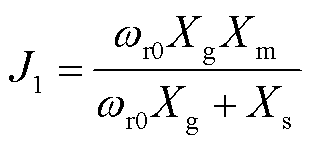 (15)
(15)
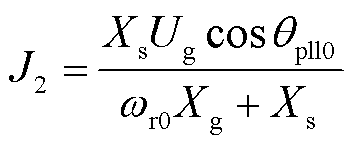 (16)
(16)
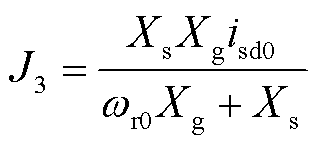 (17)
(17)
锁相环的小扰动表达式为
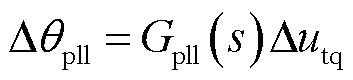 (18)
(18)
其中,锁相环传递函数Gpll(s)表达式为
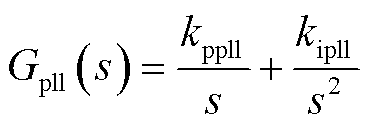 (19)
(19)
式中,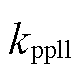 、
、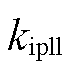 分别为锁相环的比例系数、积分系数。
分别为锁相环的比例系数、积分系数。
联立式(3)、式(14)、式(18),可得∆ird到∆θpll的传递函数
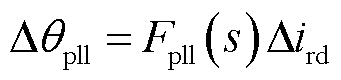 (20)
(20)
其中
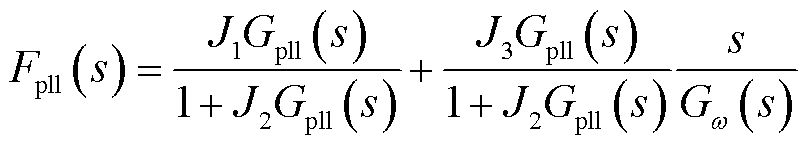 (21)
(21)
联立式(3)、式(14)、式(20),将求得∆Pt2的表达式为
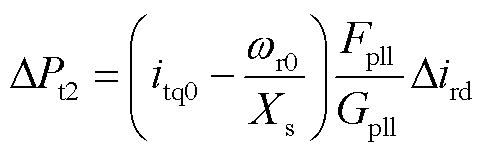 (22)
(22)
2)∆Pt3的表达式求解
联立式(12)、式(20),将求得∆Pt3的表达式描述为
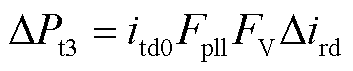 (23)
(23)
因此,以功率平衡环节为核心的双馈风机类Heffron-Phillips模型框图如图11所示。其中,∆Pt1(支路1)视为功率平衡环节的固有分量,∆Pt2(支路2)视为锁相环的直接作用,∆Pt3(支路3)则视为锁相环与端电压控制的相互作用。
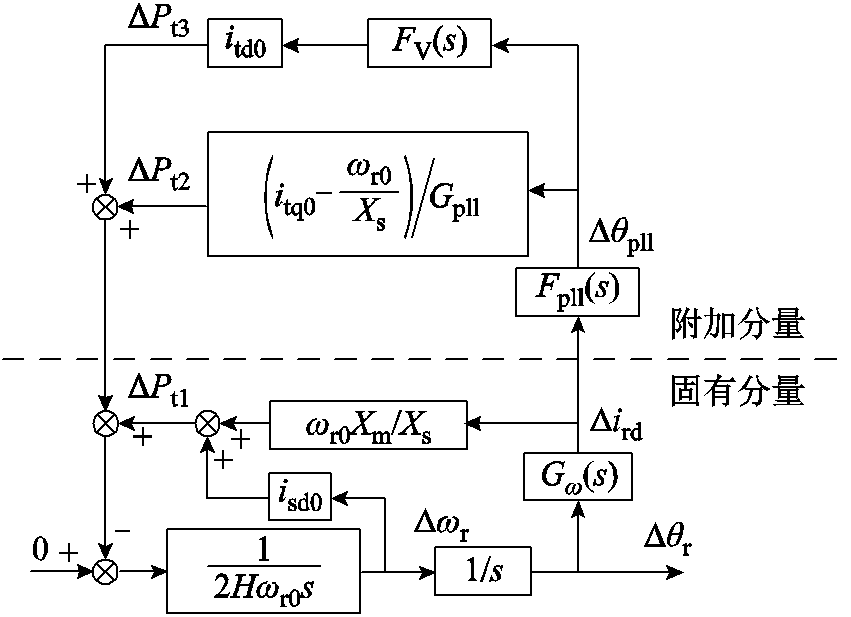
图11 双馈风机类Heffron-Phillips模型框图
Fig.11 Heffron-Phillips block diagram of a DFIG
为验证线性化之后模型的正确性,将全阶模型与线性化后的模型进行仿真对比,双馈风机与无穷大电网的连接电抗Xg=0.5(pu),各控制器参数详见附表1。仿真设置:在1 s时刻,机端输入功率骤增0.1(pu),全阶模型与线性化模型的时域仿真对比如图12所示。仿真表明,线性化模型与全阶模型在大致趋势上基本吻合。
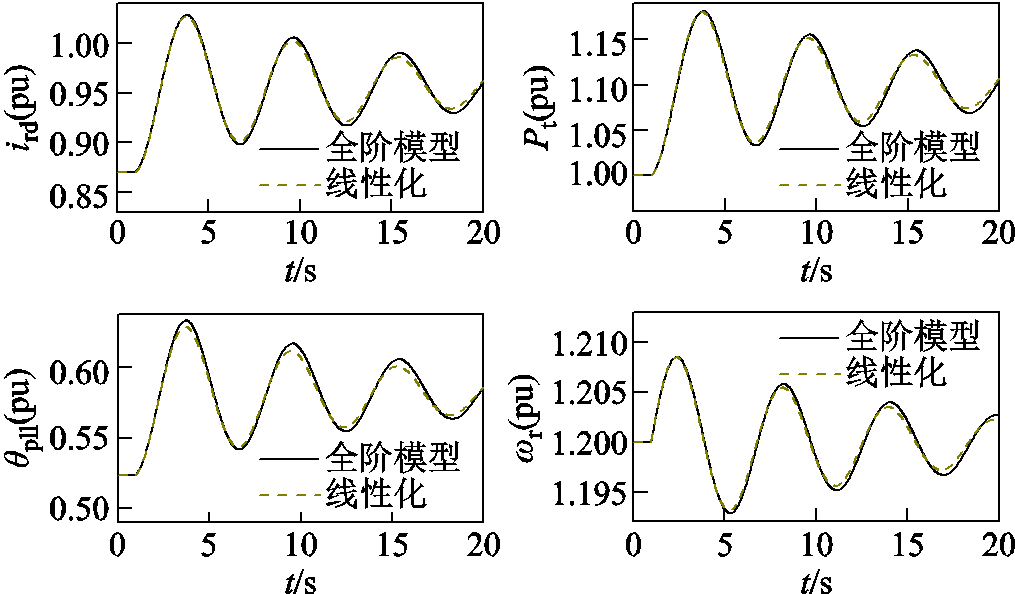
图12 线性化与全阶模型的时域仿真对比
Fig.12 Comparison of time-domain simulations between full-order model and linearized model
在功率平衡环节主导的振荡模态下,考虑特征根靠近虚轴,因此认为s≈jωd。将各支路的传递函数投影至∆ωr/∆θr方向上,得到各自的同步转矩与阻尼转矩,复转矩分析框图如图13所示。
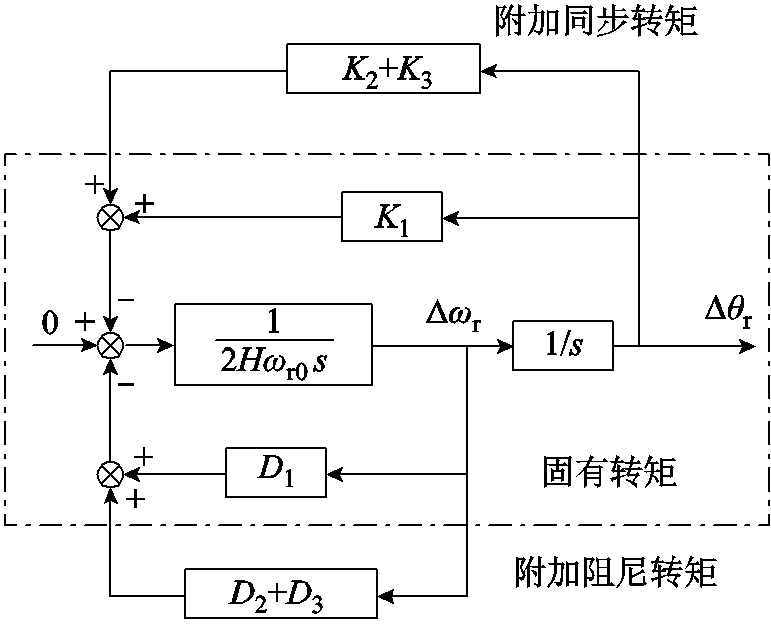
图13 复转矩分析框图
Fig.13 Complex torque analysis block diagram
根据图11的类Heffron-Phillips模型,可以推出支路1引入的固有阻尼转矩K1与同步转矩D1表达式分别为
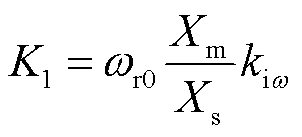 (24)
(24)
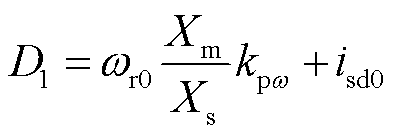 (25)
(25)
同理,支路2引入的附加同步转矩K2与附加阻尼转矩D2表达式分别为
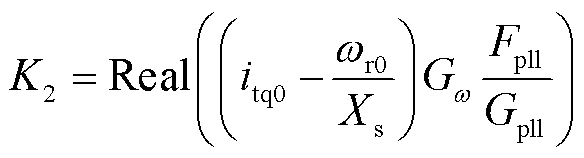 (26)
(26)
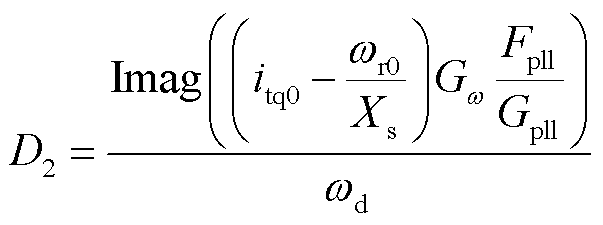 (27)
(27)
式中,ωd为振荡频率;传递函数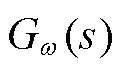 、Gpll(s)、Fpll(s)表达式详见式(4)、式(19)、式(21)。支路3引入的附加同步阻尼K3与附加阻尼转矩D3表达式为
、Gpll(s)、Fpll(s)表达式详见式(4)、式(19)、式(21)。支路3引入的附加同步阻尼K3与附加阻尼转矩D3表达式为
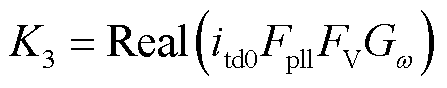 (28)
(28)
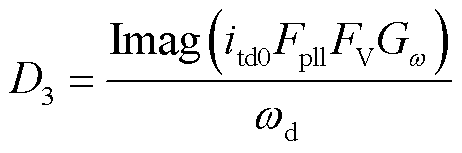 (29)
(29)
式中,FV(s)表达式详见式(13)。
在同步机中,其内电动势相位/频率直接与转子的相位/频率基本等价,其同步稳定问题可抽象成转子间的同步。而在双馈风机中,同步坐标系由锁相环采集端电压相位提供,转子上的功率不平衡由基于该坐标系的有功/无功控制来调节,转子的频率/相位与并网点处的频率/相位关系不明确,文献[27]认为风机转子与电网物理上机电耦合,但是控制环节导致了机电解耦。
本文中,考虑锁相环动态,并在转子转速尺度下,讨论转子转速/转子相位与同步相位的关系。从图11中可以发现,锁相环相位∆θpll与频率∆ωpll可以由储能元件状态量∆ωr、∆θr及不平衡功率∆Pt表征,联立式(3)、式(20),∆θpll与∆ωpll表达式分别为
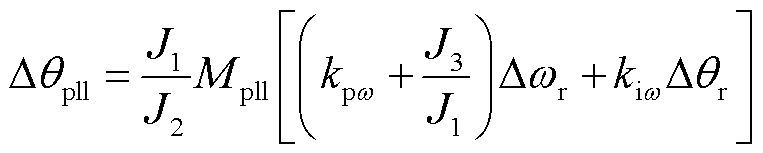 (30)
(30)
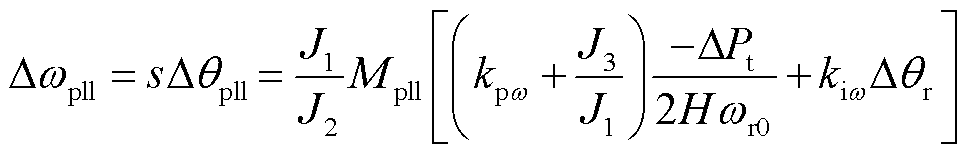 (31)
(31)
其中,传递函数Mpll表达式为
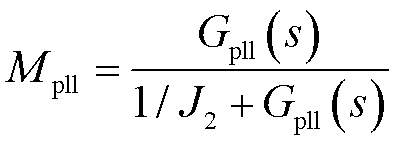 (32)
(32)
当电网发生故障时,功率不平衡将先施加于转子上,转子转速与相位发生改变,进而同步相位∆θpll发生改变。同理,频率∆ωpll动态机制与其类似。但值得注意的是,在∆ωpll的表达式中,存在不平衡功率∆Pt直接导致的频率变化,表明双馈风机的频率变化量中存在一部分快变量。
另外,式(30)、式(31)中包含的传递函数Mpll的特性与其PLL参数取值、系统振荡模态直接相关。为进一步探究PLL参数对式(30)、式(31)的影响,将研究不同参数下PLL的幅频特性与相频特性。由于本文振荡模态主要为低频振荡,重点关注1Hz以内的伯德图。在电网电抗Xg=0.5(pu)时,选取不同的锁相环参数与带宽见表2。
表2 锁相环的不同参数与带宽
Tab.2 Different parameters and bandwidths of PLL

PLL比例系数kppllPLL积分系数kipll带宽/Hz 5201.337 9 502008.591 50200 013.378 6 500200 0085.910 2
在0~1Hz以内的Mpll传函的幅频、相频特性如图14a、图14b所示。当锁相环带宽逐渐增大时,在1Hz以内,传递函数Mpll将逐渐变为幅值为1、相位为0的常数。在锁相环带宽较小时,随着频率增大,将在幅值上产生0.5(pu)以内的波动,相位发生小于90°的负角度偏置。
一般情况下,采用典型锁相环参数kppll=50, kipll= 2000时,由于锁相环带宽足够快,在转子转速尺度下,传递函数Mpll可近似为常数1。此时,式(30)中同步相位∆θpll将由储能元件状态量∆ωr、∆θr的代数表达式构成。但是,在直流电压时间尺度,锁相环带宽与之接近,上述关系可能将不成立。
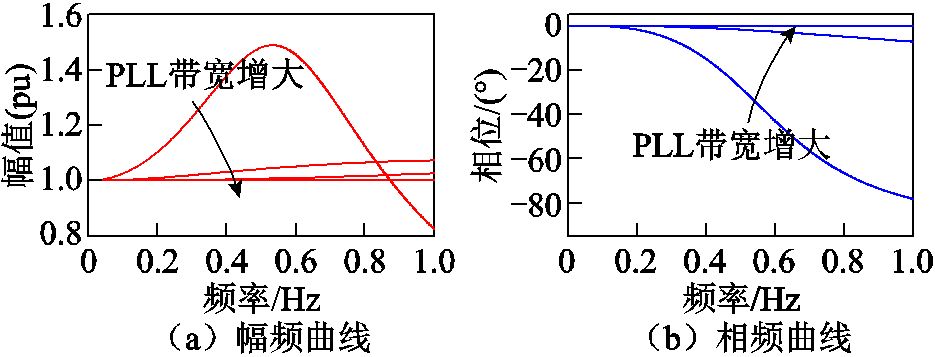
图14 不同带宽下Mpll传函的幅频相频曲线
Fig.14 Amplitude-frequency and phase-frequency curves of Mpll with different bandwidths
基于上述的小扰动同步稳定机理分析,转子转速尺度下双馈风机的同步稳定本质在于储能元件状态量∆ωr和∆θr的稳定。因此,针对图11构建类Heffron-Phillips模型,对其进行复转矩分析。
根据如图13所示的各支路同步/阻尼转矩,采用如式(24)~式(29)所示的详细表达式,分别计算各转矩随电网电抗变化的曲线,各转矩计算结果如图15和图16所示。
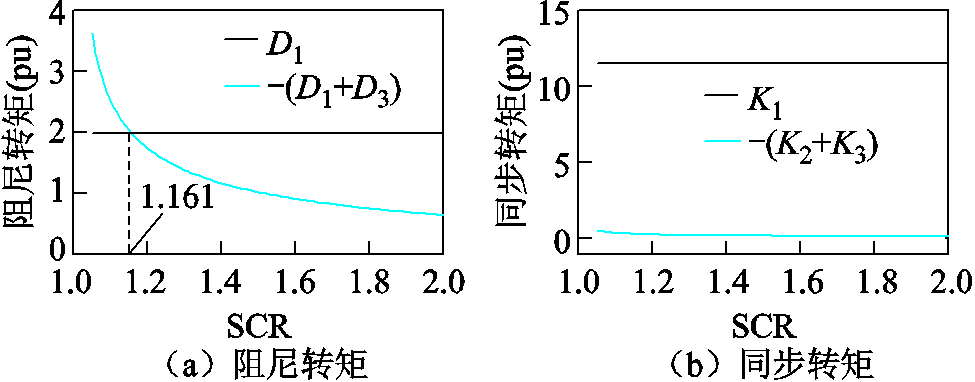
图15 转子转速尺度DFIG的同步/阻尼转矩
Fig.15 Synchronization/damping torque of DFIG within rotor speed timescale
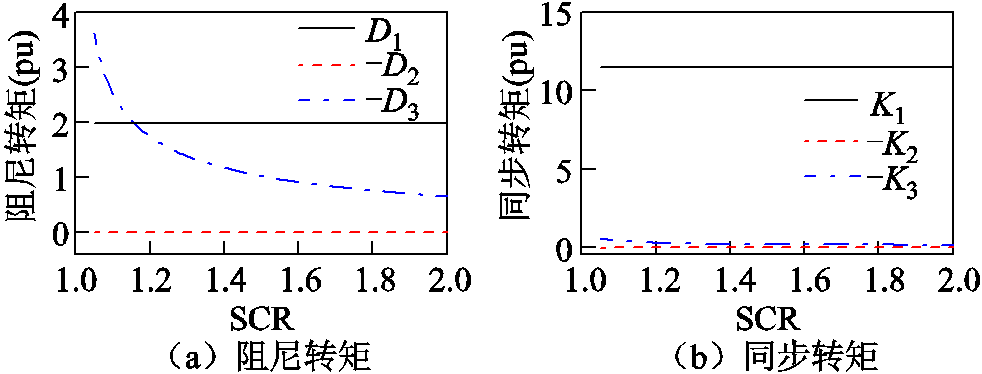
图16 转子转速尺度DFIG的各支路同步/阻尼转矩
Fig.16 The synchronization/damping torque of each branch of DFIG within rotor speed timescale
可见,在短路比SCR变化过程中,由支路1提供的同步/阻尼转矩为常值,且始终为正。表明双馈风机的功率平衡环节与同步机二阶转子方程类似,具有固有的同步/阻尼转矩。
另外,支路2和支路3共同组成的附加同步/阻尼转矩始终为负。其中,附加同步转矩在0附近,对总的同步转矩影响很小;而附加阻尼转矩将随着电网电抗的增大使得系统总阻尼不断减小,直至系统出现负阻尼。两条曲线的交点为临界短路比为1.161,此处将发生小扰动失稳,这与图7的分岔分析是基本吻合的。
进一步地,对支路2和支路3进行拆分。由支路2提供的附加同步/阻尼转矩始终在0附近,对系统小扰动同步稳定影响很小。而支路3则引入负阻尼,使得系统稳定性逐渐减弱。
上述现象反映了锁相环直接作用的支路2对系统稳定性影响很小,而端电压与锁相环相互作用的支路3向系统引入负阻尼,导致系统出现小扰动同步失稳。更进一步,支路3的阻尼转矩传递函数表达式如式(29)所示,根据3.2分析结论,其中传递函数Mpll可以近似处理为代数形式,因而端电压是负阻尼引入的主要因素。根据图11,三条支路的同步/阻尼特性均受到了Gω(s)的影响,因此有功外环参数、端电压控制参数对系统稳定性影响需要进一步分析。
根据图11的DFIG类Heffron-Phillips模型框图,端电压环节只影响支路3的附加阻尼/同步水平。式(28)、式(29)清晰地表示了该支路的附加阻尼和同步转矩,采用不同的端电压比例、积分系数对其进行定量计算。
首先,固定端电压积分系数(kiV=10),选取不同的端电压比例系数(kpV=1, 5, 10),采用式(24)~式(29)的表达式定量计算了各支路的附加阻尼转矩随短路比变化的曲线,如图17所示。端电压比例系数的增大将减小负阻尼转矩,提高系统的小扰动同步稳定性,从而减小临界失稳短路比。仿真验证如图18所示,在同等工况扰动下,端电压比例系数增大能够有效抑制小扰动振荡。
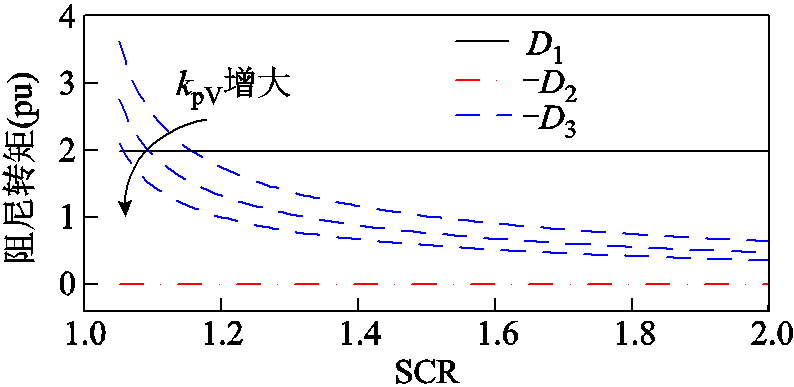
图17 不同kpV下的双馈风机各支路阻尼转矩
Fig.17 Synchronization/damping torque of each branch of DFIG under different kpV
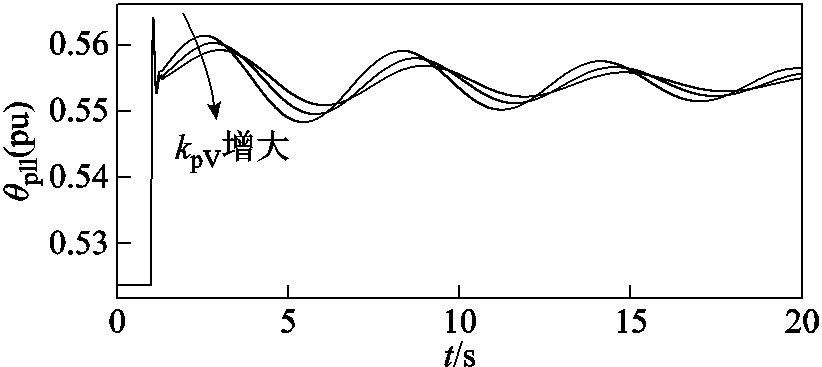
图18 不同kpV下的双馈风机时域仿真图
Fig.18 Time domain simulation of DFIG under different kpV
接着,固定端电压比例系数(kpV=1),选取不同的端电压积分系数(kiV=10, 20, 40),各支路的附加阻尼转矩如图19所示。端电压积分系数的增大将减小负阻尼转矩,提高系统的小扰动同步稳定性。仿真验证如图20所示,在同等工况扰动下,端电压积分系数增大同样可以有效抑制小扰动振荡。
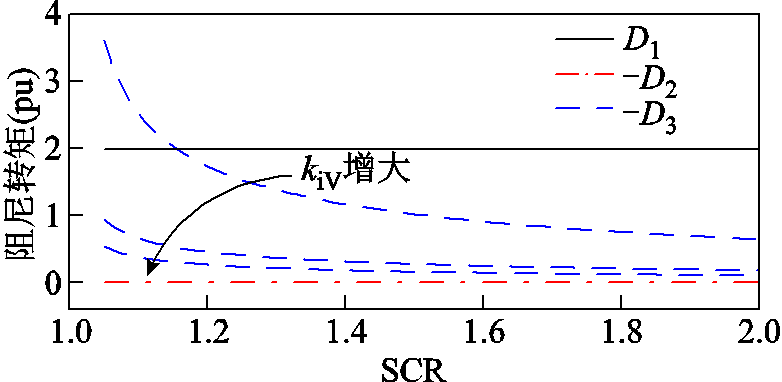
图19 不同kiV下的双馈风机各支路阻尼转矩
Fig.19 Synchronization/damping torque of each branch of DFIG under different kiV
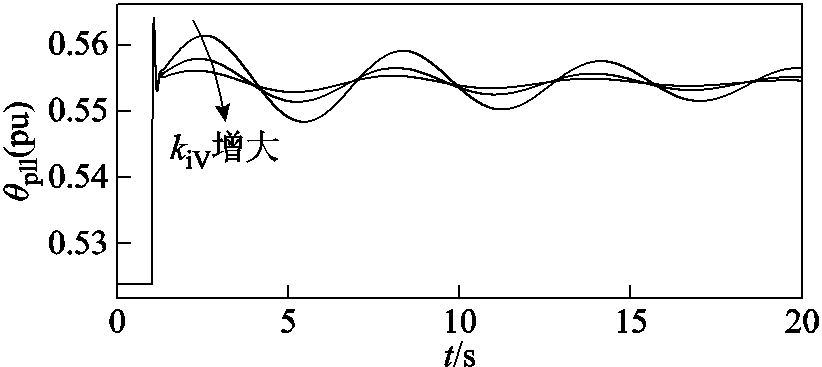
图20 不同kiV下的双馈风机时域仿真结果
Fig.20 Time domain simulation of DFIG under different kiV
同理,根据图11的DFIG类Heffron-Phillips模型框图,有支路1、2和3的同步/阻尼特性均受到了Gω(s)的影响,其中,支路1为功率不平衡环节的固有同步/阻尼转矩,而支路2和支路3表示了有功外环与锁相环、端电压环节之间的相互作用。因此,不同的有功外环比例/积分系数将影响两条支路的附加阻尼转矩水平。
首先,固定有功外环积分系数(kiω=10),选取不同的有功外环比例系数(kpω=1, 5, 8),各支路的附加阻尼转矩随短路比变化曲线如图21所示。可以明显看出,有功外环比例系数增大将提高支路1的固有正阻尼大小,同时减小支路3的负阻尼,而支路2并未发生明显变化,进而减小临界短路比。不同kpω下的双馈风机时域仿真结果如图22所示,在同等工况扰动下,有功外环比例系数增大将提高系统的小扰动稳定性。
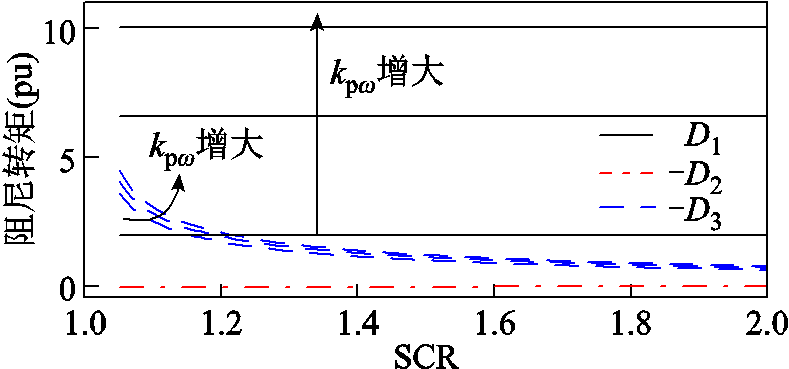
图21 不同kpω下的双馈风机各支路阻尼转矩
Fig.21 Synchronization/damping torque of each branch of DFIG under different kpω
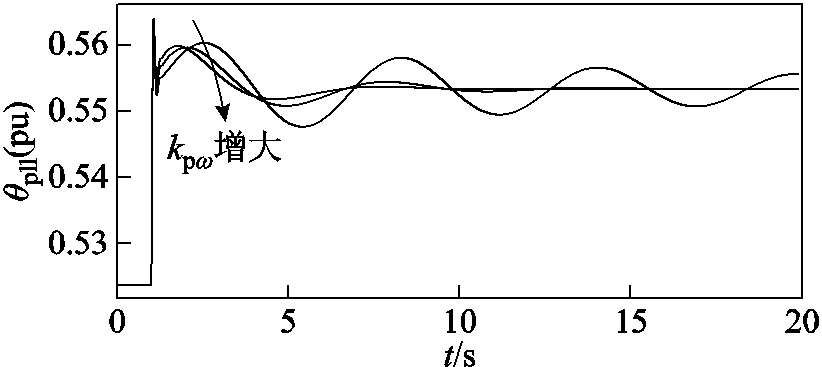
图22 不同kpω下的双馈风机时域仿真图
Fig.22 Time domain simulation of DFIG under different kpω
接着,固定有功外环比例系数(kpω=1),选取不同的有功外环积分系数(kiω=5, 10, 18),附加阻尼转矩随短路比变化曲线如图23所示。可以明显看出,有功外环积分系数增大不改变支路1和支路2的阻尼水平,同时增大支路3的负阻尼,进而增大临界短路比。不同kiω下的双馈风机各支路同步/阻尼转矩如图24所示,在同等工况扰动下,有功外环积分系数增大将削弱系统的小扰动稳定性。
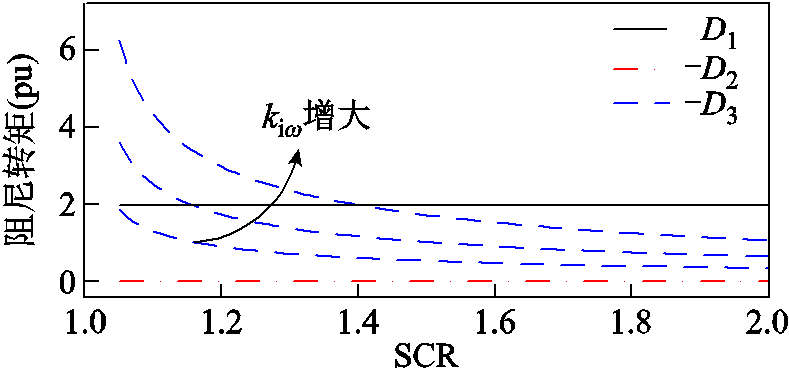
图23 不同kiω下的双馈风机各支路阻尼转矩
Fig.23 Synchronization/damping torque of each branch of DFIG under different kiω
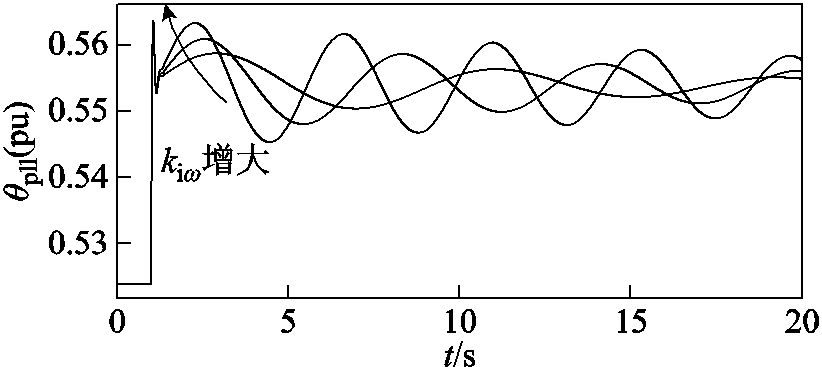
图24 不同kiω下的双馈风机时域仿真图
Fig.24 Time domain simulation of DFIG under different kiω
为验证上述结论的有效性,在SpaceR平台上进行硬件在环实验,实验平台示意图如图25所示。全阶模型的具体参数取值详见附录。分别设计了两组实验。

图25 实验平台示意图
Fig.25 Experimental platform diagram
实验一:电网短路比为SCR=1.335,电网电压骤降至0.8(pu),有功外环参数选取为:kpω=1, kiω=10;无功外环参数选取为:kpV=1, kiV=10。其他参数则采用附录第3节中的参数。系统将出现失稳现象,实验波形如图26a所示。然后,为减小负阻尼转矩,增大端电压比例参数为kpV=10以及增大端电压积分系数为kiV=20,系统将保持稳定,实验波形如图26b、图26c所示。最后,增大有功外环比例参数为kpω=5以及减小有功外环积分参数为kiω=5,系统将保持稳定,实验波形如图26d、图26e所示。
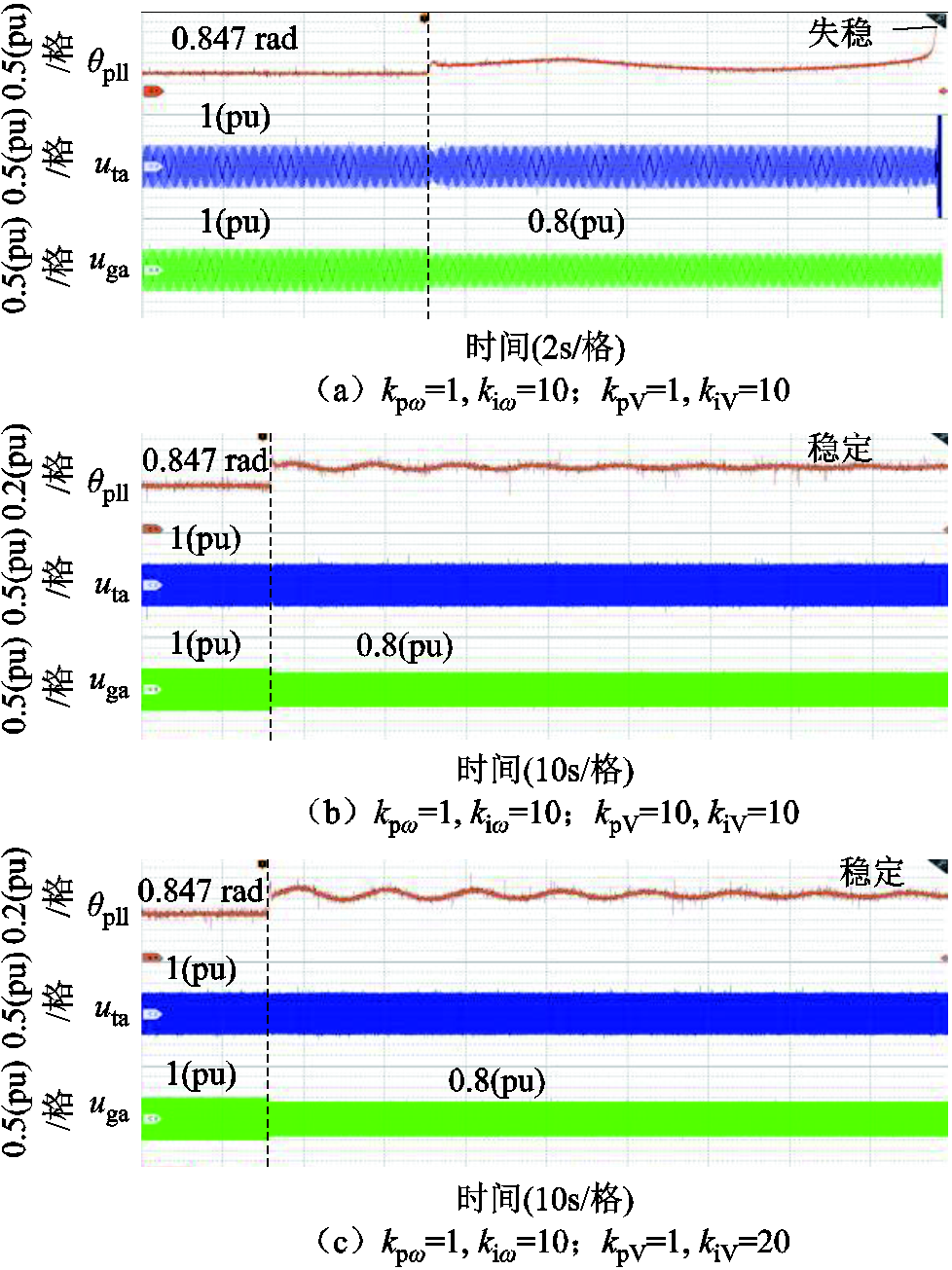

图26 第一组硬件在环实验波形
Fig.26 The first set of hardware-in-the-loop test waveform diagrams
实验二:电网短路比为SCR=1.41,电网电压骤降至0.8(pu),有功外环参数选取为:kpω=3, kiω=15;无功外环参数选取为:kpV=3, kiV=5。其他控制器参数则采用附录中的参数。系统将出现失稳现象,实验波形如图27a所示。然后,为减小负阻尼转矩,增大端电压比例参数为kpV=5以及增大端电压积分系数为kiV=10,系统将保持稳定,实验波形如图27b、图27c所示。最后,增大有功外环比例参数为kpω=7以及减小有功外环积分参数为kiω=10,系统将保持稳定,实验波形如图27d、图27e所示。实验结果与理论分析均保持一致。

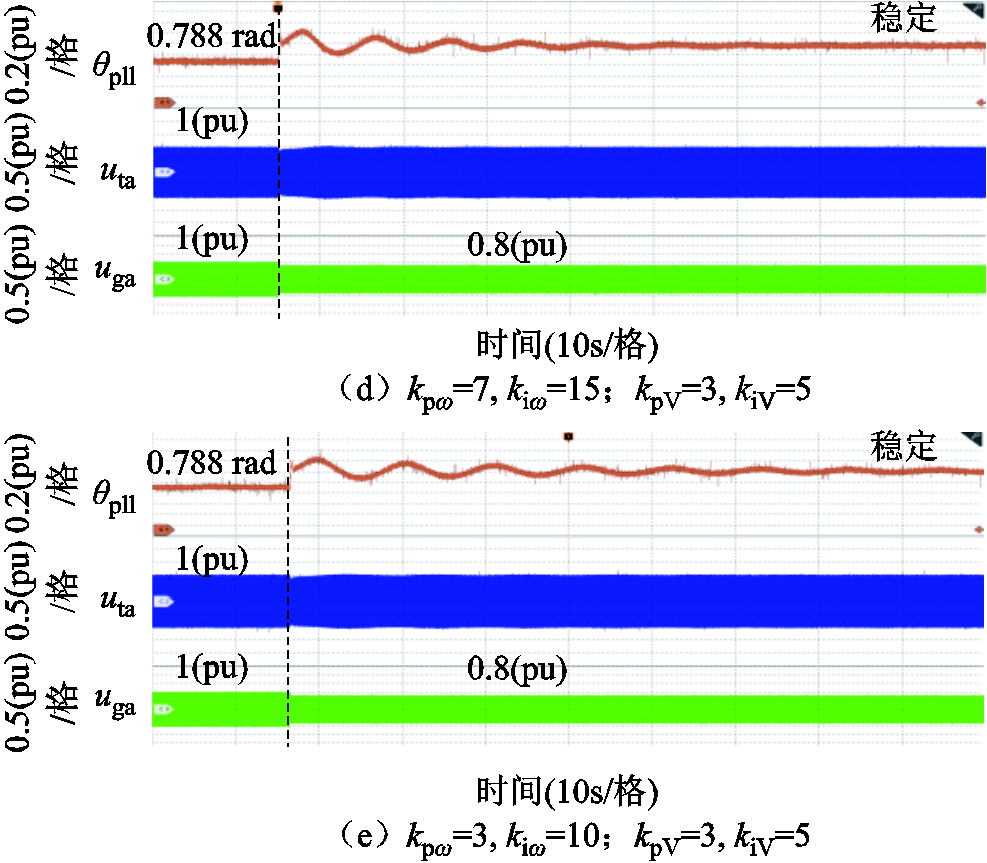
图27 第二组硬件在环实验波形
Fig.27 The second set of hardware-in-the-loop test waveform diagrams
本文研究了双馈风机转子转速尺度小扰动同步稳定性,针对DFIG小扰动失稳现象,采用复转矩法进行分析,揭示其稳定机理。详细结论如下:
1)基于主导模态分析法,发现在转子转速尺度下,双馈风机小扰动失稳由功率不平衡环节(有功外环与转子动态)主导失稳,而非锁相环为主导环节。
2)以功率不平衡环节构建了类Heffron-Phillips模型,发现转子转速尺度下同步相位由储能元件状态量∆ωr、∆θr的代数表达式近似表征,同步失稳的本质在于储能元件状态量所导致的失稳,虽然大扰动同步稳定主要由锁相环输出相位表征。
3)采用复转矩系数法分析了各支路的同步/阻尼特性,其中功率不平衡环节自身具有固有同步/阻尼转矩,锁相环对系统影响很小,而端电压环节则是引入负阻尼的主要因素。通过参数的影响分析,发现有功外环增大比例系数、减小积分系数将提高系统稳定性,端电压环节增大比例、积分系数将有利于系统稳定性。
附 录
1. 本文参数定义
附表1 参数表
App.Tab.1 Parametres of the paper
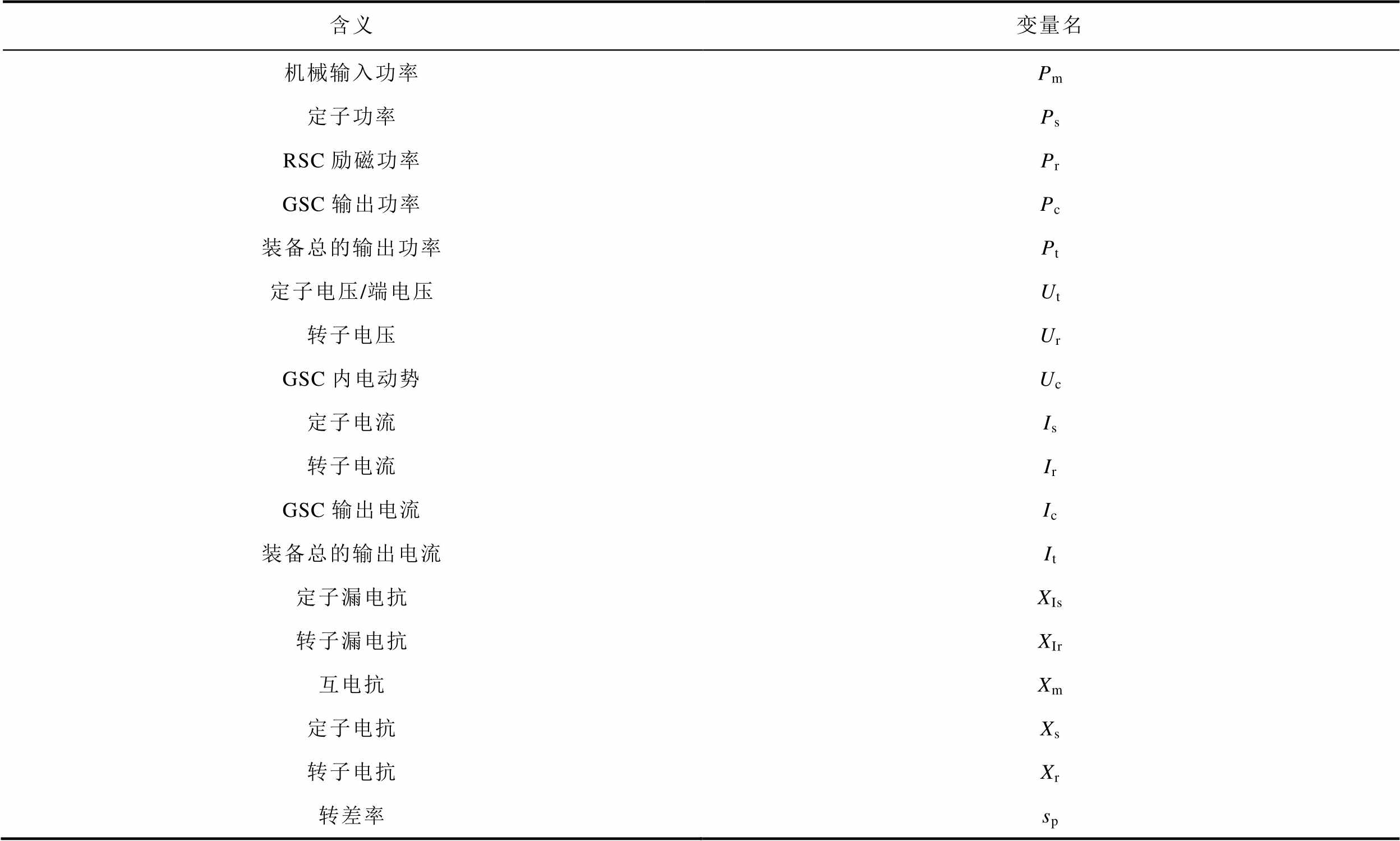
含义变量名 机械输入功率Pm 定子功率Ps RSC励磁功率Pr GSC输出功率Pc 装备总的输出功率Pt 定子电压/端电压Ut 转子电压Ur GSC内电动势Uc 定子电流Is 转子电流Ir GSC输出电流Ic 装备总的输出电流It 定子漏电抗XIs 转子漏电抗XIr 互电抗Xm 定子电抗Xs 转子电抗Xr 转差率sp
2. 双馈风机转子转速尺度五阶模型的推导过程
1)异步发电机建模
异步发电机主要包含磁链动态与转子动态两部分,转子采用单质量块模型,其动态过程用方程描述为
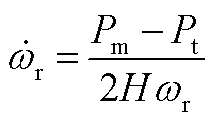 (A1)
(A1)
在锁相环提供的dq坐标下,关于磁链动态的原始微分方程与代数方程为
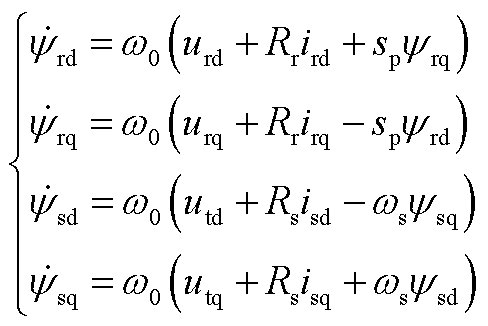 (A2)
(A2)
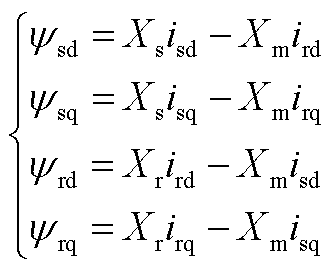 (A3)
(A3)
其中,定/转子电抗计算式为
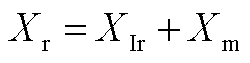 (A4)
(A4)
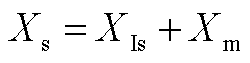 (A5)
(A5)
考虑磁链准稳态,且忽略定转子电阻大小,ωs≈1(pu),
联立式(A2)、式(A3)可以得到式(1)的定、转子电流关系。
2)机侧变换器建模
机侧变换器仅考虑外环控制,因此有功/无功外环的控制表达式为
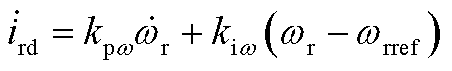 (A6)
(A6)
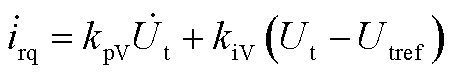 (A7)
(A7)
3)锁相环动态
锁相环二阶动态方程为
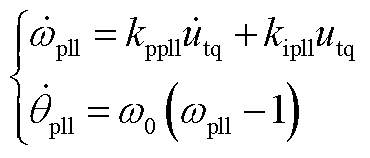 (A8)
(A8)
4)网络方程
忽略网络电感动态,在dq坐标系下,电路方程可以表示为
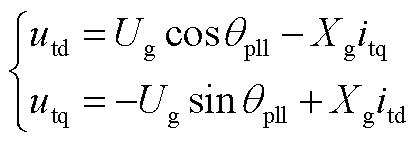 (A9)
(A9)
式(1)与式(2)联立,可知装备输出电流的表达式为
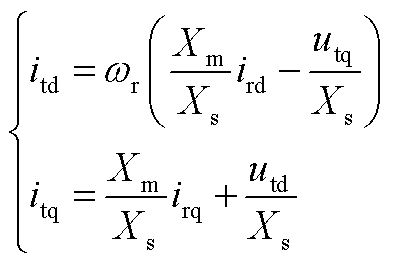 (A10)
(A10)
5)简化模型微分方程与代数方程
最终,将上述方程合并,可得微分方程为
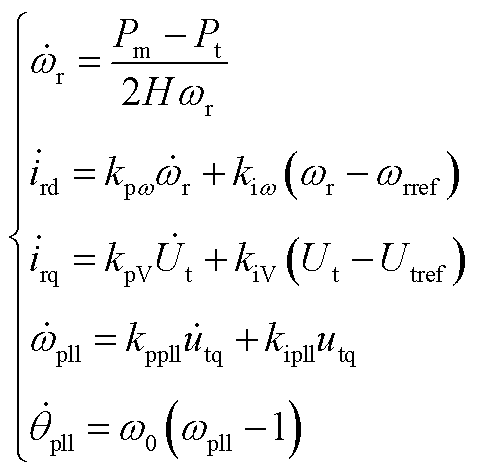 (A11)
(A11)
整个系统的代数方程为
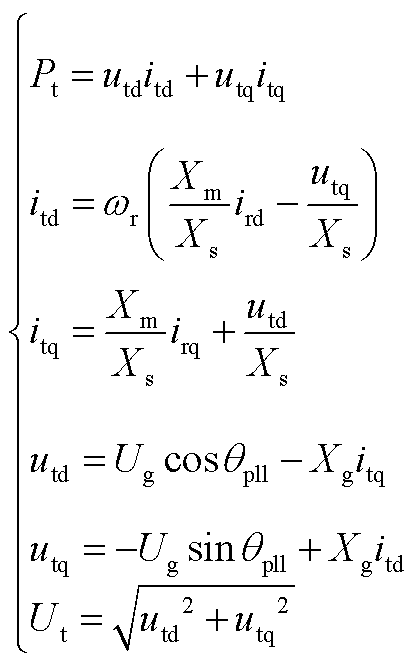 (A12)
(A12)
3. DFIG单机无穷大系统全阶模型参数取值
系统参数取值:Sbase= 2 MW,Ubase= 690 V,fbase = 50 Hz,Udcbase = 1 400 V,Udcref= 1 (pu),Utref= 1 (pu),Ug = 1 (pu),ωrref= 1.2(pu),C = 0.1 (pu),Lf= 0.1 (pu),Xg= 0.5 (pu)。
异步机参数:LIs= 0.171(pu),LIr= 0.156(pu),Lm= 3.9(pu),H= 4(pu)。
控制器参数取值如下:网侧VSC电流内环:kpucd= 0.63,kiucd= 5,kpucq= 0.63,kiucq= 5;网侧VSC直流电压外环:kpudc = 8,kiudc= 400;机侧VSC电流内环:kpurd= 0.6,kiurd = 8,kpurq = 0.6,kiurq = 8;机侧VSC转速控制器外环kpω= 1,kiω= 10;机侧VSC端电压控制器外环 kpV = 1,kiV= 10;锁相环:kppll= 50,kipll=2 000。
参考文献
[1] 继往开来,开启全球应对气候变化新征程:中华人民共和国主席习近平在气候雄心峰会上的讲话[EB/OL].中央人民政府网,(2020-12-12) . http:// www.gov.cn/gongbao/content/2020/content_5570055. htm.
Building on past achievements and launching a new journey for global climate actions-Statement by H. E. Xi Jinping president of the People’s Republic of China at the climate ambition summit[EB/OL]. The government network of the People’s Republic of China,(2020-12-13).http://www.gov.cn/gongbao/content/ 2020/content_557005 5.htm.
[2] 胡家兵, 袁小明, 程时杰. 电力电子并网装备多尺度切换控制与电力电子化电力系统多尺度暂态问题[J]. 中国电机工程学报, 2019, 39(18): 5457-5467, 5594.
Hu Jiabing, Yuan Xiaoming, Cheng Shijie. Multi-time scale transients in power-electronized power systems considering multi-time scale switching control schemes of power electronics apparatus[J]. Proceedings of the CSEE, 2019, 39(18): 5457-5467, 5594.
[3] 张兴, 战祥对, 吴孟泽, 等. 高渗透率新能源发电并网变流器跟网/构网混合模式控制综述[J]. 电力系统自动化, 2024, 48(21): 1-15.
Zhang Xing, Zhan Xiangdui, Wu Mengze, et al. Review on grid-following/grid-forming hybrid mode control for grid-connected converter in high penetration rate of renewable energy generation[J]. Automation of Electric Power Systems, 2024, 48(21): 1-15.
[4] 张天策, 李庚银, 王剑晓, 等. 基于可行域投影理论的新能源电力系统协同运行方法[J]. 电工技术学报, 2024, 39(9): 2784-2796.
Zhang Tiance, Li Gengyin, Wang Jianxiao, et al. Coordinated operation method of renewable energy power systems based on feasible region projection theory[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2784-2796.
[5] 倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002.
[6] 占萌, 张亚耀, 马锐. 以新能源为主体的新型电力系统模型体系和同步稳定研究综述[J]. 北京师范大学学报(自然科学版), 2023, 59(6): 878-886.
Zhan Meng, Zhang Yayao, Ma Rui. Review on model framework and synchronous stability of renewable-dominated new-type power systems[J]. Journal of Beijing Normal University (Natural Science), 2023, 59(6): 878-886.
[7] 王忱, 石立宝, 姚良忠, 等. 大规模双馈型风电场的小扰动稳定分析[J]. 中国电机工程学报, 2010, 30(4): 63-70.
Wang Chen, Shi Libao, Yao Liangzhong, et al. Small signal stability analysis of the large-scale wind farm with DFIGs[J]. Proceedings of the CSEE, 2010, 30(4): 63-70.
[8] 杨黎晖, 马西奎. 双馈风电机组对电力系统低频振荡特性的影响[J]. 中国电机工程学报, 2011, 31(10): 19-25.
Yang Lihui, Ma Xikui. Impact of doubly fed induction generator wind turbine on power system low-frequency oscillation characteristic[J]. Proceedings of the CSEE, 2011, 31(10): 19-25.
[9] 石佳莹, 沈沉, 刘锋. 双馈风电机组动力学特性对电力系统小干扰稳定的影响分析[J]. 电力系统自动化, 2013, 37(18): 7-13.
Shi Jiaying, Shen Chen, Liu Feng. Analysis on impact of DFIG wind turbines dynamic characteristics on power system small signal stability[J]. Automation of Electric Power Systems, 2013, 37(18): 7-13.
[10] Sahu B, Padhy B P. Evaluation of damping effect influenced by system parameters on a DFIG integrated power system[J]. IEEE Systems Journal, 2023, 17(2): 1939-1949.
[11] 马燕峰, 程有深, 赵书强, 等. 双馈风电场并网引起火电机组多模态次同步谐振机理分析[J]. 电工技术学报, 2025, 40(5): 1395-1410.
Ma Yanfeng, Cheng Youshen, Zhao Shuqiang, et al. Mechanism analysis of multi-mode SSR of thermal power unit caused by doubly fed wind farm integration [J]. Transactions of China Electrotechnical Society, 2025, 40(5): 1395-1410.
[12] 张琛, 李征, 蔡旭, 等. 双馈风电机组轴系扭振的稳定与控制[J]. 电工技术学报, 2015, 30(10): 301-310.
Zhang Chen, Li Zheng, Cai Xu, et al. Stability and control of shaft torsional oscillation for doubly-fed wind power generator[J]. Transactions of China Electrotechnical Society, 2015, 30(10): 301-310.
[13] 姚骏, 曾欣, 李嘉伟. 并网双馈感应风电系统轴系振荡特性[J]. 电工技术学报, 2017, 32(6): 123-135.
Yao Jun, Zeng Xin, Li Jiawei. Shaft oscillation characteristics of grid-connected doubly-fed induction generator-based wind power generation system[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 123-135.
[14] 刘巨, 姚伟, 文劲宇. 考虑PLL和接入电网强度影响的双馈风机小干扰稳定性分析与控制[J]. 中国电机工程学报, 2017, 37(11): 3162-3173, 3371.
Liu Ju, Yao Wei, Wen Jinyu. Small signal stability analysis and control of double-fed induction generator considering influence of PLL and power grid strength[J]. Proceedings of the CSEE, 2017, 37(11): 3162-3173, 3371.
[15] Xiong Xiaoling, Luo Bochen, Li Longcan, et al. Impedance reshaping method of DFIG system based on compensating rotor current dynamic to eliminate PLL influence[J]. IEEE Transactions on Power Electronics, 2024, 39(4): 4006-4016.
[16] Yang Yihang, Zhu Donghai, Zhou Dangsheng, et al. Synchronization instability mechanism and damping enhancement control for DFIG-based wind turbine during grid faults[J]. IEEE Transactions on Power Electronics, 2023, 38(10): 12104-12115.
[17] Buragohain U, Senroy N. Reduced order DFIG models for PLL-based grid synchronization stability assessment[J]. IEEE Transactions on Power Systems, 2023, 38(5): 4628-4639.
[18] 毕天姝, 王清, 薛安成, 等. 基于状态矩阵和摄动理论的双馈风力发电机与同步机小扰动互作用机理[J]. 电工技术学报, 2016, 31(7): 126-135.
Bi Tianshu, Wang Qing, Xue Ancheng, et al. The mechanism of small signal dynamic interaction between DFIG and synchronous generator based on state matrix and perturbation theories[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 126-135.
[19] Du Wenjuan, Wang Yang, Wang H F, et al. Collective impact of multiple doubly fed induction generators with similar dynamics on the oscillation stability of a grid-connected wind farm[J]. IEEE Transactions on Power Delivery, 2021, 36(5): 2942-2954.
[20] Zhang Yayao, Han Miao, Zhan Meng. The concept and understanding of synchronous stability in power electronic-based power systems[J]. Energies, 2023, 16(6): 2923.
[21] Xiong Liansong, Zhuo Fang, Wang Feng, et al. Static synchronous generator model: a new perspective to investigate dynamic characteristics and stability issues of grid-tied PWM inverter[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6264-6280.
[22] 康勇, 林新春, 郑云, 等. 新能源并网变换器单机无穷大系统的静态稳定极限及静态稳定工作区[J]. 中国电机工程学报, 2020, 40(14): 4506-4515, 4730.
Kang Yong, Lin Xinchun, Zheng Yun, et al. The static stable-limit and static stable-working zone for single-machine infinite-bus system of renewable-energy grid-connected converter[J]. Proceedings of the CSEE, 2020, 40(14): 4506-4515, 4730.
[23] Ma Rui, Zhang Yayao, Zhan Meng, et al. Dominant transient equations of grid-following and grid-forming converters by controlling-unstable- equilibrium-point-based participation factor analysis[J]. IEEE Transactions on Power Systems, 2024, 39(3): 4818-4834.
[24] 杜步阳, 邵德军, 朱建行, 等. 电压源型变流器并网系统多时间尺度间相互作用[J]. 电工技术学报, 2023, 38(20): 5547-5559.
Du Buyang, Shao Dejun, Zhu Jianhang, et al. The interaction between multiple timescales of the grid-tied voltage source converter[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5547- 5559.
[25] 洪国庆, 吴国旸, 金宇清, 等. 电力系统风力发电建模与仿真研究综述[J]. 电力系统自动化, 2024, 48(17): 22-36.
HongGuoqing, Wu Guoyang, Jin Yuqing, et al. Review on research of modeling and simulation for wind power generation in power system[J]. Auto-mation of Electric Power Systems, 2024, 48(17): 22-36.
[26] 贺益康, 胡家兵, 徐烈. 并网双馈异步风力发电机运行控制[M]. 北京: 中国电力出版社, 2012.
[27] 闵勇, 陈磊, 刘瑞阔, 等. 电力系统频率动态中惯量与惯量响应特性辨析[J]. 中国电机工程学报, 2023, 43(3): 855-868.
Min Yong, Chen Lei, Liu Ruikuo, et al. Analysis on characteristics of inertia and inertial response in power system frequency dynamics[J]. Proceedings of the CSEE, 2023, 43(3): 855-868.
Mechanism Analysis of Small-Signal Synchronous Stability of Double Fed Induction Generator within Rotor Speed Timescale
Abstract As the penetration rate of renewable energy sources increases, the stability mechanisms of the power system are constantly changing. The double-fed induction generator (DFIG), as a mainstream renewable energy equipment, its stability is of great significance to the safe operation of the power system. The phase-locked loop (PLL) plays an important role in synchronization, but there has been less research on simultaneously considering the dynamics of the phase-locked loop and the power balance loop. Moreover, the small-signal synchronization mechanism of DFIG within rotor speed timescale needs to be further analyzed.
Firstly, the transient model of single-DFIG infinite-bus system is constructed within the rotor speed scale. The simplified model is compared with the full-order model by Matlab/Simulink, and the results show that they match very well. Then, through bifurcation analysis, it is found that the system would experience small disturbance instability under weak grid condition. And it manifests itself in the form of low-frequency oscillatory instability. Furthermore, through the dominant modal analysis, it is found that the dominant unstable loop is the power balance loop.
In order to analyze the small-signal synchronous instability mechanism of the system, the model is linearized around the operating point. The linearized model and the full-order model are compared using Matlab under small disturbance, and the results validate the rationality of linearization. The power balance loop dominates the instability, making it considered as the core loop. Therefore, the Heffron-Philips model of the system is established for analyzing the small-signal synchronous stability mechanism. Based on the complex torque coefficient method, the terminal voltage control loop plays a dominant role by introducing negative damping. And by studying the transfer function of the PLL, it is found that the PLL with typical parameters has a negligible impact on the system in the rotor speed scale, and can be approximately regarded as a constant.
Finally, the parameters of the active outer loop and the reactive outer loop are analyzed. With the changing of the grid strength, the damping torque and synchronizing torque of each branch are quantitatively calculated. It is found that increasing the proportional coefficient of active outer loop and decreasing the integral coefficient will improve the stability of the system, and increasing the proportional/integral coefficient of the terminal voltage control loop will benefit the stability of the system. These analyses have been verified through simulations and experiments.
The conclusions of this paper are as follows: (1) In the rotor speed scale, the small-signal synchronous instability of the single-DFIG infinite-bus system is dominated by the power balance loop (active outer loop and rotor dynamic), rather than the PLL. (2) By constructing the Heffron-Philips model, it is found that the synchronous phase ∆θpll is approximately represented by an algebraic expression of the state variable ∆ωr/∆θrof the rotor. The essence of synchronous instability lies in the instability caused by the state variable of the energy storage element.3) Using complex torque coefficient method, it is found that the terminal voltage control loop is the main factor that introduces negative damping. Through the analysis of the influence of parameters, it is found that increasing the proportional coefficient of the active power outer loop and decreasing the integral coefficient will improve system stability, and increasing the proportional/integral coefficient of the terminal voltage control loop will be beneficial to system stability.
Keywords:Double fed induction generator, rotor speed time scale, dominant mode analysis, complex torque coefficient method
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.240862
南方电网公司科技项目资助036000KC23090004(GDKJXM20231026)。
收稿日期 2024-05-23
改稿日期 2024-09-13
许洪胜 男,2000年生,博士研究生,研究方向为双馈风机并网稳定性。
E-mail:xhs@hust.edu.cn
占 萌 男,1974年生,教授,博士生导师,研究方向为电力电子化电力系统动态、新能源并网稳定。
E-mail:zhanmeng@hust.edu.cn(通信作者)
(编辑 郭丽军)