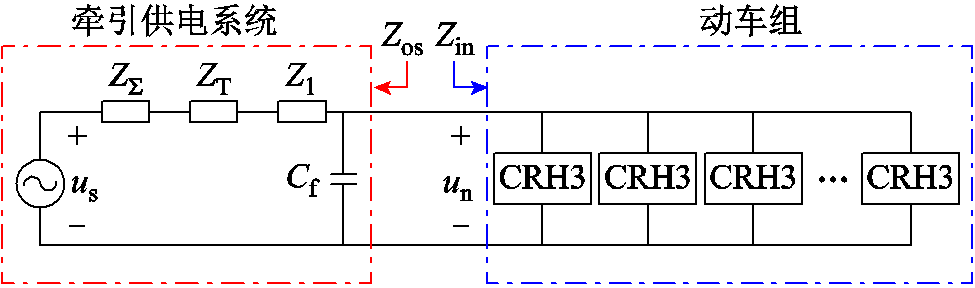
图1 车网耦合系统等效电路
Fig.1 Equivalent circuit diagram of EMUs-traction network coupling system
摘要 高速铁路车网耦合系统电压低频振荡多发生在多台动车组同时轻载启动工况下，严重时会触发牵引网牵引闭锁，威胁高速铁路的运行安全。针对高速铁路低频振荡问题，该文以CRH3型动车组为研究对象，推导了车网耦合系统阻抗模型，对车网耦合系统稳定性进行了分析，得出了系统的临界稳定条件；提出一种基于虚拟阻抗的低频振荡抑制方法，通过在动车组四象限变流器控制策略中引入并联虚拟阻抗来校正负载子系统的阻抗特性，提高系统稳定性，抑制系统低频振荡。该文还设计了一种虚拟阻抗的自适应控制方法，可以针对不同工况自适应调节虚拟阻抗参数，提升了抑制方法的适应能力。通过仿真和实验验证了所提抑制方法的有效性。
关键词：高速铁路 车网耦合系统 低频振荡 虚拟阻抗 自适应控制
随着高速铁路的发展，投入高速铁路的动车组数量不断增加，高速铁路车网系统耦合性问题也逐渐突显，其中就包括低频振荡问题。车网耦合系统低频振荡在我国多个路局时有发生，低频振荡是指当多台动车组在同一位置处于轻载启动工况时，牵引网电压、电流会出现频率为3～7 Hz的等幅振荡现象[1]，严重时会导致动车组发生牵引闭锁，无法正常运行，给高速铁路稳定运营带来严重隐患[2-4]。
目前，国内外已经有大批学者对低频振荡的机理和抑制方法进行了研究。对于低频振荡机理的研究方法主要有时域仿真法、特征值法和频域分析法。文献[5]搭建了车网耦合系统仿真模型，再现了低频振荡现象，并采用快速傅里叶分析法、空间谱估计多信号分类（Multiple Signal Classification, MUSIC）算法和Prony算法对低频振荡信号进行了分析，实现了振荡电压低频成分的辨识。文献[6]建立了考虑饱和限幅器在内的单输入单输出阻抗模型，基于描述函数法揭示了低频振荡的发生机理。文献[7]利用广义Nyquist判据在两种动车组非混运和混运工况下分析对比了关键参数对低频振荡的影响。文献[8]提出了一种改进sum-范数判据，对系统稳定性进行了进一步分析。文献[9]采用基于阻抗回差矩阵行列式的稳定性分析方法，对低频振荡的特征进行分析，给出了相关的振荡信息。
由于在牵引供电系统侧和动车组侧都会发生低频振荡现象，低频振荡抑制方法的研究也主要集中在牵引供电系统侧和动车组侧两方面。当系统两侧的阻抗比增大时，极容易引起低频振荡现象的发生。牵引供电系统侧的抑制方法主要是降低牵引供电系统等效阻抗，增大系统阻尼，以及连接网侧无功补偿装置，从而改善牵引网的供电条件。比如文献[10]通过在牵引网中增设模块化多电平换流器静态同步补偿器（Modular Multilevel Converter Synchronous Compensator, MMC_STATCOM）装置，补偿了系统的无功缺额，提高了系统的稳定性。文献[11]提出在网侧投入有源滤波器（Active Power Filter, APF）设备来提高系统稳定性，补偿系统无功功率。然而这类方法经济成本较高，不适合大范围使用。
动车组侧的抑制措施主要是围绕优化动车组的控制策略展开的，包括动车组控制参数调节、非线性控制和虚拟阻抗控制。文献[12]采用小增益定理分析，确定降低动车组四象限变流器的电压环比例参数可以抑制低频振荡，但是会降低系统的响应速度。文献[13-14]提出了一种自抗扰控制器来抑制低频振荡，但是自抗扰控制器结构复杂，参数整定难度较高。文献[15]结合自抗扰控制和传统PI控制的优点设计了一种自适应自抗扰比例积分控制器，增强了系统的鲁棒性。文献[16]提出了一种结合虚拟磁链和滑模观测器的反馈线性化虚拟惯量控制策略，在抑制低频振荡的同时减少了传感器的数量。文献[17]设计了一种模糊PI控制策略，但是模糊控制需要进行大量的仿真调试得出模糊推理规则。
虚拟阻抗控制方法的本质是通过更改变流器的控制策略，向电路提供虚拟的电阻、电感、电容等元件[18-20]，它的优点是既可以实现电路元件的功能又没有能量损耗。在振荡抑制方面，虚拟阻抗控制的实现方法主要是通过采集变流器前端的电压、电流等状态反馈量，利用不同的反馈函数实现不同的阻抗控制[21]。例如，在并网变流器系统中，针对LCL型滤波器导致的高频谐振的问题，有研究人员选取变流器前端电流[22]或者滤波电容电流[23-24]作为反馈量，通过各种PID控制[25]实现模拟串联或并联的高频阻尼电阻，有效地抑制了高频谐振问题。然而，当利用虚拟阻抗的方法去抑制低频振荡时，由于低频振荡的振荡频率与外环控制带宽接近，虚拟阻抗值选取过大会降低系统的动态性能，一些文献尝试引入滤波器到控制回路中进行阻抗补偿，比如文献[26]提出了一种基于陷波滤波器的虚拟阻抗补偿方法，但是由于低频振荡频率与基波频率相近，使用低阶滤波器无法准确提取低频分量。综上所述，目前已有的虚拟阻抗控制方法在抑制高频谐振时具有较好的效果，但是在解决低频振荡抑制问题时，还需要使用滤波器进行精确选频。因此，基于虚拟阻抗的车网耦合系统低频振荡抑制技术仍需要进一步的研究。
针对上述问题，本文引入阻抗比稳定性判据分析车网耦合系统的稳定性，探究低频振荡的产生机理和临界条件。通过改进动车组四象限变流器的控制策略，在动车组输入端口处引入并联虚拟阻抗来校正负载子系统的阻抗特性，提出了一种基于虚拟阻抗的瞬态直接电流控制策略来抑制低频振荡，并针对虚拟阻抗设计了一种自适应控制。采用带通滤波器与低通滤波器结合的方式提取低频振荡分量，根据振荡程度自适应调节虚拟阻抗值，提升了抑制方法对于不同工况的适应能力，通过仿真和实验验证了所提方法的有效性。
高速铁路车网耦合系统等效电路模型如图1所示，系统可以分为牵引供电系统和动车组两部分。Zos为牵引供电系统侧等效输出阻抗；Zin为动车组侧等效输入阻抗；us为牵引变电所输出电压；un为动车组输入电压；ZΣ为区域电网等效阻抗；ZT为牵引变压器等效阻抗；Zl为牵引网线路等效阻抗；Cf为牵引网对地分布电容。
图1 车网耦合系统等效电路
Fig.1 Equivalent circuit diagram of EMUs-traction network coupling system
将车网耦合系统分割成电源子系统和负载子系统两部分，等效成如图2所示的“源”-“荷”系统模型。图2中，in为输入电流。
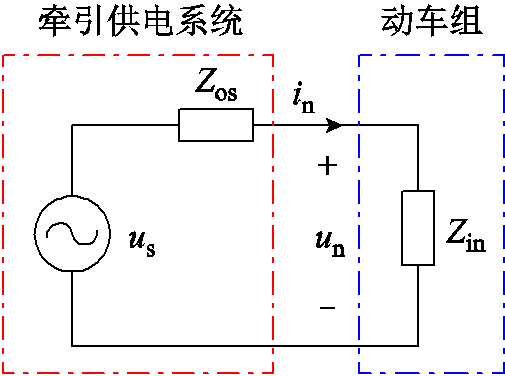
图2 “源”-“荷”系统等效模型
Fig.2 Equivalent model of “source”-“load” system
由图2可得动车组侧输入电压表达式为
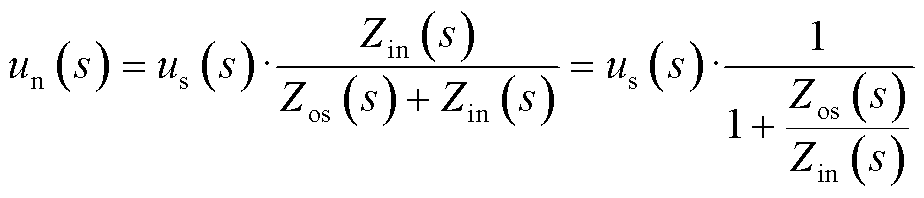（1）
可知当us为稳定的电压源时，车网耦合系统的稳定性取决于系统的闭环传递函数H(s)。
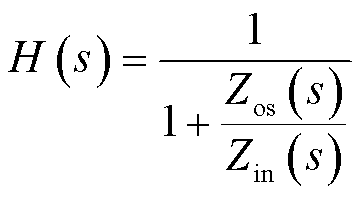（2）
该闭环传递函数的反馈增益为
（3）
式中，Tsn(s)为牵引供电系统侧等效输出阻抗与动车组侧等效输入阻抗的阻抗比。根据Middlebrook稳定性判据[27]，若要保证系统的稳定性，则需要满足条件|Tsn(s)|
1，在Bode图中表现为阻抗比幅频特性曲线与0 dB曲线不存在交截[28]，或者在交截频率fc处的相位绝对值小于180°。
根据图1可以得出牵引供电系统侧等效输出阻抗Zos在频域下的表达式为
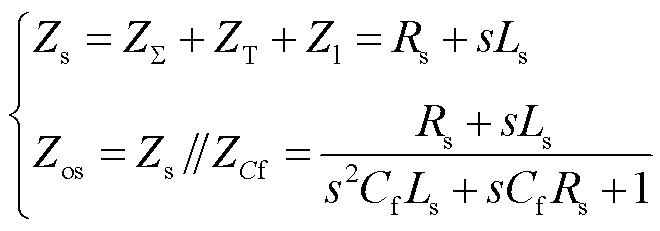（4）
式中，Rs、Ls分别为牵引供电系统的等效电阻和电感；ZCf为牵引网对地电容等效阻抗。
CRH3型动车组有4个动力单元。低频振荡发生在多台动车组同时处于轻载启动工况时，此时动车组的逆变器和牵引电机均不工作，只有辅助供电系统工作，可以将动车组直流侧负载等效成负载电阻进行建模，将对动车组的建模简化为对四象限变流器的建模。
动车组四象限变流器使用瞬态直接电流控制策略[29]，控制框图如图3所示。图3中，Ln和Rn分别为车载变压器绕组漏电感和电阻；idc为中间直流侧电流；Udc为中间直流侧电压；L2和R2分别为二次滤波回路电感和电阻；i2为滤波回路电流；Cd为支撑电容；iC为支撑电容电流；RL为等效负载；Id为负载电流；
为给定直流侧电压；In1为电压环PI环节输出电流；In2为给定电流的有效分量；
为给定内环电流幅值；KiP为电流内环比例系数；uab为产生PWM信号的调制波。
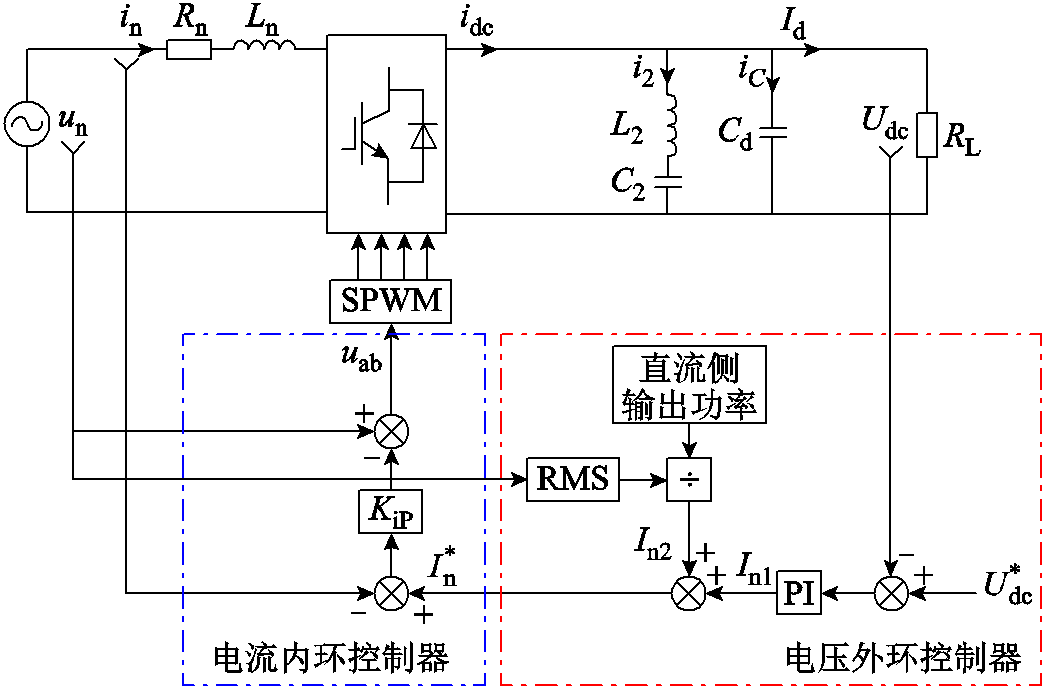
图3 瞬态直接电流控制策略控制框图
Fig.3 Control block diagram of transient direct current control strategy
瞬态直接电流控制策略的数学表达式为
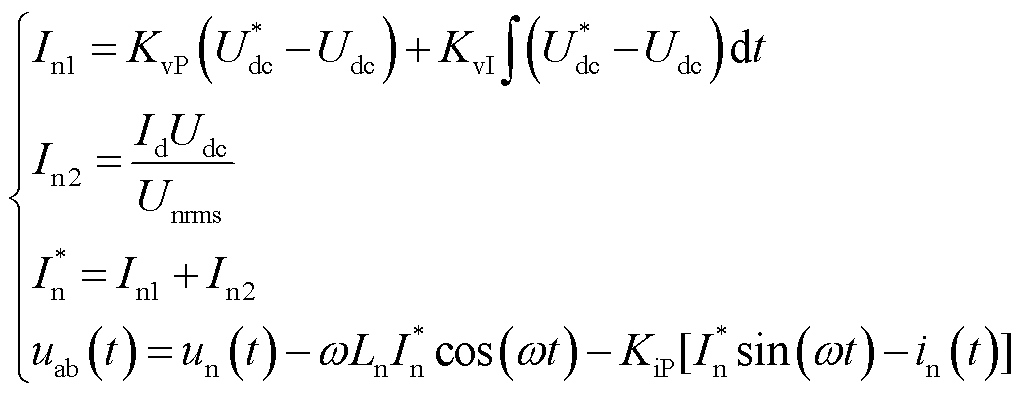（5）
式中，KvP、KvI为电压外环PI控制器参数；Unrms为网侧电压有效值；ω为网侧电压的角频率。
由于低频振荡发生在动车组轻载启动工况下，此时动车组直流侧负载电阻非常大，直流侧电流Id接近于0，导致直流侧功率IdUdc接近于0，即In2接近于0，所以可以令
，该策略传递函数框图如图4所示。图中，
为一个开关周期内开关函数Sa与Sb之差的平均值；Tv、Ti分别为电压外环和电流内环的信号采样周期；KPWM为PWM增益。将传递函数框图分成七个部分：G1代表电压外环PI控制；G2代表电流内环采样；G3代表电流内环比例增益；G4代表PWM调制；G5代表网侧阻抗参数；G6代表四象限变流器开关函数；G7代表直流侧阻抗参数。
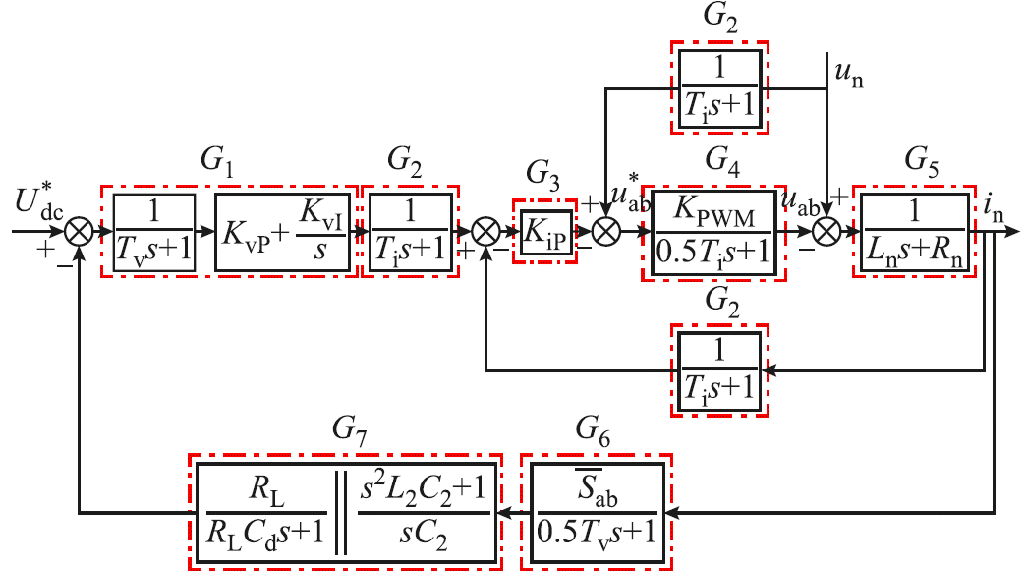
图4 瞬态直接电流控制策略传递函数框图
Fig.4 Transfer function block diagram of transient direct current control strategy
通过控制策略的传递函数框图对四象限变流器等效阻抗进行推导，得出单个动力单元的等效阻抗ZL的表达式为
（6）
1台动车组包含4个动力单元，当m台动车组同时运行时，动车组侧等效输入阻抗为
（7）
式中，k为牵引变压器电压比。
结合式（3）、式（4）、式（6）、式（7）得出车网耦合系统阻抗比Tsn(s)的表达式为
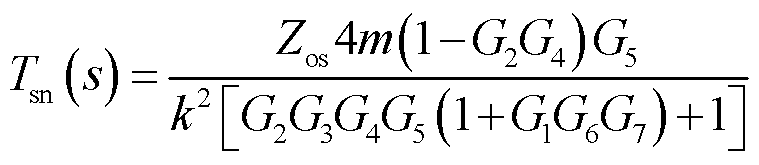（8）
根据式（8）绘制m台动车组在牵引网中同时轻载启动的阻抗比Bode图如图5所示。由图5可知，当m=1时，阻抗比的对数幅频特性曲线远离 0 dB，此时
，系统稳定；随着动车组数目m逐渐增大，幅频特性曲线逐渐靠近0 dB，系统稳定性下降；当m=6时，幅频特性曲线在7.032 Hz处穿越0 dB，且交截频率fc处的相位为182°，绝对值大于180°，|Tsn(s)|不满足远小于1的条件，系统已经处于不稳定状态，会发生低频振荡现象。
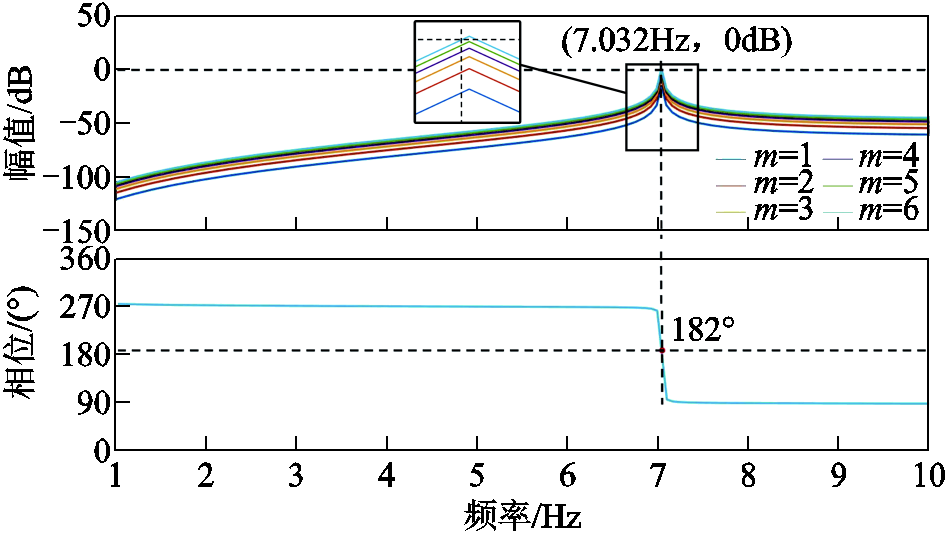
图5 阻抗比Bode图
Fig.5 Impedance ratio Bode diagram
由上述分析可知，当系统阻抗比幅频特性曲线与0 dB曲线已经存在交截时，若要保持系统稳定，交截频率处系统阻抗比的相位需要满足
（9）
Zos主要由电阻和电感组成，在工频条件下，整体上为阻感性元件，并且电阻含量较低。为了方便分析，可以将Zos视为纯感性元件，即Zos的相位等于90°，所以可将式（9）变为
（10）
整理可得
（11）
即若负载子系统的等效输入阻抗Zin在全频范围内的相位满足大于-90°且小于270°，则系统会一直保持稳定。若Zin的阻抗角出现低于-90°或者高于270°的区间，且交截频率fc落在此区间内，则系统无法满足条件式（9），系统会失去稳定。
本文考虑在系统的连接公共点（Point of Common Coupling, PCC）处并联一个校正阻抗Zp，用来补偿负载子系统的阻抗特性，使系统阻抗比的相位满足条件式（9），具体方法如图6所示。图中，ip为流过并联阻抗Zp的电流。
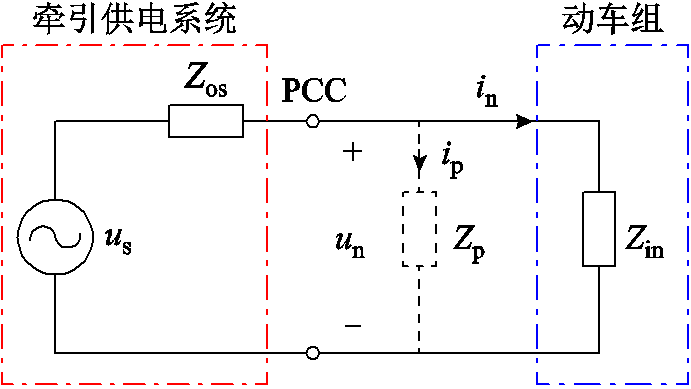
图6 在PCC处并联阻抗
Fig.6 Shunt impedance at PCC
动车组等效输入阻抗Zin和在PCC处并联的阻抗Zp可表示为
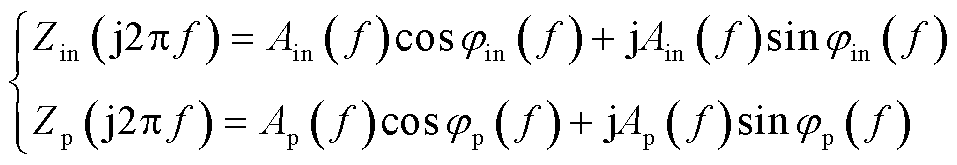（12）
式中，Ain、Ap分别为动车组等效输入阻抗和并联阻抗对应的幅值；φin和φp分别为动车组等效输入阻抗和并联阻抗对应的相位。
并联校正阻抗后，负载子系统的等效输入阻抗Zin-p的表达式为
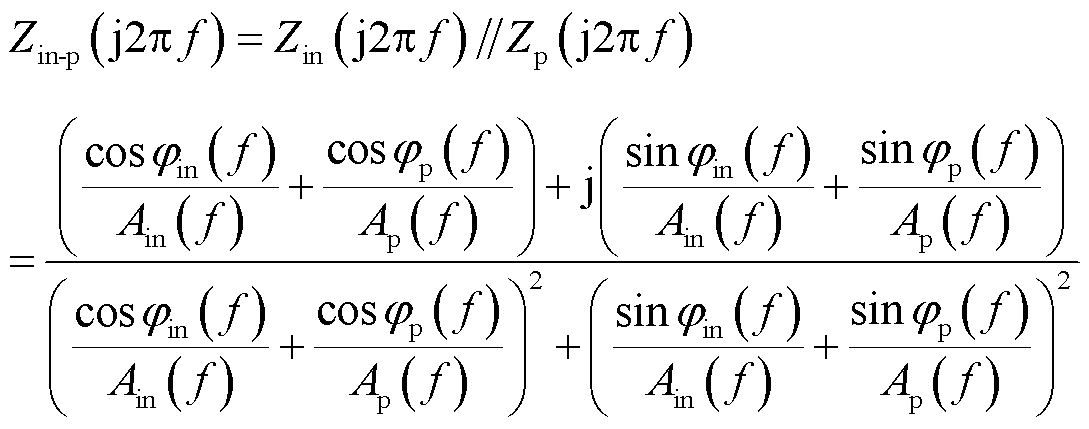（13）
结合式（11）和式（13）可知，若要保证并联阻抗后系统仍然处于稳定，需要满足并联后在交截频率fc处Zin-p的相位大于-90°且小于270°。当Zin-p具有正实部时，Zin-p的相位值处于-90°～90°之间，所以可令Zin-p的实部大于0来保证系统的稳定性，即满足如下条件
（14）
整理可得
（15）
由于Ain、Ap都是大于0的实数，且cosφin(fc)的取值范围是-1～1，所以不妨令cosφin(fc)取最小值 -1，此时式（15）可以表示为
（16）
整理可得
（17）
即此时如果保证cosφp(fc)＞0，Ap(fc)足够小，且cosφp(fc)不接近0，则可以满足式（17），并联后的系统稳定。由于阻性负载的cosφp(fc)=1，完全满足cosφp(fc)＞0且不接近0的条件，所以本文考虑在系统的公共连接点（PCC）直接并联一个电阻元件来增强系统的稳定性。
并联电阻元件后，式（17）经过整理可得
（18）
即此时只需要满足电阻元件的阻值小于动车组等效输入阻抗的幅值，则可以保证并联后的系统是稳定的。
然而在实际工程中，在系统中直接并联电阻元件会产生大量功率损耗，因为负载子系统由多台动车组并联而成，所以本文考虑通过改进动车组四象限变流器的控制策略，实现在动车组输入端口处引入并联虚拟阻抗等效在PCC端口处并联校正阻抗。车网耦合系统引入虚拟阻抗后的示意图如图7所示。图中，Rp为引入的虚拟阻抗，
为四象限变流器网侧电感电流。
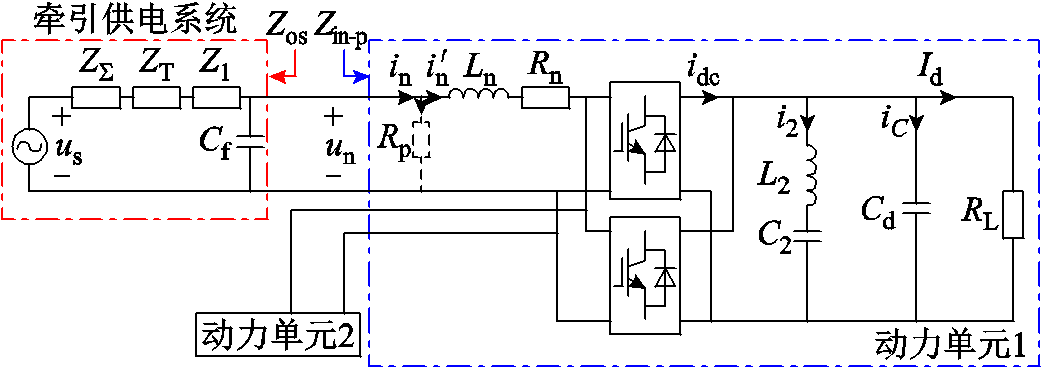
图7 在动车组接入点引入虚拟阻抗示意图
Fig.7 Schematic diagram of introducing virtual impedance into EMU access point
在四象限变流器的网侧输入端口处并联一个虚拟阻抗Rp，则此时流过Rp的电流ip为
（19）
则四象限变流器网侧电感电流值应为
（20）
通过改进瞬态直接电流控制策略，在电流环中增加网侧电流对于虚拟阻抗的反馈过程，实现虚拟阻抗的引入，得到基于虚拟阻抗的瞬态直接电流控制策略如图8所示。
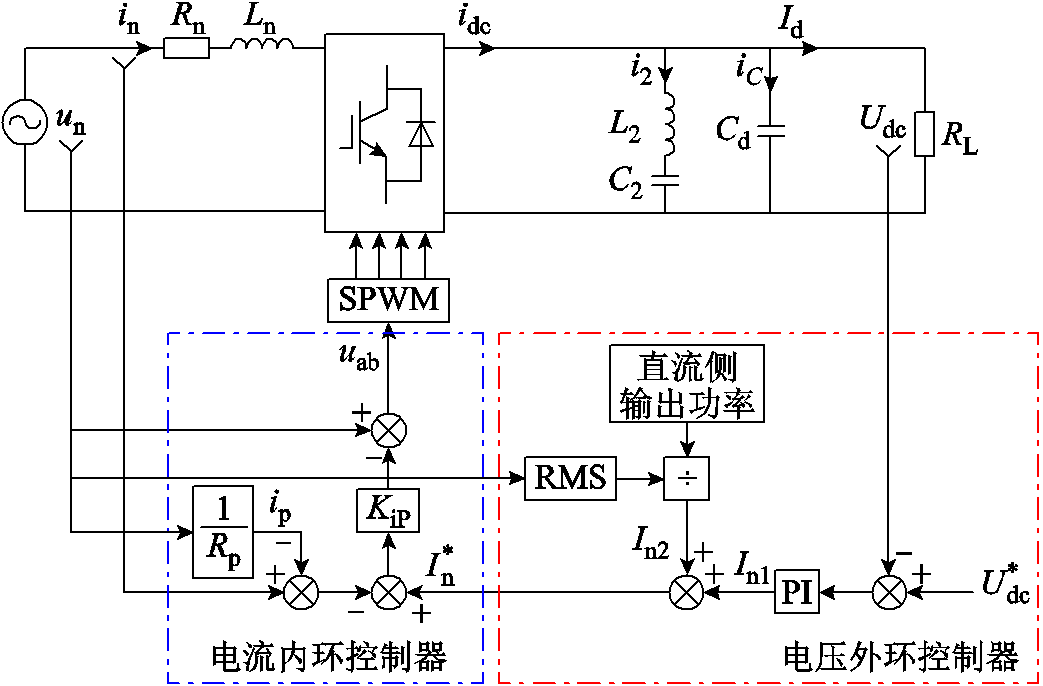
图8 基于虚拟阻抗的瞬态直接电流控制策略
Fig.8 Transient direct current control strategy based on virtual impedance
系统模型可以整理得到
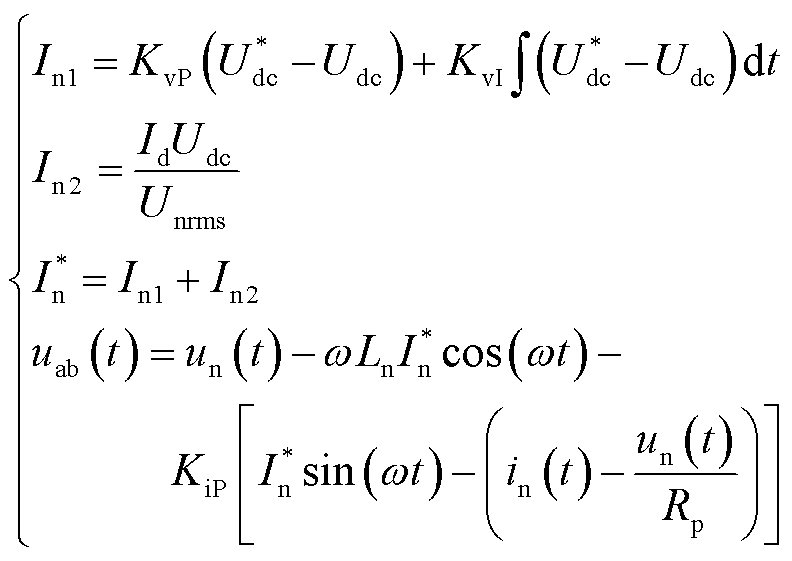（21）
根据图8和式（21）可以推导出基于虚拟阻抗的瞬态直接电流控制策略的传递函数框图如图9所示，图9中G8代表虚拟阻抗参数。
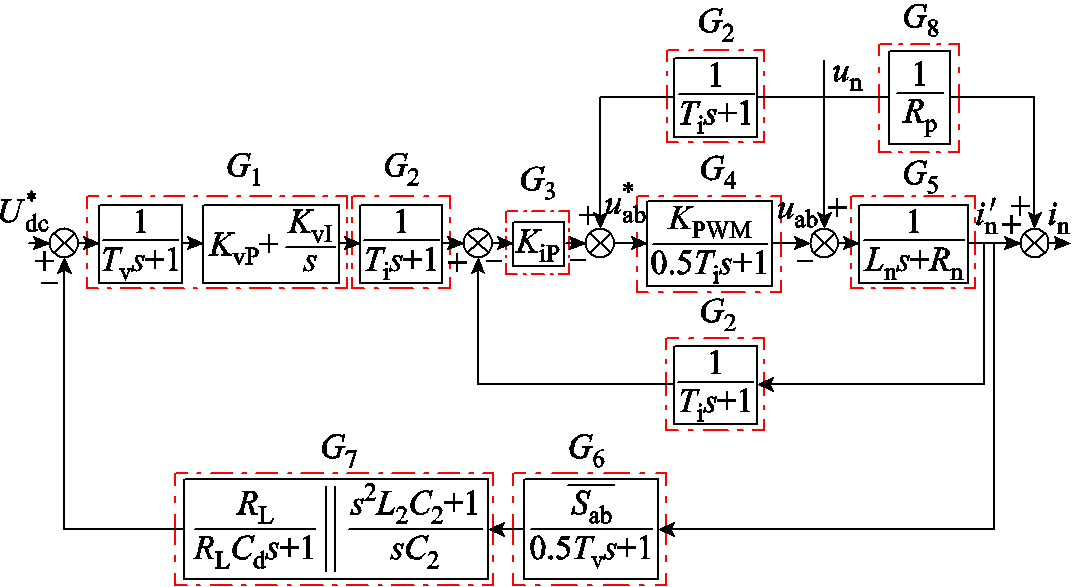
图9 虚拟阻抗控制策略传递函数框图
Fig.9 Transfer function block diagram of virtual impedance control strategy
由图9可以推导出动车组单个动力单元新的等效阻抗ZL-p为
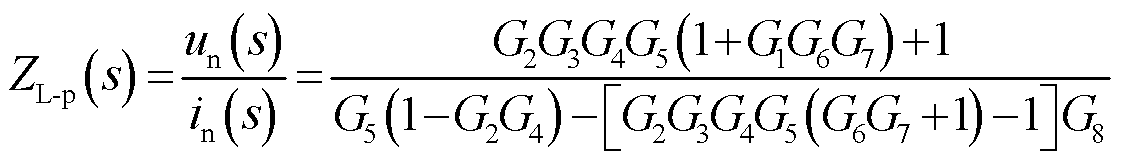（22）
当m台动车组同时接入牵引网时，引入虚拟阻抗后动车组侧的等效输入阻抗为
（23）
联立式（3）、式（4）和式（22）、式（23）可得引入虚拟阻抗后车网耦合系统阻抗比Tsn-p(s)的表达式为
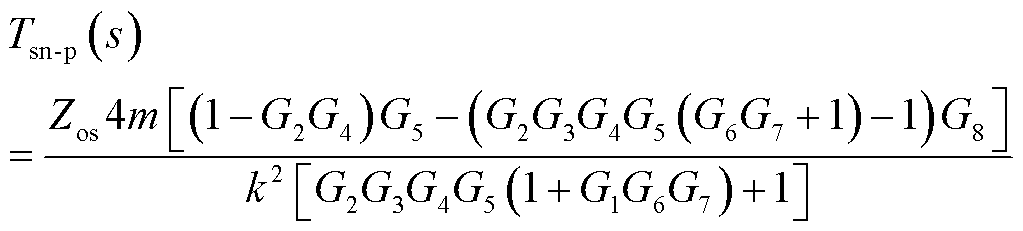（24）
根据式（24）绘制引入虚拟阻抗后的系统阻抗比Bode图进行对比分析，如图10所示，当动车组台数m=6时，分别取虚拟阻抗值Rp=0 Ω、1 Ω、2 Ω、5 Ω、10 Ω，可以发现，虽然引入虚拟阻抗后阻抗比幅频特性曲线仍然穿越0 dB曲线，但是其交截处相位绝对值小于180°，Rp取值越小，与0 dB交截处的相位绝对值越小于180°。说明引入虚拟阻抗后提高了系统的稳定性，可以抑制系统低频振荡，且Rp取值越小，抑制效果越好，系统越稳定。
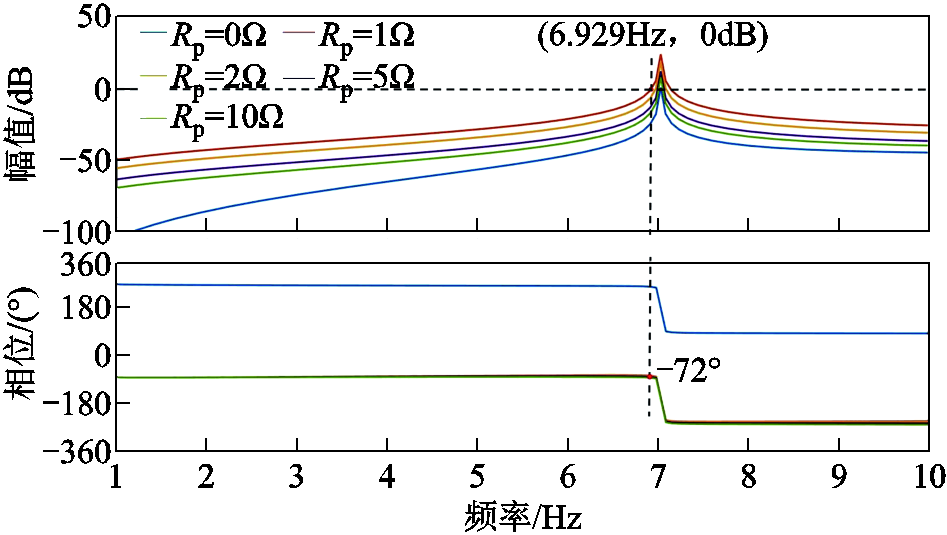
图10 引入虚拟阻抗后的阻抗比Bode图
Fig.10 Bode diagram of impedance ratio after setting virtual impedance
在实际的高速铁路系统中，工况复杂多变，若设置虚拟阻抗参数值过大，可能会导致抑制能力受限，系统中轻载启动的动车组增加后系统无法保持稳定；若设置虚拟阻抗值过小，则可能会导致四象限变流器网侧电流过小，无法使四象限变流器正常运行。将虚拟阻抗设置为固定值会导致系统灵活度较低，无法应对复杂的实际工况，所以需要设计一种自适应控制方法，提升控制策略的适应能力。
当发生低频振荡时，动车组网侧电压un同样会出现低频振荡，我国低频振荡的频率为3～7 Hz，可以将通过带通滤波器筛选采集到的动车组网侧电压信号中此频段的分量作为反馈量。设通过带通滤波器的低频电压分量为unL，其表达式为
（25）
式中，ωnL为低频电压分量的角频率；φnL为低频电压分量的相位；UnL为低频电压分量的幅值，UnL偏大，说明系统振荡幅度大，当不存在低频振荡时，UnL为0。
通过检测UnL反馈量的大小来调节Rp或者1/Rp的值，控制虚拟阻抗参数实现自适应调节，是一种可行的自适应控制方法。
将unL平方可得
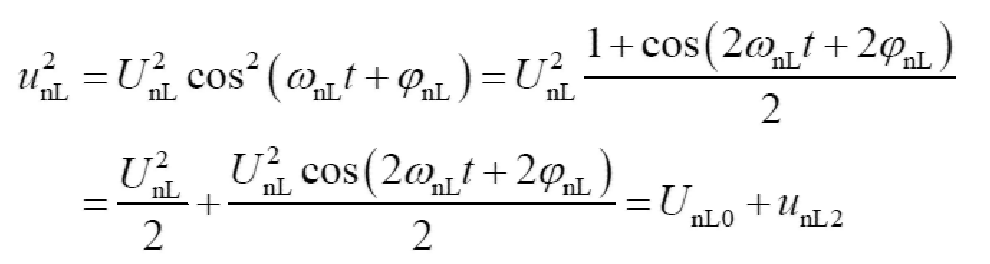（26）
将unL平方后得到一个直流分量UnL0和一个交流分量unL2，直流分量UnL0的大小与UnL的大小呈正相关，而unL2的频率比较高，可以通过低通滤波器提取直流分量UnL0来反映UnL值的变化。将检测到的UnL0送入PI控制器中，将PI控制器的输出信号1/Rp与网侧电压反馈信号un相乘后调节网侧电流信号，得到基于自适应虚拟阻抗的瞬态直接电流控制策略，控制策略如图11所示。
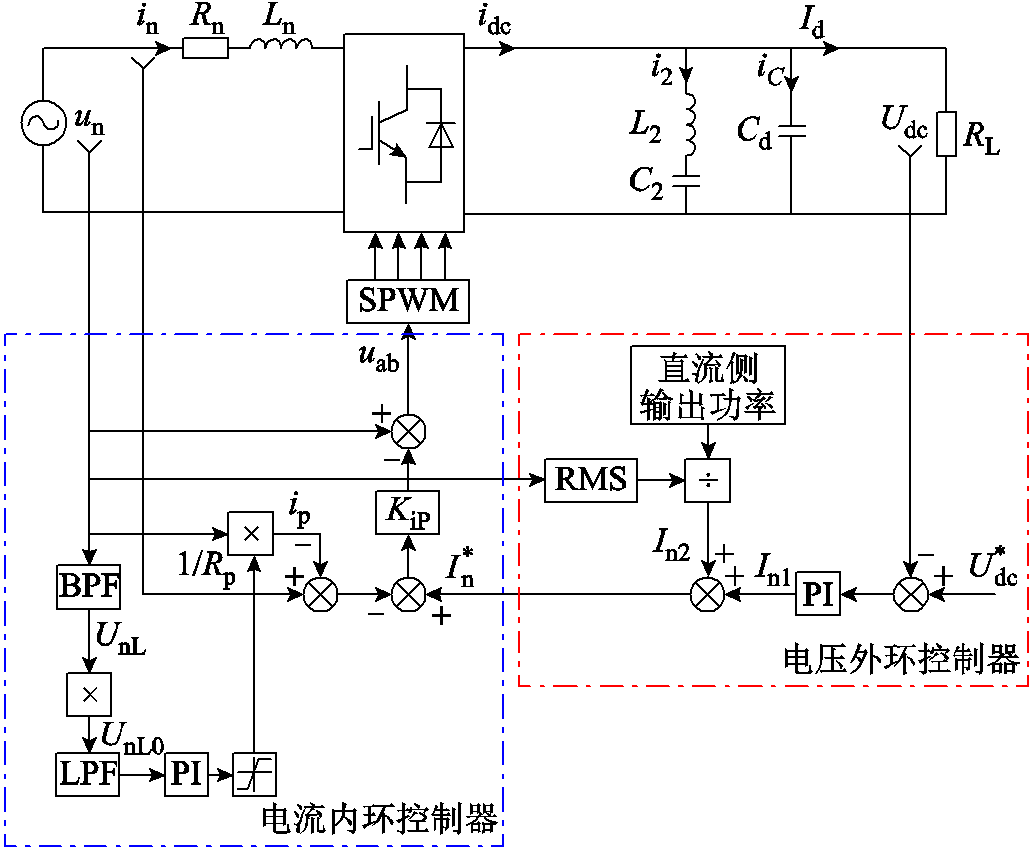
图11 基于自适应虚拟阻抗的瞬态直接电流控制策略
Fig.11 Transient direct current control strategy based on adaptive virtual impedance
系统模型的数学表达式可以整理为
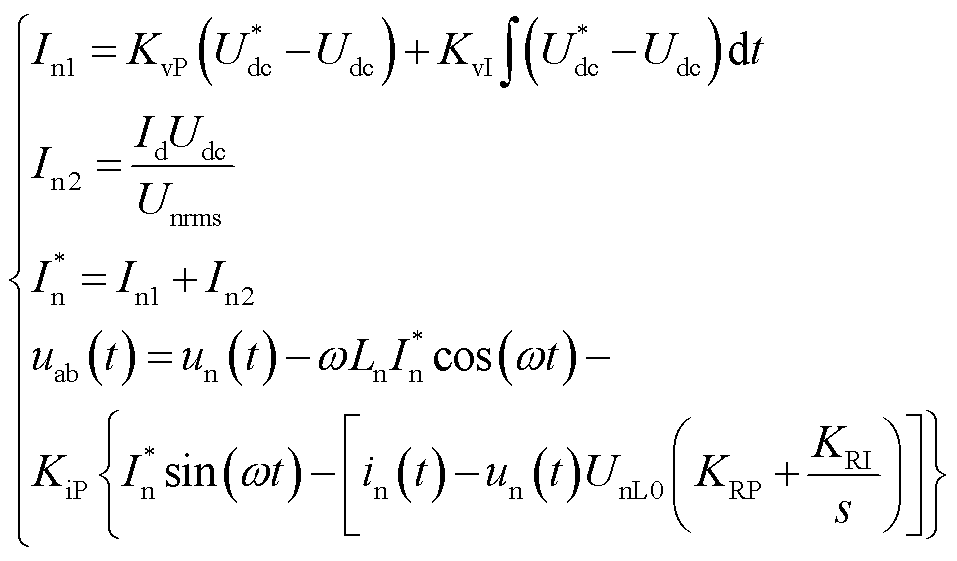（27）
式中，KRP、KRI为电阻环的PI参数。
根据图11和式（27）可以推导出基于自适应虚拟阻抗的瞬态直接电流控制策略的传递函数框图如图12所示。图中
代表自适应虚拟阻抗参数。
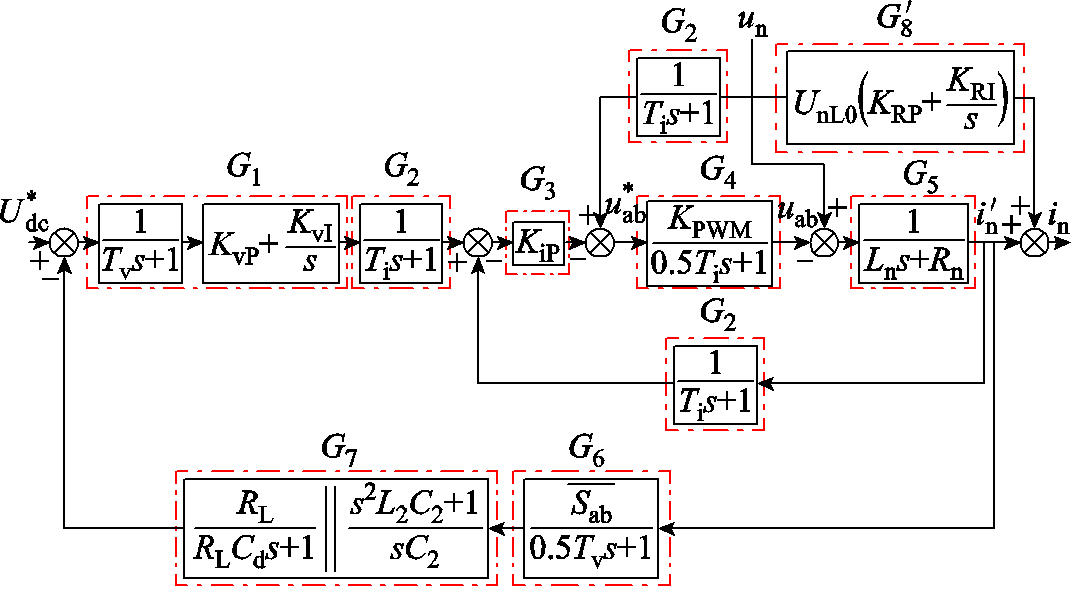
图12 自适应虚拟阻抗控制策略传递函数框图
Fig.12 Transfer function block diagram of adaptive virtual impedance control strategy
由图12和式（3）、式（4）可以得到，引入自适应虚拟阻抗后当m台动车组同时接入牵引网时车网耦合系统阻抗比
的表达式为
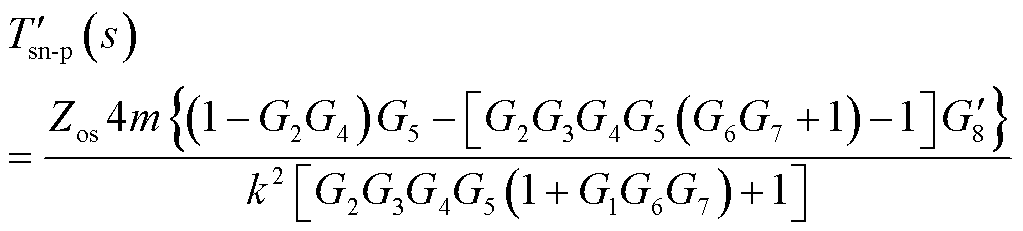（28）
根据式（28）绘制引入自适应虚拟阻抗后的系统阻抗比Bode图进行对比分析，如图13所示，当动车组台数m=6时，分别取UnL0=0(pu)、5(pu)、10(pu)、20(pu)、40(pu)，可以发现，与引入固定虚拟阻抗的结果相似，引入自适应虚拟阻抗后的系统阻抗比幅频特性曲线与0 dB的交截处相位角绝对值小于180°，且UnL0值越大，交截处的相位绝对值越小于180°，对应调节后的虚拟阻抗值越小。说明基于自适应虚拟阻抗的瞬态直接电流控制策略可以根据网侧交流电压的振荡程度调节Rp的取值，振荡越强烈，系统对于低频振荡的抑制能力越强。
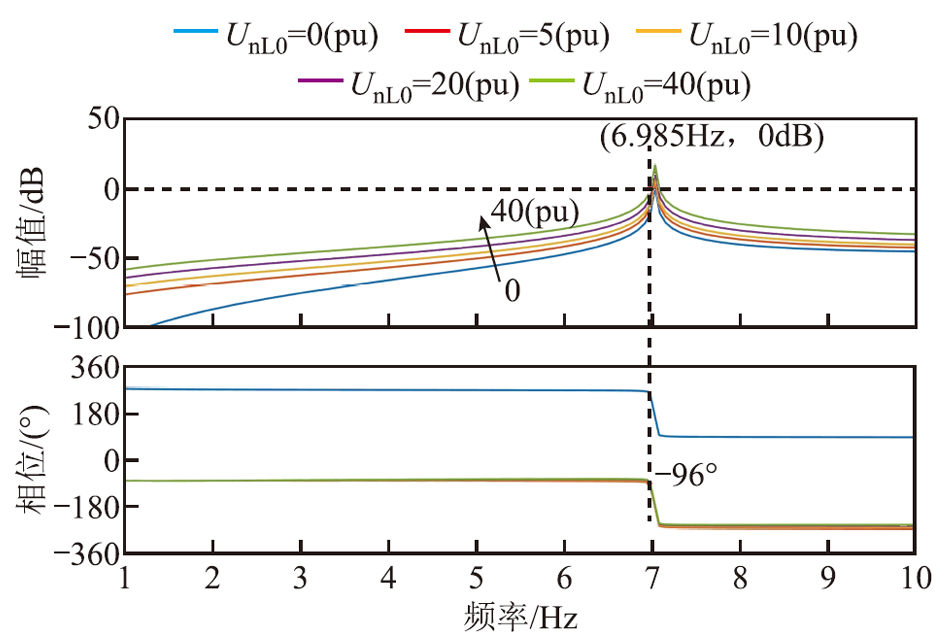
图13 引入自适应虚拟阻抗后的阻抗比Bode图
Fig.13 Bode diagram of impedance ratio after introducing adaptive virtual impedance
CRH3型动车组采用的传统控制策略为瞬态直接电流控制策略。本节搭建车网耦合系统仿真模型，对采用传统控制策略的动车组接入牵引网进行仿真分析，复现低频振荡现象。
在Matlab/Simulink环境中搭建车网耦合系统仿真模型。1台动车组包含4个动力单元，用4组四象限变流器仿真模型并联等效1台动车组，直流侧负载电阻取值为1 000 Ω。将m台动车组接入牵引网上行变电所4 km处形成车网耦合系统仿真模型如图14所示，图中T代表接触线，R代表钢轨，F代表正馈线，P代表保护线，AT代表自耦变压器。
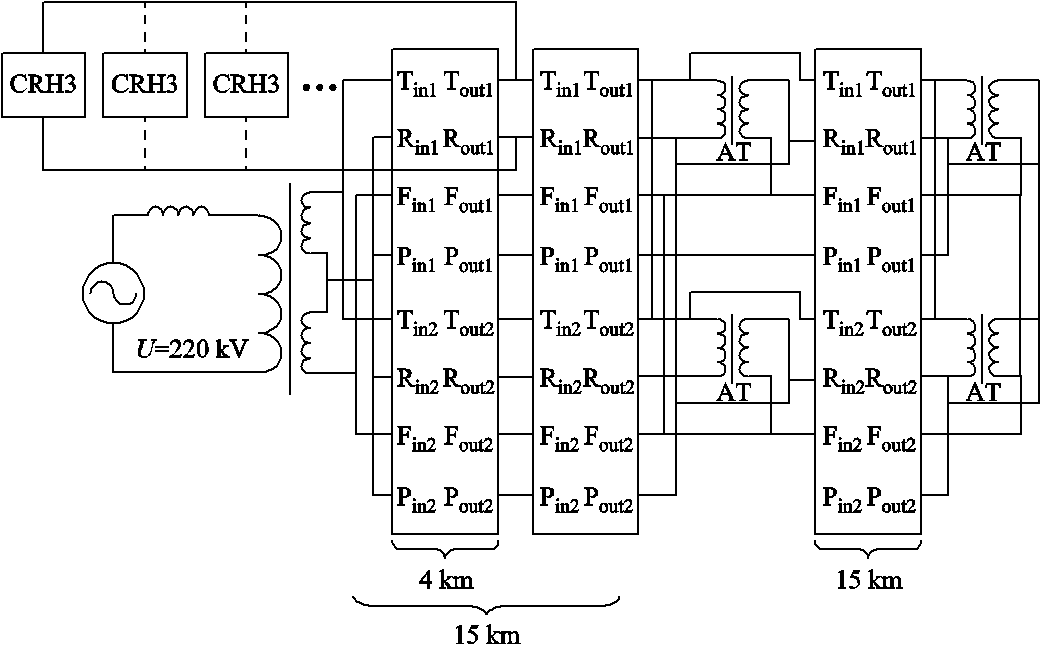
图14 车网耦合系统仿真模型
Fig.14 Simulation model of EMUs-traction network coupling system
当6台采用传统瞬态直接电流控制策略的动车组同时在牵引网中轻载启动时，系统电压电流波形如图15所示。由图15可知，动车组网侧电压电流同时出现了持续的等幅低频振荡现象，频率约为 7 Hz左右，这是由于系统电气量波动过大，传统控制策略的四象限变流器已经无法正常工作，导致系统失稳，发生低频振荡。
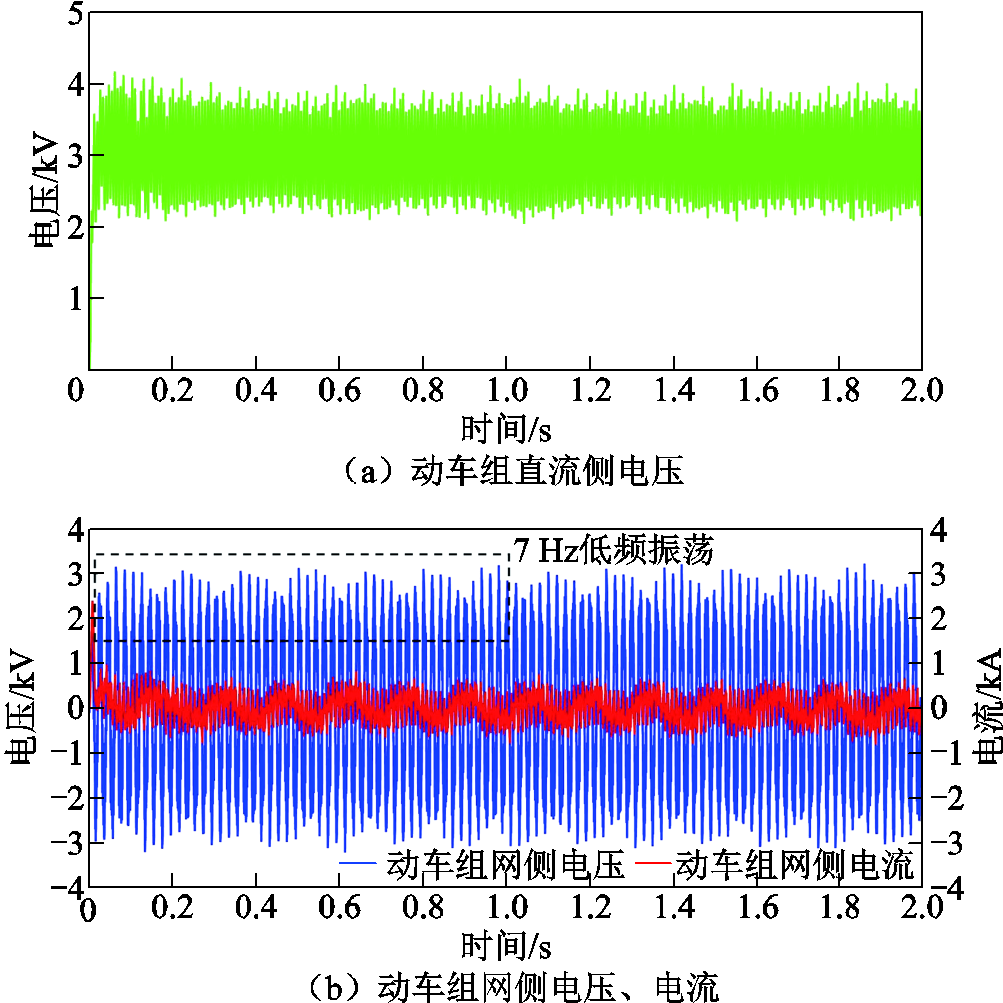
图15 接入6台动车组时电压电流波形（传统控制）
Fig.15 Voltage and current waveform diagram when connecting six EMUs (Traditional PI control)
将2.2节提出的基于虚拟阻抗的瞬态直接电流控制策略应用到动车组四象限变流器中，当m=6时，设置虚拟阻抗值分别为10 Ω、5 Ω和2 Ω，仿真结果如图16～图18所示。当Rp=10 Ω时，系统电压电流在前期仍存在一定的低频振荡，在1.6 s后系统恢复稳定，不再发生振荡；当Rp=5 Ω时，系统在1.0 s左右进入稳定状态；当Rp=2 Ω时，系统在0.3 s左右进入稳定状态。
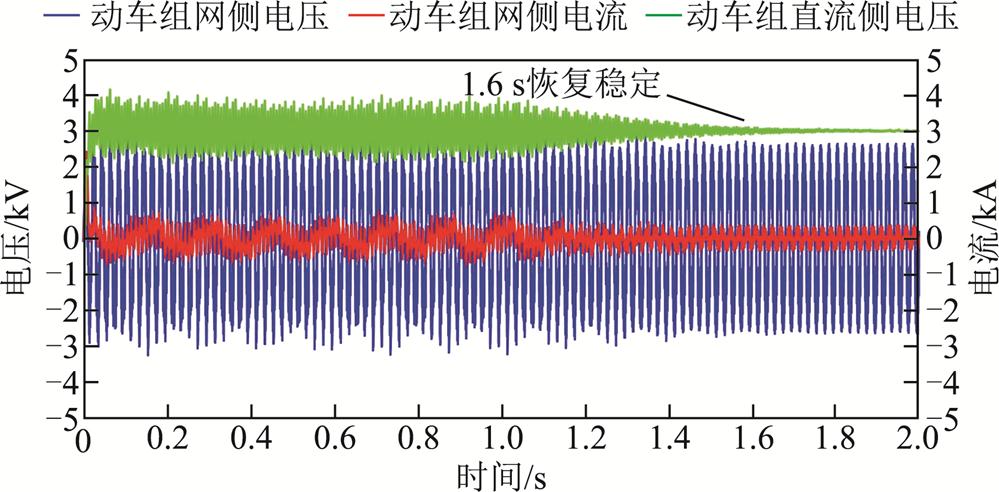
图16 接入6台动车组时电压电流波形（虚拟阻抗控制，Rp=10 Ω）
Fig.16 Voltage and current waveform diagram when connecting six EMUs (Virtual impedance control, Rp=10 Ω)
根据仿真结果可知，引入虚拟阻抗能够抑制低频振荡，虚拟阻抗值设置越小，低频振荡分量收敛越快，抑制效果越好，仿真结果与理论分析结果一致。
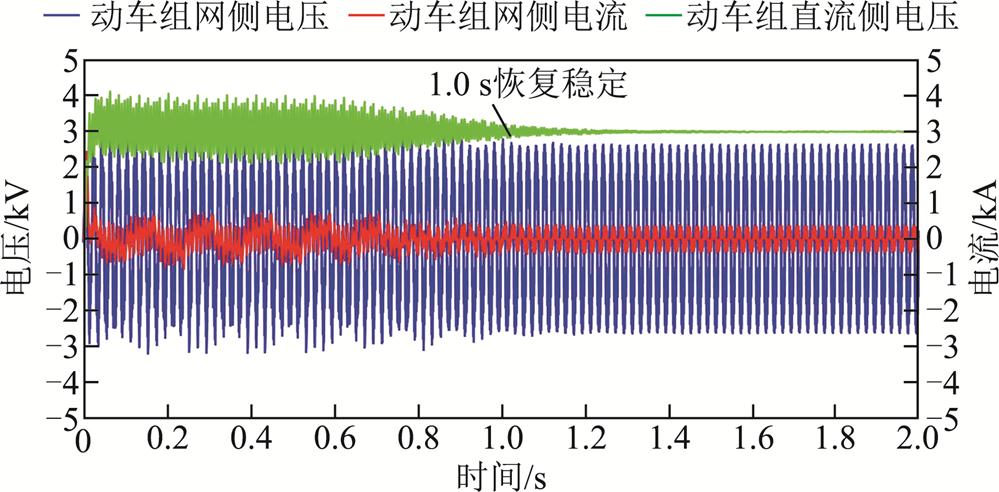
图17 接入6台动车组时电压电流波形（虚拟阻抗控制，Rp=5 Ω）
Fig.17 Voltage and current waveform diagram when connecting six EMUs (Virtual impedance control, Rp=5 Ω)
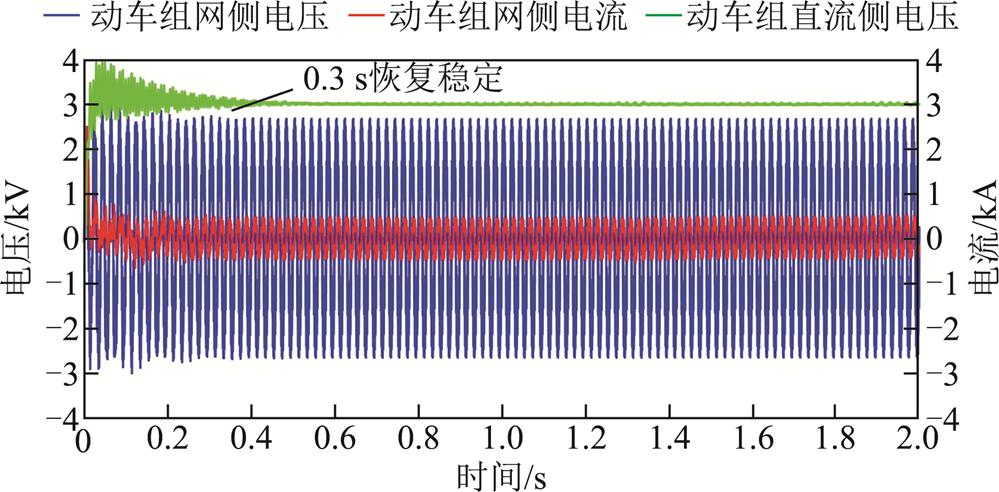
图18 接入6台动车组时电压电流波形（虚拟阻抗控制，Rp=2 Ω）
Fig.18 Voltage and current waveform diagram when connecting six EMUs (Virtual impedance control, Rp=2 Ω)
将6台动车组同时接入牵引网中，其中5台仍然沿用传统的瞬态直接电流控制策略，只有1台动车组采用2.3节提出的自适应虚拟阻抗控制策略。为了使系统能够快速稳定收敛，设置虚拟阻抗值Rp的限幅为10 Ω，仿真结果如图19所示。系统电压电流经过2.8 s后进入稳定，之后未出现低频振荡现象，同时虚拟阻抗值自适应调节至3.26 Ω，即单台动车组应用自适应虚拟阻抗控制策略对低频振荡有抑制效果，但是抑制能力较弱，系统振荡收敛时间比较慢。
将6台动车组全部应用自适应虚拟阻抗控制策略，仿真结果如图20所示，由图20可知，系统在0.5 s左右进入稳态，同时虚拟阻抗值自适应调节至4.65 Ω，动车组直流侧电压的调节时间为0.46 s，超调量为37.71 %，稳定后的电压波动为±58 V，系统随时间推移未出现大幅的低频振荡现象，抑制效果良好。
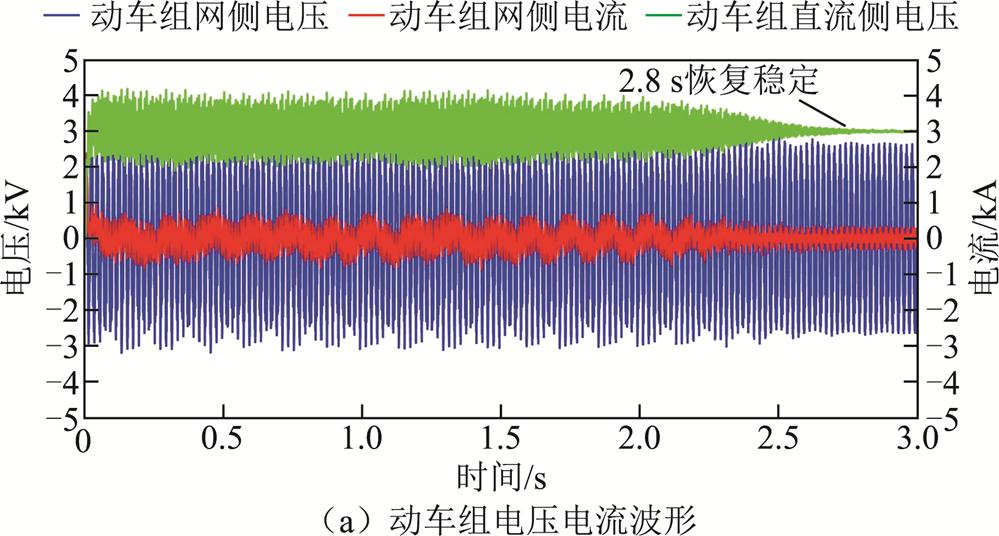
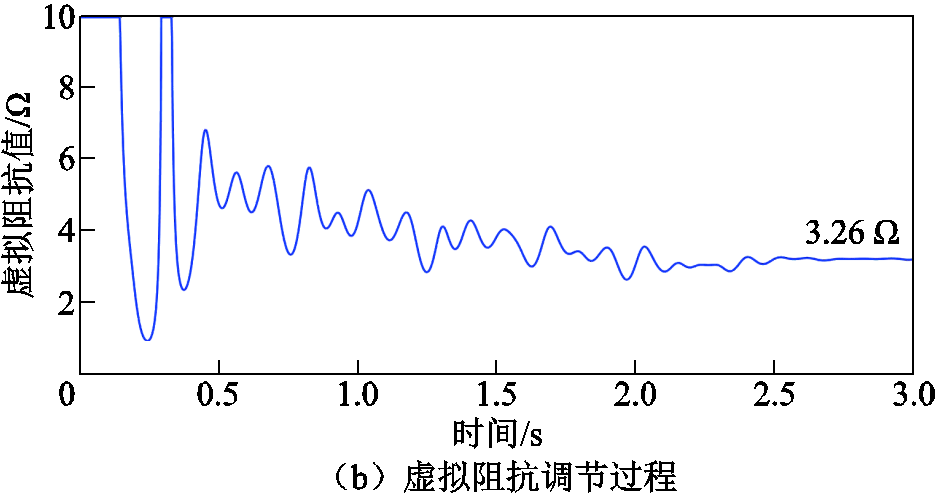
图19 接入6台动车组时仿真结果（单台采用自适应虚拟阻抗控制）
Fig.19 Simulation results when connecting six EMUs (Single unit adopts adaptive virtual impedance control)
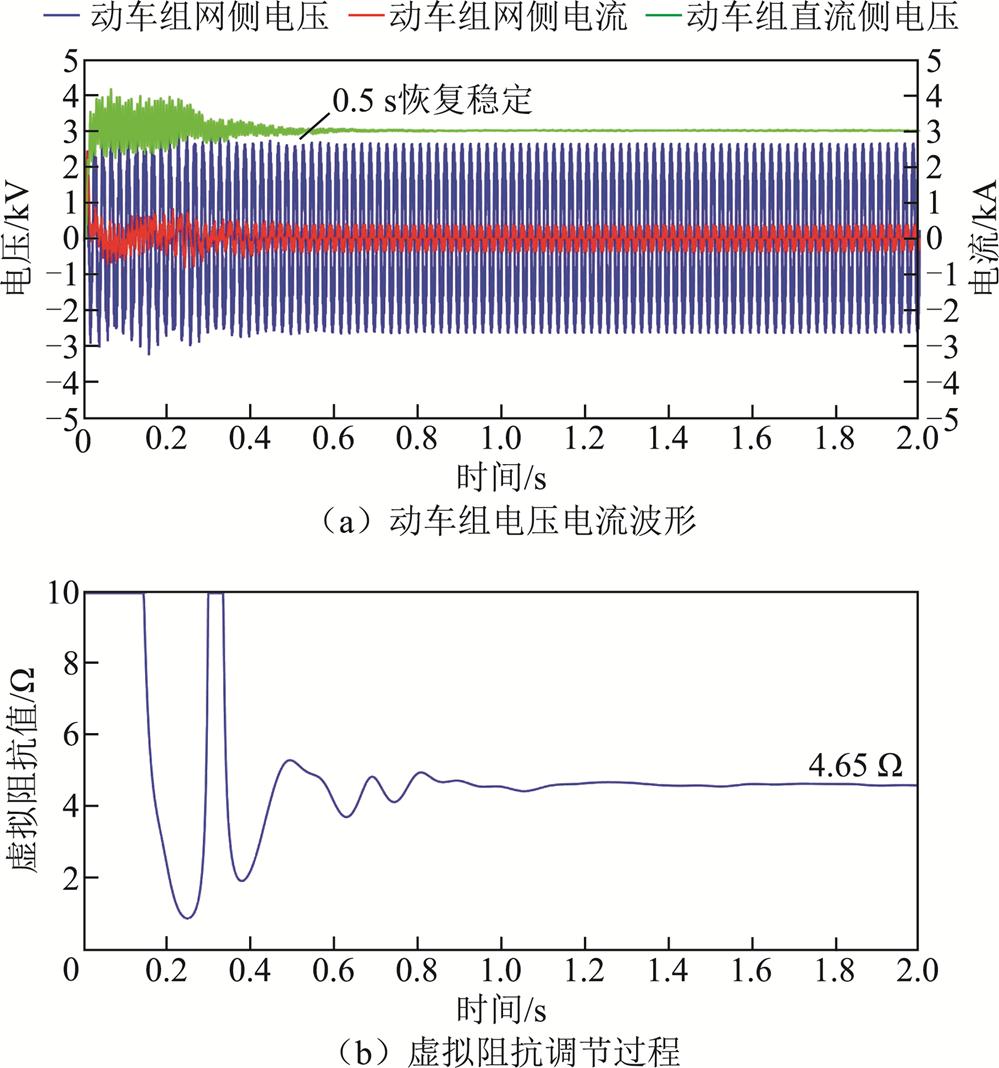
图20 接入6台动车组时仿真结果（全部采用自适应虚拟阻抗控制）
Fig.20 Simulation results when connecting 6 EMUs (All adopt adaptive virtual impedance control)
在6台采用自适应虚拟阻抗控制的动车组同时接入牵引网之后，每隔2 s继续增加接入牵引网动车组的数量，增加到11台动车组，仿真结果如图21所示。由图21可知，当动车组数量增多时，系统依然稳定运行，未发生低频振荡现象，说明在更多数量的动车组接入牵引网的情况下，基于自适应虚拟阻抗的控制方法仍然可以保证车网耦合系统的稳定运行。同时，随着动车组数量的增多，虚拟阻抗值从4.65 Ω减小到4.51 Ω，这证明了控制方法可以自动调节虚拟阻抗值的大小，虚拟阻抗值越小，抑制效果越好，仿真结果与前述理论分析一致。
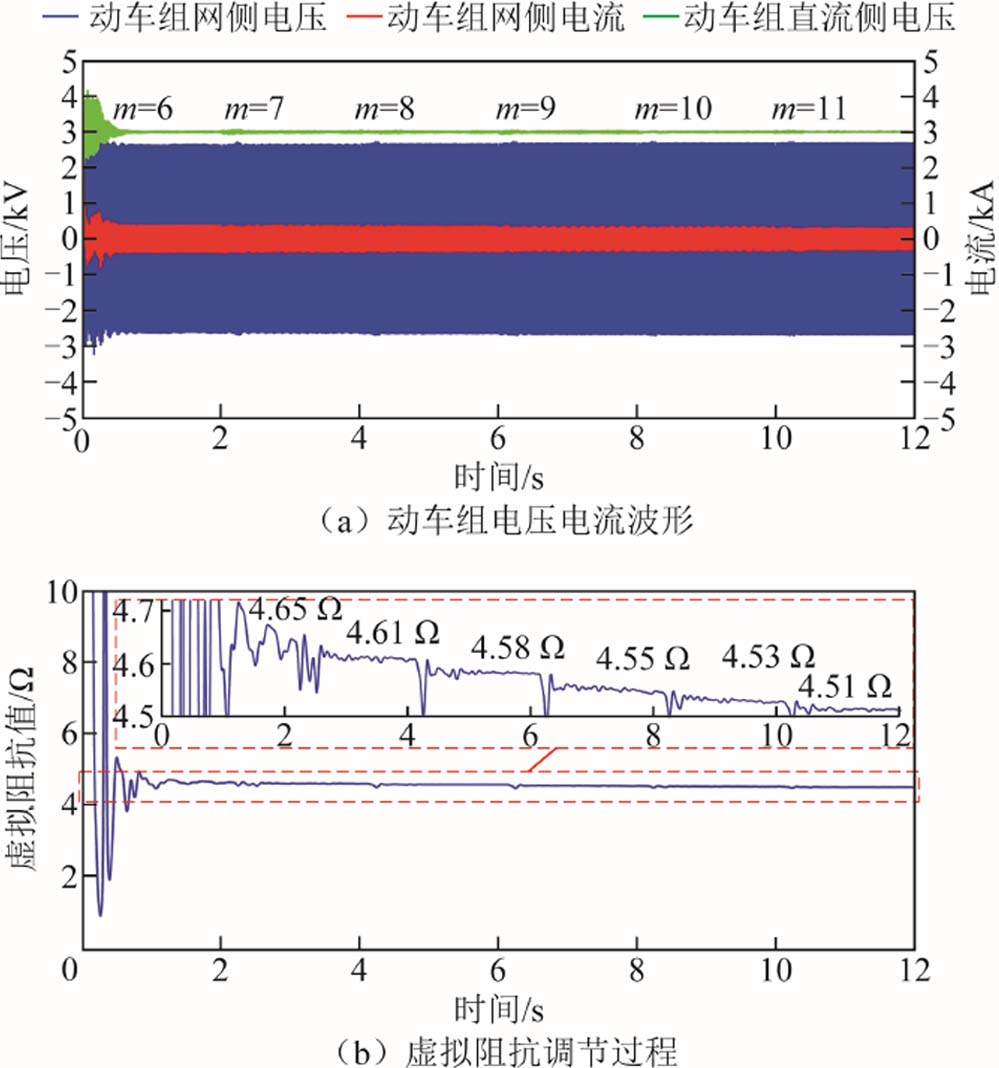
图21 增投动车组时仿真结果（全部采用自适应虚拟阻抗控制）
Fig.21 Simulation results when adding emus (All adopt adaptive virtual impedance control)
为了验证本文所提控制策略的有效性，搭建了车网耦合系统小功率实验平台如图22所示，实验系统参数见表1。
图22 小功率实验平台
Fig.22 Low-power experimental platform
表1 实验平台参数
Tab.1 Experimental platform parameters
参数数值 交流侧输入电压有效值/V20 交流侧输入电流有效值/A8 直流侧电压给定值/V40 车载变压器等效电阻/Ω2.8 车载变压器等效电感/mH1 直流侧支撑电容/mF3 直流侧等效负载/Ω20 交流侧等效可调电感/mH2
本实验用交流侧等效可调电感来模拟实际的牵引供电系统侧等效阻抗。交流侧等效可调电感为1 mH时模拟单车运行工况，增大交流侧等效可调电感到2 mH时模拟多车接入牵引网时车网耦合系统阻抗比增大的工况。
在单车运行工况下，采用传统控制策略的动车组电压电流波形如图23所示。此时交流侧电压稳定在20 V，交流侧电流为7.07 A，直流侧输出电压为40 V，系统输出稳定，电压、电流均无明显波动。
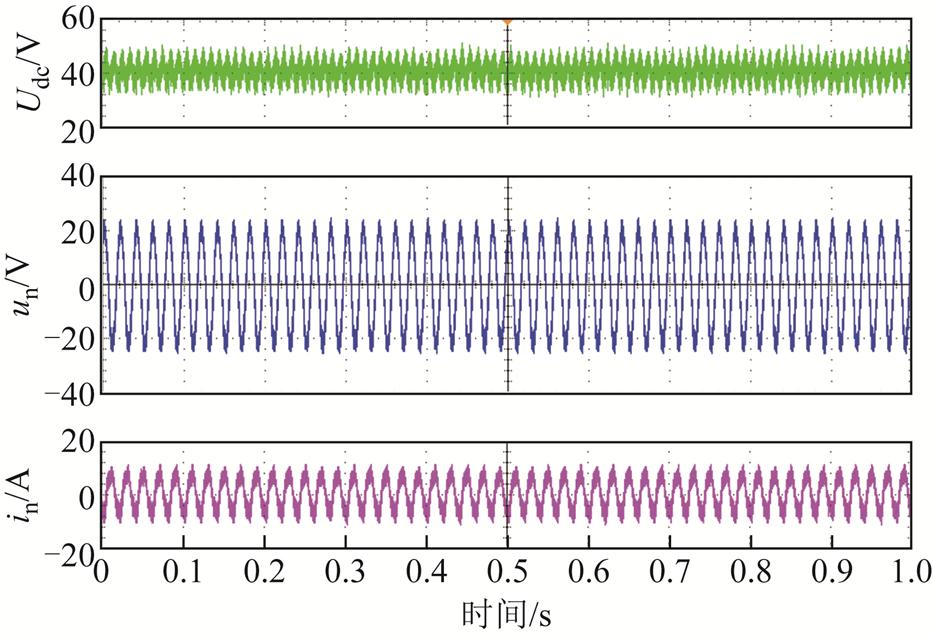
图23 单车运行工况下动车组电压电流波形（传统控制）
Fig.23 Voltage and current waveform diagram of EMU under single vehicle operation condition (Traditional PI control)
增大交流侧等效可调电感，将交流侧等效可调电感从1 mH增大到2 mH，在多车运行工况下，采用传统控制的动车组的交流侧电压电流、直流侧电压波形如图24所示。此时系统电压电流出现了7 Hz左右的明显振荡，此结果与理论分析基本相同。
将固定虚拟阻抗控制策略应用到动车组四象限变流器中，在单车工况下运行，取Rp=10 Ω，实验结果如图25所示。此时交流侧电压稳定在20 V，交流侧电流为6.71 A，直流侧输出电压为40 V。可以看出，系统电压电流均未发生低频振荡，说明引入虚拟阻抗的动车组在单车运行工况下能够正常工作。
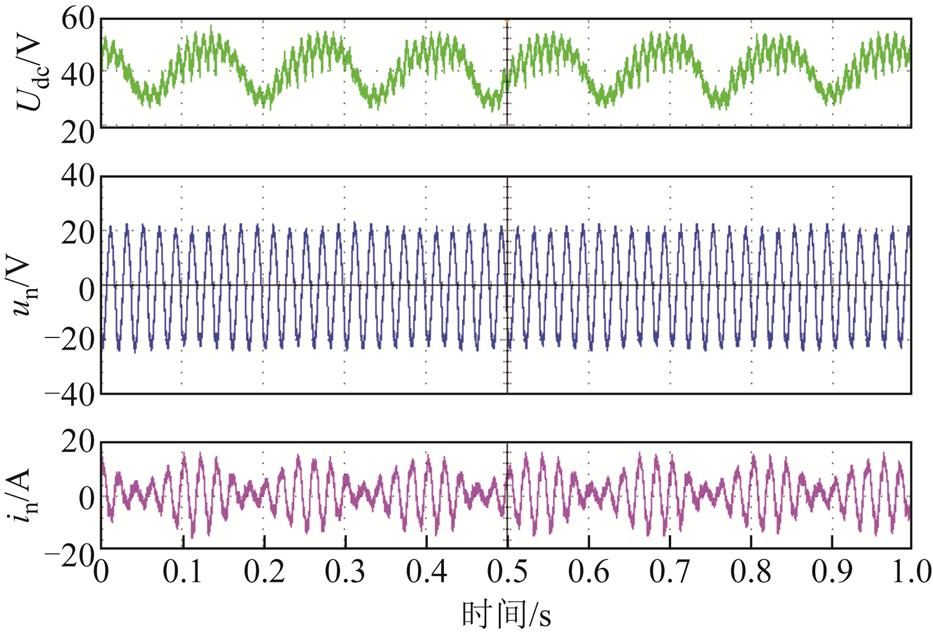
图24 多车运行工况下动车组电压电流波形（传统控制）
Fig.24 Voltage and current waveform diagram of EMU under multi-vehicle operation conditions (Traditional PI control)
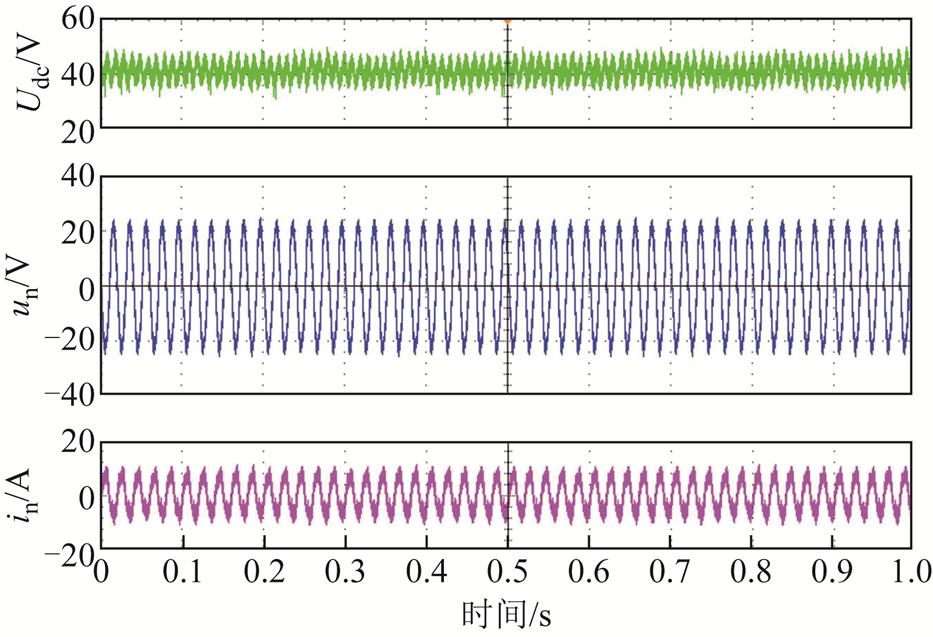
图25 单车运行工况下动车组波形（固定虚拟阻抗控制，Rp=10 Ω）
Fig.25 Waveforms of EMU under single vehicle operation condition (Fixed virtual impedance control, Rp=10 Ω)
增大交流侧等效可调电感到2 mH，系统电压电流波形如图26所示。系统电压电流均产生了7 Hz左右的明显低频振荡，这是由于虚拟阻抗值设置过大，控制策略抑制能力弱导致的。将虚拟阻抗Rp由10 Ω减小到2 Ω，此时系统快速恢复稳定，交流侧电压稳定在20 V，交流侧电流为7.70 A，直流侧输出电压为40 V，说明引入虚拟阻抗可以抑制系统低频振荡，且虚拟阻抗值越小，抑制能力越强，实验结果与理论分析吻合。
在多车工况下将应用传统控制策略的动车组四象限变流器切换到自适应虚拟阻抗控制策略，实验结果如图27所示。可以看出切换后系统电压电流迅速恢复稳定，此时交流侧电压稳定在20 V，交流侧电流为7.78 A，直流侧输出电压为40 V，说明在多车工况下基于自适应虚拟阻抗的瞬态直接电流控制策略可以抑制低频振荡，保证动车组稳定运行。
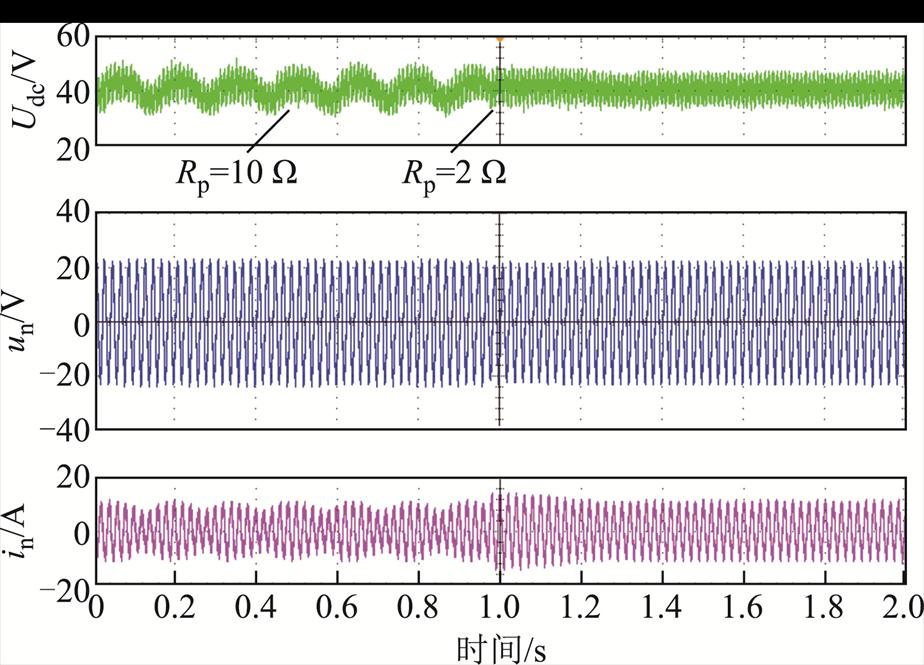
图26 多车运行工况下动车组波形（固定虚拟阻抗控制，Rp从10 Ω切换到2 Ω）
Fig.26 Waveforms of EMU under single vehicle operation condition (Fixed virtual impedance control, Rp switches from 10 Ω to 2 Ω)
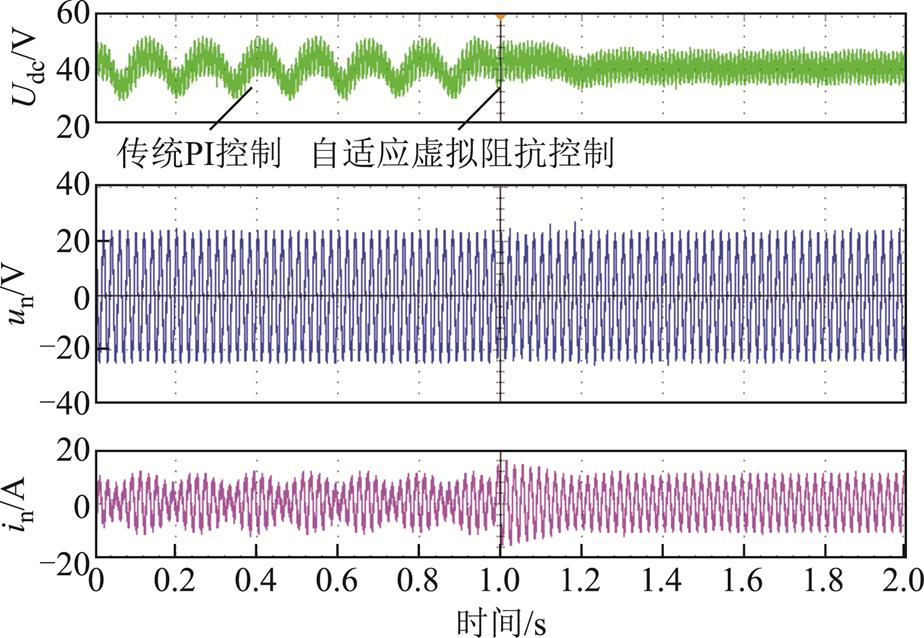
图27 多车运行工况下动车组波形（传统控制切换到自适应虚拟阻抗控制）
Fig.27 Waveforms of EMU under single vehicle operation condition (Traditional PI control is switched to adaptive virtual impedance control)
本文针对高速铁路车网耦合系统低频振荡问题，提出了一种基于虚拟阻抗的低频振荡抑制方法，并针对高速铁路复杂的工况变化，设计了一种虚拟阻抗的自适应控制方法。通过仿真和实验结果得出了下列结论：
1）在动车组四象限变流器控制策略中引入并联虚拟阻抗可以校正负载子系统的阻抗特性，提升系统稳定性，抑制低频振荡现象。当6台动车组同时接入牵引网时，全部动车组都采用基于虚拟阻抗的瞬态直接电流控制策略可以抑制低频振荡，当虚拟阻抗Rp取值为10 Ω、5 Ω、2 Ω和1 Ω时，系统电压电流分别在1.6 s、1 s、0.3 s和0.2 s进入稳态，虚拟阻抗值设置越小，抑制效果越好。
2）自适应虚拟阻抗控制方法可以通过动车组网侧电压振荡的激烈程度动态调整虚拟阻抗值，提升控制策略的适应能力，保证车网耦合系统在不同工况下的稳定运行。当6台动车组同时接入牵引网时，单台动车组应用自适应虚拟阻抗控制策略可以抑制低频振荡，系统电压电流在2.8 s进入稳态，抑制能力较弱；当全部动车组都采用自适应虚拟阻抗控制策略时，系统在0.5 s左右进入稳态，动车组直流侧电压的调节时间为0.46 s，超调量为37.71 %，稳定后的电压波动为±58 V，可以较好地抑制低频振荡现象。
参考文献
[1] 孟昭斐, 胡海涛, 周毅. 电力机车运行工况对车网系统低频振荡的影响规律研究[J]. 电气工程学报, 2022, 17(2): 131-141.
Meng Zhaofei, Hu Haitao, Zhou Yi. Study on the influence law of electric vehicle on low frequency oscillation of vehicle-network system under operating condition[J]. Journal of Electrical Engineering, 2022, 17(2): 131-141.
[2] Hu Haitao, Tao Haidong, Blaabjerg F, et al. Train–network interactions and stability evaluation in high-speed railways–part Ⅰ: phenomena and modeling[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 4627-4642.
[3] Hu Haitao, Tao Haidong, Wang Xiongfei, et al. Train-network interactions and stability evaluation in high-speed railways: part Ⅱ: influential factors and verifications[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 4643-4659.
[4] Hu Haitao, Zhou Yi, Li Xin, et al. Low-frequency oscillation in electric railway depot: a comprehensive review[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 295-314.
[5] 付莉, 张桂南, 高仕斌. 高速铁路车网耦合系统网压振荡模态分析与对策[J]. 电力系统保护与控制, 2016, 44(1): 24-32.
Fu Li, Zhang Guinan, Gao Shibin. Modal analysis and countermeasures on voltage low frequency oscillation of high-speed railway traction network and EMU coupling system[J]. Power System Protection and Control, 2016, 44(1): 24-32.
[6] 周毅, 胡海涛, 雷科, 等. 电气化铁路低频等幅振荡机理分析[J]. 中国电机工程学报, 2021, 41(9): 3024-3037.
Zhou Yi, Hu Haitao, Lei Ke, et al. Mechanism analysis of the sustained low-frequency oscillation in the electric railway system[J]. Proceedings of the CSEE, 2021, 41(9): 3024-3037.
[7] 孔睿, 吕晓琴, 王晓茹, 等. 列车混运的车网系统低频振荡建模与分析[J]. 中国电机工程学报, 2023, 43(10): 3768-3781.
Kong Rui, Lü Xiaoqin, Wang Xiaoru, et al. Modeling and analysis of low frequency oscillation in train-network system under mixed operation of trains[J]. Proceedings of the CSEE, 2023, 43(10): 3768-3781.
[8] 胡颖新, 宁志毫, 兰征, 等. 基于滑模控制的牵引网低频振荡抑制方法[J]. 电气工程学报, 2022, 17(1): 129-136.
Hu Yingxin, Ning Zhihao, Lan Zheng, et al. Low frequency oscillation suppression method of traction network based on sliding mode control[J]. Journal of Electrical Engineering, 2022, 17(1): 129-136.
[9] 唐圣德, 胡海涛, 肖冬华, 等. 基于阻抗测量信息的电气化铁路“多车共网”系统稳定性分析[J]. 电工技术学报, 2024, 39(19): 6039-6053.
Tang Shengde, Hu Haitao, Xiao Donghua, et al. Stability analysis of electrified railway multiple train-network system based on impedance measurement information[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6039-6053.
[10] Liu Zhigang, Hu Xinxuan, Liao Yicheng. Vehicle-grid system stability analysis based on norm criterion and suppression of low-frequency oscillation with MMC-STATCOM[J]. IEEE Transactions on Transportation Electrification, 2018, 4(3): 757-766.
[11] Wu Siqi, Liu Zhigang. Low-frequency stability analysis of vehicle-grid system with active power filter based on dq-frame impedance[J]. IEEE Transactions on Power Electronics, 2021, 36(8): 9027-9040.
[12] 张桂南, 刘志刚, 向川, 等. 高铁车网耦合系统电压低频振荡现象机理研究[J]. 电网技术, 2015, 39(7): 1956-1962.
Zhang Guinan, Liu Zhigang, Xiang Chuan, et al. Mechanism on voltage low frequency oscillation of high-speed railway traction network and EMU coupling system[J]. Power System Technology, 2015, 39(7): 1956-1962.
[13] 姚书龙, 刘志刚, 张桂南, 等. 基于自抗扰控制的牵引网网压低频振荡抑制方法[J]. 电网技术, 2016, 40(1): 207-213.
Yao Shulong, Liu Zhigang, Zhang Guinan, et al. A novel approach based on ADRC to traction network voltage low frequency oscillation suppression research [J]. Power System Technology, 2016, 40(1): 207-213.
[14] Zhang Guinan, Liu Zhigang, Yao Shulong, et al. Suppression of low-frequency oscillation in traction network of high-speed railway based on auto-disturbance rejection control[J]. IEEE Transactions on Transportation Electrification, 2016, 2(2): 244-255.
[15] 许加柱, 程慧婕, 黄文, 等. 自适应自抗扰比例积分控制下的高速铁路车网耦合系统低频振荡抑制方法[J]. 中国电机工程学报, 2018, 38(14): 4035-4045, 4309.
Xu Jiazhu, Cheng Huijie, Huang Wen, et al. A novel approach based on self-adaptive auto disturbance rejection proportional integral controller to suppress low frequency oscillation of high speed railway electric multiple units-traction network coupling system[J]. Proceedings of the CSEE, 2018, 38(14): 4035-4045, 4309.
[16] 喻文倩, 刘志刚, 张友刚, 等. 一种改进的高铁牵引变流器反馈线性化控制策略[J]. 电工技术学报, 2023, 38(8): 2136-2147.
Yu Wenqian, Liu Zhigang, Zhang Yougang, et al. An improved feedback linearization control strategy for high-speed railway traction converters[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2136-2147.
[17] 王颖杰, 邢涛, 焦岚轶, 等. 基于模糊PI控制的牵引网低频振荡抑制方法[J]. 铁道学报, 2021, 43(3): 62-69.
Wang Yingjie, Xing Tao, Jiao Lanyi, et al. Low-frequency oscillation suppression method for traction network based on fuzzy PI control[J]. Journal of the China Railway Society, 2021, 43(3): 62-69.
[18] 刘沁怡, 黄伟煌, 郭铸, 等. 基于自适应虚拟阻抗的多并联构网型变流器无功功率分配策略[J]. 电力系统自动化, 2024, 48(15): 122-130.
Liu Qinyi, Huang Weihuang, Guo Zhu, et al. Reactive power sharing strategy for multiple parallel grid-forming converters based on adaptive virtual impedance[J]. Automation of Electric Power Systems, 2024, 48(15): 122-130.
[19] 谢飞, 许建平, 郭夏, 等. 基于虚拟阻抗的三相Buck整流器输入不平衡控制策略[J]. 电工技术学报, 2024, 39(14): 4456-4466.
Xie Fei, Xu Jianping, Guo Xia, et al. A control strategy based on virtual impedance for three-phase buck rectifier under unbalanced phase-voltages[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4456-4466.
[20] 高磊, 吕敬, 马骏超, 等. 基于电路等效的并网逆变器失稳分析与稳定控制[J]. 电工技术学报, 2024, 39(8): 2325-2341.
Gao Lei, Lü Jing, Ma Junchao, et al. Instability analysis and stability control of grid-connected inverter based on impedance circuit equivalent[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2325-2341.
[21] Guan Yuanpeng, Xie Yunxiang, Wang Yu, et al. An active damping strategy for input impedance of bidirectional dual active bridge DC-DC converter: modeling, shaping, design, and experiment[J]. IEEE Transactions on Industrial Electronics, 2021, 68(2): 1263-1274.
[22] He Jinwei, Li Yun wei. Generalized closed-loop control schemes with embedded virtual impedances for voltage source converters with LC or LCL filters[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1850-1861.
[23] Bao Chenlei, Ruan Xinbo, Wang Xuehua, et al. Step-by-step controller design for LCL-type grid-connected inverter with capacitor–current-feedback active-damping[J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1239-1253.
[24] Pan Donghua, Ruan Xinbo, Bao Chenlei, et al. Capacitor-current-feedback active damping with reduced computation delay for improving robustness of LCL-type grid-connected inverter[J]. IEEE Tran-sactions on Power Electronics, 2014, 29(7): 3414-3427.
[25] He Yuying, Wang Xuehua, Ruan Xinbo, et al. Capacitor-current proportional-integral positive feedback active damping for LCL-type grid-connected inverter to achieve high robustness against grid impedance variation[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 12423-12436.
[26] Shuai Zhikang, Cheng Huijie, Xu Jiazhu, et al. A Notch filter-based active damping control method for low-frequency oscillation suppression in train–network interaction systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(4): 2417-2427.
[27] Brenna M, Foiadelli F, Zaninelli D. New stability analysis for tuning PI controller of power converters in railway application[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 533-543.
[28] 王晴, 刘增, 韩鹏程, 等. 基于变流器输出阻抗的直流微电网下垂并联系统振荡机理与稳定边界分析[J]. 电工技术学报, 2023, 38(8): 2148-2161.
Wang Qing, Liu Zeng, Han Pengcheng, et al. Analysis of oscillation mechanism and stability boundary of droop-controlled parallel converters based on output impedances of individual converters in DC microgrids[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2148-2161.
[29] 冯晓云. 电力牵引交流传动及其控制系统[M]. 北京: 高等教育出版社, 2009.
Low-Frequency Oscillation Suppression of EMUs-Traction Network Coupling System Based on Virtual Impedance
Abstract When multiple EMUs are simultaneously in a light-load starting condition within the traction network, it can lead to low-frequency oscillations in the traction network voltage. In severe cases, this may trigger traction locking, which poses a risk to the operational safety of high-speed trains. To address the issue of low-frequency oscillation, this study proposes a method based on virtual impedance for its suppression.
First, the impedance model of the EMUs-traction network coupling system is derived, and its stability is analyzed using the impedance ratio stability criterion and the Bode diagram. Second, based on the stability criterion, virtual impedance is incorporated into the EMU control strategy to correct the impedance characteristics of the load subsystem, thereby proposing a low-frequency oscillation suppression method. Third, an adaptive control method for virtual impedance is designed to handle the complex and dynamic working conditions, enabling the system to adjust the virtual impedance parameters and enhance the effectiveness of the suppression method. Finally, the proposed control strategy is compared with the traditional approach through a low-power experimental platform, validating the effectiveness of the suppression method.
The results of the system stability analysis indicate that the logarithmic amplitude-frequency characteristic curve of the system impedance ratio is significantly lower than 0 dB when only one unit (m=1) is connected to the traction network, and the absolute value of the system impedance ratio |Tsn(s)| is much less than 1, suggesting system stability. As the value of m increases, the amplitude-frequency characteristic curve approaches 0 dB, resulting in a decline in system stability. When m=6, the amplitude-frequency characteristic curve crosses 0 dB at 7.032 Hz, and the phase angle at the crossover frequency (fc) is 182°. The absolute value of the phase angle exceeds 180°, and the system impedance ratio |Tsn(s)| does not meet the condition of being significantly less than 1, indicating an unstable state. Simulation results with the virtual impedance control strategy indicate that when six EMUs are connected to the traction network at the same time, when the virtual impedance Rp values are 10 Ω, 5 Ω, 2 Ω and 1 Ω respectively, the system voltage and current reach a steady state at 1.6 s, 1 s, 0.3 s, and 0.2 s, respectively. The suppression effect improves as the virtual impedance decreases. The simulation results with the adaptive virtual impedance control strategy show that when six EMUs are connected to the traction network, the system reaches a steady state in approximately 0.5 s. The voltage regulation time for the DC side of the EMUs is 0.46 s, with an overshoot of 37.71% and a post-stabilization voltage fluctuation of 58 V. Subsequently, one EMU with adaptive virtual impedance control is added every 2 seconds, resulting in a total of 11 EMUs. The system remains stable, and the virtual impedance value is reduced to 4.61. The comparative experimental results indicate that, after transitioning from the traditional control strategy to the adaptive virtual impedance control strategy, the system can rapidly recover from a low-frequency oscillation at approximately 7 Hz. Furthermore, the AC-side voltage stabilizes at 20 V, while the DC-side voltage remains stable at 40 V.
Based on the analysis, the following conclusions can be drawn: (1) A higher impedance ratio between the two sides of the EMUs-traction network coupling system results in decreased system stability. When the impedance ratio does not meet the stability criterion, system instability is induced, leading to low-frequency oscillations. (2) The incorporation of parallel virtual impedance in the control strategy for the EMU's four-quadrant converter can correct the impedance characteristics of the load subsystem, enhance system stability, and suppress low-frequency oscillation. (3) The adaptive virtual impedance control method can autonomously adjust the virtual impedance value based on the intensity of voltage oscillations on the network side of the EMU, thereby suppressing low-frequency oscillations under varying load conditions, improving the adaptability of the control strategy, and ensuring the stable operation of the EMUs-traction network coupling system across different operating conditions.
Keywords：High-speed railway, EMUs-traction network coupling system, low-frequency oscillation, virtual impedance, adaptive control
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.240745
收稿日期 2024-05-08
改稿日期 2024-09-27
逯 华 男，1998年生，硕士研究生，研究方向为高速铁路车网耦合系统建模及低频振荡抑制。
E-mail：21121455@bjtu.edu.cn
王喜莲 女，1974年生，教授，博士生导师，研究方向为电机及其控制。
E-mail：xlwang1@bjtu.edu.cn（通信作者）
（编辑 郭丽军）