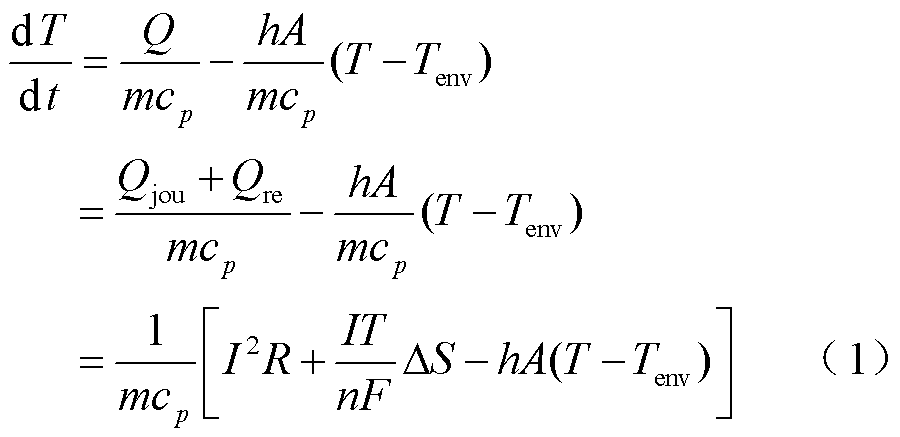
摘要 磷酸铁锂电池的开路电压与荷电状态(SOC)曲线平坦导致仅采用电信号难以实现对SOC的准确估计。鉴于此,该文从不同角度对实验获取的电-热-声多源数据进行全面特征提取,综合考虑不同特征选择方法的优势,提出了一种融合斯皮尔曼相关系数、互信息、分类提升树、最小绝对收缩和选择算法的特征选择方法,实现对电-热-声特征的联合选择,进而提高SOC估计精度。研究结果表明,相较于单一数据源特征,使用电-热-声多源关键特征构建的模型具有较高的SOC估计精度,在动态压力测试工况与新欧洲驾驶循环工况下,SOC估计的平均绝对误差分别为0.91%和0.98%,方均根误差分别为1.03%和1.13%,验证了该方法的有效性和准确性。
关键词:磷酸铁锂电池 荷电状态 多源数据 特征提取特征选择
磷酸铁锂(LiFePO4, LFP)电池因具有高安全性、优良的高温性能、大能量密度和长寿命等优点,广泛应用于乘用车、电动船舶、新能源储能和应急照明等领域[1]。电池的荷电状态(State of Charge, SOC)是电池管理系统的重要监测指标,但磷酸铁锂电池的开路电压(Open Circuit Voltage, OCV)-SOC曲线平坦,尤其在SOC为0.2~0.8的区间,并且开路电压滞回明显,导致SOC估计困难[2]。因此,研究快速准确地估计磷酸铁锂电池平台期SOC的方法至关重要。
传统SOC估计方法主要依赖电学和热学参数。近年来,一些学者开始探索基于多源数据的SOC估计方法,其中电、热、声数据的多源融合被视为一种有潜力的方法。基于电学参数的表征方法多以等效电路模型为基础,并结合数据驱动的方法实现SOC估计[3-6],短期估计误差小,但是在很大程度上依赖模型的精度和OCV-SOC曲线的准确性。而LFP电池的OCV-SOC曲线较为平坦,平台期电压误差反馈极小,易导致后验修正过程失真;同时,高SOC段和低SOC段的陡坡期电压误差反馈较大,易导致过度修正,难以得到快速准确的结果。基于热学参数的估计方法可以监测电池的温度,从而更好地理解电池的工作状态,提高SOC估计的准确性,然而,热学参数往往不能与SOC构成单一映射关系,需要同电学参数联合使用[7-9]。
近年来,超声波技术因能检测电池内部材料物理性质变化引起的声学性能差异,在电池SOC估计中受到关注。A. G. Hsieh等应用超声技术对锂离子电池进行实时监测,发现SOC与超声信号之间存在关联,并认为这是电化学循环过程中电池内材料物理性质变化的结果[10],为超声技术估算电池SOC提供了理论基础。L. Gold等进一步研究发现,超声慢波信号的传播时间(Time of Flight, TOF)和声幅值(Signal Amplitude, SA)与SOC呈近似线性的关系[11]。G. Davies等结合TOF、SA和电池电压数据,在单一实验条件下采用支持向量机构建了误差约为1%的SOC估算模型,展示了多参数融合提高估算精度的潜力[12]。P. Ladpli等结合超声波形分解后的原子参数和电压数据建立统计估算模型,SOC估算精度与仅使用单一电压特征相比提高了2倍[13]。李晓宇等通过分析超声信号特征,构建神经网络与梯度提升树的集成模型,降低SOC估算误差至2.36%以下[14]。刘素贞、蔡志端等通过提取超声特征,结合机器学习算法,减小SOC估算误差[15-16]。然而,现有研究多聚焦于超声时域特征,忽视了与其他类型参数的全面综合分析,鉴于超声信号的非线性和非平稳特性[17],仅依赖时域特征难以充分反映信号的多尺度变化。其次,超声波信号对于温度变化较为敏感,且锂离子电池的活性材料对超声波信号存在一定的散射效应和边缘效应,影响估计准确性,应考虑结合其他类型参数融合分析[18]。
综上所述,针对LFP电池OCV-SOC曲线平坦导致电信号对SOC变化不敏感和传统单一数据源的SOC估计方法存在局限性的问题,本文提出了一种综合电-热-声多源数据的估计方法。对实验采集的电-热-声数据从不同角度进行了全面的特征提取;为了更准确地选择关键特征,提出了一种融合斯皮尔曼(Spearman)相关系数、互信息、分类提升树(Category Boosting, CatBoost)、最小绝对收缩和选择算法(Least Absolute Shrinkage and Selection Operator, LASSO)的特征选择方法,进而提高SOC估计精度。为了验证所提出方法的性能,与不同特征选择方法进行了比较,并对比了使用单一数据源特征与多源数据特征的SOC估计效果,最后在不同倍率和不同工况下验证了所提方法的可行性。
考虑到电、热、声数据并非孤立存在,而是存在一定的耦合关系,使用电-热-声多源数据融合估计锂离子电池的SOC,充分利用各种数据之间的互补性,综合反映电池在复杂工作环境下的实际状态。
电学特性直接影响电池产生的热量。锂离子电池的热源包括焦耳热、可逆反应热、副反应热和混合热。焦耳热和可逆反应热作为一个循环中需要考虑的主要热源,其温度变化率表达式为[19]
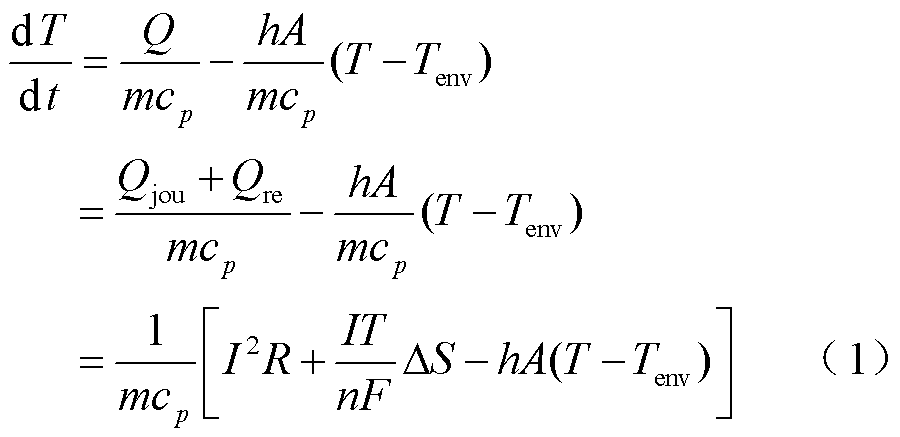
式中,Q为产热率;Qjou为焦耳热;Qre为可逆反应热;DS为熵变;m为锂离子电池质量;cp为电池比定压热容;h为表面传热系数;A为电池表面积;I为电流;R为充电或放电电阻;n为交换电子数;F为法拉第常数;T为电池温度;Tenv为环境温度。
充电时,可逆热整体呈现先增大后减小的变化趋势,而随着SOC增大,可逆热表现为吸热过程;焦耳热先减小后增大,但整体变化较为平缓,且占比大于可逆热。在二者的共同作用下,总产热曲线呈“峰状”形式,峰值点对应为恒流充电截止时间,温度随时间呈斜抛曲线式上升。放电时,电池释放能量,这是一个放热过程,同时还存在焦耳热的影响,因此,放电时电池温度仍为升高趋势[20]。反过来,温度升高会导致电池中的电解液膨胀,离子浓度降低,进而内阻增加,影响电压变化的速率[21]。
另一方面,电、热信号的变化也会影响电池内部材料的声学属性,如声速和声衰减。声阻抗是材料的关键声学属性,对声波在不同介质中的传播和交互具有重要影响。声阻抗的表达式为
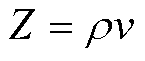 (2)
(2)
式中,Z为材料的声阻抗;ρ为材料的密度;v为超声波在介质中的传播速度。
锂离子电池由正极、负极、隔膜、电解质和集流体等几十微米厚的薄膜材料组成。根据弹性波理论,这些介质的材料杨氏模量和密度不同,将决定超声波在电池内部的传播速度[22]。介质中超声波的波速为
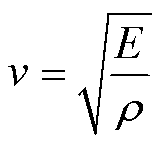 (3)
(3)
式中,E为杨氏模量。
在充放电过程中,锂离子在电极间嵌入嵌出会使得电池SOC改变,同时,电池内部材料的微观结构将发生变化,进而影响电池材料的杨氏模量、密度等物理性质,从而改变电池内部声阻抗和声速。声阻抗变化会影响声波在介质中的衰减程度,导致声波在传播过程中的能量耗散改变,从而影响接收到的声波幅值[23]。然而,由于锂离子电池属于多层多相介质,声阻抗和衰减的建模计算仍存在困难,目前尚未形成完善的数学建模与求解方法[24]。电池过热也可能导致内部材料如电解质和隔膜的物理性质发生改变,反映在超声波信号的传播特性上。因此,可将LFP电池的电化学特性、热学特性与声学特性相结合,全面反映电池状态,提高SOC估计的准确性和可靠性。
实验选取四块具有相同老化状态且高一致性的软包LFP电池,分别标记为A1、A2、A3、A4。电池采用层叠式结构,涉及多层正极、隔膜及负极的叠绕,正极主要为LFP,负极主要为石墨。电池标称电压为3.2 V,充、放电过程截止电压分别为3.8 V和2.3 V,额定容量为10 A·h。
图1为LFP电池实验平台示意图。电压、温度、超声信号的采样间隔均设置为1 min,超声每次采样的频率为250 MHz。热电偶被置于电池靠近极耳位置以监测温度变化。电池的充放电循环测试由上位机控制执行,同时连接蓝电CT6002A型电池测试系统和温度测量仪实时记录电压、电流和温度数据。采用CTS-8077PR型超声波脉冲发生接收仪,设置为“双发射”模式,发射脉宽为125 ns,电压为200 V,增益为+15 dB,配合4 MHz的4P20型压电超声直探头,对电池中心两侧施加压电加载。选用透射波模式进行超声纵波检测,当频率达到MHz时,可以检测到电极材料尺度的微小变化,分辨率为0.1 ms。Tektronix MSO44混合信号示波器实时显示超声信号,并与上位机相连,实时保存超声数据。使用高真空硅脂作为耦合剂,确保超声波的有效传输。电池夹具用于固定探头位置,保持预紧力均等。考虑环境和电池温度的影响,实验在RYHS100/2-40型复层式恒温恒湿试验箱内进行,保持温度恒定为25℃。
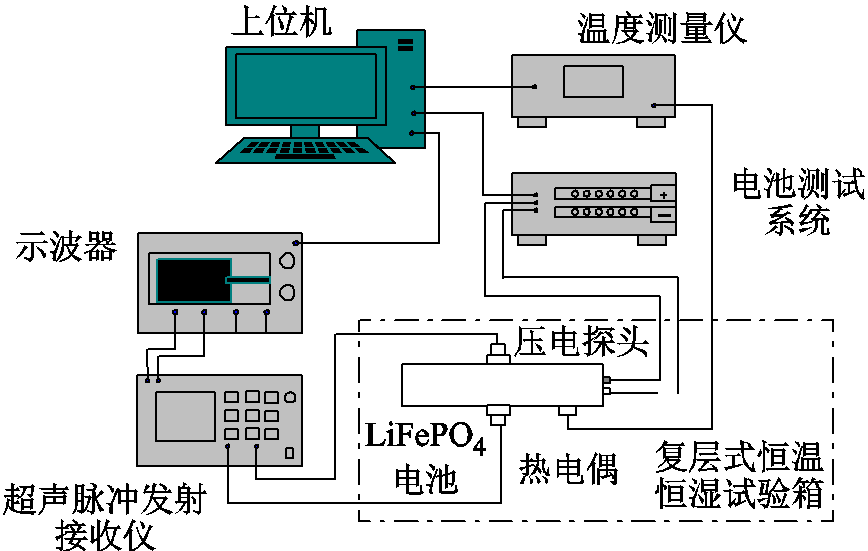
图1 LFP电池实验平台示意图
Fig.1 Schematic diagram of experimental platform for LFP battery
在实际应用中,电池的工作倍率会导致电池内部温度、电化学反应速率和应力状态的变化,影响超声透射波的传播特性。因此,对编号为A1~A4的电池分别采用0.4C、0.6C、0.8C和1.0C进行恒流充放电测试,实验所得数据具有较高的可重复性。采集的超声信号使用小波降噪方法进行预处理,经测试对比,当采用多贝西小波基,分解层数为5,并采用软阈值处理超声信号时,信号降噪效果最佳。
考虑到单一数据源的SOC估计方法存在局限性,为了准确估计锂离子电池的SOC,对电-热-声多源数据进行综合的多特征提取极为关键。本节将从多角度对采集的电-热-声信号进行全面的特征提取。本文特征均为0.8C电流倍率充放电和25℃环境下提取的特征。
为了对电-热数据进行全面的特征提取,从时间尺度的角度出发,提取了6个电信号特征和3个热信号特征,主要分为瞬时特征、短期变化特征两类。原始电信号特征电压v和电流i为瞬时特征,导数类特征dv、di、d2v、d2i为短期变化特征。与电信号特征类似,提取的热信号特征为瞬时特征温度T、短期变化特征dT、d2T。对于短期变化特征,时间尺度为1 min。考虑到电压、温度的时间积分会产生时间累计误差,因此,未提取长期累积特征。
电热信号特征如图2所示,展示了LFP电池充放电时电压v、温度T、dv和dT随SOC的变化。电压随SOC的增加而增加,但在0.2~0.8的SOC区间,电压曲线较为平坦,dv几乎为零,表明该范围内电信号对SOC变化不敏感,反映了LFP电池的OCV-SOC曲线具有平台期这一特性。由充放电电压曲线也可以看出LFP电池存在滞回特性,影响SOC估计。对于热信号变化,在充放电过程中,由于内阻和化学反应速率的影响,温度均呈轻微的升高趋势,dT较为稳定。将温度数据与其他数据结合,可以提高SOC估计的准确性和可靠性。
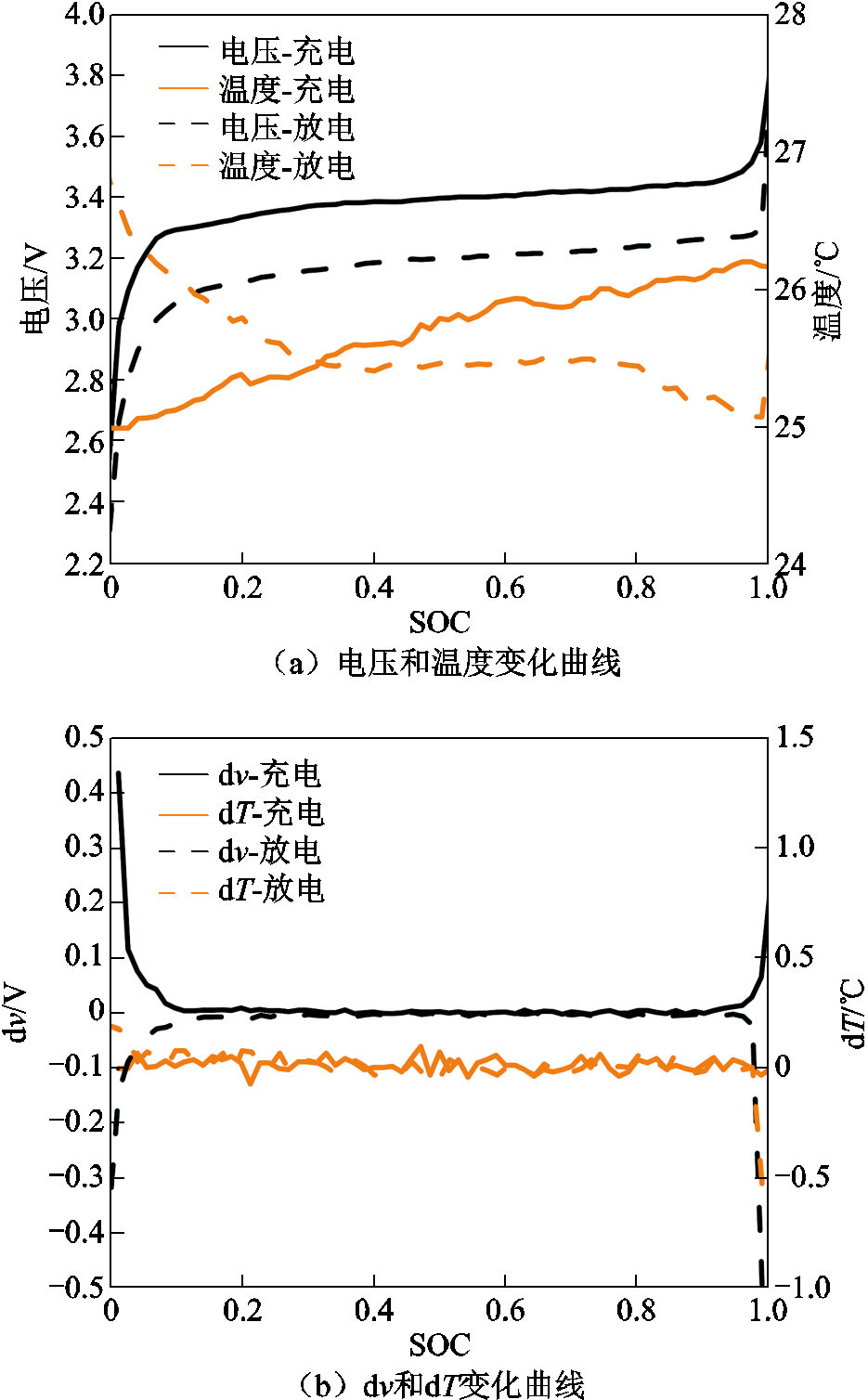
图2 电热信号特征
Fig.2 Electrical-Thermal signal characteritics
受电池温度、电化学反应速率和应力状态等影响,超声透射波信号会发生变化,直接关联超声信号与电池SOC具有挑战性。针对目前超声特征多聚焦于时域而难以充分反映信号的多尺度变化的问题,本文对主要的超声时域特征、频域特征及时频域变换特征的提取进行阐述。
3.2.1 超声时域特征提取
在时域分析中,主要通过降噪后的超声信号、绝对值信号、包络线提取特征,分别揭示信号基本属性、强度信息及振幅变化。
图3a为降噪超声信号时域图。在电池SOC变化时,超声信号波形也会发生变化,主要原因是电池充放电过程中,锂离子在正负极间转移导致电池内部材料性能改变,影响材料的阻尼和衰减特性,使得超声波在电池内部传播时的速度与衰减程度不同。基于波形和统计方法,从降噪后的超声信号中提取22种时域特征,假设超声信号第i个采样点的信号幅值为xi(i=1, 2, …, N),对应的时间为ti,采样数为N,部分超声时域特征见表1。此外,应用分段线性拟合得到截距、斜率和标准差,每段包括50个采样点,反映信号的线性关系和离散程度。
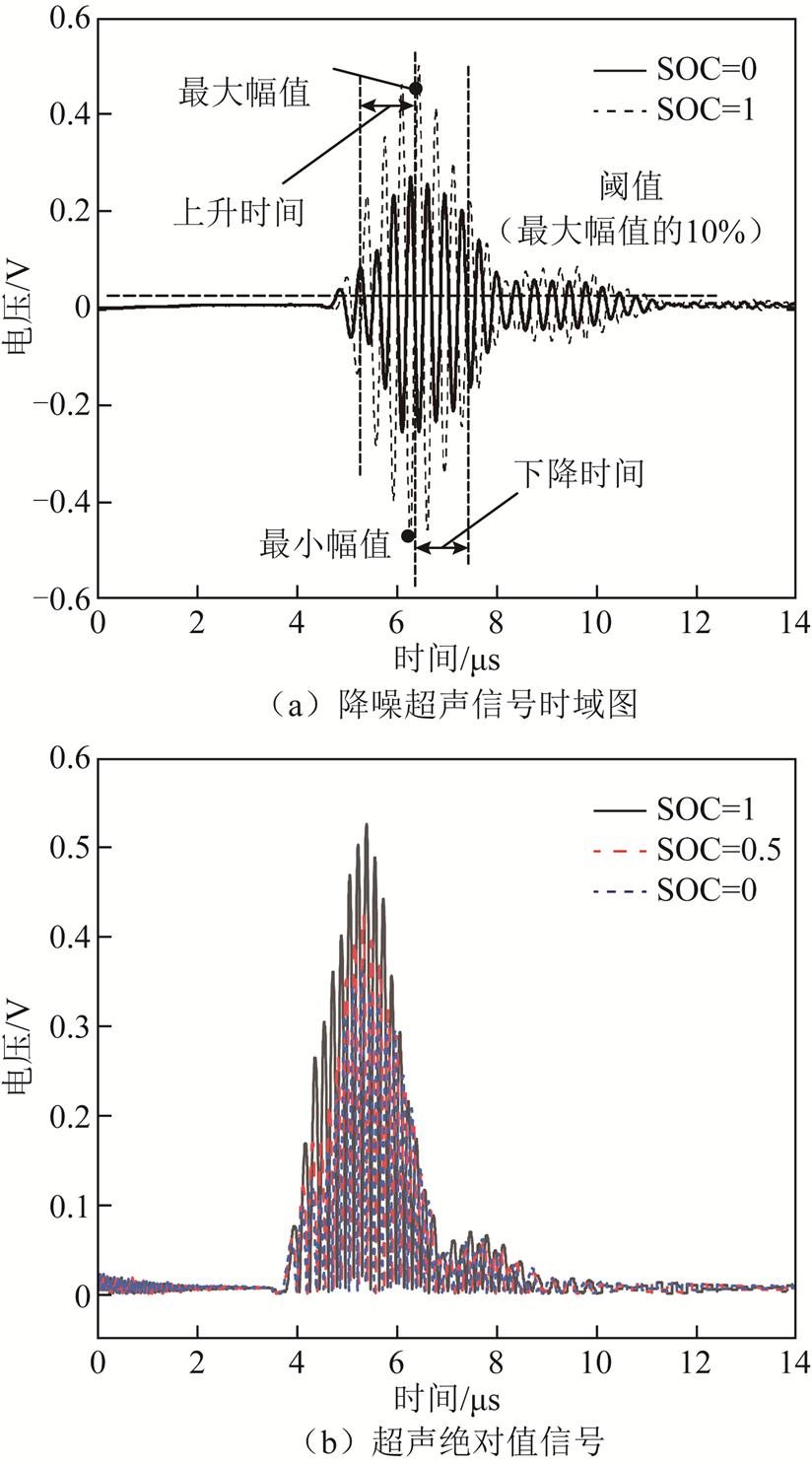
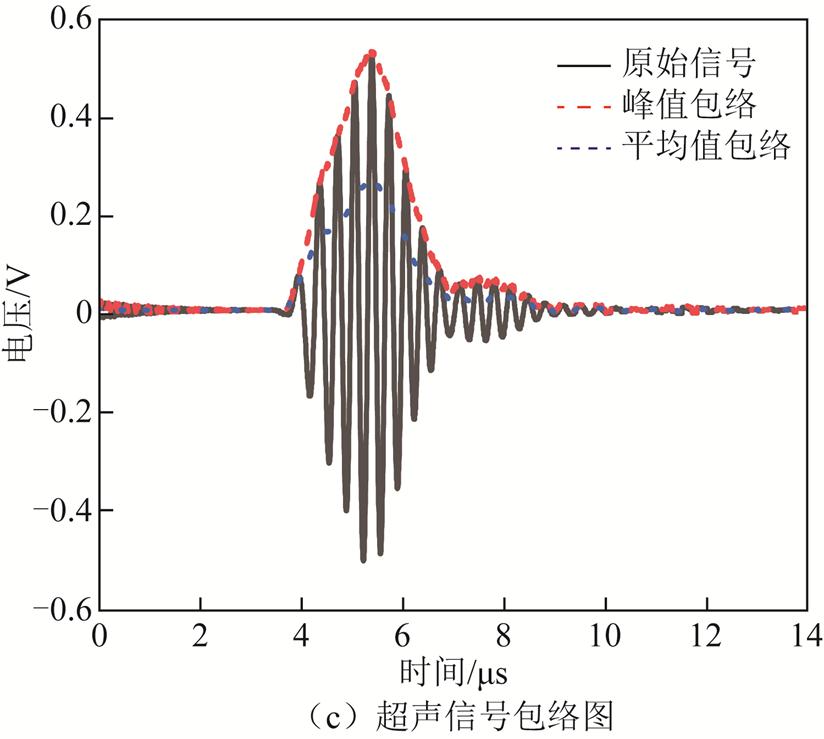
图3 超声信号时域特征
Fig.3 Time-domain characterization of ultrasound signals
表1 超声时域特征
Tab.1 Ultrasonic time domain features

特征公式 平均绝对幅值(Mean Absolute Value, MAV) 方均根(Root Mean Square, RMS) 绝对能量(Absolute Energy, AE) 时域质心(Time domain Centroid, TC) 最大幅值(Maximum Amplitude, A_max) 最小幅值(Minimum Amplitude, A_min)
为消除初始极性影响并揭示信号强度与SOC的相关性,对超声信号进行处理,将负幅值转换为正幅值。图3b为不同SOC下的超声绝对值信号,随着电池SOC增加,信号强度增强。引入第三、第四和第五时间矩(M3、M4、M5),分别反映信号强度分布的对称性、尖锐度和更高阶的信息,M3、M4、M5的绝对值定义为
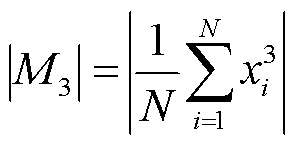 (4)
(4)
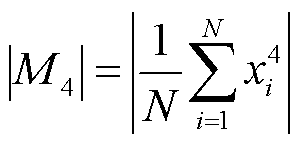 (5)
(5)
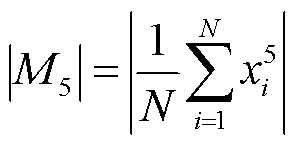 (6)
(6)
超声信号包络提取通过测量信号的局部特性产生简化波形,以便分析。通过移动窗口获取平均值、峰值等包络,如图3c所示。提取峰值、峰值位置、包络面积和不同高度(25%、50%和75%)下的宽度共六种包络特征,分别反映电池充放电过程中能量转换效率、稳定性、反应速度和一致性。
3.2.2 超声频域特征提取
时域特征虽能描述超声信号在时间轴上的特性,却难以反映频率维度的信息。因此,在频域特征提取时,主要采用频谱分析研究超声信号的频率特性。
通过快速傅里叶变换(Fast Fourier Transform, FFT)获得超声信号频谱,如图4所示。峰值频率约为3 MHz,频谱幅值和宽度随SOC增加而增加,这可能是因为电池的充放电状态会影响内部结构,从而影响声波的传播。这一结果初步表明,超声频域信号的变化与电池内部的电化学过程存在关联,为利用超声频域信号估计电池SOC提供了可能性。提取不同频点的平均幅度及16种频域特征,揭示信号的整体结构和统计特性。假设傅里叶变换后的信号频谱幅值为Xi(i=1, 2, …, N),对应的频率为fi,部分超声频域特征见表2。同时,提取不同频点的实部、虚部、模和相位,从局部反映信号频率组成和变化。
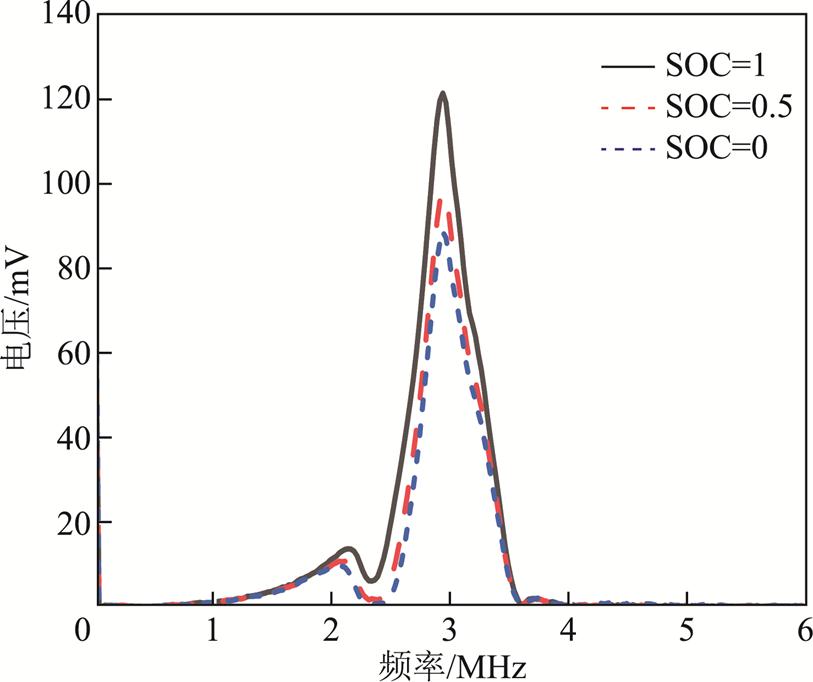
图4 超声信号FFT频谱
Fig.4 FFT spectrogram of ultrasound signals
3.2.3 超声时频域特征提取
时频域分析结合了时域和频域的信息,揭示超声信号在不同时间点上的频率成分和变化。时频分析方法主要包括短时傅里叶变换(Short Time Fourier Transform, STFT)和离散小波变换(Discrete Wavelet Transform, DWT)等。
表2 超声频域特征
Tab.2 Ultrasonic frequency domain features

特征公式 频谱质心(Spectral Centroid, SC) 频谱离散度(Spectral Spread, SS) 频谱峰度(Spectral Kurtosis, SK) 频谱熵(Spectral Entropy, SE) 频谱平坦度(Spectral Flatness, SF)
为了分析电池状态随时间变化的动态过程,采用STFT通过滑动窗口在超声信号上应用傅里叶变换,构建时频矩阵。超声信号时频域特征如图5所示。STFT得到的时频矩阵如图5a所示,各行代表特定频率下的时域信号变化,各列代表特定时间点的频谱。时间一定时,随着频率增加,信号强度减小;同样,频率一定时,随着时间增加,超声信号的强度普遍下降。提取STFT结果的方均根、标准差、能量、方差、平均绝对值、熵共六种特征,从不同角度反映信号的统计特性和能量分布情况。
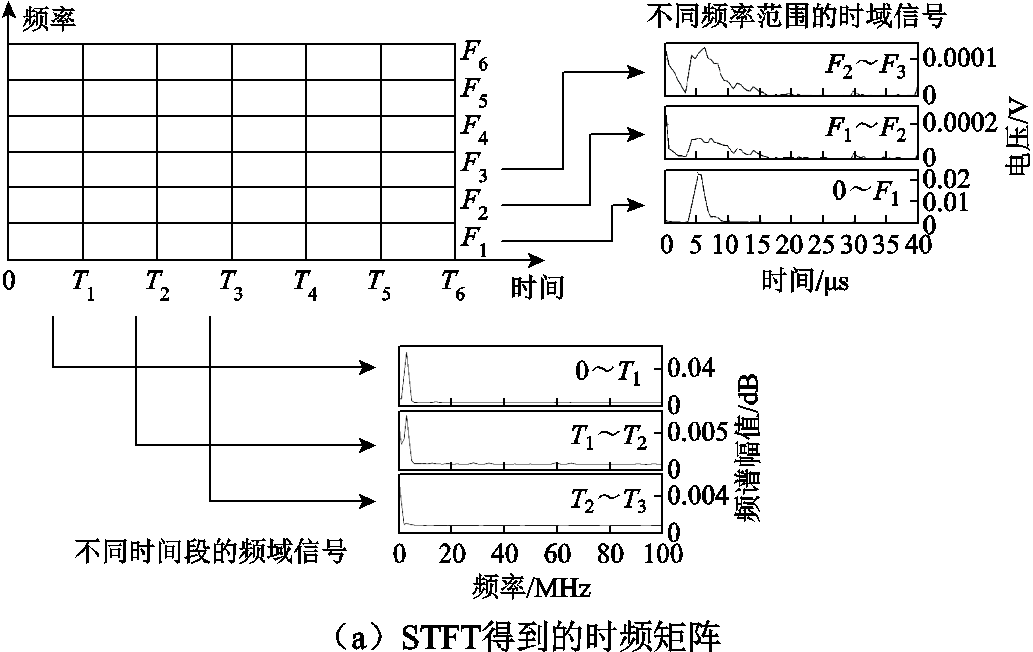
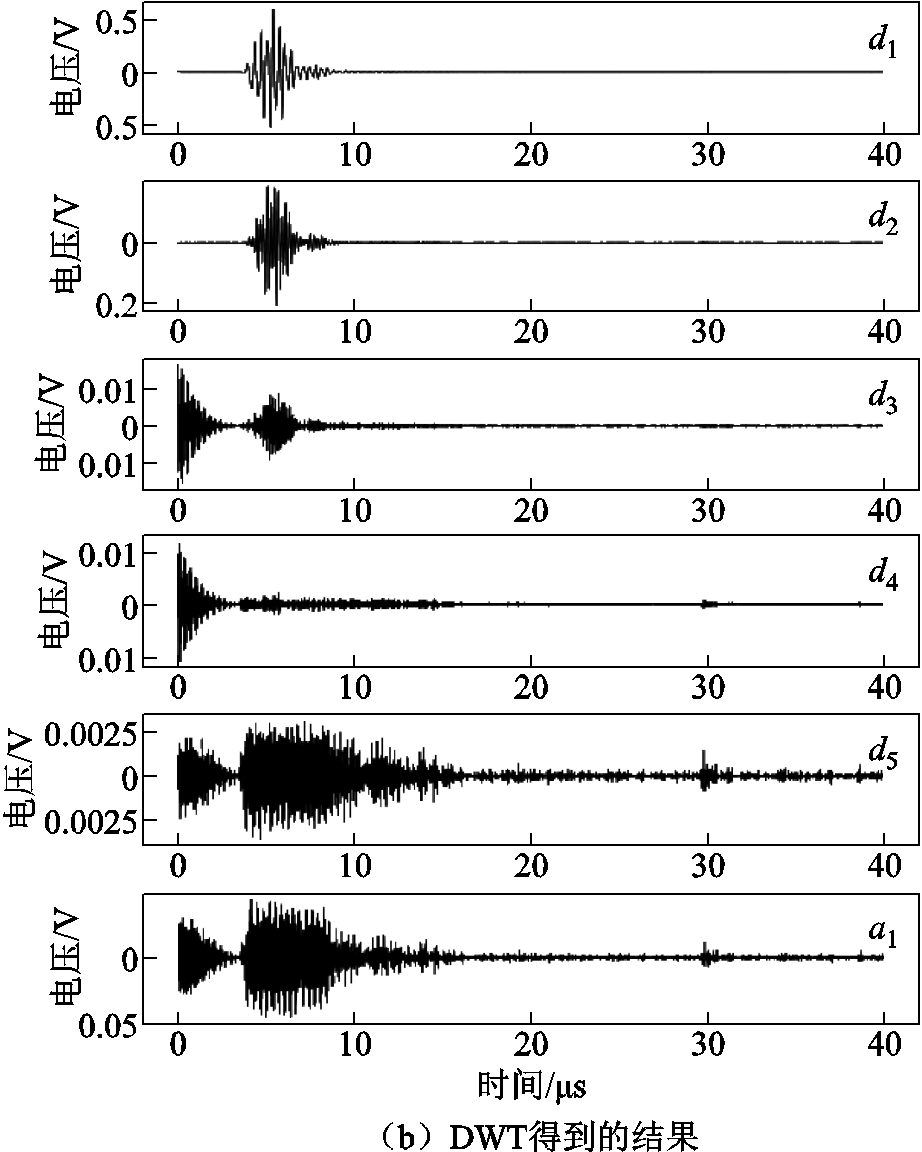
图5 超声信号时频域特征
Fig.5 Time-frequency domain characterization of ultrasound signals
考虑到DWT对信号的多分辨率分析能力,采用DWT将超声信号分解成不同频率范围的近似和细节水平,保留时间信息。图5b为使用db6小波对超声信号进行五级分解的结果。这种分解得到五个细节系数(d1、d2、d3、d4、d5)和一个近似系数(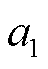 ),近似系数对应信号的低频成分,细节系数对应信号的高频成分。小波系数的变化反映了电池化学和物理状态的变化。低级别分解可以看到明显的信号活动,体现超声信号中的主要特征;而高级别分解的信号更加细腻,振幅逐渐减小,有助于捕捉超声信号的细微变化。这些近似和细节系数都可以作为特征使用。同时,计算小波绝对平均值、小波能量、小波熵、小波标准偏差和小波方差,用于评估信号动态变化和信号在不同SOC下的复杂性。
),近似系数对应信号的低频成分,细节系数对应信号的高频成分。小波系数的变化反映了电池化学和物理状态的变化。低级别分解可以看到明显的信号活动,体现超声信号中的主要特征;而高级别分解的信号更加细腻,振幅逐渐减小,有助于捕捉超声信号的细微变化。这些近似和细节系数都可以作为特征使用。同时,计算小波绝对平均值、小波能量、小波熵、小波标准偏差和小波方差,用于评估信号动态变化和信号在不同SOC下的复杂性。
考虑到高特征维度会增加模型训练的复杂度,可能导致过拟合,降低模型泛化能力,因此需对特征进行选择。同时,考虑到单一的特征选择方法可能由于其内在的局限性而对某些特征做出错误的判断,多种特征选择方法的融合有助于准确获得具有更高信息价值的特征集。综合考虑不同特征选择方法的优势,提出融合四种特征的选择方法,包括基于过滤的Spearman相关系数法、互信息法,以及基于嵌入的CatBoost、LASSO回归。
4.1.1 斯皮尔曼相关系数法
斯皮尔曼(Spearman)相关系数是描述两个数据序列之间单调关系强度的统计方法,被用来评估变量之间的相关性[25]。Spearman相关系数r的计算公式为
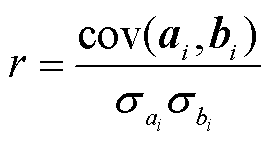 (7)
(7)
式中,ai和bi为将原始数据秩次排序后的向量;cov(ai, bi)为ai和bi的协方差;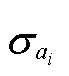 和
和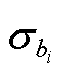 分别为ai和bi的标准差。r的取值范围为-1~1,1表示完全正单调关系,-1表示完全负单调关系,接近0表示无或极弱单调关系。
分别为ai和bi的标准差。r的取值范围为-1~1,1表示完全正单调关系,-1表示完全负单调关系,接近0表示无或极弱单调关系。
4.1.2 互信息
互信息是一种衡量两个变量间依赖强度的统计指标[26]。它不仅能捕捉线性关系,而且能量化非线性关系。在特征选择领域,尤其是处理复杂依赖结构数据时,互信息极为有用。基本原理是评估一个变量信息对减少另一个变量不确定性的程度,值越高表示两变量间依赖性越大。
4.1.3 分类提升树
分类提升树(CatBoost)是一种梯度提升决策树算法,适用于处理具有复杂关系和高维数据的问题[27]。CatBoost算法首先对数据进行训练,构建决策树,并在构建过程中根据减少损失函数的目标选择最佳特征进行分裂。训练完成后,CatBoost基于特征对模型性能的贡献评估每个特征的重要性。
4.1.4 最小绝对收缩和选择算法
LASSO是一种特征选择和正则化方法[28]。LASSO在最小二乘误差基础上添加一个与回归系数绝对值之和成比例的惩罚项,使部分回归系数的估计值收缩至零,自动进行特征选择。LASSO回归适用于处理大量变量的数据集,计算效率较高,但可能选择比最佳子集稍多的变量。因此,合理地调整正则化参数非常关键。
结合电信号、热信号和超声信号的特征,形成特征集。剔除相关系数大于0.999的冗余特征,并对其余特征进行归一化处理,以利于后续选择和模型训练。为准确选择电池SOC估计的关键特征,构建融合四种特征选择算法(Spearman相关系数法、互信息法、CatBoost、LASSO回归)的投票选择器,特征选择流程如图6所示。当超过两种方法认为某一特征应保留时,则将其选入最终关键特征集;否则,丢弃特征。为了提高方法的实用性,降低算力负担,对于四种特征选择方法,均保留重要性排名前5%的特征构成特征子集。
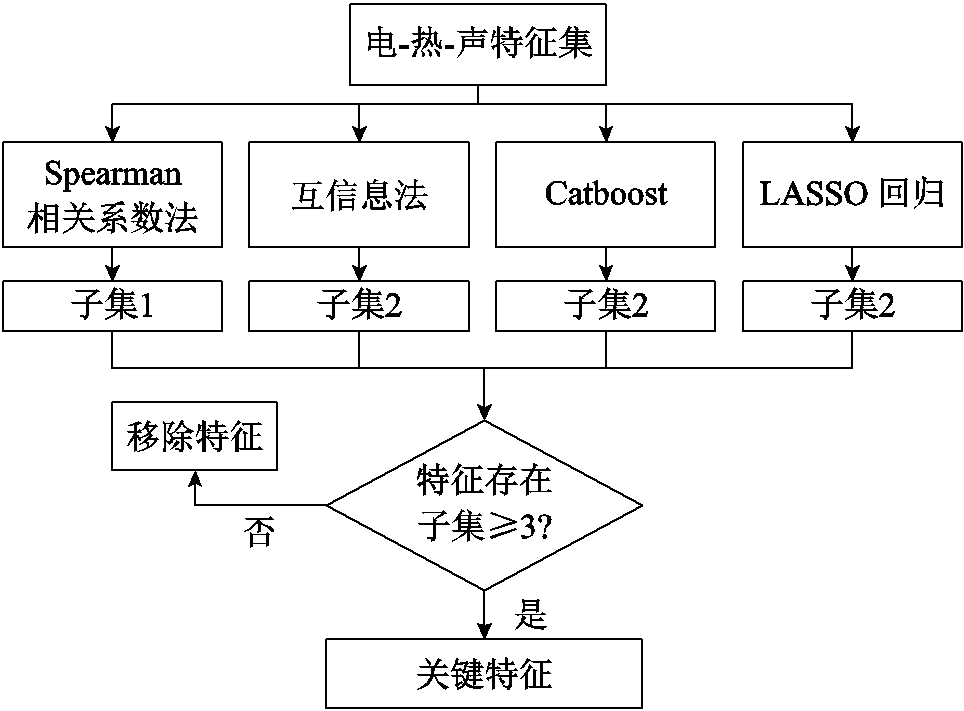
图6 特征选择流程
Fig.6 Feature selection flowchart
在0.8C电流倍率和25℃环境下实验,提取电-热-声特征组成包含1 296个特征的特征集,剔除冗余特征后特征数为998,并对特征进行归一化。特征数量多,主要是因为对于超声时频图的特征提取,在每个测量时间段内都提取了详细的特征。
使用不同方法选出的前五个关键特征见表3~表6。可以看出,不同方法识别的关键特征各异。Spearman法凭借其能捕捉线性与非线性关系的优势,识别出峰值包络的峰位置与SOC之间存在高度单调关系,得分接近0.968 3。互信息法评估变量之间相互依赖性,发现功率谱密度第2个系数与SOC共享大量信息,得分约为2.279 6。CatBoost显示电压对SOC估计至关重要,分数为8.683 1。LASSO回归通过施加L1正则化,识别出电压为关键特征,得分为0.062 7。同时,峰值包络的峰位置、电压、飞行时间等特征在多种方法中均显重要,这增加了它们对SOC估计有重要影响的可信度。因此,在进行特征选择时,最佳做法通常是融合多种方法的结果,以获得最全面的特征重要性评估。
表3 Spearman相关系数法选择的前五个特征
Tab.3 The first 5 features selected by the Spearman correlation coefficient method

特征相关系数绝对值 峰值包络的峰位置0.968 3 飞行时间0.966 4 FFT频点96对应值的相位0.962 2 FFT频点98对应值的相位0.960 1 FFT频点97对应值的相位0.957 0
表4 互信息法选择的前五个特征
Tab.4 The first 5 features selected by the mutual information method

特征互信息分数 功率谱密度第2个系数2.279 6 FFT频点5的平均幅度2.241 0 频谱熵2.222 6 绝对能量2.220 2 FFT频点99对应值的模2.216 0
表5 CatBoost法选择的前五个特征
Tab.5 The first 5 features selected by the CatBoost method

特征重要性分数 电压8.683 1 FFT频点97对应值的相位4.938 5 FFT频点96对应值的相位4.652 5 分段线性拟合曲线标准差的方差3.361 8 峰值包络的峰位置2.400 1
表6 LASSO回归法选择的前五个特征
Tab.6 The first 5 features selected by the LASSO regression method

特征重要性分数 电压0.062 7 电流0.046 9 绝对能量0.045 1 飞行时间0.033 4 FFT频点0的平均幅度0.019 1
经过筛选,Spearman相关系数法、互信息法、CatBoost、LASSO回归均保留重要性排名前5%的特征,即50个特征。通过多数投票法的集成策略,最终确定14个关键特征,包括3个超声时域特征、7个频域特征、2个时频特征、1个电特征和1个热特征。其中,超声时域特征为飞行时间、最大幅值、分段线性拟合曲线标准差的方差;超声频域特征为SE、SF、FFT频点8的平均幅度、FFT特定频点值的模(频点85、98、99)和虚部(频点96);超声时频特征为离散小波熵和离散小波变换的第一层标准差;电特征为电压;热特征为温度。这表明在估计LFP电池SOC时,超声频域特征可能更为关键。然而,电、热参数直接反映了电池的工作状态和热管理情况,在进行全面分析时同样不容忽视。
为确保实验设置的一致性,对电池A3在充放电循环中选取的特征数据进行归一化处理,其中一个循环数据作为训练集,另一个循环数据作为测试集。模型训练集和测试集大小与电池充放电时长以及超声信号采样周期有关。超声信号1 min采集一次,在电流倍率为0.8C时,每个循环采集141组超声信号数据。因此,训练集大小为14×141,测试集大小与训练集大小相同。
为验证所提特征选择方法的有效性,采用随机森林(Random Forest, RF)、门控循环单元(Gate Recurrent Unit, GRU)和双向门控循环单元(Bidirectional Gate Recurrent Unit, BiGRU)进行SOC估计。选用线性整流函数(Rectified Linear Unit, ReLU)作为激活函数,自适应矩估计(Adaptive Moment Estimation, Adam)为优化器,将迭代次数限制为1 000。经过超参数调试,确定RF的决策树数量为100,GRU和BiGRU的隐藏层大小为50,GRU层数量为1,学习率为0.01,步长为1。评估指标包括平均绝对误差(Mean Absolute Error, MAE)、方均根误差(Root Mean Square Error, RMSE)和模型运行时间。MAE和RMSE公式分别为
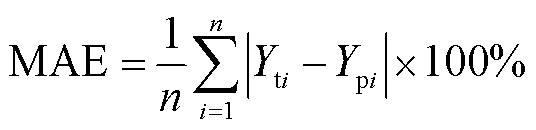 (8)
(8)
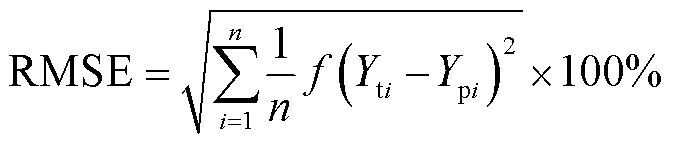 (9)
(9)
式中,n为估算样本个数;Yti为SOC实际值;Ypi为SOC估算值。
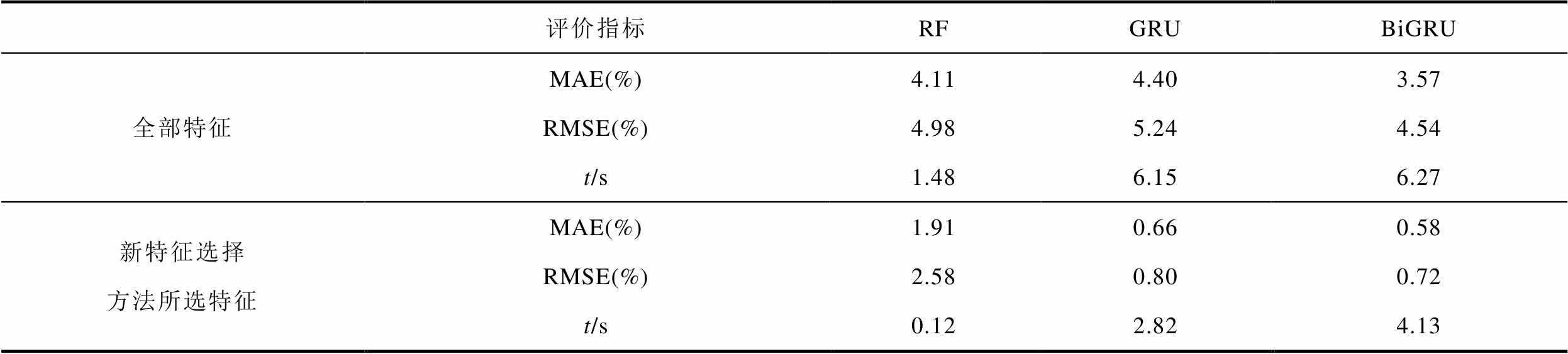
表7和图7展示了新的特征选择方法对估计结果的影响,全部特征数为998,新的特征选择方法选择的特征数为14。结果显示,相较于使用全部特征,新特征选择方法选择的特征能有效降低模型的误差,提升估计精度。在使用RF、GRU、BiGRU的情况下,MAE分别降低了2.20、3.74和2.99个百分点。这充分说明特征选择对于提升模型估计性能的重要性,从侧面证明了无效的特征会降低模型的性能。另一方面,使用提出的特征选择方法所选特征不仅提升了估计精度,还缩短了模型的训练时间。此外,BiGRU模型因能双向捕捉时间序列数据的动态特性,表现出最低的MAE和RMSE值,MAE约为0.58%,RMSE约为0.72%,然而,尽管BiGRU在估计性能上表现出色,但在时间效率上并非最优选择。
表7 所有特征与选择特征SOC估计结果
Tab.7 SOC estimates for all features and selected features
评价指标RFGRUBiGRU 全部特征MAE(%)4.114.403.57 RMSE(%)4.985.244.54 t/s1.486.156.27 新特征选择方法所选特征MAE(%)1.910.660.58 RMSE(%)2.580.800.72 t/s0.122.824.13
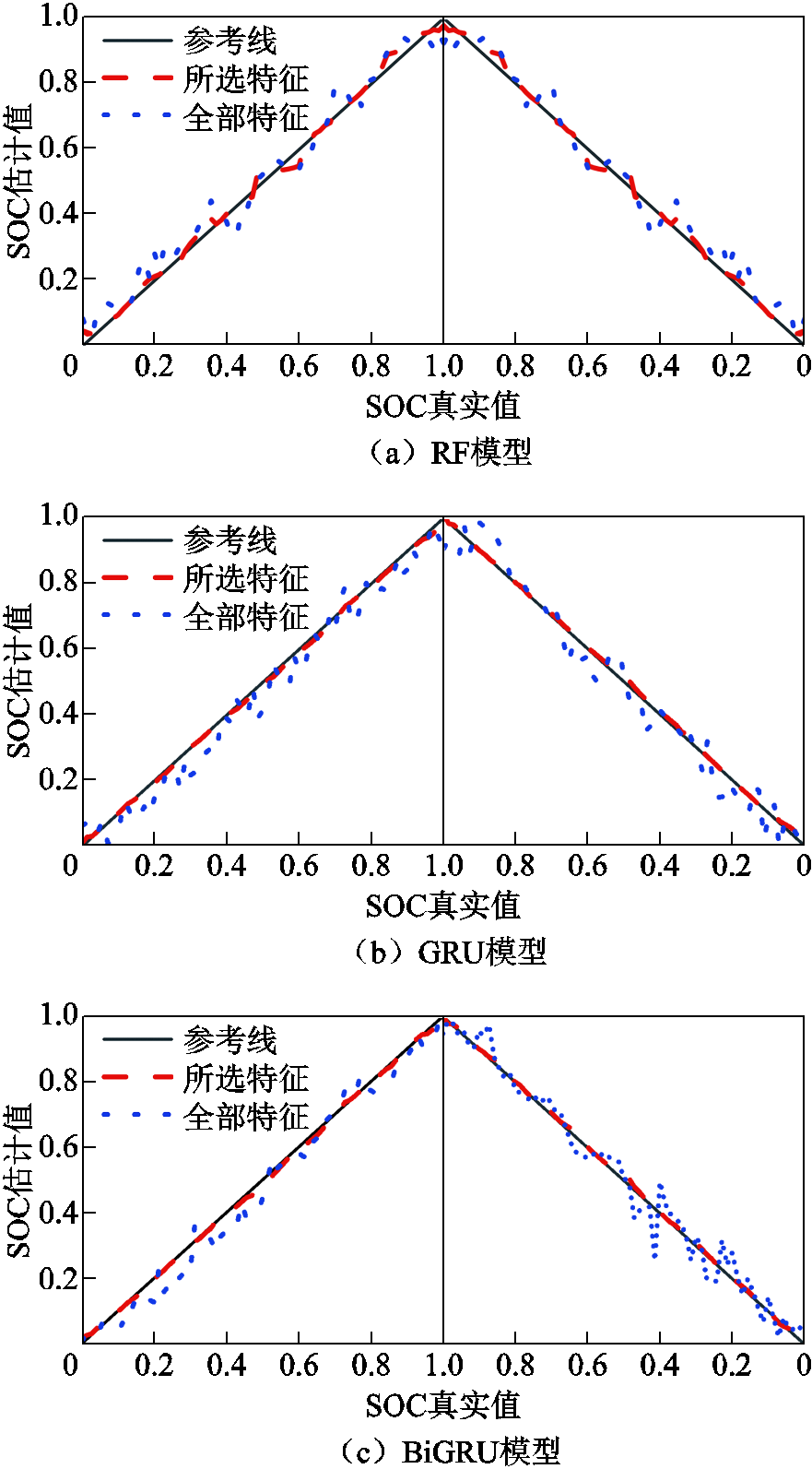
图7 所有特征与选择特征的SOC估计结果
Fig.7 SOC estimates for all features and selected features
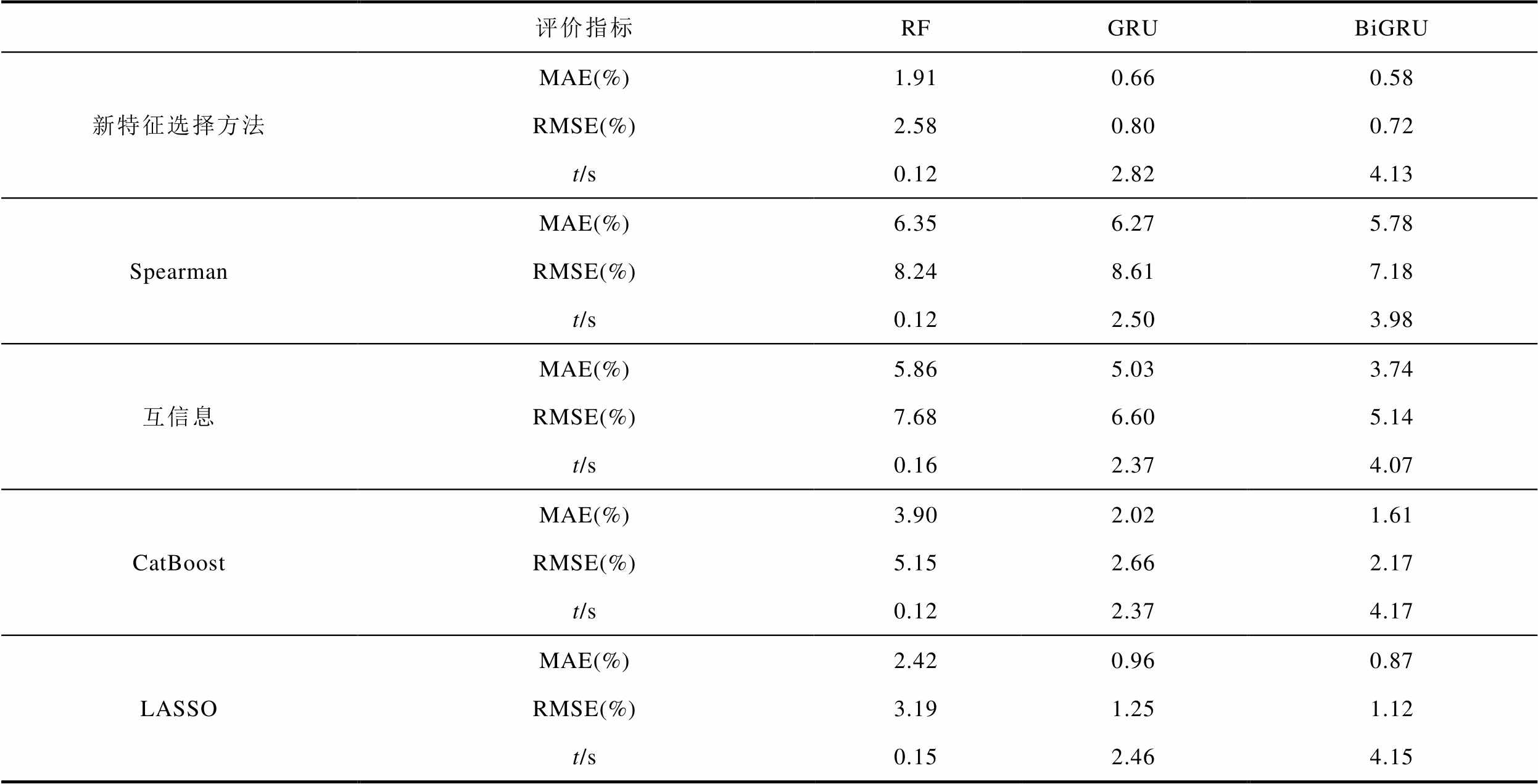
为了进一步验证所提特征选择方法的准确性,分别使用Spearman相关系数法、互信息法、CatBoost、LASSO回归选择前14个特征,进行SOC估计。表8展示了不同特征选择方法对各种模型估计结果的影响。结果显示,使用同样数量特征时,由于提出的特征选择方法集成了Spearman相关系数法、互信息法、CatBoost、LASSO回归的优点, 模型的估计精度有显著的提升,这表明提出的特征选择方法可以更为有效地从众多特征中选择出对SOC估计最关键的特征。
为了进一步证明电-热-声多源数据结合的优势,与仅使用选择的电信号特征、热信号特征、超声时域特征、超声频域特征、超声时频域特征的方法进行了比较,估计模型为BiGRU。表9和图8显示了SOC的估计结果。相较于仅使用单一信号特征,综合电-热-声多源数据的方法在SOC估计中表现最优,MAE和RMSE分别为0.58%和0.72%,显示出高度的准确性和可靠性。这得益于多源数据融合的信息互补性,电信号提供了电池内部电化学反应的直接信息,热信号反映了电池运行过程中的热状态变化,而超声信号则捕捉到了电池结构变化的声学特征,将这三种信号特征相结合,能更全面地捕捉到电池状态的变化,提高SOC估计准确度和稳健性。因此,在实际应用中,采用多源数据融合方法对SOC进行估计是一种有效的策略。
表8 不同特征选择方法下不同模型估计结果
Tab.8 Different model estimation results under different feature selection methods
评价指标RFGRUBiGRU 新特征选择方法MAE(%)1.910.660.58 RMSE(%)2.580.800.72 t/s0.122.824.13 SpearmanMAE(%)6.356.275.78 RMSE(%)8.248.617.18 t/s0.122.503.98 互信息MAE(%)5.865.033.74 RMSE(%)7.686.605.14 t/s0.162.374.07 CatBoostMAE(%)3.902.021.61 RMSE(%)5.152.662.17 t/s0.122.374.17 LASSOMAE(%)2.420.960.87 RMSE(%)3.191.251.12 t/s0.152.464.15
表9 不同特征SOC估计结果
Tab.9 SOC estimation results for different features

特征超声时域超声频域超声时频域电信号热信号电-热-声数据 MAE(%)4.823.557.566.377.530.58 RMSE(%)6.094.318.718.9013.290.72 t/s3.993.825.523.944.084.13
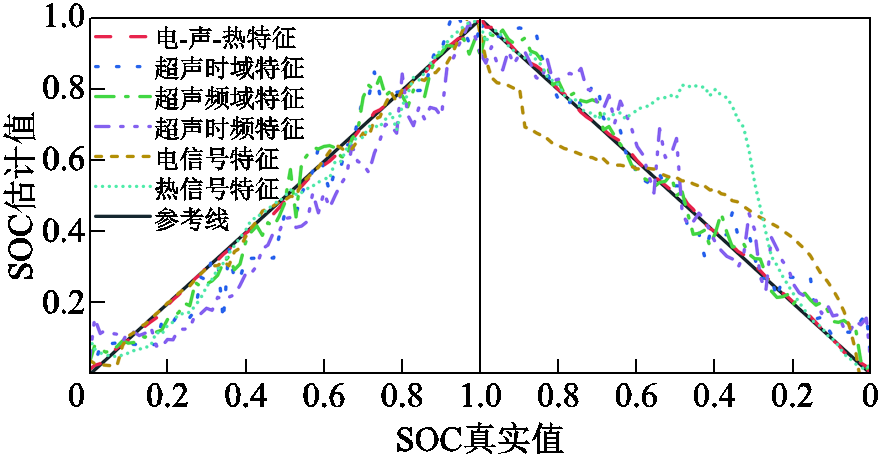
图8 不同特征下SOC估计结果
Fig.8 SOC estimation results with different characteristics
为了全面评估所提出电-热-声多源特征选择方法在不同电流充放电倍率下的SOC估计效果,使用14个关键特征和BiGRU模型对不同电流倍率(0.4C、0.6C、1.0C)下的A1、A2、A4电池进行了测试。电流倍率的增加导致电池的充放电循环时间缩短,进而减少了每个循环中采集到的数据量。在0.4C、0.6C、1.0C倍率下,每个循环分别采集到290、191、114组数据。不同倍率下SOC估计结果见表10。可以看出,模型在三个不同电流倍率下的估计效果有所不同,MAE分别为0.81%、0.46%、0.83%,RMSE分别为0.96%、0.65%、0.97%,体现出该方法的可靠性,并进一步表明超声特征的估算方法能够摆脱对电池模型的依赖。综上分析,尽管在不同倍率下所选特征的表现略有波动,但总体上显著提高了不同倍率下LFP电池平台期SOC估算的准确性和可靠性。
表10 不同倍率下SOC估计结果
Tab.10 SOC estimation results at different magnification

倍率0.4C0.6C0.8C1.0C MAE(%)0.810.460.580.83 RMSE(%)0.960.650.720.97 t/s4.564.534.133.78
为验证所提方法在复杂条件下的有效性,在动态压力测试(Dynamic Stress Test, DST)和新欧洲驾驶循环(New European Driving Cycle, NEDC)两种动态工况下进行验证,DST和NEDC工况分别循环39次和9次。不同工况下 SOC 估计结果见表11。模型在DST工况与NEDC工况下的 SOC 估计结果分别如图9a和图9b所示。由结果可知,DST工况下,提出的SOC估计方法的MAE与RMSE值分别为0.91%和1.03%;NEDC工况下,提出的SOC估计方法的MAE与RMSE值分别为0.98%和1.13%。结果表明,提出的SOC估计方法具有较好的泛化能力,可实现较高精度的SOC估计,进一步验证了提出的SOC估计方法的准确性。
表11 不同工况下SOC估计结果
Tab.11 SOC estimation results under different working conditions

工况DSTNEDC MAE(%)0.910.98 RMSE(%)1.031.13 t/s3.322.35
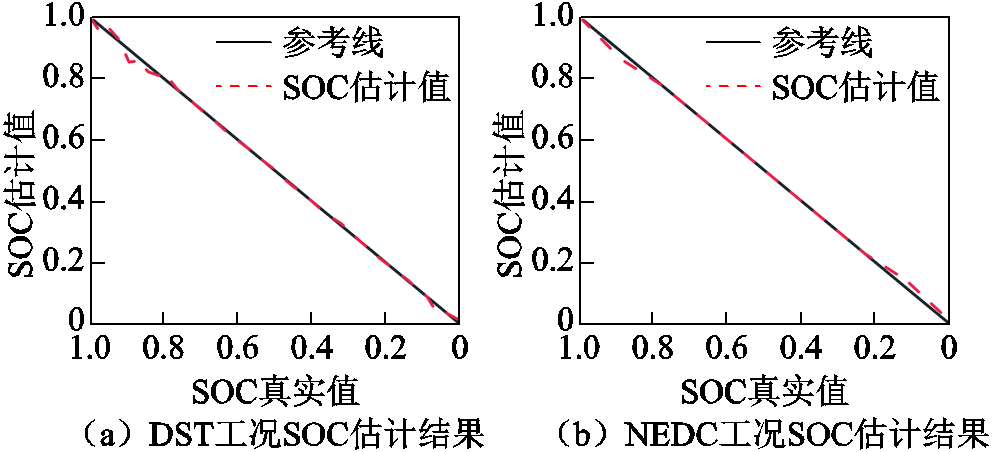
图9 不同工况下SOC估计结果
Fig.9 SOC estimation results under different working conditions
选择的14个特征中包含12个超声特征,而超声信号易受噪声影响。为了验证本文提出方法在高强度环境噪声下的适用性,在DST和NEDC工况下采集的原始超声信号中分别加入信噪比为10、4、 -2 dB 的高斯白噪声。对超声信号使用小波降噪方法进行预处理后,提取选择的12个超声特征,结合电压、温度进行SOC估计,结果见表12。
表12 不同噪声下SOC估计结果
Tab.12 SOC estimation results under different noises

信噪比/dB评价指标DSTNEDC 10MAE(%)0.981.07 RMSE(%)1.591.75 4MAE(%)1.041.10 RMSE(%)1.411.79 -2MAE(%)1.411.49 RMSE(%)2.051.93
结果显示,在不同的信噪比条件下,本文SOC估计结果依然保持较高的准确性。当信噪比为10 dB时,DST和NEDC工况下的MAE分别为0.98%和1.07%,RMSE分别为1.59%和1.75%,与无噪声条件下的结果相差不大。即使在信噪比降至-2 dB的情况下,DST与NEDC工况下的MAE和RMSE的值分别上升到了1.41%、1.49%和2.05%、1.93%,SOC估计的准确性虽有下降,但依然在一个可接受的范围内。因此,即使该方法对超声特征依赖性较大,但在小波降噪后,仍能够在一定程度上抵抗实际环境中的噪声干扰,保持SOC估计的准确度,证明了本文提出的方法具有较强的鲁棒性。
特征提取和特征选择在数据驱动的电池SOC估计方法中至关重要。本文综合电、热、声多源数据定量估计LFP电池的SOC。对电-热-声数据进行了全面的特征提取,并提出了一种融合Spearman相关系数、互信息、CatBoost和LASSO回归的特征选择新方法,显著提高了SOC估计的精度。主要结论如下:
1)提取了电、热信号的瞬时特征和短期变化特征,以及超声信号的时域、频域、时频域特征。结果表明,超声频域特征对SOC估计尤为重要,电压和温度同样不可或缺,结合电-热-声多源数据,SOC估计模型精度显著提升。
2)提出一种融合Spearman相关系数、互信息、CatBoost和LASSO回归的特征选择新方法。结果表明,使用本文提出方法能更有效地选择对SOC估计重要的特征,选择的特征比使用所有特征的SOC估计精度更高。
3)使用不同模型对SOC进行估计。结果表明,与其他模型相比,BiGRU模型具有最佳的估计效果,MAE和RMSE分别为0.58%和0.72%,为锂离子电池的状态估计提供了一种更准确、更可靠的模型。
4)在四种充放电倍率和两种工况下对所提出的方法进行了验证。结果表明,在DST与NEDC工况下,SOC估计的平均绝对误差分别为0.91%和0.98%,方均根误差分别为1.03%和1.13%,证明了本文提出的SOC估计方法具有良好的适应性和泛化能力。
参考文献
[1] Tian Jinpeng, Xiong Rui, Shen Weixiang, et al. State-of-charge estimation of LiFePO4 batteries in electric vehicles: a deep-learning enabled approach[J]. Applied Energy, 2021, 291(3): 116812.
[2] 宋磊, 陆春光, 刘琳, 等. 基于修正安时积分法的磷酸铁锂电池荷电状态估计[J]. 郑州大学学报(工学版), 2023, 44(6): 84-90.
Song Lei, Lu Chunguang, Liu Lin, et al. State of charge estimation of LiFePO4 battery based on modified amper-hour integral method[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(6): 84-90.
[3] Hou Jiayang, Xu Jun, Lin Chuanping, et al. State of charge estimation for lithium-ion batteries based on battery model and data-driven fusion method[J]. Energy, 2024, 290: 130056.
[4] 赵靖英, 胡劲, 张雪辉, 等. 基于锂电池模型和分数阶理论的SOC-SOH联合估计[J]. 电工技术学报, 2023, 38(17): 4551-4563.
Zhao Jingying, Hu Jin, Zhang Xuehui, et al. Joint estimation of the SOC-SOH based on lithium battery model and fractional order theory[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4551-4563.
[5] 李宁, 何复兴, 马文涛, 等. 基于经验模态分解的门控循环单元神经网络的锂离子电池荷电状态估计[J]. 电工技术学报, 2022, 37(17): 4528-4536.
Li Ning, He Fuxing, Ma Wentao, et al. State-of-charge estimation of lithium-ion battery based on gated recurrent unit using empirical mode decomposition[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4528-4536.
[6] 王义军, 左雪. 锂离子电池荷电状态估算方法及其应用场景综述[J]. 电力系统自动化, 2022, 46(14): 193-207.
Wang Yijun, Zuo Xue. Review on estimation methods for state of charge of lithium-ion battery and their application scenarios[J]. Automation of Electric Power Systems, 2022, 46(14): 193-207.
[7] Javid G, Ould Abdeslam D, Basset M. Adaptive online state of charge estimation of EVs lithium-ion batteries with deep recurrent neural networks[J]. Energies, 2021, 14(3): 758.
[8] Chung D W, Ko J H, Yoon K Y. State-of-charge estimation of lithium-ion batteries using LSTM deep learning method[J]. Journal of Electrical Engineering & Technology, 2022, 17(3): 1931-1945.
[9] 余杰, 廖思阳, 徐箭, 等. 考虑环境温度的磷酸铁锂电池SOC实时修正及频率控制方法[J]. 电工技术学报, 2023, 38(17): 4564-4573.
Yu Jie, Liao Siyang, Xu Jian, et al. Real-time SOC correction and frequency control method for LFP batteries considering ambient temperature[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4564-4573.
[10] Hsieh A G, Bhadra S, Hertzberg B J, et al. Electrochemical-acoustic time of flight: in operando correlation of physical dynamics with battery charge and health[J]. Energy & Environmental Science, 2015, 8(5): 1569-1577.
[11] Gold L, Bach T, Virsik W, et al. Probing lithium-ion batteries' state-of-charge using ultrasonic transmission-concept and laboratory testing[J]. Journal of Power Sources, 2017, 343: 536-544.
[12] Davies G, Knehr K W, Van Tassell B, et al. State of charge and state of health estimation using electrochemical acoustic time of flight analysis[J]. Journal of the Electrochemical Society, 2017, 164(12): A2746-A2755.
[13] Ladpli P, Liu Chen, Kopsaftopoulos F, et al. Estimating lithium-ion battery state of charge and health with ultrasonic guided waves using an efficient matching pursuit technique[C]//2018 IEEE Transpo-rtation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Bangkok, Thailand, 2018: 1-5.
[14] Li Xiaoyu, Hua Wen, Wu Chuxin, et al. State estimation of a lithium-ion battery based on multi-feature indicators of ultrasonic guided waves[J]. Journal of Energy Storage, 2022, 56: 106113.
[15] 刘素贞, 袁路航, 张闯, 等. 基于超声时域特征及随机森林的磷酸铁锂电池荷电状态估计[J]. 电工技术学报, 2022, 37(22): 5872-5885.
Liu Suzhen, Yuan Luhang, Zhang Chuang, et al. State of charge estimation of LiFeO4 batteries based on time domain features of ultrasonic waves and random forest[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5872-5885.
[16] Cai Zhiduan, Pan Tianle, Jiang Haoye, et al. State-of-charge estimation of lithium-ion batteries based on ultrasonic detection[J]. Journal of Energy Storage, 2023, 65: 107264.
[17] Shi Na, Chen Zewang, Niu Mu, et al. State-of-charge estimation for the lithium-ion battery based on adaptive extended Kalman filter using improved parameter identification[J]. Journal of Energy Storage, 2022, 45: 103518.
[18] Zhang Runnan, Li Xiaoyu, Sun Chuanyu, et al. State of charge and temperature joint estimation based on ultrasonic reflection waves for lithium-ion battery applications[J]. Batteries, 2023, 9(6): 335.
[19] Yang Sijia, Zhang Caiping, Jiang Jiuchun, et al. Review on state-of-health of lithium-ion batteries: characterizations, estimations and applications[J]. Journal of Cleaner Production, 2021, 314: 128015.
[20] 徐文军, 胡芃. 基于电化学-热耦合模型的21700型锂离子电池充放电过程热行为分析[J]. 中国科学技术大学学报, 2020, 50(5): 645-653.
Xu Wenjun, Hu Peng. Thermal behavior analysis of 21700 type lithium ion battery during charge-discharge cycles based on electrochemical-thermal model[J]. Journal of University of Science and Technology of China, 2020, 50(5): 645-653.
[21] Sun Tao, Shen Tengteng, Zheng Yuejiu, et al. Modeling the inhomogeneous lithium plating in lithium-ion batteries induced by non-uniform temperature distribution[J]. Electrochimica Acta, 2022, 425: 140701.
[22] Wu Yi, Wang Youren, Yung W K C, et al. Ultrasonic health monitoring of lithium-ion batteries[J]. Electronics, 2019, 8(7): 751.
[23] 邓哲, 黄震宇, 刘磊, 等. 超声技术在锂离子电池表征中的应用[J]. 储能科学与技术, 2019, 8(6): 1033-1039.
Deng Zhe, Huang Zhenyu, Liu Lei, et al. Applications of ultrasound technique in characterization of lithium-ion batteries[J]. Energy Storage Science and Technology, 2019, 8(6): 1033-1039.
[24] 张闯, 孙博, 金亮, 等. 基于声波时域特征的锂离子电池荷电状态表征[J]. 电工技术学报, 2021, 36(22): 4666-4676.
Zhang Chuang, Sun Bo, Jin Liang, et al. Characterization of the state of charge of lithium-ion batteries based on the time-domain characteristics of acoustic waves[J]. Transactions of China Electro-technical Society, 2021, 36(22): 4666-4676.
[25] 李永刚, 王月, 吴滨源. 基于双重Q学习的动态风速预测模型[J]. 电工技术学报, 2022, 37(7): 1810-1819.
Li Yonggang, Wang Yue, Wu Binyuan. Dynamic wind speed prediction model based on double Q learning[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1810-1819.
[26] Moslemi A. A tutorial-based survey on feature selection: Recent advancements on feature selection[J]. Engineering Applications of Artificial Intelligence, 2023, 126: 107136.
[27] Zhang Mei, Yin Jun, Chen Wanli. SOH estimation and RUL prediction of lithium batteries based on multidomain feature fusion and CatBoost model[J]. Energy Science & Engineering, 2023, 11(9): 3082-3101.
[28] Vilsen S B, Stroe D I. Battery state-of-health modelling by multiple linear regression[J]. Journal of Cleaner Production, 2021, 290: 125700.
Abstract The flat open-circuit voltage versus state of charge (SOC) curve of LiFePO4 batteries leads to difficulties in achieving an accurate estimation of SOC using only electrical signals. In addition, there are limitations in SOC estimation methods for single electrical, thermal, and acoustic data sources. In view of this, a multi-source data feature extraction method for SOC estimation of LiFePO4 battery was proposed. A comprehensive feature extraction was carried out on the electro-thermal-acoustic multi-source data obtained from different angles. Considering the advantages of different feature selection methods, a new feature selection method integrating Spearman correlation coefficient, mutual information, category boosting and least absolute shrinkage and selection operator regression was proposed. The joint selection of electro-thermal-acoustic key features was realized to improve the accuracy of SOC estimation.
Firstly, an experimental platform for LiFePO4 batteries was built. Electro-thermal-acoustic multi-source data were acquired. The transient features and short-term variation features of electrical and thermal signals, as well as the time-domain, frequency-domain, and time-frequency-domain features of ultrasonic signals were extracted, respectively. Secondly, in order to select the key features more accurately, a new method of feature selection incorporating Spearman correlation coefficient, mutual information, category boosting, and least absolute shrinkage and selection operator regression was proposed. In order to verify the performance of the proposed method, the proposed method was compared with SOC estimation results using all features and SOC estimation results under different feature selection methods. The effect of SOC estimation using single data source features versus multi-source data features was compared. The feasibility of the proposed method was verified at different magnifications and under different operating conditions. Finally, Gaussian white noise with different signal-to-noise ratios was added to the raw ultrasound signals acquired under dynamic stress test (DST) conditions and new european driving cycle (NEPC) conditions, respectively, to verify the applicability of the proposed method under high-intensity noise.
The results show that using the new method of feature selection proposed can effectively select the features that are important for SOC estimation with higher accuracy than SOC estimation using all features. With the same number of features, the SOC estimation accuracy of this method is improved compared with that of a single feature selection method. The model constructed using electric-thermal-acoustic multi-source key features has higher SOC estimation accuracy compared to single data source features. When using the BiGRU model, the mean absolute error and root-mean-square error of SOC estimates are 0.58% and 0.72%, respectively. The method performs well under a single operating condition. The method also shows good applicability at different discharge multipliers and under multiple operating conditions. Under DST conditions and NEDC conditions, the mean absolute error of SOC estimation is 0.91% and 0.98%, and the root mean square error is 1.03% and 1.13%, respectively, which verifies the validity and accuracy of the method. After adding noise with different signal-to-noise ratios to the original signals of different working conditions, the wavelet noise reduction can resist the noise interference in the actual environment to a certain extent and maintain the accuracy of SOC estimation.
Keywords:LiFePO4 battery, state of charge, multi-source data, feature extraction, feature selection
中图分类号:TM912
DOI: 10.19595/j.cnki.1000-6753.tces.240835
河北省自然科学基金项目(E2024202010)、国家自然科学基金项目(52307238)、省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学)优秀青年创新基金项目(EERI_OY2023007)资助。
收稿日期 2024-05-21
改稿日期 2024-06-04
刘素贞 女,1969年生,博士,教授,博士生导师,研究方向为锂离子电池状态评估与预测、电磁无损检测与评估等。
E-mail:szliu@hebut.edu.cn(通信作者)
任佳乐 女,2000年生,硕士研究生,研究方向为锂离子电池状态估计。
E-mail:2638180566@qq.com
(编辑 赫 蕾)