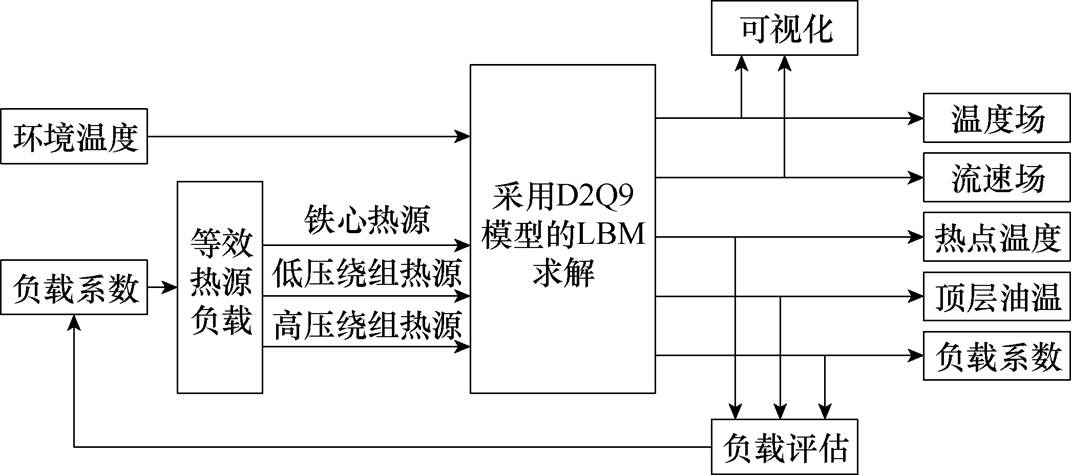
图1 基于LBM-Simulink的仿真模型
Fig.1 Simulation model based on LBM-Simulink
摘要 现场变负荷运行条件下的油浸式变压器动态载荷(DTR)和热寿命损失与设备的瞬态温升密切相关。该文提出了一种耦合电网络的格子玻耳兹曼(LBM)物理在环仿真模型,实现对电网络约束下的DTR实时评估。采用D2Q9模型对流体流动和热格子玻耳兹曼方程(LBEs)进行求解捕获变压器内部瞬态的油流和温升过程;在Simulink环境中采用等价电流源模型构建多级负载的电网络约束,并将建立的变压器LBM模型作为元件进行数值封装完成物理在环的仿真模型构建。与有限体积法(FVM)相比,所建立的模型热点温升的稳态和瞬态求解结果的误差分别为2.60%和6.44%,热点温升变化趋势与变压器负载导则吻合,验证了所提方法的有效性。基于该模型对恒定25℃、夏季和冬季典型环境温度变化下的油浸式变压器负载能力进行了评估,结果显示在相对绝缘寿命损失小于1的前提下,环境温度恒定25℃、夏季典型变化温度和冬季典型变化温度下最大的负载系数分别为1.20、1.10和1.60。所提出的基于LBM的仿真模型对油浸式变压器温升的实时监测、负载能力评估和动态增容提供了一种有效方法。
关键词:油浸式变压器 动态变压器载荷 格子玻耳兹曼方法 相对绝缘寿命
油浸式电力变压器在运行过程中产生的温升和发热现象是限制其带负载能力和安全可靠运行的重要因素[1]。目前许多现场运行的变压器为了其安全性能得到保障,大多采用保守的负载阈值进行调度和运行,造成了一定的资源浪费。对油浸式变压器进行热分析和检测是开展变压器动态载荷(Dynamic Transformer Rating, DTR)评估的基础,因此有必要对油浸式变压器的内部油流换热过程进行研究。
为了提高变压器的输送容量和节约电力资源,一些学者对变压器的负载能力进行了相关研究。Li Shuaibing等总结了变压器负载能力的评估方法,以及变压器负载能力预测和动态增容策略[2];I. Daminov等考虑了除电流和环境温度之外的热点温度和顶层温度来对变压器的负载能力进行评估,得出了不同情况下的安全运行时长[3]。也有一些学者对变压器的动态载荷量进行了研究,提出了热老化对其变压器寿命的影响并给出了计算方法[4-8]。因此,对变压器内部顶层油温,特别是热点温度的准确和快速计算是进行变压器动态负载能力评估的前提。谭又博等研究了谐波电流对热点温度的影响,并给出了热点位置[9]。刘云鹏等通过利用双峰拟合算法,结合对异常峰值曲线的边沿分析提高了布里渊光时域分析技术的空间分辨率,提高了对热点温度检测的准确性[10]。还可以通过建立磁-热-流耦合场对变压器进行仿真分析,进而准确得出变压器温度的分布和影响温升的因素[11-12]。谢裕清等应用最小二乘有限元法和迎风有限元法,与传统的有限元和有限体积法相比更加稳定,在其数值解中不会产生非物理数值振荡,进而提高了求解的精度[13]。
然而随着电力变压器数字化运维和DTR评估概念的提出,对变压器多物理场的快速计算成了研究热点[14],特别是其热-流体多物理场耦合模型的快速计算更为重要[15]。刘刚等采用基于子循环自适应串行交错的时间匹配算法,与传统计算方法相比,提高了计算速度,减少了计算冗余[16]。段辞涵等对变压器的温度场进行研究,提出了将其热传导、热对流、热辐射三种传热进行复合得出等效的传热系数,简化了传热计算,提高了计算速度[17]。荆澜涛等采用本征正交分解对温度场进行降阶运算,建立了基于物联网的油浸式变压器的数字孪生模型,提高了运行速度[18]。骆仁松等采用有限差分对高频变压器三维温升计算进行了优化,提高了计算速度[19]。目前对油浸式变压器的研究多数学者采用的是传统的有限元分析和有限体积法,而有限单元法是一种隐式求解方法,在瞬态热分析的每一个子步都需要反复进行流-热耦合方程的迭代求解,计算资源和耗时较多,难以满足快速计算的要求。通过对现场温度场的快速求解,实现变压器数字化运维并为DTR评估的提供基础。
格子玻耳兹曼方法(Lattice Boltzmann Method, LBM)作为一种显式的数值求解算法,其对变压器内部温度场的求解有着天然的优势。近年来随着LBM的发展,一些学者将LBM用于换热的研究,模拟了不同模型下流体特性及其影响因素[20-24],曾非同等利用格子玻耳兹曼方法对其变压器内部的温度场进行了研究,提出了基于流-固耦合的温度场-流场计算模型[25]。A. Tiftikci等采用格子玻耳兹曼的D3Q27晶格计算模型,研究了不同填充直径大小的颗粒对其温度场的影响,得到了不同半径下的温度场实时情况[26]。课题组前期开展了LBM在气体绝缘组合电器(Gas Insulated Switchgear, GIS)温升计算中的研究,对比了不同混合气体对GIS换热过程的影响[27]。然而LBM在变压器中的应用未考虑到电网络的约束影响,难以满足复杂电网络约束下变压器设备动态热负载能力评估的要求。
本文以油浸式电力变压器为对象,面向现场设备的瞬态温升计算和负载能力评估,提出了考虑设备与电网络约束的LBM显式求解模型,并与有限体积法(Finite Volume Method, FVM)和变压器负载导则进行了对比验证。基于该方法,对动态环境温度和不同负载系数下油浸式变压器的热点温升和负载能力进行了求解,为变压器的可靠运行和动态增容提供参考。
由于变压器实时监测和数字化运维主要由物理模型、虚拟数字模型、数据连接和应用场景等部分组成。其中虚拟数字模型必须考虑变压器内部的多物理行为,以便能够反映其实时的运行状态。因此在本文研究中考虑到了变压器的热-流耦合行为,结合LBM构建了如图1所示的LBM-Simulink仿真模型。将LBM与变压器的内部场分析相结合,实现了可视化、动态容量评估和内部温度场和流速场模拟等功能。

图1 基于LBM-Simulink的仿真模型
Fig.1 Simulation model based on LBM-Simulink
变压器简化模型如图2所示。其主要是由铁心、绕组、油箱以及绝缘套管等部分组成,铁心和绕组放置在充满着绝缘油的油箱内。变压器的传热过程包括:绕组和铁心通过热传导将热量传递到变压器表面,进而通过绝缘油自然对流传递到外壳,变压器外壳和空气之间通过大空间自然对流和辐射换热。将其传热过程等效为传热系数进行简化计算[17];绝缘油的热物性参数见表1,建模过程中的简化如下:
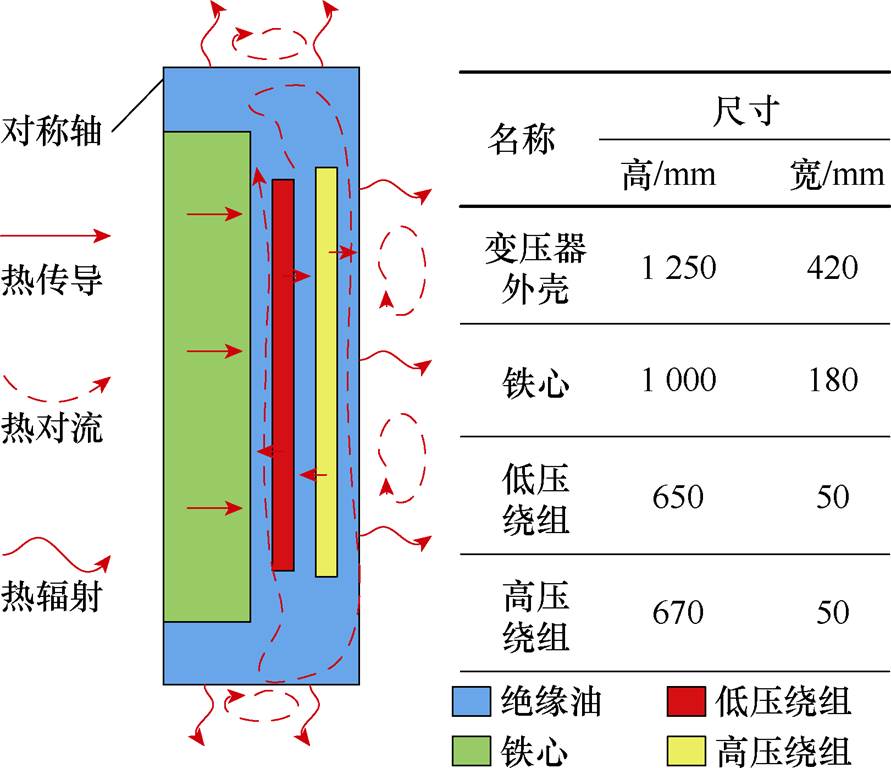
图2 变压器简化模型
Fig.2 Transformer simplified model
(1)选取变压器的单相进行分析,以铁心的中心为轴对称面。
(2)高低压绕组以及铁心沿径向的温度不变,计算时只考虑绝缘油的流动与换热过程。
表1 绝缘油的物性参数[8]
Tab.1 Insulating oil parameters[8]
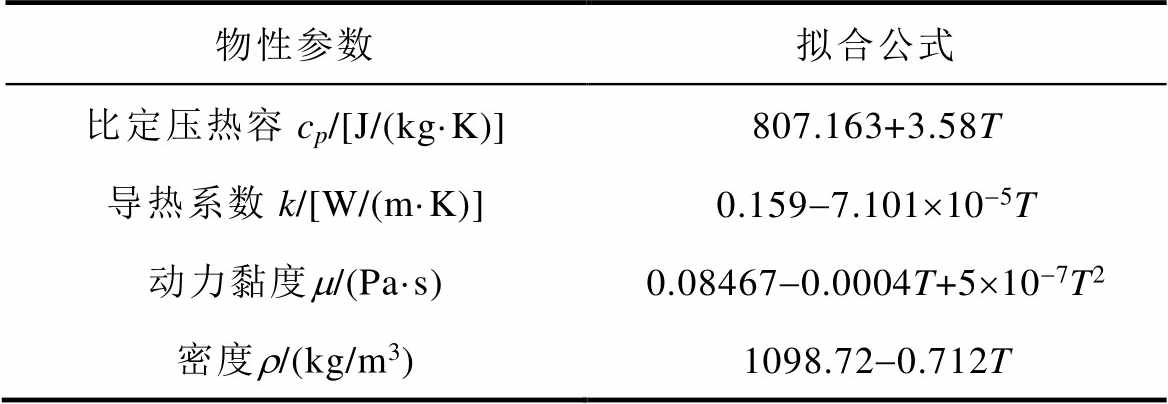
物性参数拟合公式 比定压热容cp/[J/(kg·K)]807.163+3.58T 导热系数k/[W/(m·K)]0.159-7.101´10-5T 动力黏度m/(Pa·s)0.08467-0.0004T+5´10-7T2 密度r/(kg/m3)1098.72-0.712T
(3)热源只考虑铁心和高低压绕组的产热,忽略其他装置产热。
(4)依据变压器导则[28-29],本文变压器模型采用热改性绝缘纸。
(5)除第4节中环境温度单独考虑之外,其余小节将变压器的环境温度设置为25℃(298.15K)。
变压器内部的热源主要来自绕组中电流产生的损耗和铁心中涡流产生的损耗[25]。本文对其铁心、低压绕组和高压绕组的产热功率损耗进行等效计算,计算公式为
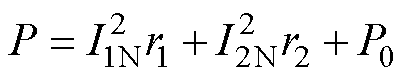 (1)
(1)
式中,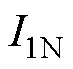 和
和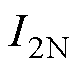 分别为低压绕组和高压绕组额定电流;
分别为低压绕组和高压绕组额定电流;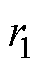 和
和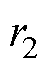 分别为低压绕组和高压绕组的等效阻值;
分别为低压绕组和高压绕组的等效阻值; 为额定情况下的铁心损耗。
为额定情况下的铁心损耗。
在后文的研究中,为了方便进行对比和定量分析,将由电流源构建的电网络约束转化为等效热源。负载系数为1.0条件下的计算结果具体数值见表2。
表2 等效热源参数
Tab.2 Equivalent parameters of heat source

参 数数 值 热导率k/[W/(m·K)]等效损耗/W 铁心213 800 低压绕组36855 000 高压绕组36843 000
LBM是一种在介观尺度上以分子动力学理论为基础,采用分布函数描述宏观物理量的方法[25],其求解流程主要包括格子域离散、格子玻耳兹曼方程(Lattice Boltzmann Equations, LBEs)求解和宏观物理场转换三个过程,如图3所示。为进行LBEs求解,首先在以开尔文为单位的宏观尺度下根据变压器的负载系数计算产热,进而得出铁心和高低压绕组的初始热源,并将其转化为流-固界面的热通量,作用在流体上。流体部分采用LBM中的格子分布函数(无量纲数)作为单位进行介观尺度下的热计算。
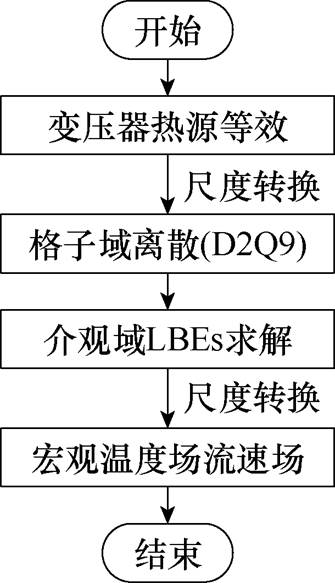
图3 LBM计算流程
Fig.3 LBM calculation process
格子域的离散是实现LBM求解的重要步骤,在格子域中基本求解单元可以用DxQy来表示,其中x表示维数,y表示格子的迁移方向。在二维模型计算中,D2Q9模型(具有9个速度方向分量的二维)可以更好地保证宏观的各向同性[30],对流体内部的流动-传热过程有很高的拟合程度。因此本文的流体流动和热LBEs都采用D2Q9晶格模型来呈现,具体晶格迁移方向如图4所示。其中各晶格的速度矢量ci可由以下公式给出。
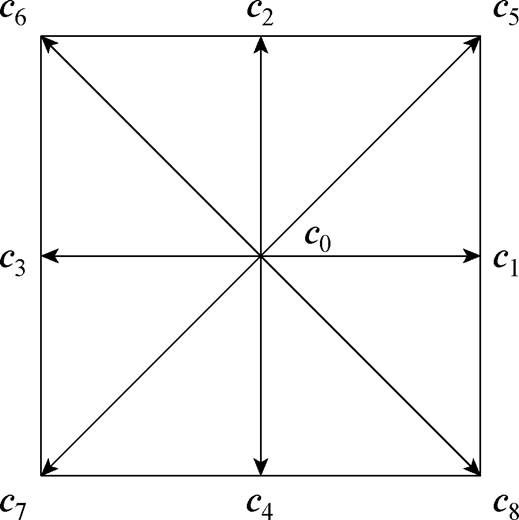
图4 D2Q9晶格模型
Fig.4 D2Q9 lattice model
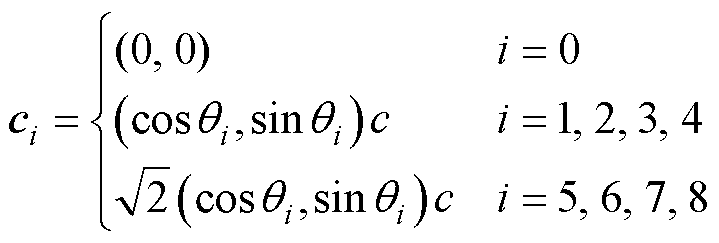 (2)
(2)
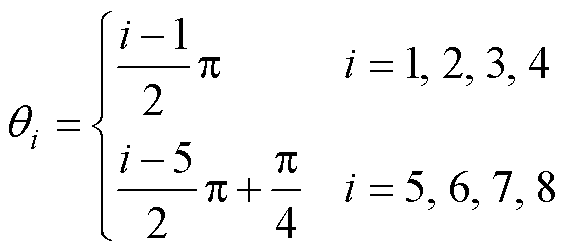 (3)
(3)
式中,c为格子声速。
油浸式变压器内部的自然对流换热过程包括流动和热两个物理场,通过浮力进行耦合。本文基于文献[31]的简化双分布模型(Double-Distribution Function, DDF)采用单一松弛时间和加入外力项的方法,在介观域分别采用流体流动和热LBEs描述流动和传热过程。通过求解LBEs获得介观动量和热分布函数fi(x, t)和gi(x, t)分别为
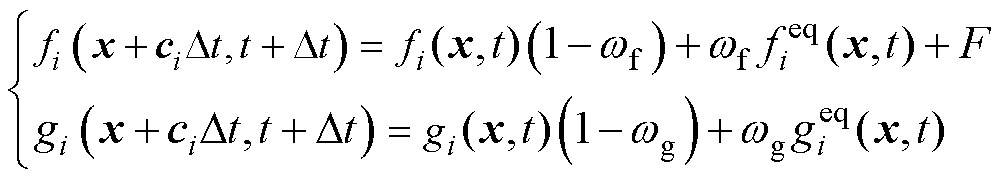 (4)
(4)
式中,Dt为晶格时间步长;wf=Dt/tf和wg=Dt/tg分别为流体松弛因子和热松弛因子;tf和tg分别为速度场和温度场的松弛时间;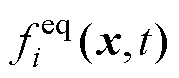 和
和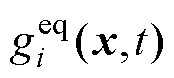 分别为流速场和温度场的平衡分布函数;F为粒子受到的外力项,采用布辛涅司克(Boussinesq)近似计算得出,即
分别为流速场和温度场的平衡分布函数;F为粒子受到的外力项,采用布辛涅司克(Boussinesq)近似计算得出,即
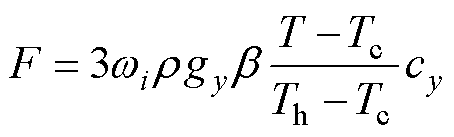 (5)
(5)
式中,r 为绝缘油密度;gy为沿-y方向的重力加速度;b 为热膨胀系数;Th和Tc分别为固体边界(热壁)和外壳(冷壁)的温度;cy为沿-y方向的速度分量。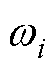 为D2Q9晶格下的各个方向的权重,其具体数值为
为D2Q9晶格下的各个方向的权重,其具体数值为
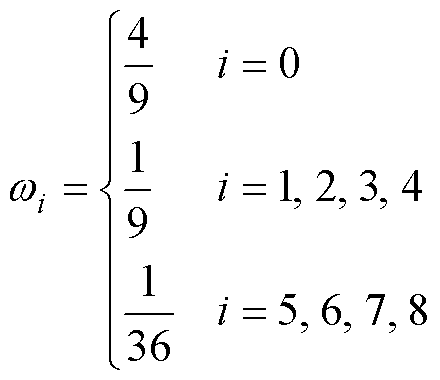 (6)
(6)
速度场和温度场的松弛时间计算式为
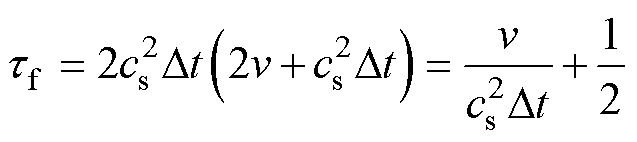 (7)
(7)
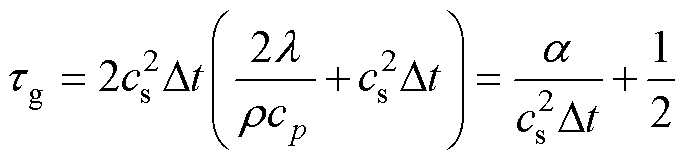 (8)
(8)
式中,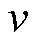 为运动黏度;
为运动黏度;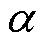 为热扩散速率;
为热扩散速率;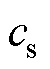 为晶格声速,对于本文的D2Q9模型而言,其
为晶格声速,对于本文的D2Q9模型而言,其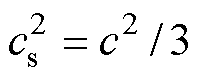 。
。
平衡动量和热分布函数为
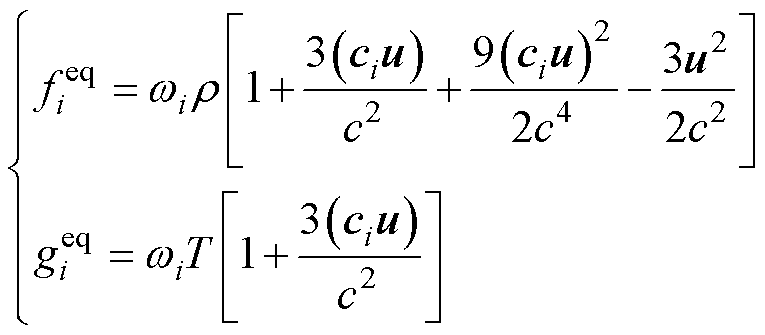 (9)
(9)
式中,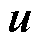 为宏观绝缘油流体流速。
为宏观绝缘油流体流速。
通过沿不同晶格方向的动量和热平衡函数的和可以计算出宏观绝缘油的密度、流体流动速度和温度分别为
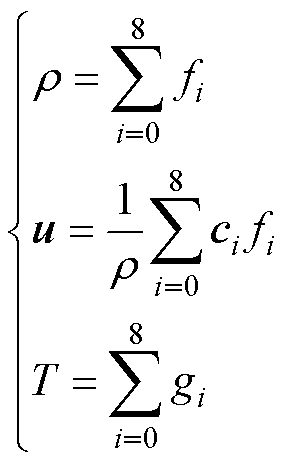 (10)
(10)
在LBM和FVM仿真计算中网格数目越多,结果将会越精确,但是计算成本和资源占用也将大大提高。本文通过进行网格无关性检验,其结果见表3,得出了随着网格数目增加,油浸式变压器LBM和FVM计算的热点温度结果将会逐渐收敛,从而确定了最佳的格子数目和网格单元数。最终本文选择格子数为1 250×420进行LBM建模仿真,选择单元数为43 654进行FVM网格划分。
表3 网格无关性检验结果
Tab.3 Grid independence test results
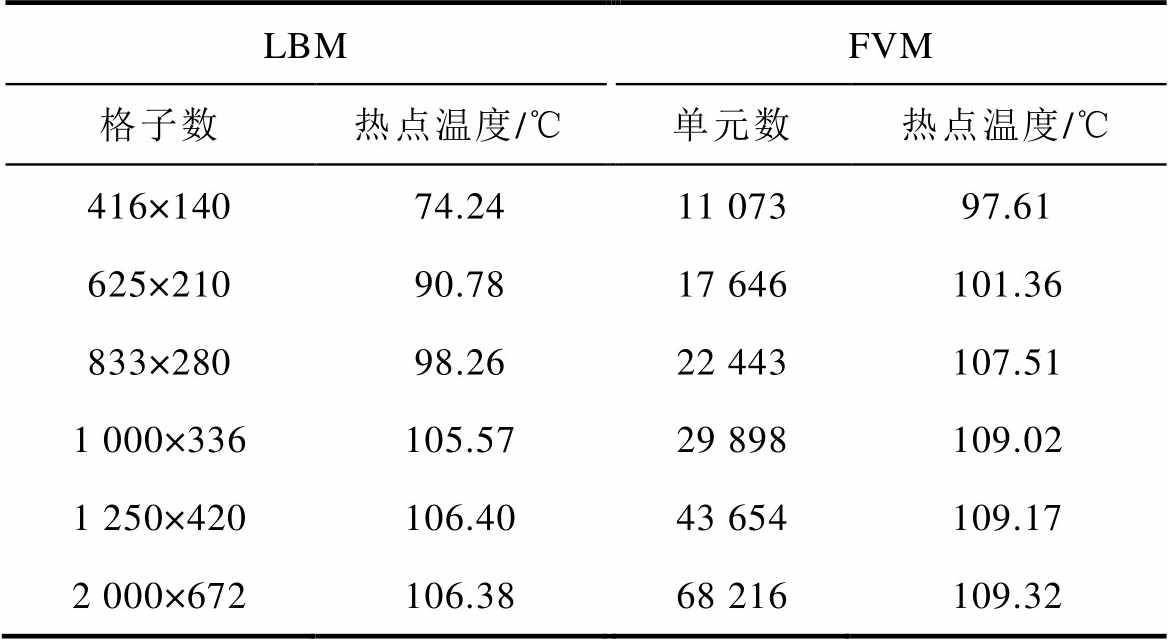
LBMFVM 格子数热点温度/℃单元数热点温度/℃ 416×14074.2411 07397.61 625×21090.7817 646101.36 833×28098.2622 443107.51 1 000×336105.5729 898109.02 1 250×420106.4043 654109.17 2 000×672106.3868 216109.32
为了验证仿真模型的有效性,进而为油浸式变压器的热-流场提供一种可视化和可预测的新途径。本文对其在稳态和瞬态条件下进行了仿真,并分别与FVM计算和变压器负载导则进行了对比。LBM和FVM的运行环境为(CPU:英特尔®酷睿TMi5-13400, 内存:32 GB),LBM完成360 s仿真的计算时长为174 s,运行内存约300 MB,FVM完成360 s仿真的计算时长为265 s,运行内存约350 MB。尽管LBM的格子数高于FVM的单元数,但是与FVM计算相比,LBM控制方程简单,且不需要处理强非线性的对流项[32],因此在速度和内存占用方面有优势,如能采用商业软件对应的加速算法和硬件,该优势还会进一步扩大。
在负载系数为1.0的运行条件下分别对LBM- Simulink模型和FVM计算进行了仿真,经过数次迭代至流速场和温度场稳态时,其LBM计算结果如图5所示,FVM计算结果如图6所示。将LBM和FVM计算所得温度进行数值对比和误差分析,结果见表4,两者顶层油温和热点温度的相对误差分别为0.04%和2.60%,且整体热-流场分布相似,可以得出该仿真模型具有有效性。然而两种方法在流体边界处的计算出现了一定的误差,尤其是在温度T5点处相对误差为22.48%,在瞬态温度场对比图8中也可以得出边界处误差较大。且通过表5中与变压器导则[29]对比不难发现FVM计算结果更接近测量值,因此FVM相较于LBM计算更为准确。但是LBM计算在格子数目较多的情况下仍然可以进行快速计算,从而使得输出的温度场云图更丰富,且能够对顶层油温和热点温度进行快速准确计算有利于进行DTR评估。
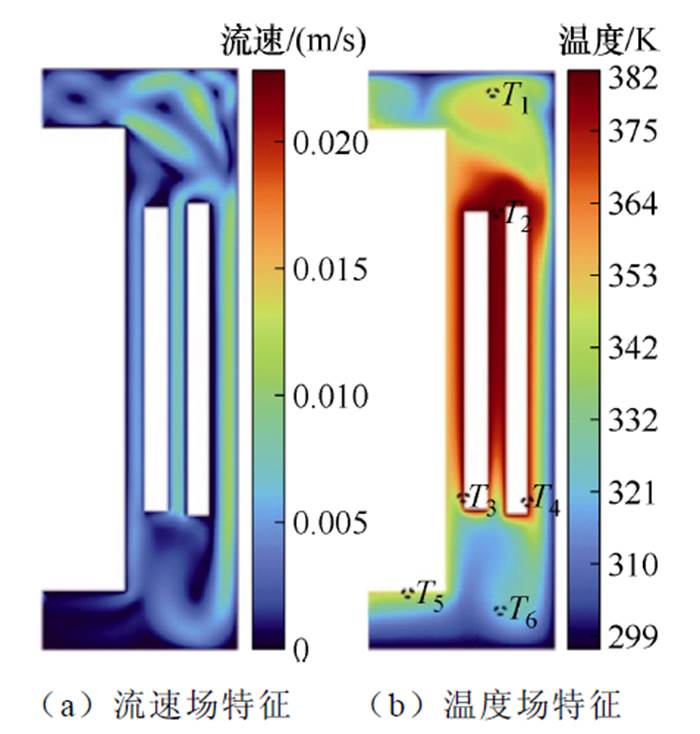
图5 LBM计算下的速度-温度场分布
Fig.5 The velocity-temperature field distribution by LBM calculation
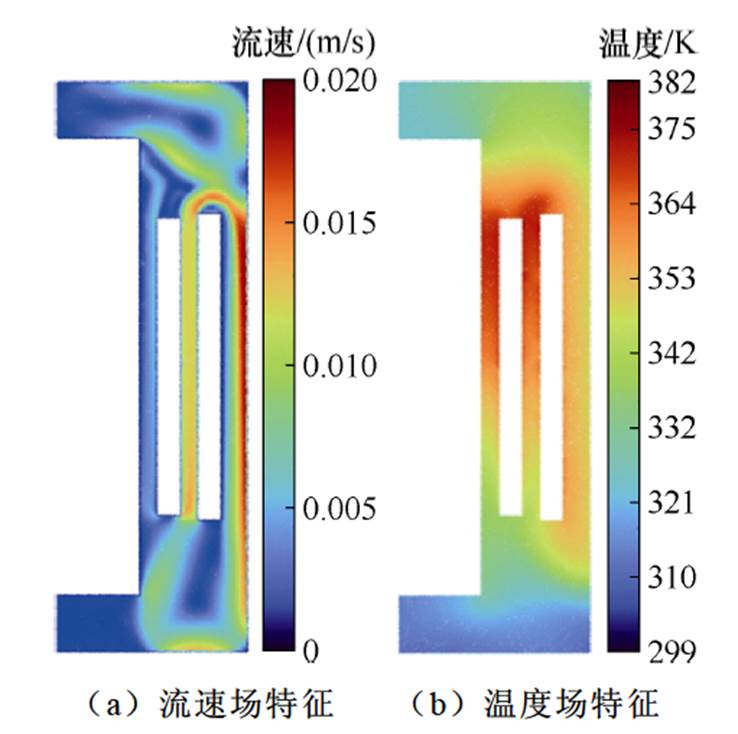
图6 FVM计算下的速度-温度场分布
Fig.6 Velocity-temperature field distribution by FVM calculation
表4 LBM与FVM计算温度结果对比
Tab.4 Comparison of LBM and FVM calculated temperature results
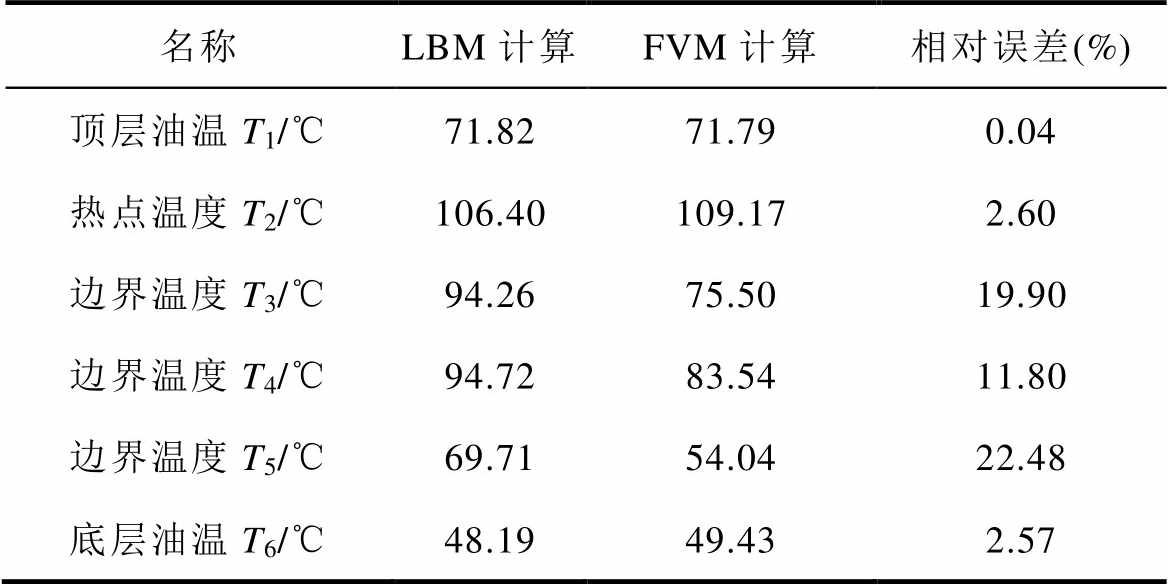
名称LBM计算FVM计算相对误差(%) 顶层油温T1/℃71.8271.790.04 热点温度T2/℃106.40109.172.60 边界温度T3/℃94.2675.5019.90 边界温度T4/℃94.7283.5411.80 边界温度T5/℃69.7154.0422.48 底层油温T6/℃48.1949.432.57
由LBM和FVM计算得出的温度场和流速场仿真结果进行对比可以看出,两种不同的计算方法所得出的热-流场分布相似,均为顶部油温较高,流速较大,低压绕组附近流体的温升最高。根据图5中的温度场可以清晰地看出变压器温升主要是高低压绕组产热,且迅速向变压器绝缘油传递热量,通过绝缘油的流动使其热量上升到变压器顶部再通过外壳进行散热,因此变压器上方温度明显高于下方。从流速场中可以看出绝缘油会因受热而向上方运动,遇冷后冷却并沿着外壳向下流动,进而形成以自然对流为主的流动换热过程,其流速较大的区域出现在绕组附近,如高低压绕组之间和油箱壁与高压绕组之间。这也使得顶层附近会出现较高的油温,且对于顶层的检测也相对容易。因此不少对油浸式变压器的温升和运行状态的检测主要是针对其顶层油温。在本文的研究中顶层油温T1和热点温度T2的检测点设置在图5中所示的位置上。
根据文献[29]中负载导则(以下简称导则)所使用的负载系数,在Simulink环境中设计出与之对应的负载模块,并将其加在搭建好的仿真模型上进行计算,可以检验本模型对不同负载系数下的瞬态温升计算的有效性和准确度。加入导则中的等效负载后,高低压绕组和铁心的温升变化曲线如图7所示,低压绕组温度曲线分布与导则中的附录C热点温度曲线分布趋势一致。
图7中的ABCDEF点分别为不同负载变化时刻,以A点为例,A点对应时刻为190 min,在此之前负载系数为1.0,之后转变为0.6。LBM计算和FVM计算每个时刻对应的热点温度与导则中的计算和测量对比结果见表5。从表中的数据可以得出本文所构建的LBM计算和FVM计算模型,相较于导则中所给出的计算公式而言,LBM计算和FVM计算结果整体相对导则测量数据的误差较小。最大误差均出现在D点时刻,此时的误差值分别为18.47%和19.28%,优于导则计算公式的相对误差。且LBM计算和FVM计算的热点温度之间差值不大,最大误差出现在F点时刻,此时的LBM计算与FVM计算之间的相对误差为6.44%。从而进一步验证了本文所构建的仿真模型的有效性,为变压器温升模拟提供了一种新的方法,这也为接下来的DTR评估提供了模型可靠性的支撑。
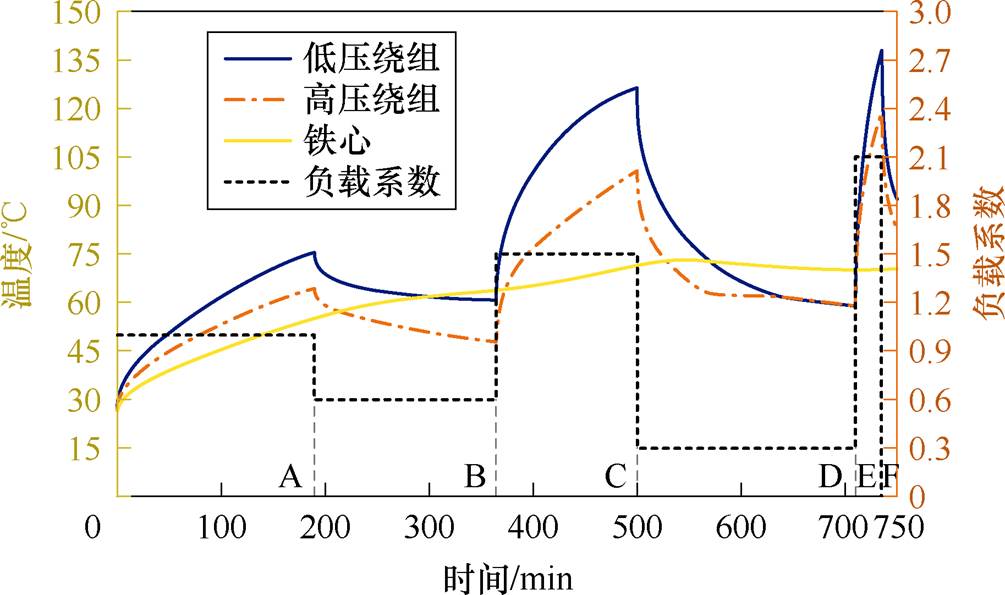
图7 负载系数按级变化时绕组铁心热点温度值
Fig.7 The hot spot temperature value of the winding core when the load coefficient changes step by step
表5 不同方法计算热点温度的结果对比
Tab.5 Comparison of the results of hot spot temperature calculated by different methods
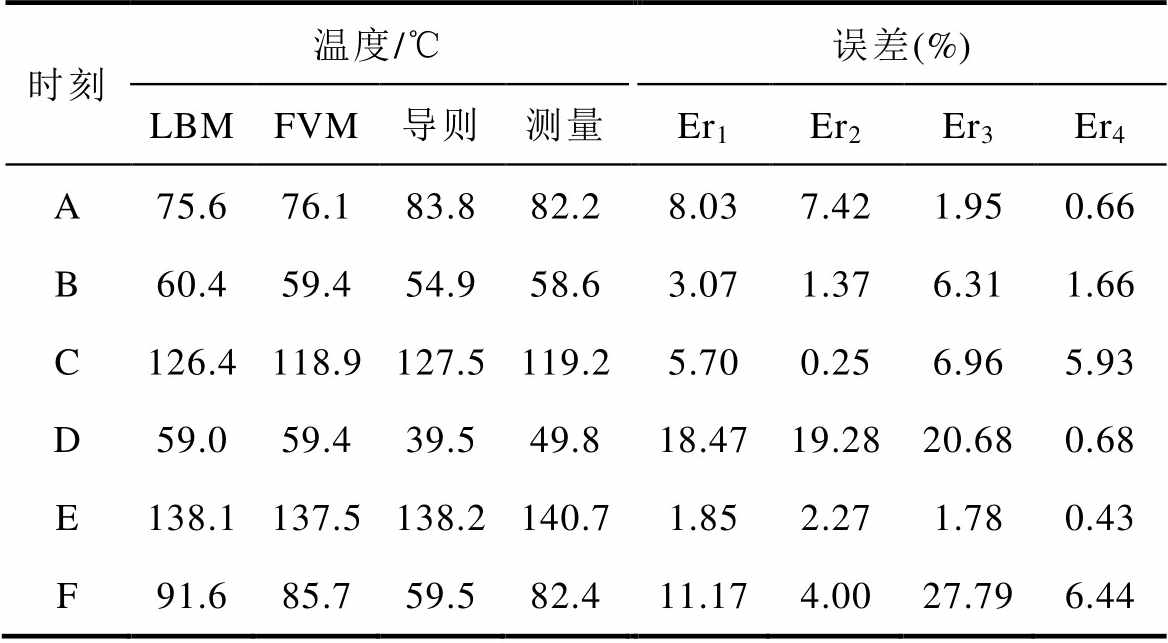
时刻温度/℃误差(%) LBMFVM导则测量Er1Er2Er3Er4 A75.676.183.882.28.037.421.950.66 B60.459.454.958.63.071.376.311.66 C126.4118.9127.5119.25.700.256.965.93 D59.059.439.549.818.4719.2820.680.68 E138.1137.5138.2140.71.852.271.780.43 F91.685.759.582.411.174.0027.796.44
注:Er1、Er2和Er3分别代表LBM、FVM和导则与测量之间的相对误差,Er4代表LBM与FVM之间的相对误差。
在不同负载约束下的LBM瞬态计算和FVM瞬态计算温度场的对比结果如图8所示,虽然在其变压器铁心边界处有一定的误差,但是从图中可以看出其整体的温度场分布相似,均为低压绕组附近的温升较大,绝缘油受热后向上运动,使得变压器上方的温度高于下方。随着负载的波动,温度场的特性与负载系数和运行的时间有关,如图8中的E点,虽然LBM和FVM计算的热点温度分别达到了138.1℃和137.5℃,但是由于是负载系数突然从0.3上升到2.1且运行时间很短,因此顶层油温并未升高过多,整体处在60~70℃之间。这时若只对顶层油温进行检测来判断变压器的运行状态,可能会出现变压器局部过热和绝缘寿命严重损失问题,因此对热点温度的快速准确预测和计算是进行DTR评估的关键。
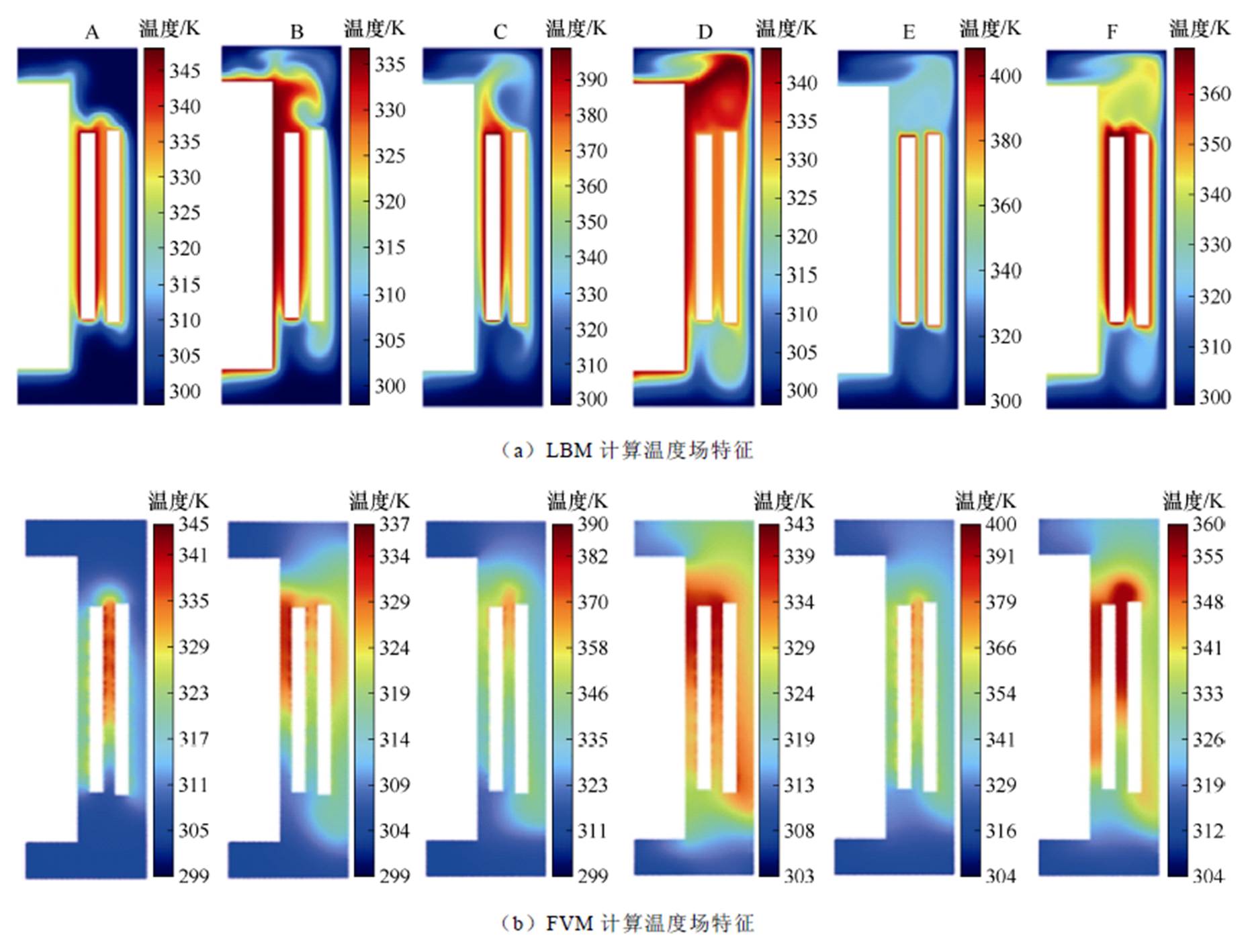
图8 负载系数按级变化时各点温度场特性
Fig.8 The temperature field characteristics of each point when the load coefficient changes step by step
为了使得变压器能够更合理的带负载运行,本文将对不同负载系数和是否考虑环境温度变化情况来对变压器进行负载评估。除了需要满足温升不超过其阈值之外,还要考虑到绝缘寿命的损失情况,变压器运行的约束条件[6]为
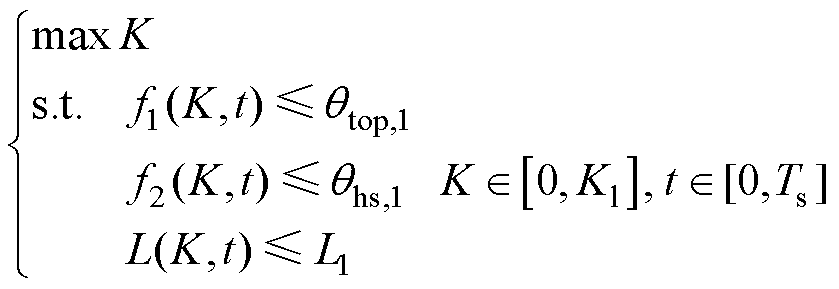 (11)
(11)
式中,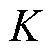 为负载系数;
为负载系数;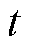 为变压器的运行时间;
为变压器的运行时间;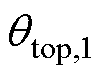 为变压器顶层油温;
为变压器顶层油温;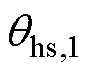 为变压器热点温度;
为变压器热点温度;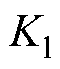 为辅助设备如分接头、套管等容量等级阈值;
为辅助设备如分接头、套管等容量等级阈值;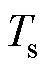 为变压器运行周期;
为变压器运行周期;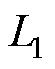 为寿命损失阈值。
为寿命损失阈值。
根据变压器导则[29],采用热改性绝缘纸的变压器,一个周期内的相对寿命损失为
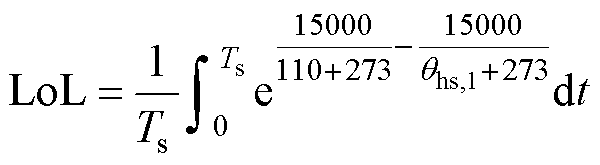 (12)
(12)
当环境温度设置为恒定的25℃时,对不同负载系数进行了顶层油温、热点温度和相对绝缘寿命损失评估进行了仿真。其中不同负载系数下的最大热点温度、顶层油温和相对绝缘寿命损失见表6。
根据表6中的结果,当负载系数超过1.20时,温升对绝缘寿命的影响将会大幅提升,从而可能对变压器造成严重的损害。且顶层油温由于流体和外界换热的因素影响,可能会出现测量误差,故不能仅对顶层油温进行测量来判断变压器的运行状态。因此建议变压器在常温环境下(25℃)时,负载系数应不超过1.20,以减少对变压器寿命的损害。
表6 环境温度25℃下仿真结果
Tab.6 Simulation results at ambient temperature of 25℃
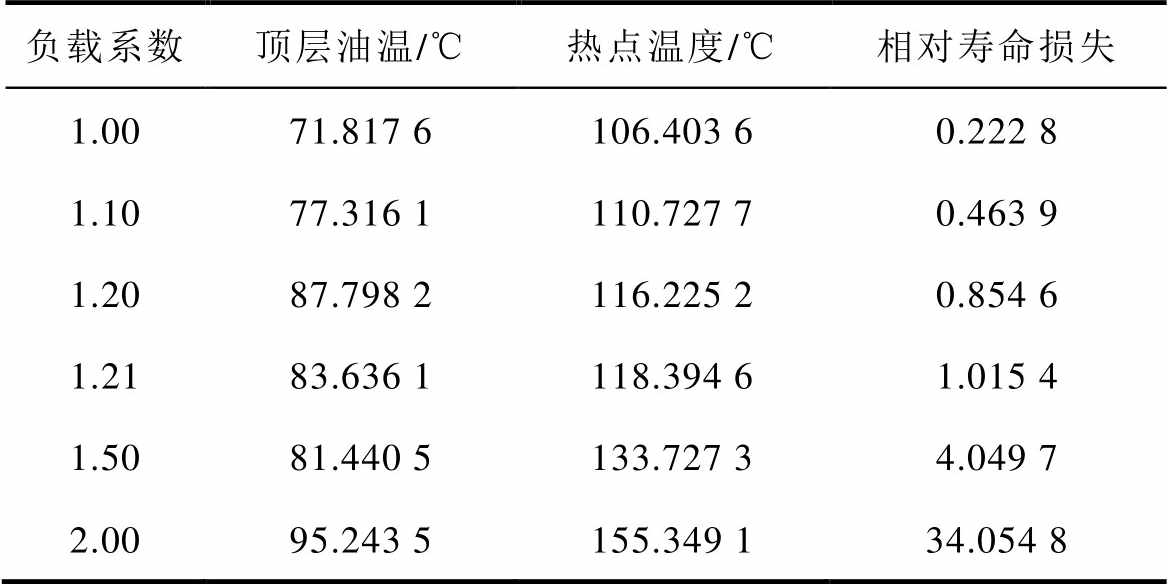
负载系数顶层油温/℃热点温度/℃相对寿命损失 1.0071.817 6106.403 60.222 8 1.1077.316 1110.727 70.463 9 1.2087.798 2116.225 20.854 6 1.2183.636 1118.394 61.015 4 1.5081.440 5133.727 34.049 7 2.0095.243 5155.349 134.054 8
考虑到变压器在实际运行过程中,环境温度的变化对其换热的影响,本文以典型的夏季和冬季温度变化曲线作为该模型的环境温度输入[6]。其温度变化曲线如图9所示,并模拟变压器在6 00—18
00—18 00的温升情况和对其不同负载系数进行仿真分析。
00的温升情况和对其不同负载系数进行仿真分析。
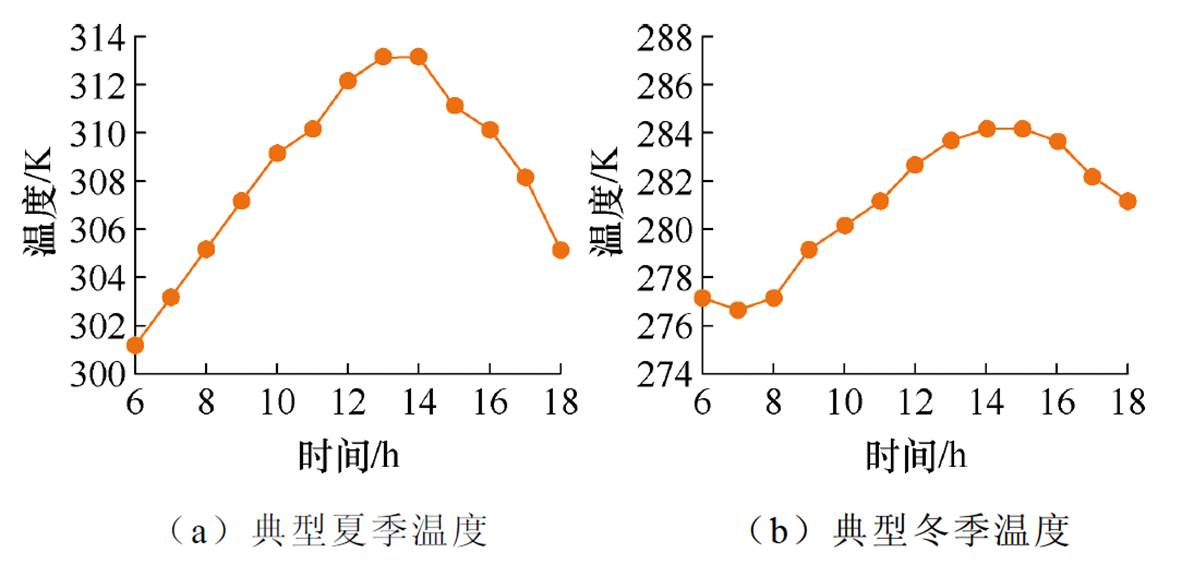
图9 典型季节温度曲线
Fig.9 Typical seasonal temperature curves
1)典型夏季温度下负载评估
在典型夏季环境温度变化下,对不同负载系数情况进行仿真分析,其结果见表7。
表7 典型夏季环境温度下仿真结果
Tab.7 Simulation results under typical summer ambient temperature
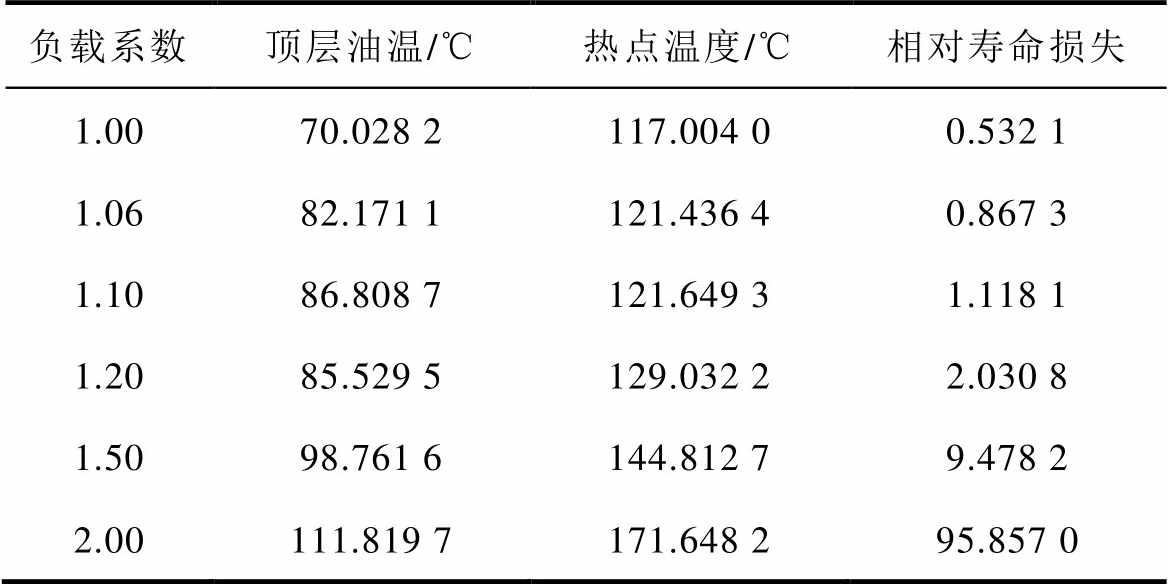
负载系数顶层油温/℃热点温度/℃相对寿命损失 1.0070.028 2117.004 00.532 1 1.0682.171 1121.436 40.867 3 1.1086.808 7121.649 31.118 1 1.2085.529 5129.032 22.030 8 1.5098.761 6144.812 79.478 2 2.00111.819 7171.648 295.857 0
从表7中可以得出环境温度的升高会使得其顶层油温和热点温度更容易升高,尤其是顶层油温相较于常温下上升的相对百分比更大。且由于散热的减小,变压器绝缘性能此时容易被损坏,如负载系数为1.0时,其热点温度已经超过了改性绝缘纸所要求的110℃,但是其一个周期内的相对寿命损失未达到阈值,这也是变压器可以在短时温升允许超过其绝缘等级所限制的温度,只需要低于其设计的阈值即可。因此在夏季时,变压器的带负载能力应不超过1.10。
2)典型冬季温度下负载评估
在典型冬季环境温度变化下,对不同负载系数情况进行仿真分析,其结果见表8。表8中可以得出环境温度的降低会使得其顶层油温和热点温度升高的速度降低。因此在冬季时,变压器的带负载能力可以得到提升,但是不应超过1.60。
表8 典型冬季环境温度下仿真结果
Tab.8 Simulation results under typical winter ambient temperature
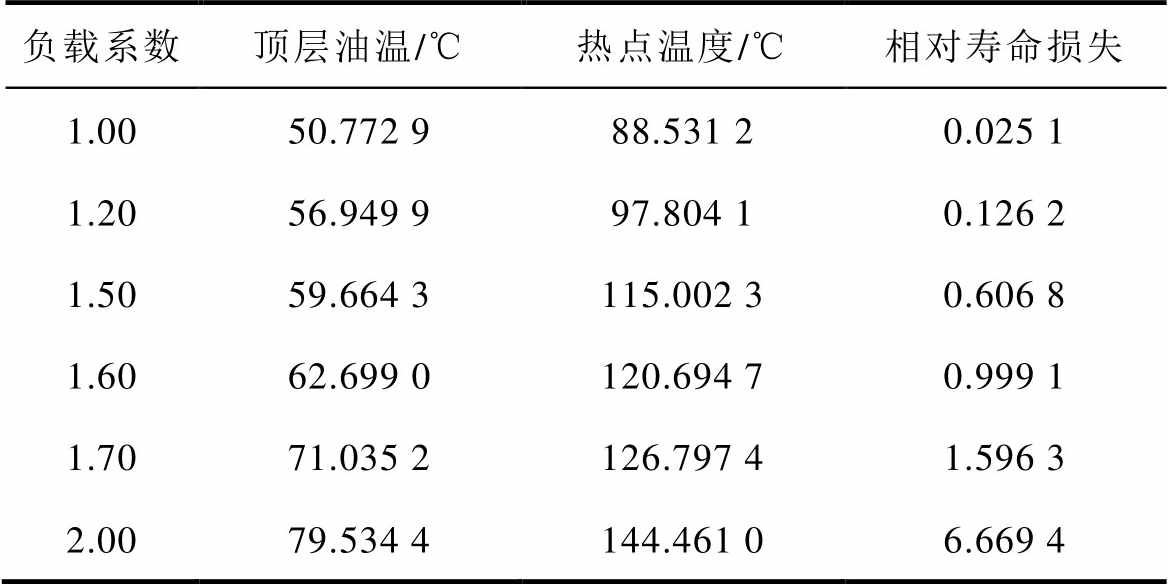
负载系数顶层油温/℃热点温度/℃相对寿命损失 1.0050.772 988.531 20.025 1 1.2056.949 997.804 10.126 2 1.5059.664 3115.002 30.606 8 1.6062.699 0120.694 70.999 1 1.7071.035 2126.797 41.596 3 2.0079.534 4144.461 06.669 4
从以上的仿真结果中可以得出,在不同的环境温度下,变压器的带负载能力发生了明显的变化,随外界温度的变化呈现负相关性,其中顶层油温受环境温度的影响较大,而热点温度主要受到负载系数的影响。这一研究结果可以为油浸式变压器在不同地区和不同季节运行时提供一定的依据,从而提高变压器的有效利用率,提高电力资源和经济效益。值得注意的是本文是对其变压器短时运行的DTR进行的评估,若现场长期定负载运行的变压器则需要严格地满足其设计限制的阈值。
1)本文构建了基于显式LBM的油浸式变压器瞬态温升计算模型,实现了变压器内部温度场和流速场的快速分析。将其稳态和瞬态计算结果与FVM计算结果对比,热点温度相对误差分别为2.60%和6.44%。验证了模型有效性,从而为现场运行变压器的负载能力评估和检测提供了一定的参考。
2)将开发的油浸式变压器LBM瞬态温升模型进行数值封装,通过与电流源等效电路仿真模型集成构建了物理在环的瞬态热仿真模型。将负载导则中对应的负载系数和运行时间作为输入,输出结果相比导则中给出的计算结果更接近于实际测量温升数值,且温升变化曲线与导则一致。
3)将搭建好的物理在环的瞬态热仿真模型应用于DTR评估。结果表明在环境温度25℃时变压器的带负载能力在相对绝缘寿命损失小于1的情况下为1.20;在以典型夏季和冬季环境温度变化时,变压器带负载能力分别为1.10和1.60。
4)后续将对考虑谐波和三相不平衡等复杂的外部等效电路和环境进行系统建模,并对所提出的LBM模型进行相应修改封装,实现对现场更为复杂运行环境约束下的DTR实时评估。
参考文献
[1] 郑玉平, 郝治国, 薛众鑫, 等. 大型电力变压器安全运行与主动保护技术探索[J]. 电力系统自动化, 2023, 47(20): 1-12.
Zheng Yuping, Hao Zhiguo, Xue Zhongxin, et al. Exploration of safe operation and active protection technology for large-capacity power transformers[J]. Automation of Electric Power Systems, 2023, 47(20): 1-12.
[2] Li Shuaibing, Li Xinchen, Kang Yongqiang, et al. Load capability assessment and enhancement for transformers with integration of large-scale renewable energy: a brief review[J]. Frontiers in Energy Research, 2022, 10: 1002973.
[3] Daminov I, Prokhorov A, Caire R, et al. Assessment of dynamic transformer rating, considering current and temperature limitations[J]. International Journal of Electrical Power & Energy Systems, 2021, 129: 106886.
[4] 李元, 刘宁, 梁钰, 等. 基于温升特性的油浸式变压器负荷能力评估模型[J]. 中国电机工程学报, 2018, 38(22): 6737-6746.
Li Yuan, Liu Ning, Liang Yu, et al. A model of load capacity assessment for oil-immersed transformer by using temperature rise characteristics[J]. Proceedings of the CSEE, 2018, 38(22): 6737-6746.
[5] Alvarez D L, Rivera S R, Mombello E E. Transformer thermal capacity estimation and prediction using dynamic rating monitoring[J]. IEEE Transactions on Power Delivery, 2019, 34(4): 1695-1705.
[6] 董旭柱, 张琛, 阮江军, 等. 油浸式电力变压器动态载荷评估技术研究与应用[J]. 高电压技术, 2021, 47(6): 1959-1968.
Dong Xuzhu, Zhang Chen, Ruan Jiangjun, et al. Research and practices of dynamic thermal rating for oil-immersed power transformer[J]. High Voltage Engineering, 2021, 47(6): 1959-1968.
[7] Zhang Chen, Dong Xuzhu, Ruan Jiangjun, et al. Dynamic thermal rating assessment of oil-immersed power transformers for multiple operating con- ditions[J]. High Voltage, 2024, 9(1): 195-205.
[8] 李大建. 油浸式变压器温度场分析与油流对内部温升影响因素研究[D]. 成都: 西南交通大学, 2013.
Li Dajian. Analysis of temperature field of oil- immersed transformer and study on influence factors of oil flow on internal temperature rise[D]. Chengdu: Southwest Jiaotong University, 2013.
[9] 谭又博, 余小玲, 臧英, 等. 谐波电流对换流变压器绕组损耗及温度分布特性的影响[J]. 电工技术学报, 2023, 38(2): 542-553.
Tan Youbo, Yu Xiaoling, Zang Ying, et al. The influence of harmonic current on the loss and temperature distribution characteristics of a converter transformer winding[J]. Transactions of China Elec- trotechnical Society, 2023, 38(2): 542-553.
[10] 刘云鹏, 黎晏霖, 李欢, 等. 基于布里渊光时域峰值边沿分析的变压器绕组局部热点检测[J]. 电工技术学报, 2024, 39(11): 3486-3498.
Liu Yunpeng, Li Yanlin, Li Huan, et al. Local hot spot detection of transformer windings based on Brillouin optical time domain peak edge analysis[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3486-3498.
[11] 张立静, 盛戈皞, 倪子瞻, 等. 油浸式电力变压器匝间故障早期的电热特性研究[J]. 中国电机工程学报, 2023, 43(15): 6124-6136.
Zhnag Lijing, Sheng Gehao, Ni Zizhan, et al. Study on electrothermal characteristics of oil-immersed power transformers in early stage of interturn faults[J]. Proceedings of the CSEE, 2023, 43(15): 6124-6136.
[12] 林晓明, 陈则徐, 陈宇, 等. 基于“磁-热-流”耦合的三绕组有载调压变压器涡流损耗与温度场仿真分析[J]. 变压器, 2023, 60(6): 20-24.
Lin Xiaoming, Chen Zexu, Chen yu, et al. Simulation analysis of eddy current loss and temperature field of three-winding transformer based on “magnetic-heat- flow” coupling[J]. Transformer, 2023, 60(6): 20-24.
[13] 谢裕清, 李琳, 宋雅吾, 等. 油浸式电力变压器绕组温升的多物理场耦合计算方法[J]. 中国电机工程学报, 2016, 36(21): 5957-5965, 6040.
Xie Yuqing, Li Lin, Song Yawu, et al. Multi-physical field coupled method for temperature rise of winding in oil-immersed power transformer[J]. Proceedings of the CSEE, 2016, 36(21): 5957-5965, 6040.
[14] 刘刚, 郝世缘, 朱章宸, 等. 基于动态模态分解-自适应变步长油浸式电力变压器绕组瞬态温升快速计算方法[J]. 电工技术学报, 2024, 39(12): 3895- 3906.
Liu Gang, Hao Shiyuan, Zhu Zhangchen, et al. Research on rapid calculation method of transient temperature rise of winding of dynamic mode decomposition-adaptive time stepping oil-immersed power transformer[J]. Transactions of China Elec- trotechnical Society, 2024, 39(12): 3895-3906.
[15] 刘云鹏, 刘一瑾, 刘刚, 等. 电力变压器智能运维的数字孪生体构想[J]. 中国电机工程学报, 2023, 43(22): 8636-8652.
Liu Yunpeng, Liu Yijin, Liu Gang, et al. Digital twin conception of intelligent operation and maintenance of power transformer[J]. Proceedings of the CSEE, 2023, 43(22): 8636-8652.
[16] 刘刚, 郝世缘, 胡万君, 等. 基于子循环自适应串行交错时间匹配算法的油浸式变压器绕组瞬态温升计算[J]. 电工技术学报, 2024, 39(4): 1185-1197.
Liu Gang, Hao Shiyuan, Hu Wanjun, et al. Transient temperature rise calculation of oil immersed transformer winding based on sub cyclic adaptive staggered time matching algorithm[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1185- 1197.
[17] 段辞涵, 阮江军, 邓永清, 等. 变压器温度场计算边界辐射-对流复合换热等效方法研究[J]. 电机与控制学报, 2020, 24(10): 120-129.
Duan Cihan, Ruan Jiangjun, Deng Yongqing, et al. Study on equivalent method of boundary radiation- convection heat transfer for transformer temperature field calculation[J]. Electric Machines and Control, 2020, 24(10): 120-129.
[18] 荆澜涛, 董雪情, 杨超, 等. 面向数字孪生应用的变压器温度场有限元降阶建模方法研究[J]. 高电压技术, 2023, 49(6): 2408-2419.
Jing Lantao, Dong Xueqing, Yang Chao, et al. Research on finite element reduced order modeling method of transformer temperature field for digital twin application[J]. High Voltage Engineering, 2023, 49(6): 2408-2419.
[19] 骆仁松, 汪涛, 文继峰, 等. 大功率高频变压器三维温升计算及优化设计方法[J]. 电工技术学报, 2023, 38(18): 4994-5005, 5016.
Luo Rensong, Wang Tao, Wen Jifeng, et al. Three- dimensional temperature calculation and optimization design method for high power high-frequency trans- former[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4994-5005, 5016.
[20] Nazarafkan H, Mehmandoust B, Toghraie D, et al. Numerical study of natural convection of nanofluid in a semi-circular cavity with lattice Boltzmann method[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2020, 30(5): 2625-2637.
[21] Hasani Malekshah E, Kolsi L. Local/volumetric entropy production analysis of natural convective flow using lattice Boltzmann method for heat exchanger application[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2024, 34(2): 520-538.
[22] Shruti B, Alam M M, Parkash A, et al. LBM study of natural convection heat transfer from a porous cylinder in an enclosure[J]. Theoretical and Com- putational Fluid Dynamics, 2022, 36(6): 943-967.
[23] Sobhani M, Ajam H. Taguchi optimization for natural convection heat transfer of Al2O3 nanofluid in a partially heated cavity using LBM[J]. Journal of Thermal Analysis and Calorimetry, 2019, 138(2): 889-904.
[24] Chelia W, Laouer A, Mezaache E H, et al. Investigation of nanofluid natural convection inside a square cavity for two orientations using lattice Boltzmann method[J]. Journal of Nanofluids, 2023, 12(4): 889-903.
[25] 曾非同, 关向雨, 黄以政, 等. 基于多尺度多物理场的油浸式变压器流动-传热数值研究[J]. 电工技术学报, 2020, 35(16): 3436-3444.
Zeng Feitong, Guan Xiangyu, Huang Yizheng, et al. Numerical study on flow-heat transfer of oil- immersed transformer based on multiple-scale and multiple-physical fields[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3436-3444.
[26] Tiftikci A, Catalbas S S, Polat E, et al. Investigation of natural convection heat transfer of self-heating packed beds[J]. International Communications in Heat and Mass Transfer, 2023, 142: 106642.
[27] Guan Xiangyu, Shu Naiqiu, Peng Hui. LBM simulation of heat transfer processes inside GIS capsule filled with different insulation gas mixtures[J]. Mathematics and Computers in Simulation, 2021, 188: 212-225.
[28] Power transformers-part 7: loading guide for oil- immersed power transformers: IEC 60076-7-2018[S]. London, England: IEC, 2018.
[29] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 电力变压器 第7部分: 油浸式电力变压器负载导则: GB/T 1094.7-2008[S]. 北京: 中国标准出版社, 2009.
[30] Mohamad A A. Lattice Boltzmann method[M]. London: Springer, 2011.
[31] Peng Y, Shu C, Chew Y T. Simplified thermal lattice Boltzmann model for incompressible thermal flows[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2003, 68(2 Pt 2): 026701.
[32] Sikdar P, Dash S M, Sinhamahapatra K P. A flexible forcing immersed boundary scheme-based one-step simplified lattice Boltzmann method for two- dimensional fluid-solid interaction problems[J]. Com- puters & Fluids, 2023, 265: 105996.
Abstract The dynamic transformer rating (DTR) and thermal life loss of oil-immersed transformers under on-site variable load operation conditions are closely related to the transient temperature rise of the equipment. However, as an implicit solution method, the traditional finite element analysis and finite volume method need to be iteratively solved in each sub-step of transient thermal analysis, which has many computational resources and is time consuming. It is challenging to meet the requirements of fast calculation. The rapid and accurate solution of the temperature field (especially the hot spot temperature rise) of the oil-immersed transformer in field operation is the premise to realize the digital operation and maintenance of the transformer and the DTR evaluation. Therefore, this paper proposes a lattice Boltzmann (LBM) physical in the loop simulation model for coupled electrical networks. The real time evaluation of DTR under electrical network constraints is realized through the rapid solution of the transformer temperature field.
Firstly, the D2Q9 model is used to solve the fluid flow and thermal lattice Boltzmann equations (LBEs) to capture the transient oil flow and temperature rise process inside the transformer. In the Simulink environment, the equivalent current source model is used to construct the electrical network constraints of multi-level load scenarios, and the established transformer LBM model is used as a component for numerical encapsulation to complete the construction of the physical-in-the-loop simulation model. Secondly, to verify the effectiveness of the proposed method, the finite volume method (FVM) is used to simulate the same oil-immersed transformer model. The grid independence test determines the optimal number of grids. The number of grids is 1 250×420 for LBM modeling and simulation, and the number of units is 43 654 for FVM meshing. Compared with the constructed LBM-Simulink model with the FVM model, LBM still has the advantages of speed and memory occupation when the number of lattices is higher than the number of FVM units. If commercial software is used, this advantage will be further expanded. Thirdly, the steady state solution results of the hot spot temperature rise of the established LBM model are compared with the FVM solution, and the error is 2.60%. According to the load curve given in the transformer guidelines, it is used as input to solve the transient temperature rise of the established LBM and FVM simulation models. Finally, the results show that the LBM and FVM calculations are better than the transformer guide calculation. The maximum error between the hot spot temperature calculated by LBM and FVM is 6.44%. Moreover, the hot spot temperature rise trend of LBM is consistent with the transformer load guidelines, which verifies the effectiveness of the proposed method.
Based on the constructed LBM model, the load capacity of oil-immersed transformers under constant 25℃ and typical ambient temperature changes in summer and winter are evaluated at 6~18 hours during the day. The results show that under the premise that the relative insulation life loss of oil-immersed transformers is less than 1. The maximum load capacity coefficients are 1.20, 1.10, and 1.60 under the constant ambient temperature of 25℃, typical temperature changes in summer, and typical temperature changes in winter. The simulation model based on the proposed LBM provides an effective method for real-time monitoring of temperature rise, load capacity evaluation, and dynamic capacity increase of oil-immersed transformers.
keywords:Oil-immersed transformer, dynamic transformer rating (DTR), Lattice Boltzmann method (LBM), relative insulation life
中图分类号:TM411
DOI: 10.19595/j.cnki.1000-6753.tces.240772
福建省自然科学基金资助项目(2020J01509)。
收稿日期 2024-05-13
改稿日期2024-07-17
于文旭 男,2000年生,硕士研究生,研究方向为电气设备在线监测技术。
E-mail: wenxuyu0919@qq.com
关向雨 男,1986年生,副教授,硕士生导师,研究方向为电气状态检测和故障诊断和设备多场耦合数值仿真技术等。
E-mail: xiangyuguan1986@163.com(通信作者)
(编辑 郭丽军)