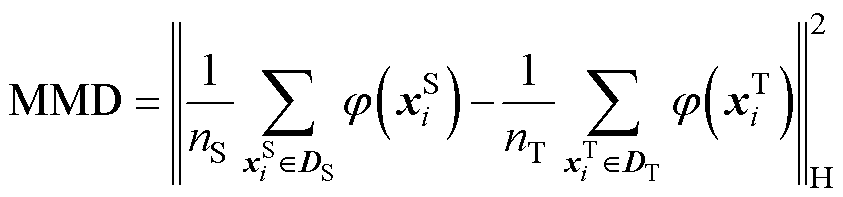 (1)
(1)
摘要 面对新能源电力系统运行场景的复杂多变性,基于深度学习的电力系统暂态稳定评估模型难以维持原有的评估性能。为此,该文提出一种面向运行场景变化的判别式域适应暂态稳定评估框架。首先,在对齐源域和目标域边缘概率分布的同时,利用贝叶斯定理进一步对齐条件概率分布,以实现最大限度的域适应。其次,在域适应中,综合考虑均值差异和方差差异,构建一种新的迁移正则项来度量域间分布差异,以进一步提高模型的域适应能力。最后,设计了一种可调参数的判别式Softmax函数,旨在通过调整参数来促使类内样本特征更加紧凑,同时迫使类间样本特征相互远离,从而获得更具判别性的暂态稳定性特征,以提高评估模型对电网的适用性。在新英格兰10机39节点系统和中国西南某省电网上的算例,验证了所提方法在新场景样本匮乏的情况下的有效性和泛化性。
关键词:暂态稳定评估 判别式域适应 边缘概率分布 条件概率分布
随着大规模可再生能源和电力电子设备的不断接入,电力系统的安全稳定机理日益复杂[1]。保障电力系统安全稳定运行已成为严峻的技术挑战,对电力系统暂态稳定性的准确评估则显得尤为重要[2]。因此,建立可靠、快速的暂态稳定评估(Transient Stability Assessment, TSA)模型,及时识别潜在的暂态稳定风险,以确保电网在新形势下安全稳定运行,变得十分迫切[3]。
在应对时变性高、复杂性强[4]的高渗透率新能源并入电网时,传统的TSA方法,如时域仿真法[5]和直接法[6]面临难以兼顾精度和速度的难题。在这种情况下,基于机器学习(Machine Learning, ML)的数据驱动型TSA方法通过离线挖掘电气量测数据与暂态稳定性之间的映射关系[7],有效地提高了分析的精度和效率,成为快速稳定性评估技术研究的热点。早期研究多局限于决策树(Decision Tree, DT)[8]、支持向量机(Support Vector Machine, SVM)[9]、随机森林(Random Forest, RF)[10]和K近邻(K Nearest Neighbor, KNN)[11]等一些浅层的ML方法。它们对特征的非线性聚合能力有限[12],求解复杂分类问题时泛化能力受到制约。近年来,深度学习(Deep Learning, DL)技术取得了迅猛发展,引起了学术界对基于DL的暂态稳定评估方法的广泛关注和研究,如堆叠自动编码器(Stacked Auto-Encoder, SAE)[13]、卷积神经网络(Convolutional Neural Network, CNN)[14]、深度置信网络[15]和长短期记忆网络(Long-Short Term Memory, LSTM)[16]等。DL方法相较于浅层的ML方法拥有更强的数据理解能力,能够有效地从高维输入特征中探索复杂和隐含的知识,已被证实在评估效果上表现得更为可靠。
DL模型能够在TSA中表现出优异的性能,这取决于一个隐含假设的成立,即模型的训练数据和实际应用中的数据服从独立同分布[17]。当然,这一假设并不总是成立,因为电力系统在运行过程中可能会遭遇不可预测的动态扰动,如关键设备的突发故障导致的非计划性停运,以及负荷需求的急剧波动等。这种情况下,会导致不同数据分布的出现,进而影响模型性能,甚至出现错误的预测结果。通常,传统方法是采集大量新场景的样本,并重新训练新模型,但这往往需要大量新场景标注样本且耗时过长[18]。在现实中,无法完全重新训练模型去适应新能源电力系统的所有运行场景的变化。
迁移学习因其强大的泛化能力和鲁棒性而成为解决这一问题的有力工具[19]。它通过减小源域与目标域的分布差异,实现了将从有标签的原始场景(源域)中获得的知识转移到有少量标签、甚至没有标签的新场景(目标域)中,从而减少对新场景样本需求[20]。域适应(Domain Adaptation, DA)作为迁移学习的主流方向之一,通过减少不同域之间的分布差异来学习域不变特征,以实现知识的跨域迁移。文献[21]采用SAE提取原始数据的特征,利用最大均值差异(Maximum Mean Discrepancy, MMD)最小化源域与目标域特征之间的差异,以增强模型对于未预见的故障的泛化能力。文献[22]通过引入域对抗训练机制,旨在缩小域间分布差异,达到域混淆的目的,提高样本匮乏阶段模型的暂态稳定评估性能。文献[23]基于对抗性训练,从不同故障的输入数据中提取域不变特征,解决未知故障的数据缺失问题。为了进一步增强域混淆能力,文献[24]通过在对抗训练过程中引入MMD准则,提升特征提取器和域判别器的学习性能,使模型快速且可靠地生成相符的风光时序功率曲线。上述基于DA的方法在迁移任务中均取得了较好的效果,但却存在两个关键问题:①在域适应过程中,它们仅仅关注了两域在特征空间中边缘概率分布的对齐,而忽略了不同域中相同类别的条件概率分布的对齐,导致域混淆能力不足;②几乎所有的DA模型在更新过程中都着重考虑如何确保特征在不同域之间保持一致,而对于特征的判别性学习关注不足,影响了最终任务模型的性能。
针对上述问题,本文提出一种面向运行场景变化的判别式域适应暂态稳定评估(Transient Stability Assessment-Discriminative Domain Adaption, TSA- DDA)框架。针对域适应存在的问题,设计了一种域间双分布自适应对齐方法,以实现更大程度域混淆。此方法提出一种新的条件概率对齐方式,在实现域间边缘概率分布对齐的同时,利用贝叶斯定理进一步对齐相关子领域,实现特征空间中域间分布的精细化对齐,降低模型迁移难度。再有,在该方法中,综合MMD和相关对齐(Correlation Alignment, CORAL),构建一种新的迁移正则项,从均值和方差两个角度衡量不同域间的分布差异,以进一步提高模型的域适应能力。针对特征的判别性学习关注不足的问题,设计了一种参数可调的判别式Softmax函数,旨在迫使同类别样本距离紧凑,不同类别样本相互远离,帮助模型学习更多高区分度的暂态稳定特征,以提高域适应框架在TSA任务中的性能表现。
基于深度学习的TSA旨在探索系统状态(如发电机转速、母线电压、功率流动等)与暂态稳定性之间的映射关系,并通过精炼的数学模型来描绘这种关系,其能够为实践应用提供坚实的理论支撑。但在新能源占比日益增长、电网运行场景复杂多变的背景下,电网暂态稳定状态具有时变性和不确定性,原有深度学习模型可能面临无法准确预测新场景下系统稳定性的挑战。
深度学习模型无法适用于新场景的主要原因是源域与目标域的数据分布不一致。为解决数据分布偏移问题,提出了迁移学习技术。迁移学习问题可以被定义为给定源域DS和源域任务TS、目标域DT和目标域任务TT,利用DS在TS上已学到的知识来辅助DT对TT的学习。在本文TSA问题中,DS指历史运行场景,DT为变化后的新场景,DS与DT的主要区别为运行场景的不同,如负荷变化、线路开断、设备投切等。在这类问题中,由于电力系统核心运行的物理机制一致,尽管DS与DT的数据分布发生了变化,但是两域的特征空间没有发生改变,迁移学习将这种情况归为域适应问题。当源域和目标域样本数据存在分布差异时,域适应需要识别和学习域间不变的特征来提升模型在新的目标域上的性能。在TSA中,域适应需要从源域和目标域之间存在差异的电气量测数据中,提取与暂态稳定评估任务相关但与运行场景无关的共性特征,从而缓解数据分布偏移的影响,进而提升暂态稳定评估模型在不同运行场景的适用性。
在域适应中,选择适当的迁移正则项以度量源域和目标域间的分布差异至关重要。MMD和CORAL是使用最为广泛的两种度量方式。
MMD可以衡量不同域数据分布之间的差异性,其定义为
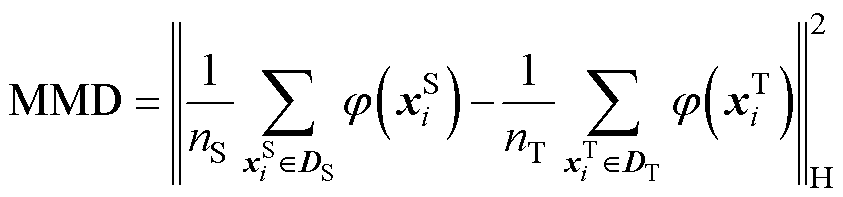 (1)
(1)
式中,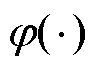 为样本数据到再生核希尔伯特空间的映射函数;
为样本数据到再生核希尔伯特空间的映射函数;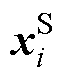 、
、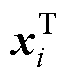 分别为源域和目标域的第
分别为源域和目标域的第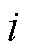 个样本;
个样本;
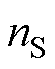 与
与
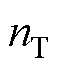 分别为源域与目标域样本个数。
分别为源域与目标域样本个数。
选择高斯核作为核函数,即
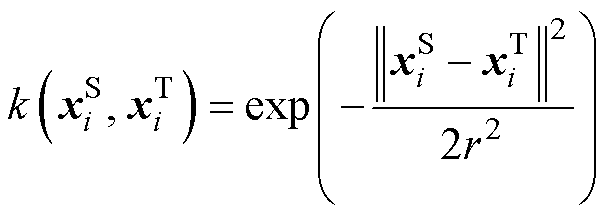 (2)
(2)
式中,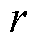 为高斯滤波器的宽度。
为高斯滤波器的宽度。
MMD的无偏估计可以定义为
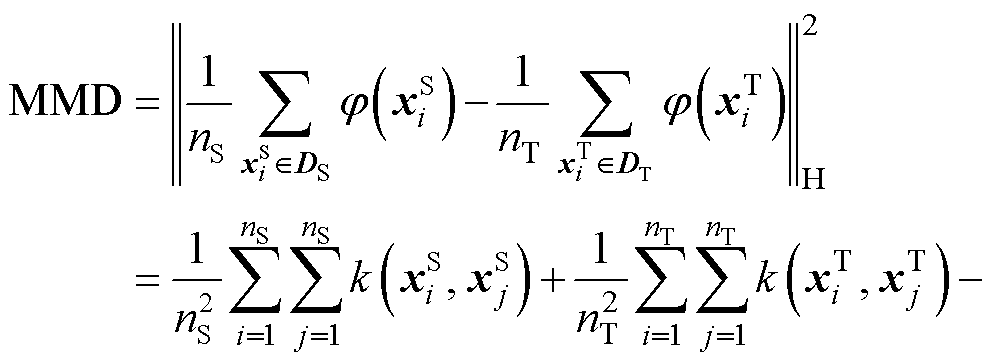
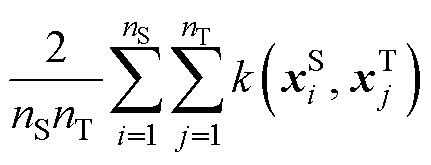 (3)
(3)
利用MMD的域适应学习方法,将源域和目标域数据映射至潜在的共同特征空间,以评估两域数据在该空间的均值差异。该学习过程通过调整模型参数,以降低源域与目标域在特征空间中的MMD值,从而实现特征表示的一致性,减少两域之间的分布差异。
与MMD在再生核希尔伯特空间中对齐源域和目标域的均值对应,CORAL旨在匹配两域的二阶协方差统计信息,其定义为
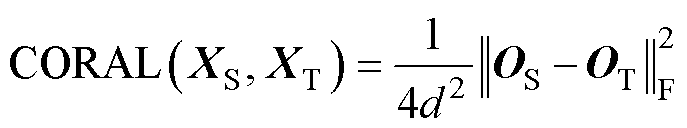 (4)
(4)
式中,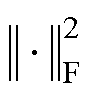 为特征矩阵的Frobenius范数;
为特征矩阵的Frobenius范数;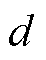 为特征的维度,用以归一化;
为特征的维度,用以归一化;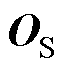 与
与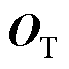 分别为源域和目标
分别为源域和目标
域的协方差矩阵,其定义为
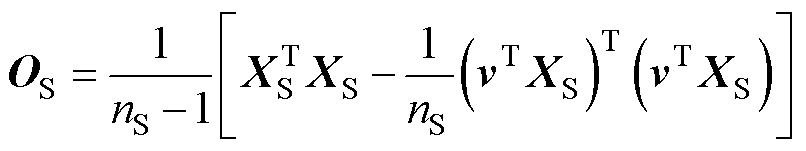 (5)
(5)
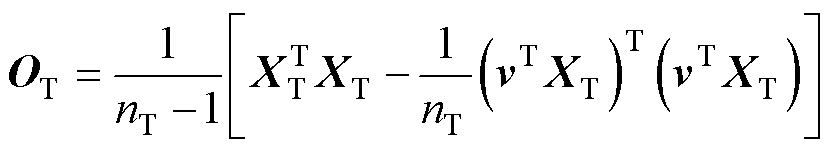 (6)
(6)
式中,XS、XT分别为源域和目标域的样本特征矩阵;v为所有元素都为1的列向量。通过最小化源域和目标域在特征空间中的协方差矩阵之间的差异,CORAL不仅对齐了两域的特征相关性(非对角元素),也对齐了两域特征的方差(对角元素)。因此,CORAL在一定程度上能够反映和减少两域间的方差差异。
由1.2节可知,MMD侧重源域和目标域之间的均值差异,CORAL则关注方差的相似性。图1展示了新英格兰10机39节点系统(源域)和调整运行方式后新场景下系统(目标域)的暂态稳定数据均值和方差的概率密度分布。可以明显看出,两域的暂态稳定数据在均值和方差上均显示出差异。若能同时考虑均值和方差信息,则可帮助模型更好地理解两域的数据分布差异。
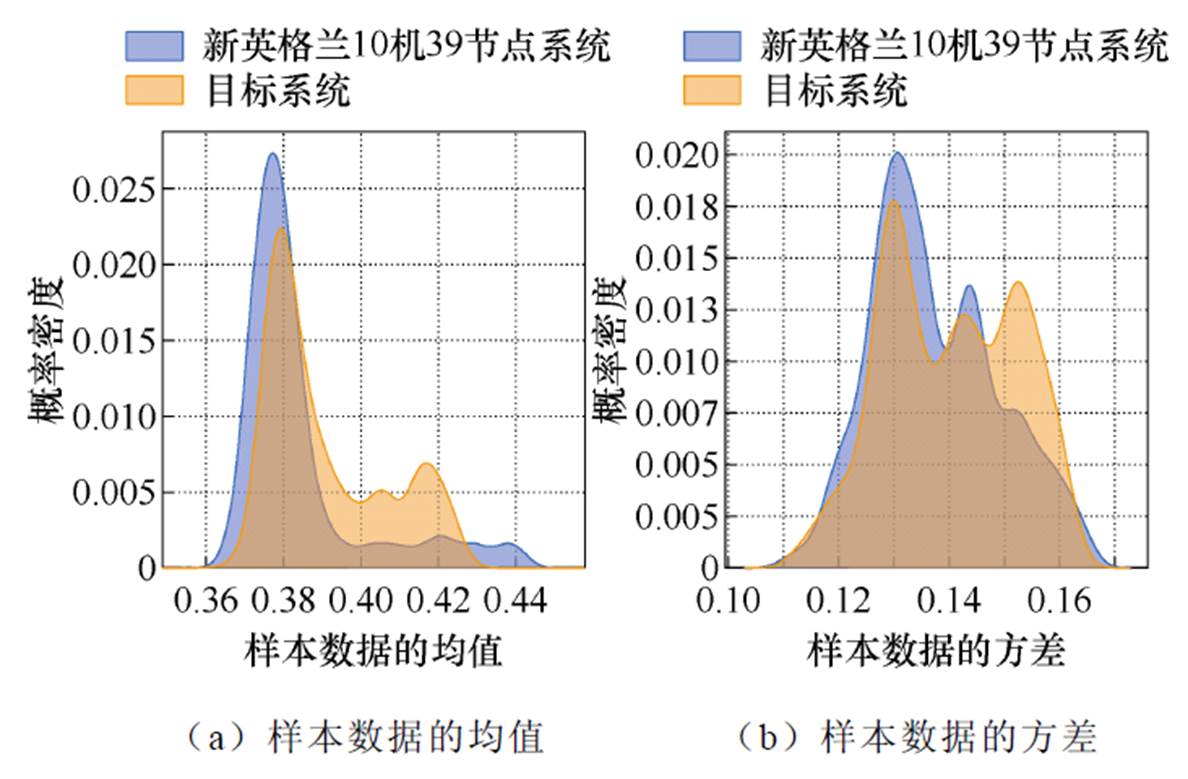
图1 均值和方差的概率密度分布
Fig.1 Probability density distribution of mean and variance
为此,结合两种统计特征,从均值和方差两个角度出发,可设计一种新的迁移正则项MC,定义为
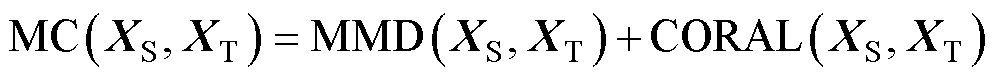 (7)
(7)
在物理意义上,MC迁移正则项不仅能够捕捉数据分布的整体偏移(均值差异),还能够计及数据波动性的不同(方差差异)。这种特性使得MC迁移正则项能够更全面、准确地衡量源域和目标域之间的分布差异,从而提升模型对不同运行场景的适应能力。
本文提出的TSA-DDA框架,如图2所示,由两个共享参数的特征提取器构成,能够在提取暂态稳定特征的同时,挖掘源域和目标域可转移的共性特征,实现自适应暂态稳定评估。其中,特征提取器由具有灵活结构的1维卷积神经网络[25](1D- CNN)构成。采用1D-CNN提取暂态过程的时间序列特征,相比循环神经网络(Recurrent Neural Network, RNN)及其衍生模型,其训练速度更快且不易受梯度问题影响。TSA-DDA框架中源域与目标域的特征对齐采用新的域间双分布自适应方法,该方法通过MC迁移正则项构造损失函数,量化并减少不同域间的边缘概率分布和条件概率分布的差异,从而对齐两域的特征,实现精细化的域适应。另外,为了增强TSA-DDA框架的判别性能,设计了一种新的判别式Softmax函数,该函数通过最大化类间距离和最小化类内距离的方式增强判别能力,从而提高域适应框架的性能表现。
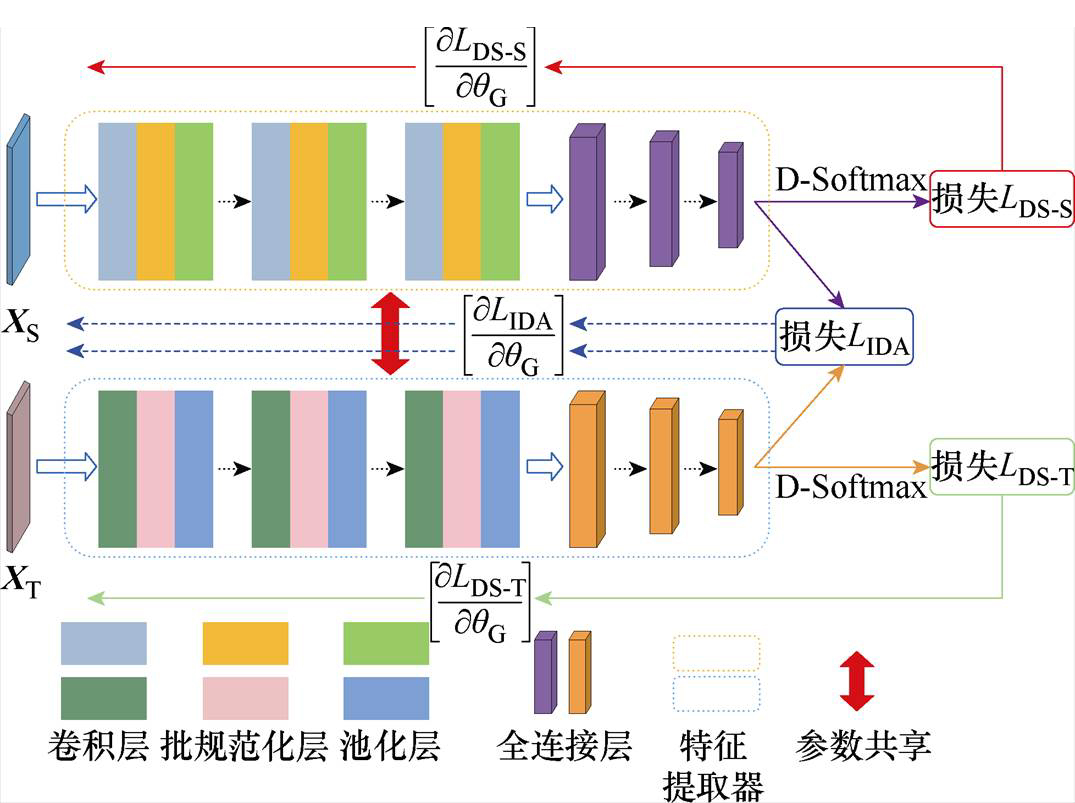
图2 TSA-DDA结构
Fig.2 The TSA-DDA structure
假设源域数据XS对应的类别标签为YS,目标域数据XT对应的类别标签为YT。在TSA中,电网运行场景的变化可能导致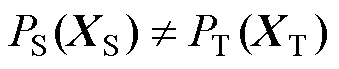 和(或)
和(或)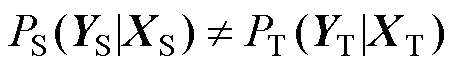 。然而,由于不同运行场景下的电力系统核心运行机制和物理规律的一致性,迁移学习通过缩小特征空间中的域间差异性,使得特征提取器可以获取域间共性的特征信息,从而提升评估模型在新运行场景下的泛化能力。为此,本文提出一种域间双分布自适应方法(Inter-Domain Dual Distribution Adaptation, IDA)。该方法利用MC迁移正则项构造损失函数来度量源域与目标域在边缘概率分布、条件概率分布的差异,并不断迫使特征提取器缩小这些差异,实现两域间特征的有效对齐,提升模型的自适应能力,降低对目标域标注样本的依赖,其具体机理如下:
。然而,由于不同运行场景下的电力系统核心运行机制和物理规律的一致性,迁移学习通过缩小特征空间中的域间差异性,使得特征提取器可以获取域间共性的特征信息,从而提升评估模型在新运行场景下的泛化能力。为此,本文提出一种域间双分布自适应方法(Inter-Domain Dual Distribution Adaptation, IDA)。该方法利用MC迁移正则项构造损失函数来度量源域与目标域在边缘概率分布、条件概率分布的差异,并不断迫使特征提取器缩小这些差异,实现两域间特征的有效对齐,提升模型的自适应能力,降低对目标域标注样本的依赖,其具体机理如下:
首先,由于边缘概率分布直接影响了样本整体的分布特征,因此引入边缘概率分布对齐机制(Marginal Probability Distribution Alignment, MPDA),其损失函数LMPDA定义为
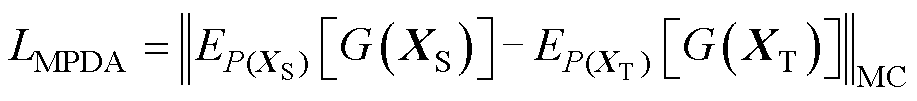 (8)
(8)
式中,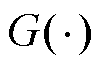 为特征提取函数;
为特征提取函数;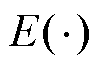 为数学期望函数;
为数学期望函数;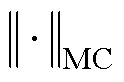 为MC迁移正则项。LMPDA被用于度量域间的边缘概率分布距离,旨在确保源域和目标域之间的整体分布一致性。LMPDA即使在不考虑类别标签的情况下,也能维持特征的相似性,从而可以提高模型的泛化性和鲁棒性。
为MC迁移正则项。LMPDA被用于度量域间的边缘概率分布距离,旨在确保源域和目标域之间的整体分布一致性。LMPDA即使在不考虑类别标签的情况下,也能维持特征的相似性,从而可以提高模型的泛化性和鲁棒性。
然而,对边缘分布对齐的重视往往导致对条件概率分布差异的忽视,这种差异在源域与目标域间可能较为明显。条件概率分布的不一致性可能会在目标域内引起不同类别样本的混淆,从而对分类任务的准确性构成挑战。尽管已有研究[26]开始尝试通过类别间关系来调整条件概率分布,以期实现更好的域适应性,但这些研究通常采用一种简化的近似策略,即用类别条件概率分布替代条件概率分布。这种策略的局限性在于,类别条件概率分布与条件概率分布之间并不总是存在一对一的对应关系。因此,在域适应的框架下,这种近似可能导致无法充分消除源域和目标域之间条件概率分布的差异,进而影响域适应性算法的整体性能。
为此,本文利用贝叶斯定理将条件概率分布转化为类条件概率分布的形式。根据贝叶斯定理,有
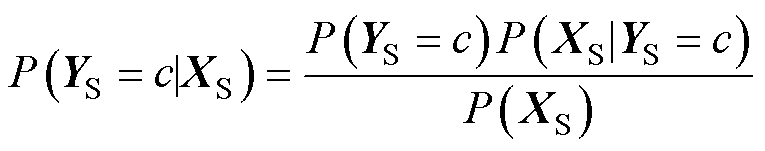 (9)
(9)
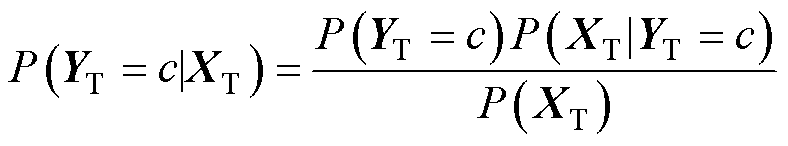 (10)
(10)
式中,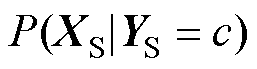 和
和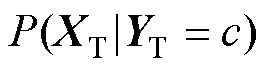 分别为源域和目标域中类别c的类别条件概率,即深度学习模型对样本进行分类的置信度;
分别为源域和目标域中类别c的类别条件概率,即深度学习模型对样本进行分类的置信度;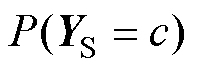 和
和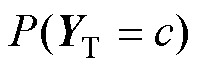 分别为两域属于类别
分别为两域属于类别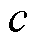 的先验概率,定义为
的先验概率,定义为
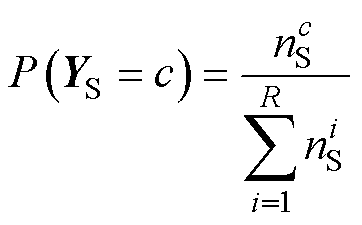 (11)
(11)
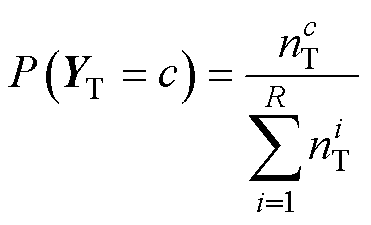 (12)
(12)
式中,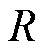 为类别数;
为类别数;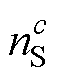 和
和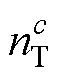 分别为源域和目标域中类别c的样本个数,即
分别为源域和目标域中类别c的样本个数,即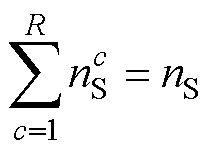 ,
, 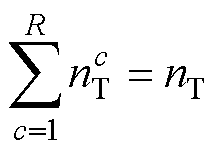 。
。
结合式(9)、式(10),设计一种新的条件概率分布对齐机制(Conditional Probability Distribution Alignment, CPDA),其损失函数 定义为
定义为
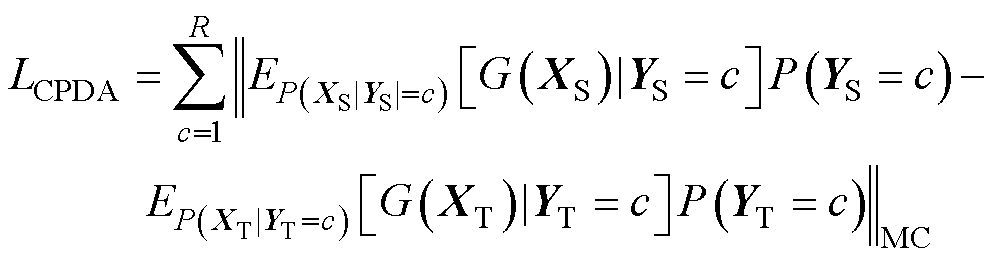 (13)
(13)
LCPDA用于度量域间的条件概率分布距离,使模型更专注于调整源域和目标域中给定类别下的分布,从而减少了类别之间的混淆,提高模型在目标域上的分类性能。此外,在LCPDA中,一个关键的策略是采用真实的条件概率分布对特征分别进行对齐,而不是简单地近似替代。这种精细化的对齐策略有助于模型更准确地捕捉源域和目标域之间的相似性和差异性,从而有效提高域混淆的能力。
综合边缘概率分布对齐机制与条件概率分布对齐机制,本文提出的域间双分布自适应方法的损失函数LIDA可以定义为
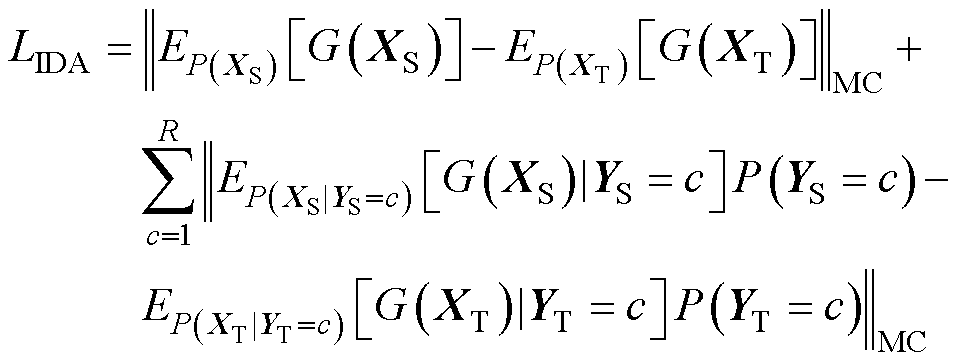 (14)
(14)
通过LIDA定义不难看出,域间双分布自适应方法采用MC迁移正则项来度量两域边缘概率分布和条件概率分布的差异,并不断减少这种差异以获得具有高度泛化的特征表示,从而实现知识的跨域迁移和表达。
Softmax函数[27]在深度学习的多类别分类任务中扮演着关键角色,其通过将模型输出转换为概率分布,为分类结果提供了直观的解释。然而,实验观察揭示了Softmax函数在特定条件下的局限性[28]。特别是在样本特征空间中,若存在类内样本分布的不一致性或类间样本的界限模糊,Softmax函数的性能可能受限。具体而言,当特征空间内同一类别的样本分布较为分散时,Softmax函数可能因缺少足够的类内紧致性而难以精确区分,这直接影响了模型的分类准确性。此外,若不同类别的样本在特征空间中过于接近,即类间区分度不高,Softmax函数同样难以区分这些类别,这进一步削弱了分类效果。
为此,本文提出了一种新颖的判别式Softmax(Discriminative Softmax, D-Softmax)函数来学习具有更多高区分度的暂态稳定性特征以提高域适应效果,其具体机理如下:
TSA问题是一个二分类问题,假设z为稳定样本的特征向量,那么为了将z预测正确,Softmax函数必须满足不等式
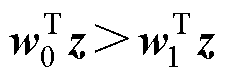 (15)
(15)
式中,w0、w1分别为权重矩阵中对应稳定类别和失稳类别的列向量。
但是,式(15)Softmax函数的特性难以确保严格的决策边界,从而无法保证类间距离的最大化和类内距离的最小化。为了能够得到更严格的决策边界,并实现正确的稳定性评估,通过引入额外的参数m和k来实现这一目的,即有
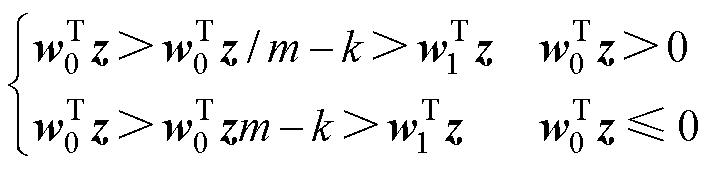 (16)
(16)
由式(16)可知,当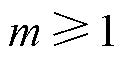 ,
,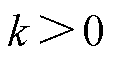 时,可以增加类别间的间隔,使得分类任务具有更严格的决策边界。因此,D-Softmax函数定义为
时,可以增加类别间的间隔,使得分类任务具有更严格的决策边界。因此,D-Softmax函数定义为
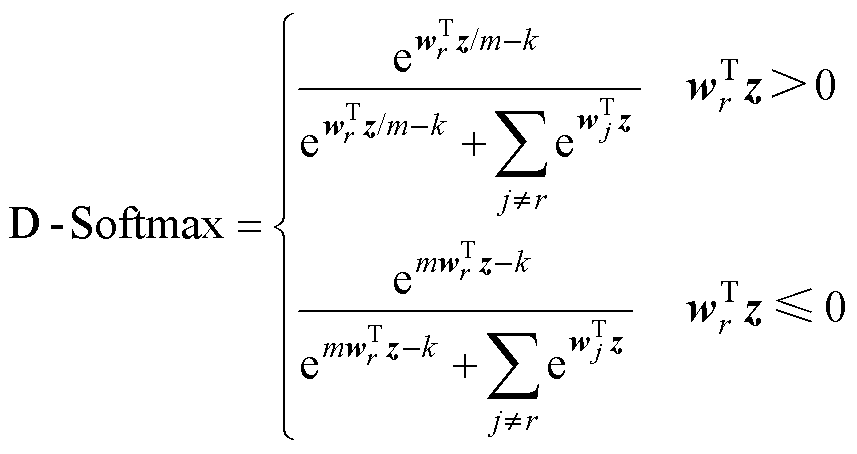 (17)
(17)
式中,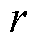 为0或1。
为0或1。
从几何的角度对其进行进一步描述,以呈现更加清晰的D-Softmax函数。根据内积概念可以将
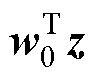 、
、
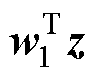 转化为向量夹角形式为
转化为向量夹角形式为
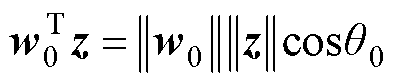 (18)
(18)
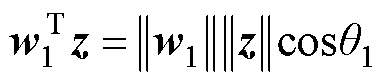 (19)
(19)
式中,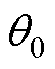 与
与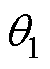 分别为
分别为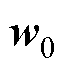 、
、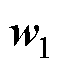 与
与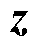 的夹角。
的夹角。
假设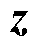 为稳定样本特征,那么
为稳定样本特征,那么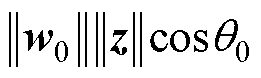 的值越大,意味着分类效果越好。当
的值越大,意味着分类效果越好。当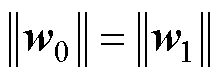 时,分类情况完全取决于角度之间的差异。Softmax与D-Softmax效果对比如图3所示,只有满足
时,分类情况完全取决于角度之间的差异。Softmax与D-Softmax效果对比如图3所示,只有满足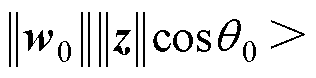
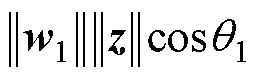 (
(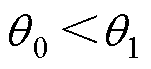 )时,才能正确分类,且只有一个决策边界。而对于D-Softmax函数,以
)时,才能正确分类,且只有一个决策边界。而对于D-Softmax函数,以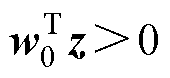 时为例,它严格满足
时为例,它严格满足
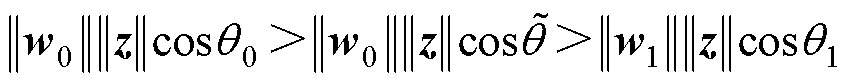 (20)
(20)
式中,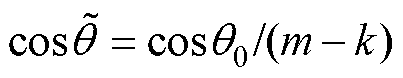 ,
,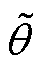 为等效边缘角。明显地,D-Softmax函数满足
为等效边缘角。明显地,D-Softmax函数满足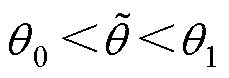 ,且稳定样本和失稳样本具有不同的决策边界。这种设计使得分类更加严格,它迫使同类别样本彼此更加紧密,而不同类别样本则相对疏远,从而为模型提供更具判别性的特征学习。
,且稳定样本和失稳样本具有不同的决策边界。这种设计使得分类更加严格,它迫使同类别样本彼此更加紧密,而不同类别样本则相对疏远,从而为模型提供更具判别性的特征学习。
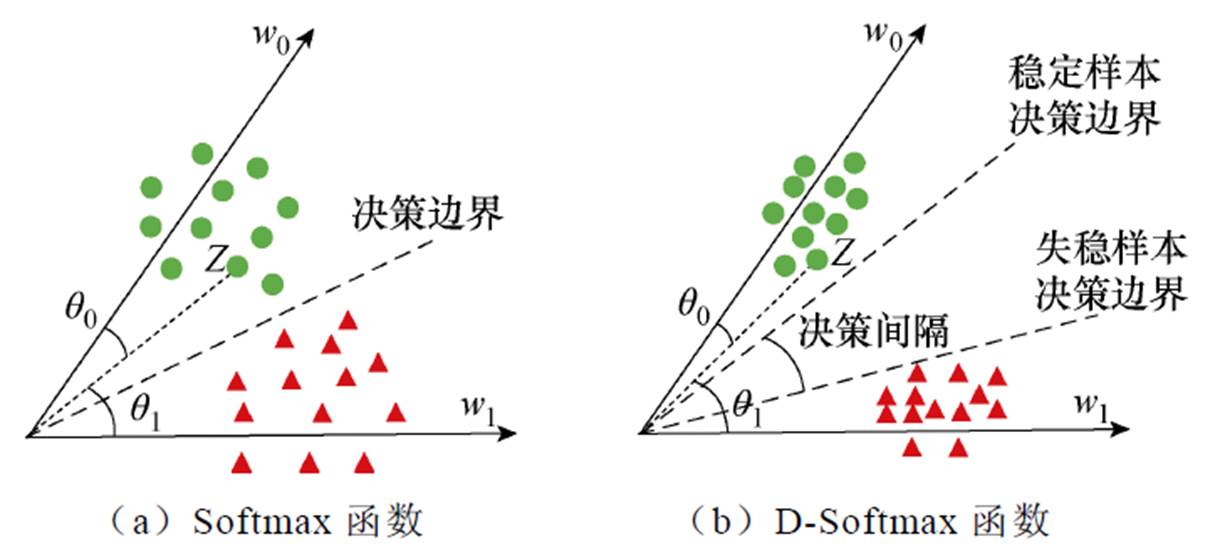
图3 Softmax与D-Softmax效果对比
Fig.3 Comparison of Softmax and D-Softmax effects
对式(17)进行权重归一化可以进一步促进更具判别性特征的学习,采用L2范数对权重向量进行归一化,即
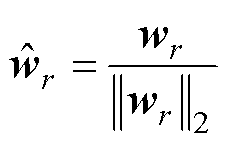 (21)
(21)
则D-Softmax函数可以最终定义为
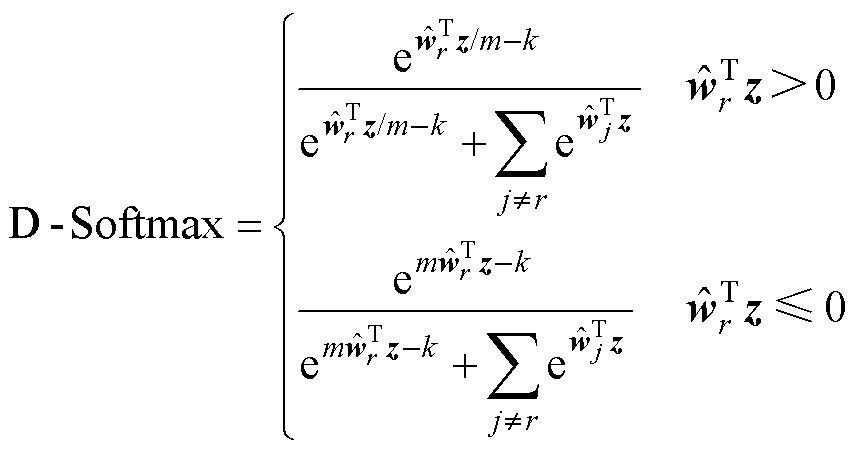 (22)
(22)
D-Softmax函数通过引入额外的可调参数m和k,并进行权重归一化,能够最大化类间距离和最小化类内距离,进而增强模型对判别性特征的学习,提高域适应框架在TSA任务中的性能表现。
基于2.1节和2.2节,综合考虑模型的评估性能和泛化能力,定义TSA-DDA的总体损失函数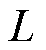 为
为
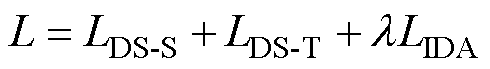 (23)
(23)
式中,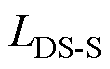 为D-Softmax函数对源域样本的分类损失;
为D-Softmax函数对源域样本的分类损失;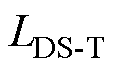 为D-Softmax函数对目标域样本的分类损失;
为D-Softmax函数对目标域样本的分类损失;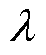 为损失函数的权重系数。通过结合
为损失函数的权重系数。通过结合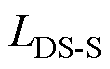 和
和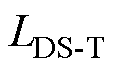 ,能够在源域和目标域的暂态稳定性评估中获得可靠的结果。
,能够在源域和目标域的暂态稳定性评估中获得可靠的结果。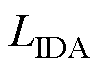 的引入旨在协助模型提取与暂态稳定评估任务相关、而与运行场景无关的共性特征,从而提升模型的自适应能力。
的引入旨在协助模型提取与暂态稳定评估任务相关、而与运行场景无关的共性特征,从而提升模型的自适应能力。
损失函数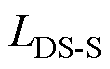 、
、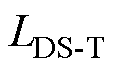 和
和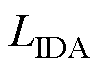 共同优化模型,在精细化提取源域和目标域共性特征的同时不断提高模型评估性能,保证模型在不同运行场景中的通用性。选择学习率
共同优化模型,在精细化提取源域和目标域共性特征的同时不断提高模型评估性能,保证模型在不同运行场景中的通用性。选择学习率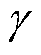 更新TSA-DDA的模型参数
更新TSA-DDA的模型参数
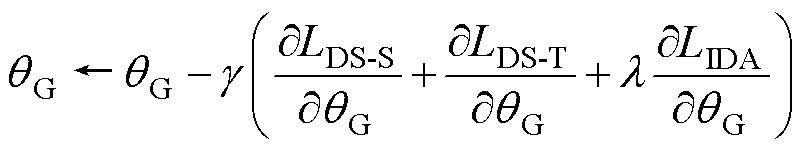 (24)
(24)
式中,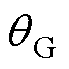 为特征提取器参数。经过样本数据的反复更新训练,所得到的参数即为TSA-DDA的模型 参数。
为特征提取器参数。经过样本数据的反复更新训练,所得到的参数即为TSA-DDA的模型 参数。
特征选择对TSA模型的评估性能至关重要[29]。电网规模的变动会显著影响节点数量,导致输入数据量急剧变化。传统的基于节点或边特征的深度学习模型难以适应这种变化。为解决这一问题,本文引入了轨迹簇特征,将故障前、故障中和故障后三个阶段的节点电压视为一个整体,并定义了29个特征作为模型输入,其构造方法见文献[30]。这种特征的优势在于其集簇性和收敛性,且维度不受电网运行场景变化的影响,为TSA-DDA的实施提供了良好基础。
本文搭建TSA-DDA框架的特征提取器参数见表1。
表1 TSA-DDA框架的特征提取器参数
Tab.1 Feature extractor parameters of TSA-DDA framework

网络层卷积池化层全连接层 层11维卷积(32, 3)、批规范化、池化(3, 4)全连接(96, 64) 层21维卷积(32, 3)、批规范化、池化(3, 4)全连接(64, 32) 层31维卷积(32, 3)、批规范化、池化(3, 4)全连接(32, 2)
基于TSA-DDA框架,面向运行场景变化的判别式域适应暂态稳定评估流程如图4所示,主要包括源域离线训练、目标域迁移更新、在线应用三个重要阶段,详细任务如下:
1)源域离线训练:利用时域仿真技术生成用于模型离线训练所需的源域数据;提取29个电压轨迹簇特征,并按照一定比例划分训练集和测试集用于训练源域任务模型。
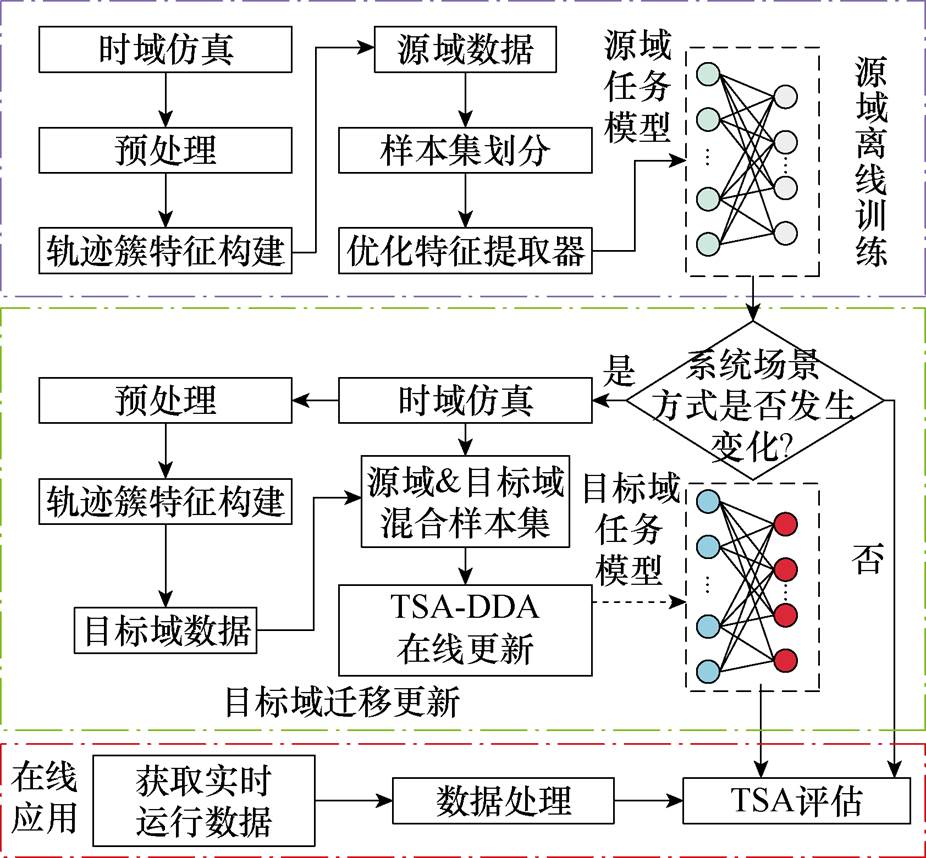
图4 TSA-DDA自适应评估流程
Fig.4 TSA-DDA adaptive assessment process
2)目标域迁移更新:当检测到电网运行场景发生变化时,通过仿真、处理获取少量目标域标注样本,并与源域样本融合建立混合样本集,随后启动TSA-DDA迁移并更新模型。
3)在线应用:获取电力系统实时运行数据并进行数据处理,通过利用已经更新后的模型,实现快速且准确的TSA。
本文基于混淆矩阵工具,使用准确率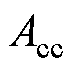 、稳定样本识别率
、稳定样本识别率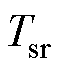 、失稳样本识别率
、失稳样本识别率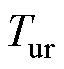 和综合性能指标
和综合性能指标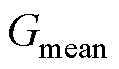 等四种评价指标对模型的性能进行全面评估。混淆矩阵见表2。
等四种评价指标对模型的性能进行全面评估。混淆矩阵见表2。
表2 暂态稳定评估混淆矩阵
Tab.2 Transient stability assessment confusion matrix

系统实际状态评估结果 稳定失稳 稳定TPFP 失稳FNTN
根据混淆矩阵,可以计算模型的Acc、Tsr、Tur和Gmean,其计算公式分别为
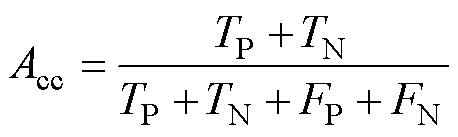 (25)
(25)
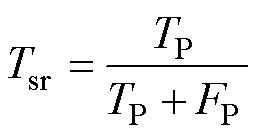 (26)
(26)
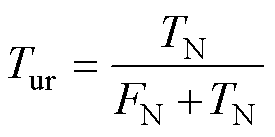 (27)
(27)
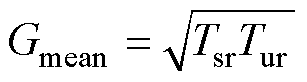 (28)
(28)
式中,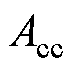 衡量了模型整体的正确预测能力;
衡量了模型整体的正确预测能力;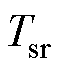 表示正确判断为稳定的样本占所有稳定样本的比例;
表示正确判断为稳定的样本占所有稳定样本的比例;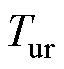 表示正确判断为失稳的样本占所有失稳样本的比例;而
表示正确判断为失稳的样本占所有失稳样本的比例;而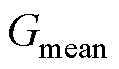 则提供了一个综合考虑稳定样本识别率和失稳样本识别率的评估指标。通过这四种指标的联合使用,能够全面地评价模型在不同方面的性能表现,从而对模型的优劣做出更加客观和全面的判断。
则提供了一个综合考虑稳定样本识别率和失稳样本识别率的评估指标。通过这四种指标的联合使用,能够全面地评价模型在不同方面的性能表现,从而对模型的优劣做出更加客观和全面的判断。
本文采用飞桨作为深度学习框架,并使用Python作为编程语言构建TSA-DDA框架。为了验证提出的TSA-DDA框架的有效性和可用性,首先选取了新英格兰10机39节点系统作为算例全面检验TSA- DDA框架性能。此外,为了进一步验证该框架的泛化性和鲁棒性,还在具有更大规模和更具复杂特性的中国西南某省级电网上进行了验证。实验仿真使用BPA和DSP软件,它们能够提供高保真的电力系统仿真数据,为模型训练和测试提供了坚实的数据基础。
设置仿真总时长为3 s,仿真步长为0.04 s。故障持续时间从1~18个周波,步长为1个周波。在不同的故障持续时间下,设置故障位于每条线路1%~99%处,步长为1%,故障类型为三相短路故障。在上述的条件下,通过仿真生成大量样本。为了避免样本不平衡对模型造成的倾向性问题,从这些样本中随机挑选出9 000个稳定样本和8 500个失稳样本,构成一个较平衡的样本集。
4.1.1 源域任务模型1D-CNN的评估性能测试与分析
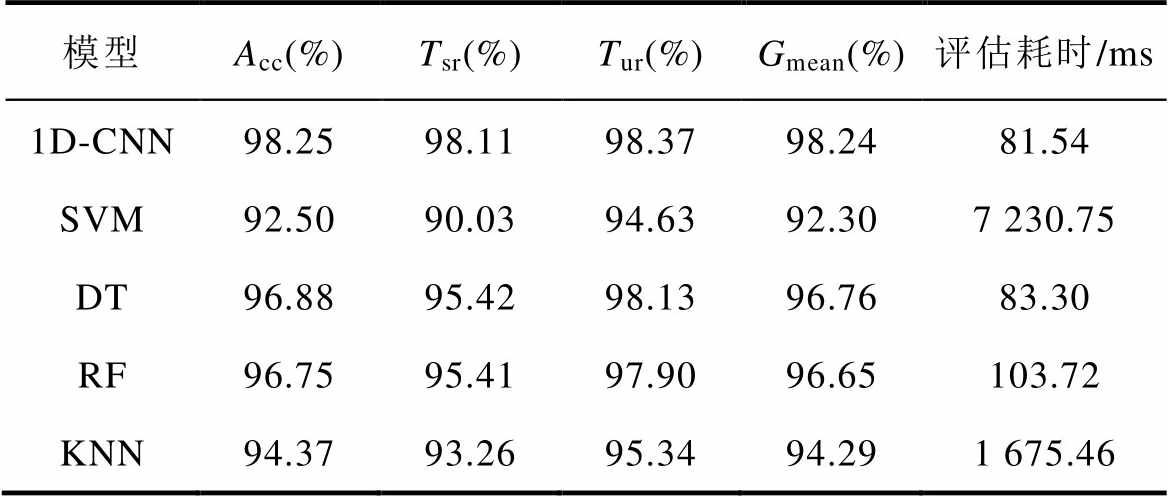
在TSA中,暂态稳定数据具有明显的时变特性,故搭建一个由3个卷积池化层和3个全连接层构成的1D-CNN作为源域任务模型。该模型具体参数见表1。为了验证1D-CNN用于TSA任务的性能,选择四种机器学习模型进行对比:SVM、DT、RF、KNN;SVM的核函数采用径向基核函数;DT采用C5.0算法;RF的基分类器个数为20;KNN中最近邻个数取为10。1D-CNN的学习率为0.001,采用交叉熵损失函数和Adam优化算法。上述五个模型的性能测试结果见表3。
结果表明,作为浅层ML模型的SVM、DT、RF、KNN等,由于其特征表达能力有限,难以充分挖掘深层次特征,因此各项评估指标上均表现不及1D-CNN。而1D-CNN模型基于其强大的非线性特征聚合,使得各项指标都达到了98%以上。此外,在对测试集2 000个样本进行评估时,1D-CNN模型的评估耗时均少于浅层ML模型,这进一步说明了其能够在保持高准确度的同时,也具有较高的计算效率。
表3 5种模型各指标评估结果
Tab.3 Assessment results of various indicators for 5 models
模型Acc(%)Tsr(%)Tur(%)Gmean(%)评估耗时/ms 1D-CNN98.2598.1198.3798.2481.54 SVM92.5090.0394.6392.307 230.75 DT96.8895.4298.1396.7683.30 RF96.7595.4197.9096.65103.72 KNN94.3793.2695.3494.291 675.46
4.1.2 TSA-DDA框架在应对运行场景变化的适用性验证
为了模拟在线应用时电网运行场景发生显著变化的情况,需假设系统中某个节点及其输电线路退出运行。具体地,通过去除4号负荷节点和相关的3条输电线路,同时将32号发电机的有功出力由300 MW调至200 MW,调整电力系统潮流及运行场景的变化。在这个条件下,共仿真生成1 500个目标域样本,并按照1 4的比例划分训练集和测试集。在4.1.1节训练所得的源域任务模型在新运行场景中的测试结果见表4。
4的比例划分训练集和测试集。在4.1.1节训练所得的源域任务模型在新运行场景中的测试结果见表4。
表4 源域任务模型在新场景中的测试结果
Tab.4 Test results of the source domain task model in new scenarios

集合新场景(%) Acc89.38 Tsr83.29 Tur94.64 Gmean88.78
由测试结果可知,通过改变电网的运行场景,源域任务模型的预测准确度显著下降,已无法满足实际需求。因此,需要采用TSA-DDA框架来提高模型在新运行场景下的性能。从目标域训练集中,分别随机挑选50、100、150、200个样本,并将它们分别与随机挑选的3 500个源域样本合并,构建混合样本集S1、S2、S3和S4。TSA-DDA框架的参数设置为:样本批次大小为130(源域样本和目标域样本数分别设置为100和30),模型训练的迭代次数为200,学习率为0.001,损失函数的权重系数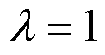 ,D-Softmax函数的参数
,D-Softmax函数的参数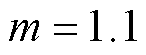 ,
, 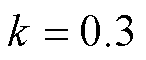 。考虑在不同混合样本集的训练下,TSA-DDA框架的迁移更新效果如图5所示。由图5可以看出,使用混合样本S1进行训练时,由于其所包含的目标样本数量有限,导致模型未能充分学习和理解数据的分布及其潜在特征,因此评估效果较差,准确率仅达到95.13%。然而,随着混合样本集中目标域样本数的增加,评估准确率逐渐升高。当混合样本集的目标域样本数量增至200时,模型的预测准确度提高至98.18%,验证了TSA-DDA框架可以有效恢复模型的评估性能。
。考虑在不同混合样本集的训练下,TSA-DDA框架的迁移更新效果如图5所示。由图5可以看出,使用混合样本S1进行训练时,由于其所包含的目标样本数量有限,导致模型未能充分学习和理解数据的分布及其潜在特征,因此评估效果较差,准确率仅达到95.13%。然而,随着混合样本集中目标域样本数的增加,评估准确率逐渐升高。当混合样本集的目标域样本数量增至200时,模型的预测准确度提高至98.18%,验证了TSA-DDA框架可以有效恢复模型的评估性能。
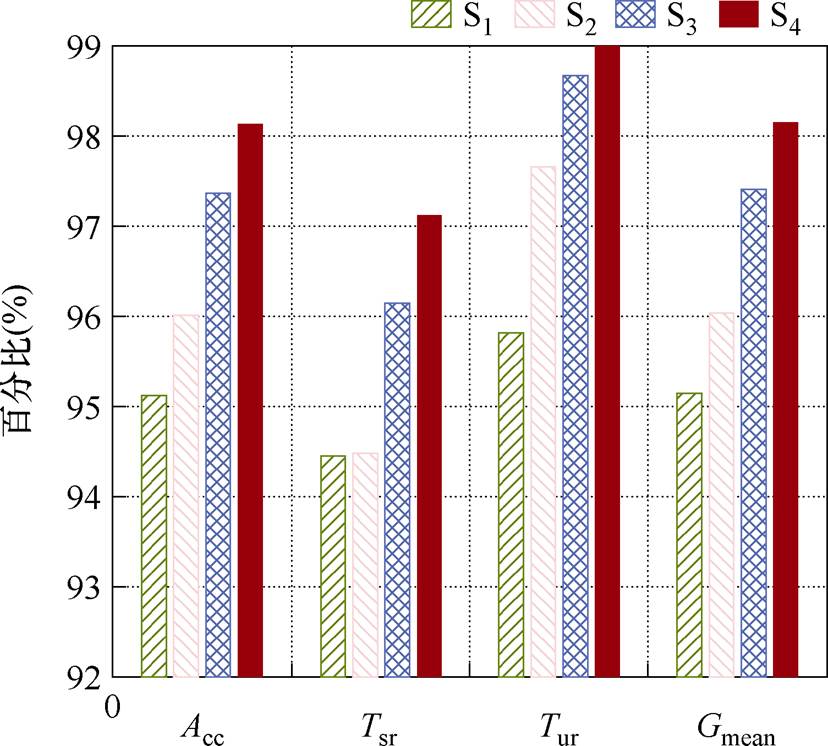
图5 TSA-DDA的适用性结果
Fig.5 Applicability results of TSA-DDA
4.1.3 消融实验
为了说明TSA-DDA框架中各模块的有效性,设置另外四个不完整的TSA-DDA框架进行消融实验:
消融模型1:模型中不包含CPDA机制,仅对源域和目标域的边缘概率分布进行对齐。采用原始Softmax函数进行激活。
消融模型2:模型中不包含MPDA机制,仅对源域和目标域的条件概率分布进行对齐。采用原始Softmax函数进行激活。
消融模型3:模型中不包含CPDA机制,仅对源域和目标域的边缘概率分布进行对齐。采用D-Softmax函数进行激活。
消融模型4:模型中不包含MPDA机制,仅对源域和目标域的条件概率分布进行对齐。采用D-Softmax函数进行激活。
测试结果见表5。表中实验结果表明,消融模型1和消融模型2在仅对齐边缘概率分布或者条件概率分布时,模型性能下降,预测准确率均未达到97.50%。在对齐特征的基础上,消融模型3和消融模型4通过引入D-Softmax函数来增强模型的判别性特征学习,预测准确率分别提升了0.25个百分点、0.62个百分点。D-Softmax函数在一定程度上增强了模型的评估性能,使其更好地适应目标域任务。
表5 五种模型各指标平均结果
Tab.5 Average results of various indicators for five models (%)
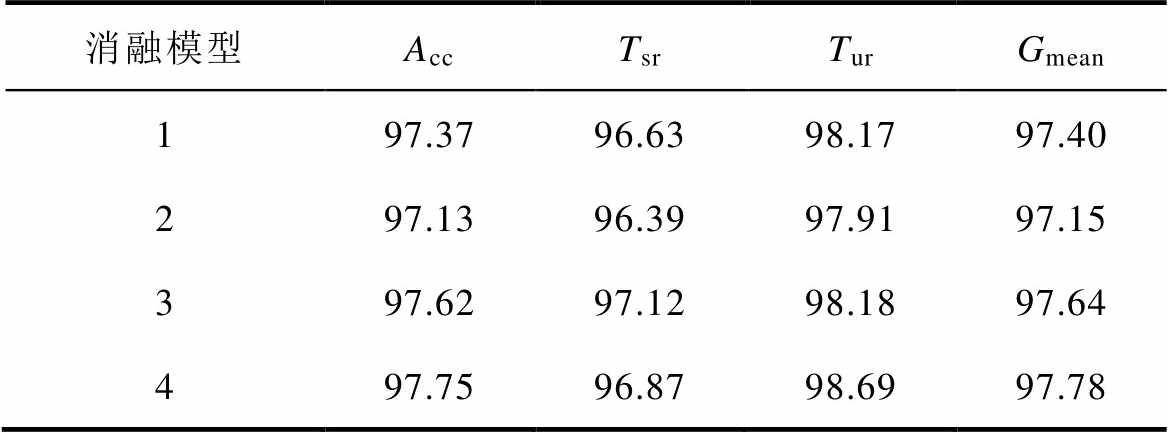
消融模型AccTsrTurGmean 197.3796.6398.1797.40 297.1396.3997.9197.15 397.6297.1298.1897.64 497.7596.8798.6997.78
4.1.4 可持续学习能力验证
为了进一步验证TSA-DDA框架在应对运行场景变化时的可持续学习能力,利用微调算法[31]和TSA-DDA连续更新模型,对目标域和源域样本测试集的预测准确率进行比较。TSA-DDA可持续学习能力验证具体结果如图6所示。其中,TSA-DDA-T、TSA-DDA-S为TSA-DDA在目标域和源域测试集上的预测准确率曲线;FT-T、FT-S为微调算法在目标域和源域测试集上的预测准确率曲线。
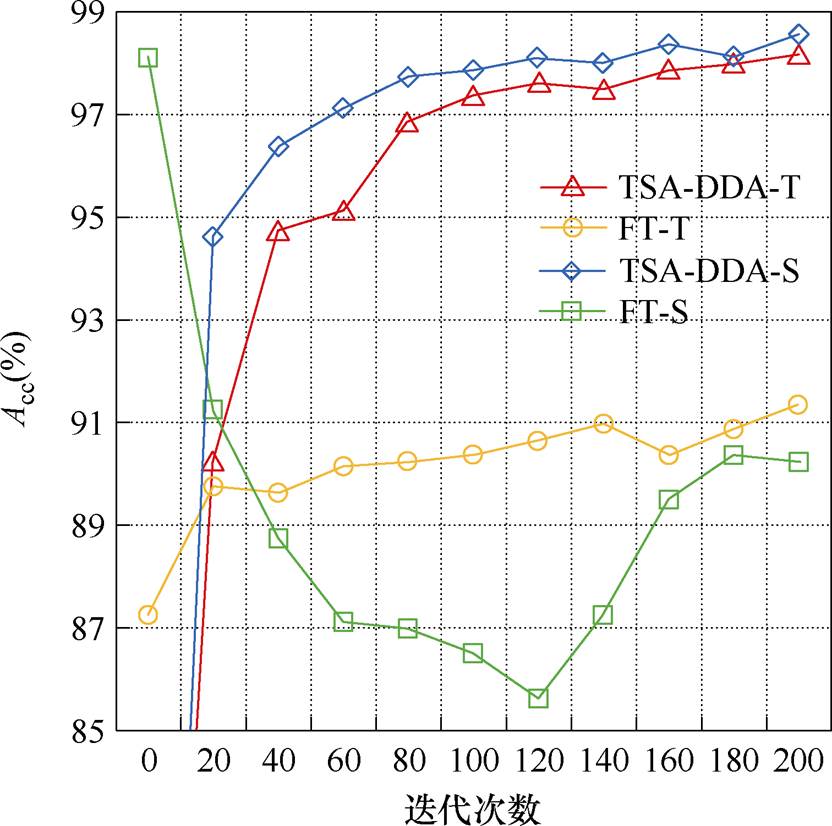
图6 TSA-DDA可持续学习能力验证
Fig.6 TSA-DDA sustainable learning capability verification
结果表明,随着训练的深入,微调算法在目标域中的预测性能逐渐升高,而在源域中的预测准确率却出现了明显下降,表现不佳。与之相反,本文提出的TSA-DDA框架在目标域和源域中的预测准确率分别达到了98.18%和98.57%。这主要归因于TSA-DDA能够最大限度地保持源域和目标域中具有高度泛化的特征,确保了源域和目标域在特征空间中的一致性,从而实现了更好的知识迁移和泛化能力。因此,TSA-DDA具有更好的可持续学习能力。
4.1.5 不同迁移方案的对比分析
为了进一步验证TSA-DDA框架的有效性,将其与一些主流的迁移学习方案的迁移效果进行比较,并包括两种不采用迁移学习的方案。
方案1:不采用迁移学习,仅通过混合样本集S4中的目标域样本进行重新训练。
方案2:不采用迁移学习,将混合样本集S4作为训练集,重新训练。
方案3:采用模型迁移,将源域模型的参数迁移至目标域,利用混合样本集S4中的目标域样本对整个网络进行微调。
方案4:采用模型迁移,将源域模型的参数迁移至目标域,冻结特征提取器层参数,初始化分类器层参数,仅利用混合样本集S4中的目标域样本进行局部微调。
方案5:结合样本迁移与模型迁移,将源域模型的参数迁移至目标域,混合样本集S4作为训练集,对整个网络进行微调。
案6:采用无监督域对抗的迁移方法,通过添加域分类器和梯度反转层,迫使特征提取器难以区分样本来源。将混合样本集S4作为训练集,目标域样本不参与分类器的训练。
方案7:采用有监督域对抗的迁移方法,模型结构、训练集与方案6保持一致,但目标域样本参与分类器的训练。
方案8:采用非对抗的域适应方法,通过添加MMD损失以对齐源域和目标域的边缘概率分布。
方案9:结合有监督域对抗和基于MMD的非对抗的域适应方法,提取源域和目标域的域不变 特征。
方案10:采用非对抗的域适应方法,通过添加MMD损失以对齐源域和目标域的边缘概率分布和类条件概率分布。
方案11:TSA-DDA框架。
上述11种方案实验结果如图7所示。
由图7可知,在新的运行场景中,方案1的性能显著较差。经过200个目标域样本的训练,其准确率未能达到95%。方案2在利用少量目标域的同时,充分利用了大量源域样本,提高了模型在有限新场景样本下的性能表现。与方案1相比,这种利用源域样本的策略使得模型的预测准确率得到了显著提高。相较于前两种方案,方案3、4、5通过共享源域任务模型的结构和参数,为构建新的目标域模型提供了一个具有良好基础特征的学习起点。这种基于模型迁移的方法使得初始应用于新场景时,模型预测准确率达到了87.25%。值得注意的是,方案5通过结合模型迁移和样本迁移技术,充分利用源域信息,有效提高了新场景标注样本匮乏阶段模型的评估性能,经过200轮次的训练后,模型预测准确率达到了96.98%。方案6采用无监督域对抗的迁移方法,只能依赖源域的分类损失和域对抗损失来进行域适应,缺乏目标域标注样本的参与。这使得模型难以有效地学习目标域的特征表示,因此在域适应方面表现不佳。方案7通过引入少量带标签的目标域样本,取得了比方案6更好的预测结果。然而,在处理过程中,忽略了域内条件概率分布的对齐,准确率达到了96.38%,但后续训练无法更进一步提升模型性能。将混合样本集S4作为训练集,方案8通过MMD对源域和目标域的边缘概率分布进行对齐,实现了97.24%的预测准确率。方案9在方案8的基础上引入了域对抗机制,增强了模型的域混淆能力,预测准确率高于方案8。方案10在对齐两域边缘概率分布的同时,采用简化的近似策略对齐类条件概率分布,相比方案8提高了0.51%的准确率。方案11,即本文方法,通过精细化对齐不同域间边缘概率分布和条件概率分布,并引入D-Softmax函数以促进模型学习更多具有高区分度的暂态稳定特征,显著提升模型的预测准确率至98.18%,实验结果证实了其性能优于前述方案。
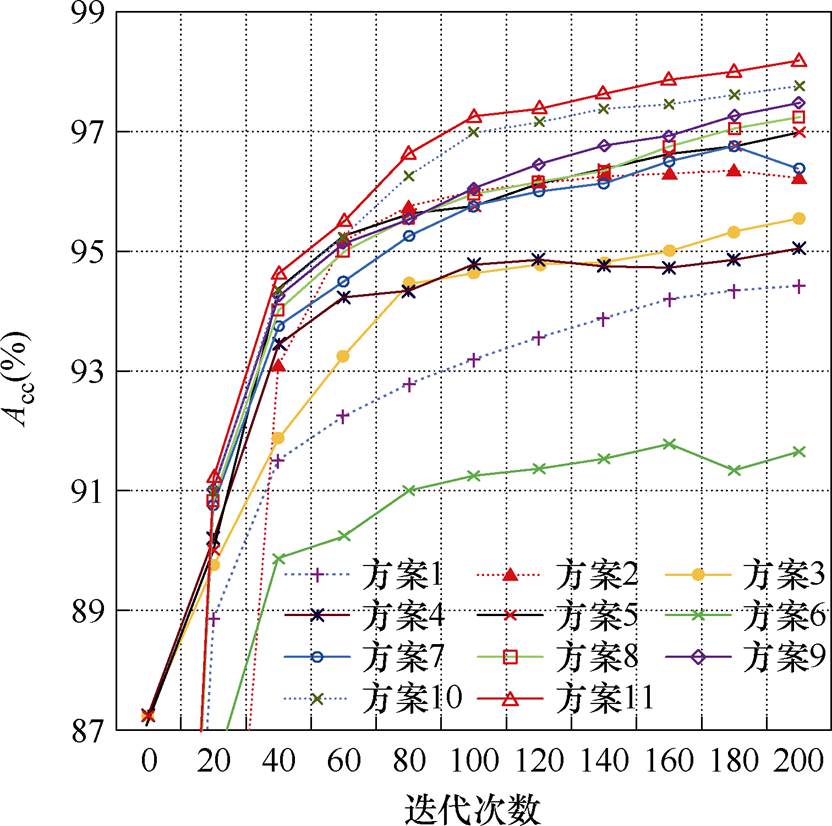
图7 不同迁移方案效果
Fig.7 Effect of different transfer schemes
为了验证本文方法对于具有高新能源渗透率的大电网有效性,选择使用西南某省实际电力系统进行有效性验证。该系统包括5 538个节点和6 154条线路,且具有40%的新能源渗透率。设置仿真时间为10 s,以0.04 s的采样间隔进行仿真数据采集。设置故障持续时间分别为0.1、0.15、0.20、0.25 s。在不同的故障持续时间下,设置线路负载在25%、50%、75%位置处的三相短路故障。在上述条件下,生成大量仿真数据。电力系统仿真软件采用DSP,共生成3 000个样本,稳定样本为2 175个,失稳样本为825个,按照1 2的比例划分训练集和测试集。其中,损失函数的权重系数
2的比例划分训练集和测试集。其中,损失函数的权重系数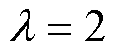 。
。
4.2.1 TSA-DDA框架在大电网的适用性分析
对于一个省级及以上规模的大型电力系统,收集或仿真生成大量标注样本,以及重新训练一个具有良好评估性能的新模型,都需要投入大量经济和时间成本。因此,对于这样的系统,利用少量的样本实现较好的TSA性能至关重要。在本节中,将新英格兰39节点系统作为源域,西南某省电力系统作为目标域。从训练集中分别随机挑选200、300、400和500个目标域样本,并将它们分别与随机挑选的4 500个源域样本组合,构成4个混合样本集作为训练集,分别标记为S5、S6、S7和S8。考虑在不同训练集下,TSA-DDA的迁移更新效果如图8所示。由测试结果可知,随着混合样本集中目标域样本数量的增加,预测准确率显著提高。当目标域样本数达到500时,模型预测准确率达到97%以上,基本满足了大电网在线应用需求。
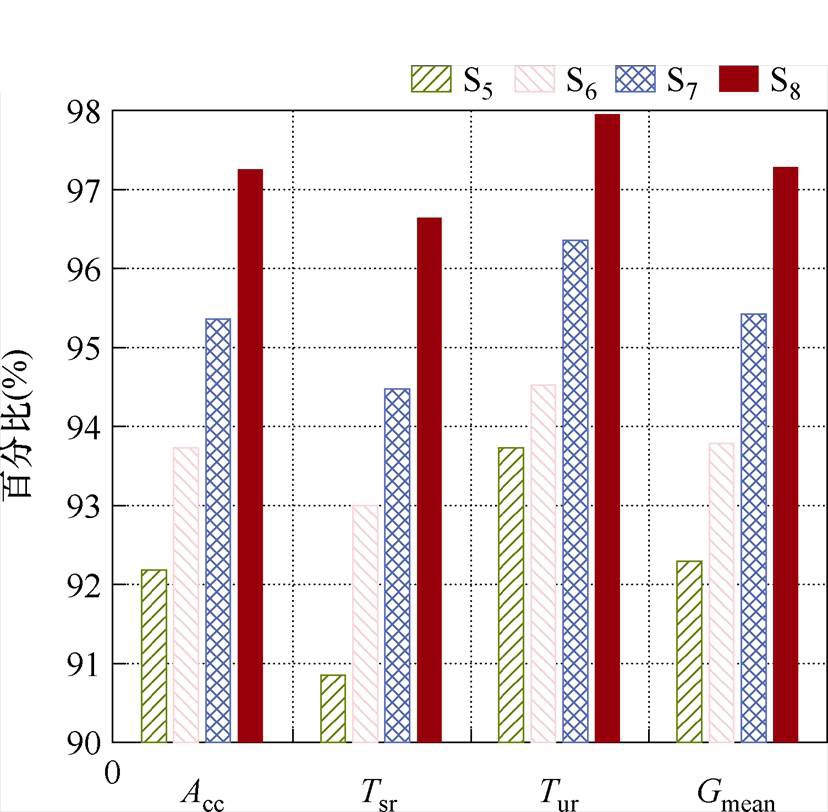
图8 TSA-DDA在大电网的适用性结果
Fig.8 Applicability results of TSA-DDA in large power grid
4.2.2 TSA-DDA框架在大电网的迁移效果验证
为了进一步验证TSA-DDA框架的泛化性能和时间成本,本节将源域任务模型、重新训练、TSA- DDA的预测结果进行比较,见表6。TSA-DDA和重新训练的耗时对比见表7。
表6 大电网采用不同模型的性能比较
Tab.6 Performance comparison of different models used in large power grids (%)
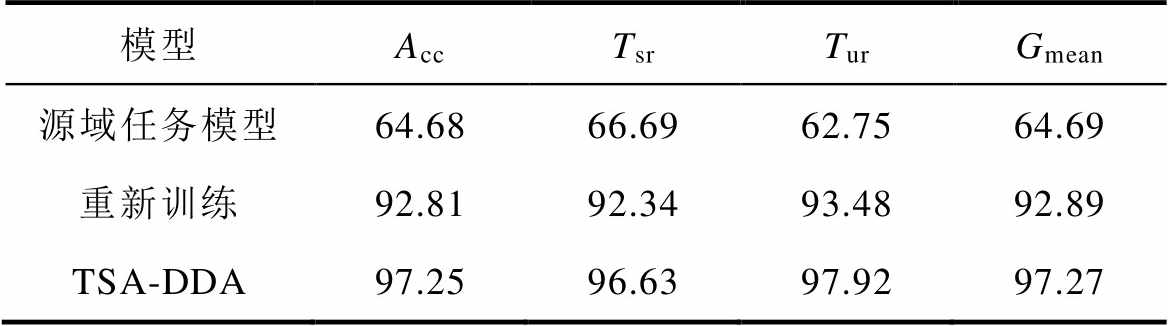
模型AccTsrTurGmean 源域任务模型64.6866.6962.7564.69 重新训练92.8192.3493.4892.89 TSA-DDA97.2596.6397.9297.27
表7 大电网采用不同模型的耗时比较
Tab.7 Comparison of time consumption for using different models in large power grids
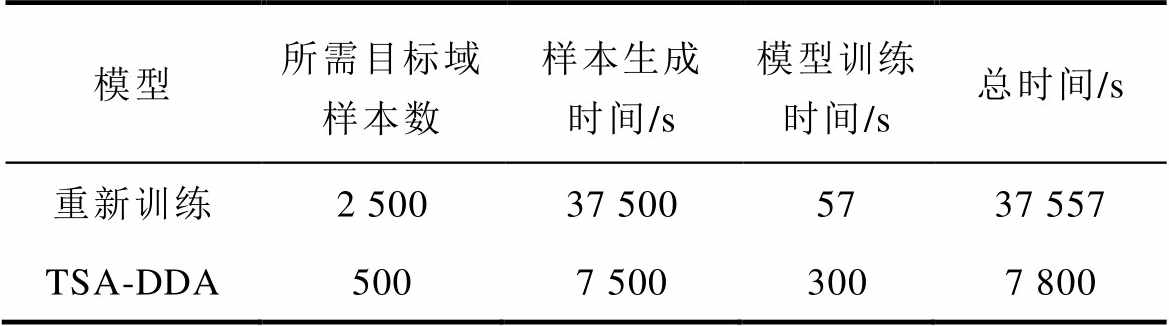
模型所需目标域样本数样本生成时间/s模型训练时间/s总时间/s 重新训练2 50037 5005737 557 TSA-DDA5007 5003007 800
由测试结果可知,本文提出的TSA-DDA框架的预测结果优于从头开始重新训练的模型。将源域任务模型直接应用于西南某省电力系统时,预测准确率仅为64.68%。然而,经过2 500个样本的训练,重新训练的模型准确率仍仅有92.81%,其样本生成时间长达37 557 s,这在新能源电网这样复杂多变的环境中明显无法满足可靠性和时效性的要求。相较之下,本文提出的TSA-DDA框架在使用500个目标域样本仅耗时7 800 s的情况下,将模型预测准确率提高至97.25%。这极大地缩短了样本生成与标注成本,有效减少在线应用的空窗期,可以有效适用于大电网运行场景多变的暂态稳定评估。
针对域适应能力不足和判别性特征学习不充分的问题,本文提出了一种面向运行场景变化的判别式域适应暂态稳定评估框架。主要结论如下:
1)提出的域间双分布自适应方法,从均值和方差两个角度综合度量了不同域边缘概率分布和条件概率分布差异,并不断减少该差异,从而实现更大程度的域适应效果,减少模型更新所需的目标域样本。
2)提出的判别式Softmax函数通过拉近类内样本特征,并迫使类间样本特征相互远离,从而获得更具判别性的暂态稳定性特征,提高了评估框架的适用性。
本文提出的评估框架能够在运用少量有标注目标域样本的基础上,快速提高模型对电网新运行场景的适应性。未来的研究将更专注于探索图神经网络在暂态稳定评估中的适应性学习,进一步提高模型在复杂多变的新能源电网中的精确评估能力。
参考文献
[1] 顾雪平, 刘彤, 李少岩, 等. 基于改进双延迟深度确定性策略梯度算法的电网有功安全校正控制[J]. 电工技术学报, 2023, 38(8): 2162-2177.
Gu Xueping, Liu Tong, Li Shaoyan, et al. Active power correction control of power grid based on improved twin delayed deep deterministic policy gradient algorithm[J]. Transactions of China Electro- technical Society, 2023, 38(8): 2162-2177.
[2] 杨金洲, 李业成, 熊鸿韬, 等. 基于阻抗的新能源接入的受端电网暂态电压失稳高风险故障快速筛选方法[J]. 电工技术学报, 2024, 39(21): 6746-6758.
Yang Jinzhou, Li Yecheng, Xiong Hongtao, et al. A fast screening method for the high-risk faults with transient voltage instability in receiving-end power grids interconnected with new energy based on impedance[J]. Journal of Electrical Engineering Technology, 2024, 39(21): 6746-6758.
[3] 钱倍奇, 陈谦, 张政伟, 等. 基于异构数据特征级融合的多任务暂态稳定评估[J]. 电力系统自动化, 2023, 47(9): 118-128.
Qian Beiqi, Chen Qian, Zhang Zhengwei, et al. Multi- task transient stability assessment based on feature- level fusion of heterogeneous data[J]. Automation of Electric Power Systems, 2023, 47(9): 118-128.
[4] 褚旭, 鲍泽宏, 许立强, 等. 基于时序卷积残差网络的主动配电系统线路短路故障诊断方案[J]. 电工技术学报, 2023, 38(8): 2178-2190.
Chu Xu, Bao Zehong, Xu Liqiang, et al. Fault line diagnosis scheme of active distribution system based on time-sequence convolution residual network[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2178-2190.
[5] Zadkhast P, Jatskevich J, Vaahedi E. A multi- decomposition approach for accelerated time-domain simulation of transient stability problems[J]. IEEE Transactions on Power Systems, 2015, 30(5): 2301- 2311.
[6] Vu T L, Turitsyn K. Lyapunov functions family approach to transient stability assessment[J]. IEEE Transactions on Power Systems, 2016, 31(2): 1269- 1277.
[7] 李宝琴, 吴俊勇, 邵美阳, 等. 基于集成深度置信网络的精细化电力系统暂态稳定评估[J]. 电力系统自动化, 2020, 44(6): 17-26.
Li Baoqin, Wu Junyong, Shao Meiyang, et al. Refined transient stability evaluation for power system based on ensemble deep belief network[J]. Automation of Electric Power Systems, 2020, 44(6): 17-26.
[8] 杨景刚, 赵科, 腾云, 等. 基于奇异谱分析与决策树的GIS振动缺陷检测方法研究[J]. 高压电器, 2024, 60(6): 33-42.
Yang Jinggang, Zhao Ke, Teng Yun, et al. Research on vibration defect detection method of GIS based on singular spectrum analysis and decision tree[J]. High Voltage Apparatus, 2024, 60(6): 33-42.
[9] 魏银图, 张旸, 温步瀛, 等. 基于支持向量机的模块化多电平换流器子模块开路故障诊断方法[J]. 电气技术, 2023, 24(10): 1-7.
Wei Yintu, Zhang Yang, Wen Buying, et al. Open circuit fault diagnosis method for modular multilevel converter submodule based on support vector machine[J]. Electrical Engineering, 2023, 24(10): 1-7.
[10] Kamwa I, Samantaray S R, Joos G. Catastrophe predictors from ensemble decision-tree learning of wide-area severity indices[J]. IEEE Transactions on Smart Grid, 2010, 1(2): 144-158.
[11] 叶圣永, 王晓茹, 刘志刚, 等. 基于受扰严重机组特征及机器学习方法的电力系统暂态稳定评估[J]. 中国电机工程学报, 2011, 31(1): 46-51.
Ye Shengyong, Wang Xiaoru, Liu Zhigang, et al. Power system transient stability assessment based on severely disturbed generator attributes and machine learning method[J]. Proceedings of the CSEE, 2011, 31(1): 46-51.
[12] 房佳姝, 刘崇茹, 苏晨博, 等. 基于自注意力Transformer编码器的多阶段电力系统暂态稳定评估方法[J]. 中国电机工程学报, 2023, 43(15): 5745- 5758.
Fang Jiashu, Liu Chongru, Su Chenbo, et al. Multi- stage power system transient stability evaluation method based on self-attention Transformer encoder[J]. Proceedings of the CSEE, 2023, 43(15): 5745-5758.
[13] 朱乔木, 陈金富, 李弘毅, 等. 基于堆叠自动编码器的电力系统暂态稳定评估[J]. 中国电机工程学报, 2018, 38(10): 2937-2946, 3144.
Zhu Qiaomu, Chen Jinfu, Li Hongyi, et al. Transient stability assessment based on stacked autoencoder[J]. Proceedings of the CSEE, 2018, 38(10): 2937-2946, 3144.
[14] 赵恺, 石立宝. 基于改进一维卷积神经网络的电力系统暂态稳定评估[J]. 电网技术, 2021, 45(8): 2945- 2957.
Zhao Kai, Shi Libao. Transient stability assessment of power system based on improved one-dimensional convolutional neural network[J]. Power System Technology, 2021, 45(8): 2945-2957.
[15] 朱乔木, 党杰, 陈金富, 等. 基于深度置信网络的电力系统暂态稳定评估方法[J]. 中国电机工程学报, 2018, 38(3): 735-743.
Zhu Qiaomu, Dang Jie, Chen Jinfu, et al. A method for power system transient stability assessment based on deep belief networks[J]. Proceedings of the CSEE, 2018, 38(3): 735-743.
[16] Yu J J Q, Hill D J, Lam A Y S, et al. Intelligent time-adaptive transient stability assessment system[J]. IEEE Transactions on Power Systems, 2018, 33(1): 1049-1058.
[17] 张若愚, 吴俊勇, 李宝琴, 等. 基于迁移学习的电力系统暂态稳定自适应预测[J]. 电网技术, 2020, 44(6): 2196-2205.
Zhang Ruoyu, Wu Junyong, Li Baoqin, et al. Self- adaptive power system transient stability prediction based on transfer learning[J]. Power System Tech- nology, 2020, 44(6): 2196-2205.
[18] 贺兴, 潘美琪, 艾芊. 小样本学习技术在新型电力系统中的应用与挑战[J]. 电力系统自动化, 2024, 48(6): 74-82.
He Xing, Pan Meiqi, Ai Qian. Applications and challenges of few-shot learning technologies in new power system[J]. Automation of Electric Power Systems, 2024, 48(6): 74-82.
[19] 金亮, 闫银刚, 杨庆新, 等. 小样本条件下永磁同步电机深度迁移学习性能预测方法[J]. 电工技术学报, 2023, 38(18): 4921-4931.
Jin Liang, Yan Yingang, Yang Qingxin, et al. Predi- ction method of deep transfer learning performance of permanent magnet synchronous motor under the con- dition of few-shot[J]. Transactions of China Electro- technical Society, 2023, 38(18): 4921- 4931.
[20] Pan S J, Yang Q. A survey on transfer learning[J]. IEEE Transactions on Knowledge and Data Engin- eering, 2010, 22(1): 1345-1359.
[21] Wen Long, Gao Liang, Li Xinyu. A new deep transfer learning based on sparse auto-encoder for fault diagnosis[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019, 49(1): 136-144.
[22] 申锦鹏, 杨军, 李蕊, 等. 基于改进域对抗迁移学习的电力系统暂态稳定自适应评估[J]. 电力系统自动化, 2022, 46(23): 67-75.
Shen Jinpeng, Yang Jun, Li Rui, et al. Self-adaptive transient stability assessment of power system based on improved domain adversarial transfer learning[J]. Automation of Electric Power Systems, 2022, 46(23): 67-75.
[23] Ren Chao, Xu Yan, Dai Bijian, et al. An integrated transfer learning method for power system dynamic security assessment of unlearned faults with missing data[J]. IEEE Transactions on Power Systems, 2021, 36(5): 4856-4859.
[24] 任佳星, 孙英云, 秦继朔, 等. 基于改进域对抗网络的新能源基地风光时序功率曲线生成方法[J]. 电网技术, 2024, 48(8): 3409-3417.
Ren Jiaxing, Sun Yingyun, Qin Jishuo, et al. Method for generating wind and solar temporal power curves innew energy bases based on improved domain adversarial networks[J]. Grid Technology, 2024, 48(8): 3409- 3417.
[25] 李延珍, 王海鑫, 杨子豪, 等. 基于非侵入式负荷分解的家庭负荷两阶段超短期负荷预测模型[J]. 电工技术学报, 2024, 39(11): 3379-3391.
Li Yanzhen, Wang Haixin, Yang Zihao, et al. Two- stage ultra-short-term load forecasting model of household appliances based on non-intrusive load disaggregation[J]. Transactions of China Electro- technical Society, 2024, 39(11): 3379-3391.
[26] Long Mingsheng, Wang Jianmin, Ding Guiguang, et al. Transfer feature learning with joint distribution adaptation[C]//2013 IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 2013: 2200-2207.
[27] 杨柏, 关焕新, 王森, 等. 基于深层卷积神经网络电动飞机主驱动电机故障诊断方法[J]. 微电机, 2020, 53(3): 49-54.
Yang Bo, Guan Huanxin, Wang Sen, et al. Fault diagnosis method for main drive motor of electric aircraft based on deep convolutional neural net- work[J]. Micromotors, 2020, 53(3): 49-54.
[28] Wang Feng, Cheng Jian, Liu Weiyang, et al. Additive margin softmax for face verification[J]. IEEE Signal Processing Letters, 2018, 25(7): 926-930.
[29] 武宇翔, 韩肖清, 牛哲文, 等. 基于变权重随机森林的暂态稳定评估方法及其可解释性分析[J]. 电力系统自动化, 2023, 47(14): 93-104.
Wu Yuxiang, Han Xiaoqing, Niu Zhewen, et al. Transient stability assessment method based on variable weight random forest and its interpretability analysis[J]. Automation of Electric Power Systems, 2023, 47(14): 93-104.
[30] 冀鲁豫, 吴俊勇, 周艳真, 等. 基于WAMS受扰电压轨迹簇特征的电力系统暂态稳定性预测[J]. 高电压技术, 2015, 41(3): 807-814.
Ji Luyu, Wu Junyong, Zhou Yanzhen, et al. Transient stability prediction of power system based on WAMS characteristic of perturbed voltage trajectory clusters[J]. High Voltage Engineering, 2015, 41(3): 807-814.
[31] 尹杰, 刘博, 孙国兵, 等. 基于迁移学习和降噪自编码器-长短时间记忆的锂离子电池剩余寿命预测[J]. 电工技术学报, 2024, 39(1): 289-302.
Yin Jie, Liu Bo, Sun Guobing, et al. Transfer learning denoising autoencoder-long short term memory for remaining useful life prediction of Li-ion batteries[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 289-302.
Abstract As China advances its dual carbon strategy, integrating new energy sources into power grids has grown significantly, making power system operations more complex and dynamic. For deep learning-based models used in transient stability assessment to be reliable, the training data and the data encountered in real-world applications must be independent and identically distributed. However, because power systems are time-varying and uncertain, models trained offline may not perform well in new operational scenarios. This paper proposes a transient stability assessment-discriminative domain adaptive (TSA-DDA) framework to address variations in operating scenarios.
Firstly, an inter-domain dual distribution adaptation method was proposed. While aligning the marginal probability distributions of the source and target domains, this method also used Bayes' theorem to align the conditional probability distributions, achieving optimal domain adaptation. Secondly, both mean and variance differences between the source and target domains were comprehensively considered in the domain adaptation process. A new transfer regularization term was constructed to measure the inter-domain distribution differences, improving the model's domain adaptation capability. Finally, a discriminant Softmax function with adjustable parameters was developed to make intra-class sample features more compact while keeping inter-class sample features away by adjusting the parameters. This improvement can enhance the applicability of the assessment model to power grids.
In the case studies, the TSA-DDA framework's ability to address variations in operational scenarios was first validated on the New England 10-machine 39-bus system. Subsequently, four alternative TSA-DDA frameworks, each with specific modules removed, were established to evaluate the effectiveness of individual components. The prediction accuracy of the target and source domain test sets was compared using a fine-tuning algorithm and the TSA-DDA. The TSA-DDA’s capacity for continual learning is confirmed. The TSA-DDA was then benchmarked against mainstream transferred learning approaches to verify its effectiveness in scenarios with limited new data. Finally, to assess the generalization capability of the proposed scheme, experiments were conducted on a larger and more complex provincial power grid in Southwest China. The experimental simulations utilized the PSD Power Tools and Dynamic Simulation Program to offer high-fidelity power system simulation data for model training and testing.
The conclusions of this paper are given as follows. (1) The inter-domain dual distribution adaptation method comprehensively measures differences in marginal and conditional probability distributions between domains from both mean and variance perspectives. It constantly forces the feature extractor to narrow these differences, ensuring effective feature alignment across domains and enhancing the model’s adaptability. (2) The discriminant Softmax function improves the model’s learning of discriminative features by compacting intra-class features and separating inter-class features, which enhances the performance of the domain adaptation framework in transient stability assessment tasks. (3) Using voltage trajectory clusters with clustering and convergence properties as model inputs, the proposed framework ensures effective transferability across systems with varying structures and scales.
keywords:Transient stability assessment, discriminative domain-adaptive, marginal probability distribution, conditional probability distribution
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.240755
国家自然科学基金资助项目(52477096)。
收稿日期 2024-05-10
改稿日期2024-08-14
王 涛 男,1976年生,教授,博士,研究方向为电力系统安全防御与恢复控制、智能技术在电力系统中的应用研究。
E-mail: wtwxx@126.com(通信作者)
杨 远 男,1997年生,硕士研究生,研究方向为智能技术在电力系统中的应用研究。
E-mail: yangyuan123654@163.com
(编辑 郭丽军)