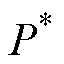 和
和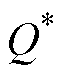 送入功率同步控制器,产生输出电压指令vref_ab。将vo_ab 与vref_ab的误差值经电压/电流双环控制,得到调制波电压vm_ab。
送入功率同步控制器,产生输出电压指令vref_ab。将vo_ab 与vref_ab的误差值经电压/电流双环控制,得到调制波电压vm_ab。摘要 随着新能源渗透率的提高,具有电压和频率支撑能力的构网型逆变器正得到广泛关注。现有研究主要聚焦于构网型逆变器的次/超同步振荡问题,但类似于跟网型逆变器,控制延时作用于电压电流控制环路,也会给系统带来中高频谐振风险。该文揭示电压电流双环控制构网型逆变器的中高频谐振机理,并分别从内部稳定性和外部稳定性两个维度,提出清晰直观的控制参数设计指导方法和虚拟阻抗构建的优化控制策略。所提出的参数优化设计方法避免了反复试凑,并可保证系统的内部稳定性和低稳态误差。通过严谨推导并分析并网电流前馈函数与输出阻抗的矢量映射关系,提出简单有效的并网电流前馈策略,提升了逆变器对电网阻抗的鲁棒性。最后,在一台10 kW的逆变器原理样机上,验证了上述理论分析的正确性和所提策略的有效性。
关键词:构网型逆变器 稳定性 谐振 控制参数 前馈策略
绿色低碳转型的能源革命正席卷全球,以同步电机为主体的传统电力系统逐步向高比例新能源和高比例电力电子化的新型电力系统演进。并网逆变器作为新能源与电网之间的能量转换接口,是电力系统中的重要的电力电子装备[1]。与同步发电机不同,并网逆变器由多时间尺度序贯调节的控制策略主导,在可控性和灵活性上具有明显优势[2-3]。从功能定位的角度,并网逆变器分为跟网型和构网型两类,其本质区别在于能否主动承担电压/频率调节[4]。跟网控制将逆变器控制为电流源,通过检测电网电压实现同步,可实现新能源发电的最大功率跟踪;构网控制则是借鉴同步发电机的物理机理,将其控制成电压源,通过调控自身输出功率或直流电压实现同步,并提供电压和频率支撑[5]。
随着未来“沙戈荒”风光新能源大基地的开发,为提升系统的稳定运行与主动支撑能力,部分新能源或储能将经构网型逆变器规模化接入,以改善电网阻尼特性、提升系统惯量、增强频率与电压支撑能力[6-7]。明晰构网型逆变器可能存在的失稳风险并提出有效的解决措施,对新能源并网发电系统的安全稳定和高质量运行起着至关重要的作用。
目前,国内外学者针对跟网型逆变器的振荡机理与抑制方法已开展了大量深入的研究,并取得了一系列卓有成效的研究成果[8-10],而对构网型逆变器的振荡机理与控制优化方面的研究仍待进一步探索与完善。在小扰动稳定性方面,现有研究则主要聚焦于其在强电网下的次同步振荡现象。文献[11]对此现象给出了直观的物理解释:电网越强,构网型逆变器与电网这两个等效电压源之间的联络阻抗越小,甚至存在“两个电压源直接并联”的失稳风险。文献[12]通过研究构网型逆变器的输出阻抗,指出其功率控制环路是上述次同步振荡的主导环节,它使得逆变器输出阻抗在低于电网额定频率段内呈负阻尼效应。为解决这一问题,学者们提出了复合同步控制[13]、有源阻尼[14]及双模式控制[15]等多种解决措施。
但值得说明的是,除了次同步振荡风险,与跟网型逆变器类似,构网型逆变器也存在中高频谐振风险。由于数字控制延时影响,构网型逆变器的输出阻抗在中高频段可能存在负阻尼,且不同的电压控制会影响输出阻抗特性,进而影响系统稳定性[16]。以输出阻抗的无源性为视角,文献[17-19]中分析了不同滤波器参数和不同控制结构下跟网型逆变器可能存在的谐振风险,并提出了一系列解决方法。文献[20]通过对比跟网型和构网型逆变器的输出阻抗,指出两者在不同频段的阻抗特性和主导因素存在较大差异。因此,有必要对构网型逆变器的谐振机理和改善方法进行详细探讨。
文献[21]分析指出,如果构网型逆变器采用电压幅值单环控制,其高频输出阻抗特性由其交流滤波器主导,控制引入的负阻抗可以忽略。然而,电压幅值控制缺乏对输出电流的控制环节,还需加入额外的故障限流措施。相比之下,矢量电压电流双闭环控制方式更受青睐,文献[22-23]对其不同内外环控制方式进行了系统的归纳和总结。文献[24]通过对比指出,若电压控制器采用纯谐振控制,电流控制器采用比例控制,更有利于系统稳定。但针对这种电压电流双环控制构网型逆变器,它的中高频谐振风险仍有待进一步阐明,亟须明晰其谐振机理并提出有效的优化控制方法。
从参数设计的角度,目前针对跟网型逆变器已形成了较为成熟的设计准则。文献[25]从低频谐波电流抑制的角度提出了跟网型逆变器的参数设计方法。文献[26]考虑数字控制延时的影响,分析了逆变器的稳定性约束并提出闭环参数可行域优化设计。然而,数字控制延时影响下的构网型逆变器稳定性约束不明。从控制策略优化设计的角度,可以沿用跟网型逆变器中的无源化理论,通过阻抗重塑来实现逆变器的谐振抑制[27-28]。对标跟网型逆变器卓有成效的无源化重塑方法[29-31],适用于构网型逆变器的阻抗重塑方法有待阐明。
综上所述,现有研究在理论和技术层面存在以下两方面不足:一方面,构网型逆变器的多控制环路大大增加了控制参数设计的复杂程度,亟须提出以稳定性为导向且清晰直观的参数设计指导方法;另一方面为了避免中高频谐振风险,通常需要引入虚拟阻抗回路,但如何优化构网型逆变器控制环节,以简便有效的方式实现虚拟阻抗的构建,仍有待阐明。因此,本文致力于构网型逆变器中高频谐振机理分析与控制优化,旨在提出保障系统稳定性的参数优化设计准则,并以阻抗重塑为视角,推导分析并网电流前馈实现形式,有效提升逆变器对电网阻抗波动的鲁棒性。
基于电压电流双环控制构网型逆变器的数学模型,首先,本文从内部稳定性和外部稳定性两个维度,分析其稳定机理和谐振风险,根据内部稳定性约束,提出控制参数优化设计方法;其次,根据外部稳定性约束,在“虚拟阻抗构建”驱动下,提出并网电流前馈优化控制策略;最后,基于一台10 kW的逆变器原理样机对理论分析和所提策略的正确性和有效性进行实验验证。
图1给出了构网型逆变器的典型控制结构示意图。图1中,Vdc为构网型逆变器的直流侧电压;L为滤波电感,C为滤波电容,它们组成LC滤波器;电网可等效为电压源vg_abc和等效电网阻抗Zg串联的戴维南等效电路。控制系统中,并网电流ig_abc和输出电压vo_abc经abc/ab 变换至静止坐标系下的ig_ab 和vo_ab,并通过功率计算,得到有功功率P和无功功率Q。将两者和功率指令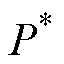 和
和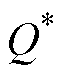 送入功率同步控制器,产生输出电压指令vref_ab。将vo_ab 与vref_ab的误差值经电压/电流双环控制,得到调制波电压vm_ab。
送入功率同步控制器,产生输出电压指令vref_ab。将vo_ab 与vref_ab的误差值经电压/电流双环控制,得到调制波电压vm_ab。
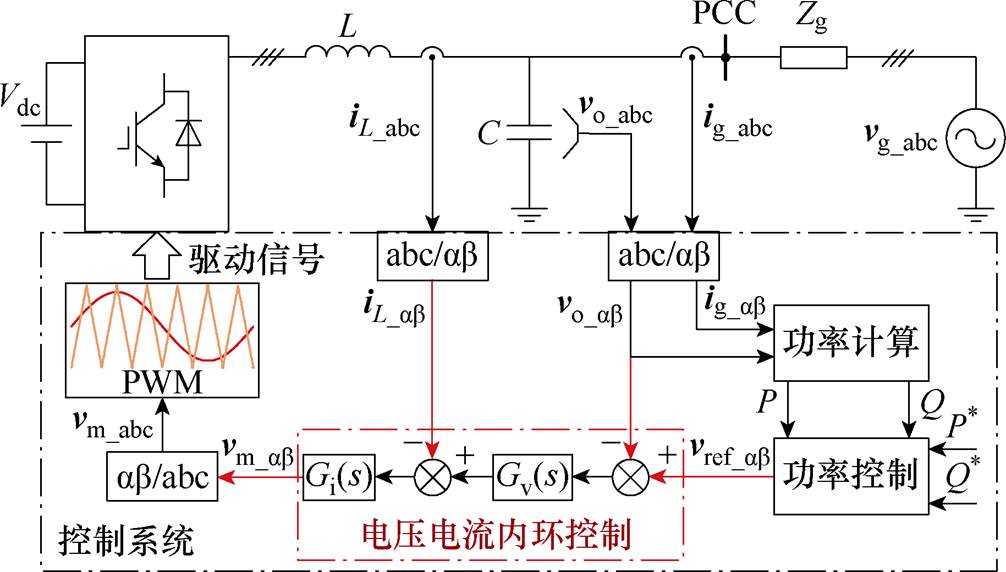
图1 构网型逆变器的结构示意图
Fig.1 Schematic diagram of the grid-forming inverter
文献[24]指出,电压控制器Gv采用纯谐振控制,电流控制器Gi采用比例控制,更有利于构网型逆变器的系统稳定性。因此本文中Gv(s)和Gi(s)分别为
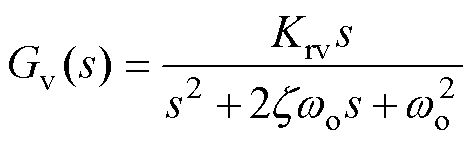 (1)
(1)
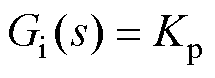 (2)
(2)
式中,Krv为电压控制器的谐振系数;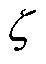 为阻尼比;wo为基波角频率;Kp为电流控制器的比例系数。
为阻尼比;wo为基波角频率;Kp为电流控制器的比例系数。
根据图1,可绘制出其控制框图如图2a所示。在静止坐标系下,由于a 轴和b 轴电压环相互解耦且模型相同,因此电压控制可用一个单输入单输出模型来表示。图中,Gd(s)为数字控制延时,表示为
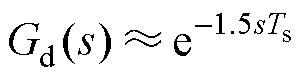 (3)
(3)
式中,Ts为采样周期。根据图2a,对原始控制框图进行如图2b~图2d所示的等效变换。
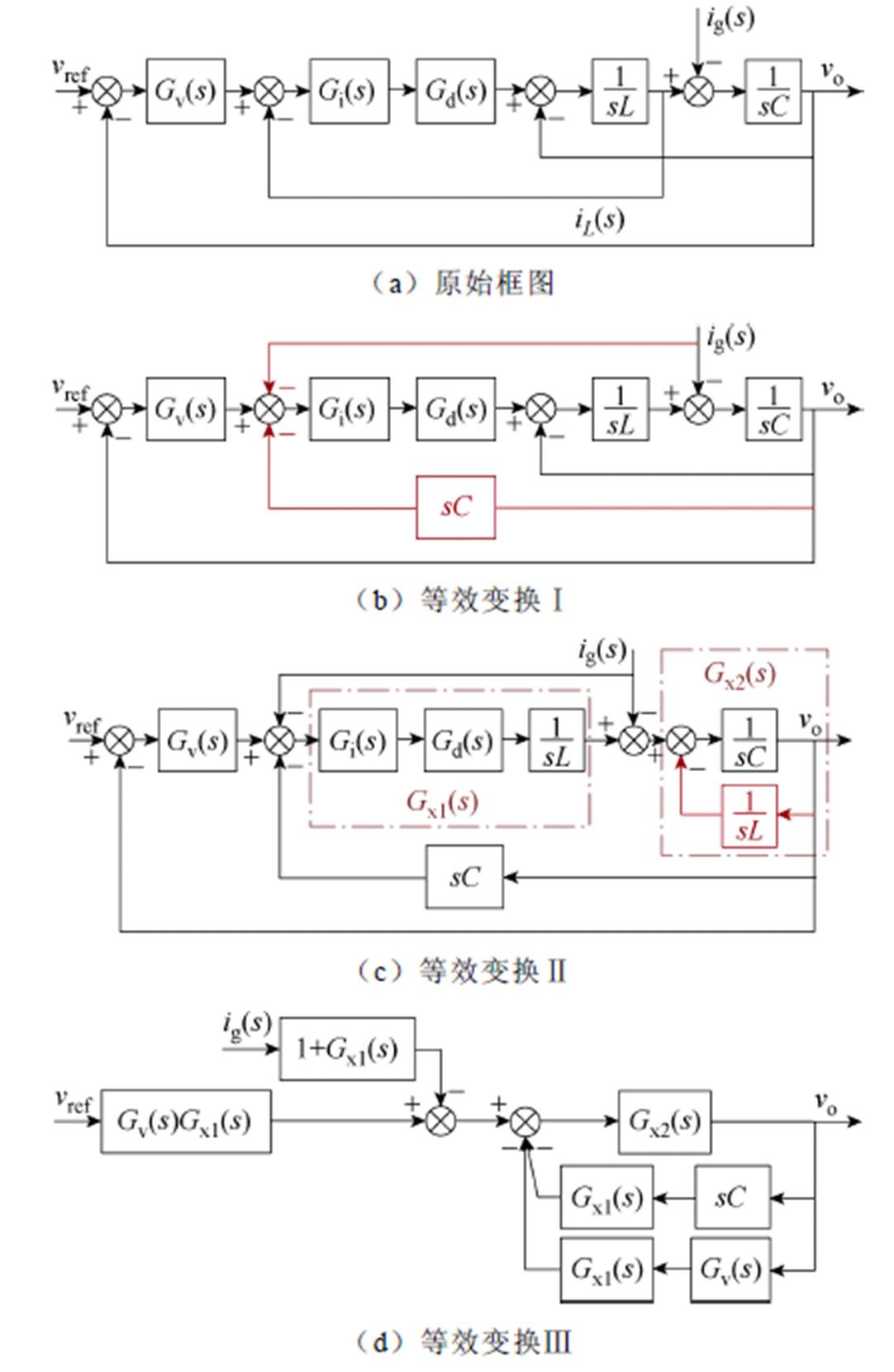
图2 构网型逆变器控制框图及其等效变换
Fig.2 Control block diagram and its equivalences of the grid-forming inverter
从图2a~图2d的等效变换过程简述如下:
(1)根据iL=ig+vosC,将图2a中iL的反馈支路用ig和vo的反馈来替代,得到图2b。
(2)将vo(s)作用于1/(sL)输入端的反馈节点移至1/(sC)的输入端,并调整其反馈函数,得到图2c。合并前向通道中的Gi(s)、Gd(s)和1/(sL)为Gx1(s),合并前向支路1/(sC)和负反馈支路1/(sL)为Gx2(s),它们分别表示为
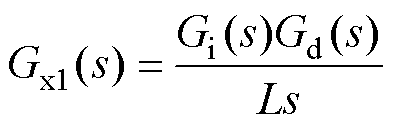 (4)
(4)
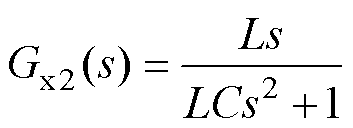 (5)
(5)
(3)将vo作用于Gv(s)输入端和输出端的两个反馈节点移至Gx2(s)的输入端,将ig(s)作用于Gv(s)输出端的反馈节点移至Gx2(s)的输入端,并调整其反馈函数,得到图2d。
根据图2d,推导出系统开环环路增益T(s)、闭环环路增益F(s)和输出电压vo(s)分别为
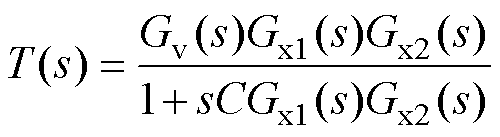 (6)
(6)
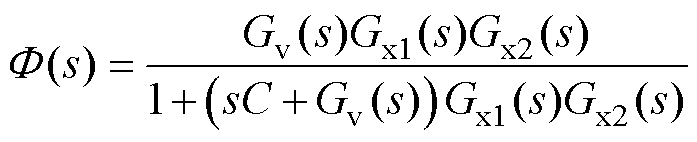 (7)
(7)
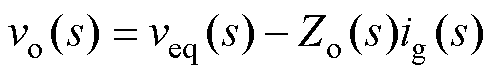 (8)
(8)
其中
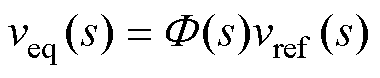
式中,Zo(s)为等效输出阻抗,表达式为
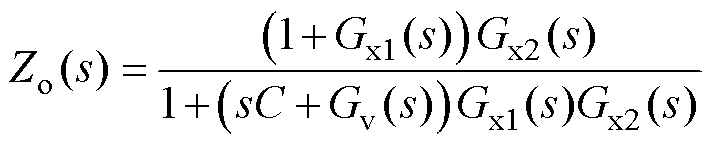 (9)
(9)
由此得到构网型逆变器的阻抗模型,即受控源veq=Fvref与输出阻抗Zo串联的形式。构网型逆变器的阻抗模型如图3所示。
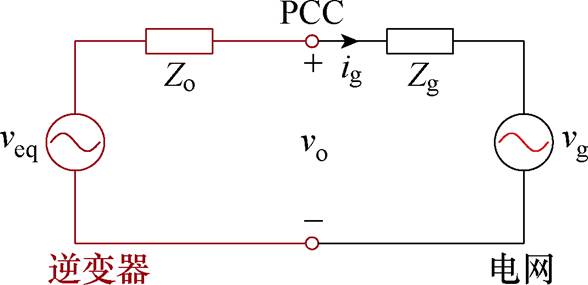
图3 构网型逆变器的阻抗模型
Fig.3 Impedance model of the grid-forming inverter
根据图3,构网型逆变器稳定并网应满足:①等效电压源veq稳定;②等效阻抗Zo与电网交互稳定。本节将基于以上两点阐述构网型逆变器的谐振失稳机理。
逆变器等效受控源自身的稳定性也被称为内部稳定性。根据veq=Fvref和Nyquist稳定判据,当且仅当系统闭环传递函数F(s)的不稳定极点数为0,即Z=P-2N=0时,逆变器内部稳定。其中,Z为F(s)的不稳定极点数;P为开环传递函数T(s)在右半s平面的极点数;N为T(s)的相频曲线与-p+2kp(k为整数)线的正负穿越次数之差,记正穿越次数为N(+),负穿越次数为N(-),则N=N(+)-N(-)。
逆变器输出阻抗与电网的交互稳定性也被称为外部稳定性。由于电网阻抗可能发生宽范围波动,导致系统谐振频率宽范围变化。根据无源性理论[32],若在所有谐振频率下等效输出阻抗Zo(s)的实部(阻性部分)都为非负,那么即使当系统受外部扰动而远离平衡点时,也能通过耗散能量的形式重新回到平衡点,此时逆变器外部稳定。
为了明晰内部稳定性是否可能被打破而带来谐振风险,即Z=P-2N=0是否成立,需要首先判别P与N的个数。
忽略扰动量ig,图2c所示的控制结构简化为如图4所示的构网型逆变器的等效双环模型。由于Gv(s)必然不包含右半平面极点,因此系统的开环右半平面极点数P由内环的稳定性所决定,即P=Zin= Pin-2Nin,下标“in”表示内环。定义内环的开环传递函数为Tin(s),其表达式为
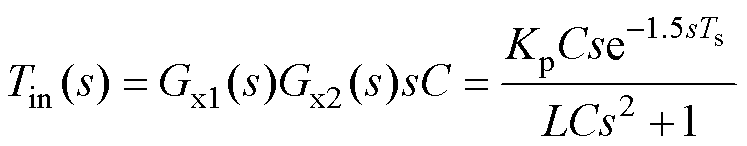 (10)
(10)
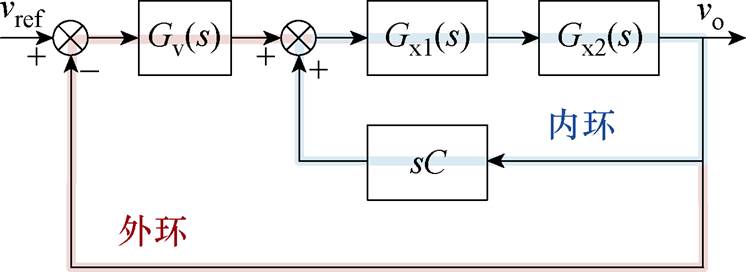
图4 构网型逆变器的等效双环模型
Fig.4 Equivalent dual-loop model of the grid-forming inverter
由式(10)可知,Tin(s)的右半平面极点数Pin=0。Tin(s)的正负穿越次数之差Nin与滤波器谐振频率fr的位置关系有关。不同滤波器谐振频率下的内环环路增益伯德图如图5所示。图中,fs为系统采样频率。
(1)0<fr<fs/6。Tin(s)的相频曲线在fs/6处穿越-180°线。若其幅值在fs/6处满足20lg|Tin( j2pfs/6)|≤0,即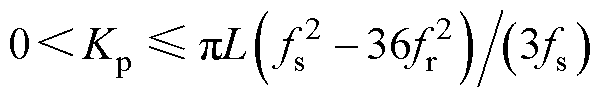 时,Nin=0,此时P= Pin-2Nin=0;反之,当
时,Nin=0,此时P= Pin-2Nin=0;反之,当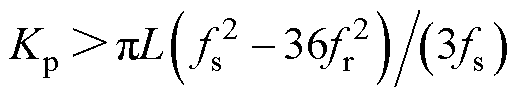 时,相频曲线仅在fs/6处有一次负穿越,即Nin=-1,于是P=Pin-2Nin=2。
时,相频曲线仅在fs/6处有一次负穿越,即Nin=-1,于是P=Pin-2Nin=2。
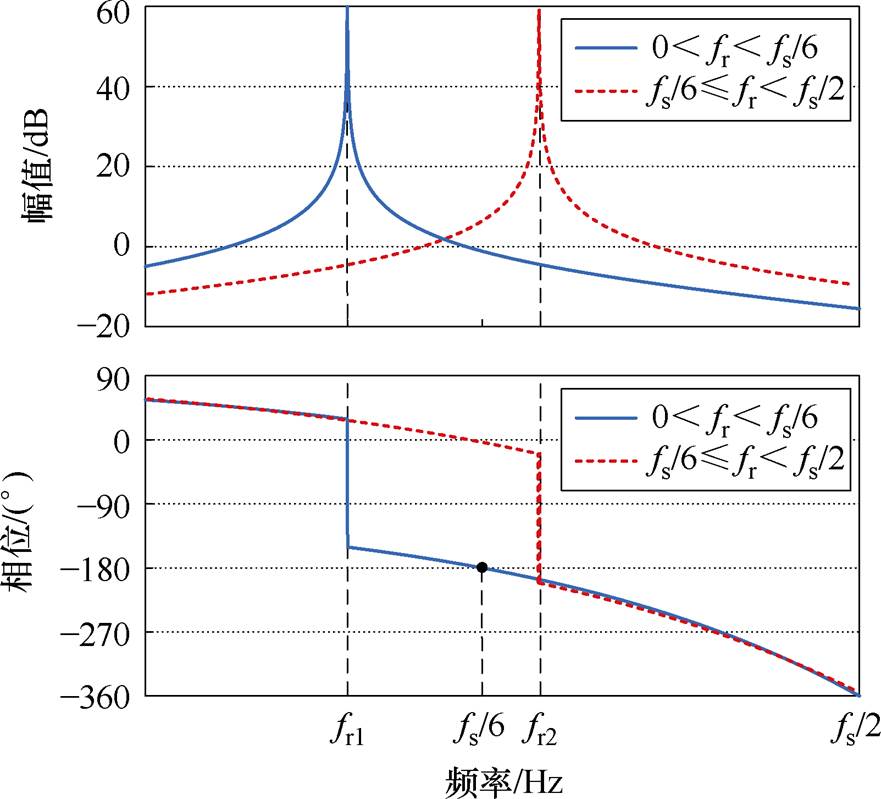
图5 不同滤波器谐振频率下的内环环路增益伯德图
Fig.5 Bode diagram of inner-loop gain with different filter resonant frequencies
(2)fs/6≤fr<fs/2。Tin(s)的相频曲线在fr处穿越-180°线,且其幅值在fr处为无穷大,因此对于任意的Kp>0,Tin(s)的相频曲线必定有一次负穿越,即Nin=-1,于是P=Zin=Pin-2Nin=2。
根据式(6),绘制出外环开环传递函数T(s)的伯德图,如图6所示,从图中可直观地看出N的个数,并由此判别P-2N=0何时成立。T(s)的相频曲线在fr和fs/6处穿越-180°线。按照上述不同P值所对应的fr和Kp取值范围,分为以下三种情况:
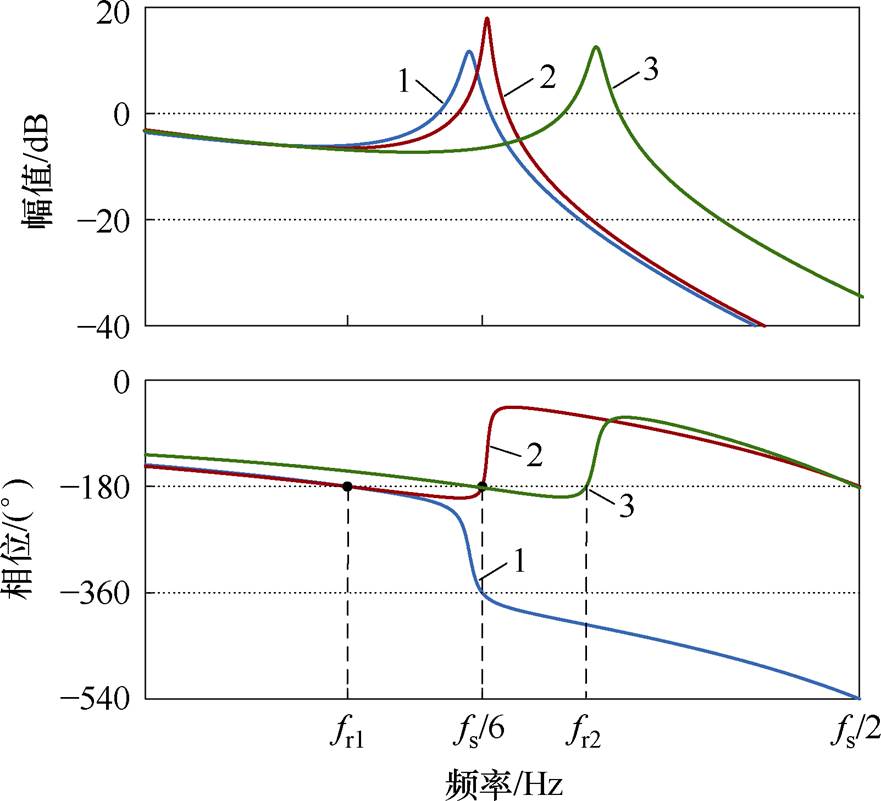
图6 不同滤波器谐振频率下的系统环路增益伯德图
Fig.6 Bode diagram of system loop gain with different filter resonant frequencies
(1)当0<fr<fs/6且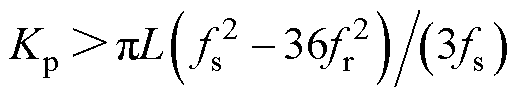 时,为了使P-2N=0成立,T(s)在fr处的幅值裕度应
时,为了使P-2N=0成立,T(s)在fr处的幅值裕度应
满足GM1>0 dB,见图6中曲线1。
(2)当0<fr<fs/6且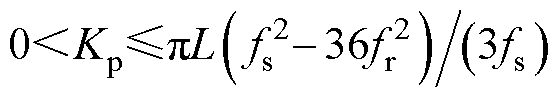 时,为了使P-2N=0成立,即N=P/2=1,应满足T(s)
时,为了使P-2N=0成立,即N=P/2=1,应满足T(s)
在fr处的幅值裕度GM1>0 dB,且在fs/6处的幅值裕度GM2<0 dB,见图6中曲线2。
(3)当fs/6≤fr<fs/2时,应有N=P/2=1,T(s)相频曲线在fs/6处负穿越-180°线,在fr处正穿越-180°线,故应满足T(s)在fr处的幅值裕度GM1<0 dB且在fs/6处的幅值裕度GM2>0 dB,见图6中曲线3。
根据上述分析,总结构网型逆变器的内部稳定性约束见表1。
表1 构网型逆变器的内部稳定性约束
Tab.1 Internal stability constraints for the grid-forming inverter

fr范围0<fr<fs/6fs/6≤fr<fs/2 Kp范围Kp>0 开环不稳定极点数P022 -180°穿越情况fr处负穿越 fr处负穿越,fs/6处正穿越 fs/6处负穿越,fr处正穿越 幅值裕度要求/dBGM1>0 GM1>0, GM2<0 GM1<0, GM2>0
从外部稳定性的角度,若构网型逆变器输出阻抗Zo具有无源性,则它与电网阻抗交互稳定。将式(4)和式(5)代入式(9)并进行整理,Zo改写为
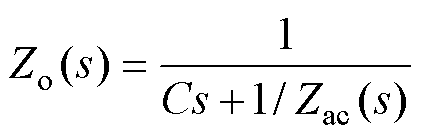 (11)
(11)
其中
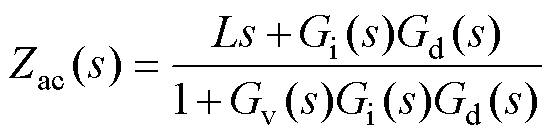 (12)
(12)
可见,逆变器输出阻抗Zo(s)可以等效为滤波电容C与有源阻抗Zac(s)的并联形式。Zo(s)的实部仅由有源阻抗Zac(s)的实部所决定,令式(12)中的s=jw,将等式左右两边同时提取实部并化简,得到
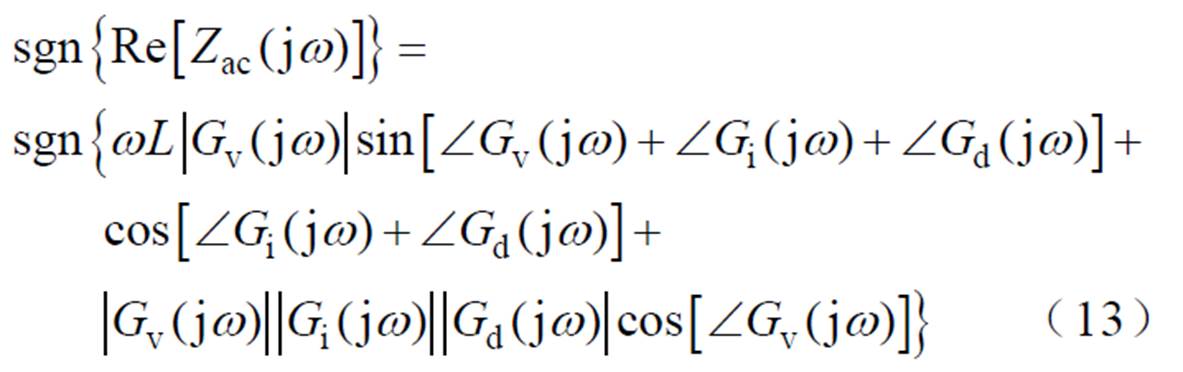
由式(1)可知,-p/2<∠Gv( jw)<p/2在全频段内恒成立,因此式(13)中等式右边第三项恒大于零,故只要使等式右边前两项之和为非负,即可保证Re[Zac( jw)]非负。观察前两项之和,可以看作[1-jwLGv( jw)]Gi( jw)Gd( jw)的实部,因此,系统具有外部稳定性的约束条件可以转换为
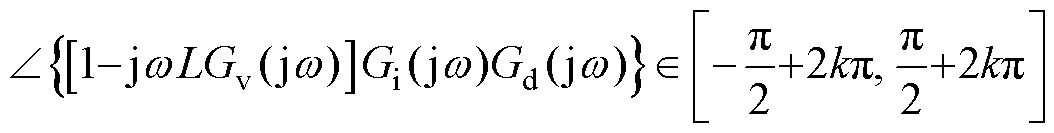 (14)
(14)
式中,k为整数。
根据式(3),得到∠Gd( jw)=-3p f/fs,将其代入式(14),上述约束条件进一步转换为
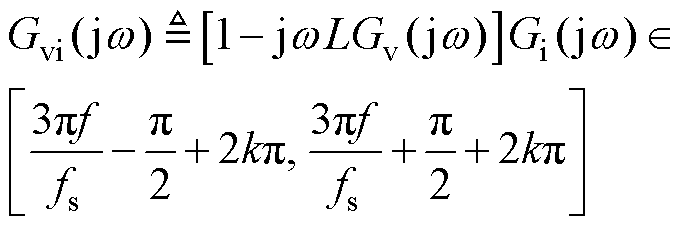 (15)
(15)
等效输出阻抗的无源性频段如图7所示。根据式(15),绘制出Gvi的约束区域,如图7中阴影区域所示。在本文中,采用比例电流调节器和谐振电压调节器,将式(1)和式(2)代入式(15)中,在图7中也绘制出它的相频曲线,如图中红色线条所示。该相频曲线与上述相位约束域交叠,落入阴影区域部分所对应的频段即为无源性频段。如图7灰色虚线所示,交叠频率点为fs/6。因此,从图7中可以看出,在采用比例电流调节器和谐振电压调节器时,构网型逆变器的输出阻抗在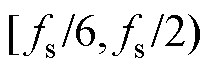 频段内不具有无源性。在该频段内,逆变器与电网的交互可能会引发谐振。
频段内不具有无源性。在该频段内,逆变器与电网的交互可能会引发谐振。
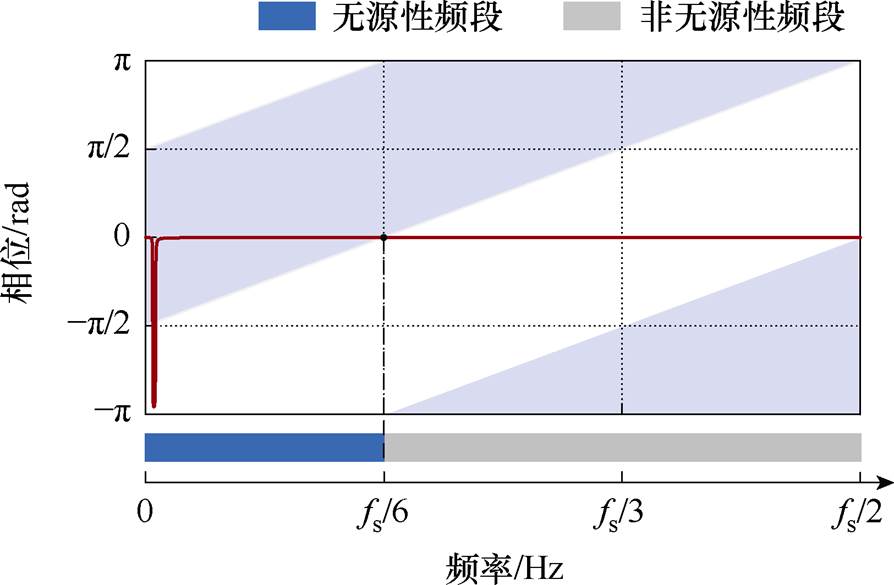
图7 等效输出阻抗的无源性频段
Fig.7 Passive frequency band of the output impedance
根据上述分析,为了规避构网型逆变器的谐振风险,需要从内部稳定性和外部稳定性两个层级对其控制进行优化设计。
本节将基于幅值裕度GM1、GM2,相位裕度PM以及基波频率处的开环增益幅值Tfo的约束,给出控制参数的优化设计步骤。
根据第2.2节的分析,T(s)的相频曲线在fr和fs/6处穿越-180°线。根据式(6),分别令s=j2p fr和s=j2p fs/6,得到T(s)的幅值裕度GM1和GM2的表达式分别为
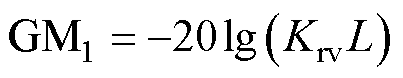 (16)
(16)
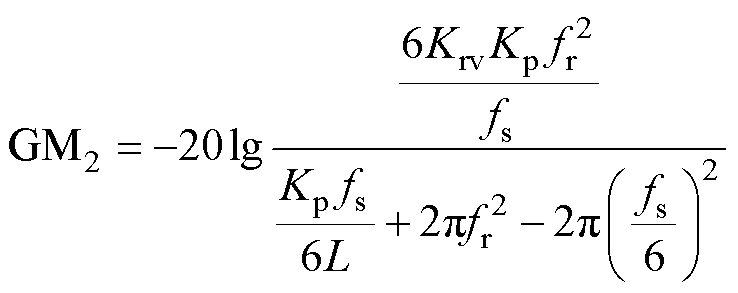 (17)
(17)
定义系统的截止频率为fc,它通常要远离谐振频率fr,以保证较好的动态性能[33],由|T( j2p fc)|=1,得到fc与控制参数Krv和Kp之间的关系式为
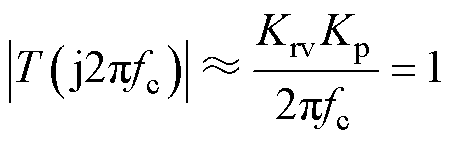 (18)
(18)
从式(18)中提取出Krv,并将其代入式(16)和式(17),得到GM1和GM2对Kp的约束条件为
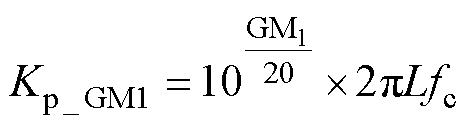 (19)
(19)
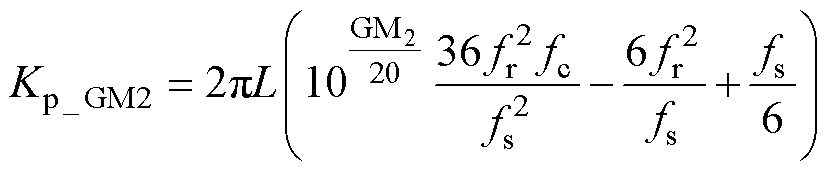 (20)
(20)
根据式(6),令s=j2p fc,可以得到T(s)的相位裕度PM对Kp的约束条件为
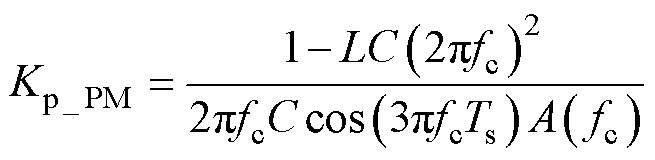 (21)
(21)
其中
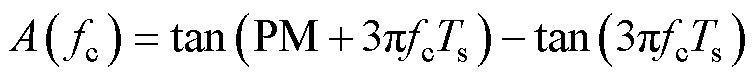 (22)
(22)
稳态误差由基波频率fo处的开环增益决定,将其定义为Tfo。将s=j2p fo代入式(6),得到
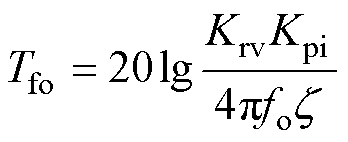 (23)
(23)
综合式(18)和式(23),得到Tfo对fc的约束为
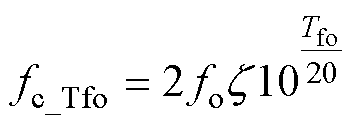 (24)
(24)
基于上述控制参数约束条件的推导并结合2.2节中内部稳定性的分析,给出构网型逆变器控制参数优化设计步骤如下:
(1)判断fr与fs/6的大小关系,根据内部稳定性的约束,由表1确定幅值裕度GM1和GM2的要求。
(2)设置期望的GM1、GM2、PM和Tfo。为保证系统具有较好的动态性能与稳态性能,一般要求|GM|>3 dB;30°<PM<60°;Tfo>40 dB[33]。
(3)根据确定的GM1、GM2、PM和Tfo,由式(19)~式(21)和式(24),得到Kp_GM1、Kp_GM2、Kp_PM和fc_Tfo四条约束曲线,进一步根据约束曲线画出Kp和fc的可选区域。
(4)从可选区域中选取合适的Kp和fc,由式(18)计算得到对应的Krv。
(5)根据选择的控制参数绘制系统的开环环路增益伯德图,检验是否满足设计要求。
由2.3节的分析可知,由于构网型逆变器的输出阻抗的非无源性,系统具有谐振风险。与跟网型逆变器引入电网电压前馈改善无源性的思想类似,本节将尝试通过引入并网电流前馈环节来拓宽无源频段,控制框图如图8a所示。图中,Gf (s)为并网电流前馈传递函数。参照与第1节相同的步骤对控制框图进行等效变换,可得到引入前馈后的等效框图如图8b所示。
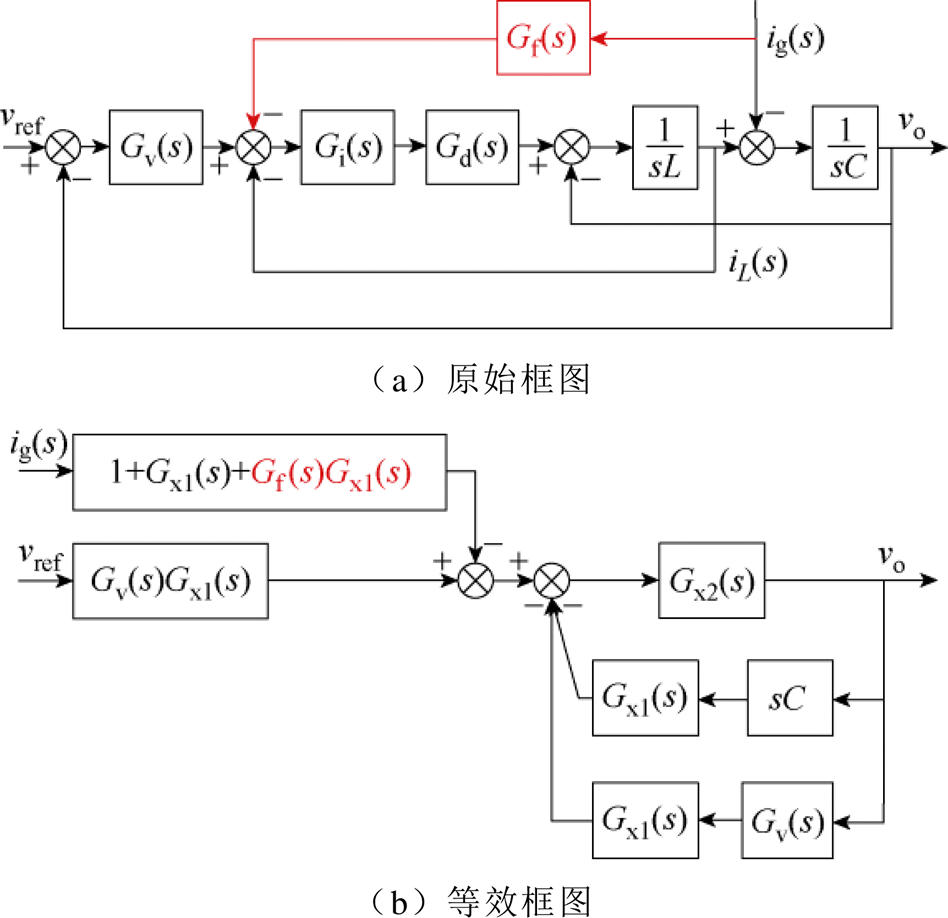
图8 引入并网电流前馈的逆变器控制框图及等效变换
Fig.8 Control block diagram and its equivalence of the grid-forming inverter with the grid current feedforward
由图8b推导出引入前馈后的输出阻抗表达式为
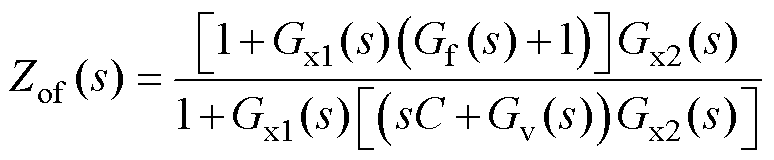 (25)
(25)
观察式(25)可以发现,只要使得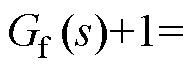
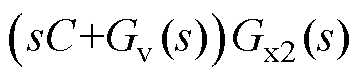 ,Zof (s)就可以简化为Gx2(s)。而根据式(5),Gx2(s)的实部为0,这意味着此时逆变器在全频段内都具有无源性。
,Zof (s)就可以简化为Gx2(s)。而根据式(5),Gx2(s)的实部为0,这意味着此时逆变器在全频段内都具有无源性。
根据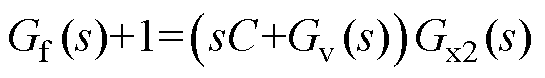 ,前馈函数应设置为
,前馈函数应设置为
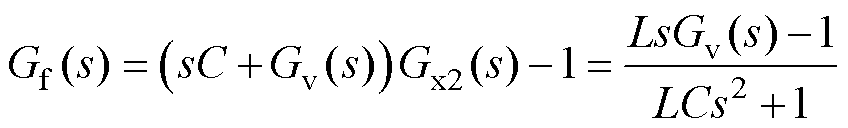 (26)
(26)
尽管此举可以增强系统的无源性,但前馈函数分母中的纯谐振项会对谐振频率fr附近的高频噪声产生放大作用。为解决这一问题,需要在保证无源性的前提下采用其他传递函数替代该谐振项。
由于1/(LCs2+1)本质上是一个无虚部的实数项,因此考虑采用实数项KR替代该谐振项。为保证引入KR后构网型逆变器仍能保证在全频段内具有无源性,首先要对谐振项1/(LCs2+1)对于输出阻抗Zof(s)的影响进行分析。
联立式(9)和式(25),Zof(s)可以分解为原始输出阻抗Zo(s)和虚拟阻抗的Zvs(s)的串联形式,即
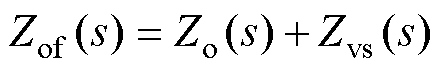 (27)
(27)
其中
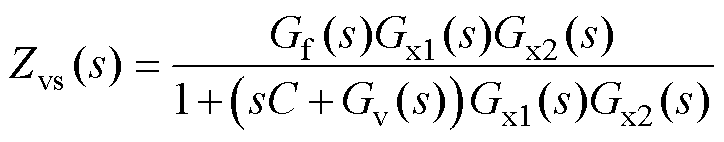 (28)
(28)
对式(27)的等式两侧同时取实部,得到
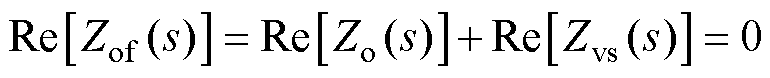 (29)
(29)
并网电流前馈策略就是通过引入Zvs(s)来抵消Zo(s)中的负阻抗成分,从而实现对构网型逆变器的无源性校正。将式(26)代入式(28),Zvs(s)的模值可以表示为
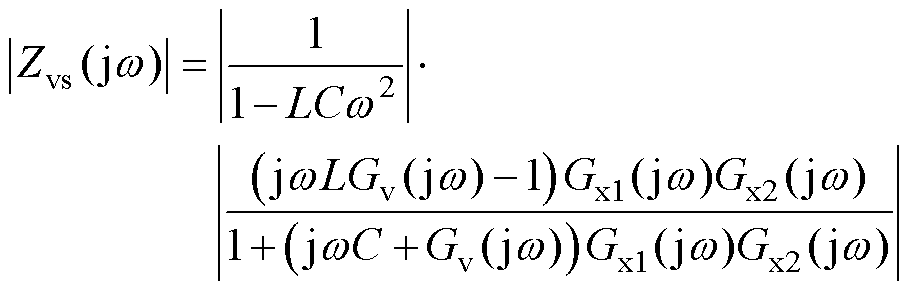 (30)
(30)
当使用KR替代1/(LCs2+1)后,虚拟串联阻抗由Zvs(s)变为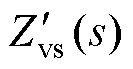 ,其相位保持不变或翻转180°,模值变为
,其相位保持不变或翻转180°,模值变为
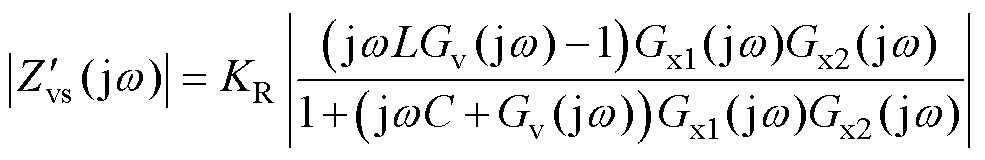 (31)
(31)
根据式(9)和式(28),以滤波器谐振频率w r和无源频段上限w s/6为分界点,矢量Zo(s)和Zvs(s)所在位置分为三种情况,Zvs( jw)和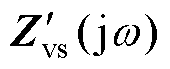 的矢量图如图9所示。根据角频率w 的位置不同,对应于(0, w r
的矢量图如图9所示。根据角频率w 的位置不同,对应于(0, w r 、(w r, w s/6
、(w r, w s/6 和(w s/6, w s/2
和(w s/6, w s/2 这三个区间,矢量Zo(s)分别位于第四象限、第一象限和第二象限。根据无源化重塑目标希望通过Zvs(s)抵消Zo(s)中的负阻抗成分,重塑后的阻抗Zof(s)简化为Gx2(s),由式(5)可知,Gx2(s)在w Î(0, w r
这三个区间,矢量Zo(s)分别位于第四象限、第一象限和第二象限。根据无源化重塑目标希望通过Zvs(s)抵消Zo(s)中的负阻抗成分,重塑后的阻抗Zof(s)简化为Gx2(s),由式(5)可知,Gx2(s)在w Î(0, w r 时落在正虚轴,在w Î(w r, w s/2
时落在正虚轴,在w Î(w r, w s/2 时落在负虚轴。
时落在负虚轴。
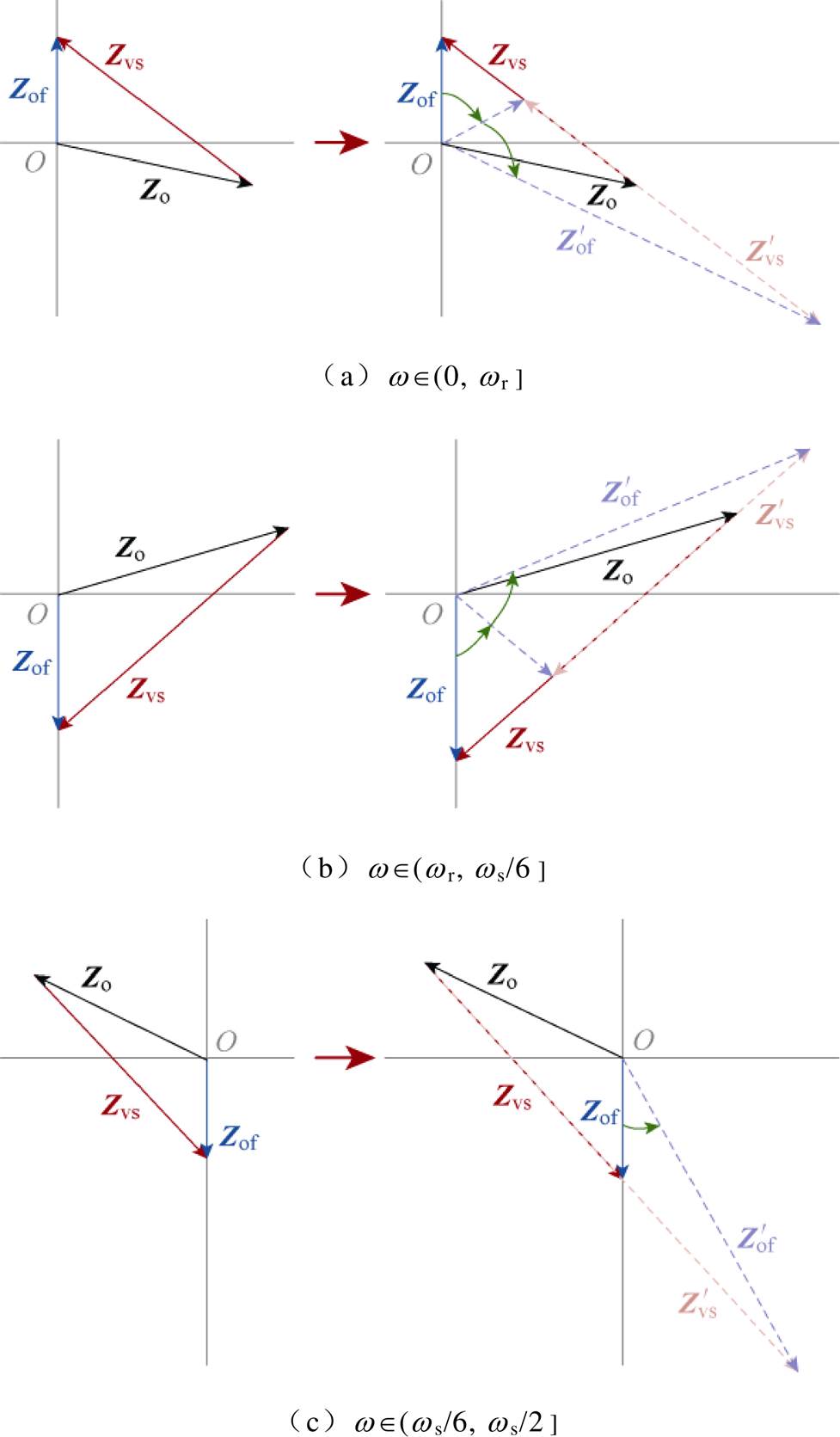
图9 Zvs( jw)和 的矢量图
的矢量图
Fig.9 Vector diagrams of Zvs( jw) and 
当w Î(0, w r 时,观察图9a,减小Zvs(s)的模值或将其进行180°翻转,所合成的矢量
时,观察图9a,减小Zvs(s)的模值或将其进行180°翻转,所合成的矢量 将落入第一象限和第四象限,其实部大于0,即阻抗无源性依然可以保证。同理,当w Î(w r, w s/6
将落入第一象限和第四象限,其实部大于0,即阻抗无源性依然可以保证。同理,当w Î(w r, w s/6 时,观察图9b,可以增大Zvs(s)的模值或将其进行180°翻转;当w Î(w s/6, w s/2
时,观察图9b,可以增大Zvs(s)的模值或将其进行180°翻转;当w Î(w s/6, w s/2 时,可以增大Zvs(s)的模值,均不影响系统的无源属性。
时,可以增大Zvs(s)的模值,均不影响系统的无源属性。
根据上述分析结论,并考虑Zvs(s)的幅值与谐振单元的模值呈正相关,可以得到谐振单元替代项KR的选取范围,如图10所示的阴影区域。可以发现,常数项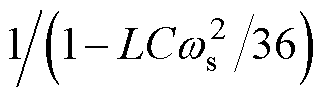 的频率特性曲线恰好可以全部落在阴影区域内。因此,谐振项可以采用该常数项替代,替代后的并网电流前馈传递函数
的频率特性曲线恰好可以全部落在阴影区域内。因此,谐振项可以采用该常数项替代,替代后的并网电流前馈传递函数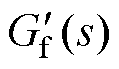 为
为
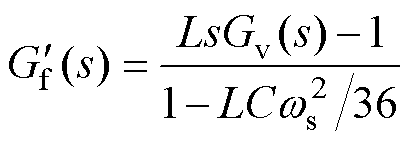 (32)
(32)
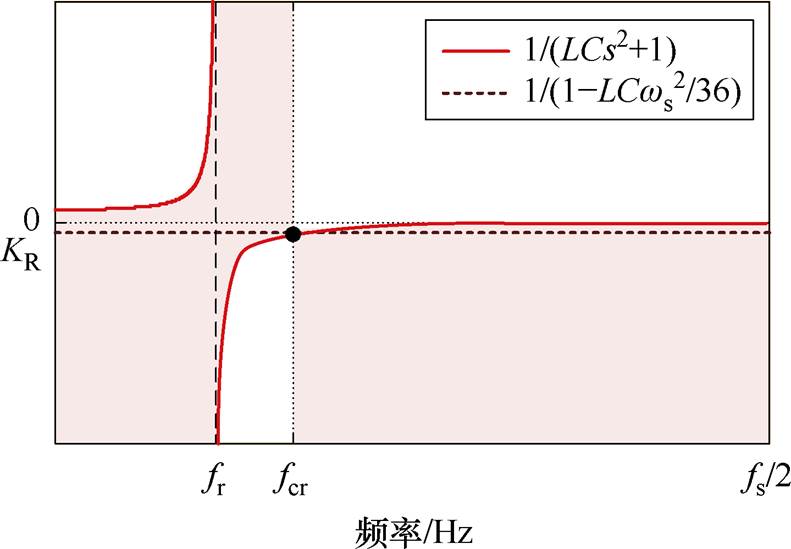
图10 KR的选取
Fig.10 Determination of KR
本节将基于表2中的构网型逆变器主电路参数,按照分析进行控制优化设计,并通过实验验证所提参数设计方法和前馈策略的有效性。实验平台如图11所示,其中,采用可编程直流电源(Chroma 62150H-600S)作为构网型逆变器的直流输入源,采用可编程交流电源(Chroma 61860)和附加电感/电容分别模拟理想电网电压和电网阻抗。
表2 构网型逆变器的主电路参数
Tab.2 Main parameters of the grid-forming inverter
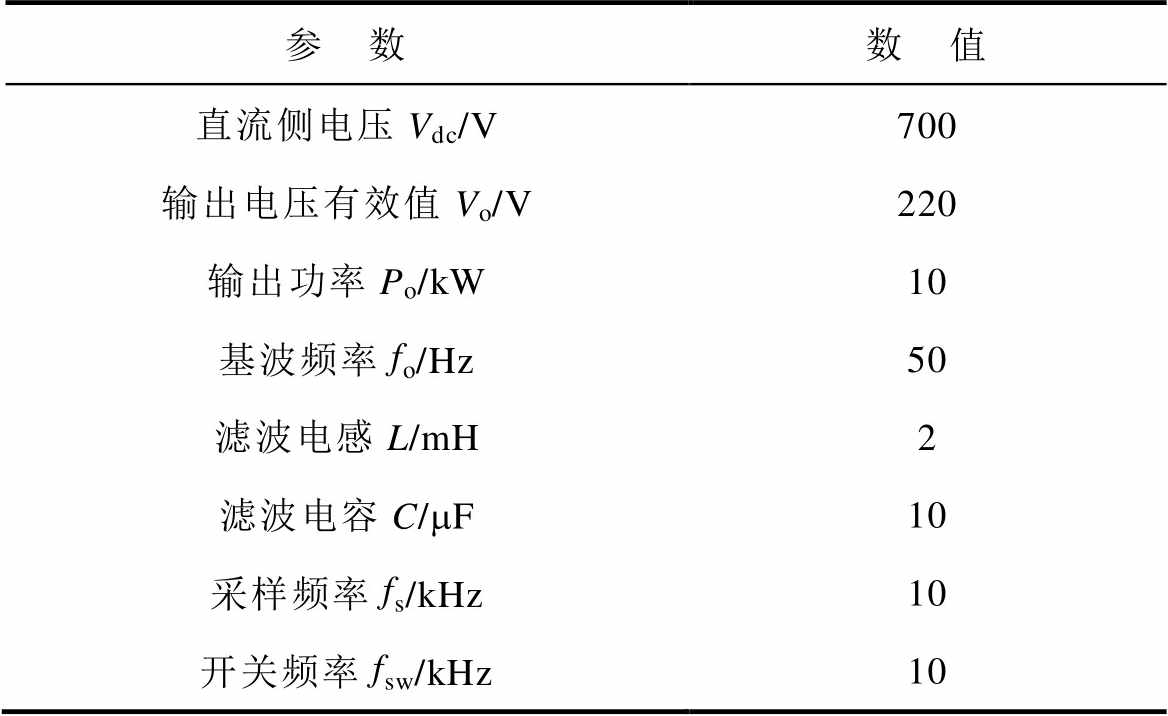
参 数数 值 直流侧电压Vdc/V700 输出电压有效值Vo/V220 输出功率Po/kW10 基波频率fo/Hz50 滤波电感L/mH2 滤波电容C/mF10 采样频率fs/kHz10 开关频率fsw/kHz10
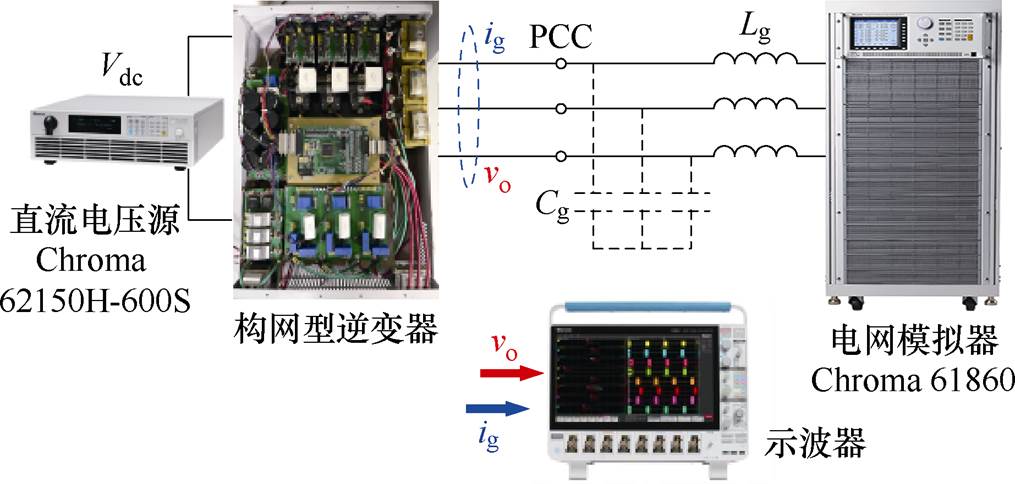
图11 实验平台
Fig.11 Experimental setup
根据表2中的主电路参数,谐振频率fr<fs/6。设置GM1>3 dB,GM2<-3 dB,PM>45°,Tfo>40 dB,参照3.2节所给出的参数设计步骤,绘制出Kp和fc的可选区域,如图12中阴影部分所示。从中选取fc=400 Hz,Kp=10(对应图12中的A点),由式(18)计算得到对应的Krv=251。根据式(32)选取并网电流前馈,在本设计案例中,Gv(z)采用纯谐振控制,在其控制带宽以上可近似为Gv(z)≈Krv/s,将其代入式(32)中,前馈函数取
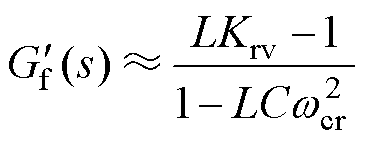 (33)
(33)
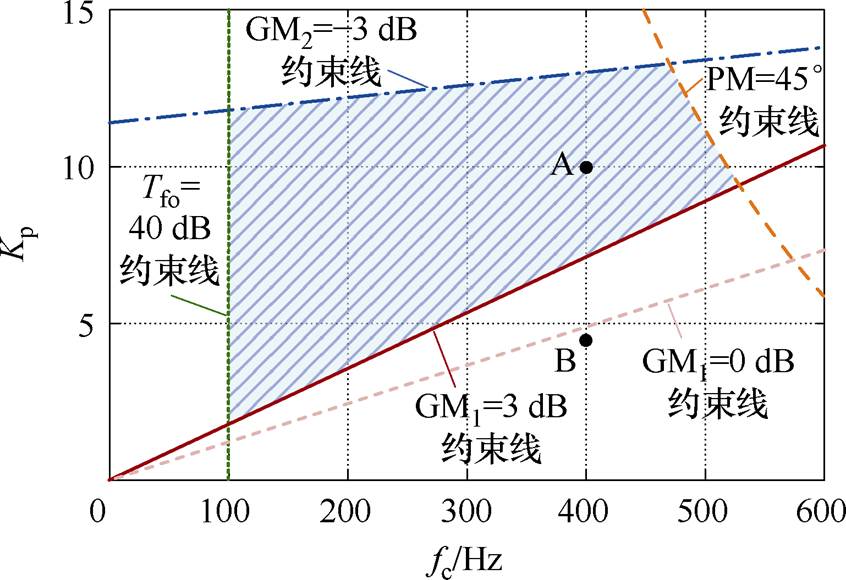
图12 控制器参数设计可选域
Fig.12 Acceptable region of controller parameters
图13绘制了系统开环环路增益伯德图。由于该设计示例中选取的Kp=10满足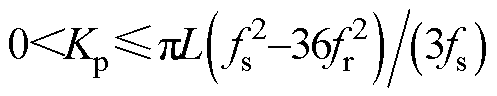 ,系统开环环路增益的相频曲线仅在fr处穿越-180°,故在检验幅值裕度时只需验证GM1是否满足要求即可。从图中得到GM1=-5.97 dB,PM=54.80°,Tfo= 52.04 dB,均满足设计要求,验证了参数设计方法的正确性。
,系统开环环路增益的相频曲线仅在fr处穿越-180°,故在检验幅值裕度时只需验证GM1是否满足要求即可。从图中得到GM1=-5.97 dB,PM=54.80°,Tfo= 52.04 dB,均满足设计要求,验证了参数设计方法的正确性。
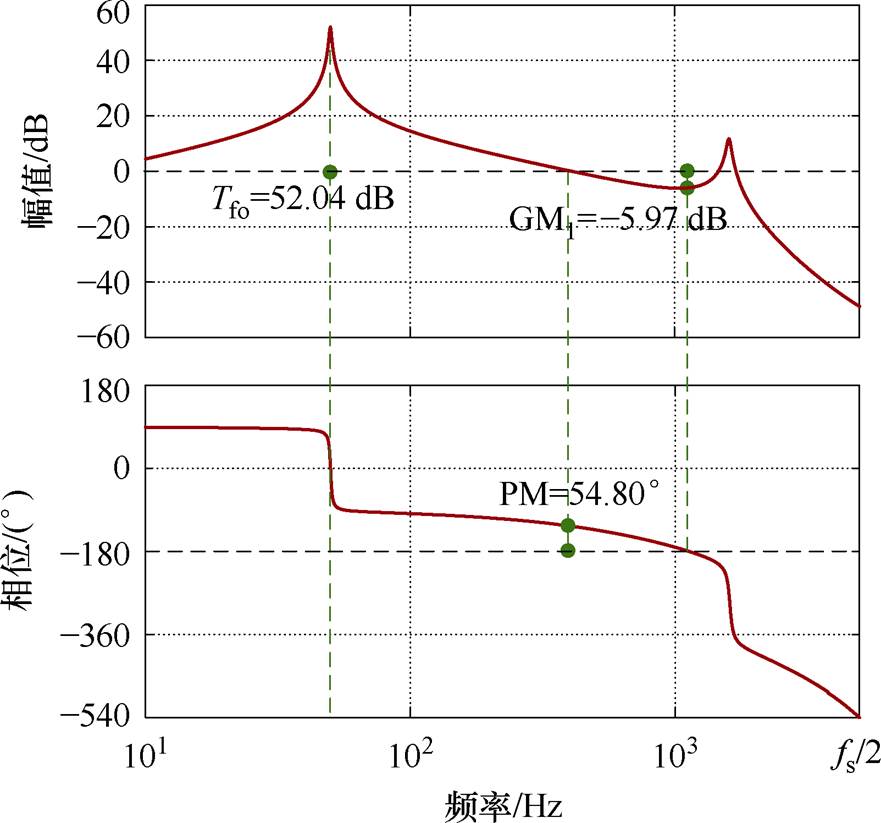
图13 控制参数优化设计下的系统环路增益伯德图
Fig.13 Bode diagram of the system loop gain with the designed controller parameters
图14绘制出了不加前馈和采用所提前馈策略后的输出阻抗伯德图。可见,当无前馈时,输出阻抗的相位在fs/6以上的频段内超过-90°,即不满足无源性要求。当电网阻抗与输出阻抗交截于该频段时,将导致并网电压谐振。当采用所提前馈策略后,逆变器输出阻抗的相位一直处于[90°, -90°]范围内,即保证了系统无源性,降低了系统的谐振风险,验证了所提前馈策略的有效性。
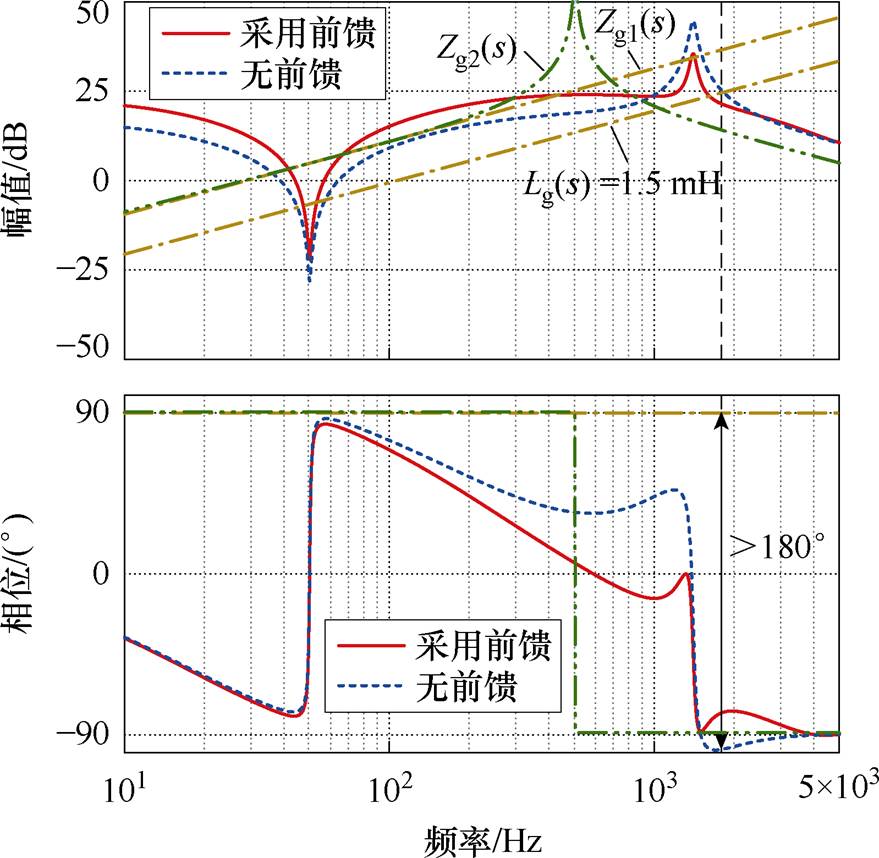
图14 逆变器输出阻抗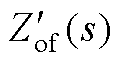 的伯德图
的伯德图
Fig.14 Plot of the inverter output impedance 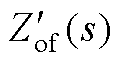
为了验证上述控制参数设计结果的正确性,首先校验系统的内部稳定性,即不考虑电网的交互影响时逆变器自身的稳定性。设置构网型逆变器离网空载运行,得到输出电压的对比实验波形如图15所示。在触发信号的下降沿时刻,将控制器参数由图12中A点对应参数改为可选域外的B点对应参数。从图15可以看出,当采用所设计的参数时,逆变器可以稳定运行并具有良好的电能质量;而当控制参数变为可选域外的B点时,输出电压出现振荡失稳,并触发保护动作、驱动闭锁。上述结果验证了所提参数设计方法的正确性和有效性。
进一步地,将构网型逆变器经1.5 mH的电网阻抗接入电网,以校验逆变器与电网交互的外部稳定性。在触发信号的下降沿时刻,切除所提出的前馈控制策略,采用所提前馈策略前后的对比实验波形如图16所示。可以看出,当采用前馈策略时,逆变器输出电压和电流保持稳定;而切除前馈后,输出电压和并网电流中开始出现1.6 kHz的振荡,该频率与图14所示的阻抗交截频率相吻合。上述实验结果验证了所提前馈策略的有效性。
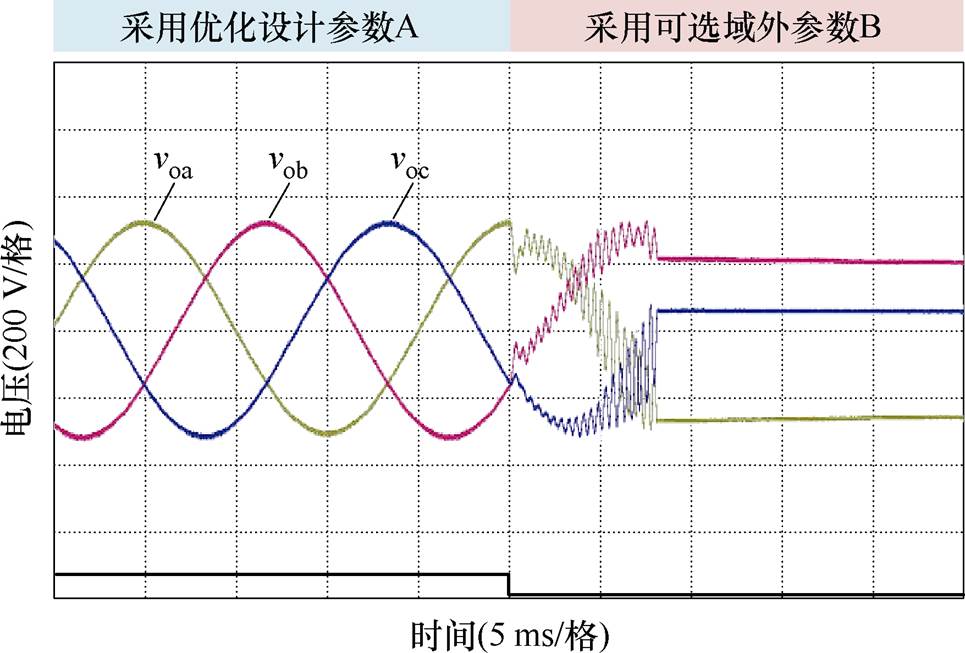
图15 采用不同控制参数的构网型逆变器对比实验波形
Fig.15 Experimental results of the grid-forming inverter with different controller parameters
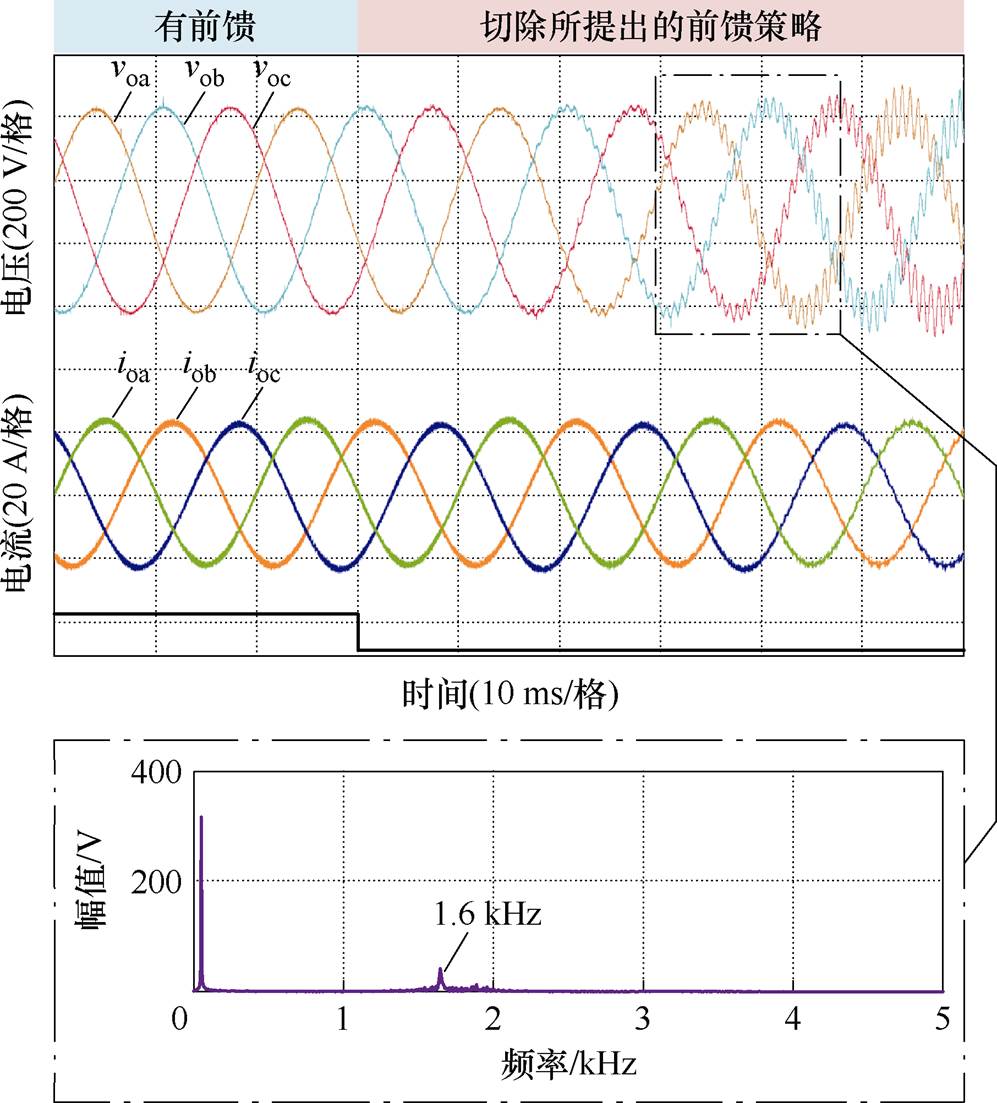
图16 采用所提前馈策略前后的对比实验波形
Fig.16 Experimental results with and without the proposed grid current feedforward scheme
接下来,验证所提设计方法和前馈策略在不同电网工况下的有效性。考虑到电网阻抗在某些情况下可能呈现容性,例如,在某些工程应用中,会在公共耦合点(Point of Common Coupling, PCC)加电容进行功率因数校正[34];海上风力发电采用远距离海底电缆将电力输送回陆地,电缆的长度和结构会增加电容总量,从而表现出电容性[35-37]。因此,本文设置另外两组电网阻抗Zg1(Lg=5 mH)和Zg2(Lg=5 mH, Cg=20 μF),在图14中也绘制出了它们与逆变器输出阻抗的交截情况。在交截频率处,逆变器输出阻抗与电网阻抗的相位差始终小于180°,因此逆变器具有较好的鲁棒性。在这两组电网工况下,构网型逆变器的实验波形如图17所示,可以看出:采用本文所提出的控制优化设计下的构网型逆变器一直保持稳定,反映了逆变器对电网强度变化的强鲁棒性,这与图14的结论一致,也说明了本文所提方法的有效性。
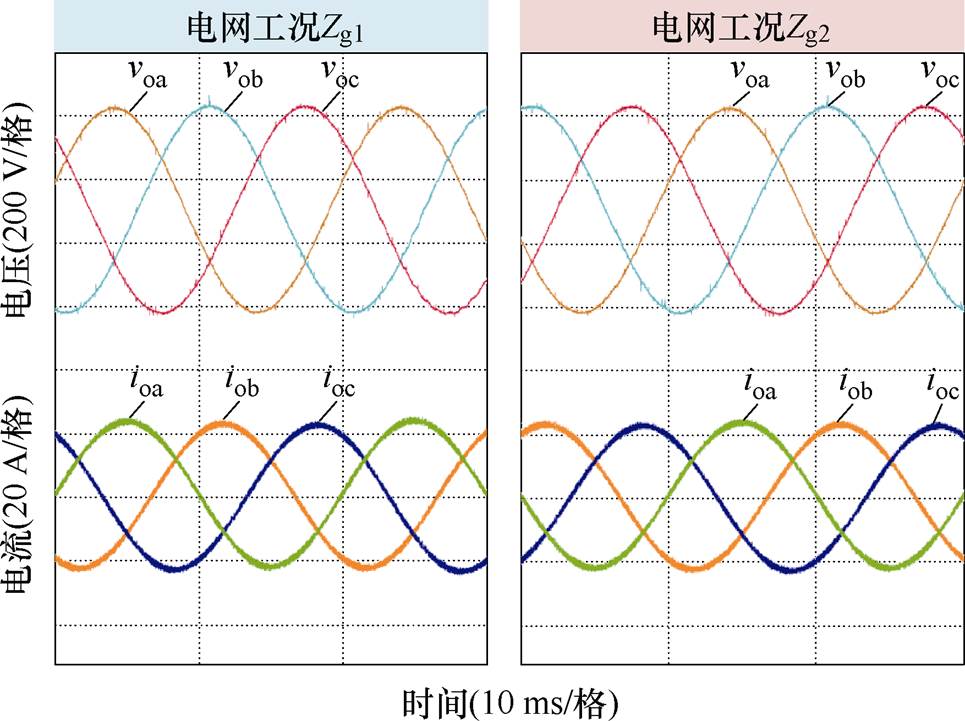
图17 在不同电网工况下控制优化后的逆变器实验波形
Fig.17 Experimental results of the grid-forming inverter with the controller optimization under different grid conditions
本文聚焦于构网型逆变器中高频谐振机理分析与控制优化,主要贡献如下:
1)通过推导电压电流双环控制构网型逆变器的环路增益和阻抗模型,分别从内部稳定性和外部稳定性这两个维度,阐释了构网型逆变器中高频谐振的产生机理。
2)基于内部稳定性约束,提出了清晰直观的控制参数设计指导方法,该方法避免了反复试凑,助力实现方便快捷高效的参数设计。
3)根据外部稳定性要求,提出了基于并网电流前馈的虚拟阻抗重构方法,通过严谨推导并分析并网电流前馈函数与输出阻抗的矢量映射关系,给出了兼具鲁棒性和简洁性的并网电流前馈实现形式。
参考文献
[1] 高磊, 吕敬, 马骏超, 等. 基于电路等效的并网逆变器失稳分析与稳定控制[J]. 电工技术学报, 2024, 39(8): 2325-2341.
Gao Lei, Lü Jing, Ma Junchao, et al. Instability analysis and stability control of grid-connected inverter based on impedance circuit equivalent[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2325-2341.
[2] 方天治, 张先云, 黄淳, 等. 输入串联输出并联LCL型并网逆变器系统的目标多重化控制策略[J]. 电工技术学报, 2019, 34(6): 1189-1200.
Fang Tianzhi, Zhang Xianyun, Huang Chun, et al. Control strategy to reach multiple objectives for input-series-output-parallel LCL-type grid-connected inverter system[J]. Transactions of China Electro- technical Society, 2019, 34(6): 1189-1200.
[3] 沈姝衡, 方天治, 章益凡. 高带宽数字控制LCL型并网逆变器及其提高并网系统鲁棒性的谐振抑制技术研究[J]. 电工技术学报, 2022, 37(21): 5548- 5561.
Shen Shuheng, Fang Tianzhi, Zhang Yifan. A high- bandwidth digital-control LCL-type grid-tied inverter and resonance-suppressing technique for improving the robustness of grid-connected system[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(21): 5548-5561.
[4] 张兴, 李明, 郭梓暄, 等. 新能源并网逆变器控制策略研究综述与展望[J]. 全球能源互联网, 2021, 4(5): 506-515.
Zhang Xing, Li Ming, Guo Zixuan, et al. Review and perspectives on control strategies for renewable energy grid-connected inverters[J]. Journal of Global Energy Interconnection, 2021, 4(5): 506-515.
[5] 葛平娟, 肖凡, 涂春鸣, 等. 考虑故障限流的下垂控制型逆变器暂态控制策略[J]. 电工技术学报, 2022, 37(14): 3676-3687.
Ge Pingjuan, Xiao Fan, Tu Chunming, et al. Transient control strategy of droop-controlled inverter con- sidering fault current limitation[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3676- 3687.
[6] 熊小玲, 李昕锐, 周琰, 等. 基于陷波器的构网型换流器同步频率谐振抑制策略[J]. 电工技术学报, 2024, 39(12): 3827-3839.
Xiong Xiaoling, Li Xinrui, Zhou Yan, et al. Syn- chronous frequency resonance suppression of grid- forming converter based on notch filter[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(12): 3827-3839.
[7] 高本锋, 邓鹏程, 梁纪峰, 等. 光伏电站与弱交流电网间次同步交互作用路径及阻尼特性分析[J]. 电工技术学报, 2023, 38(24): 6679-6694.
Gao Benfeng, Deng Pengcheng, Liang Jifeng, et al. Analysis of path and damping characteristics of subsynchronous interaction between photovoltaic plant and weak AC grid[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6679-6694.
[8] 曾祥辰, 刘青, 王嘉晨, 等. 弱电网下并网逆变器恒定带宽及稳定裕度的自适应控制策略[J]. 电工技术学报, 2024, 39(9): 2682-2695.
Zeng Xiangchen, Liu Qing, Wang Jiachen, et al. Adaptive control strategy of grid-connected inverters with constant bandwidth and stability margin in weak grids[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2682-2695.
[9] Pan Donghua, Ruan Xinbo, Bao Chenlei, et al. Capacitor-current-feedback active damping with reduced computation delay for improving robustness of LCL-type grid-connected inverter[J]. IEEE Transa- ctions on Power Electronics, 2014, 29(7): 3414-3427.
[10] 谢志为, 陈燕东, 伍文华, 等. 弱电网下多逆变器并网系统的全局高频振荡抑制方法[J]. 电工技术学报, 2020, 35(4): 885-895.
Xie Zhiwei, Chen Yandong, Wu Wenhua, et al. A global high-frequency oscillation suppression method for multi-inverter grid-connected system in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 885-895.
[11] 詹长江, 吴恒, 王雄飞, 等. 构网型变流器稳定性研究综述[J]. 中国电机工程学报, 2023, 43(6): 2339- 2358.
Zhan Changjiang, Wu Heng, Wang Xiongfei, et al. An overview of stability studies of grid-forming voltage source converters[J]. Proceedings of the CSEE, 2023, 43(6): 2339-2358.
[12] 于彦雪, 关万琳, 陈晓光, 等. 基于序阻抗的虚拟同步机同步频率谐振现象[J]. 电工技术学报, 2022, 37(10): 2584-2595.
Yu Yanxue, Guan Wanlin, Chen Xiaoguang, et al. Synchronous frequency resonance in virtual syn- chronous generator based on sequence-impedance[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2584-2595.
[13] Liu Teng, Wang Xiongfei. Physical insight into hybrid-synchronization-controlled grid-forming inverters under large disturbances[J]. IEEE Transactions on Power Electronics, 2022, 37(10): 11475-11480.
[14] 陈润, 曾君, 刘俊峰. 基于H∞滤波器的LCL型并网逆变器有源阻尼方法[J]. 电源学报, 2024, 22(4): 121-132.
Chen Run, Zeng Jun, Liu Junfeng. Active damping method based on H∞ filter of LCL grid-connected inverter[J]. Journal of Power Supply, 2024, 22(4): 121-132.
[15] Li Ming, Zhang Xing, Guo Zixuan, et al. Impedance adaptive dual-mode control of grid-connected inver- ters with large fluctuation of SCR and its stability analysis based on D-partition method[J]. IEEE Transactions on Power Electronics, 2021, 36(12): 14420-14435.
[16] 林鸿彬, 葛平娟, 徐海亮, 等. 异构逆变器并联系统改进Gershgorin圆稳定性判据及其多维谐振特性分析[J]. 电工技术学报, 2024, 39(8): 2265-2280.
Lin Hongbin, Ge Pingjuan, Xu Hailiang, et al. Improved Gershgorin circle stability criterion and multi-dimensional resonance characteristic analysis of heterogeneous inverter parallel system[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(8): 2265-2280.
[17] Wang Xuehua, He Yuying, Pan Donghua, et al. Passivity enhancement for LCL-filtered inverter with grid current control and capacitor current active damping[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 3801-3812.
[18] He Yuying, Wang Xuehua, Ruan Xinbo, et al. Passivity-based design for the plug-and-play single- loop controlled LCL-filtered inverter[C]//2020 22nd European Conference on Power Electronics and Applications (EPE'20 ECCE Europe), Lyon, France, 2020: 1-7.
[19] Wang Cheng, Wang Xuehua, He Yuying, et al. Passivity-oriented impedance shaping for LCL- filtered grid-connected inverters[J]. IEEE Transa- ctions on Industrial Electronics, 2023, 70(9): 9078- 9090.
[20] 雷雨, 李光辉, 王伟胜, 等. 跟网型和构网型新能源并网控制阻抗对比与振荡机理分析[J]. 中国电机工程学报, 2024, DOI: 11.2107.TM.20240124.1816. 011.
Lei Yu, Li Guanghui, Wang Weisheng, et al. Comparison of impedance characteristics and oscillation mechanism for grid following and grid forming renewable energy[J]. Proceedings of the CSEE, 2024, DOI: 11.2107.TM.20240124.1816. 011.
[21] Du Wei, Chen Zhe, Schneider K P, et al. A comparative study of two widely used grid-forming droop controls on microgrid small-signal stability[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 963-975.
[22] Zhang Haobo, Xiang Wang, Lin Weixing, et al. Grid forming converters in renewable energy sources dominated power grid: control strategy, stability, application, and challenges[J]. Journal of Modern Power Systems and Clean Energy, 2021, 9(6): 1239-1256.
[23] 许诘翊, 刘威, 刘树, 等. 电力系统变流器构网控制技术的现状与发展趋势[J]. 电网技术, 2022, 46(9): 3586-3594.
Xu Jieyi, Liu Wei, Liu Shu, et al. Current state and development trends of power system converter grid-forming control technology[J]. Power System Technology, 2022, 46(9): 3586-3594.
[24] Liao Yicheng, Wang Xiongfei, Blaabjerg F. Passivity- based analysis and design of linear voltage controllers for voltage-source converters[J]. IEEE Open Journal of the Industrial Electronics Society, 2020, 1: 114-126.
[25] 阚加荣, 谢少军, 吴云亚, 等. 逆变器侧电流反馈的LCL滤波并网逆变器参数设计[J]. 电力系统自动化, 2013, 37(17): 119-124.
Kan Jiarong, Xie Shaojun, Wu Yunya, et al. Para- meter design for LCL filter grid-connected inverter using inverter-side current feedback strategy[J]. Automation of Electric Power Systems, 2013, 37(17): 119-124.
[26] Pan Donghua, Ruan Xinbo, Bao Chenlei, et al. Optimized controller design for LCL-type grid- connected inverter to achieve high robustness against grid-impedance variation[J]. IEEE Transactions on Industrial Electronics, 2015, 62(3): 1537-1547.
[27] 徐海亮, 张伟杰, 林鸿彬. 一种提高并网逆变器无源性的阻抗重塑方法[J]. 电源学报, 2022, DOI: 12.1420.TM.20220908.1534.006.
Xu Hailiang, Zhang Weijie, Lin Hongbin. An improved passive impedance remodeling method for grid-connected inverters[J]. Journal of Power Supply, 2022, DOI: 12.1420.TM.20220908.1534.006.
[28] 刘昊, 方天治, 张惠丽, 等. 弱电网下应对复杂稳定性问题的并网逆变器改进电压前馈通路研究[J].电工技术学报, 2024, 39(16): 4955-4967.
Liu Hao, Fang Tianzhi, Zhang Huili, et al. Research on an improved voltage feedforward path of grid- connected inverter coping with complex stability issues in weak grid[J]. Transactions of China Elec- trotechnical Society, 2024, 39(16): 4955-4967.
[29] 杨明, 杨倬, 李玉龙, 等. 弱电网下基于电网电压前馈的并网逆变器阻抗重塑控制策略[J]. 电工技术学报, 2024, 39(8): 2553-2566.
Yang Ming, Yang Zhuo, Li Yulong, et al. Impedance remodeling control strategy of grid-connected inverter based on grid voltage feedforward in weak current network[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2553-2566.
[30] Rodriguez-Diaz E, Freijedo F D, Guerrero J M, et al. Input-admittance passivity compliance for grid- connected converters with an LCL filter[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1089-1097.
[31] Xie Chuan, Li Kai, Zou Jianxiao, et al. Passivity- based stabilization of LCL-type grid-connected inverters via a general admittance model[J]. IEEE Transactions on Power Electronics, 2020, 35(6): 6636-6648.
[32] Harnefors L, Yepes A G, Vidal A, et al. Passivity- based controller design of grid-connected VSCs for prevention of electrical resonance instability[J]. IEEE Transactions on Industrial Electronics, 2015, 62(2): 702-710.
[33] 鲍陈磊, 阮新波, 王学华, 等. 基于PI调节器和电容电流反馈有源阻尼的LCL型并网逆变器闭环参数设计[J]. 中国电机工程学报, 2012, 32(25): 133-142.
Bao Chenlei, Ruan Xinbo, Wang Xuehua, et al. Design of grid-connected inverters with LCL filter based on PI regulator and capacitor current feedback active damping[J]. Proceedings of the CSEE, 2012, 32(25): 133-142.
[34] Wang Xiongfei, Blaabjerg F, Liserre M, et al. An active damper for stabilizing power-electronics-based AC systems[J]. IEEE Transactions on Power Elec- tronics, 2014, 29(7): 3318-3329.
[35] 钱洁. 电力电缆电气参数及电气特性研究[D]. 杭州: 浙江大学, 2013.
Qian Jie. Study on electrical parameters and characteristics of power cable[D]. Hangzhou: Zhejiang University, 2013.
[36] 王仲, 唐盈盈, 贾利川. 垂直洋流下500 kV海缆电热耦合场和载流量研究[J]. 电力工程技术, 2024, 43(5): 140-149.
Wang Zhong, Tang Yingying, Jia Lichuan. Electric- thermal coupling and ampacity of 500 kV DC submarine cable under the action of vertical ocean currents[J]. Electric Power Engineering Technology, 2024, 43(5): 140-149.
[37] 曹燕明, 李亚男, 周滔, 等. 并联电抗器补偿方案对500 kV海底电缆沿线过电压的分布影响[J]. 电力工程技术, 2024, 43(4): 127-135.
Cao Yanming, Li Yanan, Zhou Tao, et al. Influence of shunt reactor compensation scheme on overvoltage distribution along 500 kV submarine cable[J]. Electric Power Engineering Technology, 2024, 43(04): 127- 135.
Abstract With the remarkable growth of renewables, distributed power generation systems (DPGSs) are starting to take over the dominant role of synchronous machines. As an essential interface between renewables and power grids, the grid-connected inverter plays an important role in the safe and stable operation of DPGSs. Among two types of grid-connected inverters, i.e., grid-following (GFL) and grid-forming (GFM) ones, attention has gradually turned to the GFM inverter in recent decades, owing to its synchronous-machine-like characteristics and capability of operating in weak grid or even forming a stand-alone grid. However, similar to the GFL inverter, the GFM inverter may exhibit non-passive characteristics in the mid/high-frequency bands, leading to mid/high-frequency resonance risk.
The existing research mainly focuses on sub-synchronous oscillation, but the mid/high-frequency resonance issue still needs to be explored. In order to mitigate the mid/high-frequency resonance and harvest the desired performance, this paper provides the optimal design procedure for controller parameters from the perspective of internal stability and the impedance reshaping method via the grid current feedforward from the perspective of external stability.
Firstly, a mathematical model of the voltage-current double-loop controlled GFM inverter is established. The control block diagram of the inverter’s control system is depicted, and its equivalent transformation is performed. Accordingly, the impedance model of the GFM inverter is obtained as a controlled source in series with the output impedance.
After that, the stability of the GFM inverter is divided into internal stability and external stability, which characterize the stability of the equivalent voltage source and the interaction stability between the equivalent impedance and the grid, respectively. From these two stability dimensions, the stability mechanism and resonance risk of the GFM inverter are analyzed based on the Nyquist stability criterion and the passivity theory, and the main factors affecting the system stability are revealed.
According to the internal stability constraints, stability margin requirements, and steady-state error, an optimal design procedure for the control parameters is provided, which avoids repeated trials and ensures internal stability and low steady-state error. Additionally, based on the external stability constraints, the impedance shaping scheme with the grid current feedforward is proposed, and the corresponding feedforward function is derived. The proposed scheme is simple to implement and can effectively enhance the inverter's robustness against grid impedance variations.
Finally, experiments are carried out on a 10 kW GFM inverter prototype. The results confirm that under different grid conditions, the inverter can with the designed parameters and the proposed scheme continuously operate stably, and the power quality is high, which verifies the theoretical analyses and the proposed scheme.
keywords:Grid-forming inverter, stability, resonance, controller parameters, feedforward scheme
中图分类号:TM614
DOI: 10.19595/j.cnki.1000-6753.tces.240719
江苏省自然科学基金项目(BK20230951)、中国博士后面上基金项目(2023M730917)和湖北省重点研发计划项目(2023BAB112)资助。
收稿日期 2024-05-07
改稿日期2024-07-10
赫玉莹 女,1997年生,博士,副教授,研究方向为并网发电系统稳定性分析及其优化控制。
E-mail: heyuying@hhu.edu.cn
王学华 男,1978年生,博士,教授,研究方向为新能源并网发电技术、柔性直流输电技术和新能源系统中的能量管理与调度。
E-mail: wang.xh@hust.edu.cn(通信作者)
(编辑 陈 诚)