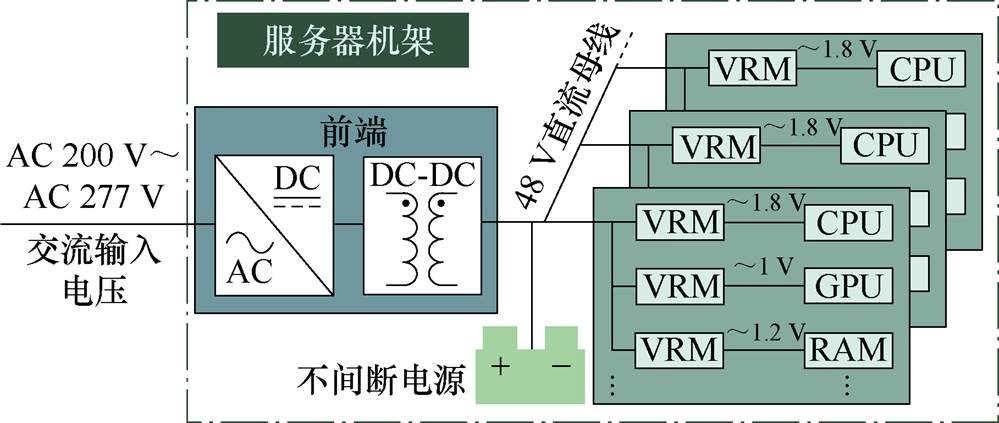
图1 48 V母线电压数据中心架构
Fig.1 Data center power architectures with 48 V bus
摘要 四开关Buck-Boost(FSBB)变换器凭借其优异的宽范围电压调节能力和输入输出电压极性相同的特点被广泛应用于电子设备中。基于四模态控制策略的FSBB变换器在输入电压和输出电压接近时会工作在过渡模式(扩展降压模式或扩展升压模式)。此时变换器的所有开关器件都将处于工作状态,变换器的开关损耗增加,变换器的转换效率降低。针对上述问题,该文提出一种低纹波-变频控制策略,当FSBB变换器工作在过渡模式时,控制两个桥臂之间的移相时间使电感电流的纹波降至最低,然后降低开关频率,提高变换器的效率。首先,分析FSBB变换器多模态控制的工作特点,指出单模态控制电感电流纹波较大、双模态控制占空比受限和三模态控制电流有效值较大的缺点,进而确定四模态控制的工作模式;其次,分析四模态控制策略下电感电流纹波与桥臂移相时间的关系,得到最小电感电流纹波的工作条件;再次,建立FSBB变换器的损耗模型,并提出低纹波-降频控制策略,降低FSBB变换器过渡模式时的开关频率,提高变换器效率;最后,搭建一个300 W的实验样机,实验结果表明,所提出的低纹波-变频控制策略的电感电流纹波在相同开关频率下仅为传统控制策略的35.6%。另外,通过实验样机实现了98.52%的峰值转换效率和98.4%的满载转换效率。相比较于传统定频控制策略,峰值效率提高了2.46%,满载效率提高了2.35%。
关键词:四开关Buck-Boost变换器 多模态控制 降频控制 高效率
随着云计算和人工智能等技术的快速发展,数据中心对供电链路的要求也越来越严格[1]。这些需求推动着数据中心电源架构朝着更高效率和更高功率密度的方向发展[2-4]。最近,电源架构的总线电压逐渐从传统的12 V提高到48 V[5-6],以减小配电线路的电流,从而降低配电损耗。48 V母线电压数据中心架构如图1所示,在48 V总线供电架构中,不间断电源(Uninterruptible Power Supply, UPS)系统与48 V总线并联,这导致总线电压在很大范围内(40~60 V)波动。为了更好地管理总线电压和能量流动,需要在UPS系统和用电系统之间插入双向DC-DC转换器[7-8]。而四开关Buck-Boost(Four- Switch Buck-Boost, FSBB)变换器因其高效率和宽电压调节能力而备受关注[9-11]。

图1 48 V母线电压数据中心架构
Fig.1 Data center power architectures with 48 V bus
图2所示为FSBB变换器的拓扑结构,FSBB变换器有3个控制自由度,图中,d1、d2分别为Buck桥臂和Boost桥臂的占空比,j 为两个桥臂之间的移相角。多个控制自由度不仅能使转换器在不同模式下运行,还能通过优化控制策略改善转换器性能[12]。
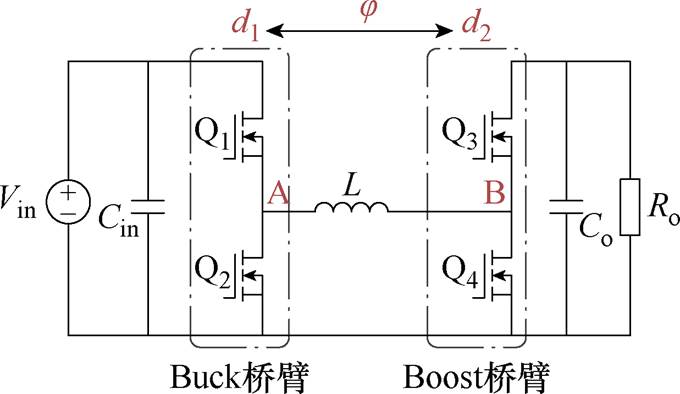
图2 四开关Buck-Boost变换器
Fig.2 Four-switch Buck-Boost converter
因此,学者们围绕FSBB变换器的控制策略展开了大量的研究。目前关于FSBB变换器的效率优化控制策略主要分为两大类:软开关控制策略研 究[13-17]和多模态控制策略研究[18-26]。
软开关控制策略可以进一步归纳为三角波电感电流控制策略和四边形电感电流控制策略两类。在文献[13]中通过控制变换器工作在同步Buck临界导通模式和同步Boost临界导通模式来实现功率器件的零电压开通(Zero Voltage Switching, ZVS)。文献[14-17]提出的四边形控制策略通过控制4个开关管使电感电流成为四边形,并引入负电流环流阶段,从而依次实现所有开关管的软开关。四边形控制策略需要同时控制3个控制自由度,增加了控制算法的复杂性。尽管软开关控制策略可以实现开关管的ZVS,提高变换器的开关频率,但是随着负载增加,电感电流的脉动变大,因此会导致电感电流有效值增加从而增加变换器的损耗。而增加的导通损耗会使软开关失去优势。
文献[18-26]研究了多模态控制策略。多模态控制策略主要通过不断优化单模态控制策略得到。在多模态控制策略中,变换器会根据不同的输入电压和输出电压将整个工作范围划分为不同的工作模式,并通过控制占空比实现电压调节功能。具体可以分为双模态控制、三模态控制和四模态控制。单模态控制策略是FSBB最简单的控制方法,开关管Q1和Q4同时开通关断,Q2和Q3同时开通关断,FSBB工作在传统的Buck-Boost模式。但是电感电流的纹波较大,因此会牺牲变换器的效率。为了减少开关损耗以及降低电感电流纹波,文献[18]提出了双模态控制策略,当输入电压高于输出电压时,FSBB工作在Buck模式(Q3常开,Q4常关);当输入电压低于输出电压时,FSBB工作在Boost模式(Q1常开,Q2常关)。虽然双模态控制可以大大提高变换器的效率,但是在输入电压和输出电压接近时,变换器会在两个不同模式之间频繁切换,因此可能会导致系统不稳定。而且受到器件寄生参数和控制器的延时影响,通常变换器的最大占空比会受到限制。因此文献[19-23]提出了三模态控制方法,当输入电压和输出电压接近时,通过引入一个额外的工作模式实现不同模式之间的平滑过渡,同时解决占空比限制的问题。在此基础上,文献[24-26]提出了四模态控制方式,在输入电压和输出电压接近时,插入两个过渡模态扩展Buck模式和扩展Boost模式。同样可以实现模式之间的平滑过渡进而提高系统稳定性,同时可以降低电感电流纹波。
当前,三模态控制方式和四模态控制方式通过在过渡模式中同时开通关断Buck桥臂和Boost桥臂很好地解决了FSBB变换器最大占空比限制的问题。但是关于过渡模式中Buck桥臂和Boost桥臂之间的移相角对变换器性能的影响尚未有学者分析。另外,对于变换器而言,整体损耗不仅会受到电感电流的影响,还会受到其他因素影响,如开关频率。然而当前并没有相关的研究,因此在多模态控制策略基础上展开移相时间和开关频率对FSBB的效率优化的研究至关重要。
针对上述问题,本文提出了一种低纹波-变频四模态控制策略优化FSBB的效率。首先研究了定频控制策略下的最小电感电流纹波控制方法。其次通过建立四模态控制策略的FSBB损耗模型,得到扩展Buck模式和扩展Boost模式时变换器的损耗与开关频率的关系。最后设计了相应的控制算法实现FSBB变换器的效率优化,并通过实验对比分析了传统控制方法和所提的低纹波变频控制方法下的FSBB的性能,证明了所提出的低纹波变频控制策略能有效减低电感电流纹波和提高FSBB变换器的转换效率。
图2所示为FSBB变换器的拓扑结构,由Buck桥臂和Boost桥臂级联滤波电感形成。其中Buck桥臂的开关管Q1的占空比定义为d1,Boost桥臂的开关管Q3的占空比定义为d2。因此,两个桥臂的中点平均电压可以分别表示为
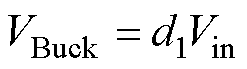 (1)
(1)
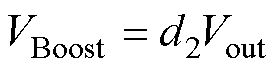 (2)
(2)
式中,VBuck为Buck桥臂中点平均电压;VBoost为Boost桥臂中点平均电压;Vin为输入电压;Vout为输出电压。
根据电感伏秒平衡可以得到FSBB输入电压Vin和输出电压Vout之间的增益M为
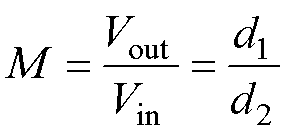 (3)
(3)
FSBB的电压增益与占空比d1和d2的变化关系如图3所示。当占空比的变化范围为[0.05, 0.95]时,变换器的输出电压增益变化范围为[0.05, 19]。因此,FSBB非常适合宽范围输入与输出的应用场景。
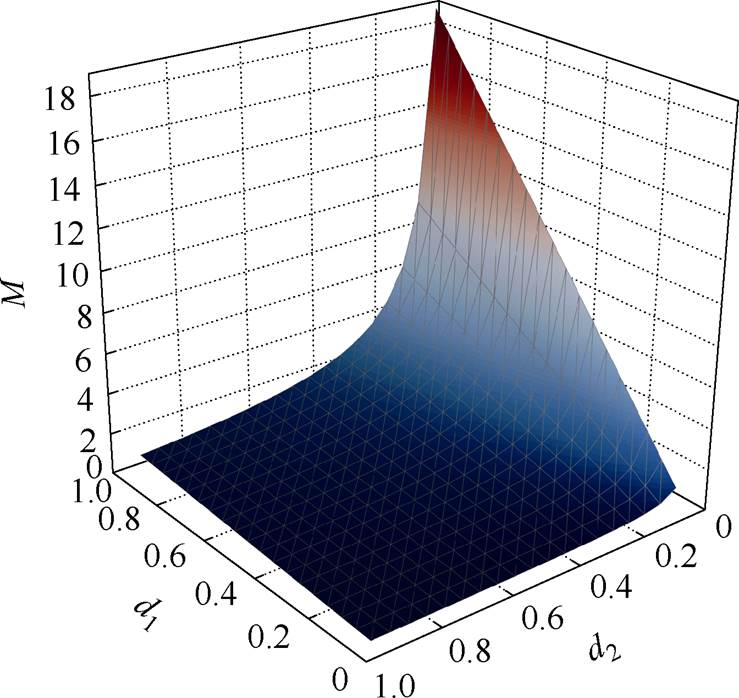
图3 FSBB变换器的电压增益
Fig.3 Voltage gain of the FSBB converter
单模态控制策略下的FSBB工作在传统Buck- Boost模式,即开关管Q1和Q4同时导通,Q2和Q3同时导通,而Q1和Q2互补导通。因此Buck桥臂和Boost桥臂的占空比满足
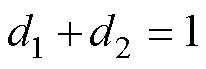 (4)
(4)
以d1为y轴变量,d2为x轴变量,可以得到FSBB变换器的单模态控制策略如图4所示。其中线段AC为工作曲线,P点为工作点,线段OP的斜率则可以表示电压增益M。
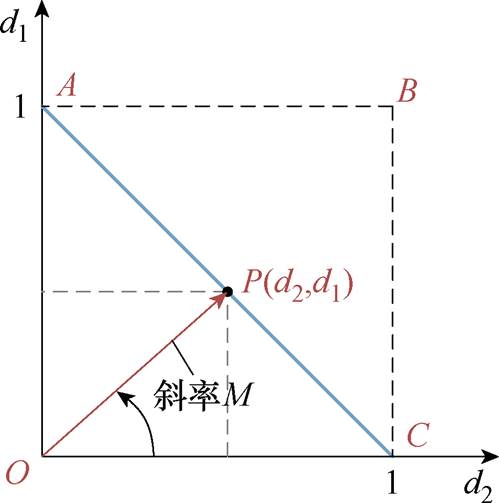
图4 FSBB变换器的单模态控制策略
Fig.4 Single-mode control strategy for FSBB converter
从图4的工作轨迹可知,单模态控制策略下可以实现FSBB的电压增益连续变化。但是电感电压始终为输入电压或者输出电压,因此电感电流的纹波较大。
根据输入电压和输出电压的大小关系将FSBB控制为Buck模式和Boost模式的控制策略称之为双模态控制。具体而言,当输入电压大于输出电压时,Boost桥臂的开关管Q3常开,而Buck桥臂的Q1作为被控管用来调节输出电压;当输入电压小于输出电压时,Buck桥臂的Q1常开,而Boost桥臂的开关管Q3作为被控管用来调节输出电压。同样可以得到FSBB变换器的双模态控制策略如图5所示。此时,工作点P将会在线段AB和BC上移动。
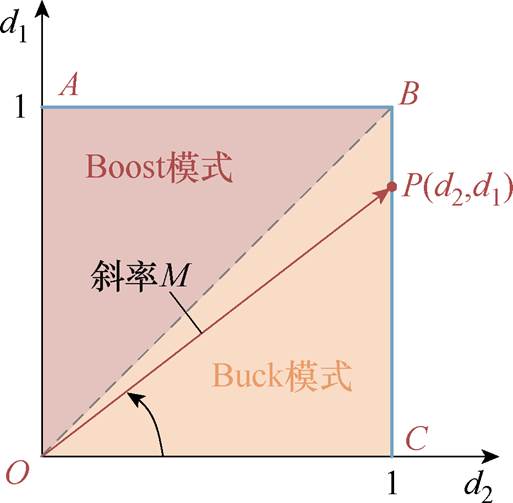
图5 FSBB变换器的双模态控制策略
Fig.5 Dual-mode control strategy for FSBB converter
双模态控制策略下FSBB的电感电压被降低到最低,仅为输入电压和输出电压的差值,因此电感电流的纹波最小。
通常由于功率器件自身的寄生参数、控制器延时和驱动芯片输出延时等问题,驱动芯片输出的方波最大占空比会受到限制。这将引起变换器的电压增益丢失问题,并且主要发生在输入电压和输出电压接近的时候。三模态控制在双模态控制的基础上通过在输入电压和输出电压接近时引入一个额外的过渡模式来避免占空比限制的问题。FSBB变换器三种典型的三模态控制策略如图6所示。
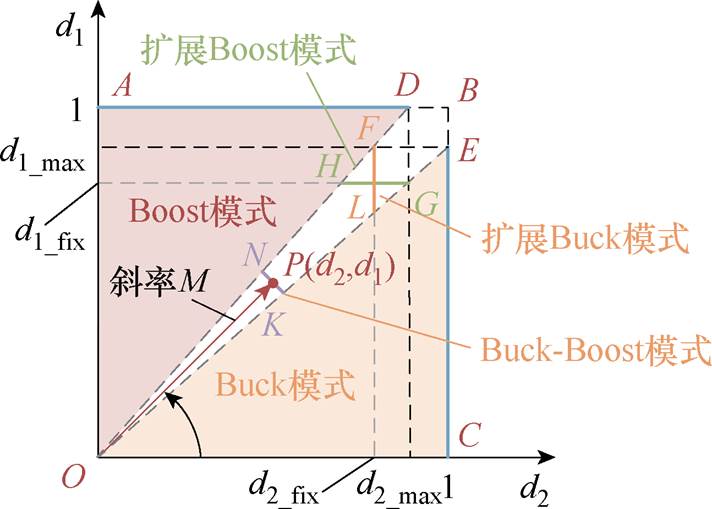
图6 FSBB变换器的三模态控制策略
Fig.6 Three-mode control strategy for FSBB converter
不同控制策略的过渡模式详细比较见表1。引入传统的Buck-Boost模式的控制方式相对简单,但是占空比变化较大,而且过渡模式的电感电流纹波较大。而引入扩展Boost模式和扩展Buck模式的两种控制方式在模式切换时不仅占空比的变化小,同时可以降低电感电流纹波,因此是常用的控制方式。
表1 三种过渡模式比较
Tab.1 Comparison of three transition models
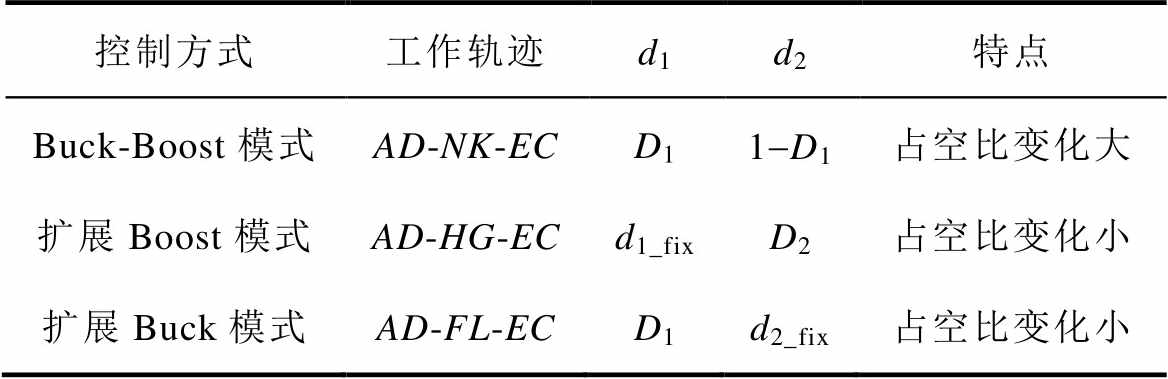
控制方式工作轨迹d1d2特点 Buck-Boost模式AD-NK-ECD11-D1占空比变化大 扩展Boost模式AD-HG-ECd1_fixD2占空比变化小 扩展Buck模式AD-FL-ECD1d2_fix占空比变化小
注:D1, D2表示被控量。
事实上,在三模态控制中由过渡模式向常规模式转换时,仍然存在较大的占空比变化,如从L点向E点切换,H点向D点切换。过大的占空比变化可能会导致系统不稳定,因此可以在过渡段增加多个控制模式实现不同模式之间的平滑转换。四模态控制策略由此而来,如图7所示。
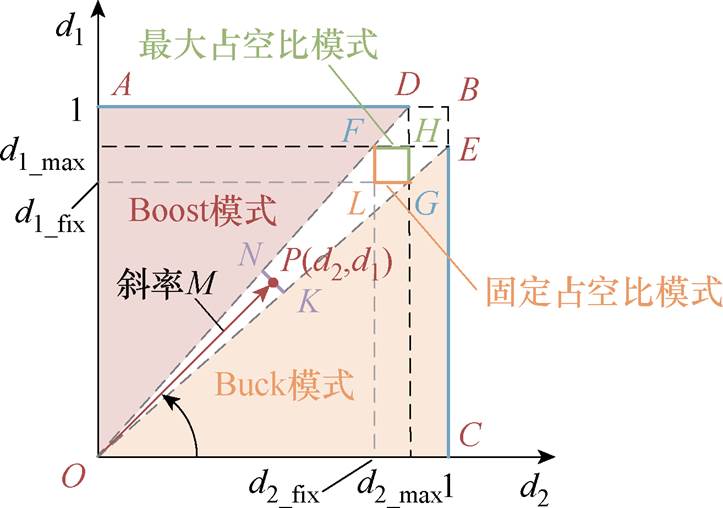
图7 FSBB变换器的四模态控制策略
Fig.7 Four-mode control strategy for FSBB converter
两种四模态控制策略的比较见表2。模式切换时两种控制方式的占空比变化一致。但是相比较于固定占空比模式,最大占空比模式中两个桥臂高电平重合时间更长,因此电感电流的纹波更小。
表2 四模态控制策略比较
Tab.2 Comparison of four-mode control strategies

控制方式工作轨迹电压关系d1d2特点 最大占空比模式ADF-H-GECVin≥VoutD1d2_max纹波小 Vin<Voutd1_maxD2 固定占空比模式ADF-L-GECVin≥Voutd1_fixD2纹波大 Vin<VoutD1d2_fix
注:D1, D2表示被控量。
综上所述,基于最大占空比模式的四模态控制方法是一种综合性能优良的控制策略,因此本文在此基础上展开进一步的研究。
在四模态控制策略中,当FSBB的输入电压和输出电压确定之后,两个桥臂的占空比大小随之被固定。此时,FSBB变换器可以等效为在滤波电感两端施加固定宽度的方波电压源,固定占空比时的FSBB变换器的等效电路如图8所示。
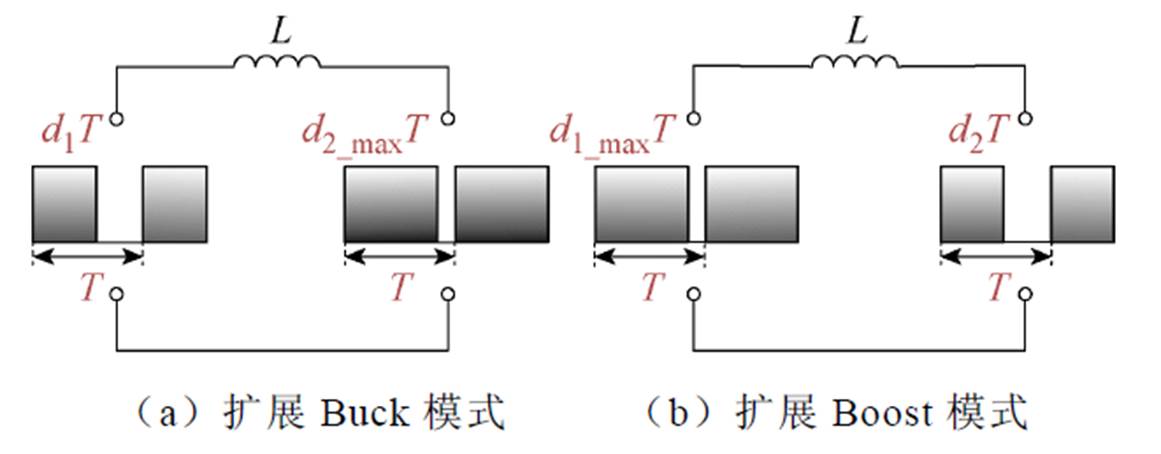
图8 固定占空比时的FSBB变换器的等效电路
Fig.8 Equivalent circuit of FSBB converter at fixed duty cycle
当桥臂之间的移相时间发生变化时,电感的端口电压改变,从而产生不同的电感电流纹波。图9给出了FSBB变换器工作在扩展Buck模式时不同桥臂移相时间的电感电流波形。
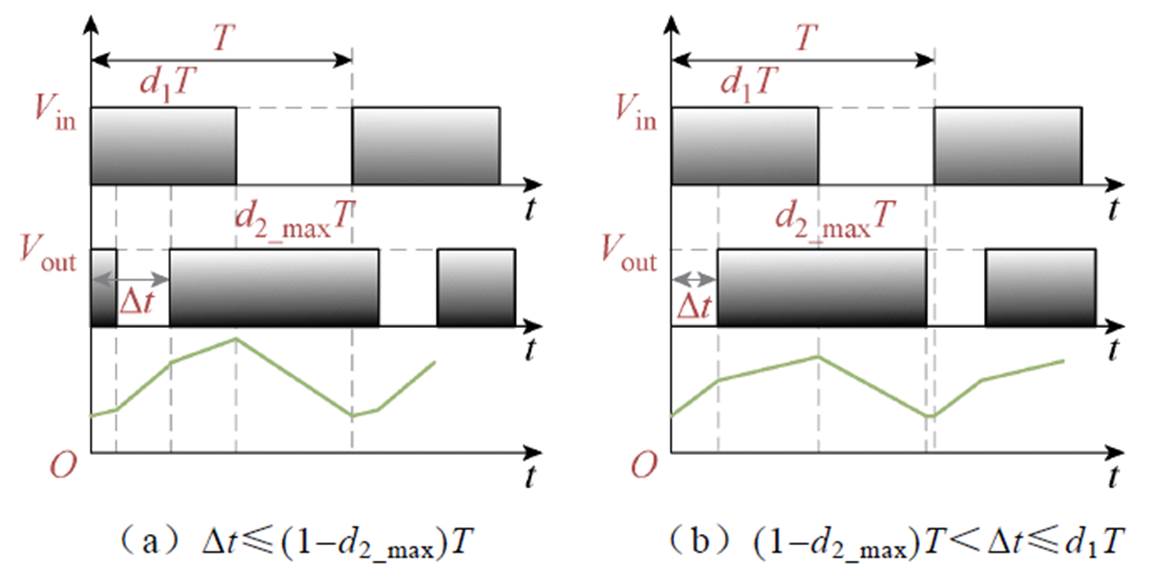
图9 不同移相时间的关键波形
Fig.9 Critical waveforms with different phase shift times
根据图9,电感电流纹波可以表示为
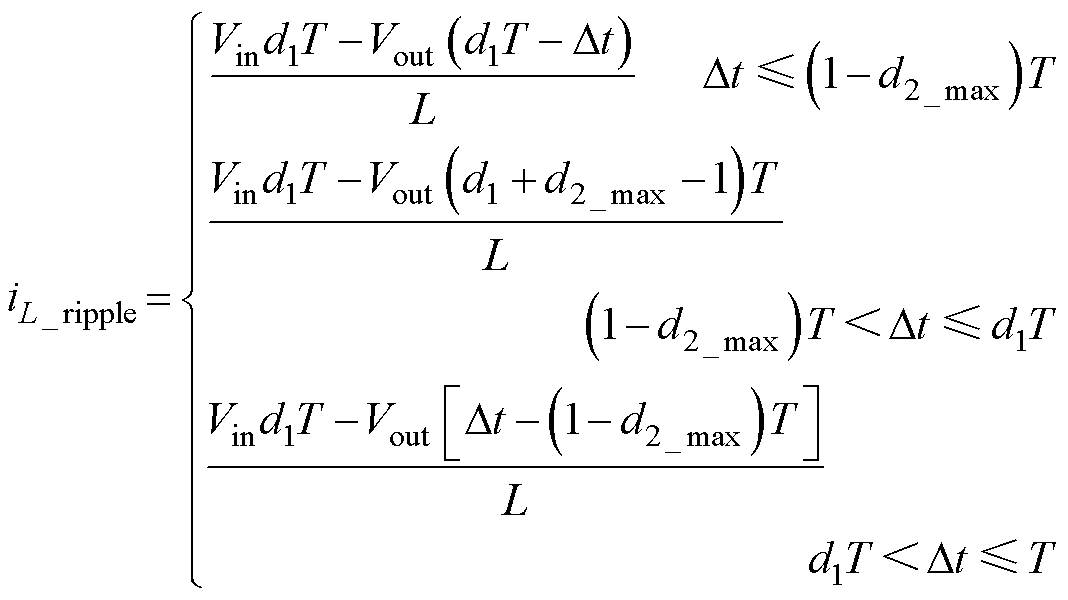 (5)
(5)
式中,iL_ripple为电感电流纹波;T为开关周期;L为电感;d2_max是Boost桥臂最大占空比。
图10给出了Vout=48 V,f=800 kHz,L=4 mH,d1_max=d2_max=0.9,模式切换阈值电压51 V(Buck模式与扩展Buck模式)时电感电流纹波随桥臂移相时间和输入电压变化的关系。从图中可以看出,随着输入电压逐渐升高,无论桥臂移相时间多大,电感电流的纹波都逐渐增加。当输入电压固定时,随着移相时间从0逐渐增加到第一边界值(1-d2_max)T,电感电流的纹波达到最大。此时若继续增加移相时间,电感电流的纹波保持不变。而随着移相时间增加到第二边界值时,电感电流的纹波又开始逐渐减小,但是仍然大于移相时间为0的时候。
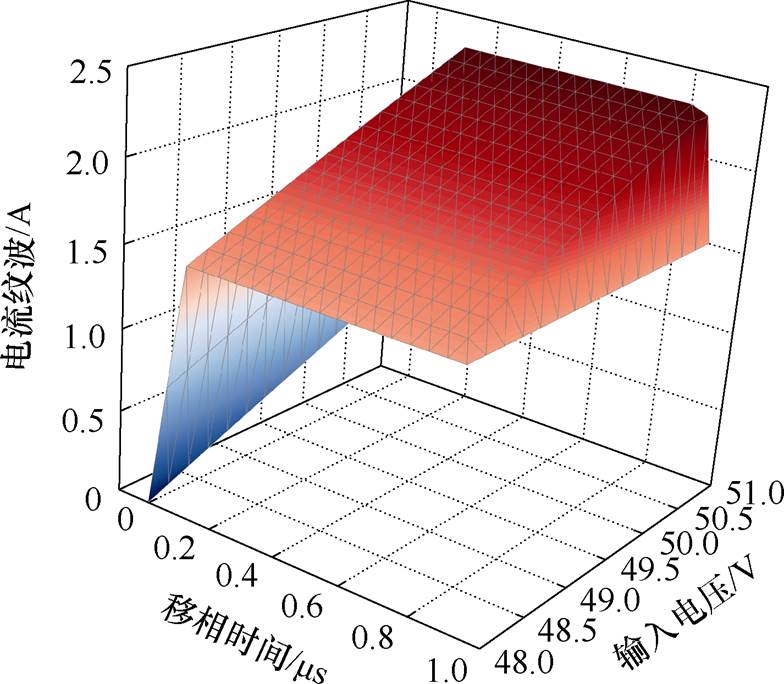
图10 电感电流纹波随桥臂移相时间和输入电压的关系(扩展Buck模式)
Fig.10 The relationship between inductor current ripple with bridge arm phase shift time and input voltage (extended Buck mode)
同样可以得到扩展Boost模式时的电感电流纹波随移相时间和输入电压的关系,如图11所示。
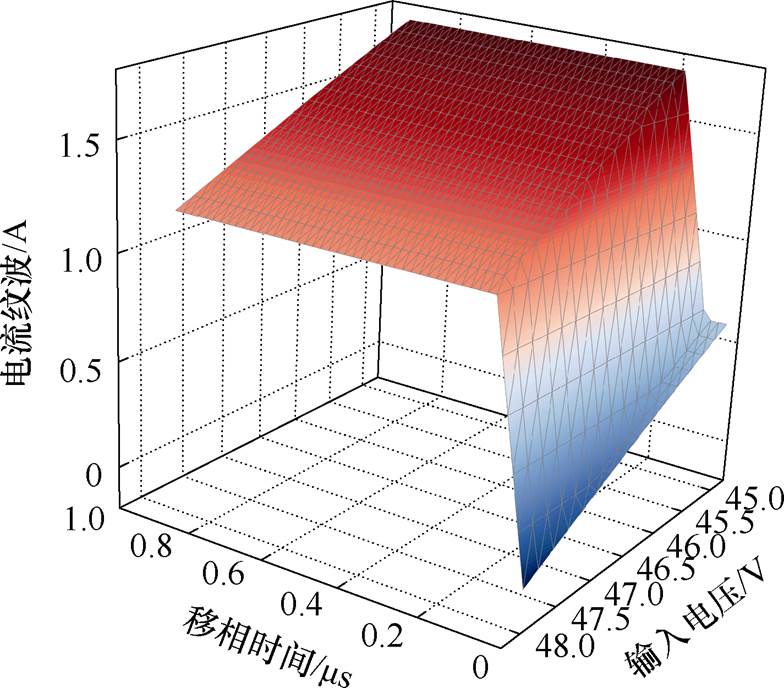
图11 电感电流纹波随桥臂移相时间和输入电压的关系(扩展Boost模式)
Fig.11 The relationship between inductor current ripple with bridge arm phase shift time and input voltage (extended Boost mode)
在扩展Boost模式中,输出电压固定时,电感电流纹波会随着输入电压升高而减小。移相时间对电感电流纹波的影响:随着移相时间逐渐增加到第一边界,在此过程中电感电流纹波不变;然后随着移相时间逐渐增加,电感电流纹波开始急剧上升,到第二边界条件时,电感电流纹波达到最大;之后移相时间对电感电流纹波再无影响。
通过上述分析,不难得出为了将电感电流纹波控制到最小,只需要将Buck桥臂和Boost桥臂之间的移相时间控制为0。
在单个开关周期中,只有当开关管Q3导通时,电感中的能量才能传递到负载端。因此电感电流与输出电流的关系可以近似表示为
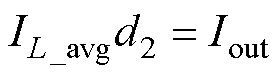 (6)
(6)
式中,IL_avg为电感电流平均值;Iout为负载电流。所以,不同工作模式的电感电流平均值可以表示为
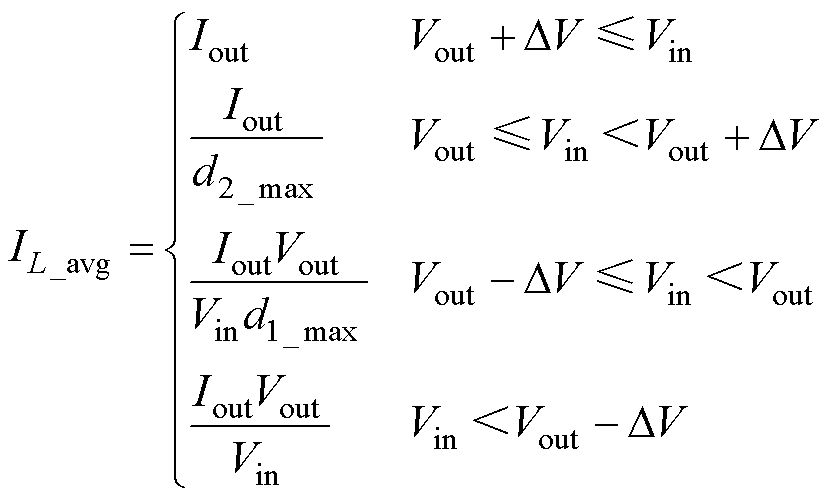 (7)
(7)
式中,DV为模式切换的电压阈值。
从式(7)可以看出,电感电流平均值只与输出电流、最大占空比、输入电压和输出电压相关,不会受到桥臂移相时间的影响。因此,可以近似认为所有四模态控制策略下电感电流的平均值相同。
电感电流有效值的大小主要与电感电流的平均值和纹波相关。当平均值相同时,纹波越小,电感电流的有效值越小。综上所述,最小电感电流控制策略是将Buck桥臂和Boost桥臂之间的移相时间控制为0,并将其定义为上升沿同步四模态控制策略。在此控制策略下,FSBB不同模式下的关键波形如图12所示。
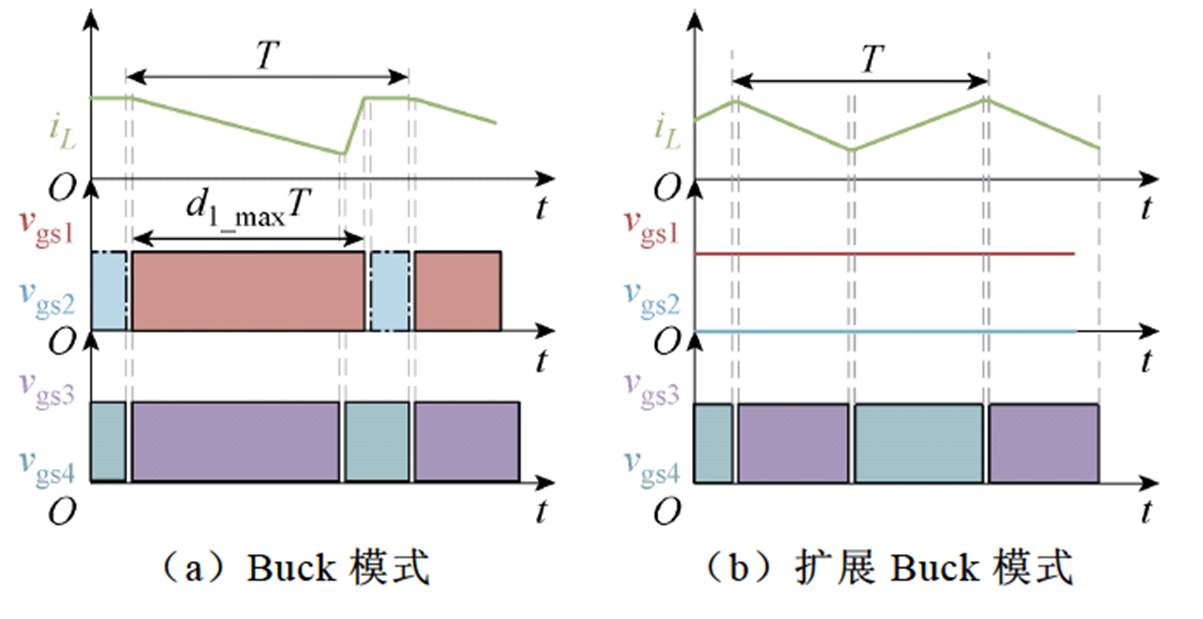
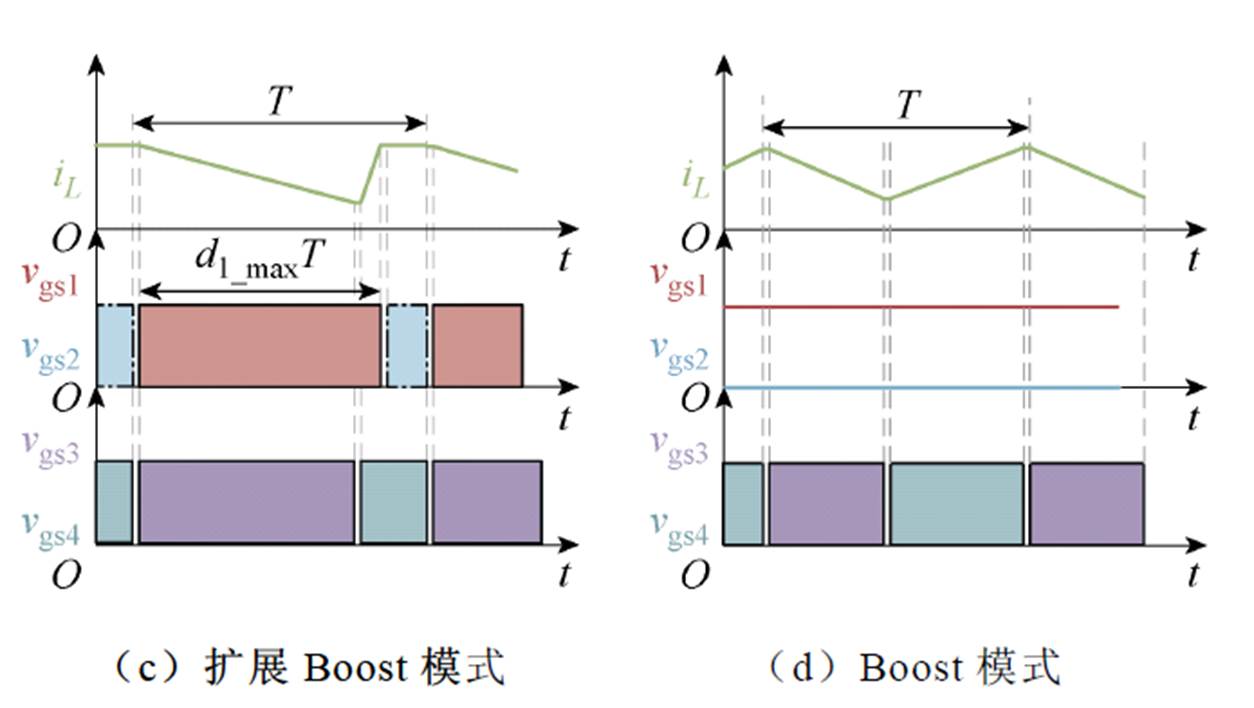
图12 FSBB变换器上升沿同步四模态控制策略的关键波形
Fig.12 Critical waveforms for a rising edge synchronized four-mode control strategy for FSBB converter
从图12的关键波形可以得到FSBB的电感电流纹波为
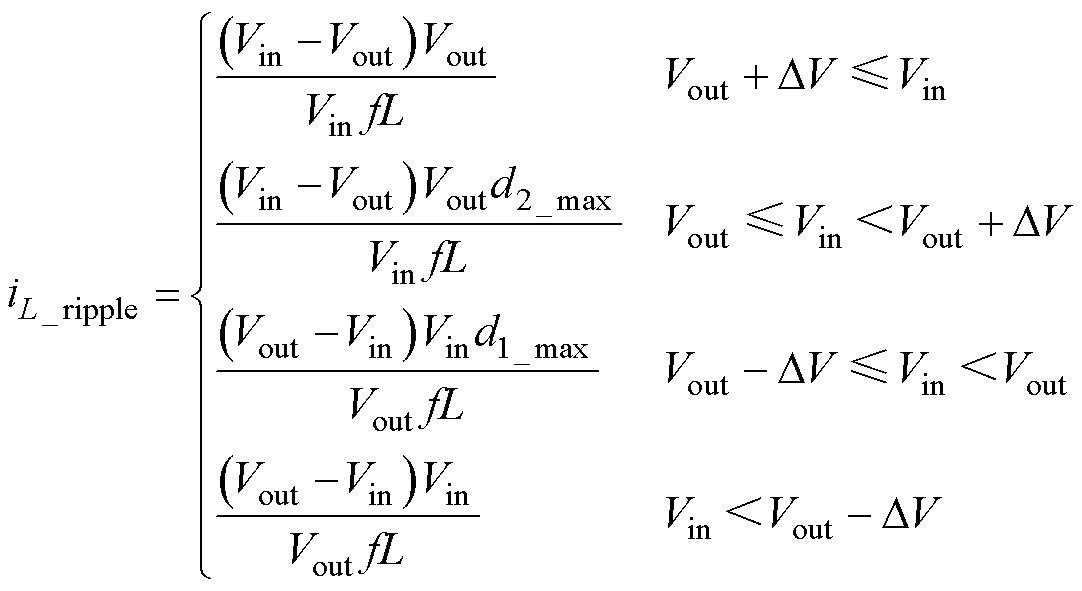 (8)
(8)
式中,f为开关频率。
为了说明所提出的控制策略的优越性,将所提出的控制方法与已有的控制策略的电感电流纹波作比较,并同时以单模态控制策略中最大电感电流纹波为基础做归一化处理,得到的结果如图13所示。
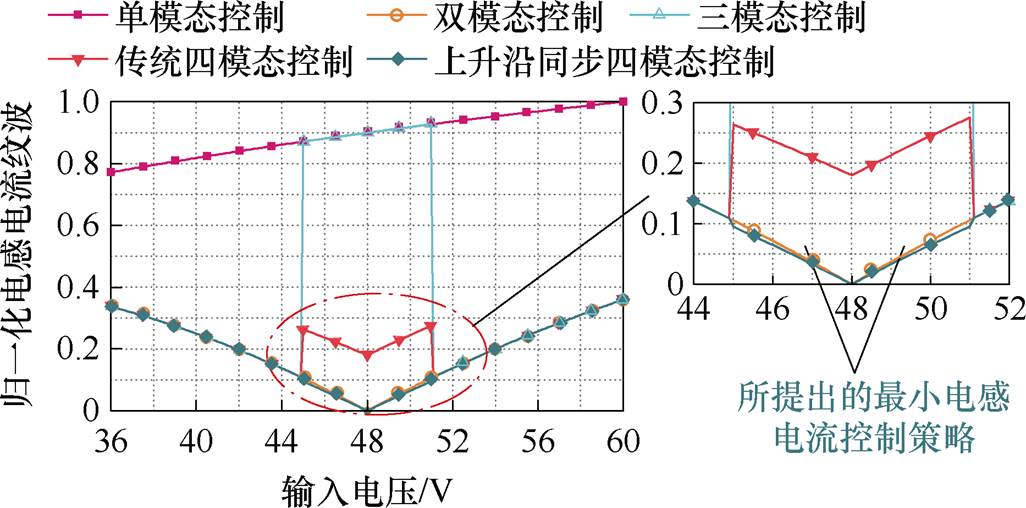
图13 不同控制策略的电感纹波对比
Fig.13 Comparison of inductor ripple with different control strategies
从图13可知,所提出的上升沿同步四模态控制策略的电感电流纹波在全范围内最小。在接近阈值电压附近时,甚至低于双模态控制策略的电感电流纹波。
在开关频率固定的情况下,电感电流的有效值越小,变换器的损耗就越小。所以通常以电感电流有效值最小作为效率优化的控制目标。但是忽略了变换器的开关损耗、驱动损耗、电感的交流铜损和磁心损耗等,这些损耗均与开关频率强相关,往往会随着开关频率降低而降低。在过渡模式中,FSBB变换器的所有功率器件都开始工作,相比于常规的Buck模式和Boost模式会产生更大的开关损耗和驱动损耗,降低了变换器的转换效率。而通过第2节所提出的最小纹波控制策略使得过渡模式中的电感电流纹波较小。因此,在此基础上可以通过在过渡模式中引入变频控制,进一步优化FSBB变换器的转换效率。
FSBB变换器的损耗主要包括功率器件损耗和电感损耗。电感损耗进一步划分为:铜损和磁心损耗。功率器件的损耗则包含导通损耗、关断损耗、开通损耗和驱动损耗。下面分别进行相关损耗的计算。电感的铜损PCu为
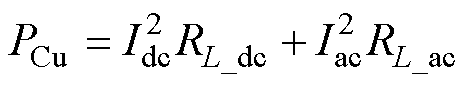 (9)
(9)
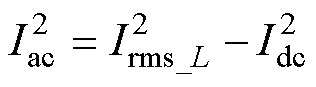 (10)
(10)
式中,Idc和Iac分别为电感电流的直流分量和交流分量;RL_dc和RL_ac分别为电感的直流电阻和交流电阻;Irms_L为电感电流有效值。
电感的磁心损耗Pcore为
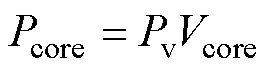 (11)
(11)
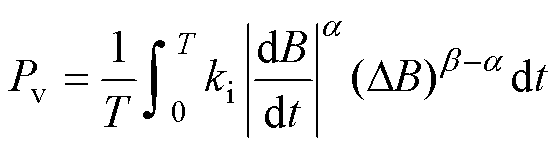 (12)
(12)
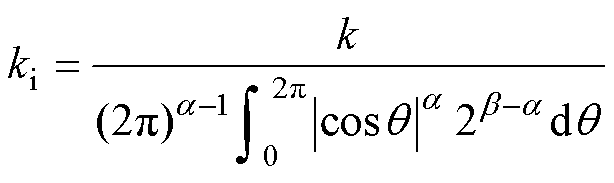 (13)
(13)
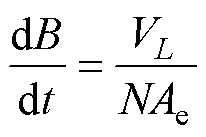 (14)
(14)
式中,k、a 和b 为磁心材料参数,根据供应商提供的数据手册得到;DB为磁通量密度变化幅值;f为开关频率;Vcore为磁心体积;VL为电感电压;N为电感匝数;Ae为磁心有效截面积。
功率器件的导通损耗Pon_MOS为
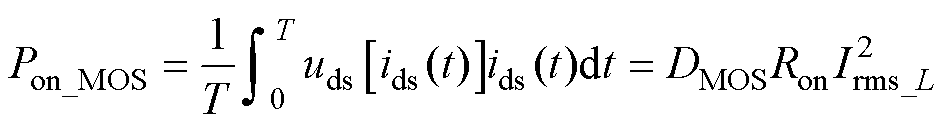 (15)
(15)
式中,uds(ids(t))为瞬时电流为ids(t)时的漏源电压;ids(t)为电流瞬时值;DMOS为功率器件平均占空比;Ron为功率器件导通电阻。
所以总的功率器件导通损耗Pon_total可表示为
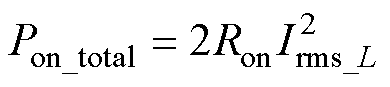 (16)
(16)
开关损耗Psw为
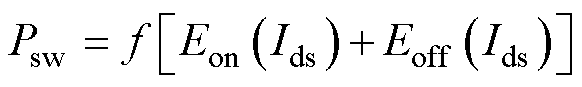 (17)
(17)
式中,Eon(Ids)和Eoff(Ids)分别为开通电流和关断电流均为Ids的开通损耗能量和关断损耗能量。
驱动损耗Pdrive为
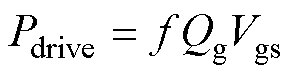 (18)
(18)
式中,Qg为MOSFET的栅极电荷;Vgs为驱动电压。
所以,过渡模式中总损耗Ploss可以表示为
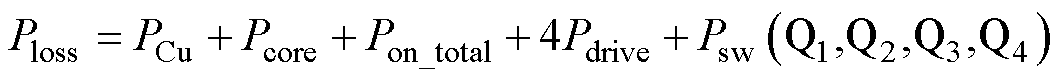 (19)
(19)
3.1节得到了FSBB变换器的损耗模型、总损耗与输入输出的电压等级、负载大小和开关频率相关。因此,首先固定输入输出电压,改变变换器的开关频率得到不同负载情况下的损耗,如图14所示。
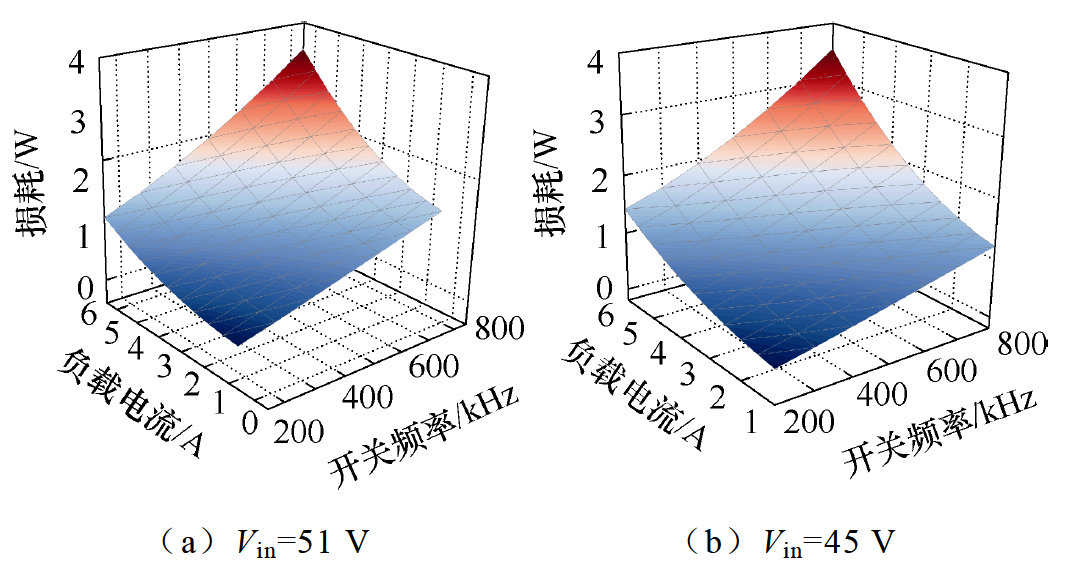
图14 损耗随负载电流和开关频率的关系(Vout=48 V)
Fig.14 Loss versus load current and switching frequency (Vout=48 V)
从图14中可以看出,当电压增益不变时,变换器的损耗会随着负载电流增加而增大。另外,当负载固定时,开关频率越低,变换器的损耗越小。
当负载固定时,改变电压增益和开关频率时,变换器的损耗变化情况如图15所示。
当M≥1时,在同一开关频率下,随着增益逐渐增加,FSBB变换器的损耗逐渐减小,直到电压增益等于1时,变换器的损耗达到最小;相反,当M≤1时,随着增益逐渐增加,变换器的损耗逐渐减小。于是,可以通过减小开关频率降低过渡模式中的变换器损耗,提高变换器的转换效率。
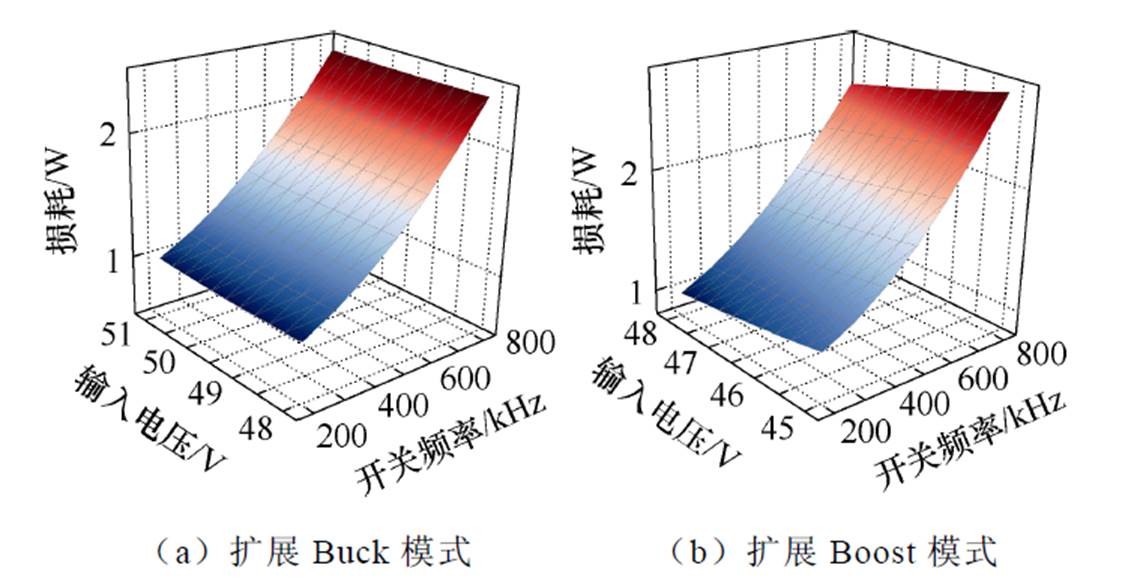
图15 损耗随输入电压和开关频率的关系(Iout=6 A)
Fig.15 Loss with input voltage and switching frequency (Iout=6 A)
对于所提出的上升沿同步变频控制策略,控制器首先对输出电压采样;然后计算输出电压误差,并经过电压环补偿得到控制信号u,Buck桥臂上管占空比与Boost桥臂下管占空比之和,即u=1+d1-d2;其次根据u的大小确定工作模式;再次根据工作模式调整开关频率以及相应桥臂的占空比;最后控制两个桥臂的移相时间并生成PWM信号。完整的控制流程如图16所示。
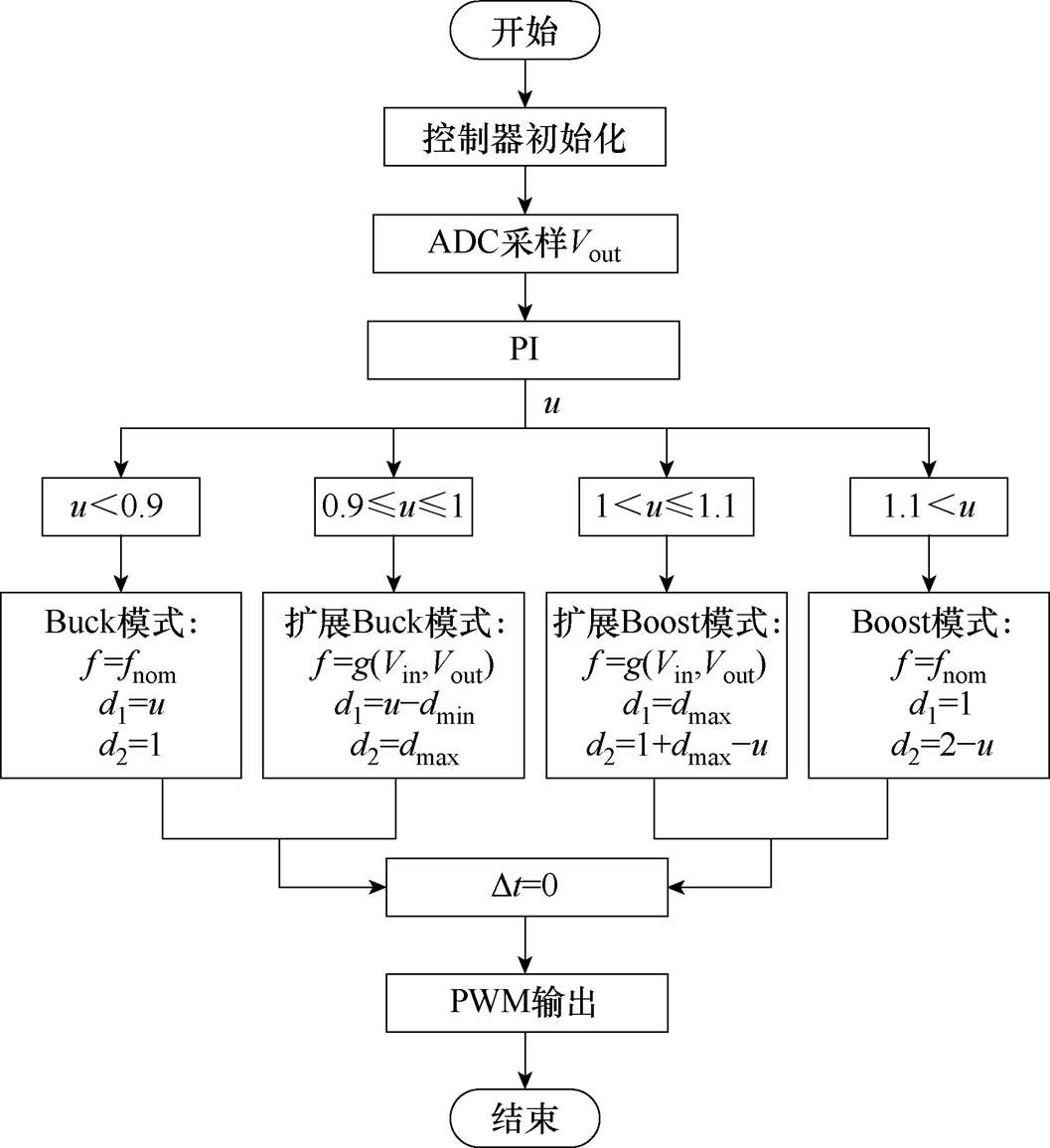
图16 低纹波-变频四模态控制流程
Fig.16 Low ripple-variable frequency four-mode control flow
考虑到GaN器件的特性和现代工业应用场景对变换器体积小的需求,本文将常规工作模式(Buck模式和Boost模式)下的开关频率设定为800 kHz[27]。而过渡模式中的开关频率取决于输入电压、输出电压和常规模式的最大电感电流纹波。需要确保过渡模式降低开关频率以后的电感电流不会使电感饱和,所以设定常规模式下最大电流纹波的一半作为过渡模式中最大电感电流纹波。然后根据电感电流纹波计算得到过渡模式在不同电压下的开关频率为
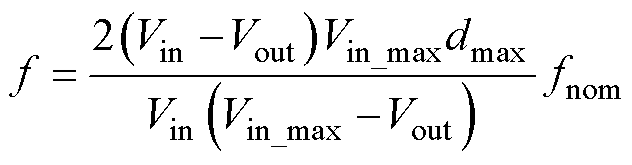 (20)
(20)
式中,Vin_max为最大输入电压;fnom为常规模式的开关频率;dmax为最大占空比限制。开关频率随输入电压变化的关系如图17所示。
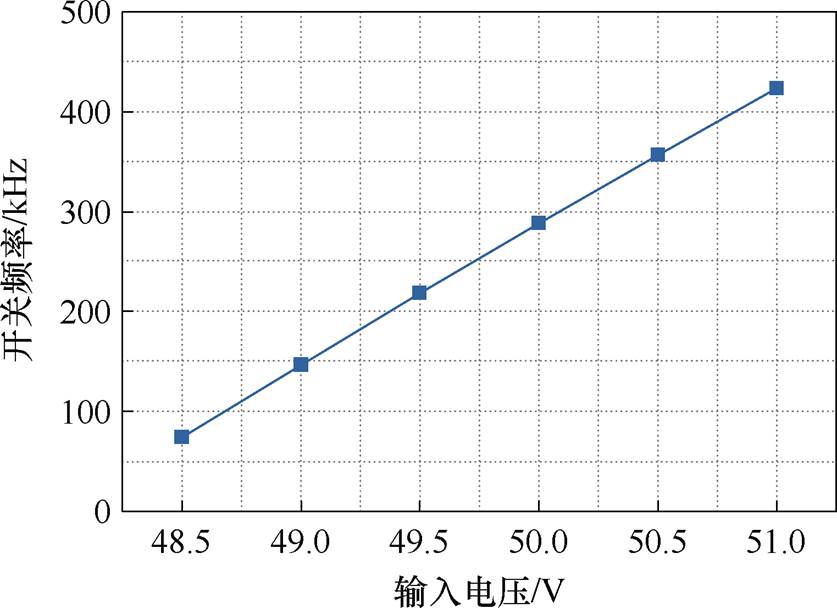
图17 过渡模式开关频率与输入电压的关系
Fig.17 Transition mode switching frequency versus input voltage
另外,在输入电压和输出电压的差值一样时设置相同的开关频率,即输出电压为48 V时,45 V输入和51 V输入开关频率一致,46 V输入和50 V输入的开关频率一致。于是可以得到整个过渡模式中的开关频率。
电感值的选取取决于电感所流过的电流的大小。在本文中不同模式下的平均值变化较小,但是电感电流纹波差异较大。即使是在降频控制策略下,常规模式下的电感电流纹波远大于过渡模式下的电感电流纹波,所以只需要按照常规模式下最大电感电流纹波设计电感值即可满足整个工况需求。
最大电感电流纹波表示为
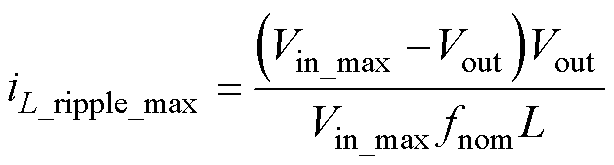 (21)
(21)
式中,iL_ripple_max为常规模式下的最大电感电流纹波。
设置电感电流纹波系数为0.5,电感可以表示为
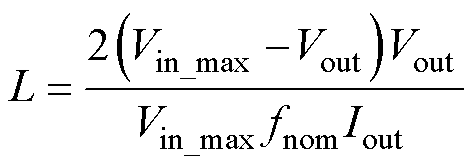 (22)
(22)
为了验证所提出的控制策略的有效性,搭建了如图18所示的实验平台,主要包括直流电压源、直流负载、示波器、功率分析仪和实验样机等。其中实验样机的主要参数见表3。

图18 实验平台
Fig.18 Experimental platforms
表3 样机参数
Tab.3 Experimental prototype parameters
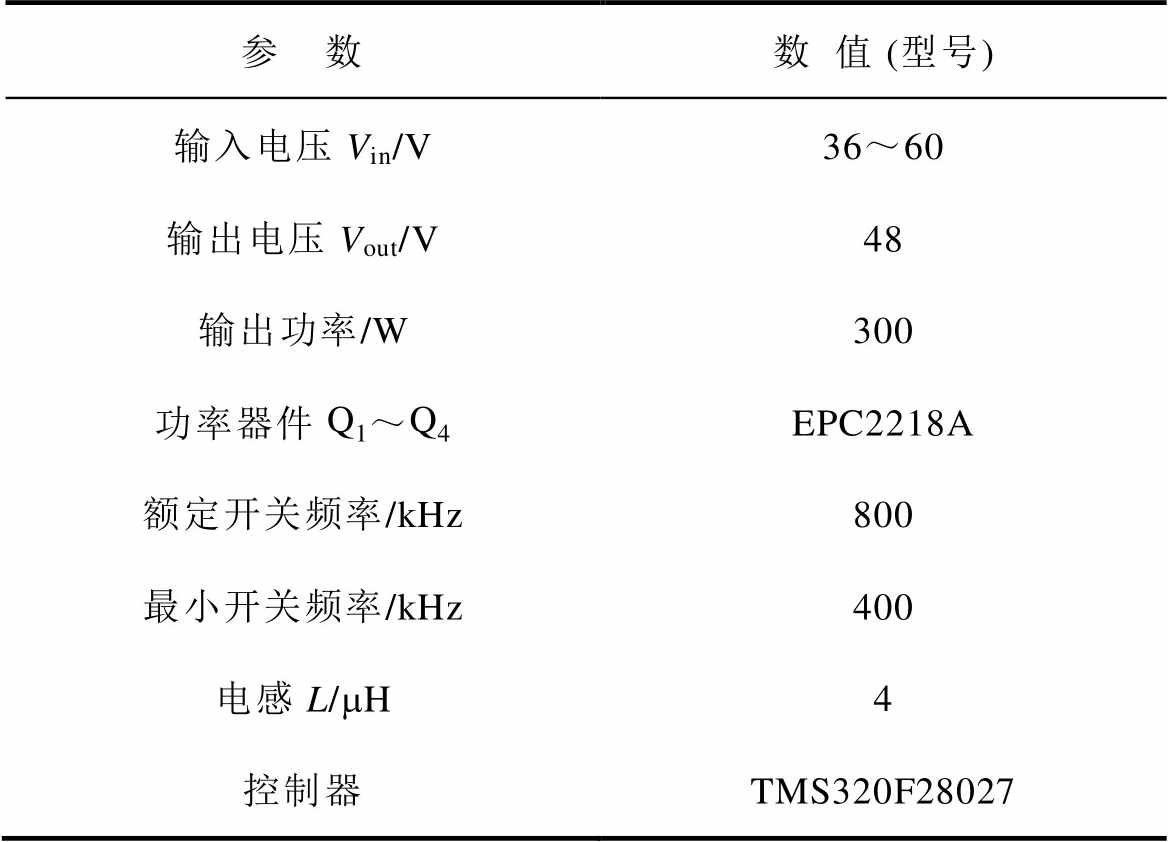
参 数数值 (型号) 输入电压Vin/V36~60 输出电压Vout/V48 输出功率/W300 功率器件Q1~Q4EPC2218A 额定开关频率/kHz800 最小开关频率/kHz400 电感L/mH4 控制器TMS320F28027
FSBB变换器不同工作模式下的稳态波形如图19所示。根据输入电压不同工作范围,FSBB变换器分别工作在四种模式下。其中常规Buck模式和Boost模式的开关频率为800 kHz,过渡模式中变换器的稳态开关频率为400 kHz。
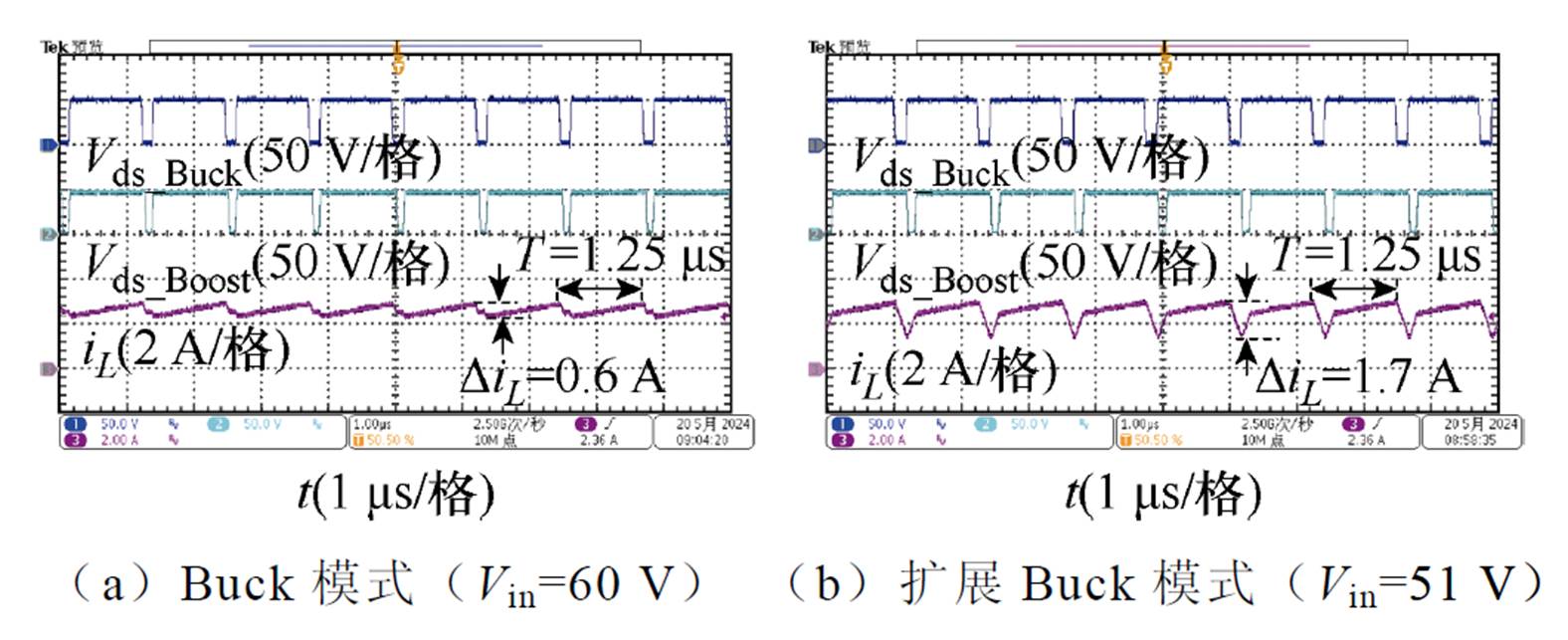
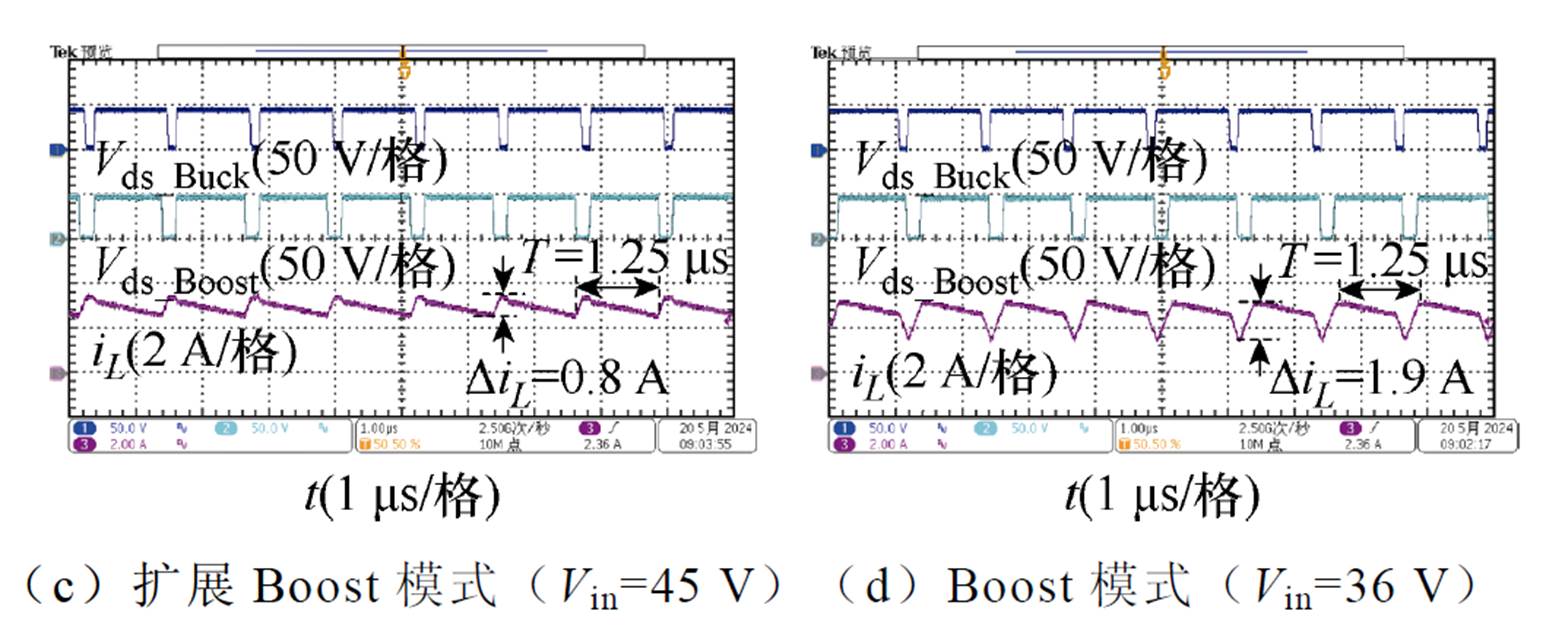
图19 不同工作模式下的稳态波形
Fig.19 Steady-state waveforms in different operating modes
为了验证所设计FSBB变换器的宽范围调压能力,分别测试了输入电压12 V和输入电压72 V时的稳态波形,如图20所示。
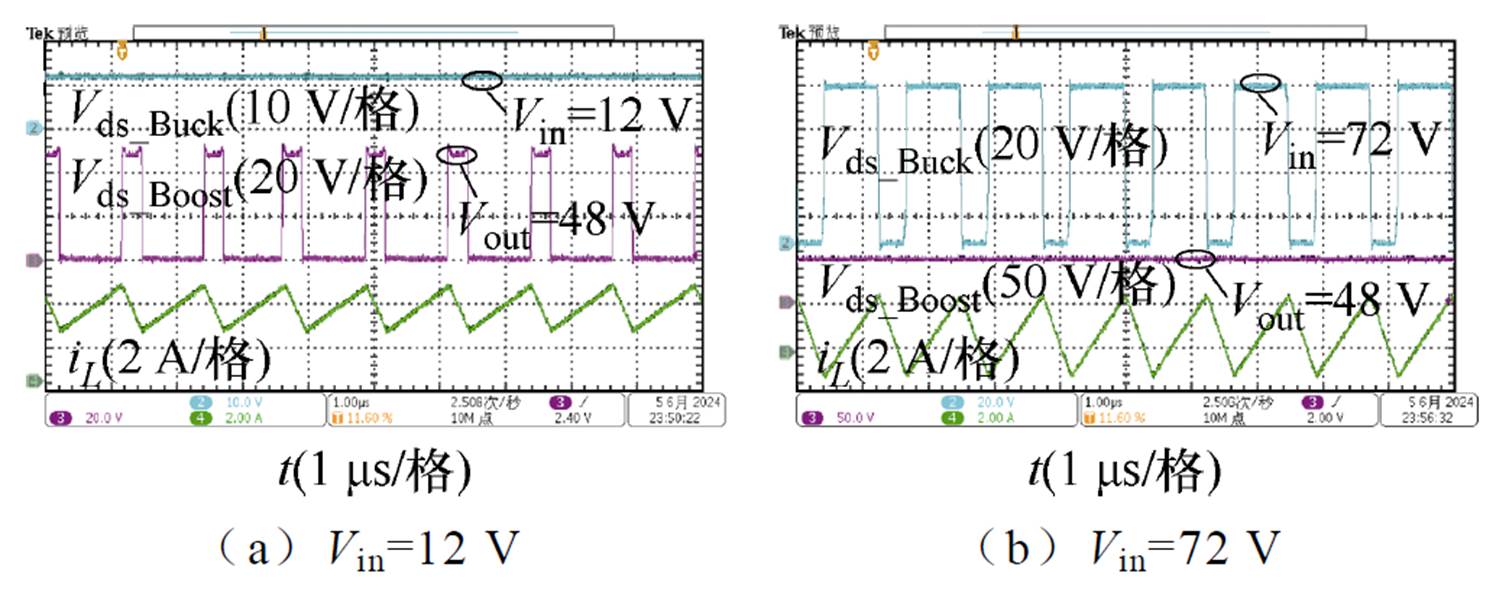
图20 宽范围输入调压波形(Vo=48 V)
Fig.20 Wide range input regulator waveforms (Vo=48 V)
从测试结果来看,所设计的FSBB可以在较宽的输入电压范围内实现稳定电压输出,具有调压范围宽的能力。
为了验证所提出的最小电感电流纹波控制策略,在同一样机中分别测试所提出的控制策略和传统四模态控制策略的电感电流波形。两种控制策略的电感电流测试比较结果如图21所示。纹波大小比较见表4。在相同开关频率和工况下,所提出的控制策略的过渡模式的电感电流纹波远小于传统四模态控制策略。其中在输入电压51 V、输出电压48 V的工况下,所提出的最小纹波控制策略的电感电流纹波仅仅为传统控制策略的35.2%。在降低开关频率后,最小纹波控制策略的电感电流纹波仍然小于传统控制策略的电感电流纹波。纹波比较结果与理论分析一致,验证了所提出的控制方法可有效降低电感电流纹波。
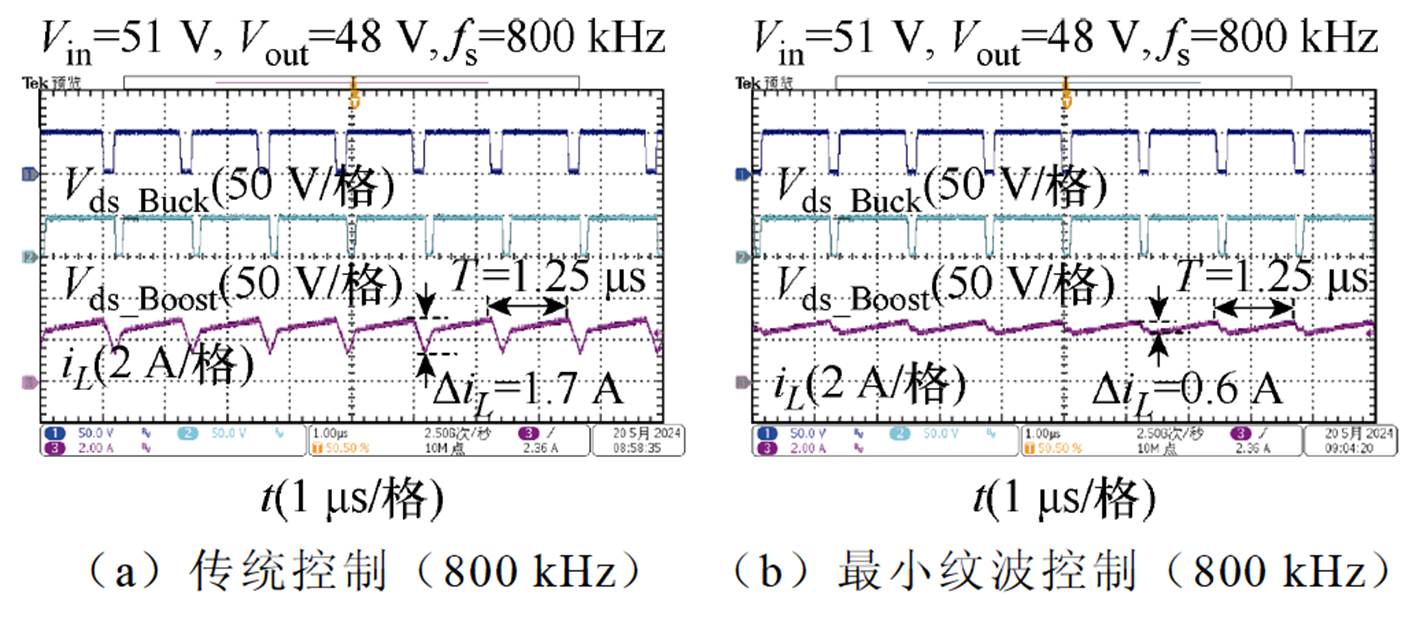

图21 电感电流纹波测试结果
Fig.21 Inductor current ripple test results
表4 不同控制策略及开关频率的纹波比较
Tab.4 Experimental prototype parameters
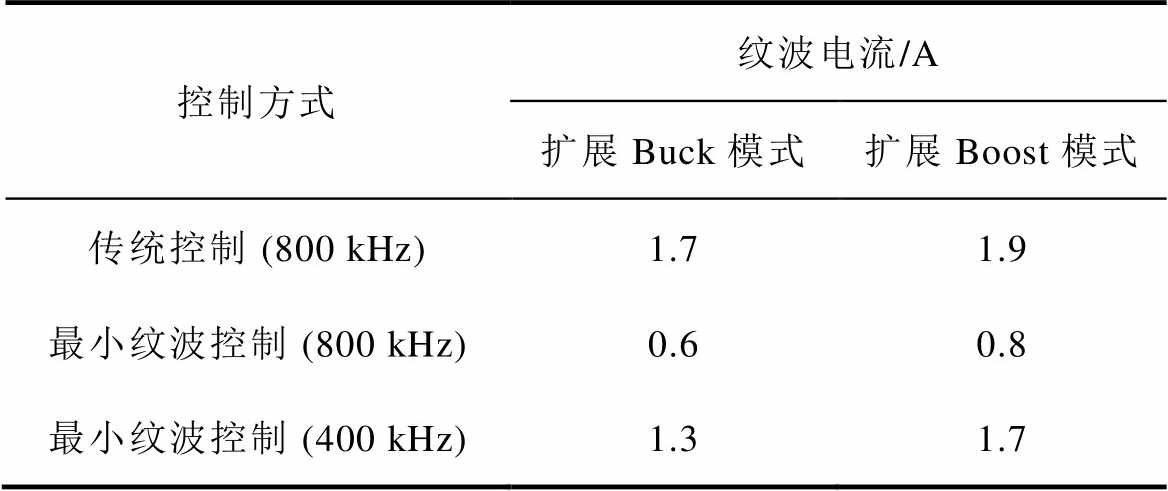
控制方式纹波电流/A 扩展Buck模式扩展Boost模式 传统控制 (800 kHz)1.71.9 最小纹波控制 (800 kHz)0.60.8 最小纹波控制 (400 kHz)1.31.7
为了说明所提出的低纹波-变频控制策略可以工作在轻载模式,而且同样适用于电流断续模式,在轻载下对所提出的控制策略进行了实验验证,分别测试负载电流0.4 A和空载下的稳态波形,测试结果如图22所示。
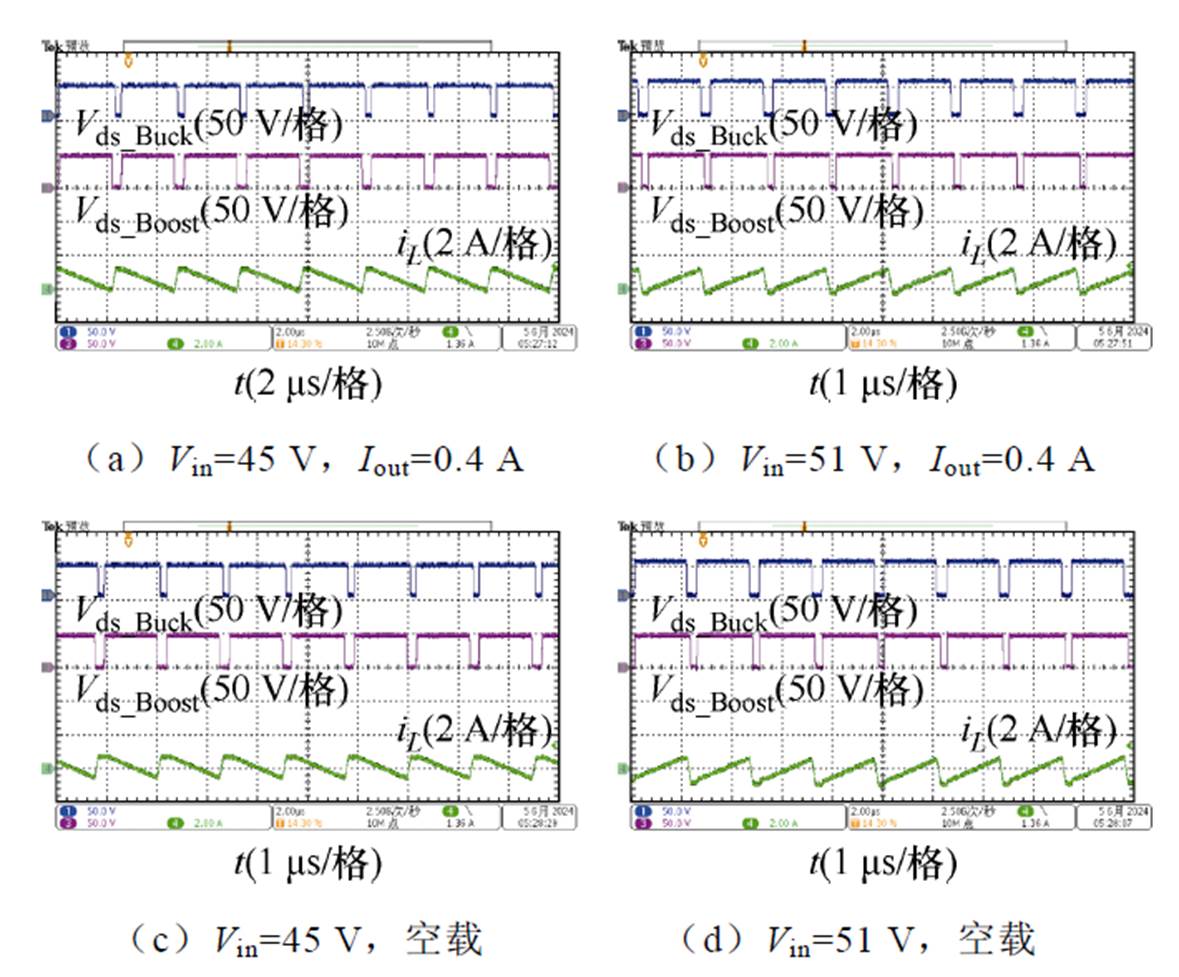
图22 轻载工况测试结果
Fig.22 Light load condition test results
为了说明所提出的控制策略可以适用于宽范围调压场景,对所提出的控制策略进行了输入电压变化的动态实验测试。分别从传统Boost模式向扩展Boost模式、扩展Buck模式和传统Buck模式跳变,得到的实验结果如图23所示。
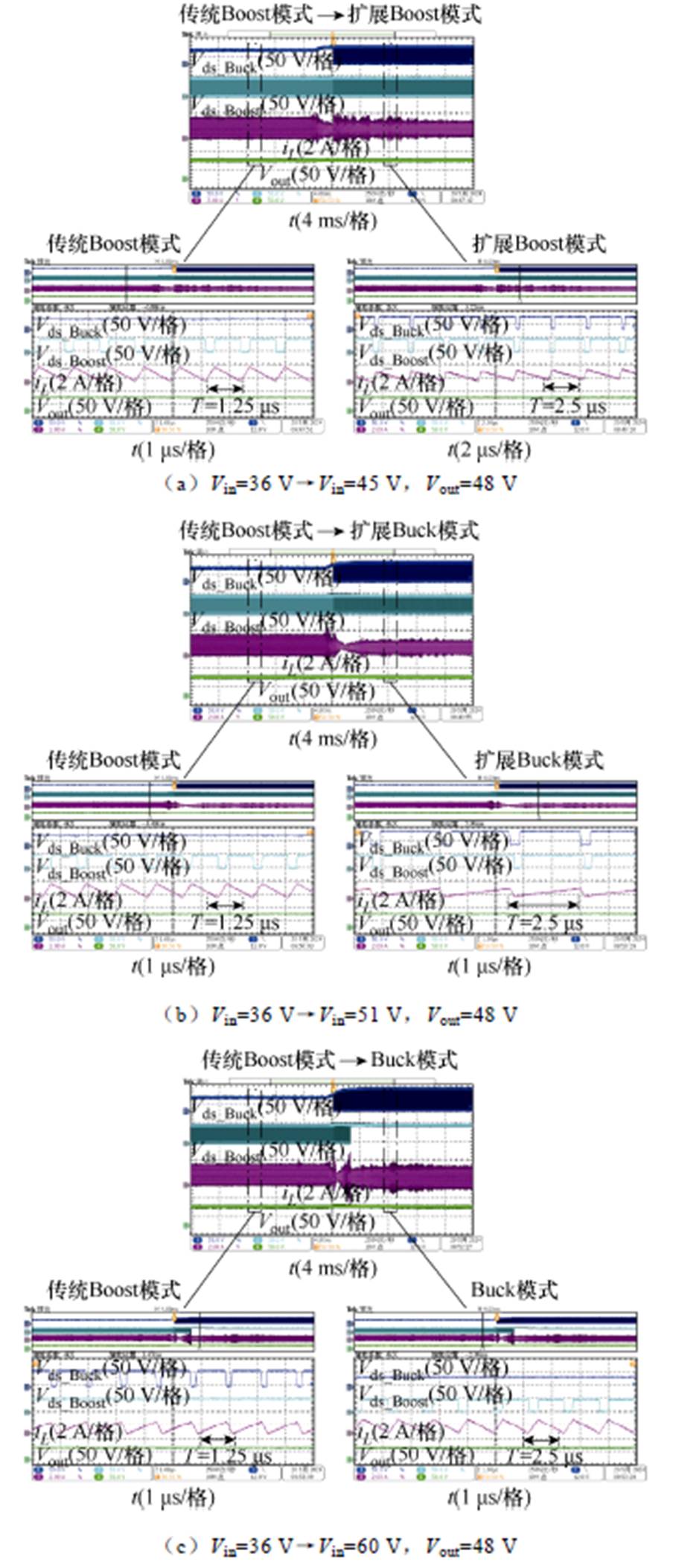
图23 输入电压变化动态实验结果
Fig.23 Experimental results of input voltage variation dynamics
从图23可以看出,所提的低纹波-变频控制策略可以很好地实现对输入电压变化的跟踪。同时完成了过渡模式中的变频控制。所以在宽范围输入的场景下提出的控制策略仍然有较好的应用性。
另外,为了验证所提出的控制策略可以满足变换器负载变化的场景,对所提出的控制策略进行了负载动态实验。分别在扩展Buck模式和扩展Boost模式下完成空载到满载和满载到空载的动态测试,测试结果如图24所示。
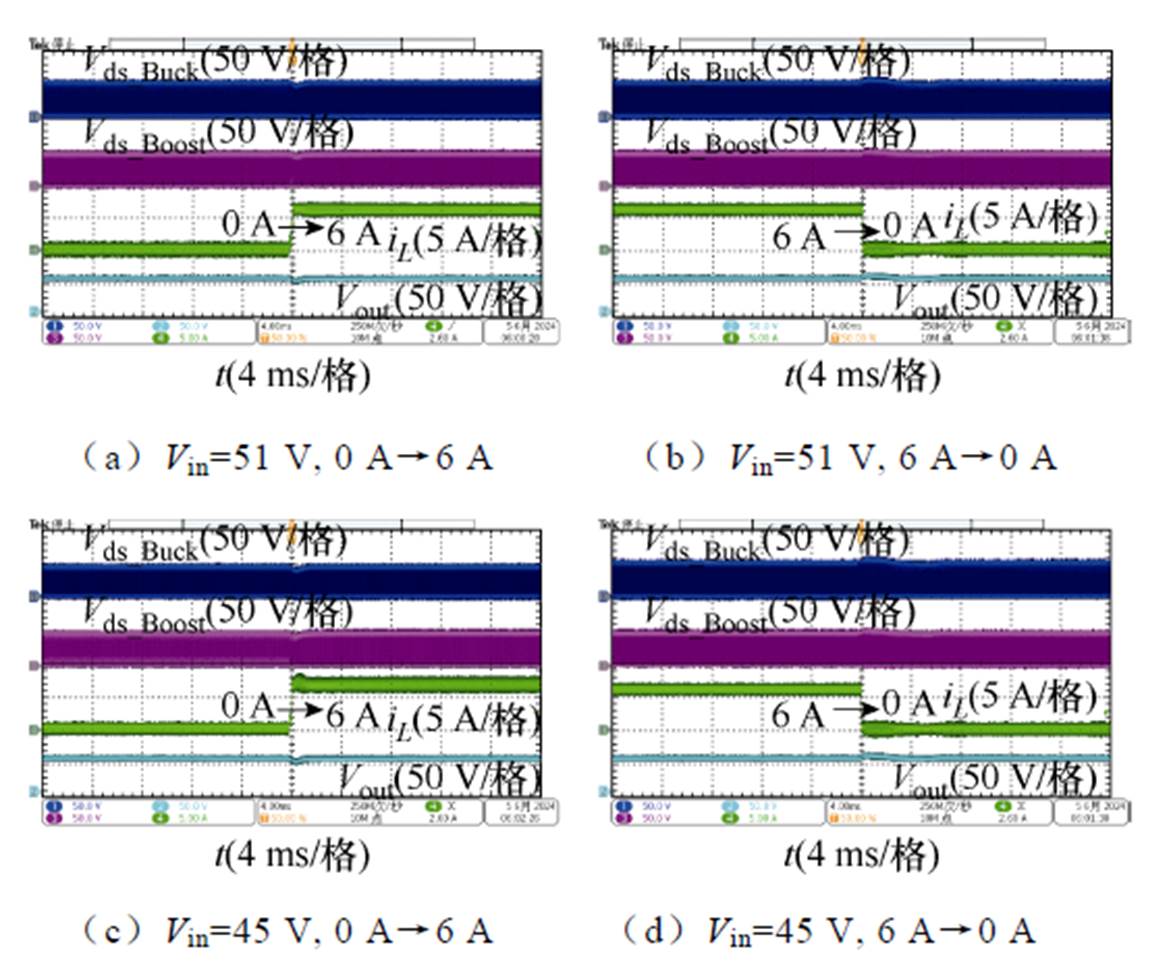
图24 负载变化动态实验结果
Fig.24 Experimental results of load variation dynamics
测试结果验证了所提出的控制策略的稳态性能和动态性能均符合理论分析,实现了FSBB变换器的低纹波-变频控制。进一步测试变换器在不同工况下的转换效率,验证所提出的高效控制策略的有效性。首先对传统定频控制策略进行测试,得到输出电压Vout=48 V,输入电压分别为36 V、48 V和60 V,开关频率为800 kHz时的效率曲线,如图25所示。
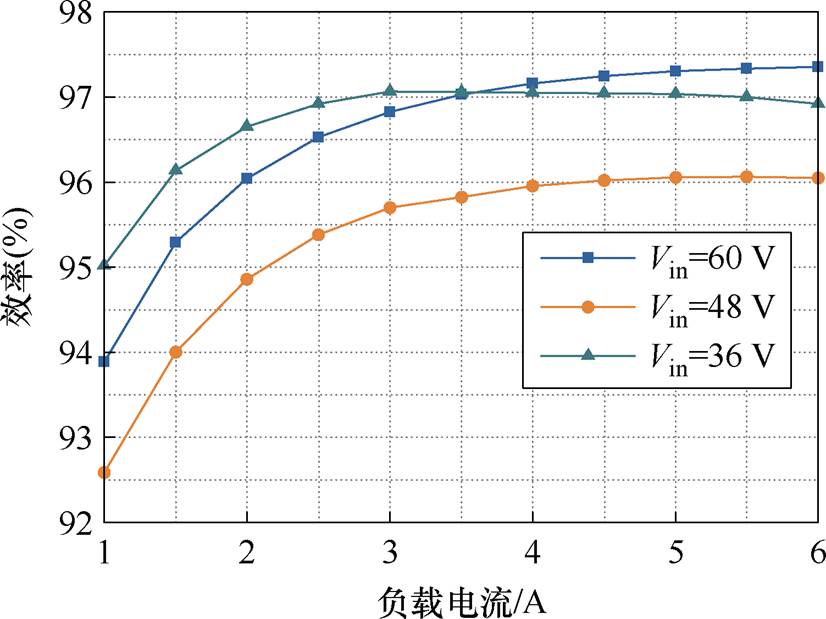
图25 定频控制策略下不同输入电压的效率比较
Fig.25 Efficiency comparison of different input voltages under fixed frequency control strategy
常规Buck模式和Boost模式下,FSBB变换器的部分功率器件开通关断,因此开关损耗和驱动损耗更小,可以实现很高的转换效率。当输入电压等于输出电压时,所有开关器件开始工作,增加额外的开关损耗,所以效率会有所降低。另外,相同输出功率下,Buck模式的电感电流更小,但是器件的开通电压更大,所以随着负载逐渐增加,Buck模式的效率逐渐高于Boost模式的效率。
对所提出的低纹波-降频控制策略进行验证,根据前面的理论分析,仅仅需要在过渡模式中根据输入电压降低变换器的开关频率。采用所提出的低纹波-变频控制策略的FSBB变换器在不同输入电压下的效率曲线如图26所示。
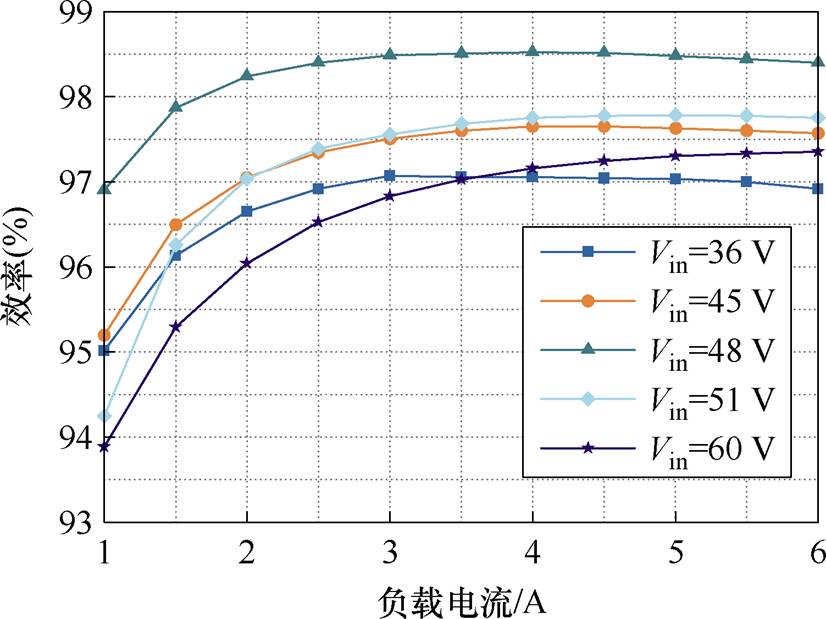
图26 变频控制策略下不同输入电压的效率比较
Fig.26 Efficiency comparison of different input voltages under variable frequency control strategy
从图26可以看出,采用所提出的控制策略后,过渡模式的转换效率相较于传统控制方式明显提高,并且高于常规Buck模式和常规Boost模式。在输入电压等于输出电压时转换效率达到最大。在重载情况下,仍然存在扩展Buck模式的效率优于扩展Boost模式的情况。
另外,为了说明所提出的控制策略的优越性能,将所提出的控制策略与文献[13]中的实验结果作比较。得到如图27所示不同控制策略的的效率比较曲线。
从图27可以看出,本文所提出的低纹波变频控制策略相比于传统的定频控制,在整个负载变化范围内的效率都有所提升。其中所提出的变频控制策略的峰值效率达到98.52%,满载效率98.4%,相比较于传统方案的峰值效率96.06%和满载效率96.05%分别提升了2.46%和2.35%。
除此之外,与现有的软开关控制策略相比,所提出的控制策略在重载段也有较大的优势。相比于文献[13]的峰值效率98.34%和满载效率97.4%,本文提出的控制策略在满载处有1%的效率提升。其主要原因是,软开关控制策略需要较大的电流纹波来实现所有开关器件的软开关,因此随着负载增加,电感电流的有效值会不可避免地增大,这导致重载效率降低较多。而在轻载时,软开关控制策略的开关损耗较小,因此会优于所提出的多模态控制策略。
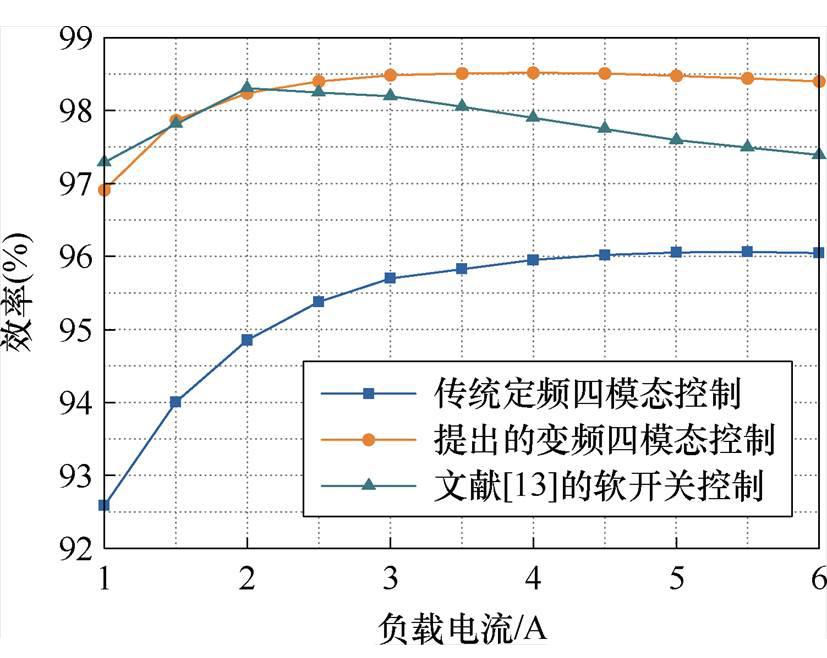
图27 不同控制策略的效率比较
Fig.27 Efficiency comparison of different control strategies
从理论分析和实验结果可知,在过渡模式中降低开关频率可以改善变换器的效率。而根据第3节的分析,过渡模式中的转换效率会随着开关频率降低而增加。对此,通过测试不同开关频率下的转换效率以验证理论分析。图28所示为不同开关频率下的转换效率比较。
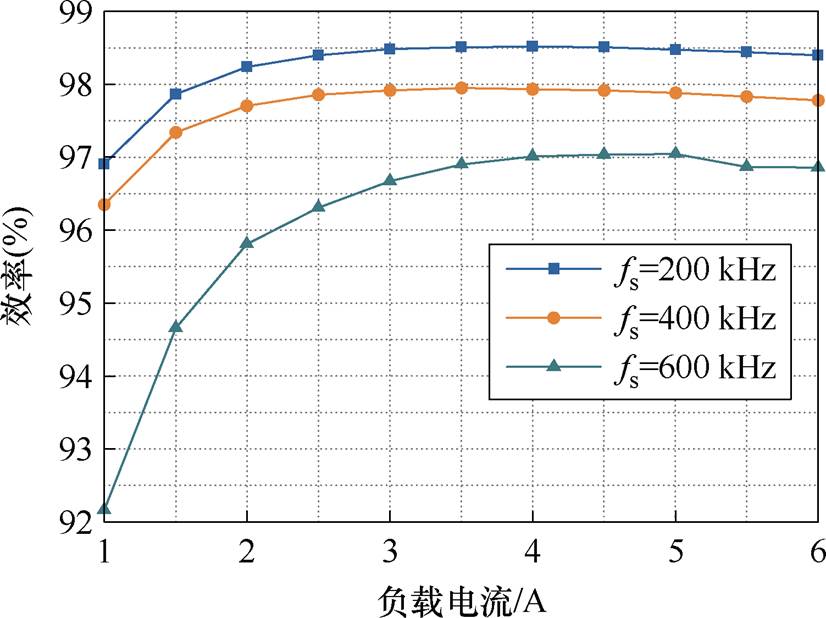
图28 不同频率的效率比较
Fig.28 Comparison of efficiency at different frequencies
根据测试结果可知,随着开关频率逐渐下降,变换器的转换效率逐渐增加,与理论分析一致。但是损耗并不会随着频率线性变化,主要是因为电感的磁心损耗和频率存在指数关系。另外器件的开关损耗和频率也是非线性关系。因此,当频率持续下降之后,效率的提升变小。
另外,为了验证电感对效率的影响,测试了在不同电感值下的转换效率曲线,如图29所示。
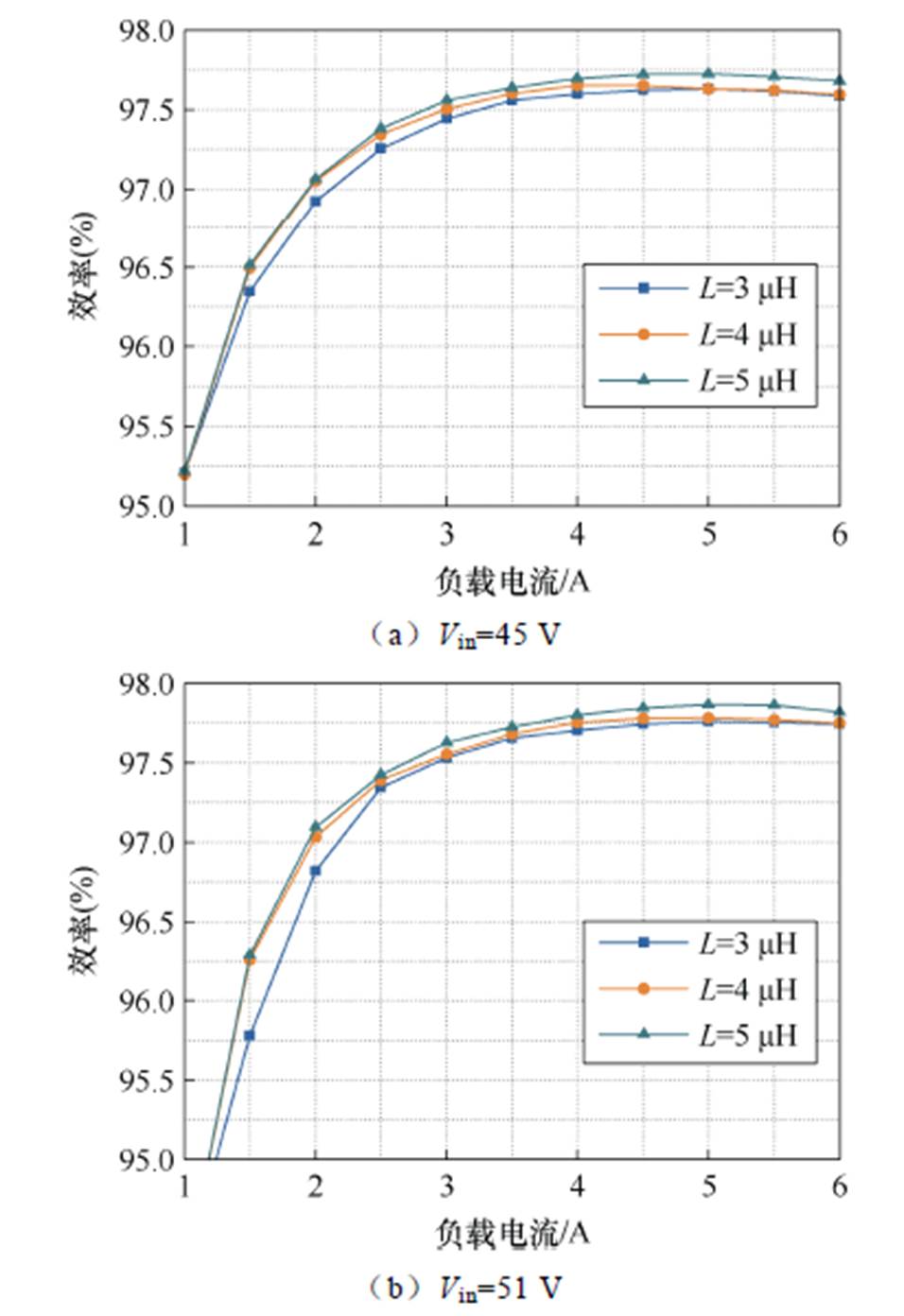
图29 损耗随负载电流和电感的关系
Fig.29 Losses with load current and inductor
从测试结果可知,相同输入输出电压下,随着电感值增加,变换器的效率略微有所变化,会随着电感增加而增加。主要原因是电感值会影响电流波形,从而影响变换器的效率。具体而言,电感越大电流纹波越小,器件的开关损耗变小。同时电感电流的有效值也会略微减小,所以导通损耗会降低。
此外,还对热分布进行了测量,图30给出了无风扇自然对流条件下的热分布。输入电压48 V、输出电压48 V、输出功率300 W。在加载3 min后测量了热图像,热分布趋于稳定。变换器的热分布主要集中在功率器件和控制芯片上,但最高温升仅为65.3℃,说明整个电路运行良好。

图30 满载热分布
Fig.30 Thermal distribution at full load
本文分析了FSBB变换器采用多模态控制策略时的电感电流纹波与桥臂移相时间的关系以及FSBB变换器效率与开关频率的关系,提出了一种低纹波变频四模态控制策略提高FSBB变换器的效率。基于理论分析与实验验证,得到以下结论:
1)当FSBB变换器工作在多模态控制策略的过渡模式时,控制Buck桥臂和Boost桥臂的移相时间为0,可以有效地减小电感电流纹波。
2)过渡模式的电感电流纹波比常规模式的纹波小,因此通过在过渡模式中降低FSBB变换器的开关频率,可以在不超过电感最大伏秒值的情况下进一步降低变换器的损耗,提高变换器的效率。
3)提出了基于最小纹波控制的降频控制策略。在相同的工况下,FSBB变换器的最高转换效率由96.06%提高到98.52%,提升2.46%。
参考文献
[1] 李金雨, 宋福龙, 马俊杰, 等. 基于5G基站可调度潜力与配电网集群划分的储能选址定容方法[J]. 电力系统自动化, 2023, 47(18): 151-160.
Li Jinyu, Song Fulong, Ma Junjie, et al. Siting and sizing method for energy storage based on dis- patchable potential of 5G base station and cluster partition of distribution network[J]. Automation of Electric Power Systems, 2023, 47(18): 151-160.
[2] 张玉莹, 曾博, 周吟雨, 等. 碳减排驱动下的数据中心与配电网交互式集成规划研究[J]. 电工技术学报, 2023, 38(23): 6433-6450.
Zhang Yuying, Zeng Bo, Zhou Yinyu, et al. Research on interactive integration planning of data centers and distribution network driven by carbon emission reduction[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6433-6450.
[3] 刘树林, 王斌, 朱高中, 等. 基于开关电感的二次型Buck-Boost变换器[J]. 电工技术学报, 2022, 37(增刊1): 190-197.
Liu Shulin, Wang Bin, Zhu Gaozhong, et al. Quadratic Buck-Boost converter based on switching inductance[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 190-197.
[4] 倪硕, 吴红飞, 陈君雨, 等. 交错并联临界导通模式Buck电感高密度集成与优化[J]. 电工技术学报, 2022, 37(18): 4688-4696.
Ni Shuo, Wu Hongfei, Chen Junyu, et al. Integration and optimization of a high power density inductor for an interleaved critical conduction mode Buck con- verter[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4688-4696.
[5] Baek J, Elasser Y, Radhakrishnan K, et al. Vertical stacked LEGO-PoL CPU voltage regulator[J]. IEEE Transactions on Power Electronics, 2022, 37(6): 6305-6322.
[6] Ahmed M H, Nabih A, Lee F C, et al. Low-loss integrated inductor and transformer structure and application in regulated LLC converter for 48-V bus converter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(1): 589-600.
[7] Akar F, Tavlasoglu Y, Ugur E, et al. A bidirectional nonisolated multi-input DC-DC converter for hybrid energy storage systems in electric vehicles[J]. IEEE Transactions on Vehicular Technology, 2016, 65(10): 7944-7955.
[8] Zhou Dehong, Wang Jiangfeng, Hou Nie, et al. Dual- port inverters with internal DC-DC conversion for adjustable DC-link voltage operation of electric vehicles[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 6917-6928.
[9] Kasper M, Bortis D, Kolar J W. Classification and comparative evaluation of PV panel-integrated DC-DC converter concepts[J]. IEEE Transactions on Power Electronics, 2014, 29(5): 2511-2526.
[10] 任林涛, 汪飞, 肖杨婷, 等. 四开关Buck-Boost变换器研究综述[J]. 电气工程学报, 2023, 18(2): 52-69.
Ren Lintao, Wang Fei, Xiao Yangting, et al. Review research on the four-switch Buck-Boost converter[J]. Journal of Electrical Engineering, 2023, 18(2): 52-69.
[11] 周国华, 邱森林, 张小兵. 宽增益高效率级联式四开关Buck-Boost LLC变换器[J]. 电工技术学报, 2024, 39(4): 1103-1115.
Zhou Guohua, Qiu Senlin, Zhang Xiaobing. Cascaded four-switch Buck-Boost LLC converter with wide gain range and high efficiency[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1103- 1115.
[12] Zhou Zongjie, Li Haiyan, Wu Xinke. A constant frequency ZVS control system for the four-switch Buck-Boost DC-DC converter with reduced inductor current[J]. IEEE Transactions on Power Electronics, 2019, 34(7): 5996-6003.
[13] 祁静静, 吴学智, 王久和, 等. 采用开关电感的Buck变换器CCM和DCM特性分析[J]. 电工技术学报, 2022, 37(16): 4155-4168.
Qi Jingjing, Wu Xuezhi, Wang Jiuhe, et al. Characteristics analysis of Buck converter with switched inductor in CCM and DCM[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4155-4168.
[14] 刘琦, 时雷雷, 徐奇, 等. 四开关升降压变换器高效控制策略研究与设计[J/OL]. 中国电机工程学报: 1-13 [2024-03-25]. https://doi.org/10.13334/j.0258-8013. pcsee.231719.
Liu Qi,Shi Leilei,Xu Qi , et al. Research and design of high-efficiency control strategy for four-switch lift-voltage converter[J/OL]. Chinese Journal of Elec- trical Engineering: 1-13 [2024-03-25]. https://doi.org/ 10.13334/j.0258-8013.pcsee.231719.
[15] 刘述喜, 邓瑞祥, 郭强, 等. 一种四开关Buck-boost变换器的模糊控制策略[J/OL]. 电气工程学报, 2023: 1-9. (2023-11-16). https://kns.cnki.net/kcms/detail/10. 1289.TM.20231115.0953.004.html.
Liu Shuxi, Deng Ruixiang, Guo Qiang, et al. A fuzzy control strategy for four-switch Buck-Boost con- verter[J/OL]. Journal of Electrical Engineering, 2023: 1-9. (2023-11-16). https://kns.cnki.net/kcms/detail/10. 1289.TM.20231115.0953.004.html.
[16] Fang Jie, Ruan Xinbo, Huang Xinze, et al. A PWM plus phase-shift control for four-switch Buck-Boost converter to achieve ZVS in full input voltage and load range[J]. IEEE Transactions on Industrial Electronics, 2022, 69(12): 12698-12709.
[17] Tian Lin, Wu Xinke, Jiang Congrang, et al. A simplified real-time digital control scheme for ZVS four-switch Buck-Boost with low inductor current[J]. IEEE Transactions on Industrial Electronics, 2022, 69(8): 7920-7929.
[18] Callegaro L, Ciobotaru M, Pagano D J, et al. A simple smooth transition technique for the noninverting Buck-Boost converter[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 4906-4915.
[19] 康家玉, 陈旭阳, 刘甲琛, 等. 基于四开关Buck- Boost的三模式平滑切换控制策略[J]. 科学技术与工程, 2019, 19(33): 193-199.
Kang Jiayu, Chen Xuyang, Liu Jiachen, et al. Research on three-mode smooth switching control strategy based on four switch Buck-Boost[J]. Science Technology and Engineering, 2019, 19(33): 193- 199.
[20] 曹以龙, 朱冬冬, 吴丹. 基于三模控制的四开关变换器设计[J]. 电源技术, 2021, 45(5): 665-668.
Cao Yilong, Zhu Dongdong, Wu Dan. Design of four-switch converter based on three-mode control[J]. Chinese Journal of Power Sources, 2021, 45(5): 665- 668.
[21] 李山, 宋立风, 章治国. 四开关Buck-Boost变换器的三模式控制方法研究[J]. 电源学报, 2019, 17(3): 111-119.
Li Shan, Song Lifeng, Zhang Zhiguo. Study on three- mode control method for four-switch Buck-Boost converter[J]. Journal of Power Supply, 2019, 17(3): 111-119.
[22] 王红斌, 陈奥博, 薛云涛, 等. 基于图形化方法的四开关Buck-Boost变换器模式平滑切换策略研究[J/OL]. 电源学报, 2023: 1-14. (2023-03-09). https:// kns.cnki.net/kcms/detail/12.1420.TM.20230309.0948.002.html.
Wang Hongbin, Chen Aobo, Xue Yuntao, et al. Research on smooth mode transition strategy of FSBB converter based on graphical method[J/OL]. Journal of Power Supply, 2023: 1-14. (2023-03-09). https:// kns.cnki.net/kcms/detail/12.1420.TM.20230309.0948.002.html.
[23] Ren Xiaoyong, Ruan Xinbo, Qian Hai, et al. Three- mode dual-frequency two-edge modulation scheme for four-switch Buck-Boost converter[J]. IEEE Transactions on Power Electronics, 2009, 24(2): 499-509.
[24] 曹以龙, 吴丹, 朱冬冬, 等. 一种基于四开关Buck- Boost变换器的四模式控制策略[J]. 电源学报, 2022, 20(5): 111-118.
Cao Yilong, Wu Dan, Zhu Dongdong, et al. Four- mode control strategy based on four-switch Buck- Boost converter[J]. Journal of Power Supply, 2022, 20(5): 111-118.
[25] 李慧慧, 皇金锋. 单电感双输出Buck-Boost变换器的非最小相位特性分析及控制策略[J]. 电工技术学报, 2023, 38(14): 3875-3887.
Li Huihui, Huang Jinfeng. Analysis of non-minimum phase characteristics and control strategies for single- inductor dual-output Buck-Boost converters[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(14): 3875-3887.
[26] Zhang Neng, Zhang Guidong, See K W. Systematic derivation of dead-zone elimination strategies for the noninverting synchronous Buck-Boost converter[J]. IEEE Transactions on Power Electronics, 2018, 33(4): 3497-3508.
[27] 樊靖轩, 施佳楠, 徐子梁, 等. 基于GaN的开关线性复合高速随动脉冲负载直流变换器[J]. 电工技术学报, 2024, 39(6): 1818-1829.
Fan Jingxuan, Shi Jianan, Xu Ziliang, et al. GaN- based switched linear composite high-speed follow-up pulse load DC converter[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1818-1829.
Abstract Recently, the bus voltage of data center power architectures has been gradually increased from the traditional 12 V to 48 V to reduce the current in the distribution lines, thus reducing distribution losses. In 48 V bus-powered architectures, the uninterruptible power supply (UPS) system is connected in parallel with the 48 V bus, which causes the bus voltage to fluctuate over a wide range (40 V to 60 V). To better manage the bus voltage and energy flow, a bidirectional DC-DC converter must be inserted between the UPS and power-using systems. The four-switch Buck-Boost converter is attractive because of its high efficiency and wide voltage regulation capability. In order to reduce the energy consumption in data centers, it becomes crucial to improve the efficiency of FSBB.
This paper analyzes the voltage gain of the FSBB converter. Then, a graphical approach compares the control strategies of the FSBB converter. The unimodal control strategy has large ripples. The bimodal control strategy system is unstable. Tri-modal solves the problems of duty cycle limitation and system stability, but the duty cycle varies greatly when the transition mode is switched. Four-mode control can add a control mode in the transition section to realize smooth conversion between different modes, and the ripple of inductor current is small. It is a control strategy with excellent performance.
Then, the minimum ripple condition of the inductor current is analyzed based on four-mode control. The inductor current ripple of the FSBB converter is minimized when the phase shift time between the Buck and Boost bridge arms is controlled to zero. The average value of the inductor current is related to the output voltage, input voltage, maximum duty cycle, and output current, and it is almost the same for all four-mode control strategies. Therefore, the control method to minimize the inductor current can be obtained by simultaneously controlling the phase shift time to zero.
Next, an accurate loss model of the FSBB converter is developed. When the voltage gain is constant, the loss of the converter increases as the load current increases. When the load is fixed, the lower the switching frequency, the lower the loss. Under the same load conditions, if the voltage gain is greater than 1, the loss decreases with the gradual increase of the gain at the same switching frequency until the loss is minimized when the voltage gain equals 1. On the contrary, if the voltage gain is less than 1, the loss gradually decreases as the gain gradually increases. Thus, this paper proposes a frequency reduction control strategy to reduce the converter loss in the transition mode and improve the conversion efficiency by reducing the switching.
Finally, an experimental platform is established to test the inverter control strategy for the FSBB converter in steady states. The minimum ripple control strategy is then validated. The results show that the transition mode’s inductor current ripple with the proposed control strategy is much smaller than the conventional four-mode control strategy. Among them, the inductor current ripple of the proposed minimum ripple control strategy is 35.2% of the conventional control strategy under the operating conditions of 51 V input voltage and 48 V output voltage. After reducing the switching frequency, the inductor current ripple of the minimum ripple control strategy is still smaller than that of the conventional control strategy. The efficiency of the proposed low ripple inverter control strategy is improved over the whole load variation range compared with the traditional fixed frequency control. Among them, the peak efficiency of the proposed inverter control strategy reaches 98.52% and full-load efficiency 98.4%, which is improved by 2.46% and 2.35% compared to the conventional scheme, respectively.
keywords:Four-switch Buck-Boost converter, multimodal control, frequency reduction control, high efficiency
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.240865
国家自然科学基金重点联合基金项目(U23B20138)和国家自然科学基金面上项目(52277198)资助。
收稿日期 2024-05-24
改稿日期2024-06-17
吴佳芮 男,1996年生,博士研究生,研究方向为高频高密度变换器。
E-mail: wujiarui123@stu.xjtu.edu.cn
杨 旭 男,1972年生,教授,博士生导师,研究方向为大功率开关电源技术、电力电子集成技术、电力系统中的电力电子装置等。
E-mail: yangxu@mail.xjtu.edu.cn(通信作者)
(编辑 陈 诚)