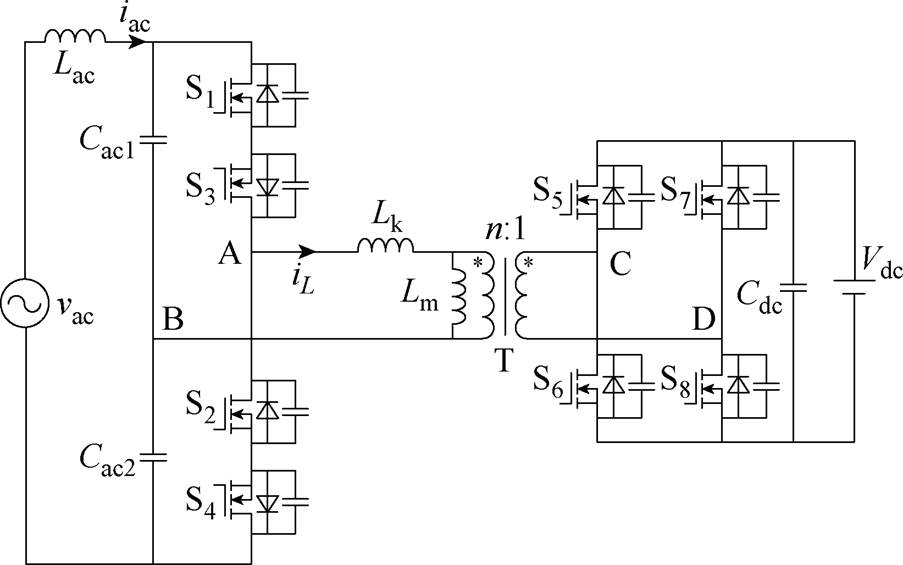
图1 单级式双有源桥AC-DC变换器拓扑
Fig.1 Single-stage dual active bridge AC-DC converter
摘要 针对单级式双有源桥AC-DC变换器调制非线性和电流应力较大的问题，该文提出一种基于线性化的变换器最小电流应力控制策略。首先，分析扩展移相（EPS）调制策略的开关特性，对于输入电流与移相比呈非线性的特点，提出一种线性化变频移相控制策略。其次，通过微分极值法实现变换器电流应力的最小化，该控制策略不仅可以降低变换器的控制复杂度，还可以在有效降低变换器电流应力的同时保证开关管具有较宽零电压开通（ZVS）范围，并且移相比和开关频率以解析形式获得，计算简单、易于实现。最后，通过仿真和实验对该文所提控制策略进行验证，证明了该控制策略的可行性。
关键词：AC-DC变换器 扩展移相 线性化 最小电流应力 零电压软开关
随着可再生能源在电网中的占比越来越大，分布式电源和分布式储能成为了必不可少的技术手段[1-4]。其中双向AC-DC变换器作为交直流混合微电网中连接直流母线与交流母线的核心装置，成为当下研究的热点[5-10]。
按照拓扑结构，双向AC-DC变换器可分为两级式和单级式[11]。在两级式拓扑结构中，前级通常采用同步整流器，后级可以采用双有源桥（Dual Active Bridge, DAB）型变换器或谐振变换器。该拓扑结构具有控制独立简单、容易实现等优势[12]。相较于两级式拓扑，单级式拓扑结构移除了中间容值较大的直流母线电容，减少了变换环节，在效率、功率密度、成本等方面都具有明显优势[13]。
在准单级式的拓扑结构中，前级AC-DC一般采用同步整流电路。后级DC-DC在采用LLC谐振变换器时，可以在全负载范围内实现开关管的零电压软开关（Zero Voltage Switching, ZVS）和二次侧整流二极管的零电流软开关（Zero Current Switching, ZCS）[14]，从而有效降低开关损耗[15]。但LLC变换器反向工作时，因其结构不对称，使得变换器工作效率降低，故仅用于单向功率传输的场合[16]。相较于谐振型AC-DC变换器，DAB型AC-DC变换器具有双向功率传输特性相同、主电路结构对称、控制简易等优点[17]。
对于DAB变换器，电流应力的大小不仅影响变换器整体效率，还与器件的选型密切相关。目前DAB变换器主要采用移相的调制策略，单移相（Single Phase Shift, SPS）调制策略因其仅有一个自由度，控制较为简单，但当变压器两侧电压幅值不匹配时，变压器漏感会产生较大的环流功率，从而导致电流有效值和峰值增大，并且变换器无法在全负载范围内实现ZVS[18]。为此，可以通过在变换器一次侧和二次侧增加自由度来实现更加灵活的调制。文献[19]基于扩展移相的调制方式优化了回流功率。文献[20-21]采用双重移相（Dual Phase Shift, DPS）调制策略给出最小电流应力的优化算法。为进一步扩大软开关范围，文献[22]采用三重移相（Triple Phase Shift, TPS）调制策略，在实现整个负载范围内电流应力最小化的同时保证了DAB全范围软开关。文献[23]则是从减小变换器系统峰值电流和磁性元件设计成本的角度给出了一种基于三重移相的最小峰值电流控制算法。
在DAB型AC-DC变换器中，仅采用SPS控制时，交流侧输入电流畸变较大，开关管电流应力也很大。采用更多自由度的调制策略，DAB变换器可以满足宽电压增益的要求，但是难以在所有范围内实现软开关。文献[24]通过采用TPS调制策略的内部模式，在一定程度上拓宽了软开关范围，但是难以保证较小的电流应力。文献[25]通过引入模式切换的调制手段，在降低变换器的电流应力的同时，拓宽了变换器的软开关范围，但会在一定程度上增加变换器调制的复杂度。
基于相移控制的优化算法会导致系统输入电流与移相比之间呈非线性关系，增加控制的复杂度，并且这种非线性关系也会使得闭环控制器设计变得较为复杂[26]。文献[27]通过采用拉格朗日算法降低了系统电流应力，并引入虚拟频率将非线性控制简化为线性控制，但计算过程较为复杂。
本文针对单级式双有源桥AC-DC变换器调制非线性和电流应力较大的问题，提出一种基于线性化的变换器最小电流应力控制策略。该控制策略实现了输入电流与移相比之间的线性化，并且在有效降低变换器电流应力的同时保证开关管具有较宽零电压开通范围。最后，通过仿真和实验对本文所提控制策略进行验证，证明了该控制策略的可行性。
图1为单级式双有源桥AC-DC变换器拓扑，S1、S3和S2、S4为一次侧的双向开关，S5～S8构成二次侧全桥，Lac和Cac构成交流滤波器，Cdc为直流稳压电容，Lk为折算到变压器一次侧的漏电感，Lm为折算到变压器一次侧的励磁电感，高频变压器T的匝数比为n。
交流侧电压工作于正半周期时，开关管S3、S4常通，S1、S2工作于高频开关状态；负半周期时开关管S1、S2常通，S3、S4工作于高频开关状态。直流侧开关管S5～S8高频导通。
图1 单级式双有源桥AC-DC变换器拓扑
Fig.1 Single-stage dual active bridge AC-DC converter
如图2所示为DAB变换器在电网电压正半周期时，EPS调制方式下的典型工作波形。所有驱动信号的占空比均为0.5，Ts为变换器的一个开关周期。D1为S6和S8之间的移相比，D2为S2和S8之间的移相比。
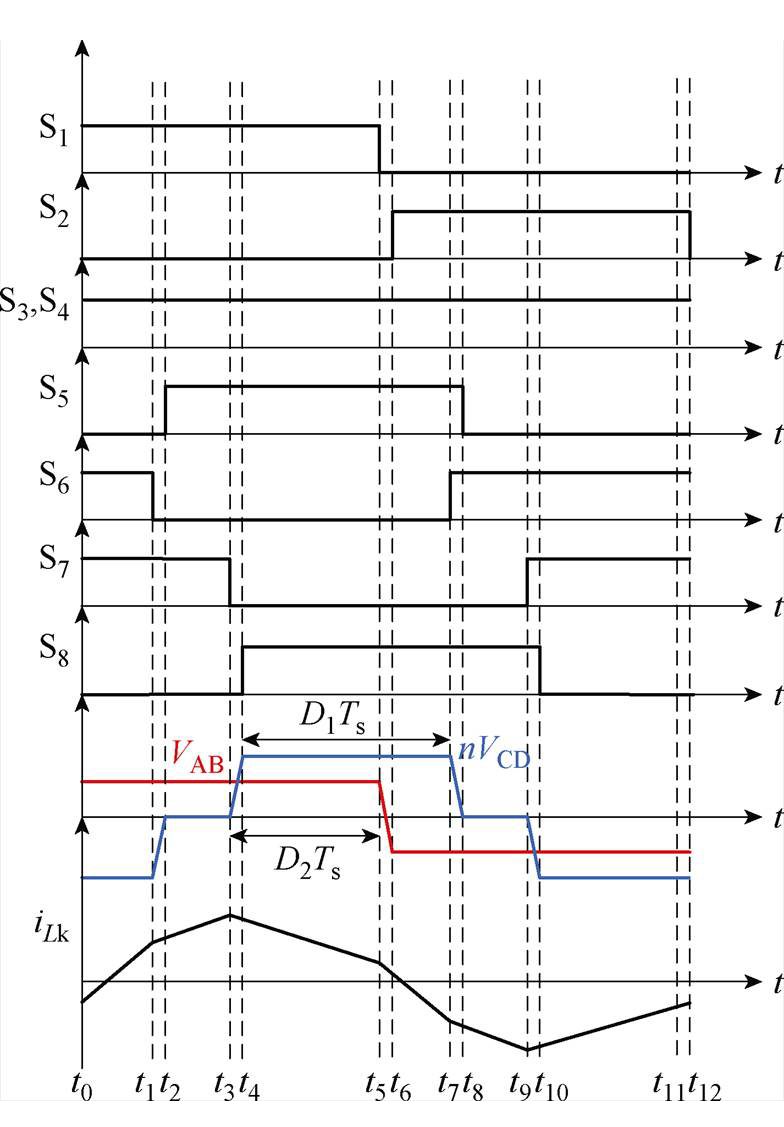
图2 扩展移相调制下DAB变换器正半周期典型工作波形
Fig.2 Typical operating waveforms of DAB converter positive half-cycle under extended phase-shift modulation
在DAB变换器进入稳态运行时，电感电流波形呈半周期中心对称。故本文只选取t0～t6时段进行分析。由于死区时间很短，可以近似认为电感电流在开关管切换过程中不发生变化。根据图2所示的工作波形，可求得电感电流在不同时段的表达式为
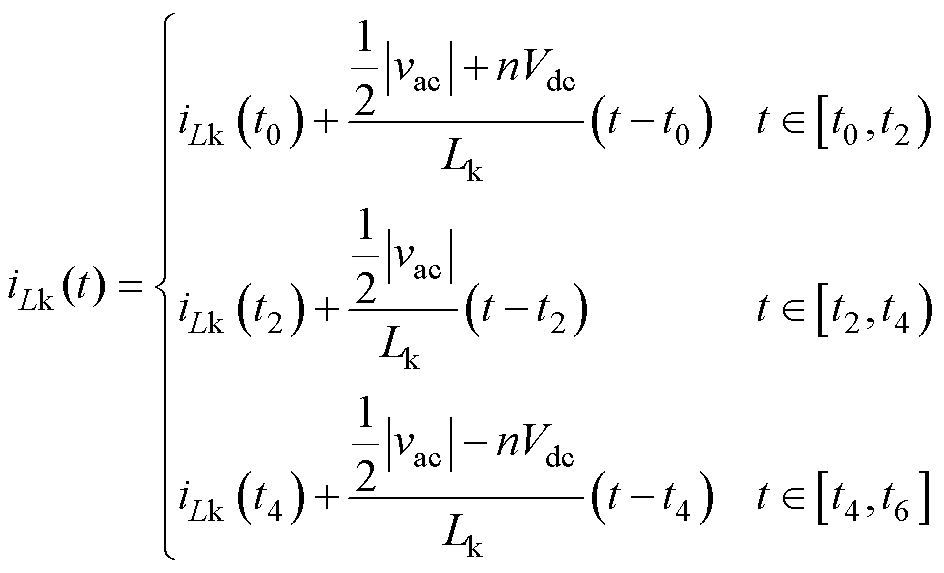（1）
式中，各时刻由占空比D1、D2表示为
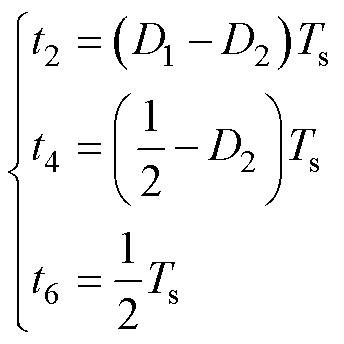（2）
结合式（1）与式（2）可以得到关键节点时刻的电感电流值分别为
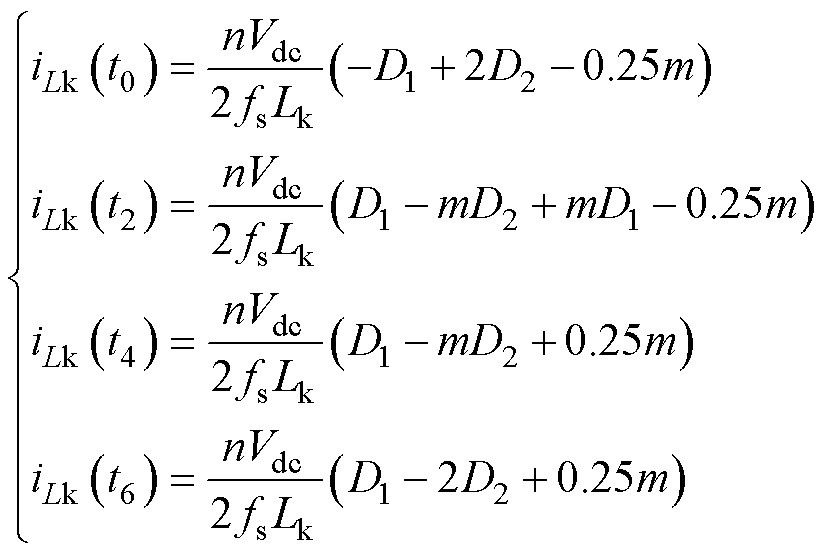（3）
式中，m为电压传输比，m=|vac|/(nVdc)；fs为变换器开关频率，满足Ts=1/fs。
由式（3）可得正半周期的输入电流为t0～t6时段开关管电流积分，表达式为
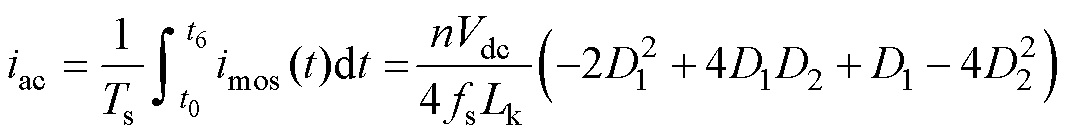（4）
变换器的平均传输功率为
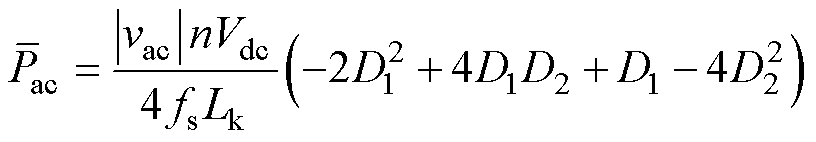（5）
基于相移控制的优化算法会导致系统输入电流与移相比之间呈非线性关系，增加控制的复杂度。通过对式（4）分析，变换器输入电流iac受移相比D1、D2以及频率fs的影响。为解决上述问题，实现变换器输入电流与移相比之间的线性化控制，在此将输入电流表达式化简为仅与其中一个变量相关的线性表达式。针对上述问题，引入移相指数k，有
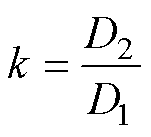（6）
将式（6）代入到式（4）可得输入电流为
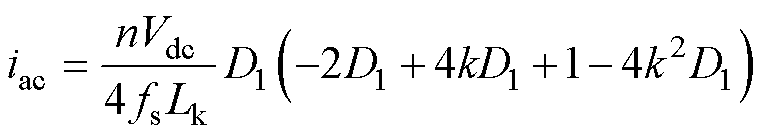（7）
由于输入电流表达式（7）依然与移相比D1和开关频率fs两个变量相关，因此输入电流iac与移相比D1的关系仍是非线性的。
输入电流iac与移相比D1和漏感Lk的函数关系如图3所示，图中两条曲线所在平面为iac与D1的非线性关系。随着移相指数k的增大，它们之间的关系变得更加非线性，并且这种非线性使得调制变得复杂，不利于提高输入电流的跟踪精度。
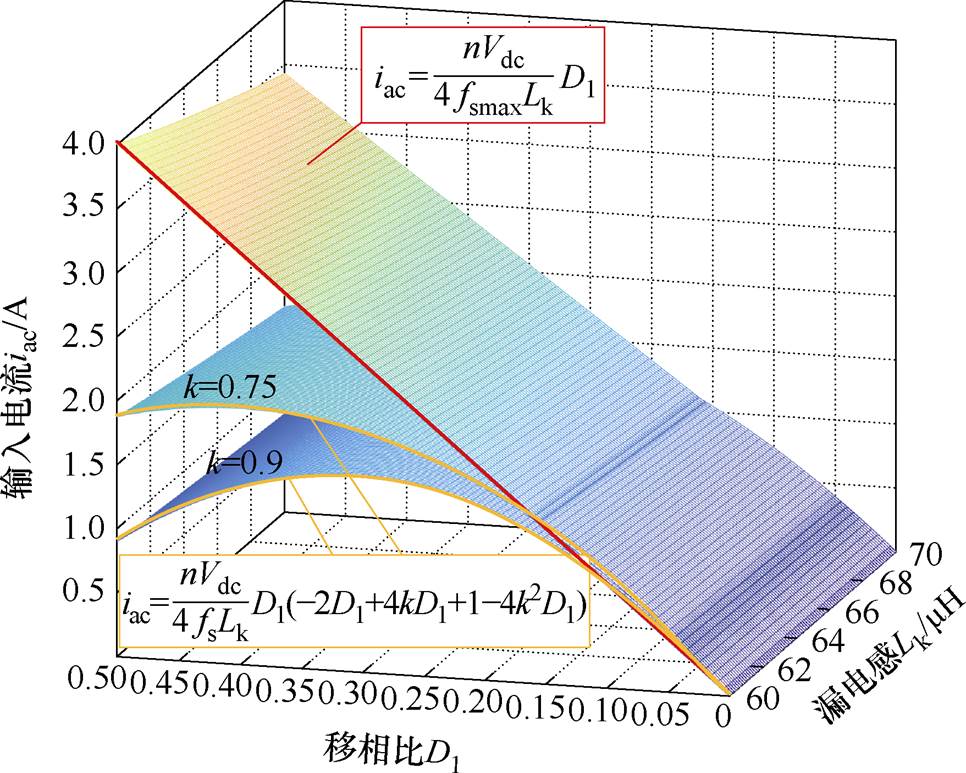
图3 输入电流iac与移相比D1和漏感Lk的函数关系
Fig.3 Input current iac as a function of shift ratio D1 and leakage inductance Lk
为了解决上述问题，通过引入最大开关频率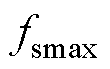
，利用移相变频控制，将开关频率
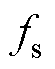通过移相比D1和最大开关频率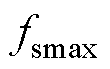表示出来，将输入电流表达式（4）化简为仅随移相比D1变化的线性表达式，此时变换器的开关频率函数
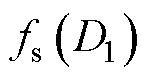为
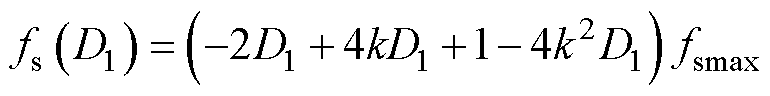（8）
将式（8）代入到式（7）可以简化为
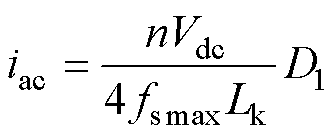（9）
如式（9）和图3所示，通过所提出的变频控制策略，输入电流iac和移相比D1变换为线性关系。
假定交流输入电流为标准正弦电流，由式（9）可以得到
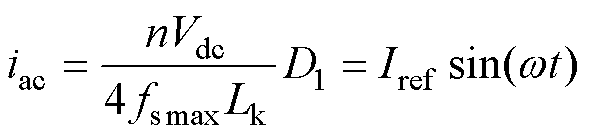（10）
式中，Iref为输入电流的参考电流幅值。
因此可以求得移相比D1为
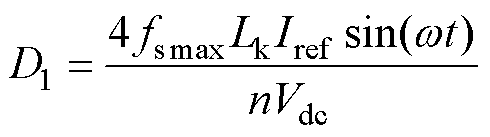（11）
其中
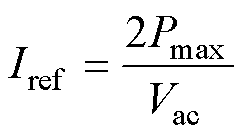（12）
式中，Pmax为变换器的最大传输功率。
假定输入交流电压与输入电流同相位，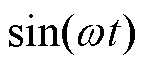
也可以用输入的交流电压表示出来，即
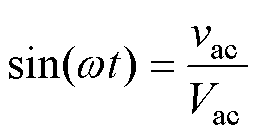（13）
将式（12）和式（13）代入式（11）可以得到D1的表达式为
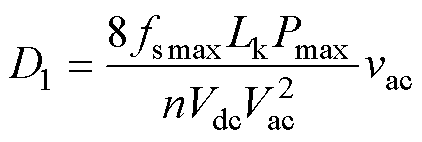（14）
通过分析电感电流表达式（3），在t4时刻，电感电流达到峰值，即
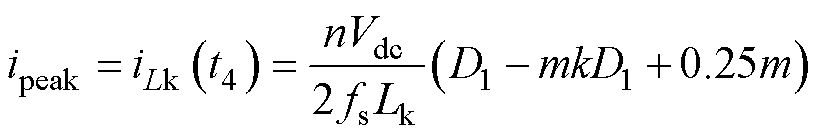（15）
式中，ipeak为电感电流峰值，即电流应力。
将式（8）代入到式（15）可以得到
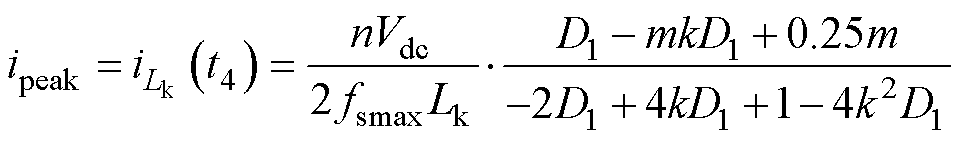（16）
式中，电压传输比m和移相比D1都与交流电压呈半正弦规律变化，因此每一时刻的m和D1都有一个固定的值相对应。对于电感电流应力表达式（15）而言，在每一时刻，因为m和D1都是固定值，故只与k的大小直接相关。
为便于后续分析，图4给出了变换器电流应力与交流输入电压vac和移相指数k之间的三维关系。
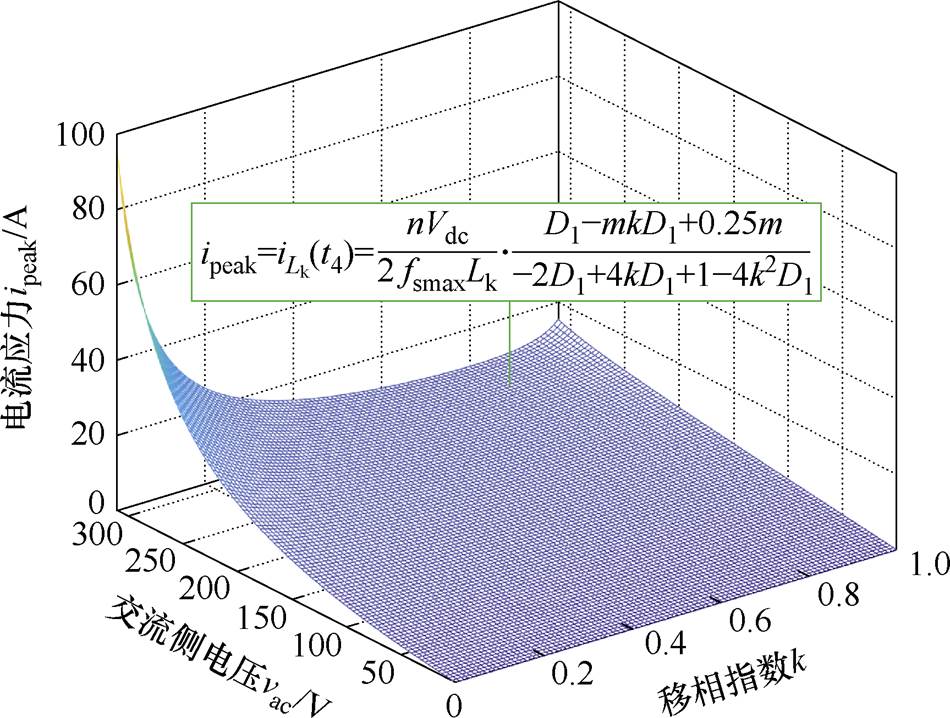
图4 电流应力在不同电压下随k的变化规律
Fig.4 Law of variation of current stress with k at different voltages
为了求得最小电流应力的轨迹，对式（16）中的k求导，可以得到
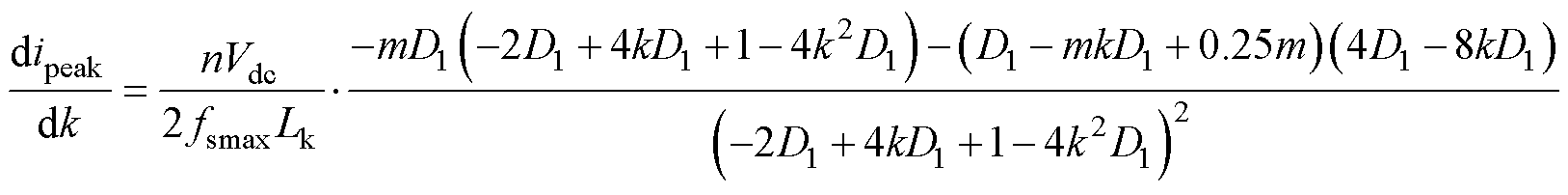（17）
图5为电流应力导数关于交流输入电压vac和移相指数k的三维图，并在图中再做一个电流应力导数为0的平面。图中，两面的交线就是最小电流应力下k关于vac变化的曲线。
令电流应力导数为0，可以求得移相指数k关于交流电压vac的表达式为
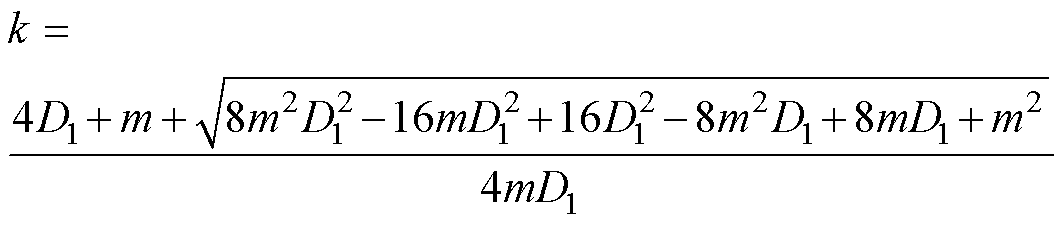（18）
将m和式（14）代入式（18）可以得到k关于vac的表达式。如图6所示为k关于vac的二维图。
将k的表达式（18）代入输入电流表达式（4），即可得到最小电流应力下的电感电流表达式。
如图7所示为所提控制策略下半个工频周期的移相比和开关频率变化曲线。其中移相比D1和D2变化范围在（0, 0.5）之间，最大开关频率为100 kHz，最小开关频率约为45 kHz。
变换器的软件控制流程如图8所示，用于解释所提出的控制策略。首先对交流电压、直流电压、输入电流进行采样，通过式（14）在DSP中计算出移相比D1的表达式，再通过式（18）计算出最小电流应力下移相指数k的表达式，最后将移相比D1和移相指数k代入到式（6）和式（8）求得移相比D2和开关频率fs。
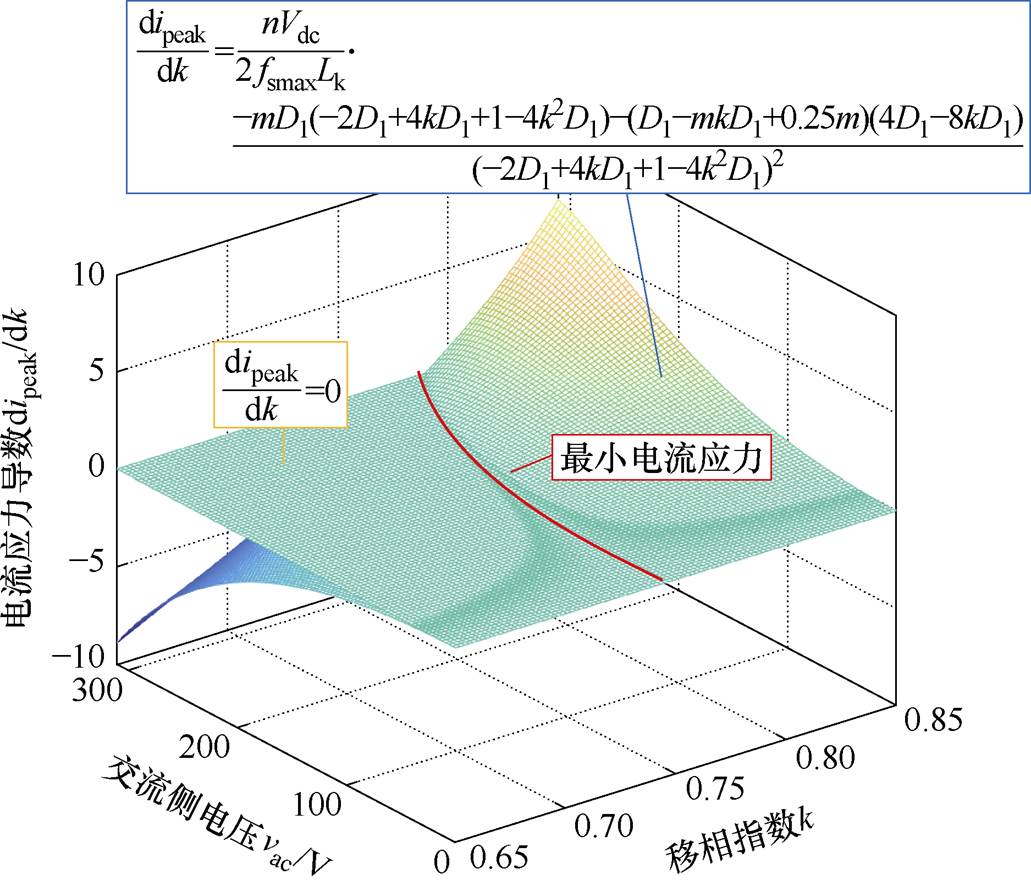
图5 最小电流应力导数关于交流电压和移相指数的轨迹图
Fig.5 Trajectories of minimum current stress with respect to AC voltage and phase shift exponent
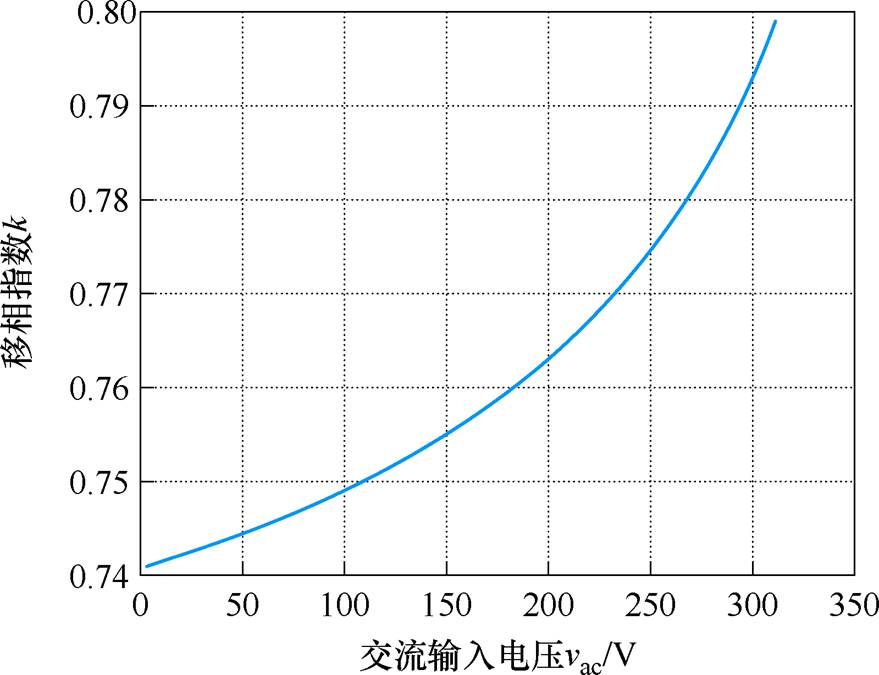
图6 最小电流应力下k的变化曲线
Fig.6 Variation curve of k under minimum current stress
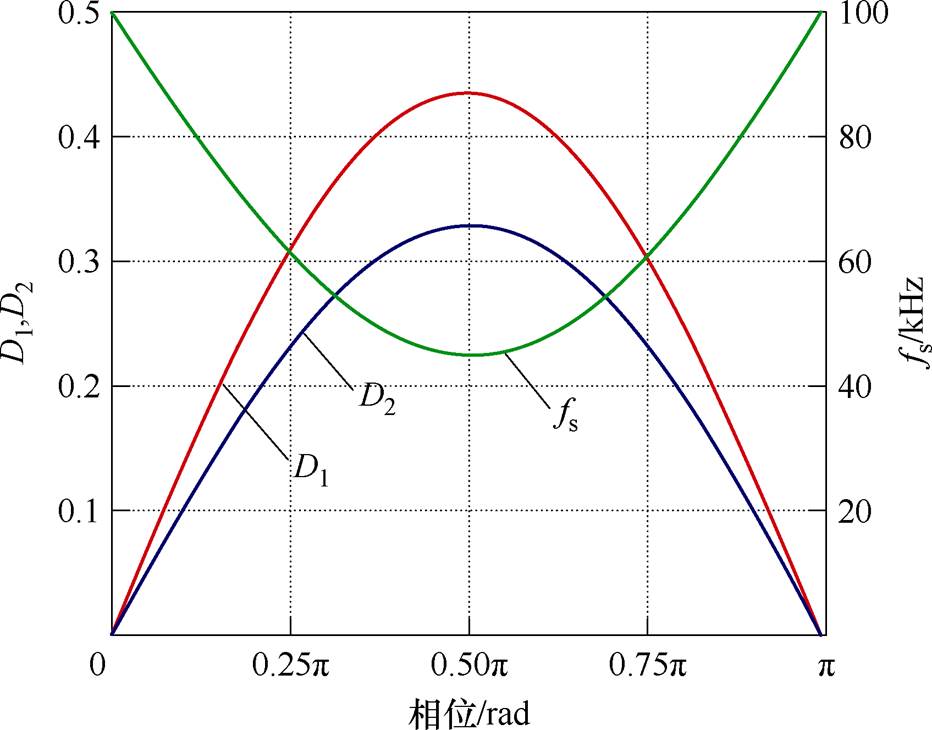
图7 所提控制方法下移相比和开关频率的变化曲线
Fig.7 Proposed control method downshift compared to and switching frequency variation curves
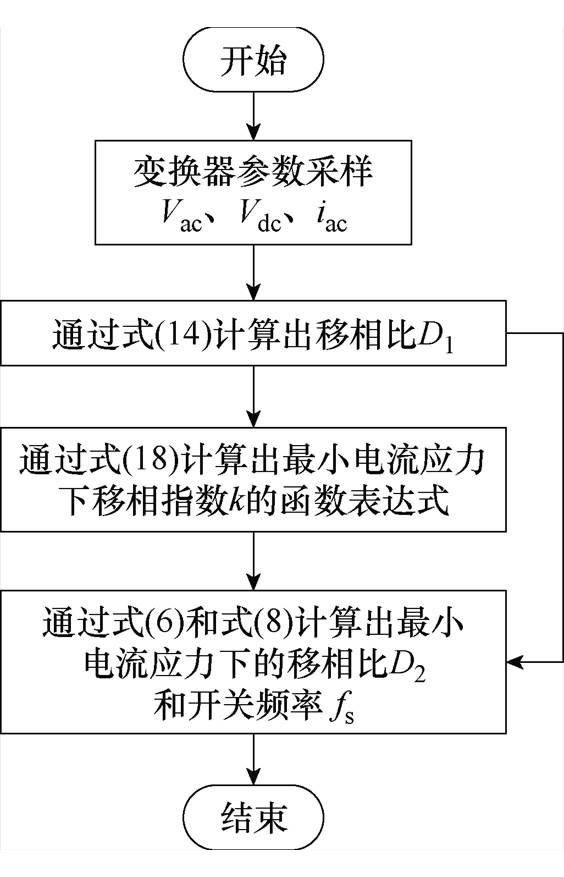
图8 基于线性化的变换器最小电流应力控制框图
Fig.8 Block diagram of linearization-based minimum current stress control for converters
根据图2分析可知，由于电感电流中心对称，想要实现所有开关管的软开关，t2时刻电感电流值需要大于一定的正值，以满足二次侧S5的软开关条件。同理，t4和t6时刻同样需要满足电感电流值大于一定的正值，以实现二次侧S8和一次侧S2的软开关条件。以t0～t6时段为例，软开关条件为
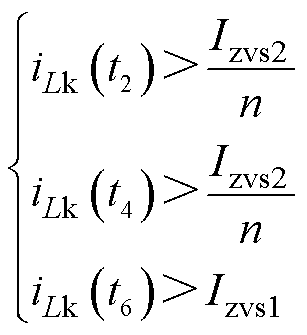（19）
式中，Izvs1和Izvs2/n为一次侧与二次侧开关管结电容完全充放电所需要的最小电感电流。
实现软开关不仅与开关管导通时刻的电感电流大小有关，还与死区时间相关。即使有足够大的电流，但是死区时间不够，结电容依然无法实现完全的充放电，也就无法实现ZVS导通；反之，如果电感电流小于实现软开关所需的最小电流，即使死区时间足够长，也无法实现ZVS导通。因此想实现ZVS导通，至少需要满足上述的两个条件。
为实现ZVS导通，死区时间需要满足
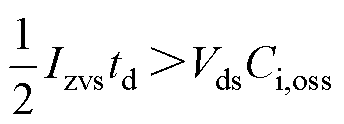（20）
式中，td为死区时间；Vds为开关管漏源极电压；Ci,oss为变换器一次侧和二次侧开关管的结电容。
表1为变换器仿真参数，由表1可求得一次侧和二次侧在最小电流下所需要的死区时间分别为322 ns和456 ns。但是死区时间过长会产生较大的死区损耗，并且还会造成输入电流在开关频率较低时刻产生畸变，因此本文的死区时间td设为100 ns。
表1 变换器仿真参数
Tab.1 Converter simulation parameters
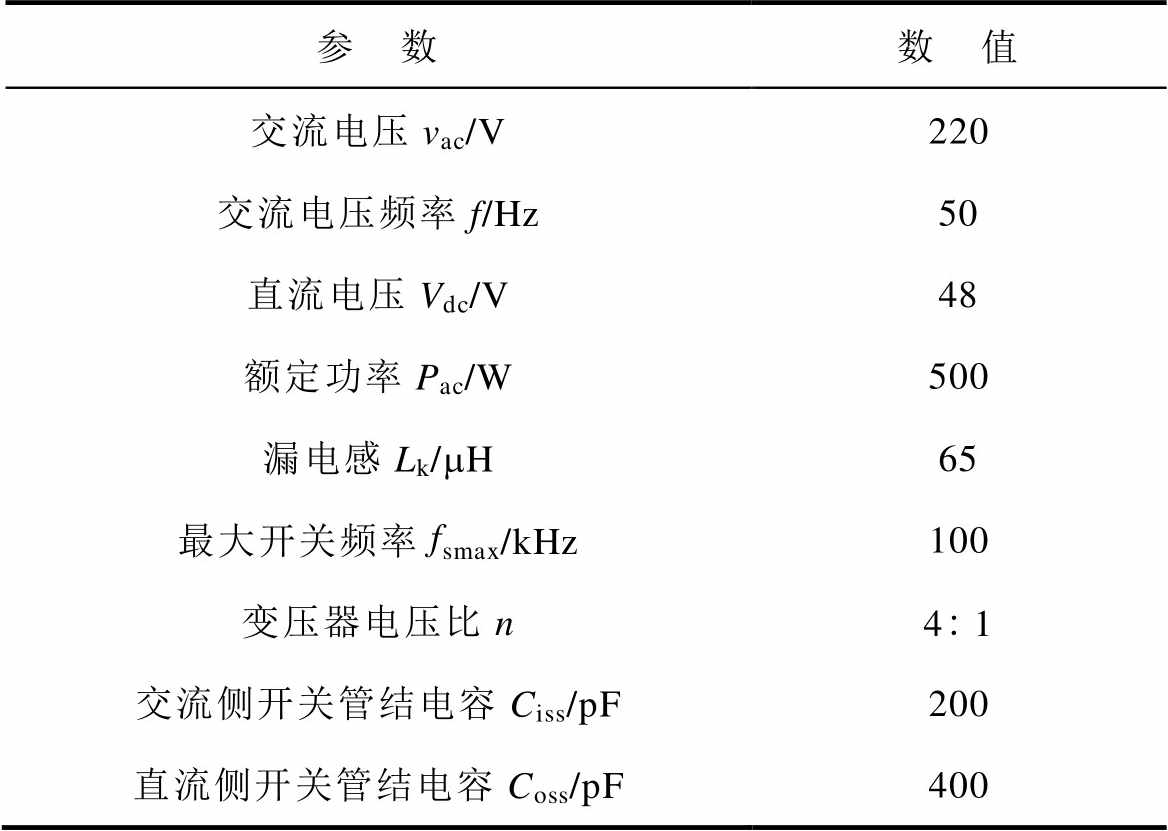
参 数数 值 交流电压vac/V220 交流电压频率f/Hz50 直流电压Vdc/V48 额定功率Pac/W500 漏电感Lk/mH65 最大开关频率fsmax/kHz100 变压器电压比n41 交流侧开关管结电容Ciss/pF200 直流侧开关管结电容Coss/pF400
对式（20）变形可得在死区时间一定时，实现软开关所需要的电流大小为
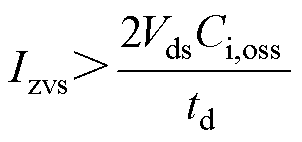（21）
一次侧开关管实现软开关的最小电流为
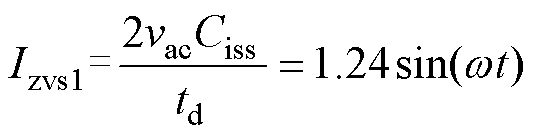（22）
二次侧开关管实现软开关的最小电流为
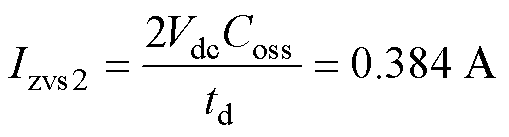（23）
根据变压器电压比的关系可以得到二次侧实现软开关所需的最小电感电流大小为0.096 A。
根据已经求得的实现软开关所需的电感电流大小和各时刻的电感电流表达式，可以作出开关管导通时刻的电感电流与实现软开关所需的电感电流的三维图，以直观清晰地判断各个开关管的ZVS导通范围。
如图9所示为一次侧开关管S2导通时刻电感电流iLk(t6)和其实现软开关所需的最小电感电流Izvs1的三维图。从图中可以看出，沿着最小电流应力下的iLk(t6)除了极端轻载下小于Izvs1，在其他时刻均能实现软开关。开关管S2几乎实现了全范围的ZVS 导通。
图9 一次侧开关管S2的软开关范围
Fig.9 Soft switching range of the primary side switching tube S2
同理，如图10所示为二次侧开关管S5导通时刻电感电流iLk(t2)和其实现软开关所需的最小电感电流Izvs2/n的三维图。从图中可以看出，沿着最小电流应力下的iLk(t2)不恒大于Izvs2/n，因此开关管S5在死区时间为100 ns下的轻载时不能实现软开关。
图10 二次侧开关管S5的软开关范围
Fig.10 Soft switching range of the secondary side switching tube S5
如图11所示为二次侧开关管S8导通时刻电感电流iLk(t4)和其实现软开关所需的最小电感电流Izvs2/n的三维图。从图中可以看出，沿着最小电流应力下的iLk(t4)除了极端轻载下小于Izvs2/n，在其他时刻均能实现软开关。开关管S8几乎实现了全范围的ZVS导通。
根据上述理论分析结果，在PSIM软件中使用表1中的参数进行仿真，验证所提出的基于线性化的变换器最小电流应力控制策略。
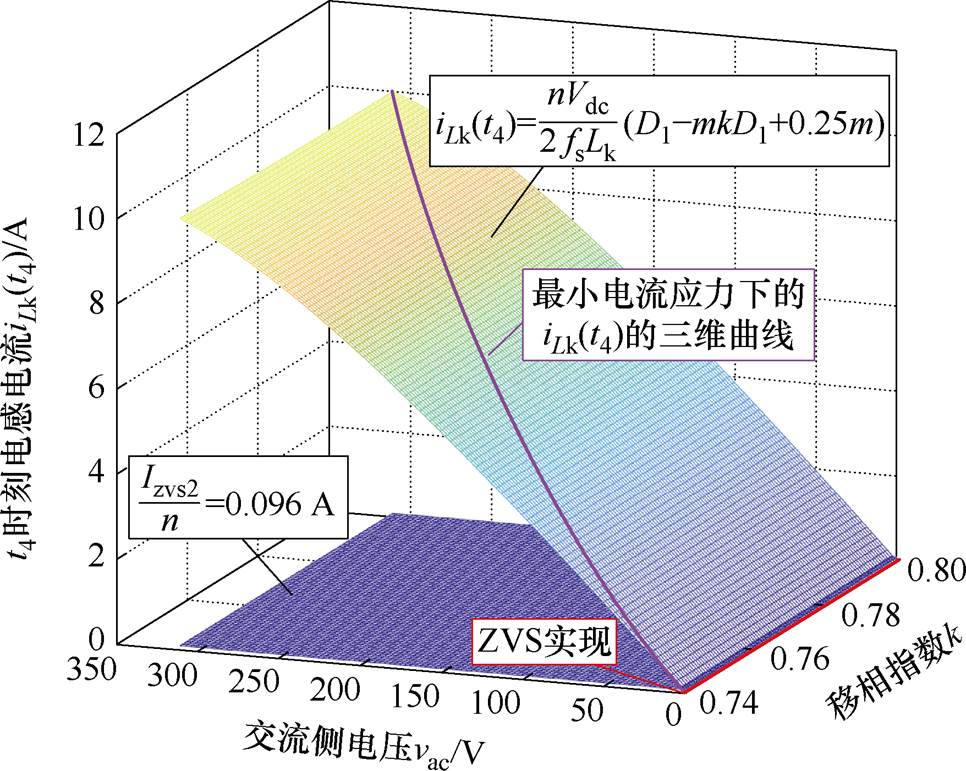
图11 二次侧开关管S8的软开关范围
Fig.11 Soft switching range of the secondary side switching tube S8
由上述分析可知，变换器的输入电流应与移相比D1呈线性关系，与移相比D1与D2成正比，且在半周期内均呈正弦变化。线性化下正向传输功率时变换器的工作波形如图12所示，输入电流与移相比D1实现了线性化。
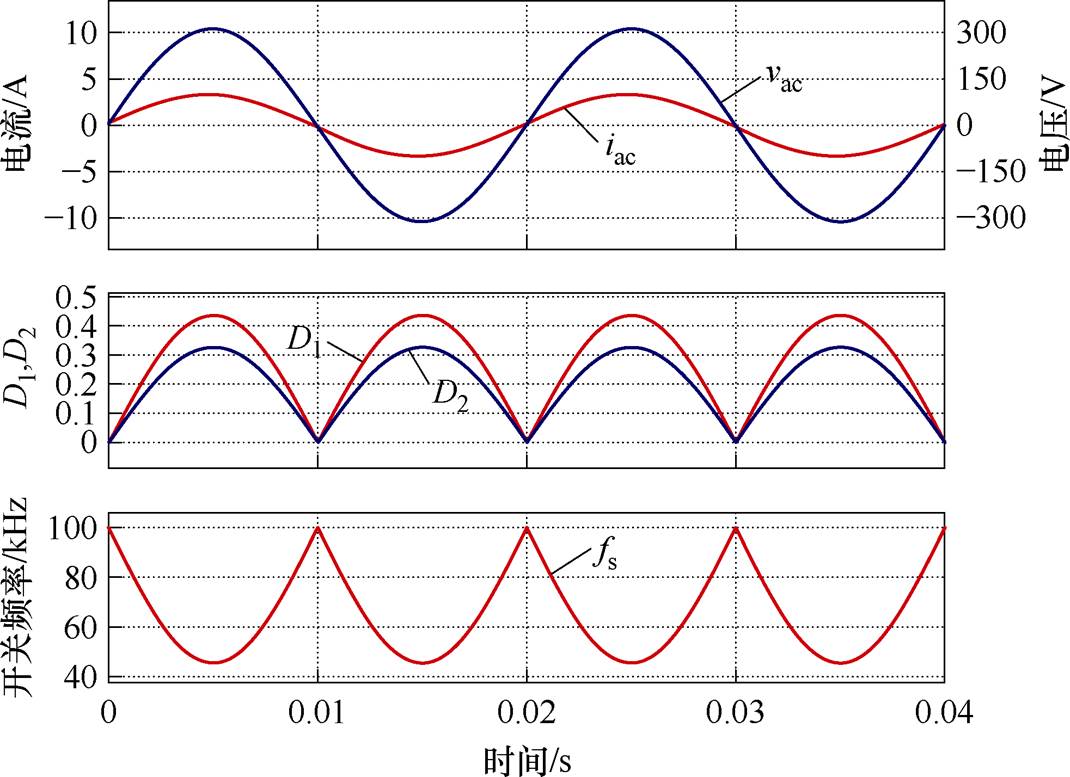
图12 线性化下正向传输功率时变换器的工作波形
Fig.12 Converter operating waveforms during forward power transmission under linearization
由图4可知，在不同电压下，变换器的电流应力随移相指数的改变而变化。为方便对比优化前后电流应力的变化情况，本文选取k=0.5作为优化前的移相指数大小。为了降低变换器的电流应力，本文通过改变移相指数k的大小来实现这一目标。
变换器在表1参数下，电流应力优化前后对比如图13所示。图13a中，当移相指数k=0.5时，变换器电感电流的最大值约为13.7 A。当移相指数k采用式（18）的最小电流应力的优化结果时，如图13b所示，变换器电感电流的最大值约为10.7 A，电流应力有明显的下降。
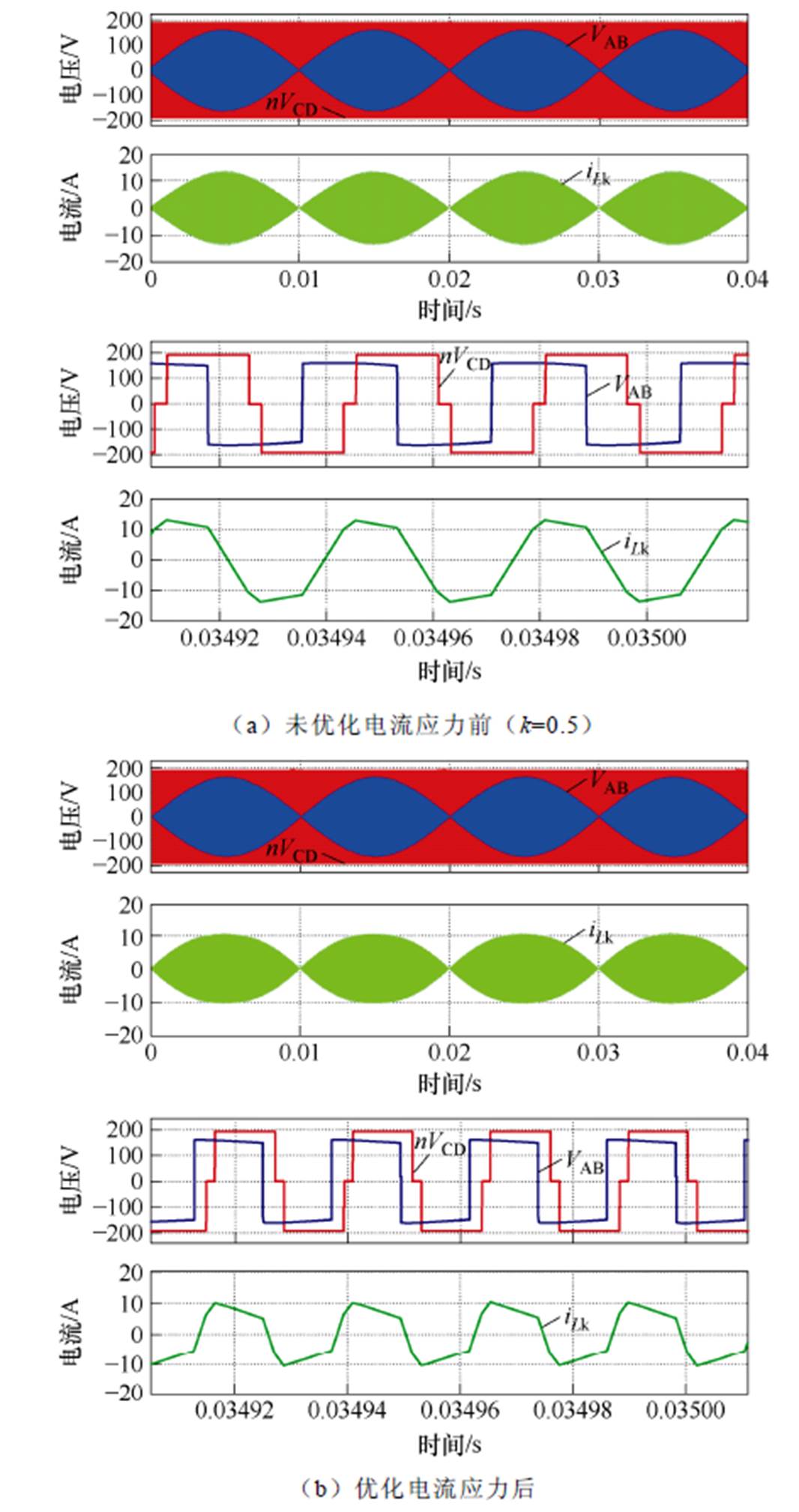
图13 变换器电感电流和端口电压的波形
Fig.13 Transducer inductive current and port voltage waveforms
本文搭建了单级式AC-DC变换器样机，表2为变换器实验参数，控制算法由TMS320F28335 DSP实现，硬件实验平台如图14所示。
图15为所提控制策略的交流输入电压vac、交流输入电流iac和DAB输出直流电压压Vdc的实验波形，与所提出的理论波形相吻合。
图16为变换器在输入电压50 V、输出功率100 W下电感电流和端口电压实验波形。由于变换器的电流应力随移相指数的改变而变化，为对比优化前后电流应力的变化情况，图16a展示了变换器在未优化电流应力、移相指数k=0.5时的变换器两端端口电压和电感电流的整体波形和细节波形，此时的电感电流的峰值为10 A左右。图16b展示了变换器在输入电压50 V，输出功率100 W下通过式（18）优化电流应力以后的变换器两端端口电压和电感电流的整体波形和细节波形，此时的电感电流的峰值为9 A左右。通过对电流应力优化前后的对比可以看到，在采用文中所提控制策略下，电流应力可以有效降低。
表2 变换器实验主要参数
Tab.2 Main parameters of converter experiment
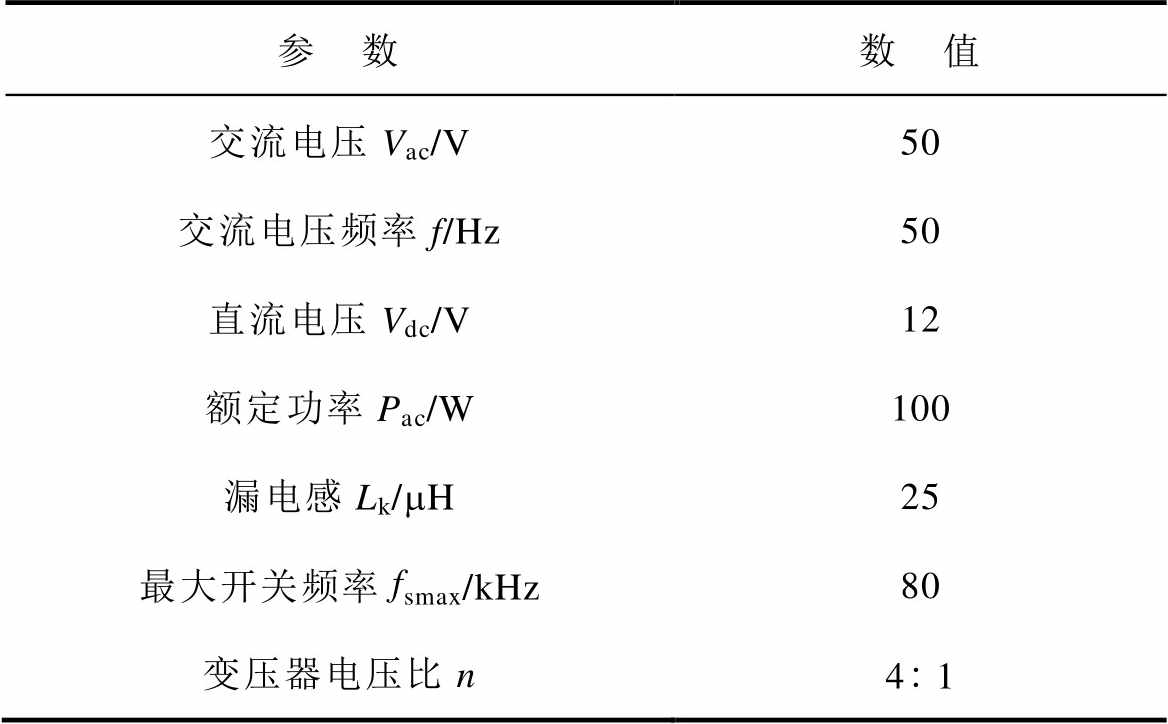
参 数数 值 交流电压Vac/V50 交流电压频率f/Hz50 直流电压Vdc/V12 额定功率Pac/W100 漏电感Lk/mH25 最大开关频率fsmax/kHz80 变压器电压比n41
图14 单级式AC-DC变换器实验平台
Fig.14 Single-stage AC-DC converter experimental platform
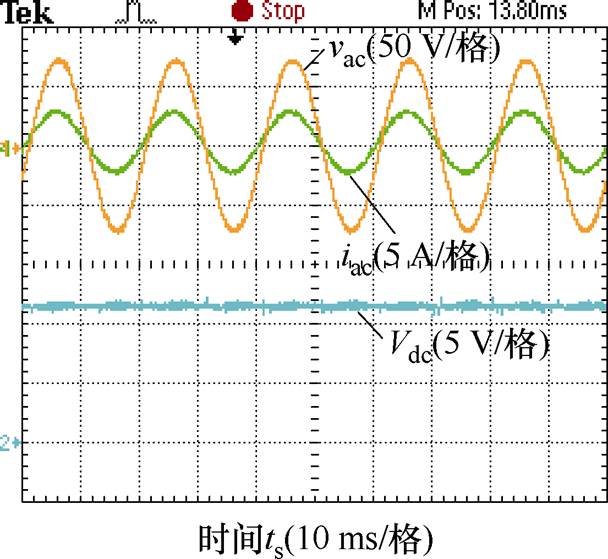
图15 单相AC-DC变换器的稳态工作波形
Fig.15 Steady-state operate waveforms of the single-phase AC-DC converter
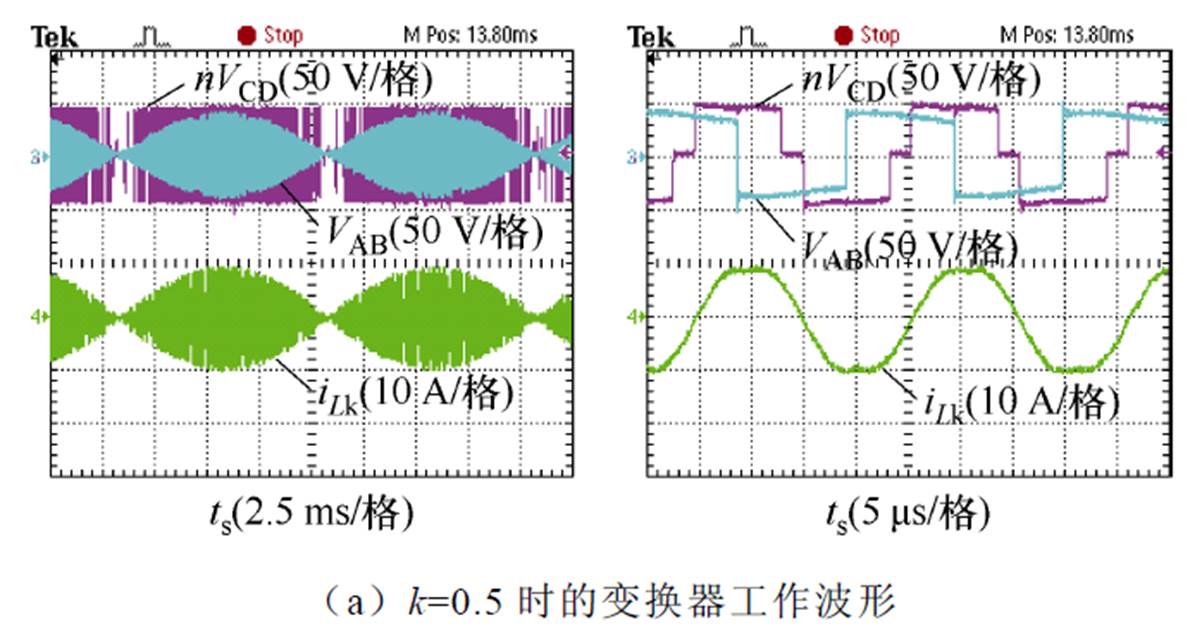
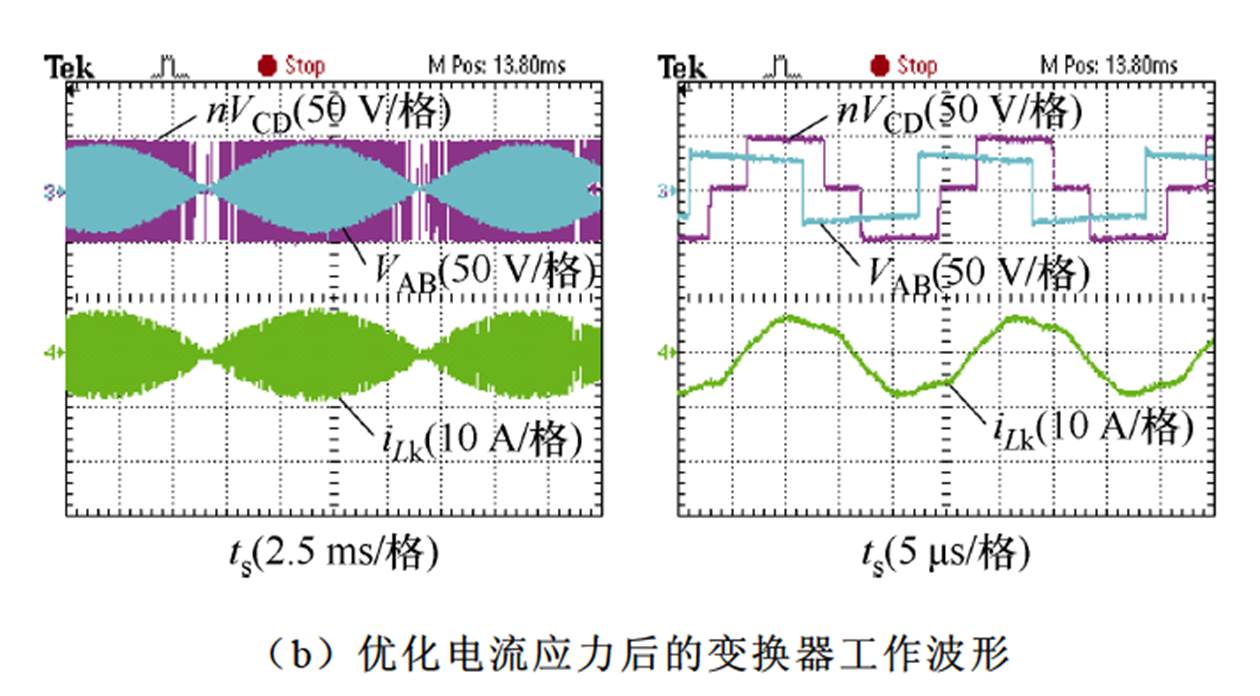
图16 输入电压50 V时变换器电感电流和端口电压波形
Fig.16 Converter inductor current and port voltage waveforms at 50 V input voltage
为进一步验证本文所提控制策略在不同输入电压下的优化情况。如图17所示为输入电压40 V下变换器电流应力优化前后对比波形。从前后对比可以看到，优化前电流应力约为9 A，通过采用本文所提控制策略后，电感电流峰值可降为7.5 A左右。
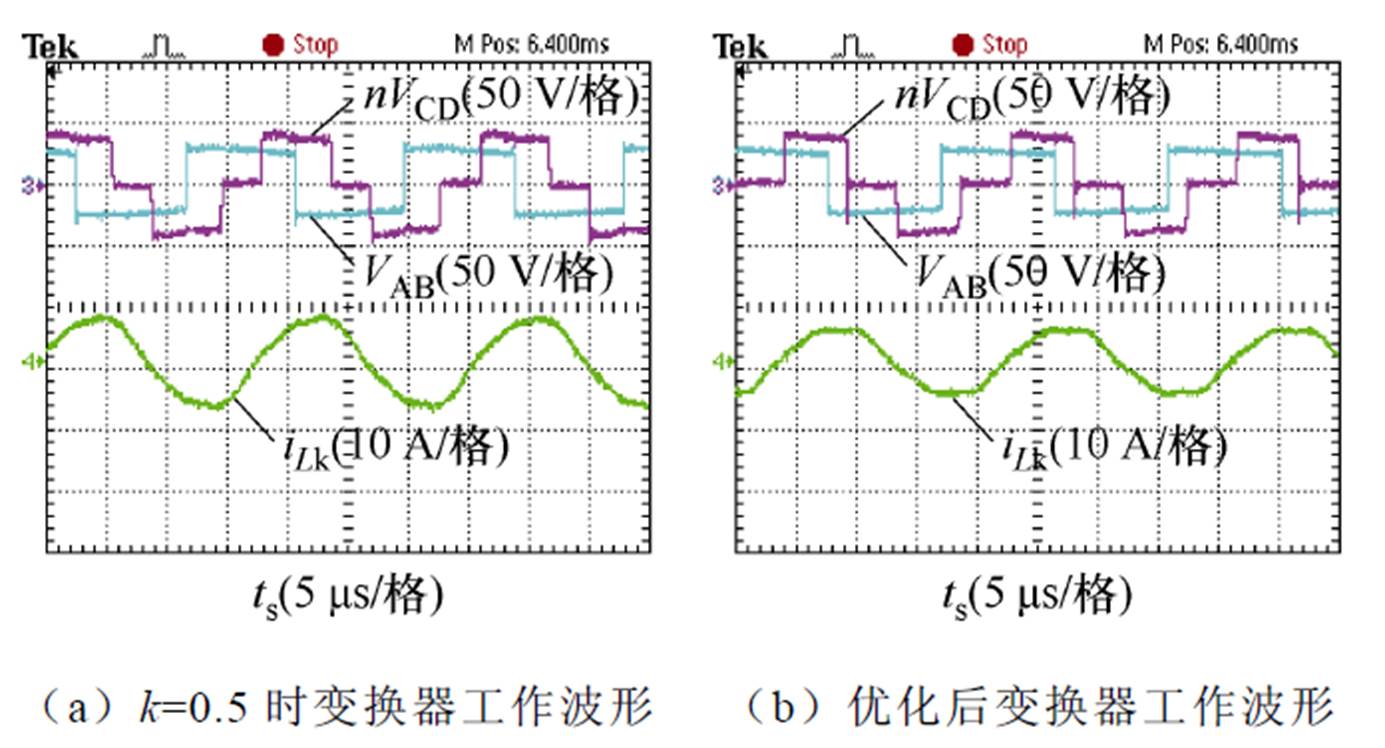
图17 输入电压40 V时变换器电流应力优化前后的工作波形
Fig.17 Operating waveforms of the converter before and after current stress optimization at input voltage 40 V
如图18所示为输入电压30 V下变换器电流应力优化前后对比波形。从前后对比可以看到，优化前电流应力约为7 A，通过采用本文所提控制策略后，电感电流峰值可降为5.4 A左右。
图19展示了交流侧开关管S2在不同工频相位时刻ZVS细节波形，其中图19a和图19b分别为重载和轻载条件下的软开关情况。可以从图中看到，S2几乎实现了全范围ZVS导通。
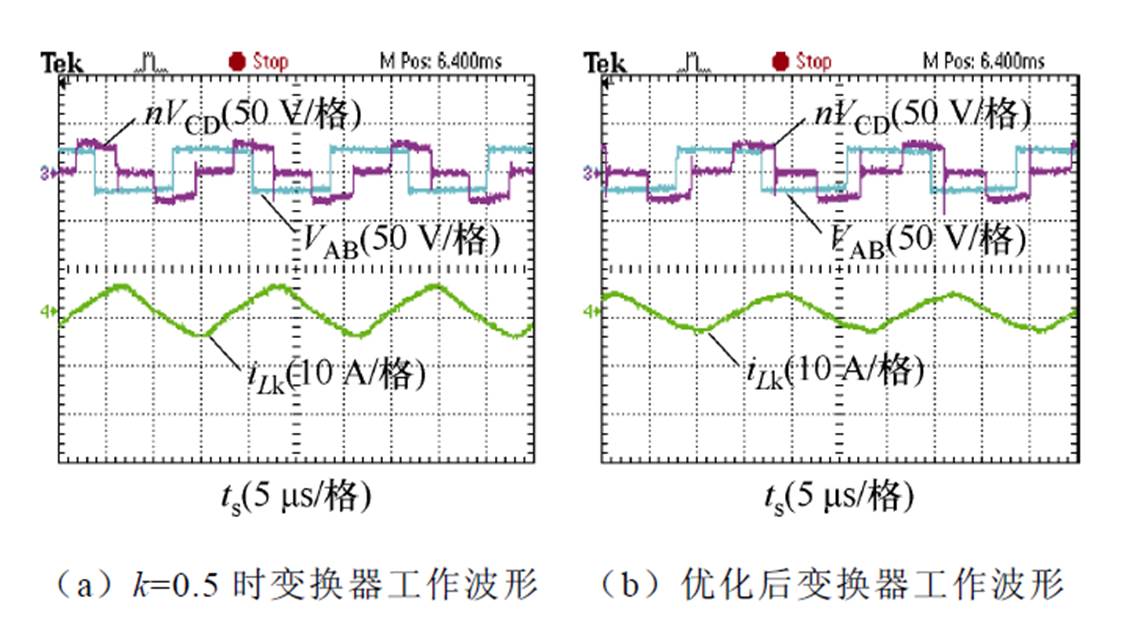
图18 输入电压30 V时变换器电流应力优化前后的工作波形
Fig.18 Operating waveforms of the converter before and after current stress optimization at input voltage 30 V
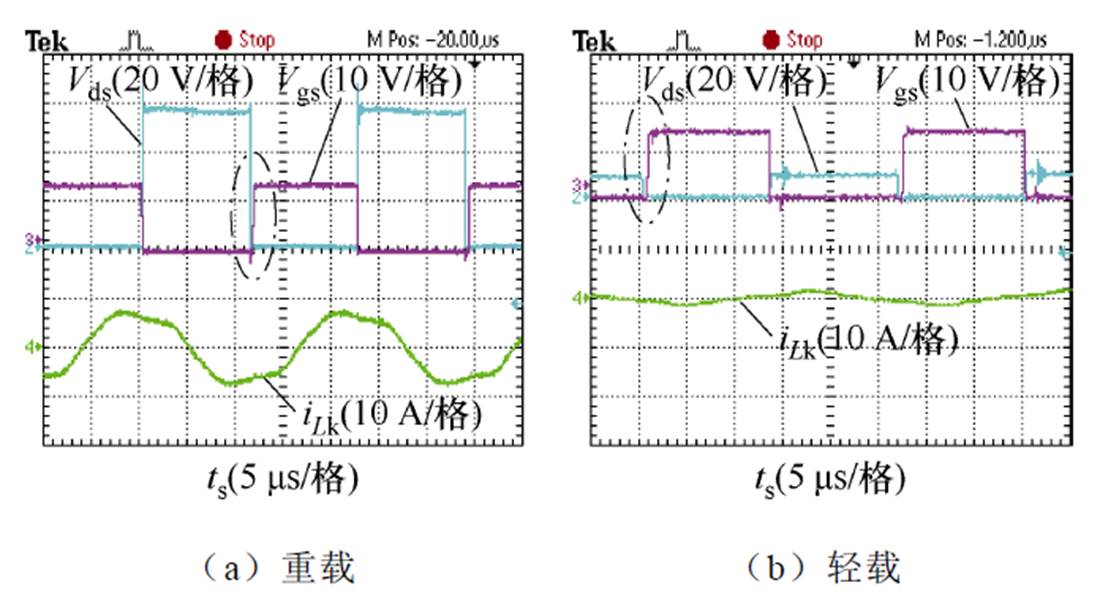
图19 一次侧开关管S2的ZVS波形
Fig.19 ZVS waveforms of the primary switching tube S2
图20展示了直流侧开关管S5在不同工频相位时刻ZVS细节波形，其中图20a和图20b分别为重载和轻载条件下的软开关情况，图20c和图20d为两种极端轻载条件下软开关细节波形的局部放大图。由式（21）在表2参数下可以求得直流开关管S5实现软开关时的最小电感电流为0.06 A。在图20c的条件下，电感电流大于0.06 A，变换器开关管S5实现ZVS导通。在图20d条件下，电感电流低于0.06 A，变换器开关管S5未实现ZVS导通。
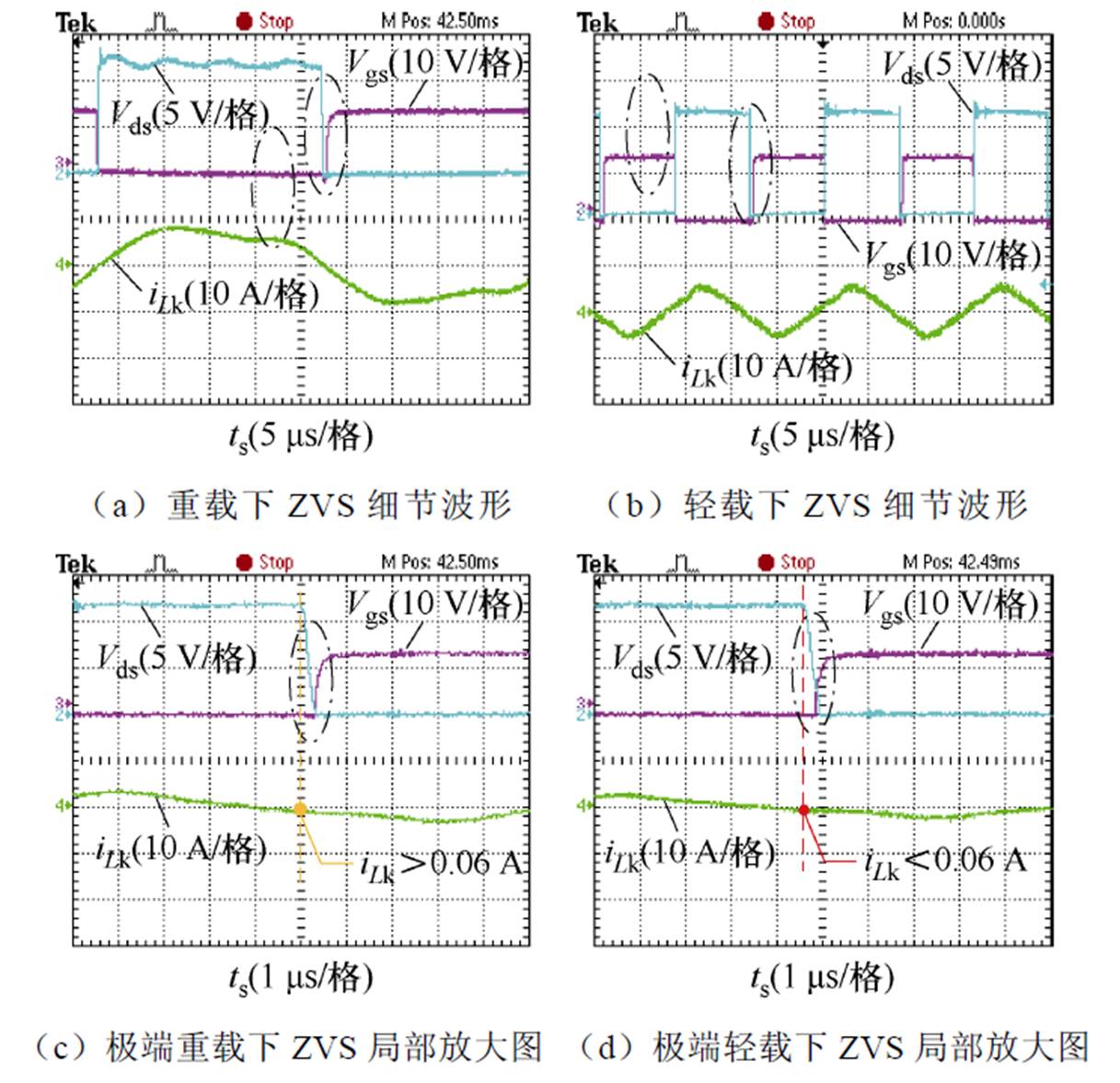
图20 二次侧开关管S5的ZVS波形
Fig.20 ZVS waveforms of the secondary side switching tube S5
图21展示了直流侧开关管S8在不同工频相位时刻ZVS细节波形，其中图21a和图21b分别为重载和轻载条件下的软开关情况。可以从图中看到，在重载和轻载条件下S8均实现了ZVS导通，几乎实现了全范围ZVS导通。
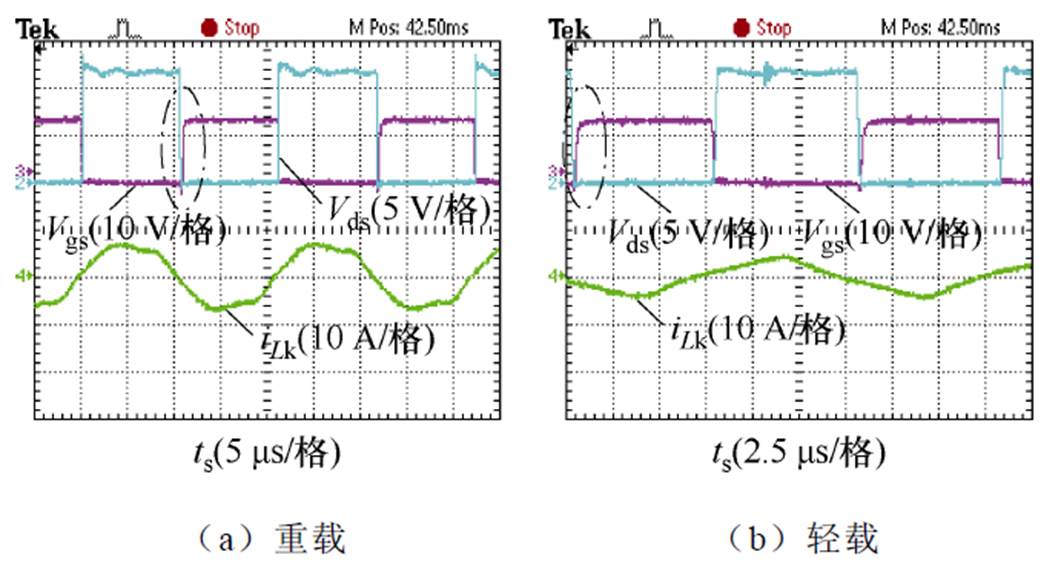
图21 二次侧开关管S8的ZVS波形
Fig.21 ZVS waveforms of the secondary side switching tube S8
图22展示了变换器在输入电压50 V，输出最大功率100 W下优化前后不同负载率效率对比。优化前在移相指数k=0.5时，变换器最高效率约为91.6%，而采用本文所提控制策略后，变换器效率最高可达93.8%，变换器整体效率越提升了约2%。
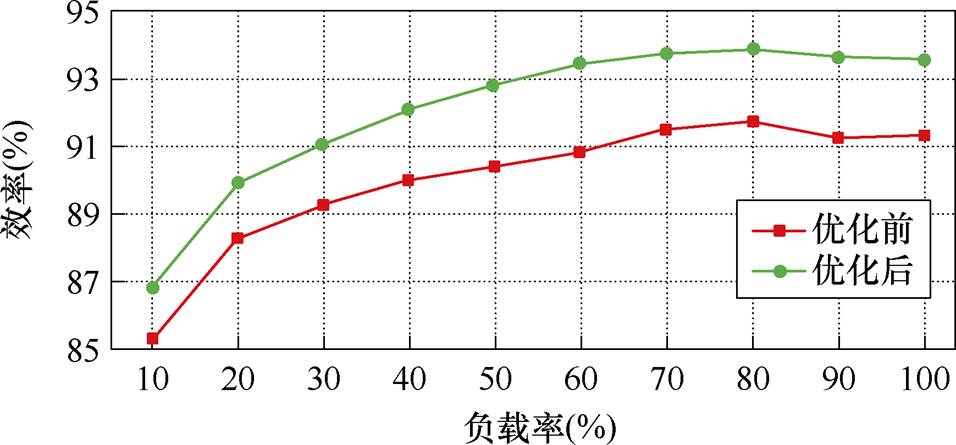
图22 变换器在不同负载下优化前后效率对比
Fig.22 Comparison of converter efficiency before and after optimization at different loads
本文针对单级式双有源桥AC-DC变换器调制非线性和电流应力较大的问题，提出了一种基于线性化的变换器最小电流应力控制策略。该控制策略可以将输入电流的非线性函数线性化，降低变换器的控制复杂度；在此基础上，通过优化移相指数，在有效降低变换器电流应力的同时保证开关管具有较宽零电压开通范围；并且移相比和开关频率以解析形式获得。最后，通过仿真和实验对本文所提控制策略进行验证，证明了该控制策略的可行性。
参考文献
[1] 高锋阳, 宋志翔, 高建宁, 等. 计及光伏和储能接入的牵引供电系统能量管理策略[J]. 电工技术学报, 2024, 39(3): 745-757.
Gao Fengyang, Song Zhixiang, Gao Jianning, et al. Energy management strategies for traction power systems with PV and energy storage access[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 745-757.
[2] 许梦阳, 郑蓬, 贺春. GW级储能电站能量管理系统关键技术试验研究[J]. 电气技术, 2023, 24(7): 56-63.
Xu Mengyang, Zheng Peng, He Chun. Experimental research on key technologies for energy management system of gigawatt-scale energy storage power station[J]. Electrical Engineering, 2023, 24(7): 56- 63.
[3] 武昭原, 刘婧宇, 周明, 等. 分散决策下分布式光伏储能系统外部性价值量化评估[J]. 电力系统自动化, 2024, 48(5): 38-47.
Wu Zhaoyuan, Liu Jingyu, Zhou Ming, et al. Quantitative evaluation of externality value for distributed photovoltaic energy storage system under decentralized decision-making[J]. Automation of Electric Power Systems, 2024, 48(5): 38-47.
[4] 康薇, 肖飞, 任强, 等. 双有源桥DC-DC变换器三移相调制及其死区效应分析和补偿[J]. 电工技术学报, 2024, 39(6): 1907-1922.
Kang Wei, Xiao Fei, Ren Qiang, et al. Three-phase- shift modulation and its dead band effect analysis and compensation of dual-active-bridge DC-DC con- verter[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1907-1922.
[5] Sun Kai, Wang Xiaosheng, Li Yunwei, et al. Parallel operation of bidirectional interfacing converters in a hybrid AC/DC microgrid under unbalanced grid voltage conditions[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 1872-1884.
[6] Khaligh A, Dusmez S. Comprehensive topological analysis of conductive and inductive charging solutions for plug-in electric vehicles[J]. IEEE Transactions on Vehicular Technology, 2012, 61(8): 3475-3489.
[7] 王要强, 李灏, 李想, 等. 基于双模式变频移相调制的单级式双有源桥型DC-AC变换器[J]. 电工技术学报, 2024, 39(21): 6865-6876.
Wang Yaoqiang, Li Hao, Li Xiang, et al. A single- stage dual active bridge DC-AC converter based on dual mode modulation of variable frequency and phase shift[J]. Transactions of China Electrotechnical Society, 2024, 39(21): 6865-6876.
[8] Gu Yunjie, Li Yitong, Yoo H J, et al. Transfverter: imbuing transformer-like properties in an interlink converter for robust control of a hybrid AC-DC microgrid[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(11): 11332-11341.
[9] 周玮, 蓝嘉豪, 麦瑞坤, 等. 无线充电电动汽车V2G模式下光储直流微电网能量管理策略[J]. 电工技术学报, 2022, 37(1): 82-91.
Zhou Wei, Lan Jiahao, Mai Ruikun, et al. Research on power management strategy of DC microgrid with photovoltaic, energy storage and EV-wireless power transfer in V2G mode[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 82-91.
[10] Su Mei, Wang Hui, Sun Yao, et al. AC/DC matrix converter with an optimized modulation strategy for V2G applications[J]. IEEE Transactions on Power Electronics, 2013, 28(12): 5736-5745.
[11] Khaligh A, D’Antonio M. Global trends in high- power on-board chargers for electric vehicles[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3306-3324.
[12] 梅杨, 黄伟超, 刘子毓. 矩阵式隔离型双向AC-DC变换器控制策略[J]. 电工技术学报, 2019, 34(12): 2499-2506.
Mei Yang, Huang Weichao, Liu Ziyu. Bidirectional and isolated AC-DC converter based on reduced matrix converter[J]. Transactions of China Electro- technical Society, 2019, 34(12): 2499-2506.
[13] 顾玲. 单级高频隔离型三相双向AC/DC变换器研究综述[J]. 中国电机工程学报, 2021, 41(21): 7434- 7449.
Gu Ling. A review of single-stage high-frequency- isolated three-phase bidirectional AC/DC converter[J]. Proceedings of the CSEE, 2021, 41(21): 7434-7449.
[14] 姜龙飞, 张展望. 一种全桥双谐振CLL谐振变换器的分析与设计[J]. 电源学报, 2017, 15(1): 92-98.
Jiang Longfei, Zhang Zhanwang. Analysis and design of a full-bridge CLL resonant converter with double resonant tanks[J]. Journal of Power Supply, 2017, 15(1): 92-98.
[15] 管乐诗, 温兆亮, 许晓志, 等. 适用于宽增益范围的可重构单级DC-DC变换器及其磁元件设计[J]. 电工技术学报, 2023, 38(6): 1571-1583.
Guan Yueshi, Wen Zhaoliang, Xu Xiaozhi, et al. A modular reconfigurable single-stage DC-DC converter suitable for wide gain range and its magnetic design[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1571-1583.
[16] Jung J H, Kim H S, Ryu M H, et al. Design metho- dology of bidirectional CLLC resonant converter for high-frequency isolation of DC distribution systems[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1741-1755.
[17] 王章毅, 陆道荣, 李想, 等. 基于移相和调频的单级双向AC-DC变换器临界电流调制策略[J]. 电工技术学报, 2023, 38(14): 3888-3897.
Wang Zhangyi, Lu Daorong, Li Xiang, et al. Boundary current modulation strategy of single-stage bidirectional AC-DC converter based on phase-shift and variable-frequency control[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3888- 3897.
[18] Zhao Biao, Song Qiang, Liu Wenhua, et al. Overview of dual-active-bridge isolated bidirectional DC-DC converter for high-frequency-link power-conversion system[J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4091-4106.
[19] 周兵凯, 杨晓峰, 张智, 等. 能量路由器中双有源桥直流变换器多目标优化控制策略[J]. 电工技术学报, 2020, 35(14): 3030-3040.
Zhou Bingkai, Yang Xiaofeng, Zhang Zhi, et al. Multi-objective optimization control strategy of dual- active-bridge DC-DC converter in electric energy router application[J]. Transactions of China Electro- technical Society, 2020, 35(14): 3030-3040.
[20] 张勋, 王广柱, 王婷. 双向全桥DC-DC变换器基于电感电流应力的双重移相优化控制[J]. 电工技术学报, 2016, 31(22): 100-106.
Zhang Xun, Wang Guangzhu, Wang Ting. Optimized control based on current-stress of bi-directional full-bridge DC-DC converters with dual-phase- shifting control[J]. Transactions of China Electro- technical Society, 2016, 31(22): 100-106.
[21] Hou Nie, Song Wensheng, Wu Mingyi. Minimum- current-stress scheme of dual active bridge DC-DC converter with unified phase-shift control[J]. IEEE Transactions on Power Electronics, 2016, 31(12): 8552-8561.
[22] Huang Jun, Wang Yue, Li Zhuoqiang, et al. Unified triple-phase-shift control to minimize current stress and achieve full soft-switching of isolated bidi- rectional DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4169-4179.
[23] 宋文胜, 侯聂, 武明义, 等. 双向全桥隔离DC/DC变换器最小峰值电流及其虚拟功率控制方法[J]. 中国电机工程学报, 2016, 36(18): 4990-4998, 5124.
Song Wensheng, Hou Nie, Wu Mingyi, et al. A current stress minimization strategy of dual-active- bridge DC/DC converters with virtual power control method[J]. Proceedings of the CSEE, 2016, 36(18): 4990-4998, 5124.
[24] Sha Deshang, Wang Sunbo. A single-stage natural power factor corrector based on dual active bridge DC-DC converter without inner current tracking loop[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 342-352.
[25] Ma Peisong, Sha Deshang, Song Keling. A single- stage semi dual-active-bridge AC-DC converter with seamless mode transition and wide soft-switching range[J]. IEEE Transactions on Industrial Electronics, 2023, 70(2): 1387-1397.
[26] Kwon O, Kim K S, Kwon B H. Highly efficient single-stage DAB microinverter using a novel modulation strategy to minimize reactive power[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(1): 544-552.
[27] Guo Dongxin, Wang Panbao, Ren Chunguang, et al. Linearized minimum current stress modulation scheme of single-phase bidirectional DAB AC-DC con- verters[J]. IEEE Transactions on Industrial Electro- nics, 2023, 70(12): 12410-12420.
Abstract In distributed power supply and distributed energy storage technologies, a bidirectional AC-DC converter is an important energy conversion device connecting AC-DC hybrid microgrids, and its performance index directly affects the overall performance and effect of hybrid microgrids. Compared with the two-stage topology, the single-stage dual active bridge (DAB) AC-DC converter removes the intermediate DC bus capacitance with a large capacitance value, reduces the conversion link, and has apparent power density and cost advantages. The traditional DAB AC-DC converter mainly adopts the modulation strategy of phase shift, which has the problems of high current stress and narrow soft-switching range. In addition, only adopting the phase shift control leads to the nonlinear relationship between the system input current and the shift ratio, increasing the control complexity. Therefore, this paper proposes a linearization-based minimum current stress control strategy for the converter to address the problems of modulation nonlinearity and high current stress in a single-stage dual active bridge AC-DC converter. This control strategy reduces the converter’s control complexity and current stress, ensuring a wide zero voltage switch (ZVS) range of the switching tubes.
Firstly, the switching characteristics of the extended phase-shift (EPS) modulation strategy are analyzed. For the nonlinearity between the input current and the shift ratio, the input current iac and the shift ratio D1 are linearly related by introducing the phase shift index k and the maximum switching frequency fsmax. The expressions of the shift ratio D1 and the switching frequency fs are obtained combined with power factor correction. The switching characteristics of the EPS modulation strategy are analyzed. The trajectory of the phase-shift index k under the minimum current stress is obtained by the differential polarity method. Then, the expression of the shift ratio D2 is obtained. Finally, the soft-switching ranges are analyzed for switch tubes S2, S5, and S8. Except for the DC-side switch tube S5, which is difficult to realize soft-switching in the small range under extreme light-load conditions, the other two switch tubes can realize ZVS in the wide range in other cases.
This paper verifies the proposed control strategy by combining simulation and experiment. Firstly, regarding simulations, the proposed control strategy can achieve the linearization between the input current and the shift ratio, effectively reducing the converter current stress. An experimental prototype is constructed with an AC 50 V input, DC 12 V output, and 100 W output power. The current stress is compared before and after optimization under different input voltages and the soft-switching realization under different load conditions. The control strategy effectively reduces the current stress of the converter while ensuring that the switching tubes have a wide ZVS turn-on range.
keywords：AC-DC converter, extended phase shift, linearization, minimum current stress, zero voltage switching
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.240825
国家自然科学基金项目（52307227）、中央引导地方科技发展资金项目（2022ZY0134）、国家资助博士后研究人员计划项目（GZB20230667）和河南省科协青年人才托举工程项目（2024HYTP020）资助。
收稿日期 2024-05-21
改稿日期2024-07-04
王要强 男，1982年生，博士，教授，博士生导师，研究方向为新能源与电力储能、电力系统运行与规划、综合能源分析与优化等方面。
E-mail: WangyqEE@163.com
李 想 男，1991年生，博士，讲师，主要研究方向为高频软开关变换器、谐振变换器、单级式AC-DC变换器拓扑及控制策略等。
E-mail: lixiang91zzu@zzu.edu.cn（通信作者）
（编辑 陈 诚）