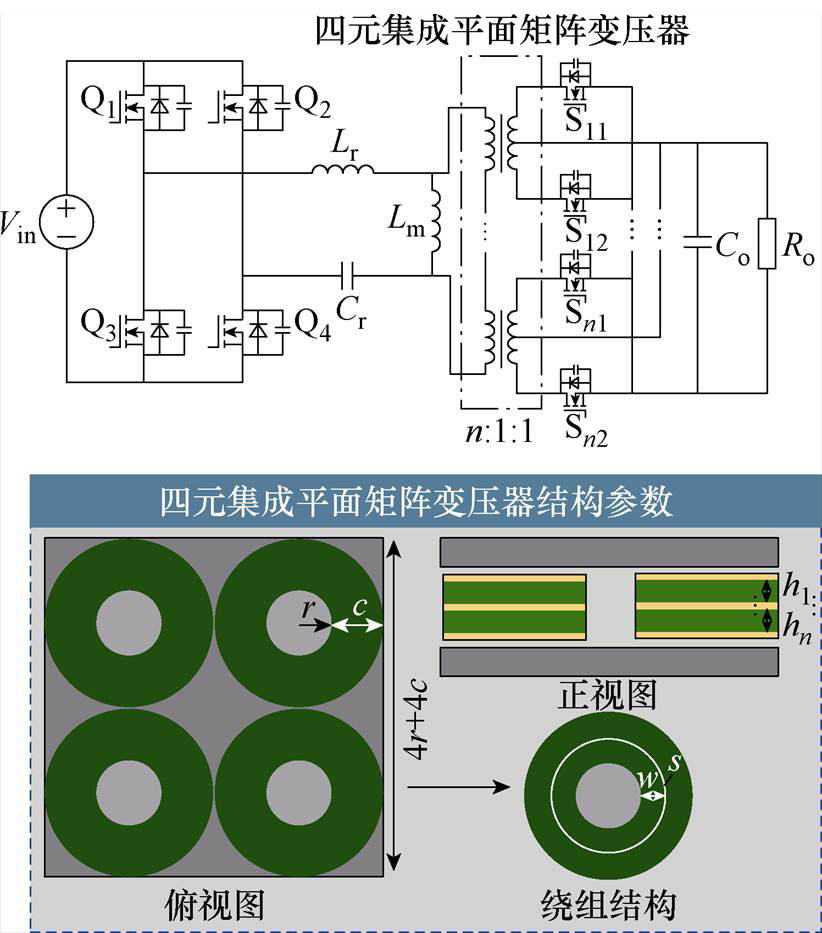
图1 全桥四路矩阵变压器LLC与变压器结构参数
Fig.1 Full bridge four-element-matrix transformer LLC and transformer structural parameters
摘要 LLC变换器因其出色的软开关性能与低输出阻抗被广泛地应用于电池储能变换器的功率级。在低压大电流工况下,LLC二次侧多采用矩阵变压器降低电流应力。在实际电路中,矩阵变压器体积占整个主功率部分25%左右,严重制约了装置功率密度的提高。且传统分立绕线式矩阵变压器寄生参数不可控,导致LLC输出电压跌落及开关尖峰,降低了装置可靠性。该文提出一种考虑损耗与寄生参数的LLC四元平面矩阵变压器集成优化设计方法。首先,基于四元集成磁心磁通分布特性提出分布式磁心损耗计算方法,建立变压器精确损耗模型。其次,通过建立变压器寄生电感和寄生电容求解模型,确定变压器结构参数与寄生参数的映射关系,实现了变压器损耗、寄生电感、寄生电容流程化解耦设计,在保证变压器高效运行前提下寄生参数可控。最后,通过有限元仿真验证并搭建了两台250 W/3.3 V/48 V储能变换器实验样机。所提方法样机在84 A输出电流下,LLC效率为95%,集成矩阵变压器一、二次侧漏感降低为原先的30%,寄生电容被有效抑制,运行性能得到进一步提升。
关键词:LLC 四元矩阵变压器 磁集成 寄生参数
随着能源需求不断增长,环境保护意识不断提高,新能源的开发和利用方兴未艾。分布式发电系统作为未来智能电网建设的重要组成部分,具有效率高、污染小、可靠性高、安装位置灵活等优点。作为分布式可再生能源接入电网的有效手段,微电网是一种小型发配电系统,其主要组成部分有分布式发电电源、储能系统等[1-2]。LLC变换器由于出色的软开关性能及较低的输出阻抗,被广泛应用于储能变换器的功率级。当LLC连接并联型储能电池组时,由于电池组输出电压低,为3.3 V左右,因此相同功率下输出电流较大。LLC采用四元平面矩阵变压器(简称LLC矩阵变压器)可有效降低二次电流应力,提高装置整体效率。然而,多路矩阵变压器占地面积大,传统的分立绕线式变压器寄生参数不可控,降低了装置可靠性。因此,研究考虑寄生参数的LLC平面化集成方法,有利于提高LLC功率密度及运行可靠性。
近年来,为解决多路矩阵变压器损耗与寄生参数不可控问题,国内外学者对LLC矩阵变压器设计与集成优化方面做了大量研究。
在LLC矩阵变压器集成方面,文献[3-7]提出了不同构型的LLC矩阵变压器集成方案。文献[3]研究了单列式集成方案,将矩阵变压器交错单列排布,实现相邻变压器之间的磁抵消。文献[4]研究了垂直集成方案,将两个矩阵变压器垂直反向堆叠,将中心公共磁柱部分磁通量抵消,但该架构垂直高度过大,且仅限两个矩阵变压器集成。文献[5-7]提出了四元矩阵变压器交错集成方法,通过磁通抵消减小集成后变压器体积。该方法可有效利用四元矩阵变压器集成空间,但兼顾损耗与寄生参数的集成设计方案有待研究。
在LLC矩阵变压器设计方面,文献[8-13]对变压器损耗或寄生参数进行建模并寻找最优设计点。其中,文献[8]基于斯坦梅茨公式建立了LLC平面变压器损耗模型,以此实现变压器效率最优设计。但该损耗计算方法应用于四元集成平面矩阵变压器时,由于磁板磁通密度分布不均匀,导致该方法计算精度低。文献[9-10]建立并拓展了LLC平面变压器漏感模型,将高频工作时的绕组趋肤效应纳入考量范围,实现了较为精确的变压器漏电感计算。文献[11-12]基于变压器绕组间电场能量,建立了变压器寄生电容模型。文献[13]分别给出了变压器损耗、漏感、寄生电感的计算方法并分析了寄生参数对于变压器性能的影响。
综上所述,以上方法仅对变压器效率、体积、寄生电感和寄生电容进行单独建模与优化。尚未有文献将变压器结构参数与性能参数进行解耦优化,在给定多个性能参数下计算变压器结构。鉴于此,本文提出一种考虑寄生参数的LLC端四元集成矩阵变压器优化设计方法。区别于对损耗、体积、寄生参数的独立建模分析,该方法将变压器各个结构参数对性能参数的影响解耦,通过所提流程化设计实现了平面化集成矩阵变压器寄生参数可控。
本文首先根据所提的分布式磁心损耗方法建立变压器精确损耗模型。其次对变压器的漏感和寄生电容建模并寻优,将变压器各个结构参数对寄生参数的影响解耦。再次通过有限元仿真进行建模与验证。最后搭建了一台250 W/3.3 V/48 V储能变换器实验样机。经验证,变压器漏电感降低为原来的30%,寄生电容所引起的二次侧开关振荡明显降低。装置功率密度为1.338 W/cm3。LLC效率为95%。
含矩阵变压器的全桥LLC拓扑及其变压器结构参数如图1所示。图中,r为磁心中柱半径,c为绕组总宽度,h1、h2、…、hn为绕组间垂直距离,w为单匝绕组宽度,s为绕组间水平距离。本文提出一种考虑寄生参数的LLC四元集成矩阵变压器平面化集成方法,如图2所示。该方法关键步骤包括:①根据变压器损耗模型选择关键结构参数r、c设计点;②基于变压器漏磁场能量建立漏感模型,确定漏感关联结构参数;③通过印制电路板(Printed Circuit Board, PCB)厚度约束判断漏感集成的可行性并设计漏感值;④基于绕组电场能量建寄生电容模型,在漏感关联参数约束下,迭代设计寄生电容关联结构参数并满足寄生电容要求。该方法实现了效率关联结构参数、漏感关联结构参数与寄生电容关联结构参数的流程化解耦设计。

图1 全桥四路矩阵变压器LLC与变压器结构参数
Fig.1 Full bridge four-element-matrix transformer LLC and transformer structural parameters

图2 一种考虑损耗与寄生参数的LLC四元矩阵平面变压器集成优化设计
Fig.2 Integrated optimization design of LLC four-element matrix planar transformer considering loss and parasitic parameters
所提方法优化结果判定的基本逻辑为基于选定参数收缩可行域:①优先选定一组效率体积组合后,可得到绕组宽度c和磁心中柱半径r的值,而c则作为与寄生电感相关的一组约束,即3w+3s=c;②选定所需寄生电感值,即可得到h1+h3之和;而h1+h3之和作为寄生电容相关的一组约束。
含矩阵变压器的全桥LLC拓扑及其变压器结构参数如图1所示。本文以一组应用于并联电池包后级混合型Sigma变换器为例。其功率级为全桥四路矩阵变压器LLC,应用所提方法对其矩阵变压器进行平面化集成设计。LLC参数见表1。
表1 LLC参数
Tab.1 LLC parameters
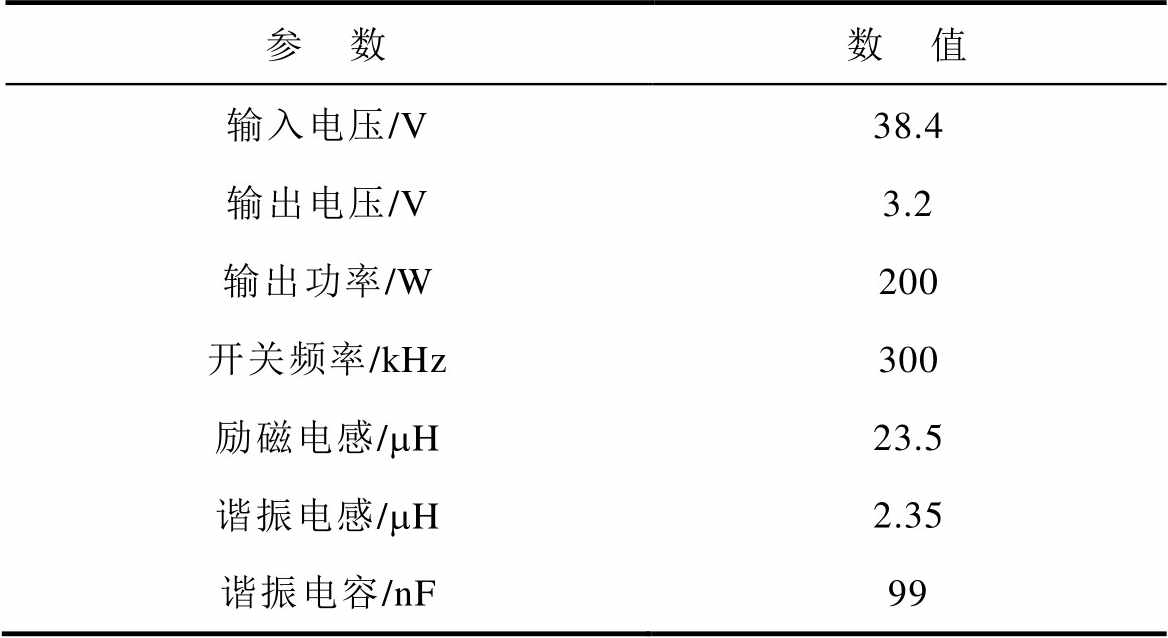
参 数数 值 输入电压/V38.4 输出电压/V3.2 输出功率/W200 开关频率/kHz300 励磁电感/mH23.5 谐振电感/mH2.35 谐振电容/nF99
集成四元矩阵变压器磁通密度分布如图3所示,变压器损耗由磁心损耗与绕组损耗两部分构成。传统的磁心损耗计算方法采用斯坦梅茨公式,首先计算磁心中柱最大磁通密度Bmax。
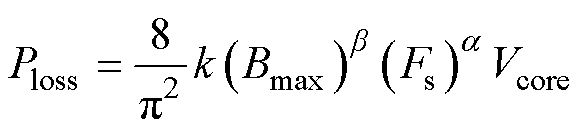 (1)
(1)
式中,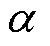 、
、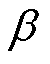 、k由磁心手册给出;Fs为变压器工作频率;Vcore为磁心体积。
、k由磁心手册给出;Fs为变压器工作频率;Vcore为磁心体积。
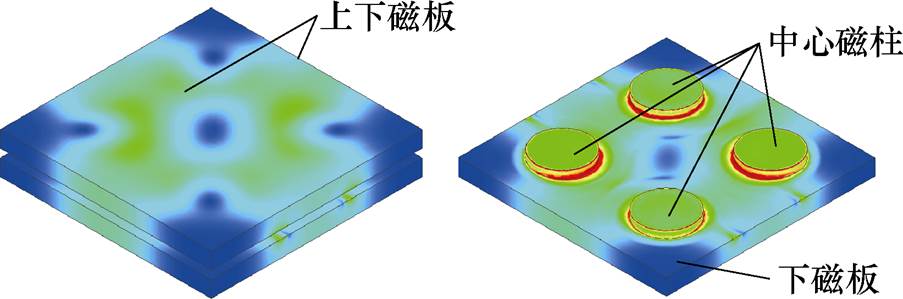
图3 集成四元矩阵变压器磁通密度分布
Fig.3 Integrated four-element-matrix transformer magnetic flux density distribution
式(1)利用磁心中柱磁通密度代替全局磁通密度,对于U型或E型等磁通密度分布均匀的磁心求解磁心损耗比较精确。但对于四元集成矩阵变压器,根据有限元仿真结果显示,变压器中柱与上、下磁板磁通密度分布不均,且磁板局部磁通密度分布也不均匀,采用斯坦梅茨公式准确度低。
本节提出一种基于单位体积损耗-磁通密度(P-B)曲线的平面变压器分布式磁心损耗计算方法,其流程如图4所示。首先,建立四元矩阵变压器的磁阻模型,利用叠加定理求解磁通分布。其次,根据磁通量,将磁心分为上、下磁板和中心磁柱三部分,这一步消除了磁心磁通密度的整体不均匀性。再次,将各部分划分为主磁路区和非磁通量区,并计算出磁通密度,这一步消除了磁心磁通密度的部分不均匀性。最后,利用P-B曲线计算磁心损耗。
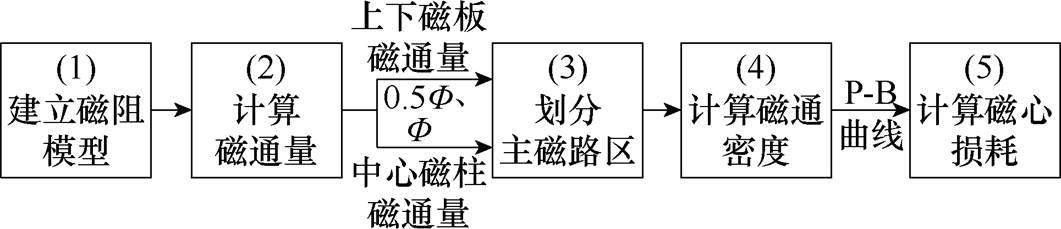
图4 基于P-B曲线的平面变压器分布式磁心损耗计算方法流程
Fig.4 Flowchart for the core loss calculation method based on the P-B curve
图5为四元矩阵变压器的简化磁阻模型。每根磁柱缠绕总匝数的1/4,每根产生0.25NIm_d磁动势,其中,N为一次侧匝数;Im_d为一次侧励磁电流峰值;各中心磁柱的气隙磁阻为Rg,忽略磁心磁阻。
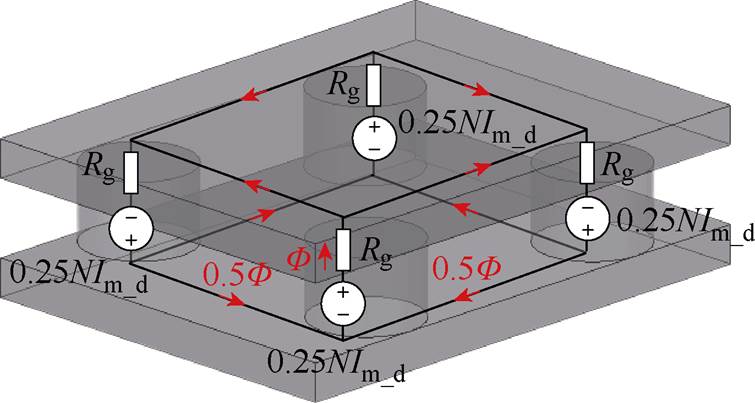
图5 集成四元矩阵变压器磁路模型
Fig.5 Simplified reluctance model of four-element matrix transformer core
中间柱磁通量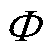 由中间柱本身产生的磁通量
由中间柱本身产生的磁通量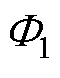 与相邻两个中间柱产生的磁通量
与相邻两个中间柱产生的磁通量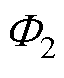 叠加形成。根据叠加定理,有
叠加形成。根据叠加定理,有
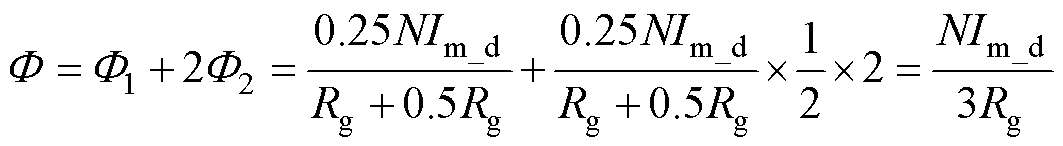 (2)
(2)
为了克服斯坦梅茨公式的不足,将磁心分为上板、中柱、下板三部分,磁心三部分结构示意图如图6所示,中间磁柱的磁通量为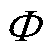 ,上、下磁板的主磁通量为0.5
,上、下磁板的主磁通量为0.5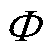 。
。
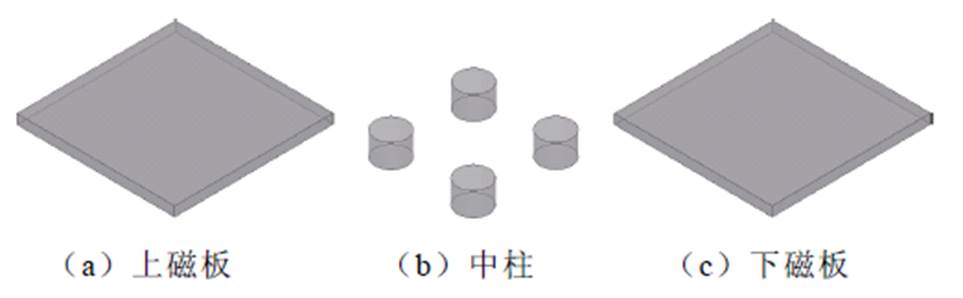
图6 磁心三部分结构示意图
Fig.6 Simplified reluctance model of four-element matrix transformer core
上、下磁板的分析需要确定磁板的主磁路面积,首先定义磁心尺寸关键参数,绕组结构示意图如图7所示。
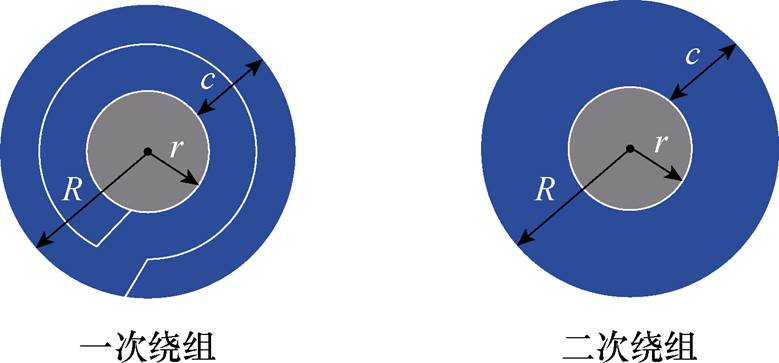
图7 绕组结构示意图
Fig.7 Schematic diagram of winding structure
结合图3中磁通密度分布,上、下磁板主磁路定义如图8a红色部分所示,其中上、下磁板主磁路宽度为c+2r。中心的低磁通密度区域可视为一个正方形,其边长为2c。磁心边缘上的低磁通密度区域的边长为c,磁板的边长为4c+4r,磁板的厚度为h1。
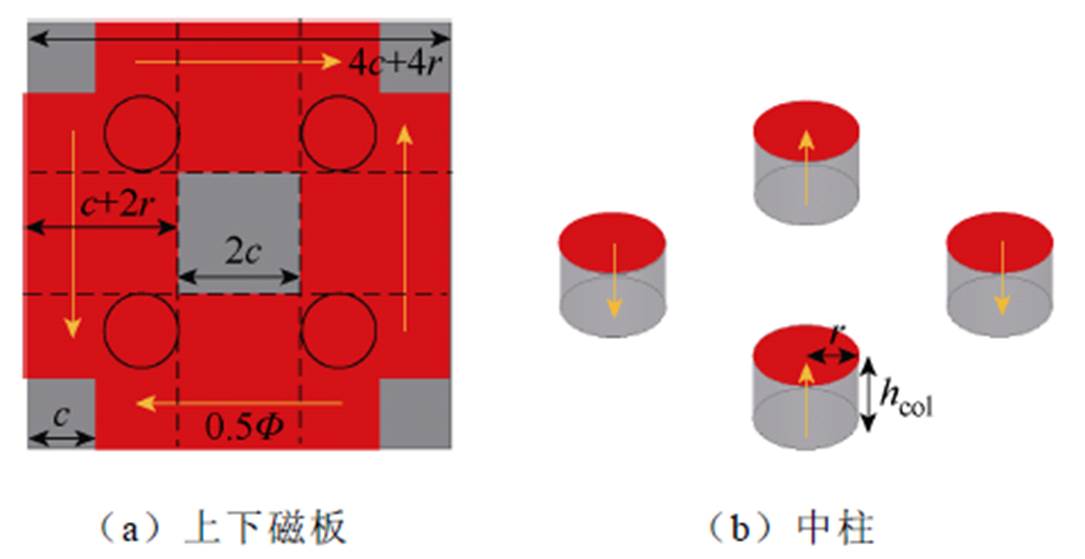
图8 主磁路划分
Fig.8 Main magnetic circuit division
上磁板主磁路的磁通密度Bup与主磁路对应的磁心体积Vup分别为
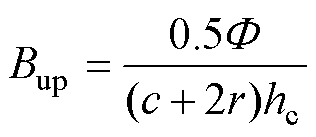 (3)
(3)
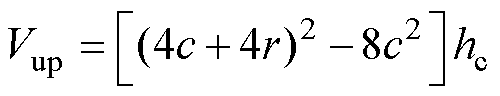 (4)
(4)
式中,hc为上、下磁板厚度。同样地,中心磁柱的磁通密度与上述分析相似。忽略边缘效应,中心磁柱横截面上的磁通密度是均匀的。如图8b所示,中心磁柱的横截面半径为r,高度为hcol。中心磁柱主磁路的磁通密度Bcol与主磁路对应的磁心体积Vcol分别为
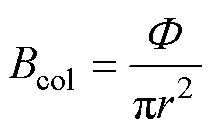 (5)
(5)
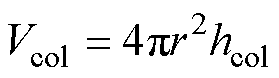 (6)
(6)
结合式(3)~式(6),参照磁心手册的P-B曲线,可得到磁通密度B与单位体积磁心损耗Pv的关系为
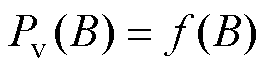 (7)
(7)
上、下磁板铁心损耗Pup为
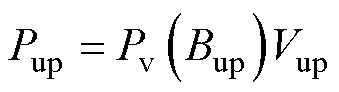 (8)
(8)
中心磁柱铁心损耗Pcol为
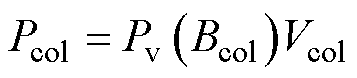 (9)
(9)
整体磁心损耗Ploss为
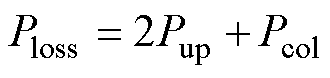 (10)
(10)
式中,Vup、Vcol分别为上磁板和中柱体积。
变压器绕组损耗计算采用一维DOWELL模型,在此不再展开。
在表1参数下,建立的变压器磁心损耗模型如图9a所示,变压器绕组损耗模型如图9b所示。变压器总损耗模型如图10a所示,图10b给出了不同r和c组合下,总损耗与占地面积的交点。根据变压器电流有效值及PCB耐流可计算变压器绕组最小铜宽cmin。选定c=7 mm。根据图3b可获得三个设计点,分别为P1、P2、P3。P1处变压器损耗和占地面积都较小,因此,选择P1点优化效果最好,此时r=5 mm。
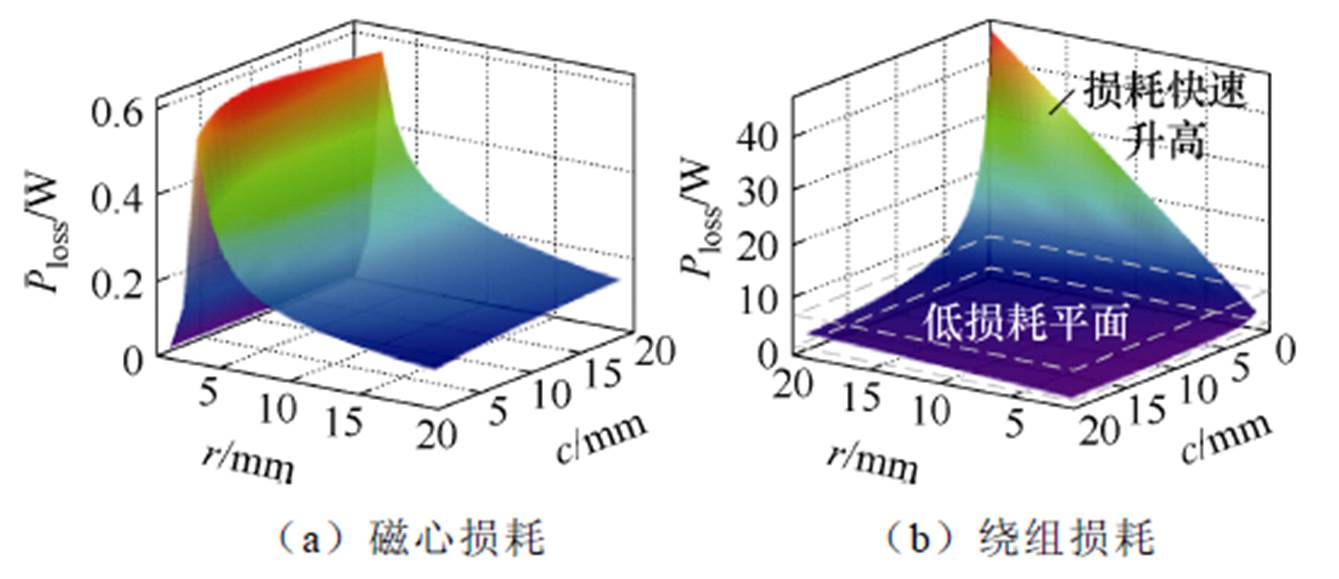
图9 四元集成矩阵变压器损耗模型
Fig.9 Integrated four-element-matrix transformer loss model
选定r、c后就确定了变压器基本参数,见表2,也确定了变压器占地面积与损耗。首先完成了四元集成矩阵变压器的初步设计,然后对变压器寄生参数进行建模与控制。
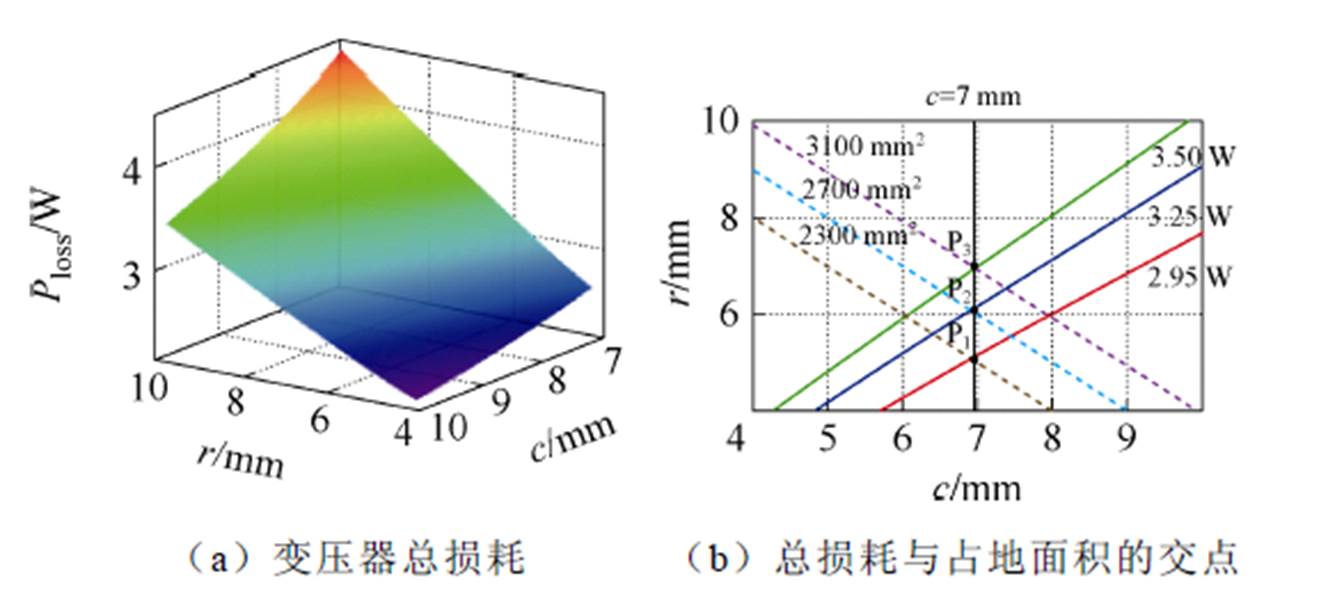
图10 四元集成矩阵变压器设计点选取
Fig.10 Integrated four-element-matrix transformer loss model
表2 变压器参数
Tab.2 Transformer parameters
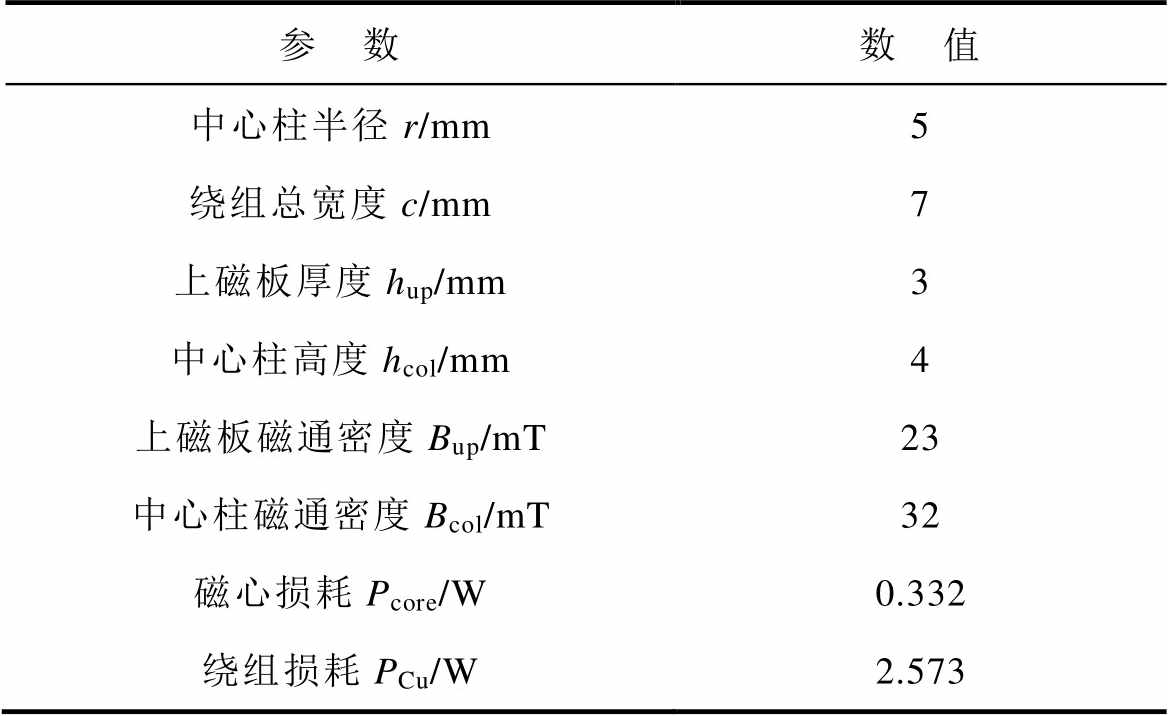
参 数数 值 中心柱半径r/mm5 绕组总宽度c/mm7 上磁板厚度hup/mm3 中心柱高度hcol/mm4 上磁板磁通密度Bup/mT23 中心柱磁通密度Bcol/mT32 磁心损耗Pcore/W0.332 绕组损耗PCu/W2.573
绕组的不同排布对变压器漏感和寄生电容都会造成影响[14-16]。由于平面变压器采用PCB绕组,绕组间垂直距离很小,因此寄生漏电感很小。由于该变压器需要一定的漏感充当谐振电感,因此绕组的排布需要绕组产生足够的漏感。图11分别给出了S-P-S和P-S-P-S-P绕组结构及其磁动势分布。其中红色为变压器二次绕组,蓝色为变压器一次绕组。变压器一次绕组同一水平方向上为串联,在垂直方向为并联。通过两种结构的磁动势对比,S-P-S绕组结构磁动势整体大于P-S-P-S-P绕组结构磁动势,对产生漏感更为有利,因此选定S-P-S绕组结构作为变压器的绕组排布顺序,以满足谐振电感值要求。
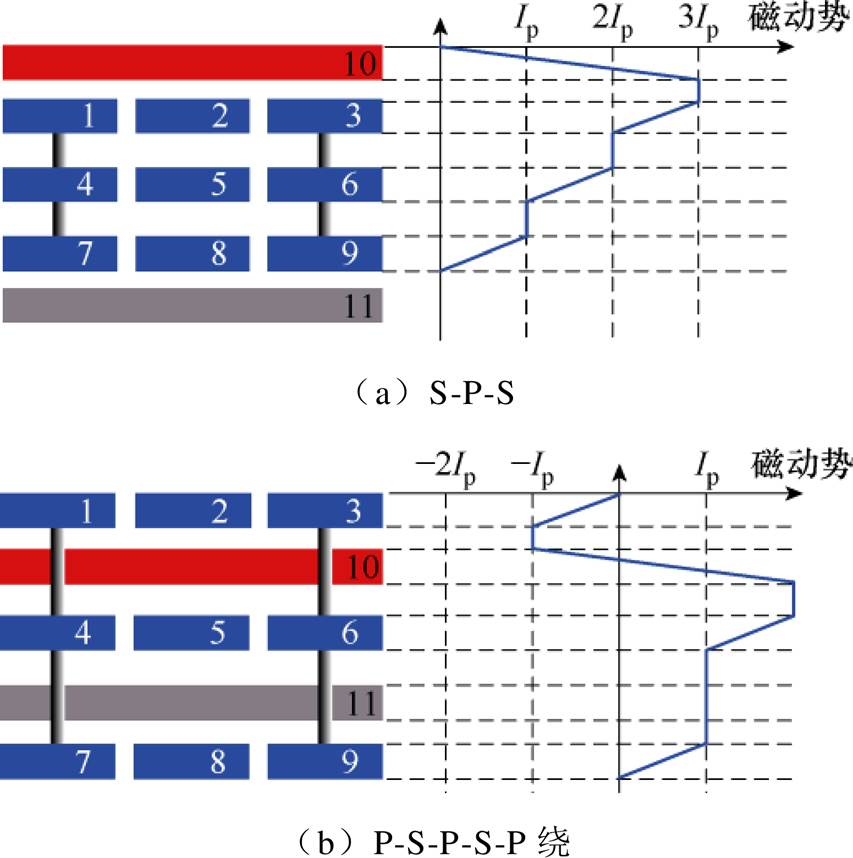
图11 绕组结构及其磁动势分布
Fig.11 Winding structure and its magnetomotive force distribution
图12展示了图11a中3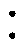 1
1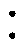 1四元变压器单柱10号绕组绕线布局。
1四元变压器单柱10号绕组绕线布局。
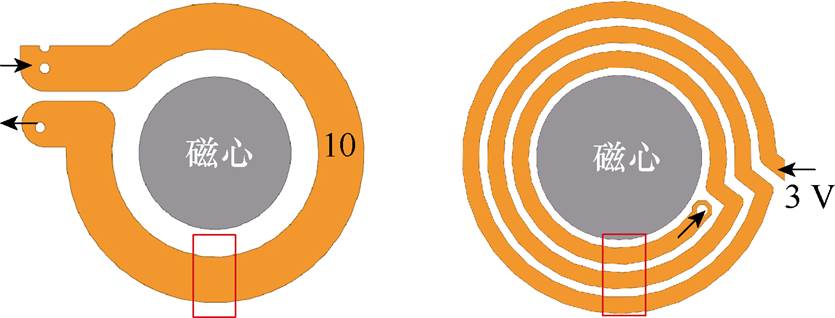
图12 3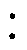 1
1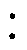 1四元变压器单柱绕线布局
1四元变压器单柱绕线布局
Fig.12 3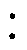 1
1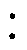 1 four-element-matrix transformer single column winding layout
1 four-element-matrix transformer single column winding layout
以第一个矩阵变压器中心柱为例。由于二次侧采用三层并联,需要在最内层设计通孔,因此二次绕组内径略大于最内层变压器一次绕组外径。
绕组垂直结构如图13a所示,根据Dowell一维模型[17-19],可以将绕组结构简化为图13b。其中,变压器一次侧单匝绕组宽度为w,绕组间距为s,绕组垂直距离如图13所示,分别为h1、h2、h3、h4。
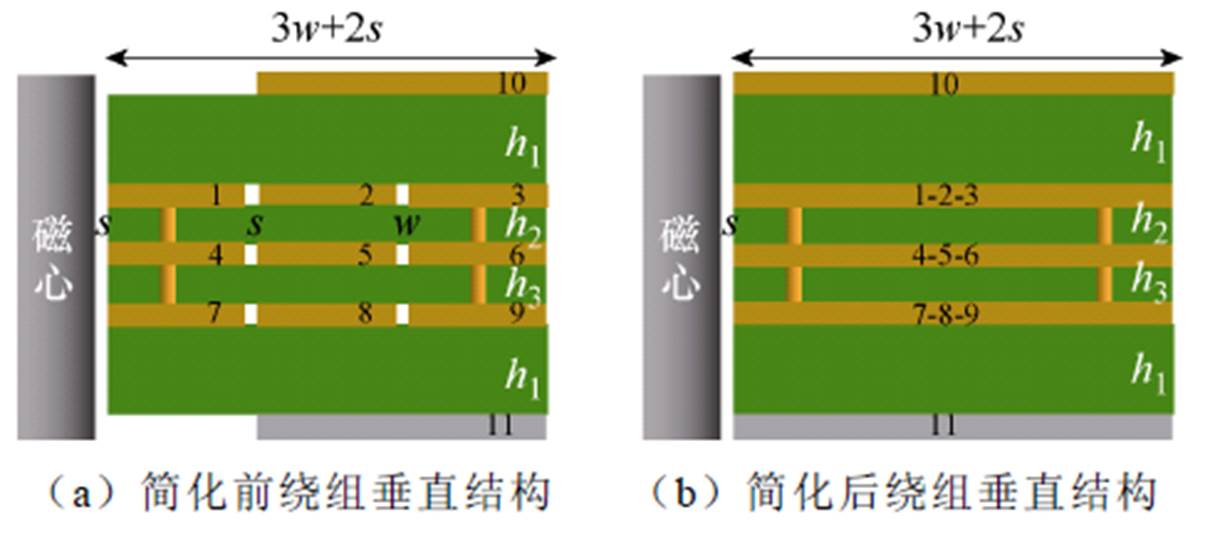
图13 S-P-S绕组垂直结构
Fig.13 Vertical structure of S-P-S winding
为计算此平面变压器的一次侧单柱漏感,应首先求得在此平面变压器绕组以及绝缘层上的磁场强度。由于中心抽头变压器二次绕组是分时工作的,因此可以忽略图13a中二次绕组11。对各个绕组建立磁场强度与位置坐标系,绕组磁场强度分布如图14所示。图中,hp为变压器一次绕组铜厚,hs为二次绕组铜厚。
根据安培环路定理,结合图3的磁动势分布,各绕组磁场强度与在其上的位置关系分别为
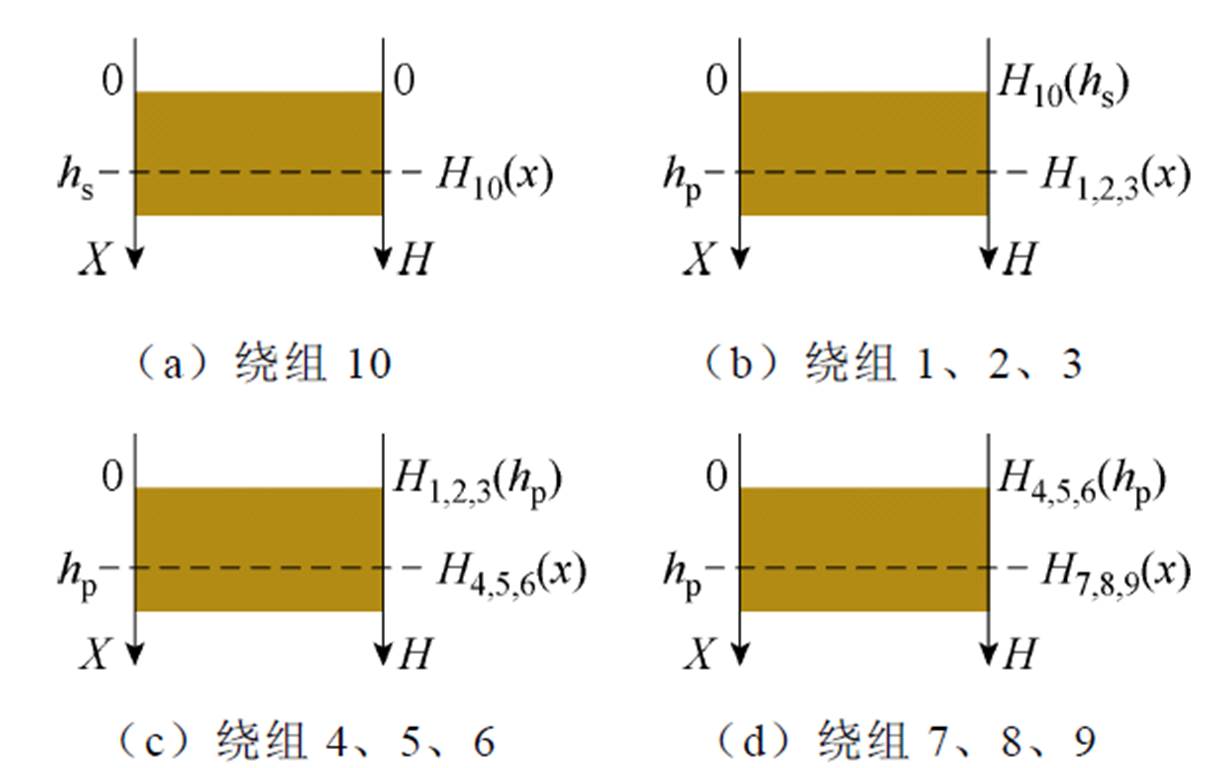
图14 绕组磁场强度分布
Fig.14 Distribution of magnetic field strength
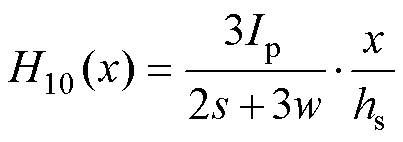 (11)
(11)
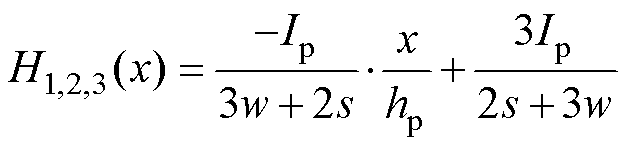 (12)
(12)
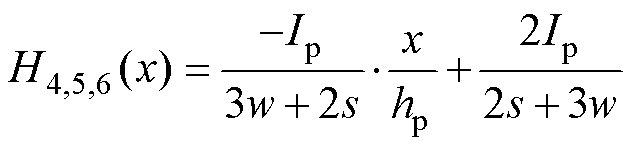 (13)
(13)
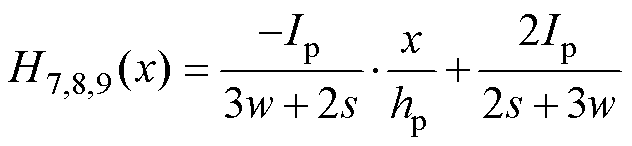 (14)
(14)
由图14可知,绝缘层内部磁场强度等于绝缘层边缘磁场强度。则绕组10与绕组1, 2, 3之间的绝缘层磁场强度为
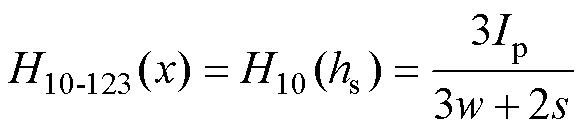 (15)
(15)
绕组1、2、3与绕组4、5、6之间的绝缘层磁场强度为
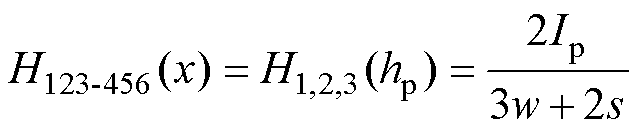 (16)
(16)
绕组4、5、6与绕组7、8、9之间的绝缘层磁场强度为
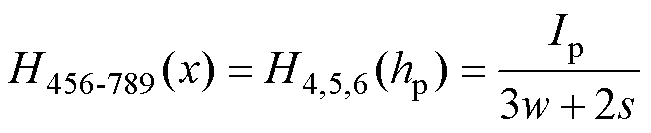 (17)
(17)
则储存在漏电感中的电场能量为
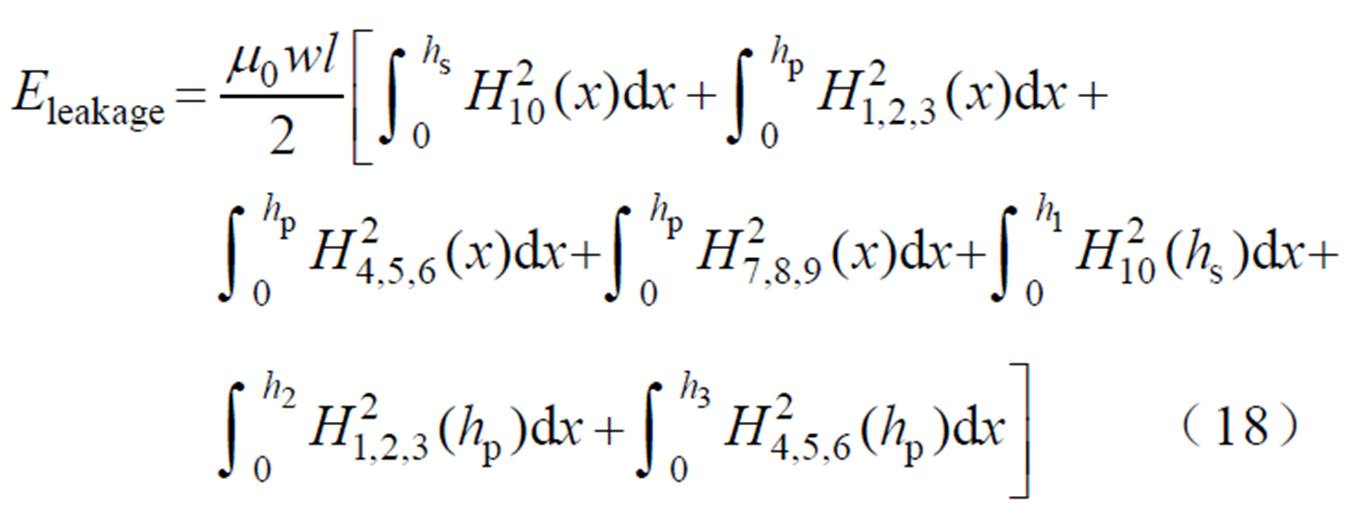
式中,m0为真空磁导率。
结合式(19)所示的电感能量公式,由于绕组间距s远小于绕组宽度w,因此当前绕组排布下漏感表达式如式(20)所示。
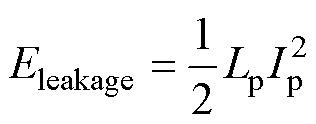 (19)
(19)
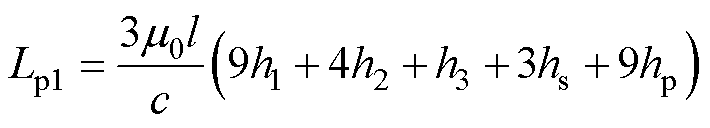 (20)
(20)
由式(20)可知,漏感大小与绕组平均周长l、二次绕组铜厚hCu1、绝缘层厚度h1、h2、h3呈正相关,与变压器一次绕组铜厚hCu2和绕组总宽度c呈负相关。由于绕组平均周长l和绕组总宽度c在2.2节中已经确定,二次侧外层位于PCB外层铜厚2 oz,变压器一次侧位于内层铜厚1 oz(1 oz=0.035 mm)。因此代入谐振电感量后即得到了绝缘层厚度h1、h2、h3的约束式。另外,PCB总厚度为hPCB,绝缘层厚度h1、h2、h3得到的约束为
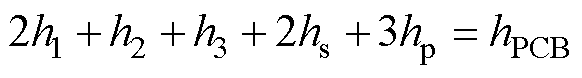 (21)
(21)
将式(20)看作h1、h2、h3的约束平面1,将式(21)看作h1、h2、h3的约束平面2。在不同的PCB总厚度情况下,图15给出了约束平面1和约束平面2的位置关系。由图可知,当hPCB较小时,约束平面1位于约束平面2下方,两者无交截。当hPCB=19 mm时,约束平面产生交截,存在多组h1、h2、h3,满足漏感设计要求。当hPCB继续增大时,约束平面1超越约束平面2,二者无交截。
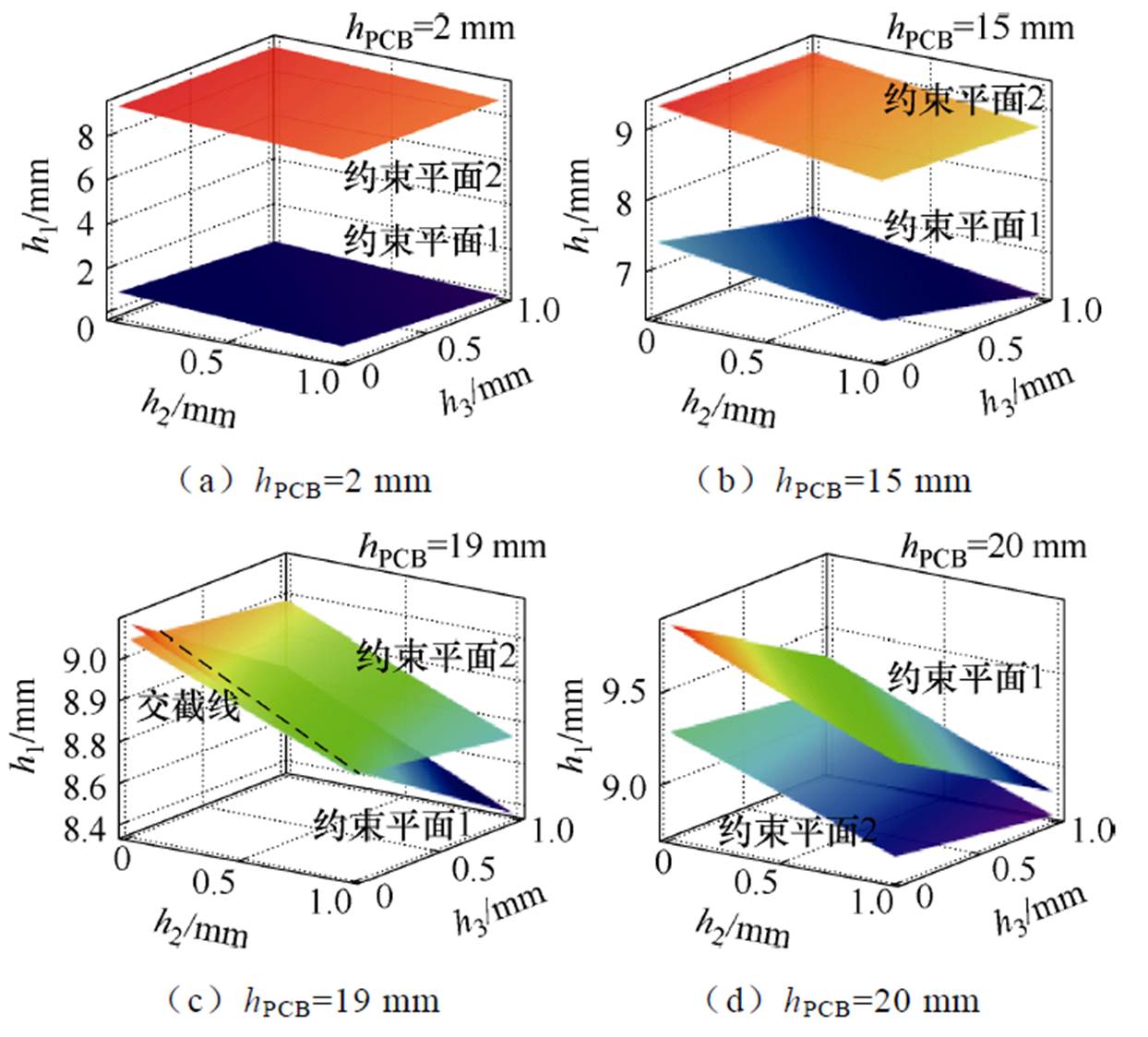
图15 不同PCB总厚度情况下约束平面的位置关系
Fig.15 The positional relationship of constraint planes for different total thicknesses of PCB
由于PCB在实际中难以制作19 mm厚度,在保证绕组PCB与功率PCB一体化制作的前提下,漏感集成方案在当前设计点无法实现。因此仍采用独立LLC谐振电感方案。根据图1的优化流程,此时选择图11所示的P-S-P-S-P绕组绕布方案对漏感重新建模,并设计h1、h2、h3使漏感尽可能减小。当前绕组垂直结构如图16所示。
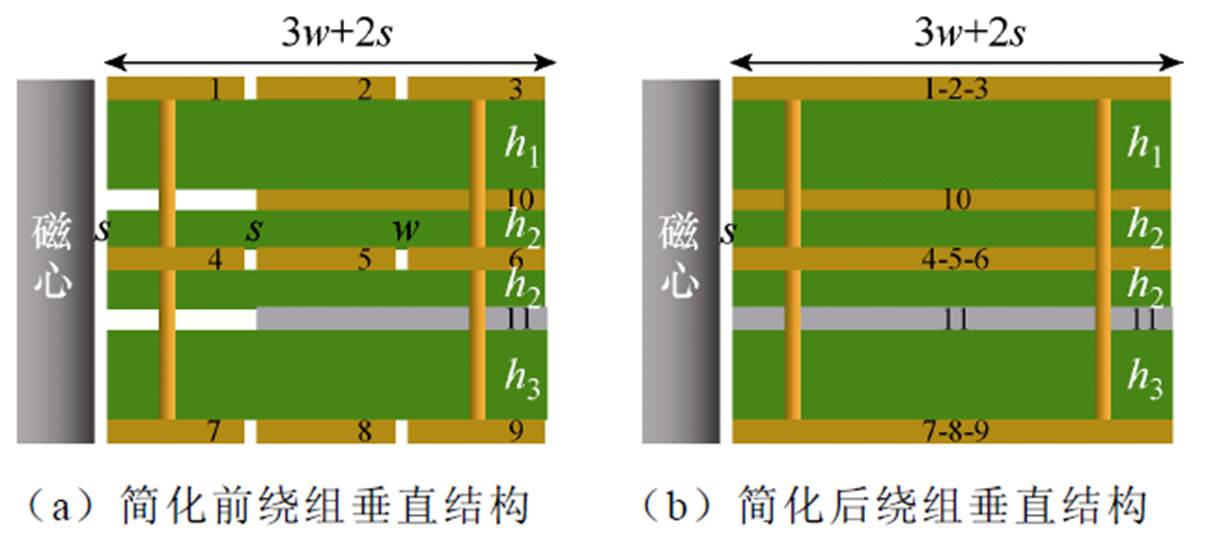
图16 P-S-P-S-P绕组垂直结构
Fig.16 Vertical structure of P-S-P-S-P winding
根据式(11)~式(20)的推导,同理可以得到当前P-S-P-S-P绕布时漏电感表达式为
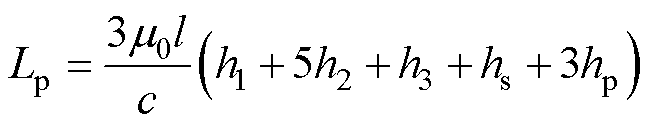 (22)
(22)
此时,由PCB总厚度hPCB所产生的约束仍然存在,如式(21)所示。将式(21)代入式(22)可得到漏感Lp与PCB总厚度hPCB和h2的关系,如图17所示。
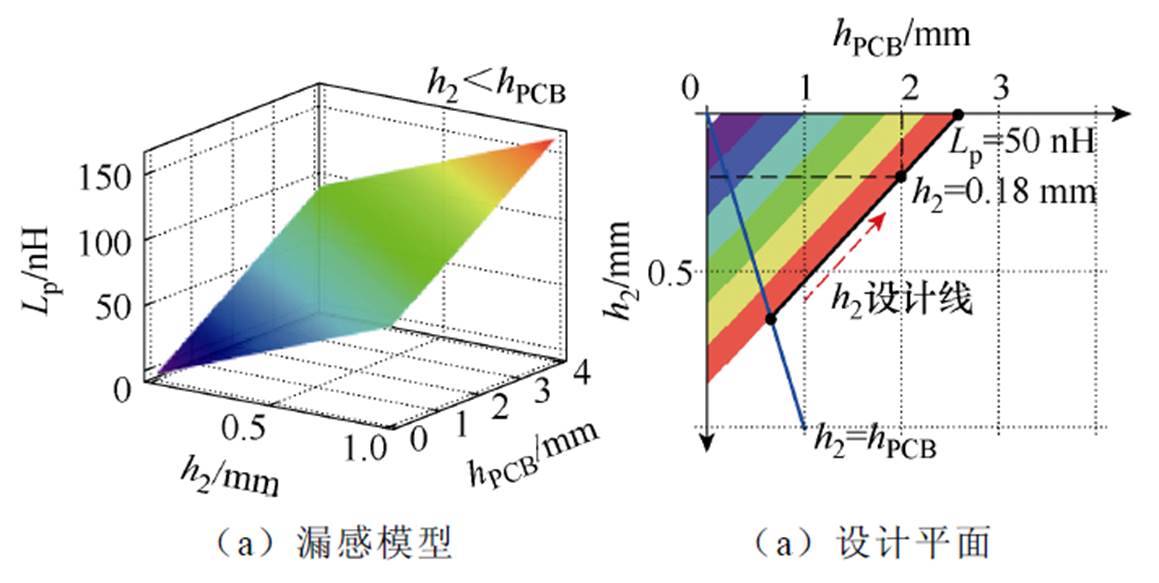
图17 漏感Lp与PCB总厚度hPCB和h2的关系
Fig.17 The relationship between leakage inductance Lp and total PCB thickness hPCB and h2
当取漏感值Lp=58 nH时,可以得到如图17b所示的h2设计线。沿设计线向上取值,PCB总厚度增大,但h1和h3取值裕量增大,对寄生电容的减小更加有利。因此,本文取设计线中段,当PCB总厚度hPCB= 2 mm时,h2=0.18 mm。此时h1+h3=1.325 mm。
绕组寄生电容根据极板位置可以分为层间电容、端接电容、边缘电容等[20-22],其中,层间电容容值较大且对LLC开关电压起主要影响,绕组层间电容示意图如图18所示。
4×(3 1
1 1) 四元变压器单柱绕线布局如图12所示,由于二次绕组每半周期交替导通,且二次侧上、下绕组对称,因此仅考虑二次侧上绕组与变压器一次绕组。以第一矩阵变压器中心柱为例,建立极坐标系,如图19a所示。假设一、二次侧共地时,第一矩阵变压器各个端口电动势如图19b所示。
1) 四元变压器单柱绕线布局如图12所示,由于二次绕组每半周期交替导通,且二次侧上、下绕组对称,因此仅考虑二次侧上绕组与变压器一次绕组。以第一矩阵变压器中心柱为例,建立极坐标系,如图19a所示。假设一、二次侧共地时,第一矩阵变压器各个端口电动势如图19b所示。
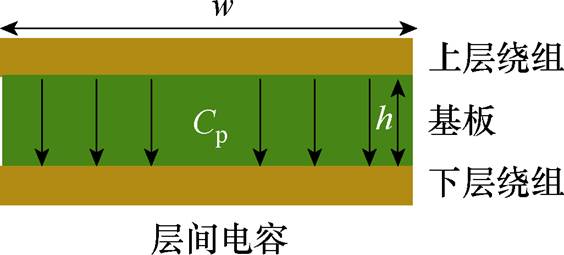
图18 绕组层间电容示意图
Fig.18 Schematic diagram of inter layer capacitance
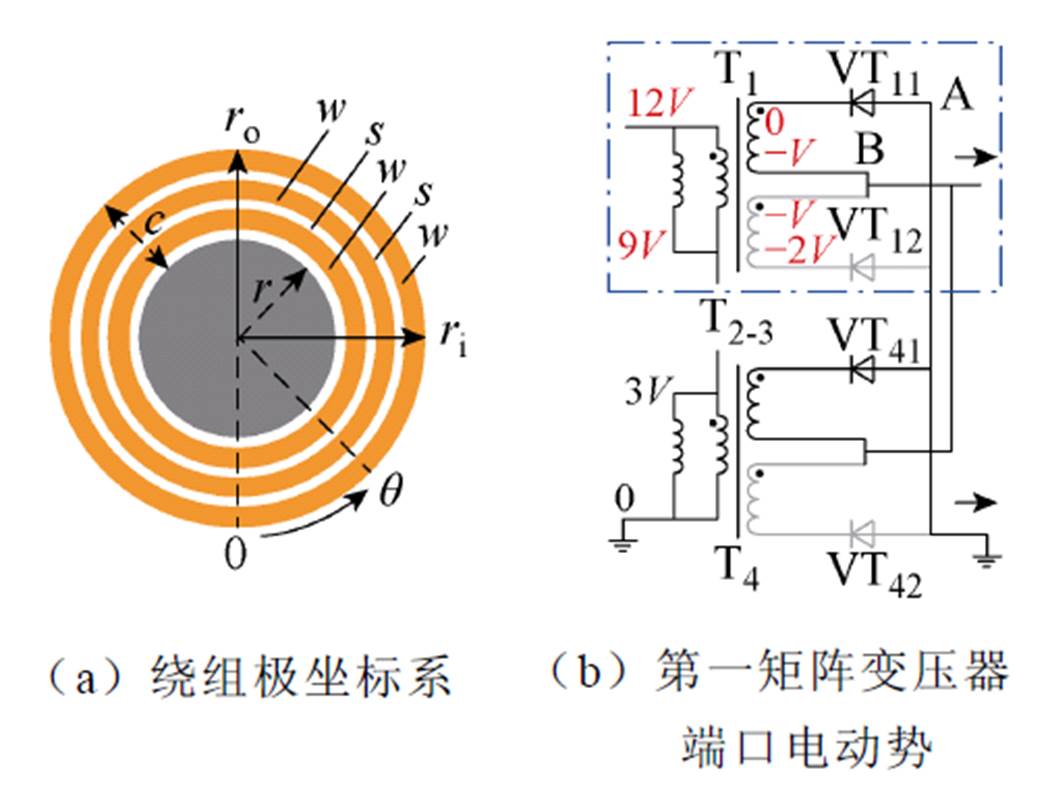
图19 绕组极坐标系及第一矩阵变压器端口电动势
Fig.19 Winding polar coordinate system and first matrix transformer port potential
根据图16给出的 P-S-P-S-P绕组垂直结构,可以得出各个绕组上电动势随极坐标系q 变化,如图20所示。
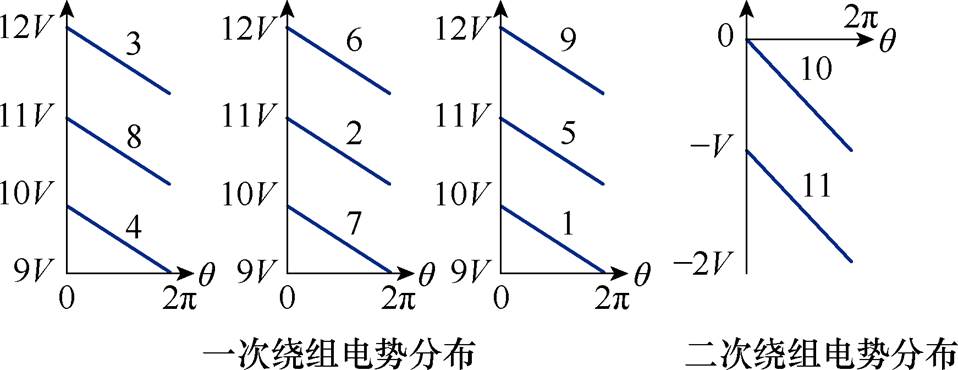
图20 各个绕组上电动势V随极坐标系q 变化
Fig.20 The potential V on each winding varies with the polar coordinate system q changing images
图21给出了一种典型的P-S层间电容示意图。P-S层间电容Cp_ps可由变压器一次绕组边缘电场能量Ep推导而得,即
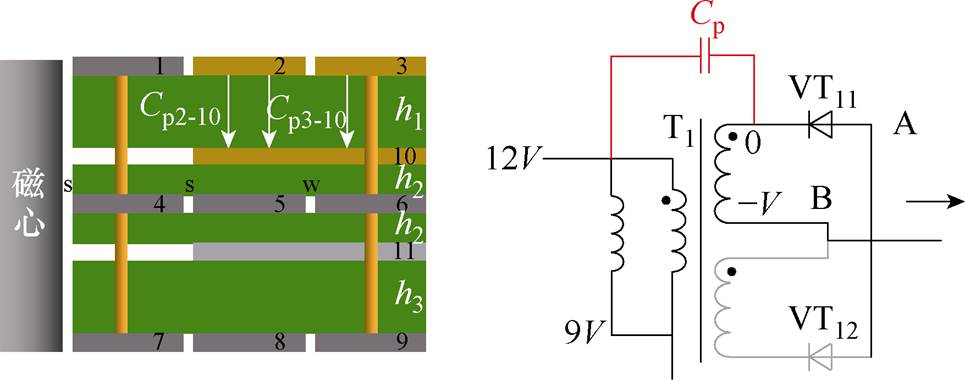
图21 典型的P-S层间电容示意图
Fig.21 Typical schematic diagram of inter layer capacitance between P-S layers
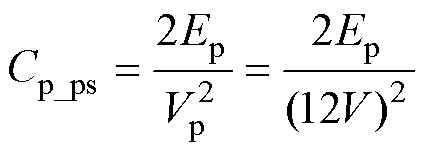 (23)
(23)
在极坐标系下,第2和第10绕组之间的电场能量Ep2-10可以表示为
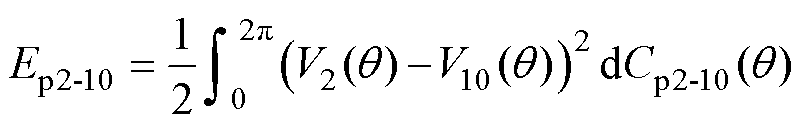 (24)
(24)
dCp2-10为每个角度电容微元,根据电容定义式可表示为
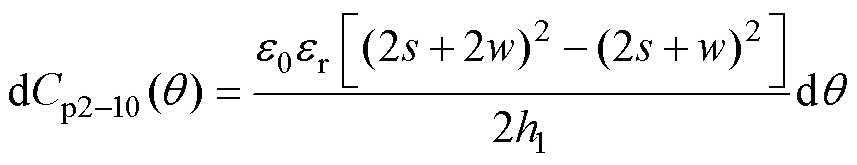 (25)
(25)
式中,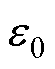 和
和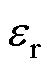 分别为真空介电常数和FR-4相对介电常数。结合式(23)~式(25),第2和第10绕组之间层间电容电场能量Ep2-10可以表示为
分别为真空介电常数和FR-4相对介电常数。结合式(23)~式(25),第2和第10绕组之间层间电容电场能量Ep2-10可以表示为
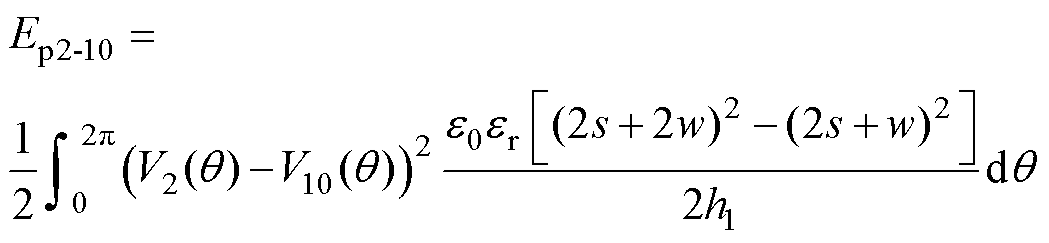 (26)
(26)
Ep2-10、Ep3-10、Ep5-10、Ep6-10、Ep8-10、Ep9-10、Ep2-11、Ep3-11、Ep5-11、Ep6-11、Ep8-11、Ep9-11计算方法相同,P-P边缘电容Cp_ps表达式为
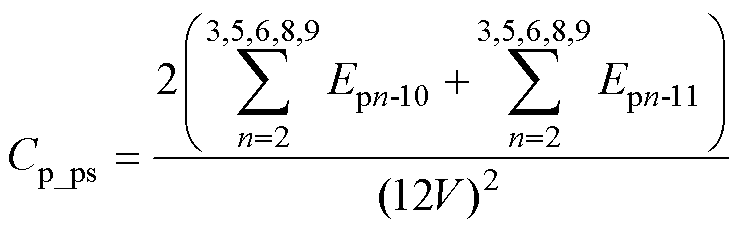 (27)
(27)
图22给出了一种典型的S-S层间电容示意图。与式(23)~式(27)同理可写出第10和第11绕组之间层间电容电场能量Ep10-11表达式为
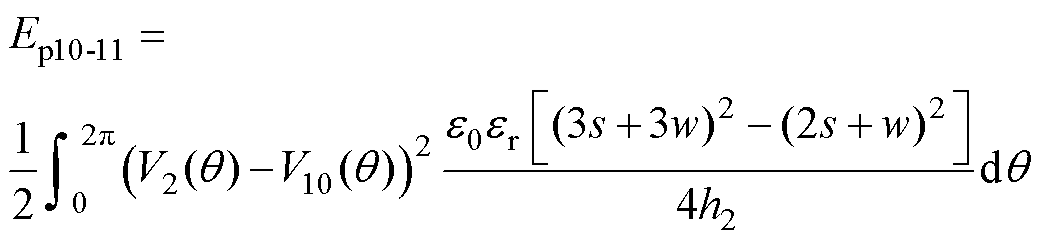 (28)
(28)
与式(27)同理,可求得S-S层间电容值。
根据3.1节、3.2节中的设计,此时h2=0.18 mm,h1+h3=1.325 mm。首先,根据对称性,依然预设h1=h3=0.662 mm。此时P-S层间电容值和S-S层间电容值是关于绕组间距s和绕组宽度w的二元函数。由于绕组间距s、绕组宽度w和绕组总宽度c存在约束关系,3s+3w=c,因此P-S层间电容值在图22a中沿黑色约束线变化,S-S层间电容值在图22b中沿黑色约束线变化。
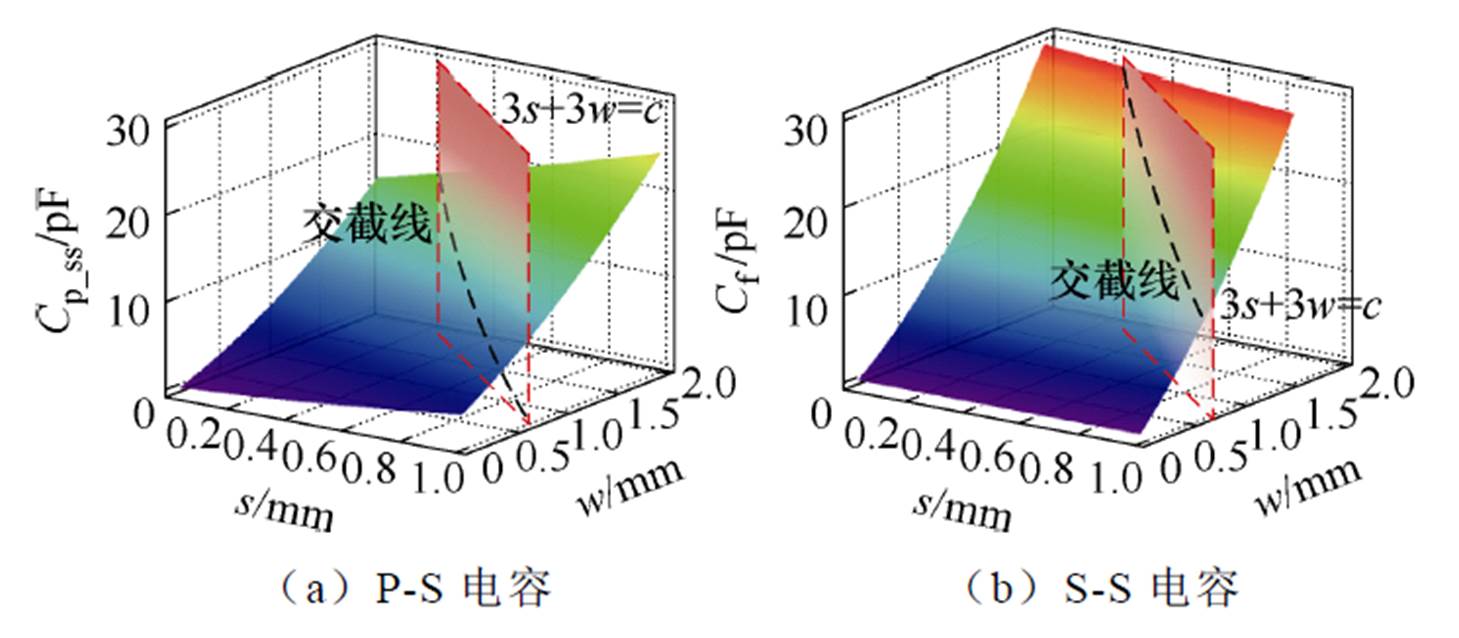
图22 P-S和S-S电容值关于绕组间距s和绕组宽度w变化关系
Fig.22 The relationship between the capacitance of P-S and S-S with respect to the s and w
寄生电感选定后,寄生电容约束随之确定。寄生电容分为P-S电容与S-S电容。其中P-S电容与二次侧开关管结电容、谐振电感共同谐振,导致二次侧Vds电压振荡。P-S电容是影响变换器性能的主因。电容平面与约束平面交截,可得到电容设计线,如图1~图6所示。为尽可能降低寄生电容值,应沿着设计线下段取值。但过窄的绕组宽度w导致较大的绕组交流损耗,因此权衡后取设计线中段,即w=1.85 mm,此时,容值为33 pF,如图23a所示。由于之前预设了h1+h3=1.325 mm,因此还需要对h1和h3进行迭代寻优,将w和s代入寄生电容模型,P-S层间电容值关于h1和h3的二元函数。将h3用h1代替,此时P-S层间电容值是关于h1的一元函数。如图23b所示。
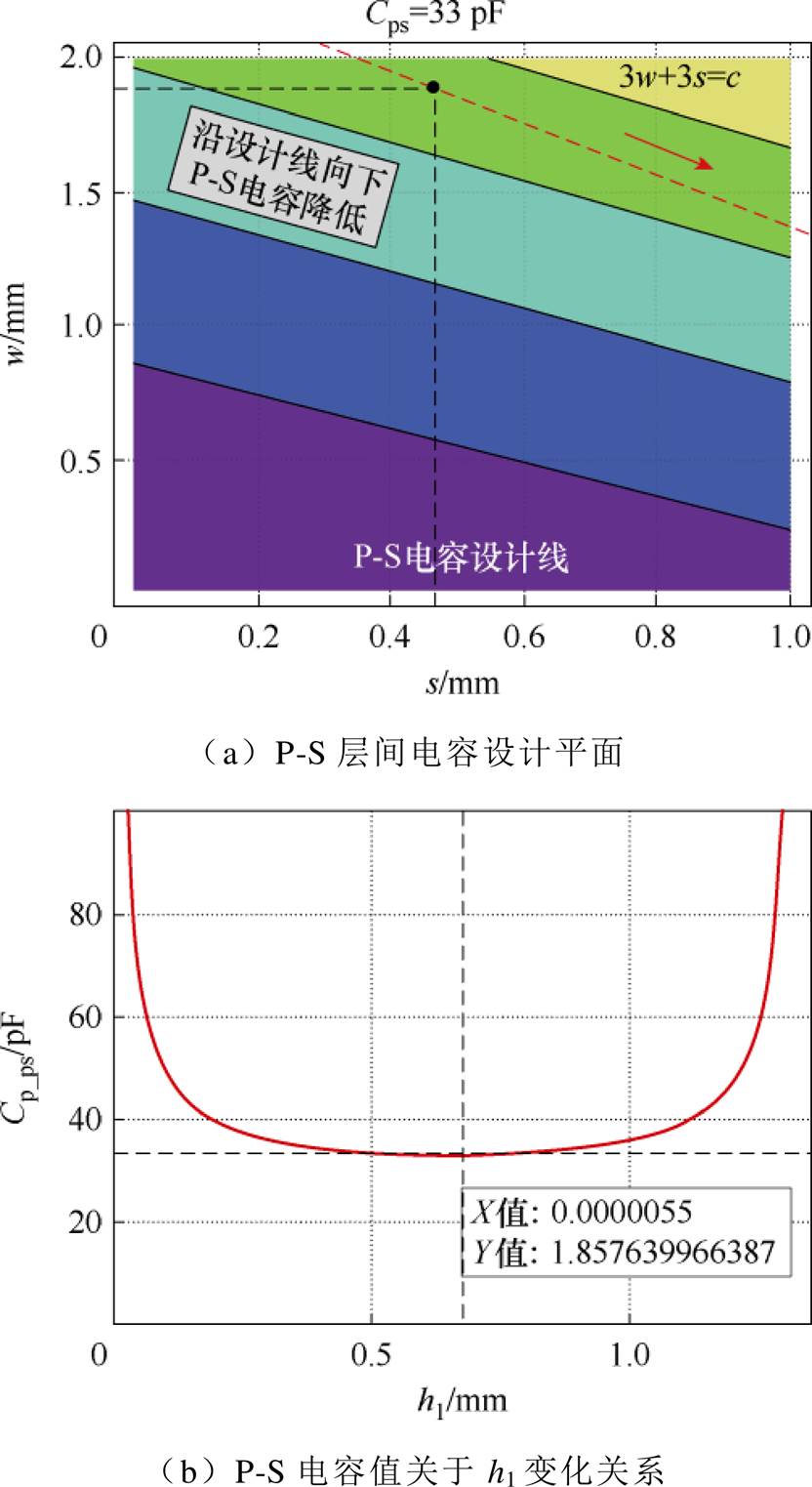
图23 P-S层间电容优化
Fig.23 P-S interlayer capacitance optimization
由图23可知,当h1=h3=0.66 mm时,P-S层间电容存在最小值。四元矩阵变压器单柱绕组尺寸设计值见表3。
表3 四元矩阵变压器尺寸参数
Tab.3 Transformer size parameters (单位: mm)
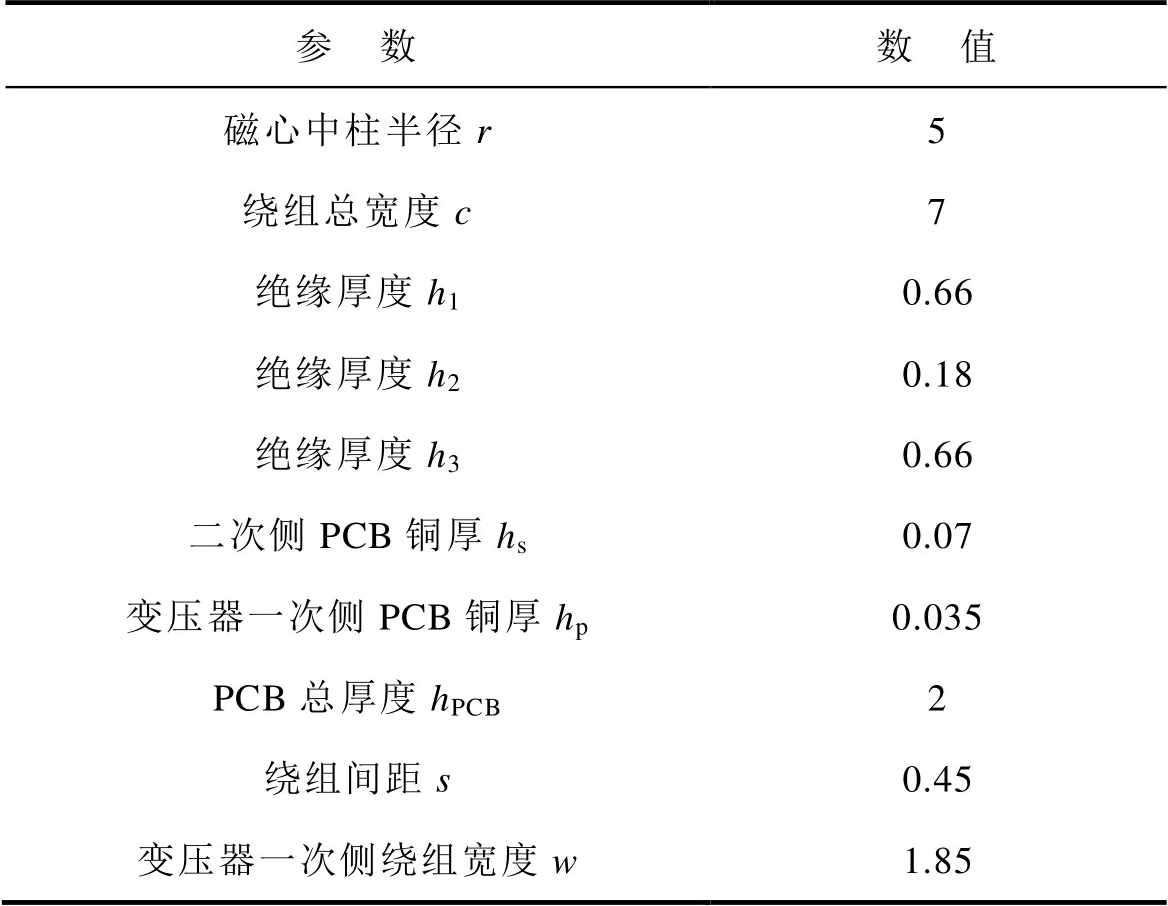
参 数数 值 磁心中柱半径r5 绕组总宽度c7 绝缘厚度h10.66 绝缘厚度h20.18 绝缘厚度h30.66 二次侧PCB铜厚hs0.07 变压器一次侧PCB铜厚hp0.035 PCB总厚度hPCB2 绕组间距s0.45 变压器一次侧绕组宽度w1.85
当前尺寸下,变压器理论寄生参数见表4。
表4 寄生参数理论值
Tab.4 Theoretical values of parasitic parameters

参 数数 值 变压器一次侧等效漏电感/nH235 P-S层间电容/pF33 S-S层间电容/pF17.3
根据3.3节的设计,本节使用Altium Designer绘制了绕组PCB并导入Ansys电磁场仿真进行验证。建立的模型如图24所示。
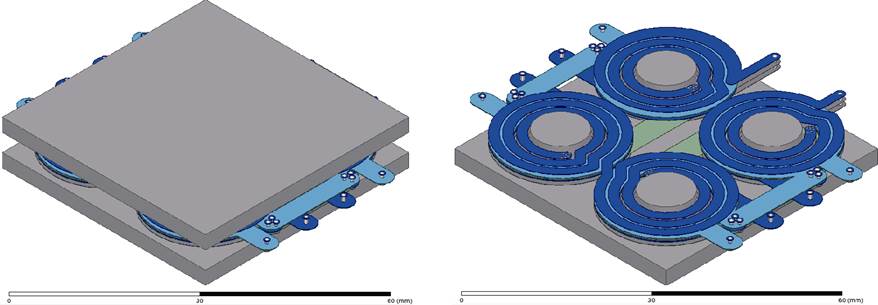
图24 四元矩阵变压器仿真模型
Fig.24 Simulation model of four-element-matrix transformer
对该模型进行涡流场磁通密度仿真,提取表1 LLC参数下的磁通密度分布情况,如图25所示。
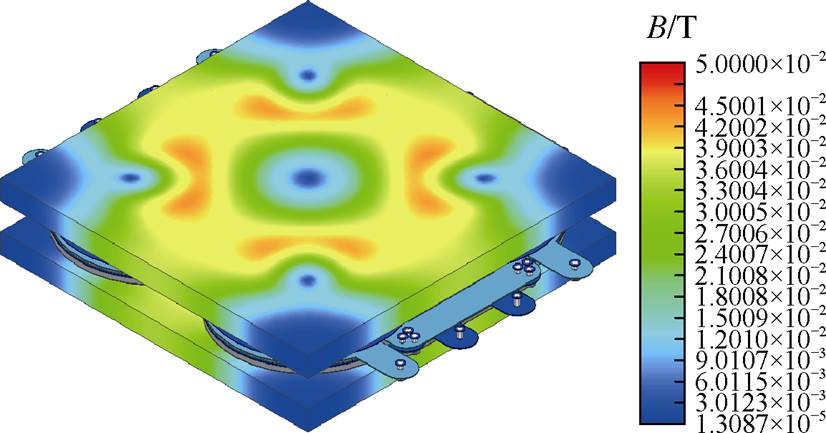
图25 四元矩阵变压器磁通密度分布情况
Fig.25 Distribution of magnetic density in four-element-matrix transformer
图25中,上磁板中心磁路区域磁通密度为18 mT,磁心中柱磁通密度为24 mT,与表2计算结果一致。使用Ansys Q3D提取单柱电容值,使用Ansys Maxwell提取所有变压器一次侧励磁电感矩阵,使用Ansys Maxwell提取四元矩阵变压器一、二次侧漏感耦合系数矩阵,提取结果见表5。
表5 Ansys Maxwell寄生参数提取结果
Tab.5 Ansys Maxwell parasitic parameter extraction results
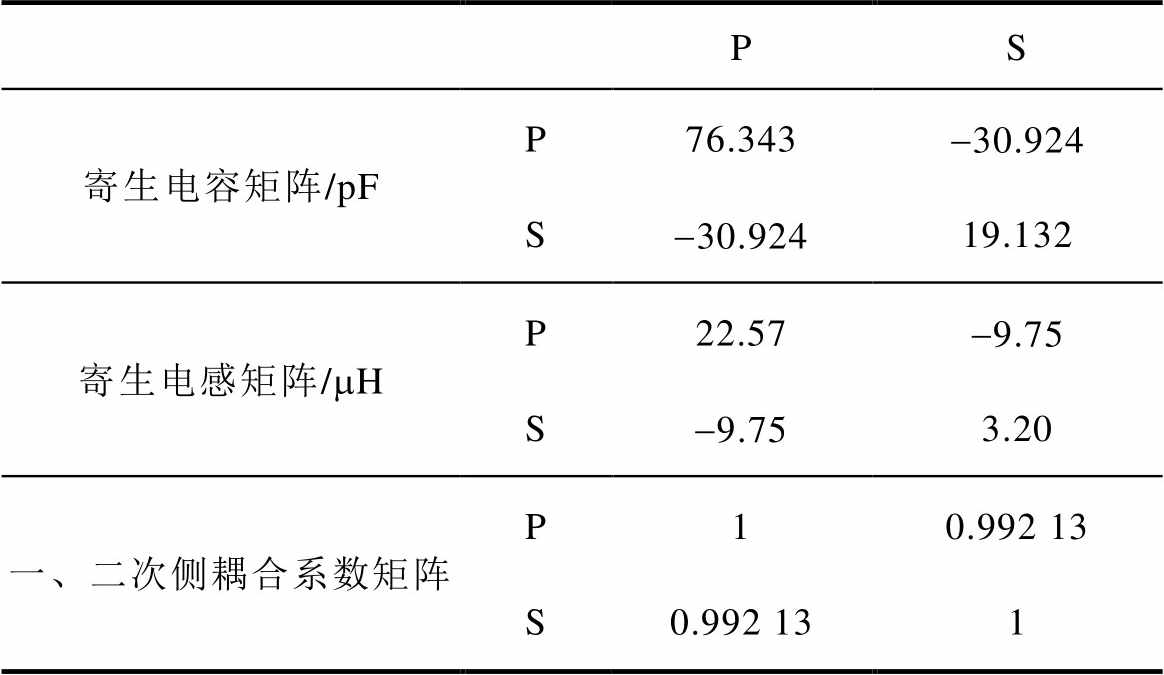
PS 寄生电容矩阵/pFP76.343-30.924 S-30.92419.132 寄生电感矩阵/mHP22.57-9.75 S-9.753.20 一、二次侧耦合系数矩阵P10.992 13 S0.992 131
电容提取值与表4理论值基本符合。变压器一次侧励磁电感大小为22.56 mH,满足设计要求。四元矩阵变压器一、二次侧耦合系数kps=0.979 8。根据式(29)可以计算出该四元矩阵变压器一次侧漏感大小为345 nH,考虑实际PCB布局与连接层带来的额外漏感,仿真值与设计值基本符合。
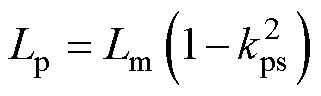 (29)
(29)
式中,Lm为励磁电感值;kps为耦合系数。
变压器磁心损耗仿真值为0.325 W,绕组损耗为2.78 W,与表2理论值符合。寄生参数计算值、仿真值与实验测量值结果见表6。
本文基于表3的参数,搭建了两台平面集成设计后的混合型Sigma变换器样机,其中LLC作为功率级,Buck作为调压级。样机如图26所示。优化后样机84 A电流输出时,装置功率密度为1.338 W/cm3。LLC效率为95%。
表6 寄生参数的理论值、仿真值、实际值对比
Tab.6 Comparison of theoretical, simulation and actual values of modified parasitic parameters
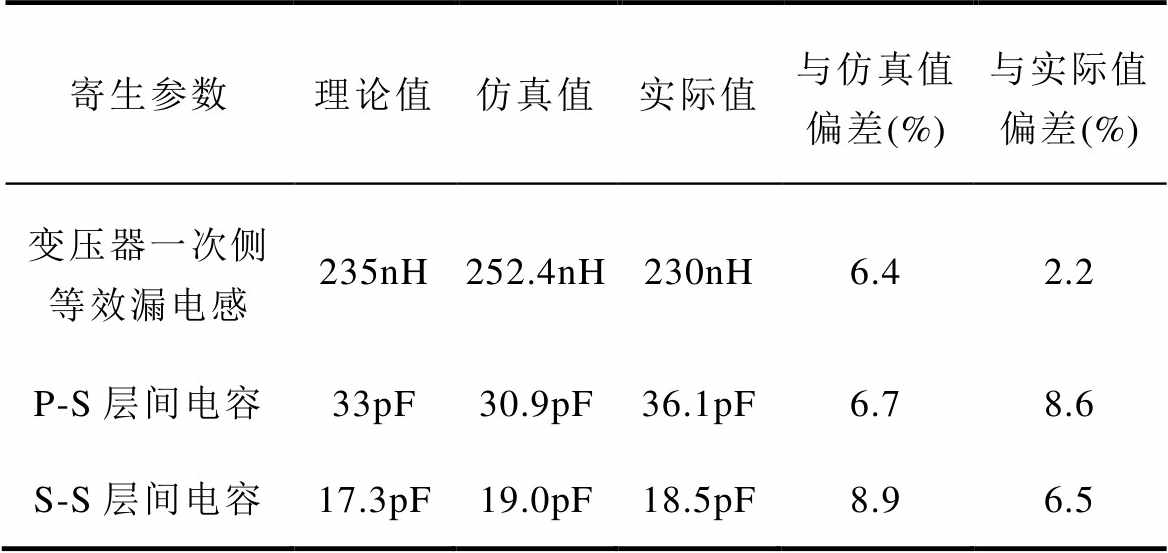
寄生参数理论值仿真值实际值与仿真值偏差(%)与实际值偏差(%) 变压器一次侧等效漏电感235nH252.4nH230nH6.42.2 P-S层间电容33pF30.9pF36.1pF6.78.6 S-S层间电容17.3pF19.0pF18.5pF8.96.5
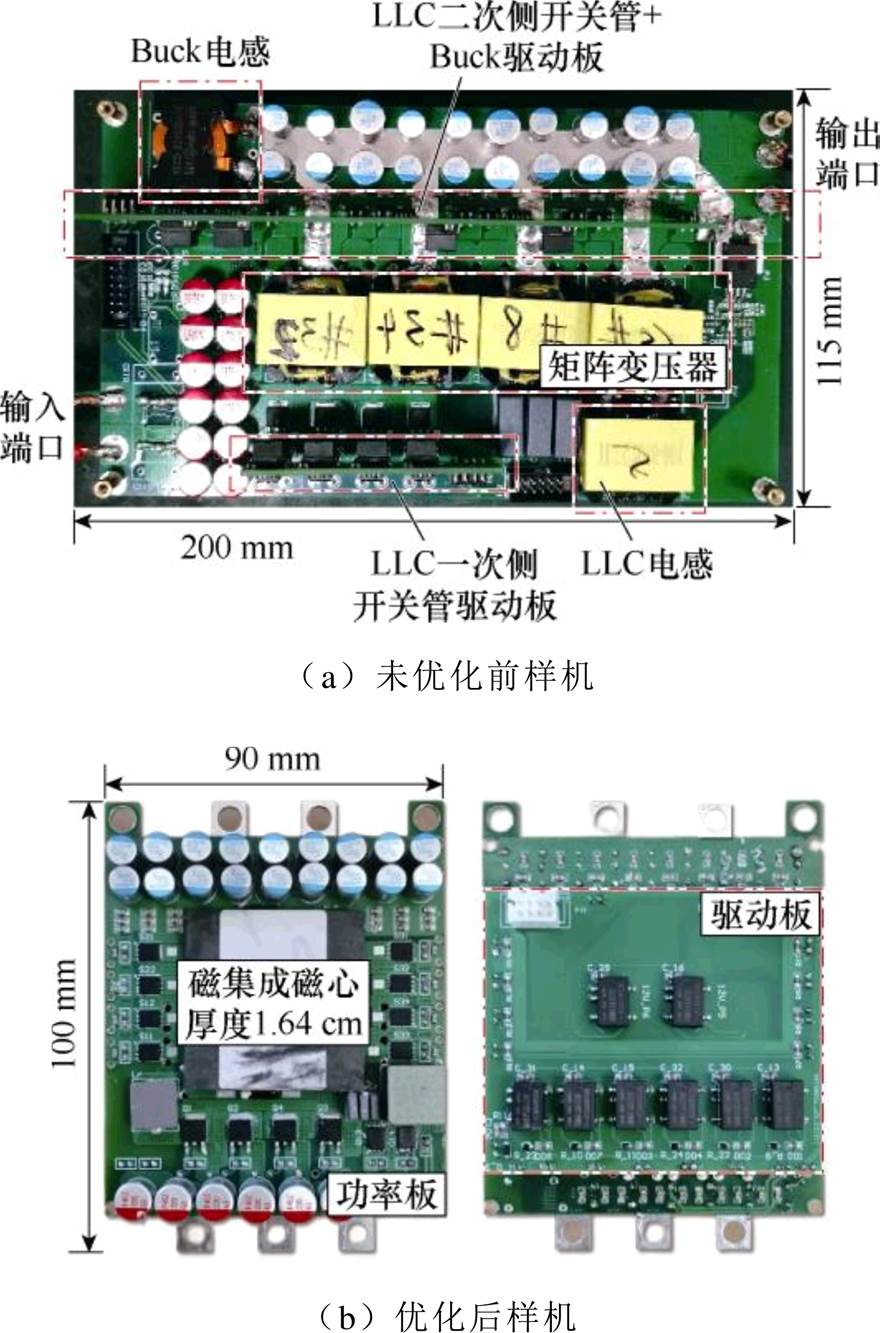
图26 LLC样机实物
Fig.26 LLC prototype physical object
优化前样机在满载250 W正向运行时,LLC承担200 W功率,与所提方法样机一致。LLC一次侧软开关波形如图27a所示。LLC二次侧软开关波形如图27b所示。在二次侧S11管关断时刻,流过二次侧S11管电流IS11已经降为0,此时二次侧实现零电流软开关(Zero Current Switching, ZCS)。该样机在LLC 200 W反向运行时,仍工作在临界连续导通模式,一次侧软开关波形如图28a所示。二次侧软开关波形如图28b所示。
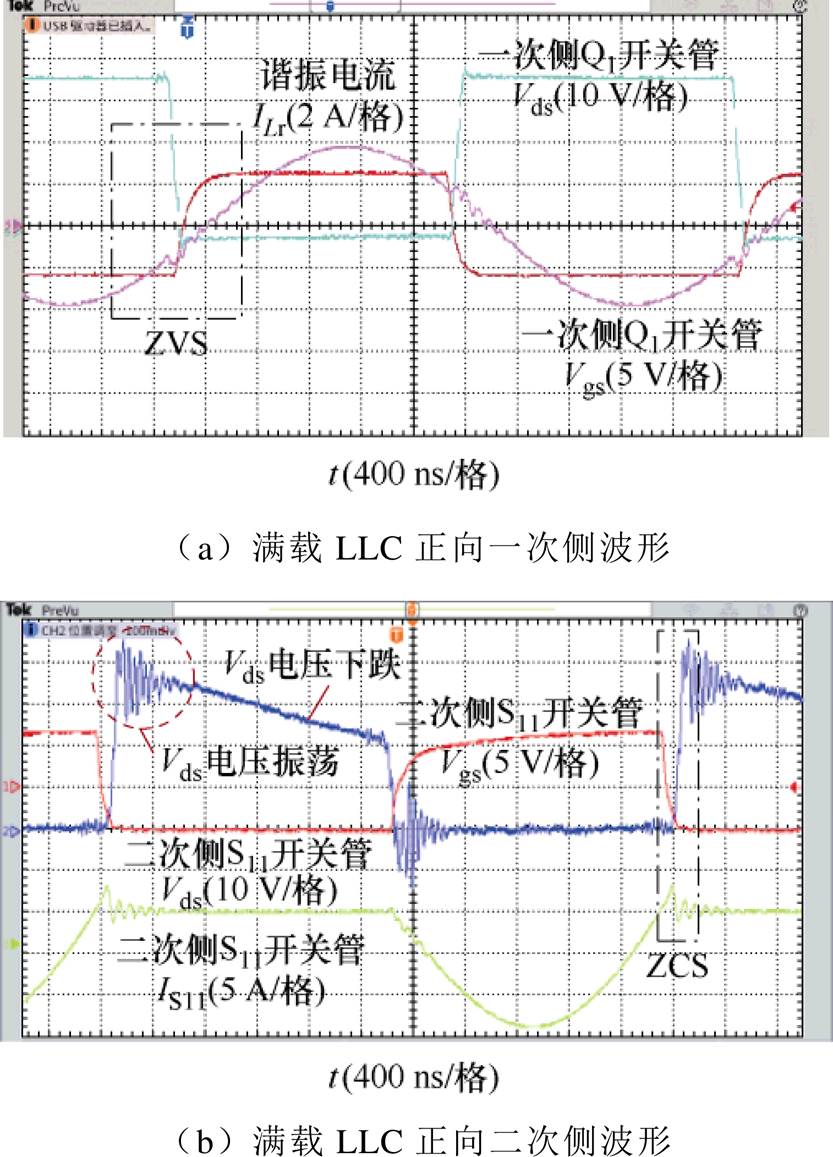
图27 优化前样机满载正向工作波形
Fig.27 Optimize the front prototype full-load forward working waveforms
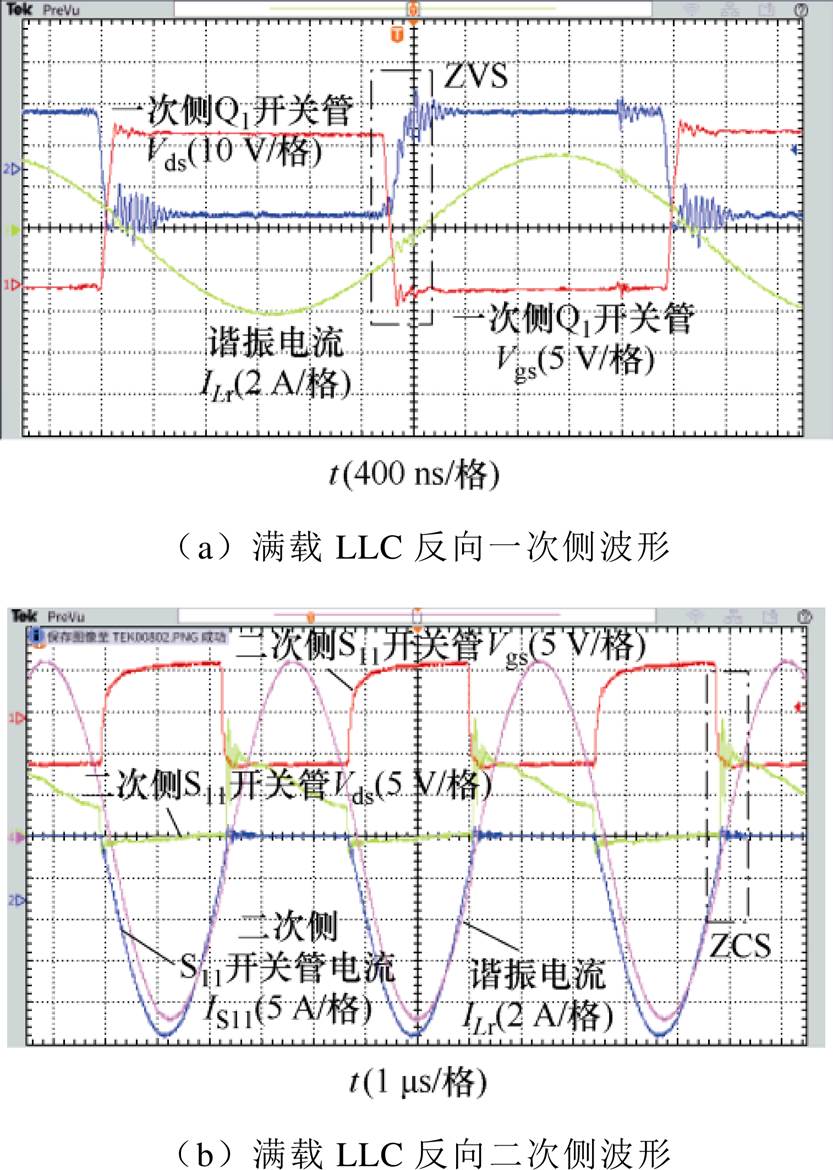
图28 优化前样机满载反向工作波形
Fig.28 Pre optimization prototype full load reverse working waveforms
优化后LLC正向运行一次侧关键波形如图29a所示。图中,在输入电压48 V时,LLC分得39 V电压。当二次侧开关管Vds降为0时,谐振电流向开关管结电容充电,LLC变压器一次侧实现ZVS。
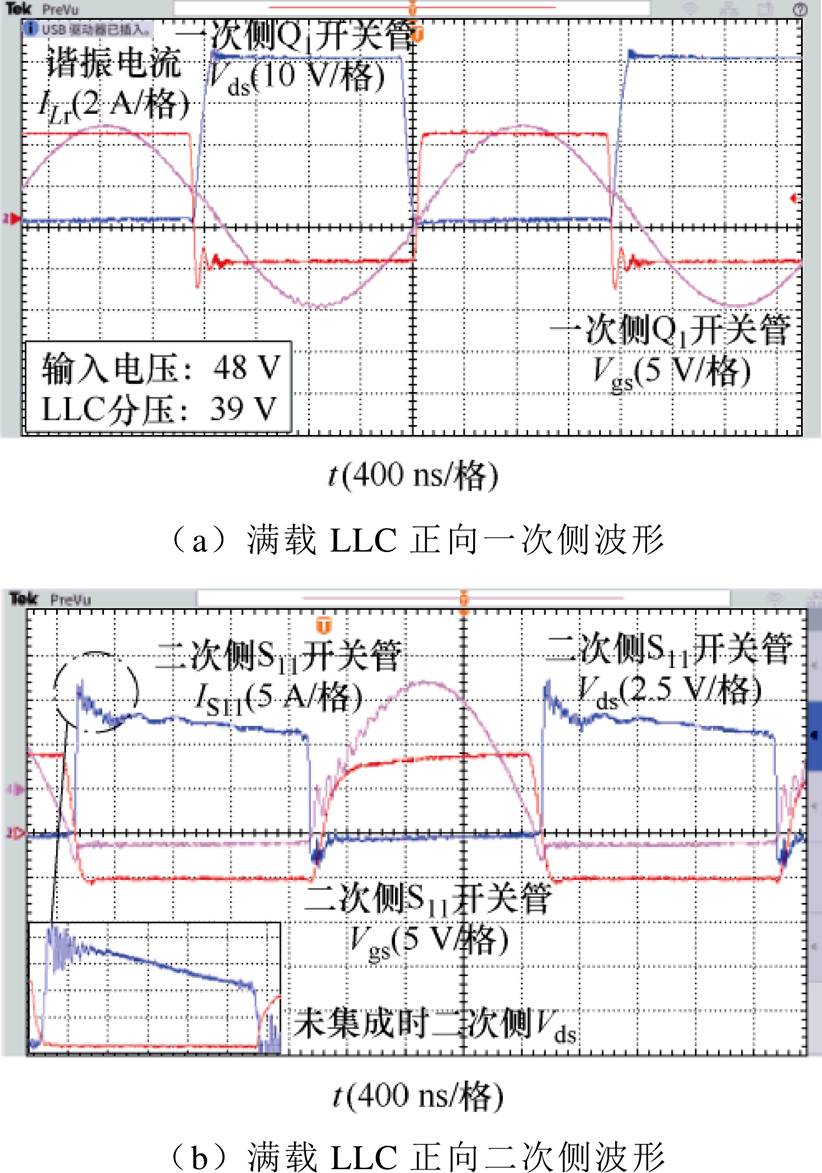
图29 优化后样机满载正向工作波形
Fig.29 Optimized prototype full load positive working waveforms
优化后LLC正向运行二次侧关键波形如图29b所示。二次侧实现ZCS。相比未集成优化前,二次侧Vds电压振荡明显降低,这意味着寄生电容值较未集成前有所减小。通过阻抗分析仪测量P-S层间电容结果显示,在低频线性段该P-S电容容值为36.1 pF,与设计值一致,如图30所示。
通过匹配谐振电感保证LLC工作在240 kHz时恰好为临界连续导通模式,可以计算出集成前后变压器一次侧漏感大小,未集成前谐振电感为1.8 mH,这意味这变压器一次侧漏感为0.7 mH。集成优化后谐振电感为2.3 mH,这表明变压器一次侧漏感大小为0.2 mH,这与理论设计一致。
优化后LLC反向运行一次侧关键波形如图31所示。变压器一次侧实现ZVS,且与未集成前相比,输入相同电压3.2 V时,LLC输出电压由34 V抬升至36 V,这意味折着二次侧漏感较之前有所减小。经过谐振点匹配,可以得到二次侧漏感由33 nH降低至12 nH。
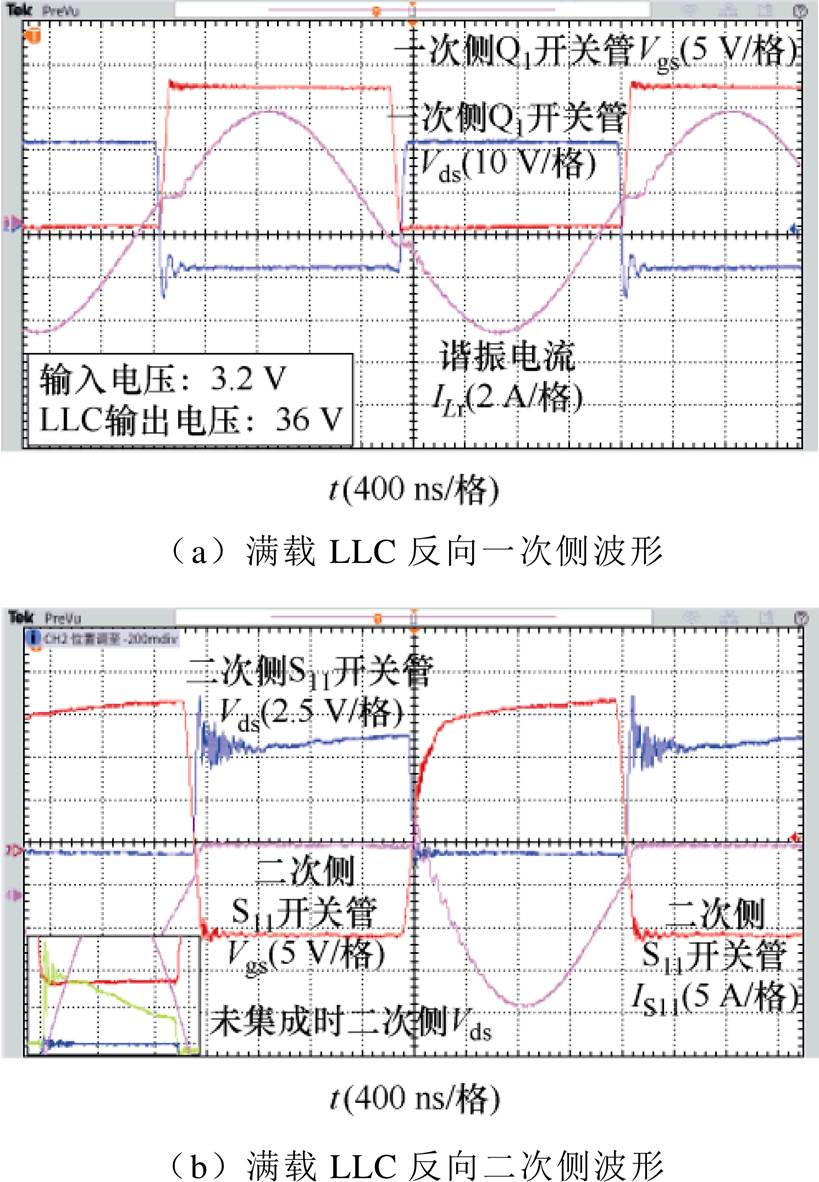
图30 优化后样机满载反向工作波形
Fig.30 Optimized prototype full load reverse working waveforms
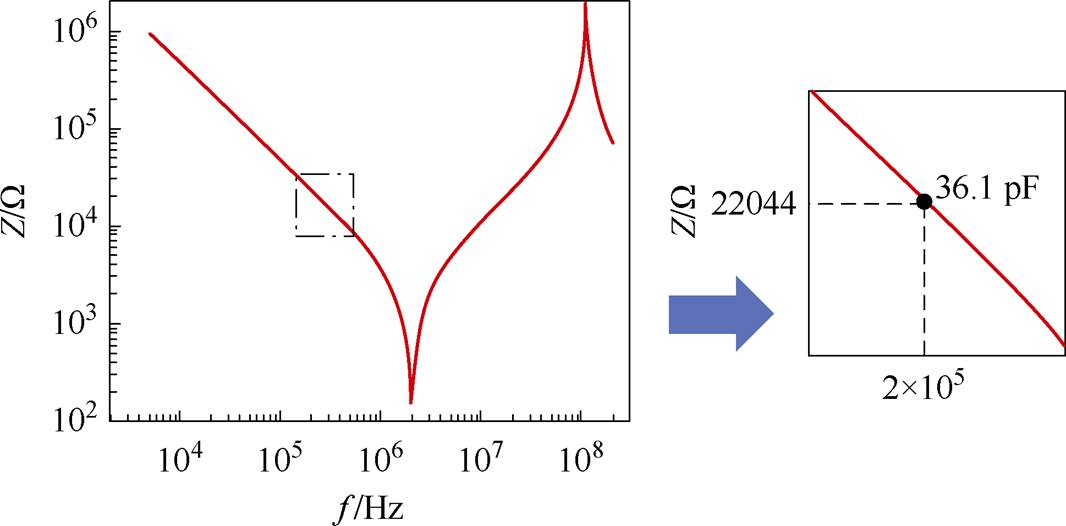
图31 变压器P-S层间电容阻抗分析仪测试结果
Fig.31 Test results of capacitance impedance analyzer between transformer P-S layerse
为验证四元集成矩阵变压器的对称性,观察该变压器上绕组连接的4个S管的Vds波形,如图32所示。从波形可知,四元矩阵变压器参数对称性良好,寄生电容所引起的二次侧Vds振荡接近且较小,验证了3.3节中寄生参数的控制效果。
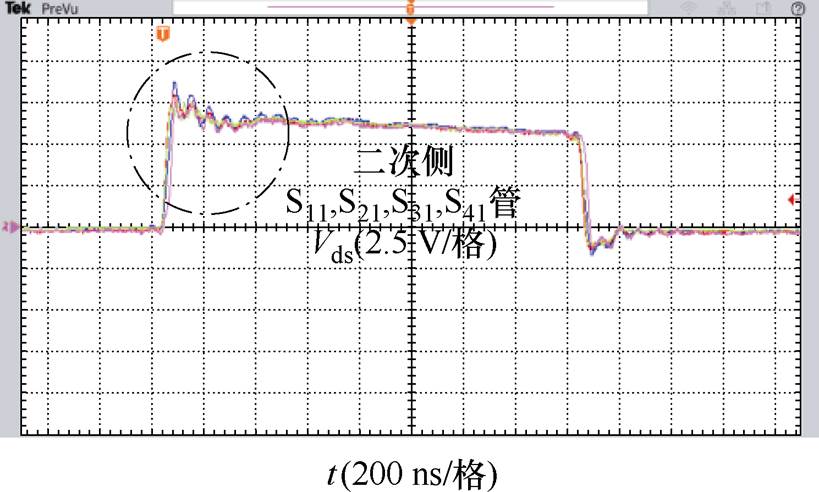
图32 变压器上绕组连接的四个SRs Vds波形
Fig.32 Four SRs Vds waveforms connected to the upper winding
在室温25℃下将样机运行30 min后观察样机温度变化情况如图33所示。二次侧整流器温度稳定在50℃,磁心温度稳定在31℃。峰值热点出现在谐振电感处,原因是采用了小封装模块化电感,承受功率较小,且散热面积较小。
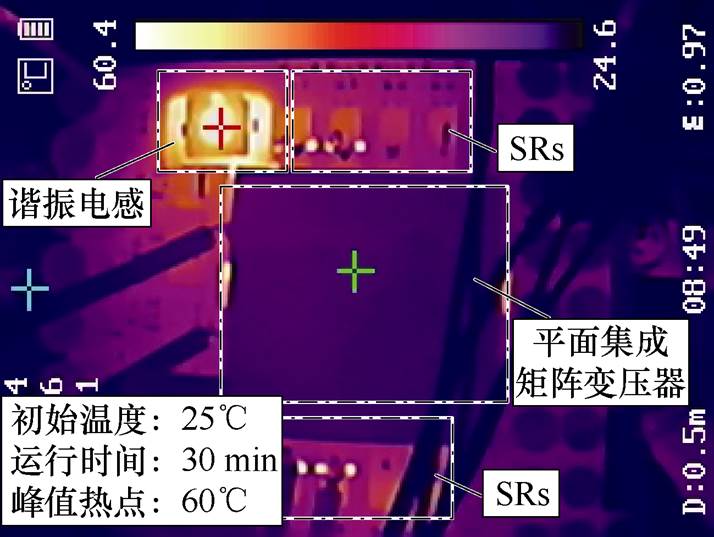
图33 样机运行30 min后热点图
Fig.33 Hotspot map after 30 minutes of prototype operation
针对低压大电流工况下LLC矩阵变压器占地面积大和寄生参数不可控的问题,本文提出一种考虑损耗与寄生参数的LLC四元矩阵平面变压器集成优化设计。通过仿真和实验分析,可以实现以下效果:
1)提出的基于P-B曲线的平面变压器分布式磁心损耗计算方法,消除了磁通密度分布不均匀度对磁心损耗模型精度的影响,实现了集成变压器损耗精准建模。
2)基于实际PCB厚度约束为漏电感可集成性提供了判据。
3)通过对漏感和寄生电感的精确建模,实现了样机尺寸参数与寄生参数的解耦映射。优化了由寄生参数引起的输出电压跌落及二次侧开关振荡。
该方法以期为LLC低压大电流场景下的储能变换器设计与集成优化提供一定的理论支撑。
参考文献
[1] 张基岳, 任洲洋, 姜云鹏, 等. 微电网定碳排运行域: 理论、构建与观测[J]. 电工技术学报, 2024, 39(8): 2342-2359.
Zhang Jiyue, Ren Zhouyang, Jiang Yunpeng, et al. Committed carbon emission operation region of microgrids: theory, construction and observation[J]. Journal of Electrical Technology, 2024, 39(8): 2342- 2359.
[2] 刘征宇, 郭乐凯, 孟辉, 等. 基于改进DBSCAN的退役动力电池分选方法[J]. 电工技术学报, 2023, 38(11): 3073-3083.
Liu Zhengyu, Guo Lekai, Meng Hui, et al. Separation method of retired power batteries based on improved DBSCAN[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 3073-3083.
[3] 陶星澳, 王丰, 卓放. 部分功率直流变换器研究综述[J]. 电工技术学报, 2024, 39(10): 3021-3037.
Tao Xing’ao, Wang Feng, Zhuo Fang. Review of partial power DC converter research[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3021-3037.
[4] Ahmed M, Fei Chao, Lee F C, et al. High-efficiency high-power-density 48/1V sigma converter voltage regulator module[C]//2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 2017: 2207-2212.
[5] Fei Chao, Lee F C, Li Qiang. High-efficiency high- power-density LLC converter with an integrated planar matrix transformer for high-output current applications[J]. IEEE Transactions on Industrial Electronics, 2017, 64(11): 9072-9082.
[6] 屠腾, 张方华, 余文浩, 等. 边界限定条件下的LLC-DCX优化设计[J]. 中国电机工程学报, 2023, 43(12): 4748-4757.
Tu Teng, Zhang Fanghua, Yu Wenhao, et al. Optimal design of LLC-DCX under boundary conditions[J]. Proceedings of the CSEE, 2023, 43(12): 4748-4757.
[7] 冒小晶. 基于LLC谐振变换器的高压母线变换器的研究[D]. 南京: 南京航空航天大学, 2012.
Mao Xiaojing. Research on high voltage bus con- verter based on LLC resonant converter[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012.
[8] 张瑜, 吴红飞, 李泽伟, 等. 面向数据中心48V供电系统的混合型母线变换器及其高密度集成[J]. 中国电机工程学报, 2024, 44(16): 6578-6587.
Zhang Yu, Wu Hongfei, Li Zewei, et al. Hybrid-type bus-converter and high-density integration for data- center 48V power supply systems[J]. Chinese Journal of Electrical Engineering, 2024, 44(16): 6578-6587.
[9] 孔瑞. 基于平面磁技术的高频DC-DC变换器磁性元件优化设计[D]. 秦皇岛: 燕山大学, 2023.
Kong Rui. Optimal design of magnetic components of high frequency DC-DC converter based on plane magnetic technology[D]. Qinhuangdao: Yanshan University, 2023.
[10] Wang Jianing, Hu Jiawen, Pei Wei, et al. In-depth design and multiobjective optimization of an integrated transformer for five-phase LLC resonant converters[J]. IEEE Transactions on Power Elec- tronics, 2022, 37(11): 13538-13553.
[11] Liu Yue, Hu Dingfan, Wu Hongfei. Magnetic integration design for input-series output-parallel LLC resonant converter[C]//IECON 2023-49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, Singapore, 2023: 1-5.
[12] Rong Enguo, Li Siqi, Zhang Rui, et al. A magnetic integration half-turn planar transformer for LLC resonant DC-DC converters[C]//2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 2018: 484-488.
[13] 李紫薇. 高频DC-DC变换器中的平面磁集成技术研究[D]. 北京: 北京交通大学, 2023.
Li Ziwei. Research on planar magnetic integration technology in high-frequency DC-DC converter[D]. Beijing: Beijing Jiaotong University, 2023.
[14] Cheng K W E. Calculation of winding losses in high frequency toroidal inductors using multistrand conductors[J]. IEE Proceedings-Electric Power Appli- cations, 1995, 142(5): 313.
[15] Hurley W G, Gath E, Breslin J G. Optimizing the AC resistance of multilayer transformer windings with arbitrary current waveforms[J].IEEE Transactions on Power Electronics, 2000, 15(2): 369-376.
[16] 旷建军, 阮新波, 任小永. 集肤和邻近效应对平面磁性元件绕组损耗影响的分析[J]. 中国电机工程学报, 2006, 26(5): 170-175.
Kuang Jianjun, Ruan Xinbo, Ren Xiaoyong. Analysis of skin and proximity effects on winding losses in planar magnetic components[J]. Proceedings of the CSEE, 2006, 26(5): 170-175.
[17] Dowell P L. Effects of eddy currents in transformer windings[J]. Proceedings of the Institution of Electrical Engineers, 1966, 113(8): 1387.
[18] Wallmeier P, Frohleke N, Grotstollen H. Improved analytical modeling of conductive losses in gapped high-frequency inductors[C]//Conference Record of 1998 IEEE Industry Applications Conference. Thirty- Third IAS Annual Meeting (Cat. No.98CH36242), St. Louis, MO, USA, 2002: 913-920.
[19] 谢东冬, 谢运祥. 平面变压器寄生参数对LLC谐振变换器性能的影响分析及优化设计验证[J]. 磁性材料及器件, 2023, 54(4): 37-42.
Xie Dongdong, Xie Yunxiang. Analysis and optimi- zation design of parasitic parameters of planar transformer for LLC resonant converter[J]. Journal of Magnetic Materials and Devices, 2023, 54(4): 37-42.
[20] 王森. 基于双向CLLLC谐振的3kW储能变流器的研制[D]. 北京: 北方工业大学, 2023.
Wang Sen. Development of 3kW energy storage converter based on bidirectional CLLLC resonance [D]. Beijing: North China University of Technology, 2023.
[21] 高圣伟, 李永宵, 田金锐, 等. 双频DC-DC变换器的磁集成技术[J].电工技术学报, 2024, 39(13): 4025- 4036.
Gao Shengwei, Li Yongxiao, Tian Jinrui, et al. Magnetic integration of double frequency DC-DC converter[J]. Journal of Electrical Technology, 2024, 39(13): 4025-4036.
[22] 单鹤洋. 基于GaN HEMT功率变换器的传导EMI建模与抑制方法研究[D]. 成都: 电子科技大学, 2023.
Shan Heyang. Research on modeling and suppression method of conducted EMI based on GaN HEMT power converter[D]. Chengdu: University of Elec- tronic Science and Technology of China, 2023.
Integrated Optimization Design of LLC Four-Element-Matrix Planar Transformer Considering Loss and Parasitic Parameters
Abstract LLC converters are widely used in the power stage of battery energy storage converters due to their excellent soft switching performance and low output impedance. Under low voltage and high current conditions, matrix transformers are often used on the secondary side of LLC to reduce current stress. In practical circuits, the volume of matrix transformers accounts for about 25% of the total main power, which seriously restricts the improvement of device power density. This paper proposes an integrated optimization design of LLC four-element-matrix planar transformer considering loss and parasitic parameters. Decoupling the influence of various structural parameters of transformers on parasitic parameters this method achieves efficient operation of transformers and controllable parasitic parameters. Voltage drop and oscillation are effectively suppressed.
Firstly, establish an accurate transformer loss model based on the proposed distributed magnetic core loss calculation method. Select the key parameters of the magnetic core that meet the efficiency and volume requirements: the radius of the magnetic core's central pillar r and the total width of the winding c. Afterward, select the winding layer structure. Establish a leakage inductance model based on transformer leakage magnetic field energy, determine the feasibility of leakage inductance integration through PCB thickness constraints, and design leakage inductance values.
The experiment shows that the secondary-side Vds voltage oscillation is significantly reduced after integration optimization, reducing the parasitic capacitance value. By matching the resonant inductance to ensure that LLC operates in critical continuous mode at 300 kHz, the magnitude of the transformer's primary leakage inductance before and after integration can be calculated. The resonant inductance before integration is 1.8 mH, indicating the original edge leakage is 0.7 mH. After integrated optimization, the resonant inductance is 2.3 mH, indicating the original edge leakage is 0.2 mH. When operating in reverse, with the same input voltage of 3.2 V, the LLC output voltage rises from 34 V to 35 V. This means that the secondary edge leakage has decreased after integration. After resonance point matching, the secondary leakage inductance can be reduced from 33 nH to 12 nH. The secondary side Vds oscillation caused by parasitic capacitance is close and small, which verifies the control effect of parasitic parameters.
This method can achieve the following effects. (1) The proposed distributed magnetic core loss calculation method for planar transformers based on P-B curves eliminates the influence of uneven magnetic density distribution on the accuracy of the magnetic core loss model, achieving accurate modeling of integrated transformer losses. (2) This method provides a judgment method for the feasibility of leakage inductance integration. (3) The prototype parasitic parameters can be controlled by accurately modeling the leakage inductance and parasitic inductance. This method provides theoretical support for designing and optimizing energy storage converters in LLC low-voltage and high-current scenarios.
keywords:LLC, four-element-matrix transformers, magnetic integration, parasitic parameters
中图分类号:TM614
DOI: 10.19595/j.cnki.1000-6753.tces.240805
国家自然科学基金(62371233)、航空科学基金(2022Z024052003, 20230058052001)、2023年江苏省高等教育教改研究课题(2023JSJG441)和国家重点实验室稳定支持基金(JBS242800150)资助项目。
收稿日期 2024-05-29
改稿日期2024-07-29
姜盟瀚 男,1999年生,博士研究生,研究方向为直流变换器集成优化。
E-mail: jmq19990502@qq.com
伍群芳 男,1989年生,副研究员,博士生导师,研究方向为高效率功率变换技术、半导体器件高效驱动理论等。
E-mail: wuqunfang@nuaa.edu.cn(通信作者)
(编辑 陈 诚)