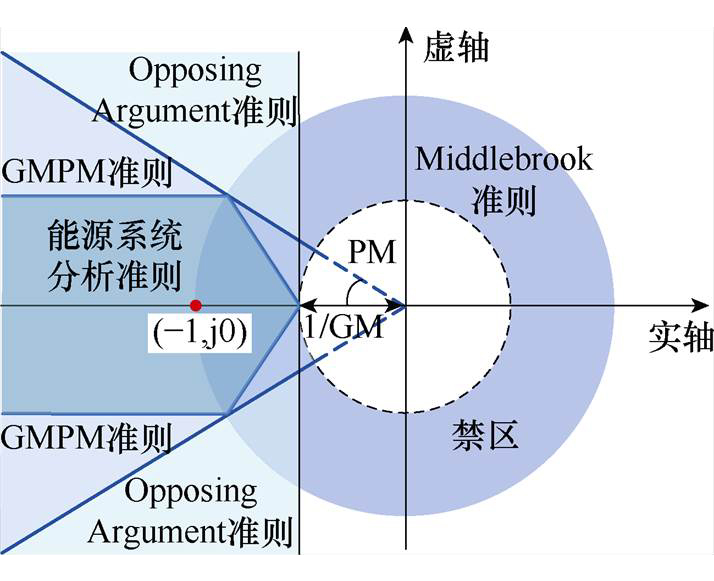
图1 不同准则的禁止区域
Fig.1 Forbidden regions of different stability criterions
摘要 传统并网变流器（GCC）控制参数设计通常在额定工况下展开，为了确保系统在非额定工况下安全运行，往往需要牺牲锁相环带宽换取稳定裕度，难以实现变流器稳定性和快速性之间的折中。此外，稳定裕度与系统输出极限的关系难以确定，二者间的定量关系依赖仿真或者实验。为此，该文提出一种基于电流稳定运行域的锁相环参数设计方法。首先，考虑控制环路之间的相互耦合，推导了复矢量开环传递函数Gs(s)，用于分析GCC不同系统参数下的稳定运行范围。其次，通过数值分析，得到了电流环与锁相环（PLL）的控制参数域，并分析了环路间耦合对锁相环控制参数取值的影响。然后，得到了不同PLL开环截止频率下GCC的电流稳定边界，并根据所需稳定运行余量选取控制参数，在保证稳定性的同时提升PLL动态性。最后，通过仿真与实验结果验证了理论分析的正确性和所提设计方法的有效性。
关键词：并网变流器 弱电网 锁相环 参数设计
为应对能源危机、推动能源结构转型，以风能、光伏为代表的可再生能源在电网中的渗透率逐渐提高[1-2]。并网变流器（Grid-Connected Converter, GCC）作为分布式能源与电网的关键接口装置，得到广泛应用。然而，由于可再生能源地理位置偏远，发电单元与电网之间的线路阻抗无法忽略，系统呈弱电网特性。在弱电网条件下，GCC的控制性能影响功率传输，甚至会对电网运行造成不利影响，因此受到了广泛关注[3-5]。
电流环和锁相环（Phase-Locked Loop, PLL）是变流器中的重要控制环节，锁相环用于跟踪公共耦合点（Point of Common Coupling, PCC）电压，电流环则参与电流反馈与控制。在弱电网条件下，电流环与PLL之间会相互耦合，影响系统稳定运 行[6-7]。此外，锁相环的负阻抗特性会减小GCC输出阻抗的幅值与相位，降低系统稳定性，甚至引起输出电流畸变、功率振荡，危害并网系统的稳定运行[8-10]。因此，合理设计PLL对提升并网变流器的控制性能具有重要意义。目前，为了提升弱电网下锁相环的性能，通常有两种实现手段：①改进PLL控制结构；②优化PLL控制参数。
一方面，通过改变锁相环控制器的结构，提升其抗干扰能力，使其在较高带宽下仍具有良好的稳定性，主要包括附加滤波器、阻抗重塑等手段。在PLL中附加滤波器可消除电网电压扰动引起的谐波，有效抑制输入干扰。典型的滤波器包括自适应谐振积分滤波器[11]、双二阶广义积分器[12]、滑动平均滤波器[13]、延迟信号抵消算子[14]等。此外，阻抗重塑也是弱化PLL负阻抗特性不利影响的有效方法。文献[15]将锁相环和直流电压环输出扰动补偿项添加到电流环控制器，减小了电网阻抗与控制器耦合的影响。文献[16-17]基于前馈控制方法，对锁相环干扰进行补偿。然而，附加环节与补偿措施会使控制结构复杂化，不利于并网系统控制参数设计，增加了并网变流器的控制难度。
另一方面，在额定工况下进行参数优化可提升锁相环的动态响应能力，降低弱电网环境带来的不利影响。文献[18-19]采用极点配置方案进行参数优化，但未知量较多且需要不断试凑。文献[20]采用根轨迹法进行参数设计，但未计及环路之间的相互耦合，且只能分析单一参数对系统的影响。文献[21]基于粒子群算法并结合特征根和振荡模态阻尼比对控制参数进行整定，但整定步骤较多。文献[22-24]提出了控制参数可行域的划分方法，得到了弱电网下满足幅值裕度（Gain Margin, GM）、相位裕度（Phase Margin, PM）、短路比（Short-Circuit Ratio, SCR）等多约束的PI参数可行域。但是，控制参数优化通常以牺牲锁相环带宽为代价换取系统稳定裕度，所得带宽往往取值较低，恶化了系统的动态 性能。
现有控制参数设计存在如下问题：①现有文献大多关注额定工作点下的参数设计，忽略了实际运行工况；②控制参数相对固定，用户难以根据对控制器动态特性和稳定裕度的不同需求分区设计参数；③参数优化往往牺牲锁相环带宽，PLL动态特性与稳定裕度难以均衡。
文献[25]提出了基于安全运行域的系统稳定性分析方法，使用数值分析法刻画了GCC不同阻抗参数下的电流稳定边界，得到了系统的电流输出极限。本文在文献[25]的基础上，开展锁相环控制参数设计工作。首先，构建了复空间矢量小信号模型，所建模型包含了工作点变量与控制参数变量。其次，通过所推导的数学模型刻画了电流环与PLL的控制参数域以及GCC输出电流稳定域。然后，运用稳定域得到了不同PLL控制参数下系统的稳定运行边界，并基于稳定运行余量设计锁相环参数。最后，根据仿真与实验验证理论分析与所提参数设计方法的有效性。
并网变流器的系统性能主要取决于物理电路和控制回路两个部分，其中，系统的响应速度与控制器参数息息相关。若控制参数设计不合理，会使得系统的响应速度较慢，降低GCC的抗干扰性能和动态性能。
现有文献通常根据准确性、稳定性、快速性等目标设计控制器参数。在建立系统小信号模型后，利用Nyquist定理、Bode图、根轨迹、仿真和实验分析GCC在该参数下的稳定性。进一步地，根据稳定裕度、电网强度、超调量等约束进行调整。然而，现有参数设计常在某一特定工况下（通常是额定工况）进行，重点分析该特定工况下系统的动态性能与稳定性。但在实际应用中，系统运行工况不断发生波动，特定工况下的系统性能难以用于表征GCC在整个运行区间的特性。同时，设计锁相环控制参数时需考虑其他控制环路对参数取值的影响，独立设计PLL控制参数会产生较大的分析误差。此外，为了保证系统在其他工况下的稳定性，通常对系统的幅值裕度和相位裕度进行设计。基于不同的PM、GM约束，划分了多种Nyquist曲线禁区，如图1所示。
图1 不同准则的禁止区域
Fig.1 Forbidden regions of different stability criterions
一方面，由GM、PM约束所得到的控制参数虽然可以提升系统的稳定性，但降低了PLL的动态性能；另一方面，稳定裕度只对最小相位系统有效，对于非最小相位系统，稳定裕度则不再具有指导意义[26]。并且稳定裕度对系统稳定性的影响缺少定量分析的方法，不同稳定裕度下GCC的极限输出需要仿真和实验才能确定。文献[27]建立了以锁相环带宽与SCR为变量的转移矩阵，可得到不同PLL带宽和电网强度下的最大有功电流，但忽略了无功分量的影响，且需要扩展模型才能考虑其他参数的影响。因此，需进一步研究稳定裕度与稳定性之间的定量关系，并探索其他方法和指标来评估变流系统的稳定裕度。
综上所述，控制参数设计需考虑控制环路间的相互耦合以及系统的运行工况，合理地设计控制参数以平衡多个方面的要求。本文所提的基于电流稳定运行域的锁相环参数设计方法，不需要试凑便可快速得到不同锁相环参数所对应的电流输出极限。在保证足够运行余量的前提下，完成参数设计，实现系统安全运行的同时提升系统的动态性能。
本节对并网系统进行小信号建模，考虑了PLL和电流内环之间的耦合对锁相环参数取值的影响，得到了可以表征并网变流系统的变系数开环传递函数，用于锁相环控制参数设计与GCC稳定性分析。
本文所研究的系统结构及其控制环路如图2所示。图2中，Vdc为变流器直流侧电压；Lf和Rf分别为变流器侧滤波器电感及其寄生电阻；Lg和Rg分别为电网阻抗中的电感与电阻；Ug为电网电压矢量；e为变流器输出电压矢量，Ut为PCC电压矢量，iL为输出电流矢量；iLd、iLq分别为电流iL的d、q轴分量，idr、iqr分别为电流d、q轴分量指令值，Utd、Utq分别为PCC电压d、q轴分量，ed、eq分别为电流环输出电压d、q轴分量；Utabc、iLabc分别为PCC处的三相电压及三相电流。本文使用的PLL为基于同步坐标系的锁相环，其控制结构如图2所示，qp为PLL输出角，w 为锁相环输出角频率，w0为额定角频率。
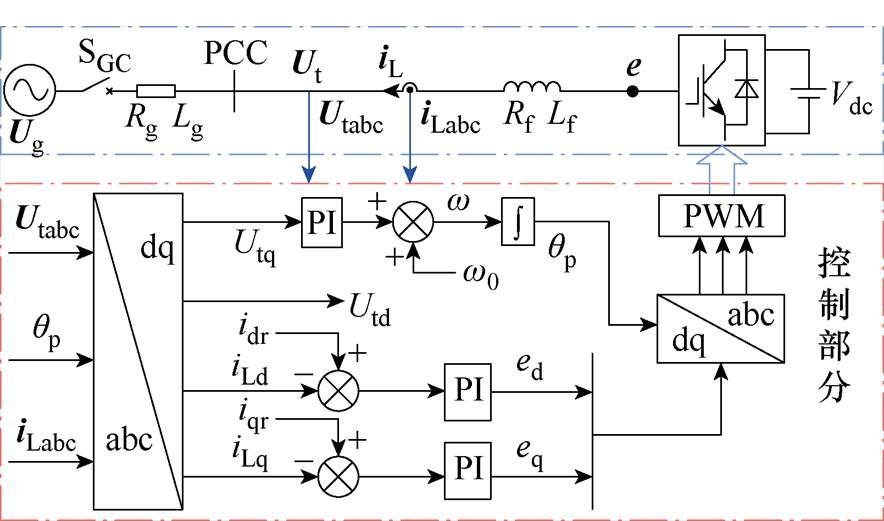
图2 三相并网变流器拓扑及控制框图
Fig.2 Topology and control block diagram of the three-phase grid-connected converter system
电流环PI控制器的表达式为
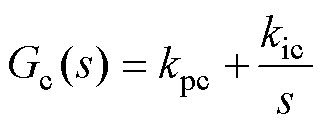（1）
式中，kpc、kic分别为电流环PI控制器的比例、积分增益。
Gde(s)为系统延时环节，可表示为
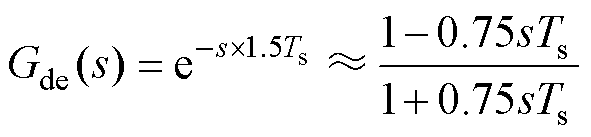（2）
式中，Ts为采样周期，Ts=1/fs。
将锁相环线性化，其模型如图3所示，qs为并网点电压实际相位，Ut0为并网点电压的稳态幅值，FPLL(s)为锁相环PI控制器，kpp、kip分别为其比例增益与积分增益。
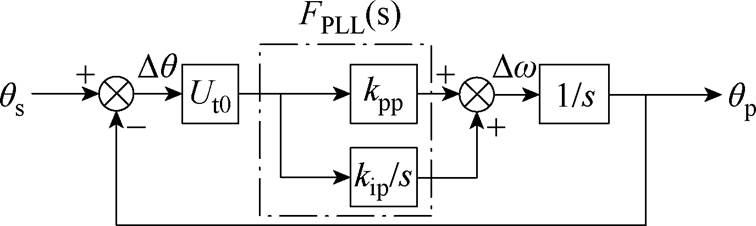
图3 PLL线性化模型
Fig.3 Linearization model of the PLL
由图3可知，PLL的开环传递函数为
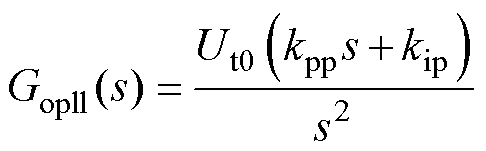（3）
在锁相环的调节过程中，由于并网点电压波动，PLL的输出角与Ut的实际位置角之间存在一个偏差角Dq。因此，系统中存在两个dq坐标系：由qp定义的控制参考系以及由qs定义的同步参考系。为了区分二者，控制参考系上标用“c”表示，而同步参考系上标用“s”表示。工作点变量x的d、q轴小扰动量在不同dq参考系下的变换关系为
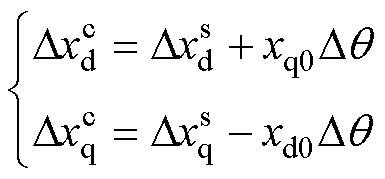（4）
式中，Dq 为控制坐标系与同步参考系之间的偏差角；Dxd、Dxq分别为工作点变量x的d、q轴小扰动量；xd0、xq0分别为电气量x的d、q轴稳态值。
式（4）用复数形式可改写为
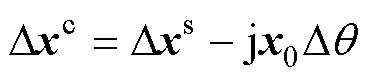（5）
式中，x0为变量x的稳态值，x0=xd0+jxq0。
并网变流器是典型的多输入多输出（Multiple Input Multiple Output, MIMO）系统，文献[25]建立了多变量复矢量单输入单输出（Single Input Single Output, SISO）模型，减少了稳定性分析的复杂性。基于文献[25]，本文推导了考虑PLL、电流环动态以及电网强度影响的系统解析表达式用于参数设计与稳定性分析。
锁相环中的线性化关系有
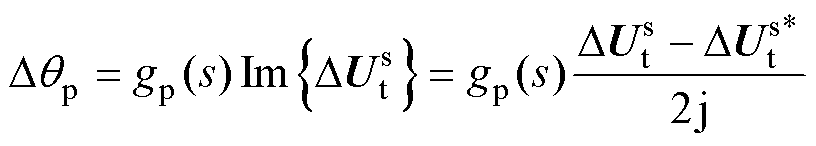（6）
式中，“*”表示共轭运算；gp(s)=FPLL(s)/(s+Ut0FPLL(s))。
在电流环中，变流器输出电压与输出电流的小扰动量之间的关系可表示为
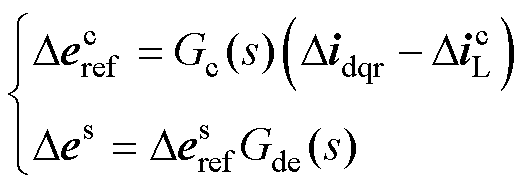（7）
式中，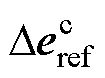
为电流环输出小扰动量；
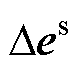为变流器输出电压小扰动量。
将两个参考系之间的小扰动量变换关系代入式（7）中，可得
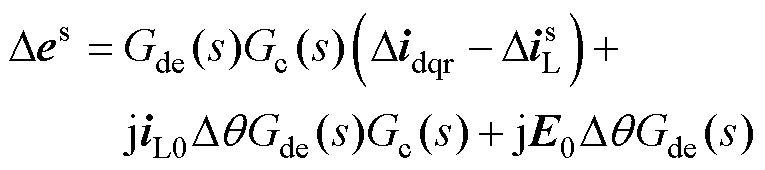（8）
式中，iL0为GCC输出电流的稳态值；E0为GCC输出电压的稳态值。
在同步参考坐标系下，物理电路中各电气参数的小扰动量之间的关系可表示为
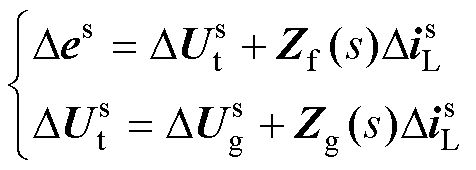（9）
式中，电网电压Ug视作为理想电源，其电压小扰动量可忽略不计，因此DUg=0。滤波阻抗Zf(s)与电网阻抗Zg(s)在dq坐标系下的表达式分别为
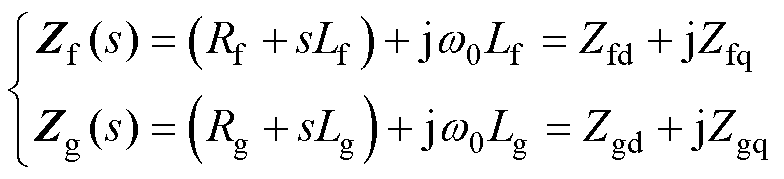（10）
将式（9）代入式（8）中，可得
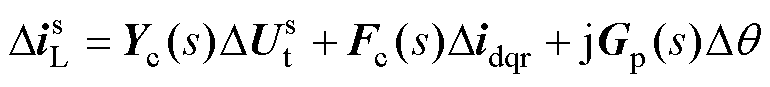（11）
其中
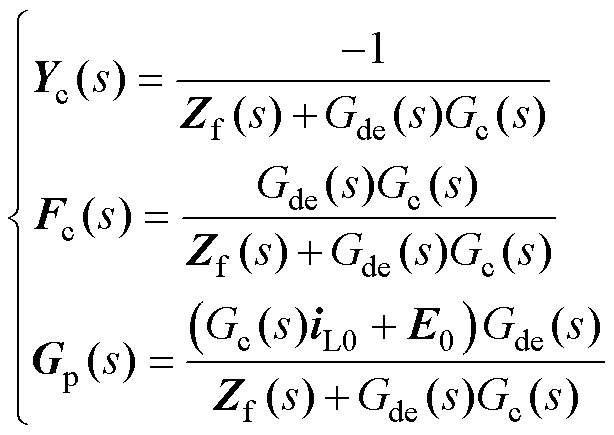
将式（6）代入式（11）中消除偏差角Dq，得
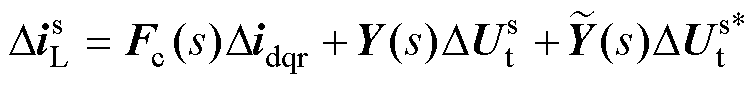（12）
其中
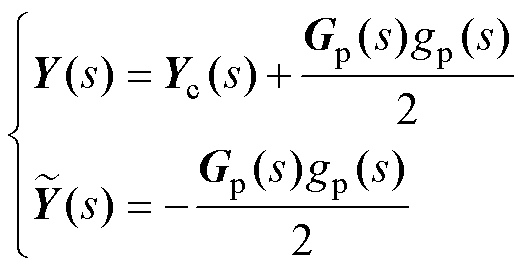
令电流参考值扰动量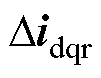
=0，由此建立了一个双输入单输出（Dual Input Single Output, DISO）模型，如图4a所示。两个输入量分别为
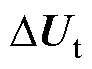和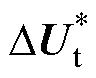
，输出量为DiL。
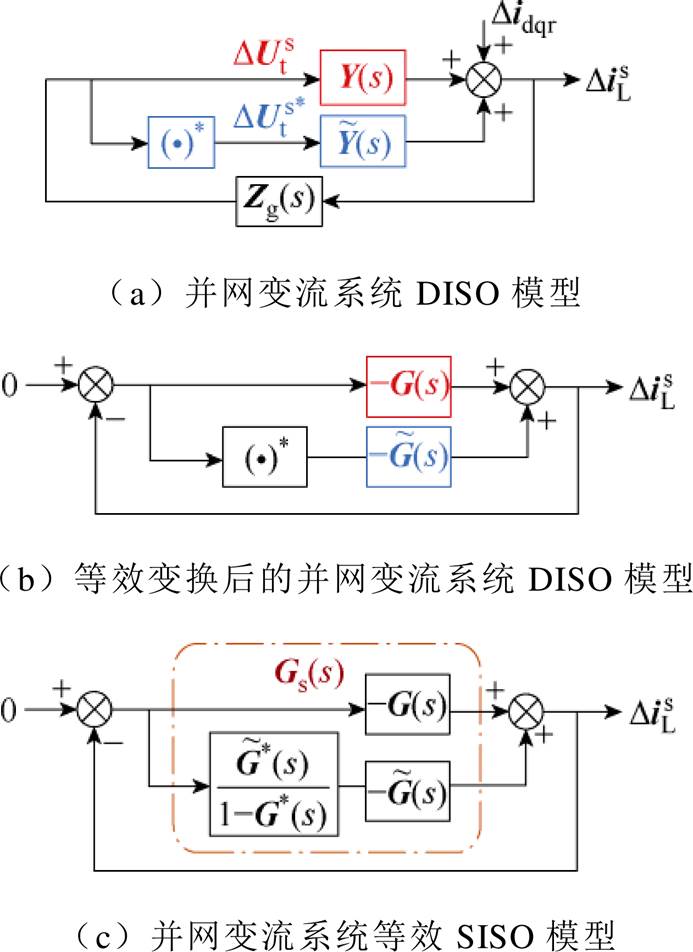
图4 并网变流系统等效SISO模型的建立
Fig.4 Establishment of the gird-connected system SISO model
进一步简化DISO模型，基于物理电路拓扑关系，将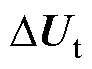和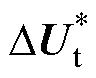用输出电流扰动量表示。消去式（12）中并网点电压扰动量后可得
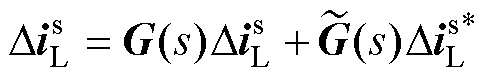（13）
其中
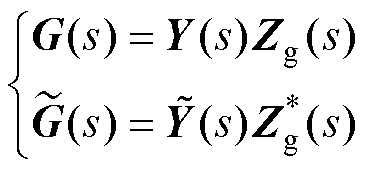
系统的两个输入量由电压小扰动量变换为电流小扰动量，如图4b所示。为了消去模型中小扰动量的共轭部分，需要得到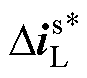
的表达式，将式（13）左右两边取共轭，可得
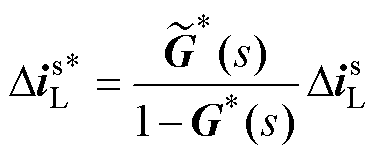（14）
需要注意的是，在求解共轭传递函数的全频率响应时，s作实数处理，因此得到共轭部分表示为
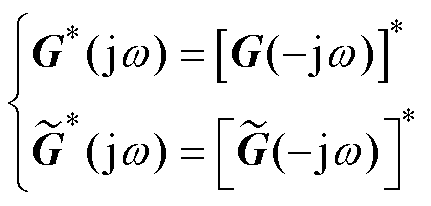（15）
将式（14）代入式（13）中，图4a由双输入单输出模型变成单输入单输出模型，如图4c所示，最后得到系统的开环传递函数为
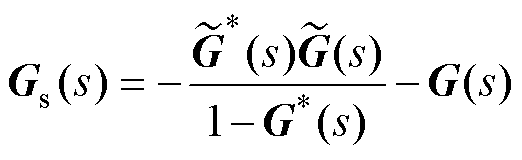（16）
与经典单边频域模型相比，复传递函数的频域响应具有双边不对称性，即w＞0时的响应通常不是w＜0时响应的共轭，复传递函数的Nyquist曲线如图5所示。其稳定性判据同样为Nyquist定理，但只有一条曲线。虽然在本文主要使用Gs(s)分析锁相环参数与电流输出极限、电流环参数与锁相环参数的关系，但该模型还可以用于研究其他参数之间的影响，如SCR与锁相环PI参数之间的约束关系、电流环参数与滤波参数优化、延时环节分析等。
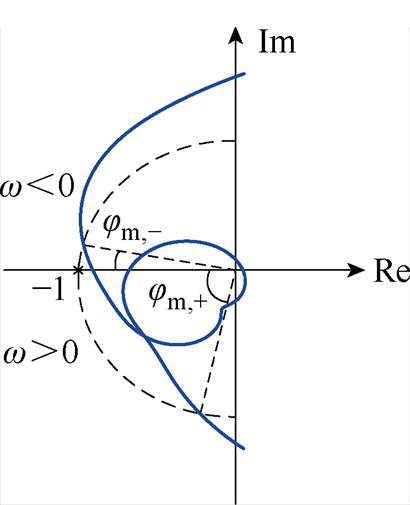
图5 复传递函数的Nyquist曲线
Fig.5 Nyquist curves of complex transfer function
本节基于所推导的复矢量开环传递函数Gs(s)开展控制参数设计。通过数值分析得到电流环-锁相环控制参数可行域，可行域的边界值为PLL参数取值上限。然而，在该组边界值下GCC的稳定裕度较低。因此，进一步刻画不同PLL参数下的稳定域，得到其稳定运行边界，并根据稳定运行余量设计PLL参数。本文中，控制参数域用于分析电流环参数对锁相环参数取值的影响，而稳定运行域则用于确定系统的稳定运行范围，保证GCC在该控制参数下具有足够的稳定裕量。
本文所提的锁相环参数设计方法步骤如下，图6给出了相应的设计流程。
（1）建立并网变流器小信号模型，得到系统复矢量等效SISO传递函数Gs(s)。
（2）求解电流环开环截止频率fci-PLL开环截止频率fcpll控制参数域。设定锁相环参数与电流环参数的分析范围，确定控制参数初始值、分析步长以及分析上限值，然后通过数值分析求解fci-fcpll控制参数域，得到给定电流环参数所对应的PLL开环截止频率的边界值。
（3）得到不同PLL参数下的稳定边界，确定控制参数取值。以第（2）步中得到的锁相环截止频率的边界值作为上限，根据稳定域的求解步骤，画出锁相环截止频率-工作点三维参数图。在三维图中，将同一fcpll数值的工作点连接起来，可得到该锁相环参数取值下的稳定运行边界。进一步地，根据所需稳定运行量确定fcpll取值，并由式（20）计算比例/积分增益，完成锁相环控制参数设计。
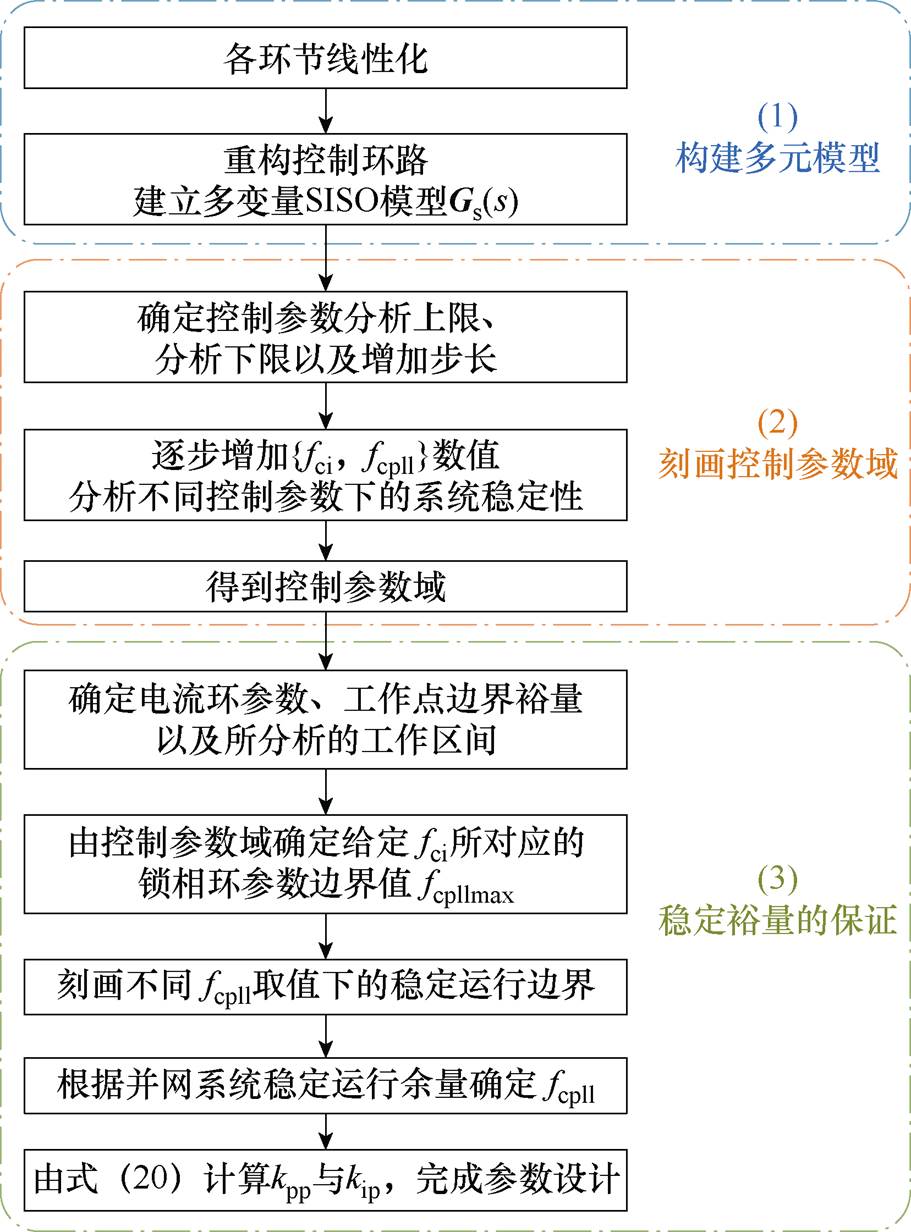
图6 控制参数设计流程
Fig.6 Flow chart of control parameter design
在后续小节中结合算例对PLL参数设计方法步骤进行详细介绍，最后综合所有设计步骤进行一个完整的锁相环参数设计。
电流环PI控制器的比例增益kpc和积分增益kic之间的关系式由文献[28]可得
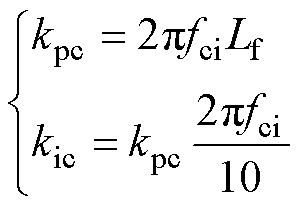（17）
式中，fci为电流环的开环截止频率。
锁相环的比例增益kpp与积分增益kip的关系由文献[29]可得
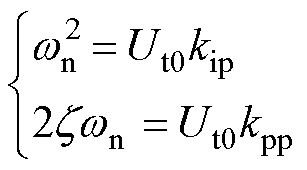（18）
式中，z 和wn分别为阻尼比和自然角频率，本文中取z=0.707。
一旦确定锁相环带宽或开环截止频率，便可相应地得到锁相环的PI参数。本文设计PLL开环截止频率为fcpll，并用fcpll表征锁相环动态响应性能。由开环截止频率的定义可得
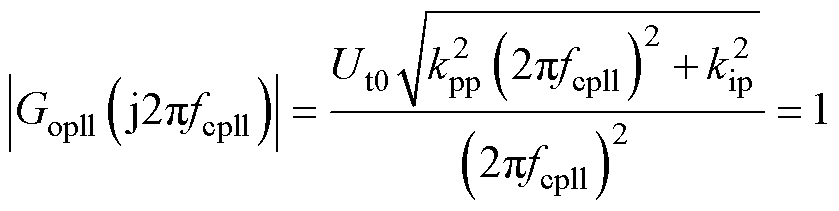（19）
根据式（18）中比例参数与积分参数的关系，可得
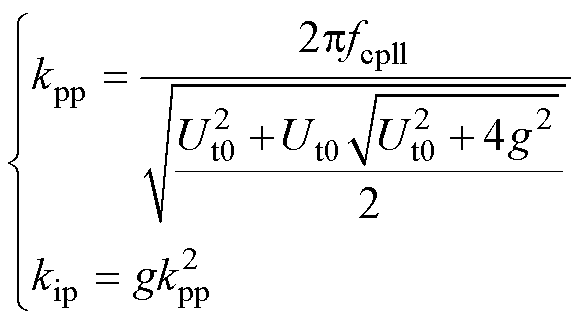（20）
式中，g=Ut0/(4z2)，由于z=0.707，则g=Ut0/2。
建立开环传递函数Gs(s)后，以fcpll、fci为变量，基于Nyqusit定理通过数值分析得到fcpll-fci控制参数可行域边界。图7为不同短路比下控制参数可行域边界，其余系统参数见表1。
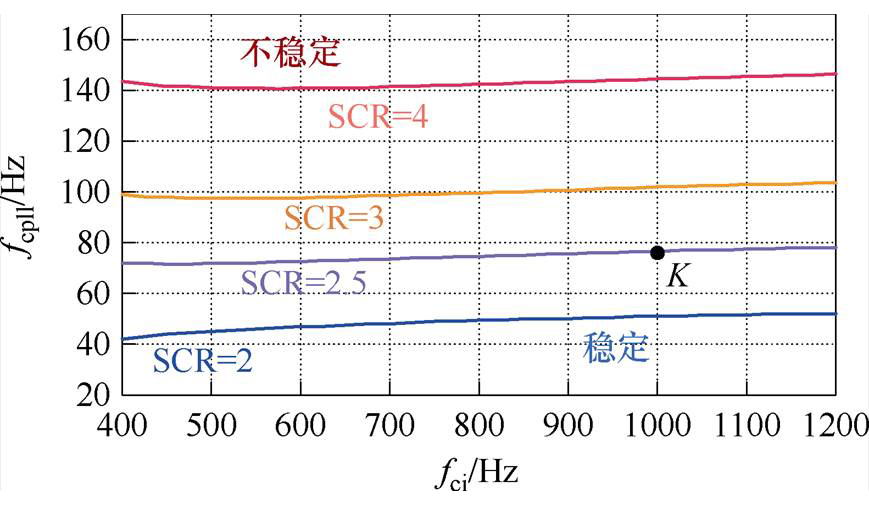
图7 系统控制参数边界
Fig.7 Boundaries of system control parameters
表1 系统额定参数
Tab.1 Rated parameters of GCC
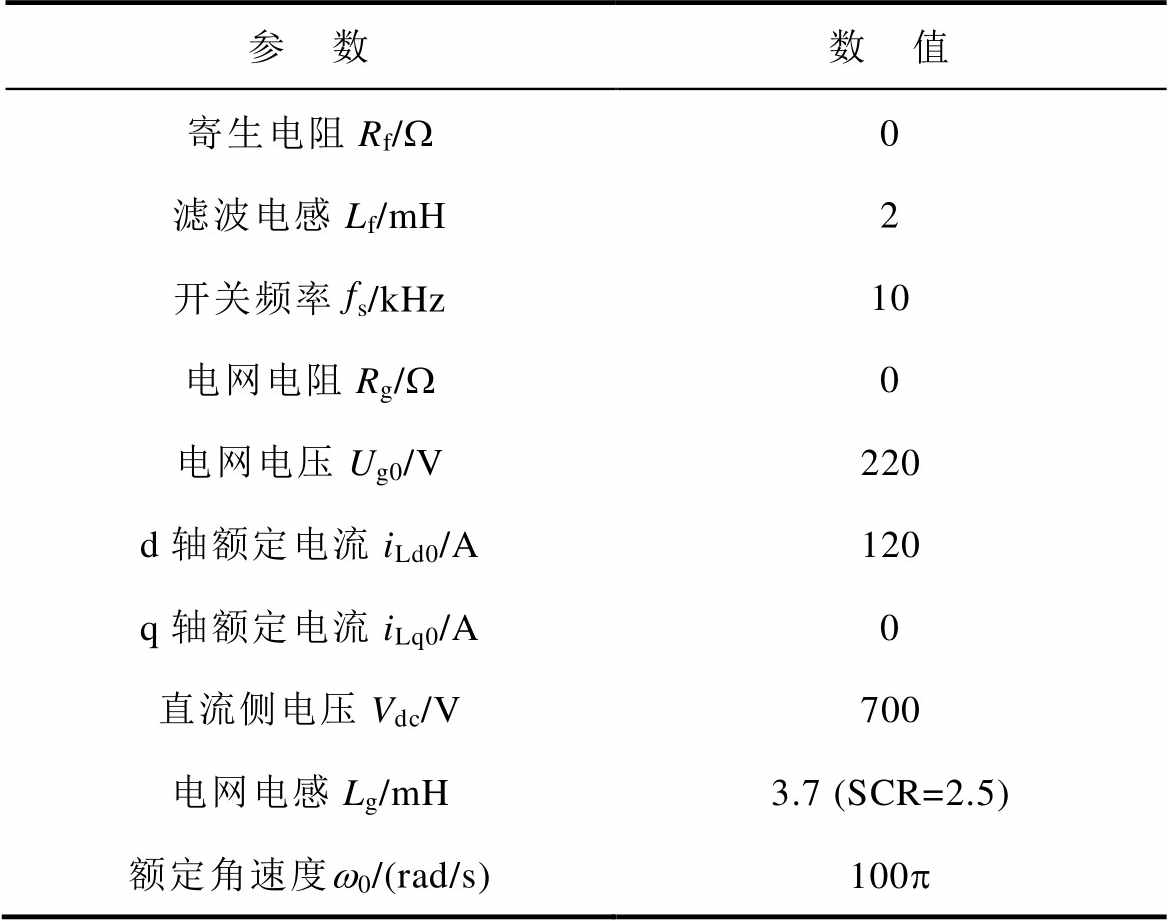
参 数数 值 寄生电阻Rf/W0 滤波电感Lf/mH2 开关频率fs/kHz10 电网电阻Rg/W0 电网电压Ug0/V220 d轴额定电流iLd0/A120 q轴额定电流iLq0/A0 直流侧电压Vdc/V700 电网电感Lg/mH3.7 (SCR=2.5) 额定角速度w0/(rad/s)100p
稳定边界之内为控制参数可行域，而边界上的点如图7中的点K，表示GCC在该设计工况下保持系统稳定的fcpll最大值。由图7可知，不同短路比（SCR）下，fcpll最大取值随着SCR的减小而减小，弱电网工况不利于系统稳定运行。
控制参数可行域能得到PLL控制参数的取值范围，但无法直接将fcpll数值设计为最大值，因为在该参数下的GCC稳定裕度较低。通过对Gs(s)的GM、PM进行设计，可保证GCC具有一定的稳定裕度。但同样地，一方面会极大地限制PLL参数取值范围；另一方面变流系统输出极限难以确定。在所有Nyquist禁区准则中，能源系统分析准则（Energy Systems Analysis Consortium, ESAC）禁区面积较小。根据ESAC禁区约束求解控制参数域，EASC准则下的参数边界如图8所示。其中SCR=2.5、GM= 6 dB、PM=30°, 60°。
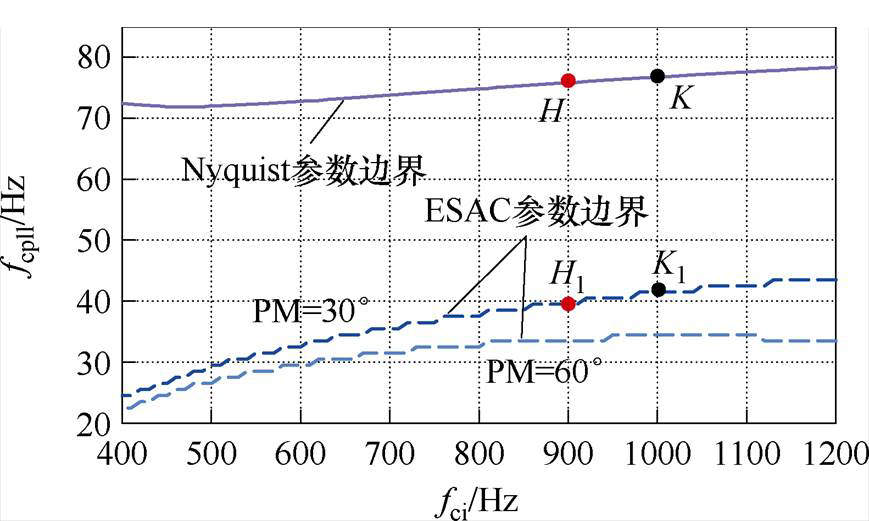
图8 EASC准则下的参数边界
Fig.8 Parameter boundaries under ESAC criteria
在图8中选取了四个边界点，其坐标值分别为：H（900 Hz, 75 Hz）、H1（900 Hz, 39 Hz）、K（1 000 Hz, 76 Hz）、K1（1 000 Hz, 41 Hz）。其中，H、K在Nyquist控制参数边界上，而H1、K1位于ESAC参数边界上。由图8可知，当电流环控制参数相同时，锁相环参数边界数值随着相位裕度的增加而减小。当fci= 900 Hz时，由Nyquist定理确定的PLL参数最大值为75 Hz，但考虑PM、GM约束后fcpll降低为39 Hz。当fci=1 000 Hz时，由Nyquist定理确定的PLL参数最大值76 Hz，而在K1点fcpll最大数值减小为41 Hz。与其他Nyquist禁区划分准则相比，ESAC的保守性更小，但是所设计的fcpll数值仍较低。开环截止频率会影响锁相环动态性能，因此在保证GCC具有足够稳定裕度的前提下提高fcpll取值具有重要意义。
现有锁相环参数设计通常在特定工作点（通常为额定工作点）下进行。然而，在实际运行时，并网变流系统的工作点不断变化。参数设计时保留的稳定裕度所对应的稳定运行范围难以确定，稳定裕度与稳定性之间缺少定量分析的方法。当偏离该特定工作点运行时，GCC的稳定性难以保证。文献[25]使用安全运行域分析GCC全工作区间的稳定性。基于稳定域开展锁相环控制参数设计，可直接得到不同稳定裕度下系统稳定运行范围的影响。同时，根据运行电流大小分区设计参数，可整体提升锁相环在全工作区间内的动态性能。
Gs(s)中嵌入了工作点变量与参数变量，为变系数传递函数。在3.2节中仅改变了控制参数值，本节中将同时改变工作点数值与控制参数值，求解系统电流稳定域得到不同PLL参数下的稳定运行边界，用于指导锁相环控制参数设计。系统稳定运行域的刻画步骤如下：
（1）构建系统复空间矢量等效SISO模型，得到开环传递函数Gs(s)。
（2）设定分析范围和分析精度，确定初始工作点、分析步长以及分析上限。
（3）确定由物理电路关系决定的系统电流传输限制域。给定工作点数值需满足物理电路拓扑约束，若不满足这一基本条件，GCC无论采用任何控制策略、任何控制参数均无法稳定运行，所选工作点不存在分析意义与研究价值。根据功率电路关系式Ugq0=-w0LgiLd0-RgiLq0，可得到约束式为
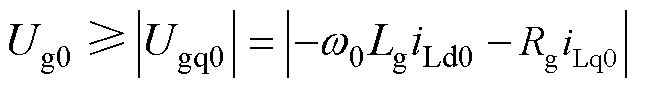（21）
式中，Ug0、Ugq0分别为电网电压的稳态幅值与其q轴分量稳态值；iLd0、iLq0分别为输出电流d、q轴分量的稳态值。
GCC电流传输限制域及稳定运行域示意图如图9所示。其中，Lml表示非定义域，在该区内的工作点不满足物理电路拓扑约束；Lde表示定义域，该域内的工作点满足电流传输限制。由图9b可知，系统稳定运行域通常由定义域与非定义域组成，而定义域中包括稳定域与失稳域两部分。
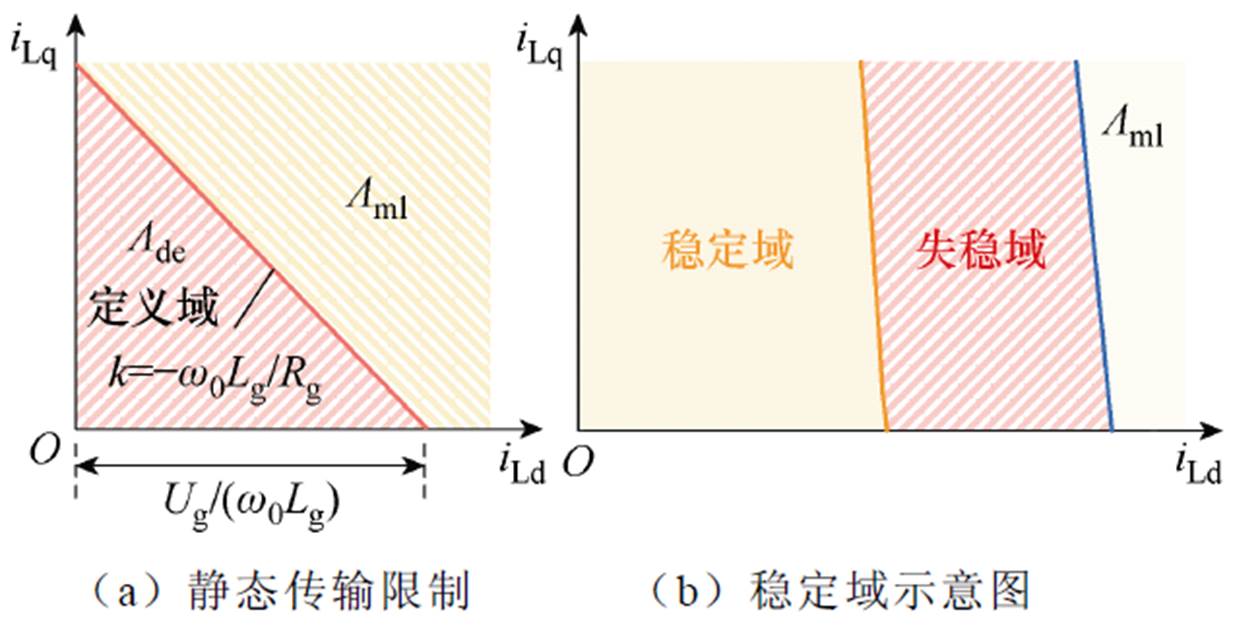
图9 变流器的静态传输限制以及稳定运行域
Fig.9 Maximum static transmission limits and stable operation domain of GCC
（4）求解不同fcpll下GCC的稳定边界，得到系统的稳定运行范围。通过求解稳定运行域，可得到并网变流器在该fcpll下的系统稳定运行范围，而工作点与稳定边界的相对位置可表征系统的稳定运行裕度。因此，本文使用稳定运行余量表征GCC的稳定裕度。为了使系统具有一定的过载能力，GCC设计时通常留有20%～50%的冗余量。因此，在参数设计时，基于有功电流、无功电流的稳定运行余量确定参数fcpll取值。运行余量可根据实际要求自行设计，且无功、有功运行余量可独立设计。本文主要开展单位功率因数下的锁相环参数设计，因此仅考虑了有功运行余量。
由图8可知，当fci=900 Hz时，fcpll最大取值为75 Hz。为了使得系统具有一定的稳定运行余量，求解了不同锁相环参数取值下的系统稳定运行边界，如图10所示。其中，X轴为输出电流d轴分量，Y轴为输出电流q轴分量，Z轴为该工作点下保持系统稳定的fcpll最大取值。图10b中，75 Hz对应Nyquist参数边界点（H点），39 Hz对应PM=30◦时ESAC边界点（H1点）。
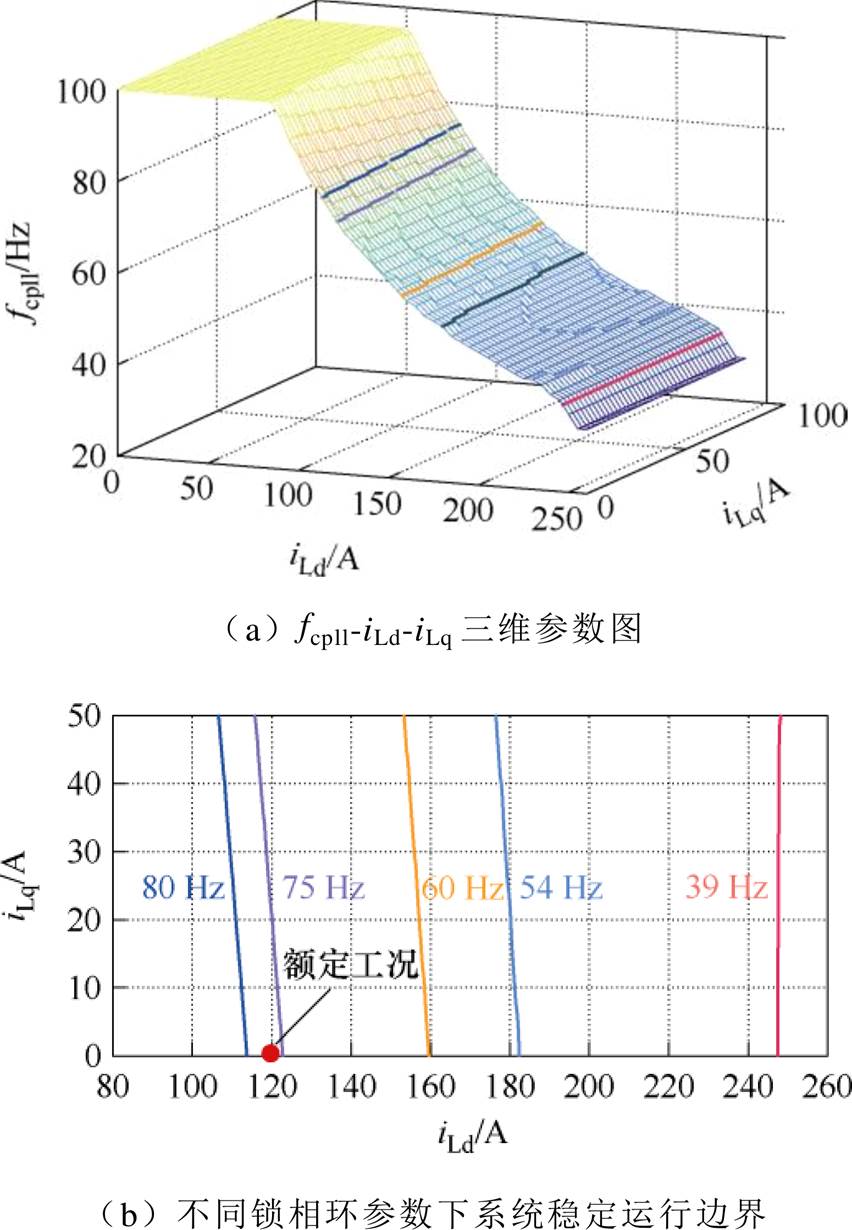
图10 系统稳定运行边界
Fig.10 Boundaries of stable operation
由图10b可知，当fcpll=75 Hz时，额定工作点在稳定域内，但离稳定边界较近；当fcpll取值超过最大值75 Hz（如fcpll=80 Hz）时，额定工作点在稳定边界的右侧，位于失稳域内。当锁相环参数取值小于75 Hz时，额定工作点与稳定边界保持一定的距离。当fcpll=60 Hz时，有功电流稳定运行余量为40 A；当fcpll=54 Hz时，有功电流稳定运行余量为61 A，具有50%的冗余量。当fcpll=39 Hz时，有功电流稳定运行余量超过了120 A，虽然具有较高的运行余量，但是牺牲了锁相环动态性能。因此，可提高锁相环参数取值。当稳定运行余量设置为20%时，PLL开环截止频率可设计为60 Hz；当稳定运行余量设置为50%时，PLL开环截止频率可设计为54 Hz。
本文以表1中的变流器锁相环参数设计作为算例。为了提升锁相环在全工作区间内的动态性能，本文将GCC全工作区间划分为轻载、中载、重载和过载四个工作区间，并对这四个区间分别开展锁相环参数设计以实现本区间稳定裕度与动态性能的均衡。以额定有功电流为基准值，这四个负载区间范围分别为：轻载区间（0～0.4(pu)）、中载区间（0.4～0.75(pu)）、重载区间（0.75～1(pu)）、过载区间（1 ～1.5(pu)）。同样地，负载区间可根据不同标准规范、设备类型、监管要求等自行划分。需注意的是，式（20）中包含并网点电压的稳态幅值Ut0，因此设计不同区间PLL开环截止频率时，Ut0需随着不同区间设计点工作电流数值的变化而变化。本文选择在区间中点工况开展锁相环参数设计，基于Gs(s)四个工作区间的控制参数边界如图11所示。
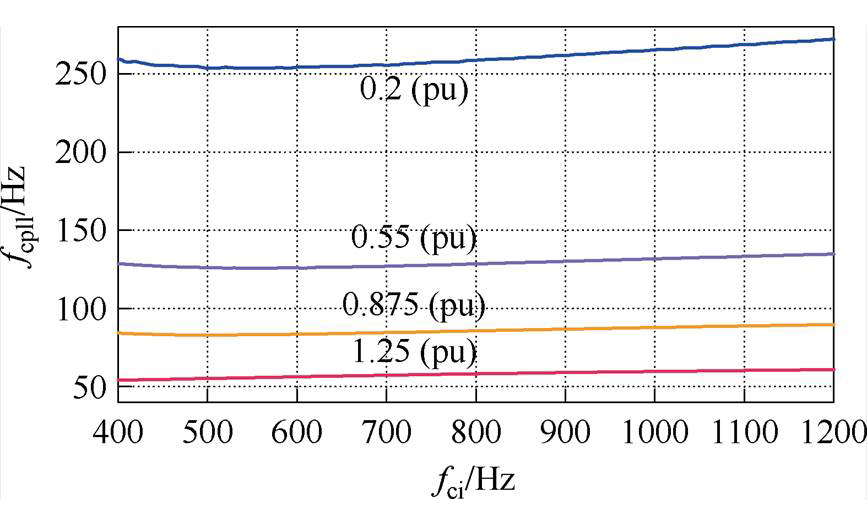
图11 不同输出电流下的控制参数可行边界
Fig.11 Feasible boundaries of control parameters under different output currents
考虑到开关频率的限制，本文中电流环参数fci= 900 Hz。在确定分析电流范围后，根据参数设计步骤确定不同区间fcpll取值。由图11可知，四个工作区间在fci=900 Hz时的锁相环边界值分别为：260、128、86、58 Hz。进一步地，求解不同锁相环参数下的系统稳定运行边界，如图12所示，最终根据运行余量设计控制参数。
在选取每个区间稳定运行余量时，以本区间最大电流作为基准值。对于中轻载负荷区间，希望锁相环具有较快的动态性能，因此运行余量取20%。由图12a、图12b可得，轻载区间锁相环参数取值为150 Hz，最大稳定运行电流约为58 A；中载区间锁相环参数取值为88 Hz，最大稳定运行电流为108 A。同样地，根据参数设计流程，重载区间锁相环参数取值为67 Hz，最大稳定运行电流为144 A。针对过载区间，由于其本身是GCC的冗余区间，因此稳定运行余量不再另取。由图12d可知，保证系统在过载区间内能稳定运行的锁相环参数最大值为50 Hz。若希望GCC稳定运行余量大于50%，可根据稳定运行边界另取控制参数值。
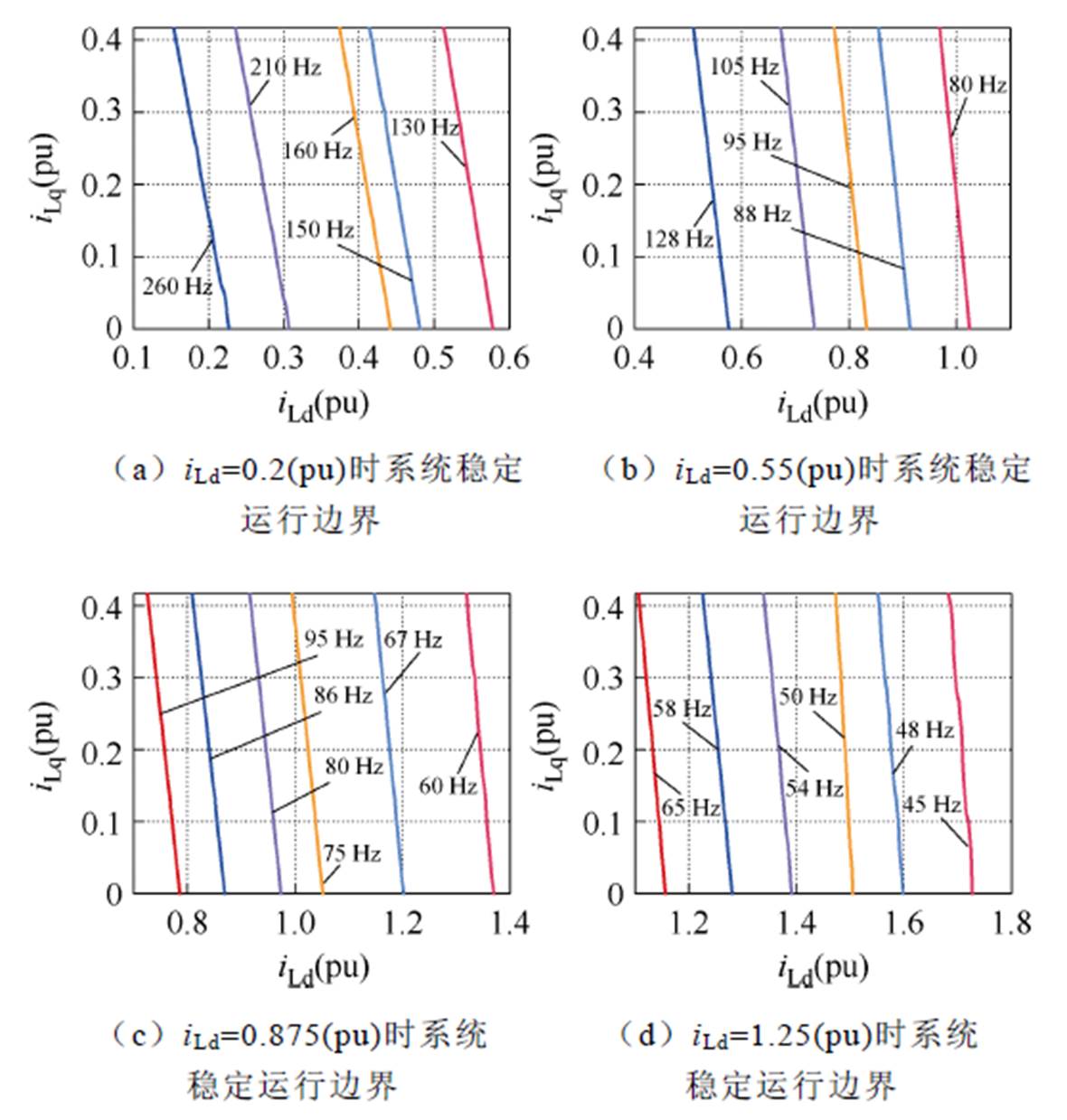
图12 不同PLL参数下稳定运行边界
Fig.12 Stable boundaries under different PLL parameters
控制理论中的PM、GM在电力电子领域中的物理意义不明晰，稳定裕度对系统极限输出的影响缺少量化表征的方法，而稳定运行域可直观表征稳定裕度对系统稳定运行范围的影响。基于稳定运行域开展参数设计，可直接得到不同控制参数下的极限输出电流，灵活设计锁相环参数，整体提升系统在全工作区间内的动态性能。
本节在Matlab中搭建了如图2所示的GCC仿真模型与小信号模型，阐明锁相环开环截止频率取值对其动态性能的影响，并验证控制参数域以及所提参数设计方法的正确性与有效性。
4.1.1 锁相环参数取值对系统动态性能的影响
在Simulink中所构建的GCC小信号数学模型如图13所示，用于分析开环截止频率对PLL动态性能的影响。图14为PLL在不同参数控制下受到两种小扰动的响应过程。其中，fci=1 000 Hz，稳态误差带设为±2%，其余参数见表1。在所选参数值中，fcpll=76 Hz与fcpll=41 Hz分别对应图8中的点K与K1。
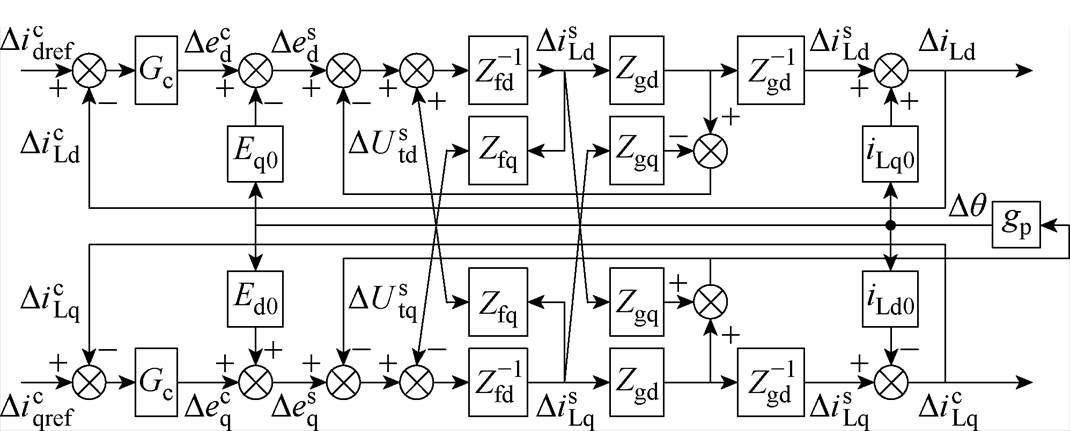
图13 小信号数学模型
Fig.13 Small signal mathematical model
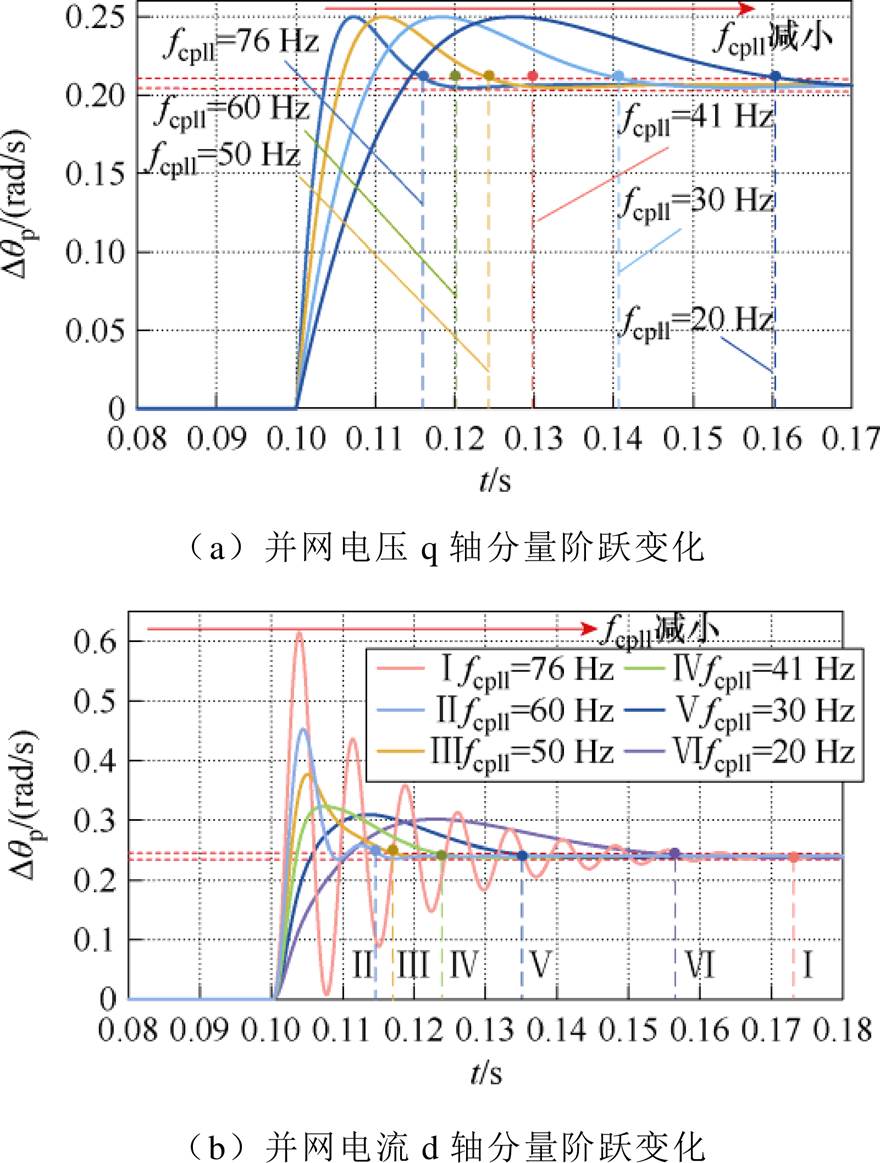
图14 锁相环的阶跃动态响应
Fig.14 Step dynamic responses of PLL
图14a中，t=0.1 s时PCC电压q轴分量Utq阶跃变化；而图14b中，t=0.1 s时输出电流d轴分量iLd阶跃变化。由图14可知，随着锁相环参数取值的降低，其动态响应时间变长。图14a中，当fcpll取最大值时，锁相环响应速度最快，其调节时间为0.016 1 s；但当fcpll取ESAC准则所得数值时，其调节时间达到为0.029 5 s，约为fcpll=76 Hz时的1.83倍。在图14b中，当锁相环参数取76 Hz时，由于该点的稳定裕度较小，锁相环经过衰减振荡后达到稳定状态，超调量较大、调节时间较长。但锁相环参数取值稍加减少后，PLL的响应速度便与开环截止频率呈正相关。当fcpll=41 Hz时，其调节时间为0.022 s，约为PLL参数取值为60 Hz时调节时间的1.56倍。通过上述分析可知，锁相环的动态响应速度与开环截止频率呈正相关，较低的锁相环开环截止频率会使得系统受到扰动时的响应时间较长。在满足稳定性的前提下增加fcpll取值，可提升并网变流器的响应速度和系统的动态性能。
4.1.2 参数设计算例仿真验证
为了验证所提锁相环参数设计方法的正确性与有效性，选择电流稳定运行域内的工作点进行仿真验证。本文主要开展单位功率因数下的锁相环参数设计，因此验证时仅考虑有功电流。观测点的选取及仿真波形如图15所示。
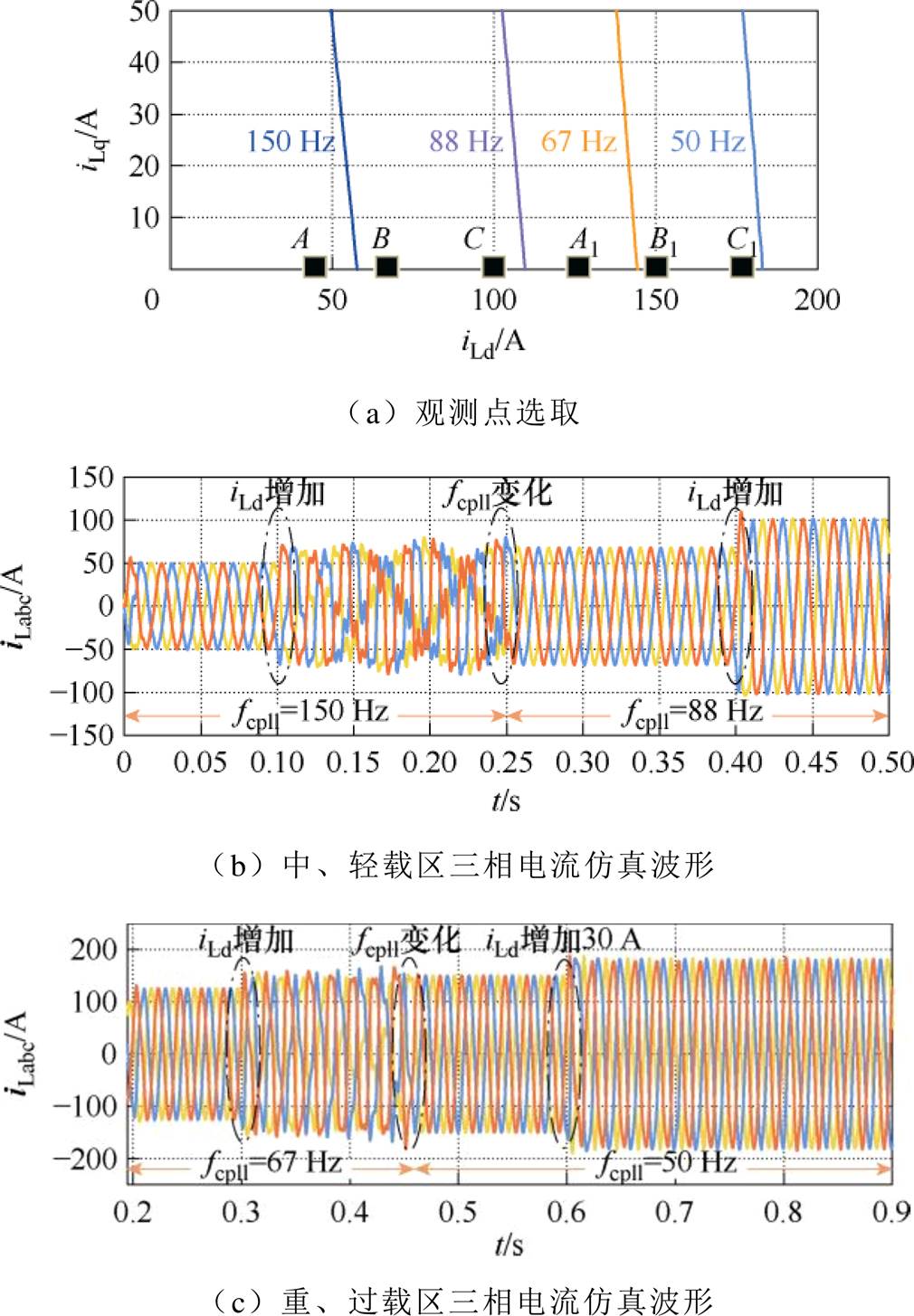
图15 观测点的选取及仿真波形
Fig.15 Selections of observed points and current simulation waveforms
图15a显示了所选择的6个验证工作点，其工作电流分别为A={48 A, 0}、B={66 A, 0}、C={100 A, 0}；A1={125 A, 0}、B1={150 A, 0}、C1={180 A, 0}。而参与仿真验证的fcpll为参数算例中4个负荷区间所设计的控制参数：fc1（0.2(pu), 150 Hz）、fc2（0.55(pu), 88 Hz）、fc3（0.875(pu), 67 Hz）、fc4（1.25(pu), 50 Hz）。在图15b中，系统初始运行于工作点A，锁相环控制参数值为150 Hz；在t=0.1 s时，有功电流增加而控制参数不变，系统运行于工作点B；在t=0.25 s时，GCC运行电流不变但控制参数减小至88 Hz；经过0.15 s后，工作电流增加34 A，系统运行于工作点C。图15c中，GCC初始运行于工作点A1，锁相环控制参数值为67 Hz；在t=0.3 s时，有功电流增加而控制参数不变，系统运行于工作点B1；经过0.15 s后，控制参数减小至50 Hz，之后数值不再改变；在t=0.6 s时，有功电流增加30 A，系统运行于工作点C1。
由图15a可知，工作点B在fc1所对应的稳定边界之外，而fc2所对应的稳定域同时包含了工作点A、B。同样地，fc3所对应的稳定域不包含工作点B1，而fc4的稳定域同时包含工作点A1、B1。在图15b、图15c的仿真波形中，当fcpll=150 Hz/67 Hz时，GCC在工作点A（A1）可稳定运行，但工作点向B（B1）迁移后，GCC的输出电流波形畸变。随着控制参数的切换，三相电流正常输出且在C（C1）仍能稳定运行。三相电流仿真波形与稳定性分析结果一致，因此，基于稳定运行域的锁相环参数设计可快速找到系统所需运行余量所对应的锁相环参数，保证GCC稳定性的同时具有较快的响应速度。
为了进一步验证本文所提控制参数设计方法的有效性，本文利用并网变流器样机开展实验验证，实验参数与仿真参数一致。
4.2.1 参数可行域边界实验验证
在图7中选取SCR=2.5时的四组控制参数在额定工况下开展实验验证，所选电流环、锁相环参数值分别为：（1 000 Hz, 75 Hz）、（1 000 Hz, 83 Hz）、（1 200 Hz, 77 Hz）、（600 Hz, 77 Hz）。图16为四组不同控制参数下的并网系统Nyquist曲线。由图16可知，在fci=1 000 Hz的情况下，fcpll取值为75 Hz时GCC由Nyquist定理判定为稳定，而fcpll=83 Hz时则判定为失稳。在fcpll=77 Hz的情况下，当fci取值为1 200 Hz时系统判定为稳定，而在fci=600 Hz时则表征为失稳。
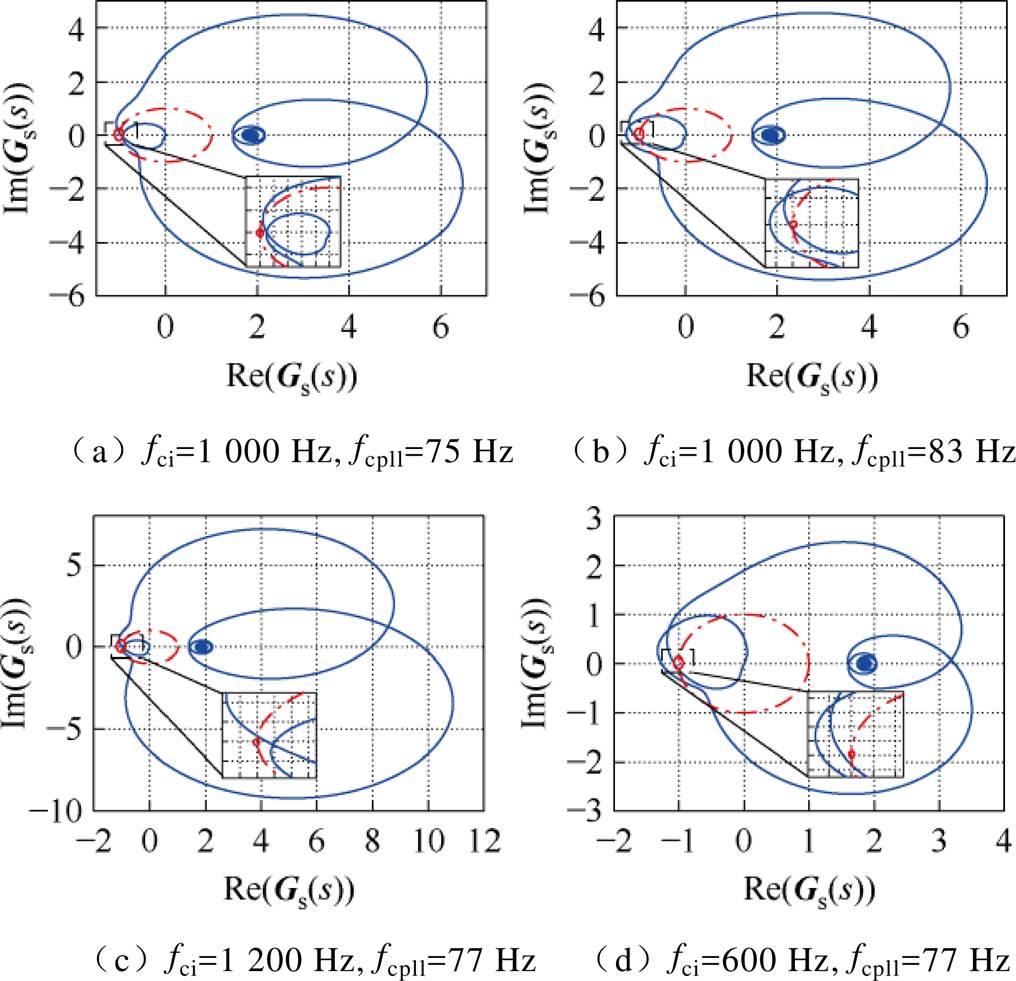
图16 不同控制参数下复传递函数的Nyquist曲线
Fig.16 Nyquist curves of complex transfer functions under different control parameters
控制参数变化时的输出电流实验波形如图17所示。图17a、图17b分别为不同锁相环参数、电流环参数下的电流d轴分量实验波形，验证时系统运行于额定工况，输出电流不变，仅切换控制参数。在图17a中，电流环参数为1 000 Hz，初始运行时锁相环参数为75 Hz，运行一段时间后fcpll增加至83 Hz。在图17b中，锁相环参数为77 Hz，初始运行时fci取值为1 200 Hz，随后减小至600 Hz。从图中可以看出，控制参数取值在可行域内时，系统能正常运行。但控制参数切换至可行边界外时，输出电流畸变振荡，并网变流系统难以稳定运行，实验结果与控制参数域的求解结果一致。
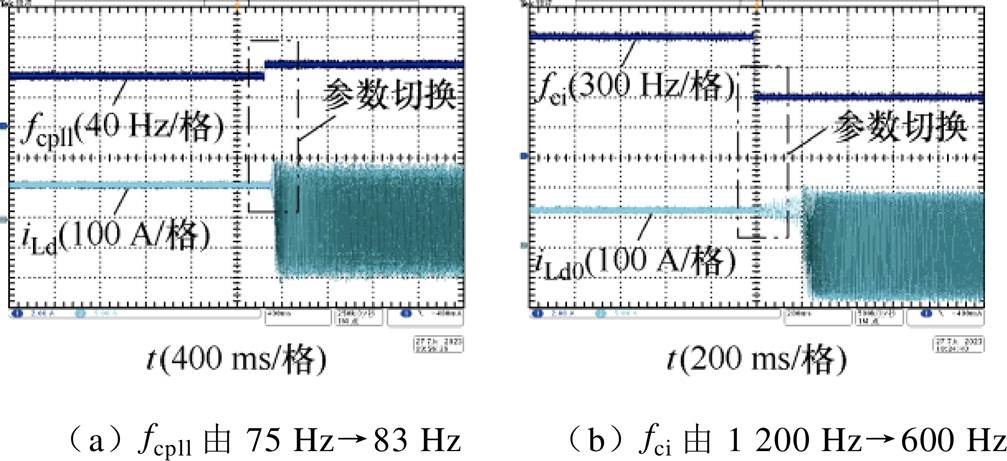
图17 控制参数变化时的输出电流实验波形
Fig.17 Output current experimental waveforms under different control parameters
4.2.2 参数设计算例实验验证
图18a、图18b分别为轻载、中载区间参数设计的实验验证波形，图19a、图19b分别为重载、过载区间参数设计的实验验证波形。在图18a、图19a中，系统分别初始运行于稳定域内的工作点A（A1），锁相环截止频率分别为150 Hz、67 Hz，运行一段时间后工况变化，工作点迁移至失稳域。图18b、图19b中锁相环截止频率分别为88 Hz、50 Hz，系统仍分别初始运行于工作点A（A1），随着时间的变化，运行电流不断增加，但始终在控制参数所对应的稳定运行边界内。
系统运行工况变化时，即使运行工作点超过所对应的载荷区间，只要工作点在锁相环参数所对应的稳定运行边界之内，变流器便可以稳定输出功率；但当运行工作点迁移至稳定运行域之外时，并网电流振荡失稳，变流器难以稳定运行。基于稳定域的控制参数设计方法，可以充分保证系统稳定性，在满足稳定裕度的同时有效弥补了仅在特定工作点设计参数的不足，提升系统动态性能。
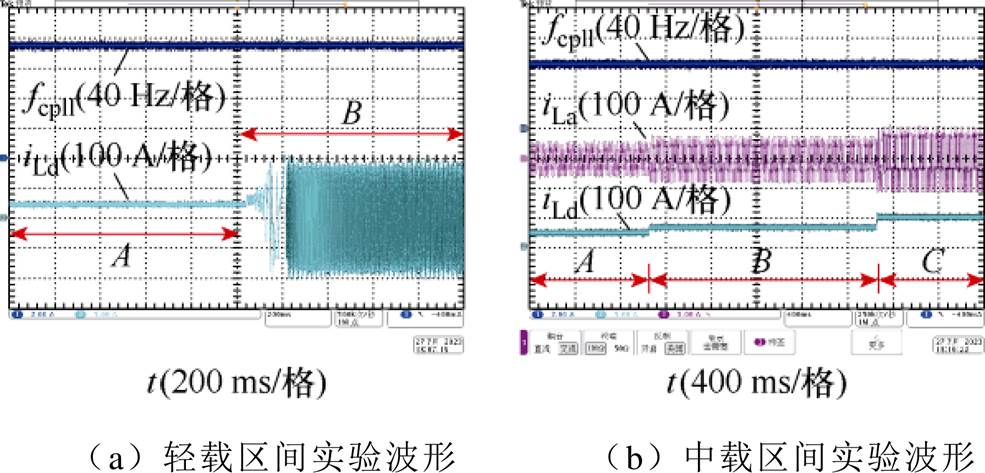
图18 中轻载区间工况变化时的实验波形
Fig.18 Experimental waveforms under variable operation conditions in medium and light load ranges
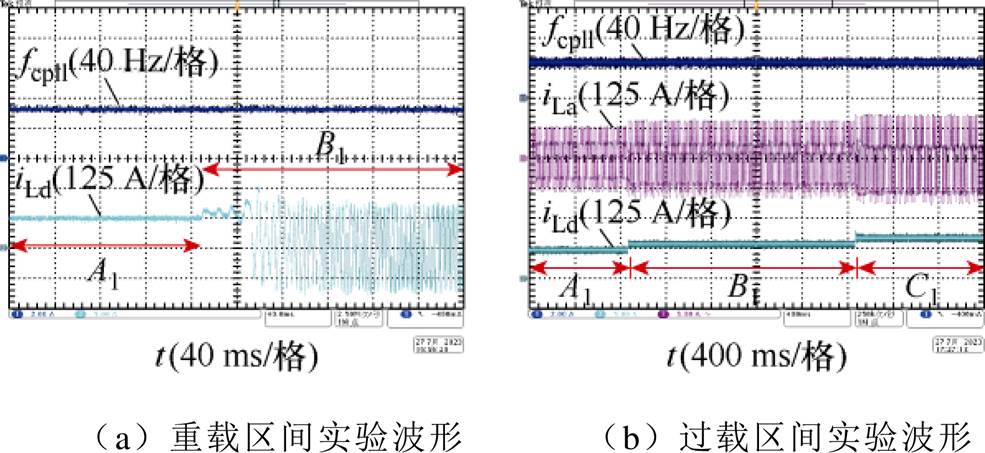
图19 重过载区间工况变化时的输出电流实验波形
Fig.19 Experimental waveforms under variable operation conditions in heavy and overload ranges
本文对并网变流系统进行建模，得到了能表征系统稳定性的开环复传递函数Gs(s)，针对锁相环动态性能与系统稳定性难以均衡的问题，提出了基于电流稳定域的锁相环开环截止频率设计方法。主要结论如下：
1）基于本文所推导的开环复传递函数，可得到电流环-锁相环控制参数域以及GCC电流稳定运行域，设计锁相环参数时不需要反复试凑，可快速得到满足稳定运行余量要求的锁相环锁参数值。
2）控制参数域与稳定运行域的分析结果可表明，电网强度与参数可行域呈正相关，锁相环开环截止频率与稳定运行域呈负相关；锁相环参数取值受电流环参数限制，且在同一电流环参数下，参数设计点的工作电流越小，所设计的锁相环参数取值更高。
3）基于稳定运行域开展锁相环参数设计，可直接定量分析稳定裕度对系统稳定运行范围的影响，同时可根据对PLL动态性能和系统稳运行余量的实际需求分区快速设计参数。
本文所提的参数设计方法只研究了电流环控制下的L型三相平衡并网变流器系统，未考虑其他控制外环或其他工况的影响。但本文提供了一套锁相环参数的设计流程以及一种稳定性分析方法，有助于提升变流器的稳定性，进一步推动变流器在工程中的应用与发展。在后续研究中，将考虑LCL型并网变流器系统，并重点关注其他控制策略以及多机并联运行等复杂情况下的参数设计。
参考文献
[1] 潘超, 范宫博, 王锦鹏, 等. 灵活性资源参与的电热综合能源系统低碳优化[J]. 电工技术学报, 2023, 38(6): 1633-1647.
Pan Chao, Fan Gongbo, Wang Jinpeng, et al. Low- carbon optimization of electric and heating integrated energy system with flexible resource participation[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1633-1647.
[2] 高锋阳, 宋志翔, 高建宁, 等. 计及光伏和储能接入的牵引供电系统能量管理策略[J]. 电工技术学报, 2024, 39(3): 745-757.
Gao Fengyang, Song Zhixiang, Gao Jianning, et al. Energy management strategies for traction power systems with PV and energy storage access[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 745-757.
[3] 高家元, 黄帅, 姜飞, 等. 弱电网下基于比例权重的控制环参数自适应调整并网逆变器稳定性提升方法[J]. 电工技术学报, 2024, 39(24): 7846-7859.
Gao Jiayuan, Huang Shuai, Jiang Fei, et al. Stability improvement method of grid-connected inverter based on proportional weight control loop parameters adaptive adjustment under weak grid[J]. Transactions of China Electro- technical Society, 2024, 39(24): 7846-7859.
[4] 曾祥辰, 刘青, 王嘉晨, 等. 弱电网下并网逆变器恒定带宽及稳定裕度的自适应控制策略[J]. 电工技术学报, 2024, 39(9): 2682-2695.
Zeng Xiangchen, Liu Qing, Wang Jiachen, et al. Adaptive control strategy of grid-connected inverters with constant bandwidth and stability margin in weak grids[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2682-2695.
[5] 高磊, 吕敬, 马骏超, 等. 基于电路等效的并网逆变器失稳分析与稳定控制[J]. 电工技术学报, 2024, 39(8): 2325-2341.
Gao Lei, LüJing, Ma Junchao, et al. Instability analysis and stability control of grid-connected inverter based on impedance circuit equivalent[J]. Transactions of China Electrotechnical Society, 2024, 39(8): 2325-2341.
[6] 韩应生, 孙海顺, 秦世耀, 等. 电压源型双馈风电并网系统小扰动低频稳定性分析[J]. 电工技术学报, 2023, 38(5): 1312-1324, 1374.
Han Yingsheng, Sun Haishun, Qin Shiyao, et al. Low-frequency stability analysis of voltage-sourced doubly-fed wind power grid-connected system under small disturbance[J]. Transactions of China Electro- technical Society, 2023, 38(5): 1312-1324, 1374.
[7] 刘昊, 方天治, 张惠丽, 等. 弱电网下应对复杂稳定性问题的并网逆变器改进电压前馈通路研究[J]. 电工技术学报, 2024, 39(16): 4955-4967.
Liu Hao, Fang Tianzhi, Zhang Huili, et al. Research on an improved voltage feedforward path of grid- connected inverter coping with complex stability issues in weak grid[J]. Transactions of China Elec- trotechnical Society, 2024, 39(16): 4955-4967.
[8] 杨苓, 陈燕东, 周乐明, 等. 弱电网下锁相环对三相LCL型并网逆变器小扰动建模影响及稳定性分析[J]. 中国电机工程学报, 2018, 38(13): 3792-3804, 4020.
Yang Ling, Chen Yandong, Zhou Leming, et al. Effect of phase locked loop on the small-signal perturbation modeling and stability analysis for three-phase LCL-type grid-connected inverter in weak grid[J]. Proceedings of the CSEE, 2018, 38(13): 3792-3804, 4020.
[9] 杨明, 杨倬, 李玉龙, 等. 高渗透率下基于并网逆变器阻抗重塑的锁相环设计方法[J]. 电工技术学报, 2024, 39(2): 554-566.
Yang Ming, Yang Zhuo, Li Yulong, et al. A phase-locked loop design method based on impedance remodeling of grid-connected inverter under high permeability[J]. Transactions of China Electro- technical Society, 2024, 39(2): 554-566.
[10] 张亚楠, 杨兴武, 徐常天. 基于环路滤波阻抗重塑的并网锁相环改进方法[J]. 电力电子技术, 2023, 57(11): 81-84.
Zhang Yanan, Yang Xingwu, Xu Changtian. Improved method of grid-connected phase-locked loop based on loop filtering impedance remodeling[J]. Power Electronics, 2023, 57(11): 81-84.
[11] 高家元, 涂春鸣, 肖凡, 等. 弱电网下基于SISO阻抗模型的LCL滤波并网逆变器在不同域下的稳定性差异分析[J]. 中国电机工程学报, 2022, 42(18): 6777-6788.
Gao Jiayuan, Tu Chunming, Xiao Fan, et al. Analysis of stability differences of LCL-filter grid-connected inverters in different domains based on SISO impedance model in weak grids[J]. Proceedings of the CSEE, 2022, 42(18): 6777-6788.
[12] 韩以鑫, 邹复民, 侯隽, 等. 两相静止坐标系下基于改进型双二阶广义积分器的锁相环控制策略[J]. 电气技术, 2024, 25(1): 23-33.
Han Yixin, Zou Fumin, Hou Jun, et al. Phase-locked loop control strategy based on improved dual second-order generalized integrator in two-phase stationary coordinate system[J]. Electrical Engin- eering, 2024, 25(1): 23-33.
[13] 周立, 刘一鸣, 刘金澍, 等. 零相位滑动平均滤波器锁相环在LCL型逆变器中的应用[J]. 电气工程学报, 2023, 18(1): 68-76, 85.
Zhou Li, Liu Yiming, Liu Jinshu, et al. Application of zero phase moving average filter in LCL inverter[J]. Journal of Electrical Engineering, 2023, 18(1): 68-76, 85.
[14] Sevilmiş F, Karaca H. Implementation of enhanced non-adaptive cascaded DSC-PLLs for renewable energy systems[J]. International Journal of Electrical Power & Energy Systems, 2022, 134: 107470.
[15] 张学广, 伏思达, 付志超, 等. 弱电网下基于电压扰动补偿的并网变换器改进控制方法[J]. 电力系统自动化, 2019, 43(18): 137-144.
Zhang Xueguang, Fu Sida, Fu Zhichao, et al. Improved control method of grid-connected converter based on voltage disturbance compensation in weak grid[J]. Automation of Electric Power Systems, 2019, 43(18): 137-144.
[16] Zhang Xueguang, Fu Sida, Chen Wenjia, et al. A symmetrical control method for grid-connected con- verters to suppress the frequency coupling under weak grid conditions[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 13488-13499.
[17] Zhang Xueguang, Xia Danni, Fu Zhichao, et al. An improved feedforward control method considering PLL dynamics to improve weak grid stability of grid-connected inverters[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 5143-5151.
[18] Turner R, Walton S, Duke R. Robust high- performance inverter control using discrete direct- design pole placement[J]. IEEE Transactions on Industrial Electronics, 2011, 58(1): 348-357.
[19] Dannehl J, Fuchs F W, Thøgersen P B. PI state space current control of grid-connected PWM converters with LCL filters[J]. IEEE Transactions on Power Electronics, 2010, 25(9): 2320-2330.
[20] 黄现莲, 冯向东. 增强变流器对电网阻抗适应性的陷波前馈控制[J]. 电气传动, 2017, 47(10): 24-28.
Huang Xianlian, Feng Xiangdong. Notch filter based grid-voltage feedforward control for enhancing grid- connected converter’s adaptive capacity to grid impe- dance variation[J]. Electric Drive, 2017, 47(10): 24-28.
[21] 黄伟煌, 李明, 郭铸, 等. 基于小干扰稳定性的多端混合高压直流输电系统控制参数分析与优化方法[J]. 电网技术, 2020, 44(8): 2941-2949.
Huang Weihuang, Li Ming, Guo Zhu, et al. Control parameter analysis and optimization method of multi-terminal hybrid HVDC transmission system based on small signal stability[J]. Power System Technology, 2020, 44(8): 2941-2949.
[22] 李明, 张兴, 郭梓暄, 等. 弱电网下基于D分割法的逆变器PI参数设计及稳定域分析[J]. 电力系统自动化, 2020, 44(15): 139-147.
Li Ming, Zhang Xing, Guo Zixuan, et al. Proportional-integral parameter design for inverter based on D-partition method and its stability region analysis in weak grid[J]. Automation of Electric Power Systems, 2020, 44(15): 139-147.
[23] Zhu Donghai, Zhou Shiying, Zou Xudong, et al. Improved design of PLL controller for LCL-type grid-connected converter in weak grid[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 4715-4727.
[24] Li Xing, Lin Hua. A design method of phase-locked loop for grid-connected converters considering the influence of current loops in weak grid[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(3): 2420-2429.
[25] 谢伟杰, 肖凡, 涂春鸣, 等. 考虑工作点时变特性的并网变流器全工作区间稳定性分析[J]. 中国电机工程学报, 2024, 44(7): 2801-2815.
Xie Weijie, Xiao Fan, Tu Chunming, et al. Full working area stability analysis of grid-connected converters considering time-varying characteristics of operating points[J]. Proceedings of the CSEE, 2024, 44(7): 2801-2815.
[26] 夏杨红, 孙勇, 韦巍. 光伏接入直流配电网时的功率振荡分析[J]. 中国电机工程学报, 2018, 38(23): 6814-6824.
Xia Yanghong, Sun Yong, Wei Wei. Power oscillation analysis of PV generators connected to DC dis- tribution network[J]. Proceedings of the CSEE, 2018, 38(23): 6814-6824.
[27] Burgos-Mellado C, Costabeber A, Sumner M, et al. Small-signal modelling and stability assessment of phase-locked loops in weak grids[J]. Energies, 2019, 12(7): 1227.
[28] Holmes D G, Lipo T A, McGrath B P, et al. Optimized design of stationary frame three phase AC current regulators[J]. IEEE Transactions on Power Electronics, 2009, 24(11): 2417-2426.
[29] Chung S K. A phase tracking system for three phase utility interface inverters[J]. IEEE Transactions on Power Electronics, 2000, 15(3): 431-438.
A Phase-Locked Loop Parameter Design Method Based on Current Stable Operation Domain of Grid-Connected Converter
Abstract Traditional control parameter design methods of grid-connected converters (GCCs) are usually carried out under rated operation conditions. The stability margin is generally characterized by the magnitude margin (GM) and phase margin (PM). The bandwidth of the phase-locked loop (PLL) needs to be sacrificed for enough system stability margin, which ensures that the system can operate safely under non-rated working conditions. Therefore, traditional parameter design methods make it difficult to achieve a compromise between the stability and rapidity of GCC. Furthermore, the relationship between the stability margin and the output limit of the system is difficult to obtain, which relies on simulations or experiments. To address this issue, this paper proposes a control parameter design method based on the system stable operation domain, which com- prehensively considers the variable working conditions and different stability requirements.
Firstly, the complex vector open-loop transfer function Gs(s) is derived, which can analyze the stability of the system in a wide operating range or under different parameters. Secondly, varying the values of the PLL and current loop control parameters, the feasible domain of control parameters can be obtained by numerical analysis. PLL and current loop are coupled to each other due to the grid impedance. Therefore, the phase-locked loop parameter has a stable parameter boundary. Thirdly, based on the upper limit of the obtained PLL parameter, the three-dimensional diagram between the PLL parameter and the output current of the dq-axis is plotted, which shows the stable operation boundaries of GCC under different PLL parameters. Finally, taking the operation margin as the stability margin, the PLL parameter can be flexibly designed to realize the balance between the stability margin and the dynamic performance. Theoretical analysis results show that the control parameter design method based on the stable domain can ensure the safe and reliable operation of the system. Compared with traditional parameter design methods, determining the value of control parameter based on operation margin can improve the dynamic performance of PLL. At the same time, the corresponding relationship between different stability margin and the output current limit of the system can be obtained. Finally, the simulation and experiment results verify the correctness of the theoretical analysis and the effectiveness of the proposed design method.
The following conclusions can be drawn from the theoretical analyses: (1) The derived open-loop complex transfer function can be used to plot the control parameter feasible domain and the stable operation domain of GCC. The PLL control parameter satisfying the operation margin can be obtained quickly without repeated trial and error in the parameter design. (2) The analysis results show that the grid strength is positively correlated with the parameter feasible domain and the PLL cutoff frequency is negatively correlated with the stable operation domain. The cutoff frequency value of PLL is limited by the current loop parameter. The smaller the operating current in the parameter design, the wider the range of PLL cutoff frequency, and the better the dynamic performance of the PLL. (3) The control parameter design method based on the stable operation domain can directly quantify the influence of stability margin on the limit of the output current, which can be used for obtaining the stable boundaries under different stability margin. At the same time, the control parameters of PLL can be flexibly designed according to the actual needs of rapidity.
keywords：Grid-connected converter, weak grid, phase-locked loop, parameter design
中图分类号：TM721
DOI: 10.19595/j.cnki.1000-6753.tces.240312
国家自然科学基金重点项目（52130704）和国家自然科学基金面上项目（52077072）资助。
收稿日期 2024-02-28
改稿日期2024-10-11
郑宇婷 女，1999年生，博士研究生，研究方向为分布式发电与电力电子技术。
E-mail: yt0107yt@hnu.edu.cn
谢伟杰 男，1995年生，博士研究生，研究方向为电力电子技术及其在电力系统中的应用。
E-mail: vijayxie@hnu.edu.cn（通信作者）
（编辑 陈 诚）