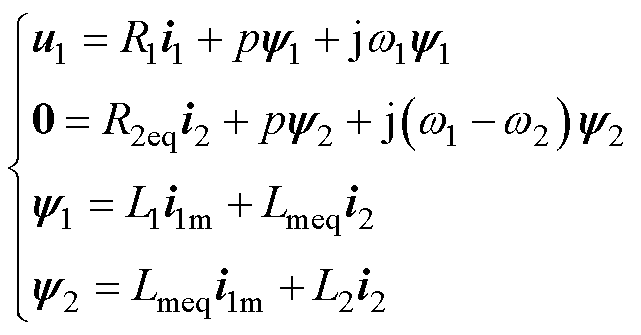（1）
摘要 因大气隙、端部效应、大功率低开关频率驱动等特点，城轨交通用直线感应电机系统运行效率偏低。现有效率优化控制策略通过损耗建模、磁链调节等过程成功提升了电机效率，但仍存在参数鲁棒性差、系统效率提升受限等问题有待解决。为此，该文针对三电平变频驱动的直线感应电机系统提出了一种适用于低开关频率的强鲁棒效率优化控制策略。首先，建立了直线感应电机初级磁链-损耗模型，分析了损耗模型参数敏感性及其局限性，进一步结合梯度下降法提出了混合式最优初级磁链搜索方法，消除了参数变化对最优磁链选择的影响；然后，推导了含初级磁链控制、开关频率约束、中点电压平衡等多个目标的价值函数，提出了基于非线性扩展状态观测器的无模型预测磁链控制，实现了低开关频率下对最优磁链的灵活调节；最后，大量实验结果表明，所提方法避免了参数变化、建模误差等在最优磁链选择和控制过程中造成的影响，有效提升了驱动系统的运行效率及鲁棒性。
关键词：直线感应电机 端部效应 效率优化 无模型预测控制 低开关频率
相较传统旋转电机牵引系统，直线感应电机（Linear Induction Machine, LIM）牵引系统可直接产生沿运动方向的电磁推力，具有选线灵活、爬坡能力强等优点，高度契合城轨交通发展需求，是直线地铁、中低速磁浮等应用的核心装备[1-2]。因其安全可靠等综合性能优良，LIM近年来得到了高度关注，是当前城轨交通领域的研究前沿和热点。同时，随着运营速度的不断提高，新建城轨交通线路大多采用DC 1 500 V供电方式，以满足大功率牵引电机需求。与两电平拓扑相比，三电平逆变器拓扑（以中点钳位型三电平逆变器拓扑最为成熟）具有输出电压正弦度高、单个功率器件电压应力小、驱动系统谐波损耗低等优点，在中压大功率牵引系统中应用广泛[3-4]。因此，三电平变频驱动的LIM牵引系统在城轨交通中具有突出的技术优势和广阔的应用前景。
然而，因初级开断，LIM运行中面临严重的端部效应：随速度增加、转差率减小，气隙磁场严重削弱，等效参数大幅变化，运行效率明显下降[5]。长期运营数据表明：城轨交通LIM运行效率偏低（额定效率仅70%左右）。同时，当前城轨交通牵引系统在额定速度以下多采用恒定励磁方式，以期获得较好的动态性能。在城轨列车巡航区间，电机长期轻载工作，恒定励磁电流将引起巨大铜耗，致使运行效率远低于额定效率。运行效率偏低已成为制约直线城轨交通快速发展和大规模应用的重要原因。
为此，相关文献提出了效率优化控制（也称最小损耗控制），以提升LIM及驱动系统的运行效率。根据技术原理的不同，效率优化控制可进一步分为模型法[6-10]和搜索法[11-12]。相比模型法，搜索法不受模型误差、参数变化等影响，参数鲁棒性更强，但也存在迭代收敛时间较长、搜索初期推力波动较大等不足[12]。然而，无论哪一类方法，现有效率优化控制都以矢量控制为基础对最优控制量（如磁链等）进行调节。在城轨交通等大功率应用场合中，逆变器开关频率仅数百赫兹，常规矢量控制及其脉宽调制方法将导致系统谐波损耗大幅增加、稳动态性能明显恶化[13]。同时，受控制自由度限制，三电平逆变器的输出电流、中点电压平衡以及低开关频率等控制目标之间相互影响和制约，加之低开关频率下模型离散化等问题，在常规矢量控制架构下开展大功率三电平牵引系统的效率优化难度极大。
不同于矢量控制，模型预测控制省略了调制环节，将电机和逆变器作为整体，结合价值函数确定最优电压矢量，只在需要时切换开关状态，能以更少的开关切换实现同样的控制性能，为大功率牵引系统提供了另一种控制方案[14]。文献[15]通过预定义的开关表确定预测控制的拟作用电压矢量，在开关频率600 Hz以内表现出良好的稳动态性能。文献[16]采用模型预测控制实现了电机高采样频率下的低开关频率运行，避免了传统低开关频率实现方法存在的模型离散困难、观测器稳定性差等问题。特别地，当采用预测磁链控制（Predictive Flux Control, PFC）时，初级磁链幅值可视为控制中的另一自由度，在相同的速度和负载条件下通过调节磁链幅值可实现损耗调节[17]。为此，文献[18-19]结合最大推力电流比（Maximum Thrust Per Ampere, MTPA）条件推导了初级磁链的参考幅值，采用PFC实现磁链调节，有效降低了电机铜耗。文献[20-21]推导了电机损耗最小的最优磁链，并结合PFC实现了电机效率优化。文献[22]对电机的谐波损耗进行分析建模，进一步提出了考虑谐波损耗的PFC，实现了磁场调制电机效率的提升。为减小铁耗建模偏差影响，文献[23]将上述两类参考磁链计算方法结合，在低速和高速时分别采用MTPA和损耗模型推导参考磁链幅值，同时在价值函数中引入开关动作项调节逆变器损耗，降低了全速度范围内的系统损耗。文献[24]以PFC为架构开展LIM效率优化，保证了低开关频率下驱动系统的稳动态性能，并通过降低谐波损耗实现了电机效率的进一步提升。然而，由于最优磁链的计算及控制均易受到参数、最优磁链难以计及逆变器损耗等因素的影响，该方法仍存在参数鲁棒性较差、系统效率有待进一步优化等问题。
鉴于此，本文针对三电平变频驱动的LIM系统，提出了一种适用于低开关频率的强鲁棒效率优化控制策略。首先，建立以初级磁链为单一优化变量的LIM损耗模型，分析了损耗模型参数敏感性，并指出该模型在实施驱动系统效率优化方面的局限性，进一步结合梯度下降法提出了混合式最优初级磁链搜索方法，消除了参数变化对最优磁链选择的影响；然后，推导了含初级磁链控制、开关频率约束、中点电压平衡等多个目标的价值函数，设计了开关频率自适应调节方法，提出了基于非线性扩展状态观测器的无模型预测磁链控制，实现了低开关频率下最优磁链的灵活调节；最后，大量实验结果表明，相比现有方法，所提方法避免了参数变化、建模误差等在最优磁链选择和控制过程中造成的影响，有效提升了驱动系统的运行效率及鲁棒性。
图1所示为同步坐标系下考虑铁损电阻的LIM等效电路，该电路采用四个修正系数Kr、Kx和Cr、Cx将纵向边端效应和横向边缘效应（后文统称“端部效应”）等效为参数的非线性变化[25]。基于该等效电路，可将LIM在同步旋转坐标系的数学模型表示为
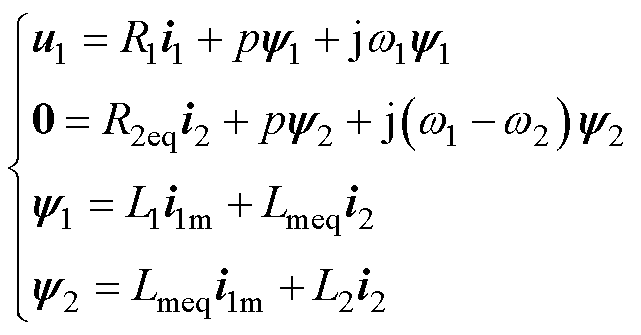（1）
其中
i1m=i1-ic Lmeq=KxCxLm0 R2eq=KrCrR20
式中，u、i、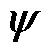
分别为电压、电流和磁链矢量；下标1和2分别为电机的初级和次级变量；R和L分别为电阻和电感；w1和w2分别为初级磁链角速度和次级角速度，w2=v2p/t，其中，v2为线速度，t 为电机极距；p为微分算子；i1m为初级漏感支路的电流；ic为铁损支路电流；Lmeq、R2eq分别为经过系数修正的等效励磁电感和次级电阻；Lm0和R20为电机静止时的参数。
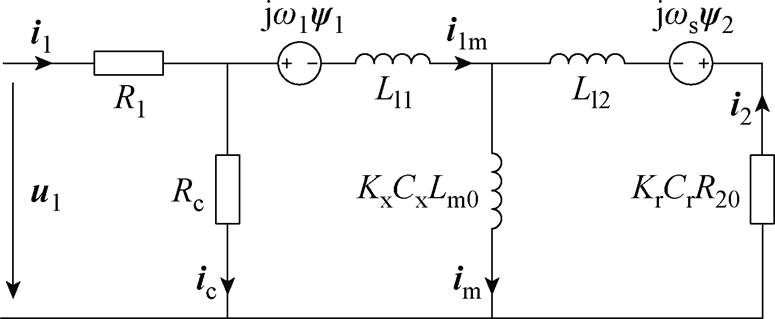
图1 同步坐标系下含铁损电阻的LIM等效电路
Fig.1 Equivalent circuit of LIM in synchronous coordinate considering core loss
图1中，铁损支路的电压和电流方程满足
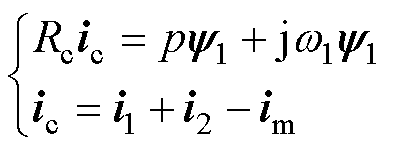（2）
式中，im为励磁电感支路电流；Rc为铁损电阻。
电机的推力方程可表示为
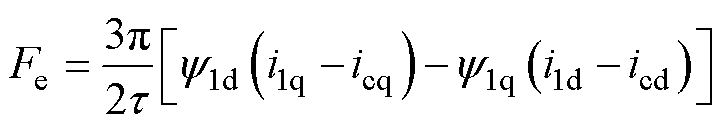（3）
中点钳位（Neutral Point Clamped, NPC）型三电平逆变器的拓扑如图2a所示。在不同的开关状态下，每一相可分别接在直流母线的正极（P）、负极（N）或中性点（O）上。如图2b所示，通过不同的开关组合，NPC型三电平逆变器可产生27个离散电压矢量。根据幅值大小分为四组：大矢量{u1, u3,…, u11}、中矢量{u2, u4,…, u12}、小矢量{u13, u14,…, u24}和零矢量{u25, u26, u27}。
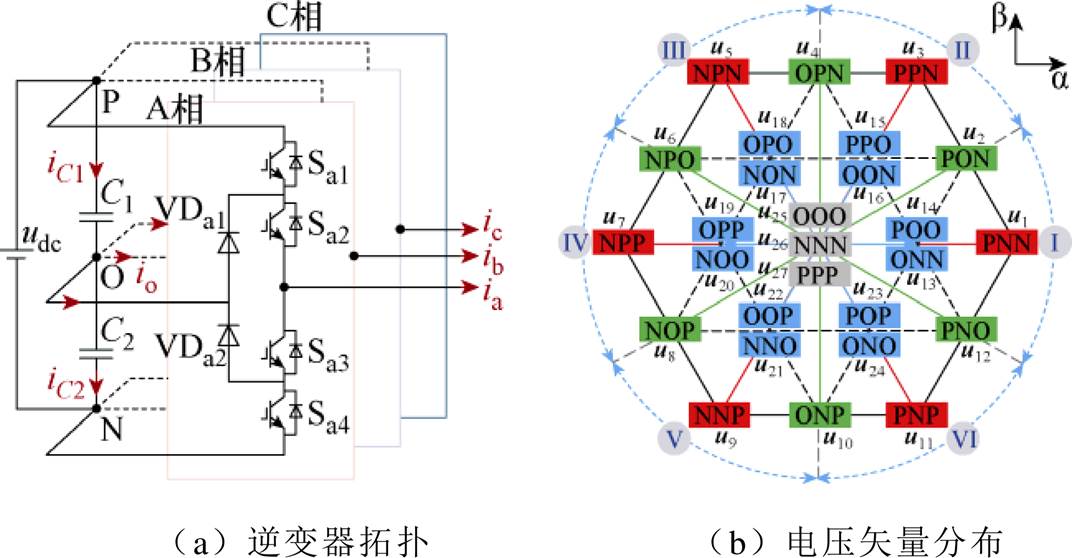
图2 NPC型三电平逆变器拓扑及空间矢量分布
Fig.2 Three level-NPC inverter topology and space distribution of all the voltage vectors
与两电平逆变器相比，NPC型三电平逆变器由于中性点引出，其中点电压在运行中将出现波动，继而引起电流和推力波动，甚至影响安全运行。为此，需要对中点电压进行控制，定义[26]为
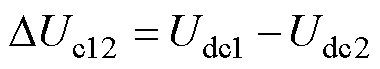（4）
式中，Udc1和Udc2分别为直流母线上、下两个电容的电压。在图2a中，基于电路基本原理，可以将k+1时刻的中点电压表示为
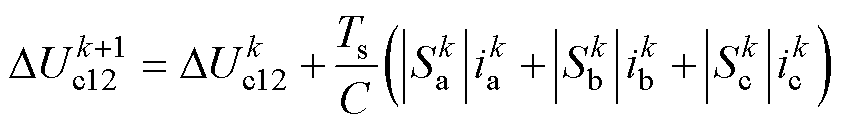（5）
式中，Sn、in（n=a, b, c）分别为各相的开关状态和电流；上标k和k+1分别代表第k和k+1时刻；C=C1=C2为直流母线上下两个电容的容值；Ts为采样周期。在本文中，分别用1、0和-1来表示开关状态P、O、N。
LIM可控损耗包含初、次级铜耗与铁耗，可表示为
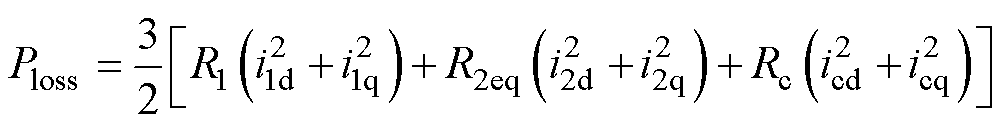（6）
由于城轨交通LIM气隙大，平均磁通密度较低，因此磁饱和现象在本文研究中未予考虑。出于以下三方面考虑，本文选择初级d轴磁链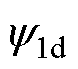
作为损耗建模的优化变量：①初级磁场定向下初级q轴磁链为零，可将电机损耗模型化简为关于初级d轴磁链的函数；②在初级磁场定向下铁损支路稳态电流计算可得到明显简化，有利于降低损耗模型阶次和最优磁链计算复杂度；③本文采用的PFC架构以初级磁链作为控制量，直接推导最优初级磁链，可避免其他优化变量向初级磁链转化时的额外推导和不必要简化。
考虑初级磁场定向（=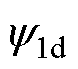
, 
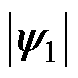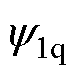=0），可从式（2）中推导得到稳态条件下铁损支路电流的dq分量满足：icd=0，icq=
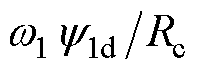。在此基础上，进一步结合式（1）和式（3）中电压、磁链和推力的基本关系，将初级电流的d、q分量表示[24]为
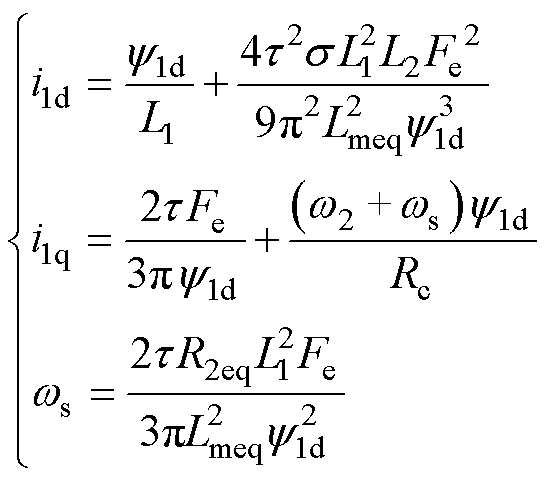（7）
其中
s=1-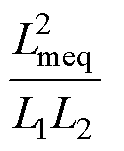
式中，s 为漏感系数；ws为转差率角速度。关于次级电流，可进一步结合输出功率表达式寻找与初级磁链的关系。LIM的输出功率可表示为
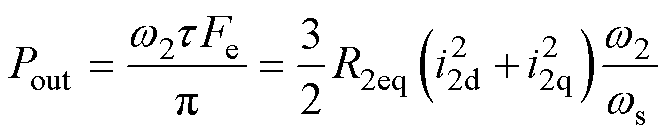（8）
将式（7）中的转差率角速度代入式（8），可建立次级电流和初级磁链的关系为
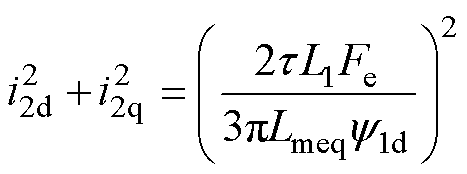（9）
将式（7）和式（9）代入式（6），化简整理可将电机可控损耗表示为初级磁链单一变量的函数，有
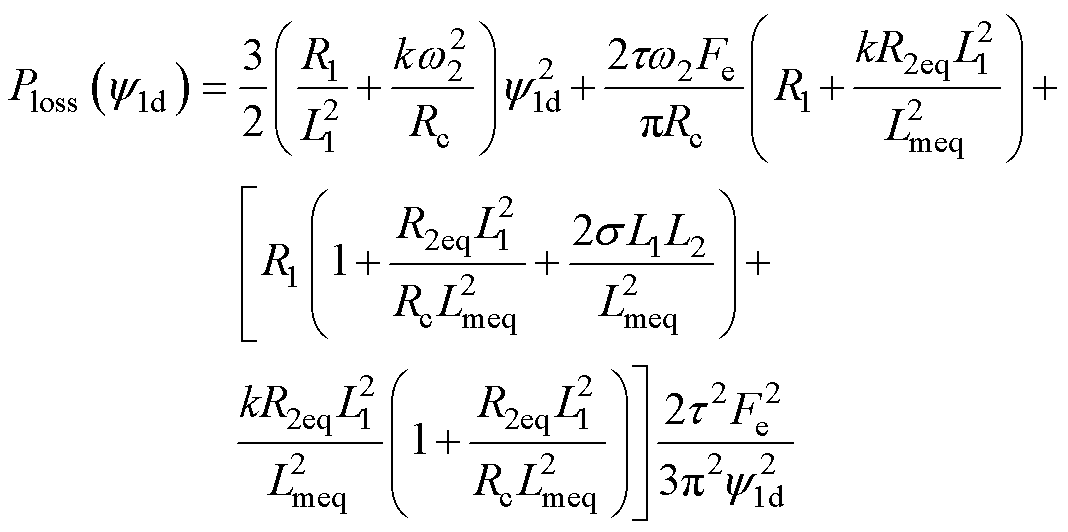
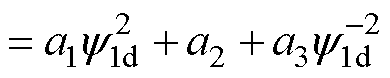（10）
其中
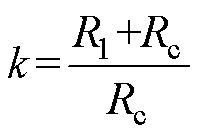
式中，a1、a2和a3为损耗系数，用于简化表达式。令式（10）的一阶导数为0，可得电机损耗最小对应的最优初级磁链解析表达式为
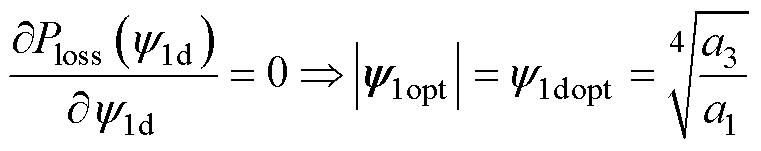（11）
式中，y1opt为最优初级磁链矢量；y1dopt为最优初级磁链矢量的d轴分量。
结合当前时刻电机速度和推力，可根据式（11）计算出理想情况下电机损耗最小对应的初级磁链，之后可进一步配合控制策略实现电机的效率优化。
从式（10）和式（11）可知，该最优磁链的计算过程需要同时使用电机初、次级电阻及电感等参数。然而，受端部效应影响，LIM的励磁电感和次级电阻等关键参数将随运行工况（速度、转差率等）发生明显的非线性变化，可能导致最优初级磁链计算结果与理论值存在偏差，进而影响效率优化策略的实施效果。为定量分析各参数影响，本文将参数偏差对初级磁链和电机损耗造成的影响定义为
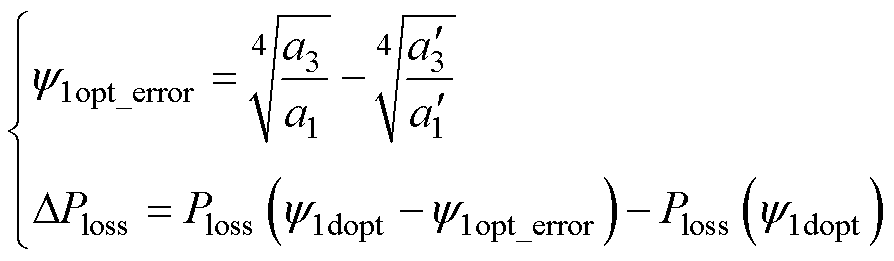（12）
式中，上标“'”表示参数存在偏差时的各个变量。
针对式（12），采用后续实验样机参数（见表1），绘制出不同速度和负载下各参数偏差的影响，如图3所示。从图3可以看出，初级电阻、次级电阻和励磁电感的变化均对最优磁链计算有较大影响，且影响程度随负载的增加而变大。以偏差的初级磁链作为参考值作用于电机系统后，将进一步导致电机损耗的增加。
图3 LIM初级磁链-损耗模型参数敏感性分析
Fig.3 Parameter sensitivity analysis of the primary flux-based LIM loss model
同时，除参数非线性变化所导致的最优磁链偏差外，仅以式（11）计算的最优初级磁链作为磁链参考值实施效率优化还存在如下不足之处：
（1）变频供电的LIM驱动系统受脉宽调制电压激励、非均匀磁路等影响，其输入电压（电流）中含有时间谐波，并在气隙中感应出丰富的空间谐波，上述损耗建模仅考虑基波损耗，在低开关频率等谐波较大工况下最优磁链将与实际情况存在一定偏差。
（2）逆变器损耗与初级磁链单一变量的映射关系难以建立，在城轨交通等大功率系统中逆变器损耗占比增加，上述最优磁链难以保证系统效率最优。
因此，有必要对基于电机初级磁链-损耗模型获取最优磁链的方法进行优化，在提升其参数鲁棒性的同时完善损耗建模中存在的不足。
针对上述不足，本文将损耗模型法与梯度下降法结合，动态时以前者计算结果作为磁链参考值保持系统快速响应能力，稳态时以前者计算结果作为搜索初值，加快搜索过程、减小搜索初期波动，以逆变器直流母线电流最小作为搜索目标，充分发挥各自优势，实现驱动系统效率优化。
为避免在逆变器直流母线侧额外安装电流传感器获取电流，本文根据电机相电流和本控制周期开关状态重构直流母线电流。针对图2a所示的NPC型三电平逆变器，直流母线电流idc可重构为
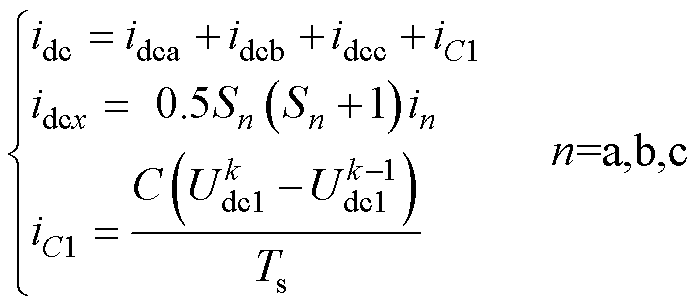（13）
式中，idcn（n=a, b, c）为逆变器各相上桥臂功率器件流过的电流；iC1为流过电容C1的充放电电流。
首先根据电机速度与指令值的偏差判断系统状态，当检测到系统进入稳态后，初级磁链参考值将通过梯度下降法更新为
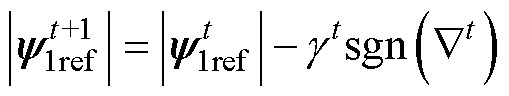（14）
式中，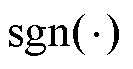
为符号函数；上标t代表搜索过程中的第t个磁链更新周期；
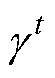为初级磁链参考值变化步长；
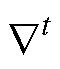为直流母线电流梯度，定义为
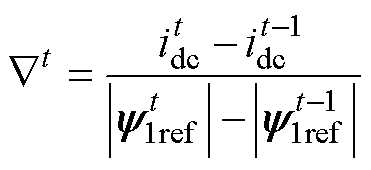（15）
由于LIM惯量较大，每一次迭代调整控制量后电机恢复至稳态的时间更长，因此本文将搜索法的磁链更新周期设为0.9 s，以使各个物理量能在初级磁链变化后稳定。在该更新周期内，为确保直流母线电流反映正确的变化趋势，仅将磁链更新0.5 s后重构的直流母线电流相加求平均，作为式（15）中的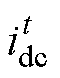
计算梯度。式（14）中的搜索初值
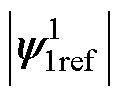设置为式（11）的计算结果，参考2.2节参数敏感性分析的结果，变化步长初值
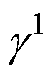设置为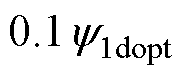
。之后每个时刻的变化步长将随着搜索状态更新为
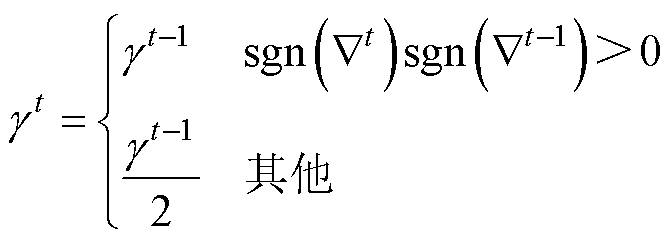（16）
式（16）表明，当第t-1和t周期的梯度方向发生变化时，极值点在两次搜索值中间，步长将变为原来的一半，进而提高搜索精度。将搜索停止的判定依据设置为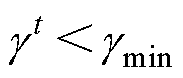
，
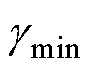为设定的最小搜索步长，应保证系统损耗最小的磁链附近直流母线电流变化不再明显。混合式最优初级磁链搜索方法的执行流程如图4所示。
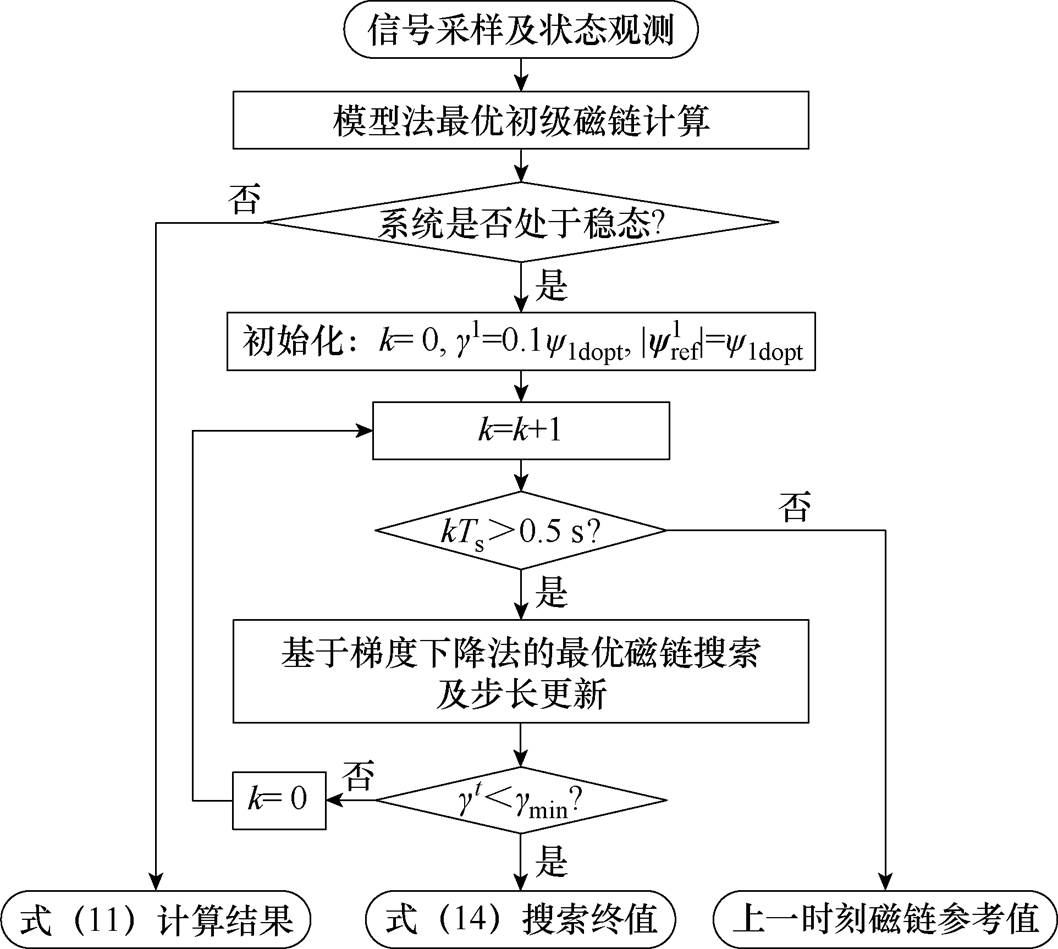
图4 混合式最优初级磁链搜索方法执行流程
Fig.4 Implementation flowchart of the hybrid optimal primary flux search method
在通过上述混合式最优初级磁链搜索方法获取初级磁链参考值后，本节将通过无模型预测磁链控制实现低开关频率下对该初级磁链的灵活调节。
为避免对推力和磁链两个量纲的物理量开展无模型预测控制，本文将文献[27]提出的参考磁链矢量发生器引入LIM进行控制目标转换。通过该矢量发生器，可将推力和磁链两个量纲的控制目标转化为参考初级磁链矢量，其中，推力控制目标将体现在该矢量相位中，和效率优化相关的磁链控制目标将体现在其幅值中。在获得参考初级磁链矢量后，考虑实际控制系统中的一拍延时，将综合初级磁链跟踪性能和开关频率约束的价值函数设计为
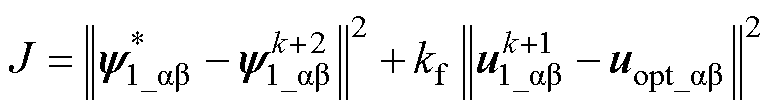（17）
式中，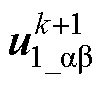
为待评价的电压矢量；
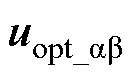为上一控制周期通过本方法确定的最优电压矢量；各变量下标_ab 用于区分该变量为两相静止坐标系下的变量；式（17）中第一项通过对初级磁链矢量的跟踪，同时实现对推力及初级磁链幅值的控制，第二项将相邻时刻所选择电压矢量的差值作为逆变器开关次数的评价标准，用以控制逆变器的开关次数，即开关频率；kf为权重参数，用以调节式（17）中前后两项的控制权重，进而达到调节开关频率的目的。
现有LIM的PFC方法[18, 24]在预测式（17）中k+2时刻初级磁链的过程中会用到大量电机参数，当模型参数不够准确或实际运行中参数非线性变化时，磁链预测结果将出现偏差，进而影响控制效果。为避免参数偏差对磁链调节过程的影响，本文采用超局部模型对电机的磁链预测模型进行修改。
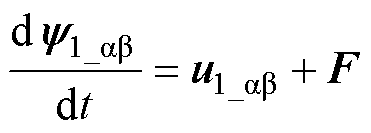（18）
式中，F为系统总扰动（包括不确定的系统变量和外部扰动）。设计非线性扩展状态观测器（Nonlinear- Extended State Observer, NL-ESO）对F进行观测，有
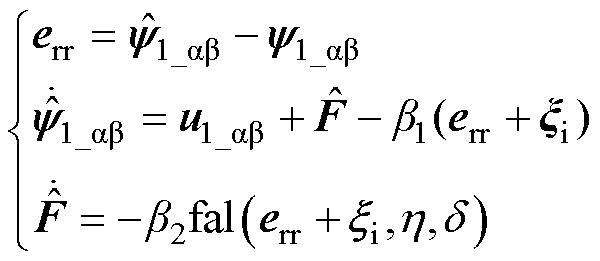（19）
式中，b1和b2为误差反馈增益；xi为测量误差及系统噪声；err为观测误差；上标“
”表示该变量通过NL-ESO观测得到；fal( · )为非线性函数，具体表达式为
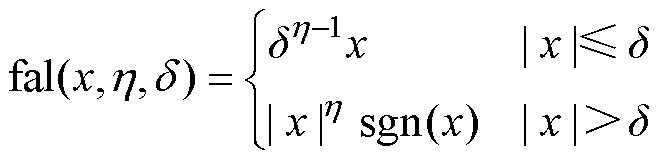（20）
式中，d 和h 为决定非线性函数特性的待整定参数，h＜1。对式（19）进行离散化并结合式（20）对增益b2处理。
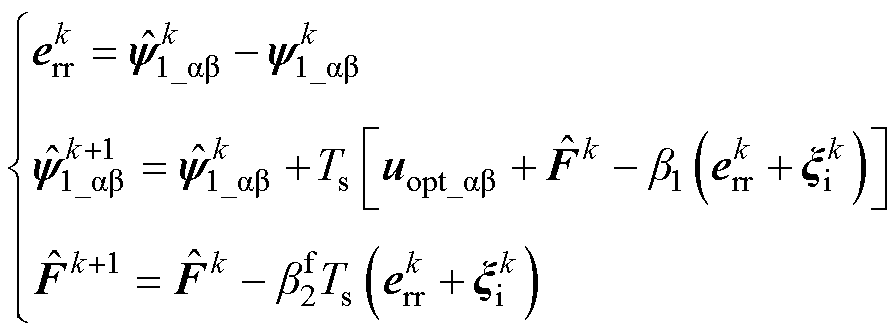（21）
式中，增益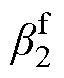
的表达式为
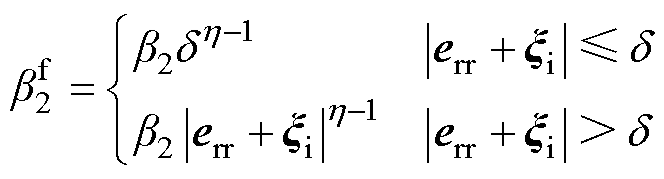（22）
从式（22）可以看出，NL-ESO中的增益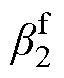大小与跟踪误差和测量噪声有关，当测量噪声过大时，增益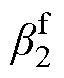会随着误差和噪声的增大而减小，避免将噪声放大；而在稳态时，增益随误差减小而增大，从而减小跟踪误差。上述增益变化规律可有效应对低开关频率引起的电流毛刺和畸变，提高观测效果。
在通过NL-ESO获得F后，可将k+2时刻的初级磁链预测为
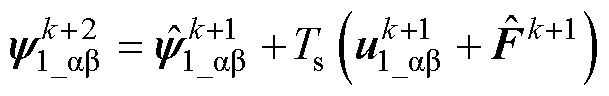（23）
式中，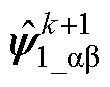
可通过NL-ESO观测得到，无需额外延时补偿。将式（23）代入式（17）中，可得
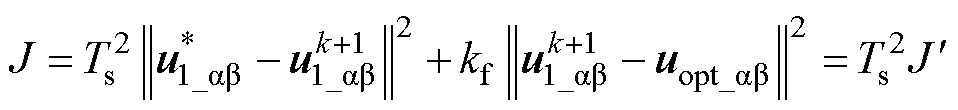
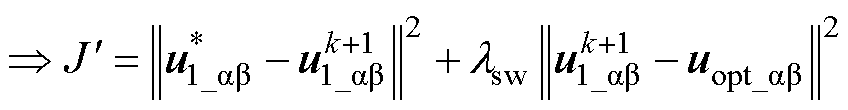（24）
其中
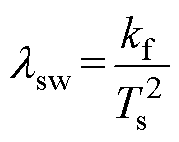
式中，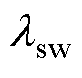
为开关频率调节因子；
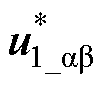为基于无差拍原理计算的能实现磁链完全跟踪参考值时对应的参考电压矢量，具体可表示为
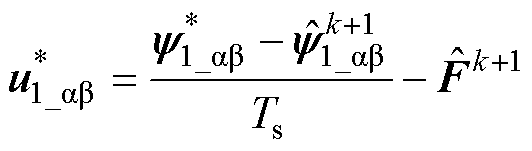（25）
采用NL-ESO完成参考电压矢量计算的完整流程如图5所示。
图5 基于NL-ESO的参考电压矢量计算流程
Fig.5 Implementation flowchart of the NL-ESO based reference voltage vector calculation
进一步地，对式（24）中的价值函数进行推导化简，可得（具体推导过程见附录）
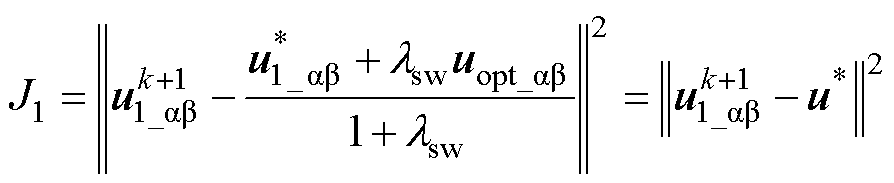（26）
式（26）表明，考虑开关频率约束时，参考电压矢量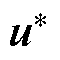
为式（25）和上一时刻作用电压矢量的合成，且随着调节因子的增加，参考电压矢量将向上一时刻作用电压矢量靠近，使得本周期倾向于选择上一时刻作用电压矢量，达到降低开关频率的目的。
除了对参考推力和初级磁链的跟踪控制外，中点电压平衡是NPC型三电平逆变器的另一个重要控制目标。通常，中点电压波动不应超过直流母线电压的5%。为了同时实现中点电压平衡及其他电机控制目标，本文采用级联优化的寻优方法，设置中点电压阈值e（本文设置为2.5%的直流母线电压），根据中点电压大小确定价值函数和待评价电压矢量。
当中点电压小于e 时，仅考虑推力和磁链的跟踪性能，价值函数即为前文推导的J1。价值函数J1的大小可等效为待评价电压矢量和参考电压矢量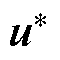之间的距离，二者距离越小，价值函数的值也越小。因此，可进一步通过几何关系对图2b中电压矢量平面进行划分，减少候选电压矢量的个数。电压矢量平面划分和候选电压矢量选择如图6所示，首先以中矢量作为边界将整个平面分为6个扇区Ⅰ～Ⅵ。在此基础上，对每个扇区内的小矢量和零矢量、小矢量和中矢量以及小矢量和大矢量的连线做垂直平分线，将其进一步划分为3个区域Q1～Q3，此时相邻扇区的边界均为正六边形的一条边，边界上的点到某两个电压矢量的距离相等，为临界点。通过这种扇区划分，可通过参考电压矢量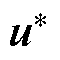位置直接确定候选电压矢量，例如，当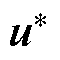处于扇区I的Q2区域时，仅以u13和u14作为候选电压矢量。
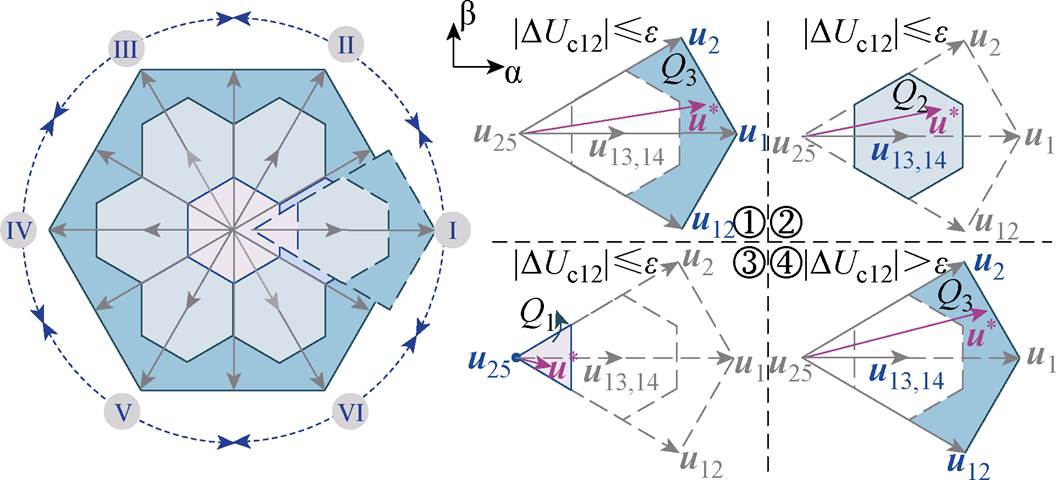
图6 电压矢量平面划分和候选电压矢量选择
Fig.6 Regions division and candidate valtage vectors selection
当中点电压大于e 时，除考虑J1给出的控制目标外，还需考虑中点电压的控制效果，对应的价值函数设计为
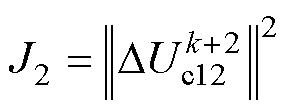（27）
式中，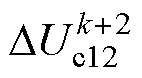
为根据式（5）考虑延时补偿后计算的中点电压预测值。由式（5）可知，只有小矢量和中矢量会影响中点电压。为综合考虑J1和J2，首先计算参考电压矢量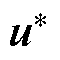并判断扇区，然后将同一扇区的小矢量和中矢量代入J2进行评价。该中点电压处理方法避免了中点电压权重系数的使用，并且可以使用参考电压矢量来降低计算量。
结合第2节提出的混合式最优初级磁链搜索方法，本文所提出的低开关频率强鲁棒效率优化控制策略框图如图7a所示。然而，为了实现低开关频率运行，仍需要在运行中人为调节式（10）中的开关频率调节因子来改变开关频率。为避免人为参数整定的繁琐过程，本文进一步提出了调节因子的自适应变化机制，实际运行中每一时刻调节因子将根据式（28）进行在线调整。
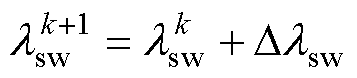（28）
式中，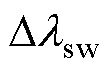
为调节因子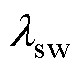
的变化步长。综合考虑开关频率的动态调节时间和稳态控制精度，将变化步长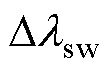设计为
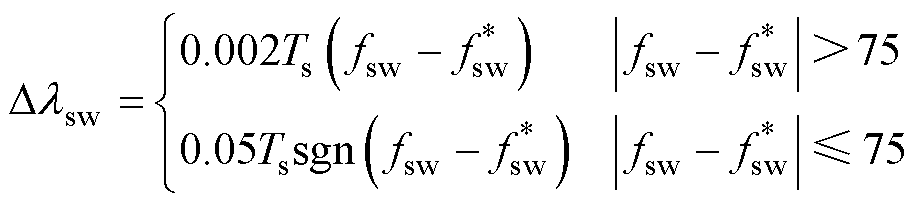（29）
式中，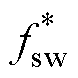
为开关频率给定值；fsw为平均开关频率，通过记录规定时间T内12个开关器件的动作次数综合N求平均得到，即fsw=N/(12T)。在式（29）中，变化步长与跟踪误差相关，当跟踪误差较大时，采用与误差成比例的大步长来快速减小跟踪误差。而当跟踪误差小于75 Hz时，步长将保持不变，从而减少在预期开关频率附近的波动。式（28）和式（29）所表示的开关频率动态调节机制如图7b所示。
最后，基于图7a所示的整体控制框图，将本文所提出的低开关频率强鲁棒效率优化控制策略的实施流程总结如下：
（1）采样电机相电流、速度及直流母线上下电容的电压，结合采样结果计算电机推力和磁链。
（2）根据式（11）计算出该推力和速度条件下电机损耗最小对应的理论最优初级磁链y1dopt。
（3）根据电机速度与指令值的偏差判断系统状态，当系统处于动态时，直接以y1dopt作为初级磁链参考值，然后执行步骤（5）；当系统处于稳态时，继续执行步骤（4）。
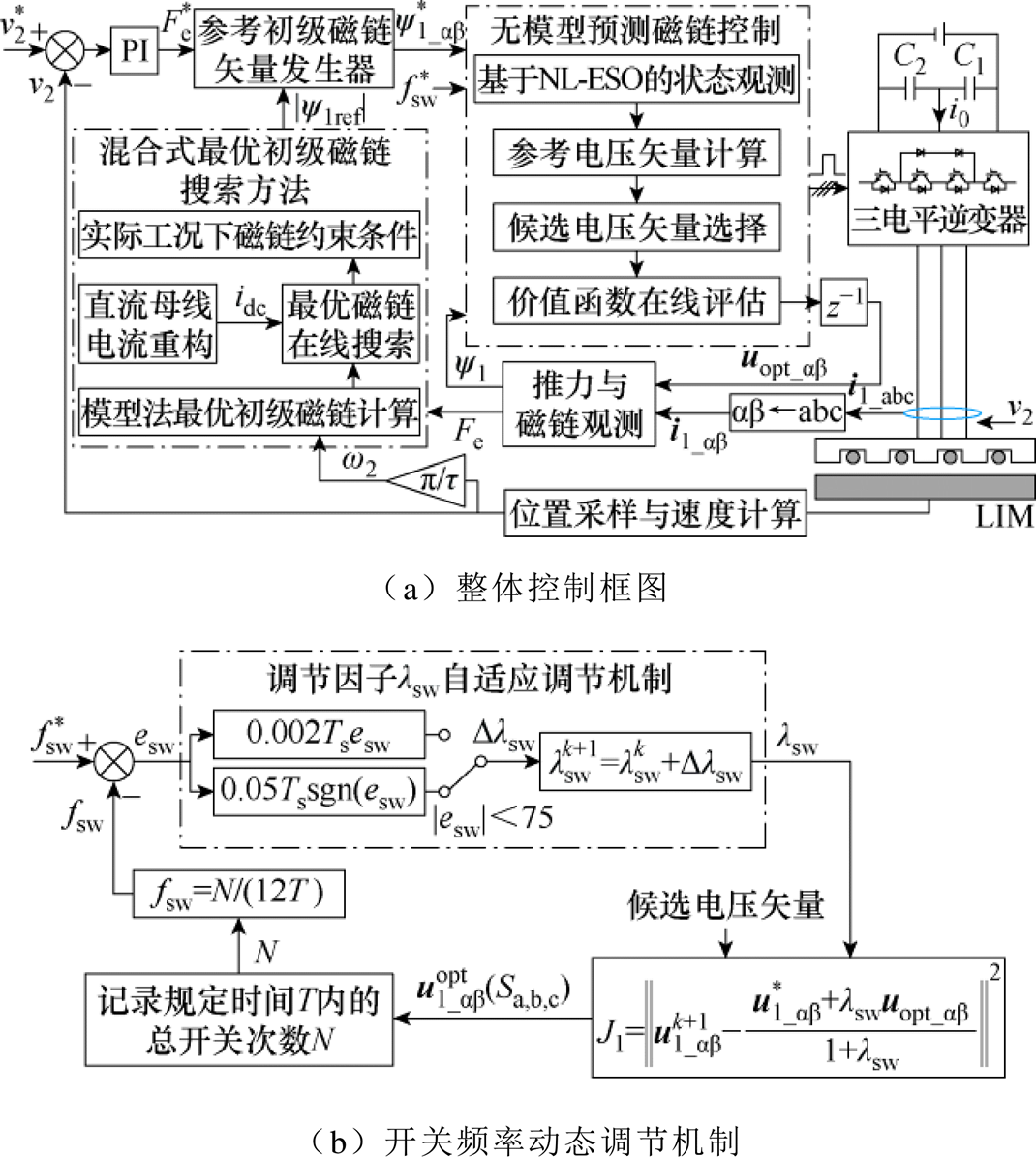
图7 所提出的低开关频率强鲁棒效率优化控制策略框图
Fig.7 Block diagram of the proposed robust efficiency optimization control strategy under low switching
（4）判断距离上一次初级磁链参考值更新是否超过0.5 s，若超过0.5 s，则开始存储重构直流母线电流，并在0.9 s时根据式（14）～式（16）对搜索步长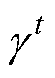
、初级磁链参考值完成一次更新，当
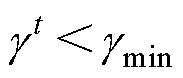后停止搜索，之后的控制周期若系统仍处于稳态则初级磁链参考值保持不变。
（5）根据初级磁链参考值、推力参考值等得到参考初级磁链矢量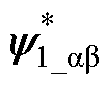
，结合NL-ESO观测的系统总扰动F计算计及开关频率约束的参考电压矢量。
（6）以参考电压矢量位置和三电平逆变器中点电压DUc12是否超过设定阈值e 为判断条件，结合图6的扇区划分确定待评价电压矢量，将待评价电压矢量依次代入J1（当DUc12＜e 时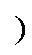
或J2（当DUc12≥e时）中，确定最优电压矢量。
（7）根据最优电压矢量产生12路PWM信号作用于三电平逆变器各相桥臂，完成电机控制。
本节将通过图8所示的3 kW LIM实验平台验证所提方法的有效性，该电机主要参数见表1。受实验空间限制，采用直径足够大（1.25 m）的弧形感应电机来模拟实际直线感应电机性能[28]。除弧形形状外，该电机与城轨交通中实际运行的直线感应电机拓扑结构无异，同样具有初级开断、半填充槽、复合次级和大气隙（10 mm）等特点。PFC的采样频率设置为12 kHz，直流母线电压设置为450 V。外围驱动系统采用IGBT全控型器件变频器，控制芯片为DSP TMS320F28335。实验中，梯度下降法和NL-ESO用到的主要参数设置如下：gmin=0.02 Wb，d =0.015 Wb，h =0.5，b1=2 000，b2=100 000。
图8 NPC型三电平逆变器驱动的LIM实验平台
Fig.8 Experimental setup for a 3L-NPC inverter-fed LIM drives
表1 LIM电机主要参数
Tab.1 Main parameters of prototyped LIM
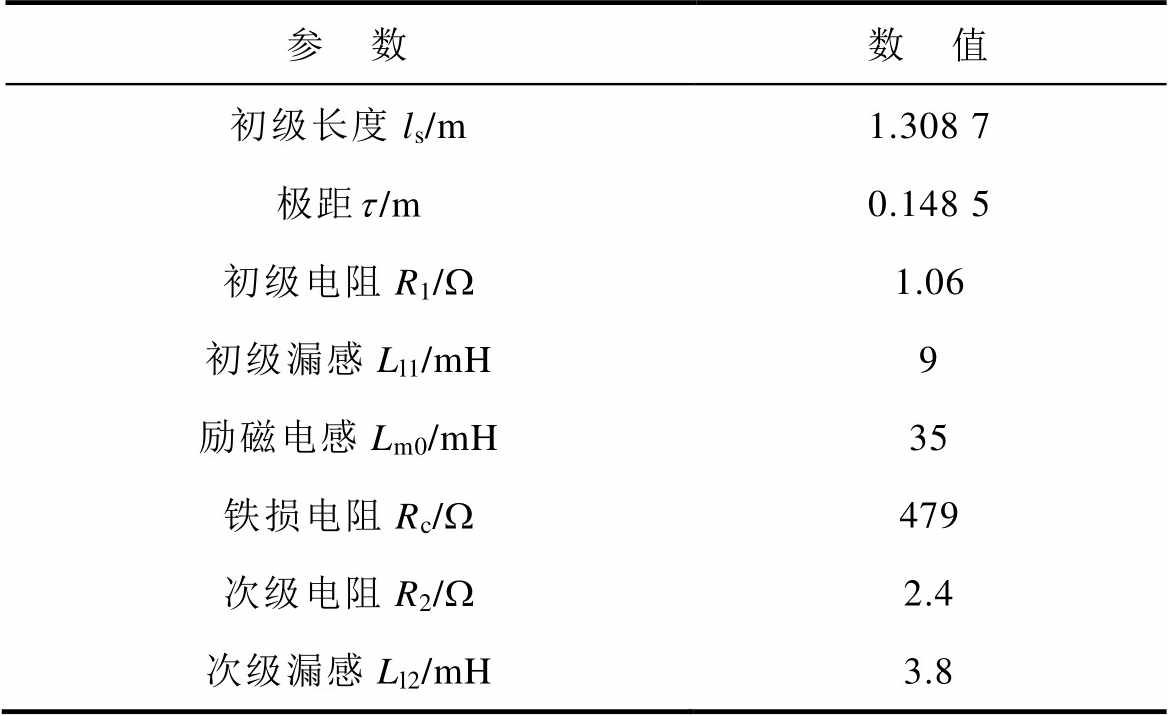
参 数数 值 初级长度ls/m1.308 7 极距t/m0.148 5 初级电阻R1/W1.06 初级漏感Ll1/mH9 励磁电感Lm0/mH35 铁损电阻Rc/W479 次级电阻R2/W2.4 次级漏感Ll2/mH3.8
除本文所提出的基于PFC的强鲁棒效率优化策略（PFC-based Robust Efficiency Optimization Strategy, PFC-REOS）外，本节还将在实验平台上应用如下两种方法进行对比：①基于PFC的恒定励磁（PFC-based Constant Excitation, PFC-CE）策略，该方法将当前城轨交通广泛采用的恒定励磁方式与PFC相结合；②文献[24]提出的基于PFC的效率优化策略（PFC-based Efficiency Optimization Strategy, PFC-EOS），此方法为该文献提出的适用于低开关频率的直线感应电机效率优化策略。
首先对所提出方法的低开关频率控制效果进行验证。图9给出了当电机速度从4 m/s到11 m/s阶跃变化过程中平均开关频率fsw和调节因子lsw的变化波形，其中，开关频率给定值设置为350 Hz，开关频率每66 ms根据所统计的总开关次数计算并更新一次。在动态过程中，开关频率将暂时偏离给定值，同时调节因子也将自适应发生变化，动态过程结束后平均开关频率将在新的调节因子下恢复至350 Hz。图9的结果表明，基于图7b所示的低开关频率自适应调节方法，可以灵活调节PFC-REOS的平均开关频率且稳定性强，为低开关频率下开展效率优化提供了可靠控制架构。
本文所提出方法对应的LIM驱动系统动态响应过程如图10所示。图10a为起动制动响应过程，电机首先从静止加速至额定速度11 m/s，稳定后制动恢复静止。当算法检测到电机起动后，直接采用式（11）计算磁链参考值，保持系统的快速响应能力。当速度达到指令值后系统恢复稳态，进一步以直流母线电流最小为目标开展搜索，直至达到搜索停止条件，全过程中磁链会随着运行工况不断发生变化。图10b为电机在额定速度下的加载过程，负载从50 N增加至150 N，加载后电机速度下降，算法检测到系统进入动态，直接计算磁链参考值，直至系统进入稳态后再次开始搜索。相较直接采用梯度下降法进行搜索，本文所提出的混合式最优初级磁链搜索方法可保持动态过程中的快速响应能力并减小搜索过程中磁链变化所引起的波动。图10c为PFC-REOS对中点电压的控制效果，起初在中点电压阈值e 设定较大时上下两个电容电压发生明显偏移，导致电机电流畸变、推力波动增加。在将中点电压阈值设置为10 V后，大约经过0.04 s中点电压就可以重新保持平衡，并被很好地稳定在10 V以内，电流和推力性能也得到明显改善。
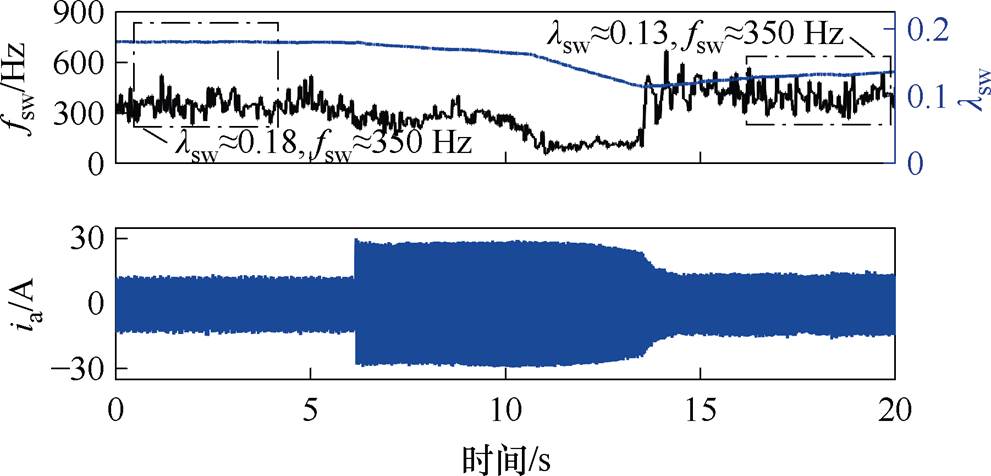
图9 速度阶跃变化时开关频率自适应调节过程
Fig.9 Switching frequency adaptive adjustment process under speed step variation
图11对比了PFC-EOS和PFC-REOS两种方法在11 m/s、150 N下的稳态性能。图中，uab为a相和b相间的线电压，Hn(%H1)为n次谐波相对基波的百分比。图11a和图11b分别为参数准确和励磁电感变为原来50%时PFC-EOS的稳态性能，由于PFC-REOS的性能不受参数影响，因此仅给出励磁电感变为原来50%时的稳态性能，如图11c所示。当励磁电感发生偏差时，PFC-EOS的稳态性能受到一定影响，直观表现为电流总谐波畸变率（Total Harmonic Distortion, THD）的增加。相反，PFC-REOS采用基于NL-ESO的无模型预测磁链控制实现初级磁链调节，根据NL-ESO观测的系统总扰动计算参考电压矢量，避免了参数偏差及建模误差等的影响。同时，由于PFC-REOS在结束搜索后磁链参考值将保持恒定，在一定程度上避免了磁链参考值波动带来的影响。
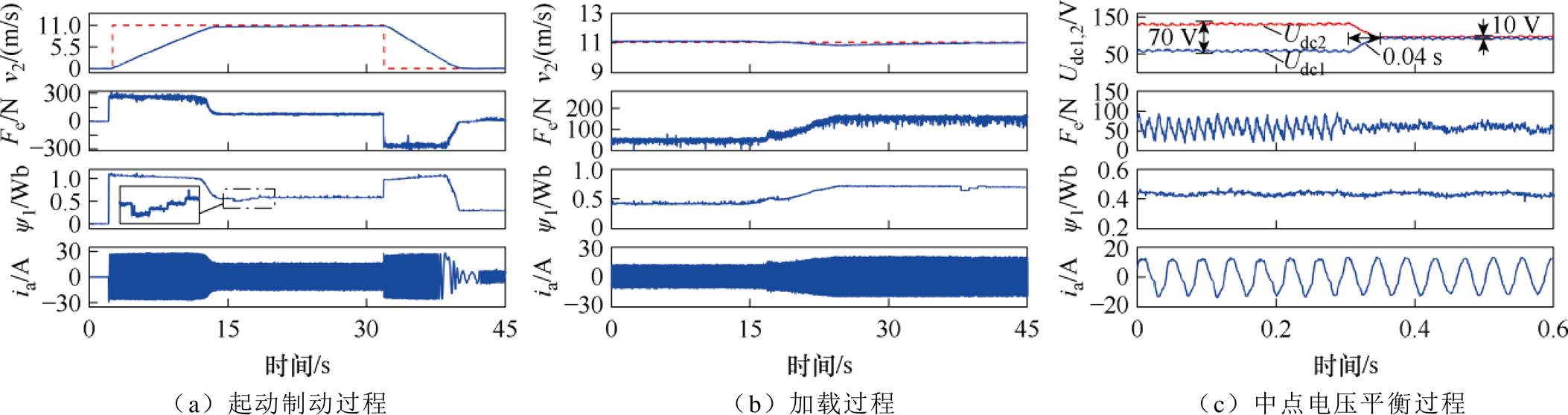
图10 所提出方法的动态响应
Fig.10 Dynamic responses for the proposed method
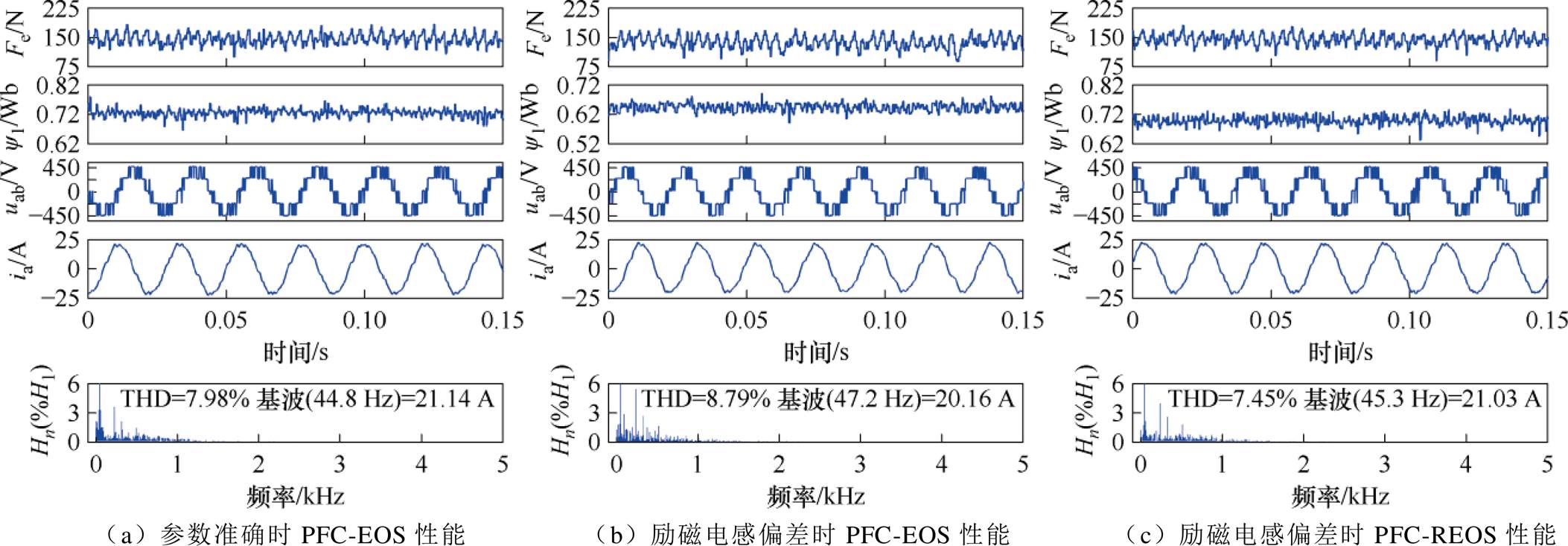
图11 PFC-EOS与PFC-REOS稳态性能对比
Fig.11 Steady-state performance comparison for PFC-EOS and PFC-REOS
图12给出了同一速度、负载条件下三种方法切换过程中的系统输入功率、初级磁链及相电流的动态变化波形。在输出功率基本相同的情况下，系统输入功率的大小可以直观反映出系统的损耗和效率情况。图12a为8 m/s、50 N且电机参数准确工况下三种方法的切换过程，驱动系统首先采用PFC-CE控制，初级磁链参考值设置为0.8 Wb，之后分别切换至PFC-EOS和PFC-REOS。如图12a所示，通过大幅降低初级电流进而降低初级铜耗，PFC-EOS和PFC-REOS在轻载下可以明显提升系统效率。对于效率优化策略而言，其本质在于调整电机的工作点来改变铜耗、铁耗和逆变器损耗的占比，从而实现总损耗最小。对于相同的工况，即相同的速度和负载，调整LIM的工作点意味着同步频率的改变，这一点可以从相电流在相同时间尺度下的放大图中得到验证。此外，由于实验平台功率较小，轻载时逆变器损耗所占比重较小，所以两类效率优化方法切换前后输入功率差别不大。
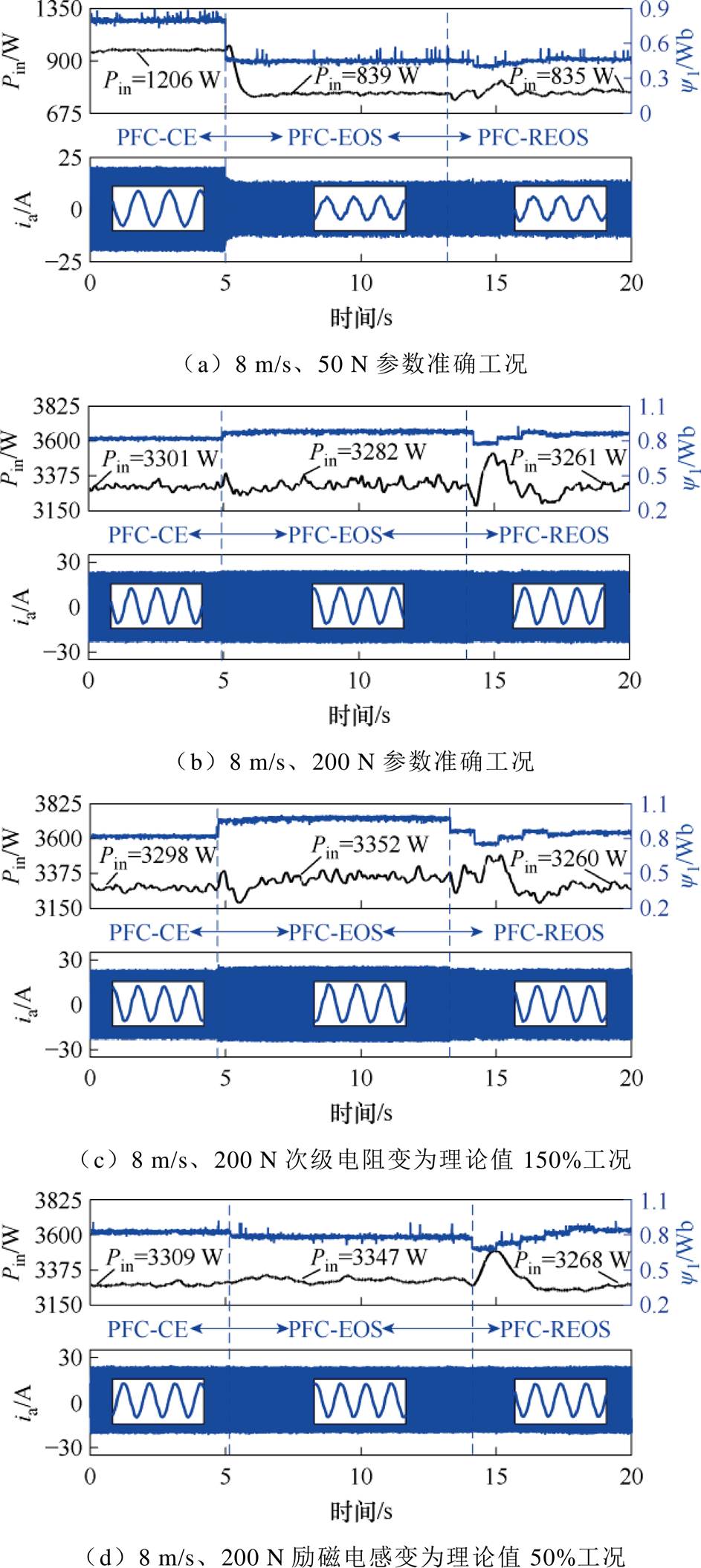
图12 不同方法动态切换过程中的实验结果
Fig.12 Experimental results of the dynamic switching between different methods
图12b为8 m/s、200 N且电机参数准确工况下三种方法的切换过程。由于此时系统最小损耗对应的初级磁链也在0.8 Wb左右，所以两类效率优化控制相比PFC-CE的损耗降低程度减小。不同于图12a中的轻载工况，此时逆变器损耗占比增加，加之端部效应所导致的电机等效次级电阻变化[24]，采用PFC-EOS时的系统效率有进一步提升的空间。相比PFC-CE和PFC-EOS，本文所提出的PFC-REOS在该工况下可分别提升系统效率1.22%和0.64%。
图12c和图12d分别给出了8 m/s、200 N下次级电阻和励磁电感与理论值发生偏差时三种方法的输入功率对比情况。受参数偏差影响，该负载条件下PFC-EOS基于式（11）计算的初级磁链参考值将与理论值存在较大偏差，进而导致输入功率明显增加。当切换至PFC-REOS后，将在PFC-EOS计算的初级磁链基础上采用梯度下降法进行搜索。此时，相比PFC-EOS，PFC-REOS可提升系统效率2.83%和2.41%。同时，对比图12b～图12d可以看到，虽然三种情况下磁链搜索初值不同，但对最终搜索结果影响不大。
图13和图14分别给出了参数准确时不同工况下PFC-REOS与PFC-CE、PFC-EOS的效率对比。图中，hmac、hinv和hsys分别为电机效率、逆变器效率和系统效率。其中，逆变器和电机的输入功率通过日置PW6001-16型功率分析仪测量，电机的输出功率通过ZHK-D型转矩传感器测量，在获得各部分输入和输出功率后可进一步计算效率。如图13所示，相比PFC-CE，不同工况下PFC-REOS均能实现系统效率提升，且以轻载工况下效果最为明显。在重载下，PFC-REOS亦可通过增加初级磁链参考值的方式降低系统损耗，但效率提升程度相对较小。由于城轨交通LIM在实际运行中长期处于轻载巡航状态，提升轻载下的系统效率具有重要意义。相比PFC-EOS，PFC-REOS可弥补PFC-EOS仅针对电机损耗建模的局限性，有效考虑到逆变器损耗、电机损耗中的未建模部分以及式（10）建模中的误差，从而在参数准确的情况下也可实现各部分效率的进一步提升，如图14所示。然而，由于实验平台功率较小，使得逆变器损耗占比较小，因此PFC- REOS相比较PFC-EOS在效率提升上的优势主要体现在重载工况下。
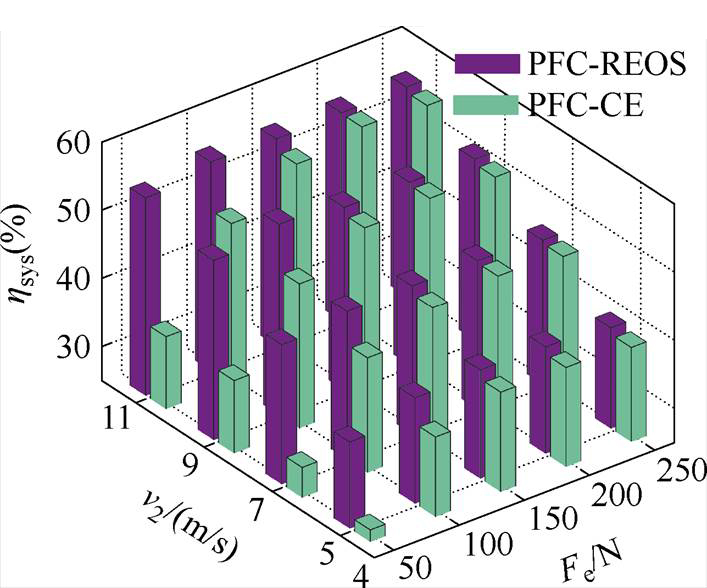
图13 不同工况下PFC-REOS与PFC-CE效率对比
Fig.13 Efficiency comparisons of PFC-REOS and PFC-CE under different conditions
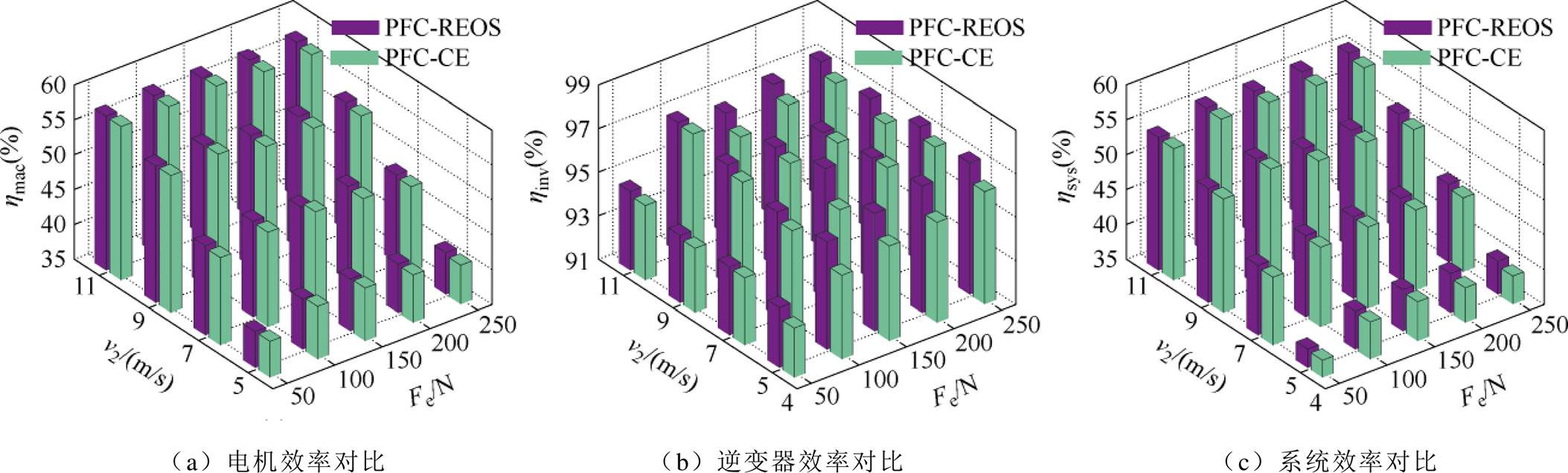
图14 参数准确时不同工况下PFC-REOS与PFC-EOS效率对比
Fig.14 Efficiency comparisons of PFC-REOS and PFC-EOS under different conditions with the accurate parameters
进一步地，图15给出了11 m/s、200 N工况下不同参数发生偏差时PFC-REOS与PFC-EOS的系统效率对比。与2.2节中的参数敏感性分析结果一致，在所有参数偏差中，励磁电感和次级电阻偏差对效率的影响最大，可分别使得系统效率降低约1.76%和1.47%。同时，LIM的励磁电感和次级电阻在电机运行中又最易受到端部效应影响，因此，本文所提出方法对提升效率优化策略的参数鲁棒性具有重要意义。
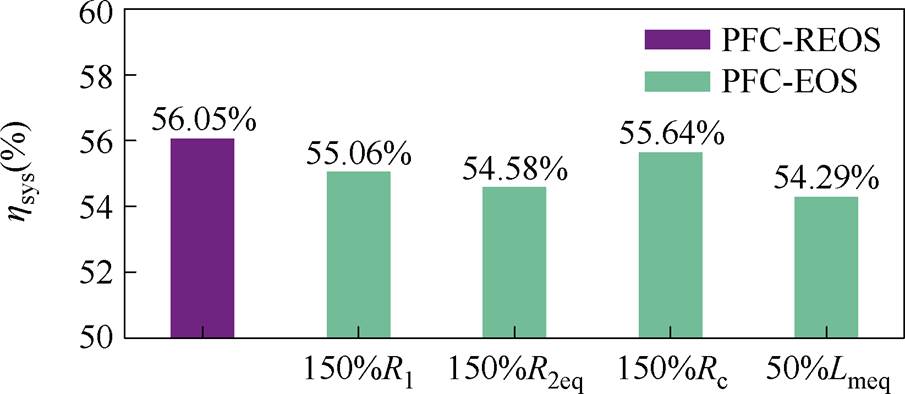
图15 参数偏差时11 m/s、200 N下PFC-REOS与PFC-EOS效率对比
Fig.15 Efficiency comparisons of PFC-REOS and PFC-EOS under 11 m/s and 200 N with the mismatched parameters
针对三电平变频驱动的LIM系统，本文提出了一种适用于低开关频率的强鲁棒效率优化控制策略。为解决现有效率优化控制策略仍存在的参数鲁棒性差、系统效率提升受限等问题，本文首先将损耗模型法与梯度下降法相结合，提出了混合式最优初级磁链搜索方法，有效避免参数变化对最优磁链的影响。在此基础上，设计NL-ESO观测模型不确定性引起的总扰动，并结合观测结果提出了开关频率自适应调节的无模型预测磁链控制，实现了低开关频率下最优磁链的灵活调节。最后，通过3 kW LIM实验平台对比验证了所提方法的有效性。主要结论如下：
1）本方法以逆变器直流母线电流最小作为搜索目标，充分考虑了损耗建模时忽略的电机谐波损耗、逆变器损耗及其他影响因素，从而进一步提升了驱动系统效率。
2）本方法推导了含开关频率约束、中点电压平衡等多个目标的价值函数，提出了开关频率自适应调节的无模型预测磁链控制，为低开关频率下实施效率优化提供了可靠的控制架构。
3）本方法通过将混合式最优初级磁链搜索方法与无模型预测磁链控制相结合，有效避免了参数变化、建模误差等在最优磁链选择和控制中造成的影响，显著增强了效率优化控制策略的参数鲁棒性。
附 录
基于如下等式对式（24）进行进一步化简。
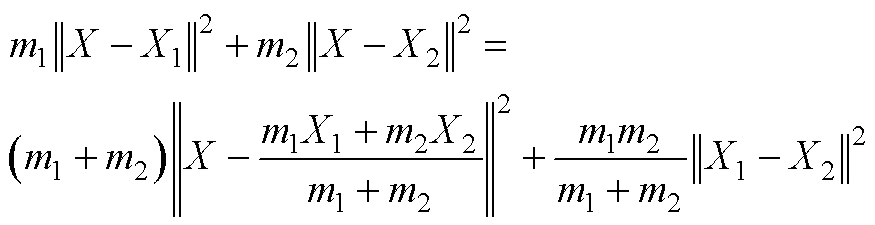（A1）
对应于式（24），可取X=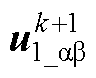
，X1=
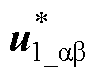，X2=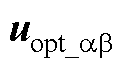
，m1=1，m2=lsw，从而将式（24）简化为
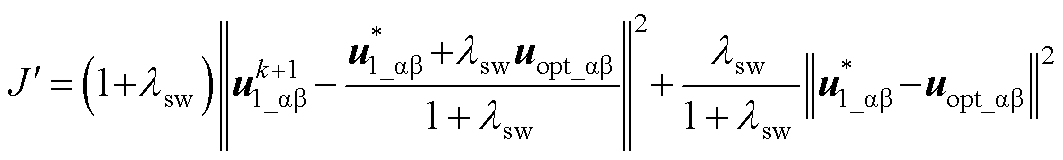（A2）
等式右边第二项为常数项，可省略。
参考文献
[1] 吕刚. 直线电机在轨道交通中的应用与关键技术综述[J]. 中国电机工程学报, 2020, 40(17): 5665-5675.
Lü Gang. Review of the application and key tech- nology in the linear motor for the rail transit[J]. Proceedings of the CSEE, 2020, 40(17): 5665- 5675.
[2] 包振, 葛健, 徐伟, 等. 同心笼次级直线双馈电机静态端部效应补偿策略[J]. 电工技术学报, 2023, 38(17): 4621-4632.
Bao Zhen, Ge Jian, Xu Wei, et al. Compensation strategy for static end effect in nest-loop secondary linear doubly-fed machine[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4621-4632.
[3] 董志强, 王琛琛, 周明磊, 等. 基于SHEPWM的三电平三相逆变器中点电位主动平衡控制策略[J]. 电工技术学报, 2024, 39(4): 1147-1158.
Dong Zhiqiang, Wang Chenchen, Zhou Minglei, et al. Active neutral-point voltage balance control strategy for three-level three-phase inverter under SHEPWM[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1147-1158.
[4] 王金平, 刘斌, 董浩, 等. 中点钳位型三电平逆变器基于调制波分解的调制策略[J]. 电工技术学报, 2023, 38(12): 3221-3233.
Wang Jinping, Liu Bin, Dong Hao, et al. A modu- lation strategy based on modulation wave decom- position for neutral point clamped three-level inverter[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3221-3233.
[5] 龙遐令. 直线感应电动机的理论和电磁设计方法[M]. 北京: 科学出版社, 2006.
[6] Accetta A, Di Piazza M C, Luna M, et al. Electrical losses minimization of linear induction motors considering the dynamic end-effects[C]//2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 2017: 4288-4294.
[7] Hu Dong, Xu Wei, Dian Renjun, et al. Loss minimi- zation control of linear induction motor drive for linear metros[J]. IEEE Transactions on Industrial Electronics, 2018, 65(9): 6870-6880.
[8] Xiao Xinyu, Xu Wei, Tang Yirong, et al. Improved loss minimization control based on time-harmonic equivalent circuit for linear induction motors adopted to linear metro[J]. IEEE Transactions on Vehicular Technology, 2023, 72(7): 8601-8612.
[9] 赵子安, 王一帆, 李凤姣, 等. 考虑铁损的同步磁阻电机最小损耗控制策略[J]. 电机与控制学报, 2023, 27(11): 1-9.
Zhao Zian, Wang Yifan, Li Fengjiao, et al. Minimum losses control strategy of synchronous reluctance motors considering iron losses[J]. Electric Machines and Control, 2023, 27(11): 1-9.
[10] 何佳佳, 周扬忠. 混合励磁型无轴承磁通切换电机损耗最小控制[J]. 电机与控制学报, 2023, 27(9): 53-62.
He Jiajia, Zhou Yangzhong. Loss minimization control of bearingless hybrid excitation motor[J]. Electric Machines and Control, 2023, 27(9): 53-62.
[11] Wang Ke, Shi Liming, Li Yaohua. A loss- minimization scheme for direct thrust-controlled linear induction motor drives[C]//2008 IEEE Inter- national Conference on Industrial Technology, Chengdu, 2008: 1-4.
[12] Balamurali A, Feng Guodong, Lai Chunyan, et al. Maximum efficiency control of PMSM drives considering system losses using gradient descent algorithm based on DC power measurement[J]. IEEE Transactions on Energy Conversion, 2018, 33(4): 2240-2249.
[13] 齐昕, 周珂, 王长松, 等. 中高功率交流电机逆变器的低开关频率控制策略综述[J]. 中国电机工程学报, 2015, 35(24): 6445-6458.
Qi Xin, Zhou Ke, Wang Changsong, et al. Control strategies for medium and high power AC machine inverters at low switching frequencies-an over- view[J]. Proceedings of the CSEE, 2015, 35(24): 6445-6458.
[14] Andersson A, Thiringer T. Assessment of an improved finite control set model predictive current controller for automotive propulsion applications[J]. IEEE Transactions on Industrial Electronics, 2020, 67(1): 91-100.
[15] Zhang Yongchang, Bai Yuning, Yang Haitao, et al. Low switching frequency model predictive control of three-level inverter-fed IM drives with speed- sensorless and field-weakening operations[J]. IEEE Transactions on Industrial Electronics, 2019, 66(6): 4262-4272.
[16] 陈荣, 翟凯淼, 舒胡平. 永磁同步电机双矢量固定开关频率模型预测控制研究[J]. 电工技术学报, 2023, 38(14): 3812-3823.
Chen Rong, Zhai Kaimiao, Shu Huping. Predictive control of dual vector fixed switching frequency model for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3812-3823.
[17] Xu Wei, Lorenz R D. Dynamic loss minimization using improved deadbeat-direct torque and flux control for interior permanent-magnet synchronous machines[J]. IEEE Transactions on Industry Appli- cations, 2014, 50(2): 1053-1065.
[18] Xu Wei, Tang Yirong, Dong Dinghao, et al. Optimal reference primary flux based model predictive control of linear induction machine with MTPA and field- weakening operations for urban transit[J]. IEEE Transactions on Industry Applications, 2022, 58(4): 4708-4721.
[19] Preindl M, Bolognani S. Model predictive direct torque control with finite control set for PMSM drive systems, part 2: field weakening operation[J]. IEEE Transactions on Industrial Informatics, 2013, 9(2): 648-657.
[20] Eftekhari S R, Davari S A, Naderi P, et al. Robust loss minimization for predictive direct torque and flux control of an induction motor with electrical circuit model[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 5417-5426.
[21] Wang Yukai, Ito T, Lorenz R D. Loss manipulation capabilities of deadbeat direct torque and flux control induction machine drives[J]. IEEE Transactions on Industry Applications, 2015, 51(6): 4554-4566.
[22] Li Xianglin, Lu Kejin, Zhao Yujian, et al. Incorporating harmonic-analysis-based loss minimi- zation into MPTC for efficiency improvement of FCFMPM motor[J]. IEEE Transactions on Industrial Electronics, 2023, 70(7): 6540-6550.
[23] Xie Wei, Wang Xiaocan, Wang Fengxiang, et al. Dynamic loss minimization of finite control set-model predictive torque control for electric drive system[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 849-860.
[24] Tang Yirong, Xu Wei, Ge Jian, et al. Predictive flux control-based efficiency optimization strategy for three-level inverter-fed linear induction machine adapted to linear metro[J]. IEEE Transactions on Power Electronics, 2024, 39(10): 13672-13685.
[25] Xu Wei, Zhu Jianguo, Zhang Yongchang, et al. Equivalent circuits for single-sided linear induction motors[J]. IEEE Transactions on Industry Appli- cations, 2010, 46(6): 2410-2423.
[26] 胡瀚林, 赵咪, 黄毅, 等. 中高调制度下NPC逆变器扇区重构型虚拟空间矢量脉宽调制及中点平衡策略[J]. 电工技术学报, 2025, 40(8): 2573-2586.
Hu Hanlin, Zhao Mi, Huang Yi, et al. Sector reconfiguration virtual space vector pulse width modulation and neutral point balance strategy of NPC inverter in medium and high modulation depth[J]. Transactions of China Electrotechnical Society, 2025, 40(8): 2573-2586.
[27] Xiao Dan, Alam K S, Osman I, et al. Low complexity model predictive flux control for three-level neutral- point clamped inverter-fed induction motor drives without weighting factor[J]. IEEE Transactions on Industry Applications, 2020, 56(6): 6496-6506.
[28] Majumdar A, Bhattacharya T K. Comparison of force developed in a linear induction machine and an equivalent arc linear induction machine at zero velocity[C]//2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 2018: 1-5.
Abstract The linear induction machine (LIM) drive system can get direct thrust and linear motions without transmission, which enjoys strong climbing capability, high acceleration or deceleration ratio, and small mechanical losses. The LIM drive systems have been developed and commercialized in over 20 linear metro lines worldwide. However, due to the large air gap, end effects, and high-power, low-switching frequency drive, the LIM drive system in urban rail transit needs better efficiency. Although the existing efficiency optimization control strategies have improved machine efficiency, the parameter robustness and system efficiency still need to be addressed. This paper proposes a robust efficiency optimization strategy for three-level inverter-fed LIM systems under low switching frequency.
Firstly, the primary flux-based LIM loss model considering end effects is built, where the loss is expressed as a convex function of primary flux. Its parameter sensitivity and limitation are analyzed. Furthermore, combined with the gradient descent method, a hybrid optimal primary flux search method is proposed to eliminate the influence of parameter changes on optimal flux selection. Then, the cost function containing multiple objectives, such as primary flux control, switching frequency constraint, and neutral point voltage balance, is derived. A model-free predictive flux control based on the nonlinear-extended state observer is proposed to manipulate optimal flux flexibly under low switching frequency.
Finally, experimental comparisons with the existing methods on a 3 kW LIM confirm that efficiency and parameter robustness can be improved for the drive system under low switching frequency. The system efficiency with the proposed method can be improved by 1.22% and 0.64% compared with the mature control strategy and the existing efficiency optimization strategy under the working conditions of 8 m/s and 200 N.
The following conclusions can be drawn. (1) The proposed method takes the minimum DC-link current as the search objective, which considers the harmonic loss and inverter loss, thus improving the system’s efficiency. (2) Considering multiple objectives, such as the switching frequency constraint and neutral point voltage balance, a model-free predictive flux control with adaptive switching frequency regulation is developed. (3) By combining the hybrid optimal primary flux search method with model-free predictive flux control, the proposed method effectively avoids the influence of parameter changes and modeling errors on optimal flux selection and manipulation. In this way, the parameter robustness of the efficiency optimization control strategy is significantly enhanced.
keywords：Linear induction machine, end effects, efficiency optimization, model-free predictive control, low switching frequency
中图分类号：TM359.4
DOI: 10.19595/j cnki.1000-6753.tces.240765
国家自然科学基金（52277050, 52407050）、中国科学院A类专项人才计划（2Q2024000076）、深圳市科技协同创新国际合作专项（GJHZ20210705142539007）、深圳市自然科学基金面上项目（JCYJ20230807143701003）和中央高校基本科研业务费专项资金（YCJJ20242205）资助项目。
收稿日期 2024-05-12
改稿日期2024-07-05
唐一融 男，1998年生，博士研究生，研究方向为直线感应电机高效高性能控制。
E-mail: yirtang@hust.edu.cn
徐 伟 男，1980年生，研究员，博士生导师，IEEE Fellow，IET Fellow，研究方向为直线电机系统。
E-mail: weixu@mail.iee.ac.cn（通信作者）
（编辑 崔文静）